Bài Tập Hình 8 Ôn Chương Đa Giác-Diện Tích Đa Giác Có Lời Giải

7. ÔN TẬP CHƯƠNG II I. BÀI TẬP
Bài 1: Cho hình chữ nhật ABCD có AB=4 cm, CD = 9cm. Trên các cạnh AB, AD, lần lượt
lấy M,N, sao cho A M = A N = x .
a) Tính diện tích hinh MBCDN theo x. b) Tìm x biết 2 S = 34cm . MBCDN
Bài 2: Cho tam giác ABC vuông tại A có AB=4cm, AC=5cm. Các điểm D,E lần lượt trên các
cạnh AB, AC sao cho BD= AE= x. Tìm x để diện tích tứ giác BDEC nhỏ nhất.
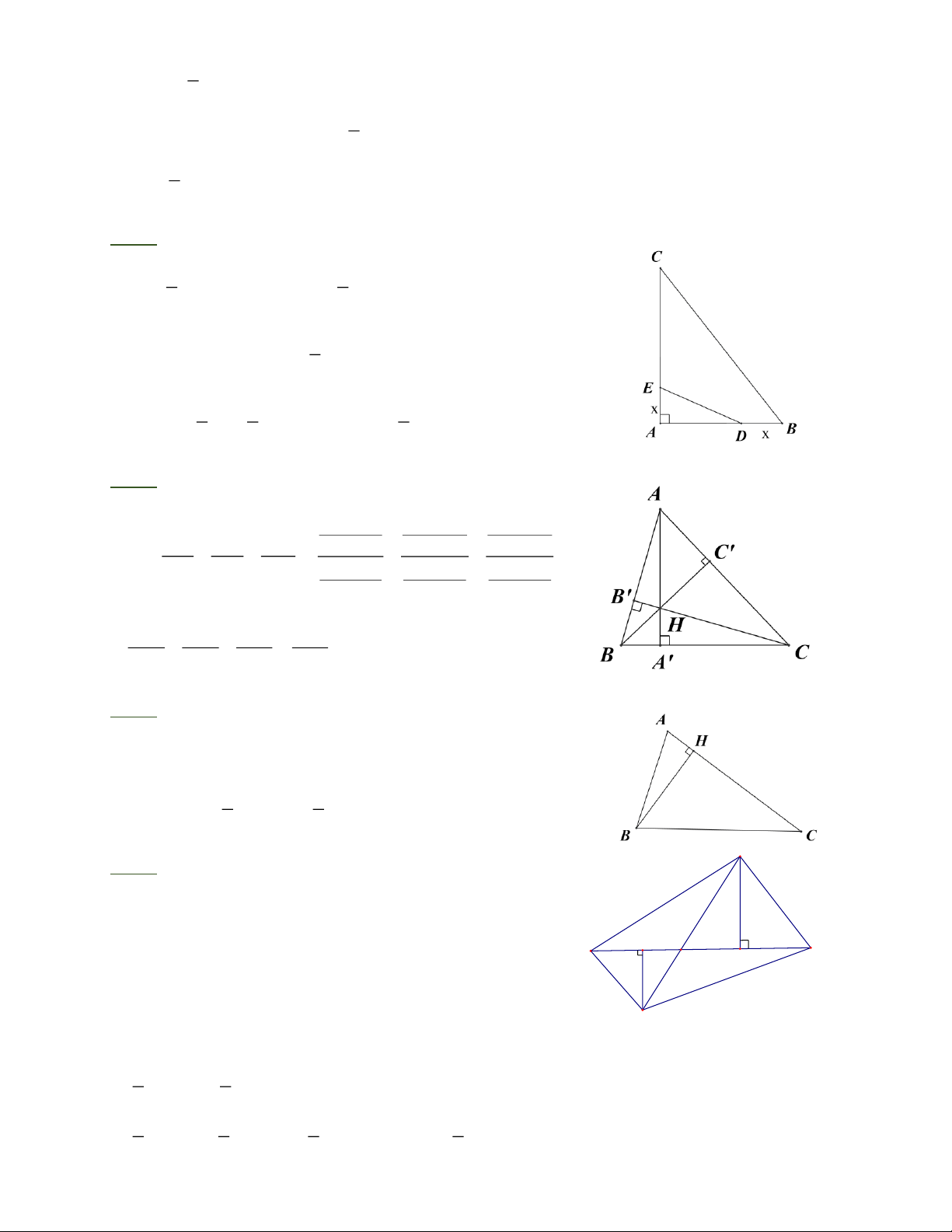
Bài 3: Cho tam giác ABC có 0
A  90 , các đường cao AA’, BB’, CC’ cắt nhau tại H. Chứng
HA' HB ' HC ' minh rằng − − =1 AA' BB ' CC ' 1
Bài 4: Cho tam giác ABC. Chứng minh rằng S  A . B AC ABC 2 1
Bài 5: Cho tứ giác ABCD. Chứng minh rằng S  AC.B . D ABCD 2
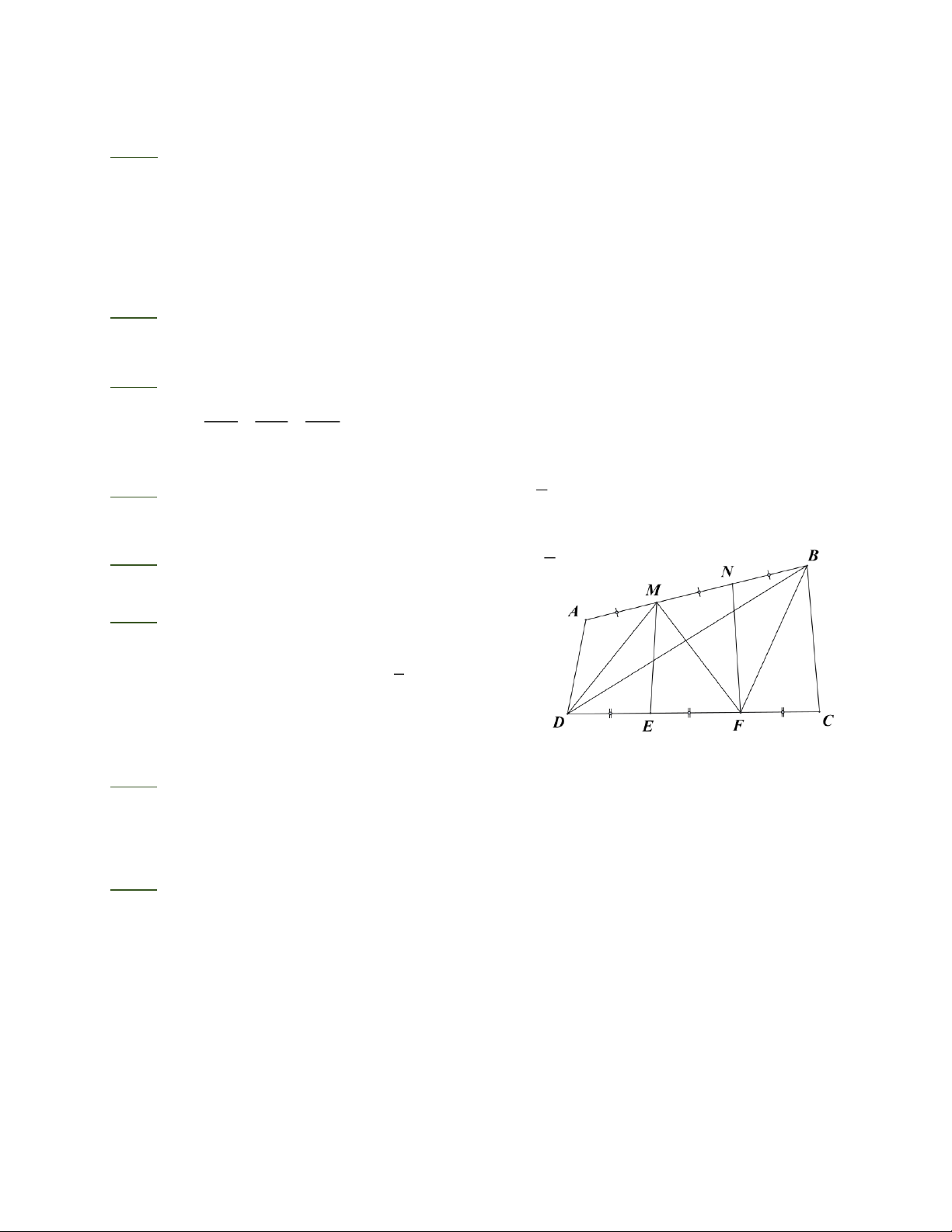
Bài 6: Cho hình bên, biết S = S. ABCD 1
a) Chứng minh rằng S + S = S. ADM BCF 3
b) Tính SMNFE theo S.
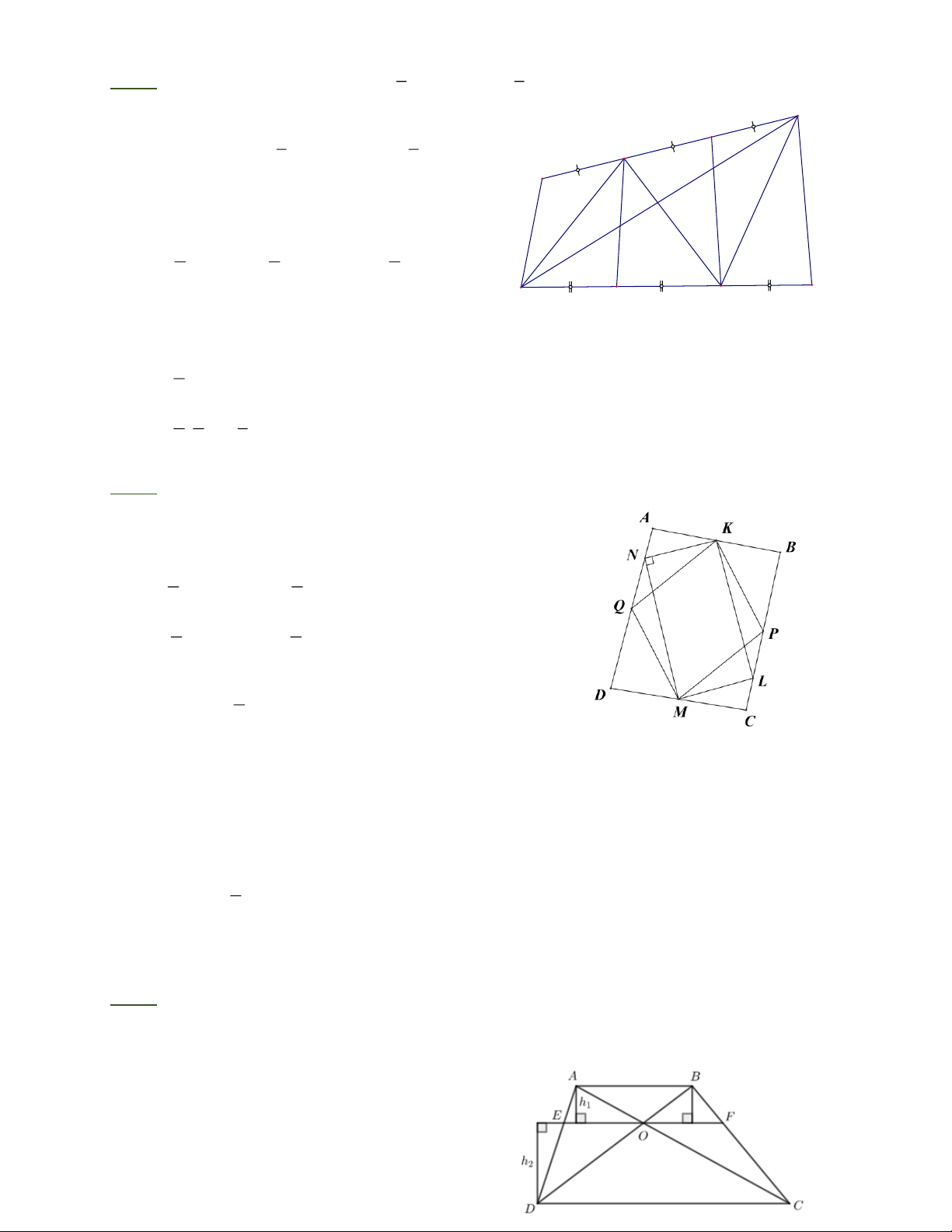
Bài 7: Gọi K và M là trung điểm của các cạnh AB, CD của tứ giác lồi ABCD, L và N nằm
trên hai cạnh kia của từ giác sao cho KLMN là hình chữ nhật. Chứng minh rằng diện tích
của hình chữ nhật KLMN bằng một nữa diện tích tứ giác ABCD.
Bài 8: Cho hình thang ABCD ( AB / /CD). Gọi O là giao điểm của AC và BD.
Qua O vẽ đường thẳng song song với AB, CD cắt các cạnh AD, BC lần lượt tại E,F. Chứng minh rằng : a) S = S b OE = F OAD OBC ) 0 . Tự luyện Trang 1
Bài 9: Cho tam giác ABC. Trên cạnh AB lấy một điểm E sao cho BE = 3 .
EA Trên cạnh BC
lấy một điểm F sao cho BF = 4FC. Gọi D là giao điểm của AF và CE. a) Chứng minh S = S . ACF AEF
b) Từ E và C kẻ EH , CK vuông góc với AF. Chứng minh EH = CK.
c) Chứng minh CD = DE. d) Chứng minh S = 2S . ABC ABD
Bài 10: Gọi G là trọng tâm của tam giác ABC. Gọi M là giao điểm của BG và AC. Chứng minh: 2 a) S = S . GBC 3 MBC b) S = S = S . GBC GAC GAB
Bài 11: Cho tam giác ABC cân tại ,
A đường cao AM . Các đường trung tuyến BD, CE cắt
nhau tại G. Gọi H , K theo thứ tự là trung điểm của BG, . CG
a) Tứ giác EHKD là hình gì? Vì sao? b) Cho 2 S = 36 cm . S ABC Tính . EHKD
Bài 12: Cho tam giác ABC vuông tại A và điểm H di chuyển trên BC. Gọi E, F lần lượt
là điểm đối xứng của H qua AB, AC. a) Chứng minh ,
A E, F thẳng hàng.
b) Chứng minh BEFC là hình thang. Có thể tìm vị trí của H để BEFC là hình bình hành, hình chữ nhật không?
c) Xác định vị trí của H để tam giác EHF có diện tích lớn nhất.
KẾT QUẢ - ĐÁP SỐ Bài 1: Trang 2 1 2 a) S = x , S = 36 AMN 2 ABCD 1 2 S = S − S = 36 − x MBCDN ABCD AMN 2 1 2 2
b) 36 − x = 34  x = 4  x = 2. ( .1 h 09) 2 Bài 2: 1 1 S = A . B AC = 10; S = x − x ABC AED (4 ) 2 2 1 S = S − S =10 − x − x BDEC ABC ADE (4 ) 2 1 1 =
− x + x = (x − x + ) 1 10 2 4 4 + 8 = (x − 2)2 2 2 + 8  8. 2 2 2 Bài 3: HA'.BC HB '.AC HC '.AB
HA' HB ' HC ' Ta có − − 2 2 2 = − − AA' BB ' CC ' AA'.BC BB '.AC CC '.AB 2 2 2 = S S S S
HBC − HAC − HAB = ABC = 1 S S S S ABC ABC ABC ABC Bài 4:
Vẽ BH ⊥ AC tại H.Ta có BH  AB 1 1 Do đó S
= BH.AC  A . B AC ( . h 112) ABC Hình 112. 2 2 B
Bài 5: Gọi O là giao điểm của AC và BD.
Vẽ BK ⊥ AC tại K, DH ⊥ AC tại H. H O A
BK  OB DH  OD C Ta có , . K Do đó D S = S + S ABCD ABC ACD 1 1 =
BK.AC + DH.AC 2 2 1 1 1
= OB AC + OD AC = AC (OB + OD) 1 . . = AC. . BD 2 2 2 2 Trang 3 1 1
Bài 6: a) Nối B với D. ta có S = AB ; D S = s ADM BCF BDC. 3 3 B N 1 1 S + S = S + S = S M Do đó ADM BCF ( ABD BDC ) 3 3 A b) Nối M với F. 2 1 1 S = S ; S = S ; S = S MBFD MEF 3 2 MDF MNF 2 MBF D C E F Do đó S = S + S MNFE MEF MNF 1 = (S + S MDF MBF ) 2 1 2 1 = . S = S. 2 3 3
Bài 7: Gọi P, Q lần lượt là trung điểm của BC, AD Chứng minh được : 1 1 S = S ; S = S AQK 4 ABD MPC 4 BCD 1 1 S = S ; S = S DQM 4 DAC DKP 4 ABC 1 Suy ra: S = S QKPM 2 ABCD
Ta có QKPM là hình bình hành, KLMN là hình chữ nhật nên nếu O là trung điểm của NL,
PQ. Suy ra AD / /BC / /MK.  S = S ; S = S  S = S QMK NMK PMK LMK KLMN QKPM 1 Do đó S = S . KLMN 2 ABCD Bài 8: S = S ADC
BDC (hai tam giác co chung đáy DC,
đường cao tương ứng bằng nhau)  S − S = S − S  S = S ADC 0DC BDC ODC OAD OBC Trang 4 Ta có: S + S = S + S E OA ODE OBF OCF
 1 h OE + 1 h OE = 1 h OF + 1 h OF 1 2 1 2 2 2 2 2  1 OE(h + 1 h OF h h 1 2 ) = ( + 1 2 ) 2 2  OE = OF. Trang 5