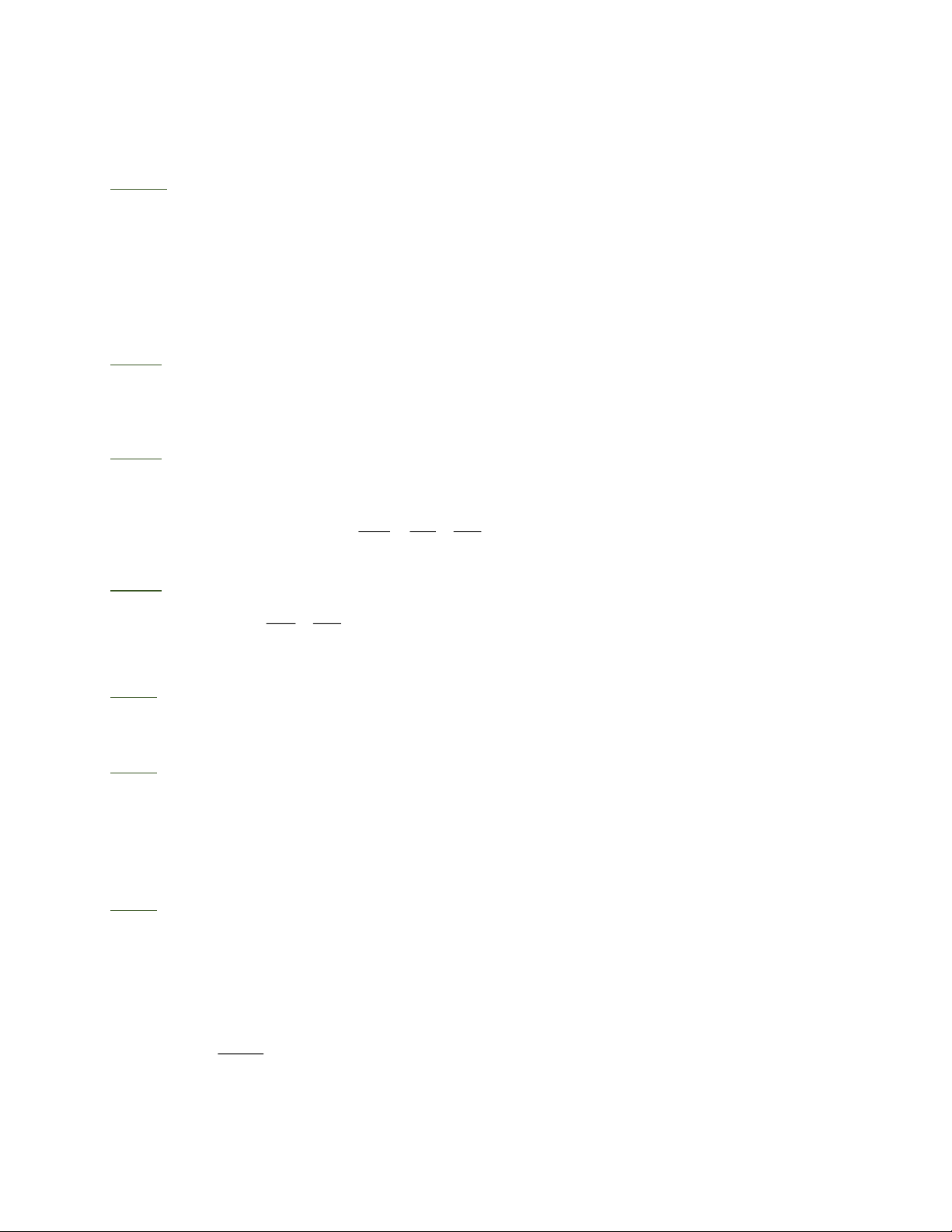
Preview text:
9. ÔN TẬP CHƯƠNG III I. BÀI TẬP
Bài 1: Cho tam giác ABC có AB = 9c , m AC = 12c .
m Các điểm D,E lần lượt trên các cạnh A ,
B AC sao cho: AD = 3c , m AE = 4c . m
a) Chứng minh rằng : DE//B . C
b) M là điểm trên cạnh BC sao cho BM = 2, 5MC . Gọi N là giao điểm của AM và DE.
Chứng minh rằng DN = 2, 5NE .
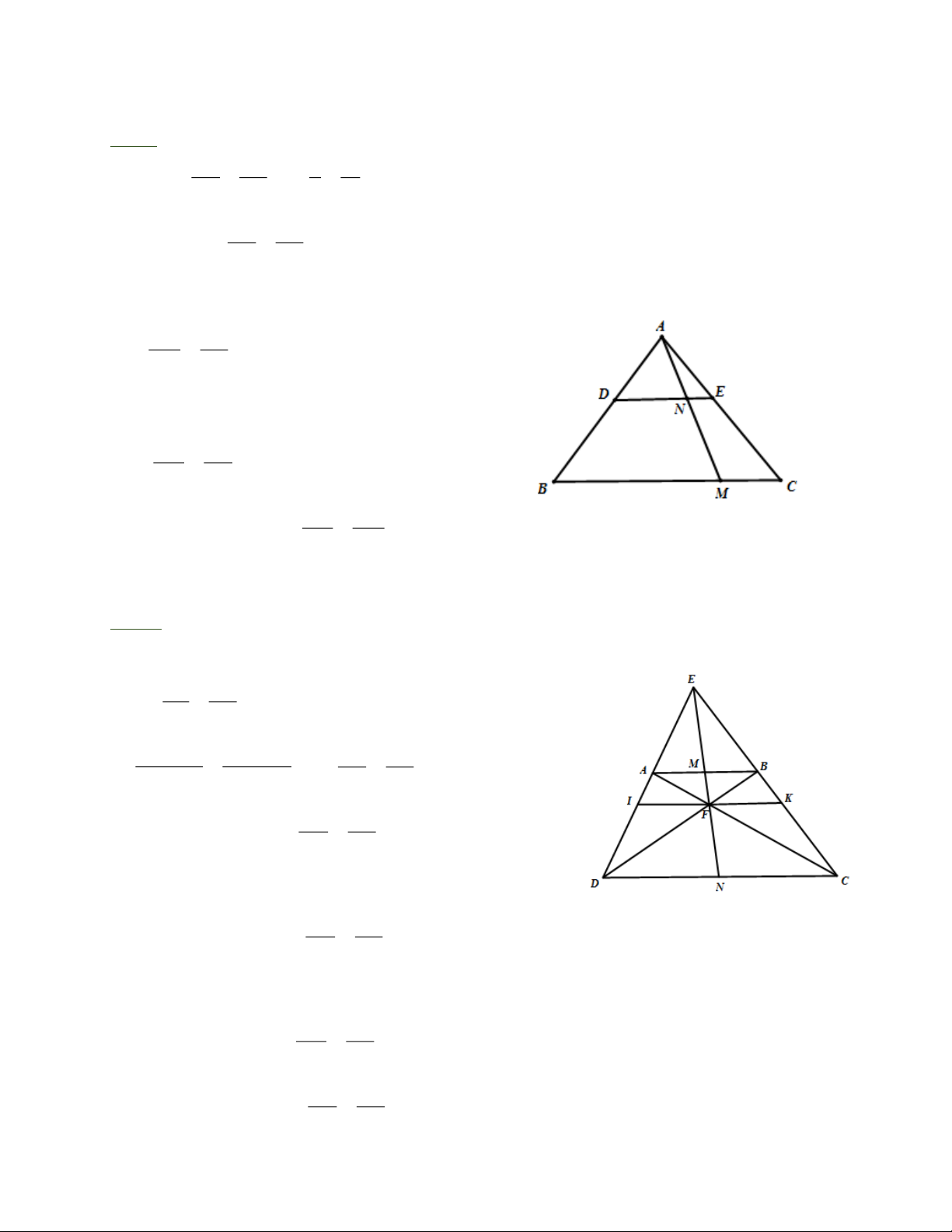
Bài 2: Cho hình thang A B CD có (AB//DC). E là giao điểm của AD và BC, F là giao điểm
của AC và BD. Chứng minh rằng đường thẳng È đi qua trung điểm của AB và qua trung điểm của DC.
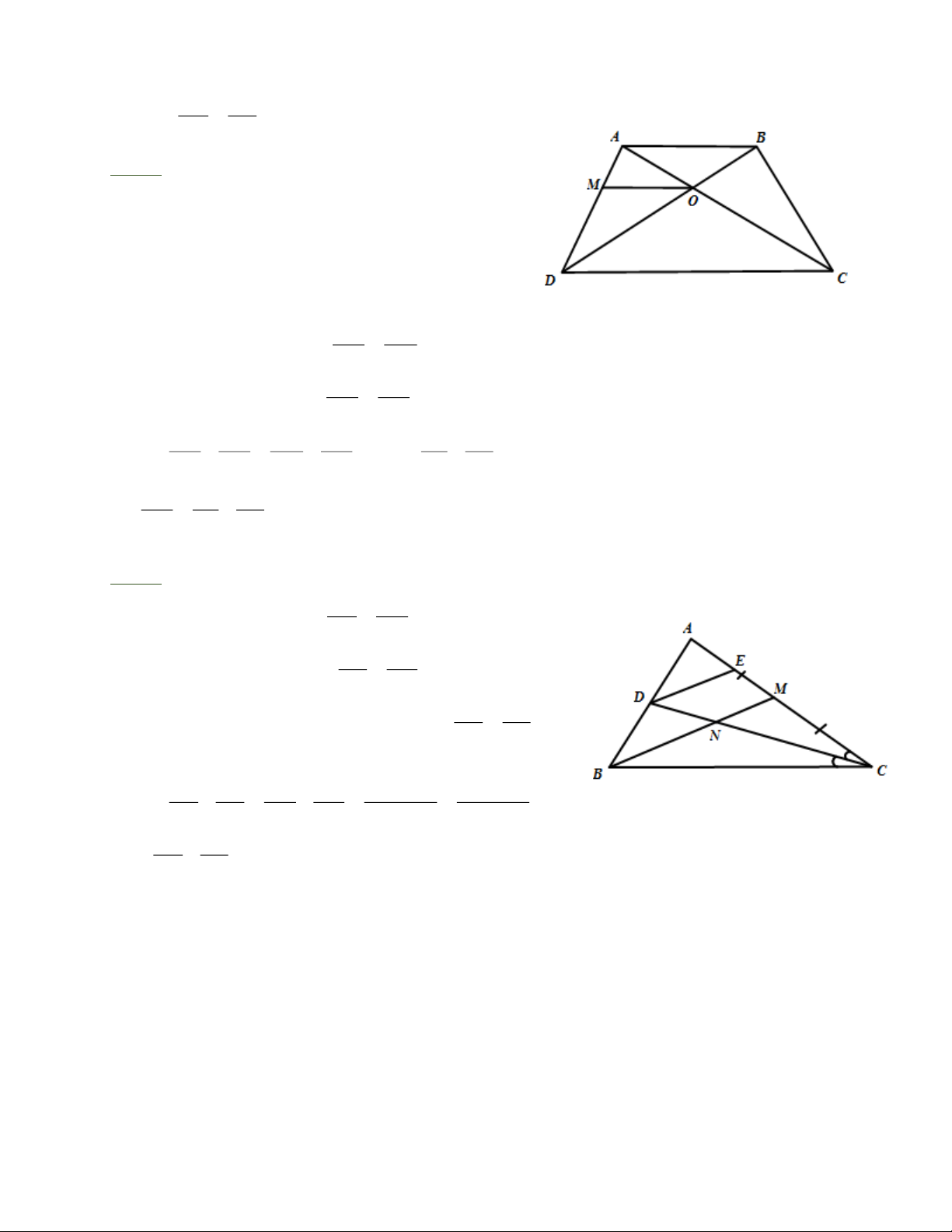
Bài 3: Cho hình thang A B CD ( AB // CD). O là giao điểm của AC và DB. Đường thẳng qua
O song song với AB cắt AD ở M. Chứng minh rằng 1 1 1
a) OAB” OCD b) = + . OM AB CD
Bài 4: Cho tam giác ABC có đường trung tuyến BM cắt đường phân giác Cd ở N. NC AC Chứng minh rằng − = 1. ND AB Tự luyện
Bài 5: Cho tam giác ABC cân tại A có các đường cao BE và CF. Gọi P là chân đường vuông
góc kẻ từ E đến AB, Q là là chân đường vuông góc kẻ từ F đến AC. Chứng minh PQ song song với BC.
Bài 6: Cho tam giác ABC vuông tại A, Ab = 1cm,AC = 3cm. Trên cạnh AC lấy các điểm D, E sao cho AD = DE = EC. a)Tính độ dài BD. b) Chứng minh BDE ∽ C DB. c) Tính DEB + DCB. 0
Bài 7: Cho hình thang vuông ABCD (A = D = 90 ) có hai đường chéo vuông góc với nhau tại O, AB = 4cm,CD = 9cm. a) Chứng minh AOB ∽ D AB. b) Tính độ dài AD.
c) Chứng minh OA.OD = OB.OC . S d) Tính tỉ số OAB . O S CD Trang 1 HƯỚNG DẪN GIẢI Bài 1: AD AE 3 4 a) Ta có : = ( vì = ) (1) AB AC 9 12 AD AE Xét ABC có =
DE / /BC ( định lý Ta- lét đảo ) AB AC
b) Xét AMC có NE / / M ( C DE / / BC) NE AE nên = . (2) MC AC
Xét ABM có DN / / BM (DE / /BC) DN AD Nên = . (3) BM AB DN NE
Từ (1) và (2) và (3) có : = . BM MC
Mà BM = 2, 5MC (gt), nên DN = 2, 5NE .
Bài 2: Qua F vẽ đường thẳng song song với DC và cắt AD tại I, cắt BC tại K, vì
IK//DC,AB//DC ( gt) nên IK//AB. FAB có AB//DC AF BF Nên : =
( hệ quả của định lý Ta – lét) CF DF AF BF = AF BF hay = . AF + CF BF + DF AC DB IF AF ADC có IF//DC, nên = DC AC
( hệ quả của định lý Ta- lét) FK BF BDC có FK//DC, nên =
( hệ quả của định lý Ta- lét) DC DB Suy ra : IF = FK. IF EF EDN có IF//DN, nên =
( hệ quả của định lý Ta- lét) DN EN FK EF ECN có FK//NC, nên =
( hệ quả của định lý Ta- lét). NC EN Trang 2 IF FK Do đó : =
, mà IF = FK DN = N . C DN NC
Bài 3: a) Xét OAB và OCD có
OAB = OCD ( đối đỉnh)
OBA = ODC ( so le trong và AB//CD).
Do đó OAB” OCD( . g ) g
b) Ta có OM//AB ( gt), AB//CD ( gt) OM//CD. OM DM Xét ABD có OM//AB =
( hệ quả của định lí Ta – lét) AB AD OM AM
Xét ACD có OM//CD =
( hệ quả của định lí Ta – lét) CD AD OM OM DM AM 1 1 Do đó + = + OM + = 1 AB CD AD AD AB CD 1 1 1 = + . OM AB CD
Bài 4: Qua D vẽ đường thẳng song song với BM cắt AC ở E. NC MC
Xét CDE có MN//DE = . ND EM AD AE
Xét ABM có DE / / BM = . BD EM AD AC
Xét ABC có CD là đường phân giác = . BD BC
Mà AM=MC( M là trung điểm của AC) NC AD MC AE MC − AE AM − AE Do đó − = − = = = 1 ND BD EM EM EM EM NC AC Hay − = 1. ND BC Trang 3




