Bài Tập Hình Học 7 Tính Chất Đường Trung Trực Của Đoạn Thẳng Có Lời Giải

 TÍNH CHẤT ĐƯỜNG TRUNG TRỰC CỦA ĐOẠN THẲNG
I. KIẾN THỨC CƠ BẢN
Định nghĩa đường trung trục: Đường trung trực của một đoạn d
thẳng là đường thẳng vuông gó với đoạn thẳng ấy tại trung M điểm của nó.
Trên hình vẽ bên, d là đường trung trực của đoạn thẳng A B . A H B
Ta cũng nói: A đối xứng với B qua d .
Định lí 1: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Định lí 2: Điểm cách đều ai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
MA = MB Þ M thuộc đường trung trực của A B
Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó. II. BÀI TẬP
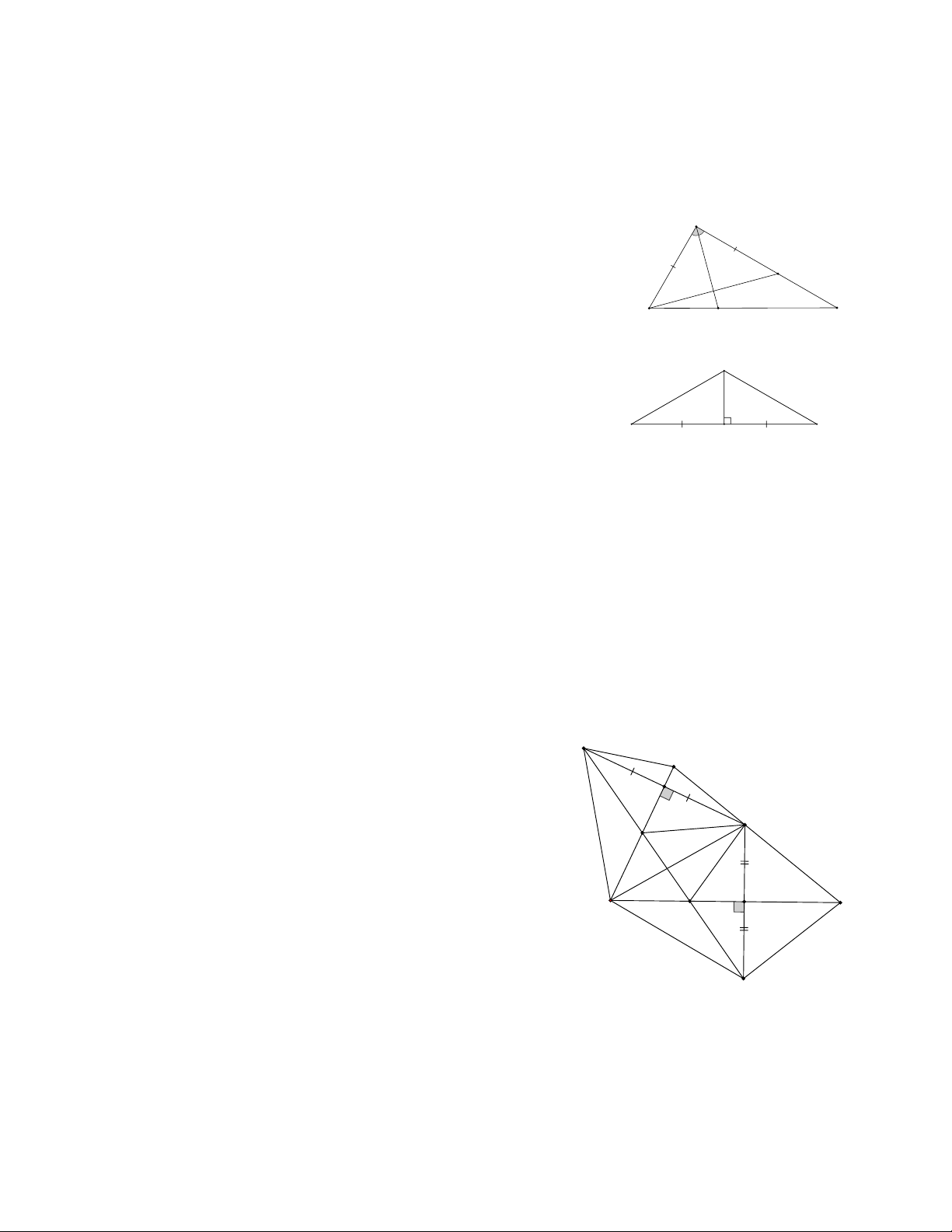
Bài 1: Cho tam giác ABC, đường phân giác AD. Trên tia AC lấy điểm E sao cho AE = AB .
Chứng minh rằng AD vuông góc với BE µ
Bài 2: Tam giác ABC vuông tại A có C = 30°. Trên tia đối của tia AC lấy điểm D sao cho ·
AD = AC. Tính số đo góc DBC.
Bài 3: Cho 3 tam giác cân MA B, NA B, PA B có chung đáy A B . Chứng minh M , N , P thẳng hàng.
Bài 4: Cho tam giác ABC có 0
A = 60 , M là điểm nằm giữa B và C. Vẽ điểm E sao cho AB là
đường trung trực của ME, điểm F sao cho AC là đường trung trực của MF.
a) Chứng minh trung trực của EF đi qua A.
b) Chứng minh BE + CF = BC .
c) Tính các góc của tam giác AEF.
d) EF cắt AB, AC lần lượt tại I, K. Chứng minh MA là phân giác của góc IMK.
e) Phải cho góc A của tam giác ABC bằng bao nhiêu độ để A là trung điểm của EF. Trang 1
Bài 5: Cho D ABC góc A nhọn, đường cao AH. Lấy các điểm P và Q lần lượt đối xứng
với H qua AB, AC.
a) Chứng minh AP = A . Q · ·
b) Cho BAC = 60°. Tính số đo góc PA . Q
c) Chứng minh API = AHI và AHK = AQK.
d) Gọi I , K lần lượt là giao điểm của PQ với AB, AC. Chứng minh HA là tia phân giác · của IHK.
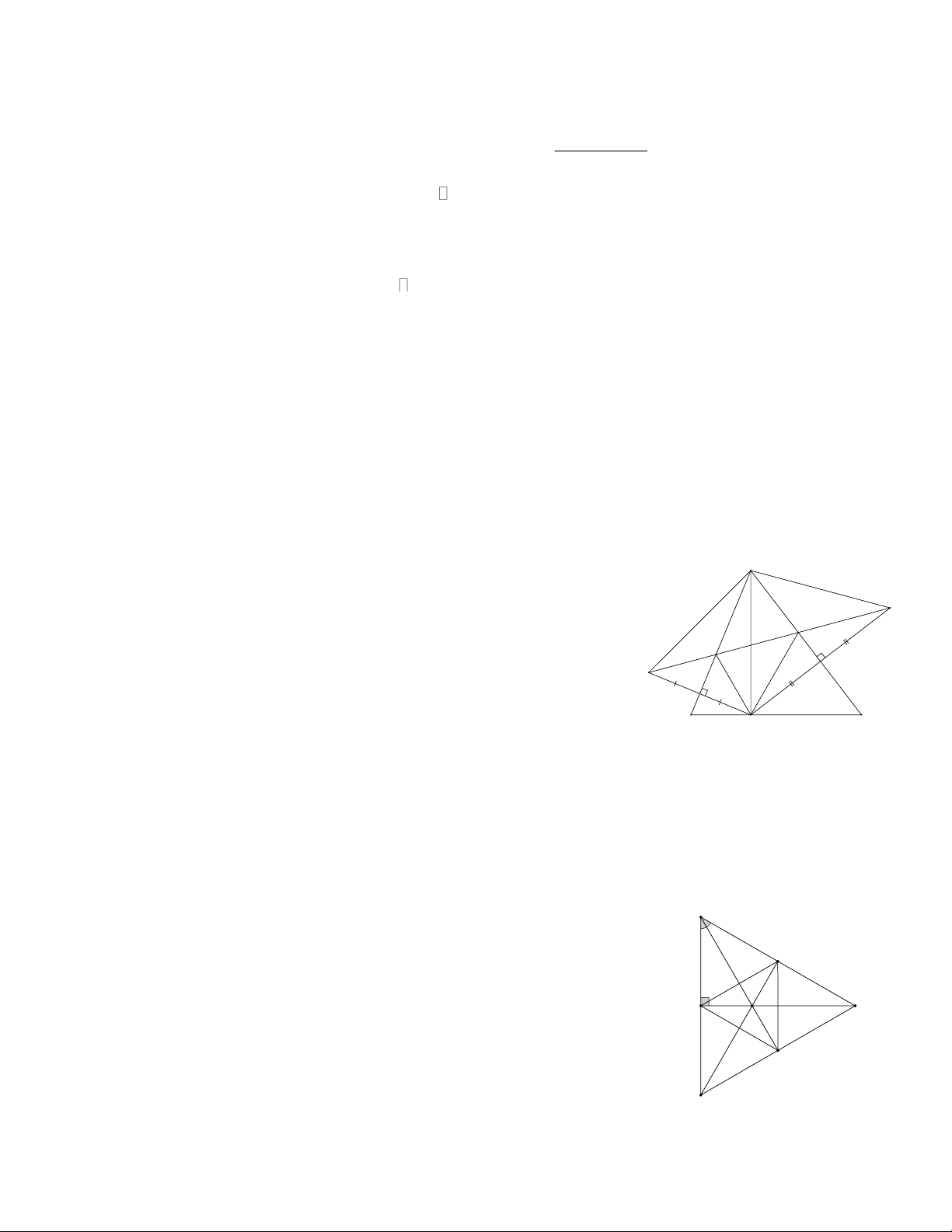
Bài 6: Cho tam giác ABC có 0
A = 90 . Trên tia BA lấy điểm M sao cho BM = BC . Phân giác
của góc ABC cắt AC tại I, MC ở K. Tia MI cắt BC ở H.
a) Chứng minh BI là trung trực của AH và AH // MC.
b) Chứng minh AK + KH = CM . c) Nếu 0
KAH = 60 , tính 0 ABC = 60 .
Bài 7: Cho tam giác ABC có 0
A = 90 , AB  AC , AH là đường cao HM, HN lần lượt là
đường phân giác của tam giác ABH và ACH. Gọi I là trung điểm của MN. Tia AI cắt BC ở K.
a) Chứng minh MN = AK và I là trung điểm của AK.
b) Chứng minh tam giác MAN là tam giác vuông. Hết Trang 2 HDG Bài 1: ABD 
= AED (c.g.c)  DB = DE (1) A
Theo giả thiết: AB = AE (2) E
Từ (1) và (2), ta chứng minh được AD là đường trung trực của C B D
BE. Suy ra A D ^ BE B
Bài 2: AB là đường trung trực của AC
Þ BD = BC Þ DDBC cân. 30o · µ D A C
Þ BDA = C = 30° ·
. Þ DBC = 180° - 60° = 120° Bài 3:
Vì MAB cân tại M Þ MA = MB Þ M Î đường trung trực của đoạn thẳng A B
NAB cân tại N Þ NA = NB Þ N Î đường trung trực của đoạn thẳng A B
PAB cân tại P Þ PA = PB Þ P Î đường trung trực của đoạn thẳng A B
 M , N , P thẳng hàng. Bài 4:
a) Vì AB là trung trực của EM Þ A E = A M
Vì AC là trung trực của MF Þ A F = A M
Þ A E = AF ( = AM) Þ A Î đường trung trực của E B
EF hay đường trung trực của EF đi qua A.
b) Vì AB là trung trực của EM Þ BE = BM
Vì AC là trung trực của MF Þ CF = CM M I
Có BC = BM + CM = BE + CF Þ BC = BE + CF
c) Xét AEM cân tại A có AB là đường trung trực
AB là phân giác EAM  A E B = MAB A K C
Xét AFM cân tại A có AC là đường trung trực
AC là phân giác FAM  FAC = MAC F Có: · · ·
BA C = BA M + MA C Trang 3 · · · · · · 0
Þ 2BA C = BA M + MA C + EAB + FAC Þ EA F = 120 · 180 - 120 0 · · 0 0
Vì AEF cân tại A và 0
EA F = 120 Þ A EF = A FE = = 30 2
d) Vì K  trung trực MF  KM = KF  KMF cân tại K  KMF = KFM
AFM cân tại A AMF = AFM  AMK = AFK
Vì I  trung trực ME  IM = IE  IEM cân tại I  IEM = E IM
AEM cân tại A AME = AEM  AEI = AMI Mà E
A I = AFK  AMK = AMI  MA là phân giác của IMK
e) Để A là trung điểm của EF 0  EAF = 180 · · · mà 0
EA F = 2BA C Þ BA C = 90 Bài 5:
a) Từ giả thiết suy ra AP = AH và AQ = AH nên AP = A . Q A b) Ta có: Q · · ·
PAQ = PAH + HAQ K · · I = 2(BAH + HAC) · P = 2BAC = 120°. · ·
c) D API = D AHI (c.c.c) Þ API = AHI ( ) 1 . B H C D · ·
AHK = D AQK (c.c.c) Þ AHK = AQK (2). · ·
d) Có AP = AQ Þ D PAQ cân Þ API = AQK ( ) 3 . · · Từ ( ) 1 , (2) và ( )
3 suy ra AHI = AHK. Þ ·
HA là tia phân giác của IHK. B · ·
Bài 6: DMBI = DCBI (c. .
g c) Þ BMI = BCI H
DBHM = DBA C (g - c - g) Þ BA = BH hay D BA H cân tại B có A I C
phân giác BI nên BI đồng thời là đường trung trực của AH K  BI ⊥ AH .
BK là phân giác trong tam giác cân MBC cân tại B nên BK cũng M Trang 4
là đường trung trực của đoạn MC  BK ⊥ MC mà B, I , K thẳng hàng  BI ⊥ MC . Từ đó suy ra AH // MC 1
b) Tam giác A MC vuông tại A, trung tuyến AK nên A K = KC = KM = MC 2 · ·
DBHM = DBA C (cmt ) Þ BHM = 90° Þ CHM = 90° 1
Tam giác CHM vuông tại H, đường trung tuyến KC nên HK = KC = KM = MC 2
Từ đó suy ra AK + KH = CM
[ Lưu ý: Xem lại bài 5 – Phiếu C304: Tính chất 3 đường trung tuyến của tam giác] c) Nếu 0
KAH = 60 thì D A HK đều (vì A K = HK ). · ·
A KM = HKC = 60° Þ DA KM ;DHKC là các tam giác đều · · · ·
Þ A MK = HCK = 60° Þ BMC = BCM = 60°
Suy ra tam giác BMC đều hay 0 ABC = 60 Trang 5