 TÍNH CHẤT BA ĐƯỜNG PHÂN GIÁC TRONG CỦA TAM GIÁC
I. KIẾN THỨC CƠ BẢN A
1. Định lí: Ba đường phân giác của một tam giác cùng đi qua một E
điểm. Điểm này cách đều ba cạnh của tam giác đó. F I
A  A , B  B , C  C 1 2 1 2 1 2  B D C
ID  IE  IF .
2. Tính chất: Trong một tam giác cân, đường phân giác của góc ở đỉnh đồng thời là đường
trung tuyến của tam giác đó. II. BÀI TẬP
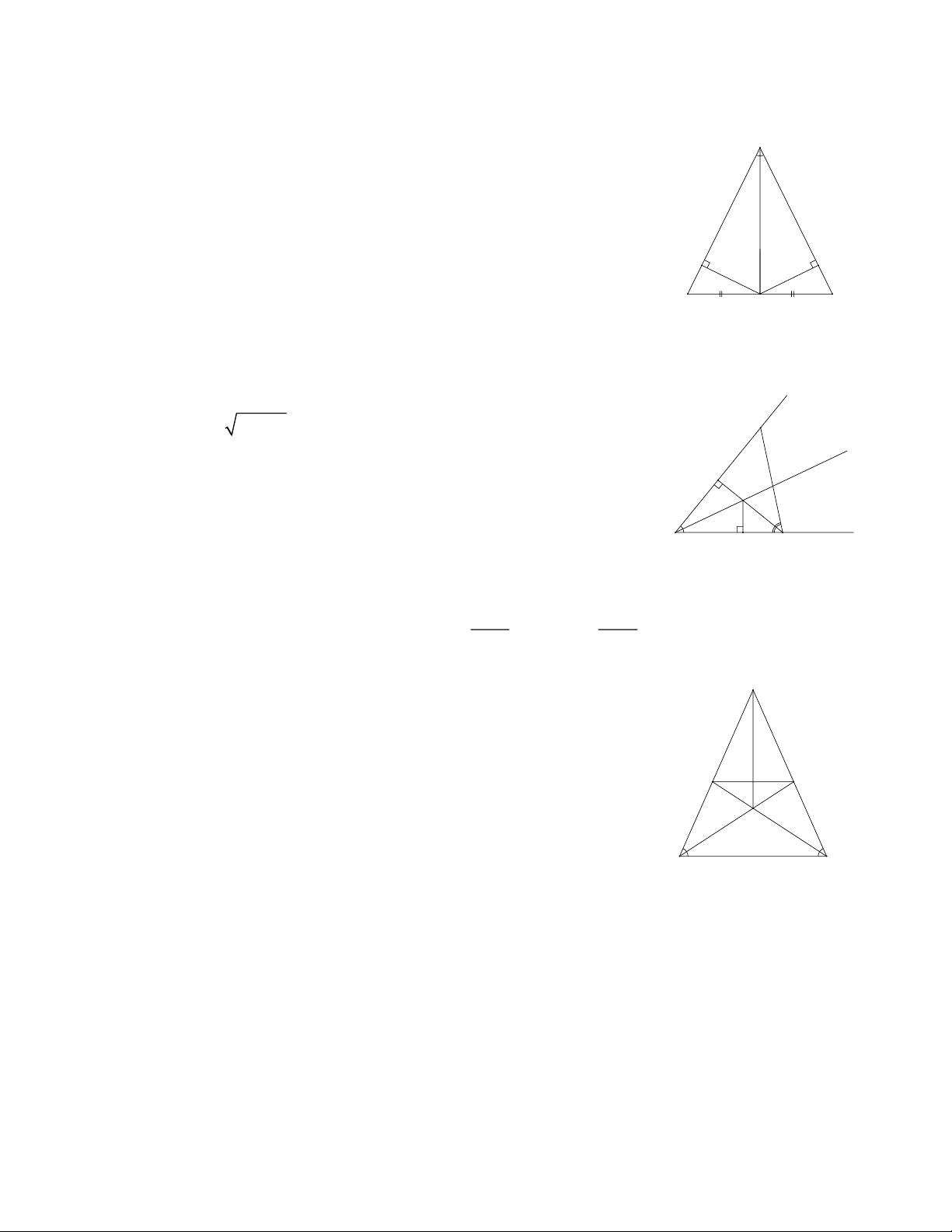
Bài 1: Cho ABC có đường trung tuyến AM đồng thời là đường phân giác của góc . A
Chứng minh rằng ABC cân tại . A
Bài 2: Cho xOy, tia phân giác .
Oz Trên tia Ox lấy điểm A sao cho OA  3 c . m Từ A kẻ
đường thẳng vuông góc với Ox cắt Oz tại H , cắt Oy tại K. Lấy điểm B trên tia Ox sao
cho KA là tia phân giác của góc OK .
B Hạ HI  OK.
a) Chứng minh AH  HI.
b) Biết OH  5 c ,
m tính khoảng cách từ điểm H đến BK.
Bài 3: Cho tam giác ABC cân tại .
A CP, BQ là các tia phân giác trong của ABC (
P  AB, Q  AC ). Gọi O là giao điểm của CP và . BQ
a) Chứng minh tam giác OBC là tam giác cân.
b) Chứng minh điểm O cách đều ba cạnh AB, AC và . BC
c) Chứng minh đường thẳng AO đi qua trung điểm của đoạn thẳng BC và vuông góc với nó.
d) Chứng minh CP  B . Q
e) Tam giác APQ là tam giác gì? Vì sao?
Bài 4: Cho tam giác MNP có N  50 ,  P  60 .
 Các tia phân giác ME, PF cắt nhau ở H.
Hãy tính số đo góc NH . P Bài 5: Cho tam giác .
ABC Các tia phân giác ở góc B và C cắt nhau ở I. a) Nếu A  70 ,
 hãy tính số đo góc BIC. b) Nếu BIC  140 ,  hãy tính số đo góc . A c) Chứng minh rằng  90  A BIC . 2 Hết Trang 1 HDG Bài 1: A
Hạ MD  AB, ME  AC.
Vì AM là tia phân giác của A nên MD  M . E D E
Do đó BDM  CEM (cạnh huyền – cạnh góc vuông).
Suy ra B  C. Vậy ABC cân tại . A B M C
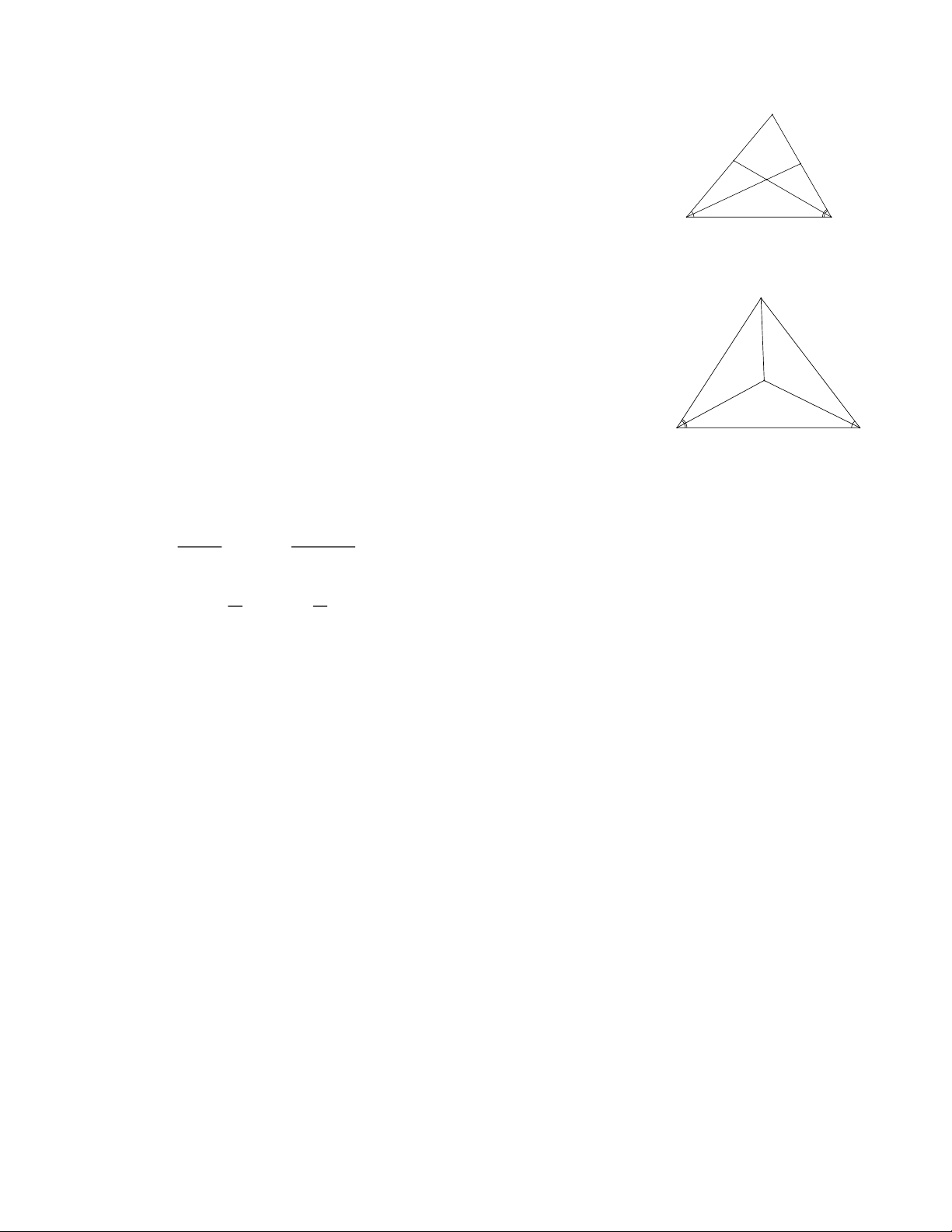
Bài 2: a) Vì H nằm trên tia phân giác của xOy nên H cách đều
Ox, Oy  AH  HI. x b) Tính 2 2
AH  5  3  4 c . m B z
Chứng minh H là giao điểm của ba đường phân giác trong A
OBK nên H cách đều ba cạnh của tam giác đó. H
Vậy khoảng cách từ điểm H đến BK bằng AH  4 c . m O y I K Bài 3:
a) Từ giả thiết suy ra ABC  ACB,   BAC B B ,   ACB C C 1 2 2 1 2 2
 B  B  C  C . A 1 2 1 2  OBC cân.
b) Vì O là giao điểm các tia phân giác CP và BQ trong ABC nên P Q
O là giao điểm ba đường phân giác trong  .
ABC Do đó, O
cách đều ba cạnh AB, AC và . BC O
c) Ta có ABC cân tại ,
A AO là tia phân giác ở đỉnh A nên AO 1 1 2 2 B C
đồng thời là trung tuyến và đường cao của  . ABC
Vậy đường thẳng AO đi qua trung điểm của đoạn thẳng BC và vuông góc với nó.
d) PBC  QCB (g.c.g)  CP  B . Q
e) Có AP  AB  BP, AQ  AC  CQ   1 .
Mà PBC  QCB  BP  C ;
Q AB  AC 2. Từ  
1 và 2 suy ra AP  A . Q
Vậy tam giác APQ cân tại A . Trang 2 Bài 4: M
Từ giả thiết suy ra N  25 và P  30 .  1 1 F E H
Do đó, ta tính được góc NHP  125 .  1 1 Bài 5: N P
a) Xét ABC, ta tính được B  C  110 .  A
Do đó, IBC  ICB  55 . 
Vậy BIC  180  55  125 . 
b) Xét BIC, từ giả thiết suy ra IBC  ICB  40 .  Do đó, ta có I
ABC  ACB  80 .  B C Vậy BAC  100 . 
c) Ta có: BIC  180  IBC  ICB B  C 180   A 180   180  2 2    A A 180   90    90  .  2  2   Bài tập bổ sung
Bài 6: Cho ABC vuông tại A có các tia phân giác của góc B, góc C cắt nhau tại I. Vẽ
ID  AB tại D, IE  AC tại E.
a) Chứng minh AB  AC – BC  2A . E
b) Cho biết AB  6 c ,
m AC  8cm . Tính IA, IB, IC ?
Bài 7: Cho ABC có BAC  120 , có các phân giác AD, BE, CF.
a) Chứng minh DE là phân giác giác của góc ADC .
b) Đường thẳng vuông góc với CF tại C cắt đường thẳng AB tại K. Chứng minh D, E, K
thẳng hàng và tính góc BED ?
c) Tính chu vi DEF biết DE  21cm , DF  20c . m Trang 3