. CÁC GÓC TẠO BỞI MỘT ĐƯỜNG THẲNG CẮT HAI ĐƯỜNG THẲNG
I. KIẾN THỨC CƠ BẢN
1. Hai cặp góc so le trong : c A4 và 2 B ; A1 và 3 B . A 2 3
2. Bốn cặp góc đồng vị : 1 4 A2 và 2 B ; A3 và 3 B ; a 2 3 1 B A 4 1 và 1 B ; A4 và 4 B
3. Hai cặp góc trong cùng phía : b A1 và 2 B ; A4 và 3 B
4. Quan hệ giữa các cặp góc: Nếu hai đường thẳng cắt một đường thẳng thứ ba và trong
các góc tạo thành có một cặp góc so le trong bằng nhau thì :
- Hai góc so le trong còn lại bằng nhau.
- Hai góc đồng vị bằng nhau.
- Hai góc trong cùng phía bù nhau. ìï µ µ ï A2 = B 2 ï µ µ ïï µ µ
A1 = B 1 Þ í A 3 = B 1 ïï µ µ ïï A o 2 + B 1 = 180 ïî II. BÀI TẬP
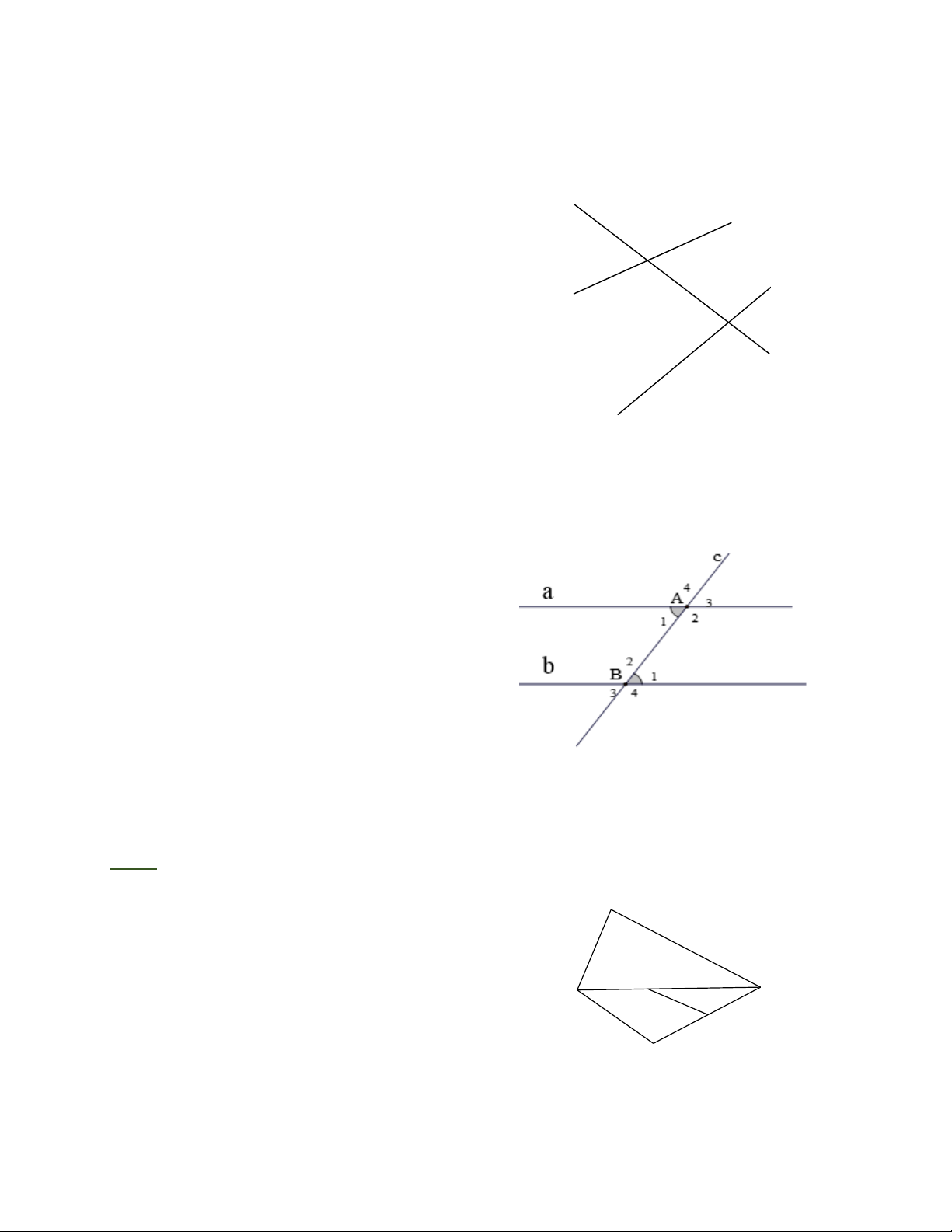
Bài 1: Xem hình vẽ bên rồi điền tên cặp góc cho đúng:
a) ABC và BCD là hai góc ………….. B
b) CMN và CAD là hai góc …………
c) CMN và DNM là hai góc ……….. M A C
d) DAC và ACB là một cặp góc ……. N
e) CBA và DAB là một cặp góc …..… D Trang 1
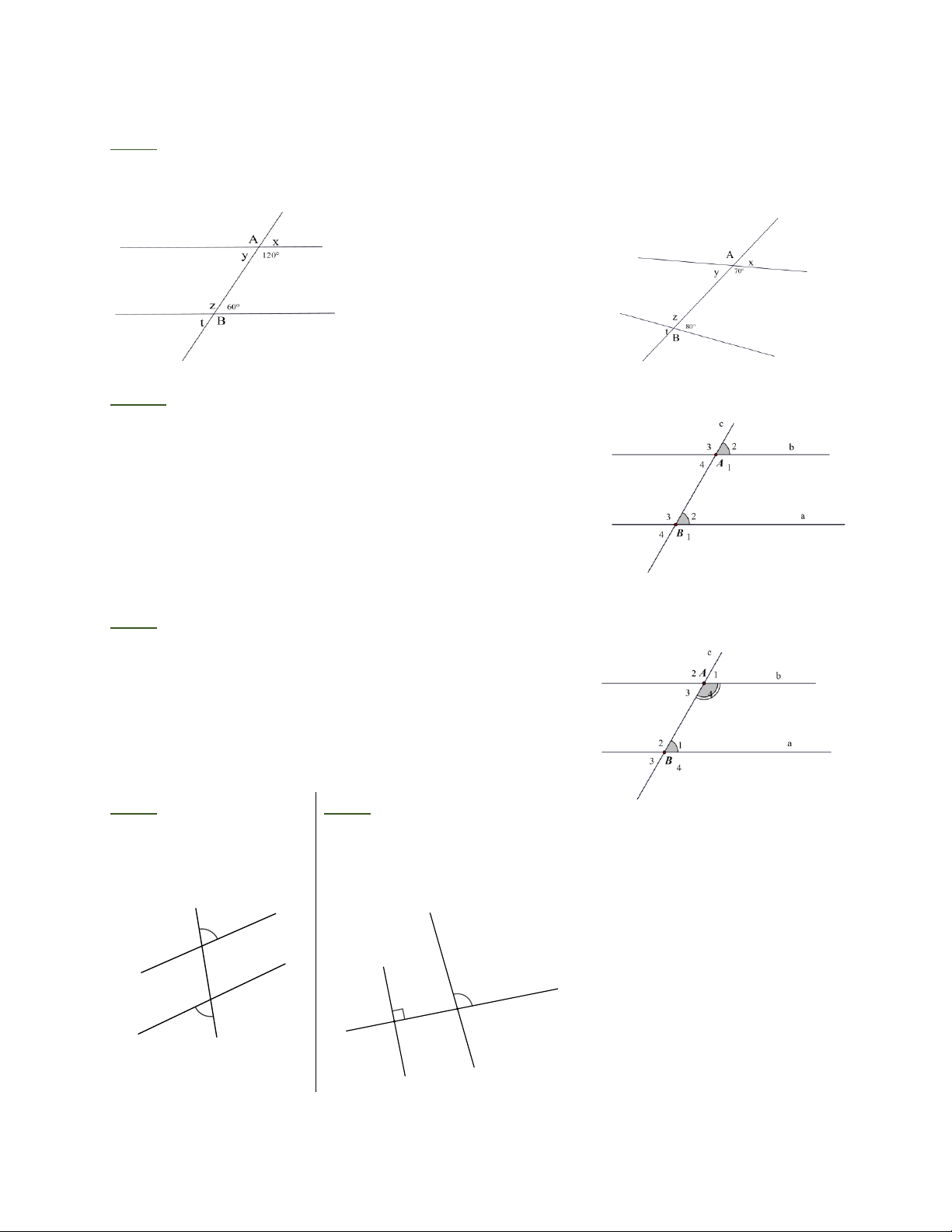
Bài 2: Tính các giá trị x,y, z,t trên mỗi hình sau: a) b)
Bài 3: Với hình vẽ bên cho biết A  B . Chứng minh rằng 2 2
a) A  B ; A  B 4 2 1 3
b) A  B ; A  B ; A  B 3 3 1 1 4 4 c) 0
A  B  180 ; 0 A  B  180 1 2 4 3
Bài 4: Cho đường thẳng c cắt hai đường thẳng a ; b tại hai điểm A và B tạo thành cặp góc
trong cùng phía bù nhau. Chứng minh rằng :
a) 2 góc so le trong (trong mỗi cặp) bằng nhau
b) 2 góc đồng vị (trong mỗi cặp) bằng nhau
c) 2 góc trong cùng phía còn lại bù nhau.
Bài 5: Cho hình vẽ. Tính Bài 6: Cho hình vẽ. các góc còn lại.
a) Kể tên các cặp góc so le trong,
Biết A  B   75 .
các cặp góc đồng vị và các cặp 2 4 góc trong cùng phía.
b) Tính các góc còn lại. A 2 y 1 4 3 x 2 z' 1 100° 3 4 B z B A y' x' Trang 2 HDG
Bài 1: a) Trong cùng phía b) đồng vị c) so le trong d) So le trong e) trong cùng phía
Bài 2: a) x = y = t = 0 , z = . 0 60 120 b) x = 0 , y = 0 , z = 0 ,t = . 0 70 110 100 80
Bài 3: a) A  A ( đối đỉnh) mà A  B (gt ) =>. A  B ( vì cùng bằng A ) 4 2 2 2 4 2 2 Ta có 0
A  A  180 ( hai góc kề bù ) 2 4 0
B  B  180 ( hai góc kề bù ) 2 3
Mà A  B (gt) . Suy ra A  B ( cùng bù với hai góc bằng nhau) 2 2 1 3 b)  Ta có 0
A  A  180 ( hai góc kề bù ) 2 1 0
B  B  180 ( hai góc kề bù ) 2 3
Mà A  B (gt) . Suy ra A  B ( cùng bù với hai góc bằng nhau) 2 2 3 3  Ta có 0
A  A  180 ( hai góc kề bù ) 2 1 0
B  B  180 ( hai góc kề bù ) 1 2
Mà A  B (gt) . Suy ra A  B ( cùng bù với hai góc bằng nhau) 2 2 1 1
 Ta có A  A (Đối đỉnh) 2 4
B  B ( Đối đỉnh) 2 4
Mà A  B (gt)  A  B 2 2 4 4 c)  Vì 0 A  A  180 1 2
mà A  B (gt) . Suy ra 0 A  B  180 2 2 1 2  Ta có 0
B  B  180 (kề bù) mà A  B (chứng minh trên) 3 2 4 2 Suy ra 0 A  B  180 4 3 Trang 3 ¶ ¶ µ ¶
Bài 4: Giải sử ta có 0
A + B = 180 . Ta cần chứng minh hai góc so le trong A 3 = B ; 4 1 1 µ ¶ ¶ ¶
Hai góc đồng vị A = B ; Hai góc trong cùng phí a 0 A + B = 180 1 1 3 2
a) 2 góc so le trong trong mỗi cặp) bằng nhau ¶ ¶ ¶ ¶ Ta có 0 A + B = 180 mà 0
A + A = 180 (hai góc kề bù) 4 1 4 3 Þ µ ¶ A 3 = B 1
b) 2 góc đồng vị ( trong mỗi cặp) bằng nhau ¶ ¶ µ ¶ Ta có 0 A + B = 180 mà 0
A + A = 180 (hai góc kề bù) 4 1 1 4 Þ µ ¶ A = B 1 1
c) 2 góc trong cùng phía còn lại bù nhau. ¶ ¶ µ ¶ µ ¶ ¶ ¶ Ta có 0
A + B = 180 mà A 0 3 = B
(c/mt) và A = B (c/mt) Þ A + B = 180 4 1 1 1 1 3 2
Bài 5: A  A  B  B  0
75 , A  A  B  B  0 180  0 75  0 105 . 2 4 4 1 1 3 1 3 Bài 6: y a) HS tự trình bày;
b) xAz  xAB  x AB  x Az  0 ' ' 90 . x z' 100° yBz  ABy  0 '
' 100 , y Bz  yBz  0 ' ' 80 . z B A y' x' Trang 4