Giải Toán 7 Bài tập cuối chương III - Kết nối tri thức với cuộc sống
Giải Toán 7 Bài tập cuối chương III - Kết nối tri thức với cuộc sống được trình bày khoa học, chi tiết giúp cho các bạn học sinh chuẩn bị bài một cách nhanh chóng và đầy đủ đồng thời giúp quý thầy cô tham khảo để soạn giáo án cho học sinh của mình. Thầy cô và các bạn xem, tải về ở bên dưới.
Chủ đề: Chương 3: Góc và đường thẳng song song (KNTT)
Môn: Toán 7
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 3: Góc và đường thẳng song song (KNTT)
Môn:
Sách:
Tác giả:
Tài liệu liên quan:
Preview text:
Giải Toán 7 Bài tập cuối chương III sách Kết nối tri thức với cuộc sống
Giải Toán 7 Kết nối tri thức với cuộc sống trang 59 tập 1 Bài 3.32
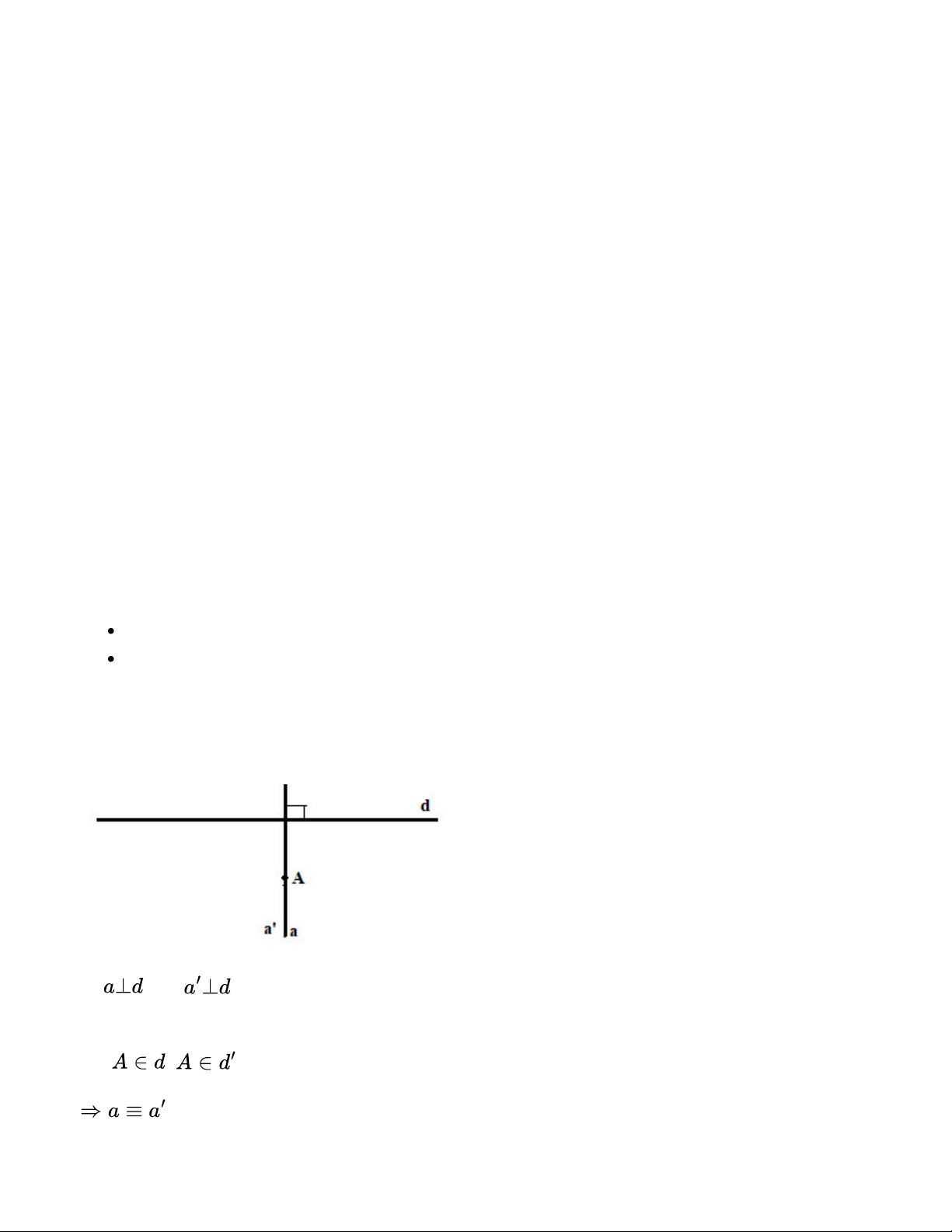
Chứng minh rằng: Cho điểm A và đường thẳng d thì có duy nhất đường thẳng đi qua A và
vuông góc với d, tức là nếu có hai đường thẳng đi qua A vuông góc với d thì chúng phải trùng nhau. Hướng dẫn giải:
- Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc
với đường thẳng còn lại
- Qua một điểm ở ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.
- Nếu một đường thẳng cắt hai đường thẳng song song thì:
Hai góc so le trong bằng nhau.
Hai góc đồng vị bằng nhau. Gợi ý đáp án:
Giả sử có 2 đường thẳng a và a’ đi qua A và vuông góc với d. Vì , mà
nên a // a’ (hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau) Mà ,
Vậy có duy nhất đường thẳng đi qua A và vuông góc với d Bài 3.33
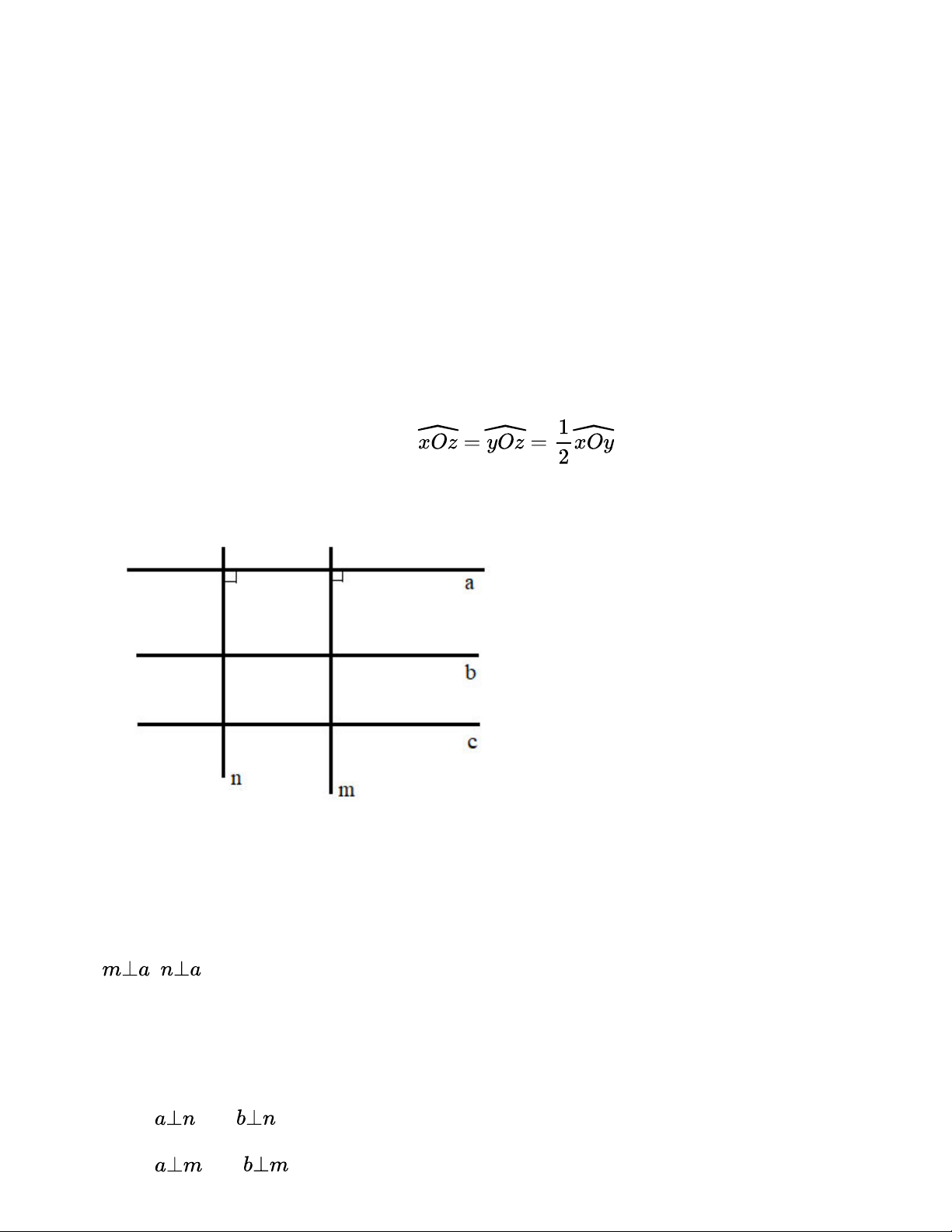
Vẽ ba đường thẳng phân biệt a, b, c sao cho a//b, b//c và hai đường thẳng phân biệt m, n cùng
vuông góc với a. Hỏi trên hình có bao nhiêu cặp đường thẳng song song, có bao nhiêu cặp đường thẳng vuông góc? Hướng dẫn giải:
- Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là hai góc kề bù.
- Hai góc kề bù có số đo bằng 1800.
- Tia nằm giữa hai cạnh của một góc và tạo với hai cạnh ấy hai góc bằng nhau được gọi là tia phân giác của góc đó.
- Khi Oz là tia phân giác của góc xOy thì Gợi ý đáp án: Ta có:
+) a // b, b // c nên a // c (Hai đường thẳng cùng song song với đường thẳng thứ ba thì chúng song song với nhau) +) ;
nên m // n (Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
Theo định lý “Đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì cũng vuông góc
với đường thẳng kia", ta có: +) a // b; nên +) a // b; nên +) a // c; nên +) a // c; nên
Vậy các cặp đường thẳng song song là: a // b ; a // c ; b // c; m // n
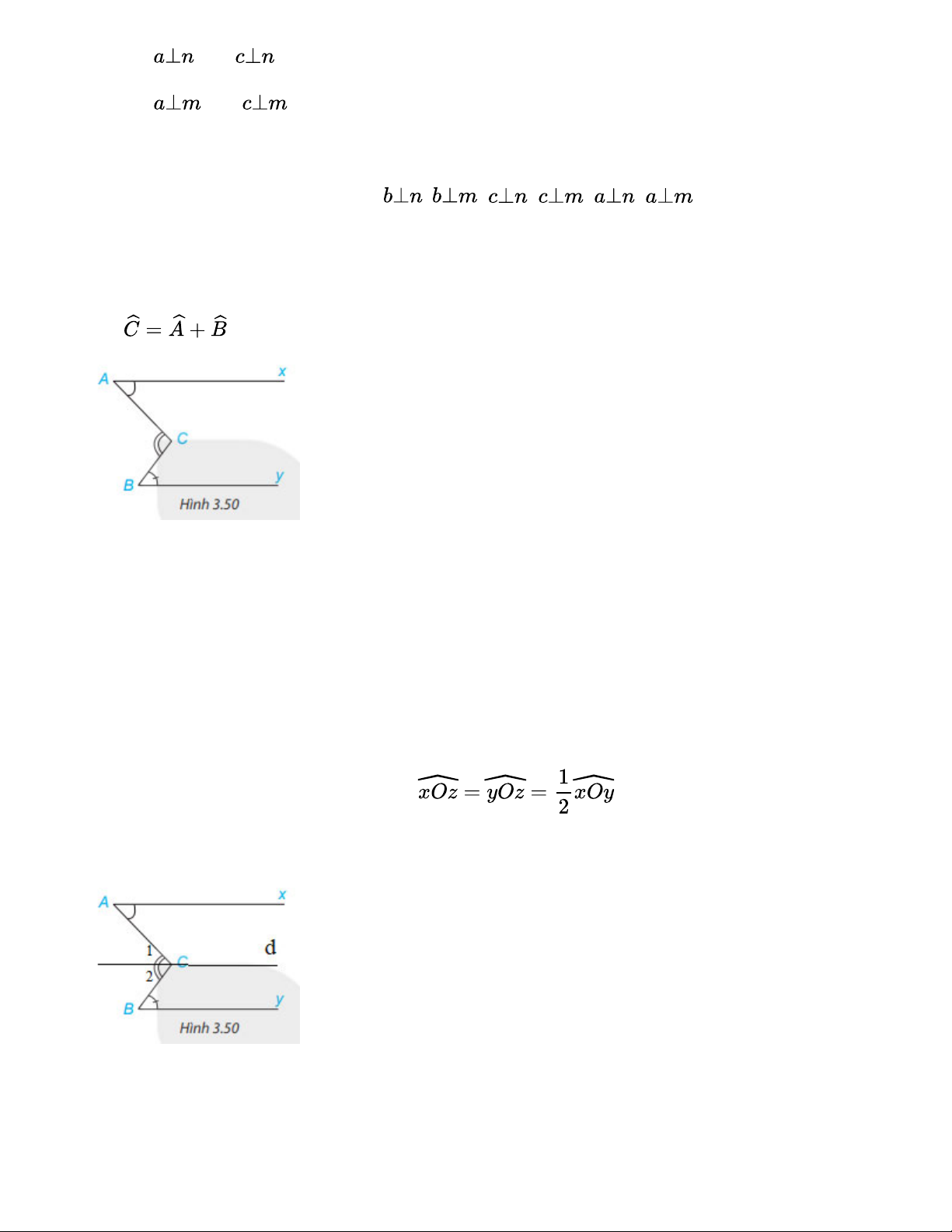
Các cặp đường thẳng vuông góc là: ; ; ; ; ; Bài 3.34
Cho Hình 3.50, trong đó hai tia Ax và By nằm trên hai đường thẳng song song. Chứng minh rằng Hướng dẫn giải:
- Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là hai góc kề bù.
- Hai góc kề bù có số đo bằng 1800.
- Tia nằm giữa hai cạnh của một góc và tạo với hai cạnh ấy hai góc bằng nhau được gọi là tia phân giác của góc đó.
- Khi Oz là tia phân giác của góc xOy thì Gợi ý đáp án:
Qua C kẻ đường thẳng d song song với Ax Vì Ax // By nên d // By Vì d // Ax nên (2 góc so le trong) Vì d // By nên (2 góc so le trong) Mà Vậy đ Bài 3.35
Cho Hình 3.51, trong đó Ox và Ox’ là hai tia đối nhau
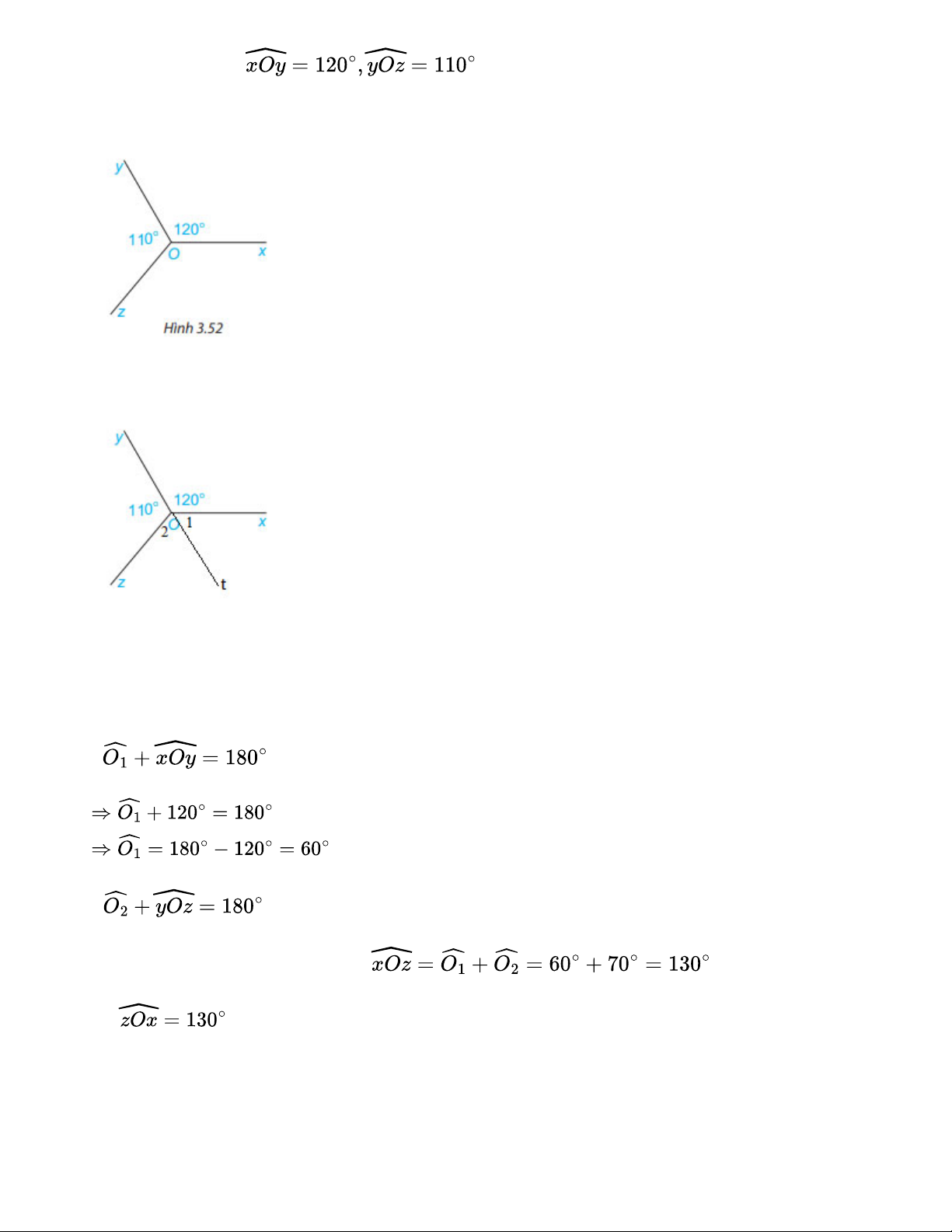
a) Tính tổng số đo ba góc O1, O2, O3 . Gợi ý: , trong đó b) Cho . Tính Gợi ý đáp án: a) Ta có: , mà (2 góc kề bù) Vậy b) Vì Vậy Bài 3.36 Cho Hình 3.52, biết . Tính số đo góc zOx.
Gợi ý: Kẻ thêm tia đối của tia Oy Gợi ý đáp án:
Kẻ Ot là tia đối của tia Oy. Ta được: +) (2 góc kề bù) +) (2 góc kề bù)
Vì Ot nằm giữa 2 tia Ox và Oz nên Vậy