Giải Toán 7 Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song | Kết nối tri thức
Giải Toán 7 Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song | Kết nối tri thức được trình bày khoa học, chi tiết giúp cho các bạn học sinh chuẩn bị bài một cách nhanh chóng và đầy đủ đồng thời giúp quý thầy cô tham khảo để soạn giáo án cho học sinh của mình. Thầy cô và các bạn xem, tải về ở bên dưới.
Chủ đề: Chương 3: Góc và đường thẳng song song (KNTT)
Môn: Toán 7
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 3: Góc và đường thẳng song song (KNTT)
Môn:
Sách:
Tác giả:
Preview text:
Giải Toán 7 bài 10: Tiên đề Euclid. Tính chất của hai đường
thẳng song song sách Kết nối tri thức với cuộc sống
Giải Toán 7 Kết nối tri thức với cuộc sống tập 1 bài 10 - Hoạt động Hoạt động 1
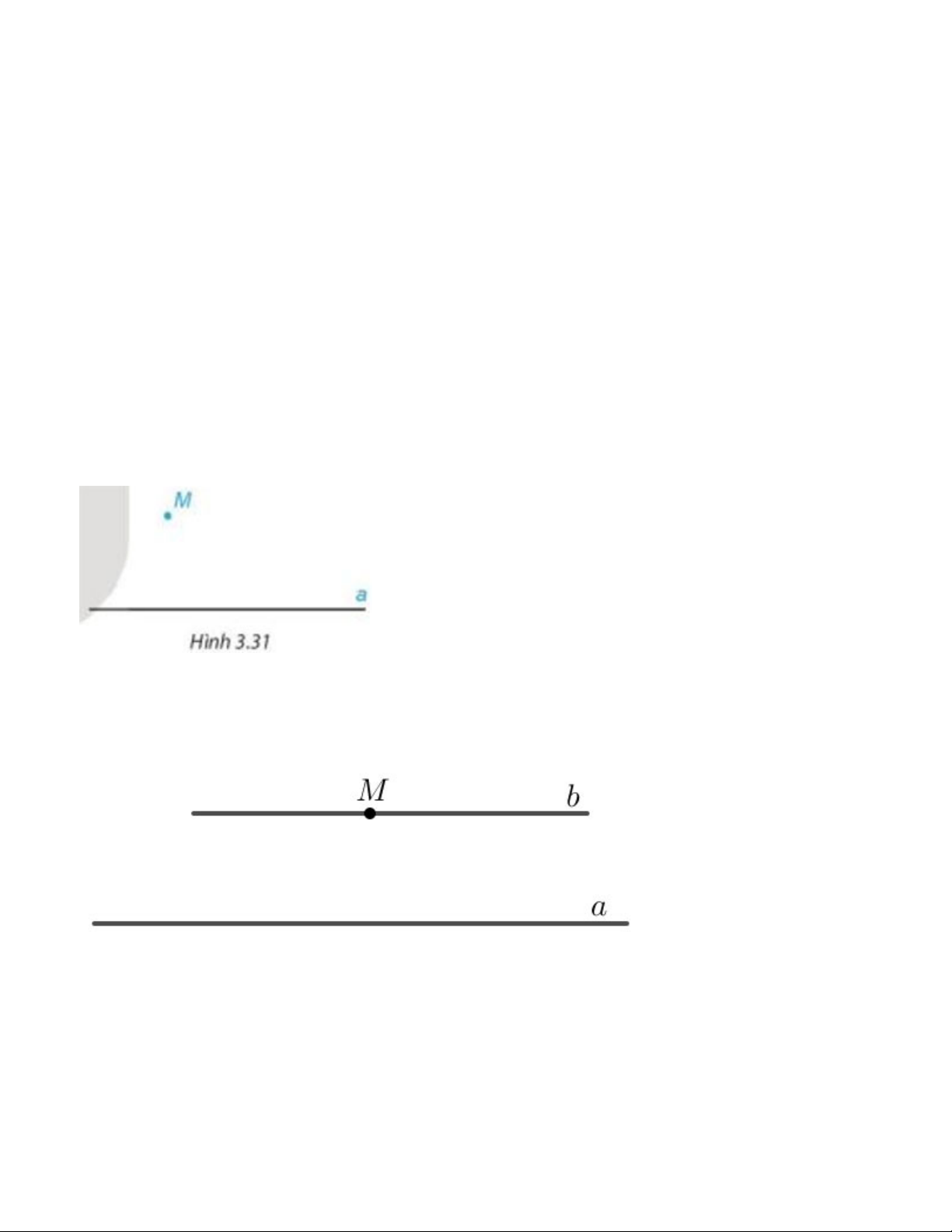
Cho trước đường thẳng a và một điểm M không nằm trên đường thẳng a (H.3.31).
Dùng bút chì vẽ đường thẳng b đi qua M và song song với đường thẳng a.
Dùng bút màu vẽ đường thẳng c đi qua M và song song với đường thẳng a.
Em có nhận xét gì về vị trí của hai đường thẳng b và c? Gợi ý đáp án:
Dùng bút chì vẽ đường thẳng b đi qua M và song song với đường thẳng a, ta được:
Dùng bút màu vẽ đường thẳng c đi qua M và song song với đường thẳng a, ta được:
Nhận xét: Hai đường thẳng b và c trùng nhau. Hoạt động 2
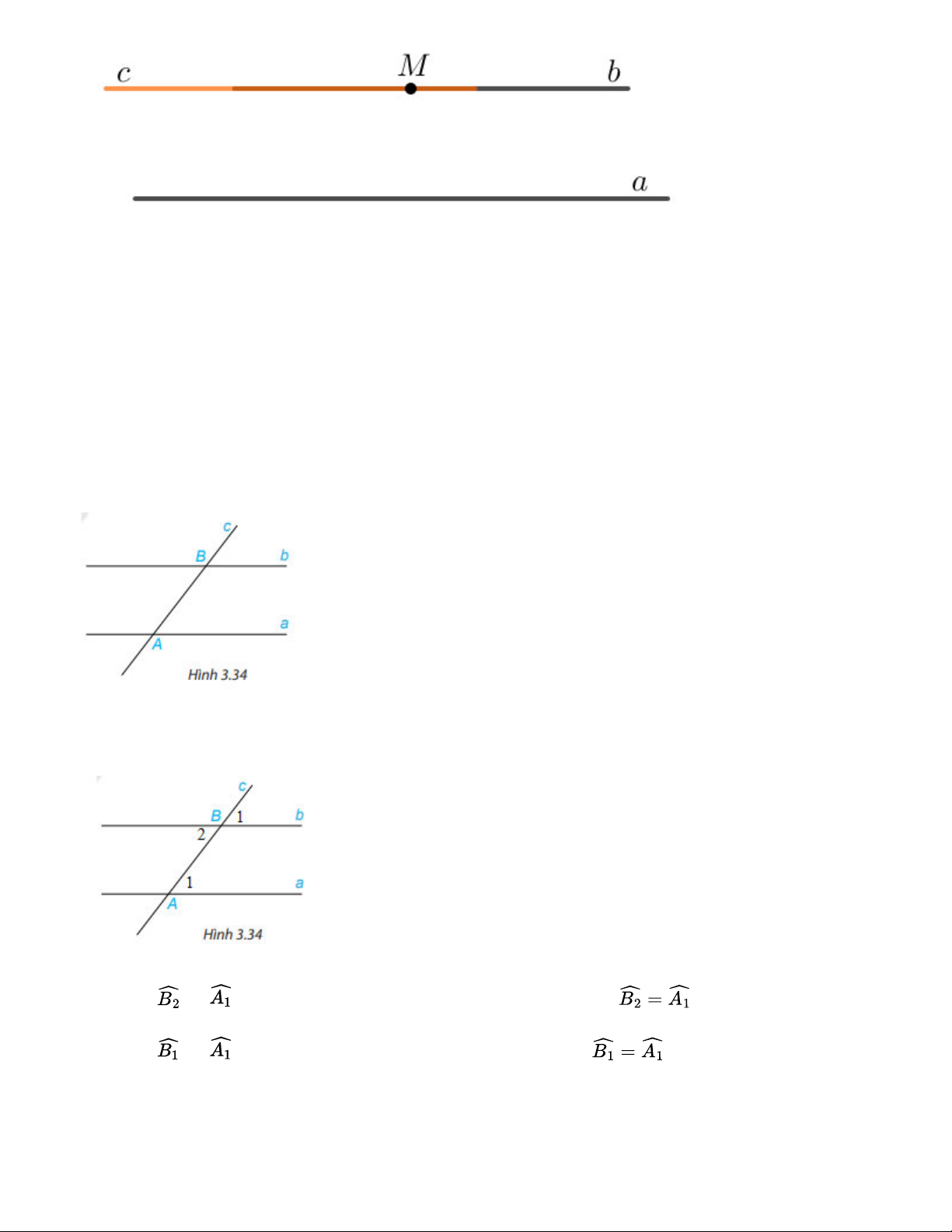
Vẽ hai đường thẳng song song a,b. Kẻ đường thẳng c cắt đường thẳng a tại A và cắt đường
thẳng b tại B. Trên Hình 3.34:
a) Em hãy đo một cặp góc so le trong rồi rút ra nhận xét.
b) Em hãy đo một cặp góc đồng vị rồi rút ra nhận xét. Gợi ý đáp án: a) Ta có: và
là hai góc ở vị trí so le trong. Đo góc ta được: b) Ta có: và
là hai góc ở vị trí đồng vị. Đo góc ta được:
Giải Toán 7 Kết nối tri thức với cuộc sống tập 1 bài 10 - Luyện tập Luyện tập 1
Phát biểu nào sau đây diễn đạt đúng nội dung của Tiên đề Euclid?
(1) Cho điểm M nằm ngoài đường thẳng a. Đường thẳng đi qua M và song song với a là duy nhất.
(2) Có duy nhất một đường thẳng song song với một đường thẳng cho trước.
(3) Qua một điểm M nằm ngoài đường thẳng a có ít nhất một đường thẳng song song với a. Gợi ý đáp án: Đáp án chính xác nhất:
(1) Cho điểm M nằm ngoài đường thẳng a. Đường thẳng đi qua M và song song với a là duy nhất. Luyện tập 2
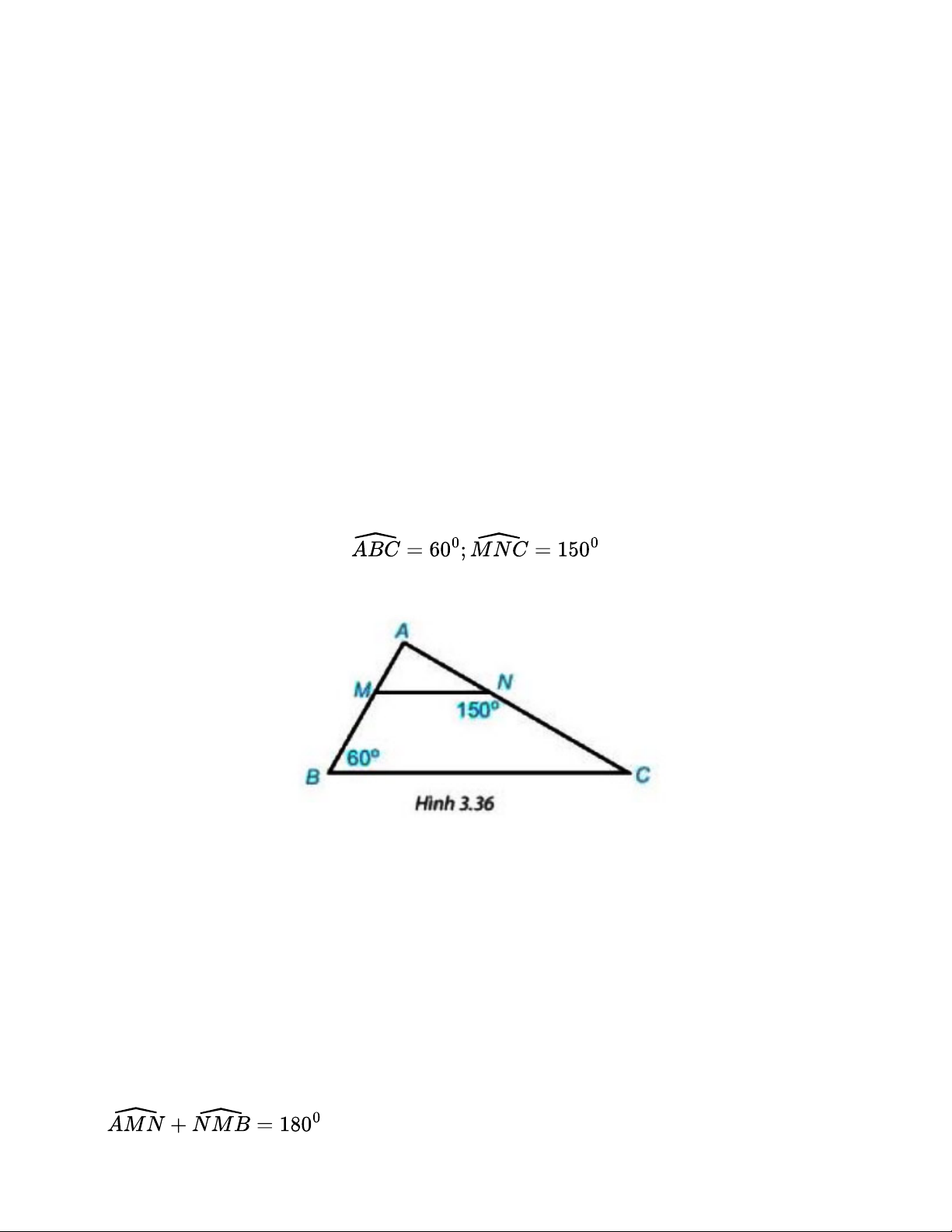
1) Cho hình 3.36. biết MN // BC,
. Hãy tính số đo các góc BMN và ACB.
2) Cho hình 3.37, biết rằng xx’ // yy’ và zz’ ⊥ xx’. Tính số đo góc ABy và cho biết zz’ có vuông góc với yy’ không. Gợi ý đáp án: 1) Ta có: MN // BC
=> (Hai góc nằm ở vị trí đồng vị)
Ta lại có: Góc AMN và góc NMB là hai góc kề bù. => => Vậy
Ta có: Góc ANM và góc MNC là hai góc kề bù. => => Mà NM // BC =>
(Hai góc ở vị trí đồng vị) Vậy
2) Ta có: zz’ ⊥ xx’ => Mà xx’ // yy’ =>
(hai góc ở vị trí đồng vị) => zz’ ⊥ yy’
Giải Toán 7 Kết nối tri thức với cuộc sống trang 53, 54 tập 1 Bài 3.17
Cho hình 3.39, biết rằng mn // pq. Tính số đo góc mHK, vHn. Gợi ý đáp án: Theo bài ra ta có: mn // pq =>
(hai góc ở vị trí so le trong) Vậy Ta lại có mn // pq =>
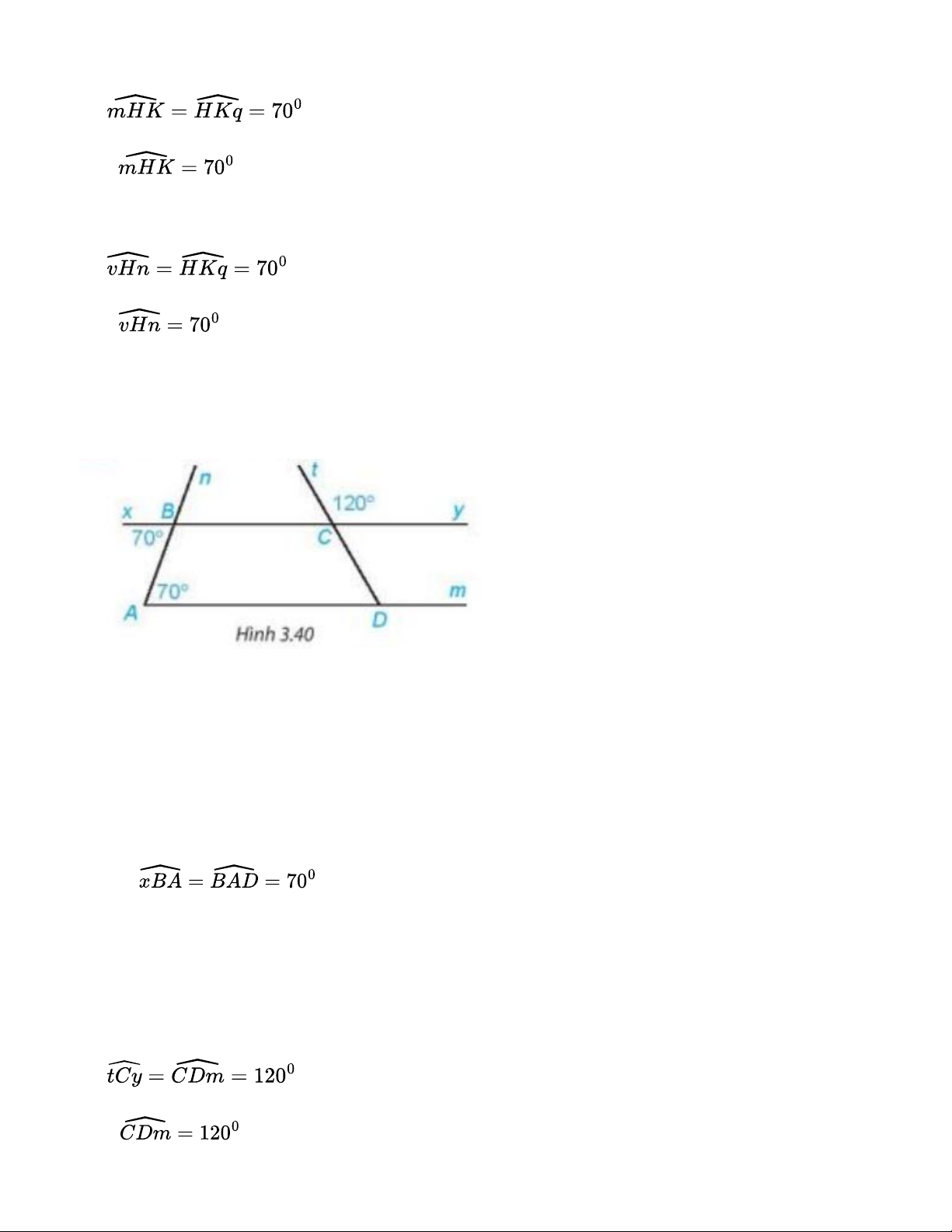
(hai góc ở vị trí đồng vị) Vậy Bài 3.18 Cho hình 3.40:
a) Giải thích tại sao Am // By. b) Tính số đo góc CDm. Gợi ý đáp án: a) Quan sát hình vẽ: Ta có:
Mà hai góc nằm ở vị trí so le trong.
=> Am // By (dấu hiệu hai đường thẳng song song)
b) Ta có: Am // By (Chứng minh câu a) =>
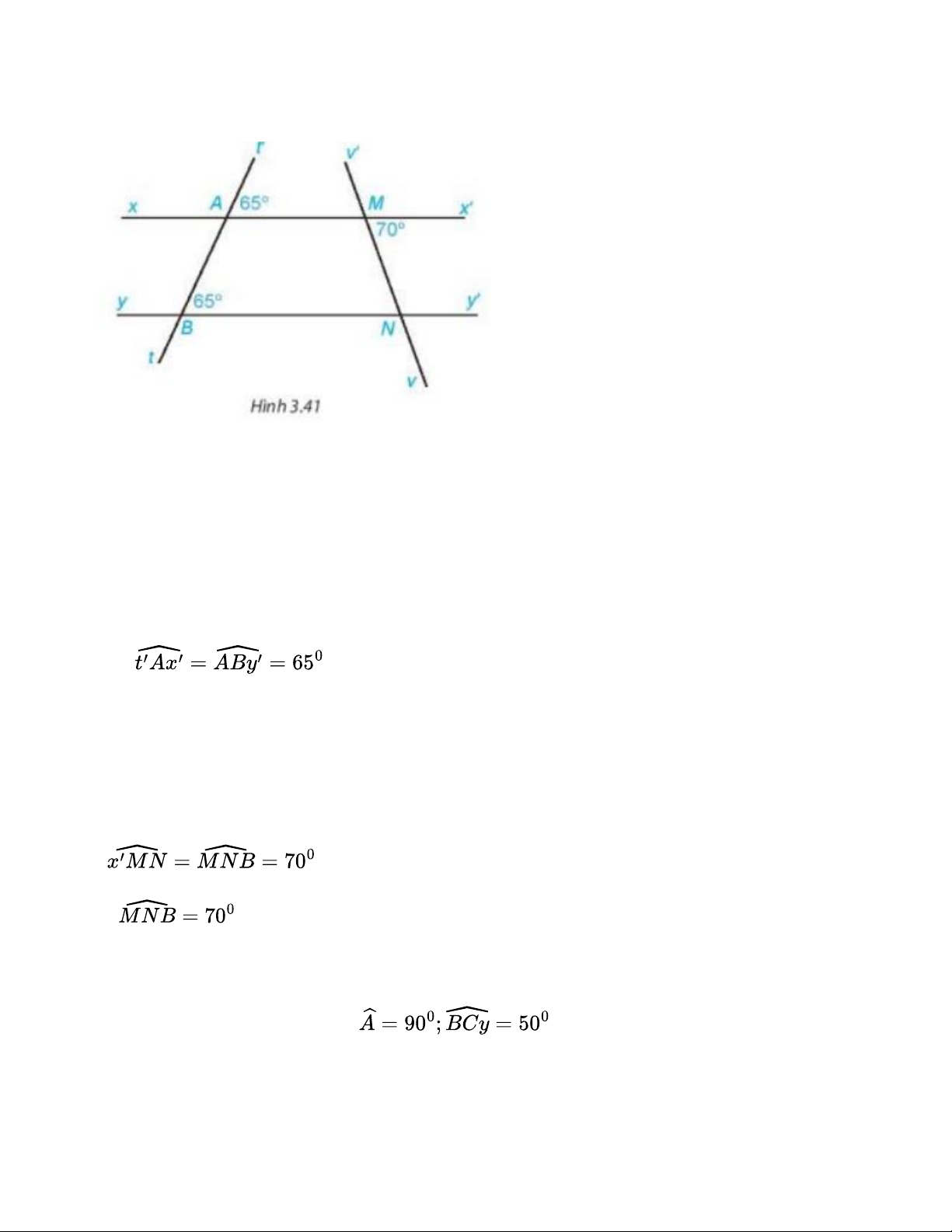
(hai góc ở vị trí đồng vị) Vậy Bài 3.19 Cho hình 3.41:
a) Giải thích tại sao xx’ // yy’. b) Tính số đo góc MNB. Gợi ý đáp án: a) Quan sát hình vẽ: Ta có:
Mà hai góc nằm ở vị trí đồng vị.
=> xx’ // yy’ (dấu hiệu hai đường thẳng song song)
b) Ta có: xx’ // yy’ (Chứng minh câu a) =>
(hai góc ở vị trí so le trong) Vậy Bài 3.20
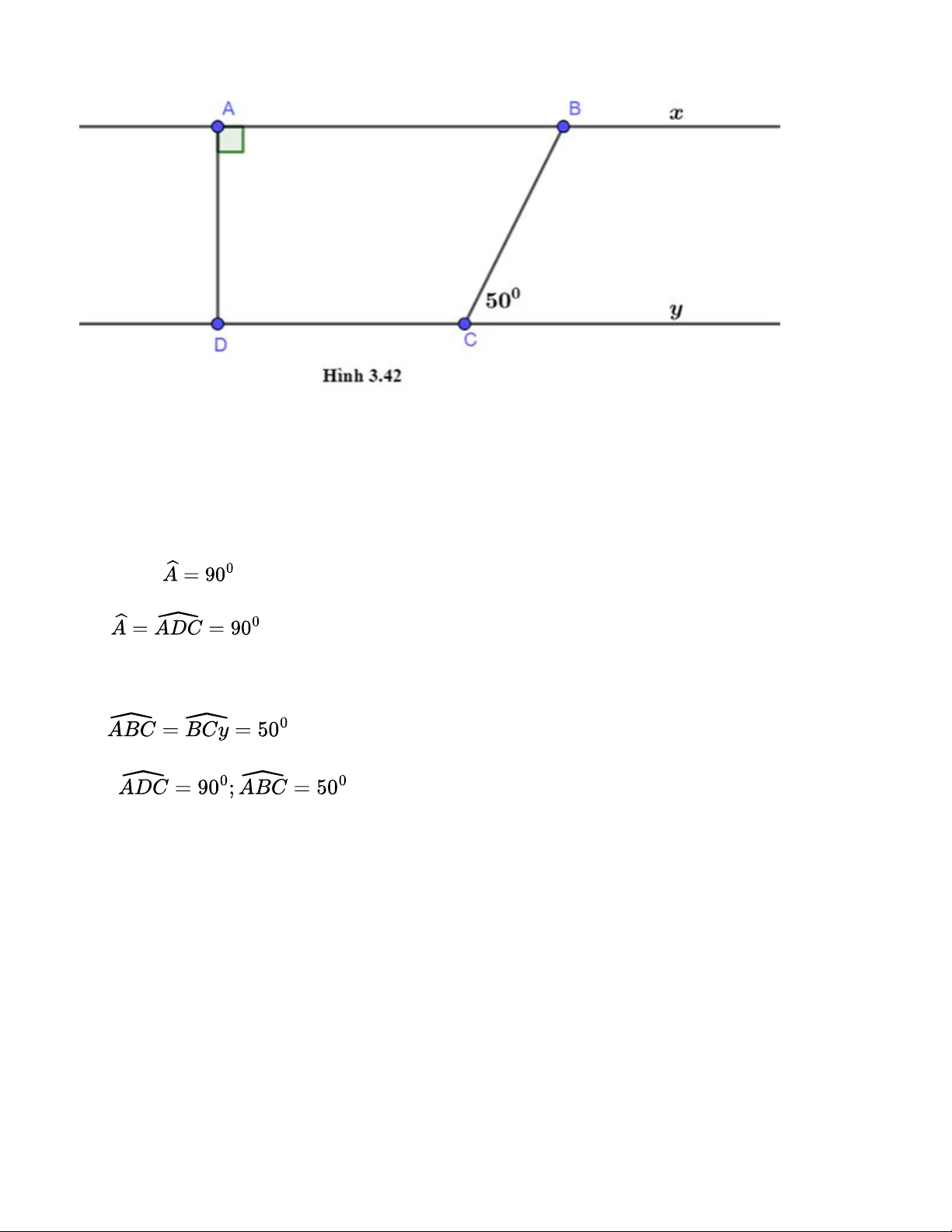
Cho hình 3.42, biết rằng Ax // Dy,
. Tính số đo các góc ADC và ABC. Gợi ý đáp án: Theo bài ra ta có: Ax // By Ta lại có: =>
(Hai góc ở vị trí đồng vị) Ta có: Ax // By =>
(Hai góc ở vị trí so le trong) Vậy Bài 3.21
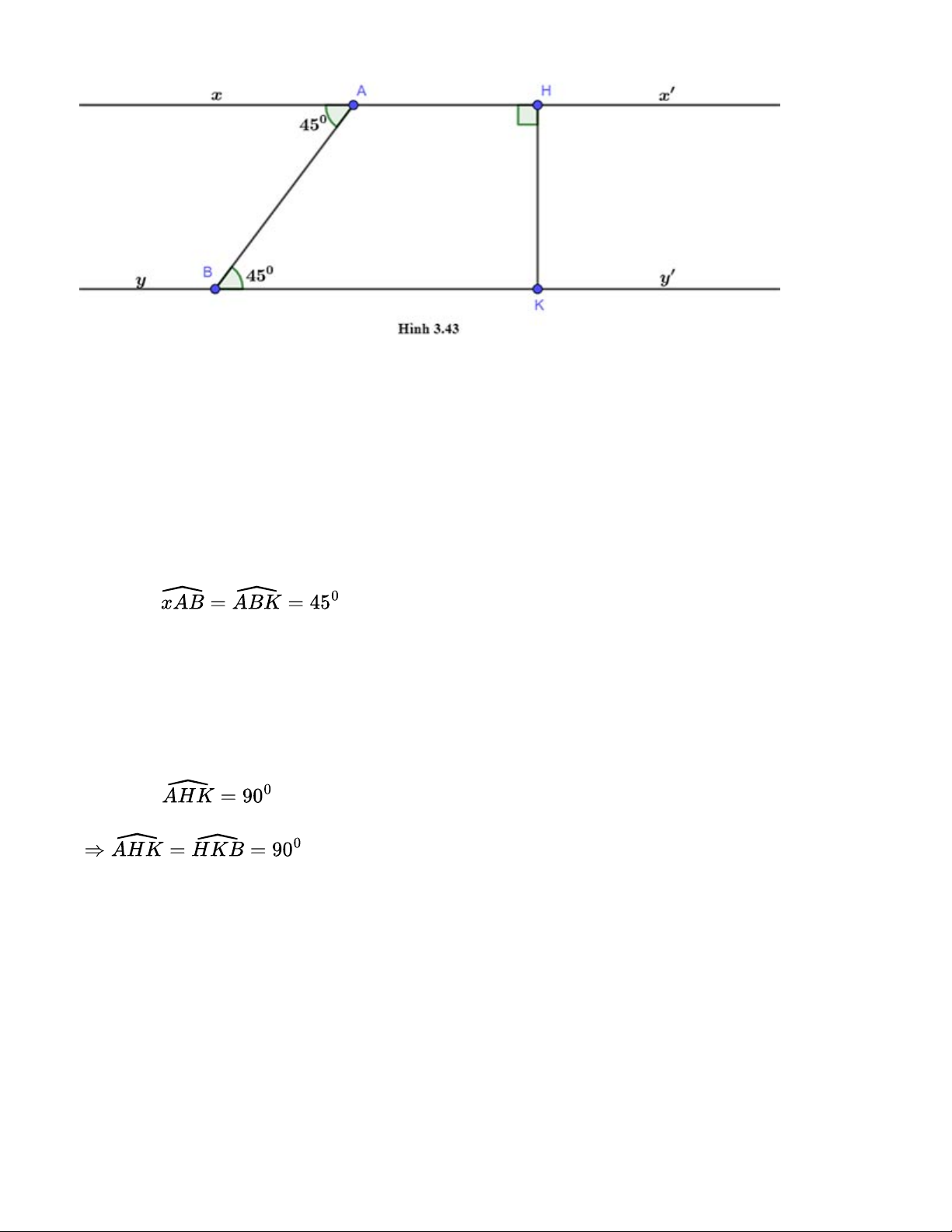
Cho hình 3.43. Giải thích tại sao: a) Ax’ // By b) By ⊥ HK Gợi ý đáp án: Quan sát hình vẽ a) Ta có:
Mà hai góc nằm ở vị trí so le trong
=> Ax’ // By (Dấu hiệu nhận biết hai đường thẳng song song)
b) Ta có: Ax’ // By (chứng minh câu a) Ta lại có:
(Hai góc đồng vị bằng nhau) => By ⊥ HK Bài 3.22
Cho tam giác ABC. Vẽ đường thẳng a đi qua A và song song với BC. Vẽ đường thẳng b đi qua
B và song song với AC. Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b? Vì sao? Gợi ý đáp án: Theo Tiên đề Euclid:
+) Qua điểm A nằm ngoài đường thẳng BC, chỉ có một đường thẳng song song với đường
thẳng BC. Đường thẳng đó là a
+) Qua điểm B nằm ngoài đường thẳng AC, chỉ có một đường thẳng song song với đường
thẳng BC. Đường thẳng đó là b
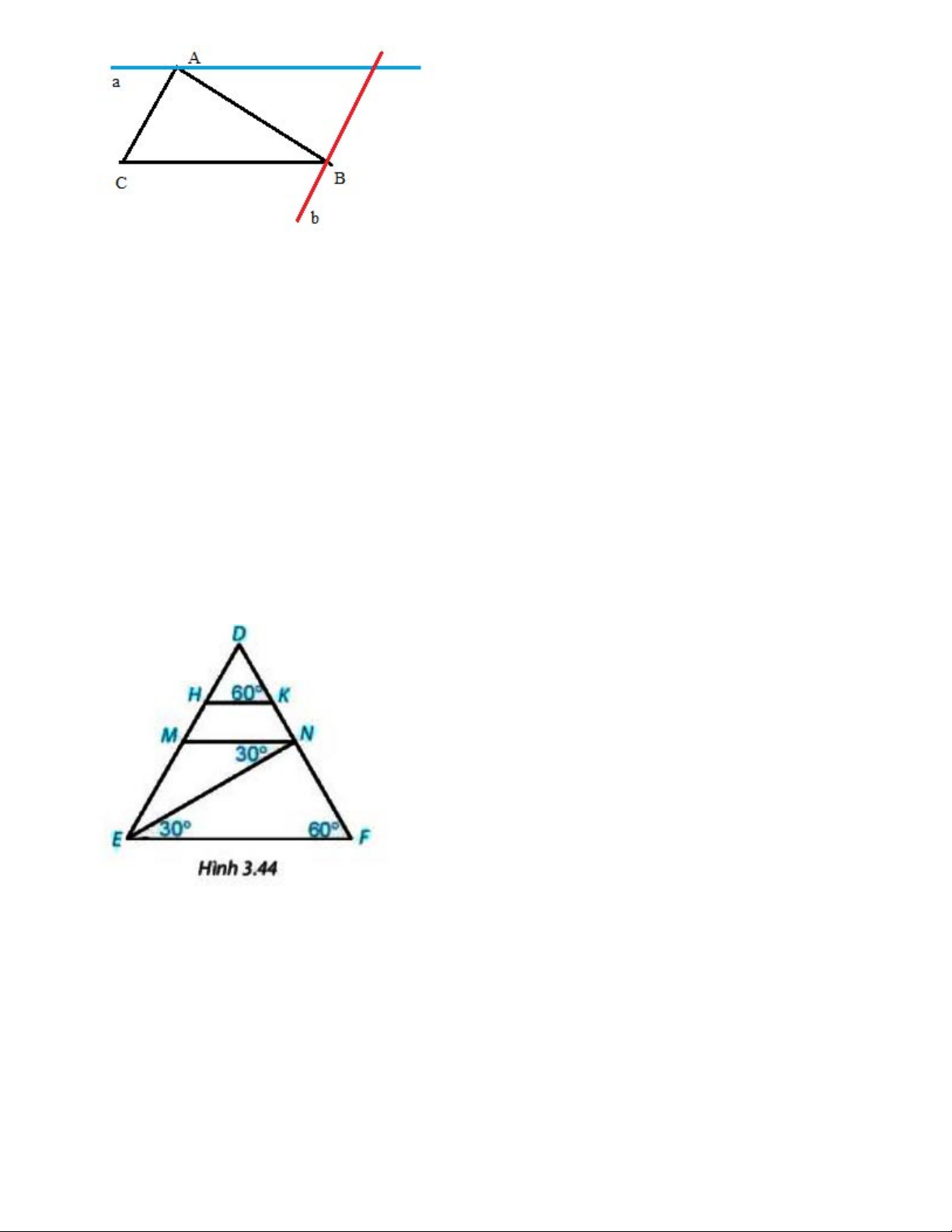
Như vậy, có thể vẽ được 1 đường thẳng a, 1 đường thẳng b. Bài 3.23 Cho hình 3.44: Giải thích tại sao: a) MN // EF; b) HK // EF; c) HK // MN. Gợi ý đáp án: Quan sát hình vẽ ta có: a) Ta có:
Mặt khác hai góc ở vị trí so le trong
=> MN // EF (Dấu hiệu nhận biết hai đường thẳng song song) b) Ta có:
Mặt khác hai góc ở vị trí đồng vị
=> HK // EF (Dấu hiệu nhận biết hai đường thẳng song song)
c) Ta có: MN // EF (chứng minh câu a) HK // EF (chứng minh câu b)
=> HK // MN (tính chất bắc cầu)