 QUAN HỆ GIỮA ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN, ĐƯỜNG XIÊN VÀ HÌNH CHIẾU
I. KIẾN THỨC CƠ BẢN
1. Quan hệ giữa đường vuông góc và đường xiên
Định lý 1. Trong các đường vuông góc và đường xiên kẻ từ một điểm nằm ngoài một
đường thẳng đến đường thẳng đó, đường vuông góc ngắn hơn mọi đường xiên.
A H ^ a Þ A H < A C , A H < A D
2. Quan hệ giữa các đường xiên và các hình chiếu của chúng
Định lý 2. Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó: A
a) Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
A H ^ a, HD > HC Þ A D > A C .
b) Đường xiên nào lớn hơn thì có hình chiếu lớn hơn. D B H C a
A H ^ a, A D > A C Þ HD > HC .
c) Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau; nếu hai hình chiếu bằng
nhau thì hai đường xien bằng nhau. A B = A C Û HB = HC . II. BÀI TẬP
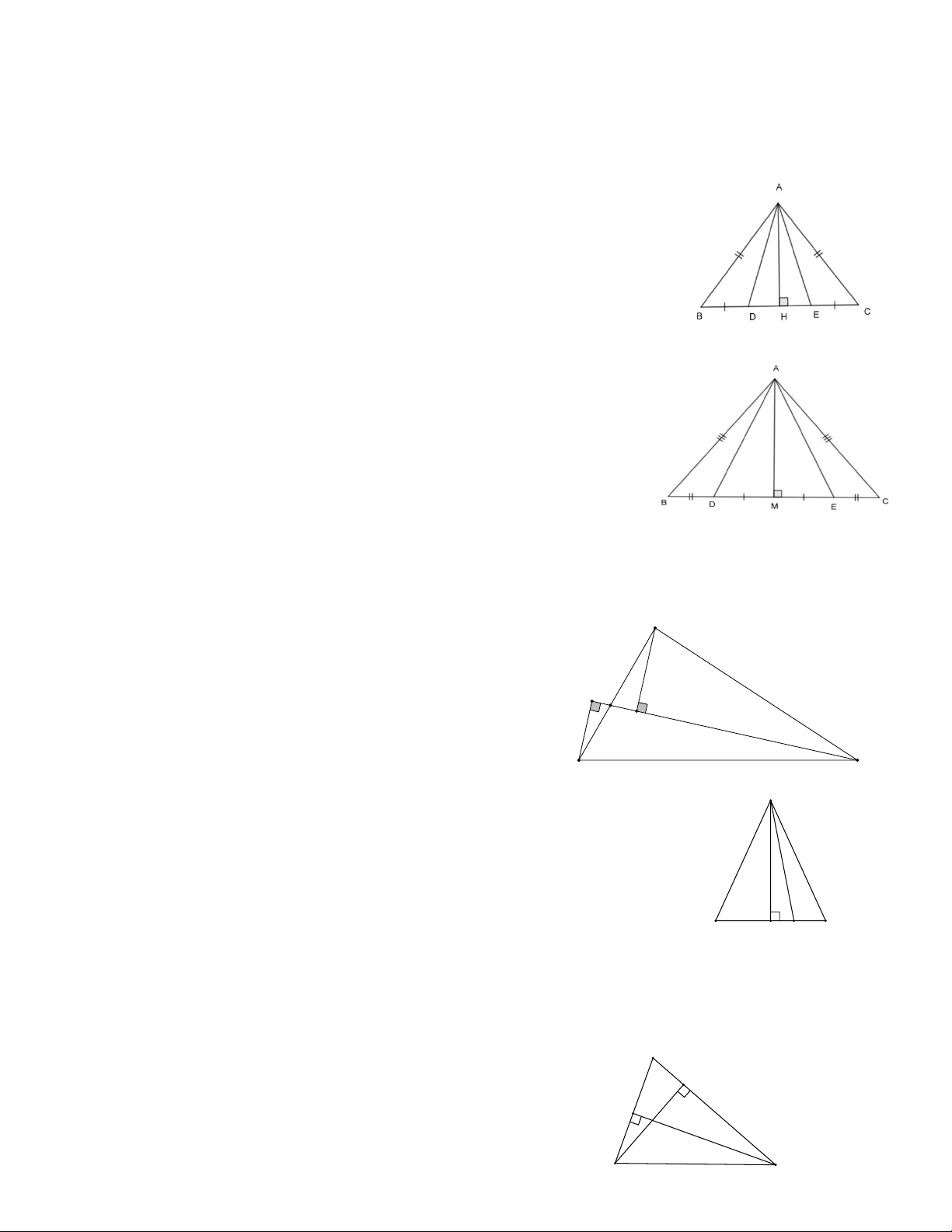
Bài 1: Cho tam giác ABC cân tại A, kẻ AH  BC H  BC . Trên các đoạn thẳng HD và
HC, lấy các điểm D và E sao cho BD  C .
E So sánh các độ dài AD, AE bằng cách xét hai hình chiếu.
Bài 2: Cho tam giác A BC cân tại A. Trên cạnh Bc lấy các điểm D và E sao cho
BD  DE  E .
C Gọi M là trung điểm của DE.
a. Chứng minh AM  BC
b. So sánh các độ dài A B, A D, AE,AC. µ µ
Bài 3: Cho D A BC có B < C , D nằm giữa A,C ( BD không vuông góc với AC). Gọi E, F
là chân các đường vuông góc kẻ từ A, C đến đường thẳng BD. So sánh A E + CF với AB và AC.
Bài 4: Cho tam giác ABC cân tại .
A Gọi H là chân đường vuông góc kẻ từ A đến BC,
điểm D thuộc cạnh BC (D khác H). Chứng minh rằng AH  AD  A . B Trang 1
Bài 5: Cho tam giác ABC không vuông. Kẻ BD vuông góc với AC tại D, kẻ CE vuông góc với AB tại .
E Chứng minh rằng BD  CE  AB  A . C
Bài 6: Cho D A BC vuông tại A, M là trung điểm BA. Vẽ A I ^ MC tại I, BK ^ MC tại K. Chứng minh: CI + CK
a. A B + A C > 3BK b. A C < < B C 2 ¶
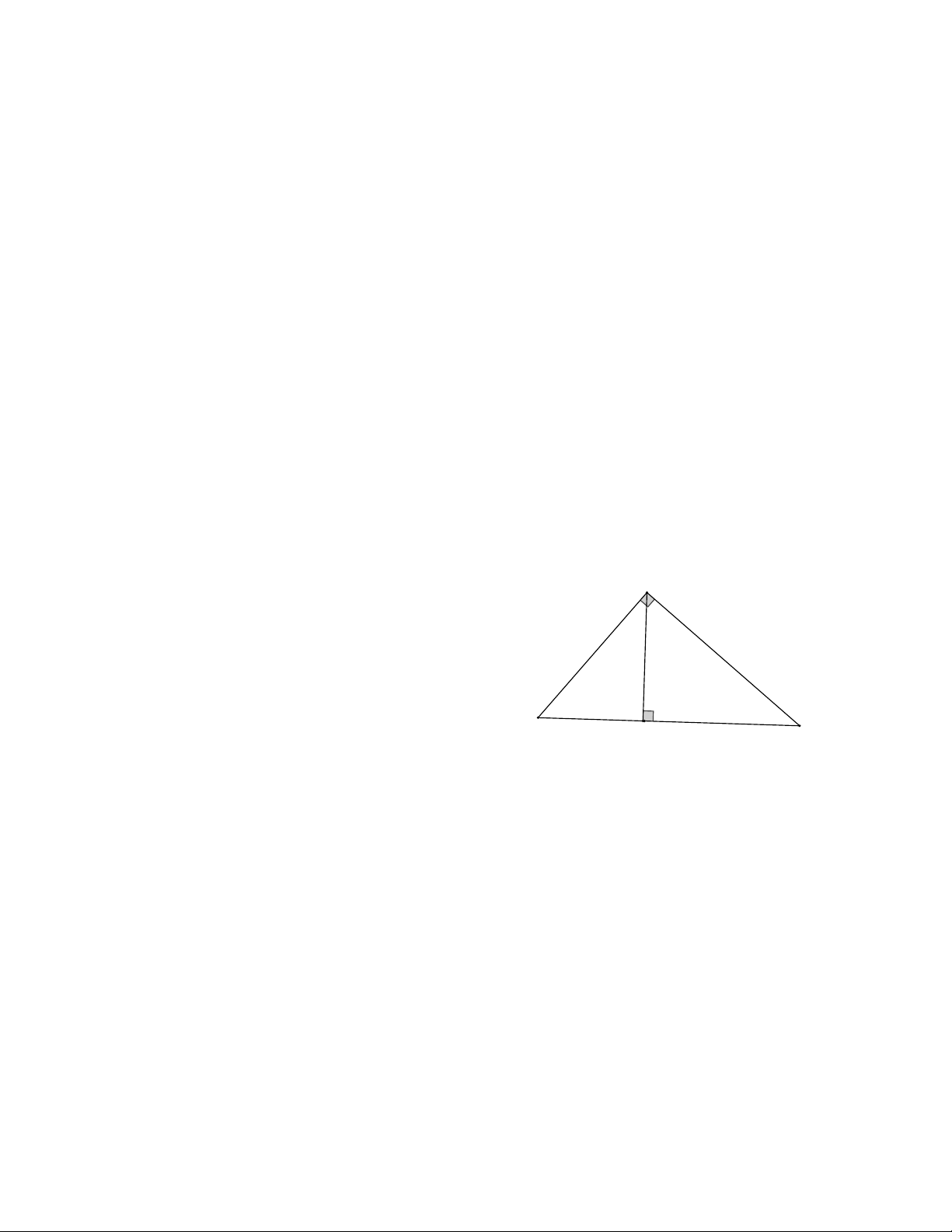
Bài 7: Cho D MNP có M = 90° , I là điểm nằm giữa N, P.
a) Chứng minh MI bé hơn ít nhất một trong 2 cạnh góc vuông.
b) Vẽ MH ^ NP tại H . Trên cạn NP lấy điểm E sao cho NE = NM , trên cạnh MP lấy
điểm F sao cho MF = MH . Chứng minh D MHE = MFE
c) Chứng minh rằng trong một tam giác vuông tổng độ dài hai cạnh góc vuông nhỏ hơn
tổng độ dài cạnh huyền và chiều cao tương ứng. Trang 2 HDG
Bài 1: Đường xiên AB  AC nên hình chiếu HB  H . C
Ta lại có BD  CE nên HD  H .
E Hình chiếu HD  HE nên
đường xiên AD  A . E Bài 2: a) A  MB  A
 MC  .c .cc  AMB  AMC . Ta lại có 0
AMB  AMC  180 suy ra 0 AMB  90 . Vậy AM  B . C
b) Hình chiếu MD  ME nên đường xiên AD  AE . Hình
chiếu MD  MB nên đường xiên AD  AB . Ta có
AD  AE  AB  AC
Bài 3: Vì D EDA vuông tai E nên A D > A E ( ) 1
Vì D CFD vuông tại F nên CD > CF (2) A Cộng theo vế ( ) 1 và (2)ta được
A D + CD > A E + CF hay A C > A E + CF (3) F D E µ µ
Mặt khác DA BC ; B < C Þ A C < A B (4) C B A
Từ (3)và (4) suy ra AB > AC > AE + CF .
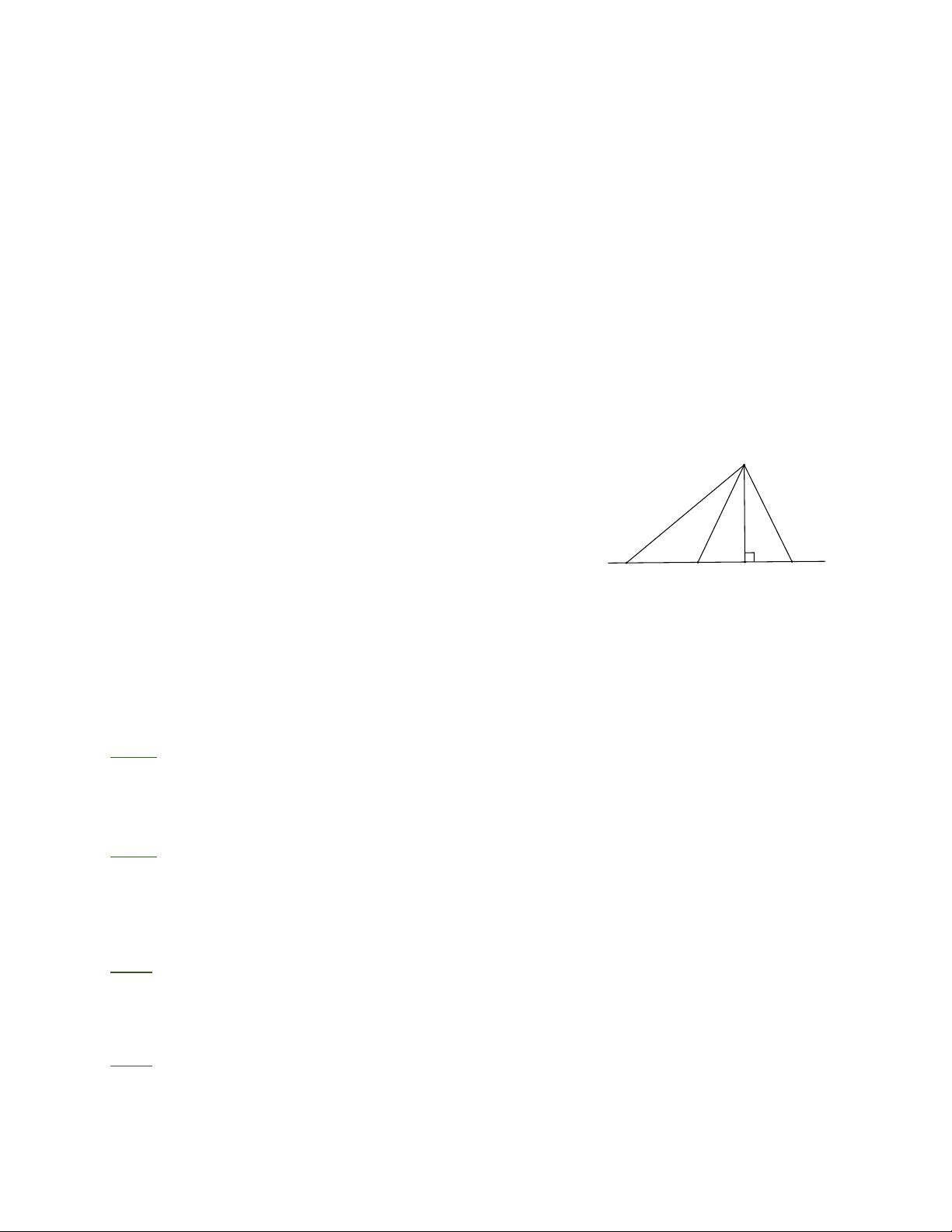
Bài 4: Ta có AH  AD (quan hệ đường vuông góc, đường xiên).
Nếu D thuộc đoạn HC  HD  HC, do đó AD  AC  A . B
Nếu D thuộc đoạn HB  HD  HB  AD  A . B B H D C
Bởi vậy AH  AD  A . B Bài 5: A
D AB D vuông tại D nên BD  AB D
D AEC vuông tại E ,CE  AC. E Trang 3 B C
Do đó BD  CE  AB  A . C Bài 6:
a) Chứng minh được D K MB = D IMA (cạnh huyền – góc nhọn) Þ A I = KB;IM = MK
D K MB vuông tại K Þ BK < BM ( ) 1
D A IM vuông tại I Þ A I < A M (2) Cộng theo vế của ( )
1 và (2)được AI + BK < BM + AM
Þ AI + BK < AB Þ 2BK < AB (3)
Vì D IA C vuông tại I nên AI < AC Þ BK < AC (4)
Cộng theo vế cuả (3)và (4)được AB + AC > 3BK IK
CI + (CI + IK ) CI + CK
b) D A MC vuông tại M có A C < CM = CI + IM = CI + = = 2 2 2 (5) ìï IC < A C ï
DA IC ;DA BC lần lượt vuông tại I, A Þ í
Þ IC < BC (6) ï A C < BC ïî
Mặt khác D BK C vuông tại K nên CK < BC (7) CI + CK
Cộng theo vế của (6)và (7)được < B C (8) 2 CI + CK
Từ (5)và (8)suy ra A C < < B C (đpcm). 2 Bài 7: ·
a) Giải sử I thuộc NH khi đó MIH < 90° Þ MIN > 90°
D MIN có MIN > 90° suy ra MN > MI
Tương tự nếu I thuộc NP suy ra MP > MI . M
Vậy MI bé hơn ít nhất một trong 2 cạnh góc vuông. · · · F
b) Ta có HMF = MNH (cùng phụ NMH ) S P N I H E Trang 4 · ·
D MNE cân tại N. D MHF cân tại M lại có HMF = MNH · ·
Suy ra các góc ở đáy bằng nhau: Þ MEH = MHF · · · ·
Có MHF + FHE = 90° Û MEH + FHE = 90° · · ·
Gọi S là giao điểm của ME và HF, D HSE có SEH + SHE = 90° suy ra HSE = 90° hay
ME ^ HF tại S
D HMS = D FMS ( cạnh huyền – cạnh góc vuông) Suy ra HS = SF
D HSE = D FSE (cạnh – góc – cạnh). Suy ra HE = FE
D MHE = D MFE (cạnh – cạnh – cạnh)
c) Ta cần chứng minh A B + A C < BC + A H . Đặt BC = a;A B = c;A C = ; b A H = h
Giải sử b + c < a + h Bình phương 2 vế ta có ( A + )2 < ( + )2 b c a h b 2 2 2 2
Þ b + c + 2bc < a + h + 2ah c Þ ( h 2 2 b + c ) 2 2
- a + 2bc - 2ah < h C
(pitago và 2bc = 2ah = S ) B H DA BC a 2
Þ 0 < h (luôn đúng)
Vậy b + c < a + h là đúng hay … (đpcm) Trang 5