Bài tập kinh tế vi mô | Trường đại học Thương mại

lOMoARcPSD|40534848 Câu 9:
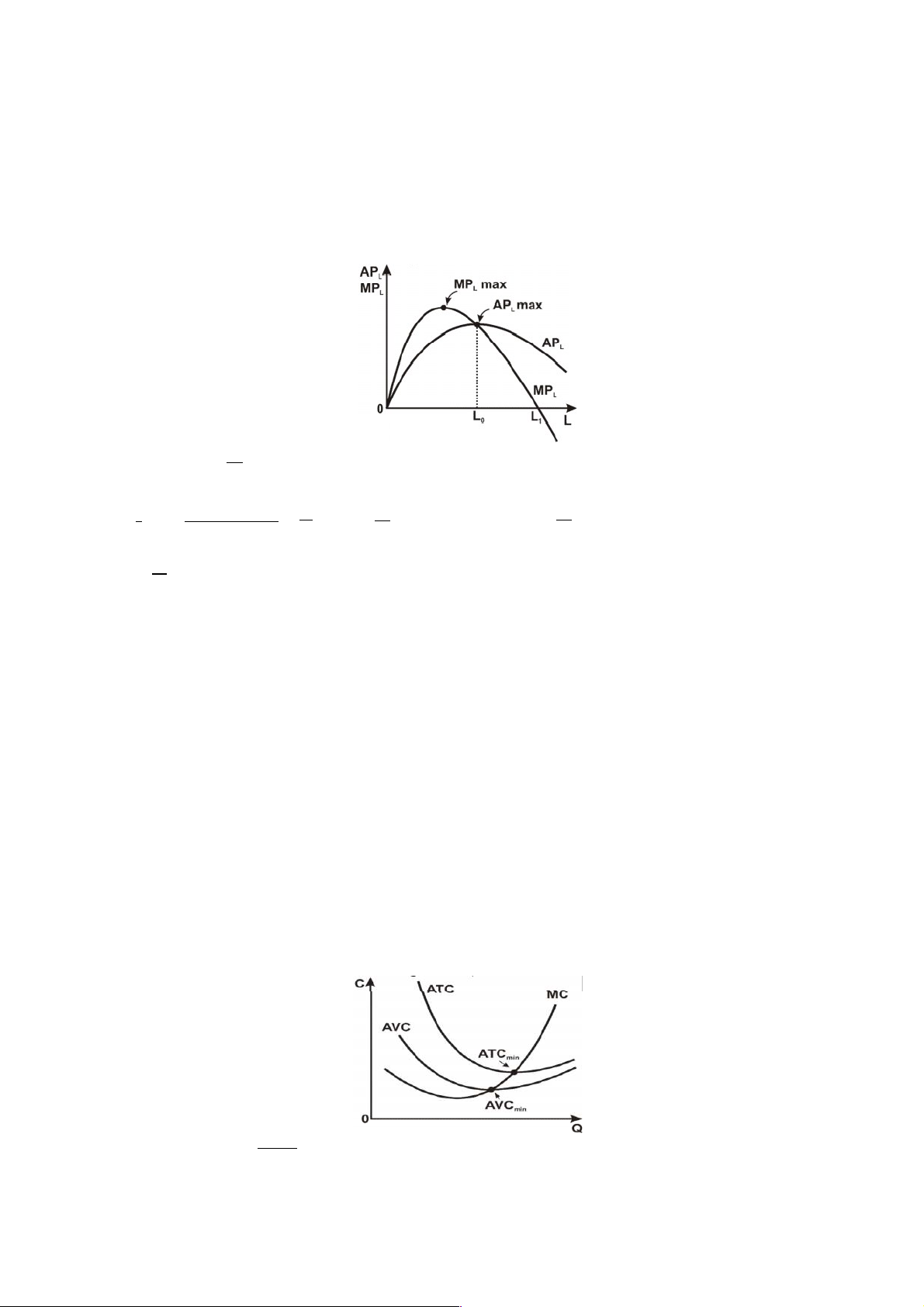
-Khi APL = MPL thì APL lớn nhất.
-Khi Khi APL > MPL thì khi tăng lao động APL sẽ giảm tương ứng với sự gia tăng của lao động.
-Khi APL < MPL thì khi tăng lao động APL sẽ tăng lên tương ứng với sự gia tăng của lao động.
Đường MPL luôn đi qua điểm cực đại của đường APL. Q
Thật vậy, ta có: APL = Q L 1 Q AP = ¢ = L Q
L L .Q .QQ ; mà Q MP và = AP = L L ∣∣∣ 𝖩L L 2 L ∣ L L 𝖩 L L = L L ⟶ AP =1 ( L ) LLL L MP AP
= 0 . Tại đó ta có: MP = AP .
Ta thấy: APL đạt cực đại khi APL L L L
Ø Vậy khi MPL = ALP thì ALP , đường MP MAX
L sẽ luôn đi qua điểm cực đại của đường AP .
L Ø Khi MP ∈ AP ⟶ MP
AP ∈ 0 AP ∈ 0 ⟶ hàm AP nghịch biến nên L L L L L L L 𝖳⟶ AP L
Ø Khi MP > AP ⟶ MP AP 0 AP 0 ⟶ hàm AP L L L L L L đồng biến
nên L 𝖳⟶ AP 𝖳 L Câu 10: Trả lời:
Chứng minh trường hợp mối quan hệ giữa MC
và AVC Khi AVC = MC thì AVC min.
• Khi AVC > MC thì khi tăng sản lượng, AVC sẽ giảm tương ứng với sự gia tăng
của sản lượng. Khi AVC < MC thì khi tăng sản lượng, AVC sẽ tăng tương ứng
với sự gia tăng của sản lượng.
Đường MC luôn đi qua điểm cực tiểu của đường AVC (xem hình dưới). TVC
Thật vậy, ta có: AVC
coi AVC là hàm với biến số Q. Q = Q lOMoARcPSD|40534848 TVC
TVC .Q TVC.Q Q Q Q T AVCQ = ¢ = 1VC = ∣TVC Q ∣ ∣∣ 2 Q Q Q 𝖩 Q 𝖩 TVC 1 mà TC = TVC = MC ⟶ = AVC ⟶ AVC Q Q QQ Q = MC AVC
Ø Vậy khi MC = AVC ⟶ AVC Q = 0 ⟶ hàm AVC đạt giá trị cực tiểu, đường MC đi qua điểm cực tiểu của AVC.
AVC∈ 0⟶ AVC 0⟶ Hàm AVC nghịch biến
Ø Khi AVC > MC ∈ ⟶ MC Q 0⟶ Hàm AVC đồng biến ⟶𝖳 Q; AVC
AVC> 0⟶ AVC
Ø Khi AVC ∈ MC > ⟶ MC Q
⟶𝖳 Q; AVC 𝖳 Câu 12:
a) Lập bảng và có kết quả: L Q P0 MPL MRPL W 1 10 20000 10 200000 40000 160000 𝖳 2 20 20000 10 200000 40000 160000 𝖳 3 28 20000 8 160000 40000 120000 𝖳 4 34 20000 6 120000 40000 80000 𝖳 5 38 20000 4 80000 40000 40000 𝖳 6 40 20000 2 40000 40000 0 MAX 7 40 20000 0 0 40000 -40000 8 30 20000 -10 -200000 40000 -2400000 9 20 20000 -10 -200000 40000 -2400000
Vậy số lao động được thuê với mức tiền công 40000/ngày ứng với giá bán sản phẩm là 20000 là 6 lao động.
b) Giá bán của sản phẩm bây giờ là 10000 L Q P0 MPL MRPL W 1 10 10000 10 100000 40000 60000 𝖳 2 20 10000 10 100000 40000 60000 𝖳 3 28 10000 8 80000 40000 40000 𝖳 4 34 10000 6 60000 40000 20000 𝖳 5 38 10000 4 40000 40000 0 MAX 6 40 10000 2 20000 40000 -20000 7 40 10000 0 0 40000 -40000 8 30 10000 -10 -100000 40000 -1400000 9 20 10000 -10 -100000 40000 -1400000
Khi giá bán sản phẩm là 10000 thì lao động sẽ giảm. Vậy số lao động được thuê với
mức tiền công 40000/ngày ứng với giá bán sản phẩm là 10000 là 5 lao động.
c) Lượng lao động được thuê sẽ tăng khi năng suất lao động của mỗi lao
động tăng lên Vì khi đó đường MRPL dịch chuyển sang phải lOMoARcPSD|40534848
Khi năng suất tăng →sản phẩm cận biên ↑,sản phẩm doanh thu ↑
→số lương lao động được thuế tăng