Bài tập lớn môn Xác suất thống kê đề tài số 5 về Bộ dữ liệu “Appliances energy prediction Data Set”

lOMoARcPSD| 36991220 MỤC LỤC
I. Hoạt động 1 ........................................................................................................................................ 1
(a) Tìm hiểu thông tin dữ liệu ............................................................................................................. 1
(b) Đọc dữ liệu và xóa bỏ các cột không cần thiết: ........................................................................... 2
(c) Mô tả dữ liệu ................................................................................................................................. 3
(d) Trực quan hóa dữ liệu và nhận xét về phân bố các biến ............................................................... 4
(e) Xác định mối quan hệ giữa năng lượng tiêu thụ và các biến giải thích/ dự báo ......................... 13
(f) Trình bày các kết quả tính toán từ mô hình trên và giải thích ý nghĩa của từng tham số ........... 16
(g) Kiểm tra giả định: ....................................................................................................................... 16
(h) Thảo luận về ý nghĩa thực tiễn của vấn đề nghiên cứu liên quan đến bộ dữ liệu ....................... 17
II. Hoạt động 2 .................................................................................................................................... 17
1. Mô tả dữ liệu ............................................................................................................................... 17
2.Phân tích dữ liệu .......................................................................................................................... 18
2.1Đọc dữ liệu .............................................................................................................................. 18
2.3 Làm sạch dữ liệu ................................................................................................................... 20
2.4 Làm rõ dữ liệu ....................................................................................................................... 21
2.5 Xây dựng các mô hình hồi quy tuyến tính .......................................................................... 23
2.6 Dự đoán ................................................................................................................................. 25 lOMoARcPSD| 36991220
TÀI LIỆU THAM KHẢO .................................................................................................................. 25 lOMoARcPSD| 36991220 I. Hoạt động 1 1. Đề bài
Bộ dữ liệu “Appliances energy prediction Data Set” chứa thông tin về các giá trị năng
lượng tiêu thụ của các thiết bị gia dụng trong một căn hộ ở châu Âu. Bộ dữ liệu bao gồm các
thông số kỹ thuật về căn hộ và các thông số môi trường bên ngoài như nhiệt độ, áp suất, độ ẩm, … Yêu cầu:
(a) Tìm hiểu thông tin về tập dữ liệu tại đây: https://archive.ics.uci.edu/ml/datasets/
Appliances+energy+prediction trình bày rõ thông tin các biến trong tập dữ liệu. Tập dữ liệu
này được dùng để nghiên cứu vấn đề gì, nêu rõ các biến phụ thuộc, biến giải thích/ dự báo trong tập dữ liệu.
(b) Đọc dữ liệu. Đọc dữ liệu vào trong R, xóa bỏ các cột không cần thiết (date, rv1, rv2)
để phân tích và đổi tên các cột dễ dàng trong quá trình phân tích.
(c) Tiến hành mô tả dữ liệu bằng cách tính toán các giá trị thống kê mô tả cho các biến
trong tập dữ liệu, bao gồm trung bình, trung vị, độ lệch chuẩn, min, max. Hãy trình bày các
kết quả tính toán trên.
(d) Trực quan hóa dữ liệu bằng cách vẽ các biểu đồ phân tán và histogram cho các biến
trong tập dữ liệu. Nhận xét về phân bố các biến.
(e) Sử dụng phân tích hồi quy đa biến để xác định mối quan hệ giữa năng lượng tiêu thụ
(Appliances) và các biến giải thích/ dự báo.
(f) Trình bày các kết quả tính toán từ mô hình trên và giải thích ý nghĩa của từng tham số.
(g) Đánh giá mô hình và các giả định của phương pháp hồi quy đa biến trong trường hợp này.
(h) Thảo luận về ý nghĩa thực tiễn của vấn đề nghiên cứu liên quan đến bộ dữ liệu. 2. Thực hiện
(a) Tìm hiểu thông tin dữ liệu
- Bộ dữ liệu bao gôm dữ liệu được ghi lại mỗi 10 phút trong 4.5 tháng bởi hệ thống cảm biến
ZigBee được lắp đặt trong một ngôi nhà và dữ liệu từ sân bay Chievres, Bỉ. Bộ dữ liệu được
dùng để nghiên cứu mối quan hệ giữa năng lượng tiêu thụ của thiết bị gia dụng đối với các yếu
tố bên ngoài và xây dựng mô hình để dự đoán năng lượng tiêu thụ trên. - Các biến có trong bộ dữ liệu: + date: thời gian
+ Appliances: năng lượng tiêu thụ của thiết bị gia dụng
+ lights: năng lượng tiêu thụ dùng cho việc chiếu sáng
+ T1: nhiệt độ nhà bếp lOMoARcPSD| 36991220 + RH_1: độ ẩm nhà bếp
+ T2: nhiệt độ phòng khách
+ RH_2: độ ẩm phòng khách
+ T3: nhiệt độ phòng giặt
+ RH_3: độ ẩm phòng giặt
+ T4: nhiệt độ phòng làm việc
+ RH_4: độ ẩm phòng làm việc
+ T5: nhiệt độ phòng tắm
+ RH_5: độ ẩm phòng tắm
+ T6: nhiệt độ bên ngoài nhà (hướng bắc)
+ RH_6: độ ẩm bên ngoài nhà (hướng bắc)
+ T7: nhiệt độ phòng ủi
+ RH_7: độ ẩm phòng ủi
+ T8: nhiệt độ phòng ngủ 1
+ RH_8: độ ẩm phòng ngủ 1
+ T9: nhiệt độ phòng ngủ 2
+ RH_9: độ ẩm phòng ngủ 2
+ To : nhiệt độ tại sân bay Chievres
+ Pressure: khí áp tại sân bay Chievres
+ RH_out: độ ẩm tại sân bay Chievres
+ Windspeed: tốc độ gió tại sân bay Chievres
+ Visibility: tầm nhìn tại sân bay Chievres + rv1: biến ngẫu nhiên 1 + rv2: biến ngẫu nhiên 2
(b) Đọc dữ liệu và xóa bỏ các cột không cần thiết:
- Sử dụng lệnh read.csv() để đọc file dữ liệu có đinh dạng .csv. Dữ liệu đọc từ file sẽ được
lưu với dạng data frame với tên biến df.
- Các biến không cần thiết là date, rv1, rv2 ứng với cột số 1, 28, 29. Để loại bỏ cột, ta có
thể dùng cấu trúc df<-df[- index cột muốn loại bỏ].
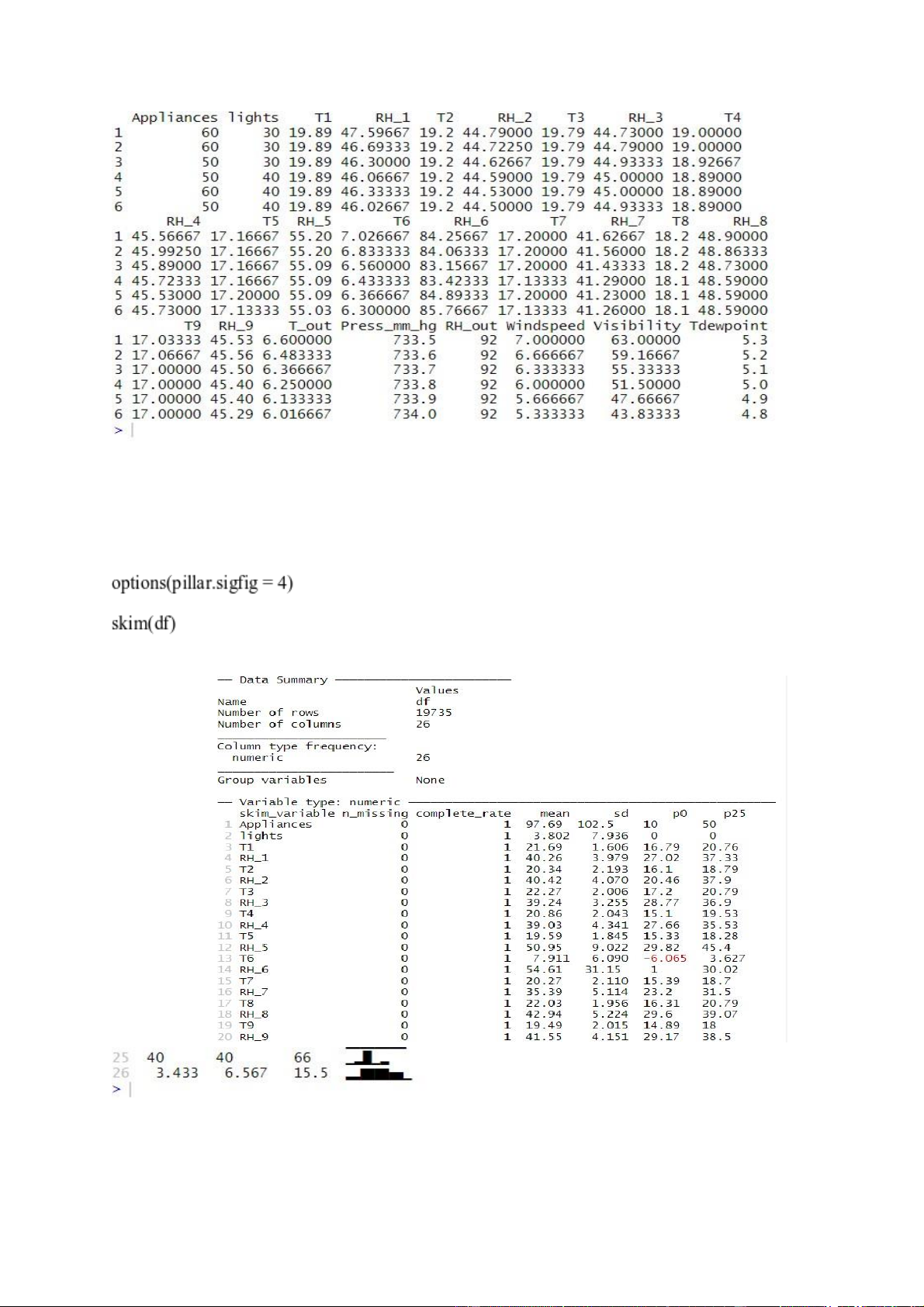
- head(df) để hiển thị 6 dòng đầu tiên của data frame df. lOMoARcPSD| 36991220 (c) Mô tả dữ liệu -
Sử dụng lệnh skim() để cho được một bảng tóm tắt của dữ liệu. Lệnh skim() nằm
trong package “skimr”, nên khi chạy cần thêm library(skimr). Nếu chưa có sẵn package
“skimr” thì có thể tải về bằng lệnh install.package(“skimr”). -
Nhìn vào kết quả, ta thấy dữ liệu gồm 26 biến với 19375 quan sát cho mỗi biến,
không có quan sát nào có dữ liệu khuyết(NA). lOMoARcPSD| 36991220 -
Cột mean biểu thị cho giá trị trung bình; sd là độ lệch chuẩn; p0, p50, p100 lần lượt
ứng với các giá trị min, trung vị, max. -
Cột hist biểu thị biểu đồ histogram đơn giản cho biến. Qua hình dạng, ta có thể thấy
một số biến quan trọng không có phân phối chuẩn như Appliances.
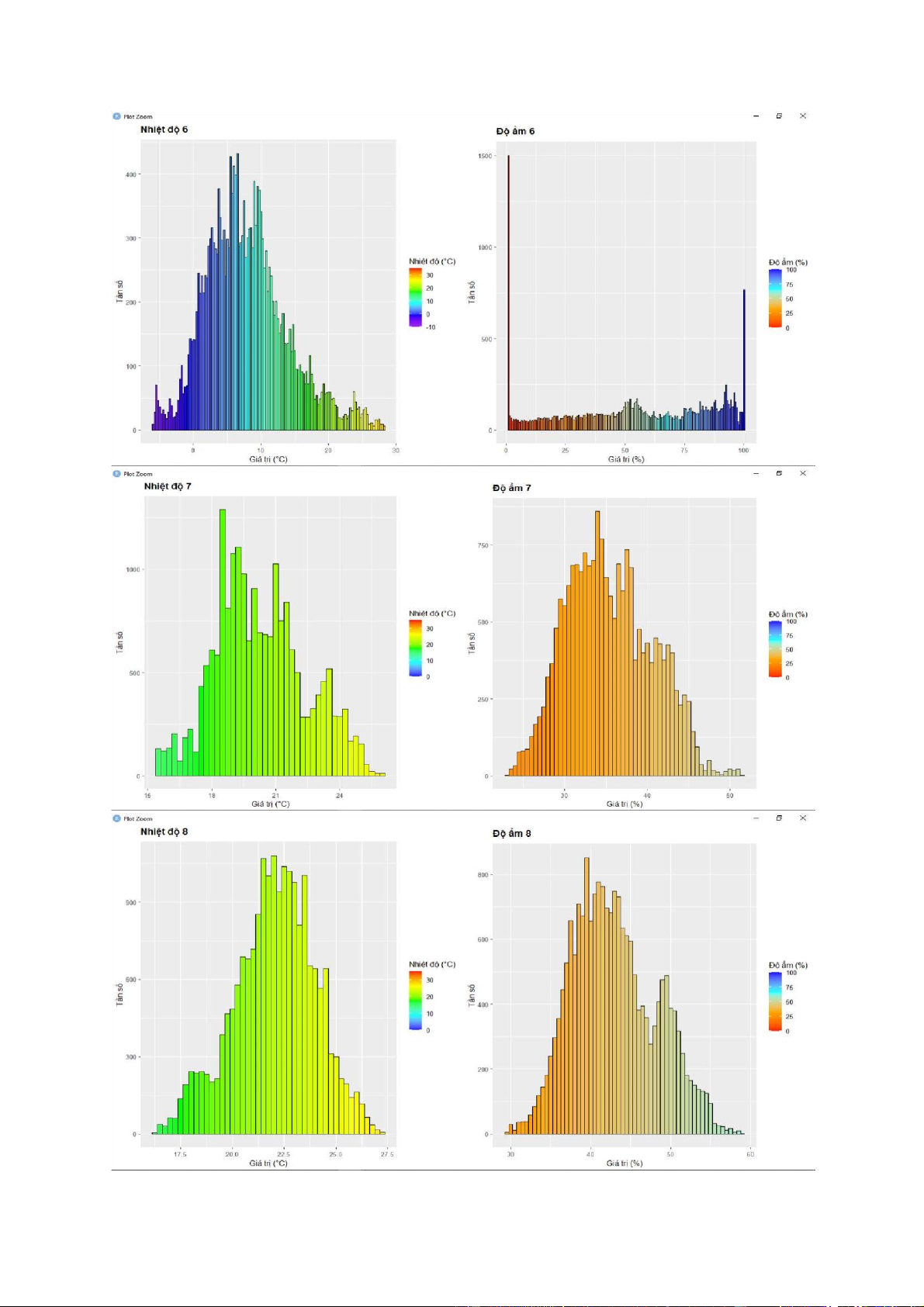
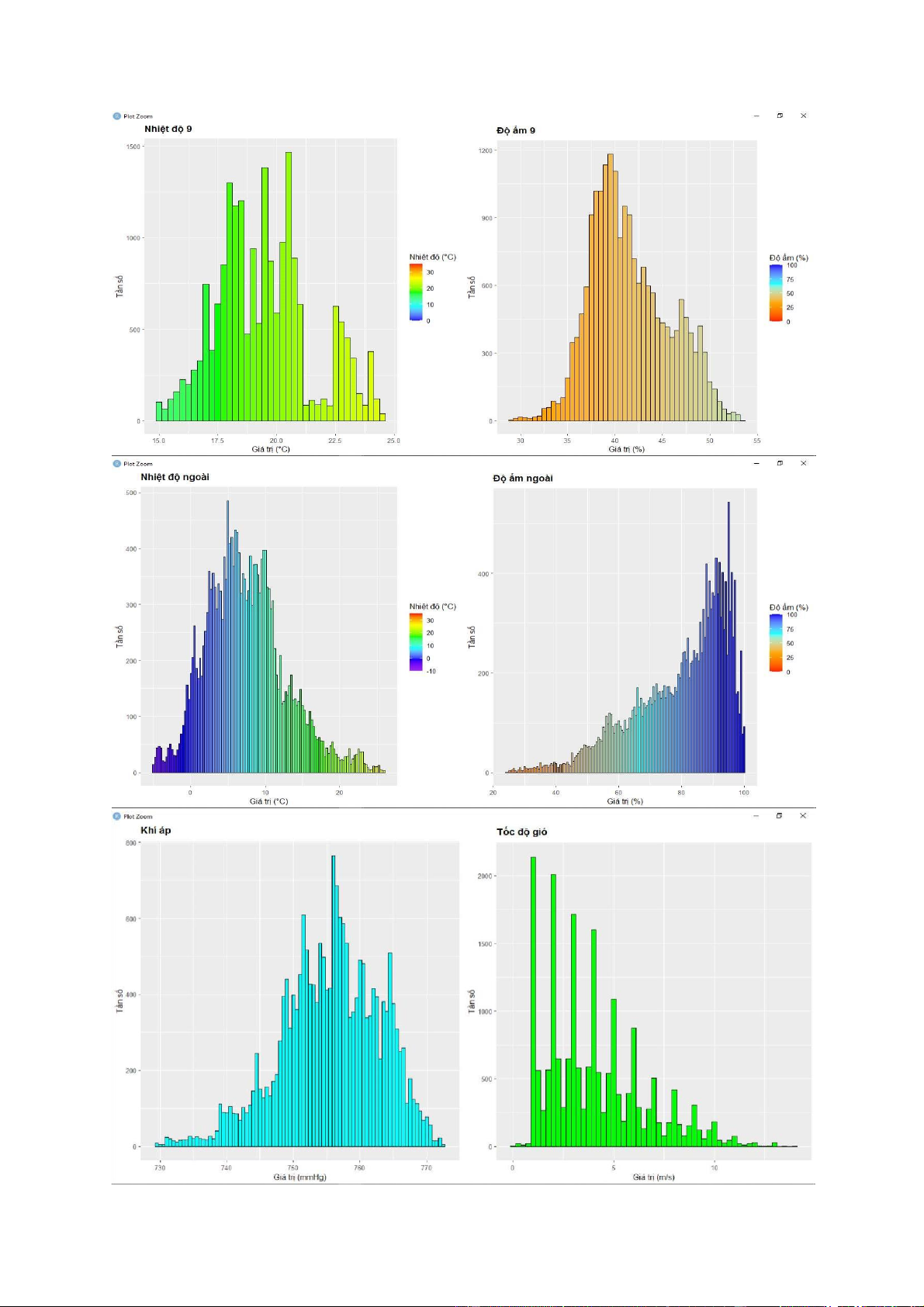
(d) Trực quan hóa dữ liệu và nhận xét về phân bố các biến
- Dùng lệnh ggplot() từ package “ggplot2” để vẽ đồ thị. Do đó, cần thêm library(ggplot2).
Dấu “+” để thêm một layer mới cho đồ thị.
- Dùng lệnh geom_histogram() để vẽ histogram. Các tham số quan trọng là data = df, để
xác định dữ liệu dùng để vẽ; mapping = aes(x = Appliances) để xác định trục hoành của
đồ thị (ở đây là biến Appliances); bins là số cột trong đồ thị histrogram; binwidth là độ
rộng cột hay khoảng giá trị của một cột (binwidth được ưu tiên hơn bins).
- Một số lệnh hỗ trợ việc hiển thị trong ggplot:
+ scale_x_continuos(): gồm một số thao tác liên quan đến giới hạn giá trị của trục hoành,
hiển thị và đặt tên (có thể dùng xlab() để thay cho việc đặt tên).
+ scale_y_continuos(): gồm một số thao tác liên quan đến giới hạn giá trị của trục tung,
hiển thị và đặt tên (có thể dùng ylab() để thay thế cho việc đặt tên).
+ ggtitle(): dùng để đặt tiêu đề cho đồ thị.
+ scale_fill_gradient(): dùng để tô màu thông qua fill = after_stat(x) (tô màu dựa theo giá
trị của x) được xác định ở trong geom_histogram(). lOMoARcPSD| 36991220 lOMoARcPSD| 36991220 lOMoARcPSD| 36991220 lOMoARcPSD| 36991220 lOMoARcPSD| 36991220
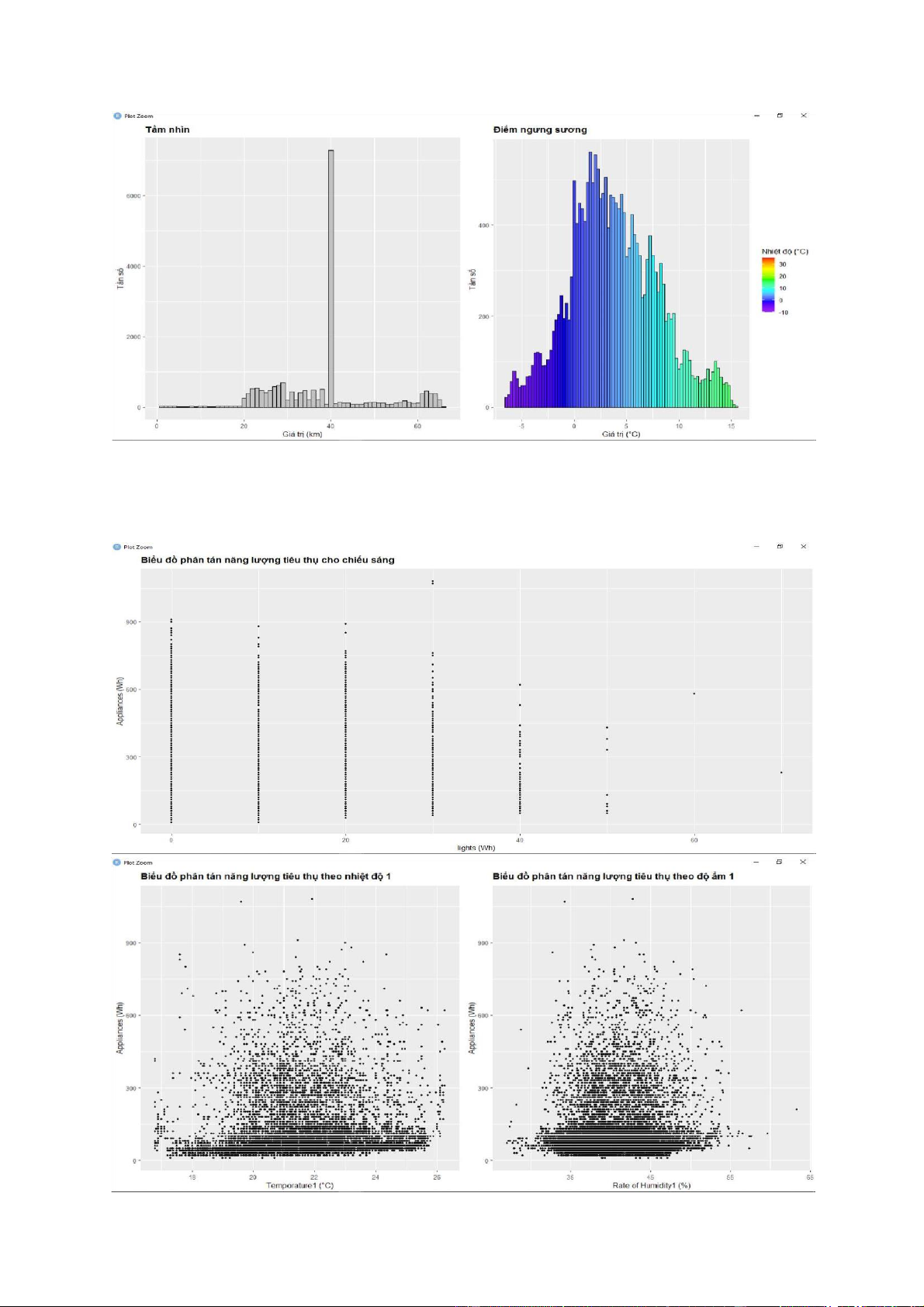
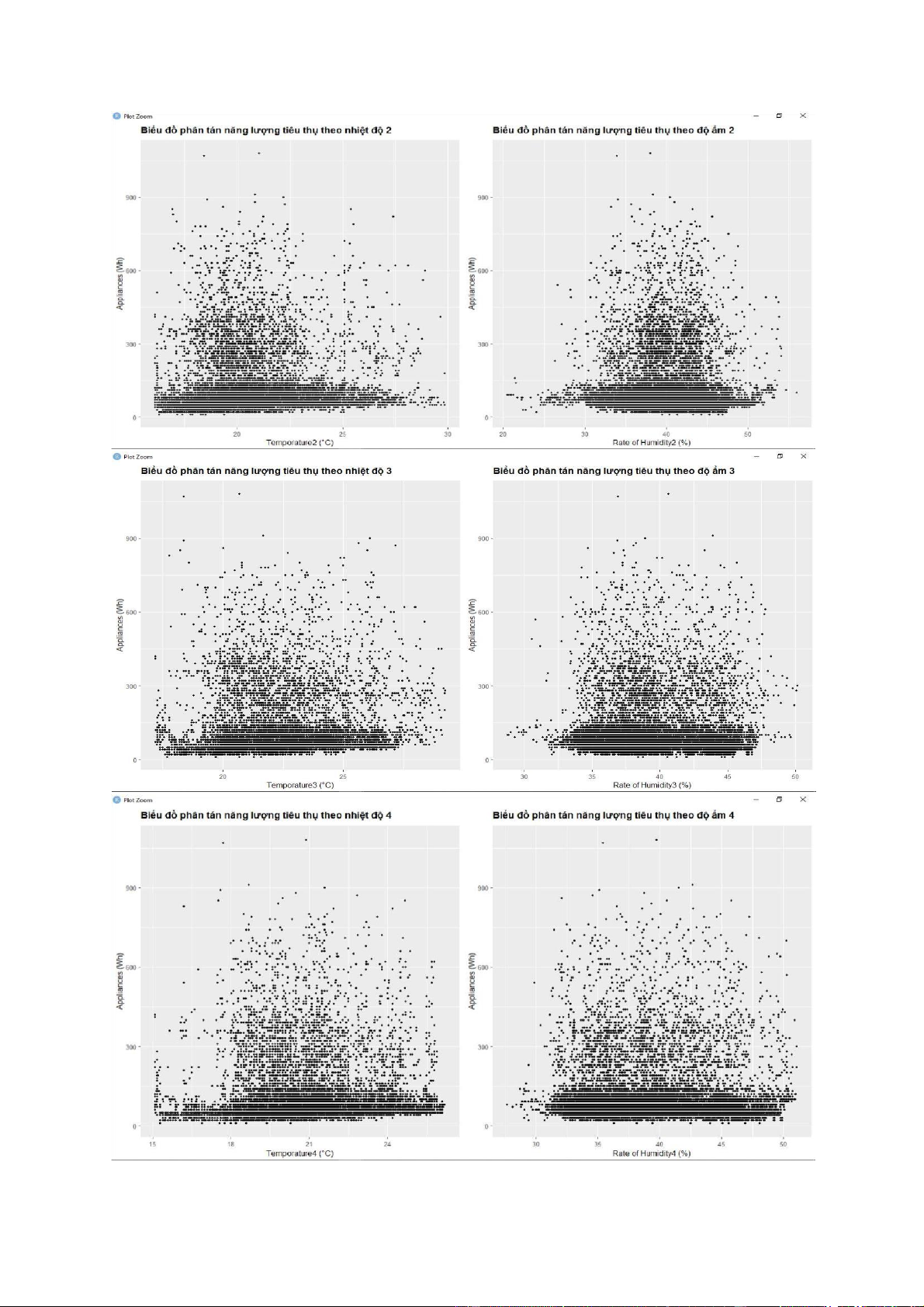
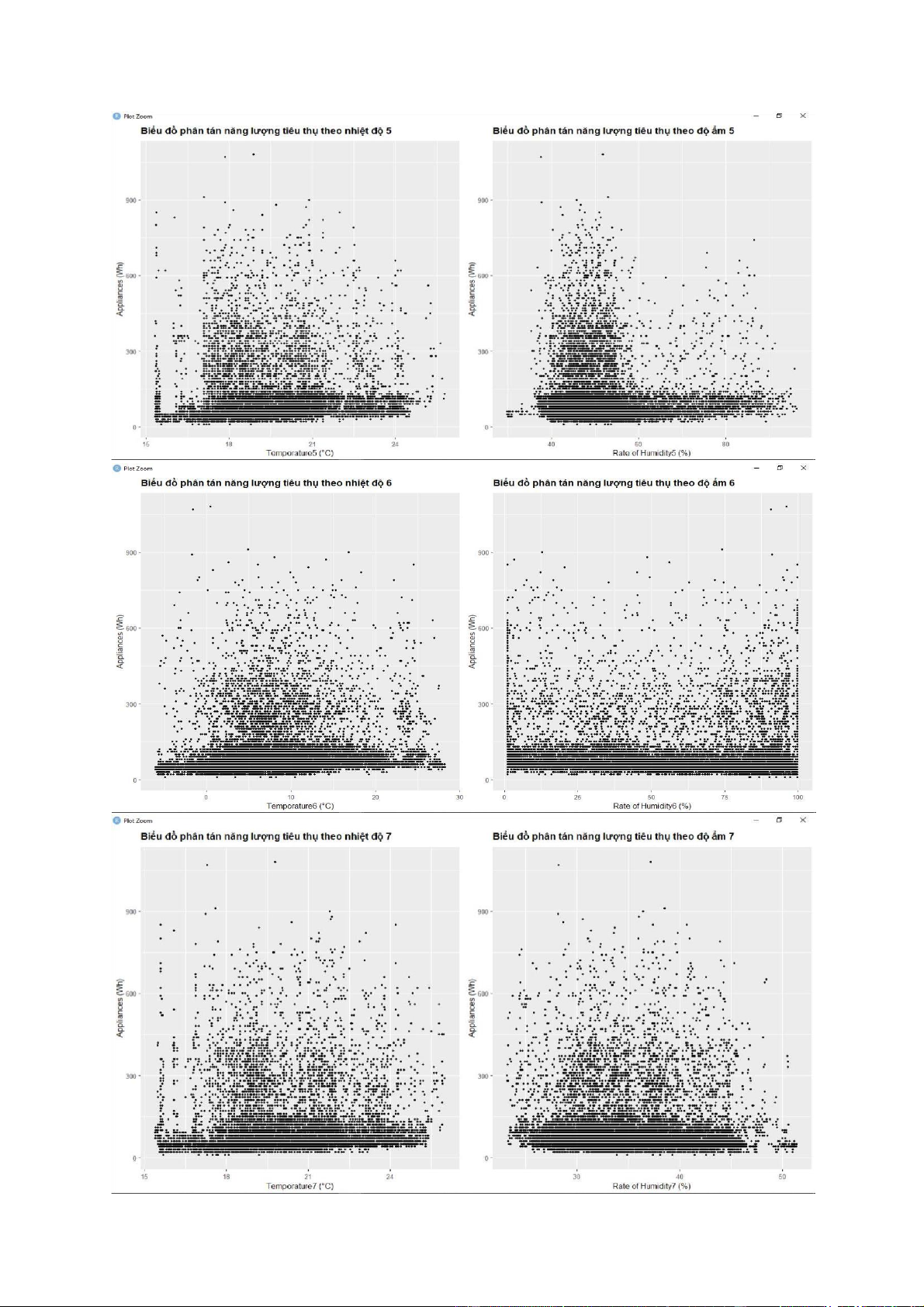
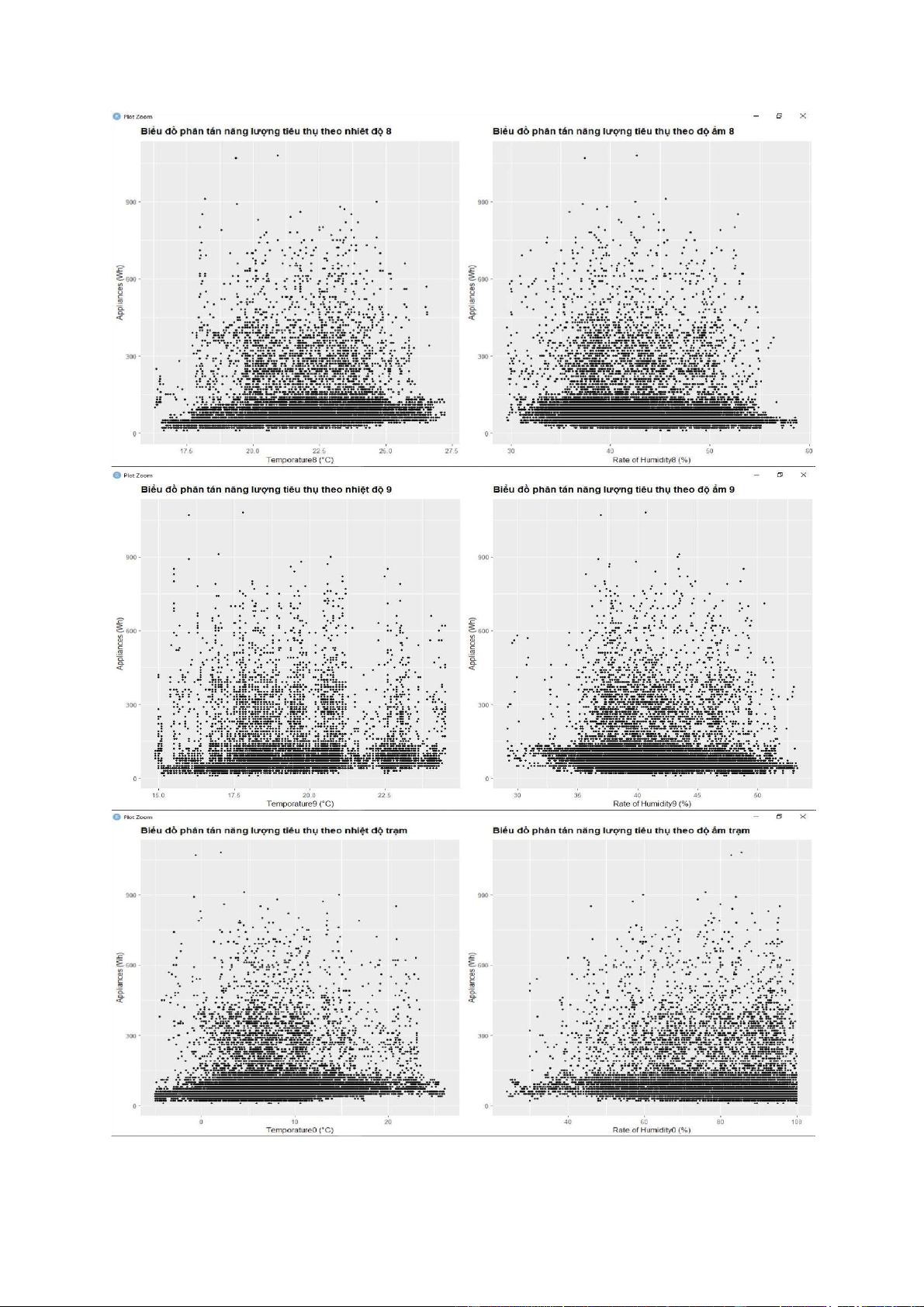
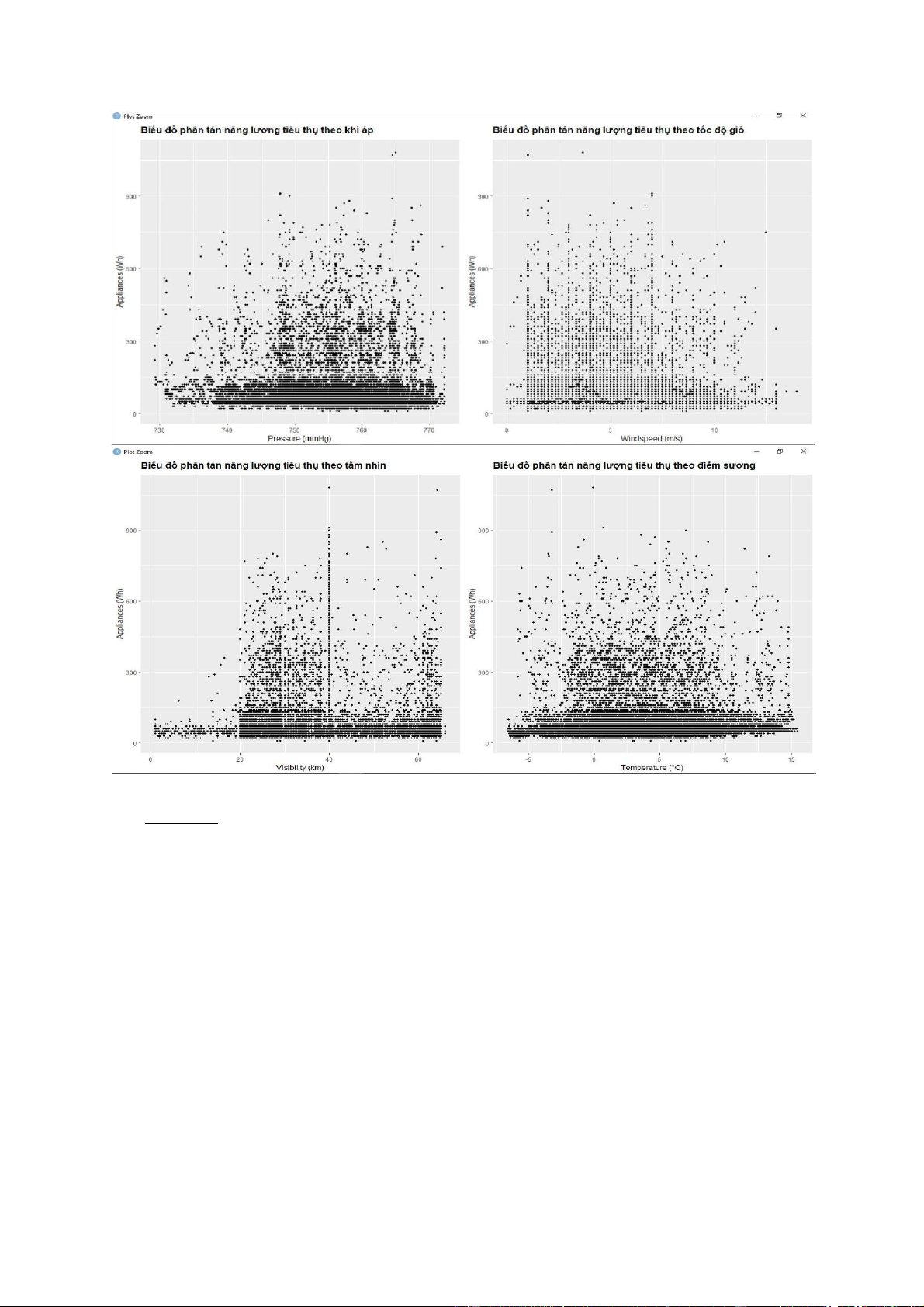
- Có thể dùng lệnh pair() để vẽ dồ thị phân tán, tuy nhiên do có quá nhiểu biến lệnh sẽ
không chạy được. Do đó, trong bài này dùng lệnh geom_point của ggplot để vẽ một số
biểu đồ phân tán nhất định. lOMoARcPSD| 36991220 lOMoARcPSD| 36991220 lOMoARcPSD| 36991220 lOMoARcPSD| 36991220 - Nhận xét:
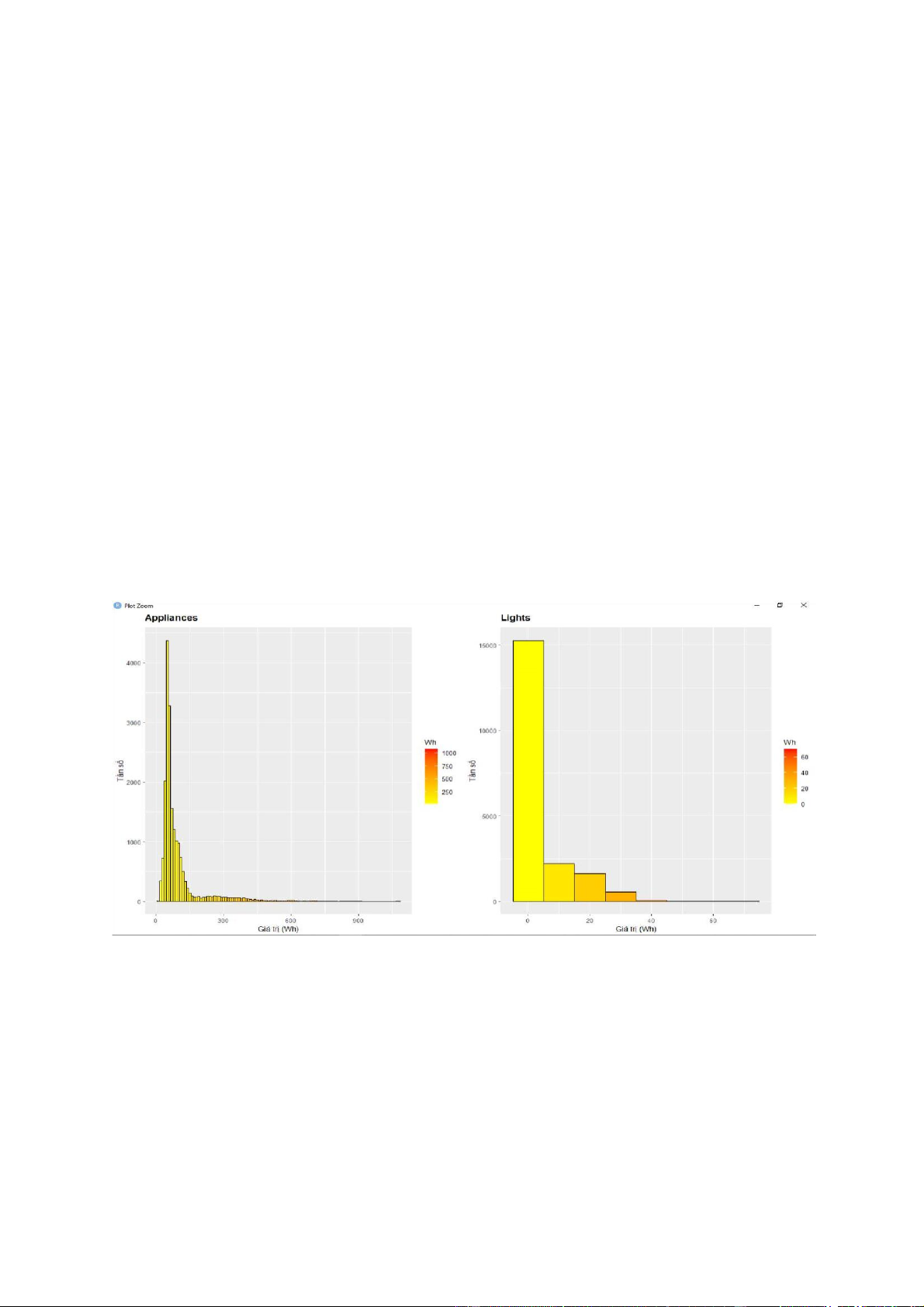
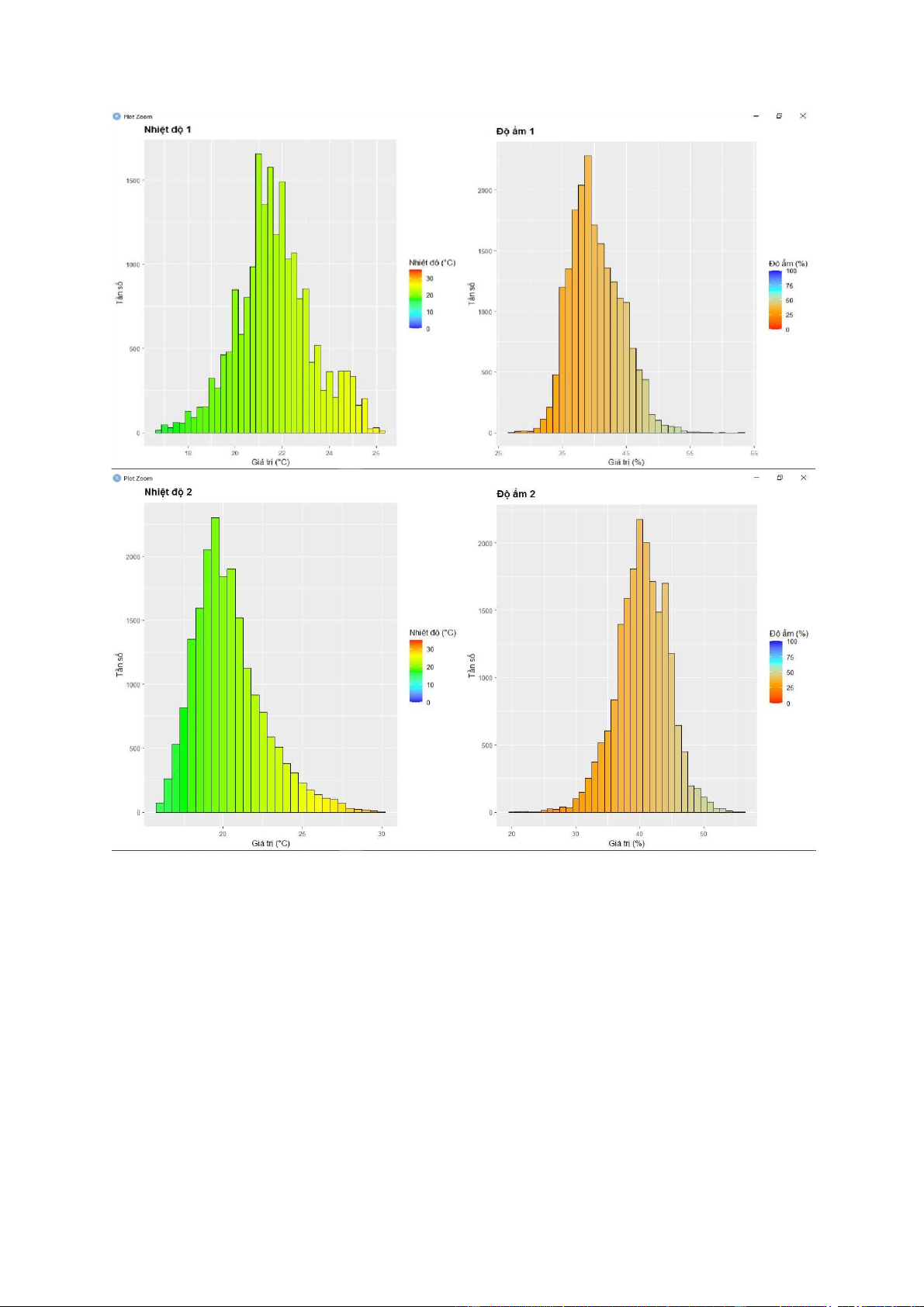
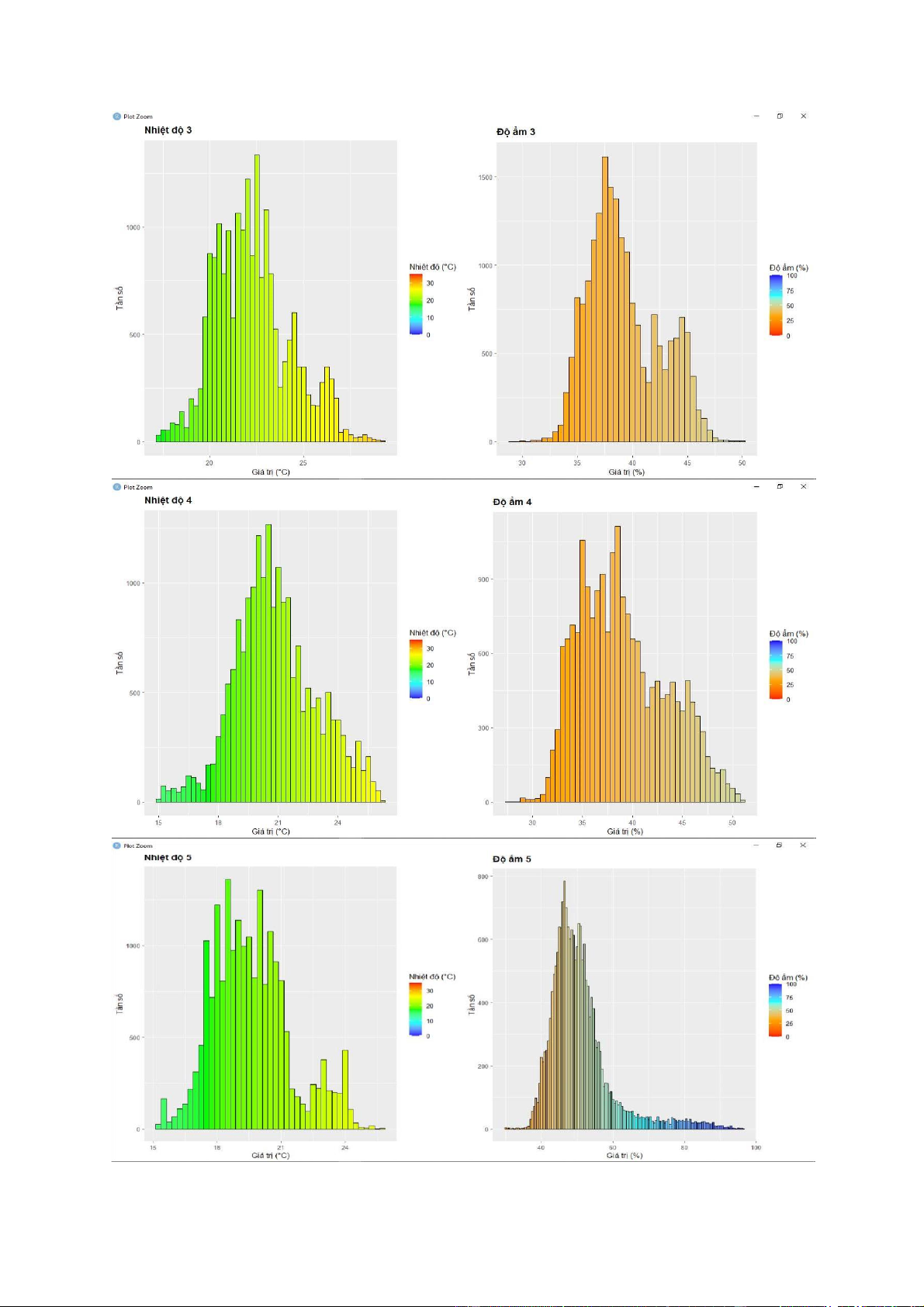
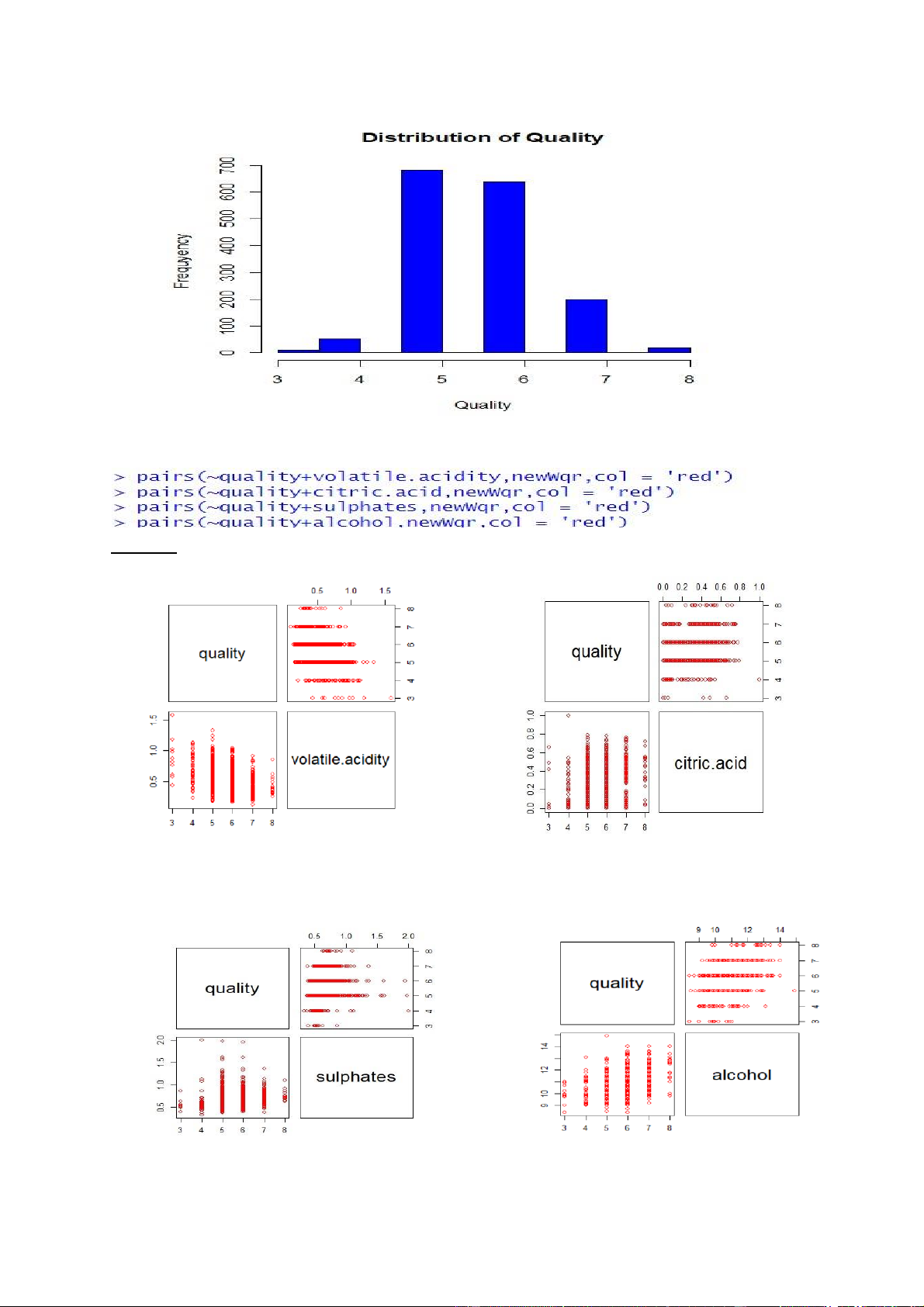
+ Nhìn vào biểu đồ histogram, ta thấy đa số các biến không có phân phối chuẩn do đồ thị bị
lệch về một bên hoặc không có dạng hình chuông.
+ Dựa vào biểu đồ phân tán, ta thấy có rất nhiều điểm tập trung thành một vệt thẳng. Điều
này thể hiện mối tương quan tuyến tính tương đối rõ giữa các biến được vẽ.
(e) Xác định mối quan hệ giữa năng lượng tiêu thụ và các biến giải thích/ dự báo.
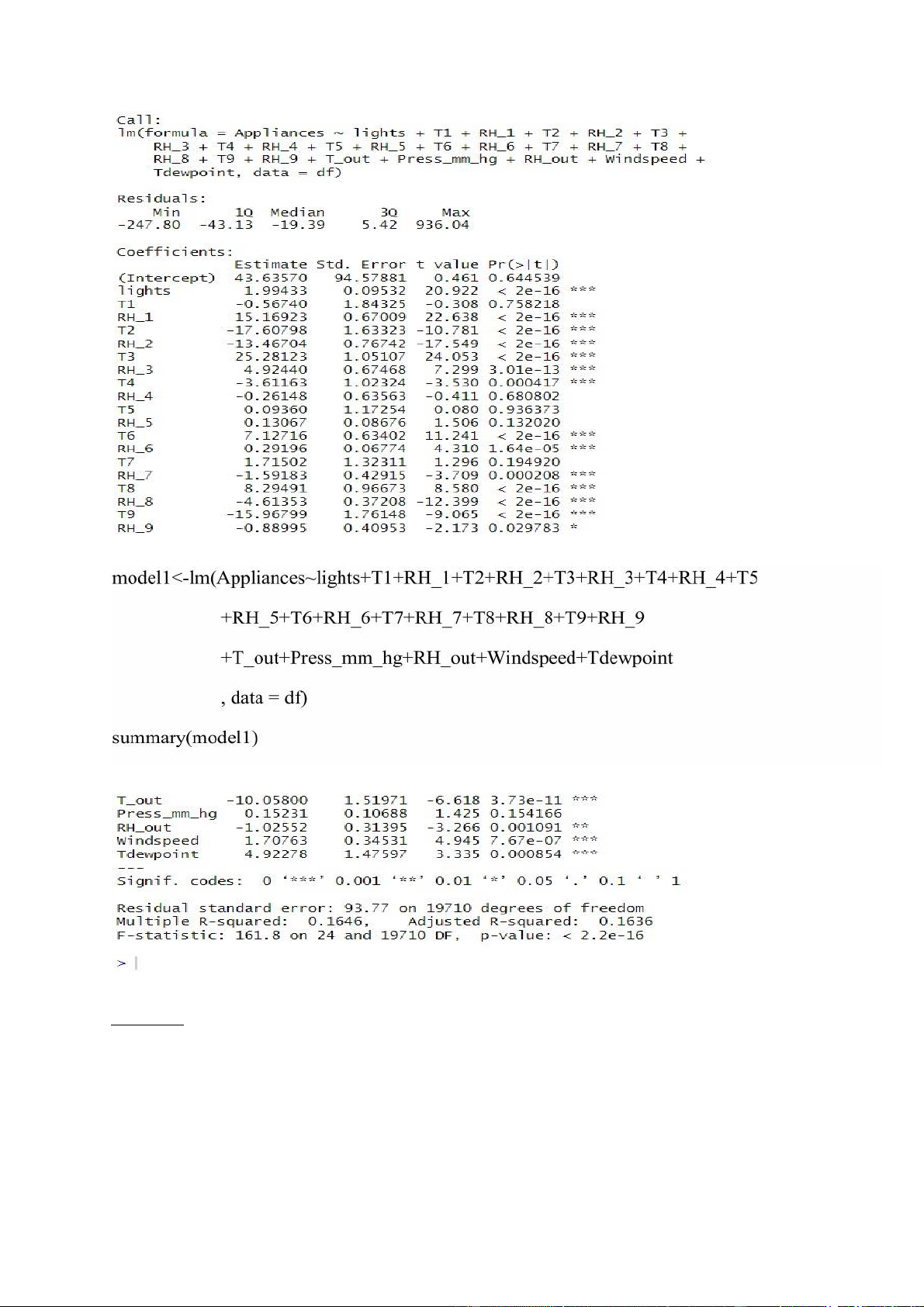
- Xét mô hình hồi quy tuyến tính gồm biến Appliances là biến phụ thuộc và các biến còn
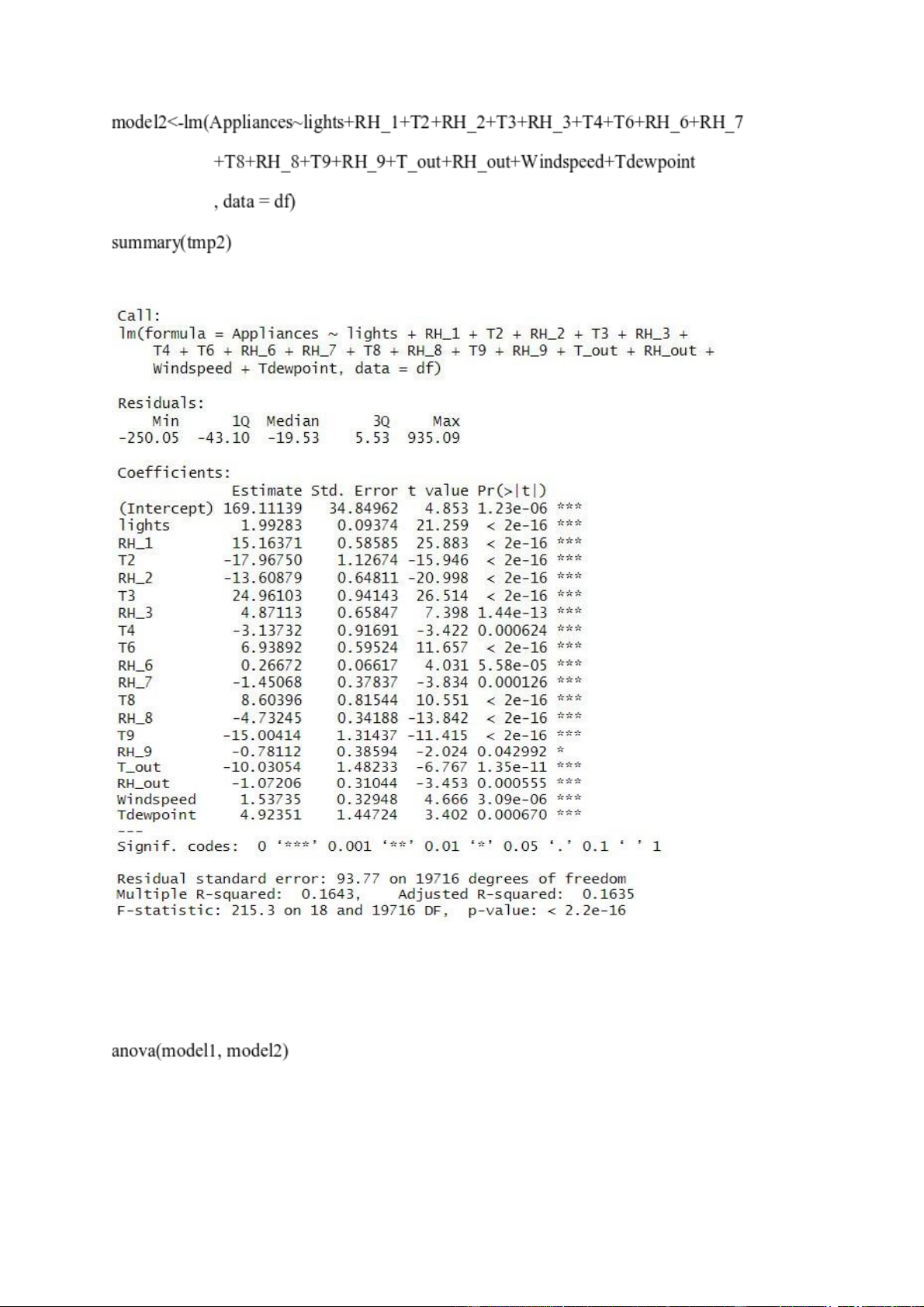
lại là biến độc lập. R: lOMoARcPSD| 36991220 Kết quả: Nhận xét:
- Từ kết quả trên giá trị R2 chỉ khoảng 0.1646, nghĩa là các biến độc lập chỉ giải thích được
16.46% sự thay đổi của biến Appliances. Bên cạnh đó, các biến T1, RH_4, T5 RH_5,
T7 có p-value > 0.05, không có ý nghĩa thống kê. Ngược lại, một số biến có p-value rất
bé, có ý nghĩa giải thích cao cho mô hình.
- Giá trị p-value của mô hình bé hơn 2.2e-16, tức là có ý nghĩa thống kê.
Xét mô hình hổi quy mới sau khi loại bỏ T1, RH_4, T5, RH_5, T7. R: lOMoARcPSD| 36991220 Kết quả:
Ta tiến hành kiểm định mô hình vừa xây dựng bằng phương pháp phân tích phương sai (ANOVA).
• H : hai mô hình có hiệu quả như nhau. 0
• H : hai mô hình có hiệu quả khác nhau. 1 lOMoARcPSD| 36991220
- Dựa vào kết quả, ta thấy p-value = 0.3496 > 0.05, chưa đủ cơ sở bác bỏ H . Cả hai mô hình 0
đều có hiệu quả như nhau, ta chọn mô hình 2 vì có ít biến hơn.
- Bên cạnh đó, giá trị R2 giữa hai mô hình chỉ sai khác 0.0003. Điều này có nghĩa các biến đã
được loại bỏ chỉ giải thích được được 0.03% sự biến thiên của biến phụ thuộc.
- Ta thu được mô hình hồi quy:
Appliances = 169.11139 + 1.99283xlights + 15.16371xRH_1 – 17.96750xT2 –
13.60879xRH_2 + 24.96103xT3 + 4.87113xRH_3 – 3.13732xT4 + 6.93892xT6 +
0.26672xRH_6 – 1.45068xRH_7 + 8.60396xT8 – 4.73245xRH_8 – 15.00414xT9 –
0.78112xRH_9 – 10.03054xT_out – 1.07206xRH_out + 1.53735xWindspeed + 4.92351xTdewpoint
(f) Trình bày các kết quả tính toán từ mô hình trên và giải thích ý nghĩa của từng tham số.
- Hệ số chặn (intercept) = 169.11139 là giá trị của biến Appliances khi vắng mặt các biến
độc lập. Ví dụ, nếu các biến độc lập = 0, biến phụ thuộc Appliances = intercept = 169.11139.
- Hệ số của biến độc lập giải thích cho mức độ ảnh hưởng của sự biến thiên của biến độc lập
đó lên biến phụ thuộc. Ví dụ, biến độc lập RH_1 có hệ số 15.16371, nghĩa là nếu tăng giá trị
RH_1 lên 1 đơn vị thì giá trị của Appliances có thể tăng lên 15.16371 đơn vị. (g) Kiểm tra giả định:
+ Tính tuyến tính của dữ liệu
+ Phần dư có phân phối chuẩn
+ Phần dư có trung bình bằng 0
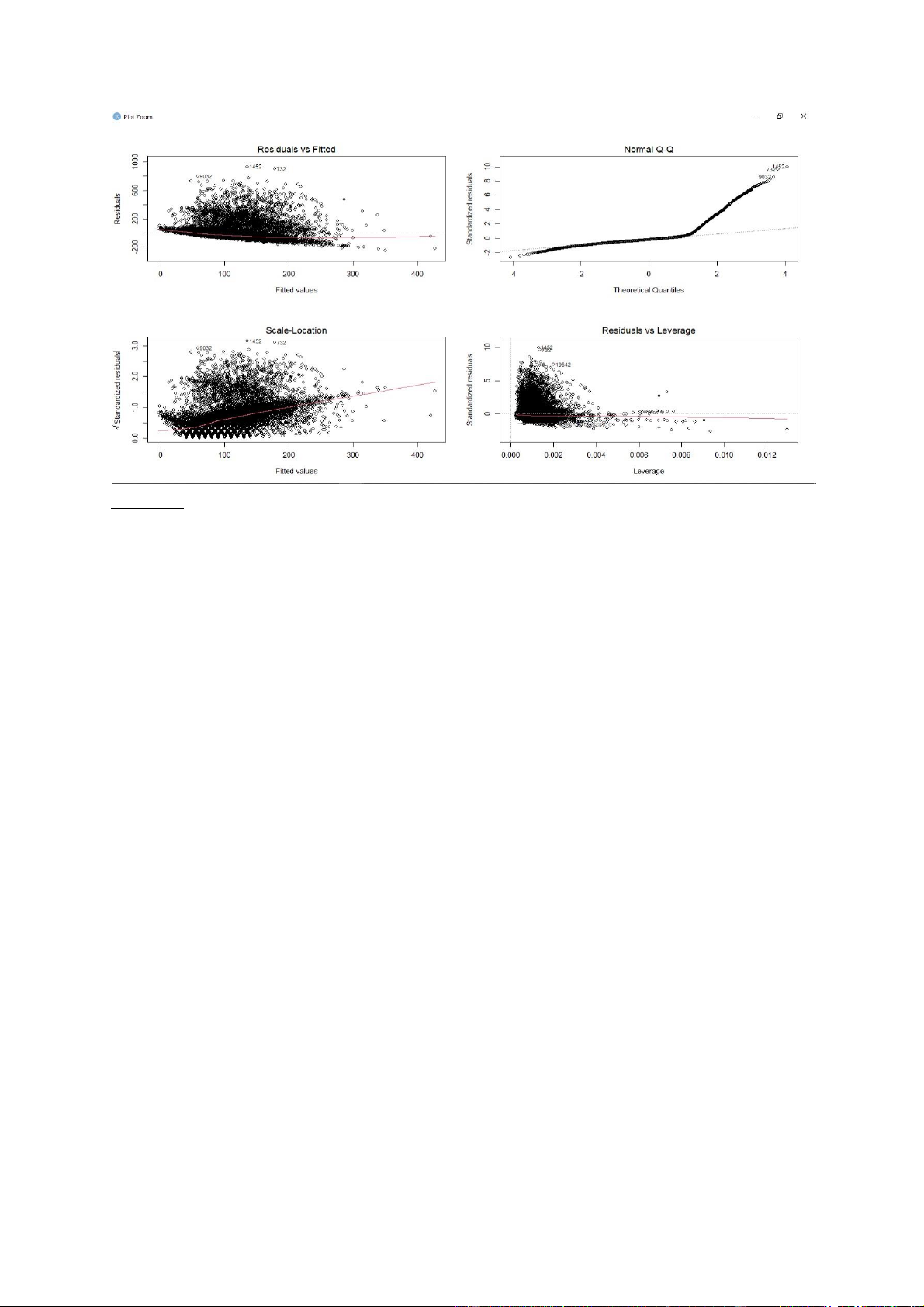
+ Phương sai của phần dư là không đổi lOMoARcPSD| 36991220 Nhận xét:
+ Biểu đồ Residuals vs Fitted cho thấy đường ngang và khá gần so với đường chuẩn, giả
định tuyến tính giữa các biến phụ thuộc và độc lập là phù hợp. Giả định 1 và 3 thỏa. +
Biểu đồ Normal Q-Q cho thấy phần dư không nằm theo đường thẳng, có nghĩa là phần
dư không tuân theo phân phối chuẩn. Giả định 2 bị vi phạm
+ Biểu đồ Scale-Location cho thấy đường màu đỏ là đường dốc, điều này chứng tỏ giả định 4 bị vi phạm.
+ Biểu đồ Residuals vs Leverage cho thấy có rất nhiều điểm vượt qua khoảng cách Cook’s
distance, có nghĩa là có nhiều điểm có ảnh hưởng cao đối với mô hình.
+ Giá trị p-value của mô hình < 2.2e-16 cho thấy mô hình hồi quy khá tốt. Tuy nhiên, mô
hình vi phạm một số giả định nên kết quả mà mô hình dự đoán có thể không chính xác.
Bên cạnh đó, do giá trị R2 = 16.43% là khá thấp, không nên dùng mô hình này để giải
thích cho sự thay đổi năng lượng tiêu thụ của các thiết bị gia dụng trong nhà.
(h) Thảo luận về ý nghĩa thực tiễn của vấn đề nghiên cứu liên quan đến bộ dữ liệu. -
Bên cạnh các thiết bị sử dụng liên tục như tủ lạnh, yếu tố thời tiết đã được chỉ ra là có
tácđộng không nhỏ lên mức điện tiêu thụ. Ví dụ như bật máy lạnh khi trời nóng và bật máy
sưởi ấm khi trời lạnh. -
Thông qua nghiên cứu bộ dữ liệu, ta có thể đưa ra mô hình dự đoán, biết được sự ảnh
hưởngcủa thời tiết đối với từng bộ phận trong hệ thống điện trong nhà. Từ đó, ta có thể cân
nhắc thay đổi bộ phận đó ít tiêu thụ năng lượng hơn. Ngoài ra, mô hình thu được có thể được
dùng để so sánh với các mô hình từ các hệ thống nhà tiết kiệm điện khác để chọn ra hệ thống
tiết kiệm điện phù hợp và hiệu quả nhất II. Hoạt động 2 1. Mô tả dữ liệu
Nhóm chọn đề tài thuộc Khoa Kỹ thuật Hóa học, làm rõ các yếu tố ảnh hưởng chất lượng
rượu vang đỏ. Tập tin winequality-red.csv chứa thông tin về các yếu tố tác động đến chất
lượng rượu vang đỏ. Các thuộc tính dữ liệu dựa trên các phép thử hóa lý bao gồm pH, acid lOMoARcPSD| 36991220
citric, SO2 tự do, độ cồn và một số yếu tố khác. Dữ liệu gốc được cung cấp tại:
https://archive.ics.uci.edu/ml/datasets/Wine+Quality
Dựa vào lý thuyết và đồ thị tương quan các yếu tố ảnh hưởng chất lượng rượu, các biến cần xem xét chính là:
Volatile.acidity: Nồng độ axit dễ bay hơi (gCH3COOH/dm3)
Citric acid: Nồng độ acid citric (g/dm3)
Sulphates: Nồng độ sulphates (g/dm3) Alcohol: Nồng độ cồn
Quality: Chất lượng rượu (3-8)
2.Phân tích dữ liệu 2.1Đọc dữ liệu
Thực hiện các lệnh sau để đọc dữ liệu từ file winequality-red.csv: Kết quả: lOMoARcPSD| 36991220 lOMoARcPSD| 36991220 2.2 Chọn biến
Vẽ biểu đồ thể hiện hệ số tương quan giữa từng biến với biến phụ thuộc là quality: Kết quả:
Qua biểu đồ, có thể thấy các biến volatile.acidity, citric acid, sulphates và alcohol có tương
quan khá lớn () với biến phụ thuộc là quality với hệ số tương quan lần lượt là: -0.39; 0.23; 0.25; 0.48.
Vậy, ta chọn volatile.acidity, citric acid, sulphates và alcohol làm các biến chính.
2.3 Làm sạch dữ liệu
- Lập ra một dữ liệu con tên newDT chỉ bao gồm các biến chính : Kết quả: lOMoARcPSD| 36991220
Kiểm tra dữ liệu khuyết:
Không có dữ liệu khuyết.
2.4 Làm rõ dữ liệu
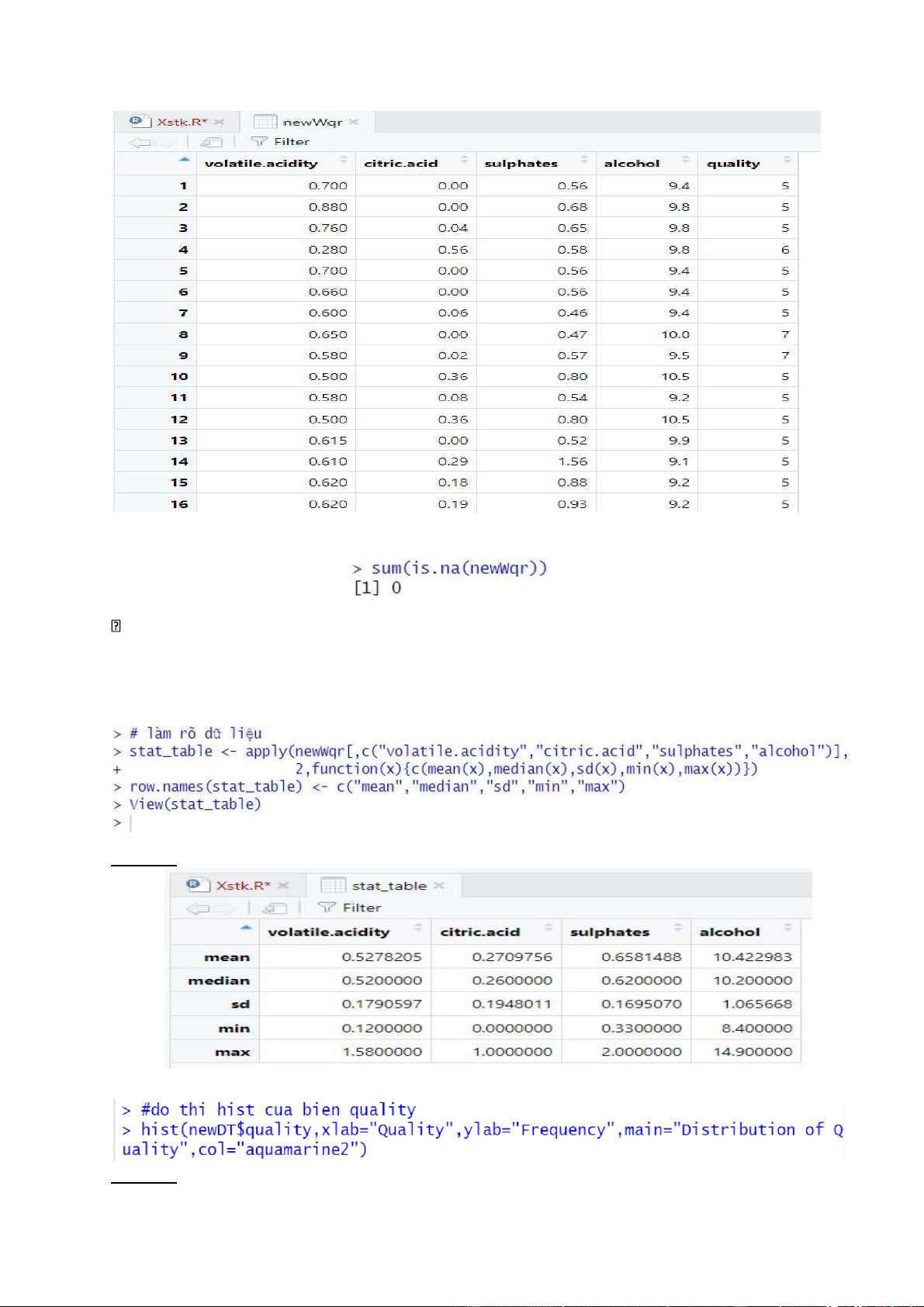
Tính các giá trị thống kê của các biến liên tục: mean (trung bình), median (trung vị), sd
(độ lệch chuẩn), min (giá trị nhỏ nhất), max (giá trị lớn nhất): Kết quả:
Vẽ đồ thị phân phối của biến quality: Kết quả: lOMoARcPSD| 36991220
- Dùng lệnh pairs() lần lượt cho các biến volatile.acidity, citric acid, sulphates và alcohol Kết quả: lOMoARcPSD| 36991220
2.5 Xây dựng các mô hình hồi quy tuyến tính
- Biến phụ thuộc: quality
- Biến độc lập (biến dự báo): volatile.acidity, citric acid, sulphates, alcohol+ Xây dựng mô hình WQR1: Sử dụng lệnh: Kết quả:
+ Xây dựng mô hình WQR2 (loại biến citric.acid), dùng Anova chọn ra mô hình hợp lý.
- Xây dựng mô hình WQR2, sử dụng lệnh: Kết quả: Nhận xét:
+ Với mức ý nghĩa 5% chúng ta đặt giả thiết
H0 là 2 mô hình hiệu quả như nhau
H1 là 2 mô hình hiệu quả khác nhau.
Để nhận xét, chúng ta quan sát cột Pr ( > | t | ) lOMoARcPSD| 36991220
Giá trị Pr = 0.4461 > 0.05 (lớn hơn mức ý nghĩa 5%) Chấp nhận giả thiết H0 và bác
bỏ giả thiết H1 2 mô hình WQR1 và WQR2 có hiệu quả tương đương nhau nhận WQR2
làm mô hình vì WQR2 có ít biến hơn.
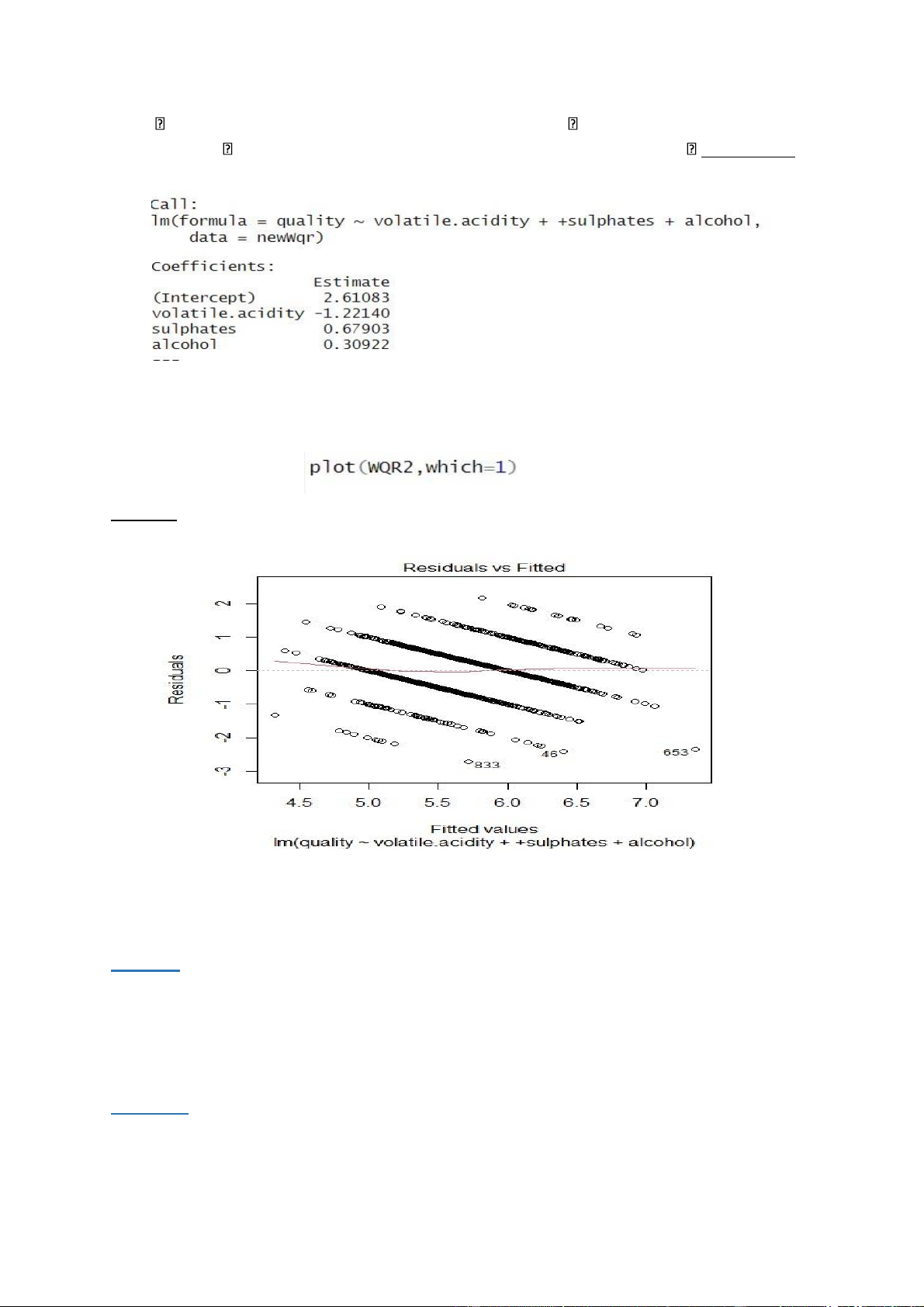
- Vẽ đồ thị hàm plot (đồ thị biểu thị sai số hồi quy và giá trị dự báo) của mô hình WQR2: - Sử dụng câu lệnh: Kết quả: Ý nghĩa:
- Fitted values là giá trị dự báo của chất lượng (quality) dựa theo các biến độc lập còn lại.
- Residuals là sai số hồi quy, là sai lệch giữa giá trị thực tế với giá trị dự báo. Nhận xét:
- Khoảng các giá trị của biến chất lượng tập trung trong khoảng từ 5 đến 6.5. lOMoARcPSD| 36991220
- Trong khoảng này các giá trị chất lượng xung quanh đường hồi quy tuyến tính, giá
trịresiduals tương đối thấp.
- Từ đồ thị ta có thể thấy đường hồi quy tuyến tính xấp xỉ đường thẳng y=0. Có thể nói
saisố tương đối thấp nên kết luận rằng nó khá chính xác.Cho thấy mô hình WQR2 khá ổn định. 2.6 Dự đoán
Điểm bé hơn 5 là không đạt chất lượng
Điểm lớn hơn hoặc bằng 5 là đạt chất lượng
Kết quả: Thu được bảng thống kê các loại rượu như sau:
- Tiến hành dự đoán tỉ lệ các loại rượu:
Kết quả: Dữ liệu về tỉ lệ dự đoán và tỉ lệ của mẫu như sau:
- Ta nhận thấy, giá trị dự báo về tỉ lệ đạt chất lượng giảm còn tỉ lệ không đạt chất
lượngtăng. Nhưng nhìn chung, mức đạt chất lượng vẫn chiếm tỉ lệ cao hơn cả.
TÀI LIỆU THAM KHẢO
1. https://archive.ics.uci.edu/ml/datasets/student+performance
2. Nguyễn Văn Tuấn. Phân tích số liệu và biểu đồ bằng R
3. Peter Dalgaard. Introductory Statistics With R