lOMoARcPSD| 36991220
ĐẠI HỌC QUỐC GIA TP. HCM
TRƯỜNG ĐẠI HỌC BÁCH KHOA
BÀI TẬP LỚN MÔN HỌC
XÁC SUẤT VÀ THỐNG KÊ ĐỀ TÀI
SO SÁNH GIÁ NHÀ TẠI BẮC KINH DỰA VÀO CÁC PHƯƠNG PHÁP THỐNG KÊ
Chương 1: Cơ sở lý thuyết.............................................................................................
1.1. Phân tích phương sai một yếu tố............................................................................2.
1.1.1 Lý thuyết về ANOVA (Phân tích phương sai)..........................................2
1.1.2 Phân tích phương sai một yếu tố................................................................2
1.2. Hồi quy tuyến tính..................................................................................................4
1.2.1 Định nghĩa................................................................................................4
1.2.2 Độ phù hợp mô hình.................................................................................5
1.2.3 Đánh giá mức độ toàn diện của mô hình...................................................6
1.2.4 Đánh giá ý nghĩa của từng biến độc lập riêng biệt....................................7
Chương 2: Hoạt động....................................................................................................
2.1. Đề bài.....................................................................................................................8
2.2. Thực hiện................................................................................................................9
2.2.1 Đọc dữ liệu...............................................................................................9
2.2.2 Làm sạch dữ liệu.......................................................................................9
2.2.3 Kiểm tra dữ liệu…………………………………………………………10
2.2.4 Loại bỏ dữ liệu ………………………………….……………………...11
2.2.5 Làm rõ dữ liệu…………………………………...……………………...12
2.2.6 ANOVA một nhân tố: đánh giá sự khác biệt về giá nhà (totalPrice) giữa
các quận (district) đã xây dựng trong năm 2012………………………………15 lOMoARcPSD| 36991220
2.2.7 Xây dựng mô hình hồi quy tuyến tính: Sử dụng mô hình hôi quy tuyến tính
phù hợp để đánh giá các nhân tố tác động đến tổng chi phí bán nhà thực
tế……………………………………………………………………………….27
TÀI LIỆU THAM KHẢO.............................................................................................
Chương 1: CƠ SỞ LÝ THUYẾT
1.1 Phân tích phương sai một yếu tố
1.1.1 Lý thuyết về phân tích phương sai ( ANOVA)
Phân tích phương sai là một mô hình để xem xét sự biến động của một biến ngẫu nhiên
định lượng X chịu tác động trực tiếp của một hay nhiều yếu tố nguyên nhân (định tính).
Mục tiêu của phân tích phương sai là so sánh trung bình của nhiều nhóm (tổng thể) dựa
trên các trị trung bình của các mẫu quan sát từ các nhóm này và thông qua kiểm định
giả thuyết củaa kết luận và sự bằng nhau của các trung bình tổng thể này.
1.1.2 Phân tích phương sai
Với các giả thuyết của bài toán ( điều kiện bài toán):
-Các tổng thể có phân phối chuẩn (với trung bình tương ứng là a ;…; a 1; a2 k chưa biết).
- Các tổng thể có phương sai bằng nhau.
- Các mẫu quan sát được lấy độc lập.
Giả sử ta muốn so sánh k nhóm X (với
j (với j = 1,2,. . . k) có kỳ vọng lần lượt là µj, ..., µk j = 1,2,. . . k)
Mô hình phân tích phương sai một yếu tố ảnh hưởng được mô tả dưới dạng kiểm định
giả thuyết như sau: Giả thiết kiểm định H0 : µ1 = µ2 = ... = µk
Giả thuyết 𝐻0 cho rằng trung bình của k tổng thể đều bằng nhau
Giả thiết đối với H ; với i 1 : a i aj j
Giả thuyết cho rằng tồn tại ít nhất một cặp trung bình tổng thể khác nhau.
Ta có các trung bình mẫu của các nhóm (xem như đại diện của các tổng thể). Trước hết
ta xem cách tính các trung bình mẫu từ những quan sát của k mẫu ngẫu nhiên độc lập (ký hiệu 𝐻̅ , … 1, 𝐻̅2
𝐻̅k) và trung bình chung của k mẫu quan sát ( ký hiệu 𝐻̅ ) từ
trường hợp tổng quát như sau:
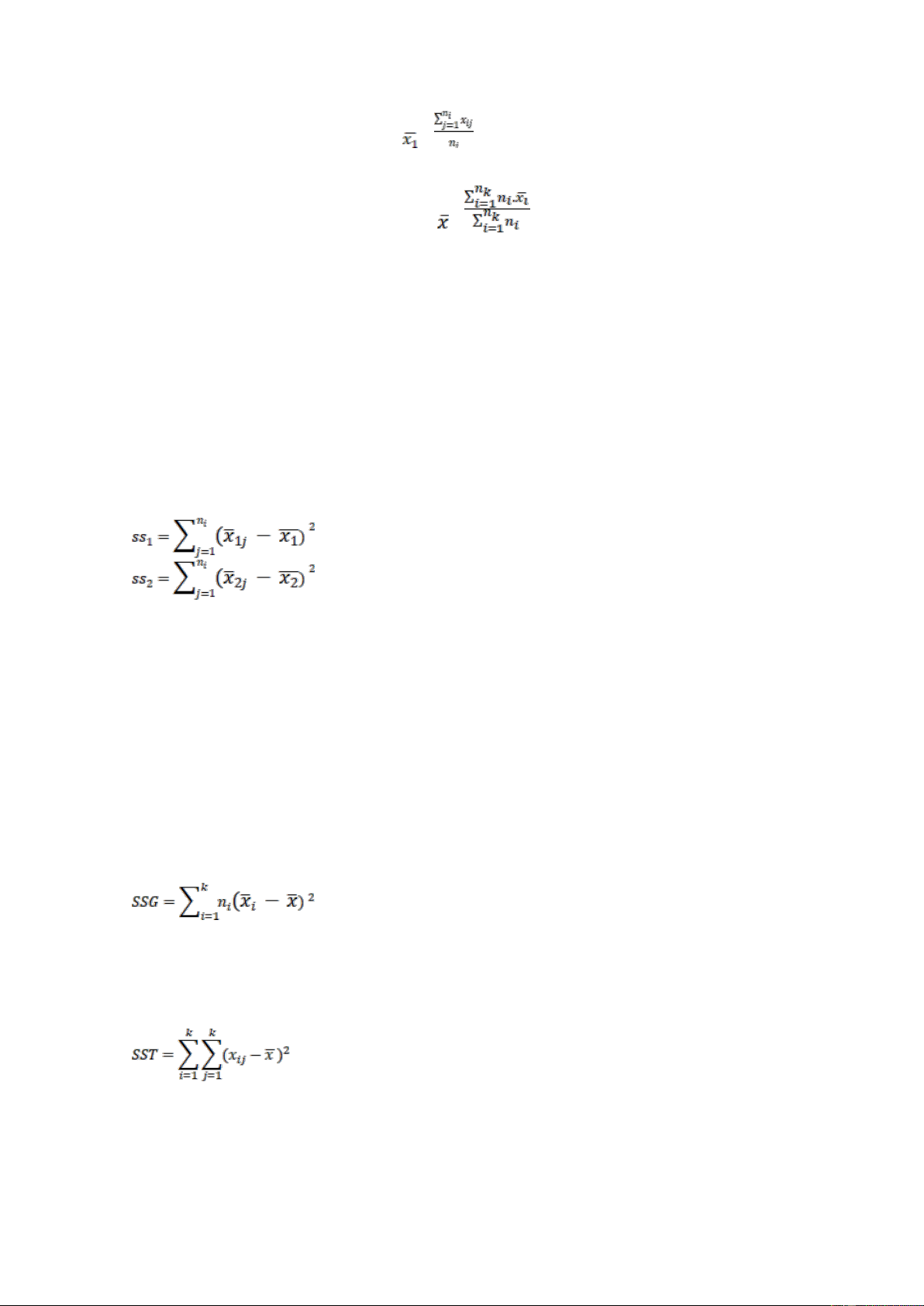
Tính trung bình mẫu của từng nhóm 𝐻̅ , … 1, 𝐻̅2 𝐻̅k theo công thức: lOMoARcPSD| 36991220 = (i= 1,2,..k)
Và trung bình chung của k mẫu =
Tính các tổng các chênh lệch bình phương (hay gọi tắt là tổng bình phương). Tính tổng
các chênh lệch bình phương trong nội bộ nhóm SSW và tổng các chênh lệch bình phương giữa các nhóm SSG.
Tổng các chênh lệch bình phương trong nội bộ nhóm (SSW) được tính bằng cách cộng
các chênh lệch bình phương giữa các giá trị quan sát với trung bình mẫu của từng nhóm,
rồi sau đó lại tính tổng cộng kết quả tất cả các nhóm lại.
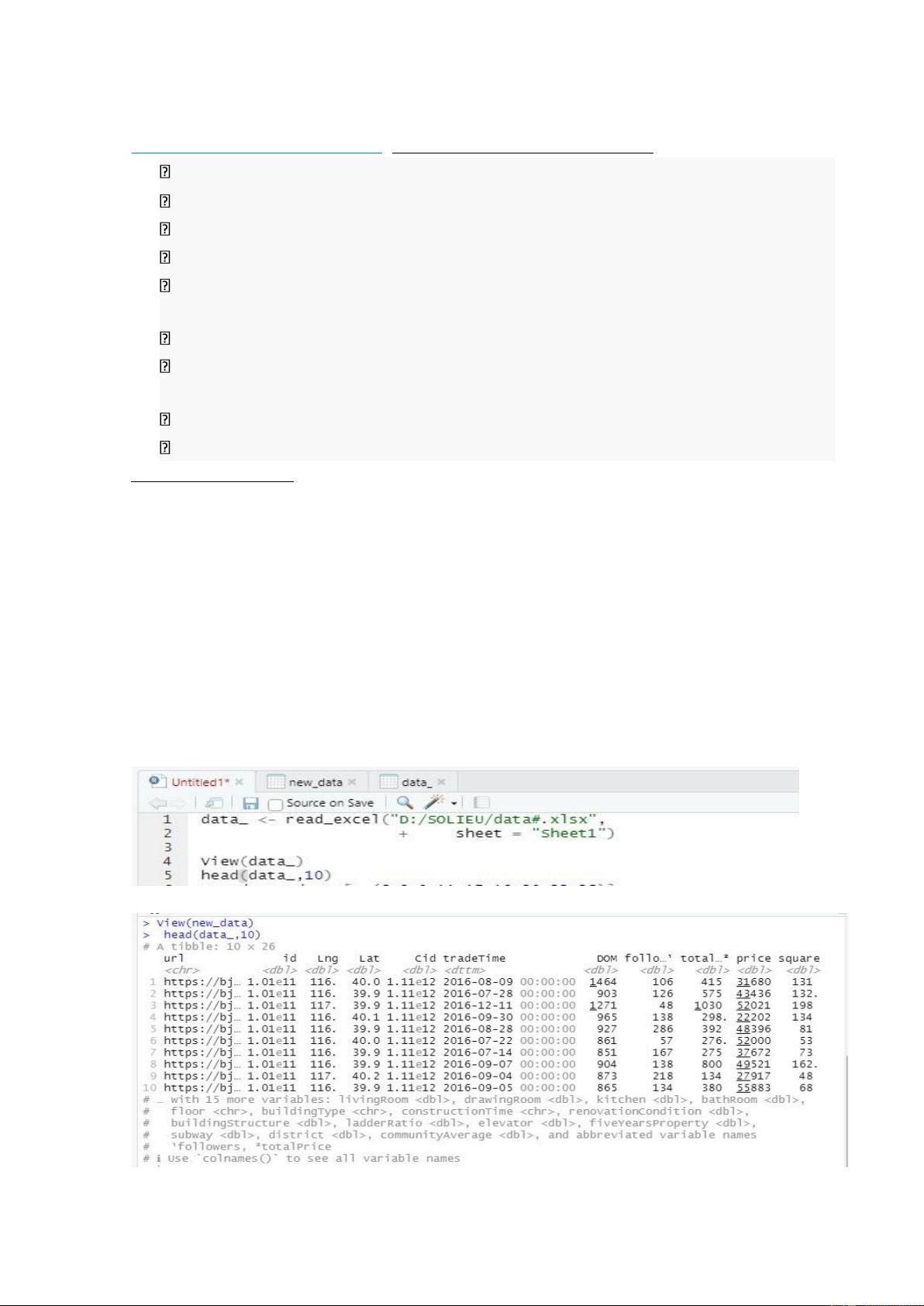
Tổng các chênh lệch bình phương của từng nhóm được tính theo công thức:
Tương tự như vậy ta tính cho đến nhóm thứ k được SSk. Vậy tổng các chênh lệch bình
phương trong nội bộ các nhóm được tính như sau:
SSW = SS1 + SS2 + ... + SSk
Tổng các chênh lệch bình phương giữa các nhóm (SSG) được tính bằng cách cộng cácc
hênh lệch được lấy bình phương giữa các trung bình mẫu của từng nhóm với trung bình
chung của k nhóm (các chênh lệch này đều được nhận thêm với số quan sát tương ứng cả từng nhóm).
Tổng các chênh lệch bình phương toàn bộ SST được tính bằng cách cộng các chênh lệch
đã lấy bình phương giữa từng giá trị quan sát của toàn bộ mẫu nghiên cứu (xij) với trung bình toàn bộ (x).
Có thể dễ dàng chứng minh là tổng các chênh lệch bình phương toàn bộ bằng tổng
cộng tổng các chênh lệch bình phương trong nội bộ các nhóm và tổng các chênh lệch
bình phương giữa các nhóm.
SST = SSW + SSG lOMoARcPSD| 36991220
-SST: Tổng các biến thiên của X do tất cả các yếu tố tạo ra.
Như vậy công thức trên cho thấy, SST là toàn bộ biến thiên của yếu tố kết quả đã được
phân tích thành hai phần: phần biến thiên do yếu tố đang nghiên cứu tạo ra (SSG) và
phần biến thiên còn lại do các yếu tố khác không nghiên cứu ở đây tạo ra (SSW). Nếu
phần biến thiên do yếu tố nguyên nhân đang xét tạo ra càng “đáng kể” so với phần biến
thiên do các yếu tố khác không cét tạo ra, thì chúng ta càng có cơ sở đe bác bỏ H0 và
kết luận là yếu tố nguyên nhân đang nghiên cứu ảnh hưởng có ý nghĩa đến yếu tố kết quả. Nhận xét:
-SSB ( hay SSG) : Phần biến thiên của giá trị X do các mức độ của yếu tố đang xem xét tạo ra.
-SSW: Phần biến thiên của giá trị X do các yếu tố nào đó không được xem xét tạo ra.
- SST: Tổng các biến thiên của X do tất cả các yếu tố tạo ra.
Tính phương sai trong nội bộ nhóm (MSW) bang cách lấy tőng các chênh lệch bình
phương trong nội bộ các nhóm (SSW) chia cho bậc tự do tương ứng là n - k (n là số
quan sát, k là số nhóm so sánh). MSW là ước lượng phần biến thiên của yếu tố kết quả
do các yếu tố khác gây ra.
Tính phương sai giữa các nhóm (MSG) bằng cách lấy tổng các chênh lệch bình phương
giữa các nhóm chia cho bậc tự do tương ứng là k - 1. MSG là ước lượng phần biến thiên
của yếu tố kết quả do yếu tố nguyên nhân đang nghiên cứu gây ra.
Để kiểm tra giả thuyết, ta cần tính một giá trị làm tiêu chuẩn kiểm định: F =
Quy tắc kiểm định: nếu F > Fk-1;nk-k;α thì ta bác bỏ giả thuyết H0 (Miền
bác bỏ: Wα = (Fk-1;nk-k;α ; +∞)).
Giá trị của Fk-1;nk-k;α được tra trong bảng Fisher.
1.2 Hồi quy tuyến tính 1.2.1 Định nghĩa
Hàm hồi quy của Y theo X chính là kỳ vọng có điều kiện của Y đối với X, tức là E (Y| X).
Việc phân tích hồi quy là nghiên cứu mối liên hệ phụ thuộc của một biến (gọi là biến
phụ thuộc) vào một hay nhiều biến khác ( gọi là các biến độc lập); với ý tưởng ước lOMoARcPSD| 36991220
lượng giá trị trung bình (tổng thể) của biến phụ thuộc trên cơ sở biết trước giá trị các
biến độc lập (qua mẫu).
Phương trình hồi quy đơn biến: Y = β0 + β1X + e
Phương trình hồi quy bội: Y = β0 + β1X1 + β2X2 + ... + βnXn + e Trong đó:
+Y là biến phụ thuộc, biến chịu tác động của biến khác. +X, X
: biến độc lập, là biến tác động lên biến khác. 1, X2, Xn
+β0 là hằng số hồi quy, hay còn được gọi là hệ số chặn.
+ β , β , β : hệ số hồi quy, hay còn được gọi là hệ số góc. 1 2 n
+e là sai số, chỉ số càng lớn càng khiến cho khả năng dự đoán của hồi quy trở nên kém
chính xác hơn hoặc sai lệch nhiều hơn so với thực tế.
1.2.2 Độ phù hợp của mô hình
Tính toán hệ số xác định bội R2: khi có nhiều biến độc lập trong mô hình đa bội thì R2
vẫn được sử dụng để xác định biến thiên của biến phụ thuộc để giải thích mối quan hệ
của biến phụ thuộc và các biến độc lập trong mô hình. Ta có:
+∑(𝐻i - )2: TSS – Total Sum of Squares
+ ∑( - )2: ESS – Explained Sum of Squares
+∑ 𝐻 2i: RSS – Residual Sum of Squares
Ta có thể viết: TSS = ESS + RSS Ý
nghĩa của các thành phần:
+ TSS là tổng bình phương của tất cả các sai lệch giữa các giá trị quan sát Yi và giá trị trung bình.
+ ESS là tổng bình phương của tất cả các sai lệch giữa các giá trị của biến phụ thuộc Y
nhận được từ hàm hồi quy mẫu và giá trị trung bình của chúng. Phần này đo độ chính xác của hàm hồi quy.
+ RSS là tổng bình phương của tất cả các sai lệch giữa các giá trị quan sát Y và các giá
trị nhận được từ hàm hồi quy.
+ TSS được chia thành 2 phần: một phần do ESS và một phần do RSS gây ra. 𝐻2 được
xác định theo công thức:
Tỷ số giữa tổng biến thiên được giải thích bởi mô hình cho tổng bình phương cần được
giải thích được gọi là hệ số xác định. 𝐻2 đo tỷ lệ hay số % của toàn bộ sai lệch Y với giá lOMoARcPSD| 36991220
trị trung bình đượcgiải thích bằng mô hình. Khi đó người ta sử dụng 𝐻2 để đo sự phù hợp của hàm hồi quy: + 0 ≤ 𝐻2 ≤ 1.
+ 𝐻2 cao nghĩa là mô hình ước lượng được giải thích được một mức độ cao biến động của biến phụ thuộc.
+ Nếu 𝐻2 = 1, nghĩa là đường hồi quy giải thích 100% thay đổi của y.
+ Nếu 𝐻2 = 0, nghĩa là mô hình không đưa ra thông tin nào về sự thay đổi của biến phụ thuộc y
1.2.3 Đánh giá ý nghĩa toàn diện của mô hình
Mô hình hồi quy mà chúng ta xây dựng là dựa trên cơ sở dữ liệu của một mẫu lấy từ
tổng thể vì vậy nó có thể bị ảnh hưởng của sai số lấy mẫu, vì vậy chúng ta phải kiểm
định lại ý nghĩa thống kê của toàn bộ mô hình. Bài toán kiểm định F: Tiêu chuẩn kiểm định: Giả thiết
H0 : R2 = 0 ( mô hình không phù hợp )
H1 : R2 ≠ 0 ( mô hình phù hợp ) Bài toán kiểm định F: Tiêu chuẩn kiểm định F = Hoặc F =
Hàm hồi quy của Y theo X chính là kỳ vọng có điều kiện của Y đối với X, tức là E(Y| X). Trong đó:
+R2 là hệ số xác định +n là cỡ mẫu
+k là số biến độc lập lOMoARcPSD| 36991220
Miền bác bỏ: Wa = (Fa(k, n - k - 1); +∞). Để tìm Fa(k, n - k - 1), ta tra bảng Fisher tại
mức ý nghĩa α = 0.05 tại cột k và hàng n - k - 1. Nếu F ∈ W
, suy ra mô hình hồi quy bội với các biến độc lập ta
a ta bác bỏ giả thiết H0
đưa vào có thể giải thích một cách có ý nghĩa cho biến phụ thuộc, hay nói cách khác là
mô hình phù hợp. Ngược lại, ta suy ra mô hình không phù hợp.
1.2.4 Đánh giá ý nghĩa của từng biến độc lập riêng biệt
Ở kiểm định F, ta đã đánh giá được rằng mô hình có ý nghĩa. Điều này có nghĩa là có ít
nhất một biến độc lập trong mô hình có thể giải thích được cho sự biến thiên của biến
phụ thuộc. Tuy nhiên, điều này không có nghĩa là tất cả các biến độc lập ta đưa vào mô
hình đều có ý nghĩa. Để có thể xác định được biến độc lập nào có ý nghĩa chúng ta phải
kiểm định giả thiết sau:
H0 : βj = 0 với j = 1, 2, ..., k H1 : βj = 0
Chúng ta có thể dùng kiểm định t để kiểm tra ý nghĩa của mỗi hệ số hồi quy với độ tin cậy 95%: T =bSSEj −0 n-k-1 Trong đó:
bj là hệ số độ dốc trong mô hình hồi quy mẫu cho biến độc lập thứ j. sbj
là sai số chuẩn ước lượng của hệ số độ dốc của biến độc lập thứ j.
Miền bác bỏ: Wa = (ta (n - k - 1); +∞). Tra bảng phân phối Student ta tìm được giá trị giới hạn t
, suy ra biến độc lập j có khả
a (n - k - 1). Nếu Tqs ∈ Wa ta bác bỏ giả thiết H0
năng giải thích cho biến phụ thuộc. Ngược lại, ta suy ra biến độc lập j không có khả
năng giải thích cho biến phụ thuộc.
Chương 2: Hoạt động 2.2 Đề bài:
Tập tin “new.xlsx” chứa thông tin về giá bán (đơn vị đô la) của 318851 ngôi nhà ở
Bắc Kinh trong giai đoạn từ 2011-2017, một số dữ liệu được giao dịch vào tháng 1
năm 2018 và một số thậm chí còn sớm hơn. Bên cạnh giá nhà, bộ dữ liệu còn bao gồm
các biến miêu tả các thuộc tính khác như số lượng người theo dõi giao dịch, loại công lOMoARcPSD| 36991220
trình, kết cầu ngôi nhà…Dữ liệu gốc được tham khảo từ trang
https://bj.lianjia.com/chengjiao. Các biến chính trong bộ dữ liệu:
tradeTime: thời điểm giao dịch
followers: số người theo dõi giao dịch.
TotalPrice: tổng giá ngôi nhà.
Square: diện tích ngôi nhà.
buildingType: loại công trình, bao gồm tháp (1), nhà gỗ (2), sự kết hợp giữa
tấm và tháp (3), tấm (4).
constructionTime: thời gian xây dựng.
buildingStructure: cấu trúc ngôi nhà, bao gồm không xác định (1), hỗn hợp
(2), gạch và gỗ (3), gạch và bê tông (4), thép (5) và hỗn hợp bê tông - thép (6).
elevator: có (1) và không có thang máy (0). district: quận Các bước thực hiện:
1/ Đọc dữ liệu (Import Data): new.xlsx
2/ Làm sạch dữ liệu (Data Cleaning): kiểm tra dữ liệu khuyết (NA).
3/ Làm rõ dữ liệu (Data visualization): thống kê mô tả - dùng thống kê mẫu và vẽ đồ thị.
4/ Sử dụng ANOVA để đánh giá sự khác biệt giá nhà giữa các quận.
5/ Xây dựng mô hình hồi quy tuyến tính để đánh giá các nhân tố có thể ảnh hưởng đến giá nhà ở Bắc Kinh. 2.2 Thực hiện:
2.2.1 Đọc Dữ Liệu (Impost Data)
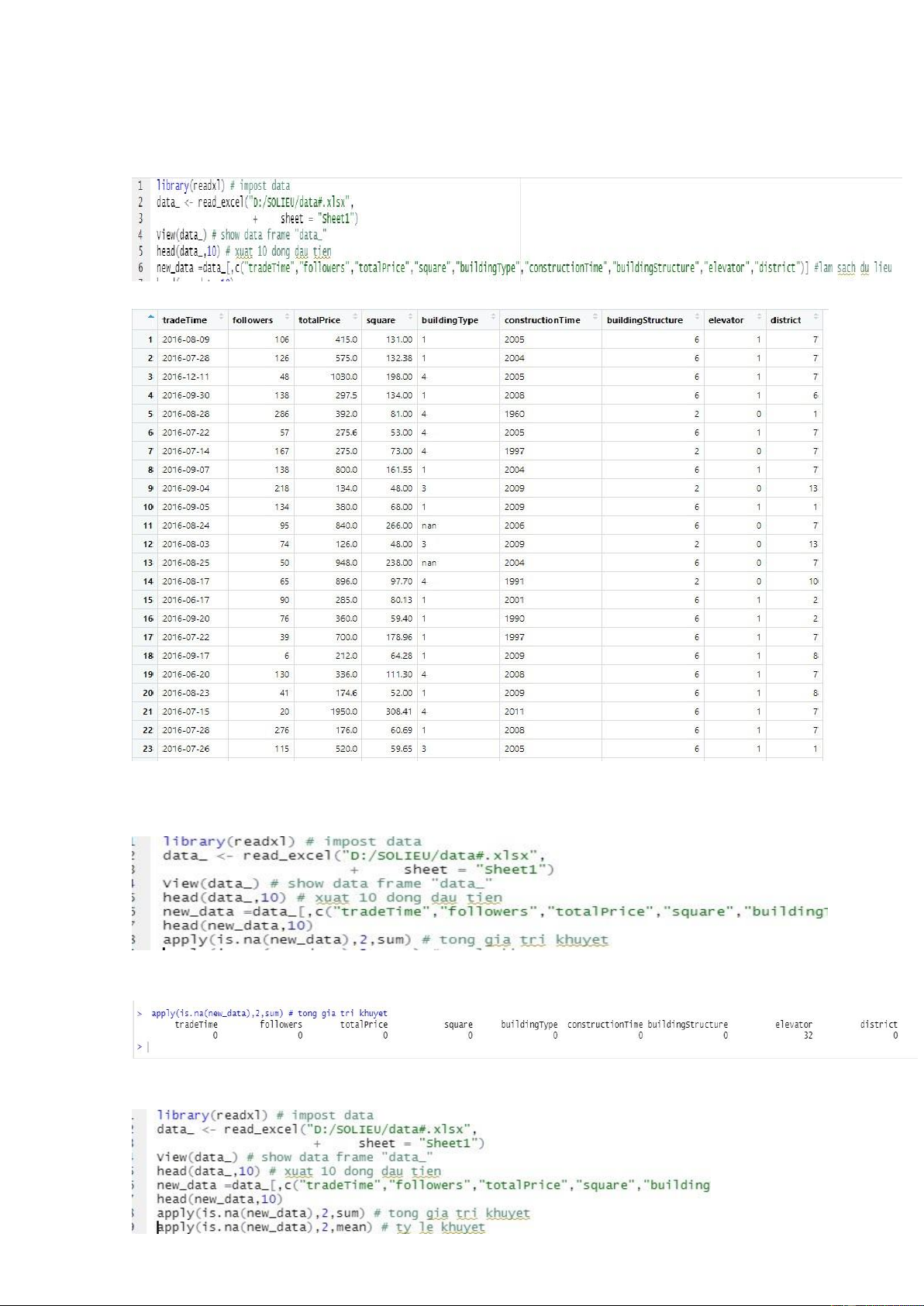
Dữ liệu cần đọc hiện đang là một tệp tin excel , có tên : data#.xlsx . Thực hiện đọc dữ liệu vào R
Xuất 10 giá trị đầu tiên , Kết quả :
2.2.2 Làm Sạch Dữ Liệu (data cleaning) lOMoARcPSD| 36991220
Yêu cầu : làm việc với những quan sát : “tradetime”, “fllower”, “total price”,
“Square” , “building type”, “ construction time”, “elevator”, “district” . nên chỉ chọn ra những qua sát trên . Kết quả : 2.2.3 Kiểm Tra Dữ liệu
Thống kê số lượng giá trị khuyết đối với từng biến : Kết quả :
Thống kê tỷ lệ giá trị khuyết đối với từng biến : lOMoARcPSD| 36991220 Kết quả
Nhận Xét : Dựa vào kết quả thu được ở bảng thống kê tỉ lệ đánh giá khuyết đối với
từng biến, ta nhận thấy có tương đối ít giá trị khuyết , chỉ xuất hiện ở biến “elevator”.
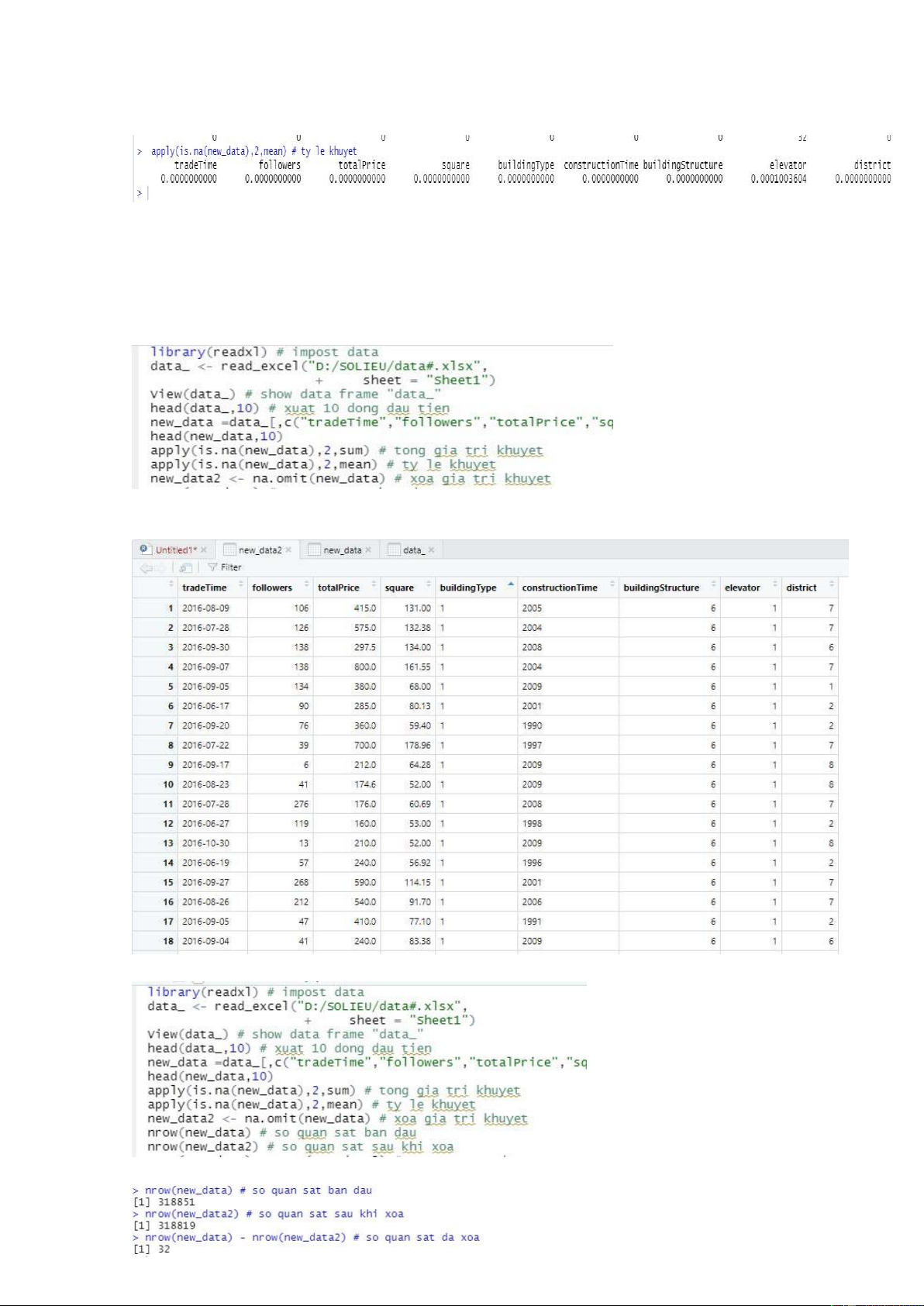
Nhưng vẫn phải lựa chọn phương pháp loại bỏ các quan sát đó . 2.2.4 Loại Bỏ dữ liệu
Tạo 1 frame data mới “new_data2” gồm những quan sát đã qua loại bỏ . Kết quả :
Để kiểm tra lại , thống kê số quan sát ban đầu và khi đã xóa : Kết quả : lOMoARcPSD| 36991220
2.2.5 Làm rõ dữ liệu (Data visualization)
Tính các giá trị thống kê mô tả (kích thước mẫu, trung bình, độ lệch chuẩn, min, max,
trung vị, các điểm tứ phân vị) của chênh lệch giữa tổng giá nhà (biến totalPrice) và cấu
trúc ngôi nhà (biến buildingStructure). Xuất kết quả dưới dạng bảng.
Hình: code R và kết quả khi tính các giá trị thống kê mô tả cho biến tổng giá ngôi nhà
(totalPrice) theo biến cấu trúc ngôi nhà (buildingStructure). Nhận xét
Biểu đồ Histogram (biểu đồ tần suất)
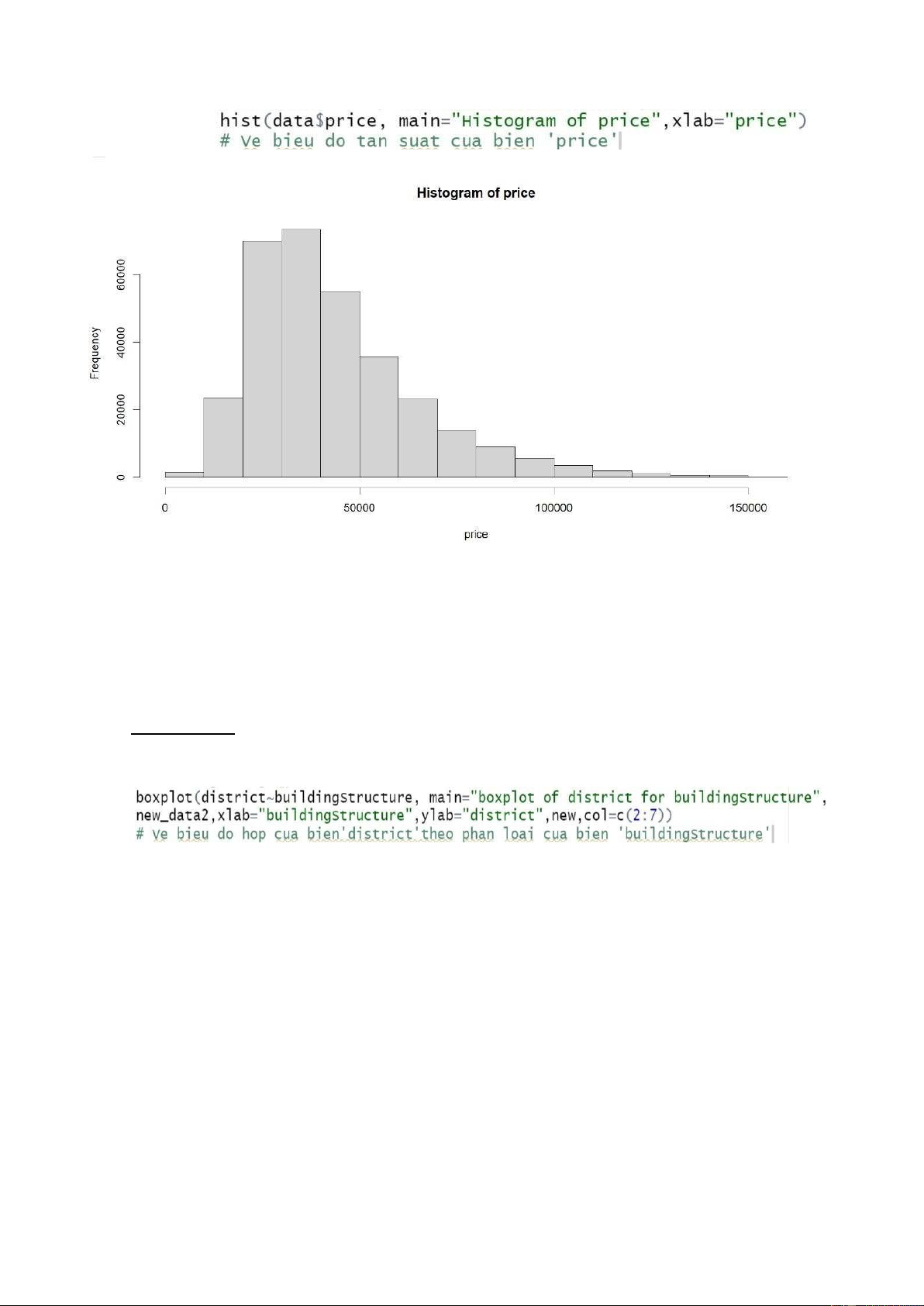
Code R: sử dụng hàm hist để vẽ biểu đồ thể hiện phân phối của biến giá nhà/m2 (price). lOMoARcPSD| 36991220 Kết quả: Nhận xét:
Dựa trên biểu đồ Histogram của biến price, ta nhận thấy phân phối của biến price đang
có xu hướng lệch trái, điều này có nghĩa là phần lớn các ngôi nhà ở Bắc Kinh có giá
nhà/m2 nằm trong khoảng từ 0 đến 75000 đô la và chỉ số ít có giá trị cao hơn. Biểu đồ hộp:
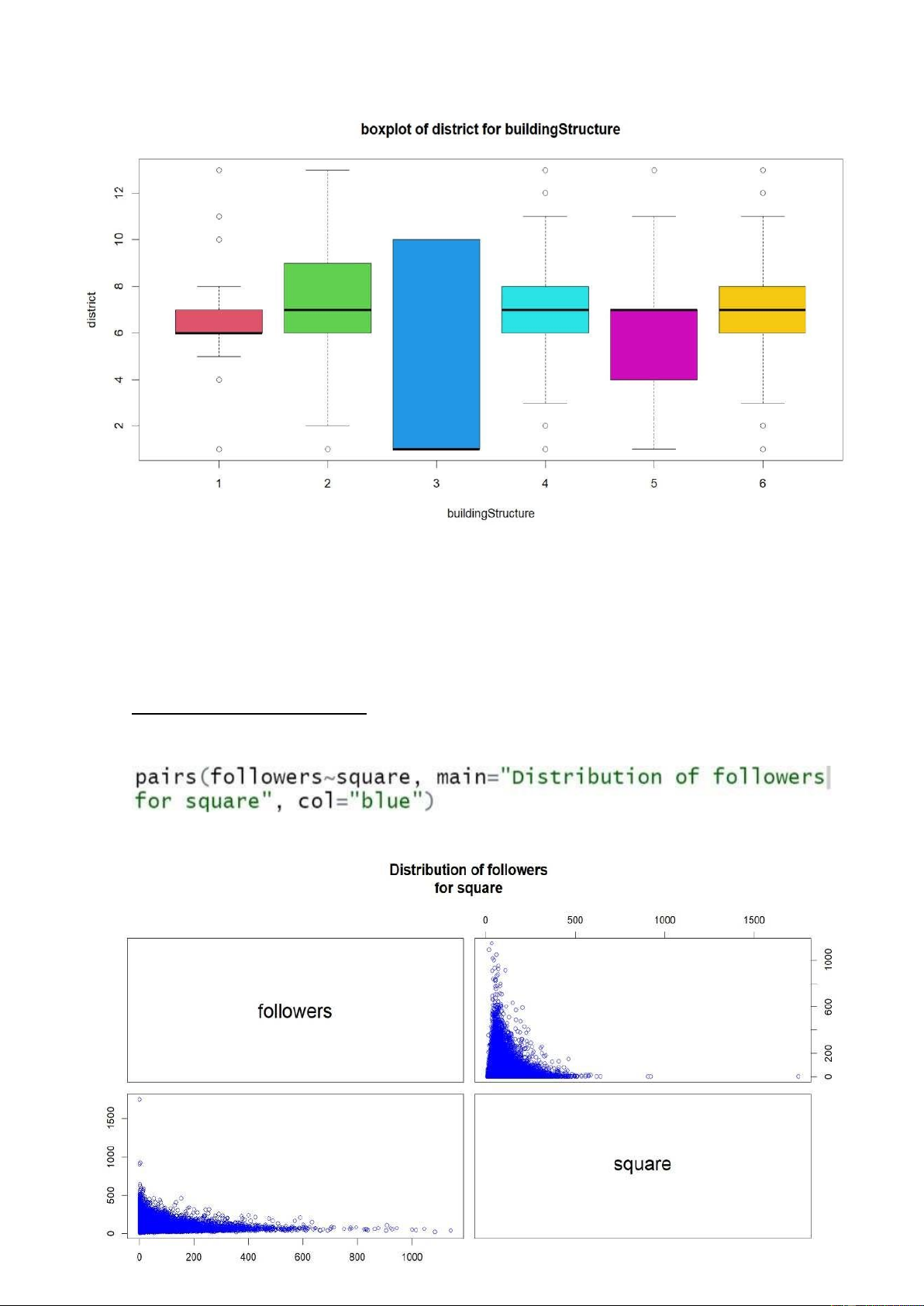
Code R: sử dụng hàm boxplot để vẽ biểu đồ hộp thể hiện phân phối của quận (district)
theo cấu trúc ngôi nhà (buildingStructure). Kết quả: lOMoARcPSD| 36991220 Nhận xét:
Dựa trên biểu đồ boxplot của biến buildingStructure theo biến district, ta có thể đọc
được 5 vị trí phân bố dữ liệu đó là: giá trị nhỏ nhất (min), tứ phân vị thứ nhất (Q1), trung
vị (median), tứ phân vị thứ 3 (Q3) và giá trị lớn nhất (max) của các cấu trúc ngôi nhà ở
các quận. Nhìn chung, ta thấy các ngôi nhà có cấu trúc được làm từ gạch và gỗ (3), được
ưa chuộng nhất so với các cấu trúc nhà còn lại.
Biểu đồ tương quan 2 biến:
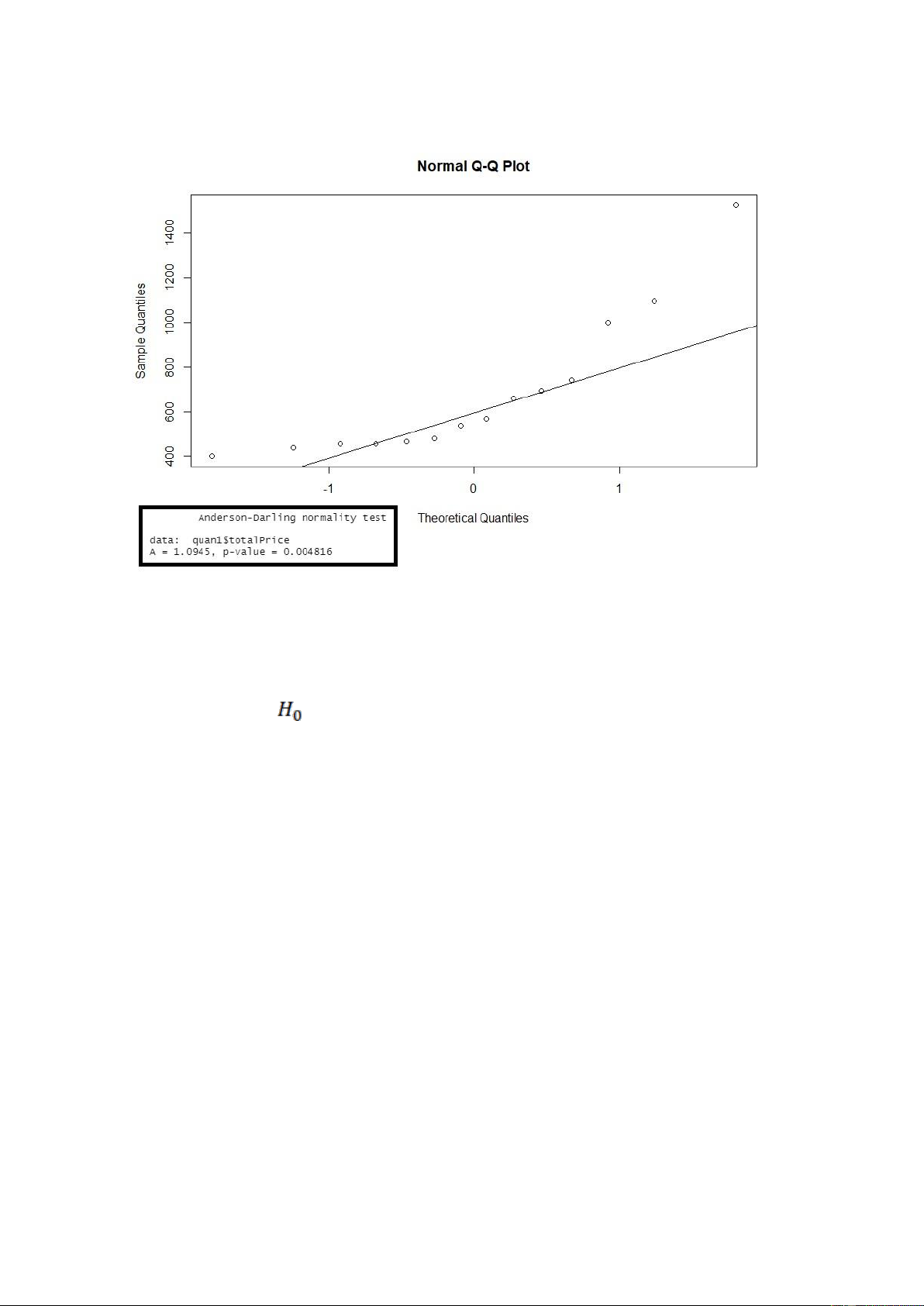
Code R: sử dụng hàm pairs để thể hiện mối tương quan giữa số lượng người theo dõi
giao dịch (followers) theo diện tích ngôi nhà (square). Kết quả: lOMoARcPSD| 36991220 Nhận xét:
Nhìn vào biểu đồ tương quan giữa 2 biến ở phía dưới (biến followers là biến chính), ta
thấy phần lớn lượng người theo dõi giao dịch tập trung ở mức từ 0-600 người với diện tích nhà là 0-500 m2.
Nhìn vào biểu đồ tương quan giữa 2 biến ở phía trên (biến square là biến chính), ta thấy
phần lớn diện tích nhà từ 0-500m2 thì lượng người theo dõi giao dịch sẽ tập trung ở mức 0-600 người.
=>Nhìn chung cả 2 đồ thị đều có xu hướng giảm dần (tỷ lệ nghịch), mức độ tập trung
của các điểm nằm trong khoảng nhất định tuy nhiên mối quan hệ tuyến tính giữa 2 biến
vẫn chưa thật sự rõ ràng, vì vậy ta cần phải xây dựng mô hình hồi quy để kiểm tra và
đưa ra đánh giá tốt hơn.
2.2.6 ANOVA một nhân tố: đánh giá sự khác biệt về giá nhà (totalPrice) giữa các quận
(district) đã xây dựng trong năm 2012
Trước khi bắt đầu tiến hành đánh giá, ta cần tìm và lọc các dữ liệu có chứ các kí hiệu không phù hợp
Hình. CodeR và kết quả khi tìm và lọc các dữ liệu có chứ các kí hiệu không phù hợp
Ta quan tâm đến việc kiểm định liệu rằng có sự khác biệt về giá nhà giữa các quận đã
xây dựng trong năm 2012 hay không?
Lọc giá cả của các nhà đã xây dựng trong năm 2012:
Hình. CodeR và kết quả khi lọc giá cả của các nhà đã xây dựng trong năm 2012 Giải
thích lý do sử dụng ANOVA một nhân tố:
Ta có nhiều quận đã xây dựng nhà trong năm 2012. Để thực hiện so sánh trung bình của
nhiều nhóm, phương pháp tối ưu nhất là dùng phân tích phương sai. Nếu chỉ so sánh 2
trung bình của 2 nhóm, ta có thể dùng t-test. Vì vậy, nếu dùng t-test cho bài toán này, ta
phải thực hiện kiểm định liên tục nhiều lần. Phương pháp phân tích phương sai cho t kết
luận sự bằng nhau hoặc khác nhau giữa các nhóm so sánh thông qua một phép kiểm định duy nhất.
Như vậy, ta sử dụng mô hình ANOVA một nhân tố: đánh giá sự khác biệt về giá nhà
(totalPrice) giữa các quận (district) đã xây dựng trong năm 2012. Trong đó:
Biến phụ thuộc: totalPrice
Biến độc lập: district lOMoARcPSD| 36991220
Hình. CodeR và kết quả khi khai báo các biến Đặt giả thuyết: + Giả thuyết
Giá nhà trung bình giữa các quận đã xây dựng
trong năm 2012 không có sự chênh lệch. + Giả thuyết
Có ít nhất 2 quận có sự chênh lệch về giá
nhà trung bình đã xây dựng trong năm 2012. Bảng ANOVA một nhân tố.
Các giả định cần kiểm tra trong ANOVA một nhân tố:
+ Giả định phân phối chuẩn: Giá nhà trung bình ở các quận đã xây dựng trong năm 2012
tuân theo phân phối chuẩn.
+ Tính đồng nhất của các phương sai: Phương sai giá nhà trung bình giữa các quận đã
xây dựng trong năm 2012 bằng nhau. Kiểm định giả định phân phối chuẩn: Giả thuyết
: Giá nhà giữa các quận đã xây dựng trong năm 2012 tuân theo phân phối chuẩn. Giả thuyết
: Giá nhà giữa các quận đã xây dựng trong năm 2012 không tuân theo phân phối chuẩn.
CodeR kiểm tra giả định phân phối chuẩn:
Hình. CodeR dùng để kiểm định giả định phân phối chuẩn cho biến ‘totalPrice’ của mỗi quận
Đây là CodeR chung để kiểm định giả định phân phối chuẩn cho biến ‘totalPrice’ của
quận X (với X là tên quận). Ở bài toán này ta có bao gồm 13 quận, vì vậy ta thực hiện
kiểm định gả định phân phối chuẩn lần lượt các quận và thu được kết quả: lOMoARcPSD| 36991220 Nhận xét:
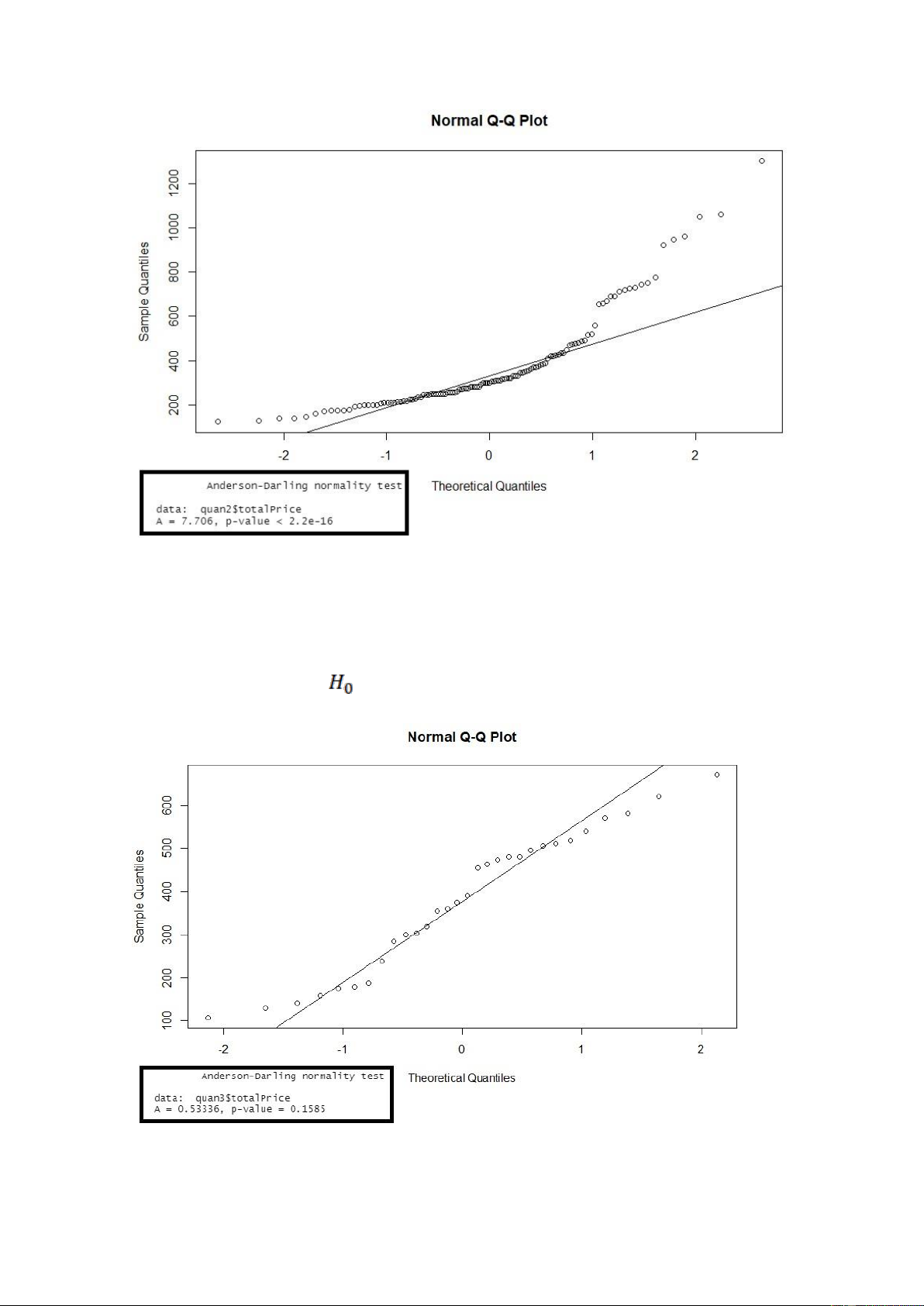
Hình. Kết quả khi kiểm định giả định phân phối chuẩn cho biến ‘totalPrice’ ở quận 1
Nhận xét: Xét biểu đồ QQ-Plot cho ta thấy có nhiều giá trị quan sát không nằm trên
đường thẳng kì vọng của phân phối chuẩn do đó biến totalPrice ở quận 1 không tuân theo phân phối chuẩn.
Ngoài ra, p-value ở các kiểm định ad.test bé hơn so với mức ý nghĩa α = 0.05, nên ta bác bỏ giả thuyết
, nên cũng đưa ra kết luận là biến totalPrice ở quận 1 không tuân theo phân phối chuẩn. lOMoARcPSD| 36991220
Kết quả khi kiểm định giả định phân phối chuẩn cho biến ‘totalPrice’ ở quận 2
Xét biểu đồ QQ-Plot cho ta thấy có nhiều giá trị quan sát không nằm trên
đường thẳng kì vọng của phân phối chuẩn do đó biến totalPrice ở quận 2 không tuân theo phân phối chuẩn.
Ngoài ra, p-value ở các kiểm định ad.test bé hơn rất nhiều so với mức ý nghĩa α = 0.05,
nên ta bác bỏ giả thuyết
, nên cũng đưa ra kết luận là biến totalPrice ở quận 2 không
tuân theo phân phối chuẩn.
Hình. Kết quả khi kiểm định giả định phân phối chuẩn cho biến ‘totalPrice’ ở quận 3 lOMoARcPSD| 36991220 Nhận xét:
Nhận xét: Xét biểu đồ QQ-Plot cho ta thấy có nhiều giá trị quan sát nằm trên đường
thẳng kì vọng của phân phối chuẩn do đó biến totalPrice ở quận 3 tuân theo phân phối chuẩn.
Ngoài ra, p-value ở các kiểm định ad.test lớn hơn so với mức ý nghĩa α = 0.05, nên ta bác bỏ giả thuyết
, nên cũng đưa ra kết luận là biến totalPrice ở quận 3 tuân theo phân phối chuẩn.
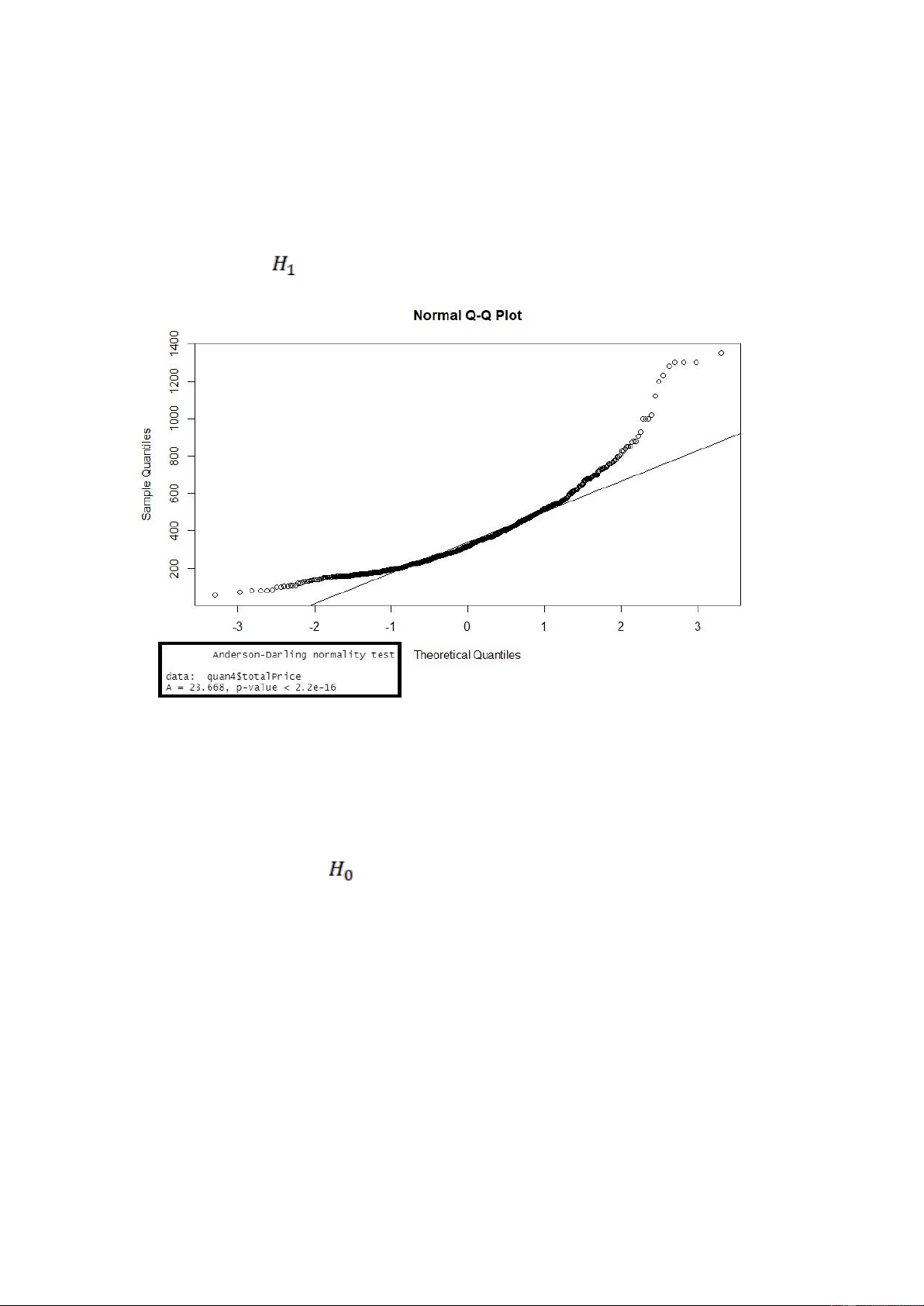
Hình. Kết quả khi kiểm định giả định phân phối chuẩn cho biến ‘totalPrice’ ở quận 4
Nhận xét: Xét biểu đồ QQ-Plot cho ta thấy có nhiều giá trị quan sát không nằm trên
đường thẳng kì vọng của phân phối chuẩn do đó biến totalPrice ở quận 4 không tuân theo phân phối chuẩn.
Ngoài ra, p-value ở các kiểm định ad.test bé hơn rất nhiều so với mức ý nghĩa α = 0.05,
nên ta bác bỏ giả thuyết
, nên cũng đưa ra kết luận là biến totalPrice ở quận 4 không
tuân theo phân phối chuẩn. lOMoARcPSD| 36991220
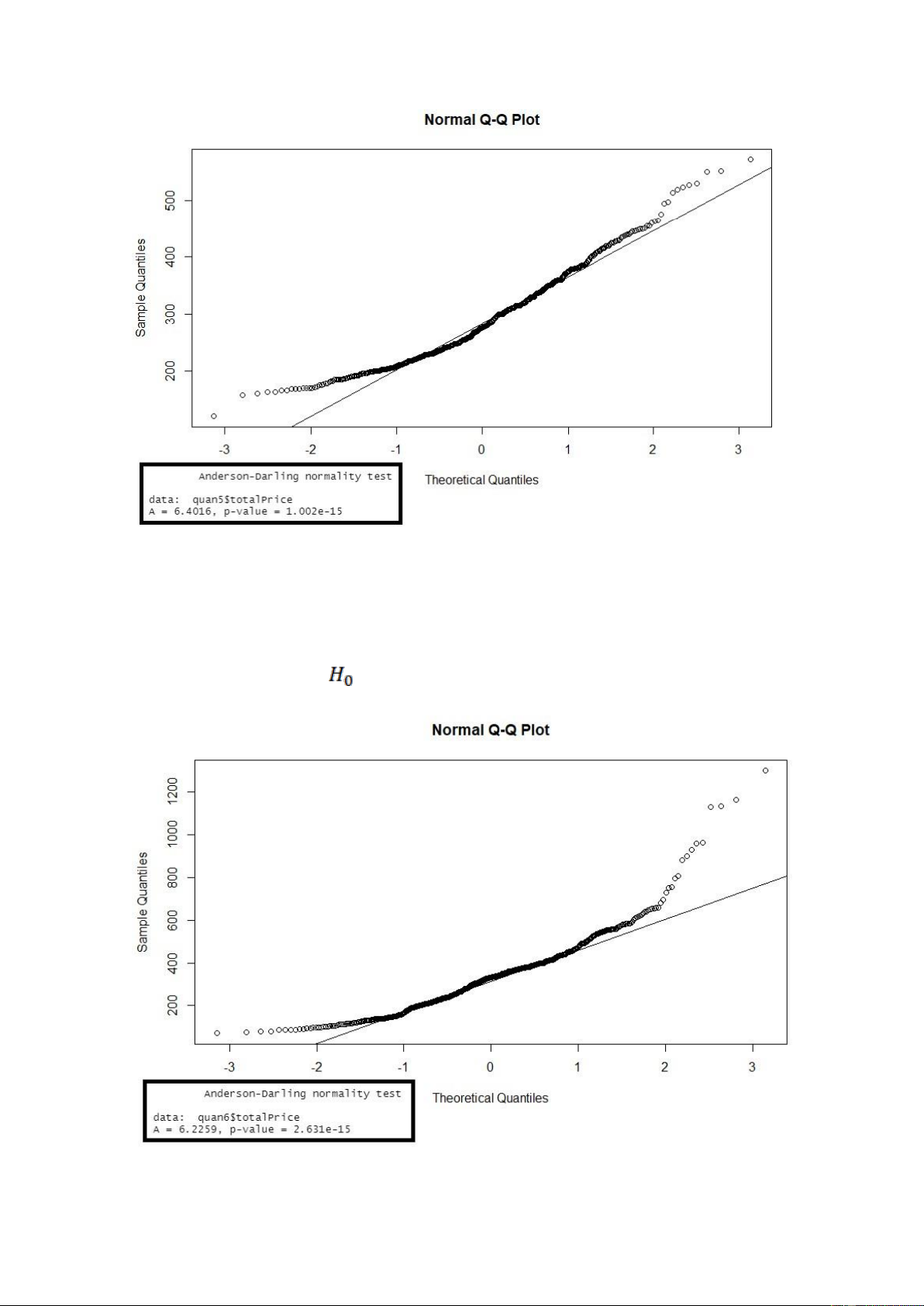
Kết quả khi kiểm định giả định phân phối chuẩn cho biến ‘totalPrice’ ở quận 5
Xét biểu đồ QQ-Plot cho ta thấy có nhiều giá trị quan sát không nằm trên
đường thẳng kì vọng của phân phối chuẩn do đó biến totalPrice ở quận 5 không tuân theo phân phối chuẩn.
Ngoài ra, p-value ở các kiểm định ad.test bé hơn rất nhiều so với mức ý nghĩa α = 0.05,
nên ta bác bỏ giả thuyết
, nên cũng đưa ra kết luận là biến totalPrice ở quận 5 không
tuân theo phân phối chuẩn. lOMoARcPSD| 36991220 Nhận xét:
Hình. Kết quả khi kiểm định giả định phân phối chuẩn cho biến ‘totalPrice’ ở quận 6
Nhận xét: Xét biểu đồ QQ-Plot cho ta thấy có nhiều giá trị quan sát không nằm trên
đường thẳng kì vọng của phân phối chuẩn do đó biến totalPrice ở quận 6 không tuân theo phân phối chuẩn.
Ngoài ra, p-value ở các kiểm định ad.test bé hơn rất nhiều so với mức ý nghĩa α = 0.05,
nên ta bác bỏ giả thuyết
, nên cũng đưa ra kết luận là biến totalPrice ở quận 6 không
tuân theo phân phối chuẩn.
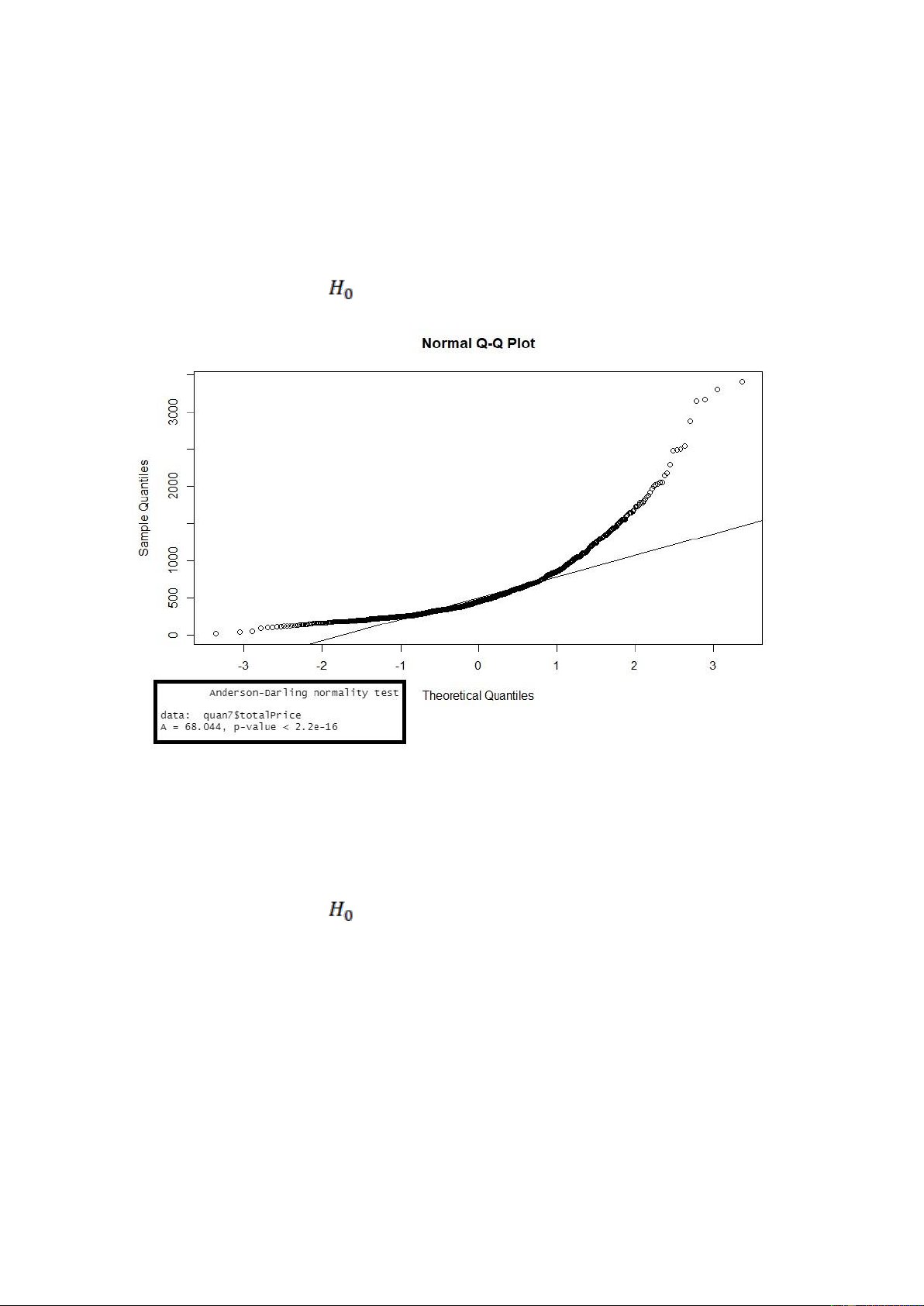
Hình. Kết quả khi kiểm định giả định phân phối chuẩn cho biến ‘totalPrice’ ở quận 7
Nhận xét: Xét biểu đồ QQ-Plot cho ta thấy có nhiều giá trị quan sát không nằm trên
đường thẳng kì vọng của phân phối chuẩn do đó biến totalPrice ở quận 7 không tuân theo phân phối chuẩn.
Ngoài ra, p-value ở các kiểm định ad.test bé hơn rất nhiều so với mức ý nghĩa α = 0.05,
nên ta bác bỏ giả thuyết
, nên cũng đưa ra kết luận là biến totalPrice ở quận 7 không
tuân theo phân phối chuẩn. lOMoARcPSD| 36991220
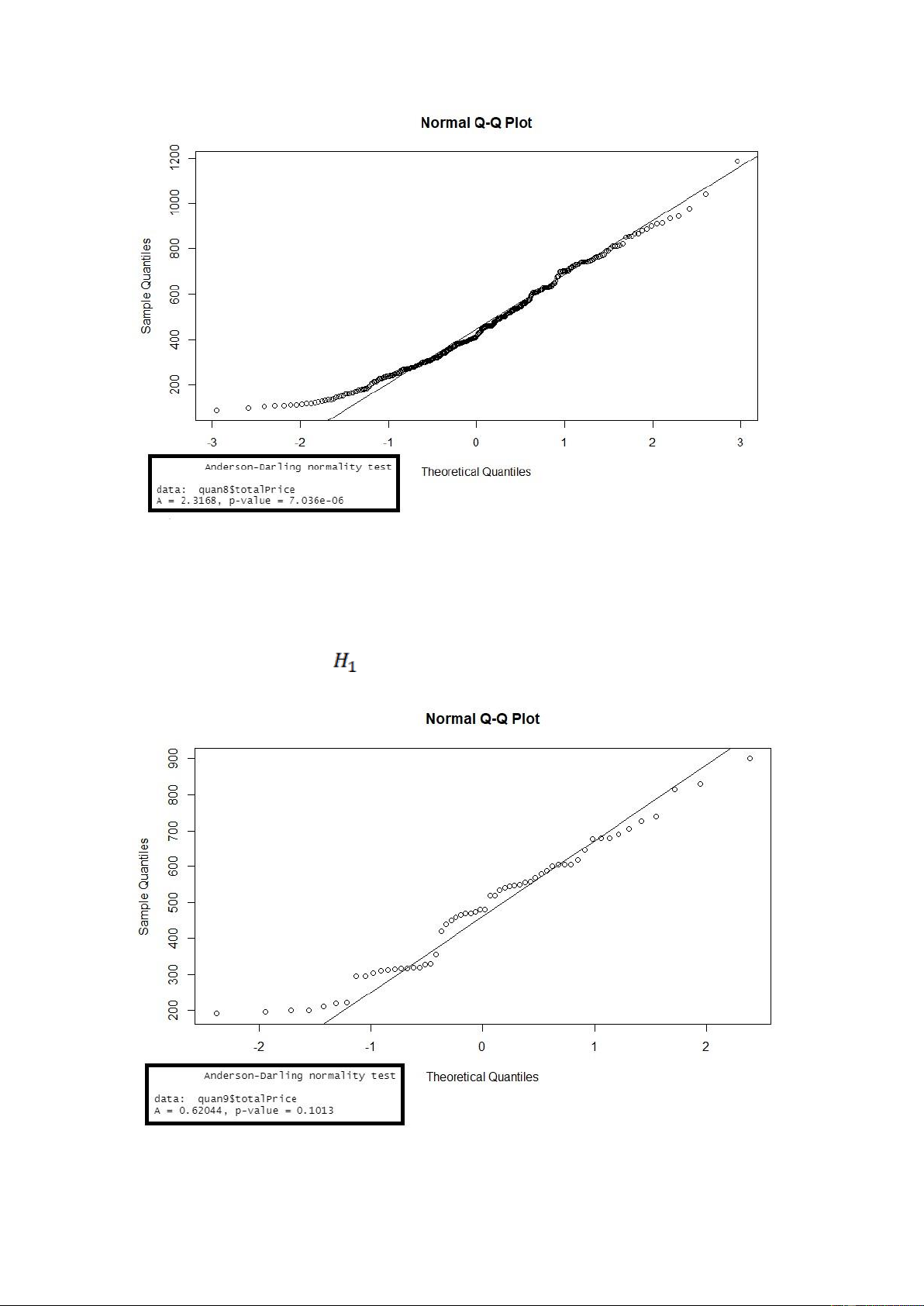
Kết quả khi kiểm định giả định phân phối chuẩn cho biến ‘totalPrice’ ở quận 8
Xét biểu đồ QQ-Plot cho ta thấy có nhiều giá trị quan sát nằm trên đường
thẳng kì vọng của phân phối chuẩn do đó biến totalPrice ở quận 8 tuân theo phân phối chuẩn.
Ngoài ra, p-value ở các kiểm định ad.test lớn hơn rất nhiều so với mức ý nghĩa α = 0.05,
nên ta bác bỏ giả thuyết
, nên cũng đưa ra kết luận là biến totalPrice ở quận 8 tuân theo phân phối chuẩn. lOMoARcPSD| 36991220 Nhận xét:
Hình. Kết quả khi kiểm định giả định phân phối chuẩn cho biến ‘totalPrice’ ở quận 9
Nhận xét: Xét biểu đồ QQ-Plot cho ta thấy có nhiều giá trị quan sát nằm trên đường
thẳng kì vọng của phân phối chuẩn do đó biến totalPrice ở quận 9 tuân theo phân phối chuẩn.
Ngoài ra, p-value ở các kiểm định ad.test lớn hơn so với mức ý nghĩa α = 0.05, nên ta bác bỏ giả thuyết
, nên cũng đưa ra kết luận là biến totalPrice ở quận 9 tuân theo phân phối chuẩn. lOMoARcPSD| 36991220
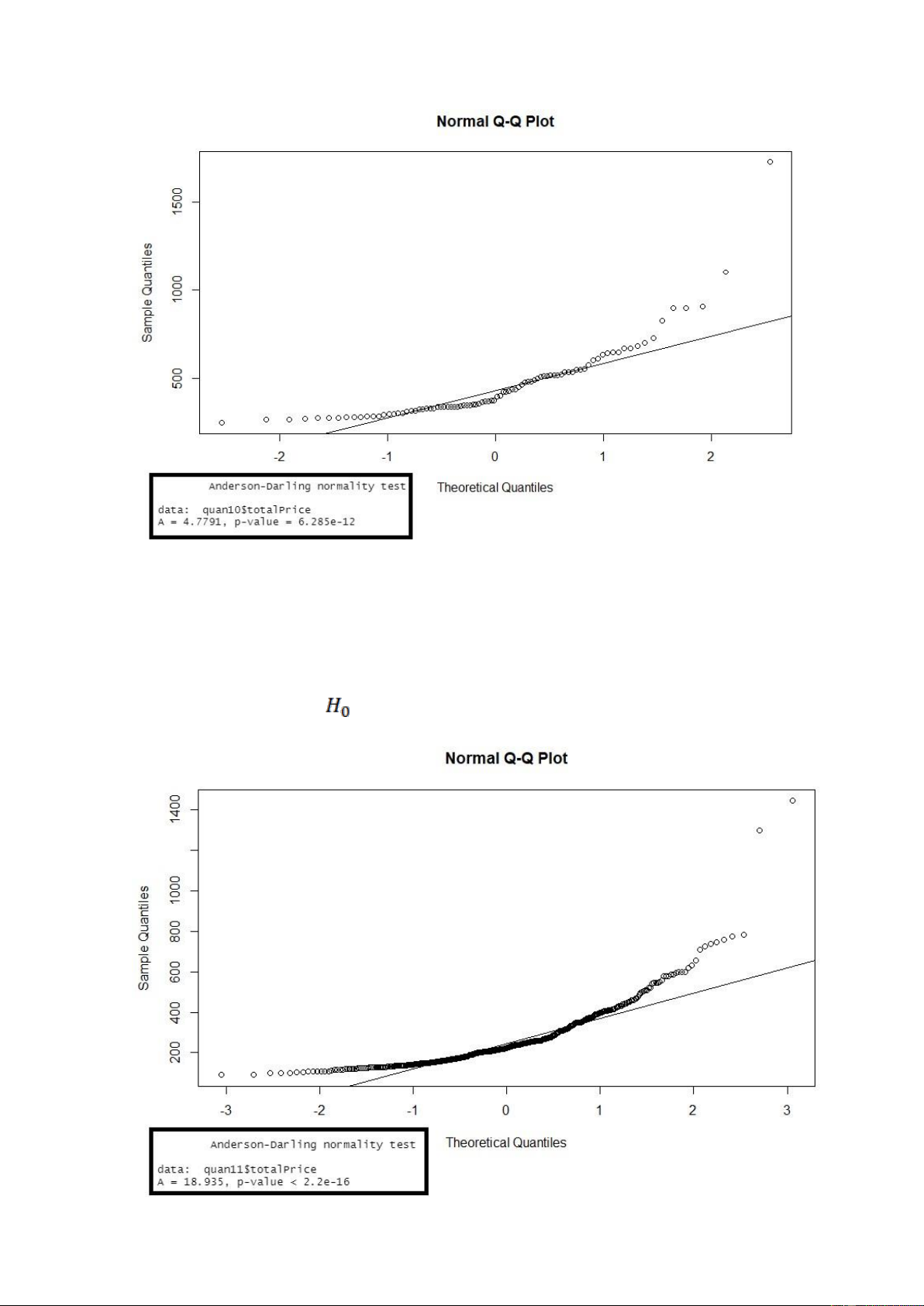
Hình. Kết quả khi kiểm định giả định phân phối chuẩn cho biến ‘totalPrice’ ở quận 10
Nhận xét: Xét biểu đồ QQ-Plot cho ta thấy có nhiều giá trị quan sát không nằm trên
đường thẳng kì vọng của phân phối chuẩn do đó biến totalPrice ở quận 10 không tuân theo phân phối chuẩn.
Ngoài ra, p-value ở các kiểm định ad.test bé hơn rất nhiều so với mức ý nghĩa α = 0.05,
nên ta bác bỏ giả thuyết
, nên cũng đưa ra kết luận là biến totalPrice ở quận 10 không
tuân theo phân phối chuẩn. lOMoARcPSD| 36991220
Hình. Kết quả khi kiểm định giả định phân phối chuẩn cho biến ‘totalPrice’ ở quận 11
Nhận xét: Xét biểu đồ QQ-Plot cho ta thấy có nhiều giá trị quan sát không nằm trên
đường thẳng kì vọng của phân phối chuẩn do đó biến totalPrice ở quận 11 không tuân theo phân phối chuẩn.
Ngoài ra, p-value ở các kiểm định ad.test bé hơn rất nhiều so với mức ý nghĩa α = 0.05,
nên ta bác bỏ giả thuyết
, nên cũng đưa ra kết luận là biến totalPrice ở quận 11 không
tuân theo phân phối chuẩn.
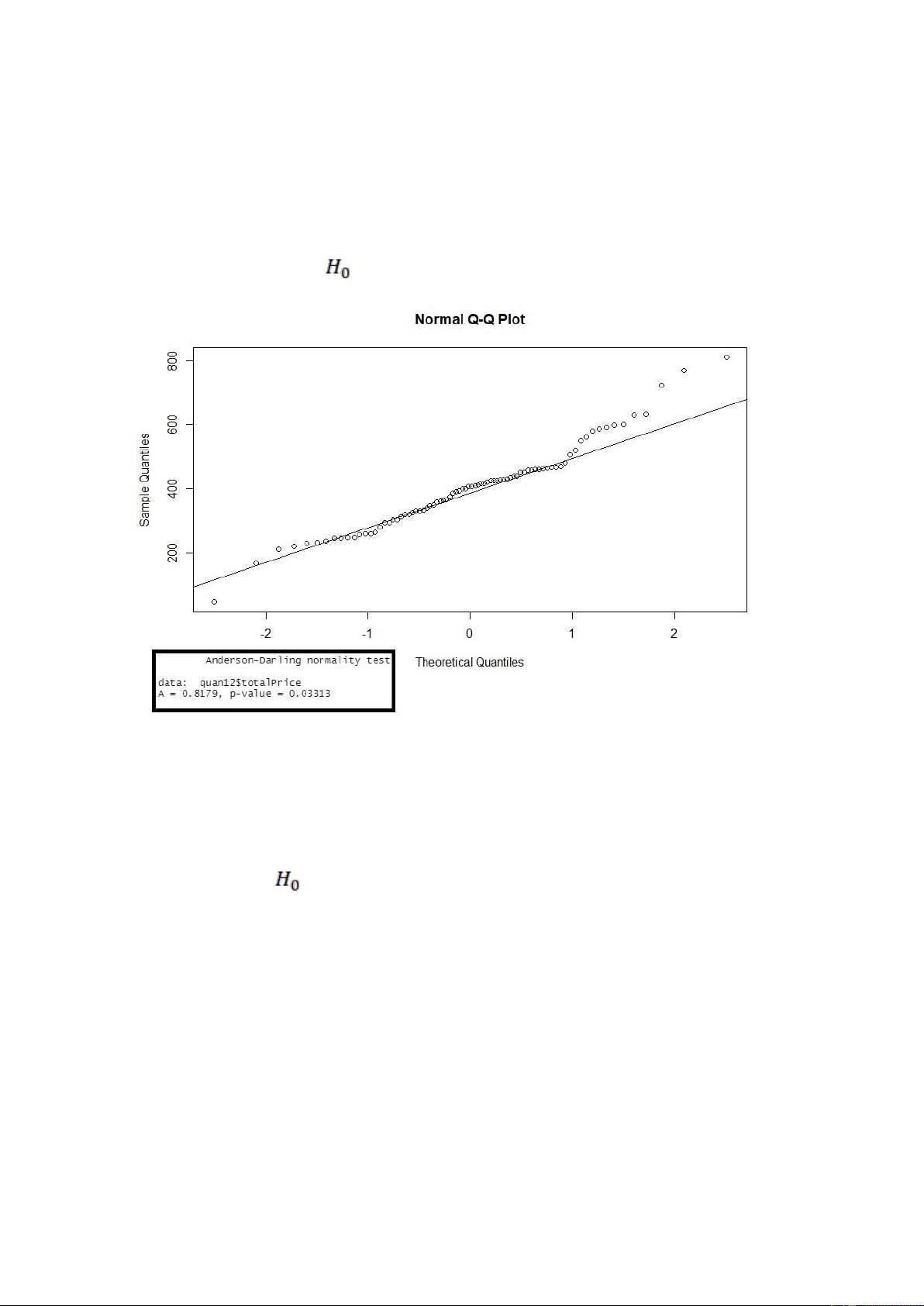
Hình. Kết quả khi kiểm định giả định phân phối chuẩn cho biến ‘totalPrice’ ở quận 12
Nhận xét: Xét biểu đồ QQ-Plot cho ta thấy có nhiều giá trị quan sát không nằm trên
đường thẳng kì vọng của phân phối chuẩn do đó biến totalPrice ở quận 12 không tuân theo phân phối chuẩn.
Ngoài ra, p-value ở các kiểm định ad.test bé hơn so với mức ý nghĩa α = 0.05, nên ta bác bỏ giả thuyết
, nên cũng đưa ra kết luận là biến totalPrice ở quận 12 không tuân theo phân phối chuẩn. lOMoARcPSD| 36991220
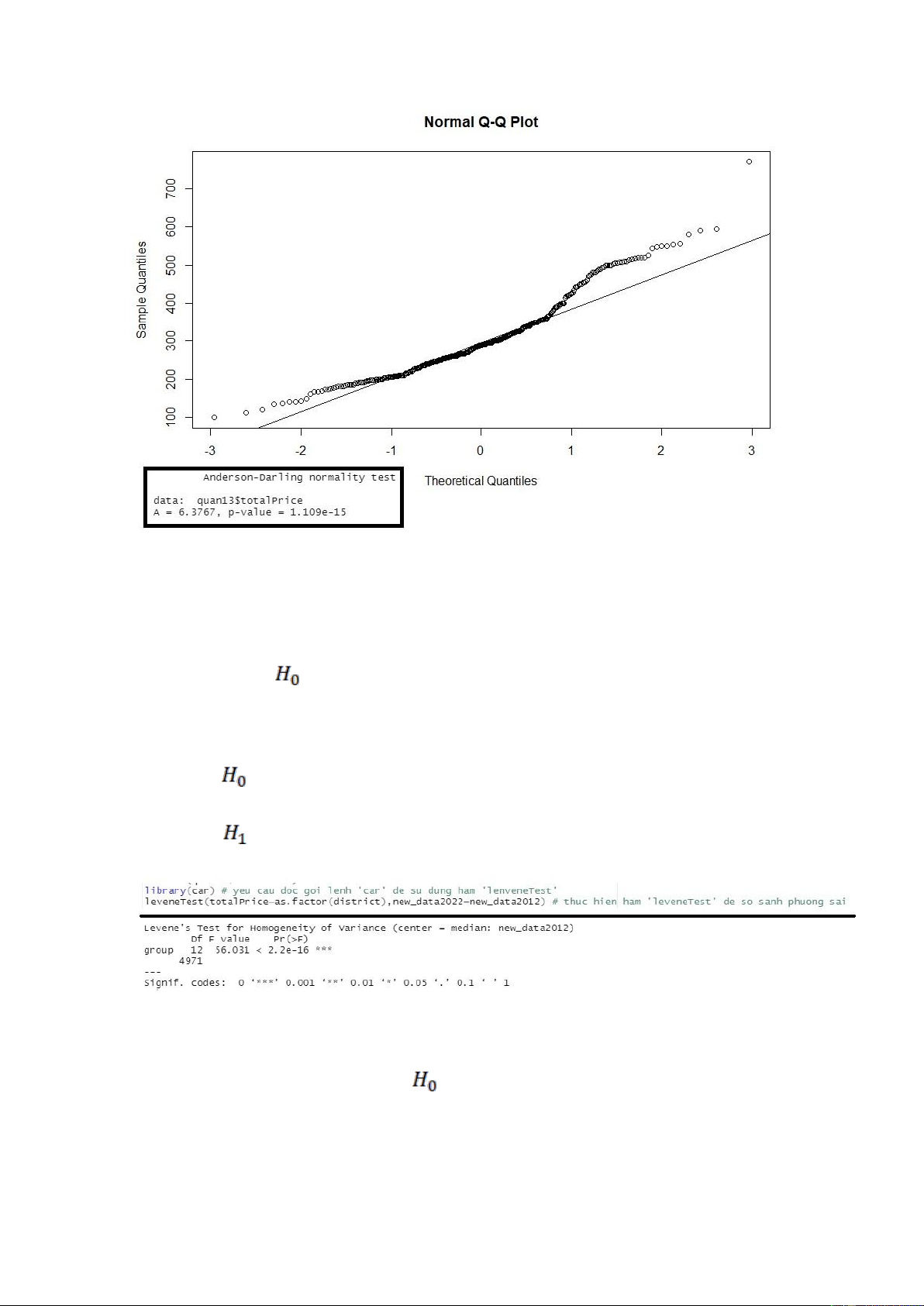
Hình. Kết quả khi kiểm định giả định phân phối chuẩn cho biến ‘totalPrice’ ở quận 13
Nhận xét: Xét biểu đồ QQ-Plot cho ta thấy có nhiều giá trị quan sát không nằm trên
đường thẳng kì vọng của phân phối chuẩn do đó biến totalPrice ở quận 13 không tuân theo phân phối chuẩn.
Ngoài ra, p-value ở các kiểm định ad.test bé hơn so với mức ý nghĩa α = 0.05, nên ta bác bỏ giả thuyết
, nên cũng đưa ra kết luận là biến totalPrice ở quận 13 không tuân theo phân phối chuẩn.
Kiểm định giả định về tính đồng nhất của các phương sai: Giả thuyết
: Phương sai giá nhà trung bình giữa các quận đã xây dựng trong năm 2012 bằng nhau. Đối thuyết
: Phương sai giá nhà trung bình giữa các quận đã xây dựng trong năm 2012 khác nhau.
Hình. CodeR và kết quả khi kiểm định giả định về tính đồng nhất của phương sai
Nhận xét: Dựa trên p-value ở kiểm định leveneTest bé hơn rất nhiều so với mức ý nghĩa
α = 0.05, nên ta bác bỏ giả thuyết
, vậy nên ta có thể đưa ra kết luận là có ít nhất 2
quận có phương sai giá nhà trung bình khác nhau. Thực hiện phân tích phương sai một nhân tố: lOMoARcPSD| 36991220
Hình. CodeR và kết quả khi thực hiện ANOVA một nhân tố
Nhận xét: Dựa trên kết quả ANOVA cho thấy:
+ SSB= 61763231, bậc tự do k-1=12 (k=13)
+ SSW= 314587596, bậc tự do N-k=4984-13=4971 (N là tổng số phần tư khảo sát ở tất cả các nhóm) + MSB=SSB/(k-1)= 5146936 + MSW=SSW/(N-k)= 63285
+ Giá trị thống kê kiểm định: f=MSB/MSW= 81.33
+ Mức ý nghĩa quan sát: p-value<2e-16
Dựa vào p-value<2e-16 rất bé so với mức ý nghĩa α = 0.05 nên ta bác bỏ được Giả thuyết .
Vậy có sự khác biệt về giá nhà trung bình giữa các quận đã xây dựng trong năm 2012.
Thực hiện so sánh bội: Nhận xét:
+ Đối với quận 2-1: Giả thuyết
: Giá nhà trung bình giữa quận 2 và quận 1 đã xây dựng trong năm 2012 bằng nhau. Đối thuyết
: Giá nhà trung bình giữa quận 2 và quận 1 đã xây dựng trong năm 2012 khác nhau. lOMoARcPSD| 36991220
Dựa vào p-value, ta thấy p-value= 0.0011583 < mức ý nghĩa 5% nên ta bác bỏ giả thuyết
, chấp nhận đối thuyết
. Vậy giá nhà trung bình giữa quận 2 và quận 1 đã xây dựng
trong năm 2012 khác nhau. Mặt khác, diff=-306.437072<0 nên ta có thể kết luận giá
nhà trung bình giữa quận 2 và quận 1 đã xây dựng trong năm 2012 khác nhau. Ngoài ra,
ta có thể đưa ra kết luận dựa vào khoảng tin cậy (-541.8117063; 71.0624377) không
chứa giá trị 0 nên giá nhà trung bình giữa quận 2 và quận 1 đã xây dựng trong năm 2012
khác nhau, và khoảng tin cậy nhận giá trị âm nên giá nhà trung bình đã xây dựng trong
năm 2012 của quận 2 thấp hơn quận 1.
Tương tự, ta sẽ thực hiện so sánh đối với từng cặp quận. Ta sẽ đưa ra kết luận rằng giá
nhà ở quận 10 cao nhất và giá nhà ở quận 13 thấp nhất.
2.2.7. Xây dựng mô hình hồi quy tuyến tính: Sử dụng mô hình hôi quy tuyến tính phù
hợp để đánh giá các nhân tố tác động đến tổng chi phí bán nhà thực tế.
Để phân tích các yếu tố ảnh hưởng đến totalPrice ta đặt biến:
• Biến phụ thuộc: totalPrice
• Biến độc lập: followers, Square, buildingType, constructionTime,
buildingStructure, elevator, district
Thực hiện vẽ đồ thị phân tán thể hiện phân tán của totalPrice theo các biến còn lại
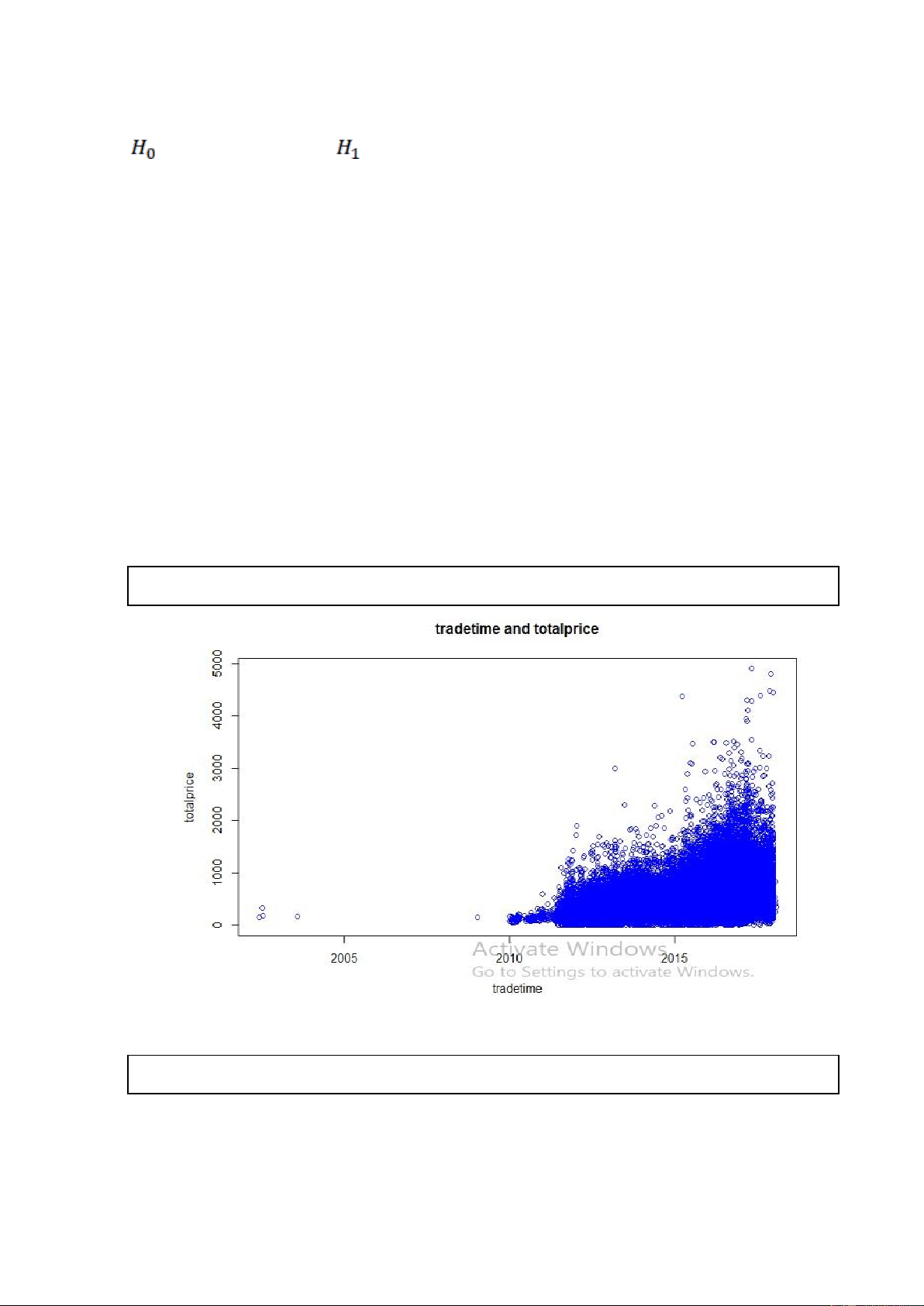
plot(new_data6$tradeTime,new_data6$totalPrice, xlab = "tradeTime",ylab = "totalprice", main = "tradetime and totalprice", col = "blue")
Hình 1. Code R và kết quả khi vẽ biểu đồ phân tán của totalPrice theo biến tradeTime
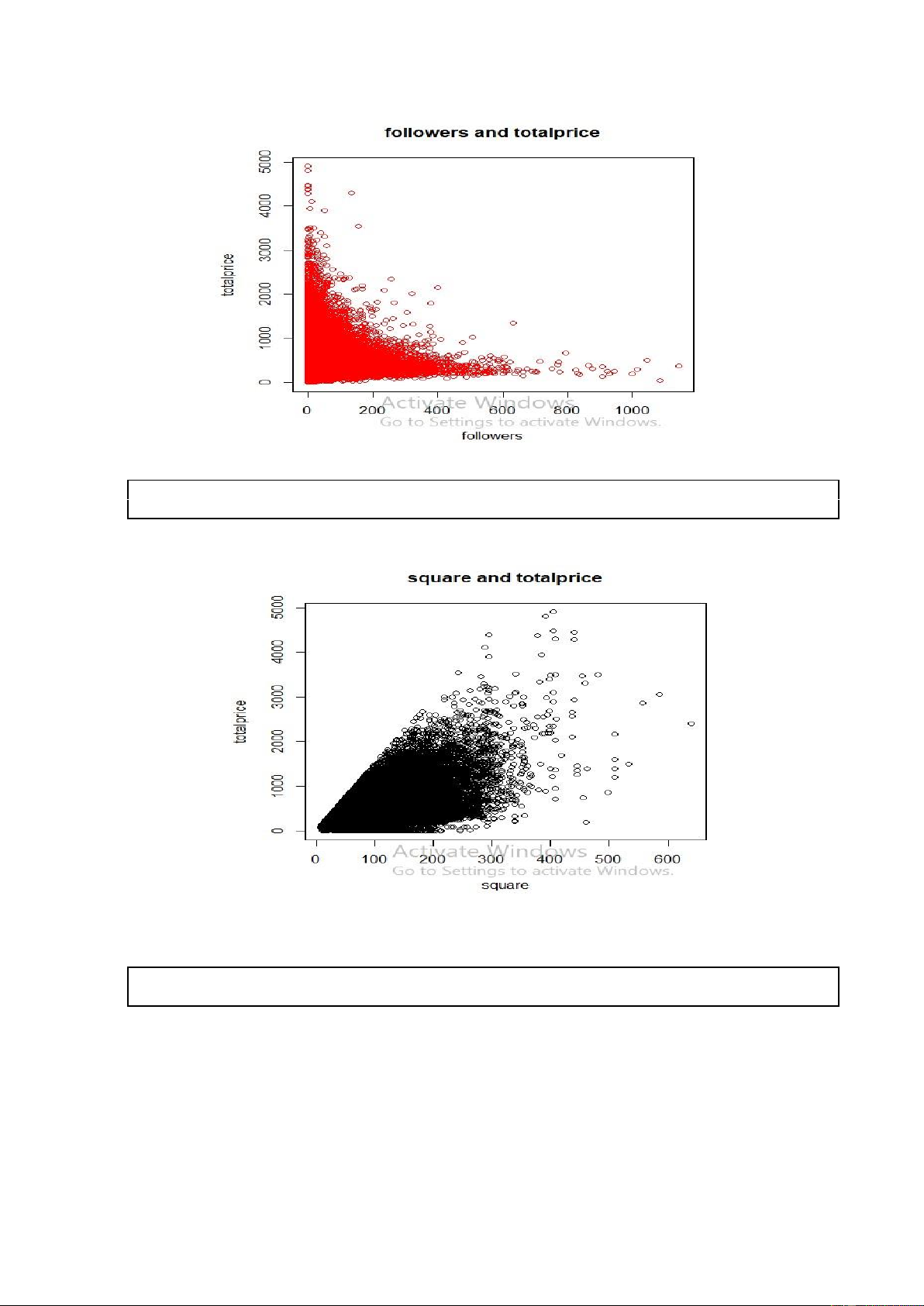
plot(new_data6$followers,new_data6$totalPrice, xlab = "followers",ylab = "totalprice", main = "followers and totalprice", col = "red") lOMoARcPSD| 36991220
Hình 2. Code R và kết quả khi vẽ biểu đồ phân tán của totalPrice theo biến followers
plot(new_data6$square,new_data6$totalPrice, xlab = "square",ylab = "totalprice", main = "square and totalprice", col = "black")
Hình 3. Code R và kết quả khi vẽ biểu đồ phân tán của totalPrice theo biến square
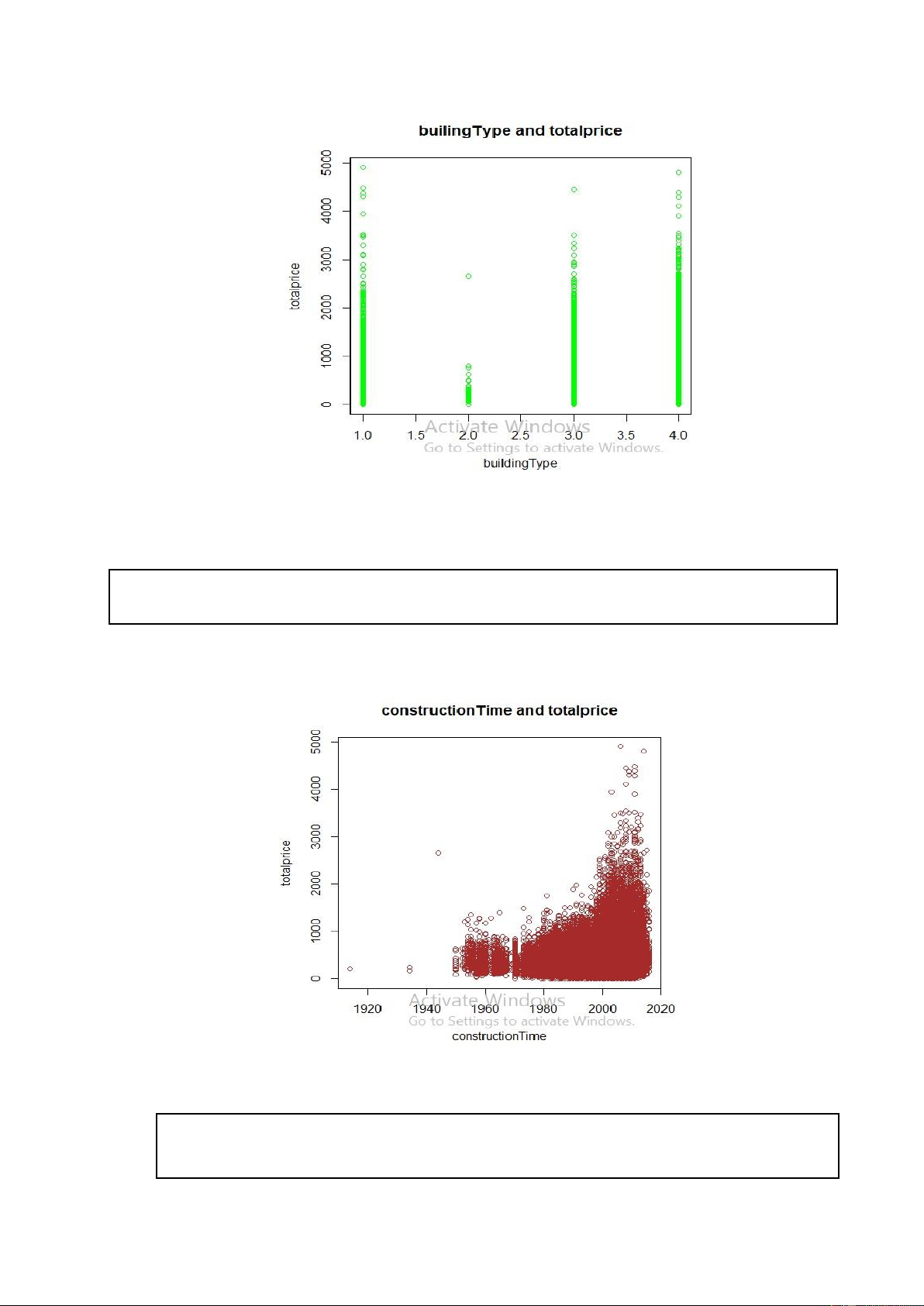
plot(new_data6$buildingType,new_data6$totalPrice, xlab = "buildingType",ylab = "totalprice", main =
"builingType and totalprice", col = "green") lOMoARcPSD| 36991220
Hình . Code R và kết quả khi vẽ biểu đồ phân tán của totalPrice theo biến buildingType
plot(new_data6$constructionTime,new_data6$totalPrice, xlab = "constructionTime",ylab = "totalprice", main =
"constructionTime and totalprice", col = "brown")
Hình . Code R và kết quả khi vẽ biểu đồ phân tán của totalPrice theo biến constructionTime
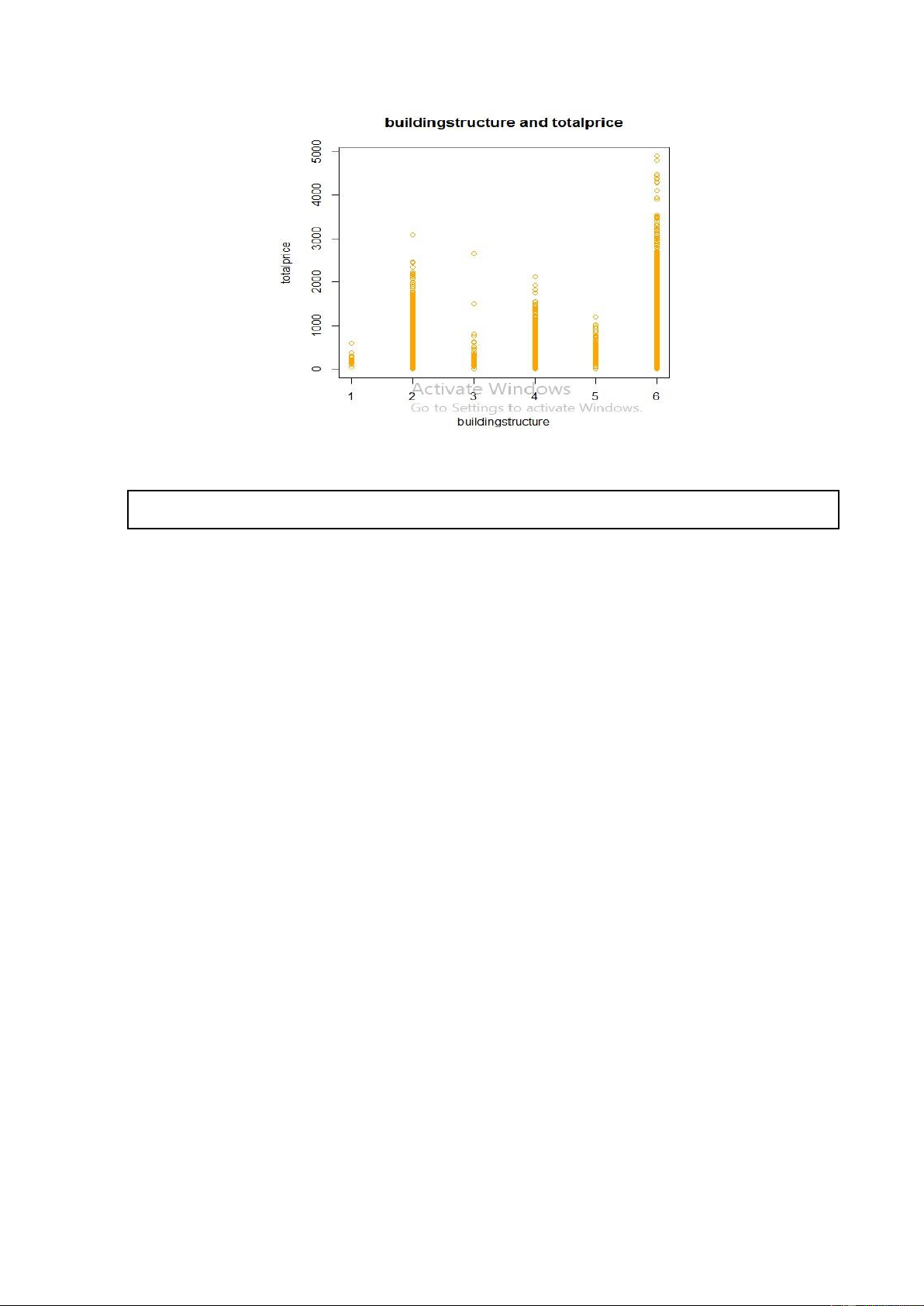
plot(new_data6$buildingStructure,new_data6$totalPrice, xlab = "buildingstructure",ylab = "totalprice",
main = "buildingstructure and totalprice", col = "orange") lOMoARcPSD| 36991220
Hình 6. Code R và kết quả khi vẽ biểu đồ phân tán của totalPrice theo biến buildingstructure
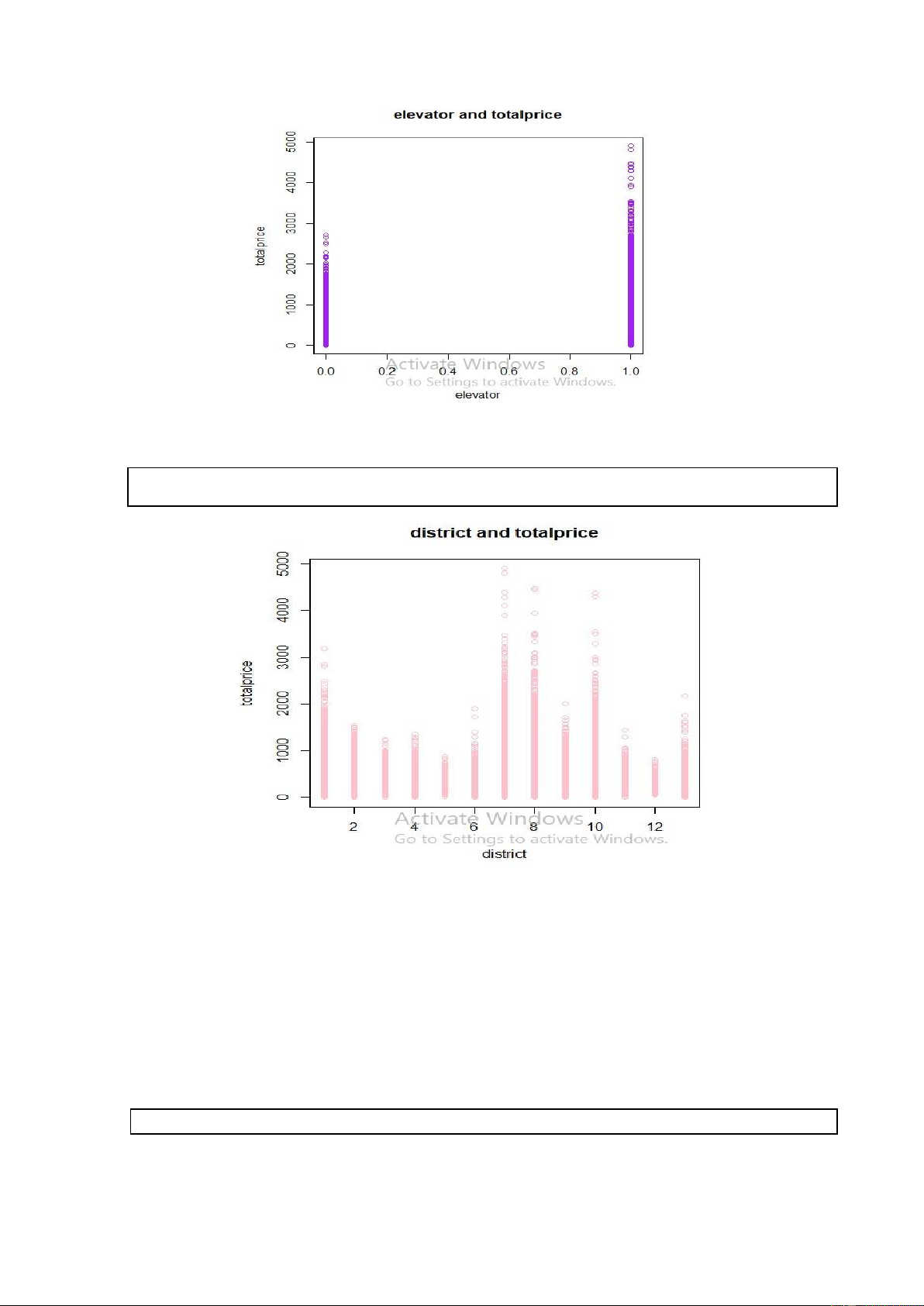
plot(new_data6$elevator,new_data6$totalPrice, xlab = "elevator",ylab = "totalprice", main = "elevator and totalprice", col = "purple") lOMoARcPSD| 36991220
Hình 7. Code R và kết quả khi vẽ biểu đồ phân tán của totalPrice theo biến elevator
plot(new_data6$district,new_data6$totalPrice, xlab = "district",ylab = "totalprice", main = "district and totalprice", col = "pink")
Hình 8. Code R và kết quả khi vẽ biểu đồ phân tán của totalPrice theo biến buildingstructure
Nhận xét: Thông qua các biểu đồ phân tán của biến totalPrice theo các biến còn lại ta
vẫn chưa nhìn thấy rõ mối quân hệ tuyến tính giữa chúng. Vậy biến totalPrice thật sự
có mối quan hệ tuyến tính với các biến còn lại hay không? Để trả lời cho câu hỏi này
chúng ta cần xây dựng mô hình hồi quy và thực hiện các kiểm định. Ta xây dựng mô
hình hồi quy tuyến tính 1: 31 model_1 =
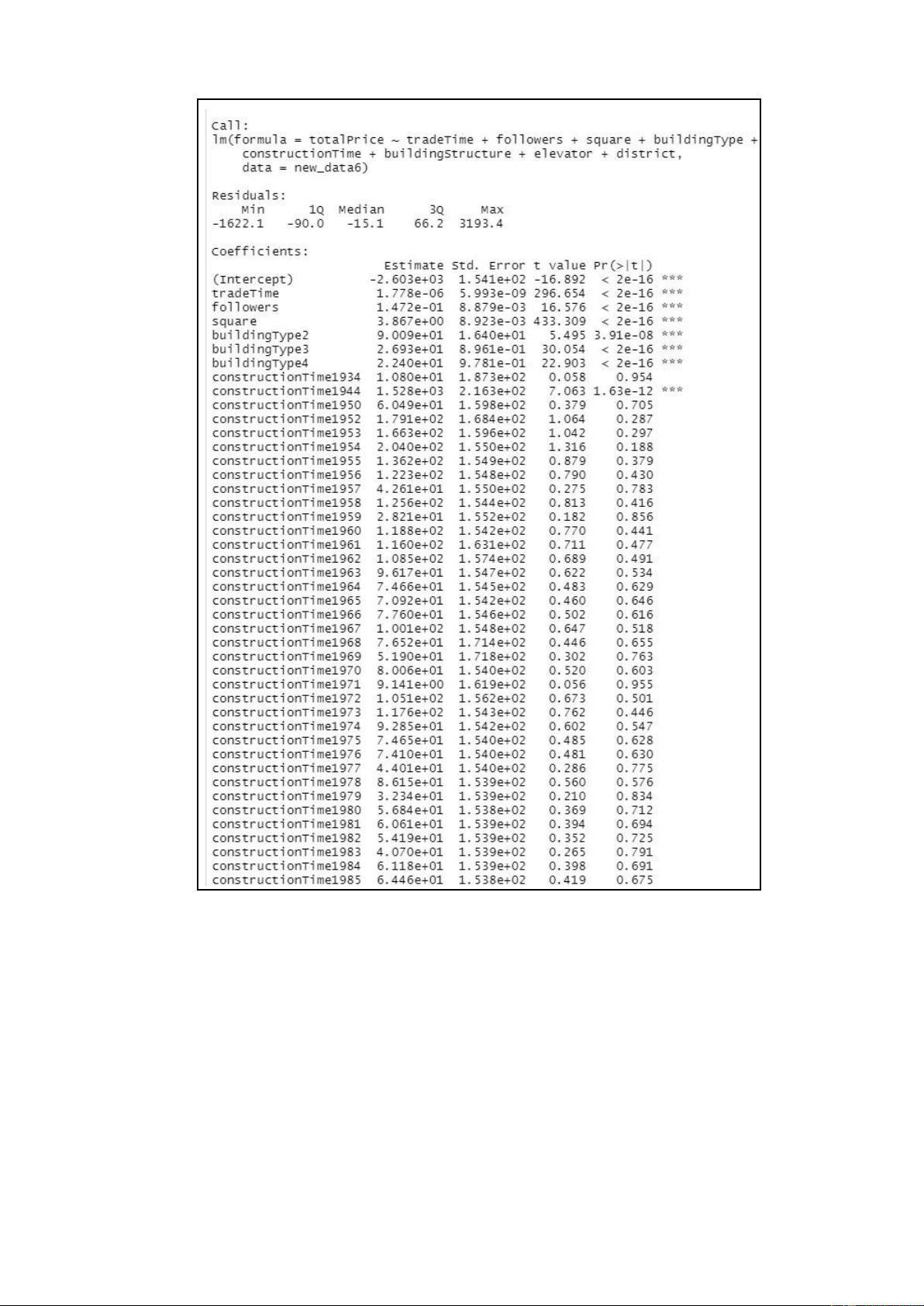
lm(totalPrice~tradeTime+followers+square+buildingType+constructionTime+buildingStructure+elevator+district, data = new_data6) summary(model_1) lOMoARcPSD| 36991220 lOMoARcPSD| 36991220
Code R và kết quả khi xây dựng mô hình hồi quy tuyến tính model_1 Nhận xét: Từ kết quả phân tích, ta thu được: 0 3 4 = - 2.603e+03; 1= 1.778e-06; 2= 1.472e- 01; = 3.867e+00; = 9.009e+01;
5= 2.693e+01; 6= 2.240e+01; 7= 1.528e+03; 8= 1.303e+01; 9= 5.340e+01); 10= 2.777e+00
Mô hình được biểu diễn như sau:
= -2.603e+03 + (1.778e-06) x tradeTime + (1.472e-01) x followers +
(3.867e+00) x square + (9.009e+01) x buildingType2 + (2.693e+01) x buildingType3
+ (2.240e+01) x buildingType4 + (1.528e+03) x constructionTime1944 + (1.303e+01)
x buildingStructure + (5.340e+01) x elevator + (2.777e+00) x district
Kiểm định các hệ số hồi quy:
Giả thuyết 𝐻0: Hệ số hồi quy không có ý nghĩa thống kê (𝐻𝐻 = 0)
Đối thuyết 𝐻1: Hệ số hồi quy có ý nghĩa thống kê (𝐻𝐻 ≠ 0)
+ Vì Pr (> |𝐻|) ứng với các biến constructionTime1934, constructionTime1950,
constructionTime1951, constructionTime1952…, constructionTime 2015,
constructionTime2016 lớn hơn mức ý nghĩa 𝐻 = 0.05 nhưng Pr (> |𝐻|) ứng với lOMoARcPSD| 36991220
constructionTime1944 bé hơn mức ý nghĩa 𝐻 = 0.05 với nên ta chưa đủ cơ sở để bác
bỏ giả thuyết 𝐻0. Ta có thể cân nhắc việc loại bỏ biến constructionTime ra khỏi mô hình.
Ta xây dựng mô hình hồi quy 2:
model_2 = lm(totalPrice~tradeTime+followers+square+buildingType+buildingStructure+elevator+district, data = new_data6) summary(model_2)
Hình 10. Code R và kết quả khi xây dựng mô hình hồi quy tuyến tính model_2
Ta so sánh các mô hình 1 và mô hình 2:
Giả thuyết 𝐻0: 𝐻1 = 𝐻2 =. . . = 𝐻10 = 0: Hai mô hình hiệu quả giống nhau (nghĩa là mô
hình 2 hiệu quả hơn mô hình 1)
Đối thuyết 𝐻1: ∃𝐻1 ≠ 0, 𝐻 = 1, … ,10: Hai mô hình hiệu quả khác nhau (nghĩa là mô hình
1 hiệu quả hơn mô hình 2) anova(model_1,model_2)
Hình 11. Code R và kết quả khi so sánh 2 mô hình model_1 và model_1
Nhận xét: Dựa trên việc so sánh 2 mô hình, ta thấy 𝐻 - 𝐻𝐻𝐻𝐻𝐻 < 2,2𝐻 - 16 rất bé so với
mức ý nghĩa 𝐻 = 0.05 nên ta bác bỏ gải thuyết 𝐻0, ta có thể kết luận 2 mô hình hiệu
quả khác nhau, tức có nghĩa là mô hình 1 hiệu quả hơn mô hình 2 (vì có ít nhất 1 hệ số
𝐻𝐻 có ý nghĩa thống kê nên mô hình đầy đủ là mô hình 1 sẽ hiệu quả hơn).
Phân tích sự tác động của các nhân tố lên tổng chi phí giá nhà đến: lOMoARcPSD| 36991220
Như vậy mô hình hồi quy tuyến tính về ảnh hưởng của các nhân tố lên việc lệch giờ đến được cho bởi:
= -2.603e+03 + (1.778e-06) x tradeTime + (1.472e-01) x followers +
(3.867e+00) x square + (9.009e+01) x buildingType2 + (2.693e+01) x buildingType3
+ (2.240e+01) x buildingType4 + (1.528e+03) x constructionTime1944 + (1.303e+01)
x buildingStructure + (5.340e+01) x elevator + (2.777e+00) x district
Trước hết, ta thấy tằng p-value tương ứng với thống kê F bé hơn 2.2e-16, có ý nghĩa
rất cao. Điều này chỉ ra rằng, ít nhất một biến dự báo trong mô hình có ý nghĩa giải
thích rất cao đến tổng chí phí giá nhà totalPrice.
Để xét ảnh hưởng cụ thể của từng biến độc lập, ta xét trong hệ số (hệ số 𝐻𝐻) và p-value
tương ứng. Ta thấy rằng p-value tương ứng với các biến followers, Square,
buildingType, buildingStructure, elevator, district bé hơn 2e-16, điều này nói lên rằng
ảnh hưởng của các biến này có ý nghĩa rất cao lên việc lệch giờ đến totalPrice. Kiểm
tra các giả định của mô hình
Nhắc lại các giả định của mô hình hồi quy: 𝐻𝐻 = 𝐻0 + 𝐻1. 𝐻1 + ⋯ 𝐻𝐻. 𝐻𝐻 + 𝐻𝐻, 𝐻 = 1, … 𝐻.
+ Tính tuyến tính của dữ liệu: mối quan hệ giữa biến dự báo X và biến phụ thuộc Y
được giả sử là tuyến tính. + Sai số có kỳ vọng bằng 0
+ Phương sai của các sai số là hằng số +
Sai số có phân phối chuẩn.
+ Các sai số _1,…, _n thì độc lập nhau.ϵ ϵ
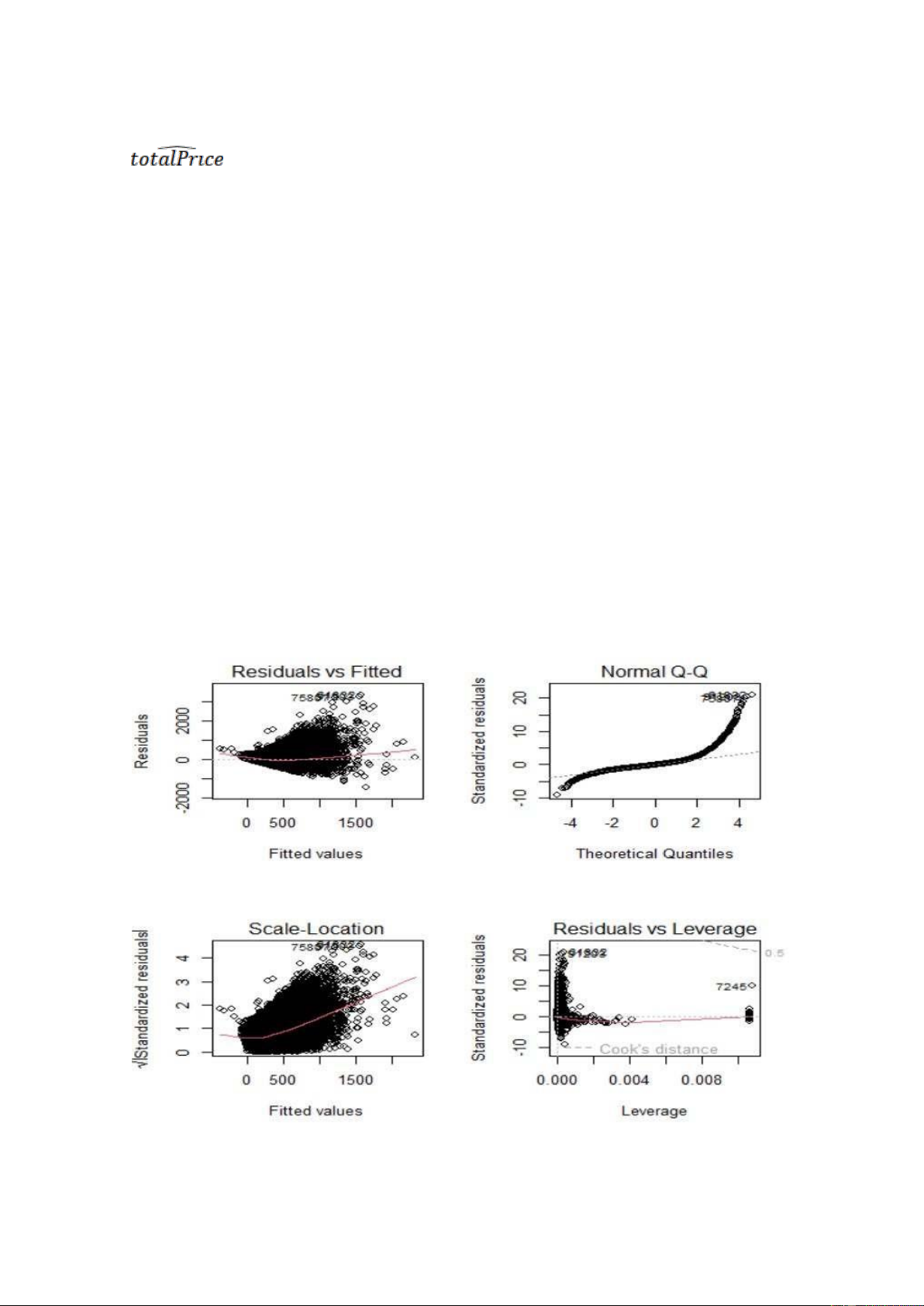
Ta thực hiện phân tích thặng dư để kiểm tra các giả định của mô hình: Nhận xét: lOMoARcPSD| 36991220
+ Đồ thị Residuals and Fitted vẽ các sai số tương ứng với các giá trị dự báo, kiểm tra giả định tuyến
tính cỉa dữ liệu, giả định sai số có kỳ vọng bằng 0, giả định phương sai cảu sai số là hằng số.
Dựa trên đồ thị ta thấy, đường màu đỏ là đường thẳng nằm ngang nên giả định tính
tuyến tính của dữ liệu thoả mãn. Đường màu đỏ nằm sát đường y=0 nên giả định sai
số có kỳ vọng bằng 0 thảo mãn. Các sai số phân tán ngẫu nhiên dọc theo đường màu
đỏ nên giả định phương sai các số là hằng số thoả mãn.
+ Đồ thị Normal Q-Q vẽ các sai số đã được chuẩn hoá, kiểm tra giả định sai số có phân phối chuẩn.
Dựa trên đồ thị ta thấy, có nhiều điểm quan trắc lệch ra khỏi dường thẳng kì vọng phân
phối chuẩn nên giả định sai số có phân phối chuẩn chưa thoả mãn.
+ Đồ thị Scale-Location vẽ căn bậc hai của các sai số đã được chuẩn hoá, kiểm tra giả
định phương sai các sai số là hằng số.
Dựa trên đồ thị ta thấy, đường màu đỏ nằm ngang, các quan trắc phân tán ngẫu nhiên
dọc theo đường màu đỏ nên giả định phương sai của các hằng số là thoả mãn.
TÀI LIỆU THAM KHẢO
[1] Giáo trình Xác suất - Thống kê & phân tích số liệu, Nguyễn Đình Huy, Đậu Thế Cấp, Lê Văn Đại