lOMoARcPSD| 36991220
ĐẠI HỌC QUỐC GIA THÀNH PHỐ HỒ CHÍ MINH
ĐẠI HỌC BÁCH KHOA ___________
BÁO CÁO BÀI TẬP LỚN MÔN XÁC SUẤT THỐNG KÊ
Câu 1: Chọn 1 biến định lượng nào đó và thực hiện:
- Tìm các đặc trưng từ mẫu dữ liệu.
- Tìm các khoảng tin cậy cho giá trị trung bình và phương sai củatổng thể.
A. Lập bài toán cụ thể:
Thực hiên khảo sát trên một nhóm sinh viên trường Đại học Bách Khoa về thời gian
giành cho việc chơi game thường ngày (đơn vị: giờ). Thu được bảng số liệu như sau: x 0 0.5 1 1.5 2 2.5 3 4 4.5 5 7 10 12 16 20 21 n 16 9 22 2 19 1 15 4 2 3 2 1 1 1 1 1 lOMoARcPSD| 36991220
Yêu cầu bài toán: Thống kê mô tả thời gian dành cho việc chơi game thường
ngày của sinh viên Bách Khoa. Với độ tin cậy 95%.
B. Cơ sở lý thuyết giải bài toán:
a.Các đặc trưng mẫu
1. Trung bình mẫu: Trung bình mẫu là trung bình cộng các giá trị của các thành phần mẫu. Với mẫu ngẫu nhiên W = (X
,…, X ), trung bình mẫu ký hiệu là . 1, X2 n
Kỳ vọng của trung bình mẫu bằng trung bình tổng thể, có thể nói xét về mặt số lớn và về mặt xác
suất thì trung bình mẫu phản ánh được giá trị của trung bình tổng thể, về cá biệt thì có sự sai lệch,
sự sai lệch nhiều hay ít được đánh giá bằng phương sai tổng thể chia cho kích thước mẫu. Khi kích
thước mẫu càng lớn thì sự sai lệch càng giảm đi, hay nói khác đi là kích thước mẫu càng lớn, thì
việc dùng trung bình mẫu để phản ánh về trung bình tổng thể là càng chính xác.
2. Phương sai mẫu: Ký hiệu là , phản ánh đúng giá trị của phương sai tổng thể.
3. Độ lệch chuẩn mẫu: Ký hiệu là , là căn bậc 2 của phương sai mẫu
4. Tỷ lệ mẫu: Ký hiệu là f, là tỉ số lần xuất hiện biến cố A trong mẫu và kích thước mẫu. lOMoARcPSD| 36991220
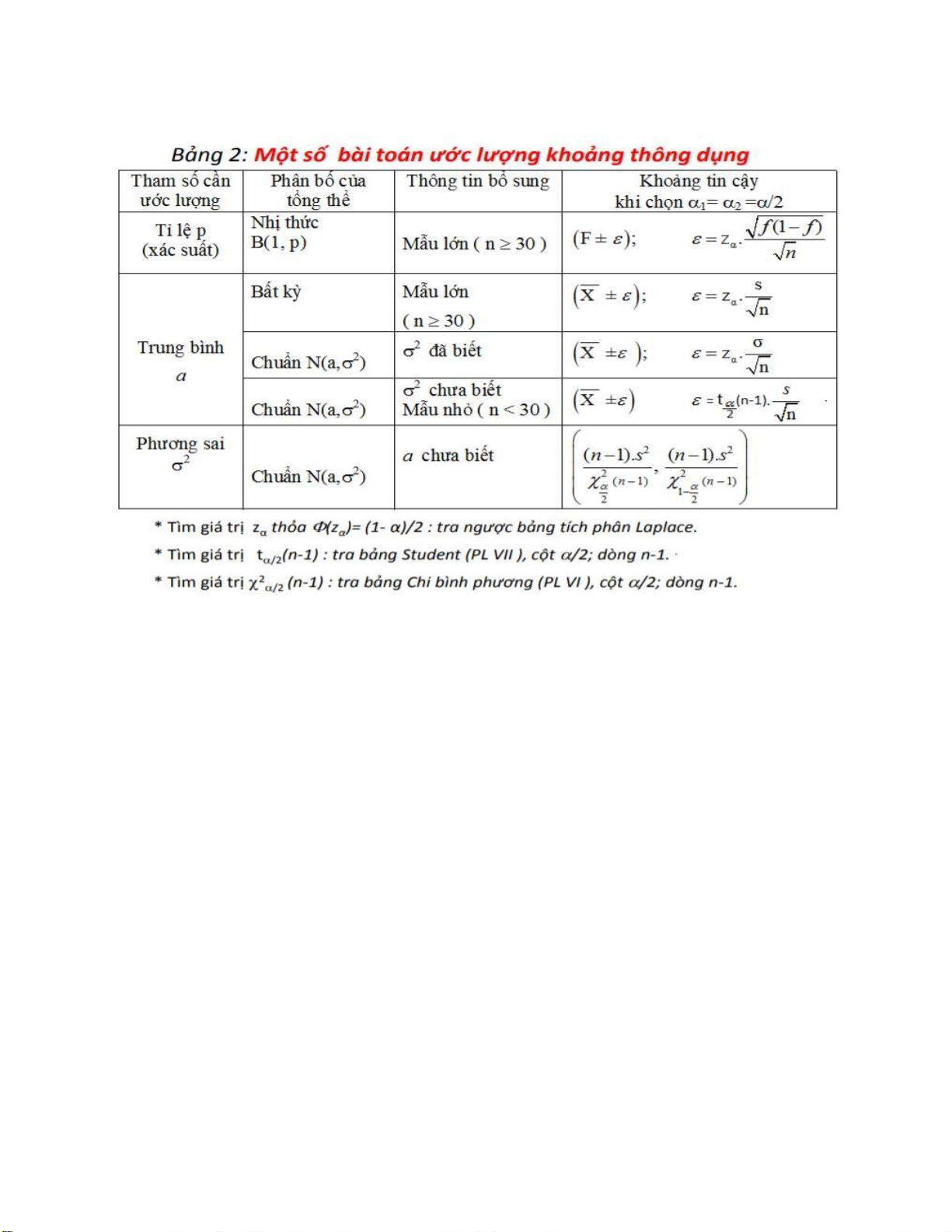
Bảng công thức ước lượng khoảng:
C. Lời giải tính tay: a/ - Trung bình mẫu: - Phương sai mẫu: ,
- Phương sai mẫu hiệu chỉnh: , - Hệ số biến thiên: CV= Trung vị mẫu (median):
Nếu thì trung vị của mẫu có giá trị
Nếu thì trung vị của mẫu có giá trị lOMoARcPSD| 36991220
Trung vị mẫu (median): Med=2 b/ Với độ tin cậy
Khoảng tin cậy cho giá trị trung bình :
*Khoảng tin cậy cho giá trị phương sai : lOMoARcPSD| 36991220
D. Lời giải từ việc sử dụng Excel:
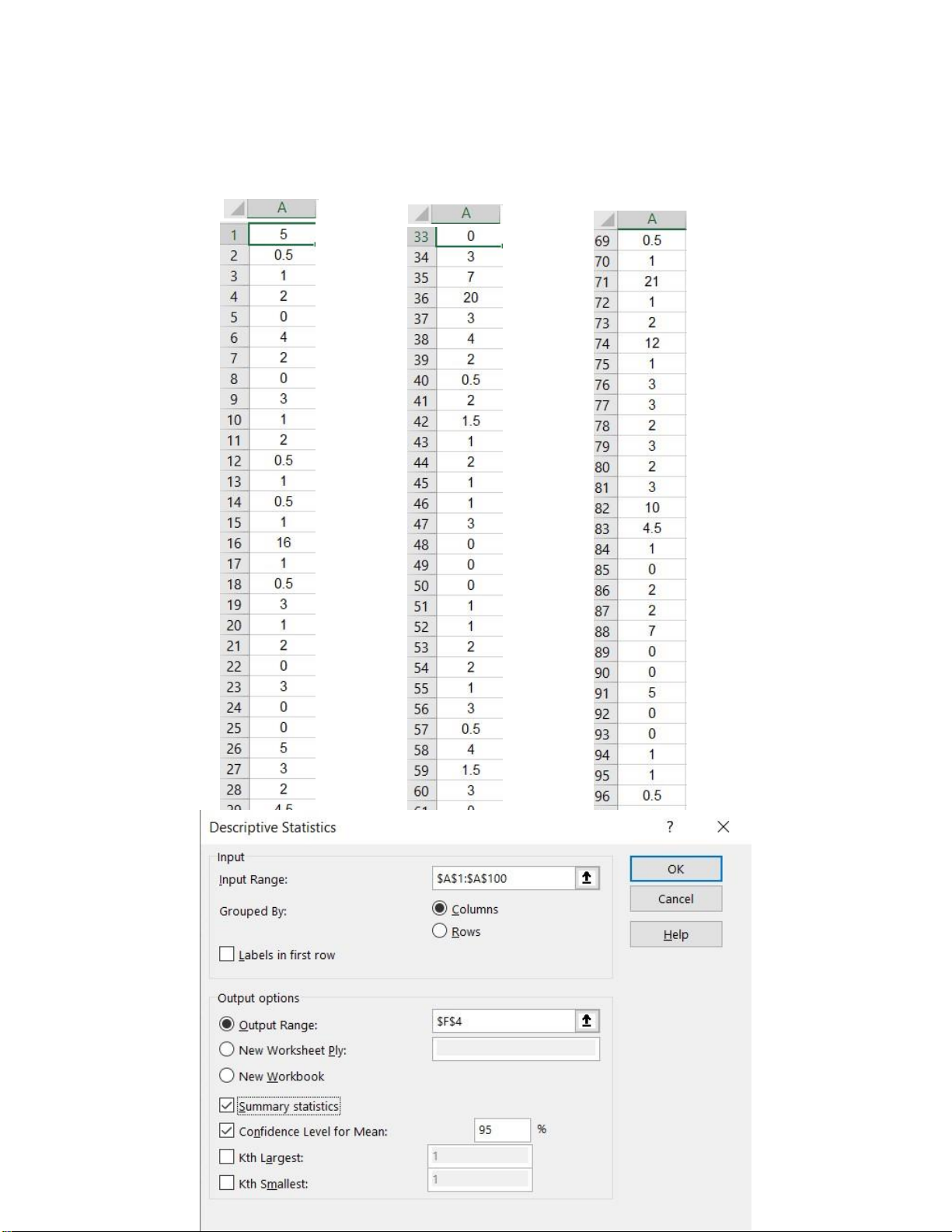
1. Nhập dữ liệu vào Excel:
2 . Chọn chức năng Data/Data Analysis/Descriptive Statistics :
+ Input Range: địa chỉ tuyệt đối chứa dữ liệu.
+ Output options: vị trí xuất kết quả.
+ Confidence Level for Mean: độ tin cậy cho trung bình. lOMoARcPSD| 36991220
3. Kết quả nhận được:
4. Tìm khoảng tin cậy của trung bình mẫu và phương sai mẫu:
*Khoảng tin cậy của trung bình mẫu:
*Khoảng tin cậy cho giá trị phương sai :
Nhập hàm =CHISQ.INV.RT(0.025,99) Và ta có kết quả là:
Nhập hàm =CHISQ.INV.RT(0.975,99): Và ta có kết quả là: lOMoARcPSD| 36991220
Câu 2: Chọn dữ liệu hai biến định lượng (hoặc xử lý số liệu số liệu theo
nhóm cho phù hợp) để lập bài toán kiểm định so sánh 2 trung bình tổng thể.
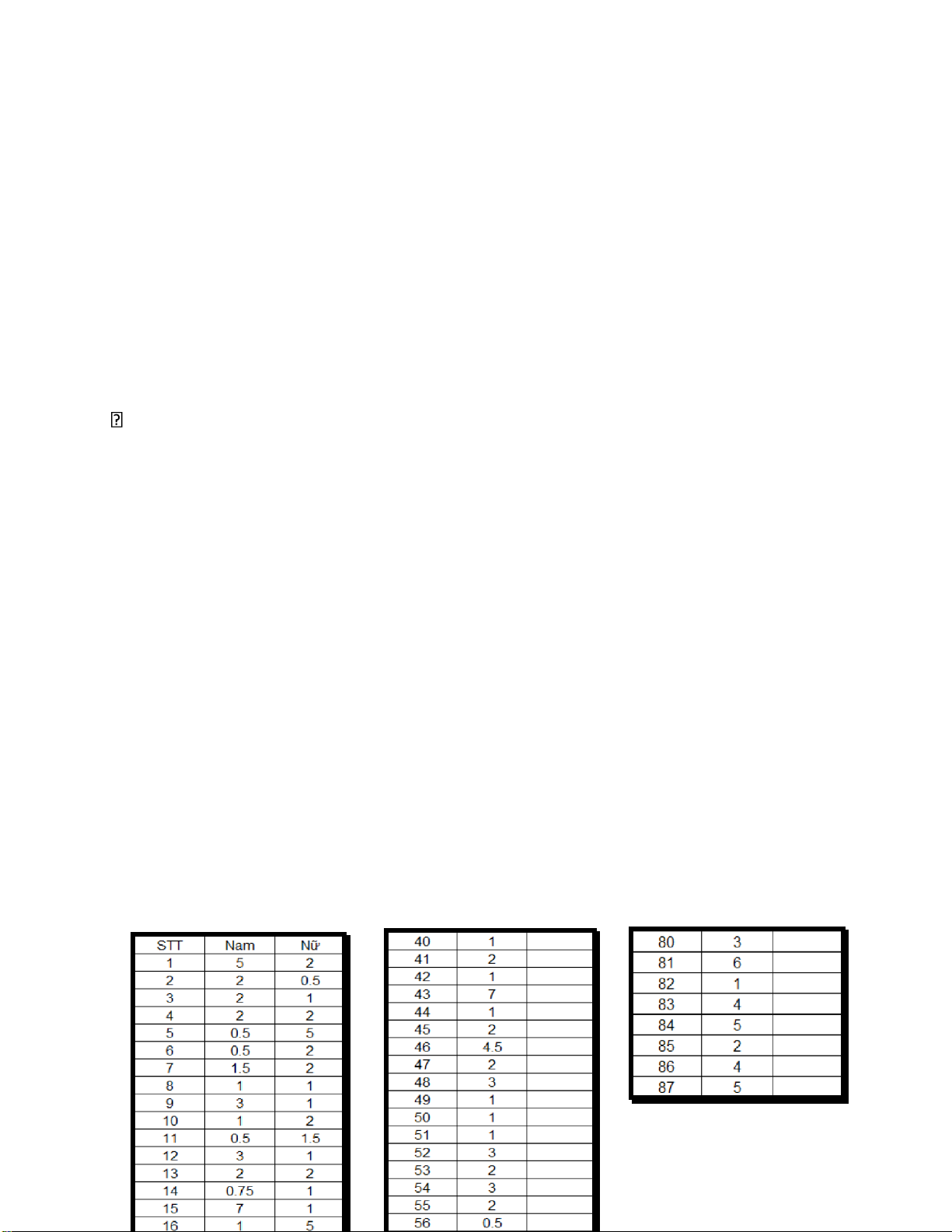
A. LẬP BÀI TOÁN CỤ THỂ: Khảo sát số giờ chơi game (đơn vị là: giờ)
của sinh viên nam và sinh viên nữ tại Đại học Bách Khoa TP.HCM:
Yêu cầu bài toán: Với mức ý nghĩa 5%, có thể cho rằng số giờ chơi game
của nam và nữ là như nhau hay không? Giả thiết số giờ chơi game như trên
có phân phối chuẩn và phương sai khác nhau. lOMoAR cPSD| 36991220
B. CƠ SỞ LÍ THUYẾT BÀI TOÁN:
- Dạng bài: Kiểm định so sánh trung bình hai tổng thể có phương sai khác nhau
- Công cụ: t-Test TWO SAMPLE ASSUMING UNEQUAL VARIANCES - Cơ sở lý thuyết:
C. TÍNH TOÁN BẰNG TAY:
Gọi ; là số giờ chơi game trung bình của nam và nữ Giả thiết kiểm định: : ; :
Có phân phối student với
+ X1,X2 có phân phối chuẩn + Chưa biết nhưng biết
+ 2 mẫu được lấy độc lập ; ; ; ; lOMoARcPSD| 36991220
Có phân phối Student với: Miền bác bỏ:
Thế vào ta được miền bác bỏ: Tiêu chuẩn kiểm định:
Sau khi tính toán như trên ta thấy được:
Có thể chấp nhận giả thiết . lOMoARcPSD| 36991220
Kết luận: Vậy số giờ chơi game trung bình của sinh viên nam và sinh viên nữ của
trường Đại học Bách Khoa là như nhau.
D. SỬ DỤNG CÔNG CỤ EXCEL:
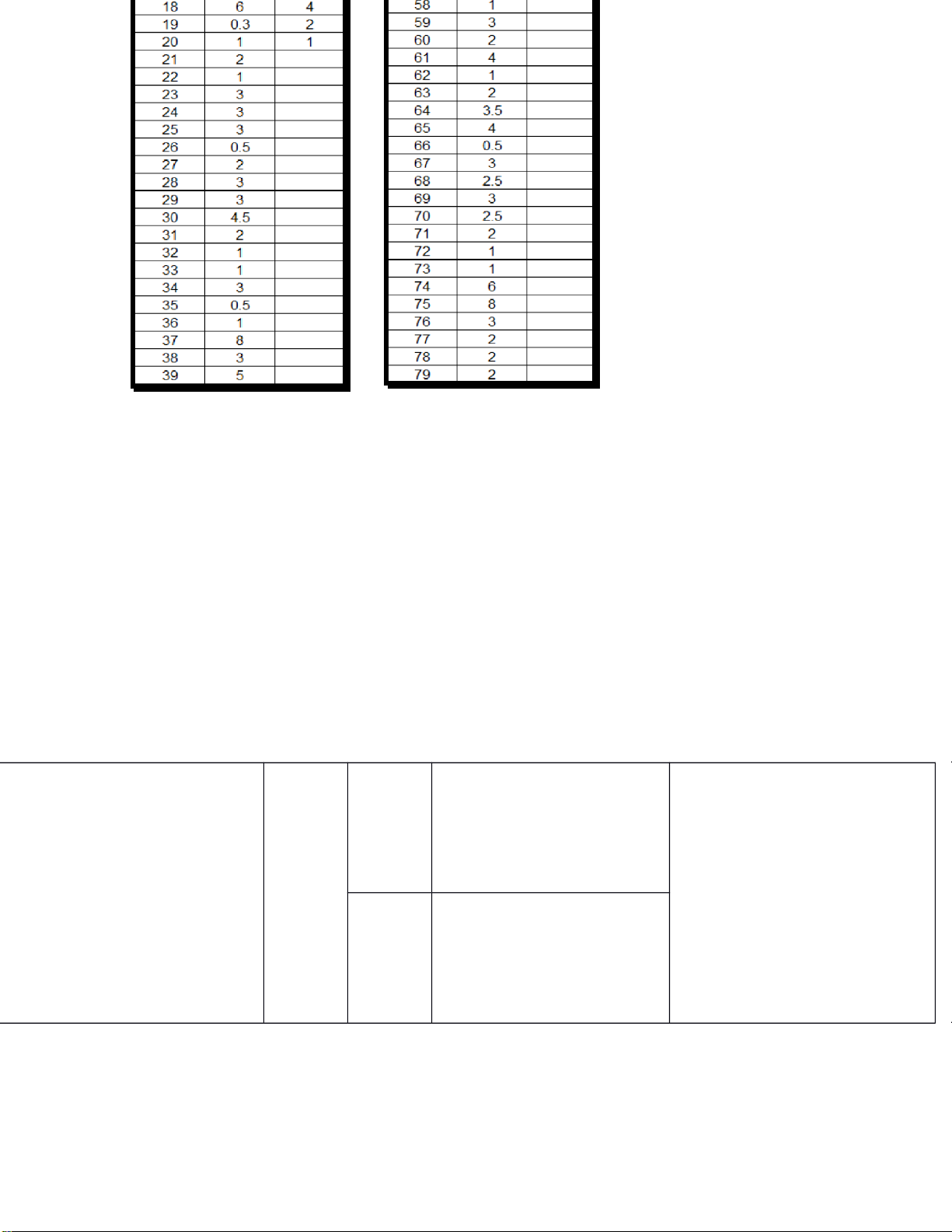
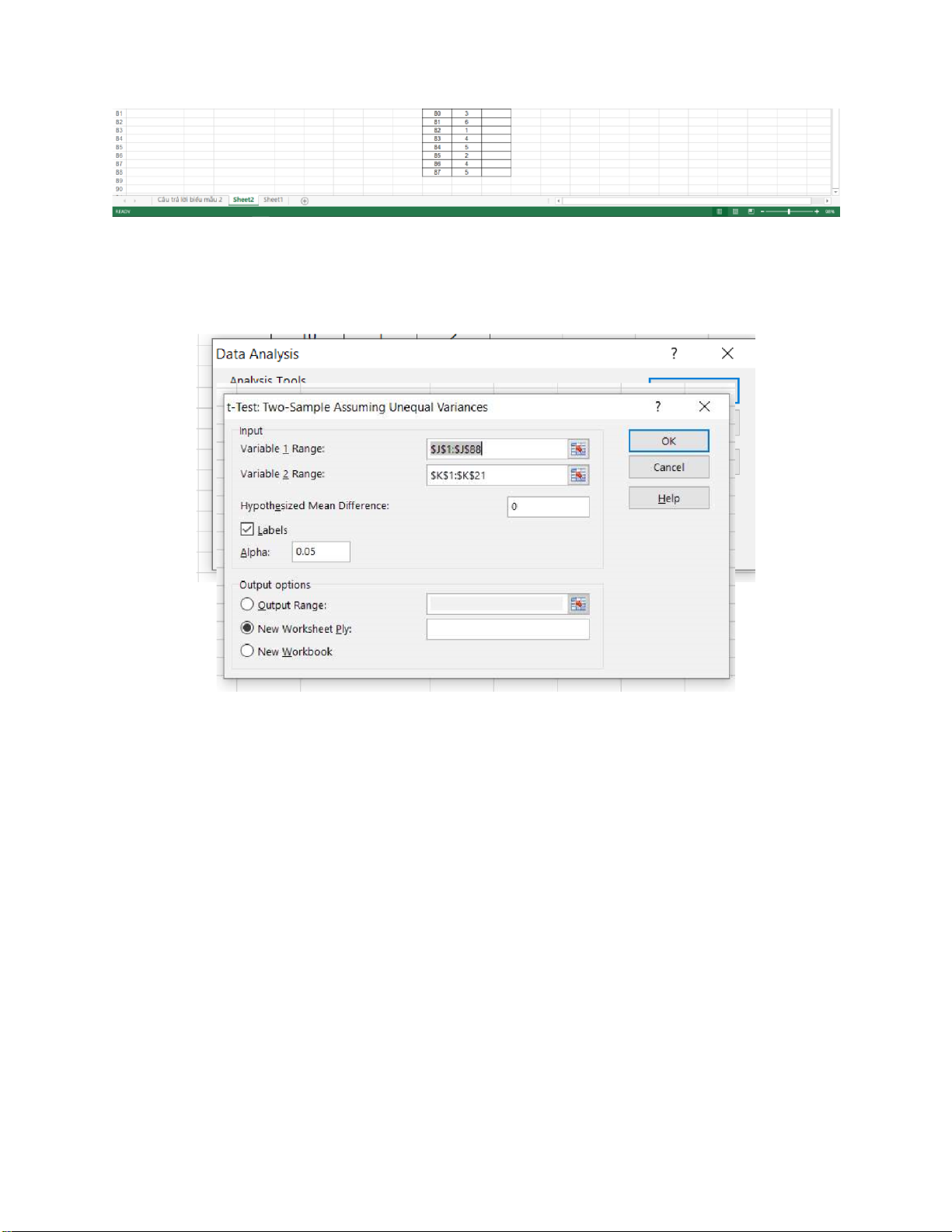
• Nhập dữ liệu vào excel: lOMoARcPSD| 36991220
• Trên thanh công cụ tìm mục Data/Data Analysist/t-Test: Two-sample Assuming Equal Variences
• Chọn các mục như hình sau:
+ Input: địa chỉ tuyệt đối chứa dữ liệu tướng ứng của mẫu 1 và mẫu 2
+ Output option: Chọn New Worksheets sẽ xuất ra 1 sheet excel mới
+ Label: Nghĩa là hàng đầu tiên của cột chứa mẫu đã chọn là tên của mẫu
nên không tính là dữ liệu để phân tích.
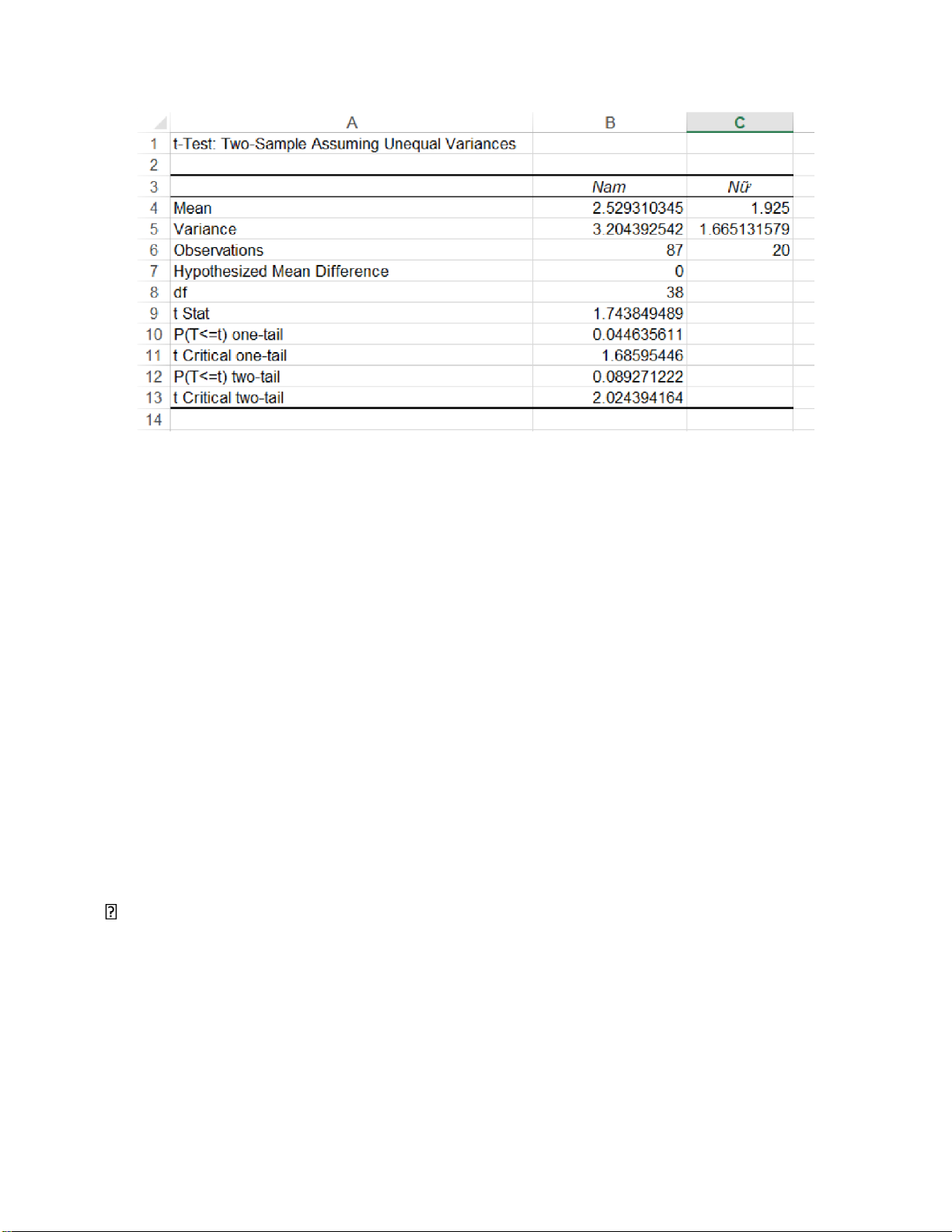
+ Alpha: là mức ý nghĩa của bài toán (0.05=5%) • Kết quả: lOMoARcPSD| 36991220
+ t Stat: là tiêu chuẩn kiểm định
+ t Critical two-tail: là miền bác bỏ
KẾT QUẢ TƯƠNG TỰ NHƯ ĐÃ TÍNH TOÁN Ở PHẦN 1
Câu 3: Chọn dữ liệu cho k biến (k>=3) (hoặc xử lý số liệu theo nhóm
cho phù hợp) để lập bài toán so sánh trung bình về k tổng thể.
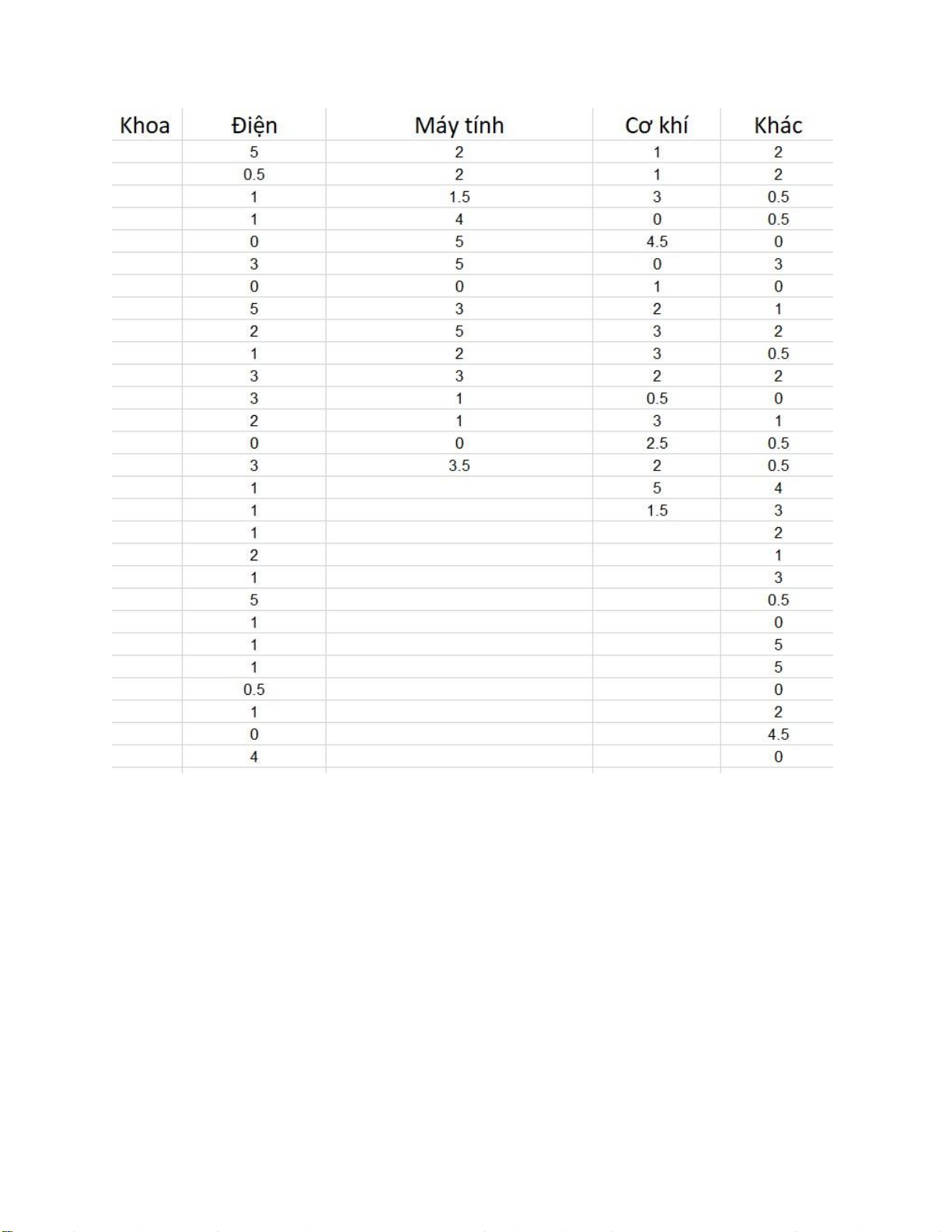
A. Lập bài toán cụ thể: lOMoARcPSD| 36991220
Thực hiên khảo sát trên một nhóm sinh viên trường Đại học Bách Khoa về thời
gian giành cho việc chơi game thường ngày (đơn vị: giờ).
Yêu cầu bài toán: Với mức ý nghĩa = 0.05, hãy kiểm định thời gian trung bình chơi
game thường ngày của các nhóm khoa có khác nhau không? Giả sử thời gian chơi
game trung bình này tuân theo phân phối chuẩn.
B. Cơ sở lý thuyết giải bài toán:
- Nhận định dạng bài: Kiểm định giá trị trung bình một nhân tố.
- Phương pháp giải: Phân tích phương sai một nhân tố.
- Công cụ giải: Anova single factor. lOMoARcPSD| 36991220 - Cơ sở lý thuyết:
Giả sử nhân tố X có k mức Y ,…,Y
(i=1,2,…,k) tuân theo phân 1,Y2 k với Yi
phối chuẩn N(), có mẫu số liệu: Thứ tự quan sát 1 2 … 3 Tổng cộng 1 2 … ( x i1 ) ( x i2 ) ( x ik ) … Kích thước mẫu .. n 1 n 2 n . k n Trung bình mẫu … của từng nhóm … Tổng bình phương chênh … lệch trong nội bộ các nhóm Tổng bình … phương chêch lệch giữa các nhóm Tổng bình phương chênh lệch toàn bộ lOMoARcPSD| 36991220 Ta có bảng Anova: Bậc tự Bình phương Giá trị thống Nguồn sai số
Tổng số bình phương do trung bình kê Giữa các nhóm k-1 Trong nội bộ n-k các nhóm Tổng cộng n-1
SSG: Phần biến thiên của giá trị X do các mức độ của yếu tố đang xem xét tạo ra.
SSW: Phần biến thiên của giá trị X do các yếu tố nào đó không được xem xét tạo ra.
SST: Tổng các biến thiên của giá trị X do tất cả các yếu tố tạo ra.
Hệ số xác định :
của mô hình Phân tích phương sai được sử dụng để đo mức độ ảnh hưởng
của yếu tố được xem xét trong mô hình đối với sự biến động của các giá trị
của biến ngẫu nhiên X quanh giá trị trung bình của nó. R2 càng lớn thì mô
hình càng gọi là thích hợp. *Giả thiết:
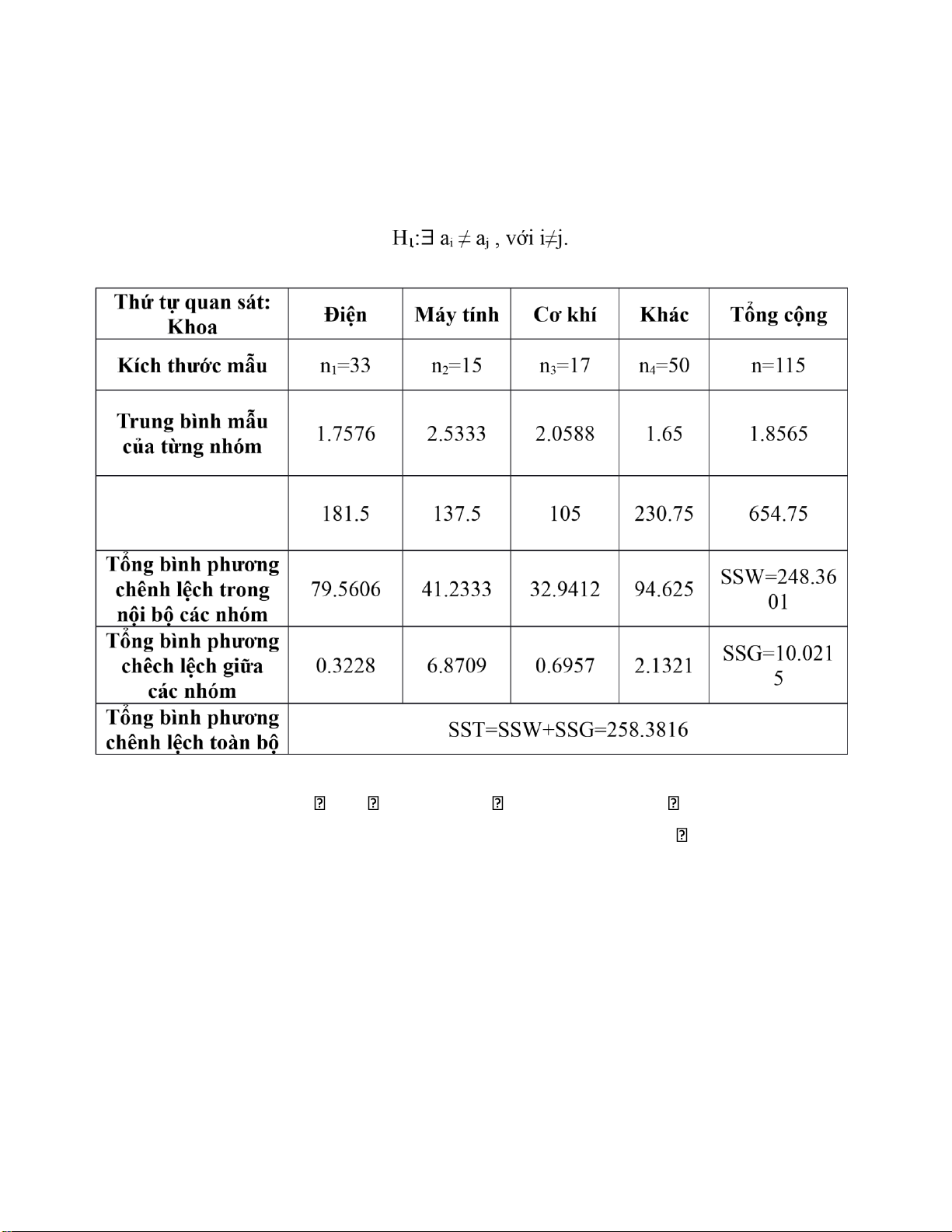
H0: a1 = a2 = … = ak “Các giá trị trung bình bằng nhau”.
H1: ai aj “Ít nhất có hai giá trị trung bình khác nhau”. *Giá trị thống kê:
*Miền bác bỏ: W = ( F (k-1; n-k) ; + ) *Biện luận:
Nếu F Chấp nhận giả thiết H0. lOMoARcPSD| 36991220
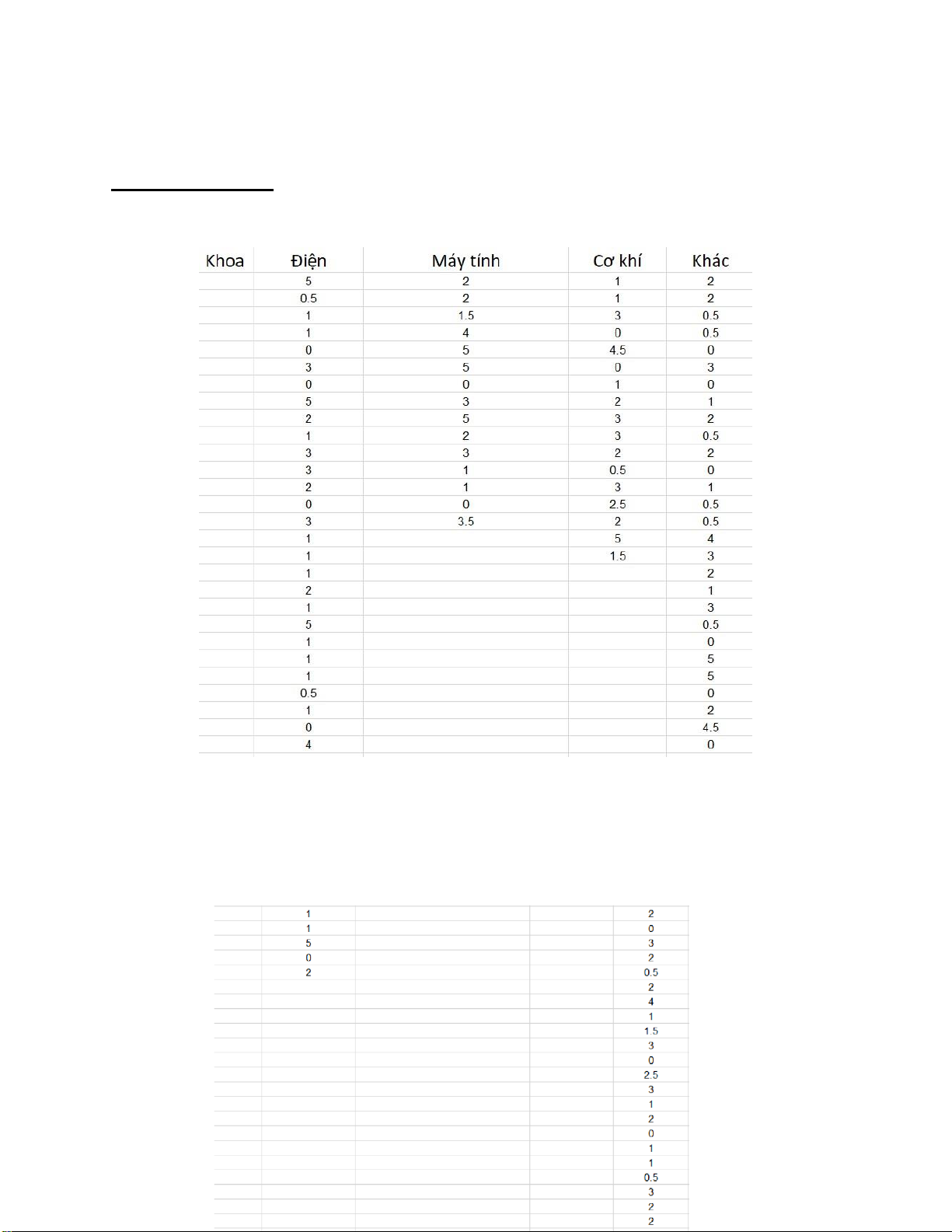
C. Lời giải tính tay:
Gọi a1, a2, a3, a4 lần lượt là thời gian trung bình chơi game thường ngày của
các khoa Điện, Máy tính, Cơ khí, Khác. Giả thiết kiểm định: H0: a1 = a2 = a3 = a4.
Miền bác bỏ: W = ( F (k-1; n-k) ; + ) = (F0.05(3;111) ; + ) = (2.69 ; + ) k-1 = 3 ; n-k=111
=> Chưa thể bác bỏ H0.
=> Có thể nói thời gian trung bình chơi game thường ngày của các nhóm khoa là như nhau. *Hệ số xác định : lOMoARcPSD| 36991220
D. Lời giải từ việc sử dụng Excel:
1. Nhập dữ liệu vào Excel: lOMoARcPSD| 36991220 lOMoARcPSD| 36991220
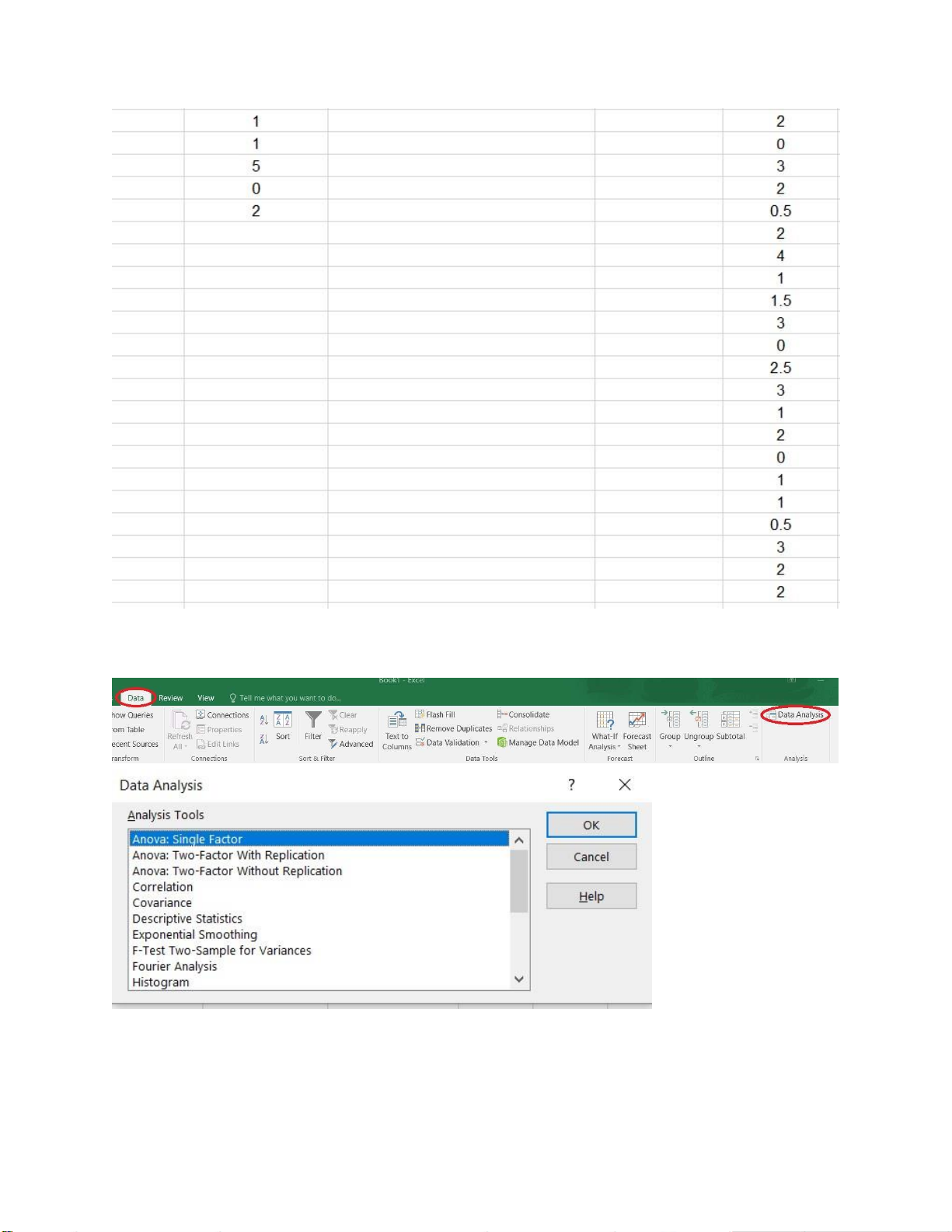
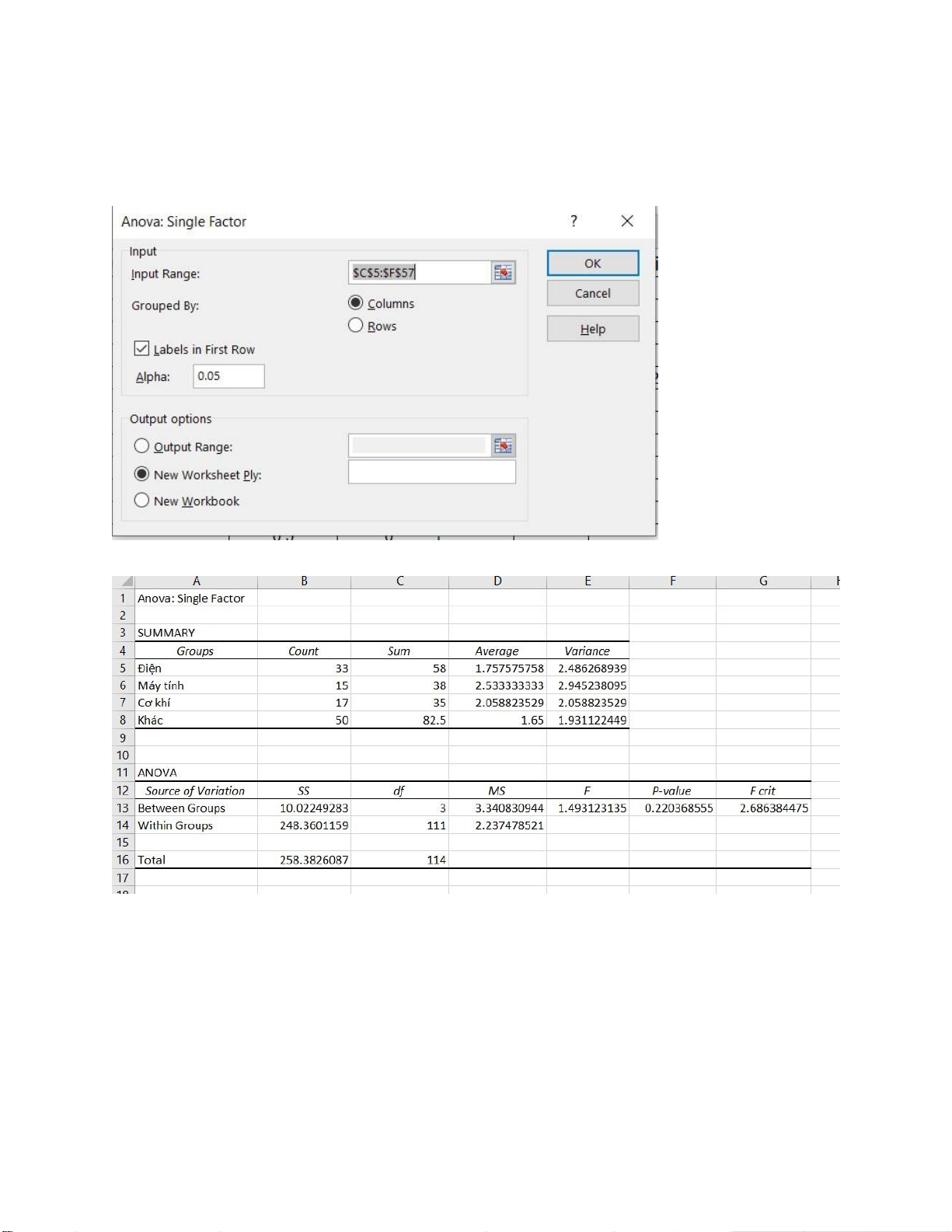
2. Chọn Data -> Data Analysis -> Anova: Single Factor -> OK
3. Hộp thoại Anova: Single Factor xuất hiện: Trong đó:
- Input Range: địa chỉ chứa dữ liệu.
- Grouped By: ở đây dữ liệu chọn theo cột. lOMoARcPSD| 36991220
- Labels in First Row: nếu Input Range có chứa hàng Tên nhóm. - Alpha: mức ý nghĩa α.
- Output options: vị trí xuất kết quả. Sau đó, chọn OK.
4. Ta được kết quả như sau: 5. Biện luận: H
“Thời gian trung bình chơi game thường ngày của các nhóm 0: a1 = a2 = a3 = a4 khoa là như nhau”. H
“Ít nhất hai khoa có thời gian trung bình chơi game thường ngày khác 1: ai aj, i j nhau”. lOMoARcPSD| 36991220
Vì P-value=0.220368555 > 0.1
F=1.493123135 < F0.05=2.686384475
=> Chưa thể bác bỏ H0.
=> Có thể nói thời gian trung bình chơi game thường ngày của các nhóm khoa là như nhau. lOMoARcPSD| 36991220
Câu 4: Chọn dữ liệu cho 2 biến (hoặc xử lý số liệu theo nhóm cho phù hợp) để
lập bài toán kiểm định so sánh về sự phân tán. Trình bày các bước thực hiện
và nhận xét kết quả. A. Lập bài toán
Bài toàn: Khảo sát điểm thi giữa kì của 117 sinh viên trường ĐHBK về kết quả thi
giữa kì đối với những sinh viên có chời game và không chơi game ta có bảng số liệu sau: Bảng 1: Điểm Điểm A Điểm B Điểm C Điểm D Chơi game (8-10) (6-8) (5-6) (0-5) Có 29 48 15 8 Không 2 13 2 0
Với mức ý nghĩa 5% có thể cho rằng điểm thi của sinh viên chơi game và không chơi
game có sự phân tán như nhau không. Giả thiết điểm thi của mỗi sinh viên tuân thủ theo quy luật chuẩn. BÀI LÀM:
Dạng bài: Kiểm định giả thuyết cho phương sai hai tổng thể.
Công cụ: F-Test Two-Sample for Variances
B. Cơ sở lý thuyết:
- Khi cần kiểm định hai tổng thể có biến động như nhau hay không chúng ta dùng
phương pháp kiểm định phương sai của hai tổng thể độc lập dựa trên một đại lượng F như sau: F = Trong đó:
là phương sai của mẫu thứ nhất, mẫu này có cỡ n1.
là phương sai của mẫu thứ hai, mẫu này có cỡ n2. lOMoARcPSD| 36991220
- Thông thường để xác địnhmaẫu nào là mẫu thứ nhất và mẫu nào là mẫu thứ hai ta làm
như sau trong khi tính đại lượng F thì giá trị phương sai lớn hơn sẽ được đặt ở tử số, và
như vậy mẫu tương ứng với phương sai đó là mẫu thứ nhất.
- Giả thiết đặt ra là kiểm định hai bên: : = : ≠
- Nếu tỉ số F rất lớn hoặc rất nhỏ ta có thể suy diễn bằng hai phương sai tổng thể khó mà
bằng nhau, ngược lại nếu tỉ số này gần đến 1 ta sẽ có bằng chứng ủng hộ giả thuyết H0.
Như vậy tỉ lệ F lớn đến đâu thì xem như là đủ bằng chứng bác bỏ H0 và ngược lại.
- Nếu tổng thể lấy mẫu được giả định có phân phối bình thường thì tỉ lệ F có phân phối
xác suất gọi tên là phân phối Fisher. Các giá trị tới hạn của phân phối F phụ thuộc và
hai giá trị bậc tự do, bậc tự do tử số ( = − 1) gắn liền với mậu thứ nhất và bậctuự do mẫu
số gắn liền với mẫu thứ hai ( = − 1).
- Quy tắc thực sự để bác bỏ H0 với kiểm định hai bên khi = − 1 và = −
1, mức ý nghĩa là: giả thiết H0 bị bác bỏ nếu giá trị kiểm định F lớn hơn giá trị tới hạn
trên = của phân phối F hoặc bé hơn giá trị tới hạn dưới = tức là < hoặc >
- Nếu chúng ta kiểm định bên phải: : : >
Quy tắc bác bỏ H0 là khi > . C. Tính tay: Giải
= 100, = 17, = 1,77452233, = 0,881812981
Gọi : lần lượt là phương sai của điểm thi giữa kì của sinh viên có và không chơi game. lOMoARcPSD| 36991220 Giả thiết kiểm định. : = : ≠
Miền bác bỏ : = (= ( 2,07: +) Tiêu chuẩn kiểm định = = = 4,049470439 Bác bỏ giả thuyết
Vậy điểm thi giữa kì của sinh viên chơi game và không chơi game có sự phân tán không
đồng đều. hay điểm thi giữa kì của sinh viên có chơi game kém đồng đều hơn so với sinh viên không chơi game.
D.Tính toán bằng excel:
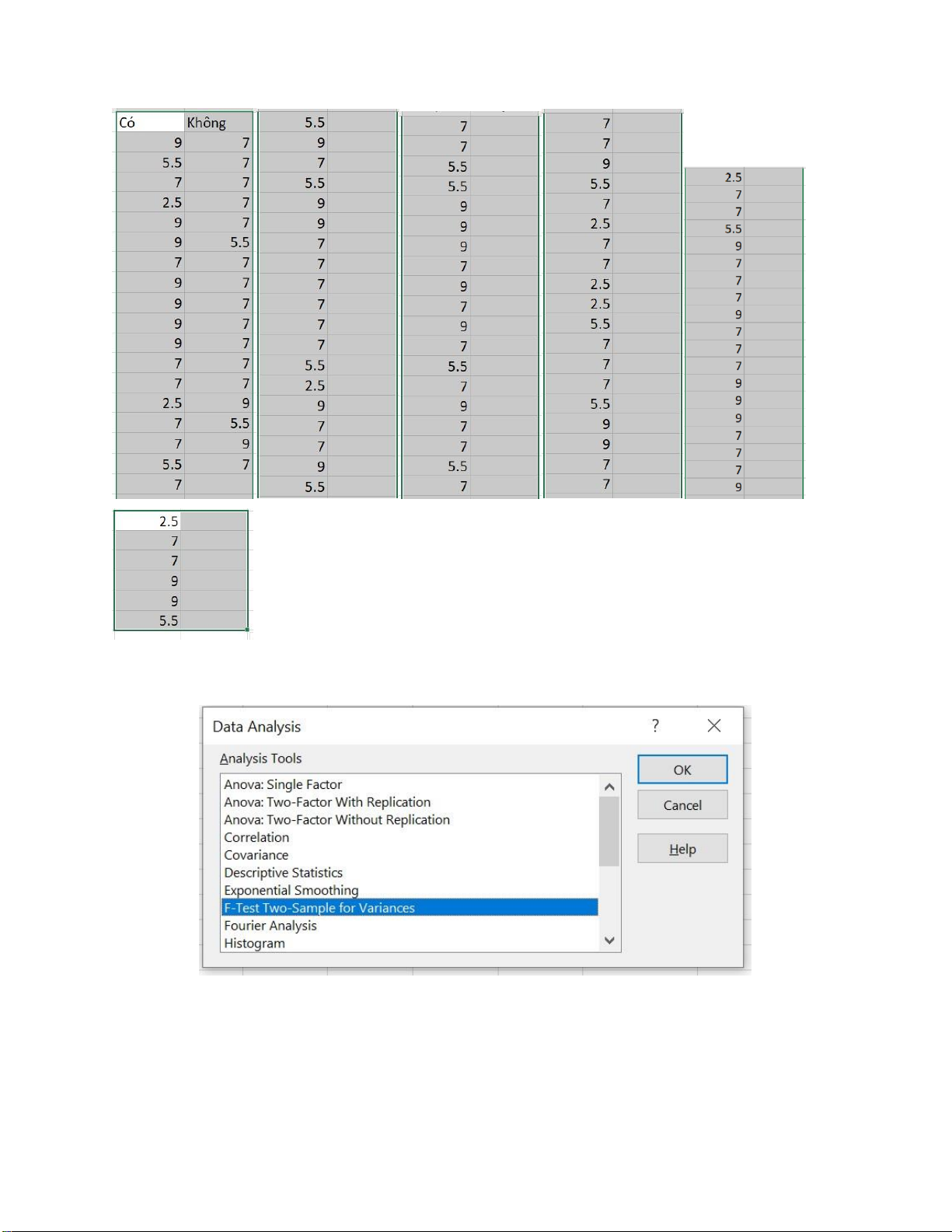
1.Nhập số liệu vào bảng tính: lOMoARcPSD| 36991220
2. Vào Data/ Data Analysis/ F-Test Two-Sample for Variances.
3.Chọn các mục như hình:
+ Input: địa chỉ tuyệt đối chứa dư liệu tương ứng của mẫu 1 và 2
+ Output options: vị trí xuất kết quả. lOMoARcPSD| 36991220 + Apha: mức ý nghĩa
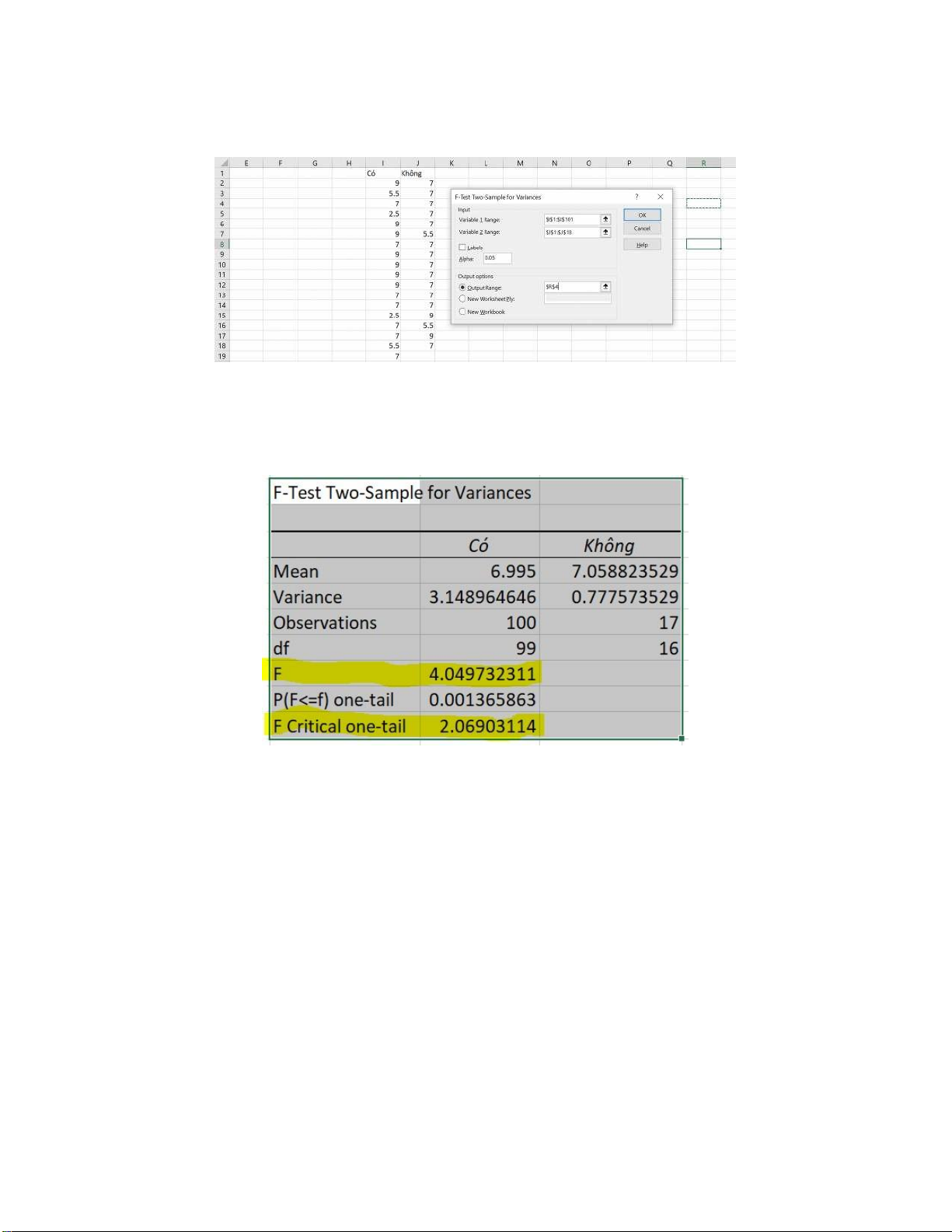
Kết quả ta nhận được: Biện luận : Giả thiết rằng:
: = ,”Điểm thi giữa kì giữa sinh viên chơi game và không chơi game có sự phân tán đồng đều”. lOMoARcPSD| 36991220
: > ,”Điểm thi giữa kì của sinh viên có chơi game kém đồng đều hơn không chơi game”. Ta có :
= 4.049732311> = 2.06903114 Bác bỏ , chấp nhận Kết luận:
Vậy điểm thi giữa kì của nhóm sinh viên có chơi game kém đồng đều hơn nhóm sinh viên không chơi game. lOMoARcPSD| 36991220
Câu 5: Chọn dữ liệu phù hợp để lập bài toán so sánh các tỉ lệ ( hay là bài toán
kiểm định tính độc lập). Trình bày các bước thực hiện và nhận xét kết quả. A. Lập bài toán:
Khảo sát ngẫu nhiên 117 sinh viên trường Đại học Bách Khoa về vấn đề giải
trí bằng game online có tương quan gì với điểm số thi giữa học kỳ, kết quả như sau: Thời gian Điểm 0 h-2h 2 h-4h >4 h Điểm A (8-10) 21 3 7 Điểm B (6-8) 43 15 3 Điểm C (5-6) 11 4 2 Điểm D (0-5) 5 2 1
Với mức ý nghĩa α=0,05, kiểm định xem thời gian chơi game có ảnh hưởng
đến điểm số thi giữa học kỳ hay không?
B. Cơ sở lý thuyết
a. Dạng bài: Kiểm định tính độc lập
b. Khái niệm thống kê:
Đối với một thí nghiệm có hai kết quả (binomial experiment) - thí dụ, đối với
một thuốc được kê đơn: có hay không – bạn thường so sánh hai tỉ số với nhau
(thực nghiệm với lí thuyết hay thực nghiệm với thực nghiệm). Song đối với một thí
nghiệm có nhiều kết quả (multinomial experiment) – thí dụ, bác sĩ đánh giá tình
trạng của các bệnh nhân được điều trị bởi thuốc trong một khoảng thời gian – bạn
cần so sánh nhiều tỉ số. Trắc nghiệm “khi” bình phương (χ2) cho phép bạn so sánh
không những hai mà còn nhiều tỉ số (hay tỉ lệ hoặc xác suất) một cách tiện lợi. χ2 là
phân phối về xác suất, không có tính đối xứng và chỉ có giá trị ≥ 0. Giả sử bạn có
một công trình nghiên cứu với N thử nghiệm độc lập, mỗi thử nghiệm có k kết quả
và mỗi kết quả mang một trong các xác suất thực nghiệm là Pi (i = 1, 2, … k). Nếu
gọi Pi,0 là các giá trị lý thuyết tương ứng với Pi thì các tần số lí thuyết sẽ là Ei =
NP . Điều kiện để áp dụng trắc nghiệm χ2 i,0
một cách thành công là các tần số lí thuyết Ei phải ≥ 5. lOMoARcPSD| 36991220 c. Giả thuyết: H ; … 0: P1 = P1,0; P2 = P2,0 ; Pk = Pk,0⇔
“Các cặp Pi và Pi,0 giống nhau”.
H1: “Ít nhất có một cặp Pi và Pi,0 khác nhau”.
Giá trị thống kê:
O : các tần số thực nghiệm (observed frequency); E i i:
các tần số lý thuyết (expected frequency). Biện luận: • Nếu
⇒ Bác bỏ giả thuyết H0 (DF = k-1)
Trong chương trình MS-EXCEL có hàm CHITEST có thể tính:
• Giá trị χ2 theo biểu thức:
Oij: tần số thực nghiệm của ô thuộc hàng i và cột j;
Eij: tần số lý thuyết của ô thuộc hàng i với cột j; r:
số hàng; c: số cột.
• Xác suất P (X >χ2) với bậc tự do DF = (r-1)(c-1); trong đó, r là số hàng và
c là số cột trong bảng ngẫu nhiên (contingency table).
• Nếu P (X >χ2) > α ⇒ Chấp nhận giả thuyết H0 và ngược lại.
C. Thực hiện bài toái bằng Excel Bước 1:
Gọi X: Điểm số thi giữa học kỳ cùa sinh viên
Gọi Y: Thời gian chơi game của sinh viên H : X, Y độc lập H 0 1: X, Y không độc lập lOMoARcPSD| 36991220
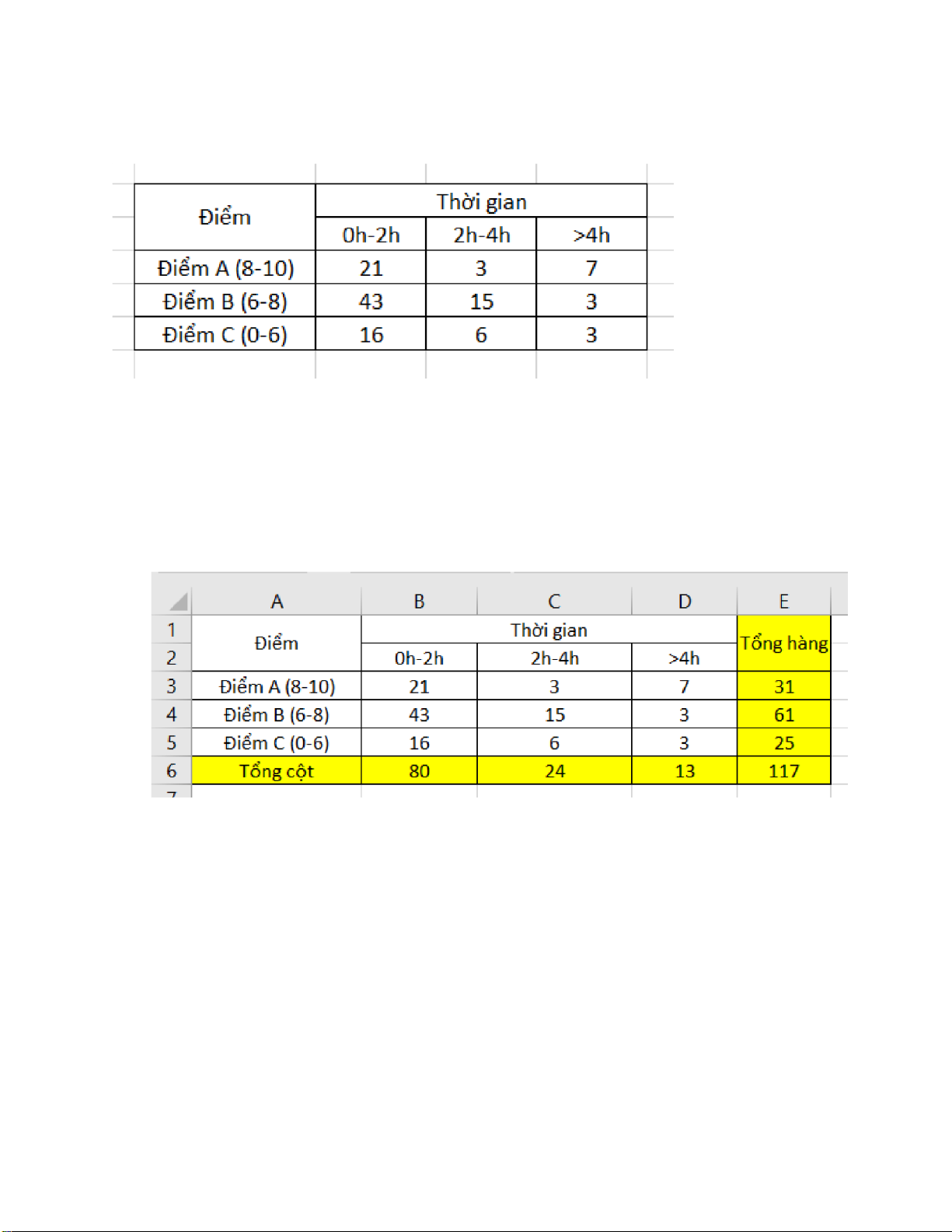
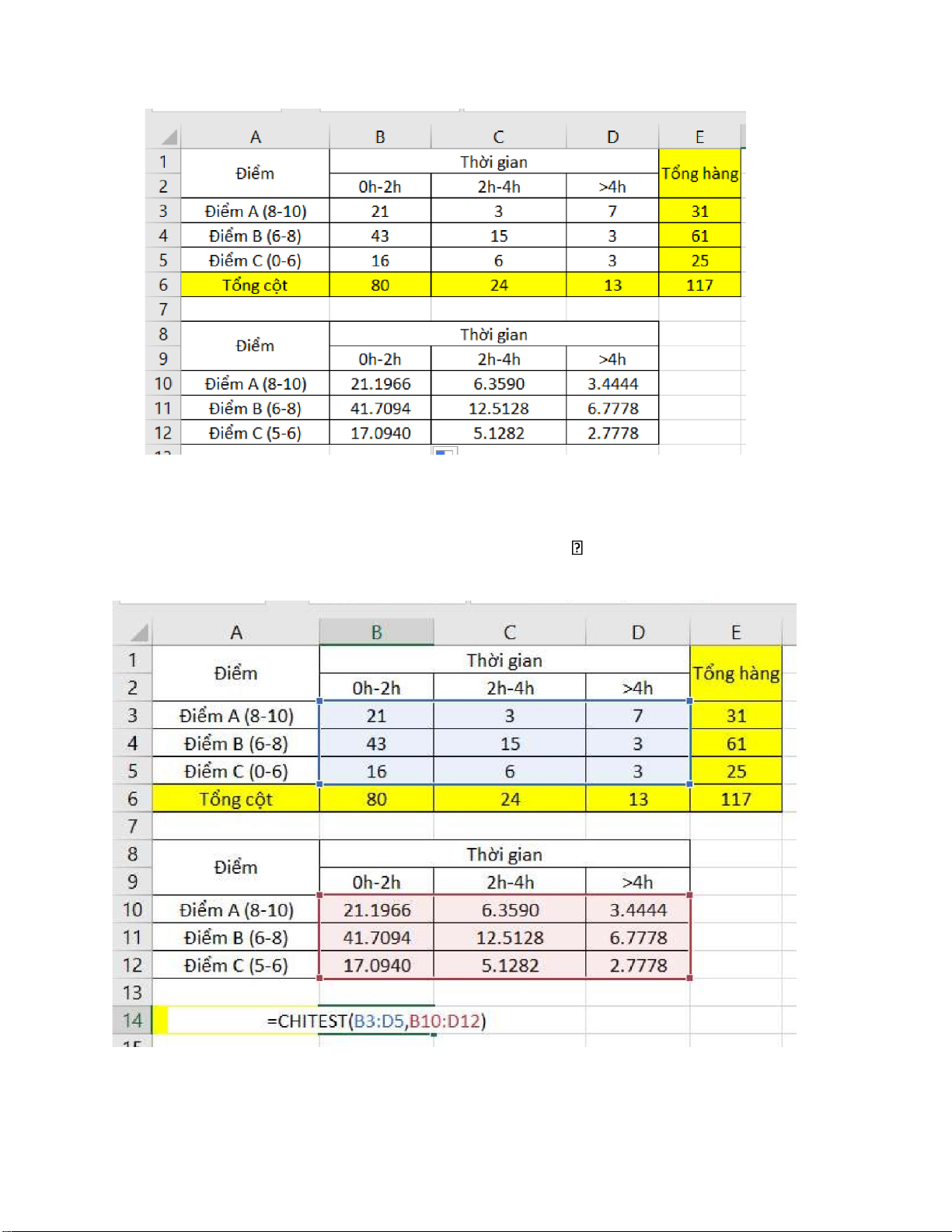
Nhập dữ liệu vào bảng tính:
Bước 2: Tính tổng các hàng và các cột.
Chọn ô E3 và nhập biểu thức =SUM(B3:D3)
Dùng con trỏ kéo kí hiệu tự điền ô E3 đến ô E5.
Chọn ô B6 và nhập biểu thức =SUM(B3:B5)
Dùng con trỏ kéo kí hiệu tự điền ô B6 đến ô E6.
Bước 3: Tính các tần số lý thuyết:
tần số lý thuyết = (Tổng hàng ×Tổng cột)/(Tổng cộng):
Ô B10 nhập lệnh = $B$6*E3/$E$6 rồi enter, sau đó kéo từ ô B10 đến ổ B12
Ô C11 nhập lệnh = $C$6*E3/$E$7 rồi enter, sau đó kéo từ ô C10 đến ổ C12
Ô D11 nhập lệnh = $D$6*E3/$E$7 rồi enter, sau đó kéo từ ô D10 đến ổ D12 lOMoARcPSD| 36991220
Bước 4: Sử dụng hàm CHITEST tính xác suất P(X> 2 ):
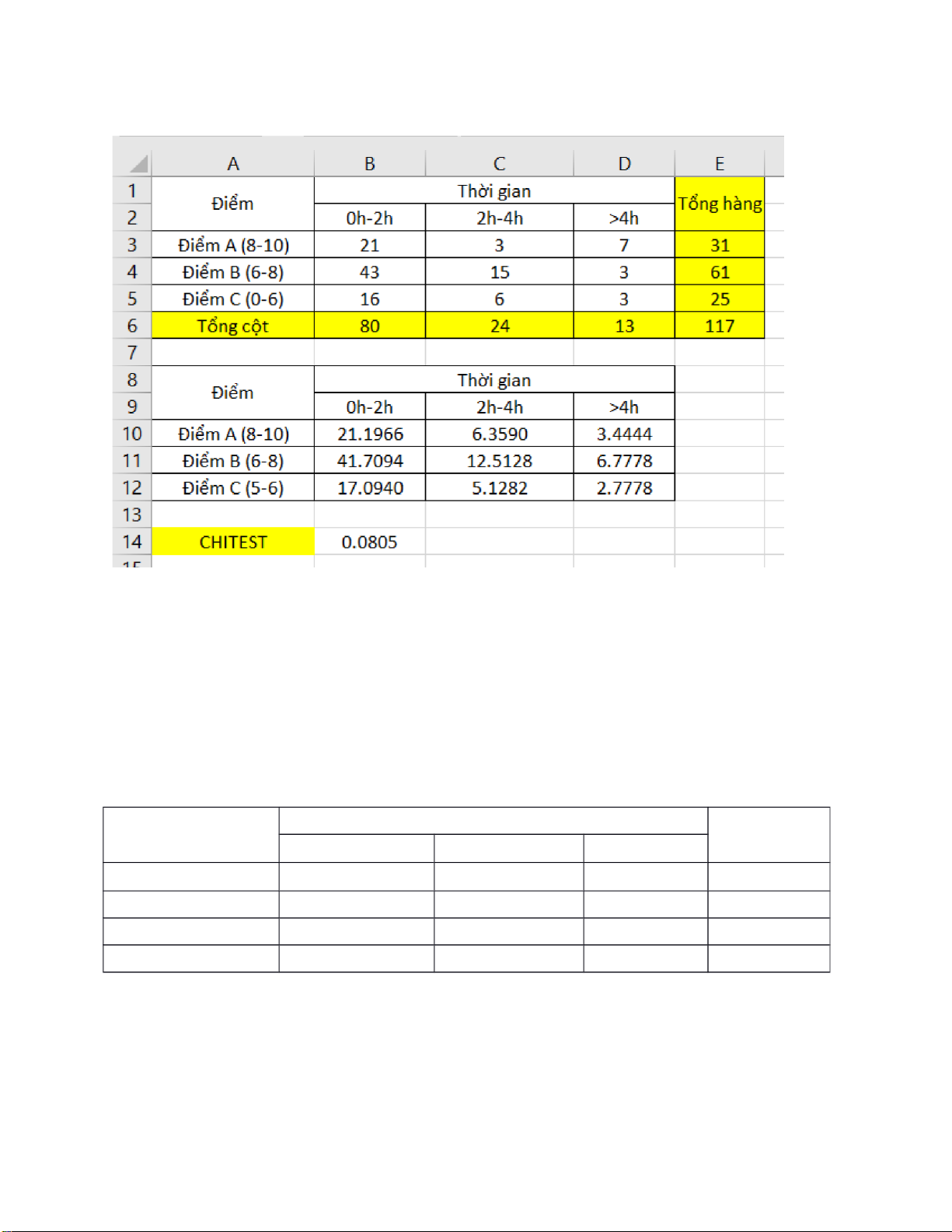
Chọn ô A14 nhập lệnh = CHITEST(B3:D5,B10:D12) lOMoARcPSD| 36991220 Ta được kết quả P: Ta có:
Kết luận: Chưa thể kết luận thời gian chơi game không ảnh hưởng đến điểm số thi
giữa học kỳ của sinh viên D.Tính bằng tay: Thời gian Điểm Tổng hàng 0 h-2h 2 h-4h >4h Điểm A (8-10) 21 3 7 31 Điểm B (6-8) 43 15 3 61 Điểm C (5-6) 16 6 3 25 Tổng cột 80 24 13 117 Với mức ý nghĩa
Gọi X: Điểm số thi giữa học kỳ cùa sinh viên
Gọi Y: Thời gian chơi game của sinh viên lOMoARcPSD| 36991220
Gỉa thiết kiểm định: H : X,Y độc lập 0
Gỉa thiết đối: H : X,Y không độc lập 1 Miền bác bỏ: Tiêu chuẩn kiểm định: 8,3223
⇒ Chưa thể bác bỏ H . Chưa thể kết luận thời gian chơi game không ảnh hưởng đến 0
điểm số thi giữa học kỳ của sinh viên.
Câu 6: Khảo sát hệ số tương quan giữa 2 biến định lượng cụ thể, dự đoán
phương trình đường hồi quy tuyến tính giữa chúng ( có hình vẽ minh họa)
và nhận xét về mối tương quan tuyến tính giữa 2 biến. Bài làm :
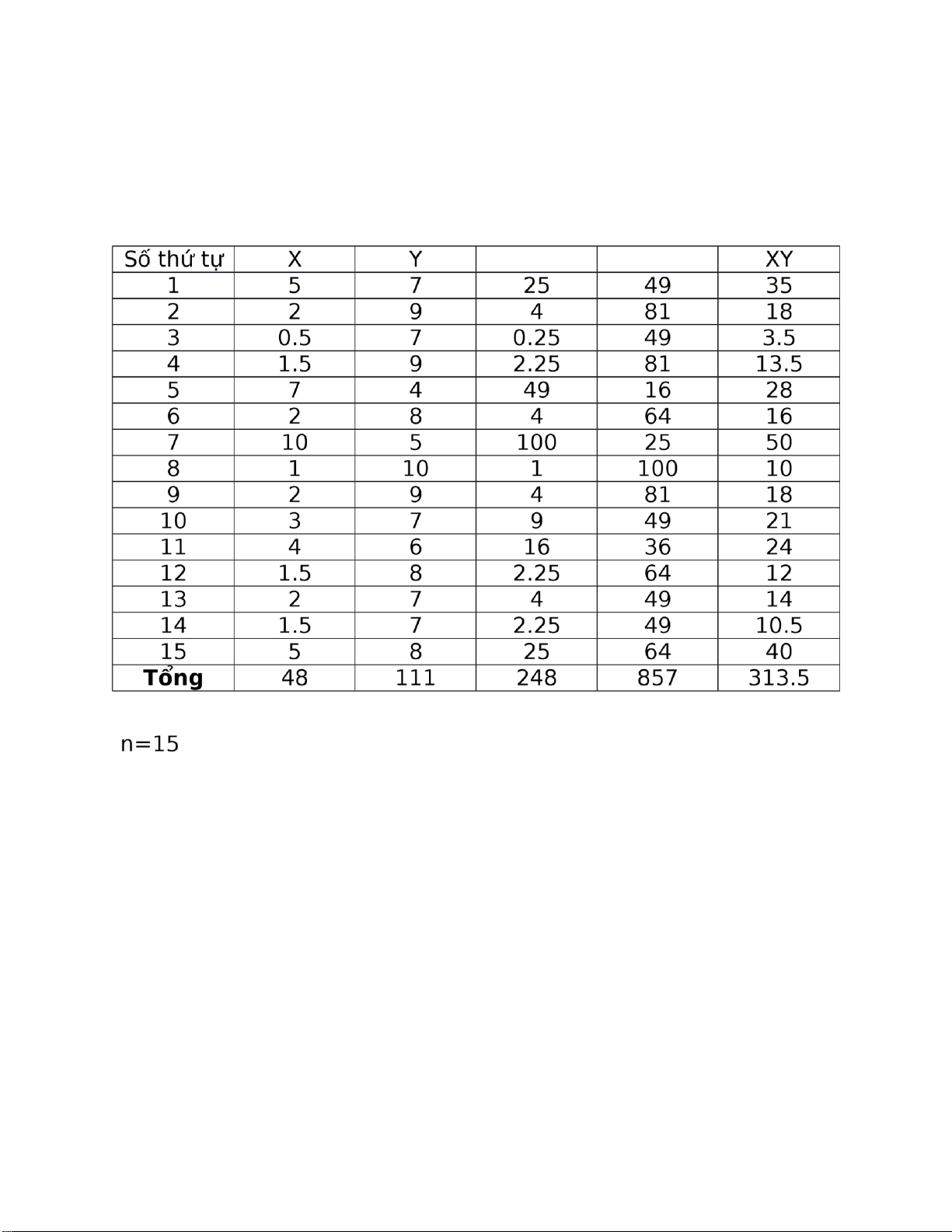
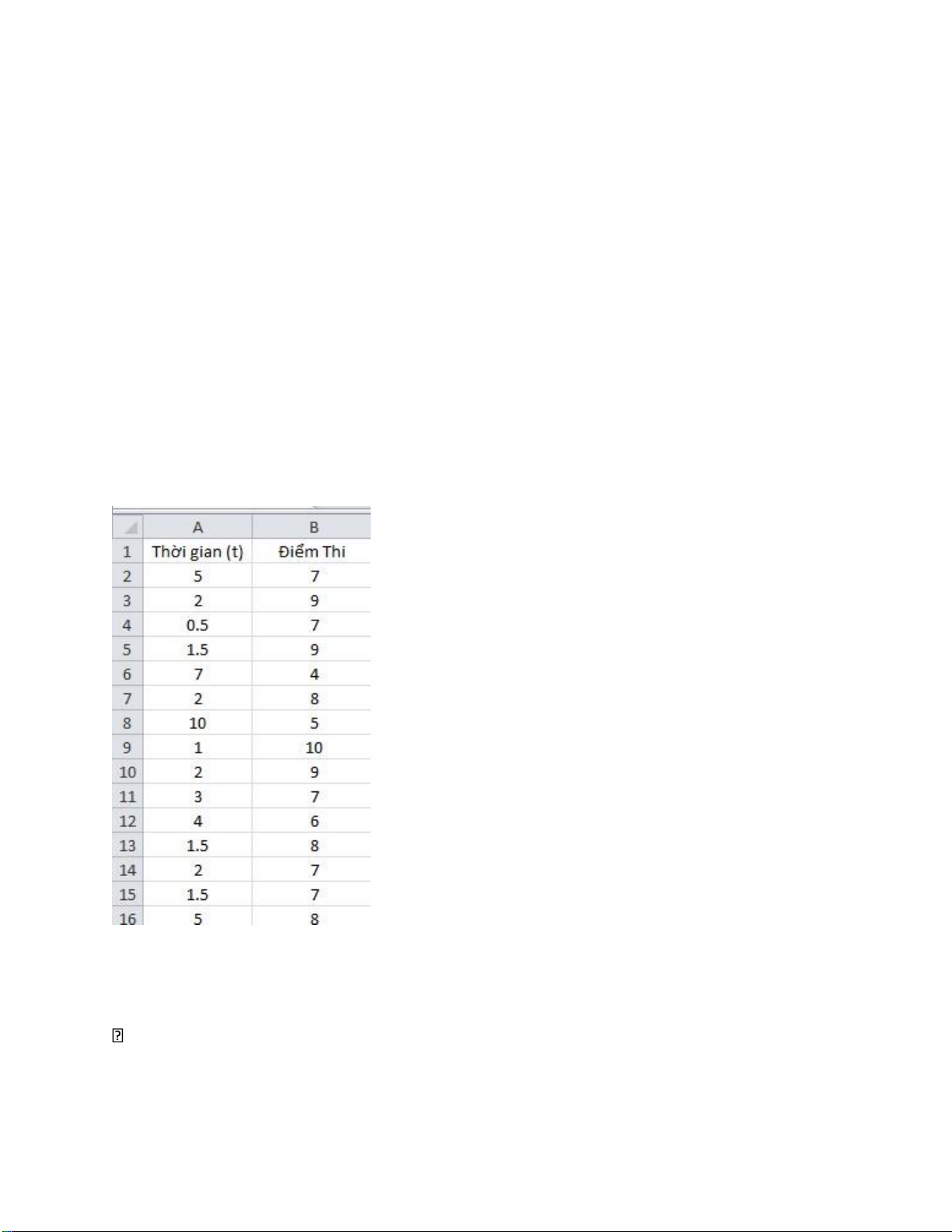
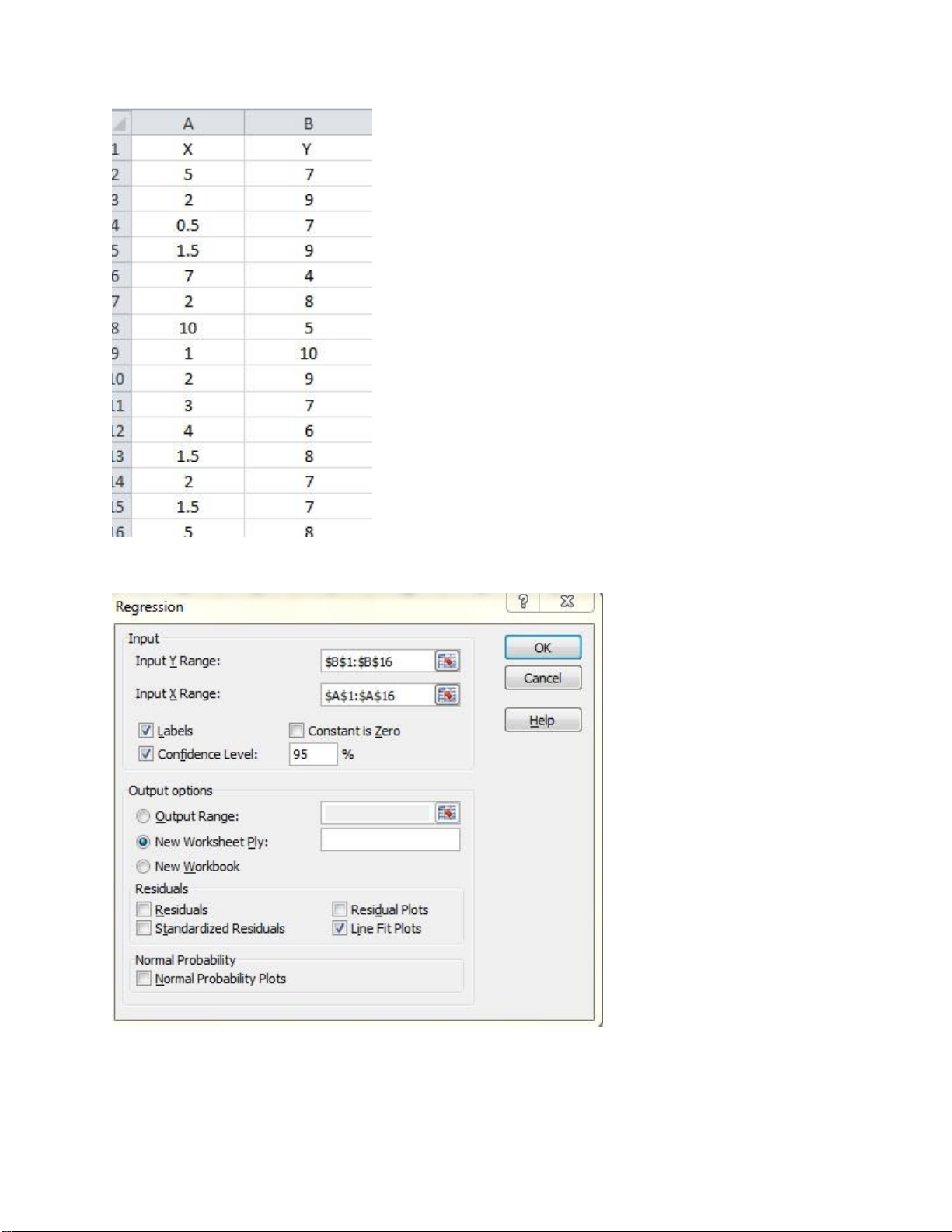
Bảng số liệu về thời gian chơi game trong một ngày và điểm thi giữa kì đạt được : Thời gian 5 2 0.5 1.5 7 2 10 1 2 3 4 1.5 2 1.5 5 ( h ) Điểm giữa kì 7 9 7 9 4 8 5 10 9 7 6 8 7 7 8
B. Cơ sở lý thuyết:
1.Tìm hệ số tương quan giữa X và Y: Hệ số tương quan: R
Các trường hợp sẽ xảy r:
• Nếu R > 0 thì X, Y tương quan thuận.
• Nếu R < 0 thì X, Y tương quan nghịch.
• Nếu R = 0 thì X, Y không tương quan.
• Nếu = 1 thì X,Y có quan hệ hàm bậc nhất. lOMoARcPSD| 36991220
• Nếu → 1 thì X, Y có tương quan chặt (tương quan mạnh).
• Nếu → 0 thì X, Y có tương quan không chặt (tương quan yếu). 2. Tương quan tuyến tính
Giả thiết: X và Y không có tương quan tuyến tính:
3 Ước lượng đường hồi quy tuyến tính Y theo X:
• Phương trình hồi quy tuyến tính: .
• Kiểm định hệ số a, b:
+ Giả thiết: Hệ số hồi quy không có ý nghĩa (=0).
+ : Hệ số hồi quy có ý nghĩa (≠0).
+ Trắc nghiệm t <: chấp nhận .
• Kiểm định phương trình hồi quy:
+ Giả thiết: “Phương trình hồi quy tuyến tính không thích hợp”.
: “Phương trình hồi quy tuyến tính thích hợp”.
+ Trắc nghiệm F <: chấp nhận . lOMoARcPSD| 36991220 C.Phần giải tay:
1.Tìm hệ số tương quan giữa X và Y: , , =, , R = => |R| ->1
Kết luận: Tương quan khá chặt chẽ , tương quan nghịch.
=> Có thể xây dựng phương trình hồi quy tuyến tính. lOMoARcPSD| 36991220 2. Tương quan tuyến tính = = Kết luận Phương trình hồi quy:
D. Thực hiện trên excel
1.Tìm hệ số tương quan giữa X và Y :
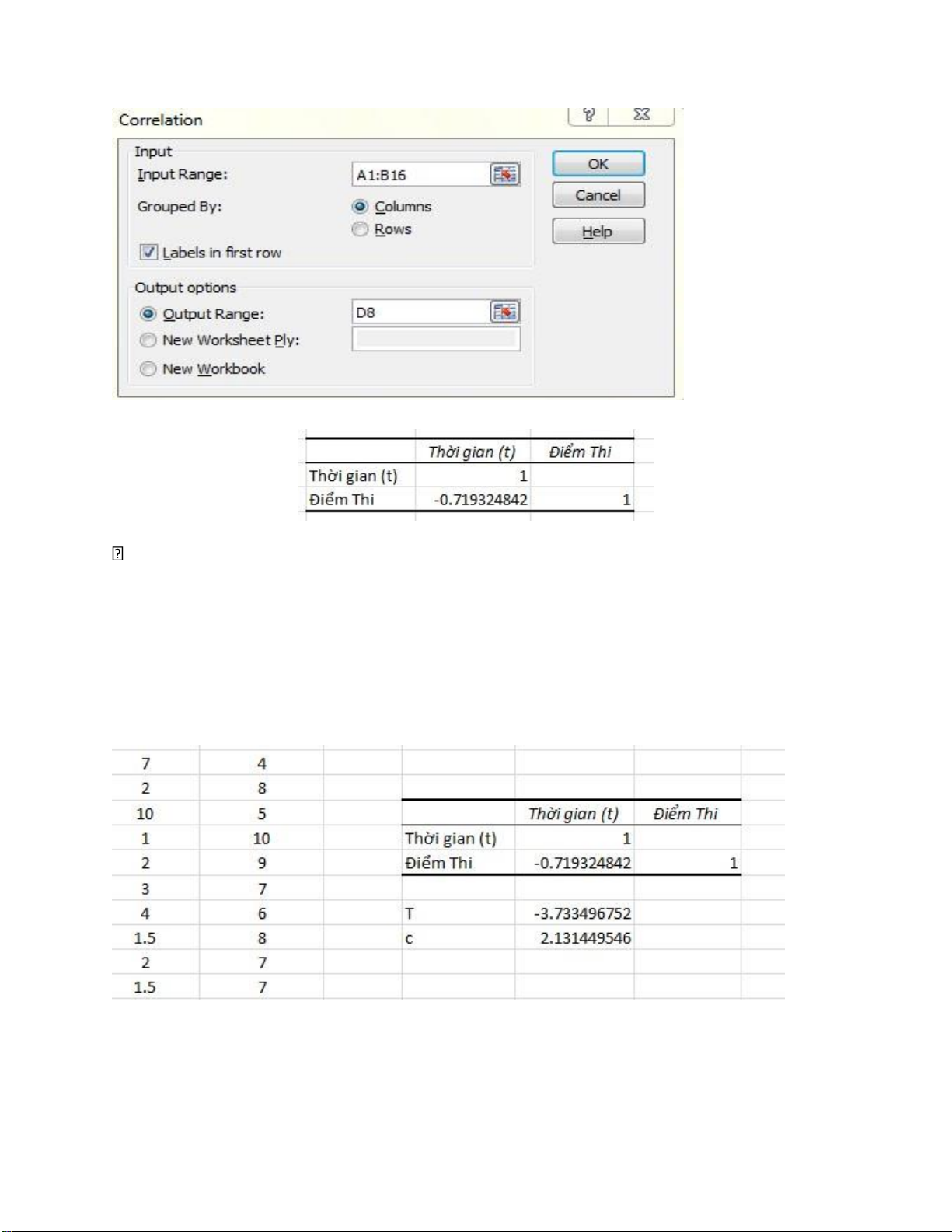
Chọn chức năng Data/Data Analysis/Correlation lOMoARcPSD| 36991220 Kết quả:
Ta có hệ số tương quan là R = chứng tỏ giữa thời gian chơi game trong một ngày
và điểm thi giữa kì có quan hệ khá chặt chẽ và có tương quan nghịch.
2. Tương quan tuyến tính:
Tính T: chọn ô E12 và nhập biểu thức =E10*SQRT(152)/SQRT(1-E10^2).
Tính c: chọn ô E13 và nhập biểu thức =TINV (0.05,15) (c là phân vị mức
α/2=0.025 của phân bố Student với n-2=15 bậc tự do)
Vì nên bác bỏ giả thiết X và Y có tương quan tuyến tính .
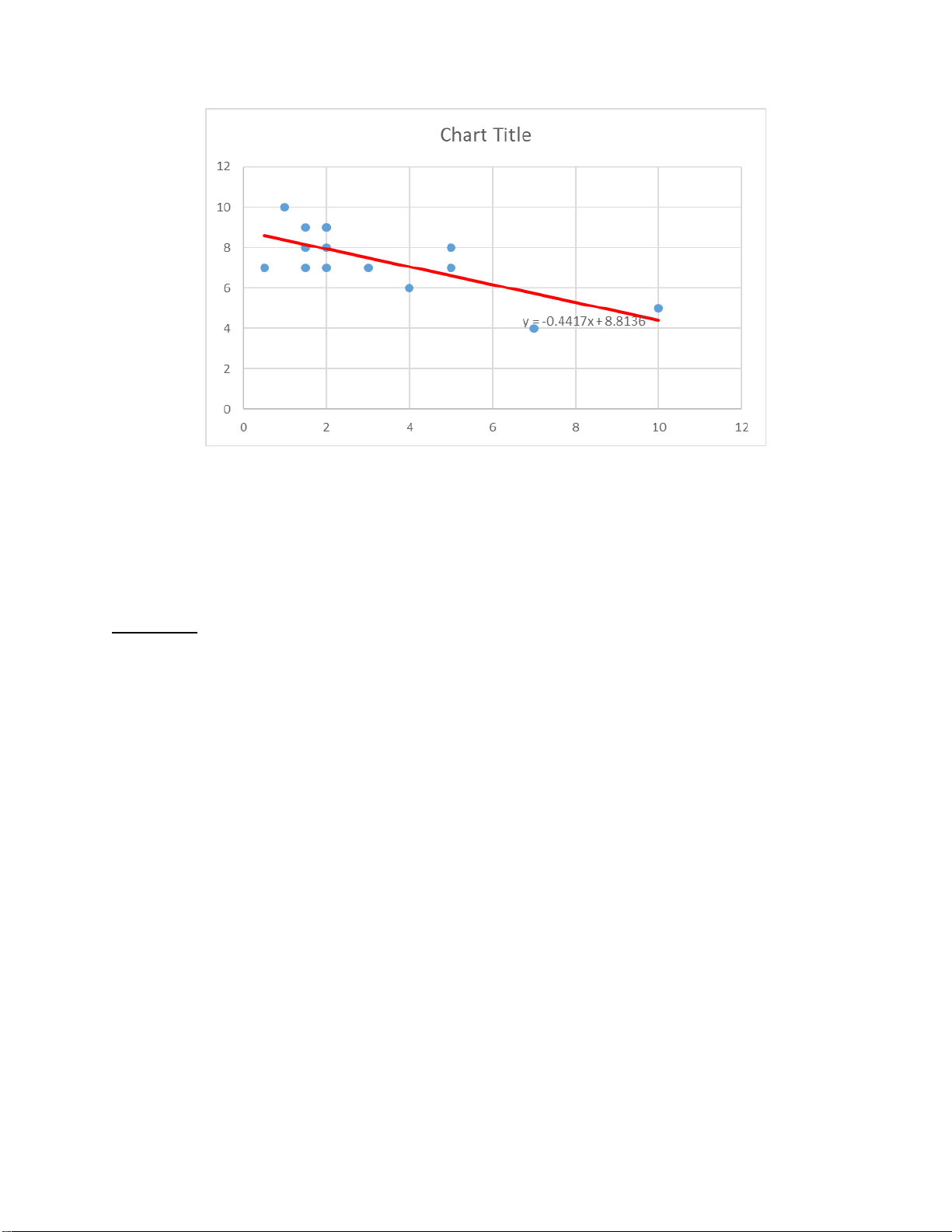
3. Ước lượng đường hồi quy tuyến tính Y theo X:
• Nhập số liệu vào bảng tính: lOMoARcPSD| 36991220
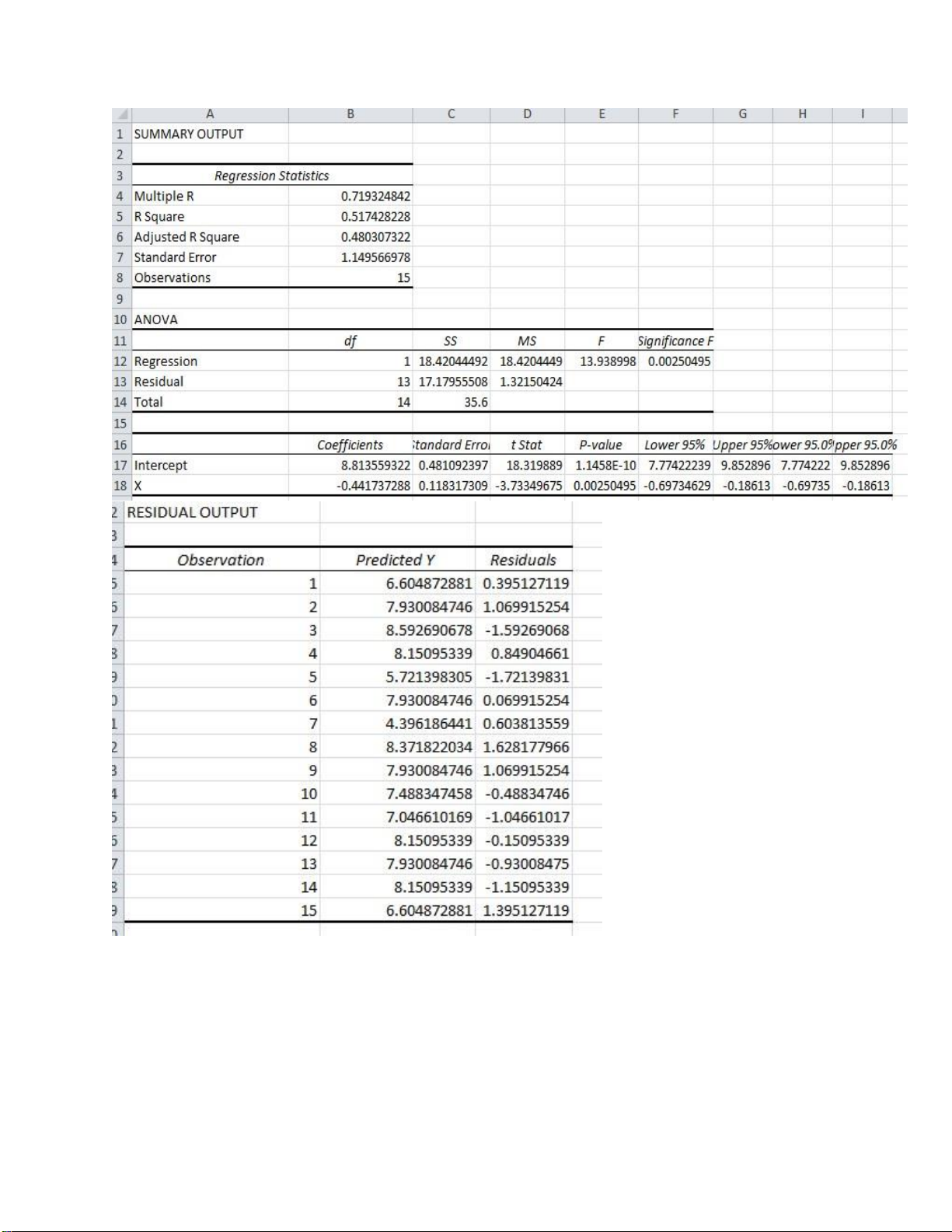
• Dùng chức năng Data/Data Analysis/Regression. Kết quả : lOMoARcPSD| 36991220 lOMoARcPSD| 36991220 Nhận xét: Phương trình hồi quy: Hệ số hồi quy:
1.14582170433113 < 0,05 hệ số tự do có ý nghĩa .
0.00250495379379856 < 0,05 hệ số của x có ý nghĩa. Phương trình hồi quy tuyến tính thích hợp bởi vì P-
value=0.00250495379379856 < 0,05. **Tài liệu tham khảo: lOMoARcPSD| 36991220
Giáo trình Xác suất và Thống kê_Nhà xuất bản Đại học Quốc gia TP.HCM