Bài Tập Lớn Thiết Kế Cơ Cấu Máy Nén Khí | Môn Nguyên lý máy - Trường Cao đẳng Công Nghệ Bách Khoa Hà Nội

lOMoAR cPSD| 59691467
Bài tập lớn Nguyên Lý Máy Đề số: 7
I. Nhiệm vụ thiết kế: Thiết kế nguyên lý cơ cấu máy nén khí kiểu piston – xylanh.
Bảng số liệu kèm theo
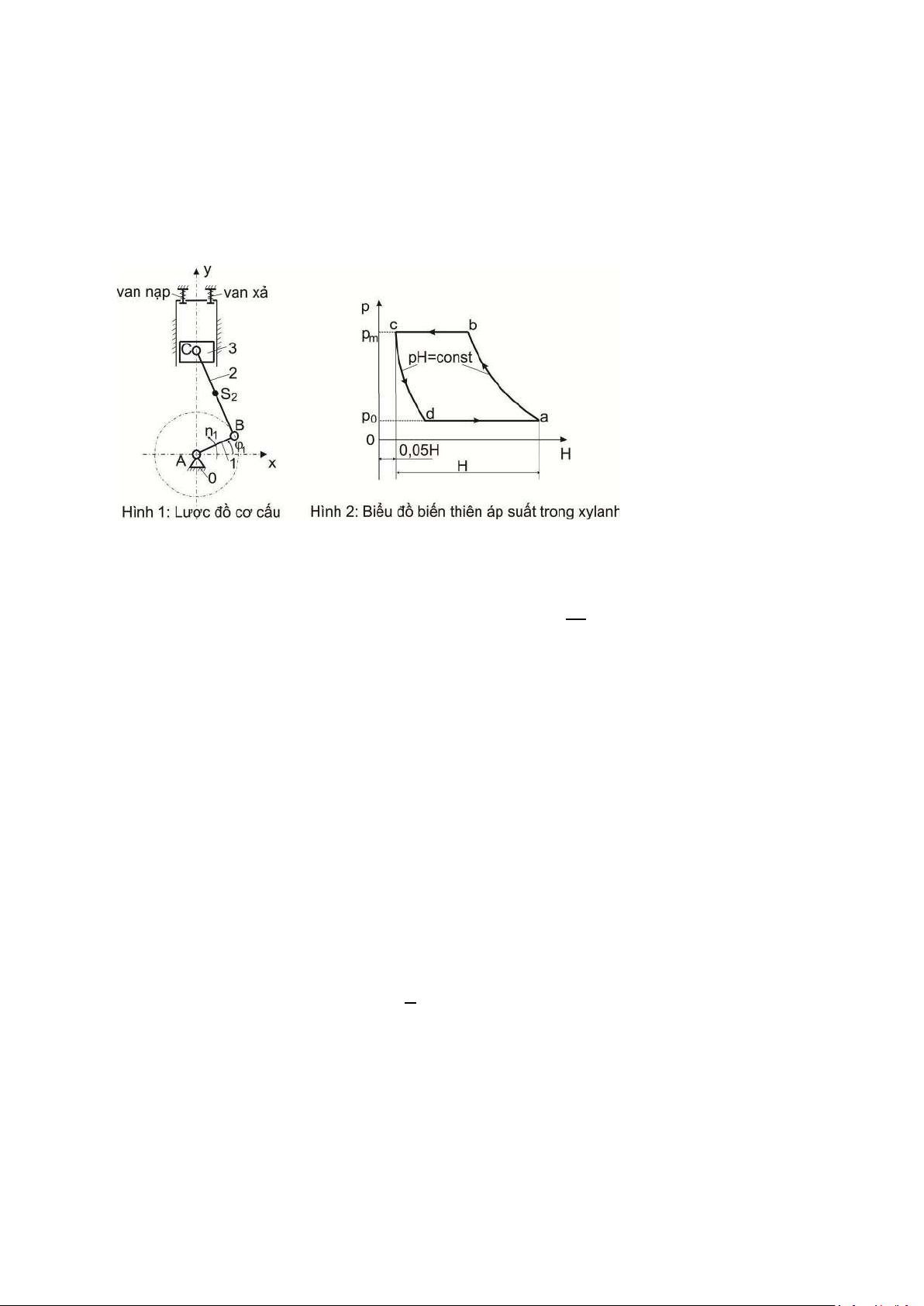
1. Hành trình piston: H = 120 (mm) BC
2. Tỷ lệ chiều dài thanh truyền khúc khuỷu: λ = = 4 AB
3. Vận tốc quay trục khuỷu: n1 = 1350 (vg/ph)
4. Gia tốc góc trục khuỷu: Ɛ1= 0 ( rad/s2¿
5. Khối lượng thanh truyền 2: m2=4 (kg )
6. Momen quán tính thanh truyền 2: Js2 = 0,12 (kgm2¿
7. Trọng tâm S2 là trung điểm của BC:
8. Khốilượng piston3:m3=¿1.5 (kg)
9. Đường kính piston 3: d3=120 (mm ) N
10. Áp suất khí quyển: po=0.1( 2) mm
11. Áp suất lớn nhất trong xy-lanh: pm=0,45¿)
Các góc φ1 = { 0 ; 12 ; 24 ; 36 ; 48 ; 60 }. lOMoAR cPSD| 59691467
II. Nội dung và yêu cầu bài tập lớn.
1. Bằng phương pháp giải tích tính vị trí, vận tốc, và gia tốc của cơ cấu ứng với
6 vị trí khâu dẫn - Tính toán các thông số chưa biết:
H = lACmax−lACmin=¿( lAB+lBC¿−(lBC−lAB) = 2lAB = 120
=> l AB=60 (mm )=l1
Mà: λ = BCAB = 4 => lBC=240( mm)=l2 n1=1350(
phvg )=141,37( rads ). a) Bài toán vị trí:
Phương trình vecto của lược đồ động: 4 ∑ li e⃗i i=1
=> l1e⃗1+l2e⃗2 + l3e⃗3 = 0
=> l1e⃗1 e⃗3 + l2e⃗2e⃗3 + l3e⃗3e⃗3 = 0 =>
l3=−l1cos(φ1−φ3)−l2cos ⁡¿) b) Bài toán vận tốc:
- Đạo hàm theo t phương trình vecto lược đồ động: d 3 3 dli d e⃗i ∑ ∑
dt = lie⃗i = = { dt e⃗i + li dt } = 0 i 1 i 1
Đặt: dli = l˙i Mà: d ⃗ei = dφi n⃗i = win⃗i dt dt dt lOMoAR cPSD| 59691467
=> Phương trình: {l˙ie⃗i + wili n⃗i} = 0 - Các
phương trình chiếu vận tốc: 3
∑{l˙i e⃗i + wili n⃗i} e⃗o=0 1 3
∑{l˙i e⃗i + wili n⃗i} n⃗o = 0 1
=> l˙3cosφ3 - w2l2sinφ2 = w1l1sinφ1 l˙3sinφ3 +
w2l2cosφ2 = −w1l1cosφ1
Ta có: l˙3 = ∆o= cosφ3 -l2sinφ2
Với sinφ3 l2cosφ2
∆2∆1= w1l1sinφ1 −l2sinφ2 w2= ∆0
−w1l1cosφ1 l2cosφ2
∆2 = cosφ3 wil1sinφ1 sinφ3 -
w1l1cosφ1
=> ∆0= l2cos(φ3 - φ1)
∆1= l1l2w1sin(φ1-φ2)
∆3= −l1w1cos(φ3-φ1) c) Bài toán gia tốc
- Đạo hàm t theo phương trình vecto vận tốc: 3
dtd ∑1 {l˙i e⃗i + wili n⃗i} = 0 lOMoAR cPSD| 59691467 Đặt: d ¨ d n⃗ ε i
i = dt wi ; l i = dt l˙i Mà: ddt = -wi ei => Phương trình: 3
∑{−w2i li e⃗i + εili n⃗i + 2wil˙i n⃗i + l¨i e⃗i } = 0 1
- Phương trình hình chiếu của gia tốc 3
∑{−w2i li e⃗i + εili n⃗i + 2wil˙i ⃗ni + l¨i e⃗i }e⃗o = 0 1
w2i li e⃗i + εili n⃗i + 2wil˙i n⃗i + l¨i e⃗i }n⃗o = 0 1
i - 2wil˙isinφi + l¨icosφi} = 0 3
∑ ¿−w2i lisin φi¿ + εili cosφi + 2wil˙icosφi + l¨isinφi} = 0 1
=> ε2l2sin φ2 - l¨3cosφ3 = b1
ε2l2cosφ2 + l¨3sinφ3 = b2
Với: b1= −w1l1cosφ1 - w22l2cosφ2 - ε1l1sin φ1
b2 = w1l1sin φ1 + w22l2sin φ2 - ε1l1cos φ1 ∆1
=> ε2 = ∆0 ∆2 l¨3 = ∆0
Với: ∆0 = l2sin φ2 (-cosφ3) = l2cos⁡(φ2−φ3)
l2cosφ2 sinφ3 lOMoAR cPSD| 59691467
∆1 = b1 (-cosφ3) = b1sinφ3+b2cosφ3 b2 sinφ3
∆3 = l2sinb2 b1 = l2(b2sinφ2 - b1cosφ2) l2cosφ2 b2
Với các thông số φ1 = { 0; 12; 24; 32; 48; 60} φ1( độ ) l3 (mm) mm a3(mm/s2¿ w2(rad/s) ε2(rad/s2) v3( s ) 0 232,38 8482,2 309613, 0 - 68 5160,22 8 12 245,19 8741.6 32276,6 3 - - 7,57819 5025,72 3 4 24 258,06 8558,2 - - - 284493, 14,7653 4637,17 9 3 7 36 270,31 7891,9 - - - 614748, 21,2121 4034,52 1 9 3 48 281,21 6745,2 - - - 927744, 26,6399 3270,59 3 8 1 60 290,08 5166,6 - - - 1193149 30,8494 2398,03 6 2
2. Bằng phương pháp họa đồ vecto, tính và vẽ họa đồ vị trí, vận tốc và gia tốc của cơ cấu. * Chọn φ1 = 0° a) Bài toán vị trí lAB 60 = 20 (mm/cm) lOMoAR cPSD| 59691467
Tacó :l AB=60(mm)Chọntỷ lệ xích μl= AB = 3 lBC = 240 (mm) => BC = 12 (cm)
Từ : φ1 = 0° ta dựng đoạn AB dài 3cm hợp với Ox 1 góc 0° => điểm B AB = 3 cm
Từ B ta dựng đường tròn tâm B bán kính R = 12(cm) . Từ A ta dựng 1 đường
thẳng vuông góc với Ox, đường thẳng này cắt đường tròn tâm B tại C => điểm C
=> Ta dựng được hình 1
- Ta đo được đoạn AC = 11,7 (cm) => lAC = 11,7 . 20 = 234 (mm)
- Ta có S2 là trung điểm BC => S2B = S2C= 6 (cm) => lS = l 2B
S2C= 6.20 = 120 (mm) 60 xS2 xS = 30 (mm) 2 -Ta có: 120 = 240 => b) Bài toán vận tốc
Theo đề ta có: ω1 = 45π = 141,27 ( rad/s )
+) Vận tốc tại điểm B:
⃗vB = ⃗v = ⃗v + ⃗v 2 B1 A1 B1 A1
mà: ⃗v A = 0 => ⃗v = ⃗v có phương vuông góc với AB 1 B1 B1 A1
chiều theo chiều ω1
độ lớn = ω1.lAB = 8482,2 (mm/s) lOMoAR cPSD| 59691467
+) Vận tốc tại điểm C
⃗vC = ⃗v = ⃗v + ⃗v 3 C2 B2 C2B2
⃗vC = ⃗v phương song song AC 3 C2 chiều từ A → C độ lớn = ?
⃗vB phương vuông góc AB 2
chiều theo chiều ω1 độ lớn = 8482,2 (mm/s)
⃗vC phương vuông góc BC 2B2
chiều = ? độ lớn = ω2.lBC +) Vận tốc điểm S:
⃗vS = ⃗v + ⃗v 2 B2 S2B2
⃗vB phương vuông góc AB 2
chiều theo chiều ω1 độ lớn = 8482,2 (mm/s)
⃗vS phương vuông góc BC chiều = 2C2
? độ lớn = ω2lBS = 12 ω2lBC = 12 vB 2C2
- Lấy điểm P bất kỳ làm gốc của họa đồ , dựng ⃗PB vuông góc AB theo chiều ω1 PB 8,482 cm
Ta chọn tỷ lệ xích: μv = vB = 2
8482,2 = 0,001 ( mm/ s )
- Từ B ta dựng đường thẳng ∆ vuông góc với BC, từ P dựng đường ∆1 song
song với AC, hai đường giao nhau tại điểm C, khi đó ta được ⃗PC biểu diễn ⃗vC 2
và ⃗BC biểu diễn ⃗vB . 2C2
Từ đó ta dựng họa đồ vận tốc như hình 2
- Ta thấy PC = PB = 8,842 (cm) lOMoAR cPSD| 59691467
=> vC = v = PC.μ 2 C3
v = 8482 (mm/s)
- Ta thấy: BC = 0 => ⃗vC = 0 => ω 2B2 2 = 0 ( rad/s)
- Ta đo được: PS = PB = PC => vS = 8482 (mm/s) 2 c) Bài toán gia tốc. - Gia tốc tại điểm B:
a⃗B = a⃗ = ⃗a + ⃗an + ⃗at 2 B1 A1 B1 A1 B1 A1 ⃗aA = 0 1 ⃗a t B =0 do ε 1 A1 1 = 0 ⃗a n B
có phương song song với AB chiều từ 1 A1
B→A độ lớn = ω21 l AB = 1199128,614 (mm/s2) - Gia tốc tại điểm C: a⃗ t
C = a⃗ = a⃗ + ⃗an + ⃗a 3 C2 B2 C2B2 C 2B2
a⃗C = a⃗ phương song song AC 3 C2 chiều = ? độ lớn = ?
a⃗B phương song song với AB chiều từ B→A 2
độ lớn = ω21 lAB = 1199128,614 (mm/s2)
⃗anC phương song song BC chiều 2B2
từ C →B độ lớn = ω22 lBC = 0 ( mm/s2)
⃗a t C phương vuông góc BC Chiều 2B2 = ?
Độ lớn = ε2.lBC - Gia tốc tại điểm S lOMoAR cPSD| 59691467
a⃗S = a⃗ + ⃗an + ⃗at 2 B2 S2B2 S2B2
a⃗B phương song song với AB chiều từ B→A 2
độ lớn = ω21 lAB = 1199128,614 (mm/s2)
⃗anS phương song song BS 2B2
chiều từ S→B độ lớn =ω22.lSB = 0 (mm/s2)
⃗atS phương vuông góc với BS 2B2 Chiều = ?
Độ lớn = ε2.lSB = ?
- Ta lấy điểm π làm gốc họa đồ
- Từ π ta dựng ⃗πB ' song song với AB , chiều từ B→ A , có độ lớn =
6 (cm), biểu diễn cho a⃗B 2 πB' 6 −6 ( cm 2 )
=> μa = aB = 2 1199128,614 = 5.10 mm/ s
- Từ B’ ta dựng ⃗B' B'' song song với BC, chiều từ B→C với B' B' ' =
0, biểu diễn cho ⃗a n C 2B2
- Từ B’’ ta dựng đường thẳng ∆2 vuông góc CB - Từ π ta dựng đường thẳng ∆3
song song với AC - 2 đường thẳng ∆3và ∆2 cắt nhau tại C’.
- ⃗πC ' biểu diễn cho a⃗C . 2
- Ta dựng họa đồ gia tốc như hình 3.
- Từ họa đồ ta đo được: B’’C’ = 6,2 (cm) => ⃗atC = = 2B2 5.10 1240000 (mm/s2) => ε2 = atC = 5166,67 ( rad/ 2B2 s2) lBC lOMoAR cPSD| 59691467
- Từ họa đồ ta đo được: πC' = 1,6 (cm) => a⃗C =¿ = 320000 2 5.10 (mm/s2).
- Do S2 là trung điểm đoạn BC, ta lấy S’ là trung điểm đoạn B”C’ từ đó ta có ⃗πS'
biểu diễn cho a⃗S . - Từ họa đồ ta đo được: πS' = 3,1 (cm) => a = = 2 S2 620000 5.10 (mm/s2). d) So sánh 2 phương pháp Các đại l3(mm) vC(mm/s) aC (mm/ 3 s2¿ ω2(rad/s) ε2(rad/s2¿ lượng Giải tích 232,38 8482,2 309613,6 0 -5160,228 8 Họa đồ 234 8482 320000 0 5166,67 Sai số 1,00697 0,99997 1,033546 0 1,001248 134 64 06 394
- Nhận xét: + Kết quả tính giữa 2 phương pháp gần như xấp xỉ và tương
đương nhau, sai số giữa 2 phương pháp rất nhỏ.
+ Sai số do quá trình làm tròn tính toán và đo đạc khi vẽ họa đồ bằng tay.
IV. Tính áp lực khớp động và momen cân bằng về khâu dẫn * Chọn φ1 = 0°. lOMoAR cPSD| 59691467 -Ta có: Pq = m
= 1,5 . 309613,68 = 464,42 (N) 3 3ac3 Pq = m = 4 . 620000 = 2480 (N) 2 2aS2 M q = J ε 2
s2 2 = 0,12 . 5160,228 = 619,2 (N)
G2 = m2.g = 4 . 10 = 40 (N)
G3 = m3.g= 1,5 . 10 = 15 (N)
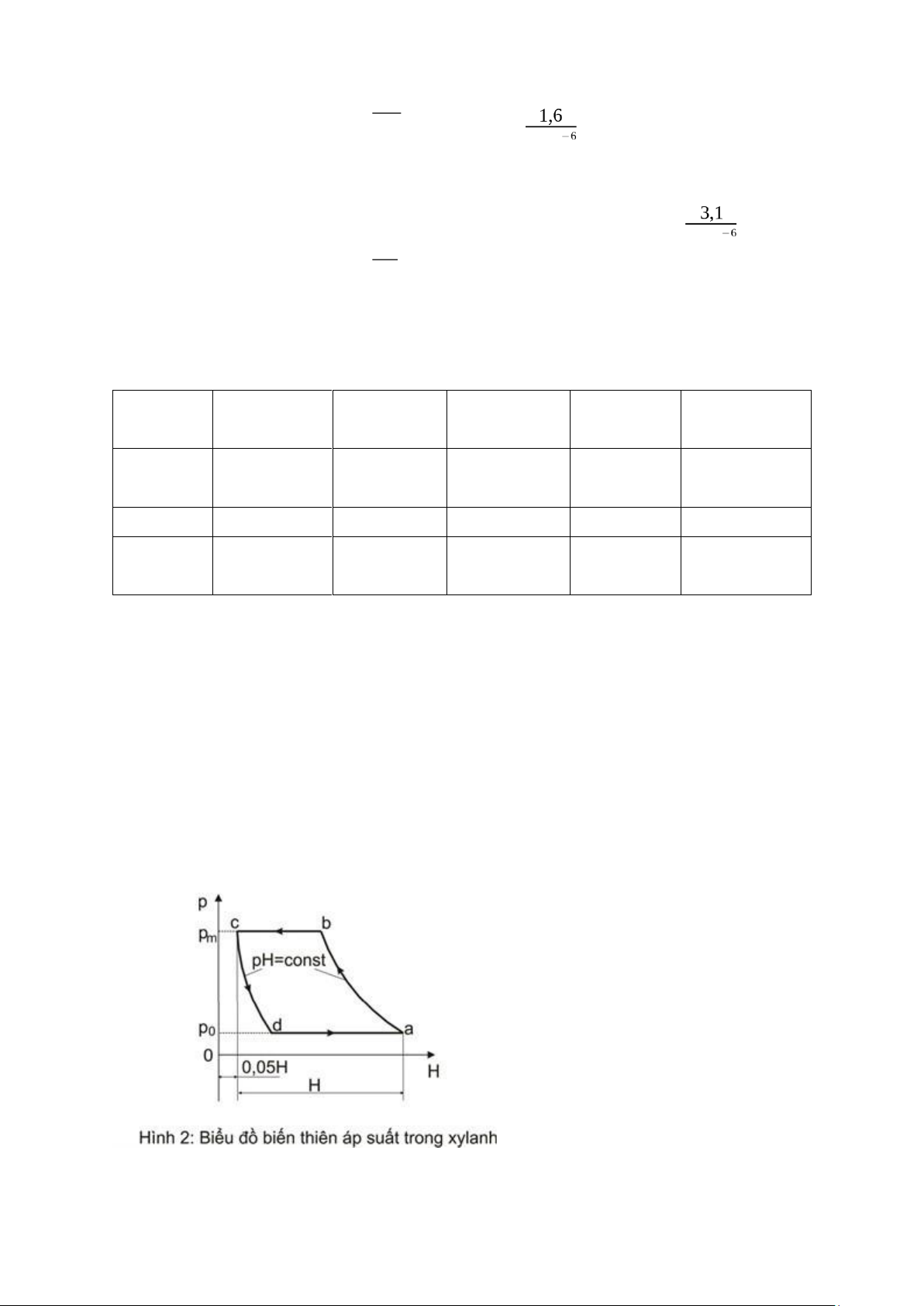
- Dựa vào đồ thị ta xét hành trình H φ1=0° = 1,05H - (l AC - l ACmin) = 1,05.120 – (232,38 – 180) = 73,62 (mm) po1,05 H 0,1.1,05.120
Ta có: pm Hb = po Ha => Hb = pm = 0,45 = 28 (mm) 1= pm H b 2)
Ta có: pm Hb = p3 Hφ 0° => p3 = H φ1=0° = 58,38 = 0.17 (N/mm 2 2
=>P3 = p3A = p3.π d = 0,17.π .120 = 1922,65 (N) 4 4
- Ta vẽ các lực của khâu 2 và khâu 3 như hình 4
- Phương trình cân bằng lực cho khâu 2 và khâu 3: ⃗ ⃗ ⃗
N 12 + ⃗P3 + ⃗Pq3 + G 3 + ⃗Pq2+ G 2 + ⃗N 43 = 0 ⃗ ⃗ ⃗
=> N n12 + ⃗N t12 + ⃗P3 + ⃗Pq3 + G 3 + ⃗Pq2+ G 2 + ⃗N43 = 0
- Xét momen tại điểm C của khâu 2:
= 0 → −Nt12.lBC - G2.hG + P .l + M = 0 2 q2 Pq2 q2 => Nt12 = −G2.hG =
2+Pq2.hPq + M −m +J 2 q2
2g.hG2+m2aS2 .hPq2 s2. ε2 lBC lBC lOMoAR cPSD| 59691467 = = 3653,685 (N)
=> Nt12đúng như giả thiết hình vẽ
- Chọn điểm a bất kỳ là gốc họa đồ
- Từ a ta dựng ⃗ab vuông góc BC, ab = 7,2 (cm) biểu diễn ⃗N t12
=> Chọn tỉ lệ xích: μP =
= 1,97.10−3 ( cm / N ) - Từ b ta dựng ⃗bc
vuông góc Ox, chiều hướng xuống dưới biểu diễn cho ⃗P3,
P3=1922,65(N),vậy ta vẽ bc=1922,65.1,97.10−3 = 3,8 (cm)
- Từ c ta dựng ⃗cd vuông góc Ox, chiều hướng lên biểu diễn cho ⃗Pq , 3 Pq = m
= 464,42 (N) , vậy ta vẽ cd = 464,52.1,97.10−3= 0.9 (cm) 3 3.aC3
- Từ d ta dựng ⃗de vuông góc Ox, chiều hướng xuống biểu diễn cho G⃗3 ,
G3 = g.m3= 15 (N) , vậy ta vẽ de = 15. 1,97.10−3 = 0,03 (cm)
- Từ e ta dựng ⃗ef có phương trùng với a⃗S và ngược chiều a⃗ biểu diễn cho 2 S2
⃗Pq , vậy ta vẽ ef = 2480. 1,97.10−3 = 4,9 (cm) - Từ f ta dựng ⃗fg vuông góc Ox, 2
chiều hướng xuống dưới biểu diễn cho G⃗2 ,
Vậy ta vẽ fg = 40. 1,97.10−3= 0,08 (cm)
- Từ g ta dựng đường thẳng ∆4 song song với Ox
- Từ a ta dựng đường thẳng ∆5 có phương vuông góc với ⃗N t12, 2 đường thẳng
∆4và ∆5 cắt nhau tại h thì ⃗ha biểu diễn cho ⃗N n12 .
- Ta vẽ họa đồ như hình 5
- Tổng hợp lực theo quy tắc hình bình hành của ⃗N n12 và ⃗N t12 ta được ⃗N 12
được biểu diễn trên ⃗hb.
- Ta đo được hb = 10 (cm) hb 10
=> N12 = μp = 1,97.10−3 = 5076,14 (N)
- Từ họa đồ lực ta thấy ⃗gh biểu diễn cho ⃗N43 và gh = 4,4 (cm) lOMoAR cPSD| 59691467 gh 4,4
=> N43 = μ p = 1,97.10−3 = 2233,5 (N)
- Gọi x là khoảng cách từ ⃗N 43 đến điểm C3.
- Xét momen tại điểm C3 : ∑ M3(C )= 0 => N43 . x = 0 => x = 0 - Ta vẽ hình 6
- Phương trình cân bằng lực cho khâu 3: ⃗ ⃗ Pq + ⃗P 3
3 + ⃗N 43 + ⃗N 23 + G 3 = 0 → ⃗Pq + 3
⃗P3 + ⃗N 43 + G⃗3 + ⃗N n23+ ⃗N t23= 0 (*)
+) chiếu phương trình (*) lên phương x:
⃗N43 = -⃗N t23 => Nt23 = 2233,5 (N)
+) chiếu phương trình (*) lên phương y ⃗ ⃗
N n23 = ⃗Pq - ⃗P 3
3 - G 3 => N n23 = 464,42 – 1922,65 – 15 = -1473,23 (N)
=> Chiều của ⃗N23 ngược chiều hình 6 = 2675,62 (N)
- Ta vẽ như hình 7 có μl = 0,05 ( cm/mm) => AB = 3 (cm)
- Ta đo được h21=¿ 1,2 (cm) => h21= 24 (mm) = 0,024 (m) - Phương trình cân
bằng lực cho khâu dẫn :
∑ M1( A) = M cb - N21.h21 = 0
=> Mcb = N21.h21= 5076,14 . 0,024 = 121,83 (Nm)