

Preview text:
CHƯƠNG 1: CẤU TRÚC VÀ XẾP LOẠI CƠ CẤU
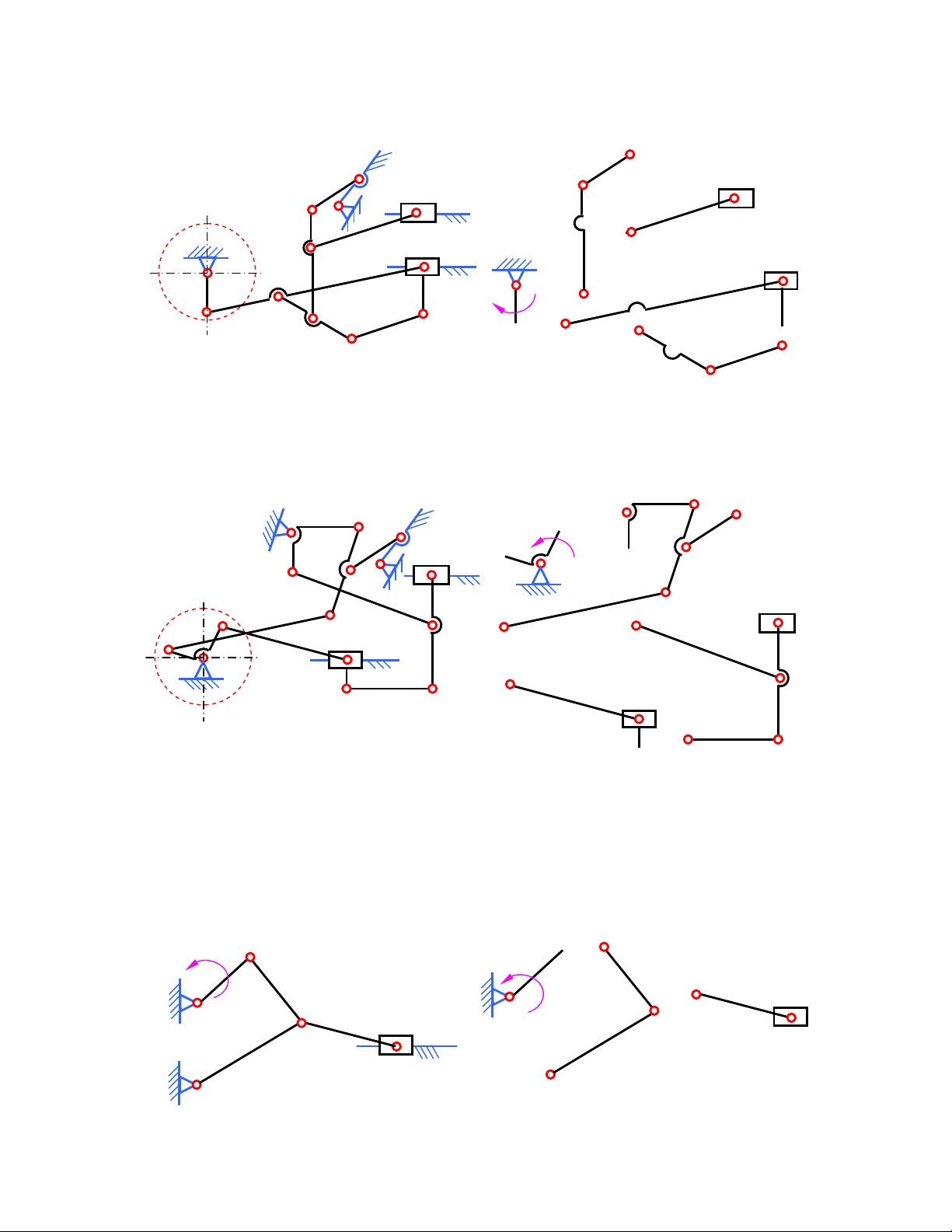
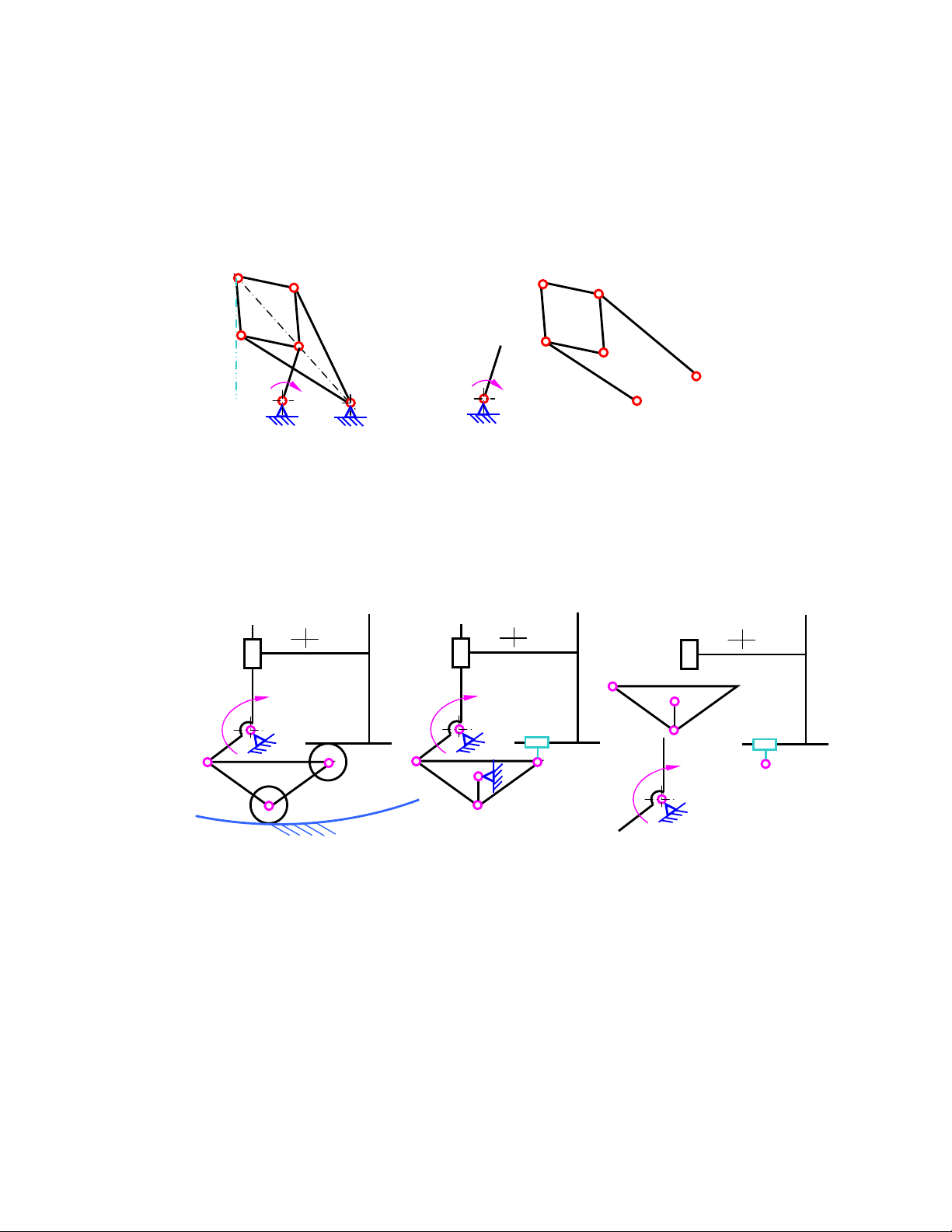
1) Tính bậc tự do và xếp loại cơ cấu phối hơi ñầu máy xe lửa trên hình 1.1a và 1.1b. K 9 K H 9 I H I O 2 G 8 8 7 G 7 6 B O1 6 2 D B D 1 2 3 E A 1 E A 3 C C A 4 5 F D E C Hình 1.1a Hình 1.1a.a 4 5 F
Bậc tự do cơ cấu ñược tính theo công thức:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 9 – (2 * 13 + 0) + 0 – 0 = 1
Chọn khâu 1 là khâu dẫn, nhóm tĩnh ñinh ñược tách ra bao gồm 4 nhóm loại 2 (6,9; 7,8; 2,3;
4,5) như hình 1.1a.a. ðây là cơ cấu loại 2.
Công thức cấu tạo cơ cấu : 1 = 1 + 0 + 0 + 0 + 0 H H A O K 2 9 10 8 O 10 K 2 9 M I 8 6 1 G I F G O3 O1 L 11 5 A L 11 7 6 M E G F M 1 7 2 B 5 O1 3 E D 2 C 4 A B C 4 3 D Hình 1.1b Hình 1.1b.b
Bậc tự do cơ cấu ñược tính theo công thức:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 11 – (2 * 16 + 0) + 0 – 0 = 1
Chọn khâu 1 là khâu dẫn, nhóm tĩnh ñinh ñược tách ra bao gồm 1 nhóm loại 2 (2,3) và 2
nhóm loại 3 (4,5,6,7; 8,9,10,11) như hình 1.1b.b. ðây là cơ cấu loại 3.
Công thức cấu tạo cơ cấu : 1 = 1 + 0 + 0 + 0
2) Tính bậc tự do và cơ cấu máy dập cơ khí (hình 1.2a) và máy ép thuỷ ñộng (hình 1.2b) A A 1 1 A 2 B 2 4 5 B O O 1 1 4 5 3 B 3 C O2 O2 C Hình 1.2a Hình 1.2a.a
Bậc tự do cơ cấu ñược tính theo công thức:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 5 – (2 * 7 + 0) + 0 – 0 = 1
Chọn khâu 1 là khâu dẫn, nhóm tĩnh ñinh ñược tách ra bao gồm 2 nhóm loại 2 (2,3; 4,5) như hình
1.2a.a. ðây là cơ cấu loại 2.
Công thức cấu tạo cơ cấu : 1 = 1 + 0 + 0 C C 3 D 3 D 4 4 B 5 B 5 2 O 2 O 2 2 A A E E A O1 1 O1 1 Hình 1.2b Hình 1.2bb
Bậc tự do cơ cấu ñược tính theo công thức:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 5 – (2 * 7 + 0) + 0 – 0 = 1
Chọn khâu 1 là khâu dẫn, khi tách nhóm ta chỉ có 1 nhóm tĩnh ñinh loại 3 (2,3,4,5 như hình
1.1bb. ðây là cơ cấu loại 3.
Công thức cấu tạo cơ cấu : 1 = 1 + 0
3) Tính bậc tự do và xếp loại cơ cấu ñộng cơ diesel (hình 1.3a) E B 3 B 5 3 E O3 5 2 C E 2 O3 6 C 4 C F 6 7 F 4 7 A A D A 1 1 O1 O 1 Hình 1.3a Hình 1.3b
Bậc tự do cơ cấu ñược tính theo công thức:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 7 – (2 * 10 + 0) + 0 – 0 = 1
Chọn khâu 1 là khâu dẫn, khi tách nhóm ta chỉ có 3 nhóm tĩnh ñinh loại 2 (2,3; 4,5; 6,7) như
hình 1.3b. ðây là cơ cấu loại 2.
Công thức cấu tạo cơ cấu : 1 = 1 + 0 + 0 + 0
4) Tính bậc tự do và xếp loại cơ cấu bơm oxy (hình 1.4a) B B 3 3 O O C C G G 2 2 4 5 4 5 H D A A D E E 2’ 6 6 K O 1 O O 1 O Hình 1.4a Hình 1.4b B B 3
Bậc tự do cơ cấu ñược tính theo công thức: O C 2 W = 3n – (2P 2 5 + P4) + rth - Wth G 1 4 5
= 3 * 6 – (2 * 8 + 1) + 0 – 0 = 1 D 2’
Chọn khâu 1 là khâu dẫn, vì có khớp loại cao là hai O E A 1 6
biên dạng răng ñang tiếp xúc với nhau tai A, do vậy ta phải O6
thay thế khớp cao thành khớp thấp (hình 1.4b).
Bậc tự do cơ cấu thay thế: Hình 1.4c
W = 3 * 7 – (2 * 8 + 0) + 0 – 0 = 1
khi tách nhóm ta có 1 nhóm tĩnh ñinh loại 2: (2’,2) và nhóm loại 3: (3,4,5,6) như hình 1.4c. ðây là cơ cấu loại 3.
Công thức cấu tạo cơ cấu : 1 = 1 + 0 + 0
5) Tính bậc tự do và xếp loại cơ cấu ñiều khiển nối trục (hình 1.5a) 1 1 2 2 2 3 3 3 5 4 5 4 5 4
Hình 1.5a Hình 1.5b Hình 15c
Bậc tự do cơ cấu Hình 1.5a ñược tính theo công thức:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 5 – (2 * 6 + 1) + 0 – 1 = 1
Chọn khâu 1 là khâu dẫn, vì có khớp loại cao là khớp cam do vậy ta phải thay thế khớp cao
thành khớp thấp (hình 1.5b).
Bậc tự do cơ cấu thay thế:
W = 3 * 5 – (2 * 7 + 0) + 0 – 0 = 1
Khi tách nhóm ta có 2 nhóm tĩnh ñinh loại 2: (2,3; 4,5) như hình 1.5c. ðây là cơ cấu loại 2.
Công thức cấu tạo cơ cấu : 1 = 1 + 0 + 0
6) Tính bậc tự do và xếp loại cơ cấu máy dệt vải dày, ñập khổ dở (hình 1.6a) O4 O O4 4 D 4 4 4 C C C D C D A B 1 B O2 B 6 O 6 2 6 O B O 1 O O A 2 1 1 1 2 2 2 1 O O O 6 6 6 O 3 3 3 O 3 O3 3
Hình 1.6a Hình 1.6b Hình 1.6c
Bậc tự do cơ cấu Hình 1.6a ñược tính theo công thức:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 8 – (2 * 10 + 2) + 0 – 1 = 1
Chọn khâu 1 là khâu dẫn, vì có khớp loại cao là khớp cam và khớp bánh răng, do vậy ta phải
thay thế khớp cao thành khớp thấp (hình 1.6b).
Bậc tự do cơ cấu thay thế:
W = 3 * 9 – (2 * 13 + 0) + 0 – 0 = 1
Khi tách nhóm ta có 4 nhóm tĩnh ñinh loại 2 như hình 1.6c. ðây là cơ cấu loại 2.
Công thức cấu tạo cơ cấu : 1 = 1 + 0 + 0 + 0 + 0
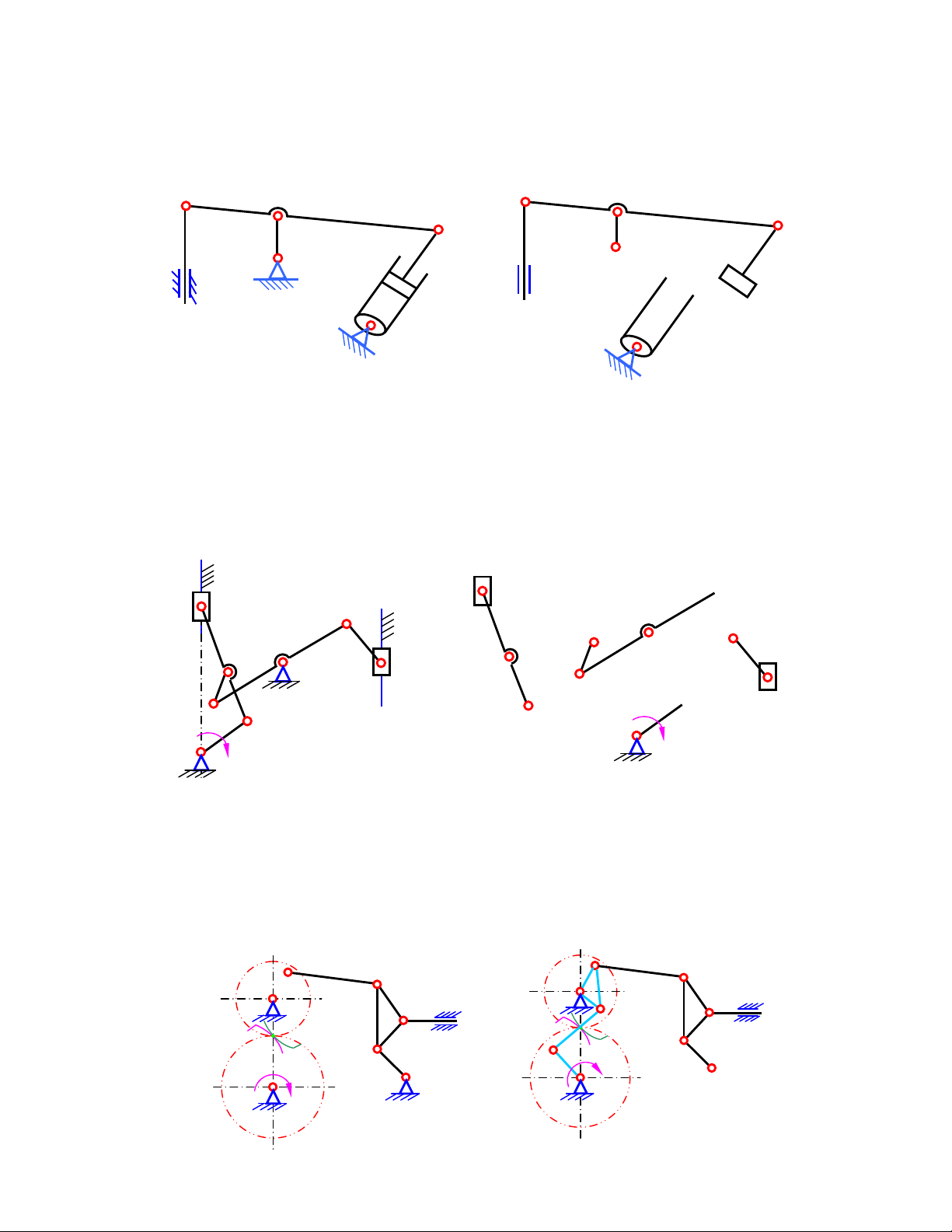
7) Tính bậc tự do và xếp loại cơ cấu cắt kẹo tự ñộng (hình 1.6a):
Bậc tự do cơ cấu Hình 1.6a ñược tính theo công thức:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 7 – (2 * 9 + 1) + 0 – 1 = 1
Chọn khâu 1 là khâu dẫn, vì có khớp O7
loại cao là khớp cam (tiếp xúc giữa cam 1 và
con lăn 2, do vậy ta phải thay thế khớp cao E D O2 A 6
thành khớp thấp (hình 1.6b). 2 4 1 5
Bậc tự do cơ cấu thay thế: O 3 O1 3
W = 3 * 7 – (2 * 10 + 0) + 0 – 0 = 1 C B
Khi tách nhóm ta có 3 nhóm tĩnh ñinh
loại 2 như hình 1.6c. ðây là cơ cấu loại 2.
Công thức cấu tạo cơ cấu : 1 = 1 + 0 + 0 + 0 + 0 Hình 1.6a A 2 O O 7 3 3 C K B O E 7 D O2 A 6 7 2 K O E 4 7 5 O3 3 O D 1 C 5 B 1 6 1 4 O1 C Hình 1.6b B Hình 1.6c
8) Tính bậc tự do và xếp loại cơ cấu máy nghiền (hình 1.8a): O 5 O O 5 5 A B B 2 2 C B B 3 A 2 C C 3 4 4 4 A O 5 3 3 5 O 5 3 1 O3 O 1 1 O 1 1 O1
Hình 1.8a Hình 1.8b Hình 1.8c
Bậc tự do cơ cấu Hình 1.8a ñược tính theo công thức:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 5 – (2 * 6 + 1) + 0 – 1 = 1
Chọn khâu 1 là khâu dẫn, vì có khớp loại cao là khớp cam (tiếp xúc giữa cam 1 và con lăn 2),
do vậy ta phải thay thế khớp cao thành khớp thấp (do biên dạng cam tại vị trí tiếp xúc là phẳng nên
thay thế khớp thấp là khớp tịnh tiến)(hình 1.8b).
Bậc tự do cơ cấu thay thế:
W = 3 * 5 – (2 * 7 + 0) + 0 – 0 = 1
Khi tách nhóm ta có 2 nhóm tĩnh ñinh loại 2 như hình 1.8c. ðây là cơ cấu loại 2.
Công thức cấu tạo cơ cấu : 1 = 1 + 0 + 0
9) Tính bậc tự do và xếp loại cơ cấu phanh má (hình 1.9a) B 2 D B 2 D B 2 D D 3 3 5 3 5 O 4 4 3 O3 A O3 5 1 A 1 1 O A 4 5 O O5 1 O1 O O 1 O5 4
Hình 1.9a Hình 1.9b Hình 1.9c
Bậc tự do cơ cấu Hình 1.9a ñược tính theo công thức:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 5 – (2 * 6 + 2) + 0 – 0 = 1
Chọn khâu 1 là khâu dẫn, vì có khớp loại cao là khớp cam (tiếp xúc giữa cam 3 và khâu 4 và
5), do vậy ta phải thay thế khớp cao thành khớp thấp (do biên dạng cam tại vị trí tiếp xúc là phẳng nên
thay thế khớp thấp là khớp tịnh tiến)(hình 1.9b).
Bậc tự do cơ cấu thay thế:
W = 3 * 7 – (2 * 10 + 0) + 0 – 0 = 1
Khi tách nhóm ta có 3 nhóm tĩnh ñinh loại 2 như hình 1.9c. ðây là cơ cấu loại 2.
Công thức cấu tạo cơ cấu : 1 = 1 + 0 + 0 + 0
10) Tính bậc tự do và xếp loại cơ cấu vẽ ñường thẳng Lipkin với các chiều dài AD = AE,
BD=DC=CE=EB, AF = FB (hình 1.11a) C D 6 C D 6 7 5 7 5 E 4 E B B 4 B 3 3 1 A 1 2 F 2 A F A Hình 1.10a Hình 1.10b
Bậc tự do cơ cấu Hình 1.10a ñược tính theo công thức:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 7 – (2 * 10 + 0) + 0 – 0 = 1
Chọn khâu 1 là khâu dẫn, vì có chuỗi ñộng kín BDCE nên khi tách nhóm ta có 1 nhóm tĩnh
ñịnh loại 4 như hình 1.10b. ðây là cơ cấu loại 4
Công thức cấu tạo cơ cấu : 1 = 1 + 0
11) Tính bậc tự do và xếp loại cơ cấu chuyển ñộng theo quỹ ñạo cho trước (hình 1.11a) G G G 5 5 C 5 2 E B A A 3 F F F 1 1 4 D 4 C C 2 C E B 2 4 B A D 3 3 1 D E
Hình 1.11a Hình 1.11b Hình 1.11c
Bậc tự do cơ cấu Hình 1.11a ñược tính theo công thức:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 5 – (2 * 5 + 2) + 0 – 2 = 1
Chọn khâu 1 là khâu dẫn, vì có khớp loại cao chỗ tiếp xúc của hai con lăn 3 và 4 với giá và
khâu 5 nên ta phải thay thế khớp cao thành khớp thấp như hình 1.11b. Bậc tự do cơ cấu thay thế:
W = 3n – (2P5 + P4) + rth - Wth = 3 * 5 – (2 * 7 + 0) + 0 – 0 = 1
Khi tách nhóm ta có 2 nhóm tĩnh ñịnh loại 2 như hình 1.11c. ðây là cơ cấu loại 2
Công thức cấu tạo cơ cấu : 1 = 1 + 0 + 0
12) Tính bậc tự do và xếp loại cơ cấu nâng thùng hạt giống (hình 1.12a) và cơ cấu nhấc lưỡi cày
của máy nông nghiệp (hình 1.12b) a) Xét hình 1.12a:
Bậc tự do cơ cấu Hình 1.12a ñược tính theo công thức:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 5 – (2 * 7 + 0) + 0 – 0 = 1
Chọn khâu 1 là khâu dẫn, tách nhóm ta có 2 nhóm tĩnh ñịnh loại 2 (2,3; 4,5) như hình 1.12aa. ðây là cơ cấu loại 2
Công thức cấu tạo cơ cấu : 1 = 1 + 0 + 0 O5 O3 3 O5 2 5 O 3 5 B A 4 4 D O1 3 D O1 1 C C 1 2 B A Hình 1.12a Hình 1.12aa b) Xét hình 1.12b: O7 B B 7 O G 7 2 1 A 1 A C 3 7 G D 2 O3 C D 6 3 O3 D F 4 4 6 E E O5 F O F 5 5 5 Hỉnh 1.12b Hình 1.12bb
Bậc tự do cơ cấu Hình 1.13b ñược tính theo công thức:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 7 – (2 * 10 + 0) + 0 – 0 = 1
Chọn khâu 1 là khâu dẫn, tách nhóm ta có 3 nhóm tĩnh ñịnh loại 2 (2,3; 4,5; 6,7) như hình
1.12bb. ðây là cơ cấu loại 2
Công thức cấu tạo cơ cấu : 1 = 1 + 0 + 0 + 0
13) Tính bậc tự do và xếp loại cơ cấu trong máy tính : cộng (hình 1.13a) và nhân (hình 1.13b) a) Xét hình 1.13a: D 5 D 3 5 C B B E 4 E 6 3 C B 1 1 1 x 4 3 E x 6 2 2x 2 A A F F a a 1 2 Hình 1.13.a Hình 1.13aa x a + x a 1 2 2 1 x3 = a + a 1 2 x + x Khi a 1 2 1 = a2 thì x3 = 2
Bậc tự do cơ cấu Hình 1.14a ñược tính theo công thức:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 6 – (2 * 8 + 0) + 0 – 0 = 2
Chứng tỏ cơ cấu co 2 khâu dẫn, Chọn khâu 1 và 2 là khâu dẫn, tách nhóm ta có 1 nhóm tĩnh
ñịnh loại 3 (3, 4, 5, 6) như hình 1.13aa. ðây là cơ cấu loại 3
Công thức cấu tạo cơ cấu : 2 = 2 + 0 b) Xét hình 1.14b: 5 5 z x 3 4 3 4 6 y x 2 6 2 1 h 1 Hình 1.13b Hình 1.13bb xy z = h − y y hi khâu 2 cố ñịnh:
= const = t , do vậy z = tx h − y
Bậc tự do cơ cấu Hình 1.13b ñược tính theo công thức:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 6 – (2 * 8 + 0) + 0 – 0 = 2
Chứng tỏ cơ cấu co 2 khâu dẫn, Chọn khâu 1 và 6 là khâu dẫn, tách nhóm ta có 1 nhóm tĩnh
ñịnh loại 3 (2, 3, 4, 5) như hình 1.13bb. ðây là cơ cấu loại 3
Công thức cấu tạo cơ cấu : 2 = 2 + 0
CHƯƠNG 2: PHÂN TÍCH ðỘNG HỌC CƠ CẤU PHẲNG LOẠI 2
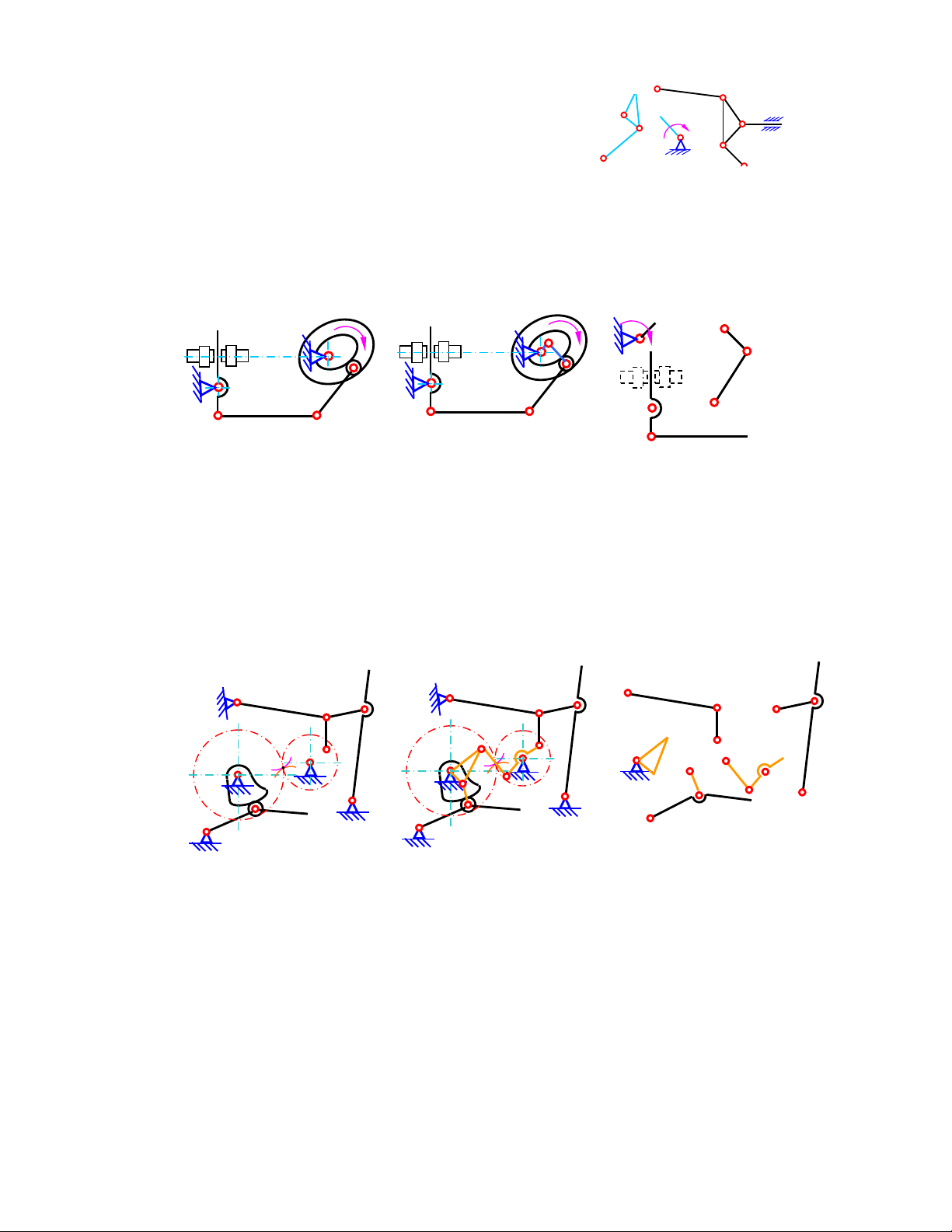
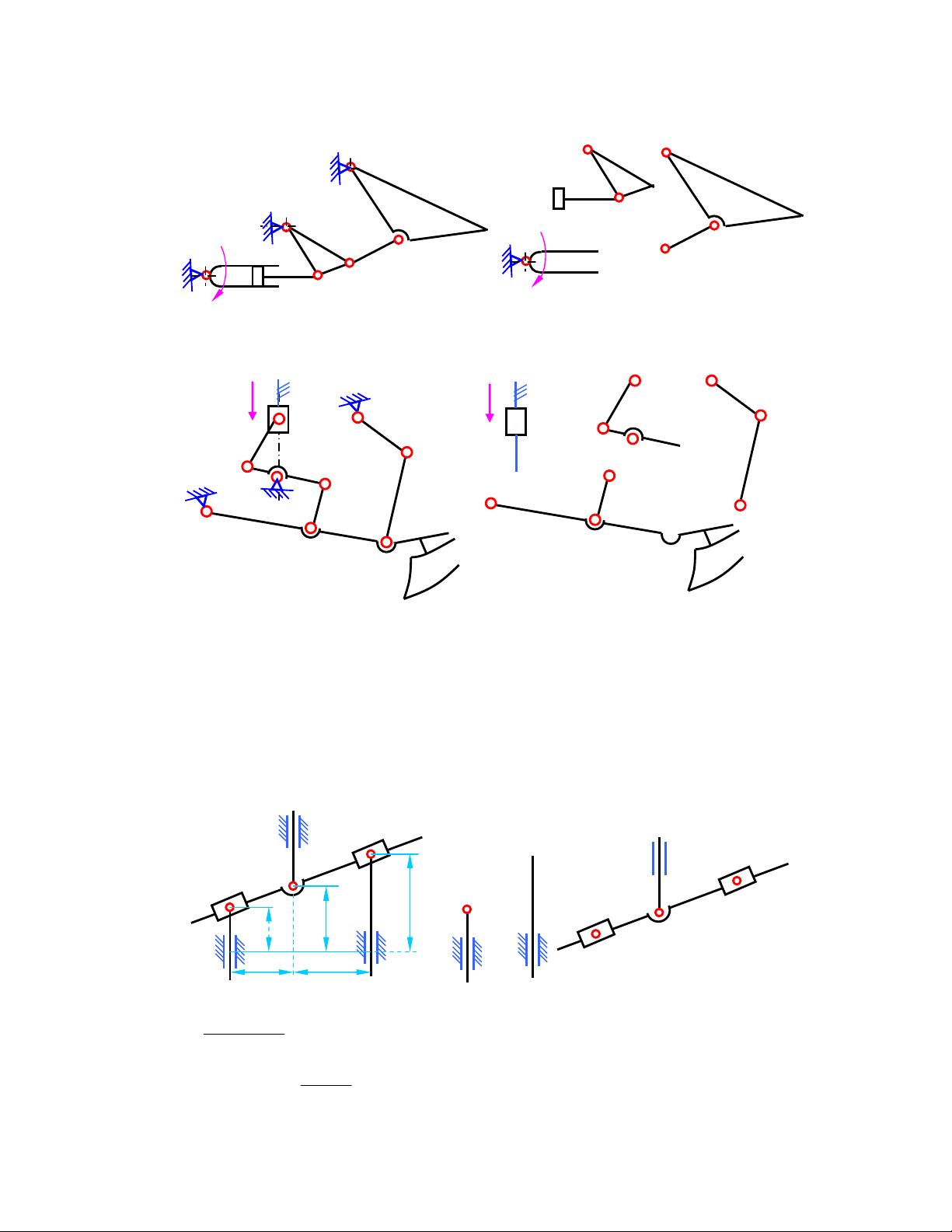
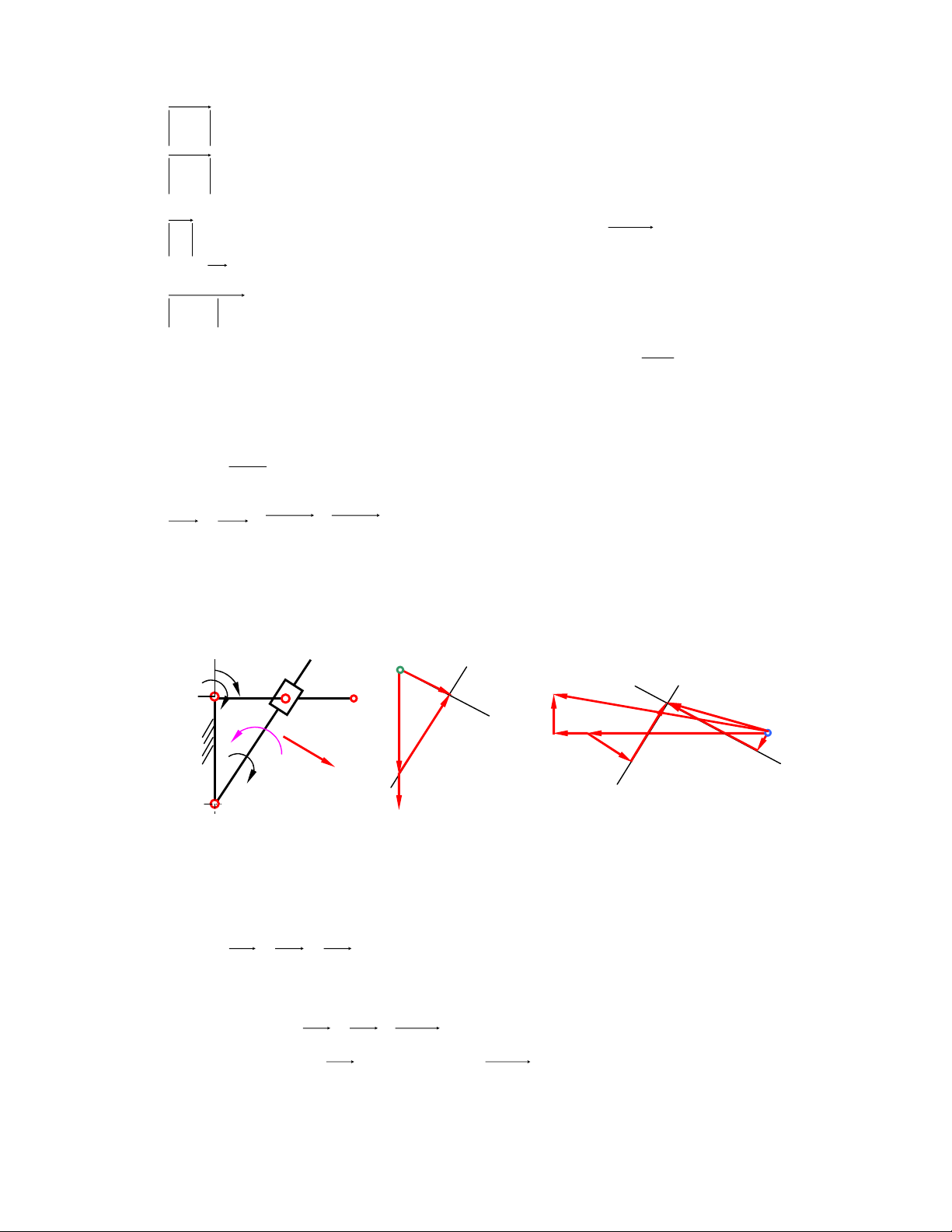
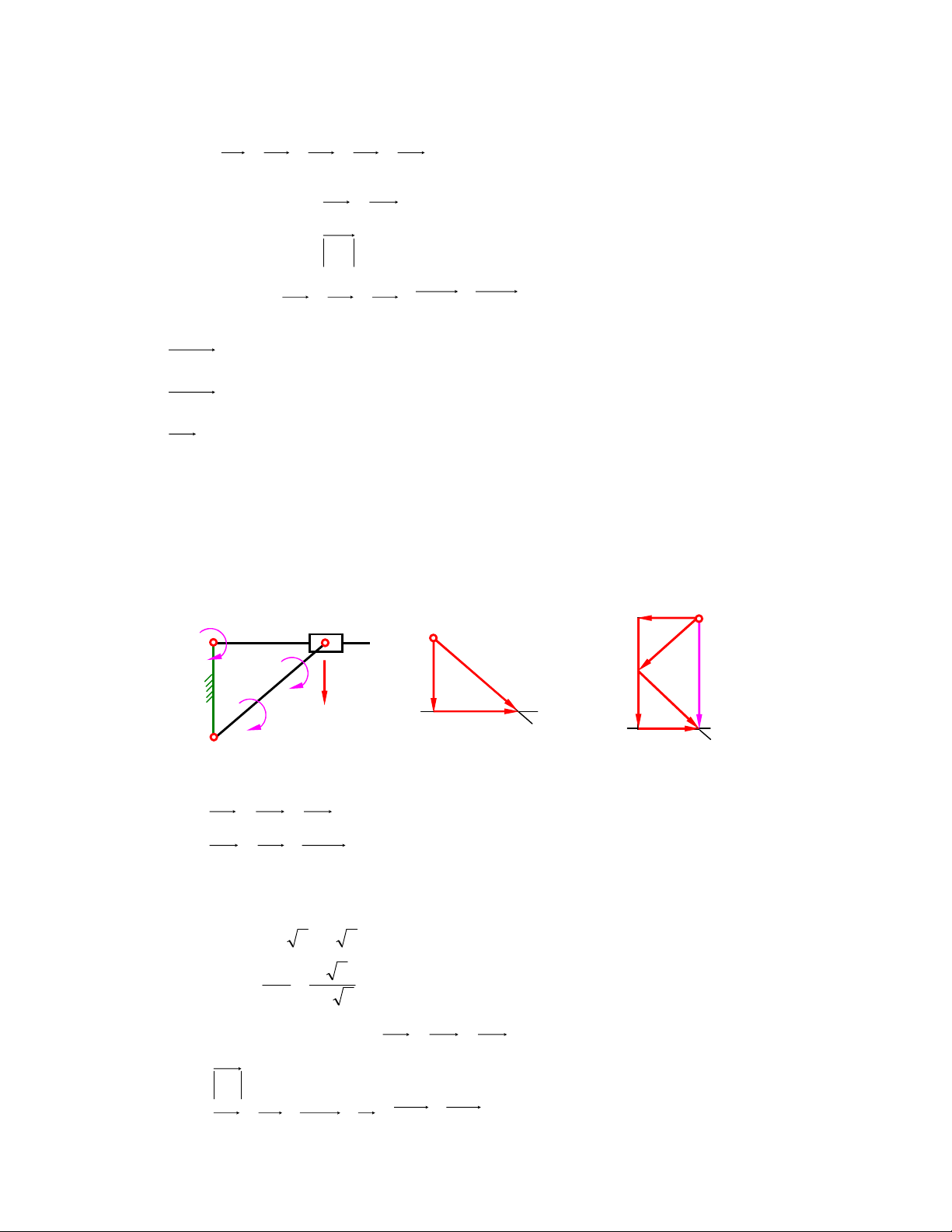
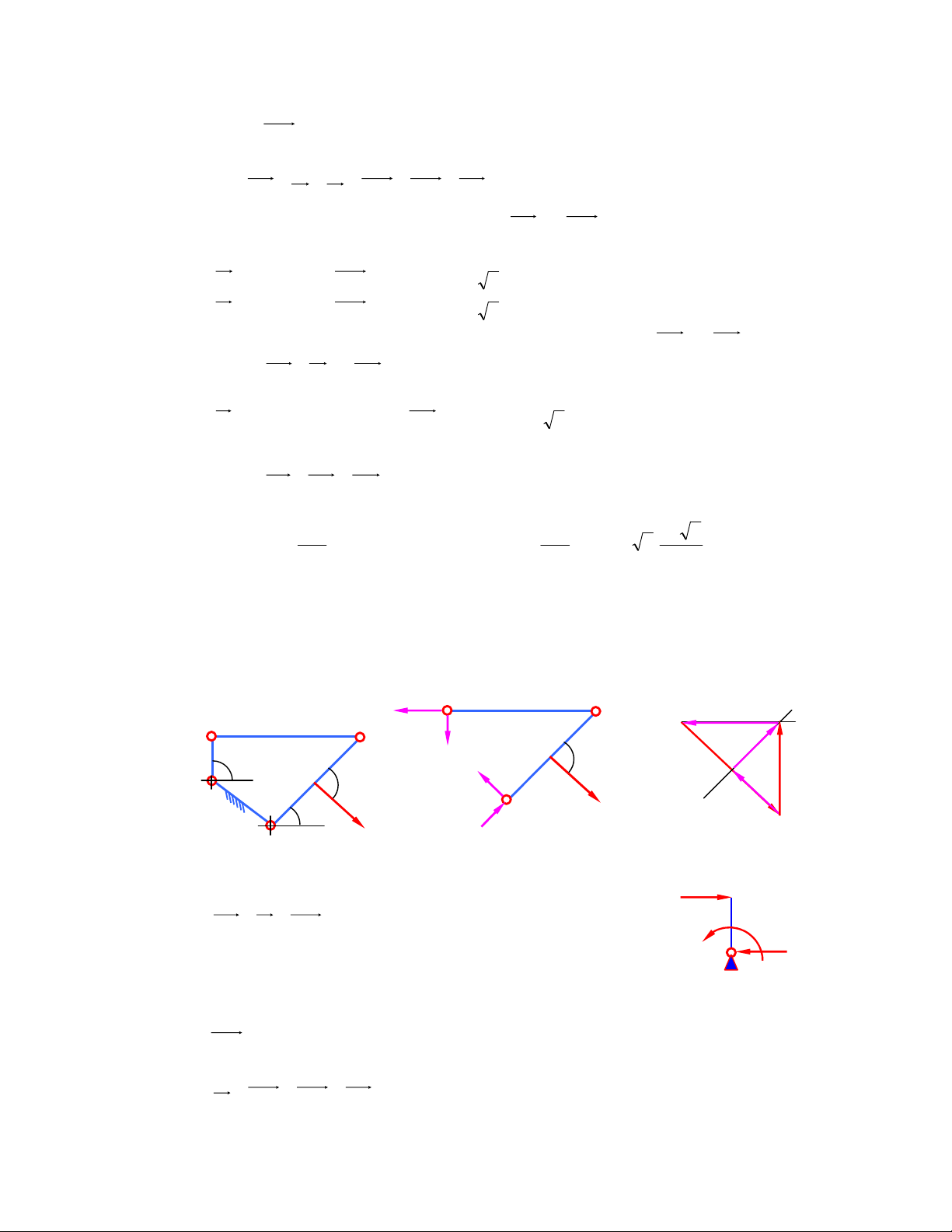
1) Xác ñịnh vận tốc và gia tốc của dao bào E trong cơ cấu máy bào xọc (hình 2.1a) khi tay quay
1 quay ñều với vận tốc góc 1 ω 10 − = s tại vị trí o
ϕ = 45 . Cho biết kích thước các khâu của 1 1 cơ cấu: l = l = , 0 2m ; l = l = m 3 , 0 ; a = 0,35m. AB ED AC CD a e5≡e4 ak B d3≡d4 2 ω E 3 1 p C ϕ1 3 4 5 A ω 1 D b1≡b2 Hình 2.1a Hình 2.1b b3
B1 ≡ B2 ≡ B3, khâu 1 nối với khâu 2 bằng khớp
quay, khâu 2 nối với khâu 3 bằng khớp trượt b3
VB = VB ≠ VB π 1 2 3 k d3 ≡d4 Giá trị : V = V = ω l . = 1 . 0 , 0 2 = 2m / s 1 , có n B B AB 1 2 b 3 n e
phương vuông góc với khâu AB, chiều theo chiều vận tốc 4 góc khâu 1. e4 ≡ e5 b (1) 1≡b2 V = V + V 3 B B2 B3B2 Hình 2.1c
Trong phương trình (1), VB vuông góc với BC, 3 VB
có phương song song với BC. 3 B2 VB
Chọn tỷ lệ xích ñể vẽ: 2 µ
(m / s / mm) V =
. Hoạ ñồ vận tốc ñược vẽ như ở hình 2.1b. p 2 b
ðo giá trị véc tơ ( p 3
b ) biểu diễn vận tốc ñiểm B3 và nhân với tỷ lệ xích ta thu ñược giá trị thực vận tốc ñiểm B3. VB pb 3 3 ω3 = = V µ . lBC lBC VB l Vì 3 BC =
, từ ñó suy ra vận tốc của ñiểm D VD lCD 3
E4 ≡ E5 và khâu 4 nối với khâu 5 bằng khớp quay: VE = V = V + V (2) 5 E4 D4 E4 D4
Trong phương trình này: VE có phương thẳng ñứng. V
có phương vuông góc với 4 E4 D4
DE. Hoạ ñồ ñược vẽ như ở hình 2.1b. Ta ño ñoạn p 5
e và nhân với tỷ lệ xích ñã chọn sẽ có giá trị vận tốc khâu 5, chiều ñi lên.
Tương tự ta cũng xác ñịnh ñược gia tốc: 2 2 a = a B B = 1 ω l = 100 , 0
. 2 = 20m / s có chiều hướng từ B ñi vào A 1 2 AB k
aB = aB + aB B + a 3 2 3 2 M n ặt khác τ aB = a + a , do vậy 3 B C B C 3 3 n τ aB = a + a = k a + a + a (3) 3 B C B C B B B 3 3 2 3 2 Trong phương trình (3) : n a 2 = ω l . 3
AB ; ñã xác ñịnh về giá trịcó phương chiều hướng từ B ñi vào C. B C 3 aτ = ε .l = ? 3 AB
; phương vuông góc với BC. 3 B C a k = 2ω2.V = 2 B B ω3. V µ 2 b 3
b ; Phương chiều lấy theo chiều V quay ñi một góc 900 theo 3 2 B3B2 chiều ω3 . a = ? B
, phương song song với BC. 3 B2 aB Ph 2 2
ương trình (3) chỉ tồn tại 2 ẩn số, chọn tỷ lệ xích hoạ ñồ gia tốc: µ =
(m / s / mm) a . b π 2
Cách giải ñược trình bày trên hình 2.1c
Các giá trị ñược ño trực tiếp trên các véc tơ biểu diễn tương ứng sau ñó nhân với tỷ lệ xích ñã chọn.
Xác ñịnh gia tốc góc khâu 3: n b b 3 3 ε 3 = µa lBC
Xác ñịnh gia tốc ñiểm D3 cũng bằng phương pháp ñồng dạng n τ aE = a + a + a (4) 4 D4 E4 D4 E4 D4
Cách lý luận cũng tương tư. Cách giải trình bày trên hình 2.1c
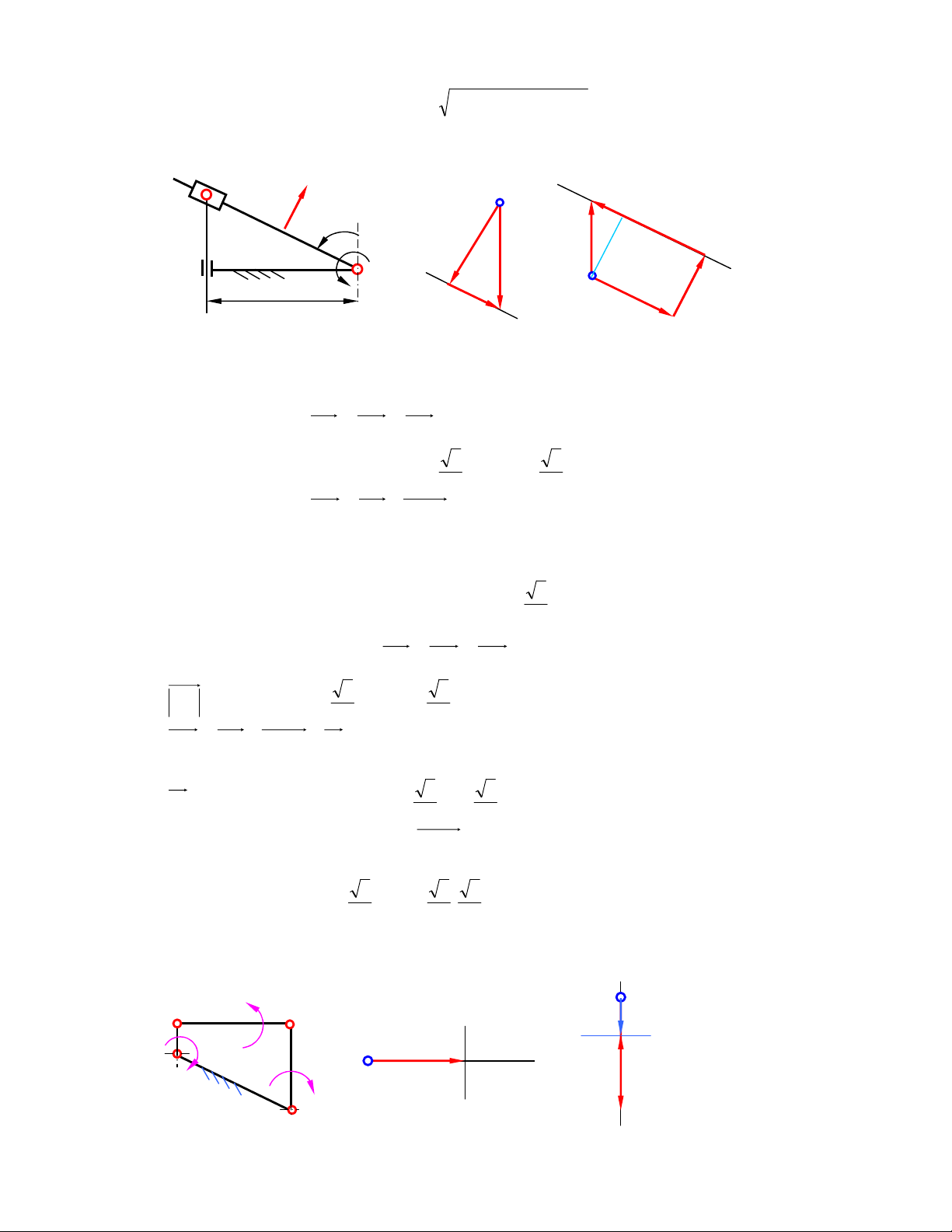
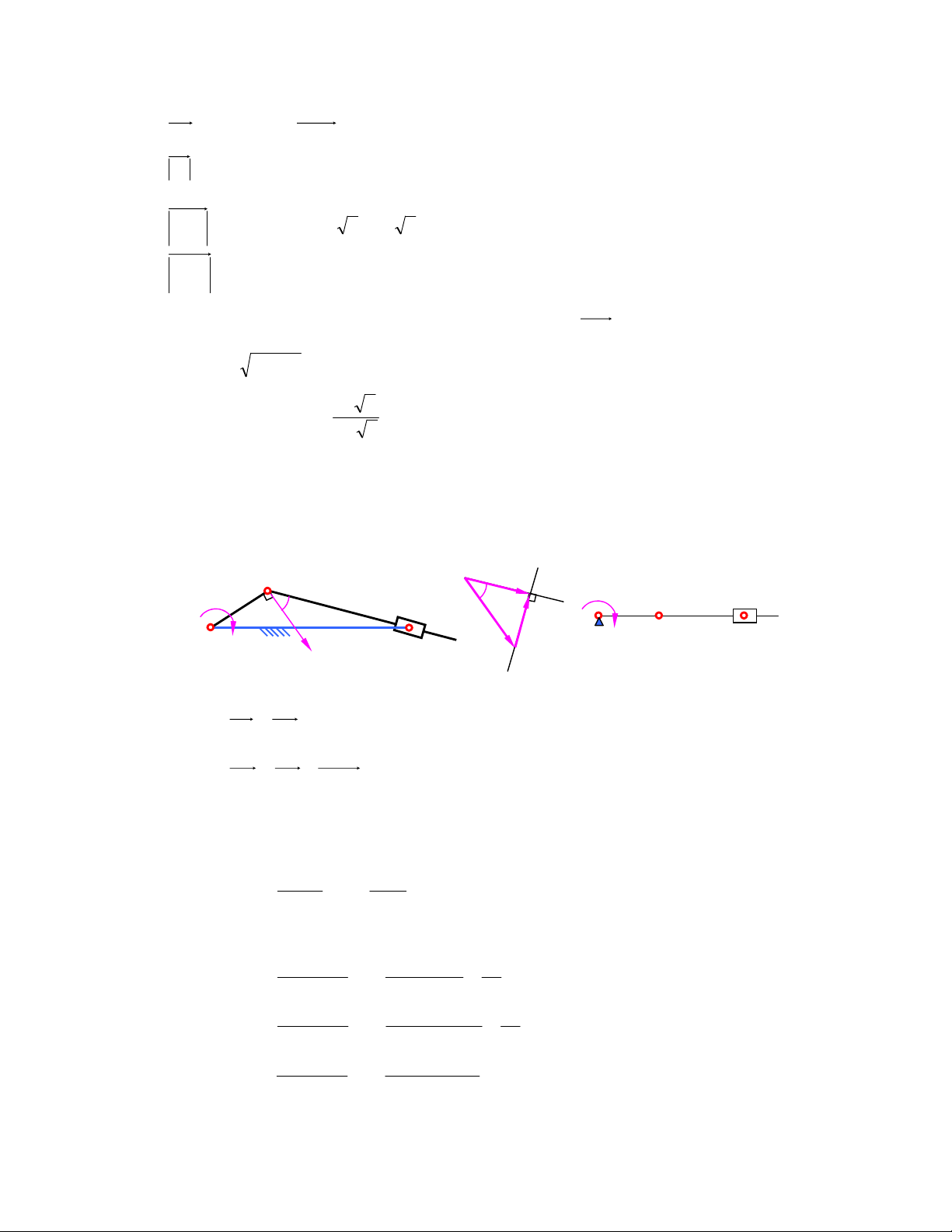
2) Tính vận tốc và gia tốc ñiểm D2 (∠ DBC = 1200) trên con trượt 2 của cơ cấu cu lít tại vị trí
ϕ1=900. Tay quay AB quay ñều với vận tốc góc ω1 = 20s-1. Cho biết kích thước các khâu của
cơ cấu: lAB = lBD = 0,5lBC = 0,2m. ϕ1 p d 2 1 2 b3 b3 A ω B D 1 ε 3 d n 2 π 3 ak b1 ≡ b2 n b3 ω k 3 b 1 ≡ b2 C d 2
Hình 2.2a Hình 2.2b Hình 2.2c
Sự tương quan kích thước ñã cho ta thấy rằng tam giác ABC là nửa tam giác ñều,
(∠ABC=600) BD thuộc khâu 2. ðể xác ñịnh vận tốc ñiểm D, trước tiên ta phải biết vận tốc ñiểm B2 và
vận tốc góc khâu 2, sau áp dụng ñịnh lý hợp vận tốc sẽ thu ñược vận tốc ñiểm D. Khâu 2 trượt trong
khâu 3 và quay theo khâu 3 cho nên tốc ñộ góc khâu 2 cũng chính là tốc ñộ góc khâu 3.
B1 ≡ B2 ≡ B3, khâu 1 nối với khâu 2 bằng khớp quay, khâu 2 nối với khâu 3 bằng khớp trượt V = V ≠ V 1 B B2 B3 Giá trị : V = V = ω l . = 20 , 0 . 2 = 4m / s B B 1 AB
, có phương vuông góc với khâu AB, chiều theo 1 2
chiều vận tốc góc khâu 1. VB = V + V (1) 3 B2 B3B2
Trong phương trình (1), VB vuông góc với BC, V
có phương song song với BC 3 B3B2
Trong trường hợp ñặc biệt này ta không cần chọn tỷ lệ xích. Hoạ ñồ vận tốc ñược vẽ như ở hình 2.2b.
Tam giác pb2b3 ñồng dạng với tam giác BCA, ta tính ñược vận tốc ñiểm b3:V = V / 2 = 2m / s B B . 3 2 VB 2
Tốc ñộ góc khâu 3 và khâu 2: 3 ω = ω = = = 5rad / s 2 3
. Chiều ñược xác ñịnh như hình vẽ lBC , 0 4 VD = V + V (2) 2 B2 D2 B2
Trong phương trình (2) ta ñã biết vận tốc ñiểm B2 , V = ω l . = 5 , 0 . 2 = m 1 / s D B 2 BD . 2 2
Chiều hướng từ trên xuống theo chiều ω2 và vuông góc với BD. Hoạ ñồ ñược vẽ tiếp như ở hình 2.2b.
Giá trị vận tốc ñiểm D ñược tính: V = V + V = 4 + 1 = m 5 / s D B D B 2 2 2 2
Tương tự ta cũng tính ñược gia tốc ñiểm D2: a = a ≠ a 1 B B2 B3 2 2 a = a B B = 1 ω .l = . 400 , 0 2 = 80m / s 1 2 AB
aB = aB + aB B + ak 3 2 3 2 n τ aB = a + a 3 B C B C 3 3 n
aB + a B B + ak = τ a + a (2) 2 3 2 B C B C 3 3
Trong phương trình trên (2) Ta có ñược:
aB : ðã xác ñịnh; a
: Giá trị chưa biết, phương song song với BC. 2 B3B2 2 a = 2 k ω3.V = . 5 . 2 2 3 = 20 3m / s B 3 B2 n 2 2 a = ω3 .l = 2 . 5 , 0 4 = 10m / s BC B3C aτ = ε .l = ? 3 BC
, có phương vuông góc với BC. B3C
Phương trình (2) tồn tại 2 ẩn số, Hoạ ñồ gia tốc ñược vẽ như ở hình 2.1c
Gia tốc góc khâu 2 và khâu 3 ñược tính như sau: aτB C ε = ε 3 2 3 = lBC n a B a τ 3 k o n o a = aB − ( + ) sin 60 + a tg60 B C 2 3 o o B cos 60 sin 60 3 3 2 = 8 ( 0 − 5 − 4 ) 0 + 10 3 = 4 , 7 63m / s 2 aτB C 47 6 , 3 3 2 ε 2 = ε3 = = = 11 , 9 075rad / s l , 0 4 BC n τ aD = a + a + a (3) 2 B2 D2 B2 D2 B2
Trong phương trình (3) Ta ñã biết: n 2 2 a = ω2 .l = 25 , 0 . 2 = 5m / s BD D2 B2 τ 2 a = ε 2.l = 11 , 9 07 . 5 , 0 2 = 28 8 , 15m / s BD D2 B
Hoạ ñồ gia tốc ñược vẽ trên hình 2,2c Giá tr 2 2
ị gia tốc ñiểm D ñược tính: aD = (80 + 5) 2 + 28 8 , 15 = 8 , 8 27m / s 2
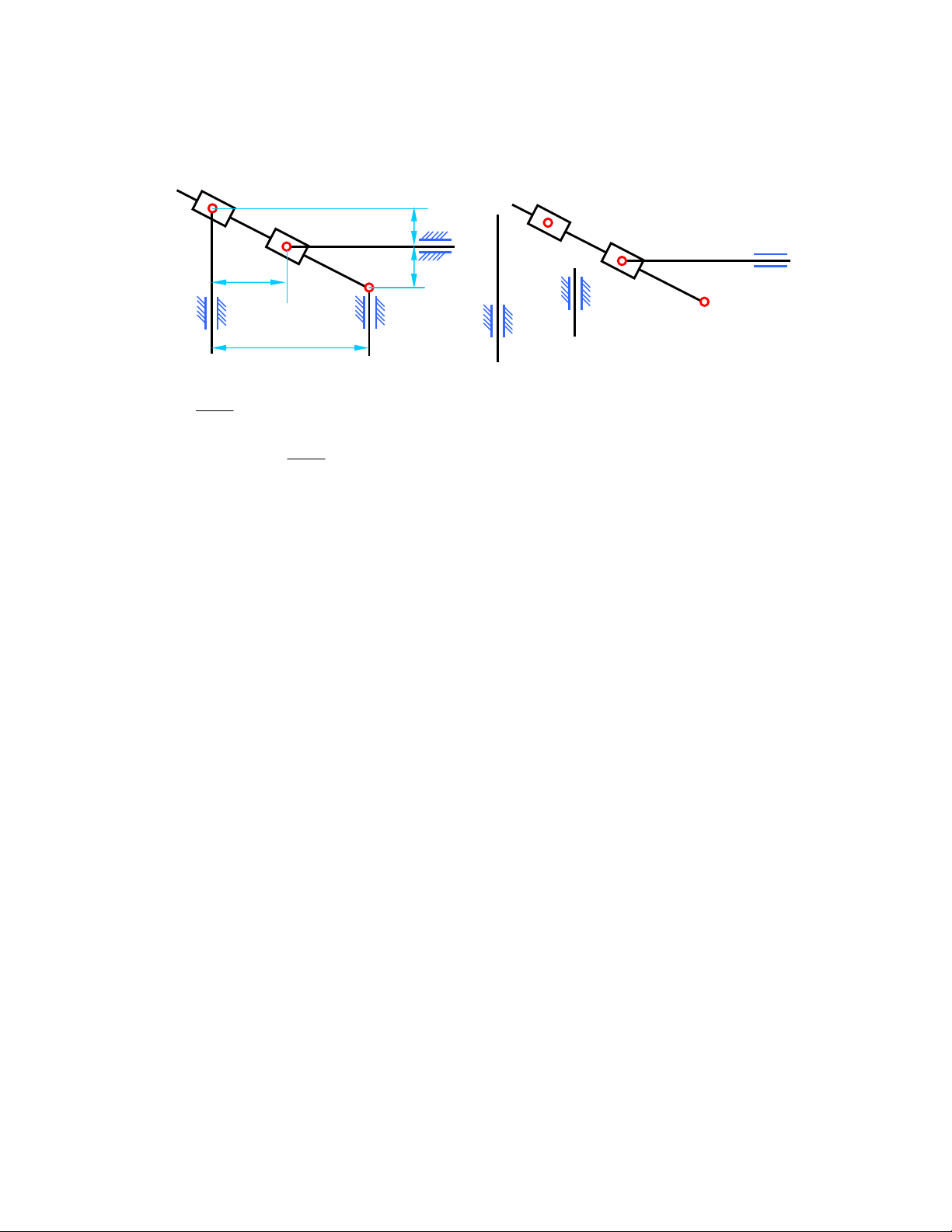
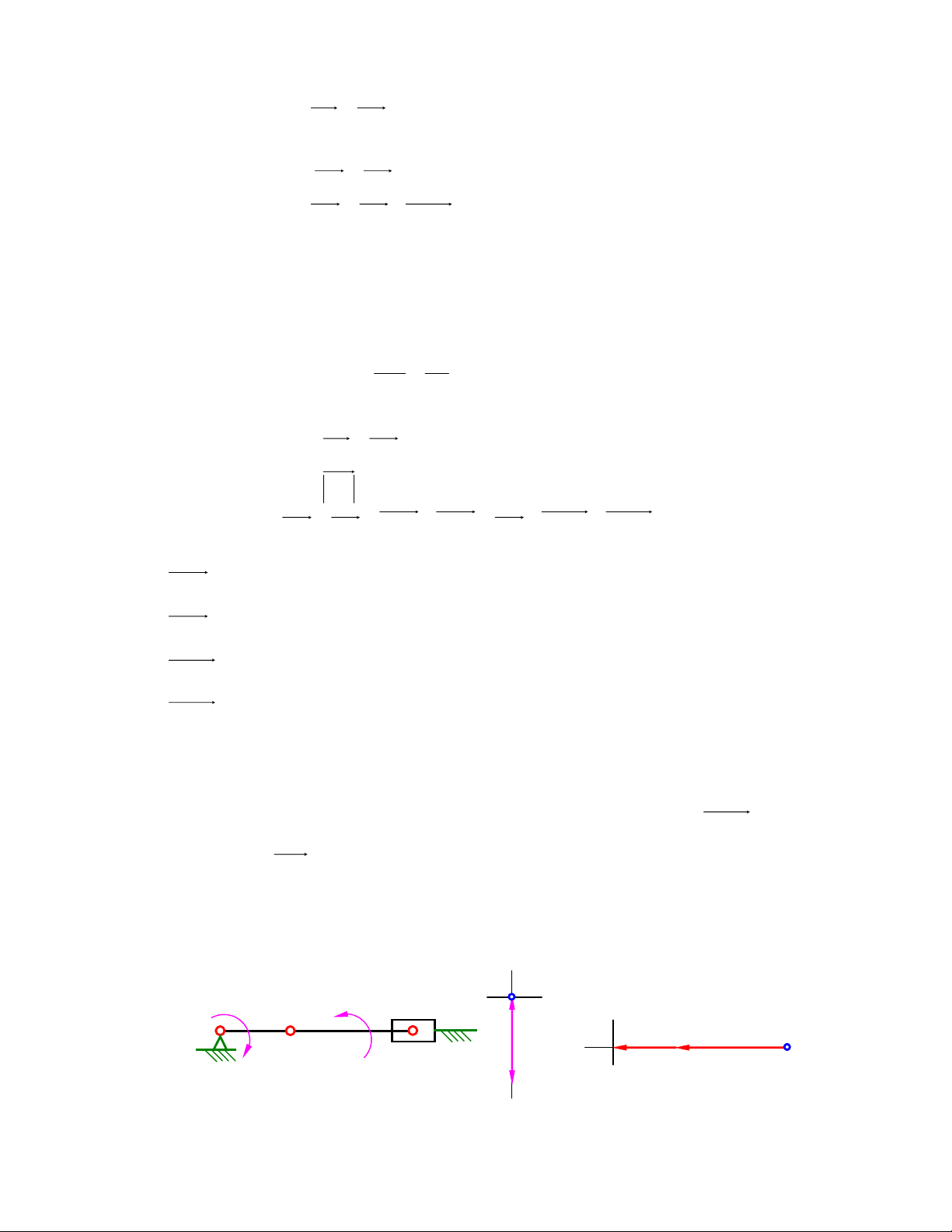
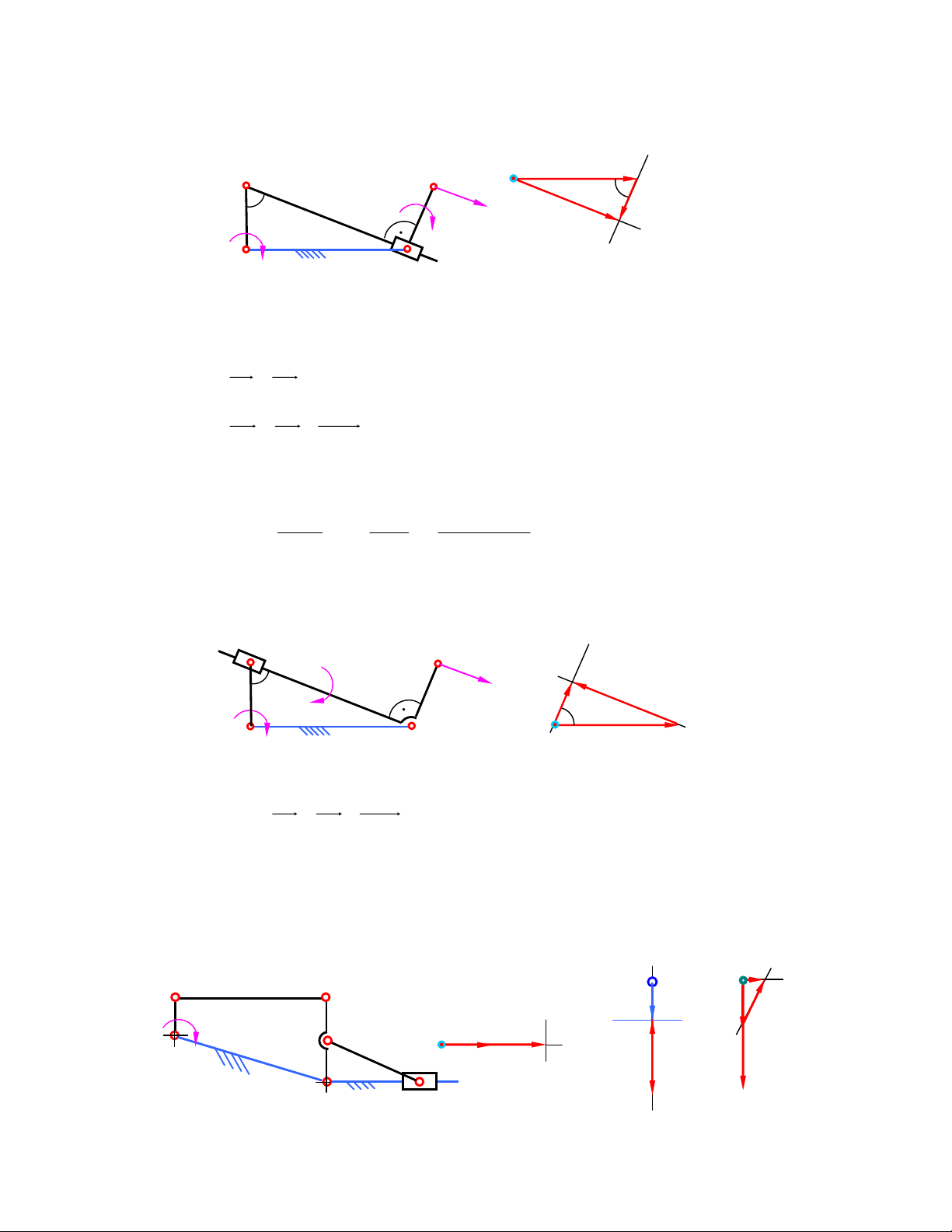
3) Tính vận tốc và gia tốc khâu 3 của cơ cấu tính tang một góc, nếu tay quay AB quay ñều với
vận tốc góc ω= 10s-1, tại vị trí ϕ1 = 60o. Cho trước h = 0,05m (hình 2.3a). B a b3, b2 2 k p ϕ 1 1 3 k C A π h b1 b2, b3 b1
Hình 2.3a Hình 2.3b Hình 2.3c
Vì khâu 3 chuyển ñộng tịnh tiến, cho nên mọi ñiểm trên khâu 3 ñều có vận tốc và gia tốc như
nhau. Chúng ta ñi xác ñịnh vận tốc và gia tốc ñiểm B3 .
B1 ≡ B2 ≡ B3 . Khâu 1 nối với khâu2 bằng khớp tịnh tiến, khâu 2 nối với khâu 3 bằng khớp quay: V ≠ V = V 1 B B2 B3 3 3 V = ω l . = 2 . , 0 05 1 . 0 = = 5 , 0 77m / s B 1 AB 1 3 3 VB = V + V (1) 2 1 B B2 1 B //BC //AB
Phương trình chỉ tồn tại hai ẩn số là giá trị vận tốc ñiểm B2 và vận tốc tương ñối giữa 2 ñiểm B1 và
B2. Hoạ ñồ véc tơ vận tốc ñược vẽ như hình 2.3b. 3
Vận tốc ñiểm B2 ñược tính như sau: V = 2V , 0 67m / . s B =
chiều ñược xác ñịnh như trên 2 B2 3
hoạ ñồ vận tốc (hình 2.3b).
Tương tự gia tốc ta cũng có: a ≠ a = a 1 B B2 B3 2 3 3 2 aB = 1 ω .l = 100 2 . . , 0 05 = 10 m / s 1 AB 3 3
aB = aB + a B B + ak 2 1 2 1 //BC // AB 3 3 a : k có giá trị là 2 . 2 1 ω .V = . 2 1 . 0 10 m / s B = . 2 1 B 6 3
Phương chiều theo chiều của VB
quay ñi một góc 90o theo chiều ω1 . Hoạ ñồ gia tốc 2 1 B
ñược vẽ như ở hình 2.3c. Giá trị gia tốc khâu 3 ñược tính: 3 3 3 2 a = a = 2a = 1 . 2 . 0 . , 6 7m / s B = 2 B3 k 3 3 3
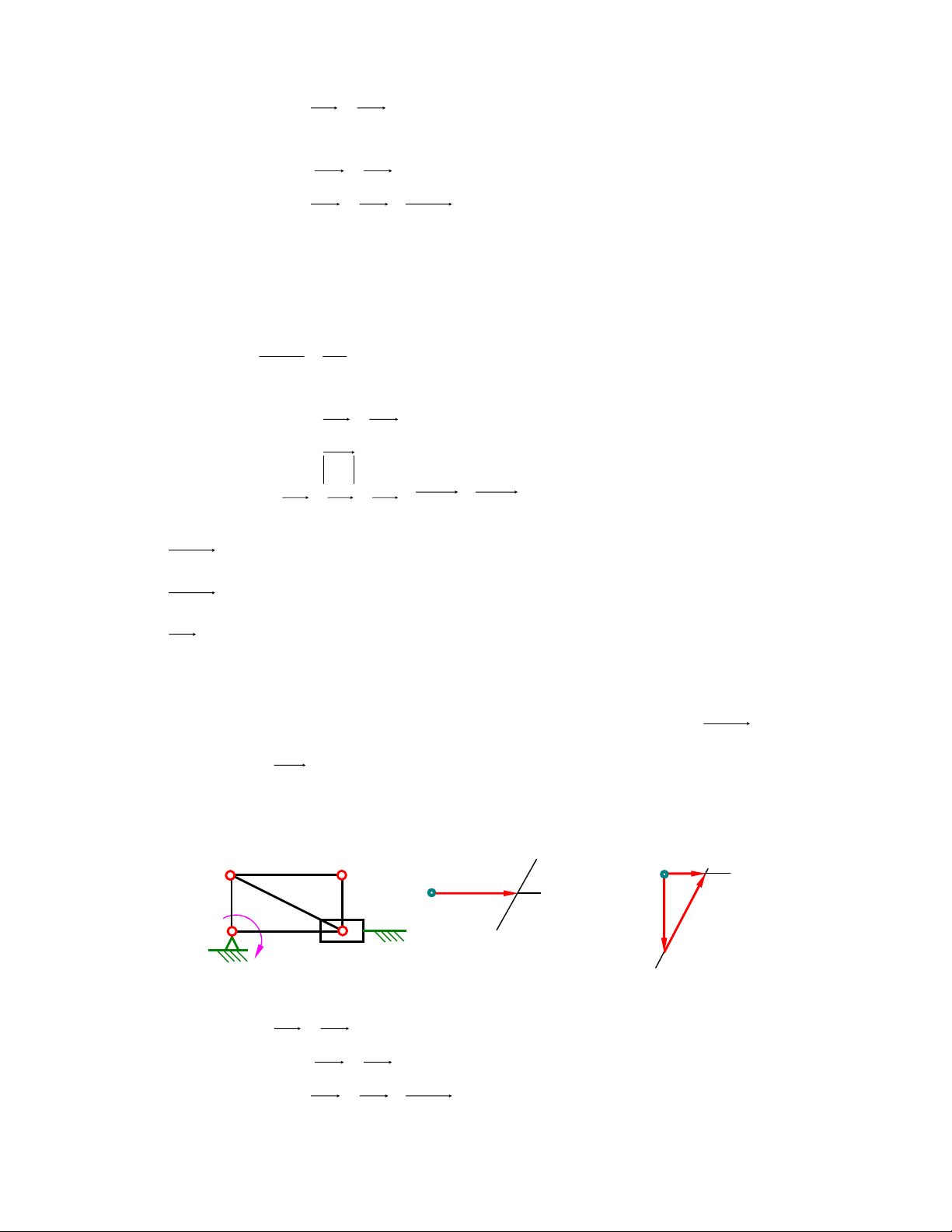
4) Tính vận tốc và gia tốc ñiểm C (hình 2.4a), vận tốc góc và gia tốc góc của các khâu 2 và 3
trong cơ cấu 4 khâu bản lề tại vị trí ∠ABC = ∠BCD = 90o , nếu tay quay AB quay ñều với vận
tốc góc ω1= 20s-1. Cho trước kích thước của các khâu 4lAB = lBC = lCD = 0,4m. π B ω2 C c 2,c3 1 2 b1, b2, c2,c3 A ω1 3 p ω 3 D b1, b2
Hình 2.4a Hình 2.4b Hình 2.4c
B1 ≡ B2. Khâu 1 nối với khâu 2 bằng khớp quay: V = 1 B VB2 V = ω l . = 20 1 , 0 . = 2m / s B 1 AB 1
Tương tự: C2 ≡ C3 và C V = V 2 C3 C V = V + V (1) 2 B2 C2 B2 ⊥CD ⊥BC
Phương trình chỉ tồn tại hai ẩn số là giá trị vận tốc ñiểm C2 và vận tốc tương ñối giữa 2 ñiểm C2
và B2. Hoạ ñồ véc tơ vận tốc ñược vẽ như hình 2.3b.
Từ hoạ ñồ ta thấy răng vận tốc ñiểm C và vận tốc ñiểm B thuộc khâu 2 là bằng nhau, do vậy khâu 2
chuyển ñộng tịnh tiến tức thời: ω2 = 0. Vận tốc góc khâu 3: VC 2 3 ω = = r 5 ad / s 3 = lCD , 0 4
Chiều ñược xác ñịnh theo chiều VC3 như hình vẽ . Xác ñịnh gia tốc: a = 1 B aB2 2 2 aB = 1 ω .l = 400 1 , 0 . = 40m / s 1 AB n τ n τ aC = a = a + a = a + a + a (2) 2 C3 B C D C D 2 3 3 C2 B2 C2 B2 Trên phương trình 2: n a : Có giá tr 2 ị bằng: ω C D 3 . lCD = 25 . 0,4 = 10m/s2 3 τ a
: Giá trị chưa biết, có phương vuông góc với CD C D 3 n a
: có giá trị bằng 0 vì ω C B 2 = 0. 2 2 τ a
: Giá trị chưa biết, có phương vuông góc với BC. C2 B2
Phương trình chỉ còn tồn tại 2 ẩn số là giá trị của 2 gia tốc tiếp. Cách giải ñược trình bày trên hình 2.4c.
Gia tốc ðiểm C bây giờ chỉ tồn tại gia tốc pháp có chiều hướng từ C ñi vào D và có giá trị là
10m/s2. Gia tốc tiếp bằng 0.
Gia tốc tiếp trong chuyển ñộng tương ñối giữa ñiểm C2 ñối với ñiểm B2 là τ a ñược biểu C2 B2 diễn bởi véc tơ 2
b c2 có giá trị là : 40 – 10 = 30m/s2.
Gia tốc góc khâu2 ñược xác ñịnh: ε2 = 30 / 0,4 = 75rad/s2. chiều xác ñịnh như trên hình vẽ.
5) Tính vận tốc và gia tốc ñiểm C và vận tốc góc và gia tốc góc của thanh truyền 2 trong cơ cấu
tay quay con trượt (hình 1.5a) khi tay quay và thanh truyền thẳng hàng. Biết tay quay AB
quay ñều với vận toccs góc ω1 = 20s-1 và kích thước các khâu : 2lAB = lBC = 0,2m. p c2, c3 B A ω2 C n 3 c 1 2 , c2, c3 2 ω π 1 b1, b2 b1, b2
Hình 2.5a Hình 2.5b Hình 2.5c
B1 ≡ B2 . Khâu 1 nối với khâu 2 bằng khớp quay: V = 1 B VB2 V = ω l . = 20 1 , 0 . = 2m / s B 1 AB 1
Tương tự: C2 ≡ C3 và C V = V 2 C3 C V = V + V (1) 2 B2 C2 B2 //AC ⊥BC
Phương trình chỉ tồn tại hai ẩn số là giá trị vận tốc ñiểm C2 và vận tốc tương ñối giữa 2 ñiểm C2
và B2. Hoạ ñồ véc tơ vận tốc ñược vẽ như hình 2.5b.
Từ hoạ ñồ ta thấy răng vận tốc ñiểm C bằng 0, vận tốc ñiểm B và vận tốc tương ñối giữa ñiểm C ñối với
ñiểm B là bằng nhau về giá trị và ngược chiều nhau. Vận tốc góc khâu 2 ñược tính: VC B 2 2 2 ω = = 10rad / s 2 = lBC , 0 2
Chiều xác ñịnh như hình vẽ (hình 2.5a) Xác ñịnh gia tốc: a = 1 B aB2 2 2 aB = 1 ω .l = 400 1 , 0 . = 40m / s 1 AB n τ C a = a = a + a + a (2) 2 3 C 2 B C2 2 B C2 2 B Trên phương trình 2: n a : có giá tr 2 ị bằng: 2 ω .l = 100 , 0 . 2 20m s C B 2 / BC = 2 2 τ a
: Giá trị chưa biết, có phương vuông góc với BC. C2 B2 a
: có phương song song với AC, giá trị chưa biết. C2
Phương trình chỉ còn tồn tại 2 ẩn số là giá trị của gia tốc tiếp tương ñối và gia tốc tuyệt ñối
ñiểm C . Cách giải ñược trình bày trên hình 2.5c.
Gia tốc ðiểm C có chiều như hình vẽ và có giá trị bằng 40 + 20 = 60m/s2.
Gia tốc tiếp trong chuyển ñộng tương ñối giữa ñiểm C2 ñối với ñiểm B2 là τ a ñược biểu C2 B2 diễn bởi véc tơ 2 cn 2
c có giá trị là 0, do vậy gia tốc góc khâu 2 bằng 0
6) Tính vận tốc và gia tốc ñiểm D trên khâu 2 của cơ cấu tay quay con trượt (hình 2.6a) tại vị trí
các góc ∠CAB = ∠CDB = 90o. Biết tay quay AB quay ñều với vận tốc góc ω1 = 20s-1 và kích thước các khâu l
AB =lCD = 0,5lBC = 0,1m. B 2 D π,d2 c2,c3 1 p b C 1,b2,c2,c3 A ω1 3 b1,b2
Hình 2.6a Hình 2.6b Hình 2.6c
B1 ≡ B2 . Khâu 1 nối với khâu 2 bằng khớp quay: V = và V = ω l . = 2 . 0 1 , 0 = 2m / s 1 B VB2 B 1 AB 1
Tương tự: C2 ≡ C3 và C V = V 2 C3 C V = V + V (1) 2 B2 C2 B2 //AC ⊥BC
Phương trình chỉ tồn tại hai ẩn số là giá trị vận tốc ñiểm C2 và vận tốc tương ñối giữa 2 ñiểm C2
và B2. Hoạ ñồ véc tơ vận tốc ñược vẽ như hình 2.6b.
Từ hoạ ñồ ta nhận thấy rằng vận tốc tại ñiểm B và ñiểm C thuộc khâu 2 ñều bằng nhau, khâu 2 chuyển
ñộng tịnh tiến tức thời, mọi ñiểm trên khâu 2 ñều có vận tốc như nhau với giá trị bằng 2m/s, ω2 = 0. V = V = V = V = 1 B V 2 B C2 3 C 2 D Xác ñịnh gia tốc: a = 1 B aB2 2 2 aB = 1 ω .l = 400 1 , 0 . = 40m / s 1 AB
Chiều hướng từ B ñi vào A n τ C a = a = a + a + a (2) 2 3 C 2 B C2 2 B C2 2 B Trên phương trình 2: n a : có giá tr 2 ị bằng: ω .l 0 C B 2 = BC 2 2 τ a
: Giá trị chưa biết, có phương vuông góc với BC. C2 B2 a
: có phương song song với AC, giá trị chưa biết. C2
Phương trình chỉ còn tồn tại 2 ẩn số là giá trị của gia tốc tiếp tương ñối và gia tốc tuyệt ñối
ñiểm C. Cách giải ñược trình bày trên hình 2.6c.
Áp dụng ñịnh lý ñồng dạng thuận: Hình nối các mút véc tơ biểu diễn gia tốc tuyệt ñối thì ñồng
dạng thuận với hình nối các ñiểm tương ứng trên cùng một khâu. Ta tìm ñược ñiểm d2 tương ứng với
ñiểm D2 trên khâu 2, ñó chính là cực hoạ ñồ gia tốc. Gia tốc ñiểm D bằng 0.
7) Tính vận tốc góc và gia tốc góc của các khâu trong cơ cấu culít (hình 2.7) ở vị trí góc ∠BAC =
90o, nếu tay quay AB quay ñều với vận tốc góc ω1 = 10rad/s và kích thước các khâu là lAB=lAC=0,2m. π b1 A 1 B p 2 ω1 3 b n 3 ak ε b 3 2,b3 ω3 b k 1 b2,b3 C
Hình 2.7a Hình 2.7b Hình 2.7c
B1 ≡ B2 ≡ B3 . Khâu 1 nối với khâu2 bằng khớp tịnh tiến, khâu 2 nối với khâu 3 bằng khớp quay: V ≠ V = V và V = ω l . = 10 , 0 . 2 = 2m / s 1 B B2 B3 B 1 AB 1 VB = V + V (1) 2 1 B B2 1 B ⊥BC //AB
Phương trình (2) tồn tại 2 ẩn số. Cách giải ñược trình bày trên hoạ ñồ vận tốc (hình 2.7b).
Vận tốc ñiểm B2 và B3 ñược xác ñịnh theo hoạ ñồ: V = V 2 = 2 2m / s B B 2 1 VB 2 2 3 1 − 3 ω = = = 10s l , 0 2 2 BC
Như vậy: ω1 = ω2 = ω3 = 10rad/s, chiều xác ñịnh như hình vẽ.
Tương tự gia tốc ta cũng có: a ≠ a = a 1 B B2 B3 2 2 aB = 1 ω .l = 100 , 0
. 2 = 20m / s có chiều hướng từ B ñi vào A. 1 AB n τ
aB = aB + aB B + k a = a + a (2) 2 1 2 1 B C B C 3 3
Trong phương trình trên (2) Ta có ñược: a : ðã xác ñịnh; a
: Giá trị chưa biết, phương song song với BC. 1 B 2 B 1 B 2 a = 2 k 1 ω .V = . 2 10 2
. = 40m / s , chiều lấy theo chiều VB2B1 quay ñi một góc 90o theo chiều 2 B 1 B ω1 (hình 2.7a). n 2 2 a = 3 ω .l = 10. ,
0 2 2 = 20 2m / s BC 3 B C aτ = ε .l = ? 3 BC
, có phương vuông góc với BC. 3 B C
Phương trình chỉ còn tồn tại 2 ẩn số. Cách giải ñược trình bày trên hình 2.7c.
Từ hình vẽ ta tính ñược gia tốc tiếp của ñiểm B3 , biểu diễn bởi 3 bn 3 b : τ 2 a = 20 2m / s 3 B C 20 2 Gia tốc góc khâu 3: 2 ε3 = = 100rad / s , 0 2 2
Do khâu 1 quay ñều và tốc ñộ góc khâu 2 luôn bằng khâu 3 cho nên: ε1 = ε2 = 0.
8) Tìm vận tốc góc lớn nhất của culits 2 (hình 2.8a) qua vận tốc góc ω1 của tay quay 1 cho trước
ứng với ba trường hợp: a) lAB = 0,075m; lAC = 0,3m b) lAB = 0,075m; lAC = 0,225m c) lAB = 0,075m; lAC = 0,150m p B c2 1 2 α α C 3 A B C A ω1 b1,b2
Hình 2.8a Hình 2.8b Hình 2.8c
B1 ≡ B2 . Khâu 1 nối với khâu 2 bằng khớp quay: V = và V = ω . 1 B V 2 B B l 1 AB 1
Chọn B2 làm cực ta viết ñược phương trình véc tơ tính vận tốc ñiểm C2. C V = V + V (1) 2 2 B C2 2 B //BC ⊥BC
Phương trình trên chỉ tồn tại 2 ẩn số giá trị. Hoạ ñồ vận tốc ñược vẽ như ở hình 2.8b.
Gọi α là góc hợp bởi phương vận tốc ñiểm B với phương của khâu BC. Tốc ñộ góc của khâu 2 ñược tính : V sinα C B ω 2 2 2 = = B V (2) l 2 BC lBC
Trong ñẳng thức (2), muốn vận tốc góc khâu 2 ñạt cực ñại thì sinα = 1 và lBC bé nhất.
Khi ñó α = 90o và A, B, C thẳng hàng (hình 2.8c) ω .l , 0 075 ω a) 1 AB 1 ω2 max = = 1 ω = l − l 3 , 0 − 0 , 0 75 3 AC AB ω .l 0 , 0 75 ω b) 1 AB 1 ω2 max = = 1 ω = l − l , 0 225 − 0 , 0 75 2 AC AB ω .l 0 , 0 75 c) 1 ω AB 2 max = = 1 ω = 1 ω l − l 1 , 0 50 − 0 , 0 75 AC AB
9) Tính vận tốc ñiểm D trên khâu 3 của cơ cấu xy lanh quay (hình 2.9a và 2.9b) tại vị trí các góc
∠BAC=∠BCD = 90o, nếu tay quay AB quay ñều với vận tốc góc ω1 = 20rad/s và kích thước các
khâu là lAB = lCD = 0,1m, lAC = 0,173m. a) Xét hình 2.9a: b 1,b2 B D p α 2 α V 1 D c2 3 A ω1 C Hình 2.9a
Ta thấy rằng ñiểm D thuộc khâu 3, khâu 3 ñang quay quanh C. Khâu 3 quay theo khâu 2 do ñó
tốc ñộ góc khâu 2 và khâu 3 là như nhau. ðể tính ñược vận tốc ñiểm D chúng ta chỉ cần xác ñịnh
ñược vận tốc góc khâu 3 thì vấn ñề coi như ñược giải quyết xong.
B1 ≡ B2 . Khâu 1 nối với khâu 2 bằng khớp quay: V = và V = ω l . = 2 . 0 1 , 0 = 2m / s 1 B V 2 B B 1 AB 1
Chọn B2 làm cực ta viết ñược phương trình véc tơ tính vận tốc ñiểm C2. C V = V + V (1) 2 2 B C2 2 B //BC ⊥BC
Phương trình trên chỉ tồn tại 2 ẩn số giá trị. Hoạ ñồ vận tốc ñược vẽ như ở hình 2.a1.
Gọi α là góc hợp bởi phương AB với phương của khâu BC. Tốc ñộ góc của khâu 2 ñược tính : V cosα 1 , 0 C B 2 2 ω = = V = 2 = , 6 2rad / s 2 B l 2 l 2 2 BC BC 1 , 0 + 1 , 0 73
Vận tốc ñiểm D ñược tính như sau: V = ω l . = , 6 1 , 0 . 2 = , 0 62m / s D 3 CD 3
Chiều ñược xác ñịnh theo chiều ω3 như hình 2.9a. b) Xét hình 2.9b: 2 D b 3 B 1 α VD α b 1,b2 3 A ω1 C p Hình 2.9b Hình 2.9b1
Tương tự ta cũng tính ñược vận tốc góc khâu 3 thông qua phương trình véc tơ: V = V + (2) 3 B V 2 B 3 B 2 B ⊥BC //BC
Hoạ ñồ vận tốc cũng giống như trường hợp trên (hình 2.9b1)
Giá trị vận tốc ñiểm D và phương chiều cùng kết quả như trên.
10) Tính vận tốc và gia tốc của ñiểm F trên cơ cấu sàng tải lắc (hình 2.10a) nếu tay quay AB
quay ñều với vận tốc góc ω1 = 20rad/s tại vị trí AB và CE thẳng ñứng. BC nằm ngang. Cho
trước kích thước các khâu: lAB = lCE = lDE = lBC/3 = 0,5lDF = 0,1m. π π f B 4,f5 C c , 1 2 2,c3 3 e3,e4 A e b ω1 4,f4,f5 1,b2,c2,c3 E p 4 F b c 1, b2 2,c3 D 5
Hình 2.10a Hình 2.10b Hình 2.10c1 Hình 2.10c2
ðây là một tổ hợp gồm 2 cơ cấu hợp thành: Cơ câu 4 khâu bản lề ABCD (tương tự bài số 4) và
cơ cấu tay quay con trượt DEF (tương tự bài số 6)
B1 ≡ B2 . Khâu 1 nối với khâu 2 bằng khớp quay: V = và V = ω l . = 2 . 0 1 , 0 = 2m / s 1 B V 2 B B 1 AB 1
Tương tư như những bài ñã giải, vị trí các khâu của cơ cấu ở vị trí ñặc biệt.Khâu 2 chuyển ñộng tịnh tiến tức thời:
ω2 = 0, Vận tốc ñiểm B và C của khâu 2 là bằng nhau VB = V = V 2 C2 C3
Tương tự trên khâu 4, vận tốc ñiểm E và ñiểm F cũng băng nhau: C V 3 VE = V = V = V = 3 E4 4 F 5 F 2
Khâu 4 tịnh tiến thức thời ω4 = 0. VF = 1m/s Vận tốc góc khâu 3: VC 2 3 ω = = 10rad / s 3 = lCD , 0 2 Xác ñịnh gia tốc: a = 1 B aB2 2 2 aB = 1 ω .l = 400 1 , 0 . = 40m / s 1 AB n τ n τ aC = a = a + a = a + a + a (2) 2 C3 B C D C D 2 3 3 C2 B2 C2 B2 Trên phương trình 2: n a : Có giá tr 2 ị bằng: ω C D 3 . lCD = 100 . 0,2 = 20m/s2 3 τ a
: Giá trị chưa biết, có phương vuông góc với CD C D 3 n a
: có giá trị bằng 0 vì ω C B 2 = 0. 2 2 τ a
: Giá trị chưa biết, có phương vuông góc với BC. C2 B2
Phương trình chỉ còn tồn tại 2 ẩn số là giá trị của 2 gia tốc tiếp. Cách giải ñược trình bày trên hình 2.10c1.
Gia tốc ðiểm C bây giờ chỉ tồn tại gia tốc pháp có chiều hướng từ C ñi vào D và có giá trị là
20m/s2. Gia tốc tiếp bằng 0.
Gia tốc ñiểm E3 bằng nửa gia tốc ñiểm C.
Xác ñịnh gia tốc ñiểm F n τ a = a = a + a + (2) 4 F a 5 F E4 4 F E4 4 F E4 Trên phương trình 2: n a : có giá tr 2 ị bằng: ω .l 0 F E 4 = EF 4 4 τ a
: Giá trị chưa biết, có phương vuông góc với EF. 4 F E4 a
: có phương song song với DF, giá trị chưa biết. F4
Phương trình chỉ còn tồn tại 2 ẩn số là giá trị của gia tốc tiếp tương ñối và gia tốc tuyệt ñối
ñiểm C. Cách giải ñược trình bày trên hình 2.10c2 ( Kế tiếp của hình 2.10c1)
Do sự tương quan ñồng dạng cới cơ cấu ta có hệ thức: a a a .DE F E 4 E 10 1 , 0 . 4 = 4 2 a = = 5m / s F = DE DF 4 DF , 0 2
CHƯƠNG 3: PHÂN TÍCH LỰC HỌC TRÊN CƠ CẤU PHẲNG LOẠI 2
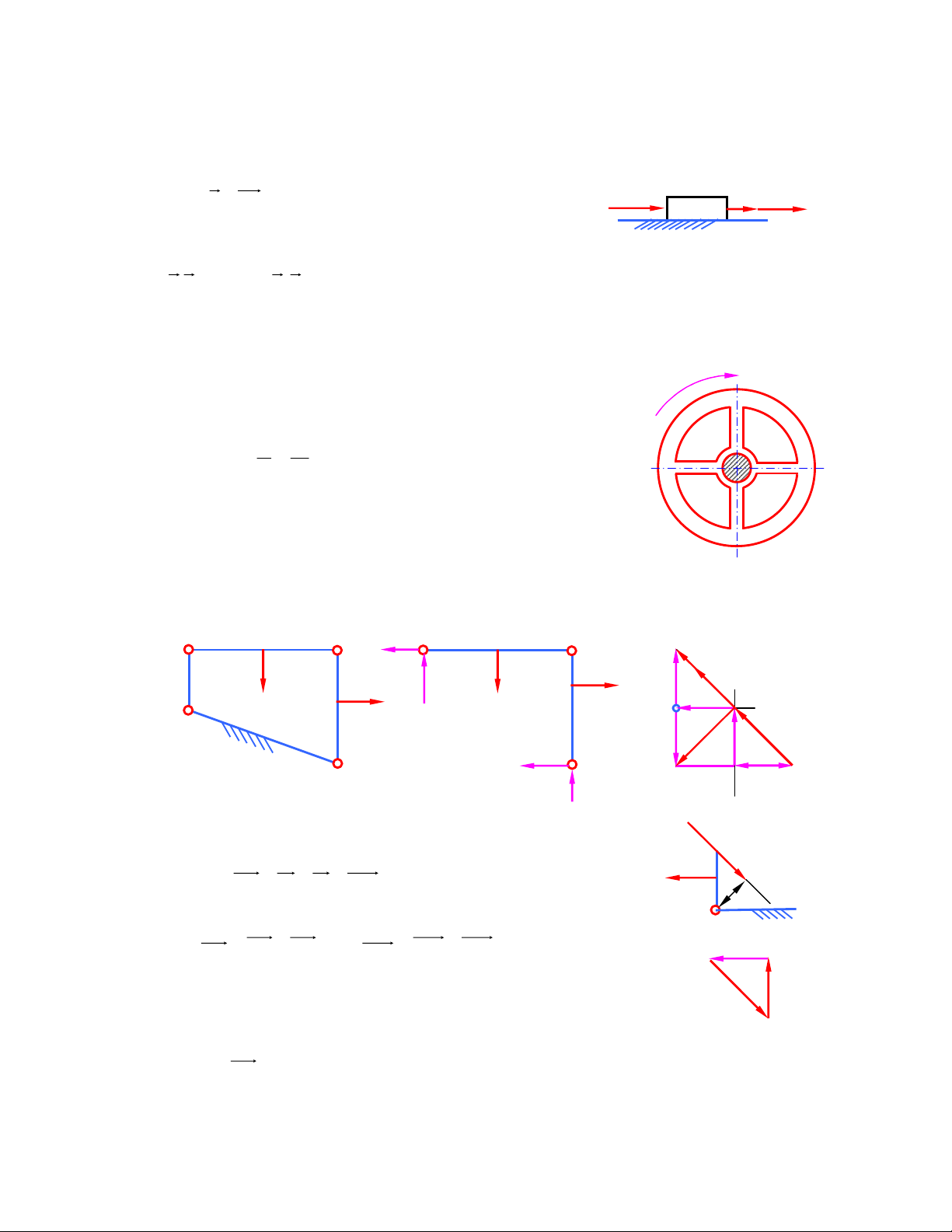
1) Một con trượt chuyển ñộng nhanh dần với gia tốc a = 10m/s2. Không kể tới ma sát trên mặt
trượt, tính công suất ngoại lực P ñẩy vật chuyển ñộng khi vật có vận tốc 5m/s. Biết khối lượng
của con trượt là m = 2 kg (hình 3.1).
Áp dụng nguyên lý D A lăm be, thu ñược: P P + P = 0 V a qt Pqt = m.a = 2.10 = 20N. P = 10N
Công suất ngoại lực P ñẩy vật chuyển ñộng với vận tốc 5m/s: Hình 3.1 P V . = PV
. cos(P,V ) = 20 5 . = 10 W 0
2) Hãy tính mômen của lực quán tính của bánh ñà trong thời gian mở máy: Biết lúc bắt ñầu mở
máy vận tốc góc bằng 0 và sau 3 giây vận tốc tăng tỷ lệ với thời gian thì máy chuyển ñộng
bình ổn, với vận tốc góc trung bình ω = 21s-1; mômen quán tính của bánh ñà là J = 2kg.m2,
trọng tâm của bánh ñà ở ngay trên trục quay (hình 3.2) ω
Phương trình chuyển ñộng của bánh ñà: ω = εt ω 21 2 ε = = = 7rad / s t 3
Mômen của lực quán tính ñược tính: M = J . ε = 2 . 7 = 14Nm Hình 3.2
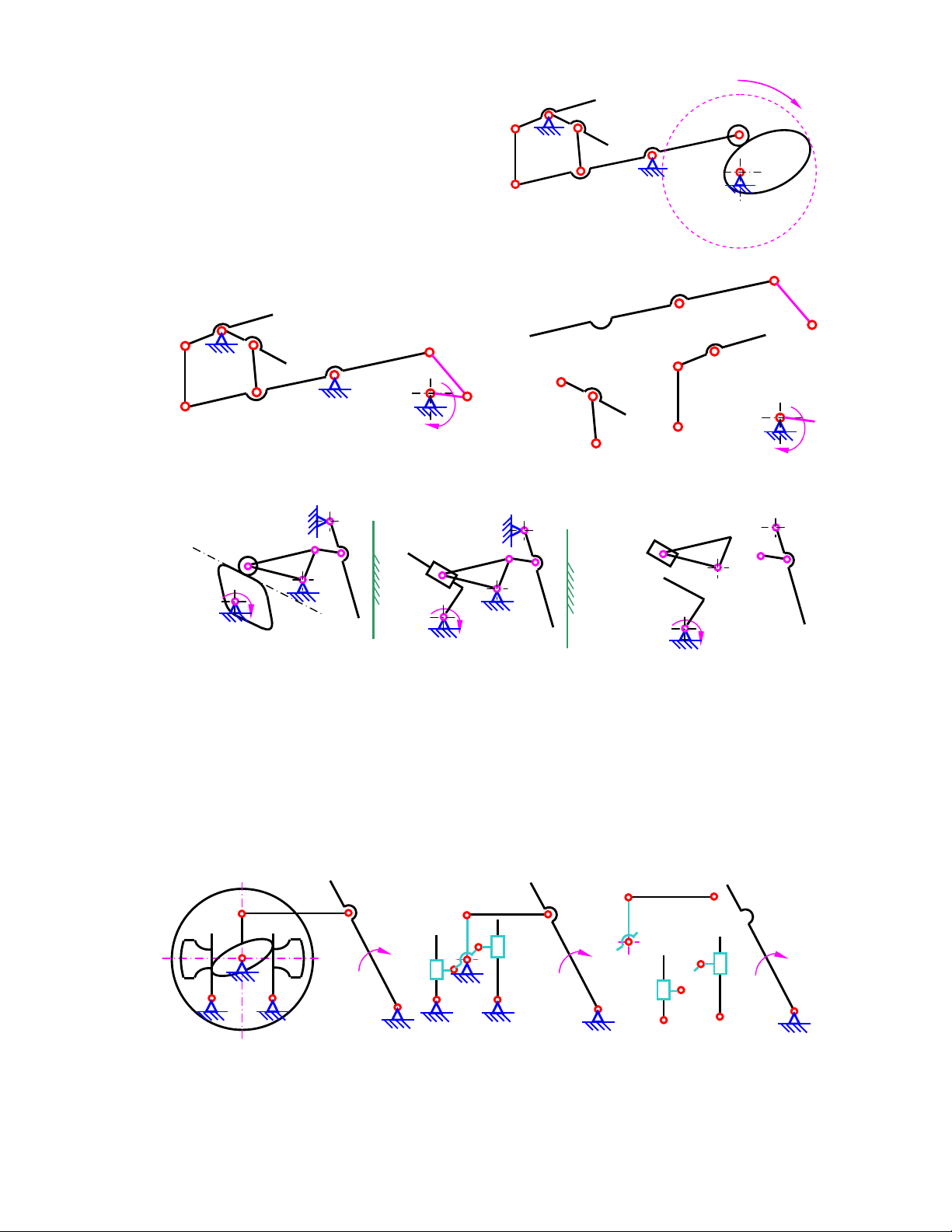
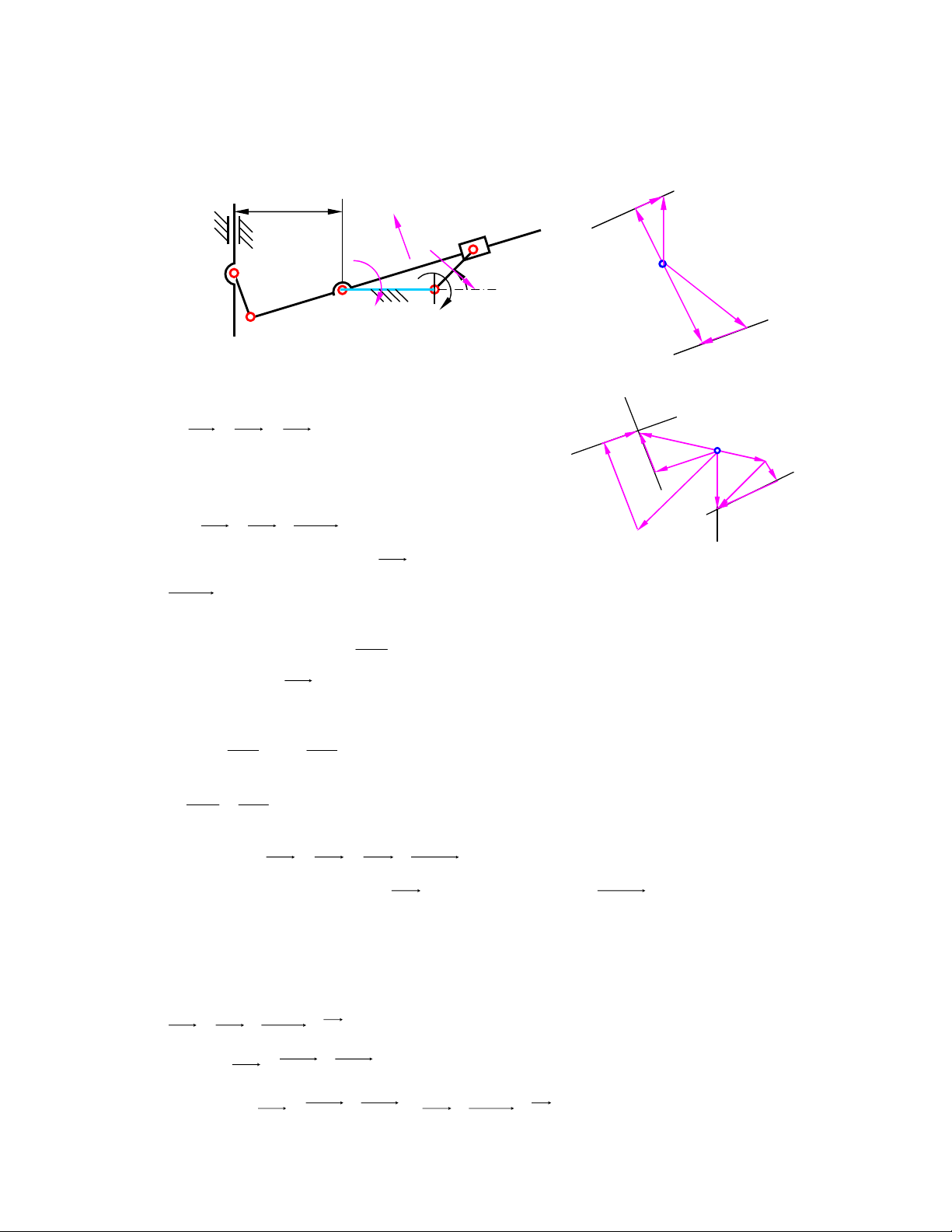
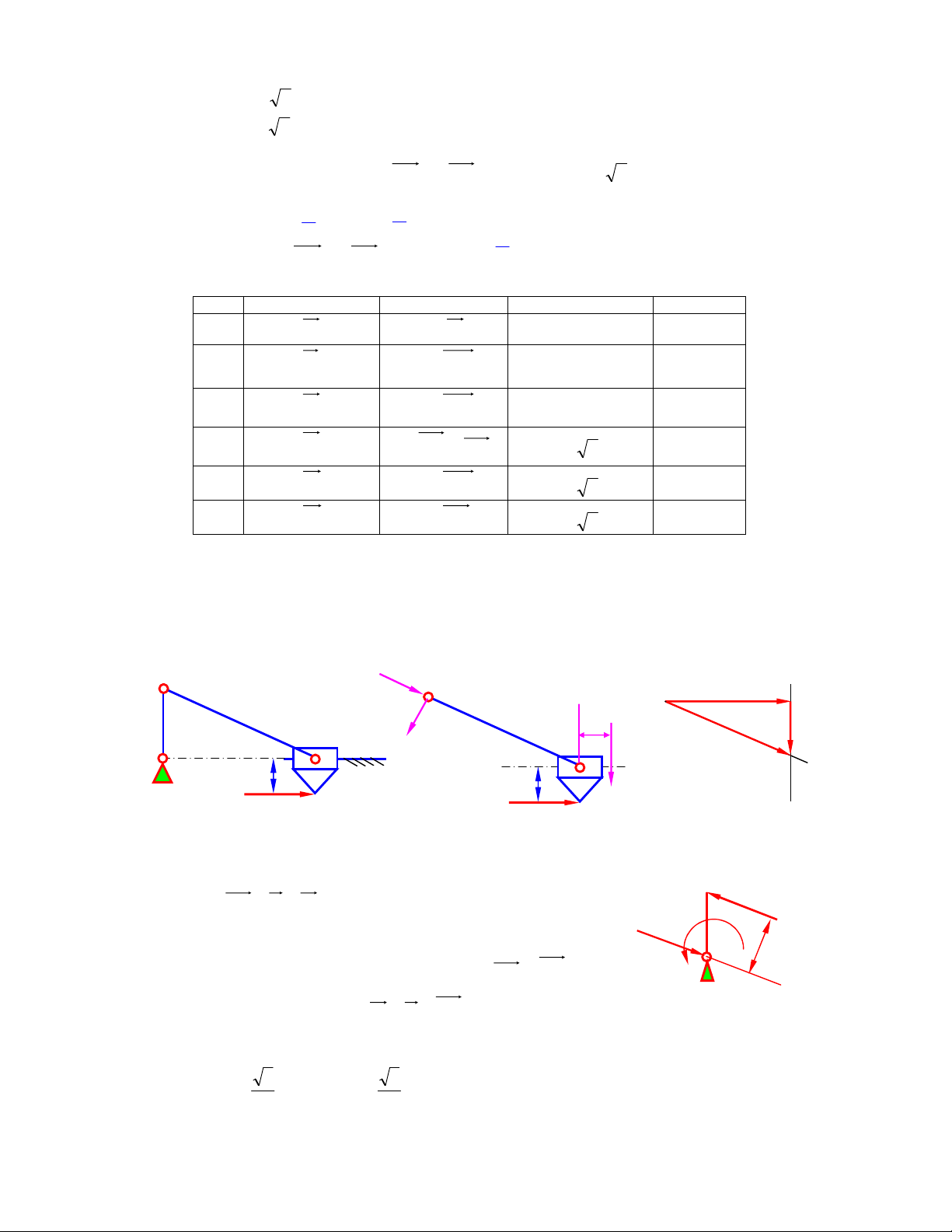
3) Tính những áp lực khớp ñộng và lực cân bằng (ñặt tại ñiểm giữa khâu AB theo phương
vuông góc với khâu này), cho trước lAB = 0,1m, lBC = lCD = 0,2m. Lực cản P2 = P3 = 1000N tác
ñộng tại trung ñiểm các khâu. Lực cản P2 hướng thẳng ñứng xuống dưới, lực P3 hướng nằm
ngang sang phải như hình 3.3a. AB, CD thẳng ñứng, BC nằm ngang B B C M C b 2 n M 2 R 12 1 P2 τ P2 N R P f A N 3 12 P a 3 3 3 D τ D R D3 c d e n R Hình 3.3a Hình 3.3b D 3 Hình 3.3c
Tách nhóm tĩnh ñịnh BCD và ñặt lực vào các khớp chờ (hình 3.3b): R R B 21
12 và RD3. Viết phương trình cân bằng lực cho toàn nhóm: R
+ P + P + R = 0 Pcb h 12 2 3 D3 (1) ph A
ương trình (1) tồn tại 4 ẩn số: Giá trị và phương chiều của 2 lực:
R12 và RD3. Chia các áp lực này ra thành 2 thành phần (hình 3.3b) τ 1 n τ = = + Pcb 1 R n + 2 R R và R R R 12 12 D3 D3 D3
Lấy tổng mômen của các lực ñối với ñiểm C thuộc khâu 2 và thuộc khâu 3: τ RA1 ΣM
(R ) = R .l − P .l = 0 (C ) R21 2 i 12 BC 2 MC τ R = 5 ,
0 P = 500N 〉0 Hình 3.3d 12 2 τ Chiều R
ñã chọn ban ñầu là ñúng. 12 τ ΣM (R ) = R .l − P .l = 0 (C ) 3 i D3 CD 3 NC τ R = 5 , 0 P = 500N 〉0 D3 3 τ Chiều R
ñã chọn ban ñầu là ñúng. D3
Viết lại phương trình cân băng lực (1): τ τ R
+ P + P + R + n R + n R = 0 (2) 12 2 3 D3 D3 12
Phương trình (2) chỉ còn tồn tại 2 ẩn số là giá trị của n R và n R
. Cách giải ñược trình bày trên 12 D3 hình 3.3c.
Véc tơ df biểu thị áp lực RD3 có giá trị là 500 2 (N) , có chiều như hình vẽ 3.3c
Véc tơ fb biểu thị áp lực RD3 có giá trị là 500 2 (N ) , có chiều như hình vẽ 3.3c
Viết phương trình cân băng lực riêng cho khâu 2 ñể tính áp lực tại khớp C: R = − 23 3 R 2 R + P + +R = 0 12 2 32 (3)
Phương trình này chỉ tồn tại 2 ẩn số là giá trị và phương chiều của R32. cách giải ñược vẽ ở hình 3.3c.
Véc tơ fc biểu thị áp lực tại khớp C 3
R 2 có giá trị là 500 2 (N ) , chiều như hình vẽ 3.3c.
Bây giờ ta ñi tính lực cân bằng ñặt tại ñiểm giữa khâu AB:
Phương trình cân băng lực của khâu 1: P + R + R = 0 cb 21 1 A (4)
Phương trình này tồn tại 3 ẩn số, ñể làm giảm bớt ẩn số, ta ñi tìm giá trị Pcb: Σ l h 1 , 0 2 M
(R ) = P . AB − R .h = 0 = = = ( A) i cb 21 P 2R . 2 .500 2 . N cb 500 21 2 l AB . 2 1 , 0
Phương trình 4 ñược giải ở hình 3.3d, và phương chiều của RA1 ñược biểu diễn như hình vẽ, giá trị ñược tính bằng 500N
4) Tính những áp lực khớp ñộng và moomen cân bằng trên khâu dẫn 1 của cơ cấu 4 khâu bản
lề phẳng; cho trước lAB = lBC / 4 = lCD / 4 = 0,1m; khâu BC nằm ngang; các góc ϕ1 = 90o, ϕ2 =
45o và lực cản P3 = 1000N tác ñộng tại trung ñiểm khâu 3 với α3 = 90o (hình 3.4a). Xét xem
việc tính những áp lực khớp ñộng ấy có phụ thuộc và vận tốc góc khâu dẫn không? Giải thích? B C n 2 R a 12 τ 3 d B C 2 R 12 M 1 α ϕ1 3 3 M c τ A α3 D P3 R D3 D P 3 ϕ2 n b R D3
Hình 3.4a Hình 3.4b Hình 3.4c
Tách nhóm tĩnh ñịnh và ñặt các áp lực tại khớp chờ.
Phương trình cân bằng lực ñược viết cho toàn nhóm: B R21 R + P + R = 0 12 3 D3 (1) Mcb
Chia áp lực tại khớp chờ ra làm 2 thành phần như hình vẽ (hình 3.4b): A Σ τ τ R M
(R ) = R .l = 0 R = A1 (C ) 0 2 i 12 BC 12 Σ τ τ M (R ) = R .l − P .l = 0 R = P = (C ) 5 , 0 500N 〉0 Hình 3.4d 3 i D3 CD 3 MC D3 3 τ Chiều R
ñã chọn ban ñầu là ñúng D3
Phương trình cân bằng lực (1) ñược viết lại như sau: τ P + R + n R + n R = 0 3 (2) D3 D3 12
Phương trình (2) chỉ tồn tại 2 ẩn số, hoạ ñồ lực ñược vẽ như ở hình 3.4c. R = 500 N D 2 3
, chiều ñược xác ñịnh như hình vẽ R = 500 2N 12
, chiều cũng ñược xác ñịnh như hình vẽ.
Tính áp lực tại khớp trong C:
Xét sự cân bằng của khâu 2: = = 3 R − 2 1
R 2 , giá trị : R 500 2N 32
Tính mômen cân bbawnoo ñặt trên khâu dẫn 1:
Chọn chiều Mcb như hình 3.4d.
Mcb = R21 . lAB = 500√ 2 . 0,1 = 50√ 2 Nm
Áp lực tại khớp A: R = − 1 R A
21 , giá trị bằng 500√ 2 N Ta lập bảng so sánh: TT Véc tơ biểu diễn Véc tơ thật Giá trị Ghi chú 1 ab 3 P 1000N 2 bc τ R 500N D3 3 cd n R 500N D3 4 da Rn = R 12 12 500 2N 5 bd RD3 500 2N 6 ad 3 R 2 500 2N
Các giá trị trên khi tính không phụ thuộc vào vận tốc góc của khâu dẫn, bởi vì chúng ta không ñi xác ñịnh lực quán tính
5) Tính những áp lực khớp ñộng và moomen cân bằng trên khâu dẫn 1 của cơ cấu tay quay con
trượt (hình 3.5a), cho trước lAB = lBC / 2 = 0,1m, AB thẳng ñứng, AC nằm ngang. Lực cản P3 =
1000N nằm ngang cách rãnh trượt một ñoạn h3 = 0,058m. Sau ñó nghiệm lại Kết quả Mcb
bằng phương pháp công suất. B n B P3 R12 2 a b 2 1 t x N R n C 12 N R12 C A c h3 3 h3 P 3 3 P3
Hình 3.5a Hình 3.5b Hình 3.5c
Tách nhóm tĩnh ñịnh ra khỏi cơ cấu và ñặt áp lực vào các khớp chờ (hình 3.5b):
Phương trình cân bằng lực ñược viết: B R 21 R + N + P = 0 12 3 (1)
Phương trình (1) có 3 ẩn số, ta cần phải giảm bớt các ẩn số. RA1 Chia áp l M
ực ở khớp chờ B ra làm 2 thành phần (hình 3.5b): cb h Σ τ τ M
(R ) = R .l = 0 R = = A (C ) 0 n R R 2 i 12 BC 12 12 12 Ph n
ương trình (1) ñược viết lại: P + N + R = 0 3 (2) Hình 3.5d 12
Hoạ ñồ lực ñược vẽ như ở hình 3.5c.
Do tam giác ABC là nửa tam giác ñều nên tam giác abc trên hình 3.5c cũng là nửa tam giác ñều: 3 3 R = 2000 N = 12 , N 1000 N 3 3
Chiều của các lực ñã chọn ban ñầu là phù hợp.
ðể tìm ñiểm ñặt của áp lực N ta viết phương trình cân bằng mômen của các lực ñối với ñiểm C3:


