Tài liệu Môn Nguyên lý máy | Trường Cao đẳng Công Nghệ Bách Khoa Hà Nội

PHẦN I: CẤU TRÚC CƠ CẤU
Chương 1. Một số khái niệm cơ bản
1.1. Cơ cấu: trong các bộ phận máy, tập hợp các vật thể có chuyển động xác định, làm
nhiệm vụ truyền hay biến đổi chuyển động gọi là cơ cấu.
1.2. Khâu: máy gồm nhiều bộ phận có chuyển động tương đối với nhau, mỗi bộ phận có
thể chuyển động riêng biệt này của máy gọi là một khâu.
 Khâu có thể là vật rắn không biến dạng, vật rắn biến dạng hoặc có dạng dây dẻo
(tuy nhiên trong phạm vi chúng ta nghiên cứu, ta xem khâu như là một vật rắn
không biến dạng hay vật rắn tuyệt đối).
 Khâu có thể là một chi tiết máy độc lập hay do một số chi tiết máy ghép cứng lại với nhau.
1.3. Nối động, thành phần khớp động, khớp động
 Để tạo thành cơ cấu, người ta phải tập hợp các khâu lại với nhau bằng cách
thực hiện các phép nối động. Nối động hai khâu là bắt chúng tiếp xúc với
nhau theo một quy cách nhất định trong suốt quá trình chuyển động.
 Chỗ trên mỗi khâu tiếp xúc với khâu được nối động với nó gọi là thành phần khớp động.
 Tập hợp 2 thành phần khớp động của hai khâu trong một phép nối động gọi là một khớp động.
1.4. Các loại khớp động và lược đồ khớp
 Các loại khớp động:
 Cách phân loại thứ I: căn cứ vào số bậc tự do tương đối bị hạn chế đi khi
nối động (còn gọi là số ràng buộc của khớp), người ta chia khớp động
thành các loại sau: khớp loại 1, loại 2, loại 3, loại 4, loại 5 lần lượt hạn chế
1, 2, 3, 4, 5 bậc tự do tương đối.
Lưu ý: Không có khớp loại 6, vì khớp này hạn chế 6 bậc tự do tương đối
giữa 2 khâu, khi đó 2 khâu ghép cứng với nhau. Không có khớp loại 0, vì
khi đó hai khâu để rời hoàn toàn trong không gian.
 Các phân loại thứ II: căn cứ vào đặc điểm tiếp xúc của 2 khâu khi nối động,
ta phân khớp động thành các loại sau:
• Khớp cao: nếu thành phần khớp động là các điểm hay các đường.
• Khớp thấp: nếu thành phần khớp động là các mặt.
 Lược đồ khớp: trên thực tế, kết cấu khâu và khớp rất phức tạp. Để thuận tiện cho
việc nghiên cứu các bài toàn về cơ cấu, người ta biểu diễn khớp động khác nhau
bằng các lược đồ quy ước. Sau đây là lược đồ một số khớp thông dụng: Lưu ý:
Trong đề thi Olympic Nguyên lý máy, đa phần các bài đều rơi vào dạng cơ cấu phẳng
rất ít khi xuất hiện cơ cấu không gian, các khớp sử dụng cũng đa phần là khớp bản lề,
khớp tịnh tiến và khớp cao phẳng. Vì cậy các bạn chú ý biểu diễn lược đồ chính xác rõ ràng nhất có thể.
Khớp bản lề cần vẽ khoanh tròn, tuyệt đối không được khoanh tô đen. Có thể nhắc hơi
thừa một chút nhưng đây là lỗi mình thấy rất nhiều người hay mắc phải. 1.5. Chuỗi
động và cơ cấu * Chuỗi động:
 Chuỗi động là tập hợp các khâu được nối với nhau bằng các khớp động.
 Dựa trên cấu trúc chuỗi động, người ta phân chuỗi động thành hai loại:
 Chuỗi động hở: là chuỗi động trong đó các khâu chỉ được nối với một khâu khác.
 Chuỗi động kín: là chuỗi động trong đó mỗi khâu được nối ít nhất với 2
khâu khác. Các khâu tạo thành các chu vi khép kín, mỗi khâu tham gia ít nhất 2 khớp động.
 Dựa trên tính chất chuyển động, ta phân biệt chuỗi động không gian và chuỗi động phẳng.
* Cơ cấu: là một chuỗi động, trong đó một khâu được chọn làm hệ quy chiếu (và gọi là
giá), các khâu còn lại có chuyển động xác định trong hệ quy chiếu này (và gọi là các
khâu động). Thông thường coi giá là cố định.
Chương 2. Bậc tự do của cơ cấu
2.1. Khái niệm về bậc tự do của cơ cấu
Số bậc tự do của cơ cấu là số thống số vị trí độc lập cần cho trước để vị trí của toàn bộ
cơ cấu hoàn toàn được xác định.
Số bậc tự do của cơ cấu cũng chính bằng số quy luật chuyển động cần cho trước để
chuyển động của cơ cấu hoàn toàn xác định.
Hiển nhiên là số bậc tự do của cơ cấu phụ thuộc vào cấu trúc cơ cấu và số khâu, số khớp và loại khớp.
2.2. Công thức tính số bậc tự do của cơ cấu phẳng Cơ cấu
phẳng, số bậc tự do được xác định theo công thức:
W = 3n – (p4 + 2p5) + Rthừa + Rtrùng – Wthừa Trong đó:
 W là số bậc tự do của cơ cấu.
 n là số khâu động của cơ cấu.
 p4 là số khớp loại cao.
 p5 là số khớp loại thấp.
 Rthừa là số ràng buộc thừa.
 Rtrùng là số ràng buộc trùng. 
Wthừa là số bậc tự do thừa.
Việc xác định số khâu động, số khớp loại cao, số khớp loại thấp tương đối dễ dàng và
không mấy khó khăn. Tuy nhiên việc xác định các ràng buộc thừa, ràng buộc trùng, số
bậc tự do thừa có khó khăn hơn đôi chút.
Nhận xét: bậc tự do của cơ cấu không phụ thuộc việc chọn khâu nào làm giá, nói một
cách khác khi thay đổi giá, bậc tự do của cơ cấu không đổi.
Sau đây là một vài ví dụ về cơ cấu có chứa ràng buộc thừa, ràng buộc trùng và bậc tự do thừa.
Chương 3. Xếp hạng cơ cấu phẳng
Mỗi cơ cấu gồm một hay nhiều khâu dẫn, nối với giá và với một số nhóm có bậc tự do bằng không.
Dưới dạng biểu thức có thể viết: W = W + 0+0+0+0+… Cơ cấu có W bậc tự do Số khâu dẫn
Các nhóm có bậc tự do bằng 0
3.1. Nhóm Atxua – Hạng của nhóm
Nhóm Atxua là nhóm có bậc tự do bằng 0 và không thể tách thành các nhóm nhỏ hơn
có bậc tự do bằng không. Hạng của nhóm Atxua:
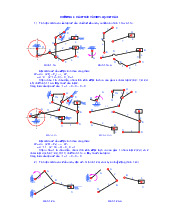
 Nhóm Atxua chỉ có hai khâu và ba khớp được gọi là nhóm Atxua hạng II. Có 5
loại nhóm nhóm Axua hạng II như sau:
Nhóm gồm có 2 khâu và 3 khớp trượt không phải là một nhóm Atxua vì bậc tự do của nó bằng 1.
 Nhóm Atxua có hạng cao hơn II:
Nếu các khớp trong của một nhóm tĩnh định tạo thành một đa giác thì hạng của
nhóm Atxua được lấy bằng số đỉnh của đa giác, nếu tạo thành nhiều đa giác thì
hạng của nhóm lấy bằng số đủnh của đa giác nhiều đỉnh nhất. 3.2. Hạng của cơ cấu
3.2.1. Nguyên tắc xếp hạng cơ cấu
Ngoài cơ cấu loại 1, không chứa một nhóm tĩnh định nào cả, tất cả các cơ cấu khác (có
chứa ít nhất một nhóm tĩnh định) được xếp loại như sau:
 Nếu cơ cấu chỉ chứa một hay nhóm tĩnh định, hạng của nhóm chính là hạng của cơ cấu.
 Nếu cơ cấu chứa nhiều nhóm tĩnh định, hạng của cơ cấu là hạng của nhóm có hạng cao nhất.
3.2.2. Nguyên tắc tách nhóm
Để xếp hạng được cơ cấu, chúng ta cần phải biết trong cơ cấu có những nhóm tĩnh định
nào. Muốn vậy, trước khi xếp hạng cơ cấu phải tách nó ra thành khâu dẫn, giá và các
nhóm tĩnh định. Nguyên tắc tách nhóm như sau:
 Khi tách nhóm, phải cho trước khâu dẫn vì cùng một cơ cấu nếu thay khâu dẫn
khác đi, các nhóm tĩnh định tách ra được trong hai trường hợp có thể khác nhau.
Điều này cũng dễ hiểu bởi vì cấu trúc nhóm tĩnh định phụ thuộc cấu trúc các khâu
trong nhóm, vậy mà khi thay khâu dẫn, ta đã lấy đi khỏi các nhóm tĩnh định, trong
cơ cấu một khâu vốn trước kia thuộc các nhóm này và thay bằng một khâu khác.
 Sau khi tách một nhóm ra khỏi cơ cấu, phần còn lại của cơ cấu vẫn phải là một
cơ cấu hoàn chỉnh, tức là phải là một chuỗi động kín, có bậc tự do bằng bậc tự do
của cơ cấu ban đầu, hoặc phải là một cơ cấu loại 1 cũng bằng số bậc tự do của cơ cấu.
 Khi tách, ta thử tách ra nhóm đơn giản, nếu không được hãy tách ra những nhóm
phức tạp hơn (tức là có loại cao hơn).  Tách từ xa đến gần.
3.2.3. Thay thế khớp cao bằng khớp thấp
Chương 4. Bài toán tính số bậc tự do và xếp hạng cơ cấu 4.1. Yêu cầu
Đề bài sẽ cho một lược đồ động của một cơ cấu phẳng. Yêu cầu:
 Xác định số bậc tự do của cơ cấu.
 Xếp hạng cơ cấu với một khâu cho trước là khâu dẫn.
 Câu này tùy từng bài: Chứng minh rằng với cơ cấu đã cho việc thay đổi khâu dẫn
có thể làm thay đổi hạng của cơ cấu. Bản chất là xếp hạng cơ cấu với các khâu dẫn khác nhau. 4.2. Hướng dẫn giải
4.2.1. Xác định số bậc tự do của cơ cấu.
Bước 1: Viết công thức tính số bậc tự do của cơ cấu phẳng.
Bước 2: Giải thích các tham số trong công thức, đồng thời xác định giá trị của chúng.
Bước 3: Thay số vào công thức trên, tính số bậc tự do của cơ cấu đã cho. Bước 4: Kết luận. 4.2.2. Xếp hạng cơ cấu
Bước 1: Thay thế chuyển tất cả các khớp cao về khớp thấp.
Bước 2: Tách cơ cấu đã cho thành khâu dẫn cộng với các nhóm Atxua theo nguyên tắc
như đã được nếu ra ở trên.
Bước 3: Biểu diễn hình vẽ và ghi rõ là nhóm Axua gồm những khâu, những khớp nào.
Đánh số các khâu,ghi tên các khớp. Lưu ý:
 Chỉ có khâu dẫn mới được nối với giá, tuyệt đối những khâu khác không được vẽ thêm giá cố định vào.
 Các khớp chỉ được biểu diễn và ghi tên một lần duy nhất, không được ghi nhiều lần.
 Lưu ý trong việc vẽ khớp trượt sẽ được nói cụ thể trong ví dụ minh họa phía dưới.
Bước 4: Kết luận hạng của cơ cấu với khâu dẫn đang xét.
4.3. Bài tập có hướng dẫn
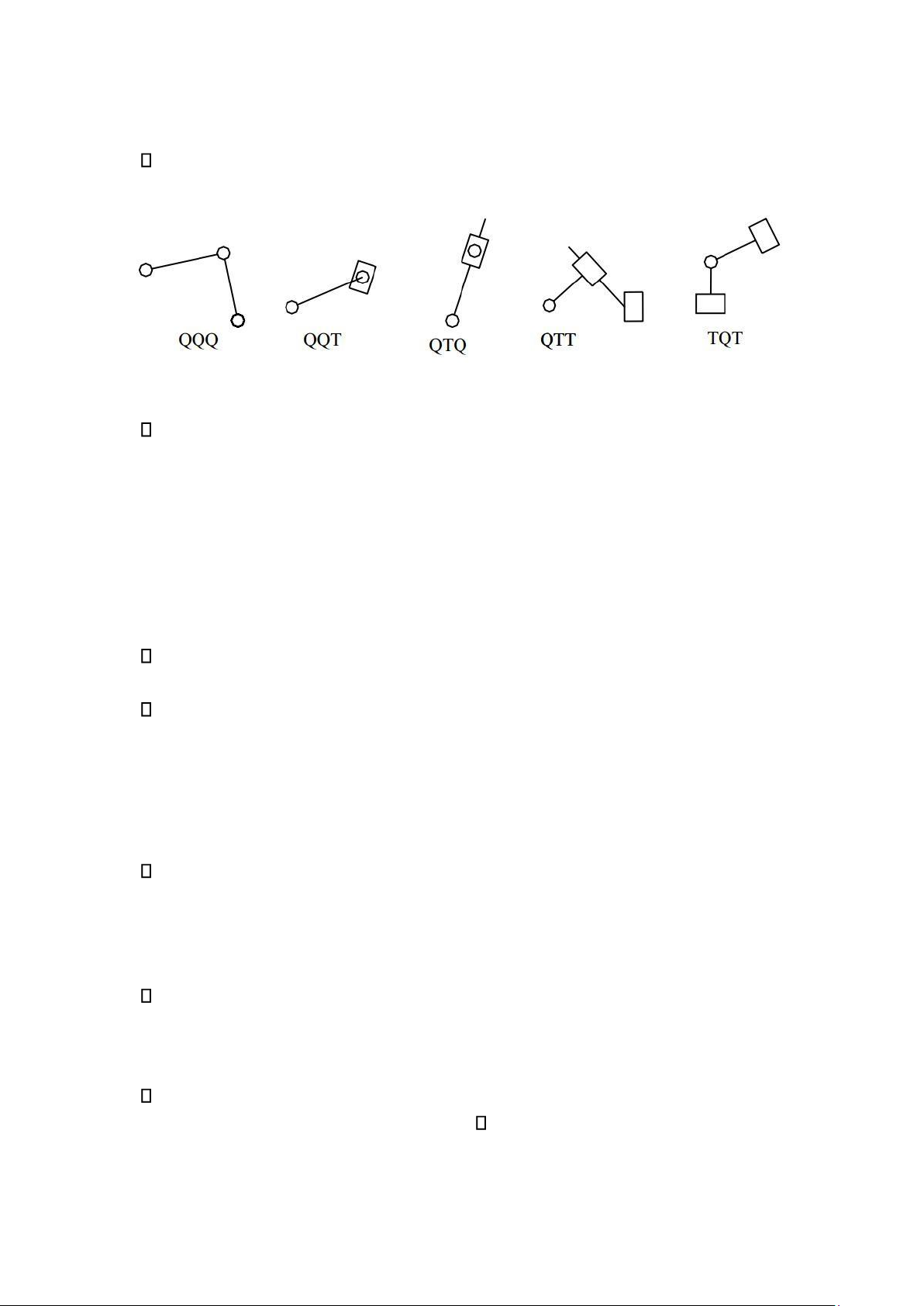
Bài 1 (Đề năm 2013): Cho cơ cấu thanh phẳng như hình vẽ, trong đó kích thước động
học và vị trí khảo sát được xác định theo lưới ô vuông , cạnh mỗi ô vuông nhỏ a = 1m.
Tính số bậc tự do và xếp hạng cơ cấu. Giải:
Công thức xác định số bậc tự do của cơ cấu phẳng:
W = 3n – (p4 + 2p5) + Rthừa + Rtrùng – Wthừa Trong đó:
 n là số khâu động, n = 5.
 p4 là số khớp loại cao, p4 = 0.
 p5 là số khớp loại thấp, p5 = 7.
 Rthừa là số ràng buộc thừa, Rthừa = 0.
 Rtrùng là số ràng buộc trùng, Rtrùng = 0. 
Wthừa là số bậc tự do thừa, Wthừa = 0.
Thay vào biểu thức tính số bậc tự do, ta có: W = 3.5 – ( 0 + 2.7) + 0 + 0 – 0 = 1 bậc tự do
Vậy cơ cấu đã cho có 1 bậc tự do. Xếp hạng cơ cấu:
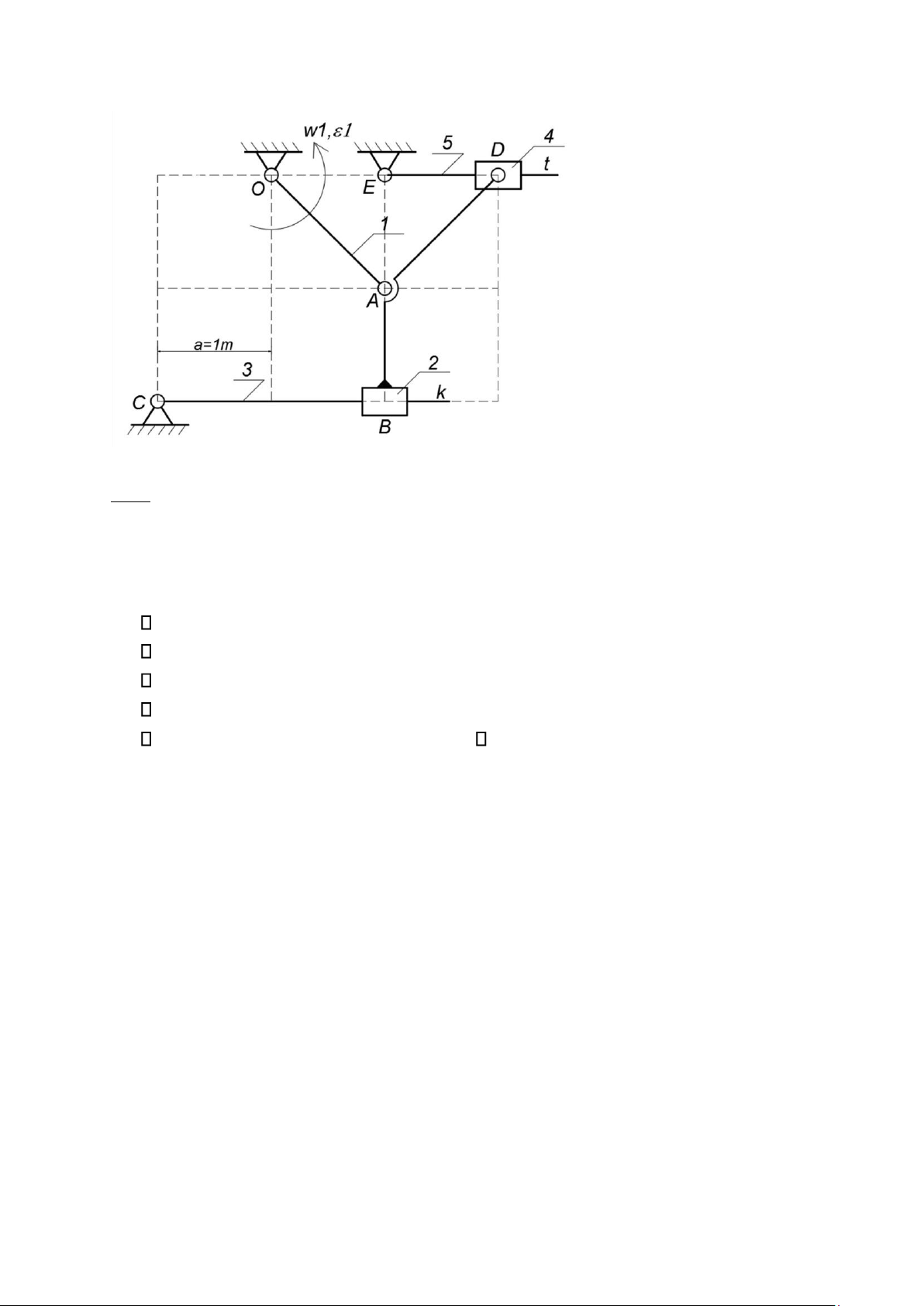
Với khâu 1 là khâu dẫn. Cơ cấu được tách thành khâu dẫn và 2 nhóm Axua hạng 2 được
biểu diễn như hình vẽ.
Nhóm Axua h ạ ng 2 th ứ nh ấ t g ồ m: khâu 4,khâu 5 và kh ớ p trư ợ t D,các kh ớ p quay E, D
Nhóm Axua h ạ ng 2 th ứ hai g ồ m: khâu 2, khâu 3 và kh ớ p trư ợ t B, các kh ớ p quay C, A
V ậ y cơ c ấ u đ ã cho là c ơ c ấ u h ạ ng 2 khi khâu 1 là khâu d ẫ n.
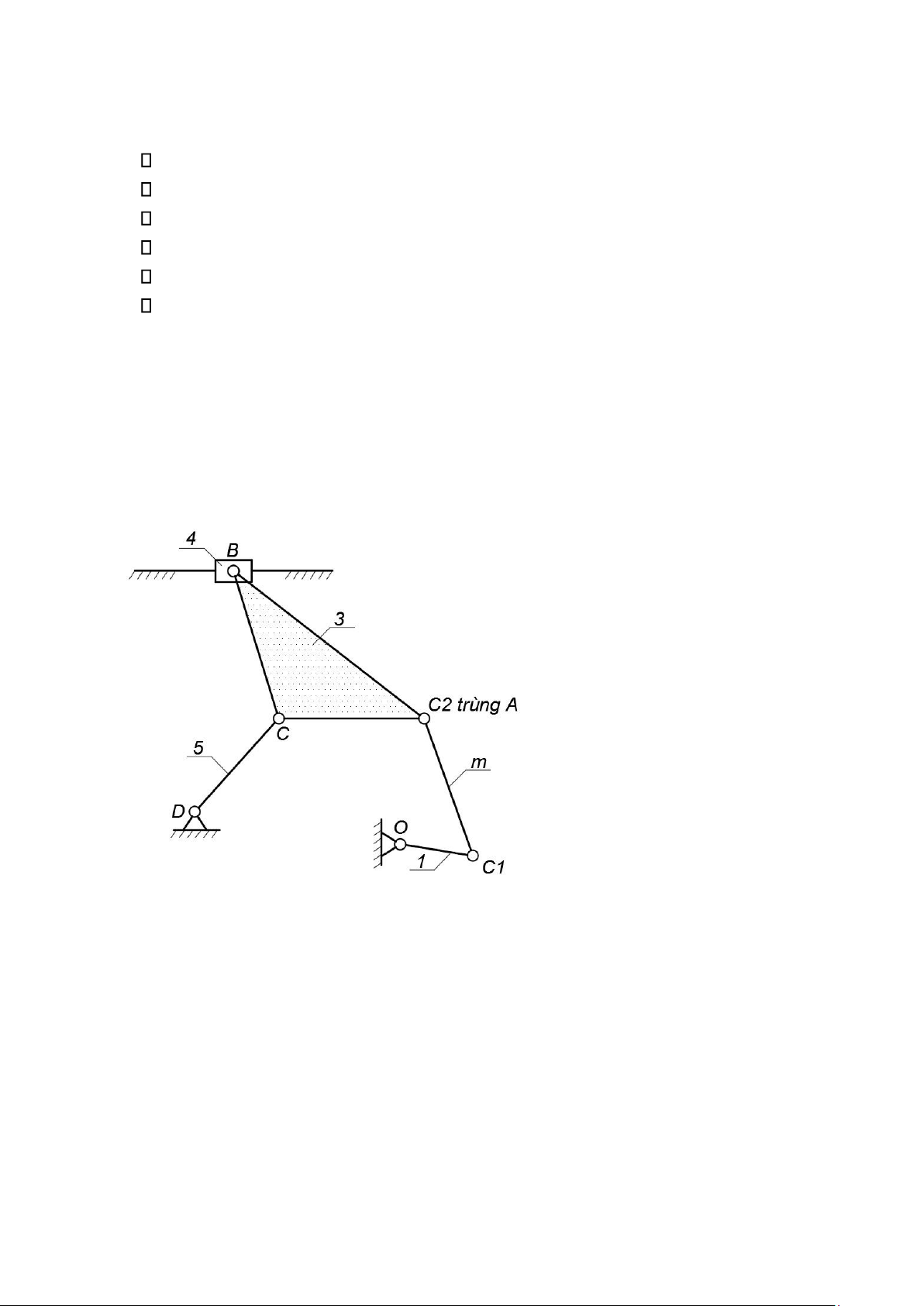
Bài 2: Cho cơ c ấ u thanh ph ẳ ng như h ình v ẽ .
a. Tính s ố b ậ c t ự do và x ế p h ạ ng cơ cáu khi khâu 1 là khâu d ẫ n.
b. Ch ứ ng minh v ớ i cơ c ấ u đ ã cho, h ạ ng c ủ a cơ c ấ u ph ụ thu ộ c vào cách l ự a ch ọ n khâu d ẫ n.
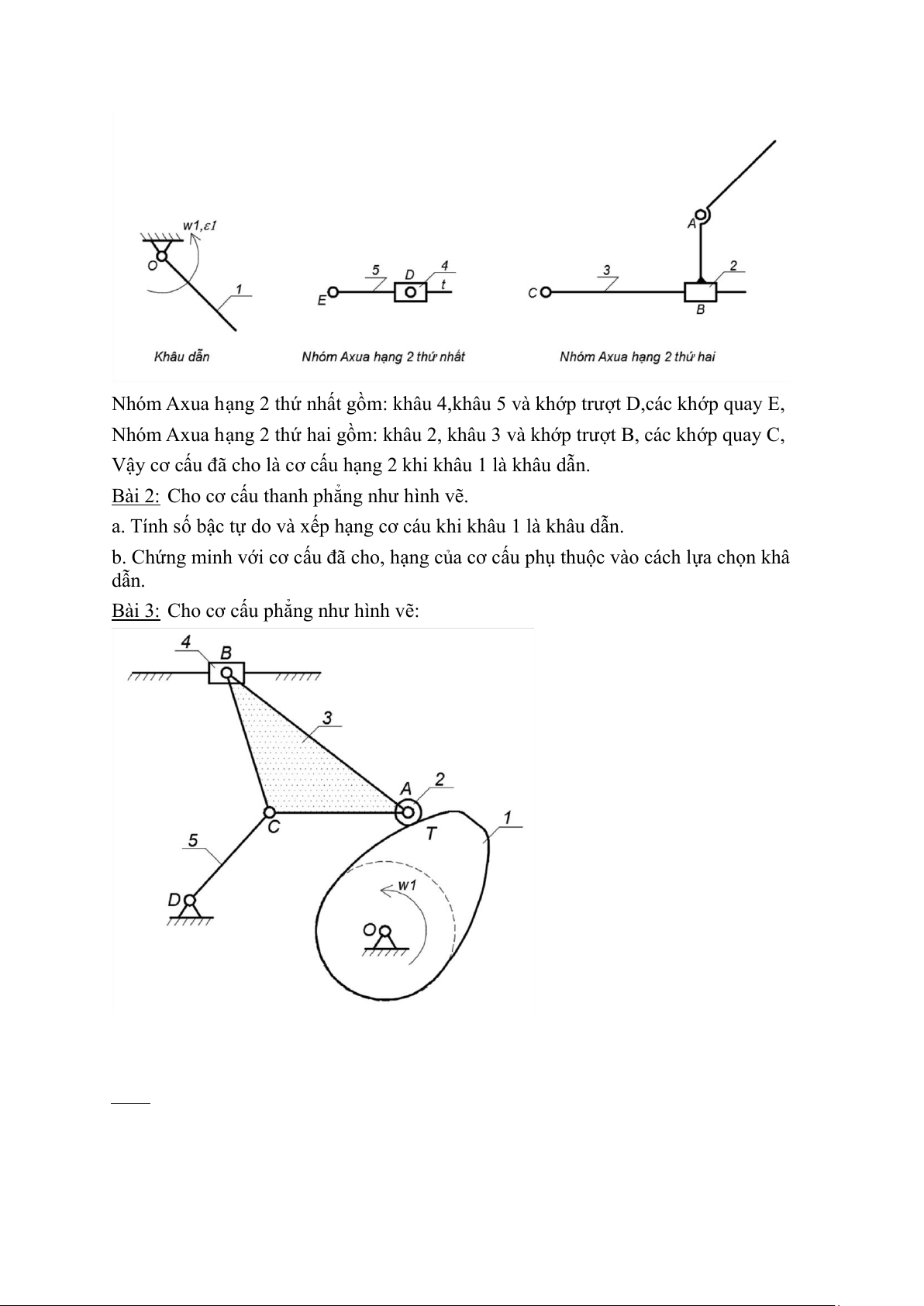
Bài 3: Cho cơ c ấ u ph ẳ ng như h ình v ẽ :
a. Tính số bậc tự do và xếp hạng cơ cấu trong trường hợp khâu 1 là khâu dẫn.
b. Hãy xếp hạng của cơ cấu trong trường hợp chọn khâu 4 làm khâu dẫn. Giải:
Công thức xác định số bậc tự do của cơ cấu phẳng:
W = 3n – (p4 + 2p5) + Rthừa + Rtrùng – Wthừa Trong đó:
 n là số khâu động, n = 5.
 p4 là số khớp loại cao, p4 = 1.
 p5 là số khớp loại thấp, p5 = 6.
 Rthừa là số ràng buộc thừa, Rthừa = 0.
 Rtrùng là số ràng buộc trùng, Rtrùng = 0.
 Wthừa là số bậc tự do thừa, Wthừa = 1 (chuyển động quay của con lăn 2 quang tâm A).
Thay vào biểu thức tính số bậc tự do, ta có: W = 3.5 – ( 1 + 2.6) + 0 + 0 – 1 = 1 bậc tự do
Vậy cơ cấu đã cho có 1 bậc tự do.
Để xếp hạng cơ cấu, trước hết phải thay thế khớp cao T bằng khâu thay thế m với hai
khớp thấp C1, C2 (C1, C2 nằm tại tâm cong của 2 biên dạng tạo khớp cao T, C2 trùng A)
và nhận được cơ cấu thay thế chỉ gồm tất cả các khớp thấp loại 5 như hình sau.
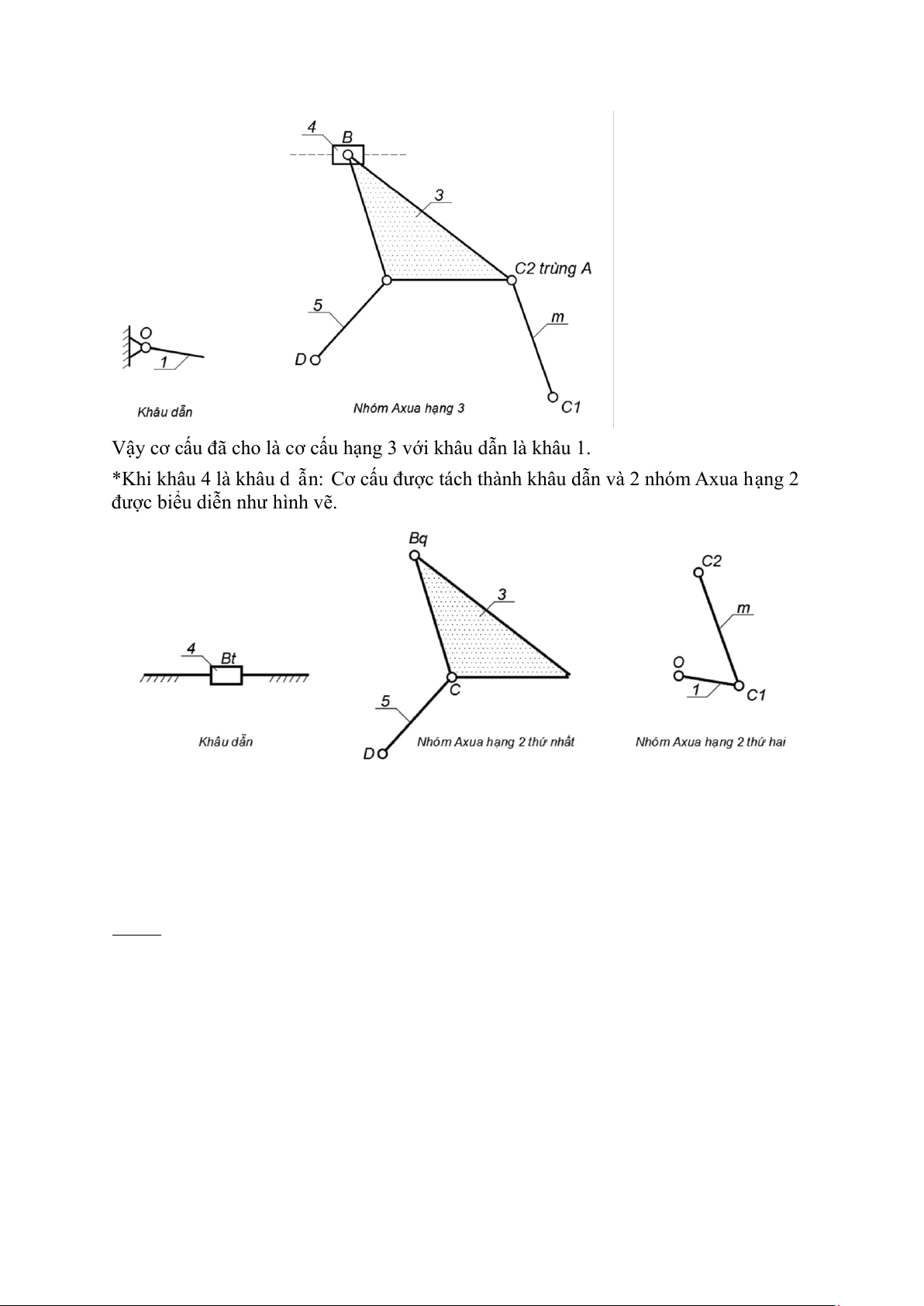
*Khi khâu 1 là khâu dẫn: Cơ cấu được tách thành khâu dẫn và nhóm Axua hạng 3
gồm các khâu m, 3, 4, 5 và các khớp C1, C2, C, Btrượt, Bquay, D được biểu diễn như hình vẽ sau.
V ậ y cơ c ấ u đ ã cho là c ơ c ấ u h ạ ng 3 v ớ i khâu d ẫ n là khâu 1.
*Khi khâu 4 là khâu d ẫ n: Cơ c ấ u đư ợ c tách thành khâu d ẫ n và 2 nhóm Axua h ạ ng 2
đư ợ c bi ể u di ễ n như h ình v ẽ .
Nhóm Axua hạng 2 thứ nhất gồm: Khâu 3, khâu 5 và khớp trượt Btrượt, khớp quay C,D
Nhóm Axua hang 2 thứ hai gồm: Khâu 1, khâu m và các khớp quay O, C1, C2.
Theo đó, với khâu 4 là khâu dẫn, cơ cấu đã cho trở thành cơ cấu hạng 2.
Vậy hạng của cơ cấu đã cho đã thay đổi khi thay đổi cách lựa chọn khâu dẫn.
Bài 4: Cho cơ cấu phẳng như hình vẽ:
*Khi khâu 1 là khâu dẫn: Cơ cấu được tách thành:  Khâu dẫn 1.
 Nhóm Axua hạng 2 bao gồm: các khâu m, 2 và các khớp C1, C2 và B.
 Nhóm Axua hạng 4 bao gồm: các khâu 3, 4, 5, 6 và các khớp C, D, E, F, G, H. được
biểu diễn như hình vẽ.
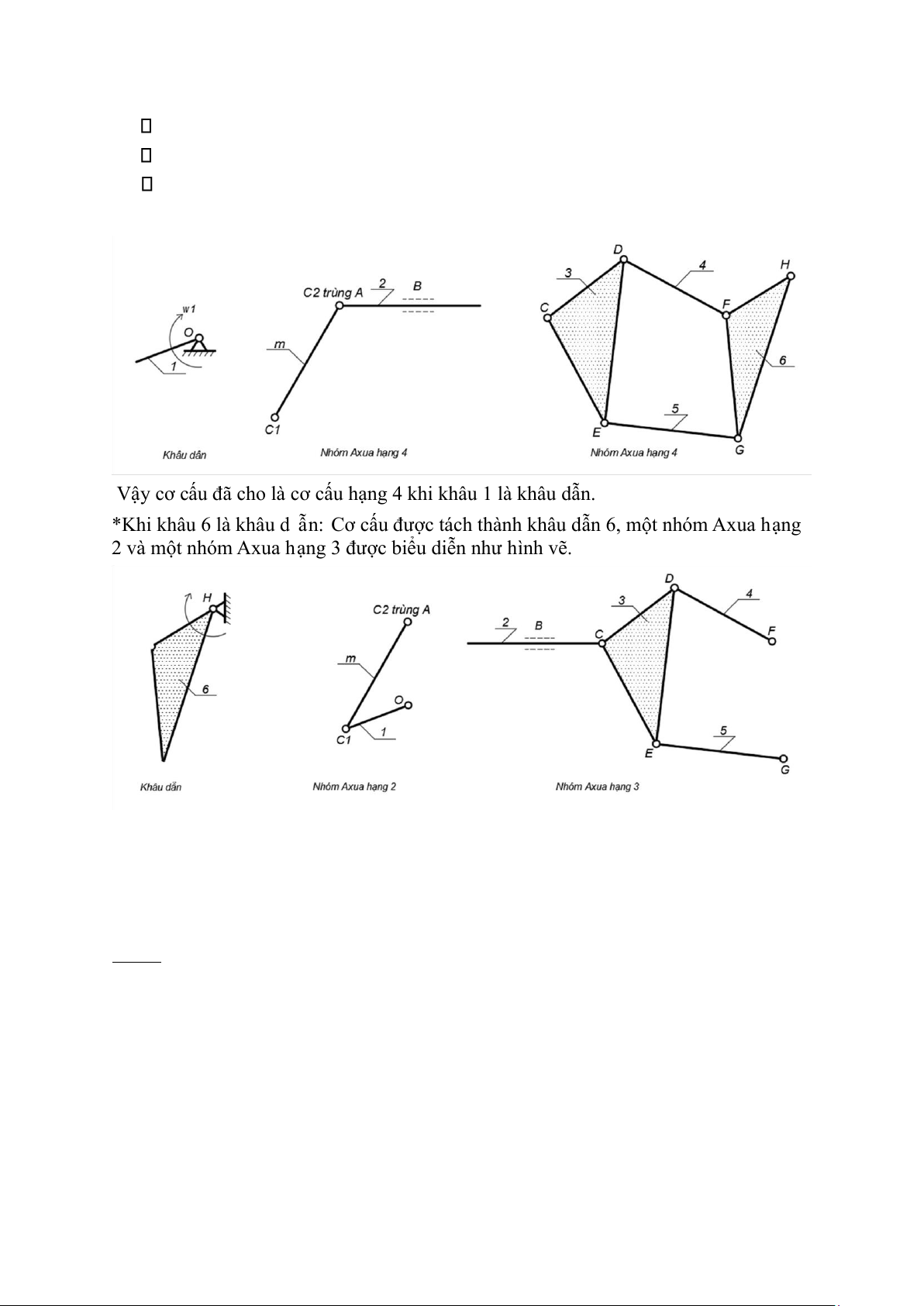
V ậ y cơ c ấ u đ ã cho là c ơ c ấ u h ạ ng 4 khi khâu 1 là khâu d ẫ n.
*Khi khâu 6 là khâu d ẫ n: Cơ c ấ u đư ợ c tách thành khâu d ẫ n 6, m ộ t nhóm Axua h ạ ng
2 và m ộ t nhóm Axua h ạ ng 3 đư ợ c bi ể u di ễ n như h ình v ẽ .
Nhóm Axua hạng 2 bao gồm: khâu 1, khâu m và 3 khớp quay A, C1, O.
Nhóm Axua hạng 3 bao gồm: các khâu 2, 3, 4, 5 và các khớp B, C, D, E, F, G.
Theo đó, với khâu 6 là khâu dẫn, cơ cấu đã cho trở thành cơ cấu hạng 3.
Vậy hạng của cơ cấu đã cho đã thay đổi (từ hạng 4 về hạng 3) khi thay đổi khâu dẫn.
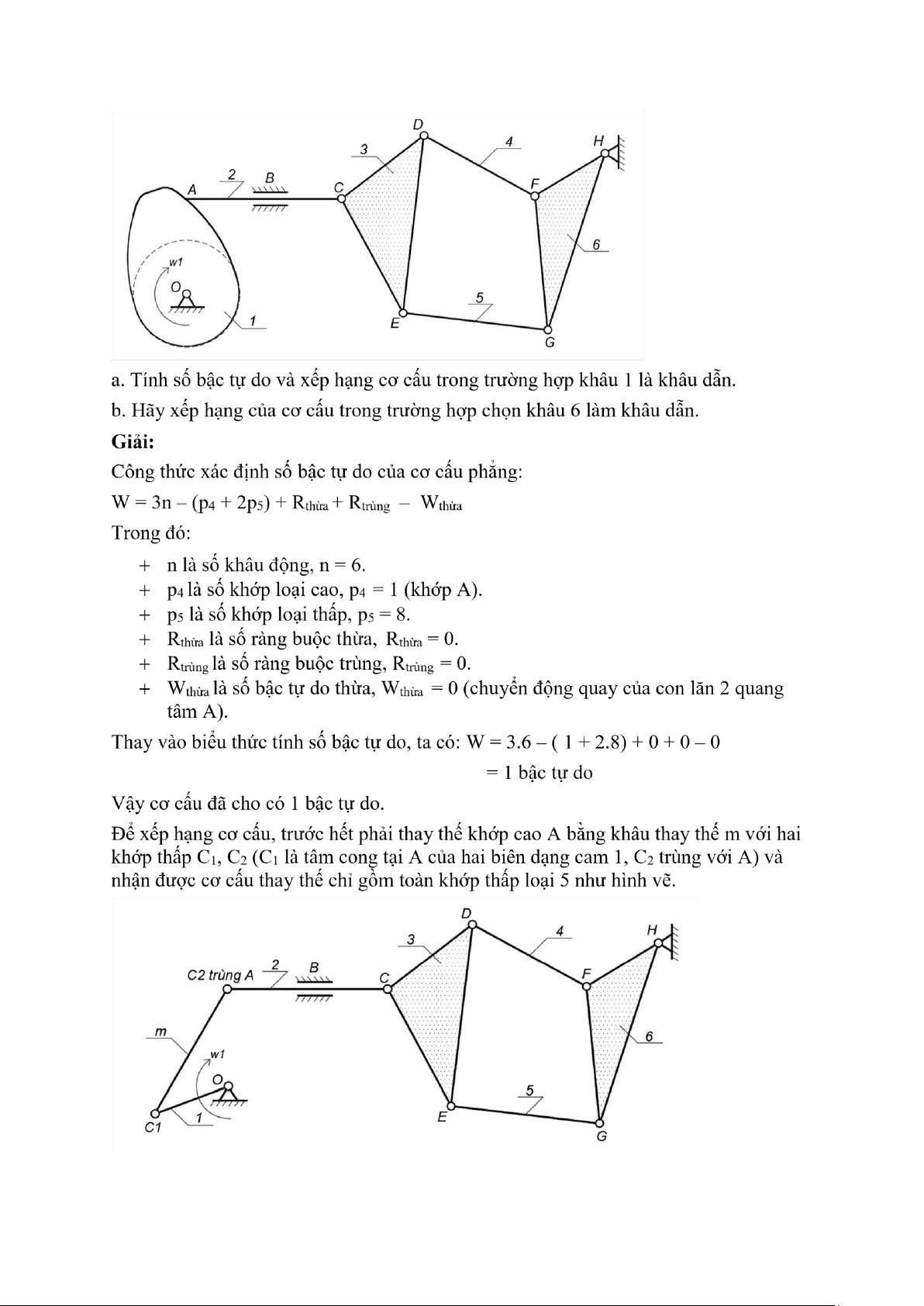
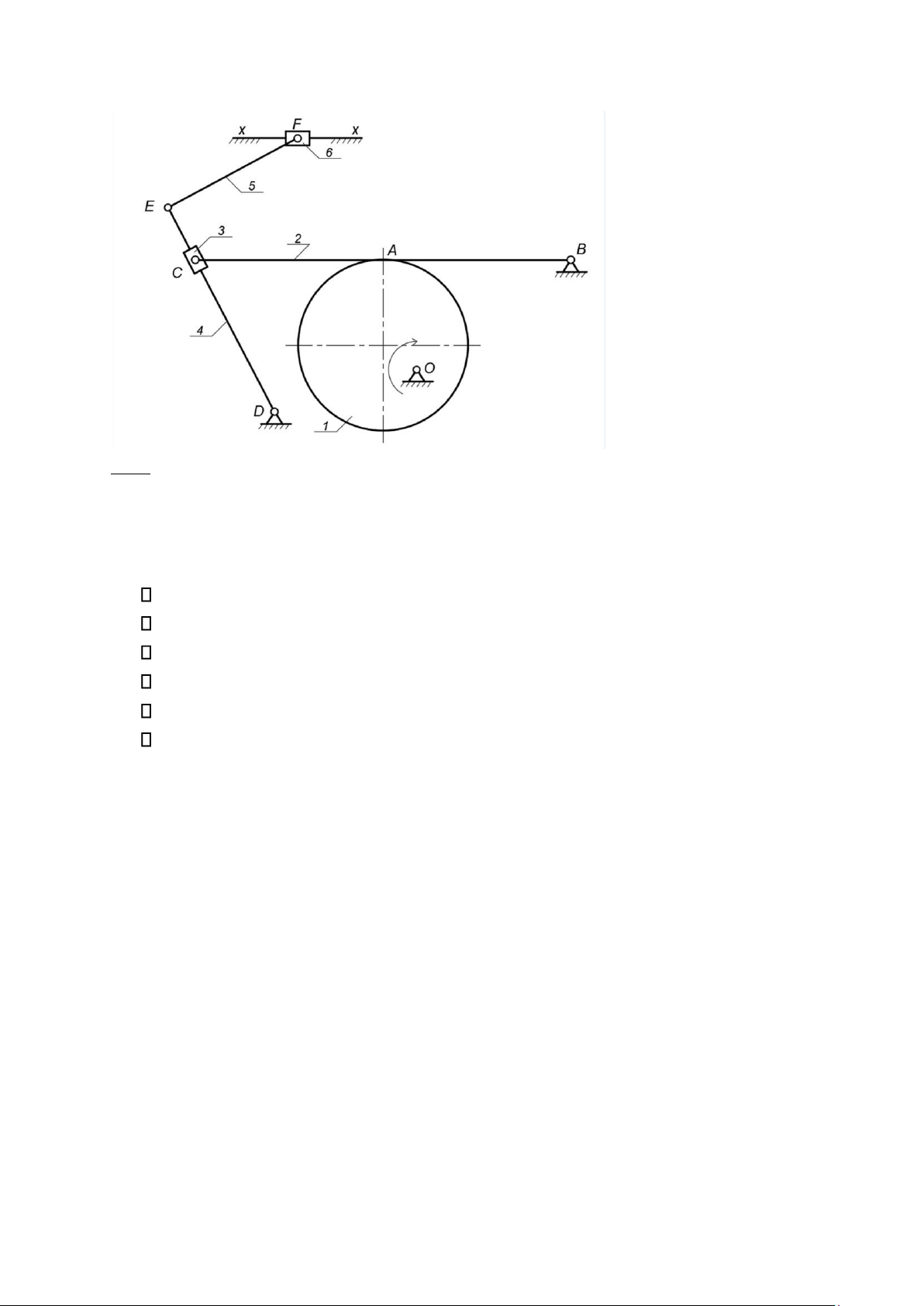
Bài 5: Cho cơ cấu phẳng như hình vẽ:
a. Tính số bậc tự do và xếp hạng cơ cấu trong trường hợp khâu 1 là khâu dẫn.
b. Chứng tỏ rằng khi đổi khâu 6 làm khâu dẫn thay cho khâu 1, hạng của cơ cấu đã cho không thay đổi. Giải:
Công thức xác định số bậc tự do của cơ cấu phẳng:
W = 3n – (p4 + 2p5) + Rthừa + Rtrùng – Wthừa Trong đó:
 n là số khâu động, n = 6.
 p4 là số khớp loại cao, p4 = 1 (khớp A).
 p5 là số khớp loại thấp, p5 = 8.
 Rthừa là số ràng buộc thừa, Rthừa = 0.
 Rtrùng là số ràng buộc trùng, Rtrùng = 0.
 Wthừa là số bậc tự do thừa, Wthừa = 0 (chuyển động quay của con lăn 2 quang tâm A).
Thay vào biểu thức tính số bậc tự do, ta có: W = 3.6 – ( 1 + 2.8) + 0 + 0 – 0 = 1 bậc tự do
Vậy cơ cấu đã cho có 1 bậc tự do.
Để xếp hạng cơ cấu, trước hết phải thay thế khớp cao A bằng khâu thay thế m với hai khớp
thấp C1 và khớp trượt A và nhận được cơ cấu chỉ gồm toàn khớp thấp loại 5 như hình vẽ.
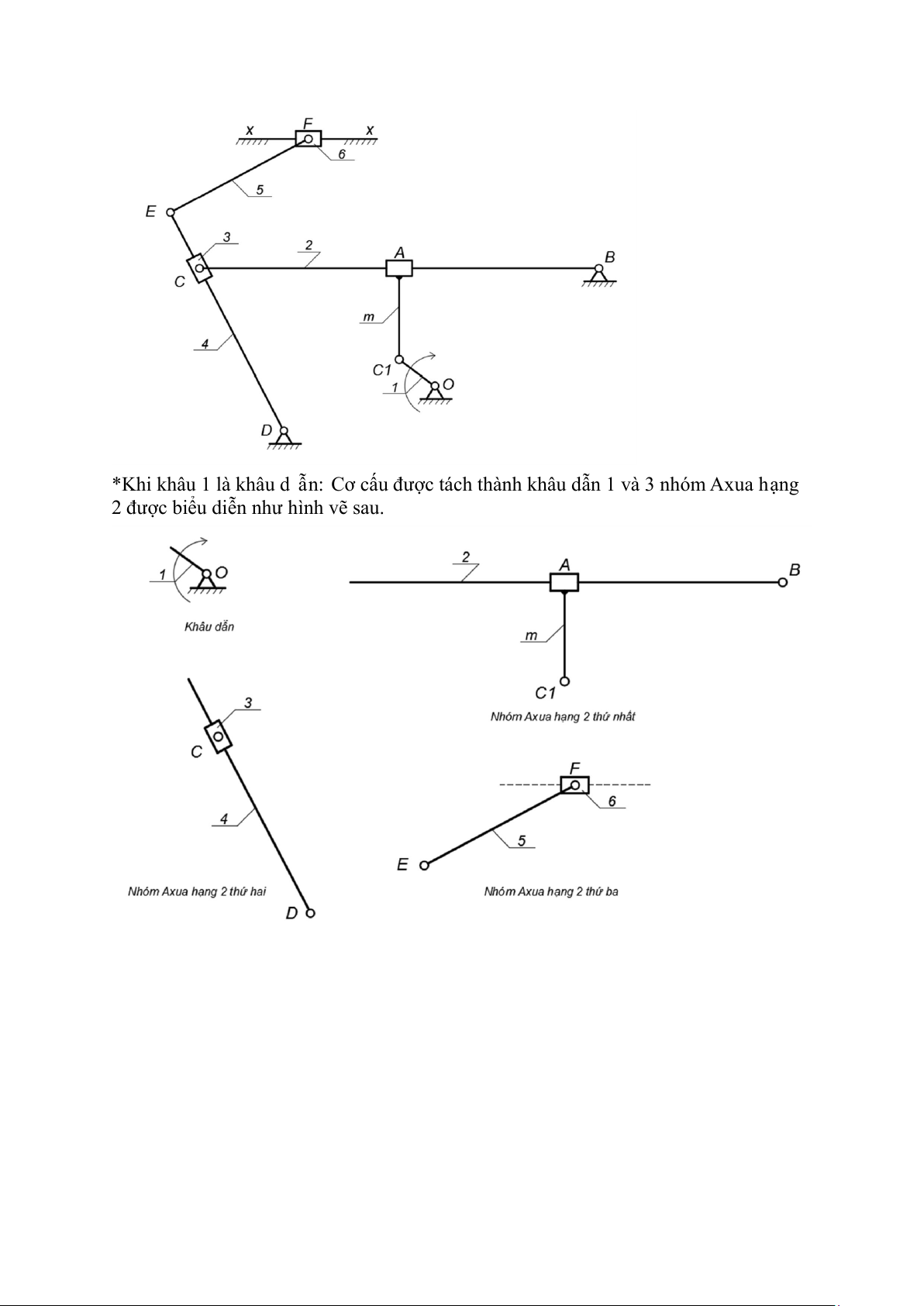
*Khi khâu 1 là khâu d ẫ n: Cơ c ấ u đư ợ c tách thành khâu d ẫ n 1 và 3 nhóm Axua h ạ ng
2 đư ợ c bi ể u di ễ n như h ình v ẽ sau.
Nhóm Axua hạng 2 thứ nhất bao gồm: các khâu m, 2 và các khớp A, B, C1.
Nhóm Axua hạng 2 thứ hai bao gồm: các khâu 3, 4 và các khớp Cquay, Ctrượt, D.
Nhóm Axua hạng 2 thứ ba bao gồm: các khâu 5, 6 và các khớp Fquay, Ftrượt, E.
Theo đó, cơ cấu là cơ cấu hạng 2 khi khâu 1 là khâu dẫn.
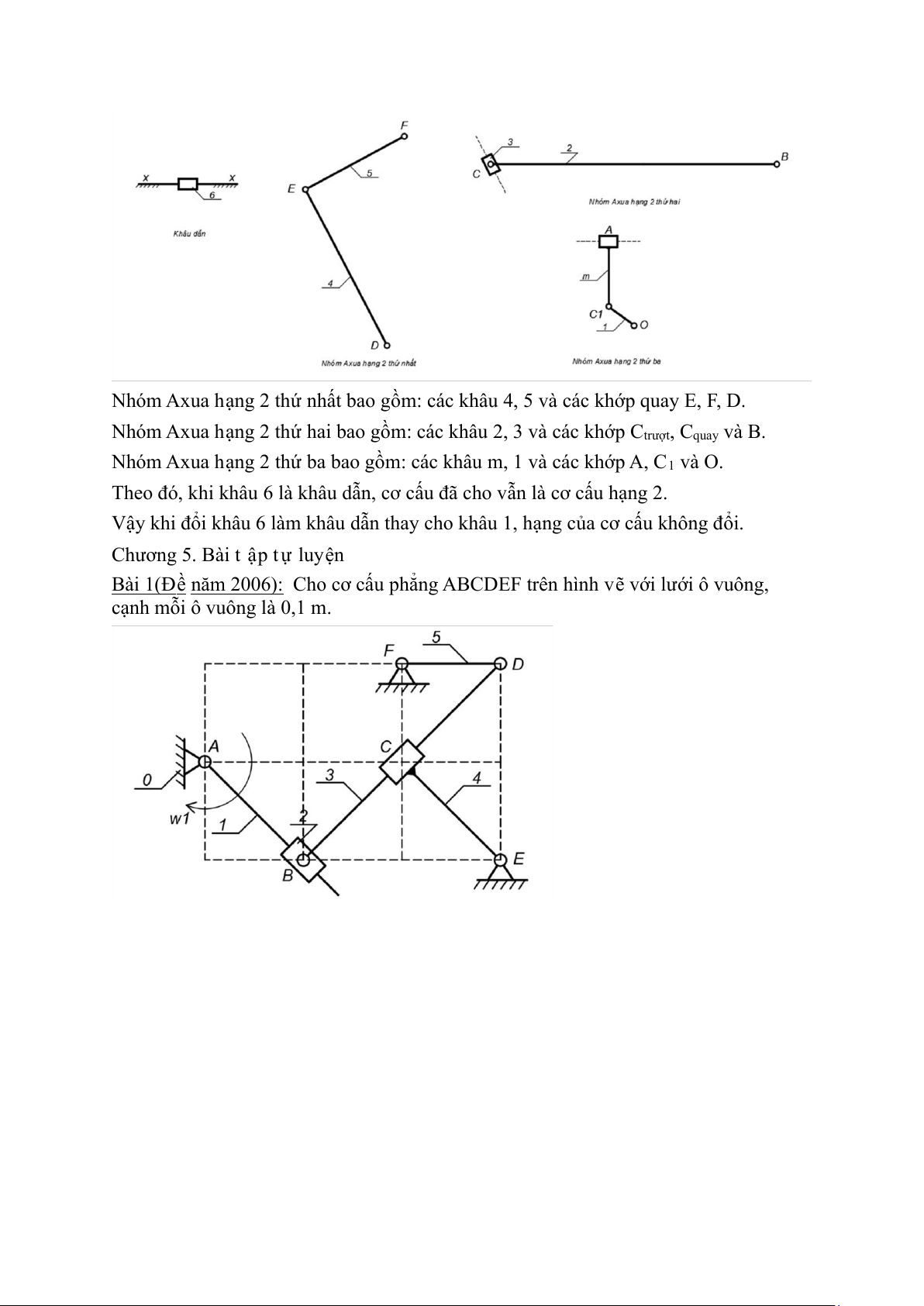
*Khi khâu 6 là khâu dẫn: Cơ cấu được tách thành khâu dẫn 6 và 3 nhóm Axua hạng 2
được biểu diễn như hình vẽ sau.
Nhóm Axua h ạ ng 2 th ứ nh ấ t bao g ồ m: các khâu 4, 5 và các kh ớ p quay E, F, D.
Nhóm Axua h ạ ng 2 th ứ hai bao g ồ m: các khâu 2, 3 và các kh ớ p C trư ợ t, C quay và B.
Nhóm Axua h ạ ng 2 th ứ ba bao g ồ m: các khâu m, 1 và các kh ớ p A, C 1 và O.
Theo đó, khi khâu 6 là khâu d ẫ n, cơ c ấ u đ ã cho v ẫ n là cơ c ấ u h ạ ng 2.
V ậ y khi đ ổ i khâu 6 làm khâu d ẫ n thay cho khâu 1, h ạ ng c ủ a cơ c ấ u không đ ổ i.
Chương 5. Bài t ậ p t ự luy ệ n
Bài 1(Đ ề năm 2006): Cho cơ c ấ u ph ẳ ng ABCDEF trên hình v ẽ v ớ i lư ớ i ô vuông,
c ạ nh m ỗ i ô vuông là 0,1 m.
1.1. Tính số bậc tự do của cơ cấu.
1.2. Xếp loại cơ cấu theo phương pháp Axua – Artobolepxki trong tất cả các trường hợp
chọn khâu nối giá 0 làm khâu dẫn. Nên chọn khâu nào nghiên cứu là tiện nhất ? Còn
phương pháp xếp loại nào nữa không (tên phương pháp, tài liệu tham khảo, đặc điểm của phương pháp) ?
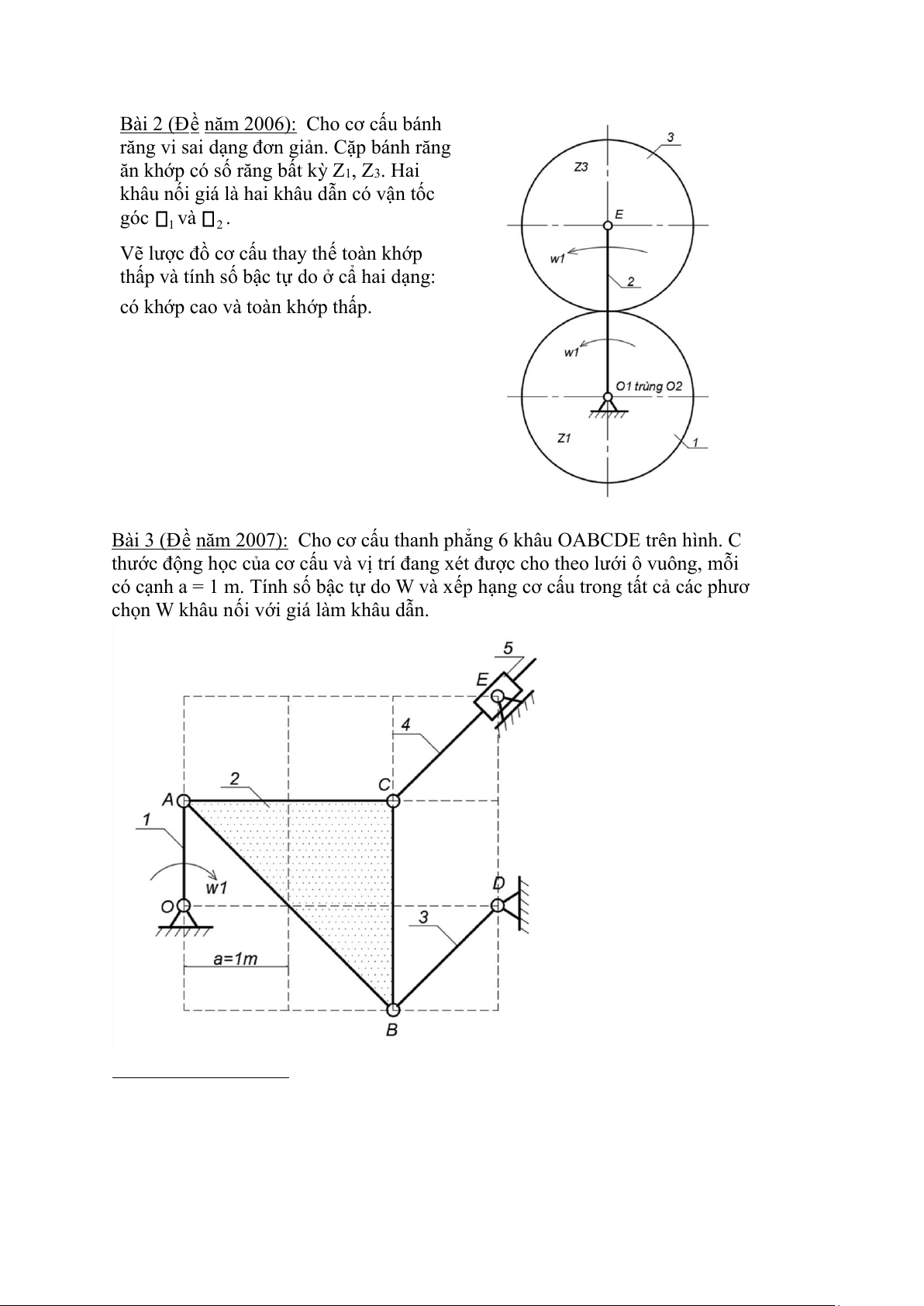
Bài 2 (Đ ề năm 2006): Cho cơ c ấ u bánh
răng vi sai d ạ ng đơn gi ả n. C ặ p bánh răng
ăn kh ớ p có s ố răng b ấ t k ỳ Z 1 , Z 3 . Hai
khâu n ố i giá là hai khâu d ẫ n có v ậ n t ố c góc  và . 1  2
V ẽ lư ợ c đ ồ cơ c ấ u thay th ế toàn kh ớ p
th ấ p và tính s ố b ậ c t ự do ở c ẩ hai d ạ ng:
có kh ớ p cao và toàn kh ớ p th ấ p.
Bài 3 (Đ ề năm 2007): Cho cơ c ấ u thanh ph ẳ ng 6 khâu OABCDE trên hình. Các kích
thư ớ c đ ộ ng h ọ c c ủ a cơ c ấ u và v ị trí đang xét đư ợ c cho theo lư ớ i ô vuông, m ỗ i ô vuông
có c ạ nh a = 1 m. Tính s ố b ậ c t ự do W và x ế p h ạ ng cơ c ấ u trong t ấ t c ả các phương án
ch ọ n W khâu n ố i v ớ i giá làm khâu d ẫ n.
Bài 4 (Đề năm 2012): Cho cơ cấu phẳng như hình vẽ. Tính số bậc tự do và xếp hạng cơ
cấu theo Axua khâu 1 là khâu dẫn.
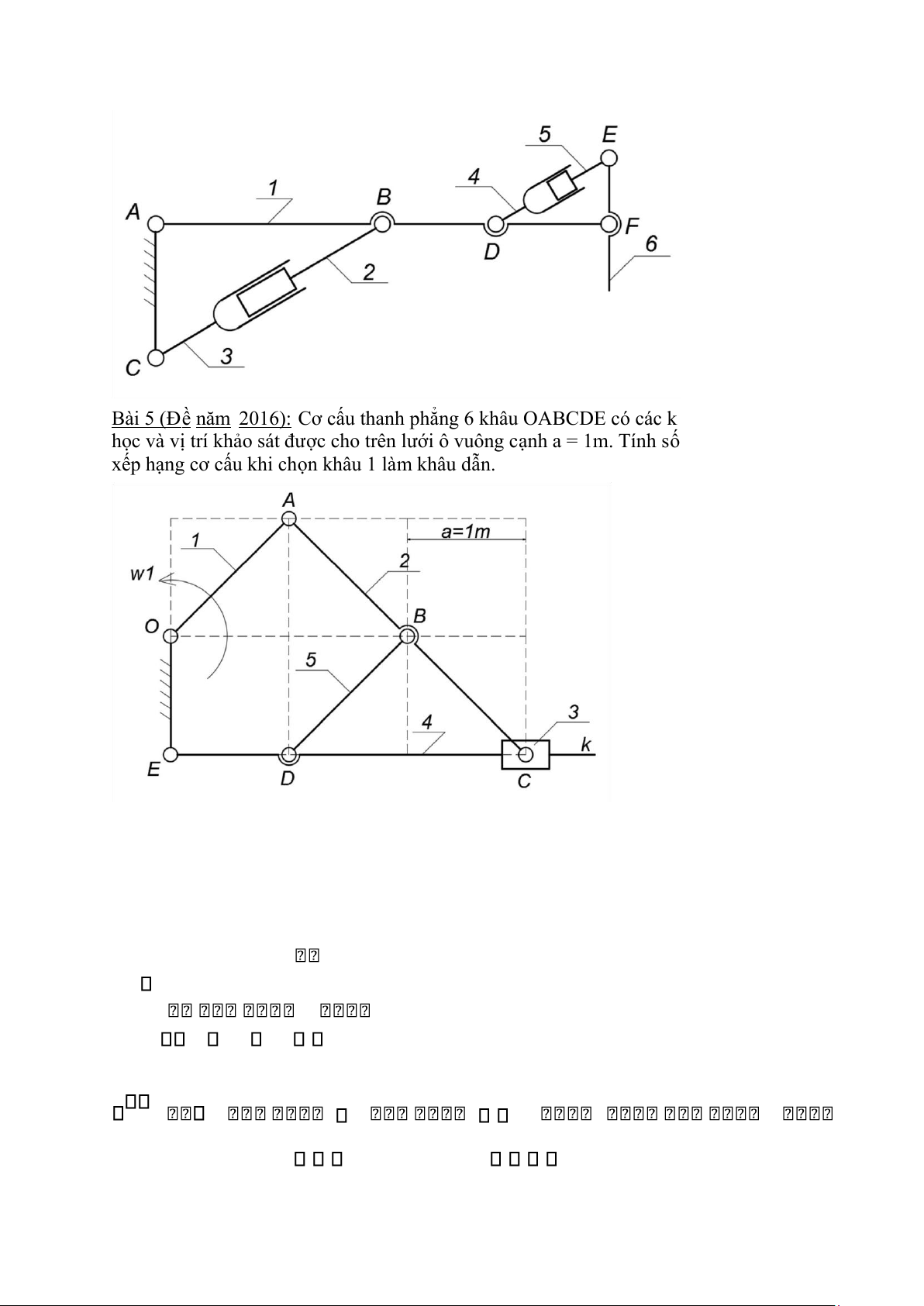
Bài 5 (Đ ề năm 2016): Cơ c ấ u thanh ph ẳ ng 6 khâu OABCDE có các kích thư ớ c đ ộ ng
h ọ c và v ị trí kh ả o sát đư ợ c cho trên lư ớ i ô vuông c ạ nh a = 1m. Tính s ố b ậ c t ự do và
x ế p h ạ ng cơ c ấ u khi ch ọ n khâu 1 là m khâu d ẫ n.
PHẦN II. PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG – BÀI TOÁN VẬN TỐC
Trước khi giải bài toán vận tốc, chúng tra ôn lại một số kiến thức đã học trong đại số và cơ học kỹ thuật.  
 Nếu một vecto m được biểu thị bằng hai tổng vecto:
            
  m  m1  m2   ...mn   m 
   m       1'  m       '2   ...m    'n                Thì suy ra: m ' 1    m2 ...mn     m1 m'2 ... m'n
Chỉ khi phương trình trên chứa 2 ẩn thì mới có thể giải được.
 Khi 2 điểm A và B thuộc cùng một khâu (tức là nằm trên cùng một vật rắn),
bao gi          ờ cũng có thể viết: vB  vA  vBA
Trong đó:     
• v    B và vA là vận tốc của 2 điểm B và A.
• vBA là vận tốc tương đối của điểm B khi quay quanh điểm A, vuông góc với AB.
 Khi 2 điểm A và B trùng nhau nhưng thuộc 2 khâu khác nhau đang chuyển
đ          ộng tương đối với nhau, bao giờ cũng có thể viết: vB  vA  vBA
Trong đó:      v •
B và vA là vận tốc của 2 điểm B và A.    
 vBA là vận tốc tương đối của điểm B khi quay quanh điểm A, vuông góc với AB.
Các phương pháp giải bài toán vận tốc:
 Phương pháp tâm vận tốc tức thời.
 Phương pháp họa đồ vận tốc.
 Phương pháp điểm Axua
 Phương pháp đổi khâu dẫn, đổi giá.  Phương pháp ảnh giả.
Trong đó 2 phương pháp được sử dụng nhiều nhất đó là: phương pháp tâm vận tốc tức
thời và phương pháp họa đồ vận tốc. Tùy từng bài toán cụ thể mà chúng ta vận dụng
một trong hai phương pháp hoặc kết hợp cả hai. Chương 1. Phương pháp tâm vận tốc tức thời 1.1. Định nghĩa
Trong cơ học kỹ thuật, một vật rắn chuyển động song phẳng, tại một thời điểm thì có
thể coi chuyển động của nó là chuyển động quay quanh 1 điểm nào đó, được gọi là tâm
quay tức thời. Các xác định tâm quay tức thời là giao điểm của các pháp tuyến của quỹ
đạo các điểm trên khâu.
Trong nguyên lý máy, tâm vận tốc tức thời Pij trong chuyển động tương đối của khâu i
đối với khâu j là đi   ểm Pi (trên khâu i) có vận tốc tương đối với trùng điểm Pj (trên
khâu j) bằng 0 (v 0ij  ).      
Hay có thể hiểu, tại thời điểm đang xét, vận tốc tuyệt đối vPi  vPj .
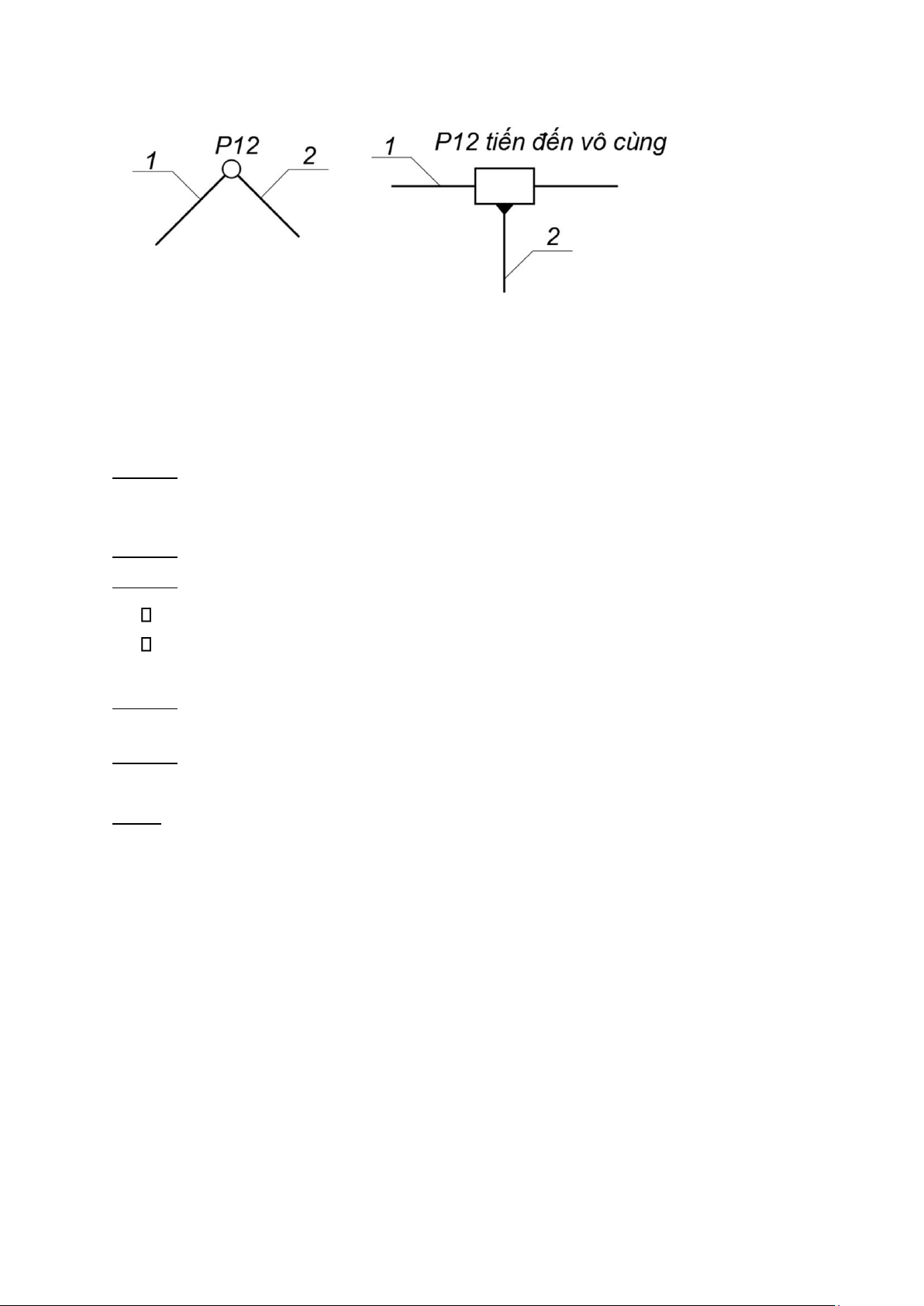
Tâm vận tốc tức thời đặc biệt:
1.2. Định lý Kenedy về 3 tâm vận tốc thức thời
Nội dung định lý Kenedy: Trong cơ cấu 4 khâu bản lề, tâm quay tức thời trong chuyển
động tương đối giữa 2 khâu đối diện là giao điểm giữa 2 đường tâm của 2 khâu còn lại. Ví dụ:
1.3. Các bước giải bài toán tìm tâm vận tốc tức thời
Bước 1: Liệt kê các tâm vận tốc tức thời đã biết, các tâm vận tốc thời chưa biết. (Cứ 2
khâu với nhau lại có 1 tâm vận tốc tức thời, vì vậy số tâm vận tốc tức thời là chỉnh hợp chập 2 của n khâu).
Bước 2: Biểu diễn các tâm vận tốc tức thời trên hình vẽ.
Bước 3: Vẽ đa giác tâm vận tốc tức thời.
 Các đỉnh đánh số các khâu có trong cơ cấu.
 Giữa 2 khâu đã biết tâm vận tốc tức thời, nối 2 đỉnh tương ứng trên đa giác bằng nét liền.
Bước 4: Áp đụng định lý Kenedy xác định các tâm vận tốc tức thời chưa biết. Biểu diễn
trên hình vẽ. Nối các đỉnh tương ứng trên đa giác bằng nét đứt. Bước 5: Kết luận.
1.4. Bài tập có hướng dẫn
Bài 1: Xác định và biểu diễn trên hình vẽ tất cả các tâm vận tốc tức thời của cơ cấu thanh
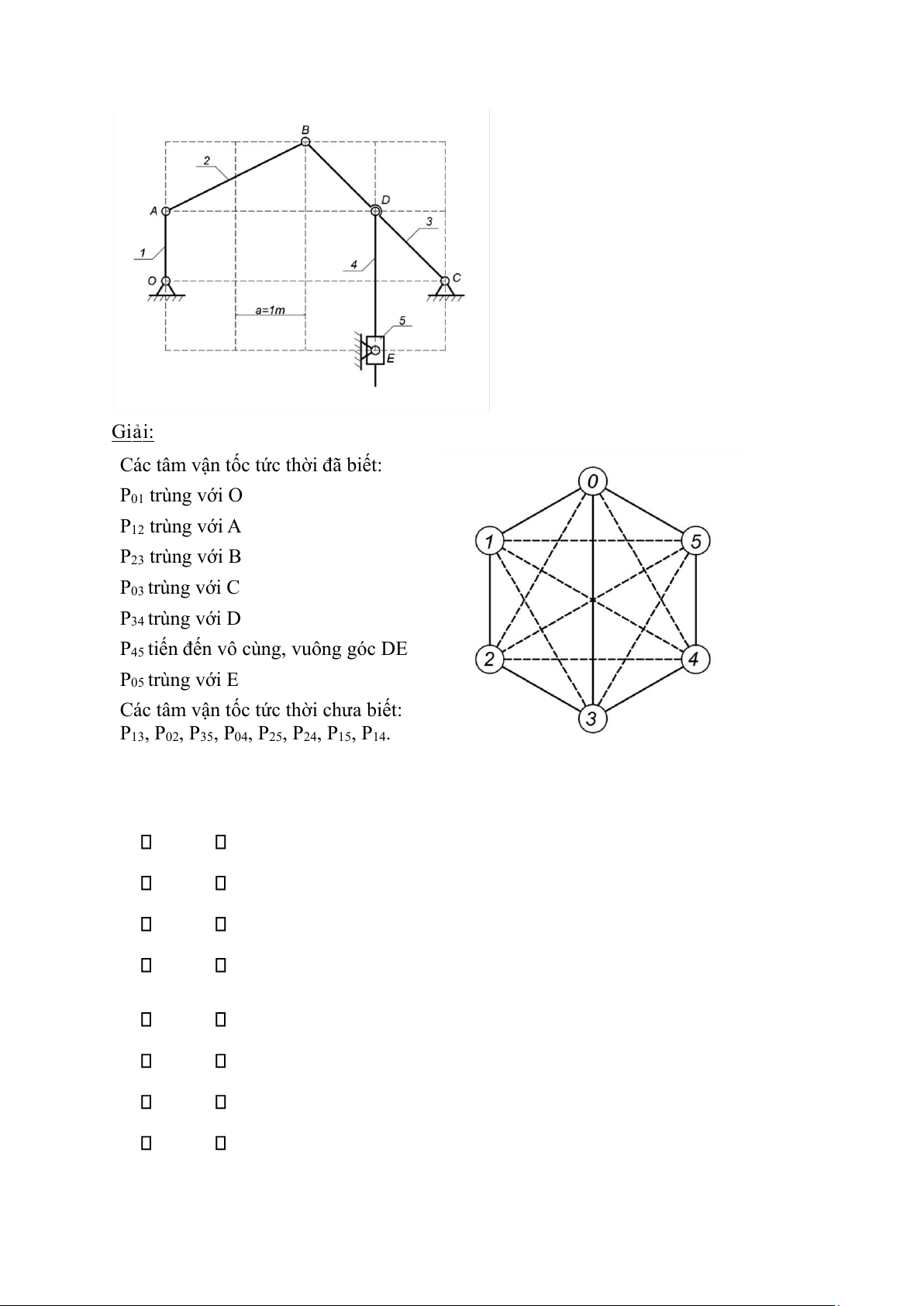
OABCDE được cho trên lưới ô vuông như hình vẽ dưới đây. Gi ả i:
Các tâm v ậ n t ố c t ứ c th ờ i đ ã bi ế t: P 01 trùng v ớ i O P 12 trùng v ớ i A P 23 trùng v ớ i B P 03 trùng v ớ i C P 34 trùng v ớ i D
P 45 ti ế n đ ế n vô cùng, vuông góc DE P 05 trùng v ớ i E
Các tâm v ậ n t ố c t ứ c th ờ i chưa bi ế t:
P 13 , P 02 , P 35 , P 04 , P 25 , P 24 , P 15 , P 14 .
Áp dụng định lý Kenedy về ba tâm vận tốc tức thời, xác định các tâm vận tốc tức thời chưa biết: P13  P P01 03  P P12 23 P02  P P01 12  P P03 23 P35  P P03 05  P P34 45 P04  P P03 34  P P25 45 P25  P P02 05  P P23 35 P24  P P02 04  P P25 45 P15  P P01 05  P P13 35 P14  P P01 04  P P13 34
Vậy tất cả các tâm vận tốc tức thời của cơ cấu được thể hiện như hình vẽ.