Bài tập LTĐK Tuần 13: Phân Tích Hệ Thống và Biểu Đồ Bode. Môn Lý thuyết điều khiển tự động (UET) | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội.

lOMoAR cPSD| 58833082
Bài tập môn LTĐK tuần 13
Họ và tên: Đào Duy Hưng-22026145 100(0.1s 1) Có G(s) = s(0.01s 1) Hàm truyền bao gồm:
1. Khâu tỉ lệ (K = 100) 2. Khâu 1 tích phân lý tưởng ( ) s
3. Khâu vi phân bậc 1 (0.1s+1)
4. Khâu quán tính bậc 1 (0.01s 1)1 Tá có: Khâu tỉ lệ (K = 100) K db = 20log(100) = 40 1
Khâu tích phân lý tưởng ( ) s 1 = -20log( ) = -20 db/dec s db
Khâu vi phân bậc 1 (0.1s+1) lOMoAR cPSD| 58833082 •  <<
10, 0.1s 1db = 20log(1) = 0 •  >>
10, 0.1s 1db = 20log(0.1 ) = 20
Khâu quán tính bậc 1 (0.01s 1)1
•  << 100, 0.01s 1db =  20log(1) = 0
•  << 100, 0.01s 1db =  20log(0.01 ) = 20
Ta có: G( j ) = 100(0.1j  1)
j  (0.01j  1)
  G( j ) =  100 + (0.1j  1)   ( j )  (0.01j  1)   G( j ) =     G( j ) = o 2 1000   0.1 1 5 10 20 40 70 100 1000  Φ( ) - - - - - - -43.12 -50.71 - -90
89.48 84.86 66.30 50.71 37.87 35.84 84.86 Matlab num = [100*0.1 100]; den = [0.01 1 0]; bode(num ,den) lOMoAR cPSD| 58833082
Họ và tên: Nguyễn Mạnh Đức lOMoAR cPSD| 58833082 Ta có: ω1 = 2 => T1 = 0.5 ω2 = 4 => T2 = 0.25 = a ω3 = 8 => T3 = 0.125 1 ω4 = 24 => T4 = 24 = b 1 ω5 = 36 => T5 = 36
Xét: Khâu tích phân lý tưởng (khâu I), với độ dốc là -20db/dec từ khoảng 1rad/s đến 2rad/s: G(s) = K = 1 => K = 1 = 8 s T3.s T3 Suy ra: K = 8, a = 0.25, b =
=> G(s) = 8(1+0.5s)(1+0.25s)s s s s(1+ )(1+ )(1+ ) 8 24 36
Nguyễn Quang Đức – 22026127
Nguyễn Trường Giang – 22026194
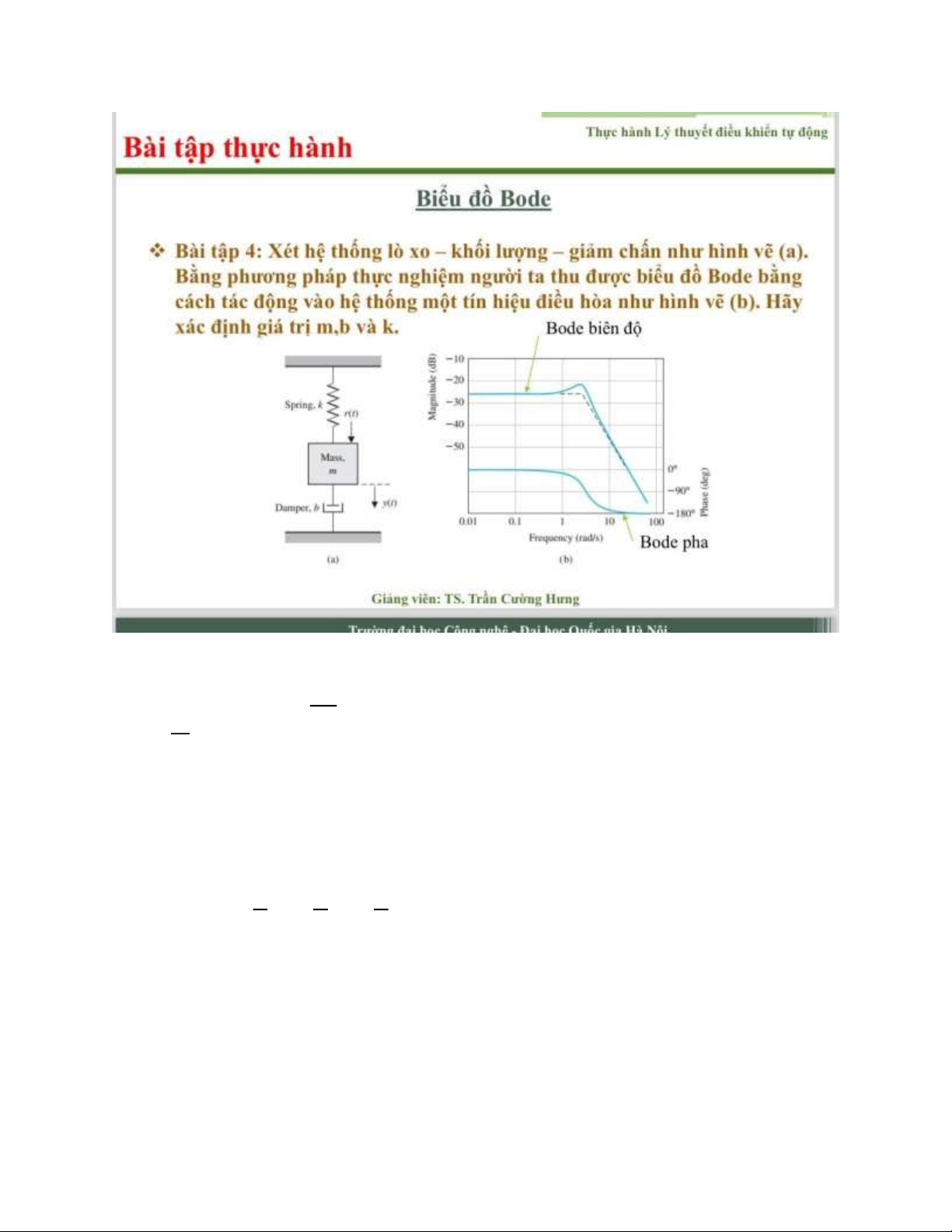
Support: Nguyễn Huy Hoàng – 22026108 lOMoAR cPSD| 58833082 *Ta có: d2y dy m dt2 = ∑Fi = F(t) - D dt – k*y(t)  mÿ + bẏ + ky = F
Ta có: x1 = y; x2 = x1̇ = ẏ => x2̇ = ÿ
 { ̇ = − kx1̇ = x 1 −xb2 x2 1 x2 + F m m m lOMoAR cPSD| 58833082  [ x1̇ ] = [−0k −1b] [x1] + [01 ] F x2̇ m m x2 m s −1 −1  G(s) = Y(s) = [1 0] [ k s + k ] [01 ] = k+ms 12+bs R(s) m m m
 Từ đồ thị ở trên, ta có:
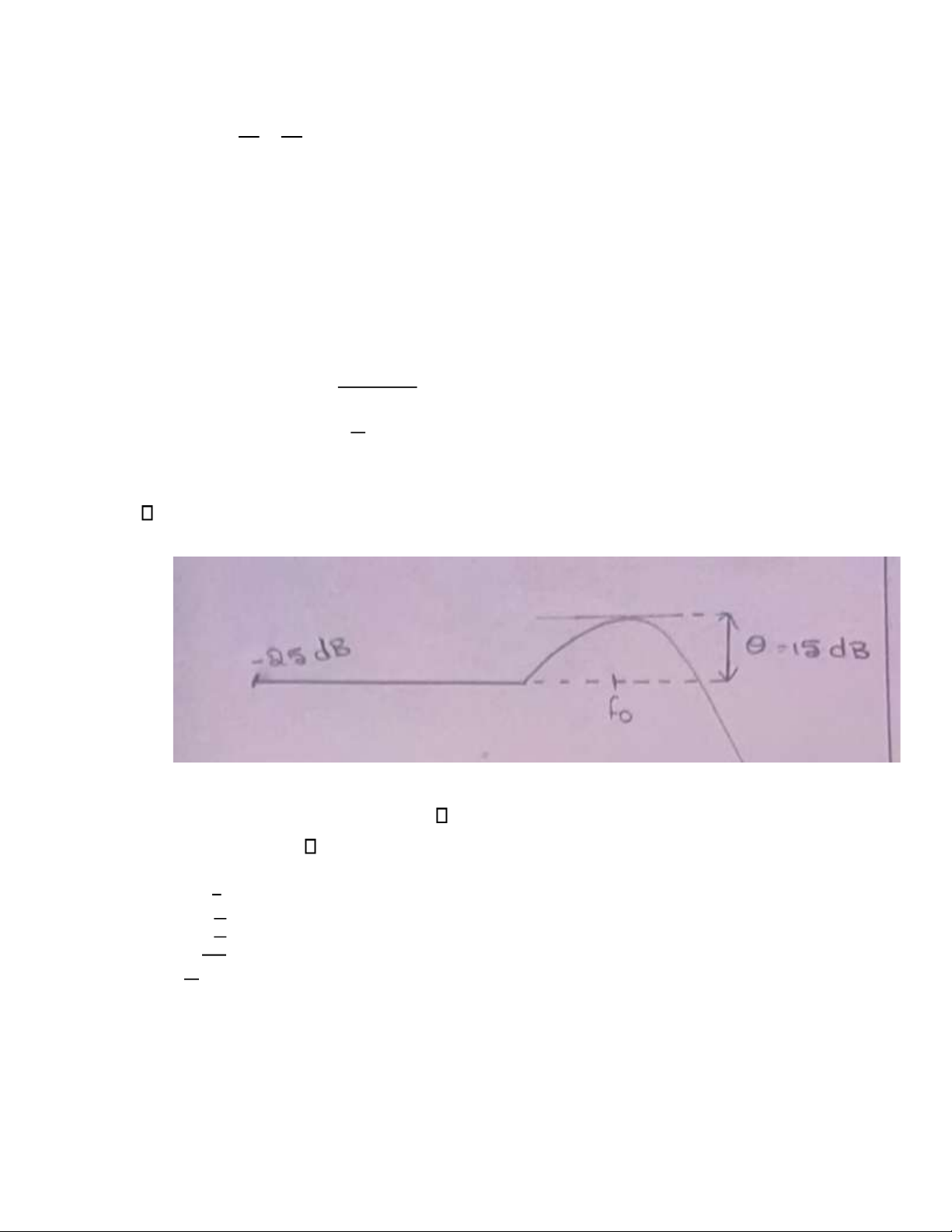
x0 = log[l + a(s)] = -25 (s  0) l + G(s) = 10 (s  0) 1 = 0.056 => k = 17.786 k √ k  0 f = m 2π  √ k = ω = 3 rad/s m k m = = 2.9758 kg g lOMoAR cPSD| 58833082 1  θ = √ mk = 5 dB b • 20log(θ) = 5 dB • θ = 10 •  mk = 1.7782 => b = 3.33 b Họ và tên:
Nguyễn Huy Hoàng 22026130
Ong Thế Anh_22026168
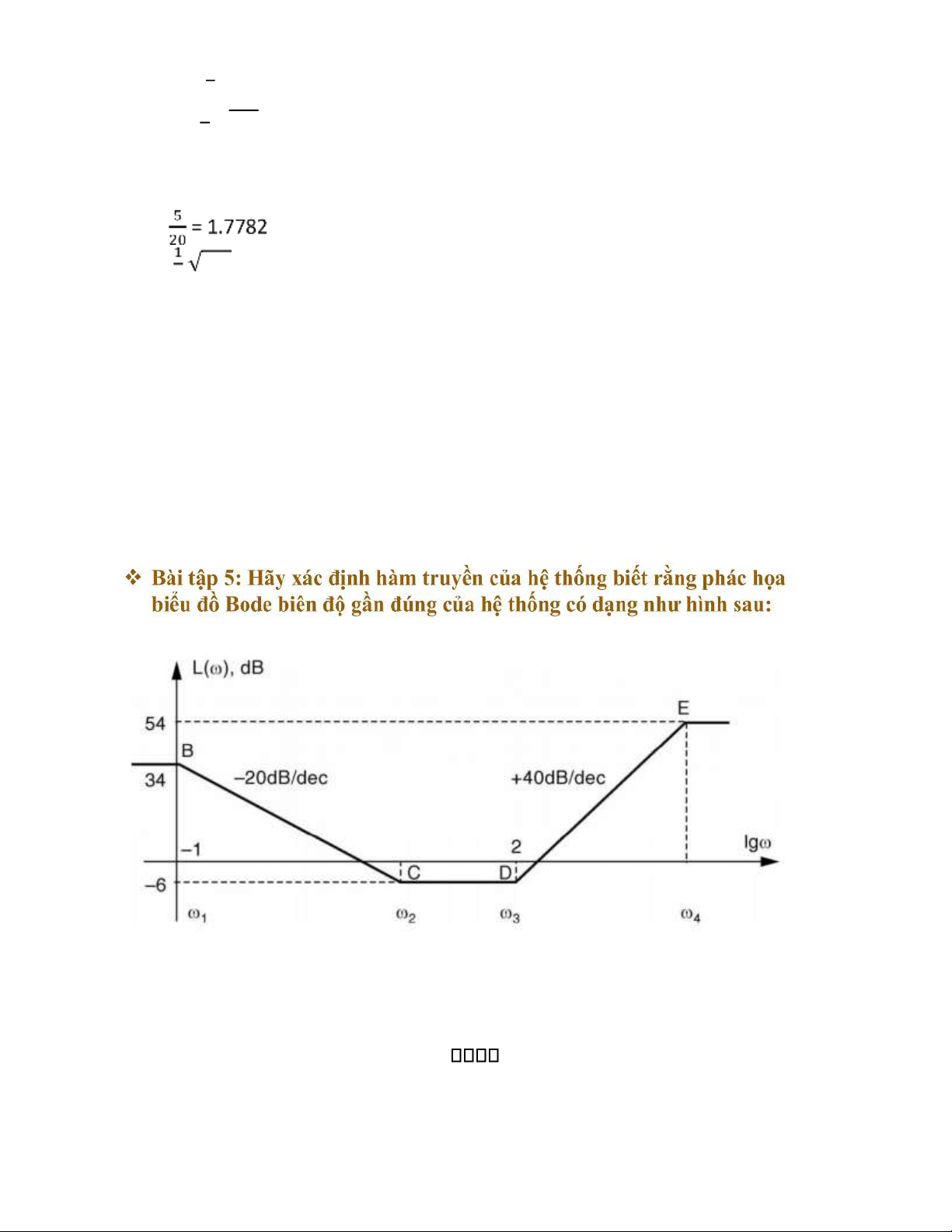
Hệ thống có bốn tần số gãy lần lượt là     1, 2, 3, 4 . lOMoAR cPSD| 58833082
Dựa vào sự thay đổi độ dốc của biểu đồ Bode của hệ thống ở ví dụ trên , ta thấy
hàm truyền của hệ thống phải có dạng:
K T s( 2  1)(Ts3  1)2 G s( ) 2
(Ts1  1)(T s4  1)
Xác định thông số của hệ thống:
Từ hình trên ta xác định được:
20lgK 34  K 50 lg 1    1  1  0,1  T1  10
Độ dốc đoạn BC là –20dB/dec, mà từ điểm B đến điểm C biên độ của biểu đồ
Bode giảm 40dB (từ 34dB giảm xuống –6dB), do đó từ B đến C tần số phải thay đổi là 2 decade.
lg  2  lg 1    2 1  2  10  T2  0,1
 lg 3   2  3  100  T3  0,01
Độ dốc đoạn DE là +40dB/dec, mà từ điểm D đến điểm E biên độ của biểu đồ Bode
tăng 60dB (từ –6dB tăng lên +54dB), do đó từ D đến E tần số phải thay đổi là 1.5 decade.
 lg  4  lg 3   1,5
3,5   4  3162   T4 0,0003
Từ các giá trị K, T T T T1 2 3 4, , ,
đã tìm được ở trên ta thay vào G(s) ở
trên để tìm hàm truyền.
Do đó hàm truyền của hệ thống là: lOMoAR cPSD| 58833082 G s( ) 
50(0,1(10s s1)(0,003 1)(0,01ss  1)1)22 Họ và tên:
Phạm Văn Huynh_22026142
Phạm Việt Hưng_22026172
Bài tập 6: Vẽ phác họa biểu bồ Bode của các hệ thống có các hàm truyền dưới đây
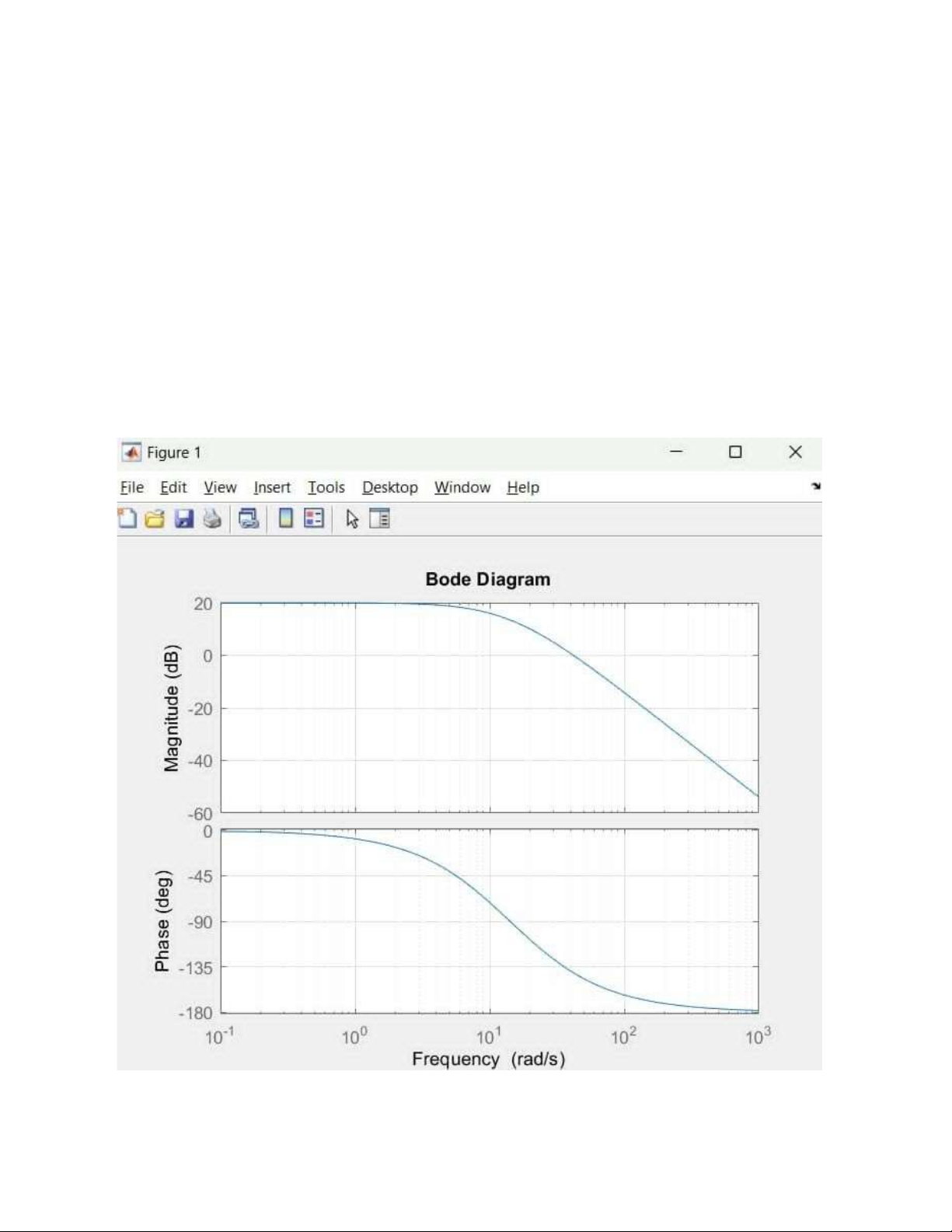
và kiểm tra lại bằng cách sử dụng lệnh « bode » trong Matlab a, G(s)= Ta có: G(s)= Hàm truyền bao gồm: 1. Khâu tỉ lệ: K=10 2. Khâu vi phân: 3. Khâu quán tính bậc 1: Khâu tỉ lệ:
 | k | dB= 20log(10)= 20 dB Khâu vi phân:
Khâu quán tính bậc 1: 0.1s + 1 → ω1 = 10 rad/s lOMoAR cPSD| 58833082 0.05s + 1 → ω2 = 20 rad/s
Vì tất cả các ω đều lớn hơn 0 nên biểu đồ Bode đi qua A co tọa độ ω=1 và L(ω)=20log(10) = 20
Log ω1 = 1 (độ dốc đường tiện cận -20dB/dec) Log
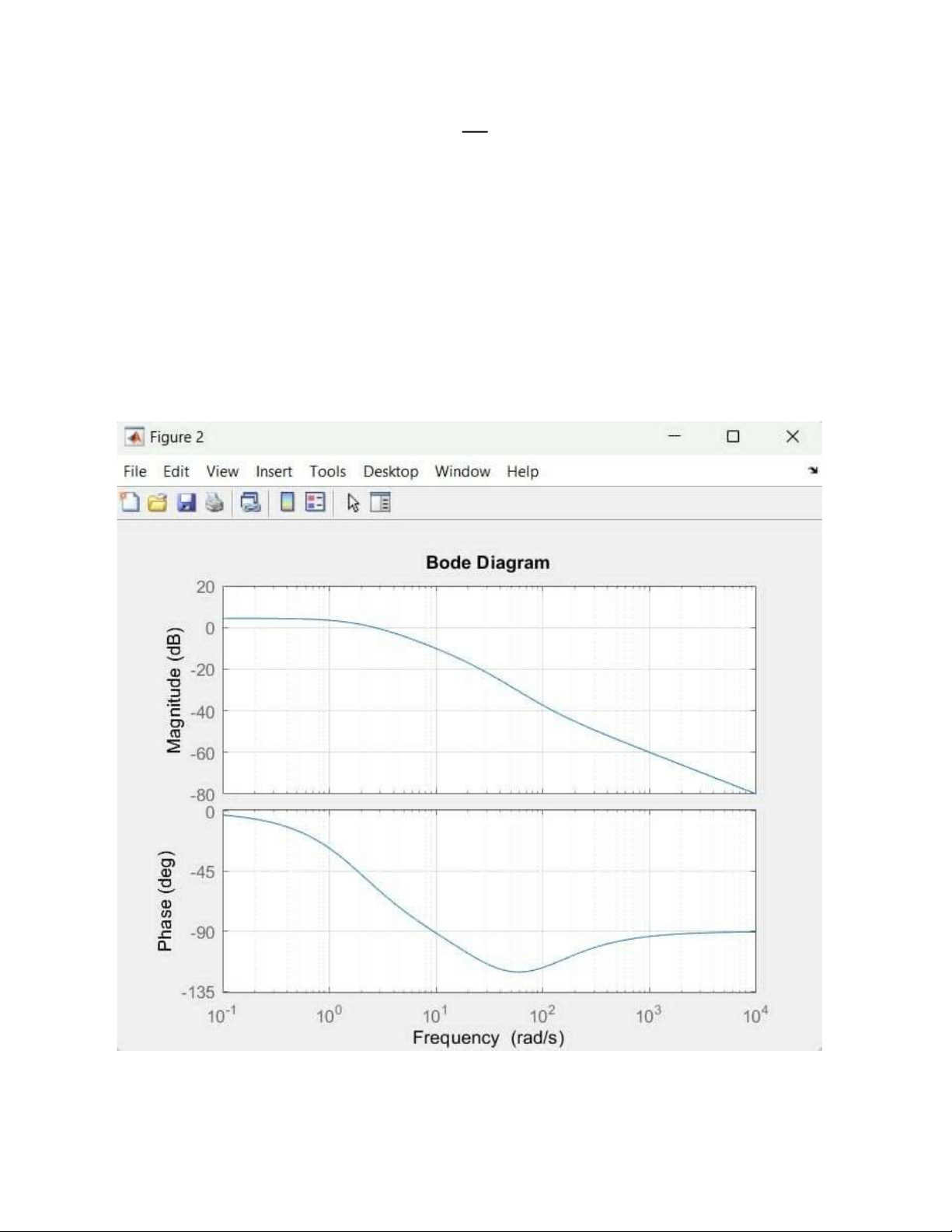
ω2 = 1.301(độ dốc đường tiện cận -20dB/dec) + Matlab: lOMoAR cPSD| 58833082 s+100 b, G(s)= (s+2)(s+30) Ta có: s 5 ( + 1 ) 100 G(s)= s s 3 ( + 1)( + 1 ) 2 30 Hàm truyền bao gồm: 1. Khâu tỉ lệ: K= → |k|db = 20log = 4.4369 2. Khâu vi phan bậc 1: s rad + 1 => ω1 = 100 ( ) => logω1 = 3(+20dB/dec) 100 s 3. Khâu quán tính bậc 1: rad 0.5s+1→ ω2 = 2 ( ) s rad 0.3( 3)s + 1 → ω3 = 30 lOMoAR cPSD| 58833082 ( ) s
Vì tất cả các ω đều lớn hơn 0 nên biểu đồ Bode đi qua A có tọa độ: ω=1 và L(ω)=20log(5/3)
→ logω2 = 0.301(độ dốc đường tiện cận -20dB/dec)
→ logω3 = 1.477(độ dốc đường tiện cận -20dB/dec) Matlab: lOMoAR cPSD| 58833082 200 2
c, G(s)=s2+2s+100= 0.01s2+2 . 0.01s+1 Khâu tỉ lệ K=2
 | k | dB= 20log(2)= 6.02 dB
A(ω)=√Re2(ω) + Im2(ω) = 〖((1−T2ω2) K2+4( Tω)2) L(ω) = 20log(A(ω))
Amax=A(ωch)=10.05(Biên độ đỉnh) 1 rad (ωch)= =10( ) T s
L(ωch)=20log (Amax)=20.044(dB) + Matlab: lOMoAR cPSD| 58833082 Họ và tên:
Trần Văn Giang – 22026138
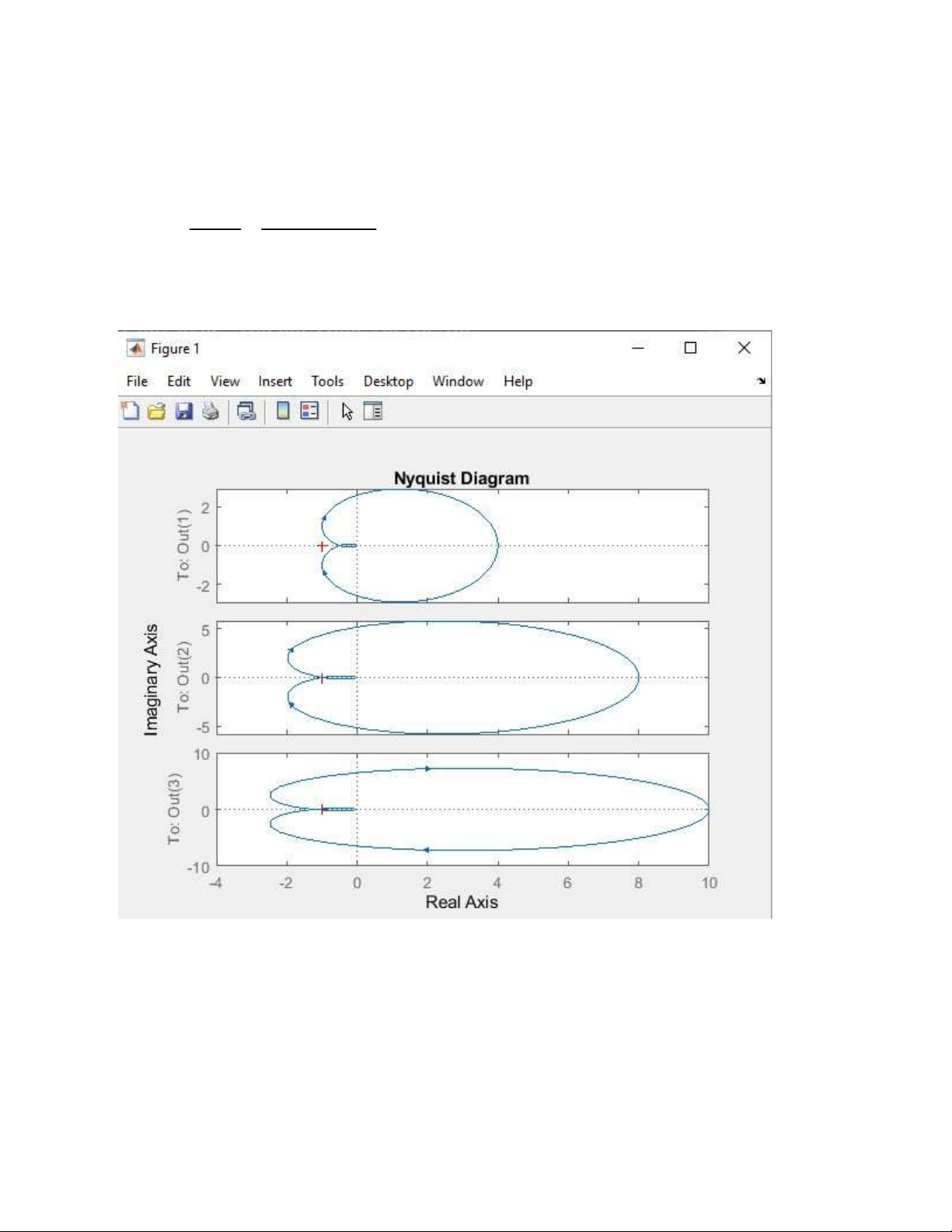
Trần Tiến Đạt – 22026189 lOMoAR cPSD| 58833082 G(s) K => SYS = 1+G(s) = s3+3∗s2+3∗s+1
Code Matlab: nyquist([4;8;10],[1 3 3 1]) Họ và tên:
Phạm Anh Đức_22026156
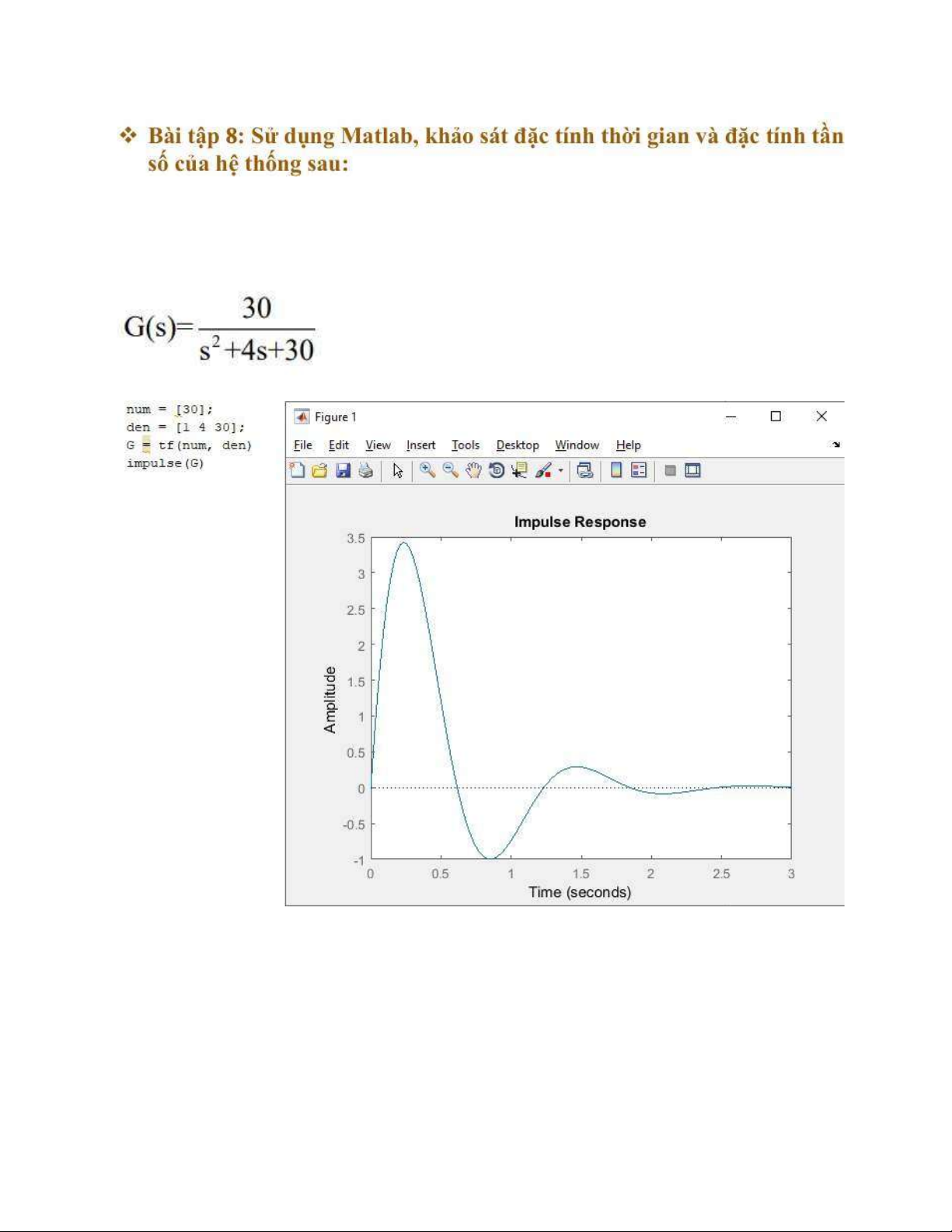
Nguyễn Quang Khánh_22026154 lOMoAR cPSD| 58833082 a, Đáp ứng xung:
Với hệ thống trên thì dao động ngõ ra từ -1 đến 3.5 và ổn định sau khoảng 3s b, Đáp ứng nấc: lOMoAR cPSD| 58833082
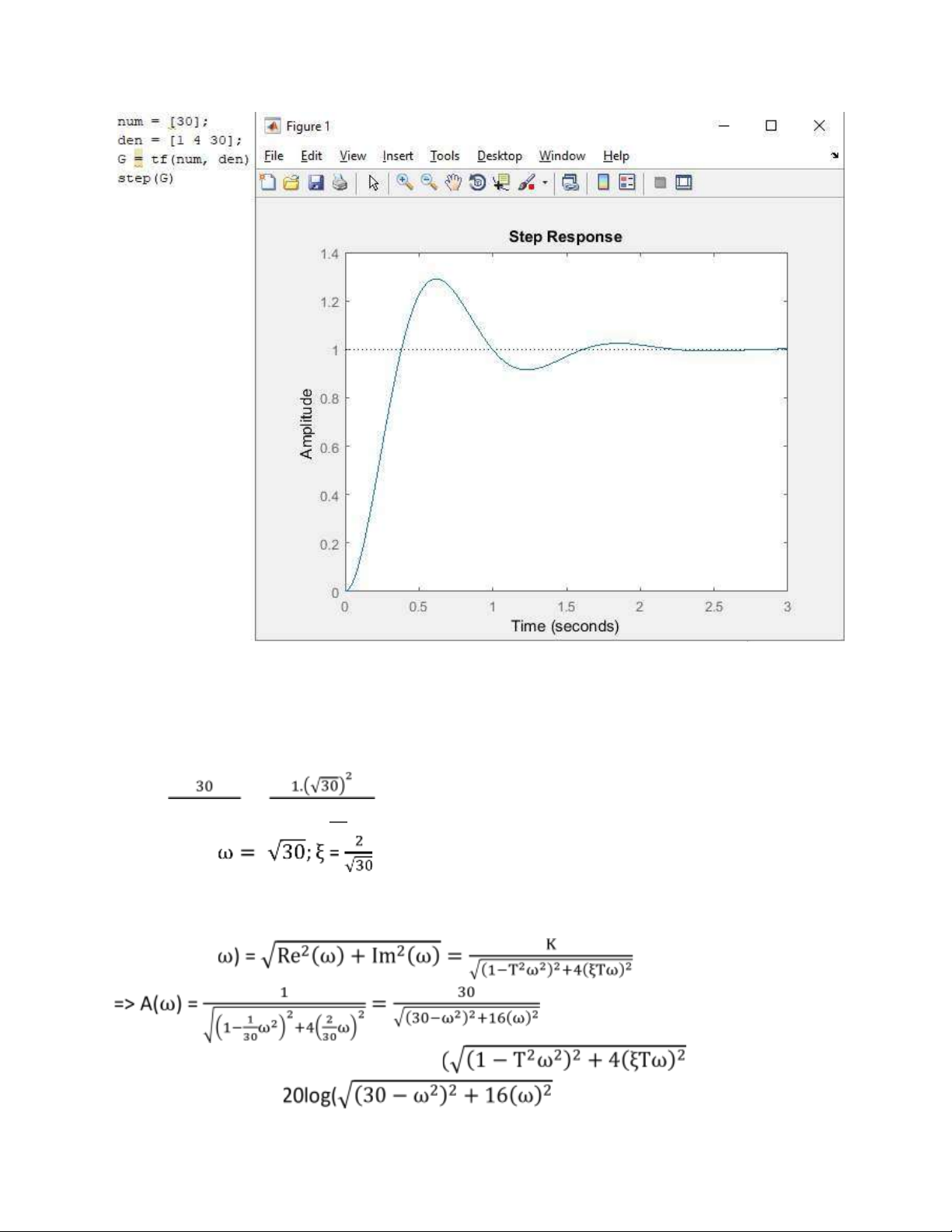
Từ hình vẽ ta thấy tin hiệu ngõ ra sẽ dao động vọt lố ch tới khoảng 1.3, giá trị xác
lập là 1 và giá trị xác lập này diễn ra trong khoản 3s c, Biểu đồ Bode:
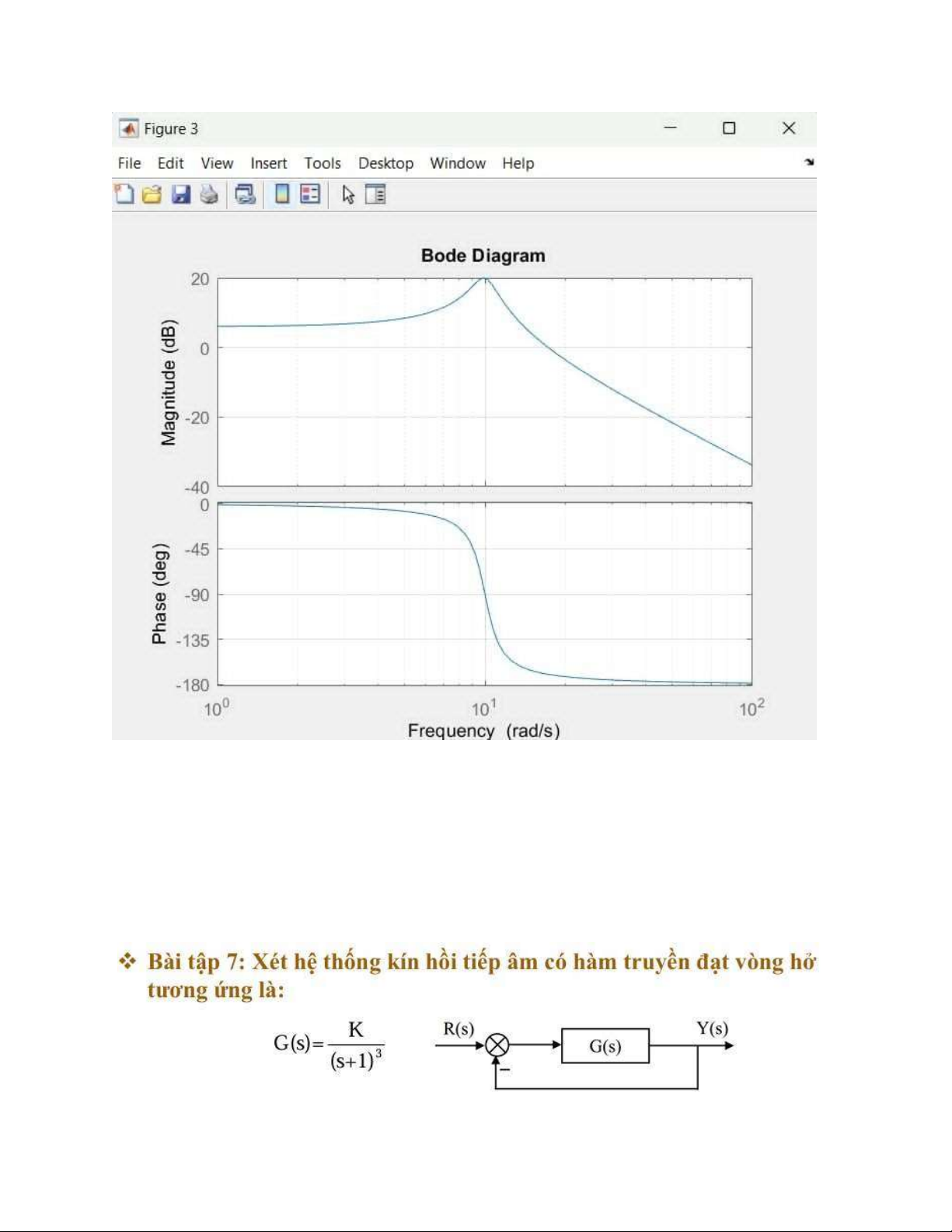
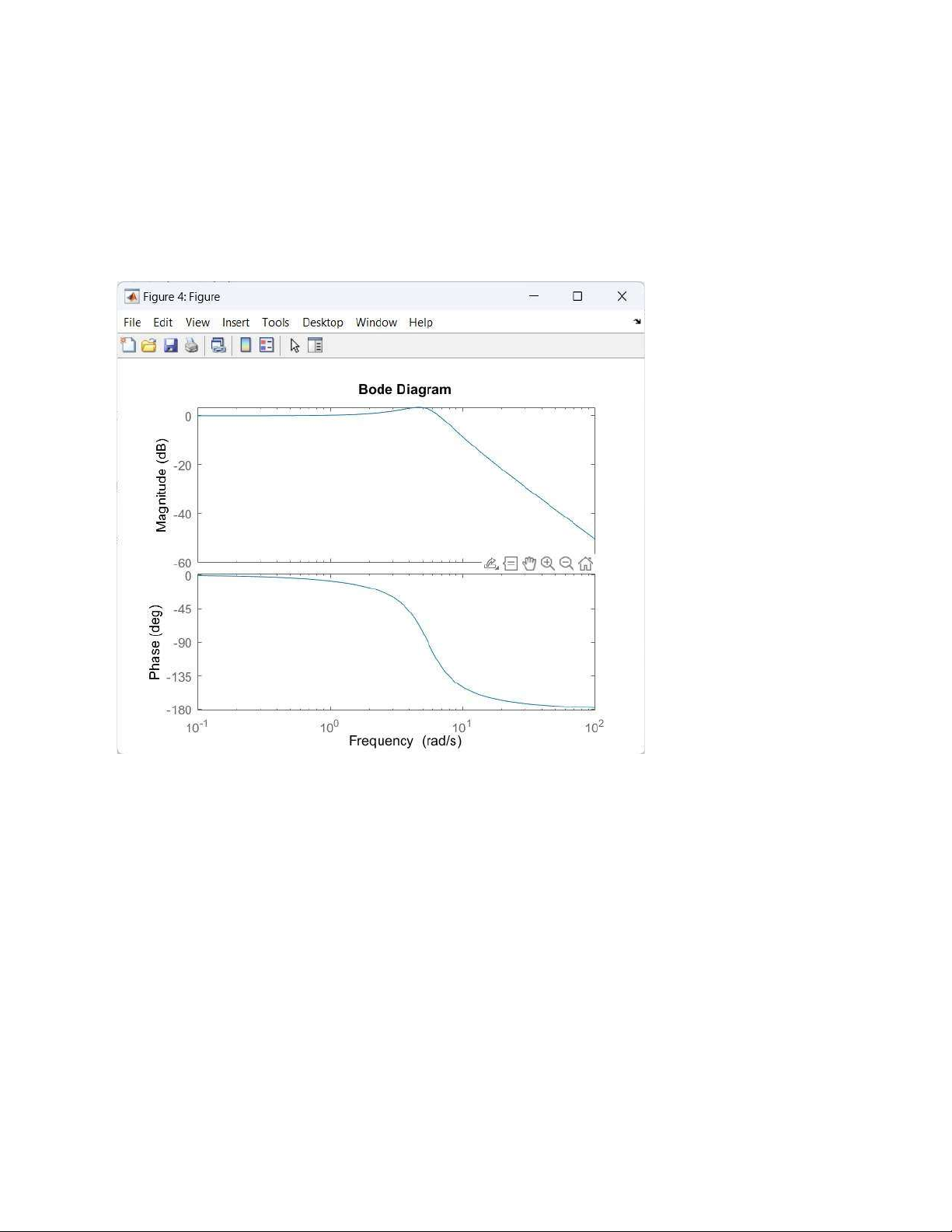
G(s) = s2+4s+30 = s2+4s+(√ 30)2 => C : K = 1; + Khâu tỉ lệ: K = 1
+ Khâu dao động bậc 2: s2 + 4s + 30 + Biên độ A(
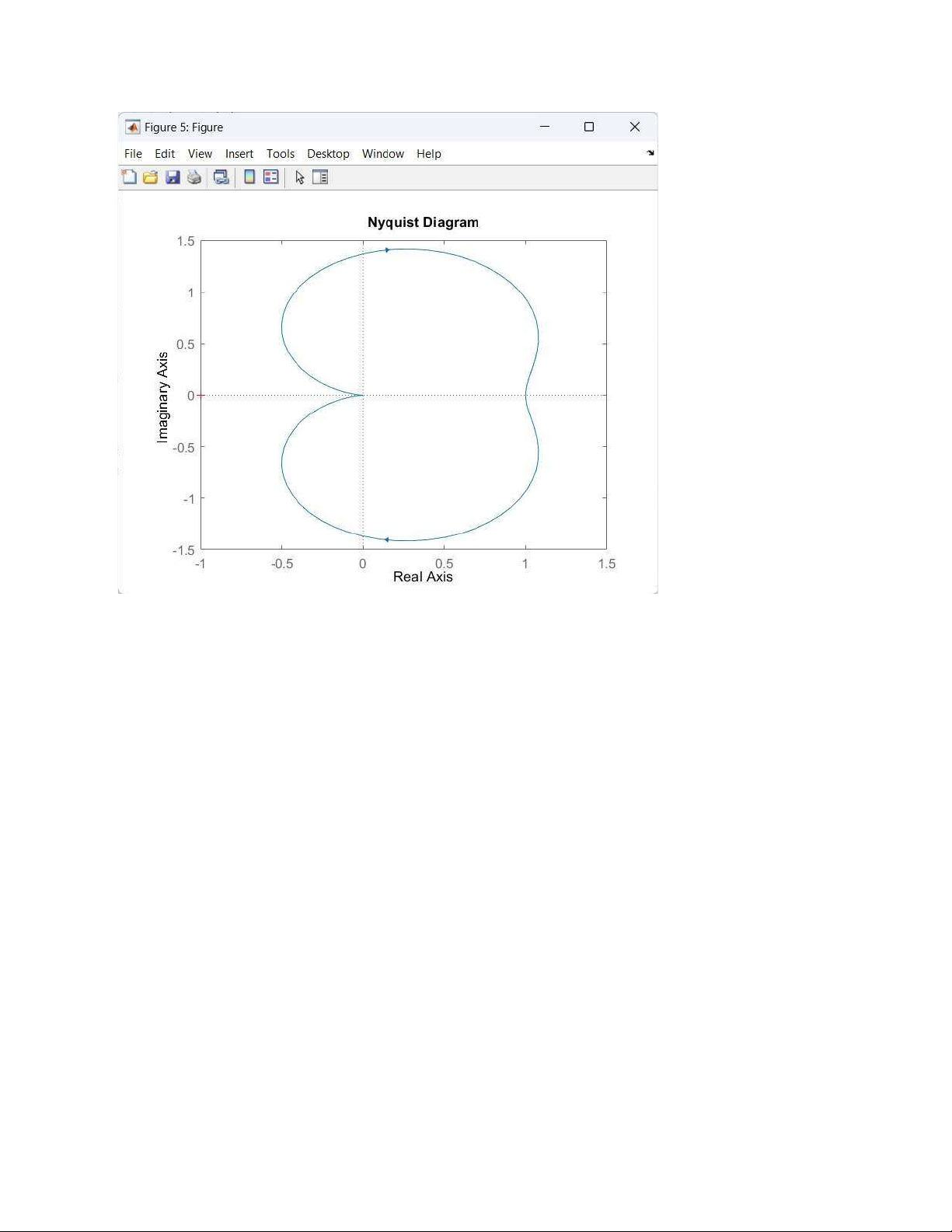
=> L(ω) = 20logA(ω) = 20logK – 20log ) => L(ω) = 20log30 – ) lOMoAR cPSD| 58833082 + Matlab num=[30]; den=[1 4 30]; sys = tf(num,den) bode(sys) d, Biểu đồ Nyquist: num=[30]; den=[1 4 30]; sys = tf(num,den) nyquist(sys) lOMoAR cPSD| 58833082
Họ và tên: Đoàn Gia Hưng lOMoAR cPSD| 58833082
a, Cho giá trị: K=100, T1=20 K G(s)= ➔ T1.s+1
Khâu tỉ lệ |k|db=20log(100)=40
Khâu quán tính bậc nhất |20s+1|=-20log(20)=-26,02 |20s+1|=-20log(1)=0 Ta có G(jω)=
∠G(jω) = ∠100 - ∠(20jω+1) ∠G(jω)= =-arctan20ω ω 0.001 0.05 0.1 1 ∞ Φ(w) -1,14 -45 -63,4 -87.1 -90 + Matlab: