lOMoARcPSD| 36067889
Bài 1. VNPT Hà Nội quay số trúng th°áng trên máy tính cho các hoá ¡n thanh toán bằng hàm Random
chọn ngẫu nhiên từ 1 trong 10 số từ 0 ến 9. Số hoá ¡n gồm 7 chữ số. Tính xác suất xảy ra các tình huống sau:
a) Số hoá ¡n trúng th°áng có số 8 ầu tiên và các chữ số sau khác nhau.
b) Hoá ¡n trúng th°áng có úng 4 chữ số trùng nhau.
Bài 2. Một cửa hàng có 3 gian bán hàng ánh số I, II, III. Có 12 khách hàng ến cùng một lúc ể mua
hàng. Tìm xác suất xảy ra các tình huống sau:
a) Gian số II có 4 ng°ßi.
Một gian có 4 ng°ßi, một gian có 5 ng°ßi và một gian có 3 ng°ßi.
Bài 3. Ba chiến sỹ mỗi ng°ßi bắn một viên ạn vào bia. Giả sử xác suất bắn trúng của ba chiến sỹ lần l°ợt là 0,6; 0,7 và 0,8.
a) Tính xác suất ể có 2 phát ạn trúng bia .
b) Cho biết có úng 2 phát trúng bia. Tính xác suất ể ng°ßi bắn tr°ợt là ng°ßi bắn kém nhất.
Bài 4. Một ng°ßi mua buôn 15 chiếc iện thoại di ộng. Anh ta ồng ý mua 15 iện thoại này với iều
kiện anh sẽ kiểm tra ngẫu nhiên 4 chiếc nếu không có chiếc nào bị lỗi. Chủ cửa hàng °a ra một lô
hàng gồm 15 máy iện thoại trong ó có 3 chiếc bị lỗi.
a) Tính xác suất chủ hàng gặp may bán °ợc lô hàng.
b) Tính xác suất khách hàng không mua hàng vì phát hiện có iện thoại bị lỗi.
c) Nếu chủ cửa hàng °a vào lô hàng 1 máy bị lỗi hoặc 4 máy bị lỗi. Tính xác suất chủ hàng
bán °ợc lô hàng trong cả 2 trußng hợp trên.
Bài 5. Trên 1 bảng quảng cáo ng°ßi ta mắc 2 hệ thống bóng èn. Hệ thống I gồm 2 bóng mắc nối
tiếp, hệ thống 2 gồm 2 bóng mắc song song. Khả năng bị hỏng của mỗi bóng èn sau 6 giß thắp sáng
liên tục là 15%, việc hỏng bóng coi nh° ộc lập. Tìm xác suất:
a) Hệ thống I bị hỏng ( °ợc hiểu là hệ thống này không sáng nữa).
b) Hệ thống II không bị hỏng.
c) Cả 2 hệ thống bị hỏng.
d) Chỉ có hệ thống I bị hỏng.
Bài 6. Một lô hàng có 9 sản phẩm. Mỗi lần kiểm tra chất l°ợng lấy ngẫu nhiên 3 sản phẩm sau khi
kiểm tra xong lại trả vào lô hàng.
Tính xác suất ể sau 3 lần kiểm tra lô hàng thì tất cả sản phẩm ều °ợc kiểm tra.
Bài 7. Một lô hàng có 4 sản phẩm loại I và 8 sản phẩm loại II. Ng°ßi thứ nhất lấy ngẫu nhiên từ lô
hàng 2 sản phẩm (không hoàn lại), ng°ßi thứ hai lấy tiếp 2 sản phẩm. Tính xác suất ể ng°ßi thứ hai
lấy °ợc 1 sản phẩm loại I. lOMoARcPSD| 36067889
Bài 8. Một lô hàng có 15 sản phẩm trong ó có 5 sản phẩm loại 1, 5 sản phẩm loại 2 và 5 sản phẩm
loại 3 (bằng mắt th°ßng không phân biệt °ợc loại của sản phẩm). Một khách hàng mua ngẫu nhiên
1 sản phẩm, sau ó một khách hàng thứ hai mua ngẫu nhiên 2 sản phẩm.
a) Tìm xác suất ể khách hàng thứ hai mua °ợc 1 sản phẩm loại 1 và 1 sản phẩm loại 2. Tìm xác
suất ể khách hàng thứ hai mua °ợc 2 sản phẩm loại 2.
Bài 9. Có 10 lọ hóa chất trong ó có 4 lọ loại I, 6 lọ loại II. Nếu dùng lọ loại I thì kết quả tốt với xác
suất 0,9, nếu dùng lọ loại II thì kết quả tốt với xác suất 0,5.
a) Lấy ngẫu nhiên 1 lọ hóa chất ể sử dụng, tìm xác suất lọ hóa chất này có kết quả tốt.
b) Tìm xác suất ể lọ hóa chất tốt này thuộc loại I.
Bài 10. Thùng thứ nhất ựng 9 sách Toán và 1 sách Lý, thùng thứ hai ựng 1 sách Toán và 5 sách Lý.
a) Từ mỗi thùng lấy ngẫu nhiên ra 1 quyển sách, tính xác suất lấy °ợc 2 cuốn sách toán.
b) Sau khi lấy ngẫu nhiên từ mỗi thùng một cuốn sách, các sách còn lại dồn hết về thùng thứ
ba. Từ thùng thứ ba lấy ngẫu nhiên 1 quyển sách. Tính xác suất sách lấy ra từ thùng ba là sách Lý.
Bài 11. Một nhà máy sản xuất một chi tiết của iện thoại di ộng có tỷ lệ sản phẩm ạt tiêu chuẩn chất
l°ợng là 87%. Tr°ớc khi xuất x°áng ng°ßi ta dùng một thiết bị kiểm tra ể kết luận sản phẩm có ạt
yêu cầu chất l°ợng hay không. Thiết bị có khả năng phát hiện úng sản phẩm ạt tiêu chuẩn với xác
suất là 0,92 và phát hiện úng sản phẩm không ạt tiêu chuẩn với xác suất là 0,96. Tìm xác suất ể 1
sản phẩm °ợc chọn ngẫu nhiên sau khi kiểm tra:
a) Đ°ợc kết luận là ạt tiêu chuẩn.
b) Đ°ợc kết luận là ạt tiêu chuẩn thì lại không ạt tiêu chuẩn.
c) Đ°ợc kết luận úng với thực chất của nó.
Bài 12. Có 3 hệ thống bóng iện A, B, C với xác suất bị hỏng trong một chu kỳ sử dụng lần l°ợt là
0,10; 0,20; 0,25 và ộc lập với nhau. Tính xác suất ể mạch không có iện do hệ thống bóng iện bị hỏng nếu chúng mắc: a) Đ°ợc mắc nối tiếp. b) Đ°ợc mắc song song. c)
2 hệ thống bóng iện A, B mắc song song, sau ó chúng °ợc mắc nối tiếp với hệ thống bóng iện C.
Bài 13. Có 3 hộp sản phẩm. Hộp thứ nhất chứa 8 sản phẩm tốt, 2 sản phẩm xấu. Hộp thứ hai chứa
7 sản phẩm tốt, 5 sản phẩm xấu. Hộp thứ 3 không có sản phẩm nào. Ng°ßi ta lấy 2 sản phẩm từ mỗi
hộp bỏ vào hộp thứ 3.
a) Trung bình lấy °ợc bao nhiêu sản phẩm tốt từ hộp thứ 2?
b) Tính xác suất ể cả bốn sản phẩm lấy từ hai hộp là tốt.
c) Giả sử hộp thứ 3 có úng 1 sản phẩm tốt, tính xác suất ể sản phẩm ó là của hộp thứ 2. lOMoARcPSD| 36067889
Bài 14. Biết rằng 1 ng°ßi có nhóm máu AB có thể nhận máu của bất kì nhóm máu nào. Nếu ng°ßi
ó có nhóm máu còn lại ( A hoặc B hoặc O) thì chỉ có thể nhận °ợc máu của ng°ßi cùng nhóm máu
với mình hoặc ng°ßi có nhóm máu O. Biết tỉ lệ ng°ßi có nhóm máu O, A, B và AB t°¡ng ứng là 33,7%; 37,5%; 20,9%; 7,9%.
a) Lấy ngẫu nhiên một ng°ßi cần tiếp máu và một ng°ßi cho máu. Tính xác suất ng°ßi cần tiếp
máu có nhóm máu A và sự truyền máu °ợc thực hiện.
b) Lấy ngẫu nhiên một ng°ßi cần tiếp máu và một ng°ßi cho máu. Tính xác suất ể sự truyền máu °ợc thực hiện.
Bài 15. Một lô sản phẩm rất lớn °ợc phân loại theo cách sau. Chọn ngẫu nhiên 30 sản phẩm làm
mẫu ại diện. Nếu mẫu không có sản phẩm nào là phế phẩm thì lô sản phẩm °ợc xếp loại 1. Nếu
mẫu có một hoặc hai sản phẩm là phế phẩm thì lô sản phẩm °ợc xếp loại 2. Trong tr°ßng hợp còn
lại (có từ ba phế phẩm trá lên) thì lô sản phẩm °ợc xếp loại 3. Giả sử tỉ lệ phế phẩm của lô hàng là 6%.
a) Hãy tính xác suất ể lô hàng °ợc xếp loại 1, loại 2, loại 3.
b) Tìm số phế phẩm chọn °ợc có khả năng nhất, tính xác suất ó.
Bài 16. Có 12 sinh viên i thi, trong ó có 2 ng°ßi thuộc loại giỏi, 6 khá và 4 trung bình. Trong số
20 câu hỏi thi, ng°ßi giỏi trả lßi °ợc tất cả, ng°ßi khá trả lßi °ợc 16 câu, ng°ßi trung bình °ợc 10 câu.
Chọn ngẫu nhiên 1 sinh viên trong số ng°ßi dự thi.
a) Mỗi ề thi có 3 câu hỏi, tính xác suất ể sinh viên ó trả lßi °ợc cả 3 câu hỏi của ề thi
b) Cho biết ng°ßi °ợc chọn trả lßi °ợc cả 3 câu hỏi. Tính xác suất ể sinh viên ó thuộc loại khá.
Bài 17. Giả sử hai biến cố A, B có xác suất P A( ) ý 0,6, PB( ) ý 0,4 và P A B( ÷ ý) 0,2. Hãy tính a) P A B( | )
b) PA B( ø ) c) P A B( ÷ ) d) P B A( | ) e) P A B( ÷ )
Bài 18. Có hai thùng ựng sản phẩm, thùng I có 80 chính phẩm và 20 phế phẩm, thùng II có 90 chính phẩm và 10 phế phẩm.
a) Lấy ngẫu nhiên từ mỗi thùng ra một sản phẩm, tính xác suất ể lấy °ợc ít nhất một chính phẩm.
b) Lấy ngẫu nhiên ra một thùng rồi từ thùng ó lấy ngẫu nhiên ra một sản phẩm. Tìm xác suất
ể sản phẩm lấy °ợc là chính phẩm.
c) Lấy ngẫu nhiên một sản phẩm từ thùng I bỏ vào thùng II trộn ều sau ó lấy từ thùng II một
sản phẩm. Tính xác suất sản phẩm lấy °ợc cuối cùng là một chính phẩm. lOMoARcPSD| 36067889 ü0 nÕu x 0 ÿ
Bài 19. Cho X là biến ngẫu nhiên với hàm mật ộ fX ( )x
ýÿýÿ2x x nÕu nÕu 10ü ü xx 21 ÿþ0 nÕu 2 ü x
a) Tìm hàm phân bố xác suất F xX ( ) .
b) Thực hiện 10 quan sát ộc lập về biến ngẫu nhiên X . Có bao nhiêu lần kết quả X nhận ù
giá trị trong khoảng ö÷ø 65; 3ú û có khả năng nhất, tìm xác suất t°¡ng ứng.
Bài 20. Cho biến ngẫu nhiên X liên tục với hàm phân bố xác suất nh° sau ü 0 nÕu xü0 F xX( )ýÿÿý 2kx nÕu 0 x k 2 x2 ÿk ÿþ 1 nÕu x kþ
a) Tìm hàm mật ộ xác suất fX ( )x . Tính P
ü ü0,5 X 2 .
b) Tính kỳ vọng EX .
Bài 21. Một phân x°áng sản xuất có 30 máy tiện hoạt ộng ộc lập nhau, xác suất các máy bị hỏng
trong một ca sản xuất là nh° nhau và ều bằng 0,07.
a) Tìm quy luật phân bố xác suất của số máy bị hỏng trong một ca sản xuất?
b) Trung bình có bao nhiêu máy bị hỏng trong một ca sản xuất ?
c) Trong một ca sản xuất có bao nhiêu máy hỏng với khả năng lớn nhất? tính xác suất này.
üÿk cos xn u Õ x
Bài 22. Biến ngẫu nhiên X có hàm mật ộ fX ( )x ýý 2 2 ÿþ 0 nÕu ng-îcl¹i
a) Xác ịnh k. Tìm hàm phân bố F xX ( ) . lOMoARcPSD| 36067889 ü
Tính Püý0ü X
ý. Tính kỳ vọng E X . b) þ 4þ
Bài 23. Gọi X là số ng°ßi gọi tới tổng ài iện thoại của công ty A trong thßi gian 5 phút. Giả sử X tuân
theo phân bố Poisson với üý3, biết e 3 ý 0,05. Tính xác suất ể trong 5 phút:
a) Có không quá 3 ng°ßi gọi tới tổng ài iện thoại của công ty A.
b) Có từ 2 ến 5 ng°ßi gọi ến tổng ài iện thoại của công ty A.
Bài 24. Một xí nghiệp sản xuất máy tính có xác suất sản phẩm là phế phẩm 0,02. Chọn ngẫu 250 máy ể kiểm tra.
a) Tính xác suất có úng 2 máy phế phẩm.
b) Tính xác suất có không quá 2 máy phế phẩm.
c) Số phế phẩm có khả năng chọn °ợc cao nhất là bao nhiêu?
Bài 25. Một trạm iện thoại tự ộng nhận °ợc trung bình với c°ßng ộ üý180 lần gọi trong 1 giß. Cho
biết e 3 0,05, e 6 0,0025. a)
Tìm xác suất ể trạm ó nhận °ợc 2 cuộc gọi trong 1 phút. b)
Tìm xác suất ể trạm ó nhận °ợc 5 cuộc gọi trong 3 phút. c)
Tìm xác suất ể trong 3 phút liên tiếp mỗi phút trạm nhận °ợc nhiều nhất 1 cuộc gọi.
Bài 26. Biến ngẫu nhiên X có hàm phân bố xác suất nh° sau ü 0 nÕu x 0
ÿ 2 kx nÕu 0ü x 1 F xX( ) ýýx ÿ þ 1 nÕu xþ1
a) Tìm k . Tìm hàm mật ộ xác suất. ü ü
Tính xác suất P÷öüýþ ü12 X 14 þ þý ýø ü X þ 12 ýþö÷ø ø
Bài 27. Chọn ngẫu nhiên 2 tấm thẻ từ một túi có chứa 10 tấm thẻ ỏ và 6 tấm thẻ xanh.
a) Gọi X là số thẻ ỏ, lập bảng phân bố xác suất của X .
b) Giả sử rút mỗi tấm thẻ ỏ °ợc 5 iểm và rút mỗi tấm thẻ xanh °ợc 8 iểm. Gọi Y là số iểm tổng
cộng của 2 tấm thẻ rút ra, tìm hàm phân bố xác suất của Y . lOMoARcPSD| 36067889
c) Tính các kỳ vọng EX , EY và các ph°¡ng sai DX , DY .
Bài 28. Cho bảng phân bố xác suất của biến ngẫu nhiên X : X 1 2 3 5 P k 2k 3k 4k
a) Tìm giá trị hằng số k . Tìm hàm phân bố xác suất F xX ( ) .
b) Tính EX , DX .
c) Lập bảng phân bố xác suất của biến ngẫu nhiên Y Xý 2 5X 5. Tính EY .
Bài 29. Cho biến ngẫu nhiên rßi rạc X có bảng phân bố xác suất: X 2 1 2 3 P 0,1 0,3 k 0,4
a) Tìm k . Tìm hàm phân bố xác suất F xX ( ) .
b) Tính kỳ vọng E X và ph°¡ng sai D X .
c) Tính P 0 ü X 2 , P X ý 2 | X 1 .
Bài 30. Một lô hàng có 14 sản phẩm trong ó 5 sản phẩm loại I và 9 sản phẩm loại II. Chọn ngẫu
nhiên 2 sản phẩm từ lô hàng, gọi X là số sản phẩm loại I chọn °ợc. a)
Lập bảng phân bố xác suất của X , tìm hàm phân bố xác suất F xX ( ) . b)
Tính kỳ vọng EX và ph°¡ng sai DX . c)
Chọn mỗi sản phẩm loại I °ợc th°áng 50USD và mỗi sản phẩm loại II °ợc th°áng
10USD, tính số tiền th°áng trung bình nhận °ợc.
Bài 31. Trong 1 hòm có 10 tấm thẻ; trong ó có 4 tấm thẻ ghi số 1, 3 thẻ ghi số 2, 2 thẻ ghi số 3 và 1
tấm thẻ ghi số 4. Chọn ngẫu nhiên 2 tấm thẻ.
a) Tính xác suất chọn °ợc một thẻ số 1 và một thẻ số 2.
b) Gọi X là tổng số ghi trên 2 tấm thẻ. Lập bảng phân bố xác suất của X và hàm phân bố xác suất F xX ( ) .
c) Với mỗi số trên thẻ chọn °ợc th°áng 20$. Gọi Y là tổng số tiền °ợc th°áng, tính EY . Bài 32.
Một xạ thủ em 5 viên ạn bắn kiểm tra tr°ớc ngày thi bắn. Xạ thủ bắn từng viên vào bia với
xác suất trúng vòng 10 là 0,85. Nếu bắn 3 viên liên tiếp trúng vòng 10 thì thôi không bắn
nữa. Gọi Y là số ạn xạ thủ này ã bắn.
a) Lập hàm phân bố xác suất của Y. b) Tính EY.
c) Xét tr°ßng hợp bắn 3 viên liên tiếp trúng vòng 10 thì ngừng bắn. Gọi Z là số ạn còn thừa.
Tìm quy luật phân bố xác suất của Z. lOMoARcPSD| 36067889
Bài 33. Một túi chứa 4 quả cầu trắng, 3 quả cầu en. Hai ng°ßi A và B lần l°ợt rút một quả cầu trong
túi ( rút xong không trả lại). Trò ch¡i kết thúc khi có ng°ßi rút °ợc quả cầu en ng°ßi ó xem nh° thua
cuộc và trả cho ng°ßi kia số tiền là X bằng số quả cầu rút ra nhân với 5 USD. Giả sử A là ng°ßi rút
tr°ớc và X là số tiền A thu °ợc.
a) Lập bảng phân bố xác suất của X . b) Tính EX .
c) Nếu ch¡i 150 ván thì trung bình A °ợc bao nhiêu?
Bài 34. Trọng l°ợng của một loại sản phẩm là biến ngẫu nhiên tuân theo quy luật phân bố chuẩn với
trọng l°ợng trung bình là 100kg và ộ lệch chuẩn là 1kg.
a) Tính tỷ lệ sản phẩm có trọng l°ợng lớn h¡n 99,35 kg.
b) Nếu cân thử 5 sản phẩm thì số sản phẩm có trọng l°ợng lớn h¡n 99,35 kg có khả năng xảy
ra cao nhất là bao nhiêu? Tính xác suất ó.
Bài 35. à một tổng ài b°u iện các cuộc iện thoại gọi ến xuất hiện một cách ngẫu nhiên, ộc lập với
nhau và trung bình có 2 cuộc gọi trong một phút. Biết rằng số cuộc gọi ến tổng ài trong khoảng
thßi gian t phút là biến ngẫu nhiên có phân bố Poisson tham số üý 2t . Tính xác suất ể:
a) Có ít nhất một cuộc gọi trong khoảng thßi gian 10 giây.
b) Trong khoảng thßi gian 3 phút có nhiều nhất ba cuộc gọi.
c) Trong khoảng thßi gian 3 phút liên tiếp mỗi phút có nhiều nhất một cuộc gọi.
Bài 36. Tín hiệu thông tin °ợc phát i 5 lần ộc lập nhau. Xác suất thu °ợc tín hiệu của mỗi lần phát là 0,7. Tính xác suất:
a) Thu °ợc tín hiệu úng 2 lần.
b) Thu °ợc tín hiệu.
c) Tìm số lần thu °ợc tín hiệu có khả năng nhất, tính xác suất ó.
Bài 37. Thßi gian phục vụ khách hàng tại một iểm dịch vụ là biến ngẫu nhiên X liên tục có hàm mật ộ xác suất ýÿýü X
5e 5x nÕu x 0 f ( )x ÿþ0 nÕu x ü0
Với X °ợc tính bằng phút/khách hàng.
a) Tìm xác suất ể thßi gian phục vụ một khách hàng nào ó nằm trong khoảng từ 0,4 ến 1 phút.
b) Tìm thßi gian trung bình ể phục vụ một khách hàng.
Bài 38. Cho X là một biến ngẫu nhiên với kỳ vọng EXýý và ộ lệch tiêu chuẩn óý DX . Hãy tính P X
ý óü3 trong các tr°ßng hợp sau: lOMoARcPSD| 36067889
a) X có phân bố mũ.
b) X có phân bố ều trên oạn 1,1 .
c) X có phân bố Poisson với tham số üý 0,09.
Bài 39. Năng suất của một loại cây ăn quả là một biến ngẫu nhiên có phân bố chuẩn với năng suất
trung bình 20kg/cây và ộ lệch chuẩn 3kg. Cây có năng suất tối thiểu 15,08kg °ợc cho là ạt tiêu chuẩn.
a)Hãy tính tỷ lệ cây ạt tiêu chuẩn. b)
Cây ạt tiêu chuẩn sẽ lãi 500 nghìn ồng/cây, ng°ợc lại cây không ạt tiêu chuẩn sẽ lỗ
1 triệu ồng/cây. Ng°ßi ta thu hoạch ngẫu nhiên một lô gồm 100 cây. Hãy tính tiền lãi trung bình cho lô cây ó.
Bài 40. Trọng l°ợng của các bao xi măng là một biến ngẫu nhiên có phân bố chuẩn với giá trị trung
bình 50kg và ộ lệch chuẩn óý 0,1(kg). Bao xi măng °ợc cho là ạt chuẩn nếu có trọng l°ợng từ 49,8 kg ến 50,2 kg.
a) Tính xác suất ể khi lấy ngẫu nhiên 1 bao thì °ợc bao ạt chuẩn.
b) Tính xác suất ể trong 5 bao °ợc lấy ngẫu nhiên thì có từ 3 ến 4 bao ạt chuẩn.
c) Trung bình có bao nhiêu bao ạt chuẩn trong số 1000 bao?
Bài 41. Cho X , Y là hai biến ngẫu nhiên rßi rạc, ộc lập có bảng phân bố xác suất nh° sau: X 2 3 5 Y 1 4 P 0,3 0,5 0,2 P 0,2 0,8
a) Lập bảng phân bố xác suất của biến ngẫu nhiên Z X Yý và T XYý .
b) Tính các kỳ vọng EZ , ET và các ph°¡ng sai DZ , DT . c) Tính P X Y þ .
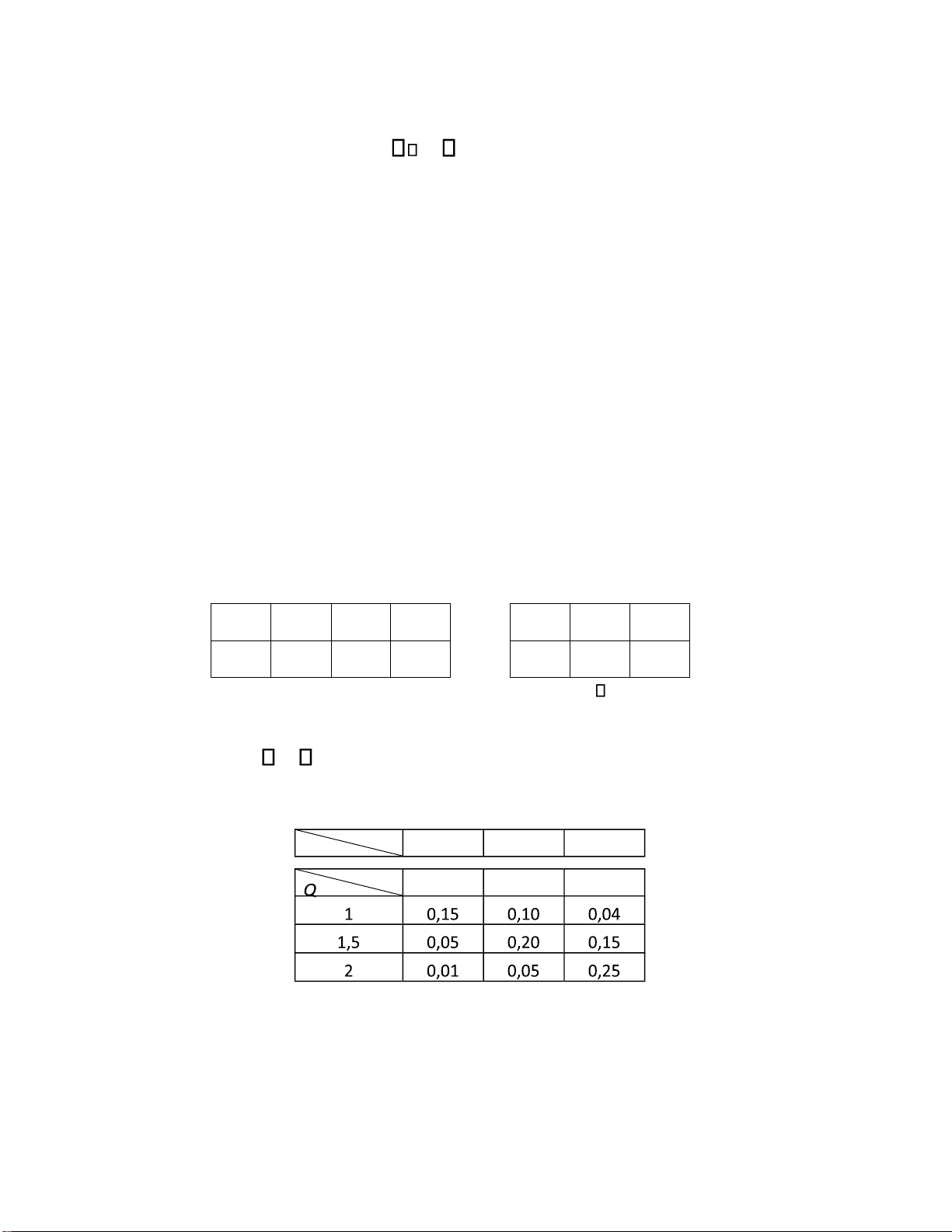
Bài 42. Thống kê về doanh số bán hàng (D) và chi phí cho tiếp thị quảng cáo (Q), ( ¡n vị: triệu ồng)
của một công ty, ng°ßi ta thu °ợc bảng phân bố xác suất ồng thßi sau ây: D 100 200 300
a) Tìm chi phí quảng cáo trung bình và ộ lệch chuẩn.
b) Tìm doanh số trung bình khi quảng cáo là 1,5 triệu ồng.
c) Doanh số có phụ thuộc vào quảng cáo hay không? Vì sao?
Bài 43. Cho X , Y là hai biến ngẫu nhiên rßi rạc có bảng phân bố xác suất ồng thßi lOMoARcPSD| 36067889 k k k
a) Tìm k. Tìm bảng phân bố xác suất của các thành phần X và Y . Hai biến ngẫu nhiên X
và Y có ộc lập không?
b) Tính ph°¡ng sai D(2X Y 3 ) . ù
c) Tìm bảng phân bố xác suất của Y với iều kiện X ý1; tính E ûY X ý ù1û .
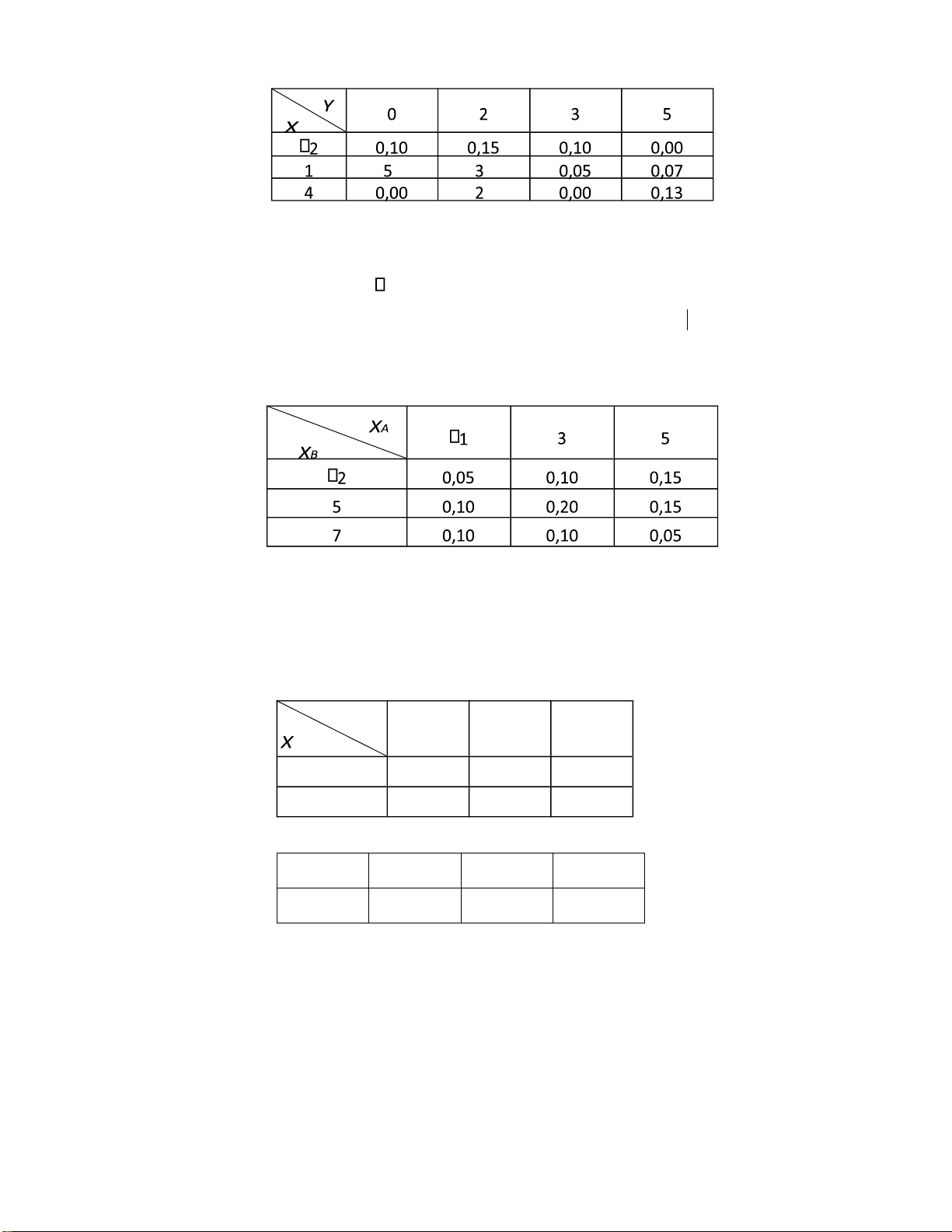
Bài 44. Một doanh nghiệp ầu t° ồng thßi vào hai thị tr°ßng A và B. Ng°ßi ta thấy lãi suất XA và XB (
¡n vị: %) là hai biến ngẫu nhiên có phân bố xác suất ồng thßi °ợc cho á bảng sau: a)
Tìm lãi suất trung bình nhận °ợc của mỗi thị tr°ßng A và B. b)
Tìm lãi suất trung bình khi ầu t° vào thị tr°ßng B, biết rằng năm ó lãi suất thị tr°ßng A là 3%? c)
Đầu t° á thị tr°ßng nào có rủi ro thấp h¡n?
Bài 45. Cho biến ngẫu nhiên 2 chiều (X Y, ) có bảng phân bố xác suất sau Y 1 2 3 1 0 17 , q 0 25 , 2 0 30 , 0 , 08 p
Và bảng phân bố xác suất của biến ngẫu nhiên Y Y 1 2 3 P 0,47 0,23 g
a) Tìm các giá trị p, q, g.
b) Hai biến ngẫu nhiên X, Y có ộc lập không?
c) Tính các kỳ vọng E X , EY và ph°¡ng sai D X , DY .
Bài 46. Cho biến ngẫu nhiên 2 chiều (X,Y) có bảng phân bố xác suất sau: lOMoARcPSD| 36067889 k
trong ó X, Y là lãi suất của 2 loại cổ phiếu A và B t°¡ng ứng. a)
Tìm k . Tính lãi suất trung bình của cổ phiếu A và lãi suất trung bình của cổ phiếu B. b)
Tính lãi suất trung bình của cổ phiếu B khi lãi suất cổ phiếu A là 2%. c)
Giả thiết mức ộ rủi ro của mỗi loại cổ phiếu °ợc xác ịnh bằng ộ lệch chuẩn (căn của
ph°¡ng sai) của lãi suất của chúng. Nếu một ng°ßi ầu t° 40% tiền ể mua cổ phiếu A và 60% tiền
ể mua cổ phiếu B thì mức ộ rủi ro ng°ßi ó gặp phải là bao nhiêu?
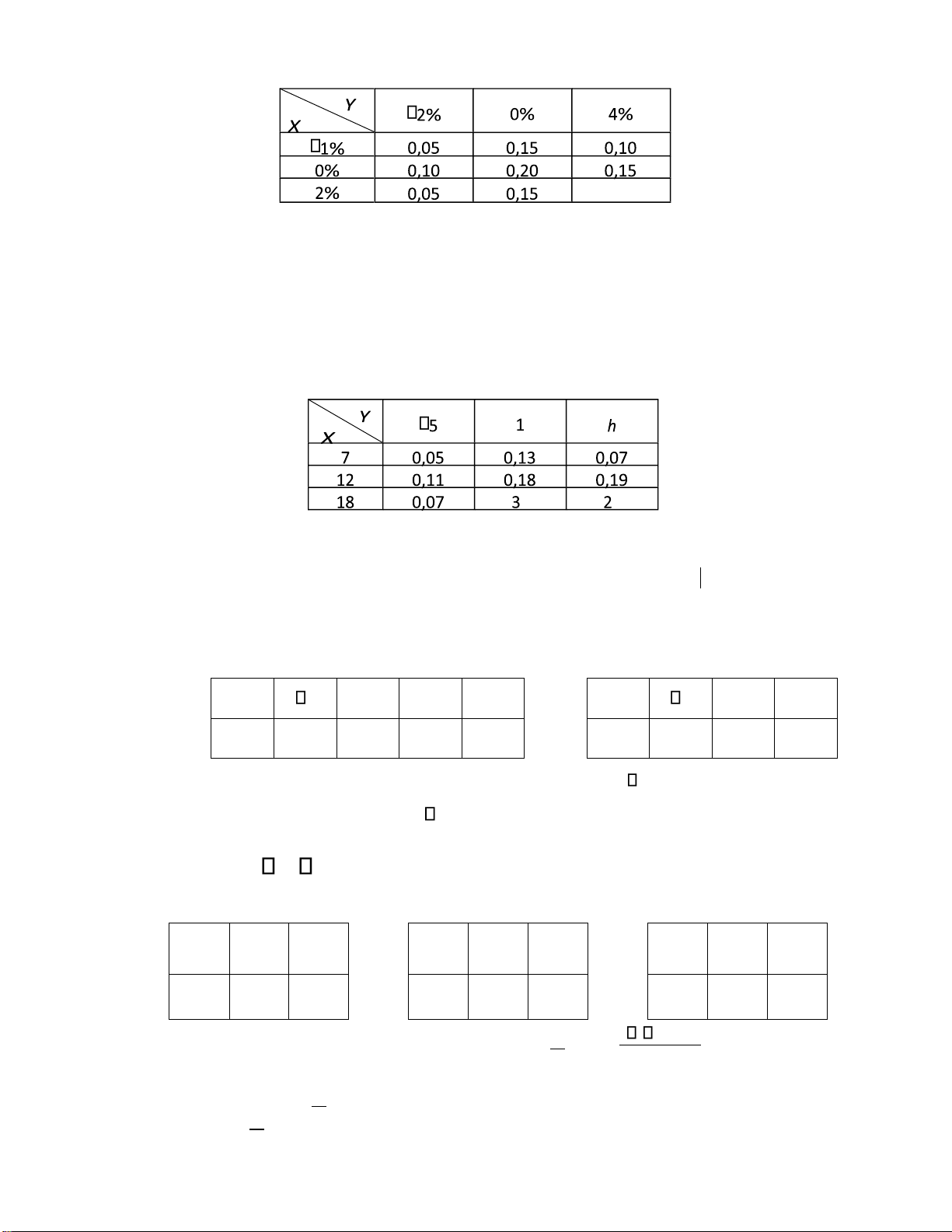
Bài 47. Cho X , Y là hai biến ngẫu nhiên rßi rạc có bảng phân bố xác suất ồng thßi k k ý a)
Tìm k. Biết EY 2, tìm h. Hai biến ngẫu nhiên X , Y có ộc lập không? ù ù
b) Tìm bảng phân bố xác suất của Y với iều kiện X ý12 và tính E ûY X ý12 û .
c) Tính hệ số t°¡ng quan òXY .
Bài 48. Cho 2 biến ngẫu nhiên X và Y ộc lập có bảng phân bố xác suất: X 1 0 1 2 Y 1 0 1 P 0,2 0,3 0,3 0,2 P 0,3 0,4 0,3
a) Lập bảng phân bố xác suất của các biến ngẫu nhiên X2 , X Y , X Y. .
b) Tính các kỳ vọng EX , EY , E(X Y ), E(XY). c) Tính P X Y þ .
Bài 49. Cho X1, X2 , X3 là ba biến ngẫu nhiên ộc lập có bảng phân bố xác suất nh° sau: X 0 2 1 2 1 2 1 X2 X3 P 0,65 0,35 P 0,4 0,6 P 0,7 0,3
a) Lập bảng phân bố xác suất của biến ngẫu nhiên XýX X X1 2 3 . 3 lOMoARcPSD| 36067889
b) Tính E(X); D(X).
c) Tính E(X1+X2+X3); D(X1+X2+X3).
Bài 50. Trọng l°ợng sản phẩm do nhà máy sản xuất ra là một biến ngẫu nhiên có phân bố chuẩn với
ộ lệch chuẩn 2 kg, trọng l°ợng trung bình theo quy ịnh là 50 kg. Nghi ngß máy hoạt ộng không bình
th°ßng làm thay ổi trọng l°ợng trung bình của sản phẩm, ng°ßi ta cân thử 100 sản phẩm và thu °ợc kết quả sau: Trọng l°ợng sản phẩm 49 50 51 52 53
Số sản phẩm t°¡ng ứng 10 60 20 5 5
Với mức ý nghĩa ý 0,05, hãy kết luận về iều nghi ngß nói trên.
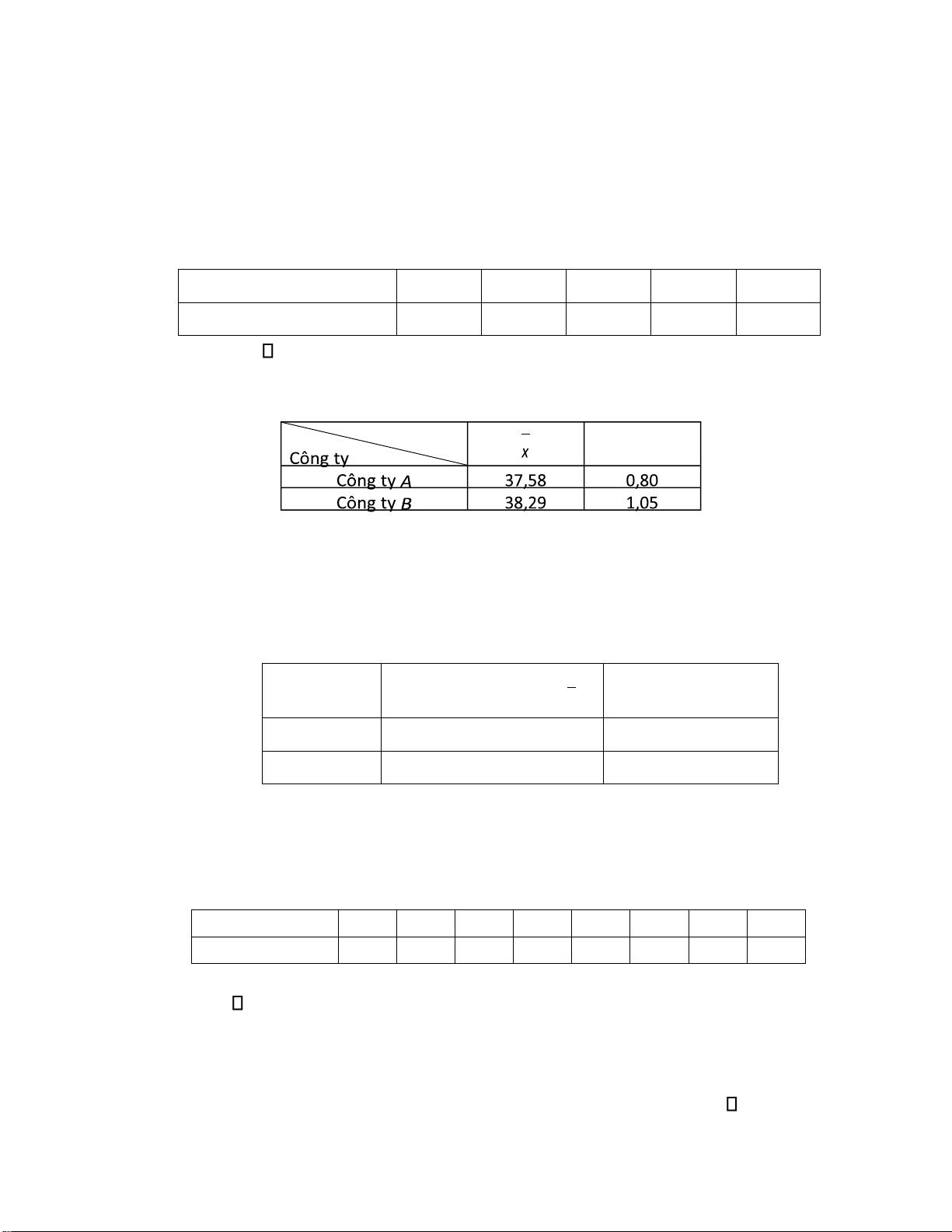
Bài 51. Theo dõi giá cổ phiếu của hai công ty A và B trong vòng 16 ngày, ng°ßi ta tính °ợc các số liệu sau: Số liệu s
Giả thiết giá cổ phiếu của hai công ty A và B là hai biến ngẫu nhiên có phân bố chuẩn có ph°¡ng sai
bằng nhau. Với mức ý nghĩa α = 0,05 hãy kiểm ịnh về nhận ịnh cho rằng có sự khác biệt thực sự
về giá cổ phiếu trung bình của hai công ty.
Bài 52. Một hợp tác xã trồng thử hai giống lúa, mỗi giống trồng trên 30 mảnh ruộng và °ợc chăm
sóc nh° nhau. Cuối vụ thu hoạch ng°ßi ta thu °ợc số liệu sau: Độ lệch chuẩn(s)
Năng suất trung bình ( x ) Giống lúa I 45 2,5 Giống lúa II 46,5 3,2
Với mức ý nghĩa α = 0,05, hãy kiểm ịnh về nhận ịnh cho rằng năng suất trung bình của hai giống
lúa có thể coi nh° bằng nhau. Biết rằng năng suất của 2 giống lúa tuân theo quy luật phân bố chuẩn
với ộ lệch tiêu chuẩn nh° nhau.
Bài 53. Để so sánh năng suất làm việc của hai tổ công nhân A và B tại một nhà máy, ng°ßi ta theo
dõi năng suất (tính theo sản phẩm/ngày) của hai tổ có số liệu sau: Tổ công nhân A 65 66 64 71 67 64 66 70 Tổ công nhân B 66 68 71 75 67 73 74
Hỏi có thể kết luận rằng 2 tổ công nhân ó có năng suất trung bình thực sự khác nhau không với
mức ý nghĩa ý 0,05. Biết rằng năng suất làm việc của hai tổ công nhân tuân theo quy luật phân
bố chuẩn với ộ lệch tiêu chuẩn nh° nhau.
Bài 54. Tỉ lệ khách hàng trá lại sử dụng dịch vụ của công ty là 60 %. Có ý kiến cho rằng tỷ lệ này giảm
do chính sách hậu mãi của công ty không tốt. Theo dõi ngẫu nhiên 300 khách hàng thấy có 162 khách ý
hàng trá lại sử dụng dịch vụ của công ty. Hãy kết luận 0,025
ý kiến trên với mức ý nghĩa . lOMoARcPSD| 36067889
Bài 55. Điều tra doanh thu hàng ngày của một số hộ kinh doanh một mặt hàng nào ó ng°ßi ta thu °ợc bảng số liệu sau
Doanh thu X (triệu ồng) 9,2 9,5 10 10,7 11 11,3 Số hộ t°¡ng ứng 2 4 7 13 9 1
Giả thiết doanh thu là biến ngẫu nhiên tuân theo quy luật phân bố chuẩn.
Với mức ý nghĩa 2,5%, có thể kết luận doanh thu trung bình trong ngày của các hộ hộ kinh doanh
mặt hàng °ợc iều tra á trên cao h¡n 10,2 triệu ồng không?
Bài 56. Một xí nghiệp hỏi ý kiến 310 khách hàng về một loại sản phẩm của xí nghiệp; kết quả có 93
ng°ßi ánh giá cao sản phẩm. Với ộ tin cậy 0,95 hãy:
a) ¯ớc l°ợng tỷ lệ khách hàng °a chuộng sản phẩm của xí nghiệp.
b) Cần hỏi bao nhiêu khách hàng ể sai số của °ớc l°ợng không v°ợt quá 0,03.
Bài 57. Một công ty có một hệ thống máy tính có thể xử lý 1300 hoá ¡n trong 1 giß. Công ty mới
nhập một hệ thống máy tính mới, hệ thống này chạy kiểm tra trong 40 giß cho thấy số hoá ¡n xử lý
trung bình trong 1 giß là 1378 với ộ lệch tiêu chuẩn 215. Với mức ý nghĩa 2,5% hãy nhận ịnh
xem hệ thống mới có tốt h¡n hệ thống cũ hay không?
Bài 58. Để xác ịnh giá trung bình ối với một loại hàng hóa trên thị tr°ßng, ng°ßi ta iều tra ngẫu
nhiên 100 cửa hàng và thu °ợc bảng số liệu sau: Giá (nghìn ồng) 36 39 40 41 45 46 50
Số cửa hàng t°¡ng ứng 15 20 45 10 2 5 3
1. Với ộ tin cậy 95% hãy °ớc l°ợng giá trung bình của loại hàng hóa ó tại thßi iểm ang xét.
Biết rằng giá hàng hóa là biến ngẫu nhiên tuân theo quy luật chuẩn.
2. Tỷ lệ tối a của loại hàng hóa ó có giá trị trên 40 nghìn ồng trên thị tr°ßng là bao nhiêu. Yêu
cầu kết luận với ộ tin cậy 95%.
Bài 59. Trọng l°ợng của một loại sản phẩm là một biến ngẫu nhiên có phân bố chuẩn. Cân thử 100
sản phẩm loại này ta thu °ợc kết quả: Trọng l°ợng (gram) 40 42 42 44 44 46 46 48 48 50 50 52
Số sản phẩm t°¡ng ứng 7 13 25 35 15 5
a) Với ộ tin cậy 95%, hãy tìm khoảng tin cậy của trọng l°ợng trung bình của loại sản phẩm trên.
b) Giả sử ộ lệch chuẩn của trọng l°ợng là 2,5 gram. Nếu muốn ộ chính xác ý 0,4 gram với ộ
tin cậy 95% thì kích th°ớc mẫu cần thiết là bao nhiêu.
Bài 60. Chọn ngẫu nhiên 129 sinh viên của Học viện Công nghệ B°u chính Viễn thông và o chiều
cao của họ ta °ợc kết quả sau: Chiều cao (cm)
152-156 156-160 160-164 164-168 168-172 172-176
Số l°ợng SV t°¡ng ứng 15 21 32 36 18 7
Giả sử chiều cao của sinh viên là biến ngẫu nhiên có phân bố chuẩn. lOMoARcPSD| 36067889
a) Hãy °ớc l°ợng chiều cao trung bình của sinh viên bằng khoảng tin cậy với ộ tin cậy 0,95.
b) Kiểm ịnh giả thuyết H0 :ýý162 ; H1:ýþ162 với mức ý nghĩa 0,05.
Bài 61. Ng°ßi ta lấy ngẫu nhiên từ lô hàng ra 200 sản phẩm thì thấy có 182 sản phẩm ạt yêu cầu chất l°ợng.
a) Với ộ tin cậy 95%, hãy °ớc l°ợng tỉ lệ sản phẩm ạt yêu cầu chất l°ợng của lô hàng.
b) Giả sử lô hàng có 6000 sản phẩm, vói ộ tin cậy 95% hãy °ớc l°ợng số sản phẩm ạt yêu cầu của cả lô hàng.
Bài 62. Năng suất lúa trung bình á vụ tr°ớc trong một vùng là 45 tạ/ha. Vụ lúa năm nay ng°ßi ta áp
dụng biện pháp kĩ thuật mới cho toàn bộ diện tích trồng lúa trong vùng. Theo dõi 31 ha, ta có bảng năng suất lúa sau ây. Năng suất (tạ/ha)
30 – 35 35 – 40 40 – 45 45 – 50 50 – 55 55 – 60 60 – 65 65 – 70
Diện tích (ha) t°¡ng ứng 1 2 6 13 4 3 1 1
Biết năng suất lúa là biến ngẫu nhiên có phân bố chuẩn.
a) Với mức ý nghĩa 2,5% hãy kiểm ịnh ý kiến cho rằng năng suất có tăng lên khi áp dụng biện pháp kĩ thuật mới.
b) ¯ớc l°ợng ph°¡ng sai của năng suất lúa với ộ tin cậy 90%.
Bài 63. Điều tra doanh thu hàng tháng của 100 hộ kinh doanh thu °ợc bảng số liệu: Doanh thu (triệu ồng) 80 85 90 95 100 105 110 115 120 125 Số hộ t°¡ng ứng 2 3 8 15 25 18 12 10 6 1
Giả sử doanh thu các hộ là biến ngẫu nhiên có phân bố chuẩn.
a) ¯ớc l°ợng giá trị doanh thu trung bình bằng khoảng tin cậy với ộ tin cậy 95%.
b) Tỷ lệ các hộ kinh doanh có doanh thu trung bình hàng tháng d°ới 100 triệu của năm ngoái
là 30%, có ý kiến cho rằng năm nay tỷ lệ hộ kinh doanh có doanh số d°ới 100 triệu thấp hợn so với
năm ngoái. Sử dụng bảng số liệu trên hãy kiểm ịnh ý kiến ó với mức ý nghĩa 2,5%.