lOMoARcPSD| 36067889 Bài tập nhóm.
1. Bằng phương pháp nghiên cứu tổng thể hãy:
- Cho biết chiều cao trung bình của sinh viên trong lớp của bạn.
- Tính độ lệch tiêu chuẩn của chiều cao sinh viên trong lớp.
- Tính tỷ lệ sinh viên có chiều cao từ 1.6m đến 1.65m.
- Tính tỷ lệ sinh viên có chiều cao 1.6m.
- Tính tỷ lệ sinh viên có chiều cao trên 1.65m. 2.
Bằng phương pháp nghiên cứu mẫu hãy cho biết chiều cao trung bình
của sinh viên trong lớp của bạn và nêu phương pháp lấy mẫu mà bạn sử dụng. 3.
So sánh giữa phương pháp nghiên cứu mẫu và phương pháp nghiên cứu tổng thể. 4.
Phát biểu các định lý về luật số lớn và định lý giới hạn trung tâm. Nếu
sự hiểu biết của bạn về mỗi định lý. Làm bài tập 4.20; 4.21; 4.22 Bài Làm
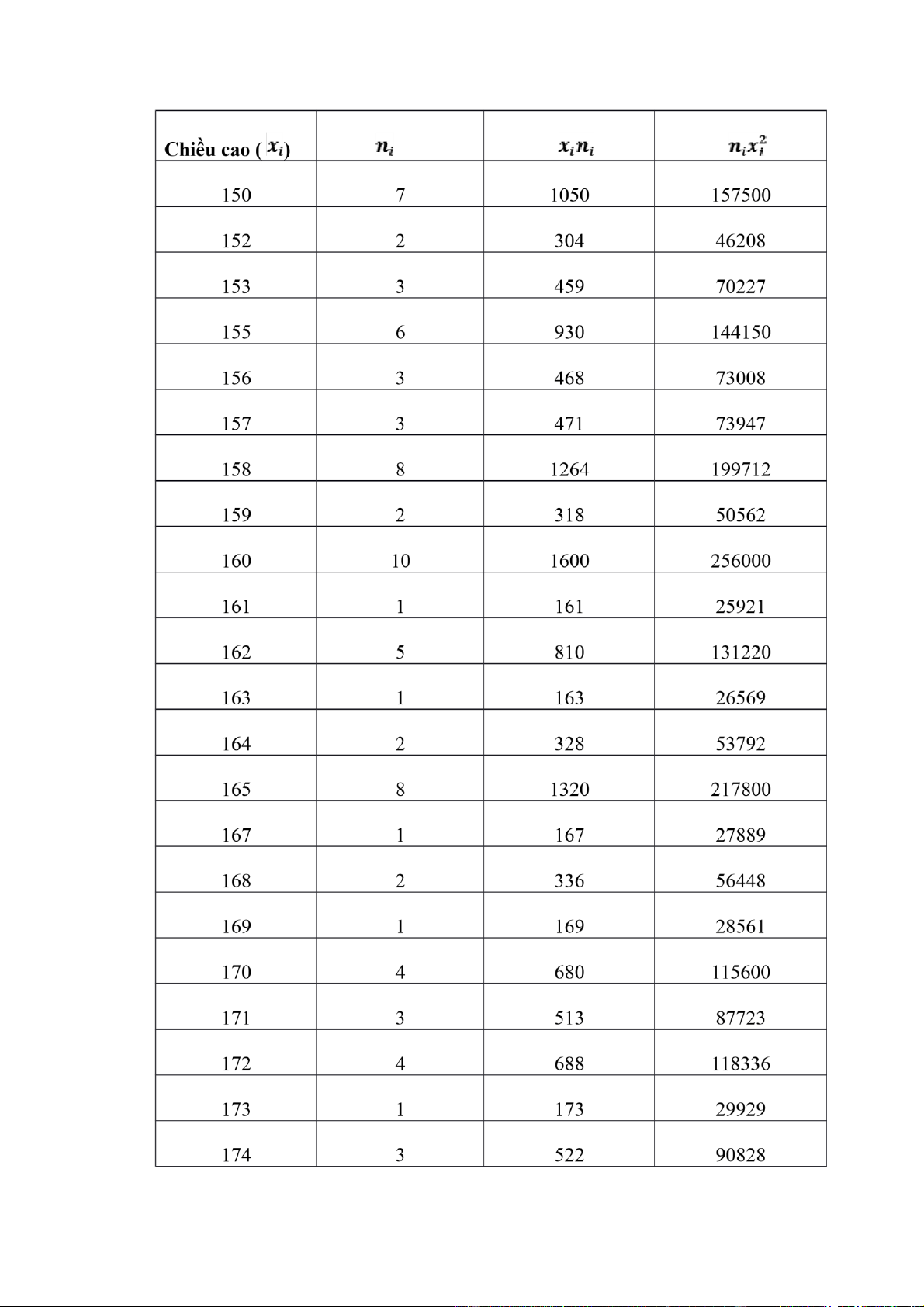
1. Điều tra chiều cao sinh viên trong lớp và có thống kê
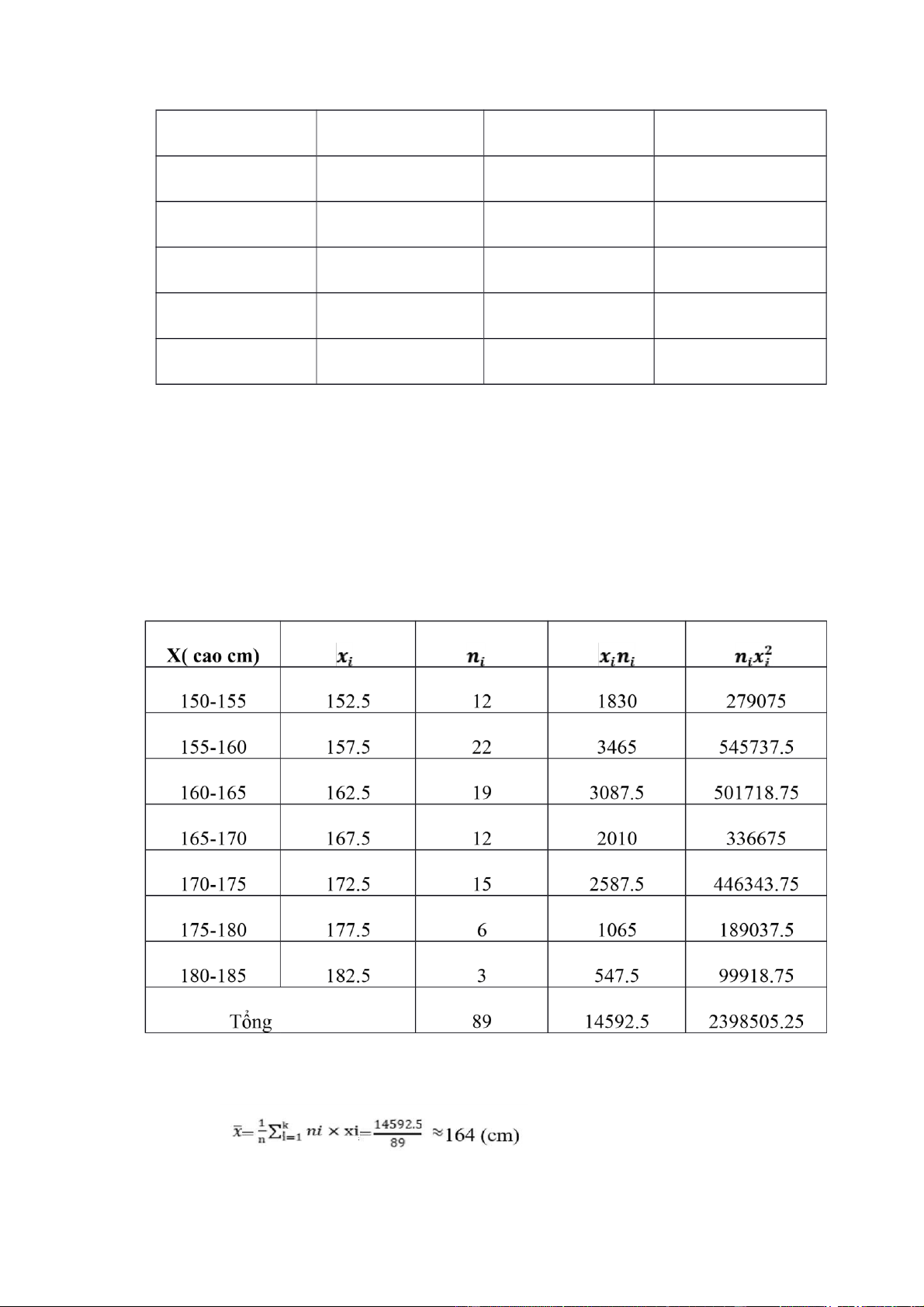
X( chiều 150-155 155-160 160-165 165-170 170-175 175-180 180-185 cao cm) Số SV 12 22 19 12 15 6 3 lOMoARcPSD| 36067889 lOMoARcPSD| 36067889 175 4 700 122500 176 1 176 30976 177 1 177 31329 180 2 360 64811 184 1 184 33856 Tổng 89 14491 2362538
- Chiều cao trung bình của sinh viên trong lớp:
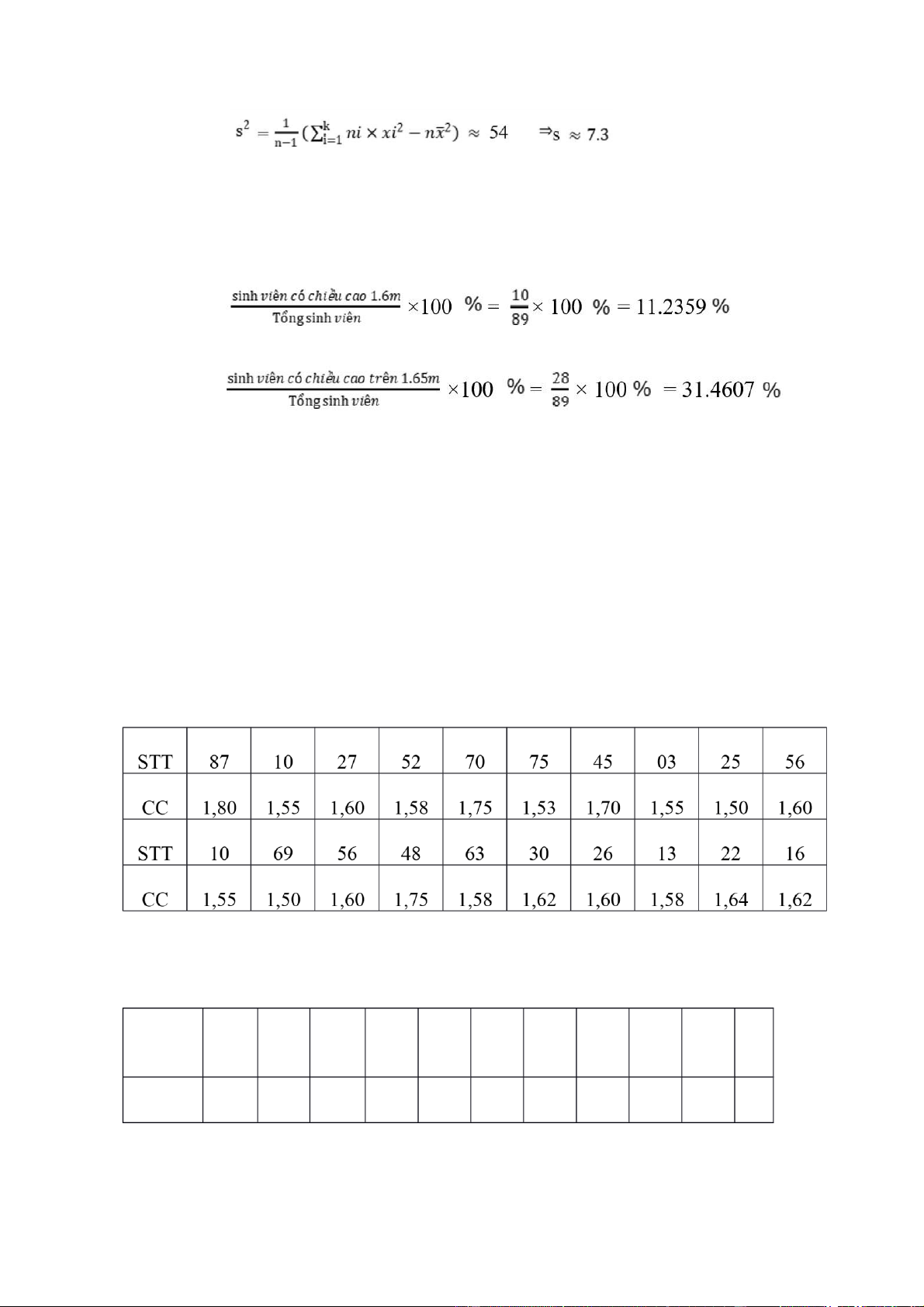
- Độ lệch tiêu chuẩn của chiều cao sinh viên trong lớp: lOMoARcPSD| 36067889
- Tỷ lệ sinh viên có chiều cao từ 1.6m- 1.65m
- Tỷ lệ sinh viên có chiều cao 1.6m
- Tỷ lệ sinh viên có chiều cao trên 1.65m
2. Bằng phương pháp nghiên cứu mẫu, ta có thể tính chiều cao trung bình của
các sinh viên trong lớp như sau:
B1: Lập bảng khảo sát thống kê lại chiều cao của toàn bộ sinh viên trong lớp,
số thứ tự của sinh viên sẽ đại diện cho sinh viên đó ( số thứ tự của sinh viên không trùng nhau).
B2: Mỗi số thứ tự của sinh viên được viết vào 1 lá thăm, tổng cộng tất cả có
89 lá. Bỏ tất cả lá thăm vào trong hộp. Chọn ngẫu nhiên, có hoàn lại, 20 lá thăm
trong 89 lá thì xác suất mỗi sinh viên được chọn là 22,5%.
Kết quả các lá thăm và chiều cao của sinh viên tương ứng với nó là:
Gọi X (m) là chiều cao sinh viên trong lớp
Từ đó ta có bảng phân bố tần số thực nghiệm: X 1 , 50 1 , 5 , 1 55
1 , 58 1 , 60 1 , 62 1 , 64 1 , 70 1 , 75 1 , 80 ∑ 3 Tần số 2 1 3 3 4 2 1 1 2 1 20
Chiều cao trung bình sinh viên trong lớp là : lOMoARcPSD| 36067889
=1/20.(2.1,50+1.1,53+3.1,55+3.1,58+4.1,60+2.1,62+1.1,64+1.1,70+2.1,75+1.1,80) =1,61
Vậy chiều cao trung bình của sinh viên trong lớp thông qua phương pháp
nghiên cứu mẫu là 1,61m.
- Phương pháp lấy mẫu được sử dụng trong bài tập là phương pháp lấy mẫu
ngẫu nhiên đơn giản.Là kĩ thuật chọn mẫu, trong đó tất cả các cá thể trong quần
thể có cùng cơ hội ( cùng xác suất) để được chọn vào mẫu.
3.So sánh giữa phương pháp nghiên cứu mẫu và phương pháp nghiên cứu tổng thể.
*Nghiên cứu tổng thể: là tập hợp tất cả các phần tử thuộc hiện tượng nghiên cứu cần
được quan sát, thu thập và phân tích. Hay nói cách khác, khi nghiên cứu một vấn đề,
ta thường quan tâm vào một dấu hiệu cụ thể, các dấu hiệu này thể hiện trên nhiều
phần tử. Tập hợp tất cả các phần tử mang dấu hiệu này được gọi là tổng thể.
*Nghiên cứu mẫu: là một phần của tổng thể được chọn ra theo những cách thức nhất
định và với một dung lượng hợp lý. Giống nhau:
- Mục đích: Thu thập dữ liệu và phân tích dữ liệu để đưa ra kết luận về một vấn đề nghiên cứu.
- Phương tiện thu thập dữ liệu: bảng câu hỏi, cuộc khảo sát, phỏng vấn, quan sát,.…
- Phân tích dữ liệu: đều sử dụng phương pháp phân tích dữ liệu như thống kê, mô tả
thống kê, suy luận, phân tích đa biến,…
- Độ chính xác: đều cần đảm bảo độ chính xác của dữ liệu thu thập, phân tích để
đưa ra kết luận chính xác.
- Độ đại diện: đều cần đảm bảo độ đại diện của mẫu hoặc tổng thể để đưa ra kết luận có tính khái quát.
- Ứng dụng: được sử dụng trong nhiều lĩnh vực khác nhau như: kinh tế, y tế, giáo
dục, khoa học xã hội,… lOMoARcPSD| 36067889 Khác nhau:
Phương pháp nghiên cứu tổng
Để đại diện cho tổng thể và giảm thể thiểu thời gian, chi phí
Mục đích Để tìm hiểu toàn bộ tổng thể và
đưa ra kết luận chính xác hơn
Sử dụng các phương pháp toán
học (đặc biệt là lý thuyết xác
Cách thức Các tham số đặc trưng của tổng
suất), người ta tiến hành suy rộng
thể có thể xác định được một
kết quả nghiên cứu trên mẫu cho cách trực tiếp. toàn bộ tổng thể.
Xác định được số lượng phần tử cần phải nghiên cứu.
Số phần tử Chưa thể xác định được toàn bộ
phần tử của tổng thể.
Không bị ảnh hưởng nếu trường
hợp bị phá hủy thì ta có thể thay
Chất Nếu các phần tử của tập hợp bị lượng
thế bằng phần tử khác.
phá huỷ trong quá trình nghiên phần tử
cứu thì phương pháp nghiên cứu
toàn bộ trở thành vô nghĩa.
- Khi tổng thể quá lớn, khó
nắmbắt được hết các phần tử Trường
- Khi tổng thể có kích thước nhỏ của tổng thể hợp sử
hoặc có thể tiếp cận được dụng
-Khi không có đủ thời gian và
- Khi mục tiêu của nghiên cứu
kinh phí để nghiên cứu tổng thể
làtìm hiểu đặc điểm của toàn bộ tổng thể
- Trong một số trường hợp
nếudung phương pháp nghiên
- Khi độ chính xác của kết quả
cứu tổng thể sẽ dẫn đến phá hủy làyếu tố quan trọng tổng thể
- Khi chi phí và thời gian
- Hạn chế được sự trùng lặp và Đ chínhộ
- Nếếu quy mô c a t ng th quáủ ổ
ể Phương pháp nghiên cứu mẫu lOMoARcPSD| 36067889
xác l n có th x y ra trớ ể ả ường h pợ sai số trong quá trình thu thập trùng ho c
b sót các phầần t ,ặ ỏ ử thông tin.
sai sót trong quá trình thu th pậ - Vẫn đảm bảo được độ chính thông
tn ban đầầu, h n chếế đạ ộ xác của kết quả, thu nhập được chính xác
c a kếết qu phần tch.ủ ả nhiều chỉ tiêu thống kê - Có thể thu thập được
các dữ -Vi c tếến hành mầết nhiếầu th iệ ờ liệu phức tạp.
gian nến có th không đ m b oể ả ả - Đảm bảo được tính kịp thời của
được tnh k p th i c a sôế li uị ờ ủ ệ số liệu thống kê. thôếng kế.
-Không thể có mẫu đại diện cho
tổng thể ở mọi khía cạnh.Do đó
luôn có sai số sinh ra từ việc chọn mẫu./ Chi phí,
-Tôến nhiếầu th i gian, chi phí, ờ -Tiết kiệm thời gian, chi phí th i gianờ
nhần l c, phự ương t n.ệ -Có thông tin nhanh hơn -Có th không kh thiể
ả-Chi phí cho công tác tổ chức
-Sai sót khi thu th p,có th phá ậ ể nghiên cứu thấp, vì vậy, phương h y
t p h p.ủ ậ ợ pháp chọn mẫu nghiên cứu tiết
kiệm được cả nhân lực, vật lực và tài chính.
-Trong nghiên cứu chọn mẫu,
khảo sát không nhiều đơn vị
nghiên cứu nên thông thường
chọn mẫu được tiến hành trong
thời gian ngắn. Dữ liệu được xử
lý và phân tích nhanh nên thông
tin thu được từ hoạt động chọn
mẫu có tính thời sự, cập nhật.
Đ đ iộ ạ -Đ m b o đ đ i di n caoả ả ộ ạ ệ , -Chỉ đảm bảo độ đại diện cao khi di nệ
-Sai sôế đ i di n v i t ng th =0 ạ ệ ớ ổ ể mẫu được lựa chọn một cách
ngẫu nhiên và đại diện cho tổng thể -Có sai số nhất định lOMoARcPSD| 36067889
Kh năngả -Được áp d ng trong các nghiến ụ -Được áp dụng trong các nghiên áp d
ngụ c u có quy mô nh , đôếi tứ ỏ ượng cứu từ nhỏ đến lớn, đối tượng nghiến c u
đ n gi n.ứ ơ ả nghiên cứu phức tạp hơn.
-Có nh ng trữường h p ta không ợ th x ể á c đnh đ c toàn b N phầần t ca tng th. ể 4.
Phát biểu định lý về luật số lớn và định lý về giới hạn trung tâm. Nêu sự
hiểubiết của bạn về mỗi định lý. Làm bài tập 4.20; 4.21; 4.22
4.1 Phát biểu của luật số lớn:
- Luật số lớn chỉ ra rằng, khi ta chọn ngẫu nhiên các giá trị (mẫu thử) trong
một dãy các giá trị (quần thể), kích thước dãy mẫu thử càng lớn thì các đặc
trưng thống kê (trung bình, phương sai,...) của mẫu thử càng "gần" với các
đặc trưng thống kê của quần thể
- Trong xác suất thống kê, quy luật số lớn chứng minh sự ổn định lâu dài của
một biến ngẫu nhiên. Cho ví dụ về các biến ngẫu nhiên độc lập phân bố đều
nhau với giá trị kì vọng khi số lần quan sát tăng lên.
- Có thể hiểu là: khi số lượng phép thử đủ lớn, tỉ lệ phép thử thành công sẽ
bằng với xác suất xảy ra và càng nhiều số liệu thì kết quả nghiên cứu càng đáng tin cậy
- Ví dụ: Khi muốn ước lượng ra chiều cao trung bình của sinh viên thì thay vì
chọn ra 100 sinh viên thì chọn ra 1000 sinh viên sẽ có kết quả ước lượng có độ tin cậy cao hơn
* Hiểu biết về luật số lớn:
- Vào thế kỉ 16, nhà toán học Gerolama Cardano đã công nhận Quy luật số lớn
nhưng chưa bao giờ chứng minh
- Năm 1713, nhà toán học người Thụy Sĩ Jakob Bernoulli đã chứng minh Quy
luật này trong cuốn sách của mình, Ars Conjectandi. Sau đó quy luật số lớn
đã được tinh chỉnh bởi các nhà toán học nổi tiếng khác
- Luật số lớn của Chebyshev lOMoARcPSD| 36067889
Thì bé tùy ý ta luôn có:
- Luật số lớn của Bernoulli là
tần suất xuất hiện biến cố A trong n phép thử độc lập và p=P(A) thì
với mọi > 0 bé tùy ý ta luôn có:
- Các nhà toán học phân biệt 2 phát biểu khác nhau của luật số lớn, là luật số
lớn yếu và luật số lớn mạnh
+ Luật số lớn yếu còn được gọi là định lý Khintchine.
Xét n biến ngẫu nhiên X_1, X_2,..., X_n độc lập, cùng phân phối với kỳ vọng E(X),
luật số lớn yếu phát biểu rằng, với mọi số thực dương, xác suất để khoảng cách giữa trung bình tích lũy
và kỳ vọng E(X) lớn hơn là tiến về 0 khi n tiến về vô cực. +Luật số lớn mạnh: lOMoARcPSD| 36067889
Xét n biến ngẫu nhiên độc lập cùng phân phối xác suất, khả tích (nghĩa là ). Luật
số lớn mạnh phát biểu rằng trung bình tích lũy Yn hội tụ hầu như
chắc chắn về E(X).
4.2.Phát biểu về định lý giới hạn trung tâm:
- Định lý Giới hạn trung tâm là một lý thuyết thống kê cho rằng kích thước
mẫu đủ lớn từ một tập hợp có phương sai hữu hạn, giá trị trung bình của tất
cả các mẫu sẽ xấp xỉ bằng giá trị trung bình tổng thể.
* Hiểu biết về định lý:
- Với một dãy các biến ngẫu nhiên độc lập và phân phối đồng nhất theo cùng
một phân phối xác suất, khi kích thước mẫu lớn hơn, phân phối của tổng của
các biến ngẫu nhiên này xấp xỉ với phân phối chuẩn (tức là “đường cong
hình chuông”) và có trung bình bằng trung bình của các biến ngẫu nhiên ban
đầu và độ lệch chuẩn bằng độ lệch chuẩn của các biến ngẫu nhiên ban đầu
chia cho căn bậc hai của kích thước mẫu
- Theo định luật giới hạn trung tâm, giá trị trung bình của một mẫu sẽ gần với
giá trị trung bình của tổng thể nói chung, khi kích thước mẫu tăng lên bất
chấp dạng phân phối dữ liệu trong thực tế. Nói cách khác, dữ liệu là chính
xác cho dù phân phối chuẩn hay phân phối khác.
- Theo nguyên tắc chung, kích thước mẫu bằng hoặc lớn hơn 30 được coi là
đủ để tuân theo CLT, có nghĩa là phân phối của các giá trị trung bình mẫu
được phân phối khá chuẩn. Do đó, càng lấy nhiều mẫu, kết quả đồ thị càng
có hình dạng phân phối chuẩn.
- Định luật giới hạn trung tâm thể hiện một hiện tượng trong đó giá trị trung
bình và độ lệch chuẩn của mẫu bằng giá trị trung bình và độ lệch chuẩn của
tổng thể, điều này cực kỳ hữu ích trong việc dự đoán các đặc điểm của tổng thể.
- Định lý giới hạn trung tâm của Liapunov lOMoARcPSD| 36067889 Trong đó:
- Định lý Lindenberg – Lewi
độc lập và cùng phân phối xác suất (iid – independent &
identically distributed) với E(Xi )=m < ; Var ( Xi )= < thì: 4.3. BÀI TẬP:
4.20. Gọi x là số phế phẩm phát hiện được. Số phế phẩm phát hiện được là số lần
thành công trong 250 sản phẩm máy. Vậy x có phân bố nhị thức X B(n.p) với n= 250 , p= 0,02 a, P(X=2) = b, P(X =P(X=0) + P(X=1) + P(X=2) 4.21.
Giả sử X là số người chọn ăn ở đợt 1. Lhi đó 1000 – X là số người chọn ăn đợt 2.
Gọi k là số chỗ ngồi trong nhà ăn. Ta phải chọn k nhỏ nhất để
P{ X < k, 1000 – X P{ 1000 – k < X < k }
0,99 Ta xem X có phân bố chuẩn với μ = 500, σ = vậy ta phải có: Từ đó : lOMoARcPSD| 36067889 Vậy k = 541 4.22.
a, Gọi X là số người trúng tuyển trong số 325 người dự tuyển X B(n.p) với n= 322, p= 0,9
Vì n= 325 > 100 và np= 325.0,9 = 292,5 >5 ,n.(1-p) = 325.0,1 = 32,5 > 5
Có thể xem X ̃ N (μ, ) với μ = n.p và σ = , q = 1-p
Xác suất số người trúng tuyển không vượt quá chỉ tiêu P ( = Ф( b, Gọi n là số
dự thi. X là BNN chỉ số người trúng tuyển trong số n người dự thi
Giả sử n khá lớn và np >5 , npq >5
Xs số người trúng tuyển không vượt quá chỉ tiêu là : P ( = Ф( Suy ra Suy ra: np + 2,3263.- 300 17,8738
Suy ra n= 320. Vậy chọn n= 320 người