Bài Tập Mã Hóa | An toàn bảo mật thông tin

lOMoAR cPSD| 61769897
BÀI TẬP MÔN MÃ HÓA & MẬT MÃ 1. BÀI TẬP
Bài 1. Mã hóa cổ điển. Cho văn bản gốc P = . Giải thích các bước thực hiện
mã hóa P và giải mã sử dụng các thuật toán mã hóa sau :
a) Mã hóa cộng với khóa K = 18 trên trường số nguyên Z26
b) Mã hóa affine với khóa k1= 7, k2 = 11 trên trường số nguyên Z26
c) Mã hóa AutoKey với K = 18 trên trường số nguyên Z26
d) Mã hóa Vigenère với khóa K = attack.
e) Mã hóa Hill Cipher với khóa K tự chọn.
f) Mã hóa Playfair với khóa K tự chọn.
g) Mã hóa Enigma với khóa K = DUT. Giải thích cơ chế mã hóa.
Bài 2. Mã hóa đối xứng hiện đại. Cho văn bản gốc P = . Thực hiện mã hoá P theo :
a) Mã hóa AES với khóa K tự chọn. Giải thích các bước thực hiện theo thuật toán.
b) Mã hóa RC6 với khóa K tự chọn. Giải thích các bước thực hiện theo thuật toán.
Bài 3. Mã hóa hàm băm. Cho văn bản gốc P = . Giải thích các bước thực hiện:
a) Tính giá trị hàm băm MD5. Giải thích các bước theo thuật toán.
b) Tính giá trị hàm băm SHA-1. Giải thích các bước theo thuật toán.
Bài 4. Mã hóa bất đối xứng. Cho văn bản gốc P = . Thực hiện mã hoá và giải mã
từng ký tự trong P theo :
a) Mã hóa RSA với (p = 7, q = 11) hoặc (p = 11, q = 17). Sử dụng lược đồ chữ
ký RSA để ký lên văn bản P.
b) Mã hóa ElGamal với p = 31, e1 = 11 và giá trị r tự chọn. Sử dụng lược đồ chữ
ký ElGamal để ký lên văn bản P.
c) Mã hóa Rabin với (p = 7, q = 11). Sử dụng lược đồ chữ ký Rabin để ký lên văn bản P.
Bài 5. Mã hóa Elliptic: Cho E23(1, 0) lOMoAR cPSD| 61769897
a) Tìm tất cả các điểm P của đường cong.
b) Chọn một điểm P. Tính các điểm 2P, 3P, 4P, 5P, …
c) Chọn một cặp điểm P, Q khác nhau: Tính R = P + Q.
b) Cho văn bản gốc M = với một số ngẫu nhiên k = 3. Hãy xác định bản mã hóa C tương ứng.
c) Thực hiện giải mã C để nhận được văn bản gốc M ban đầu.
d) Sử dụng lược đồ chữ ký ECDSA để ký lên văn bản M.
2. HƯỚNG DẪN GIẢI CÁC BÀI TẬP Các ký hiệu
P (Plan text): văn bản thuần chưa mã hóa
K (Key): khóa dùng để mã hóa
C (Cipher text): văn bản đã được mã hóa E (Encryption): hàm mã hóa
D (Decryption): hàm giải mã
2.1 Bài 1. Mã hóa cổ điển
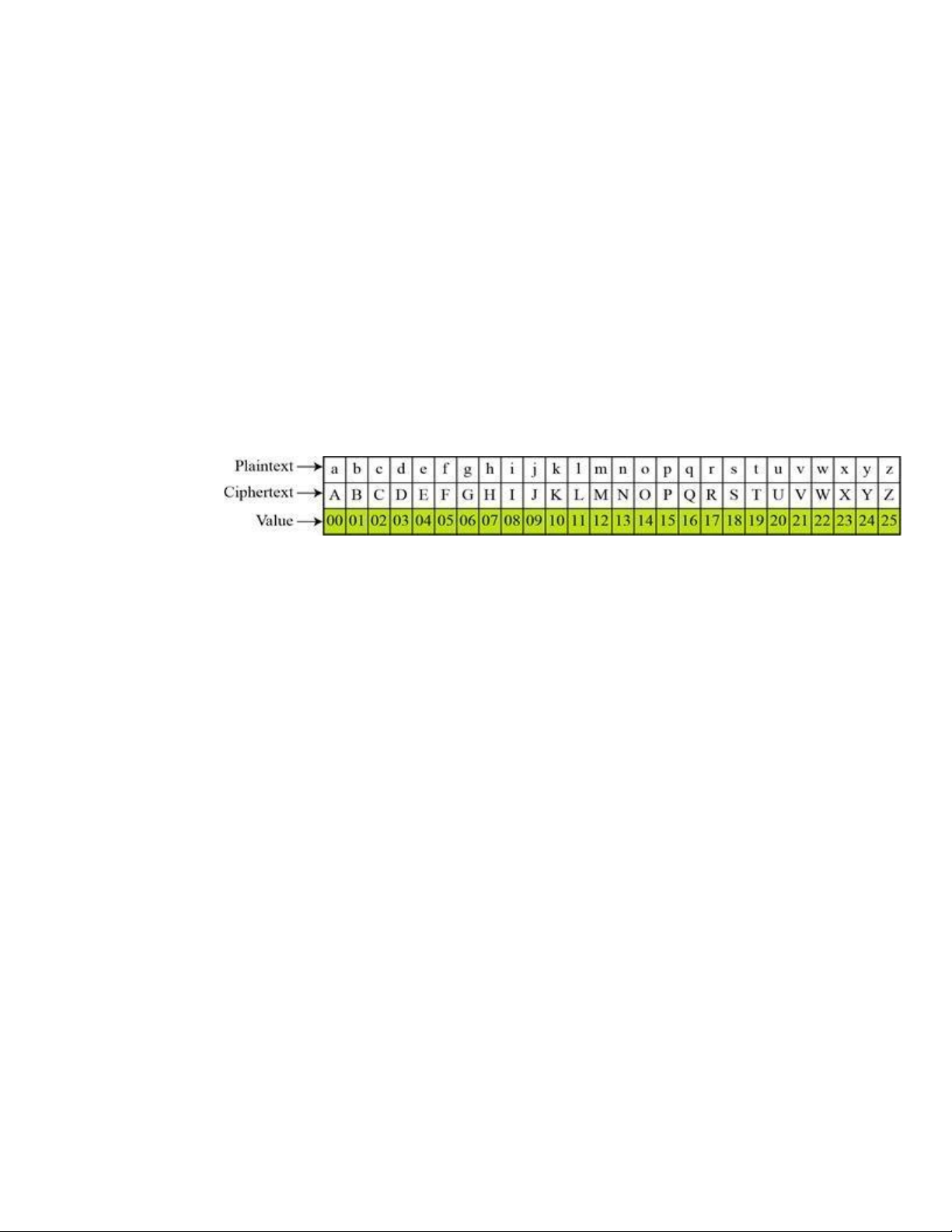
Cho P = trangiahongquan. Giải thích các bước thực hiện mã hóa P và giải mã trên trường số nguyên Z26
2.1.1 Thực hiện mã hóa cộng với K=18
Bước 1: Chuyển tất cả các chữ cái sang giá trị nguyên tương ứng. P t r a n g i a h o n g q u a n 19 17 0 13 6 8 0 7 14 13 6 16 20 0 13
Bước 2: Thực hiện cộng các giá trị nguyên này với 18 rồi chia cho 26 lấy phần dư, ghi vào bảng. 1 14 13 6 16 20 0 13 A 19 17 0 3 6 8 0 7 lOMoAR cPSD| 61769897
18 18 18 1 18 18 18 18 18 18 18 18 18 18 18 B 8 3 32 31 24 34 38 18 31 37 35 18 1 24 26 18 25 A+B 1 1 2 1 2 (A + B) mod 1 9 8 5 4
0 8 5 6 5 24 8 12 18 5 26
Bước 3: Chuyển tất cả các giá trị nguyên này về lại chữ cái.
11 9 18 5 24 0 18 25 6
5 24 8 12 18 5 L J S F Y A S Z G F Y I M S F
- Tổng hợp lại ta có bảng sau: P t r a n g i a h o n g q u a n 19 17 0 13 6 8 0 7 14 13 6 16 20 0 13 K
18 18 18 18 18 18 18 18 18 18 18 18 18 18 18 C 11
9 18 5 24 0 18 25 6 5 24 8 12 18 5 L J S F Y A S Z G F Y I M S F
2.1.2 Mã hóa affine với khóa k1= 7, k2 = 11
Bước 1: Chuyển tất cả các chữ cái sang giá trị nguyên tương ứng. P t r a n g i a h o n g q u a n 19 17 0 13 6 8 0 7 14 13 6 16 20 0 13 lOMoAR cPSD| 61769897
Bước 2: Thực hiện nhân giá trị này với 7 rồi đem kết quả này cộng với 11, kết quả sau
cùng đem chia cho 26 lấy phần dư ghi vào bảng. A 19 17 0 13 6 8 0
7 14 13 6 16 20 0 13 7 7 7 7 7 7 7 7 7 7 7
7 7 7 7 k1 1 1 1
1 11 11 11 11 11 11 11 11 11 1 11 11 1 1 1 k2 11 4 98 91 42 112 140 0 91 A*k1 133 9 0 56 91 2 0 49 14 10 5 109 102 53 123 151 11 102 A*k1 + k2 144 0 11 67 2 3 11 60 (A*k1 + k2) mod 26 14 10 11 24 1 15 11 8 5 24 1 19 20 11 24
Bước 3: Chuyển tất cả các giá trị nguyên này về lại chữ cái. P t r a n g i a h o n g q u a n 19 17 0 13 6 8 0 7 14 13 6 16 20 0 13 k1 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 k2 11 11 11 11 11 11 11 11 11 11
11 11 11 11 11 C 14 10 11 24 1 15 11 8 5 24 1 19 20 11 24 O K L Y B P L I F Y B T U L Y
2.1.3 Mã hóa Vigenère với khóa K = attack
Tra cứu bảng mã hóa Vigenère ta có: lOMoAR cPSD| 61769897 P T R A N G I A H O N G Q U A N K A T T A C K A T T A C K A T T C T K T N I S A A H N I A U T G
2.1.4 Mã hóa Hill Cipher với khóa K tự chọn T N A N U 19 13 0 13 20 )( )( )( )( ) ( )( )( )( )( ) P=R G H G A = 17 6 7 6 0 A I O Q N 0 8 14 16 13 Thực hiện tính toán 576 19 214 7 ( )( ) ) ) 654 17 = (199 mod 26 = (17 584 0 231 23 576 13 155 25 ( )( ) ) ) 654 6 = (140 mod 26 = (10 584 8 145 15 lOMoAR cPSD| 61769897 576 0 133 3 ( )( ) ) ) 654 7 = ( 91 mod 26 = (13 584 14 112 8 576 13 203 21 ( )( ) ) ) 654 6 = (172 mod 26 = (16 584 16 177 21 576 20 178 22 ( )( ) ) ) 654 0 = (172 mod 26 = (16 584 13 152 22 7 25 3 21 22 H Z D V W C
= )( )( )( )( ) ( )( )( )( )( ) 17 10 13 16 16 = R K N Q Q 23 15 8 21 22 X P I V W
P = TRANGIAHONGQUAN-> C = HRXZKPDNIVQVWQW
2.1.5 Mã hóa Playfair với khóa k tự chọn Quy
tắc thay thế của mã hóa Playfair:
- Mã hóa từng cặp hai ký tự liên tiếp nhau
- Nếu hai ký tự này giống nhau thì thêm một ký tự “X” vào giữa - Nếu dư một ký
tự thì thêm ký tự “Q“vào cuối. lOMoAR cPSD| 61769897
- Nếu hai ký tự nằm cùng dòng thì được thay thế bằng hai ký tự tương ứng bên
phải. Ký tự ở cột cuối cùng được thay thế bằng ký tự ở cột đầu tiên.
- Nếu hai ký tự nằm cùng cột thì được thay thế bằng hai ký tự tương ứng ở bên
dưới. Ký tự ở hàng dưới cùng sẽ được thay thế bằng ký tự ở hàng đầu tiên.
- Nếu hai ký tự nằm hai góc của một hình chữ nhật thì được thay thế bằng hai ký tự
nằm ở hai góc còn lại. Các bước thực hiện:
Bước 1: Tách văn bản thành từng cặp ký tự: P = TRANGIAHONGQUAN=> P = TR AN GI AH ON GQ UA NX
Bước 2: Tạo bảng mã hóa: P L A Y F I R B C D E G H K M N O Q S T U V W X Z
Bước 3: Áp dụng quy tắc mã hóa Playfair cho từng cặp - TR - OD - AN - PQ - GI - ER - AH - BQ - ON - NT - GQ - HO - UA - WP - NX - SU P = TR AN GI AH ON GQ UA NX C = OD PQ ER BQ NT HO WP SU
2.1.6 Mã hóa Autokey với K = 18 -
Bước 1: Chọn từ khóa: key. lOMoAR cPSD| 61769897
- Bước 2: Thực hiện ghép từ khóa vào văn bản thuần để có được khóa K (có độ dài
bằng với độ dài văn bản thuần): keytrangiahongq
- Bước 3: Thực hiện mã hóa theo thuật toán mã hóa Autokey với khóa K ở trên P T R A N G I A H O N G Q U A N K k e y t r a n g i a h o n g q C J N C U P I N B G G G C H U X
2.2 Bài 2. Mã hóa đối xứng hiện đại
Cho văn bản gốc P = hongquan
2.2.1 Mã hóa bằng thuật toán AES Plantext (input) Key (input) Ciphertext (output)
48 4F 4B 49 D2 F6 0C F3 89 C9 A2 2A 4 4 D 54 6E 41 D 7C CE BB 49 BB 0B 3B A 00 00 00 00 8E AC EA F3 67 7F D 6D A 00 00 00 00 F8 6C 8B D 1F 6F D8 FE
Chi tiết các bước mã hóa AES: SubBytes ShiftRows MixColumn s AddRoundKey Key Schedule 9A B9 47 BA D2 F6 0C F3 7C 23 28 8F F6 6E CE BB 0 8E AC EA F3 8E AC EA F3 lOMoAR cPSD| 61769897 F8 6C 8B AD F8 6C 8B AD B8 56 A0 F4 B8 56 A0 F4 25 75 D4 35 1C BA 17 05 39 CF C3 30 D7 2D 6A 26 34 73 42 34 73 42 26 E6 5F B4 F9 8E 47 63 1F D1 1 19 91 87 0D 87 0D 19 91 3D FC 20 AC 26 4B 7D 02 1B B7 5D AE 41 50 3D 95 95 41 50 3D 51 06 00 CA A4 9F 12 75 F5 99 12 BF 9C F4 F0 6B 9C F4 F0 6B F1 E6 2C 20 C8 10 19 25 39 F6 35 05 A0 6D 3B 8D 99 19 A0 99 19 8D 32 16 72 B5 8E 4E 87 98 49 23 2 F7 B3 FF 77 FF 77 F7 B3 5C D8 D3 DB 4F 7C 2A 8C 13 A4 F9 57 49 DB C9 9D 9D 49 DB C9 F8 FB F1 0A 09 93 8B CF F1 68 7A C5 E8 CA D4 3F E8 CA D4 3F 8F D7 9A 37 94 3A 42 EA 1B ED D8 DD D5 D5 C1 B8 AD DC 19 E2 2F 19 E2 2F 64 B8 83 FC CC 44 0D 2E 3 84 10 E5 64 E5 64 84 10 A5 E3 97 8D 10 F2 7F 32 B5 11 E8 BF 01 DC 3D 8A 8A 01 DC 3D D0 C1 6F FE 4A 33 E7 B3 9A F2 88 4D 22 80 2C 87 22 80 2C 87 30 33 F5 BC 12 FC E2 76 22 CF 17 CA 6C B0 B0 4B 6C A5 9B 8D D4 9D 4B 95 95 59 4B 35 06 F8 90 B3 4 CA 89 D2 23 D2 23 CA 89 9A EC 68 45 CC AB C7 55 56 47 AF 10 D6 C3 94 6D 6D D6 C3 94 DE 44 B6 44 85 ED 97 28 5B A9 21 6C C9 B0 98 38 C9 B0 98 38 DA A1 F6 7D 85 31 71 30 5F 90 87 4D 5D AC 0C 5D 96 6F 41 96 6F 41 9B E6 92 85 68 81 1E 8E 13 A0 5 4B 62 C6 FC C6 FC 4B 62 94 9E B0 22 92 DF 5E DC 06 41 EE FE 97 55 88 34 34 97 55 88 78 6D 13 7C 57 EB B4 B7 2F 86 A7 CB 97 C7 A3 04 97 C7 A3 04 0B 5C E2 B9 94 53 6A 7C 9F 0F 88 C5 FE A5 97 45 0C 45 0C FE 97 5C 15 7C 05 F9 3E 44 9D 2B 38 98 6 4F 9E 58 86 58 86 4F 9E 82 31 E3 38 9B 69 55 70 19 58 B6 48 5B E9 8D A9 A9 5B E9 8D F6 6E 86 04 3A 24 6B 22 CC 4A ED 26 22 ED 02 10 22 ED 02 10 E6 3D C4 16 7F AB DA CD 99 96 1E DB 1B B2 D1 99 B2 5E 1B 5E 99 A8 B4 56 26 74 50 2A F7 DC E4 7C 7 14 F9 FC 51 FC 51 14 F9 DD CF 2E E1 33 79 2E A9 EE B6 00 48 80 36 7F 93 93 80 36 7F 15 7D 20 AE 7F 5D ED 45 6A 20 CD EB D2 62 57 BD D2 62 57 BD 4D 30 15 80 44 AF 94 DA 09 9F 81 5A 8 F7 92 53 E5 92 53 E5 F7 D0 78 94 DC 75 01 09 3D A5 79 9D E1 C3 B6 31 D3 31 D3 C3 B6 90 E1 FB C2 97 50 4A 3B 07 B1 B1 F9 9 D2 4C 55 6E 6E D2 4C 55 12 99 47 37 C1 6A 79 E2 D3 F3 3E D5 lOMoAR cPSD| 61769897 1B 79 7C 22 57 1B 79 22 57 FC 6B 3E A7 ED F7 16 1E 53 59 EA 75 F4 D8 AE 9D 0C 9D 01 27 7C 01 27 1A 35 26 7B 35 3C 45 39 88 53 D6 E2 D6 E2 88 53 63 2F 08 AD 67 9A 0C 50 04 B5 04 FD 78 02 B6 98 98 78 02 B6 AC 98 CD 40 C1 06 6D 35 6D 9E A0 75 47 72 ED CB 47 72 ED CB 89 C9 BB A2 2A CE BB 4F E1 3B F7 21 96 FE 21 96 FE F7 49 0B 68 2D F5 CC 10 85 B8 FE 53 FE 53 85 B8 67 7F AD 6D 99 2C 28 D5 78 6F 3C 96 96 78 6F 3C 1F 6F D8 FE 89 17 B7 C2
2.2.2 Mã hóa bằng thuật toán RC6
Input: Plaintext được lưu trong 4 thanh ghi w-bit A, B, C & D r là số vòng
khóa vòng w-bit S[0, ... , 2r + 3]
Output: Ciphertext lưu trong A, B, C, D ' 'Hàm mã hóa' ' B = B + S[0] D = D + S[1] for i = 1 to r do {
t = (B*(2B + 1)) <<< lg w
u = (D*(2D + 1)) <<< lg w
A = ((A t) <<< u) + S[2i]
C = ((C u) <<< t) + S[2i + 1] (A, B, C, D) = (B, C, D, A) } A = A + S[2r + 2] C = C + S[2r + 3] Kết quả: Plantext: trangiahongquan
Secret key: 2b7e151628aed2a6abf71589
Ciphertext: PTtVEQvKJFj8IgdgVED2HN== lOMoAR cPSD| 61769897
2.3 Bài 3 – Mã hóa hàm băm
Cho văn bản gốc P = TRANGIAHONGQUAN
2.3.1 Tính giá trị MD5 64-ELEMENT TABLE 'T' :
T[0]=3614090360 T[1]=3905402710 T[2]=606105819 T[3]=3250441966
T[4]=4118548399 T[5]=1200080426 T[6]=2821735955 T[7]=4249261313
T[8]=1770035416 T[9]=2336552879 T[10]=4294925233 T[11]=2304563134
T[12]=1804603682 T[13]=4254626195 T[14]=2792965006 T[15]=1236535329 …
T[44]=3654602809 T[45]=3873151461 T[46]=530742520 T[47]=3299628645
T[48]=4096336452 T[49]=1126891415 T[50]=2878612391 T[51]=4237533241
T[52]=1700485571 T[53]=2399980690 T[54]=4293915773 T[55]=2240044497
T[56]=1873313359 T[57]=4264355552 T[58]=2734768916 T[59]=1309151649
T[60]=4149444226 T[61]=3174756917 T[62]=718787259 T[63]=3951481745 OPERATION TABLE 's':
s[0]=7 s[1]=1 s[2]=1 s[3]=2 s[4]=7 s[5]=1 s[6]=1 s[7]=2 s[8]=7 s[9]=1 2 7 2 2 7 2 2
s[10]= s[11]= s[12]= s[13]= s[14]= s[15]= s[16]= s[17]= s[18]= s[19]= 17 22 7 12 17 22 5 9 14 20
s[20]= s[21]= s[22]= s[23]= s[24]= s[25]= s[26]= s[27]= s[28]= s[29]= 5 9 14 20 5 9 14 20 5 9
s[30]= s[31]= s[32]= s[33]= s[34]= s[35]= s[36]= s[37]= s[38]= s[39]= 14 20 4 11 16 23 4 11 16 23
s[40]= s[41]= s[42]= s[43]= s[44]= s[45]= s[46]= s[47]= s[48]= s[49]= 4 11 16 23 4 11 16 23 6 10
s[50]= s[51]= s[52]= s[53]= s[54]= s[55]= s[56]= s[57]= s[58]= s[59]= 15 21 6 10 15 21 6 10 15 21 s[60]= s[61]= s[62]= s[63]= lOMoAR cPSD| 61769897 6 10 15 21 MDBUFFER:
words A=1732584193, B=4023233417, C=2562383102, D=271733878
Thông điệp được sau khi thêm= 'trangiahongquan?' Chiều dài=56 Tổng số khối=1 Block 0 contains: [0]1768648552 [1]1835103341 [2]128 … [12]0 [13]0 [14]64 [15]0
Chiều dài sau khi thêm =512 bits [nên là bội của 512] OPERATIONS: [Block=0]
[i = 0] A=1524079401, B=4023233417, C=2562383102, D=271733878
[i = 1] A=1524079401, B=4023233417, C=2562383102, D=4023983677
[i = 2] A=1524079401, B=4023233417, C=64826783, D=4023983677
[i = 3] A=1524079401, B=820021093, C=64826783, D=4023983677 …
[i = 59] A=1954472196, B=2426829349, C=717852174, D=1824007650
[i = 60] A=3504040046, B=2426829349, C=717852174, D=1824007650
[i = 61] A=3504040046, B=2426829349, C=717852174, D=21704235
[i = 62] A=3504040046, B=2426829349, C=364525756, D=21704235
[i = 63] A=3504040046, B=4283538711, C=364525756, D=21704235 Block=0 Processed: A=941656943 B=4011804832 C=2926908858 lOMoAR cPSD| 61769897 D=293438113 Kết quả: A_Hex=38208b6f B_Hex=ef1f48a0 C_Hex=ae7515ba D_Hex=117d82a1 Kết quả cuối cùng:
MD5("trangiahongquan") = 6f8b2038a0481fefba1575aea1827d11
2.3.2 Tính giá trị SHA-1 Giá trị ban đầu: H0=1732584193, H1=4023233417, H2=2562383102, H3=271733878, H5=3285377520
Thông điệp được sau khi thêm= 'hokimtam?' Chiều dài=56 Tổng số khối=1 Block 0 contains: [0]1752132457 [1]1836343661 [2]2147483648 … [66]2972891804 [67]3152281212 [68]3856775635 [69]2330363404 [70]2916858365 [71]3490041757 [72]2396814212 [73]2514144236 [74]316457681 [75]646975230 [76]2875846729 lOMoAR cPSD| 61769897 [77]3323451092 [78]4265846432 [79]3641639364
Chiều dài sau khi thêm =512 bits [nên là bội của 512] OPERATIONS: [Block=0]
[i = 0] A=136578076, B=1732584193, C=2079550178, D=2562383102, E=271733878
[i = 1] A=3634737659, B=136578076, C=1506887872, D=2079550178, E=2562383102
[i = 2] A=63373556, B=3634737659, C=34144519, D=1506887872, E=2079550178
[i = 3] A=1353141246, B=63373556, C=4129909886, D=34144519, E=1506887872
[i = 4] A=3410379674, B=1353141246, C=15843389, D=4129909886, E=34144519
[i = 5] A=1811763765, B=3410379674, C=2485768959, D=15843389, E=4129909886 …
[i = 73] A=552463355, B=3065140820, C=1096314285, D=2875827526, E=370522835
[i = 74] A=1838570909, B=552463355, C=766285205, D=1096314285, E=2875827526
[i = 75] A=2604744074, B=1838570909, C=3359341310, D=766285205, E=1096314285
[i = 76] A=2806940693, B=2604744074, C=1533384551, D=3359341310, E=766285205
[i = 77] A=2954330374, B=2806940693, C=2798669666, D=1533384551, E=3359341310
[i = 78] A=4006436954, B=2954330374, C=1775476997, D=2798669666, E=1533384551
[i = 79] A=1469568447, B=4006436954, C=2886066241, D=1775476997, E=2798669666 Block=0 Processed: H0=3202152640, H1=3734703075, H2=1153482047, H3=2047210875, H4=1789079890. Giá trị cuối cùng: H0_Hex=bedcf8c0 H1_Hex=de9b0be3 H2_Hex=44c0bd3f H3_Hex=7a05f57b H4_Hex=6aa33152
Kết quả: SHA1("hokimtam") = bedcf8c0de9b0be344c0bd3f7a05f57b6aa33152
2.4 Bài 4. Mã hóa bất đối xứng Cho văn bản gốc P = tam lOMoAR cPSD| 61769897
2.4.1 Mã hóa RSA với p = 7, q = 11
1) Tính n: n = p*q = 7*11 = 77
2) Tính Φ: Φ(n) = (p-1)(q-1) = (7-1)(11-1) = 60
3) Chọn e sao cho 1 < e < Φ(n), e và Φ(n) là hai số nguyên tố cùng nhau. Nghĩa là có UCLN là 1.
4) Chọn e = 7 => Khóa công khai: (7, 77) (*) Tìm d?
Ta có: d*e mod Φ(n) = 1 <=> d*e = k* Φ(n) +1 <=> d*7 = k*60 +1
Chọn k = 5 => d= 43 => Khóa bí mật: (43,60) (**) Khóa công khai (e, n) Khóa bí mật (d, Φ(n)) - Mã hóa:
+ Mã hóa ký tự T = 19: C = Me mod n = 197 mod 77 = 19
+ Mã hóa ký tự A = 0: C = Me mod n = 07 mod 77 = 0 +
Mã hóa ký tự M = 12: C = Me mod n = 127 mod 77 = 48 - Giải mã:
+ Giải mã ký tự 19: M = Cd mod n = 1943 mod 60 = 19 (≡ T : giải mã đúng)
+ Giải mã ký tự 0: M = Cd mod n = 07 mod 60 = 0 (≡ A : giải mã đúng)
+ Giải mã ký tự 48: M = Cd mod n = 487 mod 60 = 12 (≡ M : giải mã đúng)
2.4.2 Mã hóa ElGamal với p = 31, a = 11, x = 6 và k = 22
Ta có: y = xa mod p = 611 mod 31= 26
a. Mã hóa: C1 = xk mod p = 622 mod 31 = 25 + Mã hóa ký tự T = 19: C2(T=19) = (T*yk) mod p
= ((T mod p)( yk mod p)) mod p
= ((19 mod 31)( 2622 mod 31)) mod 31 = (19*5) mod 31 = 2 => ET(C1,C2) = (25,2) + Mã hóa ký tự A = 0: C2(A=0) = (A*yk) mod p lOMoAR cPSD| 61769897
= ((A mod p)( yk mod p)) mod p
= ((0 mod 31)( 2622 mod 31)) mod 31 = (0.5) mod 31 = 0 => EA(C1,C2) = (25,0) + Mã hóa ký tự M = 12: C2(M=12) = (M*yk) mod p
= ((M mod p)( yk mod p)) mod p
= ((12 mod 31)( 2622 mod 31)) mod 31 = (12.5) mod 31 = 29 => EA(C1,C2) = (25,29)
b. Giải mã: + Giải mã ký tự (25,2): (C a 2*(C1 )-1) mod p = (2*(2511)-1) mod 31
= ((2 mod 31)( (2511)-1 mod 31)) mod 31
= (2.(2531-11-1 mod 31)) mod 31 = (2.(2519 mod 31)) mod 31 = (2.25) mod 31
= 19 (≡ T : giải mã đúng) + Giải mã ký tự (25,0): (C a 2*(C1 )-1) mod p = (0*(2511)-1) mod 31
= ((0 mod 31)( (2511)-1 mod 31)) mod 31
= (0.(2531-11-1 mod 31)) mod 31 = (0.(2519 mod 31)) mod 31 = (0.25) mod 31 lOMoAR cPSD| 61769897
= 0 (≡ A : giải mã đúng)
+ Giải mã ký tự (25,29): (C a 2*(C1 )-1) mod p = (29*(2511)-1) mod 31
= ((29 mod 31)( (2511)-1 mod 31)) mod 31
= (29.(2531-11-1 mod 31)) mod 31 = (29.(2519 mod 31)) mod 31 = (29.25) mod 31 = (29.25) mod 31
= 12 (≡ M : giải mã đúng)
2.5 Bài 5. Mã hóa Elliptic Cho E71(4, -6).
P = 71, a = 4, b= -6, G= (2,9), n= 73, h = 1 d = 7
Chọn khóa riêng từ người gửi k = 1 suy ra: kG = (2,9)
Khóa riêng của người nhận d =7, người nhận tính khóa công khai: dG = 7G R = 7G: G(x, y) = (2,9) - Tính Q(x2, y2) = 2G : λ = mod p =
mod p = 64 x2 = λ2 – 2x mod p =
642 - 2*2 mod 71 = 45 y2 = λ(x – x2) – y mod p = 64(2- 45) -9 mod 71 = 8 - Tính T(x4, y4) = 2Q = 4G: λ = mod p = mod p = 56
x4 = = λ2 – 2x2 mod p = 562 - 2*45 mod 71 = 64 y4 =
λ(x2 – x4) – y2 mod p = 56(45- 64) -8 mod 71 = 64
- Tính S(x3,y3) = 3G = G(2,9) + Q(45,8) λ = mod p = mod 71 = 33
x3 = = λ2 – x2 – x mod p = 332 - 45-2 mod 71 = 48 lOMoAR cPSD| 61769897
y3 = λ(x2 – x4) – y2 mod p = 33(45- 48) -8 mod 71 = 35
- Tính R(x7, y7) = 7G = T(64,64) + S(48,35) λ = mod p = mod 71 = 24
x7 = = λ2 – x3 - x4 mod p = 242 - 48-64 mod 71 = 38 y7
= λ(x3 – x7) – y3 mod p = 24(48- 38) - 35 mod 71 = 63 Suy ra dG = (38,63) Mã hóa M(16, 6)
M + k* dG = (16,6) + 1 * 7 *(2,9) = (16,6) + (38,63) λ = mod p =
mod p = 57 * 22-1 mod 71 = 57 * 42 mod 71
= 51 x = λ2 – xM - xR mod p = 512 - 16-38 mod 71 =
62 y = λ(xR – x) – yM mod p = 51(38- 62) - 63 mod 71 = 62
Người gửi sẽ gửi bộ [kG, M+kdG] = [(2,9), (62,62)] Giải mã:
M = (M + kdG) – d*kG = (M + 7G) -7G = (62,62) – (38,63) = (62, 62) + (38, -63) Với λ = 20, x = 16, y = 6 M = (16, 6) (Đúng)
----------------------------------------------------------
@Bộ môn Mạng & Truyền thông
KHOA CÔNG NGHỆ THÔNG TIN, TRƯỜNG ĐẠI HỌC BÁCH KHOA – ĐẠI HỌC ĐÀ NẴNG