Bài tập ma trận đại số tuyến tính | Đại học Sư phạm Hà Nội

Bài tập ma trận đại số tuyến tính | Đại học Sư phạm Hà Nội với những kiến thức và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học vào thực tiễn cuộc sống.

7 4 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Nhập môn lý thuyết ma trận

Trường: Đại học Sư Phạm Hà Nội

Thông tin:

19 trang 2 tháng trước

Tác giả:

Profile Kim Oanh
BÀI T I S TUY N TÍNH ẬP ĐẠ Ố Ế
1. MA TRẬN.
1.1. Cho
A
là ma tr n vuông c p n th a mãn ậ ấ ỏ
2
n
A A I
. Ch ng minh r ngứ ằ
A
có ma trận
nghịch đả ịch đảo và tìm ma trận ngh o của
A
.
1.2. Cho
,M N
là các ma tr n vuông c p 3 th a mãn ậ ấ ỏ
5 6 2
6 7 2
6 6 1
MN
a. Tính
2
( )MN
.
b. Chứng minh
kh ngh ch. Tìm ma tr n ngh o cả ị ậ ịch đả ủa
NM
.
1.3. Cho ma trA là ậ ấ ỏn c p n th a mãn
2
A A
. Ch ng minh r ng ma tr n ứ ằ ậ
2B A I
có ma
trận ngh o. ịch đả
1.4. Cho ma trận
(
)
a. Chứ ằ ếng minh r ng n u thì
b. Tìm sao cho t ồn tại
để
(
)
1.5. Tính
a.
1 0 1
0 1 0
0 0 1
n
b.
2 1 0
0 1 0
0 0 2
n
1.6. Tính lũy thừa bậc n của
cosx sinx
sinx cosx
A
.
1.7. Cho ma trận
2017 1 2017
2016 2 2017
2016 1 2016
A
. Xác định các ph n t n ng chéo chính ầ ử ằm trên đườ
của ma trận
2 2017
S I A A A
.
1.8. Cho là ma tr ận vuông cấp
(
)
Tính , v là s
ới ố nguyên dương.
1.9. Cho
a mãn thỏ
. Ch ng minh r ng . ứ ằ
1.10. Cho
thỏa mãn Chứng minh r ng t n t i ma tr n ằ ồ ạ ậ
khác ma tr n 0 th a mãn ậ ỏ
1.11. Cho ma tr n vuông , p n. V t c a ma tr n là t ng t t c các ph n t ng ậ A B cấ ế ủ ậ A ổ ấ ả ầ ử trên đườ
chéo chính c kí hiủa A, ệu
Tr A
. ng minh rChứ ằng:
a.
Tr A B Tr A Tr B
.
b.
,Tr kA kTr A k
.
c.
Tr AB Tr BA
1.12. Chứng minh r ng không t n t i các ma tr n ằ ồ ạ ậ
, , ,A B C D
vuông c p n sao cho ấ
AC BD I
và
0CA BD
, là ma tr , 0 là ma tr n không. I ận đơn vị ậ
1.13. (Đẳ ứng th c Wagner)
a. Chứ ằ ậng minh r ng với mọi ma tr n
, ,A B C
vuông c p 2 ta luôn có ấ
2 2
0AB BA C C AB BA
b. Chứng minh rằng v i m i ma trớ ọ ận
, ,A B C
vuông c p 2 ta luôn có ấ
2016 2016
0AB BA C C AB BA
1.14. Tùy theo giá tr cị ủa
m
, hãy tìm h ng c a ma tr n ạ ủ ậ
1 2 1 1 1
1 1 1 1
1 0 1 1
1 2 2 1 1
m
A
m
1.15. Tìm
m
để ạ ủ ậ ỏ ấ h ng c a ma tr n sau nh nh t
3 1 4 1
2 3 1
3 1 1 0
3 3 7 2
m
A
1.16. Cho ma tr n vuông c p ậ ấ n:
1 0 ... 0 0
0 1 ... 0 0
... ... ... ... ... ...
0 0 ... ... 1
0 0 ... 0 1
m
m
A
m
m
. Tìm
m
để ạ ủ ậ h ng c a ma tr n A
nhỏ hơn n.
1.17. Chứng minh r ng m i ma tr n h u có th c thành t ng c a r ma ằ ọ ậ ạng r đề ể phân tích đượ ổ ủ
trậ ạ ằn có h ng b ng 1.
1.18. Giả ử ấ ỏ s A B, là các ma trận vuông c p n th a mãn
2016 2017
, 0, 0AB BA A B
.
a. Chứ ằ ồ ạ ố ựng minh r ng t n t i s t nhiên k để
0.
k
A B
b. Chứng minh rằng
r I A B r I A B n
.
2. ĐỊNH TH C Ứ
2.1. Giải phương trình:
2 3
1
1 2 4 8
0
1 3 9 27
1 4 14 64
x x x
2.2. Tính định thức :
a.
1 2 3 4
2 2 2 2
1 2 3 4
3 3 3 3
1 2 3 4
1 1 1 1
x x x x
x x x x
x x x x
b.
a b c d
b a d c
c d a b
d c b a
2.3. Tính
a b c
b c a
c a b
trong đó
, ,a b c
là 3 nghi m c c 3 : ệ ủa phương trình bậ
3
0x px q
.
2.4. Cho là các nghim, n, p, q ệm của phương trình
4
1 0x x
và
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
m
n
A
p
q
Tính
det A
.
2.5. Tính các định thức cấp n sau :
a.
1 2 2 ... 2
2 2 2 ... 2
2 2 3 ... 2
. . . ... .
2 2 2 ... 2
; b.
1 2 3 ...
1 0 3 ...
1 2 0 ...
. . . ... .
1 2 3 ... 0
n
n
n
c.
0 1 1 ... 1
1 0 ...
1 0 ...
. . . ... .
1 ...
x x
x x
x x x
;
d.
...
...
...
. . . ... .
...
a b b b
b a b b
b b a b
b b b a
e.
2
2
2
2
1 0 ... 0
1 ... 0
0 1 ... 0
. . . ... .
0 0 0 ... 1
n
x x
x x x
D
x x
x
,
n
D
là định thức cấp n mà các phần t nử ằm trên đường chéo chính b ng 1+x các phằ
2
,
ần tử
thu bộc hai đường chéo g ng chéo chính bần đườ ằng x và các phần tử còn lại ằng 0.
2.6.
a.
A
là m t ma tr n vuông cộ ậ ấp
n
thỏa mãn
1
A A
. Ch ng minh ứ
det( ) 0A I
hoặc
det( ) 2
n
A I
.
b.
,A B
là hai ma tr n vuông cùng c p ậ ấ
n
thỏa mãn
AB BA B
. Ch ng minh ứ
det( ) 0.B
2.7. Cho
,A B
là các ma tr n th c vuông c p ậ ự ấ
n
thỏa mãn
AB A B
và
2016
0A
. Chứng
minh r ng ằ
det( ) 0.B
2.8. Cho các ma tr n vuông ậ
,A B
thỏa mãn
;
t t
A A I B B I
. Biết
det detA B
. Ch ng ứ
minh r ng ằ
det( ) 0A B
.
2.9. Cho ma trậ ấn vuông c p n
; min ,
ij ij
A a a i j
. Tính
det A
.
2.10. Cho
ij
A a
là m t ma tr n vuông c p ộ ậ ấ
2n
và
11 12 1
0
n
A A A
, trong đó
1j
A
là ph i s cần bù đạ ố ủa
1 j
a
. Ch ng minh r ng t n t i s ứ ằ ồ ạ ố thực
để
11 12 1
21 22 2
1 2
...
...
2016
... ... ... ...
...
n
n
n n nn
a a a
a a a
a a a
3. HỆ N TÍNH PHƯƠNG TRÌNH TUYẾ
3.1. Giả ệi h phương trình:
3 2 1
2 7 3 5 2
3 2 5 7 3
3 2 7 5 8 3
x y z t u
x y z t u
x y z t u
x y z t u
3.2. Giả ệ ấi h n nhphương trình thuầ t sau:
1 2 3
2 3 4
3 4 5
8 9 10
1 9 10
1 2 10
0
0
0
........
0
... 0
... 0
x x x
x x x
x x x
x x x
x x x
x x x
3.3. Giả ệ ậ ệi và bi n lu n các h phương trình sau
a.
1
1
1
mx y z t
x my z t
x y mz t
b.
2 1
2 4 2
7 4 11
4 8 4 16 1
x y z t
x y z t
x y z t m
x y z t m
3.4. Cho là các s
ố nguyên. i h : Giả ệ
{
3.5. Chứ ằ ệ ệng minh r ng h m khác nghiphương trình sau có nghiệ m t : ầm thường
{
trong đó
và n l . ẻ
3.6. Tìm m để hệ sau có nghiệm duy nhất
2
8 7 1
3 2 4
5 1
5 2 2
mx z t m
x my z t m
mz t m
z mt m
3.7. Tùy theo giá tr cị ủa m, hãy biệ ậ ố ệ ủ ện lu n s nghi m c a h :
2
2 3 2 (5 3) 1
( 1) 3 2 ( ) 4
mx y z t m
x y z m t m
m x y z m m t
3.8. Tìm điề ủa m đểu kiện c hai hệ sau có nghiệm chung
2 2 3 3
1
3 3 4 2
x y z t u
x y z t u
x y z t u m
2 2 0
2
x y z mt
x y z t m
3.9. Cho
, , ,a b c d
. Ch ng minh r ng h có nghi m tứ ằ ệ phương trình sau chỉ ệ ầm thường:
2
2
2
2
1 0
1 0
1 0
1 0
a x by cz dt
bx a y dz ct
cx dy a z bt
dx cy bz a t
4. ĐA THỨC
4.1. (Xác định đa thức) Tìm tấ ảt c các đa thức
( )P x
có h s nguyên sao cho ệ ố
( '( )) '( ( )),P P x P P x x
4.2. (Nghiệm của đa thức) Cho
( )P x
là đa thức bậc n có n nghiệm phân biệt
1 2
, ,..., .
n
x x x
Chứ ằng minh r ng:
a.
1 2
1 1 1
... 0.
'( ) '( ) '( )
n
P x P x P x
b.
1 2
1 2
''( )''( ) ''( )
... 0.
'( ) '( ) '( )
n
n
P xP x P x
P x P x P x
4.3. (Đa thức với yếu tố giải tích) Với mỗi số nguyên dương
2n
xét đa thức
1
( ) ... 1.
n n
n
P x nx x x
Hỏi
( )
n
P x
có bao nhiêu nghi m th c: ệ ự
a. Khi
2; 3?n n
b. Khi
4?n
4.4. (Tính chia hết của đa thức) Cho
,m n
là các s ng minh rố nguyên dương. Chứ ằng điều
kiện c ần và đủ để đa thức
1
m n
x x
chia h t cho ế
2
1x x
là
2mn
chia h t cho 3. ế
4.5. Cho đa thức
3 2
( ) 4P x x ax bx c
trong đó
, ,a b c
là các s c. Hãy tìm ố thự
, ,a b c
sao
cho
( ) 1P x
v i m i x tho mãn ớ ọ ả
1.x
HƯỚNG D N GI I BÀI T OLIMPIC Ẫ Ả ẬP ĐS
MA TR N Ậ
1.1 Có
( )
n
A A I I
A có ma tr n ngh o là A I ậ ịch đả –
1.2 a) Có
2
3
( )MN I
b)Ta có
det( ) 1 det 1MN NM
NM có ma tr n ngh o ậ ịch đả
det( ) 0 detM 0MN
và
detN 0
N và M có ma tr n ngh o ậ ịch đả
2 1 1 1
3 3
( ) ( )MN I MNMN I NM M N NM
. V y NM có ma tr n ngh o là ậ ậ ịch đả
NM.
1.3 Ta có
2
(2 )(2A I) 4A 4 4 4A I A I A A I I
B có ma tr n ngh o là chính ậ ịch đả
nó.
1.4 a)
tính
suy ra
b) S d ng phân tích ý 1) r i tìm ra a,b,c. ử ụ ồ
1.5
1 0 1
0 1 0
0 0 1
n
1 0
0 1 0
0 0 1
n
2 1 0 2 0
0 1 0 0 1 0
0 0 2 0 0 2
n
n
n
n
1.6
cos sin
sin cos
n
nx nx
A
nx nx
1.7 Cho ma tr n ậ
2017 1 2017
2016 2 2017
2016 1 2016
A
. Xác định các ph n t n ng chéo chính cầ ử ằm trên đườ ủa
ma tr n ậ
2 2017
S I A A A
.
Ta có
2016 1 2017
, 2016 1 2017
2016 1 2017
A I B B
. D dàng ki m tra ễ ể
2
0B
. Do đó, với mọi số tự nhiên k
ta có:
k
A I kB
. T ừ đó suy ra
2018 1009.2017.S I B
.
Vậy các ph n t ng chéo chính c a ma tr n ầ ử trên đườ ủ ậ
S
là
11 22 33
2018 1009.2017.2016; 2018 1009.2017; 2018 1009.2017.2017;s s s
1.8
HD : , v
ới
.
1.9
HD: suy ra
. Suy ra .
1.10 HD: T u ki n suy ra không kh ngh n t i các ma trừ điề ệ ả ịch. Do đó tồ ạ ận
khác ma tr n 0, sao cho ậ
, đặt
là ma tr n c n tìm. ậ ầ
1.11 Dễ dàng ch ng minh ứ
1.12. s t n t i các ma tr n Giả ử ồ ạ ậ
, , ,A B C D
vuông c p n sao cho ấ
AC BD I
và
0CA BD
0 0CA BD Tr CA BD
Tr AC BD n Tr AC Tr BD n Tr CA Tr BD n Tr CA BD n
, vô lí . Suy ra đpcm.
1.13. a.
2 2
0AB BA C C AB BA
Ta có
2
2
2
2
0
0
0
x y
x yz
Tr AB BA AB BA AB BA x yz I
z x
x yz
Ta có
IC CI
, suy ra đpcm.
b. cmtt
1.14
3 1; 4 1r A m r A m
1.15
3 1 4 1 3 1 4 1 3 1 4 1
2 3 1 2 3 1 2 3 1
3 1 1 0 0 2 3 1 0 2 3 1
3 3 7 2 0 2 3 1 0 0 0 0
m m m
A
. Ta thấy
2r A
. Dấu “=”
xảy ra khi
0m
1.16 Khai tri nh th c theo cển đị ứ ột 1, ta được
1
det 1 1
n
n
A m
.
Hạng c a ma tr n ủ ậ A nhỏ hơn n khi và ch khi ỉ
1 1
det 0 1 1 0 1 1
n n
n n
A m m

Nếu n l thì ẻ
1m
. N u n ch n thì ế ẵ
1m
. .
1.17 Giả ử ậ s ma tr n A c pấ
m n
có h ng b . B ng cách sạ ằng r ằ ử d ng các phép biụ ến đổi sơ cấp
trên hàng ho c c t c có th v d ng ặ ộ ủa A ể đưa A ề ạ
0
0 0
r
m n
I
R
, t c là t n t i các ma trứ ồ ạ ận không
suy biến
,P Q
sao cho
A PRQ
( các th y cô xem ch i s tuyầ ứng minh trong giáo trình đạ ố ến tính
của th u c n ). ầy Vĩnh, nế ầ
Ta phân tích
1 2
...
r
R R R R
, trong đó
i
R
là các ma tr n có t t c các phậ ấ ả ần tử đều b ng 0 tr ằ ừ
phần t hàng i, c t i b ng 1. ử ở ộ ằ
Ta có
1
i i
r PRQ r R
(các phép bi i h ng c a ma tr n). ến đối sơ cấp không làm thay đổ ạ ủ ậ
Vậy
1 2 1
... ...
r r
A P R R R Q PR Q PR Q
là cách phân tích th a mãn yêu c u c a bt. ỏ ầ ủ
1.18 a) Do
AB BA
nên
0
k
k
i i k i
k
i
A B C A B
.
Vì
2016 2017
0, 0A B
nên
2017k
thì
0.
k
A B
b) Vì
0, 2017
k
A B k
nên ta có
1
1
...
1 det det .det ...
det 0
k k
k
I I A B I A B I A B A B
I I A B I A B A B
I A B r I A B n
Ta có:
2 1 2
... .
k k
I I A B I A B I A B A B
Tương tự như trên
suy ra
r I A B n
. Suy ra đpcm.
ĐỊNH THỨC
2.1 Khi khai tri nh th v u, ta s có v c b c 3 cển đị ức ở ế trái theo dòng đầ ẽ ế trái là đa thứ ậ ủa
x
, ký
hiệu là
( )f x
. Ta có
(2) 0f
nh th u b , có vì khi đó đị ức có 2 dòng đầ ằng nhau. Tương tự
(3) 0, (4) 0f f
. Vì
( )f x
c b c 3 nên có 3 nghi m 2, 3, 4 nên pt có 3 nghi m 2, 3, 4. là đa thứ ậ ệ ệ
2.2 a)
=
b) Ta có:
1 1 1 1
0 x
2
x
1
x
3
x
1
x
4
x
1
0 (x
2
x
1
)(x
2
x
1
) (x
3
x
1
)(x
3
x
1
) (x
4
x
1
)(x
4
x
1
)
0 (x
2
x
1
)(x
2
2
x
2
x
1
x
1
2
) (x
3
x
1
)(x
3
2
x
3
x
1
x
1
2
) (x
4
x
1
)(x
4
2
x
4
x
1
x
1
2
)
(x
2
x
1
)(x
3
x
1
)(x
4
x
1
)
1 1 1
x
2
x
1
x
3
x
1
x
4
x
1
x
2
2
x
2
x
1
x
1
2
x
3
2
x
3
x
1
x
1
2
x
4
2
x
4
x
1
x
1
2
(x
2
x
1
)(x
3
x
1
)(x
4
x
1
)
1 0 0
x
2
x
1
x
3
x
2
x
4
x
2
x
2
2
x
2
x
1
x
1
2
(x
3
x
2
)(x
3
x
2
x
1
) (x
4
x
2
)(x
4
x
2
(x
2
x
1
)(x
3
x
1
)(x
4
x
1
)(x
3
x
2
)(x
4
x
2
)
1 1
x
3
x
2
x
1
x
4
x
2
x
x
i
x
j
i j
2
2 2 2 2
2 2 2 2
2 2 2 2
2 2 2 2
4
2 2 2 2
2
2 2 2 2
.
0 0 0
0 0 0
0 0 0
0 0 0
a b c d a b c d a b c d
b a d c b a d c b a d c
c d a b c d a b c d a b
d c b a d c b a d c b a
a b c d
a b c d
a b c d
a b c d
a b c d
a b c d
b a d c
a b c d
c d a b
d c b a
2.3 nh lý Viet, ta có Theo đị
0a b c
, nên
0
0 0
0
a b c a b a b c a b
b c a b c a b c b c
c a b c a a b c c a
2.4. Ta có m, n, p, q là nghi m cệ ủa phương trình
theo định lý Viet
Nhân c t 4 v -1 r i c ng vào các c t còn l i ta có ộ ới ồ ộ ộ ạ
mnp mnq mpq npq mnpq 1 1
2.5
a) Nhân dòng 2 v i (- Ta có ớ 1) sau đó cộng vào các dòng (3), (4),…., (n).
4
1 0x x
det A
m 0 0 1
0 n 0 1
0 0 1p
q q q q 1
m
n 0 1
0 p 1
q q 1 q
q
0 0 1
n 0 1
0 p 1
(1)
1 2 2 ... 2 1 2 2 ... 2 1 2 2 ... 2
2 2 2 ... 2 2 2 2 ... 2 0 2 2 ... 2
2( 2)!2 2 3 ... 2 0 0 1 ... 0 0 0 1 ... 0
. . . ... . . . . ... . . . . ... .
2 2 2 ... 2 2 2 2 ... 2 2 2 2 ... 2
n
n n

(1) : Nhân dòng (1) v i (- ng vào dòng (2). ớ 2) sau đó cộ
b) L t c ần lượ ộng dòng (1) vào các dòng (2), (3), …., (n)
1 2 3 ... 1 2 3 ...
1 0 3 ... 0 2 6 ... 2
!
1 2 0 ... 0 0 3 ... 2
. . . ... . . . . ... .
1 2 3 ... 0 0 0 0 ...
n n
n n
nn n
n
c)
Khai tri n theo hàng 1 ta có: ể
1 x
2
D
n 1
x
2
D
n 2
;D
1
1 x
Mặt khác,
D
2
1 x
2
2
x
2
x
4
x
2
D
n
D
n 1
x
2
(D
n 1
D
n
....
D
n
D
n 1
x
2n
D
n
1 x
2
x
4
....
d) Đầ ột (2), (3), …, (n) vào cộ Sau đó nhân dòng (1) vớu tiên cộng các c t (1). i (-1) cộng vào các
dòng (2), (3), …(n). Ta có
1
... ( 1) ... ( 1) ...
... ( 1) ... 0 0 ... 0
1... ( 1) ... 0 0 ... 0
. . . ... . . . . ... . . . . ... .
... ( 1) ... 0 0 0 ...
n
a b b b a n b b b b a n b b b b
b a b b a n b a b b a b
a n b a bb b a b a n b b a b a b
b b b a a n b b b a a b
2.6
a) Ta có
2
1 2 2
( ) 2( ) det 2 det
n
A A A I A I A I A I A I
 
. Suy ra
điề ảu ph i cm.
b) Ta có
AB BA B
. Nhân c 2 v vả ế ới
1k
B
vào bên ph i các ma tr n ta có : ả ậ
1
. . .
k k k
A B B AB B
. L yấ det 2 v ế :
0 det . det det .det det
k k k
A B B A B
. Suy ra điều
phải ch ng minh. ứ
2.7
Ta có
2016 2016 2016
0 det( ) (det ) 0 det 0A A A A
( ) det det .det( ) 0AB A B B AB A B A B I B A B I
2.8
Ta có,
det 1,det 1A B 
. Do
det det det det 0A B A B
. Xét
det .det( ) det .det det( . ) det( . . )
det .det( ) det .det( )
t
t t t
B A B B A B B A I B A A A
A A B B A B

Mà
det 0 det( ) 0B A B
. Điều phải cm.
2.9. Nhân hàng 1 v -2; -3; ...;-n r i c ng vào các hàng 2, 3,....n. ới ồ ộng tương ứ
det A
1 1 1 1...
1 0 0 0...
2 1 0 0
... ... ... ....
(n 1) (n 2 (n 3) ....
Khai tri n theo c t n ể ộ
det A 1
n 1
1 0 0 0...
2 1 0 0
2 1 ...
... ...
(n 1) (n 2) (n 3) ...
=
1
n 1
. 1
n 1
1
2n
1
2.10 Cho
ij
A a
là m t ma tr n vuông c p ộ ậ ấ
2n
và
11 12 1
0
n
A A A
, trong đó
1j
A
là
phần bù đại số của
1 j
a
. Ch ng minh r ng t n t i s ứ ằ ồ ạ ố thực
để
11 12 1
21 22 2
1 2
...
...
2016
... ... ... ...
...
n
n
n n nn
a a a
a a a
a a a
Ta có
11 12 1 11 12 1
21 22 2 21 22 2 21 22 2
11 12 1
1 2 1 2 1 2
... ... ...
... ... ...
...
... ... ... ... ... ... ... ... ... ... ... ...
... ... ...
n n
n n n
n
n n nn n n nn n n nn
a a a a a a
a a a a a a a a a
A A A A
a a a a a a a a a
Suy ra
11 12 1
2016
n
A
A A A
.
HỆ N TÍNH PHƯƠNG TRÌNH TUYẾ
3.1 G i ch hai pt cu i lên trên r i gi i h b Gauss: ợi ý: Đổ ỗ ố ồ ả ệ ằng phương pháp khử
2
1
3
3
53712
11213
85723
75231
↔
2
1
3
3
53712
11213
857110
75231
3.2
T c 3(x + x )=0 nhóm 3 s h ng l i thành m t nhóm ổng 10 phương trình ta đượ
1
+…. + x
9 10
ố ạ ạ ộ
được x =0 suy ra x =0 nên x =0 suy ra x = x =0 nên x =0 nên x = x = x = x có
10 1
+x
2 3 6 9 8 7 5 2 1
=0… hệ chỉ
nghiệm t ng. ầm thườ
3.3
a) L p ma tr n h s m r ng và dùng các phép bi n v d ng b c thang: ậ ậ ệ ố ở ộ ến đổi sơ cấp đưa ma trậ ề ạ ậ
Do . Ta có các kh
ả năng sau:
N
ếu . h ệ có vô s nghiố ệm
N
ếu . h có vô s nghi ệ ố ệm
Nếu . h có vô s nghi ệ ố ệm
b) L p ma tr n h s m r ng và dùng các phép bi n v d ng b c thang: ậ ậ ệ ố ở ộ ến đổi sơ cấp đưa ma trậ ề ạ ậ
Nếu . H vô nghi ệ ệm.
N
ếu . H ệ ố có vô s nghiệm
3.4 H ệ phương trình tương đương với:
Gọi
là ma tr n h s cậ ệ ố ủa phương trình trên. Ta có:
Do đó
là một số chẵn. Suy ra và có cùng tính ch n l ,
ẵ ẻ
với m i n. Mà ọ
là s l nên ố ẻ
cũng là số ẻ. do đó l
. Vậy hệ
trên là h Cramer và có nghi m duy nh t : ệ ệ ấ
.
3.5
Gọi A là ma tr n các h s . Ta cóậ ệ ố
do đó
.
Mà nên
(do n l ) ẻ
Bởi v y detA = 0 t nh lý Cronecker Capelly h có vô s nghi m ph ậ ức là r(A) < n. Theo đị – ệ ố ệ ụ
thuộc vào (n r ) tham s có nghi m khác 0. – ố. Do đó hệ ệ
3.6 detA=
2 2
2
0 8 7
3 2 4 0 5
0 0 5
0 0 5
5
3 5
m
m m
m
m
m m
m
m
m
Hệ có nghi m duy nh ệ ất ↔ detA≠0↔m≠0
3.7
4
1m
m
mm1m23
3m5223
1m11
txzy
2
↔
4m3
1m2
m
3mm1m210
m562m310
1m11
txzy
2
↔
m3
1m2
m
3m4m3m00
m562m310
1m11
txzy
2
Với m=3 h có vô s nghi m x, t l y giá tr tùy ý ệ ố ệ ấ ị
Với m≠3 hệ có vô số nghiệm t lấy giá trị tùy ý
3.8 Gợi ý: Hai h có nghi m chung khi và ch khi h sau có nghi m ệ ệ ỉ ệ ệ
mtzyx2
0mt2z2yx
m2u4t3zyx3
1utzyx
3u3t2zyx2
m
0
4m2
0
1
1
m2
1
1
2
5
1
1
3
2
1
1
0
0
0
14410
11111
tzyxu
m
0
m2
3
1
1
m2
3
1
2
1
1
1
1
2
1
3
0
0
4
21123
11111
tzyxu
HS t làm ti p ự ế
3.9 Gọi A là ma tr n h s c a h . nh th c c a ma tr n này b ng cách làm gi ng ậ ệ ố ủ ệ Ta đi tính đị ứ ủ ậ ằ ố
trong bài 2.2 b), và t c det( ) khác ừ đó thấy đượ A 0. Suy ra đpcm.
ĐA THỨC
4.1
s Suy ra Giả ử
- N ếu thì th a s b c cao nh t c ừ ố ậ ấ ủa P(P’(x)) là:
Thừ ố ấa s bậc cao nh t của P’(P(x)) là:
. Do đó từ P(P’(x)) =
P’(P(x)) ta suy ra nghĩa là n = 1 và
nguyên) , suy ra mâu
thuẫn.
- N ếu n = 0 thì t ừ P(P’(x)) = P’(P(x)) ta suy ra P(x) = 0 với mọi x.
- N ếu n = 1 thì P(x) = ax + b, nên t . ừ P(P’(x)) = P’(P(x)) ta suy ra
Vậy c tho mãn yêu c u bài toán là P(x) = 0 ho c P(x) = ax + v i a nguyên. các đa thứ ả ầ ặ
ớ
4.2
a) Ta có
Đặt
khi đó
Ta có
Xét đa thức:
Ta có b c c a Q(x) < n và Q có n nghi m là Suy ra Q(x) = 0 v i m i x, nên h ậ ủ ệ ớ ọ ệ
số cao nh t c a Q(x) là ấ ủ
b) Ta có
Suy ra
Do
nên
theo đị
nh lý Rolle t n tồ ại
sao cho
L i có
ạ
Suy ra
4.3
a) Khi n = 2:
– có 2 nghi m th c x = 1 và x = - ½. ệ ự
Khi n = 3:
có duy nh t nghi m th c x = 1. ấ ệ ự
Ta s ẽ chứng minh đa thức
x
1
,x
2
,...,x
n
1
P
'(x
1
)
1
P
'(x
2
)
...
1
P
'(x
n
)
0.
Q(x) = có duy nh
ất m t nghi m th c x = a < 0 n u n ch n và ộ ệ ự ế ẵ
không có nghi m th c n u n l . ệ ự ế ẻ
Nh
ận xét Q(x) = R’(x) trong đó
.
V
ậy Q(x) = R’(x) =
. Kh o sát t s R(x) = ả ử ố
Ta th ấy
Nếu n l thì S(x) 0 v i m i x, d u b ng x y ra khi x = 1 (dung BDT Cauchy). Tuy nhiên Q(1) ẻ ớ ọ ấ ằ ả
khác 1. V y Q(x) không có nghi m th ậ ệ ực.
Nếu n ch n kh o sát hàm s ta th y S(x) có 2 nghi m, x = 1 và m t nghi m x = a < 0 . V y Q(x) ẵ ả ố ấ ệ ộ ệ ậ
có duy nh t m t nghi m th c x = a < 0. ấ ộ ệ ự
4.4. Biể ễu di n m = 3k + r và n = 3l + s, với Khi đó
Vì
và
cùng chia hết cho
nên
chia h t cho ế
khi và ch khi ỉ
chia h t cho ế
Do nên
chia hết cho khi và
chỉ khi r = 2, s = 1 ho c r = 1, s = 2. ặ
Mặt khác mn 2= (3k + r)(3l + s) 2 = 3(3kl + ks + lr) + rs – – – 2. Nhưng rs – 2 chia hết cho 3 khi
và ch khi r = 2, s = 1 ho c r = 1, s = 2. ỉ ặ
4.5. Thay x = 1 và x = -1 ta có:
.
Thay x = 1/2 và x = -1/2 ta có:
. Suy ra b = - 3.
Lại thay x = 1; x = - c 1 ta đượ
Thay x = 1/2 và x = -1/2 ta có:
Suy ra a = c = 0. V ậy
Thử l t x = cost, ta có |P(x)| = |cos3t| ại đặ
| 1/19
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

BÀI T I
ẬP ĐẠ SỐ TUYẾN TÍNH
1. MA TRẬN.
1.1. Cho A là ma trận vuông cấp n th a ỏ mãn 2
A A I . Ch ng ứ
minh rằng A có ma trận n
nghịch đảo và tìm ma trận nghịch đảo của A . 5 6 2 1.2.  
Cho M , N là các ma trận vuông cấp 3 thỏa mãn MN  6 7  2   6 6 1   a. Tính 2 (MN) .
b. Chứng minh NM khả nghịch. Tìm ma trận nghịch đảo của NM .
1.3. Cho A là ma trận cấp n thỏa mãn 2 A A . Ch ng
ứ minh rằng ma trận B  2AI có ma trận nghịch đảo. 1.4. Cho ma trận ( ) a. Chứng minh rằ ế ng n u thì
b. Tìm sao cho tồn tại để ( ) 1.5. Tính nn 1 0 1 2 1 0     a. 0 1 0   b. 0 1 0   0 0 1   0 0 2   cosx sinx
1.6. Tính lũy thừa bậc n của A  . s  inx cosx    2017 1 2  017 1.7.  
Cho ma trận A  2016 2 2  017 
 . Xác định các phần tử nằm trên đường chéo chính 2016 1 2  016   của ma trận 2 2017
S I A A    A .
1.8. Cho là ma trận vuông cấp ( ) Tính , với là s ố nguyên dương. 1.9. Cho th a
ỏ mãn . Chứng minh rằng .
1.10. Cho thỏa mãn Chứng minh rằng tồn tại ma trận
khác ma trận 0 thỏa mãn
1.11. Cho ma trận vuông A, B cấp n. Vết của ma trận A là t ng ổ
tất cả các phần tử trên đường
chéo chính của A, kí hiệu Tr  A . Ch ng m ứ inh rằng:
a. TrA  B Tr  A Tr  B . b. Trk A kTr  A , k  . c. TrA
B TrB A
1.12. Chứng minh rằng không t n t ồ ại các ma trận ,
A B,C, D vuông cấp n sao cho
AC BD I và CABD  0 , I là ma trận đơn vị, 0 là ma trận không.
1.13. (Đẳng thức Wagner)
a. Chứng minh rằng với mọi ma trận ,
A B,C vuông cấp 2 ta luôn có
AB BA2 C CAB B 2 A  0
b. Chứng minh rằng với mọi ma trận ,
A B,C vuông cấp 2 ta luôn có
AB BA2016 C C AB BA2016  0  1  2 1 1  1    m 1  1 1  1 
1.14. Tùy theo giá trị của m , hãy tìm hạng của ma trận A     1 m 0 1 1    1 2 2 1 1    3 1 4 1   m 2 3 1
1.15. Tìm m để ạ
h ng của ma trận sau nhỏ ấ nh t A     3 1 1 0   3 3 7 2    1 m 0 ... 0 0   0 1 m ... 0 0  
1.16. Cho ma trận vuông cấp n: A  ... ... ... ... ... ... . Tìm m để ạ h ng của ma trận A   0 0 ... ... 1 m   m 0 0 ... 0 1    nhỏ hơn n.
1.17. Chứng minh rằng m i
ọ ma trận hạng r đều có thể phân tích được thành t ng ổ của r ma trận có hạ ằ ng b ng 1.
1.18. Giả sử A, B là các ma trận vuông cấp n thỏa mãn 2016 2017 AB B , A A  0, B  0.
a. Chứng minh rằng tồn tại số tự nhiên k để   k A B  0.
b. Chứng minh rằng r I AB  r I AB  n .
2. ĐỊNH THỨC 2 3 1 x x x 2.1. 1 2 4 8 Giải phương trình:  0 1 3 9 27 1 4 14 64
2.2. Tính định thức : 1 1 1 1 a b c d x x x x ba d c  a. 1 2 3 4 b. 2 2 2 2 x x x x cda b 1 2 3 4 3 3 3 3 x x x xd cb a 1 2 3 4 a b c
2.3. Tính b c a trong đó , 3 a ,
b c là 3 nghiệm của phương trình bậc 3 : x px q  0. c a b
2.4. Cho m, n, p, q là các nghiệm của phương trình 4
x x 1  0 và m 1 1 1 1    1 n 1 1 1 A     1 1 p  1 1    1 1 1 q   1 Tính det A.
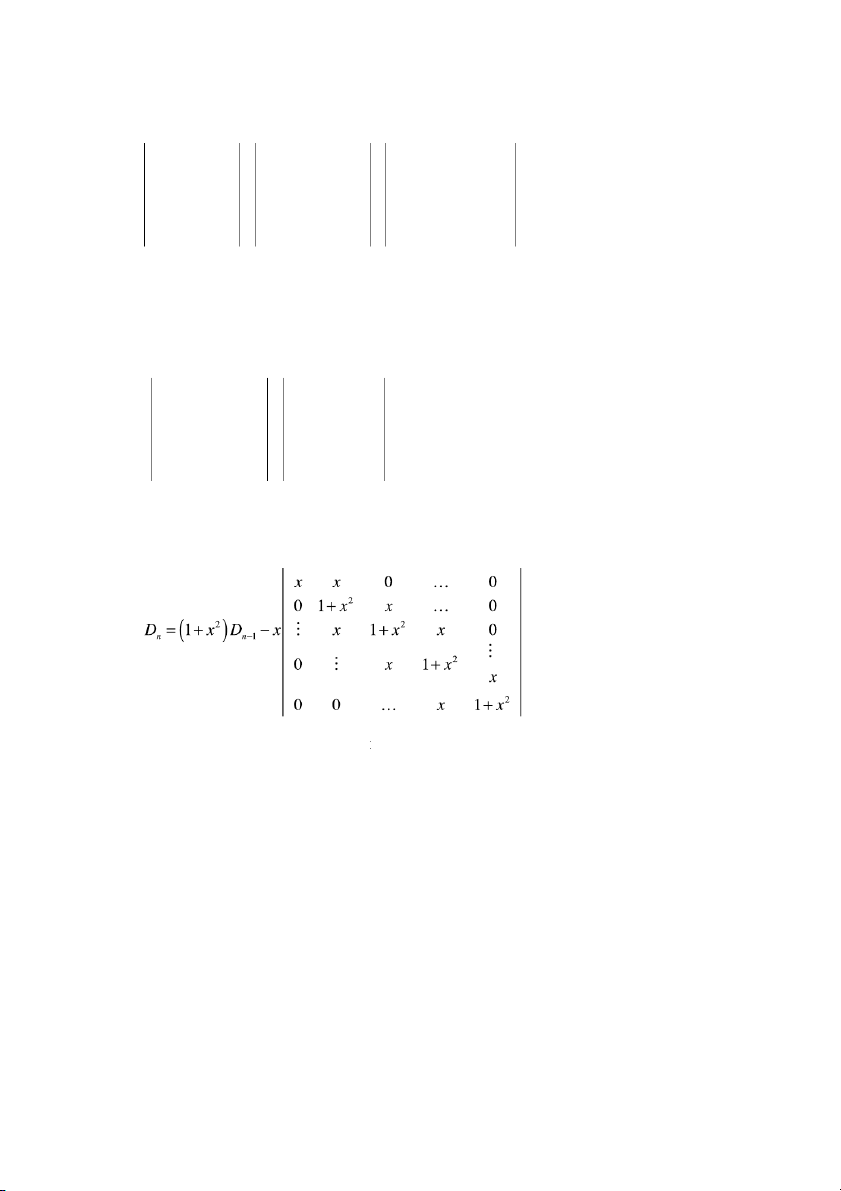
2.5. Tính các định thức cấp n sau : 1 2 2 ... 2 1 2 3 ... n 2 2 2 ... 2 1  0 3 ... n a. 2 2 3 ... 2 ; b. 1  2  0 ... n . . . ... . . . . ... . 2 2 2 ... 2 1  2  3  ... 0 0 1 1 ... 1 a b b ... b 1 0 x ... x b a b ... b c. 1 x 0 ... x ; d. b b a ... b . . . ... . . . . ... . 1 x x ... x b b b ... a 2 1 x x 0 ... 0 2 x 1 x x ... 0 e. 2 D   , n 0 x 1 x ... 0 . . . ... . 2 0 0 0 ... 1  x
D là định thức cấp n mà các phần t
ử nằm trên đường chéo chính bằng 1+x2, các phần tử n thuộc hai đường chéo g ng chéo chính b ần đườ
ằng x và các phần tử còn lại bằng 0. 2.6. a.  A là m t
ộ ma trận vuông cấp n thỏa mãn 1 A A . Ch ng ứ
minh det( A I )  0 hoặc det(  ) 2n A I . b. ,
A B là hai ma trận vuông cùng cấp n thỏa mãn AB BA B . Ch ng ứ minh det( ) B  0. 2.7. Cho ,
A B là các ma trận thực vuông cấp n thỏa mãn AB A B và 2016 A  0. Chứng minh rằng det( ) B  0.
2.8. Cho các ma trận vuông , A B thỏa mãn t  ; t A A
I B B I . Biết det A  det B . Ch ng ứ minh rằng det(A ) B  0 .
2.9. Cho ma trận vuông cấp n A  a ; a  min ,i j . Tính det  A . ij ij
2.10. Cho A  a là m t
ộ ma trận vuông cấp n  2 và A A   A  0 , trong đó A ij  11 12 1n 1j là phần bù đại s c ố ủa a . Ch ng m ứ inh rằng tồn tại s ố thực  để 1 j a   a   ... a   11 12 1 n a a ... a 21 22 2n  2016 ... ... ... ... a a ... a n1 n 2 nn
3. HỆ PHƯƠNG TRÌNH TUYẾN TÍNH 3.1. Giải hệ phương trình:
 3xy 2ztu  1 
 2 x y  7 z 3t 5u  2
x 3y 2z 5t 7u 3  3
x 2 y 7z 5t 8u   3
3.2. Giải hệ phương trình thuầ ấ n nh t sau:
x x x  0 1 2 3
x x x  0 2 3 4 
x x x  0 3 4 5   ........
x x x  0 8 9 10 
x ...  x x  0 1 9 10
x x ... x  0  1 2 10
3.3. Giải và biện luận các hệ phương trình sau 
2x y z t 1
mx y z t  1   
x  2 y z  4t  2
a. x my z t  1 b.  
x  7 y  4z 11t m
x y mz t  1
4x  8y  4z 16t m   1 3.4. Cho là các s ố nguyên. Giải hệ: { 3.5. Chứng minh rằ ệ ng h m
phương trình sau có nghiệ khác nghiệm tầm thường: { trong đó và n lẻ.
3.6. Tìm m để hệ sau có nghiệm duy nhất
mx 8z  7t m 1 3
x my  2z  4t m  2
mz  5t m 1 
 5z mt  2m   2
3.7. Tùy theo giá trị của m, hãy biện luận số nghiệm của ệ h : 
mx y z t m
 2x  3y  2z  (5m  3)t m  1  2
(m  1)x  3y  2z  (m m )t  4 
3.8. Tìm điều kiện của m để hai hệ sau có nghiệm chung
 2x y z  2t 3u  3  
x y z t u  1 3
x y z 3t 4u  2m
x y  2z  2mt  0 
2x y z t   m 3.9. Cho , a , b , c d  . Ch ng m ứ
inh rằng hệ phương trình sau chỉ có nghiệm tầm thường:   2
1 a x by cz dt  0  bx    2
1 a y dz ct  0 
cx dy   2
1 a z bt  0 
 dx cy bz    2
1 a t  0 4. ĐA THỨC
4.1. (Xác định đa thức) Tìm tất cả các đa thức ( P ) x có hệ s nguyê ố n sao cho ( P P '( ) x )  P '( ( P x)), x  
4.2. (Nghiệm của đa thức) Cho P(x) là đa thức bậc n có n nghiệm phân biệt x , x ,..., x . 1 2 n Chứng minh rằng: 1 1 1 a.   ...  0. P'( x ) P'( x ) P'( x ) 1 2 n P' ( x ) P' ( x ) P ' (x ) b. 1 2  ... n   0. P '(x ) P '(x ) P '(x ) 1 2 n
4.3. (Đa thức với yếu tố giải tích) Với mỗi số
nguyên dương n  2 xét đa thức n n 1 P (x) nx x    ... x 1
 . Hỏi P (x) có bao nhiêu nghiệm th c ự : n n
a. Khi n  2; n  3? b. Khi n  4?
4.4. (Tính chia hết của đa thức) Cho ,
m n là các số nguyên dương. Chứng minh rằng điều kiện c
ần và đủ để đa thức m n
x x 1chia hết cho 2
x x 1 là mn  2 chia hết cho 3. 4.5. Cho đa thức 3 2
P(x)  4x ax bx c trong đó , a ,
b c là các số thực. Hãy tìm , a , b c sao
cho P(x) 1 với m i
ọ x thoả mãn x 1.
HƯỚNG DẪN GIẢI BÀI TẬP ĐS OLIMPIC MA TRẬN
1.1 Có A(A I ) I
A có ma trận nghịch đảo là A I – n 2 1.2 (MN) I a) Có 3 b)Ta có det(MN ) 1 det NM 1
NM có ma trận nghịch đảo det(MN) 0 detM 0 và detN 0
N và M có ma trận nghịch đảo 2 1 1 1 (MN) I MNMN I NM M N
(NM ) . Vậy NM có ma trận nghịch đảo là 3 3 NM. 1.3 Ta có 2 (2A I )(2 A I) 4 A 4A I 4A 4A I I
B có ma trận nghịch đảo là chính nó. 1.4 a) tính suy ra b) S d ử ng phân tích ý 1) ụ r i ồ tìm ra a,b,c. 1.5 n 1 0 1 1 0 n 0 1 0 0 1 0 0 0 1 0 0 1 n 2 1 0 2n n 0 0 1 0 0 1 0 0 0 2 0 0 2 n cos nx sin nx n A 1.6 nx nx sin cos 2017 1 2017
1.7 Cho ma trận A 2016 2
2017 . Xác định các phần t
ử nằm trên đường chéo chính của 2016 1 2016 ma trận 2 2017 S I A A A . 2016 1 2017 Ta có A I , B B 2016 1 2017 . Dễ dàng kiểm tra 2 B
0 . Do đó, với mọi số tự nhiên k 2016 1 2017 ta có: k A I kB . T
ừ đó suy ra S 2018I 1009.2017.B . Vậy các phần t
ử trên đường chéo chính của ma trận S là s 2018 1009.2017.2016; s 2018 1009.2017; s 2018 1009.2017.2017; 11 22 33 1.8 HD : , với . 1.9 HD: suy ra . Suy ra . 1.10 HD: T ừ điều kiện s uy ra không khả ngh n t
ịch. Do đó tồ ại các ma trận
khác ma trận 0, sao cho , đặt là ma trận cần tìm.
1.11 Dễ dàng chứng minh 1.12. Giả sử t n t ồ ại các ma trận ,
A B,C, D vuông cấp n sao cho AC BD I và CA BD 0 CA BD 0 Tr CA BD 0 Tr AC BD n Tr AC Tr BD n Tr CA Tr BD n Tr CA BD n , vô lí . Suy ra đpcm. 1.13. a. 2 2 AB BA C C AB BA 0 2 x y x yz 0 Ta có 2 2 Tr AB BA 0 AB BA AB BA x yz I 2 z x 0 x yz Ta có IC CI , suy ra đpcm. b. cmtt 1.14 r A 3 m 1; r A 4 m 1 3 1 4 1 3 1 4 1 3 1 4 1 m 2 3 1 m 2 3 1 m 2 3 1 1.15 A . Ta thấy r A 2 . Dấu “=” 3 1 1 0 0 2 3 1 0 2 3 1 3 3 7 2 0 2 3 1 0 0 0 0 xảy ra khi m 0 1.16 Khai tri nh t ển đị h c ứ theo cột 1, ta được 1 det 1 1 n n A m . Hạng c a
ủ ma trận A nhỏ hơn n khi và chỉ khi n 1 n 1 det 0 1 1 n 0 1 n A m m 1 Nếu n lẻ thì m
1. Nếu n chẵn thì m 1. .
1.17 Giả sử ma trận A cấp m n có hạng bằng r. Bằng cách sử d ng ụ
các phép biến đổi sơ cấp I 0 trên hàng hoặc c t
ộ của A có thể đưa A về dạng r R , t c ứ là t n
ồ tại các ma trận không 0 0 m n suy biến , P Q sao cho A
PRQ( các thầy cô xem chứng minh trong giáo trình đại s t ố uyến tính
của thầy Vĩnh, nếu cần ). Ta phân tích R R R
... R , trong đó R là các ma trận có tất cả các phần tử đều bằng 0 trừ 1 2 r i phần t ử ở hàng i, c t ộ i bằng 1. Ta có r PR Q r R
1 (các phép biến đối sơ cấp không làm thay đổi hạng c a ủ ma trận). i i Vậy A P R R ... R Q PR Q ...
PR Q là cách phân tích th a ỏ mãn yêu cầu của bt. 1 2 r 1 r k 1.18 k a) Do AB BA i i k i nên A B C A B . k i 0 Vì 2016 2017 k A 0, B 0 nên k 2017 thì A B 0. b) Vì k A B 0, k 2017 nên ta có k k 1 I I A B I A B I A B ... A B k 1 1 det I det I A B .det I A B ... A B det I A B 0 r I A B n Ta có: 2k 1 2 ... k I I A B I A B I A B A B . Tương tự như trên suy ra r I A B n . Suy ra đpcm. ĐỊNH THỨC 2.1 Khi khai tri nh t ển đị hức ở vế u, t trái theo dòng đầ
a sẽ có vế trái là đa thức bậc 3 của x , ký
hiệu là f (x) . Ta có f (2) 0 vì khi đó định thức có 2 dòng đầu bằng nhau. , c Tương tự ó f (3)
0, f (4) 0. Vì f (x) là đa thức bậc 3 nên có 3 nghiệm 2, 3, 4 nên pt có 3 nghiệm 2, 3, 4. 2.2 a) 1 1 1 1 0 x x x x x x 2 1 3 1 4 1 0 (x x )(x x ) (x x )(x x ) (x x )(x x ) 2 1 2 1 3 1 3 1 4 1 4 1 0 (x x )(x2 x x x2 ) (x x )(x2 x x x2 ) (x x )(x2 x x x2 2 1 2 2 1 1 3 1 3 3 1 1 4 1 4 4 1 1) 1 1 1 (x x )(x x )(x x ) x x x x x x 2 1 3 1 4 1 2 1 3 1 4 1 x2 x x x2 x2 x x x2 x2 x x x2 2 2 1 1 3 3 1 1 4 4 1 1 1 0 0 (x x )(x x )(x x ) x x x x x x 2 1 3 1 4 1 2 1 3 2 4 2 x2 x x x2 (x x )(x x x ) (x x )(x x 2 2 1 1 3 2 3 2 1 4 2 4 2 1 1 (x x )(x x )(x x )(x x )(x x ) 2 1 3 1 4 1 3 2 4 2 x x x x x x 3 2 1 4 2 = x x i j i j b) Ta có: 2 a b c d a b c d a b c d b a d c b a d c b a d c . c d a b c d a b c d a b d c b a d c b a d c b a 2 2 2 2 a b c d 0 0 0 2 2 2 2 0 a b c d 0 0 2 2 2 2 0 0 a b c d 0 2 2 2 2 0 0 0 a b c d 4 2 2 2 2 a b c d a b c d b a d c 2 2 2 2 2 a b c d c d a b d c b a
2.3 Theo định lý Viet, ta có a b c 0 , nên a b c a b a b c a b 0 b c a b c a b c b c 0 0 c a b c a a b c c a 0
2.4. Ta có m, n, p, q là nghiệm của phương trình 4 x x 1 0 theo định lý Viet Nhân c t ộ 4 với -1 r i ồ c ng và ộ o các c t ộ còn lại ta có m 0 0 1 n 0 1 0 0 1 det A 0 n 0 1 m q n 0 0 p 1 0 p 1 0 1 q q q q q q 1 q 1 0 p 1 mnp mnq mpq npq mnpq 1 1 2.5
a) Nhân dòng 2 với (-1) sau đó cộng vào các dòng (3), (4),…., (n). Ta có 1 2 2 ... 2 1 2 2 ... 2 1 2 2 ... 2 2 2 2 ... 2 2 2 2 ... 2 0 2 2 ... 2 (1) 2 2 3 ... 2 0 0 1 ... 0 0 0 1 ... 0 2(n 2)! . . . ... . . . . ... . . . . ... . 2 2 2 ... 2 2 2 2 ... n 2 2 2 2 ... n 2
(1) : Nhân dòng (1) với (-2) sau đó cộng vào dòng (2).
b) Lần lượt cộng dòng (1) vào các dòng (2), (3), …., (n) 1 2 3 ... n 1 2 3 ... n 1 0 3 ... n 0 2 6 ... 2n 1 2 0 ... n 0 0 3 ... 2n n! . . . ... . . . . ... . 1 2 3 ... 0 0 0 0 ... n
Khai triển theo hàng 1 ta có: c) 1 x2 D x2D 1 x n ; D 1 n 2 1 Mặt khác, D 1 x2 2 x2 x4 x2 2 D D x2(D D n n 1 n 1 n.... D D x2n D n n 1 n 1 x2 x4 ....
d) Đầu tiên cộng các cột (2), (3), …, (n) vào cột (1). Sau đó nhân dòng (1) với (-1) cộng vào các
dòng (2), (3), …(n). Ta có a b b ... b a
(n 1)b b b ... b a (n 1)b b b ... b b a b ... b a
(n 1)b a b ... b 0 a b 0 ... 0 n 1 b b a ... b a
(n 1)b b a ... b 0 0 a b ... 0 a n 1 b a b . . . ... . . . . ... . . . . ... . b b b ... a a
(n 1)b b b ... a 0 0 0 ... a b 2.6 a) Ta có 2 1 2 2 ( ) 2( ) det 2n A A A I A I A I A I
det A I . Suy ra điề ả u ph i cm.
b) Ta có AB BA B. Nhân cả 2 vế với k 1 B
vào bên phải các ma trận ta có : k k 1 . . . k k k k A B B A B
B . Lấy det 2 vế : 0 det . A det B det B .det A det B . Suy ra điều phải ch ng m ứ inh. 2.7 Ta có 2016 2016 2016 A 0 det(A ) (det ) A 0 det A 0 AB A B B AB A B ( A B I ) det B det . A det(B I ) 0 2.8 Ta có, det A 1, det B
1. Do det A det B
det A det B 0 . Xét t det .det( ) det .det det( . t ) det( . t . t B A B B A B B A I B A A A ) det . A det( A ) B det . B det( A ) B Mà det B 0 det(A ) B 0 . Điều phải cm.
2.9. Nhân hàng 1 với -2; -3; ...;-n r i ồ c
ng vào các hàng 2, 3,....n. ộng tương ứ 1 1 1 ... 1 1 0 0 ... 0 det A 2 1 0 0 ... ... ... .... (n 1) (n 2 (n 3) .... 1 0 0 ... 0 2 1 0 0 Khai triển theo c t ộ n det A 1n 1 2 1 ... = ... ... (n 1) (n 2) (n 3) ... 1n 1 n . 1 1 12n 1 2.10 Cho A
a là một ma trận vuông cấp n 2 và A A A 0, trong đó A là ij 11 12 1n 1j
phần bù đại số của a . Ch ng m ứ inh rằng t n t ồ ại s ố thực để 1 j a a ... a 11 12 1 n a a ... a 21 22 2n 2016 ... ... ... ... a a ... a n1 n 2 nn Ta có a a ... a a a a n ... n ... 11 12 1 11 12 1 a a ... a a a a a a a n ... n ... 21 22 2 21 22 2 21 22 2n A A A ... A 11 12 1 ... ... ... ... ... ... ... ... ... ... ... ... n a a ... a a a ... a a a ... a n1 n 2 nn n1 n 2 nn n1 n 2 nn 2016 A Suy ra . A A A 11 12 1n
HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
3.1 Gợi ý: Đổi ch ha ỗ i pt cu i ố lên trên r i
ồ giải hệ bằng phương pháp khử Gauss: 1 3 2 5 7 3 1 3 2 5 7 3 3 2 7 5
8 3 ↔0 11 7 5 8 3 3 1 2 1 1 1 3 1 2 1 1 1 2 1 7 3 5 2 2 1 7 3 5 2 3.2
Tổng 10 phương trình ta được 3(x1+…. + x9+ x10)=0 nhóm 3 s h ố ạng lại thành m t ộ nhóm được x1 =
0 0 suy ra x1+x2=0 nên x3=0 suy ra x6= x9=0 nên x8=0 nên x7= x5= x2= x1 =0… hệ chỉ có nghiệm t ng. ầm thườ 3.3 a) Lập ma trận hệ s m ố ở r ng và dùng cá ộ
c phép biến đổi sơ cấp đưa ma trận về dạng bậc thang: Do . T a có các khả năng sau: Nếu . hệ có vô s nghi ố ệm
Nếu . hệ có vô số nghiệm Nếu . h ệ có vô s nghi ố ệm b) Lập ma trận hệ s m
ố ở rộng và dùng các phép biến đổi sơ cấp đưa ma trận về dạng bậc thang: Nếu . H ệ vô nghiệm.
Nếu . Hệ có vô số nghiệm
3.4 Hệ phương trình tương đương với: Gọi là ma trận hệ s c
ố ủa phương trình trên. Ta có:
Do đó là một số chẵn. Suy ra và có cùng tính chẵn lẻ, với m i ọ n. Mà là s l
ố ẻ nên cũng là số lẻ. do đó . Vậy hệ
trên là hệ Cramer và có nghiệm duy nhất : .
3.5 Gọi A là ma trận các hệ s . T ố a có do đó . Mà nê n (do n lẻ)
Bởi vậy detA = 0 tức là r(A) < n. Theo định lý Cronecker C
– apelly hệ có vô số nghiệm ph ụ thuộc vào (n r – ) tham s c
ố. Do đó hệ ó nghiệm khác 0. m 0 8 7 3 m 2 4 m 0 m 5 3.6 detA= 2 2 m m 25 0 0 m 5 3 m 5 m 0 0 5 m Hệ có nghiệm duy nh ất ↔ detA≠0↔m≠0 y z x t y z x t 1 1 m 1 m 1 1 m 1 m 3.7 ↔ 3 2 2 m 5 3 m 1 0 1 3m 2 6 5m 2m 1 3 2 m 1 m 2 m 4 0 1 2m 1 m 2 m 3 3m 4 y z x t 1 1 m 1 m ↔ 0 1 3m 2 6 5m 2m 1 0 0 m 3 m2 4m 3 3 m Với m=3 hệ có vô s nghi ố
ệm x, t lấy giá trị tùy ý
Với m≠3 hệ có vô số nghiệm t lấy giá trị tùy ý
3.8 Gợi ý: Hai hệ có nghiệm chung khi và chỉ khi hệ sau có nghiệm 2x y z t 2 u 3 3 x y z t u 1 3x y z t 3 4u 2m x y 2 z 2mt 0 2x y z t m u x y z t u x y z t 1 1 1 1 1 1 1 1 1 1 1 1 3 0 3 2 1 1 2 0 1 4 4 1 4 3 1 1 3 2m 0 1 3 5 1 2m 4 0 1 1 2 2m 0 0 1 1 2 2m 0 0 2 1 1 1 m 0 2 1 1 1 m HS t l ự àm tiếp
3.9 Gọi A là ma trận hệ số c a
ủ hệ. Ta đi tính định th c ứ c a
ủ ma trận này bằng cách làm gi ng ố
trong bài 2.2 b), và từ đó thấy được det(A) khác 0. Suy ra đpcm. ĐA THỨC 4.1 Giả sử Suy ra - Nếu t hì thừa s b
ố ậc cao nhất của P(P’(x)) là: Thừa số bậc cao ấ nh t của P’(P(x)) là: . Do đó từ P(P’(x)) = P’(P(x)) ta suy ra nghĩa
là n = 1 và nguyên) , suy ra mâu thuẫn.
- Nếu n = 0 thì từ P(P’(x)) = P’(P(x)) ta suy ra P(x) = 0 với mọi x.
- Nếu n = 1 thì P(x) = ax + b, nên t
ừ P(P’(x)) = P’(P(x)) ta suy ra .
Vậy các đa thức thoả mãn yêu cầu bài toán là P(x) = 0 hoặc P(x) = ax + v ới a nguyên. 4.2 a) Ta có Đặt khi đó Ta có Xét đa thức: Ta có bậc c a
ủ Q(x) < n và Q có n nghiệm là x ,x ,..., x Suy ra Q(x) = 0 với mọi x, nên hệ 1 2 n 1 1 1
số cao nhất của Q(x) là ... 0. P'(x ) P'(x ) P'(x ) 1 2 n b) Ta có Suy ra Do nên theo định lý Rolle t n ồ tại sao cho Lại có Suy ra 4.3
a) Khi n = 2: – có 2 nghiệm thực x = 1 và x = - ½.
Khi n = 3: có duy nhất nghiệm thực x = 1.
Ta sẽ chứng minh đa thức Q(x) = có duy nhất m t
ộ nghiệm thực x = a < 0 nếu n chẵn và không có nghiệm th c ự nếu n lẻ.
Nhận xét Q(x) = R’(x) trong đó . Vậy Q(x) = R’(x) = . Khảo sát tử s R ố (x) = Ta thấy
Nếu n lẻ thì S(x) 0 với m i
ọ x, dấu bằng xảy ra khi x = 1 (dung BDT Cauchy). Tuy nhiên Q(1)
khác 1. Vậy Q(x) không có nghiệm thực .
Nếu n chẵn khảo sát hàm s t
ố a thấy S(x) có 2 nghiệm, x = 1 và m t
ộ nghiệm x = a < 0 . Vậy Q(x) có duy nhất m t ộ nghiệm th c ự x = a < 0.
4.4. Biểu diễn m = 3k + r và n = 3l + s, với Khi đó Vì và cùng chia hết cho
nên chia hết cho khi và chỉ khi
chia hết cho Do nên chia hết cho khi và
chỉ khi r = 2, s = 1 hoặc r = 1, s = 2. Mặt khác mn 2= – (3k + r)(3l + s) 2
– = 3(3kl + ks + lr) + rs – 2. Nhưng rs – 2 chia hết cho 3 khi
và chỉ khi r = 2, s = 1 hoặc r = 1, s = 2.
4.5. Thay x = 1 và x = -1 ta có: .
Thay x = 1/2 và x = -1/2 ta có: . Suy ra b = - 3.
Lại thay x = 1; x = -1 ta được
Thay x = 1/2 và x = -1/2 ta có: Suy ra a = c = 0. Vậy
Thử lại đặt x = cost, ta có |P(x)| = |cos3t|