Bài tập mẫu: Chương 1 - Mô hình Kinh tế và Tối đa hóa Lợi nhuận | Môn Kinh tế lượng - Học viện Chính sách và Phát triển

lOMoAR cPSD| 59452058
Bài tập mẫu: Chương 1: MÔ HÌNH KINH TẾ
Bài số 1: Mục tiêu doanh nghiệp
Công ty Trung Thành có hàm cầu là P = 100 - Q và hàm tổng chi phí là TC = 200 20Q + Q2, 1.
Xác định giá và sản lượng tối đa hoá lợi nhuận của công ty. Hãy xác định lợinhuận tối đa đó? 2.
Xác định giá và sản lượng tối đa hoá tổng doanh thu? Tính lợi nhuận trongtrường hợp này? 3.
Xác định giá và sản lượng tối đa hoá doanh thu nếu như lợi nhuận mục tiêu
củacông ty phải kiếm được là 1400 triệu đồng. Lời giải
1. Ta có MR = TR(Q)’. Với TR= PxQ = (100 - Q)xQ = 100Q - Q2, vì thế MR = 100- 2Q
MC = TC(Q)’, do đó MC = 2Q - 20. Điều kiện để tối đa hóa lợi nhuận là MR = MC.
Giải phương trình MR = MC, ta có Q = 30. Thay Q = 30 vào phương trình đường
cầu, P = 70 (triệu đồng). Lợi nhuận của công ty là = TR - TC = 70x30 - (200 20x30 + 302) = 1600 (triệu)
2. Điều kiện tối đa hóa doanh thu là: MR = 0
Giải phương trình 100- 2Q = 0, ta có Q = 50 và P = 100 - 50 = 50
Lợi nhuận của công ty Trung Thành trong trường hợp này là
= TR - TC = 50 x 50 - (200 – 20 x 50 + 502) = 800 (triệu đồng)
3. Điều kiện lợi nhuận phải đạt là 1400 triệu đồng: TR - TC = 1400
Giải phương trình 100Q - Q2 - (200 - 20Q + Q2) = 1400. Ta có Q1 = 20 và Q2 = 40.
Thay các giá trị sản lượng đó vào phương trình cầu được P1 = 80 và P2 = 60 Tổng
doanh thu tương ứng là TR1 = P1 x Q1 = 1600 (triệu đồng) và TR2 = P2 x Q2 = 2400
(triệu đồng). Với mục tiêu tối đa hóa doanh thu trong điều kiện có ràng buộc, ta lựa
chọn mức sản lượng Q2 = 40 và P2 = 60
Bài số 2: Tối đa hóa lợi nhuận
Cho hàm lợi nhuận ( ) của công ty Thu Phương phụ thuộc sản lượng của hai hàng
hoá do công ty sản xuất Q 2 2
1 và Q2 như sau : = f(Q1,Q2) = 50Q1 - 2Q1 - Q1Q2 - 4Q2 lOMoAR cPSD| 59452058 + 80Q2
1. Xác định mức sản lượng Q
1,Q2 để tối đa hoá lợi nhuận của công ty.
2. Hãy xác định sản lượng và lợi nhuận khi công ty đối mặt với ràng buộc là Q1 + Q2 = 20. Lời giải
1. Xác định Q1,Q2 để lợi nhuận lớn nhất, ta đặt / Q1 và / Q2 bằng 0: / Q1 = 50 - 4Q1 - Q2 = 0 / Q2 = - Q1 - 8Q2 + 80 = 0
Giải hệ hai phương trình trên, có: Q1= 10,3 và Q2 = 8,7; = 606,45
2. Để giải bài toán tối ưu hoá này, ta có thể giải theo hai phương pháp thế và Lagrange. Phương pháp thế:
Từ ràng buộc sản lượng, ta có Q1 = 20 - Q2 . Thay vào hàm lợi nhuận, ta có = 50(20 - Q 2 2
2) - 2(20 - Q2)2 - (20 - Q2)Q2 - 4Q2 + 80Q2 = - 5Q2 + 90Q2 + 200 Như vậy hàm
lợi nhuận là hàm số có môt biến và không có ràng buộc, ta tính đạo hàm của theo
Q2 và đặt bằng 0 : d /dQ2 = -10Q2 + 90 = 0 Vậy Q2 = 9, và do đó Q1 = 20 - Q2 = 11.
Khi đó lợi nhuận công ty thu được là = 605. Phương pháp Lagrange:
Ta xác lập hàm Lagrange (L ) theo dạng sau: L 2 2
= 50Q1 - 2Q1 - Q1Q2 - 4Q2 + 80Q2 + (Q1 + Q2 - 20)
Hàm Lagrange L có thể coi như là hàm không bị ràng buộc với 3 biến số : Q1, Q2 và
. Vì thế để tối đa hoá L , ta đặt đạo hàm riêng của L theo Q1, Q2 và bằng 0 để tìm Q1, Q2 và . L / Q1 = 50 - 4Q1 - Q2 + = 0
L / Q2 = - Q1 - 8Q2 + 80 + = 0 L / = Q1 + Q2 - 20 = 0
Giải hệ ba phương trình trên, ta cũng xác định được các giá trị Q1, Q2 như phương pháp thế.
Bài tập mẫu: Ch 2: Lý thuyết CẦU lOMoAR cPSD| 59452058
Bài 1. (Lựa chọn kết hợp tiêu dùng tối ưu - Ứng dụng rút ra đường cầu hàng hóa)
Hàm lợi ích dạng Coob Douglas của một người tiêu dùng là U(X,Y) = X1/2Y1/2. Thu
nhập bằng tiềncủa người tiêu dùng là I = 36$, giá của hàng hóa X và Y là PX = 1$, PY = 3$.
a. Hãy xác định kết hợp tiêu dùng tối ưu của người này.
b. Nếu giá hàng hóa X tăng lên gấp ba, ceteris paribus, thì kết hợp tiêu dùng tối ưu
hóa của người này thay đổi thế nào ?
c. Nếu thu nhập tăng gấp đôi (ceteris) kết hợp (X,Y) tối ưu là gì
d. Minh họa đường cầu hàng hóa X dựa vào kết quả câu a và b.
Lời giải :
a. Điểm tiêu dùng tối ưu là điểm tiếp xúc giữa đường bàng quan và đường ngân sách.
Tại đó độ dốc của đường IC và BL phải bằng nhau. Độ dốc của đường bàng quan
là tỷ lệ lợi ích cận biên của hai hàng hóa. Độ dốc của đường ngân sách (còn gọi
là giá tương đối) là tỷ số giá của hai hàng hóa.
Với dữ liệu đầu bài ra phương trình đường ngân sách là (BL) 36 = X + 3Y hay Y = 12 – X/3.
Độ dốc của đường ngân sách là tỉ số 2 giá = -1/3 U 0,5 0,5X 0,5 0,5Y 0,5 MU X X Y X 0,5
MUY UY X 0,50,5Y 0,5 0,Y5X0,50,5 MUX 0,5Y : 0,5 0,5X 0,5 Y
Độ dốc của đường bàng quan là MUY X 0,5 Y 0,5 X
Số lượng X và Y tối ưu là nghiệm của hệ phương trình sau: 36 = X + 3Y Y 1 X 3 lOMoAR cPSD| 59452058
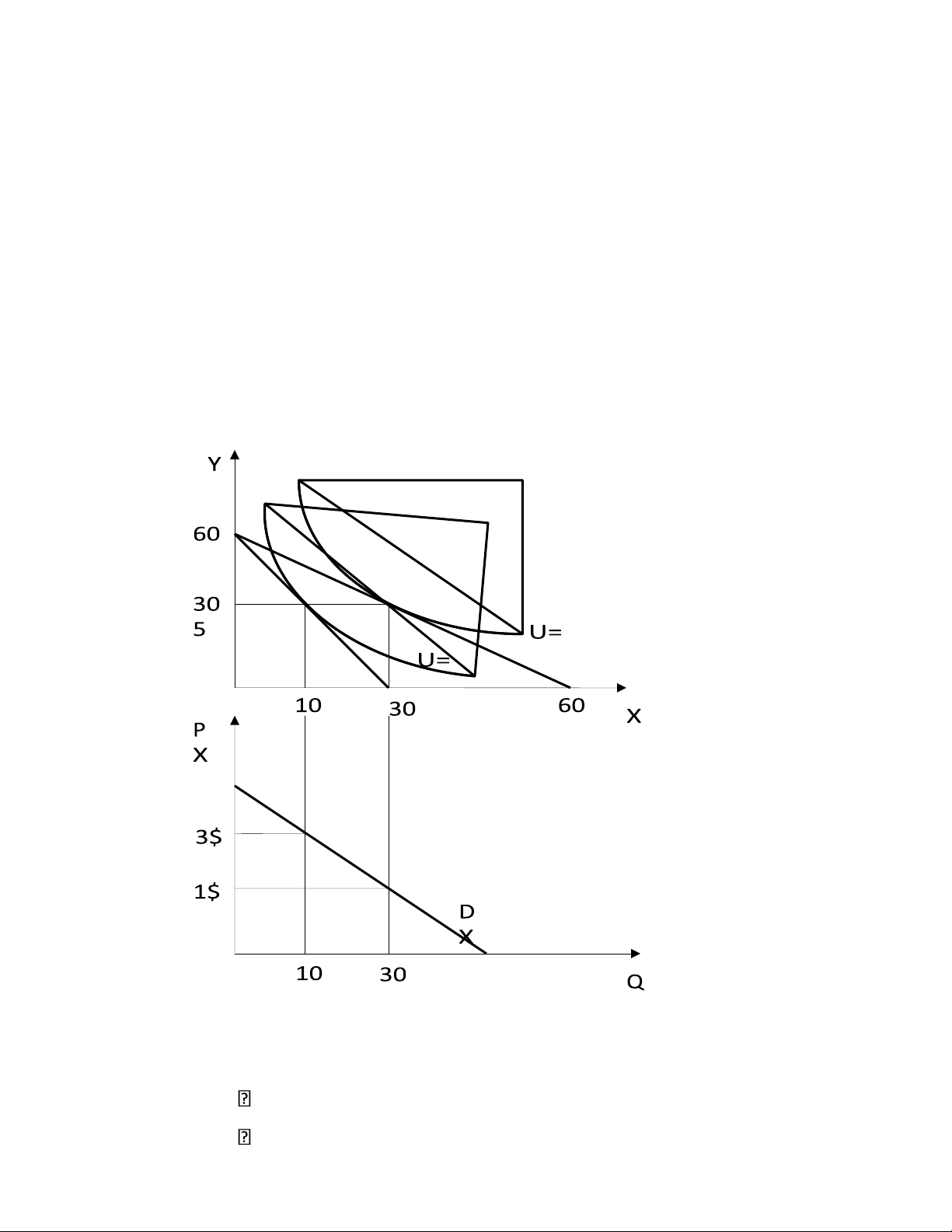
Giải hệ hai phương trình này ta được X1 = 6, Y1 = 18.
b. Tương tự, điểm tiêu dùng tối ưu khi giá hàng hóa X tăng lên gấp ba là nghiệmcủa hệ sau: 36 = 3X + 3Y Y 3 X 3
c. Tương tự, giải hệ phương trình sau ta được X3 = 12, Y3 = 36. 72 = X + 3Y Y 1 X 3 d. Đồ thị minh họa
Bài 2. (Xác định hàm cầu Marshall)
Một người tiêu dùng có ngân sách hạn chế là I để chi tiêu cho 2 hàng hóa X và Y
với giá tương ứng là PX và PY. Hàm lợi ích của người tiêu dùng này có dạng U(X;Y)= X.Y.
Hãy xác định hàm cầu của các hàng hóa X và Y bằng phương pháp nhân tử Lagrange? lOMoAR cPSD| 59452058
Lời giải :
Mục tiêu của người tiêu dùng là tối đa hóa lợi ích trong việc tiêu dùng hàng hóa,
dịch vụ ta có hàm mục tiêu: U(X;Y)= X.Y max.
Ràng buộc ngân sách của người tiêu dùng có dạng I = X PX + Y PY Ta
có hàm Lagrange tương đương như sau:
L = XY + λ(X PX + Y PY - I) Max
Đạo hàm riêng theo các biến số X, Y và λ ta có: L 0 Y PX 0 X L 0 X PY 0 Y L
0 P XX. P YY. I 0
Trong đó λ được gọi là số nhân Lagrange.
Giải hệ phương trình trên ta có hàm cầu của các hàng hóa tương ứng như sau: 1 1 Q X QY 2P và X 2PY Bài 3 .
Hàm lợi ích Coob Douglas với 2 hàng hoá X và Y (dạng Coob – Douglas) được cho
bởi phương trình U = X1/2 Y1/2 hay U = √XY
Người tiêu dùng này có thu nhập là 60 $. Giá của hàng hoá X là 3$ và giá của hàng hoá Y là 1$
a. Hãy xác định kết hợp tiêu dùng 2 hàng hoá X và Y. Lời giải:
đường ngân sách BL: 60 = 3X + 1Y hay Y = 60 - 3X (1)
Lợi ích cận biên: MUX = (U)’X = 0,5√Y/ X & MUY = (U)’Y = 0,5√X/Y Điều
kiện tối ưu là: MUX/Px = MUY/Py.
Ta có: 0,5√Y/ X /3 = 0,5√X/Y /1 suy ra Y = 3X (2)
Từ (1) và (2) ta có: X* = 30 và Y* = 10; UMax = 10√3 lOMoAR cPSD| 59452058
b. Nếu giá của hàng hoá X giảm xuống còn 1& thì kết hợp tiêu dùng sẽ thay
đổi như thế nào? LỜI GIẢI:
BL khi giá hhoá X thay đổi 60 = 1X + 1Y (3).
Điều kiện MUX/Px = MUY/PY sẽ là: 0,5√Y/X /1 = 0,5√X/Y /1 suy ra Y = X (4)
Từ (3) và (4) ta có: X* = 30 và Y* = 30; UMax = 30 c. TE = 30 - 10 = 20 SE = 10 (√3 -1) IE = 10√3 (√3 -1)
(TE = SE + IE = 10 (√3 -1) + 10√3 (√3 -1) = 20
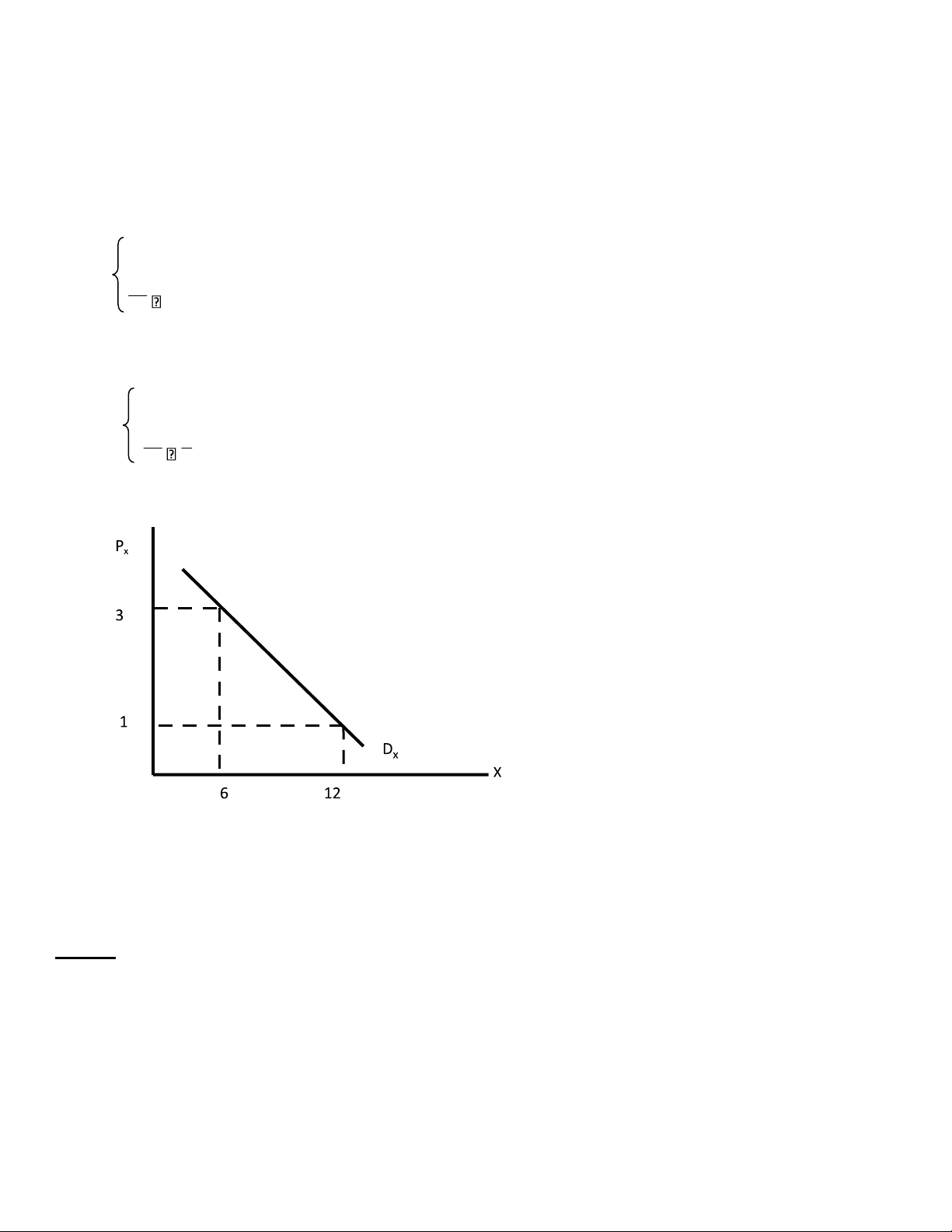
d. Hãy minh hoạ các kết quả tính toán trên bằng đồ thị 30 √ 10 3 d. X
Biểu cầu đối với hàng hoá X, ta có: P = 3$ Qx = 10 P = 1$ Qx = 30 lOMoAR cPSD| 59452058
Bài 2. Một người tiêu dùng có ngân sách hạn chế là I để chi tiêu cho 2 hàng hoá X
và Y với giá tương ứng là PX và PY. Hàm lợi ích của người tiêu dùng này có dạng U(X;Y) = √X.Y.
Hãy xác định hàm cầu của các hàng hoá X và Y bằng phương pháp nhân tử Lagrange? Lời giải
Căn cứ vào mục tiêu của người tiêu dùng là tối đa hoá lợi ích trong việc tiêu dùng
hàng hoá, dịch vụ chúng ta có hàm mục tiêu: U(X;Y) = √X.Y max
Ràng buộc ngân sách của người tiêu dùng có dạng I = PX.X + PY.Y
Như vậy, chúng ta phải giải bài toán cực trị có điều kiện ràng buộc là: U(X;Y) = √X.Y max với I = PX.X + PY.Y
Ta có hàm Lagrange tương đương như sau: L = √X.Y + [ I – (PX.X + PY.Y)] Đạo
hàm riêng theo các biến số X, Y và ta có: L’X = 0 hay 0,5√Y/X = PX L’Y = 0 hay 0,5√X/Y = PY L
0 PX .X PY .Y I 0
Trong đó được gọi là số nhân Lagrange.
Giải hệ phương trình trên ta có hàm cầu của các hàng hoá tương ứng như sau: I I Q X QY Cầu hàng hoá X là
2P và cầu hàng hoá Y là 2P X Y
• K/luận 1: Dx và Dy dốc xuống theo qui luật về cầu
• K/luận2: X và Y là các hàng hóa thông thường
• K/luận 3: X và Y là các hàng hóa độc lập
Bài 4. (Ứng dụng các co giãn để quyết định lượng bán)
Theo hiệp hội sản xuất thép Việt Nam (VSA) dự đoán rằng co giãn của cầu theo
giá đối với thép ở Việt Nam là -1,2, trong khi đó co giãn của cầu theo thu nhập là 3.
Trong năm tới, các nhà sản xuất thép tại Việt Nam dự định tăng giá trung bình của lOMoAR cPSD| 59452058
thép lên 5%, và họ kỳ vọng thu nhập dùng để chi tiêu của người tiêu dùng sẽ tăng khoảng 3%. a.
Nếu lượng bán thép được sản xuất trong nước năm nay là 300 triệu tấn, các
nhàsản xuất của Việt Nam bán được bao nhiêu vào năm tới? b.
Các nhà sản xuất trong nước nên tăng giá thép lên bao nhiêu nếu họ muốn
tănglượng bán lên 5% trong năm tới ?
Lời giải :
a. Lượng bán thép thay đổi khi giá tăng 5% là: 5% x (-2) = -10%
Lượng bán thép thay đổi khi thu nhập tăng 3% là: 3% x 3 = 9%
Tổng lượng bán ô tô thay đổi khi các biến thay đổi là -1%.
Như vậy năm tới lượng bán sẽ giảm đi 1%. Năm nay lượng bán là 300 triệu tấn thì
năm tới là 297 triệu tấn.
b. Nếu VSA muốn tăng lượng bán lên 5% giá phải tăng lên 2%. Vì thu nhập củangười
tiêu dùng là yếu tố nằm ngoài khả năng kiểm soát của VSA, nên họ phải tăng giá
để triệt tiêu ảnh hưởng của thu nhập tăng làm cho lượng bán thép tăng lên 5%.
Bài 5. (Co giãn của doanh thu theo giá)
Tổng doanh thu hoạt động của hãng vận tải công cộng số 19 là 1 tỷ đồng trong
khi tổng chi phí hoạt động là 1,2 tỷ đồng. Giá của một lần đi là 7 ngàn đồng, và co
giãn của cầu theo giá được ước lượng là -0,6. Theo luật, các nhà chức trách của ngành
giao thông công cộng phải từng bước thực hiện loại bỏ thua lỗ. a.
Hãng nên áp dụng chính sách giá nào (tăng hay giảm giá vé để tăng Tổng doanhthu)? Tại sao? b.
Hãng phải áp dụng giá cho mỗi lượt đi là bao nhiêu để bù được những thâm
hụtnếu hãng không thể giảm được chi phí?
Lời giải :
Một vấn đề rất được quan tâm trong phân tích kinh tế là phản ứng của doanh thu
đối với sự biến động giá hàng hóa trên thị trường. Nếu ký hiệu ER là co giãn của tổng lOMoAR cPSD| 59452058
doanh thu theo giá P thì có thể hiểu đó là thước đo sự nhạy cảm của tổng doanh thu
về hàng hóa này trước sự thay đổi 1% của giá.
Công thức: ER = (dTR/dQ)x(Q/TR) = [d(PxQ)/dQ)] x(1/P)
= [P x1 + (dP/dQ) x (1/Q)] x (1/P) = 1 + E Áp dụng:
a. Hãng nên tăng giá sẽ làm tăng tổng doanh thu vì cầu không co giãn: EP = - 0,6
b. Nếu hãng không thể giảm được chi phí thì cần phải tăng doanh thu lên 200 triệutức
là doanh thu phải tăng 20% hay (%∆TR = + 20).
Vì hệ số co giãn của doanh thu theo giá là S = ER = 1 + ED = 0,4 tức là giá tăng 1%
sẽ làm doanh thu tăng 0,4%. Mặt khác theo định nghĩa ER = 0,4 = (%∆TR)/(%∆P) =
(%20)/(%∆P) do đó (%∆P) = 50. Vậy để doanh thu tăng 20% thì giá vé phải tăng 50%.
Do đó hãng BRT phải đặt giá mới là P = 7 x 1,5 = 10,5 ngàn đồng/lượt.
Bài 6 . (Ứng dụng hệ số co giãn EDP, EDI, EDxPy, EDxPs, EDA)
Phương trình đường cầu xuất khẩu sản phẩm cacao của Công ty C & C được cho bởi.
Qx = 1,5 - 3Px + 0,08I + 2Py - 0,6Ps + 0,12A Trong đó:
Qx: Lượng cacao xuất khẩu hàng năm (nghìn tấn) Px: Giá cacao ($/kg)
I: Thu nhập của người tiêu dùng (nghìn $/năm)
Py: Giá cacao của hãng cạnh tranh ($/kg) Ps: Giá đường ($/kg)
A: Chi phí quảng cáo của hãng (nghìn $/năm) Giả sử
rằng PX = 2, I = 25, PY = 1,8, PS = 0,5, A = 10
a. Tính lượng cacao xuất khẩu của công ty C & C trong năm.
b. Tính các hệ số co giãn EDP, EDI, EDxPy, EDxPs, EDA
c. Giả sử trong năm tới hãng tăng giá cacao lên 5% và tăng chi phí quảng cáo lên
12%. Đồng thời Công ty C & C dự báo thu nhập của người tiêu dùng trong năm
tới tăng 4%, giá PY tăng 7% và PS giảm 8%. lOMoAR cPSD| 59452058
Dự tính lượng xuất khẩu cacao của công ty trong năm tới. Đáp số:
a. Lượng cacao xuất khẩu của công ty C & C trong năm nay là:
Q = 1,5 – 3 x 2 + 0,08 x 25 + 2 x 1,8 - 0,6 x 0,5 + 0,12 x 10 = 2
b. Các hệ số co giãn EDP, EDI, EDxPy, EDxPs, EDA
EDP = (∂Q/∂P).(P/Q) = -3 x (2/2) = -3
EDI = (∂Q/∂I).(I/Q) = 0,08 x (25/2) = 1
EDxPy = (∂QX/∂PY).(PY/QX) = 2 x (1,8/2) = 1,8
EDxPs = (∂QX/∂PS).(PS/QX) = -0,6 x (0,5/2) = - 0,15
EDA = (∂Q/∂A).(A/Q) = 0,12 x (10/2) = 0,6
c. Giá cacao tăng 5% sẽ làm cho lượng cacao giảm 3 x 5% = 15%
Quảng cáo tăng 12% sẽ làm cho lượng cacao tăng 0,6 x 12% = 7,2%
Thu nhập tăng 4% sẽ làm cho lượng cacao tăng 1 x 4% = 4%
PY tăng 7% sẽ làm cho lượng cacao tăng 1,8 x 7% = 12,6%
PS giảm 8% sẽ làm cho lượng cacao tăng (- 0,15) x (- 8%) = 1,2%
Tổng hợp lại tổng lượng cacao thay đổi là:
Q% = -15% + 7,2% + 4% + 12,6% + 1,2% = 10%
Vậy lượng cacao xuất khẩu sẽ tăng 10% (so với năm trước Q = 2 (nghìn tấn) hay
lượng cacao trong năm tới của C & C) là: 2 x (1 + 0,1) = 2,2 (nghìn tấn).