

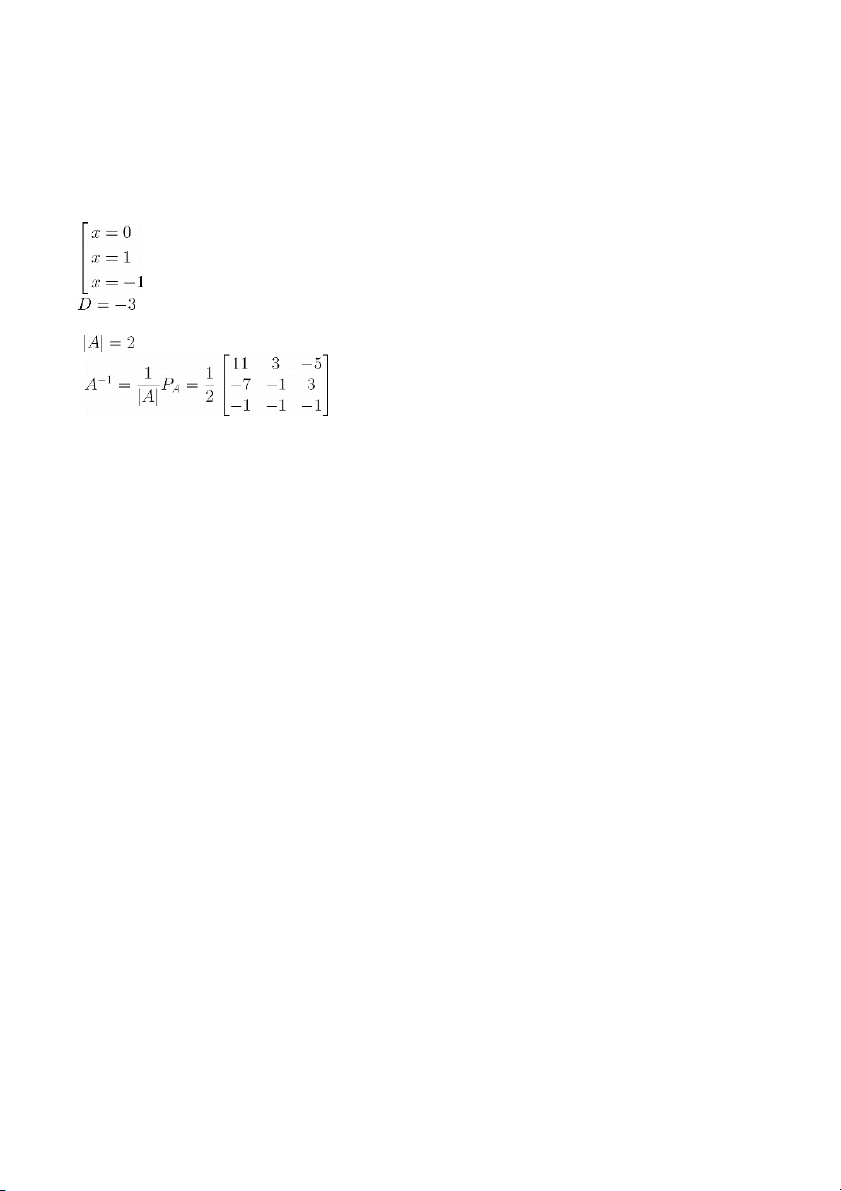


Preview text:
TRƯỜNG ĐH DUY TÂN BÀI TẬP QUA MẠNG KHOA KHTN
MÔN: TOÁN CAO CẤP C2
= = == = = = = = = = = = Bài mẫu số 2 = = = = = = = = = = = =
Phần 1: Câu hỏi trắc nghiệm I. Phần tùy chọn:
1. Xác định ma trận con cấp 2, của ma trận (a) (b) (c) (d)
2. Xác định giá trị của định thức (a) (b) (c) (d)
3. Xác định giá trị của định thức (a) (b) (c) (d)
4. Xác định giá trị của định thức (a) (b) (c) (d) 5. Xác định (a) (b) (c) (d) 6. Xác định (a) (b) (c) (d) 7. Xác định (a) (b) (c) (d) 8. Xác định (a) (b) (c) (d) 9. Xác định (a) (b) (c) (d)
10. Xác định ma trận nào sau đây là ma trận khả nghịch (a) (b) (c) (d) II.
Xác định các phát biểu sau đây đúng hay sai.
1. Định thức chỉ xác định đối với ma trận vuông.
2. Phép biến đổi sơ cấp không làm thay đổi giá trị của định thức.
3. Định thức không thay đổi qua phép chuyển vị.
4. Mọi ma trận vuông có định thức khác không đều khả nghịch.
5. Định thức của một tổng hai ma trận bằng tổng hai định thức.
Phần 2: Câu hỏi ngắn.
1. Sử dụng tính chất của định thức để chứng minh đẳng thức 2. Giải phương trình 3. Tính định thức 4. Cho ma trận (a) Tính .
(b) A có khả nghịch hay không? Trong trường hợp A khả nghịch hãy sử dụng phương pháp ứng dụng của định thức để tìm . ĐÁP ÁN ĐỀ MẪU SỐ 2
Phần 1: Câu hỏi trắc nghiệm I. Phần tùy chọn:
1. (c), 2. (a), 3. (c), 4. (c), 5. (c), 6. (a), 7. (d), 8. (c), 9. (d), 10. (b) II.
Câu hỏi đúng – sai.
1. Đúng, 2. Sai, 3. Đúng, 4. Đúng, 5. Sai.
Phần 2. Câu hỏi ngắn. 1. 2. 3. 4. (a) (b) TRƯỜNG ĐH DUY TÂN
BÀI GIẢI BÀI TẬP QUA MẠNG KHOA KHTN
MÔN: TOÁN CAO CẤP C2
= = == = = = = = = = = = Bài tập mẫu số 2 = = = = = = = = = = = =
Phần 1: Câu hỏi trắc nghiệm I. Phần tùy chọn: 1.
là ma trận nhận được từ ma trận A bằng cách bỏ đi hàng 1 và cột 2. Vậy đáp án (c) là đáp án đúng.
2. Trong định thức có một hàng không thì định thức bằng 0. Đáp án (a)
3. Định thức của tam giác bằng tích các phần tử nằm trên đường chéo chính. Đáp án (c)
4. Trong định thức có hai hàng bằng nhau thì định thức bằng 0. Đáp án (c).
5. Đảo vị trí hai hàng thì định thức đổi dấu. Đáp án (c)
6. Nhân một số với một hàng, định thức nhân với số được nhân. Đáp án (a).
7. Phép biến đổi sơ cấp thứ ba không làm thay đổi giá trị của định thức. Đáp án (d).
8. Định thức có thể tách một hàng hoặc một cột thành hai định thức. Định thức tạo thành có hàng 1
bằng 0 nên định thức bằng 0. Đáp án (c).
9. Phép chuyển vị không làm thay đổi giá trị của định thức. Đáp án (d).
10. Ma trận vuông khả nghịch khi và chỉ khi định thức của nó khác 0. Đáp án (b). II.
Câu hỏi đúng – sai. 1. Đúng.
2. Sai. Vì phép biến đổi sơ cấp thứ nhất và thứ hai làm thay đổi giá trị của định thức.
3. Đúng. Theo tính chất của định thức.
4. Đúng. Theo tính chất của định thức.
5. Sai. Theo tính chất của định thức.
Phần 2. Câu hỏi ngắn. 1.
Định thức thứ nhất có hàng 2 bằng hàng 3, định thức thứ hai có hàng 1 và hàng 2 tỷ lệ nên chúng bằng 0.
2. Bằng cách khai triển định thức ta nhận được phương trình
3. Sử dụng tổng hợp phương pháp biến đổi sơ cấp và khai triển theo cột 4.
(a) Bằng cách khai triển trực tiếp ta nhận được (b) Vì
nên A khả nghịch. Tìm ma trận phụ hợp
Hoàn toàn tương tự, ta có
5. Biến đổi sơ cấp đưa
về dạng bậc thang rút gọn.
Dạng bậc thang rút gọn của A là ma trận đơn vị nên A khả nghịch và




