













Preview text:
lOMoAR cPSD| 58504431
BÀI TẬP MÔN THỐNG KÊ TRONG KINH TẾ VÀ KINH DOANH Chương 1
1. Môt nhà nghiên cứu muốn tìm hiểu về kết quả kinh doanh của các doanh nghiệp tại ĐBSCL.
Dựa vào số liệu của các Sở Kế hoạch – Đầu tư các tỉnh, nhà nghiên cứu có danh sách ngẫu nhiên 10.000 doanh nghiệp.
a. Nhà nghiên cứu muốn chọn một mẫu ngẫu với cỡ mẫu n = 500 doanh nghiệp. Giả sử
nhànghiên cứu chọn quan sát đầu tiên trong mẫu có số thứ tự là 10, những quan sát tiếp theo
trong mẫu sẽ có số thứ tự là gì?
b. Giả sử, nhà nghiên cứu muốn chọn một mẫu ngẫu với cỡ mẫu n = 1.000 doanh nghiệp
vàdoanh nghiệp đầu tiên trong mẫu có số thứ tự là 5, những quan sát tiếp theo trong mẫu sẽ có số thứ tự là gì?
c. Tại sao nhà nghiên cứu cần chọn mẫu mà không thu thập số liệu của tổng thể?
d. Điều gì sẽ xảy ra đối với số liệu mẫu nếu thứ tự của các doanh nghiệp trong danh sáchkhông
được xếp một cách ngẫu nhiên?
2. Giả sử bạn đang tìm hiểu về kết quả học tập của sinh viên ĐHCT. Dựa vào số liệu của Phòng
Đào tạo, bạn được cung cấp danh sách ngẫu nhiên 40.000 sinh viên của trường. a.
Bạn hãy mô tả quy trình bạn sẽ áp dụng để chọn một mẫu ngẫu nhiên gồm 200 sinh
viêncho nghiên cứu của bạn. b.
Nếu bạn muốn chọn một mẫu ngẫu với cỡ mẫu n = 500 sinh viên. Giả sử bạn chọn quan
sátđầu tiên trong mẫu có số thứ tự là 20, những sinh viên tiếp theo trong mẫu sẽ có số thứ tự là gì? c.
Nếu bạn chỉ chọn mẫu gồm những sinh viên đang lên lớp học thì mẫu mà bạn chọn
đượccó phải là mẫu ngẫu nhiên không? Số liệu từ mẫu này có đại diện cho tổng thể các sinh viên không? Chương 2
1. Một công ty thế chấp lấy mẫu ngẫu nhiên các tài khoản của khách hàng về kết quả kinh
doanh. Cho biết mỗi biến sau đây là phân loại hay số. Nếu phân loại, đưa ra mức độ đo lường.
Nếu bằng số, nó rời rạc hay liên tục?
a. Giá mua ban đầu của các căn hộ của khách hàng.
b. Thành phố/tỉnh cư trú của khách hàng
c. Mức độ hài lòng của chủ sở hữu đối với dịch vụ của công ty (1: rất không hài lòng; đến 5:rất hài lòng)
d. Số lần thanh toán trên mạng của khách hàng bị trễ.
2. Một số câu hỏi được đặt ra cho một mẫu khách ngẫu nhiên đến một trung tâm thông tin du
lịch ở London. Đối với mỗi câu hỏi dưới đây, mô tả loại dữ liệu thu được.
a. Bạn có đang ở qua đêm ở London không?
b. Đã bao nhiêu lần bạn đến thăm London trước đây? lOMoAR cPSD| 58504431
c. Những điểm thu hút nào sau đây bạn đã ghé thăm? Tòa tháp ở Luân Đôn Cung điện Buckingham Big Ben Vườn hoa Covent Tu viện Westminster
d. Bạn có khả năng đến thăm London một lần nữa trong 12 tháng tới: (1) không có khả năng,(2)
rất có thể, (3) rất có thể?
3. Một quản trị viên đại học yêu cầu phân chia chi phí đi lại cho giảng viên để tham dự các
cuộc họp chuyên môn khác nhau. Các khoản phì được ước tính như sau 31% chi phí đi lại được
chi cho chi phí vận chuyển, 25% được chi cho nhà ở, 17% được chi cho thực phẩm và 20%
được chi cho phí đăng ký hội nghị; phần còn lại được chi cho các chi phí linh tinh. a. Xây dựng
một biểu đồ bánh (Pie chart) cho các khoản chi phí.
b. Xây dựng biểu đồ cột (bar chart) cho các khoản chi phí.
4. Người giám sát của một nhà máy thu được một mẫu ngẫu nhiên về kinh nghiệm của nhân
viên (tính theo tháng) và thời gian hoàn thành một nhiệm vụ (tính bằng phút). Vẽ đồ thị dữ liệu
với một thành phần (kinh nghiệm hay thời gian).
Kinh nghiệm/thời gian < 5 phút 5 và < 10 phút 10 và < 15 phút Ít hơn 3 tháng 10 13 25 3 < 6 tháng 10 13 12 6 < 9 tháng 9 22 8 9 < 12 tháng 12 18 19 12 và > 12 tháng 15 12 10
5. Tóm tắt thống kê của Hoa Kỳ cung cấp một bản tóm tắt thống kê đáng tin cậy và đầy đủ về
số lượng các loài động vật hoang dã đang bị đe dọa ở cả trong và ngoài nước Mỹ kể từ tháng
4 năm 2010 (Bảng 383, Tóm tắt thống kê của Hoa Kỳ 2011): Loài
Các loài động vật hoang dã có
Các loài động vật hoang dã có
nguy cơ tuyệt chủng ở Hoa Kỳ
nguy cơ tuyệt chủng bên ngoài Hoa Kỳ Động vật có vú 70 255 Chim 76 182 Bò sát 13 66 Động vật lưỡng cư 14 8 Cá 74 11 lOMoAR cPSD| 58504431 a.
Xây dựng một biểu đồ cột về số lượng các loài động vật hoang dã đang bị đe dọa ở HoaKỳ. b.
Xây dựng một biểu đồ cột về số lượng các loài động vật hoang dã có nguy cơ tuyệt chủngbên ngoài Hoa Kỳ. c.
Xây dựng một biểu đồ cột để so sánh số lượng các loài có nguy cơ tuyệt chủng ở Hoa
Kỳvới số lượng các loài có nguy cơ tuyệt chủng bên ngoài Hoa Kỳ.
6. Số lượng nam và nữ theo học tại các trường đại học (đại học và sau cử nhân) tại Hoa Kỳ
từnăm 2000 đến 2008 được trình bày bên dưới. Trình bày đồ thị những dữ liệu này với một chuỗi thời gian. S nh p h c (ngànố ậ ọ Nam Nữ sinh viên) 2000 6721, 8590,5 8 2001 6960, 967,2 8 2002 7202, 9409,6 1 2003 7255, 9644,9 6 2004 7387, 9884,4 3 2005 7455, 10031, 9 6 2006 7574, 10184, 8 1 2007 7815, 10432, 9 2 2008 8188, 10913, 9 9
7. Sinh viên tự thu thập số liệu chuỗi thời gian về GDP, kim ngạch xuất, nhập khẩu, dân sốcủa
Việt Nam trên Niên giám thống kê của Tổng cục thống kê và vẽ các đồ thị chuỗi thời gian cho những dữ liệu này.
8. Hãy xem xét các dữ liệu sau đây về tuổi của 28 thành viên một câu lạc bộ bơi lội. 17 62 15 65 28 51 24 65 39 41 35 15 39 32 36 37 40 21 44 37 59 13 44 56 12 54 64 59
a. Xây dựng phân phối tần số.
b. Xây dựng biểu đồ histogram. lOMoAR cPSD| 58504431 c. Xây dựng một ogive.
d. Xây dựng một biểu đồ thân và lá (stem and leaf).
9. Xây dựng một biểu đồ thân và lá cho những giờ mà 20 sinh viên đã dành để học cho một bài kiểm tra Thống kê. 3, 2, 4, 6, 4, 2, 2, 3, 4, 5,5 5 8 5 2 8 3 6 9 4 5, 6, 3, 2, 5, 3, 2, 1, 2, 3,6 2 7 0 4 0 6 9 0 8
10. Xây dựng một biểu đồ phân tán (scatter plot) cho dữ liệu sau:
(5, 53) (21, 65) (14, 48) (11, 66) (9, 46) (4, 56)
(7, 53) (21, 57) (17, 49) (14, 66) (9, 54) (7, 56)
(9, 53) (21, 52) (13, 49) (14, 56) (9, 59) (4, 56)
11. Bảng dưới đây cho thấy tuổi của các đối thủ trong một sự kiện quần vợt từ thiện ở Rome: Tu iổ Ph nầ trăm 18–24 18,26 25–34 16,25 35–44 25,88 45–54 19,26 55+ 20,35
a. Xây dựng một phân phối tần số tích lũy tương đối.
b. Bao nhiêu phần trăm đối thủ cạnh tranh dưới 35 tuổi?
c. Bao nhiêu phần trăm đối thủ cạnh tranh từ 45 tuổi trở lên? 12.
Một công ty đặt giá khác nhau cho một bộ DVD cụ thể ở tám vùng khác nhau của
đấtnước. Bảng kèm theo cho thấy số lượng bộ được bán và giá tương ứng (tính bằng đô la). Vẽ
sơ đồ dữ liệu bằng cách sử dụng biểu đồ phân tán với doanh số là biến phụ thuộc và giá là biến độc lập. Lượng bán
420 380 350 400 440 380 450 420 Giá 104 195 148 204 96 256 141 109 13.
Bảng sau liệt kê số lượng khách truy cập hàng ngày vào trang web của một doanh
nghiệpmới trong năm đầu tiên. Thán Số Thán Số g lượt g lượt 1 5.400 7 5.600 2 5.372 8 5.520 3 5.265 9 5.280 4 5.250 10 5.400 5 5.289 11 5.448 6 5.350 12 5.500
a. Vẽ đồ thị dữ liệu với một chuỗi thời gian sử dụng giá trị từ 5.000 đến 5.700 trên trục tung.
b. Vẽ đồ thị dữ liệu với một chuỗi thời gian sử dụng tỷ lệ xích từ 4.000 đến 7.000. lOMoAR cPSD| 58504431
c. Nhận xét về sự khác biệt giữa hai đồ thị thời gian này.
14. Một mẫu gồm 20 nhà phân tích tài chính đã được yêu cầu cung cấp dự báo thu nhập trên
mỗi cổ phiếu của một công ty cho năm tới. Các kết quả được tóm tắt trong bảng sau:
D báoự ($/cổ S nhà phânố phi uế ) tích 9,95 < 10,45 2 10,45 < 10,95 8 10,95 < 11,45 6 11,45 < 11,95 3 11,95 < 12,45 1
a. Xây dựng biểu đồ histogram.
b. Xác định tần số tương đối.
c. Xác định tần số tích lũy.
d. Xác định và giải thích các tần số tích lũy tương đối.
15. Một công ty thực hiện một bài kiểm tra năng lực cho tất cả các đại diện bán hàng mới. Ban
quản lý quan tâm đến điểm kiểm tra này có thể dự đoán doanh số hàng tuần của các đại diện
mới. Điểm kiểm tra năng lực nằm trong khoảng từ 0 đến 30 với điểm số lớn hơn cho thấy năng
khiếu cao hơn. Doanh số hàng tuần được ghi nhận bằng trăm đô la. Xây dựng một biểu đồ phân
tán các điểm kiểm tra và doanh số hàng tuần cho một mẫu ngẫu nhiên gồm 10 đại diện sau đây. Đi m ki m tra (ể ể 12 30 15 24 14 18 28 26 19 27 x)
Doanh s tu n (ố ầ y) 20 60 27 50 21 30 61 54 32 57 Chương 3
1. Một chuỗi cửa hàng bách hóa lấy mẫu ngẫu nhiên 10 cửa hàng ở một tiểu bang. Sau khi xem
xét hồ sơ bán hàng, người ta thấy rằng, so với cùng kỳ năm ngoái, % tăng doanh số đô la sau
đây đã đạt được trong giai đoạn Giáng sinh năm nay: 10,2 3,1 5,9 7,0 3,7 2,9 6,8 7,3 8,2 4,3
a. Tính phần trăm tăng trung bình trong doanh số đô la. b. Tính trung vị.
2. Độ tuổi của một mẫu gồm 12 sinh viên đăng ký khóa học kinh tế vĩ mô trực tuyến như sau: 21 22 27 36 18 19 22 23 22 28 36 33
a. Tuổi trung bình của mẫu này là bao nhiêu? b. Tìm tuổi trung vị. c. Giá trị mode là gì?
d. Tính 5 chỉ số mô tả số liệu.
3. Độ tuổi của một mẫu ngẫu nhiên những người tham dự một trận bóng đá gần đây như sau: 23 35 14 37 38 15 45 12 40 27 13 18 19 lOMoAR cPSD| 58504431 23 37 20 29 49 40 65 53 18 17 23 27 29 31 42 35 38 22 20 15 17 21 a. Tìm tuổi trung bình. b. Tìm độ lệch chuẩn.
c. Tìm hệ số biến động.
4. Một mẫu dữ liệu ngẫu nhiên có giá trị trung bình là 75 và phương sai là 25. a.
Sử dụng định lý Chebyshev để xác định phần trăm quan sát có giá trị trong khoảng từ 65đến 85. b.
Nếu dữ liệu có tính đối xứng, sử dụng quy tắc thực nghiệm để tìm phần trăm xấp xỉ
củacác quan sát có giá trị trong khoảng từ 65 đến 85.
5. Bao nhiêu thời gian để giám đốc điều hành công ty tập thể dục hàng ngày? Các chương trình
đào tạo tồn tại để giúp các giám đốc điều hành cải thiện sức khỏe của họ để họ có thể suy nghĩ
rõ ràng hơn và đưa ra quyết định kinh doanh tốt hơn. Giả sử rằng chúng tôi lấy mẫu ngẫu nhiên
mười giám đốc điều hành và có được thời gian tập thể dục hàng ngày sau đây (tính bằng phút): 20 35 28 22 10 40 23 32 28 30
a. Tính thời gian tập thể dục trung bình hàng ngày.
b. Tính độ lệch chuẩn sử dụng các công thức khác nhau được trình bày trong lý thuyết.c.
Tìm hệ số biến động. 6.
Một nhà xuất bản nhận được một bản sao của sách giáo khoa 500 trang từ máy in.
Bằngchứng trang được đọc cẩn thận và số lỗi trên mỗi trang được ghi lại, tạo ra dữ liệu trong bảng sau: Số lỗi 0 1 2 3 4 5 Số trang 102 138 140 79 33 8
Tìm giá trị trung bình và độ lệch chuẩn trong số lỗi trên mỗi trang. 7.
Sau đây là một mẫu ngẫu nhiên về giá cho mỗi miếng gỗ dán, X và số lượng được bán, Y(tính bằng nghìn): Đ n giáơ Lượng (x) bán (y) $6 80 7 60 8 70 9 40 10 0
a. Tính hiệp phương sai giữa x và y.
b. Tính hệ số tương quan. Giá và lượng bán có mối quan hệ như thế nào?
8. Bệnh viện River Hills quan tâm đến việc xác định hiệu quả của một loại thuốc mới để giảm
thời gian cần thiết để phục hồi hoàn toàn sau phẫu thuật đầu gối. Phục hồi hoàn toàn được đo
bằng một loạt các bài kiểm tra sức mạnh so sánh đầu gối được điều trị với đầu gối không được
điều trị. Thuốc đã được dùng với số lượng khác nhau cho 18 bệnh nhân trong khoảng thời gian lOMoAR cPSD| 58504431
6 tháng. Đối với mỗi bệnh nhân, số đơn vị thuốc, X và ngày phục hồi hoàn toàn, Y, được cung
cấp bởi dữ liệu (x, y) sau đây:
(5, 53) (21, 65) (14, 48) (11, 66) (9, 46) (4, 56)
(7, 53) (21, 57) (17, 49) (14, 66) (9, 54) (7, 56)
(9, 53) (21, 52) (13, 49) (14, 56) (9, 59) (4, 56)
a. Tính toán hiệp phương sai. B nhệ nhân X Y Xi - X Yi - Y (Xi - X)(Yi - Y) (Xi - X)2 (Yi - Y)2 1 5 53 -6.61 -2.22 14.69 43.71 4.94 2 21 65 9.39 9.78 91.80 88.15 95.60 3 14 48 2.39 -7.22 -17.25 5.71 52.16 4 11 66 -0.61 10.78 -6.59 0.37 116.16 5 9 46 -2.61 -9.22 24.08 6.82 85.05 6 4 56 -7.61 0.78 -5.92 57.93 0.60 7 7 53 -4.61 -2.22 10.25 21.26 4.94 8 21 57 9.39 1.78 16.69 88.15 3.16 9 17 49 5.39 -6.22 -33.53 29.04 38.72 10 14 66 2.39 10.78 25.75 5.71 116.16 11 9 54 -2.61 -1.22 3.19 6.82 1.49 12 7 56 -4.61 0.78 -3.59 21.26 0.60 13 9 53 -2.61 -2.22 5.80 6.82 4.94 14 21 52 9.39 -3.22 -30.25 88.15 10.38 15 13 49 1.39 -6.22 -8.64 1.93 38.72 16 14 56 2.39 0.78 1.86 5.71 0.60 17 9 59 -2.61 3.78 -9.86 6.82 14.27 18 4 56 -7.61 0.78 -5.92 57.93 0.60 Trung bình 11.6 55.2 30.13 32.73 1 2 4.03
Cov(X, Y) = E(Xi - X)(Yi - Y) = 4,03 > 0 : X và Y có tương quan dươ ớng v i nhau 2
x = E(Xi - X)2 = 30,13 => x = 5,49 2
y = E(Yi - Y)2 = 32,73 => y = 5,72 b. Tính hệ số tương quan. > 0 lOMoAR cPSD| 58504431
c. Thảo luận ngắn gọn về mối quan hệ giữa số lượng đơn vị thuốc và thời gian phục hồi. Liều
lượng nào chúng ta có thể đề nghị dựa trên phân tích ban đầu này?
Hiệp phương sai và hệ số tương quan giữa số đơn vị thuốc được dùng và số ngày hồi phục có
giá trị dương, chứng tỏ hai biến số này có mối tương quan dương, có nghĩa là số đơn vị thuốc
được dùng tăng thì số ngày hồi phục cũng tăng. Tuy nhiên, hệ số tương quan gần bằng 0, chứng
tỏ mối quan hệ giữa 2 biến không được chặt chẽ hay là, số đơn vị thuốc được dùng không có
nhiều tác dụng chữa trị. Do vậy, có thể dùng thuốc ít cũng không ảnh hưởng đến quá trình phục hồi.
9. Một sân bay lớn gần đây đã thuê chuyên gia tư vấn John Cadariu để nghiên cứu vấn đề chậm
trễ giao thông hàng không. Ông đã ghi lại số phút máy bay bị trễ cho một mẫu các chuyến bay trong bảng sau: Số phút trễ 0 < 10 10 < 20 20 < 30 30 < 40 40 < 50 50 < 60 Số chuyến bay 30 25 13 6 5 4
a. Ước tính số phút trễ trung bình.
b. Ước tính phương sai mẫu và độ lệch chuẩn.
10. Mô tả dữ liệu sau đây bằng số: (4, 53) (10, 65) (15, 48) (10, 66) (8, 46) (5, 56) (7, 60) (11, 57) (12, 49) (14, 70) (10, 54) (7, 56) (9, 50) (8, 52) (11, 59) (10, 66) (8, 49) (5, 50)
11. Trong một năm, tăng trưởng thu nhập của 500 tập đoàn lớn nhất Hoa Kỳ trung bình 9,2%;độ lệch chuẩn là 3,5%.
a. Có thể đảm bảo rằng 84% các số liệu tăng trưởng thu nhập này sẽ nằm trong khoảng nào?
b. Sử dụng quy tắc thực nghiệm, có thể ước tính rằng khoảng 68% các số liệu tăng trưởng
thunhập này sẽ nằm trong khoảng nào?
12. Hãy xem xét bốn tổng thể sau: a. 1, 2, 3, 4, 5, 6, 7, 8 b. 1, 1, 1, 1, 8, 8, 8, 8 c. 1, 1, 4, 4, 5, 5, 8, 8, d. -6, -3, 0, 3, 6, 9, 12, 15
Tất cả các tổng thể này có cùng một trung bình. Không thực hiện các phép tính, sắp xếp các
tổng thể theo độ lớn của phương sai của chúng, từ nhỏ nhất đến lớn nhất. Sau đó tính toán từng phương sai bằng tay. Chương 4.
1. Cho một không gian mẫu S = [E1, E2, E3, E4, E5, E6, E7, E8, E9, E10]
a. Cho trước A = [E1, E3, E6, E9], hãy xác định A.
b. Cho trước A = [E1, E3, E7, E9] và B = [E2, E3, E8, E9], hãy xác định:
b1. Phần giao giữa A và B. b2.
Phần hội giữa A và B. lOMoAR cPSD| 58504431
b3. Phần hội giữa A và B có phải là một hệ đầy đủ không?
2. Một công ty nhận giao một số máy móc mới phải được lắp đặt và kiểm tra trước khi nó có
sẵn để sử dụng. Công ty chắc chắn rằng sẽ mất không quá 7 ngày để lắp đặt và kiểm tra. Đặt A
là sự kiện “sẽ mất hơn 4 ngày trước khi máy móc sẵn sàng” và B là sự kiện “trong vòng chưa
đầy 6 ngày trước khi máy móc sẵn sàng”. a. Mô tả sự kiện là phần bù của sự kiện A.
b. Mô tả sự kiện là phần giao của sự kiện A và B.
c. Mô tả sự kiện là phần hội của các sự kiện A và B.
d. Sự kiện A và B có loại trừ lẫn nhau không?
e. Sự kiện A và B có phải là tập hợp đầy đủ không?
f. Chứng minh: (A B) ( A B) = B
g. Chứng minh: A ( A B) = A B
3. Florin Frenti vận hành một shop xe nhỏ, đã qua sử dụng có ba chiếc Mercedes (M1, M2,
M3) và hai Toyota (T1, T2). Hai khách hàng, Cezara và Anda, đến shop, và mỗi người chọn
một chiếc xe. Các khách hàng không biết nhau và không có giao tiếp giữa họ. Đặt các sự kiện
A và B được định nghĩa như sau:
A: Khách hàng chọn ít nhất một chiếc Toyota.
B: Khách hàng chọn hai chiếc xe cùng mẫu.
a. Xác định tất cả các cặp ô tô trong không gian mẫu.
b. Xác định sự kiện A.
c. Xác định sự kiện B.
d. Xác định phần bù của A.
e. Chứng minh: (A B) ( A B) = B
f. Chứng minh: A ( A B) = A B 4.
Không gian mẫu chứa 5 A và 7 B. Xác suất mà một bộ 2 đối tượng được chọn ngẫu
nhiên sẽ bao gồm 1 A và 1 B là bao nhiêu? 5.
Trong một thành phố 120.000 người có 20.000 người Na Uy. Xác suất mà một người
được chọn ngẫu nhiên từ thành phố sẽ là người Na Uy là bao nhiêu? 6.
Một công ty vừa nhận được máy móc mới phải được cài đặt và kiểm tra trước khi nó đi
vàohoạt động. Bảng kèm theo hiển thị đánh giá xác suất của người quản lý cho số ngày cần
thiết trước khi máy móc hoạt động. Số ngày 3 4 5 6 7 Xác suất 0,08 0,24 0,41 0,20 0,07
Đặt A là sự kiện “mất hơn bốn ngày trước khi máy móc hoạt động” và B là sự kiện “mất chưa
đầy sáu ngày trước khi máy móc sẵn sàng”. a. Tìm xác suất của sự kiện A.
b. Tìm xác suất của sự kiện B. lOMoAR cPSD| 58504431
c. Tìm xác suất của phần bù của sự kiện A.
d. Tìm xác suất của phần giao của sự kiện A và B.
e. Tìm xác suất của phần hội của các sự kiện A và B.
7. Một người quản lý có sẵn một nhóm 8 nhân viên có thể được giao cho một nhiệm vụ giám
sát dự án. 4 nhân viên là nữ và 4 là nam. 2 người đàn ông là anh em. Người quản lý phải thực
hiện nhiệm vụ một cách ngẫu nhiên để mỗi trong số 8 nhân viên có khả năng được lựa chọn
như nhau. Hãy coi A là sự kiện mà nhân viên được chọn là một người đàn ông và B là sự kiện
mà nhân viên được chọn là một trong những người anh em. a. Tìm xác suất của A. b. Tìm xác suất của B.
c. Tìm xác suất của phần giao của A và B.
8. Một công ty nhận được một phần cụ thể trong các lô hàng là 100. Nghiên cứu chỉ ra các xác
suất được cho trong bảng sau đối với số lượng các bộ phận bị lỗi trong một lô hàng. Số lỗi 0 1 2 3 >3 Xác suất 0,29 0,36 0,22 0,10 0,03
a. Xác suất sẽ có ít hơn ba phần bị lỗi trong một lô hàng là bao nhiêu?
b. Xác suất sẽ có nhiều hơn một phần bị lỗi trong một lô hàng là bao nhiêu?
c. Năm xác suất trong bảng có tổng bằng 1. Tại sao phải như vậy? 9.
Xác suất của A là 0,60, xác suất của B là 0,45 và xác suất của một trong hai là 0,80. Xác
suất của cả A và B là bao nhiêu? 10.
Xác suất của A là 0,60, xác suất của B là 0,45 và xác suất của cả hai là 0,30. Xác suất hộicủa A và B là gì? 11.
Xác suất của A là 0,80, xác suất của B là 0,10 và xác suất của cả hai là 0,08. Xác suất
cóđiều kiện của A, cho trước B là gì? A và B có độc lập về mặt xác suất không? 12.
Một nhà phân tích tài chính đã được yêu cầu đánh giá triển vọng thu nhập của bảy tập
đoàn trong năm tới và xếp hạng chúng theo tỷ lệ tăng trưởng thu nhập dự đoán. a. Có bao nhiêu
cách xếp hạng khác nhau có thể có?
b. Trong thực tế, nếu một thứ tự cụ thể là kết quả của một phỏng đoán, xác suất mà dự đoán
này sẽ trở thành chính xác là gì? 13.
Một công ty có 50 đại diện bán hàng. Nó quyết định rằng người đại diện thành công
nhấttrong năm trước sẽ được thưởng một kỳ nghỉ tháng 1 ở Hawaii, trong khi người đại diện
thứ hai sẽ giành được một kỳ nghỉ ở Las Vegas. Các đại diện khác sẽ được yêu cầu tham dự
một hội nghị về phương thức bán hàng hiện đại tại Buffalo. Có bao nhiêu kết quả có thể? 14.
Người ta ước tính rằng 30% tất cả sinh viên năm cuối trong trường đều quan tâm
nghiêmtúc đến triển vọng việc làm, 25% quan tâm nghiêm túc đến điểm số và 20% quan tâm
nghiêm túc đến cả hai. Xác suất mà một sinh viên năm cuối được chọn ngẫu nhiên từ trường
này quan tâm nghiêm túc đến ít nhất một trong hai điều này là gì? lOMoAR cPSD| 58504431 15.
Một ngân hàng phân loại người vay là rủi ro cao hoặc rủi ro thấp. Chỉ 15% các khoản
vaycủa nó được cho vay những người thuộc nhóm rủi ro cao. Trong tất cả các khoản vay của
nó, 5% bị vỡ nợ và 40% các khoản vỡ nợ được cho vay những người có rủi ro cao. Xác suất
mà một người vay có rủi ro cao sẽ vỡ nợ là bao nhiêu? 16.
Một biên tập viên có thể sử dụng tất cả, một số hoặc không một trong ba chiến lược
khảthi để tăng doanh số bán sách:
a. Một chương trình khuyến mãi tiền xuất bản đắt tiền
b. Một thiết kế bìa đắt tiền
c. Phần thưởng dành cho đại diện bán hàng đáp ứng các mức doanh số được xác định trước.
Trước đây, ba chiến lược này đã được áp dụng đồng thời chỉ với 2% số sách của công ty.
Hai mươi phần trăm các cuốn sách đã có thiết kế bìa đắt tiền, và trong số này, 80% đã có chương
trình khuyến mãi tiền xuất bản đắt tiền. Một biên tập viên đối thủ biết rằng một cuốn sách mới
sẽ có cả chương trình khuyến mãi tiền xuất bản đắt tiền và thiết kế bìa đắt tiền và bây giờ muốn
biết khả năng mà chương trình thưởng cho đại diện bán hàng sẽ được giới thiệu như thế nào.
Tính xác suất này của biên tập viên đối thủ.
Giải: gọi A, B, và C lần lượt là các sự kiện chương trình khuyến mãi, thiết kế bìa và
thưởng cho đại diện được thực hiện:
Ta có: P(A B C) = 0,02, P(B) = 0,2, và P(A|B) = 0,8, ta tìm: P(C|(A B) =
P(A B C)/[PA|B)P(B)] = .02/.16 = .125
17. Bảng kèm theo cho thấy tỷ lệ nhân viên bán hàng máy tính được phân loại theo tình trạng
hôn nhân và liệu họ có rời bỏ công việc hay ở lại trong khoảng thời gian 1 năm. Tình trạng hôn nhân Thời gian làm việc 1 năm < 1 năm Lập gia đình 0,64 0,13 Độc thân 0 , 17 0 , 06
a. Xác suất mà một nhân viên bán hàng được chọn ngẫu nhiên đã kết hôn là bao nhiêu?
b. Xác suất mà một nhân viên bán hàng được chọn ngẫu nhiên rời bỏ công việc trong năm làbao nhiêu?
c. Xác suất mà một nhân viên bán hàng được chọn ngẫu nhiên ở lại công việc trên 1 năm làbao nhiêu?
d. Xác suất mà một nhân viên bán hàng được chọn ngẫu nhiên ở lại công việc trong năm đãkết hôn là bao nhiêu?
18. Điểm của một lớp sinh viên năm nhất đại học, được thu thập sau năm đầu tiên, đã được
phân tích. Bảy mươi phần trăm sinh viên trong nhóm tứ phân vị đầu của lớp đại học đã tốt
nghiệp trung học ở trên 10% cao nhất của lớp trung học của họ, 50% học sinh ở nửa giữa của
lớp đại học đã tốt nghiệp trung học ở trên 10% cao nhất của lớp trung học và 20% học sinh ở
tứ phân vị dưới đáy của lớp đại học đã tốt nghiệp trung học ở trên 10% cao nhất của lớp trung học. lOMoAR cPSD| 58504431 a.
Xác suất mà một sinh viên năm nhất được chọn ngẫu nhiên tốt nghiệp trong 10% trên
củalớp trung học của mình là bao nhiêu? b.
Xác suất mà một sinh viên năm nhất được chọn ngẫu nhiên tốt nghiệp trong 10% trên
củalớp trung học sẽ nằm trong top 25% đầu của lớp đại học là bao nhiêu? c.
Xác suất mà một sinh viên năm nhất được chọn ngẫu nhiên không tốt nghiệp trong
10%trên của lớp trung học sẽ không nằm trong top đầu của lớp đại học?
19. (3.77) Một sinh viên cảm thấy rằng 70% các khóa học đại học của cô là thú vị và phần còn
lại nhàm chán. Sinh viên này được tiếp cận với các đánh giá của sinh viên về các giáo sư và
phát hiện ra rằng 60% các khóa học thú vị do các giáo sư trước đây đã nhận được những đánh
giá tích cực dạy và 25% các khóa học nhàm chán cũng do những ông như vậy dạy. Học kỳ tiếp
theo, sinh viên quyết định tham gia ba khóa học, tất cả từ các giáo sư đã nhận được đánh giá
tích cực của sinh viên. Giả sử rằng sinh viên này phản ứng với ba khóa học là độc lập với nhau.
a. Xác suất mà sinh viên này sẽ tìm thấy cả ba khóa học thú vị là gì?
b. Xác suất mà sinh viên này sẽ tìm thấy ít nhất một trong những khóa học thú vị là gì?
20. Một nhà xuất bản gửi tài liệu quảng cáo cho một văn bản kế toán đến 80% tất cả các giáosư
giảng dạy khóa học kế toán phù hợp. Ba mươi phần trăm các giáo sư nhận được tài liệu này
đã sử dụng cuốn sách, 10% các giáo sư không nhận được tài liệu này có sử dụng quyển
sách. Xác suất mà một giáo sư chấp nhận cuốn sách đã nhận được tài liệu quảng cáo là gì?
21. Một nhà phân tích thị trường chứng khoán đã kiểm tra triển vọng cổ phiếu của một sốlượng
lớn các tập đoàn. Khi hiệu suất của các cổ phiếu này được điều tra một năm sau đó, hóa ra
25% hoạt động tốt hơn nhiều so với mức trung bình của thị trường, 25%, kém hơn nhiều
và 50% còn lại, tương đương với mức trung bình. Bốn mươi phần trăm các cổ phiếu hóa ra
làm tốt hơn nhiều so với thị trường được các nhà phân tích đánh giá là mua tốt, cũng như
20% trong số đó đã làm tốt cũng như thị trường và 10% trong số đó làm tồi tệ hơn nhiều.
Xác suất mà một cổ phiếu đánh giá mua tốt bởi nhà phân tích thực hiện tốt hơn nhiều so
với mức trung bình là gì?
22. Bạn và một người bạn là những người hâm mộ bóng đá lớn và đang tranh luận về khảnăng
FC Barcelona sẽ giành chiến thắng trong trận chung kết UEFA Champions League với
Manchester United. Bạn đang ủng hộ Manchester United, nhưng bạn của bạn nói với bạn
rằng các nhà cái đã đưa ra tỷ lệ cược sau cho trò chơi: 2: 8 (Manchester United vs FC
Barcelona). Xác suất mà Manchester United sẽ giành chiến thắng là gì?
23. Bạn là người quản lý sản phẩm thịt cho Gigantic Food, một nhà phân phối thực phẩm siêuthị
bán lẻ lớn, người đang nghiên cứu các đặc tính của hỗn hợp sản phẩm gà. Gà được mua từ
cả Free Range Farms và Big Food Ltd. Free Range Farms sản xuất gà được nuôi bằng ngũ
cốc tự nhiên và thức ăn trong khu vực cho ăn mở. Trong hỗn hợp sản phẩm của họ, 10% gà
chế biến có trọng lượng dưới 3 pound. Big Food Ltd. sản xuất gà trong chuồng bằng cách
sử dụng ngũ cốc thực phẩm làm giàu để tăng trưởng nhanh. Họ lưu ý rằng 20% gà chế biến
của họ nặng ít hơn ba cân. Gigantic mua 40% gà của họ từ Free Range và trộn các sản phẩm
với nhau mà không có nhận dạng của nhà cung cấp. Giả sử bạn mua một con gà nặng hơn
ba cân. Xác suất gà đến từ Free Range là gì? Nếu bạn mua 5 con gà, xác suất có ít nhất 3
con đến từ Free Range là bao nhiêu? lOMoAR cPSD| 58504431
24. Giả sử rằng bạn có một người bạn thông minh chưa nghiên cứu xác suất. Làm thế nào bạnsẽ
giải thích cho bạn của bạn sự phân biệt giữa các sự kiện loại trừ lẫn nhau và các sự kiện
độc lập? Minh họa câu trả lời của bạn với các ví dụ phù hợp.
25. Phát biểu, với bằng chứng, liệu rằng mỗi nhận định sau là đúng hay sai:
a. Xác suất phần hội của hai sự kiện không thể nhỏ hơn xác suất giao nhau của chúng.
b. Xác suất phần hội của hai sự kiện không thể lớn hơn tổng xác suất riêng lẻ của chúng.
c. Xác suất của phần giao của hai sự kiện không thể lớn hơn một trong hai xác suất riêng lẻcủa chúng.
d. Một sự kiện và phần bù của nó là loại trừ lẫn nhau.
e. Xác suất riêng lẻ của một cặp sự kiện không thể tổng bằng hơn 1.
f. Nếu hai sự kiện là loại trừ lẫn nhau, chúng cũng phải được tập hợp đầy đủ.
g. Nếu hai sự kiện là đầy đủ, chúng cũng phải loại trừ lẫn nhau.
26. Được biết, 20% tất cả các trang trại trong một tiểu bang vượt quá 160 mẫu Anh và 60% tất
cả các trang trại trong tiểu bang đó thuộc sở hữu của những người trên 50 tuổi. Trong số tất cả
các trang trại ở bang vượt quá 160 mẫu Anh, 55% thuộc sở hữu của những người trên 50 tuổi. a.
Xác suất mà một trang trại được chọn ngẫu nhiên ở tiểu bang này vượt quá 160 mẫu
Anhvà thuộc sở hữu của một người trên 50 tuổi là gì? b.
Xác suất mà một trang trại ở tiểu bang này lớn hơn 160 mẫu Anh hoặc thuộc sở hữu
củamột người trên 50 tuổi (hoặc cả hai) là gì? c.
Xác suất mà một trang trại ở tiểu bang này, thuộc sở hữu của một người trên 50 tuổi,
vượtquá 160 mẫu Anh là gì? d.
Quy mô của trang trại và tuổi của chủ sở hữu trong tiểu bang này có độc lập thống kêkhông?
27. Trong một tập đoàn lớn, 80% nhân viên là nam và 20% là nữ. Các bậc giáo dục cao nhất
mà người lao động có được là sau đại học đối với 10% nam giới, đại học đối với 30% nam giới
và trung học cho 60% nam giới. Các bậc giáo dục cao nhất là sau đại học cho 15% phụ nữ, đại
học cho 40% phụ nữ và trung học cho 45% phụ nữ.
a. Xác suất mà một nhân viên được chọn ngẫu nhiên sẽ là một người đàn ông chỉ có trình độhọc vấn trung học là gì?
b. Xác suất mà một nhân viên được chọn ngẫu nhiên có trình độ sau đại học là gì?
c. Xác suất mà một nhân viên được chọn ngẫu nhiên có trình độ sau đại học là một người đànông là gì?
d. Giới tính và trình độ học vấn của nhân viên trong tập đoàn này có độc lập thống kê không?
e. Xác suất mà một nhân viên được chọn ngẫu nhiên chưa được đào tạo sau đại học là phụ nữlà gì? 28.
Một nhân viên bán bảo hiểm nhân thọ nhận thấy rằng, trong số doanh số mà anh ta
kiếmđược, 70% là dành cho những người đã sở hữu chính sách. Ông cũng nhận thấy rằng, lOMoAR cPSD| 58504431
trong số tất cả các liên hệ mà không bán được sản phẩm, 50% đã sở hữu chính sách bảo hiểm
nhân thọ. Hơn nữa, 40% của tất cả các liên hệ dẫn đến doanh số bán hàng. Xác suất bán hàng
sẽ được thực hiện cho một người liên hệ đã sở hữu một chính sách là gì? 29.
Bạn có trách nhiệm phát hiện nguồn lỗi khi hệ thống máy tính bị lỗi. Từ phân tích
củabạn, bạn biết rằng nguồn lỗi là ổ đĩa, bộ nhớ máy tính hoặc hệ điều hành. Bạn biết rằng
50% lỗi là lỗi ổ đĩa, 30% là lỗi bộ nhớ máy tính và phần còn lại là lỗi hệ điều hành. Từ các tiêu
chuẩn hiệu suất thành phần, bạn biết rằng khi xảy ra lỗi ổ đĩa, xác suất xảy ra lỗi là 0,60; khi
xảy ra lỗi bộ nhớ máy tính, xác suất thất bại là 0,7; và khi xảy ra lỗi hệ điều hành, xác suất xảy
ra lỗi là 0,3. Với thông tin từ các tiêu chuẩn hiệu suất thành phần, xác suất xảy ra lỗi ổ đĩa là
gì, cho rằng đã xảy ra lỗi? 30.
Robert Smith sử dụng cày thường xuyên hoặc cày tối thiểu để chuẩn bị các cánh
đồngngô trong trang trại ở bang Minnesota của mình. Cày thường xuyên được sử dụng cho
40% diện tích. Phân tích sau khi vụ mùa được thu hoạch cho thấy 50% mẫu đất năng suất cao
là từ các cánh đồng cày tối thiểu và 40% các cánh đồng năng suất thấp là từ các cánh đồng với
việc cày thường xuyên. Xác suất của cánh đồng có năng suất cao nếu được cày thường xuyên
là bao nhiêu? Xác suất mà một cánh đồng có năng suất cao đã được chuẩn bị bằng cách sử
dụng cày thường xuyên là bao nhiêu?
Chương 5. Phân phối xác suất của biến rời rạc 1.
Trình bày hàm phân phối xác suất của số lượng mặt hình khi tung ba đồng xu đồng
nhấtmột cách độc lập. 2.
Số lượng máy tính được bán mỗi ngày tại Công ty máy tính F được xác định theo phânphối xác suất sau: x 0 1 2 3 4 5 6 P(x) 0,05 0,10 0,20 0,20 0,20 0,15 0,10 Hãy tính:
a. P(3 x < 6) = ?
b. P(x > 3) = ? c. P(x 4) = ?
d. P(2 < x 5) = ?
3. Cho hàm phân phối xác suất của biến ngẫu nhiên X: x 0 1 2 P(x) 0,25 0,5 0,25
a. Vẽ đồ thị hàm phân phối xác suất.
b. Tính toán và vẽ đồ thị phân phối xác suất tích lũy.
c. Tìm giá trị trung bình của biến ngẫu nhiên X.
d. Tìm phương sai của X
4. Một đại lý ô tô tính toán tỷ lệ ô tô mới đã bán bị trả lại nhiều lần khác nhau để sửa lỗi
trong thời gian bảo hành. Các kết quả được hiển thị trong bảng sau.
Số lần trả lại (x) 0 1 2 3 4
Tỷ lệ (P(x)) 0,28 0,36 0,23 0,09 0,04
a. Vẽ đồ thị hàm phân phối xác suất.
b. Tính toán và vẽ đồ thị phân phối xác suất tích lũy. lOMoAR cPSD| 58504431
c. Tính xác suất ít nhất một lần bị trả lại của một ô tô đả được bán.
d. Tìm giá trị trung bình của số lần trả lại của ô tô để sửa lỗi cho các lỗi trong thờigian bảo hành.
e. Tìm phương sai của số lượng bị trả của ô tô để sửa chữa các khiếm khuyết trongthời gian bảo hành.
5. Công ty A sản xuất túi phân. Trọng lượng tính bằng kg trên mỗi túi khác nhau, được trình bày trong bảng sau. Trọng lượng (kg) 44 45 46 47 48 49 50
Tỷ lệ túi (P(x)) 0,04 0,13 0,21 0,29 0,20 0,10 0,03
a. Vẽ đồ thị phân phối xác suất.
b. Tính toán và vẽ đồ thị phân phối xác suất tích lũy.
c. Xác suất mà một túi được chọn ngẫu nhiên sẽ chứa hơn 45 và ít hơn hay bằng 49 kglà bao nhiêu?
d. Hai gói được chọn ngẫu nhiên. Xác suất mà ít nhất một trong số chúng chứa ít nhất47 kg là bao nhiêu?
e. Tính toán, bằng cách sử dụng máy tính, độ lệch trung bình và độ lệch chuẩn củatrọng lượng trên mỗi túi.
f. Chi phí (tính bằng đồng) của việc sản xuất một túi màng phủ là 75 + 2X, trong đó X
là số kg mỗi túi. Doanh thu từ việc bán chiếc túi, bất kể trọng lượng, là 2,50 ngàn
đồng. Nếu lợi nhuận được tính bằng chênh lệch giữa doanh thu và chi phí, hãy tìm
giá trị trung bình và độ lệch chuẩn của lợi nhuận trên mỗi túi. 6.
a. Một lô hàng rất lớn của các phụ tùng chứa 10% sản phẩm lỗi. Hai sản phẩm đượcchọn
ngẫu nhiên từ lô hàng và kiểm tra. Đặt biến ngẫu nhiên X biểu thị số lượng sản phẩm
lỗi được tìm thấy. Tìm phân phối xác suất của biến ngẫu nhiên này.
b. Một lô hàng gồm 20 sản phẩm chứa 2 sản phẩm lỗi. Hai sản phẩm được chọn
ngẫunhiên từ lô hàng và kiểm tra. Đặt biến ngẫu nhiên Y biểu thị số lượng sản phẩm
lỗi được tìm thấy. Tìm phân phối xác suất của biến ngẫu nhiên này. Giải thích tại sao
câu trả lời của bạn khác với câu trả lời cho phần (a).
c. Tìm giá trị trung bình và phương sai của biến ngẫu nhiên X trong phần (a).
d. Tìm giá trị trung bình và phương sai của biến ngẫu nhiên Y trong phần (b).
7. Một học sinh cần biết chi tiết về một bài tập lớp đến hạn vào ngày hôm sau và quyết
định gọi cho các thành viên trong lớp để biết thông tin này. Cô tin rằng đối với bất kỳ
cuộc gọi cụ thể nào, xác suất có được thông tin cần thiết là 0,40. Cô quyết định tiếp tục
gọi các thành viên trong lớp cho đến khi có được thông tin. Nhưng pin điện thoại của
cô sẽ không cho phép hơn 8 cuộc gọi. Đặt biến ngẫu nhiên X biểu thị số lượng cuộc gọi
cần thiết để có được thông tin. a. Tìm phân phối xác suất của X.
b. Tìm phân phối xác suất tích lũy của X.
c. Tìm xác suất để có ít nhất ba cuộc gọi được thực hiện để có được thông tin. lOMoAR cPSD| 58504431
8. Một nhà đầu tư đang xem xét ba chiến lược cho khoản đầu tư $ 1.000. Lợi nhuận có
thể xảy ra được ước tính như sau: •
Chiến lược 1: Lợi nhuận 10.000 đô la với xác suất 0,15 và lỗ 1.000 đô la với xác suất0,85 •
Chiến lược 2: Lợi nhuận 1.000 đô la với xác suất 0,5, lợi nhuận 500 đô la với
xácsuất 0,30 và mất 500 đô la với xác suất 0,20 • Chiến lược 3: Lợi nhuận nhất định là $ 400
Chiến lược nào có lợi nhuận kỳ vọng cao nhất? Giải thích lý do tại sao bạn muốn hoặc
không muốn khuyên nhà đầu tư áp dụng chiến lược này. 9.
Đối với phân phối xác suất nhị thức với P = 0,5 và n = 12, hãy tìm xác suất số
lần thành công bằng 7 và xác suất số lần thành công nhỏ hơn 6. 10.
Đối với phân phối xác suất nhị thức với P = 0,4 và n = 20, hãy tìm xác suất số
lần thành công bằng 9 và xác suất số lần thành công nhỏ hơn 7. 11.
Một giám đốc sản xuất biết rằng 5% linh kiện được sản xuất bởi một quy trình
sản xuất cụ thể có một số khiếm khuyết. Sáu trong số các linh kiện này, có đặc điểm có
thể được coi là độc lập với nhau, được kiểm tra.
a. Xác suất mà không có linh kiện nào trong số này có khiếm khuyết là bao nhiêu?
b. Xác suất mà một trong những linh kiện này có khiếm khuyết là bao nhiêu?
c. Xác suất mà ít nhất hai trong số các linh kiện này có một khiếm khuyết là baonhiêu?
12. Một nhóm lợi ích công cộng thuê sinh viên để thu hút quyên góp qua điện thoại.
Sau một thời gian đào tạo ngắn, sinh viên gọi điện cho các nhà tài trợ tiềm năng và được
trả tiền trên cơ sở hoa hồng. Kinh nghiệm chỉ ra rằng những sinh viên này có xu hướng
chỉ thành công khiêm tốn và 70% trong số họ từ bỏ công việc trong hai tuần đầu làm
việc. Nhóm thuê 6 sinh viên, có thể được xem như một mẫu ngẫu nhiên. a. Xác suất mà
ít nhất 2 trong số 6 sẽ bỏ cuộc trong hai tuần đầu tiên là gì?
b. Xác suất mà ít nhất 2 trong số 6 sẽ không từ bỏ trong hai tuần đầu tiên là gì? 13.
Một hãng hàng không nhỏ đi máy bay có thể chứa tới 8 hành khách. Hãng
hàngkhông đã xác định rằng xác suất một hành khách đã bán vé sẽ không đến cho
chuyến bay là 0,2. Đối với mỗi chuyến bay, hãng hàng không bán vé cho 10 người đầu
tiên đặt vé. Phân phối xác suất cho số lượng vé được bán trên mỗi chuyến bay được
hiển thị trong bảng đi kèm. Tỷ lệ các chuyến bay của hãng hàng không mà số lượng
hành khách đã bán vé xuất hiện vượt quá số lượng ghế có sẵn là bao nhiêu? (Giả sử sự
độc lập giữa số lượng vé được bán và xác suất một hành khách được bán vé sẽ xuất hiện.) Số vé bán 6 7 8 9 10 Xác suất 0,25 0,35 0,25 0,10 0,05 14.
Một đại lý máy tính xách tay tung ra một chiến dịch quảng cáo mới. Người mua
máy tính mới có thể, nếu không hài lòng vì bất kỳ lý do gì, trả lại chúng trong vòng 2
ngày kể từ ngày mua và được hoàn lại tiền đầy đủ. Chi phí cho đại lý hoàn trả như vậy lOMoAR cPSD| 58504431
là 100 đô la. Các đại lý ước tính rằng 15% của tất cả người mua sẽ, thực sự, trả lại máy
tính và được hoàn lại tiền. Giả sử rằng 50 máy tính được mua trong thời gian chiến dịch. a.
Tìm giá trị trung bình và độ lệch chuẩn của số lượng các máy tính này sẽ được
trảlại để hoàn lại tiền. b.
Tìm giá trị trung bình và độ lệch chuẩn của tổng chi phí hoàn trả sẽ tích lũy theo
kếtquả của 50 lần mua này.
15. Một công ty nhận được một lô hàng linh kiện rất lớn. Một mẫu ngẫu nhiên gồm 16
linh kiện trong lô hàng này sẽ được kiểm tra và lô hàng sẽ được chấp nhận nếu có ít hơn
2 trong số các linh kiện này bị lỗi. Xác suất chấp nhận mỗi lô hàng là bao nhiêu nếu nó chứa tỷ lệ lỗi? a. 5% b. 15% c. 25% 16.
Một công ty nhận được lô hàng lớn các bộ phận từ hai nguồn. Bảy mươi phần
trămcác lô hàng đến từ một nhà cung cấp có lô hàng thường chứa 10% khiếm khuyết,
phần còn lại là từ một nhà cung cấp có lô hàng thường chứa 20% khiếm khuyết. Một
người quản lý nhận được một lô hàng nhưng không biết nguồn. Một mẫu ngẫu nhiên gồm 20
mặt hàng từ lô hàng này được kiểm tra và 1 trong số các bộ phận được phát hiện là bị
lỗi. Xác suất mà lô hàng này đến từ nhà cung cấp đáng tin cậy hơn là gì? (Gợi ý: Sử dụng định lý Bayes.) 17.
Xác định xác suất của chính xác bốn thành công cho một biến ngẫu nhiên có
phân phối Poisson với tham số = 2,4. 18.
Xác định xác suất nhỏ hơn hoặc bằng 9 lần thành công cho một biến ngẫu nhiên
có phân phối Poisson với tham số = 8,0. 19.
Số vụ tai nạn trong một cơ sở sản xuất có phân phối Poisson với trung bình 2,6 vụ mỗi tháng.
a. Trong một tháng nhất định, xác suất sẽ có ít hơn 2 vụ tai nạn là bao nhiêu?
b. Trong một tháng nhất định, xác suất sẽ có nhiều hơn 3 vụ tai nạn là bao nhiêu?
20. Một công ty có 250 máy tính cá nhân. Xác suất mà bất kỳ 1 trong số chúng cần được
sửa chữa trong một tuần nhất định là 0,01. Tìm xác suất để có ít hơn 4 máy tính cá
nhân cần được sửa chữa trong một tuần cụ thể. Sử dụng phân phối xấp xỉ Poisson
cho phân phối nhị thức.
21. Một quốc gia có luật yêu cầu người lái xe phải mang bảo hiểm. Người ta ước tính
rằng, bất chấp luật này, 6,0% những người lái xe trong quốc gia không được bảo
hiểm. Một mẫu ngẫu nhiên của 100 người lái xe đã được thực hiện. Sử dụng xấp xỉ
Poisson cho phân phối nhị thức để ước tính xác suất có ít nhất 3 người lái xe trong
mẫu này không được bảo hiểm. Cũng chỉ ra những tính toán nào sẽ cần thiết để tìm
xác suất này chính xác nếu phép tính gần đúng Poisson không được sử dụng. lOMoAR cPSD| 58504431
22. Xem xét phân phối xác suất kết hợp sau: X 1 2 Y 0 0,3 0,2 1 0,25 0,25
a. Tính toán phân phối xác suất cận biên cho X và Y.
b. Tính toán hiệp phương sai và tương quan cho X và Y.
c. Tính giá trị trung bình và phương sai cho hàm tuyến tính W = 2X + Y.
23. Một nhà nghiên cứu nghi ngờ rằng số lượng giữa các bữa ăn nhẹ mà học sinh ăn
trong một ngày trong các kỳ thi cuối cùng có thể phụ thuộc vào số lượng bài kiểm tra
mà học sinh phải thực hiện vào ngày hôm đó. Bảng đi kèm cho thấy xác suất kết hợp,
được ước tính từ một khảo sát. Số bữa ăn (Y)
Số bài kiểm tra (X) 0 1 2 3 0 0,07 0,09 0,06 0,01 1 0,07 0,06 0,07 0,01 2 0,06 0,07 0,14 0,03 3 0,02 0,04 0,16 0,04
a. Tìm phân phối xác suất của X và tính số bài kiểm tra trung bình mà học sinh thựchiện vào ngày hôm đó.
b. Tìm phân phối xác suất của Y và, do đó, số lượng bữa ăn nhẹ trung bình mà họcsinh ăn vào ngày hôm đó.
c. Tìm và giải thích phân phối xác suất có điều kiện của Y, với X = 3.
d. Tìm hiệp phương sai giữa X và Y.
e. Số bữa ăn nhẹ và số bài kiểm tra có độc lập với nhau không?
24. Một nhà nghiên cứu thị trường muốn xác định xem một mẫu máy tính cá nhân mới
được quảng cáo trên chương trình trò chuyện đêm khuya có đạt được sự công nhận
thương hiệu nhiều hơn trong số những người xem chương trình thường xuyên hơn so
với những người không xem. Sau khi tiến hành một cuộc khảo sát, người ta thấy rằng
15% tất cả mọi người đều xem chương trình thường xuyên và có thể xác định chính xác
sản phẩm. Ngoài ra, 16% tất cả mọi người thường xuyên xem chương trình và 45% tất
cả mọi người có thể xác định chính xác sản phẩm. Xác định một cặp biến ngẫu nhiên như sau:
X = 1, nếu xem thường xuyên
X = 0, nếu xem không thường xuyên
Y = 1, nếu sản phẩn được xác định chính Y = 0, nếu sản phẩm không được xác định xác chính xác lOMoAR cPSD| 58504431
a. Tìm phân phối xác suất kết hợp của X và Y.
b. Tìm phân phối xác suất có điều kiện của Y, cho X = 1.
c. Tìm và giải thích hiệp phương sai giữa X và Y. 25.
Một quản lý nhà hàng nhận được những khiếu nại thường xuyên về chất lượng
của cả thực phẩm và dịch vụ. Phân phối xác suất cận biên cho số lượng khiếu nại hàng
tuần trong mỗi danh mục được hiển thị trong bảng đi kèm. Nếu các khiếu nại về thực
phẩm và dịch vụ độc lập với nhau, hãy tìm phân phối xác suất kết hợp. Số khiếu nại về Xác suất Số khiếu nại về Xác suất thực phẩm dịch vụ 0 0,12 0 0,18 1 0,29 1 0,38 2 0,42 2 0,34 3 0,17 3 0,10 26.
Một nhà thầu ước tính xác suất cho số ngày cần thiết để hoàn thành một loại dự
án xây dựng nhất định như sau: Thời gian (ngày) 1 2 3 4 5 Xác suất 0,05 0,20 0,35 0,30 0,10
a. Xác suất mà một dự án được chọn ngẫu nhiên sẽ mất ít hơn 3 ngày để hoàn thành làbao nhiêu?
b. Tìm thời gian kỳ vọng để hoàn thành một dự án.
c. Tìm độ lệch chuẩn của thời gian cần thiết để hoàn thành một dự án.
d. Chi phí dự án của nhà thầu khác được tạo thành từ hai phần: chi phí cố định là20.000
đô la, cộng với 2.000 đô la mỗi ngày để hoàn thành dự án. Tìm giá trị trung bình và
độ lệch chuẩn của tổng chi phí dự án.
e. Nếu ba dự án được thực hiện, xác suất mà ít nhất hai trong số chúng sẽ mất ít nhất
4ngày để hoàn thành, giả sử có sự độc lập của thời gian hoàn thành của từng dự án, là bao nhiêu?
27. Một bài kiểm tra trắc nghiệm có chín câu hỏi. Đối với mỗi câu hỏi, có bốn câu trả
lời có thể được chọn. Một điểm được trao cho mỗi câu trả lời đúng và không có điểm
trừ cho câu trả lời sai. Gíao thưởng một điểm thưởng nếu các sinh viên đánh vần đúng
tên của họ. Một sinh viên chưa học bài kiểm tra này quyết định chọn một câu trả lời cho
mỗi câu hỏi một cách ngẫu nhiên.
a. Tìm số câu trả lời đúng kỳ vọng cho học sinh trong chín câu hỏi này.
b. Tìm độ lệch chuẩn của số câu trả lời đúng cho học sinh trong chín câu hỏi này.
c. Học sinh đánh vần đúng tên của mình:
i) Tìm tổng số điểm kỳ vọng trong bài kiểm tra cho học sinh này.
ii) Tìm độ lệch chuẩn của tổng điểm của anh ấy trong bài kiểm tra. lOMoAR cPSD| 58504431
28. Máy tính của bạn đang cần sửa chữa nghiêm trọng. Bạn đã ước tính rằng các sự cố
xảy ra trung bình 3,5 lần mỗi tuần. Nếu bạn đúng và số sự cố theo phân phối Poisson,
hãy tính toán các xác suất sau.
a. Xác suất trong cả tuần máy tính của bạn chạy không có vấn đề gì.
b. Xác suất chỉ nhận được 1 lần tắt máy.
c. Xác suất nhận được 5 lần tắt máy.
29. Yoshida Toimi là một ứng cử viên cho thị trưởng của một thành phố Trung Tây. Nếu
anh ta nhận được hơn 50% số phiếu, anh ta sẽ giành chiến thắng trong cuộc bầu cử.
Trước cuộc bầu cử, nhân viên chiến dịch của ông đang lên kế hoạch hỏi 100 cử tri được
chọn ngẫu nhiên liệu rằng họ ủng hộ Yoshida hay không. a.
Cần bao nhiêu phản hồi tích cực từ mẫu 100 này để xác suất 50% trở lên cử tri
ủnghộ ông là 0,95 trở lên? b.
Giả sử chiến dịch có thể hỏi 400 cử tri được chọn ngẫu nhiên. Bây giờ câu trả
lờicủa bạn cho câu hỏi trong phần (a) là gì?
30. Faschip, Ltd., là nhà sản xuất máy tính xách tay mới của châu Phi. Mục tiêu chất
lượng của họ là 99,999% máy tính họ sản xuất sẽ hoạt động chính xác như đã hứa trong
tài liệu mô tả. Để theo dõi hiệu suất chất lượng của chúng, người ta đính kèm mỗi máy
tính một tờ giấy lớn bao gồm số điện thoại trực tiếp miễn phí trực tiếp trên đường dây
điện tử cho Phó chủ tịch sản xuất để thông báo nếu máy tính không hoạt động như đã
hứa. Trong năm đầu tiên Faschip bán 1.000.000 máy tính. a.
Nếu họ đang đạt được mục tiêu chất lượng của họ, xác suất mà họ sẽ nhận được
íthơn 5 cuộc gọi là gì? Nếu điều này xảy ra, kết luận hợp lý về chương trình chất lượng của họ là gì? b.
Nếu họ đang đạt được mục tiêu chất lượng của họ, xác suất mà họ sẽ nhận
đượchơn 15 cuộc gọi là gì? Nếu điều này xảy ra, điều gì sẽ là một kết luận hợp lý về
chương trình chất lượng của họ?
Chương 6. PHÂN PHỐI XÁC SUẤT BIẾN LIÊN TỤC
1. Một nhà phân tích đã có sẵn hai dự báo, F1 và F2, thu nhập trên mỗi cổ phiếu của một
công ty vào năm tới. Ông dự định hình thành một dự báo kết hợp như là một trung bình
có trọng số của hai dự báo riêng lẻ. Khi hình thành dự báo kết hợp, trọng số X sẽ được
gán cho dự báo F1 và trọng số (1 - X) được gán cho dự báo thứ hai, giá trị trung bình
của dự báo kết hợp là XF1 + (1 - X)F. Nhà phân tích muốn chọn giá trị từ 0 đến 1 cho
trọng số X, nhưng anh ta không chắc chắn đâu sẽ là lựa chọn tốt nhất. Giả sử rằng sự
lựa chọn tốt nhất có thể có của trọng số X có thể được xem như một biến ngẫu nhiên
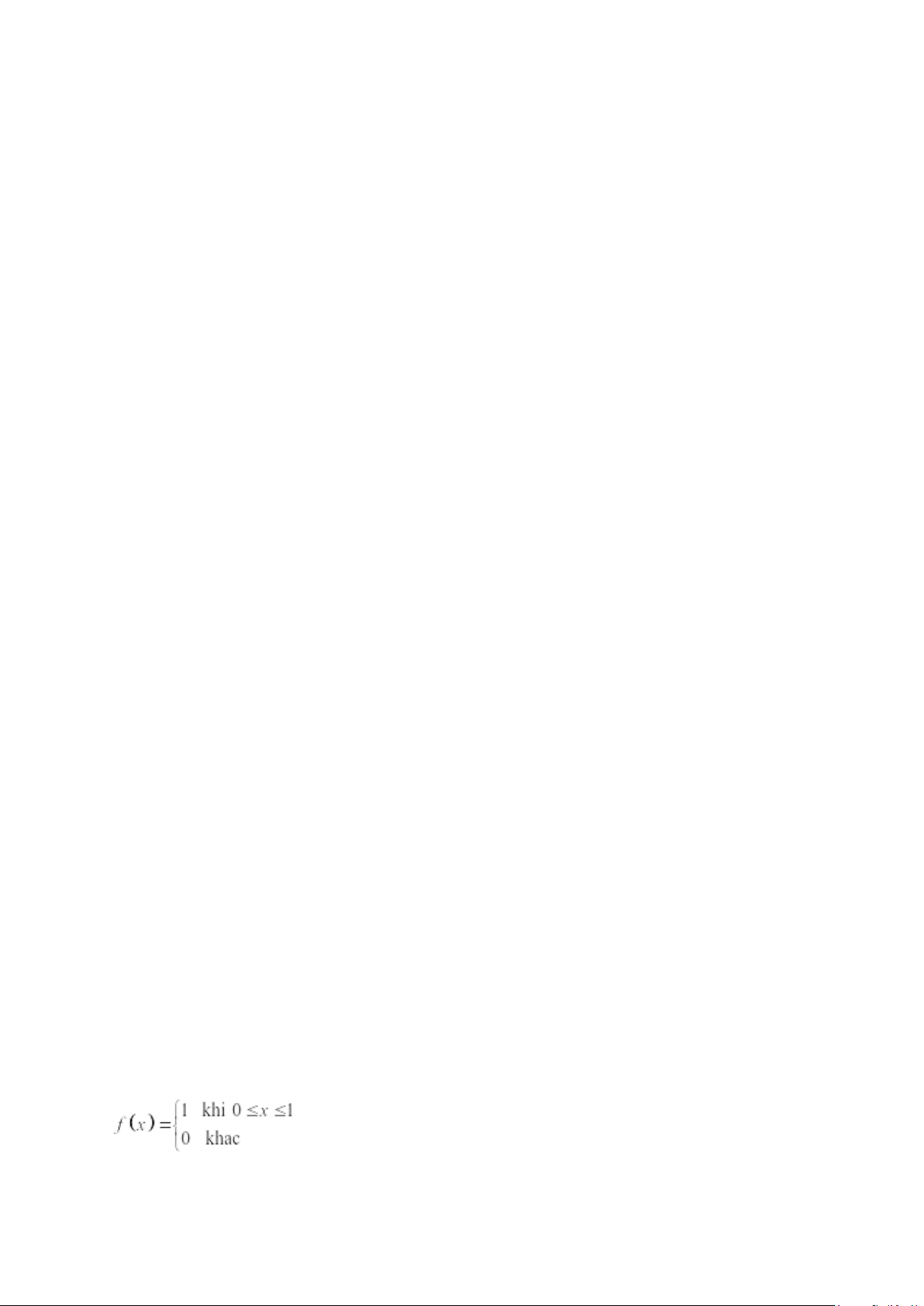
được phân bố đồng đều giữa 0 và 1, có hàm mật độ xác suất:
a. Vẽ đồ thị hàm mật độ xác suất.