




































Preview text:
lOMoARcPSD| 37922327
HỌC VIỆN CÔNG NGHỆ BƯU CHÍNH VIỄN THÔNG BÀI TẬP TOÁN KINH TẾ
Biên soạn: TS. Lê Thị Ngọc Diệp
Khoa Quản trị Kinh doanh 1 Hà Nội, Năm 2021 lOMoARcPSD| 37922327 MỤC LỤC
CHƯƠNG 1. MÔ HÌNH TOÁN KINH TẾ.................................................................2
CHƯƠNG 2. MÔ HÌNH QUY HOẠCH TUYẾN TÍNH...........................................7
CHƯƠNG 3. MÔ HÌNH BÀI TOÁN VẬN TẢI.......................................................14
CHƯƠNG 4. MÔ HÌNH BÀI TOÁN TỐI ƯU TRÊN MẠNG................................19
CHƯƠNG 5. MÔ HÌNH HỆ THỐNG PHỤC VỤ CÔNG CỘNG..........................23
CHƯƠNG 6. MÔ HÌNH QUẢN LÝ DỰ TRỮ.........................................................26 lOMoARcPSD| 37922327
CHƯƠNG 1. MÔ HÌNH TOÁN KINH TẾ
1.1. Cho hàm tổng chi phí TC = 5000 + (Q là sản lượng) a/
Tìm hàm chi phí cận biên MC. b/ Tính chi phí trung
bình AC tại Q = 100. c/ Vẽ đồ thị hàm chi phí biến
đổi trung bình (VC/Q). d/ Tính hệ số co giãn của TC
theo Q tại Q = 17. Đáp số: b/ 54,85437; d/ 0,01638
1.2. Cho hàm tổng chi phí TC = 4000 + 10Q + 0,1Q2 (Q là sản lượng).
Giá P được xác định bởi phương trình Q = 800 – 2,5 P.
a/ Tìm hàm chi phí cận biên MC.
b/ Tìm hàm chi phí trung bình AC, khảo sát sự thay đổi của nó.
c/ Tìm hệ số co giãn của TC tại P = 80. Đáp số: c/ 1,695652
1.3. Một doanh nghiệp có hàm tổng doanh thu TR = - 10Q2 + 1000Q và hàm tổng chi phí TC =
Q3 – 25Q2 + 600Q + , trong đó Q là sản lượng. Hãy xác định mức sản lượng tối đa hóa lợi nhuận
và mức lợi nhuận tối đa. Lời giải có phù hợp với quy luật lợi ích cận biên giảm dần hay không?
Đáp số: Q* = 40 (đơn vị sản lượng); π* = 18000 (đơn vị tiền tệ)
1.4. Cho hàm sản xuất Y(t) = 0,2K0,4L0,8, trong đó: K = 120 + 0,1t; L = 200 + 0,3t.
a/ Tính hệ số co giãn của Y theo K và L. b/ Tính hệ số tăng trưởng của vốn
K, lao động L và kết quả sản xuất Y. c/ Hãy cho biết hiệu quả của việc tăng
quy mô sản xuất trong trường hợp này.
1.5. Xét mô hình lợi nhuận (Q) = TR(Q) – TC(Q) – a.TR(Q). Trong đó: TR là tổng doanh thu,
TC là tổng chi phí, a là thuế suất theo doanh thu.
a/ Xác định biểu thức điều kiện của Q để lợi nhuận đạt cực đại.
b/ Khi thuế suất tăng, mức Q tối ưu biến động như thế nào?
1.6. Một doanh nghiệp cạnh tranh hoàn hảo có hàm sản xuất dạng:
Q = K0,65 + L0,35 với pK = 8, pL = 6 và p = 4 Trong đó Q là sản lượng; K là vốn;
L là lao động. a/ Hãy xác định mức sử dụng vốn và lao động tối ưu. b/ Hãy
phân tích tác động của giá vốn, giá lao động đến mức sản lượng của DN. lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
Đáp số: a/ K* = 0,04; L* = 0,1066
1.7. Một doanh nghiệp cạnh tranh hoàn hảo có hàm chi phí biên: MC = 2Q2 - 12Q + 25, chi phí
cố định FC và giá bán sản phẩm p.
a/ Hãy xác định hàm tổng chi phí TC với FC = 20. Với p = 39 hãy xác định mức sản
lượng và mức lợi nhuận tối ưu.
b/ Nếu giá p tăng 10% thì mức sản lượng và mức lợi nhuận tối ưu sẽ biến động như thế nào?
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
Đáp số: a/ Q* = 7; Π* = 143,3. b/ Khi giá tăng 10% thì sản lượng tối ưu tăng 3,48% và
lợi nhuận tối ưu tăng 19%
1.8. Một doanh nghiệp có công nghệ sản xuất cho bởi hàm sản xuất: Y(t) = 0,4 K(t) + 0,7 L(t)
Trong đó Y(t) là kết quả sản xuất năm t; K(t) là vốn đầu tư năm t; L(t) là sức lao động năm t (K > 0, L > 0).
a/ Phân tích xu hướng thay đổi của kết quả sản xuất theo vốn đầu tư và theo sức lao
động. Hàm sản xuất có tính chất hiệu quả thay đổi theo quy mô không? Vì sao?
b/ Xác định hệ số thay thế của sức lao động cho vốn và ngược lại.
Đáp số: b/ MRTS(L,K) = - 0,5714, MRTS(K,L) = -1,75.
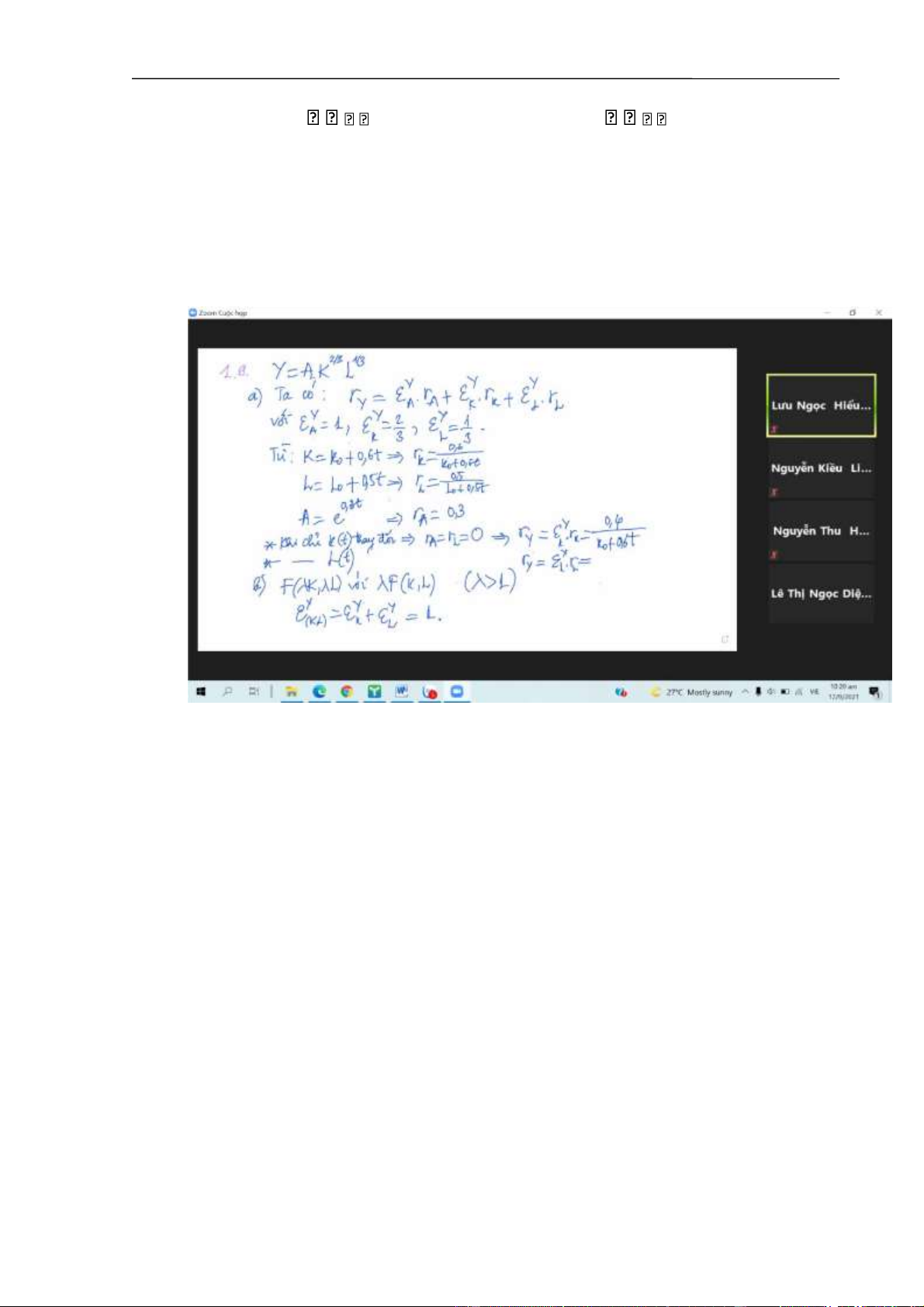
1.9. Một doanh nghiệp có công nghệ sản xuất cho bởi hàm sản xuất: Y t A t .K 23 t
.L13 t , trong đó Y(t) là kết quả sản xuất năm t, A t e0.3t là tác động của tiến bộ khoa học
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
– công nghệ năm t, K t K0 0.6t là vốn đầu tư năm t; L t L0 0.5t là sức lao động
năm t. a/ Xác định xu hướng thay đổi của hệ số tăng trưởng của kết quả sản xuất năm t khi chỉ
K(t) thay đổi? Khi chỉ L(t) thay đổi? Khi chỉ A(t) thay đổi? Khi cả A(t), K(t), L(t) cùng thay đổi?
b/ Quá trình sản xuất của doanh nghiệp có biến đổi theo quy luật hiệu quả thay đổi theo quy mô không? Vì sao?
1.10. Tổng chi phí sản xuất của một doanh nghiệp được cho bởi hàm: C(Q) =
Q3 – 5Q2 + 14Q + 144 (Q > 0), trong đó Q là kết quả sản xuất.
a/ Khảo sát sự thay đổi tuyệt đối của tổng chi phí sản xuất theo kết quả sản xuất, từ đó
có nhận xét gì về sự mở rộng sản xuất của doanh nghiệp.
b/ Tính hệ số co dãn của tổng chi phí sản xuất theo kết quả sản xuất tại Q = 4. Với Q =
4, thuế doanh thu là 20%, tìm điều kiện để doanh nghiệp có lãi? doanh nghiệp hòa vốn? doanh nghiệp lỗ vốn?
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
Đáp số: b/ Hệ số co dãn của C(Q) theo Q tại Q = 4 là 0,4783. Với Q 4 , thuế doanh
thu là 20%, doanh nghiệp có lãi khi p > 57,5, hòa vốn khi p = 57,5, lỗ vốn p < 57,5.
1.11. Một công ty có thể sản xuất và cung ứng cho thị trường hai mặt hàng với hàm tổng doanh
thu và hàm tổng chi phí như sau: TR = P 2 2
1Q1 + P2Q2 , TC = 2Q1 + Q1Q2 + 3Q2 .
Trong đó: Pi, Qi là giá cả và sản lượng hàng hoá thứ i (i = 1,2).
a/ Xác định công thức tính tổng lợi nhuận cực đại.
b/ Áp dụng công thức tìm được ở câu a, tìm sản lượng cực đại lợi nhuận c/ Tính hệ số
co giãn của tổng chi phí theo từng mặt hàng và hệ số co giãn đồng thời
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
theo cả hai mặt hàng tại điểm cực đại lợi nhuận tìm được ở câu b. Đáp số : c/ 2
1.12. Nhu cầu hai mặt hàng phụ thuộc giá như sau: Q1 = 40 – 2P1 – P2 ; Q2 = 35 – P1 – P2 .
Tổng chi phí là hàm của các sản lượng: TC = Q 2 2 1 + 2Q2 + 12.
Trong đó: Pi , Qi là giá cả và sản lượng hàng hoá thứ i (i = 1,2).
a/ Xác định mức Q1, Q2 sao cho tổng lợi nhuận đạt cực đại.
b/ Tính chi phí cận biên cho từng mặt hàng tại mức tối ưu tìm được ở câu a.
c/ Hai mặt hàng này có thay thế lẫn nhau trong tiêu dùng không?
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế Đáp số : a/ Q
* = 65/14 c/ Hai mặt hàng không thay thế cho nhau. 1* = 25/7 ; Q2
1.13. Độ hữu dụng (U) của người tiêu dùng khi tiêu thụ hai loại hàng hoá a và b có dạng:
U = 1,2A0,4B0,2 (trong đó A và B là mức tiêu thụ hàng hoá a và b).
a/ Độ hữu dụng sẽ biến động như thế nào nếu người tiêu dùng tăng mức tiêu thụ cả hai loại hàng hoá lên 10%?
b/ Có thể nói rằng hai loại hàng hoá trên có thể thay thế được cho nhau với tỷ lệ 1:1 hay không?
1.14. Hàm lợi ích của người tiêu dùng (U) khi tiêu dùng hai loại hàng hoá 1, 2 có dạng: U = (x1
+ 2)(x2 + 1) (trong đó x1 và x2 là mức tiêu thụ hàng hoá 1 và 2).
a/ Hai loại hàng hoá trên có thể thay thế cho nhau theo tỷ lệ 1:1 hay không? Lợi ích
biên của chúng có như nhau không?
b/ Cho biết giá của hai loại hàng hoá lần lượt là p1 = 4, p2 = 6 và thu nhập của người
tiêu dùng là M = 130. Hãy xác định mức cầu hai loại hàng hoá trên nhằm tối đa hoá lợi ích của người tiêu dùng?
Đáp số: b/ X1* = 16 ; X2* = 11.
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
1.15. Mức cung một loại nông sản (S) phụ thuộc vào giá của nông sản (P), lượng mưa (R) và
có dạng: S = a + bP2 + R0,5, trong đó a < 0, b > 0.
a/ Hãy xác định các biểu thức phân tích tác động (tương đối) riêng và đồng thời của
giá, lượng mưa tới mức cung.
b/ Theo dự báo có khả năng thời tiết khô hạn nên mưa sẽ giảm. Để ổn định mức cung
nông sản, Nhà nước sẽ trợ giá cho nông dân. Hãy xác định biểu thức tính mức trợ giá cần thiết
theo dự đoán về mức giảm sút của lượng mưa.
1.16. Mức cầu tiền tệ (M) phụ thuộc vào thu nhập (Y) và lãi suất (r) có dạng như sau: M = 0,1Y0,02r -0,2
a/ Hãy xác định mối quan hệ giữa mức cầu tiền tệ với thu nhập và lãi suất.
b/ Trong trường hợp thu nhập không đổi, nếu muốn giảm mức cầu tiền tệ 5% thì phải
điều chỉnh lãi suất như thế nào?
Đáp số : b/ Muốn M giảm 5% thì cần tăng lãi suất lên 25%.
1.17. Hàm cầu (D) và hàm cung (S) về một loại hàng hoá có dạng như sau:
D = 0,2p-0,1M0,2 ; S = 0,1p0,4q-0,05
Trong đó: p là giá hàng hoá, M là thu nhập của người tiêu dùng, q là mức giá chung của
các yếu tố được sử dụng để sản xuất hàng hoá. Với mô hình trên:
a/ Nếu giá hàng hoá tăng 10% thì mức cầu sẽ biến động như thế nào?
b/ Có thể cho rằng nếu giá hàng hoá và mức giá chung của các yếu tố được sử dụng để
sản xuất hàng hoá tăng cùng tỷ lệ thì mức cung không đổi hay không?
c/ Hãy phân tích tác động của thu nhập, mức giá chung của các yếu tố được sử dụng
để sản xuất hàng hoá tới mức giá cân bằng.
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
1.18. Hàm cầu (D) và hàm cung (S) về một loại hàng hoá có dạng như sau: D
= 100 – 0,3p ; S = – 50 + 0,2(p – t)
Trong đó: p là giá hàng hoá, t là thuế đánh vào một đơn vị hàng hoá bán ra. Cho t = 10.
a/ Tính độ co giãn của giá cân bằng theo thuế t và nêu ý nghĩa của kết quả thu được.
b/ Nếu Chính phủ muốn giá cân bằng ở mức p = 280 và trợ cấp hàng hoá cho phía cầu
thì số trợ cấp cần thiết là bao nhiêu?
c/ Chính phủ muốn lượng cân bằng là 10. Để đạt được mục tiêu đó, Chính phủ có thể
giảm thuế phía cung hoặc trợ cấp cho phía cầu. Cách làm nào sẽ lợi hơn nếu xét trên quan điểm thu – chi ngân sách?
1.19. Cho mô hình: Y = C + I + G + EX – IM
Trong đó: C = βYd (0 < β < 1) ; IM = ρYd (0 < ρ < 1) ; Yd = (1 – t)Y; với Y là thu nhập
quốc dân, Yd là thu nhập khả dụng, C là tiêu dùng, I là đầu tư, G là chi tiêu của Chính phủ, EX
là xuất khẩu, IM là nhập khẩu, t là thuế suất thuế thu nhập; β và ρ là các tham số.
a/ Với β = 0,85; ρ = 0,3; I = 200; G = 500; EX = 150; t = 0,1, hãy xác định thu nhập
quốc dân, cán cân thương mại ở tình huống cân bằng.
b/ Với các chỉ tiêu ở câu a, có ý kiến cho rằng: Nếu Chính phủ tăng thuế suất 10% thì
có thể tăng chi tiêu 10% mà không ảnh hưởng tới thu nhập quốc dân ở trạng thái cân bằng. Hãy nhận xét ý kiến này.
1.20. Một số chỉ tiêu của nền kinh tế quốc dân có mối liên hệ như sau: Y = C + I + G + EX – IM
Trong đó: C = 0,9Yd; IM = 0,15Yd ; Yd = (1 – t)Y; với Y là thu nhập quốc dân, Yd là
thu nhập khả dụng, C là tiêu dùng, I là đầu tư, G là chi tiêu của Chính phủ, EX là xuất khẩu, IM
là nhập khẩu, t là thuế suất thuế thu nhập.
Cho I0 = 200; G0 = 270; EX0 = 180; t0 = 0,15 a/ Tại mức thu nhập quốc dân cân bằng,
có thặng dư hay thâm hụt ngân sách, có thặng
dư hay thâm hụt thương mại hay không?
b/ Có thể nói rằng nếu giảm xuất khẩu 10% thì Chính phủ có thể tăng chi tiêu 10% mà
không ảnh hưởng tới thu nhập quốc dân ở trạng thái cân bằng hay không?
c/ Chi tiêu của Chính phủ cần tăng thêm bao nhiêu để thu nhập quốc dân đạt mức Y = 1800,
khi đó các chỉ tiêu khác (đo bằng các biến nội sinh của mô hình) thay đổi như thế nào?
1.21. Một số chỉ tiêu của nền kinh tế quốc dân có mối liên hệ như sau: Y = C + I + G + NX
C = 20 + 0,75Yd; G = 20 + 0,1Y ; Yd = (1 – t)Y
với Y là thu nhập quốc dân, Yd là thu nhập khả dụng, C là tiêu dùng, I là đầu tư, G là chi tiêu
của Chính phủ, NX là xuất khẩu ròng, t là thuế suất thuế thu nhập. Cho I0 = 25; NX0 = 15.
a/ Nếu Nhà nước muốn cân đối ngân sách thì phải định thuế suất t là bao nhiêu?
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
b/ Có ý kiến cho rằng: việc gia tăng đầu tư I không ảnh hưởng tới tình huống cân đối
ngân sách ở câu a. Ý kiến này đúng hay sai? Tại sao? CHƯƠNG 2.
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
CHƯƠNG 3. MÔ HÌNH QUY HOẠCH TUYẾN TÍNH
2.1. Cho bài toán QHTT: f(x) = 6x1 - 7x2 + 4x3 – x4 max 3x1 - 2x2 + 3x3 + x4 = 8 x1 + 2x2 - 4x3 + 3x4 = 3 - 2x1 + x3 + 3x4 = 5 xj 0 ( j = 1 ÷ 4)
a/ Chứng minh hệ véc tơ A1, A2, A3 - hệ véc tơ cột lập bởi hệ số các ẩn x1, x2, x3 ở hệ
ràng buộc là độc lập tuyến tính.
b/ Tìm PACB ứng với hệ véc tơ A1, A2, A3 nếu có.
2.2. Cho bài toán QHTT: f(x) = x1 + 2x2 - x3 + 3x4 max 6x1 + 4x2 - 2x3 + 2x4 = 16 x1 + 2x2 - x4 = 4 - x1 + 2x3 + 5x4 = 10 xj 0 ( j = 1 ÷ 4)
Tìm tất cả các PACB suy biến của bài toán và cơ sở tương ứng của nó.
Đáp số: Vậy x = (0, 3, 0, 2) là PACB suy biến (duy nhất) với các cơ sở tương ứng là
A1, A2, A4 hoặc A2, A3, A4 .
2.3. Cho bài toán QHTT: f(x) = 6x1 - 7x2 + 4x3 – x4 + x5 max
3x1 - 2x2 + 3x3 + 5x4 – x5 = 10
- 2x1 + x2 + 2x3 + x4 – 3x5 = 1 4x1 + 3x2 – x3 – 7x4 + x5 = 9 xj 0 ( j = 1÷ 5)
a/ Chứng minh hệ véc tơ A1, A2, A3 - hệ véc tơ cột lập bởi hệ số các ẩn x1, x2, x3 ở hệ
ràng buộc là độc lập tuyến tính.
b/ Tìm PACB ứng với hệ véc tơ A1, A2, A3 nếu có.
2.4. Cho bài toán QHTT:
f(x) = 2x1 + x2 - 3x3 + 5x4 + x5 max 3x1 + 4x2 - x3 + x4 = 11 x1 - 3x2 - x4 + x5 = 0 -2x1 + x3 + 3x4 = 9 xj 0 ( j = 1÷ 5)
Tìm một PACB của bài toán và cơ sở của nó.
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
2.5. Cho bài toán QHTT: f(x) = 2x1 – x2 + 4x3 max x1 + 2x2 – x3 ≥ 1 3x1 – x2 + 4x3 ≤ 12 x1 + 2x3 ≤ 10 xj 0 (j = 1÷3)
a/ Chứng minh bài toán có phương án tối ưu.
b/ Với f(x) min, chứng minh bài toán không có phương án tối ưu. Hãy chỉ ra một
dãy các phương án mà trên đó f(x) giảm vô hạn.
2.6. Cho bài toán QHTT: f(x) = x1 + 8x2 + 10x3 min x1 + x2 + 4x3 = 2 x1 - x2 + 2x3 = 0 xj 0 ( j = )
Không giải, hãy chứng minh bài toán có PACB tối ưu.
2.7. Cho bài toán QHTT sau: f(x) = x1 + 4x2 + x3 max 4x1 + 11x2 + 3x3 ≥ - 7 x1 + x2 - x3 = 0 x ≤ 0 (j = ) j
Không giải, hãy chứng minh bài toán có PACB tối ưu và xác định một PACB tối ưu.
2.8. Cho bài toán QHTT: f(x) = x1 + 8x2 + x3 min x1 + x2 + 4x3 = 10 - x1 - 2x2 + x3 = 0 xj 0 ( j = 1 ÷ 3)
a/ Không giải, hãy chứng minh bài toán có PACB tối ưu. b/
Tìm tập hợp các PACB của bài toán.
Đáp số: b/ Tập hợp các PACB: X = {x1, x2} với x1 = (0, 10/9, 20/9) và x2 = (2, 0, 2)
2.9. Giải bài toán QHTT sau đây bằng phương pháp đơn hình: (nhân với -1 trc khi đổi) f(x) = x1 - x2 - 3x3 min 2x1 - x2 + x3 2 4x1 - 2x2 + x3 - 4 3x1 + x3 10 xj 0 ( j = 1 ÷ 3) Đáp số: Phương
án tối ưu: x* = (2/3, 22/3, 8) với fmin = - 92/3
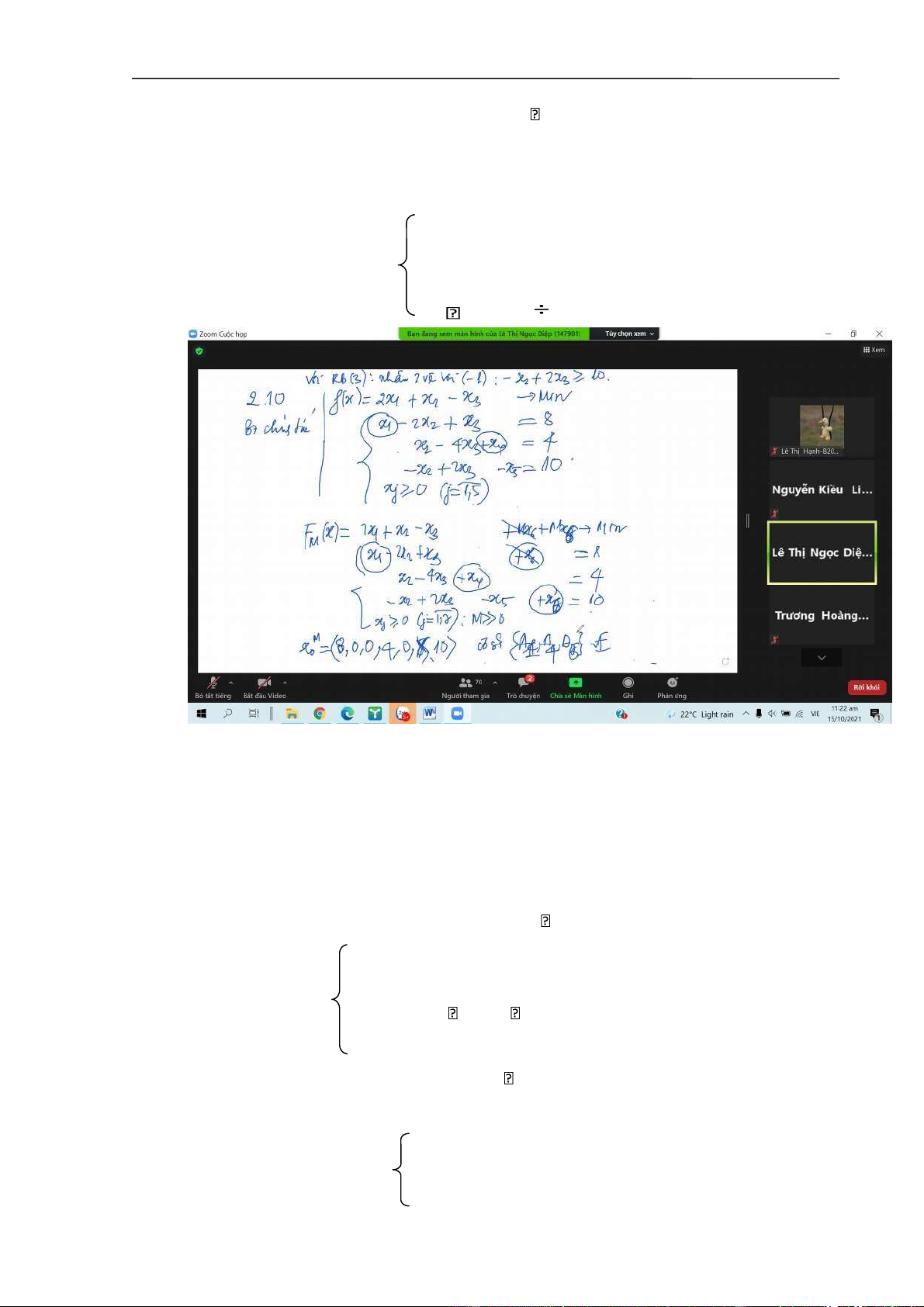
2.10. Giải bài toán QHTT sau bằng phương pháp đơn hình :
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
f(x) = 2x1 + x2 - x3 min ( cần nhân 2 vế với -1 vào pt 3 trc
khi dùng biến phụ để xd btoan ctac)
Chỉ có 2 biến cô lập là X1, X4 ( biến có hệ số +1, X5 là hệ số -1) nên cần 1 biến giả để xây dựng. x 1 - 2x 2 + x 3 = 8 x 2 - 4x 3 4 x 2 - 2x 3 - 10 x j 0 (j = 1 3)
Hướng dẫn: Đưa bài toán về dạng chính tắc. Sau đó lập bài toán M, giải bằng phương pháp
đơn hình. Từ bảng cuối cùng xác định được bài toán M không có lời giải nên bài toán chính tắc
cũng không có lời giải. Vậy bài toán gốc cũng không có lời giải.
2.11. Giải bài toán QHTT sau đây bằng phương pháp đơn hình:
f(x) = x1 + 5x2 + 4x3 - 6x4 max 2x1 + 3x2 - 4x3 - 5x4 1 5x1 - 6x2 + x3 - x4 3 4x1 + x2 - 2x3 + 3x4 2 xj 0 ( j = )
2.12. Cho bài toán QHTT: f(x) = - 10x1 + 3x2 min mx1 + 3x2 8 mx1 + x2 15
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế x1 0 , x2 0 với m 0
a/ Bằng phương pháp đơn hình, giải và biện luận bài toán theo tham số m. b/
Áp dụng giải bài toán khi m = 8.
Hướng dẫn: Đưa về dạng chính tắc; lập bảng đơn hình, giải và biện luận theo bảng đơn
hình. Kết quả: với m < 0 thì bài toán không có lời giải; với m > 0 thì lời giải của bài toán là: xopt = (8/m, 0); fopt = - 80/m .
2.13. Cho bài toán QHTT: f(x) = x1 + 2x2 + 2x3 + x4 + 6x5 max x1 + 3x2 + 3x3 + x4 + 9x5 = 18 x1 + 5x2 + 2x4 +
8x5 = 13 x3 + x5 = 3 xj 0 ( j = ) a/ Chứng tỏ véc tơ x0 =
(0, 1, 2, 0, 1) là phương án cực biên. b/ Giải bài toán bằng
phương pháp đơn hình xuất phát từ x0.
2.14. Cho bài toán QHTT: f(x) = 2x1 - x2 - x3 + 3x4 min x1 + ax2 +
x3 = 16 bx2 - 4x3 + x4 8 x2 - 2x3 + 3x4 - 20 xj 0 ( j = )
Với b 0, chỉ ra một khoảng giá trị của a để bài toán vô nghiệm.
2.15. Giải bài toán QHTT sau đây bằng phương pháp đơn hình:
f(x) = 2x1 + x2 - x3 + 3x4 min (1) x1 - 2x2 + x3 = 16 (a) x2 - 4x3 + x4 8 (b) (2) x2 - 2x3 + 3x4 - 20 (c) xj 0 ( j = ) (3)
2.16. Cho bài toán QHTT: f(x) = -2x1 + 5x2 - 4x3 + x4 max (1) 2ax1 + 3x2 - x3 + x4 = 3 ax1 - 6x2 + x3 = 1 (2) xj 0 ( j = ) (3) với a R; a 0
a/ Giải và biện luận bài toán theo a
b/ Giải bài toán với a = 2.
c/ Với a = 3, giải bài toán, đồng thời tìm các phương án của bài toán sao cho giá trị hàm mục tiêu bằng 0,1.
2.17. Cho bài toán QHTT: f(x) = 8x1 - 2x2 - 6x3 → min
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế 2x1 + 6x2 - 8x3 ≥ - 4 (1) 2x2 - 2x3 ≤ 10 (2) 4x1 - 8x2 + 6x3 ≥ - 6 (3) 2x1 - 6x2 ≥ - 15 (4) - 2x1 + 4x3 ≤ 6 (5)
và véc tơ x0 = (-1, 1, 1) a/
Viết bài toán đối ngẫu, các cặp ràng buộc đối ngẫu. b/
Phân tích các tính chất của x0 đối với bài toán đã cho.
c/ Xác định tập phương án tối ưu và các PACB của bài toán đối ngẫu. Đáp số:
b/ x0 là PACB không suy biến và là phương án tối ưu của bài toán gốc.
c/ Tập PA tối ưu của bài toán đối ngẫu: y* = {y0 = (1, 0, 1, 0, -1)}. PACB chính là y0.
2.18. Cho bài toán QHTT:
f(x) = 7x1 - 3x2 - 6x3 + 2x4 + 4x5 – 9x6 Min x1 - x2 - 2x3 + x5 - 3x6 = - 16 (1) 2x2 + 5x3 + x4 + 2x6 19 (2)
-2x1+ 2x2 + 4x3 + x4 + 3x5 + 6x6 ≤ 32 (3) xj ≥ 0 (j = 1 ÷ 6)
và phương án x0 = (0, 2, 1, 0, 0, 4) a/ Viết bài toán đối ngẫu, các cặp ràng buộc
đối ngẫu. b/ Nêu những tính chất có thể có của x0 đối với bài toán đã cho. c/
Xác định tập phương án tối ưu và các PACB tối ưu của bài toán đối ngẫu. Đáp
số: b/ x0 là phương án tối ưu của bài toán gốc nhưng không phải là PACB.
c/ Tập phương án tối ưu của bài toán đối ngẫu là: y* = {y = (3+ 2y3, 0, y3), y3 ≤ 0} PACB tối ưu: y0 = (3, 0, 0).
2.19. Cho bài toán QHTT:
f(x) = - 9x1+ 5x2 + 15x3 + 6x4 + 7x5 Min 4x2 + x3 - x4 + 2x5 = 4 (1)
3x1 + x2 – x3 + x4 - x5 ≤ 1 (2)
- x1 – x2 + x3 - 2x4 ≥ - 1 (3) xj 0 (j = 2 ÷ 5)
a/ Viết bài toán đối ngẫu. Chỉ ra các cặp ràng buộc đối ngẫu.
b/ Cho véc tơ x0 = (1, 0, 0, 0, 2). Phân tích tính chất của x0 đối với bài toán gốc. c/
Xác định tập phương án tối ưu và các PACB tối ưu của bài toán đối ngẫu.
Đáp số: b/ x0 là phương án cực biên tối ưu. c/ Tập phương án tối ưu của bài toán
đối ngẫu: y* = {y=(, y2, 9+3y2), - 3≤ y2 ≤ 0} Các PACB tối ưu: y1 = (7/2, 0, 9), y2 = (2, -3, 0).
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
2.20. Cho bài toán quy hoạch tuyến tính và véc tơ x* = (0, 1, 0, 2, 3):
f(x) = x1 + x2 + x3 + x4 + x5 → min 3x1 + x2 + x3 = 1 5x1 + x2 + x3 + x4 = 3 2x1 + 5x2 + x3 + x5 = 8
xj ≥ 0 (j = 1÷5). a/ Viết bài toán đối ngẫu, các cặp ràng buộc
đối ngẫu. b/ Phân tích các tính chất của x* đối với bài toán đã cho.
2.21. Cho bài toán QHTT:
f(x) = 11x1 + 7x2 - 4x3 - 16x4 min x1 -
2x2 + x3 + 3x4 ≤ - 12 (1) - x1 + 4x2 -
3x3 - 8x4 20 (2) - 2x1 + x2 - x3 -
x4 ≤ - 2 (3) xj 0 ( j = 1÷4)
a/ Viết bài toán đối ngẫu. Chứng tỏ véc tơ y0 = (-1, 2, -3) là phương án cực biên của bài toán đối ngẫu.
b/ Xuất phát từ y0, dùng thuật toán đơn hình đối ngẫu tìm lời giải của bài toán gốc. Xác
định phương án tối ưu của bài toán đối ngẫu.
2.22. Dùng phương pháp đơn hình giải quy hoạch gốc sau đây, từ đó suy ra lời giải của bài toán
đối ngẫu tương ứng với nó.
f(x) = x1 – x2 – 2x4 + 2x5 – 3x6 → min x1 + x4 + x5 – x6 = 2 x2 + x4 + x6 = 12 x3 + 2x4 + 4x5 + 3x6 = 9 xj 0 (j = 1÷6) 2.23. Cho bài toán:
f(x) = – 5x1 + 2x2 – 4x3 + 9x4 + 6x5 – 7x6 Min
3x1 + 2x2 – x3 + x4 + 2x5 – 2x6 4 (1)
– x1 – x2 – x4 – x5 + 3x6 = – 1 (2) 4x1
+ 2x3 – 3x4 – 3x5 – x6 – 7 (3) x1, x3, x6 0; x2, x5 0
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
a/ Viết bài toán đối ngẫu, các cặp ràng buộc đối ngẫu b/ Nêu những tính chất có thể có
của véc tơ x0 = (2, 0, 1, 5, 0, 2) đối với bài toán đã
cho. Xác định phương án tối ưu của bài toán đối ngẫu và các tính chất của nó.
2.24. Cho bài toán QHTT: f(x) = x1 + 4x2 + px3 Max 3x1 + 4x2 + 4x3 = 10 (1) - x1 + x2 + x3 = - 1 (2) xj 0 (j = 1÷3); p là tham số
a/ Viết bài toán đối ngẫu và các cặp ràng buộc đối ngẫu.
b/ Với điều kiện nào của p thì véc tơ x0 = (2, 1, 0) sẽ là phương án tối ưu của bài toán
gốc và bài toán đối ngẫu có PACB tối ưu không suy biến.
c/ Với giá trị của p tìm được ở câu b, chứng tỏ x0 là PACB tối ưu duy nhất.
2.25. Cho bài toán QHTT:
f(x) = 2x1+ 16x2 - 25x3 + 2x4 Max
2x1 - 2x2 - 3x3 + 2x4 = 4 (1) 3x2 + 5x3 - 2x4 ≥ - 2 (2) 2x1 - 2x3 + x4 = 5 (3) xj 0(j = 1÷4)
a/ Viết bài toán đối ngẫu. Chỉ ra các cặp ràng buộc đối ngẫu. b/ Cho véc tơ
x0 = (0, 3, 0, 5). Phân tích tính chất của x0 đối với bài toán gốc. c/ Xác định
tập phương án tối ưu và các PACB tối ưu của hai bài toán.
2.26. Giải bằng phương pháp đơn hình đối ngẫu bài toán:
f(x) = 5x1 + 7x2 + 3x3 + 2x4 Min x1 + x3 - x4 = 4 - x1 + 2x2 + x4 18 2x1 + x2 - 3x4 5 xj 0 (j = 1÷4)
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
2.27. Cho bài toán QHTT sau:
f(x) = 3x1 – x2 – 8x3 – 2x4 + 2x5 → Min
– 2x1 + 5x3 + 3x4 – 3x5 – 11 x1 –
4x3 + 4x4 – x5 = 14 x1 – 2x3 – 2x4 +
x5 = – 4 – 2x1 + x2 + 4x3 + 2x5 = 20
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
xj 0 (j = 1÷5) a/ Giải bằng phương
pháp đơn hình. Tìm một phương án có f(x) = - 48.
b/ Xác định tập phương án tối ưu và phương án tối ưu của bài toán đối ngẫu khi hàm
mục tiêu là: h(x) = x1 + x2 + 2x3 – 6x4 + 5x5 → min. CHƯƠNG 4.
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
CHƯƠNG 5. MÔ HÌNH BÀI TOÁN VẬN TẢI
3.1. Cho bài toán vận tải tiêu chuẩn cước phí. 0 0 50 /15 thu Ui B 1 : 30 B 2 : 20 B 3 : 70 Phát 20 8 2 5 0 A 1 : 40 -9 20 20 7 5 6 -1 A 2 : 35 -7 -2 35 15 4 11 10 -5 A 3 : 45 30 -4 15 Vj -1 2 5
Ta có: 5=m+n-1 => đây là PACB không suy biến Ta kẻ thêm Ui và Vj.
Ta thấy tất cả dentaij đều <0 nên đây là PACB tối ưu.
Giải bài toán vận tải đã cho. Phương án tối ưu của bài toán có duy nhất không? Vì sao?
3.2. Cho bài toán vận tải theo tiêu chuẩn cước phí với số liệu như sau: 30/0 80/0 240 0
Giải bài toán bằng phương pháp thế vị. Nhận xét về phương án tối ưu của bài toán.
Ta có tổng phát = tổng thu = 1160
Ta thấy 8=m+n-1 => PACB không suy biến
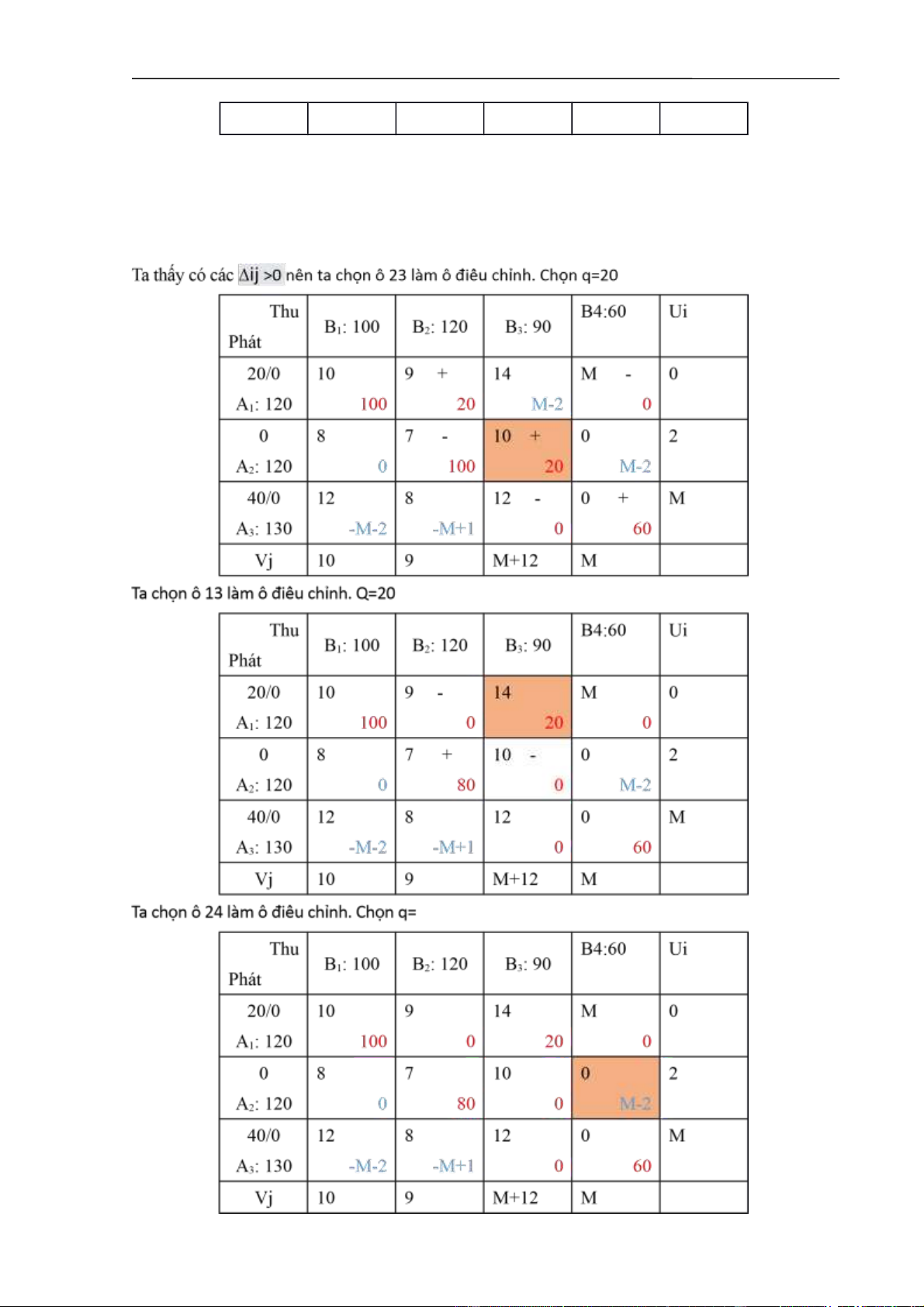
Ta có các denta ij>0 nên ta chọn ô điều chỉnh. Ta chọn ô 15 làm ô điều chỉnh. Ta chọn q=100
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
3.3 . Cho bài toán vận tải tiêu chuẩn cước phí: Thu B 1 : 85 B 2 : 75 B 3 : 70 B 4 : 60 B 5 : 45 Phát A 1 : 80 8 2 5 4 12 A 2 : 110 7 5 6 8 10 A 3 : 90 4 11 10 9 6 A 4 : 120 6 3 12 7 5
Giải bài toán vận tải trên với điều kiện lượng hàng giữ lại ở trạm phát A2 không vượt
quá 10. Phương án tối ưu tìm được có phải là duy nhất không? Vì sao?
Hướng dẫn: Chuyển bài toán về dạng đóng, tách trạm phát A 1 2 thành 2 trạm A2 = 100 và A 2
2 = 10 (với chi phí tại điểm thu giả tương ứng với là M >> 0 để không thể phân hàng dư vào ô này).
Phương án vận chuyển tối ưu: X* = ; f (X*) = 1490 (ĐV tiền) Tồn
kho ở A : 10 đơn vị hàng; A : 5 đơn vị hàng; A : 50 đơn vị hàng. 2 3 4
Phương án X* tìm được là duy nhất.
3.4. Cho bài toán vận tải tiêu chuẩn cước phí:
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế Thu B B B B B 1 : 85 2 : 115 3 : 130 4 : 70 5 : 95 Phát A 1 : 90 2 6 5 10 9 A 2 :110 4 7 3 6 12 A 3 : 75 7 9 8 12 5 A 4 : 80 5 3 7 8 4
Giải bài toán vận tải đã cho với điều kiện lượng hàng chở đến B3 không được ít hơn 130
đơn vị hàng. Phương án tối ưu của bài toán có duy nhất không? Vì sao? Tìm tập phương án tối ưu (nếu có).
Hướng dẫn: đưa về bài toán vận tải với chi phí tại điểm phát giả tương ứng với B3 là
M>> 0 để không thể phân thiếu hàng vào ô này. Phương án tối ưu X* tìm được là không duy
nhất. Tập phương án tối ưu của bài toán vận tải đã cho: D = {}, trong đó , X* = và =
3.5. Cho bài toán vận tải tiêu chuẩn cước phí: Thu B 1 : 30 B 2 : 20 B 3 : 70 Phát A 1 : 40 4 2 1 A 2 : 30 9 4 6 A 3 : 30 8 2 3
a/ Giải bài toán vận tải đã cho. Phương án tối ưu của bài toán có duy nhất không? Vì
sao? Tìm tập phương án tối ưu (nếu có).
b/ Thay cước phí c’13 = c13 + và c’33 = c33 + , còn giữ nguyên cước phí các cung đường
còn lại. Tìm điều kiện của để phương án tối ưu của bài toán đã cho vẫn là phương án tối ưu của
bài toán khi thay cước phí mới.
3.6. Cho bài toán vận tải theo tiêu chuẩn tổng chi phí nhỏ nhất với số liệu như sau: Thu: b j 105 85 80 100 60 Phát: a i 12 11 15 8 12 115 (35) (80) 90 8 14 17 6 14 c ij
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế (65) (25)
( x ij ) 5 11 16 5 9 100 (40) (60) 7 10 19 4 11 125 (50) (75)
a/ Chứng tỏ rằng hệ {x } là phương án cực biên tối ưu của bài toán vận tải trên. ij
b/ Thực hiện phép biến đổi: c’33 = c33 + α ; c’43 = c43 + α ; còn các cij khác giữ nguyên.
Xác định α để phương án đã cho vẫn tối ưu. Với trị số nào của α thì bài toán có vô số phương
án tối ưu? Khi đó hãy chỉ ra một phương án cực biên tối ưu khác và một phương án tối ưu không cực biên.
c/ Nếu phép biến đổi có dạng c’i3 = ci3 + α (i = 1÷ 4); còn các cij khác giữ nguyên,
trong đó α > - 15 thì có kết luận gì về phương án tối ưu của bài toán vận tải mới?
3.7. Cho bài toán vận tải và tập phương án cực biên được đánh dấu *. Thu: b j 150 85 75 115 90 Phát: a i 100 3 2* 11 4* 7 245 4* 7 12* 10 9* c ij 120 7* 8* 19 14 16 55 17 19 25 18* 22
a/ Hãy xác định một phương án tương ứng với các ô chọn được đánh dấu *. Giải bài
toán xuất phát từ phương án đó.
b/ Giả sử b4 = 115+α, a2 = 245+α, hãy tìm trị số của α để phương án tối ưu của bài
toán mới có tập ô chọn trùng với lời giải ở câu a.
PP: Với lượng hàng b4 và a2 được thay đổi theo đề bài. Thực hiện phân hàng vào tập ô chọn
của PATU ở câu a (cách phân hàng tương tự như cách phân hàng ở câu a). PA thu được sẽ có
lượng hàng ở 1 số ô chọn có dạng Xij (anpha). Cần tìm anpha sao cho
3.8. Cho bài toán vận tải và tập phương án cực biên được đánh dấu * ở bảng dưới đây.
a/ Hãy xác định phương án tối ưu của bài toán. Tổng phát =290=tổng thu. b/ Giảm cước phí c
’ = 14, chứng minh rằng bài toán có vô số phương án 42 xuống còn c42
tối ưu. Tìm phương án tối ưu mà trạm phát A2 chuyển cho trạm thu B1 một lượng hàng là 45
đơn vị, phương án đó có phải là phương án cực biên tối ưu hay không?
PP: Khi thay c42=17 còn c42’=14 thì denta ij của c42 lúc đầu là -3, sau đó thành 0. Chỉ cần tính
lại denta 42. Lấy ô 42 làm ô điều chỉnh, thực hiện điều chỉnh sẽ thu được PACB tối ưu t2
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế => tập PATU Thu: b j 51 54 60 45 80 Phát: a i 10* 11 10 9* 8 50 5 45 12* 12* 5 13 11 c ij 90 46 44 19 18* 6* 14 15 70 10 60 18 17 7 15 12* 80 80
3.9. Cho bài toán vận tải tiêu chuẩn cước phí: 0 0 0 0 Thu B4:60 Ui B 1 : 100 B 2 : 120 B 3 : 90 Phát 20 / 0 10 9 14 M 0 A 1 : 120 100 0* M-2 20 0 8 7 10 0 2 A 2 : 120 0 120 M M-2 / 40 0 12 8 12 0 M A 3 : 130 - M -2 - +1 M 90 40
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế Vj 10 9 M+12 M
Giải bài toán vận tải đã cho với điều kiện trạm phát A1 phải được ưu tiên phát hết hàng.
Ta có tổng phát là 370 > Tổng thu 310. Khi đó bổ sung thêm B4 = 60 Ta
có 5 < m+n-1 nên ta bổ sung thêm 1 ô chọn và không tạo thành chu trình Kẻ thêm Ui và Vj.
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
3.10. Cho bài toán vận tải tiêu chuẩn cước phí: Thu B 1 : 110 B 2 : 90 B 3 : 110 Phát A 1 : 80 15 17 14 A 2 : 60 12 10 11 A 3 : 100 20 16 21
Giải bài toán vận tải đã cho với điều kiện trạm thu B1 phải được ưu tiên nhận đủ hàng.
3.11. Cho bài toán vận tải tiêu chuẩn cước phí: Thu B 1 : 60 B 2 : 50 B 3 : 100 B 4 : 60 Phát A 1 : 60 3 5 2 5 A 2 : 80 15 6 12 7 A 3 : 90 14 8 11 13 A 4 : 90 10 5 8 9
Hãy tìm phương án vận chuyển tối ưu với điều kiện trạm phát A2 không được phát hàng cho trạm thu B2.
PP: Ô 22 bị cấm, đặt M vào
3.12. Cho bài toán vận tải tiêu chuẩn cước phí: Thu B 1 : 200 B 2 : 50 B 3 : 300 Phát A 1 : 250 20 21 24 A 2 : 250 18 15 14 A 3 : 70 11 11 9 A 4 : 130 15 12 13
a/ Hãy tìm phương án vận chuyển tối ưu với điều kiện trạm phát A1 không được tồn kho quá 80 đơn vị hàng. Thêm trạm B4
Tách trạm a1 là 170 và 80. Đặt M vào ô 170, còn lại đặt 0 b/ Phương án tối ưu có duy nhất
không? Vì sao? Tìm tập phương án tối ưu (nếu có).
3.13. Cho bài toán vận tải tiêu chuẩn cước phí: Thu B 1 : 20 B 2 : 40 B 3 : 35 B 4 : 30
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế Phát A 1 : 30 11 18 12 19 A 2 : 18 3 6 2 5 A 3 : 20 8 14 20 15 A 4 : 37 6 16 10 11
a/ Chứng minh rằng bài toán có vô số phương án tối ưu.
b/ Hãy tìm một phương án tối ưu với điều kiện trạm phát A3 chuyển cho trạm thu B1
một lượng hàng là 6 đơn vị hàng. Phương án đó có phải là phương án cực biên hay không?
3.14. Giải bài toán vận tải tiêu chuẩn thời gian với số liệu cho ở bảng sau (tij – thời gian vận
chuyển hết hàng từ Ai đến Bj). Thu B 1 : 40 Phát A 1 : 50 3 tij A 2 : 70 5 A 3 : 60 4 CHƯƠNG 6.
CHƯƠNG 7. MÔ HÌNH BÀI TOÁN TỐI ƯU TRÊN MẠNG
4.1. Đồ thị trọng số G = (X, A) như hình vẽ sau đây. Tìm đường đi ngắn nhất từ X . Vẽ 1 đến X7
đồ thị đối ngẫu của đồ thị trên. 60 X2 X5 50 30 40 20 X1 X4 20 X7 40 10 70 Đáp số: 40
Đường đi ngắn nhất từ x
50 1 đến x 7 là x 1 x 3 x 4 x 7 với chiều dài là 100 X6 đơn vị độ dài X3 ( ).
4.2. Cho đồ thị trọng số G = (X, A) như hình vẽ. Tìm đường đi ngắn nhất từ X1 đến X6 và vẽ đồ thị đối ngẫu.
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế 5 X2 X5 2 6 X1 1 8 3 X6 6 3 4
Đáp số: x 1 x 3 x 4 x 6 với chiều dài là 12 (đơn vị độ dài). X3 X4 5
4.3. Cho đồ thị G = (X, A) như sau: 3 4 x2 x3 x4 3 7 5 2 2 2 2 Nguồn Đích 2 6 5 8 x1 x5 x7 x8 x6 2 4 5 1 3 4 3 6 5 x1 x9 x1 10 0 00 0
a/ Tìm đường đi ngắn nhất từ x1 x8 b/
Tìm đường đi ngắn nhất từ x2 x11 c/
Tìm đường đi ngắn nhất từ x Đáp 5 x8 số:
a/ x1 x2 → x3 → x4 → x8 hoặc x1 x5 → x6 → x4 → x8 với
chiều dài là 17 đơn vị độ dài.
b/ Không có đường đi từ đỉnh x2 x11 c/ x5 → x6 → x4
→ x8 với chiều dài là 11 đơn vị độ dài.
4.4. Hãy xác định phương án kết nối các điểm trên đồ thị dưới đây sao cho tổng chiều dài mạng
liên thông là ngắn nhất.
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế A 9 I 8 6 14 2 B G L 5 12 9 11 C 6 5 H 2 E 2 J 8 10 N 9 4 D 5 3 11 6 M 9 F
4.5. Cho đồ thị như hình vẽ sau. Nguồn là đỉnh 1, đích là đỉnh 6, tổng số hàng vận chuyển từ
nguồn đến đích là 6 đơn vị. Trên mỗi cạnh có một cặp số thứ tự mà số thứ nhất là chi phí vận
chuyển một đơn vị hàng hoá trên cạnh, số thứ hai là khả năng thông qua của cạnh này. Hãy xác
định phương án vận chuyển sao cho vận chuyển hết lượng hàng theo yêu cầu từ nguồn đến đích
với tổng chi phí vận chuyển là nhỏ nhất. 4 , (4 1) (3 4) , (2 , 4) 6 (1 2) , 1 3 (6 3) ,
Đáp số : Luồng hàng cần vận c, (1 hu
4) yển là: x 12 = 2; x 14 = 4; x 32 = 1; x = 3; x = 2; x = (1 , 2) 3 ; x
= 3 với tổng chi phí vận c huyển bằ (5 n , g 3) 60 (đơn vị 46 = 1; x 56 ti ền). 2 5 Đích Nguồn 25 36 43
4.6. Cho đồ thị hữu hạn G X A ( , )
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
(Các số ghi trên mỗi cạnh, cung là khả năng thông qua của cạnh, cung đó) a/
Từ đồ thị đã cho G = (X,A):
- Xác định ma trận liên hệ cung nút của đồ thị. , )
- Bỏ cung (x x5 7 . Vẽ đồ thị đối ngẫu với đồ thị còn lại. Xác định một cặp điều
kiện đối ngẫu của hai đồ thị này. b/ Xác định luồng lớn nhất trên mạng cho bởi đồ thị G =
(X,A), trong đó x là đỉnh nguồn, x 1 8 là đỉnh đích.
4.7. Tính các chỉ tiêu thời gian, tìm đường găng và độ dài đường găng của sơ đồ mạng sau:
Đáp số: Đường găng: x1 → x4 → x6 → x7 → x8 với độ dài 22 (đơn vị độ dài) 4.8.
Tìm đường găng và độ dài đường găng của sơ đồ mạng sau:
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế 6 8 2 6 11 0 3 8 5 3 8 5 1 6 7 12 9 1 9 2 1 4 7 10 1 1 0 1 6 6 1 2 1 5 9 1 1 1 21
Đáp số: Đường găng: x1 → x3 → x7 → x10 → x12 với độ dài là 29 (đơn vị độ dài).
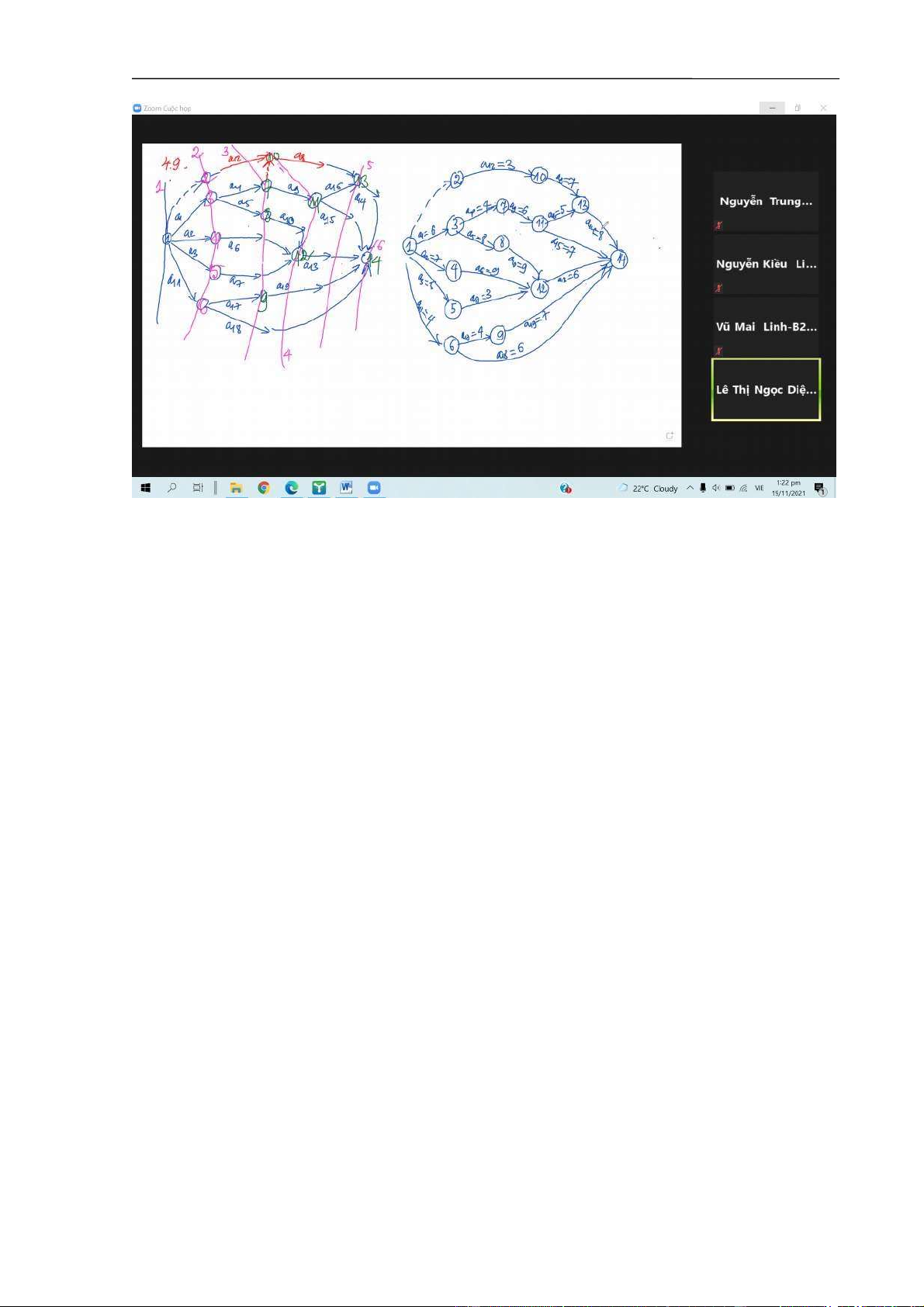
4.9. Lập sơ đồ mạng lưới cho dự án gồm các công việc từ a1 đến a19 với trình tự thực hiện các công việc như sau: Công việc a đầu ngay.
1, a2, a3 và a11 có thể bắt
Công việc a1 làm trước a4 và a5 ; a3 làm trước a7. Công
việc a4 làm trước a8 và a9 ; a6 làm sau a2.
Công việc a9 làm trước a15 và a16 ; a10 làm sau a5.
Công việc a11 làm trước a17 và a18 .
Công việc a12 làm trước a8 ; công việc a13 làm sau a6, a7 và a10.
Công việc a14 làm sau a8 và a16 ; a17 làm trước a19. Các công việc a làm cuối cùng. 13, a14, a15, a18 và a19
Cho biết thời gian hoàn thành các công việc: a1 – 6h; a2 – 7h; a3 – 5h; a4 – 4h; a5 – 8h; a6
– 9h; a7 – 3h; a8 – 7h; a9 – 6h; a10 – 9h; a11 – 4h; a12 – 3h; a13 – 6h; a14 – 8h; a15 – 7h; a16 – 5h; a17
– 4h; a18 – 6h; a19 – 7h.
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
Tìm đường găng và tính độ dài đường găng tìm được.
4.10. Lập sơ đồ mạng lưới cho dự án gồm các công việc từ a1 đến a20 với trình tự thực hiện các công việc như sau: Công việc a đầu ngay.
1, a2, a3 và a4 có thể bắt
Công việc a1 làm trước a5 ; a2 làm trước a6, a7 và a8.
Các công việc a3 làm trước a9 và a10 ; a11 làm sau a4. Công việc a ; các công việc a 12 làm sau a5 và a6
13 và a14 làm sau a8 và a9.
Các công việc a15 và a20 làm sau a10 và a11.
Các công việc a16 và a18 làm sau a7 và a13.
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
Công việc a19 làm sau a14 và a15.
Công việc a17 làm sau a12 và a16. Các công việc a làm cuối cùng. 17, a18, a19 và a20
Thời gian hoàn thành các công việc như sau: a1 – 1h; a2 – 5h; a3 – 2h; a4 – 2h; a5 – 6h;
a6 – 3h; a7 – 8h; a8 – 6h; a9 – 1h; a10 – 4h; a11 – 2h; a12 – 8h; a13 – 7h; a14 – 9h; a15 – 6h; a16 – 5h;
a17 – 3h; a18 – 5h; a19 – 9h; a20 – 6h.
Tìm đường găng và tính độ dài đường găng tìm được. CHƯƠNG 8.
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
CHƯƠNG 9. MÔ HÌNH HỆ THỐNG PHỤC VỤ CÔNG CỘNG
5.1. Một trạm xử lý tin nóng có 10 máy làm việc tự động, mỗi máy xử lý trung bình
được 4 bản tin một giờ. Trạm làm việc theo chế độ của hệ thống Eclang, dòng các bản tin cần
xử lý là dòng Poát xông dừng với tốc độ trung bình 30 bản tin giờ. Hãy xác định các chỉ tiêu
đánh giá chất lượng xử lý tin của trạm.
5.2. Bộ phận kiểm tra sản phẩm có 4 máy làm việc tự động, năng suất các máy đều là 3
sản phẩm một phút. Mỗi sản phẩm ra khỏi dây chuyền đến bộ phận kiểm tra nếu gặp lúc có máy
rỗi sẽ được kiểm tra một trong các máy rỗi, ngược lại sản phẩm được nhập kho không qua kiểm
tra. Dòng sản phẩm ra khỏi dây chuyền là dòng Poát xông dừng, mật độ trung bình là 10 sản
phẩm/phút. Thời gian kiểm tra một sản phẩm phân phối theo luật chỉ số.
Người ta muốn nâng tỷ lệ sản phẩm được kiểm tra và dự định hai phương án như sau:
a/ Tăng thêm 3 máy có năng suất như các máy cũ.
nA=7, nuy=3 sp/phút, tính lại Po => Ppv b/ Nâng năng
suất gấp 2 lần cho 4 máy hiện có. nB=4, nuy = 6 sp/phút, tính lại po =>Ppv
Hãy chọn phương án đáp ứng yêu cầu đặt ra cao hơn?
5.3. Một phòng khám có 3 bác sỹ, thời gian mỗi bác sỹ khám cho một bệnh nhân trung
bình là 15 phút. Giả sử dòng bệnh nhân đến khám là dòng Poát xông dừng, mỗi giờ trung bình
có 9 bệnh nhân đến phòng khám. Phòng khám có 6 chỗ chờ tối đa cho 6 bệnh nhân. Hãy tính
các chỉ tiêu đánh giá hoạt động của phòng khám này.
5.4. Một cửa hàng bảo dưỡng xe máy có 5 công nhân làm việc và một diện tích để 10
xe chờ. Mỗi công nhân bảo dưỡng một xe. Dòng xe có nhu cầu bảo dưỡng giả thiết là dòng tối
giản, trung bình 4 xe/giờ. Thời gian bảo dưỡng trung bình mỗi xe của một công nhân hết 1 giờ. Hãy tính các chỉ tiêu: - Xác suất phục vụ.
- Số công nhân bận trung bình.
- Số xe chờ trung bình và thời gian chờ trung bình.
5.5. Một bưu cục trung tâm có 6 ghi sê làm việc độc lập, mỗi ghi sê do một nhân viên
đảm nhận, trung bình một giờ giải quyết được 8 giao dịch. Trung bình mỗi giờ có 36 khách
hàng đến giao dịch tại bưu cục. Nếu khách hàng đến bưu cục gặp lúc có ghi sê rỗi thì được nhận
vào phục vụ ngay, ngược lại khách hàng phải xếp hàng chờ. Diện tích của bưu cục đủ lớn, dòng
yêu cầu đến bưu cục là dòng Poát xông dừng, thời gian phục vụ một khách hàng là một biến
ngẫu nhiên tuân theo quy luật chỉ số. Hãy xác định các chỉ tiêu đánh giá chất lượng phục vụ của bưu cục đó.
N=6, năng suất = 8 giao dịch/giờ, lamda=36. Đây là hệ thống chờ thuần nhất. Có 2 loại trạng thái.
Xk(t) chạy từ 0 đến 6. Xn+s(t) chạy từ 1 đến vô cùng.
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
A, Tính xác suất để tính được ít nhất 2 quầy rỗi.
Tính hệ thống phục vụ ngay, hệ thống đang yêu cầu chờ => ra xác suất kênh bận
Ít nhất 2 quầy rỗi = nhiều nhất 4 kênh bận.
Tính (1 bận+2 bận...+ 4 bận) => ít nhất 2 quầy rỗi = 1-tổng bận.
5.6. Một bưu cục (bưu kiện) có 2 tổ làm việc độc lập, năng suất mỗi tổ là 20 bưu kiện
một giờ. Dòng bưu kiện về bưu cục là dòng Poát xông dừng với cường độ là 100 bưu kiện một
ngày, mỗi ngày làm việc 10 giờ. Thời gian khai thác một túi bưu kiện là một biến ngẫu nhiên
tuân theo quy luật chỉ số.
Một bưu kiện về đến bưu cục gặp lúc có tổ rỗi thì được nhận vào khai thác ngay tại đó,
ngược lại bưu kiện được xếp vào kho theo thứ tự với dung tích kho không hạn chế.
a/ Vẽ sơ đồ trạng thái, cho biết hệ thống nói trên là hệ thống phục vụ loại gì? b/
Hãy xác định các chỉ tiêu đánh giá chất lượng phục vụ của hệ thống.
5.7. Một Trung tâm Bưu Điện có 6 nhân viên làm các gói dịch vụ về điện thoại, mỗigiờ
một người hoàn thành được các gói dịch vụ của 4 khách hàng. Trung bình mỗi giờ có 18 khách
hàng đến Trung tâm Bưu Điện để yêu cầu được phục vụ. Nếu khách đến Trung tâm gặp lúc có
nhân viên rỗi thì được phục vụ ngay, ngược lại thì phải xếp hàng chờ ở phòng chờ. Phòng chờ
đủ lớn cho mọi khách hàng đã đến Trung tâm Bưu Điện để được phục vụ. Giả sử dòng khách
hàng đến Trung tâm Bưu Điện là dòng Poát-xông dừng, thời gian làm xong các gói dịch vụ cho
một khách hàng là biến ngẫu nhiên tuân theo quy luật số mũ.
a/ Vẽ sơ đồ trạng thái của hệ dịch vụ. Trạng thái của hệ thống thay đổi theo quy luật gì? Vì sao?
b/ Tính các chỉ tiêu đánh giá chất lượng phục vụ của hệ thống: P , , , , . Từ các chỉ 0 , Pc , Ppv
tiêu tính được, nhận xét về chất lượng phục vụ của hệ thống.
5.8. Một bộ phận kiểm tra sản phẩm của một cơ sở sản xuất có 6 máy làm việc tự động,
năng suất mỗi máy đều là 12 sản phẩm/giờ. Mỗi sản phẩm ra khỏi dây chuyền sản xuất đến bộ
phận kiểm tra, nếu gặp lúc có máy rỗi thì sẽ được kiểm tra tại một trong các máy rỗi, ngược lại
sản phẩm được nhập kho không qua kiểm tra. Dòng sản phẩm ra khỏi dây chuyền sản xuất là
dòng Poát – xông dừng, mật độ trung bình 24 sản phẩm/giờ. Thời gian kiểm tra một sản phẩm
tuân theo quy luật số mũ.
a/ Vẽ sơ đồ trạng thái của hệ thống. Trạng thái của hệ thống biến đổi theo quy luật gì? Vì sao?
b/ Tính các chỉ tiêu đánh giá chất lượng phục vụ của bộ phận kiểm tra.
c/ Nếu muốn tỷ lệ sản phẩm được kiểm tra không nhỏ hơn 99% thì tối thiểu cần bao
nhiêu máy tự động ở bộ phận kiểm tra.
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
5.9. Một trung tâm xử lý tin nhanh có 3 tổ làm việc độc lập, năng suất mỗi tổ là 6
bảntin/giờ. Mỗi bản tin đến trung tâm, nếu gặp lúc có tổ rỗi thì sẽ được xử lý tại một trong các
tổ rỗi, ngược lại bản tin sẽ bị loại ra khỏi trung tâm. Dòng bản tin đến trung tâm xử lý là dòng
Poát – xông dừng, mật độ trung bình 12 bản tin/giờ. Thời gian xử lý một bản tin tuân theo quy
luật số mũ. a/ Vẽ sơ đồ trạng thái của hệ thống. Trạng thái của hệ thống biến đổi theo quy luật gì? Vì sao?
b/ Tính các chỉ tiêu đánh giá chất lượng phục vụ của hệ thống.
c/ Nếu muốn tỷ lệ bản tin được xử lý không nhỏ hơn 95% thì tối thiểu cần bao nhiêu tổ xử lý tin.
5.10. Một siêu thị gồm có 6 quầy thu ngân, mỗi giờ mỗi quầy trung bình thanh toánđược
6 khách hàng. Trung bình mỗi giờ có 27 khách hàng đến xếp hàng thanh toán. Nếu một khách
hàng đến gặp quầy rỗi thì được thanh toán ngay, ngược lại phải xếp hàng chờ. Không gian xếp
hàng chờ đủ lớn. Giả sử dòng khách đến thanh toán là dòng Poát xông dừng, còn thời gian thanh
toán tuân theo quy luật mũ.
a/ Hệ thống trên thuộc loại hệ thống phục vụ công cộng nào? Vẽ sơ đồ trạng thái của
hệ thống. Trạng thái của hệ thống biến đổi theo quy luật “huỷ và sinh” không?
b/ Tính các chỉ tiêu đánh giá chất lượng phục vụ của hệ thống.
CHƯƠNG 10. MÔ HÌNH QUẢN LÝ DỰ TRỮ
6.1. Một cửa hàng kinh doanh một mặt hàng điện tử, nhu cầu về mặt hàng này trongkhu
vực là 40.000 đơn vị/ năm. Giá mua mỗi đơn vị là 14 nghìn đồng, chi phí bảo quản mỗi đơn vị
tính tỷ lệ với giá mua theo hệ số 0,05. Chi phí cho mỗi lần đặt hàng là 120 nghìn đồng. Thời
gian từ lúc bắt đầu làm hợp đồng đến khi có hàng về cửa hàng là 3 tháng.
a/ Tính lượng hàng đặt mỗi lần sao cho tổng chi phí là nhỏ nhất. Xác định thời gian mỗi
chu kỳ mua và tiêu thụ hàng, mức hàng còn lại trong kho vào thời điểm cần tiến hành làm thủ tục mua hàng cho kỳ sau.
b/ Nếu cửa hàng nhận được một báo giá mới của một nhà cung cấp khác với đơn giá
13,5 nghìn đồng nhưng chi phí cho mỗi lần đặt hàng là 125 nghìn đồng thì có nên lựa chọn mua ở nơi mới này không?
6.2. Một doanh nghiệp cung cấp thuốc bảo vệ thực vật dự báo trên địa bàn mình
cungcấp lượng tiêu thụ mỗi năm là 30.000 đơn vị. Công suất thực tế của doanh nghiệp là 45.000
đơn vị/năm. Chi phí cho một lần chuẩn bị sản xuất là 2 triệu, chi phí sản xuất tính trực tiếp cho
mỗi đơn vị thuốc bảo vệ thực vật này là 200 nghìn đồng. Chi phí bảo quản bằng 15% chi phí
sản xuất trực tiếp. Thời gian chuẩn bị một đợt sản xuất là 1 tháng.
Hãy xác định số đơn vị thuốc cần sản xuất cho mỗi đợt sao cho tổng chi phí là nhỏ nhất.
Xác định điểm (lượng thuốc còn trong dự trữ) chuẩn bị sản xuất.
6.3. Nhu cầu một loại thuốc chữa bệnh thông thường hàng năm là 960.000 hộp.
Mộtcông ty dược có một cơ sở sản xuất với công suất 1.600.000 hộp/năm, dự định cung cấp
loại thuốc này. Chi phí cho mỗi đợt chuẩn bị sản xuất là 250$, chi phí sản xuất mỗi hộp là 12$,
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
chi phí bảo quản bằng 20% chi phí sản xuất. Công ty có một kho đủ lớn để bảo quản thuốc. Giả
sử việc tiêu thụ là đều đặn và cường độ sản xuất trong mỗi kỳ là không đổi.
Trong năm đầu, công ty đã chia thành 6 đợt sản xuất bằng nhau và cung cấp vừa đủ nhu
cầu. Kiểm tra thấy lượng thuốc qua kho là 500.000 hộp.
Hãy xác định lại khả năng sản xuất của công ty và đặt kế hoạch sản xuất cho năm sau
với giả thiết các yếu tố khác không thay đổi.
6.4. Một cơ sở sản xuất và cung ứng cho thị trường một loại sản phẩm với tổng nhu
cầu là 30.000 tấn/năm. Cơ sở này có khả năng sản xuất hàng năm 40.000 tấn một cách đều đặn,
ngoài ra có thể mua sản phẩm cùng loại. Nếu tự sản xuất thì chi phí cho một tấn là 140$, nếu
mua ngoài thì giá một tấn là 138$, giá bán là 160$/tấn. Trong trường hợp mua ngoài, cơ sở phải
chịu một khoản thiệt hại do không sử dụng thiết bị là 20.000 $/năm. Hệ số chi phí dự trữ tính
theo giá mua hoặc theo chi phí sản xuất là 10%. Chi phí đặt hàng khi mua ngoài là 150$ mỗi
lần, thời gian nhập hàng là không đáng kể. Chi phí chuẩn bị sản xuất mỗi lần là 100$.
a/ Cơ sở nên mua ngoài hay tự sản xuất để cung ứng?
b/ Mỗi lần mua hoặc sản xuất là bao nhiêu để tổng lãi là lớn nhất?
6.5. Một nhà in có tổng nhu cầu 120 tấn giấy/năm. Nhà in có thể mua giấy từ một cơ
sở sản xuất có công suất đủ lớn. Chi phí cho một lần giao dịch mua hàng là 60$, giá mỗi tấn
giấy là 160$ nếu mua lô hàng dưới 30 tấn, 158$ nếu mua lô hàng từ 30 tấn trở lên. Chi phí bảo
quản tính theo giá với hệ số 10%.
a/ Xác định lô hàng nên mua mỗi lần sao cho tổng chi phí là nhỏ nhất.
b/ Nếu bên bán chào giá 155$/tấn đối với lô hàng 40 tấn thì có nên mua theo cách này không?
6.6. Một công ty phát hành một mặt hàng văn hoá phẩm với nhu cầu thường xuyên
vàđều đặn. Mỗi lần tổ chức sản xuất phát sinh một chi phí cố định là 200$, chi phí trực tiếp cho
mỗi đơn vị phụ thuộc vào lượng phát hành mỗi lần như sau: nếu mỗi lần phát hành dưới 1.000
đơn vị thì giá là 8$/ đơn vị, từ 1.000 đơn vị đến dưới 3.000 thì giá là 7,2$/ đơn vị, từ 3.000 trở
lên thì giá là 7$/ đơn vị. Chi phí bảo quản tính theo giá với hệ số là 5%.
Hãy xác định lượng phát hành mỗi lần sao cho tổng chi phí là nhỏ nhất, biết rằng tổng
nhu cầu hàng năm là 25.000 đơn vị.
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com) lOMoARcPSD| 37922327
Bài tập Toán Kinh tế Chương 1 – Mô hình Toán kinh tế
TÀI LIỆU THAM KHẢO
1. TS. Nguyễn Thượng Thái, TS. Nguyễn Quảng
Giáo trình Toán chuyên ngành (dùng cho ngành quản trị kinh doanh BCVT) Nhà
xuất bản Bưu Điện, năm 2003.
2. PGS.TS. Nguyễn Quang Dong – Ngô Văn Thứ - PGS.TS Hoàng Đình Tuấn Giáo
trình Mô hình Toán Kinh tế Nhà xuất bản Thống kế, năm 2006. 3. GS. Trần Túc
Quy hoạch tuyến tính
Nhà xuất bản Đại học Kinh tế Quốc dân, năm 2001. 4. GS. Trần Túc
Bài tập Quy hoạch tuyến tính
Nhà xuất bản khoa học và kỹ thuật, năm 2001. 5. TS. Hoàng Đình Tuấn
Lý thuyết mô hình toán kinh tế
Nhà xuất bản khoa học và kỹ thuật, năm 2003. 6. Lê Đình Thúy
Toán cao cấp cho các nhà kinh tế: phần 1 – Đại số tuyến tính, phần 2 – Giải tích toán học
Nhà xuất bản Đại học kinh tế Quốc dân, năm 2007
7. Bộ Giáo dục và Đào tạo
Kinh tế học Vi mô – Giáo trình dùng trong các trường đại học và cao đẳng khối kinh tế.
Nhà xuất bản Giáo dục, năm 2004.
TS. Lê Thị Ngọc Diệp – Khoa QTKD1 – Học viện CNBCVT
Downloaded by Rot Ca (rotca780@gmail.com)




