Bài tập Môn Toán rời rạc | Đại học Cần Thơ

lOMoAR cPSD| 58488183 1 Bài tập Chương 1
Bài 1.1. Cho các mệnh đề sau A = "hôm nay là chủ nhật", B = ”3+1 = 7”,C = "hôm nay trời không mưa". Hãy lập các mệnh
đề sau và tìm chân giá trị của chúng: ¬A,¬B,¬C,A → B,¬A ↔ B,A∨B,B∧¬C,(A∨B) → ¬C.
Bài 1.2. Cho A = "bạn lái xe với tốc độ trên 65 km/h" và B = "bạn bị phạt vì vượt quá tốc độ cho phép".
Hãy viết các mệnh đề sau bằng cách biểu diễn theo các công thức A và B.
1) "Bạn không lái xe với tốc độ vượt quá 65 km/h."
2) "Bạn lái xe với tốc độ trên 65 km/h nhưng bạn không bị phạt vì vượt quá tốc độ cho phép".
3) "Nếu bạn lái xe vượt quá 65 km/h thì bạn không bị phạt vì vượt quá tốc độ cho phép."
4) "Nếu bạn bị phạt vì vượt quá tốc độ cho phép thì bạn lái xe với tốc độ trên 65 km/h."
5) "Bạn bị phạt vì vượt quá tốc độ cho phép nếu và chỉ nếu bạn lái xe với tốc độ trên 65 km/h." 6) " Nếu bạn không lái xe
với tốc độ trên 65 km/h thì bạn không bị phạt vì vượt quá tốc độ cho phép. "
Bài 1.3. Lập bảng giá trị chân lý đầy đủ và thu gọn của các công thức mệnh đề sau:
1) (A → (B → C)) → ((A → B) → (A → C)).
2) ¬(¬A → B) ↔ (A → (¬B ∨ C)).
3) (A → B) ↔ (¬A ∨ B).
4) ¬(A ∧ ¬(B ∨ C)) → (B ∧ ¬C).
Bài 1.4. Chứng minh các công thức tương đương sau:
A ∧ (B ∨ C) ≡ (A ∧ B) ∨ (A ∧ C),
A ∨ (B ∧ C) ≡ (A ∨ B) ∧ (A ∨ C),
A ∨ B ≡ ¬(¬A ∧ ¬B),
A ∧ B ≡ ¬(¬A ∨ ¬B),
A → B ≡ ¬A ∨ B ≡ ¬(A ∧ ¬), ((A ↔
B) ↔ B) ≡ A,
(A ∧ B) ∨ ¬B ≡ A ∨ ¬B,
A ∧ (A ∨ B) ≡ A,
(A ↔ B) ↔ C ≡ A ↔ (B ↔ C).
Bài 1.5. Kiểm tra các công thức sau đúng hay sai?
1) (A ↔ B) logic kéo theo (A → B)?
2) ¬A ∨ B và ¬B ∨ A logic tương đương?
3) (A → B) → ((B → C) → (A → C)) ≡ 1.
4) A ∧ (¬(A ∨ B)) ≡ 0.
5) |= ((A → B) → B) → B.
6) |= (A ↔ B) ↔ (A ↔ (B ↔ A)).
Bài 1.6. Chứng minh các định lý sau:
1) |= (A → B) ∨ (B → C).
2) |= ((A ∧ B) → C) → ((A → C) ∨ (B → C)).
Bài 1.7. Hãy xác định công thức nào là đồng nhất đúng, đồng nhất sai?
1. A ↔ (A ∨ A),
2. (A → B) → ((B → C) → (A → C)),
3. (A → B) ↔ ((¬A) ∨ B),
4. (A → B) ↔ ¬(A ∧ ¬B).
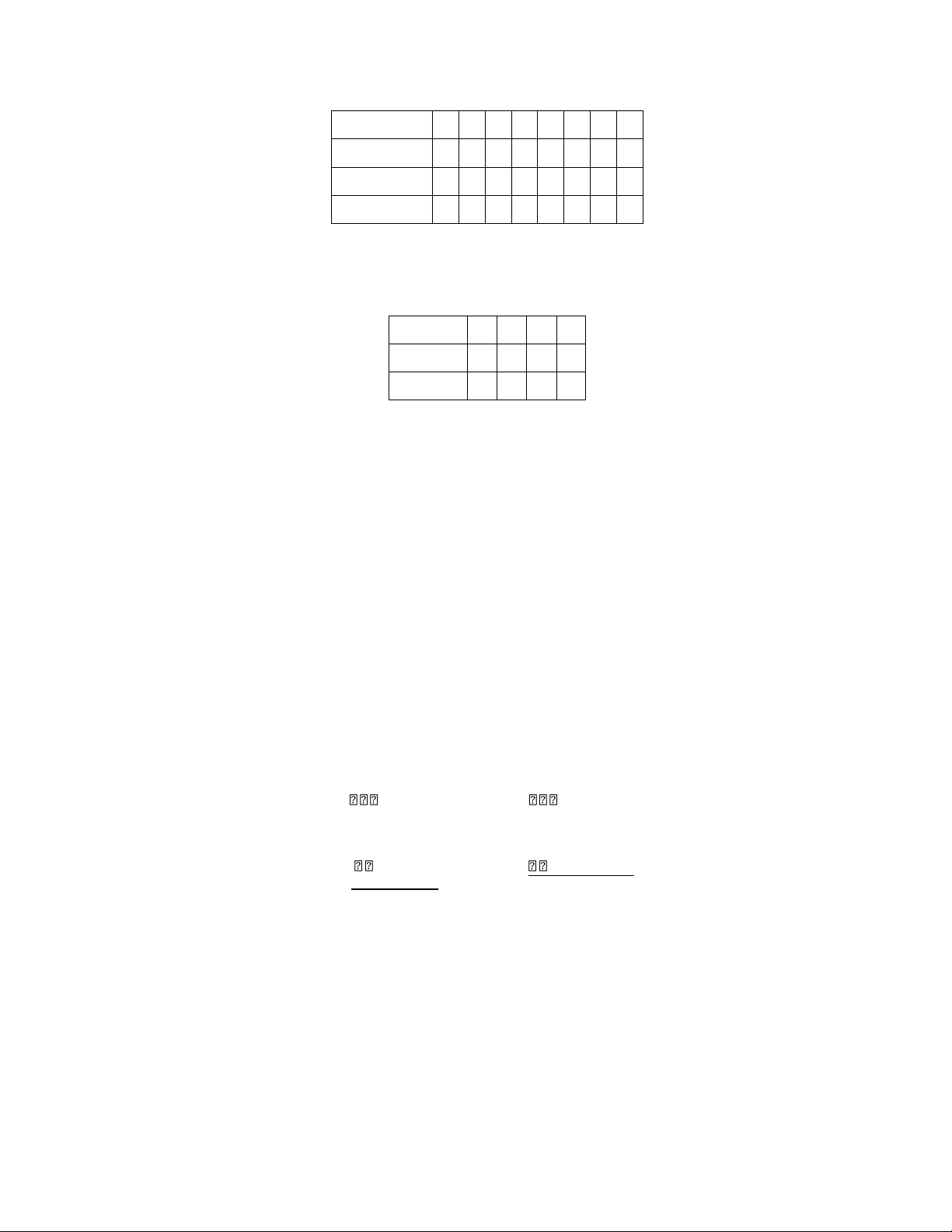
Bài 1.8. Cho hàm đại số logic f : {0,1}3 → {0,1} như sau:
1. Tìm dạng chuẩn tắc hội A tương ứng với f(x1,x2,x3). 1 lOMoAR cPSD| 58488183 x1 1 1 1 1 0 0 0 0 x2 1 1 0 0 1 1 0 0 x3 1 0 1 0 1 0 1 0
f(x1,x2,x3) 1 1 0 0 0 0 1 0
2. Tìm dạng chuẩn tắc tuyển B tương ứng với f(x1,x2,x3).
3. Hãy biểu diễn A qua 2 phép toán {¬,→}.
4. Hãy biểu diễn B qua 2 phép toán {6=,∧}.
Bài 1.9. Cho hàm đại số logic f : {T,F}2 → {T,F} như sau: x1 T T F F x2 T F T F f(x1,x2) F T F F
1. Tìm dạng chuẩn tắc hội A tương ứng với f(x1,x2).
2. Tìm dạng chuẩn tắc tuyển B tương ứng với f(x1,x2).
3. Hãy biểu diễn A qua 2 phép toán {¬,→}.
4. Hãy biểu diễn B qua 2 phép toán {6=,∨}.
Bài 1.10. Kiểm tra các công thức sau có phải định lý không?
1. (A → B) ∧ (B → C) ∧ (D ∨ ¬C) ∧ (¬D ∨ E) ∧ ¬E → (¬A ∨ B).
2. (A → B) ∧ ¬B ∧ ¬C → ¬(A ∨ C).
3. A ∧ (A → B) ∧ (C ∨ D) ∧ (D → ¬B) → (C ∨ E).
Bài 1.11. Chứng minh các định lý sau bằng qui tắc suy diễn:
1. (A → (B → C)) ∧ A ∧ B → A.
2. (A → (B → C)) ∧ A ∧ B → B.
3. A ∧ B ∧ (A → (B → C)) → C.
4. (A → B) ∧ (B → C) ∧ ¬C → A.
5. (A → B) ∧ (B → C) ∧ (D ∨ ¬C) ∧ (¬D ∨ E) ∧ ¬E → ¬A.
6. (A → B) ∧ (¬A → C) ∧ (C → D) → (¬B → D).
7. ((A ∨ B) → C) ∧ (C → (A ∨ D) ∧ ¬A ∧ ¬E ∧ (¬E → ¬D)) → A.
Bài 1.12. Chỉ ra suy luận sau là đúng A → B,
A ∧ B → C, ¬A → C, C → D, C → D ¬D 1)2) ∴ ¬B → D ∴ ¬A ∨ ¬B
Bài 1.13. "Nếu An đi làm về muộn thì vợ An sẽ rất giận dữ. Nếu Bình thường xuyên vắng nhà thì vợ Bình cũng sẽ rất giận
dữ. Nếu vợ Bình hoặc vợ An giận dữ thì cô Hà bạn họ nhận được than phiền, mà cô Hà không
hệ nhận được lời than phiền. Vậy An đi làm về sớm và Bình rất ít khi vắng nhà." Dùng quy tắc
suy diễn để chỉ suy luận trên là đúng.
Bài 1.14. Kiểm tra công thức sau có phải hằng đúng hay không
A = (¬X ∨ Y ) ∧ (¬Z ∨ D) ∧ (¬X ∨ Z) → (Y ∨ D). bằng cách: 1. Lập bảng chân lý.
2. Đưa về dạng chuẩn tắc hội hoặc dạng chuẩn tắc tuyển.
3. Dùng qui tắc suy diễn. lOMoAR cPSD| 58488183 2
Bài 1.15. Chứng minh định lý sau
(A → B) ∧ (¬C ∨ D) ∧ (A ∨ C) → (¬B → D) bằng các phương pháp: 1. Lập bảng chân lý;
2. Đưa về dạng chuẩn tắc hội hoặc dạng chuẩn tắc tuyển;
3. Dùng qui tắc suy diễn.
Bài 1.16. Chứng minh rằng các công thức sau không là hằng đúng:
1. (A ↔ B) ∧ (B → C) ∧ (C ∨ D) ∧ (D → B) → ¬D.
2. A ∧ (A → B) ∧ (A → (C ∨ ¬B)) ∧ (¬C ∨ D) → ¬D.
3. (A → B) ∧ ((B ∧ C) → D) ∧ (E → C) ∧ ¬A → (¬D → ¬E).
Bài 1.17. Suy luận sau đây có đúng không? A → B, B → C, C → D A ∴ D
Bài 1.18. "Nếu muốn đi học sáng thứ 2 thì Mai phải dạy sớm. Nếu Mai đi nghe nhạc tối thứ chủ nhật thì Mai sẽ về muộn.
Nếu Mai về muộn và thức dậy sớm thì Mai phải đi học sáng thứ 2 và chỉ được ngủ dưới 7 giờ trong ngày. Nhưng Mai
không thể đi học nếu chỉ ngủ dưới 7 giờ. Vậy hoặc Mai không đi nghe nhạc tối chủ nhật hoặc
Mai phải nghỉ học sáng thứ 2." Suy
luận trên có đúng không? Bài 1.19. Chứng minh
(A → B) ∧ (B → C) ∧ (D ∨ ¬C) ∧ (¬D ∨ E) ∧ ¬E → ¬A ≡ 1.
Bài 1.20. Tìm phản ví dụ cho các suy luận sau: A ↔ B, B → C, C ∨ ¬D, ¬D → B ∴ D và A, A → B,
A → (C ∨ ¬B), ¬C ∨ ¬D ∴ D lOMoAR cPSD| 58488183 2 Bài tập chương 2
Bài 2.1. Cho công thức vị từ 1 biến A(x) = {x > 5}. Hãy tìm giá trị chân lý của các công vị từ sau: A(2),A(7),∀xA(x) trên
trường số thực R, ∃xA(x) trên trường số thực R.
Bài 2.2. Cho công thức vị từ A(x,y,x) = {x + y < 2z}.
Tìm giá trị chân lý của các vị từ sau A(1,2,3),A(−3,5,6),∀x∃y∃zA(x,y,z)trên trường số nguyên Z, ∀x∀y∀zA(x,y,z) trên trường
số thực R,∃xA(x,x,x) trên trường số tự nhiên N và ∃x∃y∃z¬A(x,y,z) trên trường số thực R. 3
Bài 2.3. Cho P(x) là câu "x học ở lớp từ 7h00 đến 12h00 mỗi ngày" trên trường các sinh viên. Hãy diễn đạt các lượng từ
sau thành câu thông thường:
1. ∃xP(x).
2. ∀xP(x).
3. ∀x¬P(x).
4. ∃xP(x) → P(An).
5. P(Thu) → ∃xP(x).
6. ∀xP(x) ∨ ∃x¬P(x).
7. P(Mai) ∧ ¬P(Thu).
8. P(Mai) ↔ ¬P(Huy).
Bài 2.4. Hãy biểu diễn các câu sau thành một công thức logic vị từ thích hợp.
1. Nếu Nam là bạn của Mai và Mai là bạn của Nga, thì Nam là bạn của Nga.
2. Nếu Nam là bạn của Mai và Mai là bạn của Nga, thì Nga không là bạn của Nam.
3. Nếu Huy không là bạn của Mai hoặc mọi bạn của Mai không là bạn của Nam, thì Nam là bạn của Huy.
4. Mọi bạn của Nam là bạn của Nga. Huy là bạn của Nam, nên Huy là bạn của Nga.
Bài 2.5. Cho P(x),Q(x),R(x) là các câu tương ứng sau: "x là giáo sư", " x là kẻ ngu ngốc" và "x là kẻ vô tích sự". Hãy biểu
diễn các câu sau qua các công thức logic vị từ liên quan tới P(x),Q(x),R(x) :
1. " Không có giáo sư nào là kẻ ngu ngốc".
2. "Mọi kẻ ngu ngốc đều vô tích sự".
3. "Không có giáo sư nào là kẻ vô tích sự".
4. "An là một giáo sư. Mọi giáo sư là không vô tích sự, nên An không là một kẻ vô tích sự".
5. "Mọi kẻ vô tích sự đều không là giáo sư, nên tồn tại một giáo sư không là kẻ vô tích sự".
6. "Nếu một kẻ vô tích sự là giáo sư thì tồn tại một giáo sư là kẻ ngu ngốc".
Bài 2.6. Hãy viết các dấu ngoặc cho các công thức sau:
1. ∃x¬A(x) → ∀x∃yB(x,y) ∨ ∃z¬C(z).
2. ∀x∃y∀zA(x,y,z) ↔ ∀xB(x) ∧ ∃xC(x).
3. A(5,x) → ∃xB(x) ∨ ∀xC(x) ↔ ∀x∃yA(x,y).
Bài 2.7. Tìm dạng chuẩn tắc tuyển và dạng chuẩn tắc hội của logic vị từ sau: .
Bài 2.8. Đưa công thức logic vị từ sau về dạng chuẩn tắc hội và dạng chuẩn tắc tuyển .
Từ đó có thể kết luận được tích chất gì của công thức logic vị từ trên?
Bài 2.9. Đưa các công thức logic vị từ sau về dạng chuẩn tắc hội và dạng chuẩn tắc tuyển:
1. (∀xA(x) ∧ ∀xQ(x) ∨ ∃x¬A(x) ∨ ∃x(Q(x) ∧ ¬A(x))) → (M → (B ∧ C) → M).
2. ¬(∀xA(x) ∧ ∀xB(x)) → (∃xC(x) ∨ ∃x(¬B(x) ∨ A(x)) ∨ (X → (Y → ¬Z))). Bài 2.10. Chứng minh các công
thức logic vị từ sau là hằng đúng:
1. ∃x(A(x) → B(x)) ↔ (∀xA(x) → ∃xB(x)). 2.
(∃xA(x) → ∀xB(x)) → ∀x(A(x) → B(x)).
3. ∀x(A(x) ∨ B(x)) → (∀xA(x) ∨ ∃xB(x)).
4. ∀x(A(x) → B(x)) → (∃xA(x) → ∃xB(x)). lOMoAR cPSD| 58488183
5. ∀x(A → B(x)) ↔ (A → ∀xB(x)), trong đó A là công thức vị từ không chứa biến vị từ x.
6. ∃x(A → B(x)) ↔ (A → ∃xB(x)), trong đó A là công thức vị từ không chứa biến vị từ x.
Bài 2.11. Chứng minh rằng các công thức sau đây không logic đồng nhất đúng:
1. ∃x∀y (A(x,y) ∧ ¬A(y,x) → (A(x,x) ↔ A(y,y))).
2. ∀x¬A(x,x) ∧ ∀x∀y∀z(A(x,y) ∧ A(y,z) → A(x,z)) → ∃x∀y¬A(x,y). Bài 2.12. Các công thức sau có phải
là hằng đúng hay không? Vì sao?
1. ∃x∀y ((p(x,y) ∧ ¬p(y,x)) → (p(x,x) ↔ p(y,y))).
2. ∀x∀y∀z (p(x,x) ∧ (p(x,z) → (p(x,x) ∨ p(y,z)))) → ∃y∀zp(y,z). 4