BNN RR BNN LT ĐN
Là BNN có tập giá trị hữu hạn hoặc đếm Là BNN có tập giá trị lập đấy (a , b) ⊂ R được PPX Bảng PPXS Hàm mật độ XS: f(x) S X x1 x2 … xn a)
f ( x )≥ 0, ∀x P p +∞ 1 p2 … pn b) ∫ a)
f ( x ) dx=1 p ≥ 0 i −∞ b b) ∑ p =1 i c) i
P (a< X < b)=∫ f (x )dx c)
P (a< x <b)=… . a
Hàm phân phối XS: F (x )=P( X <x)
Hàm phân phối XS: F (x )=P( X <x)
Tham Kì vọng toán (trung bình): +∞ số
Kì vọng toán (trung bình): E (X )=∫ xf ( x) dx
E (X )=∑ x p i i −∞ đặc i trưng
T/c: E(a.X+b.Y+c) = a.E(X) + b.E(Y) + c; X và Y độc lập thì E(X.Y) = E(X).E(Y)
Phương sai: V ( X )=E ( X2)−[E( X )]2
Phương sai: V ( X )=E ( X2)−[E( X )]2 +∞
E (X2 )=∑ x2i pi
E (X2 )=∫ x2 f ( x )dx i −∞
T/c: X và Y độc lập thì V(a.X+b.Y+c) = a2V(X) + b2V(Y)
X và Y không độc lập thì V(a.X+b.Y+c) = a2V(X) + b2V(Y) + 2ab.Cov(X,Y) PPX
Không – Một (Bernoulli): A(p) Đều: U(a,b) S
P (X=x )= px (1−p )1−x ; x=0 ;1 thông
E (X )= p ; V (X ) =p (1−p )
f ( x )={ 0n uếx∉(a,b) 1 dụng n u ế x ∈(a , b) b−a (b−a )2
E (X )= a+ b ; V (X ) = 2 12 Nhị thức: B(n,p)
Chuẩn: N (μ ,σ2)
P (X=x )=C x px (1− p)n−x ; x=0,1 , … n −( x− μ) 2 n a) 2 σ2
E (X )=np ; V ( X )=np (1−p ) f ( x )= 1 e σ√ 2 π
Mode : m ∈ N ; np+ p−1≤ m ≤ np + p 0 0 b)
E (X )=m =m
μ ; V (X ) =σ2 d 0= c)
P (X <b ) =Φ(b−μ);tc:Φ(−u)+Φ(u)=1 σ d)
X ∼ N ( μ , σ2 ) 2 ) và độc lập với 1
1 ; Y ∼ N ( μ , σ 2 2
nhau thì Z =aX +bY ∼ N (a μ +b μ , a2 σ2+b2 σ2) 1 2 1 2 Poisson: P(λ) Lũy thừa Student
P (X=x )= e−λ λx ; x=0,1,2 , … x ! Khi – bình phương
E (X )= λ ; V ( X )=λ ; λ−1 ≤ m ≤ λ Fisher - Snedecor 0
BNN 2 chiều: công thức, tính chất của Hiệp phương sai, Hệ số tương quan
Biết cách tính kì vọng điều kiện và khái niệm hàm hồi quy; + … Ví dụ
Cho biết điểm thi của sinh viên nam là X ∼ N (7,5 ;1,44) ; điểm thi của nữ là Y ∼ N (7,7;2,25) . Tìm
XS để điểm thi của 1 sv nam bất kì (X) cao hơn 1 sv nữ bất kì (Y).
Cần P (X >Y )=P(Y −X <0)
Y ∼ N (7,7 ; 1,52) ; X ∼ N (7,5 ; 1,22) và độc lập nên Y − X ∼ N (0,2; 12 .1,52+(−1 )2 . 1,22=3,69)
P (X >Y )=P (Y − X <0) =Φ ( 0−0,2)=Φ (−0,104)=0,4602 √ 3,69
Gọi Nguyễn Anh Phương (vắng); Nguyễn Linh Chi (có, làm đúng)
Ví dụ: Tỷ suất lợi nhuận (%) khi đầu tư cổ phiếu A là X ∼ N (3 ;0,32) , của cổ phiếu B là
Y ∼ N (3,2; 0,42) và độc lập. Đầu tư 64% vốn và A và 36% vốn vào B. Tìm XS tỷ suất LN thu được cao hơn 5%.
Z =0,64 X +0,36 Y ∼ N (0,64.3+0,36.3,2 ; 0,642 . 0,32+ 0,362 .0,42 ); tìm P(Z >5 )=?
13h53 gọi bạn Liên (có, đúng); Yến (vắng); Phụng (có, dúng) Giá trị tới hạn Fisher ( ) (24 ;39)
VD: f 19;29 =1,958 ;f = 1 = 1 0,05 0,975 (Thanh Vân, có, ) f (39;24 ) 2,151 0,025 BÀI 5 VD 5.2.
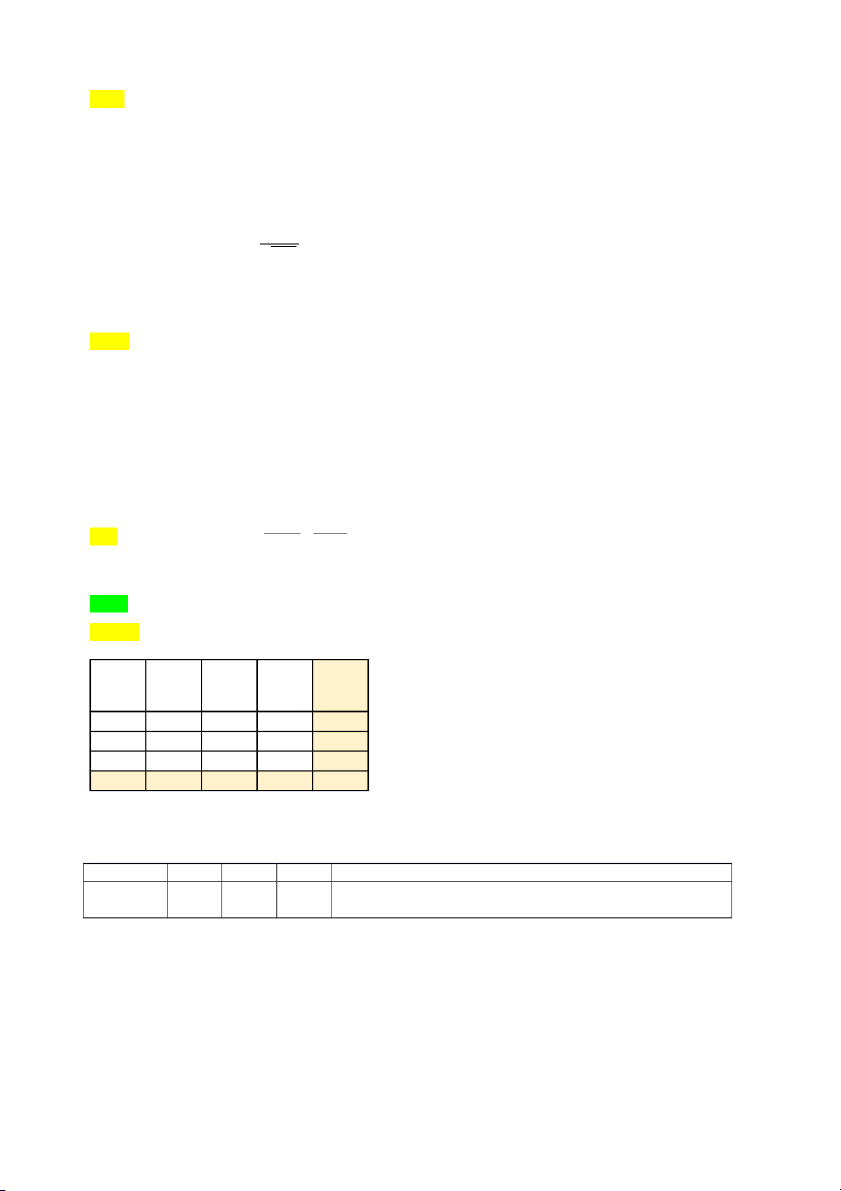
X : Số người lao động (người), Y : Số người phụ thuộc của hộ (người) 0 1 2 Y X 2 0,1 0,02 0,01 0,13 3 0,16 0,12 0,08 0,36 4 0,2 0,17 0,14 0,51 0,46 0,31 0,23 1
P (X=2 , Y =0)=0,1 ≠ 0,13× 0,46=P (X =2 ) P( Y =0)⇒ X và Y không độc lập Bảng pp biên của X: X (người) 2 3 4
E(X)=2.0,13+…+4.0,51 = 3,38 (Duyên) P 0,13 0,36 0,51
V(X)=22.0,13+ …+ 42.0,51-3,382=0,4956 (Dũng-1; L.Anh đúng) Bảng pp biên của Y: X (người) 0 1 2 E(Y)= 0,77 (Nhàn) P 0,46 0,31 0,23 V(X)= 0,6371 (Nhàn)
Bảng PPXS có điều kiện của X khi Y = 0: X | Y = 0 2 3 4 0,1 0,16 0,2 E(X|Y=0)=E(X|0)= 2⋅ +3 ⋅ +4 ⋅ =3,22 0,46 0,46 0,46 P 0,1 0,16 0,2 V(X|Y=0) V(X|0)= 0,1 0,16 0,2 22⋅ +32 ⋅ +42 ⋅ −3,222=? 0,46 0,46 0,46 0,46 0,46 0,46 + + E(X|Y=0)=E(X|0)= 0,1 0,16 0,2 2⋅ +3 ⋅ +4 ⋅ = 2.0,1 3.0,16 4.0,2 =3,22 0,46 0,46 0,46 0,46
Bảng PPXS có điều kiện của X khi Y = 1: X | Y = 1 2 3 4 0,02 E(X|Y=1)=E(X|1)= 0,12 0,17 2⋅ +3 ⋅ +4 ⋅ =3,48 0,31 0,31 0,31 P 0,02 0,12 0,17 0,31 0,31 0,31
Bảng PPXS có điều kiện của X khi Y = 2: X | Y = 2 2 3 4
E(X|Y=2)=E(X|2)= …=2,96 P 0,01 0,08 0,14 0,23 0,23 0,23 E(X|Y=0)=3,22 E(X|Y=1)=3,48 E(X|Y=2)=2,96
E(X|Y=y) = f(y): Hàm hồi quy
Các bảng PP có điều kiện của Y Y|X=2 0 1 2 P 0,1 0,02 0,01 0,13 0,13 0,13 Y|X=3 0 1 2 P 0,16 0,12 0,08 0,36 0,36 0,36 Y|X=4 0 1 2 P 0,2 0,17 0,14 0,51 0,51 0,51 Bài tập
Cho biến ngẫu nhiên 2 chiều (X, Y) có bảng PPXS đồng thời như sau: X Y 0,5 2 4 20 0,04 0,26 0,1 0,4 50 0,12 0,3 0,18 0,6 Tổng 0,16 0,56 0,28
X là chi phí quảng cáo (triệu đồng); Y là doanh thu (tỉ).
a. X và Y có độc lập không?
P (X=20 , Y =0,5 )=0,04 ≠ 0,4 × 0,16=P ( X=20) . P(Y =0,5 )⇒ X và Y không độc lập
b. Tìm trung bình và phương sai của chi phí quảng cáo?
Tính Đ.Văn E (X )=20× 0,4+50 × 0,6=38 (tr.đ)
Tính Đ.Thành V ( X )=202.0,4+502.0,6−382=216(tr . đ )2
c. Tìm trung bình và phương sai của doanh thu?
Tính T.Trung E (Y )=2,32( tỉ) ;V ( Y )=1,378(tỉ)2
d. So sánh doanh thu trung bình khi chi phí quảng cáo tương ứng là 20 và 50.
Thắm (v); Trà My (v), Ng Phượng (có) 0,04 0,26 0,1
E (Y |X =20 )=0,5 ⋅ +2 ⋅ +4 ⋅ =2,35(tỉ ) 0,4 0,4 0,4
T.Thùy Trang (v), Lê Thu Hằng E (Y|X =50)=2,3(tỉ )
Vậy E (Y|20) >E(Y ∨50)
e. Cho biết chi phí khác là 1,8 tỉ. Tìm lợi nhuận trung bình khi chi phí quảng cáo là 20 tr.đ ln=Y −t ng ổ
CP=Y − X −1,8 1000
E (ln )=E ( Y ∨X =20)−0,02−1,8=2,35− = 1,82 ?
f. X và Y tương quan dương hay tương quan âm? Cov(X,Y)
E (X .Y )=20.0,5 .0,04+20.2 .0,26+20.4 .0,1+50.0,5 .0,12+ 50.2.0,3+50.4 .0,18=87,8
Cov( X , Y )=E (X . Y )−E (X ). E( Y )=87,8−38.2,32=−0,36<0 X và Y tương quan âm
g. X và Y liên hệ với nhau chặt chẽ đến mức độ nào? Hệ số tương quan Cov (X , Y ) −0,36 ρ = = =−0,021 X ,Y σ . σ √216. √1,378 X Y
X và Y có tương quan âm với mức độ tương quan rất yếu. BÀI 6 ĐL giới hạn trung tâm
Y −E (Y )
Khi n tiến ra vô cùng thì Z = √ ∼ N( 0 ;1) V (Y )
Y =E (Y )+√V (Y ). Z=μ+σZ ∼ N ( μ ,σ 2)
Sử dụng: có X ,…, X độc lập cùng pp, kì vọng, ps hữu hạn, với ∼ N (,) 1 n
n ≥30 thì Y =∑ Xi Ví dụ 4.6.
Xác suất để một khách hàng vào siêu thị mua sản phẩm của hãng A là 0,3. Tính xác suất để trong
200 khách vào siêu thị có:
a) Nhiều hơn 70 khách mua hàng của hãng A.
b) Từ 40 đến 50 khách mua hàng của hãng A.
Cách 1: Dễ thấy số khách mua là X ∼B ( 200 ;0,3)
Do n > 100 nên X ∼ N (200.0,3 ;200.0,3.0,7)
Cách 2: Dùng ĐL giới hạn trung tâm
Xét khách số 1 vào siêu thị, gọi X là số người mua sp A, dễ thấy X ∼ A (0,3) 1 1
Xét khách thứ i vào siêu thị, số người mua sp A là X ∼ A (0,3) i X , X ,… , X
) =0,3;V( X )=0,3.0,7=0,21 1 2 200
độc lập, có E (Xi i (t/m ĐL GHTT)
Khi đó, X =∑ X ∼N (μ , σ2) i i
μ=∑ E ( X )=∑ 0,3=200.0,3=60 i i i
σ2=∑ V (X )=∑ 0,21=200.0,21=42 i i i − a.
P (X >70)=1−Φ (70 60)=? √42 − − b.
P (40 ≤ X ≤ 50)=Φ (50 60)−Φ (40 60)=? √42 √42