Bài tập ôn luyện đội tuyển TST môn Toán | Đại học Su Phạm Hà Nội

BÀI TẬP ÔN LUYỆN ĐỘI TUYỂN TST MÔN TOÁN Ngày 10/4/2023
Bài 1. Tìm các số nguyên dương n sao cho tồn tại số nguyên dương m và các số nguyên
tố 1  p  q thỏa mãn q  p | m và , | m p q n 1.
Bài 2. Xác định số nguyên tố p và các số nguyên dương x, y thỏa mãn 3 3
x  y  p  xy  p. 2   q n 1
Bài 3. Cho các số nguyên dương n và số nguyên tố q, chứng minh n    không  2  thể là lũy thừa của . q
Bài 4. Cho x, y và a ,a ,... là các số nguyên thỏa mãn a  a  0 và 0 1 0 1 a      a ,a bằng 1 p p 1    xa  ya
1, n 0. Xét số nguyên tố p bất kỳ. Chứng minh n 2 n 1 n hoặc lớn hơn p.
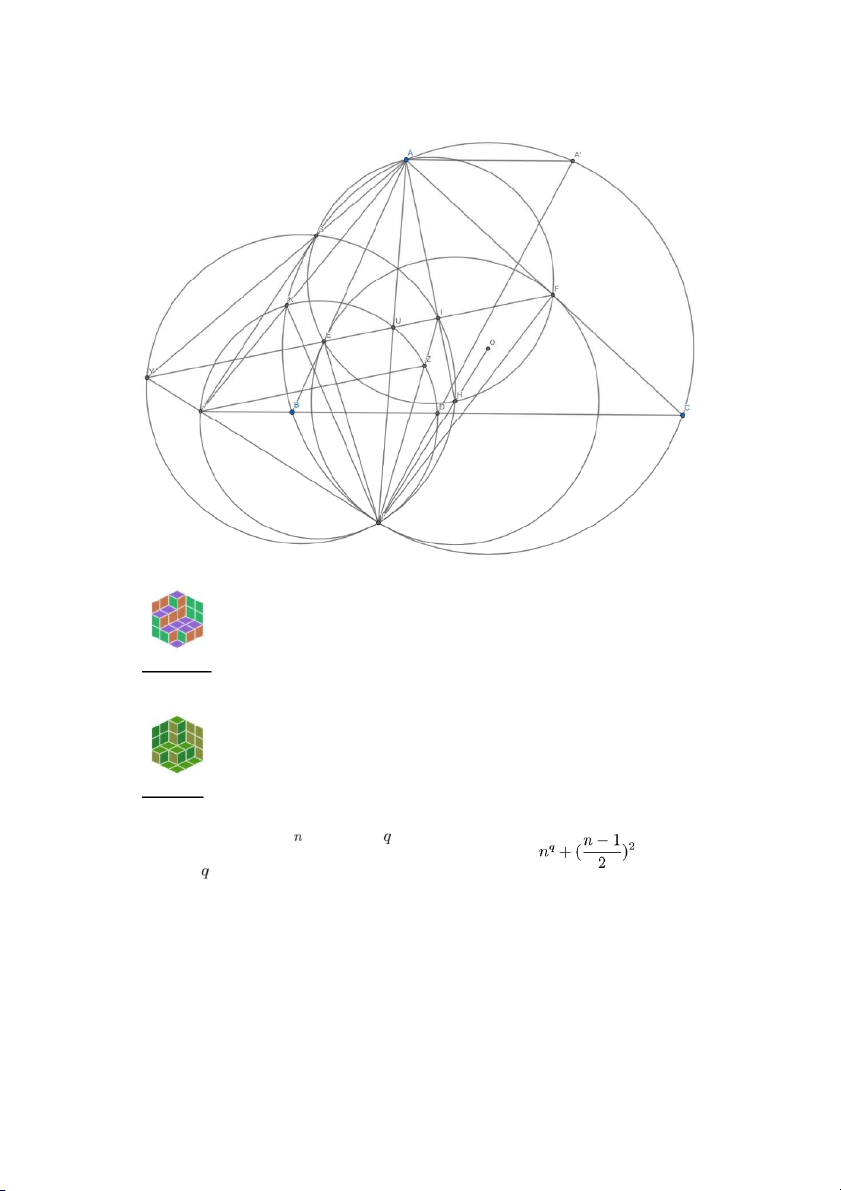
Bài 5. Cho tam giác ABC nội tiếp đường tròn O và ngoại tiếp đường tròn  I. Đường
tròn I  tiếp xúc với BC tại D. Đường thẳng qua I và vuông góc AI cắt AB, AC tại E, F.
Đường tròn  AEF cắt O và AI tại G, H. Tiếp tuyến tại G của O cắt BC tại J và AJ
cắt O tại K. Chứng minh DJK  và GIH  tiếp xúc.
Bài 6. Cho tam giác ABC cân tại A nội tiếp đường tròn O. Trung tuyến đỉnh B cắt O
tại D. Đường tròn qua C, D và tiếp xúc với BC cắt đường tròn đi qua A, D và tiếp xúc với
CD tại D, X. Chứng minh BCX  đi qua tâm đường tròn nội tiếp tam giác ABC.
Bài 7. Cho n người tham gia 1 bữa tiệc. Không có nhiều hơn n cặp là bạn bè. Hai người
bắt tay nhau nếu và chỉ nếu họ có ít nhất 1 người bạn chung. Xét số nguyên m  3 và 3
n  m . Chứng minh tồn tại người A, số người bắt tay với A không lớn hơn m 1 lần số người bạn của A.
Bài 8. Trong nhóm học sinh A có n bạn nữ và n bạn nam mà mỗi bạn nữ quen tất cả các
bạn nam. Nhóm học sinh B có n bạn nữ g ,g ,..., bạn nam b ,b ,..., 1 2 g và 2n 1 b n 1 2 2 n 1  .
Biết rằng bạn nữ g quen với các bạn nam b , b ,..., b
và không quen những bạn nam i 1 2 2i 1 
còn lại. Với mỗi số r  1, 2,..., n ta kí hiệu Ar  và B r  là số cách chọn r cặp nam nữ
trong nhóm A và B tương ứng mà có thể nhảy với nhau (2 bạn nhảy được với nhau nếu
quen nhau). Chứng minh A r  B r ,r  1, 2,..., . n ar 26, 2023, 5:03 AM
Find all positive integers , such that there exists a positive integer and . A , W h g If , F g g o so N g ) fo fo F , , we get
, which was already treated above. Serbia MO 2023 P6 a_507_bc 240 posts #1Apr 3, 2023, 4:16 AM• 1 Y Given is a triangle
with incenter and circumcircle . The incircle is tangent e . enter onal . It sends to so and are tangent at . Attachments: Z K Y SPHS1234 462 posts Serbia MO 2023 P4 a_507_bc 240 posts #1Apr 3, 2023, 4:11 AM
Given a positive integer and a prime , prove that the number can't be a power of . d , then it is easy to see that
is the minimal period of this sequence, that is, means that , as , we get , then as , we get for all prime divisors of which finishes. Remark: Mar 14, 2023, 8:52 PM
people attend a party. There are no more than pairs of friends among them.
Two people shake hands if and only if they have at least common friend. Given integer such that .
Prove that there exists a person , the number of people that shake hands with is no that , which is absurd since
. Otherwise, all trees have depth
at most 1. We pick that maximizes . Then clearly . We can see that , which is absurd given .
Now the conclusion readily follows by picking a connected component with . It is
either a tree or a pseudotree. IMO Shortlist 1997, Q13 orl 3649 posts
#1Aug 10, 2008, 10:17 AM• 1 Y town there For in which girls town, for from town A and h girl can then be
paired with any of the remaining boys. Case2: When is not dancing. We simply have . Therefore, and . It may be observed that and
satisfy the same recurrence relation with
same initial values and hence the conclusion. 2023 Israel TST Test 5 P2 Phorphyrion 201 posts #1Mar 24, 2023, 5:55 AM Let be an isosceles triangle, inscribed in a circle . The -symmedian
intersects again at . The circle through and tangent to and the circle through and tangent to intersect at points . The incenter of is denoted . Prove that are concyclic. Z K Y trinhquockhanh 299 posts #2Mar 24, 2023, 10:01 AM
My solution with angle chasing and similar triangles, the critical step is to construct and .