lOMoAR cPSD| 45148588
BÀI TẬP VẬT LÝ 1 – PHẦN CƠ HỌC
CHƯƠNG 1. ĐỘNG HỌC CHẤT ĐIỂM
1.1 Từ một đỉnh tháp cao H = 25 m người ta ném một hòn đá theo phương ngang với vận tốc
ban đầu v0 = 15 m/s. Tìm: a. Quỹ đạo của hòn đá.
b. Thời gian chuyển động của hòn đá.
c. Khoảng cách từ chân tháp đến điểm hòn đá chạm đất.
d. Vận tốc, gia tốc tiếp tuyến, gia tốc pháp tuyến của hòn đá khi chạm đất.
e. Bán kính cong của quỹ đạo tại điểm bắt đầu ném và điểm chạm đất. Bỏqua sức cản không khí lấy g = 10 m/s2.
1.2 Một viên đạn được bắn lên từ mặt đất với vận tốc ban đầu v0 = 200 m/s hợp với phương
ngang một góc α = 30°. Tìm: a.
Độ cao cực đại và tầm xa mà viên đạn đạt được. b.
Gia tốc tiếp tuyến và gia tốc pháp tuyến của viên đạn sau lúc bắn 1 giây.Với góc bắn α
bằng bao nhiêu để: tầm xa của đạn là cực đại; độ cao cực đại và tầm xa của đạn bằng nhau.
1.3 Trong một quy trình chế tạo, một con lăn hình trụ được sử dụng để cán phẳng vật liệu nằm
dưới nó. Cho đường kính của con lăn là 1 m. Con lăn được điều khiển để quay xung quanh một
trục cố định với tọa độ góc được xác định bởi phương trình: θ = 2,5t2 – 0,6t3 trong đó θ được
tính bằng rad và t tính bằng giây. (a) Xác định tốc độ góc cực đại của con lăn. (b) Xác định tốc
độ dài cực đại của một điểm nằm trên mặt ngoài của con lăn?
CHƯƠNG 2. ĐỘNG LỰC HỌC CHẤT ĐIỂM
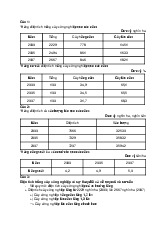
2.1 Có hai vật khối lượng m1, m2 liên kết với nhau bằng một sợi
dây vắt qua ròng rọc ở đỉnh của mặt phẳng nghiêng hợp với mặt
ngang một góc α (Hình 2.1). Vật m1 nằm trên mặt phẳng nghiêng. Hình 2.1
Hệ số ma sát giữa m1 và mặt nghiêng là k. Giả thiết lúc
đầu hai vật đứng yên. a.
Với điều kiện nào của tỉ số các khối lượng (m2/m1) để cho vật m2: đi xuống; đi lên; đứng yên. b.
Xác định gia tốc của hệ vật trong hai trường hợp đầu. Bỏ qua khối lượngròng rọc và dây,
ma sát ở ròng rọc không có. 1 lOMoAR cPSD| 45148588 2.2
Trên một cái bàn có khối lượng M, đặt
một hệ gồm ba vật có khối lượng: m, 2m, 3m
được liên kết với nhau bằng các sợi dây (Hình
2.2). Hệ số ma sát giữa vật 2m và bàn là k = 0,1.
Hỏi hệ số ma sát giữa bàn và mặt sàn phải có giá trị nhỏ nhất Hình 2.2
bằng bao nhiêu để bàn đứng yên khi hệ
vật chuyển động. Bỏ qua khối lượng dây và ròng rọc, ma sát ở các ròng rọc là không đáng kể. 2.3
Trên trần một thang máy đang đi lên với gia tốc a0 = 1,2 m/s2 có gắn một lực kế.
Đầu dưới lực kế có treo một ròng rọc, người ta vắt qua ròng rọc một sợi dây và hai đầu
dây treo hai vật khối lượng lần lượt là m1 = 200 g; m2 = 300 g. Bỏ qua khối lượng và ma
sát ở ròng rọc, dây không dãn và có khối lượng không đáng kể đáng kể. Xác định:
a. Gia tốc của vật m1 so với đất và với thang máy.
b. Số chỉ trên lực kế. 2.4
Cho hệ vật như Hình 2.3. Cần phải dịch chuyển một
chiếc xe theo phương ngang với gia tốc nhỏ nhất bằng
bao nhiêu để cho các vật m1 và m2 không chuyển động đối
với xe. Cho khối lượng các
vật m1 = 300 g; m2 = 500 g; hệ số ma sát giữa vật Hình 2.3 m1, m2 và xe là k = 0,2. Bỏ qua khối
lượng ròng rọc và dây nối, ma sát ở ròng rọc không đáng kể. 2.5
Cho hai vật đều có khối lượng là m = 3,5 kg được treo trên
trần của một thang máy như Hình 2.4. (a) Nếu thang máy dịch
chuyển với gia tốc hướng lên a⃗ có độ lớn 1,6 m/s2, hãy tìm lực căng
dây T1 và T2 của hai sợi dây phía trên và phía dưới. (b) Nếu sợi dây
chỉ chịu được lực căng lớn nhất là 85 N thì gia tốc lớn nhất mà thang
máy có thể đạt được trước khi dây đứt là bao nhiêu? Hình 2.4 2.6
Một khối vật có khối lượng 3 kg được giữ trên tường
bằng một lực ⃗P hợp với phương ngang một góc θ = 50° như ở Hình 2.5. Hệ số ma sát
tĩnh giữa khối vật và tường là 0,25. Xác định giá trị lớn nhất và nhỏ
nhất của ⃗P để khối vật đứng yên. 2 lOMoAR cPSD| 45148588
CHƯƠNG 3. ĐỘNG LỰC HỌC HỆ CHẤT ĐIỂM – VẬT RẮN Hình 2.5
3.1 Trên một đĩa tròn mỏng, phẳng, đồng chất bán kính R có
khoét một lỗ tròn nhỏ bán kính r, tâm O’ của lỗ khoét cách tâm
O của đĩa tròn một khoảng
. Xác định vị trí khối tâm của đĩa.
3.2 Cho một ròng rọc cố định là một hình trụ đặc có khối lượng
m1 = 200 g; trên hình trụ có cuốn một sợi dây mềm, không giãn,
khối lượng không Hình 3.1
đáng kể. Đầu tự do của sợi dây được nối với một
vật có khối lượng m2 = 500 g, vật được đặt trên một mặt phẳng nghiêng góc α = 45°. Ma sát
giữa m2 và mặt phẳng nghiêng có hệ số k = 0,1. Thả nhẹ m2 cho hệ chuyển động, lấy g = 10 m/s2.
a. Tính gia tốc chuyển động của vật m2.
b. Tìm quãng đường m2 đi được sau 2 giây kể từ khi bắt đầu chuyển động.
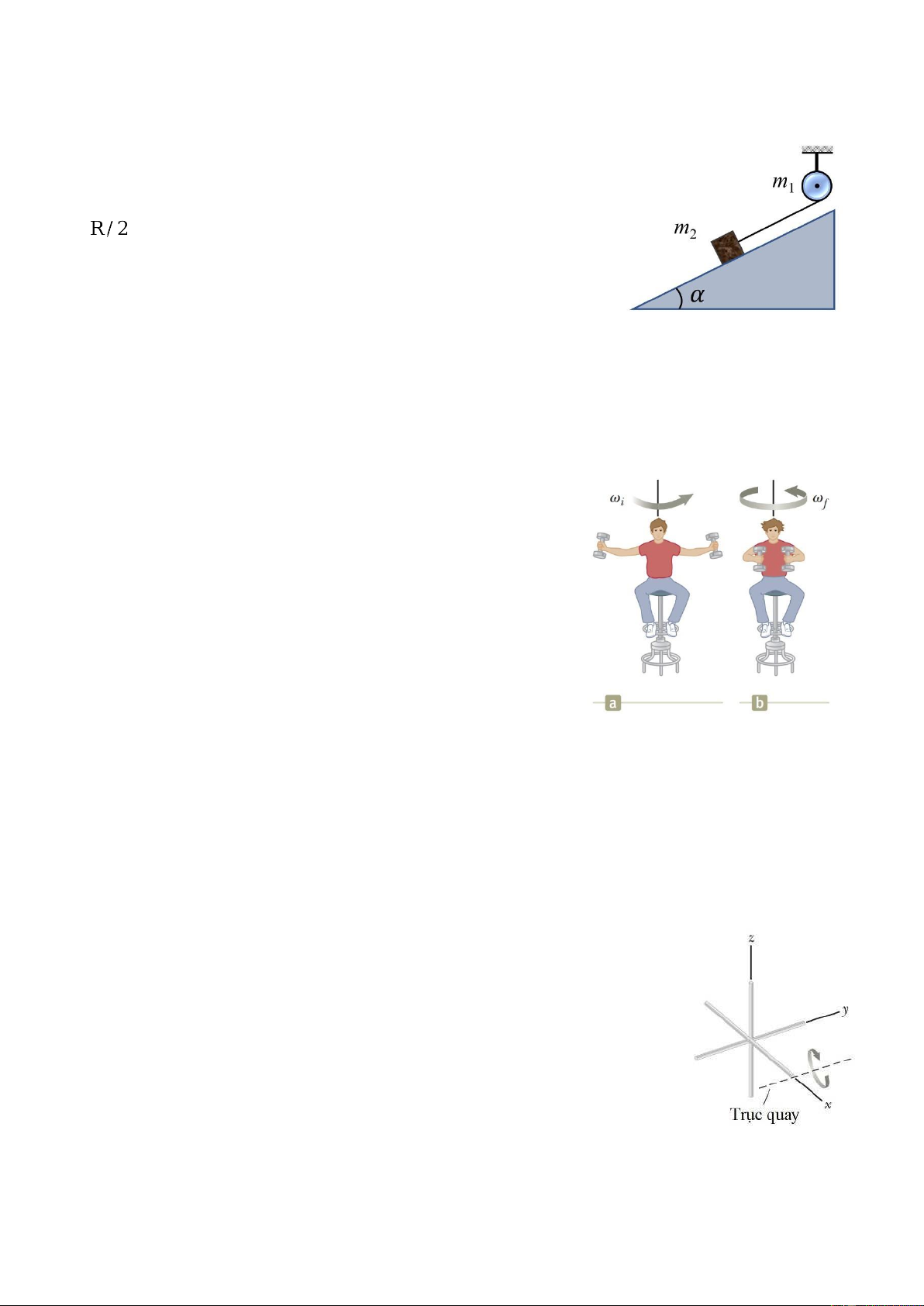
3.3 Một sinh viên ngồi trên một chiếc ghế quay tự do, cầm
hai quả tạ, mỗi quả có khối lượng 3 kg (Hình 3.2). Khi hai
tay dang ngang (Hình 3.2a), thì quả tạ cách trục quay 1 m
và sinh viên quay với tốc độ góc 0,75 rad/s. Moment quán
tính của sinh viên cộng với ghế là 3 kg∙m2 và giả thiết là
không đổi. Sinh viên Hình 3.2 kéo các quả tạ vào trong theo phương ngang
đến vị trí cách trục quay 0,3 m (Hình 3.2b). Tìm tốc độ góc mới của sinh viên.
3.4 Một khẩu pháo có khối lượng m1 = 104 kg có thể chuyển động không ma sát trên đường
nằm ngang, khi chuyển động khẩu pháo mang một quả đạn có khối lượng m2 = 100 kg, viên đạn
có thể được bắn ra khỏi nòng với vận tốc u = 500 m/s so với nòng pháo. Hãy xác định vận tốc
của khẩu pháo ngay sau khi bắn trong các trường hợp sau:
a. Khi bắn khẩu pháo đứng yên, quả đạn được bắn theo phương ngang.
b. Khi bắn khẩu pháo đứng yên, quả đạn được bắnhướng lên trên hợp
với phương ngang một góc α = 60°.
c. Khi bắn khẩu pháo chuyển động với vận tốc v0 = 18 km/h, quả đạn
được bắn theo phương ngang về phía trước. Hình 3.3
3.5 Cho ba thanh mỏng giống nhau, có chiều dài L và khối lượng m được dính chặt vào nhau tại
trung điểm mỗi thanh sao cho các thanh đôi một vuông góc với nhau (Hình 3.3). Hãy xác định 3 lOMoAR cPSD| 45148588
moment quán tính của hệ ba thanh này đối với trục quay đi qua một đầu của một thanh và
song song với một trong hai thanh còn lại.
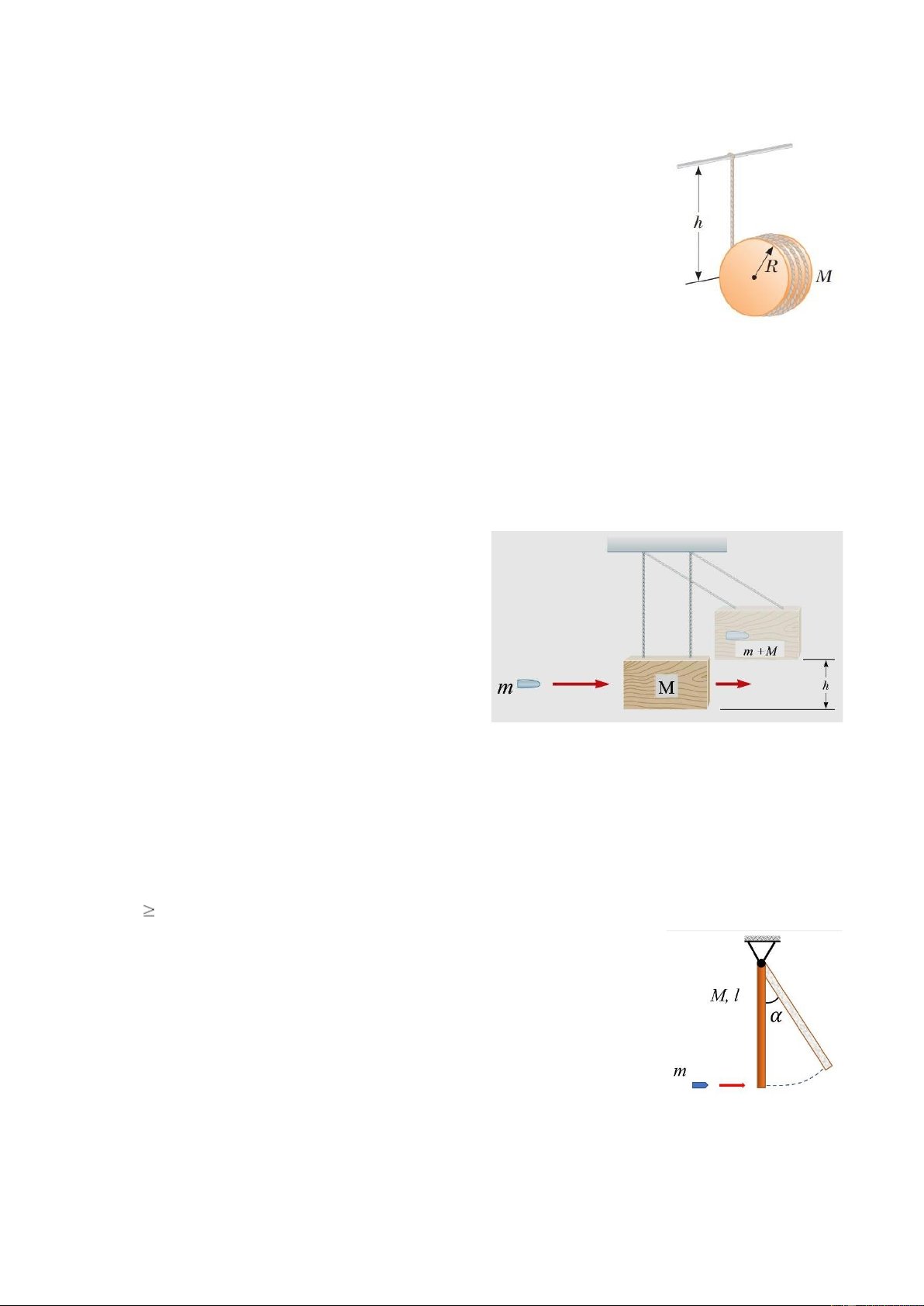
3.6 Cho một sợi dây quấn quanh một cái đĩa đồng chất bán kính R và
khối lượng M. Một đầu sợi dây được treo cố dịnh, đĩa được thả cho
rơi không vận tốc ban đầu theo phương thẳng đứng (Hình 3.4). Chứng
tỏ rằng (a) lực căng của sợi dây bằng 1/3 trọng lượng của đĩa, (b) độ
lớn của gia tốc khối tâm đĩa là 2g/3, và (c) tốc độ của khối tâm đĩa là
(4gh/3)1/2 sau khi đĩa rơi được một đoạn h. Hình 3.4
CHƯƠNG 4. NĂNG LƯỢNG
4.1. Một con lắc thử đạn khối lượng M, viên đạn
khối lượng m bay theo phương nằm ngang,
xuyên vào khối gỗ (con lắc) và bị mắc lại trong
khối gỗ đồng thời khối gỗ được nâng lên độ cao h.
a. Hãy lập biểu thức tính vận tốc viên Hình 4.1
đạn ngay trước va chạm với khối gỗ.
b. Tính tỉ số phần trăm động năng của viên đạn biến thành nhiệt khi vachạm. Cho m = 20 g; M = 1,2 kg.
c. Khối lượng viên đạn m = 20 g. Hỏi khối lượng khối gỗ tối đa là bao nhiêuđể khối gỗ chuyển
động được. Biết khối gỗ (có cả viên đạn bên trong) chuyển động được khi động năng khối
gỗ 1% động năng viên đạn trước va chạm.
4.2. Một thanh đồng chất có chiều dài l và khối lượng M, có thể quay
xung quanh một trục nằm ngang đi qua đầu trên của thanh. Một viên
đạn có khối lượng m bay theo phương ngang tới xuyên vào đầu dưới của thanh Hình 4.2
và bị mắc lại trong thanh. Biết sau va chạm thanh bị lệch đi góc α so với phương thẳng đứng,
coi m << M. Tìm vận tốc viên đạn trước lúc va chạm. 4 lOMoAR cPSD| 45148588
4.3. Một chiếc bút chì có chiều dài l = 20 cm được giữ thẳng đứng, sau đó buông nhẹ để nó đổ
xuống mặt bàn nằm ngang, coi rằng trong quá trình đổ đầu bút chì không bị trượt trên bàn. Hãy
xác định vận tốc góc của bút chì tại thời điểm bút chì hợp với phương thẳng đứng một góc α.
Áp dụng tại thời điểm bút chì nằm ngang. Lấy g = 10 m/s2.
4.4. Một quả cầu đặc, đồng chất bán kính r bắt đầu lăn không trượt
từ đỉnh một bán cầu bán kính R. Xác định vị trí quả cầu rời mặt bán
cầu và vận tốc góc của quả cầu ở đó. Hình 4.3
4.5. Sử dụng hệ thống ròng rọc được gắn vào mái của
tòa nhà, ba công nhân nâng một chiếc đàn piano có trọng lượng 3,5 kN lên một căn hộ cách
mặt đường 25 m với tốc độ không đổi. Công suất của mỗi công nhân có được là 165 W và hệ
thống ròng rọc có hiệu suất 75% (25% cơ năng chuyển hóa thành các dạng khác do ma sát trong
ròng rọc). Bỏ qua khối lượng của ròng rọc, tìm thời gian cần thiết để nâng cây đàn từ mặt đường lên đến căn hộ.
4.6. Cho hai vật m1 = 5 kg và m2 = 10 kg có
thể trượt không ma sát trên mặt đường như
trong Hình 4.4. Vật m1 được thả cho trượt
không vận tốc ban đầu từ vị trí có độ cao h đến va chạm hoàn Hình 4.4
toàn đàn hồi với vật m2 đang đứng
yên trên mặt đường nằm ngang. Xác định độ cao cực đại của m1 sau va chạm.
CHƯƠNG 5. DAO ĐỘNG CƠ HỌC
5.1. Chu kỳ dao động tắt dần là 4 s. Giảm lượng loga là 1,6. Pha ban đầu bằng 0.
a. Viết phương trình dao động, biết rằng khi t = T/4 thì độ dời của chất điểm bằng 4,5 cm.
b. Dùng kết quả trên vẽ đồ thị của dao động trong 2 chu kỳ. 5.2.
Xác định giảm lượng loga của một con lắc toán học có chiều dài l = 50 cm, biết
rằng sau thời gian Δt = 5 phút, cơ năng toàn phần của nó giảm đi n = 4.104 lần. 5.3.
Một vật có khối lượng m = 10 g đang thực hiện dao động tắt dần với biên độ cực
đại A0 = 7 cm, pha ban đầu bằng 0, hệ số tắt dần β = 1,6 s-1. Tác dụng lên vật một lực kích
thích tuần hoàn và vật sẽ dao động cưỡng bức với phương trình: x = 5cos(10πt + 0,75π)
(cm) a. Tìm phương trình dao động riêng tắt dần
b. Tìm phương trình của ngoại lực kích thích tuần hoàn. 5 lOMoAR cPSD| 45148588
5.4. Một chiếc xe trẻ em có khối lượng m = 10 kg, được đặt trên 2 lò xo đàn hồi. Biết rằng cứ
dưới một sức đè F = 9,8 N thì lò xo co lại một đoạn 2 cm. Xe chạy trên đường nằm ngang gồ
ghề cứ cách 30 cm lại có ổ gà. Hỏi vận tốc của xe bằng bao nhiêu thì xe bị rung động mạnh nhất.
5.5. Cho một khối hộp P được gắn với một lò xo nhẹ thực hiện một dao động điều hòa theo
phương ngang, trên một mặt phẳng không ma sát với tần số f =
1,5 Hz. Một khối hộp B đặt nằm yên trên P, hệ số
ma sát giữa hai khối hộp là µs = 0,6. Biên độ dao Hình 5.1 động cực
đại của P là bao nhiêu để B không trượt trên P. 6