Bài tập ôn tập thi lần 3 năm 2022 - Tài liệu tham khảo | Đại học Hoa Sen

Lê Uyên Thi - 22011346 BÀI T P LẦẦN 3 Ậ 10. Cho bài toán QHTT  Hàm mục tiêu: D  Các ràng buộc E C B
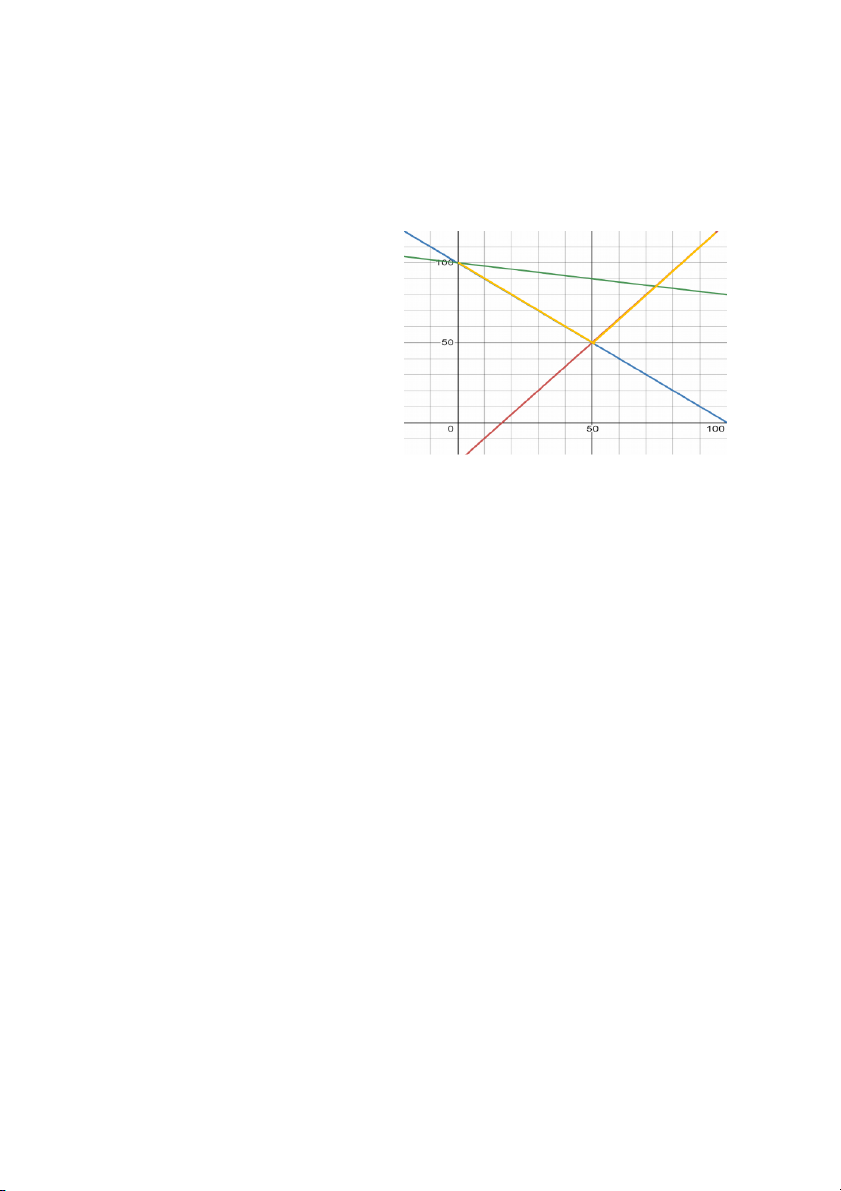
Dựa vào đồ thị bên cạnh, hãy: A
a) Chỉ ra miền xác định của bài toán, giải thích?
Miền xác định của bài toán DCE là vì có đồ thị của: 3x -2y = 50 x + y = 100 0,2x + y = 100
b) Tìm tọa độ các điểm cực biên của miền xác định?
C, D, E là các điểm cực biên của miền xác định 0 (0; 0) x + y =100 x = 0 => D (0, 100) x + y = 100 3x – 2y = 50 => C (50, 50) 3x – 2y = 50 0,2x + y = 100 => E (73,53; 85,3)
c) Tìm nghiệm tối ưu và giá trị tối ưu của bài toán?
Với D (0, 100) => 5*0 + 2*100 = 200 Lê Uyên Thi - 22011346
Với C (50, 50) => 5*50 + 2*50 = 350
Với E (73,53; 85,3) => 5*73,53 + 2*85,3 = 538,25
Lần lượt thế tọa độ các điểm cực biên vào hàm mục tiêu 5x + 2y, ta được hàm mục
tiêu đạt giá trị lớn nhất tại (x = 73,53; y = 85,3)
Mức lợi nhuận tối đa khi đó là: 5 × 73,53 + 2 × 85,3 = 538,25
11. Công ty Hartman sản xuất 2 sản phẩm nguyên khối, Ban quản lý công ty muốn xác
định số lượng từng loại sản phẩm sẽ sản xuất trong giai đoạn sắp tới. Các thông tin sau
đây liên quan đến tính sẵn có của lao động, sử dụng lao động và lợi nhuận của sản phẩm:
Phát triển một mô hình quy hoạch tuyến tính cho bài toán của công ty Hartman với mục
tiêu là tối đa hóa lợi nhuận. Giải mô hình để xác định số lượng sản xuất tối ưu của sản
phẩm 1 và 2. Tìm mức lợi nhuận tối đa dự kiến. Mô hình bài toán
Gọi x là số lượng sản phẩm 1
Gọi y là số lượng sản phẩm 2 Hàm mục tiêu Max {30x + 15y} Với các ràng buộc: 1. x + 0,35y ≤ 100 2. 0,3x + 0,2y ≤ 36 3. 0,2x + 0,5y ≤ 50 4. x, y ≥ 0
Dùng excel solver ta được x = 77,98; y =63,16
Giá trị lợi nhuận tối đa là 3284,211 Lê Uyên Thi - 22011346
12. Hiệp hội tín dụng nhân viên tại các trường đại học nhà nước đang lên kế hoạch phân
bổ vốn cho năm tới. Hiệp hội thực hiện bốn loại cho vay đối với các thành viên của mình.
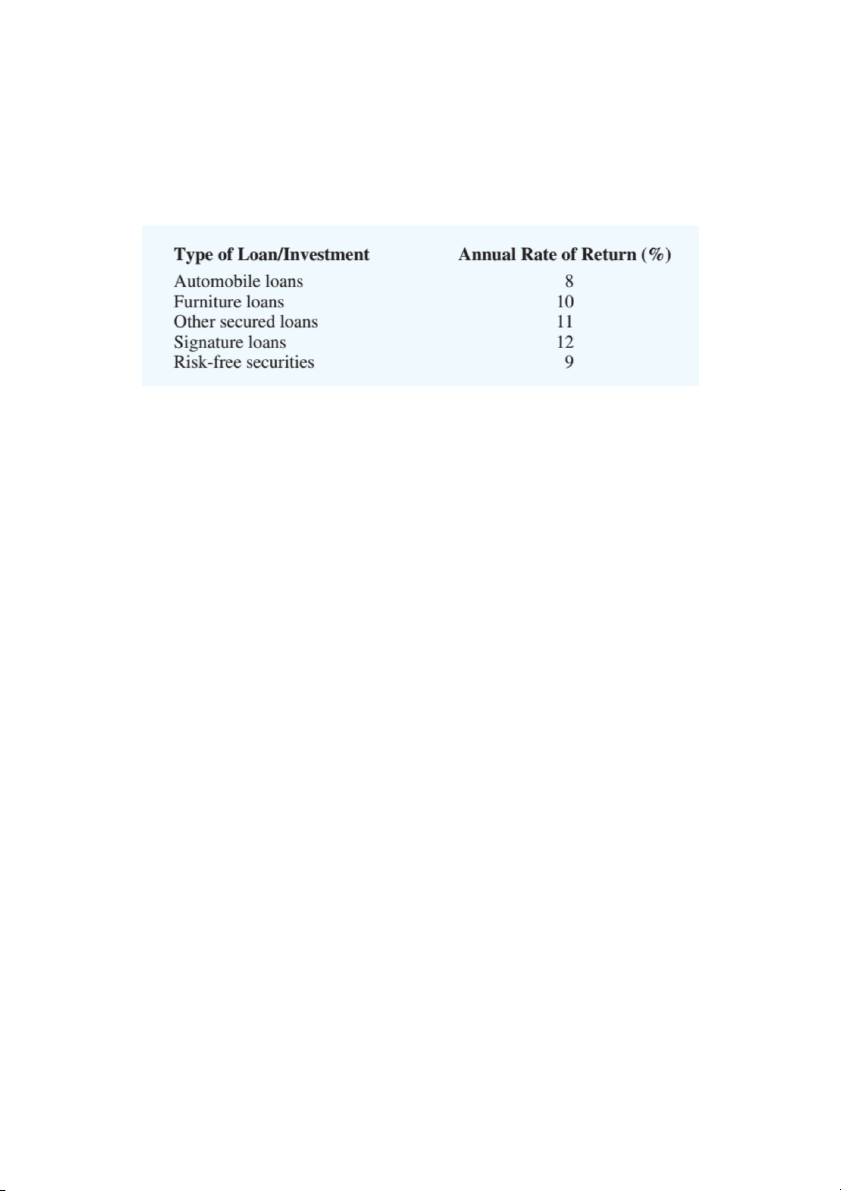
Ngoài ra, hiệp hội còn đầu tư vào chứng khoán phi rủi ro để ổn định thu nhập. Các khoản
đầu tư doanh thu khác nhau cùng với tỷ suất lợi nhuận hàng năm như sau:
Hiệp hội có sẵn 2 triệu đô la để đầu tư trong năm tới. Luật pháp tiểu bang và chính sách
của Hiệp hội áp đặt các hạn chế sau đây đối với các khoản vay và đầu tư:
 Chứng khoán không rủi ro không được vượt quá 30% tổng số tiền.
 Khoản vay tín chấp (Signature loans) không được vượt quá 10% số tiền đầu tư vào
tất cả các khoản vay (ô tô, nội thất, các khoản vay có bảo đảm khác và tín chấp).
 Các khoản vay nội thất cộng với các khoản vay có bảo đảm khác không được vượt quá các khoản vay ô tô.
 Các khoản vay có bảo đảm khác cộng với các khoản vay tín chấp không được vượt
quá số tiền đầu tư vào chứng khoán phi rủi ro.
Nên phân bổ 2 triệu đô la cho mỗi phương án cho vay / đầu tư như thế nào để tối đa hóa
tổng lợi nhuận hàng năm? Tổng lợi nhuận hàng năm dự kiến là gì? Lê Uyên Thi - 22011346 Mô hình: Các biến của mô hình: A = Automobile loans F = Furniture loans O = Other secured loans S = Signature loans R = Risk-free securities Hàm mục tiêu:
Max {0,08A + 0,1F + 0,11O + 0,12S + 0,09R} Với các ràng buộc: 1. A + F + O + S + R = 2000000 2. R ≤ 0,3*2000000
3. – 0,1A – 0,1F – 0,1O + 0,9S ≤ 0 4. F + O – A ≤ 0 5. O + S – R ≤ 0 6. A, F, O, S, R ≥ 0
Dùng excel solver ta được A = 630000 F = 170000 O = 460000 S = 140000 R = 600000
Tổng lợi nhuận hàng năm dự kiến là 188800 $
13. Sở Cảnh sát Hạt Clark sắp xếp các sĩ quan cảnh sát làm việc theo ca 8 tiếng. Thời
gian bắt đầu cho ca làm việc là: 8:00 sáng, 12:00 trưa, 4:00 chiều, 8:00 tối, nửa đêm và 4:00 sáng.
Một sĩ quan bắt đầu ca làm việc tại một trong những thời điểm này và làm việc trong 8
giờ tiếp theo. Trong các hoạt động ngày thường, số lượng sĩ quan cần thay đổi tùy thuộc
vào thời gian trong ngày. Dưới đây là yêu cầu số lượng sĩ quan tối thiểu làm nhiệm vụ
trong từng khoảng thời gian trong ngày: Lê Uyên Thi - 22011346
Hãy xác định số lượng sĩ quan cảnh sát nên được lên lịch để bắt đầu ca làm việc 8 giờ tại
từng thời điểm (8:00 sáng, 12:00 trưa, 4:00 chiều, 8:00 tối, nửa đêm và 4:00 sáng) để tối
thiểu hóa tổng số sĩ quan cần thiết.
(Gợi ý: Hãy đặt là số lượng sĩ quan bắt đầu làm việc lúc 8:00 sáng, là số lượng sĩ quan
bắt đầu làm việc vào 12:00 trưa, v.v.) Gọi:
x1 là số lượng sĩ quan bắt đầu làm việc lúc 8:00 sáng
x2 là số lượng sĩ quan bắt đầu làm việc vào 12:00 trưa
x3 là số lượng sĩ quan bắt đầu làm việc vào 4:00 chiều
x4 là số lượng sĩ quan bắt đầu làm việc vào 8:00 tối
x5 là số lượng sĩ quan bắt đầu làm việc vào 12:00 đêm
x6 là số lượng sĩ quan bắt đầu làm việc vào 4:00 sáng Hàm mục tiêu:
Min {x1 + x2 + x3 + x4 + x5 + x6} Các ràng buộc: 1. x6 + x1 ≥ 5 2. x1 + x2 ≥ 6 3. x2 + x3 ≥ 10 4. x3 + x4 ≥ 7 5. x4 + x5 ≥ 4 6. x5 + x6 ≥ 6
7. x1, x2, x3, x4, x5, x6  N
Dùng excel solver ta được
Vậy có 19 sĩ quan cảnh sát nên được lên lịch để bắt đầu ca làm việc 8 giờ tại từng thời
điểm để tối thiểu hóa tổng số sĩ quan cần thiết như sau: Lê Uyên Thi - 22011346 x1 = 3 x2 = 3 x3 = 7 x4 = 0 x5 = 4 x6 = 2
14. Một công ty nhập khẩu hàng hóa tại 2 cảng ở Philadelphia và New Orleans. Hàng hóa
sau đó được vận chuyển đến 4 đại lý ở Atlanta, Dallas, Columbus và Boston. Trong kỳ kế
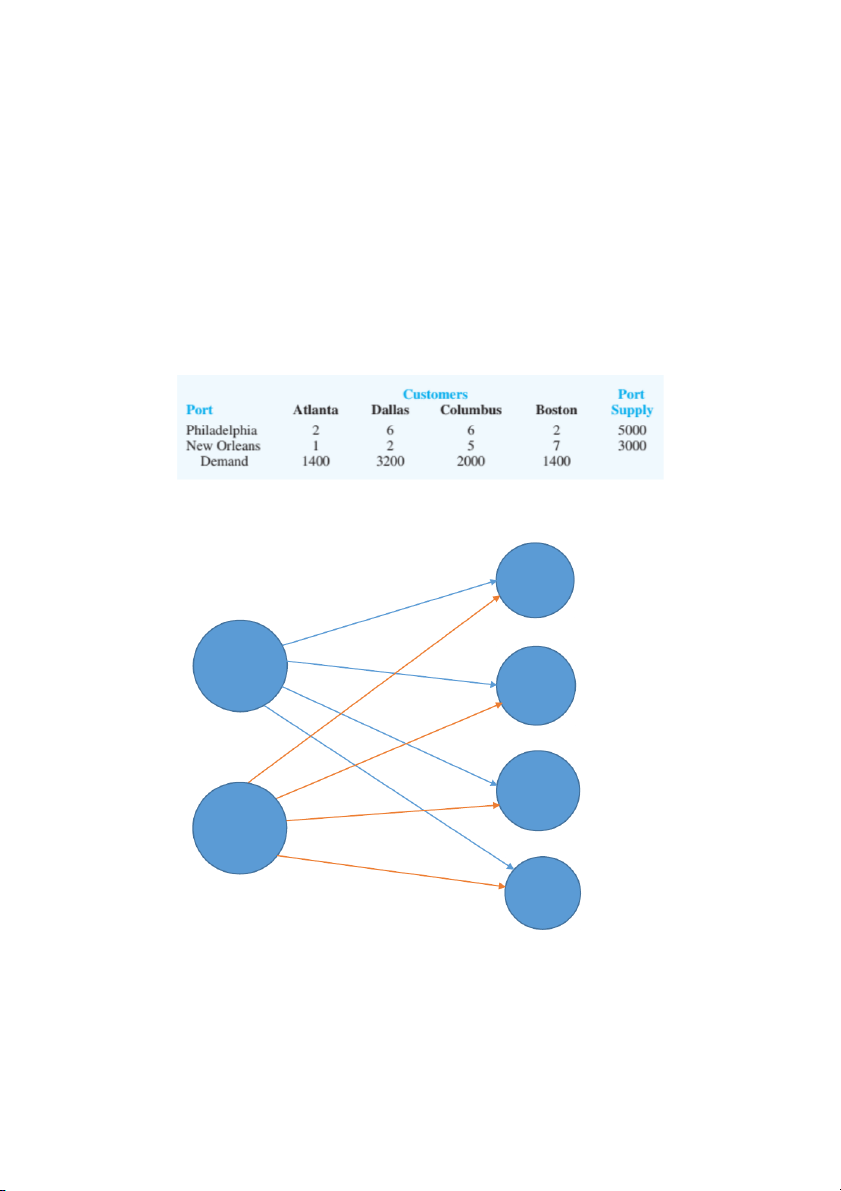
hoạch tiếp theo, nguồn cung cấp tại mỗi cảng, nhu cầu của các đại lý và chi phí vận
chuyển cho mỗi đơn vị hàng hóa từ mỗi cảng đến từng đại lý như sau:
a) Hãy vẽ 1 network cho bài toán phân phối hàng hóa ở trên. Atlanta 140 2 5000 6 Philadelphia 6 3200 Dallas 2 1 2 Columbus 2000 5 New 3000 Orleans 7 Boston 1400 Lê Uyên Thi - 22011346
b) Xây dựng mô hình QHTT của bài toán và giải bằng excel solver, với mục tiêu
là tối thiểu tổng chi phí vận chuyển nhưng vẫn đáp ứng được nhu cầu của các đại lý. Mô hình
Biến: Gọi xIJ là số lượng hàng hóa vận chuyển từ điểm cung I đến điểm cầu J (I = 1,2; J =1,2,3,4) Hàm mục tiêu Min {2x 11 + 6x + 6x 12 + 2x 13 + x 14 + 2x 21 22 + 5x + 7x 23 } 24 Các ràng buộc: Về phía điểm cung: x11 + x + x 12 + x 13 14 ≤ 5000 x21 + x + x 22 + x 23 ≤ 3000 24 Về phía điểm cầu x11 + x = 140 21 x12 + x = 3200 22 x13 + x = 2000 23 x14 + x = 1400 24 xIJ ≥ 0
Dùng excel solver ta được Route Units Shipped Cost per Unit Total cost From To Philadelphia Atlanta 140 2 $ 280 $ Philadelphia Dallas 200 6 $ 1,200 $ Philadelphia Columbus 2000 6 $ 12,000 $ Philadelphia Boston 1400 2 $ 2,800 $ New Orleans Dallas 3000 2 $ 6,000 $ 22,280 $ Lê Uyên Thi - 22011346
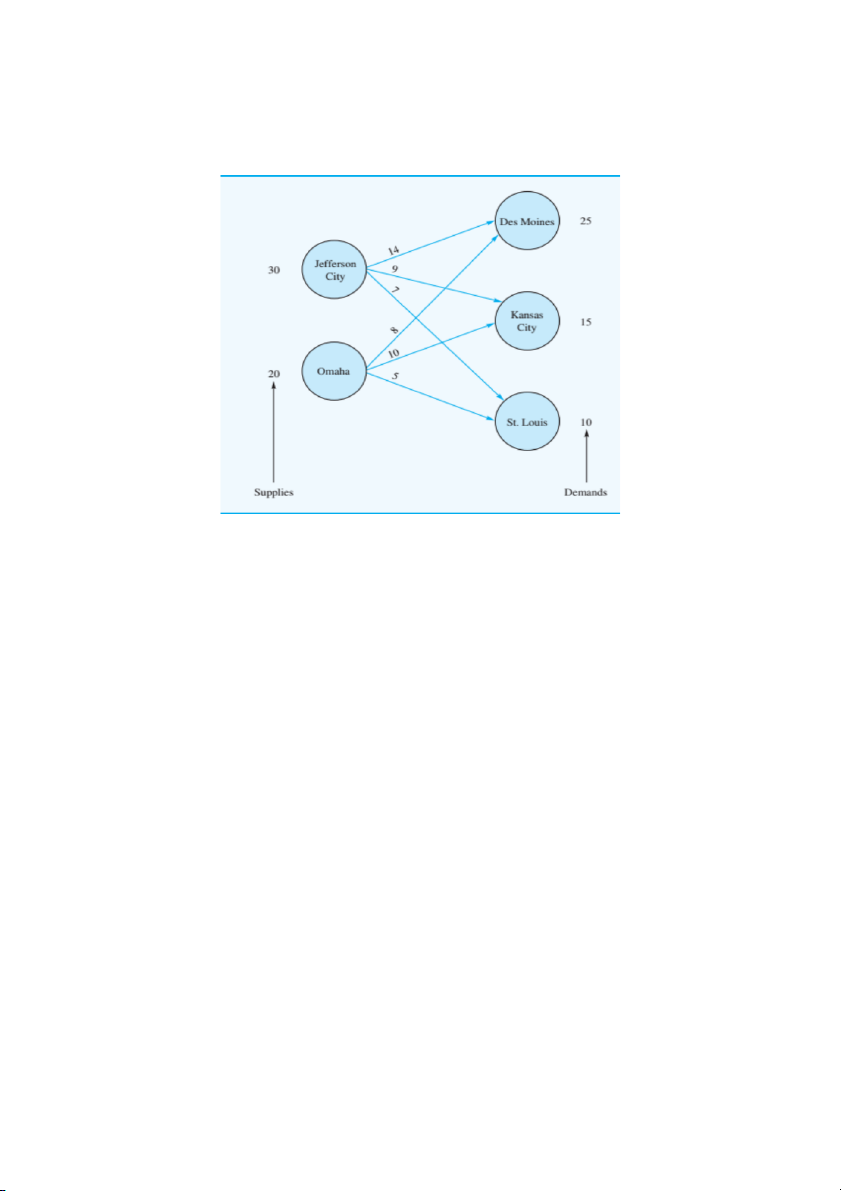
15. Giả sử bài toán vận chuyển có sơ đồ mạng (network) như hình bên dưới.
a) Hãy xác định tổng cung, tổng cầu, cung đường có chi phí vận chuyển thấp
nhất và cao nhất trên mỗi đơn vị sản phẩm. Tổng cung: 50 Tổng cầu: 50
Cung đường có chi phí vận chuyển thấp nhất: Omaha – St. Louis
Cung đường có chi phí vận chuyển cao nhất: Jefferson City – Des Moines Lê Uyên Thi - 22011346
b) Hãy xây dựng mô hình QHTT của bài toán và giải bằng excel solver, với mục
tiêu là tối thiểu tổng chi phí vận chuyển nhưng vẫn đáp ứng được nhu cầu của các đại lý. Mô hình
Biến: Gọi xIJ là số lượng hàng hóa vận chuyển từ điểm cung I đến điểm cầu J (I = 1,2; J =1,2,3) Hàm mục tiêu Min {14x 11 + 9x + 7x 12 13 + 8x + 10x 21 22 + 5x } 23 Các ràng buộc: Về phía điểm cung: x11 + x + x 12 ≤ 30 13 x21 + x + x 22 ≤ 20 23 Về phía điểm cầu x11 + x = 25 21 x12 + x = 15 22 x13 + x = 10 23 xIJ ≥ 0
Dùng excel solver ta được: Route Units Shipped Cost per Unit Total cost From To Jefferson City Des Moines 5 14 $ 70 $ Jefferson City Kansas City 15 9 $ 135 $ Jefferson City St. Louis 10 7 $ 70 $ Omaha Des Moines 20 8 $ 160 $ 435 $