



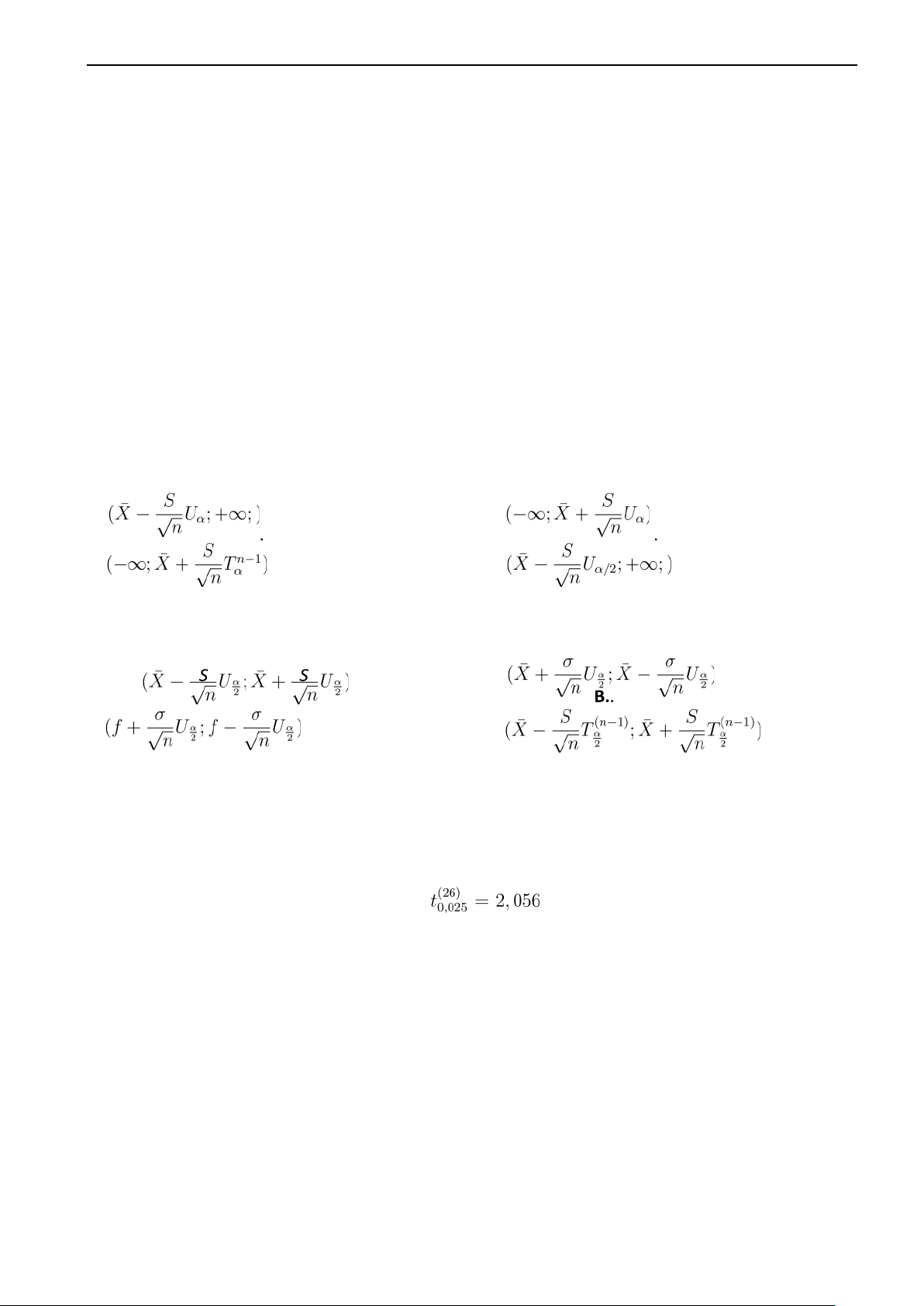







Preview text:
lOMoAR cPSD| 40425501
BàitậpXSTK(Bổsung) BộmônToán
BÀITẬPXÁCSUẤTTHỐNGKÊ
1 Biếncốngẫunhiênvàxácsuất
Câu 1. Tòa nhà có 3 chuông báo cháy hoạt động độc lập, A là biến cố chuông 1 kêu khi có cháy, B là biến
cố chuông 2 kêu khi có cháy, C là biến cố chuông 3 kêu khi có cháy. Biến cố có chuông kêu khi có cháy là:
A. A + B + C. B. ABC .
C. A.B.C + A.B.C + A.B.C . D. ABC.
Câu 2. Cho A,B là hai biến xung khắc có xác suất P(A) = 0,1;P(B) = 0,3. Khi đó P(A + B) bằng: A. 0,03. B. 0,4 . C. 0,2 . D. 0,37.
Câu 3. Cho A,B là hai biến cố độc lập có xác suất P(A) = 0,4;P(B) = 0,2. Tính P(A+B). A. P(A + B) = 0,6. B.
P(A + B) = 0,08 . C. P(A + B) = 0,52 . D. P(A + B) = 0,4.
Câu 4. A1,B1 là các biến cố, có P(A1) = 0,5 và P(B1|A1) = 0,4. Tính P(A1B1). A. 0,2. B. 0,3 . C. 0,9 . D. 0,1.
Câu 5. Cho A1,B1,C1 là 3 biến cố tạo thành một hệ đầy đủ. Biết P(A1) = 0,1;P(B1) = 0,7.
Giá trị của P(C1) là : A. 0,6. B. 0,2 . C. 0,8 . D. 0,07.
Câu 6. Cho 2 biến cố độc lập. Khẳng định nào sau đây sai?
A. P(B|A) = P(B).
B. P(A|B) = P(A) .
C. P(AB) = P(A)P(B) .
D. P(A + B) = P(A) + P(B).
Câu 7. Ba người cùng bắn vào 1 bia, mỗi người bắn một viên. Gọi Ai là biến cố người thứ i bắn trúng
bia. Biến cố có đúng một người bắn trúng là
A. A1A2A3.
B. A1 + A2 + A3 .
C. A1.A2.A3 + A1.A2.A3 + A1.A2.A3 .
D. A1.A2.A3 + A1.A2.A3 + A1.A2.A3.
Câu 8. Đại kiện tướng cờ vua Nguyễn Ngọc Trường Sơn tham gia một giải cờ chớp và nằm cùng bảng
với 6 người nữa ngang tài, ngang sức với Sơn. Mỗi ván đấu quy định luôn có thắngthua, không có ván
hòa. Hỏi xác suất khi thi đấu một lượt với 6 kỳ thủ, Sơn thắng được đúng 3 ván bằng bao nhiêu? 1 lOMoAR cPSD| 40425501
BàitậpXSTK(Bổsung) BộmônToán A. 0,5. B. 0,53 . C. . D. 0,56.
Câu 9. Cho 2 biến cố độc lập. Khẳng định nào sau đây sai?
A. P(B|A) = P(B) và P(A|B) = P(A) .
B. P(AB) = P(A).P(B) .
C. P(A + B) = 1 − P(A).P(B) .
D. P(A + B) = P(A) + P(B).
Câu 10. Từ bộ bài chuẩn 52 quân bài ta chọn ngẫu nhiên 4 quân bài. Xác suất 4 quân bài đó chứa ít nhất một quân 2 là: A. . B. . C. . D. .
Câu 11. Biết rằng học phần Toán 1 chỉ được thi nhiều nhất hai lần (nếu lần một không đạt thì phải thi
lại). Theo đánh giá của giáo viên bộ môn, khả năng thi đạt ở lần 1 của Việt là 70%, nếu phải thi lại thì
khả năng đạt ở lần 2 là 90%. Tính xác suất Việt vượt qua được môn Toán 1 ở kỳ thi kết thúc học phần sắp tới. A. 0,97. B. 0,63 . C. 0,9 . D. 0,8.
Câu 12. Trong 10 sản phẩm có 2 phế phẩm. Lấy ngẫu nhiên có hoàn lại 2 sản phẩm. Xác suất để lấy
được cả 2 phế phẩm là: A. 0,4. B. 0,56 . C. 0,04 . D. 0,044.
Câu 13. Ba người cùng bắn vào một mục 琀椀 êu, mỗi người bắn một viên. Xác suất bắn trúng của mỗi
người lần lượt là 0,7; 0,8 và 0,9. Xác suất mục 琀椀 êu bị trúng đạn là: A. 0,504. B. 0,994 . C. 0,0153 . D. 0,9.
Câu 14. Giả sử 4 quả trứng nở thành 4 con gà. Tính xác suất để trong đó có 2 con trống. A. 0,5. B. 0,25 . C. 0,375 . D. 0,0625.
Câu 15. Cho A,B là 2 biến cố độc lập. Biết P(A) = 0,4;P(A + B) = 0,6. Tính P(B). A. 0,2. B. . C. . D. 0,5.
Câu 16. Một người bán hàng thực hiện phương thức bán hàng theo các bước sau:
Bước 1: Giao dịch với khách hàng trên điện thoại; Bước 2: Giao dịch với khách hàng tại nhà nếu giao
dịch trên điện thoại thành công. Kinh nghiệm cho thấy rằng 25% các cuộc giao dịch với khách hàng trên
điện thoại ở bước 1 sẽ dẫn tới việc giao dịch với khách hàng tại nhà ở bước 2. Giả sử người bán hàng
thực hiện 16 cuộc giao dịch trên điện thoại, hãy 琀 nh xác suất để có đúng 4 cuộc giao dịch tại nhà với khách hàng. A. . B. . C. . D. 0,25.
Câu 17. Một người chơi bóng rổ thực hiện ném độc lập 3 lần. Xác suất ném trúng rổ trong mỗi lần ném
của người này là 0,8. Gọi X là số lần ném trúng rổ của người này. Tính P(X ≥ 1). 2 lOMoAR cPSD| 40425501
BàitậpXSTK(Bổsung) BộmônToán A. 0,8. B. 0,488 . C. 0,512. D. 0,992 . 2
Biếnngẫunhiênvàquyluậtphânphốixácsuất
Câu 18. Nhà thầu quan tâm đến tổng giá thành của một dự án ông ta bỏ thầu. Ông ước đoán giá vật
liệu là 500 triệu và 琀椀 ền công lao động là 15 triệu một ngày, từ đó giá tổng thể của dự án là G = 500 +
15X. Ông đánh giá một cách chủ quan thời gia hoàn thành dự án theo bảng xácsuất Thời gian (X ngày) 15 16 17 18 19
20 .Tínhgiá thànhtrungbìnhcủa dựán P
0,1 0,2 0,3 0,15 0,15 0,1
(theo đánh giá của nhà thầu)? A. 550 triệu.
B. 662,75 triệu . C. 700 triệu .
D. 760,25 triệu.
Câu 19. Nhà bán lẻ điện thoại 琀 nh số lần khách hàng mua điện thoại phải quay lại sửa chữa trong thời gian bảo hành tuân theobảng phân phối xác suất sau:
X(số lần sửa chữa) 0 1 2 3 . P
0,3 0,3 0,25 0,15
Nếu phải quay lại sửa chữa X lần thì số 琀椀 ền thiệt hại là T = 0,1.X2 (triệu đồng). Tính số 琀椀 ền thiệt
hại trung bình cho việc phải bảo hành khi bán mỗi chiếc điện thoại.
A. 0,265 triệu.
B. 0,15625 triệu .
C. 0,15 triệu .
D. 0,3 triệu .
Câu 20. Giám đốc đang 琀 m hiểu có cần thay thế lò sấy nhà máy hay không. Ghi nhận số lần hỏng lò
sấy trong một tuần tuân theo bảng phân phối xác suất sau: . X(số lần hỏng) 0 1 2 3 4 P
0,10 0,26 0,42 0,16 0,06 Mỗi lần hỏng, nhà
máy thiệt hại cỡ 15 triệu.
Tìm số 琀椀 ền thiệt hại trung bình cho việc sửa chữa lò sấy trong một tuần.
A. 28,8 triệu.
B. 27,3 triệu . C. 15 triệu . D. 30 triệu.
Câu 21. Tuổi thọ của một loại sản phẩm là biến ngẫu nhiên có phân phối chuẩn, qua nghiên cứu thấy
tuổi thọ trung bình là 8 năm và độ lệch chuẩn là 1,5 năm. Người ta quy định thời hạn bảo hành là 5
năm. Tìm tỉ lệ sản phẩm phải bảo hành. Biết Φ0(3,33) = 0,4995;Φ0(2) = 0,4773. A. 2,22%. B. 52,27% . C. 47,73% . D. 2,27%.
Câu 22. Một công ty cho ra đời một con chíp có tuổi thọ (琀 nh theo năm) là một biến ngẫu nhiên X có 3 lOMoAR cPSD| 40425501
BàitậpXSTK(Bổsung) BộmônToán
hàm mật độ xác suất là nếu x ≥ 0 . Tuổi thọ trung bình của con chíp là: nếu x < 0 A. 0,2 năm. B. 5 năm . C. 10 năm . D. 2 năm .
Câu 23. Cho X,Y là 2 biến ngẫu nhiên độc lập. Biết V (X) = 3,V (Y ) = 1. Khi đó V (X − 3Y ) bằng:
A. 12. B. 0 . C. 4 . D. −6.
Câu 24. Giả sử X là biến ngẫu nhiên liên tục có hàm phân bố xác suất nếu
x < 1 nếu 1 ≤ x < 5. Xác suất P(2 < X < 3) là: nếu x ≥ 5 B. . C. . D. .
Câu 25. Tuổi thọ của một loại côn trùng (琀 nh theo tháng) là một biến ngẫu nhiên liên tục X 3 2(2 − x) nếu x ∈ [0;2] x
có hàm mật độ xác suất như sau: f(x) = 4
Tỷ lệ loại côn trùng đó 0 nếu x /∈ [0;2]
chết trước 1 tháng được 琀 nh bởi: A. . B. . C. .
Câu 26. Biến ngẫu nhiên liên tục X có hàm mật độ xác suất như sau: 3 2(2 − x)
nếu x ∈ [0;2] x f(x) = 4 Tính mốt của X. 0 nếu x /∈ [0;2] A. . B. m0 = 1 . C. . D. m0 = 2.
Câu 27. Biết X ∼ B(50;0,5) và Y ∼ N(30;4). Tính E(X + Y ).
A. E(X + Y ) = 80.
B. E(X + Y ) = 4,5 .
C. E(X + Y ) = 55 .
D. E(X + Y ) = 20.
Câu 28. Trọng lượng sản phẩm do một máy sản xuất tự động là biến ngẫu nhiên X (琀 nh theo gam) có
phân phối chuẩn X ∼ N(100;1). Sản phẩm được coi là đạt 琀椀 êu chuẩn nếu trọng lượng của nó nằm
trong khoảng từ 99 gam đến 101 gam. Cho máy sản xuất ra 20 sản phẩm, 琀 nh xác suất để có ít nhất
một sản phẩm đạt 琀椀 êu chuẩn. A. B. . 4 lOMoAR cPSD| 40425501
BàitậpXSTK(Bổsung) BộmônToán C. . D.
Câu 29. Một dự án xây dựng được viện thiết kế A soạn thảo cho bên B xét duyệt. Xác suất để B chấp
nhận dự án khi xét duyệt là 0,45. Nếu chấp nhận dự án thì B phải trả cho A là 500 triệu đồng, còn ngược
B phải trả cho A là 100 triệu đồng, biết rằng chi phí cho thiết kế là 250 triệu và thuế 10% doanh thu.
Gọi X là số lợi nhuận mà A có thể nhận được sau khi trừ đi 琀椀 ền thuế và chi phí thiết kế. Tìm tập giá trị của X. X 2 4 6 9
P 0,2 0,4 0,1 0,3
A. {−160 triệu, 200 triệu }.
B. { 100 triệu, 500 triệu } .
C. {−160 triệu, 250 triệu } .
D. { 250 triệu, 500 triệu }.
Câu 30. Cho biến ngẫu nhiên rời rạc X có bảng phân phối xác suất.
Từ bảng trên ta 琀 nh được E(X) = 5,3. Tính P(|X − E(X)| ≤ 3). A. 0,2. B. 0,5 . C. 0,6 . D. 0,7.
3 Ướclượngthamsố
Câu 31. Lãi suất cổ phiếu của một công ty trong vòng 20 ngày liên 琀椀 ếp được cho bởi bảng sau Lãi suất(%) 0,7 0,9 1 1,3 1,4 1,6 1,7 Số ngày 3 2 5 4 3 2 1
Biết lãi suất cổ phiếu của công ty tuân theo luật phân phối chuẩn. Cổ phiếu được coi là đạt kì vọng của
nhà đầu tư nếu lãi suất theo ngày đạt trên 1%. Hãy ước lượng tỉ lệ tối đa những ngày đạt kì vọng của
nhà đầu tư với độ 琀椀 n cậy 0,95, biết u0,025 = 1,96, u0,05 = 1,65. A. 0,684. B. 0,696 . C. 0,335 . D. 0,5.
Câu 32. Thời gian tự học X (giờ/tuần) của sinh viên hệ chính quy ở trường đại học A là biến ngẫu nhiên
có phân bố chuẩn. Điều tra một mẫu gồm 25 sinh viên chính quy, người ta nhận được thời gian tự học
trung bình là 7,44 giờ và độ lệch chuẩn mẫu hiệu chỉnh s = 2,467. Cho trước
. Nếu ước lượng thời gian tự học của sinh viên chính quy với độ dài
khoảng 琀椀 n cậy 1,946 thì độ 琀椀 n cậy đạt được bao nhiêu? A. 0,9. B. 0,87 . C. 0,9397 . D. 0,95.
Câu 33. Sản lượng trong một ngày của một phân xưởng là biến ngẫu nhiên có phân bố chuẩn. Một mẫu
kích thước 10 cho ta phương sai mẫu hiệu chỉnh s2 = 2,6352. Giả sử sản lượng trung bình được ước
lượng với độ chính xác 1,152 thì độ 琀椀 n cậy đạt được bao nhiêu? Cho trước . A. 0,8. B. 0,76 . C. 0,9 . D. 0,95. 5 lOMoAR cPSD| 40425501
BàitậpXSTK(Bổsung) BộmônToán
Câu 34. Mở thử 200 hộp của một kho đồ hộp, người ta thấy có 8 hộp bị biến chất. Nếu muốn ước
lượng tỷ lệ đồ hộp bị biến chất của kho đó với độ dài khoảng 琀椀 n cậy 0,0544 thì độ 琀椀 n cậy đạt
được bao nhiêu? Biết u0,025 = 1,96;u0,05 = 1,64.
A. 1 − α = 0,05.
B. 1 − α = 1,96 .
C. 1 − α = 0,025 .
D. 1 − α = 0,95.
Câu 35. Khảo sát về thời gian tự học X (giờ/tuần) của sinh viên hệ chính quy ở Trường đại học Công
nghệ GTVT trong thời gian gần đây, một nhóm nghiên cứu đã điều tra ngẫu nhiên 108 sinh viên chính
quy thì thấy thời gian tự học trung bình là 7,47 và độ lệch 琀椀 êu chuẩn hiệu chỉnh là 2,206. Biết rằng
u0,05 = 1,64;u0,025 = 1,96;u0,0537 = 1,61, với độ 琀椀 n cậy 95%, thời gian tự học trong tuần của sinh viên
chính quy có khoảng 琀椀 n cậy là:
A. (7,254;7,886).
B. (7,054;8,186) .
C. (6,954;7,886).
D. (7,054;7,886) .
Câu 36. Khoảng 琀椀 n cậy phải với độ 琀椀 n cậy là 1 − α cho kì vọng của biến ngẫu nhiên không có
giả thiết phân bố chuẩn, phương sai chưa biết là (điều kiện mẫu lớn hơn 30) : A. B. C. . D. .
Câu 37. Khoảng 琀椀 n cậy đối xứng với độ 琀椀 n cậy 1 − α cho kì vọng của biến ngẫu
nhiên X ∼ N (µ,σ2) với σ2 chưa biết là: A.. C. . D. .
Câu 38. Thời gian tự học X (giờ/tuần) của sinh viên hệ chính quy ở trường đại học A là biến ngẫu nhiên
có phân bố chuẩn. Để khảo sát về thời gian tự học của sinh viên trong thời gian gần đây, nhóm nghiên
cứu đã điều tra một mẫu gồm 27 sinh viên chính quy, nhận được thời gian tự học trung bình là 7,3 giờ
và phương sai mẫu hiệu chỉnh s = 2,46. Biết
, khoảng ước lượng cho thời gian tự học
trung bình trong tuần của một sinh viên hệ chính quy của trường đại học A với độ 琀椀 n cậy 95% là:
A. (6,327;8,273).
B. (6,327;8,873) .
C. (6,027;8,273) .
D. (6,25;8,95) .
Câu 39. Khi chế tạo 150 chi 琀椀 ết máy thì thấy 30 chi 琀椀 ết không đạt 琀椀 êu chuẩn. Biết u0,242 =
0,7;u0,121 = 1,17.Với độ 琀椀 n cậy 0,758, tỷ lệ tối đa các chi 琀椀 ết không đạt 琀椀 êu chuẩn là: A. 0,2228. B. 0,2528 . C. 0,3228 . D. 0,4228 .
Câu 40. Khoảng 琀椀 n cậy phải với độ 琀椀 n cậy là 1 − α cho kì vọng của biến ngẫu nhiên không có
giả thiết phân bố chuẩn, phương sai chưa biết là (điều kiện mẫu lớn hơn 30): 6 lOMoAR cPSD| 40425501
BàitậpXSTK(Bổsung) BộmônToán A. B. C. . D. .
Câu 41. Khi ước lượng kì vọng của biến ngẫu
nhiên có phân phối chuẩn N(µ,σ2) với σ2 chưa biết, kích thước mẫu n và độ chính xác ε cho trước thì độ
琀椀 n cậy 1−α của ước lượng được suy ra từ công thức: A. . B. . C. . D. .
Câu 42. Kiểm tra ngẫu nhiên 16 bóng đèn loại A 琀 nh được tuổi thọ trung bình của chúng là 1200 (giờ)
và độ lệch chuẩn mẫu s = 26,094 giờ. Giả sử tuổi thọ của bóng đèn loại A là biến ngẫu nhiên có phân phối chuẩn. Biết
.Với độ 琀椀 n cậy 0,95 khoảng 琀椀 n cậy đối xứng cho tuổi thọ trung
bình của bóng đèn loại A là: A. . B. . C. . D. .
Câu 43. Sảnlượngtrongmộtngàycủamộtphânxưởnglàbiếnngẫunhiêntuântheoquyluật chuẩn với độ lệch
琀椀 êu chuẩn σ = 2,6. Từ kết quả thống kê của 10 ngày ta thu được sản lượng
trung bình của mẫu x = 25,5. Biết .Với độ
琀椀 n cậy 90%, 琀 m khoảng ước lượng bên phải cho sản lượng trung bình trong một ngày của phân xưởng đó. . C.
Câu 44. Năng suất X của một loại cây trồng là biến ngẫu nhiên tuân theo quy luật phân phối chuẩn.
Thống kê năng suất của 25 mảnh vườn được trung bình mẫu x = 23,28 và phương sai
mẫu s2 = 1,54. Biết
, với độ 琀椀 n cậy 90%, khoảng 琀椀 n cậy cho năng
suất trung bình của loại cây trồng trên là:
A. (20,85;26,7).
B. (22,85;23,7) .
C. (12,85;13,7) .
D. (22,85;+∞).
Câu 45. Kiểm tra chất lượng của 1.000 chi 琀椀 ết máy cùng loại thì thấy 3% số chi 琀椀 ết không đạt
琀椀 êu chuẩn. Biết u0,05 = 1,64;u0,1 = 1,28;u0,025 = 1,96.Với độ 琀椀 n cậy 95%, khoảng 琀椀 n cây bên
phải cho tỷ lệ chi 琀椀 ết không đạt 琀椀 êu chuẩn là: 7 lOMoAR cPSD| 40425501
BàitậpXSTK(Bổsung) BộmônToán A. . B. . C. . D. Câu 46. Biết
rằng tần suất thực nghiệm để xuất hiện phế phẩm của nhà máy là 0,1. Biết rằng u0,05 =
1,65;u0,025 = 1,96. Để ước lượng tỷ lệ chính phẩm với độ 琀椀 n cậy 0,95 và độ sai lệch không vượt quá
0,058 thì số sản phẩm cần kiểm tra ít nhất là: A. 104. B. 103 . C. 101 . D. 105.
Câu 47. Trong bài toán xác định cỡ mẫu khi ước lượng khoảng đối xứng cho giá trị trung bình, giả sử
với cỡ mẫu n = 30 ta 琀 nh được sai số ε = 0,3, vậy muốn sai số là ε = 0,1 thì cần lấy cỡ mẫu là A. 90. B. 270 . C. 10 . D. 120.
Câu 48. Biết rằng tần suất thực nghiệm để xuất hiện phế phẩm của nhà máy là f. Để ước lượng tỷ lệ
chính phẩm của nhà máy với độ 琀椀 n cậy 1 − α và độ sai lệch không vượt quá ε0 thì kích thược mẫu
n cần thiết được xác định bằng công thức nào sau đây? A. . B. . C. . D. .
Câu 49. Người ta chọn một mẫu gồm 100 琀椀 vi trong một kho thì thấy có 80 琀椀 vi Sony. Dựa vào
mẫu trên nếu muốn độ chính xác cho ước lượng số 琀椀 vi Sony trong kho nhỏ hơn 0,0392, với độ 琀
椀 n cậy 95% thì cần chọn ít nhất bao nhiêu 琀椀 vi ? Biết u0,025 = 1,96, u0,05 = 1,65, u0,01 = 2,33 A. 200. B. 180 . C. 300 . D. 400.
Câu 50. Tại một vùng núi khu vực vùng cao 10000 người. Tiến hành khám bệnh cho 1600 người bất kỳ
thấy có 320 bị mắc bệnh đau mắt hột. Hãy ước lượng số người bị bệnh đau mắt hột ở vùng cao nói
trên với độ 琀椀 n cậy 95%, biết u0,025 = 1,96, u0,05 = 1,65.
A. (0,1804;0,2196).
B. (0,19;0,21) . C. (1804;2196) . D. (1900;2100).
4 Kiểmđịnhgiảthuyế 琀琀 hốngkê
Câu 51. Định mức thời gian hoàn thành sản phẩm là 14 phút. Theo dõi thời gian hoàn thành sản phẩm
ở 250 công nhân, người ta thấy thời gian hoàn thành sản phẩm trung bình là 15 phút.Có cần thay đổi
định mức 14 phút trước đây hay không?Để kết luận về ý định này, cặp giả thuyết thống kê là:
A. H0 : µ = 14;H1 : µ < 14.
B. H0 : µ = 15;H1 : µ > 15 .
C. H0 : µ = 14;H1 : µ 6= 14 .
D. H0 : µ = 15;H1 : µ 6= 15.
Câu 52. CótàiliệunóirằngtrọnglượngtrungbìnhX củamộtloạisảnphẩmlà70kg.Đểkiểm định lại ý kiến trên
(với mức ý nghĩa 5%) người ta điều tra một mẫu kích thước 100, nhận được trung bình mẫu 67,07 và 8 lOMoAR cPSD| 40425501
BàitậpXSTK(Bổsung) BộmônToán
độ lệch chuẩn mẫu hiệu chỉnh s = 7,057. Cho biết 65; giá trị quan sát là: A. −4,15. B. −5 . C. 5 . D. 3,2.
Câu 53. Nhà sản xuất cho rằng trọng lượng trung bình của một loại sản phẩm là 70 kg. Nghi ngờ thông
琀椀 n đưa ra cao hơn so với thực tế, người ta điều tra một mẫu kích thước 100, được trọng lượng
trung bình 67,07 và độ lệch chuẩn hiệu chỉnh s = 7,057. Với mức ý nghĩa 5%, cặp giả thuyết thống kê
cho bài toán kiểm định là:
A. H0 : µ = 70;H1 : µ < 70.
B. H0 : µ = 70;H1 : µ > 70 .
C. H0 : µ = 67,07;H1 : µ < 67,07 .
D. H0 : µ = 70;H1 : µ 6= 70.
Câu 54. Trọng lượng 琀椀 êu chuẩn của một loại sản phẩm là 27,5 kg. Nghi nghờ do điều kiện máy móc
xuống cấp đã làm cho trọng lượng của sản phẩm thay đổi, người ta lấy mẫu kích thước 41 và nhận
được trọng lượng trung bình 26,8 và độ lệch 琀椀 êu chuẩn 1,308. Để kết luận về điều nghi ngờ trên,
dùng cặp giả thuyết thống kê nào sau đây: A. .
Câu 55. Tuổi thọ của bóng đèn là một biến ngẫu nhiên tuân theo luật phân phối chuẩn. Một dây chuyền
sản xuất bóng đèn có tuổi thọ 750 giờ. Nghi ngờ do dây chuyền hoạt động đã lâu nên sản xuất kém
chất lượng, người ta chọn ngẫu nhiên 41 bóng đèn thì thấy tuổi thọ trung bình đạt 740 giờ với s = 30
giờ. Với mức ý nghĩa α = 0,05 hãy đưa ra cặp giả thuyêt và đối thuyết của bài toán trên.
A. H0 : µ = 750; H1 : µ < 750.
B. H0 : µ = 750; H1 : µ > 750 .
C. H0 : µ = 740; H1 : µ < 740 .
D. H0 : µ = 740; H1 : µ > 740.
Câu 56. Xét bài toán: Tuổi thọ của bóng đèn là một biến ngẫu nhiên tuân theo luật phân phối chuẩn.
Một dây chuyền sản xuất bóng đèn có tuổi thọ 750 giờ. Nghi ngờ do dây chuyền hoạt động đã lâu nên
sản xuất kém chất lượng, người ta chọn ngẫu nhiên 41 bóng đèn thì thấy tuổi thọ trung bình đạt 740
giờ với s = 30 giờ. Với mức ý nghĩa α = 0,05 có thể kết luận rằng chất lượng của dây truyền trên kém đi
hay không? Thống kê kiểm định cần sử dụng cho bài toán trên là: A.. B. C.. D. .
Câu 57. Tỉ lệ học sinh đỗ tốt nghiệp phổ thông trung học chung của toàn quốc là 80%. Điều tra ngẫu
nhiên 400 học sinh thi tốt nghiệp phổ thông trung học ở một tỉnh thấy có 290 học sinh đỗ tốt nghiệp.
Với mức ý nghĩa 5%, có thể coi tỉ lệ học sinh đỗ tốt nghiệp của tỉnh này thấp hơn mức chung của toàn 9 lOMoAR cPSD| 40425501
BàitậpXSTK(Bổsung) BộmônToán
quốc hay không? Biết u0,05 = 1,65;u0,025 = 1,96. Bài toán kiểm định trên có miền bác bỏ được 琀 nh bằng công thức sau:
A. Wα = (−∞;−u0,025).
B. Wα = (−∞;−u0,05) .
C. Wα = (−u0,05;+∞) .
D. Wα = (−u0,025;+∞).
Câu 58. ĐộbềnX củamộtloạidâythéplàđạilượngngẫunhiêncóquyluậtphânphốichuẩn với độ bền quy
định là 165, độ lệch chuẩn 15. Với công nghệ mới, người ta lấy ngẫu nhiên 25 sợi, đo độ bền của
chúng và nhận được x = 170. Với mức ý nghĩa α = 0,05, có thể cho rằng độ bền trung bình của loại dây
thép này đã tăng không? Biết u0,05 = 1,65;u0,025 = 1,96. A. Uqs = 1,67 < u0,025 = 1,96 tức độ bền dây thép tăng lên.
B. |Uqs| = 1,67 > U0,025 = 1,65, tức độ bền dây thép giảm đi . C. |Uqs| = 1,67
< U0.025 = 1,96, tức độ bền dây thép giảm đi .
D. Uqs = 1,67 > u0,05 = 1,65, tức độ bền dây thép tăng lên. .
Câu 59. Mức hao phí xăng X của một loại ô tô chạy từ A đến B là một đại lượng ngẫu nhiên tuân theo
quy luật phân phối chuẩn với định mức hao phí 20 lít, độ lệch chuẩn 4 lít. Đoạn đường được sửa lại,
người ta cho rằng mức hao phí xăng trung bình đã giảm xuống. Với mức ý nghĩa α = 0,05 giả thuyết và
đối thuyết cho bài toán trên là:
A. H0 : µ = 20;H1 : µ > 20.
B. H0 : µ = 4;H1 : µ < 4 .
C. H0 : µ = 20;H1 : µ < 20 .
D. H0 : µ = 20;H1 : µ 6= 20.
Câu 60. Mức hao phí xăng của một loại ô tô chạy từ A đến B là một đại lượng ngẫu nhiên tuân theo
quy luật phân phối chuẩn với định mức hao phí là 50 (lít), độ lệch chuẩn là 4 (lít). Đoạn đường được
sửa lại, người ta cho rằng mức hao phí xăng đã giảm xuống. Quan sát 30 ô tô loại trên, người ta thu
được bảng số liệu sau đây: Mức hao phí
48,5 − 49 49,5 − 50 50 − 50,5 50,5 − 51
51 − 51,5 51,5 − 52 Số xe 5 10 10 3 1 1
Với mức ý nghĩa α = 0,05, biết u0.05 = 1,64;u0,01 = 2,32;u0,025 = 1,96, miền bác bỏ Wα cho bài toán kiểm định trên là:
A. (1,96;+∞).
B. (1,64;+∞) .
C. (−∞;−1,96) ∪ (1,96;+∞) .
D. (−∞;−1,64).
Câu 61. Mức hao phí xăng của một loại ô tô chạy từ A đến B là một đại lượng ngẫu nhiên tuân theo quy
luật phân phối chuẩn với định mức hao phí là 50 lít, độ lệch chuẩn là 4 lít. Đoạn đường được sửa lại,
người ta cho rằng mức hao phí xăng đã giảm xuống. Quan sát 30 ô tô loại trên, người ta thu được
trung bình mẫu x = 48 và 琀 nh được giá trị Uqs = −2,738, và Wα = (−∞;−1,64). Với mức ý nghĩa α = 0,05
hãy kết luận về ý kiến trên.
A. Chưa có đủ cơ sở bác bỏ H0.
B. Bác bỏ H0, tức là H1 đúng . 10 lOMoAR cPSD| 40425501
BàitậpXSTK(Bổsung) BộmônToán
C. Cả H0;H1 đều đúng .
D. Bài toán chưa đủ dữ kiện.
Câu 62. Một máy sản xuất tự động, lúc đầu tỷ lệ sản phẩm bị lỗi là 5%. Để đánh giá quy trình cải 琀椀
ến kỹ thuật mới được áp dụng, người ta lấy 400 sản phẩm mang kiểm tra thì thấy có 10 sản phẩm bị
lỗi. Từ đó, với mức ý nghĩa 5%, người ta 琀 nh được giá trị quan sát uqs = −2,294 và miền bác bỏ Wα =
(−∞; −1,65).Trong các kết luận dưới đây, kết luận nào đúng nhất? A. Tỷ lệ sản phẩm lỗi đã giảm. B. Tỷ
lệ sản phẩm lỗi đã tăng .
C. Tỷ lệ sản phẩm lỗi không thay đổi .
D. Tỷ lệ sản phẩm lỗi đã thay đổi.
Câu 63. ĐộbềnX củamộtloạidâythéplàđạilượngngẫunhiêncóquyluậtphânphốichuẩn với độ bền quy
định là 165, độ lệch chuẩn 15. Công nghệ mới được áp dụng. Người ta lấy ngẫu nhiên ra 25 sợi, đo độ
bền của chúng và nhận được x = 170. Với mức ý nghĩa α = 0,05, bài toán kiểm định có giá trị quan sát
được xác định bởi công thức sau: A. . B. . C. . D. .
Câu 64. Chiều dài của một loại sản phẩm là đại lượng ngẫu nhiên có phân phối chuẩn với chiều dài 琀
椀 êu chuẩn là 35cm. Nghi ngờ chiều dài của sản phẩm thay đổi người ta đo thử 41
sảnphẩmvàthuđượctrungbìnhmẫux = 34,488vàđộlệchchuẩnmẫuhiệuchỉnhs = 1,362.
Vớimứcýnghĩa0,05biết,giátrịTqs µ 0 qs. x − µ0 ≈− 0, 109 qs = qs = √ .s n
chobàitoánkiểmđịnhtrênlà: qs = A. T. B. T. C. T. D. T .
Câu 65. Thông thường hạt giống để trong kho có tỷ lệ nảy mầm là 0,95. Một hôm phát hiện thấy trong
kho có một thiết bị bị hỏng. Nghi ngờ tỷ lệ nảy mầm đã giảm sau sự cố đó, người ta gieo 100 hạt thì
thấy có 90 hạt nảy mầm. Hãy cho biết suy luận nào sau đây đúng với mức ý nghĩa 0,05? A. Tỷ lệ nảy
mầm mới là f = 0,9 < 0,95, chứng tỏ tỷ lệ nảy mầm bị giảm thực sự. 11 lOMoAR cPSD| 40425501
BàitậpXSTK(Bổsung) BộmônToán B.
, tỷ lệ nảy mầm thực sự giảm .
, tỷ lệ nảy mầm thực sự giảm . D. Tính được
, tỷ lệ nảy mầm thực sự giảm.
Câu 66. Trọng lượng X của một bao gạo được máy đóng gói tự động là biến ngẫu nhiên có quy luật
phân phối chuẩn, trọng lượng theo quy định là 20 kg với độ lệch chuẩn 0,1kg. Sau thời gian khá dài đưa
vào vận hành, nghi ngờ trọng lượng trung bình của các bao thay đổi, người ta lấy ngẫu nhiên 25 bao
gạo đem cân thì thấy trọng lượng trung bình của chúng là x = 19,7kg. Cho biết u0,05 = 1,65;u0,025 = 1,96,
với mức ý nghĩa α = 0,05, miền bác bỏ giả thuyết là
A. Wα = (−∞;−1,65) ∪ (1,65;+∞).
B. Wα = (−∞;−1,96) ∪ (1,96;+∞) .
C. Wα = (−∞;−1,65) .
D. Wα = (−∞;−1,96).
Câu 67. Một máy sản suất tự động với tỉ lệ chính phẩm là 99%. Sau một thời gian hoạt động, người ta
nghi ngờ tỉ lệ trên bị giảm. Kiểm tra ngẫu nhiên 900 sản phẩm thấy có 18 phế phẩm. Với mức ý nghĩa
5%, nếu kiểm định xem máy móc có hoạt động bình thường không thì giá trị quan sát là A. −3,02. B. −2,143. C. −0,1. D. 2,143.
Câu 68. Thông thường hạt giống để trong kho có tỷ lệ nảy mầm là 0,8. Một hôm phát hiện thấy trong
kho có một thiết bị bị hỏng. Nghi ngờ tỷ lệ nảy mầm đã giảm sau sự cố đó, người ta gieo 400 hạt thì
thấy có 300 hạt nảy mầm. Hãy cho biết suy luận nào sau đây đúng? (với mức ý nghĩa 5%). A. Vì tỷ lệ
nảy mầm mới là f = 0,75 < 0,8 chứng tỏ tỷ lệ nảy mầm bị giảm thực sự. B. Tính được
nên tỷ lệ nảy mầm thực sự giảm. C. Tính được
nên tỷ lệ nảy mầm thực sự giảm. D.
) nên tỷ lệ nảy mầm thực sự giảm. ĐÁP SỐ 1 A 7 C 13 B 32 C
38 A 44 B 50 C 56 A 62 A 2 B 8 C 14 C
33 A 39 A 45 B 51 C 57 B 63 C 64 A 12 lOMoAR cPSD| 40425501
BàitậpXSTK(Bổsung) BộmônToán 3 C 9 D 15 B 34 D 40 A 46 B 52 A 58 D 65 C 4 A 10 C 16 B 35 C 41 D 47 B 53 A 59 C 66 B 5 A 11 A 17 D 36 A 42 B 48 A 54 B 60 D 67 A 6 D 12 C 31 A 37 D 43 A 49 D 55 A 61 B 68 B 13



