lOMoAR cPSD| 40425501 ĐỀ ÔN TẬP SỐ 1
Bài 1: Một công ty có 3 cửa hàng kinh doanh ộc lâp. Trong tháng, xác suất hoàn
thành mục tiêu doanh số của cửa hàng thứ nhất, thứ hai, thứ ba lần lượt là: 0,8 ; 0,9;
0,93. Tính xác suất trong tháng có:
a) Đúng hai cửa hàng hoàn thành mục tiêu doanh số.
b) Cửa hàng thứ 2 không hoàn thành mục tiêu doanh số, biết rằng có úng 2 cửa
hàng hoàn thành mục tiêu doanh số.
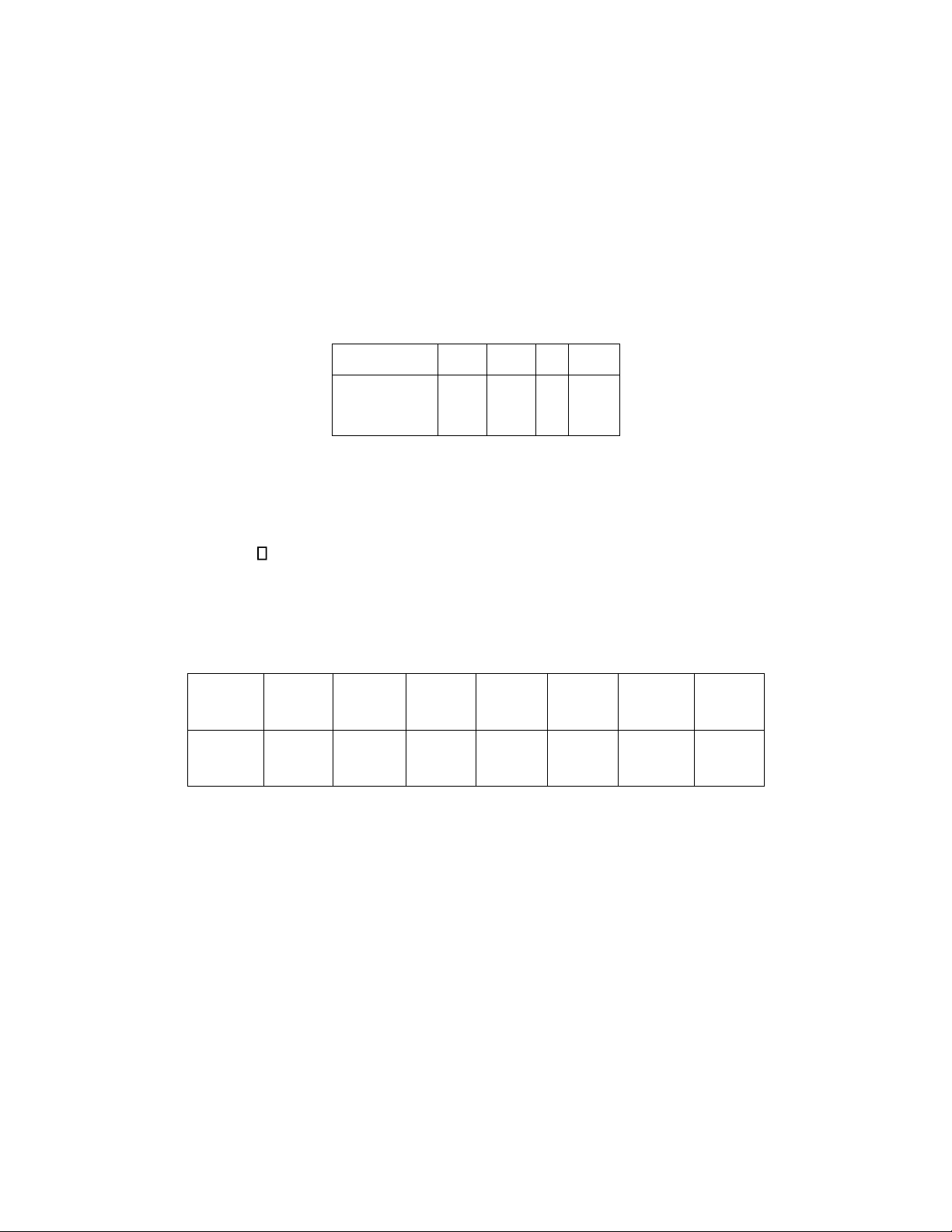
Bài 2: Cho X là biến ngẫu nhiên rời rạc có bảng phân phối xác suất: X x= i -2 1 2 4 0,2 0,3 a 0,4 P X x( = i ) .
a) Tìm giá trị của tham số a
b) Tính Mod(X), E(X), D(X)
c) Tính P X( 2)
Bài 3: Người ta ịnh mức thời gian trung bình ể một công nhân hoàn thành công
việc A là 24 phút. Một mẫu iều tra về thời gian X (phút) hoàn thành công việc A
qua theo dõi một số công nhân cùng thực hiện công viêc này ược cho trong bảng sau: X
[18;2 [20;2 [22;2 [24;2 [26;2 [28; [30;3 0) 2) 4) 6) 8) 30) 2] Số 7 16 30 45 27 18 8 người
a) Với ộ tin cậy 98%, hãy ước lượng khoảng tin cậy ối xứng cho tỷ lệ những
công nhân có thời gian hoàn thành công việc A chưa tới 26 phút.
b) Với mức ý nghĩa 3%, dựa vào kết quả iều tra, hãy xác minh xem ịnh mức nói
trên có gây khó khăn cho công nhân hay không? ĐỀ ÔN TẬP SỐ 2
Bài 1: Lớp có 50 học sinh, trong ó có 20 học sinh giỏi toán, 15 học sinh giỏi Văn
và có 10 học sinh giỏi cả 2 môn. Chọn ngẫu nhiên một học sinh trong lớp. Tính xác suất:
a) Học sinh này giỏi ít nhất một môn. lOMoAR cPSD| 40425501
b) Học sinh này chỉ giỏi úng một môn.
Bài 2: Tuổi thọ (năm) của một loại bóng èn là biến ngẫu nhiên liên tục X có hàm
a x. (5− x), x [0;5]
mật ộ xác suất: f x( ) = 0 , x [0;5]
a) Tìm giá trị của tham số a và tính tuổi thọ trung bình của loại sản phẩm này.
b) Thời gian bảo hành của sản phẩm là 1 năm. Khách hàng sẽ ược ổi bóng èn
mới nếu nó bị hỏng trong thời gian gian bảo hành. Tính xác suất khách hàng
ược ổi bóng èn mới nếu bóng èn bị hỏng.
Bài 3: Để nghiên cứu ường kính X (mm) của một loại sản phẩm do xí nghiệp A sản
xuất, người ta o ường kính của một số sản phẩm loại này của do xí nghiệp A sản xuất có kết quả sau:
[9,80;9,82 [9,82;9,84 [9,84;9,86 [9,86;9,88 [9,88;9,90 X ) ) ) ) ] Số sản 10 phẩm 25 60 75 30
a) Với ộ tin cậy 98%, dựa vào mẫu quan sát, hãy tìm khoảng tin cậy ối xứng cho
ường kính trung bình của sản phẩm do xí nghiệp A sản xuất.
b) Theo qui ịnh, những sản phẩm có ường kính trong khoảng [9,82;9,88) là những
sản phẩm ạt tiêu chuẩn kỹ thuật. Đo ường kính của 250 sản phẩm cùng loại
do xí nghiệp B sản xuất thấy có 187 sản phẩm ạt tiêu chuẩn kỹ thuật. Với mức
ý nghĩa 3%, dựa vào các mẫu quan sát, có thể xem tỷ lệ sản phẩm ạt tiêu chuẩn
kỹ thuật do xí nghiệp A sản xuất cao hơn xí nghiệp B không?
ĐỀ ÔN TẬP SỐ 3
Bài 1: Có ba sinh viên cùng làm bài thi môn xác suất thống kê. Xác suất làm ược
bài thi của từng người lần lượt là 0,5; 0,75 và 0,9.
a) Tìm xác suất ể có 1 sinh viên làm ược bài thi.
b) Tính xác suất có ít nhất một sinh viên làm ược bài thi
Bài 2: Cho biến ngẫu nhiên liên tục X có hàm mật ộ xác suất như sau: 0 , x [0;3] f x( ) = 2
k x.( +1) ,0 x 3 lOMoAR cPSD| 40425501
a) Tìm hằng số k và tính phương sai D X( ).
b) Tìm hàm phân phối F x( ).
Bài 3: Chiều cao của một giống cây trồng là biến ngẫu nhiên X (cm) có phân phối
chuẩn. Qua quan sát một số cây trên khu ất A ta có kết quả sau: X [62;6 [67- [72- [77- [82- [87- [92- (cm) 7) 72) 77) 82) 87) 92) 97] Số cây 9 15 26 39 26 19 6
Những cây trồng có chiều cao từ 72cm trở lên ược gọi là loại 1.
a) Với ộ tin cậy 95%, hãy ước lượng khoảng tin cậy ối xứng cho chiều cao trung
bình của giống cây trồng trên.
b) Quan sát 200 cây trồng cùng loại trên khu ất B thấy có 170 cây loại I. Với mức
ý nghĩa 4%, hãy so sánh tỷ lệ cây loại I trên hai khu ất A và B ĐỀ ÔN TẬP SỐ 4
Bài 1: Một lô hàng có 20 sản phẩm trong ó có 5 sản phẩm lỗi. Một khách hàng lấy
ngẫu nhiên lần lượt ra ngoài 4 sản phẩm ể kiểm tra. Nếu cả 4 sản phẩm ều không
bị lỗi thì khách hàng chấp nhận lô hàng.
a) Tính xác suất khách hàng chấp nhận lô hàng nếu mỗi lần kiểm tra sản phẩm xong ều hoàn lại
b) Tính xác suất khách hàng không chấp nhận lô hàng nếu mỗi lần kiểm tra sản
phẩm xong ều không hoàn lại.
Bài 2: Cho biến ngẫu nhiên rời rạc X có bảng phân phối xác suất sau ây: X 1 a 5 7 10
P 0,2 0,3 b 0,1 0,25
a) Tìm a b, biết E X( ) = 4,75. b) Tính Mod(X), D(X)
c) Tính các xác suất P(3 X 10).
Bài 3: hảo sát thu nhập X ( ơn vị: triệu ồng/tháng) của một số viên chức tại
TP.HCM, thu ược bảng số liệu sau: lOMoAR cPSD| 40425501 Thu [2; [4; [6; [8; [10; [12; [14;1 nhập X 4) 6) 8) 10) 12) 14) 6] Số 4 21 35 90 77 28 13 người
a) Hãy ước lượng khoảng tin cậy ối xứng cho thu nhập trung bình của viên chức
tại TP.HCM với ộ tin cậy 95%.
b) Có ý kiến cho rằng thu nhập bình quân của viên chức tại TP.HCM là hơn 9
triệu ồng/ tháng. Với mức ý nghĩa 3%, hãy cho biết ý kiến này có ược chấp nhận không? ĐỀ ÔN TẬP SỐ 5
Bài 1: Một máy sản xuất với tỉ lệ sản phẩm ạt tiêu chuẩn là 60%.
a) Cho máy sản xuất ra 10 sản phẩm. Tính xác suất ược ít nhất 4 sản phẩm ạt tiêu chuẩn.
b) Nếu máy sản xuất ra 210 sản phẩm thì số sản phẩm ạt tiêu chuẩn có khả năng nhất là bao nhiêu?
Bài 2: Tỷ lệ ứng viên lọt vào vòng 2 khi ứng tuyển tại công ty A là 20%. Giả sử tại
một kỳ tuyển dụng có 300 ứng viên thi tuyển, hãy:
a) Gọi biến ngẫu nhiên X là số ứng viên lọt vào vòng 2, hãy xác ịnh phân phối của X, giải thích.
b) Tính xác suất có ít nhất một ứng viên lọt vào vòng 2.
Áp dụng phương pháp xấp xỉ phân phối chuẩn, tính xác suất có từ 20 ến 50 ứng
viên lọt vào vòng 2.
Bài 3: Để nghiên cứu ộ bền chịu nén X (kg/cm2) của một loại bê tông do xưởng A
sản xuất, người ta o ộ bền chịu nén của một số mẫu bê tông của xưởng A, có kết quả sau: X
[260;264) [264;268) [268;272) [272;276) [276;280] Số mẫu 10 25 60 75 30
a) Với ộ tin cậy 97%, dựa vào mẫu quan sát, hãy tìm khoảng tin cậy ối xứng cho
ộ bền chịu nén trung bình của loại bê tông này do xưởng A sản xuất.
b) Các mẫu bê tông có ộ bền chịu nén 268(kg/cm2) ược gọi là mẫu bê tông loại
1. Đo ộ bền chịu nén của 160 mẫu bê tông cùng loại do xưởng B sản xuất thấy lOMoAR cPSD| 40425501
có 120 mẫu bê tông loại 1. Với mức ý nghĩa 5%, dựa vào các mẫu quan sát, có
thể coi tỷ lệ mẫu bê tông loại 1 do xưởng A sản xuất cao hơn xưởng B không?