


































Preview text:
PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG TRONG MẶT PHẲNG PHÉP BIẾN HÌNH A. LÝ THUYẾT 1. Định nghĩa:
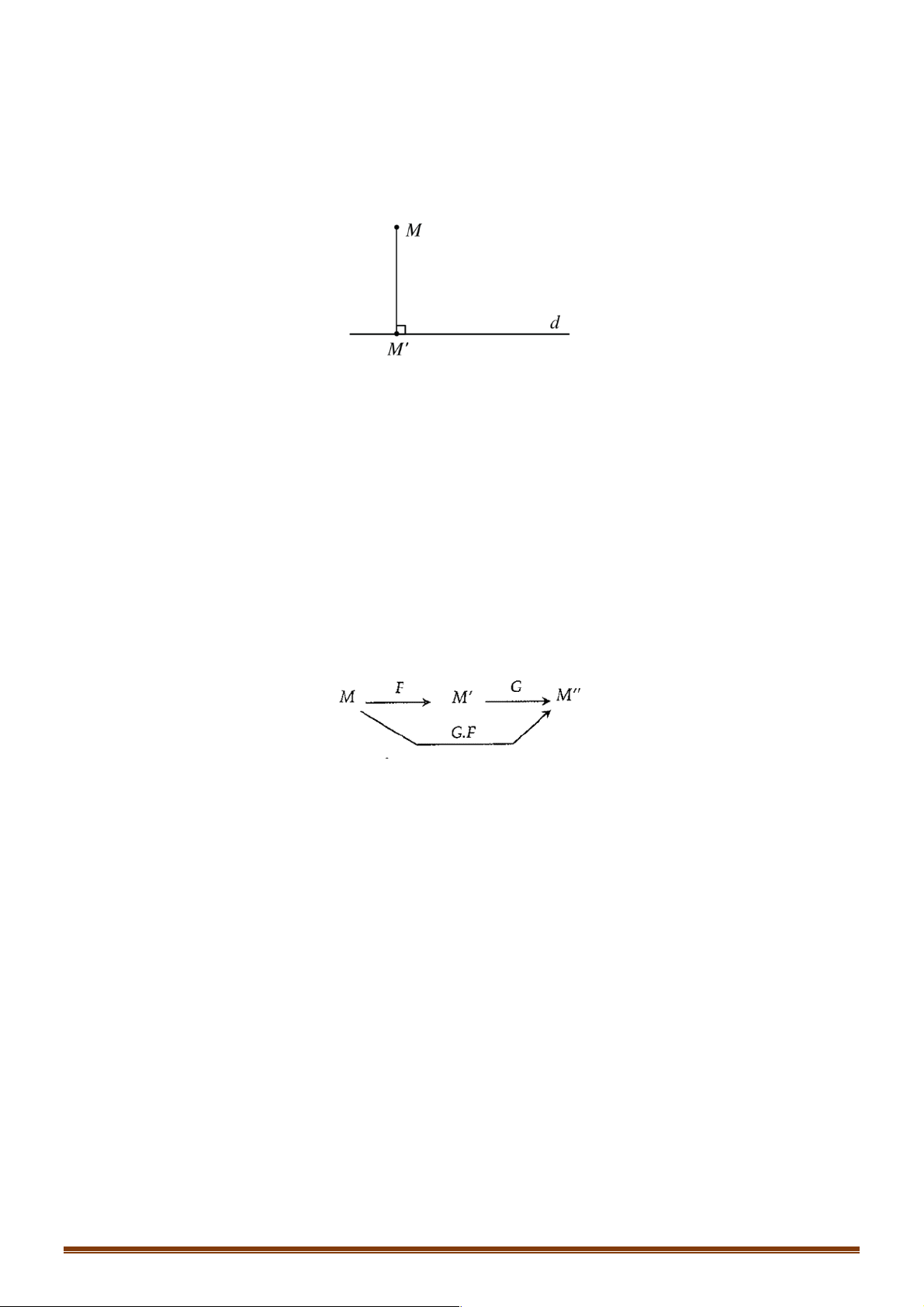
Phép biến hình là một quy tắc để mỗi điểm M của mặt phẳng xác định được một điểm duy nhất M ¢ thuộc mặt phẳng đó .
2. Kí hiệu và thuật ngữ:
Gọi P là tập hợp các điểm trong mặt phẳng và một phép biến hình F :
F : P ® P
M ® M ¢ = F (M )
- Điểm M ¢ gọi là ảnh của điểm M qua phép biến hình F , hay M là điểm tạo ảnh của điểm M ¢ .
- Nếu H là một hình nào đó thì H ¢ ( gồm các điểm M ¢ là ảnh của M ÎH ) được gọi là anh của H qua
phép biến hình F .
- Phép biến hình biến mỗi điểm M thành chính nó được gọi là phép đồng nhất.
3. Tích của hai phép biến hình
Cho hai phép biến hình F và G . Gọi M là điểm bất kỳ trong mặt phẳng. M ¢ là ảnh của M qua F ,
M ¢¢ là ảnh của M ¢ qua G .
Ta nói, M ¢¢ là ảnh của M trong tích của hai phép biến hình F và G . Ký hiệu . G F
M ¢¢ = G(F (M )) Trang 1 PHÉP TỊNH TIẾN A. Lý thuyết 1. Định nghĩa ! !!!!!" "
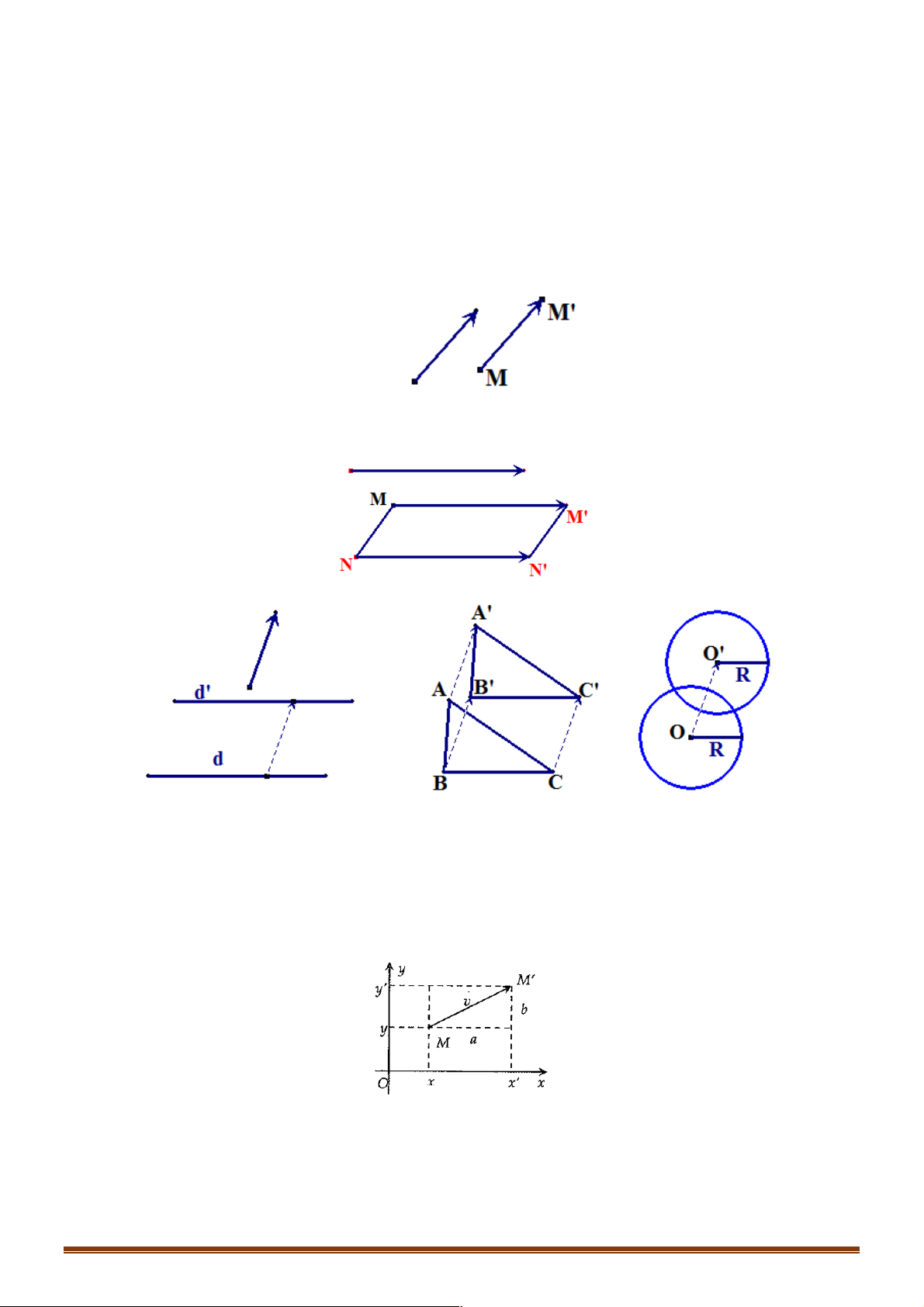
Trong mặt phẳng cho vectơ v . Phép biến hình biến mỗi điểm M thành điểm M ¢ sao cho MM¢ = v !
được gọi là phép tịnh tiến theo vectơ v . ! !
• Phép tịnh tiến theo vectơ v kí hiệu là: T! , v được gọi là vectơ tịnh tiến. v """""! !
• Ta có: T! (M ) = M ¢ Û MM ¢ = v v
• Phép tịnh tiến theo vecto – không chính là phép đồng nhất. !" v 2. Tính chất: !!!!!" !!!!"
Tính chất 1: Nếu phép tịnh tiến biến hai điểm M , N thành hai điểm M ,¢ N¢ thì M N
¢ ¢ = MN , từ đó suy ra M N ¢ ¢ = MN . !" v !" v !" v Tính chất 2:
Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn
thẳng thành đoạn thẳng bằng nó, biến một tam giác thành một tam giác bằng nó, đường tròn
thành đường tròn có cùng bán kính. STUDY TIP
Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
3. Biểu thức tọa độ: !
Trong mặt phẳng tọa độ Oxy cho vectơ v = ( ; a b), M ( ;
x y). Khi đó phép tịnh tiến theo vectơ !
ìx ' = x + a
v :T! (M ) = M'( x'; y ') có biểu thức tọa độ: í v
îy ' = y + b
B. CÁC DẠNG TOÁN VỀ PHÉP TỊNH TIẾN Trang 2
DẠNG 1. CÁC BÀI TOÁN KHAI THÁC ĐỊNH NGHĨA, TÍNH CHẤT VÀ ỨNG DỤNG CỦA PHÉP TỊNH TIẾN Phương pháp:
Sử dụng định nghĩa hoặc tính chất của phép tịnh tiến.
Xác định ảnh của một điểm, một hình qua phép tịnh tiến.
Tìm quĩ tích điểm thông qua phép tịnh tiến.
Ứng dụng phép tịnh tiến vào các bài toán hình học khác ...
Ví dụ 1: Kết luận nào sau đây là sai? """! ! A.T! ( )
A = B Û AB = u
B. T!!!" (A) = B u AB !!!" !!!!"
C. T! (B) = B
C. T !!!" (M ) = N Û AB = 2MN 0 2 AB
Lời giải: Đáp án D !!!!" !!!"
Ta có T !!!" (M ) = N Û MN = 2AB . Vậy D sai. 2 AB STUDY TIP """""! !
Định nghĩa phép tịnh tiến: T! M = M ¢ Û MM ¢ = v v ( ) .
Ví dụ 2: Giả sử T! (M ) = M ';T! (N) = N '. Mệnh đề nào sau đây sai? v v !!!!!!" !!!!" !!!!!" !!!!"
A. M ' N ' = MN .
B. MM ' = NN '
C. MM ' = NN '.
D. MNM ' N ' là hình bình hành.
Lời giải: Đáp án D
Theo tính chất của một phép tịnh tiến thì các đáp án A, B, C là đúng.
MNM ' N ' không theo thứ tự các đỉnh của hình bình hành nên D sai.
Ví dụ 3: Cho hai đường thẳng d và d cắt nhau. Có bao nhiêu phép tịnh tiến biến d thành d 1 2 1 2 A. Không. B. Một. C. Hai. D. Vô số. Đáp án A
Lời giải:
Do phép tịnh tiến biến một đường thẳng thành đường thẳng song song hoặc trùng với nó nên
không có phép tịnh tiến nào biến d thành d . 1 2
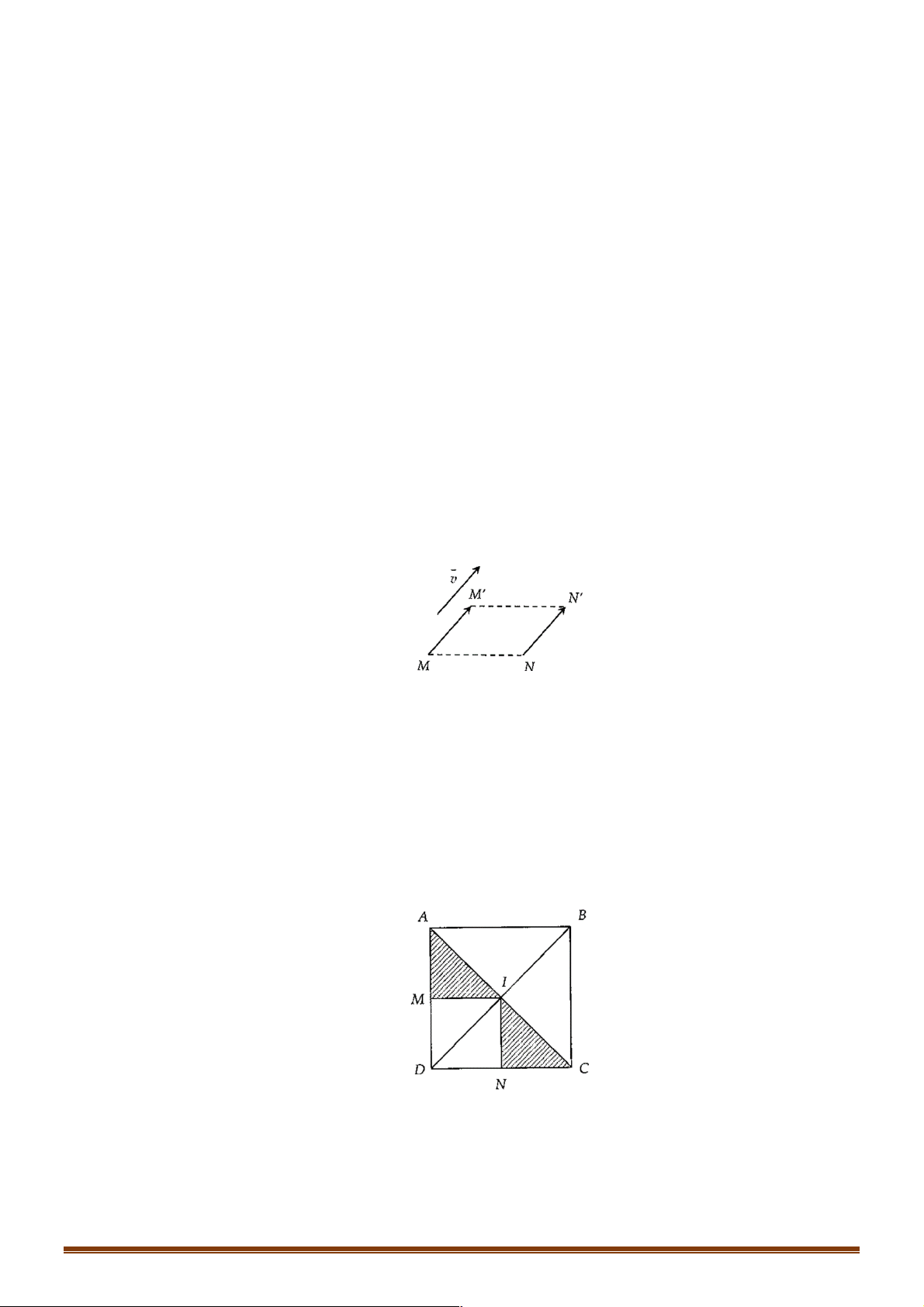
Ví dụ 4: Cho hình vuông ABCD tâm I . Gọi M , N lần lượt là trung điểm AD, DC . Phép tịnh tiến theo
vectơ nào sau đây biến tam giác AMI thành INC !!!!" !!" !!!" !!!!" A. AM . B. IN . C. AC . D. MN .
Lời giải: Đáp án D !!!!" !!" !!"
Ta có MN = AI = IC Þ T!!!!" ( A D MI) = I D NC MN
Ví dụ 5: Cho hình bình hành ABCD tâm I . Kết luận nào sau đây là sai? Trang 3
A. T!!!" (D) = C .
B. T!!!" (B) = A .
C. T!!" (I ) = C .
D. T!!" (I ) = B. AB CD AI ID
Lời giải: Đáp án D !!" !!"
Ta có T!!" (I) = I ' Û II ' = ID Û I ' º D . Vậy D sai ID
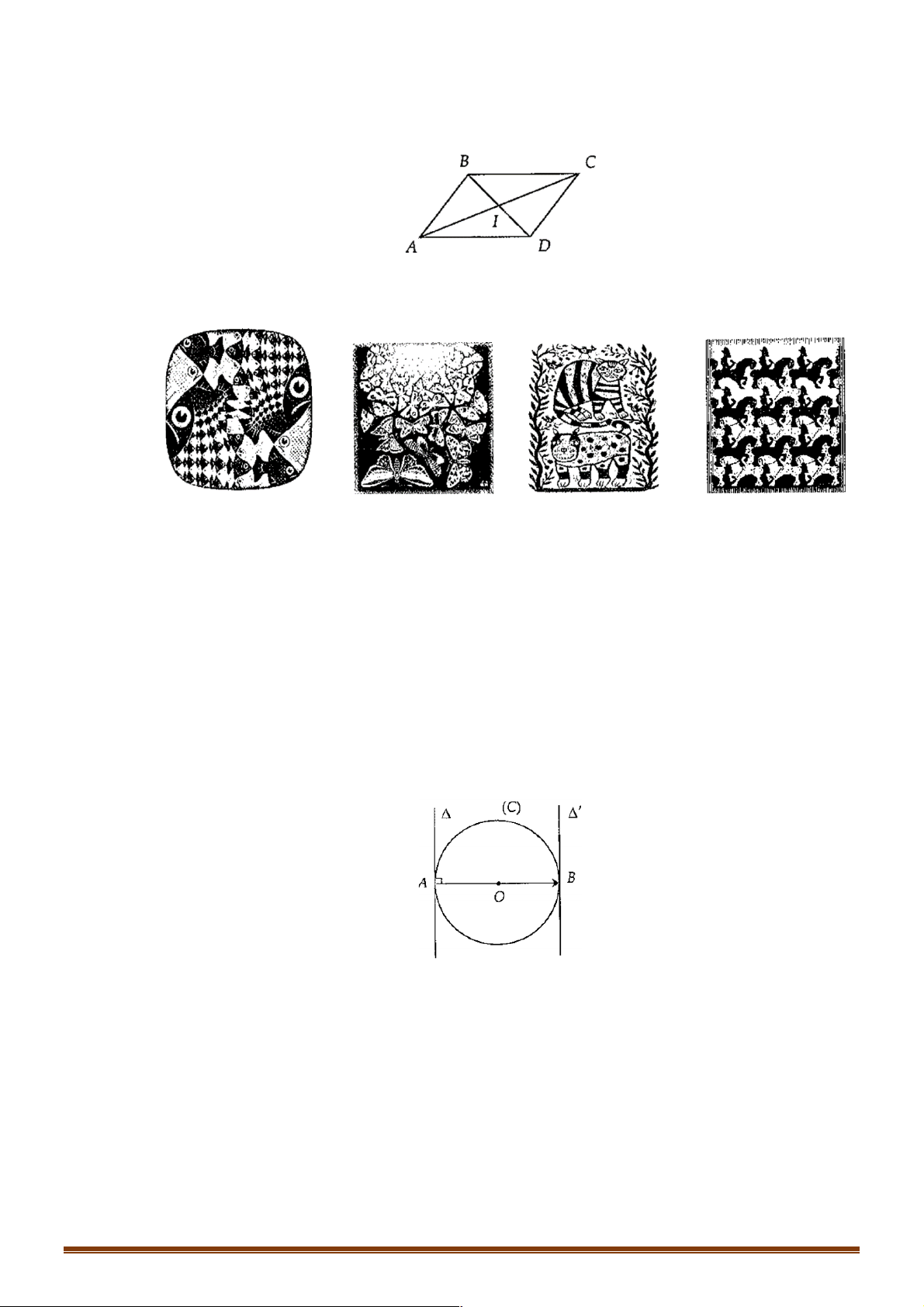
Ví dụ 6: Trong các đối tượng: con cá (hình A), con bướm (hình B), con mèo (hình C), con ngựa (hình
D), hình nào có phép tịnh tiến? A. B. C. D.
Lời giải: Đáp án D
Trong hình D đối tượng con ngựa này là ảnh của con ngựa kia qua một phép tịnh tiến theo một hướng xác định.
Ví dụ 7: Cho đường tròn (C)có tâm O và đường kính AB . Gọi D là tiếp tuyến của (C) tại điểm A . !!!"
Phép tịnh tiến theo vectơ AB biến D thành:
A. Đường kính của đường tròn (C) song song với D.
B. Tiếp tuyến của (C) tại điểm B .
C. Tiếp tuyến của (C) song song với AB .
D. Đường thẳng song song với D và đi qua O
Lời giải: Đáp án B.
Theo tính chất 2 của phép tịnh tiến nên T!!!" (D) = ¢ D Þ ¢ D // , D ¢
D là tiếp tuyến của đường tròn AB
(C) tại điểm B .
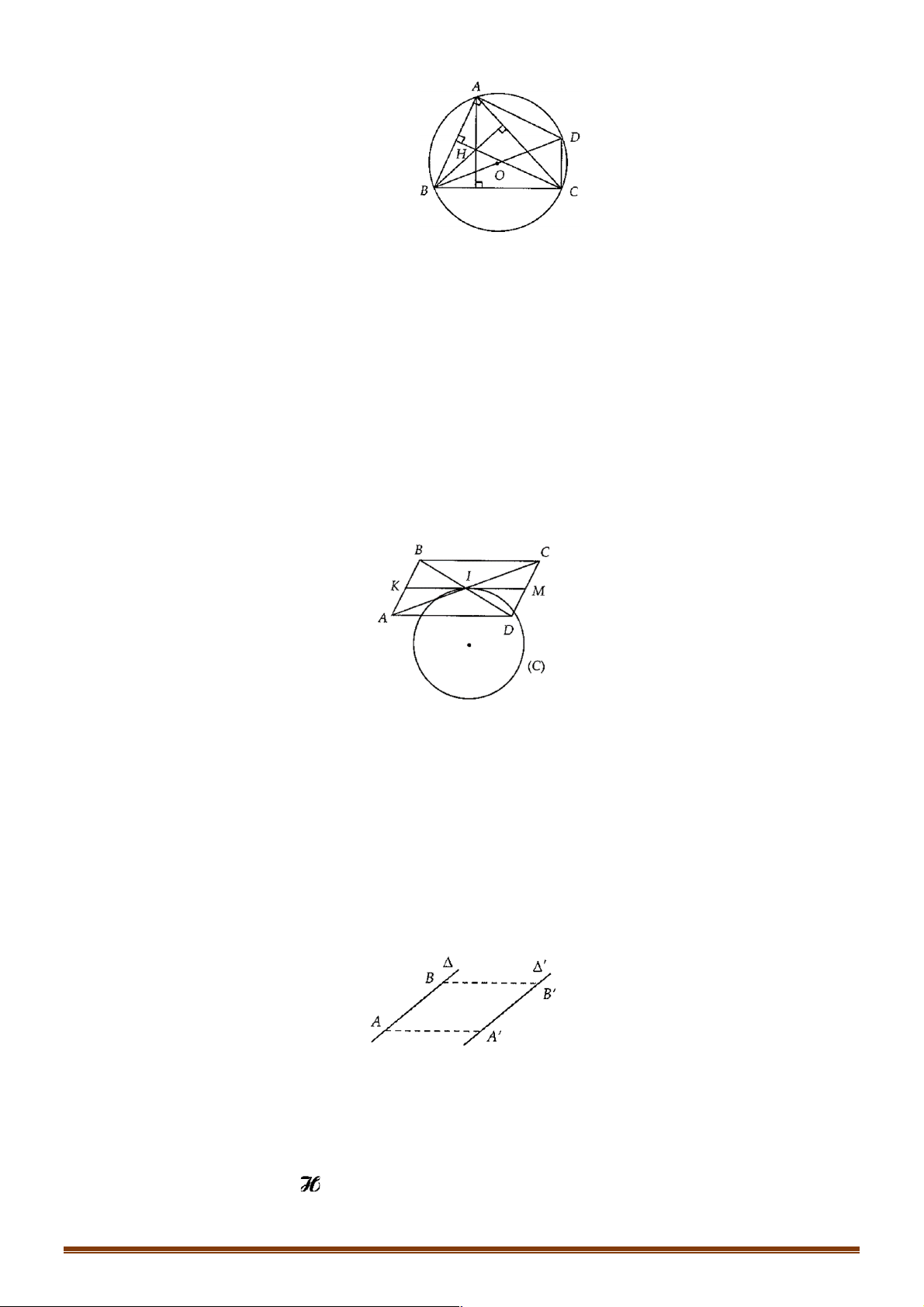
Ví dụ 8: Cho hai điểm B,C cố định trên đường tròn ( ,
O R) và A thay đổi trên đường tròn đó, BD là
đường kính. Khi đó quỹ tích trực tâm H của ABC D là:
A. Đoạn thẳng nối từ A tới chân đường cao thuộc BC của ABC D .
B. Cung tròn của đường tròn đường kính BC .
C. Đường tròn tâm O¢ bán kính R là ảnh của ( , O R) qua T!!!". HA
D. Đường tròn tâm O ' , bán kính R là ảnh của ( ,
O R) qua T!!!!". DC
Lời giải: Đáp án D. Trang 4
Kẻ đường kính BD Þ ADCH là hình bình hành(Vì AD//CH và AH //DC cùng vuông góc
với một đường thẳng) !!!" !!!"
Þ AH = DC Þ T!!!!" ( A) = H . DC
Vậy H thuộc đường tròn tâm O ' , bán kính R là ảnh của ( ,
O R) qua T!!!!". DC
Ví dụ 9: Cho hình bình hành ABCD , hai điểm ,
A B cố định, tâm I di động trên đường tròn (C). Khi
đó quỹ tích trung điểm M của cạnh DC :
A. là đường tròn (C¢) là ảnh của (C) qua T!!!", K là trung điểm của BC . KI
B. là đường tròn (C¢) là ảnh của (C) qua T!!!", K là trung điểm của AB . KI
C. là đường thẳng BD .
D. là đường tròn tâm I bán kính ID .
Lời giải: Đáp án B.
Gọi K là trung điểm của AB Þ K cố định.
Ta có T!!!" (I ) = M Þ M Î(C¢) = T!!!" C KI KI (( )).
DẠNG 2. XÁC ĐỊNH ẢNH CỦA MỘT ĐIỂM HOẶC MỘT HÌNH QUA PHÉP TỊNH TIẾN BẰNG
PHƯƠNG PHÁP TỌA ĐỘ Phương pháp
1. Xác định ảnh của một điểm qua phép tịnh tiến
- Sử dụng biểu thức tọa độ. !
2. Xác định ảnh D¢ của đường thẳng D qua phép tịnh tiến theo véctơ v .
Cách 1. Chọn hai điểm ,
A B phân biệt trên D , xác định ảnh A ,¢ B¢ tương ứng. Đường thẳng D¢ cần tìm là
đường thẳng qua hai ảnh A ,¢ B¢.
Cách 2. Án dụng tính chất phép tịnh tiến biến đường thẳng thành đường thẳng cùng phương với nó.
Cách 3. Sử dụng quỹ tích. Với mọi M ( ; x y) ,
ÎD T! (M ) = M¢(x ;¢ y¢ M ¢Î D¢ v ) thì .
ìx¢ = x + a
ìx = x¢ - a
Từ biểu thức tọa độ í ta được í
thế x, y và phương trình D ta được phương trình D¢.
îy¢ = y + b
îy = y¢ - b
3. Xác định ảnh của một hình (đường tròn, elip, parabol…) Trang 5
- Sử dụng quỹ tích: Với mọi điểm M ( ;
x y) thuộc hình , T! (M ) = M¢(x ;¢ y¢ M ¢ v
) thì thuộc ảnh ’ của hình .
- Với đường tròn: áp dụng tình chất phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính
hoặc sử dụng quỹ tích.
Ví dụ 1. Trong mặt phẳng tọa độ Oxy , cho điểm A(3; 3
- ). Tìm tọa độ diểm A¢ là ảnh của A qua phép !
tịnh tiến theo véctơ v = ( 1 - ;3). A. A¢(2; 6 - ). B. A¢(2;0). C. A¢(4;0). D. A¢( 2; - 0).
Lời giải: Đáp án B. """! ! ìx = + ì = ¢ x x! x ¢ 2 Ta có T A A v A ! A = A¢ x Û ¢ = Û Û í Þ A¢(2;0) ¢ y ¢ AA v v ( ) ( A A ) í . y = + î = ¢ y y! y î ¢ 0 A A v A STUDY TIP
ìx¢ = x + a
Biểu thức tọa độ của phép tịnh tiến: í
îy¢ = y + b
Ví dụ 2. Trong mặt phẳng tọa độ Oxy , cho điểm M¢( 4;
- 2), biết M ¢ là ảnh của M qua phép tịnh tiến ! theo véctơ v = (1; 5
- ). Tìm tọa độ điểm M . A. M ( 3; - 5). B. M (3;7). C. M ( 5; - 7). D. M ( 5; - - ) 3 .
Lời giải: Đáp án C. """""! !
Ta có: T! (M ) = M ¢(x Û ¢ = ¢; y ¢ MM v v M M ) ìx! = x - ì = - ! ì = - ¢ x x x ¢ x x 5 v M M Û í M M v M Û í Û í Þ M ( 5; - 7). y! = y - î = - ! = ¢ y y y î ¢ y y 7 v M M M M v î M
Ví dụ 3. Trong mặt phẳng tọa độ Oxy , cho điểm M ( 5;
- 2) và điểm M¢( 3;
- 2) là ảnh cảu M qua phép ! !
tịnh tiến theo véctơ v . Tìm tọa độ véctơ v . ! ! ! ! A. v = ( 2; - 0). B. v = (0;2). C. v = ( 1 - ;0). D. v = (2;0).
Lời giải: Đáp án D. """""! ! ìx! = x - ì ! = ¢ x x 2 ! Ta có: T v M M v
! (M ) = M ¢( x Û ¢ = Û Û í Þ v = (2;0) ¢; y ¢ MM v v M M ) í . y! = y - î ! = ¢ y y 0 v M M î v !
Ví dụ 4. Trong mặt phẳng tọa độ Oxy , cho hai điểm M (0;2), N ( 2; - )
1 và véctơ v = (1;2). Ơ. Phép tịnh !
tiến theo véctơ v biến M , N thành hai điểm M ,¢ N¢ tương ứng. Tính độ dài M N ¢ ¢. A. M N ¢ ¢ = 5 . B. M N ¢ ¢ = 7 . C. M N ¢ ¢ =1. D. M N ¢ ¢ = 3 .
Lời giải: Đáp án A. T ì ! M = M ¢ ï v ( ) Ta có í Þ MN = M N ¢ ¢ = (- - )2 + ( - )2 2 0 1 2 = 5 . T ï ! N = N¢ î v ( ) STUDY TIP
Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm
Ví dụ 5. Trong mặt phẳng tọa độ Oxy , cho ABC D
biết A(2;4), B(5; ) 1 , C ( 1 - ; 2 - ). Phép tịnh tiến theo !!!"
véctơ BC biến ABC D thành A D ¢B C
¢ ¢ tương ứng các điểm. Tọa độ trọng tâm G¢ của A D ¢B C ¢ ¢ là: Trang 6 A. G¢( 4; - 2 - ). B. G¢(4;2). C. G¢(4; 2 - ). D. G¢( 4; - 4).
Lời giải: Đáp án A. !!!"
Ta có tọa độ trọng tâm ABC D là G(2; ) 1 ; BC = ( 6; - 3 - ). !!!!" !!!" ìx = + ï ¢ x x!!!" ì = - G G x ¢ 4
T!!!" (G) = G¢(x Û ¢ = BC G Û í Û í Þ G¢( 4; - 2 - ) ¢; y ¢ GG BC BC G G ) . ïy = + !!!" = - ¢ y y y î î ¢ 2 G G BC G STUDY TIP
Phép tịnh tiến biến trọng tâm G của ABC D
thành trọng tâm G¢ của A D ¢B C ¢ ¢
Ví dụ 6. Trong mặt phẳng tọa độ Oxy , tìm phương trình đườn thẳng D¢ là ảnh của đường thẳng D !
: x + 2y -1 = 0 qua phép tịnh tiến theo véctơ v = (1;- ) 1 .
A. D¢ : x + 2y = 0.
B. D¢ : x + 2y - 3 = 0 . C. ¢
D : x + 2y +1 = 0. D. D¢: x + 2y + 2 = 0.
Lời giải: Đáp án A. Cách 1:
Chọn A(1;0)ÎD ÞT! A = A¢ - ¢ ÎD v ( ) (2; )1 . Chọn B( 1 - ; )
1 ÎD Þ T! (B) = B¢(0;0 Î ¢ D v ) .
Þ đường thẳng D¢ chính là đường thẳng A¢B¢ . !
Đường thẳng D¢ qua A¢(2;- )
1 và có một véctơ pháp tuyến n = (1;2) có phương trình là: ¢ D (
:1 x - 2) + 2( y + )
1 = 0 Û x + 2y = 0 . STUDY TIP
Hai đường thẳng cùng phương thì có hai véctơ pháp tuyến cùng phương. Cách 2. T! D = ¢ D Þ ¢ D D D¢
x + 2y + m = 0 v ( )
, là hai đường thẳng cùng phương nên có dạng .
Chọn A(1;0)ÎD ÞT! A = A¢ - ¢ ÎD Þ m = v ( ) (2; )1 0.
Vậy phương trình D¢ : x + 2y = 0.
Cách 3: Sử dụng quỹ tích
Lấy M (x ; y ÎD Û x + y - = M M ) 2 1 0 M M ( )1. ìx¢ = x + ìx = x¢ -
Ta có T! M = M ¢ x¢ y¢ Î ¢ D Û í Û v ( ) ( ) 1 1 ; M M í y¢ = y -1 y = y¢ +1 î M î M Thay vào ( ) 1 ta được (x¢ - ) 1 + 2( y¢+ )
1 -1 = 0 Û x¢ + 2y¢ = 0.
Vậy D¢ : x + 2y = 0.
Nhận xét: Độc giả sử dụng cách 3 tỏ ra có tính tư duy cao hơn, nhanh hơn và áp dụng cho
nhiều loại hình khác nhau.
Ví dụ 7. Trong mặt phẳng tọa độ Oxy , tìm phương trình đường tròn (C¢) là ảnh cảu đường tròn ( ! C) 2 2
: x + y - 2x + 4y -1 = 0 qua T! với v = (1;2). v A. (x + )2 2 2 + y = 6. B. (x - )2 2 2 + y = 6. C. 2 2
x + y - 2x -5 = 0. D. 2 2
2x + 2y -8x + 4 = 0.
Lời giải: Đáp án B.
Cách 1: Theo tính chất của phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính.
Ta có: đường tròn (C) có tâm I (1; 2
- ), bán kính R = 6 .
Suy ra: T! (I ) = I¢(2;0). v Trang 7
Vậy đường tròn (C¢)có tâm I¢(2;0), bán kính R¢ = R = 6 có phương trình: (x- )2 2 2 + y = 6.
Cách 2: Sử dụng quỹ tích: Gọi M ( ;
x y)Î(C) ÞT! (M ) = M¢(x ;¢ y¢) v ìx¢ = x +1 ìx = x¢ -1 Þ í Û í îy¢ = y + 2 îy = y¢ - 2
Thế x, y vào phương trình đường tròn (C), ta có:
(x¢- )2 +(y¢- )2 - (x¢- )+ (y¢- )- = Û (x¢)2 +(y¢)2 1 2 2 1 4 2 1 0 - 4x¢- 2 = 0
Vậy (C¢) (x - )2 2 : 2 + y = 6. Study Tip
Phương trình đường tròn ( - )2 + ( - )2 2 x a
y b = R có tâm I ( ; a b) bán kính . R
Phương trình đường tròn 2 2
x + y - 2ax - 2by + c = 0 có tâm I ( ; a b) bán kính 2 2
R = a + b - c . ! !
Ví dụ 8. Cho vectơ v = ( ;
a b) sao cho khi tịnh tiến đồ thị y = f (x) 3
= x + 3x +1 theo vectơ v ta nhận
được đồ thị hàm số y = g (x) 3 2
= x -3x + 6x - . T
1 ính P = a + b . A. P = 3. B. P = 1 - . C. P = 2 . D. P = 3 - .
Lời giải: Đáp án A.
Từ giả thiết ta có: g (x) = f (x - a) + b Û x - x + x - = é(x - a)3 3 2 3 6 1
+ 3(x - a) +1ù + b ë û 3 2 3 2
Û x - x + x - = x - ax + ( 2 a + ) 3 3 6 1 3 3
1 x - a -3a +1+ b ìa =1
Đồng nhất thức ta được: í
Þ P = a + b = 3. b î = 2 Study Tip
Đồng nhất thức của 2 đa thức Û các hệ số của các đa thức tương ứng bằng nhau.
Ví dụ 9. Trong mặt phẳng tọa độ Oxy , cho hai điểm A( 5; - 2), C( 1
- ;0) . Biết B = T! ( A), C =T! (B). u v ! !
Tìm tọa độ của vectơ u + v để có thể thực hiện phép tịnh tiến T! ! biến điểm A thành điểm C. u+v A. ( 6; - 2). B. (2; 4 - ). C. (4; 2 - ). D. (4;2).
Lời giải: Đáp án C. """! !
Ta có: T! ( A) = B Û AB = u u """! !
T! (B) = C Û BC = v v !!!" !!!" !!!" " "
Mà AC = AB + BC = u + v """! ! !
Do đó: T! ! ( A) = C Û AC = u + v = - + (4; 2). u v Study Tip
Ta có sơ đồ tổng quát: T T v u A B C Tu+v Trang 8
Ví dụ 10. Trong mặt phẳng tọa độ Oxy , cho hình bình hành OABC với điểm A( 2 - )
;1 , điểm B thuộc
đường thẳng D : 2x - y - 5 = 0. Tìm quỹ tích đỉnh C ?
A. Là đường thẳng có phương trình 2x - y -10 = 0 .
B. Là đường thẳng có phương trình x + 2y - 7 = 0 .
C. Là đường thẳng có phương trình 2x - y + 7 = 0.
D. Là đường tròn có phương trình 2 2
x + y - 2x + y = 0. Đáp án A.
Lời giải:
Vì OABC hình bình hành nên T!!!" (B) = C AO
Vậy quỹ tích điểm C là đường thẳng D ' song song với D . Ta tìm được phương trình
D ': 2x - y -10 = 0.
Ví dụ 11. Trong mặt phẳng tọa độ Oxy , cho đường thẳng d : 3x + y - 9 = 0. Tìm phép tịnh tiến theo véc tơ
!v có giá song song với Oy biến d thành d ' đi qua A(1; )1 ! ! ! !
A. v = (0;5) . B. v = (1; 5 - ) . C. v = (2; 3 - ). D. v = (0; 5 - ). Đáp án D.
Lời giải: ! !
Véc tơ v có giá song song với Oy Þ v = (0;k ),k ¹ 0 ìx = x
Gọi M (x y)Îd Þ T! (M ) = M (x ) ' ; ' '; y' Û í v
îy ' = y + k
Thế vào phương trình d Þ d ': 3x '+ ´
y -k - 9 = 0 mà d ' đi qua A(1; ) 1 nên k = 5 - .
Ví dụ 12. Ví dụ 12: Trong mặt phẳng tọa độOxy , cho hai đường thẳng d : 2x - 3y + 3 = 0 và !
d': 2x - 3y - 5 = 0. Tìm tọa độ v có phương vuông góc với d và T! biến đường thẳng d thành v d '. ! æ 6- 4 ö ! æ 1 - 2 ö ! æ 16 - 24 - ö ! æ16 24 - ö A. v = ; . B. v = ; . C. v = ; . D. v = ; . ç ÷ ç ÷ ç ÷ ç ÷ è 13 13 ø è 13 13 ø è 13 13 ø è13 13 ø Đáp án D.
Lời giải: !
ìx = x '- a
Gọi v = (a;b), ta có T! (M ) = M '(x';y')Îd ' Þ í v
îy = y '- b
Thế vào phương trình đường thẳng d : 2x '- 3y '- 2a + 3b + 3 = 0 Từ giả thiết suy ra 2 - a +3b +3 = 5 - Û 2 - a + 3b = 8 - ( )1 ! ! ! ! !
Véc tơ chỉ phương của d là u = (3;2). Do u ^ v Þ .
u v = 0 Û 3a + 2b = 0 (2) 16 24 - Giải hệ ( )
1 và (2) ta được a = ;b = . 13 13
C. BÀI TẬP RÈN LUYỆN KỸ NĂNG
DẠNG 1. CÁC BÀI TOÁN KHAI THÁC ĐỊNH NGHĨA, TÍNH CHẤT VÀ ỨNG DỤNG CỦA PHÉP TỊNH TIẾN
Câu 1: Có bao nhiêu phép tịnh tiến biến đường thẳng thành chính nó? A. 0 . B.1. C. 2 . D. Vô số.
Câu 2: Có bao nhiêu phép tịnh tiến biến đường tròn thành chính nó? A. 0 . B.1. C. 2 . D. Vô số.
Câu 3: Có bao nhiêu phép tịnh tiến biến hình vuông thành chính nó? A. 0 . B.1. C. 2 . D. Vô số.
Câu 4: Phép tịnh tiến không bảo toàn yếu tố nào sau đây? Trang 9
A. Khoảng cách giữa hai điểm.
B. Thứ tự ba điểm thẳng hàng.
C. Tọa độ của điểm. D. Diện tích. ! !
Câu 5: Với hai điểm ,
A B phân biệt và T! ( A) = A ,¢ T! (B) = B¢ với v ¹ 0. Mệnh đề nào sau đây đúng? v v !!!!" " !!!!" !!!" !!!" " !!!!" !!!" " A. A B ¢ ¢ = v.
B. A¢B¢ = AB.
C. AB = v. D. A B ¢ ¢+ AB = 0.
Câu 6: Cho hai đường thẳng d và d song song với nhau. Có bao nhiêu phép tịnh tiến theo vectơ 1 2 ! !
v ¹ 0 biến d thành d ? 1 2 A. 0 . B.1. C. 2 . D. Vô số.
Câu 7: Cho hình bình hành ABCD . Phép tịnh tiến T!!!" !!!" biến điểm A thành điểm nào? AB+ AD
A. A¢ đối xứng với A qua C .
B. A¢ đối xứng với D qua C .
C. O là giao điểm của AC qua BD . D. C .
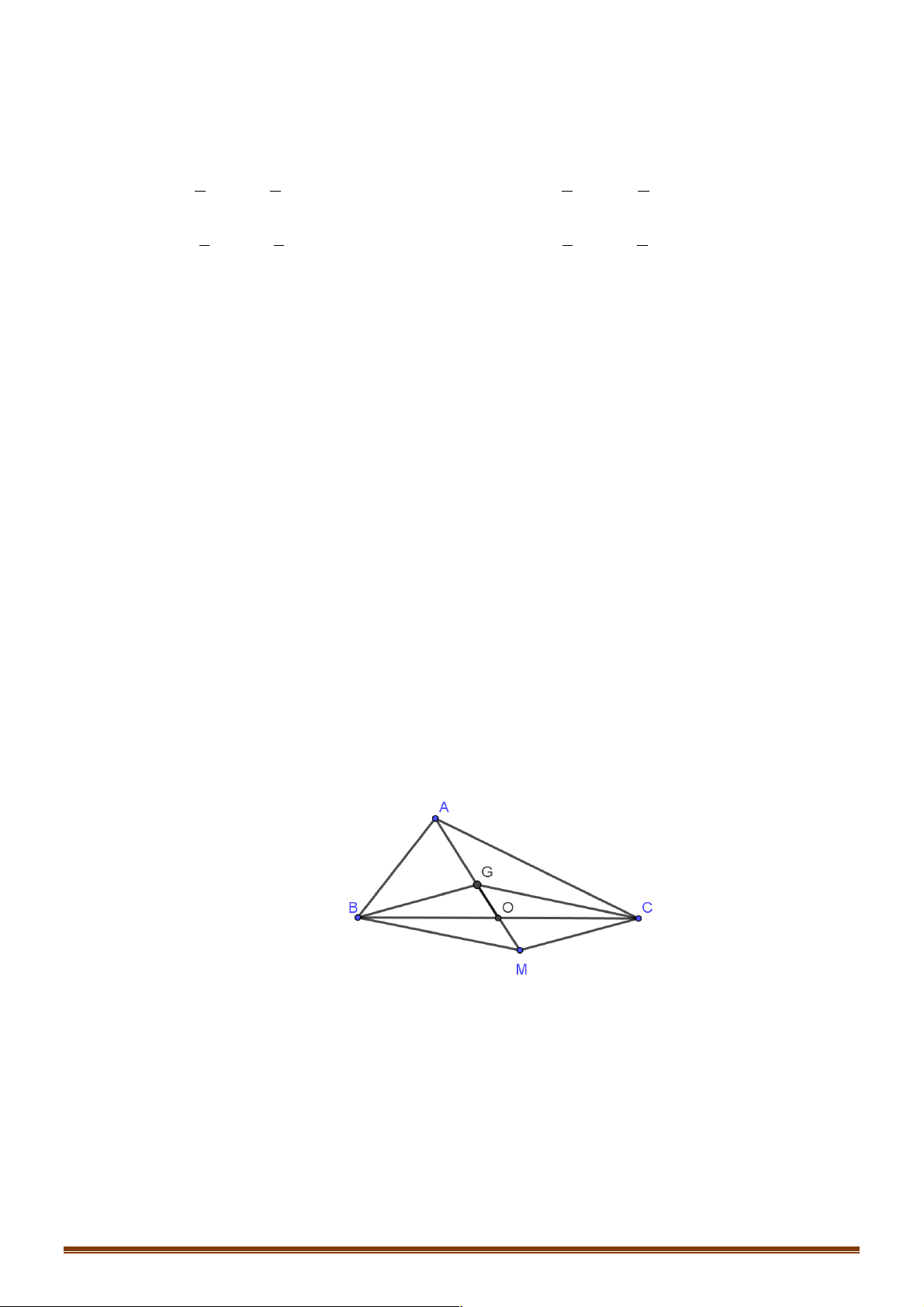
Câu 8: Cho tam giác ABC có trọng tâm G , T!!!" (G) = M . Mệnh đề nào là đúng? AG
A. M là trung điểm BC .
B. M trùng với A .
C. M là đỉnh thứ tư của hình bình hành BGCM .
D. M là đỉnh thứ tư của hình bình hành BCGM . !!!"
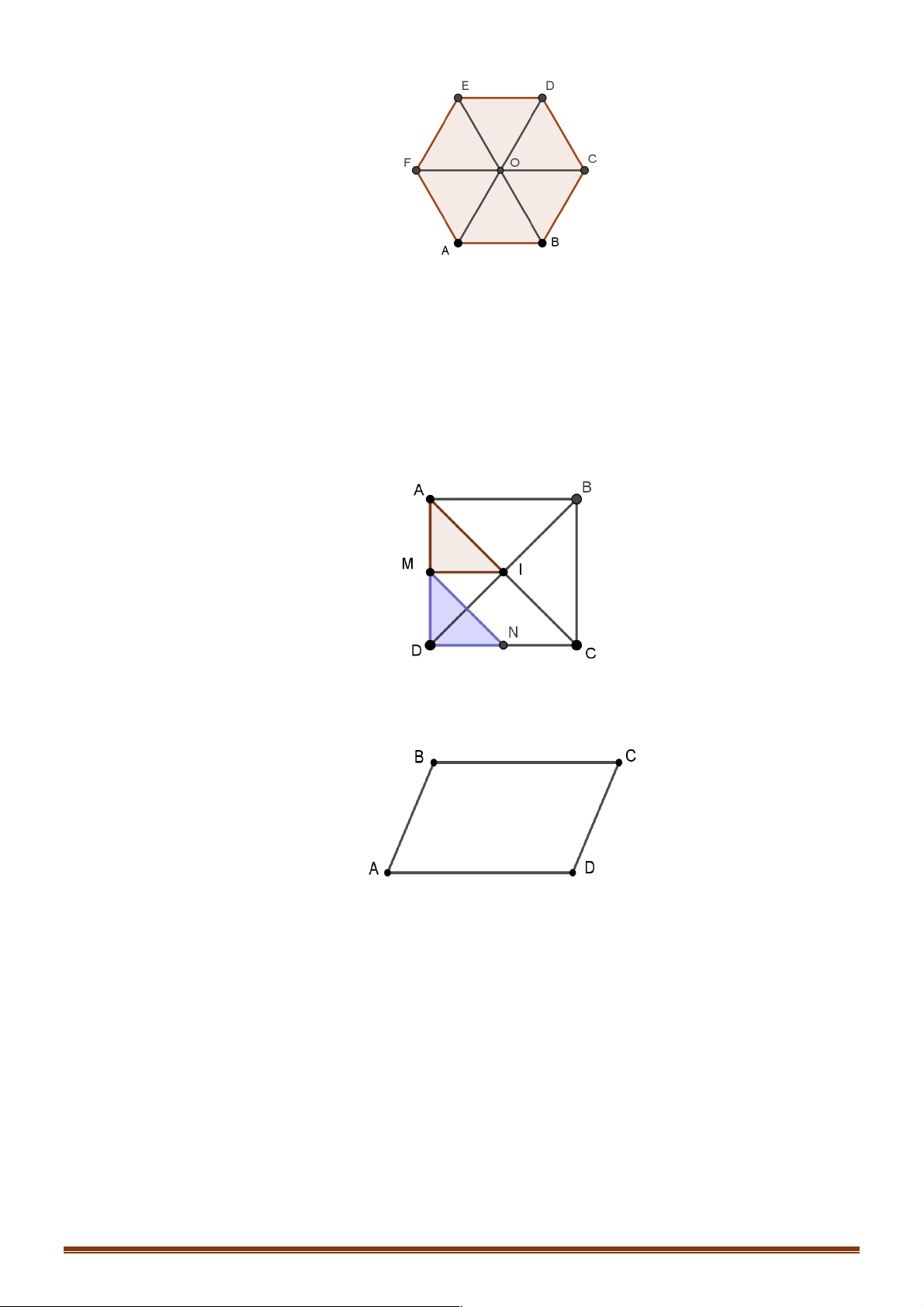
Câu 9: Cho lục giác đều ABCDEF tâm O . Tìm ảnh của AO D
F qua phép tịnh tiến theo vectơ AB . A. AO D B . B. BO D C . C. CD D O . D. D D EO .
Câu 10: Cho hình bình hành ABCD tâm I . Kết luận nào sau đây sai?
A. T!!!!" ( A) = B.
B. T!!!" (B) = A.
C. T!!!" (I ) = B.
D. T!!" (I ) = C . DC CD DI IA
Câu 11: Cho hình vuông ABCD tâm I . Gọi M , N lần lượt là trung điểm của AD, DC . Phép tịnh tiến
theo vectơ nào sau đây biến AM D I thành MD D N ? !!!!" !!" !!!" !!!!" A. AM . B. NI . C. AC . D. MN .
Câu 12: Cho hình bình hành ABCD . Có bao nhiêu phép tịnh tiến biến đường thẳng AB thành đường
thẳng CD và biến đường thẳng AD thành đường thẳng BC ? A. 0 . B.1. C. 2 . D. Vô số.
Câu 13: Cho đường tròn (O) và hai điểm ,
A B . Một điểm M thay đổi trên đường tròn (O). Tìm quỹ !!!!!" !!!" !!!"
tích điểm M ¢ sao cho MM ¢ + MA = MB.
A. (O¢) = T!!!" O
(O¢) =T!!!!" O
(O¢) =T!!!" O
(O¢) =T!!!!" O BM (( )) BA (( )) AM (( )) AB (( )). B. . C. . D. .
Câu 14: Cho tứ giác lồi ABCD có AB = BC = CD = a , ∑ BAD = 75° và ∑
ADC = 45°.Tính độ dài AD . A. a 2 + 5 . B. a 3 . C. a 2 + 3 . D. a 5 .
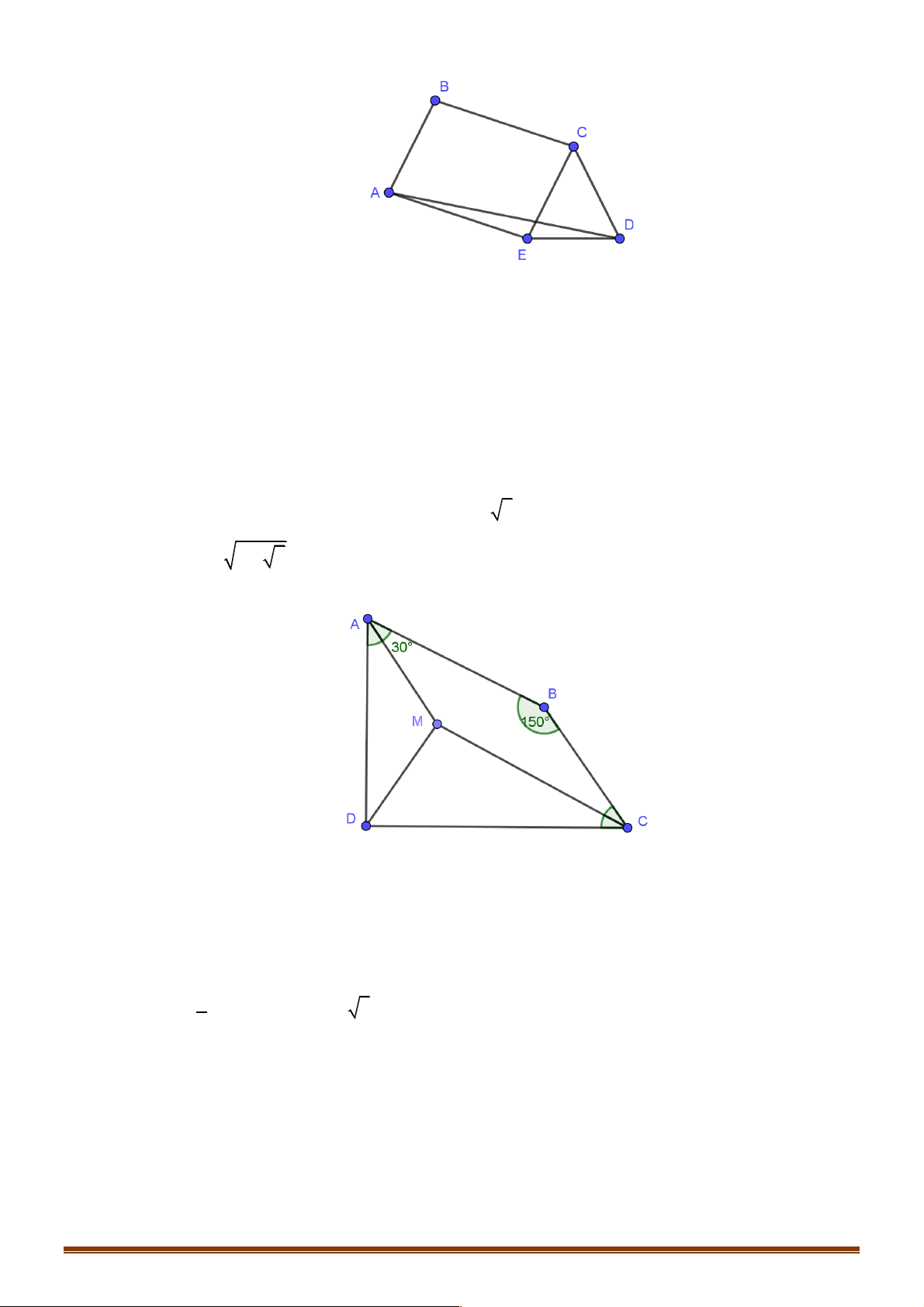
Câu 15: Cho tứ giác ABCD có AB = 6 3, CD = 12, ! ! ! A = 60 ,
° B =150 ,° D = 90°. Tính độ dài BC . A. 4 . B. 5 . C. 6 . D. 2 . AC BD
Câu 16: Trên đoạn AD cố định dựng hình bình hành ABCD sao cho =
. Tìm quỹ tích đỉnh C . AD AB
A. Đường tròn tâm A , bán kính là AB 3 .
B. Đường tròn tâm A , bán kính là AC .
C. Đường tròn tâm A , bán kính là AD .
D. Đường tròn tâm A , bán kính là AD 2 .
Câu 17: Cho hai đường tròn có bán kính R cắt nhau tại M , N . Đường trung trực của MN cắt các
đường tròn tại A và B sao cho ,
A B nằm cùng một phía với MN . Tính 2 2
P = MN + AB . A. 2 P = 2R . B. 2 P = 3R . C. 2 P = 4R . D. 2 P = 6R .
Câu 18: Cho hai đường tròn có bán kính R tiếp xúc ngoài với nhau tại K . Trên đường tròn này lấy
điểm A , trên đường tròn kia lấy điểm B sao cho ∑
AKB = 90°. Độ dài AB bằng bao nhiêu? A. R . B. R 2 . C. R 3. D. 2R .
Câu 19: Từ đỉnh B của hình bình hành ABCD kẻ các đường cao BK và BH của nó biết
KH = 3, BD = 5. Khoảng cách từ B đến trực tâm H của tam giác BKH có giá trị bằng bao 1 nhiêu? Trang 10 A. 4 . B. 5 . C. 6 . D. 4,5.
DẠNG 2. XAC DỊNH ẢNH CỦA MỘT DIỂM HOẶC HINH QUA PHEP TỊNH TIẾN BẰNG PHƯƠNG PHAP TỌA DỘ
Câu 1: Trong mặt phẳng tọa độ Oxy , tìm tọa độ điểm M ¢ là ảnh của điểm M (1;2) qua phép tịnh tiến ! theo vectơ v = (3 ) ;1 . A. M¢(4; 2 - ) . B. M ¢(4;2). C. M ¢(2 ) ;1 . D. M ¢(4;- ) 1 . !
Câu 3: Trong mặt phẳng tọa độ Oxy , cho vectơ v = (2; )
1 và điểm A(4;5) .Hỏi A là ảnh của điểm nào !
sau đây qua phép tịnh tiến theo vectơ . v A. (1;6) . B. (2;4). C. (4;7). D. (6;6). !
Câu 6: Trong mặt phẳng tọa độ Oxy , cho điểm A(2;2), B(4;6) và T! ( A) = B . Tìm vectơ . v v A. (1;2) . B. (2;4). C. (4;2). D. ( 2; - 4 - ).
Câu 7: Trong mặt phẳng tọa độOxy , biết điểm M¢( 3;
- 0) là ảnh của điểm M (1; 2 - ) qua T! và điểm u ! ! M¢¢(2; )
3 là ảnh của M ¢ qua T! . Tìm tọa độ vectơ u + . v v A. (1;5) . B. ( 2; - 2 - ). C. (1; ) 1 - . D. ( 1 - ;5).
Câu 8: Trong mặt phẳng tọa độ Oxy , cho các điểm A ,¢ B¢ lần lượt là ảnh của các điểm A(2;3), B(1; ) 1 ! !!!!"
qua phép tịnh tiến theo vectơ v = (3 )
;1 . Tính độ dài vectơ A B ¢ .¢ A. 2 . B. 3 . C. 5 . D. 2 .
Câu 9: Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có các điểm A(3;0), B( 2 - ;4),C( 4 - ;5) . G ! !
là trọng tâm tam giác ABC và phép tịnh tiến theo vectơ u ¹ 0 biến điểm A thành G . Tìm tọa
độ G¢ biết G¢ = T! (G). u A. G¢( 5; - 6) . B. G¢(5;6). C. G¢(3; ) 1 . D. G¢( 1 - ;3). !
Câu 10: Trong mặt phẳng tọa độOxy , cho đường thẳng D : x + 5y -1 = 0 và vectơ v = (4;2). Khi đó ảnh !
của đường thẳng D qua phép tịnh tiến theo vectơ v là
A. x + 5y -15 = 0 .
B. x + 5y +15 = 0.
C. x + 5y + 6 = 0.
D. -x - 5y + 7 = 0. !
Câu 11: Trong mặt phẳng tọa độ Oxy , cho v = (-4;2) và đường thẳng D¢: 2x + y -5 = 0. Hỏi D¢ là ảnh
của đường thẳng D nào sau đây qua T!. v
A. D : 2x + y + 5 = 0 .
B. D : 2x + y - 9 = 0. C. D : 2x + y -15 = 0. D. D : 2x + y -11 = 0. ìx =1+ 2t
Câu 12: Trong mặt phẳng tọa độOxy , cho đường thẳng D : í và đường thẳng ¢
D : x + 2y -1 = 0 îy = 1 - - t !
. Tìm tọa độ vectơ v biết T! (D) = D .¢ v ! ! ! ! A. v = (0;- ) 1 . B. v = (0;2). C. v = (0; ) 1 . D. v = ( 1 - ; ) 1 .
Câu 13: Trong mặt phẳng tọa độ Oxy , tìm phương trình đường tròn (C¢) là ảnh của đường tròn ( ! C) 2 2
: x + y - 4x - 2y +1 = 0 qua phép tịnh tiến theo v = (1;3).
A. (C¢) (x - )2 +( y - )2 : 3 4 = 2 .
B. (C¢) (x - )2 +( y - )2 : 3 4 = 4.
C. (C¢) (x + )2 +( y + )2 : 3 4 = 4.
D. (C¢) (x + )2 +( y - )2 : 3 4 = 4. !
Câu 14: Trong mặt phẳng tọa độ Oxy , cho v = (3;- )
1 và đường tròn (C) (x - )2 2 :
4 + y =16 . Ảnh của
(C) qua phép tịnh tiến T! là v Trang 11
A. (x - )2 +( y - )2 1 1 =16 .
B. (x + )2 +( y + )2 1 1 =16.
C. (x - )2 +( y + )2 7 1 =16.
D. (x + )2 +( y - )2 7 1 =16. !
Câu 15: Trong mặt phẳng tọa độOxy , cho v = (1; 2
- ) và đường cong (C) 2 2 : 2x + 4y = 1 . Ảnh của (C)
qua phép tịn tiến T! là v A. 2 2
2x + 4y + 4x +16y -17 = 0 . B. 2 2
2x + 4y - 4x +16y +17 = 0. C. 2 2
2x + 4y - 4x -16y +17 = 0. D. 2 2
2x + 4y - 4x -16y - 7 = 0. 2 2 x y !
Câu 16: Trong mặt phẳng tọa độOxy , cho elip (E) : +
=1 và véc tơ v = (2; )
1 . Ảnh của (E) qua 16 9
phép tịn tiến T! là: v 2 2 x - 2 y -1 2 2 x + 2 y +1 A. (E) ( ) ( ) : + =1 . B. (E) ( ) ( ) : + = . 1 16 9 16 9 2 2 x y 2 2 x - 2 y -1 C. (E) : + =1. D. (E) : + =1. 4 9 16 9
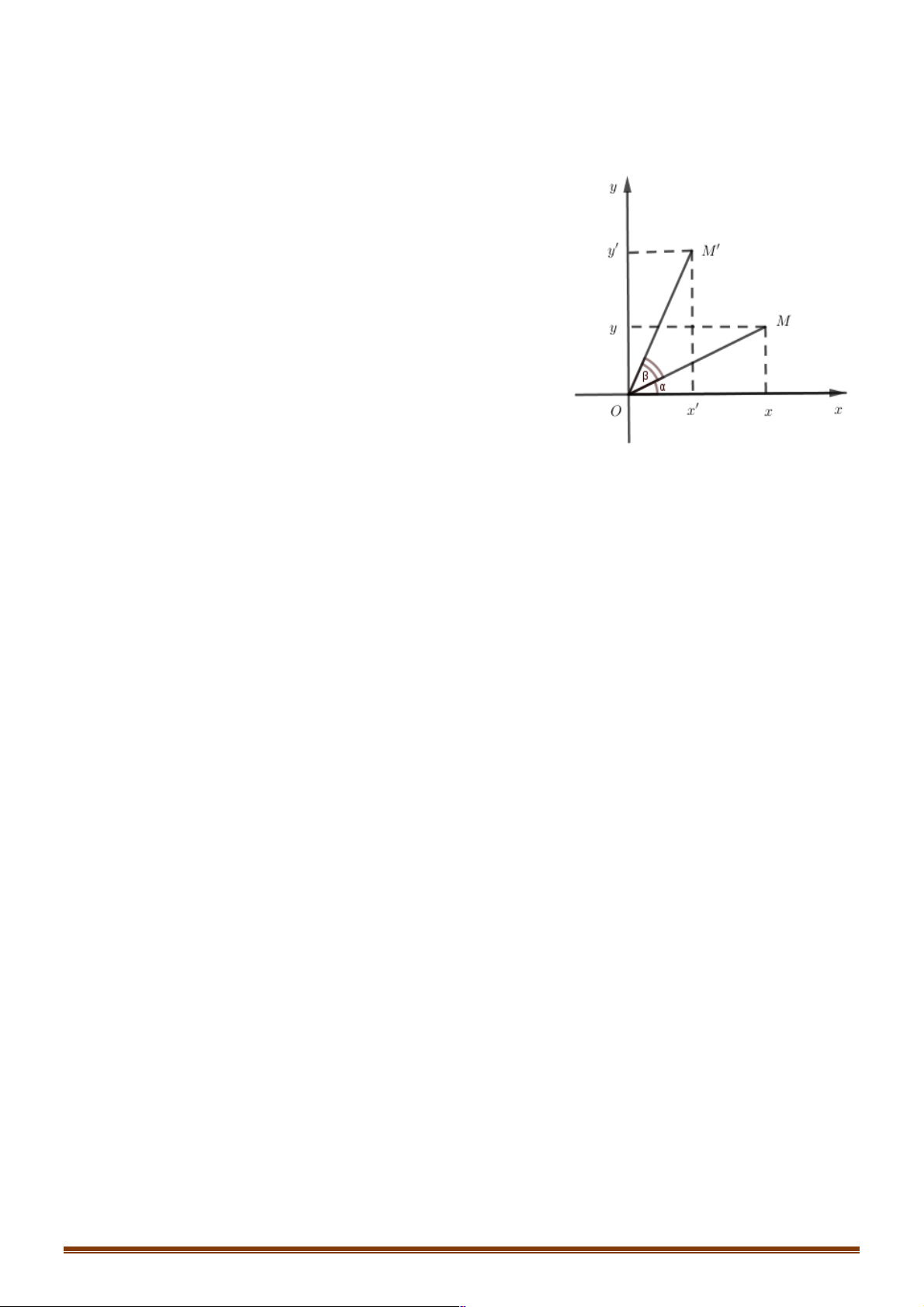
Câu 17: Trong mặt phẳng tọa độ Oxy , với a,a, b là những số cho trước, xét phép biến hình F biến mỗi ìx ' = . x cosa - . y sina + a điểm M ( ;
x y) thành điểm M '(x'; y ') trong đó: í . Cho hai điểm îy ' = . x sina + . y cosa + b M (x ; y N (x ; y M ', N ' M , N F 2 2 ) 1 1 ) , , gọi
lần lượt là ảnh của qua phép biến hình . Khi đó
khoảng cách d giữa M ' và N ' bằng:
A. d = (x - x + y - y
d = (x + x + y + y 2 1 )2 ( 2 1)2 2 1 )2 ( 2 1)2 . B. .
C. d = (x + x + y - y
d = (x - x + y + y 2 1 )2 ( 2 1)2 2 1 )2 ( 2 1)2 . D. . ! 2 x - x +1 !
Câu 18: Cho véc tơ v = (a;b) sao cho khi phép tịnh tiến đồ thị y = f (x) = theo véc tơ v ta x -1 2 x
nhận đồ thị hàm số y = g (x) = . Khi đó tích . a b bằng: x +1 A. 1 . B. 5 . C. 6 . D. 4 . !
Câu 19: Trong mặt phẳng tọa độOxy , cho v = ( 2 - )
;1 và đường thẳng d : 2x - 3y + 3 = 0, !"
d : 2x -3y -5 = 0. Tìm tọa độ w = (a;b) có phương vuông góc với đường thẳng d để d là 1 1
ảnh của d qua phép tịnh tiến T!" . Khi đó a + b bằng: w 6 16 -8 5 A. . B. . C. . D. . 13 13 13 13
Câu 20: Trong mặt phẳng tọa độ Oxy , cho phép biến hình F xác định như sau: Với mỗi điểm M ( ; x y)
ta có điểm M ' = F (M ) sao cho M '(x'; y ') thỏa mãn: x' = x + 2; y ' = y -3. Mệnh đề nào sau đây đúng: ! !
A. F là phép tịnh tiến theo v = (2;3) .
B. F là phép tịnh tiến theo v = (-2;3). ! !
C. F là phép tịnh tiến theo v = (2; 3 - ).
D. F là phép tịnh tiến theo v = ( 2; - 3 - ) .
Câu 21: Trong mặt phẳng tọa độ Oxy , cho hai điểm A(1;6); B( 1 - ; 4
- ). Gọi C, D lần lượt là ảnh của ! ,
A B qua phép tịnh tiến theo v = (1;5). Kết luận nào sau đây là đúng:
A. ABCD là hình vuông.
B. ABCD là hình bình hành.
C. ABDC là hình bình hành. D. ,
A B,C, D thẳng hàng. Trang 12
Câu 22: Trong mặt phẳng tọa độ Oxy , cho đường thẳng có phương trình d : y = 2, và hai điểm A(1;3); B(3; 4
- ). Lấy M trên d , N trên trục hoành sao cho MN vuông góc với d và
AM + MN + NB nhỏ nhất. Tìm tọa độ M , N ? æ 6 ö æ 6 ö æ 7 ö æ 7 ö A. M ;2 , N ;0 . B. M ;2 , N ;0 . ç ÷ ç ÷ ç ÷ ç ÷ è 5 ø è 5 ø è 5 ø è 5 ø æ 8 ö æ 8 ö æ 9 ö æ 9 ö C. M ;2 , N ;0 . D. M ;2 , N ;0 . ç ÷ ç ÷ ç ÷ ç ÷ è 5 ø è 5 ø è 5 ø è 5 ø
HƯỚNG DẪN GIẢI CHI TIẾT
DẠNG 1: CÁC BÀI TOÁN KHAI THÁC ĐỊNH NGHĨA, TÍNH CHẤT VÀ CÁC ỨNG DỤNG CỦA PHÉP TỊNH TIẾN
Câu 1: Đáp án D. !
Khi véc tơ v của phép tịnh tiến T! có giá song song hoặc trùng với đường thẳng đã cho thì sẽ v
có vô số phép tịnh tiến biến đường thẳng thành chính nó. Câu 2: Đáp án B. ! !
Khi v = 0: Đường tròn (C) có tâm I thì T! biến đường tròn (C) thành chính nó. v Câu 3: Đáp án B. ! !
Khi v = 0 có một phép tịnh tiến biến hình vuông thành chính nó. Câu 4: Đáp án C. ! !
Khi tọa độ của véc tơ tịnh tiến v ¹ 0. Câu 5: Đáp án B. !!!!!" !!!"
Ta chỉ ra được ABB ' A' là hình bình hành Þ A'B' = AB Câu 6: Đáp án D.
Chẳng hạn lấy bất kỳ AÎd , B Î d Þ T!!!" (d d AB 1 ) thành
nên có vô số phép tịnh tiến thỏa 1 2 2 mãn. Câu 7. Đáp án D. !!!" !!!" !!!"
Ta có AB + AD = AC Þ T!!!" A = C AC ( ) . Câu 8. Đáp án C. !!!" !!!!"
Ta có T!!!" G = M Û AG = GM Þ BGCM AG ( ) là hình bình hành. Câu 9. Đáp án B. Trang 13 T ì !!!" A = B AB ( ) ïï Ta có T
í !!!" O = C Þ T!!!" A D OF = DBCO AB ( ) AB ( ) .
ïT!!!" F =O ïî AB ( ) Câu 10. Đáp án D.
Ta có T!!" I = A IA ( ) nên đáp án D sai. Câu 11. Đáp án A.
Từ hình vẽ ta có T!!!!" A D MI = M D DN AM ( ) . Câu 12. Đáp án B. Từ hình vẽ ta có
T!!!" AB = CD , AB CD BC ( ) với là các đoạn thẳng.
T!!!" AB = CD , AD BC BC ( ) , với
là đoạn thẳng nên có một phép tịnh tiến thỏa mãn. Câu 13. Đáp án A. !!!!!" !!!" !!!" !!!!!" !!!" !!!" !!!"
Ta có : MM¢ + MA = MB Û MM¢ = MB - MA = AB Û T!!!" M = M¢ AB ( ) .
Vậy tập hợp điểm M¢ là ảnh của đường tròn (O) qua T!!!" . AB Câu 14. Đáp án C. Trang 14
Xét T!!!" A = A¢ BC ( ) .
Khi đó CA¢ = BA = CD Þ C D A D ¢ cân tại C . ∑ Þ ¢ A CD = 0 60 Þ DC ¢ A D đều. ∑ Þ ¢ A DA = 0
15 và AA¢ = BC = CD = A D ¢ = a ∑ Þ ¢ AA D = 0 150 Do đó 2 2 2 2 2 AD = 2A A ¢ - 2A A ¢ cos AA D
¢ = 2a + 3a (áp dụng định lí cosin).
Þ AD = a 2 + 3 . Câu 15. Đáp án C.
Xét T!!!" A = M Þ ABCM BC ( ) là hình bình hành. ∑ 0 ∑ Þ BCM = Þ BCD = 0 30 60 và ∑ MCD = 0 30 Ta có 2 2 2 0
MD = MC + DC -2 . MC D .
C cos30 = 36 Þ MD = 6 1
MD = CD và MC = MD 3 Þ MD D
C là nửa tam giác đều. 2 ∑ 0 ∑ Þ DMC = Þ MDA = 0 90 30 Vậy ∑ ∑ ∑
MDA = MAD = MAB = 0
30 Þ DAMD cân tại M Þ BC = MA = MD = 6 . Câu 16. Đáp án D.
Chọn hệ trục về chiều dương như hình vẽ. Trang 15 vuong Hide Luoi y B(x,y) C(x+1,y) I x A D
Cố định D(1;0). Với B( ;
x y) ÞC(x +1;y)
Từ giả thiết AC.AB = AD.BD Û (x + )2
1 + y . x + y = (x - )2 2 2 2 2 1 + y Û ( 2 2 x + y )( 2 2
x + y + 2x) =1- 2x Û ( 2 2 x + y + ) 1 ( 2 2
x + y + 2x) 2 2
- x - y - 2x = 1- 2x Û ( 2 x + 2 y + )( 2 x + 2 1 y + 2x - ) 1 = 0 (do 2 2
x + y +1 > 0).
Û x + y + x - = Û (x + )2 2 2 2 2 1 0 1 + y = 2 (1).
Suy ra quỹ tích B là đường tròn tâm I , bán kính 2 ( I là điểm đối xứng của D qua A )
Ta có T!!!" B = C BC ( )
Vậy quỹ tích của C là đường tròn tâm A , bán kính AD 2 . Câu 17. Đáp án C.
Giả sử trung trực MN cắt (O A (O B O , A B 2 ) 1 ) tại , cắt tại ( ở giữa ) 1
(Bạn đọc tự vẽ hình) !!!!!"
Thực hiện phép trịnh tiến theo vectơ O O đường tròn (O (O1)
2 ) biến thành đường tròn . vì 2 1
vậy B biến thành A , M biến trhành M , N biến thành N . 1 1
MNN M là hình bình hành nội tiếp nên là hình chữ nhật. Vậy 1 1 2 2 2 2 2
MN + M M = MN + AB = 4R . 1 Câu 18. Đáp án D.
(Bạn đọc tự vẽ hình). !!!!!"
Sử dụng phép tịnh tiến theo vectơ O O thì K biến thành C , KA thành CB . Vì vậy AB = 2R 1 2 . Câu 19. Đáp án A. Trang 16 B P C H H 1 A D K !!!"
Thực hiện phép tịnh tiến theo vectơ KD ta có :
K biến thành D , H biến thành H , B biến thành P 1 Ta có PH D
K vuông tại H và KH = 3,KP = BD = 5 nên PH = 25- 9 = 4 Þ BH = PH = 4. 1
DẠNG 2. XÁC ĐỊNH ẢNH CỦA MỘT ĐIỂM HOẶC MỘT HÌNH QUA PHÉP TỊNH TIẾN BẰNG
PHƯƠNG PHÁP TỌA ĐỘ. Câu 1. Đáp án B. ìx¢ =
T! M = M¢ x¢ y¢ Û í Þ M¢ v ( ) ( ) 4 ; (4;2) îy¢ = 2 Câu 3. Đáp án B.
ìïx = x + x! ìx = 2
Theo biểu thức tọa độ Þ í A v Û í ïy = y + î y! y A v î = 4 Câu 6. Đáp án B.
ìx! = x - x ìx! = ï v B A ï 2 Ta có í Û í v
y! = y - y y! = ïî v B A ïî 4 v Câu 7. Đáp án A. ! """""! ! """"""! ! ! """""!
Ta có u = MM ,¢ v = M M
¢ ¢ Þ u + v = MM¢¢ = (1;5). Câu 8. Đáp án C.
T! A = A¢ v ( ) Ta có Þ A B ¢ ¢ = AB = .
T! B = B¢ v ( ) 5 Câu 9. Đáp án A. ! """! Ta tìm được G( 1
- ;3) Þ u = AG = ( 4 - ;3) !!!" !!!!"
T!!!" (G) = G¢ Þ AG = GG¢ Þ G¢( 5; - 6 AG ) . Câu 10. Đáp án A.
Ảnh của D có dạng x + 5y + c = 0 ( ¢ D )
Chọn A(1;0)ÎD : T! (A) = A¢( ; x y) ¢ ÎD Þ A¢(5;2
D¢ : 5 +10 + c = 0 Þ c = 15 - v ) thế vào Þ ¢
D : x + 5y -15 = 0 . Trang 17 Câu 11. Đáp án D. ìx¢ = x - Điểm M ( ;
x y)ÎD biến thành M(x ;¢y¢) ¢ ÎD 4 Þ í
thay x ,¢ y¢ vào îy¢ = y + 2
D¢ : 2x + y -11 = 0 . Câu 12. Đáp án C. Chọn A(1;- ) 1 ÎD
Thử đáp án C Þ T! (A) = A¢ Þ A¢(1;0 Î ¢ D v ) (thỏa mãn) Câu 13. Đáp án B.
Đường tròn (C) có tâm I (2; ) 1 , bán kính R = 2
Ta có I¢ = T! I Þ I¢ Þ C¢ x - + y - = v ( ) ( ) ( ) ( )2 ( )2 3;4 : 3 4 4 . Câu 14. Đáp án C.
Đường tròn (C) có tâm I (4;0) , bán kính R = 4
Ta có T! I = I¢ - v ( ) (7; )1
Vậy đường tròn ảnh là (C¢) (x - )2 +(y + )2 : 7 1 = 16 Câu 15. Đáp án B. ìx¢ = x +1 ìx = x¢ -1
Sử dụng quỹ tích điểm M ( ;
x y)Î(C) : T! (M) = M¢(x ;¢y¢ Î C¢ Þ í Þ í v ) ( ) îy¢ = y - 2 îy = y¢ + 2
Thay vào (C) ta được đáp án B. Câu 16. Đáp án A. ìx = x¢ - 2
Sử dụng quỹ tích điểm : T! (M) = M¢(x ;¢y¢ M ( ; x y)Î(E)Þ í v ) với mọi điểm îy = y¢ - 2
Thay vào (E) ta được đáp án A. Câu 17. Đáp án A.
ìïx ¢ = x .cosa - y .sina + a
ìïx ¢ = x .cosa - y .sina + a Ta có 1 1 1 í 2 2 2 í
ïy ¢ = x .sina - y .cosa + b î
ïy ¢ = x .sina - y .cosa + b 1 1 1 î 2 2 2 2 2 Þ M N ¢ ¢ =
x ¢ - x ¢ + y ¢ - y ¢ ( 2 1 ) ( 2 1 ) 2 2 2 2 2 2 2 2 =
x ¢ - x ¢ cos a + y ¢ - y ¢ sin a + x ¢ - x ¢ sin a + y ¢ - y ¢ cos a ( 2 1 ) ( 2 1 ) ( 2 1 ) ( 2 1 )
= (x - x + y - y Þ d = x - x + y - y 2 1 )2 ( 2 1)2 ( 2 1)2 ( 2 1)2 . Câu 18. Đáp án C.
Ta có g(x) = f (x -a)+ b Trang 18 x (x -a)2 2 - (x - a)+1 Û = + b x +1 x - a -1 2 x x + ( 2 - a + b - ) 2 2
1 x + a - ab + a - b +1 Û = x +1 x - a -1 ìa = 2 - Þ í Þ . a b = 6 . îb = 3 - Câu 19. Đáp án C. ! !"
Đường thẳng d có vectơ pháp tuyến là n = (2; 3 - ) Þ w = (2 ; m 3 - m)
T!" (M) = M¢(2 ; m 1-3m M Î d w ) , với
T!" d = d¢ Þ d¢ 2x - 3y + b = 0 w ( ) có dạng
Vì d¢ qua M Þ 4m - 3 + 9m + b = 0 Û b = 3 -13m.
Þ d¢ : 2x - 3y + 3 -13m = 0 8 ! æ16 24 ö 8
Để d º d¢ Þ 3 -13m = 5 - Û m = Þ w = ;- Þ a + b = - . 1 ç ÷ 13 è 13 13 ø 13 Câu 20. Đáp án C.
ìx¢ = x + a ìa = 2 !
Thật vậy theo biểu thức tọa độ của T! M = M¢ í Þ í Þ v = (2; 3 - ) v ( ) .
îy¢ = y + b îb = 3 - Câu 21. Đáp án D.
T! A = C Þ C v ( ) (2;1 )1
T! B = D Þ D v ( ) (0; )1 !!!" !!!" !!!" AB = ( 2; - 1 - 0), CD = ( 2; - 1 - 0), BC = (3;15) !!!" !!!" !!!" !!!" !!!" AD = ( 1 - ; 5 - ) Þ BC = 3 - , AD AB = CD Þ , A ,
B C,D thẳng hàng. Câu 22. Đáp án B.
Cách 1 : Thử các tọa độ M, N ta được kết quả AM + MN + NB nhỏ nhất với M Îd, N ÎOx và MN ^ d . Cách 2 : A d A M 1 H 1 d2 K N B
Gọi H Î d , K Î d sao cho HK ^ d . 1 2 1 !!!"
Gọi T là phép tịnh tiến theo vectơ HK
Gọi A = T!!!!" A , A B Çd = N, M Îd MN ^ d 1 HK ( ) với 1 2 1 1
AM + MN + NB nhỏ nhất Û AM + NB nhỏ nhất ( MN không đổi)
AM + NB = A N + NB ³ A B 1 1
Dấu " = " xảy ra khi N = A B Ç d 1 2 Trang 19 Lấy A 1;1 N A B 1 (
), điểm cần tìm là giao điểm của và trục hoành. 1 !!!!" !!!"
Gọi N (x ;0 Þ A N = x -1; 1 - , A B = 2; 5 - 0 ) 1 ( 0 ) 1 ( ) !!!!" !!!" x -1 1 - 7 æ 7 ö æ 7 ö
Vì A N và A B cùng phương nên 0 = Þ x = Þ N ;0 và M ;2 . 1 1 0 ç ÷ ç ÷ 2 5 - 5 è 5 ø è 5 ø Trang 20
PHÉP ĐỐI XỨNG TRỤC. PHÉP ĐỐI XỨNG TÂM A. LÝ THUYẾT
I. Phép đối xứng trục 1. Định nghĩa
Phép đối xứng qua một đường thẳng a là phép biến hình biến điểm M thành điểm M¢ đối xứng với M
qua đường thẳng a .
Kí hiệu : — ( a là trục đối xứng) a !!!!!!" !!!!!"
— M = M¢ Û M M¢ = -M M M M a a ( ) với là hình chiếu của trên . 0 0 0 M
— M = M Û M Îa M a ( ) 0 a
— M = M¢ Û — M¢ = M a ( ) a ( ) M'
a là trung trực của đoạn MM¢ . 2. Tính chất
Tính chất 1 : Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kỳ.
Tính chất 2 : Phép đối xứng trục biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng
bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính. A O R d B C a B' C' d' O' R' A'
Phép đối xứng trục biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
3. Trục đối xứng của một hình
Đường thẳng a gọi là trục đối xứng của hình H nếu — biến hình H thành chính nó. Khi đó H được gọi a
là hình có trục đối xứng.
4. Biểu thức tọa độ
Trong mặt phẳng tọa độ Oxy: — : M ( ;
x y) ® M¢(x ;¢y¢ a ) ìx = x¢
Nếu a º Ox Þ í îy = -y¢ Trang 21 ìx = -x¢
Nếu a º Oy Þ í îy = y¢ y y y M M' y M x y' x O x' y' x x M' x' O
II. Phép đối xứng tâm 1. Định nghĩa
Cho điểm I . Phép biến hình biến điểm I thành chính nó, biến mỗi điểm M khác I thành M¢ sao cho I
là trung điểm MM¢ được gọi là phép đối xứng tâm I .
Kí hiệu: — ( I là tâm đối xứng) I !!!" !!!"
— M = M¢ Û IM¢ = -IM I ( ) M' I M
Nếu M º I Û M¢ º I .
Nếu M ¹ I Û I là trung điểm của MM¢ . 2. Tính chất !!!!!" !!!!"
Tính chất 1 : Nếu — M = M¢ — N = N¢ M N ¢ ¢ = -MN M N ¢ ¢ = MN I ( ) I ( ) và thì , từ đó suy ra .
Tính chất 2 : Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến
đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nóm biến đường tròn thành
đường tròn có cùng bán kính.
Phép đối xứng tâm biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
Phép đối xứng tâm bảo toàn khoảng cách giữa hai điểm bất kì. Trang 22 A A B O B C A I B' A' I C' B' I A' A' O'
3. Tâm đối xứng của một hình.
Điểm I được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm I biến hình H thành chính nó. Khi
đó H được gọi là hình có tâm đối xứng.
4. Biểu thức tọa độ
Trong mặt phẳng tọa độ Oxy , cho I x ; y M ( ; x y)
M¢(x ;¢y¢) 0 ( 0 0 ) , gọi và với
ìïx¢ = x - x
— M = M¢ Þ í I ( ) 2 0
ïy¢ = 2y - y î 0 I M(x;y) M'(x';y')
B. CÁC DẠNG TOÁN VỀ PHÉP ĐỐI XỨNG TRỤC, ĐỐI XỨNG TÂM
DẠNG 1. KHAI THÁC DỊNH NGHĨA, TINH CHẤT VA ỨNG DỤNG CỦA PHÉP ĐỐI XỨNG TRỤC
VÀ ĐỐI XỨNG TÂM. Phương pháp :
- Sử dụng định nghĩa hoặc tính chất của phép đối xứng trục, đối xứng tâm.
- Xác định ảnh của một điểm, một hình qua phép đối xứng trục, đối xứng tâm.
- Tìm quỹ tích điểm thông qua phép đối xứng trục, đối xứng tâm.
- Vận dụng đối xứng trục, đối xứng tâm để giải các bài toán hình học khác…
Ví dụ 10: Cho đường thẳng a . Qua phép đối xứng trục a , đường thẳng nào biến thành chính nó.
A. Các đường thẳng song song với a .
B. Các đường thẳng vuông góc với a .
C. Các đường thẳng hợp với a một góc 0 60 .
D. Các đường thẳng hợp với a một góc 0 30 . Đáp án B. Lời giải: Trang 23 l A a A'
Giả sử l là đường thẳng vuông góc với a .
Lấy AÎl và D A º A¢ Þ AA¢ ^ a Þ A¢Îl Þ D l = l a ( ) a ( )
và ngược lại vẫn thỏa mãn .
Ví dụ 11: Cho hai đường thẳng cắt nhau d và d¢ . có bao nhiêu phép đối xứng trục biến đường thẳng
này thành đường thẳng kia? A. Không có. B. Một. C. Hai. D. Vô số. Lời giải: Đáp án C.
Có 2 phép đối xứng trục với các trục là hai đường phân giác của góc tạo bởi hai đường thẳng
cắt nhau d và d¢ . a' d d'
Ví dụ 12: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hình vuông có vô số trục đối xứng.
B. Hình chữ nhật có 4 trục đối xứng.
C. Tam giác đều có vô số trục đối xứng .
D. Tam giác cân nhưng không đều có 1 trục đối xứng. Lời giải: Đáp án D.
Tam giác cân nhưng không đều có một trục đối xứng là đường cao ứng với đỉnh của tam giác cân đó.
Ví dụ 13: Hình nào dưới đây có một tâm đối xứng? A. . B. . C. . D. . Lời giải: Đáp án C.
Hình C có một tâm đối xứng tại giao điểm của hai đường chéo.
Ví dụ 14: Giải sử phép đối xứng tâm O biến đường thẳng d thành d . Trong các mệnh đề sau, mệnh đề 1 nào đúng? Trang 24
A. d cắt d .
B. Nếu O Ï d thì d ! d . 1 1
C. Nếu d qua O thì d cắt d .
D. d và d cắt nhau tại O . 1 1 Lời giải: Đáp án B d' d A O B B' A' Thật vậy, ,
A B Î d . Qua phép đối xứng tâm O Ï d ta được ảnh là A ,¢ B¢Îd , AB ! A B ¢ ¢ . 1
Ví dụ 15: Mệnh đề nào sau đây là sai:
A. Hình gồm hai đường thẳng cắt nhau có một tâm đối xứng.
B. Hình vuông có một tâm đối xứng.
C. Hình gồm hai đường tròn bằng nhau có một tâm đối xứng.
D. Đường elip có vô số tâm đối xứng. Lời giải: Đáp án D
Đường elip có một tâm đối xứng.
Ví dụ 16: Cho đường thẳng d và hai điểm ,
A B nằm cùng phía với d . Gọi A đối xứng với A , B đối 1 1
xứng với B qua d . M là điểm trên d thỏa mãn MA + MB nhỏ nhất. Chọn mệnh đề sai:
A. Góc giữa AM và d bằng góc giữa BM và d .
B. M là giao điểm của A B và d . 1
C. M là giao điểm của AB và d . 1
D. M là giao điểm của AB và d. Lời giải: Đáp án D B A d M A1 B1 Với N
" Îd : A N + BN ³ A B do A N = AN, A M = AM 1 1 1 1
Þ AN + BN = A N + BN ³ A B = A M + MB = AM + MB. 1 1 1
Đẳng thức xảy ra khi M º N . Vậy A B Ç d . 1
Ví dụ 17: Với mọi tứ giác ABCD , kí hiệu S là diện tích tứ giác ABCD . Chọn mệnh đề đúng: 1 1
A. S = ( A .
B CD + BC.AD)
B. S £ ( A .
B CD + BC.AD) 2 2 1 C. S > .
AB CD + BC.AD
D. S ³ ( A .
B CD + BC.AD) . 2 Lời giải: Đáp án B. Trang 25 B A C D D' 1
Sử dụng phép đối xứng trục qua đường trung trực AC Þ S £ A .
B AC . Gọi D¢ đối xứng ABC 2
với D qua trung trực của AC Þ S = S = + ¢ S ¢ S ABCD ABCD BAD BCD¢ 1 1 Do S £ ¢ £ ¢ ¢ A . B AD , S ¢ BC.CD ABD 2 BCD 2 1 1 Þ 1 S £ A .
B AD¢ + BC.CD¢ = ( .
AB CD + BC.AD) ABCD 2 2 2
Ví dụ 18: Cho hai điểm ,
A B phân biệt. Gọi S , S là phép đối xứng qua ,
A B . Với điểm M bất kì, gọi A B M = S M M = S M F M M 2 B ( 1 ) 1 A ( ), . Gọi
là phép biến hình biến thành . Chọn mệnh đề 2 đúng:
A. F không là phép dời hình
B. F là phép đối xứng trục.
C. F là phép đối xứng tâm.
D. F là phép tịnh tiến. Lời giải: Đáp án D M1 A B M M2 !!!" !!!!" !!!!" !!!!"
Ta có: MA = AM , M B = BM . 1 1 2 !!!!!" !!!" !!!!" !!!!" !!!!" !!!!" !!!!" !!!!" !!!!" !!!!" !!!!" !!!"
MM = MA+ AM + M B + BM = AM + AM + M B + M B = 2AM + 2M B = 2AB . Vậy F 1 1 1 2 1 1 1 1 1 1 !!!"
là phép tịnh tiến theo vectơ 2AB .
Ví dụ 19: Cho ABC D
và đường tròn tâm O . Trên đoạn AB , lấy điểm E sao cho BE = 2AE , F là
trung điểm của AC và I là đỉnh thứ tư của hình bình hành AEIF . Với mỗi điểm P trên (O) !!" !!!" !!!" !!"
ta dựng điểm Q sao cho PA + 2PB + 3PC = 6IQ . Khi đó tập hợp điểm Q khi P thay đổi là:
A. Đường tròn tâm O¢ là ảnh của đường tròn (O) qua Đ . I
B. Đường tròn tâm O¢ là ảnh của đường tròn (O) qua Đ E
C. Đường tròn tâm O¢ là ảnh của đường tròn (O) qua phép đối xứng tâm Đ F
D. Đường tròn tâm O¢ là ảnh của đường tròn (O) qua phép đối xứng tâm Đ . B Lời giải: Đáp án A !!!" !!!" !!!" "
Gọi K là điểm xác định bởi KA+ 2KB +3KC = 0 . !!!" !!!" !!!" !!!" !!!" " !!!" 1 !!!" 1 !!!"
Khi đó KA + 2(KA+ AB) + 3(KA+ AC) = 0 Û AK = AB + AC . 3 2 Trang 26 !!" !!!" !!!" 1 !!!" 1 !!!"
Mặt khác AEIF là hình bình hành nên AI = AE + AF = AB + AC nên K º I . 3 2 !!!" !!!" !!!" !!!" !!" !!!" !!" !!" !!"
Từ giả thiết Þ 6PK + (KA+ 2KB + 3KC) = 6IQ Û PK = IQ hay PI = IQ Þ Đ P = Q Þ P (O) Q (O¢) (O) I ( ) khi di động trên
thì di động trên đường là ảnh của qua
phép đối xứng tâm I .
DẠNG 2. TÌM ẢNH CỦA ĐIỂM, ĐƯỜNG THẲNG QUA PHÉP ĐỐI XỨNG TRỤC, ĐỐI XỨNG
TÂM BẰNG PHƯƠNG PHÁP TỌA ĐỘ Phương pháp:
1. Xác định ảnh của một điểm qua phép đối xứng trục, đối xứng tâm.
- Sử dụng biểu thức tọa độ.
2. Xác định ảnh D¢ của đường thẳng D qua hình qua phép đối xứng trục, đối xứng tâm.
Cách 1: Chọn hai điểm ,
A B phân biệt trên D , xác định ảnh A ,¢ B¢ tương ứng qua phép đối xứng trục, đối
xứng tâm. Đường thẳng D¢ cần tìm là đường thẳng qua hai ảnh A ,¢ B¢. Cách 2:
Dựa vào vị trí tương đối của đường thẳng D và trục đối xứng để tìm ảnh D¢ .
Áp dụng tính chất phép đối xứng tâm biến đường thẳng D thành đường thẳng D¢ song song hoặc trùng với nó.
Cách 3: Sử dụng quỹ tích
Với mọi điểm M ( ;
x y)ÎD qua phép đối xứng trục hoặc đối xứng tâm sẽ biến M thành M¢(x ;¢ y¢) ¢ ÎD .
Từ biểu thức tọa độ rút x, y thế vào phương trình đường thẳng D ta được phương trình đường thẳng ảnh D¢ .
3. Xác định ảnh của một hình H (đường tròn, elips, parabol..)
Sử dụng quỹ tích: với mọi điểm M ( ;
x y) thuộc hình H , qua phép đối xứng trục hoặc đối xứng tâm sẽ
biến M thành M ¢(x ;¢ y¢) thì M ¢ thuộc ảnh H ¢ của hình H .
Với đường tròn áp dụng tính chất phép đối xứng trục hoặc đối xứng tâm biến đường tròn thành đường
tròn có cùng bán kính hoặc sử dụng quỹ tích.
Ví dụ 1. Trong mặt phẳng tọa độ Oxy , cho phép biến hình F : M ( ; x y) ® M¢( ; y x) . Chọn mệnh đề đúng:
A. F là phép đối xứng trục Oy .
B. F là phép đối xứng trục Ox .
C. F là phép đối xứng với trục đối xứng là đường phân giác của góc phần tư thứ nhất.
D. F là phép đối xứng trục với trục là đường phân giác của góc phần tư thứ hai. Lời giải: Đáp án C y a y' M' y=x y M O x 1 x x' Trang 27
Ví dụ 2. Trong mặt phẳng tọa độ Oxy , cho phép đối xứng trục Đ , với a là đường thẳng có phương a
trình: 2x - y = 0. Lấy A(2;2); Đ A a (
) thành điểm có tọa độ bao nhiêu? æ ö æ 2 14 ö æ14 2 ö A. ( 2; - 1 1 2) . B. ; . C. ; . D. ; . ç ÷ ç ÷ ç ÷ è 2 2 ø è 5 5 ø è 5 5 ø Lời giải: Đáp án C y a y' M' y M O x 1
æ x + 2 y + 2 ö Ta có ß ( ) A = ¢ A ( ; x y H AA¢ Þ H ; a ). Gọi là trung điểm ç ÷ è 2 2 ø ! !!!" ! n = (2;- )
1 là vectơ pháp tuyến của a , AA 'và n cùng phương và H Î a
(ìx - 2).1+ 2( y - 2) = 0 ì 2 = ï ìx + 2y = 6 x ï Þ ï í Û 5 í Û í x + 2 y + 2 ï2. - = 0 î2x - y = 2 - 14 î ï 2 2 y = ïî 5
Ví dụ 3. Trong mặt phẳng tọa độ Oxy , cho A( 1
- ;3). Tìm ảnh của A qua phép đối xứng tâm O. A. A'( 1 - ; 3 - ) . B. A'( 1 - ; ) 3 . C. A'(1; 3 - ) . D. A'(1;3) . Lời giải: Đáp án C ìx' =1
Ta có: Đ A = A Þ í Þ A - O ( ) ' '(1; 3). îy = 3 -
Ví dụ 4. Trong mặt phẳng tọa độ Oxy , phép đối xứng tâm I biến A(1;3) thành A'(5; )
1 thì I có tọa độ là: A. I (6;4) . B. I (4; 2 - ) . C. I (12;8) . D. I (3;2) . Lời giải: Đáp án D
ìx = 2x - x ìx = 3 Ta có: A' I A I í Þ í
y = 2y - y y = 2 î A' I A î I
Ví dụ 5. Trong mặt phẳng tọa độ Oxy , cho hai điểm M (1;3) và M '( 1 - ; )
1 .Phép đối xứng trục Đ biến a
điểm M thành M ' có trục a có phương trình:
A. x - y + 2 = 0 .
B. x - y - 2 = 0 .
C. x + y + 2 = 0 .
D. x + y - 2 = 0 . Lời giải: Đáp án D Trang 28 a A x; ( y) M' M
Ta có: a là trung trực của MM ' Gọi A(x y) 2 2
; Îa Û AM = AM '
Û (x - )2 +( y - )2 = (x + )2 +( y - )2 1 3 1
1 Û x + y - 2 = 0
Ví dụ 6. Trong mặt phẳng tọa độ Oxy , cho đường thẳng d : x - y - 2 = 0. Ảnh của d qua phép đối xứng
trục tung có phương trình:
A. x - y + 2 = 0 .
B. x + y + 2 = 0 .
C. x + y - 2 = 0 .
D. x + 2y - 2 = 0 . Lời giải: Đáp án B Lấy M ( ; x y) Þ M '(- ;
x y) đối xứng với M qua Oy .
Vậy ảnh của d qua phép đối xứng trục tung là:
-x - y - 2 = 0 Þ x + y + 2 = 0
Ví dụ 7. Trong mặt phẳng tọa độ Oxy , cho hai đường thẳng l : y - 2 = 0 , d : x + 2y + 2 = 0. Gọi d ' là
ảnh của d qua phép đối xứng trục l . Phương trình của d ' là:
A. x - 2y +10 = 0 .
B. x + 2y +10 = 0 .
C. x - 2y -10 = 0 .
D. x + 2y -10 = 0 . Lời giải: Đáp án A y y M' y=2 y1 M x 1 O x1 x Lấy M ( ;
x y) qua phép đối xứng trục l là M (x ; y 1 1 ) . ìx = x ìx = x Với 1 1 í Û í y = 4 - y y = 4 - y î 1 î 1
M Îd Û x + 2y + 2 = 0 Û x - 2y +10 = 0 1 1
Û M 'Î d ' có phương trình x - 2y +10 = 0
Ví dụ 8. Trong mặt phẳng tọa độ Oxy , cho đường thẳng D : x + y - 2 = 0 . Tìm ảnh D ' đối xứng với D
qua đường thẳng d : 3x + y - 4 = 0.
A. 7x - y + 6 = 0.
B. x - 7 y + 5 = 0.
C. 7x + y + 6 = 0.
D. 5x - 2y - 6 = 0. Lời giải: Đáp án A Trang 29 N d M N' ' ìx + y - 2 = 0 ìx =1 Xét hệ phương trình: í Û í
Þ D Ç d = M (1 ) ;1 3 î x + y - 4 = 0 îy =1 æ 4 2 ö
Chọn N (2;0)ÎD . Gọi N ' là ảnh của N qua Đ ta tìm được N ' ;- d ç ÷ è 5 5 ø !!!!!" æ 1 7 ö " Þ N 'M = ; Þ n = (7;- ç ÷
)1 là vectơ pháp tuyến của D'. è 5 5 ø
Vậy phương trình đường thẳng D ' là: 7x - y - 6 = 0
Ví dụ 20: Trong mặt phẳng tọa độ Oxy , ảnh của đường thẳng d : x + 2y - 3 = 0 qua phép đối xứng tâm I (4;3) là:
A. x + 2y -17 = 0.
B. x + 2y +17 = 0.
C. x + 2y - 7 = 0.
D. x + 2y -15 = 0 . Lời giải: Đáp án A.
Sử dụng phương pháp quỹ tích, ta có: ìx¢ = - x ìx = - x¢
Ð M x y ® M ¢ x¢ ¢ Þ í Þ d ( ) ( ) 8 8 : ; ; y í îy¢ = 6 - y îy = 6 - y¢
Thế vào phương trình d ta có: 8- x¢ + 2(6- y¢) -3 = 0 Û -x¢- 2y¢+17 = 0 Û x¢+ 2y -17 = 0.
Ví dụ 21: Trong mặt phẳng tọa độ Oxy , cho đường tròn (C) có phương trình: 2 2
x + y - 4x + 5y +1 = 0.
Tìm ảnh đường tròn (C¢) của (C) qua phép đối xứng trục Oy . A. 2 2
x + y - 4x - 5y +1 = 0. B. 2 2
x + y + 4x + 5y +1 = 0. C. 2 2
2x + 2y + 8x +10y - 2 = 0. D. 2 2
x + y + 4x - 5y +1 = 0. Lời giải: Đáp án B.
Phương pháp quỹ tích: từ biểu thức tọa độ Ð : M ( ;
x y) ® M¢(x ;¢ y¢ Î C¢ Oy ) ( ) ìx = -x¢ Þ í
Þ (-x¢)2 + ( y¢)2 + 4x¢+ 5y¢+1= 0. îy = y¢
Vậy phương trình đường tròn (C¢) là 2 2
x + y + 4x + 5y +1 = 0. ìx = -x¢
Study tip: Phép đối xứng trục Oy : Ð : M ( ;
x y) ® M¢(x ;¢ y¢ Î C¢ Þ í Oy ) ( ) îy = y¢
Ví dụ 22: Trong mặt phẳng tọa độ Oxy , cho đường tròn (C) có phương trình: 2 2
x + y - 4x - 2y - 4 = 0 .
Tìm ảnh đường tròn (C¢) của (C) qua phép đối xứng tâm I (1;3). A. 2 2
x + y -10x -16 = 0. B. 2 2
x + y -10y -16 = 0. C. 2 2
x + y -10y +16 = 0. D. 2 2
x + y - x -10y + 9 = 0. Lời giải: Đáp án C. Trang 30
Cách 1: Ð C = C¢ M ( ; x y) I I (( )) ( ): Với mọi
qua phép đối xứng tâm ta được ¢( ì ¢ = - = - ì = - ¢ ¢ y¢)Î(C¢) x 2x x 2 x x 2 x M x ; I Þ í Û í
. Thế vào (C) ta có:
y¢ = 2y - y = 6 - y î îy = 6 - y¢ I
( - x¢)2 +( - y¢)2 - ( - x¢)- ( - y¢)- = Û(x¢)2 +(y¢)2 2 6 4 2 2 6 4 0 -10y¢+16 = 0
Vậy đường tròn (C¢): 2 2
x + y -10y +16 = 0.
Cách 2: Đường tròn (C) có tâm M (2; )
1 , bán kính R = 3, Ð M = M ¢ Þ M ¢ I ( ) (0;5 .)
Vậy đường tròn (C¢): 2 2
x + y -10y +16 = 0. Trang 31 PHÉP QUAY A. LÝ THUYẾT 1. Định nghĩa.
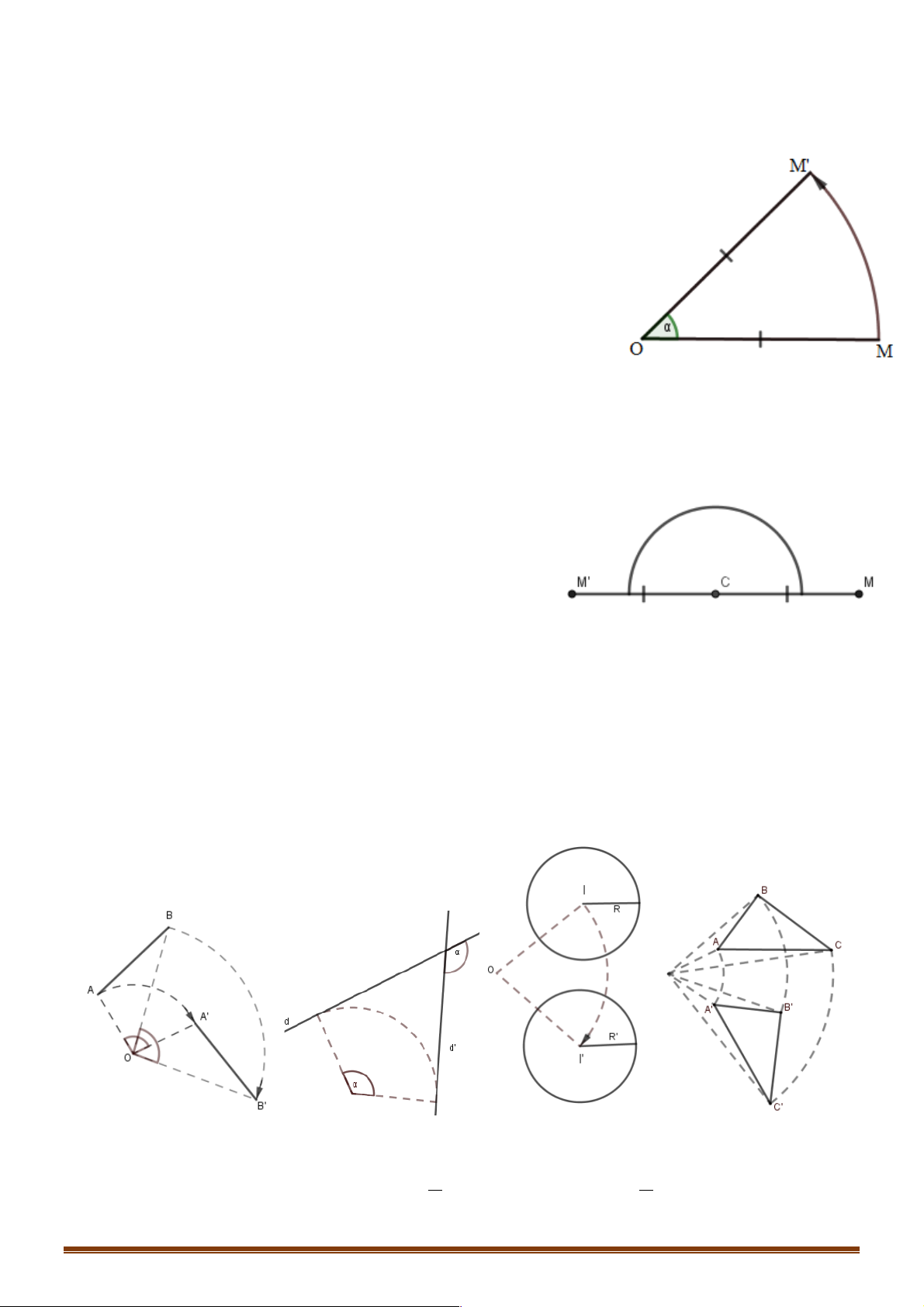
Trong mặt phẳng cho điểm O cố định và góc lượng giác a không đổi.
Phép biến hình biến mỗi điểm M
thành điểm M ¢ sao cho OM = OM ¢ và (OM,OM¢) =a được gọi là
phép quay tâm O góc quay a . Kí hiệu: Q
( O là tâm phép quay, a là góc quay lượng giác). (O,a) OM ì = OM¢ ï Q M = M ¢ Û í O,a ( ) ( ) (ïOM ,¢OM î ) =a Nhận xét:
• Chiều dương của phép quay là chiều dương của đường tròn lượng giác (chiều kim đồng hồ).
• Với k Î! ta luôn có: Phép quay: Q là phép đồng nhất; (O,2kp ) Q
là phép đối xứng tâm. (O,(2k+ )1p) ìx¢ = -y
Study tip: j = 90° Þ í îy¢ = x 2. Tính chất.
Tính chất 1: Phép quay bảo toàn khoảng cách giữa hai điểm bất kì.
Tính chất 1: Phép quay biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó,
biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.
Study tip. Phép quay biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự.
Nhận xét: Gọi a là góc của phép quay biến đường thẳng d thành đường thẳng d¢ : p p Q d = d¢ Þ (d,d¢) =a 0 £ a £ (d,d¢) =p -a < a < p O,a ( ) Góc nếu ; góc nếu . ( ) 2 2 Trang 32
3. Biểu thức tọa độ của phép quay
Trong mặt phẳng với hệ trục Oxy , xét phép quay Q (I,j)
Trường hợp 1: Khi tâm quay I trùng với gốc tọa độ O .
Đặt OM = r và góc ( , Ox OM ) =a Þ góc ( , Ox OM ¢) = a +j ìx¢ = r cos ï (a +j) Þ M ¢ : í ïy¢ = r sin î (a +j)
ìx¢ = xcosj - ysinj Hay M ¢ : í ( )1
îy¢ = xsinj + ycosj Nếu Q M ¢ ;
x y ® M x, y I , j - ( ) ( ) thì ( )
ìx = x¢cosj + y¢sinj M : í (2)
îy = -x¢sinj + y c¢osj Study tip: ìx¢ = -y • Nếu j = 90° Þ í îy¢ = x ìx¢ = y • Nếu j = 90 - ° Þ í îy¢ = -x ìx¢ = -x • Nếu j =180° Þ í îy¢ = -y
Trường hợp 2: Khi tâm quay I (x ; y 0 0 ). Ta có:
ìx¢ - x = x - x cosj - y - y sinj ï 0 ( 0 ) ( 0 ) í (3)
ïy¢ - y = x - x sinj + y - y cosj î 0 ( 0 ) ( 0 )
ìx - x = x¢ - x cosj + y¢ - y sinj ï 0 ( 0 ) ( 0 ) í (4)
ïy - y = - x - x sinj + y - y cosj î 0 ( 0 ) ( 0 ) Study tip: Q : M ;
x y ® M ¢ x ;¢ y¢ Þ 3 I ,j ( ) ( ) ( ) ( ) Q
: M ¢ x ;¢ y¢ ® M ; x y Þ 4 I ,-j ( ) ( ) ( ) ( )
B. CÁC DẠNG TOÁN VỀ PHÉP QUAY
DẠNG 1: KHAI THÁC ĐỊNH NGHĨA, TÍNH CHẤT VÀ ỨNG DỤNG PHÉP QUAY Phương pháp chung:
• Sử dụng định nghĩa hoặc tính chất của phép quay.
• Xác định ảnh của một điểm, một hình qua phép quay.
• Tìm quỹ tích điểm thông qua phép quay. Trang 33
• Các yếu tố liên quan đến phép quay là tam giác đều, tam giác cân, tam giác vuông… từ đó ứng dụng
phép quay để giải các bài toán hình học khác.
Ví dụ 1: Giả sử Q
M ® M ,¢Q N ® N¢ O,j ( ) O,j ( )
. Khi đó mệnh đề nào sau đây sai? ( ) ( ) !!!!" !!!!"
A. (OM ,OM¢) = j . B. ∑ ∑ MON = M O ¢ N¢.
C. MN = M N ¢ ¢ . D. MO D N = M D O ¢ N¢. Lời giải: Đáp án A. OM ì ¢ = OM ï Q M ® M ¢ Û í j O,j ( )
với là góc lượng giác. ( ) (ïOM,OM¢ î ) =j
Trong khi đó đáp án A: (OM ,OM ¢) = j (không là góc lượng giác)
Ví dụ 2: Có bao nhiêu điểm biến thành chính nó qua phép quay tâm O , góc quay a ¹ k2p , k Î! . A. Không có. B. Một. C. Hai. D. Vô số. Lời giải: Đáp án B. Q M ® M M º O O,a ( ) khi tâm quay. ( )
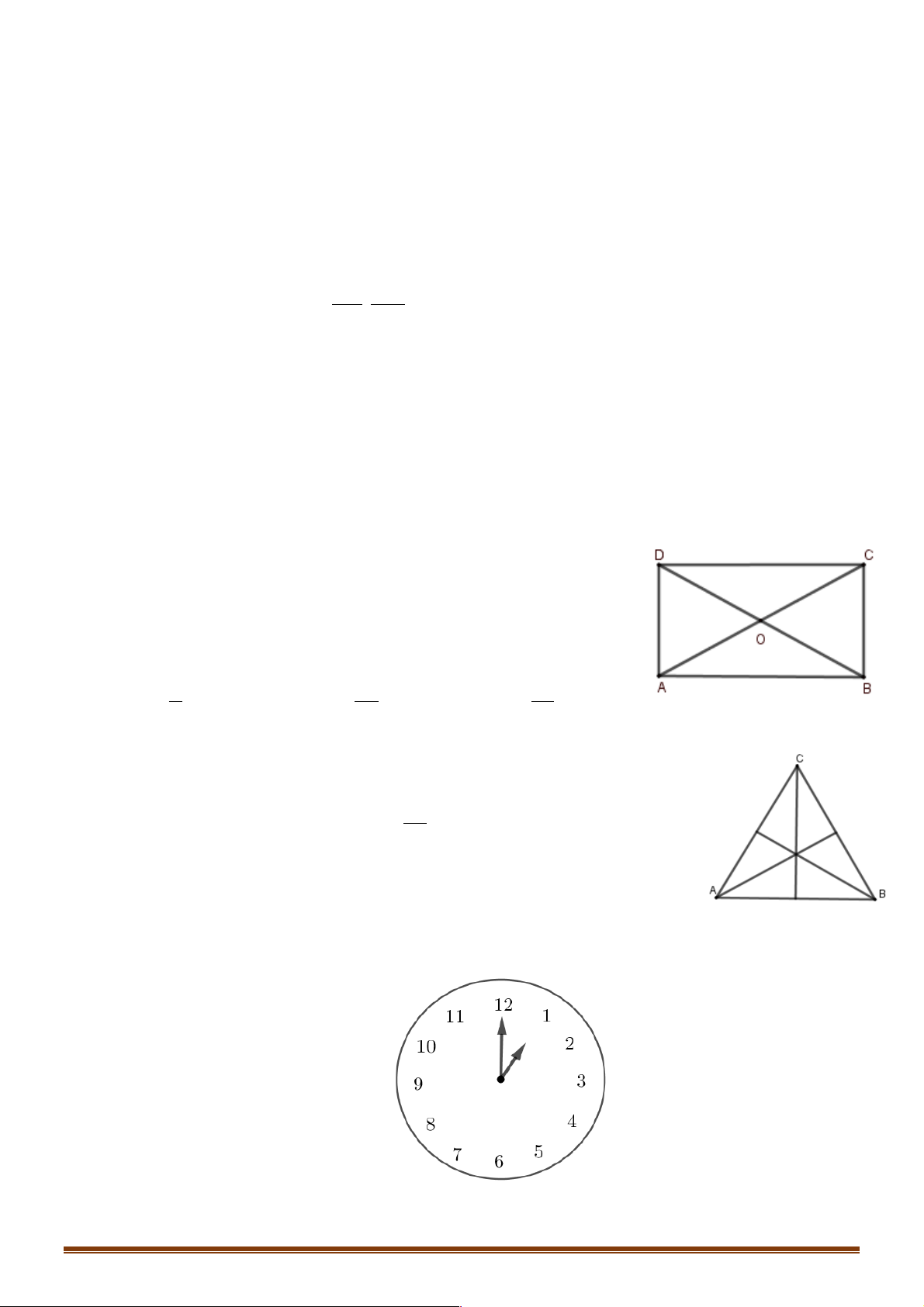
Ví dụ 3: Cho hình chữ nhật ABCD có tâm O . Hỏi có bao nhiêu phép quay tâm O , góc quay a ,
0 £ a £ 2p , biến hình chữ nhật thành chính nó? A. Không có. B. Một. C. Hai. D. Vô số. Lời giải: Đáp án C.
Khi góc quay a = 0 hoặc a = 2p thì phép quay biến hình chữ nhật thành chính nó.
Ví dụ 4: Cho tam giác đều ABC có tâm O . Phép quay tâm O , góc quay
j biến tam giác đều thành chính nó thì góc quay j là góc nào sau đây: p 2p 3p A. . B. . C. . D. . 3 3 2 Lời giải: Đáp án B. OA ì = OB ï Q A = B Û í p O,j ( ) 2 ( ) ( , OA OB) = j = ïî 3
Ví dụ 5: Chọn 12 giờ làm mốc, khi kim giờ chỉ một giờ đúng thì kim phút đã quay được một góc bao nhiêu độ? A. 360° . B. 360 - ° . C. 180 - ° . D. 720° . Lời giải: Trang 34 Đáp án B.
Khi kim giờ chỉ đến một giờ đúng thì kim phút quay được đúng một vòng theo chiều âm và được một góc là 360 - ° .
Study tip: Chiều dương của góc quay là chiều ngược chiều kim đồng hồ, chiều âm của góc
quay là chiều cùng chiều kim đồng hồ.
Ví dụ 6: Trong các chữ cái và số sau, dãy các chữ cái và số khi ta thực hiện phép quay tâm A , góc quay
180° thì ta được một phép đồng nhất ( A là tâm đối xứng của các chữ cái hoặc số đó). A. X , , L 6,1,U . B. , O Z,V ,9,5.
C. X , I,O,8,S.
D. H, J, K, 4,8. Lời giải: Đáp án C. Ta có: Q X = X ; Q I = I; Q O = ; O A,180° ( ) A,180° ( ) A,180° ( ) ( ) ( ) ( ) Q 8 = 8; Q S = S. A,180° ( ) A,180° ( ) ( ) ( )
Study tip: Phép biến hình H thành chính nó ta được phép đồng nhất.
Ví dụ 7: Cho hình vuông ABCD tâm O , M là trung điểm của AB , N là trung điểm của OA . Tìm ảnh
của tam giác AMN qua phép quay tâm O góc quay 90° . A. BM D N
¢ ¢ với M ,¢ N¢ lần lượt là trung điểm của BC,OB. B. CM D N
¢ ¢ với M ,¢ N¢ lần lượt là trung điểm của BC,OC . C. DM D N
¢ ¢ với M ,¢ N¢ lần lượt là trung điểm của DC,OD. D. DM D N
¢ ¢ với M ,¢ N¢ lần lượt là trung điểm của AD,OD. Lời giải: Đáp án D. Ta có: Q A = D O,90° ( ) ( ) Q M = M ¢ AD O,90° ( ) là trung điểm . ( ) Q N = N¢ OD O,90° ( ) là trung điểm . ( )
Ví dụ 8: Gọi I là tâm đối xứng của các hình ,
A B,C, D . Khi thực hiện phép quay tâm I góc quay 180°
thì hình nào luôn được phép đồng nhất? A. B. C. D. Lời giải: Đáp án C.
Từ hình C ta có qua phép Q
ta luôn được một hình là chính nó. (I,180°) Trang 35
Ví dụ 9: Cho hình vuông ABCD có cạnh 2 và có các đỉnh vẽ theo chiều dương. Các đường chéo cắt !!" !!!"
nhau tại I . Trên cạnh BC lấy BJ = 1. Xác định phép biến đổi AI thành BJ biết O là tâm quay. !!!" !!" !!!" !!" !!!" !!" !!!" !!" A. BJ = Q AI BJ = Q AI BJ = Q AI BJ = Q AI O, 1 - 35° ( ) O,135° ( ) O, 45 - ° ( ) O,45° ( ). B. . C. . D. . ( ) ( ) ( ) ( ) Lời giải: Đáp án A. AB 2 Ta có: AI = =
=1Þ AI = BJ lại có ( AI, BJ ) = 45° 2 2 Þ BJ = Q AI O AB O,45° (
) tâm là giao điểm của trung trực và cung ( ) !!!" !!" chứa góc 45° đi qua ,
A B Þ BJ = Q AI O,45° ( ). ( )
Ví dụ 10: Cho đường thẳng d và điểm O cố định không thuộc d , M là điểm di
động trên d . Tìm tập hợp điểm N sao cho tam giác MON đều.
A. N chạy trên d¢ là ảnh của d qua phép quay Q . (O,60°)
B. N chạy trên d¢ là ảnh của d qua phép quay Q . (O, 6 - 0°)
C. N chạy trên d¢ và d¢¢ lần lượt là ảnh của d qua phép quay Q và Q . (O,60°) (O, 6 - 0°)
D. N là ảnh của O qua phép quay Q . (O,60°) Đáp án C d'' O - 600 d' N 600 M 1 OM D
N đều Þ OM = ON và ∑ 0 NOM = 60
Vì vậy khi chạy trên d thì N chạy trên d ' là ảnh của d qua Q N d " 0 và chạy trên là ảnh (O,60 ) của d qua Q 0 . (O,-60 )
DẠNG 2. Xác định ảnh của điểm, đường thẳng qua phép quay bằng phương pháp tọa độ
Phương pháp chung:
1.Xác định ảnh của một điểm qua phép quay.
- Sử dụng biểu thức tọa độ trong các biểu thức đã nêu.
2. Xác định ảnh D ' của đường thẳng D qua phép quay.
Cách 1: Chọn hai điểm ,
A B phân biệt trên D , Xác định ảnh A', B ' tương ứng. Đường thẳng D ' cần tìm
là đường thẳng qua hai ảnh A', B ' . Trang 36
Cách 2: Áp dụng tính chất phép quay Q
biến đường thẳng D thành đường thẳng D ' có góc (O,a) ( ,
D D') =a hoặc p -a (đơn vị radian)
Cách 3: Sử dụng quỹ tích
- Với mọi điểm M ( ; x y)ÎD :Q
M = M ' x '; y ' M 'Î D ' O,a ( ) ( ) thì ( )
- Từ biểu thức tọa độ rút x, y thế vào phương trình đường thẳng D ta được phương trình ảnh D '
3. Xác định ảnh của một hình H (đường tròn, elip, parabol…)
- Sử dụng quỹ tích: Với mọi điểm M ( ;
x y) thuộc hình H , Q
M = M ' x '; y '
M '(x'; y ') O,a ( ) ( ) thì thuộc ( ) ảnh H' của hình H .
- Với đường tròn áp dụng tính chất phép quay biến đường tròn thành đường tròn có cùng bán kính hoặc sử dụng quỹ tích.
Ví dụ 1: Trong mặt phẳng tọa độ Oxy , Qua phép quay tâm O , góc quay 0
90 biến điểm M ( 3; - 5) thành điểm nào? A. (3;4) B. ( 5; - 3 - ) . C. (5; 3 - ) . D. ( 3; - 5 - ). Lời giải: Đáp án B ìx' = -y Q : M ;
x y ® M ' x '; y ' Þ í 0 (O,90 ) ( ) ( ) îy'= x ìx ' = 5 -
Cách 1: Dùng biểu thức tọa độ Þ M ' : í îy ' = 3 -
Cách 2: Vẽ biễu diễn tọa độ của điểm trên hệ trục Oxy Þ M '( 5 - ; ) 3 . 2 2 OM ì = OM ' ì ï ï 34 = x' + y ' ìx' = 5 -
Cách 3: Ta có Q
M = M ' Û í!!!!"!!!!!" Û í Þ í ( 0 O;90 ) ( ) OM ïî OM ' = 0 ïî 3 - x'+ 5y ' = 0 îy ' = 3 -
Nhận xét: Độc giả vận dụng cách 1 nhanh hơn, các cách 2 và cách 3 khá dễ hiểu nhưng dài hơn.
Ví dụ 2: Trong mặt phẳng tọa độ Oxy , cho điểm M (1; )
1 . Hỏi điểm nào sau đây là ảnh của điểm M
qua phép quay tâm O(0;0) , góc quay 0 45 ? A. M '(0; 2). B. M '( 2;0). C. M '(0; ) 1 . D. M '(1;- ) 1 . Lời giải: Đáp án A
ìx' = xcosj - ysinj Q : M ;
x y ® M ' x '; y ' Þ í 0 (O,90 ) ( ) (
) îy'= xsinj+ycosj ìx' = 0 ï
Cách 1: Theo biểu thức tọa độ: í Þ M '(0; 2) ïîy' = 2 Trang 37 xx '+ yy '
Góc giữa 2 vecto: cosj = 2 2 2 2
x + y . x ' + y ' OM ì = OM ' ï Cách 2: Q M ;
x y ® M ' x '; y ' Û= í 0 (O;45 ) ( ) ( ) (ïOM,OM ' î ) 0 = 45 2 2 2 2
ì 1 +1 = x' + y' 2 2 ï ìïx' + y' = 2 Û í x '+ y ' Û í 0 cos45 = ï ïîx'+ y ' = 2 2 2 2 x ' + y ' î
Giải hệ trên Þ M '(0; 2)
Ví dụ 3: Trong mặt phẳng tọa độ Oxy , cho đường thẳng d có phương trình 5x - 3y +15 - 0 . Tìm ảnh
d’ của d qua phép quay Q O 0 với là gốc tọa độ. ? (O,90 )
A. 5x - 3y + 6 = 0 .
B. 3x + 5y +15 = 0 .
C. 5x + y - 7 = 0. D. 3
- x + 5y + 7 = 0. Lời giải: Đáp án B d' A' B' d O A B
Cách 1: Chọn A(0;5)Îd , B( 3; - 0)Îd ' ( Q A = A' 5 - ;0 Îd ' 0 O,90 ) ( ) ( ) ( Q B = B ' 0; 3 - Îd ' 0 O,90 ) ( ) ( )
Đường thẳng d’ là đường thẳng ’ A ’
B :3x + 5y +15 = 0
Cách 2: Vì góc quay là 0
90 Þ d ^ d ' Þ d ' có dạng 3x + 5y + c = 0
Chọn A(0;5)Îd qua phép quay Q ’ A ( 5;
- 0)Îd ' Þ c = 5 1 0 ta được (O,90 )
Cách 3: Sử dụng quỹ tích
Với mọi điểm M ( ;
x y)Îd ta có Q
M = M ' x '; y ' Îd ' ( 0 O,90 ) ( ) ( ) Trang 38 ìx' = -y ìx = y '
Từ biểu thức tọa độ í Û í
.Thế x, y vào phương trình đường thẳng d ta được îy ' = x îy = -x ' d’ :
d ': 3x + 5y +15 = 0
Ví dụ 4: Trong mặt phẳng tọa độ Oxy , viết phương trình đường tròn ( ’ C ) là ảnh của (C) 2 2
: x + y - 2x + 4y - 4 = 0 qua phép quay Q . æ p ö O,- ç ÷ è 2 ø
A. (x + )2 +( y + )2 2 1 = 9.
B. (x - )2 +( y - )2 2 1 = 9.
C. (x - ) +( y + )2 2 2 3 1 = 9.
D. (x - )2 +( y + )2 1 2 = 9 . Lời giải: Đáp án A
Cách 1: Đường tròn (C) có tâm I (1; 2
- ), bán kính R = 3 . Q = Þ - - æ p ö ( I ) I ' I '( 2; ) 1 O,- ç ÷ è 2 ø
Đường tròn (C ') có tâm I '( 2 - ;- )
1 , bán kính R ' = R = 3 có phương trình: (x+ )2 +(y + )2 2 1 = 9
Cách 2: Phương pháp quỹ tích Ta có Q : M ® M
" Î(C) Þ M 'Î(C') æ p ö
( ;x y) M '(x'; y') với O,- ç ÷ è 2 ø ìx' = y ìx = -y '
Từ biểu thức tọa độ í Û í îy ' = -x îy = x '
Thế vào (C) (-y )2 +(x )2 : '
' + 2y '+ 4x'- 4 = 0
Û (x )2 + ( y )2 '
' + 4x '+ 2y '- 4 = 0
Û (x'+ 2)2 + ( y '+ )2 1 = 9
Ví dụ 5: Trong mặt phẳng tọa độ Oxy , cho các điểm A( 2; - ) 3 , ’
A (1;5) và B(5; 3 - ), ’ B (7; 2 - ). Phép quay tâm I ( ;
x y) biến A thành ’
A và B thành ’
B , ta có x + y bằng: A. 1 - . B. 2 C. 1 D. 3 - Lời giải: Đáp án D Q
A = A' Þ IA = IA' 1 O,a ( ) ( ) ( ) Q
B = B ' Þ IB = IB ' 2 O,a ( ) ( ) ( ) ì ï ( 2
- - x)2 + (3- y)2 = (1- x)2 + (5- y)2 Từ ( ) 1 và(2) Þ í ï (5- x)2 +( 3
- - y)2 = (7 - x)2 + (-2 - y)2 î Trang 39 ì 25 = ì6 + 4 =13 x x y ïï 2 Û í Û í Þ x + y = 3 - î4x +12y =19 31 ïy = - ïî 2
C. BÀI TẬP RÈN LUYỆN KỸ NĂNG
DẠNG 1: KHAI THÁC ĐỊNH NGHĨA, TÍNH CHẤT VÀ ỨNG DỤNG CỦA PHÉP QUAY
Câu 1: Cho 2 đường thẳng bất kì d và d’ . Có bao nhiêu phép quay biến đường thẳng d thành đường thẳng d’ ?
A. không có phép nào. B. có 1 phép duy nhất. C. chỉ có 2 phép. D. có vô phép số.
Câu 2: Cho hình vuông tâm O . Hỏi có bao nhiêu phép quay tâm O góc a , 0 £ a < 2p biến hình vuông thành chính nó ? A.1 . B. 2 . C.3 . D. 4.
Câu 3: Gọi d’ là hình ảnh của d qua tâm I góc quay j (biết I không nằm trên d ), đường thẳng d’ song với d khi: p p p A. j = . B. j = 2 . C. j = . D. j = p - . 3 6 3
Câu 4: Cho hai đường tròn cùng bán kính (O) và (O ') tiếp xúc ngoài nhau. Có bao nhiêu phép quay
góc 90° biến hình tròn (O) thành (O ')? A. 0 . B.1 . C. 2 . D. Vô số.
Câu 5: Cho hình lục giác đều ABCDE tâm O . Tìm ảnh của tam giác AOF qua phép quay tâm O góc quay 0 120 . A. O D AB . B. BO D C . C. DOC D . D. EO D D .
Câu 6: Chọn 12 giờ làm mốc, khi đồng hồ chỉ năm giờ đúng thì kim giờ đã quay được một góc bao nhiêu độ ? A. 0 270 . B. 0 360 - . C. 0 150 - . D. 0 135 .
Câu 7: Cho hai đường thẳng D và D biết Q
D = D . Mệnh đề nào sau đây đúng ? 1 2 ( 0 O - ) ( 1) 2 ; 120 A (D ,D =120 D D (D ,D = 1 - 20 (D ,D = 60 1 2 ) 0 1 2 ) 0 1 2 ) 0 . B. // . C. . D. . 1 2
Câu 8: Cho hai điểm phân biệt , A B và Q
B = C. Mệnh đề nào sau đây đúng ? ( 0 ;3 A 0 ) ( ) A. 0 ABC = 30 . B. 0 ABC = 90 . C. 0 ABC = 45 . D. 0 ABC = 75 .
Câu 9: Cho hai điểm phân biệt I, M và Q M = N I; 3 - 2p ( )
. Mệnh đề nào sau đây đúng ? ( )
A. M là trung điểm của đoạn IN .
B. N là trung điểm của đoạn IM .
C. I là trung điểm của đoạn MN .
D. M º N . Câu 10: Cho ABC D
đều (thứ tự các đỉnh theo chiều dương lượng giác). Kết luận nào sau đây sai ? A. Q = Q = Q C = B Q A = C æ 7p ö ( ) æ 7p ö ( ) æ p ö (C ) B æ p ö ( B) C . B. . C. . D. . A, ç ÷ A,- ç ÷ A, ç ÷ A,- ç ÷ è 3 ø è 3 ø è 3 ø è 3 ø
Câu 11: Gọi I là tâm hình vuông ABCD (thứ tự các đỉnh theo chiều dương lượng giác). Kết luận nào sau đây sai ? Trang 40 A. Q I D BC = I D CD. B. Q I D BC = I D AB . ( 0 I ,90 ) ( ) ( 0 I , 9 - 0 ) ( ) C. Q I D BC = I D DA. D. Q I D BC = I D DA. ( 0 I ,180 ) ( ) ( 0 I ,360 ) ( )
Câu 12: Gọi I là tâm ngũ giác đều ABCDE (thứ tự các đỉnh theo chiều dương lượng giác). Kết luận nào sau đây là sai ? A. Q
CD = EA. B. Q
AB = BC . C. Q
AB = DE . D. Q CD = BC. ( 0 I,144 ) ( ) ( 0 I,72 ) ( ) ( 0 I,144 ) ( ) ( 0 I,72 ) ( )
Câu 13: Gọi I là tâm lục giác đều ABCDEF (thứ tự các đỉnh theo chiều dương lượng giác). Kết luận nào sau đây là sai ? A. Q I D ED = I D BA. B. Q I D AB = I D BC . ( 0 I , 1 - 20 ) ( ) ( 0 I , 6 - 0 ) ( ) C. Q AB = BC . D. Q I D CD = I D FA. ( 0 I ,60 ) ( ) ( 0 I ,180 ) ( )
Câu 14: Cho hai tam giác vuông cân OAB và ’ OA ’
B có chung đỉnh O sao cho O nằm trên đoạn ’ AB
và nằm ngoài đoạn thẳng ’
A B . Gọi G và ’
G lần lượt là trọng tâm các tam giác O ’ AA và O ’
BB . Xác định dạng của tam giác ’ GOG A. cân. B. vuông. C. vuông cân. D. đều.
Câu 15: Cho 3 điểm A , B , C , điểm B nằm giữa A và C . Dựng về phía đường thẳng AC các tam
giác đều ABE và BCF . Gọi M và N lần lượt là trung điểm của AF và EC . Xác định dạng của BM D N . A. cân. B. vuông. C. vuông cân. D. đều.
Câu 16: Cho đường thẳng d và điểm O cố định không thuộc d . M là điểm di động trên d . Xác định
quỹ tích điểm N sao cho OM D N đều.
A. N Î d¢ với d¢ = Q d N Î d¢ d¢ = Q d O,180° ( ) O,60° ( ). B. với . ( ) ( )
C. N Î d¢ với d¢ = Q d N Î d¢ d¢ = Q d O, 1 - 20° ( ) O,120° ( ). D. với . ( ) ( )
Câu 17: Cho hình vuông ABCD , M Î BC , K Î DC sao cho ∑ ∑
BAM = MAK . Khi đó mệnh đề nào sau đây là đúng ?
A. AD = AK - KD .
B. AB = AM + DK . C. AK = BM + KD . D. AM = BM + AB . Câu 18: Cho ABC D
. Dựng về phía ngoài tam giác các hình vuông BCIJ , ACMN . Gọi O, P lần lượt là
tâm đối xứng của chúng, D là trung điểm của AB . Xác định dạng của DOP D . A. cân . B. vuông. C. vuông cân. D. đều.
DẠNG 2: XÁC ĐỊNH ẢNH CỦA ĐIỂM, ĐƯỜNG QUA PHÉP QUAY BẰNG PHƯƠNG PHÁP TỌA ĐỘ
Câu 19: Trong mặt phẳng tọa độ Oxy , cho điểm A( ;
x y). Biểu thức tọa độ của điểm A' = Q A ( 0 O,90 ) ( ) là: ìx ' = y ìx ' = - y ìx ' = - y ìx ' = y A. í . B. í . C. í . D. í . î y ' = -x î y ' = x î y ' = -x îy ' = x
Câu 20: Trong mặt phẳng tọa độ Oxy , cho điểm A( ;
x y) . Biểu thức tọa độ của điểm A' = Q A ( 0 O, 9 - 0 ) ( ) là: ìx ' = y ìx ' = - y ìx ' = - y ìx ' = y A. í . B. í . C. í . D. í . î y ' = -x î y ' = x î y ' = -x îy ' = x
Câu 21: Trong mặt phẳng tọa độ Oxy , cho điểm A( ;
x y) . Biểu thức tọa độ của điểm A' = Q A O,j ( ) ( ) là: Trang 41
ìx ' = x cosj - y sinj
ìx ' = x cosj + y sinj A. í . B. í .
îy ' = xsinj + y cosj
îy ' = xsinj - y cosj
ìx ' = xsinj - y cosj
ìx ' = x cosj - y sinj C. í . D. í .
îy ' = xsinj + y cosj
îy ' = x cosj + y sinj
Câu 22: Trong mặt phẳng tọa độ Oxy , cho điểm A(4; )
1 . Biểu thức tọa độ của điểm A' = Q A ( 0 O, 9 - 0 ) ( ) là: A. A( 1 - ;4). B. A(1; 4 - ). C. A(4;- ) 1 . D. A( 4; - - ) 1 .
Câu 23: Trong mặt phẳng tọa độ Oxy , cho điểm A( ;
x y) . Biểu thức tọa độ của điểm A' = Q A ( 0 O,60 ) ( ) là: ì 1 3 ì 1 3 ì 1 3 ì 1 3 ïx ' = x - y ïx ' = x - y ïx ' = x + y ïx ' = - x - y ï ï ï ï A. 2 2 2 2 2 2 2 2 í . B. í . C. í . D. í . ï 3 1 ï 3 1 ï 3 1 ï 3 1 y ' = x + y ï y ' = x - y y ' = x + y y ' = - x + y î 2 2 ïî 2 2 ïî 2 2 ïî 2 2
Câu 24: Trong mặt phẳng tọa độ Oxy , cho hình vuông ABCD tâm I (1;2), biết điểm A(4;5) . Khi đó
với B(x ; y C (x ; y D(x ; y x .x .x D D ) C C ) B B ) , , thì bằng: B C D A. 12. B. 8. C. 16. D. 32.
Câu 25: Trong mặt phẳng tọa độ Oxy , cho đường thẳng d : x + y +1 = 0 , điểm I (1; 2 - ), phép quay Q
d = d ' . Xác định phương trình đường thẳng d¢ . ( 0 O,90 ) ( )
A. -x + y - 2 = 0 .
B. x - y -1 = 0.
C. x - y + 3 = 0.
D. x - y - 3 = 0.
Câu 26: Trong mặt phẳng tọa độ Oxy , cho điểm A(0;3). Tìm tọa độ điểm ’
A là ảnh của A qua phép quay Q . ( 0 O,-45 ) æ 1 3 ö æ 3 1 ö æ 3 - 1 ö æ 3 3 ö A. A' ; . B. A' ; . C. A' ; . D. A' ; . ç ÷ ç ÷ ç ÷ ç ÷ è 2 2 ø è 4 4 ø è 2 2 ø è 2 2 ø
Câu 27: Trong mặt phẳng tọa độ Oxy , tìm phép quay Q biến điểm A( 1
- ;5) thành điểm A'(5; ) 1 A. Q A = A' . B. Q A = A' . C. Q
A = A' . D. Q A = A'. ( 0 O, 9 - 0 ) ( ) ( 0 O,90 ) ( ) ( 0 O,180 ) ( ) ( 0 O, 2 - 70 ) ( )
Câu 28: Trong mặt phẳng tọa độ Oxy , cho phép quay tâm O góc quay a biến điểm M ( ; x y) thành æ 1 3 3 1 ö
điểm M 'ç x - y;
x + y ÷ . Tìm a . ç 2 2 2 2 ÷ è ø p p p p A.a = . B. a = 2 . C. a = 3 . D. a = . 6 3 3 4
Câu 29: Trong mặt phẳng tọa độ Oxy , cho I (2; )
1 và đường thẳng d : 2x + 3y + 4 = 0. Tìm ảnh của d qua Q 0 (I,45 )
A. -x + 5y - 2 + 3 2 = 0 .
B. -x + 5y - 3 +10 2 = 0.
C. x - 5y + 3 + 2 = 0.
D. -x + 5y - 3 +11 2 = 0.
Câu 30: Trong mặt phẳng tọa độ Oxy , cho đường tròn (C) 2 2
:x + y + 6x + 5 = 0. Tìm ảnh đường tròn
(C¢) của (C) qua Q . ( 0 O,90 )
A. x + ( y - )2 2 3 = 4. B. (C) 2 2
:x + y + 6y - 6 = 0.
C. x + ( y + )2 2 3 = 4. D. (C) 2 2
:x + y + 6x -5 = 0. Trang 42
Câu 31: Trong mặt phẳng tọa độ Oxy , cho phép quay tâm O góc quay 0 45 Q . Tìm ảnh của ( 0 O,45 )
đường tròn (C) (x - )2 2 : 1 + y = 4. 2 2 æ 2 2 2 ö æ 2 ö æ 2 ö æ 2 ö A. ç x - ÷ + ç y - ÷ = 4 . B. ç x + ÷ + ç y + ÷ = 4. ç 2 ÷ ç 2 ÷ ç ÷ ç ÷ è ø è ø 2 2 è ø è ø 2 2 æ 2 ö æ 2 ö C. ç x - ÷ + ç y + ÷ = 4. D. 2 2
x + y + 2x + 2y - 2 = 0. ç 2 ÷ ç 2 ÷ è ø è ø
Câu 32: Trong mặt phẳng tọa độ Oxy , viết phương trình các cạnh AB, BC của DABC biết A(1;2 , ) 2 3 B(3;4 ) và cos A = ,cos B = . 5 10
A. AC :x - y -1 = 0, BC :x - y + 5 = 0.
B. AC :3x - y - 2 = 0, BC :x - 2y + 3 = 0.
C. AC :3x - y -1 = 0, BC :x - 2y + 5 = 0.
D. AC :3x - y - 4 = 0, BC :x - 2y + 2 = 0 .
D. HƯỚNG DẪN GIẢI CHI TIẾT
DẠNG 1: KHAI THÁC ĐỊNH NGHĨA, TÍNH CHẤT VÀ ỨNG DỤNG PHÉP QUAY Câu 1: Đáp án D. Câu 2: Đáp án D.
Thật vậy, các phép quay biến hình vuông thành chính nó: Q ,Q ,Q ,Q . ( 0 O ) ( 0 O ) ( 0 O ) ( 0 ,0 ,90 ,180 O,270 ) Câu 3: Đáp án D.
Khi j = -p , phép quay trở thành phép đối xứng tâm I Þ d / /d¢. Câu 4: Đáp án B. (O') O I I 1 2 I
Gọi I là tâm của phép quay, I , I là tâm các đường tròn (O) và (O¢). 1 2 ìII = II ï 1 2 Q I = I Û í
. Vậy chỉ có 1 phép quay thỏa mãn. ( 0 I ,90 ) ( 1 ) 2 ( ï II , II = 90 î 1 2 ) 0 Câu 5: Đáp án D. Q A = E , Q F = D , Q
O = O Þ Q A D OF = E D OD. ( 0 O,120 ) ( ) ( 0 O,120 ) ( ) ( 0 O ) ( ) ( 0 ,120 O,120 ) ( ) Câu 6: Đáp án C.
Khi kim giờ chỉ đến năm giờ đúng thì kim giờ quay được đúng 0 150 - tức theo chiều âm. Trang 43 Câu 7: Đáp án D.
Vì góc quay 1200 nên góc giữa hai đường thẳng là: 1800 – 1200 = 600 Câu 8: Đáp án D. Câu 9: Đáp án D. Câu 10: Đáp án C. Câu 11: Đáp án D. Câu 12: Đáp án C. Câu 13: Đáp án B. Câu 14: Đáp án C. B A' G' G B' A O ì ï ( Q A = B 0 O,90 ) ( ) í Þ Q O D AA¢ = O D BB¢ Þ Q G = G¢ OG = OG¢ 0 0 . Do đó và O,90 O,90 ïî (Q A¢ = B¢ 0 O,90 ) ( ) ( ) ( ) ( ) ( ) ∑ 0 GOG¢ = 90 Câu 15: Đáp án D. F E M N A C B
Phép quay tâm B góc quay 0
60 biến các điểm E,C lần lượt thành ,
A F biến đoạn EC thành
AF nên biến trung điểm N của EC thành trung điểm M của AF Þ BN = BM và (BN BM ) 0 , = 60 Þ BM D N đều.
Câu 16: Đáp án A. O d 60o M N
Vì DOMN đều và O cố định Þ N = Q M . ( 0 O,60 ) ( ) Câu 17: Đáp án C. Trang 44 M' 1 D A 2 3 1 K 1 B M C Ta có: Q :B ® ; D Q
:M ® M ¢ Þ Q
:BM ® DM ¢ Þ BM = DM ¢ 0 0 0 . (A,90 ) (A,90 ) (A,90 )
Vậy, BM + KD = DM ¢ + KD .
Cần chứng minh: M ,¢ D, K thẳng hàng và AKM D
¢ cân tại K Þ DM ¢ + KD = KM ¢. Thật vậy: Q
BM = DM ¢ Þ BM ^ DM ¢ Þ ^ ¢ ∑ 0 BM // AD
AD DM Þ ADM¢ = 90 0 . Mà ( ,9 A 0 ) ( )
M ,¢ D, K thẳng hàng. Ta có: D ®D ¢ ∂ ∂ Q : ABM
ADM Þ M = M ¢ . ( 0 A ) 1 1 ,90 Có: ∑¢ ! 0 ∑ + = Þ ¢ ! 0 M AK A 90
M AK + A = 90 (do ! ! A = A ) ∑ Þ ¢ ∂
M AK = M Þ A
D KM cân tại K 1 3 1 3 1
Þ KM ¢ = KD + DM ¢ = KA Þ KD + BM = AK Câu 18: Đáp án C. Ta có: Q :M ® ;
A B ® I Þ Q
:MB ® AI Þ MB = AI 0 0 . (C,90 ) (O,90 ) N M ì 1 P
DP // BM , DP = BM ï A ï Mà 2 í
Þ DO = DP và DO ^ DP C D 1
ïDO // AI,DO = AI ïî 2 B Þ DOP D là tam giác vuông cân. O I J
DẠNG 2: XÁC ĐỊNH ẢNH CỦA MỘT ĐIỂM HOẶC MỘT HÌNH QUA PHÉP QUAY BẰNG
PHƯƠNG PHÁP TỌA ĐỘ Câu 19: Đáp án B. Câu 20: Đáp án A. Câu 21: Đáp án A. Trang 45 Câu 22: Đáp án B. Câu 23: Đáp án A.
Vận dụng biểu thức tọa độ của phép quay tâm O và góc quay j ta được đáp án A . Câu 24: Đáp án C. Ta có: Q
A = B Þ B 2;
- 5 . I là trung điểm AC Þ C ( 2; - - )
1 ; I là trung điểm ( BD 0 I ,90 ) ( ) ( ) Þ D(4;- ) 1
Þ x .x .x =16. B C D Câu 25: Đáp án D.
Ta có: I Î d Þ I Î d¢ Đường thẳng d
¢ có dạng: x - y + c = 0. Vì d¢ đi qua I nên 1+ 2 + c = 0 Þ c = 3
- Þ d¢:x - y - 3 = 0 Câu 26: Đáp án D. æ 3 3 ö
Áp dụng biểu thức tọa độ Þ A¢ ; ç ÷ è 2 2 ø Câu 27: Đáp án A. OA ìï = OA¢ = 26 Ta có: í!!!" !!!" Þ Q A = A¢ ( 0 , 90 - ) ( ) ïî . OA OA¢ = 0 O
(Do A nằm ở góc phần tư thứ hai, A¢ nằm ở góc phần tư thứ nhất) Câu 28: Đáp án B. ìx¢ = . x cos a - . y sin a p
Theo biểu thức tọa độ: í
. Do giá trị tọa độ M ¢ Þ a = îy¢ = . x sin a + . y cos a 3 Câu 29: Đáp án D. Chọn 2 điểm M ( 2; - 0), N (1; 2
- )Îd . Gọi M¢(x ; y N¢(x ; y M , N 2 2 ) 1 1 ) và là ảnh của qua Q
0 . Áp dụng biểu thức tọa độ: (I,45 )
ìx¢ - x = x - x cosj - y - y sin j ï æ ö 0 ( 0 ) ( 0 ) 3 2 5 2 í Þ M ¢ç2 - ;1- ÷, N¢ ç ÷ (2+ 2;1-2 2)
ïy¢ - y = x - x sin j + y - y cosj 2 2 î 0 ( 0 ) ( 0 ) è ø !!!!!" æ 5 2 2 ö Þ M N ¢ ¢ = ç ; ÷ ç 2 2 ÷ è ø ! Gọi d¢ = Q
d Þd¢ đi qua M ,¢ N¢ và có vtcp u = (5; )
1 Þ d¢ :- x + 5y - 3 +11 2 = ( 0. 0 I ,45 ) ( ) Câu 30: Đáp án C.
Đường tròn (C) có tâm I ( 3;
- 0) và bán kính R = 2. Q
I = I¢ ÞI¢ 0; 3 - . ( 0 O,90 ) ( ) ( )
Phương trình đường tròn (C¢) x +( y + )2 2 : 3 = 4. Câu 31: Đáp án A. Trang 46
Đường tròn (C) có tâm I (1;0) và bán kính R = 2 . ì 2 0 ïx¢ =1.cos 45 = ï 2 Q
I = I¢ x ;¢ y¢ Þ í 0 . (O,45 ) ( ) ( ) ï 2 0 y¢ = 1.sin 45 = ïî 2 2 2 æ 2 ö æ 2 ö
Phương trình đường tròn: ç x - ÷ + ç y - ÷ = 4 ç 2 ÷ ç 2 ÷ è ø è ø Câu 32: Đáp án C.
Sử dụng tính chất của phép quay tâm I ( ;
a b)Îd :Ax + By +C = 0 thành
d¢ :( A- B tan j)(x - a) +( Atan j+ B)( y -b) = 0. Khi đó ta được phương trình:
AC :3x - y -1 = 0, BC :x - 2y + 5 = 0 Trang 47
PHÉP DỜI HÌNH VÀ HAI HÌNH BẰNG NHAU A. LÝ THUYẾT 1. Định nghĩa.
Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kỳ. Nhận xét:
- Các phép Đồng nhất, tịnh tiến, đối xứng tâm, đối xứng trục và phép quay là những phép dời hình
- Phép biến hình có được bằng cách thực hiện liên tiếp hai phép dời hình cũng là một phép dời hình. 2. Tính chất. Phép dời hình:
- Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bào toàn thứ tự giữa chúng
- Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng bằng nó
- Biến tam giác thành tam giác bằng nó, biến góc thành góc bằng nó
- Biến đường tròn thành đường tròn có cùng bán kính
3. Hai hình bằng nhau
Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia
B. CÁC BÀI TOÁN VỀ PHÉP DỜI HÌNH Ví dụ 1:
Phép biến hình nào sau đây là một phép dời hình?
A. Phép biến mọi điểm M thành điểm M
¢ sao cho O là trung điểm MM ,
¢ với O là điểm cố định cho trước.
B. Phép chiếu vuông góc lên đường thẳng d.
C. Phép biến mọi điểm M thành điểm O cho trước.
D. Phép biến mọi điểm M thành điểm M
¢ là trung điểm của đoạn OM , với O là một điểm cho trước. Lời giải: Đáp án A Với mọi điểm ,
A B tương ứng có ảnh A ,¢ B
¢ qua phép biến hình với quy tắc O là trung điểm
tương ứng Þ AB = A¢B¢ Þ Đây là phép dời hình. Ví dụ 2:
Xét hai phép biến hình sau, đâu là phép dời hình?
(I) Phép biến hình F :M x ; y ® M ¢ -y ; x 1 1 ( 1 1 ) 1 ( 1 1 )
(II) Phép biến hình F :M x ; y ® M ¢ 2x ;2y 2 2 ( 2 2 ) 2 ( 2 2 )
A. Chỉ phép biến hình (I).
B. Chỉ phép biến hình (II).
C. Cả hai phép biến hình (I) và (II).
D. Cả hai phép biến hình (I) và (II) đều không là phép dời hình. Trang 48 Lời giải: Đáp án A
Chọn hai điểm M (x ; y ), N (x ; y M M N N ) bất kỳ. Xét phép biến hình (I) có:
F M = M ¢ -y ; x
; F N = N¢ -y ; x Þ MN = M N ¢ ¢ = x - x + y - y 1 ( ) ( M M ) 1( ) ( N N )
( M N )2 ( M N )2
Xét tương tự với phép biến hình (II) không là phép dời hình. Ví dụ 3:
Cho hình vuông tâm O . Gọi M , N, ,
P Q lần lượt là trung điểm của các cạnh AB, BC,CD, DA
. Phép dời hình nào sau đây biến tam giác AMO thành tam giác CPO ? !!!!"
A. Phép tịnh tiến theo véc tơ AM .
B. Phép đối xứng trục MP .
C. Phép quay tâm O góc quay 0 180 .
D. Phép quay tâm O góc quay 0 - 180 . Lời giải: Đáp án D ì M ï ( Q A = C A 0 B O; 1 - 80 ) ( ) ï Ta có: Q í
M = P Þ Q : A D MO ® CP D O ( 0 O; 1 - 80 ) ( ) ( 0 O; 1 - 80 ) ï Q ï O N î ( Q O = O 0 O; 1 - 80 ) ( ) D C P Ví dụ 4:
Cho hai hình bình hành. Hãy chỉ ra một đường thẳng chia hai hình bình hành đó thành hai phần bằng nhau.
A. Đường thẳng đi qua hai tâm của hai hình bình hành.
B. Đường thẳng đi qua hai đỉnh của hai hình bình hành.
C. Đường thẳng đi qua tâm của hình bình hành thứ nhất và một đỉnh của hình bình hành còn lại.
D. Đường chéo của một trong hai hình bình hành đó. Lời giải: Đáp án A Ví dụ 5:
Trong mặt phẳng tọa độ Oxy , cho các điểm A( 3;
- 2), B(4;5),C( 1 - ;3). Gọi A D B C là ảnh 1 1 1 của ABC D
qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc ! 0
- 90 và phép tịnh tiến theo véc tơ v = (0 )
;1 . Khi đó tọa độ các đỉnh của A D B C là: 1 1 1
A. A 1;2 , B 1 - ;4 ,C 3;5 A 2; 3 - , B 5; 4 - ,C 3; 1 - 1 ( ) 1( ) 1( ) 1 ( ) 1( ) 1( ). B. . C. A 5; 4 - , B 2; 3 - ,C 3; 1 - A 2;4 , B 5; 3 - ,C 3;2 1 ( ) 1( ) 1( ) 1 ( ) 1( ) 1( ). D. . Lời giải: Đáp án D Q : A D BC ® A D B ¢ C
¢ ¢ Þ A¢ 2;3 , B¢ 5; 4 - ,C¢ 3;1 ( 0 O;90 ) ( ) ( ) ( ) Trang 49 T! : A D B ¢ C ¢ ¢ ® A
D B C Þ A 2;4 , B 5; 3 - ,C 3;2 v 1 1 1 1 ( ) 1( ) 1( ) Ví dụ 6:
Trong mặt phẳng tọa độ Oxy , cho đường thẳng d :3x + y + 3 = 0. Viết phương trình đường !
thẳng d¢ là ảnh của d qua phép tịnh tiến theo véc tơ v ( 2 - )
;1 và phép quay tâm O góc quay 0 180 . A. 6
- x - 2y - 7 = 0 . B. 3
- x - y + 8 = 0.
C. 3x + y - 6 = 0.
D. 6x + 2y -15 = 0. Lời giải: Đáp án B.
T! (d ) = d¢ Þd¢ :3x + y +8 = 0; v Q
d¢ = d¢Þd¢ là ảnh của d¢¢ qua phép đối xứng tâm O . ( 0 O;180 ) ( )
Þd¢:-3x - y + 8 = 0
Lời giải: Tr (d)= d ', Q d = d ' fi d ' 3x + y + c = 0 0 ( ) có dạng . v (O,180 ) Chọn M(0;- ) 3 d Œ fi Tr (M)= M '(- 2;- 2) d
Π' fi c = 8 fi d ': 3x + y + 8 = 0 v
fi Đường thẳng d ' :- 3x - y + 8 = 0 .
Ví dụ 7: Nếu thực hiện liên tiếp hai phép quay cùng tâm Q và phép Q thì kết quả là: (O,j 1) (O,j 2)
A. một phép đồng nhất.
B. phép tịnh tiến.
C. phép quay tâm O góc quay j + j .
D. phép quay tâm O góc quay là j + j . 1 2 1 2 Lời giải:: Gọi M ' = Q M M ' = Q M ' O,j ( ) O,j ( , ) ( 1) ( 2 ) Ta có: OM' = OM,(OM,OM ) ' = j và OM' = OM',(OM',OM') ' = j 1 2 fi OM ' = OM và (OM', ) OM = j + j hay Q M = M ' O,j + j ( ) . 1 2 ( 1 2 )
C. BÀI TẬP RÈN LUYỆN KỸ NĂNG
Câu 1: Phép biến hình nào sau đây là một phép dời hình?
A. Phép đồng nhất.
B. Phép chiếu lên một đường thẳng.
C. Phép biến mọi điểm M thành điểm O cho trước.
D. Phép biến mọi điểm M thành điểm là trung điểm của đoạn OM với O là điểm cho trước.
Câu 2: Phép biến hình F là phép dời hình khi và chỉ khi:
A. F biến đường thẳng thành đường thẳng song song với nó.
B. F biến đường thẳng thành chính nó.
C. F biến đường thẳng thành đường thẳng cắt nó.
D. F biến tam giác thành tam giác bằng nó.
Câu 3: Cho hai phép biến hình: F :M x; y Æ M' x + 1; y- 3 F :M x; y Æ M' - y;x 2 ( ) ( ) 1 ( ) ( , ) . Phép biến
hình nào trong hai phép biến hình trên là phép dời hình.
A. Chỉ phép biến hình F . 1
B. Chỉ phép biến hình F . 2
C. Cả hai phép biến hình F và F . 1 1
D. Cả hai phép biến hình F và F đều không là phép dời hình. 1 1 Trang 50
Câu 4: Cho một ngũ giác đều và một phép dời hình f . Biết rằng f ( ) A = C, f (E)= Bvà f ( ) D = A . Ảnh của điểm C là: A. A . B. B . C. C . D. E .
Câu 5: Cho hình chữ nhật và một phép dời hình F trong mặt phẳng. Biết rằng qua phép dời hình F
tam giác ABC biến thành tam giác BAD , tam giác ADC biến thành tam giác nào sau đây? A. CBA . B. BCD . C. DAB . D. BMD . Ê ˆ
Câu 6: Trong mặt phẳng tọa độ Oxy, xét biến hình ( ) 1 F : M x; y Æ M 'Á x;my˜ Á
˜ . Với giá trị nào của m 2 Á ˜ Ë ¯ thì F là phép dời hình? A. m = 2 . B. m = - 2 . C. m = 1.
D. không tồn tại m.
Câu 7: Cho hai điểm phân biệt A, B và F là phép dời hình, biết F(A)= A;F( ) B = B. Giả sử N thuôc
đường thẳng AB , N π A, N π B và F(N)= M. Chọn khẳng định đúng? A. M ∫ A . B. M ∫ B . C. M ∫ N .
D. Các khẳng định trên đều sai. uuur uuur
Câu 8: Cho DABC và điểm M thỏa mãn BM = 2CM . F là phép dời hình. Gọi F( )
A = A ;F B = B ;F C = C ;F M = M AB = 4, BC = 5, CA = 6 1 ( ) 1 ( ) 1 ( ) , biết . Độ dài đoạn 1 A M bằng: 1 1 A. 116 . B. 106 . C. 57 . D. 74 .
Câu 9: Mệnh đề nào sau đây là sai?
A. Hai hình bằng nhau thì luôn phải trùng khít lên nhau.
B. Hai hình bằng nhau khi có phép dời hình biến hình này thành hình kia.
C. Gọi A, B tương ứng là tập hợp điểm của hình H và H ' .
D. Hai hình trùng khít lên nhau thì luôn phải bằng nhau.
Câu 10: Cho hai điểm A, B và phép dời hình F thỏa mãn F( ) A = A; F( )
B = B. Gọi C là điểm không
thuộc đường thẳng AB. Biết F(C
) và C nằm cùng phía với AB. Với mọi M bất kì chọn khẳng định đúng. A. F(M
) và M đối xứng nhau qua AB. B. F(M
) và M đối xứng nhau qua BC .
C. F(M)= M với mọi M . D. F(M)= A.
Câu 11: Trong mặt phẳng xét hình (H
) là hình gồm hai đường tròn tâm O và tâm O' có bán kính tương
ứng là R và R ' (với R > R ' ). Khi đó:
A. Đường nối tâm OO ' sẽ chia hình (H
) thành hai phần bằng nhau.
B. Đường vuông góc với đường nối tâm OO ' và đi qua trung điểm của OO ' sẽ chia hình (H )
thành hai phần bằng nhau.
C. Đường nối hai điểm bất kì A, B (không trùng với OO ' ) với A thuộc (O , ) B thuộc ( ) O' sẽ chia hình (H
) thành hai phần bằng nhau.
D. Mỗi đường thẳng bất kì đi qua O hoặc O ' chia hình (H
) thành hai phần bằng nhau.
Câu 12: Cho hình chữ nhật ABCD . Gọi E, F, H, K, O, I, J lần lượt là trung điểm của các cạnh AB, BC,
CD, DA, KF, HC, KO. Mệnh đề nào sau đây đúng:
A. Hai hình thang AEJK và FOIC bằng nhau.
B. Hai hình thang BEJO và FOIC bằng nhau.
C. Hai hình thang AEJK và DHOK bằng nhau.
D. Hai hình thang BJEF và ODKH bằng nhau.
Câu 13: Cho phép dời hình: F: M(x; ) y Æ M'(x- 3; y+ )
1 . Xác định ảnh của đường tròn ( ) ( + )2 + ( - )2 C : x 1
y 2 = 2 qua phép dời hình F. Trang 51 A. ( - )2 + ( + )2 x 4 y 3 = 2. B. ( + )2 + ( - )2 x 2 y 1 = 2. C. ( + )2 + ( - )2 x 4 y 3 = 2. D. ( - )2 + ( + )2 x 2 y 1 = 2.
Câu 14: Trong mặt phẳng Oxy, cho các phép dời hình: F :M x; y Æ M' x + 2; y- 4 1 ( ) ( ) và F :M ; x y ® M ' - ; x -y A(4;- ) 1 F F 2 ( ) (
). Tìm tọa độ ảnh của điểm qua rồi đến , nghĩa là 1 2 F F È A ˘ 2 1 ( ) . Î ˚ A. (4;1 . ) B. (0;5 . ) C. (- 6;5 . ) D. (6;5 . )
Câu 15: Mệnh đề nào sau đây là sai: Phép biến hình thực hiện:
A. qua hai phép đối xứng trục có các trục cắt nhau là một phép quay.
B. qua hai phép tịnh tiến ta được một phép tịnh tiến.
C. qua hai phép đối xứng tâm ta được phép tịnh tiến hoặc đối xứng tâm.
D. qua hai phép quay ta luôn được một phép đồng nhất. D. HƯỚNG DẪN GIẢI Câu 1: Đáp án A.
Phép đồng nhất bảo toàn khoảng cách hai điểm bất kì Câu 2: Đáp án D.
F biến tam giác thành tam giác bằng nó tức bảo toàn khoảng cách hay độ dài các cạnh. Câu 3: Đáp án C. Xét hai điểm A(x ; y B(x ; y F F B B ) A A ) và
qua hai phép biến hình và . Với phép biến hình 1 2 F : A Æ A'(x + 1; y - 3 ; B Æ B'(x + 1; y - 3 B B ) A A ) 1 fi AB = A 'B' = (x - x + y - y B A )2 ( B A )2
Tương tự với phép biến hình F thì AB = A 'B' nên ta chọn đáp án C 2 Câu 4: Đáp án D Nếu M = f (C ) ta có CA = CM (do f ( ) A = C) ( ) 1 CE = MB (do f (E)= B) (2 ) CD = MA (do f ( ) D = A ) ( ) 3 ( )
1 € M thuộc đường tròn tâm C bán kính CA
(2)€ M thuộc đường tròn tâm B bán kính CE = BE ( )
3 € M thuộc đường tròn tâm A bán kính CD = AE. Vậy M ∫ E Câu 5: Đáp án B
Theo giả thiết F :DABC Æ DBAD fi F(A)= B;F( ) B = A;F( ) C = D.
Ta xác định ảnh của D qua phép dời hình F. Giả sử F( ) D = E, ta có AD = BE, BD = AE,CD = DE
Vậy điểm E là điểm chung của ba đường tròn. Đường
tròn tâm B bán kính AD, tâm A bán kính BD và tâm D bán kính b. Vậy E ∫ C hay F( ) D = C fi DADC Æ DBCD qua F Câu 6: Đáp án D. Lấy O(0; ) 0 ;A(2;2 ) ta có: F( ) O = O;F(A)= A'(1;2m ) Trang 52 7 F là phép dời hình 2 2 € OA = OA ' 2 2 € 8 = 1+ 4m € m = . 4 Lấy điểm B(2; ) 1 fi F( ) B = B'(1;m ) 7 2 2 2
OB = OB' € 5 = 1+ m € 5 = 1+ (vô lí) fi OB π OB'. Nên F không là phép dời hình 4 Câu 7: Đáp án C Ta có F(A )
B = AB € F là phép đồng nhất fi M ∫ N Câu 8: Đáp án B.
Theo tính chất phép dời hình AM = A M 1 1 uuur uuur uuur uuur uuur uuur uuur uuur uuur
BM = 2CM € AM- AB = 2(AM- AC)€ AM = 2AC- AB uuur uuur 2 2 2 fi AM = 4AC + AB - 4AC.AB ( ) * uuur uuur uuur uuur uuur Ta có: 2 2 2
BC = AC- AB fi BC = AC + AB - 2AC.AB uuur uuur 2 2 2 fi 2AC.AB = AC + AB - BC , thế vào ( ) * ta có: 2 2 2 2
AM = 2AC - AB + 2BC = 72- 16 + 50 = 106 fi AM = 106 Câu 9: Đáp án A r r Ví dụ: Tr (DAB )
C = DA'B'C', v π 0 € DABC = DA 'B'C' và phân biệt. v Câu 10: Đáp án C Gọi C = F C F(A)= A,F( ) B = B 1 ( ) và
nên theo tính chất phép dời hình ta có DABC = DABC 1
Có 2 khả năng xảy ra: C và C đối xứng với nhau qua AB hoặc C ∫ C 1 1
Theo giả thiết C và C cùng phía so với AB fi C ∫ C . 1 1
Với mọi M ta vẽ đường thẳng qua M cắt AB, AC tại D và E. Theo câu 7: F( )
D = D,F(E)= E fi F(M)= M. Câu 11: Đáp án A Câu 12: Đáp án A
Ta có hình thang AEJK biến thành hình thang FOIC qua hai
phép dời hình là phép tịnh tiến Tuuur và phép đối xứng trục EH. EO Câu 13: Đáp án C Ï x Ô ' = x - 3 Ï x Ô = x '+ 3
Ta có F: M(x; y)Æ M'(x '; y ) ' Ô Ô fi Ì € Ì y Ô ' = y + 1 y Ô = y'- 1 Ô Ó Ô Ó ( ) ( Œ ) ( + )2 + ( - )2 M x; y C : x 1 y 2 = 2 € ( + )2 + ( - )2 x ' 4 y' 3 = 2. Vậy phương trình ( ) C' là: ( + )2 + ( - )2 x 4 y 3 = 2 Câu 14: Đáp án C Ï x Ô ' = 6 Ta có: F :A 4; 1 A ' x '; y ' Ô - Æ fi 1 ( ) ( ) Ì y Ô ' = - 5 Ô Ó Ï x Ô ' = - 6 F :A ' 6; 5 A ' x '; y ' Ô - Æ fi 2 ( ) ( ) Ì y Ô ' = 5 Ô Ó Câu 15: Đáp án D Trang 53 Ï OM Ô = OM ' Thật vậy xét 2 phép quay: Q : M M ' Ô Æ € Ì và (O,a ) ( ÔOM,OM ) ' = a Ô Ó Ï IM Ô ' = IM ' Q : M ' M ' Ô Æ € Ì
(với tâm O π I,a π j )fi $ M π M ' fi Không có phép (I,j ) ( ÔIM',IM') ' = j Ô Ó đồng nhất thỏa mãn. Trang 54 PHÉP VỊ TỰ A. LÝ THUYẾT 1. Định nghĩa.
Cho điểm O cố định và số k không đổi, k π 0 . Phép biến hình biến mỗi điểm M thành điểm M ' sao cho uuuur uuur
OM' = kOM được gọi là phép vị tự tâm O, tỉ số k. Kí hiệu: V
(O là tâm vị tự, k là tỉ số vị tự) (O,k) uuuur uuur V M = M ' € OM ' = kOM o,k ( ) ( ) Nhận xét:
- Khi k > 0, M và M ' nằm cùng phía đối với điểm O
- Khi k < 0, M và M ' nằm khác phía đối với điểm O
Khi k = - 1, M và M ' đối xứng nhau qua tâm O nên V ÆÐ (O,- ) 1 O
- Khi k = 1fi M ∫ M ' phép vị tự V
trở thành phép đồng nhất (O, ) 1 2. Tính chất.
Tính chất 1: Nếu phép vị tự tỉ số k biến hai điểm M, N tùy ý theo thứ tự thành M ', N ' thì uuuuur uuur
M' N' = kMN và M' N' = k MN .
Tính chất 2: Phép vị tự tỉ số k:
a) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa chúng.
b) Biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.
c) Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó.
d) Biến đường tròn bán kính R thành đường tròn có bán kính k .R
3. Biểu thức tọa độ của phép vị tự.
Trong mặt phẳng tọa độ Oxy cho phép vị tự V ;I x ; y I,k ( 0 0 ) ( ) uuur uur Ï x Ô ' = kx + (1- k)x V :M(x; y) M '(x '; y ) 0 ' IM ' kIM Ô Æ Æ = € Ì 1 I,k ( ) ( ) y Ô ' = ky + Ô (1- k)y0 Ó
@Đọc thêm: Tâm vị tự của hai đường tròn
Định lý: Với hai đường tròn bất kì luôn có một phép vị tự biến đường tròn này thành đường tròn kia.
Tâm của phép vị tự như thế được gọi là tâm vị tự của hai đường tròn. Trang 55 M' M' M M' R' M M R' R R O I' I O I' I 1 I O1 M'' M'' Hình a Hình b Hình c
Cho hai đường tròn (I; R) và (I '; R') các trường hợp: R¢
TH1: Nếu I º I ' thì phép vị tự tâm I tỉ số -
biến đường tròn (I; R) thành đường tròn (I '; R') ( R Hình a). R¢ R¢
TH2: Nếu I ¹ I ' và R ¹ R ' thì phép vị tự tâm O tỉ số k =
và phép vị tự tâm O tỉ số k = - sẽ R 1 1 R
biến (I; R) thành(I '; R') ( Hình b) .
Ta gọi O là tâm vị tự ngoài, O là tâm vị tự trong của hai đường tròn. 1 R¢
TH3: Nếu I ¹ I' và R = R' thì có một phép vị tự tâm O tỉ số k = - = 1
- biến đường tròn (I;R) thành 1 R
(I';R') hay phép đối xứng tâm (Hình c).
B. CÁC DẠNG TOÁN VỀ PHÉP VỊ TỰ
DẠNG 1. KHAI THÁC ĐỊNH NGHĨA, TÍNH CHẤT VÀ ỨNG DỤNG CỦA PHÉP VỊ TỰ Phương pháp:
- Sử dụng định nghĩa hoặc tính chất của phép vị tự.
- Xác định ảnh của một điểm, một hình qua phép vị tự.
- Tìm quỹ tích điểm thông qua phép vị tự.
- Các yếu tố liên quan phép vị tự là thẳng hàng, tỉ số không đổi…từ đó ứng dụng phép vị tự
để giải các bài toán hình học khác…
Ví dụ 1: Cho điểm O và k ¹ 0 . Gọi M ¢ là ảnh của M qua phép vị tự tâm O tỉ số k . Mệnh đề nào sau đây là sai? !!!!" !!!!"
A. Phép vị tự biến tâm vị tự thành chính nó.
B. OM¢ = kOM .
C. Khi k = 1 phép vị tự là phép đối xứng tâm. D. M ¢ = V Û M =V M ¢ O,k æ 1 ö ( ). ( ) c, ç ÷ è k ø Lời giải:: Đáp án C.
Khi k = 1: phép vị tự V
M = M ¢ Û M º M ¢ O,1 ( ) ( )
Ví dụ 2: Cho ABC D
có trọng tâm G . Gọi M , N, P lần lượt là trung điểm của các cạnh AB, BC,CA .
Phép vị tự nào sau đây biến ABC D thành N D PM ? A. V . B. V . C. V . D. V . æ 1 ö æ 1 ö (G, 2 - ) æ 1 ö A,- ç ÷ M, ç ÷ G,- ç ÷ è 2 ø è 2 ø è 2 ø Lời giải:: Đáp án D. Trang 56 !!!!" 1 !!!" !!!" 1 !!!" !!!" 1 !!!"
Ta có GM = - GC,GP = - GB,GN = - GA Þ V A D BC = N D PM æ 1 ö ( ) 2 2 2 G,- ç ÷ è 2 ø ! ""!
Ví dụ 3: Cho hai điểm O, I . Xét phép vị tự V tâm I tỉ số k ¹ 1 và phép tịnh tiến theo u = (1- k ) IO .
Lấy điểm M bất kì, M =V M , M = T M F M M 1 ( ) 2
( 1). Phép biến hình biến thành . Chọn 2 mệnh đề đúng:
A. F là phép vị tự tâm O tỉ số 1- k .
B. F là phép vị tự tâm O tỉ số k . 1 1
C. F là phép vị tự tâm O tỉ số .
D. F là phép vị tự tâm O tỉ số - . k k Lời giải:: Đáp án B. !!!!" !!!"
IM = K.IM 1 1 ( ) !!!!!!" " !!" !!!!" !!!!" !!" !!!!" !!!!" !!"
M M = u = 1- k IO Þ IM - IM = 1- k IO Û IM = IM + 1- k IO 2 1 2 ( ) 2 1 ( ) 2 1 ( ) ( ) !!!!" !!!" !!" !!!!!" !!!!" Thế ( )
1 vào (2): IM = kIM + 1- k IO Þ OM = kOM 2 ( ) 2
Vậy F là phép vị tự tâm O tỉ số k .
Ví dụ 4: Cho ABC D
có cạnh 3,5,7. Phép đồng dạng tỉ số k = 2 biến ABC D thành A D ¢B C ¢ ¢ có diện tích là: 15 3 15 3 15 3 A. . B. 15 3 . C. . D. . 2 4 8 Lời giải:: Đáp án B. 15 3 Ta có: S = ABC D 4
Tỉ số diện tích hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng. S A D ¢B C ¢ ¢ Þ = 4 Û S = D ¢ ¢ ¢ 15 3 . A B C S ABC D
Ví dụ 5: Có bao nhiêu phép vị tự biến đường tròn (C) thành đường tròn (C¢)? A. 3 . B. 1 . C. 2 .
D. không xác định. Lời giải:: Đáp án D.
Không xác định vì thiếu giả thiết về phép vị tự.
Ví dụ 6: Cho đường tròn tâm O và hai đường kính AA¢ và BB¢ vuông góc với nhau. M là điểm bất kì
trên đường kính BB¢ , M ¢ là hình chiếu vuông góc của M xuống tiếp tuyến với đường tròn tại
A . I là giao điểm của AM và A¢M ¢ . Khi đó I là ảnh của M trong phép vị tự tâm A tỉ số bao nhiêu? 2 2 1 A. . B. - 1 . C. . D. - . 3 3 3 3 Lời giải:: Đáp án A. Trang 57 AI MM ¢ AI 2 2 = = 2 Þ = = AM AA¢ IM + AI 2 +1 3 !!" 2 !!!!" Þ 2
AI = AM . Vậy I là ảnh của M trong phép vị tự tâm A tỉ số . 3 3
DẠNG 2. TÌM ẢNH CỦA MỘT ĐIỂM HOẶC HÌNH QUA PHÉP VỊ TỰ BẰNG PHƯƠNG PHÁP TỌA ĐỘ Phương pháp:
1. Xác định ảnh của một điểm qua phép vị tự.
- Sử dụng biểu thức tọa độ của phép vị tự.
2. Xác định ảnh D¢ của đường thẳng D qua phép vị tự.
Cách 1: Chọn hai điểm ,
A B phân biệt trên D , xác định ảnh A ,¢ B¢ tương ứng. Đường thẳng D¢ cần
tìm là đường thẳng qua hai ảnh A ,¢ B¢.
Cách 2: Áp dụng tính chất phép vị tự V
biến đường thẳng D thành đường thẳng D¢ song song (O,k) hoặc trùng với nó.
Cách 3: Sử dụng quỹ tích
- Với mọi điểm M ( ; x y)ÎD :V
M = M ¢ x ;¢ y¢ M ¢Î D¢ O,k ( ) ( ) thì . ( )
- Từ biểu thức tọa độ rút x, y thế vào phương trình đường thẳng D ta được phương trình ảnh D¢.
3. Xác định ảnh của một hình H ( đường tròn, elip, parabol…)
- Sử dụng quỹ tích: Với mọi điểm M ( ;
x y) thuộc hình H , V
M = M ¢ x ;¢ y¢ M ¢ O,k ( ) ( ) thì thuộc ảnh ( )
H ¢ của hình H .
- Với đường tròn áp dụng tính chất phép vị tự biến đường tròn bán kính R thành đường tròn bán
kính k R hoặc sử dụng quỹ tích.
Ví dụ 1: Trong mặt phẳng tọa độ Oxy , cho điểm A(3;2). Ảnh của A qua phép vị tự tâm O tỉ số k = 1 - là: A. (3;2) . B. (2;3). C. ( 2; - - ) 3 . D. ( 3; - 2 - ). Lời giải:: Đáp án D. ìx¢ = 3 -
Áp dụng biểu thức tọa độ của phép vị tự: V
A = A¢ Þ A¢ : í O, 1 - ( ) ( ) îy¢ = 2 -
Ví dụ 2: Trong mặt phẳng tọa độ Oxy , cho đường thẳng d : 5x + 2y - 7 = 0. Tìm ảnh d¢ của d qua
phép vị tự tâm O tỉ số k = 2 - .
A. 5x + 2y +14 = 0.
B. 5x + 4y + 28 = 0 . C. 5x - 2y - 7 = 0.
D. 5x + 2y -14 = 0. Lời giải:: Đáp án A. Trang 58 M O
Cách 1: Chọn hai điểm ,
A B phân biệt trên d , xác định ảnh A ,¢ B¢ tương ứng. Đường thẳng
d¢ cần tìm là đường thẳng qua hai ảnh A ,¢ B¢ (học sinh tự làm).
Cách 2: Do d¢ song song hoặc trùng với d. Nên d¢ có dạng 5x + 2y + c = 0. !!!!" !!!!" Lấy M (1; )
1 Îd . Khi đó: V
M = M¢ x ;¢ y¢ Û OM¢ = 2 - OM Þ M¢ 2 - ; 2 - O, 2 - ( ) ( ) ( ) ( )
Thay vào d¢ Þ c = 14 . Vậy d¢ : 5x + 2y +14 = 0 ì 1 = - ¢ ì ¢ = 2 x x x - x ïï
Cách 3: Gọi M (x y) 2 ; Îd :V
M = M ¢ x ;¢ y¢ Þ í Û y = í O, 2 - ( ) ( ) ( ) îy¢ = 2 - y 1 ïy = - y¢ ïî 2 5
Thế vào phương trình đường thẳng d : - x¢ - y '- 7 = 0 Û 5x¢ + 2y¢ +14 = 0 2
Vậy d¢ : 5x + 2y +14 = 0.
Ví dụ 3: Trong mặt phẳng tọa độ Oxy , cho đường tròn (C) (x - )2 +( y - )2 : 1
1 = 4. Tìm ảnh (C¢) của
(C) qua phép vị tự tâm I ( 1 - ;2) tỉ số k = 3? A. 2 2
x + y -14x + 4y -1 = 0 . B. 2 2
x + y + 4x - 7y - 5 = 0.
C. (x - )2 +( y + )2 5 1 = 36.
D. (x - )2 +( y - )2 7 2 = 9. Lời giải:: Đáp án C. M' M R' R O I' I O1 M''
Đường tròn (C) có tâm J (1; ) 1 , bán kính R = 2 . ìx¢ = 1 - + 3 ï (1+ )1 = 5 V
J = J ¢ x ;¢ y¢ Þ í Þ J¢ 5; 1 - I,3 ( ) ( ) ( ) ( ) ïy¢ = 2 + 3 î (1- 2) = 1 -
R¢ = R = Þ (C¢) (x - )2 +( y + )2 3 6 : 5 1 = 36 1
Ví dụ 4: Trong mặt phẳng tọa độ Oxy , cho phép vị tự tâm O tỉ số k = . Tìm ảnh (S¢) của đường cong 2 ( + S ) 2x 1 : y = qua phép vị tự trên. 1- x 4x +1 4x +1 2x +1 2x -1 A. y = . B. y = . C. y = . D. y = . 2 - 4x 1- 4x 1- 2x 1- 4x Lời giải:: Trang 59 Đáp án A. V : M ;
x y ® M ¢ x ;¢ y¢ æ 1 ö ( ) ( ) O, ç ÷ è 2 ø M " ( ;
x y)Î(S) Þ M¢(x ;¢ y¢)Î(S¢) ì 1 x¢ = x 1 ïï ìx = 2 2x¢ + 2 x¢ ¢ + Þ 2.2x 1 í Û y = í thế vào (S ) 2 Þ 2y¢ = Û y¢ = 1 ï îy = 2y¢ 1- 2x¢ 1- 2x¢ y¢ = y ïî 2 x + Vậy (S¢) 4 1 : y = 2 - 4x
C. BÀI TẬP RÈN LUYỆN KỸ NĂNG
DẠNG 1. KHAI THÁC ĐỊNH NGHĨA, TÍNH CHẤT VÀ ỨNG DỤNG CỦA PHÉP VỊ TỰ
Câu 1: Mệnh đề nào sau đây sai về phép vị tự:
A. Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy.
B. Biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
C. Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó.
D. Biến đường tròn thành đường tròn cùng bán kính.
Câu 2: Cho hai đường thẳng song song d và d¢ . Có bao nhiêu phép vị tự đối với tỉ số k = 20 biến
đường thẳng d thành d¢ ?
A. Không có phép nào.
B. Có một phép duy nhất. C. Chỉ có 2 phép. D. Có vô số phép.
Câu 3: Cho hai đường thẳng cắt nhau d và d¢ . Có bao nhiêu phép vị tự biến đường thẳng d thành d¢ ?
A. Không có phép nào.
B. Có một phép duy nhất. C. Chỉ có 2 phép. D. Có vô số phép.
Câu 4: Cho hai đường thẳng song song d và d¢ , và một điểm O không nằm trên chúng. Có bao nhiêu
phép vị tự tâm O biến đường thẳng d thành d¢ ? A. 0 . B. 1 . C. 2 . D. Vô số.
Câu 5: Cho hai đường tròn bằng nhau ( ;
O R) và (O ;¢R) với tâm O và tâm O¢ phân biệt. Có bao
nhiêu phép vị tự biến ( ;
O R) thành (O ;¢R)? A. 0 . B. 1 . C. 2 . D. Vô số.
Câu 6: Cho hai phép vị tự V và V
với O và O¢ là hai điểm phân biệt và k.k¢ = 1. Hợp của hai (O,k) (O¢,k¢)
phép vị tự đó là phép nào sau đây?
A. Phép tịnh tiến.
B. Phép đối xứng trục.
C. Phép đối xứng tâm. D. Phép quay. 3 Câu 7: Cho ABC D
vuông tại A , AB = 6, AC = 8. Phép vị tự tâm A tỉ số biến B thành B¢, biến C 2
thành C¢ . Mệnh đề nào sau đây sai? A. BB C ¢ C ¢ là hình thang. B. B C ¢ ¢ =12 . 3 C. S = 2 . D. Chu vi ABC D = chu vi A D ¢B C ¢ ¢. A B ¢ C ¢ ¢ 4 3
Câu 8: Cho hình thang ABCD ( AB / /CD). Đáy lớn AB = 8 , đáy nhỏ CD = 4. Gọi I là giao điểm của !!!" !!!"
hai đường chéo và J là giao điểm của hai cạnh bên. Phép biến hình AB thành CD là phép vị tự nào? A. V . B. V . C. V . D. V . æ 1 ö æ 1 ö æ 1 ö æ 1 ö I, ç ÷ J, ç ÷ I,- ç ÷ J,- ç ÷ è 2 ø è 2 ø è 2 ø è 2 ø Trang 60
Câu 9: Cho đường tròn ( ;
O R) và một điểm A cố định trên đường tròn. BC là dây cung di động và
BC có độ dài không đổi bằng 2a (a < R). Gọi M là trung điểm BC . Khi đó tập hợp trọng
tâm G của ABC D là: A. G = V M æ 2 ö (
), tập hợp là một đường tròn. A, ç ÷ è 3 ø B. G = V M æ 1 ö (
), tập hợp là một đường thẳng. O, ç ÷ è 2 ø C. G = V M æ 1 ö (
), tập hợp là một đường tròn. A, ç ÷ è 3ø D. G = V M æ 2 ö (
), tập hợp là một đường thẳng. B, ç ÷ è 3 ø
Câu 10: Cho đường tròn ( ;
O R) đường kính AB . Một đường tròn (O¢) tiếp xúc với đường tròn (O)
và đoạn AB lần lượt tại C và D . Đường thẳng CD cắt ( ;
O R) tại I . Tính độ dài đoạn AI . A. 2R 3 . B. R 2 . C. R 3 . D. 2R 2.
Câu 11: Cho hai đường tròn ( ;
O R) và (O ;¢ R¢) tiếp xúc trong tại A (R > R¢). Đường kính qua A cắt ( ;
O R) tại B và cắt (O ;¢ R¢) tại C . Một đường thẳng di động qua A cắt ( ;
O R) tại M và cắt
(O ;¢R¢) tại N . Gọi I là giao điểm của BN và CM . Mệnh đề nào sau đây là đúng?
A. Tập hợp điểm I là đường tròn: (O¢¢) =Væ ¢ ö (( , O R R )). C, ç ÷ è R+R¢ ø
B. Tập hợp điểm I là đường tròn: (O¢¢) =V ö (( , O R æ R )). C, ç ÷ è R+R¢ ø
C. Tập hợp điểm I là đường tròn: (O¢¢) =Væ ¢ ö (( , O R R )). M, ç ÷ è R+R¢ ø
D. Tập hợp điểm I là đường tròn: (O¢¢) =V ö (( , O R æ R )). M, ç ÷ è R+R¢ ø
DẠNG 2: TÌM ẢNH CỦA MỘT ĐIỂM HOẶC MỘT HÌNH QUA PHÉP VỊ TỰ BẰNG PHƯƠNG PHÁP TỌA ĐỘ.
Câu 1: Trong mặt phẳng tọa độ Oxy , tìm ảnh A¢ của điểm A(1; 3
- ) qua phép vị tự tâm O tỉ số 2 - A. A¢(2;6). B. A¢(1;3). C. A¢( 2; - 6). D. A¢( 2; - 6 - ) .
Câu 2: Trong mặt phẳng tọa độ Oxy, cho A(1;2) . Tìm ảnh A¢ của A qua phép vị tự tâm I (3;- ) 1 tỉ số k = 2. A. A¢(3;4). B. A¢(1;5). C. A¢( 5; - - ) 1 . D. A¢( 1 - ;5).
Câu 3: Trong mặt phẳng tọa độ Oxy, cho P( 3; - 2),Q(1; ) 1 , R(2; 4
- ). Gọi P ,¢Q ,¢ R¢ lần lượt là ảnh của 1 , P ,
Q R qua phép vị tự tâm O tỉ số k = - . Khi đó tọa độ trọng tâm của tam giác P Q ¢ R ¢ ¢ là: 3 æ 1 1 ö æ 1 ö æ 2 1 ö æ 2 ö A. ; . B. 0; . C. ; - . D. ;0 . ç ÷ ç ÷ ç ÷ ç ÷ è 9 3 ø è 9 ø è 3 3 ø è 9 ø
Câu 4: Trong mặt phẳng tọa độ Oxy, cho ba điểm A(0; ) 3 , B(2;- ) 1 ,C ( 1
- ;5) .Phép vị tự tâm A tỉ số
k biến B thành C . Khi đó giá trị k là: 1 A. k = - . B. k = 1 - 1 . C. k = . D. k = 2 . 2 2
Câu 5: Trong mặt phẳng tọa độ Oxy, cho ba điểm A(0; ) 3 , B(2;- ) 1 ,C ( 1
- ;5) .Phép vị tự tâm A tỉ số
k biến B thành C . Khi đó giá trị k là: A. k = 2 . B. k = 1 - . C. k = 1. D. k ÎÆ . Trang 61
Câu 6: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d : 2x + y - 4 = 0, I ( 1
- ;2). Tìm ảnh d¢ của d
qua phép vị tự tâm I tỉ số k = 2 -
A. 2x - y + 4 = 0. B. 2
- x + y + 8 = 0.
C. 2x + y + 8 = 1 0.
D. x + y + 2 = 0. 2
Câu 7: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d : 3x - y - 5 = 0. Tìm ảnh d¢ của d qua phép 2
vị tự tâm O tỉ số k = - 3 A. 3
- x + y - 9 = 0.
B. 3x - y -10 = 0.
C. 9x - 3y +15 = 0 .
D. 9x - 3y +!0 = 0. x y
Câu 8: Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d : - =
1 và d¢ : 2x - y - 6 = 0 . Phép vị 2 4 tự V d = d .¢ k O,k ( ) Tìm ( ) 3 A. k = 2 . B. k = - 1 . C. k = 1 . D. k = - . 2 3 3 3
Câu 9: Trong mặt phẳng Oxy, tìm ảnh đường tròn (C¢)của đường tròn (C) (x - )2 +( y + )2 : 1 2 = 5 qua
phép vị tự tâm 0 tỉ số k = 2 - .
A. (C¢) (x + )2 +( y + )2 : 2 4 =10.
B. (C¢) (x - )2 +( y - )2 : 2 4 =10.
C. (C¢) (x + )2 +( y - )2 : 2 4 = 20.
D. (C¢) (x - )2 +( y + )2 : 2 4 = 20.
Câu 10: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) (x - )2 +( y + )2 : 3
1 = 5. Tìm ảnh đường tròn
(C¢) của đường tròn (C) qua phép vị tự tâm I (1;2) và tỉ số k = 2 - A. 2 2
x + y + 6x -16y + 4 = 0. B. 2 2
x + y - 6x +!6y - 4 = 0 .
C. (x + )2 +( y - )2 3 8 = 20.
D. (x - )2 +( y + )2 3 8 = 20. Câu 11: Trong mặt phẳng Oxy, cho hai đường tròn
(C : x-1 + y -3 =1 1 ) ( )2 ( )2 ;
(C : x-4 + y -3 = 4 2 ) ( )2 (
)2 . Tìm tâm vị tự ngoài của hai đường tròn đó A. ( 2; - 3). B. (2;3). C. (3; 2 - ). D. (1; 3 - ).
Câu 12: Trong mặt phẳng Oxy, cho hai đường tròn (C : x -3 + y -3 = 9 1 ) ( )2 ( )2 và đường tròn
(C : x-10 + y -7 =9 (C) (C¢) 2 ) ( )2 ( )2
. Tìm tâm vị tự trong biến thành . æ 36 27 ö æ13 ö æ 32 24 ö æ 13 ö A. ; . B. ;5 . C. ; . D. 5; ç ÷ ç ÷ ç ÷ ç ÷ è 5 5 ø è 2 ø è 5 5 ø è 2 ø
D. HƯỚNG DẪN GIẢI CHI TIẾT
Dạng 1: Khai thác định nghĩa, tính chất và ứng dụng của phép vị tự. Câu 1: Đáp án D. Câu 2: Đáp án D. Câu 3: Đáp án A
Theo tính chất phépv ị tự biến đường thẳng thành đường thẳng song song hoặc trùng nhay,
không có trường hợp d cắt d¢ . Câu 4: Đáp án B. Câu 5: Đáp án B. Câu 6: Đáp án A M1 M2 M O I O' Trang 62 !!!!" !!!!" !!!!!" !!!!!"
Lấy điểm M bất kỳ: V M = M V
M = M Þ OM = kOM O M ¢ = k O ¢ M ¢ O ;¢k¢ ( 1 ) O;k ( ) và và ( ) 1 ( ) 2 1 2 1 !!!" !!!!"
Khi đó phép hợp thành F (M ) = M . Gọi I là ảnh của O qua phép hợp V Þ O I¢ = kO O ¢ 2 (O ;¢k) !!!!" !!!!" !!!!" !!!!!" !!" !!!!" !!!" !!!!"
Khi đó IM = k O
¢ M = k.k O
¢ M nên: MM = OI = OO¢ + O I¢ = 1- k¢ OO¢ 2 ( ) 2 1 ! """"!
Vậy F là phép tịnh tiến theo vectơ u = (1- k¢)OO¢. Câu 7: Đáp án B B' B 6 A 8 C C' V = ¢ Þ ¢ = = = ¢ Þ ¢ = = Þ ¢ ¢ = + = æ ö ( B) (B ) 3 AB
AB 9;Væ ö (C) (C ) 3 2 2 AC AC 12 B C 9 12 15 3 3 ; A ç ÷ 2 ; A ç ÷ 2 è 2 ø è 2 ø . Câu 8: Đáp án C J 4 D C 8 A B Ta có AB 1 !!" 1 !!" !!" 1 !!" = ;V
A = C Û IC = - I ; A V
B = D Û ID = - IB æ 1 ö ( ) æ 1 ö ( ) CD 2 I , ç ÷ 2 I , ç ÷ 2 è 2 ø è 2 ø . !!" !!" 1 !!" !!" !!!" !!!"
Þ IC - ID = - (IA- IB) 1 Û CD = - AB 2 2 Câu 9: Đáp án A A G O B M C Ta có: 2 2 2 2
OM ^ BC Þ OM = R - a Þ M Î ; O R - a ( ) !!!" 2 !!!!"
Ta có: AG = AM Þ G = V M æ 2 ö ( ) 3 A, ç ÷ è 3 ø
Khi M di động trên đường tròn 2 2 ;
O R - a thì G chạy trên đường tròn (O¢) là ảnh của ( )
đường tròn (O) qua phép vị tự V . æ 2 ö A, ç ÷ è 3 ø Câu 10: Đáp án B Trang 63 C O' B A D O I R¢ Ta có: V
O = O¢ Û CO¢ = CO æ R¢ ö ( ) ( ) 1 C, ç ÷ R è R ø ¢ = Û = æ ¢ ö ( ) R V I D CD CI (2 R ) C, ç ÷ R è R ø CD¢ CO Từ ( ) 1 và (2) Þ = Þ OIÄO D
¢ Þ OI ^ AB Þ I là điểm chính giữa của cung AB . CD CI Câu 11: Đáp án A M N I B A C O O' Ta dự đoán V M = I M (O) Þ I æ CI ö (
) mà nắm trên đường tròn nằm trên đường tròn C; ç ÷ è CM ø (O =V O 1 ) æ CI ö ( ) C; ç ÷ è CM ø CI Ta cần chứng minh
theo R và R¢ CM CM CI + IM IM ¢ Ta có = =1+ IM IB BM AB R CI R mà = = = = Þ = CI CI CI CI IN CN AC R¢ CM R + R¢ Þ V = æ ¢ ö ( M ) I R çC, ÷ è R+R¢ ø
DẠNG 2: TÌM ẢNH CỦA ĐIỂM, ĐƯỜNG QUA PHÉ VỊ TỰ BẰNG PHƯƠNG PHÁP TỌA ĐỘ.
Câu 1: Đáp án C !!!" !!!" V
A = A¢ Û OA¢ = 2 - OA Þ A¢ 2 - ;6 O; 2 - ( ) ( ). ( ) Câu 2: Đáp án D !!" !!" ìx¢ - 3 = 4 V
A = A¢ Û IA¢ = 2IA Û í Þ A 1 - ;5 I ,2 ( ) ( ). ( ) îy¢ +1 = 6 Câu 3: Đáp án B V
P = P ;¢V
Q = Q ;¢V R = R¢ Þ æ 1 ö ( ) æ 1 ö ( ) æ 1 ö ( ) tọa độ các điểm O,- O,- O,- ç ÷ ç ÷ ç ÷ è 3 ø è 3 ø è 3 ø æ 2 - ö æ 1 1 ö æ 2 4 ö æ ö P¢ 1; ;Q¢ - ;- ; R¢ - ;
. Nên tọa độ trọng tâm P D 1 Q ¢ R ¢ ¢ là 0; . ç ÷ ç ÷ ç ÷ ç ÷ è 3 ø è 3 3 ø è 3 3 ø è 9 ø Câu 4: Đáp án A Trang 64 !!!" !!!" ì 1 - = 2k ï 1 Giả sử V
B = C Û AC = k AB Û í Þ k = - A,k ( ) . ( ) ï2 = k î ( 4 - ) 2 Câu 5: Đáp án D ì 5 !!!" !!!" 5 ì = k.4 ïk = Giả sử V
B = C Û AC = k AB Û í Þ í Þ Þ k ÎÆ A k 4 , ( ) không thỏa mãn . ( ) 1 î = -k ïîk = 1 - Câu 6: Đáp án C V
d = d¢ Þ dÄ d¢ d¢
2x + y + c = 0 I , 2 - ( ) nên có dạng ( ) ìx¢ = 5 Chọn điểm
M (2;0)Îd ÞV M = M ¢ ; x y Î d¢ Þ í I ; 2 - ( ) ( ) thế vào ( ) îy ' = 2 -
d¢ :10 - 2 + c = 0 Þ c = 8
Vậy d¢ : 2x + y + 8 = 0. Câu 7: Đáp án D
Tương tự câu 6 Þ d¢ : 9x - 3y +10 = 0 . Câu 8: Đáp án A
d : 2x - y - 4 = 0 Þ dÄd¢ ìx¢ = 2k
Chọn M (2;0)Îd ÞV
M = M ¢ x ;¢ y¢ Þ í O,k ( ) ( ) ( ) îy¢ = 0 3
Do M ¢Îd¢ Þ 2.2k - 0 - 6 = 0 Û k = . 2 Câu 9: Đáp án C
Đường tròn (C) có tâm I (1; 2
- ) và bán kính R = 5 ìx¢ = 2 - ÞV
I = I¢ x ;¢ y¢ Þ í Þ I¢ 2 - ;4
R¢ = k .R = 2 5 O, 2 - ( ) ( ) ( ). Bán kính ( ) îy¢ = 4
Þ đường tròn (C¢) (x + )2 +( y - )2 : 2 4 = 20. Câu 10: Đáp án C !!" !!" ìx¢ = 3 -
Đường tròn (C) có tâm I (8 ) ;1 :V
J = J ¢ x ;¢ y¢ Û IJ ¢ = 2 - IJ Þ í Þ J¢ 3 - ;8 I , 2 - ( ) ( ) ( ) ( ) îy¢ = 8
Bán kính R¢ = k R = 2 5 Þ phương trình (C¢) (x - )2 +( y - )2 : 3 8 = 20. Câu 11: Đáp án A Đường tròn (C I 1;3 R = 1 1 ( ) 1 ) có tâm và bán kính 1 Đường tròn (C I 4;3 R = 2 2 ( ) 2 ) có tâm và bán kính 2 Gọi I là tâm vị tự ngoài của phép vị tự R !!" !!" V C = C Þ V
I = I , k =
= 2 Û II = 2II Þ I 2 - ;3 I ,k (( )) ( ) I ,k ( ) 2 1 2 1 2 2 1 ( ). ( ) ( ) R1 Câu 12: Đáp án A
Đường tròn (C) có tâm I (3;3) và bán kính R = 3
Đường tròn (C¢) có tâm I¢(10;7) và bán kính R¢ = 2
Þ I ¹ I ,¢ R ¹ R¢ Þ 2
tỉ số vị tự k = - 3 Trang 65 !!!!" !!!" V
I = I¢ Û O I¢ = kO I O ; x y 1 ( ) O ,k ( ) với là tâm vị tự trong ( 1 1 1 ) ì 2 ì x - = - (x - ) 36 10 3 x = ï 3 ï ï ï 5 Û í Þ í 2 ïx ( y ) 27 7 3 ï - = - - y = ïî 3 ïî 5 æ 36 27 ö Vậy O ; 1 ç ÷ è 5 5 ø Trang 66 PHÉP ĐỒNG DẠNG A. LÝ THUYẾT 1. Định nghĩa
Một phép biến hình F được gọi là phép đồng dạng tỉ số k (k > 0)nếu với hai điểm bất kỳ M , N và ảnh
M ,¢ N¢ tương ứng của chúng ta luôn có M N ¢ ¢ = kMN. A A' M Phép đồng dạng M' B N C B' N' C' Nhận xét:
- Phép dời hình là phép đồng dạng tỉ số k = 1.
- Phép vị tự tỉ số k là phép đồng dạng tỉ số k .
- Nếu thực hiện liên tiếp hai phép đồng dạng thì ta được một phép đồng dạng. 2. Tinh chất
Phép đồng dạng tỉ số k :
a) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toán thứ tự giữa chúng.
b) Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.
c) Biến một tam giác thành tam giác đồng dạng với tam giác đã cho, biến góc thành góc bằng nó.
d) Biến một đường tròn bán kính R thành đường tròn bán kính k .R. STUDY TIP
a) Nếu một phép đồng dạng biến tam giác thành tam giác A¢B C
¢ ¢ thì nó cũng biến trọng tâm, trực tâm,
tâm các đường tròn nội tiếp, ngoại tiếp của tam giác ABC thành tương ứng của tam giác A¢B C ¢ ¢ .
b) Phép đồng dạng biến đa giác n cạnh thành đa giác n cạnh, biến đỉnh thành đỉnh, cạnh thành cạnh. 3. Hình đồng dạng
Hai hình được gọi là đồng dạng với nhau nếu có một phép đồng dạng biến hình này thành hình kia
B. CÁC DẠNG BÀI TOÁN VỀ PHÉP ĐỒNG DẠNG
Ví dụ 1: Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai đường thẳng bất kỳ luôn đồng dạng.
B. Hai đường tròn bất kỳ luôn đồng dạng.
C. Hai hình vuông bất kỳ luôn đồng dạng.
D. Hai hình chữ nhật bất kỳ luôn đồng dạng. Đáp án D
Lời giải:
Với hai hình chữ nhật bất kỳ ta chọn từng cặp cạnh tương ứng khi đó tỉ lệ giữa chúng chưa chắc
đã bằng nhau. Vì vậy không phải lúc nào cũng tồn tại phép đồng dạng biến hình chữ nhật này
thành hình chữ nhật kia.
Ví dụ 2: Cho hình chữ nhật ABCD có tâm I. Gọi H, K, ,
L J lần lượt là trung điểm của ,
AD BC, KC, IC. Tứ giác IHCD đồng dạng với tứ giác nào sau đây? A. JLKI . B. ILJH . C. JLBA . D. ALJH Đáp án A
Lời giải: M L B C I J A H D Trang 67 1
Tứ giác IHDC là hình thang vuông. Ta thấy IHDC đồng dạng với JLKI theo tỉ số 2
Ví dụ 3: Mệnh đề nào sau đây là đúng?
A. Phép đồng dạng tỉ số k = 1 là phép dời hình.
B. Phép đồng dạng tỉ số k = 1
- là phép đối xứng tâm.
C. Phép đồng dạng tỉ số k = 1 là phép tịnh tiến.
D. Phép đồng dạng tỉ số k = 1 là phép vị tự tỉ số k = 1 Đáp án A
Lời giải:
Khi k = 1 phép đồng dạng bảo toàn khoảng cách nên là phép dời hình.
Ví dụ 4: Cho ABC D
có đường cao AH, H nằm giữa BC. Biết AH = 4, HB = 2, HC = 8. Phép đồng
dạng F biến H D BA thành H
D AC . F được hình thành bởi hai phép biến hình nào? 1
A. Phép đối xứng tâm H và phép vị tự tâm H tỉ số k = . 2 !!!"
B. Phép tịnh tiến theo BA và phép vị tự tâm H tỉ số k = 2 .
C. Phép vị tự tâm H tỉ số k - 2 và phép quay tâm H góc quay là góc ( , HB HA).
D. Phép vị tự tâm H tỉ số k = 2 và phép đối xứng trục Đáp án C
Lời giải: A 4 φ B 2 H C Ta có V và Q với j = ( ,
HB HA) biến B thành A và A thành C, vậy F là phép đồng (H,2) (H;j)
dạng hợp thành của V và Q biến H D BA thành H D AC . (H,2) (H;j)
Ví dụ 5: Trong mặt phẳng Oxy, cho điểm M (2;4). Hỏi phép đồng dạng có được bằng cách thực hiện 1
liên tiếp phép vị tự tâm O tỉ số k = và phép quay tâm O góc quay 90
- ° sẽ biến điểm M 2
thành điểm nào sau đây? A. (2; ) 1 - . B. (2 ) ;1 . C. ( 1 - ;2). D. (1;2) Đáp án A
Lời giải: !!!!" 1 !!!!" Ta có V
M = M ¢ x ;¢ y¢ Û OM ¢ = OM Þ M ¢ 2; 1 - æ 1 ö ( ) ( ) ( ) O; ç ÷ 2 è 2 ø
ìx¢¢ = y¢ = 2 Q
M ¢ = M ¢ x¢ ;¢ y¢ Þ í Þ M ¢ 2; 1 - . O; 9 - 0° ( ) ( ) ( ) ( )
îy¢¢ = -x¢ = 1 -
Ví dụ 6: Trong mặt phẳng Oxy, cho đường thẳng d : 2x - y = 0 thỏa mãn phép đồng dạng có được bằng
cách thực hiện llieen tiếp phép vị tự tâm O tỉ số k = 2
- và phép đối xứng trục Oy sẽ biến
đường thẳng d thành đường thẳng nào sau đây? A. 2 - x - y = 0.
B. 2x + y = 0 .
C. 4x - y = 0.
D. 2x + y - 2 = 0 Đáp án A Lời giải: Ta có: V
d = d¢ Þ d¢ ! d O; 2 - ( ) ( )
Þ d¢ có dạng: 2x - y + c = 0 Trang 68
Chọn N (1;2)Îd :V N = N¢ 2 - ; 4 - Îd¢ Þ 4
- + 4 + c = 0 Þ c = 0 O; 2 - ( ) ( ) ( )
+ phương trình đường thẳng d¢ : 2x - y = 0
Qua phép đối xứng trục Oy : Đ d¢ = d¢ oy ( )
Suy ra phương trình ảnh d¢¢ cần tìm là: 2 - x - y = 0
Ví dụ 7. Trong mặt phẳng Oxy , cho đường tròn (C) (x - )2 +( y - )2 : 2
2 = 4. Hỏi phép đồng dạng có 1
được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = và phép quay tâm O góc quay 2 0
90 sẽ biến (C) thành đường tròn nào sau đây?
A. (x - )2 +( y - )2 2 2 = . 1
B. (x - )2 +( y - )2 1 1 = . 1
C. (x + )2 +( y - )2 2 1 =1.
D. (x + )2 +( y - )2 1 1 =1 Đáp án D. Lời giải: Gọi V C = C¢ (C¢) I¢(1 ) ;1 R¢ = 1 æ 1 ö (( )) ( ) nên đường tròn có tâm và bán kính . O; ç ÷ è 2 ø Ta lại có Q C¢ = C¢ R¢¢ = 1
I¢ (x¢;¢ y¢ ) 0 ( ) ( ) có bán kính và tâm được xác định (O;90 ) ( ) ìx¢ = -y¢ = 1 - í Þ I¢ ( 1 - ) ;1 îy¢ = x¢ =1
Vậy phương trình đường tròn (C¢ ) là: (x + )2 +( y - )2 1 1 =1.
C. BÀI TẬP RÈN LUYỆN KỸ NĂNG
Câu 1: Mệnh đề nào sau đây là đúng?
A. Phép dời hình là phép đồng dạng, tỉ số k = 1 - .
B. Phép vị tự tỉ số k là một phép đồng dạng với tỉ số -k .
C. Phép vị tự tỉ số k ¹ 0 là phép đồng dạng tỉ số k .
D. Phép đồng dạng là phép dời hình với k ¹ 0 .
Câu 2: Trong các mệnh đề sau, mệnh đề nào đúng?
I. “ Mỗi phép vị tự tỉ số k là một phép đồng dạng tỉ số k ”.
II. “ Mỗi phép đồng dạng là một phép dời hình”.
III. “ Thực hiện liên tiếp hai phép đồng dạng ta được một phép đồng dạng” A. Chỉ I. B. Chỉ II. C. Chỉ III. D. Cả I và III.
Câu 3: Giả sử phép đồng dạng F biến tam giác ABC thành tam giác A B C . Giả sử F biến trung 1 1 1
tuyến AM của ABC D
thành đường cao A M của A
D B C . Mệnh đề nào sau đây là đúng? 1 1 1 1 1 A. A
D B C là tam giác đều. B. A
D B C là tam giác cân. 1 1 1 1 1 1 C. A
D B C là tam giác vuông tại B . D. A
D B C là tam giác vuông tại C . 1 1 1 1 1 1 1 1
Câu 4: Cho hình chữ nhật ABCD và AC = 2AB . Gọi Q là phép quay tâm A góc quay j = ( , AB AC)
V là phép vị tự tâm A tỉ số 2, F là phép hợp thành của V và Q . F biến đường tròn tâm B
bán kính BA thành đường tròn nào sau đây?
A. Đường tròn tâm D bán kính DB .
B. Đường tròn tâm C bán kính CA .
C. Đường tròn tâm D bán kính DC .
D. Đường tròn tâm A bán kính AC .
Câu 5: Cho hai đường tròn (I; R) và (I ;2
¢ R) tiếp xúc ngoài nhau tại O . d là đường thẳng tiếp xúc
với hai đường tròn tại O . Gọi V là phép vị tự tâm O tỉ số k , Đ là phép đối xứng qua đường
thẳng d , F là phép hợp thành của Đd và V
. Với giá trị k bằng bao nhiêu thì F biến (O;k)
(I;R) thành (I ;2 ¢ R)? Trang 69 A. k = 2 . B. k = 2 - 1 . C. k = - 1 . D. k = . 2 2
Câu 6: Cho hình vuông ABCD tâm O (điểm được đặt theo chiều kim đồng hồ). A ,¢ B ,¢C ,¢ D¢ theo thứ
tự là trung điểm của AB, BC,CD, DA. Gọi V là phép vị tự tâm O tỉ số k = 2 và Q là phép p
quay tâm O góc quay - . Phép biến hình F được xác định là hợp thành liên tiếp của phép 4
quay và phép vị tự. Khi đó qua F ảnh của đoạn thẳng B D ¢ ¢ là: A. Đoạn D B ¢ ¢ .
B. Đoạn A¢C¢ . C. Đoạn CA . D. Đoạn BD . !!" !!" "
Câu 7: Cho hình bình hành ABCD tâm O . Trên cạnh AB lấy điểm I sao cho IA+ 2IB = 0. Gọi G là trọng tâm ABD D
. F là phép đồng dạng biến AG D I thành CO D
D . Khi đó F là hợp bởi hai phép biến hình nào? !!!"
A. Phép tịnh tiến theo GD và phép V . B. Phép Q và phép V . (B;- )1 ( 0 G;108 ) æ 1 ö B; ç ÷ è 2 ø C. Phép V và phép Q . D. Phép V và phép Q . æ 3 ö ( 0 O; 108 - ) æ 3 ö ( 0 G; 108 - ) A; ç ÷ A; ç ÷ è 2 ø è 2 ø
Câu 8: Phép đồng dạng với tỉ số k nào dưới đây thì được một hình bằng hình ban đầu? 1 A. 1. B. 0. C. 2. D. . 2
Câu 9: Phóng to một hình chữ nhật kích thước là 4 và 5 theo phép đồng dạng tỉ số k = 3 thì được hình có diện tích là:
A. 60 đơn vị diện tích.
B. 180 đơn vị diện tích.
C. 120 đơn vị diện tích.
D. 20 đơn vị diện tích. Câu 10: Cho ABC D và A D ¢B C
¢ ¢ đồng dạng với nhau theo tỉ số k . Chọn câu sai:
A. k là tỉ số hai trung tuyến tương ứng.
B. k là tỉ số hai đường cao tương ứng.
C. k là tỉ số hai góc tương ứng.
D. k là tỉ số hai bán kính đường tròn ngoại tiếp tương ứng.
Câu 11: Cho hình vuông ABCD , P thuộc cạnh AB , H là chân đường vuông góc hạ từ B đến PC .
Phép đồng dạng viến BH D C thành PH D
B . Khi đó ảnh của B và D lần lượt là:
A. P và Q(QÎBC;BQ = BH ).
B. C và Q(QÎBC;BQ = BH ).
C. H và Q(QÎBC;BQ = BH ).
D. P và C .
Câu 12: Mệnh đề nào sau đây là đúng?
A. Mọi phép đồng dạng đều biến đường thẳng thành đường thẳng song song hoặc trùng với nó
B. Mọi phép đồng dạng biến hình vuông thành hình vuông.
C. Tồn tại phép đồng dạng biến hình chữ nhật (không phải hình vuông) thành hình vuông.
D. Phép đồng dạng biến tam giác thành tam giác có cùng diện tích.
Câu 13: Trong hệ trục tọa độ Oxy , cho điểm M (1;2). Phép đồng dạng là hợp thành của phép vị tự tâm p
I (1;2) tỉ số k = 2 và phép quay tâm O góc quay sẽ biến M thành điểm có tọa độ: 4 A. (2; ) 1 - B. (2 2; 2) C. (2;2 2) D. (2 2;- 2)
Câu 14: Trong mặt phẳng tọa độ Oxy , cho đường thẳng d : x + 2y = 0. Phép đồng dạng là phép thực p
hiện liên tiếp qua phép vị tự tâm I (1; 2
- ) tỉ số k = 3 và phép quay tâm O góc quay sẽ biến 2
đường thẳng d thành đường thẳng nào sau đây?
A. 2x - y - 6 = 0
B. x + 2y - 6 = 0
C. 2x - y + 6 = 0
D. 2x - y - 3 = 0
Câu 15: Trong mặt phẳng tọa độ Oxy , cho điểm M (0 )
;1 . Phép đồng dạng là phép thực hiện liên tiếp
qua phép vị tự tâm I (4;2) tỉ số k = 3
- và phép đối xứng qua trục d : x - 2y + 4 = 0 sẽ biến M
thành điểm nào sau đây? Trang 70 A. (16;5) B. (14;9) C. (12;13) D. (18; ) 1
Câu 16: Trong mặt phẳng tọa độ Oxy , cho đường tròn (C) (x - )2 +( y - )2 : 1
2 = 4. Phép đồng dạng là
phép thực hiện liên tiếp qua phép vị tự tâm O tỉ số k = 2
- và phép quay tâm O góc quay 0 180
sẽ biến đường tròn (C) thành đường tròn nào sau đây? ( O là gốc tọa độ) A. 2 2
x + y - 4x -8y - 2 = 0 B. 2 2
x + y + 4x + 8y + 2 = 0
C. (x + )2 +( y + )2 2 4 =16
D. (x - )2 +( y - )2 2 4 =16
Câu 17: Trong mặt phẳng tọa độ Oxy , cho đường tròn (C) (x - )2 +( y - )2 : 1
2 = 9. Phép đồng dạng là 1
phép thực hiện liên tiếp qua phép vị tự tâm I (1;- )
1 tỉ số k = và phép tịnh tiến theo 3
!v =(3;4) sẽ biến đường tròn (C) thành đường tròn có phương trình:
A. (x - )2 +( y - )2 4 4 = 9
B. (x - )2 +( y - )2 4 4 = 1
C. (x + )2 +( y + )2 4 4 = 1 D. (x - )2 2 1 + y = 1 D. HƯỚNG DẪN GIẢI Câu 1: Đáp án C. Câu 2: Đáp án C. Câu 3: Đáp án D.
Theo tính chất phép đồng dạng thì A M là đường trung tuyến của A
D B C , theo giả thiết 1 1 1 1 1
A M lại là đường cao nên A
D B C là tam giác cân tại A . Vì vậy ABC D cân tại A . 1 1 1 1 1 1 Câu 4: Đáp án B. V B = B ;Q B = C ;2 A ( ) 1 ; A j ( 1 ) ( ) ( ) Qua V
biến đường tròn tâm B bán kính BA thành đường tròn tâm B bán kính B A. (A;2) 1 1 Qua Q
biến đường tròn tâm B bán kính B A thành đường tròn tâm C bán kính CA . ( ; A j ) 1 1 A D I B C B1 Câu 5: Đáp án A. d O I' I I1
Ta có: Đ ((I )) = (I ;V I = I¢ k = 2 d 1 ) O;2 (( 1 )) ( ) . Vậy ( ) Câu 6. Đáp án C. Trang 71 A' A B D' B' O D C' C Ta có: Q
biến B ,¢ D¢ thành B , D : B D = B D
¢ ¢ và B , D nằm trên đường thẳng qua AC æ p ö 1 1 1 1 1 1 O; ç ÷ è 4 ø ( V B = B V
D = D Þ OB = OB OD = OD Þ B D = B D = B D ¢ ¢ = AC O ) ( ; 2 , 2 2 2 1 ) 2 (O ) ( 1) 2 2 1 2 1 2 2 1 1 ; 2 ; 2 . Câu 7. Đáp án C. A I B G O D C - Phép V A D GI = A D OB æ 3 ö ( ) ; A ç ÷ è 2 ø - Phép Q A D OB = C D OD ( 0 O; 1 - 80 ) ( ) Câu 8. Đáp án A. Đáp án B.
Qua phép đồng dạng tỉ số k = 3 ta được các cạnh tương ứng của hình chữ nhật là 12 và 15.
Þ Diện tích của hình chữ nhật ảnh là: 12.15 = 180. Câu 10. Đáp án C. Câu 11. Đáp án A. A P B H Q D C Câu 12. Đáp án B. Câu 13. Đáp án B. !!!!" !!!" ìx¢ = 3 Ta có: V M = M ¢ ;
x y Û IM ¢ = 2IM Þ í Þ M ¢ 3; 1 - I ;2 ( ) ( ) ( ). ( ) îy¢ = 1 - ì 3 2 2 ïx¢¢ = + = 2 2 ï Q ¢ = ¢ ¢ ¢ Þ í Þ ¢ æ p ö ( M ) M ( x y ) 2 2 ; M (2 2; 2) O; ç ÷ è 4 ø ï 3 2 2 y¢¢ = - = 2 ïî 2 2 Câu 14. Đáp án C. Ta có: V
d = d¢ Û d¢ ! d Þ d¢
x + 2y + c = 0 I ;3 ( ) có dạng: . ( ) Chọn M (2;- ) 1 Î d Þ V
M = M ¢ x ;¢ y¢ Þ M ¢ 4;1 Îd¢ Þ 4 + 2 + c = 0 Þ c = 6 - I ;3 ( ) ( ) ( ) ( )
Þ d¢: x + 2y - 6 = 0. Trang 72 Có Q ¢ = ¢ æ p ö (d ) d . O; ç ÷ è 4 ø ìx¢ = -y ìx = y¢
Gọi N (x ;¢ y¢)Îd¢ Þ Q ¢ = ¢ ¢ ¢ Þ í Þ æ p ö ( N )
N (x ; y ) í O; ç ÷ îy¢ = x îy = -x¢ è 2 ø
Thế vào phương trình d¢¢ : y¢¢ - 2x¢¢ - 6 = 0.
Vậy phương trình d¢ : 2x - y + 6 = 0. Câu 15. Đáp án C. !!!!" !!!" Ta có: V M = M¢ ; x y Û IM¢ = 3 - IM Þ M¢ 16;5 I ; 3 - ( ) ( ) ( ). ( )
Đ (M¢) = M¢ (x¢;¢ y¢ Þ d M M ¢ ¢ Þ M M ¢ ¢
2x + y + c = 0 d ) là trung trực của có dạng: đi qua M ¢ Þ c = 37 - Þ M M
¢ ¢ : 2x + y -37 = 0
Gọi H là trung điểm của M M ¢ ¢
ì2x + y - 37 = 0
Þ tọa độ H là nghiệm của hệ í
Þ H (14;9) Þ M¢ (12;13). îx - 2y + 4 = 0 Câu 16. Đáp án D.
Đường tròn (C) có tâm J (1;2) bán kính R = 2 V
J = J x ;¢ y¢ Þ J 2 - ; 4 - R = 2R = 4 O; 2 - ( ) 1( ) 1 ( ), bán kính ( ) 1
Þ Phương trình (C : x + 2 + y + 4 =16 1 ) ( )2 ( )2 Q
J = J x¢;¢ y¢ Þ J 2;4 , bán kính R = R = 4 ( 0 O;180 ) ( 1 ) 2 ( ) 2 ( ) 2 1
Vậy phương trình đường tròn cẩn tìm là: (x - )2 +( y - )2 2 4 =16 Câu 17. Đáp án B.
Đường tròn (C) có tâm J (1;2) bán kính R = 3 !!" 1 !" 1 V
J = J Û IJ = IJ Þ J 1;0 , R = R = 1 æ 1 ö ( ) 1 1 1 ( ) 1 I ; ç ÷ 3 3 è 3 ø """"! !
T! (J = J Þ J J = v Þ J 4;4 R =1 v 1 ) 2 1 2 2 ( ), bán kính 2
Vậy đường tròn ảnh qua hai phép V và T 2 2
! là: ( x - 4) + ( y - 4) = . 1 æ 1 ö I ; v ç ÷ è 3 ø Trang 73




