Bài tập phương pháp lũy thừa giải hệ phương trình có lời giải chi tiết

Tài liệu gồm 19 trang hướng dẫn phương pháp lũy thừa giải hệ phương trình thông qua các bài toán được giải chi tiết.

Cùng với phương pháp hàm số đã trình bày ở bài trước thì phương pháp lũy thừa cũng là một phương pháp phổ biến trong việc giải phương trình. Có thể nói đây là phương pháp được nghĩ đến đầu tiên khi giải các hệ phương trình chứa dấu căn, vì ta có thể ngay lập tức loại bỏ dấu căn bằng cách nâng lũy thừa tương ứng. Tuy nhiên cần phải “thận trọng” khi sử dụng phương pháp này vì việc nâng lũy thừa có thể khiến cho các phương trình hệ quả có số mũ lớn và khó giải.

68 34 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 10

Môn: Toán 10

Thông tin:

19 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
1.PHƯƠNG PHÁP LŨY THỪA
Giải:
Điều kiện :
0
x y
x y
. Nhận xét : Vế trái của phương trình (1) không âm.
Bình phương 2 vế từng phương trình ta được
2
2 4 2
2
8
x x y
x x y
2
4 2 2
2 3
8 4
x y x
x y x
Điều kiện :
x
Phương trình
2 2
3 4 4
x y x x
4 4
y x
Phương trình
4 2 2 4
4 64 16
x y x x
2
4 2 4
4 4 64 16
x x x x
5
32 80 0 6
2
x x y
Vậy nghiệm của hệ phương trình đã cho là
5
;6
2
Giải:
Điều kiện :
1
1
x
y
Bài toán 1.
2 2
2 (1)
4 2
x y x y
x y x y
Bài toán 3.
5
1 (1)
2
3
2 3 1 2
4
x y
y x x
Phương trình
2 2
2 2 2 4 4
x x y
2 2
4 2 3
x y x
Điều kiện tương đương :
2
x
. Phương trình
2 2 2
3 4 4 4
x y x x
.
2 2
1 1, 1 4
y x x y x
Thế (4) vào phương trình (3) ta được :
3
2 3 2 2
1 2 1 1 0
y y y y y y
6 5 4 3 2
2 4 2 1 0
y y y y y y
2
4 3 2
1 3 1 0
y y y y y
4 3 2
1 2
3 1 0
y x
y y y y
Xét phương trình :
4 3 2
3 1 0
y y y y
Nếu
0 1
y x
, không thỏa hệ.
Xét
0 :
y
phương trình
2
2
1 1
3 0
y y
y y
Đặt
1
, 2.
t y t
y
Phương trình trên trở thành :
2
1 0
t t
, vô nghiệm.
Vậy nghiệm của hệ phương trình đã cho là
1;2
Giải:
Điều kiện :
3 2 0
x y
x y
. Phương trình
2 1 3 2
x y x y
.
2 2 1 3
x y x y
.Điều kiện :
2 1
x y
.
Thế (3) vào phương trình (1) ta được :
Bài toán 5.
0 (1)
3 2 1 2
x y x y
x y x y
4 1 0 4 1 4
x y y x
Thế (4) vào phương trình (3) ta được :
2 5 1 6 2
x x
2
1
3
5 1 9 6 1
x
x x x
2
1
2
,
3
9
1 3
9 11 2 0
x
x loai
x y
x x
Vậy nghiệm của hệ phương trình đã cho là
1;3
Giải:
Điều kiện :
1
1
y
x
. Phương trình
1 2 2 1 5
x y
.
2 1 2 5
y x
2
5
2
4 1 4 20 25 3
x
y x x
Phương trình
2 4 4 8 3 1 1 4
y x x
Thế (3) vào phương trình (4) ta được :
2
4 20 24 8 3 1 0
x x x x
4 3 2 8 3 1 0
x x x x
4 3 2 2 1 0
x x x
3
3
4
5
2 1 2 , vi x
2
x y
x x loai
Vậy nghiệm của hệ phương trình đã cho là
3
3;
4
Bài toán 6.
5
1 (1)
2
3
2 3 1 2
4
x y
y x x
Giải: Hệ phương trình
3 3
2 2
1
- 12y 2
= 9 + y
3 - 3x = -6y
x
x
Lấy phương trình (1) trừ phương trình (2) ta được :
3 2 3 2
3 3 6 12 9
x x x y y y
3 3
1 2
x y
1 2
x y
3 3
y x
Thế Phương trình (3) vào Phương trình (1) ta được
3
3
9 3
x x
2
9 27 18 0
x x
1 2
2 1
x y
x y
Hệ phương trìnhcó 2 nghiệm
1; 2 , 2; 1
Giải: Lấy phương trình (1) cộng với phương trình (2) ta được :
2 2 2 2
2 250
x y x y
3
2 2
125
x y
2 2
5 3
x y
Thế Phương trình (3) vào Phương trình (1) ta được
5 25 = 185 xy = 12
xy . Khi đó ta có hệ phương trình :
2
2
2 2
12
5
5
12
12
x
x y
x
xy
y
x
Bài toán 50 .
3 3
2 2
= 9
= x - 4y
- y
+ 2y
x
x
Bài toán 66.
2 2 2 2
2 2 2 2
185 1
65 2
x xy y x y
x xy y x y
4 2
25 144 0
12
x x
y
x
2
2
4 3
16
3 4
9
4 3
12
3 4
x y
x
x y
x
x y
y
x y
x
Hệ phương trình có 4 nghiệm
4;3 , 3;4 , 3; 4 , 4; 3
Giải: Điều kiện :
0
0
x
y
x y
y x
Vì :
0 0
x x y x y x
Suy ra, vế trái của (2) dương.Bình phương 2 vế 2 phương trình của hệ ta được :
2
2
2 2 4
1
2y+
x x y
y x
2
2
2 3
2 1 2 4
x y x
y x y
2 2
0 2
3
4 4
x
x y x x
0 2
4 4
x
y x
2 2
1
0
2
4
4 1 4
y
y x y y
2
1
0
2
3 4 4 1 0
y
y x y
2
1
0
2
3 3 5 0
y
y y
1
0
2
,
3 69
6
y
loai
y
Hệ phương trìnhvô nghiệm
Bài toán 67.
2 1
1 2
x y x y
y x y x
Giải:
Do phương trình(1)
x y x y
0
y y y
Điều kiện :
0
x y
Bình phương 2 vế từng phương trình ta được
2 2
2 4 4
2 2 1
2 2 1
x x y
x x y
2 2
4 4 2
2 1 2
2 1 2 3
x y x
x y x
Điều kiện :
1
0
2
x
. Phương trình
2 2 2
2 4 1 4 4
x y x x
2
4 4 1
y x
2
4 1
4
4
x
y
Thế (4) vào phương trình(3) ta được :
2
4 2
4 1
2 1 2
4
x
x x
2
4 2 4
16 8 1
4 1 4 4
16
x x
x x x
5
8 5 0
8
x x
Suy ra
2
3 3
8
2 2
y y
Vậy nghiệm của hệ phương trình đã cho là
5 3
;
8
2 2
Giải: Phương trình
2 2
1 2 3
x y x
Bài toán 76.
2 2 2 2
= 1 1
1 2
x y x y
x y x y
Bài toán 82(THTT)..
2 2
2 2 2
1 2 1
y + xy = 3x - 1 2
x y
x
Thế (3) vào (phương trình(2) ta được :
2 2
2 3 1
x xy x
2
4 3 0
x xy
. Ta có x = 0, loại.
Xét
0
x
:
2
4 3
x
y
x
. Thế
2
4 3
x
y
x
vào (1) ta được :
2
2
2
4 3
1 2
x
x
x
2
2 2
4 3 2
x x
4 2
16 23 7 0
x x
2
2
1
7
16
x
x
1 1
1 1
7 5
4
7
7 5
4
7
x y
x y
x y
x y
Vậy hệ phương trình có 4 nghiệm
7 5 7 5
1;1 , 1; 1 , ; , ;
4 4
7 7
Giải: Thế phương trình(2) vàophương trình (1) ta được :
3 3 2 2
2 9 2
x y x y xy x xy y
3 3 2 2 3 3
2 9
x y x y x xy y x y
3 3
8 3
x y
Ta có y = 0 thì x = 0, không thỏa (2), loại
Xét
0
y
: phương trình
3
3 8 2 2
x x
x y
y y
.
Thế
2
x y
vào phương trình(2) ta được :
2
2 2
2 2 3
y y y
2
1 2
1
1 2
y x
y
y x
Bài toán 83(THTT)..
3 3
2 2
2 9 2 3 1
- xy + y = 3 2
x y x y xy
x
Vậy hệ phương trình có 2 nghiệm
1;2 , 1; 2
.
Giải: Điều kiện :
0
x y
Bình phương 2 vế của phương trình (1) ta được :
2
3 4
x y xy
2 2
3 10 3 0 3
x xy y
TH 1 :
0 0
y x
: không thỏa hệphương trình.
TH 2 :
0
y
: phương trình
2
3 3 10 3 0
x x
y y
3
3
1 3
3
x
x y
y
x y x
y
x = 3y
: phương trình
2
2 6 8 0
y y
4 12
2 6
y x
y x
y = 3x
: phương trình
2
2 9 2 8 0
x x
, vô nghiệm.
Vậy hệ phương trình có 2 nghiệm
12;4 , 6;2
.
Giải: Điều kiện :
x y
. Bình phương 2 vế củaphương trình (1) ta được :
2 2 2
4 2 2 3
x x y y
Thế phương trình (2) vàophương trình (3) ta được :
2
8 24 4
x y .
Bài toán 95.
2
3 x - y = 2 1
2 8 2
xy
x y
Bài toán 96.
2 2
2 - = y 1
9 2
x y x y
x y
Điều kiện :
3
x
. Thế (4) vàophương trình (1) ta được :
2
4 2 2 8 24 8 24
x x x x
2
8 24 3
x x x x
2
8 24 3
x x
2
8 15 0
x x
5 4
3 0
x y
x y
Vậy hệ phương trình có 3 nghiệm :
5; 4 , 3;0 , 5;4
.
Giải: Điều kiện :
2 2
y x
. Bình phương 2 vế của phương trình (1) ta được :
2 2 2 2
2 144 24
y x y x y y
2 2
72 12 3
x y x y
Thế (3) vào phương trình (2) ta được :
12 72 12 5
y y
Bình phương 2 vế của phương trình (2) ta được :
2 2 2
144
x y x
2 2
25 144
x x
2
2
16
4; 3
9
x
x x
x
Vậy hệ phương trình có 4 nghiệm :
3;5 , 3;5 , 4;5 , 4;5
.
Giải: Điều kiện :
1 0
xy x
TH 1 :
0
x
: không thỏaphương trình (2).
TH 2 :
0
x
: phương trình
2
1
2 1 3
x
y
x
Thế (3) vào phương trình (2) ta được :
Bài toán 97.
2 2
2 2
= 12 - y 1
= 12 2
x y x
x y x
Bài toán 98.
2 2
2
1 1 =3x - 4x +1 1
1 2
x y y x
xy x x
2 2
2 2
1 1
3 4 1
x x
x x x x
x x
2 2 2
1 2 1 3 4 1
x x x x
3
2 6 4 0
x x x
1 1
5
2
2
x y
x y
Vậy hệ phương trình có 4 nghiệm
5
1; 1 , 2;
2
.
Giải: Điều kiện :
2 2
0
x y
Hệ phương trình
2 2 2 2
2 2
3 =3 1
3 = 0 2
x x y x y x y
y x y x y
Xét
0
x
:hệ phương trình trở thành :
2
3
3 = 0
0
3 = 0
y y
y
y y
, loại.
Xét
0
y
:hệ tphương trình rở thành :
3 2
3 3 = 0
0
-x = 0
x x x
x
, loại
Xét
, 0
x y
: Hệ phương trình
2 2 2 2 2
2 2 2
3 =3y 3
3 = 0 4
xy x y xy y x y
xy x y x xy
Cộngphương trình (3) và phương trình (4) lại với nhau ta được :
2 2 2 2 2 2
2 3
xy x y y x y x y
Bài toán 99.
2 2
2 2
3
=3
3
= 0
x y
x
x y
x y
y
x y
2 2
2 3 1 0
xy y x y
3 1
2 3 1 0 5
2
y
xy y x
y
Thế (5) vào phương trình (2) ta được :
2
2
3 1 3 1
3 0
2 2
y y
y y y
y y
3 2 2
4 9 6 1 2 3 1 12 0
y y y y y
3 2
4 3 1 0
y y
1 1
y x
Vậy hệ phương trình có nghiệm duy nhất
1;1
.
Giải: Hệ phương trình trở thành
Cộng phương trình (1) và phương trình (2) lại với nhau ta được :
Xem x là ẩn của phương trình, y là tham số.
. Phương trình có nghiệm :
: Phương trình
, vô nghiệm.
2 2
2
16 4 = 12 1
16 8 56 10 36 2
x xy y
x xy x y
2 2
32 2 6 28 10 24 0
x y x y y
2
2 4
y
6
6 4
4
4 4 4
4
y
x
y x
y y x
x
6 4
y x
2
2
1 16 4 6 4 6 4 12 0
x x x x
2
16 24 24 0
x x
Bài toán 104(HSGHCM 2013-2014).
2 2
2
16 4 = 12 1
8 4 28 5 18 2
x xy y
x xy x y
: Phương trình
.
Vậy hệ phương trình có nghiệm .
Giải : Hệ phương trình (I)
Ta thấy nếu x = 0 thì không thỏa hệphương trình. Vậy
TH 1: y = 0 : Hệ phương trình (I)
TH 2: x = 1: Hệ phương trình (I)
Vậy (1; 0) là một nghiệm của hệ phương trình.
TH 3: x = -1: Hệ phương trình (I)
Vậy (-1; 0) là một nghiệm của hệ phương trình.
TH 4: : Lấy phương trình (1) chia cho phương trình (2), vế theo vế, ta được :
(2) (3)
Thế (3) vào phương trình 2) ta được :
4 4
y x
2
2
1 16 4 4 4 4 4 12 0
x x x x
2
1
16 16 4 0 2
2
x x x y
1
;2
2
2 4
2
- 1
2
x y x - y = x 1
2
y x + 1 = x - 1
x
0
x
4
2
1 0
1
1 0
x
x
x
1 0
0
2 0
y y
y
y
1 0
0
2 0
y y
y
y
1
0
x
y
2
2
1
1
x y
x x
x
4 2
1
xy x x
2 4 2 2
1 1 1
x x x x
2 6 4 2
1 2 2 1
x x x x
Bài toán 107.
4 3 2 2
- x y + x y = 1
3 2
y - x + xy = -1
x
x
, vô nghiệm.
Hệ phương trình đã cho có nghiệm : .
Giải : Dễ thấy y = 0 không thỏa hệphương trình. Vậy .
Hệ phương trình
Từ phương trình (2) . Phương trình (2)
Thế (3) vào phương trình (1) ta được :
6 4 2
2 3 0
x x x
2 4 2
2 3 0
x x x
1;0 , 1;0
0
y
3
3
2
2
27 7
8
2
4
+ =
x
+ 6 = 1
x
y
x
y y
3
3
3 7
2
2
3
2 2x
+ =
+ = 1
x
y
x
y y
2
2
3 9 6 7
2 4 1
2
3
2 2x 2
=
+ = 1
x
x x
y y y
x
y y

0
x
3
2 3
2
y
x
y x
2
2
9 6 7
4
2 2
=
y x
x
x y y
2
2
9 6 7
4
2 2
=
y x
x
x y y
2
2
7
2
9 6
2
4
=
y
x
x
x
y y
2
2
9 6
7 4
= y
x
x x
y y
2
9
7 4 6
=
x x y x
y
2
4 13 0
+ 9 =
xy xy
Bài toán 111.
3 3 3
2 2
7
8 y
2
4 y
+ 27 =
+ 6x = y
x y
x
Phương trình (3)
(3)
Hệ phương trình đã cho có 2 nghiệm : .
Giải : Thế phương trình (2) vàophương trình (1) ta được :
Thế : x = 2y vàophương trình (2) ta được :
Hệphương trình đã cho có 2 nghiệm : .
Giải: Điều kiện :
Phương trình (1) (3)
1
9
4
xy
xy
1
9
4
y
x
xy
x
1
:
y
x
2
9
5
2
x
x
3
3 3
9 10
10 9
10 9
x x y
9
:
4
y
x
2
10 9
3 8
x
x
3
3
3
27 3 3 80
80 4
80
x x y
3
3 3
3
9 10 3 3 80
; , ;
10 9 4
80
3 3 2 2
2 - 9y + xy
= + x x y x y
3 3 3 3
2 - 9y -
=
x x y
3 3
=
8
x y
=
2
x y
2
3 3 1 2
y y x
2;1 , 2; 1
1 0 1
2 0 2
x x
y y
2 2
7 12 0
y y x x
Bài toán 114.
3 3
2 2
2 - 9y 2 3 1
- xy 2
=
+ = 3
x x y xy
x y
Bài toán 151.
2
3 4 7 1
1
= 2
1 2
x x y y
y x
x y
Xem phương trình (3) là phương trình theo ẩn y, còn x là tham số.
. Nghiệm là :
, thế vào phương trình 2) ta được : . ,loại
, thế vào phương trình (2) ta được :
Hệ phương trình có 2 nghiệm :
Giải : Ta có :
y = 0 không thỏa hệ
Xét . Chia 2 vế của phương trình (2) cho y, ta được :
Hệ phương trình có 2 nghiệm :
2
1
4
2
x
4
3
y x
y x
y = x + 4
2
4
1
=
1 2
x
x
x x
y = 3 - x
2
3
1
=
1 1
x
x
x x
2
9 6 = x - 1
x x
2
5 2
10 7 = 0
2 1
x y
x x
x y
021
01
2
2
yyxx
yxyx
2
2
1
1 2 0
x y x y
x x y y
0
y
2
2
1
2 1 0
x y x y
x y x y
01
1
2
2
yx
yxyx
1
1
2
yx
yxyx
1
1
2
yx
yx
xy
xx
1
11
2
xy
xx
1
0
2
xy
xx
1
10
0;1 ; 1;2
Bài toán 181.
2
2
1 0 1
1 2 0 2
x y x y
x x y y
Giải : Điều kiện :
Hệ phương trình
Từ phương trình (1) ta có :
y = 0 không thỏa hệ
Xét . Chia 2 vế của phương trình (2) cho , ta được :
Thế vào phương trình (1), ta được :
, thỏa điều kiện ban đầu.
Hệ phương trình có nghiệm :
2
2 3 0
x y
2
2
3 3
2 3 2 3 3 2 1
2 2 3 1 6 1 2 0 2
x y y y
y x y x x x
3
3 2 0
2
y y
0
y
3
y
3 2
2
3 2 2 2 3 3 3
3 2
2 4 3 6 6 6 0
x x x x x
y y y y y y y
3 2
2
3 3 3 3 2 2 2
2 3
2 6 6 3 6 4 0
x x x x x
y y y y y y y
3 2
2
3 3 3 3 2 2 2
1 1
2 3 3 3 2 4 0
x x x x x
y y y y y y y
04
1
3
1
2
23
y
x
y
x
2
1
y
x
2 1
x y
2
4 6 4 3 2
y y y
2
2
4 6 4 3 2
y y y
5 14
18 5 0
18 9
y y x
14 5
;
9 18
Bài toán 182.
2
2
3 3
2 3 2 3 0
2 2 3 1 6 1 2 0
x y y
y x y x x x
Bài toán 188.
2 2
2 2
7 1
2 2 2
x xy y
x xy y x y
Giải : Phương trình (2)
Xem đây là phương trình theo ẩn x, còn y là tham số.
. Nghiệm là :
,thay vào phương trình (1) ta được :
, thay vào phương trình (1) ta được :
Vậy hệ phương trình có 4 nghiệm :
Giải : Điều kiện :
Phương trình (2) (3)
Xemphương trình (3) là phương trình theo ẩn y, còn x là tham số.
. Nghiệm là :
,t hế y = 2x -2 vào phương trình (1) ta có phương trình :
(4)
2 2
(1 ) 2 2 0
x y x y y
2
(3 1)
y
2
1
x y
x y
2
x y
2
x y
2
1 2
7 7
1 2
y x
y
y x
1
x y
2
2
1 1 7
y y y y
2
3 2
6 0
2 3
y x
y y
y x
2;1 ; 2; 1 ; 2; 3 ; 3;2
2
2
2 1 0
3 0
x xy x
x y y
2 2
3 4 4 6 2 0
y x y x x
1
4 3 1
2 2
2
4 3 1
2 1
2
x
y x
x
y x
2 2
y x
2 2
4 1 4 2 3
x x x x x
2 2
3
3
4 1 4 2
x
x x x x
Bài toán 197.
2 2
2 2
2 1 3 2 1
4 4 6 3 2 0 2
x xy x y x y x y
x y xy x y
(5)
Do nên từ phương trình trên ta có : x > 0.
Cộng phương trình(4) và phương trình(5), vế theo vế, ta được :
, thỏa phương trình
,thế y = 2x -1 vào phương trình (1) ta có phương trình :
(6)
Điều kiện :
Vì không thỏa phương trình nên .
(7)
Cộng phương trình(6) và phương trình(7), vế theo vế, ta được :
, thỏa phương trình. Vậy hệ phương trình có 2 nghiệm
2 2
1
0
4 1 4 2
x
x x x x
2 2
1
4 1 4 2x x x x
x
2 2
4 1 4 2,x x x x x
2
1
2 4 1 3x x x
x
2
2
1
4 4 1 3x x x
x
4 3 2
7 4 2 1 0
x x x
3 2
1 7 3 1 0
x x x x
1 0
x y
2 1
y x
2 2
4 1 4 3 2 3 1
x x x x
2
4 3 2 0
3 41
0
8
3 1 0
x x
x
x
1
x
1
x
2 2
3 3
6 3 1
4 1 4 3 2
x
x
x x x
2 2
3 3
4 1 4 3 2
3 1
x
x x x
x
2 2
4
4 1 4 3 2 1
3 1
x x x
x
2
4
2 4 1 3
3 1
x x
x
2
2
4
4 4 1 3
3 1
x x
x
2 2
2
16 24
16 4 9
3 1
3 1
x
x x
x
x
2
2
7 4 3 1 16 24 3 1
x x x x
4 3 2
63 42 29 12 0
x x x
3 2
2
63 84 27 18 0
3
x x x x
2 1
3 3
x y
2 1
1;0 ; ;
3 3
| 1/19
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

1.PHƯƠNG PHÁP LŨY THỪA
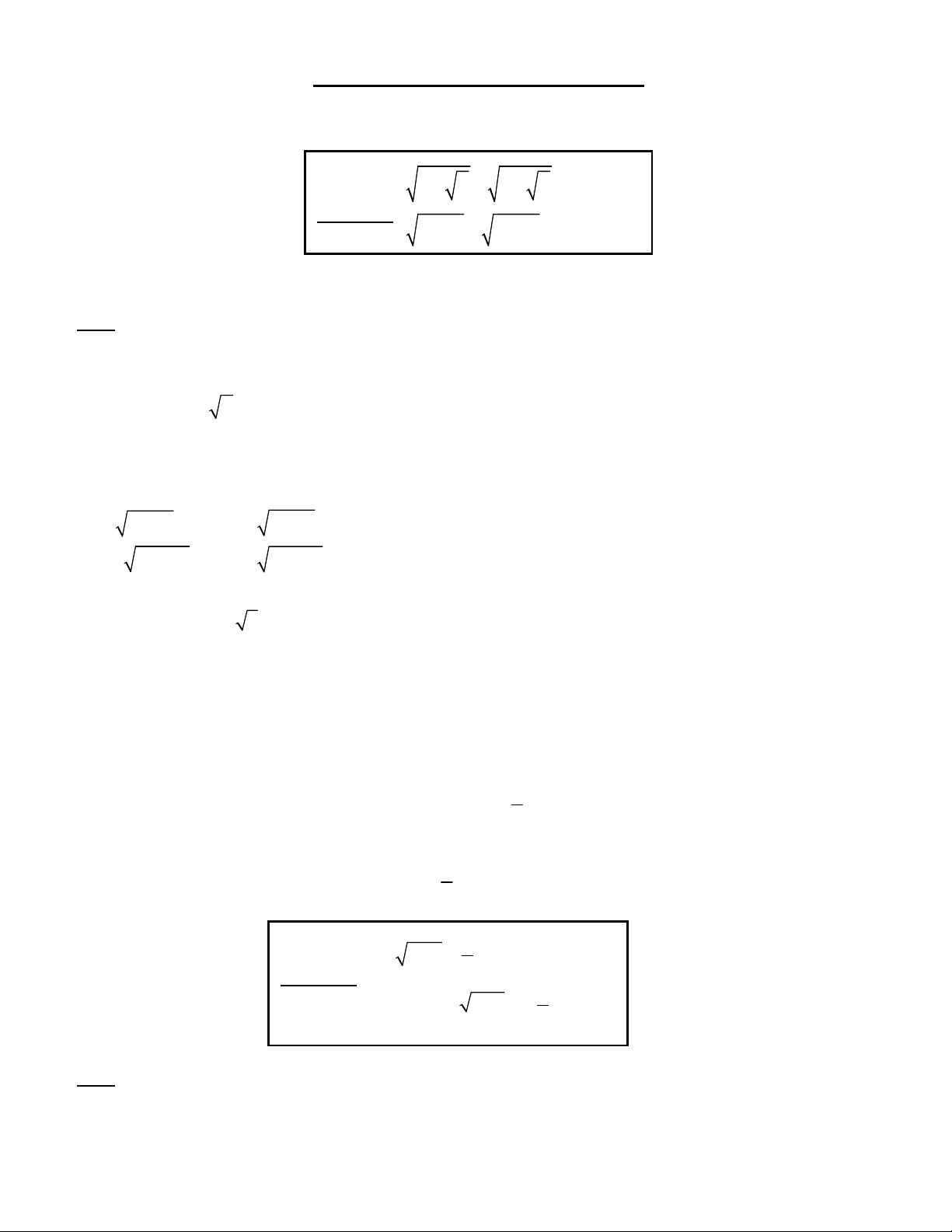
xy xy 2 (1)  Bài toán 1.  2 2
x y x y 4   2  Giải:x y  0  Điều kiện : 
. Nhận xét : Vế trái của phương trình (1) không âm. x y
Bình phương 2 vế từng phương trình ta được 2
x x y  2 2  
x y x  2  3    2 4 2 x x y  8 4 2 2 
x y  8  x 4 
Điều kiện : 0  x  2 2 Phương trình   2 2
3  x y  4  4x x y  4x  4 Phương trình   4 2 2 4
4  x y  64 16x x 5
x   x  2 4 2 4 4 4
 64 16x x  32x  80  0  x   y  6 2  5
Vậy nghiệm của hệ phương trình đã cho là  ; 6    2   5 x  1 y  (1)   2 Bài toán 3.  3
y  2 x  3 x 1   2   4 Giải:x  1 Điều kiện :  y  1  Phương trình   2 2
2  2x  2 x  4 y  4 2 2 
x  4 y  2  x 3
Điều kiện tương đương : x  2 . Phương trình   2 2 2
3  x  4 y  4  4x x . 2 2
y x 1  x y  1, x  1 4
Thế (4) vào phương trình (3) ta được :  y  3 2 3  y   2
y   y  2 1 2 1 y y   1  0 6 5 4 3 2
y y  2 y  4 y  2 y y 1  0  y  1   x  2
  y  2  4 3 2 1
y y  3y y   1  0   4 3 2
y y  3y y 1  0  Xét phương trình : 4 3 2
y y  3y y  1  0 
Nếu y  0  x  1, không thỏa hệ. 1  1 
Xét y  0 : phương trình  2  y   y   3  0 2   y y   1
Đặt t y  , t  2. Phương trình trên trở thành : 2
t t 1  0 , vô nghiệm. y
Vậy nghiệm của hệ phương trình đã cho là  1  ; 2
x y x y  0 (1)  Bài toán 5.
x y  3x  2 y  1  2  Giải:x   y Điều kiện : 
. Phương trình 2  x y 1  3x  2y . 3x  2 y  0 
 2 x y  2x y 13 .Điều kiện : 2x y  1.
Thế (3) vào phương trình (1) ta được :
4x y 1  0  y  4x 14
Thế (4) vào phương trình (3) ta được :  1 x
2 5x 1  6x  2   3 2
5x 1  9x  6x 1   1  2 x x  ,loai  3    9  2
9x 11x  2  0
x  1  y  3  
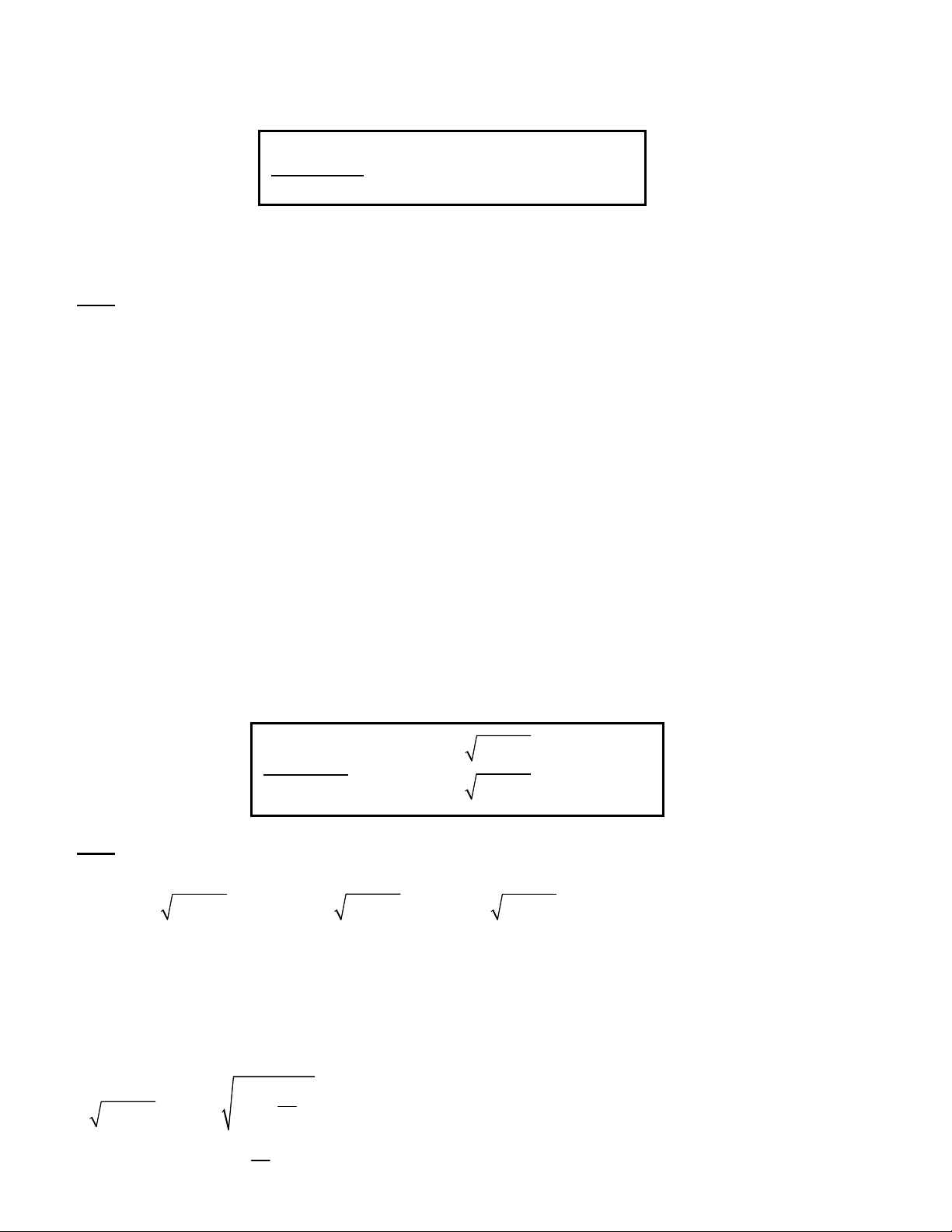
Vậy nghiệm của hệ phương trình đã cho là 1;3  5 x  1 y  (1)   2 Bài toán 6.  3
y  2 x  3 x 1   2   4 Giải:y  1  Điều kiện :  . Phương trình  
1  2x  2 1 y  5 . x  1    5 x  
 2 1 y  2x  5  2  4 y   2
1  4x  20x  253 
Phương trình 2  4y  4  8 x  3 1 x  14
Thế (3) vào phương trình (4) ta được : 2
4x  20x  24  8 x  3 x 1  0  4 x  3 x  2  8 x  3 x 1  0  3
x  3  y    4
 4  x  3 x  2  2 x 1  0   5
2 x 1  2  x,loai vi x   2  3
Vậy nghiệm của hệ phương trình đã cho là  3;     4  3 3  x - y = 9 Bài toán 50 .  2 2  x + 2y = x - 4y  3 3 x = 9 + y    1
Giải: Hệ phương trình   2 2
 3x - 3x = -6y - 12y 2 
Lấy phương trình (1) trừ phương trình (2) ta được : 3 2 3 2 3 3
x  3x  3x y  6 y 12 y  9   x   1   y  2
x 1  y  2
y x  3 3
Thế Phương trình (3) vào Phương trình (1) ta được
x  1  y  2
x    x  3 3 9 3 2  9
x  27x 18  0
 x  2  y  1  
Hệ phương trìnhcó 2 nghiệm 1; 2  ,2;  1  2 2
x xy y   2 2
x y  185   1 Bài toán 66.  2 2 2 2
x xy y x y  65 2 
Giải: Lấy phương trình (1) cộng với phương trình (2) ta được :  2 2 x y  2 2 2 x y  250
  x y 3 2 2  125 2 2 
x y  5 3
Thế Phương trình (3) vào Phương trình (1) ta được
525  xy = 185  xy = 12 . Khi đó ta có hệ phương trình : 2   12 2   2 2 x   5 
x y  5     x     xy  12   12 y    x 2  x  16
x  4  y  3 4 2
x  25x 144  0    2 
x  3  y  4  x  9  12      y  
x  4  y  3  12  x y   
x  3  y  4  x
Hệ phương trình có 4 nghiệm 4;3,3; 4, 3  ; 4  , 4  ; 3  
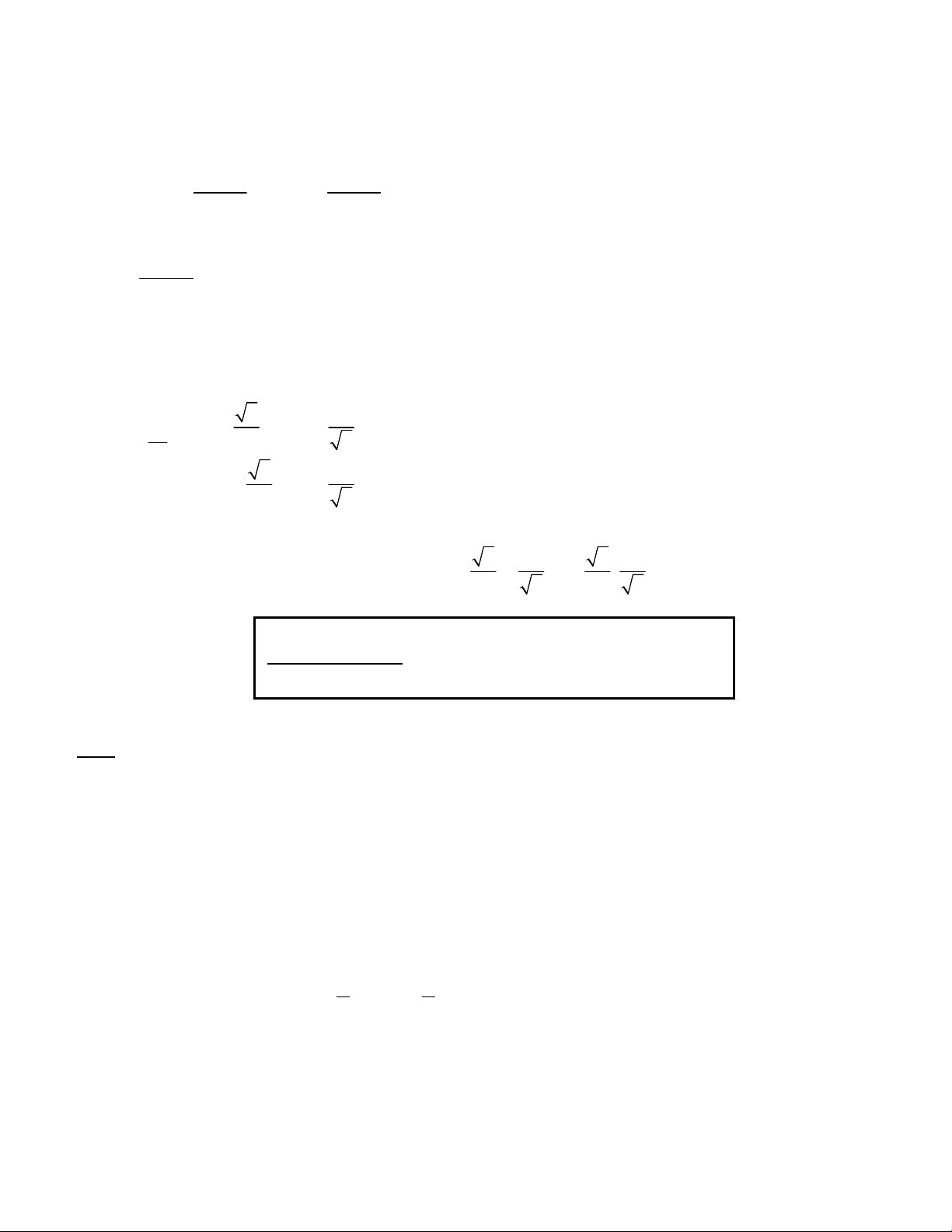
x y x y  2    1 Bài toán 67.
y x y x  1 2  x  0  y  0 
Giải: Điều kiện :  x y   y x
Vì : x x  0   y x   y x   0
Suy ra, vế trái của (2) dương.Bình phương 2 vế 2 phương trình của hệ ta được : 2
2x  2 x y  4 2  
x y  2  x  3    2
2y+ y x  1 2 
2 y x  1 2y 4  0  x  2 0  x  2 3     2 2
x y  4  4x xy  4  4x   1  1 0  y  0  y    4  2    2 4 2 y x 2
 1 4 y y 2  
3y  4x  4 y 1  0   1  1 0  y  0  y    2   2   , loai 2  3   69
3y  3y  5  0   y    6
Hệ phương trìnhvô nghiệm
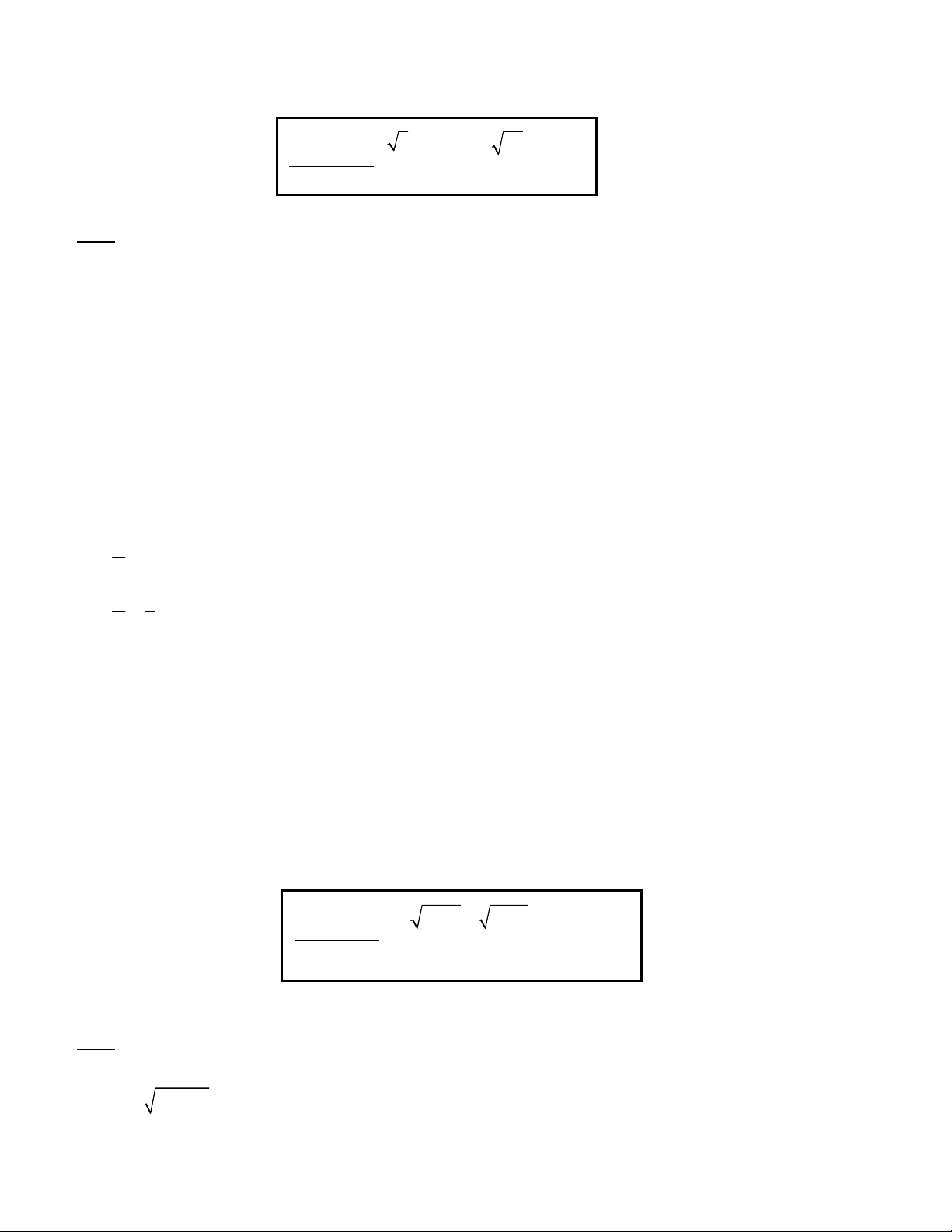
x y x y = 1   1  Bài toán 76.  2 2 2 2  x y
x y  1 2  Giải:
Do phương trình(1)  x y x y y   y y  0
Điều kiện : x y  0
Bình phương 2 vế từng phương trình ta được 2 2
2x  2 x y  1 2 2  
2 x y  1 2x     2 4 4
2x  2 x y  1 4 4 2 
2 x y  1 2x 3  1
Điều kiện : 0  x  . Phương trình     2 2 x y  2 2 4
 1 4x  4x 2 2 4x 1
 4 y  4x 1 2  y  4 4
Thế (4) vào phương trình(3) ta được : 2  4x 1 4  2 2 x   1 2x    4  2 
16x  8x 1  5 4 2 4  4 x
 1 4x  4x  
 8x  5  0  x  16   8 3 3 Suy ra 2 y   y  8 2 2  5 3 
Vậy nghiệm của hệ phương trình đã cho là  ;   8 2 2    2 x   2
1 y   2   1
Bài toán 82(THTT)..  2 2 2
x y + xy = 3x - 1  2 
Giải: Phương trình   2 2
1  x y  2  x 3
Thế (3) vào (phương trình(2) ta được : 2 2
2  x xy  3x 1 2
 4x xy  3  0 . Ta có x = 0, loại. 2 4x  3 2 4x  3
Xét x  0 : y  . Thế y  vào (1) ta được : x x 2 2  4x  3    2 x 1     2  
x   x  2 2 2 4 3  2 4 2
 16x  23x  7  0  x     
x  1  y  1
x  1 y  1  2   x  1   7 5  7   x   y   2  x  4  7  16  7 5  x    y   4 7  7 5   7 5 
Vậy hệ phương trình có 4 nghiệm 1;  1 ,  1  ;   1 ,  ;  ,   ;   4 7   4 7      3 3
2x  9 y  
x y2xy  3   1
Bài toán 83(THTT)..  2 2
x - xy + y = 3 2 
Giải: Thế phương trình(2) vàophương trình (1) ta được : 3 3
x y   x y 2 2 2 9
2xy x xy y  3 3
x y   x y 2 2
x xy y  3 3 2 9  x y 3 3
x  8 y 3
Ta có y = 0 thì x = 0, không thỏa (2), loại 3  x x
Xét y  0 : phương trình 3   8 
 2  x  2 y   . y y  
Thế x  2 y vào phương trình(2) ta được :
y  1  x  2  y2 2 2 2
 2 y y  3 2  y  1   y  1   x  2  
Vậy hệ phương trình có 2 nghiệm 1; 2, 1  ; 2   .  3 
x - y  = 2 xy   1 Bài toán 95.  2
2x y  8 2 
Giải: Điều kiện : x y  0
Bình phương 2 vế của phương trình (1) ta được :  x y2 3  4xy 2 2
 3x 10xy  3y  0 3
TH 1 : y  0  x  0 : không thỏa hệphương trình. 2  x x
TH 2 : y  0 : phương trình 3  3 10  3  0   y y    x  3  yx  3y      x 1 y  3x    y 3 
y  4  x  12
 x = 3y : phương trình   2
2   y  6 y  8  0  
y  2  x  6 
 y = 3x : phương trình   2 2  9
x  2x  8  0 , vô nghiệm.
Vậy hệ phương trình có 2 nghiệm 12; 4,6; 2 . 2
  x y - x y  = y   1 Bài toán 96.  2 2
x y  9 2 
Giải: Điều kiện : x   y . Bình phương 2 vế củaphương trình (1) ta được :  2 2 x x y  2 4 2 2  y 3
Thế phương trình (2) vàophương trình (3) ta được : 2
8x  24  y 4 .
Điều kiện : x  3 . Thế (4) vàophương trình (1) ta được :  2
4 2x  2 x  8x  24   8x  24 2
x x  8x  24  x  3
x  5  y  4 2 
x  8x  24  3 2
x  8x  15  0  
x  3  y  0 
Vậy hệ phương trình có 3 nghiệm : 5;4,3;0,5; 4 . 2 2
x y x = 12 - y    1 Bài toán 97. 2 2
x y x = 12 2 
Giải: Điều kiện : 2 2
y x . Bình phương 2 vế của phương trình (1) ta được : 2 2 2 2
y  2x y x  144  24 y y 2 2
x y x  72 12 y 3
Thế (3) vào phương trình (2) ta được : 12  72 12 y y  5
Bình phương 2 vế của phương trình (2) ta được : 2 x  16 2  x  2 2
y x   144 2  x  2
25  x   144    x  4  ; x  3 2 x  9 
Vậy hệ phương trình có 4 nghiệm : 3;5, 3
 ;5,4;5 ,4;5 . 2 x   y  
1  y x 1  2 =3x - 4x +1   1 Bài toán 98.  2
xy x 1  x 2 
Giải: Điều kiện : xy x 1  0
TH 1 : x  0 : không thỏaphương trình (2). 2 x 1
TH 2 : x  0 : phương trình 2  y 1  3 x
Thế (3) vào phương trình (2) ta được : 2 2  x 1  x 1  2 2 x x
 3x  4x 1 2 2 2       x   1 2x  
1  3x  4x 1 x x    
x  1  y  1  x  3
2x  6x  4  0   5
x  2  y    2  5
Vậy hệ phương trình có 4 nghiệm   1;   1 , 2  ;    .  2   3x y x  =3  2 2  x y Bài toán 99. x  3yy  = 0 2 2  x y
Giải: Điều kiện : 2 2
x y  0 x   2 2
x y   3x y=3 2 2
x y    1 Hệ phương trình   y  2 2
x y   x  3y = 0 2 
Xét x  0 :hệ phương trình trở thành : 2 3   y y= 0 
y  0 , loại. 3  y  3y = 0 
Xét y  0 :hệ tphương trình rở thành : 3 2
x  3x  3x = 0   x  0 , loại -x = 0 
Xét x, y  0 : Hệ phương trình xy   2 2 x y  2
 3xy y =3y  2 2
x y  3   xy  2 2 x y  2
x  3xy = 0 4 
Cộngphương trình (3) và phương trình (4) lại với nhau ta được : xy  2 2 x y  2 2
y x y  2 2 2 3 x y  3y 1
  xy y    2 2 2 3
1 x y   0  2xy  3y 1  0  x  5 2 y
Thế (5) vào phương trình (2) ta được : 2  3y 1    3y 1 2  y   y    3y  0   2 y 2 y      3 2
y y y    y   2 4 9 6 1 2 3 1 12 y  0 3 2
 4 y  3y 1  0  y  1  x  1
Vậy hệ phương trình có nghiệm duy nhất 1;  1 .
Bài toán 104(HSGHCM 2013-2014). 2 2 1
 6x  4xy y = 12    1  2 8
x  4xy  28x  5 y  1  8 2 
Giải: Hệ phương trình trở thành 2 2 1
 6x  4xy y = 12    1  2 1
 6x  8xy  56x 10 y  3  6 2 
Cộng phương trình (1) và phương trình (2) lại với nhau ta được : 2 x   y   2 32 2 6
28 x y 10y  24  0
Xem x là ẩn của phương trình, y là tham số.  6  y x    y  6  4 4 x    y  2 2
4 . Phương trình có nghiệm :    4  y y  4  4xx    4
y  6  4x : Phương trình   
x x   x    x2 2 1 16 4 6 4 6 4 12  0 2
 16x  24x  24  0 , vô nghiệm.
y  4  4x : Phương trình   
x x   x    x2 2 1 16 4 4 4 4 4 12  0 1 2
 16x 16x  4  0  x   y  2 . 2  1
Vậy hệ phương trình có nghiệm  ; 2 .    2   4 3 2 2 x - x y + x y = 1 Bài toán 107.  3 2 x y - x + xy = -1  2 x y  x - y 4 = x - 1   1
Giải : Hệ phương trình    (I) x   2 y x +  2 1 = x - 1 2 
Ta thấy nếu x = 0 thì không thỏa hệphương trình. Vậy x  0 4  x 1  0
TH 1: y = 0 : Hệ phương trình (I)    x  1 2 x 1  0  
y 1 y   0
TH 2: x = 1: Hệ phương trình (I)    y  0 2 y  0 
Vậy (1; 0) là một nghiệm của hệ phương trình.   y  1   y   0
TH 3: x = -1: Hệ phương trình (I)    y  0  2  y  0 
Vậy (-1; 0) là một nghiệm của hệ phương trình. x  1 TH 4: 
: Lấy phương trình (1) chia cho phương trình (2), vế theo vế, ta được : y  0   x y (2)  2 x
x 1  xy    4 2 x x   1 (3)  2   x 1 
Thế (3) vào phương trình 2) ta được : 2 x     4 2
x x   2 1 1 x   1 2  x     6 4 2 1
x  2x  2x   1 6 4 2
x  2x  3x  0 2  x  4 2
x  2x  3  0, vô nghiệm.
Hệ phương trình đã cho có nghiệm :  1  ;0,1;0 .  7 3 3 3 8  x y + 27 = y Bài toán 111.  2 2 2 4x y + 6x = y 
Giải : Dễ thấy y = 0 không thỏa hệphương trình. Vậy y  0 . 3  27 7  3   8x + = 3 3 7  2x + = 3 y 2    y 2 Hệ phương trình        2 x x 4 + 6 = 1  x  3  2  2 2x + = 1 y y     y y     3   9 6x  7 2 2x  4x   = 1    2    y y y 2       x  3  2 2x + = 1   2  y y    3 y
Từ phương trình (2)  x  0 . Phương trình (2)  2x   3 y 2x
Thế (3) vào phương trình (1) ta được : y  9 6x  7 y  9 6x  7 2 4x   = 2  4x   =  2    2x y y 2 2   2x y y 2   7 y 2  9 6x   = 2
 7x = y 4x     2x 2 2 9 6x y y 4x     2 y y 9 2
 7x = 4x y
 6x   xy2 4 13xy + 9 = 0 y  1  xy  1 y    x  9    xy  9   4 xy   4x 1 9 9 10  y
:Phương trình (3)  5x  3 3 3
 10x  9  x   y x 2 2x 10 9 9 10 9 3 27 3 3 80  y  :(3)  x  3  x   x   y  4x 2 3 8x 3 80 80 4 3  9 10   3 3 80 
Hệ phương trình đã cho có 2 nghiệm : 3 3  ;  ,  ;  .    3 10 9 80 4      3 3 2x - 9y = 
x y2xy  3   1 Bài toán 114.  2 2
x + y - xy = 3  2
Giải : Thế phương trình (2) vàophương trình (1) ta được : 3 3 x
=  x y  2 2 2 - 9y x + y + xy 3 3 3 3
 2x - 9y = x - y 3 3
x = 8y x = 2y
Thế : x = 2y vàophương trình (2) ta được : 2
3y  3  y  1   x  2 
Hệphương trình đã cho có 2 nghiệm : 2;  1 , 2  ;   1 . Bài toán 151.
x  3 x  4  y y  7   1  2  y x 1 = 2  x 1 2  y  x 1  0 x  1
Giải: Điều kiện :    2  y  0 y  2   Phương trình (1) 2 2
y  7 y x x 12  0 (3)
Xem phương trình (3) là phương trình theo ẩn y, còn x là tham số. 2  1 
y x  4   4 x  . Nghiệm là :     2  y  3  x   x  2 4 x 1
 y = x + 4 , thế vào phương trình 2) ta được : = . ,loại x 1 x  2
 y = 3 - x , thế vào phương trình (2) ta được :   x2 3 x 1
x  5  y  2  = 2
 9  6x x = x - 1 2
 10  7x x = 0   x 1 x 1
x  2  y  1 
Hệ phương trình có 2 nghiệm : 5; 2  ;2;  1 2
x y x y 1  0   1  Bài toán 181. 2 x   
1  x y  2  y  0 2  2 2 
x yx y  1  0
x 1  y x yGiải : Ta có :       2 2  x  
1 x y  2  y  0  x  
1  x y  2  y  0   y = 0 không thỏa hệ
 Xét y  0 . Chia 2 vế của phương trình (2) cho y, ta được : 2
x 1  y x y 2  
x  1  yx y     2
x y 2  2 x y  1  0   
x y   1  0  2
x  1  yx y  2 x  1  y     x y  1 x y  1
x2  1  1  x
x2  x  0
x  0  x  1      
y  1  xy  1  xy  1  x
Hệ phương trình có 2 nghiệm : 0;  1 ;1;2 2
x  2 y  3  2 y  3  0  Bài toán 182.
22 y x   3y x  2 3 3
1  6x x   1  2  0
Giải : Điều kiện : 2
x  2 y  3  0 2
x  2y  3  2y  3  3  2y    1 Hệ phương trình  
22 y x   3y x  2 3 3 1
 6x x   1  2  0 2  3
Từ phương trình (1) ta có : 3  2 y  0  y  2  y = 0 không thỏa hệ
 Xét y  0 . Chia 2 vế của phương trình (2) cho 3 y , ta được : 3 2 2 x x x 3 x x 2  2  4  3  6   6  6   0 3 2 2 2 3 3 3 y y y y y y y 3 2 2 x x x 2 x x 3  2  6  6   3  6   4  0 3 3 3 3 2 2 2 y y y y y y y 3 2 2  x x x 1   x x 1   2   3  3    3  2    4  0 3 3 3 3 2 2 2 y y y y y y y     3 2  x  1  x  1 x  1  2  3  4  0   2  x  2  y 1      y   y y
Thế vào phương trình (1), ta được : 2
4 y  6 y  4  3  2 y 5 14
y y     y2 2 4 6 4 3 2
 18y  5  0  y   x  
, thỏa điều kiện ban đầu. 18 9  14 5
Hệ phương trình có nghiệm :   ;    9 18  2 2
x xy y  7    1 Bài toán 188. 2 2
x xy  2 y  x  2 y 2 
Giải : Phương trình (2) 2 2
x  (1 y)x  2y  2 y  0
Xem đây là phương trình theo ẩn x, còn y là tham số.  x  2 y 2
  (3y 1) . Nghiệm là :
x  y 1 
x  2 y ,thay x  2 y vào phương trình (1) ta được :
y  1  x  2 2 7 y  7 
y  1 x  2 
x   y 1 , thay vào phương trình (1) ta được :  y  3   x  2
y  2   y   2 1 1 y y  7 2
y y  6  0 
y  2  x  3 
Vậy hệ phương trình có 4 nghiệm : 2;  1 ; 2;  
1 ; 2; 3;3; 2 2 2 
 2x xy x 1 
y x  3y x y  2   1 Bài toán 197.  2 2
4x y  4xy  6x  3 y  2  0 2  2 
2x xy x 1  0
Giải : Điều kiện :  2
x  3y y  0  Phương trình (2) 2
y    x 2 3 4
y  4x  6x  2  0 (3)
Xemphương trình (3) là phương trình theo ẩn y, còn x là tham số.  4x  3 1 y   2x  2    2 1. Nghiệm là :  4x  3 1  y   2x 1  2
y  2x  2 ,t hế y = 2x -2 vào phương trình (1) ta có phương trình : 3 2 2
4x x 1  4x x  2  3x (4)   3x 2 2
4x x 1  4x x  2 1 1   x  0 2 2 
4x x 1  4x x  2  (5) 2 2
4x x 1  4x x  2 x Do 2 2
4x x 1  4x x  2, x
   nên từ phương trình trên ta có : x > 0.
Cộng phương trình(4) và phương trình(5), vế theo vế, ta được : 2 1 2  1 
2 4x x 1  3x   4 2 4x x   1  3x    xx  4 3 2
 7 x  4x  2x 1  0   x   3 2
1 7x  3x x  
1  0  x  1  y  0 , thỏa phương trình
y  2x 1 ,thế y = 2x -1 vào phương trình (1) ta có phương trình : 2 2 4x 1 
4x  3x  2  3x 1 (6) 2
4x  3x  2  0 Điều kiện : 3   41   x   0 3x 1  0 8  Vì 3x  3
x  1 không thỏa phương trình nên x  1 . 6   3x 1 2 2
4x 1  4x  3x  2 3  x  3 4 2 2 
4x 1  4x  3x  2  2 2 
4x 1  4x  3x  2  1 (7) 3x 1 3x 1
Cộng phương trình(6) và phương trình(7), vế theo vế, ta được : 2 4 2  4 
2 4x 1  3x   4 2 4x   1  3x    3x 1  3x 1  16 24x 2 2 2
 16x  4  9x     2
7 x  43x   1
 16  24x 3x   1 3x  2 1 3x 1 4 3 2  2 
 63x  42x  29x 12  0  x     3 2
63x  84x  27 x 18  0  3  2 1  2 1   x   y
, thỏa phương trình. Vậy hệ phương trình có 2 nghiệm 1;0; ;   3 3  3 3 