Bài tập quản lí giáo dục trong nhà nước | Đại học Sư Phạm Hà Nội
Bài tập quản lí giáo dục trong nhà nước | Đại học Sư Phạm Hà Nội với những kiến thức và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học vào thực tiễn cuộc sống. Mời bạn đọc đón xem!
Môn: Tâm lý học giáo dục 278 tài liệu
Trường: Đại học Sư Phạm Hà Nội 2.1 K tài liệu
Tác giả:
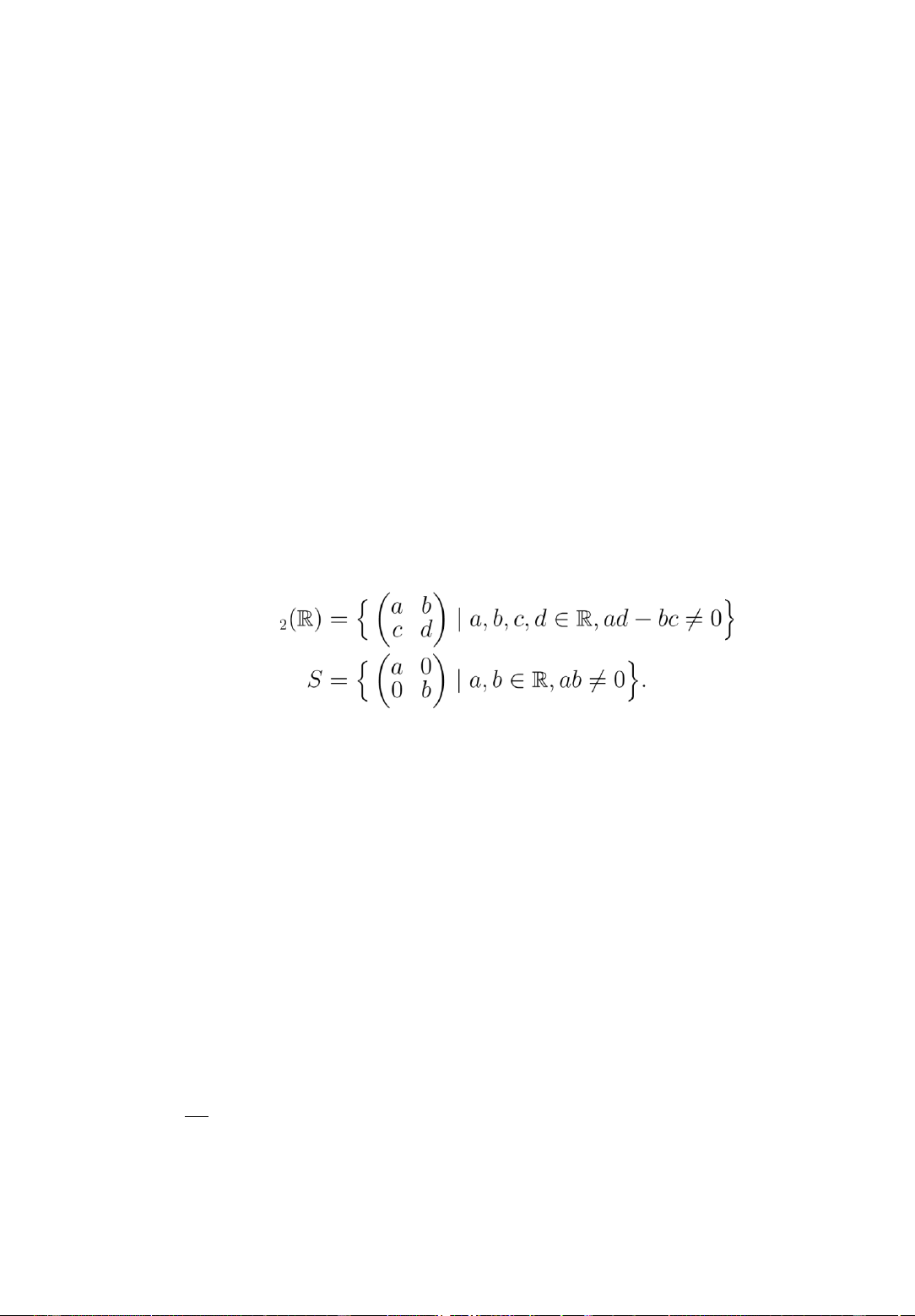
Preview text:
TRƯỜNG ĐẠI HỌC SƯ PHẠM HÀ NỘI
ĐỀ THI KẾT THÚC HỌC PHẦN Khoa Toán -
Tin Môn thi: CẤU TRÚC ĐẠI SỐ CƠ BẢN ————–
Thời gian làm bài: 120 phút Câu 1. (2 điểm)
(a) Hãy chỉ ra ví dụ (kèm giải thích) về một nhóm hữu hạn không giaohoán.
(b) Hãy chỉ ra (kèm giải thích) một nhóm con cyclic cấp 10 của nhómnhân
C∗ các số phức khác 0.
Câu 2. (3 điểm) Cho GL2(R) là nhóm nhân các ma trận vuông thực cấp 2 không suy
biến, và S là tập con gồm các ma trận chéo trong GL2(R): GL
(a) Chứng minh S là một nhóm con của nhóm GL2(R).
(b) Nhóm con S có phải là một nhóm con chuẩn tắc của GL2(R) hay không? Tại sao?
(c) Cho nhóm nhân R∗ ×R∗ = {(a,b) | a,b ∈ R,a 6= 0 ,b = 06 }, với phép
nhân: (a,b).(c,d) = (ac,bd). Chứng minh đẳng cấu nhóm:
S ∼= R∗ × R∗.
Câu 3. (5 điểm) Cho tập con I của vành đa thức hệ số hữu tỉ Z[x], và tập con
Z[i√10] của trường số phức C như sau:
(a) Chứng minh I là một ideal của vành Z[x].
(b) Chứng minh Z[i√10] là một vành con của trường số phức C.
(c) Chứng minh đẳng cấu vành Z[x]/I ∼= Z[i√10].
(d) Ideal I có là một ideal nguyên tố hay ideal cực đại của Z[x] không? Tại sao? Z
(e) [i√10] có phải là một vành Euclid hay không? Tại sao?
—————————————————————–
Lưu ý: - Cán bộ coi thi không giải thích gì thêm.
- Người thi ĐƯỢC PHÉP sử dụng tài liệu giấy.