-
Thông tin
-
Hỏi đáp
Bài Tập Quang học - Vật Lí Đại Cương 2 | Trường Đại học Kiến trúc Hà Nội
Điều kiện cực đại: Hiệu quang lộ của hai sóng ánh sáng tại nơi gặp nhau bằng một số nguyên lần bước sóng ánh sáng 21 (Với k = 0, ±1,±2,……) (1.1). Điều kiện cực tiểu: Hiệu quang lộ của hai sóng ánh sáng tại nơi gặp nhau bằng một số bán nguyên lần bước sóng ánh sáng. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem !
Trường:
Đại học Kiến trúc Hà Nội (193)
Thông tin:
75 trang
1 tháng trước
Tác giả:
Bài Tập Quang học - Vật Lí Đại Cương 2 | Trường Đại học Kiến trúc Hà Nội
Điều kiện cực đại: Hiệu quang lộ của hai sóng ánh sáng tại nơi gặp nhau bằng một số nguyên lần bước sóng ánh sáng 21 (Với k = 0, ±1,±2,……) (1.1). Điều kiện cực tiểu: Hiệu quang lộ của hai sóng ánh sáng tại nơi gặp nhau bằng một số bán nguyên lần bước sóng ánh sáng. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem !
n
2
- sin
2
i
1
1
Chương 1: GIAO THOA ÁNH SÁNG
I. TÓM TẮT LÝ THUYẾT
1. Điều kiện cực đại và cực tiểu giao thoa
* Điều kiện cực đại: Hiệu quang lộ của hai sóng ánh sáng tại nơi gặp nhau bằng
một số nguyên lần bước sóng ánh sáng
L
1
-
L
2
=kλ
(Với k = 0, ±1,±2,……) (1.1)
* Điều kiện cực tiểu: Hiệu quang lộ của hai sóng ánh sáng tại nơi gặp nhau bằng
một số bán nguyên lần bước sóng ánh sáng
L
1
-
1
L
2
=(k + )λ
2
(k = 0, ±1,±2,……) (1.2)
Trong đó: L
1
, L
2
là quang lộ của tia sáng từ nguồn thứ cấp thứ nhất và thứ 2 tới điểm
quan sát. λ là bước sóng ánh sáng trong chân không.
Nếu giao thoa thực hiện trong không gian thì điều kiện cực đại và cực tiểu giao thoa
lần lượt là:
r
1
– r
2
= kλ (1.3)
r
1
– r
2
= (k + ½)λ (1.4)
2. Vân giao thoa trong máy giao thoa Yang
* Vị trí vân sáng:
(1.5)
x
=k
Dλ
s
a
(Với
k
=
0,
±1,±2,……)
* Vị trí vân tối:
x
=(k +
1
)
D
λ
(Với k = 0, ±1,±2,……) (1.6)
t
2 a
* Khoảng vân (bề rộng của vân giao thoa):
i =x
k +1
-
x
=
D λ
k
a
(1.7)
Trong đó: λ là bước sóng ánh sáng tới.
a là khoảng cách giữa 2 nguồn kết hợp
D là khoảng cách từ mặt phẳng chứa hai nguồn sáng tới màn quan sát.
3. Giao thoa khi dùng ánh sáng trắng
Hình ảnh giao thoa: chính giữa là một vân trắng, gọi là vân trắng chính giữa hay vân
trung tâm. Ở 2 bên vân trung tâm có các dải màu sắc như ở cầu vồng, tím ở trong,
đỏ ở ngoài gọi là phổ của ánh sáng trắng.
Độ rộng phổ bậc k: Δx = x
đ
(k) – x
t
(k) (1.8)
4. Giao thoa do phản xạ
a, Kết luận của Lloyd: Sau khi phản xạ trên môi trường chiết quang hơn môi trường
ánh sáng tới, quang lộ của tia phản xạ dài thêm một đoạn là
λ
.
2
b, Bản mỏng có bề dày thay đổi
Hiệu quang lộ giữa 2 tia phản xạ trên hai mặt bản mỏng:
L
1
-
λ
L
2
=2d -
2
(1.9)
Trong đó : d là bề dày của bản mỏng tại điểm quan sát n
là chiết suất của bản mỏng
i là góc tới của tia sáng trên bản mỏng. λ
là bước sóng ánh sáng tới
c. Vân của nên không khí
Hiệu quang lộ giữa 2 tia phản xạ trên hai mặt nêm:
L
-
L
=
2d
+
λ
(1.10)
1 2
2
Những vân tối thỏa mãn:
d
=
k
λ
( k = 0, 1,2,……) (1.11)
t
2
Những vân sáng thỏa mãn:
d
=
(2k
-
1)
λ
( k = 0, 1,2,……)
s
4
(1.12)
Trong đó : d là bề dày của nêm.
d. Vân tròn Niuton
Những vân tối thỏa mãn:
d
=
k
λ
( k = 0, 1,2,……)
t
2
(1.13)
Những vân sáng thỏa mãn:
d
=
(2k
-
1)
λ
( k = 0, 1,2,……)
s
4
(1.14)
Bán kính vân tối thứ k :
rk
=
Rλ .
k
( k = 0, 1,2,……) (1.15)
Trong đó R là án kính cong của thấu kính
e.Bản mỏng có bề dày không đổi – Vân cùng độ nghiêng
Hiệu quang lộ giữa 2 tia phản xạ trên hai mặt bản mỏng:
L
-
L
=
2d n2
-
sin 2 i
-
λ
(1.16)
1 2 1
2
Trong đó : d là bề dày của bản mỏng tại điểm quan sát
n là chiết suất của bản mỏng
i là góc tới của tia sáng trên bản mỏng.
λ là bước sóng ánh sáng tới
II. BÀI TẬP MẪU
1. Khoảng cách giữa 2 máy trong khe giao thoa Yang là 1mm. Khoảng cách từ màn
quan sát tới mặt phẳng chứa 2 khe là 3m. Khi toàn bộ hệ thống đặt trong không khí,
người ta đo được khoảng cách giữa 2 vân sáng liên tiếp i = 1,5 mm.
a, Tìm bước sóng ánh sáng tới
b, Xác định vị trí vân sáng thứ 3 và vân tối thứ 4
c, Đặt trước một trong hai khe sáng một bản mỏng phẳng có 2 mặt song song, chiết
suất n = 1.5, bề dày e = 10 μm. Xác định độ dịch chuyển của vân giao thoa trên màn
quan sát.
d, Trong câu hỏi c nếu đổ đầy nước (n = 1,33) vào khoảng cách giữa màn quan sát
và mặt phẳng khe thì hệ thống vân giao thoa có gì thay đổi ? Hãy tính khoảng cách
giữa 2 vân sáng liên tiếp trong trường hợp này.
Giải
Cho a = 1 mm ; D = 3m ; i = 1,5 mm
Tìm: a, λ = ?
b, x
s3
=?; x
t4
=?
c, đặt trước một trong 2 khe bản mỏng n = 1.5, e = 10 μm, độ dịch chuyển hệ
vân
d, Đổ nước vào khoảng cách giữa màn và khe, i
’
= ?
a, Áp dụng công thức:
i
=
D
λ
⟶
λ
=
ai
=
0,5
m
a D
b, Vị trí vân sáng thứ 3 ứng với k = 3: x
s3
= 3i = 4,5 mm
2
x
x
'
Vị trí vân sáng thứ 4 ứng với k = 3: x
t4
= (3+1/2)i = 5,25 mm
c,
Khi đặt một bản mỏng trong suốt trước một trong hai khe hở, hiệu quang lộ giữa
các tia sáng từ hai khe đến một điểm trên màn thay đổi. Khi đó hệ thống vân sẽ thay
đổi.
Hiệu quang lộ của hai tia sáng tại một điểm trên màn:
L
1
– L
2
=[( r
1
–e) +ne]– r
2
=(r
1
– r
2
) + (n-1)e
Ta đã có:
x
'
r
1
- r
2
=a
D
⟶
L
1
-
'
L
2
=a
D
+ ⟶n - 13e
Vị trí vân sáng được xác định bởi:
L
-
L
=a
x
s
+
⟶
n
-
1
3
e
=k
λ
⟶
=k
D
λ
-
s
a
⟶
n
-
1
3
eD
a
1 2
D
(1)
x '
1
Vị trí vân tối được xác định bởi:
L
1
-
L =a
t
+ ⟶n - 13e =(k + )λ
2
D 2
⟶
x
'
=(k +
1
)
Dλ
-
⟶n
-
13eD
(2)
t
2 a a
Mặt khác, khi chưa có bản mỏng, vị trí vân sáng và vân tối là:
x
=k
D
λ
s
a
x
=(k +
1
)
Dλ
(3)
(4)
t
2 a
So sánh (1), (2), (3), và (4) ta thấy:
- Khoảng vân mới là:
i '
=
[(k +1)
Dλ
-
⟶
n
-
1
3
e
D
]
-
[k
Dλ
-
⟶
n
-
1
3
eD
]
=
D
λ
=
i
a a
- Hệ thống vân dịch chuyển một đoạn:
a a a
Δx =x
'
- x
=[k
Dλ
-
⟶
n
-
1
3
eD
]
-
k
D
λ
=-
⟶
n
-
1
3
eD
s s
a a a a
Vì n>1
⟶
Δx
=-
⟶
n
-
1
3
eD
∈
0
a
(dịch chuyển xuống phía
'
3
dưới, cùng phía với khe có
bản mỏng)
ình 1.1
Độ dịch chuyển:
Δx
=
⟶
n
-
1
3
eD
=1,5(cm)
a
d, Khi đổ nước vào giữa màn quan sát và mặt phẳng khe thì Hiệu quang lộ của hai
tia sáng tại một điểm M trên màn là:
L - L =n⟶r - r
3
=na
x
s
1 2 1 2
D
Vị trí vân sáng xác định bởi:
L
-
L
=n⟶r
-
r
3
=na
x
s
=kλ
⟶
x
'
=k
λD
=k
i
1 2
Vị trí vân tối xác định bởi:
x'
1
1 2
D
1
λD
s
na n
1 i
L - L =n⟶r - r
3
=na
t
=(k + )λ
⟶
x
'
=(k + )
=(k + )
1 2 1 2
D 2
t
2 na 2
n
Khoảng vân là:
i
'
=
i
=1,125mm
n
Vậy các vân sáng đã sít lại gần nhau một đoạn bằng 1,15 – 1,125 = 0,025 mm
2.Hai gương Fresnel đặt nghiêng góc với nhau một góc
α =5.10
-
3
rad;
Khoảng cách
từ giao tuyến I của 2 gương đến khe sáng S và màn quan sát E lần lượt là
d1, d 2
.
Cho
d1
=
d 2
=
1m
. Ánh sáng do khe S phát ra có bước
sóng
λ =0,54μm
a, Tính khoảng vân, bề rông trường giao thoa và số vân sáng quan sát được
trong trường giao thoa
b, Nếu thí nghiệm tiến hành với ánh sáng trắng (
0,4
⟶
λ
⟶
0,76
μ
m)
thì tại
điểm
M cách vân trung tâm một khoảng x = 0,8 mm có những bức xạ nào cho vân tối.
Giải
Cho hai gương Fresnel có:
α
=
5.10
-
3 rad;
d
Tìm: a, i=?,MN=?; N
s
=?
=d
2
=1m
;
λ =0,54μm
a, S
1
, S
2
là ảnh ảo của ảnh S cho bởi 2 gương, được coi là 2 nguồn sáng kết hợp.
S
1
, S
2
và S cùng nằm trên đường tròn bán kính r
Từ hình vẽ ta có:
⟶
S
1
IS
2
=2
α
; S
1
S
2
=a =2d
1
sin
α
⟶2d
1
α
'
'
1
Khoảng cách từ nguồn kết hợp đến màn:
D = HO = 2d
1
cosα + d
2
= d
1
+ d
2
= 2
m
Khoảng vân:
4
Hình 1.2
i =
D
λ
=
λ
⟶
d
1
+
d
2
3
=10
-
4
m =0,1mm
a 2d
1
α
Bề rộng trường giao thoa trên màn:
MN
=2l
=2d
2
cosα
⟶2d
2
α
⟶0,01m Số vân sáng quan sát
được:
N =
2l
+1
=
i
4αd
1
d
2
λ
⟶
d
1
+ d
2
3
+1 =101
b, Các bức xạ cho vân tối tại M
Vị trí vân tối:
x
=
(k
+
1
)
D
λ
với a = 2d α và
d
=
d
=1
m
ta có:
t
x =(k +
1
)
λ
⟶
λ
=
2 a
2αx
1
1 2
t
2 α 2k +1
Với ánh sáng trắng
0,4
⟶λ
⟶0,76μm
⟶
0,4
⟶
2
α
x
⟶0,76
\ 2k +1
⟶
4,7
⟶k
⟶9,5
Vậy k = 5, 6, 7, 8, 9
Với k=5 →λ = 0,727 μm
Với k=6 →λ = 0,692 μm
Với k=7 →λ = 0,0,6 μm
Với k=8 →λ = 0,471 μm
Với k=9 →λ = 0,4102 μm
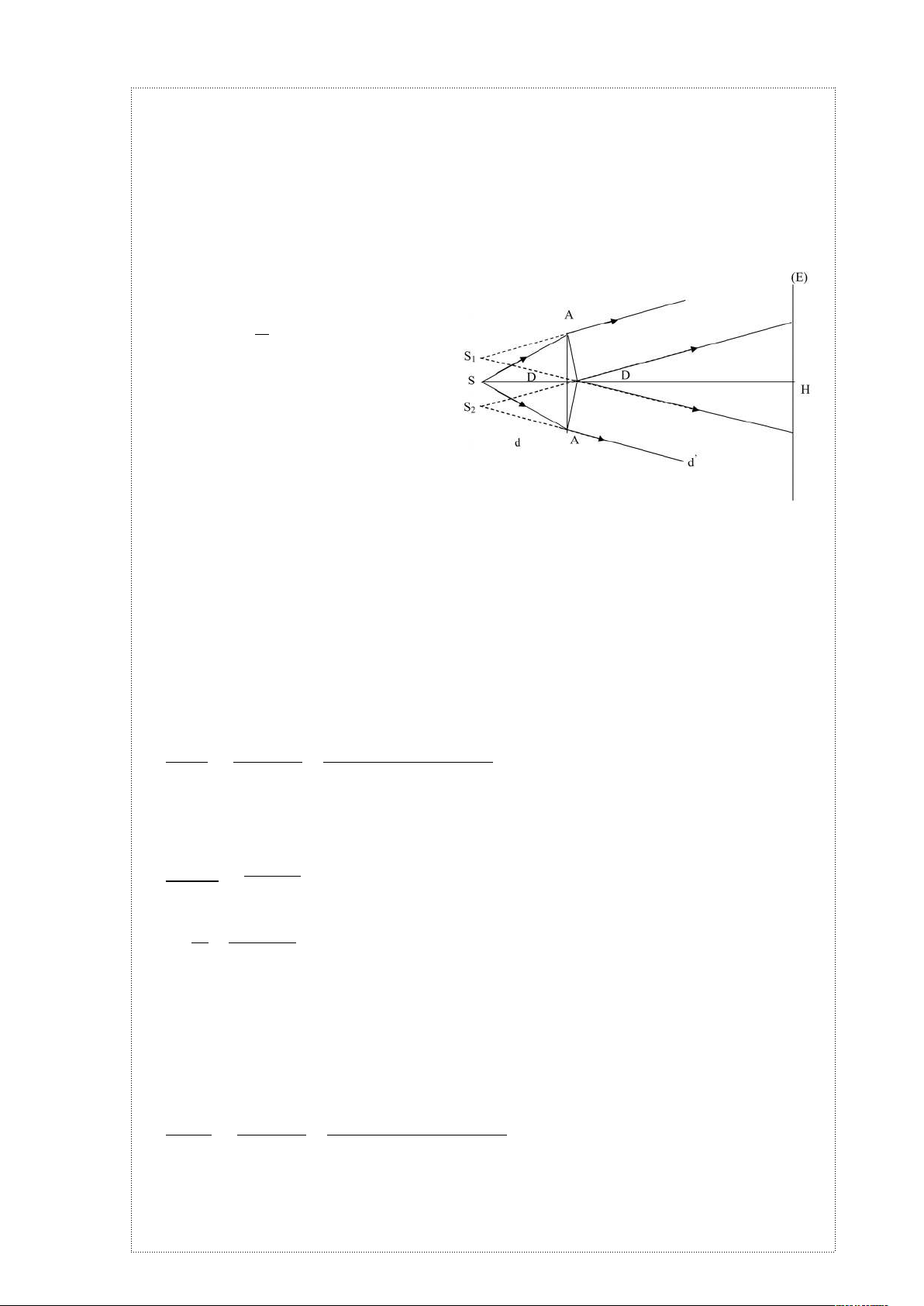
2. Hai lăng kính có cùng góc ở đỉnh A = 20
’
, làm bằng thủy thinh có chiết suất n =
1,5 có đáy gắn chung với nhau tạo thành một lưỡng lăng kính. Một khe sáng S phát
ánh sáng có bước sóng λ = 0,5 μm đặt trên mặt đáy chung, cách hai lăng kính
khoảng d = 50 cm.
a, Tính khoảng cách giữa hai ảnh S
1
, S
2
của ảnh S tạo bởi hai lăng kính (coi S
1
, S
2
cùng nằm trong một mặt phẳng với S).
b, Chứng tỏ rằng trên màn E đặt song song với mặt phẳng chứa S
1
, S
2
ta quan sát
được một hệ vân giao thoa. Tính khoảng vân và số vân quan sát được trên màn, biết
khoảng cách từ màn đến lưỡng lăng kính là d
’
=200 cm.
5
c, Khoảng vân và số vân quan sát được sẽ thay đổi như thế nào nếu:
* Thay nguồn sáng S bằng nguồn sáng S
’
phát ra bước sóng λ
’
= 0,45 μm đặt tại vị trí
của nguồn S?
* Nguồn S
’
nói trên đi xa dần lưỡng lăng kính theo phương vuông góc với màn E?
Giải
a, Ta có: A = 20
’
= 20.3.10
-4
rad
Khi đó:
tagD
=
2
⟶
D
⟶
S S
=
2Dd
d
1 2
Với D = (n-1)A = 3.10
-3
rad( góc lệch
của tia sáng trong lăng kính)
- 5
⟶
S
1
S
2
=2Dd =300.10
m =3mm
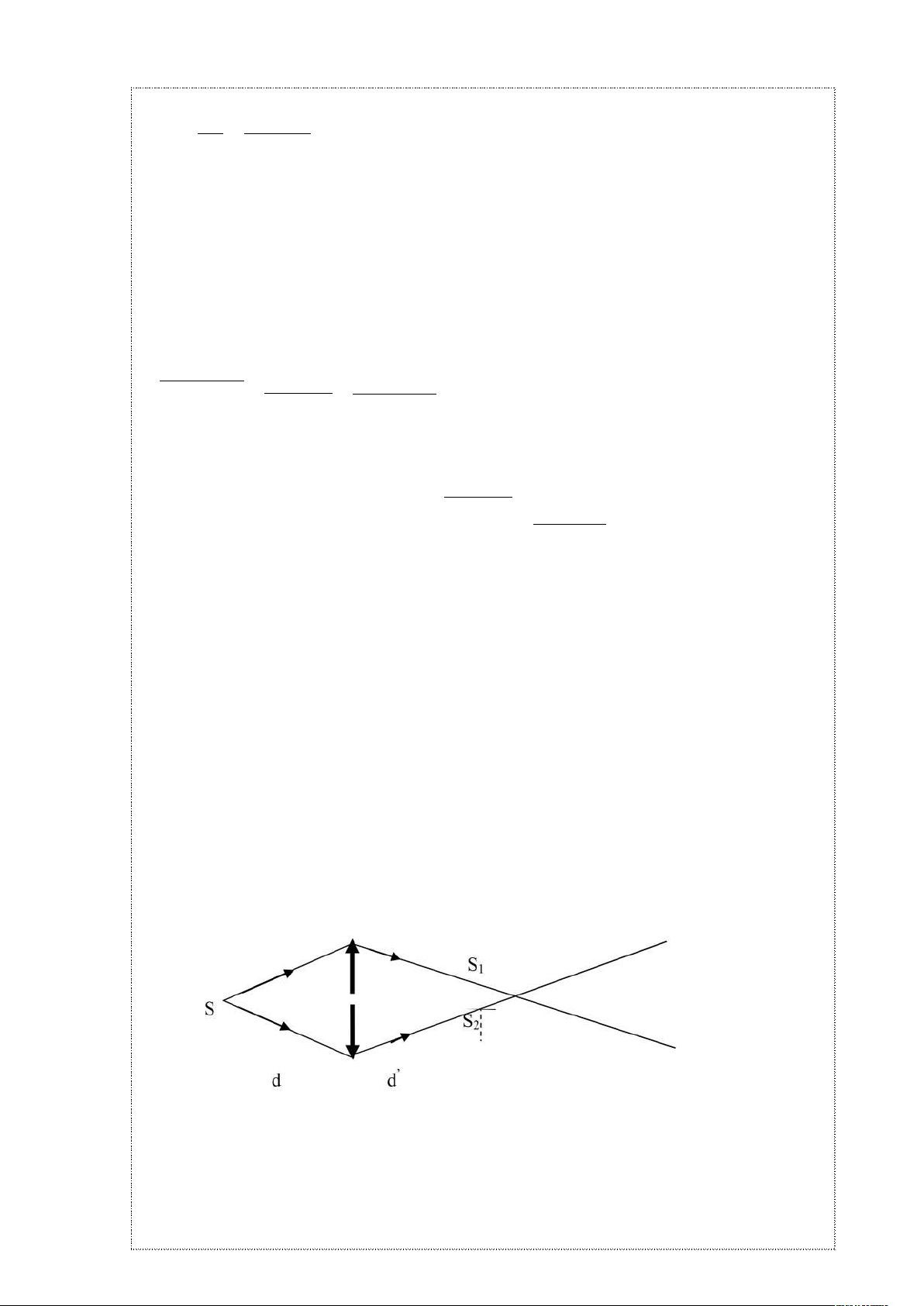
b, S
1
, S
2
là của ảnh S tạo bởi 2 lăng
kính, 2 ảnh này đối xứng nhau qua S
và hoàn toàn giống nhau nên chúng
Hình 1.3
được coi là 2 nguồn kết hợp. Do đó tại vùng sáng chung của 2 nguồn sẽ có hiện
tượng giao thoa ánh sáng.
* Nếu 2 sóng tới cùng pha => vân sáng.
* Nếu 2 sóng tới ngược pha => vân tối
Khoảng vân giao thoa:
λ.SH
λ
⟶d
+
d
'
3
0,5.10
-
6
⟶50 +
200
3
10
-
2
.
i = . = =
⟶416.10
-
6
m
=0,416mm S S S S
3.10
-
3
1 2 1 2
Bề rộng giao thoa trường:
d '.S S
200.0,3
L =
1
2
= =1,2cm
d 50
L 1,2
Ta có:
2i
=
2.0,0416
=
14,4cm
Số vân sáng trong giao thoa trường: n = 2.14+1 = 29 vân
Số vân tối trong giao thoa trường: n = 2(14+1) = 30 vân
c,* nếu nguồn sáng thay đổi bước sóng thì khoảng vân cũng thay đổi:
λ
'
.SH
λ
⟶d
+
d
'
3
0,45.10
-
6
⟶50 +
200
3
10
-
2
i =
.
= =
⟶375.10
-
6
m =0,0375cm
1
S S S S 3.10
-
3
1 2 1 2
6
⟶
7
Khi đó:
L
2i
1
1,2
= =16,2cm
2.0,0375
Số vân sáng trong giao thoa trường: n = 2.16+1 = 33 vân
Số vân tối trong giao thoa trường: n = 2(16+1) = 34 vân
Vậy số vân sáng quan sát được trên màn tăng thêm 4 vân
* Khi nguồn S
’
di chuyển ra màn thì d
1
tăng. Ta có:
λ
'
d
i =
1
+
d '
3
λ
'
=
λ
'
d
'
+
2
⟶
n - 1
3
d
1
A
2
⟶
n - 1
3
A
2
⟶
n
-
1
3
d
1
A
λ
'
Khi d
1
→
∞
thì i đạt giá trị cực tiểu:
i
=
2
⟶
n
-
1
3
A
=
Tương tự như trên ta tính được:
- Số vân sáng: 2.80+1 = 161 Vân
- Số vân tối: 2.80 = 160 vân.
0,45.10
-
4
6.10
-
3
=0,0075cm
4. Một thấu kính mỏng có tiêu cự f = 50 cm được cắt ra làm 2 phần bằng nhau theo
mặt phẳng qua trục chính và vuông góc với tiết diện của thấu kính. Một nguồn sáng
điểm S phát ra ánh sáng đơn sắc đặt trên trục chính và cách thấu kính một khoảng d
= 1m.
a, Phải tách hai nửa thấu kính này ra đến khoảng nào (một cách đối xứng qua trục
chính), để nhận được hai ảnh S
1
, S
2
cách nhau 4 mm.
b, Đặt một màn quan sát E vuông góc với trục chính và cách các nguồn S
1
, S
2
một
khoảng D = 3m. Tìm độ rộng của vùng giao thoa trên màn E. Người ta đo được
khoảng cách từ vân trung tâm (vân thứ không) đến vân sáng thứ 10 là 4,10 mm. Tìm
bước sóng λ của ánh sáng.
Giải
a,
Hình 1.4
Ta có:
d
'
=
df
=
(- 100)50
=
100cm
d + f (- 100) + 50
Hai tam giác SO
1
O
2
và SS
1
S
2
đồng dạng nên:
O
1
O
2
=
SO
1
⟶
O O =
SO
1
.S S
100.0,4
=0,2cm
S S SS
1
2
SS
1
2
=
200
1 2 1 1
Vậy phải tách 2 nửa thấu kính ra một đoạn 0,2 cm.
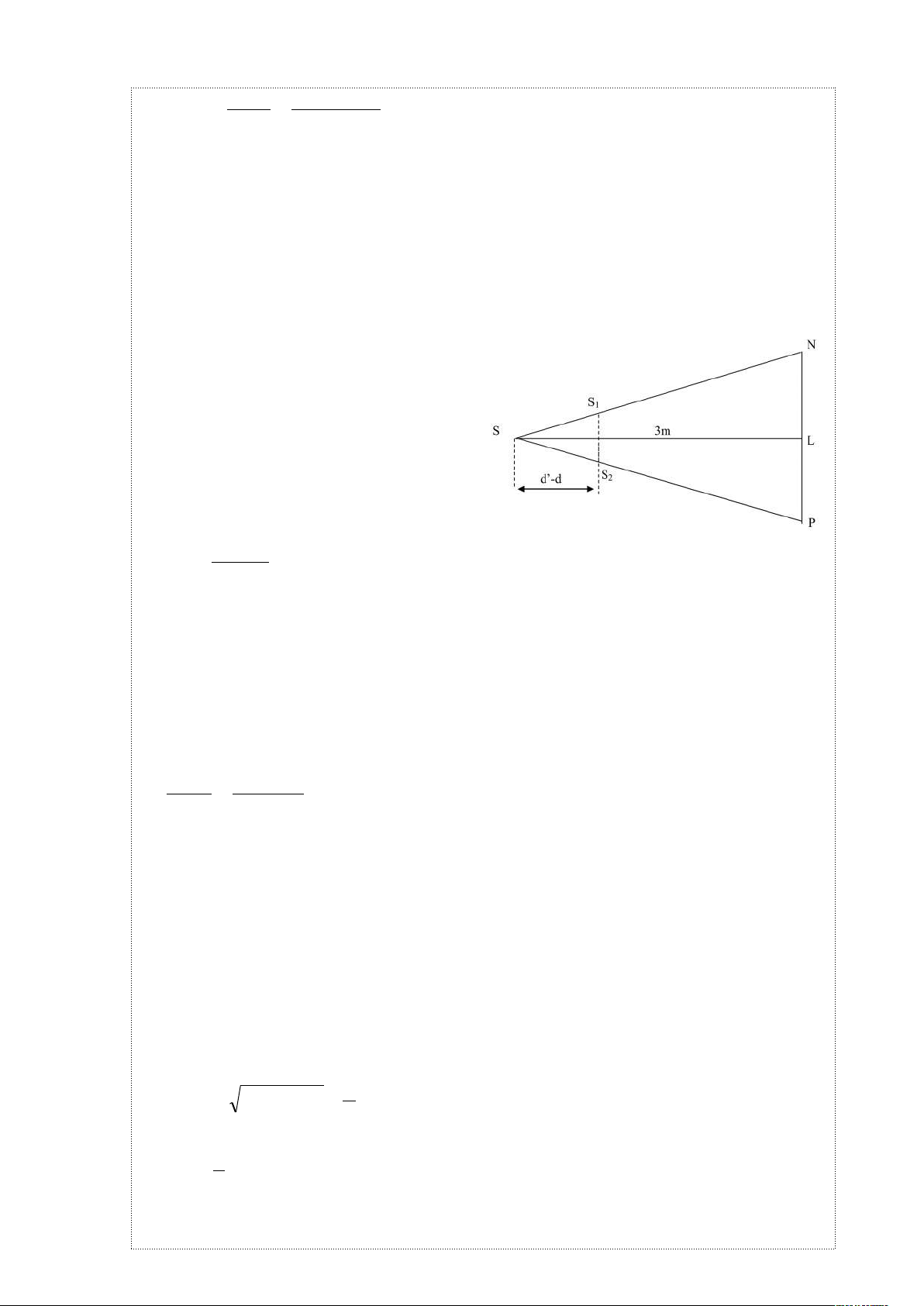
b, Δ SS
1
S
2
đồng dạng với Δ SNP nên:
S
1
S
2
=
SM
⟶
NP =
SL
.S S
NP SL SM
1
2
Với SM = d
’
– d = 100 +100 = 200 cm
SL = SM + ML = 200+300 = 500 cm
Bề rộng giao thoa trường:
L =NP =
0,2.500
=0,5cm
Hình 1.5
200
Vậy bề rộng giao thoa trường: L = 0,5 cm.
Khoảng cách vân:
10i = 0,41 cm
⟶
i =0,041cm
Bước sóng của ánh sáng thực hiện:
i.S S
0,041.0,4
λ =
1
2
= =5.10
-
5
cm =0,55μm
ML 300
3.
Chiếu một chùm tia sáng đơn sắc, song song có bước sóng
λ
=
0,6
μ
m
vàomột bản mỏng hai mặt song song có độ dày d, chiết suất n = 1,3. Biết góc tới là
i =30
0
. Hỏi bề dày nhỏ nhất của bản phải bằng bao nhiêu để chùm tia phản xạ có:
a, Cường độ sáng cực tiểu
b, Cường độ sáng cực đại
Giải:
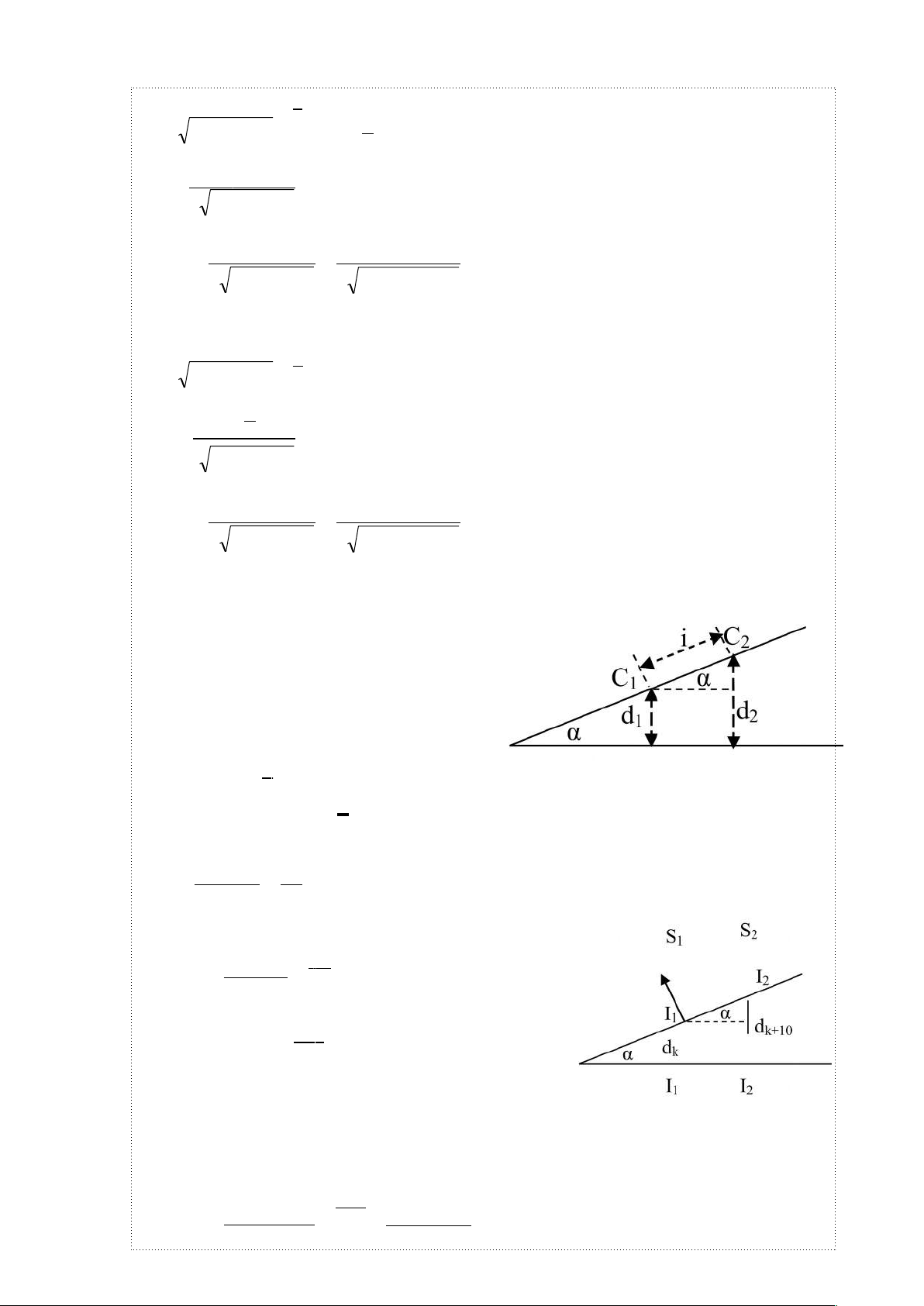
Hiệu quang lộ giữa tia phản xạ tại mặt dưới và tia tới gặp nhau tại điểm C ở mặt trên
của bản mỏng là:
L - L
=2d n
2
- sin
2
i
-
λ
1 2 1
2
Chùm tia phản xạ có cường độ sáng cực tiểu khi:
/
1
⟶
ΔL =
∣
k +
2
∣
λ
⟶ ⟶
8
n
2
- sin
2
i
1
n
2
- sin
2
i
1
2 n
2
- sin
2
i
1
2 C1,332 -
⟶0,532
n
2
- sin
2
i
1
n
2
- sin
2
i
1
4 n
2
- sin
2
i
1
4 ⟶1,332 -
⟶0,532
2
2 2
⟶
2d
-
λ
/
k +
1
⟶
λ
=
∣ ∣
⟶ ⟶
⟶
d
=
(
k
+
1 )
λ
2
Bề dày d nhỏ nhất ứng với k = 0
λ
⟶
d
min
=
0,6
=
⟶0,25
μ
m
Chùm tia phản xạ có cường độ sáng cực đại khi:
ΔL =k
λ
⟶
2d
-
(k +
1
)λ
λ
=kλ
2
⟶
d =
2
2
Bề dày d nhỏ nhất ứng với k = 0
λ
⟶
d
min
=
0,6
=
⟶0,125
μ
m
4. Một chùm tia sáng có bước sóng
λ =0,6μm
rọi vuông góc với mặt nêm thủy
tinh (chiết suất n = 1,5). Quan sát hệ thống vân giao thoa của chùm phản xạ thấy
rằng số vân giao thoa chứa trong khoảng l = 1 cm là N = 10.
a, Công thức xác định khoảng cách giữa 2
vân sáng liên tiếp ?
b, Xác định góc nghiêng α của nêm ?
Giải
Ta có : hiệu quang lộ của 2 tia phản xạ là
Tại M là vân tối nếu :
L - L
=2nd
-
λ
/
k
'
+
1
⟶
λ
1
⟶
d
t
2 t
=
∣
∣
⟶ ⟶
(k
'
+1)λ kλ
= =
2n 2n
Hình 1.6
Giả sử C
1
và C
2
ứng với hai vân tối cạnh nhau, ta
có :
sin
α
⟶α
=
d
t 2
-
d
t1
i
λ
=
2ni
Khoảng vân là :
i
=
λ
2nα
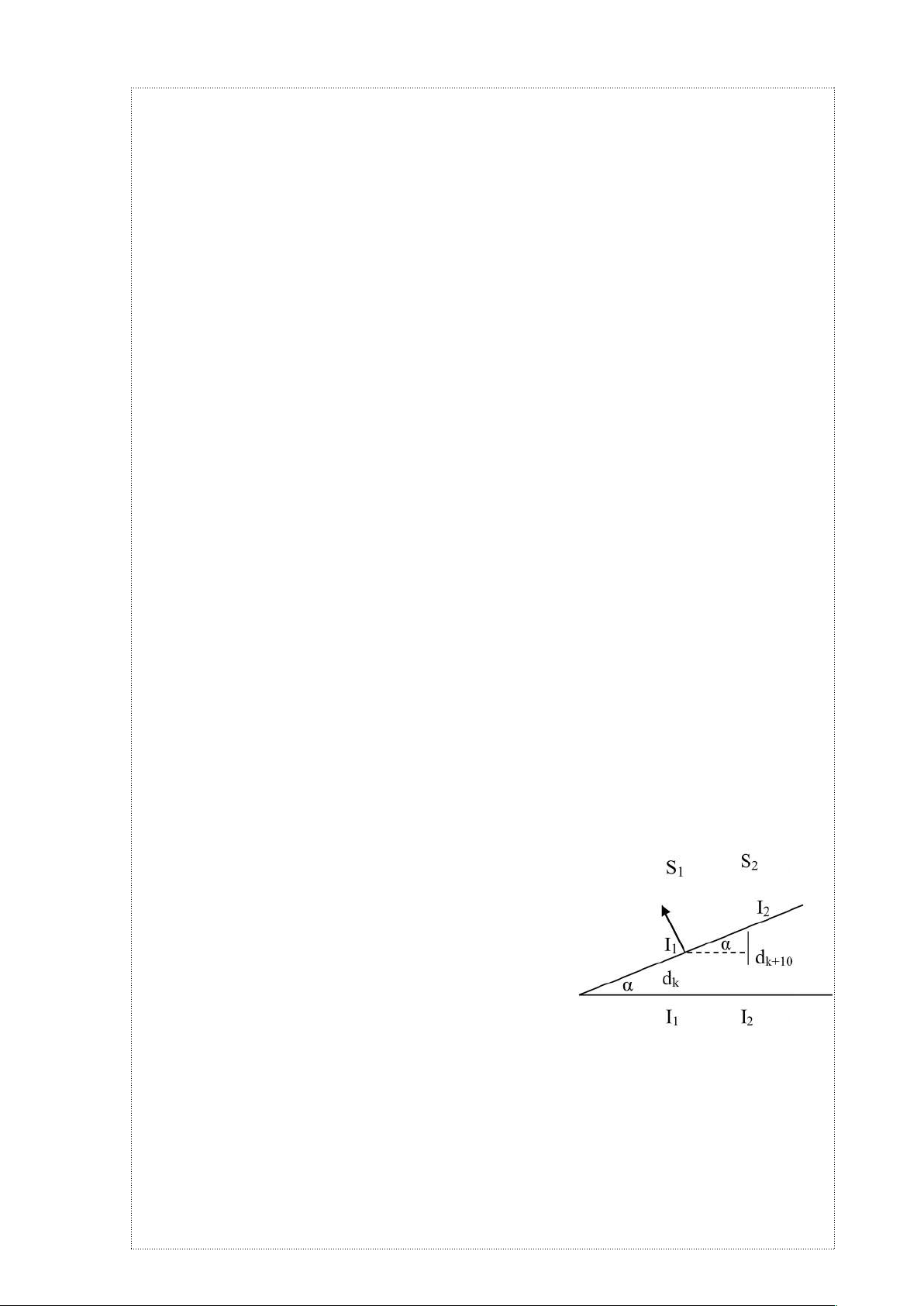
b, Từ hình vẽ ta có :
α ⟶sin α
=
d
t (k +10)
-
d
tk
I I
10λ
=
2nl
10.0,6.10
-
6
=
2.1,5.10
-
2
=2.10
-
4
rad
Hình 1.7
1
2
6. Chiếu chùm tia sáng đơn sắc bước sóng
2
9
λ =0,546μm
được rọi
vuông góc với một
bản thủy tinh phẳng của 1 hệ thống cho vân tròn niuton. Người ta đo được đường
kính của vân tối thứ năm và thứ mười năm lần lượt là 9,34 mm và 16,18 mm.
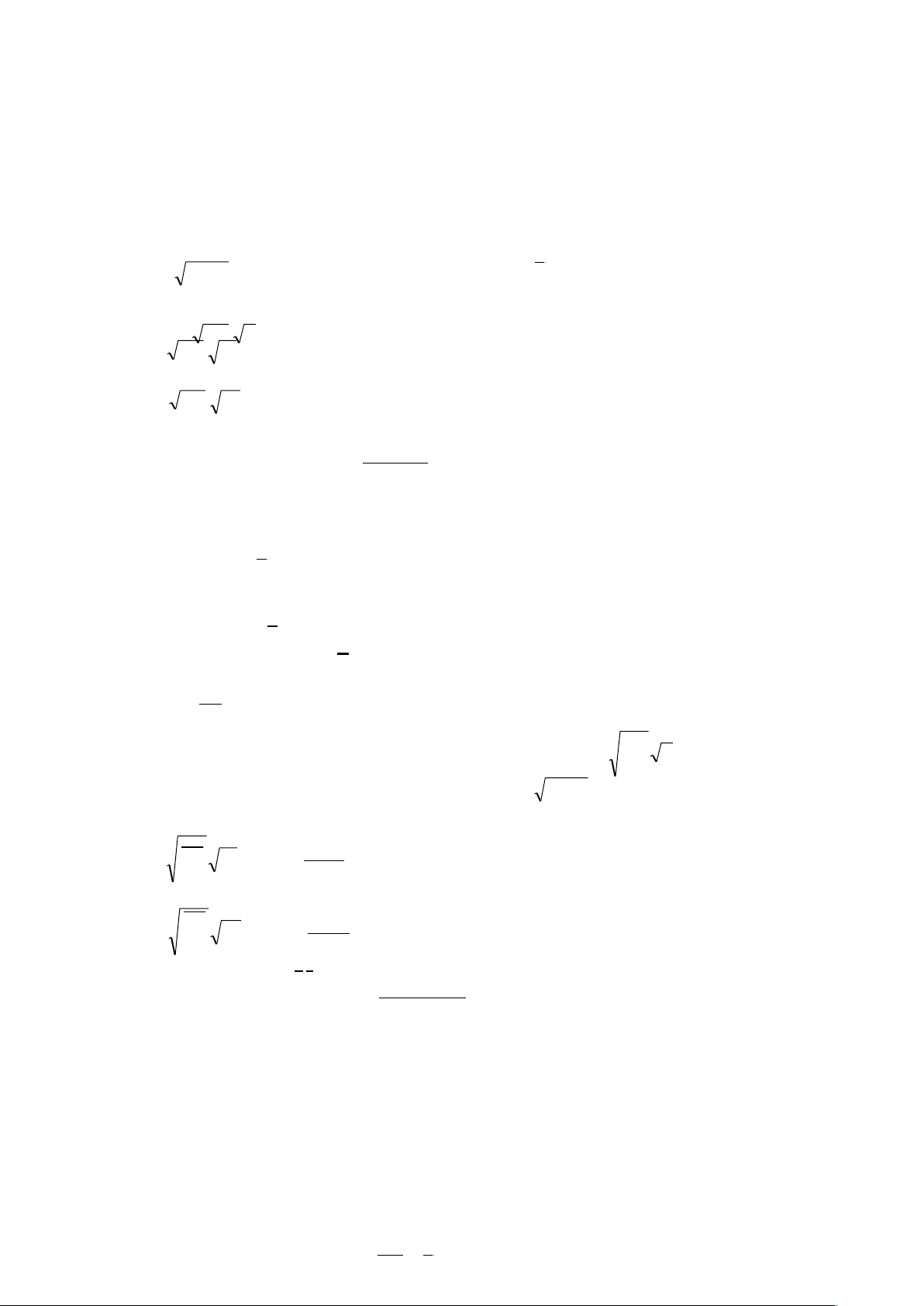
2Rdk
Rλ . k
Rλ . k1
Rλ . k2
2Rdk
Rλk n
1
2
2 2
a, Tính bán kính R của thấu kính
b, Cho một chất lỏng chiếm đầy khoảng giữa thấu kính và bản phẳng (chất lỏng có
chiết suất nhỏ hơn chiết suất của thủy tinh), người ta thấy đường kính của vân tối
thứ năm và thứ mười năm bây giờ lần lượt là 8,09 mm và 14 mm. Tìm chiết suất
chất lỏng đó.
Giải
a, Bán kính vân tối thứ k được xác định bởi :
rk
⟶
với vân tối thứ k ta
có
d =k
λ
k
2
⟶
r
k
=
r
1
=
do đó:
⟶
r
2
=Rλk
(1)
r
2
=
⟶
r
2
=Rλk
(2)
Hình 1.8
Lấy (2) – (1) ta được :
r
2
- r
2
r
2
- r
2
=
⟶
k - k
3
R
λ
⟶
R =
2
1
=8m
2 1 2 1
⟶
k
2
- k
1
3
λ
b, Vì chất lỏng có chiết suất nhỏ hơn chiết suất của thủy tinh nên hiệu quang lộ của 2
tia sáng tại M trên mặt cong thấu kính là:
L
1
-
L
=2nd +
λ
2
2
Tại M là vân tối nếu :
L - L
=2nd
+
λ
/
k +
1
⟶
λ
1 2 t
=
∣ ∣
⟶ ⟶
kλ
⟶
d
t
=
2n
Khi đó bán kính vân tối thứ k được tính bởi :
r
k
⟶
=
Ta có :
r
=
R λ
k
⟶
r
2
=
Rλk
1
1
n
1 1
n
r
=
R λ
k
⟶
r
2
=
Rλk
2
2
n
2 2
n
⟶
r
2
- r
2
=⟶k - k
3
Rλ
⟶
n =
⟶
k
2
-
k
1
3
Rλ
=1,33
2 1 2 1
n
r
2
- r
2
2 1
7. Trên một bản thủy tinh phẳng (n = 1,5), người ta phủ một màng mỏng chiết suất n
’
= 1,4. Một chùm tia sáng đơn sắc song song, bước sóng
λ =0,6μm
được chiếu gần
thẳng góc với mặt bản. Tính bề dày của màng mỏng biết rằng do hiện tượng giao
thoa, chùm tia phản xạ có cường độ sáng cực tiểu.
Giải
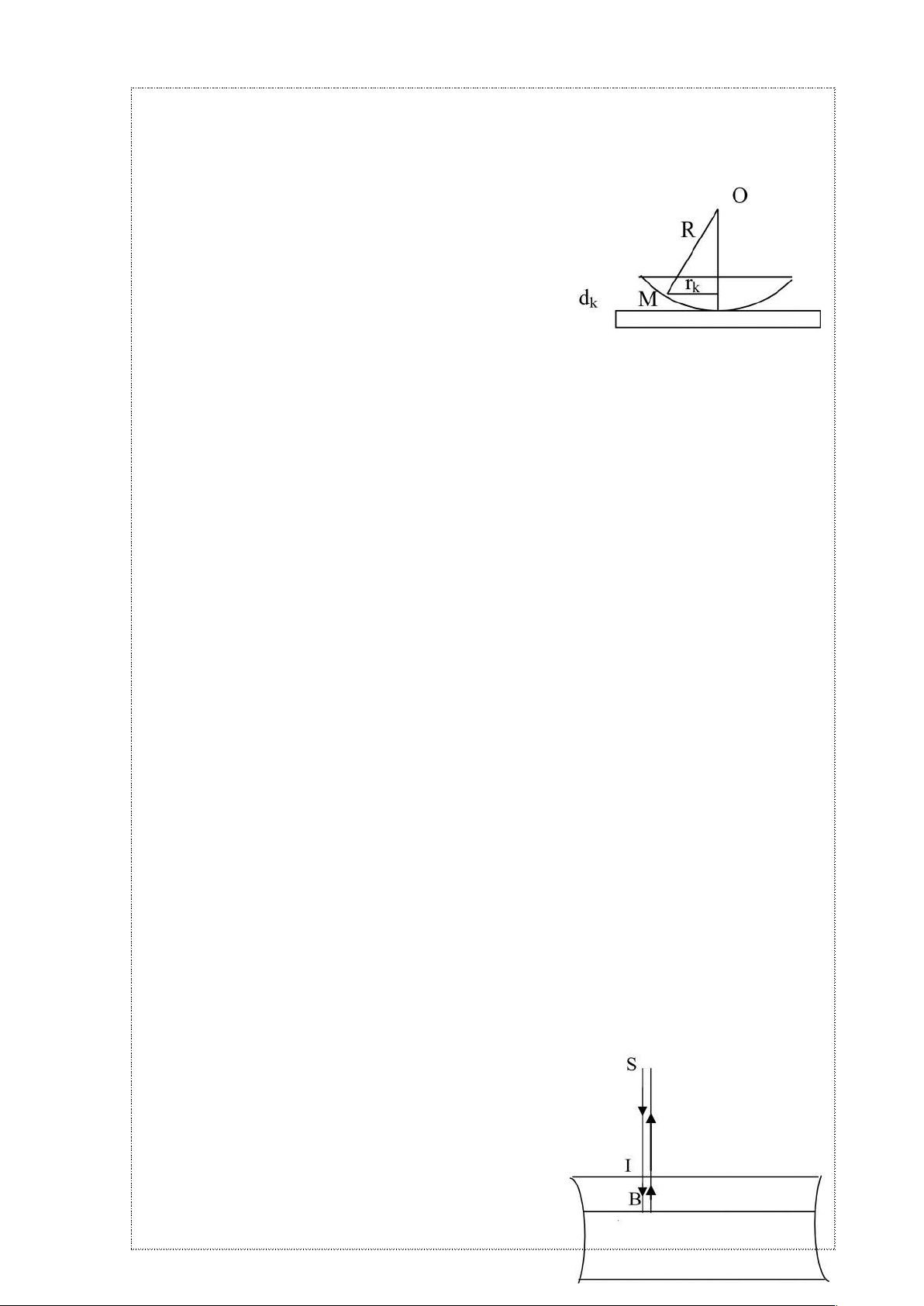
Xét tia sáng tới SI. Khi tới mặt của bản mỏng, một phần tia sáng này sẽ phản xạ ở
mặt trước của màng (tại I), 1 phần qua màng mỏng
và phản xạ tại mặt sau của màng (tại B trên mặt
thủy tinh). Hai tia phản xạ này giao thoa với nhau.
Quang lộ của tia SIS là :
L
=SIS +
λ
1
2
1
2
10
Hình 1.9
1
2
⟶⟶
Quang lộ của tia SIBIS là :
L
=
SIS
+
2n' IB
+
λ
=
SIS
+
2n'e
+
λ
2
Hiệu quang lộ của 2 tia phản xạ :
L
2
-
2 2
L =2n
'
e
Do 2 tia phản xạ giao thoa cho cực tiểu nên:
L - L =2n
'
e
/
k +
1
⟶
λ
⟶
e
/
k
+
1
⟶
λ
2 1
=
∣ ∣
⟶ ⟶
=
∣
2
∣
2n
'
Nếu k = 0 thì
e
0
λ
=
4n
'
=
0,6
4.1,4
=0,11μm
Nếu k = 1 thì
e
=
3
λ
3.0,6
= =0,33μm
1
4n
'
4.1,4
8. Trong một thí nghiệm dùng giao thoa kế Maikenxon, khi dịch chuyển gương di
động một khoảng L = 0,161 mm, người ta quan sát thấy hình giao thoa dịch đi 500
vân. Tìm bước sóng của ánh sáng dùng trong thí nghiệm.
Giải
Khi dịch chuyển gương di động một khoảng
λ
thì hiệu quang lộ của hai tia thay đổi
2
là λ và hệ thống dịch chuyển một khoảng vân. Do đó nếu khi gương di động dịch
chuyển một khoảng L và hệ thống vân dịch chuyển đi m khoảng vân thì có :
L =m
λ
⟶
2
λ =
2L
=0,644μm
m
III. BÀI TẬP CHƯƠNG 1
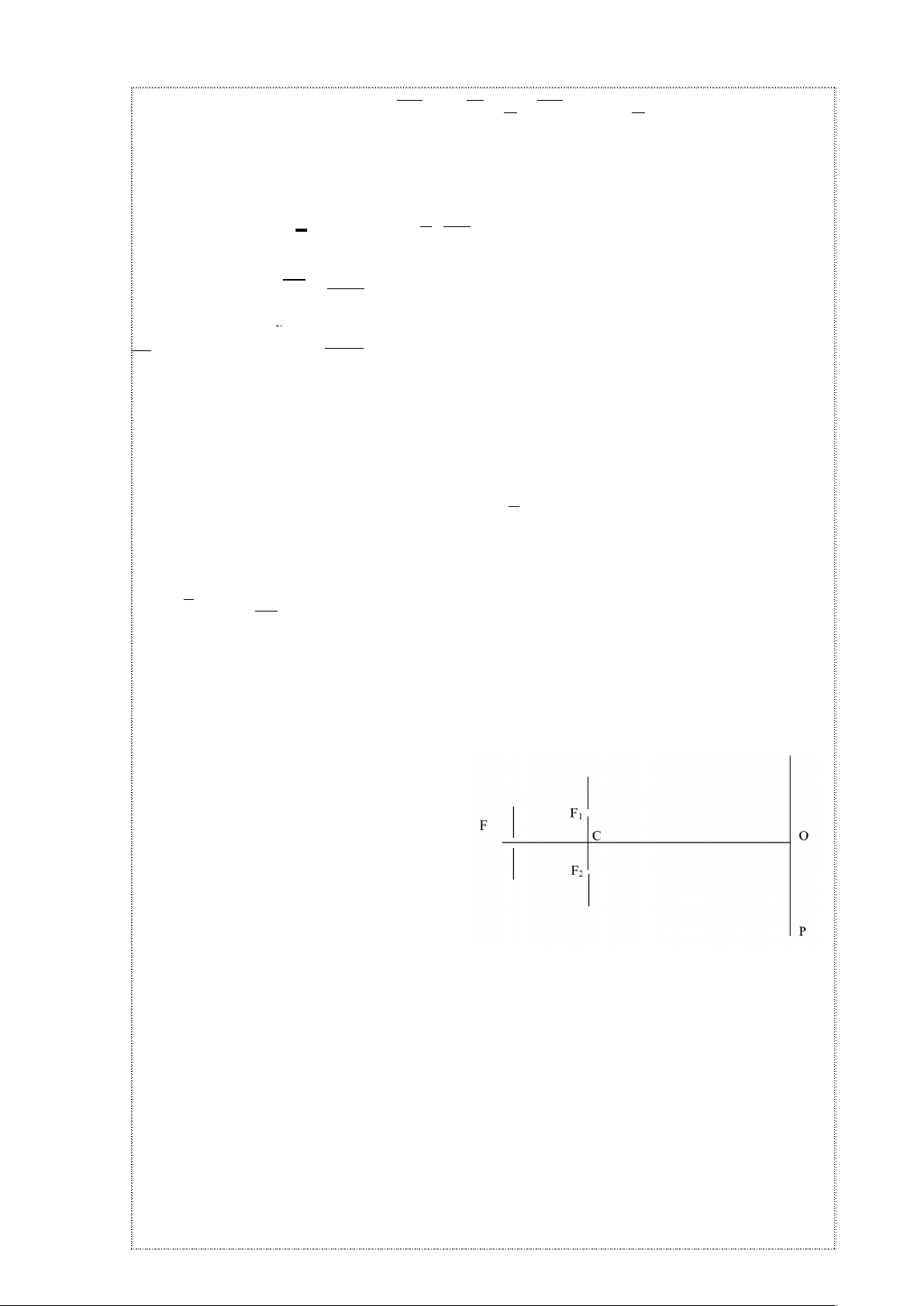
1. Chùm ánh sáng đơn sắc phát ra từ khe hẹp F được rọi vào một màn E
cách khe sáng một đoạn FC = 1 m. Trên mnaf e có hai khe hẹp F
1
và F
2
song song
với nhau và cách đều khe sáng F. Khoảng cách giữa hai khe sáng F
1
và F
2
là
a=1mm, song song với màn E và cách màn E một đoạn 1,2 m người ta đặt một màn
quan sát P.
a, Khoảng cách giữa 2 vân sáng liên
tiếp là i = 0,6 mm. Tìm bước sóng của
ánh sáng phát ra từ khe F.
b, Trước khe F
1
người ta đặt một bản
mỏng trong suốt hai mặt song song,
dày e = 2μm và có chiết suất n = 1,5.
Xác định vị trí mới của vân sáng giữa.
Phải dịch chuyển khe F một đoạn bằng
bao nhiêu và theo chiều nào theo
phương vuông góc với CO để đưa vân
sáng giữa về lại vị trí O.
c, Đưa khe F về vị trí ban đầu, bản
Hình 1.10
mỏng được lấy ra khỏi hệ thống. Giả sử khe F phát ra ánh sáng trắng. Thì tại vị trí
vân tối thứ 15 có vân tối của các bức xạ nào ? biết ánh sáng trắng có bước sóng từ
0,4 μm đến 0,7 μm
Đáp số :
a,
λ =0,5μm
b, * Vân trung tâm dịch chuyển về phía F
1
một đoạn 1,32 mm.
*Dịch F một đoạn 1,1 mm về phía F
1
c, Có vân tối của 8 bức xạ có bước sóng : 0,580 ; 0,63 ; 0,69 μm.
λ =0,414;
0,439 ;
0,468 ;
0,5 ;
0,537 ;
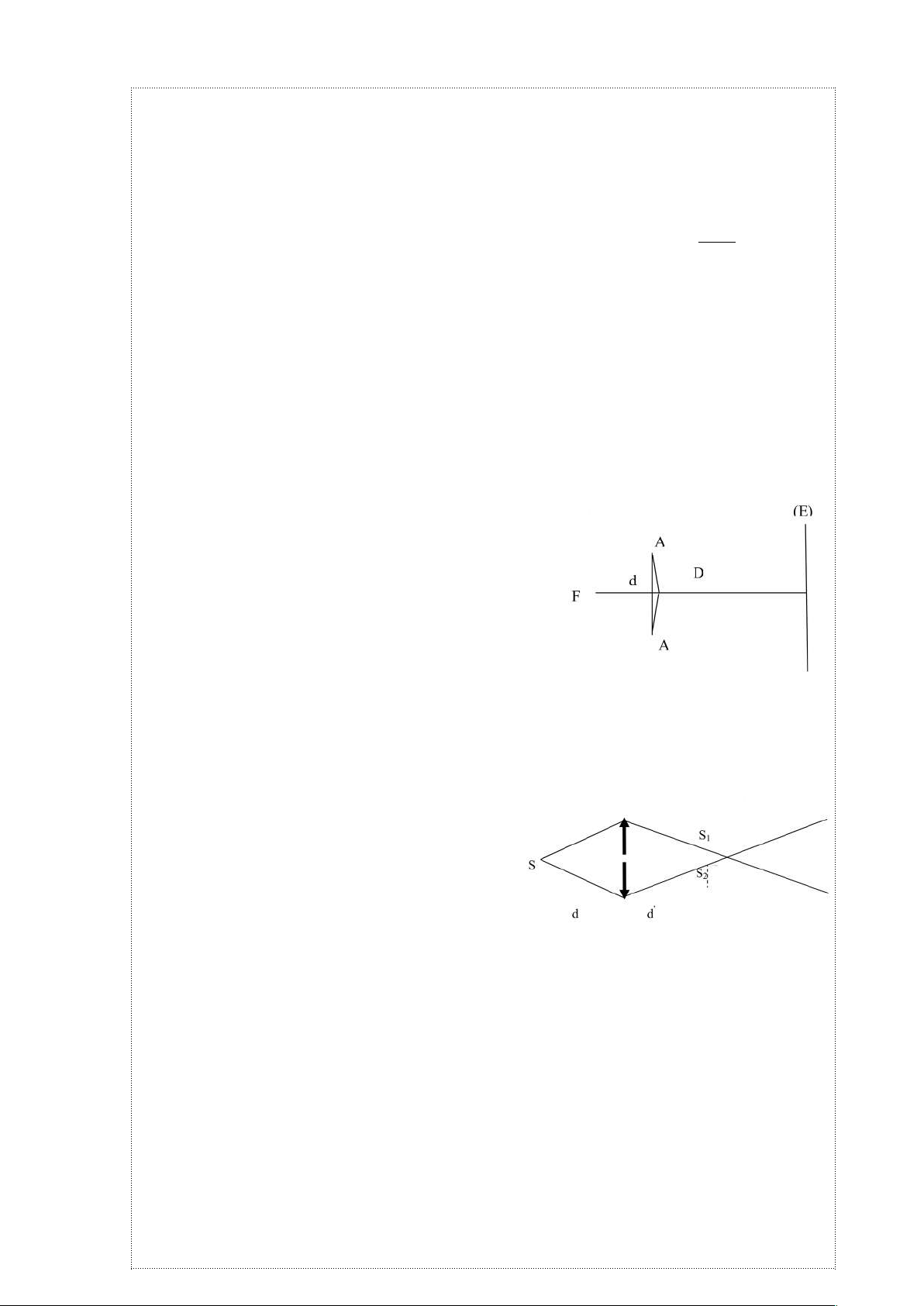
2. Trong thí nghiệm gương phẳng Frenen, khoảng cách giữa các ảnh ảo S
1
S
2
của
nguồn sáng là a = 0,5 mm. Màn quan sát cách S
1
S
2
một đoạn D = 5m. Với ánh
sáng xanh thì khảng cách giữa 2 vân sáng liên tiếp trên màn quan sát i=5mm. Tính
bước sóng của ánh sáng xanh.
Đáp số :
λ =0,500μm
3. Cho hệ thống gương Frenen G G
đặt nghiêng nhau một góc
α
=
2,62
rad
. Nguồn
1
2
1000
điểm O đặt trước hai gương, cách giao tuyến C của 2 gương một đoạn r=1m và phát
ra ánh sáng xanh có bước sóng
λ
=
0,55
μ
m
. Góc
G CO =300
, bề rộng của
mỗi
1
gương bằng 25 mm. Tính :
a, Khoảng cách giữa các ảnh ảo O
1
O
2
cho bởi 2 gương
b, Bề rộng của các vân giao thoa, biết màn E đặt song song với O
1
O
2
và cách giao
tuyến một đoạn d = 1m.
c, Số vân sáng có trên màn quan sát.
Đáp số : a, O
1
O
2
= 5,24 mm
b, i = 0,21mm
c, N = 26 vân
4. Hệ thống lưỡng lăng kính Frenen được bố trí
như hình vẽ. Lưỡng lăng kính có bề rộng AA
’
=1
cm, các góc chiết quang A = A
’
= 30
’
, chiết suất n
= 1,5 và được chiếu sáng bởi khe sáng F đặt cách
lưỡng lăng kính một đoạn d = 25 cm. Màn quan
sát P đặt cách F một đoạn E = 1m. Xác định:
a, Bề rộng của miền giao thoa ở trên màn quan
sát.
b, Số vân sáng chứa trên màn nếu bước sóng
của ánh sáng tới
λ
=
0,66μm
Hình 1.11
Đáp số : a, L = 6,54 mm
B, N = 21
5. Dùng một lưỡng thấu kính Biê để quan sát hiện tượng giao thoa như hình vẽ
a, Vẽ đường đi của các tia sáng xuất phát từ khe sáng S.
b, Xác định vị trí và khoảng cách 2 ảnh thực
S
1
, S
2
của khe sáng s qua 2 nửa thấu kính
L
1
, L
2
. Biết rằng tiêu cự thấu kính f=20 cm.
Bề rộng của khe hở giữa 2 nửa thấu kính a =
1 mm, khoảng cách từ khe sáng S tới lưỡng
thấu kính d=40cm.
c, Màn quan sát đặt cách lưỡng thấu kính
một đoạn S = 80 cm. Tính bề rộng của miền
Hình 1.12
giao thoa, khoảng cách giữa hai vân sáng
liên tiếp và tổng số vân sáng có trên màn quan sát. Cho biết bước sóng dùng trong
thí nghiệm
λ
=
0,55
μ
m
d, Sau ảnh S
1
, người ta đặt một bản thủy tinh mỏng, 2 mặt song song, có bề dày e =
8μm, chiết suất n = 1,5, vuông góc với quang trục lưỡng thấu kính và mặt phẳng
chứa ảnh S
1
. Xác định độ dịch chuyển của hệ thống vân giao thoa.
Đáp số : b, l = 2 mm
c, L = 3 mm ; i = 0,11 mm ; N = 27 vân sáng.
d, hệ thống vân dịch về phía đặt bản mỏng một đoạn 0,8 mm.
12
13
6. Chiếu một chùm ánh sáng xiên một góc 45
0
lên một màng nước xà phòng. Tìm bề
dày nhỏ nhất của màng để những tia phản chiếu có màu vàng. Cho biết bước sóng
của ánh sáng màu vàng là 6.10
-5
cm. Chiết suất của màng là n=1,33.
Đáp số : d = 1,31.10
-5
cm.
7. Chiếu một chùm tia song song
λ =0,6μm
lên một màng xà phòng (n = 1,3) dưới
góc tới 30
0
. Hỏi bề dày nhỏ nhất của màng phải là bao nhiêu để chùm tia phản xạ có:
a, Cường độ sáng cực tiểu
b, Cường độ sáng cực đại
Đáp số : a, d = 0,25 μm; : b, d = 0,125 μm
8. Một chùm tia sáng song song đơn sắc bước sóng
λ =0,6μm
được rọi vuông góc
với một nêm thủy tinh (n = 1,5). Xác định góc nghiêng của nêm, biết rằng số vân giao
thoa chứa trong khoảng l = 1 cm là N = 10.
Đáp số:
α =2.10
-
4
rad
9. Một màng mỏng nước xà phòng chiết suất n = 1,33 được đặt thẳng đứng, vì nước
xà phòng dồn xuống dưới nên màng có dạng hình nêm. Quan sát những vân giao
thoa của ánh sáng phản chiếu màu xanh (
λ
=
0,5461
μ
m
) người ta thấy khoảng cách
giữa 6 vân bằng 2 cm. Xác định:
a, Góc nghiêng của nêm.
b, Vị trí của ban vân tối đầu tiên (coi vân số 1 là vân nằm ở giao tuyến của 2 mặt
nêm). Biết hướng quan sát vuông góc với mặt nêm.
Đáp số: a,
α
=
0,52.10- 4 rad
b, x = 0; 0,4; 0,8 cm
10. Chiếu một chùm tia sáng song song đơn sắc (
λ
=
0,5
μ
m
) vuông góc với mặt nêm
không khí và quan sát ánh sáng phản xạ trên mặt nêm, người ta thấy bề rộng của
mỗi vân là 0,05 cm.
a, Tìm góc nghiêng giữa 2 mặt nêm.
b, Nếu chiếu đồng thời 2 chùm sáng đơn sắc, bước sóng lần lượt bằng
λ1
=
0,5μm
,
λ
2
=0,6μm
xuống mặt nêm thì hệ thống vân trên mặt nêm có gì thay đổi? Xác định vị
trí tại đó các vân tối của hai hệ thống vân trùng nhau.
Đáp số: a,
α
=
0,5.10- 3 rad
b, Trên mặt nêm có 2 hệ thống vân giao thoa, cách cạnh nêm một khoảng l=n.0,3
(cm) (với n là số nguyên) thì vân tối của 2 ánh sáng trùng nhau.
11. Một chùm tia sáng đơn sắc bước sóng
λ =0,6μm
được rọi vuông góc với một
bản vân tròn Niuton. Tìm bề dày của lớp không khí tại vị trí của vân tối thứ tư của
chùm tia phản xạ.
Bấm Tải xuống để xem toàn bộ.