




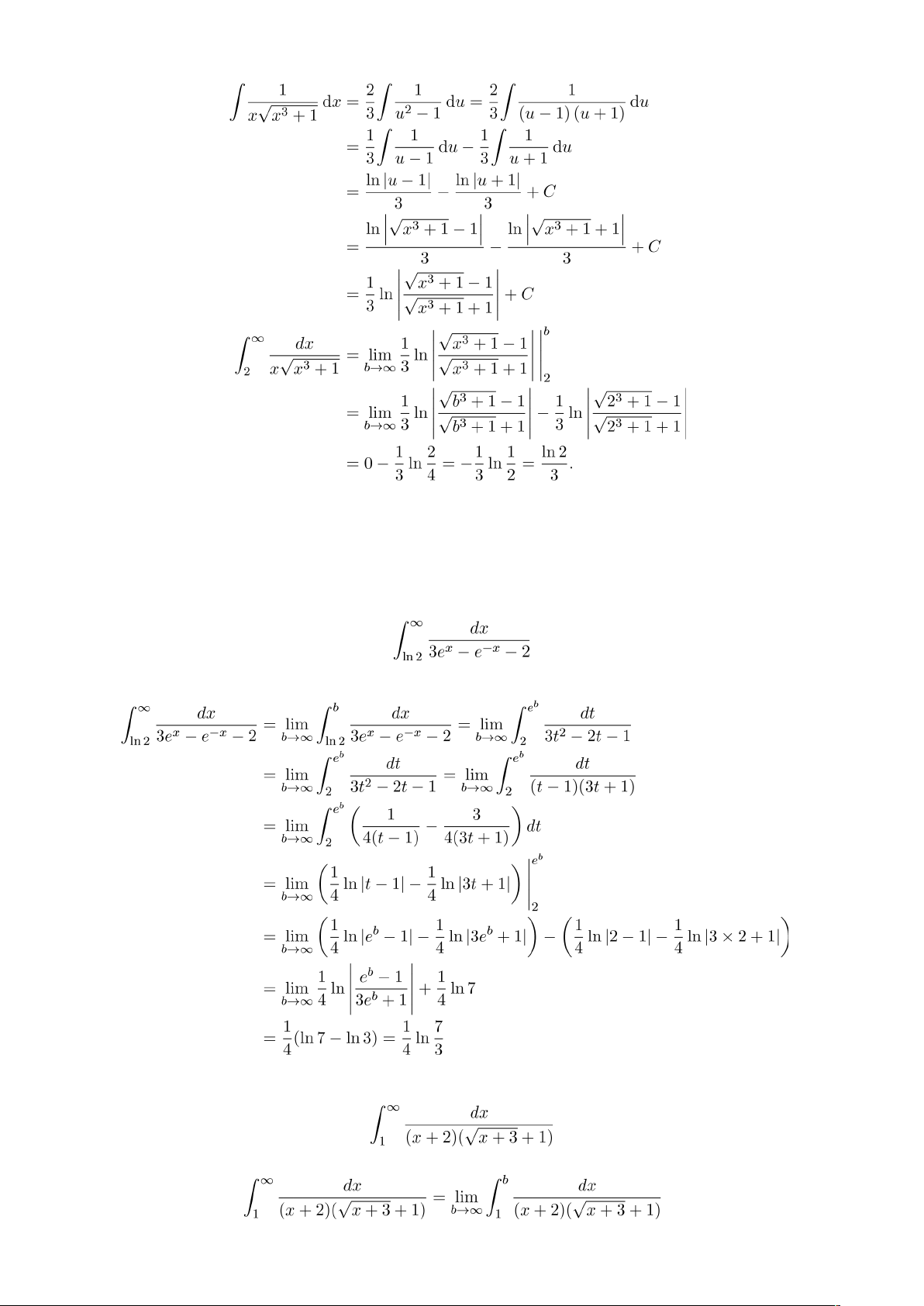





















Preview text:
1 Tóm tắt lý thuyết
Tích phân 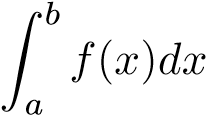 được gọi là suy rộng nếu ít nhất một trong các điều sau xảy ra:
được gọi là suy rộng nếu ít nhất một trong các điều sau xảy ra:
- a = −∞ hoặc b = +∞ hoặc cả hai.
- hàm f(x) không bị chặn tại một hoặc nhiều điểm (cô lập) thuộc đoạn [a,b].
1.1 Tích phân suy rộng cận vô hạn
Định nghĩa 1 (Tích phân suy rộng loại I). Hiểu một cách đơn giản như sau (bỏ qua một số giả thiết):
- Z +∞ f(x)dx = lim+ Z b f(x)dx
- b→ ∞ a
- b
- f(x)dx = lim Z f(x)dx
Z
a→−∞ a −∞
- Z +∞ f(x)dx = Z c f(x)dx + Z +∞ f(x)dx
−∞ −∞ c
Nếu các giới hạn trên tồn tại hữu hạn thì ta nói tích phân suy rộng hội tụ. Ngược lại, ta nói tích phân phân kỳ (Tức là nếu giới hạn trên không tồn tại hoặc bằng ±∞ thì ta nói tích phân phân kỳ).
Ví dụ 1. Hãy chỉ ra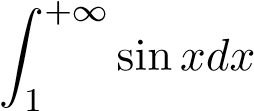 phân kỳ.
phân kỳ.
Định lý 1 (Dấu hiệu so sánh I- So sánh trực tiếp). Cho hàm số f(x),g(x) liên tục trên [a,+∞) và 0 ≤ f(x) ≤ g(x), ∀x ∈ [a,+∞). Khi đó:
i. Nếu 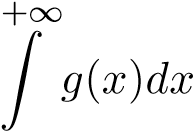 hội tụ thì
hội tụ thì 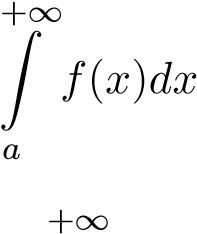 hội tụ. ii. Nếu
hội tụ. ii. Nếu 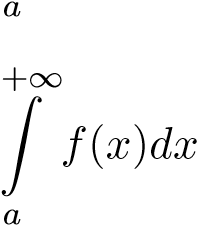 phân kỳ thì
phân kỳ thì 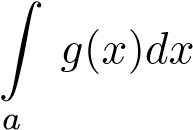 phân kỳ.
phân kỳ.
Định lý 2 (Dấu hiệu so sánh II- So sánh qua giới hạn). Cho hàm số f(x),g(x) liên tục trên [a,+∞) và 0 ≤ f(x),g(x), ∀x ∈ [a,+∞). Giả sử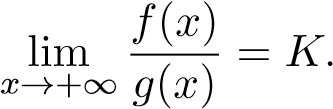 Khi đó:
Khi đó:
- Nếu
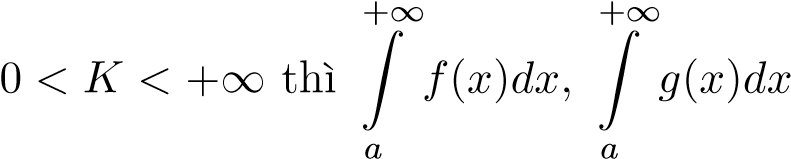 cùng hội tụ hoặc cùng phân kỳ.
cùng hội tụ hoặc cùng phân kỳ. - Nếu
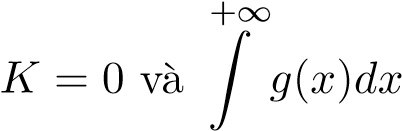 hội tụ thì
hội tụ thì 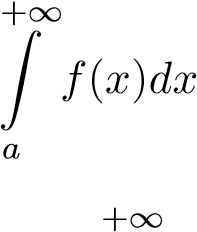 hội tụ.
hội tụ. - Nếu
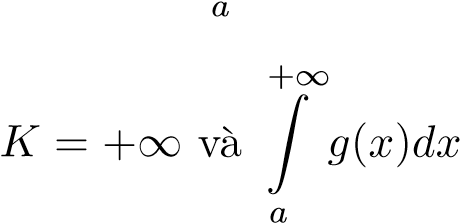 phân kỳ thì
phân kỳ thì 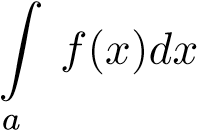 phân kỳ.
phân kỳ.
1.2 Tích phân suy rộng của hàm không bị chặn
Định nghĩa 2 (Tích phân suy rộng loại II). Cho a và b là các số thực hữu hạn.
b
- Giả sử tích phânf(x)dx tồn tại hữu hạn với mọi t ∈ (a,b] và f không bị chặn tại a
Z
t
(nghĩa là |f(x)| → ∞ khi x → a+). Khi đó ta định nghĩa
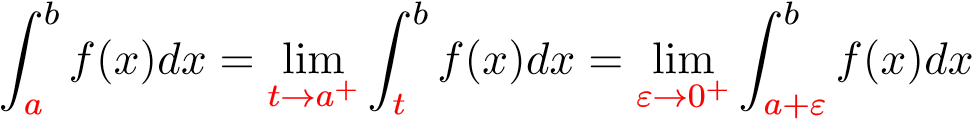
nếu giới hạn trên tồn tại. Nếu giới hạn trên tồn tại hữu hạn ta nói tích phân suy rộng loại II hội tụ, ngược lại ta nói nó phân kỳ.
b
- Giả sử tích phânf(x)dx tồn tại hữu hạn với mọi t ∈ [a,b) và f không bị chặn tại b
Z
t
(nghĩa là |f(x)| → ∞ khi x → b−). Khi đó ta định nghĩa
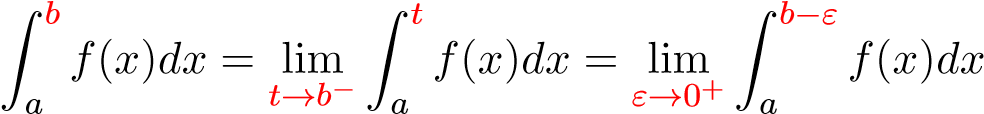
nếu giới hạn trên tồn tại. Nếu giới hạn trên tồn tại hữu hạn ta nói hữu hạn ta nói tích phân suy rộng loại II hội tụ, ngược lại ta nói nó phân kỳ.
- Giả sử f không bị chặn tại điểm c với a < c < b và các tích phân
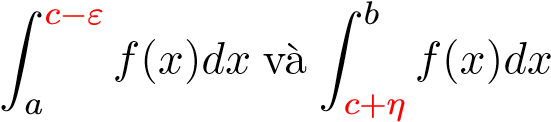 tồn tại với mọi 0 < ε < c − a và 0 < η < b − c. Khi đó ta định nghĩa:
tồn tại với mọi 0 < ε < c − a và 0 < η < b − c. Khi đó ta định nghĩa:

nếu các giới hạn trên tồn tại. Nếu cả hai giới hạn ở vế phải tồn tại hữu hạn thì ta nói 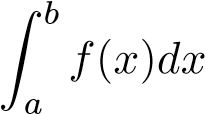 hội tụ, ngược lại ta nói tích phân phân kỳ.
hội tụ, ngược lại ta nói tích phân phân kỳ.
Định lý 3 (Dấu hiệu so sánh I- So sánh trực tiếp). Giả sử f(x),g(x) là hai hàm khả tích trên 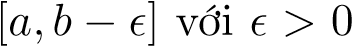 bé tùy ý, có giới hạn bằng vô cùng tại x = b và giả sử 0 ≤ f(x) ≤ g(x) với mọi x ∈ [a,b). Khi đó
bé tùy ý, có giới hạn bằng vô cùng tại x = b và giả sử 0 ≤ f(x) ≤ g(x) với mọi x ∈ [a,b). Khi đó
- Nếu
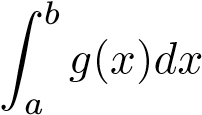 hội tụ thì
hội tụ thì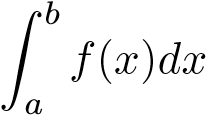 hội tụ.
hội tụ. - Nếu
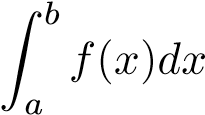 phân kỳ thì
phân kỳ thì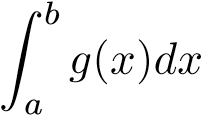 phân kỳ.
phân kỳ.
- Nếu
Định lý 4 (Dấu hiệu so sánh II- So sánh qua giới hạn). Giả sử f(x),g(x) là hai hàm khả tích trên 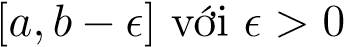 bé tùy ý, có giới hạn bằng vô cùng tại x = b, không âm với mọi x ∈ [a,b) và giả sử
bé tùy ý, có giới hạn bằng vô cùng tại x = b, không âm với mọi x ∈ [a,b) và giả sử . Khi đó
. Khi đó
- Nếu
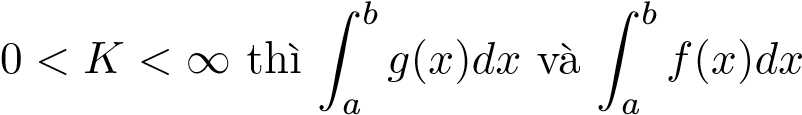 cùng hội tụ hoặc cùng phân kỳ.
cùng hội tụ hoặc cùng phân kỳ. - Nếu
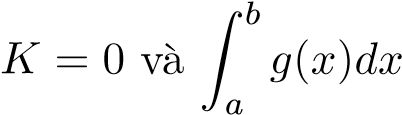 hội tụ thì
hội tụ thì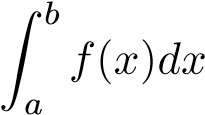 hội tụ.
hội tụ. - Nếu
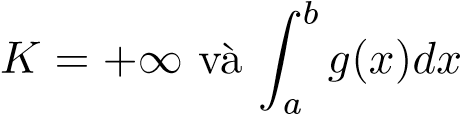 phân kỳ thì
phân kỳ thì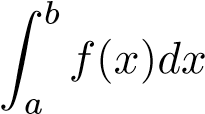 phân kỳ.
phân kỳ.
- Nếu
Ví dụ 2. Xét sự hội tụ của tích phân
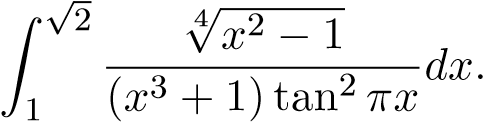
Ta thấy đây là tích phân suy rộng loại II.
Cách 1
Xét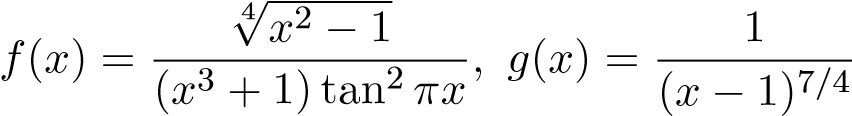 . Ta có f,g ≥ 0 và
. Ta có f,g ≥ 0 và
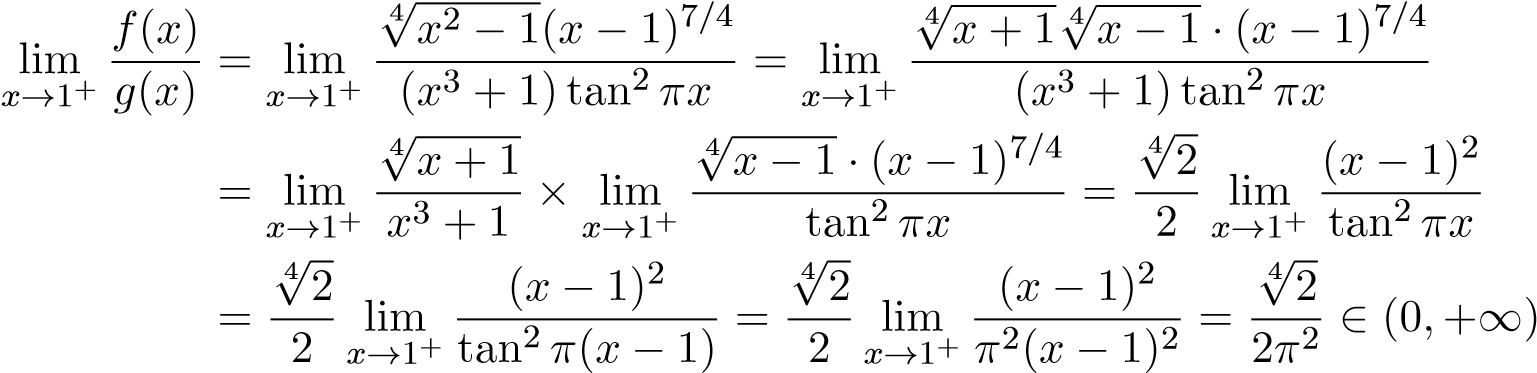
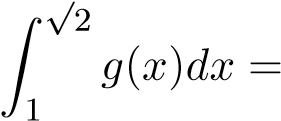
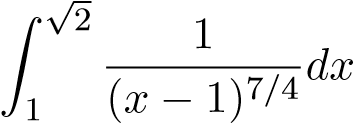 √2 √2
√2 √2
Z
nên hai tích phânf(x)dx và Z g(x)dx cùng hội tụ hoặc cùng phân kỳ. Mà
1 1
phân kỳ nên tích phân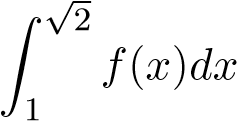 phân kỳ.
phân kỳ.
Cách 2. Cách 1 không cho chúng ta biết tại sao lại chọn hàm g như vậy. Cách sau sẽ phân tích bản chất của hàm f trong lân cận điểm 1 từ đó sẽ nhìn thấy cách chọn hàm g ở trên. Khi x → 1+ ta có:
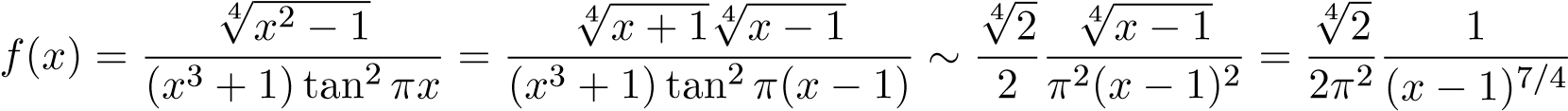 .
.
Mà tích phân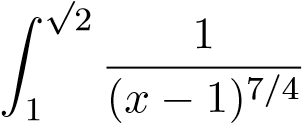 phân kỳ nên tích phân ban đầu phân kỳ.
phân kỳ nên tích phân ban đầu phân kỳ.
(Giải thích thêm việc phân tích trên tương đương với việc chọn hàm 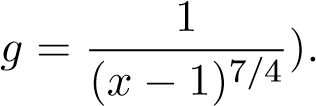
Ví dụ 3. Xét sự hội tụ của tích phân
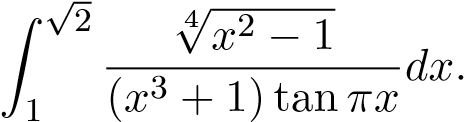
Làm tương tự như ví dụ trên ta được tích phân hội tụ (hàm g trong trường hợp này là
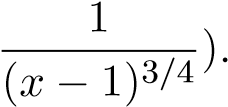
Ví dụ 4. Xét sự hội tụ của tích phân
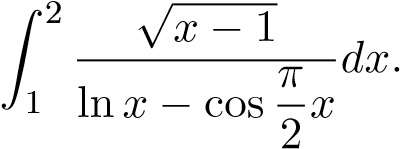
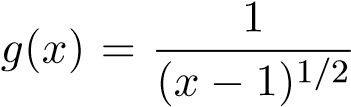 Cách 1. Dùng dấu hiệu so sánh qua giới hạn với hàm(làm tương tự như ví dụ trên).
Cách 1. Dùng dấu hiệu so sánh qua giới hạn với hàm(làm tương tự như ví dụ trên).
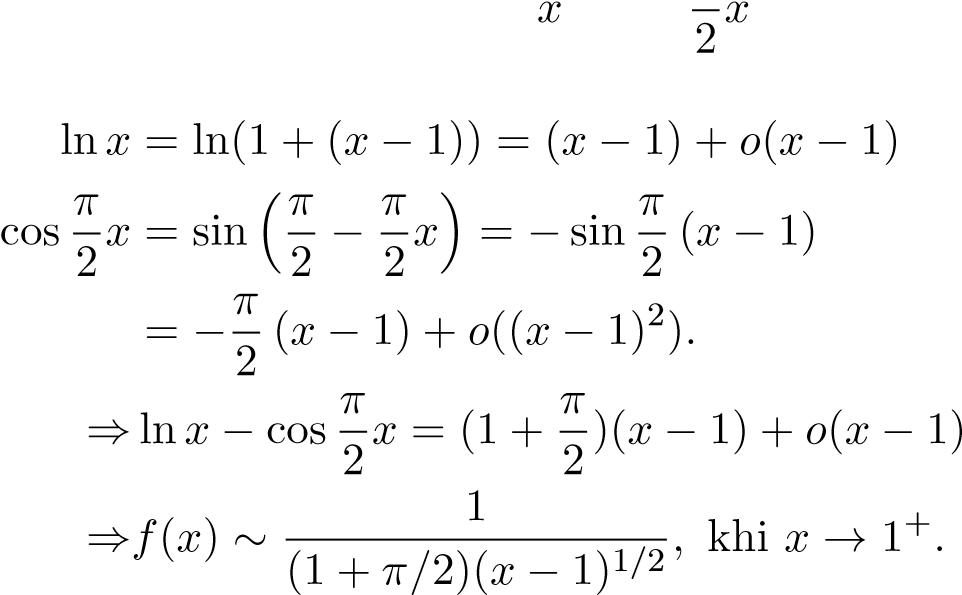 Cách 2. Ta sẽ phân tích dáng điệu hàm
Cách 2. Ta sẽ phân tích dáng điệu hàm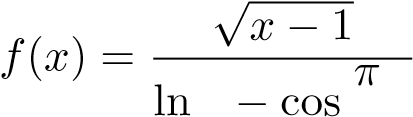 khi x → 1+. Ta có:
khi x → 1+. Ta có:
Mà tích phân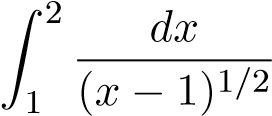 hội tụ nên tích phân suy rộng ban đầu hội tụ.
hội tụ nên tích phân suy rộng ban đầu hội tụ.
Chú ý 1. Nhiều bạn mắc sai lầm khi khai triển Taylor hàm 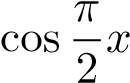 tại điểm x0 = 1.
tại điểm x0 = 1.
Ví dụ 5. Xét sự hội tụ của tích phân sau
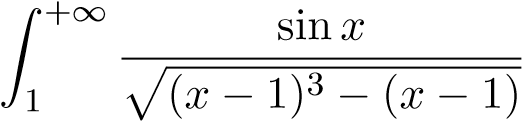 .
.
ĐS: Hội tụ (tuyệt đối).
2 Bài tập tích phân suy rộng
2.1 Tính tích phân sau
Ví dụ 6. Tính tích phân suy rộng sau
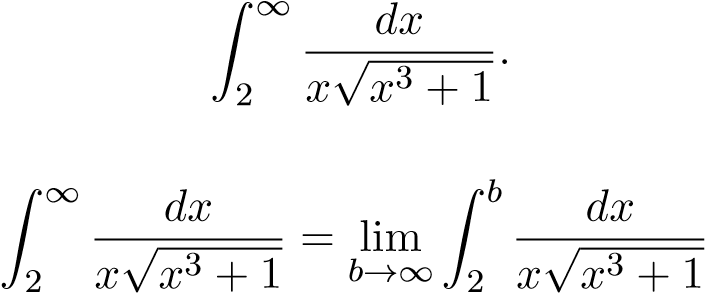 Theo đn ta có
Theo đn ta có
.
Xét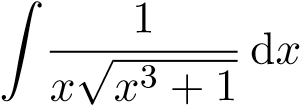
Cách 1. Đặt u = √x3 + 1 ta có

Chú ý 2. Ta có thể làm theo nhiều cách khác nhau, chẳng hạn đặt
u = x3 + 1.
Ví dụ 7. Tính tích phân suy rộng sau
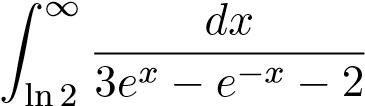 .
.
Giải:
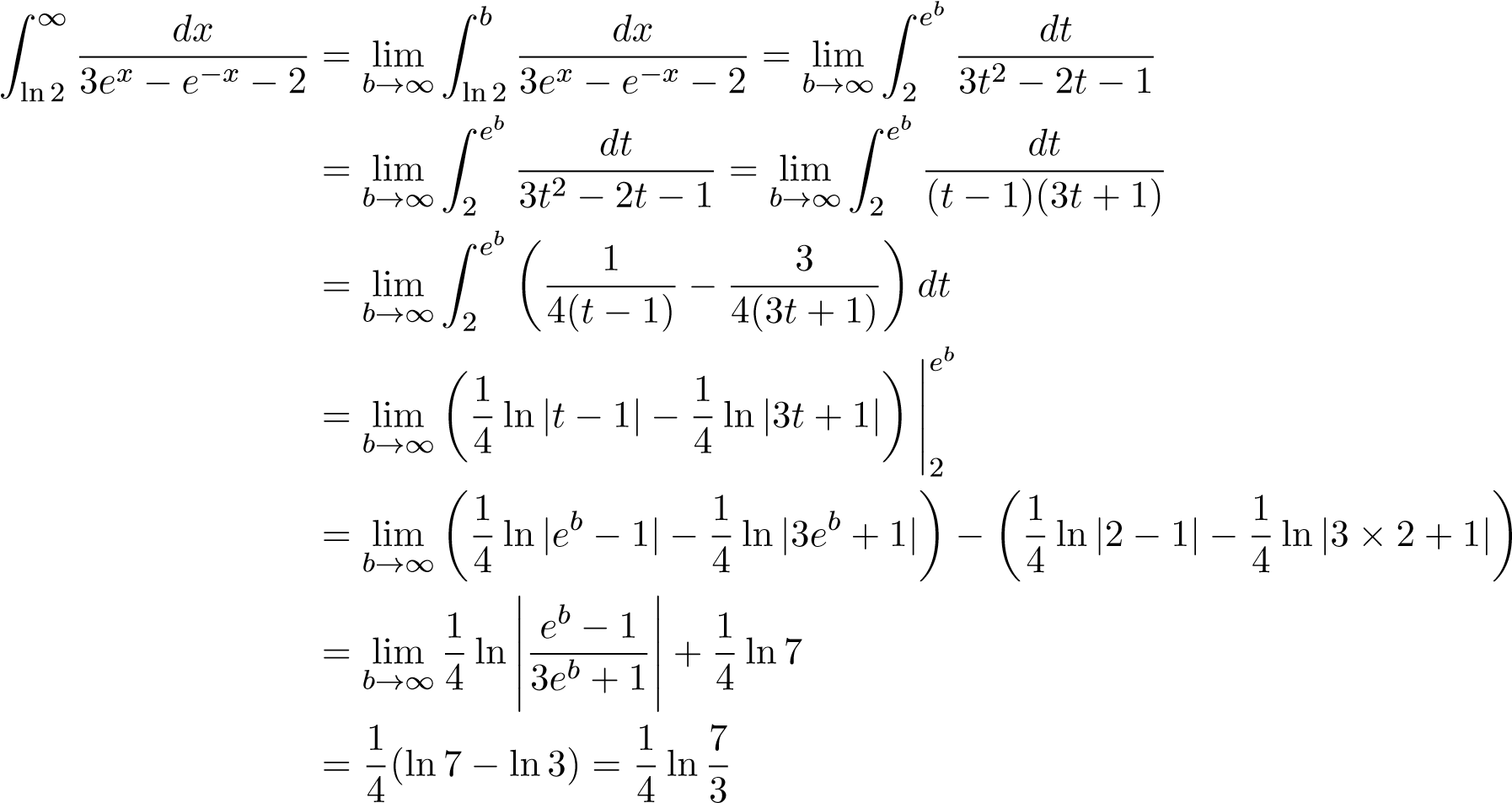
Ví dụ 8. Tính tích phân suy rộng sau
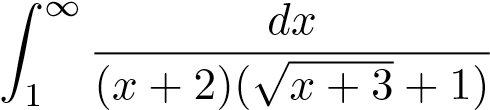 .
.
Theo đn ta có
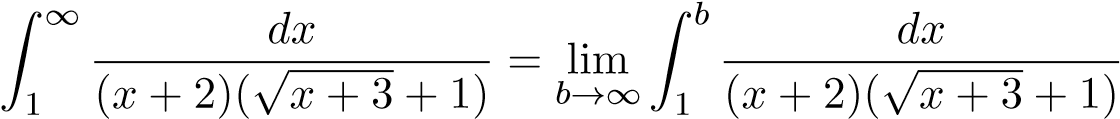 .
.
Xét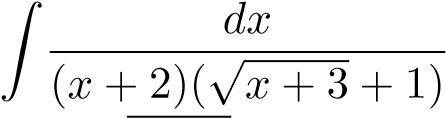
Đặt u = √x + 3, suy ra u2 = x + 3,2udu = dx. Ta có
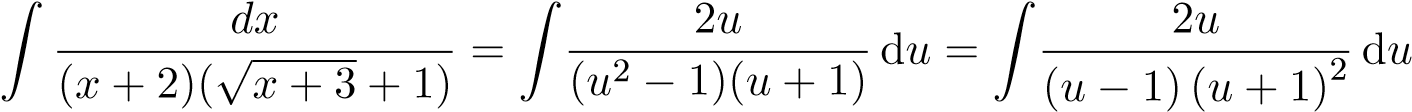
Ta phân tích
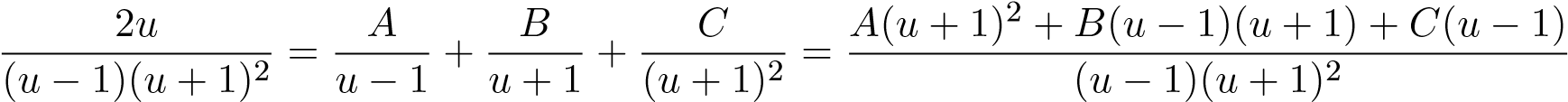 .
.
Suy ra đồng nhất thức
2u ≡ A(u + 1)2 + B(u − 1)(u + 1) + C(u − 1) . (*)
Để tính các hệ số A,B,C ta có thể dùng phương pháp hệ số bất định hoặc chọn các giá trị đặt biệt của u. Ta sẽ làm theo cách thứ hai. Từ đồng nhất thức (∗) lần lượt cho u = 1,−1,0 ta được:
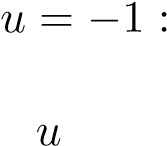 u = 1 : 2 = 4A + 0 + 0 ⇒ .
u = 1 : 2 = 4A + 0 + 0 ⇒ .
A
=
1
2
⇒
C
=1
.
−
1
2
−2 = 0 + 0 − 2C
1
= 0 : 0 = A − B − C ⇒ B = A − C = 2 − 1 = .
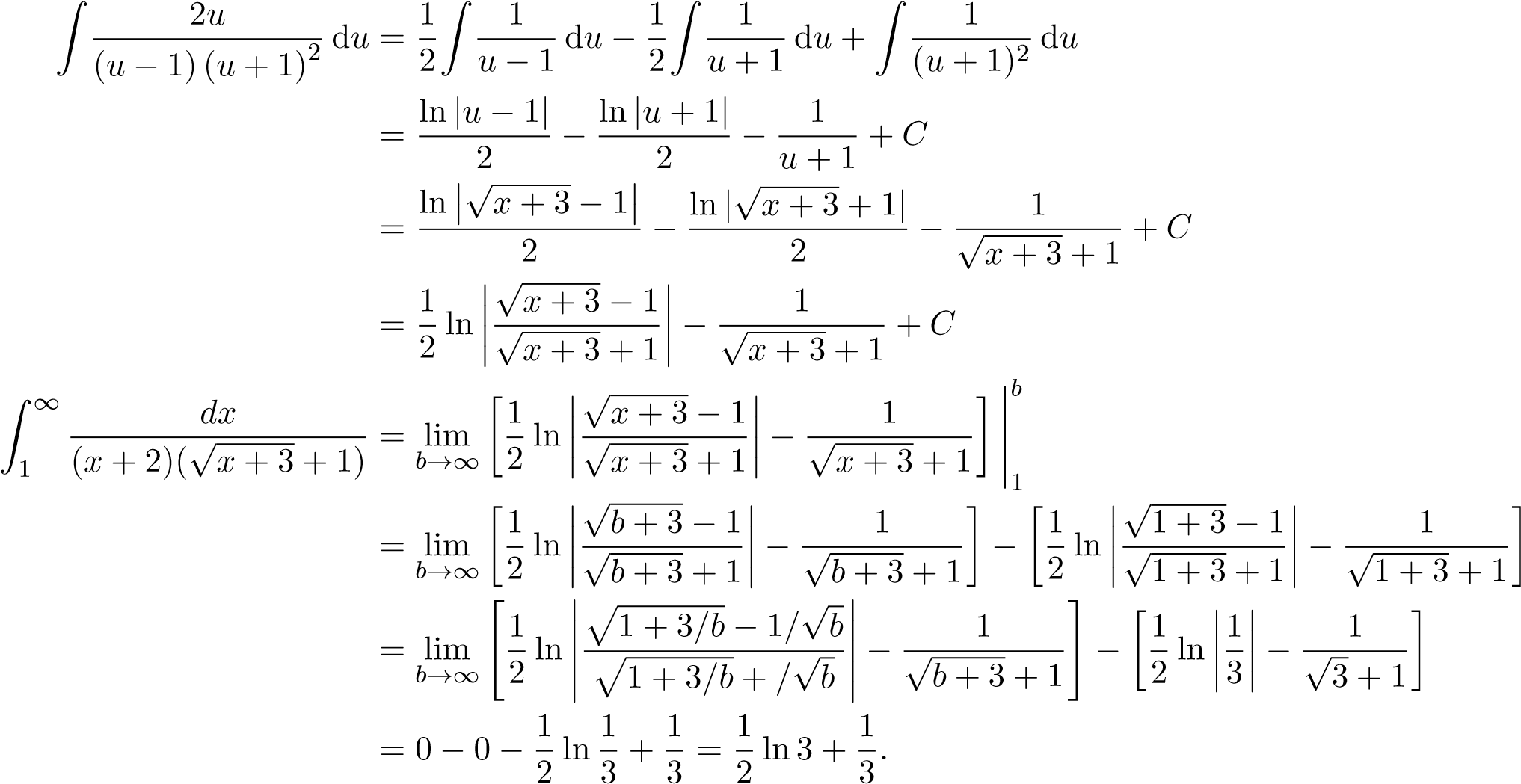
Chú ý 3. Đây chỉ là một cách làm. Ta cũng có thể đổi biến theo cách khác miễn là kết quả vẫn đúng.
Ví dụ 9. Tính tích phân suy rộng sau
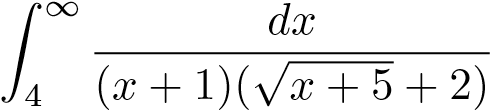 .
.
Theo đn ta có
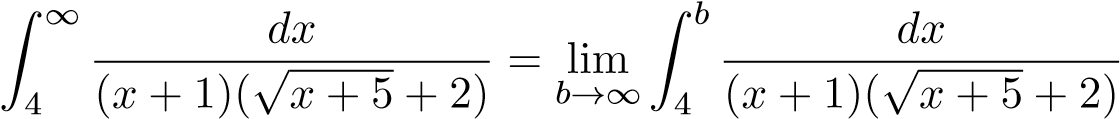 .
.
Xét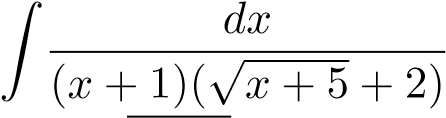
Đặt u = √x + 5, suy ra u2 = x + 5,2udu = dx. Ta có
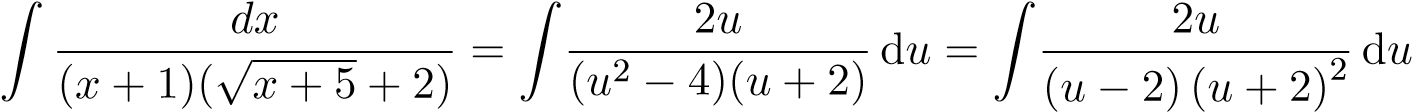
Ta phân tích
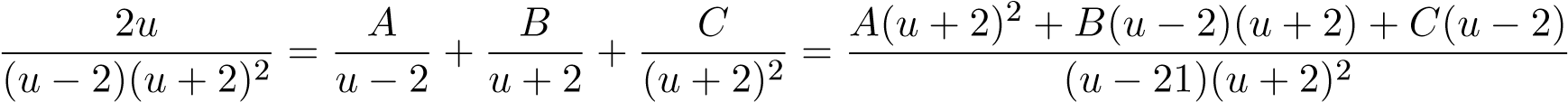 .
.
Suy ra đồng nhất thức
2u ≡ A(u + 2)2 + B(u − 2)(u + 2) + C(u − 2) . (*)
Từ đồng nhất thức (∗) lần lượt cho u = 2,−2,0 ta được:
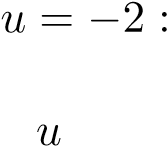 u = 2 : 4 = 16A + 0 + 0.
u = 2 : 4 = 16A + 0 + 0.
⇒
A
=
1
4
⇒
C
=1
.
4
A
−
2
C
4
=
1
−
2
4
=
−
1
4
−4 = 0 + 0 − 4C
= 0 : 0 = 4A − 4B − 2C ⇒ B =.

Ví dụ 10. Tính tích phân suy rộng sau
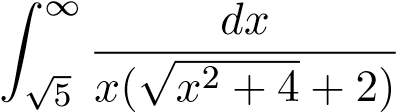 .
.
Theo đn ta có
.
Xét
x | 5 | b |
u | 3 | √b2 + 4 |
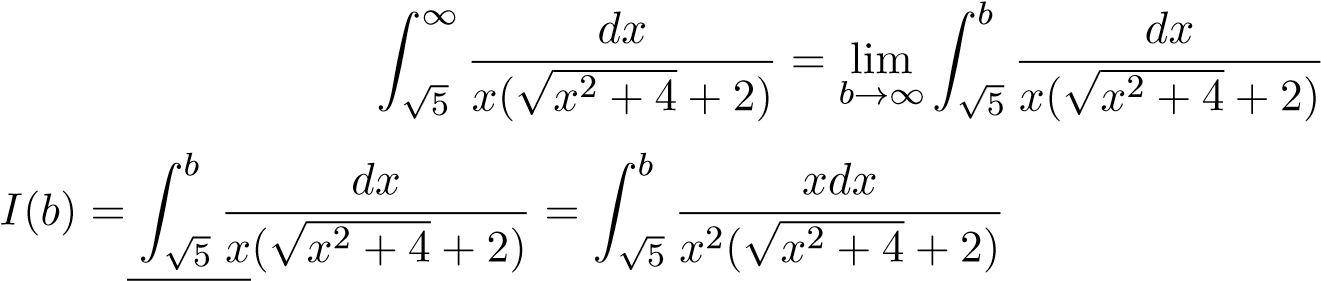 Đặt u = √x2 + 4, suy ra u2 = x2 + 4,udu = xdx. √
Đặt u = √x2 + 4, suy ra u2 = x2 + 4,udu = xdx. √
Ta có
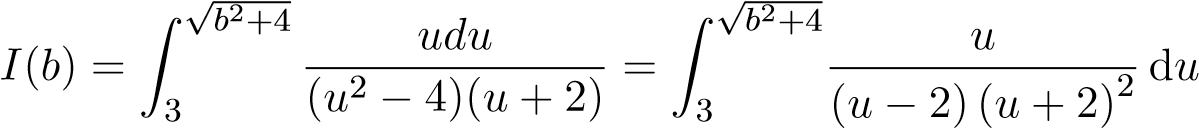
Ta phân tích
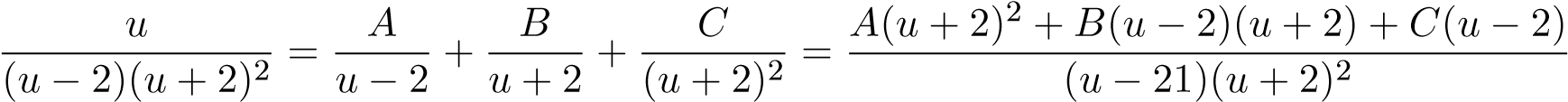 .
.
Suy ra đồng nhất thức
u ≡ A(u + 2)2 + B(u − 2)(u + 2) + C(u − 2) . (*)
Từ đồng nhất thức (∗) lần lượt cho u = 2,−2,0 ta được:
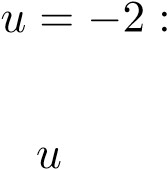 u = 2 : 2 = 16A + 0 + 0
u = 2 : 2 = 16A + 0 + 0
⇒
A
=
1
8
.
⇒
C
=
1
2
.
⇒
B
=
4
A
−
2
C
4
=
1
/
2
−
1
4
=
−
1
8
.
−2 = 0 + 0 − 4C
= 0 : 0 = 4A − 4B − 2C
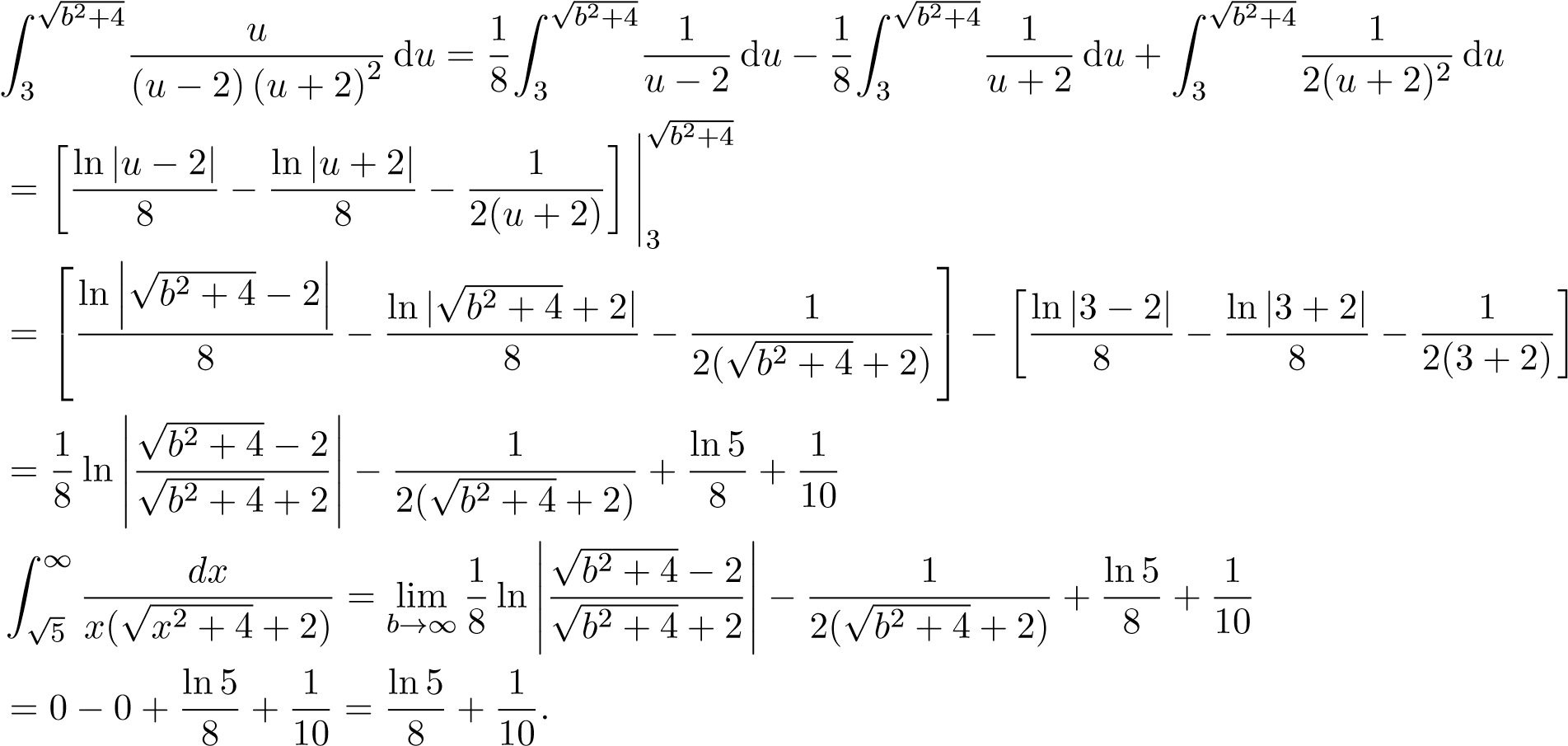
Ví dụ 11. Tính tích phân suy rộng sau
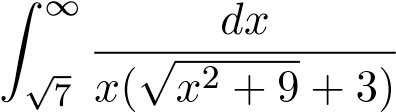 .
.
Cách làm tương tự mấy câu trước.
ĐS: 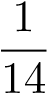 +
+ 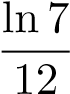
Ví dụ 12. Tính các tích phân sau
1.
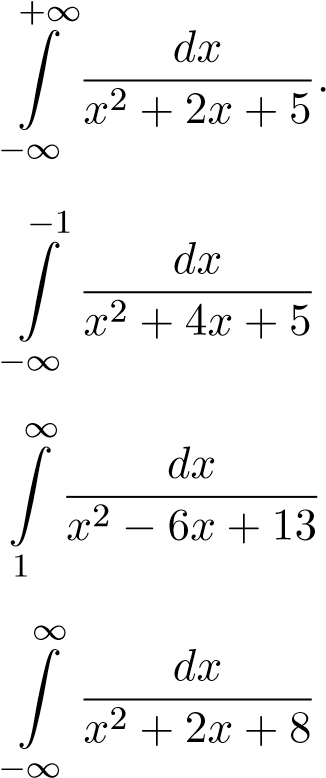 2..
2..
3.
4.
Ví dụ 13. Tính các tích phân sau
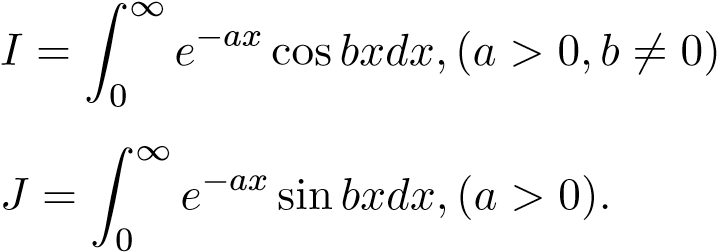 1..
1..
2.
ĐS: (Sử dụng tích phân từng phần)
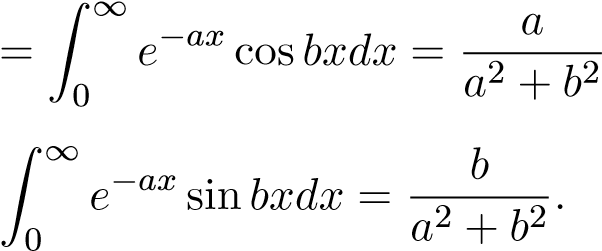 1..
1..
2.
Giải
1. Xét tích phân bất định I = Z e−ax cosbxdx, (a > 0,b 6= 0). Sử dụng tích phân từng phần
đặt u = cosbx,dv = e−axdx, suy ra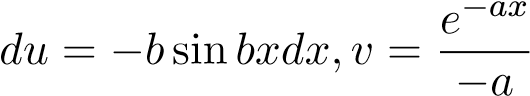 , ta có
, ta có
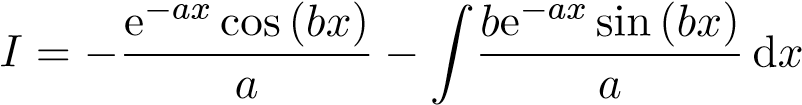
Tiếp tục sử dụng công thức tích phân từng phần một lần nữa. Đặt u = bsinbx,dv =
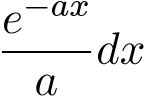 , suy ra
, suy ra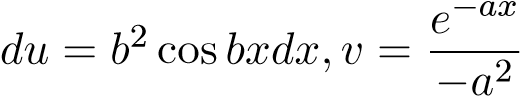 ta được
ta được
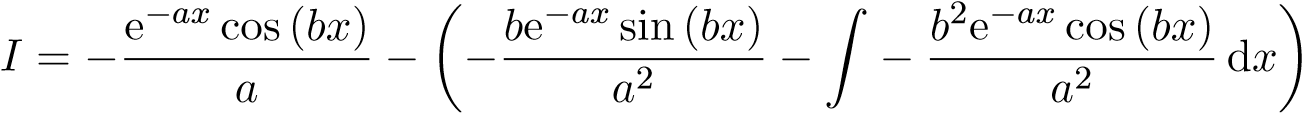
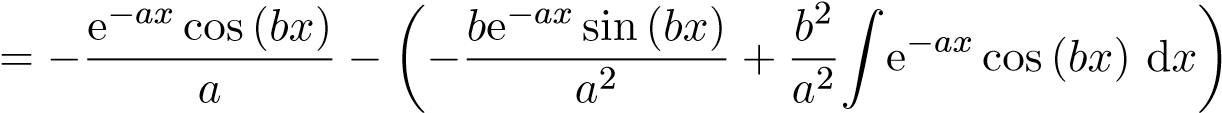
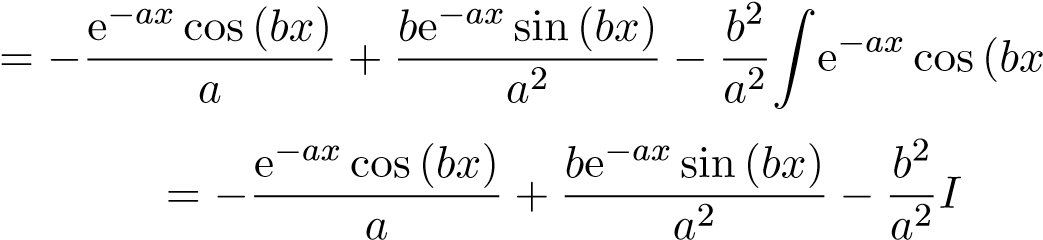 ) dx
) dx
Suy ra
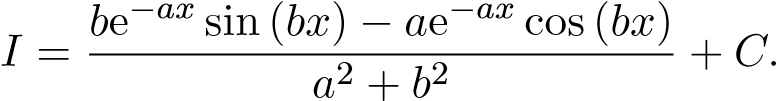
The định nghĩa ta có
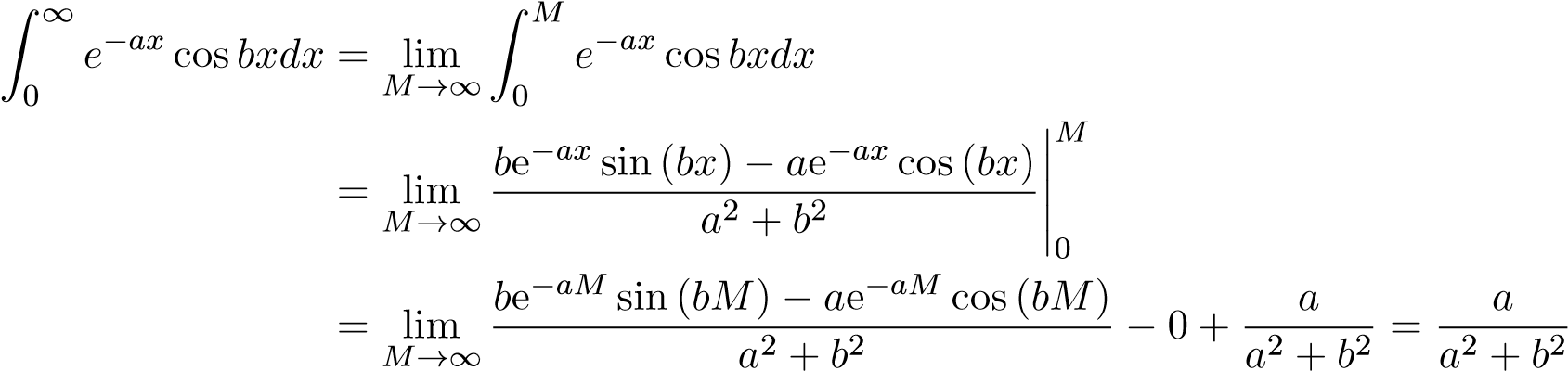 .
.
Chú ý: Để tính giới hạn trên ta có sử dụng định lý kẹp (tự làm).
Ví dụ 14. Tính các tích phân sau
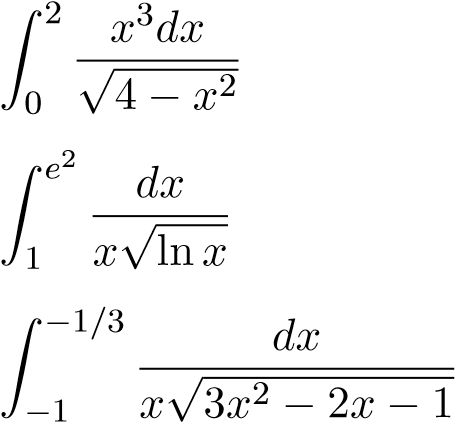 1.
1.
2.
3.
Ví dụ 15. Tính tích phân sau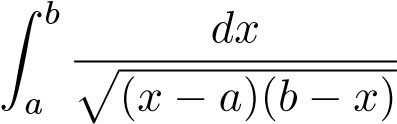 .
.
Ví dụ 16 (?). Tính tích phân sau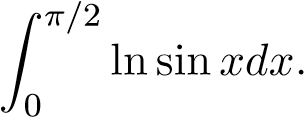
Giải
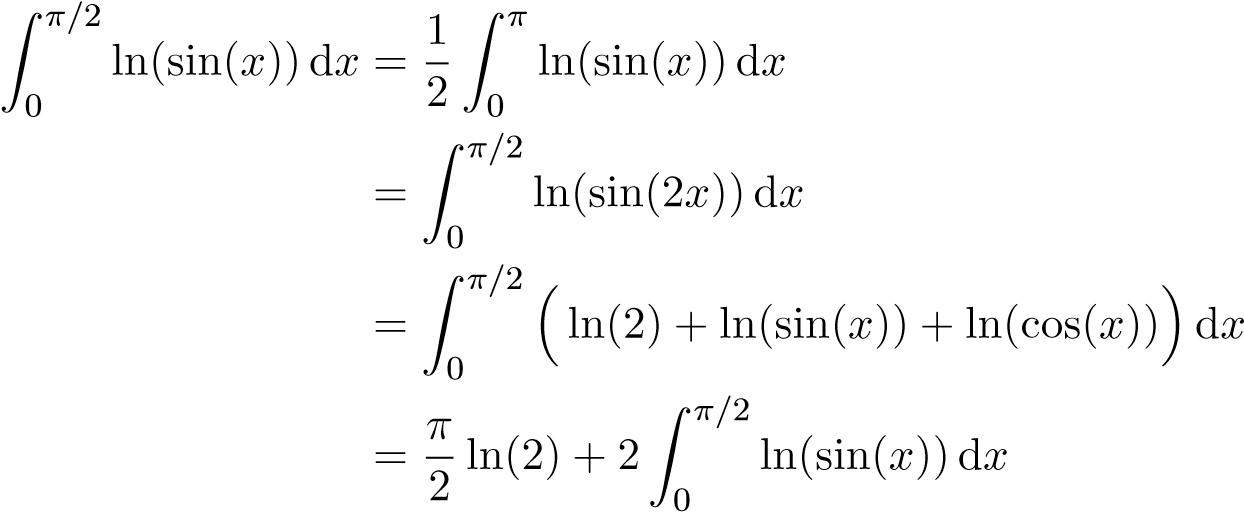
Do đó
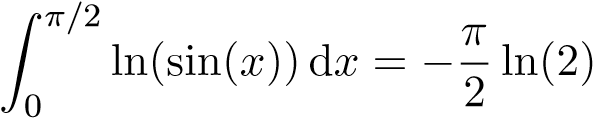
Ví dụ 17 (?). Tính tích phân sau: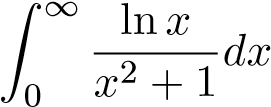
Giải 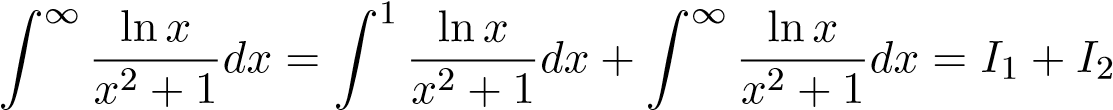 . Trước hết ta chứng minh hai tích phân
. Trước hết ta chứng minh hai tích phân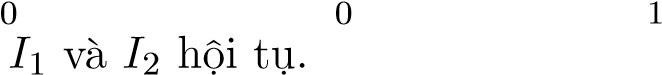
Xét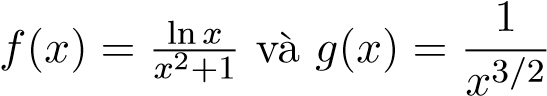 . Khi đó, ta có
. Khi đó, ta có
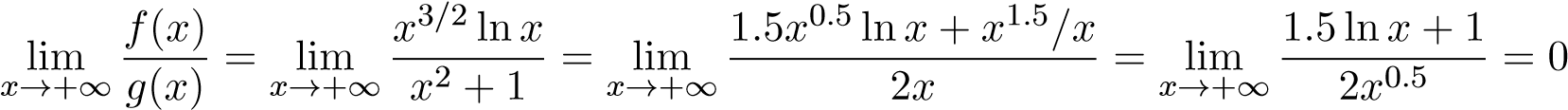 .
.
Mà tích phân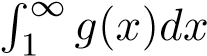 hội tụ nên tích phân I2 hội tụ.
hội tụ nên tích phân I2 hội tụ.
Tương tự ta có
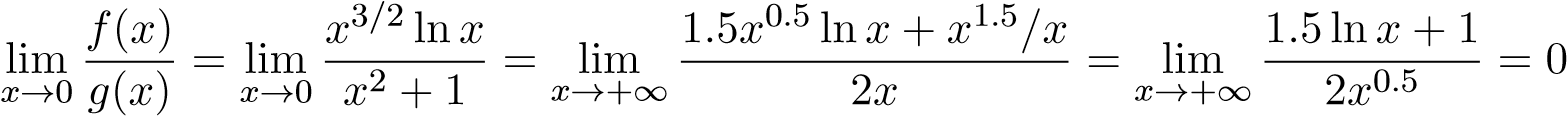 .
.
Mà tích phân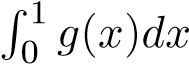 hội tụ nên tích phân I1 hội tụ.
hội tụ nên tích phân I1 hội tụ.
Đổi biến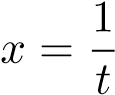 ta có
ta có
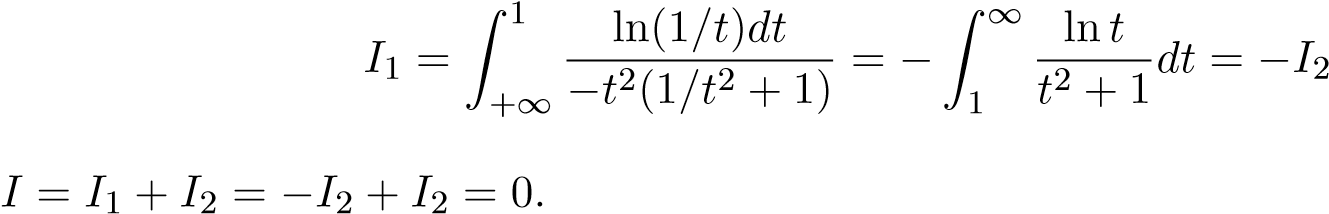 .
.
Vậy
Tổng quát hơn ta có:
Z
∞
0
ln(
x
)
dx
x
2
+
a
2
=
π
ln(
a
)
2
a
,
(
a>
0)
.
Thật vậy
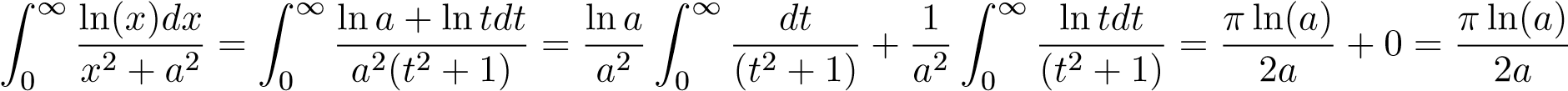 .
.
Ví dụ 18 (?). Tính tích phân sau
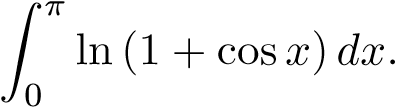
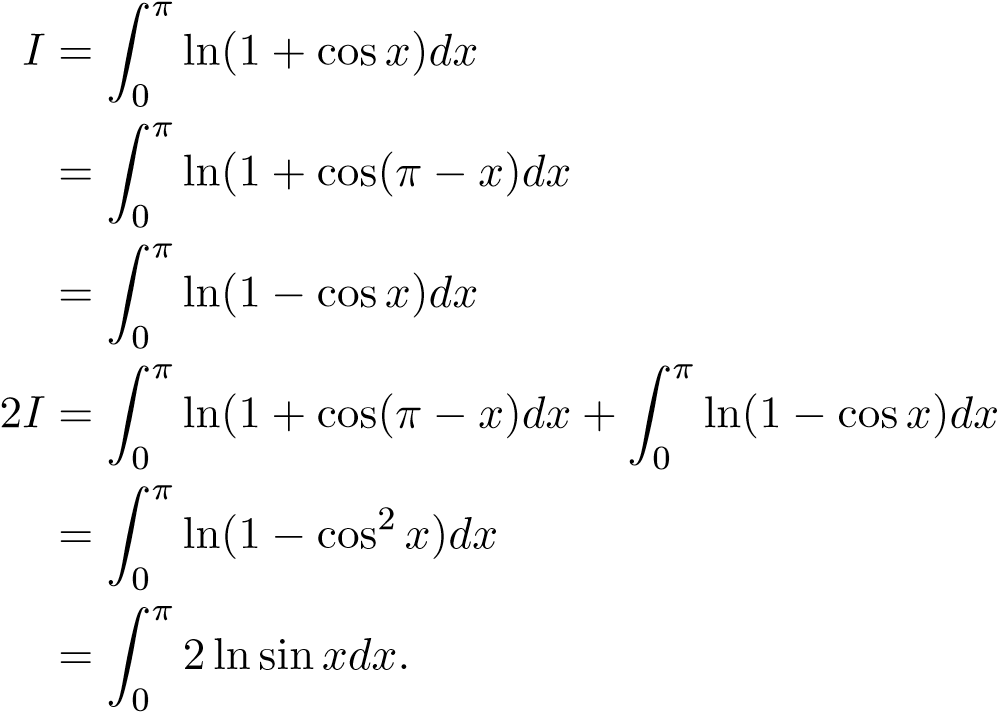 (Sử dụng tc:
(Sử dụng tc: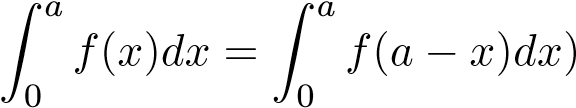
Suy ra
π
Z
Z
I =ln(sinx)dx (1)
0
π/2 π
=ln(sinx)dx + Z ln(sinx)dx (2)
0 π/2
Từ (1) bằng cách đổi biến x = 2t ta có
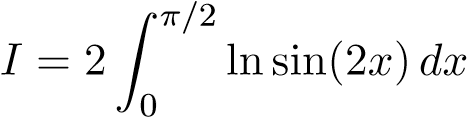
Từ (2) bằng cách đổi biến t = π − x ở tích phân thứ 2 ta có
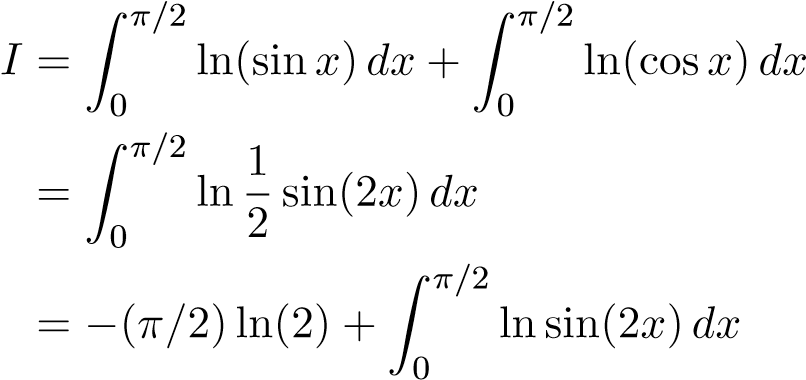 (4)
(4)
Từ đó suy ra
π/2
Z
0 lnsin(2x)dx = −(π/2)ln2 ⇒ I = −π ln2
Ví dụ 19. Tính tích phân sau
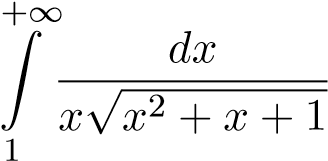 .
.
Giải:
Đặt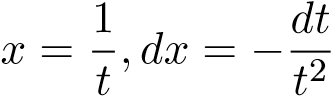 ,
,
x | 1 | b |
t | 1 | 1/b |
ta có
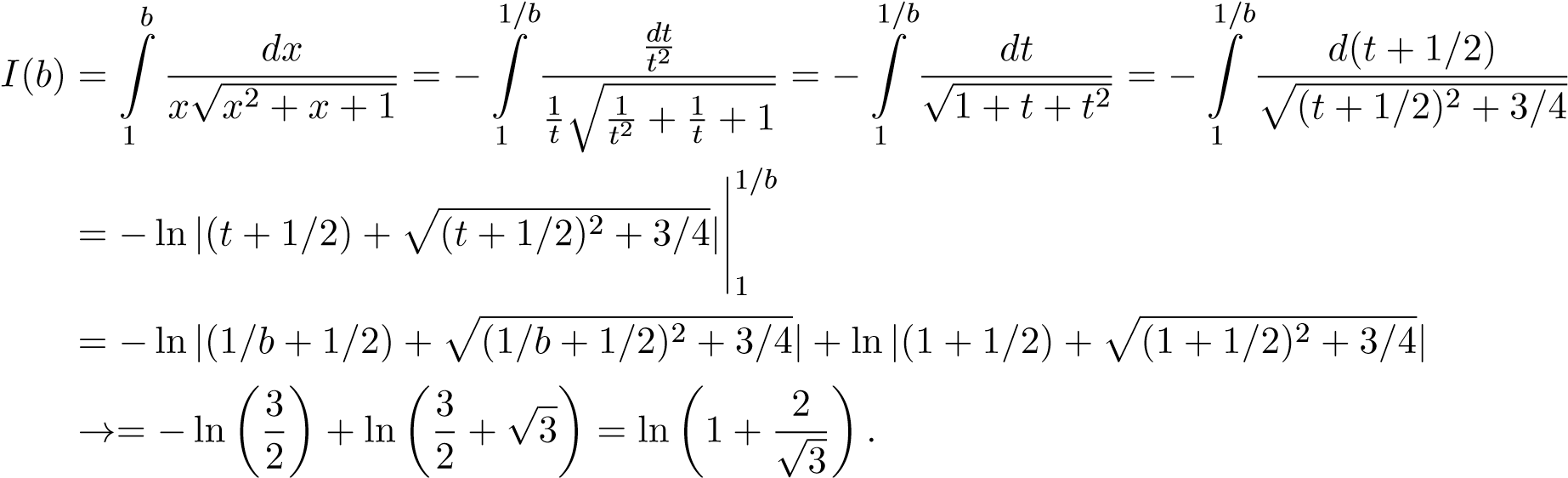
Cách 2. Ta cũng có thể làm trực tiếp như sau: Đặt 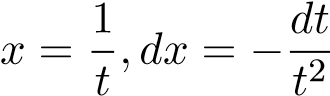 ,
,
x | 1 | +∞ |
t | 1 | 0 |
ta có
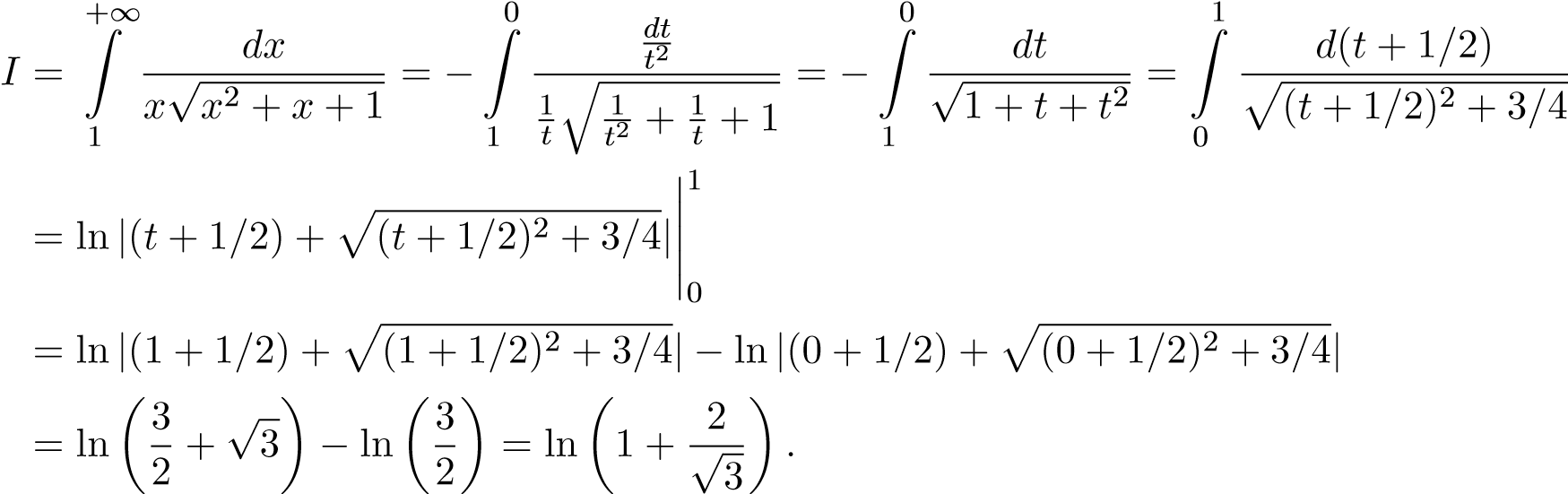
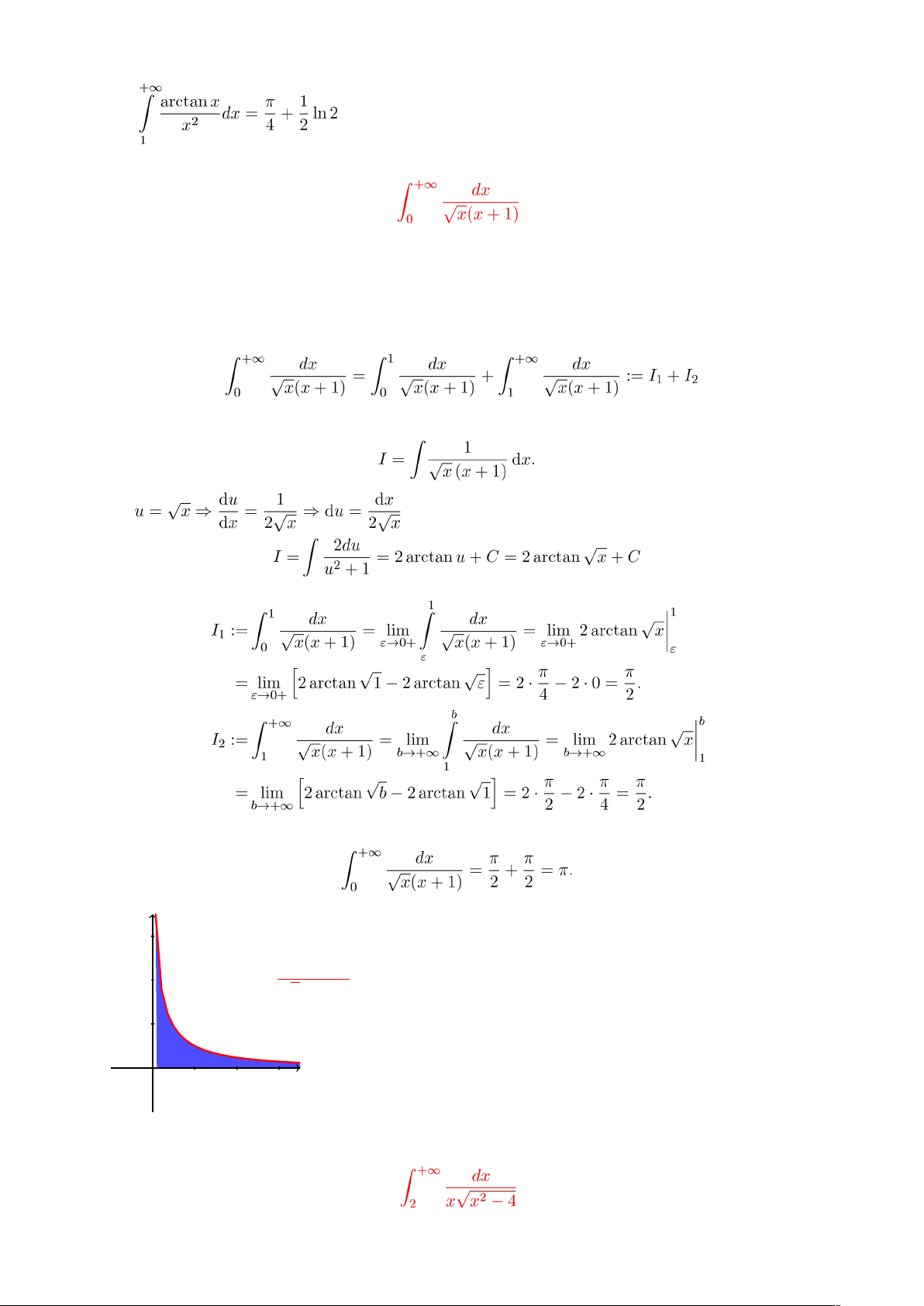
Ví dụ 20. Tính tích phân sau
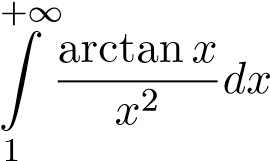
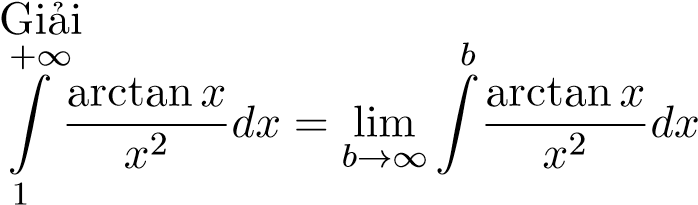 . Ta có
. Ta có
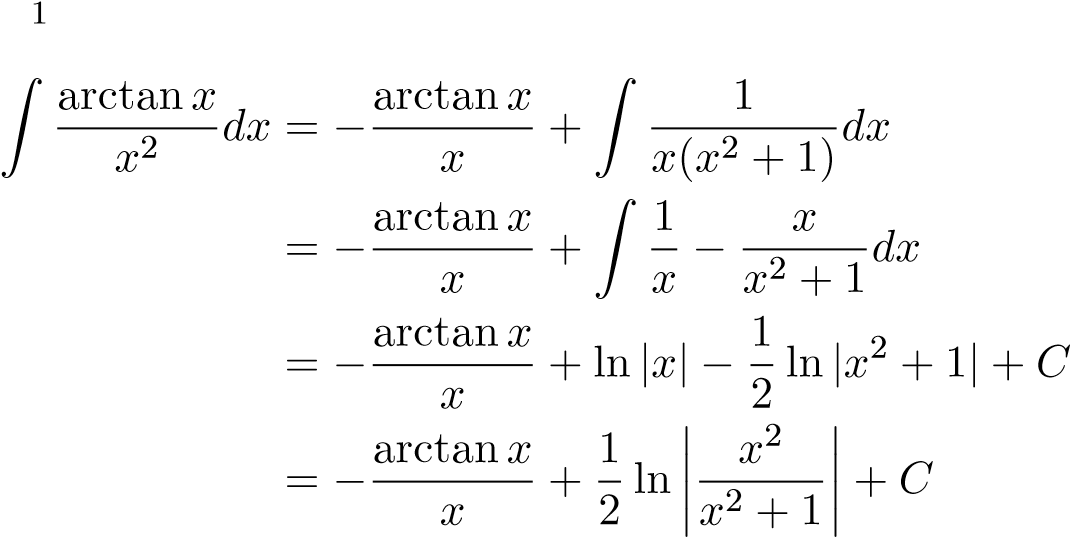
Suy ra
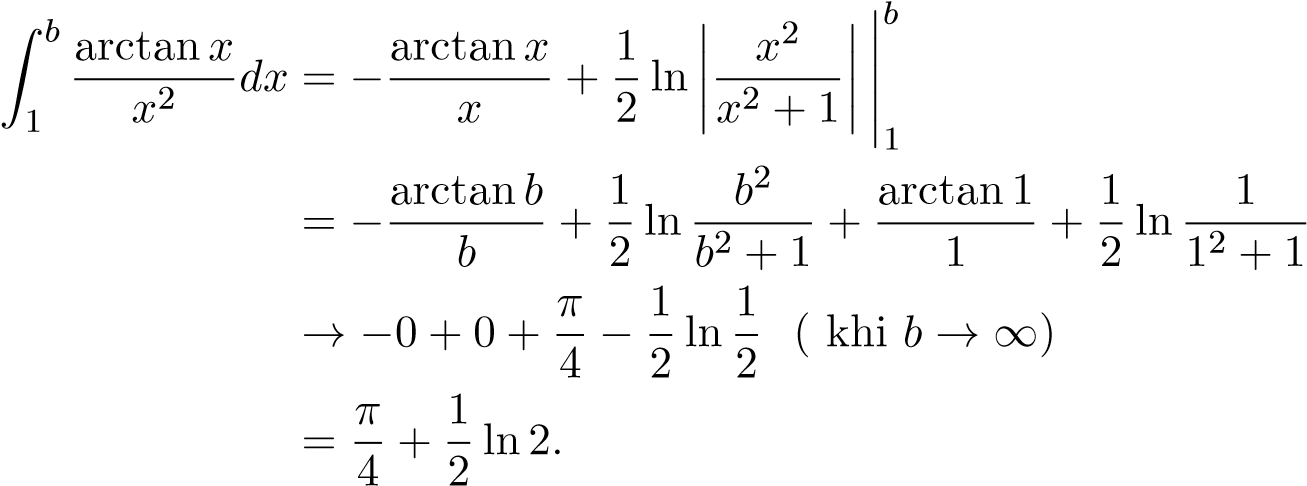
Vậy 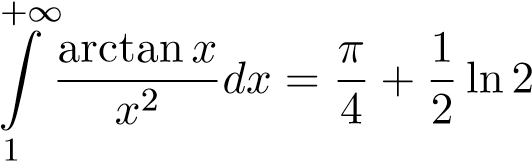 .
.
Ví dụ 21. Tính tích phân
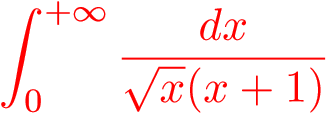 .
.
Giải:
Chú ý rằng tích phân suy rộng là tích phân suy rộng cả hai loại (cận vô hạn và hàm không bị chặn tại 0). Ta tách ra như sau
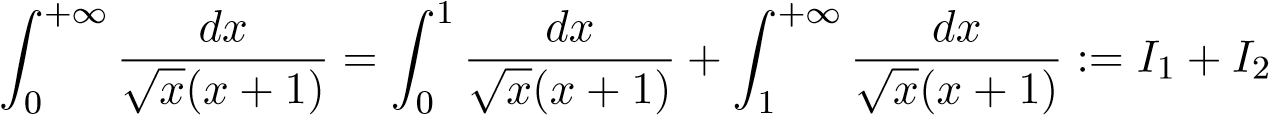 .
.
Xét nguyên hàm
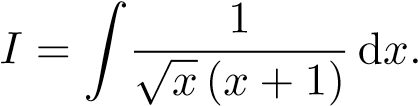
Đặt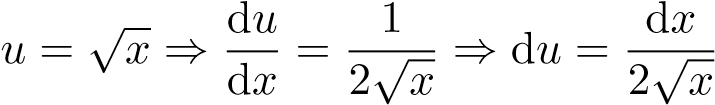 . Khi đó
. Khi đó
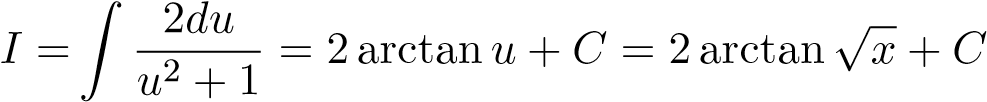
Ta có
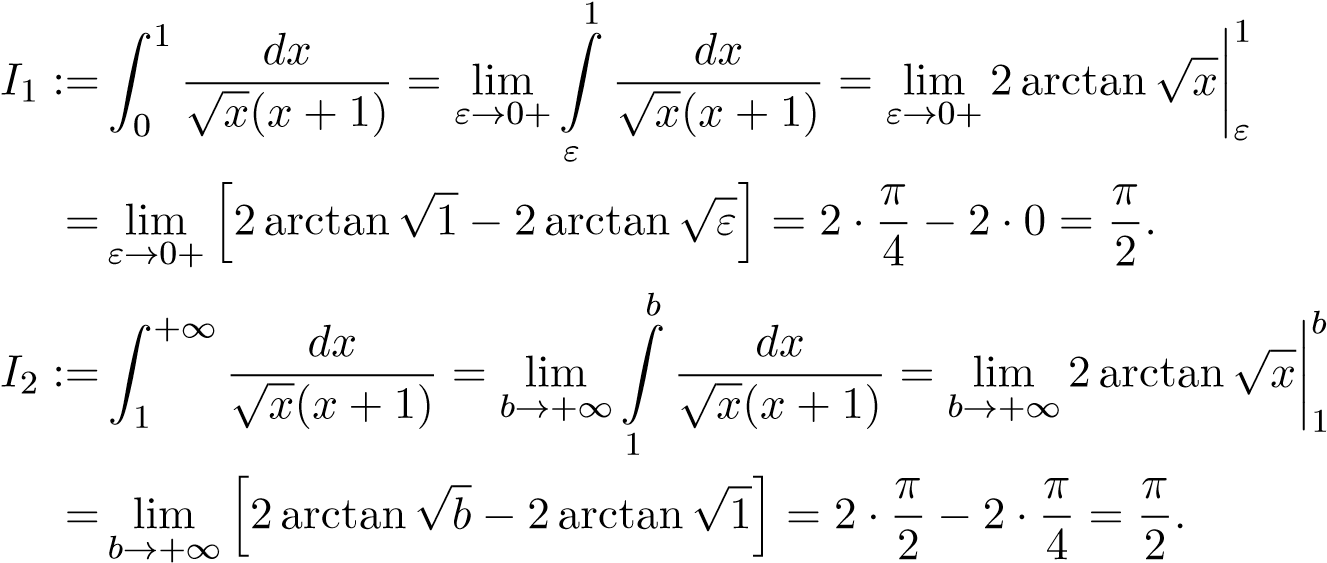
Vậy
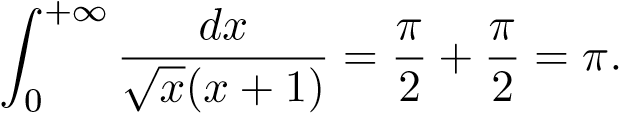
x
1
2
3
y
1
2
3
f
(
x
)=
1
√
x
(
x
+1)
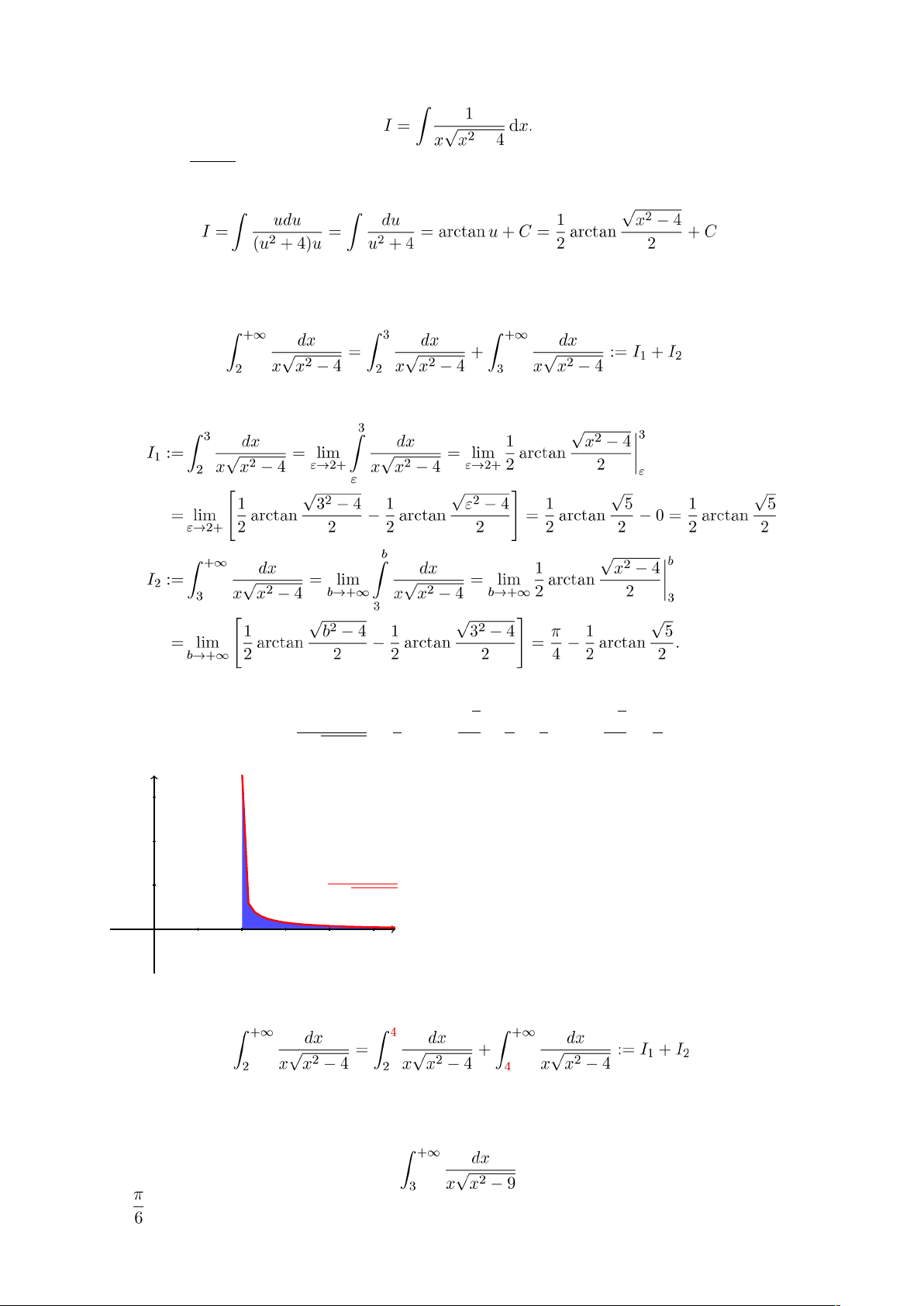
Ví dụ 22. Tính tích phân suy rộng sau:
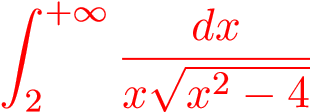 .
.
Giải:
Xét nguyên hàm
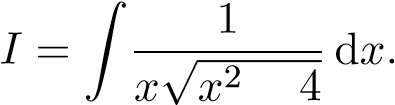 − Đặt u = √x2 − 4 ⇒ u2 = x2 − 4 ⇒ udu = xdx. Khi đó
− Đặt u = √x2 − 4 ⇒ u2 = x2 − 4 ⇒ udu = xdx. Khi đó
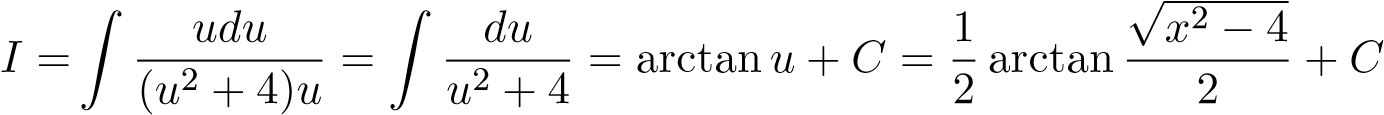
Chú ý rằng tích phân suy rộng là tích phân suy rộng cả hai loại (cận vô hạn và hàm không bị chặn tại 2). Ta tách ra như sau
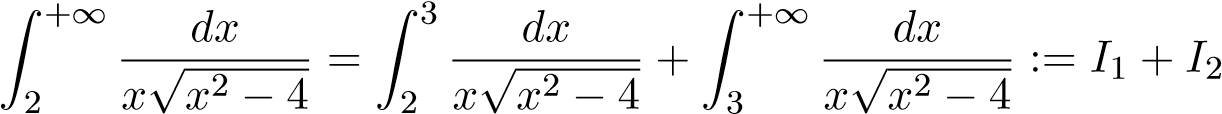 .
.
Ta có
 .
.
2
Vậy
Z
+
∞
2
dx
x
√
x
2
−
4
=
1
2
arctan
√
5
2
+
π
4
−
1
2
arctan
√
5
2
=
π
4
.
x
1
2
3
4
5
y
1
3
f
(
x
)=
1
x
√
x
2
−
4
Chú ý 4. Nếu ta tách
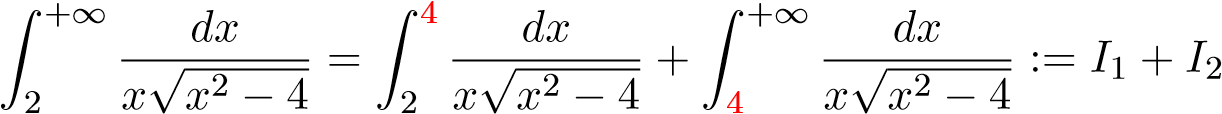 .
.
thì kết quả tính toán sẽ nhanh gọn hơn (Hãy thử xem!!!) Ví dụ 23. Tính tích phân suy rộng sau:
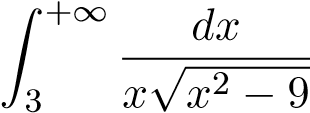
ĐS: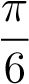
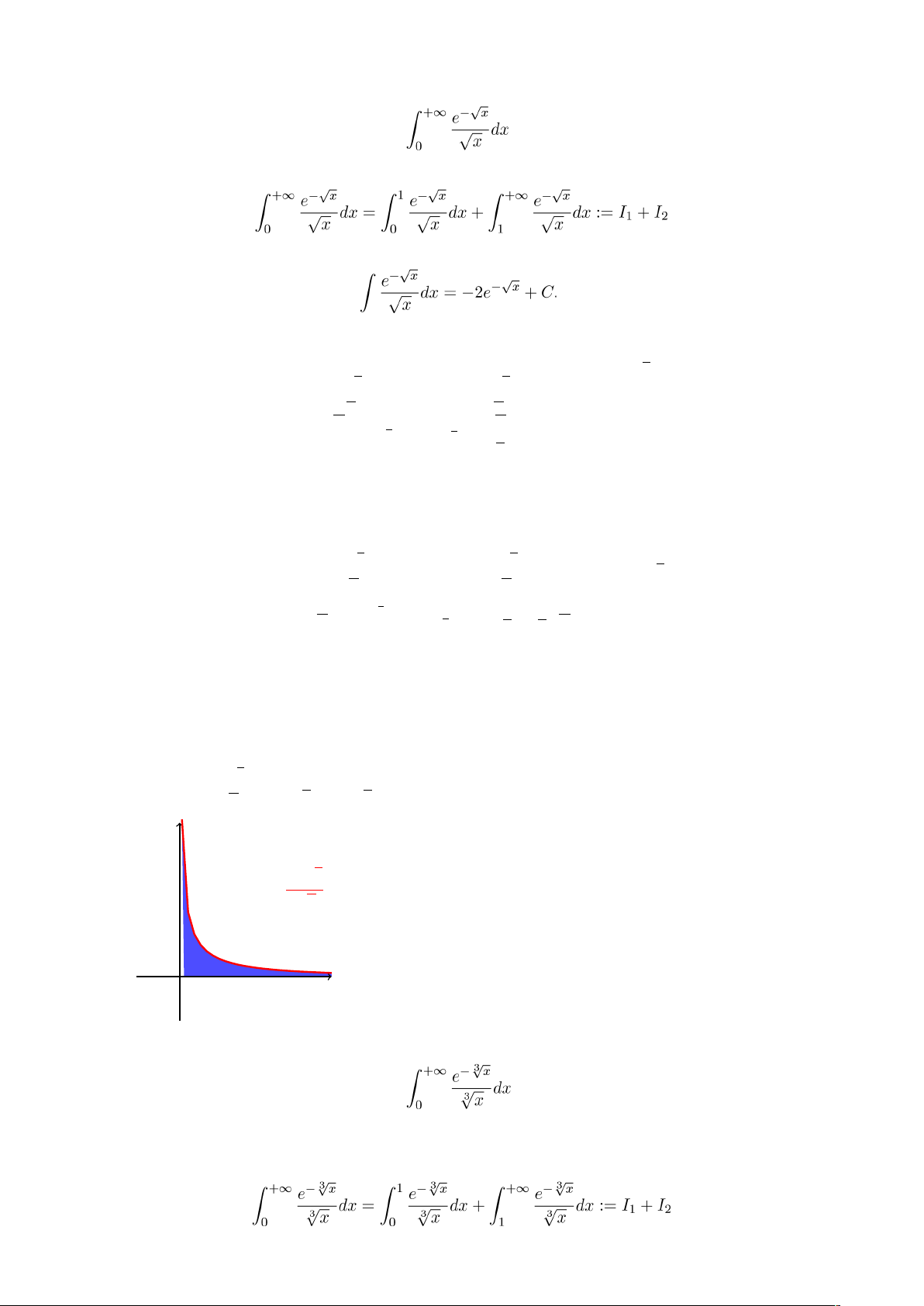
Ví dụ 24. Tính tích phân suy rộng sau:
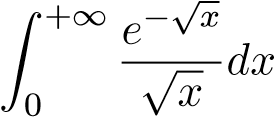
Giải: Ta có
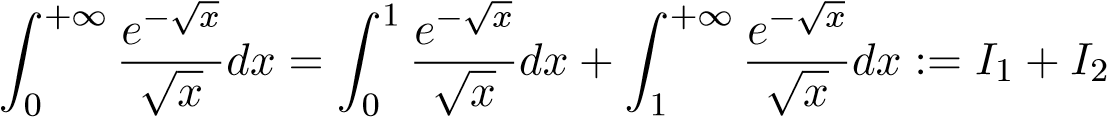 .
.
Dễ thấy rằng
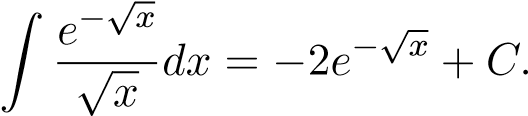
Suy ra
1 e−√x 1 e−√x √x 1
Z
I1 =0 √x dx = ε→lim0+ Zε √x dx = ε→lim0+ −2e− ε
= lim0+ −2e−√1 + 2e−√ε = −2e + 2. ε→
I2 = 1+∞ e√−√xx dx = b→lim+∞1 Z1b e√−√xx dx = b→lim+∞−2e−√xb1
Z
= lim+ −2e−√b + 2e−√ = 0 + 2e = 2e. b→ ∞
Suy ra
Z
+
∞
0
e
−
√
x
√
x
dx
=
−
2
e
+2+
2
e
=2
.
O
x
y
f
(
x
)=
e
−
√
x
√
x
Ví dụ 25. Tính tích phân suy rộng sau:
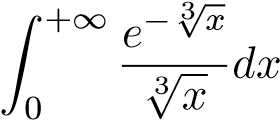
Giải:
(Gợi ý: Đổi biến sau đó tích phân từng phần.) Ta có
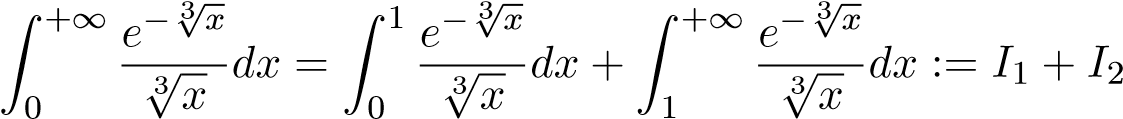 .
.
Trước hết ta tính tích phân bất định sau:
dx
Z
e
−
3
√
x
3
√
x
Đặt t = √3 x suy ra t3 = x, suy ra 3t2dt = dx. Tích phân trên trở thành
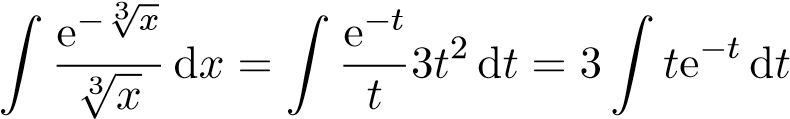
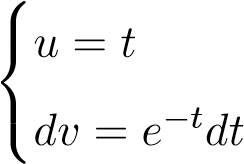 du = dt
du = dt
Đặtsuy ra. Theo công thức tích phân từng phần ta có:
v = −e−t
Z te−t dt = −te−t + Z e−tdt = −te−t − e−t + C.
Do đó
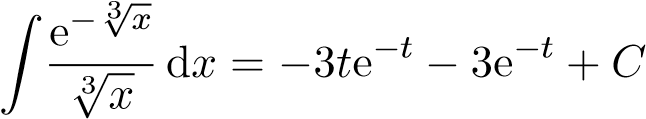
Từ đó
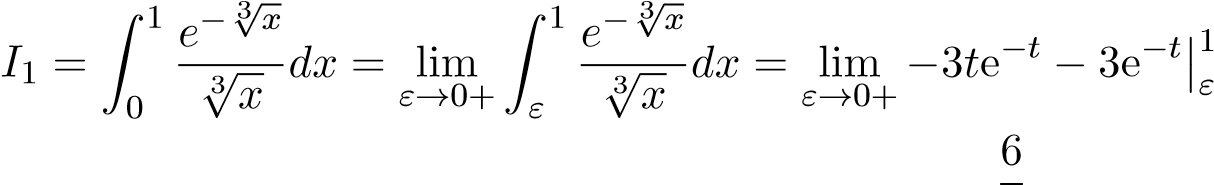
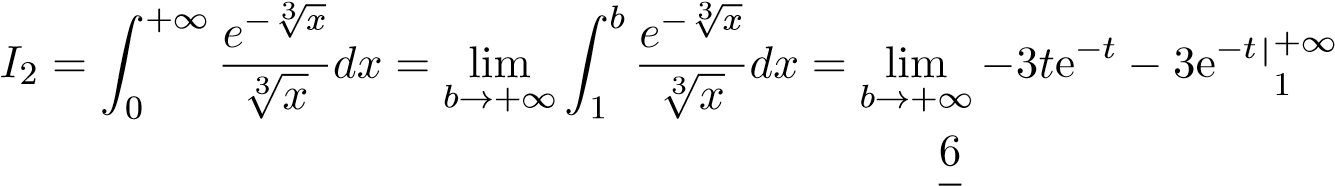
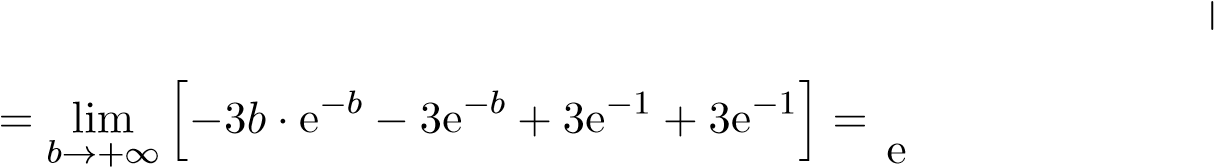
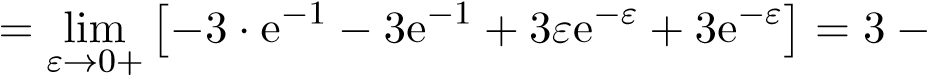 e
e
và
Vậy
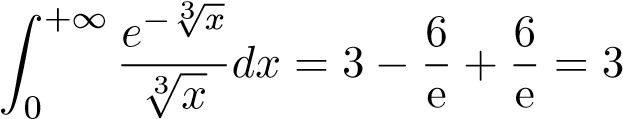 .
.
O
x
y
f
(
x
)=
e
−
3
√
x
3
√
x
Ví dụ 26. Tính tích phân suy rộng sau
Giải: Ta có 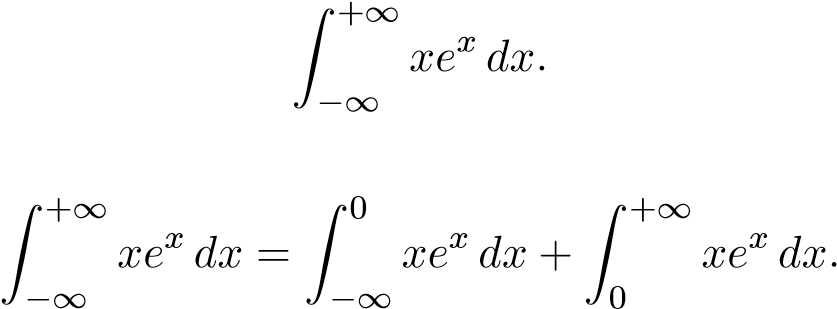
Xét tính phân thứ nhất ta có
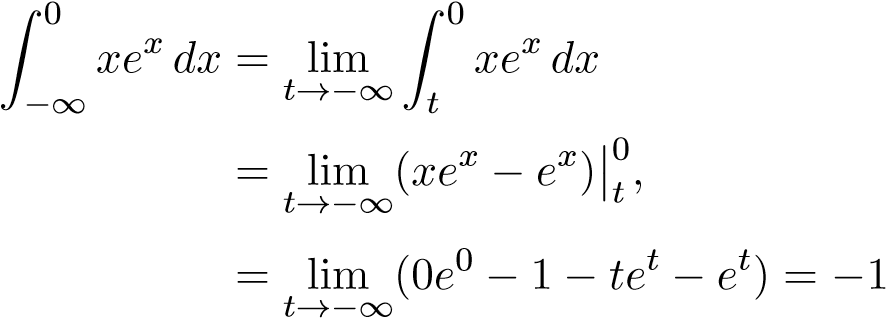 (tích phân từng phần)
(tích phân từng phần)
.
Chú ý rằng
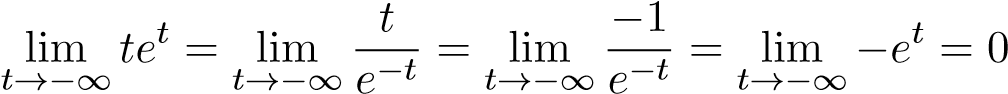 .
.
Xét tích phân thứ hai
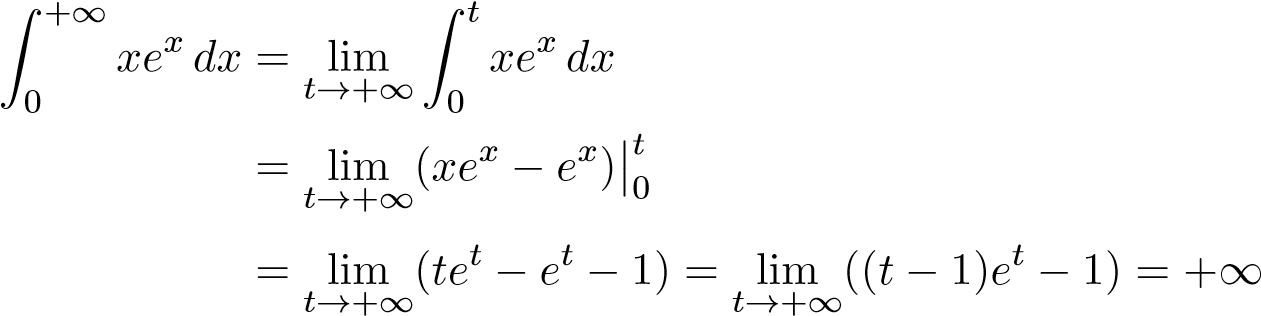 .
.
Vậy tích phân 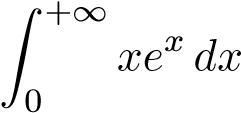 phân kỳ nên tích phân
phân kỳ nên tích phân 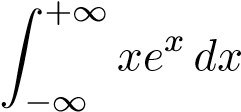 phân kỳ.
phân kỳ.
Ví dụ 27. Tính tích phân:
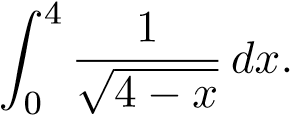
Giải: Hàm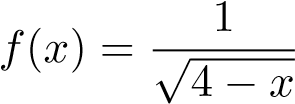 liên tục trên [0,4) và gián đoạn tại 4. Ta có
liên tục trên [0,4) và gián đoạn tại 4. Ta có
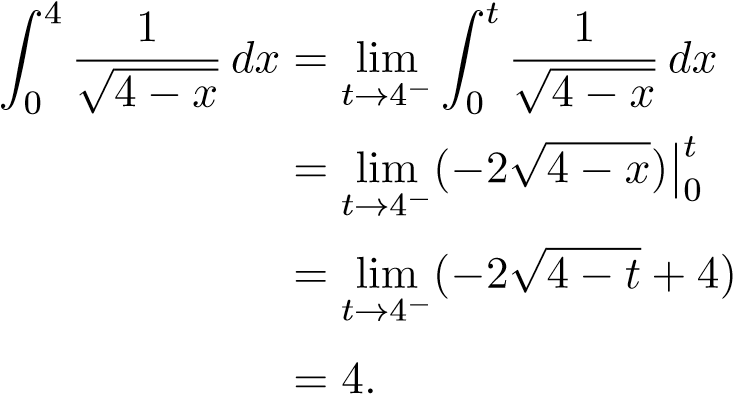
2.2 Xét sự hội tụ, phân kỳ của tích phân sau Ví dụ 28. Xét sự hội tụ của tích phân:
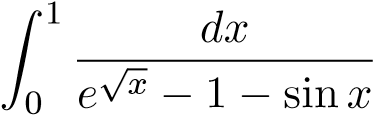 .
.
Gợi ý: Khai triển Taylor ta được trong lân cận điểm 0
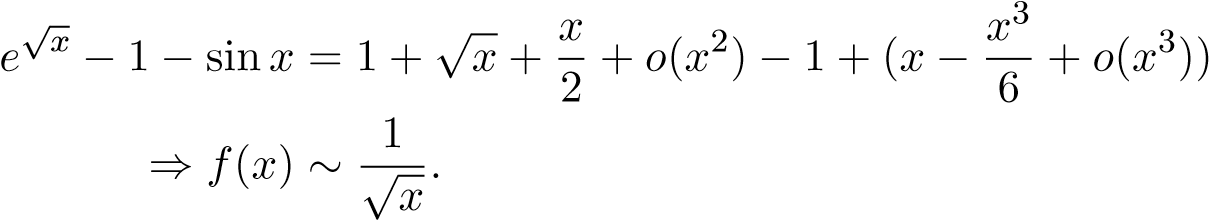
Mà tích phân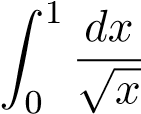 hội tụ nên tp ban đầu hội tụ.
hội tụ nên tp ban đầu hội tụ.
Ví dụ 29. Xét sự hội tụ của tích phân:
Giải: Dễ thấy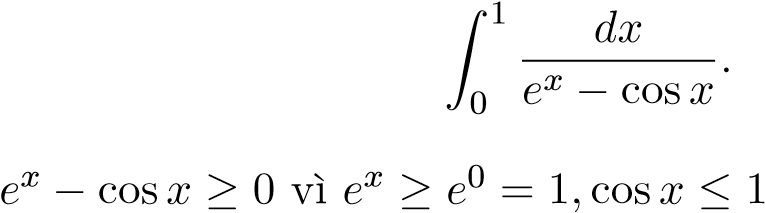 . Ta có
. Ta có
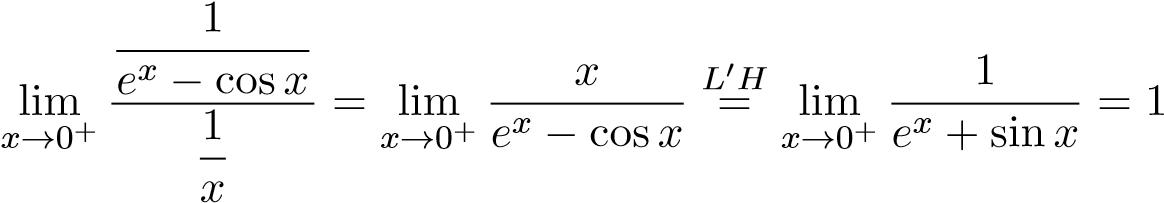 .
.
Mà tích phân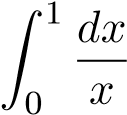 phân kỳ nên tích phân đã cho phân kỳ.
phân kỳ nên tích phân đã cho phân kỳ.
Ví dụ 30. Xét sự hội tụ của tích phân:
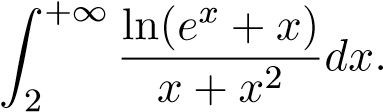
Giải
Đặt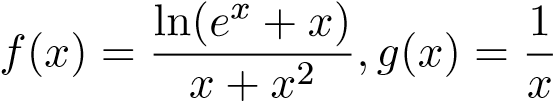 . Xét
. Xét
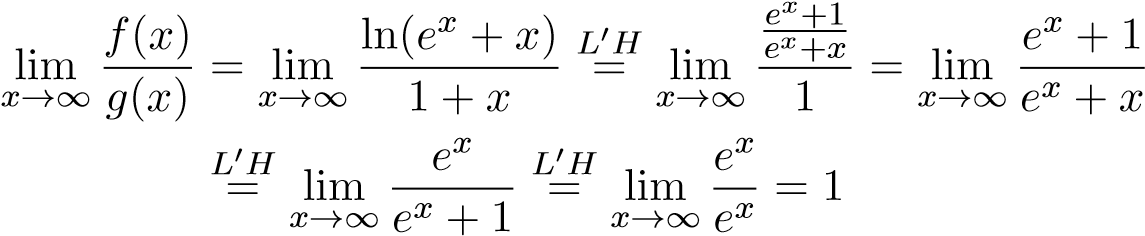
Mà tích phân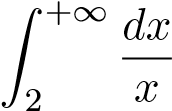 phân kỳ nên tích phân
phân kỳ nên tích phân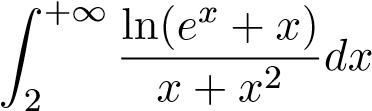 phân kỳ.
phân kỳ.
Ví dụ 31. Xét sự hội tụ của tích phân:
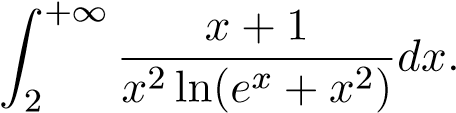
Giải
Đặt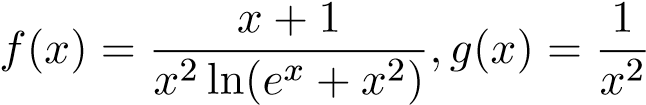 . Xét
. Xét
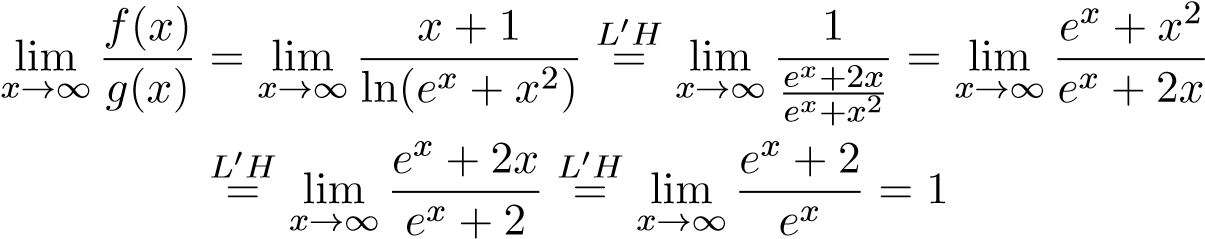
Mà tích phân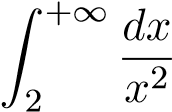 HT nên tích phân ban đầu hội tụ.
HT nên tích phân ban đầu hội tụ.
Ví dụ 32. Xét sự hội tụ của tích phân:
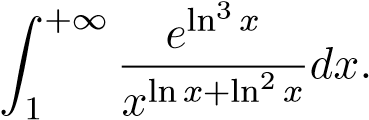
ĐS: HT
Gợi ý:
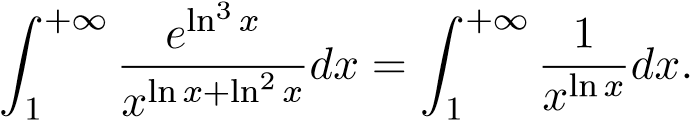
Ta có
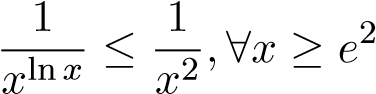
Mà tích phân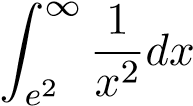 hội tụ nên tích phân
hội tụ nên tích phân
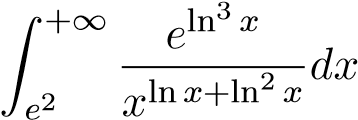
hội tụ. Suy ra tích phân ban đầu
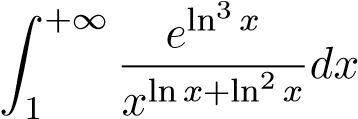
hội tụ.
Ví dụ 33. Xét sự hội tụ của tích phân sau
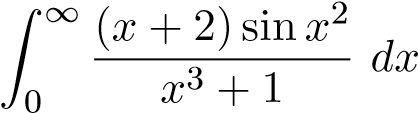
Giải:
Với x ≥ 1 ta có
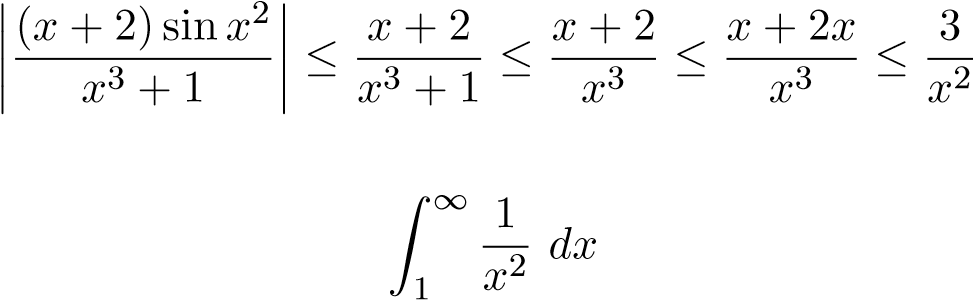 .
.
Mà
hội tụ nên tích phân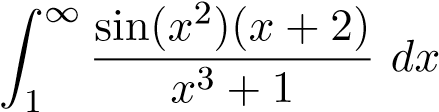 hội tụ tuyệt đối. Suy ra tích phân ban đầu hội tụ. Ví dụ 34. Xét sự hội tụ của tích phân sau
hội tụ tuyệt đối. Suy ra tích phân ban đầu hội tụ. Ví dụ 34. Xét sự hội tụ của tích phân sau
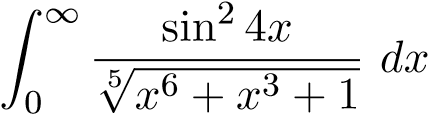 ĐS: Hội tụ, so sánh với
ĐS: Hội tụ, so sánh với 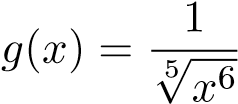 .
.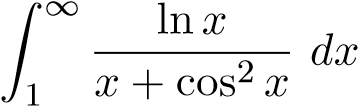 ĐS: phân kỳ, so sánh trực tiếp với
ĐS: phân kỳ, so sánh trực tiếp với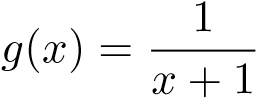 .
.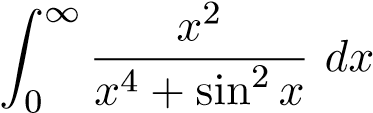 . ĐS: Hội tụ.
. ĐS: Hội tụ.
Gợi ý:
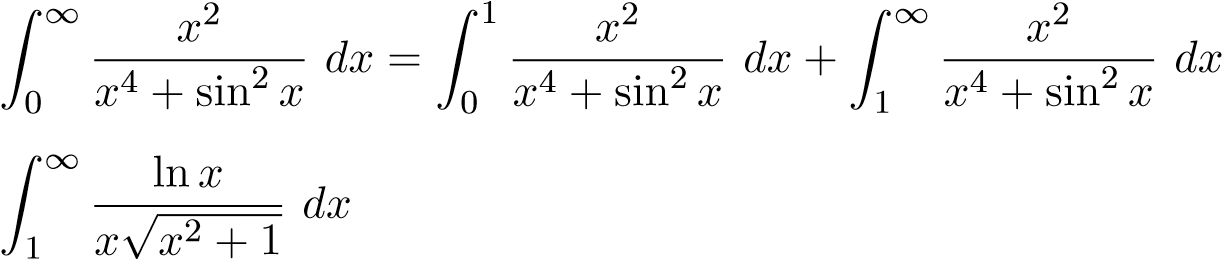 .
.
- Hội tụ, ss với
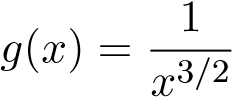
Gợi ý:
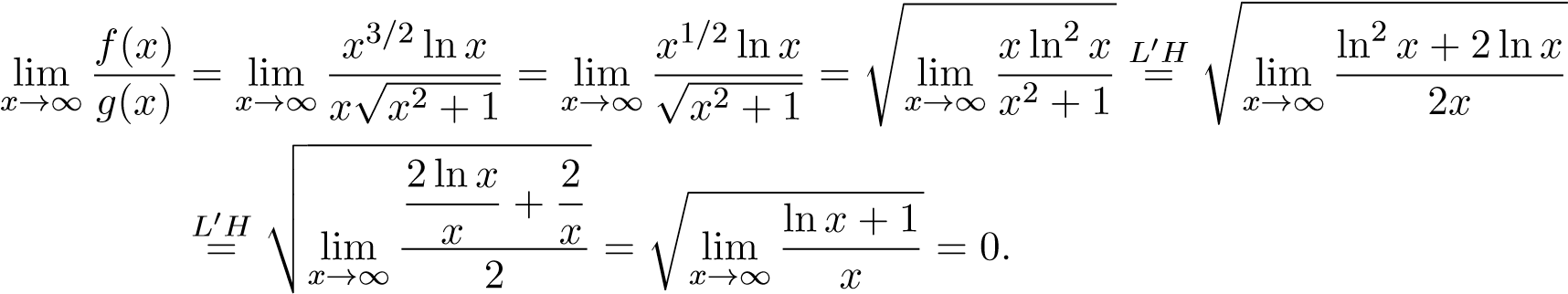
Ví dụ 35. Xét sự hội tụ của tích phân sau
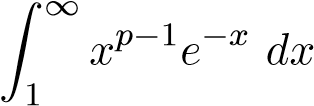
Giải: Bằng cách sử dụng quy tắc L’Hospital p+1 lần ta có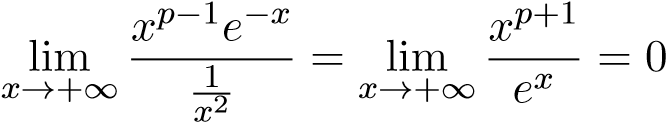 .
.
Mà tích phân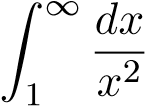 hội tụ nên tích phân ban đầu hội tụ.
hội tụ nên tích phân ban đầu hội tụ.
Ví dụ 36. Xét sự hội tụ của tích phân sau
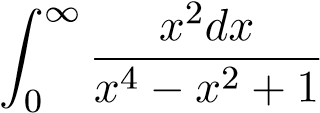
Giải
Ta có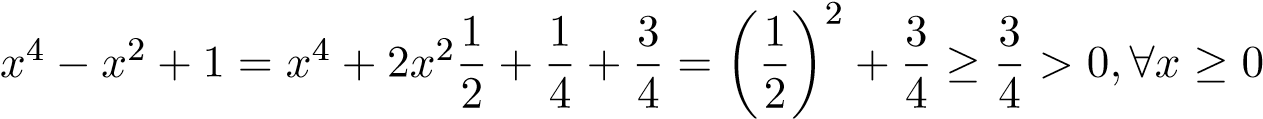 . Ta lại có
. Ta lại có
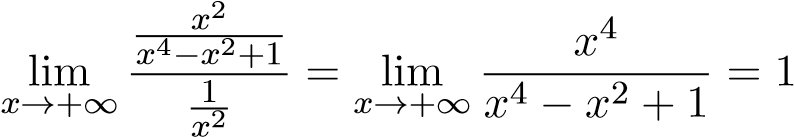 .
.
Mà tích phân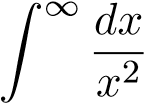 hội tụ nên tích phân
hội tụ nên tích phân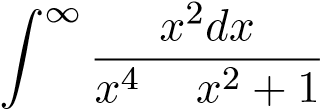 hội tụ. Suy ra tích phân
hội tụ. Suy ra tích phân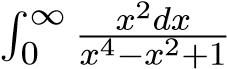
hội tụ vì 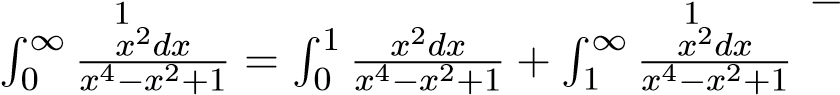 trong đó tích phân thứ nhất là tích phân xác định, còn tích phân thứ hai hội tụ. Ví dụ 37. Xét sự hội tụ của tích phân sau
trong đó tích phân thứ nhất là tích phân xác định, còn tích phân thứ hai hội tụ. Ví dụ 37. Xét sự hội tụ của tích phân sau

Sử dụng vô cùng bé tương đương ta có
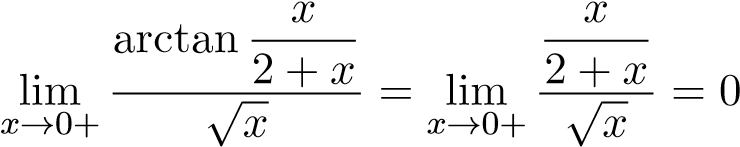 .
.
Do đó x = 0 không phải điểm kỳ dị của hàm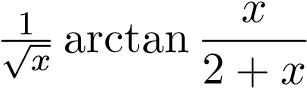 nên tích phân đang xét chỉ là tích phân suy rộng cận vô hạn. Ta lại có
nên tích phân đang xét chỉ là tích phân suy rộng cận vô hạn. Ta lại có
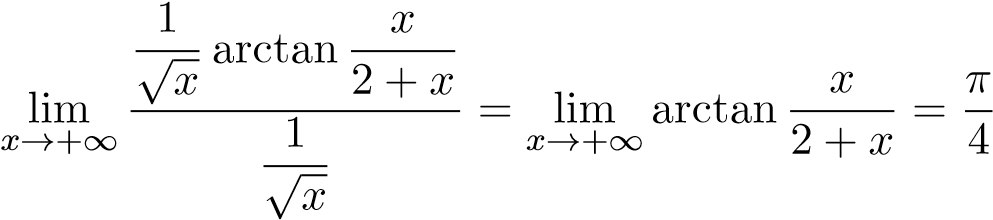 .
.
Mà tích phân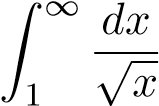 phân kỳ nên tích phân
phân kỳ nên tích phân phân kỳ nên
phân kỳ nên 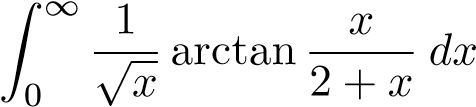 phân kỳ.
phân kỳ.
Ví dụ 38. Xét sự hội tụ của tích phân sau
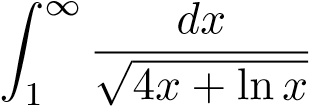
Gợi ý: Phân kỳ, so sánh với hàm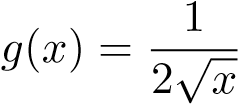 .
.
Ví dụ 39. Xét sự hội tụ của tích phân sau
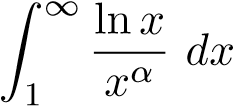
ĐS:
- α > 1 hội tụ
- α ≤ 1 phân kỳ
Ví dụ 40. Xét sự hội tụ của tích phân sau
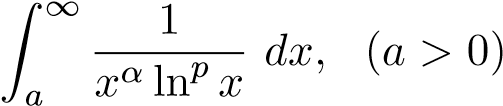 .
.
ĐS:
- α = 1:
- p > 1 hội tụ
- p ≤ 1 phân kỳ
- α > [1] tích phân hội tụ với mọi p.
- α < 1 tích phân phân kỳ với mọi p. Ví dụ 41. Xét sự hội tụ của tích phân sau
1. 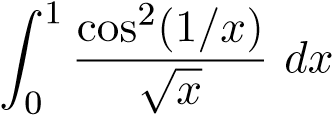
HT, so sánh trực tiếp với hàm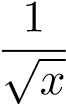 .
.
2. 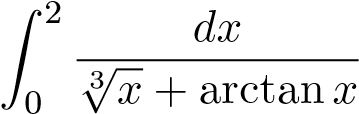 HT, so sánh trực tiếp với hàm
HT, so sánh trực tiếp với hàm 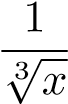 . 3.
. 3. 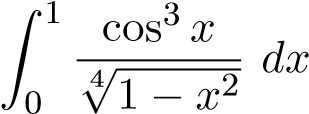 HT, so sánh trực tiếp
HT, so sánh trực tiếp 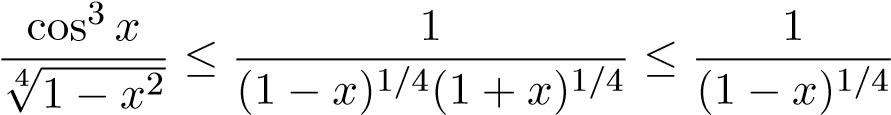 .
.
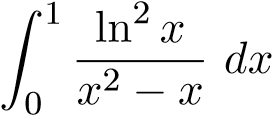 phân kỳ.
phân kỳ.
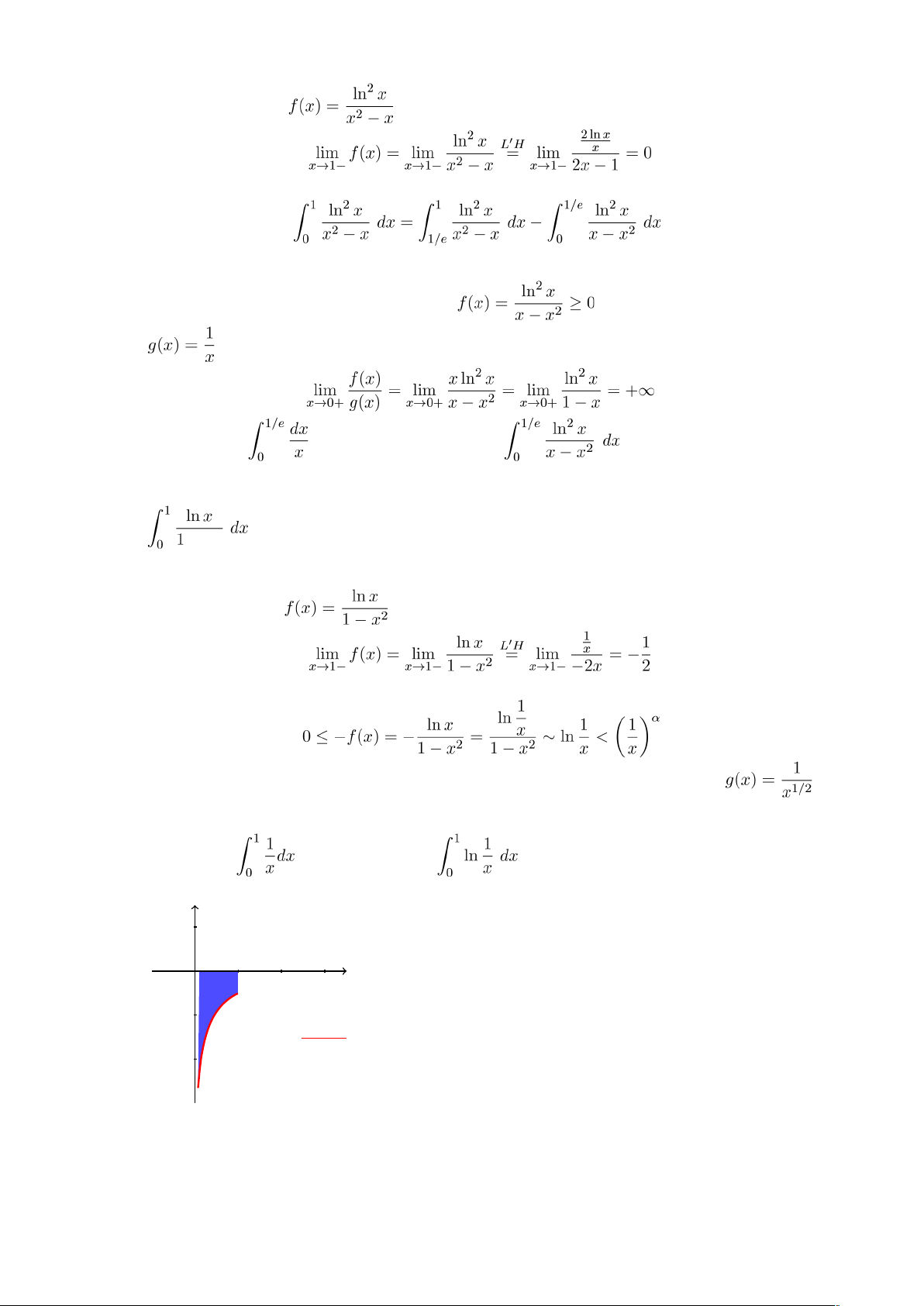
Gợi ý: Tại x = 0 hàm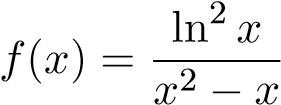 không bị chặn. Tuy nhiên tại x = 1, ta có
không bị chặn. Tuy nhiên tại x = 1, ta có
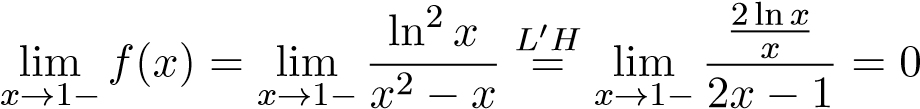 .
.
Nên tích phân đã cho chỉ suy rộng tại đầu mút x = 0. Ta có
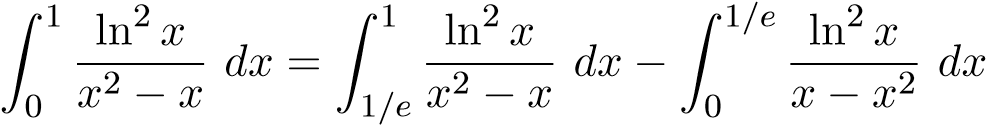
trong đó tích phân thứ nhất là tích phân xác định thông thường còn tích phân thứ 2 là
tích phân suy rộng tại cận dưới x = 0 và hàm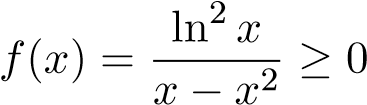 trên khoảng [0,1/e]. Đặt
trên khoảng [0,1/e]. Đặt
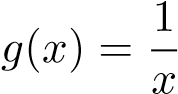 ta có
ta có
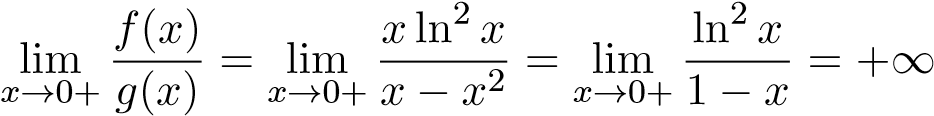 .
.
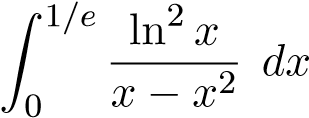 Mà tích phân
Mà tích phân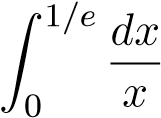 phân kỳ nên tích phân . Vậy tích phân ban đầu phân kỳ.
phân kỳ nên tích phân . Vậy tích phân ban đầu phân kỳ.
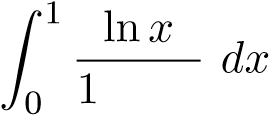 2 phân kỳ.
2 phân kỳ.
− x
Gợi ý:Tại x = 0 hàm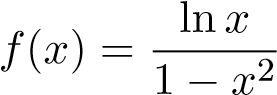 không bị chặn. Tuy nhiên tại x = 1, ta có
không bị chặn. Tuy nhiên tại x = 1, ta có
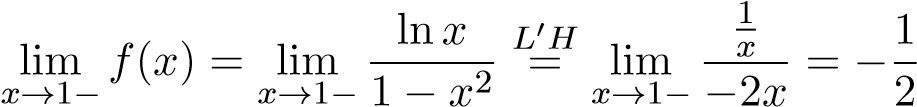 .
.
Nhận xét rằng f(x) < 0 trên khoảng (0,1]. Nên ta có ước lượng sau
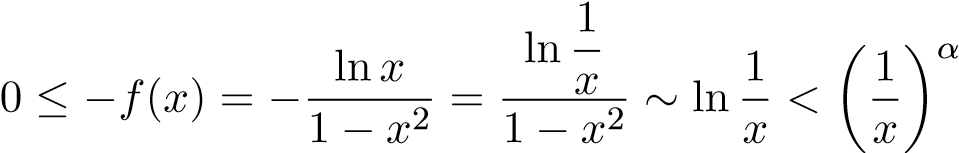
khi x → 0+ với mọi α > 0. Vì vậy, để cho đơn giản và dễ làm ta chọn α = 1/2. Đặt 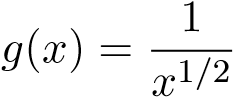 . Do tích phân
. Do tích phân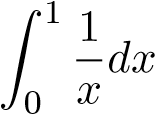 hội tụ nên tích phân
hội tụ nên tích phân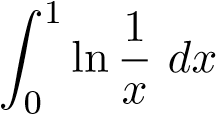 hội tụ nên tích phân
hội tụ nên tích phân
x
1
2
3
y
−
2
−
1
1
f
(
x
)=
ln
x
1
−
x
2
Ví dụ 42. Sử dụng tiêu chuẩn so sánh qua giới hạn, xét sự hội tụ của các tích phân sau
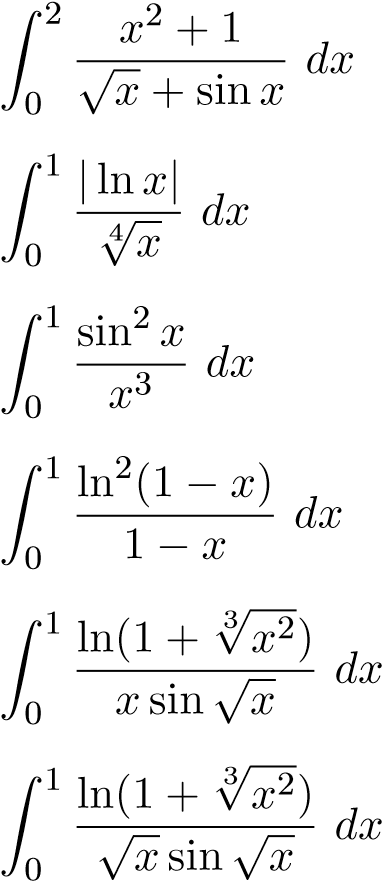 HT, so sánh với hàm
HT, so sánh với hàm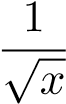 .
.- HT, so sánh với hàm
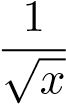 . 3. phân kỳ, so sánh với hàm
. 3. phân kỳ, so sánh với hàm 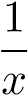 .
.
4. phân kỳ, so sánh với hàm 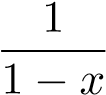 . 5. HT, so sánh với hàm
. 5. HT, so sánh với hàm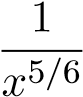 .
.
- HT, so sánh với hàm
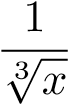 .
.
Ví dụ 43. Xét sự hội tụ của tích phân sau
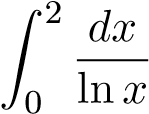
Giải
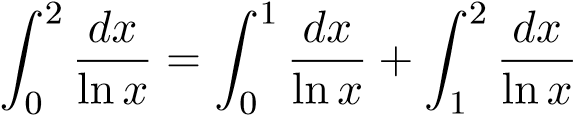 .
.
Ta có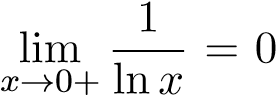 nên tích phân thứ nhất chỉ là tích phân xác định thông thường. Xét tích phân thứ hai ta có:
nên tích phân thứ nhất chỉ là tích phân xác định thông thường. Xét tích phân thứ hai ta có:
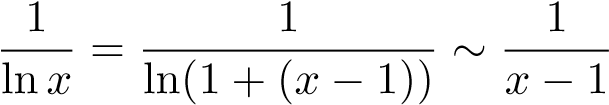 khi x → 1 + .
khi x → 1 + .
Mà tích phân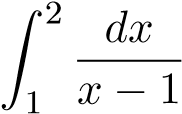 phân kỳ nên tích phân ban đầu phân kỳ.
phân kỳ nên tích phân ban đầu phân kỳ.
Ví dụ 44. Xét sự hội tụ của tích phân sau
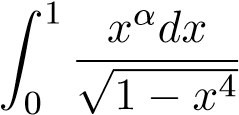
Giải
Xét tại hai đầu mút, ta có
- Tại
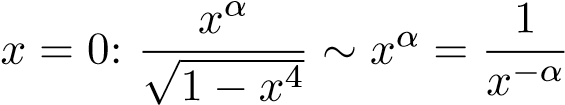
- α > −1 tích phân
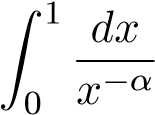 hội tụ.
hội tụ. - α ≤ −1 tích phân
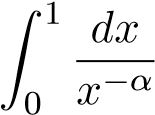 phân kỳ.
phân kỳ.
- α > −1 tích phân
- Tại
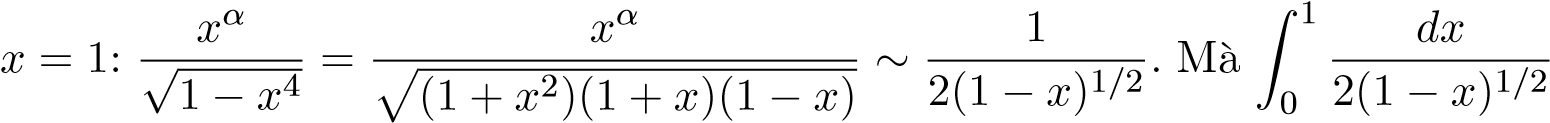 hội tụ.
hội tụ.
Kết luận
- α > −1 tích phân
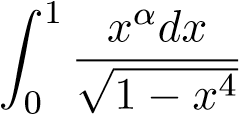 hội tụ.
hội tụ. - α ≤ −1 tích phân
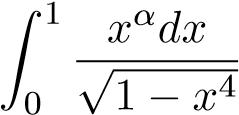 phân kỳ.
phân kỳ.
Ví dụ 45. Xét sự hội tụ của tích phân sau
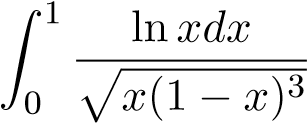
Ví dụ 46. Xét sự hội tụ của tích phân sau
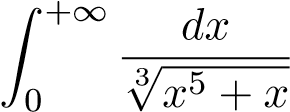
Giải
Ta có
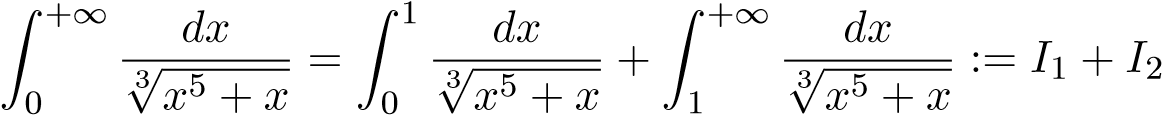 .
.
- Với I1, đặt
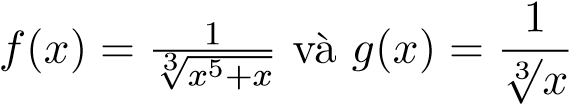 . Ta có
. Ta có
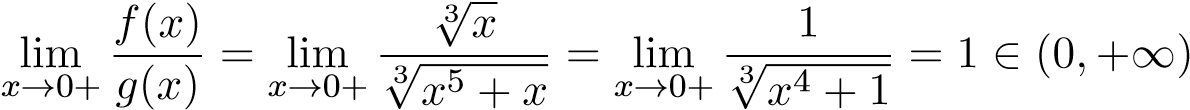 .
.
Mà tích phân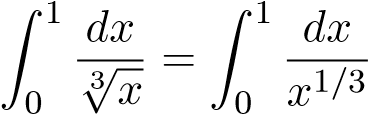 hội tụ (α = 1/3 < 1) nên I1 hội tụ.
hội tụ (α = 1/3 < 1) nên I1 hội tụ.
- Với I2, đặt
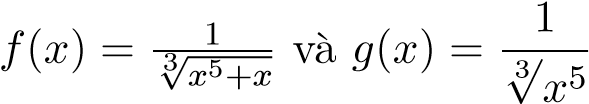 . Ta có
. Ta có
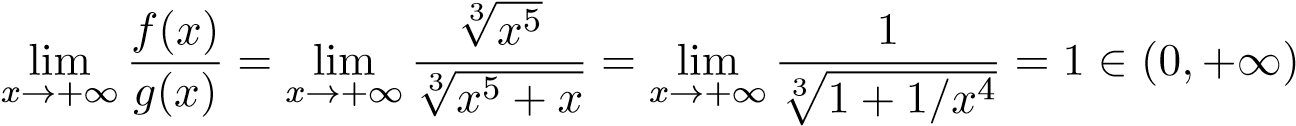 .
.
Mà tích phân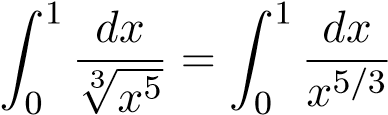 hội tụ (α = 5/3 > 1) nên I2 hội tụ.
hội tụ (α = 5/3 > 1) nên I2 hội tụ.
Vậy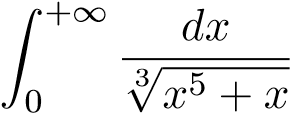 hội tụ.
hội tụ.
Ví dụ 47. Xét sự hội tụ của tích phân sau
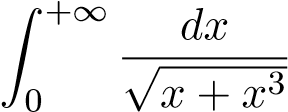
Gợi ý: Làm tương tự câu trên
Ví dụ 48. Xét sự hội tụ của tích phân sau
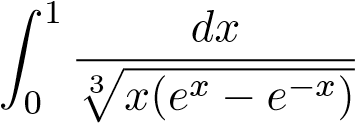 .
.
Nhận xét: Hàm dưới dấu tích phân không bị chặn khi x → 0+ và theo công thức khai triển Maclaurin ta có:
ex − e−x = 1 + x + o(x) − (1 − x + o(x)) = 2x + o(x).
Điều này gợi ý ta chọn hàm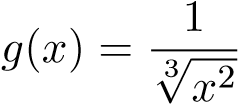 . Vì vậy ta có thể giải bài toán trên như sau:
. Vì vậy ta có thể giải bài toán trên như sau:
Giải:
Đặt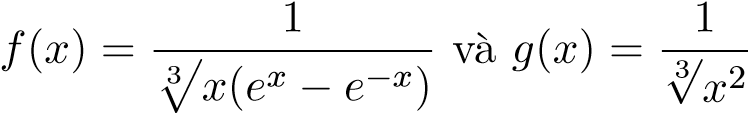 . Ta có
. Ta có
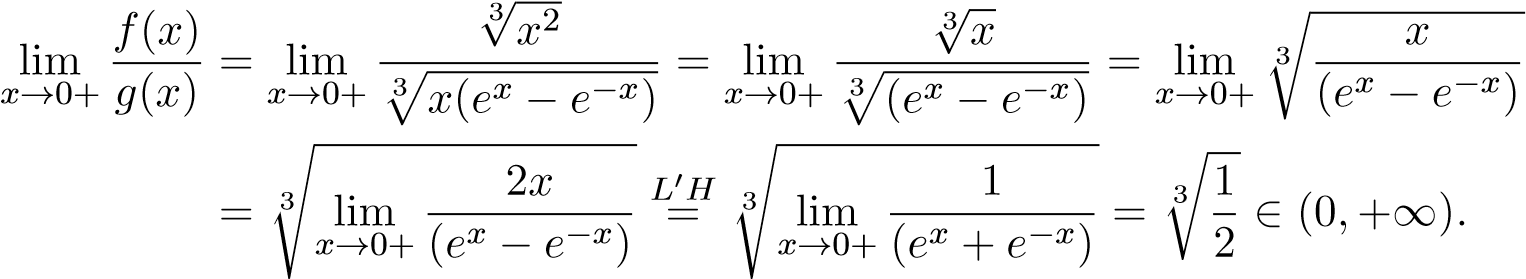
Mà tích phân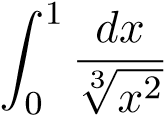 hội tụ nên tích phân
hội tụ nên tích phân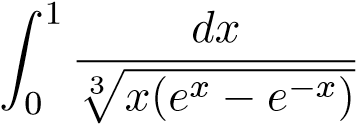 hội tụ.
hội tụ.
Các em sửa lại các lỗi sai nếu phát hiện. Một số ví dụ liên quan đến tham số và các ví dụ 16,17 có thể bỏ qua khi ôn tập (nếu không hiểu).
Bản thảo còn nhiều lỗi, các em sử dụng cá nhân không post lên mạng nhé!
3 Bài tập tích phân suy rộng
Câu 1. Tính các tích phân suy rộng sau nếu nó hội tụ.
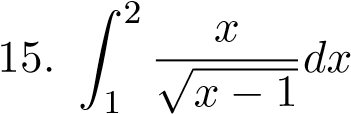 Z 1 xα lnxdx; 8.
Z 1 xα lnxdx; 8. 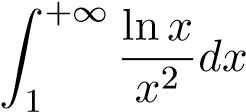 ; ;
; ;
0
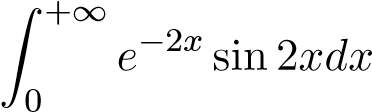 ; 9.
; 9. 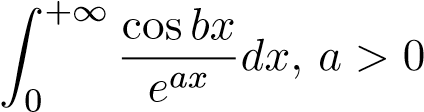 ;
; 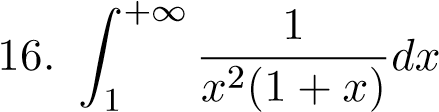 ;
;
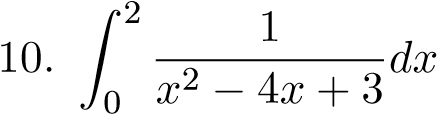
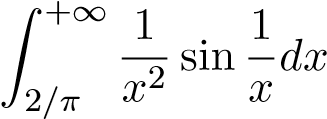 3.;; 17. Z 1 xlnxdx;
3.;; 17. Z 1 xlnxdx;
0
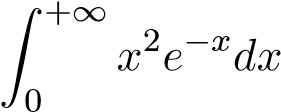 ;
; 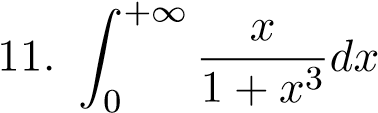 ;
; 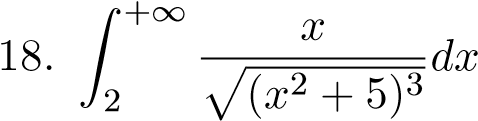 ;
;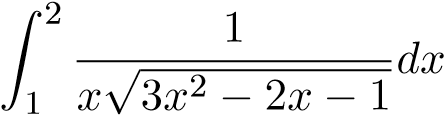 ;
; 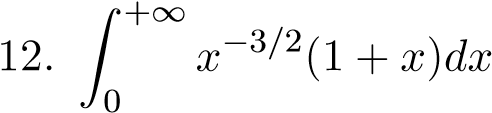 ;
; 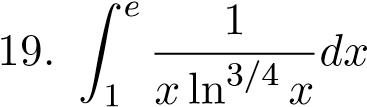 ;
;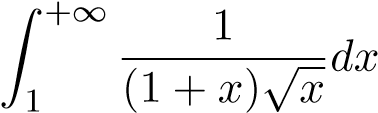 ;
; 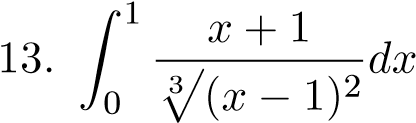 ;
; 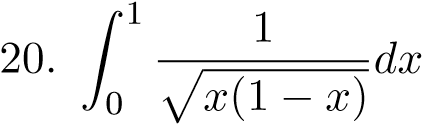 ;
;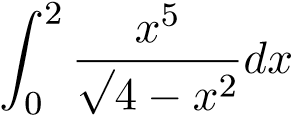 ;
; 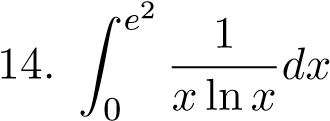 ;
; 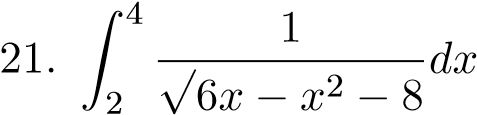 ;
;
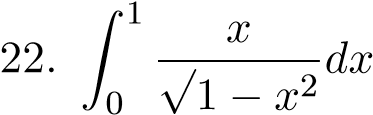 ;
; 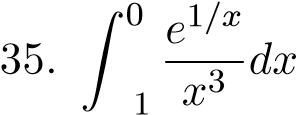 ;
; 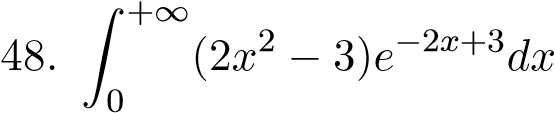 ;
;
−
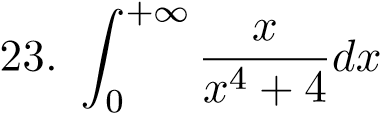 ;
; 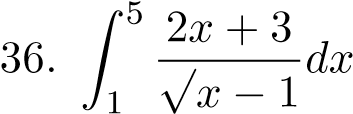 ;
; 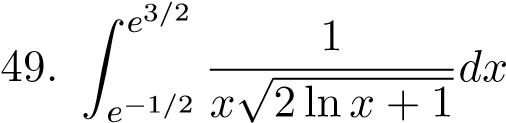 ;
;
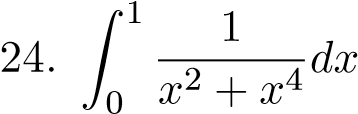 ;
; 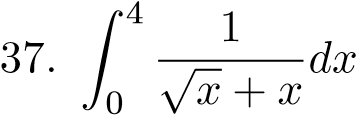 ; ;
; ;
50.
Z
5
1
1
2
x
+
√
x
−
1+2
dx
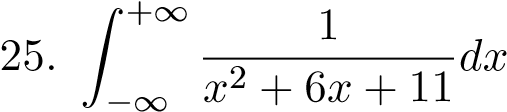
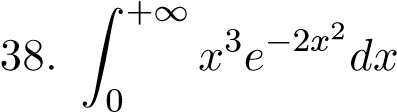
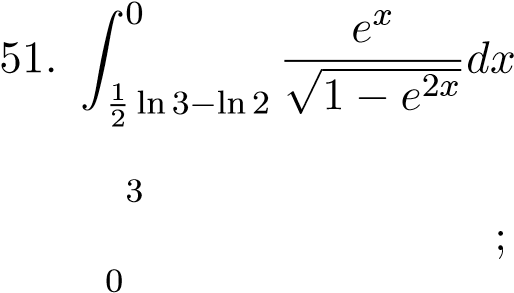
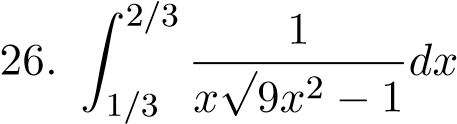
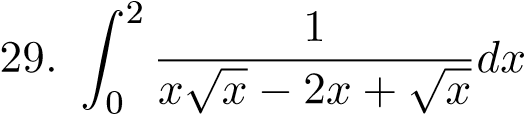
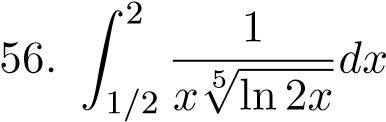

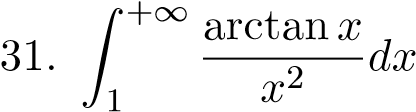 ;;
;;
53.
Z
+
∞
√
e
arctan(2ln
x
)
x
(1+4
ln
2
x
)
dx
Z
55.
Z
+
∞
1
1
x
√
1+
x
dx
43.
Z
1
0
ln
2
x
√
x
dx
;
; 39. Z√422 1√x2 − 2dx;
(x − 1)
; 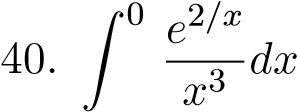 ;
;
;
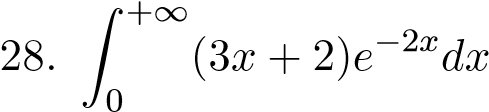 ; ;
; ;
;
; 42. +∞ 2 1 dx;
3 x − x − 2 ;
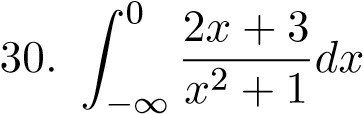 ; ;
; ;
;
;; 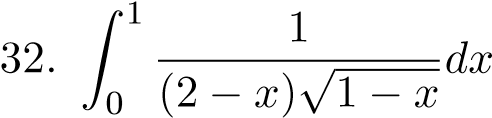 ;
; 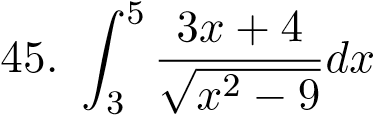 ;
; 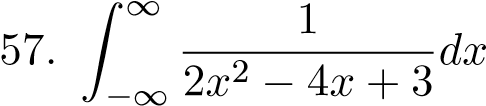 ;
;
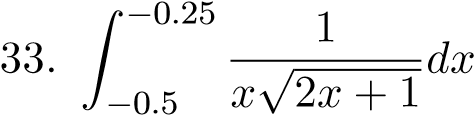 ; 46. Z01(3x2 + 8x − 3)lnxdx;
; 46. Z01(3x2 + 8x − 3)lnxdx; 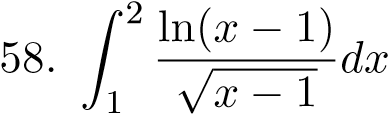 ;
;
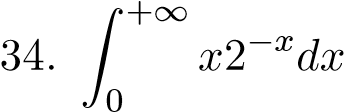 ;
; 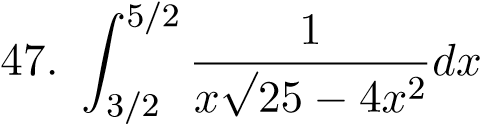 ;
; 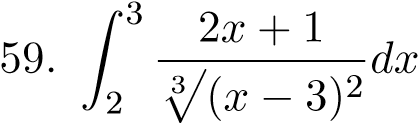 ;
;
Câu 2. Xét sự hội tụ phân kỳ của các tích phân suy rộng sau:
1. 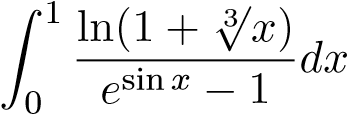 ; 7.
; 7. 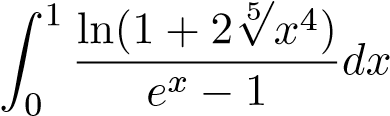 ;
; 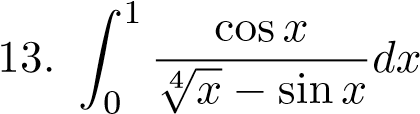 ;
;
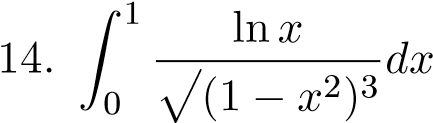 ;
;
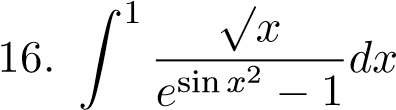
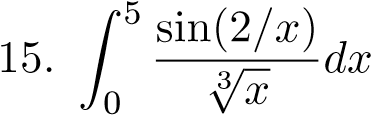 ;
;
2.
Z
π/
4
0
ln(1+
x
)
3
√
π
2
−
16
x
2
√
sin
x
dx
;
3.
Z
1
0
√
x
√
1
−
x
2
dx
;
4.
Z
1
0
cos
2
x
3
√
1
−
x
2
dx
;
8.
Z
√
2
/π
0
1
x
3
cos
1
x
2
dx
;
9.
Z
1
0
x
2
3
√
1
−
x
2
dx
;
10.
Z
1
0
ln(1
−
x
)
dx
;
;
0
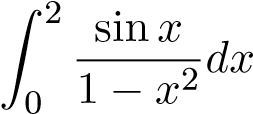 ;
; 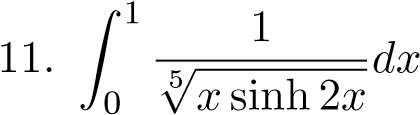 ;
; 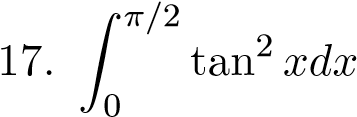 ;
;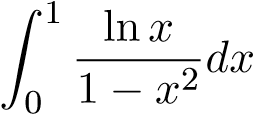 ;
; 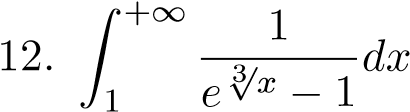 ;
; 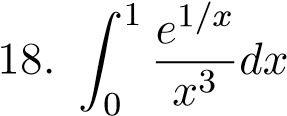 ;
;
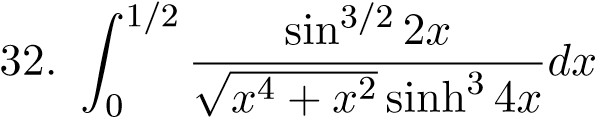
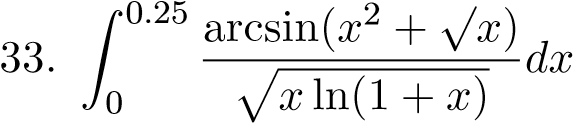 ;
; 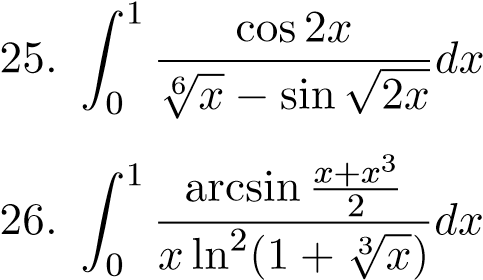 ;
; 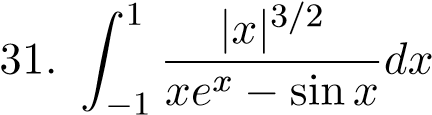 ;
;
19.
Z
1
0
1
3
p
x
(
e
x
−
e
−
x
)
dx
20.
Z
3
0
ln(1+
5
√
x
2
)
e
tan
x
−
1
dx
;
21.
Z
1
/
2
0
arcsin(
x
2
+
x
3
)
x
ln
2
(1+
x
)
dx
;
22.
Z
π
0
sinh
x
e
x
2
−
cos
x
dx
23.
Z
1
0
1
5
√
1
−
x
10
dx
24.
Z
2
0
s
16+
x
4
16
−
x
4
dx
;
27.
Z
1
0
e
2
x
−
cos
x
sin
x
−
x
dx
;
28.
Z
1
/
3
0
arcsin(2
x
+
x
2
)
x
2
ln
2
(1+
x
2
)
dx
;
29.
Z
1
0
x
+
sinh
x
e
x
2
−
cos
x
dx
30.
Z
2
0
sin(1
−
x
2
)
(1
−
x
2
)
2
+
3
√
1
−
x
2
dx
;
;
34.
Z
π/
4
0
e
−
2
x
−
cos2
x
x
3
/
2
sin2
x
dx
;
;
; ;
; ;
Câu 3. Xét sự hội tụ, phân kỳ của tích phân suy rộng cận vô hạn sau.
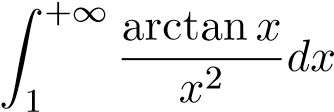 ; 14.
; 14. 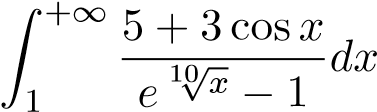 ;
;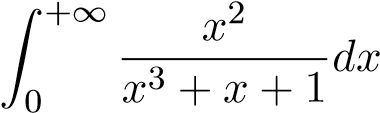 ; 15.
; 15. 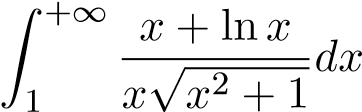 ;
;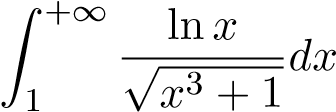 ; 16.
; 16. 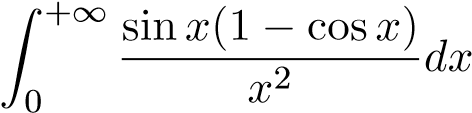 ;
;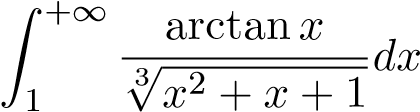 ; 17.
; 17. 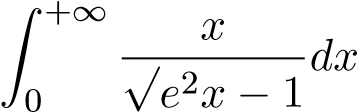 ;
;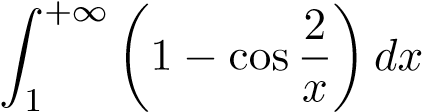 ; 18.
; 18. 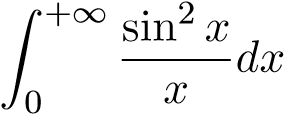 ;
;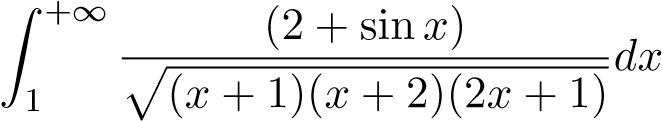 ; 19.
; 19. 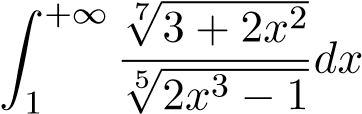 ;
;- Z1+∞ √x +1cos2 xdx; 20.
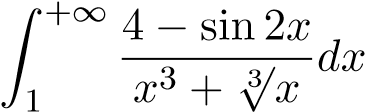 ;
; 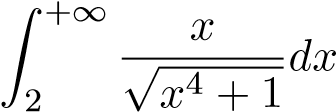 ; 21.
; 21. 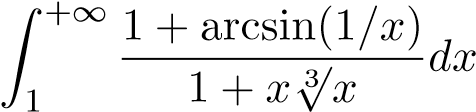 ; 9.
; 9. 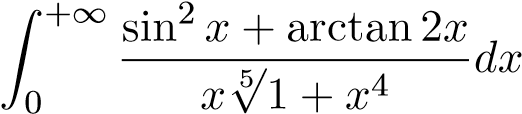 ; 22.
; 22. 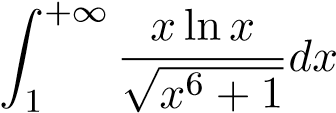 ;
;
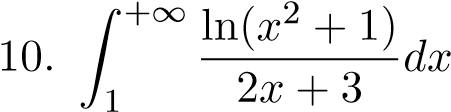 ; 23.
; 23. 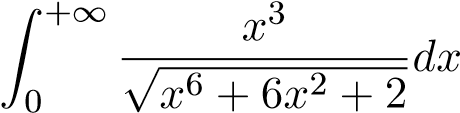 ;
;
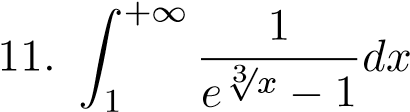 ; 24.
; 24. 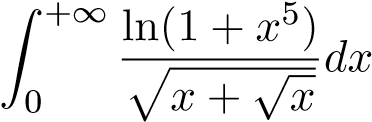 ;
;
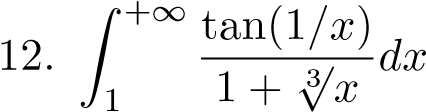 ; 25.
; 25. 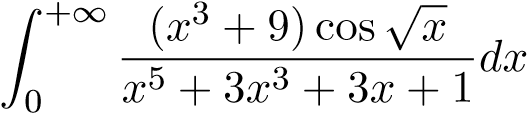 ;
;
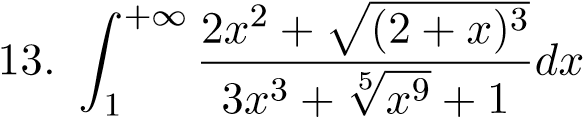 ; 26.
; 26. 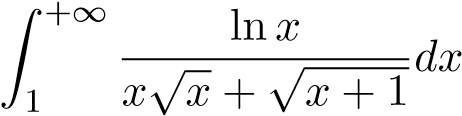 ;
;
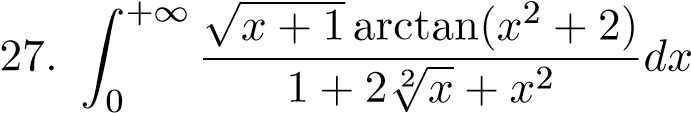 ; 39.
; 39. 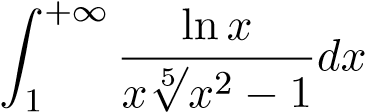 ;
;
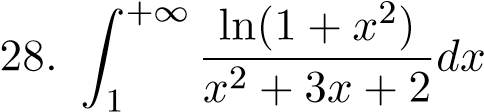 ; 40.
; 40. 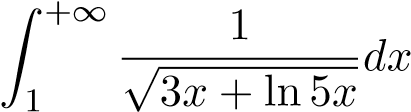 ;
;
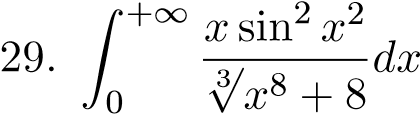 ; 41.
; 41. 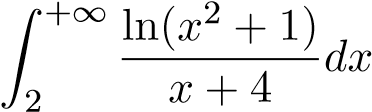 ;
;
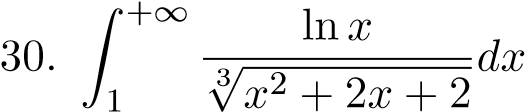 ; 42. ;
; 42. ; 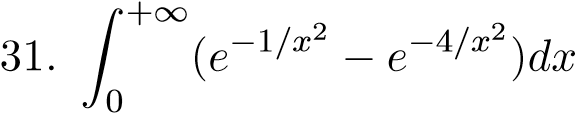 ; 43.
; 43. 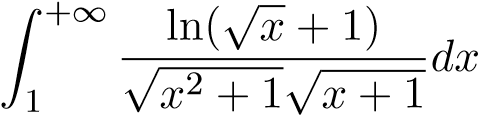 ;
;
Z
+
∞
2
√
x
sin
2
(
x
2
+2)
3
√
x
5
+
x
3
+15
dx
32. Z2+∞ √3 x2 +1cos2 2xdx; 44. 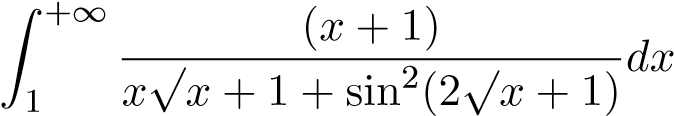 ;
;
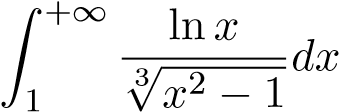 45.
45. 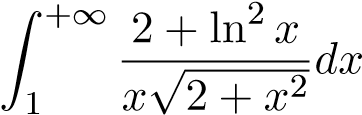 ;
;
33.
Z
+
∞
1
x
arccos(1
/x
2
)
6
√
x
13
+2
x
7
+4
x
+1
dx
;
34.
Z
+
∞
0
3
√
x
2
+3
x
+7
4
√
x
3
+8
x
+17
dx
;
;
46.;
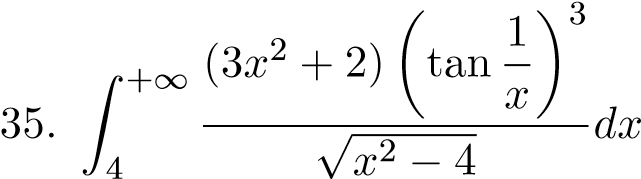 47.
47. 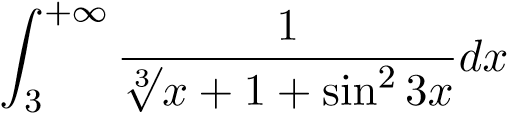 ;
;
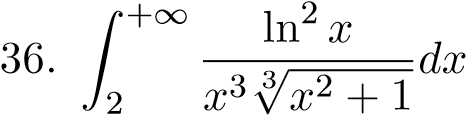 ; 48.
; 48. 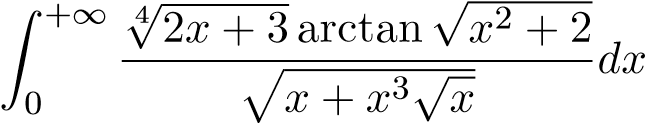 ;
;
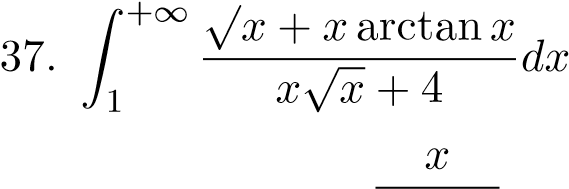 ;
;
49.
Z
+
∞
0
1
2
√
x
+3
cos
x
dx
;
50.
Z
+
∞
4
2
x
3
+
p
(
x
3
+1)
3
3
x
5
3
p
(
x
2
+1)
dx
;
 ;
;
Yêu cầu:
- Học thuộc bảng nguyên hàm cơ bản .
- Đọc lý thuyết trong slide bài giảng hoặc giáo trình.
- Một số ví dụ khó, ví dụ có tham số sẽ không thi (có thể bỏ qua nếu không hiểu)
- Mỗi bài làm ÍT NHẤT 25 câu vào vở.
Z0 −f(x)dx hội tụ. Vậy tích phân ban đầu hội tụ. ↑

