Bài tập sử dụng phương pháp hàm số để giải hệ phương trình

Tài liệu gồm 64 trang hướng dẫn sử dụng phương pháp hàm số giải hệ phương trình, các bài toán hệ phương trình được chọn lọc và giải chi tiết.

Phương pháp hàm số là một phương pháp quan trọng và rất hay được sử dụng để giải các bài toán hệ phương trình, đây là một trong những phương pháp được “yêu thích” trong các đề thi THPT Quốc gia môn Toán bởi tính sáng tạo, khả năng nhận dạng và nhạy bén trong việc chọn hàm số.

Thông qua tài liệu, bạn đọc sẽ nắm được một số tư duy biến đổi điển hình để có thể đưa về dạng bài quen thuộc, từ đó có thể chọn một hàm số thích hợp và làm đơn giản bài toán.

56 28 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 10

Môn: Toán 10

Thông tin:

64 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
3.PHƯƠNG PHÁP XÉT CHIỀU BIẾN THIÊN HÀM SỐ
Giải: Điều kiện :
1
x
. Phương trình
4
4
1 1 1 2
x x y y
.
Đặt
4
1, 0
u x u
4 4
1 1 2
x u x u
Khi đó,phương trình (1) trở thành :
4 4
2 2 3
u u y y
Xét phương trình (2) :
2 2
2 1 6 1 0
x y x y y
Xem x là ẩn, y là tham số, ta có :
4
y
Phương trình có nghiệm
0
y
Xét hàm số
4
2, 0;f t t t t
2
4
2
' 1 0, 0;
2
t
f t t
t
Suy ra hàm số liên tục và đồng biến trên
0;

Từ đó, phương trình
4
3 1
u y x y
.
4
1
y x
4
1 4
x y
Thế (4) vào phương trình (2) ta được :
2
4 4 2
1 2 1 1 6 1 0
y y y y y
8 5 2
2 4 0
y y y y
6 5 4 3 2
1 3 3 3 4 0
y y y y y y y y
Bài toán 7(A – 2013).
4
4
2 2
1 1 2 (1)
2 1 6 1 0 2
x x y y
x x y y y
0 1
1 0,
y x
y x loai
Vậy nghiệm của hệ phương trình đã cho là
1;0
Giải:
Điều kiện :
1
1
x
y
. Xét hàm số
2
1, 1;f t t t t

1
' 2 0, 1;
2 1
f t t t
t

. Suy ra hàm số đồng biến trên
1;

Từ đó, phương trình
2
x y
.
1 2 1 4
x x
2
1 4
x x
3 2
4 0
x x
2
x y
Vậy hệ phương trình có nghiệm
2;2
.
Giải: Điều kiện :
0 , 1
x y
Lấy phương trình (1) trừ phương trình (2) vế với vế, ta được :
2
2
1
1
y
x
x y
. Xét hàm số
2
1
, 0;1
t
f t t
t
2 2
1
' 0, 0;1
1
f t t
t t
Suy ra hàm số liên tục và nghịch biến trên [0; 1]
Bài toán 11.
2 2
1 1 4 1
1 + 1 2
x y y x
x x y y
Bài toán 2.
0 (1)
3 2 1 2
x y x y
x y x y
Từ đó, phương trình
x y
. Khi đó
2
1
1 1
2
x x
2 2
1
1
4
x x
4 2
4 4 1 0
x x
2
2
,
1
2
2
2
2
x loai
x
x y
Vậy nghiệm của hệ phương trình đã cho là
2 2
;
2 2
Giải:
Điều kiện :
2 0
2 8
16 2 0
x
x
x
Áp dụng bất đẳng thức Bu-nhia-cop-xki cho 4 số :
2 2
1, 1,3, 1
x y
ta được
2 2 2 2 2 2
1 3 1 1 3 . 1 1
x y x y
2 2 2 2
1 3 1 10
x y x y
Do phương trình (1) nên dấu “ =” xảy ra. Khi đó ta có :
2
2
1
1
1 3
y
x
2 2
9 1 1
x y
2 2
9 10
x y
Thế
2 2
9 10
x y
vào phương trình (2), ta được :
2
2 16 2 2 9 10 - 628 = 0
x x x
(3)
Xét hàm số :
2
2 16 2 2 9 10 - 628, x 2;8
f x x x x
1 1
' 36 0, x 2;8
2 2 16 2
f x x
x x
Bài toán 17.
2 2 2 2
2
1 3 1 10 1
2 16 2 2 - 628 = 0 2
x y x y
x x y
Vậy hàm số
f x
đồng biến trên (2; 8) và
6 0
f
do đó phương trình (3) có nghiệm duy nhất x
= 6. Với x = 6 ta có
314
y
Vậy hệ phương trình có 2 nghiệm :
6; 314 ; 6; 314
Giải: Điều kiện :
2
2
x
y
Lấy phương trình (1) trừ đi phương trình (2) vế với vế, ta được :
5 2 5 2 3
x x y y
Xét hàm số :
5 2 ,t 2;f t t t

2 5
' 0, 2
2 5. 2
t t
f t t
t t
Vậy hàm số nghịch biến trên
2;

.
Phương trình
3
f x f y x y
Khi đó, hệ phương trìnhtrở thành :
5 2 7
x x
2 3 2 5. 2 49
x x x
5. 2 23
x x x
2
2 23
5 2 23
x
x x x
2 23
539
49 539 0
49
x
x y
x
Hệ phương trình có 1 nghiệm
539 539
;
49 49
Bài toán 65.
5 2 7 1
2 5 7 2
x y
x y
Bài toán 78.
2 2 4 2
2
+ y = y 1+ y 1
4 5 8=6 2
x x
x y
Giải: Điều kiện :
0
x
Nếu y = 0 thì phương trình(1) tương đương :
3
0 0
x x
, không thỏa hệ.
Xét
0 :
y
phương trình
3
3
1 3
x x
y y
y y
Xét hàm số
3
( ) , f t t t t
;
2
' 3 1 0,f t t t
Suy ra, hàm số f(t) đồng biến trên
2
3 4
x
y x y
y
. Thế (4) vào phương trình(2) ta được :
2 2
4 5 18 6
y y
2 2 2
2 4 5 18 23 5
y y y
Điều kiện :
2
115 115
23 5 0
5 5
y y
Bình phương 2 vế của phương trình trên, ta được :
2
4 2 2
4 4 37 40 23 5
y y y
4 2
9 378 369 0
y y
2
2
1
1
41,
y x
y
y loai
Vậy nghiệm của hệ phương trình đã cho là
1;1 , 1; 1
Giải: Điều kiện :
2
2 0
y x
Phương trình(1)
3 2
2 2 2 1 1 0
x x y x y
2 2
2 2 1 2 0
x x y x
2
2 1 2 0
x y x
2 1 3
y x
Bài toán 89.
3 2
3 2
2 2 1 1 1
4 1 ln 2 0 2
x x y x y
y x y x
Thế (3) vào phương trình(2) ta được :
3 2
2 1 4 1 ln 2 1 2 0
x x x x
3 2
2 1 4 1 ln 2 1 2 0
x x x x
Xét hàm số
3 2
2 1 4 1 ln 2 1 2 ,
f x x x x x
x
2
2
8 2
' 3 2 1 4
4 2 1
x
f x x
x x
2
2 2
2
3 2 1 4 2 1 16 2
' 0,
4 2 1
x x x x
f x x
x x
Suy ra, hàm số f(x) đồng biến và liên tục trên
. Mặt khác , f(0) = 0
Vậy phương trình
có nghiệm duy nhất x = 0, suy ra y = -1
Vậy nghiệm của hệ phương trình đã cho là
0; 1
.
Giải:
Hệ phương trìnhtương đương với
3 3
2
=278 1
100 2
y x y
y x y
Từphương trình (2) suy ra y > 0.Viết lạiphương trình (1) :
2 2
278
y x y x xy y . . Vì y > 0 và
2 2
0, ,x xy y x y
nên (1)
0 0
x y x y
.Phương trình(2)
10
3
x y
y
Thế (3) vào phương trình(1) ta được :
Bài toán 90.
3 4
2 2 3
=278
2 100
x y y
x y xy y
3
3
10
278
y y y
y
. Đặt
, 0
t y t
, ta có phương trình :
3
2 2 6
10
278
t t t
t
3
9 3
10 278 0
t t t
Xét hàm số
3
9 3
10 278 0, 0;f t t t t t

2
8 2 3
' 9 9 10 278 0, 0;f t t t t t

Suy ra, hàm số f(t) đồng biến và liên tục trên
0;

. Mặt khác , f(1) = 0
Vậy phương trình
có nghiệm duy nhất t = 1.
Từ đó,
1 1 9
y y x
. Vậy nghiệm của hệ phương trình đã cho là
9;1
.
Giải : Điều kiện : . Phương trình (1)
(3)
Đặt
Phương trình (3)
Xét hàm số ;
Suy ra, hàm số đồng biến trên .
Phương trình
1
2
2
y
x
3 2 2 2 1
x x y y
1 2 2 1 2 1 2 1
x x y y
2
, 0
= 2 1
=
x
u v
v y
u
2 2 3 3
1 1
u u v v u u v v
3
, 0
f t t t t
2
' 3 1 0, 0
f t t t
f t
0;

2 2 1
u v x y
Bài toán 109.
3
3 2 - 2y 2 1 1
2 2 1 2
= 0
2 - = 1
x x y
x y
Thế : x = 3 – 2y vào phương trình (2) ta được :
Đặt , phương trình trở thành :
Hệ phương trình đã cho có 2 nghiệm : .
Giải : Điều kiện :
Hệ phương trình
Xét phương trình (1) :
2 2 1 3 2
x y x y
3
2 2 1 2 1 1
y y
2 1 0
X y
3
1
5 1
2 1 0
2
5 1
,
2
X
X X X
X loai
1 2 1 1 1 1
X y y x
5 1 5 1
2 1
2 2
X y
6 2 5 5 5 1 5
2 1
4 4 2
y y x
1 5 5 5
1;1 , ;
3 4
1
0
x
y
3
2
1 8
1
- =
= y
x y x
x
2
3
2
1 1 8 1
1
- =
= y
x x x
x
2
3
1 1 8 - =
x x x
Bài toán 115.
3
4
1 8
1
- =
= y
x y x
x
Xét hàm số :
Xét hàm số :
Hàm số g(x) đồng biến trên
Vậy hàm số f(x) đồng biến trên
Mặt khác, f(2) = 0.Suy ra, phương trình có nghiệm duy nhất x = 2, y = 1
Hệ phương trình đã cho có 1 nghiệm : .
Giải : Điều kiện :
2
0
x
y
Phương trình (2)
2 2 3 2
1 x
x y x x y y x y
2 2 3 2
x
x xy x y x y y x y
2 2
x 0
xy x x y y xy
2 3
1 + 2x - 1 8 - x =
x x
3 2
- x + 2x + 1 - 9
x = 0
x
3 2
- x + 2x + 1 - 9, x 1
f = xx x
2
1
x - 2x + 2 + , x 1
2 1
f' = 3x
x
2
x - 2x , x 1
= 3g x
' x - 2 > 0 , x 1
= 6g x
1;

1 , 1
g x g x
1, 1
g x x
' 0, 1
f x x
1;
2;1
Bài toán 121(THPTQG 2014-2015).
2
2
2
2
1 2 2 1
1
2
y
y y x
x
x y
x y y
y x
2 2
0
xy x x y x y
2
1 0
xy x x y
2
0
1 0
x y
xy x
2
1 1
x y
x y
2
0
x y
, thế vàophương trình (1) ta được :
2
2
2 2
2
1 2 2
y
y y y
y
2 2
2 2 2 2 0
y y y y
2 2
2 2 2 2 0
y y y y
2 2
2 2 2 2
y y y y
Đặt
2
, 0
2
u y
u v
v y
, Phương trình trở thành :
2 2
2 3
u u v v
Xét hàm số :
2
( ) 2 , t 0;f x t t
' 2 2 0, 0
f t t t
Suy ra, hàm số f(t) đồng biến và liên tục trên
0;

Phương trình
2
2
u v y y
2 2
2 2 0
y y y y
1,
2 4
y loai
y x
1
1 1
1
x y x
y
Do x ≥ 2
1 1
2 2 2 1
1 2
y y
y
, vô lý.
Vậy hệ phương trình có nghiệm :
4;2
Bài toán 128(Chuyên Lê Hồng Phong)
2 2 2
1 1 + 1 1
4 1 1 1
4 3 +8 2
1 3 2
xy x y y
y
xy xy
y y
Giải : Phương trình (2) (3)
Với , đặt ,ta có :
Từ phương trình (3) ta có :
Ta lại có :
Từ phương trình (1) ta suy ra : . Điều kiện :
Ta có :
. Xét hàm số :
Suy ra, hàm số f(t) đồng biến và liên tục trên
Xét 2 điểm thuộc đồ thị hàm số f(t).
Ta có : và hàm số f(t) đồng biến và liên tục trên nên
4 1 1 1
4 3 + 8
1 3 2
y
xy xy
y y
0
xy
1
3, 0
u u
xy
2
1 1
- 4 3 + 8 = u 4 5
u
xy xy
2
1 1
- 4 3 + 8= u - 2 1 0
xy xy
1
4 1 0
4
y y
2 2
2
1
1 0,
y y y
y y y
y y
0
x
0
1
2
4
x
y
2 2 2
1 1 + 1
xy x y y
2
2
1
1 1
1 1 +
y
x x
y y y
2
2
2
1 1 1
1 1 +
y
x x
y y y
2
2
1 1 1
1 + 1
x x x
y y y
1
f x f
y
2
( ) 1 tf t t t t
2
2
2
' 1 1 0,
1
t
f t t t
t
1 1
, , ,M x f x N f
y y
M N
y y
(3)
Xét phương trình (1) :
Thế (3) vào phương trình (1) ta được :
(4)
Nếu x = 0, không thỏa phương trình (4), xét x ≠0.
Chia 2 vế củaphương trình (4) cho ta đựợc :
Đặt , phương trình trở thành :
thỏa điều kiện :
Hệphương trìnhphương trình có nghiệm duy nhất :
1
M N
x x x
y
1
xy
3
4
2 4 2 3 +3x - 1
y y x
4 2 3
4 3 + 3x - 1
x x x
4 3 2
3 4 3 1 0
x x x x
2
x
2
2
1 3
3 4 0
x x
x x
2
2
1 1 1
2. . 3 2 0
x x x
x x x
2
2
1 1 1
2. . 3 2 0
x x x
x x x
2
1 1
3 2 0
x x
x x
1
t x
x
2
3 2 0
t t
1
2
t
t
1
1 =1
t x
x
2
1=0,VN
x x
1
2 =2
t x
x
2
2 1 = 0 x = 1 y = -1
x x
2
y
1; 1
Bài toán 134.(Chuyên Hạ long)
3 2 3
3 2+8 2 = 10y - 3xy + 12 1
5 2 8 6 2 2
y x x
y x y xy x
Giải : Điều kiện :
không thỏa phương trình (2).
Chia 2 vế của phương trình (2) cho ta được :
(3)
Xét hàm số : ;
Hàm số f(t) đồng biến và liên tục trên và
(4)
Thế (4) vào phương trình (1) ta được :
(5)
Đặt :
(6)
Thế (6) vào phương trình (5) ta được :
2 0
2 2
2 0
x
x
x
0
y
3
y
3
8 6
5 2 2
x x x
y y
3
6 2
2 2 2 5 2x x x
y y
3
3
2 2
2 3 2 3.
x x
y y
3
3 ,f t t t t
2
' 3 3 0,f t t t
2
3 2f x f
y
2
2 x
y
0, 2
2
2
y x
y
x
6 20 6
2+8 2 = - x + 12
2 2 2
x x
x x x
2
3 2 - 6 2 +4 4 = 10 - 3x
x x x
3 2 - 6 2
t x x
2 2
3 2 - 6 2 9 2 36 2 36 4
t x x t x x x
2
90 27 36 4
x x
2
2
90 27
4 4
9
x t
x
2
90 27
+ = 10 - 3x
9
x t
t
2
0
+9 = 0
9
t
t t
t
, vô nghiệm vì : 5x – 15 < 0,
Hệ phương trình có nghiệm duy nhất :
Giải : Điều kiện :
Phương trình (1)
Xét hàm số : ;
Hàm số f(t) đồng biến và liên tục trên và
Phương trình
0 3 2 - 6 2 0
t x x
3 2 = 6 2 9 2 36 2
x x x x
6
45 54 0 5
5
x x y
9 3 2 - 6 2 9
t x x
3 2 9 6 2
x x
9 2 81 36 2 108 2
x x x
5 15 12 2
x x
2;2
x
6
; 5
5
2
1
3 1 0
3
6 4 0
2 10 2 10
x
x
y y
y
3 2
25 9
2 6 9 2 4
2 2
y y y x x
3 2
1 1
2 6 12 8 1 2 4 4
2 2
y y y y x x
3
3
2 2 2 2 4 4 3
y y x x
3
2 ,f t t t t
2
' 6 1 0,f t t t
3 2 4
f y f x
4 2
x y
2
2 2 10
4 4 4
y
y y x
Bài toán 135.(THPT Nghi Sơn)
3 2
2 2
2 12 25 18 2 9 4 1
3 1 3 14 8 6 4 2
y y y x x
x x x y y
Thế (4) vào phương trình (2) ta được :
Hệphương trình có nghiệm duy nhất :
Giải Điều kiện :
Phương trình (2)
Xét hàm số : ;
Hàm số f(t) đồng biến và liên tục trên và
.Điều kiện :
Thế (4) vào phương trình (1) ta được :
2
2 2 10
4 4
y
y y x
2
3 1 3 14 8 6
x x x x
2
3 1 6 3 14 8 0
x x x x
2
3 1 4 1 6 3 14 5 0
x x x x
3 5
5
5 3 1 0
3 1 4 1 6
x
x
x x
x x
3 1
5 3 1 0
3 1 4 1 6
x x
x x
5 1
3 1 1
3 1 0,
3
3 1 4 1 6
x y
x VN x
x x
5;1
2 2
2 0 2
x y x y
3 6 3 2 2
3 6 3 4 0
y x y yx y y
3 6 2 3 2
3 3 6 4
y x yx y y y
3
3
2 2
3 1 3 1 3
yx yx y y
3
3 ,f t t t t
2
' 3 3 0,f t t t
2
3 1
f yx f y
2
1 4
x y y
1 2 1
y y
Bài toán 136.(Sở GDĐT Thanh Hóa)
2 2 2
3 6 2 2
1 2 2 1
1 3 2 3 4 0 2
x y x x x y
y x y x y
Thế (5) vàophương trình (4) ta được :
Thế (6) vào phương trình (4) ta được :
2
2 1
y x x y
2
1 1 2 1 0
y x x y
2
1 1 0
x y
1 1 1 1 0
x y x y
1 1 0
1 1 0
x y
x y
1 1 0 1 1
x y y x
2 2
1 1
1 1 1 1
x x
y x y x
2
1
2 5
x
y x x
2 2 2
2 2 1
x x x x x
4 3 2 2
2 2 2 1 0
x x x x x
2
2 2
2 1 0
x x x x
2
2 2
1 0 1 0
x x x x
1 5 1 5
2 2
1 5
,
2
x y
x loai
1 1 0 1 1
x y y x
2 2
1 1
1 1 1 1
x x
y x y x
2
1
2 6
x
y x x
2 2 2
2 2 1
x x x x x
4 3 2
2 2 1 0
x x x x
4 3 2 2
2 2 2 1 0
x x x x x
2
2 2
1 0 1 0
x x x x
1 5 1 5
2 2
1 5
,
2
x y
x loai
Hệ phương trình có 2 nghiệm :
Giải : Từ phương trình (2) suy ra :
(1)
Xét hàm số : ;
Hàm số f(t) đồng biến và liên tục trên và
.Điều kiện :
Thế y = 2x vào phương trình (2) ta được :
Hệ có 2 nghiệm :
Giải : (1) . Vì
1 5 1 5 1 5 1 5
; ; ;
2 2 2 2
2 0 2
y y
3 3 2 2
2 6 - y 3 3x y + 3xy 0
x x y
3 3 3 2 2
3 + x - y 3x y + 3xy 3 3 0
x x y x
3
3
3 + x - y 3 3 0
x x y x
3
3
3 = y - x 3 3
x x y x
3
3 ,
f t t t t
2
' 3 3 0,
f t t t
3 =
f x f y x
= y - x y = 2x
x
2 2 1
x x
2
2
2 4 2 2
x x
2
4
4 1
x x
2
2
2 1
2 1
x x
x x
2
2
2 2 0,
2 2 0
x x VN
x x
1 3 2 2 3
1 3 2 2 3
x y
x y
1 3; 2 2 3 ; 1 3; 2 2 3
2
y 2 2 3
x x
2
2 0, 0
x x x y
Bài toán 139.(THPT Can Lộc)
2 2
2
2
2 3 - y 3 = 3xy 1
2 4 2 2
x x y x y
x y
Bài toán 142.
2
2 2 2
2 = y 2
1
2 1 2 3 = 2x - 4x 2
xy x
y x x x
Phương trình (3)
Thế (4) vào phương trình (2), ta được :
.
Xét hàm số :
Hàm số f(t) đồng biến và liên tục trên và
Phương trình
Hệ phương trình có 1 nghiệm :
Giải
Điều kiện :
Phương trình (1)
Xét hàm số :
Hàm số f(t) đồng biến và liên tục trên và
2
2
2
2
y
x x
2
2 4
y x x
2
2 2 2
2 2 1 2 3 = 2x - 4x
x x x x x
2 2
1 2 2 1 2 3 = 0
x x x x x x
2
2
2 1 1 2 - 1 5
x x x x x x
2
2 ,f t t t t t
2
2
2
' 2 1 0,
2
t
f t t t
t
5 1 1
f x f x x x
1
1
2
x y
1
;1
2
1 0 1
2 0 2 0
x x
y x y x
3
2 = 3 1 2x - 1 + 1 1
y y x x
3
2 = 1 2 1 1
y y x x x
3
3
2 = 2 1 1 3
y y x x
3
2 ,f t t t t
2
' 6 1 0,f t t t
Bài toán 143.(THPT Triệu Sơn 4)
3
2
2 + 2x 1 = 3 1 1
2 1 - y = 2 - x 2
y y x x
y
Phương trình
Thế (4) vào phương trình (2), ta được :
Hệ phương trình có nghiệm duy nhất :
Giải : Điều kiện : . Phương trình (1)
. Thế vào phương trình (2) ta được :
3 1 1 , 0
f y f x y x y
2 2
1 1 4
y x x y
2 2
2 1 - y = 2 - 1
y y
2 2
2 1 - y - y - 1= 0
y
2
2
2
1
- y + 1 = 0
2 1 + y
y
y
2
2
1
-1 y + 1 = 0
2 1 + yy
2
1
-1= 0
2 1 + yy
2
2 1 + y= 1
y
2
2 1 = 1 - y
y
2
2
1
2 1 1
y
y y
2
1
2,
0 1
2 0
y
y loai
y x
y y
1;0
0
1
5
x
y
3 2 2
x y y xy x
2
1 1 0
x xy y xy
2
1 0
x y xy
2
1
x y
xy
2
x y
2
5 1 - x = 1
x x
2
5 1 = 1 + x 3
x x
Bài toán 144.
2
1
5 1 1
x
x y
x y
y x y
TH 1 :
TH 2 :
.Thế vào (2) ta được :
(do vế trái không âm, vế phải âm)
Hệ phương trình có 4 nghiệm :
Giải :Phương trình (1) (3)
Vì : nên :
0:
x
2 2
3 5 1 = 1 + x
x
2 2 4
5 1 = 1 + 2x
x x
2
4 2
2
1
3 2 = 0
2
x
x x
x
1 1
2 2
x y
x y
0:
x
2 2
3 5 1 = 1 - x
x
2 2 4
5 1 = 1 - 2x
x x
2
4 2
2
7 41
2
7 2 = 0
7 41
2
x
x x
x
7 41 7 41
2 2
7 41 7 41
2 2
x y
x y
1
1xy x
y
1
5 1 1
y y
y
1
5 1 1
y
y
5 1 1
y y y
5 1 1 2 5 1
y y y y y
2
2 5 1 5 2 1,
y y y y VN
7 41 7 41 7 41 7 41
1;1 ; 2;2 ; ; ; ;
2 2 2 2
2
2
2
4
1
x x
y y
2
1 0,y y y
2
2
2 1
3 4
1
y y
x x
2
2
4 2 4 2 4
x x y y
Bài toán 145.
2 2
32 3
4 1 2 1
12 10 2 2 1 2
x x y y
y y x
Xét hàm số :
Hàm số f(t) đồng biến và liên tục trên và
Thế x = -2y vào phương trình (2), ta được :
Xét hàm số :
Hàm số g(t) đồng biến và liên tục trên và
Phương trình
Hệ phương trình có 2 nghiệm :
Giải : Điều kiện :
phương trình (1)
(3)
Xét hàm số :
2
4,f t t t t
2
' 1 0,
4
t
f t t
t
4 2
f x f y
2
x y
32 3
3 5 2 2 1
x x x
3
3
3 3
1 2 1 1 2 1 5
x x x x
3
2 ,g t t t t
2
' 3 2 0,g t t t
3 3
5 1 1
g x g x
3 3
1 1
x x
3
3 2
1 1 3 3 0
x x x x
0 0
1
1
2
x y
x y
1
0;0 ; 1;
2
2
2
1 0 1 1
1 1 1
0 2
2 0
x x
y
y
y y
3 3 2
3 3 3 1 3 3
x x y y y y
3
3
3 1 3 1
x x y y
3
3 , 1;1
f t t t t
2
' 3 3, 1;1
f t t t
Bài toán 146.
3 3 2
2 2 2
3 3 2 0 1
1 3 2 2 0 2
x y y x
x x y y
' 0, 1;1
f t t
Hàm số f(t) nghịch biến và liên tục trên và
Phương trình
Thế x +1 = y vào phương trình (2), ta được :
Hệ phương trình có 1 nghiệm :
Giải : Do y = 0 không thõa hệ phương trình nên
Hệ phương trình
Cộng 2 phương trình của hệ với nhau ta được :
(3)
2
' 0 3 3 0 1
f t t t
1;1
3 1 1 1
f x f y x y y x
2 2 2
1 3 1 2 0
x x x
2 2
2 1 2 0
x x
2 2
1 2 1 1 0
x x
2 2
1 1 0 1 1 0
x x x
0;1
0
y
2
3 2
3
2
8 4
3 2 1
4 6
4 5
x x
y y
x x
y y
3 2
3
8 6
3 6 4x x x
y y
3
3 2
2 2
3 3 1 3 3 3x x x x
y y
3
3
2 2
1 3 1 3x x
y y
-
1
2
t
f(t)
f’(t)
-
1
0
-
2
Bài toán 146
3 2
2 3 2 2
3 2 1 4 8 1
4 6 5 4 2
y x x y
y x y x y y
Xét hàm số :
2
' 3 3 0,f t t t
Hàm số f(t) đồng biến và liên tục trên và
Thế (4) vào phương trình , ta được :
Hệ phương trình có nghiệm :
Giải : Điều kiện :
Phương trình (1)
(3)
Xét hàm số :
2
' 6 1 0,f t t t
Hàm số f(t) đồng biến và liên tục trên
Phương trình
Thế vào phương trình (2) ta được :
3
3 ,f t t t t
2 2
1 1 4
f x f x
y y
2
3
4 5 1 3 1
x x x x
3 2
1 0
x x x
1 1
1,
x y
x loai
1;1
2
1
1 0
3 3
9 4 0
2 2
x
x
y
y
3
2 = 3 1 2 2 2 1
y y x x x
3
2 = 2 1 1 1
y y x x x
3
3
2 = 2 1 1
y y x x
3
2 ,
f t t t t
3 1 1 0
f y f x y x
2
4 5 2 6 1
x x x
2
2 4 5 4 12 2
x x x
2
2 4 5 4 5 1 4 8 4
x x x x
2
2
4 5 1 2 2
x x
4 5 1 2 2
4 5 1 2 2, vì:2 2 0, 1
x x
x x loai x x
Bài toán 155.
3
2 2 2
2 2 1 = 3 1 1
9 4 2 6 - 7 2
y y x x x
y x y
Hệ phương trình có 2 nghiệm :
Giải : Điều kiện :
Phương trình (2) (3)
Thế (3) vào phương trình (1) ta được :
(4)
Xét hàm số :
Bảng biến thiên :
2
1 2 0
4 5 1 2
x
x x
2
4
1
1
2
2
1 2,
4 8 4 0
1 2 2
x
x
x loai
x x
x y
4 4
1 2; 2 ; 1 2; 2
2
2 0
1
2 1 0
2
x
x
y
y
2 2
2 2 2
x y x y
2 2 2
2 2 2 2 = 2y + y + 2 1
x y x y x x y
2 2
3 2 2 = 4y + 2y + 2 1
x x x y
2 2
1 1 1 1 = 2y + 2y + 2 1
x x x y
2
1, 1;
f t t t t t
1
' 2 1 ,t -1
2 1
f t t
t
1
'' 2
4 1 1
f t
t t
1
'' 0 2 =0
4 1 1
f t
t t
8 1 1=1
t t
3
1
1 =
8
t
1 3
1= t = -
2 4
t
Bài toán 156.
2 2
2 2
2 2 = 2y + y + 2 1 1
2 2 2 0 2
x x x y
x y x y
1/2
f’(t)
t
f’’(t)
+
∞
+
∞
+
∞
-3/4
-1
0 + -
Ta thấy . Hàm số f(t) đồng biến và liên tục trên
Phương trình
Thế vào phương trình (2) ta được :
Hệ phương trình có 2 nghiệm :
Giải : Điều kiện : . Phương trình (1)
(3)
Xét hàm số :
Hàm số f(t) đồng biến và liên tục trên
Phương trình
Thế vào phương trình (2) ta được :
' 0, 1;f t t

1;

4 1 = f 2y 1 2 2 1
f x x y x y
2
2
2 1 2 2 2 1 2 0
y y y y
2
6 7 1 0
y y
1 1
1 2
6 3
y x
y x
2 1
1;1 ; ;
3 6
1
2
x
3
2 1 3 2 1 = y + 3y
x x
3
3
2 1 3 2 1 = y + 3y
x x
3
3 ,
f t t t t
2
' 3 +3 > 0, t
f t t
1;

2
2
1
3 2 1, 0 2 1
2
y
y x y y x x
2
2
2
1
1
5 5 6
2 2
y y
y
y y
3 2
3 11 5 0
y y y
Bài toán 157.
3
2
2 2 2 1 = y + 3y 1
5 5 6 2
x x
y xy x y
Hệ phương trình có 1 nghiệm :
Giải :Điều kiện :
Phương trình (1) (3)
Xét hàm số :
Hàm số f(t) đồng biến và liên tục trên
Phương trình
Thế vào phương trình (2) ta được :
Xét : không thỏa phương trình trên.
Chia 2 vế của phương trình trên cho ta được
Đặt : ,phương trình trên trở thành :
2
5 2 1 0
y y y
5,
1 2 2 2
1 2,
y loai
y x
y loai
2 2;1 2
2
1
1 3 3
1 0
3 3
6 6 0 3 3
3 3
3 0 3
3
x
x
x
x
x x x
x
y y
y
3
3
1 1 1 = 2 + 2 1
x x y y
3
1 ,
f t t t t
2
3
3
' 1 0,
2 1
t
f t t
t
3 3
3 1 2 1 2
f x f y x y
2
3 1 6 6 =
x x x x
2
3 1 = 1 1 1 4 1
x x x x
1
x
1
x
1 1
1 + + 1 4 3
1
1
x x
x
x
1
1 + > 0
1
t x
x
Bài toán 158
2
3
2
3
3 3 = 2 + 3 + 1 1
3 1 6 6 = 2 + 1 2
x x x x y y
x x x y
1 5
1
2
1
x
x
2
2 1 5 1 2 0
x x
1 2
1
1
2
x
x
5 62
5 127
4 64
x y
x y
Hệ phương trình có 2 nghiệm :
Giải : Điều kiện : . Ta thấy không thỏa hệ phương trình.
Xét ,Phương trình (1) , suy ra
(3)
Xét hàm số :
2
1, 0
f t t t t t
2
2
2
' 1 1 0, 0
1
t
f t t t
t
Hàm số f(t) đồng biến và liên tục trên
Phương trình
2 2
+ 6 =3 6 3
t t t t
2
2
3 0
3
5
t =
6 15 0
2
6 3
t
t
t
t t
5 127
5;62 ; ;
4 64
0
x
0
x
0
x
2
1
3 1 9 1 =
1
y y
x x x
0
y
2
1
3 3 9 1 =
x x
y y y
x
2
1 1 1
3 3 3 1 = +
x
y y y
x x x
2
2
1 1 1
3 3 3 1 = + 1
y y y
x x x
0;

1 1
3 3 3f y f y
x x
Bài toán 159.
2
3 2 2
1
3 1 9 1 = 1
1
9 1 4 1 = 10 2
xy y
x x
x y x x
Thế vào phương trình (2) ta được :
(4)
Xét hàm số :
Hàm số f(t) đồng biến trên và g(1) = 0. Vậy (4) có nghiệm duy nhất :
Hệ phương trình có nghiệm duy nhất :
Giải : Điều kiện :
Phương trình (1)
. Ta có :
Thế vào phương trình (2) ta được :
3 2
1
1 4 1 = 10
x x x
x
3 2 2
4 1 - 10 = 0
x x x x
3 2 2
4 1 - 10, x > 0
g x x x x x
2 2
2
' 3 2 1 8 > 0, x > 0
g x x x x x x
x
0;

1
1
3
x y
1
1;
3
2
0
0
2 0
2 2
x
x
x
x
2 2 2
2 1 = 2 2 2
x x x xy x y
3 2 2 2
2 2 2 0
x x x xy y
2 2 2 2
2 2 0
x x y x y x
2 2
2 2 0
x x y x
2 2
2 1 0
x x y
2 2
2 2
2,
1
1
x loai
x y
x y
1
1
x
y
2 2 3 2
4 3 2 1 1
y y x x y
Bài toán 160.
2
2
2
2 2 3 2
1
1 = 2 1 1
4 3 2 2 1 2
y
x y
x
y y x x x
(3)
Xét hàm số :
Bảng biến thiên :
Theo Bảng biến thiên ta có : và
Xét hàm số :
Bảng biến thiên :
2 2 3 2
4 1 1 3 2 1 1
y y x x y
2 2 2 3 2
4 1 1 1 1 3 2 1 1
y y y x x y
2 2 3
4 1 1 3 2
y y x x
2 2 3
4 1 3 2
y y x x
3
3 2, 1;0 0;1
f x x x x
2
' 3 3
f x x
2
' 0 3 3 0 1
f x x x
4, 1;0 0;1
f x x
1;0 0;1
min 4 1
f x x
2 2
4 1, 1;1
g y y y y
2
4
' 2
1
y
g y y
y
2
4
' 0 2 0
1
y
g y y
y
2
2
2 1 0
1
y
y
2
0
0
2
1
3,
1
y
y
y loai
y
-2
0
f(x)
x
f’(x)
-4
1
0
-1
-
-4
1-4
√
2
g(y)
y
g’(y)
1
0
-1
0 - +
1-4
√
2
Theo Bảng biến thiên ta có : và
. Hệ phương trình có nghiệm duy nhất :
Giải : Điều kiện :
Phương trình (1) (3)
Xem phương trình (3) là phương trình theo ẩn , còn là tham số.
. Phương trình có nghiệm :
Thế vào (2) ta được :
(4)
Xét hàm số :
Hàm số f(t) đồng biến trên
(5)
4, 1;1
g y y
1;1
max 4 0
g y y
1
3 4
0
x
f x g y
y
1;0
4 4
0
5 0
xy
y x
2
2 2 2 2
5 2 5 12 36 = 0
x y xy x y xy
2 2
5
x y
xy
2
' 6
xy
2 2
2 2
5 6
5 2 6,
x y
x y xy loai
4 4 2 2 2 2
5 5 + 2xy
y x x y x y
4 4 4 2 2 4
5 4 5 2
y x x x y y xy
4 4 4 4 2 2
5 5 4 2
y x y x x y xy
2
2
4 4 4 4
5 5 2 2
y x y x xy xy
2
, 0;f t t t t
' 2 1 0, 0
f t t t
0;
4 4 4 4
4 5 2 2 5
f y x f xy xy y x
4 2 2 4
4 5 0
x x y y
Bài toán 161.
2
2 2 2 2
4 4 2 2
5 2 6 5 +36 1
5 6 + 2xy - 6y 2
x y xy x y
y x x
Nếu , không thỏa hệ đã cho.
Xét , chia 2 vế của phương trình (5) cho ta được :
Từ
Hệ phương trình có 2nghiệm :
Giải : Điều kiện :
Phương trình (1)
(3). Dễ thấy :
Xét hàm số :
Bảng biến thiên :
0 0
y x
0
y
4
y
4 2
4 5 0
x x
y y
2
2
1
5,
x
y
x y
x
loai
y
2 2 2
1
5 6 6 6
1
x y
x y x
x y
1;1 ; 1; 1
2
2
1 0 1 1
0 2
2 0
x x
y
y y
3 3 2
3 2 3
x x y y
3 2 2 3 2
3 3 1 3 2 1 3
x x x x x y y
3 2
3 2
1 3 1 3
x x y y
0 1 2
0 2
x
y
3 2
3 , 0;2
f t t t t
2
' 3 6
f t t t
2
0
' 0 3 6 0
2
t
f t t t
t
Bài toán 162.
3 3 2
2 2 2
3 3 2 1
1 -3 2y - y = 2 2
x y y x
x x
0
t
f’(t)
2
0
- 0
Hàm số f(t) nghịch biến trên .
Thế vào phương trình (2) ta được :
, loai.
Hệ phương trình vô nghiệm.
Giải :Điều kiện : .Ta thấy không thỏa hệ phương trình.
Xét ,Phương trình (1)
, suy ra
(3)
Xét hàm số :
Hàm số f(t) đồng biến và liên tục trên
0;2
3 1 1
f x f y x y
2
2 2
1 -3 2 1 - 1 = 2
x x x x
2 2
- 2 1 - = 2
x x
2 2
1 - +2 1 - 1 0
x x
2
2
1 - 1 0
x
0
x
0
x
0
x
2
2
2
1
2 2 4 1
x x
y y
x
2
2
2
1
2 2 4 1
x x
y y y
x
0
y
2
2
2
1 1 1
2 2 2 1
x
y y y
x x x
2
2
1 1 1
2 2 2 1 1
y y y
x x x
2
1, t 0;
f t t t t

2
2
2
' 1 1+ >0, t 0;
1
t
f t t
t

0;

Bài toán 163
.
2 2 2
2 2 2
2 2 4 1 1 1
4 1 +2 1 = 6 2
x y y x x
y x x x
Phương trình
Thế vào phương trình (2) ta được :
(4)
Xét hàm số :
Hàm số g(x) đồng biến trên và g(1) = 0. Vậy (4) có nghiệm duy nhất :
Hệ phương trình có nghiệm duy nhất :
Giải : Phương trình (1)
(3)
Xét hàm số :
Hàm số f(t) đồng biến trên . Phương trình
Thế vàophương trình (2) ta được :
1 1
3 2
2
f y f y
x x
2 2
2
1
1 +2 1 = 6
x x x
x
2 2
1 +2x 2 - 6 = 0
x x x
2 2
1 +2x 2 - 6 = 0,x > 0
g x x x x
2
1
' 2 +4x > 0, x > 0
x
g x x x
x x
0;
1
1
2
x y
1
1;
2
3 2 3
3 3 1 3 1 3
x x x x y y
3
3
1 3 1 3
x x y y
3
3 , t
f t t t
2
' 3 +3 > 0, t
f t t
3 1 1
f y f x y x
3
3 2
3 1 7 = 1- 1
x x x
3
3 2
3 4 = 1 - 1
x x x
3 2 2 2
3 4 = 1 - 1 1 + x + 1 1
x x x x
Bài toán 164
.
3 2 3
3
3 2
3 6 4 3 1
3 7 = 1- 1 2
x x x y y
y x x
Xét phương trình :
Vì nên vế trái của phương trình trên luôn dương.
Vậy phương trình trên vô nghiệm. Hệ phương trình có nghiệm duy nhất : (0; 1)
Giải : Điều kiện :
0
0
x y
x y
x y
2 2 2
3
2
1 + x + 1 1
3 4 + 0
1 + 1
x x
x x
x
2 2
2 2
2
1 + x + 1 1
3 - 4x + 0
1 + 1
x
x x
x
2 2
2
2
0 1
1 + x + 1 1
3 - 4x + 0
1 + 1
x y
x
x
x
2 2
2
2
1 + x + 1 1
3 - 4x + 0
1 + 1
x
x
x
2 2
2
2
2 4 4 1 + x + 1 1
3 - 2. x + + 0
3 9 9
1 + 1
x
x
x
2
2 2 2
2
2 4 1 -2 1 + 1 + x +3 1
3 - - + 0
3 3
1 + 1
x x
x
x
2
2
2
2
1 - 1 3
2 4
3 - - + 3+ 0
3 3
1 + 1
x
x
x
2
2
2
2 2
1 - 1
2 5 3
3 - + 0
3 3
1 + 1 1 + 1
x
x
x x
2
2
2
2
2 2
1 - 1
2 5 1 4
3 - + 0
3
1 + 1 1 + 1
x
x
x
x x
2 2
5 1 5, 5 1 4 0,x x x x
Bài toán 165
.
2
2
3 2 1
2 3 2
x y x y x y x y
x x y x y
Đặt : ,Phương trình (1) trở thành :
Thế : y = 1- x vào phương trình (2) ta được :
Hệ phương trình có nghiệm duy nhất : (1; 0)
Giải : Điều kiện :
Phương trình (1)
Đặt , phương trình trên trở thành :
, 0
t x y t
2
3 2
t t t t
2
2 3 0
t t t t
3 1
1 0
2 3
t
t t
t t
3
1 0
2 3
t t
t t
1
3
0,
2 3
t
t VN
t t
1
1 1
2
x y y x x x
2
3 2 1 3
x x
2
3 2 2 1 1 0
x x
2
2
2 1
1
0
2 1 1
3 2
x
x
x
x
2
1 2
1 0
2 1 1
3 2
x
x
x
x
2
1 0
1 2
0,
2 1 1
3 2
x y
x
VN
x
x
2 0 2
2 0 2
x x
y y
2 2 2 2
2 2
2
2 2
x y
x xy y y xy x
y y y
2 2
2 2 1 2 2
x x x x x
y y y y y
, 1
x
t t
y
Bài toán 166
.
2 2 2 2
2 2 2 1
8 6 1 2 2 4 2 3 2
x xy y y xy x x y
y x y y x
Bình phương 2 vế của phương trình trên, ta được :
, thế : y = x vào phương trình (2) ta được :
(3)
Xét hàm số :
Hàm số f(t) đồng biến trên .
Hệ phương trình có 2 nghiệm :
2 2
2 2 1 2 2
t t t t t
2 2 2 2
3 2 3 2 2 2 1 4 8 4
t t t t t t t t
2 2 2
2 2 2 1 6 1
t t t t t t
2
2 2 2
4 2 2 1 6 1
t t t t t t
4 2 2
7 14 7 0 1 1
t t t t
x y
8 6 1 2 2 4 2 3
x x x x x
8 1 2 1 2 2 2 4 2 5
x x x x x
3 2
2 1 2 1 2 2 2 4 2 4 1
x x x x x
3 2
2 1 2 1 2 2 2 2 1
x x x x
3 3
2 1 2 1 2 2 2 2
x x x x
3
, 2
f t t t t
2
' 3 1 0, 2
f t t t
2;

3 2 1 2 2
f x f x
3 2 1 2 2
x x
4 1 4 4 2 2
x x x
3 6 4 2
x x
2
3 6 16 2
x x
2
9 52 68 0
x x
34
9
2
x y
x y
39 39
2;2 ; ;
4 4
Bài toán 167
.
4 3 4 2
4 1 y + 4y = 1 1
x y x
Giải : Phương trình (1)
, thay vào phương trình (2) ta được :
(3)
Xét hàm số :
Bảng biến thiên :
4 4 3 2
4 + 4y - y = 1
x x y y
4 2
1 4 y + 1 - y + 1 = 0
x y y
4 2
4 1 1 = 0
x y y
4 2
1
4 1 0
y
x y
1
y
2 2
4 1 4
x x
2
2 2
16 1 4
x x
4 2
8 0 0; 2 2
x x x x
4
4 2
2
1 1
1
4 1
1 1
4 1
2 2
x
x
x y
y
y
3 2 2
2 8 6 2 4 1
y y x x
2 2
4 1, 1;1
f x x x x
2
4
' 2
1
x
f x x
x
2 2
4 2
' 0 2 0 2 1 0
1 1
x
f x x x
x x
2
0
2
1 0
1
x
x
2
0
1 2
x
x
2
0
0
3,
1 2
x
x
x loai
x
0
+
f(x)
x
f’(x)
1
-1
0
-
-4
Theo Bảng biến thiên ta có :
Xét hàm số :
Bảng biến thiên :
Theo Bảng biến thiên ta có :
Phương trình (3)
Hệ phương trình có 4 nghiệm :
Giải : Điều kiện :
Phương trình (1)
0 4, 1;1
f x f x
3
1 1
8 6 2, ;
2 2
g y y y y
2
' 24 6
g y y
2
1
' 0 24 6 0
2
g y y y
1 1 1
4, ;
2 2 2
g y g y
0
4
1
4
2
x
f x
f x g y
y
g y
1
0; ; 0; 1 ; 2 2; 1 ; 2 2; 1
2
2 3
8 0
x y
3 3 2
1 8 12 8 1
x x y y y
3
3 2
1 2 12 6 1 2 1 1
x x y y y y
0
g(y)
y
g’(y)
1/2
-1/2
-
-4
Bài toán 168
.
3 2 3
2 3
12 2 8 8 1
8 5 2 2
x y x y y
x y x y
(3)
Xét hàm số :
Hàm số f(t) đồng biến trên . Phương trình
Thế : 2y – 1 = x vào phương trình (2) ta được :
.
Hệ phương trình có 2 nghiệm :
Giải : Điều kiện :
Từ phương trình (2) . Đặt
3
3
1 2 1 2 1 1
x x y y
3
1,f t t t t
2
' 3 1 0,f t t t
3 2 1 2 1
f x f y x y
2
3
2 1 8 5 2 1 2
y y y y
3 2
8 4 4 1 8 5
y y y y
2
3 2
8 5 0
8 4 4 1 8 5
y
y y y y
3 2
5
8
8 60 76 24 0
y
y y y
5
8
6 11
1 1
1
,
2
y
y x
y x
y loai
11;6 ; 1;1
1
3 1 0
3
5 4 0 4
5
y
y
x
x
0
x y
2 2
2 2
2 2
; , 0
4
3
u x y
u v
x xy y
v
Bài toán 169
.
2 2
2 2
3 1 5 4 3 3 1
4
2 2 2 2
3
y x xy y
x xy y
x y x y
Phương trình (2) trở thành :
Thế : y = x vào phương trình (1) ta được :
(3)
. Vì . Từ
2 2 2
2 2 2 2
2 2
2
2 2
3
2 2 2 2
4
2
3
u x y
v x xy y u xy
x xy y
v
2 2
3
2
2
v u xy
2 2
2
2 2 2 2 2
3 3
2
2 2 2 2
u u
x y x y x xy y v u v
2
2
3
2
2 2
u
u v v
2 2
3 2 5 0
u uv v
2 2 2
3 2 2 3 0
u uv v v
2 2
2 3 0
v u v u v
3 5 0
u v u v
3 5 0
u v
u v
u v
2
2 2
2 0 0
x xy y x y x y
2
3 1 5 4 3 3
x x x x
2
3 1 1 5 4 2 3 3
x x x x x x
2 2
2
3 1 1 5 4 2
3 3
3 1 1 5 4 2
x x x x
x x
x x x x
2 2
2
3 0
3 1 1 5 4 2
x x x x
x x
x x x x
2
1 1
3 0
3 1 1 5 4 2
x x
x x x x
2
0
1 1
3 0,
3 1 1 5 4 2
x x
VN
x x x x
0
1
x y
x y
3 5 0
u v
, 0 0
u v u v
0 0
xy x y
Hệ phương trình có 2 nghiệm :
Chú ý. Để có phương trình (3) ta làm như sau : Dùng máy tính ta biết được phương trình có 2
nghiệm : 0 và 1và cũng là nghiệm của phương trình : . Ta biến đổi phương trình :
như sau:
Ta phải có :
Giải : Phương trình (2) (3)
Thế phương trình (3) vào phương trình (1) ta được :
(4)
0;0 ; 1;1
2
0
x x
2
3 1 5 4 3 3
x x x x
2
3 1 5 4 3 3
x x x x
2
3 1 5 4 3 3
x x a x x b x x x a x b
2 2
2
3 1 5 4
3 3 3
3 1 5 4
x x a x x b
x x a b
x x a x x b
2 2 2 2
2
3 2 1 5 2 4
3 3 3
3 1 5 4
x a x a x b x b
x x a b
x x a x x b
2 2 2
2 2 2
3 2 1
5 2 4
x a x a x x
x b x b x x
2
2
3 2 1
1 0 1
5 2 1 2
4 0
a
a a
b b
b
2 2
2 2 3 3
y x y x y x
2 2 2 2
2 5 2 5 2 2
x x y y y x y x
2 2 2 2
1 4 1 4 1 1
x y y x
2 2 2 2
1 4 1 1 4 1
x x y y
Bài toán 172
.
2 2
2 2
2 5 2 5 3 3 1
3 3 2
x x y y y x
y y x x
Xét hàm số :
Hàm số f(t) đồng biến trên
,thế vào phương trình (2) ta được :
,thế vào phương trình (2) ta được :
Hệ phương trình có 2 nghiệm :
Giải Điều kiện :
Phương trình (1)
(3)
Xét hàm số :
Hàm số f(t) đồng biến trên
Phương trình (4)
4 , 0;f t t t t
1
' 1 0, 0;
2 4
f t t
t

0;
2 2
4 1 1
x y
2
x y
x y
x y
3 3
4 3 0
4 4
y y x
2
x y
2
2
3 3 2 2
y y y y
3 1
2 3 0
2 2
y y x
1 3 3 3
; ; ;
2 2 4 4
3 2
2
3 0
2
8 0
0
2 0
y y
x
y y
y
x
3 2
3 2 3
x x y y
3 2
3 3 1 3 1 3 3 3
x x x x y y
3
3
1 3 1 3 3 3
x x y y
3
3 , 1;f t t t t

2
' 3 3 0, 1;f t t t

1;

3 1 3 1 3
f x f y x y
Bài toán 173
.
3 2 3 2
2
3 2 3 1
3 2 8 2
x x y y
x y y
Phương trình (2) (5)
Thế (4) vàophương trình (5) ta được :
Hệ phương trình có 1 nghiệm duy nhất :
Giải : Điều kiện :
Phương trình (1)
(4)
Xét hàm số :
Hàm số f(t) đồng biến trên
Thế phương trình (5) vào phương trình (2) ta được :
2
9 2 8
x y y
2
9 3 1 8
y y y
2
8 9 9 3
y y y
2
2
8 9 81 3
y y y
4 3 2
16 82 63 162 0
y y y y
3 2
1 17 99 162 0
y y y y
3 2
1 3
17 99 162 0,
y x
y y y VN
3;1
3 2 3 2
1 0 1
1 0 1 0
y y
x x x x
2 2
3 3
1 2 1
x x y y x x y y
2
3
1 0
x x y y
3
1
x x y y
3
1 1 1
x x y y
3
3
1 1
x x y y
3
,f t t t t
2
' 3 1 0,f t t t
3 3
4 1 1
f x f y x y
3 2
0
1
x
x y
3
2
0
1 5
x
x y
Bài toán 174.
3 32 2 4 2 3
3
3
4 3 2
2 2 1 1
1 1 1 2
x y x x y y y x x
x x x x y
. Hệ phương trình có 2 nghiệm :
Giải : Điều kiện : . Phương trình (2)
Từ phương trình trên suy ra :
Phương trình (3)
Đặt :
(4)
Xét hàm số :
Hàm số f(u) đồng biến trên
Phương trình
Hệ phương trình có 2 nghiệm :
4 3 2 3
1 1
x x x x
4 3 3 2
1 1 0
x x x x
3 2
3
3 2
1 0
1 1
x x
x x
x x
2
3 2
1
1 0
1 1
x x x
x x
3 2
0 1
1 2
1
0, do x 0
1 1
x y
x y
x VN
x x
0;1 ; 1;2
2
x
2
2
2 2 2 4
x x y y y
2
2 4
x y y
0
y
4
4
1 3 2 = 5 y
x x y
4 4 4
4
2, 0 2 3 5 3 5
t x t t x x t x t
4 4
3 5 = 5 y
t t y
4
5 , 0;
f u u u u

3
4
2
' 1 0, 0;
5
u
f u u
u

0;
4
3 2
f y f t y t y x
0;1 ; 1;2
Bài toán 175.
4
4
2 2
3 2 - 5 = y 1
2 2 8 4 0 2
x x y
x x y y y
Bài toán 176.
3 2
3 2 3
2 5 3 3 10 6 1
6 13 10 2
x y x y x x y
x x x y y
Giải Điều kiện :
Phương trình (2)
(3)
Xét hàm số :
Hàm số f(t) đồng biến trên .
Thế vàophương trình (1) ta được : (4)
Xét hàm số :
Ta có :
Suy ra , vậy hàm số g(x) đồng biến trên
Và g(2) = 0, do đó phương trình (4) có nghiệm duy nhất x = 2
Hệ phương trình có nghiệm duy nhất :
Giải : Điều kiện :
Phương trình (1)
2 5 0
3 0
x y
x y
3 2 3
6 12 8 2 10 10
x x x x y y
3
3
2 2 10 10
x x y y
3
10,f t t t t
2
' 3 1 0,f t t t
3 2 2
f x f y y x
3 2
3 3 5 2 3 10 26
x x x x x
3 2
5
3 3 5 2 3 10 26, 1;
2
g x x x x x x x
3
3 1 5
' 3 6 10, 1;
2
2 3 3 5 2
g x x x x
x x
2
5
3 6 10 0, 1;
2
x x x
5
' 0, 1;
2
g x x
5
1;
2
0
y
2;0
3 2 0
x y
3 3 2 2 3 2
3 3 8 12 6 1 0
y x x y xy x x x
Bài toán 178.
3 3 2
3
7 3 12 6 1 0 1
4 1 3 2 = 4 2
x y xy x y x x
x y x y
Thế vào phương trình (2) ta được : (3)
Xét hàm số :
Hàm số f(t) đồng biến trên
Phương trình (3) có nghiệm duy nhất , thỏa điều kiện
Hệ phương trình có nghiệm duy nhất :
Giải : Điều kiện :
Phương trình (1)
(3)
Xét hàm số :
Hàm số f(t) đồng biến trên . Phương trình
Thế vào phương trình (2) ta được :
(4)
Do
Từ phương trình (4), suy ra : ;
3 3
2 1 0
y x x
3 3
2 1
x y x
2 1 1
x y x y x
3
3 2 2 4 0
x x
3
3 2 2 4, 2
f x x x x
2
3
1 1
' 3. 3 2 0, 2
3
2 2
f x x x
x
2;
2 0
f
2 1
x y
2; 1
2
8 0
x y
6 2 3 2
3 4 3 3 1 3 1
x x y y y y
3
3
2 2
3 4 1 3 1 4
x x y y
3
3 4,tf t t t
2
' 3 3 0, tf t t
2 2
3 1 x -1
f x f y y
2 2
2 1 1 2 7 + 7 - x = 0
x x x
2 2
2 5 1 2 7
x x x x
2 2 2
2 5 4 1 0,x x x x x x
1 0
x
2
2 2
4 2 5 1 2 7
x x x x
4 3 2
x x x x
2
3 1 2 6 0
x x x
Bài toán 179.
6 2 3 2
2
3 4 3 6 1
2 1 8+7 = x 2
x x y y y
y x x y
.Hệ phương trình có nghiệm duy nhất :
Giải : Điều kiện :
Phương trình (1)
(3)
Xét hàm số :
Hàm số f(t) đồng biến trên .
Phương trình
Thế vào phương trình (2) ta được :
(4)
Xét hàm số :
. Hàm số f(x) đồng biến trên và
Nên phương trình (4) có nghiệm duy nhất :
Hệ phương trình có nghiệm duy nhất :
3 8
1 0, ( thoa)
x y
x y loai khong
3;8
4 1
x
3 2
2 3 3 1 1 3 1 2 1 1 1
y y y y x x x
3
2 1 1 2 1 1 1
y y x x x
3
2 ,f t t t t
2
' 6 1 0, tf t t
3 1 1 1 1
f x f y x y
1 1
x y
3 2 4 1 4
x x x
4 1 3 2 4 0
x x x
4 1 3 2 4, 4;1
f x x x x x
1 1 1
' 0, 4;1
2 4 2 1 3 2
f x x
x x x
4;1
3 0
f
3 3
x y
3;3
Bài toán 180.
3 2
2
2 7 2 1 3 1 3 2 1 1
2 4 3 5 4 2
y y x x x y
y y y x
Bài toán 185.
3 2 3 2
3 2 3 (1)
3 2 (2)
x x y y
x y x
Giải : Điều kiện :
Phương trình (1)
(3)
Ta thấy :
Xét hàm số:
Hàm số f(t) đồng biến trên
Thay vào phương trình (2), ta được :
Vậy hệ phương trình có nghiệm duy nhất là:
Giải Phương trình (1)
(3). Mặt khác, ta có :
3 2
3
3
3 0
2
2
x
x
y y
y x
y x
3 2
3 2 3
x x y y
3 3
( 1) 3( 1) ( 3) 3 3
x x y y
1 2
3 1 2
2 2 3 2 1
3 4 2
x
x x
y x y x
y
3
( ) 3 , 2
f t t t t
2
2
'( ) 3 3 3 2 3 0, 2
f t t t
2;
3 ( 1) 3 1 3
f x f y x y
2
2 2
x x y
2
3 3
x x x
2
4 3 0
x x
1,
3 1
x loai
x y
(3;1)
2
2
1
4 1
1
y y
x x
2
1 0,
x x x
2 2
4 1
y y x x
2 2
1 4 1
x x y y
2
2
4
1 1
4
x x
y y
2
4 0,
y y y
Bài toán 195.
2 2
3
2
3
1 4 1 1
2 5 5 2 6 1 10 2
x x y y
y y x x
(4)
Lấy phương trình (3) trừphương trình (4), vế với vế, ta được :
(5)
Thế (5) vàophương trình (2) ta có phương trình : (6)
Xét hàm số :
Hàm số đồng biến trên và
Suy ra, phương trình (6) có nghiệm duy nhất
Vậy hệ phương trình có 1 nghiệm .
Giải : Điều kiện :
Phương trình (2)
2 2
4 1 4
x x y y
2
2 3 1 5
y x x
2
4 6 1 10
y x x
3
3
2 5 5 2 4
y y y
3
3
2 5 5 2 4 ,f y y y y y
2
2
3
2 5
' 6 2 5 4 0,
2
5 2
f y y y
y
f y
3
0
2
f
3
2
y
2
3 3 1 5
x x
2
3 1 3 5
x x
2
2
3 5 0
9 1 3 5
x
x x
2
3
5
16 30 0
x
x x
0
x
3
0;
2
2
x
x y
2 4 1 2 4 0
x y y x y y
3
2 4 2 4 0
x y y x y x y y
Bài toán 205.
3
4 3 2 2 1
5 2 4 0 2
y y x x x
x y x y y
(3)
Xét hàm số :
Hàm số : đồng biến trên .Phương trình
. Ta có hệ phương trình :
Xét phương trình :
2
2 4 1 1 0
y x y x y x y
1 2 4 1 0
x y y x y x y
4 0
x y x y
4
x y x y
0
x y
3
1 3 2 2 4 2 2
y y x x x
2 3 2
3
2 2 2 2 2 2 1
y y x x x x
2 3
3
3 2 2 3 2 1 2 1
y y x x x x
3
3
2 1 2 1
y y x x
3
,f t t t t
2
' 3 1 0,f t t t
f t
2
1 0
3 2 1
2 2 1
y
y x
x y y
2
1
2 3
y
x y y
2
4 0
1
2 3
x y x y
y
x y y
2 2
2
1 3 3 0
1
2 3
y y y y
y
x y y
2 2
1 3 3 0
y y y y
2 2
2 1 3 3 0
y y y y
2
2
2
3 2
2 0
1 3 3
y y
y y
y y
2
1 2
1 2 0
1 3 3
y y
y y
y y
2
1
2 1 0
1 3 3
y
y y
y y
Vậy hệ phương trình có nghiệm duy nhất :
Giải Điều kiện :
Phương trình (1) (3)
Xét hàm số trên
(3) (4)
Thay (4) vào phương trình (2) ta được :
.Hệ phương trình có nghiệm duy nhất:
Giải Phương trình (1) (3)
Phương trình (2)
Xét hàm số :
Hàm số f(t) đồng biến trên
(3) . Thay vào phương trình (2) ta được :
2 2
2
3 3 3 3 2
2 0
1 3 3
y y y y y
y
y y
2 3
y x
3;2
0
5
x
y
2 4 5 5 2 5 4
x x x y y y
2 4
f t t t t
0;
1 1 1
0, 0;
2 2 2 2 4
f t t
t t t
5 5 5
f x f y x y y x
2
2
5 5 44
x x x x
2
1 6
2 12 14 0
7,
x y
x x
x loai
1;6
3
3
3 1 3 1
x x y y
2
1
xy y x
1 0 1
x x
3
3 , 1;f t t t t

2
' 3 3 0, 1;f t t t

1;
1
f x f y x y
Bài toán 209.
2 2
2 4 1 3 5 1
44
2
x x x y y y
x y x y
Bài toán 210.
3 3 2
2 2 2 2
3 3 2 1
2 1 0 2
x x y y
x y y xy x
Hệ phương trình có 2 nghiệm : .
Giải : Phương trình
Xét hàm số :
Hàm số đồng biến trên . Phương trình (3)
Thay y=x+2 vào phương trình (2) ta có :
Vậy hệ phương trình có 2 nghiệm là (-3;-1), (3;5).
Giải : Phương trình (2)
(3)
Xét hàm số
2
2 2 2
1 2 1 1 1 0
y y y y y y
4 3
0 1
0 1 0
1 2
y x
y y y y
y x
1;0 ; 2;1
3 2 3 2
(1) 3 4 4 3 4
x x x y y y
3 3
( 1) 1 ( 1) 1 (3)
x x y y
3
,f t t t t
2
' 3 1 0,f t t t
f t
( 1) ( 1) x 1 y 1 2
f x f y y x
2
2
2 2(2 2) 18
x x x
2
3 5
2 18 0
3 1
x y
x
x y
3 2 2 3
7 12 6 0
x x y xy y x y
3 3 2 2 3
8 12 6 2 0
y x x y xy x x y x
3 3
2 2
y x y x x x
3
,f t t t t
2
' 3 1 0,f t t t
Bài toán 216.
3 3 2 2
2 2
3( ) 4( ) 4 0
( , )
2( ) 18
x y x y x y
x y
x y x y
Bài toán 220.
2 2
3 2 2 3
2 7 2 6 0 1
7 12 6 0 2
x y x y
x x y xy y x y
Suy ra hàm số đồng biến trên . Phương trình
Thế vào phương trình (1) ta được :
Vậy hệ phương trình có 2 nghiệm .
Giải : Điều kiện:
Nếu , để hệ phương trình có nghiệm thì : .
hệphương trình vô nghiệm.
Nếu y<0, từ (2) suy ra x>0
Ta có :
Xét hàm số
Suy ra hàm số đồng biến trên
Phương trình
Thế vào phương trình (1) ta có phương trình : (4).
Xét hàm số : trên
f t
3 2
y x x x y
2
3
5 6 0
2
x
x x
x
2;2
; 3;3
6 0
1
x y
x
0
y
0 1
y
(1) 2 6 2 5
(1) (1)
(1) 1 1
VT x y
VT VP
VP y
2
9 1 9 0
x xy y
2
2
3 3
9 9 (3)
y y
x x
2
( ) 9 , 0;f t t t t

2
2
9 2
'( ) 0. 0
9
t
f t t
t
f t
0;

2
3 3 9
(3) ( )f f y y x
y
x x
2
9
2 6 1
y y
y
2
9
( ) 2 6
g y y
y
;0

Bài toán 221.
2
2 6 1 (1)
9 1 9 0 (2)
x y y
x xy y
Suy ra hàm số đồng biếntrên
Xét hàm số : trên có
Suy ra hàm số nghịch biến trên và phương trình (4) có nghiệm duy nhất y= -3, vậy x
= 1.
Cách 2. (Dùng lượng liên hợp)
Xét phương trình :
Vì phương trình vô nghiệm và có hệ số a = 1 > 0, nên
Do đó vế trái của (*) luôn dương, với mọi y < 0, (*)vô nghiệm.
Vậy hệ phương trình có nghiệm duy nhất (1;-3).
2
3
3
2 2
9
6 '
18
'( ) 0, 0
9 9
6 6
y
y
y
g y y
y y y
y y
( )
g y
;0

h( ) 1
y y
;0

h'( ) 1 0, 0
y y
h( )
y
;0

2
9
2 6 1
y y
y
2
9
2 6 2 3 0
y y
y
2
2
9
6 4
2 3 0
9
6 2
y
y
y
y
y
3 2
2
2
2 9
2 3 0
9
6 2
y y
y
y y
y
2
2
2
3 3
2 3 0
9
6 2
y y y
y
y y
y
2
2
2
3
2 3 1 0
9
6 2
y y
y
y y
y
2
2
2
3 1
3
1 0
9
6 2
y x
y y
y y
y
2
3 0
y y
2
3 0,y y y
Giải : Điều kiện : . Phương trình (1)
(3)
Xét hàm số :
Suy ra hàm số đồng biến trên .
Thế vào phương trình (2) ta được :
Đặt với
Ta có
Khi đó, phương trình (2) trở thành :
Nghiệm của hệ phương trình là : .
1 1
x
3
2 3 1 2 1 1 1
y y x x x
3
3
2 2 1 1
y y x x
3
2 ,f t t t t
2
' 6 1 0,f t t t
3 1
f y f x
1
y x
2 2
1 1 2 2 1
x x x x
2 2
2 2 1 1 1 0
x x x x
cos
x t
2
0; 0; sin sin
2 2 2 2
t t t
t
2
cos 1 2sin 1 2 sin
2 2
t t
x t x
2
2 os 2cos sin 2 sin 1 0
2
t
c t t t
1 os2 sin2 2 sin 1 0
2
t
c t t
sin 2 sin
4 2
t
t
2 2
4 2
2 2
4 2
t
t k
t
t k
3
2
2 4
5 3
2
2 4
t k
t k
4
3 3
3 4
10 5
k
t
k
k
t
3 3
3
os 2 sin
10 5
10
cos 1 2,
x c y
t
t
x y loai
3 3
os ; 2 sin
10 5
c
Bài toán 228.
3
2
2 2 1 3 1 1
1 2 2 1 2
y x x x y
y x xy x
Giải : Điều kiện : . Phương trình (1)
(3)
Xét hàm số:
Hàm số
f t
đồng biến trên
0;

Phương trình
Thay vào phương trình (2) ta được: (4)
Xét hàm số :
nên g(y) đồng biến trên
Hơn nữa g(6) = 0 nên phương trình (4) có nghiệm duy nhất là
Vậy nghiệm của hệ phương trình là : .
Giải : Điều kiện:
2
x
.Phương trình:
3 3 2
2 3 4
x x y y y
1
2
2
x
y
3
2(2 1) 2 1 (2 4 1) 2
x x y y
3
2(2 1) 2 1 2 2 2 2
x x y y y
3
3
2(2 1) 2 1 2 2 2
x x y y
3
( ) 2 , 0;f t t t t

2
'( ) 6 1 0, 0;f t t t

3 (2 1) ( 2) 2 1 2
f x f y x y
4
4 8 2 4 6
y y
4
( ) 4 8 2 4 6, 2;g y y y y

4
1 1
'( ) 0 2;
4 8 2 4

g y y
y y
2;
1
6
2
y x
1
;6
2
Bài toán 229.
3
2(2 1) 2 1 (2 3) 2 1
4 2 2 4 6 2
x x y y
x y
Bài toán 231.
3 3 2
3
3 4 2 0 1
3 2 2 2
x y y x y
x x x y
(3)
Xét hàm số trên . Ta có: .
Suy ra hàm số đồng biến trên .
Phương trình
Thay vào phương trình (2) ta được:
Xét phương trình : (*)
Ta có
Do đó phương trình (*) vô nghiệm. Vậy hệ phương trình đã cho có nghiệm duy nhất .
3
3
2 1 1 2
x x y y
3
2
f t t t
2;

2
' 3 1 0, 2;f t t t

f t
2;

3 1 1 1
f x f y x y y x
1
y x
3
3 2 2 1
x x
3
8 2 2 2
x x
2
2 2 2 2 2
2 2 4
2 2
x x
x x x
x
2
2 2
2 2 4
2 2
x
x x x
x
2
2
2 2 4 0
2 2
x x x
x
2
2
2
2 4 0
2 2
x
x x
x
2 0 2 3
x x y
2 2
2 2
2 4 0 2 4
2 2 2 2
x x x x
x x
2
2
2
2 4 1 3 3; 1, 2;
2 2
VT x x x VP x
x

2;3
Bài toán 245.
2 3 3 3 3
8 12 12 4 y + 3xy
8 2
3 1 4
1
x x xy xy y x
x x
xy x y
x y
Giải : Hệ phương trình
Điều kiện :
Phương trình (1)
(3)
Xét hàm số : . Ta có :
Hàm số đồng biến trên . Phương trình (3)
(4)
Thế vào phương trình (2) ta được :
Đặt , phương trình trên trở thành :
2 3 3 3 3
8 12 12 4 y + 3xy 1
8 2
3 1 1 4 2
1
x x xy xy y x
x x
x y
x y
0
0
1 1 0
1
0
x
x
x y
y
y
3
3 2
8 12 12
4 + 3x
x x x x
x
y y y
3 2
2 3 3
2 2 2 2
3 .1 3 .1 1 3 3 + 3x
x x x x
x
y y y y
3
3
2 2
1 3 1 + 3x
x x
x
y y
3
3,f t t t t
2
' 3 3 0,f t t t
f t
2 2
1 1
x x
f f x x
y y
2
1
x
x
y
2
0
1
x
y
x
3 1 1 4 4 1
x y y x
3 1 1 4 1 1 0
x y y x
1 1
3 4 1 0
1 1
y y
x x
1
0
1
y
t
x
Thế vào phương trình (4) ta được :
Vậy hệ phương trình có nghiệm duy nhất:
Giải : Điều kiện :
Phương trình (1)
(3)
Xét hàm số : . Hàm số đồng biến trên
Phương trình (3)
Ta có : . Thế : y = x – 2 vào phương trình (2) ta được :
2
4 3 1 0
t t
1
1
,
4
t
t loai
1
1 1 1
1
y
y x y x
x
2
0 ,
2
2 0
1
1
x y loai
x
x x x x
x y
x
1;1
2
2 0
16
16 3 0
3
x
x
y
y
3 2 3 2
9 27 27 5 15 3 3 1 5 5
x x x x y y y y
3 3
3 5 3 1 5 1
x x y y
3
5,f t t t t
2
' 3 5 0,f t t t
f t
3 1 3 1 2
f x f y x y y x
16 16 22
2
3 3 3
y x x
2
4 2 22 3 8
x x x
2
4 2 2 22 3 4 4 0
x x x
2
2 6 3
4 4 0
2 2 22 3 4
x x
x
x x
4 3
2 2 0
2 2 22 3 4
x x
x x
Bài toán 246.
3 3 2 2
2
3 32 9 + 8y+36 1
4 2 16 3 8 2
x y y x x
x y x
Xét hàm số :
Hàm số nghịch biến trên
và
, suy ra phương trình (*) có nghiệm
duy nhất x = -1, khi đó y = -3. Vậy hệ phương trình có 2 nghiệm :
Giải : Điều kiện :
Phương trình (1)
(3)
Xét hàm số : . Ta có
Hàm số đồng biến trên
.
Phương trình (3)
Thế vào phương trình (2) ta được :
2 0
4 3
2 0
2 2 22 3 4
x y
x
x x
4 3 22
2,x 2;
3
2 2 22 3 4
f x x
x x
2 2
2 9 22
' 1 0, x 2;
3
2 2 2 2 22 3 22 3 4
f x
x x x x
f x
22
2;
3
1 0
f
2;0 ; 1; 3
2 8 0 4
y y
6 4 2 2 3 2 3
3 3 4 4 4
x x y x y y x y y y
3
2 2 3
4 4
x y x y y y
3
4t,tf t t
2
' 3 4 0, tf t t
f t
2 2 2
2 , 0
f x y f y x y y y x y
2
2
y x
Bài toán 249.
6 4 2 2 3 2
2
3
3 3 2 4 8 0 1
3 2 3 2 2 8 2
x x y x y y x y
y x y
Phương trình (*)
Vì
. Phương trình (*) vô nghiệm.
Vậy hệ phương trình có 2 nghiệm :
3 2 2 2
3 3 2 8
x x x
3 2 2 2
3 1 3 2 8 3 0
x x x
2 2 2
3 3
4 2 2 2
1 1 1
3 0
1 3 2 8 3
x x x
x x x x
2
3 34 2 2 2
3 1 1
1 0
1 3 2 3
x
x x x x
3 3
4 2 2 2
1
1
2
3 1 1
0
1 3 2 8 3
x y
x x x x
3 34 2 2 2
3 1 1
: 0
1 3 2 8 3x x x x
2 2 2 2
2 2
1 1
: 8 3 8 3 3 2
3 2 8 3
x x x x x
x x
3 34 2 2 2
3 1 1
0,
1 3 2 8 3
x
x x x x
1 1
1; ; 1;
2 2
| 1/64
| | Tải xuống

Có thể bạn quan tâm:

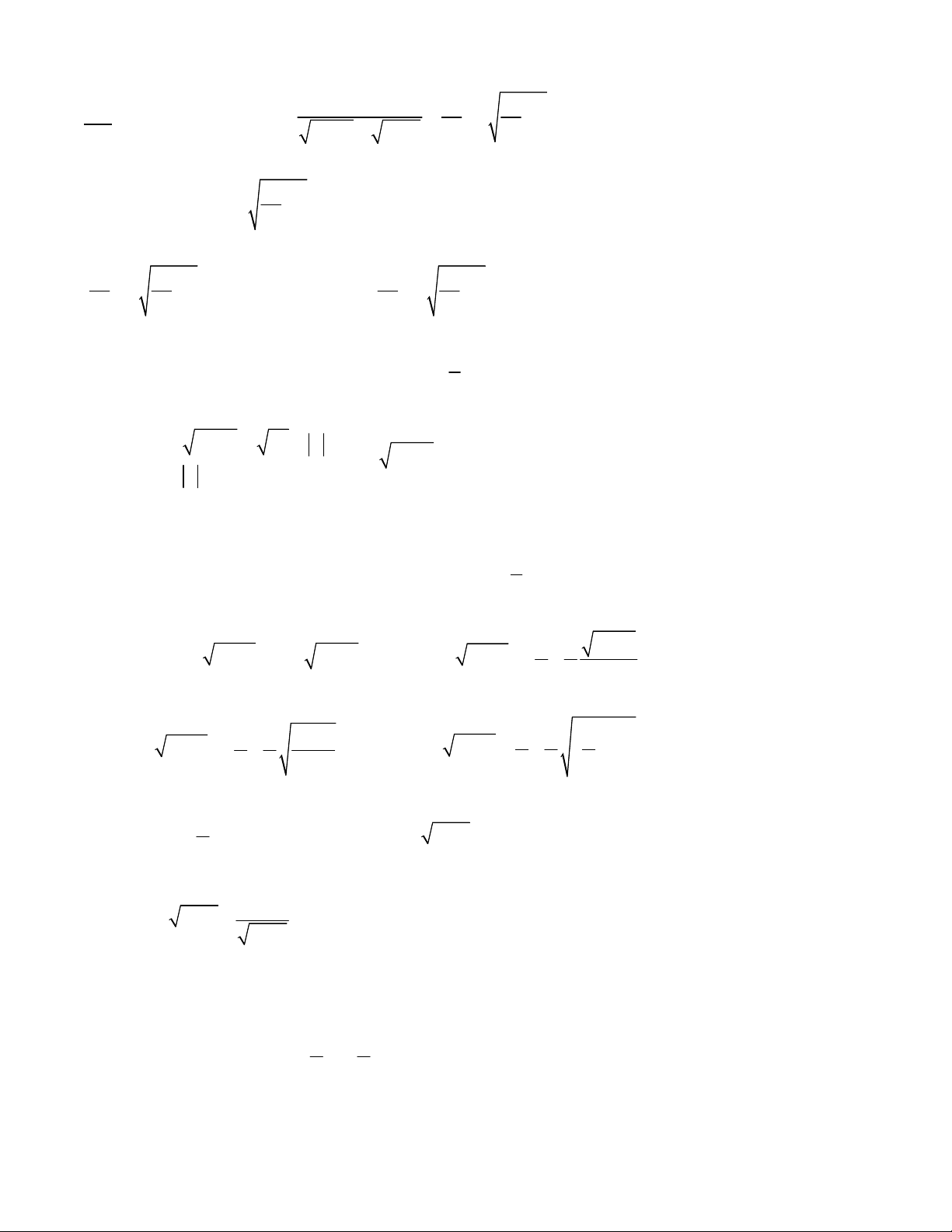
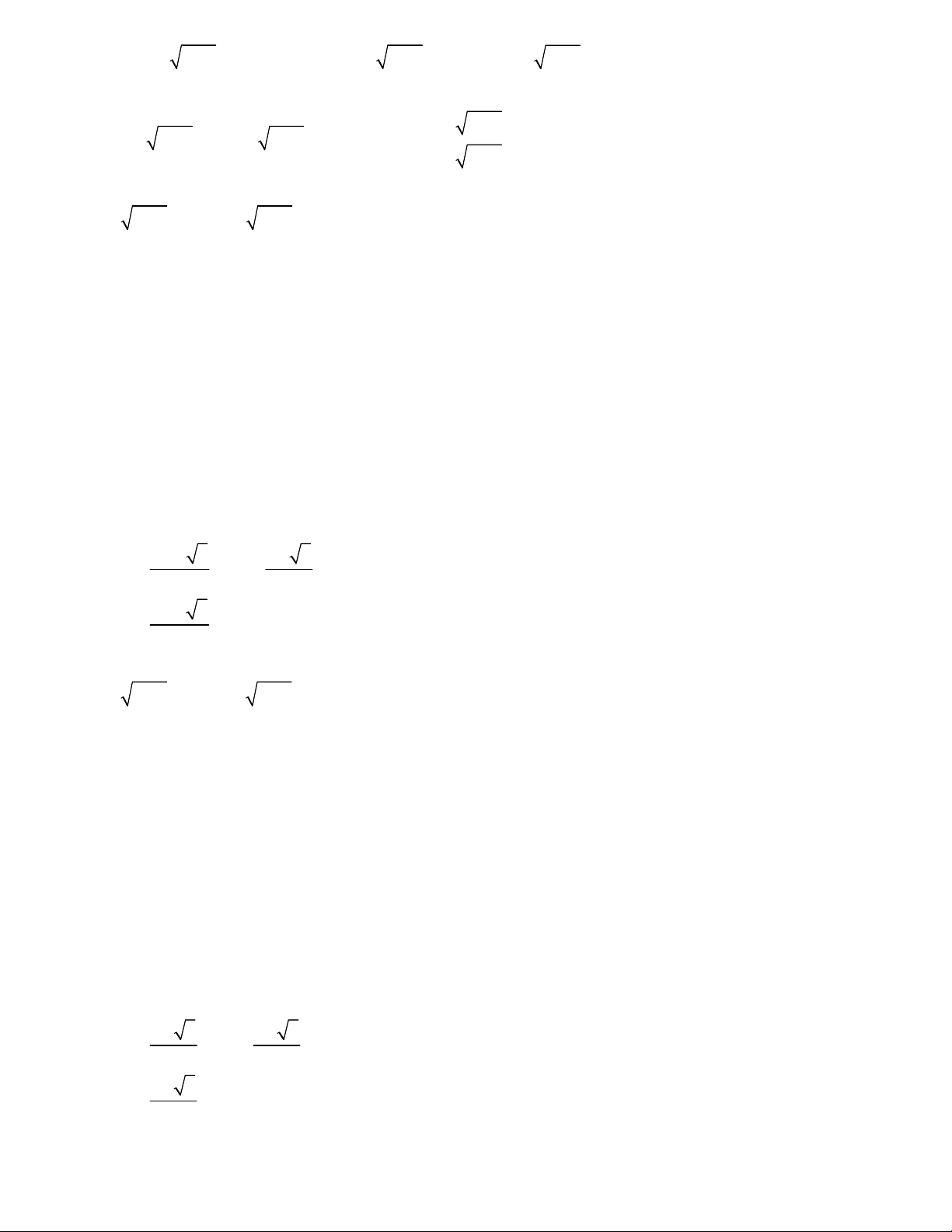
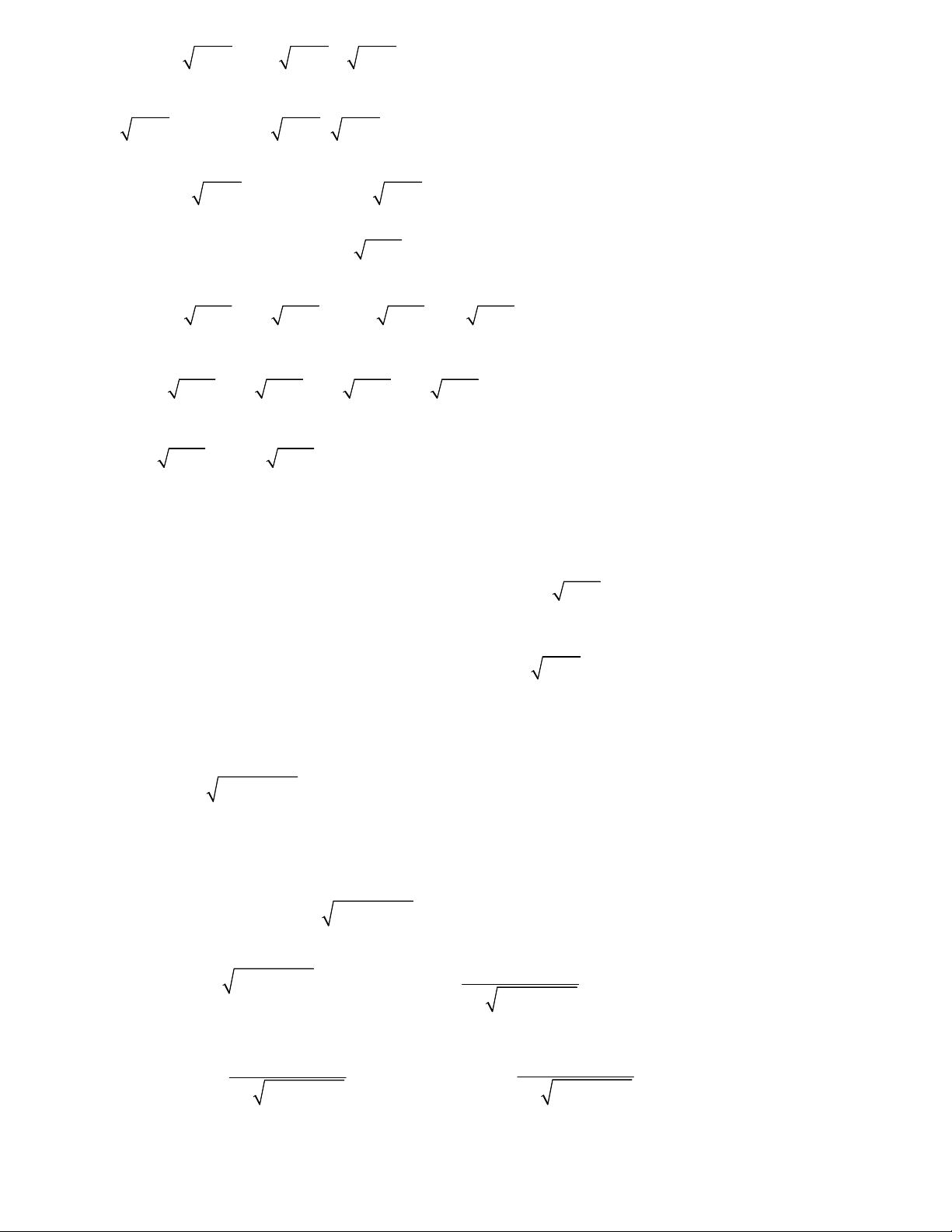
Preview text:

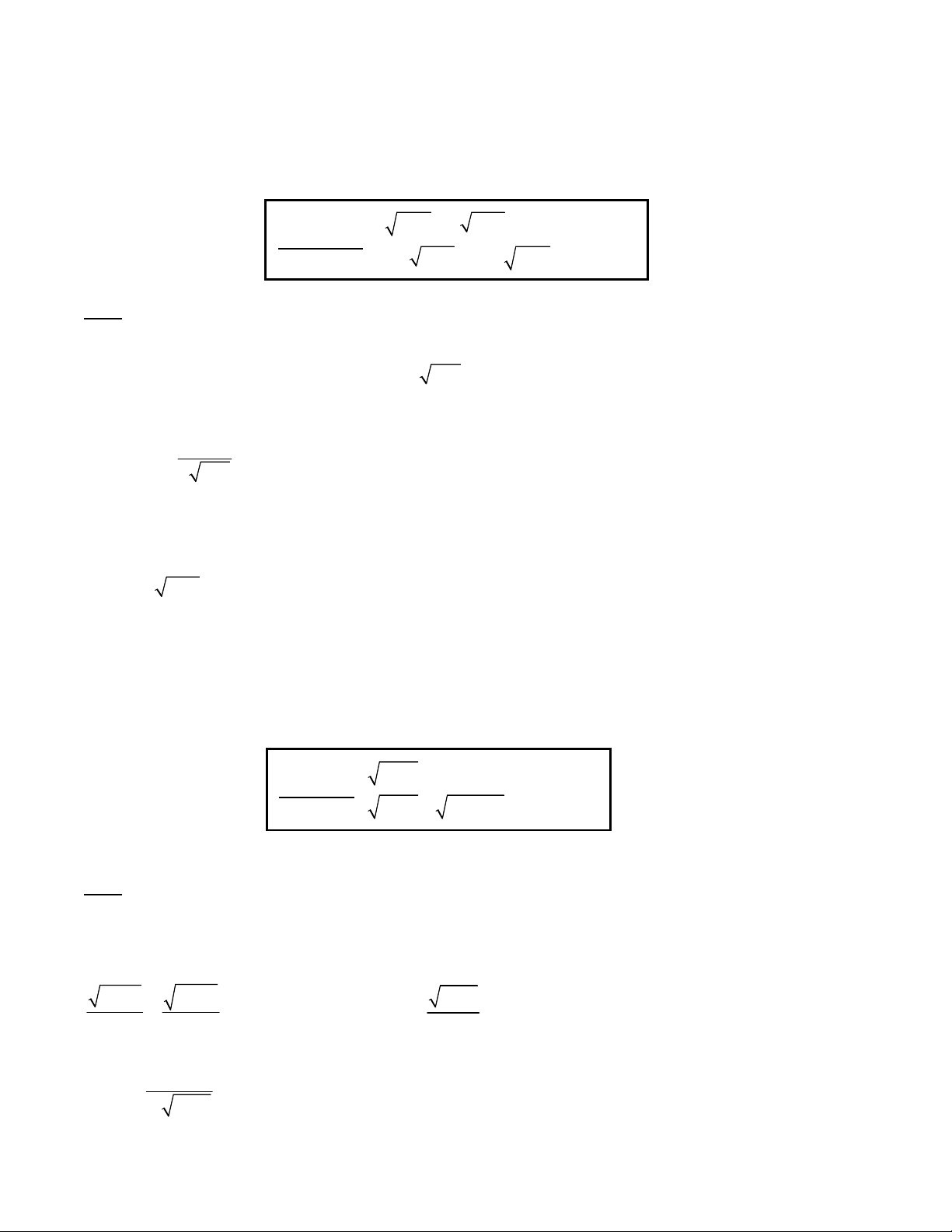
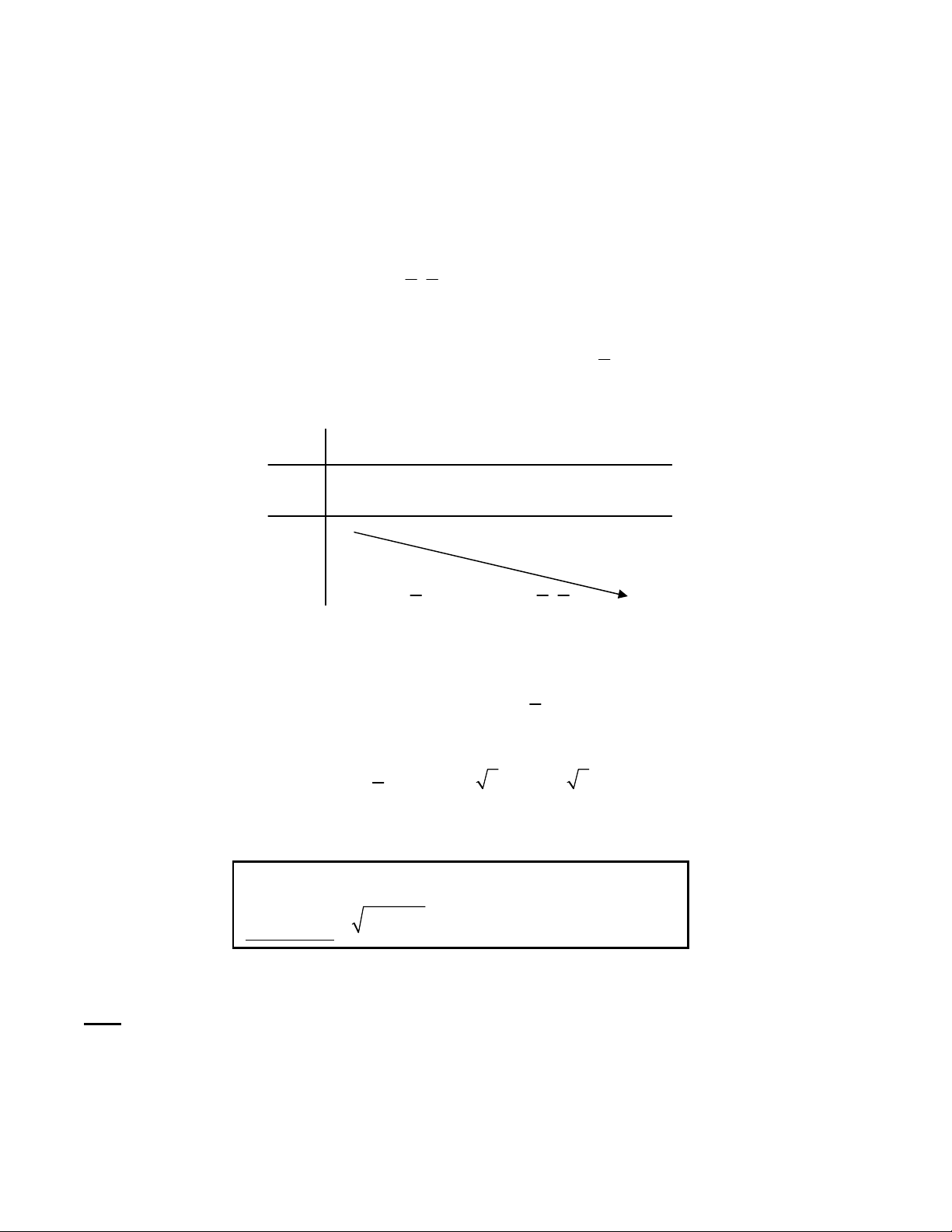
3.PHƯƠNG PHÁP XÉT CHIỀU BIẾN THIÊN HÀM SỐ 4 4 
 1 x x 1 
y  2  y (1)
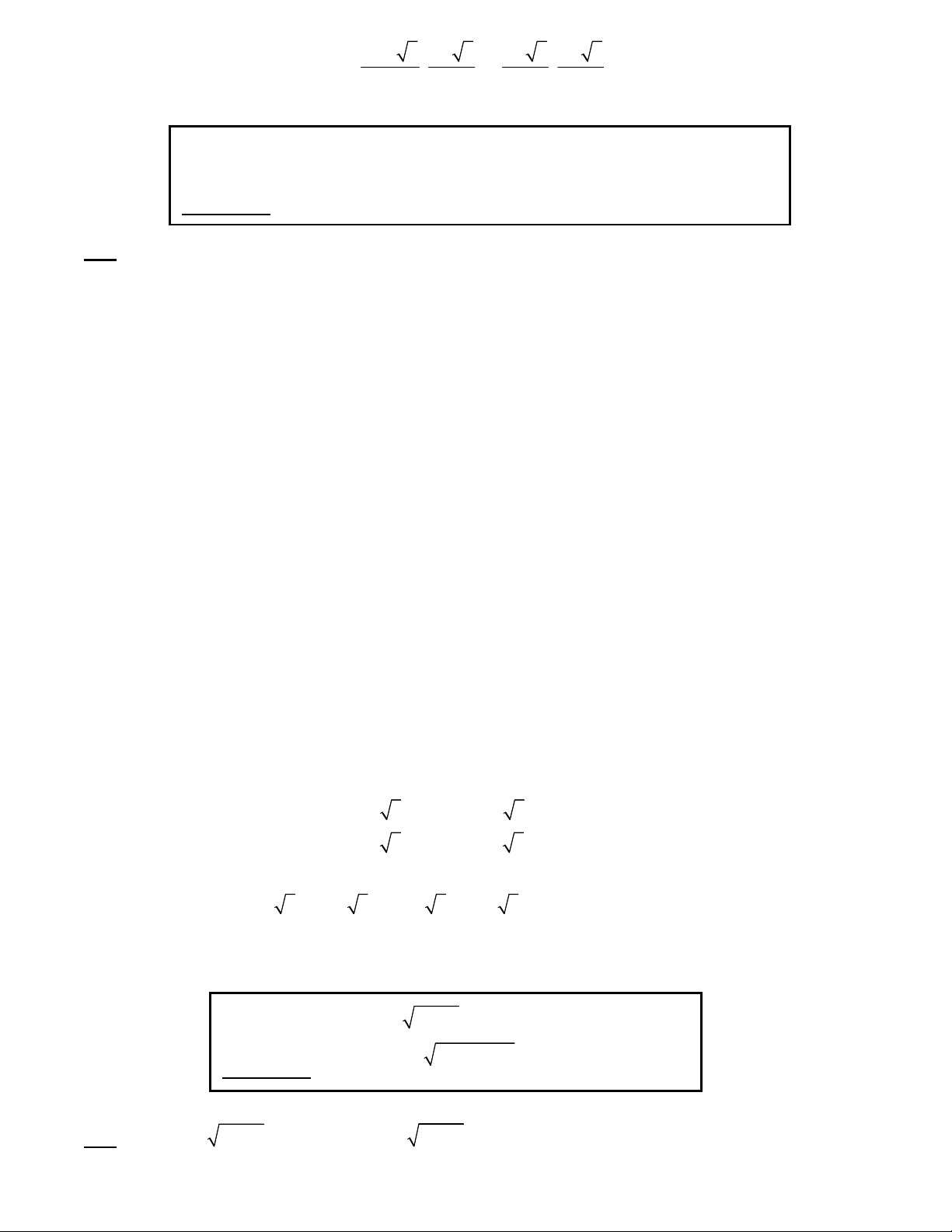
Bài toán 7(A – 2013).  2
x  2x y   2
1  y  6 y  1  0 2 
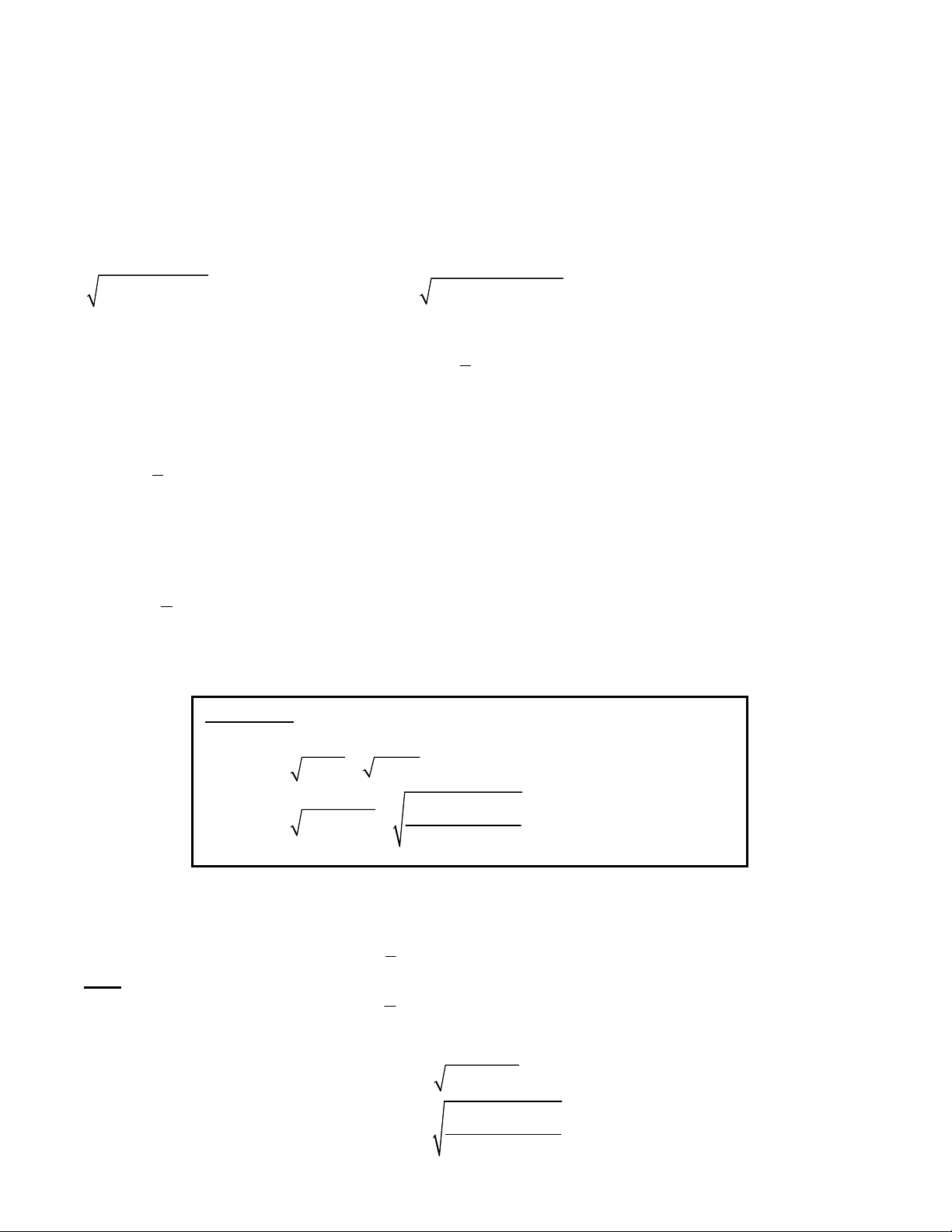
Giải: Điều kiện : x 1. Phương trình   4 4
1  1 x x 1  y y  2 . Đặt 4 u x 1, u  0 4 4
x u 1  x 1  u  2
Khi đó,phương trình (1) trở thành : 4 4
u u  2  y y  2 3 Xét phương trình (2) : 2
x   y   2 2
1 x y  6 y 1  0
Xem x là ẩn, y là tham số, ta có :   4y
Phương trình có nghiệm y  0
Xét hàm số f t 4
t t  2,t 0; 2 2t
f 't   1
 0,t 0;  4 t  2
Suy ra hàm số liên tục và đồng biến trên 0; 
Từ đó, phương trình   4
3  u y x 1  y . 4  y x 1 4
x y  14
Thế (4) vào phương trình (2) ta được :  y  2 4   4
y   y   2 1 2 1
1  y  6 y 1  0 8 5 2
y  2 y y  4 y  0  y y   6 5 4 3 2 1
y y y  3y  3y  3y  4  0
y  0  x  1  
y  1  x  0, loai
Vậy nghiệm của hệ phương trình đã cho là 1;0
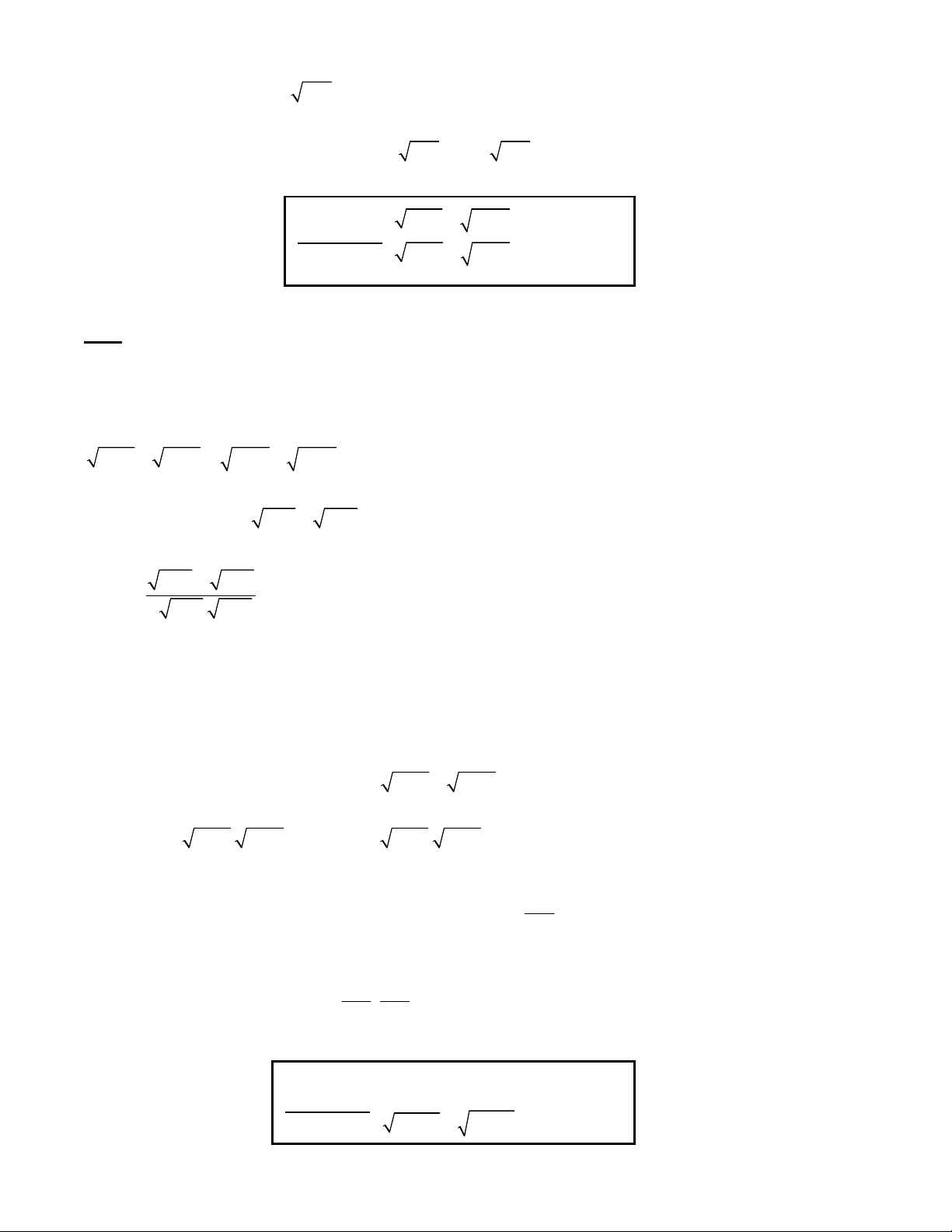
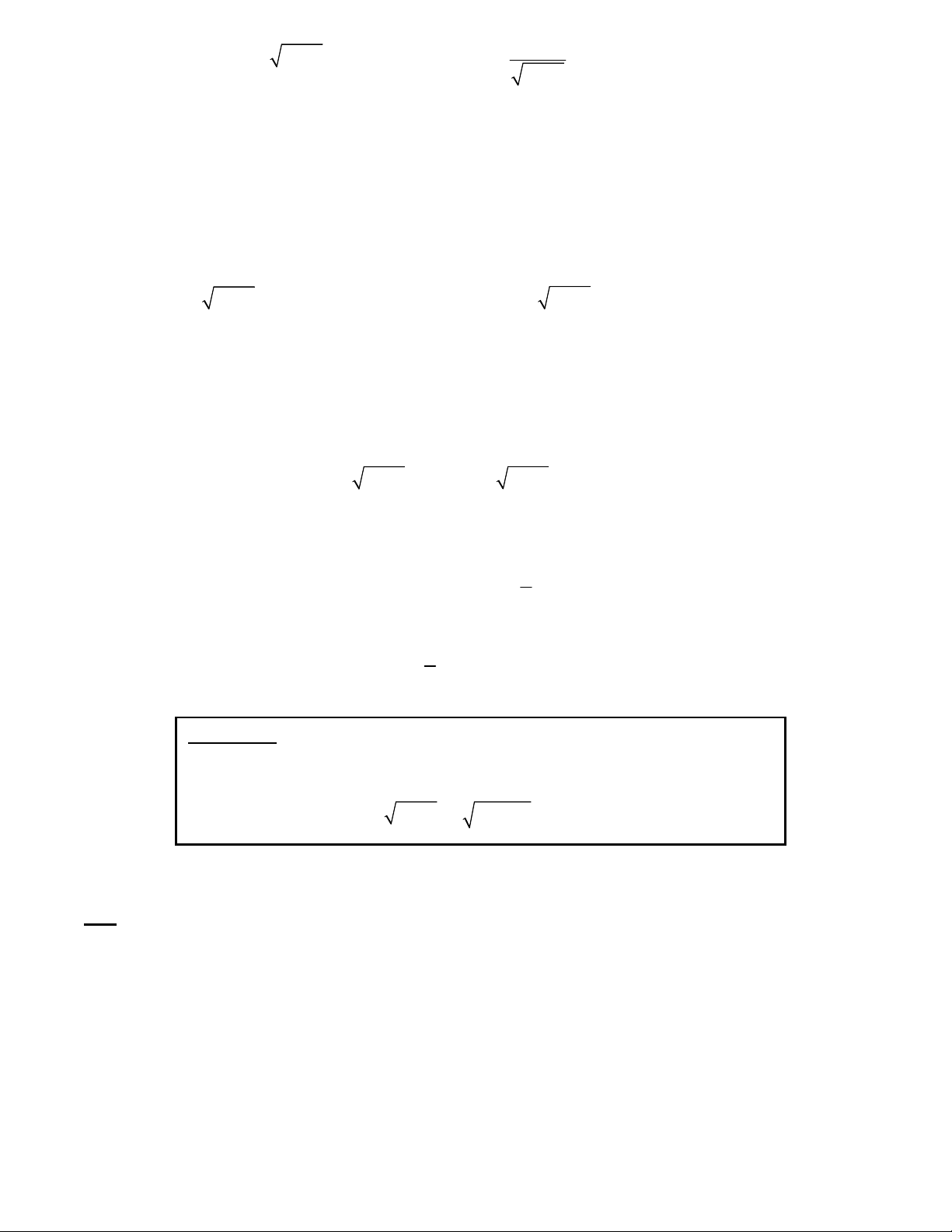
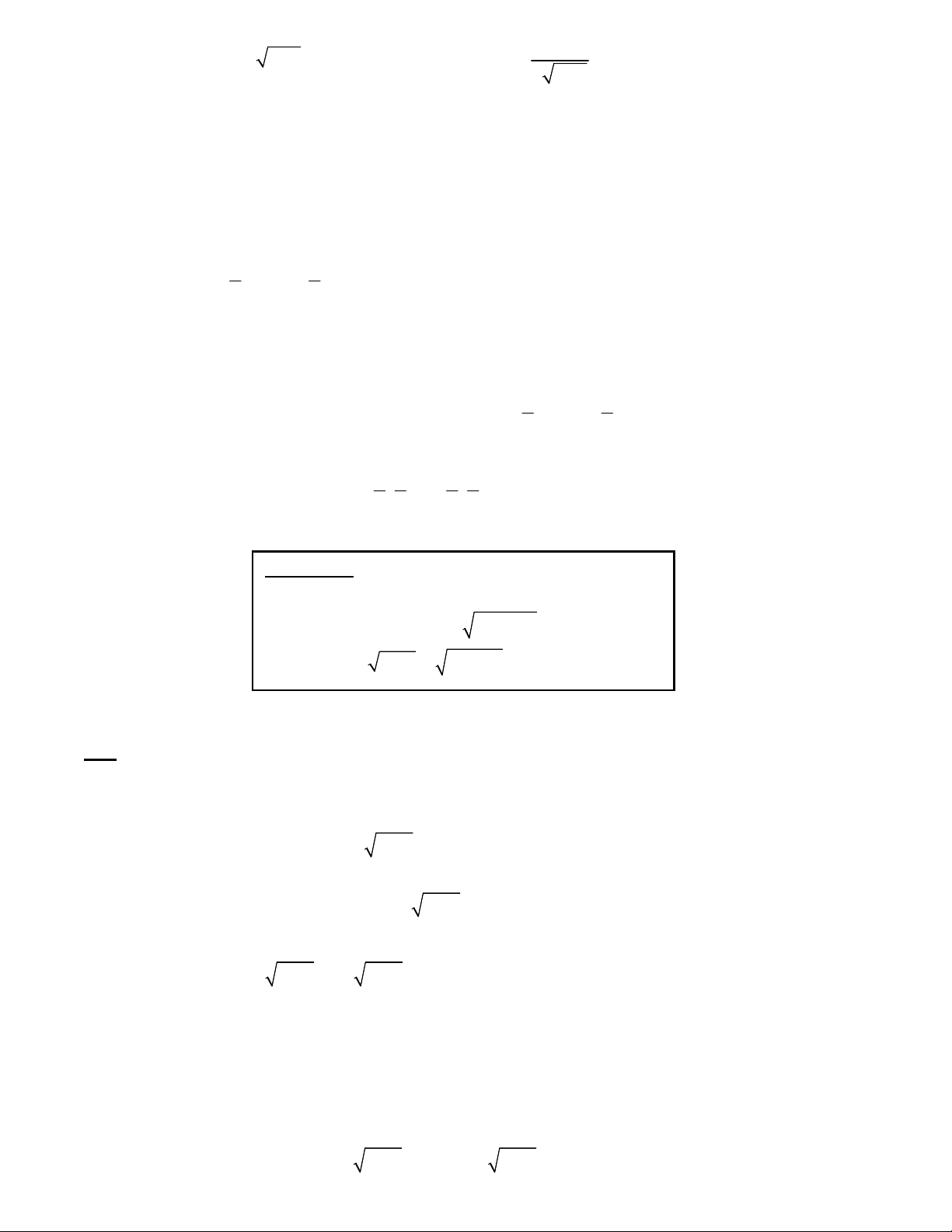
x y 1  y x 1  4    1 Bài toán 11.  2 2
x x 1  y + y 1 2  Giải:x  1 Điều kiện : 2 
. Xét hàm số f t   t t 1,t 1; y  1  1
f 't  2t   0, t
 1;  . Suy ra hàm số đồng biến trên 1;  2 t 1
Từ đó, phương trình 2  x y .   1  2x x 1  4 2
x x   1  4 3 2
x x  4  0  x  2  y
Vậy hệ phương trình có nghiệm 2; 2 .
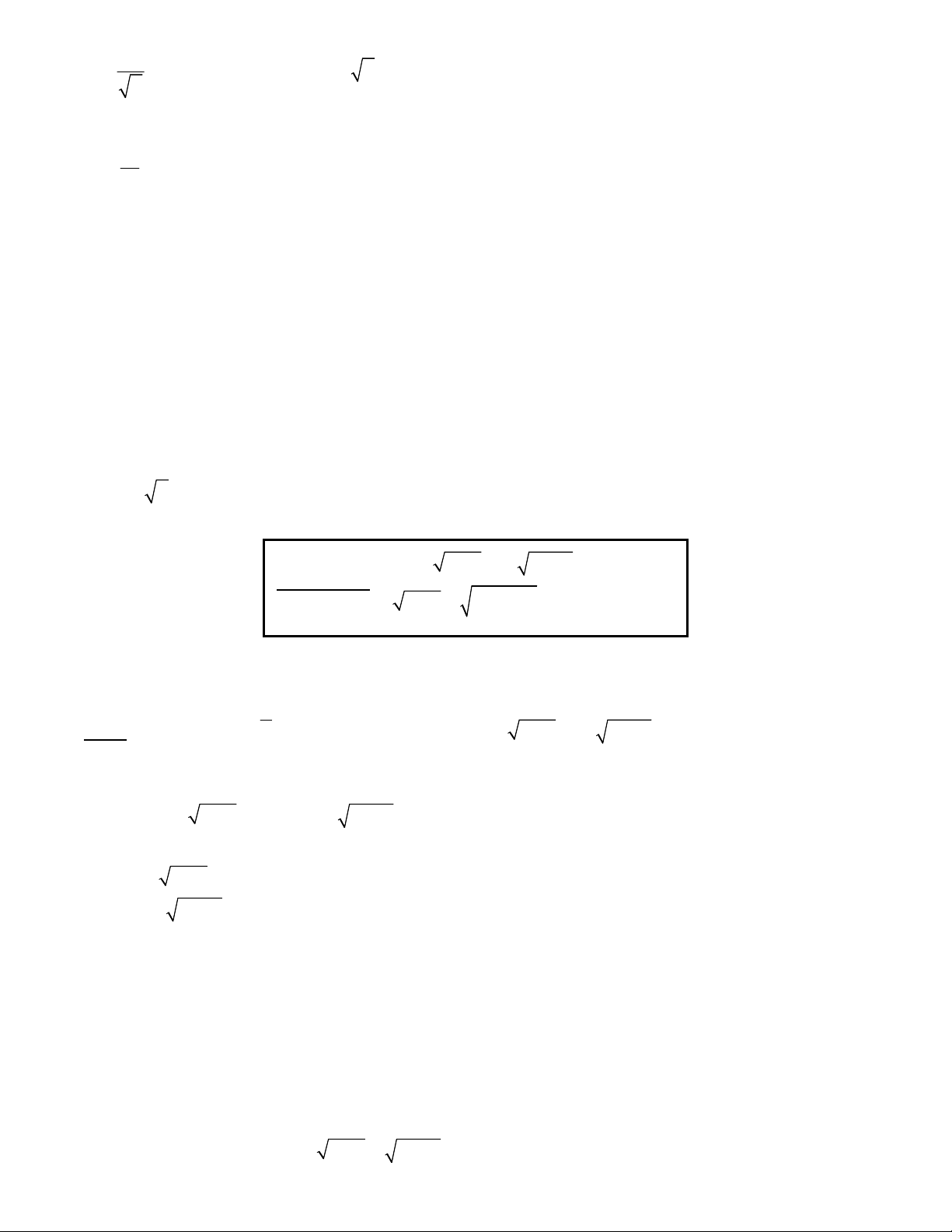
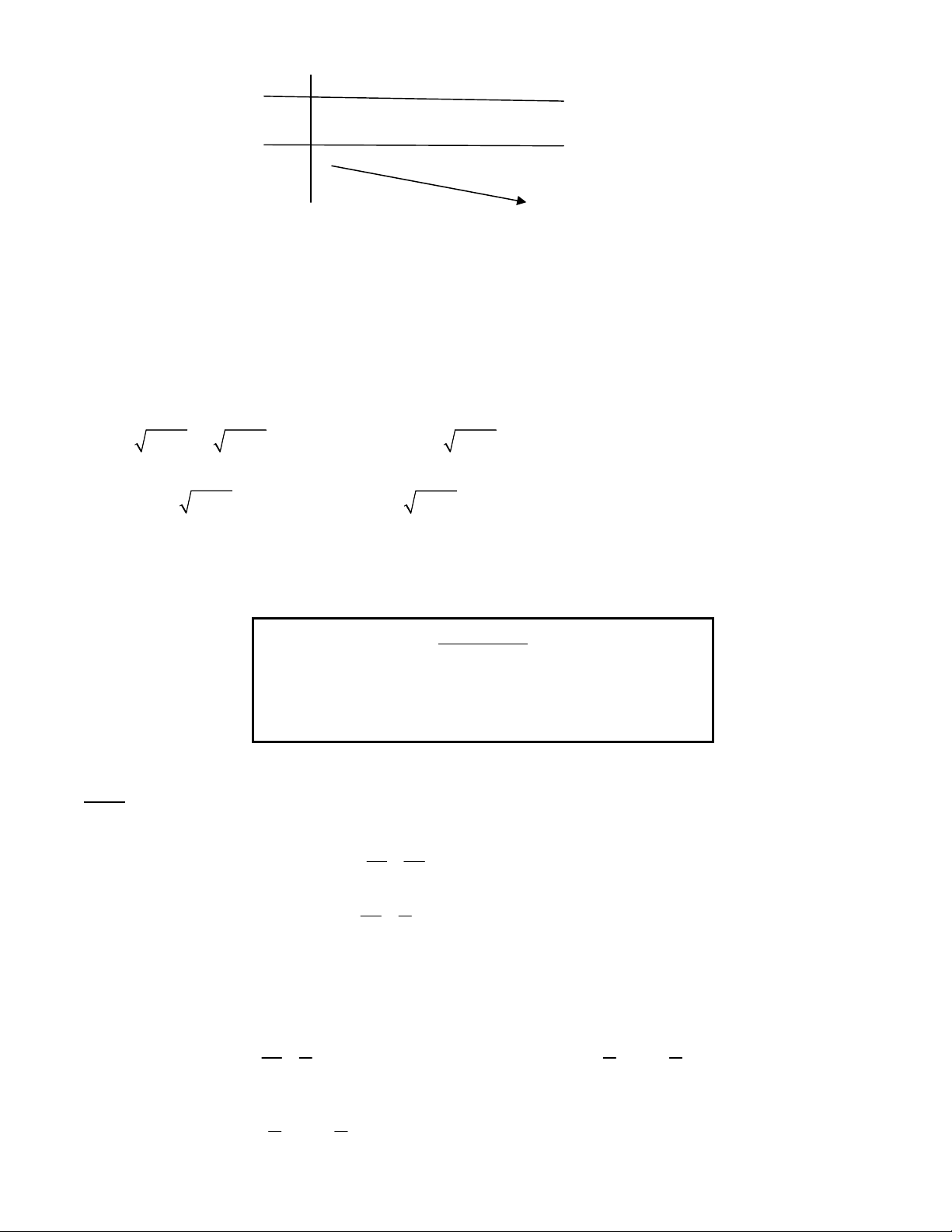
x y x y  0 (1)  Bài toán 2.
x y  3x  2 y  1  2 
Giải: Điều kiện : 0  x, y  1
Lấy phương trình (1) trừ phương trình (2) vế với vế, ta được : 2 2 1 x 1 y 2 1 t
 . Xét hàm số f t  ,t 0;  1 x y t 1 f 't    0, t  0;  1 2 2 t 1 t
Suy ra hàm số liên tục và nghịch biến trên [0; 1]
Từ đó, phương trình   x y . Khi đó 1 1   2
1  x 1 x  2  x  2 1 x   2 4  2  x   , loai 1 4 2 2  4
x  4x 1  0 2  x    2  2  x   y  2  2 2 
Vậy nghiệm của hệ phương trình đã cho là  ;   2 2    2 2
x 1  3 y 1  10   2 2
x y    1 Bài toán 17. 2
x  2  16  2x  2 y - 628 = 0 2  x  2  0
Giải: Điều kiện :   2  x  8 16  2x  0 
Áp dụng bất đẳng thức Bu-nhia-cop-xki cho 4 số : 2 2
1, x 1,3, y 1 ta được 2 x    2 y   2 2 2 2 1 3
1  1  3 . x 1 y 1 2  x    2 y     2 2 1 3 1 10 x y
Do phương trình (1) nên dấu “ =” xảy ra. Khi đó ta có : 2 2 x 1 y 1    2 x   2 9 1  y 1 2 2
 9x 10  y 1 3 Thế 2 2
9x 10  y vào phương trình (2), ta được : x    x   2 2 16 2
2 9x 10 - 628 = 0 (3)
Xét hàm số : f x  x    x   2 2 16 2
2 9x 10 - 628, x 2;  8 1 1 f ' x  
 36x  0, x  2;8 2 x  2 16  2x
Vậy hàm số f x đồng biến trên (2; 8) và f 6  0 do đó phương trình (3) có nghiệm duy nhất x
= 6. Với x = 6 ta có y   314
Vậy hệ phương trình có 2 nghiệm : 6; 314;6; 314
x  5  y  2  7    1 Bài toán 65.   x  2  y  5  7 2  x  2
Giải: Điều kiện : y  2 
Lấy phương trình (1) trừ đi phương trình (2) vế với vế, ta được : x  5  x  2  y  5  y  2 3
Xét hàm số : f t  t  5  t  2 ,t  2;
t  2  t  5 f 't    0, t   2
2 t  5. t  2
Vậy hàm số nghịch biến trên2;  .
Phương trình 3  f x  f y  x y
Khi đó, hệ phương trìnhtrở thành : x  5  x  2  7
 2x  3  2 x  5. x  2  49 
x  5. x  2  23  x 2  x  23  2  x  23 539      x   yx  5 
 x  2  23  x2  49x  539  0 49   539 539 
Hệ phương trình có 1 nghiệm ;    49 49  x   2 2 x + y  4 = y  2 1+ y    1 Bài toán 78.  2  4x  5  y  8=6 2 
Giải: Điều kiện : x  0
Nếu y = 0 thì phương trình(1) tương đương : 3
x  0  x  0 , không thỏa hệ. 3  x x
Xét y  0 :phương trình   3 1    y y   3 y y   Xét hàm số 3
f (t)  t t, t   ; f t  2 '
 3t 1  0, t  
Suy ra, hàm số f(t) đồng biến trên  x   2 3 
y x y 4 . Thế (4) vào phương trình(2) ta được : y 2 2 4 y  5  y 18  6   2 y   2 y   2 2 4 5 18  23  5y 115 115 Điều kiện : 2
23  5 y  0    y  5 5
Bình phương 2 vế của phương trình trên, ta được :
y y      y 2 4 2 2 4 4 37 40 23 5 4 2
 9 y  378 y  369  0 2
y  1  x    y  1  2 y  41,loai
Vậy nghiệm của hệ phương trình đã cho là 1;  1 , 1;   1 2   3
x  2x y   2
1  x y   1   1 Bài toán 89.  3 2
y  4x 1 ln  y  2x  0 2 
Giải: Điều kiện : 2
y  2x  0 Phương trình(1)   3
x x   y   2 2 2 2
1  x y   1  0  x  2
x     y   2 2 2
1 x  2  0   x y   2 2 1 x  2  0
y  2x 1 3
Thế (3) vào phương trình(2) ta được :
x  3  x    x  2 2 1 4 1 ln 2 1  2x  0  
  x  3  x    x  2 2 1 4 1 ln 2
1  2x  0   
Xét hàm số f x   x  3  x    x  2 2 1 4 1 ln 2
1  2x , x     8x  2
f ' x  32x  2 1  4  2 4x  2x  1 32x  2 1  2
4x  2x   2 1 16x  2 f ' x   0, x    2 4x  2x 1
Suy ra, hàm số f(x) đồng biến và liên tục trên  . Mặt khác , f(0) = 0
Vậy phương trình  có nghiệm duy nhất x = 0, suy ra y = -1
Vậy nghiệm của hệ phương trình đã cho là 0;  1  . 3 4 
x y y =278 Bài toán 90. 2 2 3
x y  2xy y  100  Giải: y   3 3
x y  =278   1
Hệ phương trìnhtương đương với 
y x y2  100 2 
Từphương trình (2) suy ra y > 0.Viết lạiphương trình (1) :
y x y  2 2
x xy y   278 . . Vì y > 0 và 2 2
x xy y  0, x  , y   10
nên (1) x y  0  x y  0 .Phương trình(2)  x   y 3 y
Thế (3) vào phương trình(1) ta được : 3    10  3 y 
y   y   278 . Đặt t y,t  0 , ta có phương trình :  y        3 10  3 2 2  6 t 9 3   tt  
  278  t  10  t   278t  0   t     3
Xét hàm số f t 9  t   3
10  t   278t  0,t 0; 2 f t  8 2  t t  3 ' 9 9
10  t   278  0, t  0;
Suy ra, hàm số f(t) đồng biến và liên tục trên 0; . Mặt khác , f(1) = 0
Vậy phương trình  có nghiệm duy nhất t = 1.
Từ đó, y  1  y  1 x  9 . Vậy nghiệm của hệ phương trình đã cho là 9;1 . 
 3  x 2  x - 2y 2 y 1 = 0   1  Bài toán 109. 3
2 2  x - 2 y   1 = 1 2   1  y
Giải : Điều kiện : 
2 . Phương trình (1)  3  x 2  x  2 y 2 y 1 x  2 
 1 2  x 2  x  1 2y   1 2 y 1 (3) u  = 2  x Đặt   u, v  0
v = 2 y 1  Phương trình (3)   2
u u   2  v  3 3 1 1
v u u v v 
Xét hàm số f t 3
t t,t  0 ; f t  2 '
 3t 1  0, t   0
Suy ra, hàm số f t  đồng biến trên 0; .
Phương trình   u v  2  x  2y 1
 2  x  2 y 1  x  3  2 y
Thế : x = 3 – 2y vào phương trình (2) ta được :
y    y  3 2 2 1 2 1  1
Đặt X  2 y 1  0 , phương trình trở thành :   X  1   5 1 3
X  2 X 1  0  X   2    5 1 X  ,loai  2
X  1  2 y 1  1  y  1  x  1 5 1 5 1 X   2 y 1  2 2 6  2 5 5  5 1 5  2 y 1   y   x  4 4 2  1 5 5  5 
Hệ phương trình đã cho có 2 nghiệm : 1;  1 ,  ;  .  3 4    3
x 1 - y = 8  x Bài toán 115.  4   x   1 = y  x  1
Giải : Điều kiện :  y  0  3
x 1 - y = 8  x Hệ phương trình      x  2 1 = y   x 1 -   x  2 3 1 = 8  x   1    x  2 1 = y 
Xét phương trình (1) : x  -  x  2 3 1 1 = 8  x 2 3 
x 1 - x + 2x - 1= 8  x 3 2
 x - x + 2x + x 1 - 9= 0 
Xét hàm số : f  x 3 2
= x - x + 2x + x 1 - 9, x  1 1 f' x 2 = x 3 - 2x + 2 + , x  1 2 x 1
Xét hàm số : g x 2 = x 3 - 2x , x 1 g ' x = x 6 - 2 > 0 , x   1
Hàm số g(x) đồng biến trên 1;
g x  g   1 , x
  1  g x  1, x   1
f ' x  0, x   1
Vậy hàm số f(x) đồng biến trên 1;
Mặt khác, f(2) = 0.Suy ra, phương trình  có nghiệm duy nhất x = 2, y = 1
Hệ phương trình đã cho có 1 nghiệm : 2;  1 . 2  y 1 y  2 2 
y  2 x  2   1  x
Bài toán 121(THPTQG 2014-2015). x 1 y 2 x  
y y 2  y x x  2
Giải : Điều kiện :  y  0  Phương trình (2) 2
x y x x   2 3 2
1  y y x y x
x xy x 2 2
y x y  3 2 y x y x 
  xy x 2 x y  2
y xy  x  0
  xy x 2
x y    2
x y   0   xy x   2
1 x y   0 2  2 x y  0 x y    
xy x 1  0 
x y   1  1  2
x y  0 , thế vàophương trình (1) ta được : 2  y  2 y 2 2 1 
y  2 y  2 2 2
y  2 y  2  y  2 y  2  0 2 yy y   2 y   2 2
2  2 y  2  0  y y   2 y   2 2 2  2 y  2 u   y  Đặt 2 2 
u, v  0 , Phương trình trở thành : u  2u v  3v  2 v y  2  Xét hàm số : 2
f (x)  t  2t, t  0; 
f 't   2t  2  0,t  0
Suy ra, hàm số f(t) đồng biến và liên tục trên 0;  Phương trình  2  u v y y  2  y  1  ,loai 2 2
y y  2  y y  2  0
  y  2  x  4  1
x y   1  1  x y 1 1 1 Do x ≥ 2 
 2  2 y  2  1  y   , vô lý. y 1 2
Vậy hệ phương trình có nghiệm : 4; 2 2 xy   2  x   2 1
1  y+ 1 y   1 
Bài toán 128(Chuyên Lê Hồng Phong) 4 y 1 1 1   4  3  +8 2
 1 3y  2  y xy xy 4 y 1 1 1
Giải : Phương trình (2)    4  3 + 8 (3)
1 3y  2  y xy xy 1
Với xy  0, đặt u
 3,u  0 ,ta có : xy 1 1 1 1 2 - 4
 3 + 8 = u  4u  5  - 4
 3 + 8= u - 22 1  0 xy xy xy xy 1
Từ phương trình (3) ta có : 4y 1  0  y  4 2 2   y 1  y y Ta lại có : 2   y y 1  0, y     y y  x  0
Từ phương trình (1) ta suy ra : 
x  0 . Điều kiện : 1  y  2   4 2 1 1 1 y Ta có : 2 xy  2  x   2 1 1  y+ 1 yx  2 1 x 1  + y y y 2 2  1 1  1   x  1 1 1 y 2 1 x 1  + 2
x x x 1  + 1 2   y y y y y y    1 
f x  f . Xét hàm số : 2  
f (t)  t t t 1 t   y   2 t f 't  2  1  t  1   0, t   2 t  1
Suy ra, hàm số f(t) đồng biến và liên tục trên     
Xét 2 điểm M x f x 1 1 , , N , f
thuộc đồ thị hàm số f(t).     y y    
Ta có : y y và hàm số f(t) đồng biến và liên tục trên  nên M N 1
x x x   xy  1 M N (3) y Xét phương trình (1) : 3 4
y  2  4 y  2  3x +3x - 1
Thế (3) vào phương trình (1) ta được : 4 2 3
x  4x  3x + 3x - 1 4 3 2
x  3x  4x  3x 1  0 (4)
Nếu x = 0, không thỏa phương trình (4), xét x ≠ 0.
Chia 2 vế củaphương trình (4) cho 2 x ta đựợc : 1 3  1 1   1 2  x   3x   4  0 2  x  2. . x   3 x   2  0 2     x x 2  x x   x   1 1   1 2   x  2. . x   3 x   2  0  2     x x   x  2  1   1   x   3 x   2  0      x   x  1
Đặt t x  , phương trình trở thành : xt  1 2
t  3t  2  0  t  2  1 t   1  x  =1 2
x x 1=0,VN x 1 t   2  x  =2 2
x  2x 1 = 0  x = 1 y = -1 thỏa điều kiện : y  2  x
Hệphương trìnhphương trình có nghiệm duy nhất : 1;  1 3
y x  2+8 x  2 = 10y - 3xy + 12    1
Bài toán 134.(Chuyên Hạ long)  3 2 3 5  y
2  x  8  6 y xy 2  x 2  x  2  0
Giải : Điều kiện :   2
  x  2 2  x  0 
y  0 không thỏa phương trình (2).
Chia 2 vế của phương trình (2) cho 3 y ta được : 3 8 6 6  2  5 2  x  
x 2  x  2  x  2 2  x  5 2  x   3   y y y y   3 3  2  2  2  x  3 2  x   3. (3)     y y  
Xét hàm số : f t 3
t  3t,t   ; f t  2 '
 3t  3  0, t   
Hàm số f(t) đồng biến và liên tục trên  và
y  0, x  2   2     f   x  2 3 2  f  2  x    2 (4)   y   y y    2  x
Thế (4) vào phương trình (1) ta được : 6 20 6
x  2 +8 x  2 = - x + 12 2  x 2  x 2  x 2
 3 x  2 - 6 2  x +4 4  x = 10 - 3x (5)
Đặt : t  3 x  2 - 6 2  x 2 t x
x t   x      x 2 3 2 - 6 2 9 2 36 2  36 4  x 2
 90  27x  36 4  x 2 90  27x t 2   4 4  x (6) 9
Thế (6) vào phương trình (5) ta được : 2 90  27x t t   0 t+ = 10 - 3x 2  t  +9t = 0   9 t  9 
t  0  3 x  2 - 6 2  x  0 6
 3 x  2 = 6 2  x  9 x  2  362  x
 45x  54  0  x   y  5 5
t  9  3 x  2 - 6 2  x  9  3 x  2  9  6 2  x
 9  x  2  81 362  x 108 2  x
 5x 15  12 2  x , vô nghiệm vì : 5x – 15 < 0, x   2  ;2  6
Hệ phương trình có nghiệm duy nhất :  ; 5    5  3 2 2
y 12y  25y 18  2x  9 x  4   1 
Bài toán 135.(THPT Nghi Sơn)  2 2
 3x 1  3x 14x  8  6  4 y y 2   1 3  x 1  0 x   
Giải : Điều kiện :    3  2
6  4 y y  0   2
  10  y  2  10   25   9 Phương trình (1) 3 2 
 2 y  6 y
y  9  2 x x  4      2   2   1   1 3 2 
 2 y  6 y 12 y  8 
y 1  2 x  4  x  4      2   2  3   y  3 2 2
  y  2  2 x  4  x  4 3
Xét hàm số : f t 3
 2t t,t   ; f t  2 '
 6t 1  0, t   
Hàm số f(t) đồng biến và liên tục trên  và
Phương trình 3  f y  2  f x  4   2   y  2   10 
x  4  y  2   2
y  4y  4  x  4    2   y  2   10   2
y  4 y  x  4 
Thế (4) vào phương trình (2) ta được : 2
3x  1  3x 14x  8  6  x 2
 3x 1  6  x  3x 14x  8  0 2
 3x 1  4 1 6  x  3x 14x  5  0 3 x  5 x  5  
  x  5 3x   1  0 3x 1  4 1 6  x  3 1    x  5   3x 1  0  
 3x 1  4 1 6  x
x  5  y  1   3 1 1  
 3x 1  0, VN x   
 3x 1  4 1 6  x 3
Hệphương trình có nghiệm duy nhất : 5;  1 2 2 2
x y x 1  2x x y  2    1
Bài toán 136.(Sở GDĐT Thanh Hóa)  3  y  6 x   1  3y  2 x  2 2
 3y  4  0 2 
Giải Điều kiện : 2 2
x y  2  0  x y  2 Phương trình (2) 3 6 3 2 2
y x y  3yx  6 y  3y  4  0 3 3 6 2 3 2 3
y x  3yx y  3y  6 y  4   2 yx  2
 3yx   y   1  3 y   1 3
Xét hàm số : f t 3
t  3t,t   ; f t  2 '
 3t  3  0, t   
Hàm số f(t) đồng biến và liên tục trên  và    f  2 3
yx   f y   1 2
x y y 1 4 .Điều kiện : y 1  2   y  1
Thế (4) vào phương trình (1) ta được : 2
y x  2x y 1 2
y 1 x 1 2x y 1  0  x y  2 1 1  0
x y 1 1  0
  x y 1  
1 x y 1   1  0   x y 1 1  0 
x y 1 1  0 
y 1  x 1 x  1  x  1    x  1       2  2 
y 1   x   1
y 1   x  2     1 
y x  2x  5 
Thế (5) vàophương trình (4) ta được : 2 x  2 x x 2 2
x  2x 1 4 3 2 2
x  2x x  2x  2x 1  0
  x x2 2   2
2 x x 1  0  x x  2 2 2
1  0  x x 1  0  1   5 1 5 x   y   2 2    1   5 x  ,loai  2
x y 1 1  0 
y 1  x 1 x  1 x  1   x  1      2  2 
y 1   x   1
y 1   x  2     1 
y x  2x  6 
Thế (6) vào phương trình (4) ta được : 2 x  2 x x 2 2
x  2x 1 4 3 2
x  2x x  2x 1  0 4 3 2 2
x  2x x  2x  2x 1  0  x x  2 2 2
1  0  x x 1  0  1 5 1 5 x   y   2 2    1 5 x  ,loai  2  1
  5 1 5  1 5 1 5 
Hệ phương trình có 2 nghiệm :  ; ; ;   2 2   2 2      2x  2 x  3 - y 2
y  3 = 3xy x y   1   2 2
x  2  42  y 2
Bài toán 139.(THPT Can Lộc)
Giải : Từ phương trình (2) suy ra : 2  y  0  y  2 (1) 3 3 2 2
 2x  6x - y  3y  3x y + 3xy  0 3  x x  3 3 2 2
3 + x - y  3x y + 3xy   3y  3x  0 3  x x  3 3 3 + x - y
 3y  3x  0 3
x  3x =  y - x  3 y x 3
Xét hàm số : f t 3
t  3t,t   ; f t 2 '
 3t  3  0, t   
Hàm số f(t) đồng biến và liên tục trên  và
3  f x = f y x  x = y - x  y = 2x .Điều kiện : 2x  2  x 1
Thế y = 2x vào phương trình (2) ta được : 2
x  2 x   1 x  2 2 2
 42  2x  x   x  2 4 4 1   2
x  2 x   1  2
x  2x  2  0,VNx  1   3  y  2   2 3     2
x  2x  2  0  x  1   3  y  2   2 3  Hệ có 2 nghiệm :  1   3; 2   2 3; 1   3; 2   2 3  2
xy  2 = y x  2    1  2
y  2 x   2 2 1
x  2x  3 = 2x - 4x 2  Bài toán 142. Giải : (1) 2  y
x  2  x  2 3 . Vì 2
x  2  x  0, x
    y  0     2 y Phương trình (3)   2 2
y x  2  x 4 2 x  2  x
Thế (4) vào phương trình (2), ta được : 2 2 2 2 x  2  x  2 x 1
x  2x  3 = 2x - 4x .     2
  x x   x   x   2 1 2 2 1
x  2x  3 = 0
x x   x    x    x   2 2 2 1
1   2 - x   1 5   2 t
Xét hàm số : f t 2
t t  2  t,t   2 
f 't  t  2  1  0, t   2 t  2
Hàm số f(t) đồng biến và liên tục trên  và 1
Phương trình 5  f x  f  x  
1   x  x 1  x    y  1 2  1
Hệ phương trình có 1 nghiệm :   ;1    2  3
2y y + 2x 1 x = 3 1 x   1   2
 2 y 1 - y = 2 - x 2
Bài toán 143.(THPT Triệu Sơn 4) Giải 1   x  0 x  1 Điều kiện :   
y  2  x  0
y  2  x  0   Phương trình (1) 3
 2y y = 3 1 x  2x - 1 +  1 1 x 3 3
 2y y = 1 x  21 x 1 x 3
 2 y y = 2 1 x   1 x 3
Xét hàm số : f t 3
 2t t,t   f t 2 '
 6t 1  0, t  
Hàm số f(t) đồng biến và liên tục trên  và
Phương trình 3  f y  f  1 x  y  1 x, y  0 2 2
y  1 x x  1 y 4
Thế (4) vào phương trình (2), ta được : 2 y   2 2 1 - y = 2 - 1 y  2 2
 2 y 1 - y - y - 1= 0 2 y 1  1   -  2 y +  1 = 0   -1   2 y +  1 = 0 2 2 y 1 + y 2  2y 1 + y     1  -1= 0 2  2 y 1 + y= 1 2 2 y 1 + y  y  1 2 
 2y 1 = 1 - y  2y 1  1 y2 2  y  1  y  2  ,loai    2  y  2y  0
y  0  x  1  
Hệ phương trình có nghiệm duy nhất : 1;0  1 x 2 x   y   Bài toán 144. x y
 5y 1  x y 1  x  0 
Giải : Điều kiện : 3 2 2 
1 . Phương trình (1)  x y yxy x y    5 2 x y 2
x xy  
1  y xy   1  0   2
x y xy   1  0  xy  1   2
x y . Thế vào phương trình (2) ta được : 2
5x 1 - x x = 1 2
 5x 1 = 1 + x x 3
TH 1 : x  0 :   2 2 3  5x 1 = 1 + x 2 2 4
 5x 1 = 1 + 2x  x 2 x  1
x  1 y  1 4 2
x  3x  2 = 0     2 x  2 
x  2  y  2 
TH 2 : x  0 :   2 2 3  5x 1 = 1 - x 2 2 4
 5x 1 = 1 - 2x  x   7  41 7  41 7  41 2 x   x    y  4 2 2  2 2
x  7x  2 = 0      7  41 2 7  41 7  41 x  x    y   2  2 2 1 xy  1   x   .Thế vào (2) ta được : y 1 1 5y 1 
y  1  5y 1   1  y 5y   1 1  y y y
y 5y  
1 1 2 y 5y   1  yy y   2 2 5 1  5
y  2 y 1,VN (do vế trái không âm, vế phải âm)        
Hệ phương trình có 4 nghiệm :     7 41 7 41 7 41 7 41 1;1 ; 2; 2 ;  ; ;  ;   2 2   2 2       2
x x  4   2 y y 1  2   1 Bài toán 145. 2 3 3 12 
y 10 y  2  2 x 1 2  2
Giải :Phương trình (1) 2
x x  4  (3) 2 y y 1 2 2 y y 1 2  Vì : 2 y y 1  0, y
   nên : 3  x x  4  1  x x    y2 2 4 2  4   2  y 4 t
Xét hàm số : f t 2
t t  4,t   
f 't   1  0, t   2 t  4
Hàm số f(t) đồng biến và liên tục trên  và
4  f x  f  2
y  x  2  y
Thế x = -2y vào phương trình (2), ta được : 2 3 3 3
3x  5x  2  2 x 1 3 3 3   x   1  2 x   1   x   1  2 x 1 5
Xét hàm số : g t 3
t  2t,t   g t 2 '
 3t  2  0, t   
Hàm số g(t) đồng biến và liên tục trên  và
Phương trình    g x    g  3 3 5 1 x 1 3 3  x 1  x 1
x  0  y  0   x  3 3 2
1  x 1  3x  3x  0   1
x  1 y   2  1
Hệ phương trình có 2 nghiệm :   0; 0; 1  ;    2  Bài toán 146. 3 3 2
x y  3y  3x  2  0   1   2 2 2
x  1 x  3 2 y y  2  0 2  2 1    x  0  1   x  1
Giải : Điều kiện :     1
  y 1  1 2
2y y  0 0  y  2   phương trình (1) 3 3 2
x  3x y  3y  3y 1 3  3y
x x   y  3 3 3 1  3 y   1 (3)
Xét hàm số : f t 3
t  3t,t  1  ;  1 f t  2 '
 3t  3,t  1  ;  1 f t  2 '
 0  3t  3  0  t  1
  f 't   0, t  1;  1 t -1 1 f’(t) - 0 2 f(t) -2
Hàm số f(t) nghịch biến và liên tục trên  1  ;  1 và
Phương trình 3  f x  f y  
1  x y 1  y x 1
Thế x +1 = y vào phương trình (2), ta được : 2 2 2
x  1 x  3 1 x  2  0 2 2
 x  2 1 x  2  0 2 2
 1 x  2 1 x 1  0   2   x  2 1 1
 0  1 x  1  x  0
Hệ phương trình có 1 nghiệm : 0;  1 Bài toán 146 3 2  y
3x  2x   1  4 y  8   1  2 3 2 2
y x  4 y x  6 y  5 y  4 2 
Giải : Do y = 0 không thõa hệ phương trình nên y  0  8 4 2
3x  2x 1    3 2  y y Hệ phương trình   4 6 3
x  4x  5    2    y y
Cộng 2 phương trình của hệ với nhau ta được : 3 8 6  2   2  3 2
x  3x  6x  4   3 2
x  3x  3x 1 3x  3   3 3     y y y y     3       x  3 2 2 1  3 x   1   3 (3)     y y    
Xét hàm số : f t 3
t  3t, t   f t 2 '
 3t  3  0, t   
Hàm số f(t) đồng biến và liên tục trên  và  2  2
f x   1  fx 1    4 y y  
Thế (4) vào phương trình  , ta được :
x  1  y  1
x x    x  2 3 4 5 1  3 x   1 3 2
x x x 1  0   x  1,loai
Hệ phương trình có nghiệm : 1;  1 3
2y y  2x 1 x = 3 1 x   1  Bài toán 155. 2 2 2
 9  4y  2x  6 y - 7 2  x  1 1   x  0 
Giải : Điều kiện :    3 3 2 9  4 y  0   y     2 2 Phương trình (1) 3
 2 y y = 3 1 x  2  2x  2 1 x 3
 2y y = 21 x 1 x  1 xy y   x3 3 2 = 2 1  1 x (3)
Xét hàm số : f t 3
 2t t,t   f t 2 '
 6t  1  0, t   
Hàm số f(t) đồng biến và liên tục trên 
Phương trình 3  f y  f  1 x   y  1 x  0
Thế vào phương trình (2) ta được : 2
4x  5  2x  6x 1 2 2
 2 4x  5  4x 12x  2  2 4x  5  4x  5 1  4x 8x  4
 4x  5 1  2  2x
  x   2   x  2 4 5 1 2 2  
 4x  5 1  2x  2,loai vì : 2x  2  0, x   1   1  1 x   1   2x  0 2  x       2   4x  5 
x  1 2, loai  1 2x2  2 4x 8x 4 0       4
x 1 2  y   2 
Hệ phương trình có 2 nghiệm :  4    4 1 2; 2 ; 1 2;  2  Bài toán 156. 2 2
2x x x  2 = 2y + y + 2y 1    1  2 2
x  2 y  2x y  2  0  2  x  2  x  2  0 
Giải : Điều kiện :    1 2y 1  0 y      2 Phương trình (2) 2 2  x  2
y  2x y  2 (3)
Thế (3) vào phương trình (1) ta được : 2 x   2
y x y   2 2 2
2  x x  2 = 2y + y + 2y 1 2 2
x  3x  2  x  2 = 4y + 2y + 2y 1
  x  2  x    x     2 1 1 1 1 = 2y + 2y + 2y 1 (4) 1
Xét hàm số : f t 2
t t t 1,t  1
 ;  f 't   2t 1 ,t  -1 2 t 1 1 1
f ' t  2 
f ' t  0  2  =0 4t   1 t 1 4t   1 t 1 1 3  8t   1
t 1=1   t  3 1 1 =  t 1=  t = - 8 2 4 Bảng biến thiên : t -3/4 -1 +∞ f’’(t) - 0 + +∞ +∞ f’(t) 1/2
Ta thấy f 't  0, t   1
 ;  . Hàm số f(t) đồng biến và liên tục trên  1  ; 
Phương trình 4  f x  
1 = f 2y  x 1  2y x  2y 1
Thế vào phương trình (2) ta được :
y  1 x  1  y  2 2 2
1  2y  22y   1  y  2  0 2
 6y  7 y 1  0   1 2
y   x    6 3  2 1 
Hệ phương trình có 2 nghiệm : 1;  1 ;  ;    3 6  Bài toán 157.   2x  2   3
2x 1 = y + 3y   1  2
y xy  5  5x  6 y  2  1
Giải : Điều kiện : x . Phương trình (1) 2   x    3 2 1 3
2x 1 = y + 3y x   x  (3)  3 3 2 1 3 2 1 = y + 3y
Xét hàm số : f t 3
t  3t,t   f t 2 '  3t +3 > 0, t   
Hàm số f(t) đồng biến và liên tục trên  1  ;  2 y 1 Phương trình 3 2
y  2x 1, y  0  y  2x 1  x  2
Thế vào phương trình (2) ta được : 2  y   2 1 y y 1 2 y   5  5  6 y 3 2
y  3y 11y  5  0 2 2  y  5  ,loai    y   2
5 y  2y   1  0
y  1 2  x  2  2 
y 1 2,loai
Hệ phương trình có 1 nghiệm : 2  2;1 2 Bài toán 158 x x   2
x  3x  3 3
= y  2 + y  3 + 1   1  2 3 3 
x 1  x  6x  6 = y  2 + 1 2  x  1 x 1  0 1   x  3  3    x  3  3  
Giải :Điều kiện : 2
x  6x  6  0    x  3 3  x  3  3 y  3  0   y  3     y 3    
Phương trình (1)   x     x  3 3 1
1 1 = y  2 +  y  2 1 (3) 2 3t
Xét hàm số : f t 3
t 1  t,t   f 't   1  0, t    3 2 t 1
Hàm số f(t) đồng biến và liên tục trên 
Phương trình    f x    f  3 y   3 3 1 2  x 1  y  2
Thế vào phương trình (2) ta được : 2 2
3 x 1  x  6x  6 = x  3 x 1 =  x   1 1  x   1  4 x   1
Xét : x  1 không thỏa phương trình trên.
Chia 2 vế của phương trình trên cho x 1 ta được 1 1  x 1 + + x 1 4   3 x 1 x 1 1
Đặt : t x 1 +
> 0 ,phương trình trên trở thành : x 1 3   t  0  t   3 5 2 2
t+ t  6 =3  t  6  3  t      t = t  6   3t2 2 6t 15  0 2   1 5 2  x 1  
 2 x 1 5 x 1 2  0 x 1 2  x 1  2
x  5  y  62    1   5 127 x 1   x   y   2  4 64  5 127 
Hệ phương trình có 2 nghiệm : 5;62; ;     4 64  Bài toán 159. 3xy   1 2 1 9y 1 =   1 x 1  x  3 x  2 9 y   1  4 2 x   1 x = 10 2 
Giải : Điều kiện : x  0 . Ta thấy x  0 không thỏa hệ phương trình. 1
Xét x  0 ,Phương trình (1) 2
 3y 1 9y 1 = , suy ra   y  0
x x 1  x x 1  x x  2
 3y  3y 9y 1 =
y y y2 1 1 1 3 3 3 1 = + x x x x 2  
y y y2 1 1 1 3 3 3 1 = + 1 (3)   x xx  2 t
Xét hàm số : f t 2
t t t 1, t  0 f 't  2  1 t 1   0, t   0 2 t 1
Hàm số f(t) đồng biến và liên tục trên 0;  1  1
Phương trình 3  f 3y  f  3y     x x
Thế vào phương trình (2) ta được :  1 3  x 1  4 2 x  3 2 2    1
x = 10  x x  4 x   1 x - 10 = 0 (4)  x
Xét hàm số : g x 3 2
x x   2 4 x   1 x - 10, x > 0 2 g ' x 2
 3x  2x   2 x   1  8x x > 0, x  > 0 x 1
Hàm số f(t) đồng biến trên 0; và g(1) = 0. Vậy (4) có nghiệm duy nhất : x 1 y  3  1 
Hệ phương trình có nghiệm duy nhất : 1;    3  Bài toán 160. 2   1 y   x   2 2 1  y = 2 1     1  x     2 4 y   2 3
y x  3x  2 2 2  x   1 2  x  0 x  0 
Giải : Điều kiện :    2 2  x  0   2  x  2 
Phương trình (1)  x  2 x x   2 2 2
1  xy = 2x  2 y  2 3 2 2 2
x  2x x xy  2 y  2  0  x  2 2
x y    2 2
2 x y    x  2  0   x   2 2 2
x y    x  2  0   x   2 2 2 x y   1  0 x  2  , loaix  1 2 2   
x 1 y . Ta có :  2 2 x y 1  y  1  
Thế vào phương trình (2) ta được : 2 y   2 3
y x x   2 4 3 2 y 1 1     2 y      2 3
y x x   2 4 1 1 3 2 y 1   1   2 y    2 y      2 3
y x x   2 4 1 1 1 1 3 2 y 1   1 2 2 3  4
y 1 1   y x  3x  2 2 2 3
y  4 y 1  x  3x  2 (3)  
Xét hàm số : f x 3
x  3x  2, x  1  ;0 0;  1 f x 2 '  3x  3 f x 2 '
 0  3x  3  0  x  1  Bảng biến thiên : x 0 1 -1 f’(x) - 0 f(x) -2 -4
Theo Bảng biến thiên ta có : f x  4  , x   1  ;0 0;  1 và min f x  4   x  1  1  ;0   0;  1
Xét hàm số : g y 2 2
y  4 y 1, y  1  ;  1 4y 4y
g ' y  2y
g ' y  0  2y   0 2 y 1 2 y 1  y  0  2   y  0   2 y 1   0  2   2  1   y 1     y   3,loai 2 y 1     Bảng biến thiên : y 0 -1 1 g’(y) + 0 - -4 g(y) 1-4√2 1-4√2
Theo Bảng biến thiên ta có : g y  4  , y   1  ; 
1 và max g y  4   y  0  1  ;  1 x  1
 3  f x  g y  4   
. Hệ phương trình có nghiệm duy nhất : 1;0 y  0  Bài toán 161. 2  2 2  x  5y    2 xy  2 2
6  x  5y  +36   1  4 4 2 2
 5y x  6x + 2xy - 6y 2  xy  0
Giải : Điều kiện :  4 4 5y x  0  2 Phương trình (1)   2 2 x y   xy  2 2 5 2
x  5y  12 xy  36 = 0 (3)
Xem phương trình (3) là phương trình theo ẩn  2 2
x  5 y , còn xy là tham số. 2 2
x  5y  6    xy  2 '
6 . Phương trình có nghiệm :  2 2
x  5y  2  xy  6,loai  Thế vào (2) ta được : 4 4
y x   2 2 x y  2 2 5 5
x y  + 2xy 4 4 4 2 2 4
 5y x x  4x y 5y  2xy 4 4 
y x   4 4 y x  2 2 5 5
 4x y  2xy 2 2 4 4 4 4  5y x  5y x  2xy  2xy (4)    
Xét hàm số : f t 2
t t,t 0; f 't  2t 1 0, t   0
Hàm số f(t) đồng biến trên 0;    f  4 4
y x   f xy 4 4 4 5 2
 2xy  5y x 4 2 2 4
x  4x y  5y  0 (5)
Nếu y  0  x  0 , không thỏa hệ đã cho.
Xét y  0 , chia 2 vế của phương trình (5) cho 4 y ta được : 2  x    1 4 2    x   x y     4  5  0       x y y y 2      x    5  , loai    y   x  1  y Từ 2 2 2
x  5y  6  6x  6  x  1   y
Hệ phương trình có 2nghiệm : 1;  1 ; 1  ;  1 3 3 2
x y  3y  3x  2   1   2 2 2
 1 x x -3 2y - y = 2 2 Bài toán 162. 2 1    x  0  1   x  1
Giải : Điều kiện :    2 2
y y  0 0  y  2   Phương trình (1) 3 3 2
x  3x  2  y  3y   3 2
x x x     2 x x   3 2 3 3 1 3 2 1  y  3y 0   x 1  2
  x  3   x  2 3 2 1 3
1  y 3y (3). Dễ thấy :  0  y  2 
Xét hàm số : f t 3 2
t  3t ,t 0;  2 t   0 f t 2 '  3t  6t f 't  2
 0  3t  6t  0   t  2  Bảng biến thiên : t 2 0 f’(t) 0 - 0
Hàm số f(t) nghịch biến trên 0;2 . 3  f x  
1  f y  x 1  y
Thế vào phương trình (2) ta được :  x x
x    x  2 2 2 1 -3 2 1 - 1 = 2 2 2
x - 2 1 - x = 2 2 2
 1 - x +2 1 - x 1  0  x   , loai.  2 2 1 - 1 0
Hệ phương trình vô nghiệm. Bài toán 163. 2 x y   2 2  2 4 y 1 2
x x 1   1  2  4y   2 1 x +2 2 x   1 x = 6 2 
Giải :Điều kiện : x  0 .Ta thấy x  0 không thỏa hệ phương trình. 2 x x 1
Xét x  0 ,Phương trình (1) 2
y 2  2 4y 1    2 x 2 x x 1 2
 2y  2y 4y 1  , suy ra y  0 2 x 2 2 1 1 x 1 2 1 1  1 
 2 y  2 y 2y2 1  
 2 y  2 y 2y 1   1 (3) 2   x x x x x x  2 t
Xét hàm số : f t 2
t t t 1, t 0; f 't  2  1 t 1+ >0, t  0;  2 t 1
Hàm số f(t) đồng biến và liên tục trên 0;  1  1
Phương trình 3  f 2y  fy     x  2x
Thế vào phương trình (2) ta được :  1  2 1 x +2 2 2    2 x 1 x = 6  1 x +2x
x  2 x - 6 = 0 2  (4)  x
Xét hàm số : g x 2 2  1 x +2x
x  2 x - 6 = 0,x > 0 2 x 1
g ' x  2x +4x x   > 0, x  > 0 x x 1
Hàm số g(x) đồng biến trên 0; và g(1) = 0. Vậy (4) có nghiệm duy nhất : x 1 y  2  1 
Hệ phương trình có nghiệm duy nhất : 1;    2  Bài toán 164. 3 2 3
x  3x  6x  4  y  3y   1   3   3y  7 3 x = 1-  2 1 x  2 
Giải : Phương trình (1)   3 2
x x x     x   3 3 3 1 3
1  y  3y
  x  3   x   3 1 3
1  y  3y (3)
Xét hàm số : f t 3
t  3t, t   f t 2 '  3t +3 > 0, t   
Hàm số f(t) đồng biến trên  . Phương trình 3  f y  f x  
1  y x 1
Thế vàophương trình (2) ta được :   x     x     x 3 3 2 3 1 7 = 1- 1
  x   x   x 3 3 2 3 4 = 1 - 1   x   3 2 2 2 3
4 x = 1 - 1 x 1 + x + 1 x 1    2 x  2 2 1 + x + 1 x 1 2 2  1 + x + 1 x 1    3 
 3x  4 x +  0 2 2
x 3x - 4x +   0 2 1 + 1 x  2 1 + 1 x    
x  0  y  1  2 2   1 + x + 1 x 1 2 3x - 4x +  0   2  1 + 1 x 2 2 1 + x + 1 x 1 Xét phương trình : 2 3x - 4x +  0 2 1 + 1 x 2 2  2 4 4  1 + x + 1 x 1 2  3 x - 2. x +  +  0   2  3 9 9  1 + 1 x 2 2 2 2  2  4
1 -2 1 x + 1 + x +3 1 x  3 - x - +  0   2  3  3 1 + 1 x   1 - 1 x 2 2 2  3 2 4  3 x- - + 3+  0   2  3  3 1 + 1 x   1 - 1 x 2 2 2 2 5 3  3 - x +    0   2 2  3  3 1 + 1 x 1 + 1 x     1 - 1 x x 2 2 2 2 2 5 1 4  3 x- +   0   2 2  3  1 + 1 x 1 + 1 x Vì 2 2
5 1 x  5, x
    5 1 x  4  0, x
   nên vế trái của phương trình trên luôn dương.
Vậy phương trình trên vô nghiệm. Hệ phương trình có nghiệm duy nhất : (0; 1) Bài toán 165.
x y x y  3  
x y2  2 x y   1  2
x x y  2 
x y  3 2  x y  0
Giải : Điều kiện : 
x   y x y  0 
Đặt : t x y,t  0 ,Phương trình (1) trở thành : 2
t t  3  t  2 t 2
t t  2 t t  3  0 3t   1  3 
t t   1   0  t   1 t   0   2 t t  3 
2 t t  3  t  1  1  3
x y  1  y  1 x x x  t   0,VN 2  2 t t  3
Thế : y = 1- x vào phương trình (2) ta được : 2
x  3  2x 1  3 2
x  3  2  2x 1 1  0 2 x 1 2  x   1  x 1 2     0   x   1     0 2 x  3  2 2x 1 1 2  x  3  2 2x 1 1 
x  1  y  0   x 1 2    0,VN 2  x  3  2 2x 1 1
Hệ phương trình có nghiệm duy nhất : (1; 0) Bài toán 166. 2 2 2 2
x xy  2 y y xy  2x  2x y   1 
8y 6 x1  2 y2y4 x2 3 2  x  2  0 x  2
Giải : Điều kiện :    y  2  0 y  2   2 2 2 2
x xy  2 y
y xy  2x
2  x y  Phương trình (1)    2 2 y y y 2 2  x   x   x   x   x     2  2  1  2  2           y y y y y           x
Đặt t  ,t  1 , phương trình trên trở thành : y 2 2
t t  2  2t t 1  2t  2
Bình phương 2 vế của phương trình trên, ta được : 2 2 2 2
3t  2t  3  2 t t  2 2t t 1  4t  8t  4 2 2 2
 2 t t  2 2t t 1  t  6t 1
 t t   t t    t t  2 2 2 2 4 2 2 1 6 1 4 2 2
 7t 14t  7  0  t  1  t  1
x y , thế : y = x vào phương trình (2) ta được :
8x  6 x 1  2  x  2 x  4 x  2  3     8   x   1  2 x 1   
2 x  2x  2 4 x  2 5   x  3 
x     x   x  2 2 1 2 1 2 2 2
 4 x  2  4   1   x  3 
x     x    x  2 2 1 2 1 2 2 2 2 1    x  3  
x      x  3 2 1 2 1 2 2
 2  x  2  (3)
Xét hàm số : f t 3
t t,t  2 f t  2 '
 3t 1  0, t   2
Hàm số f(t) đồng biến trên 2; . 3  f 2 x 1  f 2  x  2    
3  2 x 1  2  x  2  4  x  
1  4  4 x  2  x  2  34 2 x   y
 3x  6  4 x  2  3x  6  16 x  2 2
 9x  52x  68  0   9
x  2  y   39 39
Hệ phương trình có 2 nghiệm :   2; 2; ;    4 4  Bài toán 167. 4 3
x y   4 x    2 4 1 y + 4y = 1   1
Giải : Phương trình (1) 4 4 3 2
x x y  4 y + 4y - y = 1 4
x y   2 1  4 y  y +  1 -  y +  1 = 0  y  1   4 2
x  4 y   1  y   1 = 0   4 2
x  4 y 1  0 
y  1 , thay vào phương trình (2) ta được : 2 2
4 x  1  x  4 
x    x  2 2 2 16 1 4 4 2
x  8x  0  x  0; x  2 2 4  1   x  1  x  1 4 2 
x  4 y  1     1 1 2 4 y  1   y     2 2   3 2 2
2  8y  6 y  2  x  4 x 1 (3) 4x
Xét hàm số : f x 2 2
x  4 x 1, x 1;  1
f ' x  2x  2 x 1 4x  2 
f ' x  0  2x   0  2x 1   0 2 2 x 1  x 1   x  0 x  0 x  0 x  0   2       1    0 2 2  x 1  2  x 1  2
x   3, loai 2      x 1 Bảng biến thiên : x -1 0 1 f’(x) + 0 - -4 f(x)
Theo Bảng biến thiên ta có : f x  f 0  4, x   1  ;  1  1 1 Xét hàm số :  g y 3
 8y  6 y  2, y   ;  2 2   1 g y 2 '  24y  6 g ' y 2
 0  24 y  6  0  y   2 Bảng biến thiên : y -1/2 1/2 g’(y) - 0 g(y)  1   1 1
Theo Bảng biến thiên ta có : 
g y  g  4  , y    ;   -4  2    2 2      f   xx 0  4  Phương trình (3) 
f x  g y     1 g   y   4  y     2  1
Hệ phương trình có 4 nghiệm :  0; ;0;   1 ;2 2;  1 ; 2  2;    1  2  3 2 3
x 12y x  2  8y  8y   1   2 3
x  8y  5x  2 y 2 Bài toán 168.
Giải : Điều kiện : 2 3
x  8y  0 Phương trình (1) 3 3 2
x x 1  8 y 12 y  8 y 1
x x    y3 3 2 1 2
12y  6 y 1 2 y 11
x x    y  3 3 1 2 1  2 y   1 1(3)
Xét hàm số : f t 3
t t 1,t   f t 2 '
 3t 1  0, t   
Hàm số f(t) đồng biến trên  . Phương trình 3  f x  f 2y  
1  x  2y 1
Thế : 2y – 1 = x vào phương trình (2) ta được :  y  2 3 2
1  8y  52 y   1  2 y 3 2
 8y  4y  4y 1  8y  5 8  5  y  5  0   y      8
8y  4y  4 y 1   8y 52 3 2  3 2 8
y  60y  76y  24  0   5 y   8    
y  6  x  11 
Hệ phương trình có 2 nghiệm : 11;6;1;  1  .
y  1 x 1   1
y  ,loai   2 Bài toán 169.
 3y 1  5x  4  3xy y  3   1    4 2 2
x xy y 2 2 
 2x  2y
 2 x y  2   3  1 y   3  y 1  0 
Giải : Điều kiện :  3    5x  4  0 4  x     5 2 2 u
  2x  2y  
Từ phương trình (2)  x y  0 . Đặt 2 2  ;u, v  0
4 x xy y v     3 2 2 2 u   2x  2 y  3       2 2 2 2 2 2 
v  2x  2xy  2 y u  2 4 xy x xy y 2 2 v    3 3 2 2 
v u  2xy    2 2 2 u 3 3 u
x y   x y2 2 2 2 2 2 
x  2xy y   v u v  2 2 2 2 2 3 u
Phương trình (2) trở thành : 2 u v  2 v  2 2 2 2
 3u  2uv  5v  0 2 2 2
 3u  2uv  2v  3v  0 u v
v u v   2 2 2
3 u v   0
 u v3u  5v  0  3u 5v  0  u
  v x xy y    x y2 2 2 2 0
 0  x y
Thế : y = x vào phương trình (1) ta được : 2
3x 1  5x  4  3x x  3 
x    x   
x    x   2 3 1 1 5 4
2  3x  3x (3)
3x 1  x  2 1
5x  4   x  22 2    3x  3x
3x 1   x   1
5x  4   x  2 2 2 x x x x     2
3 x x   0
3x 1   x   1
5x  4   x  2     1 1 2 x x    3  0
 3x 1 x  1 5x 4  x 2          2 x x  0  x  0  y  1 1     3  0,VN x 1 y  
3x 1   x   1
5x  4   x  2  3
u  5v  0 . Vì u, v  0  u v  0 . Từ   xy  0  x y  0
Hệ phương trình có 2 nghiệm : 0;0;1;  1
Chú ý. Để có phương trình (3) ta làm như sau : Dùng máy tính ta biết được phương trình có 2
nghiệm : 0 và 1và cũng là nghiệm của phương trình : 2
x x  0 . Ta biến đổi phương trình : 2
3x 1  5x  4  3x x  3 như sau: 2
3x 1  5x  4  3x x  3 
x    x a 
x    x b 2 3 1 5 4
 3x x  3   x a   x b
3x 1  x a2
5x  4   x b2 2  
 3x  3x  3  a b
3x 1   x a
5x  4   x b 2
x  3  2a 2 2 x 1 a
x  5  2b 2 x  4  b 2  
 3x  3x  3  a b
3x 1   x a
5x  4   x b 3   2a  1 2   x  2  3  2a 2 2
x 1 a  x x 1   a  0 a  1 Ta phải có :      2 x   5  2b 2 2
x  4  b  x x 5  2b  1 b  2    2 4  b  0  Bài toán 172. 2 2 
x  2x  5  y  2y  5  y  3x  3   1  2 2
y  3y  3  x x 2 
Giải : Phương trình (2) 2 2
y x  2 y  2x y  3x  3 (3)
Thế phương trình (3) vào phương trình (1) ta được : 2 2 2 2
x  2x  5 
y  2 y  5  y x  2 y  2x
  x  2    y  2    y  2   x  2 1 4 1 4 1 1
  x  2    x  2   y  2    y  2 1 4 1 1 4 1 (4) 1
Xét hàm số : f t  t  4  t,t 0; f 't  1  0, t  0; 2 t  4 x   y
Hàm số f(t) đồng biến trên  2 2
0;  4   x   1   y   1  x y  2 
x   y ,thế vào phương trình (2) ta được : 3 3 4
y  3  0  y   x   4 4
x y  2 ,thế vào phương trình (2) ta được : 3 1
y y    y  2 2 3 3 2
  y  2  2 y  3  0  y   x   2 2  1 3   3 3
Hệ phương trình có 2 nghiệm :   ; ;  ;      2 2   4 4  Bài toán 173. 3 2 3 2
x  3x  2  y  3y    1  2 3  x  2 
y  8 y 2  3 2
y  3y  0  x  2
Giải Điều kiện : 2
y  8y  0   y  0   x  2  0  Phương trình (1) 3 2
x  3x  2  y y  3   3 2
x  3x  3x   1  3 x  
1   y  3  3 y  3
  x     x    y   y  (3)  3 3 1 3 1 3 3 3
Xét hàm số : f t 3
t  3t, t 1; f t  2 '
 3t  3  0, t  1;
Hàm số f(t) đồng biến trên 1;
Phương trình 3  f x  
1  f y 3  x 1 y  3(4)
Phương trình (2)   x   2 9
2  y  8y (5)
Thế (4) vàophương trình (5) ta được :  y    2 9 3 1  y  8y 2
y  8y  9  9 y  3
  y y  2 2 8 9  8  1 y  3 4 3 2
y 16 y  82 y  63y 162  0
y 1  x  3   y    3 2
1 y 17 y  99y 162  0   3 2
y 17 y  99y 162  0,VN
Hệ phương trình có 1 nghiệm duy nhất : 3;  1 2 2 3 4 3 2 3
x y  2 x x y  2y y 1   3
x x    1 
x x x 1  x y  3 4 3 2 1 1 2 Bài toán 174. y 1  0 y 1
Giải : Điều kiện :    3 2 3 2
x x 1  0
x x 1  0   2 2 Phương trình (1)   3
x x    y y     3 1
2 x x y y 1
 x x y y  2 3 1  0 3
x x y y 1 3
x x   y 1  1
y 1  x x y   y  (4)  3 3 1 1
Xét hàm số : f t 3
t t,t   f t 2 '
 3t 1  0, t   
Hàm số f(t) đồng biến trên 
   f  3 x  f y   3 4 1  x y 1 x  0  x  0      3 2 3 2  x y 1  x   y    1 5 
Thế phương trình (5) vào phương trình (2) ta được : 4 3 2 3
x x x 1  x 1 4 3 3 2
x x x x 1 1  0 3 2 x x  1  3
x x   1   0 2
x x   1 x   0   3 2
x x 1 1 3 2 
x x 1 1 
x  0  y 1 
 x  1  y  2
. Hệ phương trình có 2 nghiệm : 0;  1 ;1; 2  1 x   0,VN do x  0 3 2 
x x 1 1 4 4 
x  3  x  2 - y  5 = y   1  2
x  2x y  2 2
y  8y  4  0 2 Bài toán 175.
Giải : Điều kiện : x  2 . Phương trình (2)
x x y     y  2 2 2 2 2
 4 y   x y  2 2  4 y
Từ phương trình trên suy ra : y  0 Phương trình   4 4
1  x  3  x  2 = y  5  y (3) Đặt : 4 4 4 4
t x  2,t  0  t x  2  x  3  t  5  x  3  t  5   4 4
3  t  5  t = y  5  y (4) 3 2u
Xét hàm số : f u 4
u  5  u,u 0; f 'u  1  0, u  0; 4 u  5
Hàm số f(u) đồng biến trên 0;
Phương trình    f y  f t 4 3
y t y x  2
Hệ phương trình có 2 nghiệm : 0;  1 ;1; 2 3 2
 2x y  5  3  x y x  3x 10y  6    1 Bài toán 176. 3 2 3
x  6x 13x y y 10  2  2
x y  5  0
Giải Điều kiện : 
3  x y  0  Phương trình (2) 3 2 3
x  6x 12x 8  x  2 10  y y 10
  x  3   x   3 2
2 10  y y 10 (3)
Xét hàm số : f t 3
t t 10,t   f t 2 '
 3t 1  0, t   
Hàm số f(t) đồng biến trên  .
3  f x  2  f y  y x  2
Thế vàophương trình (1) ta được : 3 2
3x  3  5  2x x  3x 10x  26 (4)  5 Xét hàm số :  g x 3 2
 3x  3  5  2x x  3x 10x  26, x  1  ;   2   3 1  5  g ' x 3  
 3x  6x 10, x  1;   2 3x  3 5  2x  2   5 Ta có : 2  3
x  6x 10  0, x   1  ;  2     5  5 Suy ra  
g ' x  0, x   1  ;
, vậy hàm số g(x) đồng biến trên  1  ;    2   2  
Và g(2) = 0, do đó phương trình (4) có nghiệm duy nhất x = 2  y  0
Hệ phương trình có nghiệm duy nhất : 2;0 3 3 7
x y  3xy   x y 2
12x  6x 1  0   1 Bài toán 178.
3 4x y 1  3x  2y = 4  2 
Giải : Điều kiện : 3x  2y  0 Phương trình (1) 3 3 2 2 3 2
y x  3x y  3xy  8x 12x  6x 1  0 3 3
  y x3   x  3 2
1  0   x y  2x   1
x y  2x 1  y x 1
Thế vào phương trình (2) ta được : 3 3x  2  x  2  4  0 (3)
Xét hàm số : f x 3
 3x  2  x  2  4, x  2 2 1  1
f ' x  3. 3x  2 3   0, x   2  3 2 x  2
Hàm số f(t) đồng biến trên  2
 ; f 2  0
Phương trình (3) có nghiệm duy nhất x  2  y  1  , thỏa điều kiện
Hệ phương trình có nghiệm duy nhất : 2;  1 6 2 3 2
x  3x  4  y  3y  6y   1  Bài toán 179. 2
y   x   2 1
x y  8+7 = x 2 
Giải : Điều kiện : 2
x y  8  0 Phương trình (1) 6 2 3 2
x  3x  4  y  3y  3y 1 3y 1
 x 3  x    y  3 2 2 3 4 1  3 y   1  4 (3)
Xét hàm số : f t  3
t  3t  4, t   f t  2 '
 3t  3  0, t  
Hàm số f(t) đồng biến trên  . Phương trình    f  2
x   f y   2 3 1  y  x -1
Thế vào phương trình (2) ta được :  2
x     x   2 2 1 1 2x  7 + 7 - x = 0 2
x x    x   2 2 5 1 2x  7 (4) Do 2 2 2
2x x  5  x  4  x x 1  0, x   
Từ phương trình (4), suy ra : 2
x 1  0 ;     2
x x    x    2 4 2 5 1 2x  7 4 3 2
 2x  8x 12x  24x 18  0   x   x   2 3 1 2x  6  0
x  3  y  8 
.Hệ phương trình có nghiệm duy nhất : 3;8
x 1 y  0,loai(khong thoa)  3
2y  7 y  2x 1 x  3 1 x  3 2 2 y    1   1 Bài toán 180. 2
 2 y  4 y  3  5  y x  4 2 
Giải : Điều kiện : 4
  x  1 Phương trình (1)   3 2
2 y  3 y  3 y  
1  y 1  3 1 x  2 1 x   1 1 x   y  3 2
1  y 1  21 x 1 x  1 x (3)
Xét hàm số : f t 3
 2t t,t   f t  2 '
 6t 1  0, t  
Hàm số f(t) đồng biến trên  .
Phương trình 3  f  1 x  f y  
1  1 x y 1  1 x 1  y
Thế vào phương trình (2) ta được :
3  2x  4  1 x x  4 
x  4  1 x  3  2x  4  0 (4)
Xét hàm số : f x  x  4  1 x  3  2x  4, x 4;  1 1 1 1 f ' x     0, x   4; 
1 . Hàm số f(x) đồng biến trên  4  ;  1 và f   3  0 2 x  4 2 1 x 3  2x
Nên phương trình (4) có nghiệm duy nhất : x  3   y  3
Hệ phương trình có nghiệm duy nhất :  3  ;3 3 2 3 2 
x  3x  2  y  3y (1) Bài toán 185. x  3 
y x  2 (2)  x  3  x  3
Giải : Điều kiện : 3 2
y  3y  0   y x  2   y x  2  Phương trình (1) 3 2
x  3x  2  y y  3 3 3
 (x 1)  3(x 1)  ( y  3)  3 y  3 (3) x  3 x 1  2 x 1  2 Ta thấy :       y x  2
y x  2  3  2  1    y  3  4  2  Xét hàm số: 3
f (t)  t  3t, t
  2 f t t    2 2 '( ) 3 3 3 2  3  0, t   2
Hàm số f(t) đồng biến trên 2;
3  f (x 1)  f y  3  x 1 y  3 2
x  2x  2  y
Thay vào phương trình (2), ta được :  x  1,loai 2 x  3  x  3x 2
x  4x  3  0 
x  3  y 1 
Vậy hệ phương trình có nghiệm duy nhất là: (3;1)  2  x x 1   2 y
y  4  1   1 Bài toán 195.    2 y  53 2 3
 5  2 y  6 x 1 10x 2   
Giải Phương trình (1) 1 2  2   y y  4  1
x 1  x  0, x      2    x 1  x  2 2  y y  4 
x 1  x (3). Mặt khác, ta có : 2 2 x x 1 y y  4  1     4  2
x x 1    1 2
y  4  y  0, y        2  y 4 y      2 2
 4 x x 1 
y  4  y (4)  
Lấy phương trình (3) trừphương trình (4), vế với vế, ta được : 2 2 y  3  x 1  5x 2  4
y  6 x 1 10x (5)
Thế (5) vàophương trình (2) ta có phương trình :  y  3 3 2 5
 5  2 y  4 y (6)
Xét hàm số : f y   y  3 3 2 5
 5  2 y  4 y, y   2 5
f ' y  62 y  52   4  0, y    y2 3 2 5 2 Hàm số  
f y đồng biến trên  3 và f   0    2  3
Suy ra, phương trình (6) có nghiệm duy nhất y   2 2  3   3  x 1  5x 2
 3 x 1  3  5x  3 3   5x  0  x      5  x  0 9
x 1  3  5x 2 2  2 16  x  30x  0   3
Vậy hệ phương trình có 1 nghiệm  0;  .    2  3
y y  4  3x  
x  2 x  2   1 Bài toán 205.
x y  5 x y  2 y  4  0  2   x  2
Giải : Điều kiện : x y
Phương trình (2)   x y  2y  4   1
x y  2 y  4  0 3  x y  2 y  4
x y x y  2 y  4  0      yx y x y x y              2 2 4 1 1 0    
x y 1 2 y  4  x y x y 1  0    
x y  4 
x y  0  x y  4 x y x y  0   3
1  y y  3 x  2   x  2  4 x  2  2
y y   x  2   x  3   x  2 3 2 2 2 2  2 x  2   1
y y   x  2   x  3 3 3 2 2  3 x  2 1 x  2 1 3 3 y y x  2 1  x  2 1 (3)    
Xét hàm số : f t 3
t t, t   f t  2 '
 3t  1  0, t    y 1  0
Hàm số : f t  đồng biến trên  .Phương trình 3  y x  2 1   2
x  2  y  2 y 1 
x y  4  x y  0  y  1  
. Ta có hệ phương trình :   y  1 2
x y  2 y  3   2
x y  2 y  3  2 2
y y 1 y  3y  3  0     y  1  2
x y  2 y  3   Xét phương trình : 2 2 y y 1 
y  3y  3  0 2 2 2
y  3 y  2
y y  2  1 
y  3 y  3  0 2
y y  2   0 2 1 y  3 y  3
y 1 y  2  y 1  
  y 1 y  2 
 0   y  2 y 1   0 2 1  y  3 y  3 2  1 y 3y 3       2 2  y y 3y 3 y 3y 3 2          y  2
  0  y  2  x  3 2  1 y 3 y 3      
Vậy hệ phương trình có nghiệm duy nhất : 3;2
x x  2  x  4  y 1  y  3  y  5    1 Bài toán 209. 2 2
x y x y  44 2  x  0
Giải Điều kiện :  y  5 
Phương trình (1)  x x  2  x  4  y  5   y  5  2   y  5  4 (3) 1 1 1
Xét hàm số f t   t t  2  t  4 trên 0;  f t     0, t   0;   2 t 2 t  2 2 t  4
(3)  f x  f y 5  x y  5  y x  5 (4)
Thay (4) vào phương trình (2) ta được : x x   x   x  2 2 5 5  44
x  1  y  6 2
 2x 12x 14  0 
.Hệ phương trình có nghiệm duy nhất: 1;6
x  7,loai  3 3 2
x  3x y  3y  2    1 Bài toán 210. 2 2 2 2
x y y  2xy x 1  0 2 
Giải Phương trình (1)  x x   y  3 3 3 1  3 y   1 (3)
Phương trình (2)   xy y2  x 1  x 1 0  x 1
Xét hàm số : f t 3
t  3t,t 1; f t  2 '
 3t  3  0, t  1; 
Hàm số f(t) đồng biến trên 1;
(3)  f x  f y  x y 1. Thay vào phương trình (2) ta được :
y  0  x  1  y  2 2 2
y y   y   2 1 2
1 y   y   1 1  0 4
y y  0  y  3 y   1  0 
y 1 x  2 
Hệ phương trình có 2 nghiệm : 1;0;2;  1 . 3 3 2 2 
x y  3(x y )  4(x y)  4  0 Bài toán 216.  ( , x y  ) 2 2
x y  2(x y)  18 
Giải : Phương trình 3 2 3 2
(1)  x  3x  4x  4  y  3y  4 y 3 3
 (x 1)  x 1  ( y 1)  y 1 (3)
Xét hàm số : f t 3
t t,t   f t 2 '
 3t 1  0, t   
Hàm số f t  đồng biến trên  . Phương trình (3)  f (x 1)  f (y 1)  x1  y1  y x  2
Thay y=x+2 vào phương trình (2) ta có :
x  3  y  5
x   x  2 2 2  2(2x  2)  18 2
 2x 18  0  x  3   y  1  
Vậy hệ phương trình có 2 nghiệm là (-3;-1), (3;5). 2 2
2x y  7x  2 y  6  0    1 Bài toán 220.  3 2 2 3
7x  12x y  6xy y x y  0  2 
Giải : Phương trình (2) 3 2 2 3
 7x  12x y  6xy y x y  0   3 3 2 2 y x x y xy  3 8 12 6
x  2x y x  0
  y x3   y x  x3 2 2  x (3)
Xét hàm số f t  3
t t,t   f t  2 '
 3t  1  0, t   
Suy ra hàm số f t đồng biến trên  . Phương trình 3  y  2x  x x y x  3
Thế vào phương trình (1) ta được : 2
x  5x  6  0   x  2 
Vậy hệ phương trình có 2 nghiệm 2;2 ;3;3 .
2 x y  6  1 y (1)  Bài toán 221. 2 9 
1  x xy 9  y  0 (2) 
x y  6  0
Giải : Điều kiện:  x  1 
Nếu y  0 , để hệ phương trình có nghiệm thì : 0  y  1.
VT (1)  2 x y  6  2 5  
  VT (1)  VP(1) hệphương trình vô nghiệm.
VP(1)  1  y  1  
 Nếu y<0, từ (2) suy ra x>0 2  3   3  Ta có : 2
9 1 x xy 9  y  0  9      
 y 9   y2 (3)  x   x  2 9  2t Xét hàm số 2
f (t)  t 9  t ,t  0; f '(t)   0. t   0 2 9  t
Suy ra hàm số f t đồng biến trên 0;   3  3 9
Phương trình (3)  f
f ( y) 
  y x    2  x x y 9
Thế vào phương trình (1) ta có phương trình : 2
y  6  1 y (4). 2 y 9
Xét hàm số : g( y)  2
y  6 trên  ;  0 2 y  9   y  6 '  2  3 y y 18   g '( y)    0, y   0 9 3 9  y  6 yy  6 2 2 y y
Suy ra hàm số g( y) đồng biếntrên  ;  0
Xét hàm số : h( y)  1  y trên  ;
 0 có h'( y)  1  0,y  0
Suy ra hàm số h( y) nghịch biến trên  ;
 0 và phương trình (4) có nghiệm duy nhất y= -3, vậy x = 1.
Cách 2. (Dùng lượng liên hợp) 9  9  Xét phương trình : 2
y  6  1 y  2 
y  6  2   y  3  0 2 y 2 y    9      y  6  4    2 y 3 2 y  2 y  9 2    y  3  0 2    y  3  0  9   9  2   y  6  2  yy  6  2 2   y 2   y         y 3 2 y y 3       2 y y  3 2    y  3  0 2  y 3 1     0  9   9  2 2  yy  6  2  yy  6  2 2   y 2   y    y  3   x  1  2 y y  3   1  0   9 2 yy  6  2  2 y  Vì phương trình 2
y y  3  0 vô nghiệm và có hệ số a = 1 > 0, nên 2
y y  3  0, y   
Do đó vế trái của (*) luôn dương, với mọi y < 0, (*)vô nghiệm.
Vậy hệ phương trình có nghiệm duy nhất (1;-3). 3
2y  2x 1 x  3 1 x y    1 Bài toán 228. 2
y 1  2x  2xy 1 x 2 
Giải : Điều kiện : 1
  x  1. Phương trình (1) 3
 2 y y  3 1 x  2 1 x   1 1 x y y   x   x (3)  3 3 2 2 1 1
Xét hàm số : f t 3
 2t t,t   f t  2 '
 6t 1  0, t   
Suy ra hàm số đồng biến trên  . 3  f y  f  1 x   y  1 x
Thế vào phương trình (2) ta được : 2 2
1 x 1  2x  2x 1 x 2 2
 2x  2x 1 x  1 x 1  0 tt t
Đặt x  cost với t   2 0;   0;  sin  sin 2  2    2 2 t t Ta có 2
x  cos t  1 2 s in  1 x  2 sin 2 2 t
Khi đó, phương trình (2) trở thành : 2 2 o
c s t  2 cos t sin t  2 sin 1  0 2  t 2t    k 2 tt   4 2 1 o
c s2t  sin 2t  2 sin
1  0  sin 2t   sin     2  4  2 t  2t     k 2  4 2  3 k 4 t    k 2 t     3  3 3  2 4  3 3 t x  o c s  y  2 sin      k    10  10 5  5 3  3 k 4t   k 2t t   
x  cos 1  y  2,loai    2 4  10 5  3 3
Nghiệm của hệ phương trình là :  os c ; 2 sin .    10 5  3
2(2x 1)  2x 1  (2 y  3) y  2    1 Bài toán 229.
4x  2  2 y  4  6  2   1 x  
Giải : Điều kiện : 3 
2 . Phương trình (1)  2(2x 1)  2x 1  (2 y  4 1) y  2 y  2  3
 2(2x 1)  2x  
1  2 y  2 y  2  y  2  x    x    y   y  (3)  3 3 2(2 1) 2 1 2 2 2 Xét hàm số: 3
f (t)  2t t , t 0; 2
f '(t)  6t 1  0, t  0;
Hàm số f t  đồng biến trên 0; 
Phương trình 3  f (2x 1)  f ( y  2)  2x 1  y  2
Thay vào phương trình (2) ta được: 4 4 y  8  2 y  4  6 (4) Xét hàm số : 4 g( y) 
4 y  8  2 y  4  6, y  2; 1 1 g '( y)  
 0 y  2;  nên g(y) đồng biến trên 2; 4 4 y  8 2 y  4 1
Hơn nữa g(6) = 0 nên phương trình (4) có nghiệm duy nhất là y  6  x  2  1
Vậy nghiệm của hệ phương trình là :  ; 6 .    2  3 3 2
x y  3y x  4 y  2  0    1 Bài toán 231. 3
x x  3  
2 x  2  y 2
Giải : Điều kiện: x  2  .Phương trình: 3 3 2
x x  2  y  3y  4 y
x x    y  3 3 2 1   y   1  2 (3)
Xét hàm số f t 3
t t  2 trên  2
 ; . Ta có: f t 2 '
 3t 1  0, t   2  ;  .
Suy ra hàm số f t đồng biến trên  2  ; .
Phương trình 3  f x  f y 1  x y 1  y x 1
Thay y x 1 vào phương trình (2) ta được: 3
x  3  2 x  2 1 3
x  8  2  x  2  2 2 x  2  2 x  2  2 2 x  2 2   
  x  2 x  2x  4    x  2 2
x  2x  4     x  2  2  x  2  2  x  2   2   x 2 2 x 2x 4        0 2  2  
x  2x  4   0 x 2 2       x  2  2 
x  2  0  x  2  y  3  2 2 Xét phương trình : 2 2
x  2x  4 
 0  x  2x  4  (*)  x  2  2  x  2  2 2
Ta có VT x  2x  4   x  2 2 1  3  3;VP   1, x  2;  x  2  2
Do đó phương trình (*) vô nghiệm. Vậy hệ phương trình đã cho có nghiệm duy nhất 2;3. 2 3 3 3 3 8  x x 1  2xy 1
 2 xy 4y x y + 3xy Bài toán 245.  8 x 2 x
3 xyxy 1    4  x 1  y  2 3 3 3 3 8  x x 1  2xy 1
 2 xy 4y x y + 3xy   1 
Giải : Hệ phương trình  8 x 2 x 3   x  1  y  1   4   2 x 1  yx  0  x  0 Điều kiện :   x  1  y  1 0y 1    y 0 
8x x 12x 12 x 3 Phương trình (1)    4 x + 3x 3 2 y y y 3 2  2 x   2 x  2 x 2 x 2 3 3   3  .13 .1 1  3 3   x + 3x y   y y y     3  2 x   2 x  3  1   3 1
   x + 3x(3) y   y     
Xét hàm số : f t 3 t 3 , t t
 . Ta có : f t 2 '
3t 30, t  
Hàm số f t đồng biến trên . Phương trình (3)  2 x  2 x 2 x 2 xf  1   f   x  1   x   x 1    y 0(4)  yy   y x 1 
Thế vào phương trình (2) ta được : 3  x  1  y 
1 4y 4 x  1 y 1  y 1  3  x  1  y  1   4 y  1  x  1 0 3  4 1  0 x 1  x 1  y 1  Đặt t   ,
0 phương trình trên trở thành : x 1  t  1  y 1  2 4  t 3t 1   0  1  1  y 1   x 1
 y x t   ,loai x 1   4 2 xx 0 , y loai 2
Thế vào phương trình (4) ta được :
x x x2 x 0 x 1  x 1   y
Vậy hệ phương trình có nghiệm duy nhất: 1;  1 3 3 2 2 x
  y 3y 32x 9x + 8y+36    1 Bài toán 246.  2
4 x2 163y x 8    2  x   2  x  20 
Giải : Điều kiện :   16 163y 0 y     3 Phương trình (1) 3 2 3 2 x 9
x 27x275x 1  5 y 3  y 3y 1  5y5 
x 3   x   y 3 3 5 3 1   5 y  1 (3)
Xét hàm số : f t 3 t 5 ,
t t  f t 2 '
3t 50, t   .
 Hàm số f tđồng biến trên 
Phương trình (3)  f x 
3  f y 
1 x3 y 1
  y x2 16 16 22 Ta có : y  x2 x
. Thế : y = x – 2 vào phương trình (2) ta được : 3 3 3 2 2
4 x2  223x x 8   4 x2  2  22 3  x 4   x   4 0 x2  63x  4 3  4      2x   4 0   x  2  x2 0   x2 2 223x 4  x22 223x 4  x  2y 0   4 3   x20     x22 223x 4 4 3  22
Xét hàm số : f   x   x2,x 2  ;   x2 2 223x 4  3  2 9  22 f '  x   1  0, x   2  ; 2 2   xxxx   3 2 2 2 2 22 3 22 3 4         22 Hàm số f  
x nghịch biến trên 2  ;   và f  
1 0, suy ra phương trình (*) có nghiệm  3 
duy nhất x = -1, khi đó y = -3. Vậy hệ phương trình có 2 nghiệm : 2;  0 ; 1  ;  3 6 4 2 2 3 2 x
 3x y3x y 2y 4x 8y 0   1  Bài toán 249. 2 3 3
 2y x 32 2y8   2 
Giải : Điều kiện : 2y 8  0y 4  Phương trình (1) 6 4 2 2 3 2 3
x 3x y3x y y 4x 4y y 4y   x  3 2 y   2 x   3 4
y y 4y(3)
Xét hàm số : f t 3
t 4t,t. Ta có f t 2 ' 3t 4 0, t  
Hàm số f t đồng biến trên . Phương trình (3)  f  2 x   y f   2 2
y x y y 2y x , y  0 2
Thế 2y x vào phương trình (2) ta được : 3 2 2 2
3 x x 32 x 8 3 2 2 2  
3 x  1 x 3  2  x 8  3 0 2 2 2  x 1    x 1    x 1   3      0 3 4 3 2 2 2  x x 1
   x 32  x 83   3 1 1  2  x   1   0   3 4 3 2 2 2  x x 1  x 32 x  3  1 x  1  y   2  3 1 1    0    3 4 3 2 2 2  x x 1  x 32 x 83 3 1 1 Phương trình (*) :   0 3 4 3 2 2 2 x x 1  x 32 x 83 1 1 2 2 2 2 Vì x
 : x 8  x 3 x 83 x 32  2 2 x 32 x 83 3 1 1    0, x   .
Phương trình (*) vô nghiệm. 3 4 3 2 2 2 x x 1  x 32 x 83  1  1
Vậy hệ phương trình có 2 nghiệm : 1  ; ; 1;      2  2