BỘ GIÁO DỤC VÀ ĐÀO TẠO ĐẠI HỌC DUY TÂN
-----  ----- 
BÀI TẬP THỰC HÀNH
TOÁN RỜI RẠC & ỨNG DỤNG
LỚP K15CMUTPM, K16CMUTCD
TỔ BỘ MÔN CƠ SỞ TIN HỌC
GIẢNG VIÊN: ĐẶNG VIỆT HÙNG ĐÀ NẴNG 09/2022 BUỔI 1 TẬP HỢP
Bài 1. Viết chương trình nhập một mảng các số nguyên, viết hàm kiểm tra một mảng
các phần tử nguyên có phải là một tập hợp hay không.
Bài 2. Viết chương trình nhập các phần tử của tập hợp A (các phần tử không được
giống nhau). Viết hàm in ra tất cả các phần tử của tập hợp A.
Bài 3. Viết chương trình nhập các phần tử nguyên dương cho tập hợp A và B. Viết
chương trình kiểm tra 2 tập A, B có bằng nhau không
Gợi ý: so sánh lượng của 2 tập và kiểm tra xem A có là tập con của B.
Bài 4. Viết chương trình tính hợp, giao, hiệu của 2 tập số nguyên A và B.
Bài 5. Viết chương trình xuất ra tích Descartes của 2 tập A (kí tự chữ cái), B (số nguyên).
Bài 6. Giải quyết bài 4 với cấu trúc danh sách liên kết (đơn, đôi)
Bài 7. Viết chương trình tính hợp, giao, hiệu và tích Descartes của 3 tập A, B, C.
Gợi ý: Sử dụng nguyên lý bù trừ.
Viết chương trình in ra tất cả các từ có 4 kí tự từ tập {‘a’, ‘b’, ‘c’, ‘d’, ‘e’ ,’f’, ‘g’}
trong đó mỗi kí tự chỉ xuất hiện nhiều nhất 1 lần. 2 BUỔI 2 ĐỆ QUI Bài 1: tính tổng S=1+3+5+7+…+(2n-1)
bằng phương pháp đệ qui.
Bài 2:Tính tổng của các chữ số của một số nguyên bất kỳ. (n>=0) Thuật toán:
Cài đặt Giải thuật: int Tong(int n) { if (n==0) return n; else return n%10 + Tong(n/10); }
Bài 3: Viết chương trình tìm ước chung lớn nhất của hai số a,b bằng kĩ thuật đệ qui. int ucln(int a,int b) { if(a==b) return a;
else if (a>b) return ucln(a-b,b); else return ucln(a,b-a); }
Bài 3: Viết chương trình tính n!
Bài 4: Dãy số Fibonacci được định nghĩa như sau: A(0) = A(1) =1
A(n) = A(n-2) + A(n-1) với n >1
a. Nhập một số n và in ra n số Fibonacci đầu tiên
b. Nhập một số n và in ra các số Fibonacci <=n
c. Nhập một số m, kiểm tra xem m có phải số Fibonacci?
Bài 5: Viết chương trình liệt kê các hoán vị của
các số từ 1 đến n (với n >0 và được nhập vào từ bàn phím). 3 BTN: b
Bài 6: Giả sử a,b là những số nguyên dương.
Q là hàm số của a và b, được định nghĩa như sau: 0 nếu aQ(a,b) = Q(a-b, b) +1 nếu a>=b
Hãy viết chương trình và tính Q(2,3) và Q(14,3).
Bài 7: Viết chương trình sử dụng giải thuật đệ quy và giải thuật lặp cho các yêu cầu sau đây:
a. Tính tổng S = 1 + 2 + …+n
b. Tính tổng S= 1 +3 + 5+ …+ (2k+1) với (2k+1)<=n
c. Đổi số n hệ thập phân sang hệ bất kỳ(chỉ dùng đệ quy)
d. Nhập vào một số nguyên dương n và in số đảo ngược của n ra màn hình. (ví dụ
nhập n= 12345 thì in ra màn hình 54321)
Bài 8: Một số nguyên dương được gọi là đối xứng nếu chữ số thứ nhất bằng chữ số
cuối, chữ số thứ hai bằng chữ số gần cuối,… Viết hàm để kiểm tra số nguyên dương n
có phải là số đối xứng hay không.
Bài 9: Tìm các số đối xứng bé hơn hoặc bằng n mà bình phương cũng là một số đối xứng. B ài 10
: Xét định nghĩa đệ qui  n 1 , m 0  A(m,n) =  ( A m  ) 1 , 1 , n 0   ( A  m , 1 ( A , m n  )) 1 , m  0  n  0
Hàm này được gọi là hàm Ackermann. 1. Tính A(1,2)?
2. Viết hàm đệ qui để tính A(m,n).
Bài 11: Viết chương trình cài đặt bài toán Tháp Hà Nội.
Trước tiên ta xét một vài trường hợp đơn giản:
1. Trường hợp n=1: ta chỉ cần 1 phép chuyển
- Chuyển đĩa từ cột A sang cột C (ký hiệu A C)
2. Trường hợp n=2: ta chỉ cần thực hiện 3 phép chuyển:
- Chuyển đĩa thứ nhất từ cọc A sang cọc B: A B 
- Chuyển đĩa thứ hai từ cọc A sang cọc C: A C  4
- Chuyển đĩa thứ nhất từ cọc B sang cọc C: B C 
3. Trường hợp n>2: Ta coi (n-1) đĩa ở trên đóng vai trò như đĩa thứ nhất thì có
thể hình dung đang có 2 đĩa trên cọc A. Nếu mô phỏng như trường hợp có 2 đĩa thì ta có giải thuật như sau:
- Chuyển (n-1) đĩa từ cọc A sang cọc B
- Chuyển đĩa thứ n từ cọc A sang C
- Chuyển (n-1) đĩa từ B sang C
Và lược đồ 3 bước cơ bản trên ứng với n đĩa, ta lại đưa bài toán về với (n-1)
đĩa rồi đến (n-2) đĩa và cho đến khi bài toán ứng với 1 đĩa: chuyển 1 đĩa từ cọc này sang cọc kia.
Như vậy giải thuật này mang tính chất đệ quy và giải thuật theo ngôn ngữ C
như sau: Dùng B làm cọc trung gian
void hn_tower(int n, char A, char B, char C) { if(n==1)
cout<< "chuyen 1 dia tu coc "<< A <<" qua coc "<< C <else{ hn_tower(n-1,A,C,B); hn_tower(1,A,B,C); hn_tower(n-1,B,A,C); } }
Kết quả chạy chương trình với số đĩa n=3 như sau: 5 BUỔI 3 HỆ THỨC TRUY HỒI
Bài 8. Viết chương trình cài đặt bài toán lãi kép Bài mẫu:
(Xem lại lý thuyết phần công thức truy hồi)
Ta có P =1000000, lãi suất d=0,1 0 1 Pn=Pn-1+d*Pn-1 #include #include using namespace std; int n=10,p0=5,d=2; int a(int n){ if(n==0)return p0; else return ...*a(n-1); }
int main(int argc, char *argv[]) {
cout<<"P("< system("PAUSE"); return EXIT_SUCCESS; }
Sinh viên điền vào phần ... để hoàn thành phần chương trình
Bài 9. Viết chương trình cài đặt bài toán tháp Hanoi
Gợi ý: Xem lại phần lý thuyết Có Cn=2Cn-1+1 , Cn=2 -1 n Bài mẫu: #include #include using namespace std;
char Peg1='A', Peg2='B', Peg3='C'; int NumDisks,Count; void Move(int char n,
StarPeg,char AuxPeg,char EndPeg){ 6
if(n==1){cout<<"chuyen:"<"< Count=Count+1;} { else Move(n-1,StarPeg,...,AuxPeg); Move(1,StarPeg,...,EndPeg); Move(n-1,...,StarPeg,EndPeg); } }
int main(int argc, char *argv[]) {
cout<<"n=";cin>>NumDisks;
Move(NumDisks,Peg1,Peg2,Peg3);
cout<<"So lan chuyen:"< system("PAUSE"); return EXIT_SUCCESS; }
Bài 10. Giả sử dân số thế giới năm 2007 là 8 tỉ người và tốc độ tăng dân số là 0,2% mỗi năm.
a) Lập hệ thức truy hồi cho dân số thế giới n năm sau năm 2004.
b) Giải hệ thức truy hồi cho dân số thế giới n năm sau năm 2004.
c) Dân số thế giới năm 2020 là bao nhiêu ?
d) Viết hàm A(n) để tính kết quả.
Bài 11. Cho dãy số {an} thoả mãn hệ thức truy hồi:
an= 5an-1- 6an-2; a0=0 và a1=1.
a) Giải hệ thức truy hồi trên.
b) Viết hàm A(n) để tính a .n
Bài 12. Cho dãy số {an} thoả mãn hệ thức truy hồi:
an= 6an-1- 9an-2; a0=1 và a1=3.
a) Giải hệ thức truy hồi trên.
b) Viết hàm A(n) để tính a .n 7 BUỔI 4, 5
Dùng phương pháp đệ qui quay lui sinh ra Chỉnh hợp n<=6 chập
k<=n từ tập các số {3, 5, 7, 9, 12, 14, 10}
PHƯƠNG PHÁP SINH VÀ QUAY LUI
Gợi ý: sinh viên xem bài giải mẫu bên dưới và phần lý thuyết phương pháp liệt kê cấu
hình tổ hợp bằng đệ qui quay lui và phương pháp sinh để sử dụng thuật toán cài đặt các bài toán sau
Bài 13. Viết chương trình sinh tất cả các hoán vị của tập X={1..n}.
Bài 14. Viết chương trình sinh tất cả các chỉnh hợp lặp chập k của tập X={1..n}.
Bài 15. Viết chương trình sinh tất cả các chỉnh hợp chập k của tập X={1..n}.
Bài 16. Viết chương trình phát sinh tất cả các tổ hợp chập k của tập X={1..n}.
Bài 17. Viết chương trình phát sinh tất cả các tổ hợp lặp chập k của tập X={1..n}.
Bài 18. Dùng thuật toán phát sinh cấu hình để viết chương trình liệt kê và đếm tất cả
các nghiệm của phương trình x1+x2+x3+x4+x5 = 21. So sánh với công thức đếm tìm được.
Bài 19. Dùng thuật toán phát sinh cấu hình tổ hợp để viết chương trình liệt kê tất cả
các số từ 1000000 đến 9999999 có tổng các chữ số bằng 20.
Bài 20. Viết chương trình liệt kê tất cả các nghiệm nguyên không âm của phương
trình x1+x2+…+xk = n. Với n, k nhập từ bàn phím.
Bài 21. Viết lại các chương trình trên bằng phương pháp lặp.
Gợi ý Xem thuật toán phần lý thuyết tại lớp
BÀI MẪU (theo gợi ý của giáo viên hướng dẫn, sinh viên hoàn thiện phần ... để
chương trình cho ra kết quả) 8
LIỆT KÊ DÃY NHỊ PHÂN BẰNG PHƯƠNG PHÁP SINH #include #include int n,b[20],stop; void Init() {
cout<<"\n Nhap do dai xau nhi phan: "; cin>>n;
for(int i=1;i<=n;i++) b[i]=0; stop=0; } void Next_Bit_String() { int i=n;
while(i>0 && b[i]==1) { b[i]=0; i--; }
if(i<1) stop=1; else b[i]=1; } void Generate() { Init(); while(!stop) {
for(int i=1;i<=n;i++) cout< cout<<"\n"; Next_Bit_String(); } } int main() { Generate(); getch(); }
LIỆT KÊ HOÁN VỊ BẰNG PHƯƠNG PHÁP SINH #include 9 #include //Dao mang tu vi tri k den n //(3)
void Dao(int M[100],int k,int n) { int j=n,i=k,tam=0; while(j>=i) { tam=M[i]; M[i]=M[j]; M[j]=tam; j--;i++; } } //hien thi mang //(4) void Display(int M[100],int n) { int i=0;
for(i=1;i<=n;i++)printf("%d ",M[i]); printf("\n"); } //khoi tao mang void Create(int M[100],int n) { int i=0; for(i=1;i<=n;i++)M[i]=i; } //dao vi tri i, j //(2)
void DaoPostion(int M[100],int int n, i,int j) { int tam; 10 tam=M[i]; M[i]=M[j]; M[j]=tam; }
// tim vi tri phan tu co gia tri nho nhat trong cac
//phan tu tu k den n va co gia tri lon hon M[k] //(1) int min(int M[100],int int k, n) { int min=32767,postion=0; for(int i=k+1;i<=n;i++) if(...) { min=M[i]; postion=i; } return postion; }
//liet ke cac hoan vi cua n phan tu //(5)
void LietKeHoanvi(int M[100],int n) { int i,k, ok; Create(M,n);
Display(M,n);//liet ke hoan vi dau tien 1 2 3 ... n while(1) { ok=0; for(i=n-1;i>=1;i--) { if(M[i+1]>M[i]) { ... 11
DaoPostion(M,n,i,k);//tham chieu den (2)
Dao(M,i+1,n);//tham chieu den (3)
Display(M,n);//tham chieu den (4) ... ... } } if(!ok)break; } } //main function int main() { int M[100],n; while(1) {
printf("n=");scanf("%d",&n); if(n==0)break;
else LietKeHoanvi(M,n);//tham chieu den (5) } return 0; }
LIỆT KÊ TỔ HỢP BẰNG PHƯƠNG PHÁP SINH #include #include #define TRUE 1 #define FALSE 0 #define MAX 100 int n, k, Count, C[MAX], Stop; void Init(){ int i; 12
printf("\n Nhap n="); scanf("%d", &n);
printf("\n Nhap k="); scanf("%d", &k); for(i=1; i<=k; i++) C[i]=i; } void Print(){ int i;Count++;
printf("\n Tap con thu %d:", Count); for(i=1; i<=…; i++) printf("%3d", C[i]); } void Next_Combination(){ int i,j; i = k;
while(i>0 && C[i]= =…)i--; if(i>0) { C[i]= C[i]+1;
for(j=i+1; j<=k; j++) C[j]=…; } else Stop = TRUE; } void Combination(){ Stop=FALSE; while (!Stop){ Print(); Next_Combination(); } }
int main(int argc, char *argv[]) { Init(); Combination(); printf("\n"); system("PAUSE"); 13 return EXIT_SUCCESS; } PHƯƠNG PHÁP QUAY LUI
Bài 12: Viết chương trình liệt kê các dãy nhị phân có độ dài n (với n >0 và được nhập vào từ bàn phím). #include #include int n,b[20]; void InKetQua() {
for(int i=1;i<=n;i++) cout< cout<<"\n"; } void Thu(int k) { int j; for(j=0;j<=1;j++) { b[k]=j; if(k==n) InKetQua(); else Thu(k+1); //Quay lui } } int main() {
cout<<"\n Nhap do dai xau nhi phan: "; cin>>n; Thu(1); getch(); return 0; }
Bài 13*: Viết chương trình cài đặt cho bài toán 8 quân hậu. Cách giải: 14
Đánh số cột và dòng của bàn cờ là từ 1 cho đến n. Mỗi dòng chỉ xếp 1 quân
hậu. Như vậy vấn đề của chúng ta bây giờ là tìm xem mỗi quân hậu trên mỗi dòng sẽ
được xếp vào cột nào trên bàn cờ thì thỏa mãn là chúng không ăn được lẫn nhau.
Theo như luật chơi cờ thì quân Hậu ăn theo đường ngang, dọc và hai đường
chéo. Như vậy yêu cầu bài toán được đưa về dạng tìm các cách xếp hậu trên bàn cờ
hay nói cách khác là tìm các bộ gồm n thành phần (x1, x2,…,x ) n trong đó xi = j nghĩa
là quân hậu của hàng i được xếp vào cột j. Như vậy các giá trị đề cử cho xi là từ 1 cho
đến n. Giá trị j này được chấp nhận nếu các quân hậu trước đó chưa chiếu đến (hay
nói cách khác là vị trí ô (i,j) này chỉ được chấp nhận khi các quân hậu đã xếp trước đó không ăn được)
Các nước chiếu của quân hậu Xét n=8
Đối với mỗi ô trong hàng, sẽ có 1 cột và 2 đường chéo đi qua nó là đường chéo
trái và đường chéo phải.
Ta sẽ dùng 3 mảng kiểu boolean để biểu thị cho các cột, các đường chéo trái,
và các đường chéo phải (có tất cả 15 đường chéo trái và 15 đường chéo phải).
int a[8]; với các giá trị ban đầu của nó là true hay a[i]=1
int b[15], c[15];với các giá trị ban đầu của nó là true hay b[i]=1, c[i]=1 Trong đó:
a[i] = true: hàng i chưa bị chiếm bởi quân hậu nào.
b[k]=true: Đường chéo trái k chưa bị chiếm bởi quân hậu nào với 2<=k<=2*n
c[k] = true: Đường chéo phải k chưa bị chiếm bởi quân hậu nào với 1- n<=k<=n-1
Chú ý rằng các ô (i, j) cùng nằm trên 1 đường chéo trái thì có cùng giá trị i + j,
và cùng nằm trên đường chéo phải thì có cùng giá trị i - j.
Để kiểm tra xem ô (i, j) có an toàn không, ta chỉ cần kiểm tra xem hàng i và
các đường chéo (i +j), (i - j) đã bị chiếm chưa, tức là kiểm tra a[i], b[i + j], và c[i - j].
Ngoài ra, ta cần có 1 mảng x để lưu giữ chỉ số hàng của quân hậu trong cột j. int x[8];
Vậy với thao tác đặt hậu vào vị trí hàng i cột j, ta cần thực hiện các công việc:
x[j] = i; a[i] = false; b[i + j] = false; c[i - j] = false;
Với thao tác bỏ hậu ra khỏi cột j trong hàng i, ta cần thực hiện các công việc:
a[i] = true; b[i + j] = true; c[i - j ] = true;
Còn điều kiện để kiểm tra xem vị trí tại cột j trong hàng i có an toàn không là: 15
(a[i] = =true) && (b[i + j] == true) && (c[i - j] == true)
Như vậy, hàm Try sẽ được thể hiện cụ thể bằng ngôn ngữ C như sau: void In_kq() {
cout<<"\n -Cach xep: "<<++d<<":\n"; for(int i=1;i<=n;i++)
cout<<"("< cout<<"\n"; } void Try(int j) { for(int i=1;i<=n;i++)
if(a[i]&&b[i+j]&&c[i-j]) { x[j]=i; a[i]=false; b[i+j]=false; c[i-j]=false; if(j==8)In_kq(); else Try(j+1); a[i]=true; b[i+j]=true; c[i-j]=true; } }
Kết quả thực thi chương trình bài toán 8 hậu cho ra 92 cách. Xem hình vẽ về demo bài toán: 16 BUỔI 6
CÁC PHƯƠNG PHÁP DUYỆT ĐỒ THỊ
Bài 22. Viết chương trình lưu trữ và duyệt (sâu, rộng) đồ thị vô hướng(có hướng) G(V,E)
Bài mẫu: Sinh viên hoàn thiện phần … để cho ra kết quả, sau đó áp dụng thuật toán
trên để viết chương trình duyệt đồ thị có hướng
DUYỆT ĐỒ THỊ VÔ HƯỚNG THEO CHIỀU SÂU #include #include #include #define MAX 100 #define TRUE 1 #define FALSE 0 int G[MAX][MAX],//Ma tran ke n,//So dinh
C[MAX];//Mang danh dau cac dinh chua xet FILE *fptr; //Khoi dung void Init (char *path){ … }
//Depth first search(duyet theo chieu sau) void DFS (int v){ int u; printf("%3d",v); C[v]=…; for(u=1; u<=n; u++){
if(… && C[u]= =FALSE) DFS(u); } }
int main(int argc, char *argv[]) 17 { int i; Init("Graph.INP");
for(i=1; i<=n;i++) if(…)DFS(i); system("PAUSE"); return EXIT_SUCCESS; }
DUYỆT ĐỒ THỊ VÔ HƯỚNG THEO CHIỀU RỘNG #include #include #include #define MAX 100 #define TRUE 1 #define FALSE 0
int G[MAX][MAX],n,C[MAX],QUEUE[MAX],FirstQ=1, LastQ=1; FILE *fptr; //DUYET DO THI THEO CHIEU RONG //Khoi dung void Init (char *path){ … }
/* Duyet theo chieu rong (Breadth First Search)*/ void BFS (int i){
int u, j;FirstQ=… ; LastQ=…;
QUEUE[LastQ]=i;//Tao hang doi voi dinh dau la i C[i]=TRUE;//Danh dau dinh i while(…){ u=QUEUE[FirstQ]; printf("%3d",u);
FirstQ=FirstQ+1; /*Duyet dinh dau hang doi*/ for(j=1; j<=n;j++){
if(G[u][j]= =1 && C[j]= =FALSE ){ LastQ=LastQ+1; QUEUE[LastQ]=…; 18 C[j]=…; } } } }
int main(int argc, char *argv[]) { int i; Init("Graph.INP"); printf("\n\n"); for(i=1; i<=n; i++) if (C[i]= =…)BFS(i); system("PAUSE"); return EXIT_SUCCESS; }
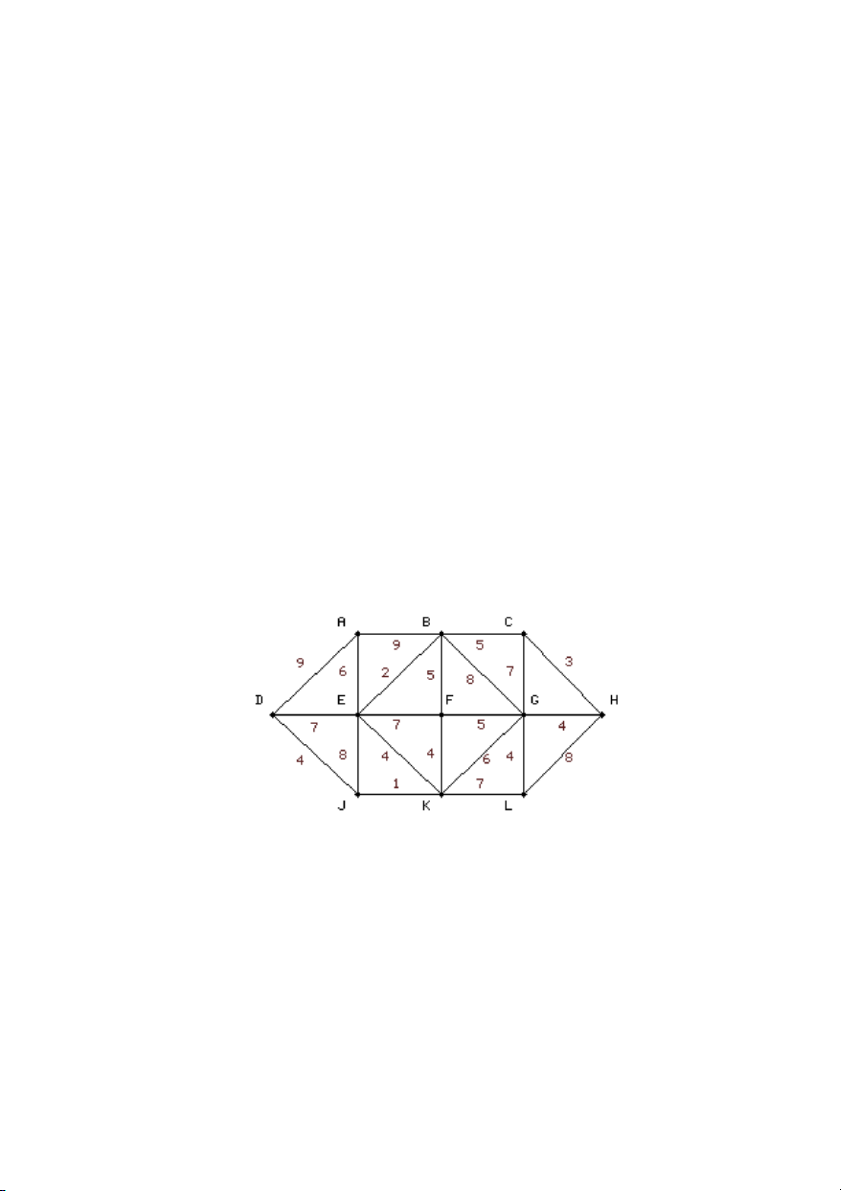
Bài 23. Cho đồ thị G=(V,E,W)
a) Tìm đường đi ngắn nhất từ A đến H.
b) Tìm cây phủ nhỏ nhất của G.
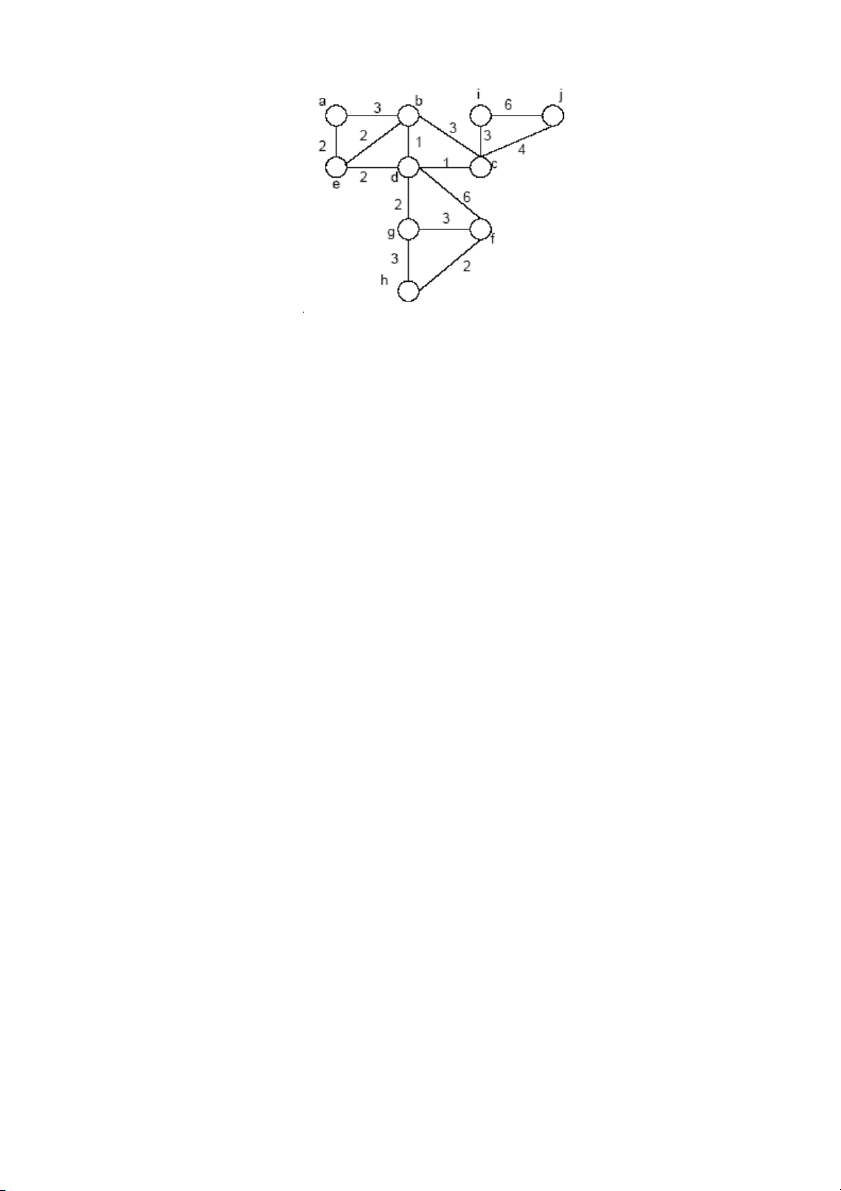
Bài 24. Cho đồ thị G=(V,E,W) 19
a) Tìm đường đi ngắn nhất từ a đến j.
b) Tìm cây phủ nhỏ nhất của G. 20