Bài tập Tín hiệu, mã hóa PCM và ghép kênh TDM/FDM môn Thông tin số | Trường Đại học Bách Khoa Hà Nội

Bài 2: Tín hiệu g(t) có phổ rộng 1.0 KHz và tần số trung tâm fc=10KHz. Hãy tìm tần số lấy mẫu để G(f) không bị
chồng phổ. Sai số tối đa cho phép của tần số lấy mẫu là bao nhiêu? GIẢI
Ta thấy tần số trung tâm fc=10 KHz >> 0 do đó đây là tín hiệu thông dải, áp dụng định lý lấy mẫu cho tín hiệu thông dải: ,
Trong đó fmax và fmin lần lượt là giới hạn trên và dưới của dải tần và n′ = INT
Với phổ B = 1.0 KHz. Ta có: fmax = fc + 0.5B = 10.5 KHz, fmin = fc − 0.5B = 9.5 KHz =⇒ n′ = INT INT . Khi đó: KHz KHz
Như vậy: 2.1 KHz ≤ fs ≤ 2.33 KHz thì không xảy ra chồng phổ.
Lý tưởng nhất ta muốn lấy mẫu ở chính giữa dải này để sai số cho phép là tối đa =⇒ fs = 0.5 · (2.1 + 2.33) = 2.215 KHz
2.215 ± 0.115 KHz
Bài 3: Một hệ thống thông tin số truyền tín hiệu thoại sử dụng phương pháp mã hoá PCM tuyến tính. Hệ thống
này sử dụng bộ lọc lý tưởng có tần số cắt 3,4 KHz để chống nhiễu chồng phổ. Tính tốc độ truyền của dòng bit
PCM này để tỷ số SNqR, thoả mãn điều kiện SNqR ≥ 50dB biết rằng trong tín hiệu thoại: GIẢI Ta có: với
mà SNqR ≥ 50dB (bài cho) hay SNqR ≥ 105, từ đó ta có:
n ≥ 9.173 chọn n = 10
Tín hiệu thoại là tín hiệu băng cơ sở và hệ thống sử dụng bộ lọc lý tưởng với tần số cắt 3,4 KHz nên tín hiệu
sẽ có dải tần 0−3.4 KHz, theo định lý lấy mẫu tín hiệu băng cơ sở, ta có tần số lấy mẫu tối thiểu là:
fs = 2B = 6.8 KHz
Tốc độ dòng bit tối thiểu để thỏa mãn điều kiện đề bài là:
Rb = nfs = 68 Kbps
Bài 4: Tìm tỷ số SNR sau giải mã tại đầu thu của tín hiệu trong bài tập 3, với giả thiết cứ 106 bit truyền sẽ có 1 bit lỗi. GIẢI
Cứ 106 bit truyền sẽ có 1 bit lỗi =⇒ xác suất lỗi là:
Giả sử SNRTX = SNqR, với SNRTX là tỉ số tín hiệu trên nhiễu của tín hiệu được phát đi. Nói cách khác nhiễu
trong hệ thống chỉ đến từ lượng tử hóa.
Tỷ số SNR tại đầu thu là: hay 51.44 dB
Bài 5: Giả sử tín hiệu số trong bài tập 3 được truyền theo dạng nhị phân qua một kênh truyền dẫn có băng tần
cho phép từ 0-1,1MHz, đường truyền không có nhiễu. Có thể có tối đa bao nhiêu kênh thoại được truyền trên
đường truyền này? Trong trường hợp sử dụng phương pháp mã hoá PCM phi tuyến với từ mã 8 bit, tốc độ lấy
mẫu 8 KHz thì có tối đã bao nhiêu kênh? GIẢI
Dung lượng của đường truyền là:
C = 2W log2 M,
với W = 1,1 MHz, M = 2 (truyền theo dạng nhị phân). Do đó:
C = 2 · 1.1 · log2 2 ≈ 2.2 Mbps
Số kênh thoại truyền được trên đường truyền với tốc dòng như bài 3 là: C 2.2 Mbps = ≈ 32.35 kênh Rb 68 Kbps
Làm tròn xuống vì không truyền được lẻ kênh =⇒ 32 kênh.
Trong trường hợp sử dụng phương pháp mã hoá PCM phi tuyến với từ mã 8 bit (n = 8), tốc độ lấy mẫu 8 KHz
(fs = 8 KHz), tốc độ luồng bit sẽ là:
Rb = nfs = 64Kbps
Số kênh thoại truyền được trên đường truyền trong trường hợp này là: C 2.2 Mbps
= ≈ 34 kênh (đã làm tròn xuống) Rb 64 Kbps
*LƯU Ý: SNR trong công thức Shannon: C = W log2 (1 + SNR) là SNR của kênh truyền, không liên quan đến
SNR của quá trình ADC. Vì đề cho là đường truyền không nhiễu (lý tưởng) do đó ta sẽ dùng công thức tính dung lượng của Nyquist.
Bài 6: Phương pháp lượng tử hóa phí tuyến theo luật A(A = 87,6) với hàm y = f(x) được xây dựng theo nguyên
tắc lượng tử hóa phi tuyến theo x chính là lượng tử hóa phi(?) tuyến tính đối với y. Tín hiệu x = sin(t) được lấy
mẫu tín hiệu tại thời điểm t = (a + b + c)/10. Nếu tín hiệu này thành chuỗi bit nhị phân. Xác định chuỗi bit nhị phân này. Giải
t = (a + b + c)/10 ? chắc là mã số sinh viên hay gì à a = 4, b = 0, c = 6
=⇒ t = 1 =⇒ x = sin(t) = sin(1) ≈ 0,841. Theo A-law
thì y được tính như sau: nếu ,
nếu |x| > A1
với sgn(x) là hàm dấu của x, sgn(x) = 1 khi x > 0 và sgn(x) = −1 khi x < 0. A là hằng số được quy
định trước (bởi chuẩn nào đó). Trong bài này
. Thay vào công thức đã cho ta có:
Dễ thấy y = f(x) là hàm đơn điệu tăng, nên dải biên độ của y là y = [f(−1),f(1)] hay y = [−1,1]. A-law dùng
8 bits (256 mức) để lượng tử hoá tuyến tính y. Do đó ta có bước lượng tử là:
Giả dụ như mã hoá theo kiểu đánh tăng dần với -1 là 8 bit 0 (mức thứ nhất) và 1 là 8 bit 1 (mức thứ 256). có
thể làm theo các cách mã hoá khác: bù 2, gray, ...
Mã hoá kiểu này cơ bản là đang dịch dải lên y = [0,2] (cộng 1 vào giá trị biên độ) để viết số nhị phân cho tiện.
Khi đó mức lượng tử sẽ được tính như sau: Mức lượng tử = round round
Theo cách mã hoá của ta thì chuỗi bit sẽ tương ứng với mức lượng tử ở dạng nhị phân: 252(10) → 11111100(2) 3 Mã đường truyền
Bài 1: Tín hiệu băng tần cơ bản với 4 mức biên độ có độ rộng một ký hiệu là 100µs.
1. Hãy tính độ rộng băng tần tối thiểu để truyền tín hiệu trên, với giả thiết bộ lọc cos nâng được dùngvới hệ số α = 0.3.
2. Để truyền 1 triệu bit cần bao nhiêu thời gian?
3. Nếu muốn truyền số bit trên với một nửa thời gian thì cần mã hoá bao nhiêu mức, giả thiết độ rộngbăng
tần để truyền không thay đổi. GIẢI 1. Ta có:
Tsymbol = 100µs =⇒ Rsymbol = 100M symbol/s Tín hiệu
có 4 mức (M = 4) do đó số bit trong mỗi mức là:
n = log2 M = log2 4 = 2 bits Tốc độ dòng bit là:
Rb = n · Rsymbol = 200 Mbps
Như vậy cần 1 kênh có dung lượng ít nhât là 200 Mbps để truyền được tín hiệu này. Theo định lý kênh Nyquist, ta có: C 200 Mbps
C = 2W log2 M =⇒ W = = = 25 MHz 2log2 M 2 × 4
Khi dùng bộ lọc cos nâng, độ rộng băng thông tối thiểu cần thiết để truyền tín hiệu mở rộng ra 1 + α lần:
W ′ = W(1 + α) = 25 MHz × 1.3 = 32.5 MHz
2. Thời gian để truyền 1 triệu bit là: 1M 1M = = 5 ms Rb 200 Mbps
3. Truyền với thời gian bằng một nửa thời gian chính là truyền với tốc độ bit gấp đôi:
C′ = 2C = 2 · 2W log2 M
Vì ta giữ nguyên độ rộng băng tần W nên đại lượng cần thay đổi là số mức của tín hiệu. Ta có:
C′ = 2C = 2 · 2W log2 M = 2W log2 M′
Như vậy M′ = M2 = 42 = 16 mức, ta cần mã hóa 16 mức nếu muốn truyền với 1 nửa thời gian. OR
Muốn truyền với 1 nửa thời gian mà vẫn giữ nguyên độ rộng băng tần thì mỗi mức cần phải truyền được
gấp đôi số bits: n′ = 2n = 2 × 2 = 4 như vậy cần mã hóa với số mức là :M = 24 = 16 mức Bài 2: Cho tín
hiệu băng tần cơ bản với 4 mức biên độ sử dụng mã NRZ lưỡng cực (polar NRZ). Tín hiệu này được
truyền trên đường truyền với độ suy giảm 15dB. Tại đầu thu, công suất nhiễu tại đầu vào là 10mW và
trở kháng đầu vào là 50Ω. Bên phát phải có công suất phát tín hiệu trung bình tối thiểu là bao nhiêu để
xác suất lỗi ký hiệu là Pe = 10−4. GIẢI
Giả sử xác suất xuất hiện của 4 biên độ mã polar NRZ là đồng khả năng, ta có: PS,avg
Lại có, công suất nhiễu trung bình là: δ2 √ PN,avg = = R ⇒ δ = p P N,avgR = 10−2R
Xác suất lỗi ký hiệu là: erfc là số mức: M = 4 √ √ 10 r ! 3 10 = p 20 10 − 2 4 2 ! erfc erfc erfc PS,avg
Lại có, Pe = 10−4 (đề bài cho), do đó: √ !! 10 √ p 10 p erfc 2 2
PS,avg =⇒ 0.00013 = erfc PS,avg Tra bảng erfc: Ta thấy: √ 10 p 2
PS,avg ≈ 2.69 =⇒ PS,avg ≈ 2.89W
Vì đường truyền suy hao 15dB nên ta có: P TX 1.5 1.5 1.5 1.5 = 10 =⇒ PTX = PRX × 10 = PS,avg × 10 = 2.89W × 10 ≈ 91.39W PRX
Như vậy ta cần phát với công suất 91.39W để tỷ lệ lỗi ký tự là Pe = 10−4
Bài 3: Mã NRZ lưỡng cực (polar NRZ) dưới dạng nhị phân, xung vuông được truyền trên đường truyền dài 15
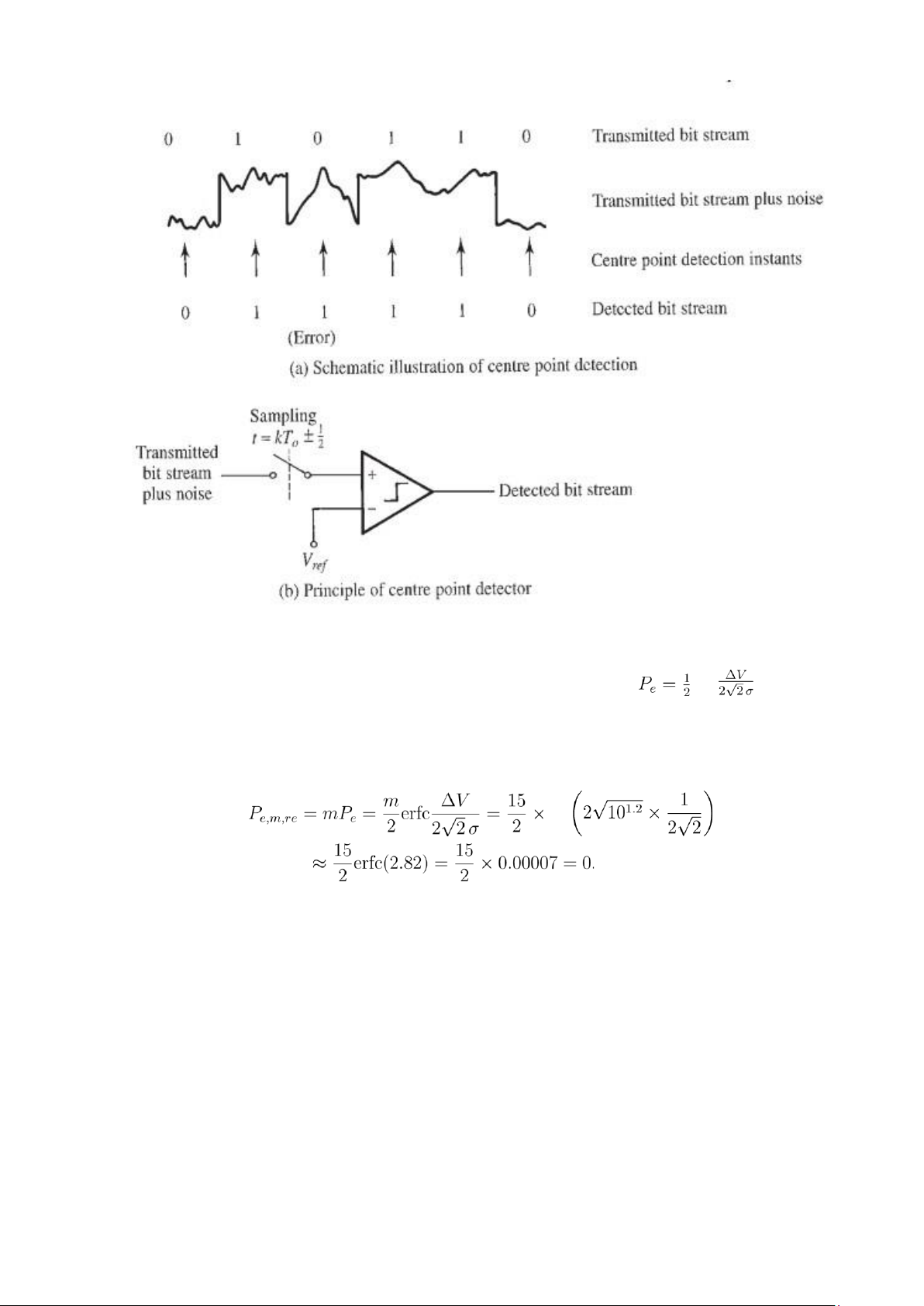
chặng. Biết rằng tỷ số SNR tại đầu vào trạm lặp tại mỗi chặng đo được là 12dB. Hãy tính xác suất bit lỗi Pe trong các trường hợp:
1. Sử dụng trạm lặp khuếch đại.
2. Sử dụng trạm lặp khôi phục. 3. So sánh kết quả. GIẢI
Giả sử xác suất xuất hiện các mức của mã polar NRZ là đồng khả năng ta có công suất trung bình của tín hiệu là: PS,avg
=⇒ ∆V = 2pPS,avgR(1)
Công suất nhiễu trung bình là: PN,avg PN,avgR(2) r = ⇒ ∆ V Từ (1) và (2) P σ =2 P N,avgS,avg . Lại có: s √ P ∆ V S,avg P =10 1 .2 = ⇒ =2 =2 10 1 .2 SNR = PN,avg σ PN,avg
1. Với trạm lặp khuếch đại, công suất nhiễu được khuếch đại cùng với công suất tín hiệu bị suy hao
trên kênh truyền. Giả sử mỗi chặng đều gây ra công suất nhiễu với giá trị như nhau thì với m chặng, √ công suất
nhiễu được khuếch đại m lần, do đó điện áp nhiễu tương đương σ tăng lên m lần, trong khi đó thì điện
áp của tín hiệu ở điểm thu giống với ở điểm phát. Ở điểm thu, điện áp nhiễu tương đương và điện áp tín hiệu là:
Tại điểm thu tỷ số tín hiệu trên nhiễu là: erfc erfc erfc erfc(0.73) 095%
2. Với trạm lặp tái tạo, thay vì khuếch đại, tín hiệu được "lặp" thông qua quá trình nhận diện (detection) để
quyết đinh xem đầu vào là gì:
Khi này, tín hiệu đi ra khỏi trạm lặp sẽ là 1 chuỗi xung vuông noiseless (lý tưởng), nhưng quá trình này vẫn
có lỗi xảy ra khi quá trình nhận diện (detection) phát hiện sai với xác suất erfc .
Với điều kiện là mPe << 1, ta có thể bỏ qua trường hợp cùng 1 ký hiệu được nhận sai nhiều hơn 1 lần qua
m chặng và khi đó thì dễ thấy lỗi của quá trình nhận diện sẽ tích lũy tuyến tính qua từng chặng, xác suất lỗi ở điểm thu là: erfc 0525%
3. Dùng bộ lặp tái tạo OK hơn nhiều so với bộ lặp khuếch đại: tốt hơn khoảng gần 300 lần. 4 Ghép kênh
Bài 1: WLAN hoạt động ở tần số 2,4 GHz sử dụng phương pháp FHSS với 75 kênh tần số. Chu kỳ lặp lại của các
kênh tần số là 30s. Tốc độ truyền số liệu là 2Mbit/s. Biết rằng độ dài tối đa của một gói Ethernet WLAN là 1518 byte. Hãy cho biết:
1. Tại một kênh tần số có tối thiểu bao nhiêu gói được truyền đi?
2. Phương pháp nhảy tần ở đây là nhảy tần nhanh hay nhảy tần chậm? GIẢI
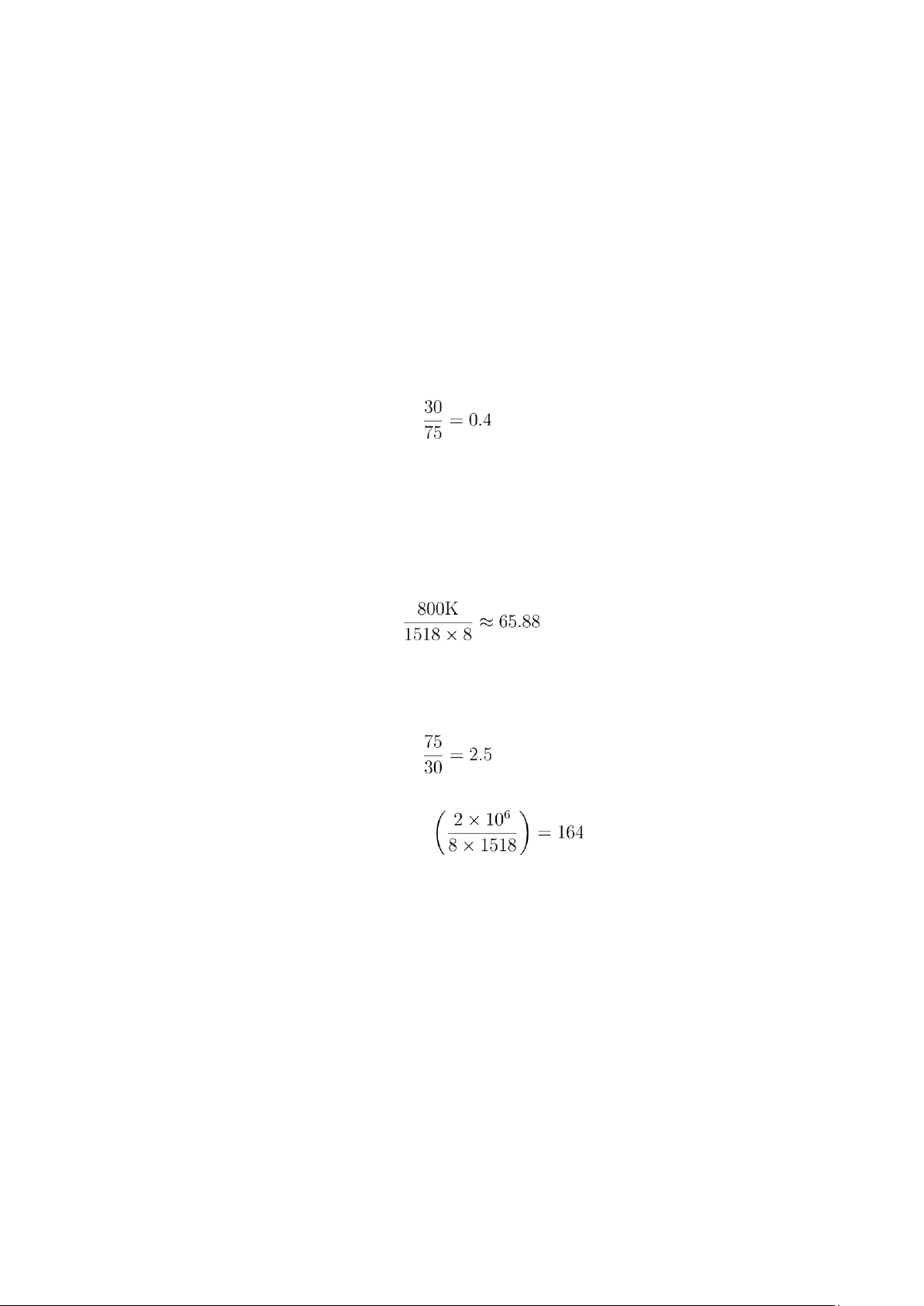
1. Số gói truyền tối thiểu trên mỗi kênh được tính trong một chu kỳ lặp lại, vì trong khoảng thời gian này, tất
cả 75 kênh đều được sử dụng một lần duy nhất, không lặp lại.
Thời gian dành cho 1 kênh trong 1 chu kì lặp lại là: s/kênh
Tại tốc độ 2 Mbps, số bit truyền được trong 0,4 s là:
2 × 106 × 0.4 = 800 Kbit
Số gói mà mỗi kênh truyền được trong 1 chu kì (số gói tối thiểu) là: gói
Làm tròn xuống vì không truyền được lẻ gói =⇒ 65 gói.
2. Tốc độ nhảy kênh là: kênh/s
Tốc độ truyền gói là: round down gói/s
Vì tốc độ nhảy kênh chậm hơn truyền gói =⇒ nhảy tần chậm
Bài 2: Cho tín hiệu thoại với dải tần từ 0 – 4 KHz. Giả sử 12 tín hiệu thoại được ghép kênh theo kiểu FDM và
TDM. Trước khi được ghép kênh TDM, giả sử các kênh thoại đã được mã hoá PCM phi tuyến với tần số lấy mẫu
8KHz, độ dài từ mã 8 bit.
1. Tính độ rộng 1 khe thời gian khi ghép kênh kiểu TDM.
2. Tính độ rộng băng thông cần thiết khi trong hệ thống ghép kênh TDM có sử dụng bộ lọc cos nângvới hệ
số α=0,3 để hạn chế ISI.
3. Tính độ rộng băng thông cần thiết khi trong hệ thống ghép kênh FDM có sử dụng băng tần bảo vệgiữa hai
kênh thoại kề nhau là Bguard = 0.5 KHz. GIẢI
1. Tốc độ mỗi luồng trước khi ghép kênh kiểu TDM là:
Rb = nfs = 8 × 8K = 64 Kbps
Tốc độ sau khi ghép 12 kênh kiểu TDM là: Kbps
Độ rộng mỗi khe thời gian (khi ghép xen byte) là: s
2. Coi như tín hiệu được truyền kiểu nhị phân (binary signalling) băng thông cần thiết theo định lýkênh Nyquist là: KHz
Một công thức khác có thể dùng để tính W
Băng thông cần thiết khi dùng bộ lọc cos nâng với α = 0.3 là:
W ′ = W(1 + α) = 384 KHz × 1.3 = 499.2 KHz
3. Băng thông cần thiết khi ghép 12 kênh theo kiểu FDM với Bguard = 0.5 KHz là:
W = 12B + 11Bguard = 12 × 4K + 11 × 0.5K = 53.5 KHz
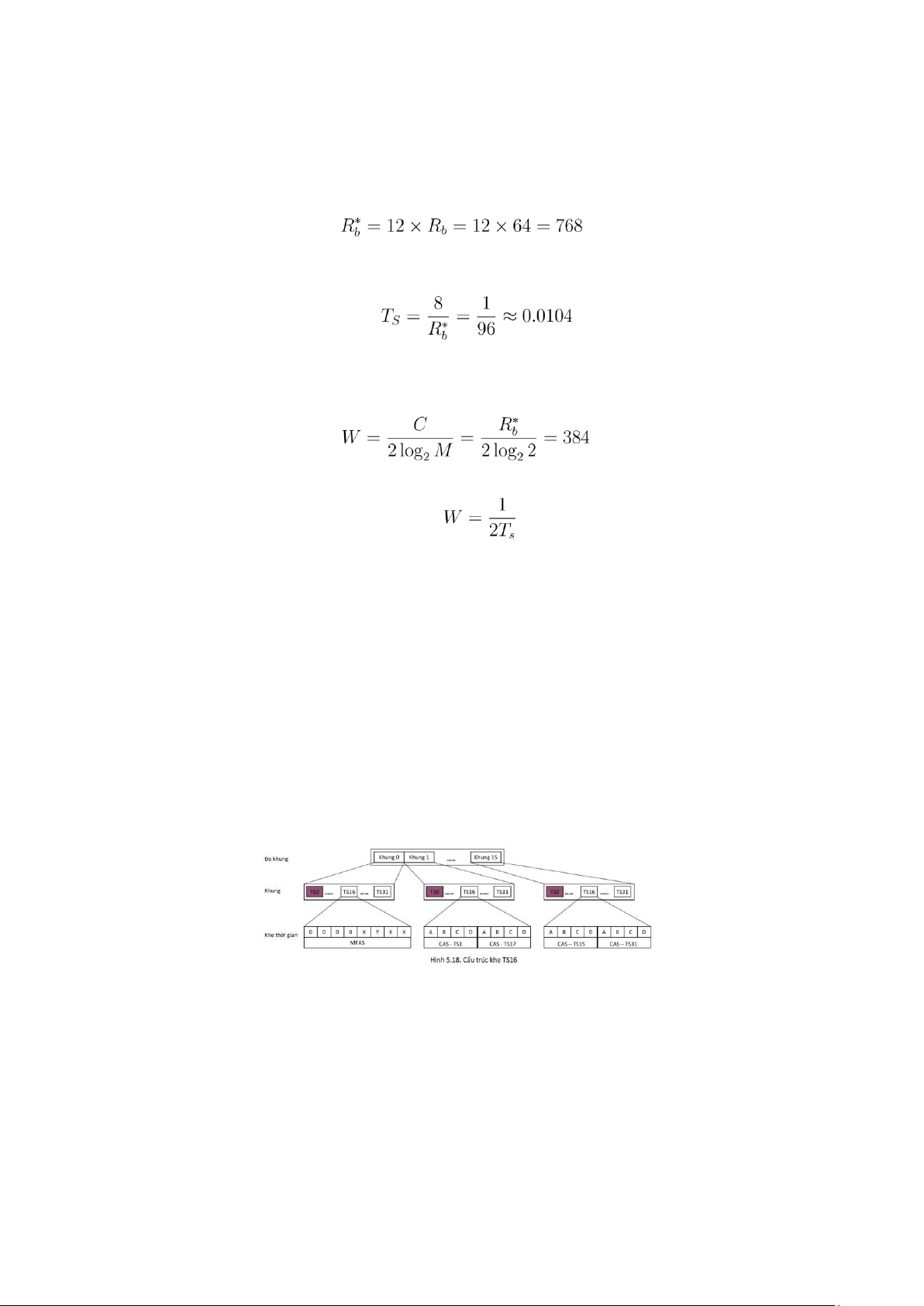
Bài 3: Trong hệ thống ghép kênh PCM32, tín hiệu báo hiệu CAS cho khe thời gian thứ 5 và thứ 20 nằm ở vị trí
nào (khung và khe thời gian số mấy trong đa khung)? GIẢI
Figure 1: nhờ cái hình đây để nhớ ô ạ :V
Tín hiệu CAS nằm ở khe thứ 16.
Vị trí khung = (vị trí khe < 16)? : vị trí khe : vị trí khe - 16
Do đó tín hiệu CAS của khe thời gian thứ 5 nằm ở khe thứ 16 của khung thứ 5, khe thời gian thứ 20 nằm ở
khe thứ 16 của khung thứ 4.
(bản ôn tập của trường =))) :)
Tín hiệu báo hiệu Cas luôn nằm ở khe thứ 16 . Ở trong một khung khe thứ 16 có độ dài 8 bit được chia đôi
để 4 bit đầu báo hiệu cho chính cái khe đó và báo hiệu cho khe thứ n + 1. Làm như vậy để báo hiệu cho 30 khe
giống nhau tại mỗi khung vì có 15 khung mang thông tin và một khung đầu tiên không liên quan vì nó dùng để điều khiển. Bài 4:
Tính tốc độ truyền của dòng số liệu báo hiệu (CAS) cho mỗi kênh thoại trên đường PCM32. GIẢI
PCM32 ghép 32 kênh thoại 64 Kbps thành các khung và đa khung. 1 khung PCM32 gồm 32 khe thời gian, mỗi
khe 1 byte (8 bit), mỗi đa khung có 16 khung. Do đó:
Tốc độ sau khi ghép là: Kbps = 2048 Kbps
Độ rộng 1 khe thời gian là: ms Rb 2048K 256 Độ rộng 1 đa khung là:
TMF = TS × 32 × 16 = 2 ms
Trong PCM32, dòng số liệu báo hiệu (CAS) cho mỗi kênh trong 1 đa khung có độ lớn là 4 bit/kênh. Như vậy
trong mỗi 2 ms, có 4 bit CAS được truyền cho mỗi kênh (tổng cộng có 120 kênh cho 30 kênh thoại). Tốc độ truyền
dòng số liệu báo hiệu (CAS) cho mỗi kênh là: 4 bit = 2 Kbps 2 ms
Bài 5: 4 luồng 2048 Kbps được ghép TDM xen byte theo kiểu PDH thành 1 luồng 8448 Kbps, biết mỗi khung dài
125 µs. Hỏi trong 1 khung các bit FANCR chiếm bao nhiêu khe thời gian. GIẢI
Tốc độ truyền các bit FANCR là:
vFANCR = v∗ − nv = 8448K − 4 × 2048K = 256Kbps
Số bit FANCR trong 1 khung là:
vFANCR × TF = 32 bit =⇒ 4TS 5 Điều chế số
Bài 1: Cho hệ thống điều chế BPSK có sóng mang sBPSK(t) = ±Acos(2πfct) truyền qua kênh AWGN với tốc độ
truyền Rb = 1 Mbps. Biết biên độ A = 10mV và mật độ công suất nhiễu N0 = 10−11 W/Hz. Hãy tính xác suất lỗi bit Pbe? GIẢI
Thời gian để truyền 1 bit là:
Công suất trung bình của sóng mang là: W
Năng lượng bit/ký hiệu là:
Eb = P × Tb = 5 × 10−5 × 10−6 = 5 × 10−11 W.s (hay chính là 5 × 10−11 J)
Áp dụng công thức tính xác suất lỗi của BPSK: erfc erfc erfc 077%
Bài 2: Xét hệ thống sử dụng điều chế QPSK có các thông số như sau: công suất tín hiệu (trung bình) là P = 3 ×
10−6 W, mật độ phổ công suất của nhiễu là N0/2 = 10−14 W/Hz
1. Tìm tốc độ bit tối đa để xác suất lỗi bit của hệ thống không lớn hơn 10−7.
2. Với tốc độ bit như câu a, xác định băng thông lý tưởng Bmin (mức băng thông nhỏ nhất) của hệ thống và
băng thông B của hệ thống khi không sử dụng bộ lọc tạo dạng xung. GIẢI
1. Điều chế QPSK =⇒ mức điều chế M = 4, tốc độ kí hiệu là: Rbit Rbit Rsymbol = = symbol/s log2 M 2
Năng lượng trung bình mỗi ký hiệu là: Esymbol bit
Xác suất lỗi bit đối với điều chế QPSK (M = 4) là: r E ! P · sin π bit error N 0 M erfc Với , thay vào: ! √ r E 2 · N 2 P 0 bit error erfc Thay Esymbol
và N0 = 2 × 10−14 W/Hz ta được: bit Pbit error erfc erfc
Ta có điều kiện bài ra là: Pbit error erfc Như vậy: erfc
(Giá trị này khá bé và không có trong bảng erfc nên ta phải dùng những công thức xấp xỉ như của 2 Abramowitz and Stegun: erfc(
Giải bất phương trình trên ta tìm được: Rbit ≤ 11.08 Mbps
Như vậy tốc độ bit tối đa để xác suất lỗi bit của hệ thống không lớn hơn 10−7 là 11.08 Mbps .
2. Mức băng thông tối thiểu lý tưởng là:
Bmin = Rsymbol = Rbit log2 M = 11.08 × 2 = 22.16 MHz
Băng thông thực tế khi không sử dụng bộ lọc tạo dạng xung là:
B = 2Rsymbol = 2 × 22.16 = 44.32 MHz
Bài 3: Một hệ thống điều chế M-PSK có tốc độ bit là Rb = 100 Kbps, băng thông (đã lọc tạo dạng xung) B = 35
KHz, kênh truyền là AWGN, hệ thống dùng bộ lọc cos nâng (Raised Cosine Filter) để tạo dạng xung trước khi thực
hiện điều chế với hệ số uốn (Roll-off Factor) α = 0.4 và dùng mã Gray để mã hóa các kí tự.
1. Xác định số mức điều chế M ?
2. Hãy xác định tỷ số Es/N0 cần thiết để đảm bảo mức xác suất lỗi bit Pbe = 10−6
3. Xác định hiệu suất phổ ηs và hiệu suất công suất ηp (với mức xác suất lỗi bit yêu cầu như câu b) của hệ thống. GIẢI 1. Ta có:
mà B = 35 KHz, Rb = 100 Kbps và α
= 0.4, do đó mức điều chế là: 2. Xác suất lỗi bit là: ! erfc Thay M = 16 ta có: ! erfc Điều kiện bài ra: erfc erfc 2
Dùng công thức xấp xỉ Abramowitz and Stegun: erfc( , ta được:
Như vậy tỉ số khoảng 277.35 thì tỉ số lỗi bit Pbe = 10−6 3. Hiệu suất phổ là: RS 25K ηs = log2 M · = 4 · ≈ 2.86 bps/Hz B 35K
Hiệu suất công suất là:
Bài 4: Xét hệ thống thông tin số có tốc độ bit Rb = 500 Kb/s dùng bộ điều chế 16-QAM vuông, mỗi kênh I và Q
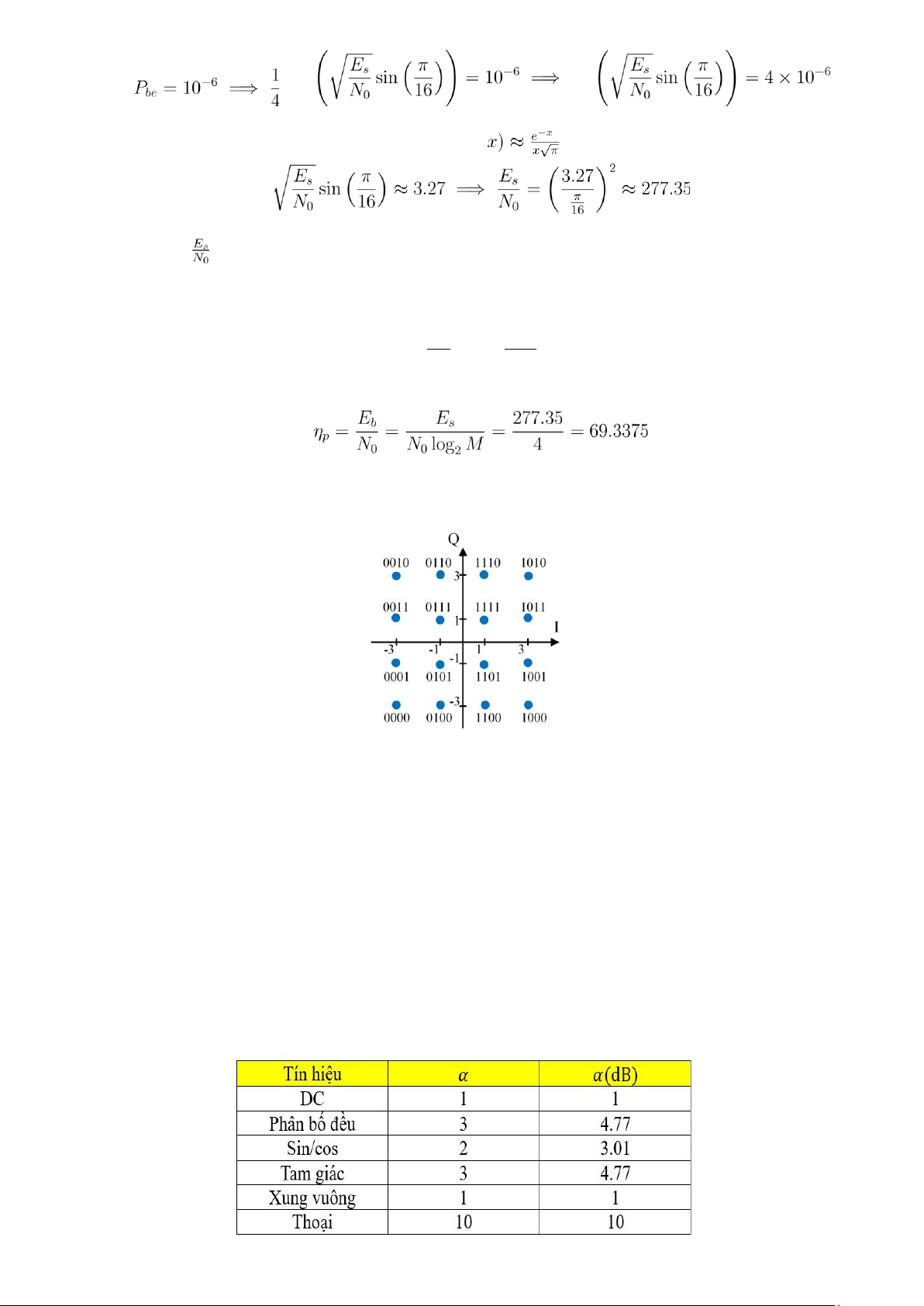
có 4 mức biên độ -3V, -1V, 1V, 3V và sử dụng mã Gray để mã hóa các ký hiệu điều chế (như hình vẽ). Tín hiệu
sau điều chế được truyền qua kênh AWGN với mật độ phổ công suất của nhiễu là N0 = 3.63 × 10−7 W/Hz.
1. Trong 16 ký tự điều chế thì ký tự nào nhạy với nhiễu nhất? (Tức là khả năng giải mã sai cao nhấtso với các ký tự còn lại)
2. Xác định năng lượng ký hiệu trung bình.
3. Tính xác suất lỗi bit.
4. Giả thiết phía thu nhận được 2 ký tự có biên độ kênh I và Q là sr1 (1.5,1.7) và sr2(3.2,-1,6). Xác định dòng
bit sau giải mã ứng với 2 ký tự này 6 bảng chọn α