Bài Tập Toán 7 Đại Lượng Tỉ Lệ Nghịch Có Lời Giải

 ĐẠI LƯỢNG TỈ LỆ NGHỊCH I. LÍ THUYẾT 1. Định nghĩa
Nếu đại lượng y liên hệ với đại lượng x theo công thức a y =
hay xy = a với a là một hằng x
số khác 0 thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a . 2. Tính chất
Nếu hai đại lượng tỉ lệ nghịch với nhau thì:
- Tích hai giá trị tương ứng của chúng luôn không đổi (bằng hệ số tỉ lệ): x .y = x .y = ... = . a 1 1 2 2
- Tỉ số hai giá trị bất kì của đại lượng này bằng nghịch đảo tỉ số hai giá trị tương ứng của x y x y đại lượng kia: 1 2 1 3 = ; = ;... x y x y 2 1 3 1 II. BÀI TẬP
Bài 1: Chu vi và độ dài một cạnh của hình vuông có phải là
hai đại lượng tỉ lệ thuận không? Nếu có, hệ số tỉ lệ là bao nhiêu?
……………………………………………………………………..
……………………………………………………………………..
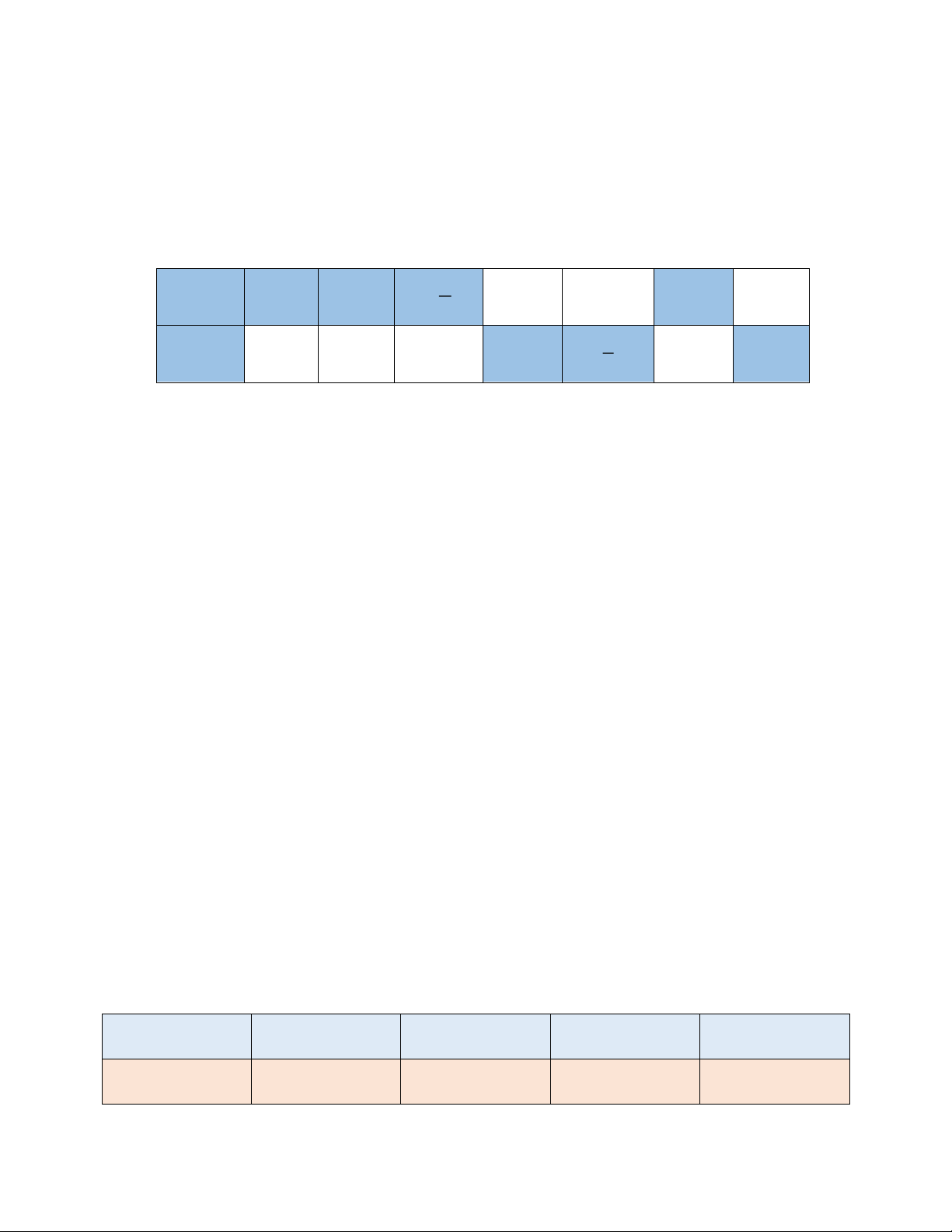
Bài 2: Cho bảng sau: x 8 − 6 − −2 6 4 y 6 8 24 −8 −12
Hai đại lượng x và y được cho ở trên có phải là hai đại lượng tỉ lệ nghịch không? Vì sao?
………………………………………………………………………………………………….
………………………………………………………………………………………………….
Bài 3: Cho biết x và y là hai đại lượng tỉ lệ thuận.
a) Biết rằng với hai giá trị x x − y 1 ,
2 của x có tổng bằng
2 thì hai giá trị tương ứng 1,
y2 của y có tổng bằng 6 . Hỏi hai đại lượng x và y liên hệ với nhau bởi công thức nào? Trang 1
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
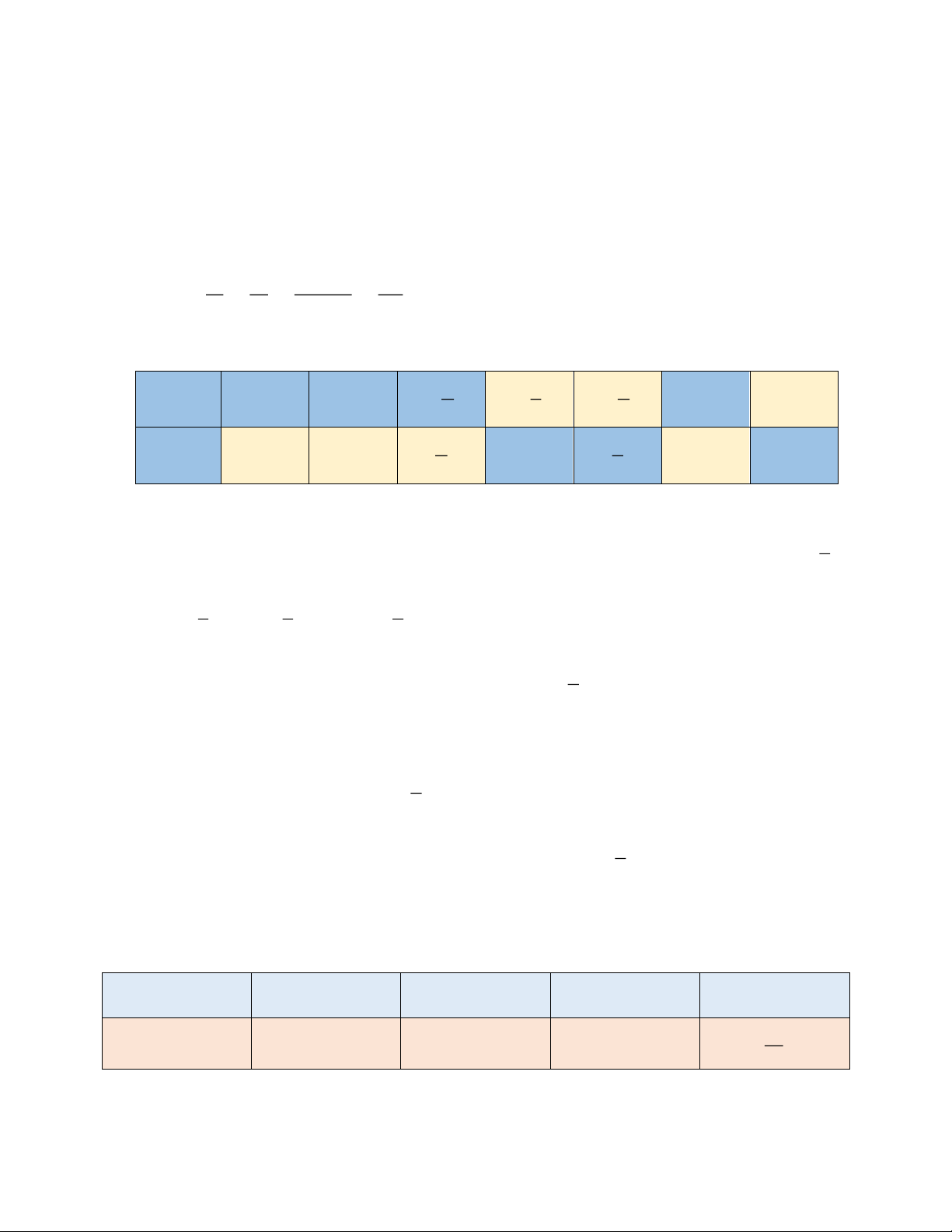
b) Từ đó, hãy điền số thích hợp vào các ô trống trong bảng sau: 1 x −2 −1 − 0 2 1 y 1 −6 3
Bài 4: Cho 3 đại lượng x, y, z . Hãy cho biết mối liên hệ giữa hai đại lượng x và z biết:
a) x và y tỉ lệ nghịch; y và z tỉ lệ nghịch
b) x và y tỉ lệ nghịch; y và z tỉ lệ thuận.
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
Bài 5: Một hình chữ nhật có diện tích 2
100m . Các kích thước x, y (mét) của hình
chữ nhật có liên hệ gì? Lập bảng các giá trị của y tương ứng với các giá trị sau của x : 10, 20, 25, 30
………………………………………………………………………………………………….
…………………………………………………………………………………………………. x y Trang 2 HDG:
Bài 1: Chu vi C và độ dài a của một cạnh hình vuông là hai đại lượng tỉ lệ thuận vì
C = 4a. . Hệ số tỉ lệ là 4 .
Bài 2: Ta thấy trong các cột tích . x y −
đều bằng 48 nên x và y là hai đại lượng tỉ lệ nghịch. y y y + y 6 Bài 3: a) 1 2 1 2 = = =
= - 3 . Ta có y = −3x x x x + x - 2 1 2 1 2 b) 1 1 1 x – 2 – 1 − − − 0 2 2 3 9 3 1 y 6 3 1 0 – 6 2 3 Bài 4: b
a) x và y tỉ lệ nghịch; Þ xy = a
y và z tỉ lệ nghịchÞ yz = b Þ y = z b b a Thay y =
ta có x. = a Þ x = z z z b a
Vậy x và z là hai đại lượng tỉ lệ thuận theo hệ số b
b) x và y tỉ lệ nghịch Þ xy = a
y và z tỉ lệ thuậnÞ y = kz a
Thay y = kz ta có x.kz = a Þ xz = k a
Vậy x và z là hai đại lượng tỉ lệ nghịch theo hệ số tỉ lệ k Bài 5:
Hai đại lượng x và y là hai đại lượng tỉ lệ nghịch và xy = 100 x 10 20 25 30 y 10 10 5 4 3 Trang 3