Bài Tập Toán 8 Tuần 11 Có Lời Giải Chi Tiết

PHIẾU BÀI TẬP TOÁN 8 TUẦN 11 Bài 1. Làm tính chia. a) ( 3 2
x + x + x + ) ( 2 6 3 4 2 : 3x + 2). b) ( 5 4 2
x + x + + x + x − ) ( 2 2 3 3 : x + ) 1 . c) ( 5 3 2
x + x + + x − x + ) ( 3 4 3 5
15 : x − x + 3) . Bài 2.
Dùng định nghĩa hai phân thức bằng nhau chứng minh các đẳng thức sau: 3 4 4 xy 5x y 2 x ( x + 3) x a) = ; b) = ; 3 7 35x y x( x + 3)2 x + 3 2 2 − x x − 4x + 4 3 2 x − 9x −x − 3x c) = ; d) = ; 2 2 + x 4 − x 15 − 5x 5 Bài 3.
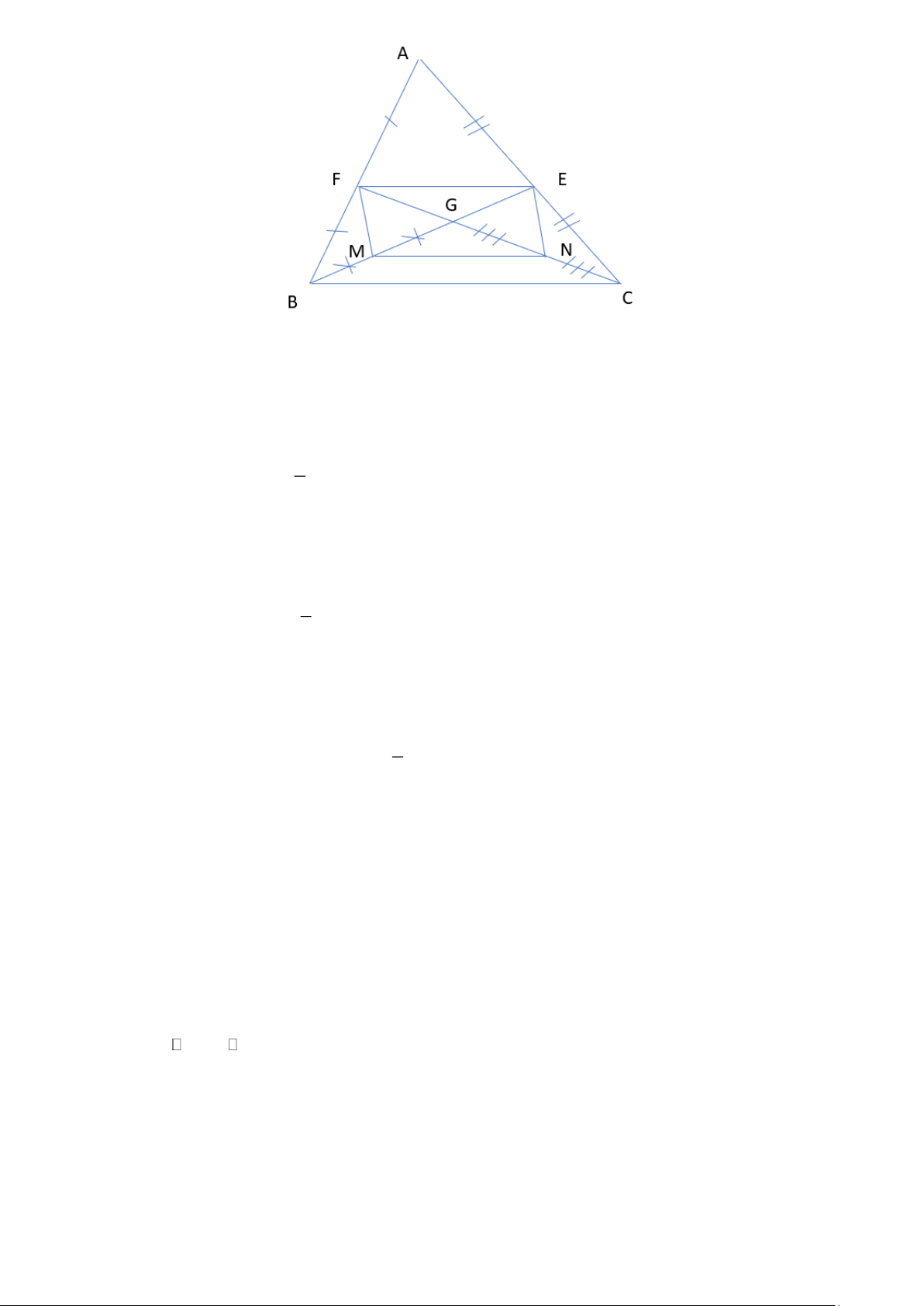
Cho tam giác ABC , các trung tuyến BE và CF cắt nhau ở G . Gọi M , N theo thứ tự là trung
điểm BG và CG .
a) Tứ giác MNEF là hình gì? Vì sao?
b) Tìm điều kiện của tam giác ABC để tứ giác MNEF là hình thoi? Bài 4.
Cho hình bình hành ABCD có B = 60 , AB = 2AD . Gọi E và F theo thứ tự là trung điểm của
AB và BC . Đường EF cắt DA tại I . Chứng minh : a) EAI = EBF .
b) Tứ giác AIBF là hình bình hành.
c) Tứ giác AIFC là hình bình hành.
d) Tứ giác AIFC là hình chữ nhật. Bài 5.
Cho hình chữ nhật ABCD . Nối C với một điểm E bất kì trên đường chéo BD . Trên tia đối
của tia EC lấy điểm F sao cho EF = EC . Vẽ FH và FK lần lượt vuông góc với AB và AD . Chứng minh rằng :
a) Tứ giác AHFK là hình chữ nhật.
b) AF // BD và KH // AC .
c) Ba điểm F , H , K thẳng hàng. Bài 6.
Tìm giá trị nhỏ nhất của các phân thức. 2 x + 4x + 6 4 + 2 1− 2x a) b) 3 5 Bài 7. Chứng minh rằng: a) 51 2 −1 chia hết cho 7 . b) 19 17 17 +19 chia hết cho18 . c) 3
36 −1 chia hết cho 7 nhưng không chia hết cho 37 . Trang 1
ĐÁP ÁN BÀI TẬP TĂNG CƯỜNGTOÁN 8 TUẦN 11
HƯỚNG DẪN GIẢI CHI TIẾT Bài 1. Làm tính chia. a) ( 3 2
x + x + x + ) ( 2 6 3 4 2 : 3x + 2). b) ( 5 4 2
x + x + + x + x − ) ( 2 2 3 3 : x + ) 1 . c) ( 5 3 2
x + x + + x − x + ) ( 3 4 3 5
15 : x − x + 3) . Lời giải a) ( 3 2
x + x + x + ) ( 2 6 3 4 2 : 3x + 2) 3 6x + 2 3x + 4x + 2 − 2 3x + 2 3 6x + 4x 2x + 1 2 3x + − 2 2 3x + 2 0 b) ( 5 4 2
x + x + + x + x − ) ( 2 2 3 3 : x + ) 1 . 5 x + 4 2x + + 2 3x + x − − 3 2 x +1 5 x + 3 x 3 x + 2 2x − x +1 4 2x − 3 x + 2 3x − − 9 4 2x + 2 2x − 3 x + 2 x + x − − 3 3 2
Thương x + 2x − x + 1, phép chia có dư 2x − 4 . − 3 x − x 2 x + 2x − − 3 2 x +1 2x − 4 c) ( 5 3 2
x + x + + x − x + ) ( 3 4 3 5
15 : x − x + 3) . 5 x + 3 4x + + 2 3x − 5x + − 15 3 x − x + 3 5 x − 3 x + 2 3x 2 x + 5 Trang 2 3 5x − 5x − − 9 3 5x − 5x − 9 0 Bài 2.
Dùng định nghĩa hai phân thức bằng nhau chứng minh các đẳng thức sau: 3 4 4 xy 5x y 2 x ( x + 3) x a) = ; b) = ; 3 7 35x y x( x + 3)2 x + 3 2 2 − x x − 4x + 4 3 2 x − 9x −x − 3x c) = ; d) = ; 2 2 + x 4 − x 15 − 5x 5 Lời giải a) Ta có: ( 3 xy )( 3 x y) 4 4 35 = 35x y 4 4 4 4
 7.5x y = 35x y 3 4 4 xy 5x y Do đó: = 3 7 35x y
b) Ta có: x ( x + ) ( x ) x (x + )2 2 2 3 3 3  =  −  x
 ( x + ) x = x ( x +  )2 2 3 3 2 x ( x + 3) x Do đó: = x( x + 3)2 x + 3 c) Ta có: ( − x)( 2 − x ) 2 3 2 4
= 8 − 2x − 4x + x
( + x)( 2x − x + ) 2 3 2 2 4
4 = 2x − 8x + 8 + x − 4x + 4x 2 3
= 8 − 2x − 4x + x 2 2 − x x − 4x + 4 Do đó: = 2 2 + x 4 − x d) Ta có: ( 3 x − x) 3
9 .5 = 5x − 45x ( − x)( 2 −x − x) 2 3 2 3 15 5 3 = 1
− 5x − 45x + 5x +15x = 5x − 45x 3 2 x − 9x −x − 3x Do đó: = 15 − 5x 5 Bài 3.
Cho tam giác ABC , các trung tuyến BE và CF cắt nhau ở G . Gọi M , N theo thứ tự là
trung điểm BG và CG .
a) Tứ giác MNEF là hình gì? Vì sao?
b) Tìm điều kiện của tam giác ABC để tứ giác MNEF là hình thoi? Lời giải Trang 3
a) +) Vì BE, CF là các đường trung tuyến
E, F lần lượt là trung điểm của AC, AB .
EF là đường trung bình của ABC 1
EF / /BC và E F = BC 2
+) Vì M là trung điểm của GB , N là trung điểm của GC
MN là đường trung bình của GBC 1
MN / /BC và MN = BC 2
Xét tứ giác MNEF có:
MN / / EF (cùng / / BC ) 1
MN = EF ( cùng = BC ) 2
Do đó tứ giác MNEF là hình bình hành.
b) Để tứ giác MNEF là hình thoi  ME ⊥ NF (hai đường chéo vuông góc)  ME ⊥ CF .
Vậy ABC cần thêm điều kiện hai đường trung tuyến BE, CF vuông góc với nhau thìtứ giác MNEF là hình thoi. Bài 4.
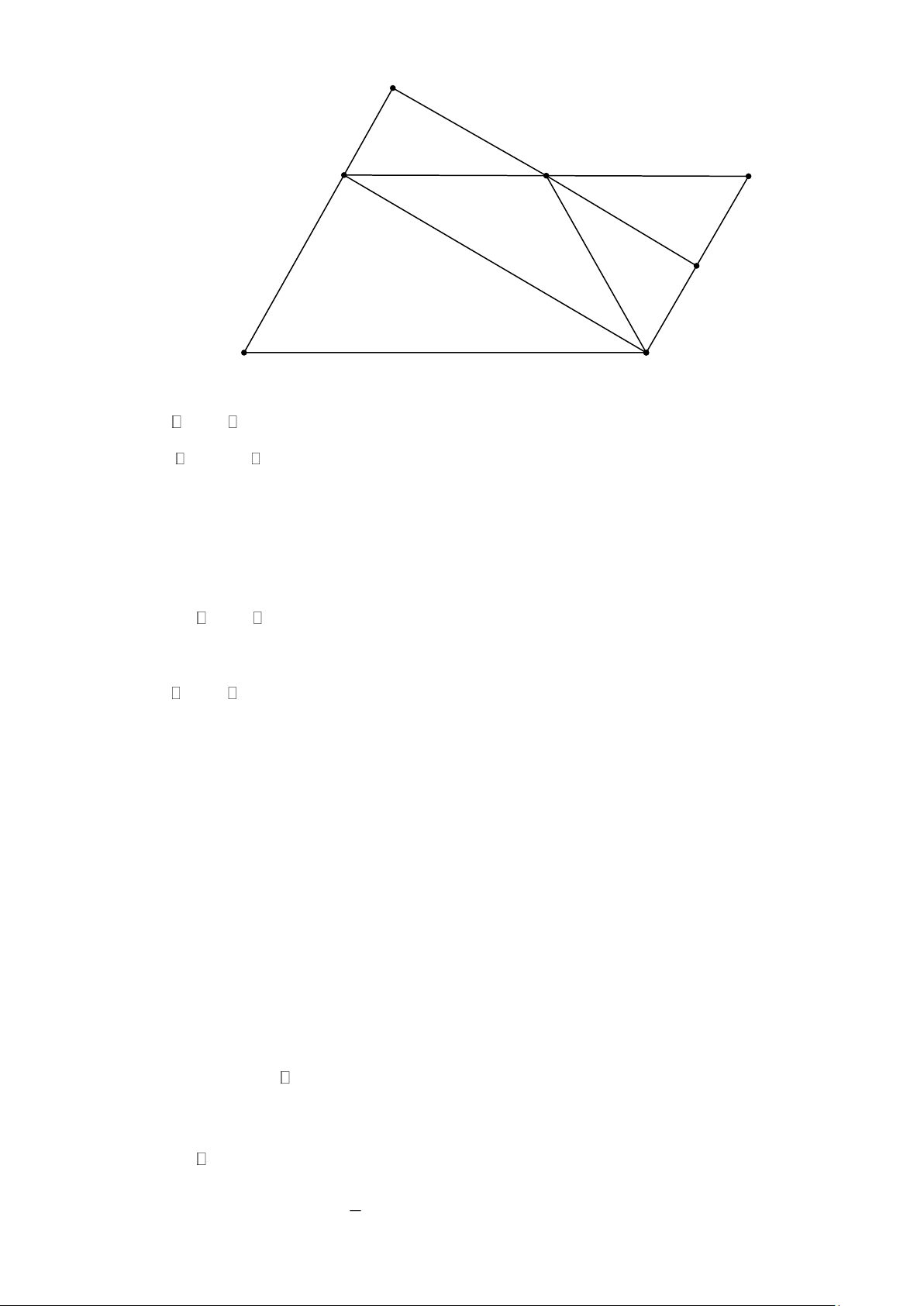
Cho hình bình hành ABCD có B = 60 , AB = 2AD . Gọi E và F theo thứ tự là trung
điểm của AB và BC . Đường EF cắt DA tại I . Chứng minh : a) EAI = EBF .
b) Tứ giác AIBF là hình bình hành.
c) Tứ giác AIFC là hình bình hành.
d) Tứ giác AIFC là hình chữ nhật. Lời giải Trang 4 I E B A F D C a) EAI = EBF .
Xét EAI và EBF có: EA = EB (gt)
IEA = FEB (đối đỉnh)
IAE = FBE (so le trong)
Suy ra EAI = EBF (g – c – g). Đpcm
b) Tứ giác AIBF là hình bình hành.
Do EAI = EBF (c/m a) nên AI = BF (cạnh tương ứng)
Mà AI // BF (do AD // BC )
Suy ra tứ giác AIBF là hình bình hành (tứ giác có một cặp cạnh đối song song và bằng nhau). Đpcm
c) Tứ giác AIFC là hình bình hành.
Ta có: AI = BF mà BF = FC (gt) nên AI = FC .
Mặt khác AI // FC (do AD // BC )
Suy ra tứ giác AIFC là hình bình hành (tứ giác có một cặp cạnh đối song song và bằng nhau). Đpcm
d) Tứ giác AIFC là hình chữ nhật.
Do AB = 2AD (gt) nên AB = 2BC mà AB = 2BE (do E là trung điểm của AB ) nên
BE = BC . Suy ra BEC cân tại B .
Mặt khác EBC = 60 (gt) Suy ra BEC đều. 1
Suy ra CE = EB hay CE = AB . 2 Trang 5
Suy ra ACB vuông tại C (trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền).
Suy ra Tứ giác AIFC là hình chữ nhật (hình bình hành có một góc vuông) Đpcm Bài 5.
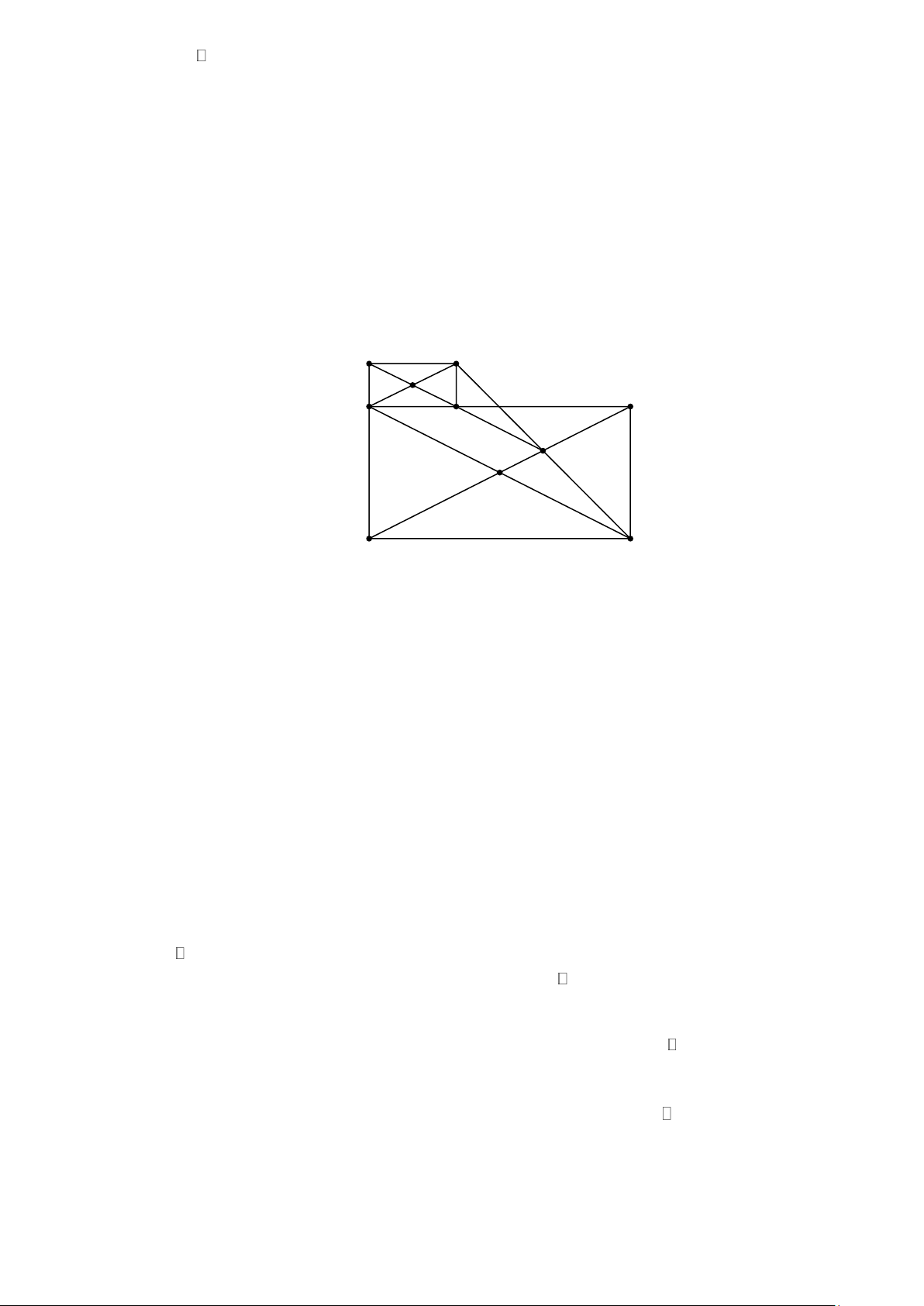
Cho hình chữ nhật ABCD , nối C với một điểm E bất kì trên đường chéo BD . Trên tia
đối của tia EC lấy điểm F sao cho EF = EC . Vẽ FH và FK lần lượt vuông góc với
AB và AD . Chứng minh rằng :
a) Tứ giác AHFK là hình chữ nhật.
b) AF // BD và KH // AC .
c) Ba điểm E , H , K thẳng hàng. Lời giải K F M A B H E N D C
a) Tứ giác AHFK là hình chữ nhật.
Xét tứ giác AHFK có :
HAK = 90 (do AB ⊥ AD )
AKF = 90 (do FK ⊥ AD )
FHA = 90 (do FH ⊥ AB )
Suy ra tứ giác AHFK là hình chữ nhật (tứ giác có 3 góc vuông). Đpcm
b) AF // BD và KH // AC .
Gọi N là giao điểm của AC và BD ; M là giao điểm của AF và HK .
Xét CAF có N là trung điểm của AC (tính chất đường chéo của hình chữ nhật) ; E là trung
điểm của CF (gt). Suy ra NE là đường trung bình của CAF . Suy ra NE // AF hay AF // BD . Đpcm
Do NA = ND (tính chất đường chéo của hình chữ nhật) nên NAD cân tại N nên NAD = NDA .
Do MA = MK (tính chất đường chéo của hình chữ nhật) nên MAK cân tại M nên MAK = MKA .
Mà AF // BD nên KAM = ADN (đồng vị). Suy ra NAD = MKA là cặp góc ở vị trí đồng vị. Trang 6
Suy ra KH // AC . Đpcm
c) Ba điểm E , H , K thẳng hàng.
Xét FAC có M là trung điểm của AF (tính chất đường chéo của hình chữ nhật) ; E là
trung điểm của FC (gt). Suy ra ME là đường trung bình của FAC . Suy ra ME // AC .
Mặt khác KH // AC (c/m b). Suy ra K , M , H , E thẳng hàng ( vì qua điểm M có một và chỉ
một đường thẳng song song với AC ) hay ba điểm E , H , K thẳng hàng. Đpcm Bài 6.
Tìm giá trị nhỏ nhất của các phân thức. 2 x + 4x + 6 4 + 2 1− 2x a) b) 3 5 Lời giải
a) Ta có : x + x + = x + x + + = ( x + )2 2 2 4 6 4 4 2 2 + 2 . 1 2
Có ( x + 2)2  0  ( x + 2)2 + 2  2  ( x + 2)2 + 2  3   . 3
Dấu " = " xảy ra khi x + 2 = 0  x = −2 . 2
Phân thức đạt giá trị min = khi x = −2 . 3 1 4
b) Ta có: 1− 2x  0  4 + 2 1− 2x  4  (4 + 2 1− 2x )  . 5 5 1
Dấu " = " xảy ra khi 1− 2x = 0  x = 2 4 1
Phân thức đạt giá trị min = khi x = . 5 2 Bài 7. Chứng minh rằng: d) 51 2 −1 chia hết cho 7 . e) 19 17 17 +19 chia hết cho18 . f) 3
36 −1 chia hết cho 7 nhưng không chia hết cho 37 . Lời giải 17 17 a) Ta có : 51  − = ( 3)  − ( 3 − )   ( 3)  51 2 1 2 1 2 1 2 −1 7  2 −1 7      b) Ta có : 19 17 + = ( 19 + ) +( 17 17 19 17 1 19 − ) 1 Có : ( 19 + ) ( + )  ( 19 17 1 17 1 17 + ) 1 18 ( 17 − ) ( − )  ( 17 19 1 19 1 19 − ) 1 18  ( 19 17 17 +19 ) 18 . Trang 7
c) Ta có : ( 63 − ) ( − )  ( 63 − )  ( 63 36 1 36 1 36 1 35 36 − ) 1 7 . Có: ( 63 − ) = ( 63 36 1 36 + ) 1 − 2 ( 63 + ) ( + ) ( 63 36 1 36 1 36 + )
1 − 2 không chia hết cho 37.  HẾT  Trang 8