Bài Tập Toán 8 Tuần 17 Có Lời Giải Chi Tiết

PHIẾU BÀI TẬP TOÁN 8 TUẦN 17 Bài 1.
Tìm điều kiện của x để giá trị các phân thức xác định 7x 3 3x a) b) c) 2x − 5 2 3x − 2x 3 2
8x −12x + 6x −1 Bài 2. Cho biểu thức: 2 x + 2x x − 5 50 − 5x A = + + 2x +10 x 2x(x + 5)
a) Tìm điều kiện xác định của biều thức A
b) Rút gọn biểu thức A
c) Tìm x để A =1, A =3 Bài 3. Cho biểu thức: (x + )2 2 2 2 
x  x + 6x + 4 B = 1−  − x  x + 2  x
a)Rút gọn biểu thức B
b)Tìm giá trị của x để biểu thức B đạt giá trị lớn nhất Bài 4.
Tính diện tích mảnh đất hình thang vuông ABCD theo các độ dài cho trên hình bên và biết
diện tích tam giác vuông BEC bằng 2 13,5cm . Bài 5.
Cho tam giác OAB vuông tại O với đường cao OM . Hãy giải thích vì sao ta có đẳng thức: . AB OM = . OA . OB 2 2x − 8x + 9 Bài 6.
a) Tìm giá trị nhỏ nhất của A = 2 x − 4x + 5 2 2x + 6x + 7
b) Tìm giá trị lớn nhất của B = 2 x + 3x + 3 Bài 7. Rút gọn biểu thức 1 a b 2 2 − − x y
c (a + c) − a (a − c)
a) a + b b) a − b a + b c) d) x 1 b a + c a − 1 1 − 2 2 a − b a − b a + b a − c a + c x y Trang 1
ĐÁP ÁN BÀI TẬP TĂNG CƯỜNG TOÁN 8 TUẦN 18
HƯỚNG DẪN GIẢI CHI TIẾT Bài 1.
Tìm điều kiện của x để giá trị các phân thức xác định 7x 3 3x a) b) c) 2x − 5 2 3x − 2x 3 2
8x −12x + 6x −1 Lời giải 7x a)
xác định  2x − 5  0  2x  5 5  x  2x − 5 2 3 b) xác định 2
 3x − 2x  0  x(3 − 2x)  3
0  x  0, x  2 3x − 2x 2 3x c) xác định 3 2
 8x −12x + 6x −1  0 3
 (2x −1)  0  2x −1  0 3 2
8x −12x + 6x −1 1  x  2 Bài 2. Cho biểu thức: 2 x + 2x x − 5 50 − 5x A = + + 2x +10 x 2x(x + 5)
a) Tìm điều kiện xác định của biều thức A
b) Rút gọn biểu thức A
c) Tìm x để A =1, A =3 Lời giải
a) ĐKXĐ: x  0, x  −5 2 x + 2x x − 5 50 − 5x 2 x + 2x x − 5 50 − 5x b) A = + + = + +
MTC : 2x(x + 5) 2x +10 x 2x(x + 5) 2(x + 5) x 2x(x + 5) 2
x(x + 2x) 2(x − 5)(x + 5) 50 − 5x 3 2 2 + − − = + + x 2x 2x 50 50 5x = + + 2x(x + 5) 2x(x + 5) 2x(x + 5)
2x(x + 5) 2x(x + 5) 2x(x + 5) 3 2 2
x + 2x + 2x − 50 + 50 − 5x = 2x(x + 5) 3 2
x + 4x − 5x 2 + − 2 + − − + − + − + = x 4x 5 = x 5x 1x 5 =
x(x 5) (x 5) − = (x 1)(x 5) = x 1 = 2x(x + 5) 2(x + 5) 2x(x + 5) 2x(x + 5) 2x(x + 5) 2x c) x −1 *Để A =1 thì
=1  x −1 = 2x  x − 2x = 1  x = −1 2x Trang 2 x −1 − *Để A =3 thì
= 3  x −1 = 6x  x − 6x = 1  −5x = 1 1  x = 2x 5 Bài 3. Cho biểu thức: (x + )2 2 2 2 
x  x + 6x + 4 B = 1−  − x  x + 2  x
a)Rút gọn biểu thức B
b)Tìm giá trị của x để biểu thức B đạt giá trị lớn nhất Lời giải a) (x + )2 2 2 2 
x  x + 6x + 4 (x + )2 2 2
2  x + 2 − x  x + 6x + 4 B = 1−  − =   − x  x + 2  x x  x + 2  x (x + )( 2 x + − x ) 2 2 2 x + 6x + 4 2 3 2 2 + − + + − − − − = − x 2x x 2x 4 2x x 6x 4 = x x x 3 2
−x − 2x − 2x 2 − − − = x( x 2x 2) = 2
= −x − 2x − 2 x x b) 2
B = −x − 2x − 2 = −( 2
x + 2x + 2) = −( 2 x + 2x +1+ ) 1 = −( 2 x + 2x + ) 1 −1 = −( x + )2 1 −1  −1 B = 1 − khi đó (x + )2
1 = 0  x +1 = 0  x = −1 max Bài 4.
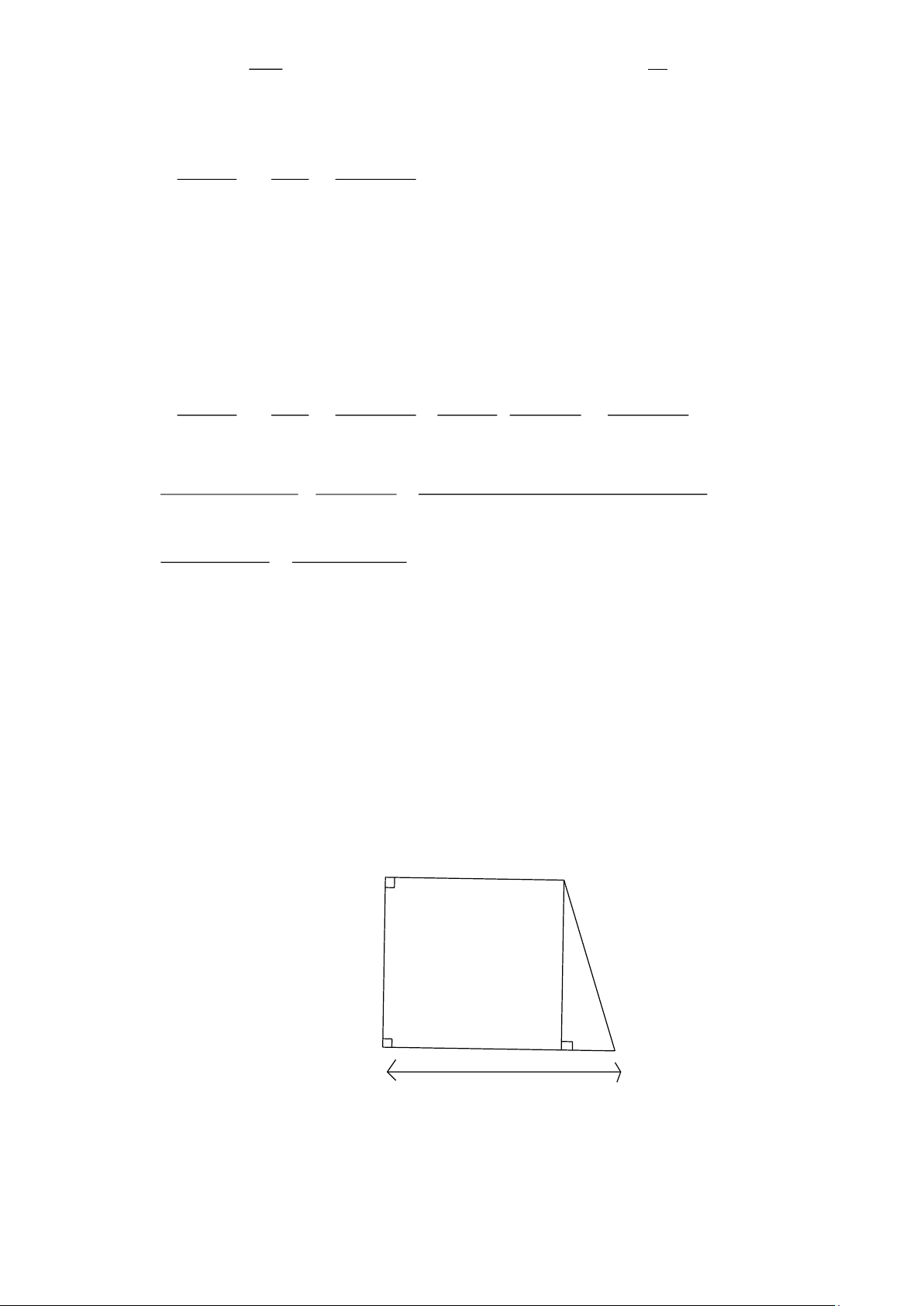
Tính diện tích mảnh đất hình thang vuông ABCD theo các độ dài cho trên hình bên và biết
diện tích tam giác vuông BEC bằng 2 13,5cm . Lời giải 10cm A B C D E 13cm
Tứ giác ABED có BAD = ADE = DEB = 90 (gt) nên ABED là hình chữ nhật suy ra AB = DE
Ta lại có AB = 10cm (gt) nên DE = 10cm
Ta có DE + EC = DC  10 + EC = 13 EC = 3cm Trang 3 1
Diện tích BEC là BE.EC = 13,5  BE.EC = 13,5.2  BE.3 = 27  BE = 9cm 2 1 1
Diện tích hình thang vuông ABCD là ( AB + CD) BE = (10 +13) 2 9 =103,5cm 2 2
Vậy diện tích hình thang vuông ABCD là 2 103,5cm . Bài 5.
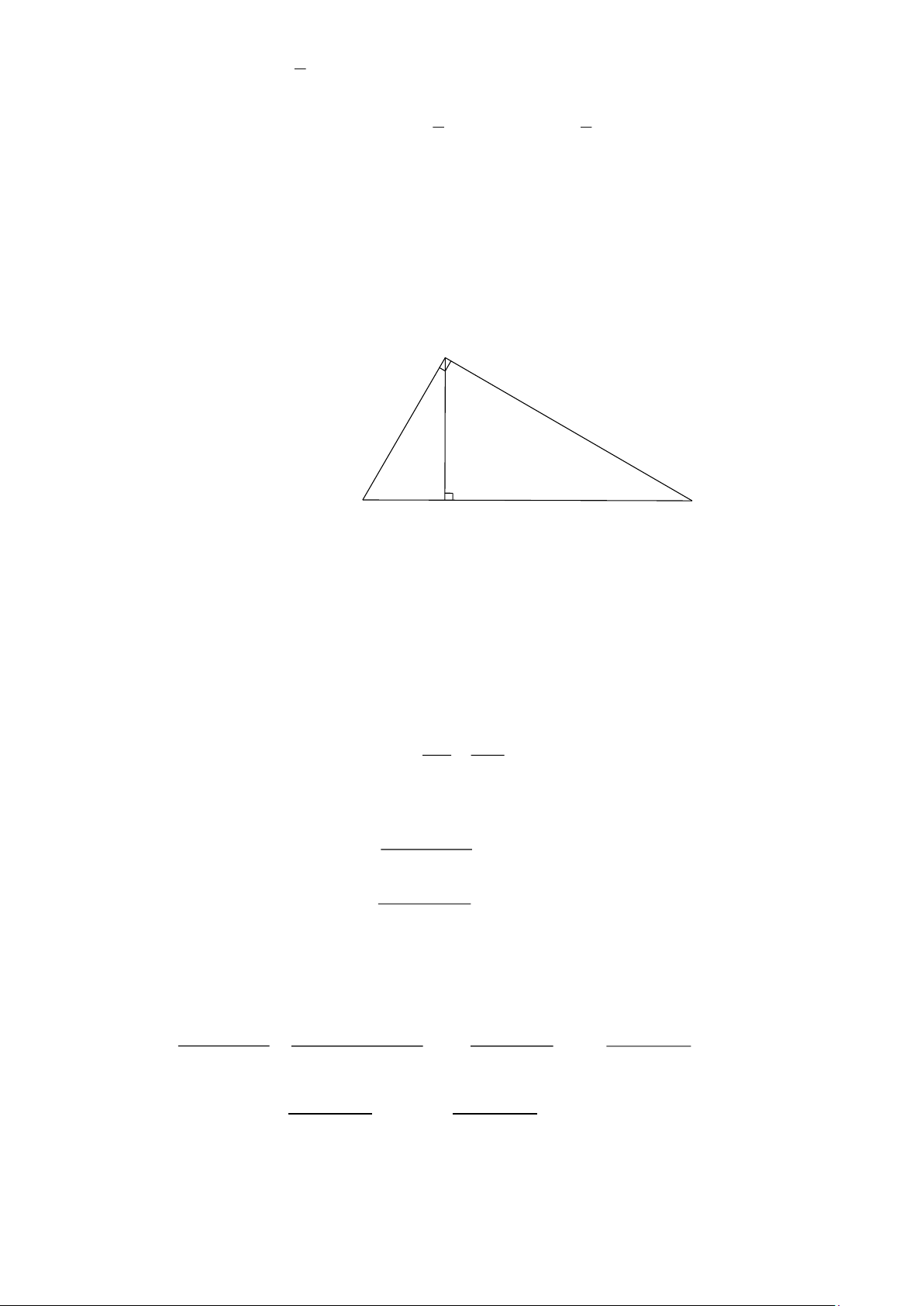
Cho tam giác OAB vuông tại O với đường cao OM . Hãy giải thích vì sao ta có đẳng thức: . AB OM = . OA . OB Lời giải O A B M
Vì AOB vuông tại O nên AOB = 90
Mà OM là đường cao của tam giác AOB nên AMO = 90
Xét AOB và AMO có:
AOB = AMO = 90 (chứng minh trên) Góc A chung AB OB
Do đó AOB  AMO (g – g) suy ra = AO OM
Hay AB.OM = AO.OB (Đpcm). 2 2x − 8x + 9 Bài 6.
a) Tìm giá trị nhỏ nhất của A = 2 x − 4x + 5 2 2x + 6x + 7
b) Tìm giá trị lớn nhất của B = 2 x + 3x + 3 Lời giải a) Ta có: 2 2x − 8x + 9 2( 2
x − 4x + 5) −1 1 1 A = = = 2 − = 2 − 2 x − 4x + 5 2 2 x − 4x + 5 x − 4x + 5 (x − 2)2 +1 1 1
Do ( x − 2)2  0   1  2 −
 1, tức A  1 , với mọi x. (x − 2)2 +1 (x − 2)2 +1
Dấu “=” xảy ra khi ( x − )2 2 = 0  x = 2 .
Vậy giá trị nhỏ nhất của A bằng 1 khi x = 2 . Trang 4 b) Ta có 2 2x + 6x + 7 2( 2 x + 3x + 3) +1 1 1 B = = = 2 + = 2 + 2 x + 3x + 3 2 2 2 x + 3x + 3 x + 3x + 3  3  3 x + +    2  4 2  3  1 4 1 10 10 Do x −  0    2 +    , tức B  , với mọi x . 2 2  2   3  3 3  3  3 3 3 x − + x − +      2  4  2  4 2  3  3
Dấu “=” xảy ra khi x − = 0  x =    2  2 10 3
Vậy giá trị lớn nhất của B bằng khi x = . 3 2 Bài 7. Rút gọn biểu thức 1 a b 2 2 − − x y
c (a + c) − a (a − c)
a) a + b b) a − b a + b c) d) x 1 b a + c a − 1 1 − 2 2 a − b a − b a + b a − c a + c x y Lời giải 1 2 2 1 a − b
(a + b)(a −b) a) a + b = . = = a − b 1 a + b 1 a + b 2 2 a − b a b −
a (a + b) − b(a − b)
(a −b)(a + b) 2 2 2 2
a + ab − ba + b a + b b) a − b a + b = . = = = 1 b a 2 2 2 2 +
(a −b)(a + b) b(a + b) + a(a −b) ba + b + a − ab a + b a − b a + b
c (a + c) − a (a − c)
c a + c − a a − c c) = c
 (a + c) − a(a − c) ( ) ( )  : c a  −
(a − c)(a + c) a − c a + c − + = c
 (a + c) − a(a − c) (a c)(a c) .  = ( − )( + ) 2 2
a c a c = a − c
c(a + c) − a(a − c) 2 2 x − y
(x − y)(x + y) y − x (x − y)(x + y) −xy d) x = : =
= −y (x + y) 2 . = −xy − y 1 1 − x xy x x − y x y  HẾT  Trang 5