

























Preview text:
ĐÀO HOÀNG DŨNG BÀI TẬP
TOÁN KINH TẾ 2 - 2020 - Bài tập Toán kinh tế 2 Đào Hoàng Dũng Chương 1
Biến cố và xác su t ấ
Tính xác suất bằng định nghĩa. Mối quan hệ giữa các biến cố
1. Một người rút tiền ở cây ATM nhưng quên mất 3 số cuối của mã PIN và chỉ nhớ rằng
chúng khác nhau. Tìm xác suất ể
đ người đó nhập một lượt được đúng mã PIN của mình.
2. Một công ty cần tuyển ba nhân viên. Có 30 người nộp đơn, trong đó có 18 nam và 12 nữ.
Giả sử rằng khả năng trúng tuyển của 30 người là như nhau.
a) Tính xác suất để 3 người trúng tuyển đều là nam.
b) Tính xác suất để cả 3 người trúng tuyển đều là nữ.
c) Tính xác suất để có ít nhất một nữ trúng tuyển.
3. Thang máy của một tòa nhà 10 tầng xuất phát từ tầng 1 với 5 khách. Coi như mọi người
chọn tầng một cách ngẫu nhiên và độc lập. Tìm khả năng xảy ra các tình huống sau:
a) Tất cả cùng ra ở tầng 7.
b) Tất cả cùng ra ở một tầng.
c) Mỗi người ra ở một tầng khác nhau.
4. Có 10 khách bước ngẫu nhiên vào một cửa hàng có 3 quầy. Tính xác suất để có 3 người vào quầy số 1.
5. Tìm xác suất để gặp ngẫu nhiên ba người không quen biết nhau ở ngoài đường (giả thiết
những người này đều không sinh vào năm nhuận) thì họ:
a) Có ngày sinh nhật khác nhau.
b) Có ngày sinh nhật trùng nhau. 6. Một ng ờ
ư i bỏ ngẫu nhiên 3 lá thư vào 3 phong bì đã ghi sẵn địa chỉ. Tính xác suất để:
a) Chỉ có một lá thư bỏ đúng địa chỉ.
b) Cả 3 lá thư đều được bỏ không đúng địa chỉ.
7. Một công ty tham gia đấu thầu 2 dự án. Gọi A là biến cố công ty đó thắng thầu dự án k k
(k 1, 2). Hãy viết bằng kí hiệu các biến cố biểu thị rằng:
a) Công ty chỉ thắng thầu một dự án.
b) Công ty không thắng thầu dự án nào.
8. Ba người cùng bắn vào một mục tiêu. Gọi A là biến cố người thứ k bắn trúng mục tiêu k
(k 1, 2,3) . Hãy viết bằng kí hiệu các biến cố biểu thị rằng:
a) Chỉ có người thứ nhất bắn trúng mục tiêu.
b) Chỉ có một người bắn trúng mục tiêu. 1 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
c) Chỉ có hai người bắn trúng mục tiêu.
d) Có người bắn trúng mục tiêu.
Công thức cộng, công thức nhân xác suất, công thức Becnulli 9. Một ng ờ
ư i mua ngẫu nhiên một vé xổ số có 5 chữ số.
a) Tính xác suất để được vé không có chứ số 1 hoặc không có chữ số 5. b) Tính xác suất ể
đ được vé có chữ số 2 và có chữ số lẻ.
10. Ba người chia nhau 2 vé đi xem phim. Chứng minh bốc thăm là phương thức công bằng.
11. Một sinh viên phải thi 3 môn một cách độc lập nhau. Xác suất nhận cùng một điểm số nào
đó ở cả 3 môn đều như nhau. Xác suất để thu được một môn điểm 8 là 0,18, dưới 8 là
0,65, xác suất cả 3 môn đều được điểm 10 là 0,000343. Tính xác suất để sinh viên thi 3
môn được ít nhất là 28 điểm. Điểm thi được cho theo thang điểm 10, không có điểm lẻ.
12. Một công ty đầu tư vào hai dự án A và B. Khả năng gặp rủi ro khi đầu tư vào 2 dự án này
tương ứng là 9%, 7% và gặp rủi ro đồng thời khi đầu tư cả hai dự án là 4%. Nếu đầu tư cả
hai dự án, tính xác suất để:
a) Ít nhất một dự án gặp rủi ro.
b) Chỉ dự án A gặp rủi ro.
13. Một lô hàng có 100 sản phẩm, trong đó có 10 phế phẩm. Kiểm tra ngẫu nhiên lần lượt 3
sản phẩm. Nếu có phế phẩm trong 3 sản phẩm kiểm tra thì không mua lô hàng. Tính xác
suất lô hàng được mua.
14. Một máy có ba bộ phận hoạt động độc lập với nhau. Xác suất để các bộ phận bị hỏng lần
lượt là 0,1; 0,3 và 0,2. Tính xác suất của các biến cố sau:
a) Có đúng 2 bộ phận bị hỏng.
b) Có ít nhất 1 bộ phận bị hỏng.
15. Có ba người A, B và C cùng phỏng vấn xin việc ở một công ty. Xác suất trúng tuyển của
mỗi người lần lượt là 0,8; 0,6 và 0,7. Việc trúng tuyển của mỗi người là độc lập.
a) Tính xác suất có hai người trúng tuyển.
b) Biết rằng có hai người trúng tuyển. Tính xác suất để hai người đó là A và B.
16. Một tờ tiền giả lần lượt được hai người A và B kiểm tra. Xác suất để người A phát hiện ra
tờ này giả là 0,7. Nếu người A cho rằng tờ này là giả, thì xác suất để người B cũng nhận
định như thế là 0,8. Ngược lại, nếu người A cho rằng tờ này là tiền thật thì xác suất để
người B cũng nhận định như thế là 0,4.
a) Tính xác suất để chỉ đúng một trong hai người A hoặc B phát hiện ra tờ này giả.
b) Biết tờ tiền đó đã bị ít nhất một trong hai người này phát hiện là giả, tính xác suất để
A phát hiện ra nó là giả. 2 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
17. Xác suất bắn trúng mục tiêu của 3 người đi săn tương ứng là 0,7; 0,6 và 0,5. Ba người này
cùng bắn một con nai và con nai bị trúng 1 viên đạn. Tính xác suất bắn trúng của mỗi người.
18. Tỉ lệ phế phẩm của một lô hàng là 3%. Chọn ngẫu nhiên có hoàn lại lần lượt từng sản phẩm:
a) Tính xác suất phải chọn đến lần thứ tư mới được phế phẩm.
b) Phải chọn bao nhiêu lần để xác suất chọn được ít nhất 1 phế phẩm không nhỏ hơn 0,9.
19. Một sinh viên phải thi 6 môn kết thúc học kì. Khả năng thi được trên 5 điểm của mỗi môn
là 0,8 và độc lập nhau. Tính xác suất để trong học kì này người đó:
a) Được 5 môn trên 5 điểm.
b) Được ít nhất 4 môn trên 5 điểm.
20. Một máy sản xuất lần lượt từng sản phẩm. Xác suất l àm ra một phế phẩm của máy là 0,01.
a) Cho máy xản suất 10 sản phẩm. Tính xác suất có 2 phế phẩm; có ít hơn 3 phế phẩm.
b) Máy cần sản xuất ít nhất bao nhiêu sản phẩm để xác suất có ít nhất một chính phẩm trên 0,99.
21. A chơi cờ với B với xác suất thắng mỗi ván là p. Tìm giá trị của p để A thắng chung cuộc
trong bốn ván dễ hơn trong sáu ván. Biết rằng để thắng chung cuộc thì phải thắng ít nhất 1 nửa tổng số ván.
22. Có 2 xạ thủ, mỗi người bắn 10 viên đạn vào cùng một bia. Xác suất bắn trúng đích mỗi lần
của 2 xạ thủ tương ứng là 0,7 và 0,8. Tính xác suất: a) Bia bị trúng đạn.
b) Bia bị trúng 2 viên đạn.
23. Theo điều tra của một ngân hàng về sử dụng thẻ tín dụng ở công ty, có 50% dùng thẻ A,
40% dùng thẻ B, 30% dùng thẻ C, 20% dùng thẻ A và B, 15% dùng thẻ A và C, 10% dùng
thẻ B và C, 5% dùng cả ba thẻ A, B, C. Tính xác suất để khi chọn ngẫu nhiên một người ở công ty đó, thì:
a) Người ấy dùng ít nhất một trong ba loại thẻ nói trên.
b) Người ấy dùng thẻ B, biết rằng người ấy dùng thẻ A.
24. Một nhân viên bán hàng mỗi năm đến chào hàng ở công ty Phương Đông ba lần. Xác suất
để lần đầu bán được hàng là 0,8. Nếu lần trước bán được hàng thì xác suất để lần sau bán
được hàng là 0,9, còn nếu lần trước không bán được hàng thì xác suất để lần sau bán được
hàng chỉ là 0,4. Tìm xác suất ể đ :
a) Cả ba lần đều bán được hàng.
b) Có đúng hai lần bán được hàng. 3 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
Công thức xác suất đầy đủ. Công thức Bayes
25. Có 2 máy cùng sản xuất một loại sản phẩm. Tỉ lệ chính phẩm của máy thứ nhất là 0,9; của
máy thứ hai là 0,85. Từ một kho chứa 1 sản phẩm của máy thứ nhất (còn lại của máy thứ 3
hai) lấy ngẫu nhiên một sản phẩm để kiểm tra .
a) Tính xác suất lấy được phế phẩm.
b) Nếu sản phẩm lấy ra là chính phẩm. Tính xác suất sản phẩm đó do máy thứ hai sản xuất.
26. Trong 20 tờ tiền có 3 tờ giả. Một tờ bị rút đi không rõ thật hay giả. Người ta rút ngẫu
nhiên trong các tờ còn lại ha itờ.
a) Tính xác suất để hai tờ tiền được rút ra ở lần thứ hai là tiền thật .
b) Nếu biết rằng hai tờ tiền rút ra ở lần thứ hai là tiền thật. Tìm xác suất để tờ tiền bị rút đi
trước đó cũng là tiền thật.
27. Người ta đã phỏng vấn ngẫu nhiên 500 khách hàng về một loại sản sẩm mới dự định đưa
ra thị trường và thấy có: 160 người trả lời “Sẽ mua”, 240 người trả lời “Có thể sẽ mua”,
100 người trả lời “Không mua”. Kinh nghiệm cho thấy tỉ lệ khách hàng thực sự mua sản
phẩm tương ứng với những cách trả lời trên là 40%, 20% và 2%.
a) Hãy ước tính tỉ lệ người thực sự mua sản phẩm đó?
b) Trong số khách hàng thực sự mua sản phẩm thì có khoảng bao nhiêu phần trăm đã trả lời “Sẽ mua”?
28. Một công ty bảo hiểm chia dân cư (đối tượng bảo hiểm) làm 3 loại: ít rủi ro, rủi ro trung
bình, rủi ro cao. Theo thống kê cho thấy tỉ lệ dân cư gặp rủi ro trong 1 năm tương ứng với
các loại trên là: 5%, 10%, 25% và trong toàn bộ dân cư có 20% ít rủi ro; 50% rủi ro trung bình; 30% rủi ro cao.
a) Tính tỉ lệ dân gặp rủi ro trong một năm.
b) Nếu một người không gặp rủi ro trong năm thì xác suất người đó thuộc loại ít rủi ro là bao nhiêu?
29. Một người có 3 chỗ ưa thích như nhau để câu cá. Xác suất để câu được cá ở những chỗ đó
tương ứng là: 0,6; 0,8 và 0,7. Biết rằng ở một chỗ người đó đã thả câu ầ và chỉ đượ ộ
Tìm xác suất để cá được câu ở chỗ thứ nhất.
30. Trong một kho rượu ố lượng chai rượ ạ ạ ằng nhau. Người ta ấ ẫ
nhiên 1 chai rượu trong kho và đưa cho 4 người sành rượ ế
ử để xác định xem đây ại rượ . Giả sử ỗi ngườ
ả năng đoán đúng là 0,8. Có 3 người kết luận chai 4 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
rượu thuộc loại A và một người kết luận chai rượu thuộc loại B. Vậy chai rượu được chọn
thuộc loại A với xác suất bằng bao nhiêu?
31. Trong những hộ vay tiền ngân hàng để nuôi tôm, tỉ lệ hộ làm ăn không có lãi là 5%. Trong
các hộ vay tiền ngân hàng để nuôi tôm mà làm ăn không có lãi, tỉ lệ trả nợ ngân hàng
không đúng hạn là 88%. Trong các hộ vay tiền ngân hàng để nuôi tôm mà làm ăn có lãi, tỉ
lệ trả nợ ngân hàng không đúng hạn là 2%.
a) Một hộ đã vay tiền ngân hàng để nuôi tôm, thì xác suất hộ đó không trả nợ ngân hàng đúng hạn là bao nhiêu.
b) Một hộ nuôi tôm đã không trả nợ ngân hàng đúng hạn, thì xác suất hộ đó làm ăn không có lãi là bao nhiêu.
32. Tỷ lệ phế phẩm của một máy là 5%. Người ta dùng một thiết bị kiểm tra tự động đạt được
độ chính xác khá cao song vẫn có sai sót. Tỷ lệ sai sót đối với chính phẩm là 4% còn đối
với phế phẩm là 1%. Nếu sản phẩm bị kết luận là phế phẩm thì bị loại.
a) Tìm tỷ lệ sản phẩm được kết luận là chính phẩm mà thực ra là phế phẩm.
b) Tìm tỷ lệ sản phẩm bị kết luận là phế phẩm mà thực ra là chính phẩm.
33. Sản phẩm sản xuất ra phải qua hai máy kiểm tra 1 và 2. Nếu được máy 1 chấp nhận thì
mới được chọn để máy 2 kiểm tra tiếp. Sau khi máy 2 chấp nhận thì sản phẩm mới được
đưa ra thị trường. Xác suất máy 1 chấp nhận là 0,9 và xác suất để máy 2 chấp nhận là 0,8.
Biết rằng việc kiểm tra của 2 máy là độc lập.
a) Tính tỉ lệ sản phẩm sản xuất ra không được đưa ra thị trường.
b) Chọn ngẫu nhiên một sản phẩm không được đưa ra thị trường. Tính xác suất để sản
phẩm đó bị loại là do máy 2.
34. Một túi chứa 9 nhẫn bạc và 1 nhẫn vàng. Túi kia có 1 nhẫn bạc và 5 nhẫn vàng. Từ mỗi túi
rút ra ngẫu nhiên một nhẫn. Những chiếc nhẫn còn lại được dồn vào một túi thứ ba. Từ túi
thứ ba này lại rút ngẫu nhiên một chiếc nhẫn. Tính xác suất để ta rút ra được nhẫn vàng ở túi thứ ba. 5 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
HƯỚNG DẪN, ĐÁP SỐ 1 1. 10.9.8 2. a) b) c) 3. a) b) c) 4. 5. 6. a) b) 7. a) b)
10. a) Gọi A = “vé có chữ số 1”, B = “vé có chữ số 5” 5 5 Xs cần tìm là
P A B 9 8
P(A) P(B ) P(A.B ) 2 10 10
b) Gọi C = “vé có chữ số 2”, D = “vé có chữ số lẻ”. Cần tính P(CD) 1 P(C ) D
11. HD: Có 3 lá thăm, lần lượt mỗi người rút 1 lá. Chứng minh xác suất để mỗi người bốc
thăm được vé xem phim đều bằng . 12. 0,002415
15. a) Gọi A, B, C lần lượt là các biến cố người A, B, C trúng tuyển và K là biến cố có 2
người trúng tuyển.
Xs cần tính là P(K) PABC ABC ABC, đ/ s0,452. P(ABK ) P(ABC) 36
b) Xs cần tính là P(AB | K ) , đ/ s . P(K ) P(K ) 113
16. Gọi A, B lần lượt là các biến cố người A, B phát hiện tiền giả. Từ giả thiết có: P(A) =
0,7; P(B|A) = 0,8; P(B | ) A 0,4.
a) Cần tính P( AB AB )
b) Gọi K = “ít nhất một trong hai người phát hiện tờ tiền là giả”, cần tính P(AK )
P(AB AB) ( P A| K) ,tương tự ý b bài 15. ( P K) ( P K) 18. a) ≈ 0,0274
b) P(“có ít nhất một phế phẩm trong n lần chọn”) = 1 - P(“không có phế phẩm nào
trong n lần chọn”) ≥ 0,9. Đ/s: ít nhất 76 lần. 20. a) ≈ 0,0274
b) P(“có ít nhất một phế phẩm trong n lần chọn”) = 1 - P(“không có phế phẩm nào
trong n lần chọn”) ≥ 0,9. 6 Bài tập Toán kinh tế 2 Đào Hoàng Dũng Đ/s: ít nhất 76 lần.
21. Cần tìm p để: P(“A thắng chung cuộc trong bốn ván”) > P(“A thắng chung cuộc trong sáu ván”) 2 2 2 3 3 1 4 4 0 3 3 3 4 4 2 5 5 1 6 6 0 C p (1 ) p C p (1 )
p C p (1 ) p C p (1 ) p C p (1 ) p C p (1 )
p C p (1 ) 4 4 4 6 6 6 6 p
28. Chọn ngẫu nhiên một người. Gọi H1, H2, H3 lần lượt là các biến cố người được chọn
thuộc loại ít rủi ro, rủi ro trung bình và rủi ro cao. {H1, H2, H3} lập nên một nhóm đầy
đủ các biến cố. Gọi A = “chọn được người gặp rủi ro . ”
a) Tính P(A) bằng công thức xs đầy đủ. Tính được P(A) = 0,135. Suy ra, tỉ lệ dân gặp rủi
ro trong một năm là 13,5%.
b) Xác suất cần tính là P(H1| ), sử dụng công thức Bayes để tính.
29. Gọi H1, H2, H3 lần lượt là các biến cố người đó chọn câu chỗ thứ nhất, thứ hai và thứ 3
tương ứng. {H1, H2, H3}lập nên một nhóm đầy đủ các biến cố.
Gọi A = “thả câu ba lần và chỉ câu được 1 con cá”, tính P(A) theo công thức xs đầy
đủ, các xs P(A|Hi) có thể tính theo công thức Becnulli.
Xác suất cần tính là: P(H1|A), sử dụng công thức Bayes để tính xs này.
30. Gọi H1, H2, H3 lần lượt là các biến cố người thứ nhất, người thứ hai và người thứ ba
bắn trúng mục tiêu. A = “con nai bị trúng một viên đạn” =
H H H H H H H H H . 1 2 3 1 2 3 1 2 3
Cần tính các xác suất P(H1|A), P(H2|A) và P(H3|A)
31. Gọi A = “chai rượu lấy ra thuộc loại A”, B = “chai rượu lấy ra thuộc loại B”, K = “3
người kết luận chai rượu loại A và 1 người kết luận loại B”. XS cần tính là P(A|K),
tính xs này theo công thức Bayes (nhóm đầy đủ các biến cố là A, B).
Chú ý, biến cố (K|A) = “3 người kết luận đúng và 1 người kết luận sai” và (K|B) = “3
người kết luận sai và một người kết luận đúng” do đó các xs P(K|A) và P(K|B) có thể
tính theo công thức Becnulli. Đ/s: 16 ( P A| K) 17
35. Gọi H1 = “Hai nhẫn được ra từ mỗi túi là nhẫn vàng”, H1 = “Hai nhẫn được rút ra từ
mỗi túi là nhẫn bạc”, H3 = “Hai nhẫn được rút ra từ mỗi túi gồm 1 vàng và 1 bạc”.
{H1, H2, H3}lập nên nhóm đầy đủ các biến cố.
Gọi A = “rút ra được nhẫn vàng ở túi thứ ba”. Tính P(A) theo công thức xs đầy đủ. 7 Bài tập Toán kinh tế 2 Đào Hoàng Dũng Chương 2 Biến ng u nhi ẫ ên và phân ph i
ố xác suất
1. Một thiết bị gồm 3 bộ phận hoạt động độc lập với nhau, xác suất trong thời gian t các bộ
phận bị hỏng tương ứng là 0,15; 0,1; 0,13. Gọi X là số bộ phận bị hỏng trong thời gian t.
a) Lập bảng phân phối xác suất của X .
b) Viết biểu thức hàm phân phối của X .
c) Tìm xác suất trong thời gian t thiết bị có không quá một bộ phận bị hỏng.
d) Tìm E(X ),V(X ),m và m . 0
2. Biến ngẫu nhiên rời rạc X có quy luật phân phối xác suất như sau: X x 1 x 2 P 1 p 0,7 Tìm x , E
và V (X ) 0, 21 (x x ) . 1 2 x và 1 p biết (X) 2, 7 2 1
3. Ba máy ATM 1, 2, 3 có xác suất không cho giao dịch tại cùng một thời điểm lần lượt là
0,02; 0,03; 0,05. Tại thời điểm đó, mỗi máy được một người rút tiền. Tính số máy không
cho giao dịch tin chắc nhất trong ba máy trên vào thời điểm đó, biết rằng ba máy ATM
này hoạt động độc lập.
4. Trong 100 000 vé xổ số phát hành có 1 giải trị giá 100 triệu đồng, 1 giải trị giá 20 triệu
đồng, 5 giải trị giá 5 triệu đồng, 15 giải trị giá 1 triệu đồng. Tìm số tiền lãi kì vọng của
một người khi mua một vé xổ số, biết giá vé là 10 000 đồng.
5. Có hai hộp sản phẩm; hộp thứ nhất có 7 chính phẩm và 3 phế phẩm, hộp thứ hai có 8
chính phẩm và 2 phế phẩm. Lấy ngẫu nhiên một hộp rồi từ đó lấy ngẫu nhiên ra 3 sản phẩm.
a) Lập bảng phân phối xác suất của số chính phẩm được lấy ra.
b) Tìm xác suất để sai lệch giữa số chính phẩm được lấy ra và kỳ vọng toán của nó nhỏ hơn 1.
6. Một hộp có 10 sản phẩm gồm chính phẩm và phế phẩm. Gọi X là số phế phẩm có trong
hộp. X có bảng phân phối xác suất như sau: X 0 1 2 P 0,6 0,3 0,1
Lấy ngẫu nhiên từ hộp 2 sản phẩm. Gọi Y là số phế phẩm có trong 2 sản phẩm lấy ra. Tìm
quy luật phân phối xác suất của Y . 8 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
7. Tại một cửa hàng, lượng hàng bán được trong ngày về một loại thực phẩm có bảng phân phối xác suất như sau: Lượng bán (kg) 30 31 32 33 34 35 36 Xác suất 0,05 0,1 0,2 0,3 0,15 0,12 0,08
Mỗi kg thực phẩm mua vào với giá 20 ngàn đồng, bán ra với giá 25 ngàn đồng song nếu
bị ế thì cuối ngày phải bán với giá 15 ngàn đồng mới bán hết. Để lợi nhuận trung bình là
lớn nhất thì mỗi ngày cửa hàng nên đặt mua bao nhiêu kg thực phẩm.
8. Một công ty thuê một luật sư trong một vụ kiện với hai phương án trả công như sau:
Phương án 1: Trả 7 triệu đồng bất kể thắng hay thua kiện.
Phương án 2: Trả 1 triệu đồng nếu thu kiện và 15 triệu đồng nếu thắng kiện.
Luật sư đã chọn phương án 2. Vậy theo đánh giá của luật sư thì khả năng thắng kiện của
công ty tối thiểu là bao nhiêu.
9. Theo thống kê, một người ở độ tuổi 40 sẽ ố ột năm nữ ớ ấ . Một
công ty bảo hiểm nhân thọ bán bảo hiểm một năm cho những người ở độ tuổi đó với giá là
ệ đồng. Trong trường hợp người mua bảo hiểm bị chết thì ố ề ồi thườ
ệu đồ . Giả thiết bỏ qua toàn bộ các chi phí khác ngoài việc chi trả tiền bảo hiểm cho khác thì ợ ậ ủ ỗ ẻ ả ể ạ này là bao nhiêu.
10. Trong một cuộc thi, người ta có hai hình thức thi như sau:
Hình thức thứ nhất: Mỗi người phải trả lời hai câu hỏi, mỗi câu trả lời đúng được 5 điểm.
Hình thức thứ hai: Nếu trả lời đúng câu thứ nhất thì mới được trả lời câu thứ hai, nếu
không thì dừng. Trả lời đúng câu thứ nhất được 5 điểm, trả lời đúng câu thứ hai được 10 điểm.
Trong cả hai hình thức thi, các câu trả lời sai đều không được điểm. Giả sử xác suất trả lời
đúng mỗi câu đều là 0,8; việc trả lời đúng mỗi câu là độc lập với nhau. Theo bạn, nên
chọn hình thức nào để số điểm trung bình đạt được nhiều hơn.
11. Biến ngẫu nhiên X có phân phối xác suất như sau:
P(X k) k k
C p (1 p)nk , (k 0,1, 2,..., ) n n
Tìm m (mốt) của X . 0
12. Biến ngẫu nhiên X có phân phối xác suất như sau: k (
P X k) e . , (k 0,1, 2,...) k !
với là số dương cho trước. Tìm m (mốt) của X . 0
13. Theo dõi hiệu quả kinh doanh của một công ty qua nhiều năm, các chuyên gia thiết lập
bảng phân phối xác suất của lãi suất đầu tư của công ty như sau: 9 Bài tập Toán kinh tế 2 Đào Hoàng Dũng X (%) 8 9 10 11 12 13 14 P 0,07 0,14 0,2 0,3 0,16 0,1 0,03
a) Khả năng đầu tư vào công ty đó để đạt lãi suất ít nhất 11% là bao nhiêu?
b) Tìm mức lãi suất nhiều khả năng nhất và mức lãi suất trung bình khi đầu tư vào công ty đó.
c) Tìm mức độ rủi ro khi đầu tư vào công ty đó.
14. Thống kê về tai nạn giao thông cho thấy tỉ lệ tai nạn xe máy (vụ/tổng số xe/năm) chia theo
mức độ nhẹ và nặng tương ứng là 0,001 và 0,005. Một công ty bán bảo hiểm xe máy với
mức thu phí hàng năm là 30 000 đồng và số tiền bảo hiểm trung bình một vụ là 1 triệu
đồng đối với trường hợp nhẹ và 3 triệu đồng đối với trường hợp nặng. Hỏi lợi nhuận trung
bình hàng năm mà công ty thu được đối với mỗi hợp đồng bảo hiểm là bao nhiêu? Biết
rằng thuế doanh thu phải nộp là 10% và tổng tất cả các chi phí khác chiếm 15% doanh thu.
15. Một cửa hàng mua vào bốn thùng hàng với giá 120 nghìn đồng/thùng. Số thùng hàng chưa
bán được, khi hết hạn sử dụng được nhà phân phối mua lại với số tiền bằng 3 số tiền cửa 4
hàng đã mua vào. Gọi X là số thùng hàng bán được của cửa hàng, X có phân phối xác suất như sau: X 0 1 2 3 4 1 P 2 2 6 4 15 15 15 15 15
Nếu giá bán ra của mỗi thùng hàng trên như nhau, thì giá đó là bao nhiêu để lợi nhuận kì
vọng đối với 4 thùng hàng này là 40 nghìn đồng/thùng.
16. Thống kê về mức độ hỏng và chi phí sửa chữa của hai loại động cơ A và B, có bảng số liệu sau: Mức độ hỏng 1 2 3
Chi phí sửa chữa (triệu A 5,5 7,2 12,5
đồng/năm) của một động cơ B 6,0 7,5 10,8 Tỉ lệ hỏng (%/năm) A 2 5 3 B 1 4 5
Một công ty đang sử dụng 6 động cơ loại A và 4 động cơ loại B. Tính chi phí sửa chữa
trung bình hàng năm cho cả hai loại động cơ trên của công ty.
17. Cơ quan dự báo khí tượng thủy văn chia thời tiết thành các loại “xấu”, “bình thường”,
“tốt” với xác suất tương ứng là 0,25; 0,45; 0,3. Với tình trạng trên thì khả năng nông
nghiệp được mùa tương ứng là 0,2; 0,6; 0,7. Nếu như sản xuất nông nghiệp được mùa thì
mức xuất khẩu lương thực tương ứng với tình trạng trên là: 2,5 triệu tấn, 3,3 triệu tấn, 3,8
triệu tấn. Hãy tìm mức xuất khẩu lương thực có khả năng nhất. 10 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
18. Tuổi thọ của một loại sản phẩm (đơn vị: năm) là biến ngẫu nhiên liên tục có hàm phân phối xác suất dạng 0 khi x 5 ( ) 1 k khi x 5 2 x
a) Tìm k ? Tính xác suất để trong 10 sản phẩm có 3 sản phẩm hỏng trước 6 năm.
b) Một công ty kinh doanh sản phẩm này khi bán được một sản phẩm lãi 500.000 đồng.
Nếu sản phẩm bị hỏng trong thời gian bảo hành thì phải bỏ ra 1.000.000 đồng cho
chi phí sửa chữa. Muốn có tiền lãi trung bình là 300.000 đồng cho một sản phẩm bán
được thì công ty phải quy định thời gian bảo hành là bao nhiêu năm.
19. Thời gian (phút) xếp hàng chờ mua hàng của khách là biến ngẫu nhiên liên tục với hàm
phân phối xác suất như sau: 0 voi x 0 3 2 F(x) a
x 3x 2x voi 0 x 1 1 voi x 1 a) Tìm a .
b) Tìm thời gian xếp hàng trung bình.
20. Tuổi thọ của một loại sản phẩm (đơn vị: năm) là biến ngẫu nhiên liên tục có hàm mật độ xác suất: 0 khi x 5
f (x) k khi x 5 3 x
a) Tìm k ? Tính tuổi thọ trung bình của sản phẩm.
b) Nếu muốn tỉ lệ sản phẩm phải bảo hành là 20% thì phải quy định thời gian bảo hành là bao nhiêu?
21. Tuổi thọ (tính theo năm) của một thiết bị điện tử là biến ngẫu nhiên có hàm mật độ xác suất như sau: 2 . x k e víi x 0 f (x) 0 víi x 0
Xác định k và tính xác suất ể
đ thiết bị này sử dụng được ít nhất 2 năm. 22. Cho hàm số k
(1 x), x 1 ;0 f ( ) x k
(1 x), x 0; 1 0, x 1 ; 1 11 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
a) Xác định k để f (x) là hàm mật độ xác suất của biến ngẫu nhiên X và tìm hàm phân phối xác suất.
b) Tìm kỳ vọng và phương sai của X .
23. Nhu cầu hàng năm về mặt hàng A là biến ngẫu nhiên liên tục X có hàm mật độ xác suất
như sau (đơn vị: ngàn sản phẩm): k
(30 x), x 0;3 0 f (x) 0, x 0;3 0 a) Xác định k ?
b) Tìm xác suất để nhu cầu về loại hàng đó không vượt quá 12 ngàn sản phẩm trong một năm.
c) Tìm nhu cầu trung bình hàng năm về mặt hàng A.
24. Cho biến ngẫu nhiên X có hàm mật độ xác suất như sau: k .sin , x víi x 0; 2 f (x )
0, víi x 0; 2 a) Xác định k.
b) Tính xác suất để khi thực hiện 3 phép thử độc lập X nhận giá trị trong khoảng ; ít nhất một lần. 6 3
25. Cho biến ngẫu nhiên X có hàm mật độ xác suất ax 2 bx , víi x 0;1 f (x ) 0, víi x 0;1 Biết
E(X ) 0, 6 . Tìm hàm phân phối xác suất của X ; tính 1 P 1 X
và V (X ) . 2
26. Giả sử hàm mật độ của biến ngẫu nhiên X là : . x A e víi x f x 0 ( ) ( 0) 0 víi x 0 a) Tìm A .
b) Tìm hàm phân phối của X .
c) Tìm kì vọng và phương sai của X .
27. Thống kê về lãi cổ phần tính cho 100 USD của 2 ngân hàng A và B trong một số năm
tương ứng là X (đơn vị %), Y (đơn vị %) kết quả cho trong bảng: 12 Bài tập Toán kinh tế 2 Đào Hoàng Dũng Y X -2 5 10 -1 0,1 0,15 0,1 4 0,05 0,2 0,1 10 0,1 0,15 0,05
a) Lập bảng phân phối biên của X, của Y. Tính lãi cổ phần trung bình cho từng ngân hàng.
b) Khi Y = 5%, tính lãi cổ phần trung bình của X.
c) X và Y có độc lập với nhau không? Tính .
d) Lập bảng phân phối của T = X + Y. Tính E(T) và V(T).
28. Chọn ngẫu nhiên 3 quả cầu từ hộp có 3 cầu đỏ, 4 cầu trắng, 5 cầu vàng. Gọi X, Y tương
ứng là số cầu đỏ, cầu vàng có trong 3 quả chọn ra.
a) Lập bảng phân phối ồ đ ng thời của X và Y
b) Tìm các phân phối biên của X và Y.
c) Tìm phân phối của số cầu đỏ biết số cầu vàng đã chọn được là 1. d) Tính .
29. Điều tra thu nhập hàng năm (đơn vị 10 triệu đồng) của các cặp vợ chồng đang làm việc.
Thu nhập của vợ, chồng tương ứng là X, Y được cho trong bảng: Y 10 20 30 40 X 10 0,2 0,04 0,01 0 20 0,1 0,36 0,09 0 30 0 0,05 0,1 0 40 0 0 0 0,05
a) Tìm phân phối biên của thu nhập của chồng, của vợ; thu nhập trung bình hàng năm của họ.
b) Tìm phân phối thu nhập của vợ có chồng thu nhập 20 triệu/năm; thu nhập trung bình của họ.
c) Tìm , từ đó cho kết luận về sự phụ thuộc giữa thu nhập của vợ chồng
d) Lập bảng phân phối xác suất của tổng thu nhập của các cặp vợ chồng. Tính trung
bình của tổng thu nhập đó. 13 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
Hướng dẫn, đáp số
1. b) Hàm phân phối xác suất của X: ( ) {
4. Gọi X là tiền lãi (ngàn đồng) khi mua 1 vé xổ số, lập bảng phân phối xác suất của X, tính E(X).
6. HD: (X 0),(X 1),(X 2) là các biến cố tạo nên một nhóm đầy đủ các biến cố. Tính
xs của các biến cố (Y 0),(Y 1),(Y 2) qua nhóm đầy đủ này. ( P Y 0) ( P X 0). (
P Y 0 | X 0) ( P X 1). (
P Y 0 | X 1) ( P X 2). (
P Y 0 | X 2) 2 2 9 C 8 0, 61 0,3 0,1 C 2 2 1 C 0 1 C 0
8 . HD: Luật sư lựa chọn phương án 2, như vậy theo đánh giá của luật sự thì :
E(“lợi nhuận khi lựa chọn phương án 2”) E(“lợi nhuận khi lựa chọn phương án 1”).
9. Gọi X là lợi nhuận (triệu đồng) của công ty khi bán 1 thẻ bảo hiểm, lập bảng phân phối
xác suất của X, tính E(X).
10. Gọi X, Y lần lượt là số điểm đạt được khi chọn hình thức thi 1 và 2 tương ứng. Lập
bảng ppxs của X, Y, tính và so sánh E(X), E(Y).
14. Lợi nhuận trung bình hàng năm mà công ty thu được đối với mỗi hợp đồng bảo hiểm là 6.500 đồng
17. HD: Gọi H1, H2, H3 tương ứng là các biến cố tình trạng thời tiết năm đó là “xấu”, “bình
thường” và “tốt”, { H1, H2, H3} tạo nên một nhóm đầy đủ các biến cố; A = “sản xuất
nông nghiệp được mùa” và X = “mức xuất khẩu lương thực” (triệu tấn).
Khi đó: (X = 2,5) = (H1|A); (X = 3,3) = (H2|A); (X = 3,8) = (H3|A).
18. a) . Sử dụng công thức công thức Becnulli. 19. a)
b) Gọi X là thời gian (phút) xếp hàng chờ mua hàng của khách, cần tính E(X).
20. a) . Gọi X là tuổi thọ (năm) của sản phẩm, cần tính E(X).
b) Gọi t (năm) là thời gian bảo hành sản phẩm. Cần tìm t sao cho: P(X ≤ t) = 0,2. 21. 22. 14 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
23. a) b) Cần tính ( ) c) Cần tính ( ) 24. a)
25. . Hàm phân phối xác suất của X: ( ) { 27. a) ( ) ( ) b) ( | ) c) 15 Bài tập Toán kinh tế 2 Đào Hoàng Dũng Chương 3
Một số quy lu t ậ phân ph i ố xác su t
ấ thông dụng
Phân phối nhị thức – B(n, p )
1. Thống kê cho thấy cứ 3 lần chào hàng thì có một lần bán được hàng. Nếu chào hàng 20
lần và gọi X là số lần bán được hàng thì X tuân theo quy luật gì ?
2. Một người trả lời ngẫu nhiên 30 câu hỏi trắc nghiệm, mỗi câu hỏi có 4 phương án trả lời
trong đó chỉ có 1 phương án đúng. Gọi X là số câu trả lời đúng của người đó.
a) Nêu quy luật phân phối xác suất của X.
b) Tìm số câu trả lời đúng trung bình của người đó.
c) Tìm số câu trả lời đúng có xác suất cao nhất của người đó.
3. Gieo 100 hạt đậu tương. Xác suất nảy mầm của mỗi hạt là 0,9. Tính xác suất để trong 100 hạt.
a) Có đúng 80 hạt nảy mầm.
b) Có ít nhất 1 hạt nảy mầm.
c) Có nhiều nhất 98 hạt nảy mầm .
4. Một xạ thủ bắn ngẫu nhiên độc lập 14 viên đạn vào một mục tiêu với xác suất bắn trúng
đích của mỗi viên là 0,2. Tìm số viên đạn trúng đích với khả năng lớn nhất.
5. Một lô hàng chứa rất nhiều sản phẩm với tỷ lệ phế phẩm là 0,02. Cần phải lấy một mẫu cỡ
bằng bao nhiêu, sao cho xác suất để có ít nhất một phế phẩm trong mẫu đó không bé hơn 0,95.
6. Xác suất để máy bị hỏng trong một ngày hoạt động là 0,01. Mỗi lần máy hỏng chi phí sửa
chữa hết 1 triệu đồng. Vậy có nên kí một hợp đồng bảo dưỡng là 120 ngàn đồng một
tháng (30 ngày) để giảm xác suất hỏng của máy đi một nửa hay không và nếu kí thì hiệu
quả mang lại là bao nhiêu.
Phân phối siêu bội – H(N, M, n)
7. Trong 20 giấy báo thuế có 3 giấy mắc sai sót. Lấy ngẫu nhiên 5 giấy để kiểm tra. Tìm
phân phối xác suất; trung bình và phương sai của số giấy mắc sai sót có trong 5 giấy lấy ra.
8. Để thanh toán 10 triệu đồng tiền hàng, một khách hàng gian lận đã xếp lẫn 10 tờ 100 ngàn
tiền giả với 90 tờ tiền thật. Chủ cửa hàng rút ngẫu nhiên 3 tờ đem đi kiểm tra và giao hẹn,
nếu phát hiện có tiền giả thì cứ mỗi tờ giả khách hàng phải đền năm tờ thật. Tìm số tiền
phạt trung bình mà khách hàng phải trả. 16 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
Phân phối Poisson – P(λ)
9. Một cửa hàng có 4 chiếc ô tô cho thuê, lượng cầu (đơn vị chiếc) thuê xe trong một ngày là
biến ngẫu nhiên X có phân phối Poisson với E(X ) 2 .
a) Tìm luật phân phối xác suất của số ô tô cửa hàng này cho thuê được trong một ngày.
b) Tính số ô tô trung bình mà cửa hàng cho thuê trong một ngày?
10. Số khách hàng vào một siêu thị trong 20 phút là biến ngẫu nhiên phân phối Poisson với số
khách trung bình là 6. Tính xác suất để trong 10 phút nào đó có hơn 2 khách vào siêu thị.
11. Một trung tâm bưu điện nhận được trung bình 150 cú điện thoại trong 1 giờ. Tìm xác suất
để trung tâm này nhận được không quá 2 cuộc điện thoại trong 1 phút.
12. Một cửa hàng có 3 xe ô tô cho thuê. Hàng ngày phải nộp thuế 50 ngàn đồng/1 xe dù xe có
được thuê hay không. Mỗi chiếc xe được thuê với giá 700 ngàn đồng/1 ngày. Giả sử yêu
cầu thuê xe của cửa hàng là biến ngẫu nhiên X có phân phối Poisson với tham số 2,8 .
Tính số tiền lãi trung bình của trạm thu được trong một ngày.
Phân phối đều – U(a; b)
13. Một xe buýt xuất hiện tại bến đợi lúc 7 giờ sáng, cứ 15 phút một chuyến. Giả sử thời gian
xuất hiện tại bến đợi ( kí hiệu là X ) tại bến đợi của một hành khách có phân phối đều từ 7 giờ đến 7 giờ 30.
a) Viết hàm phân phối xác suất của X .
b) Tìm xác suất để hành khách đó phải ợi
đ ít hơn 5 phút; nhiều hơn 10 phút.
14. Một nhà kinh doanh muốn đầu tư 10 triệu đồng vào một công ty mà nếu trong năm tới
công ty làm ăn thuận lợi có thể sẽ mang lại lãi suất đến 14% còn nếu gặp khó khăn thì lãi
suất có thể giảm đến mức 4%. Trong khi đó nếu gửi tiền vào ngân hàng thì lãi suất đảm
bảo 8%/năm. Vậy nếu dùng tiền để đầu tư thì khả năng có lãi hơn gửi ngân hàng là bao nhiêu.
Phân phố mũ – E(λ)
15. Thời gian phục vụ mỗi khách hàng (phút/khách hàng) tại một cửa hàng là biến ngẫu nhiên
có phân phối mũ với hàm mật độ xác suất như sau: 5 5
e x voi x 0 f (x) 0 voi x 0
a) Tìm xác suất để thời gian phục vụ khách hàng nào đó sẽ nằm trong khoảng từ 0,4 đến 1 phút.
b) Tìm thời gian trung bình để phục vụ một khách hàng. 17 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
16. Khoảng thời gian mà hai khách hàng kế tiếp nhau đến ngân hàng là biến ngẫu nhiên phân
phối mũ với trung bình là 3 phút. Giả sử vừa có một khách đến. Tìm xác suất để trong
vòng ít nhất 2 phút nữa mới có người khách tiếp theo đến ngân hàng.
Phân phối chuẩn – N(μ; σ2)
17. Chiều cao của một người trưởng thành có phân phối chuẩn với trung bình 175 cm và độ
lệch chuẩn 4 cm. Hãy xác định:
a) Tỉ lệ người trưởng thành có tầm vóc trên 180 cm.
b) Tỉ lệ người trưởng thành có chiều cao từ 166 cm đến 177 cm.
c) Giá trị , biết 33% người trưởng thành có chiều cao dưới mức .
d) Giới hạn biến động chiều cao của 90% người trưởng thành xung quanh giá trị trung bình.
18. Thời gian (tính bằng tháng) từ lúc vay tới lúc trả tiền của một khách hàng tại một ngân
hàng là biến ngẫu nhiên có phân phối chuẩn trung bình 18 tháng, độ lệch tiêu chuẩn 4 tháng.
a) Tính tỉ lệ khách hàng trả tiền cho ngân hàng trong khoảng từ 10 đến 19 tháng; không
ít hơn một năm; ít hơn 9 tháng.
b) Khoảng thời gian tối thiểu là bao nhiêu để tỉ lệ khách hàng trả tiền cho ngân hàng
vượt thời gian đó không quá 1%.
19. Gọi X là lượng điện tiêu thụ (tính bằng kWh) hàng tháng của một hộ gia đình.Giả sử X là
biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn với tham số 70 kWh và 40 kWh. Giá
tiền điện một tháng là 1500 đồng/kWh nếu lượng điện tiêu thụ trong tháng đó không quá
50 kWh. Tháng nào dùng quá mức này sẽ phải trả 700 đồng cho 1 kWh dôi ra. Gọi Y là
tiền điện (nghìn đồng) phải trả hàng tháng của một hộ gia đình. Tính các xác suất: a) (6
P 0 Y 317) b) P(Y 251)
HD: a) (60 Y 317) (60 Y 75) (75 Y 317) (4 X 50) (50 X 160) .
20. Thời gian hoạt động tốt (không phải sửa chữa) của một máy tính là biến ngẫu nhiên có
phân phối (xấp xỉ) chuẩn với 4300giờ và 250giờ. Giả thiết mỗi ngày một chiếc
máy loại này được dùng trong 10 giờ.
a) Tìm tỉ lệ máy tính loại này phải bảo hành, nếu thời gian bảo hành là 360 ngày.
b) Phải nâng chất lượng máy tính loại này bằng cách làm cho thời gian hoạt động tốt
trung bình của sản phẩm lên bao nhiêu để tỉ lệ sản phẩm phải bảo hành và vẫn như
trên song có thể nâng thời gian bảo hành lên thành 720 ngày.
21. Khi thâm nhập một thị trường mới, doanh nghiệp chỉ dự kiến được rằng doanh số hàng
tháng có thể đạt tuân theo luật phân phối (xấp xỉ) chuẩn. Khả năng đạt được doanh số trên
40 triệu là 0,2 và dưới 25 triệu là 0,1. 18 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
a) Tìm kì vọng và phương sai của doanh số hàng tháng này.
b) Tìm xác suất để doanh nghiệp đạt được doanh số ít nhất là 32 triệu/tháng.
22. Tuổi thọ của một loại bóng đèn (đơn vị: năm) là biến ngẫu nhiên có phân phối chuẩn trung
bình 4,2 năm, phương sai 2,25 (năm)2. Khi bán một bóng đèn thì công ty lãi 100 ngàn
đồng, song nếu đèn phải bảo hành thì lỗ 300 ngàn đồng.
a) Nếu quy định thời gian bảo hành là 3 năm thì tiền lãi trung bình khi công ty bán một bóng đèn là bao nhiêu.
b) Để tiền lãi trung bình khi bán một bóng đèn là 30 ngàn đồng thì phải quy định thời
gian bảo hành là bao nhiêu?
23. Độ dài chi tiết (cm) do một máy tự động sản xuất là biến ngẫu nhiên phân phối (xấp xỉ)
chuẩn với độ lệch chuẩn là 9 cm. Nếu được biết 84,13% chi tiết do máy sản xuất có độ dài
không vượt quá 84 cm thì xác suất để lấy ngẫu nhiên 3 chi tiết được ít nhất 1 chi tiết có độ
dài không dưới 80 cm là bao nhiêu.
24. Đầu tư vào hai thị trường A và B, có lãi suất là các biến ngẫu nhiên độc lập và phân phối chuẩn.
Lãi trung bình Độ lệch chuẩn
Thị trường A 10% 4%
Thị trường B 9% 3%
a) Muốn có lãi hơn 8%, trong ba phương án sau phương án nào là tốt nhất:
Phương án 1: Đầu tư toàn bộ tiền vào thị trường A.
Phương án 2: Đầu tư toàn bộ tiền vào thị trường B.
Phương án 3: Chia đều vốn vào cả hai thị trường.
b) Muốn rủi ro (phương sai) là nhỏ nhất thì phải đầu tư vào hai thị trường theo tỉ lệ nào.
Hướng dẫn, đáp số 1. ( ) 2. ( )
6. Tính chi phí trung bình cho sửa chữa và bảo dưỡng máy trong tháng trong trường hợp
không kí hợp đồng bảo dưỡng và trường hợp kí hợp đồng bảo dưỡng, so sánh 2 chi phí
này rồi chọn trường hợp có chi phí thấp hơn. Đ/s: Nên kí hợp đồng bảo dưỡng.
7. Gọi là số giấy báo thuế sai sót trong 5 giấy lấy ra. ( )
8. Số tiền phạt trung bình là 150 ngàn đồng. 19 Bài tập Toán kinh tế 2 Đào Hoàng Dũng Chương 4
Cơ sở lý thuyết mẫu
2. Tính trung bình mẫu và độ lệch tiêu chuẩn từ mẫu số liệu sau: X 2 3 4 5 6 7 8 9 10 11 ni 15 30 25 12 41 11 52 8 33 23
3. Tính trung bình mẫu và độ lệch tiêu chuẩn từ mẫu số liệu sau: X 114 115 116 117 118 119 120 Tần số 22 67 54 73 45 18 13
4. Tính trung bình mẫu và độ lệch chuẩn mẫu từ các số liệu sau: a)
Khoảng 0 – 10 10 – 20 20 – 30 30 – 40 40 – 50 50 – 60 60 – 70 70 – 80 80 – 90 Tần số 7 15 30 28 42 19 34 18 7 b) Khoảng 0,5 – 3,5 3,5 – 6,5 6,5 – 9,5
9,6 – 12,5 12,5 – 15,5 15,5 – 18,5 18,5 – 21,5 Tần số 25 30 5 9 3 0 3 20 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
HƯỚNG DẪN SỬ DỤNG MÁY TÍNH CASIO fx – 570VN PLUS 21 Bài tập Toán kinh tế 2 Đào Hoàng Dũng 22 Bài tập Toán kinh tế 2 Đào Hoàng Dũng Chương 5
Ước lượng tham số
Phương pháp ước lượng điểm 1. Cho W (X
là một mẫu ngẫu nhiên từ tổng thể có phân phối chuẩn N(μ, σ2). Lập 1, X 2, X 3) các thống kê 1 1 1 và 1 1 1 . 1 G X1 X 2 X3 G X X X 4 2 4 2 1 2 3 3 6 2
a) Chứng minh rằng G , ủ μ. 1 2
G là các ước lượng không chệch c a
b) Trong hai ước lượng trên, ước lượng nào tốt hơn cho μ?
2. Cho W (X , X , X ) là một mẫu ngẫu nhiên từ tổng thể có phân phối chuẩn N(μ, σ2). Lập 1 2 3 thống kê 1 1 1 G . 1 X X2 X3 3 6 2
a) Tính kì vọng và phương sai của G .
b) G có phải là ước lượng hiệu quả của μ không? Tại sao?
3. Từ một mẫu ngẫu nhiên kích thước 5, xét ba thống kê sau: X
X 2X 3X 4X 5 1 1 1 1 X 2 , 1 2 3 4 X5 và 1 G G G X X X 2 2 15 3 1 2 3 2 3 6
Chứng minh ba thống kê trên là các ước lượng không chệch của trung bình tổng thể m.
Ước lượng nào hiệu quả hơn cả?
Phương pháp ước lượng bằng khoảng tin cậy
4. Trong một cuộc khảo sát 64 khách hàng ở một tiệm ăn nhanh, thời gian đợi trung bình là 3
phút và độc lệch chuẩn là 1,5 phút. Với độ tin cậy , tìm khoảng tin cậy cho thời gian
đợi phục vụ trung bình của tiệm ăn này. Biết thời gian đợi phục vụ là biến ngẫu nhiên có
phân phối (xấp xỉ) chuẩn.
5. Trong một cuộc điều tra 150 người nghiện thuốc lá được chọn ngẫu nhiên. Người ta tính
được số điếu thuốc hút trong một tuần của họ có trung bình là 97 và độ lệch tiêu chuẩn là
36. Tìm khoảng tin cậy 99% cho số điếu thuốc hút trung bình trong 1 tuần của người
nghiện thuốc lá. Biết số điếu thuốc hút trong một tuần của người nghiện thuốc là biến
ngẫu nhiên có phân phối (xấp xỉ) chuẩn.
6. Tuổi thọ của một loại bóng đèn do một dây chuyền sản xuất ra có độ lệch chuẩn là 95 giờ.
Điều tra 50 bóng đèn loại này tính được tuổi thọ trung bình là 350 giờ. Giả th ế i t tuổi thọ
của bóng đèn là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn.
a) Với độ tin cậy 95%, hãy ước lượng tuổi thọ trung bình tối đa của loại bóng đèn này. 23 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
b) Nếu muốn ước lượng tuổi thọ trung bình của loại bóng đèn đạt độ chính xác là 25 giờ
và độ tin cậy 98% thì cần điều tra bao nhiêu bóng?
7. Chỉ tiêu A của một loại sản phẩm là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn. Mẫu
điều tra về chỉ tiêu A (tính bằng %) của sản phẩm này được cho trong bảng Xi 0 – 5
5 – 10 10 – 15 15 – 20 20 – 25 25 – 30 30 – 35 35 – 40 ni 7 12 20 25 18 12 5 1
a) Hãy ước lượng trung bình chỉ tiêu A với độ tin cậy 95%.
b) Hãy ước lượng trung bình tối thiểu của chỉ tiêu A với độ tin cậy 95%.
c) Nếu muốn ước lượng trung bình chỉ tiêu A đạt độ tin cậy 95% và độ chính xác 1,2%
thì cần điều tra thêm bao nhiêu sản phẩm nữa?
d) Nếu sử dụng mẫu này để ước lượng trung bình các sản phẩm đạt độ chính xác 1% thì
đảm bảo độ tin cậy là bao nhiêu?
e) Những sản phẩm có chỉ tiêu A không quá 10% là loại 2. Hãy ước lượng trung bình chỉ
tiêu A các sản phẩm loại 2 với độ tin cậy 95%, biết rằng chỉ tiêu A các sản phẩm loại 2
là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn.
8. Cơ quan cảnh sát giao thông kiểm tra hệ thống phanh của 100 chiếc xe tải trên đường
quốc lộ. Họ phát hiện 35 chiếc có phanh chưa đảm bảo.
a) Tìm khoảng tin cậy 95% cho tỉ lệ xe tải có phanh chưa an toàn.
b) Tìm khoảng tin cậy 98% cho tỉ lệ xe tải có phanh tốt.
9. Điều tra ngẫu nhiên thu nhập/tháng của 100 nhân viên công ty A thu được kết quả sau:
Thu nhập (triệu đồng) 3,0 3,2 3,4 3,6 3,8 4,0 Số nhân viên 5 15 25 30 20 5
a) Ước lượng mức thu nhập/tháng trung bình của nhân viên công ty A với độ tin cậy 0,95.
b) Hãy ước lượng tỉ lệ nhân viên công ty A có thu nhập không quá 3,6 triệu đồng/tháng với độ tin cậy 0,95.
Biết thu nhập/tháng của nhân viên công ty này là biến ngẫu nhiên có phân phôi (xấpxỉ) chuẩn.
10. Điều tra doanh thu trong tuần (triệu đồng) của một số cửa hàng bán tạp phẩm ở vùng A, người ta thu đ ợ ư c số liệu sau: Doanh thu trong tuần 21 22 23 24 25 26 Số cửa hàng 7 17 29 27 15 5 Với ộ đ tin cậy 95% hãy:
a) Tìm khoảng tin cậy cho doanh thu/tuần trung bình tối thiểu của mỗi cửa hàng tạp phẩm ở vùng A.
b) Tìm khoảng tin cậy cho độ phân tán của doanh thu/tuần. 24 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
c) Tìm khoảng tin cậy cho tỉ lệ số cửa hàng có doanh thu/tuần dưới 23 triệu đồng.
11. Để nghiên cứu nhu cầu về một loại hàng ở một khu vực, người ta tiến hành khảo sát về
nhu cầu mặt hàng này ở 400 hộ gia đình, kết quả cho trong bảng:
Nhu cầu (kg/tháng) 0 – 1 1 – 2 2 – 3 3 – 4 4 – 5 5 – 6 6 – 7 7 – 8 Số hộ 10 35 86 132 78 31 18 10
Giả sử khu vực nghiên cứu có 4000 hộ và nhu cầu về loại hàng này là biến ngẫu nhiên có
phân phối (xấp xỉ) chuẩn.
a) Ước lượng nhu cầu trung bình về mặt hàng này của toàn khu vực trong một năm với độ tin cậy 95%.
b) Khi ước lượng nhu cầu trung bình về mặt hàng này của toàn khu vực trong một năm,
nếu ta muốn độ tin cậy đạt được 99% và độ chính xác là 4,8 tấn thì cần khảo sát nhu
cầu loại hàng này thêm bao nhiêu hộ gia đình trong vùng này nữa?
12. Lãi suất cổ phiếu của một công ty là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn. Giá trị
trong 10 năm qua (đơn vị: %) là: 15, 12, 20, 8,10, 16, 14, 22, 18, 19. Với độ tin cậy 95%, hãy ước lượng:
a) Độ phân tán (phương sai) của lãi suất cổ phiếu này.
b) Độ phân tán tối đa của lãi suất cổ phiếu này.
c) Độ phân tán tối thiểu của lãi suất cổ phiếu này.
13. Một nông dân muốn ước lượng tỉ lệ nảy mầm cho một giống lúa mới. Mẫu điều tra của
ông cho kết quả trong 1000 hạt đem gieo có 640 hạt nảy mầm .
a) Với độ tin cậy 95%, hãy ước lượng tỉ lệ nảy mầm của giống lúa này.
b) Nếu muốn ước lượng tỉ lệ hạt nảy mầm có sai số không vượt quá 2% và đạt độ tin cậy
95% thì cần gieo ít nhất bao nhiêu hạt ?
c) Với độ tin cậy 97% hãy ước lượng số hạt giống nảy mầm tối thiểu khi gieo 10000 hạt.
14. Kết quả quan sát về hàm lượng vitamin C của một loại trái cây cho ở bảng sau: Hàm lượng vitamin C(%) 3 – 7 8 – 10 11 – 13 14 – 16 17 – 19 20 – 24 Số trái cây 5 10 20 35 25 5
Biết hàm lượng vitamin C ở trái cây này là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn.
a) Với độ tin cậy 95%, hãy tìm khoảng tin cậy đối xứng của hàm lượng vitamin C trung bình trong mỗi trái;
b) Qui ước những trái cây có hàm lượng vitamin C từ 17% trở lên là loại 1. Nếu muốn độ
chính xác khi ước lượng hàm lượng vitamin C trung bình là 0,5 và độ chính xác 1
khi ước lượng tỉ lệ trái cây loại 1 là 0,05 với cùng độ tin cậy 95% thì cần mẫu có 2
kích thước tối thiểu bao nhiêu? 25 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
15. Để đánh giá trữ lượng cá trong hồ người ta đánh bắt 2000 con cá, đánh dấu rồi thả xuống
hồ. Sau đó bắt lại 400 con thì thấy có 80 con có dấu.
a) Với độ tin cậy 95%, hãy ước lượng trữ lượng cá trong hồ.
b) Nếu muốn sai số của ước lượng giảm đi một nửa thì lần sau phải đánh bắt bao nhiêu con?
16. Lô hàng có rất nhiều sản phẩm loại A và 1000 sản phẩm loại B. Lấy ngẫu nhiên 400 sản
phẩm từ lô hàng để kiểm tra thì thấy có 36 sản phẩm loại B.
a) Hãy ước lượng số sản phẩm loại A có trong lô hàng.
b) Nếu muốn ước lượng tỉ lệ sản phẩm loại A có trong lô hàng đạt được độ chính xác 5%
thì độ tin cậy đạt được bao nhiêu %?
17. Để ước lượng số tờ bạc giả của một loại giấy bạc người ta đánh dấu 200 tờ bạc giả l ạ o i
này rồi tung vào lưu thông. Sau một thời gian ngắn kiểm tra 600 tờ bạc giả loại này có 15
tờ được đánh dấu. Với độ tin cậy 95%, hãy ước lượng số tờ bạc giả loại này. 26 Bài tập Toán kinh tế 2 Đào Hoàng Dũng Chương 6
Kiểm định giả thuyết thống kê
1. Khối lượng trung bình của một gói đường do một máy tự động đóng gói theo thiết kế là
500 gam/gói. Nghi ngờ máy đóng gói đường làm việc không bình thường làm cho khối
lượng của gói đường có xu hướng giảm sút. Người ta lấy ngẫu nhiên 30 gói cân thử được
khối lượng trung bình là 495 gam và độ lệch chuẩn s =10 gam. Với mức ý nghĩa 5%, hãy
kết luận về nghi ngờ trên.
2. Chỉ tiêu chất lượng A của một loại sản phẩm là biến ngẫu nhiên có phân phối (xấp xỉ)
chuẩn. Một mẫu điều tra được kết quả cho trong bảng: xi (gam) 200 220 240 260 280 Số sản phẩm 3 7 16 17 7
a) Có tài liệu cho rằng trung bình chỉ tiêu A các sản phẩm loại này là 250 gam. Cho nhận
xét về tài liệu này với mức ý nghĩa 5%.
b) Những sản phẩm có chỉ tiêu A nhỏ hơn 240 gam là loại 2. Có tài liệu cho rằng trung
bình chỉ tiêu A các sản phẩm loại 2 là 220 gam. Hãy cho nhận xét về tài liệu này với
mức ý nghĩa 2%. Giả thiết chỉ tiêu A của sản phẩm loại 2 có phân phối chuẩn.
3. Điều tra doanh số bán hàng X (đơn vị: triệu đồng/tháng) của các hộ kinh doanh một loại
hàng năm nay cho số liệu:
Doanh số (tr.đồng/tháng) 11 11,5 12 12,5 13 13,5 Số hộ 10 15 20 30 15 10
a) Những hộ có doanh số trên 12,5 triệu đồng/tháng là những hộ có doanh số cao. Có tài
liệu cho rằng tỉ lệ hộ có doanh số cao là 35%. Cho nhận xét về tỉ lệ trong tài liệu đó với mức ý nghĩa 5%?
b) Năm trước doanh số bán hàng trung bình của các hộ này là 120 triệu/1 năm. Có thể
cho rằng doanh số bán hàng của các hộ này năm nay tăng lên không, với mức ý nghĩa 1%?
4. Nếu áp dụng phương pháp công nghệ thứ nhất thì tỉ lệ phế phẩm là 9%, còn áp dụng
phương pháp công nghệ thứ hai thì trong 100 sản phẩm có 4 phế phẩm. Với mức ý nghĩa
5%, có thể cho rằng áp dụng phương pháp công nghệ thứ hai cho tỉ lệ phế phẩm thấp hơn không?
5. Lô hàng đủ tiêu chuẩn xuất khẩu nếu tỉ lệ phế phẩm không vượt quá 3%. Kiểm tra ngẫu
nhiên 400 sản phẩm của lô hàng thấy có 14 phế phẩm. Với mức ý nghĩa 0,05 có cho phép
lô hàng xuất khẩu được không? 27 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
6. Tỉ lệ phế phẩm do một máy tự động sản xuất là 5%. Kiểm tra một mẫu ngẫu nhiên 300 sản
phẩm thấy có 24 sản phẩm là phế phẩm. Từ đó có ý kiến cho rằng tỉ lệ phế phẩm do máy
đó sản xuất có chiều hướng tăng lên. Hãy kết luận ý kiến nêu trên với mức ý nghĩa 0,05.
7. Một nhà máy sản xuất bóng đèn cho rằng chất lượng bóng đèn loại này được coi là đồng
đều nếu tuổi thọ của các bóng đèn có độ lệch chuẩn bằng 1000 giờ hoặc ít hơn. Lấy ngẫu
nhiên 10 bóng để kiểm tra thì tìm được độ lệch chuẩn mẫu s = 1150. Vậy với mức ý nghĩa
5% có thể coi chất lượng bóng đèn loại này do công ty sản xuất là đồng đều hay không.
Biết tuổi thọ của bóng đèn là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn.
8. Khối lượng của con gà lúc mới nở là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn. Nghi
ngờ độ đồng đều về trọng lượng gà con giảm sút người ta cân thử 12 con và tìm được s2 =
11,41 (gam)2. Với mức ý nghĩa 0,05, hãy kết luận về điều nghi ngờ trên biết rằng độ phân
tán của khối lượng gà con là σ2 = 10 (gam)2.
9. Chiều cao thanh niên ở hai vùng A và B là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn. Ở
vùng A, chiều cao trung bình của thanh niên là 164 cm và độ lệch chuẩn 5,63 cm. Điều tra 200 200
ngẫu nhiên 200 thanh niên ở vùng B, tính được x 32900, 2 x 541840 , trong đó B B i i i 1 i 1
x là chiều cao thanh niên thứ i (i 1, 200) . Có thể cho rằng độ đồng đều về chiều cao của Bi
thanh niên vùng A là hơn vùng B hay không? Kết luận với mức ý nghĩa 5%.
Bài tập tổng hợp phần ước lượng và kiểm định giả thuyết
10. Năng suất lúa của vùng A là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn. Thu hoạch
ngẫu nhiên 100 ha của vùng trong vụ này tính được năng suất trung bình là x 37,9 100 (tạ/ha) và
x x2 1059. i i 1
a) Hãy ước lượng năng suất lúa trung bình của vùng với độ tin cậy 95%.
b) Nếu vụ trước năng suất lúa trung bình của vùng này là 35 (tạ/ha), thì với mức ý nghĩa
5% có thể cho rằng năng suất lúa vụ này cao hơn được không?
11. Năng suất một giống lúa chất lượng cao tại vùng A là biến ngẫu nhiên có phân phối (xấp
xỉ) chuẩn. Thu hoạch ngẫu nhiên 256 ha lúa vùng được các số liệu: x 15, 027 (tạ/ha),
256 x x . i 2 148,809 i 1
a) Hãy ước lượng năng suất trung bình tối thiểu của giống lúa trên với độ tin cậy 0,95.
b) Khi mới đưa ra sản xuất, phương sai của năng suất giống lúa trên tại vùng A là 5
(tạ/ha)2. Người ta nghi ngờ giống lúa trên đã bị thoái hóa nên nó không ổn định so với
trước đây. Dựa vào mẫu trên hãy kết luận về nghi ngờ trên với mức ý nghĩa 5%. 28 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
12. Khảo sát về thu nhập của một số người làm việc ở một công ty, người ta thu được bảng số liệu: Thu nhập ( –
26 – 30 30 – 34 34 – 38 38 – 42 42 – 50 triệu đồng/năm) 20 26 Số người 20 50 130 110 60 30
a) Những người có thu nhập không quá 30 triệu đồng/năm là những người có thu nhập
thấp. Với độ tin cậy 96%, hãy tìm khoảng tin cậy đối xứng của tỉ lệ người có thu nhập thấp của công ty.
b) Nếu công ty báo cáo mức thu nhập bình quân của một người là 3 triệu đồng/tháng thì
có tin cậy được không (kết luận với mức ý nghĩa 5%)?
c) Nếu muốn ước lượng thu nhập trung bình của một người ở công ty này với độ chính
xác 0,5 triệu đồng/năm thì độ tin cậy đạt được bao nhiêu?
13. Thu nhập hàng tháng của một công nhân ở xí nghiệp N là biến ngẫu nhiên có phân phối
(xấp xỉ) chuẩn. Năm nay, điều tra ngẫu nhiên 100 công nhân thu được số liệu sau: Thu nhập ( 5 5,5 6 6,5 7 7,5 8
triệu đồng/tháng) Số công nhân 5 15 20 30 15 9 6
a) Biết xí nghiệp N có 1000 công nhân, ước tính thu nhập hàng tháng trung bình của toàn
bộ công nhân ở xí nghiệp này;
b) Với độ tin cậy 95%, ước lượng thu nhập hàng tháng trung bình tối thiểu của 1 công nhân xí nghiệp N.
c) Nếu trước đó 1 năm tỉ lệ công nhân có thu nhập trên 7 triệu đồng/tháng là 10% thì với
mức ý nghĩa 5% có thể cho rằng tỉ lệ này năm nay đã tăng lên không?
14. Mẫu điều tra về giá bán X (đơn vị: 1000 đồng) của mỗi cổ phiếu A trên thị trường chứng
khoán trong các phiên giao dịch được cho ở bảng sau: xi
11 – 13 13 – 15 15 – 17 17 – 19 19 – 21 21 – 23 23 – 25 Số phiên 5 17 23 33 25 16 2
Biết giá bán X là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn.
a) Với độ tin cậy 95%, hãy tìm khoảng tin cậy đối xứng của doanh thu trung bình khi bán
10000 cổ phiếu A trên thị tr ờ ư ng với ộ đ tin cậy 95%.
b) Nếu muốn ước lượng giá bán của một cổ phiếu A đạt độ chính xác là 500 đồng với độ
tin cậy 95% thì cần điều tra thêm bao nhiêu phiên nữa?
c) Với độ tin cậy 95%, hãy ước lượng tỉ lệ tối thiểu cổ phiếu A có giá bán từ 17 nghìn đồng trở lên.
d) Với độ tin cậy 90%, hãy tìm khoảng tin cậy của phương sai giá bán một cổ phiếu A. 29 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
e) Biết rằng trước kia độ phân tán của giá bán cổ phiếu A là 11 nghìn đồng. Với mức ý
nghĩa 2%, có thể cho rằng độ phân tán về giá bán của loại cổ phiếu này có xu hướng
giảm xuống so với trước đây không?
15. Xét nghiệm 100 chai nước Luvia trong một nhà kho, thấy tỉ lệ chất A trong một chai như sau:
Tỉ lệ chất A (%)
[0; 5) [5; 10) [10; 15) [15; 20) [20; 25) [25; 30) [30; 35) [35; 40) Số chai 7 12 20 25 18 12 5 1
Biết rằng tỉ lệ chất A (%) ở một chai nước Luvia là biến ngẫu nhiên X có phân phối (xấp xỉ) chuẩn.
a) Với độ tin cậy 95%, trung bình tỉ lệ chất A trong mỗi chai nước Luvia không bé hơn bao nhiêu?
b) Nếu dùng mẫu này để ước tính trung bình tỉ lệ chất A của mỗi chai nước Luvia với độ
chính xác là 1% thì độ tin cậy là bao nhiêu? (biếtu 1,2393 ). 0,11
c) Nếu muốn ước tính trung bình tỉ lệ chất A đạt độ tin cậy 96% và độ chính xác là 1,2%
thì phải xét nghiệm thêm bao nhiêu chai nước Luvia nữa?
d) Những chai nước Luvia có lượng chất A nhỏ hơn 10% thì không đạt yêu cầu. Biết rằng
nhà kho có 1000 chai nước Luvia, hãy ước tính số chai Luvia không đạt yêu cầu cảu
kho ấy với độ tin cậy 96%.
e) Với mức ý nghĩa 5%, cho biết tỉ lệ chai nước Louvia đạt yêu cầu trong kho có trên 80% không?
16. Khảo sát về mức thưởng của một số ngườ
i làm việc ở một công ti, người ta thu được bảng s ố liệu:
Mức thưởng (triệu đồng/năm) 20 – 26 26 – 30 30 - 34 34 – 38 38 – 42 42 - 50 Số người 20 50 130 110 60 30
a) Những người có mức thưởng không quá 30 triệu đ/năm là những người có mức thưởng thấp.
Với độ tin cậy 95%, hãy tìm khoảng tin cậy đối xứng của tỉ lệ người có mức thưởng thấp của công ti;
b) Nếu công ti báo cáo mức mức thưởng bình quân của một người là 3 triệu đồng/tháng thì có tin
cậy được không (kết luận với mức ý nghĩa 5%)?
c) Nếu muốn ước lượng mức thưởng trung bình của một người ở công ti này với độ chính xác
0,5 triệu đồng/năm thì độ tin cậy đạt được bao nhiêu?
17. Từ một lô hàng gồm 4000 sản phẩm, người ta chọn ngẫu nhiên 400 sản phẩm để kiểm tra thì thấy
có 350 sản phẩm loại I.
a) Nếu cho rằng số sản phẩm loại I của lô hàng là 3700 thì có chấp nhận được không (với mức ý nghĩa 5%)? b) Nếu muốn ước n
lượ g tỉ lệ sản phẩm loại I của lô hàng đạt được độ chính xác 3,5% và độ tin
cậy 95% thì cần kiểm tra bao nhiêu sản phẩm nữa ? 30 Bài tập Toán kinh tế 2 Đào Hoàng Dũng 2 1 u z
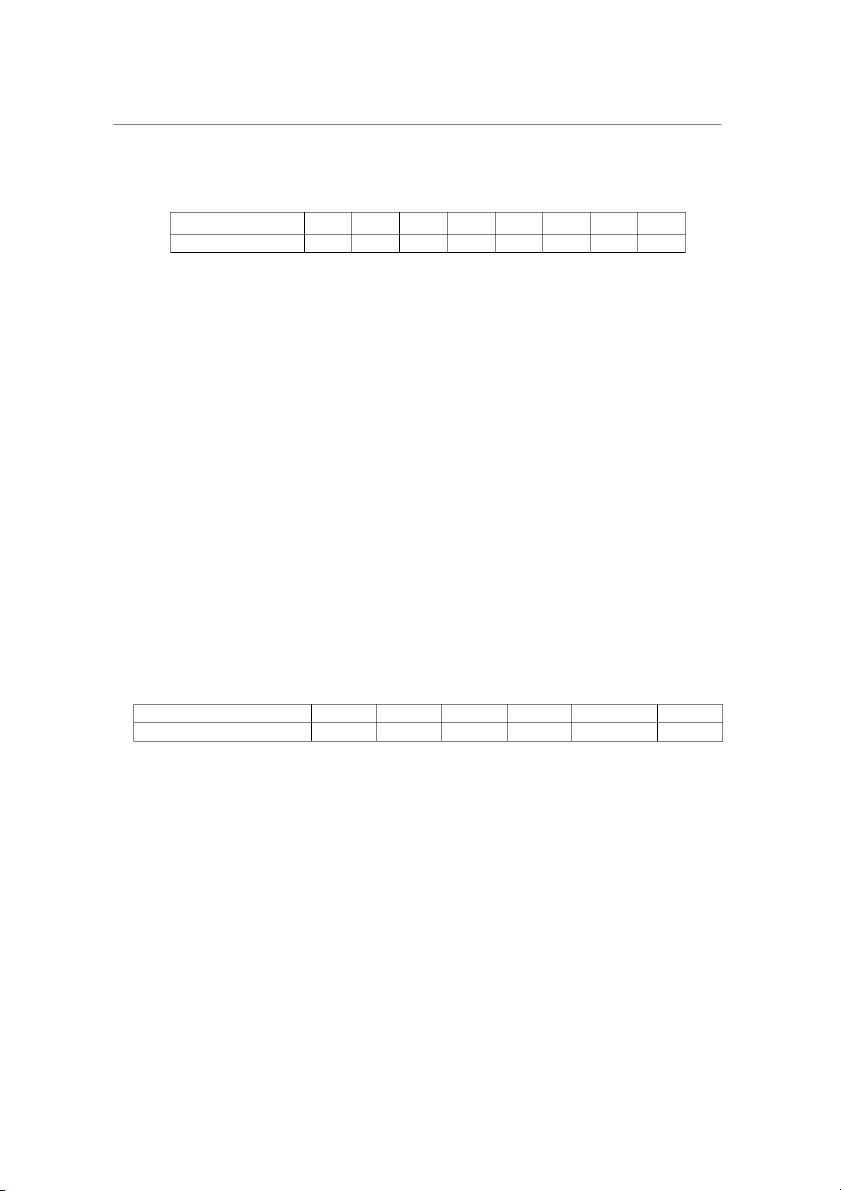
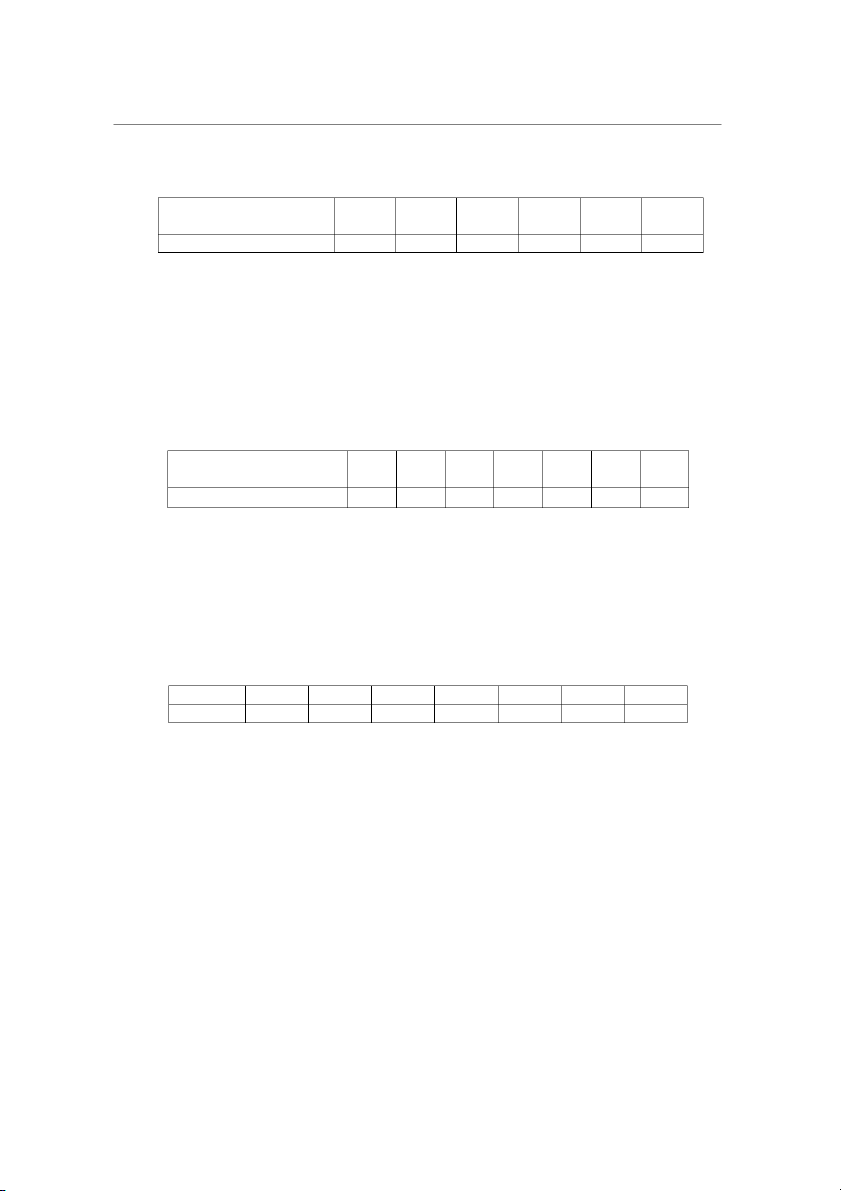
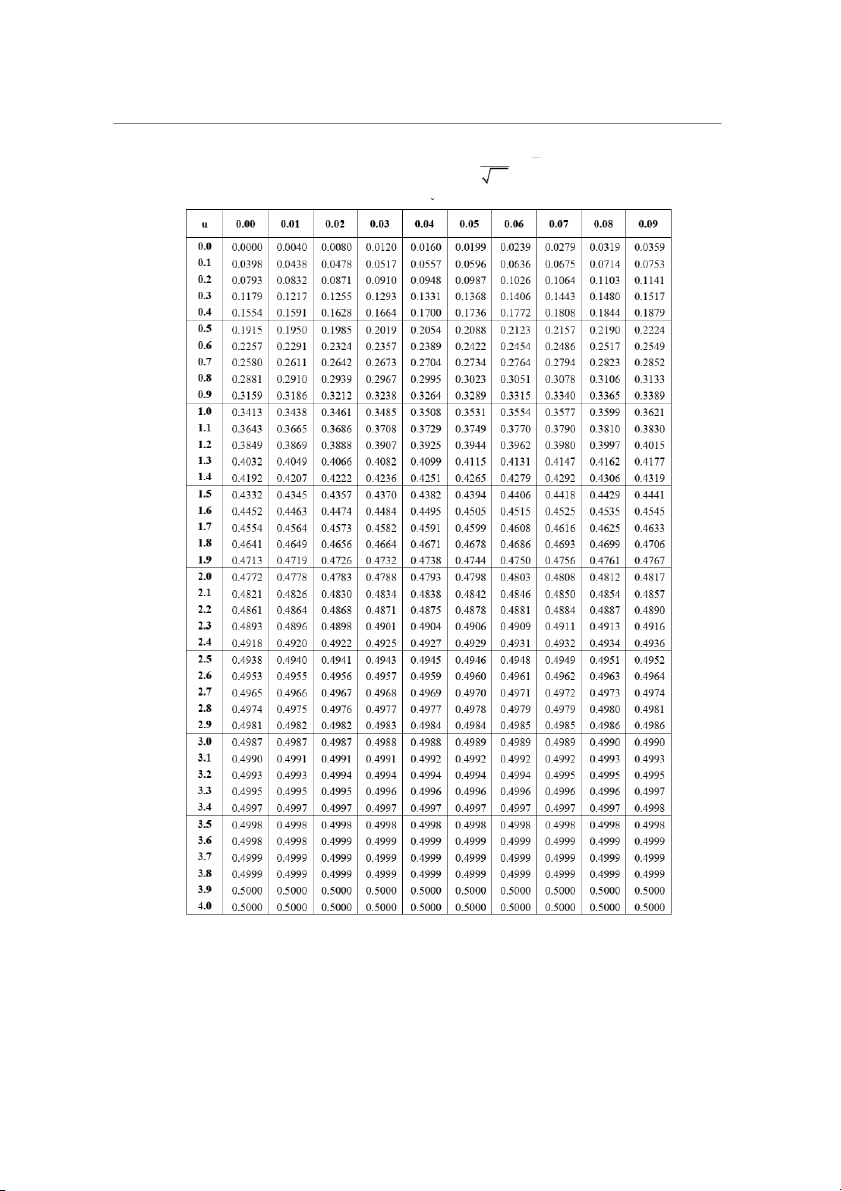
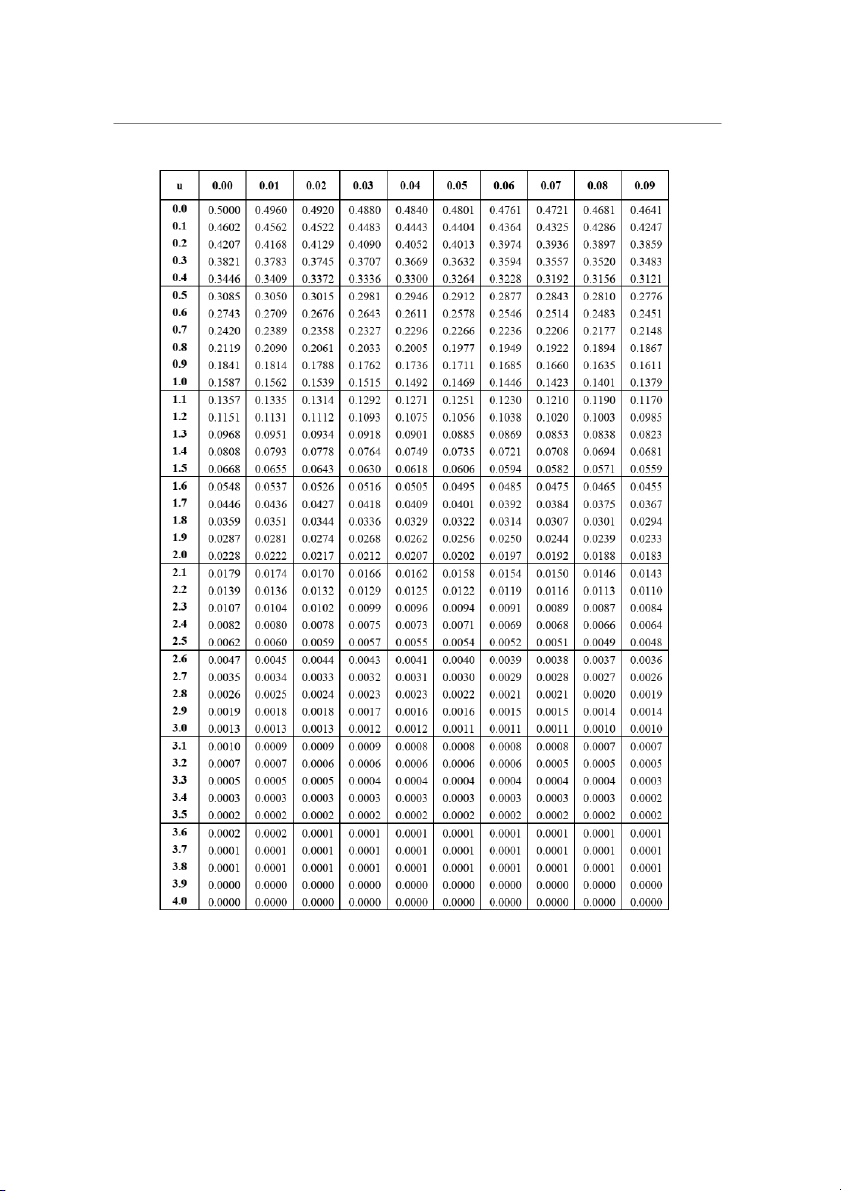
Bảng giá trị hàm 2 0 u e dz 2 0 31 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
Bảng giá trị tới hạn chu n
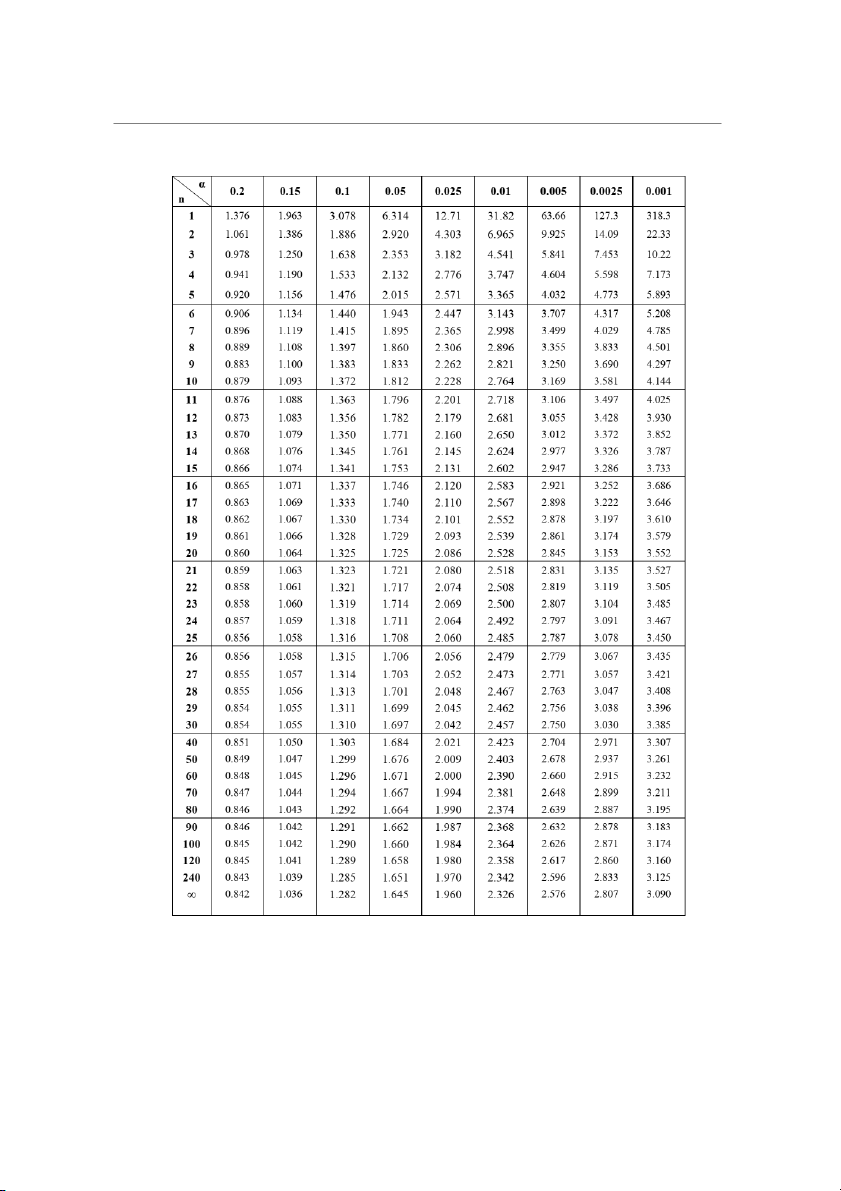
ẩ : PU u 32 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
Bảng giá trị tới hạn phân phối Student ( ) 33 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
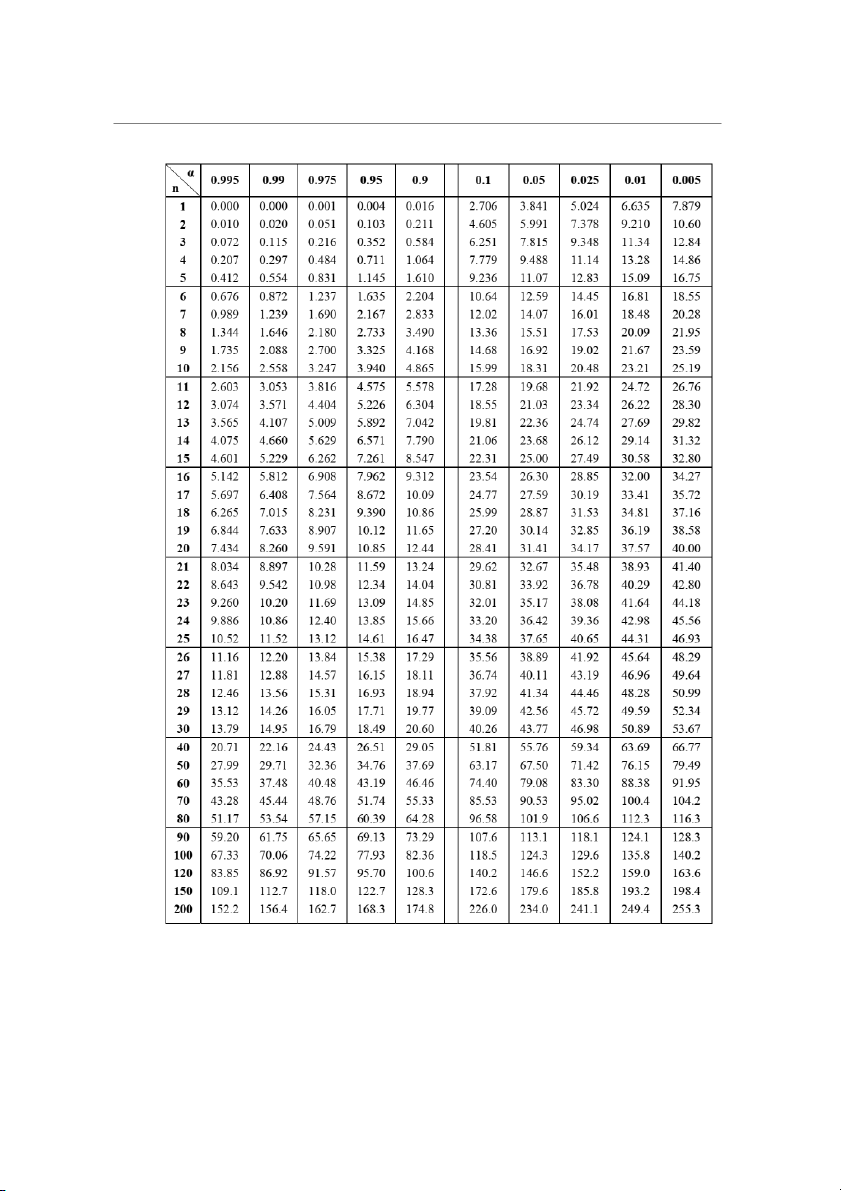
Bảng giá trị tới hạn phân phối Khi bình phương ( ) 34 Bài tập Toán kinh tế 2 Đào Hoàng Dũng
SỬ DỤNG EXCEL 2010 ĐỂ TRA CÁC GIÁ TRỊ TỚI HẠN
1. (u) NORM.S.DIST( , u TRUE) 0.5 0
2. Giá trị tới hạn chuẩn: u 1*NORM.S.INV( )
3. Tìm khi biết u : 1 NORM.S.DIST(u ,TRUE)
4. Giá trị tới hạn Student: (n) t T.INV.2T(2*, ) n
5. Giá trị tới hạn Khi bình phương: 2(n)
CHISQ.INV.RT( ,n)
6. Tìm giá trị tới hạn Fisher: ( ) ( ) (n ) (n ) 7. t : T.DIST.RT(t , )
Tìm α khi biết n và n
SỬ DỤNG MÁY TÍNH CASIO 570 VN PLUS TÍNH CÁC GIÁ TRỊ
CỦA PHÂN PHỐI CHUẨN
1. Tính (u) , chẳng hạn với u 1,26 0
MODE 3 1 AC SHIFT 1 5 2 1.26 =
Kết quả hiển thị trên màn hình, giá trị (1.26) là: 0.39617 0
2. Tìm u khi biết (u) 0.17 0
MODE ▼ 3 3 0.33 = = =
Kết quả hiển thị trên màn hình: –0.4399131231.
Giá trị của u là: –1 (–0.4399131231) = 0.4399131231.
(chú ý: 0.33 là kết quả của phép toán 0.5 – 0.17).
3. Tính giá trị của u khi biết , chẳng hạn 0.025
MODE ▼ 3 3 0.025 = = =
Kết quả hiện thị trên màn hình: : –1.959964028
Giá trị cần tìm là: u 1 – ( 1.959964028) 1.959964028 0.025
4. Tìm khi biết giá trị của u . Ví dụ: Biết u , tìm ? 1.65
MODE 3 1 AC 0.5 – (dấu trừ) SHIFT 1 5 2 1.65 =
Kết quả hiển thị trên màn hình, giá trị là: 0.04947 35




