. SỐ THỰC
I. KIẾN THỨC CƠ BẢN 1. Số thực
 Số hữu tỉ và số vô tỉ được gọi chung là số thực
Tập hợp các số thực được ký hiệu là
 Nếu a là số thực thì a biểu diễn dưới dạng số thập phân hữu hạn hoặc vô hạn. Khi đó, ta
có thể so sánh hai số thực tương tự nhu so sánh hai số hữu tỉ viết dưới dạng thập phân
 Với a, b là hai số thực dương, nếu a  b thì a  b 2. Trục số thực
 Mỗi số thực được biểu diễn bởi mọt điểm trên trục số
 Mỗi điểm trên trục số biểu diễn một số thực 3. Các phép toán
Trong tập hợp số thực , ta cũng định nghĩa các phép toán cộng, trừ, nhân, chia, nâng lên
lũy thừa và khai căn. Các phép toán trong tập hợp số thực cũng có các tính chất như các
phép toán tring tập hợp các số hữu tỉ. II. BÀI TẬP
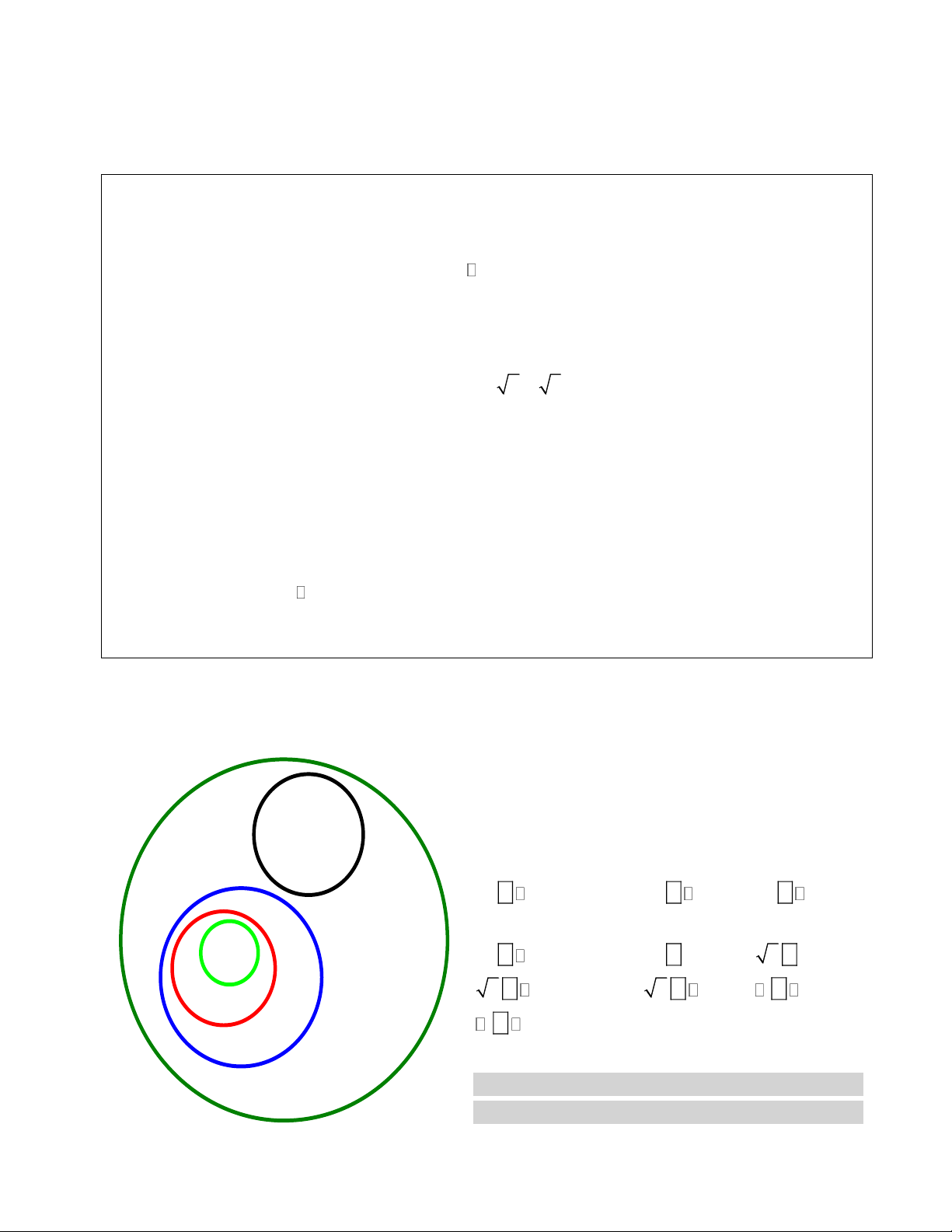
Bài 1: Điền tên các tập hợp ¥ ;¢ ;¤ ; I; ¡ vào sơ đồ Ven cho phù hợp
Bài 2: Điền các dấu  ,  ,
  thích hợp vào ô vuông. 2  ; 2  ; 2  ; 2  ; 2  I 2 I ; 2 ; 2 ; ;
Nếu a là số hữu tỉ thì a viết được dưới dạng
số thập phân …………………………………….… Trang 1
hoặc …………………………..………….………… Bài 3: So sánh 2 a) 0,135 0,(135) b) 0,(3) 7 43 c) 2,1(467) d)    2 0, 3     2 0, 3 20 Bài 4  16 e)    2 0, 21     2 0, 21 f)    2 0,3 59    121
Bài 4: Sắp xếp các số thực sau theo thứ tự tăng dần 7 0,466 ;
; 0,4636363… ; 0,463736 ; 0,4656365…  15 7 Ta có :
 ................................ 15
Bài 5: Thực hiện phép tính 2     5 5  A      10 5 7 2 : 3, 72 0, 02 . :  2,8     B  13, 25  2 10 .230, 04  46, 75   3  37  6  15  27 6 
Bài 6: Chứng minh 7 là số vô tỉ
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
………………………………………………………………………………………………… Trang 2
………………………………………………………………………………………………… HDG: Bài 1:    ; I  Bài 2: 2   ; 2   ; 2   ; 2   ; 2    2  ;  2  ; 2  ;  ; 
Nếu a là số hữu tỉ thì a viết được dưới dạng số thập phân hữu hạn hoặc số thập phân vô hạn tuần hoàn.
Bài 3: a) 0,135  0,135 b)   1 2 0, 3   3 7 2 2 c)   43 2,1 467  2,15  ; d) 0,3    0,3 20 2 2 2 16  4  2 2 e) 0,2  1     0,2  1 ; f) 
 0,36  0,359       121 11 7
Bài 4: 0, 4636363... < 0, 463736 < 0, 4656565... < 0, 466 < 15 Bài 5: A = 0,2 B = 100
Bài 6: Giả sử 7 là số hữu tỉ, như vậy 7 có thể được viết dưới dạng phân số tối m m 2 m giản tức là 7  . Suy ra 7  hay 2 2
7n  m (1). Đẳng thức (1) chứng tỏ: n n 2 n 2
m 7 mà 7 là số nguyên tố nên m 7 . Đặt m = 7k k   ta có: 2 2
m  49k (2). Từ (1) và (2) suy ra 2 2
7n  49k nên 2 2
n  7k (3). Từ (3) ta lại có 2
n 7 . Như vậy m và n cùng m
chia hết cho 7 nên phân số
không tối giản, trái giả thiết. Vậy 7 không phải là số n
hữu tỉ, do đó 7 là số vô tỉ.
Nhận xét: Bằng phương pháp nêu trên, ta có thể chứng minh được rằng: Nếu
số nguyên dương a không phải là số chính phương thì
a là số vô tỉ. Chẳng hạn:
2; 3; 5; 6; 8;... là những số vô tỉ. Trang 3