Bài tập tổng hợp Chương 4 Xác suất thống kê | Học viện Chính sách và Phát triển
Bài tập tổng hợp Chương 4 Xác suất thống kê | Học viện Chính sách và Phát triển được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Tài liệu liên quan:
Preview text:
CHƯƠNG 4. BIẾN NGẪU NHIÊN HAI CHIỀU, HÀM CÁC BIẾN NGẪU NHIÊN September 7, 2016
BÀI TẬP TỔNG HỢP CHƯƠNG 4
Bài 1.(4.46/tr261). Một nhân viên bán hàng mỗi ngày đi chào hàng ở ba nơi với xác suất
bán được hàng mỗi nơi là 0,2. Nếu bán được hàng ở nơi thứ nhất và thứ hai thì tiền lãi
mỗi nơi là 100USD còn nếu bán được ở nơi thứ ba thì do hàng có chất lượng cao hơn nên lãi được 200USD.
a. Thiết lập bảng phân phối xác suất đồng thời của số lần bán được hàng X và tổng số tiền lãi Y.
b. Tìm số lần bán được hàng trung bình và số tiền lãi trung bình của mỗi ngày bán hàng.
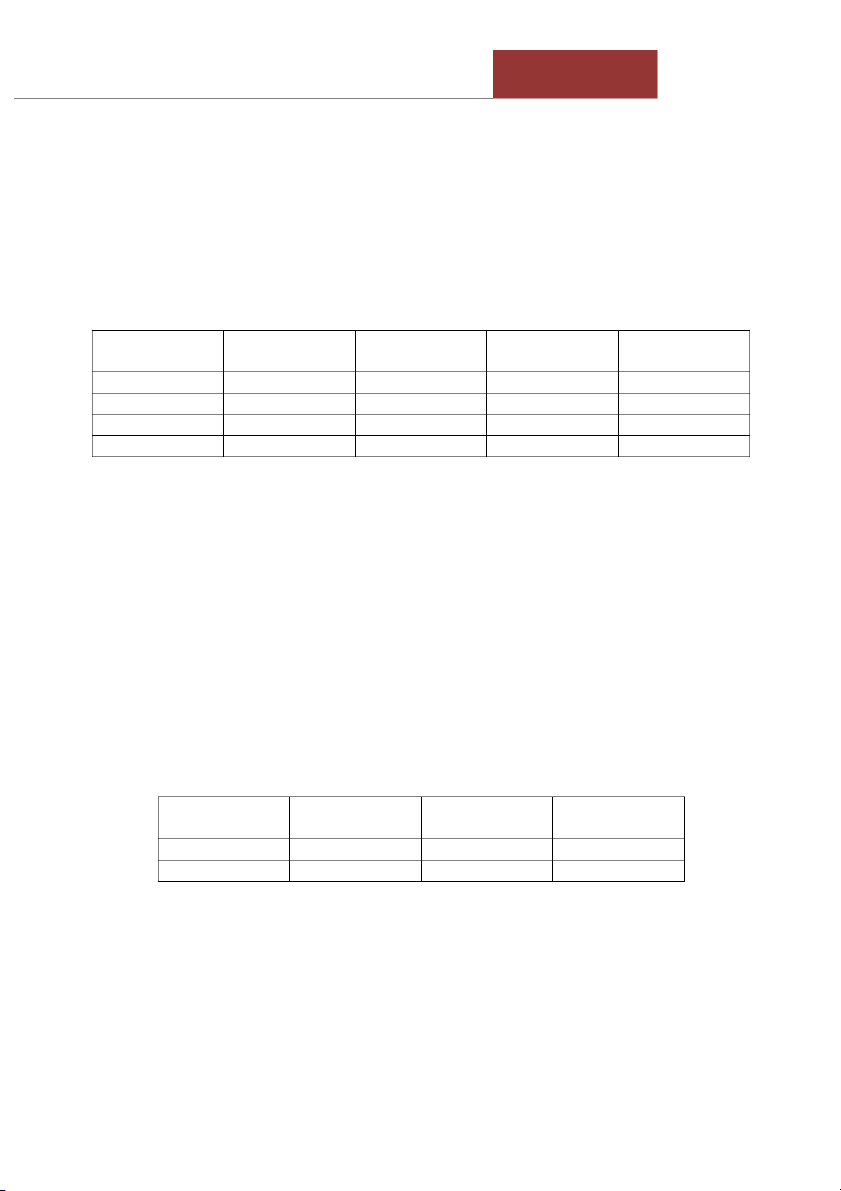
Bài 2. (4.47/tr261). Cho bảng phân phối xác suất đồng thời của biến ngẫu nhiên rời rạc hai chiều (X, Y) như sau: Y 1 2 3 P(x) X -2 0,05 0,4 -1 0,2 P(y) 0,2 0,5
a. Hãy điền vào các giá trị còn thiếu của bảng. b. Tìm E(X + Y) c. Tìm V(X - Y)
Bài 3. (4.48/tr261).Cho biến ngẫu nhiên rời rạc hai chiều có xác suất đồng thời được xác
định bằng biểu thức sau:
, 2 y ) với x =1 ; 2 ; 3 và y =0 ; 1 ; 2
P( x , y )={C(xi i i i i i 0
với các giá trị khác của x , y i i
Hãy thiết lập bảng phân phối xác suất đồng thời của (X, Y)
Bài 4. (4.49/tr262). Thống kê những người tuổi trưởng thành ở một nước theo hai chỉ tiêu sau:
X: thu nhập sau thuế (ngàn USD/ năm)
Y: mức độ hạnh phúc của người đó
Thu được bảng số liệu sau:
CHƯƠNG 4. BIẾN NGẪU NHIÊN HAI CHIỀU, HÀM CÁC BIẾN NGẪU NHIÊN September 7, 2016 Y Bất hạnh
Hạnh phúc vừa Rất hạnh phúc X phải 2,5 0,03 0,12 0,07 7,5 0,02 0,13 0,11 12,5 0,01 0,13 0,14 17,5 0,01 0,09 0,14
a. Tìm mức độ hạnh phúc trung bình tương ứng với mỗi mức thu nhập. Vẽ đồ thị và cho nhận xét.
b. Tìm hệ số tương quan và cho nhận xét.
Bài 5. (4.50/tr262). Một chủ cửa hàng điện tử dự kiến doanh thu của cửa hàn trong tháng
có phân phối xác suất như sau. Cột cuối cùng là mức thuế doanh thu tương ứng Doanh thu x Xác suất P(x) Thuế T(x) 20 0,10 4 30 0,30 6 40 0,40 9 50 0,20 13 a. Tìm doanh thu kỳ vọng
b. Tìm mức thuế kỳ vọng
c. Tìm doanh thu sau thuế kỳ vọng
Bài 6. (4.51-4.54/tr263). Thống kê dân số của một nước theo hai chỉ tiêu học vấn X và
giới tính Z thu được kết quả sau: Z Nam 0 Nữ 1 X Thất học 0 0,04 0,05 Tiểu học 1 0,10 0,12 Trung học 2 0,23 0,29 Đại học 3 0,10 0,07
a. Lập bảng phân phối xác suất biên của học vấn.
b. Tìm xác suất để lấy ngẫu nhiên một người thì người đó tốt nghiệp từ trung học trở lên.
c. Tìm trình độ học vấn trung bình.
d. Lập bảng phân phối xác suất biên của Z và tính E(Z). Cho nhận xét.
CHƯƠNG 4. BIẾN NGẪU NHIÊN HAI CHIỀU, HÀM CÁC BIẾN NGẪU NHIÊN September 7, 2016
e. Lập bảng phân phối xác suất về học vấn của nam.
f. Học vấn có độc lập với giới tính không.
g. Tìm trình độ học vấn trung bình của nam.
h. Tìm trình độ học vấn trung bình của nữ và so sánh với trình độ học vấn trung bình của nam.
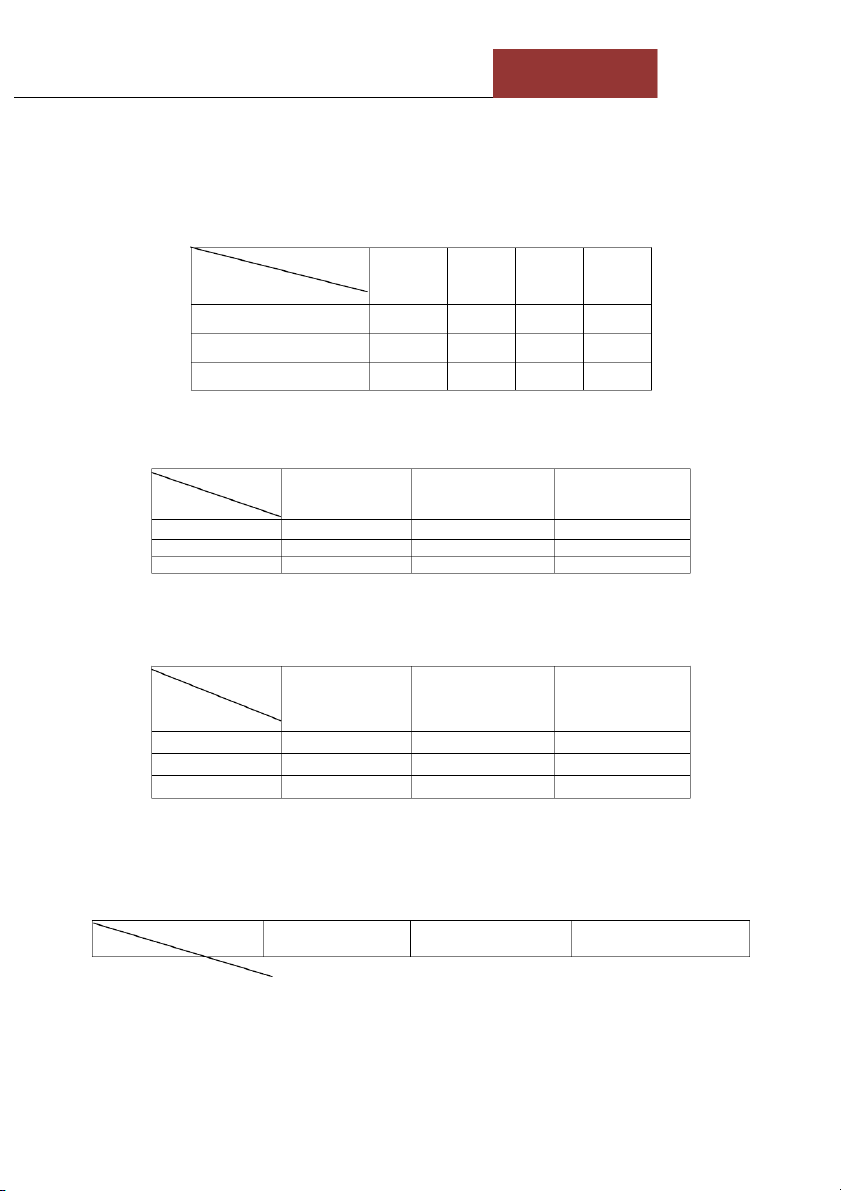
Bài 7. (4.55/tr264). Cho bảng phân phối xác suất đồng thời của biến ngẫu nhiên rời rạc hai chiều (X, Y) như sau: Y 0 1 2 3 X 1 0,08 0,12 0,16 0,4 2 0,06 0,09 0,12 0,3 3 0,06 0,09 0,12 0,3 Tổng số 0,2 0,3 0,4 1
a. X và Y có độc lập với nhau không? Tại sao? Tính Cov(X, Y), E(X), E(Y), V(X-Y)
b. Lập bảng phân phối xác suất của (X – Y). Tính xác suất để (X + Y) bé hơn 2.
Bài 8. (4.56/tr264). Một hộp đựng 5 sản phẩm, trong đó có 3 phế phẩm. Các sản phẩm
được lấy ra để kiểm tra cho tới khi phát hiện thấy phế phẩm.
Ký hiệu Xi là số lần kiểm tra tới khi phế phẩm đầu tiên bị phát hiện, X là 2 số lần kiểm tra
thêm cho tới khi phế phẩm thứ hai bị phát hiện.
a. Lập bảng phân phối xác suất đồng thời của (X1, X2)
b. Tính hiệp phương sai giữa X và X 1 .2
Bài 9. (4.57/tr265). Cho bảng phân phối xác suất đồng thời của biến ngẫu nhiên hai
chiều (X, Y) như sau: (trong đó y,a,b là các số chưa biết) Y y 0 1 X 0 1/4 a 1/8 1 1/5 b 1/10
a. Xác định a và b sao cho X và Y là độc lập với nhau
b. Quy luật phân bố xác suất có điều kiện của X đối với các giá trị khác nhau của y
trong trường hợp này như thế nào?
CHƯƠNG 4. BIẾN NGẪU NHIÊN HAI CHIỀU, HÀM CÁC BIẾN NGẪU NHIÊN September 7, 2016
c. Giả thiết rằng a = 1/5, xác định giá trị y sao cho hiệp phương sai của (X, Y) bằng
không. X và Y trong trường hợp này có độc lập với nhau không?
Câu 1. Giả sử bạn đầu tư vào hai cổ phiếu A và B có lãi suất theo tháng (đơn vị: %) được cho
dưới dạng bảng phân phối xác suất đồng thời như sau: B -2 1 3 5 A -1 0,01 0,04 0,1 0,05 3 0,05 0,25 0,15 0,1 6 0,1 0,05 0,1 0
Tính lãi suất trung bình khi đầu tư vào cổ phiếu A nếu lãi suất cổ phiếu B bằng 3%.
Câu 2. Tỷ suất lợi nhuận (%/phiên giao dịch) của hai cổ phiếu A và B là hai biến ngẫu nhiên X, Y có bảng phân phối như sau: X -4 1 2 Y -3 0,1 0,12 0,1 -1 0,06 0,18 0,14 3 0,15 0,1 0,05
Nếu tỷ suất lợi nhuận của cổ phiếu A là 1%/phiên thì tỷ suất lợi nhuận trung bình của cổ phiếu B là bao nhiêu?
Câu 3. Tỷ suất lợi nhuận (%/ phiên giao dịch) của hai loại cổ phiếu A và B lần lượt là biến ngẫu
nhiên X, Y có bảng phân phối xác suất như sau: X -3 -1 5 Y -4 0,1 0,13 0,1 -1 0,15 0,2 0,12 6 0,02 0,12 0,06
Nếu tỷ suất lợi nhuận của cổ phiếu B là -1%/ phiên thì tỷ suất lợi nhuận trung bình của cổ phiếu A là bao nhiêu?
Câu 4 Khi đầu tư vào hai thị trường A và B lãi suất XA và XB (đơn vị: %/phiên) là các biến ngẫu
nhiên có bảng phân phối xác suất đồng thời như sau: XA -4 -1 6
CHƯƠNG 4. BIẾN NGẪU NHIÊN HAI CHIỀU, HÀM CÁC BIẾN NGẪU NHIÊN September 7, 2016 XB -3 0,05 0,1 0,15 -1 0,1 0,2 0,15 5 0,1 0,1 0,05
Tìm lãi suất trung bình khi đầu tư vào thị trường B biết năm đó lãi suất thị trường A là 6%.
Câu 5 Khi đầu tư vào thị trường Vàng và Ngoại tệ thì lãi suất X và Y (đơn vị: %) là các biến
ngẫu nhiên có bảng phân phối xác suất đồng thời như sau: X -3 2 3 Y -2 0,05 0,1 0,15 1 0,1 0,2 0,15 4 0,1 0,1 0,05
Tìm lãi suất trung bình khi đầu tư vào thị trường ngoại tệ biết năm đó lãi suất thị trường vàng là 2%.