



























































































Preview text:
lOMoARcPSD|36340008 1 Bài tập
Bài 0.1. Cho biết các dữ liệu sau đây là tổng thể hay mẫu, tương ứng với mục đích nghiên cứu:
a) Nghiên cứu về tuổi của sinh viên K62 của Trường Đại học Kinh tế
Quốc dân qua hồ sơ toàn bộ sinh viên tại phòng Quản lý đào tạo.
b) Nghiên cứu về sự hài lòng của khách hàng tại một ngân hàng qua dữ
liệu phỏng vấn ngẫu nhiên 300 khách hàng của ngân hàng đó.
c) Nghiên cứu về thị trường chứng khoán qua dữ liệu giá đóng cửa của
các chứng khoán vào ngày 31/12/2020.
d) Nghiên cứu về tổng khối lượng cổ phiếu giao dịch chính thức trong
năm 2020 của các ngân hàng niêm yết trên sàn chứng khoán qua số
liệu của Ủy ban Chứng khoán.
e) Nghiên cứu về kết quả học tập của sinh viên một trường đại học thông
qua số liệu của các sinh viên năm cuối.
Bài 0.2. Cho biết dữ liệu cho nghiên cứu sau đây thuộc loại sơ cấp hay thứ
cấp, là dữ liệu chéo hay dữ liệu chuỗi thời gian:
a) Một sinh viên nghiên cứu khoa học thực hiện khảo sát bằng bảng hỏi
với 300 sinh viên khác về thời gian tự học.
b) Một sinh viên nghiên cứu các biến vĩ mô tác động đến tăng trưởng
GDP của Việt Nam giai đoạn 1990 - 2020.
c) Trưởng phòng đếm số nhân viên đi muộn hằng ngày tại văn phòng mình quản lý.
d) Nghiên cứu viên phân tích so sánh lợi thế cạnh tranh các tỉnh thành
Việt Nam năm 2020 qua chỉ số cạnh tranh cấp tỉnh PCI do VCCI tính toán công bố.
e) Giảng viên đánh giá so sánh các sinh viên mình giảng dạy qua điểm
một bài kiểm tra giữa kì.
Bài 0.3. Cho biết các biến trong Ví dụ ?? và Ví dụ ?? trang ?? thuộc loại
nào theo cách phân loại biến trong Bảng ??.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 2
Bài 0.4. Cho biết các biến sau là định tính hay định lượng, nếu định tính
thì là định danh hay thứ bậc, nếu định lượng thì rời rạc hay liên tục:
a) Điểm thi cuối kì môn Lý thuyết xác suất và Thống kê toán
b) Thời gian để hoàn thành bài thi một học phần
c) Loại tốt nghiệp của cử nhân Trường Đại học Kinh tế Quốc dân
d) Cỡ giày của các đôi giày trong kho
e) Xếp hạng cạnh tranh cấp tỉnh năm 2020
f) Xếp hạng cạnh tranh của các tỉnh ở Việt Nam năm 2020
g) Chỉ số cạnh tranh của các tỉnh ở Việt Nam năm 2020
h) Hình thức sở hữu của các doanh nghiệp trên địa bàn Hà Nội
i) Nhiệt độ trung bình của các ngày trong năm tại Hà Nội
Bài 0.5. Cho biết với số liệu chứa các thông tin sau, có thể thực hiện các
công việc gì trong số sau: nhóm, gộp, liệt kê, so sánh, xếp thứ tự, tính toán
a) Ngành học và điểm kiểm tra của các sinh viên trong một lớp tín chỉ.
b) Giới tính và trình độ (cao đẳng, đại học, cao học, tiến sĩ) của các nhân
viên tại một cơ sở đào tạo.
c) Thu nhập và vị trí công việc của người lao động tại một công ty.
d) Năm sinh và tuổi của các thí sinh trong một cuộc thi.
e) Vị trí về đích và thời gian hoàn thành chặng đua của các vận động
viên trong một cuộc thi chạy.
f) Hình thức sở hữu và vốn điều lệ của các công ty thành lập mới trong năm 2020.
Bài 0.6. Cho biết trong những phát biểu sau, phát biểu nào là đúng
a) Kích thước mẫu càng lớn thì kết quả càng chính xác.
b) Trong một lớp học, tỉ lệ số nam/số nữ gọi là tần suất.
c) Tổng các giá trị tần suất trong bảng tần suất bằng 1.
d) Tần suất chỉ áp dụng cho biến định tính.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 3
e) Kích thước mẫu không vượt quá kích thước tổng thể.
f) Số liệu mẫu thứ cấp luôn nhiều quan sát hơn mẫu sơ cấp.
Bài 0.7. Cho biết trong những phát biểu sau, phát biểu nào là đúng
a) Đồ thị cột với biến định danh có thể đổi thứ tự các cột cho nhau.
b) Đồ thị cột với biến thứ bậc không thể đổi thứ tự các cột cho nhau.
c) Đồ thị phân phối giá trị không thể đổi thứ tự các cột cho nhau.
d) Đồ thị phân phối giá trị luôn có các cột ở giữa cao nhất.
e) Đồ thị phân phối giá trị không có cột nào nằm bên trái trục tung.
f) Đồ thị phân phối giá trị có tổng giá trị đại diện bởi chiều cao các cột
bằng kích thước của bộ số liệu.
Bài 0.8. Cho biết trong những phát biểu sau, phát biểu nào là đúng
a) Điểm số có phân phối lệch trái thì tỉ lệ sinh viên nhận điểm cao sẽ
nhiều hơn tỉ lệ sinh viên nhận điểm thấp.
b) Giá cả có phân phối lệch phải thì tỉ lệ người mua với giá đắt sẽ nhiều
hơn tỉ lệ người mua với giá rẻ.
c) Lợi nhuận có phân phối hoàn toàn đối xứng quanh giá trị 0 thì khả
năng có lãi và khả năng lỗ bằng nhau.
d) Nhiệt độ chỉ nằm trong khoảng từ 10 đến 30 độ và lệch phải, thì tỉ lệ
ngày trên 20 độ sẽ nhiều hơn tỉ lệ ngày dưới 20 độ.
e) Lợi nhuận nằm trong khoảng từ (-10 tỉ) đến +40 tỉ và lệch trái thì khả
năng lợi nhuận dưới 15 tỉ sẽ ít hơn khả năng lợi nhuận trên 15 tỉ.
f) Doanh thu phân phối đối xứng hình chuông, đỉnh tại 100 tỉ, thì khả
năng doanh thu trên 110 tỉ sẽ lớn hơn khả năng doanh thu dưới 90 tỉ.
Bài 0.9. Cho biết với các đồ thị rải điểm của các cặp biến sau, biểu đồ tương
quan cùng chiều hay ngược chiều thì hợp lý hơn?
a) Điểm bài kiểm tra và điểm bài thi cuối kì học phần Kinh tế vi mô của 50 sinh viên.
b) Tỉ lệ thất nghiệp và tỉ lệ lạm phát của 100 quốc gia vào năm 2010.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 4
c) Chi phí quảng cáo và doanh thu trong năm 2020 của 100 doanh nghiệp bán lẻ.
d) GDP và tổng giá trị xuất khẩu hàng hóa của Việt Nam hằng năm, giai đoạn 1990 - 2020.
e) Nhiệt độ trung bình và lượng tiêu thụ bia hằng ngày tại một khu vực.
f) Thuế suất thuế nhập khẩu và lượng nhập khẩu của 50 loại hàng hóa xa xỉ.
Bài 0.10. Cho số liệu về kết quả hai môn thi của một số sinh viên, với đánh
giá ở ba mức 𝐴, 𝐵, 𝐶, như sau:
𝐴𝐴, 𝐴𝐴, 𝐴𝐵, 𝐴𝐵, 𝐴𝐵, 𝐴𝐶, 𝐴𝐶, 𝐵 𝐴, 𝐵 𝐴, 𝐵𝐵,
𝐵𝐵, 𝐵𝐵, 𝐵𝐵, 𝐵𝐶, 𝐵𝐶, 𝐶 𝐴, 𝐶 𝐵, 𝐶𝐶, 𝐶𝐶, 𝐶𝐶
Tính tần số và tần suất của a) Sinh viên có điểm 𝐴
b) Sinh viên chỉ có điểm 𝐴
c) Sinh viên có điểm 𝐴 và 𝐵
d) Sinh viên có điểm 𝐴 hoặc 𝐵
e) Sinh viên có điểm 𝐴 và không có điểm 𝐵
f) Sinh viên không có điểm 𝐴 và không có điểm 𝐵
g) Sinh viên không có điểm 𝐴 hoặc không có điểm 𝐵
h) Điền tần số vào các bảng tần số một chiều và hai chiều sau:
(1) Có điểm 𝐴 Không có 𝐴
(2) Có điểm 𝐵 Không có 𝐵 𝑓 ? ? 𝑓 ? ? (3)
Có điểm 𝐵 Không có 𝐵 Có điểm 𝐴 ? ? Không có 𝐴 ? ?
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 5
Bài 0.11. Cho số liệu mẫu sau
10, 11, 14, 14, 15, 18, 19, 19, 20, 22, 25, 40
a) Tính các thống kê xu thế trung tâm: trung bình, trung vị, mốt.
b) Tính các điểm phân vị và vẽ đồ thị hộp.
c) Tính phương sai, độ lệch chuẩn, khoảng tứ phân vị.
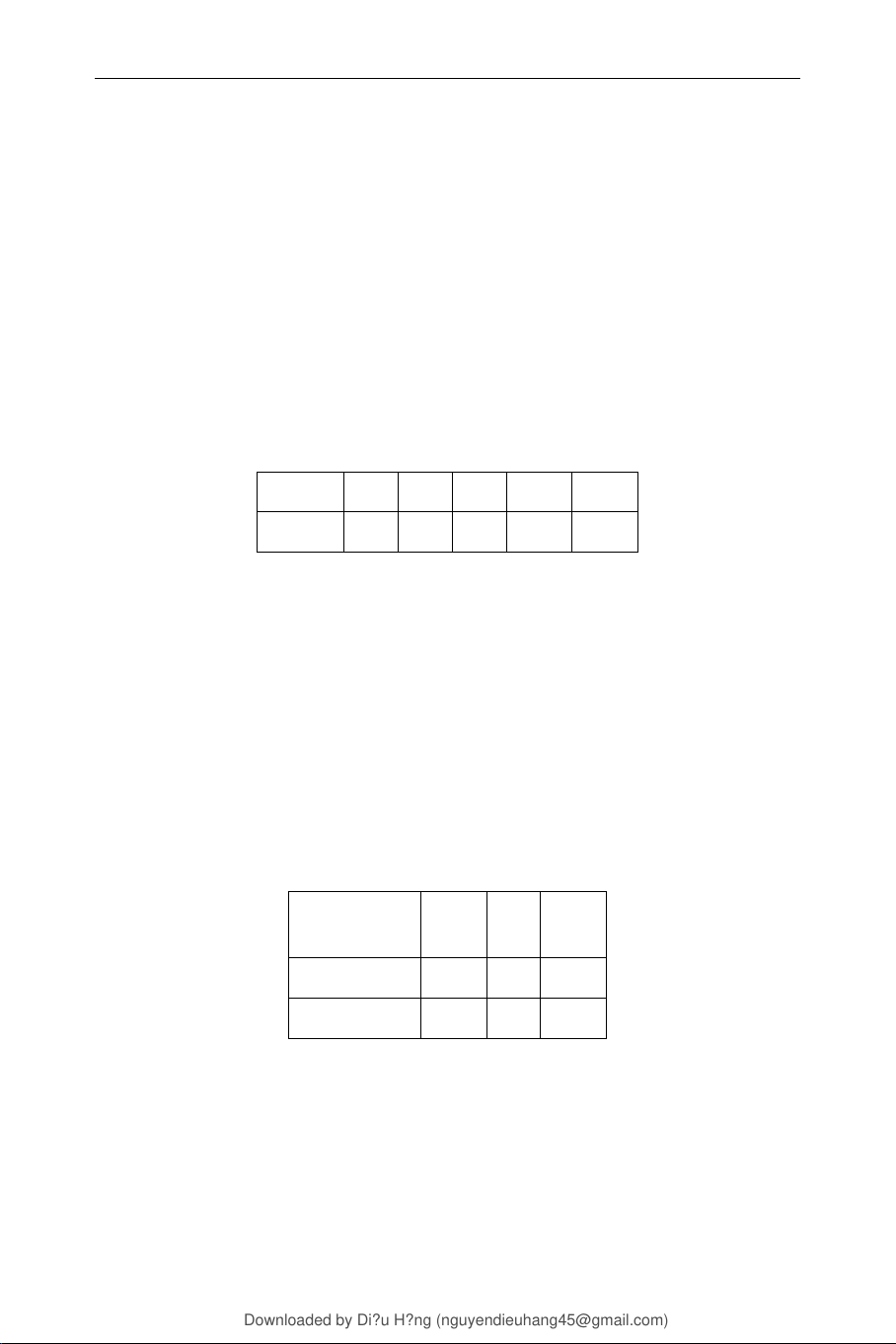
Bài 0.12. Cho số liệu sau về thu nhập của một số hộ gia đình (triệu VND/tháng) Thu nhập 18 19 20 21 22 Số hộ 2 5 8 7 3
a) Tính trung bình, phương sai khi coi đây là số liệu mẫu, và khi coi đây là số liệu tổng thể.
b) So sánh hệ số biến thiên của của số liệu khi coi là số liệu mẫu và khi
coi là số liệu tổng thể.
d) Tính hệ số bất đối xứng, hệ số nhọn của số liệu.
Bài 0.13. Cho số liệu mẫu về giá bán buôn (nghìn đồng/sản phẩm) và lượng
bán (nghìn sản phẩm) của một công ty trong 8 tháng như sau:
Tháng Một Hai Ba Bốn Năm Sáu Bảy Tám Giá 120 125 122 118 116 116 112 119 Lượng 20 21 22 24 24 26 25 27
a) Tính trung bình, phương sai, độ lệch chuẩn của giá và lượng.
b) Tính hiệp phương sai của giá và lượng.
c) Tính hệ số tương quan giữa giá và lượng, và nhận xét về tương quan của hai biến.
d) Nếu hệ số tương quan giữa lượng bán và chi phí quảng cáo là 0,73 thì
có thể nhận xét thế nào về tương quan giữa hai cặp biến: lượng- giá
và lượng - chi phí quảng cáo?
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 6 Bài tập tổng hợp
Bài 0.14. Một cửa hàng sau khi hoạt động một thời gian thực hiện khảo
sát khách hàng và có phiếu khảo sát sau đây (chỉ có tính minh họa).
PHIẾU KHẢO SÁT KHÁCH HÀNG
Xin Quý khách vui lòng cho biết các thông tin
(1) Họ tên:....................................... (2) Nam / Nữ (3) Tuổi:.....
(4) Số lần đến cửa hàng Lần đầu Lần hai Từ 3 trở lên
(5) Số sản phẩm đã mua:......... (6) Số tiền thanh toán (nghìn đồng):............. (7) Thanh toán bằng Tiền mặt Thẻ Chuyển khoản Khác
(8) Thời gian chọn hàng (phút):......... (9) Thời gian thanh toán (phút):.........
Với các câu sau, các đánh giá: 1: rất không hài lòng, 2: không hài lòng,
3: bình thường, 4: hài lòng, 5: rất hài lòng 1 2 3 4 5
(10) Chủng loại hàng, số lượng hàng: (12) Giá cả hàng hóa:
(13) Chính sách khuyến mại:
(14) Thái độ, sự chỉ dẫn của nhân viên:
(15) Đánh giá chung về cửa hàng:
Xin chân thành cảm ơn.
a) Dữ liệu thu thập được là sơ cấp hay thứ cấp, là tổng thể hay mẫu?
b) Các biến tương ứng với các câu hỏi từ 1 đến 15 thuộc loại nào?
c) Với thông tin từ mỗi câu hỏi, bạn sẽ đề xuất các phân tích như thế
nào, tính các thống kê nào?
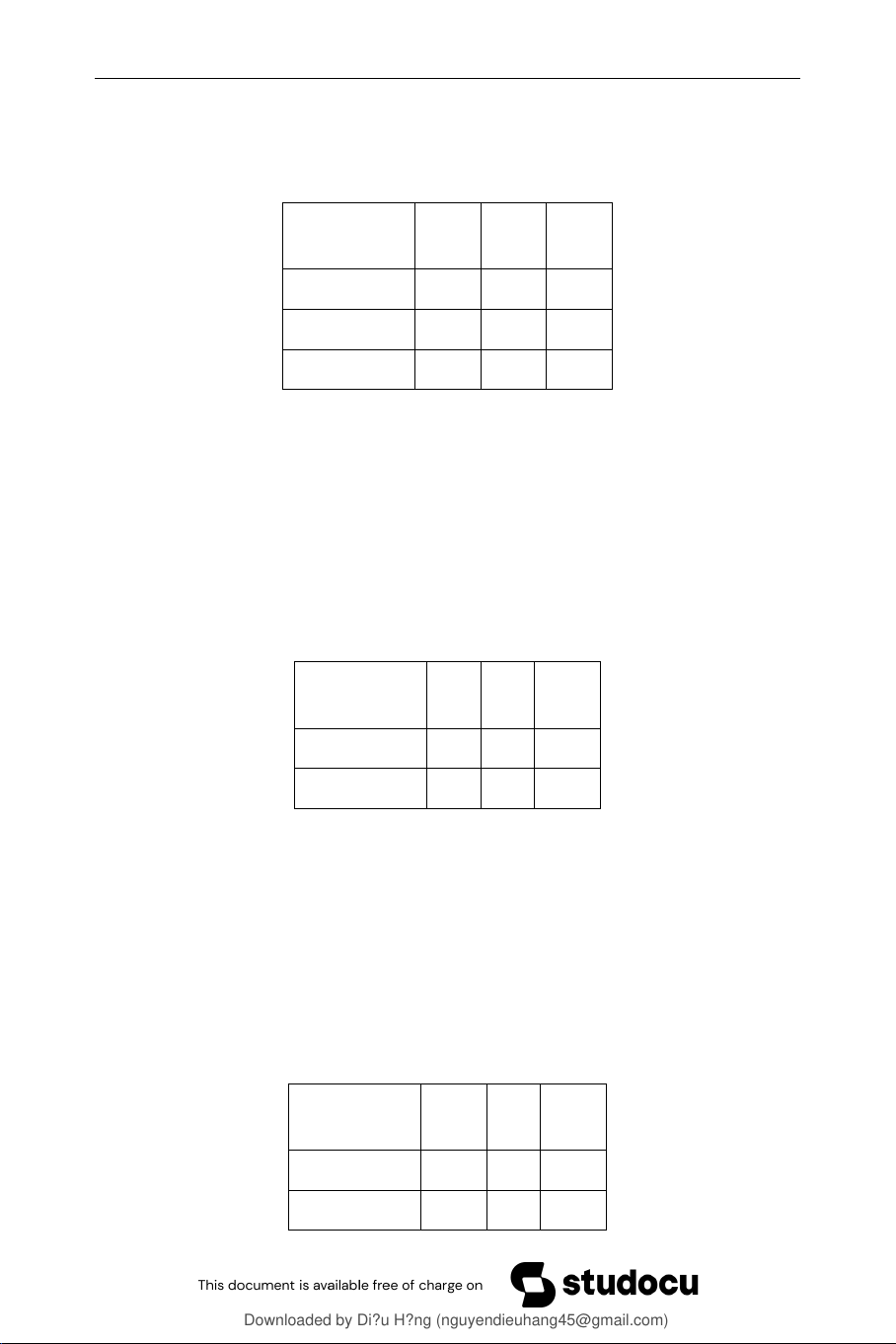
Bài 0.15. Với cuộc khảo sát khách hàng, có bảng tần số như sau: Số lần đến cửa hàng Giới 1 2 ≥3 Nam 20 50 30 Nữ 40 50 110
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 7
Hãy tính tần số và tần suất của a) Khách là nam
b) Khách đến cửa hàng 1 lần
c) Khách đến cửa hàng ít nhất 2 lần
d) Khách nữ và đến cửa hàng 2 lần
e) Khách nữ hoặc đến cửa hàng 2 lần
f) Khách đến cửa hàng 1 lần trong số khách nam
g) Khách nữ trong số khách đến cửa hàng ít nhất 2 lần
Bài 0.16. Cho hai số liệu mẫu sau về thu nhập của hai khu vực I và II
• Số liệu khu vực I: (12, 15, 18, 20, 26);
• Số liệu khu vực II: (8, 9, 9, 12, 15, 40).
a) Nếu so sánh về trung bình thì khu vực nào có thu nhập cao hơn?
b) Nếu so sánh về trung vị thì khu vực nào thu nhập cao hơn?
c) Theo bạn, trung bình hay trung vị tốt hơn khi so sánh thu nhập ở hai khu vực?
d) So sánh phương sai và độ lệch chuẩn của hai mẫu.
e) So sánh hai hệ số biến thiên của hai mẫu.
Bài 0.17. Cho biểu đồ phân phối giá trị của lương một số lao động trong
cuộc khảo sát như sau, với tần số là người 30 27 25 19 20 15 15 12 10 8 8 5 5 3 1 1 0 20 21 22 23 24 25 26 27 28 29
Hình 1 – Lương người lao động
a) Không tính toán, so sánh giữa trung bình và trung vị.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 8
b) Tính toán và so sánh giữa trung bình, trung vị, mốt.
c) Tính phương sai và độ lệch chuẩn của mẫu.
d) Xác định các tứ phân vị, cho biết mẫu có giá trị ngoại lai hay không?
d) Tính hệ số bất đối xứng.
e) Tính tần suất lao động có thu nhập chênh lệch so với trung bình không quá độ lệch chuẩn.
Bài 0.18. Lương hằng tháng của người lao động tại một công ty có trung
bình bằng 18 (triệu đồng) và phương sai bằng 16 (triệu đồng)2.
a) Nếu lương tính bằng nghìn đồng thì có trung bình, phương sai, độ
lệch chuẩn bằng bao nhiêu?
b) Nếu tháng cuối năm công ty thưởng cho mỗi người lao động là 10
triệu đồng, thì trung bình, phương sai của lương + thưởng của tháng
cuối năm bằng bao nhiêu? Hệ số biến thiên thay đổi như thế nào?
c) Lương cả năm của người lao động tại công ty có trung bình, độ lệch chuẩn bằng bao nhiêu?
d) Giả sử lương hằng tháng có phân phối hoàn toàn đối xứng, và mức
lương hằng tháng 30 triệu đồng là giá trị ngoại lai. Vậy, giá trị tứ
phân vị thứ nhất tối thiểu bằng bao nhiêu?
Bài 0.19. Cho mẫu theo bảng sau về giá vàng nhập khẩu (USD/ounce) Giá
1850-1860 1860-1870 1870-1880 1880-1890 1890-1900 Số ngày 5 12 8 7 4
a) Vẽ đồ thị phân phối giá trị và nhận xét về hình dáng của phân phối.
b) Tính trung bình và độ lệch chuẩn mẫu.
c) Tính hệ số bất đối xứng và cho biết mẫu lệch dương hay lệch âm.
Bài 0.20. Để xác định giá trị ngoại lai, bên cạnh cách dùng tứ phân vị và
khoảng tứ phân vị, còn có cách thứ hai như sau: Khoảng bình thường là
khoảng giá trị chênh lệch so với trung bình không quá 3 lần độ lệch chuẩn;
những phần tử chênh lệch so với trung bình quá 3 lần độ lệch chuẩn là giá trị ngoại lai.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 9 Cho bộ số liệu sau:
2, 4, 6, 6, 7, 8, 8, 8, 9, 9, 10, 11, 14, 14, 16, 17, 19, 20, 25, 30.
Hãy xác định khoảng bình thường và các giá trị ngoại lai theo hai cách.
Bài 0.21. Chứng minh các tính chất của các thống kê và về mối quan hệ
giữa thống kê và tham số trong mục ??.
Bài 0.22. Với một bộ số liệu mẫu (𝑥1, 𝑥2, ..., 𝑥𝑛), có số liệu chuẩn hóa, là
bộ số (𝑧1, 𝑧2, ..., 𝑧𝑛) như sau: 𝑥𝑖 − ¯𝑥 𝑧𝑖 = , 𝑖 = 1, 𝑛 𝑠𝑥
a) Chứng minh rằng bộ số liệu chuẩn hóa có trung bình bằng 0 và phương sai bằng 1.
b) Nếu số liệu là số liệu tổng thể, thay ¯𝑥 bởi 𝜇 và 𝑠 bởi 𝜎, thì chứng
minh tính chất trên vẫn đúng.
c) Hãy tính bộ số liệu chuẩn hóa của bộ số liệu mẫu sau:
10, 11, 14, 14, 15, 18, 19, 19, 20, 22, 25, 40.
Bài 0.23. Với số liệu mẫu theo cặp {(𝑥𝑖, 𝑦𝑖), 𝑖 = 1, 𝑛}, cho biết hệ số tương
quan sẽ thay đổi thế nào nếu:
a) Tất cả phần tử của 𝑥 tăng thêm 𝑎
b) Tất cả phần tử của 𝑥 tăng thêm 𝑎 , của 1 𝑦 tăng thêm 𝑎2
c) Tất cả phần tử của 𝑥 nhân thêm với 𝑏1
d) So sánh 𝑐𝑜𝑣(𝑥∗, 𝑦∗) với 𝑐𝑜𝑣(𝑥, 𝑦); 𝑟 , nếu
𝑥∗,𝑦∗ với 𝑟𝑥,𝑦 𝑥∗ = 𝑎1 +
𝑏1𝑥, 𝑦∗ = 𝑎2 + 𝑏2𝑦 .
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 10
Câu hỏi trắc nghiệm
Câu 0.1. Mẫu khảo sát năm sinh viên về điểm tổng kết bốn môn học, điều nào sau đây là đúng?
A. Mẫu có 5 biến và 4 quan sát C. Mẫu có 9 quan sát
B. Mẫu có 4 biến và 5 quan sát D. Mẫu có 20 quan sát
Câu 0.2. Mẫu khảo sát năm sinh viên về điểm tổng kết bốn môn học, có
thể tính được bao nhiêu hệ số tương quan? A. 4 C. 6 B. 5 D. 10
Câu 0.3. Tăng giá trị của phần tử lớn nhất trong một bộ số liệu thêm một
đơn vị, đại lượng nào thay đổi nhiều nhất? A. Khoảng giá trị C. Khoảng tứ phân vị B. Trung bình D. Độ lệch chuẩn
Câu 0.4. Số liệu gồm tiền lương của 10 người, khi mức lương thấp nhất
tăng thêm 1 đơn vị, điều nào sau đây là đúng?
A. Khoảng biến thiên giảm 1 C. Trung bình tăng 0,1
B. Độ lệch chuẩn giảm 1 D. Phương sai giảm 0,1
Câu 0.5. Với mẫu có hơn 3 phần tử, khi giảm giá trị của phần tử nhỏ nhất,
điều nào sau đây là đúng?
A. ¯𝑥 và 𝑚 không đổi C. thay đổi 𝑒 ¯ 𝑥 không đổi, 𝑚𝑒
B. ¯𝑥 thay đổi, 𝑚 không đổi D. thay đổi 𝑒 ¯ 𝑥 và 𝑚𝑒
Câu 0.6. Cho thông tin về giá gas (𝑥), giá điện (𝑦), lượng gas tiêu thụ (𝑧)
như dưới đây. Cho biết cặp biến nào tương quan chặt nhất? 𝑠𝑥 = 4,2 𝑠𝑦 = 6,3 𝑠𝑧 = 5,1
𝑐𝑜𝑣 (𝑥, 𝑦) = 20,6 𝑐(𝑦, 𝑧) = 16,3
𝑐𝑜𝑣 (𝑥, 𝑧) = −19,5 A. Giá gas và giá điện
C. Giá gas và lượng gas tiêu thụ
B. Giá điện và lượng gas tiêu thụ
D. Cả ba cặp chặt như nhau
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 11
Câu 0.7. Cho thời gian họp mỗi tuần (đơn vị: giờ/tuần) của một mẫu từ 25
CEO (Chief Excutive Officer – Quản lý cao cấp) trong bảng sau: 14 15 18 23 15 19 20 13 15 23 23 21 15 20 21 16 15 18 18 19 19 22 23 21 12
Phương sai mẫu của tập dữ liệu trên bằng A. 11,56 B. 11,1 C. 3,4 D. 3,3
Câu 0.8. Cho hai số liệu mẫu sau về hóa đơn thanh toán của hai cửa hàng I và II
• I: (15, 17, 18, 14, 14, 19, 23, 25, 17, 24, 23, 17, 19, 27);
• II: (22, 24, 21, 22, 26, 28, 15, 14, 16, 18, 25, 11, 12, 13).
Dựa vào dữ liệu này, đâu là phát biểu đúng:
A. Trung bình hóa đơn thanh toán của cửa hàng I lớn hơn II nhưng phương sai mẫu nhỏ hơn.
B. Trung bình hóa đơn thanh toán của cửa hàng II lớn hơn I nhưng phương sai mẫu nhỏ hơn.
C. Cả trung bình và phương sai mẫu hóa đơn thanh toán của cửa hàng I đều lớn hơn II.
D. Cả trung bình và phương sai mẫu hóa đơn thanh toán của cửa hàng II đều lớn hơn I.
Câu 0.9. Cho bộ dữ liệu về mức độ hài lòng về công tác của Ban Quản lý
từ một số cư dân tại khu chung cư với bảng sau: Rất hài lòng Hài lòng Rất hài lòng Không hài lòng Rất hài lòng Hài lòng
Không hài lòng Rất không hài lòng Hài lòng
Rất hài lòng Không hài lòng Hài lòng
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 12
Loại biến xuất hiện trong bộ dữ liệu là?
A. Biến định lượng liên tục
B. Biến định lượng rời rạc
C. Biến định tính thứ bậc
D. Biến định tính danh nghĩa
Câu 0.10. Cho bộ dữ liệu về số lần quay lại mua hàng tại shop/tuần gần
nhất (dựa trên tích điểm) từ một số khách hàng như sau:
2, 1, 0, 2, 3, 3, 2, 2, 1, 0, 0, 1, 2, 2, 3, 1
Loại biến xuất hiện trong bộ dữ liệu là?
A. Biến định lượng liên tục
B. Biến định lượng rời rạc
C. Biến định tính thứ bậc
D. Biến định tính danh nghĩa
Câu 0.11. Cho dữ liệu điểm thi của một số sinh viên trong bảng sau: 8 7 9 7 8 7 10 6 6 3
Trung vị của dữ liệu là: A. 8 B. 7,5 C. 6,5 D. 7,2
Câu 0.12. Điểm của một bài thi gồm nhiều câu hỏi dễ đối với sinh viên thường có xu hướng: A. Lệch trái B. Lệch phải C. Đối xứng D. Không xác định
Câu 0.13. Cho bộ dữ liệu về mức độ hài lòng về công tác của Ban Quản lý
từ một số cư dân tại khu chung cư với bảng sau: Rất hài lòng Hài lòng Rất hài lòng Không hài lòng Rất hài lòng Hài lòng
Không hài lòng Rất không hài lòng Hài lòng
Rất hài lòng Không hài lòng Hài lòng
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 13
Cách biểu diễn nào sau đây KHÔNG thích hợp để mô tả thông tin của bộ dữ liệu? A. Biểu đồ Histogram
B. Biểu đồ Cột (Bar chart)
C. Biểu đồ Bánh xe (Pie chart)
D. Bảng tần số (Frequency table)
Câu 0.14. Số liệu về hóa đơn thanh toán (triệu đồng) và giới tính từ một số
khách hàng của cửa hàng A và B trong bảng sau: Hóa đơn CH A Giới tính KH Hóa đơn CH B Giới tính KH 15 Nam 22 Nam 17 Nam 24 Nữ 18 Nữ 21 Nữ 14 Nam 22 Nam 14 Nam 26 Nữ 19 Nữ 28 Nam 23 Nam 15 Nam 25 Nam 18 Nam 17 Nam 16 Nữ 24 Nữ 18 Nữ 23 Nữ 25 Nam 17 Nữ 11 Nam 19 Nam 12 Nam 27 Nữ 13 Nam
Dựa vào dữ liệu này, đâu là phát biểu đúng:
A. Tỷ lệ hóa đơn trên 17 triệu của cửa hàng A cao hơn cửa hàng B và tỷ lệ
khách hàng nữ của cửa hàng A thấp hơn cửa hàng B.
B. Tỷ lệ hóa đơn trên 17 triệu của cửa hàng A cao hơn cửa hàng B và tỷ lệ
khách hàng nữ của cửa hàng A cao hơn cửa hàng B.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 14
C. Tỷ lệ hóa đơn trên 17 triệu của cửa hàng A thấp hơn cửa hàng B và tỷ lệ
khách hàng nữ của cửa hàng A thấp hơn cửa hàng B.
D. Tỷ lệ hóa đơn trên 17 triệu của cửa hàng A thấp hơn cửa hàng B và tỷ lệ
khách hàng nữ của cửa hàng A cao hơn cửa hàng B.
Câu 0.15. Dữ liệu về thời gian chờ (phút) được khám của 39 bệnh nhân tại
một bệnh viện đa khoa cho trong bảng sau: 3 4 5 7 7 7 7 8 8 9 9 10 10
10 10 10 11 12 12 13 14 14 15 15 17 17
18 19 19 19 21 21 22 22 23 24 24 24 24
Thời gian chờ trung bình và độ lệch chuẩn mẫu của dữ liệu là:
A. Trung bình = 13,95 và độ lệch chuẩn mẫu = 40,42
B. Trung bình = 13,95 và độ lệch chuẩn mẫu = 39,38
C. Trung bình = 13,95 và độ lệch chuẩn mẫu = 6,36
D. Trung bình = 13,95 và độ lệch chuẩn mẫu = 6,28
Câu 0.16. Dữ liệu về thời gian chơi game (giờ/tuần) của 38 thiếu niên cho trong bảng sau:
Thời gian chơi game Tần số 0-3,5 3 3,5-7,5 7 7,5-11,5 12 11,5-15,5 7 15,5-19,5 9
Thời gian chờ trung bình và độ lệch chuẩn mẫu của dữ liệu là:
A. Trung bình = 10,78 và độ lệch chuẩn mẫu = 24,15
B. Trung bình = 10,78 và độ lệch chuẩn mẫu = 24,8
C. Trung bình = 10,78 và độ lệch chuẩn mẫu = 4,91
D. Trung bình = 10,78 và độ lệch chuẩn mẫu = 4,98
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 1 Bài tập
Bài 0.1. Giả sử một lớp tín chỉ có 30 sinh viên (gồm 20 sinh viên nữ và 10
sinh viên nam). Giảng viên chọn ngẫu nhiên một sinh viên lên bảng. Hãy
xác định không gian mẫu của phép thử này.
Bài 0.2. Rút ngẫu nhiên một quân bài từ bộ bài tây có 52 quân.
a) Xác định không gian mẫu Ω của phép thử này.
b) Biểu diễn biến cố “Rút được quân K” là tập con của Ω.
Bài 0.3. Cổ phiếu A đang giao dịch tại Sở giao dịch chứng khoán Hồ Chí
Minh (HOSE) với biên độ giao dịch là 7% và bước giá 0,1 nghìn đồng. Giả
sử trong phiên sắp tới giá mở cửa của cổ phiếu A là 10 nghìn đồng. Coi
việc quan sát giá đóng cửa của cổ phiếu A trong phiên đang xét là một phép
thử. Hãy xác định không gian mẫu của phép thử này.
(Biên độ giao dịch là 7% có nghĩa là cổ phiếu A có thể đóng cửa với giá
cao hơn hoặc thấp hơn tối đa là 7% so với giá mở cửa; bước giá 0,1 nghìn
đồng có nghĩa là cổ phiếu A có thể giao dịch ở các mức giá 9,3 nghìn đồng,
9,4 nghìn đồng, ..., 10,7 nghìn đồng nhưng không thể giao dịch ở mức giá 9,55 nghìn đồng).
Bài 0.4. Tung đồng thời hai đồng xu hình tròn (đối xứng, đồng chất, có rìa
mảnh) trên một mặt phẳng cứng.
a) Xác định không gian mẫu của phép thử.
b) Biểu diễn biến cố “xuất hiện hai mặt giống nhau” là tập con của không gian mẫu.
Bài 0.5. Một sinh viên làm ba câu hỏi trắc nghiệm bằng cách chọn bừa.
Các kết cục sau có phải là kết cục duy nhất không? Tại sao?
a) “Sinh viên làm đúng 1 câu“
b) “Sinh viên làm đúng câu 1“
Bài 0.6. Một xạ thủ dùng 5 viên đạn để tập bắn cho đến khi trúng bia hoặc
hết đạn thì dừng. Hãy xác định không gian mẫu của phép thử này.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 2
Bài 0.7. Tung đồng thời hai con xúc xắc hình lập phương đồng chất trên
mặt phẳng cứng, trên các mặt của mỗi con xúc xắc đều đánh số chấm từ 1 đến 6.
a) Tính xác suất tổng số chấm xuất hiện là 9.
b) Tính xác suất tổng số chấm xuất hiện vượt quá 9.
c) Tính xác suất tổng số chấm xuất hiện là 9 biết rằng sau khi tung có ít
nhất một con xúc xắc xuất hiện mặt 6 chấm. 1 1 2 Đáp số: a) , b) , c) 9 6 11
Bài 0.8. Giả sử xác suất sinh con trai và sinh con gái bằng nhau và đều
bằng 0,5. Chọn ngẫu nhiên một gia đình có 3 người con.
a) Tìm xác suất gia đình đó có đúng hai con gái.
b) Tìm xác suất gia đình đó có đúng hai con gái biết rằng con đầu lòng là con gái.
c) Tìm xác suất gia đình đó có đúng hai con gái biết rằng con đầu lòng là con trai.
Đáp số: a) 0,375, b) 0,5, c) 0,25
Bài 0.9. Một lớp có 50 sinh viên, trong đó có 35 sinh viên nữ và 15 sinh
viên nam. Chọn ngẫu nhiên 3 sinh viên.
a) Tìm xác suất chọn được 3 sinh viên nam.
b) Tìm xác suất chọn được đúng một sinh viên nam. Đáp số: a) 0,023, b) 0,455
Bài 0.10. Kiểm tra ngẫu nhiên 100.000 sản phẩm của một công ty thì thấy
có 1.560 sản phẩm bị lỗi. Nếu coi 100.000 là đủ lớn thì khi chọn ngẫu nhiên
1 sản phẩm của công ty, xác suất chọn được sản phẩm lỗi bằng bao nhiêu? Đáp số: 0,156
Bài 0.11. Mức xác suất 0,97 có thể coi là lớn hay không? Hãy cho ví dụ
minh họa phù hợp với câu trả lời của bạn.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 3
Bài 0.12. Chứng minh rằng nếu hai biến cố 𝐴 và 𝐵 độc lập thì các cặp biến cố sau cũng độc lập: a) 𝐴 và ¯ 𝐵 b) ¯ 𝐴 và 𝐵 c) ¯ 𝐴 và ¯ 𝐵
Bài 0.13. Hãy cho một ví dụ hai biến cố 𝐴 và 𝐵 vừa không độc lập vừa không xung khắc.
Bài 0.14. Hãy cho một ví dụ một nhóm 3 biến cố độc lập từng đôi nhưng
không độc lập toàn phần với nhau.
Bài 0.15. Có hai sinh viên cùng tham gia một kì thi. Đặt biến cố: 𝐴 = “sinh
viên thứ nhất thi đạt” và 𝐵 = “sinh viên thứ hai thi đạt”. Hãy biểu diễn các
biến cố sau qua 𝐴 và 𝐵. a) Có người thi đạt.
b) Có người thi không đạt.
c) Có đúng 1 sinh viên thi đạt.
d) Không có sinh viên nào thi không đạt.
Bài 0.16. Cho ví dụ một nhóm có n biến cố có tổng các xác suất của các
biến cố trong nhóm bằng 1 nhưng không phải là nhóm đầy đủ các biến cố. Với a) n = 2 b) n = 3
Bài 0.17. Với 𝐴 và 𝐵 là hai biến cố bất kì có xác suất dương. Chứng minh
rằng nếu 𝐴 và 𝐵 xung khắc thì 𝐴 và 𝐵 phụ thuộc. (Khi đó, theo logic thì
nếu 𝐴 và 𝐵 độc lập thì 𝐴 và 𝐵 không xung khắc).
Bài 0.18. Có hai sinh viên cùng tham gia một kì thi với xác suất cả hai cùng
thi đạt là 0,3. Đặt biến cố: 𝐴 = “sinh viên thứ nhất thi đạt” và 𝐵 = “sinh
viên thứ hai thi đạt” và các biến cố 𝐶𝑖 = “có i sinh viên thi đạt” (𝑖 = 0, 1, 2).
a) 𝐴 và 𝐵 có xung khắc không? có độc lập không? tại sao?
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 4
b) Hãy biểu diễn 𝐶0, 𝐶1, 𝐶2 qua 𝐴 và 𝐵.
c) 𝐶0, 𝐶1, 𝐶2 có xung khắc từng đôi với nhau không? có phải là nhóm
đầy đủ các biến cố không? có độc lập từng đôi với nhau không? có độc lập
toàn phần với nhau không? tại sao?
Bài 0.19. Một mạch điện gồm 2 bóng điện hoạt động độc lập với xác suất
hỏng lần lượt là 0,2 và 0,15. Tìm xác suất mạch bị mất điện do bóng điện
hỏng trong hai trường hợp: a) Mạch mắc song song. b) Mạch mắc nối tiếp. Đáp số: a) 0,03, b) 0,32
Bài 0.20. Một sinh viên đi từ nhà tới trường phải qua ba ngã tư có đèn giao
thông. Xác suất sinh viên gặp đèn đỏ ở ngã tư thứ nhất là 0,3. Nếu gặp đèn
đỏ ở ngã tư nào đó thì xác suất gặp đèn đỏ ở ngã tư tiếp theo là 0,6. Nếu
không gặp đèn đỏ ở ngã tư nào đó thì xác suất gặp đèn đỏ ở ngã tư tiếp theo là 0,5.
a) Tìm xác suất sinh viên này gặp đúng 1 đèn đỏ.
b) Biết sinh viên này gặp đúng 1 đèn đỏ, tìm xác suất người đó gặp đèn đỏ ở ngã tư thứ ba. Đáp số: a) 0,375, b) 0,467
Bài 0.21. Một công ty tổ chức thi tuyển nhân viên mới qua hai vòng với
quy định nếu qua vòng trước mới được dự thi ở vòng sau. Ở vòng 1 có 60%
thí sinh bị loại. Ở vòng 2 có 50% thí sinh bị loại.
a) Tìm tỉ lệ thí sinh bị loại.
b) Tìm tỉ lệ thí sinh bị loại ở vòng 1 trong số thí sinh bị loại. Đáp số: a) 80%, b) 75%
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 5 Bài tập tổng hợp
Bài 0.22. Một trường có 1000 học sinh, trong đó có 200 em đăng kí tham
gia câu lạc bộ cờ vua, 300 em đăng kí câu lạc bộ bóng rổ, 400 em đăng kí
câu lạc bộ nhảy hiện đại, 70 em đăng kí cả cờ vua và bóng rổ, 80 em đăng
kí cả cờ vua và nhảy hiện đại, 90 em đăng kí cả bóng rổ và nhảy hiện đại
và 30 em đăng kí cả ba câu lạc bộ đang xét. Chọn ngẫu nhiên một học sinh
trường này, tìm xác suất:
a) Chọn được học sinh không đăng kí câu lạc bộ nào trong ba câu lạc bộ trên.
b) Chọn được học sinh đăng kí đúng một trong ba câu lạc bộ trên.
c) Chọn được học sinh đăng kí câu lạc bộ bóng rổ biết rằng học sinh đó
đã đăng kí câu lạc bộ cờ vua.
Đáp số: a) 0,31, b) 0,51, c) 0,35.
Bài 0.23. Một lô sản phẩm có 2 sản phẩm màu xanh, 4 sản phẩm màu vàng và 6 sản phẩm màu đỏ.
a) Lấy đồng thời 4 sản phẩm từ hộp. Tìm xác suất lấy được đủ ba màu.
b) Lấy đồng thời 5 sản phẩm từ hộp. Tìm xác suất lấy được đủ ba màu. Đáp số: a) 0,436, b) 0,611
Bài 0.24. Một công ty đấu thầu 2 dự án. Xác suất trúng thầu dự án thứ nhất
là 0,6 và xác suất trúng thầu dự án thứ hai là 0,7. Xác suất chỉ trúng thầu
dự án thứ nhất là 0,06.
a) Tính xác suất công ty trúng thầu cả hai dự án.
b) Biết công ty trúng thầu dự án thứ nhất, tìm xác suất công ty trúng thầu dự án thứ hai.
c) Biết công ty không trúng thầu dự án thứ nhất, tìm xác suất công ty
trúng thầu dự án thứ hai.
Đáp số: a) 0,54, b) 0,77, c) 0,4
Bài 0.25. Một nhân viên nộp kế hoạch ra mắt sản phẩm mới cho trưởng
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 6
phòng và phó phòng. Xác suất trưởng phòng đồng ý là 0,6. Xác suất phó
phòng đồng ý là 0,5, nhưng nếu trưởng phòng đã đồng ý thì xác suất phó
phòng sẽ đồng ý là 0,7.
a) Tính xác suất cả trưởng phòng và phó phòng đều đồng ý.
b) Tính xác suất cả trưởng phòng và phó phòng đều không đồng ý.
c) Biết rằng phó phòng đã đồng ý. Tìm xác suất trưởng phòng cũng đồng ý.
Đáp số: a) 0,42, b) 0,32, c) 0,84
Bài 0.26. Một cửa hàng cho biết tỉ lệ khách vào cửa hàng quyết định mua
hàng là 40%. Quan sát ngẫu nhiên 10 người khách vào cửa hàng này, tìm xác suất:
a) Trong đó có không quá 2 người mua hàng bằng bao nhiêu?
b) Trong đó có 8 người mua hàng biết rằng đã có từ 5 người mua hàng trở lên. Đáp số: a) 0,167, b) 0,029
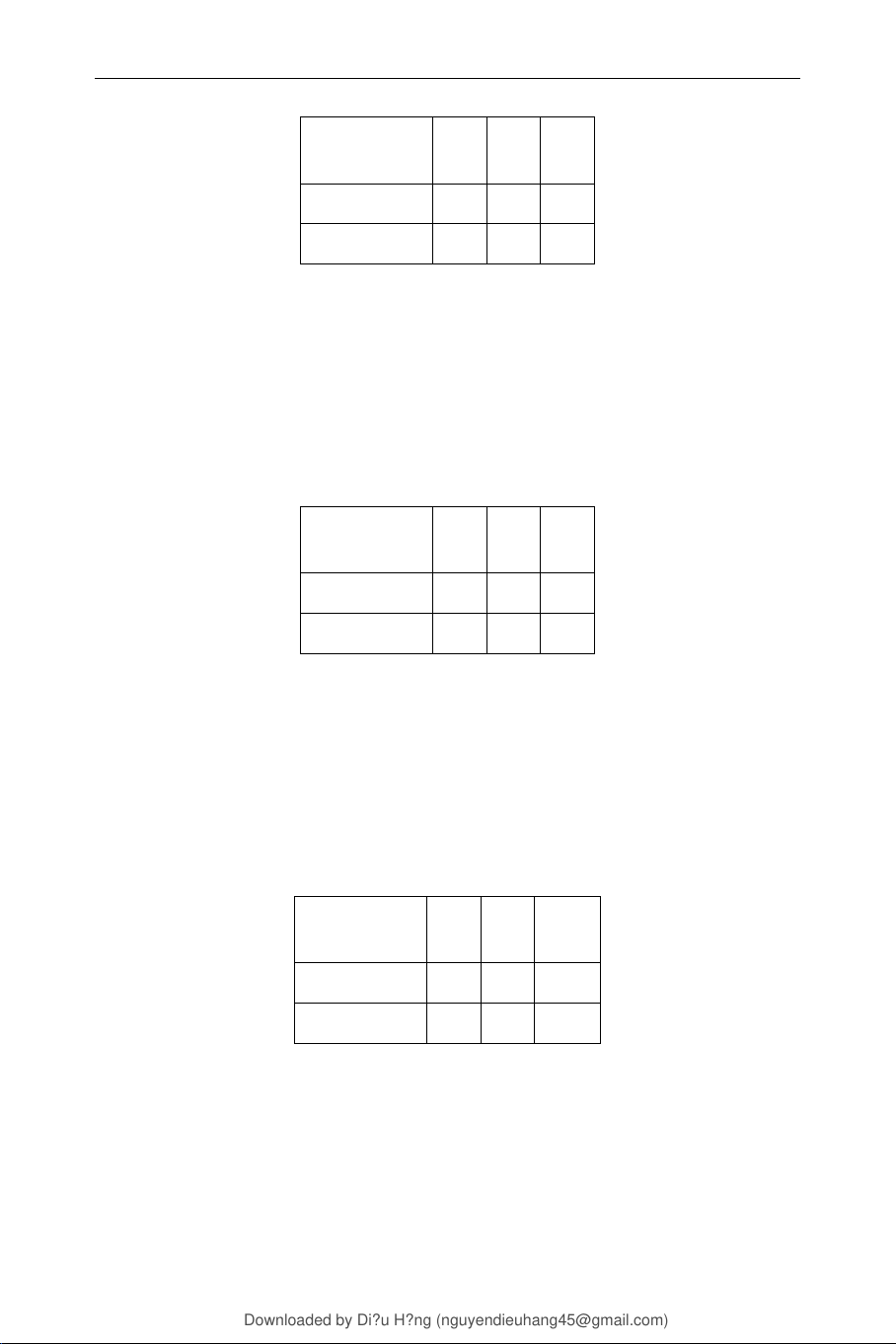
Bài 0.27. Thống kê về nhóm ngành học (Kinh tế và kinh doanh) và giới
tính của sinh viên của một trường đại học, có bảng sau: Kinh tế Kinh doanh Nam 800 1200 Nữ 2700 300
Chọn ngẫu nhiên một sinh viên của trường này. Sử dụng định nghĩa cổ
điển về xác suất, hãy tính xác suất:
a) Chọn được sinh viên nam.
b) Chọn được sinh viên học kinh tế.
c) Chọn được sinh viên nam biết rằng người đó học kinh tế.
d) Chọn được sinh viên học kinh tế biết rằng người đó là sinh viên nam.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 7
Đáp số: a) 0,4, b) 0,7, c) 0,229, d) 0,4
Bài 0.28. Thống kê về nhóm ngành học (Kinh tế và kinh doanh) và giới
tính của sinh viên của một trường đại học, có bảng sau: Kinh tế Kinh doanh Nam 𝑎 2000 − 𝑎 Nữ 3500 − 𝑎 𝑎 − 500
Chọn ngẫu nhiên một sinh viên, gọi 𝐴 là biến cố “chọn được sinh viên
nam”, 𝐵 là biến cố “chọn được sinh viên học kinh tế”.
a) Với 𝑎 = 800 thì hai biến cố 𝐴 và 𝐵 có độc lập với nhau không?
b) Với giá trị nào của 𝑎 thì 𝐴 và 𝐵 độc lập. Đáp số: a) Không, b) 1400
Bài 0.29. Tại một nhà hàng có 80% khách hàng đi theo nhóm 2 người trở
lên, còn lại là khách hàng đi một mình. Giả sử sau khi sử dụng dịch vụ tại
nhà hàng, mọi khách hàng đều đánh giá chất lượng dịch vụ là tốt hay không
tốt. Tỉ lệ khách hàng đánh giá chất lượng dịch vụ tốt trong số khách đi theo
nhóm là 70% và trong số khách đi một mình là 80%.
a) Chọn ngẫu nhiên một khách hàng đã sử dụng dịch vụ tại nhà hàng.
Tìm xác suất chọn được khách hàng đánh giá chất lượng tốt.
b) Giả sử việc đánh giá chất lượng dịch vụ của các vị khách là độc lập
với nhau. Chọn ngẫu nhiên ba khách hàng đã đánh giá chất lượng dịch vụ
của nhà hàng là không tốt. Tìm xác suất cả ba khách đều đi một mình. Đáp số: a) 0,72, b) 0,011
Bài 0.30. Một nhà máy có tỷ lệ sản phẩm tốt là 80%. Trước khi đưa ra thị
trường người ta sử dụng một thiết bị kiểm tra chất lượng để loại sản phẩm
xấu. Thiết bị kiểm tra nhận biết đúng sản phẩm tốt với xác suất là 0,9 và
nhận biết đúng sản phẩm xấu với xác suất là 0,95. Mua một sản phẩm trên
thị trường. Tìm xác suất mua phải sản phẩm xấu. Đáp số: 0,014
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 8
Câu hỏi trắc nghiệm
Câu 0.1. Không gian mẫu Ω là: A. Một phép thử
C. Một biến cố ngẫu nhiên
B. Một biến cố chắc chắn
D. Một biến định lượng
Câu 0.2. Chọn ngẫu nhiên một sinh viên K63 Trường Đại học Kinh tế Quốc
dân, trúng tuyển sử dụng điểm thi Trung học phổ thông ở Việt Nam. Biến
cố “chọn được sinh viên có điểm thi Trung học phổ thông môn Toán bằng 0” thuộc loại nào? A. Biến cố chắc chắn
C. Biến cố không thể có B. Biến cố ngẫu nhiên D. Biến cố sơ cấp
Câu 0.3. Xác suất của một biến cố ngẫu nhiên bất kì không có đặc điểm nào sau đây? A. Có thể bằng 0
C. Phụ thuộc vào điều kiện cơ bản của phép thử B. Có thể bằng 1
D. Phụ thuộc vào người thực hiện phép thử
Câu 0.4. Tung đồng thời hai con xúc xắc đối xứng, đồng chất trên mặt
phẳng cứng (trên các mặt của mỗi con xúc xắc đều có số chấm từ 1 đến 6).
Biến cố “tổng số chấm xuất hiện bé hơn 12” thuộc loại: A. Biến cố chắc chắn
C. Biến cố không thể có B. Biến cố ngẫu nhiên D. Biến cố sơ cấp
Câu 0.5. Tung đồng thời 3 đồng xu tròn, đối xứng, đồng chất trên mặt
phẳng cứng. Số kết cục duy nhất của phép thử này là: A. 8 C. 3 B. 6 D. 2
Câu 0.6. Hộp có 4 chính phẩm, 6 phế phẩm. Lấy đồng thời 3 sản phẩm thì
xác suất lấy được đúng 1 chính phẩm là: A. 0,033 C. 0,083 B. 0,25 D. 0,5
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 9
Câu 0.7. Một hộp có 2 sản phẩm màu xanh, 3 sản phẩm màu đỏ, 5 sản
phẩm màu vàng. Lấy đồng thời ba sản phẩm thì xác suất lấy được đúng một
sản phẩm màu xanh gần bằng: A. 0,533 C. 0,467 B. 0,017 D. 0,5
Câu 0.8. Một hộp có 2 sản phẩm màu xanh, 3 sản phẩm màu đỏ, 5 sản
phẩm màu vàng. Lấy đồng thời ba sản phẩm thì xác suất lấy được sản phẩm màu xanh gần bằng: A. 0,533 C. 0,467 B. 0,017 D. 0,5
Câu 0.9. Lô hàng gồm 14 sản phẩm sản xuất trong nước và 6 sản phẩm
nhập ngoại. Lấy ngẫu nhiên cùng lúc 3 sản phẩm thì xác suất được 2 sản
phẩm trong nước và 1 sản phẩm nhập ngoại bằng bao nhiêu? A. 0,18 C. 0,08 B. 0,48 D. 0,16
Câu 0.10. Một công ty đấu thầu 2 dự án, gọi 𝐴 là biến cố “công ty trúng
thầu dự án thứ nhất”, 𝐵 là biến cố “công ty trúng thầu dự án thứ hai”. Biến
cố “công ty không trúng thầu dự án nào” biểu diễn qua 𝐴 và 𝐵 là: A. ¯ 𝐴 ∩ ¯ 𝐵 C. 𝐴 ∩ 𝐵 B. ¯ 𝐴 ∪ ¯ 𝐵 D. ( ¯
𝐴 ∩ 𝐵) ∪ ( 𝐴 ∩ ¯ 𝐵)
Câu 0.11. Một công ty đấu thầu 2 dự án, gọi 𝐴 là biến cố “công ty trúng
thầu dự án thứ nhất”, 𝐵 là biến cố “công ty trúng thầu dự án thứ hai”. Biến cố ¯ 𝐴 ∩ 𝐵 có nghĩa là:
A. Công ty trúng thầu đúng 1 dự án. B. Công ty có trúng thầu.
C. Công ty chỉ trúng thầu dự án thứ hai.
D. Công ty trúng thầu dự án thứ hai.
Câu 0.12. Công thức nào sau đây sai:
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 10 A. 𝑃(( 𝐴 ∩ ¯ 𝐵) ∪ ( ¯
𝐴 ∩ 𝐵)) = 𝑃( 𝐴) · 𝑃( ¯ 𝐵) + 𝑃( ¯ 𝐴) · 𝑃(𝐵) B. 𝑃(( 𝐴 ∩ ¯ 𝐵) ∪ ( ¯
𝐴 ∩ 𝐵)) = 𝑃( 𝐴) + 𝑃(𝐵) − 2𝑃( 𝐴 ∩ 𝐵) C. 𝑃(( 𝐴 ∩ ¯ 𝐵) ∪ ( ¯
𝐴 ∩ 𝐵)) = 𝑃( 𝐴) · 𝑃( ¯ 𝐵| 𝐴) + 𝑃( ¯ 𝐴) · 𝑃(𝐵| ¯ 𝐴) D. 𝑃(( 𝐴 ∩ ¯ 𝐵) ∪ ( ¯
𝐴 ∩ 𝐵)) = 𝑃( 𝐴 ∩ ¯ 𝐵) + 𝑃( ¯ 𝐴 ∩ 𝐵)
Câu 0.13. Công ty tham gia đấu thầu 2 dự án, với xác suất trúng thầu dự án
một là 0,6, xác suất trúng thầu cả hai dự án là 0,4 và xác suất không trúng
thầu dự án nào là 0,1. Xác suất công ty trúng thầu dự án hai biết rằng đã
trúng thầu dự án một là: A. 0,7 C. 0,43 B. 0,3 D. 0,75
Câu 0.14. Một người thi tuyển nhân viên tại hai công ty. Xác suất trúng
tuyển công ty thứ nhất là 0,45. Xác suất trúng tuyển cả hai công ty là 0,25.
Xác suất không trúng tuyển công ty nào là 0,2. Xác suất người đó trúng
tuyển công ty thứ hai là: A. 0,2 C. 0,1 B. 0,6 D. 0,5
Câu 0.15. Một học sinh làm hai câu hỏi thi. Xác suất làm đúng câu 1 là
0,4. Xác suất làm đúng câu 2 là 0,3. Xác suất làm đúng câu 2 biết rằng đã
làm đúng câu 1 là 0,6. Xác suất người đó chỉ làm đúng một câu là: A. 0,22 C. 0,40 B. 0,76 D. 0,46
Câu 0.16. Một cửa hàng bán hàng online, bán hai loại hàng là đồ gia dụng
và quần áo trẻ em. Qua ghi nhận các đơn đặt hàng của cửa hàng thì có 60%
đơn hàng có đặt đồ gia dụng, 65% đơn hàng có đặt quần áo trẻ em, có đơn
hàng đặt cả hai loại. Xác suất đơn đặt hàng sắp tới đặt cả hai loại hàng hóa trên bằng bao nhiêu? A. 0,25 C. 0,05 B. 0,39 D. 1,00
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 11
Câu 0.17. Một cửa hàng bán hàng online, bán hai loại hàng là đồ gia dụng
và quần áo trẻ em. Qua ghi nhận các đơn đặt hàng của cửa hàng thì có 60%
đơn hàng có đặt đồ gia dụng, 65% đơn hàng có đặt quần áo trẻ em, có đơn
hàng đặt cả hai loại. Xác suất đơn đặt hàng sắp tới chỉ đặt đúng một trong
hai loại hàng hóa trên bằng bao nhiêu? A. 0,25 C. 0,47 B. 0,05 D. 0,75
Câu 0.18. Một công ty có 40% nhân viên là nam, còn lại là nữ. Chọn ngẫu
nhiên 5 nhân viên của công ty thì xác suất trong đó có đúng 2 nhân viên nam gần bằng: A. 0,16 C. 0,346 B. 0,035 D. 0,158
Câu 0.19. Một đề thi trắc nghiệm có 10 câu hỏi độc lập, mỗi câu có bốn
phương án lựa chọn, trong đó chỉ có một phương án đúng. Một học sinh trả
lời bừa tất cả 10 câu hỏi. Xác suất học sinh đó trả lời đúng 5 câu gần bằng: A. 0,5 C. 0,0002 B. 0,058 D. 0,001
Câu 0.20. Một đề thi trắc nghiệm có 10 câu hỏi độc lập, mỗi câu có bốn
phương án lựa chọn, trong đó chỉ có một phương án đúng. Mỗi câu trả lời
đúng được cộng 1 điểm, câu trả lời sai bị trừ 1 điểm. Nếu học sinh đạt 4
điểm trở lên thì qua. Một học sinh trả lời bừa cả 10 câu thì xác suất học
sinh đó thi qua gần bằng: A. 0,0031 C. 0,224 B. 0,146 D. 0,0035
Câu 0.21. Xác suất để một người từng nghe quảng cáo về sản phẩm A là
0,75. Khả năng người nào đó mua sản phẩm A khi từng nghe và chưa từng
nghe quảng cáo lần lượt là 0,28 và 0,08. Chọn ngẫu nhiên một người mua
sản phẩm A, xác suất người đó từng nghe quảng cáo về sản phẩm này là: A. 0,087 C. 0,23 B. 0,913 D. 0,462
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 12
Câu 0.22. Một kho hàng có 70% sản phẩm do nhà máy A cung cấp và 30%
sản phẩm do nhà máy B cung cấp. Tỉ lệ chính phẩm nhà máy A và nhà máy
B tương ứng là 90% và 82%. Tỉ lệ phế phẩm của kho hàng là: A. 12,4% C. 14% B. 87,6% D. 86%
Câu 0.23. Một kho hàng có 70% sản phẩm do nhà máy A cung cấp và 30%
sản phẩm do nhà máy B cung cấp. Tỉ lệ chính phẩm nhà máy A và nhà máy
B tương ứng là 90% và 82%. Lấy ngẫu nhiên 5 sản phẩm của kho hàng thì
xác suất trong đó có phế phẩm là: A. 0,124 C. 0,484 B. 0,53 D. 0,476
Câu 0.24. Một công ty có 60% nhân viên là nam, còn lại là nữ. Tỉ lệ nhân
viên không hoàn thành nhiệm vụ trong tháng trước của nam là 10%, của nữ
là 8%. Chọn một nhân viên không hoàn thành nhiệm vụ trong tháng trước
thì xác suất chọn được nhân viên nữ là: A. 0,092 C. 0,348 B. 0,400 D. 0,652
Câu 0.25. Tỷ lệ nam giới mắc bệnh loãng xương là 25%. Nam giới hút
thuốc lá có nguy cơ mắc bệnh loãng xương cao gấp 2 lần so với nam giới
không hút thuốc. Tỷ lệ nam giới hút thuốc lá là 25%. Biết rằng một nam
giới bị mắc bệnh loãng xương, khi đó xác suất người này có hút thuốc lá là: A. 0,20 C. 0,25 B. 0,67 D. 0,40
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 1 Bài tập
Bài 0.1. Lấy ví dụ biến ngẫu nhiên tương ứng với các phép thử sau.
a) Tung ngẫu nhiên hai con xúc xắc.
b) Lấy ngẫu nhiên 2 sản phẩm từ một kho hàng có 10 sản phẩm tốt và 3 sản phẩm xấu.
c) Làm một bài thi trắc nghiệm.
Bài 0.2. Một hộp kín đựng 7 viên bi xanh, 3 viên bi đỏ. Lấy ngẫu nhiên 2
viên. Gọi 𝑋 là số bi đỏ lấy được.
a) 𝑋 nhận những giá trị nào? b) Tính 𝑃(𝑋 = 2). c) Tính 𝑃(𝑋 ≤ 3).
Bài 0.3. Có 10 lô đất được đánh số từ 1 đến 10. Một người bốc ngẫu nhiên
2 lô. Gọi 𝑋 là số lô được đánh số chẵn.
a) Tính xác suất người đó bốc được cả hai lô đều được đánh số chẵn.
b) Lập bảng phân phối xác suất của 𝑋.
Bài 0.4. Cho biến ngẫu nhiên 𝑋 có bảng phân phối xác suất như sau: 𝑋 2 3 7 𝑃 0,1 0,2 0,7 a) Tính 𝑃(𝑋 < 5).
b) Giả sử 𝐹 (𝑥) là hàm phân phối xác suất của 𝑋. Vẽ đồ thị của 𝐹 (𝑥) và tính 𝐹 (3) − 𝐹 (2).
Bài 0.5. Biến ngẫu nhiên 𝑋 có bảng phân phối xác suất như sau: 𝑋 0 1 3 5 𝑃 0,2 0,3 𝑎 0,15
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 2 a) Xác định 𝑎. b) Tính 𝑃(𝑋 > 2).
Bài 0.6. Một học sinh làm bài kiểm tra gồm 2 câu hỏi. Nếu làm đúng câu
1 được 7 điểm, đúng câu 2 được 3 điểm. Xác suất học sinh làm đúng câu 1
là 0,6; xác suất làm đúng câu 2 là 0,2.
a) Lập bảng phân phối xác suất của số điểm của học sinh.
b) Tính xác suất để học sinh được ít nhất 5 điểm.
Bài 0.7. Một hộp có 6 sản phẩm tốt và 2 sản phẩm xấu. Lấy ngẫu nhiên 2
sản phẩm, gọi X là số sản phẩm tốt lấy được.
a) Lập bảng phân phối xác suất của X.
b) Tính trung bình và phương sai của số sản phẩm tốt lấy được.
Bài 0.8. Lợi nhuận (đơn vị: tỷ đồng) của một công ty có bảng phân phối xác suất như sau: 𝑋 −20 0 10 30 𝑃 0,1 0,5 0,25 0,15
a) Tính xác suất để công ty có lãi.
b) Tính kì vọng và độ lệch chuẩn của lợi nhuận.
c) Biết rằng nếu lợi nhuận của công ty cao hơn 5 tỷ thì giám đốc được
thưởng 200 triệu; nếu công ty lỗ thì giám đốc bị phạt 100 triệu; còn
lại được thưởng 50 triệu. Tính trung bình tiền thưởng của giám đốc công ty.
Bài 0.9. Tỷ suất lợi nhuận nếu đầu tư vào 2 dự án 𝐴 và 𝐵 có bảng phân phối xác suất như sau: 𝑋𝐴 30 40 42 𝑃 0,2 0,6 0,2
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 3 𝑋𝐵 −10 40 120 𝑃 0,2 0,6 0,2
a) Để kỳ vọng lợi nhuận cao hơn, nên đầu tư toàn bộ vốn vào công ty nào?
b) Nên đầu tư vào công ty nào để rủi ro thấp hơn?
c) Nếu đầu tư vào cả hai ngành (giả sử lợi nhuận hai ngành độc lập), thì
nên chia vốn theo tỷ lệ nào để rủi ro thấp nhất?
Bài 0.10. Biết rằng tỷ lệ người dân Hà Nội đã tiêm Vắc-xin ngừa Covid là
97%. Chọn ngẫu nhiên 5 người.
a) Gọi 𝑋 là số người đã tiêm Vắc-xin. 𝑋 có phân phối xác suất theo quy luật gì?
b) Tính trung bình; độ lệch chuẩn và mốt của số người đã tiêm Vắc-xin.
Bài 0.11. Một nhà kho lắp 3 chuông báo cháy hoạt động độc lập. Xác suất
mỗi chuông kêu khi có cháy là 0,92.
a) Tính xác suất có chuông kêu khi có cháy.
b) Tính trung bình và độ rủi ro của số chuông kêu khi có cháy.
Bài 0.12. Một sinh viên làm bài kiểm tra gồm 2 câu, nếu làm đúng câu 1
được 6 điểm, đúng câu 2 được 4 điểm. Xác suất sinh viên làm đúng câu 1
là 0,7, xác suất làm đúng câu 2 là 0,2.
a) Lập bảng phân phối xác suất số điểm của sinh viên đó.
b) Từ bảng phân phối xác suất ở câu (a), tính xác suất sinh viên đó được trên 5 điểm.
Bài 0.13. Cho 𝑋, 𝑌 lần lượt là số làn đường và số vụ va chạm giao thông
trong 1 tháng, có bảng phân phối xác suất đồng thời HH 𝑌 HH 5 8 10 H 𝑋 H H 1 0,16 0,2 0,4 2 0,2 0,1 0,04
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 4
a) Tính trung bình số vụ va chạm giao thông.
b) Tính xác suất có nhiều hơn 5 vụ va chạm giao thông trên đoạn đường có hai làn.
c) Tính trung bình số vụ va chạm giao thông trên đoạn đường chỉ có đúng một làn.
d) Tính hệ số tương quan giữa số vụ va chạm giao thông và số làn đường và nhận xét kết quả.
Bài 0.14. Một người chào bán sản phẩm với hai khách hàng. Mỗi khách
mua hàng thì người bán lãi 3 triệu đồng; xác suất để khách hàng mua hàng
là 0,6. Lập bảng phân phối xác suất đồng thời của số khách mua hàng và số tiền lãi.
Bài 0.15. Cho 𝐸 (𝑋) = 15, 𝑉 (𝑋) = 9, 𝐸 (𝑌) = 40, 𝑉 (𝑌) = 64, 𝐸 (𝑋 · 𝑌) =
615. Tính hệ số tương quan của 𝑋 và 𝑌 và nhận xét kết quả. Bài tập tổng hợp
Bài 0.16. Phát biểu sau đúng hay sai
a) Kì vọng của biến ngẫu nhiên là hằng số không âm.
b) Quy luật phân phối Không-một là quy luật nhị thức.
c) Phương sai của hiệu 2 biến ngẫu nhiên độc lập bằng hiệu phương sai của 2 biến ngẫu nhiên.
d) Phương sai phản ánh độ dao động của biến ngẫu nhiên.
e) Kì vọng của biến ngẫu nhiên rời rạc là giá trị nằm giữa giá trị nhỏ
nhất và giá trị lớn nhất mà biến ngẫu nhiên đó có thể nhận.
Bài 0.17. Lấy ví dụ biến ngẫu nhiên tương ứng với các phép thử sau:
a) Chọn 1 số tự nhiên trong các số tự nhiên từ 1 đến 10.
b) Đầu tư 500 triệu vào một dự án.
c) Bắn một viên đạn vào bia.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 5
Bài 0.18. Một người bán hàng ở 5 nơi, xác suất bán được hàng ở mỗi nơi là
0,8. Gọi X là số nơi bán được hàng.
a) X là biến ngẫu nhiên rời rạc hay liên tục, X nhận những giá trị nào? b) Tính 𝑃(𝑋 = 3). c) Tính 𝑃(𝑋 > 1).
Bài 0.19. Số bộ quần áo bán được mỗi ngày của một cửa hàng thời trang có
bảng phân phối xác suất như sau: 𝑋 0 3 5 6 𝑃 0,1 0,4 0,35 0,15
a) Tính xác suất để trong một ngày cửa hàng bán được nhiều hơn 3 bộ quần áo.
b) Thông thường mỗi ngày cửa hàng bán được bao nhiêu bộ quần áo?
c) Tính xác suất để trong 3 ngày bất kì có 2 ngày cửa hàng bán được ít
nhất một bộ quần áo. Biết số bộ quần áo bán được của các ngày khác
nhau là độc lập với nhau.
Bài 0.20. Một đề thi trắc nghiệm có 10 câu. Mỗi câu có 4 đáp án, trong đó
có 1 đáp án đúng. Một học sinh khoanh ngẫu nhiên tất cả các câu.
a) Tính xác suất học sinh đó được nhiều nhất 2 câu.
b) Tính kì vọng và phương sai của số câu của học sinh đó.
Bài 0.21. Một công ty A, theo quy định mỗi tháng trả lương cho công nhân
một lần vào cuối tháng. Xác suất công ty trả chậm lương cho công nhân trong một tháng là 0,4.
a) Cho biết quy luật phân phối xác suất của số lần trả chậm lương cho
công nhân trong 12 tháng của công ty A.
b) Tính xác suất để trong 12 tháng có không quá 2 lần công ty A trả
chậm lương cho công nhân.
c) Tính số lần trả chậm lương trung bình của công ty A trong 12 tháng.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 6
d) Tìm số lần trả chậm lương có thể xảy ra nhiều nhất trong 12 tháng của công ty A.
Bài 0.22. Một xạ thủ cấp 4 viên đạn. Anh ta bắn từng viên vào bia với xác
suất trúng mỗi lần bắn là 0,9. Nếu anh ta bắn trúng thì thôi không bắn nữa.
a) Tính xác suất để người đó sử dụng hết 3 viên.
b) Tính trung bình số viên đạn mà xạ thủ không sử dụng.
Bài 0.23. Lượng bán thực phẩm hàng ngày tại một cửa hàng có bảng phân phối xác suất như sau: 𝑋 (𝑘𝑔) 21 22 23 24 25 𝑃 0,1 0,2 0,3 0,35 0,05
a) Tính kì vọng, phương sai của lượng bán.
b) Tính xác suất để tổng lượng bán 2 ngày bất kì nhiều hơn 48 kg. Biết
rằng lượng bán của các ngày là độc lập với nhau.
c) Giá mua mỗi kg thực phẩm là 23 ngàn, giá bán 28 ngàn. Song nếu
hàng còn đến cuối ngày thì phải bán với giá 17 ngàn mới bán hết.
Muốn có lãi cao hơn nên nhập về 22 hay 23 kg mỗi ngày.
Bài 0.24. Cho biến ngẫu nhiên 2 chiều 𝑋, 𝑌 có bảng phân phối xác suất như sau: HH 𝑋 HH 3 5 7 H 𝑌 H H 1 0,1 0,2 0,04 2 0,15 0,3 0,21
a) Lập bảng phân phối xác suất của 𝑋. b) Tính 𝐸 (𝑋 |𝑌 = 2)
c) Tính hệ số tương quan của 𝑋 và 𝑌.
d) Tính 𝑃(𝑋 + 𝑌 > 5).
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 7
Bài 0.25. Cho biến ngẫu nhiên 2 chiều 𝑋, 𝑌 có bảng phân phối xác suất như sau: HH 𝑋 HH 3 5 7 H 𝑌 H H 1 0,1 0,2 0,04 2 0,2 0,1 0,06 4 0,25 0,05 0
a) Lập bảng phân phối xác suất của biến ngẫu nhiên 𝑋 trong điều kiện 𝑌 = 2.
b) Hai biến 𝑋 và 𝑌 độc lập hay phụ thuộc?
c) Tính kì vọng và phương sai của biến ngẫu nhiên 𝑍, biết 𝑍 = 0,3𝑋 + 0,7𝑌 .
Bài 0.26. Cho X là thu nhập, Y là chi tiêu của hộ gia đình (đơn vị: triệu/tháng). HH 𝑌 HH 8 9 11 H 𝑋 H H 10 0,1 0,2 0,02 15 0,1 0,3 0,28
a) Tính kì vọng và độ rủi ro của chi tiêu.
b) Tính kì vọng của thu nhập biết chi tiêu là 8 triệu.
c) Tính xác suất để thu nhập cao hơn chi tiêu.
Bài 0.27. Cho 𝑋𝐴, 𝑋𝐵 (triệu) lần lượt là giá bán hai sản phẩm 𝐴 và 𝐵 trên
thị trường, có bảng phân phối xác suất đồng thời như sau: HH 𝑋 H 𝐴 H 50 60 80 H 𝑋 H 𝐵 H 60 0,12 0,2 0,08 80 0,18 0,3 0,12
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 8
a) Tính kì vọng giá bán sản phẩm 𝐴 biết giá sản phẩm 𝐵 là 60 (triệu).
b) Tính hiệp phương sai giữa giá bán hai sản phẩm.
c) Tính xác suất để giá bán sản phẩm 𝐴 cao hơn giá bán sản phẩm 𝐵.
Bài 0.28. Lợi nhuận khi đầu tư vào ngành 𝐴 là 𝑋 (đơn vị: triệu đồng) và
ngành 𝐵 là 𝑌 (đơn vị: triệu đồng). Có bảng phân phối xác suất như sau: HH 𝑋 HH 100 200 300 H 𝑌 H H 10 0, 15 0, 1 0, 04 15 0, 05 0, 2 0, 15 20 0, 01 0, 05 0, 25
a) Tính kì vọng, phương sai của lợi nhuận khi đầu tư vào ngành 𝐴.
b) Tính kì vọng của lợi nhuận khi đầu tư vào ngành 𝐴 biết lợi nhuận khi
đầu tư vào ngành 𝐵 là 20 triệu đồng.
c) Tính kì vọng và độ phân tán của lợi nhuận khi chia vốn theo tỷ lệ 7 : 3
để đầu tư vào hai ngành.
Bài 0.29. Cho biết giá bán (kí hiệu là 𝑃) có trung bình là 20 và độ lệch
chuẩn là 3, lượng bán (kí hiệu là 𝑄) có trung bình là 800 và độ lệch chuẩn
là 90. Doanh thu (kí hiệu là 𝑇 𝑅, tính là 𝑇 𝑅 = 𝑃 × 𝑄) có trung bình là
15.780. Tính hệ số tương quan giữa giá bán và lượng bán. Hãy nhận xét về kết quả đó.
Bài 0.30. Cho biết thu nhập (kí hiệu là 𝑇 𝑁) có trung bình là 20 triệu đồng
và độ lệch chuẩn là 2 triệu đồng, chi tiêu (kí hiệu là 𝐶𝑇) có trung bình là
9,5 triệu đồng và độ lệch chuẩn là 1,2 triệu đồng. Hệ số tương quan giữa
thu nhập và chi tiêu là 0,6. Tính trung bình và phương sai của tiết kiệm (kí
hiệu là 𝑇 𝐾 và 𝑇 𝐾 = 𝑇 𝑁 − 𝐶𝑇).
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 9 Câu hỏi trắc nghiệm
Câu 0.1. Tung ngẫu nhiên một con xúc xắc. Gọi 𝑋 là số chấm xuất hiện.
Phát biểu nào sau đây là đúng?
A. 𝑋 là biến ngẫu nhiên rời rạc.
B. 𝑋 là biến ngẫu nhiên liên tục.
C. 𝑋 là biến cố ngẫu nhiên.
D. 𝑋 là xác suất xuất hiện số chấm.
Câu 0.2. Một sinh viên thi hết học phần, gọi:
𝑋 = “Sinh viên đạt điểm tối đa”
𝑌 = “Điểm số của sinh viên”
𝑍 = “Số câu làm đúng của sinh viên”
𝑊 = “Số câu làm sai của sinh viên”
Khái niệm nào không phải là biến ngẫu nhiên? A. 𝑋 B. 𝑌 C. 𝑍 D. 𝑊
Câu 0.3. Một biến số có thể nhận giá trị bất kì trên khoảng (0; 1) thì gọi là:
A. Biến ngẫu nhiên rời rạc. B. Biến cố ngẫu nhiên.
C. Biến ngẫu nhiên liên tục.
D. Biến ngẫu nhiên phân phối Không – một.
Câu 0.4. Qua thống kê của một cửa hàng thì xác suất một khách bất kì mua
hàng là 0,15. Quan sát ngẫu nhiên 5 khách vào cửa hàng. Số khách không
mua hàng trong số 5 người được quan sát là:
A. Biến ngẫu nhiên phân phối A(0,15)
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 10
B. Biến ngẫu nhiên phân phối A(0,75).
C. Biến ngẫu nhiên phân phối B(5;0,15).
D. Biến ngẫu nhiên phân phối B(5;0,85).
Câu 0.5. Thu nhập các hộ gia đình ở vùng thứ nhất là biến ngẫu nhiên kí
hiệu là 𝑋, ở vùng thứ hai là biến ngẫu nhiên kí hiệu là 𝑌 . Câu nói “thu nhập
vùng thứ nhất không cao hơn nhưng ổn định hơn ở vùng thứ hai” được viết
dưới dạng kì vọng và phương sai như thế nào?
A. 𝐸 (𝑋) ≥ 𝐸 (𝑌) và 𝑉 (𝑋) < 𝑉 (𝑌).
B. 𝐸 (𝑋) ≥ 𝐸 (𝑌) và 𝑉 (𝑋) > 𝑉 (𝑌)
C. 𝐸 (𝑋) ≤ 𝐸 (𝑌) và 𝑉 (𝑋) < 𝑉 (𝑌)
D. 𝐸 (𝑋) ≤ 𝐸 (𝑌) và 𝑉 (𝑋) > 𝑉 (𝑌)
Câu 0.6. Cho bảng phân phối xác suất của số người đến cửa hàng trong 1 giờ như sau: 𝑋 4 5 6 𝑃 0,2 0,3 0,5
Tính kì vọng và phương sai của 𝑋
A. 𝐸 (𝑋) = 5 và 𝑉 (𝑋) = 77.
B. 𝐸 (𝑋) = 5 và 𝑉 (𝑋) = 28,7.
C. 𝐸 (𝑋) = 5,3 và 𝑉 (𝑋) = 28,7.
D. 𝐸 (𝑋) = 5,3 và 𝑉 (𝑋) = 0,61.
Câu 0.7. Xác suất để một sản phẩm của hãng A hỏng trong một năm đầu
sử dụng là 0,1. Trong 100 sản phẩm của hãng A có trung bình số sản phẩm
hỏng trong năm đầu sử dụng là: A. 7 B. 10 C. 11 D. 12
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 11
Câu 0.8. Tỷ lệ chính phẩm của một nhà máy là 70%. Lấy ngẫu nhiên 4 sản
phẩm của nhà máy để kiểm tra. Số chính phẩm lấy được có khả năng xảy ra cao nhất là: A. 1 B. 2 C. 3 D. 4
Câu 0.9. Số lần gặp đèn đỏ của một người khi đi từ nhà đến cơ quan là biến
ngẫu nhiên phân phối nhị thức với n = 3 và p = 0,3. Xác suất người đó gặp
đúng 1 đèn đỏ khi đi từ nhà đến cơ quan là: A. 0,127 B. 0,3 C. 0,441 D. 0,657
Câu 0.10. Cho bảng phân phối xác suất về lợi nhuận ròng (X: đơn vị là tỉ
đồng) của doanh nghiệp như sau: 𝑋 −0, 3 −0, 1 0,2 0,6 𝑃 0,1 0,2 0,3 0,4
Khi đó, khả năng doanh nghiệp có lãi là: A. 0,4 B. 0,6 C. 0,7 D. 0,8
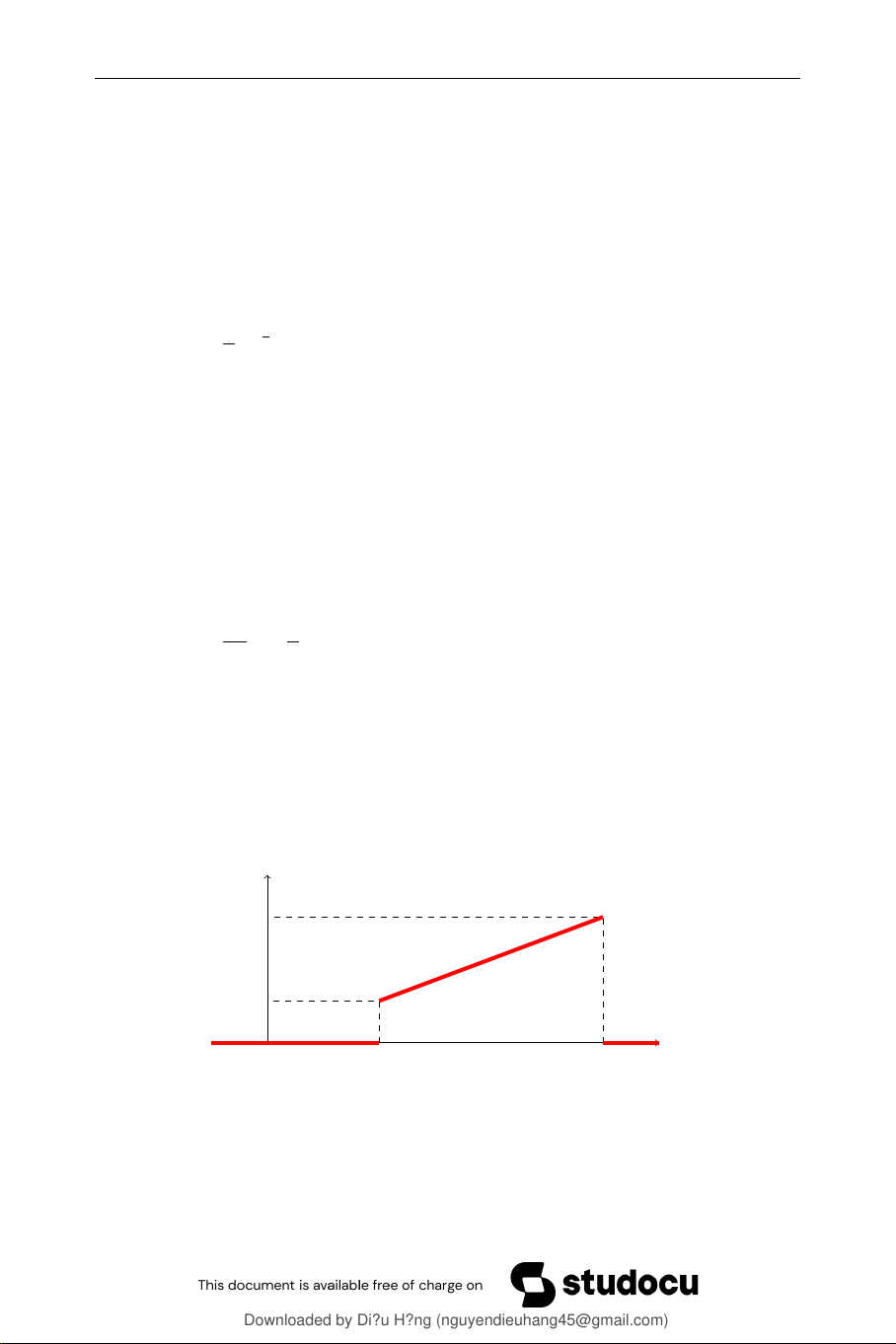
Câu 0.11. Lợi nhuận (tỷ đồng) của một công ty là biến ngẫu nhiên rời rạc
𝑋 có đồ thị hàm phân phối xác suất như sau: 𝐹 (𝑥) 1 1 2 3 5 𝑥 0 Mốt của lợi nhuận là A. 1 B. 2 C. 3 D. 5
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 12
Câu 0.12. Một người dự định đầu tư vào một dự án. Nếu dự án thành công
thì lãi là 7 (tỷ VND), nếu không thành công thì lỗ 2 (tỷ VND). Biết xác suất
thành công là 0,6; khi đó kì vọng và phương sai của lợi nhuận là: A. 3,4 và 19,44 B. 3,4 và 31 C. 2,5 và 31 D. 5 và 19,44
Câu 0.13. Một người đi bán hàng ở hai nơi độc lập nhau, xác suất bán được
ở mỗi nơi đều bằng 0,7. Tại mỗi nơi nếu bán được hàng thì người đó được
lãi 5 triệu. Tính kì vọng và phương sai của tiền lãi: A. 7 và 10,5 B. 7 và 2,1 C. 3,5 và 2,1 D. 3,5 và 10,5
Câu 0.14. Theo quảng cáo của một công ty thì tỉ lệ khách hàng đánh giá
sản phẩm của công ty tốt là 93%. Giả sử quảng cáo đúng, nếu phỏng vấn
ngẫu nhiên 50 khách hàng đã dùng sản phẩm của công ty thì số người đánh
giá tốt có khả năng cao nhất là mấy người? A. 46,5 B. 47 C. 50 D. 46
Câu 0.15. Khi bán được một sản phẩm, nhân viên bán hàng được nhận tiền
hoa hồng là 200 nghìn, xác suất để nhân viên bán được hàng cho mỗi lần
gặp khách hàng là 0,4. Nếu một ngày nhân viên đi gặp 10 khách hàng thì
số tiền hoa hồng trung bình của nhân viên bằng bao nhiêu? Giả thiết mỗi
khách hàng mua không quá 1 sản phẩm. A. 480 nghìn B. 800 nghìn C. 600 nghìn D. 840 nghìn
Câu 0.16. Một đề thi có 2 câu hỏi độc lập, mỗi câu 5 điểm. Xác suất học
sinh trả lời đúng câu 1, 2 tương ứng là 0,6 và 0,7. Kì vọng số câu trả lời
đúng của học sinh đó là: A. 1,3 B. 1 C. 2 D. 1,5
Câu 0.17. Một cửa hàng cho rằng xác suất bán được hàng trong 1 tuần là
0,4. Nếu bán được hàng thì lợi nhuận là 10 triệu đồng; nếu không bán được
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 13
hàng thì lỗ 1 triệu đồng. Phương sai của lợi nhuận là: A. 40,6 (triệu đồng)2 B. 27,84 (triệu đồng)2 C. 29,04 (triệu đồng)2 D. 6,37 (triệu đồng)
Câu 0.18. Công ty bán sản phẩm cho khách hàng với thời gian bảo hành
miễn phí quy định là 1 năm. Tỷ lệ sản phẩm của công ty bị hỏng trong 1
năm đầu sử dụng là 10%. Khi bán 1 sản phẩm thì công ty thu lãi 120 nghìn
đồng. Nếu sản phẩm bị hỏng trong thời gian bảo hành miễn phí thì công ty
phải chi 100 nghìn đồng cho việc bảo hành. Tiền lãi trung bình trên mỗi
sản phẩm bán được của công ty là: A. 120 (nghìn đồng) B. 110 (nghìn đồng) C. 98 (nghìn đồng) D.20 (nghìn đồng)
Câu 0.19. Theo thống kê, số suất đồ ăn sáng hằng ngày bán được tại cửa
hàng A là biến ngẫu nhiên X có bảng phân phối xác suất như sau: 𝑋 80 100 120 150 𝑃 0,25 0,6 0,1 0,05
Mỗi ngày chủ cửa hàng chuẩn bị 120 suất. Mỗi suất bán được thì lãi 12
nghìn đồng, nếu bị ế thì phải chịu lỗ 20 nghìn đồng. Tìm số tiền lãi trung
bình mỗi ngày của chủ cửa hàng. A. 664 nghìn đồng B. 754 nghìn đồng C. 784 nghìn đồng D.736 nghìn đồng
Câu 0.20. Một xạ thủ dùng 4 viên đạn để tập bắn với quy định nếu bắn
trúng hai viên liên tiếp hoặc hết đạn thì dừng bắn. Các viên đạn được bắn
độc lập với xác suất trúng đều là 0,8. Khi đó, số viên đạn xạ thủ sử dụng trung bình là: A. 3,2 (viên) B. 2 (viên) C. 3 (viên) D.2,6 (viên)
Câu 0.21. Cho X là thu nhập, Y là chi tiêu của hộ gia đình (đơn vị: triệu/tháng).
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 14 HH 𝑌 HH 8 9 10 H 𝑋 H H 10 0,1 0,2 0 15 0,1 0,3 0,3
Mức chi tiêu trung bình trong tháng của hộ gia đình có thu nhập 15 triệu là: A. 6,5 (triệu) B. 9,29 (triệu) C. 9,1 (triệu) D.8,7 (triệu)
Câu 0.22. Cho X là thu nhập, Y là chi tiêu của hộ gia đình (đơn vị: triệu/tháng). HH 𝑌 HH 8 9 10 H 𝑋 H H 10 0,1 0,2 0 15 0,1 0,3 0,3
Hệ số tương quan giữa thu nhập và chi tiêu là A. 0,253 B. -0,253 C. -0,405 D. 0,405
Câu 0.23. Cho 𝑋𝐴, 𝑋𝐵 lần lượt là lãi suất trong một năm của hai cổ phiếu 𝐴 và 𝐵. HH 𝑋 H 𝐴 H 4 8 12 H 𝑋 H 𝐵 H 6 0,1 0,2 0,15 12 0,2 0,3 0,05
Một người đầu tư 200 triệu vào cổ phiếu A và 400 triệu vào cổ phiếu B.
Tiền lãi trung bình một năm của người đó là: A. 52 B. 52,4 C. 48 D. 50,2
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 15
Câu 0.24. Một sản phẩm có trung bình và đô lệch chuẩn của giá bán lần
lượt là 10 và 3; trung bình và phương sai của lượng bán lần lượt là 120 và
100; doanh thu trung bình là 1185. Tính hệ số tương quan giữa giá bán và lượng bán: A. 15 B. -15 C. -0,5 D. 0,5
Câu 0.25. Cho 𝑋𝐴, 𝑋𝐵 lần lượt là giá bán hai sản phẩm 𝐴 và 𝐵 trên thị
trường, có bảng phân phối xác suất đồng thời như sau: HH 𝑋 H 𝐴 H 50 60 80 H 𝑋 H 𝐵 H 60 0,12 0,2 0,08 80 0,18 0,3 0,12
Xác suất để giá bán sản phẩm B cao hơn giá bán sản phẩm A là: A. 0,6 B. 0,3 C. 0,48 D. 0,42
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 1 Bài tập 0 nếu 𝑥 ∉ (0; 4)
Bài 0.1. Cho hàm số 𝑓 (𝑥) = 1 1 𝑥 + nếu 𝑥 ∈ (0; 4) 16 8
a) Chứng minh 𝑓 (𝑥) là hàm mật độ xác suất của biến ngẫu nhiên liên tục 𝑋.
b) Tính xác suất để trong một phép thử 𝑋 nhận giá trị lớn hơn 2.
c) Tính xác suất để trong 3 phép thử độc lập có đúng 1 lần 𝑋 nhận giá trị nhỏ hơn 2.
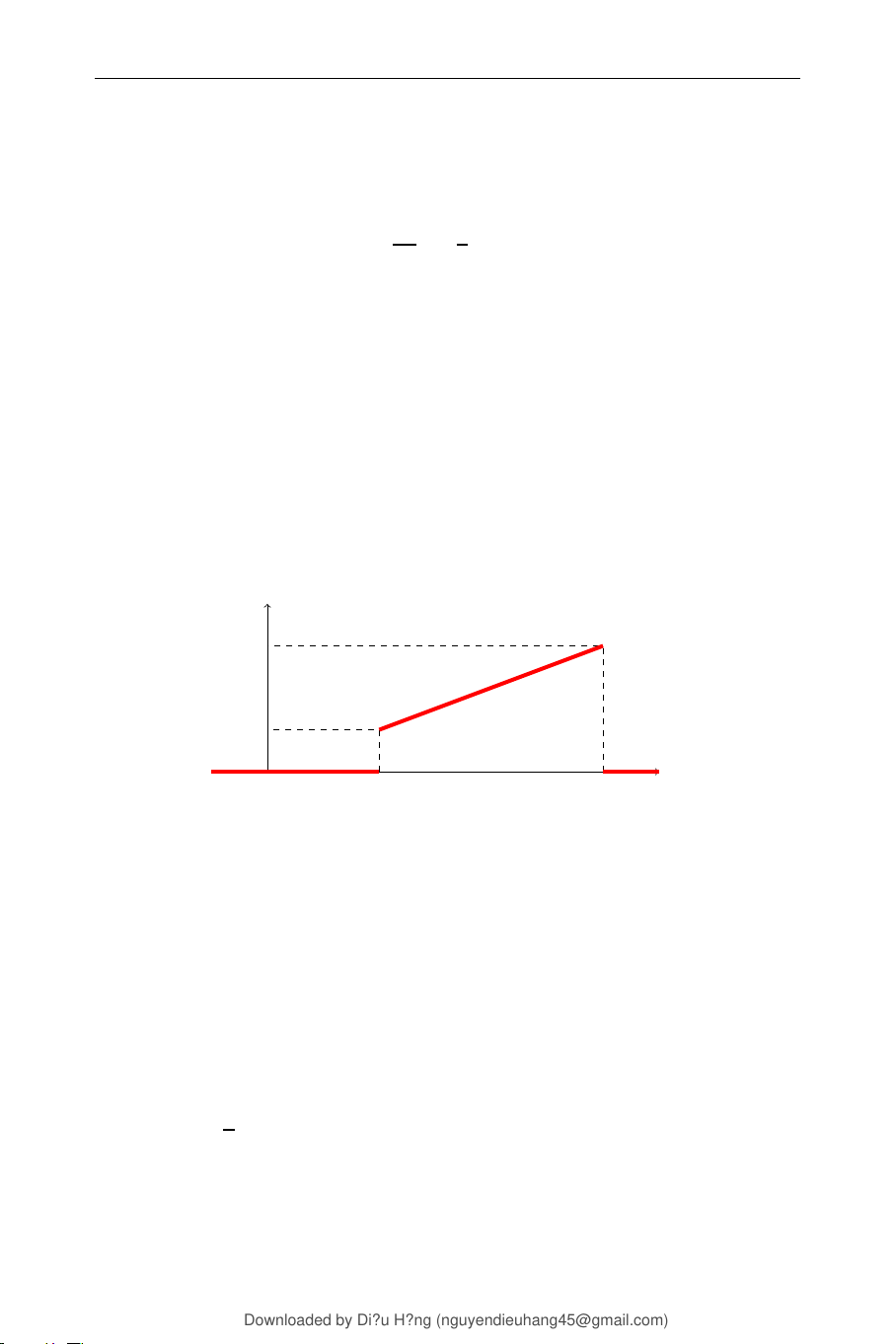
Bài 0.2. Cho biến ngẫu nhiên liên tục 𝑋 có đồ thị hàm mật độ xác suất 𝑓 (𝑥) như hình vẽ 𝑓 (𝑥) 0, 75 0, 25 𝑥 0 1 3
a) Tính xác suất để trong một phép thử 𝑋 nhận giá trị không quá 2.
b) Tính xác suất để trong 5 phép thử độc lập có không quá 1 lần X nhận giá trị lớn hơn 2.
Bài 0.3. Thời gian (đơn vị: phút) để thí sinh hoàn thành một câu hỏi trắc
nghiệm là biến ngẫu nhiên liên tục có hàm mật độ xác suất: 0 nếu 𝑥 ∉ (0; 3) 𝑓 (𝑥) = 2 𝑥(3 − 𝑥) nếu 𝑥 ∈ (0; 3) 9
a) Tìm tỷ lệ câu hỏi có thời gian hoàn thành nhiều hơn 2 phút.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 2
b) Biết đề thi có 10 câu có nội dung độc lập nhau, tính xác suất để có ít
nhất 2 câu hỏi có thời gian hoàn thành nhiều hơn 2 phút.
Bài 0.4. Thời gian (đơn vị: phút) giữa hai khách hàng liên tiếp vào một cửa
hàng là biến ngẫu nhiên liên tục có hàm mật độ xác suất: 0 nếu 𝑥 < 0 𝑓 (𝑥) = 1 𝑒−1𝑥 4 nếu 𝑥 ≥ 0 4
a) Tính thời gian trung bình giữa hai khách hàng liên tiếp vào cửa hàng.
b) Tính xác suất để khoảng thời gian giữa 2 khách hàng liên tiếp vào cửa hàng nhỏ hơn 3 phút.
Bài 0.5. Biến ngẫu nhiên liên tục 𝑋 có hàm mật độ xác suất: 0 nếu 𝑥 ∉ (0; 4) 𝑓 (𝑥) = 1 1 𝑥 + nếu 𝑥 ∈ (0; 4) 16 8
a) Tính kì vọng và phương sai của 𝑋.
b) Tìm giá trị trung vị của 𝑋.
Bài 0.6. Cho biến ngẫu nhiên liên tục 𝑋 có đồ thị hàm mật độ xác suất 𝑓 (𝑥) như hình vẽ: 𝑓 (𝑥) 0, 75 0, 25 𝑥 0 1 3
a) Tính kì vọng và phương sai của 𝑋.
b) Tính xác suất để trong một phép thử 𝑋 nhận giá trị lớn hơn giá trị trung bình của nó.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 3
Bài 0.7. Thời gian (đơn vị: phút) để thí sinh hoàn thành một câu hỏi trắc
nghiệm là biến ngẫu nhiên liên tục có hàm mật độ xác suất: 0 nếu 𝑥 ∉ (0; 3) 𝑓 (𝑥) = 2 𝑥(3 − 𝑥) nếu 𝑥 ∈ (0; 3) 9
a) Tính thời gian trung bình và độ lệch chuẩn để hoàn thành một câu hỏi trắc nghiệm.
b) Tính thời gian hoàn thành một câu có khả năng xuất hiện nhiều nhất.
Bài 0.8. Cho X là biến ngẫu nhiên có phân phối đều trên đoạn [2; 12].
a) Tìm hàm mật độ xác suất của X.
b) Tính xác suất để X nhận giá trị từ 4 đến 8.
c) Tính xác suất để trong 5 phép thử độc lập có đúng 2 lần X nhận giá trị nhỏ hơn 4.
Bài 0.9. Thời gian hoàn thành một sản phẩm của công nhân là biến ngẫu
nhiên có phân phối đều. Sản phẩm có thời gian hoàn thành ít nhất là 5 phút,
sản phẩm có thời gian hoàn thành nhiều nhất là 10 phút.
a) Tính thời gian hoàn thành sản phẩm trung bình của công nhân.
b) Tìm trung vị của thời gian hoàn thành sản phẩm của công nhân.
c) Tìm tỷ lệ sản phẩm có thời gian hoàn thành nhiều hơn 8 phút.
Bài 0.10. Biến ngẫu nhiên Z có phân phối chuẩn hóa. Tính xác suất: a) 𝑃(𝑍 > −1,96) b) 𝑃(𝑍 < 1,65)
c) 𝑃(1,28 < 𝑍 < 1,96)
Bài 0.11. Biến ngẫu nhiên 𝑋 ∼ 𝑁(10; 9). Tính xác suất:
a) 𝑋 nhận giá trị lớn hơn 17,5.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 4
b) 𝑋 nhận giá trị không quá 7.
c) 𝑋 nhận giá trị trong khoảng từ 5,5 đến 16.
Bài 0.12. Biến ngẫu nhiên 𝑋 có phân phối Chuẩn, trung bình bằng 20,
phương sai bằng 4. Tính xác suất để:
a) 𝑋 nhận giá trị sai lệch so với giá trị trung bình của nó không quá 3 đơn vị.
b) Trong 3 phép thử độc lập, có đúng 1 lần 𝑋 nhận giá trị lớn hơn giá trị trung bình của nó.
Bài 0.13. Cho 𝑋, 𝑌 là các biến ngẫu nhiên độc lập, 𝑋 ∼ 𝑁(20; 9),𝑌 ∼
𝑁 (30; 25). Tính xác suất: a) 𝑃(𝑋 < 𝑌) b) 𝑃(3𝑋 ≥ 2𝑌 + 15)
Bài 0.14. Doanh thu trong một ngày tại một cửa hàng là biến ngẫu nhiên
có phân phối Chuẩn, doanh thu trung bình là 100 triệu, độ lệch chuẩn là 20
triệu. Tính xác suất để:
a) Doanh thu trong một ngày cao hơn 130 triệu.
b) Doanh thu trong một ngày không quá 80 triệu.
c) Doanh thu chênh lệch so với doanh thu trung bình nhiều hơn 10 triệu.
Bài 0.15. Tại một trang trại nuôi lợn, qua theo dõi người ta thấy số kg tăng
thêm trong một tháng của mỗi con lợn là biến ngẫu nhiên có phân phối
Chuẩn, trung bình là 20 kg. Tỷ lệ lợn có cân nặng tăng thêm nhiều hơn 24 kg là 2,28%.
a) Tìm tỷ lệ lợn có cân nặng tăng thêm trong một tháng ít hơn 18 kg.
b) Tính xác suất để trong 5 con lợn thì có đúng 1 con có cân nặng tăng
thêm trong tháng từ 19 kg đến 25 kg.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 5
Bài 0.16. Một cửa hàng chuyên bán điện thoại xách tay với chế độ bảo hành
tại cửa hàng, thời gian quy định bảo hành là 12 tháng. Khi bán được một
chiếc điện thoại cửa hàng có lãi 2 triệu, song nếu điện thoại hỏng trong thời
gian bảo hành thì cửa hàng phải chi phí 1,5 triệu cho việc bảo hành. Tính
tiền lãi trung bình của mỗi chiếc điện thoại, biết thời gian không phải sửa
chữa là biến ngẫu nhiên có phân phối Chuẩn, trung bình là 24 tháng, độ lệch chuẩn là 6 tháng.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 6 Bài tập tổng hợp Bài tập tự luận
Bài 0.17. Thời gian hoàn thành một sản phẩm (đơn vị: phút) là biến ngẫu
nhiên liên tục có hàm mật độ xác suất 0 nếu 𝑥 ∈ (1; 5) 𝑓 (𝑥) = 1 (5 − 𝑥) nếu 𝑥 ∉ (1; 5) 8
a) Tính xác suất để để một sản phẩm có thời gian hoàn thành nhiều hơn 4 phút.
b) Tính xác suất để trong 6 sản phẩm thì có không quá 2 sản phẩm có
thời gian hoàn thành ít hơn 3 phút.
c) Tính thời gian hoàn thành sản phẩm trung bình và phương sai thời
gian hoàn thành sản phẩm. 7 8
Đáp số: a) 0,0625 b) 0,0376 c) 𝐸 (𝑋) = , 𝑉 (𝑋) = 3 9
Bài 0.18. Thời gian chờ để thanh toán (đơn vị: phút) của khách hàng tại
một siêu thị là biến ngẫu nhiên liên tục X có hàm mật độ xác suất: 0 nếu 𝑥 ∉ (0; 30) 𝑓 (𝑥) = 30 − 𝑥 nếu 𝑥 ∈ (0; 30) 450
a) Nếu tỷ lệ khách hàng phải chờ từ 10 phút trở lên vượt quá 50% thì
siêu thị sẽ tăng thêm quầy thanh toán. Hỏi siêu thị có cần tăng thêm quầy thanh toán không?
b) Nếu xác suất trong 5 khách có từ 2 khách trở lên phải chờ quá 10
phút lớn hơn 50% phải thêm quầy thanh toán thì kết luận ở câu a có thay đổi không?
c) Tính trung bình và độ lệch chuẩn thời gian chờ để thanh toán của khách hàng.
Đáp số: a) 0,4444 b) 0,7354 c) 𝐸 (𝑋) = 10, 𝑉 (𝑋) = 50
Bài 0.19. Một nhà đầu tư dự định mua cổ phiếu A và nắm giữ trong vòng
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 7
1 tháng. Biết tỷ suất sinh lời của cổ phiếu A là biến ngẫu nhiên liên tục 𝑋.
Nếu thị trường thuận lợi thì X có thể lên đến 10%. Nếu thị trường khó khăn
thì X có thể xuống −6%. Vì không có thêm thông tin gì nên nhà đầu tư coi như X phân phối Đều.
a) Xác suất để tỷ suất sinh lời dương bằng bao nhiêu?
b) Biết lãi suất tiền gửi ngân hàng kì hạn 1 tháng là 0,375%. Nếu nhà
đầu tư quan tâm đến lãi trung bình thì nên dùng toàn bộ vốn để mua cổ
phiếu A hay gửi ngân hàng?
Đáp số: a) 𝑃(𝑋 > 0) = 0, 625 b) 𝐸 (𝑋) = 2%
Bài 0.20. Thời gian (đơn vị: giờ) từ lúc khách hàng đặt hàng thành công
trên mạng đến khi nhận được hàng là biến ngẫu nhiên liên tục có hàm mật độ xác suất: 1 𝑒−𝑥/48 nếu 𝑥 > 0 𝑓 (𝑥) = 48 0 nếu 𝑥 < 0
a) Tính xác suất để khách hàng nhận được hàng trong vòng 24 giờ kể từ lúc đặt hàng.
b) Tính thời gian chờ trung bình của khách hàng cho mỗi đơn đặt hàng.
Đáp số: a) 𝑃(𝑋 ≤ 24) = 0,3935 , b) 𝐸 (𝑋) = 48
Bài 0.21. Một người cân nhắc giữa việc mua nhà bây giờ hay gửi tiền vào
tiết kiệm với lãi suất 9% một năm để chờ một năm sau mới mua. Biết mức
tăng giá nhà là biến ngẫu nhiên có phân phối Chuẩn, trung bình là 6%, độ
lệch chuẩn là 4%. Tìm khả năng rủi ro của người đó nếu gửi tiền vào tiết
kiệm để một năm sau mua nhà. Đáp số: 0,0668
Bài 0.22. Một người cân nhắc giữa việc mua cổ phiếu của hai công ty A và
B. Tỷ suất lợi nhuận (đơn vị: %) của cổ phiếu hai công ty là các biến ngẫu
nhiên độc lập 𝑋𝐴, 𝑋𝐵, biết 𝑋𝐴 ∼ 𝑁 (12; 16), 𝑋𝐵 ∼ 𝑁 (10; 9).
a) Người đó muốn tỷ suất lợi nhuận tối thiểu là 11% thì nên mua cổ phiếu của công ty nào?
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 8
b) Người đó muốn hạn chế rủi ro bằng cách mua cổ phiếu của cả hai
công ty thì nên mua theo tỷ lệ như thế nào?
Đáp số: a) 𝑃(𝑋𝐴 > 11) = 0,5987, 𝑃(𝑋𝐵 > 11) = 0,3694
b) 36% công ty A và 84% công ty B.
Bài 0.23. Tuổi thọ của một loại sản phẩm là biến ngẫu nhiên phân phối
Chuẩn với trung bình là 4,5 năm và độ lệch chuẩn là 1,6 năm. Khi bán được
một sản phẩm thì hãng sản xuất lãi 300 nghìn đồng. Nếu sản phẩm bị hỏng
trong thời gian bảo hành miễn phí thì hãng phải chi trung bình 900 nghìn
đồng cho mỗi sản phẩm hỏng đó.
a) Tìm tỷ lệ sản phẩm có tuổi thọ dưới 18 tháng.
d) Nếu quy định thời gian bảo hành miễn phí là 18 tháng thì số tiền lãi
hãng thu được từ mỗi sản phẩm bán ra là bao nhiêu?
c) Muốn bảo hành miễn phí cho 2% số sản phẩm thì nên quy định thời
gian bảo hành miễn phí là bao nhiêu năm?
d) Nếu muốn tiền lãi trung bình trên nỗi sản phẩm bán ra là 273 nghìn
đồng thì nên quy định thời gian bảo hành miễn phí bao lâu? Đáp số:
a) 𝑃(𝑋 < 18) = 0,0304 b) 272,64 c) 1,214 năm d) 1,491 năm
Bài 0.24. Chiều cao của học sinh lớp 12 là biến ngẫu nhiên có phân phối
Chuẩn, chiều cao trung bình là 162 cm, độ lệch chuẩn là 5 cm. Một học
sinh lớp 12 được coi là có chiều cao bình thường nếu sai lệch so với chiều
cao trung bình không quá 10 cm.
a) Tìm tỷ lệ học sinh lớp 12 có chiều cao bình thường.
b) Chọn ngẫu nhiên 100 học sinh lớp 12 thì số học sinh có chiều cao
không bình thường xuất hiện nhiều nhất là bao nhiêu?
Đáp số: a) 95,45%; b) 5 học sinh
Bài 0.25. Chiều dài của một loại sản phẩm là biến ngẫu nhiên có phân phối
Chuẩn, độ lệch chuẩn là 4 cm. Tỷ lệ sản phẩm có chiều dài lớn hơn 20 cm là 10,56%.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 9
a) Tìm chiều dài trung bình của sản phẩm.
b) Lấy ngẫu nhiên 10 sản phẩm thì xác suất để có nhiều nhất 2 sản phẩm
có chiều dài nhỏ hơn 12 cm là bao nhiêu? Đáp số: a) 15 b) 0,5967
Bài 0.26. Số tiền chi cho cước điện thoại di động hằng tháng của người dân
là biến ngẫu nhiên có phân phối Chuẩn. Theo khảo sát thì số người chi cho
cước điện thoại di động hằng tháng nhiều hơn 300 nghìn đồng là 2,28%, ít
hơn 250 nghìn đồng là 84,13%. Số tiền trung bình chi cho cước điện thoại
di động hằng tháng của người dân bằng bao nhiêu?
Đáp số: 200 nghìn đồng.
Bài 0.27. Thời gian sử dụng điện thoại trong một ngày của sinh viên là biến
ngẫu nhiên có phân phối Chuẩn, trung bình là 3 tiếng. Theo khảo sát thì có
15,87% sinh viên sử dụng điện thoại nhiều hơn 5 tiếng một ngày. Tìm tỷ lệ
sinh viên sử dụng điện thoại trong một ngày: a) Ít hơn 2 tiếng
b) Từ 1 tiếng đến 6 tiếng
Đáp số: a) 30,87% b) 77,45%
Bài 0.28. Tỷ lệ người sử dụng điện thoại thông minh có vào mạng xã hội ít
nhất một lần trong một ngày là 80%. Tính xác suất để trong 400 người sử
dụng điện thoại thông minh thì có:
a) Nhiều nhất 310 người vào mạng xã hội ít nhất một lần trong ngày.
b) Ít nhất 70 người không vào mạng xã hội trong một ngày.
Đáp số: a) 0,1056 b) 0,8944
Bài 0.29. Cho 𝑋, 𝑌 là các biến ngẫu nhiên độc lập. 𝑋 ∼ 𝑁(15; 4),𝑌 ∼ 𝑁 (20; 9)
a) Tìm phân phân phối xác suất của biến ngẫu nhiên 2𝑋 − 𝑌
b) Tính 𝑃(2𝑋 − 𝑌 > 6)
Đáp số a) 2𝑋 − 𝑌 ∼ 𝑁 (10; 25) b) 0,7881
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 10
Bài 0.30. Biết lợi suất trái phiếu hai công ty A, B là các biến ngẫu nhiên
độc lập 𝑋𝐴 ∼ (11; 4), 𝑋𝐵 ∼ 𝑁 (12; 9). Một người đầu tư 40% vốn vào trái
phiếu công ty A và 60% vốn vào trái phiếu công ty B. Tính xác suất để lợi
suất thu được cao hơn 13%. Đáp số: 0,2386 Câu hỏi đúng sai
Câu 0.1. Các khẳng định dưới đây đúng hay sai? Hãy giải thích vì sao.
a) Giá trị của hàm mật độ xác suất 𝑓 (𝑥) là xác suất để biến ngẫu nhiên
liên tục 𝑋 nhận giá trị bằng 𝑥.
b) Nếu tỷ suất lợi nhuận cổ phiếu công ty Hòa Phát (mã cổ phiếu HPG)
trong một phiên giao dịch là biến ngẫu nhiên liên tục 𝑋 ∈ (−7%; 7%) thì 𝑃(𝑋 = 5%) > 0.
c) Bài thi môn Xác suất thống kê toán có 40 câu hỏi trắc nghiệm, mỗi
câu có 4 phương án trả lời và chỉ có 1 đáp án đúng. Điểm thi của sinh viên
có thể đạt được là biến ngẫu nhiên liên tục.
d) Thời gian để vận động viên chạy về đích trên quãng đường 100 m là
biến ngẫu nhiên liên tục.
Câu 0.2. Các khẳng định dưới đây đúng hay sai? Hãy giải thích vì sao.
a) Nếu 𝑈 là biến ngẫu nhiên có phân phối Đều trên khoảng (𝑎; 𝑏) thì
xác suất để 𝑈 nhận giá trị trong mọi khoảng con của (𝑎; 𝑏) đều bằng nhau.
b) Khi tham gia thị trường một công ty có thể dự đoán được lợi nhuận
thấp nhất là 𝑎 và lợi nhuận cao nhất là 𝑏, mà không có thêm thông tin gì
khác thì có thể coi lợi nhuận có phân phối Đều trên khoảng (𝑎; 𝑏).
Câu 0.3. Các khẳng định dưới đây đúng hay sai? Hãy giải thích vì sao.
a) Nếu 𝑋 ∼ 𝑁 (𝜇; 𝜎2) thì 𝜇 là giá trị có khả năng xuất hiện nhiều nhất
b) Cho 𝑋 ∼ 𝑁 (𝜇; 𝜎2). Nếu 𝜎 giảm thì đồ thị hàm mật độ xác suất có
độ rộng giảm đi và độ cao tăng lên.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 11
c) Cho 𝑍 ∼ 𝑁 (0; 1) và có hàm phân phối xác suất Φ(𝑧). Ta có: Φ(𝑧) + Φ(−𝑧) = 1
d) Nếu 𝑧𝛼 là giá trị tới hạn Chuẩn mức 𝛼 thì Φ(𝑧𝛼) = 1 − 𝛼
e) Cho 𝑋 ∼ 𝑁 (𝜇𝑋; 𝜎2𝑋),𝑌 ∼ 𝑁(𝜇𝑌; 𝜎2𝑌). Ta có: 𝑉 (2𝑋+3𝑌) = 4𝜎2𝑋+9𝜎2𝑌
Câu hỏi trắc nghiệm
Câu 0.4. Trong các phát biểu sau, phát biểu nào được đại diện bởi biến ngẫu nhiên liên tục?
A. Số tín chỉ sinh viên đăng ký trong một học kỳ
B. Số khách vào một cửa hàng trong một giờ
C. Cân nặng của sinh viên
D. Nhiệt độ sôi của nước tinh khiết
Câu 0.5. Trong các biến ngẫu nhiên dưới đây, biến ngẫu nhiên nào không
phải là biến ngẫu nhiên liên tục?
A. Số trẻ em sinh ra trong một giờ tại một bệnh viện
B. Cân nặng của trẻ sơ sinh
C. Thời gian hoàn thành một bài thi của sinh viên
D. Lợi tức trong một tháng của một loại cổ phiếu
Câu 0.6. Trong các hàm số dưới đây, hàm số nào là hàm mật độ xác suất
của biến ngẫu nhiên liên tục? 0 nếu 𝑥 ∉ (2; 6) A. 𝑓 (𝑥) = 1 𝑥 nếu 𝑥 ∈ (2; 6) 36 0 nếu 𝑥 ∉ (2; 6) B. 𝑓 (𝑥) = 1 𝑥 nếu 𝑥 ∈ (2; 6) 4
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 12 0 nếu 𝑥 ∉ (2; 6) C. 𝑓 (𝑥) = 1 𝑥 nếu 𝑥 ∈ (2; 6) 32 0 nếu 𝑥 ∉ (2; 6) D. 𝑓 (𝑥) = 1 𝑥 nếu 𝑥 ∈ (2; 6) 16
Câu 0.7. Tuổi thọ của một loại sản phẩm (đơn vị: năm) là biến ngẫu nhiên
liên tục có hàm mật độ xác suất: 0 nếu 𝑥 ∉ (0; 4) 𝑓 (𝑥) = 3 𝑥 (4 − 𝑥) nếu 𝑥 ∈ (0; 4) 32
Xác suất để sản phẩm có tuổi thọ nhiều hơn 3 năm là: A. 0,5234 C. 0,15625 B. 0,25 D. 0,5324
Câu 0.8. Tuổi thọ của một loại sản phẩm (đơn vị: năm) là biến ngẫu nhiên
liên tục có hàm mật độ xác suất: 0 nếu 𝑥 ∉ (0; 4) 𝑓 (𝑥) = 3 𝑥 (4 − 𝑥) nếu 𝑥 ∈ (0; 4) 32
Tỷ lệ sản phẩm có tuổi thọ từ 2 đến 5 năm là: A. 50% C. 75% B. 28,125% D. 71,75%
Câu 0.9. Tuổi thọ của một loại sản phẩm (đơn vị: năm) là biến ngẫu nhiên
liên tục có hàm mật độ xác suất: 0 nếu 𝑥 ∉ (0; 4) 𝑓 (𝑥) = 3 𝑥 (4 − 𝑥) nếu 𝑥 ∈ (0; 4) 32
Xác suất để trong 5 sản phẩm loại đó có đúng 1 sản phẩm có tuổi thọ nhiều hơn 2 năm là: A. 0,5 C. 0,3215 B. 0,15625 D. 0,0625
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 13
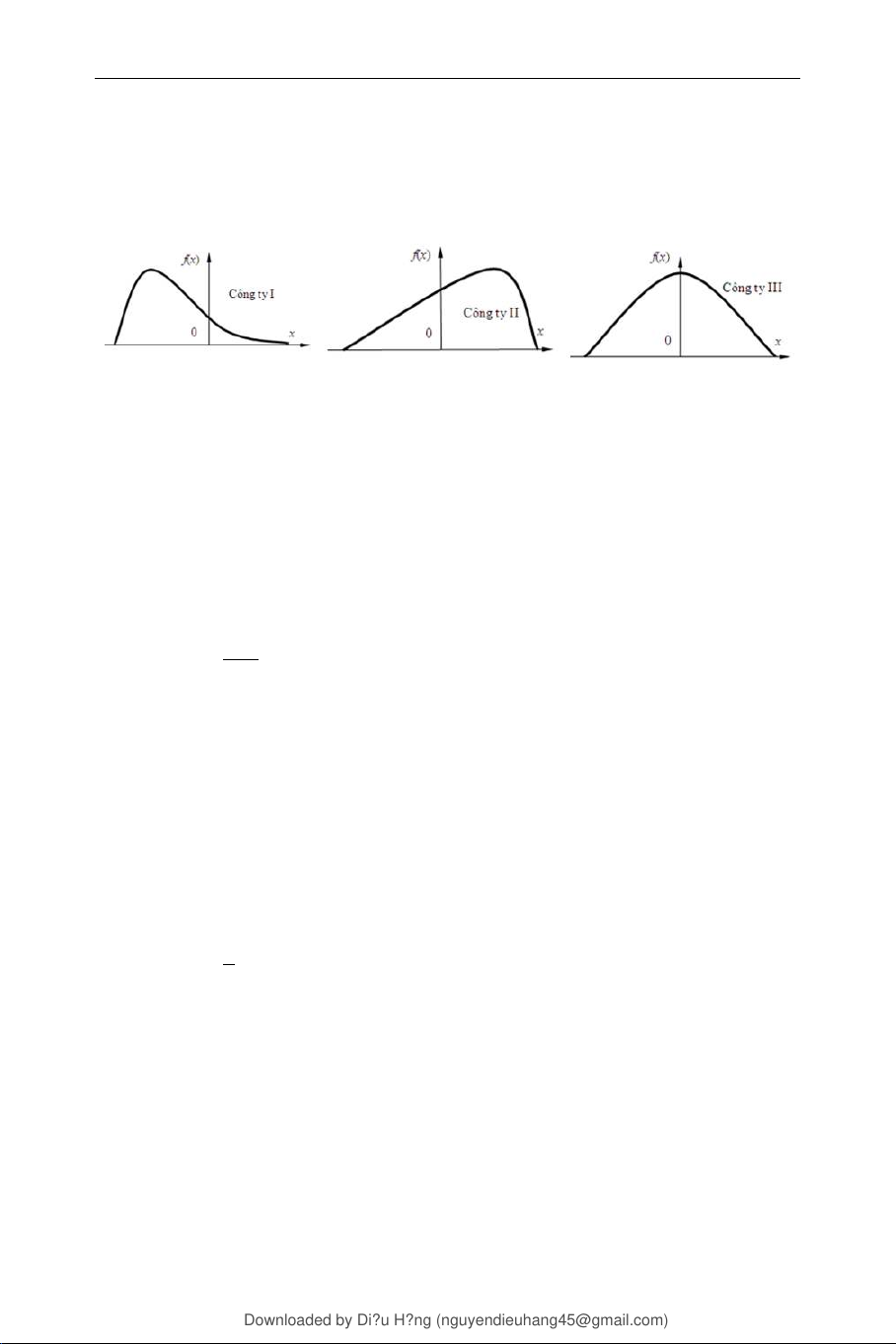
Câu 0.10. Lợi nhuận của ba công ty là ba biến ngẫu nhiên liên tục có đồ
thị hàm mật độ xác suất dưới đây:
Để xác suất có lợi nhuận dương là cao hơn thì nên chọn công ty nào? A. Công ty I. C. Công ty III. B. Công ty II.
D. Chọn công ty nào cũng được.
Câu 0.11. Biến ngẫu nhiên liên tục X có hàm mật độ xác suất: 0 nếu 𝑥 ∉ (0; 5) 𝑓 (𝑥) = 3 𝑥2 nếu 𝑥 ∈ (0; 5) 125
Giá trị kì vọng của X bằng: A. 3,75 C. 4,75 B. 2,5 D. 2,75
Câu 0.12. Mức tiêu thụ nhiên liệu (đơn vị: lít) của một loại xe máy trên
quãng đường 100 km là biến ngẫu nhiên liên tục có hàm mật độ xác suất: 0 nếu 𝑥 ∉ (2; 4) 𝑓 (𝑥) = 3 (𝑥 − 2)(4 − 𝑥) nếu 𝑥 ∈ (2; 4) 4
Mức tiêu thụ nhiên liệu trung bình trên quãng đường 100 km của loại xe máy đó là: A. 3,2 lít C. 3 lít B. 2,8 lít D. 2,5 lít
Câu 0.13. Biến ngẫu nhiên liên tục X có hàm mật độ xác suất:
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 14 0 nếu 𝑥 ∉ (0; 5) 𝑓 (𝑥) = 3 𝑥2 nếu 𝑥 ∈ (0; 5) 125 Phương sai của X bằng: A. 15 C. 11,25 B. 0,9375 D. 3,83
Câu 0.14. Mức tiêu thụ nhiên liệu của một loại xe máy trên quãng đường
100 km là biến ngẫu nhiên liên tục có hàm mật độ xác suất: 0 nếu 𝑥 ∉ (2; 4) 𝑓 (𝑥) = 3 (𝑥 − 2)(4 − 𝑥) nếu 𝑥 ∈ (2; 4) 4
Độ lệch chuẩn mức tiêu thụ nhiên liệu trên quãng đường 100 km của loại xe máy đó là: A. 0,2 C. 3,033 B. 2,49 D. 0,447
Câu 0.15. Biến ngẫu nhiên liên tục X có hàm mật độ xác suất: 0 nếu 𝑥 ∉ (1; 4) 𝑓 (𝑥) = 2 (𝑥 − 1)(4 − 𝑥) nếu 𝑥 ∈ (1; 4) 9
Giá trị mốt của biến ngẫu nhiên bằng: A. 2,8 C. 3 B. 2,5 D. 3,2
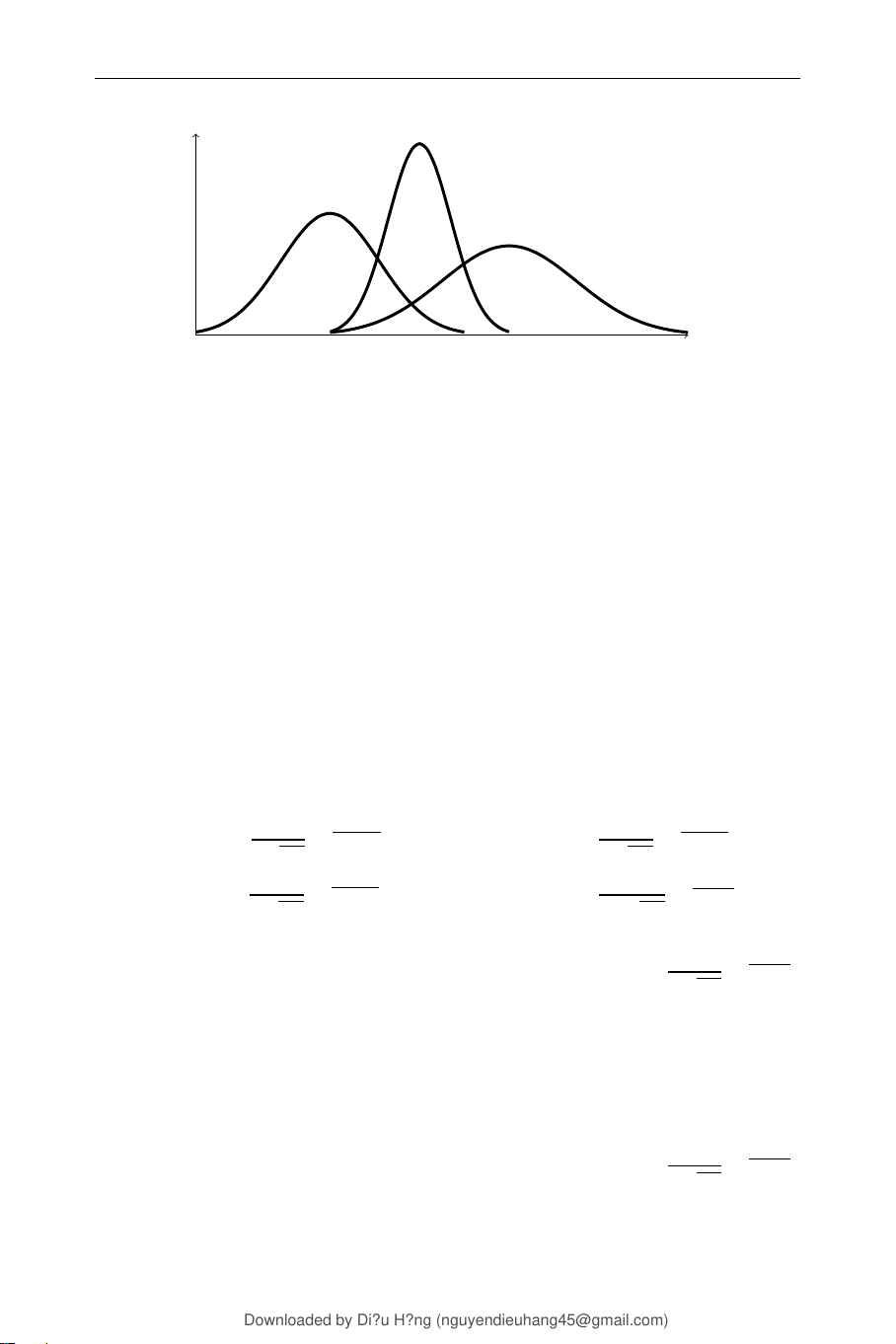
Câu 0.16. Lợi nhuận của ba công ty I, II, III là các biến ngẫu nhiên phân
phối Chuẩn, có đồ thị hàm mật độ xác suất như Hình 1. Nếu muốn chọn
công ty có lợi nhuận ổn định nhất thì chọn công ty nào? A. Công ty I C. Công ty III B. Công ty II
D. Không chọn được công ty nào
Câu 0.17. Cho lợi nhuận của ba công ty I, II, III là các biến ngẫu nhiên
phân phối Chuẩn, đồ thị hàm mật độ xác suất như trong Hình 1. Nếu muốn
chọn công ty có lợi nhuận trung bình cao nhất thì chọn công ty nào?
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 15 𝑓 (𝑥) Công ty II Công ty I Công ty III 𝑥
Hình 1 – Lợi nhuận 3 công ty A. công ty I C. công ty III B. công ty II
D. Không chọn được công ty nào
Câu 0.18. Cho 𝑋 ∼ 𝑁(𝜇; 𝜎2). Khi tăng 𝜇 và giảm 𝜎2 thì kết luận nào sau
đây đúng về đồ thị của hàm mật độ xác suất 𝑓 (𝑥)?
A. Đồ thị dịch chuyển sang phải và đỉnh của đồ thị cao lên.
B. Đồ thị dịch chuyển sang phải và đỉnh của đồ thị thấp xuống.
C. Đồ thị dịch chuyển sang trái và đỉnh của đồ thị cao lên.
D. Đồ thị dịch chuyển sang trái và đỉnh của đồ thị thấp xuống.
Câu 0.19. Cho 𝑋 ∼ 𝑁(12; 9), khi đó hàm mật độ xác suất của 𝑋 là: 1 1
A. 𝑓 (𝑥) = √ 𝑒− (𝑥−12)2 18
C. 𝑓 (𝑥) = √ 𝑒− (𝑥−12)2 6 9 2𝜋 3 2𝜋 1 1
B. 𝑓 (𝑥) = √ 𝑒− (𝑥−12)2 18 D. 𝑓 (𝑥) = √ 𝑒− (𝑥−9)2 24 3 2𝜋 12 2𝜋 1
Câu 0.20. Cho 𝑋 ∼ 𝑁(𝜇; 𝜎2) có hàm mật độ là: 𝑓 (𝑥) = √ 𝑒− (𝑥−5)2 8 . 2 2𝜋
Điều nào sau đây là đúng? A. 𝜇 = 5; 𝜎 = 4 C. 𝜇 = 4; 𝜎 = 25 B. 𝜇 = 4; 𝜎 = 5 D. 𝜇 = 5; 𝜎 = 2 1
Câu 0.21. Cho 𝑋 ∼ 𝑁(𝜇; 𝜎2) có hàm mật độ là: 𝑓 (𝑥) = √ 𝑒− (𝑥−8)2 32 . 4 2𝜋 Điều nào sau đây đúng?
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 16 A. 𝑚0 = 32 C. 𝑚0 = 8 B. 𝑚0 = 16 D. 𝑚0 = 4
Câu 0.22. Cho 𝑋 ∼ 𝑁(16; 𝜎2) . Khẳng định nào sau đây đúng?
A. 𝑃(𝑋 < 16) = 0,5
C. 𝑃(𝑋 > 4) = 0,5
B. 𝑃(𝑋 = 16) = 0,5 D. 𝑃(𝑋 = 4) = 0,5
Câu 0.23. Cho 𝑍 ∼ 𝑁(0; 1) có hàm mật độ xác suất 𝜑(𝑧) Khẳng định nào sau đây sai?
A. Giá trị lớn nhất của 𝜑(𝑧) bằng 1
B. Đồ thị hàm 𝜑(𝑧) nhận trục tung làm trục đối xứng
C. 𝑃(𝑍 > 0) = 0,5
D. 𝑃(𝑍 > 1) = 𝑃(𝑍 < −1)
Câu 0.24. Nhiệt độ trong ngày là biến ngẫu nhiên có phân phối Chuẩn với
trung bình 25 độ C, phương sai là 6,25 độ2. Xác suất để vào một thời điểm
ngẫu nhiên nhiệt độ lớn hơn 30 độ C là: A. 0,9772 C. 0,2119 B. 0,7881 D. 0,0228
Câu 0.25. Cho 𝑋 ∼ 𝑁(30; 16). Giá trị 𝑃(𝑋 > 28) là: A. 0,3085 C. 0,5497 B. 0,6915 D. 0,4503
Câu 0.26. Thời gian chờ khám bệnh tại một bệnh viện là biến ngẫu nhiên
có phân phối Chuẩn, thời gian chờ trung bình là 20 phút, phương sai là 16.
Xác suất để một bệnh nhân phải chờ không quá 15 phút là: A. 0,6227 C. 0,8944 B. 0,3773 D. 0,1056
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 17
Câu 0.27. Thời gian chờ khám bệnh tại một bệnh viện là biến ngẫu nhiên
có phân phối Chuẩn, thời gian chờ trung bình là 20 phút, phương sai là 4.
Xác suất để trong 5 bệnh nhân đến khám có không quá 2 bệnh nhân phải
chờ nhiều hơn 22 phút là: A. 0,1587 C. 0,5475 B. 0,9689 D. 0,15
Câu 0.28. Thời gian chờ khám bệnh tại một bệnh viện là biến ngẫu nhiên
có phân phối Chuẩn, thời gian chờ trung bình là 20 phút. Tỷ lệ bệnh nhân
phải chờ nhiều hơn 25 phút là 15,87%. Tỷ lệ bệnh nhân phải chờ ít hơn 15 phút là: A. 15,87% C. 42,07% B. 84,13% D. 57,93%
Câu 0.29. Thời gian chờ khám bệnh tại một bệnh viện là biến ngẫu nhiên
có phân phối Chuẩn. Biết có 15,87% bệnh nhân phải chờ ít hơn 14 phút và
2,28% bệnh nhân phải chờ nhiều hơn 26 phút. Thời gian chờ khám trung bình tại bệnh viện là: A. 17% C. 15% B. 16% D. 14%
Câu 0.30. Thời gian hoạt động tốt không phải sửa chữa của một loại điện
thoại là biến ngẫu nhiên có phân phối Chuẩn, trung bình là 5 năm, độ lệch
chuẩn là 2 năm. Nhà sản xuất quy định thời gian bảo hành là 1 năm. Khi
bán được một chiếc điện thoại nhà sản xuất có lãi 400 nghìn đồng, nếu điện
thoại hỏng trong thời gian bảo hành thì nhà sản xuất phải chi phí 700 nghìn
đồng để sửa chữa. Tiền lãi trung bình của mỗi chiếc điện thoại là:
A. 393,16 nghìn đồng
C. 384,04 nghìn đồng
B. 390,88 nghìn đồng
D. 339,16 nghìn đồng
Câu 0.31. Thời gian hoạt động tốt không phải sửa chữa của một loại điện
thoại là biến ngẫu nhiên có phân phối Chuẩn, trung bình là 5 năm, độ lệch
chuẩn là 2 năm. Nhà sản xuất muốn bảo hành cho 4% sản phẩm bán được
thì cần quy định thời gian bảo hành là:
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 18 A. 1,5 năm C. 1,2 năm B. 1 năm D. 2 năm
Câu 0.32. Thời gian hoạt động tốt không phải sửa chữa của một loại điện
thoại là biến ngẫu nhiên có phân phối Chuẩn, trung bình là 5 năm, độ lệch
chuẩn là 2 năm. Khi bán được một chiếc điện thoại nhà sản xuất có lãi 400
nghìn đồng, nếu điện thoại hỏng trong thời gian bảo hành thì nhà sản xuất
phải chi 600 nghìn cho việc bảo hành. Để tiền lãi kì vọng của mỗi sản phẩm
là 376 nghìn đồng thì thời gian quy định bảo hành là bao lâu? A. 1,5 năm C. 1,2 năm B. 1 năm D. 2 năm
Câu 0.33. Cho X, Y là các biến ngẫu nhiên độc lập, 𝑋 ∼ 𝑁(40; 16);𝑌 ∼ 𝑁 (20; 4)
Tính 𝑃(2𝑋 − 3𝑌 > 15) A. 0,8276 C. 0,5709 B. 0,6915 D. 0,5199
Câu 0.34. Giá bán sản phẩm trên thị trường là biến ngẫu nhiên có phân
phối Chuẩn. Sản phẩm A có giá bán trung bình là 200 nghìn, độ lệch chuẩn
là 30 nghìn; sản phẩm B có giá bán trung bình là 250 nghìn, độ lệch chuẩn
là 40 nghìn, giá bán hai loại sản phẩm A, B độc lập nhau. Tỷ lệ sản phẩm
A có giá bán thấp hơn sản phẩm B là: A. 97,06% C. 84,13% B. 52,58% D. 15,87%
Câu 0.35. Tỷ lệ người có xem quảng cáo về sản phẩm của công ty A trên
mạng là 15%. Xác suất để trong 200 người vào mạng có nhiều hơn 35 người
xem quảng cáo về sản phẩm của công ty A là: A. 57,77% C. 16,11% B. 42,23% D. 83,89%
Câu 0.36. Thu nhập hằng tháng của người dân tỉnh A là biến ngẫu nhiên
có phân phối Chuẩn, trung bình là 15 triệu, độ lệch chuẩn là 4 triệu. Một
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 19
người có mức thu nhập bình thường nếu thu nhập hằng tháng chênh lệch so
với thu nhập trung bình không quá 5 triệu. Tỷ lệ người có thu nhập bình thường của tỉnh A là: A. 21,13% C. 24,53% B. 78,87% D. 75,47%
Câu 0.37. Cân nặng một loại sản phẩm là biến ngẫu nhiên có phân phối
Chuẩn. Sản phẩm đạt tiêu chuẩn nếu cân nặng chênh lệch so với trung bình
không quá hai lần độ lệch chuẩn. Trong 1000 sản phẩm thì số sản phẩm đạt tiêu chuẩn trung bình là: A. 683 sản phẩm. C. 954 sản phẩm. B. 997 sản phẩm. D. 865 sản phẩm.
Câu 0.38. Cho 𝑍 ∼ 𝑁(0; 1). Biết 𝑃(𝑍 < 1, 23) = 0, 8907, khẳng định nào dưới đây đúng? A. 𝑧0,1093 = 1, 23 C. 𝑧1,23 = 0, 1093 B. 𝑧0,8907 = 1, 23 D. 𝑧1,23 = 0, 8907
Câu 0.39. Cho 𝑇 ∼ 𝑇 (20), 𝑡(20) = 1, 725. Khẳng định nào sau đây đúng? 0,05
A. 𝑃(𝑇 < −1,725) = 0,05
C. 𝑃(𝑇 > 1,725) = 0,95
B. 𝑃(𝑇 < 1,725) = 0, 05
D. 𝑃(𝑇 > −1,725) = 0,05
Câu 0.40. Cho 𝑇 ∼ 𝑇 (10). Tính 𝑃(𝑇 < 2, 228) ta được:
A. 𝑃(𝑇 < 2,228) = 0,025
C. 𝑃(𝑇 < 2,228) = 0,05
B. 𝑃(𝑇 < 2,228) = 0,975
D. 𝑃(𝑇 < 2,228) = 0,95 Câu 0.41. Cho 2
𝜒2 ∼ 𝜒2(10), 𝜒 (10) = 18,307. 0,05
Khẳng định nào sau đây đúng?
A. 𝑃(𝜒2 < 18,307) = 0,05
C. 𝑃(𝜒2 < −18,307) = 0,05
B. 𝑃(𝜒2 > 18,307) = 0,95
D. 𝑃(𝜒2 < 18,307) = 0,95
Câu 0.42. Cho 𝜒2 ∼ 𝜒2(6). Tính 𝑃(𝜒2 > 10, 64) ta được:
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 20
A. 𝑃(𝜒2 > 10,64) = 0,95
C. 𝑃(𝜒2 > 10,64) = 0,1
B. 𝑃(𝜒2 > 10,64) = 0,975
D. 𝑃(𝜒2 > 10,64) = 0,9
Câu 0.43. Cho 𝐹 ∼ 𝐹(10; 8), 𝑓 (10,8) = 4,295. 0,025
Khẳng định nào sau đây đúng?
A. 𝑃(𝐹 < −4,295) = 0,025
C. 𝑃(𝐹 > 4,295) = 0,025
B. 𝑃(𝐹 > 4,295) = 0,975
D. 𝑃(𝐹 < 4,295) = 0,025
Câu 0.44. Cho 𝑍1 ∼ 𝑁(0; 1), 𝑍2 ∼ 𝑁(0; 1), 𝑍1, 𝑍2 là các biến ngẫu nhiên
độc lập. Đặt 𝑋 = 𝑍2 + 𝑍2. Tính 𝑃(𝑋 > 0, 211) ta được: 1 2
A. 𝑃(𝑋 > 0,2107) = 0,95
C. 𝑃(𝑋 > 0,2107) = 0,975
B. 𝑃(𝑋 > 0,2107) = 0,9
D. 𝑃(𝑋 > 0,2107) = 0,1
Câu 0.45. Cho 𝜒2 ∼ 𝜒2(3), 𝜒2 ∼ 𝜒2(3), 𝜒2, 𝜒2 là các biến ngẫu nhiên độc 1 2 1 2 𝜒2
lập. Đặt 𝑋 = 1 . Tính 𝑃(𝑋 > 15, 44) ta được: 𝜒22
A. 𝑃(𝑋 > 15,44) = 0,25
C. 𝑃(𝑋 > 15,44) = 0,025
B. 𝑃(𝑋 > 15,44) = 0,01
D. 𝑃(𝑋 > 15,44) = 0,05
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 1 Bài tập
Bài 0.1. Xét tổng thể là tất cả thanh niên Việt Nam 19 tuổi ở thời điểm hiện
tại. Hãy trả lời các câu hỏi sau:
a) Kích thước tổng thể là hữu hạn hay vô hạn?
b) Cho ví dụ một dấu hiệu nghiên cứu định tính có thể thu thập dữ liệu
từ tổng thể trên. Hãy dùng biến ngẫu nhiên để đại diện và lượng hóa
cho dấu hiệu nghiên cứu vừa lấy ví dụ, cho biết biến ngẫu nhiên có
thể nhận những giá trị nào?
c) Cho ví dụ một dấu hiệu nghiên cứu định lượng có thể thu thập dữ liệu
từ tổng thể trên. Hãy dùng biến ngẫu nhiên để đại diện và lượng hóa
cho dấu hiệu nghiên cứu vừa lấy ví dụ, cho biết biến ngẫu nhiên có
thể nhận những giá trị nào?
d) Nếu muốn thu thập dữ liệu cho hai biến ở câu (a) và câu (b) trên toàn
bộ của tổng thể thì có thể gặp khó khăn thế nào?
Bài 0.2. Sử dụng số liệu của ví dụ ?? trang ??, hãy:
a) Xác định dấu hiệu nghiên cứu và cho biết dấu hiệu đó thuộc loại định tính hay định lượng.
b) Lập bảng phân phối tần số của tổng thể. Tính các tham số đặc trưng
của tổng thể: trung bình, phương sai, độ lệch chuẩn, hệ số biến thiên,
hệ số bất đối xứng, hệ số nhọn.
c) Dùng biến ngẫu nhiên gốc 𝑋 để đại diện cho dấu hiệu nghiên cứu.
Tính các tham số đặc trưng của 𝑋: trung bình, phương sai, độ lệch
chuẩn, hệ số biến thiên, hệ số bất đối xứng, hệ số nhọn. So sánh kết
quả tính toán được với kết quả ở câu (b).
Bài 0.3. Giả sử tổng thể là tất cả học sinh dự thi môn Toán trong kì thi
Trung học phổ thông năm 2022. Sử dụng dữ liệu trong bài báo "Điểm thi
Toán tốt nghiệp THPT 2022: Có 35 điểm 10, hơn 12.000 điểm 9", báo
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 2
điện tử dantri.com.vn (https://dantri.com.vn/giao-duc-huong-nghiep/diem-
thi-toan-tot-nghiep-thpt-2022-co-35-diem-10-hon-12000-diem-9-2022072 3224937276.htm).
a) Dựa vào đồ thị trong bài báo, cho biết giá trị Mốt của điểm thi Toán
bằng bao nhiêu? Tần số tương ứng của giá trị đó.
b) Dựa vào hình dáng đồ thị trong bài báo, hãy dự đoán dấu của hệ số
bất đối xứng của điểm thi Toán.
c) Dựa vào đồ thị trong bài báo, hãy lập bảng phân phối tần số của điểm thi Toán.
d) Tính trung bình, phương sai, độ lệch chuẩn, hệ số bất đối xứng, hệ
số nhọn của điểm thi Toán (có thể sử dụng phần mềm Excel để tính
toán). Hệ số bất đối xứng tính được có dấu giống như dự đoán ở câu (b) hay không? Bài 0.4.
a) Hãy phân biệt khái niệm, kí hiệu của mẫu ngẫu nhiên và mẫu cụ thể.
b) Xét tổng thể tất cả sinh viên đang học năm thứ nhất đại học tại Việt
Nam, dấu hiệu nghiên cứu là tuổi của sinh viên. Hãy lấy ví dụ mẫu
ngẫu nhiên kích thước 10 và một mẫu cụ thể kích thước 10 được rút từ tổng thể này.
Bài 0.5. Hãy cho ví dụ một mẫu cụ thể kích thước 5 được rút từ (các) tổng thể sau:
a) Tổng thể tất cả các cuốn sách đã được xuất bản trong năm vừa qua,
dấu hiệu nghiên cứu chiều rộng của sách.
b) Tổng thể tất cả các tờ báo điện tử ở Việt Nam.
c) Tổng thể tất cả người lao động làm việc tại một tập đoàn lớn, dấu hiệu
nghiên cứu là lương hằng tháng theo hợp đồng lao động.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 3
Bài 0.6. Sử dụng số liệu trong ví dụ 5.5, theo cách 3 ta có bảng sau: Nhóm tuổi
20 - 29 30 - 39 40 - 49 50 - 59 Số người ( 𝑓𝑖) 25 60 80 35
Hãy tính các thống kê trên mẫu: trung bình, phương sai, độ lệch chuẩn, hệ
số biến thiên, hệ số bất đối xứng, hệ số nhọn.
Bài 0.7. Tung một con xúc xắc cân đối, đồng chất trên mặt phẳng cứng hai
lần độc lập với nhau thì số chấm xuất hiện tương ứng là 𝑋1, 𝑋2. Lập bảng
phân phối xác suất, tính kì vọng toán và phương sai của trung bình mẫu 𝑋 ¯ 1 + 𝑋2 𝑋 = . 2
Bài 0.8. Sử dụng số liệu của Bài tập 0.2 trang 1. Từ tổng thể đang xét, chọn
ngẫu nhiên hai lao động thì lương của họ lần lượt là 𝑋1 và 𝑋2 và độc lập với nhau.
a) Lập bảng phân phối xác suất của 𝑋1 và 𝑋2.
b) Lập bảng phân phối xác suất của lương trung bình của hai lao động
đã chọn (đây là trung bình mẫu của mẫu kích thước 2, kí hiệu ¯ 𝑋). Từ
đó, tính kì vọng toán và phương sai của của ¯
𝑋, so sánh với kì vọng
toán và phương sai của biến ngẫu nhiên 𝑋 trong Bài tập 0.2.
c) Lập bảng phân phối xác suất của phương sai của lương của hai lao
động đã chọn (đây là phương sai mẫu của mẫu kích thước 2, kí hiệu
là 𝑆2). Tính kì vọng toán của 𝑆2 và so sánh với phương sai của biến
ngẫu nhiên 𝑋 trong Bài tập 0.2.
Bài 0.9. Tiền chi trên mỗi hóa đơn của khách hàng vào mua sắm tại siêu
thị A là biến ngẫu nhiên phân phối Chuẩn với trung bình là 485 nghìn đồng
và độ lệch chuẩn là 64 nghìn đồng. Người quản lý siêu thị lấy ngẫu nhiên
bốn hóa đơn vừa được thanh toán.
a) Hãy xác định phân phối xác suất của tổng số tiền thanh toán của bốn hóa đơn.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 4
b) Tính xác suất để tổng số tiền thanh toán trên bốn hóa đơn ít hơn 2 triệu đồng.
Bài 0.10. Số tiền chi cho việc khám chữa bệnh của một hộ gia đình ở khu
vực A trong một năm có trung bình là 4,62 triệu đồng và độ lệch chuẩn là 0,75 triệu đồng.
a) Cần thêm điều kiện gì để có thể trả lời câu hỏi "với xác suất 0,95, số
tiền chi cho việc khám chữa bệnh trung bình của 4 hộ gia đình tối
thiểu bằng bao nhiêu?". Giả sử điều kiện được thỏa mãn, hãy trả lời câu hỏi trên.
b) Với xác suất 0,95, số tiền chi cho việc khám chữa bệnh trung bình
của 64 hộ gia đình tối thiểu bằng bao nhiêu? Trong trường hợp này
có cần thiết thêm điều kiện ở câu (a) hay không? Tại sao?
Bài 0.11. Giả sử thu nhập hằng tháng của nhân viên giao hàng tại công ty
A phân phối Chuẩn với trung bình là 10 triệu đồng và độ lệch chuẩn là 1,2 triệu đồng.
a) Chọn ngẫu nhiên 16 nhân viên giao hàng của công ty A, với xác suất
0,99 thì lương trung bình của họ tối đa là bao nhiêu triệu đồng?
b) Chọn ngẫu nhiên 100 nhân viên giao hàng của công ty A, với xác suất
0,99 thì lương trung bình của họ tối đa là bao nhiêu triệu đồng?
c) So sánh kết quả của câu (a) và câu (b) và nhận xét.
Bài 0.12. Chiều cao của thanh niên ở một vùng phân phối Chuẩn với trung
bình là 167 cm và phương sai là 64 cm2. Đo chiều cao của 16 thanh niên:
a) Tìm xác suất để chiều cao trung bình của họ vượt quá 1,7 m.
b) Với xác suất 0,95 thì chiều cao trung bình của họ tối đa là bao nhiêu?
c) Với xác suất 0,9 thì chiều cao trung bình của họ nằm trong khoảng
đối xứng nào xung quanh giá trị trung bình 167 cm. So sánh cận trên
của khoảng vừa tìm được với kết quả ở câu (b) và nhận xét.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 5
Bài 0.13. Chuỗi cửa hàng thời trang A cho biết cứ 10 người khách vào cửa
hàng của chuỗi thì có đến 7 người quyết định mua hàng. Giả sử thông tin
trên là đúng. Quan sát ngẫu nhiên 100 khách vừa vào một cửa hàng của chuỗi này:
a) Tìm xác suất trong đó có không quá 65 người quyết định mua hàng.
b) Với xác suất 0,95, trong số 100 khách đó sẽ có tối thiểu bao nhiêu người mua hàng.
c) Nếu sau khi quan sát thì chỉ thấy có 50 khách mua hàng, ít hơn so với
kết quả ở câu (b), bạn hãy dự đoán nguyên nhân của sự sai lệch này.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 6 Bài tập tổng hợp
Bài 0.14. Thời gian sử dụng mạng xã hội trong ngày của người Việt Nam
có phân phối Chuẩn với trung bình là 4 giờ, độ lệch chuẩn là 0,8 giờ.
a) Hỏi ngẫu nhiên một người, tính xác suất để thời gian sử dụng mạng
xã hội của người này nằm trong khoảng từ 3 giờ đến 6 giờ mỗi ngày?
b) Khảo sát ngẫu nhiên 100 người, tính xác suất để thời gian sử dụng
mạng xã hội trung bình của 100 người này trên 4,2 giờ mỗi ngày?
Đáp số: a) 0,8882, b) 0,9938
Bài 0.15. Theo một khảo sát thì 83% hộ gia đình có máy tính cá nhân.
a) Trong một mẫu ngẫu nhiên với 175 hộ được chọn, hãy tính xác suất
để có từ 140 đến 150 hộ gia đình có máy tính cá nhân.
b) Với xác suất là 95% thì tỉ lệ hộ có máy tính cá nhân trong 200 hộ
được chọn ngẫu nhiên tối đa là bao nhiêu?
Đáp số: a) 0,7108. b) 87,37%
Bài 0.16. Thu nhập hằng tháng của nhân viên một công ty phân phối Chuẩn
với trung bình là 15 triệu đồng, phương sai là 4 (triệu đồng2). Lấy ngẫu
nhiên 16 nhân viên để khảo sát về thu nhập. Xác suất để thu nhập trung
bình hằng tháng của 16 nhân viên này không vượt quá 15,5 triệu đồng là bao nhiêu? Đáp số: 0,8413
Bài 0.17. Tỉ lệ phế phẩm của nhà máy A là 10%. Lấy ngẫu nhiên 100 sản
phẩm, xác suất để tỉ lệ phế phẩm của mẫu ít nhất bằng 16% là bao nhiêu? Đáp số: 0,0228
Bài 0.18. Tỷ lệ học sinh xếp loại học tập trung bình của một trường là 10%.
Với xác suất 0,9772, lấy ngẫu nhiên 400 học sinh của trường thì có tối đa là
bao nhiêu học sinh có xếp loại học tập trung bình? Đáp số: 52
Bài 0.19. Cân nặng của một loại sản phẩm là biến ngẫu nhiên phân phối
Chuẩn với trung bình là 20 kg và độ phân tán là 1,6 kg. Lấy ngẫu nhiên 36
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 7
sản phẩm, với xác suất 0,9332 thì cân nặng trung bình của 36 sản phẩm này tối đa là bao nhiêu? Đáp số: 20,4
Bài 0.20. Chiều dài của một loại sản phẩm là một biến ngẫu nhiên phân
phối chuẩn với trung bình là 100 cm và phương sai là 16 cm2. Kiểm tra
ngẫu nhiên 25 sản phẩm loại này.
a) Tính khả năng để chiều dài trung bình của 25 sản phẩm này nhỏ hơn 101 cm.
b) Với xác suất là 0,9452 thì chiều dài trung bình của 25 sản phẩm trên ít nhất là bao nhiêu?
Đáp số: a) 0,8944 ; b) 98,72 cm
Bài 0.21. Tỉ lệ chính phẩm của nhà máy A là 90%. Lấy ngẫu nhiên 100 sản phẩm của nhà máy này.
a) Tính xác suất để trong mẫu trên có ít nhất 85% là chính phẩm.
b) Với xác suất là 0,9192, trong số sản phẩm được lấy ra có tối đa bao nhiêu chính phẩm? Đáp số: a) 0,9525; b) 94
Bài 0.22. Chiều cao của thanh niên vùng A là biến ngẫu nhiên có phân phối
Chuẩn, với độ lệch chuẩn là 5 cm. Chọn ngẫu nhiên 25 thanh niên.
a) Tính xác suất để chiều cao trung bình của 25 thanh niên này sai lệch
so với chiều cao trung bình của thanh niên toàn vùng trên 2 cm.
b) Tính xác suất để độ phân tán của chiều cao của 25 thanh niên này không vượt quá 3,8 cm. Đáp số: a) 0,0456; b) 0,05
Bài 0.23. Tỉ lệ phế phẩm của nhà máy A là 10%. Lấy ngẫu nhiên 100 sản
phẩm của nhà máy để xem xét.
a) Tính xác suất để tỉ lệ phế phẩm trong mẫu sai lệch so với tỉ lệ tổng thể không vượt quá 6%?
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 8
b) Với xác suất là 0,3174 thì tỉ lệ phế phẩm trong số 100 sản phẩm này ít nhất là bao nhiêu? Câu hỏi trắc nghiệm
Câu 0.1. Đại lượng được tính toán trên số liệu tổng thể được gọi là: A. Biến ngẫu nhiên C. Thống kê B. Tham số D. Quy luật
Câu 0.2. Độ lệch chuẩn của thống kê trung bình mẫu có kích thước từ 2 trở lên:
A. Bằng với độ lệch chuẩn của tổng thể
B. Tăng lên khi kích thước mẫu tăng lên
C. Luôn luôn nhỏ hơn độ lệch chuẩn tổng thể
D. Lớn hơn độ lệch chuẩn tổng thể
Câu 0.3. Điều nào sau đây đúng với thống kê trung bình mẫu
A. Luôn phân phối Chuẩn
B. Có phương sai bằng phương sai tổng thể
C. Có kì vọng toán là trung bình tổng thể
D. Luôn bằng trung bình tổng thể
Câu 0.4. Phát biểu nào là đúng đối với thống kê tỉ lệ mẫu ˆ𝑝
A. Bằng tỉ lệ tổng thể
B. Có phương sai tăng lên khi tăng kích thước mẫu
C. Có kì vọng bằng tỉ lệ tổng thể
D. Luôn có phân phối Chuẩn
Câu 0.5. Trung bình tổng thể là 30, phương sai tổng thể là 20. Từ tổng thể
đó rút ra một mẫu ngẫu nhiên kích thước là 10. Khi đó, độ lệch chuẩn của
trung bình mẫu xấp xỉ bằng:
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 9 A. 2 B. 3 C. 1, 4 D. 1, 7
Câu 0.6. Tổng thể phân phối chuẩn với trung bình là 200 và phương sai là
25. Từ tổng thể lập một mẫu ngẫu nhiên kích thước 100 thì trung bình mẫu
sẽ có quy luật phân phối là: A. 𝑁 (200; 25) C. 𝑁 (2; 25) B. 𝑁 (200; 0,25) D. 𝑁 (2; 0,25)
Câu 0.7. Tỉ lệ người bị mắc bệnh phổi ở vùng A là 15%. Điều tra một mẫu
400 người dân sống trong vùng được chọn ngẫu nhiên. Xác suất để trong
mẫu có trên 45 người bị mắc bệnh phổi xấp xỉ bằng: A. 0,0179 B. 0,9821 C. 0,0094 D. 0,9906
Câu 0.8. Tỷ lệ sinh viên nữ của một trường đại học là 50%. Nếu lấy mẫu
ngẫu nhiên 100 sinh viên của trường này thì xác suất tỉ lệ sinh viên nữ trong
mẫu đó nhỏ hơn 45% gần bằng: A. 0,8413 B. 0,1587 C. 0,0228 D. 0,9772
Câu 0.9. Mức chi cho tiền điện trong tháng của hộ gia đình có phân phối
Chuẩn với trung bình là 2,5 triệu đồng, độ lệch chuẩn là 0,6 triệu đồng.
Chọn một mẫu ngẫu nhiên 36 hộ gia đình. Xác suất để mức chi cho tiền
trung bình của 36 hộ này nhỏ hơn 2,2 triệu đồng là bao nhiêu? A. 0,9987 B. 0,0013 C. 0,3085 D. 0,6915
Câu 0.10. Tiền lương của nhân viên phân phối Chuẩn với trung bình là
200$ / tuần, độ lệch chuẩn là 50$ / tuần. Chọn ngẫu nhiên 100 nhân viên
để phỏng vấn. Xác suất để lương trung bình của họ nằm trong khoảng 195
đến 205 $/ tuần là bao nhiêu? A. 84,13% B. 68,26% C. 34,13% D. 15,87%
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 1 Bài tập
Bài 0.1. Cho tổng thể với biến ngẫu nhiên gốc 𝑋 có trung bình là 𝜇, phương
sai là 𝜎2. Từ tổng thể, lấy mẫu ngẫu nhiên 𝑊 = (𝑋1, 𝑋2, 𝑋3, 𝑋4). Trong các
thống kê sau, thống kê nào là ước lượng không chệch của trung bình tổng
thể? Thống kê nào là ước lượng hiệu quả nhất của trung bình tổng thể? 𝑋 a) 1 + 2𝑋2 + 3𝑋3 + 4𝑋4 𝐺1 = 10 𝑋 b) 1 + 𝑋2 + 𝑋3 + 𝑋4 𝐺2 = 10 𝑋 c) 1 + 𝑋2 + 𝑋3 𝐺3 = 3
d) 𝐺4 = 0, 15𝑋1 + 0, 25𝑋2 + 0, 5𝑋3 + 0, 1𝑋4
Bài 0.2. Chứng minh các kết luận sau:
a) Trung bình mẫu là ước lượng vững của trung bình tổng thể.
b) Tỉ lệ mẫu là ước lượng vững của tỉ lệ tổng thể.
Bài 0.3. Từ tổng thể lập hai mẫu ngẫu nhiên độc lập với kích thước mẫu,
trung bình mẫu, phương sai mẫu và tỉ lệ mẫu lần lượt là 𝑛1, 𝑛2, ¯ 𝑋1, ¯ 𝑋2, 𝑆2, 𝑆2, ˆ 𝑝 1 2 1, ˆ 𝑝2.
Với giá trị nào của 𝛼 (0 ≤ 𝛼 ≤ 1) thì ước lượng 𝐺𝛼 là hiệu quả nhất trong
các lớp ước lượng sau:
a) 𝐺𝛼 = 𝛼 ¯𝑋1 + (1 − 𝛼) ¯𝑋2
b) 𝐺𝛼 = 𝛼 ˆ𝑝1 + (1 − 𝛼) ˆ𝑝2 2𝜎4
c) 𝐺𝛼 = 𝛼𝑆2 + (1 − 𝛼)𝑆2, trong đó 𝑉 (𝑆2 , 𝑖 1 2 𝑖 ) = = 1, 2. 𝑛𝑖 − 1
Bài 0.4. Gọi 𝑝 là tỉ lệ phế phẩm do một máy sản xuất, 𝑋 = 1 nếu sản phẩm
là phế phẩm, 𝑋 = 0 nếu sản phẩm là chính phẩm.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 2
a) Nếu 𝑝 = 0,17 thì mẫu nào sau đây là hợp lí nhất? 𝑤1 = (0, 1, 1, 0, 0, 0, 1); 𝑤2 = (0, 1, 1, 0, 0, 1, 1) 𝑤3 = (0, 1, 1, 0, 1, 1, 1); 𝑤4 = (0, 1, 1, 0, 1, 1, 1)
b) Nếu mẫu điều tra được là 𝑤0 = (0, 1, 1, 0, 0, 1, 0) thì giá trị nào sau
đây là hợp lí nhất cho 𝑝? ˆ 𝑝1 = 0,3; ˆ 𝑝2 = 0,4; ˆ 𝑝3 = 0,5; ˆ 𝑝4 = 0,6
Bài 0.5. Để ước lượng tỉ lệ sinh viên hiện có công việc làm thêm hay không,
người ta hỏi ngẫu nhiên 10 sinh viên thì 7 em trả lời có.
a) Dùng biến ngẫu nhiên 𝑋 để đại diện và lượng hóa cho dấu hiệu nghiên
cứu sinh viên có đi làm thêm hay không. Hãy xác định phân phối xác suất của 𝑋.
b) Viết công thức hàm hợp lí cho bài toán này, từ đó cho biết giá trị nào
sau đây là ước lượng hợp lí nhất cho tỉ lệ sinh viên hiện có công việc làm thêm: 0,6; 0,7; 0,8.
Bài 0.6. Giả sử cân nặng của sản phẩm phân phối Chuẩn. Cân ngẫu nhiên
25 sản phẩm thì tìm được trung bình là 186 g và độ lệch chuẩn mẫu là 16 g. Với độ tin cậy 95%.
a) Hãy ước lượng khoảng tin cậy đối xứng của cân nặng trung bình của sản phẩm.
b) Muốn giữ nguyên độ tin cậy ở câu (a) và độ dài khoảng tin cậy giảm
2 lần thì phải cân bao nhiêu sản phẩm? Tổng quát câu trả lời trong
trường hợp muốn độ dài khoảng tin cậy giảm 𝑘 lần.
Bài 0.7. Biết chi tiêu hằng tháng của hộ gia đình phân phối Chuẩn. Điều
tra chi tiêu của 50 hộ gia đình thì tính được trung bình là 13 triệu/tháng và
phương sai là 4,5 (triệu/tháng)2. Với độ tin cậy 95%, hãy ước lượng độ phân
tán về chi tiêu hằng tháng của hộ gia đình?
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 3
Bài 0.8. Điều tra ngẫu nhiên 200 người dân ở một vùng thì có 176 người có bảo hiểm y tế.
a) Với độ tin cậy 95% hãy ước lượng bằng khoảng tin cậy đối xứng tỷ lệ
người dân vùng này có bảo hiểm y tế.
b) Muốn giữ nguyên độ tin cậy ở câu (a) mà sai số của ước lượng không
vượt quá 2% thì phải điều tra thêm bao nhiêu người nữa?
c) Biết cả khu dân cư này có 12.000 người. Với độ tin cậy 90%, hãy ước
lượng số người dân của khu này chưa có bảo hiểm y tế.
Bài 0.9. Tại một khu vực dân cư, điều tra ngẫu nhiên 400 hộ gia đình về
mức chi tiền điện hằng tháng, tìm được trung bình mẫu là 945 nghìn đồng
và độ lệch chuẩn mẫu là 158 nghìn đồng, trong đó có 38 hộ chi tiền điện
từ 1,2 triệu đồng/tháng trở lên. Giả sử mức chi tiền điện hằng tháng của hộ
gia đình phân phối Chuẩn. Với độ tin cậy 90%, hãy ước lượng
a) Mức chi tiền điện trung bình tối đa của một hộ gia đình.
b) Độ phân tán tối thiểu của mức chi tiền điện hằng tháng của các hộ gia đình ở khu này.
c) Tỉ lệ hộ gia đình chi tiền điện hằng tháng từ 1,2 triệu đồng trở lên tối
thiểu là bao nhiêu phần trăm?
Bài 0.10. Sau khi thử nghiệm trên 160 bệnh nhân thì nhóm nghiên cứu báo
cáo rằng tỉ lệ bệnh nhân khỏi bệnh A khi dùng loại thuốc B là từ 82,06%
đến 87,94%. Biết đây là kết quả ước lượng bằng khoảng tin cậy đối xứng.
a) Hãy tìm số bệnh nhân đã khỏi bệnh trong 160 người thử nghiệm.
b) Cho biết độ tin cậy của ước lượng bằng bao nhiêu?
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 4 Bài tập tổng hợp Câu hỏi đúng sai
Bài 0.11. Cho biết các kết luận dưới đây đúng hay sai, giải thích?
a) Trong các ước lượng điểm của một tham số tổng thể, ước lượng nào
có phương sai bé hơn là ước lượng tốt hơn.
b) Trong các ước lượng điểm của một tham số tổng thể, ước lượng nào
có phương sai bé nhất là ước lượng hiệu quả nhất.
c) Trong hai ước lượng điểm không chệch, ước lượng nào có phương sai
nhỏ hơn là ước lượng tốt hơn.
d) Trung bình mẫu là ước lượng đủ của trung bình tổng thể.
e) Các giá trị của một thống kê là ước lượng không chệch tính trên các
mẫu cụ thể đều đúng bằng giá trị của tham số tổng thể.
f) Dựa trên một mẫu ngẫu nhiên, ta có thể tìm được nhiều ước lượng
không chệch cho một tham số của tổng thể.
g) Trong các bài toán ước lượng khoảng, với một độ tin cậy cho trước,
ta có vô số khoảng tin cậy cho các tham số đang cần ước lượng.
h) Muốn giảm sai số của ước lượng khi ước lượng tỉ lệ tổng thể bằng
khoảng tin cậy đối xứng thì cần giảm bớt kích thước mẫu (nếu độ tin cậy không đổi).
i) Trung bình mẫu là ước lượng không chệch cho trung bình của tổng thể phân phối Chuẩn.
j) Phương sai mẫu là ước lượng không chệch cho phương sai của một
tổng thể có phân phối Chuẩn.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 5 Bài tập tự luận
Bài 0.12. Nghiên cứu thời gian làm các thủ tục hành chính của người bệnh
để vào nhập viện ở một bệnh viện, người ta tiến hành khảo sát 50 người
bệnh thì tính được thời gian làm thủ tục hành chính trung bình là 20,5 phút,
độ lệch chuẩn là 4,2 phút. Giả thiết thời gian làm thủ tục hành chính để
nhập viện là biến ngẫu nhiên có phân phối chuẩn. Cho 𝑡(𝑛>30) 0,01 = 2,326; 𝑡 (𝑛>30) 0,025 = 1,96; 𝑡 (𝑛>30) 0,05 = 1,645; 𝑡 (𝑛>30) 0,1 = 1,282; 2 2 2 2 𝜒 (49) (49) (49) (49)
0,025 = 70,22; 𝜒0,975 = 31,55; 𝜒0,05 = 66,34; 𝜒0,95 = 33,93
a) Thời gian làm thủ tục hành chính nhập viện trung bình của người
bệnh nằm trong khoảng nào với độ tin cậy 95%.
b) Ước lượng thời gian làm thủ tục hành chính nhập viện trung bình tối
thiểu của người bệnh với độ tin cậy 0,9?
c) Để sai số của ước lượng không vượt quá 0,8 (phút) và giữ nguyên độ
tin cậy ở câu (a) thì cần phải khảo sát ít nhất bao nhiêu người bệnh?
d) Ước lượng phương sai thời gian làm thủ tục hành chính nhập viện của
bệnh nhân với độ tin cậy 0,95 bằng khoảng tin cậy hai phía.
Đáp số: a) (19,336 ; 21,664); b) 19,739; c) 106 ; d) (12,309 ; 27,396)
Bài 0.13. Kiểm tra ngẫu nhiên 500 sản phẩm trong một lô hàng, thấy có
205 sản phẩm do nhà máy A sản xuất.
Cho 𝑧0,025 = 1, 96; 𝑧0,01 = 2,33; 𝑧0,025 = 1,96; 𝑧0,05 = 1,645; 𝑧0,1 = 1,28
a) Ước lượng tỉ lệ sản phẩm do nhà máy A sản xuất trong lô hàng này
bằng khoảng tin cậy đối xứng với độ tin cậy 0,95.
b) Nếu muốn độ dài khoảng tin cậy ở câu (a) không vượt quá 4% thì cần
kiểm tra ít nhất bao nhiêu sản phẩm của lô hàng?
c) Nếu lô hàng có tổng cộng 100.000 sản phẩm, thì sẽ có tối đa bao
nhiêu sản phẩm do nhà máy A sản xuất, với độ tin cậy 90%.
d) Biết rằng nhà máy A đã cung cấp 2800 sản phẩm vào lô hàng này.
Với độ tin cậy 99% hãy ước lượng tối thiểu số lượng sản phẩm của toàn bộ lô hàng.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 6
Đáp số: a) (0,3669 ; 0,4531); b) 2324; c) 44618; d) 6071
Bài 0.14. Mức chi cho y tế trong một năm của hộ gia đình ở khu vực thành
phố là biến ngẫu nhiên có phân phối Chuẩn. Điều tra ngẫu nhiên 100 hộ
gia đình ở khu vực thành phố thì thấy mức chi cho y tế bình quân là 15,8
triệu/năm với độ lệch chuẩn 2,5 triệu/năm. Cho 2 2 𝑡 (𝑛>30) (99) (99) 0,025 = 1,96; 𝑡 (𝑛>30) 0,05
= 1,645; 𝜒0,025 = 128,4; 𝜒0,975 = 73,36; 2 2 𝜒 (99) (99) 0,1 = 117,44; 𝜒0,9 = 81,45
a) Hãy ước lượng độ biến động của mức chi cho y tế trong năm của các
hộ gia đình thành phố (đo bằng phương sai) với độ tin cậy 0,95.
b) Ước lượng tối đa độ lệch chuẩn của mức chi tiêu cho y tế của các hộ
gia đình khu vực thành phố với độ tin cậy 90%.
c) Hãy tìm độ dài khoảng tin cậy khi ước lượng mức chi tiêu cho y tế
trung bình của các hộ gia đình khu vực thành phố với độ tin cậy 95%.
Đáp số: a) (4,819 ; 8,434); b) 2,756; c) 0,98
Bài 0.15. Quan sát ngẫu nhiên 150 khách hàng vào siêu thị A thì tính được
mức chi tiêu bình quân trong lần mua sắm tại siêu thị là 132,5 nghìn đồng,
độ lệch chuẩn là 22,5 nghìn đồng; và thấy có 24 khách có mức chi tiêu trên
2 triệu đồng. Mức chi tiêu của khách hàng tại siêu thị được giả sử là có phân phối Chuẩn. Cho 2 2 𝑡 (𝑛>30) (149) (149) 0,025 = 1,96; 𝑡 (𝑛>30) 0,05 = 1,645; 𝜒0,05 = 179,6; 𝜒0,95 = 122,7
a) Ước lượng mức chi tiêu trung bình của khách hàng tại siêu thị A với độ tin cậy 0,95.
b) Với độ tin cậy 90%, độ đồng đều (đo bằng độ lệch chuẩn) của mức
chi tiêu các khách hàng nằm trong khoảng nào?
c) Hãy ước lượng tỉ lệ tối đa khách hàng có mức chi tiêu mỗi lần tại siêu
thị A nhiều hơn 2 triệu đồng, với độ tin cậy 0,95.
Đáp số: a) (128,899 ; 136,101); b) (20,494 ; 24,794); c) 0,2092
Bài 0.16. Khảo sát ngẫu nhiên 100 sinh viên trường đại học A về việc học
môn Xác suất thống kê thì thấy điểm tổng kết môn học của các sinh viên
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 7
này bình quân là 7,65 và độ lệch chuẩn là 0,5 điểm; trong đó có 88 sinh
viên cho rằng việc học môn này ở trường mình là thực sự hữu ích. Cho 2 𝑡 (𝑛>30) (99) 0,025 = 1,96; 𝑡 (𝑛>30) 0,05 = 1,645; 𝑡 (𝑛>30) 0,01 = 2,33; 𝜒0,1 = 117,4; 2 𝜒 (99) 0,9
= 81,45; 𝑧0,01 = 2,33; 𝑧0,1 = 1,28
a) Ước lượng điểm tổng kết trung bình môn Xác suất thống kê của sinh
viên trường đại học A với độ tin cậy 98%.
b) Tìm khoảng tin cậy 80% cho độ phân tán (đo bằng độ lệch chuẩn)
điểm tổng kết môn Xác suất thống kê của sinh viên trường đại học A.
c) Ước lượng tối thiểu số sinh viên của trường đại học A cho rằng việc
học môn Xác suất thống kê là thực sự hữu ích với độ tin cậy 99%,
biết rằng trường đại học A có 5500 sinh viên có học môn này.
Đáp số: a) (7,5335 ; 7,7665); b) (0,459 ; 0,551); c) 4424
Câu hỏi trắc nghiệm
Câu 0.1. Cho các thống kê: 𝐺 2 1 1 = 𝑋 𝑋 𝑋 𝑋 3 1 + 13 2 ; 𝐺2 = 5 1 + 45 2 được
xây dựng trên mẫu kích thước 𝑛 = 2 lập từ tổng thể có trung bình là 𝜇 và
phương sai là 𝜎2. Đâu là ước lượng không chệch của trung bình tổng thể:
A. Chỉ thống kê 𝐺1
C. Chỉ thống kê 𝐺2
B. Cả hai thống kê 𝐺1 và 𝐺2
D. Không có thống kê nào
Câu 0.2. Xét mẫu ngẫu nhiên kích thước 𝑛 = 3, 𝑊 = (𝑋1, 𝑋2, 𝑋3) được lập
từ tổng thể có trung bình là 𝜇 và phương sai là 𝜎2. Trong số các ước lượng
không chệch của trung bình tổng thể dưới đây, ước lượng nào là ước lượng tốt nhất: 1 3 1 1 1 1 1 1 𝐺1 = 𝑋1 + 𝑋2 + 𝑋3; 𝐺2 = 𝑋1 + 𝑋2; 𝐺3 = 𝑋1 + 𝑋2 + 𝑋3 5 5 5 2 2 4 2 4 A. Thống kê 𝐺1 C. Thống kê 𝐺3 B. Thống kê 𝐺2
D. Cả 3 thống kê tốt như nhau
Câu 0.3. Một ước lượng điểm được gọi là ước lượng hiệu quả nếu nó là:
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 8
A. Ước lượng không chệch
C. Ước lượng không chệch và có phương sai bé nhất
B. Ước lượng có phương sai bé nhất
D. Ước lượng chệch nhưng phương sai bé nhất
Câu 0.4. Khi cần ước lượng tỉ lệ chuyến xe tốn nhiên liệu của một công ty
vận tải thì tham số cần ước lượng là:
A. Phương sai tổng thể
B. Tỉ lệ tổng thể
C. Trung bình tổng thể
D. Độ lệch chuẩn tổng thể
Câu 0.5. Ước lượng khoảng đối xứng cho tỉ lệ tổng thể, có thể giảm độ dài
khoảng tin cậy bằng cách (nếu các yếu tố khác giữ nguyên)
A. Tăng kích thước mẫu
C. Giảm độ tin cậy
B. Giảm kích thước mẫu
D. Cả A và C đều đúng
Câu 0.6. Khi ước lượng cho trung bình của tổng thể phân phối Chuẩn, nếu
giữ nguyên các yếu tố khác, và trung bình mẫu tăng lên, thì độ dài khoảng tin cậy sẽ: A. Tăng lên C. Không thay đổi B. Giảm xuống
D. Có thể tăng hoặc giảm
Câu 0.7. Điều tra ngẫu nhiên 40 người tại một vùng thấy có 15 người có sử
dụng sản phẩm của doanh nghiệp. Với độ tin cậy 90%, khoảng tin cậy tỉ lệ
người có sử dụng sản phẩm của doanh nghiệp trong vùng là: A. (0, 2993; 0, 3406) C. (0, 2249; 0, 3251) B. (0, 0563; 0, 1237) D. (0, 2491; 0, 5009)
Cho 𝑧0,01 = 2,33; 𝑧0,025 = 1,96; 𝑧0,05 = 1,645; 𝑧0,1 = 1,28
Câu 0.8. Cân nặng của trẻ sơ sinh được cho là có phân phối chuẩn. Điều
tra cân nặng 100 trẻ sơ sinh tại một bệnh viện thấy trung bình mẫu bằng
3,2 kg; độ lệch chuẩn mẫu 0,2 kg. Cho 2 2 𝜒 (99) (99)
0,025 = 128,4; 𝜒0,975 = 73,36; 2 2 𝜒 (99) (99) 0,05
= 123,2; 𝜒0,95 = 77,05 Với độ tin cậy 90%, độ lệch chuẩn của cân
nặng trẻ sơ sinh nằm trong khoảng:
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 9
A. (0, 1754; 0, 2321) (kg)
C. (0, 0321; 0, 0513) (kg2)
B. (0, 1792; 0, 2264) (kg)
D. (0, 0308; 0, 0539) (kg2)
Câu 0.9. Tạp chí USA Today khảo sát 369 cha mẹ làm việc thì thấy có 200
người cho biết họ dành quá ít thời gian cho con cái của họ bởi các cam kết
về công việc. Cho 𝑧0,01 = 2,33; 𝑧0,025 = 1,96; 𝑧0,05 = 1,645; 𝑧0,1 = 1,28.
Khoảng tin cậy 95% của tỉ lệ tổng thể các cha mẹ làm việc mà họ cảm thấy
dành quá ít thời gian cho con cái bởi các cam kết công việc là? A. (0, 491; 0, 593) C. (0, 556; 0, 586) B. (0, 499; 0, 585) D. (0, 498; 0, 526)
Câu 0.10. Ước lượng mức giá trung bình trên thị trường của 1 loại hàng
hóa thông qua một mẫu kích thước 20 với trung bình mẫu 30 USD, phương
sai mẫu là 9 USD2. Biết rằng giá của hàng hóa này có phân phối chuẩn. Cho 𝑡(19) 0,025 = 2, 093; 𝑡 (19)
0,05 = 1, 729. Với độ tin cậy 95% thì sai số biên của
ước lượng trong khoảng đối xứng là: A. 2, 808 B. 4, 212 C. 1, 404 D. 1, 315
Câu 0.11. Ước lượng cho tỉ lệ sinh viên có việc làm sau 1 năm tốt nghiệp,
khảo sát trên một mẫu 200 sinh viên, thu được tỉ lệ mẫu là 85%. Trong
các khoảng sau, khoảng nào có thể là kết quả ước lượng khoảng tin cậy đối
xứng cho tỉ lệ tổng thể? A. 80%-88% B. 86%-92% C. 74%-82% D. 80%-90%
Câu 0.12. Giá đóng cửa của một loại cổ phiếu niêm yết trên sàn chứng
khoán HOSE được giả sử là có phân phối chuẩn. Theo dõi giá đóng cửa
của cổ phiếu này trong 100 phiên giao dịch thì thấy giá bình quân là 32,85
(nghìn đồng), phương sai mẫu là 7,5625 (nghìn đồng)2. Với độ tin cậy
95%, giá đóng cửa trung bình của loại cổ phiếu này nằm trong khoảng nào? Cho 𝑡(99) 0,025 = 1, 96; 𝑡 (99) 0,05 = 1, 645
A. (32,311 ; 33,389) nghìn đồng
B. (31,367 ; 34,333) nghìn đồng
C. (32,397 ; 33,303) nghìn đồng
D. (31,606 ; 34,094) nghìn đồng
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 10
Câu 0.13. Khi ước lượng tối đa độ dao động của giá một loại cổ phiếu với
độ tin cậy 0,9; sử dụng số liệu về giá đóng cửa của cổ phiếu đó trong 50
phiên giao dịch thì cần giá trị tới hạn nào dưới đây? Biết rằng giá cổ phiếu
đó có phân phối chuẩn và chưa biết kì vọng. A. 2 2 2 2 𝜒 (49) B. 𝜒 (49) C. 𝜒 (49) D. 𝜒 (49) 0,05 0,95 0,9 0,95
Câu 0.14. Đâu là công thức đúng cần sử dụng để ước lượng tối đa cho tỉ lệ của tổng thể: √ √ A. ˆ 𝑝 (1− ˆ𝑝) ˆ 𝑝 (1− ˆ𝑝) ˆ 𝑝 − √ 𝑧 √ 𝑧 𝑛 𝛼 B. ˆ𝑝 + 𝑛 𝛼 √ √ C. ˆ 𝑝 (1− ˆ𝑝) ˆ 𝑝 (1− ˆ𝑝) ˆ 𝑝 + √ 𝑧 𝛼 D. ˆ𝑝 − √ 𝑧 𝛼 𝑛 2 𝑛 2
Câu 0.15. Đâu là công thức đúng của độ dài khoảng tin cậy trong bài toán
ước lượng trung bình của tổng thể phân phối chuẩn, chưa biết phương sai tổng thể: A. 𝑆 √ 𝑡 (𝑛−1) B. 2 𝑆 𝑡(𝑛−1) 𝑛 𝛼 𝑛 𝛼 2 2 √ C. ˆ 𝑝 (1− ˆ𝑝) √ 𝑧 𝛼 D. 2 𝑆 √ 𝑡 (𝑛−1) 𝑛 𝛼 2 𝑛 2
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 1 Bài tập
Bài 0.1. Phát biểu nào đúng/sai và giải thích:
a) Sai lầm loại I là chấp nhận giả thuyết 𝐻0 trong khi 𝐻0 đúng.
b) Sai lầm loại I là chấp nhận giả thuyết 𝐻0 trong khi 𝐻0 sai.
c) Sai lầm loại I là bác bỏ giả thuyết 𝐻0 trong khi 𝐻0 đúng.
d) Sai lầm loại I là bác bỏ giả thuyết 𝐻0 trong khi 𝐻0 sai
Bài 0.2. Các mệnh đề sau đúng/sai và giải thích
a) Khi thực hiện kiểm định giả thuyết nếu giá trị 𝑃-value lớn hơn mức ý
nghĩa cho trước thì bác bỏ 𝐻0.
b) Khi thực hiện kiểm định nếu kết luận là bác bỏ 𝐻0 thì có thể bị mắc sai lầm loại II.
c) P(sai lầm loại I) + P(sai lầm loại II) = 1.
d) Xác suất bác bỏ giả thuyết 𝐻0 khi 𝐻0 sai gọi là lực kiểm định.
e) Tăng mức ý nghĩa thì làm tăng mức xác suất mắc sai lầm loại II.
Bài 0.3. Các mệnh đề sau đúng/sai và giải thích:
a) Việc bác bỏ giả thuyết 𝐻0 khi giả thuyết 𝐻0 đúng gọi là mắc sai lầm loại I.
b) Việc chấp nhận giả thuyết 𝐻0 khi giả thuyết 𝐻0 sai gọi là mắc sai lầm loại I.
c) Nếu giả thuyết 𝐻0 bị bác bỏ ở mức ý nghĩa 5% thì cũng bị bác bỏ ở mức ý nghĩa 1%.
d) Nếu giả thuyết 𝐻0 bị bác bỏ ở mức ý nghĩa 1% thì cũng bị bác bỏ ở mức ý nghĩa 5%.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 2
e) Lực kiểm định tỷ lệ nghịch với xác suất mắc sai lầm loại II.
Bài 0.4. Năm ngoái giá một loại hàng hóa trung bình là 20, độ lệch chuẩn
là 4. Viết cặp giả thuyết để kiểm định hai ý kiến sau:
a) Năm nay giá trung bình sẽ tăng lên.
b) Năm nay giá sẽ ổn định hơn.
Bài 0.5. Viết cặp giả thuyết phù hợp cho các bài toán kiểm định giả thuyết
thống kê đối với các nhận định sau:
a) Độ dao động của giá vàng trên thị trường trong năm qua là chưa đến 30 𝑢𝑠𝑑.
b) Mức độ biến động của giá vàng là quá 500 𝑢𝑠𝑑2.
c) Mức độ biến động của giá vàng ở thị trường Việt Nam và thị trường Trung Quốc như nhau.
Bài 0.6. Viết cặp giả thuyết phù hợp cho các bài toán kiểm định giả thuyết
thống kê đối với các nhận định sau:
a) Tỷ lệ khách quay lại mua hàng lần hai là 60%.
b) Tỷ lệ nữ khách hàng trong ngày của một cửa hàng là ít hơn nam.
c) Tỷ lệ nam mua hàng của khảo sát tháng 1 nhiều hơn tỷ lệ nam mua
hàng của khảo sát tháng 2.
Bài 0.7. Đo chiều cao của 200 thanh niên được chọn ngẫu nhiên ở vùng
dân cư A thu được số liệu sau:
Chiều cao (cm) 155 160 165 170 175 Số thanh niên 30 50 60 50 10
Với mức ý nghĩa 5% thì có thể cho rằng tỉ lệ số thanh niên vùng A có chiều
cao dưới 170 cm là trên 50% hay không?
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 3
Bài 0.8. Kiểm tra ngẫu nhiên 100 sản phẩm của 1 lô hàng có 12 phế phẩm.
Nếu tỉ lệ phế phẩm của lô hàng vượt quá 10% thì không được xuất kho. Với
ý nghĩa 5% hãy kết luận xem lô hàng có được xuất kho không?
Bài 0.9. Thí nghiệm dùng loại thuốc A để chữa bệnh T thì trong số 400
người mắc bệnh T có 300 người khỏi bệnh. Nếu dùng thuốc B để chữa
bệnh T thì tỉ lệ khỏi là 80%. Có thể cho rằng thuốc B là hiệu quả như thuốc
A hay không? Hãy kết luận với mức ý nghĩa 5%.
Bài 0.10. Năm trước chi phí sinh hoạt bình quân của mỗi sinh viên học tại
Hà Nội là 3 triệu đồng/ tháng và độ dao động là 1 triệu đồng/ tháng. Năm
nay điều tra mức chi phí của 50 sinh viên thấy chi phí sinh hoạt bình quân
trung bình mỗi sinh viên là 3,7 triệu đồng/ tháng, độ dao động là 0,9 triệu
đồng/ tháng. Giả định mức chi tiêu là biến ngẫu nhiên phân phối chuẩn.
Phải chăng mức chi tiêu hằng tháng của sinh viên năm nay đã tăng lên và
đồng đều hơn, cho kết luận với mức ý nghĩa 10%.
Bài 0.11. Theo số liệu điều tra mức sống dân cư năm 2014 thì Tổng cục
Thống kê đã khảo sát 420 hộ gia đình ở Hà Nội trong đó có 183 hộ ở thành
thị và 237 hộ ở nông thôn. Thu nhập trung bình và độ lệch chuẩn mẫu của
các hộ gia đình tương ứng là 11,8 (triệu đồng/ tháng) và 9,16 (triệu đồng/
tháng). Chi tiêu trung bình và độ lệch chuẩn mẫu của các hộ gia đình tương
ứng là 8,58 (triệu đồng/ tháng) và 6,58 (triệu đồng/ tháng). Giả thiết thu
nhập và chi tiêu của các hộ gia đình ở Hà Nội là các biến ngẫu nhiên có
phân phối Chuẩn. Với mức ý nghĩa 𝛼 = 5%.
a) Có thể cho rằng thu nhập trung bình theo tháng của các hộ gia đình ở
Hà Nội cao hơn 10 triệu đồng hay không?
b) Có thể cho rằng chi tiêu trung bình theo tháng của các hộ gia đình ở
Hà Nội là 8 triệu đồng hay không?
c) Số hộ thành thị có thấp hơn số hộ ở nông thôn hay không?
d) Liệu độ biến động thu nhập của các hộ (đo bằng độ lệch chuẩn) có
bằng 10 triệu đồng/ tháng hay không?
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 4
e) Tìm khoảng hoặc tính toán giá trị 𝑃-value của các kiểm định trên.
Bài 0.12. Cân thử 40 quả trồng theo phương pháp truyền thống thì trọng
lượng trung bình là 30,32 gam, phương sai 7,572 𝑔𝑎𝑚2; cân thử 50 quả
trồng theo phương pháp cải tiến thì trọng lượng trung bình là 32,5 gam,
phương sai 6,722 𝑔𝑎𝑚2. Biết trọng lượng quả phân phối chuẩn, với mức ý nghĩa 5%.
a) Trọng lượng loại quả trồng theo phương pháp truyền thống và cải tiến có như nhau không?
b) Phải chăng loại quả trồng theo phương pháp cải tiến nặng hơn?
c) Có thể nói loại quả trồng theo phương pháp cải tiến có trọng lượng đồng đều hơn không?
d) Cho biết 𝑃-value của các kiểm định trong khoảng nào?
Bài 0.13. Điều tra thị trường cho thấy trong một ngày có 400 khách hàng
nam vào trung tâm, trong đó có 212 người mua hàng; và có 500 khách hàng
nữ vào trung tâm, trong đó có 285 người mua hàng. Với mức ý nghĩa 1%
có thể cho rằng nói chung trong dài hạn tỉ lệ khách nam mua hàng là ít hơn khách nữ hay không?
Bài 0.14. Nếu áp dụng cách thức quảng cáo sản phẩm theo phương thức cũ
thì khi khảo sát 90 ngày người ta tính được doanh thu trung bình của công
ty là 30 (triệu đồng/ngày) và mức ổn định của doanh thu là 3 (triệu đồng/
ngày). Sau khi thực hiện phương thức quảng cáo mới, điều tra doanh thu
của công ty cũng trong 100 ngày và có kết quả là doanh thu trung bình của
công ty là 40 (triệu đồng/ngày) và mức ổn định của doanh thu là 5 (triệu
đồng/ ngày). Biết doanh thu là biến ngẫu nhiên phân phối chuẩn.
a) Phải chăng phương thức quảng cáo mới mang lại doanh thu cho công
ty cao hơn với mức ý nghĩa 10%.
b) Với mức ý nghĩa 5%, có thể nói độ biến động doanh thu của 2 phương
thức quảng cáo đều như nhau?
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 5
Bài 0.15. Năm ngoái tiến hành điều tra 31 cửa hàng thì giá bán trung bình
của sản phẩm A là 120 𝑈𝑆𝐷 và phương sai là 30 𝑈𝑆𝐷2. Năm nay cũng
tiến hành điều tra 31 cửa hàng thì thấy giá bán trung bình tăng lên là 122
𝑈𝑆𝐷 và phương sai là 21,8 𝑈𝑆𝐷2. Giả sử giá bán phân phối theo quy luật
Chuẩn. Với mức ý nghĩa 10%:
a) Kiểm định giả thuyết cho rằng phương sai giá bán của năm ngoái và năm nay bằng nhau.
b) Giả sử phương sai giá bán 2 năm là khác nhau, khi kiểm định ý kiến
cho rằng về trung bình giá bán sản phẩm A năm nay đã tăng lên so với năm ngoái.
Bài 0.16. Cho kết quả tính toán như sau với hai biến phân phối chuẩn: trong
đó X là thu nhập của người lao động ở khu vực nông thôn, Y là thu nhập
của người lao động ở khu vực thành thị (triệu đồng/ năm) X Y Mean 15 20 Variance 12 18 Observations 80 100
a) Với mức ý nghĩa 5%, kiểm định giả thuyết cho rằng thu nhập khu vực
nông thôn đồng đều hơn khu vực thành thị (mức độ bất bình đẳng nông thôn ít hơn)?
b) Với mức ý nghĩa 5% có thể cho rằng trung bình của thu nhập 2 khu
vực là khác nhau? (yêu cầu sinh viên sử dụng kết luận từ câu a để thực hiện câu b)
c) Cho biết P-value của kiểm định trong câu a và câu b trên nằm trong khoảng nào?
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 6 Bài tập tổng hợp Bài tập tự luận
Bài 0.17. Tổng điều tra trên một khu vực A vào 5 năm trước cho thấy có
10% dân số ở độ tuổi trưởng thành không biết chữ. Năm nay điều tra ngẫu
nhiên 400 người thì có 30 người ở độ tuổi trưởng thành không biết chữ. Với mức ý nghĩa 5%:
a) Hãy nhận xét ý kiến cho rằng tỉ lệ mù chữ không giảm đi so với 5 năm trước.
b) Phải chăng tỉ lệ mù chữ vẫn còn trên 3%?
c) Để so sánh tỉ lệ mù chữ khu vực A với khu vực B, tiến hành điều tra
400 người ở khu vực B thì thấy có 40 người ở độ tuổi trưởng thành
không biết chữ. Có thể kết luận rằng tỉ lệ mù chữ ở khu vực A là thấp hơn khu vực B không?
d) Có thể nói tỉ lệ dân số ở độ tuổi trưởng thành ở cả khu vực A và B là 95% không?
Bài 0.18. Điều tra ngẫu nhiên 200 sinh viên của một trường đại học thấy
có 110 sinh viên nữ và 90 sinh viên nam, trong số sinh viên nữ có 20 người
đi làm thêm ngoài giờ học còn trong số sinh viên nam có 18 người đi làm
thêm ngoài giờ học. Với mức ý nghĩa 5% hãy cho kết luận về các điều nghi ngờ sau:
a) Tỉ lệ giới của trường đại học đó là như nhau.
b) Tỉ lệ sinh viên nam đi làm thêm ngoài giờ cao hơn tỉ lệ sinh viên nữ đi làm thêm ngoài giờ.
c) Tỉ lệ sinh viên nam đi làm thêm ngoài giờ là không quá 25%.
d) Tỉ lệ sinh viên không đi làm thêm của trường đại học đó là 80%.
Bài 0.19. Mức chi cho y tế trong một năm của hộ gia đình ở khu vực thành
phố là biến ngẫu nhiên có phân phối Chuẩn. Điều tra ngẫu nhiên 50 hộ
gia đình ở khu vực thành phố thì thấy mức chi cho y tế bình quân là 15,8
triệu/năm với độ lệch chuẩn 2,5 triệu.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 7
a) Với mức ý nghĩa 1%, có thể nói mức chi tiêu cho y tế bình quân của
các hộ trung bình là trên 12 triệu/ năm.
b) Với mức ý nghĩa 5%, độ dao động chi tiêu cho y tế của các hộ chưa đến 3 triệu/ năm.
Bài 0.20. Quan sát ngẫu nhiên 120 khách hàng vào siêu thị A thì tính được
mức chi tiêu bình quân mỗi lần vào mua sắm tại siêu thị là 150 nghìn đồng,
độ lệch chuẩn là 12,5 nghìn đồng; và thấy có 20 khách có mức chi tiêu trên
2 triệu đồng. Mức chi tiêu của khách hàng tại siêu thị được giả sử là có phân phối Chuẩn.
a) Với mức ý nghĩa 1%, kiểm định giả thuyết mức chi tiêu bình quân
mỗi lần mua sắm tại siêu thị là chưa đến 200 nghìn đồng.
b) Với mức ý nghĩa 10%, kiểm định giả thuyết tỉ lệ khách có mức chi tiêu trên 2 triệu đồng.
c) Với mức ý nghĩa 5%, kiểm định giả thuyết độ phân tán mức độ chi
tiêu bình quân mỗi lần mua sắm tại siêu thị là 10 nghìn đồng.
Câu hỏi trắc nghiệm
Câu 0.1. Đâu là mức xác suất mắc sai lầm loại I? A. 𝛼 C. 1-𝛼 B. 𝛽 D. 1-𝛽
Câu 0.2. Miền bác bỏ giả thuyết 𝐻0 kí hiệu là 𝑊𝛼 được xây dựng theo công thức nào sau đây:
A. 𝑃(𝐺 ∈ 𝑊𝛼/𝐻0 đúng) = 1 − 𝛼
B. 𝑃(𝐺 ∈ 𝑊𝛼/𝐻0 đúng) = 𝛼
C. 𝑃(𝐺 ∈ 𝑊𝛼/𝐻0 đúng) = 𝛽
D. 𝑃(𝐺 ∈ 𝑊𝛼/𝐻0 đúng) = 1 − 𝛽
Câu 0.3. Đâu là lực kiểm định?
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 8 A. 𝛼 C. 1-𝛼 B. 𝛽 D. 1-𝛽
Câu 0.4. Năm ngoái chi cho điện của các hộ gia đình trung bình là 200,
phương sai là 24. Kiểm định ý kiến “năm nay mức chi biến động hơn so với
trước". Giả thiết mức chi phân phối Chuẩn. Khi đó cặp giả thuyết là:
A. H0: 𝜇 = 200; H1: 𝜇 > 200
B. H0: 𝜇 = 200; H1: 𝜇 < 200
C. H0: 𝜎2 = 24; H1: 𝜎2 > 24
D. H0: 𝜎2 = 24; H1: 𝜎2 < 24
Câu 0.5. Năm ngoái chi cho điện của các hộ gia đình trung bình là 220, độ
lệch chuẩn là 20. Kiểm định ý kiến “năm nay mức chi ổn định hơn so với
trước". Giả thiết mức chi phân phối Chuẩn. Khi đó, cặp giả thuyết là:
A. H0: 𝜎2 = 20; H1: 𝜎2 > 20
B. H0: 𝜎2 = 20; H1: 𝜎2 < 20
C. H0: 𝜎2 = 400; H1: 𝜎2 > 400
D. H0: 𝜎2 = 400; H1: 𝜎2 < 400
Câu 0.6. Kiểm định cặp giả thuyết: H0: 𝜎2 = 100; H1: 𝜎2 < 100. Với mẫu
kích thước 20, mức ý nghĩa 5%, khi đó cần tra bảng giá trị tới hạn nào? A. 2(19) 2(19) 𝜒 C. 𝜒 0,05 0,95 B. 2(20) 2(20) 𝜒 D. 𝜒 0,05 0,95
Câu 0.7. Cần kiểm định giả thuyết "Độ phân tán của chi tiêu là chưa đến
8 (triệu)2", với chi tiêu phân phối Chuẩn. Điều tra mẫu kích thước 50 được
trung bình mẫu 30 và phương sai mẫu là 5 (triệu)2. Giá trị quan sát của kiểm định là: A. 39,53 C. 38,74 B. 31,25 D. 30,63
Câu 0.8. Khi kiểm định cặp giả thuyết: H0: 𝜎2 = 100; H1: 𝜎2 < 100, với
mẫu kích thước 27, mức ý nghĩa 5%, tính được giá trị quan sát là 14, vậy kết luận là:
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 9 A. 2( 𝜒2 𝑛−1) : bác bỏ H 𝑞𝑠 < 𝜒1−𝛼 0 B. 2( 𝜒2
𝑛−1) : chưa có cơ sở bác bỏ H 𝑞𝑠 > 𝜒1−𝛼 0 C. 2(19) 𝜒2
: chưa có cơ sở bác bỏ H 𝑞𝑠 < 𝜒𝛼 0 D. 2( 𝜒2 𝑛−1) 𝑞𝑠 > 𝜒𝛼 : bác bỏ H0
Câu 0.9. Kiểm tra 100 sản phẩm của nhà máy thì có 90 chính phẩm. Khi
kiểm định xem tỷ lệ chính phẩm của nhà máy có đạt 95% thì giá trị quan sát của kiểm định là: A. 𝑍𝑞𝑠 = 2,293 C. 𝑍𝑞𝑠= 1,183
B. 𝑍𝑞𝑠 = -1,183
D. 𝑍𝑞𝑠 = -2,293
Câu 0.10. Với mức ý nghĩa 5%, mẫu gồm 100 quan sát thì tính được giá trị
quan sát của tiêu chuẩn kiểm định là -2,15. Khi kiểm định cặp giả thuyết: ( 𝐻0 : 𝑝 = 𝑝0 = 0, 5
kết luận nào dưới đây là phù hợp? 𝐻1 : 𝑝 ≠ 0, 5
Cho 𝑍0,05 = 1, 645; 𝑍0,025 = 1, 96. A. Bác bỏ 𝐻0 C. Bác bỏ 𝐻1
B. Không bác bỏ 𝐻0
D. Chưa đủ thông tin kết luận
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 1 Bài tập
Bài 0.1. Cho biết trong các trường hợp sau, trường hợp nào kiểm định tính
phân phối Chuẩn là phù hợp với biến trong số liệu.
a) Số liệu của 100 hộ gia đình, biến là số lượng xe máy hộ sở hữu
b) Số liệu của 50 doanh nghiệp, biến là doanh thu trong năm 2020
c) Số liệu của 3 người lao động, biến là năng suất lao động/ngày khảo sát trong một ngày
d) Số liệu của một người lao động, biến là năng suất lao động/ngày khảo sát trong 1 năm
e) Số liệu của 100 doanh nghiệp về việc doanh nghiệp có sở hữu trang web riêng hay không
Bài 0.2. Trong kiểm định tính phân phối Chuẩn của một biến, cho biết các
câu sau đúng hay sai, giải thích.
a) Nếu hệ số bất đối xứng không đổi, hệ số nhọn càng nhỏ thì càng dễ
kết luận biến phân phối Chuẩn
b) Nếu hệ số nhọn không đổi, hệ số bất đối xứng càng gần 0 thì càng dễ
kết luận biến phân phối Chuẩn
c) Thống kê JB càng lớn thì càng dễ kết luận biến phân phối Chuẩn
d) Kiểm định kết luận biến phân phối Chuẩn với mọi mức ý nghĩa khi
hệ số bất đối xứng bằng 0 và hệ số nhọn bằng 3
Bài 0.3. Những trường hợp nào sau đây có thể thực hiện kiểm định tính độc
lập bằng bảng tiếp liên trực tiếp?
a) Thu nhập và năng suất của người lao động
b) Xếp loại tốt nghiệp và chức vụ của cử nhân ĐHKTQD sau khi tốt nghiệp 5 năm
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 2
c) Trình độ và thu nhập của người lao động
d) Giới tính và năng suất của người lao động
e) Quy mô vốn và lợi nhuận của doanh nghiệp
f) Lĩnh vực kinh doanh và hình thức sở hữu của doanh nghiệp
Với các trường hợp không thực hiện trực tiếp, nêu cách để có thể sử dụng
bảng tiếp liên để kiểm định.
Bài 0.4. Xác định bậc tự do của giá trị tới hạn 𝜒2 khi kiểm định tính độc
lập của hai dấu hiệu định tính sau:
a) Giới tính và tay thuận
b) Xếp loại tốt nghiệp của cử nhân ĐHKTQD (Xuất sắc, giỏi, khá, trung
bình khá, trung bình) và tình trạng sau 1 năm (chỉ đi làm, chỉ học tiếp, vừa học vừa làm, khác)
c) Học bổng (có, không) và tham gia câu lạc bộ (không tham gia, tham
gia 1 câu lạc bộ, tham gia từ 2 câu lạc bộ trở lên) của sinh viên trong một học kì
d) Quy mô vốn của doanh nghiệp (tăng, giữ nguyên, giảm) và kết quả
kinh doanh (có lãi, hòa vốn, lỗ) trong một năm
Câu 0.1. Giả sử ta muốn kiểm định xem một biến ngẫu nhiên có phân phối
Chuẩn hay không. Khi đó, giá trị tới hạn 𝜒2 cần sử dụng sẽ có bậc tự do là: A. Bậc 1 B. Bậc 2 C. Bậc 3 D. Bậc 6
Câu 0.2. Giả sử ta muốn kiểm định xem Tuổi thọ của một loại sản phẩm
(X) có phân phối chuẩn hay không. Với mẫu cụ thể ta tính được giá trị quan
sát là 6,13. Khi đó, kết luận ở mức ý nghĩa 5% sẽ là:
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 3
A. Bác bỏ H0; X phân phối chuẩn
B. Bác bỏ H0; X không phân phối chuẩn
C. Chưa bác bỏ H0; X có phân phối chuẩn
D. Chưa bác bỏ H0; X không phân phối chuẩn
Câu 0.3. Khi kiểm định về tính phân phối Chuẩn của một biến ngẫu nhiên
bằng kiểm định Jarque-Bera, nếu các hệ số nhọn và hệ số bất đối xứng của
mẫu không đổi, kích thước mẫu tăng lên thì khả năng bác bỏ giả thuyết H0 sẽ như thế nào? A. Tăng lên. B. Giảm xuống C. Không thay đổi D. Không xác định
Câu 0.4. Kiểm định sự độc lập của 2 dấu hiệu định tính: dấu hiệu “thành
phần kinh tế" có 5 phạm trù (nhà nước, tập thể, tư nhân, hộ gia đình và có
vốn đầu tư nước ngoài), dấu hiệu “kết quả kinh doanh" có 3 phạm trù (có
lãi, hòa vốn, thua lỗ), với mức ý nghĩa 𝛼 thì giá trị tới hạn cần sử dụng là: A. 2(8) 𝜒𝛼/2 B. 2(8) 𝜒𝛼 C. 2(8) 𝜒1−𝛼 D. 2(15) 𝜒𝛼
Câu 0.5. Giả sử ta có 2 dấu hiệu định tính 𝐴 và B, trong đó dấu hiệu A có
3 phạm trù, dấu hiệu B có 2 phạm trù. Khi đó, nếu muốn kiểm định xem
hai dấu hiệu này có độc lập với nhau hay không ở mức ý nghĩa 5%, mà tính
được giá trị quan sát là 4,56 thì kết luận sẽ là:
A. Bác bỏ H0; hai dấu hiệu A,B độc lập
B. Bác bỏ H0; hai dấu hiệu không độc lập
C. Chưa bác bỏ H0; hai dấu hiệu độc lập
D. Chưa bác bỏ H0; hai dấu hiệu không độc lập
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 4
Câu 0.6. Giả sử ta muốn kiểm định xem Tuổi thọ của một loại sản phẩm
(X) có phân phối chuẩn hay không. Với mẫu cụ thể ta tính được giá trị quan
sát là 6,13. Khi đó, kết luận ở mức ý nghĩa 5% sẽ là:
A. Bác bỏ H0; X phân phối chuẩn
B. Bác bỏ H0; X không phân phối chuẩn
C. Chưa bác bỏ H0; X có phân phối chuẩn
D. Chưa bác bỏ H0; X không phân phối chuẩn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 5 Bài tập tổng hợp
Bài 0.5. Cho dữ liệu về thương hiệu xe và quyết định mua lại cùng thương
hiệu xe khi đổi ô tô mới của 500 khách hàng: Thương hiệu Quyết định Tổng BMW Frod Honda Có mua lại 69 120 123 312 Không mua lại 56 80 52 188 Tổng 125 200 175 500
a) Tỷ lệ quyết định mua lại cùng thương hiệu xe khi đổi xe mới của
thương hiệu xe nào cao nhất?
b) Với mức ý nghĩa 𝛼 = 5%, có thể nói quyết định mua lại cùng thương
hiệu xe khi đổi xe mới và loại xe độc lập hay không?
c) Với mức ý nghĩa 𝛼 = 1%, có thể nói quyết định mua lại cùng thương
hiệu xe khi đổi xe mới và loại xe độc lập hay không? Tính 𝑃-value của kiểm định.
Bài 0.6. Cho dữ liệu về đánh giá của nhân viên về quản lý doanh nghiệp và
quy mô của doanh nghiệp từ 200 nhân viên: Quy mô doanh nghiệp Đánh giá về quản lý Tổng Nhỏ Vừa Lớn Xuất sắc 40 25 5 70 Giỏi 35 35 10 80 Bình thường 25 10 15 50 Tổng 100 70 30 200
a) Tỷ lệ đánh giá “Xuất sắc” của nhân viên về quản lý của doanh nghiệp
quy mô nào là thấp nhất?
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 6
b) Xây dựng cặp giả thuyết để kiểm tra sự phụ thuộc của quy mô doanh
nghiệp và đánh giá về quản lý doanh nghiệp từ nhân viên.
c) Với mức ý nghĩa 𝛼 = 10%, có thể nói quy mô doanh nghiệp và đánh
giá của nhân viên về quản lý doanh nghiệp độc lập với nhau?
d) Với mức ý nghĩa 𝛼 = 5%, có thể nói quy mô doanh nghiệp và đánh
giá của nhân viên về quản lý doanh nghiệp độc lập với nhau? Tính 𝑃- value của kiểm định.
Bài 0.7. Cho dữ liệu về thời gian chờ khám bệnh của 35 bệnh nhân (phút) trong bảng sau: 3 3 4 4 6 7 7 8 8 9 9 10 10 11 12 12 12 12 15 16 16 17 18 19 19 20 22 25 26 26 28 30 31 32 34
a) Xây dựng cặp giả thuyết để kiểm tra tính phân phối Chuẩn của thời
gian chờ khám bệnh của bệnh nhân.
b) Với mức ý nghĩa 𝛼 = 10%, kiểm định tính phân phối Chuẩn của thời gian chờ khám bệnh.
c) Với mức ý nghĩa 𝛼 = 5%, kiểm định tính phân phối Chuẩn của thời
gian chờ khám bệnh. Tính 𝑃-value của kiểm định.
d) Theo Cơ quan quản lý Y tế, tỷ lệ bệnh nhân phải chờ từ 15 đến 20
phút là 20%, tỷ lệ bệnh nhân phải chờ trên 20 phút là 15%, còn lại
là chờ dưới 15 phút. Với mức ý nghĩa 5% và sử dụng số liệu trong
bảng trên kiểm tra tính xác thực về phát biểu của Cơ quan quản lý Y
tế. Tính 𝑃 – value của kiểm định.
Bài 0.8. Cho dữ liệu về điểm kiểm tra đầu vào (thang 100 điểm) của 50 ứng
viên xin việc trong bảng sau:
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 7 71 66 61 65 54 93 60 86 70 70 73 73 55 63 56 62 76 54 82 79 76 68 53 58 85 80 56 61 61 64 65 62 90 69 76 79 77 54 64 74 65 65 61 56 63 80 56 71 79 84
a) Xây dựng cặp giả thuyết để kiểm tra tính phân phối Chuẩn của điểm
kiểm tra đầu vào của ứng viên xin việc.
b) Với mức ý nghĩa 𝛼 = 10%, kiểm định tính phân phối Chuẩn của điểm
kiểm tra đầu vào của ứng viên xin việc.
c) Với mức ý nghĩa 𝛼 = 5%, kiểm định tính phân phối Chuẩn của điểm
kiểm tra đầu vào của ứng viên xin việc. Tính 𝑃-value của kiểm định.
d) Theo cơ quan quản lý lao động, tỷ lệ kiểm tra có điểm đạt 50-60 là
20%, tỷ lệ kiểm tra có điểm từ 61-70 là 40%, tỷ lệ kiểm tra có điểm
từ 71-80 là 32%, tỷ lệ trên 80 điểm là 8%. Với mức ý nghĩa 5% và
sử dụng dữ liệu trong bảng trên để kiếm định tỷ lệ điểm kiểm tra đã
thay đổi hay không? Tính 𝑃-value của kiểm định.
Bài 0.9. Cho dữ liệu từ một cuộc điều tra năm 2020 về số lượng người sử
dụng Twitter từ 4 nước: Anh, Nhật, Nga và Mỹ trong bảng sau:
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 8 Quốc gia Mạng xã hội Twitter Tổng Anh Nhật Nga Mỹ Có sử dụng 480 215 343 640 1678 Không sử dụng 320 285 357 360 1322 Tổng 800 500 700 1000 3000
a) Tỷ lệ sử dụng mạng xã hội trên của quốc gia nào là cao nhất.
b) Xây dựng cặp giả thuyết để kiểm tra sự phụ thuộc của việc sử dụng
mạng xã hội Twitter và quốc gia.
c) Với mức ý nghĩa 𝛼 = 10%, có thể nói quốc gia và việc sử dụng mạng
xã hội Twitter độc lập với nhau?
d) Với mức ý nghĩa 𝛼 = 5%, có thể nói quốc gia và việc sử dụng mạng
xã hội Twitter độc lập với nhau? Tính 𝑃-value của kiểm định.
e) Cùng năm 2020, các tỷ lệ sử dụng mạng xã hội Instagram trên tổng
số người sử dụng Instagram của các quốc gia trên lần lượt là: 35%,
10%, 22% và 33%. Có thể nói tỷ lệ sử dụng hai mạng xã hội nói trên
của 4 quốc gia là như nhau hay không?
Câu hỏi trắc nghiệm
Câu 0.7. Kích thước mẫu 𝑛 cần để kiểm tra phân phối Chuẩn của dữ liệu A. 𝑛 ≥ 30 B. 𝑛 ≥ 50 C. 𝑛 ≥ 100
D. Không yêu cầu cụ thể
Câu 0.8. Cho dữ liệu từ một cuộc điều tra năm 2020 về số lượng người sử
dụng loại bia Heineken từ 3 quốc gia: Anh, Nga và Mỹ trong bảng sau:
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 9 Quốc gia Loại bia Tổng Anh Nga Mỹ Nhẹ 212 215 983 1678 Nặng 320 285 717 1322 Tổng 800 500 1700 3000
Kiểm định tính độc lập của loại bia sử dụng và quốc gia thì thống kê kiểm định bằng: A. 70,58 B. 2801,59 C. 1,03 D. 2802,59
Câu 0.9. Cho dữ liệu từ một cuộc điều tra năm 2020 về số lượng người sử
dụng loại bia Heineken từ 3 quốc gia: Anh, Nga và Mỹ trong bảng sau: Quốc gia Loại bia Tổng Anh Nga Mỹ Nhẹ 212 215 983 1678 Nặng 320 285 717 1322 Tổng 800 500 1700 3000
Kiểm định tính độc lập của loại bia sử dụng và quốc gia thì 𝑃-value của kiểm định bằng: A. Xấp xỉ 1 B. Xấp xỉ 0 C. 0,5 D. 0,015
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 10
Câu 0.10. Cho dữ liệu về điểm kiểm tra đầu vào (thang 100 điểm) của 28
ứng viên xin việc trong bảng sau: 71 66 61 65 54 93 60 86 70 70 73 73 55 63 56 62 76 54 82 79 76 68 53 58 85 80 56 61
Kiểm định tính phân phối Chuẩn của điểm kiểm tra đầu vào của ứng
viên xin việc thì thống kê kiểm định bằng: A. 1,5 B. 3 C. 2,77 D. 16,6
Câu 0.11. Cho dữ liệu về điểm kiểm tra đầu vào (thang 100 điểm) của 28
ứng viên xin việc trong bảng sau: 71 66 61 65 54 93 60 86 70 70 73 73 55 63 56 62 76 54 82 79 76 68 53 58 85 80 56 61
Kiểm định tính phân phối Chuẩn của điểm kiểm tra đầu vào của ứng
viên xin việc thì 𝑃-value của kiểm định bằng: A. 0,47 B. 0,53 C. 0,75 D. 0,25
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 1 Bài tập
Bài 0.1. Cho biết trong các bộ số liệu sau, bộ nào có thể sử dụng phân tích
phương sai để kiểm định trung bình bằng nhau.
a) Khảo sát sinh viên năm thứ 1, 2, 3, 4 về chi cho tài liệu học tập trong
một năm; mỗi năm học khảo sát 20 sinh viên
b) Khảo sát 25 sinh viên về điểm các học phần Kinh tế Vi mô, Nguyên lý kế toán, Marketing
c) Khảo sát về việc đồng ý (gán giá trị 1) hay không đồng ý (gán giá trị
0) với một chính sách của nhà nước, với 3 nhóm đối tượng: 100 người
thất nghiệp, 200 người đang làm việc, 120 người đã nghỉ hưu
d) Khảo sát về số con trong các hộ gia đình, với 4 quận, mỗi quận 50 hộ
e) Khảo sát về thu nhập của các hộ gia đình: 120 hộ tại Hà Nội, 150 hộ
tại TP.HCM, 100 hộ tại Đà Nẵng
Bài 0.2. Xác định các bậc tự do trong bảng ANOVA tương ứng với các bộ số liệu sau
a) Số liệu khảo sát về thời gian tự học của 10 sinh viên ở một mình, 15
sinh viên ở với bạn, 12 sinh viên ở với người thân.
b) Số liệu khảo sát tỉ suất lợi nhuận của các doanh nghiệp có vốn đầu
tư trực tiếp nước ngoài tại các thành phố trực thuộc trung ương, mỗi
thành phố 20 doanh nghiệp.
c) Số liệu khảo sát thu nhập / tháng của người lao động trong các lĩnh
vực: tài chính, marketing, công nghệ, luật; mỗi lĩnh vực 15 người.
Bài 0.3. Cho biết các câu sau, câu nào đúng, câu nào sai, tại sao?
a) Đại lượng SSB luôn nhỏ hơn SSW
b) Đại lượng MSB luôn lớn hơn MSW nên thống kê F luôn lớn hơn 1
c) Bậc tự do của SST luôn lớn hơn bậc tự do của SSW
d) Bậc tự do của SST là tổng hai bậc tự do của SSB và SSW
Bài 0.4. Xác định bậc tự do trong bảng ANOVA tương ứng với số liệu sau:
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 2
a) Khảo sát các sinh viên về thu nhập từ làm thêm, với sinh viên các
năm từ 1 đến 3, với ba ngành: kinh tế, kinh doanh, luật.
b) Khảo sát tỉ suất lợi nhuận của các doanh nghiệp với 5 hình thức sở
hữu, gồm cả doanh nghiệp đã lên sàn và chưa lên sàn chứng khoán.
c) Khảo sát thu nhập bình quân đầu người với 420 hộ gia đình tại Hà
Nội, 350 hộ tại TP.Hồ Chí Minh, gồm cả hộ ở thành thị và nông thôn.
Bài 0.5. Cho biết các câu sau, câu nào đúng, câu nào sai, tại sao?
a) Số liệu của ANOVA hai nhân tố có thể dùng để kiểm định ANOVA một nhân tố.
b) Bậc tự do của SSA luôn nhỏ hơn bậc tự do của SSW.
c) Thống kê 𝐹 của nhân tố nào lớn hơn thì sẽ dễ bác bỏ giả thuyết 𝐻0
trong cặp giả thuyết tương ứng với nhân tố đó hơn.
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 3
Câu hỏi trắc nghiệm
Câu 0.1. Mục đích của bài toán phân tích phương sai là
A. Tính toán các phương sai mẫu
B. Kiểm định về sự bằng nhau của các phương sai
C. Kiểm định về sự bằng nhau của các trung bình
D. So sánh các trung bình với phương sai
Câu 0.2. Đâu không phải giả thiết của bài toán phân tích phương sai một nhân tố
A. Các tổng thể con phân phối Chuẩn
B. Các mẫu con có phương sai bằng nhau
C. Các mẫu con độc lập
D. Các tổng thể con có phương sai bằng nhau
Câu 0.3. Trong bài toán phân tích phương sai một nhân tố, nếu các trung
bình mẫu con bằng nhau thì
A. Thống kê 𝐹 bằng 0
B. SST bằng với SSB
C. Phương sai các mẫu con sẽ bằng nhau
D. Bác bỏ giả thuyết 𝐻0 với mọi mức ý nghĩa
Câu 0.4. Khảo sát 18 doanh nghiệp chia thành ba nhóm: rất nhỏ, nhỏ, vừa;
và phân tích phương sai để kiểm định về sự bằng nhau của năng suất trung
bình. Bậc tự do của SSB và SSW lần lượt là A. 3 và 18 C. 2 và 15 B. 2 và 17 D. 3 và 15
Câu 0.5. Phân tích phương sai với thu nhập trung bình của người lao động
chia theo độ tuổi (dưới 30, 30 đến 40, 40 đến 50, trên 50) và trình độ (dưới
đại học, đại học, sau đại học), các bậc tự do nào sẽ có trong bảng ANOVA A. 3, 4, 12 C. 2, 8, 12 B. 3, 6, 11 D. 2, 6, 12
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 4
Câu 0.6. Để kiểm định thời gian chờ trung bình của người dân tại một quầy
dịch vụ công có như nhau không giữa năm ngày làm việc trong tuần, khảo
sát ngẫu nhiên mỗi ngày 20 người và thực hiện phân tích phương sai, thì
thống kê 𝐹 bằng 2,3. Cho biết kết luận nào là đúng:
A. Chưa bác bỏ 𝐻0, thời gian chờ trung bình bằng nhau
B. Chưa bác bỏ 𝐻0, thời gian chờ trung bình không bằng nhau
C. Bác bỏ 𝐻0, thời gian chờ trung bình bằng nhau
D. Bác bỏ 𝐻0, thời gian chờ trung bình không bằng nhau
Câu 0.7. Kiểm định trung bình lượng chi của khách hàng trong ba loại: chỉ
đặt hàng qua mạng, chi mua hàng trực tiếp, vừa đặt qua mạng vừa đến trực
tiếp, tổng số khách là 21, thì thống kê 𝐹 bằng 5,1. 𝑃-value của kiểm định trong khoảng nào? A. Dưới 2,5% C. 5% đến 10% B. 2,5% đến 5% D. Trên 10%
Câu 0.8. Từ bộ số liệu VHLSS2018 khảo sát mức sống hộ gia đình Việt
Nam, tính biến Thu nhập bình quân đầu người, viết tắt là TNBQ, đơn vị:
triệu VND, tính trung bình cho ba thành phố là Hà Nội, TP.Hồ Chí Minh,
Đà Nẵng; và theo quy mô hộ, chia làm 4 mức, được số liệu sau
Hà Nội TP.Hồ Chí Minh Đà Nẵng 1-2 người 70 93 75 3-4 người 77 76 76 5-6 người 59 69 60 > 6 người 69 47 75
Với mức ý nghĩa 5%, thực hiện kiểm định trung bình bằng nhau với biến TNBQ khi
a) Thực hiện phân tích phương sai một nhân tố là Thành phố
b) Thực hiện phân tích phương sai một nhân tố là Quy mô
c) Thực hiện phân tích phương sai hai nhân tố Thành phố và Quy mô
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com)




