
Câu 1: [0D4-1-1] Nếu
ab
và
cd
thì bất đẳng thức nào sau đây luôn đúng?
A.
ac bd
. B.
a c b d
. C.
a c b d
. D.
ab
cd
.
Lời giải
Chọn C
Cộng 2 vế bất đẳng thức ta được
a c b d
.
Câu 2: [0D4-1-1] Cho bất đẳng thức
a b a b
. Dấu đẳng thức xảy ra khi nào?
A.
ab
. B.
0ab
. C.
0ab
. D.
0ab
.
Lời giải
Chọn B
Tính chất của bất đẳng thức.
Câu 3: [0D4-1-1] (Chỉnh sửa 1.5 thành 1.8) Giá trị nhỏ nhất của biểu thức
2
3xx
với
x
là:
A.
9
4
. B.
3
2
. C.
0
. D.
3
2
.
Lời giải
Chọn C
Ta có:
2
0
0
x
x
2
30xx
.
Câu 4: [0D4-1-1] Cho biểu thức
2
1f x x
. Kết luận nào sau đây đúng?
A. Hàm số
fx
chỉ có giá trị lớn nhất, không có giá trị nhỏ nhất.
B. Hàm số
fx
chỉ có giá trị nhỏ nhất, không có giá trị lớn nhất.
C. Hàm số
fx
có giá trị nhỏ nhất và giá trị lớn nhất.
D. Hàm số
fx
không có giá trị nhỏ nhất và không có giá trị lớn nhất.
Lời giải
Chọn C
Ta có:
0fx
và
10f
;
1fx
và
01f
.

Vậy hàm số
fx
có giá trị nhỏ nhất bằng
0
và giá trị lớn nhấtbằng
1
.
Câu 5: [0D4-1-1] Cho hàm số
2
1
1
fx
x
. Mệnh đề nào sau đây là đúng?
A.
fx
có giá trị nhỏ nhất là
0
, giá trị lớn nhất bằng
1
.
B.
fx
không có giá trị nhỏ nhất, giá trị lớn nhất bằng
1
.
C.
fx
có giá trị nhỏ nhất là
1
, giá trị lớn nhất bằng
2
.
D.
fx
không có giá trị nhỏ nhất và giá trị lớn nhất.
Lời giải
Chọn B
Ta có:
0 1;f x x
và
01f
. Vậy
fx
không có giá trị nhỏ nhất, giá
trị lớn nhất bằng
1
.
Câu 6: [0D4-1-1] Cho biết hai số
a
và
b
có tổng bằng
3
. Khi đó, tích hai số
a
và
b
A. có giá trị nhỏ nhất là
9
4
. B. có giá trị lớn nhất là
9
4
.
C. có giá trị lớn nhất là
3
2
. D. không có giá trị lớn nhất.
Lời giải
Chọn D
Vì
a
và
b
là hai số bất kì nên không xác định được giá trị lớn nhất của tích
ab
.
Câu 7: [0D4-1-1] Cho ba số
a
;
b
;
c
thoả mãn đồng thời:
0a b c
;
0b c a
;
0c a b
. Để ba số
a
;
b
;
c
là ba cạnh của một tam giác thì cần thêm đều kiện gì
?
A. Cần có cả
, , 0abc
. B. Cần có cả
, , 0abc
.
C. Chỉ cần một trong ba số
,,abc
dương D. Không cần thêm điều kiện gì.
Lời giải
Chọn B
Câu 8: [0D4-1-1] Tìm mệnh đề đúng?
A.
a b ac bc
. B.
11
.ab
ab

C.
ab
và
c d ac bd
. D.
, 0a b ac bc c
.
Lời giải
Chọn D
Tính chất của bất đẳng thức.
Câu 9: [0D4-1-1] Suy luận nào sau đây đúng?
A.
ab
cd
ac bd
. B.
ab
cd
ab
cd
.
C.
ab
cd
a c b d
. D.
0
0
ab
cd
ac bd
.
Lời giải
Chọn D
Tính chất của bất đẳng thức.
Câu 10: [0D4-1-1] Trong các tính chất sau, tính chất nào sai?
A.
ab
cd
a c b d
. B.
0
0
ab
cd
ab
dc
.
C.
0
0
ab
cd
ac bd
. D.
ab
cd
a c b d
.
Lời giải
Chọn D
Tính chất của bất đẳng thức.
Câu 11: [0D4-1-1] Tìm mệnh đề đúng trong các mệnh đề sau?
A.
ab
11
ab
. B.
ab
ac bc
.
C.
ab
cd
ac bd
. D. Cả A, B, C đều sai.
Lời giải
Chọn D
Tính chất của bất đẳng thức.
Câu 12: [0D4-1-1] Mệnh đề nào sau đây sai?

A.
ab
cd
a c b d
. B.
ab
cd
ac bd
.
C.
ab
cd
a c b d
. D.
ac bc
ab
.
0c
Lời giải
Chọn B
Tính chất của bất đẳng thức.
Câu 13: [0D4-1-1] Cho
, , , a b c d
với
ab
và
cd
. Bất đẳng thức nào sau đây đúng .
A.
a c b d
. B.
a c b d
. C.
ac bd
. D.
22
ab
.
Lời giải
Chọn A
A đúng vì
0BDT a b c d
B sai với
5, 4, 3, 2a b c d
C sai với
5, 3, 1, 2a b c d
D sai với
1, 3ab
.
Câu 14: [0D4-1-1] Tìm giá trị nhỏ nhất của hàm số
2
2
3
yx
x
(
0x
).
A.
23
. B.
4
3
. C.
4
23
. D.
3
.
Lời giải
Chọn A
Với
0x
thì
2
0x
nên
22
22
33
2 . 2 3y x x
xx
.
Câu 15: [0D4-1-1] Tìm giá trị nhỏ nhất của hàm số
8
2
x
y
x
với
0x
.
A.
16
. B.
8
. C.
4
. D.
2
.
Lời giải
Chọn C
Áp dụng BĐT AM-GM, được
88
2 . 4
22
xx
y
xx
.
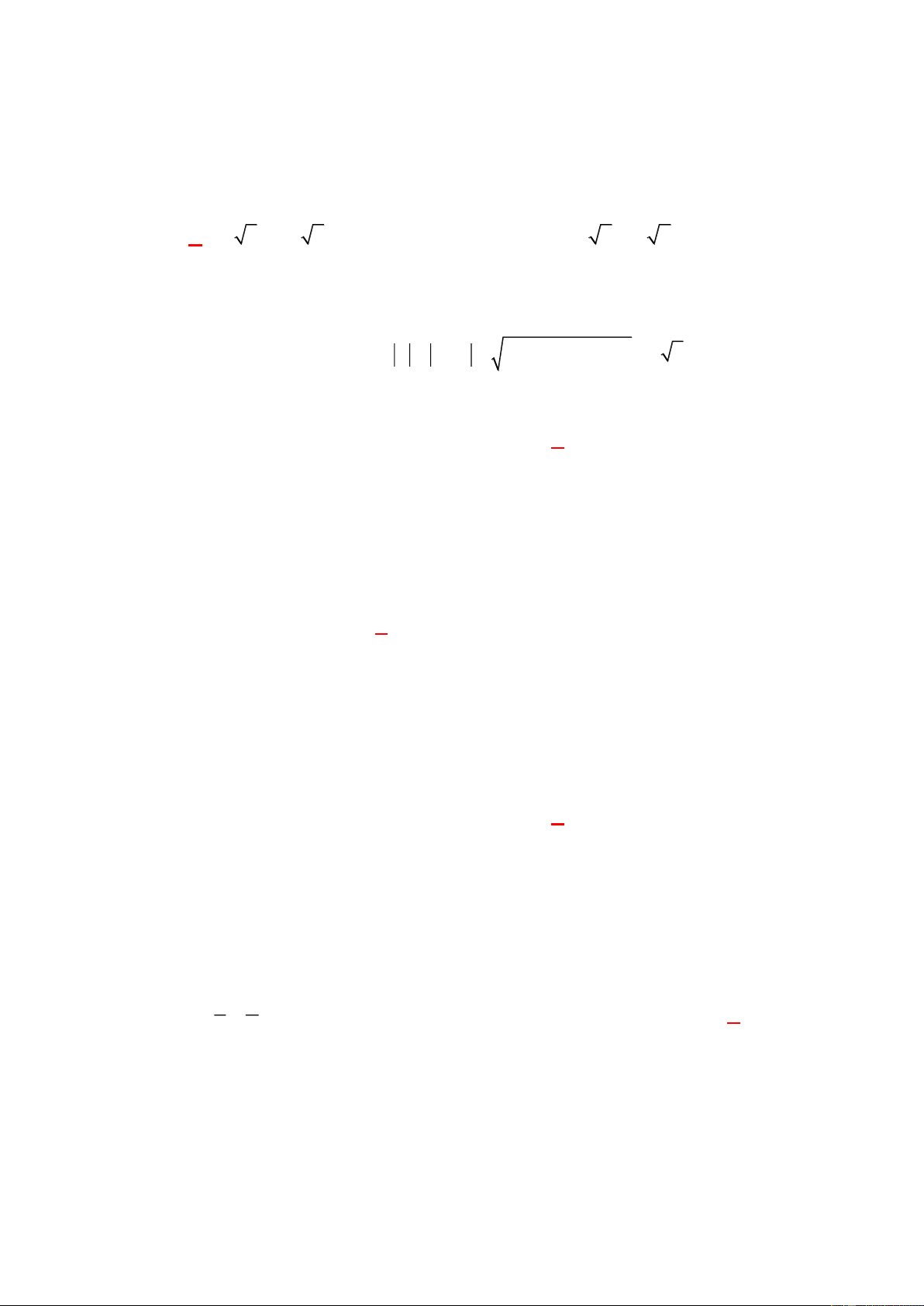
Câu 16: [0D4-1-1] Cho
x
và
y
thỏa mãn
22
4xy
. Tìm giá trị nhỏ nhất và giá trị lớn nhất
của
T x y
.
A.
8
và
8
. B.
2
và
2
.
C.
22
và
22
. D.
2
và
2
.
Lời giải
Chọn C
Áp dụng BĐT BCS, được
2 2 2 2
1 1 2 2T x y x y
.
Câu 17: [0D4-1-1] Nếu
ab
và
cd
thì bất đẳng thức nào sau đây luôn đúng?
A.
ac bd
. B.
a c b d
. C.
a d b c
. D.
ac bd
.
Lời giải
Chọn C
ab
và
cd
a c b d a d b c
.
Câu 18: [0D4-1-1] Nếu
0m
,
0n
thì bất đẳng thức nào sau đây luôn đúng?
A.
mn
. B.
–0nm
. C.
––mn
. D.
–0mn
.
Lời giải
Chọn B
0m
,
0n
thì
0, 0 ( ) 0 0m n n m n m
.
Câu 19: [0D4-1-1] Nếu
,ab
và
c
là các số bất kì và
ab
thì bất đẳng nào sau đây đúng?
A.
ac bc
. B.
22
ab
.
C.
a c b c
. D.
c a c b
.
Lời giải
Chọn C
ab
a c b c
(Tính chất cộng 1 số cho 2 vế của bất đẳng thức).
Câu 20: [0D4-1-1] Nếu
ab
và
cd
thì bất đẳng thức nào sau đây luôn đúng?
A.
ab
cd
. B.
a c b d
. C.
ac bd
. D.
a c b d
.
Lời giải
Chọn D
ab
và
cd
a c b d
(Tính chất cộng 2 vế của 2 bất đẳng thức cùng chiều).
Câu 21: [0D4-1-1] Bất đẳng thức nào sau đây đúng với mọi số thực
a
?

A.
63aa
. B.
36aa
. C.
6 3 3 6 aa
. D.
63 aa
.
Lời giải
Chọn D
6 3 6 3aa
(luôn đúng).
Câu 22: [0D4-1-1] Nếu
,,abc
là các số bất kì và
ab
thì bất đẳng thức nào sau đây luôn
đúng?
A.
3 2 3 2 a c b c
. B.
22
ab
. C.
ac bc
. D.
ac bc
.
Lời giải
Chọn A
3 3 3 2 3 2a b a b a c b c
.
Câu 23: [0D4-1-1] Nếu
0ab
,
0cd
thì bất đẳng thức nào sau đây không đúng?
A.
ac bc
. B.
a c b d
. C.
22
ab
.
D.
ac bd
.
Lời giải
Chọn D
a c b d
không đúng vì trừ 2 bất đẳng thức cùng chiều thi không được kết quả
đúng.
Ví dụ:
7 8; 5 1
nhưng
7 5 2 7 8 1
.
Câu 24: [0D4-1-1] Nếu
0ab
,
0.cd
thì bất đẳng thức nào sau đây không đúng?
A.
a c b d
. B.
ac bd
. C.
ab
cd
. D.
ad
bc
.
Lời giải
Chọn C
ab
cd
không đúng vì chia 2 bất đẳng thưc cùng chiều thì không được kết quả đúng.
Ví dụ:
7 8; 5 1
nhưng
78
51
.
Câu 25: [0D4-1-1] Sắp xếp ba số
6 13
,
19
và
3 16
theo thứ tự từ bé đến lớn thì
thứ tự đúng là
A.
19
,
3 16
,
6 13
. B.
3 16
,
19
,
6 13
.
C.
19
,
6 13
,
3 16
. D.
6 13
,
3 16
,
19
.
Lời giải
Chọn A
Dùng máy tính cầm tay kiểm tra ta được
19 3 16 6 13
.

Câu 26: [0D4-1-1] Nếu
22 a c b c
thì bất đẳng thức nào sau đây đúng?
A.
33 ab
. B.
22
ab
.
C.
22ab
. D.
11
ab
.
Lời giải
Chọn C
2 2 2 2a c b c a b a b
.
Câu 27: [0D4-1-1] Nếu
22ab
và
33 bc
thì bất đẳng thức nào sau đây đúng?
A.
ac
. B.
ac
. C.
33 ac
. D.
22
ac
.
Lời giải
Chọn B
22
33
a b a b
ac
b c b c
.
Câu 28: [0D4-1-1] Một tam giác có độ dài các cạnh là
1,2,x
trong đó
x
là số nguyên. Khi đó,
x
bằng
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn B
Ta có
1,2,x
là độ dài 3 cạnh tam giác nên ta có
2 1 2 1x
(một cạnh luôn lớn
hơn hiệu 2 cạnh và nhỏ hơn tổng 2 cạnh).
Suy ra
13x
và
x
là số nguyên nên
2x
.
Câu 29: [0D4-1-1] Cho
, , ,a b c d
là các số thực trong đó
,0ac
. Nghiệm của phương trình
0ax b
nhỏ hơn nghiệm của phương trình
0cx d
khi và chỉ khi
A.
bc
ad
. B.
bc
ad
. C.
ba
dc
. D.
bd
ac
.
Lời giải
Chọn D
0ax b
có nghiệm
b
x
a
;
0cx d
có nghiệm
d
x
c
Suy ra
b d b d
a c a c
.
Câu 30: [0D4-1-1] Cho hai số thực
,ab
tùy ý. Mệnh đề nào sau đây là đúng?
A.
a b a b
. B.
a b a b
. C.
a b a b
. D.
a b a b
.
Lời giải

Chọn B
Đáp án A sai khi
1; 1.ab
Đáp án B và D sai khi
0.ab
Xét :
2 2 2 2
22a b a b a ab b a ab b ab ab
luôn đúng với
mọi số thực
,ab
.
Vậy,chọn B.
Câu 31: [0D4-1-1] Mệnh đề nào sau đây là mệnh đề đúng?
A. Nếu
2
0a
thì
0a
. B. Nếu
2
aa
thì
0a
.
C. Nếu
2
aa
thì
0a
. D. Nếu
0a
thì
2
aa
.
Lời giải
Chọn D
Đáp án D đúng, do
22
0 1 0a a a a a a
đúng với
0a
.
Câu 32: [0D4-1-1] Trong các tính chất sau, tính chất nào sai
A.
.
ab
a c b d
cd
B.
0
.
0
ab
ab
cd
cd
C.
0
. . .
0
ab
a c b d
cd
D.
0
. . .
0
ab
a c b d
cd
Lời giải
Chọn B
Vì không thể chia vế với vế của hai bất đẳng thức cùng chiều.
Câu 33: [0D4-1-1] Tìm mệnh đề đúng trong các mệnh đề sau
A.
11
.ab
ab
B.
.a b ac bc
C.
.
ab
ac bd
cd
D.
0
. . .
0
ab
a c b d
cd
Lời giải
Chọn D
A sai vì thiếu đk
11
0 ab
ab
, B sai vì thiếu đk
0c
,
C sai vì thiếu đk
0
0
ab
ac bd
cd

Câu 34: [0D4-1-1] Mệnh đề nào sau đây sai?
A.
.
ab
a c b d
cd
B.
.
ab
ac bd
cd
C.
.
ab
a c b d
cd
D.
ac bc a b
, với
0.c
Lời giải
Chọn B
B sai vì thiếu đk
0
0
ab
ac bd
cd
Câu 35: [0D4-1-1] Cho ba số
,,abc
thoả mãn đồng thời
0a b c
,
0a b c
,
0a b c
. Để ba số
,,abc
là ba cạnh của một tam giác thì cần thêm đều kiện gì?
A. Cần có cả
, , 0abc
. B. Cần có cả
, , 0abc
.
C. Chỉ cần một trong ba số
,,abc
dương . D. Không cần thêm điều kiện gì.
Lời giải
Chọn B

Câu 1: [0D4-1-2] Cho
,xy
là hai số bất kì thỏa mãn
2 5xy
ta có bất đẳng thức nào sau
đây đúng:
A.
22
5.xy
B.
2
– 2 0.x
C.
2
2
5 – 2 5.xx
D. Tất cả đều đúng.
Lời giải
Chọn D
Từ giả thiết ta có
2
2 2 2 2
5 2 5 20 25x y x x x x
2
2
5 4 4 5 5 2 5x x x
Dễ thấy biểu thức trên lớn hơn hoặc bằng 5, và tất cả các đáp án A, B, C đều đúng
nên chọn D.
Câu 2: [0D4-1-2] Cho
, , 0abc
và
1 abc
. Dùng bất đẳng thức Côsi ta chứng minh
được
1 1 1
1 1 1 64
abc
. Dấu đẳng thức xảy ra khi và chỉ khi nào:
A.
.abc
B.
1.abc
C.
1
.
3
abc
D.
1, 0.a b c
Lời giải
Chọn C
Cách 1: Thử chọn dễ thấy C là đáp án thỏa mãn.
Cách 2: Giải chi tiết:
Xét
1 1 1 1 1 1 1
1VT
a b c ab bc ca abc
Áp dụng BĐT Cauchy cho các số dương trên ta có
3
1 1 1 3
abc
abc
;
2
3
1 1 1 3
ab bc ca
abc
và
3
1
3 27
abc
abc
Suy ra
1 9 27 27 64VT
Dấu bằng xảy ra khi và chỉ khi
1
3
abc
.
Câu 3: [0D4-1-2] đề nghị sửa thành dạng 1.1 Xét các bất đẳng thức:

22
2a b ab
;
2
22
2a b a b
2a b ab
;
2 2 2
a b c ab bc ca
Trong các bất đẳng thức trên, số bất đẳng thức đúng với mọi số thực a, b, c là:
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn C
Ta có
2
22
20 a b ab a b
luôn đúng với mọi số thực a, b
Ta có
22
22
20 a b a b a b
luôn đúng với mọi số thực a, b
Ta có
2 2 2
2 2 2 2 2 2
2 2 0a b c ab bc ca a b c ab bc ca a b b c c a
luôn đúng với mọi số thực a, b, c.
Ta có
2a b ab
không đúng khi a, b âm
Vậy có 3 bất đẳng thức đúng.
Câu 4: [0D4-1-2] Giá trị nhỏ nhất của biểu thức
1
2
Px
x
với
2x
là:
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn D
Ta có
2 2 0 xx
Áp dụng bất đẳng thức Cauchy ta có
1 1 1
2 2 2 2 . 2 4
2 2 2
P x x x
x x x
Vậy GTNN của
4P
Dấu bằng xảy ra khi
1
23
2
xx
x
.
Câu 5: [0D4-1-2] Cho
0ab
. Xét các mệnh đề sau
3 3 2 2
: ( )( )I a b a b a b
.
2 2 2 2
: ( 3 ) ( 3 )II a a b b b a
.
22
: ( 3 ) ( 3 )III a a b b b a
.
3 3 3 2 2 3
: 3 3 0IV a b b a b ab a
.

Số mệnh đề đúng là.
A.
4
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn D
A đúng vì
2 2 2 2
00BDT a b a ab b a b a b ab a b
B đúng vì
3
3 2 2 3
3 3 0 0BDT a a b ab b a b
C đúng vì
3
3 2 2 3
3 3 0 0BDT a a b ab b a b
.
D sai vì
3
33
0BDT a b b a
.
Câu 6: [0D4-1-2] Cho
2
số
a
và
b
. Xét các mệnh đề sau đây.
: ( ) ( )I b a b a a b
.
22
:2(1 ) 1 2II a a
.
2 2 2
:(1 )(1 ) (1 )III a b ab
.
2
2 2 2 2
:4IV a b a b
Số mệnh đề đúng là.
A.
1
. B.
2
. C.
4
. D.
3
.
Lời giải
Chọn D
A đúng vì
2
22
2 0 0BDT a ab b a b
B đúng vì
2
2
4 2 1 0 2 1 0BDT a a a
C đúng vì
2
2 2 2 2 2 2 2 2
1 1 2 2 0 0BDT a b a b ab a b a ab b a b
D sai vì
22
0BDT a b
.
Câu 7: [0D4-1-2]Cho
, , a b c
với
ab
và
ac
. Câu nào sau đây đúng?
2
bc
a
.
a c b a
.
2 2 2
2a b c
.
0a b c a
.
Số mệnh đề đúng là.
A.
1
. B.
3
. C.
4
. D.
2
.
Lời giải
Chọn D

A đúng vì
20BDT a b c a b a c
B đúng vì
0BDT a b a c
C sai với
1, 2, 3a b c
.
D sai vì
ab
và
ac
nên
0a b c a
Câu 8: [0D4-1-2] Trong các hình chữ nhật có cùng chi vi thì
A. Hình vuông có diện tích nhỏ nhất.
B. Hình vuông có diện tích lớn nhất.
C. Không xác định được hình có diện tích lớn nhất.
D. Cả A, B, C đều sai.
Lời giải
Chọn B
Ý nghĩa hình học của bất đẳng thức Cô si.
Câu 9: [0D4-1-2] Cho biểu thức
P a a
với
0a
. Mệnh đề nào sau đây là mệnh đề
đúng?
A.Giá trị nhỏ nhất của P là
1
4
. B.Giá trị lớn nhất của P là
1
4
.
C.Giá trị lớn nhất của P là
1
2
. D. P đạt giá trị lớn nhất tại
1
4
a
.
Lời giải
Chọn B
Ta có:
2
2
1 1 1
4 2 4
P a a a a a
.
Câu 10: [0D4-1-2] Giá trị lớn nhất của hàm số
2
2
59
fx
xx
bằng
A.
11
4
. B.
4
11
. C.
11
8
. D.
8
11
.
Lời giải
Chọn D
Ta có:
2
2
5 11 11
5 9 ;
2 4 4
x x x x
.

Suy ra:
2
28
5 9 11
fx
xx
. Vậy giá trị lớn nhất của hàm số bằng
8
11
.
Câu 11: [0D4-1-2] Cho
2
f x x x
. Kết luận nào sau đây là đúng?
A.
fx
có giá trị nhỏ nhất bằng
1
4
. B.
fx
có giá trị lớn nhất bằng
1
2
.
C.
fx
có giá trị nhỏ nhất bằng
1
4
. D.
fx
có giá trị lớn nhất bằng
1
4
.
Lời giải
Chọn D
2
22
1 1 1 1 1
4 4 4 2 4
f x x x x x x
và
11
24
f
.
Câu 12: [0D4-1-2] Bất đẳng thức
2
4m n mn
tương đương với bất đẳng thức nào sau
đây?
A.
22
1 1 0n m m n
. B.
22
2m n mn
.
C.
2
0m n m n
. D.
2
2m n mn
.
Lời giải
Chọn B
2
4m n mn
22
24m mn n mn
22
2m n mn
.
Câu 13: [0D4-1-2] Với mọi
,0ab
, ta có bất đẳng thức nào sau đây luôn đúng?
A.
0ab
. B.
22
0a ab b
. C.
22
0a ab b
. D.
0ab
.
Lời giải
Chọn C
22
22
2 2 2
33
2 0; 0
2 2 4 2 4
b b b b b
a ab b a a a b
.
Câu 14: [0D4-1-2] Với hai số
x
,
y
dương thoả thức
36xy
, bất đẳng nào sau đây đúng?
A.
2 12x y xy
. B.
2 72x y xy
.
C.
22
4xy x y
. D.
2
36
2
xy
xy
.

Lời giải
Chọn A
Áp dụng bất đẳng thức Cô – si cho hai số không âm
x
,
y
. Ta có:
2 2 36 12x y xy
.
Câu 15: [0D4-1-2] Cho hai số
x
,
y
dương thoả
12xy
, bất đẳng thức nào sau đây đúng?
A.
6xy
. B.
2
36
2
xy
xy
.
C.
22
2xy x y
. D.
6xy
.
Lời giải
Chọn A
Áp dụng bất đẳng thức Cô – si cho hai số không âm
x
,
y
. Ta có:
6
2
xy
xy
.
Câu 16: [0D4-1-2] Cho
x
,
y
là hai số thực bất kỳ thỏavà
2xy
. Giá trị nhỏ nhất của
22
A x y
.
A.
2
. B.
1
. C.
0
. D.
4
.
Lời giải
Chọn D
Áp dụng bất đẳng thức Cô – si cho hai số không âm
2
x
và
2
y
. Ta có:
2
2 2 2 2
2 2 4A x y x y xy
. Đẳng thức xảy ra
2xy
.
Câu 17: [0D4-1-2] Với
, , , 0a b c d
. Trong các mệnh đề sau đây mệnh đề sai?
A.
1
a a a c
b b b c
. B.
1
a a a c
b b b c
.
C.
a c a a c c
b d b b d d
. D. Có t nhất hai trong ba mệnh đề
trên sai.
Lời giải
Chọn D
Ta có:
a b c
a a c
b b c b b c
suy ra A, B đúng.

Câu 18: [0D4-1-2] Hai số
,ab
thoả bất đẳng thức
2
22
22
a b a b
thì
A.
ab
. B.
ab
. C.
ab
. D.
ab
.
Lời giải
Chọn C
2
22
22
a b a b
2
22
22a b a b
2
0ab
ab
.
Câu 19: [0D4-1-2] Cho
,0ab
. Chứng minh
2
ab
ba
. Một học sinh làm như sau:
I)
2
ab
ba
22
21
ab
ab
II)
1
22
2a b ab
22
20a b ab
2
( ) 0ab
.
III) và
2
0ab
đúng
,0ab
nên
2
ab
ba
.
Cách làm trên :
A. Sai từ I). B. Sai từ II).
C. Sai ở III). D. Cả I), II), III) đều đúng.
Lời giải
Chọn D
Câu 20: [0D4-1-2] Cho các bất đẳng thức:
2
ab
I
ba
,
3
a b c
II
b c a
,
1 1 1 9
III
a b c a b c
(với
, , 0abc
). Bất đẳng thức nào trong các bất đẳng
thức trên là đúng?
A. chỉ
I
đúng. B. chỉ
II
đúng.
C. chỉ
III
đúng. D.
,,I II III
đều đúng.
Lời giải
Chọn D
Ta có:
2 . 2
a b a b
I
b a b a
đúng;
3
3 . . 3
a b c a b c
II
b c a b c a
đúng;

3
3
1 1 1 1
3
3
a b c abc
a b c abc
1 1 1
9abc
abc
1 1 1 9
a b c a b c
III
đúng.
Câu 21: [0D4-1-2] Với
m
,
0n
, bất đẳng thức:
33
mn m n m n
tương đương với bất
đẳng thức
A.
22
0m n m n
. B.
22
0m n m n mn
.
C.
2
0m n m n
. D. Tất cả đều sai.
Lời giải
Chọn C
3 3 2 3 2 3
0mn m n m n m n m mn n
22
0m m n n m n
2
0m n m n
.
Câu 22: [0D4-1-2] Cho
, 0xy
. Tìm bất đẳng thức sai?
A.
2
4x y xy
. B.
1 1 4
x y x y
.
C.
2
14
xy
xy
. D.
2
22
2x y x y
.
Lời giải
Chọn B
1 1 1 1 4
4xy
x y x y x y
đẳng thức xảy ra
xy
.
Câu 23: [0D4-1-2] Cho
22
1xy
, gọi
S x y
. Khi đó ta có
A.
2S
. B.
2S
. C.
22S
. D.
11S
.
Lời giải
Chọn C
Ta có:
22
12x y xy
21xy
.
Mặt khác:
2
2 2 2
22S x y x xy y
22S
.

Câu 24: [0D4-1-2] Cho
,xy
là hai số thực thay đổi sao cho
2xy
. Gọi
22
m x y
. Khi
đó ta có:
A. giá trị nhỏ nhất của
m
là
2
. B.giá trị nhỏ nhất của
m
là
4
.
C. giá trị lớn nhất của
m
là
2
. D.giá trị lớn nhất của
m
là
4
.
Lời giải
Chọn A
Ta có:
22x y y x
.
Do đó:
22
2 2 2 2
2 2 4 4 2 1 2 2;m x y x x x x x x
.
Vậy giá trị nhỏ nhất của
m
là
2
.
Câu 25: [0D4-1-2] Với mỗi
2x
, trong các biểu thức:
2
x
,
2
1x
,
2
1x
,
1
2
x
,
2
x
giá trị biểu
thức nào là nhỏ nhất?
A.
2
x
. B.
2
1x
. C.
2
1x
. D.
2
x
.
Lời giải
Chọn B
Ta có:
2 2 2
11x x x
và
1
22
xx
.
Mặt khác:
2
22
24
0; 2
2 1 2 1 2 1
x x x
x x x
x
x x x
2
21
x
x
.
Câu 26: [0D4-1-2] Giá trị nhỏ nhất của hàm số
2
21
x
fx
x
với
1 x
là
A.
2
. B.
5
2
. C.
22
. D. 3.
Lời giải
Chọn B
Ta có:
2 1 2 1 1 2 1 5
2.
2 1 2 1 2 2 1 2 2
x x x
fx
x x x
.
Vậy hàm số
fx
có giá trị nhỏ nhất bằng
5
2
.
Câu 27: [0D4-1-2] Giá trị nhỏ nhất của hàm số
1
2f x x
x
với
0x
là

A.
2
. B.
1
2
. C.
2
. D.
22
.
Lời giải
Chọn D
Ta có:
11
2 2 2 . 2 2f x x x
xx
.
Vậy hàm số
fx
có giá trị nhỏ nhất bằng
22
.
Câu 28: [0D4-1-2] Xét các mệnh đề sau đây:
I.
22
2a b ab
II.
33
()ab a b a b
III.
44ab ab
Mệnh đề nào đúng?
A. Chỉ I. B. Chỉ II. C. I và III. D. I, II và
III.
Lời giải
Chọn A
I đúng vì
2
0BDT a b
II, III sai với
0, 1ab
.
Câu 29: [0D4-1-2] Xét các mệnh đề sau
2
4
1
.
12
a
a
1
.
12
ab
ab
2
2
11
.
22
a
a
2
1
ab
ab
.
Số mệnh đề đúng là .
A.
1
. B.
3
. C.
4
. D.
2
.
Lời giải
Chọn D
A đúng vì
2
2 4 2
2 1 1 0BDT a a a
B sai với
1, 2ab
C đúng vì
2
2
2 2 2
2
11
2 2 1 1 1 0
22
a
a a a
a
.
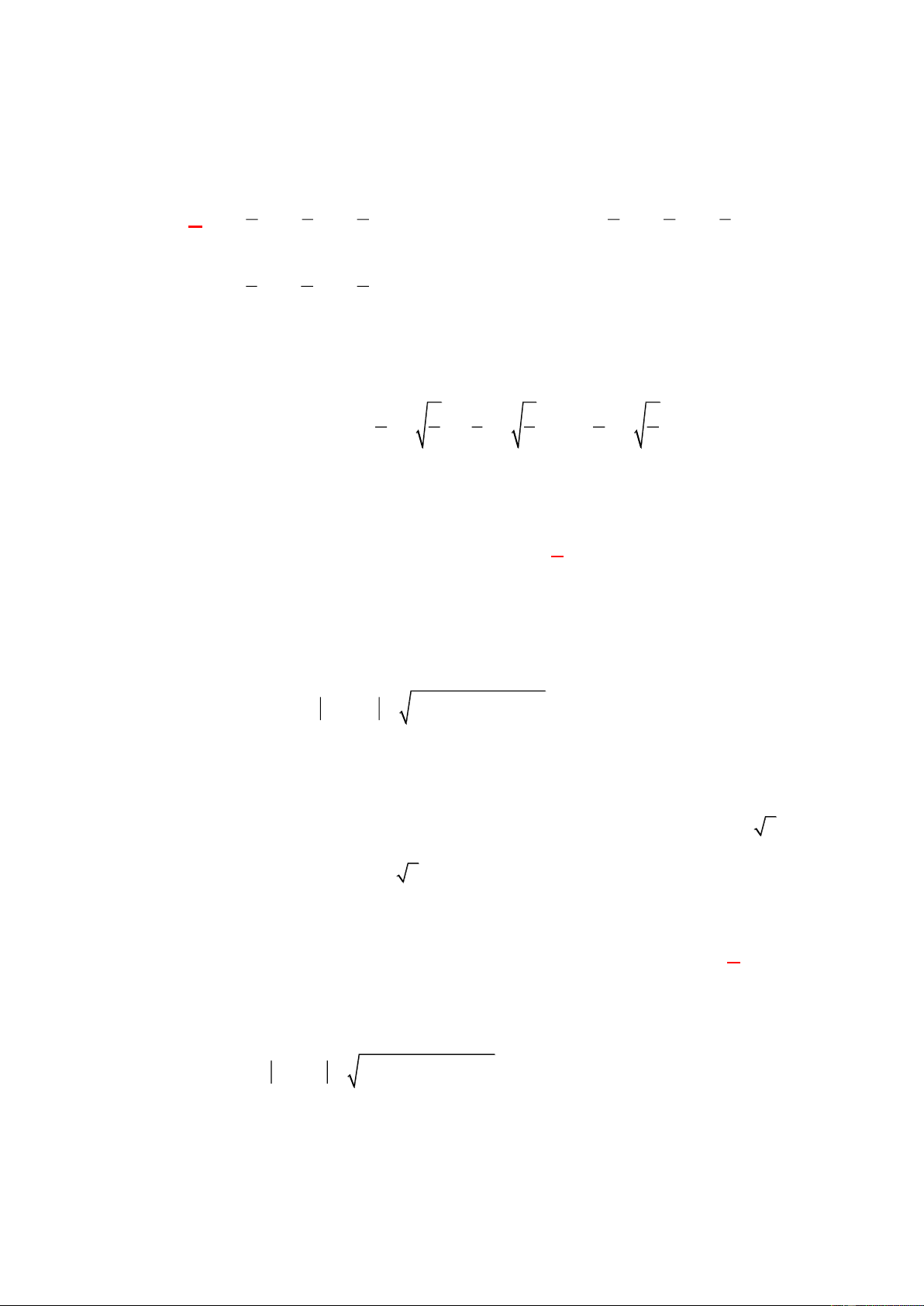
D sai với
1; 1ab
Câu 30: [0D4-1-2] Cho
, , a b c
dương. Bất đẳng thức nào đúng?
A.
1 1 1 8
a b c
b c a
. B.
1 1 1 3
a b c
c a b
.
C.
1 1 1 3
b c a
c a b
. D.
6a b b c c a abc
.
Lời giải
Chọn A
Với
,,abc
dương thì
1 2 ,1 2
a a b b
b b c c
và
12
cc
aa
, nhân vế theo vế ta
chọn A
Câu 31: [0D4-1-2] Cho
22
4xy
. Câu nào sau đây sai ?
A.
|3 4 | 10xy
. B.
|3 4 | 5xy
.
C.
|3 4 | 25xy
. D.
|3 4 | 20xy
.
Lời giải
Chọn B
Với mọi
,xy
thì
2 2 2 2
3 4 3 4 10x y x y
nên B sai.
Câu 32: [0D4-1-2] Cho bốn số
, , , a b x y
thỏa mãn
2 2 2 2
1a b x y
. Tìm bất đẳng
thức đúng.
:| | 1I ax by
.
:| ( ) ( ) | 2II a x y b x y
.
:| ( ) ( ) | 2III a x y b x y
.
:| | 1IV ay bx
.
Số mệnh đề đúng là .
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn D
A đúng vì
2 2 2 2
1ax by a b x y
.

B đúng vì
22
2 2 2 2 2 2
22a x y b x y a b x y x y a b x y
.
Tương tự C, D đúng.
Câu 33: [0D4-1-2] Tìm giá trị lớn nhất của hàm số
2
56y x x
trên đoạn
2;3
.
A.
5
2
. B.
1
4
. C.
1
. D.
1
2
.
Lời giải
Chọn D
Ta có:
2
1 5 1
, 2;3
4 2 4
y x x
và
15
42
yx
.
Câu 34: [0D4-1-2] Tìm giá trị lớn nhất của hàm số
63
8y x x
trên đoạn
0;2
.
A.
8
B.
16
. C.
4
. D.
3
4
.
Lời giải
Chọn B
Ta có:
2
3
16 4 16, 0;2y x x
và
3
16 4 0;2yx
.
Câu 35: [0D4-1-2] Trong các số
32
,
15
,
23
,
4
A. số nhỏ nhất là
15
, số lớn nhất là
23
.
B. số nhỏ nhất là
23
, số lớn nhất là
4
.
C. số nhỏ nhất là
15
, số lớn nhất là
32
.
D. số nhỏ nhất là
23
, số lớn nhất là
32
.
Lời giải
Chọn D
Dùng máy tính cầm tay kiểm tra ta được
2 3 15 4 3 2
.
Câu 36: [0D4-1-2] Cho hai số thực
,ab
sao cho
ab
. Bất đẳng thức nào sau đây không
đúng?
A.
44
ab
. B.
2 1 2 1 ab
. C.
0ba
. D.
22 ab
.
Lời giải
Chọn A

44
a b a b
không đúng. V dụ
3; 4;a b a b
nhưng
44
44
34ab
.
Câu 37: [0D4-1-2] Nếu
01a
thì bất đẳng thức nào sau đây đúng?
A.
1
a
a
. B.
1
a
a
. C.
aa
. D.
32
aa
.
Lời giải
Chọn A
Lấy ví dụ cụ thể với
1
4
a
ta sẽ thấy được chỉ có kết quả
1
a
a
là đúng.
Câu 38: [0D4-1-2] Nếu
a b a
và
b a b
thì bất đẳng thức nào sau đây đúng?
A.
0ab
. B.
ba
. C.
0ab
. D.
0a
và
0b
.
Lời giải
Chọn A
0a b a b
;
00b a b a a
Suy ra
0ab
.
Câu 39: [0D4-1-2] Cho
,,abc
là độ dài ba cạnh của một tam giác. Mệnh đề nào sau đây
không đúng?
A.
2
a ab ac
.
B.
2
ab bc b
.
C.
2 2 2
2 b c a bc
. D.
2 2 2
2 b c a bc
.
Lời giải
Chọn D
2
2 2 2 2 2 2 2
22b c a bc b c bc a b c a
0b c a a c b
(Vô lý).
Câu 40: [0D4-1-2] Cho
2
f x x x
. Kết luận nào sau đây là đúng?
A.
()fx
có giá trị nhỏ nhất bằng
1
4
. B.
()fx
có giá trị lớn nhất bằng
1
2
.
C.
()fx
có giá trị nhỏ nhất bằng
1
4
. D.
()fx
có giá trị lớn nhất bằng
1
4
.
Lời giải
Chọn D

Ta có:
2
22
1 1 1 1 1
2. .
2 4 4 2 4
f xx xxxx
1
4
.
Đẳng thức xảy ra khi
1
2
x
.
Vậy,
()fx
có giá trị lớn nhất bằng
1
4
.
Câu 41: [0D4-1-2] Cho hàm số
2
1
1
fx
x
. Mệnh đề nào sau đây là đúng?
A.
()fx
có giá trị nhỏ nhất là
0
, giá trị lớn nhất bằng
1
.
B.
()fx
không có giá trị nhỏ nhất, giá trị lớn nhất bằng
1
.
C.
()fx
có giá trị nhỏ nhất là
1
, giá trị lớn nhất bằng
2
.
D.
()fx
không có giá trị nhỏ nhất và giá trị lớn nhất.
Lời giải
Chọn B
Ta có:
0fx
nên không có giá trị nhỏ nhất.
Ta có:
2
1 1x
2
1
1
1
x
. Đẳng thức xảy ra khi
0x
.
Vậy,
()fx
không có giá trị nhỏ nhất, giá trị lớn nhất bằng
1
.
Câu 42: [0D4-1-2] Với giá trị nào của
a
thì hệ phương trình
1
21
xy
x y a
có nghiệm
( ; )xy
với
.xy
lớn nhất
A.
1
4
a
. B.
1
2
a
. C.
1
2
a
. D.
1a
.
Lời giải
Chọn B
Hệ phương trình có nghiệm
xa
,
1ya
Ta có:
22
2.
1 1 1
1
2 4 4
axy a a a a a
2
1 1 1
2 4 4
a
Đẳng thức xảy ra khi
1
2
a
.
Vậy
xy
lớn nhất khi
1
2
a
.
Câu 43: [0D4-1-2] Cho biết hai số
a
và
b
có tổng bằng
3
. Khi đó, tch hai số
a
và
b

A. có giá trị nhỏ nhất là
9
4
. B. có giá trị lớn nhất là
9
4
.
C. có giá trị lớn nhất là
3
2
. D. không có giá trị lớn nhất.
Lời giải
Chọn B
Ta có:
2
33ab a a a a
2
22
3 9 9 3 9 9
2
3
2
2
4
.
4 4 4
a aaaa
Đẳng thức xảy ra khi
3
2
a
.
Vậy,
ab
có giá trị lớn nhất là
9
4
.
Câu 44: [0D4-1-2] Cho
2ab
. Khi đó, tch hai số
a
và
b
A. có giá trị nhỏ nhất là
1
. B. có giá trị lớn nhất là
1
.
C. có giá trị nhỏ nhất khi
ab
. D. không có giá trị nhỏ nhất.
Lời giải
Chọn A
Ta có:
2
2
2 1 112ab a a aaa
Đẳng thức xảy ra khi
1a
Vậy,
ab
đạt giá trị nhỏ nhất là
1
.
Câu 45: [0D4-1-2] Với mỗi
2x
, trong các biểu thức:
2
x
,
2
1x
,
2
1x
,
1
2
x
,
2
x
giá trị biểu
thức nào là nhỏ nhất?
A.
2
x
. B.
2
1x
. C.
2
1x
. D.
2
x
.
Lời giải
Chọn B
Nếu
2x
thì
2
1
x
,
22
13x
,
2
2
1x
,
13
22
x
,
1
2
x
.
Vậy giá trị của biểu thức
2
1x
là nhỏ nhất.
Câu 46: [0D4-1-2] Giá trị nhỏ nhất của biểu thức
2
3xx
với
x
là:
A.
3
2
. B.
9
4
. C.
27
4
. D.
81
8
.

Lời giải
Chọn B
Ta có:
22
2
3 9 9 3 9
3
2 4 4
.
4
2.
2
x x x xx
9
4
Đẳng thức xảy ra khi
3
2
x
Vậy giá trị nhỏ nhất của biểu thức là
9
4
.
Câu 47: [0D4-1-2] Giá trị nhỏ nhất của biểu thức
2
3xx
với
x
là:
A.
9
4
. B.
3
2
. C.
0
. D.
3
2
.
Lời giải
Chọn C
Ta có:
2
30xx
Đẳng thức xảy ra khi
0x
.
Câu 48: [0D4-1-2] Giá trị nhỏ nhất của biểu thức
2
6A x x
với
x
là:
A.
9
. B.
6
. C.
0
. D.
3
.
Lời giải
Chọn A
Ta có :
2
22
2
6 6 6 9 9 3 9 9A x x x x x x x
min
9A
khi
3 0 3xx
.
Câu 49: [0D4-1-2] Cho biểu thức
P a a
với
0a
. Mệnh đề nào sau đây là mệnh đề
đúng?
A. Giá trị lớn nhất của
P
là
1
4
. B. Giá trị nhỏ nhất của
P
là
1
4
.
C. Giá trị lớn nhất của
P
là
1
2
. D.
P
đạt giá trị nhỏ nhất tại
1
4
a
.
Lời giải
Chọn A
Ta có :
2
1 1 1 1 1
4 4 4 2 4
P a a a a a a a

1
4
max
P
khi
11
0
24
aa
.
Câu 50: [0D4-1-2] Giá trị lớn nhất của hàm số
2
2
59
fx
xx
bằng
A.
11
4
. B.
4
11
. C.
11
8
. D.
8
11
.
Lời giải
Chọn D
Ta có :
2
2
59
f x f x
xx
đạt giá trị lớn nhất khi
2
59A x x
đạt giá
trị nhỏ nhất.
2
22
min
25 11 5 11 11 11
5 9 5
4 4 2 4 4 4
A x x x x x A
khi
5
2
x
Vậy
fx
đạt giá trị lớn nhất là
8
11
khi
5
2
x
.
Câu 51: [0D4-1-2] Cho biểu thức
2
1f x x
. Kết luận nào sau đây đúng?
A. Hàm số
()fx
chỉ có giá trị lớn nhất, không có giá trị nhỏ nhất.
B. Hàm số
()fx
chỉ có giá trị nhỏ nhất, không có giá trị lớn nhất.
C. Hàm số
()fx
có giá trị nhỏ nhất và giá trị lớn nhất.
D. Hàm số
()fx
không có giá trị nhỏ nhất và không có giá trị lớn nhất.
Lời giải
Chọn C
TXĐ :
1;1D
2
min max
0 1 1 0; 1x D x y y
.
Vậy hàm số có GTLN và GTNN.
Câu 52: [0D4-1-2] Cho
a
là số thực bất kì,
2
2
1
a
P
a
. Bất đẳng thức nào sau đây đúng với
mọi a?
A.
1P
. B.
1P
. C.
1P
. D.
1P
.
Lời giải
Chọn D
Cách 1. Xét
2
2
2 2 2
1
2 2 1
10
1 1 1
1 1
a
a a a
P
a a a
P
.

Vậy, chọn đáp án D.
Cách 2. Khi
11aP
loại đáp án A, B và C.
Câu 53: [0D4-1-2] Cho
2 2 2
Q a b c ab bc ca
với
,,abc
là ba số thực. Khẳng định nào
sau đây là đúng?
A.
0Q
chỉ đúng khi
,,abc
là những số dương.
B.
0Q
chỉ đúng khi
,,abc
là những số không âm.
C.
0.Q
với
,,abc
là những số bất kì.
D.
0Q
với
,,abc
là những số bất kì.
Lời giải
Chọn D
2 2 2
22Q a b c ab bc ca
2 2 2 2 2 2
2 2 2a ab b b bc c c ca a
2 2 2
0 , ,
0 , ,
a b b c c a a b c
Q a b c
Vậy, chọn đáp án D.
Câu 54: [0D4-1-2] Số nguyên
a
lớn nhất sao cho
200 300
3a
là:
A.
3
. B.
4
. C.
5
. D.
6
.
Lời giải
Chọn C
Ta có :
100 100
200 300 2 3 2 3 2
3 3 3 27 5a a a a a
.
Câu 55: [0D4-1-2] Cho hai số thực
a
,
b
tùy ý. Mệnh đề nào sau đây là đúng?
A.
.ab a b
. B.
a
a
bb
với
0b
.
C. Nếu
ab
thì
22
ab
. D.
a b a b
.
Lời giải
Chọn C
+Ta có
22
a b a b
,
,ab
hay ta có C đúng.
+ Chọn
2a
,
1b
thay vào các phương án chỉ có phương án C đúng.
Câu 56: [0D4-1-2] Cho hai số thực
a
,
b
tùy ý. Mệnh đề nào sau đây là đúng?
A.
a b a b
. B.
a b a b
. C.
a b a b
. D.
a b a b
.

Lời giải
Chọn A
+ Với mọi số thực
a
,
b
ta có
a b a b a b
hay ta có A đúng.
+ Chọn
3a
,
2b
ta có B, D sai chỉ có A, C đúng. Chọn
3a
,
2b
thay
vào A, C chỉ có A đúng.
Câu 57: [0D4-1-2] Bất đẳng thức nào sau đây đúng với mọi số thực
x
?
A.
xx
. B.
xx
. C.
2
2
xx
. D.
xx
.
Lời giải
Chọn D
Chọn
0x
thay vào các phương án ta có D đúng.
Câu 58: [0D4-1-2] Nếu
a
,
b
là những số thực và
ab
thì bất đẳng thức nào sau đây luôn
đúng?
A.
22
ab
. B.
11
ab
với
0ab
.
C.
b a b
. D.
ab
.
Lời giải
Chọn A
+Ta có
22
a b a b
,
,ab
hay ta có A đúng.
+ Chọn
1
2
a
,
4b
ta có B, C, D sai chỉ có A đúng.
Câu 59: [0D4-1-2] Cho
0a
. Nếu
xa
thì bất đẳng thức nào sau đây luôn đúng?
A.
xa
. B.
xx
. C.
xa
. D.
11
xa
.
Lời giải
Chọn B
+ Ta có
,x x x
vậy B đúng.
+ Chọn
4x
,
3a
ta có A, C, D đều sai, Vậy chọn. A.
Câu 60: [0D4-1-2] Nếu
xa
, với
0a
thì bất đẳng thức nào sau đây luôn đúng?
A.
xa
. B.
11
xa
. C.
xa
. D.
xa
.
Lời giải
Chọn D
Chọn
1x
,
2a
thay vào ta có A, B, C đều sai chọn. D.
Câu 61: [0D4-1-2] Cho
1a
,
1b
. Bất đẳng thức nào sau đây Sai?

A.
21aa
. B.
21ab a b
. C.
21ab b a
. D.
21bb
.
Lời giải
Chọn C
Chọn
1a
,
1b
thay vào ta có A, B, D đúng chỉ C sai.
Câu 62: [0D4-1-2] Giá trị nhỏ nhất của hàm số
2
()f x x
x
với
0x
là
A.
4
. B.
1
2
. C.
2
. D.
22
.
Lời giải
Chọn D
Vì
0x
nên ta có
2
0
x
.
Áp dụng BĐT Cô-Si cho hai số
x
và
2
x
ta có
22
2 . 2 2xx
xx
. Dấu
""
xảy ra khi và chỉ khi
2
2, 0x x x
x
.
Vậy giá trị nhỏ nhất của hàm số là
22
khi
2x
.
Câu 63: [0D4-1-2] Giá trị nhỏ nhất của hàm số
3
( ) 2f x x
x
với
0x
là
A.
43
. B.
6
. C.
23
. D.
26
.
Lời giải
Chọn D
Vì
0x
nên ta có
20x
và
3
0
x
.
Áp dụng BĐT Cô-Si cho hai số
2x
và
3
x
ta có
33
2 2 2 . 2 6xx
xx
. Dấu
""
xảy ra khi và chỉ khi
33
2 , 0
2
x x x
x
.
Vậy giá trị nhỏ nhất của hàm số là
26
khi
3
2
x
.
Câu 64: [0D4-1-2] Giá trị nhỏ nhất của hàm số
2
()
21
x
fx
x
với
1 x
là
A.
2
. B.
5
2
. C.
22
. D.
3
.
Lời giải
Chọn B

Ta có
2
21
x
fx
x
1 2 1
2 1 2
x
x
1 2 1 5
2.
2 1 2 2
x
x
.
Dấu
""
xảy ra khi và chỉ khi
12
3, 1
21
x
xx
x
.
Vậy giá trị nhỏ nhất của hàm số là
5
2
khi
3x
.
Câu 65: [0D4-1-2] Cho
2x
. Giá trị lớn nhất của hàm số
2
()
x
fx
x
bằng
A.
1
22
. B.
2
2
. C.
2
2
. D.
1
2
.
Lời giải
Chọn A
Cách 1:
Với
20xy
.
Ta có
22
2
. 2 0
x
y y x x
x
,
Nếu
02yx
.
Nếu
0y
khi đó hàm số đạt giá trị lớn nhất, nhỏ nhất khi
có nghiệm
Vậy ta có
2
0 1 8 0y
11
2 2 2 2
y
.
Dấu
""
xảy ra khi và chỉ khi
2
4
8 16 0
1, ktm
x
xx
x
.
Vậy hàm số đạt giá trị lớn nhất
1
22
y
khi
4x
.
Cách 2: (Sử dụng kiến thức 12).
Ta có
2
4
22
x
y
xx
;
04yx
.
Lập BBT và dựa vào BBT ta có hàm số đạt giá trị lớn nhất
1
22
y
khi
4x
.
Câu 66: [0D4-1-2] Giá trị nhỏ nhất của hàm số
1
( ) 2f x x
x
với
0x
là
A.
2
. B.
1
2
. C.
2
. D.
22
.
Lời giải
Chọn D
Ta có
1
2f x x
x
1
2 2 . 2 2x
x
.

Dấu
""
xảy ra khi và chỉ khi
12
2 , 0
2
x x x
x
.
Vậy giá trị nhỏ nhất của hàm số là
22
khi
2
2
x
.
Câu 67: [0D4-1-2] Giá trị nhỏ nhất của hàm số
2
1
( ) 2f x x
x
với
0x
là
A.
1
. B.
2
. C.
3
. D.
22
.
Lời giải
Chọn C
Ta có
2
1
2f x x
x
2
1
xx
x
3
2
1
3 . . 3xx
x
. Dấu
""
xảy ra khi và chỉ khi
2
1
xx
x
2
1x
1 0x do x
.
Vậy giá trị nhỏ nhất của hàm số là
3
khi
1x
.
Câu 68: [0D4-1-2] Cho
a
,
b
,
c
,
d
là các số dương. Mệnh đề nào sau đây là đúng?
A. Nếu
ac
bd
thì
a b c d
ac
. B. Nếu
ac
bd
thì
a b c d
bd
.
C.
a b c ab bc ca
. D.
2 ( ) 2ab a b ab a b
.
Lời giải
Chọn A
Ta có
ac
bd
bd
ac
11
bd
ac
b a d c
a a c c
a b c d
ac
.
Ta có
ac
bd
a b c d a b c d
b b d d b d
.
Ta có
2a b ab
,
2b c bc
,
2c a ca
.
Cộng vế theo vế ta có
a b c ab bc ca
Dấu
""
xảy ra khi và chỉ khi
abc
.
Ta có
2a ab a b
;
2b ab b a
.
Cộng vế theo vế ta có
22a b ab ab a b
, Dấu
""
xảy ra khi và chỉ
khi
1ab
.
Câu 69: [0D4-1-2] Chọn mệnh đề đúng.
A. Giá trị lớn nhất của hàm số
13y x x
với
13x
là
2 khi 2x
B. Giá trị nhỏ nhất của hàm số
13y x x
với
13x
là
2 khi 2x

C. Giá trị nhỏ nhất của hàm số
2
2 5 1y x x
là
17 5
khi
84
x
D. Giá trị lớn nhất của hàm số
2
2 5 1y x x
là
17 5
khi
84
x
Lời giải
Chọn A
Với
13x
thì ta có
0y
1
.
Khi đó ta có
2 2 2
2 2 1
1 3 1 3 1 1 4y x x x x
.
Dấu
""
xảy ra khi và chỉ khi
1 3 2x x x
.
Hay ta có
2
4 2 2yy
2
.
Từ
1
và
2
ta có
02y
.
Vậy giá trị lớn nhất của hàm số là
2y
khi
2x
.
Câu C,D sai vì:
Ta có
2
2 5 1y x x
2
5 17
2
48
x
17
8
.
Vậy giá trị nhỏ nhất của hàm số là
17
8
y
khi
5
4
x
.
Câu 70: [0D4-1-2] Cho
2 2 2
1abc
. Hãy chọn mệnh đề đúng.
A.
0ab bc ca
. B.
1
2
ab bc ca
.
C.
1ab bc ca
. D.
1ab bc ca
.
Lời giải
Chọn B
+ Ta có
22
2a b ab
;
22
2b c bc
;
22
2c a ac
.
Cộng vế theo vế ta có
2 2 2
22a b c ab bc ca
1ab bc ca
.
+ Ta có
2
0abc
2 2 2
20a b c ab bc ca
1
2
ab bc ca
.
Bài 2: Bất phương trình, hệ bất phương trình bậc nhất một ẩn.
Câu 71: [0D4-1-2] Nếu
ab
và
.cd
thì bất đẳng thức nào sau đây luôn đúng?
A.
ac bd
. B.
a c b d
. C.
a d b c
. D.
ac bd
.
Lời giải
Chọn C
Có
c d c d

Lại có
ab
Cộng vế theo vế ta có:
a d b c
.
Câu 72: [0D4-1-2] Bất đẳng thức nào sau đây đúng với mọi số thực a?
A.
63aa
. B.
36aa
. C.
6 3 3 6 aa
. D.
63 aa
.
Lời giải
Chọn D
0:6 3a a a
loại A
0:3 6a a a
loại B
6 3 3 6 3 3 1a a a a
loại C
6 3 6 3aa
(luôn đúng).
Câu 73: [0D4-1-2] Nếu
,,abc
là các số bất kì và
ab
thì bất đẳng thức nào sau đây luôn
đúng?
A.
3 2 3 2 a c b c
. B.
22
ab
. C.
ac bc
. D.
ac bc
.
Lời giải
Chọn A
3 3 3 2 3 2a b a b a c b c
(luôn đúng)
22
0a b a b
loại B
;0a b c ac bc
loại C
;0a b c ac bc
loại D.
Câu 74: [0D4-1-2] Nếu
0ab
,
0cd
thì bất đẳng thức nào sau đây không đúng?
A.
ac bc
. B.
a c b d
. C.
22
ab
. D.
ac bd
.
Lời giải
Chọn B
A, C, D luôn đúng.
Câu 75: [0D4-1-2] Nếu
0ab
,
0.cd
thì bất đẳng thức nào sau đây không đúng?
A.
a c b d
. B.
ac bd
. C.
ab
cd
. D.
ad
bc
.
Lời giải
Chọn C
A, B luôn đúng.
Ta có:
0
ac bd
ac bd a d
bc bc b
b
c
c
D đúng.
Câu 76: [0D4-1-2] Nếu
22 a c b c
thì bất đẳng thức nào sau đây đúng?

A.
33 ab
. B.
22
ab
. C.
22ab
. D.
11
ab
.
Lời giải
Chọn C
2 2 2 2a c b c a b a b
(luôn đúng).
Câu 77: [0D4-1-2] Nếu
22ab
và
33 bc
thì bất đẳng thức nào sau đây đúng?
A.
ac
. B.
ac
. C.
33 ac
. D.
22
ac
.
Lời giải
Chọn B
22
33
a b a b
ac
b c b c
.
Câu 78: [0D4-1-2] Với số thực
a
bất kì, biểu thức nào sau đây có thể nhận giá trị âm?
A.
2
21aa
. B.
2
1aa
. C.
2
21aa
. D.
2
21aa
.
Lời giải
Chọn D
2
21aa
có
'2
0 2 1 0aa
aR
loại A
2
1aa
có
'2
3 0 1 0aa
aR
loại B
2
21aa
có
'2
0 2 1 0aa
aR
loại C
2
21aa
có
'2
2 0 2 1 0aa
12
;a a a
(với a
1
;a
2
là nghiệm của
phương trình).
Câu 79: [0D4-1-2] Với số thực
a
bất kì, biểu thức nào sau đây luôn luôn dương.
A.
2
21aa
. B.
2
1aa
. C.
2
21aa
. D.
2
21aa
.
Lời giải
Chọn B
Giải thch thương tự như câu 12
2
1aa
có
2
3 0 1 0aa
aR
.
Câu 80: [0D4-1-2] Tìm khẳng định đúng:
A.
..a b ac bc
. B.
11
ab
ab
. C.
ab
ab cd
cd
. D.
a b a c b c
.
Lời giải
Chọn C
Theo lý thuyết ta chọn C.

Câu 81: [0D4-1-2] Suy luận nào sau đây đúng:
A.
ab
ac bd
cd
. B.
ab
ab
cd
cd
.
C.
ab
a c b d
cd
. D.
0
0
ab
ac bd
cd
.
Lời giải
Chọn D
Theo BĐT ta chọn D.
Câu 82: [0D4-1-2] Với mọi
,0ab
, ta có bất đẳng thức nào sau đây luôn đúng?
A.
0ab
. B.
22
0a ab b
. C.
22
0a ab b
. D.
0ab
.
Lời giải
Chọn C
Ta có:
2
222
13
2
0
4
a b ba ab b
( do
,0ab
).
Câu 83: [0D4-1-2 Với hai số
,xy
dương thỏa
36xy
, bất đẳng thức sau đây đúng?
A.
2 12x y xy
. B.
2 72x y xy
. C.
2
36
2
xy
xy
. D.
2 72x y xy
.
Lời giải
Chọn A
Ta có
2 2. 36 12x y xy
.
Câu 84: [0D4-1-2] Cho
0x
;
0y
và
2xy
. Gía trị nhỏ nhất của
22
A x y
là:
A.
2
. B.
1
. C.
0
. D.
4
.
Lời giải
Chọn D
22
2
2 4 0, 0, 2x y xy x y xAx yy
.
Câu 85: [0D4-1-2] Cho
, , , 0a b c d
, tìm mệnh đề sai.
A.
1.
a a a c
b b b c
B.
1.
a a a c
b b b c

C.
.
a c a a c c
b d b b c d
D. Có ít nhất một trong ba mệnh
đề trên sai.
Lời giải
Chọn C
Với
, , , 0a b c d
A đúng vì
1
a
ab
b
ac bc
ab ac ab bc
a b c b a c
a a c
b b c
.
Tương tự B cũng đúng.
Dễ thấy C sai vì phản ví dụ
1 2 1 1 2 2 1 3 2
2 3 2 2 2 3 2 4 3
(vô lí).
Câu 86: [0D4-1-2] Với
,0mn
, bất đẳng thức
33
.mn m n m n
tương đương với bất
đẳng thức
A.
22
. 0.m n m n
B.
22
. 0.m n m n mn
C.
2
0.m n m n
D. Tất cả đều sai.
Lời giải
Chọn C
Ta có
3 3 2 2
..mn m n m n mn m n m n m n mn
2
0m n m n
Câu 87: [0D4-1-2] Cho
, 0xy
. Tìm bất đẳng thức sai.
A.
2
4.x y xy
B.
1 1 4
.
x y x y
C.
2
14
.
()xy x y
D.
2.x y xy
Lời giải
Chọn B
Dễ thấy
22
40x y xy x y
, nên A đúng. Từ đó kéo theo C đúng.
B sai vì bđt đúng là
1 1 4
x y x y

Câu 88: [0D4-1-2] Với hai số
,xy
dương thoả
36xy
. Bất đẳng thức nào sau đây đúng?
A.
2 12.x y xy
B.
22
2 72.x y xy
C.
2
36.
2
xy
xy
D. Tất cả đều đúng.
Lời giải
Chọn D
Áp dụng bất đẳng thức AM-GM cho 2 số dương x,y ta thấy cả 3 phương án trên đều
đúng.
Câu 89: [0D4-1-2] Cho bất đẳng thức
a b a b
. Dấu đẳng thức xảy ra khi nào?
A.
.ab
B.
. 0.ab
C.
. 0.ab
D.
. 0.ab
Lời giải
Chọn B
Ta có bất đẳng thức
x y x y
, dấu đẳng thức xảy ra khi
.0xy
.
Khi đó
a b a b a b a b
, dấu đẳng thức xảy ra khi
a( b) 0 0ab
Câu 90: [0D4-1-2] Cho
, , 0abc
Xét các bất đẳng thức sau
I)
2
ab
ba
II)
3
a b c
bca
III)
11
4ab
ab
Chọn khẳng định đúng.
A. Chỉ I) đúng. B. Chỉ II) đúng. C. Chỉ III) đúng. D. Cả I),
II), III) đúng.
Lời giải
Chọn D
Áp dụng bất đẳng thức AM-GM cho các số dương
,,abc
2 . 2
a b a b
b a b a
, đẳng thức xảy ra khi
ab
.
3
3 . . 3
a b c a b c
b c a b c a
, đẳng thức xảy ra khi
abc
.
1 1 1
2 .2 4a b ab
a b ab
đẳng thức xảy ra khi
ab
.

Câu 91: [0D4-1-2] Cho
, , 0x y z
. Xét các bất đẳng thức sau
I)
3 3 3
3x y z xyz
II)
1 1 1 9
x y z x y z
III)
3
x y z
y z x
Chọn khẳng định đúng.
A. Chỉ I) đúng . B. Chỉ I) và III) đúng . C. Cả I), II), III) đúng. D. Chỉ III)
đúng.
Lời giải
Chọn B
Dễ thấy I) và III) đúng.
Lại có
3
3
1 1 1 1 1 1 1 9
3 .3 9x y z xyz
x y z xyz x y z x y z
. Vậy II)
sai.
Câu 92: [0D4-1-2] Cho
, , 0abc
. Xét các bất đẳng thức sau
I)
2
ab
ba
II)
3
a b c
bca
III)
1 1 1 9
a b c a b c
Bất đẳng thức nào đúng?
A. Chỉ I) đúng. B. Chỉ II) đúng. C. Chỉ III) đúng. D. Cả I),
II), III) đúng.
Lời giải
Chọn D
Dễ thấy I) và III) đúng.
Lại có
3
3
1 1 1 1
3. .3. 9a b c abc
a b c abc
1 1 1 9
a b c a b c
.Vậy
III) cũng đúng.
Câu 93: [0D4-1-2] Cho
,0ab
. Chứng minh
2
ab
ba
. Một học sinh làm như sau
I)
2
ab
ba
22
2
ab
ab
(1)
II) (1)
2 2 2 2 2
2 2 0 ( ) 0a b ab a b ab a b
III) vì
2
0ab
đúng
, 0ab
nên
2
ab
ba
Cách làm trên

A. Sai từ I). B. Sai từ II). C. Sai ở III). D. Cả I),
II), III) đúng.
Lời giải
Chọn D
Câu 94: [0D4-1-2] Cho
, , 0abc
. Xét các bất đẳng thức
I)
3
3a b c abc
II)
1 1 1
9abc
abc
III)
9a b b c c a
.
Bất đẳng thức nào đúng
A. Chỉ I) và II) đúng. B. Chỉ I) và III) đúng. C. Chỉ I) đúng. D. Cả I),
II), III) đúng.
Lời giải
Chọn A
Dễ thấy bđt I) và II) đúng còn bđt III) sai.
Câu 95: [0D4-1-2] Trong các hình chữ nhật có cùng chu vi thì
A. Hình vuông có diện tích nhỏ nhất .
B. Hình vuông có diện tích lớn nhất.
C. Không xác định được hình có diện tích lớn nhất .
D. Cả A, B, C đều sai.
Lời giải
Chọn B
Gọi kch thước hai cạnh hình chữ nhật là
, , 0a b a b
và chu vi là P. Ta có
2 a b P
.
Diện tch hình chữ nhật là
22
2
.
2 4 16
a b P P
S ab
Khi đó
2
maxS
16
P
ab
.
§ 2. ĐẠI CƯƠNG VỀ BẤT PHƯƠNG TRÌNH.

Câu 1: [0D4-1-3] Bất đẳng thức
2 2 2 2 2
()a b c d e a b c d e
, , , ,a b c d e
tương
đương với bất đẳng thức nào sau đây?
A.
2 2 2 2
0.
2 2 2 2
b c d e
a a a a
B.
2 2 2 2
0.
2 2 2 2
a a a a
b c d e
C.
2 2 2 2
0.
2 2 2 2
a a a a
b c d e
D.
2 2 2 2
0.a b a c a d a e
Lời giải
Chọn B
2 2 2 2 2
()a b c d e a b c d e
2 2 2 2
2 2 2 2
0
4 4 4 4
a a a a
ab b ac c ad d ae e
2 2 2 2
0
2 2 2 2
a a a a
b c d e
Câu 2: [0D4-1-3] Cho
,0ab
và
ab a b
. Mệnh đề nào đúng?
A.
4.ab
B.
4.ab
C.
4.ab
D.
4.ab
Lời giải
Chọn B
Vì
,0ab
, ta có
2
2
ab
a b ab
2
2
4
2
ab
a b a b a b
(*).
Lại có
,0ab
nên chia hai vế của (*) cho
0ab
, ta được
4ab
.
Câu 3: [0D4-1-3] Cho
, , 0a b c
và
a b c
P
a b b c c a
. Khi đó
A.
0 1.P
B.
2 3.P
C.
1 2.P
D.
3
.
2
P
Lời giải
Chọn C

AD bđt ở câu 4 :
1
a a a c
b b b c
, ta có
1
a a a c
a b a b a b c
.
Tương tự
b b a
b c a b c
,
c c b
c a a b c
.Suy ra
2P
.
Lại có
,
a a b b
a b a b c b c a b c
,
cc
c a a b c
. Suy ra
1P
.
Vậy
12P
.
Câu 4: [0D4-1-3] cho
, , 0abc
. Xét các bất đẳng thức
I)
1 1 1 8
a b c
b c a
II)
2 2 2
64b c c a a b
a b c
III)
a b c abc
Chọn khẳng định đúng.
A. Chỉ I) đúng. B. Chỉ II) đúng. C. Chỉ I) và II) đúng. D. Cả I),
II), III) đúng.
Lời giải
Chọn C
1 1 1 . .
a b c b a c b a c
b c a b c a
2 2 2
8
ba cb ac
b c a
nên I) đúng .
Lại có
4
22
24
bc
b c bc
aa
a
,
tương tự
44
22
4 , 4
ca ab
c a a b
bc
bc
,
suy ra
4 4 4
2 2 2
4 4 4 64
bc ca ab
b c c a a b
a b c
a b c
nên II) đúng.
Dễ thấy III) sai.
Câu 5: [0D4-1-3] Cho x, y là những số thực dương thỏa mãn
5
4
xy
. Giá trị nhỏ nhất của biểu
thức
41
4
P
xy
là:

A.
2
. B.
3
. C.
5
. D.
65
4
.
Lời giải
Chọn C
Áp dụng bất đẳng thức Cauchy schwarz ta có
22
2
11
25
2
4 1 2
22
4
5
5
4
4
P
x y x y x y
Dấu bằng xảy ra khi
1
1,
4
xy
.
Câu 6: [0D4-1-3] Cho
0ab
và
2
1
1
a
x
aa
,
2
1
1
b
y
bb
. Mệnh đề nào sau đây đúng?
A.
xy
. B.
xy
.
C.
xy
. D. Không so snh được.
Lời giải
Chọn B
Ta có:
11
1
a
xa
và
11
1
b
yb
.
Suy ra:
1 1 1
1
11
ab
x y a b
Do
0ab
nên
11a
và
11b
suy ra:
1
1
11ab
1
10
11ab
.
Vậy
11
0
xy
11
xy
do
0x
và
0y
nên
11
xy
xy
.
Câu 7: [0D4-1-3] Cho
, , 0abc
. Xét các bất đẳng thức sau:
I)
2
ab
ba
. II)
3
a b c
b c a
. III)
11
4ab
ab
.
Bất đẳng thức nào đúng?
A. Chỉ I) đúng. B. Chỉ II) đúng. C. Chỉ III) đúng. D. Cả ba
đều đúng.
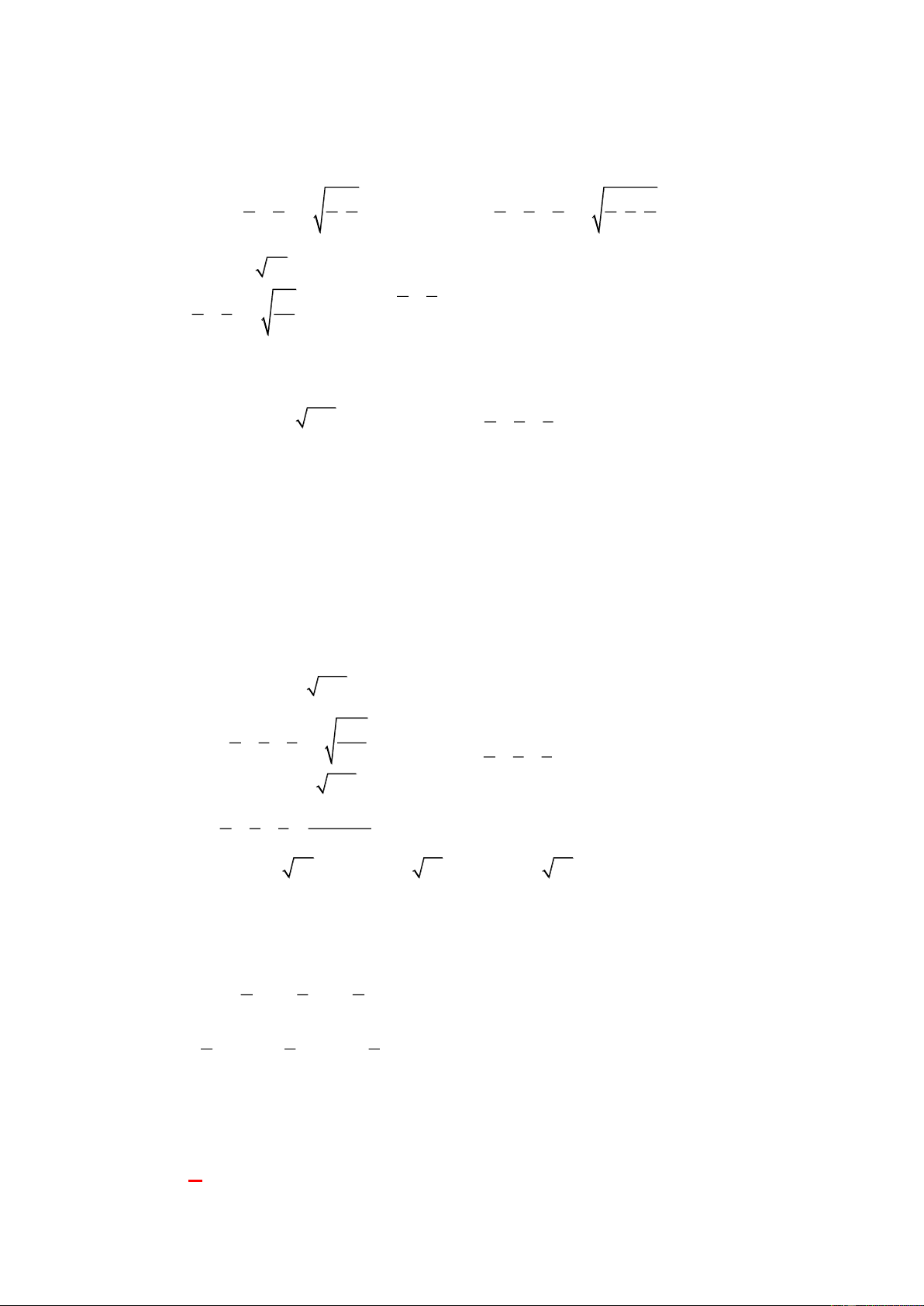
Lời giải
Chọn D
Ta có:
2 . 2
a b a b
I
b a b a
đúng;
3
3 . . 3
a b c a b c
II
b c a b c a
đúng;
2
1 1 1
2
a b ab
a b ab
11
4ab
ab
()III
đúng.
Câu 8: [0D4-1-3] Cho
, , 0abc
. Xét các bất đẳng thức:
I)
3
3a b c abc
II)
1 1 1
9abc
abc
III)
9a b b c c a
.
Bất đẳng thức nào đúng:
A. Chỉ I) và II) đúng. B. Chỉ I) và III) đúng.
C. Chỉ I) đúng. D. Cả ba đều đúng.
Lời giải
Chọn A
3
3a b c abc I
đúng;
3
3
1 1 1 1
3
3
a b c abc
a b c abc
1 1 1
9abc
abc
1 1 1 9
II
a b c a b c
đúng;
2a b ab
;
2b c bc
;
2c a ca
8a b b c c a abc
III
sai.
Câu 9: [0D4-1-3] Cho
, , 0abc
. Xét các bất đẳng thức:
I)
1 1 1 8
a b c
b c a
. II)
2 2 2
64b c c a a b
a b c
.
III)
a b c abc
. Bất đẳng thức nào đúng?
A. Chỉ I) đúng. B. Chỉ II) đúng.
C. Chỉ I) và II) đúng. D. Cả ba đều đúng.

Lời giải
Chọn C
12
aa
bb
;
12
bb
cc
;
12
cc
aa
1 1 1 8 8
a b c a b c
b c a b c a
I
đúng.
1
2
b
b
aa
;
1
2
c
c
aa
4
22
2
2 4 4
bc bc
bc
a a a
.
Tương tự:
4
2
2
4
ac
ca
bb
;
4
2
2
4
ab
ab
cc
.
Suy ra:
2 2 2
64b c c a a b II
a b c
đúng.
Ta có:
2
3
3
33abc a b c abc abc
33abc III
sai.
Câu 10: [0D4-1-3] Cho
, , 0x y z
và xt ba bất đẳng thức(I)
3 3 3
3x y z xyz
; (II)
1 1 1 9
x y z x y z
; (III)
3
x y z
y z x
. Bất đẳng thức nào là đúng?
A. Chỉ I đúng. B. Chỉ I và III đúng. C. Chỉ III đúng. D. Cả ba
đều đúng.
Lời giải
Chọn B
3 3 3 3 3 3
3
33x y z x y z xyz I
đúng;
3
3
1 1 1 1
3
3
x y z xyz
x y z xyz
1 1 1
9x y z
x y z
1 1 1 9
II
x y z x y z
sai;
3
3 . . 3
x y z x y z
III
y z x y z x
đúng.
Câu 11: [0D4-1-3] Cho
,0ab
và
ab a b
. Mệnh đề nào sau đây đúng?
A.
4ab
. B.
4ab
. C.
4ab
. D.
4ab
.
Lời giải
Chọn B

Áp dụng bất đẳng thức Cô – si ta có:
2
4
ab
ab
.
Do đó:
ab a b
2
4
ab
ab
2
4 0 4 0a b a b a b a b
40ab
(vì
0ab
)
4ab
.
Câu 12: [0D4-1-3] Cho
a b c d
và
x a b c d
,
y a c b d
,
z a d b c
. Mệnh đề nào sau đây là đúng?
A.
x y z
. B.
y x z
. C.
z x y
. D.
x z y
.
Lời giải
Chọn A
Ta có:
x y a b c d a c b d a c d b c d a b d c b d
0a c b bd cd d a b c
.
Suy ra:
xy
.
Tương tự:
0x z a c d b x z
;
0y z a b d c y z
.
Câu 13: [0D4-1-3] Bất đẳng thức:
2 2 2 2 2
a b c d e a b c d e
,
, , , a b c d
tương đương với bất đẳng thức nào sau đây?
A.
2 2 2 2
0
2 2 2 2
b c d e
a a a a
.
B.
2 2 2 2
0
2 2 2 2
a a a a
b c d e
.
C.
2 2 2 2
0
2 2 2 2
a a a a
b c d e
.
D.
2 2 2 2
0a b a c a d a d
.
Lời giải
Chọn B
2 2 2 2 2
a b c d e a b c d e

2 2 2 2
2 2 2 2
0
4 4 4 4
a a a a
ab b ac c ad d ae e
2 2 2 2
0
2 2 2 2
a a a a
b c d e
.
Câu 14: [0D4-1-3] Cho
2x
. Giá trị lớn nhất của hàm số
2x
fx
x
bằng:
A.
1
22
. B.
2
2
. C.
2
2
. D.
1
2
.
Lời giải
Chọn A
Ta có
0fx
và
2
2
22
2 1 2 1 1 1 1 1
20
8 4 8
22
x
f x f x
x x x x
.
Vậy giá trị lớn nhất của hàm số bằng
1
22
.
Câu 15: [0D4-1-3] Với
, , 0abc
. Biểu thức
a b c
P
b c c a a b
. Mệnh đề nào sau đây
đúng?
A.
3
0
2
P
. B.
3
2
P
. C.
4
3
P
. D.
3
2
P
.
Lời giải
Chọn D
Ta có:
1 1 1
3P a b c
b c c a a b
.
Áp dụng bất đẳng thức
1 1 1 9
x y z x y z
suy ra:
1 1 1 9
2b c c a a b a b c
.
Do đó
93
3
22
PP
; đẳng thức xảy ra khi
abc
.

Câu 16: [0D4-1-3] Cho
3
số
, , a b c
. Bất đẳng thức nào sau đây đúng?
A.
2a b ab
. B.
2 2 2 2
( 2 3 ) 14( )a b c a b c
.
C.
2 2 2
ab bc ca a b c
. D.
1 1 4
a b a b
.
Lời giải
Chọn C
C đúng vì
2 2 2
2 2 2
0ab bc ca a b c a b b c c a
.
Câu 17: [0D4-1-3] Cho
, , a b c
là
3
cạnh của tam giác. Xét các bất đẳng thức sau đây:
I.
2 2 2
2( ).a b c ab bc ca
II.
2 2 2
2( ).a b c ab bc ca
III.
2 2 2
.a b c ab bc ca
Bất đẳng thức nào đúng?
A. Chỉ I. B. Chỉ II. C. Chỉ III. D. II và
III.
Lời giải
Chọn B
II đúng vì
2 2 2 2
2 2 2 2 0BDT a ac c b b ab bc
20a c b a c b b b a c
I và III sai với
3, 4, 5a b c
.
Câu 18: [0D4-1-3] Cho
, , a b c
là
3
số không âm. Xét bất đẳng thức nào sau đây đúng?
33
: ( )I ab b a a b
.
:( )( 1) 4II a b ab ab
.
:III a b c ab bc ca
.
2 2 2
:9IV a b c a b c abc
.
Các mệnh đề đúng là .

A. Chỉ I. B. Chỉ II, III. C. Chỉ III. D. II và
III, IV.
Lời giải
Chọn D
A sai với
0, 1ab
.
B đúng vì
20a b ab
và
1 2 0ab ab
nên
14a b ab ab
.
C đúng vì
2 , 2a b ab b c bc
và
2c a ca
, cộng vế theo vế ta được
đpcm.
Câu 19: [0D4-1-3] Câu nào sau đây đúng với mọi số
x
và
y
?
A.
22
2 4 6x y xy
B.
2 2 2 2
4 ( ) ( )xy x y x y
.
C.
12xy xy
. D.
22
30x y xy
.
Lời giải
Chọn B
A sai với
1, 2xy
.
C sai với
0, 0xy
.
D sai với
1; 2xy
.
Câu 20: [0D4-1-3] Cho
, , a b c
dương. Câu nào sau đây sai ?
A.
(1 2 )(2 3 )(3 1) 48a a b b ab
.
B.
(1 2 )(2 3 )(3 1) 48b b a a ab
.
C.
2 2 2
1 1 1 1 1 1 1
1 1 1 2a b c a b c
.
D.
1 1 1 8
a b c
b c a
.
Lời giải
Chọn C
A đúng khi p dụng BĐT Cauchy có
1 2 2 2aa
;
2 3 2 6a b ab
;
3 1 2 3bb
B đúng khi p dụng BĐT Cauchy có
1 2 2 2bb
;
2 3 2 6b a ab
;
3 1 2 3aa

C sai với
1, 2, 3a b c
.
D đúng khi p dụng BĐT Cauchy có
12
aa
bb
;
12
bb
cc
;
12
cc
aa
Câu 21: [0D4-1-3] Cho
, , a b c
dương. Bất đẳng thức nào đúng?
A.
1 1 1
( ) 3abc
abc
. B.
1 1 1
( ) 9abc
abc
.
C.
1 1 1
( ) 9abc
abc
. D.
1 1 1
( ) 3abc
abc
.
Lời giải
Chọn C
C đúng vì
3
3a b c abc
và
3
1 1 1 1
3
a b c abc
, nhân vế theo vế ta chọn C .
Câu 22: [0D4-1-3] Cho
22
1xy
, gọi
S x y
. Khi đó ta có
A.
2S
. B.
2S
. C.
22S
. D.
11S
.
Lời giải
Chọn C
2 2 2 2 2
2 2 2x y xy yS x
Đẳng thức xảy ra khi
xy
.
Vậy,
22S
.
Câu 23: [0D4-1-3] Cho
,xy
là hai số thực thay đổi sao cho
2xy
. Gọi
22
m x y
. Khi
đó ta có:
A. giá trị nhỏ nhất của
m
là
2
. B. giá trị nhỏ nhất của
m
là
4
.
C. giá trị lớn nhất của
m
là
2
. D. giá trị lớn nhất của
m
là
4
.
Lời giải
Chọn A
Ta có:
2
22
2 4 2m xyx y x y xy
4
2
m
xy
22
4
2 2. 4
2
m
m x xy my
2m
Vậy giá trị nhỏ nhất của
m
là 2.
Câu 24: [0D4-1-3] Bất đẳng thức nào sau đây là đúng ?
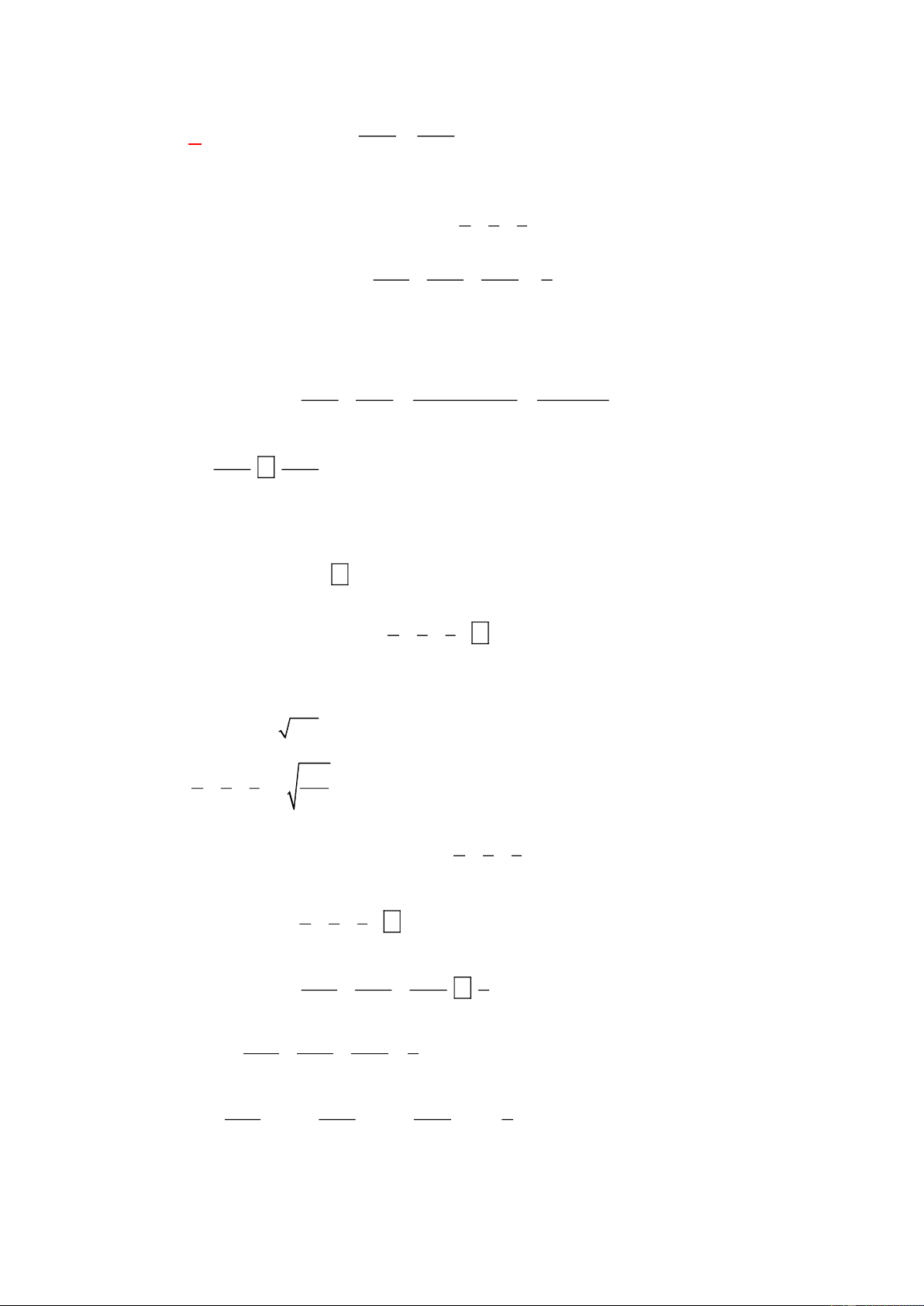
A. Nếu
,ab
dương thì
4
ab a b
ab
.
B. Với
,ab
bất kỳ
2 2 2 2
2 a ab b a b
.
C. Nếu
,,abc
dương thì
1 1 1
9.abc
abc
.
D. Nếu
,,abc
dương thì
3
2
a b c
b c c a a b
.
Lời giải
Chọn A
Xét đáp án A
22
4
0
4 4 4
ab a b a b
ab a b
a b a b a b
4
ab a b
ab
Xét đáp án B
2
2 2 2 2 2 2
2 2 0a ab b a b a ab b a b
2 2 2 2
2 a ab b a b
Xét đáp án C
1 1 1
9.abc
abc
Áp dụng bất đẳng thức Côsi cho 3 số dương
3
3a b c abc
3
1 1 1 1
3
a b c abc
Nhân vế theo vế suy ra
1 1 1
9abc
abc
1 1 1
9.abc
abc
Xét đáp án D
3
2
a b c
b c c a a b
Ta có:
3
2
a b c
b c c a a b
3
1 1 1 3
2
a b c
b c c a a b

9
2
a b c a b c a b c
b c b c b c
1 1 1 9
2
abc
b c b c b c
Áp dụng bất đẳng thức Côsi cho 3 số dương
3
13
0
22
a b c a b b c c a a b b c c a
3
1 1 1 1
30
b c b c b c a b b c c a
Nhân vế theo vế suy ra
1 1 1 9
2
abc
b c b c b c
Vậy
3
2
a b c
b c c a a b
với
, , 0abc
là bất đẳng thức đúng
3
2
a b c
b c c a a b
.
Câu 25: [0D4-1-3] Cho
,ab
là các số thực. Bất đẳng thức nào sau đây là đúng ?
A.
2
ab
ab
với
, 0.ab
. B.
2
22
22
a b a b
.
C.
22
1a b a b ab
. D.
22
93a b a b ab
.
Lời giải
Chọn C
Xét :
2
2 2 0 0
2
ab
ab a b ab a b ab a b
Đáp án A sai khi
0ab
.
Xét:
2
2 2 2 2 2 2
2
2 2 4 2
a b a b a ab b a b
2
2 2 2 2
2 2 0.a ab b a b a b
Đáp án B sai khi
ab
.
Xét :
2 2 2 2
1 2 1 2a b a b ab a b a b ab
2 2 2 2
2 2 1 2 1 0a ab b a a b b

2 2 2
1 2 0 , .a b a b a b
.
Đáp án C đúng
Xét :
2 2 2 2
9 3 2 9 2 3a b a b ab a b a b ab
2 2 2 2
2 2 2
2 6 9 6 9 0
3 3 0
a ab b a a b b
a b a b
Đáp án D sai khi
3ab
.
Câu 26: [0D4-1-3] Giá trị nhỏ nhất của hàm số
2
1
( ) 2f x x
x
với
0x
là
A.
1
. B.
2
. C.
3
. D.
22
.
Lời giải
Chọn C
0x
20x
,
2
1
0
x
.
Áp dụng bdt cosi ta có:
3
2 2 2
1 1 1
( ) 2 3 . . 3f x x x x x x
x x x
.
Dấu “=” xảy ra khi
3
2
1
11x x x x
x
.
Câu 27: [0D4-1-3] Cho hai số
,xy
dương thỏa
12xy
, bất đẳng thức nào sau đây đúng?
A.
2 12xy x y
. B.
2
36
2
xy
xy
. C.
22
2xy x y
. D.
2 12xy x y
.
Lời giải
Chọn A
Ta có:
2x y xy
nên A đúng.
Câu 28: [0D4-1-3] Cho
,0mn
, bất đẳng thức
2
( ) 4m n mn
tương đương với bất đẳng
thức nào sau đây.
A.
22
( 1) ( 1) 0n m m n
. B.
2
( ) 0m n m n
.

C.
2
( ) 0m n m n
. D.
2
( ) 8m n mn
.
Lời giải
Chọn C
Ta có
2
2 2 2
( ) 4 2 0m n mn m n mn m n
. (Luôn đúng)
2
( ) 0m n m n
(Luôn đúng với mọi
,0mn
)
Vậy
22
( ) 4 ( ) 0m n mn m n m n
.
Câu 29: [0D4-1-3] (THPT Lê Quý Đôn - Quảng Trị - Lần 1 - 2017 - 2018 - BTN) Cho
hai số thực
0x
,
0y
thay đổi và thỏa mãn điều kiện:
22
x y xy x y xy
.
Giá trị lớn nhất của biểu thức:
33
11
M
xy
là:
A.
9
. B.
18
. C.
16
. D.
1
.
Lời giải
Chọn C
Ta có:
22
-x y xy x y xy
2
3x y xy x y xy
(1)
2
3x y xy x y
2
3
xy
xy
xy
(vì nếu
3xy
thì
09
vô lý)
Đặt
xyt
suy ra
2
3
t
xy
t
.
Dễ thấy
0t
vì nếu
0t
thì từ (1) cho ta
0xy
trái giả thiết.
Mặt khác:
2
2
xy
xy
22
34
tt
t
11
34t
(Vì
0t
nên
2
0t
)
1
3
t
t
.
Khi đó
33
11
M
xy
33
33
xy
xy
3
33
3x y xy x y
xy
2
2
69tt
t
.
Xét hàm số
2
2
69
tt
ft
t
trên khoảng
; 3 1;
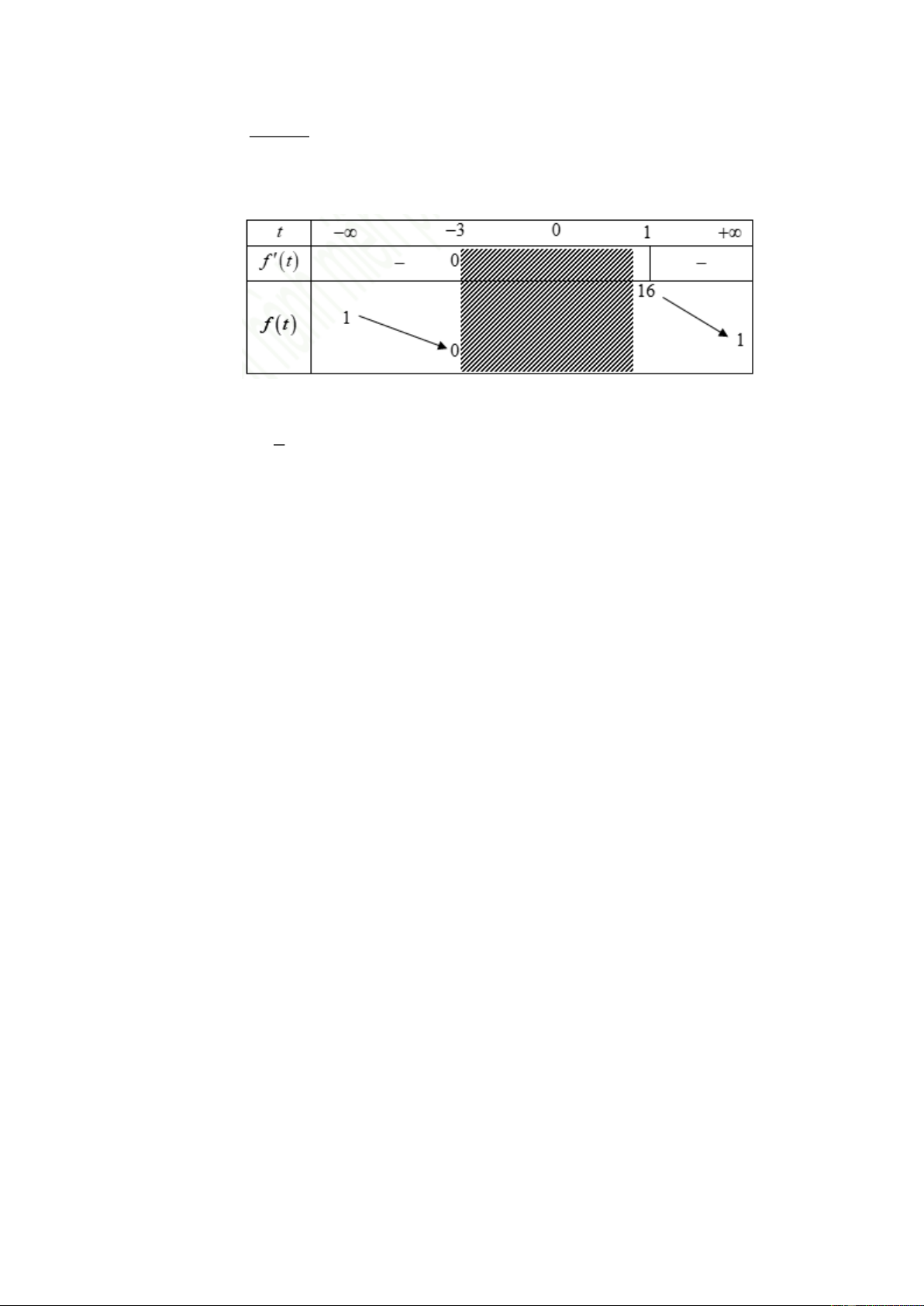
3
6 18
t
ft
t
,
03f t t
.
Ta có bảng biến thiên:
Từ bảng biến thiên ta thấy giá trị lớn nhất của hàm số là
16
, đạt được khi
1t
1
2
xy
.

Câu 1: [0D4-1-4] Cho
, , 0abc
và
a b c
P
b c c a a b
. Khi đó
A.
01P
. B.
12P
. C.
23P
. D.
3
.
2
P
Lời giải
Chọn D
Thật vậy
1 1 1
3 1 1 1
a b c
P a b c
b c c a a b a b b c c a
1 1 1 1
2
a b b c c a
a b b c c a
3
3
1 1 9 9 3
3 3 3
2 2 2 2
a b b c c a P
a b b c c a
Câu 2: [0D4-1-4] Cho 3 số
, , a b c
dương. Câu nào sau đây sai?
A.
ab bc ca
abc
c a b
. B.
. . 8
a b b c c a
b c c a a b
.
C.
ac cb ba
abc
b a c
. D. Có 1 câu sai trong 3 câu trên.
Lời giải.
Chọn C
Vì 3 số
, , a b c
dương nên:
2 2 2
2 2 2 2 2 2
1 1 1 1 1 1 1 1 1
(1)
ac cb ba abc acb cba
a b c a b c
b a c b a c
abc
b a c abc b a c ab bc ca
Mặt khác: áp dụng bất đẳng thức Bunhiacopxki ta có:
2
2 2 2 2 2 2
1 1 1 1 1 1 1 1 1
ab bc ca a b c b c a
2 2 2
1 1 1 1 1 1
ab bc ca a b c
Do đó: bất đẳng thức (1) sai.
Câu 3: [0D4-1-4] Cho 3 số
, , a b c
dương. Câu nào sau đây đúng.
A.
3
a b c
bca
. B.
2 2 2
1 . 1 . 1 8 2
abc
b c a
.
C.
2 2 2 2
5 3 4 5a b a b a b
. D. 2 câu B và C đúng.

Lời giải.
Chọn D
A. Đúng vì
, , a b c
dương nên áp dụng BĐT Cô-si ta có:
3
3 . . 3.
a b c a b c a b c
b c a b c a b c a
Dấu "=" xảy ra khi:
.abc
B. Sai vì:
2 2 2 2 2 2
1 . 1 . 1 2 .2 .2
a b c a b c
b c a b c a
2 2 2
1 . 1 . 1 16 2
abc
b c a
C. Sai vì:
3 4 0ab
.
Câu 4: [0D4-1-4] Cho 3 số
, , a b c
bất kì. Chọn đáp án sai.
A.
2
22
22
a b a b
. B.
2
( ) 4a b ab
.
C.
2
2 2 2
33
a b c a b c
. D. Có 1 câu sai trong 3 câu trên.
Lời giải.
Chọn D
A. Đúng vì áp dụng bất đẳng thức Bunhiacopxki ta có:
2
22
2
2 2 2 2
1 1 .
22
a b a b
a b a b
B. Đúng vì:
22
0 4 .a b a b ab
C. Đúng vì áp dụng bất đẳng thức Bunhiacopxki ta có:
2
2 2 2
2
2 2 2 2 2 2
111
33
a b c a b c
a b c a b c
.
Câu 5: [0D4-1-4] Cho
3 4 15.ab
Xét các câu sau đây?
I.
22
9.ab
II.
22
9 4 45.ab
III.
22
4 17.ab
Câu nào đúng?
A. Chỉ I. B. Có I, II và III C. Có I và III. D. Có I và
II.
Lời giải.
Chọn B
I. Đúng vì áp dụng bất đẳng thức Bunhiacopxki ta có:
2
2 2 2 2 2 2
3 4 3 4 9.a b a b a b
II. Đúng vì áp dụng bất đẳng thức Bunhiacopxki ta có:

2
2 2 2 2 2 2
1.3 2.2 1 2 9 4 9 4 45.a b a b a b
III. Đúng vì áp dụng bất đẳng thức Bunhiacopxki ta có:
2
2
2 2 2 2 2 2 2 2
15
3. 2.2 3 2 4 4 4 17
13
a b a b a b a b
.
Câu 6: [0D4-1-4] Cho
, ab
dương thỏa mãn
4 4.ab
Câu nào sau đây đúng?
A.
1ab
. B.
2
16
27
ab
. C.
2
64
27
ab
. D. Cả 3
đáp án trên.
Lời giải
Chọn D
Áp dụng bất đẳng thức Cô si cho 2 số dương
a
và
4b
ta có :
4 2 .4a b a b
44ab
1ab
. A đúng.
Áp dụng bất đẳng thức Cô si cho 3 số dương
a
,
2b
và
2b
ta có :
3
22
.2 .2
3
a b b
a b b
3
22
4 16
4
3 27
ab ab
. B đúng.
Áp dụng bất đẳng thức Cô si cho 3 số dương
,
22
aa
,
4b
ta có:
3
4
22
. .4
2 2 3
aa
b
aa
b
3
22
4 64
3 27
a b a b
. C đúng.
Câu 7: [0D4-1-4] Xét bất đẳng thức
a b a b
. Dấu “ =” xảy ra khi và chỉ khi:
A.
ab
. B.
0ab
. C.
0ab
. D. 2 câu A
và C.
Lời giải
Chọn D
Ta có:
a b a b
2
22
2a b a b ab
22ab ab ab ab
Dấu bằng xảy ra khi và chỉ khi
ab
hoặc
0ab
.
Câu 8: [0D4-1-4]Tìm giá trị lớn nhất của hàm số
2
2
53
3
xx
y
x
với
0x
.
A.
5 3 3
3
. B.
5 3 6
6
. C.
53
3
. D.
53
6
.

Lời giải
Chọn B
Ta có
2
22
2
5 3 1 2 3 5 6 5 3
1 5. 1 5. 1 5.
3 3 6
2 3 2 3
2 .3
x x x x
y
xx
x
.
Câu 9: [0D4-1-4] Cho 2 số dương
, xy
thay đổi thỏa mãn điều kiện
1xy
. Tìm giá trị
nhỏ nhất của biểu thức
1
.P xy
xy
A.
17
4
. B.
2
. C.
4
. D.
1
2
.
Lời giải
Chọn A
Ta có:
2
1
24
xy
xy xy
Đặt
xy t
, điều kiện
1
4
t
Khi đó
1 1 15 1 15 1 15 17
2 . .4
16 16 16 16 2 4 4
P t t t
t t t t
.
Câu 10: [0D4-1-4] Cho
, , , a b c d
thỏa mãn
2 2 2 2
4a d b c
. Câu nào sau đây đúng ?
A.
4ac bd
. B.
4ac bd
.
C.
22ac bd
. D.
44ac bd
.
Lời giải
Chọn D
Ta có
2
2 2 2 2
ac bd a d c b
2
16 4 4ac bd ac bd
.
Câu 11: [0D4-1-4] Cho
n
số dương
1 2 3
, , ,...,
n
a a a a
thỏa mãn
1 2 3
... 1
n
a a a a
. Câu nào sau
đây đúng ? Cho biết
1.2.3.... !nn
A.
1
12
(1 )(1 )...(1 ) 2
n
n
a a a
. B.
2
1 2 3
(1 )(4 )(9 )...( ) 2 . !
n
n
a a a n a n
.
C.
12
(1 )(1 )...(1 ) 2
n
n
a a a
. D. Hai câu B và C.
Lời giải
Chọn D

Áp dụng bất đẳng thức Cô si cho 2 số dương ta có :
11
12aa
22
12aa
…
12
nn
aa
1 2 1 2 3 1 2 3
(1 )(1 )...(1 ) 2 ... 2 ... 1
nn
n n n
a a a a a a a a a a a
Vậy C đúng.
Tương tự áp dụng bất đẳng thức Cô si cho 2 số dương ta có :
11
12aa
22
4 2.2aa
22
9 2.3aa
…
2
2
nn
n a n a
2
1 2 3
(1 )(4 )(9 )...( ) 2 .1.2.3... 2 . !
nn
n
a a a n a n n
Kết luận B và C đúng.
Câu 12: [0D4-1-4] (THPT Thanh Miện - Hải Dương - Lần 1 - 2018 - BTN) Cho các số
thực dương
x
,
y
,
z
thỏa mãn
x y xyz z
. Giá trị lớn nhất của biểu thức
2
2
2
3
2
1
2
1
1
x yz
x
P
y z x
x
thuộc khoảng nào trong các khoảng sau:
A.
1,3;1,4
. B.
0,8;0,9
. C.
1,7;1,8
. D.
1,4;1,5
.
Lời giải
Chọn D
Từ giả thiết
11
. . 1x y xyz z x y xy
zz
.
Đặt
tan
2
A
x
,
tan
2
B
y
và
1
tan
2
C
z
thay vào hệ thức trên ta được
tan tan tan tan tan tan 1
2 2 2 2 2 2
A B B C C A
, suy ra
A
,
B
,
C
là ba góc của tam giác.
Từ đó ta có
2
3
2
2
2sin cos
22
1
x A A
x
và
2
2
2
sin
2
1
xA
x
.

2
2
tan tan
1
22
tan tan 1
22
CB
yz
BC
yz
cos cos tan tan 2 tan tan
2 2 2 2 2 2
cos cos tan tan 1
2 2 2 2
B C B C B C
B C B C
sin sin sin
2
cos
2
BC
BC
BC
1
cos cos cos
22
cos
2
A
B C B C
BC
22
cos cos 1 cos
2 2 2
cos
2
A B C A
BC
2
cos 1 1 cos
22
2cos
12
AA
A
.
Vậy
22
2sin cos 2sin cos
2 2 2 2
A A A A
P
sin sin cos
22
AA
A
2sin .sin 2
24
A
A
.
Dấu bằng đạt được khi
sin 1
sin 1
24
BC
A
A
2
4
A
BC
1
21
21
x
y
z
.

Câu 1: [0D4-3-1] Khẳng định nào sau đây đúng?
A.
2
3xx
3x
. B.
1
0
x
1x
.
C.
2
1
0
x
x
10x
. D.
x x x
0x
.
Lời giải
Chọn D
Vì
ab
a c b c
,
c
. Trong trường hợp này
cx
.
Câu 2: [0D4-3-1] Cho bt phương trnh:
8
1 1
3 x
. Mt hc sinh gii như sau:
I
11
1
38x
II
3
38
x
x
III
3
5
x
x
.
Hi hc sinh này gii sai ở bước nào?
A.
I
. B.
II
. C.
III
. D.
II
và
III
.
Lời giải
Chọn B
I
11
1
38x
.
Đúng v chia hai vế cho mt số dương
80
ta được bt thức tương đương cùng
chiều.
11
38x
II
3
38
x
x
( chỉ đúng khi:
30x
3x
).
Với
4x
thì
11
3 4 8
1
1
8
(sai) nhưng
43
3 4 8
43
18
(đúng).Vậy
II
sai.
3
38
x
x
III
3
5
x
x
. Đúng v đây chỉ là bước thu gn bt phương trnh bậc nht đơn
gin.
Câu 3: [0D4-3-1] Tập nghiệm của bt phương trnh
2 2 2x x x
là:

A.
. B.
;2
. C.
2
. D.
2;
.
Lời giải
Chọn C
Ta có:
2 2 2x x x
20
2
x
x
2
2
x
x
2x
.
Câu 4: [0D4-3-1] Giá trị
3x
thuc tập nghiệm của bt phương trnh nào trong các bt
phương trnh sau đây?
A.
3 2 0xx
. B.
2
3 2 0xx
. C.
2
10xx
. D.
12
0
1 3 2xx
.
Lời giải
Chọn B
Ta có:
2
3 2 0xx
20x
2x
;2x
và
3 ; 2
.
Câu 5: [0D4-3-1] Bt phương trnh
2
5 1 3
5
x
x
có nghiệm là
A.
x
. B.
2x
. C.
5
2
x
. D.
20
23
x
.
Lời giải
Chọn D
2
5 1 3
5
x
x
2
5 3 1
5
x
x
23
4
5
x
20
23
x
.
Câu 6: [0D4-3-1] Tìm tập nghiệm
S
của bt phương trnh
2
40xx
.
A.
S
. B.
0S
. C.
0;4S
. D.
;0 4;
.
Lời giải
Chọn A
Vì
2
4 0,x x x
.
Câu 7: [0D4-3-1] Bt phương trnh
33
23
2 4 2 4
x
xx
tương đương với:

A.
23x
. B.
3
2
x
và
2x
. C.
3
2
x
. D. Tt c
đều đúng.
Lời giải
Chọn D
33
23
2 4 2 4
x
xx
2 4 0
23
x
x
2
23
x
x
2
3
2
x
x
3
2
x
.
23x
3
2
x
.
Vậy A, B, C đều đúng.
Câu 8: [0D4-3-1] Các giá trị của
x
tho mãn điều kiện của bt phương trnh
3
1
2 3 2 3x x x
x
là
A.
2x
. B.
3x
. C.
3x
và
0x
. D.
2x
và
0x
.
Lời giải
Chọn C
Điều kiện:
30
0
x
x
3
0
x
x
(
3
2x
có nghĩa
x
).
Câu 9: [0D4-3-1] Hệ bt phương trnh
3
32
5
63
21
2
xx
x
x
có nghiệm là
A.
5
2
x
. B.
75
10 2
x
. C.
7
10
x
. D. Vô
nghiệm.
Lời giải
Chọn C
3
32
5
63
21
2
xx
x
x
3
32
5
6 3 4 2
xx
xx
7
2
5
25
x
x
7
10
5
2
x
x
7
10
x
.
Câu 10: [0D4-3-1] Khẳng định nào sau đây là khẳng định sai?

A. Bt phương trnh bậc nht mt ẩn luôn có nghiệm.
B. Bt phương trnh
0ax b
vô nghiệm khi
0a
và
0b
.
C. Bt phương trnh
0ax b
có tập nghiệm là khi
0a
và
0b
.
D. Bt phương trnh
0ax b
vô nghiệm khi
0a
.
Lời giải
Chọn D
Vì
0 1 0 1 0x
( đúng
x
).
Câu 11: [0D4-3-1] Số
3x
là nghiệm của bt phương trnh nào sau đây?
A.
51x
. B.
3 1 4x
. C.
4 11xx
. D.
2 1 3x
.
Lời giải
Chọn D
Thay
3x
vào các bt phương trnh ta có phương án D đúng.
Câu 12: [0D4-3-1] Số
1x
là nghiệm của bt phương trnh nào sau đây?
A.
30x
. B.
2 1 0x
. C.
2 1 0x
. D.
10x
.
Lời giải
Chọn B
Thay
1x
vào các bt phương trnh ta có phương án B đúng.
Câu 13: [0D4-3-1] Số nào sau đây là nghiệm của bt phương trnh
1
1
33
x
x
xx
?
A.
2
. B.
1
. C.
0
. D.
3
2
.
Lời giải
Chọn C
Thay các giá trị
3
2;1;0;
2
x
vào bt phương trnh th ta có
0x
là nghiệm.
Câu 14: [0D4-3-1] Số
1x
là nghiệm của bt phương trnh
2
2mx
khi và chỉ khi
A.
3m
. B.
3m
. C.
3m
. D.
1 m
.
Lời giải

Chọn B
Vì
1x
là nghiệm của bt phương trnh nên ta có
2
1 2 3mm
.
Câu 15: [0D4-3-1] Số
1 x
là nghiệm của bt phương trnh
2
2 3 1m mx
khi và chỉ khi
A.
1m
. B.
1m
. C.
11m
. D.
1m
.
Lời giải
Chọn A
Với
1 x
bt phương trnh trở thành:
2 3 1 1.m m m
Câu 16: [0D4-3-1] Tập nghiệm của bt phương trnh
2 1 3 2xx
là
A.
1;
. B.
;5
. C.
5;
. D.
;5
.
Lời giải
Chọn A
2 1 3 2 5 5 1.x x x x
Vậy bt phương trnh đã cho có tập nghiệm là:
1; .S
.
Câu 17: [0D4-3-1] Tập nghiệm của bt phương trnh
5 2 4 0xx
là:
A.
8
;
7
. B.
8
;
3
. C.
8
;
7
. D.
8
;
7
.
Lời giải
Chọn A
8
5 2 4 0 7 8 .
7
x x x x
Vậy bt phương trnh đã cho có tập nghiệm là:
8
;.
7
S
Câu 18: [0D4-3-1] Tập nghiệm của bt phương trnh
3 5 1xx
là:
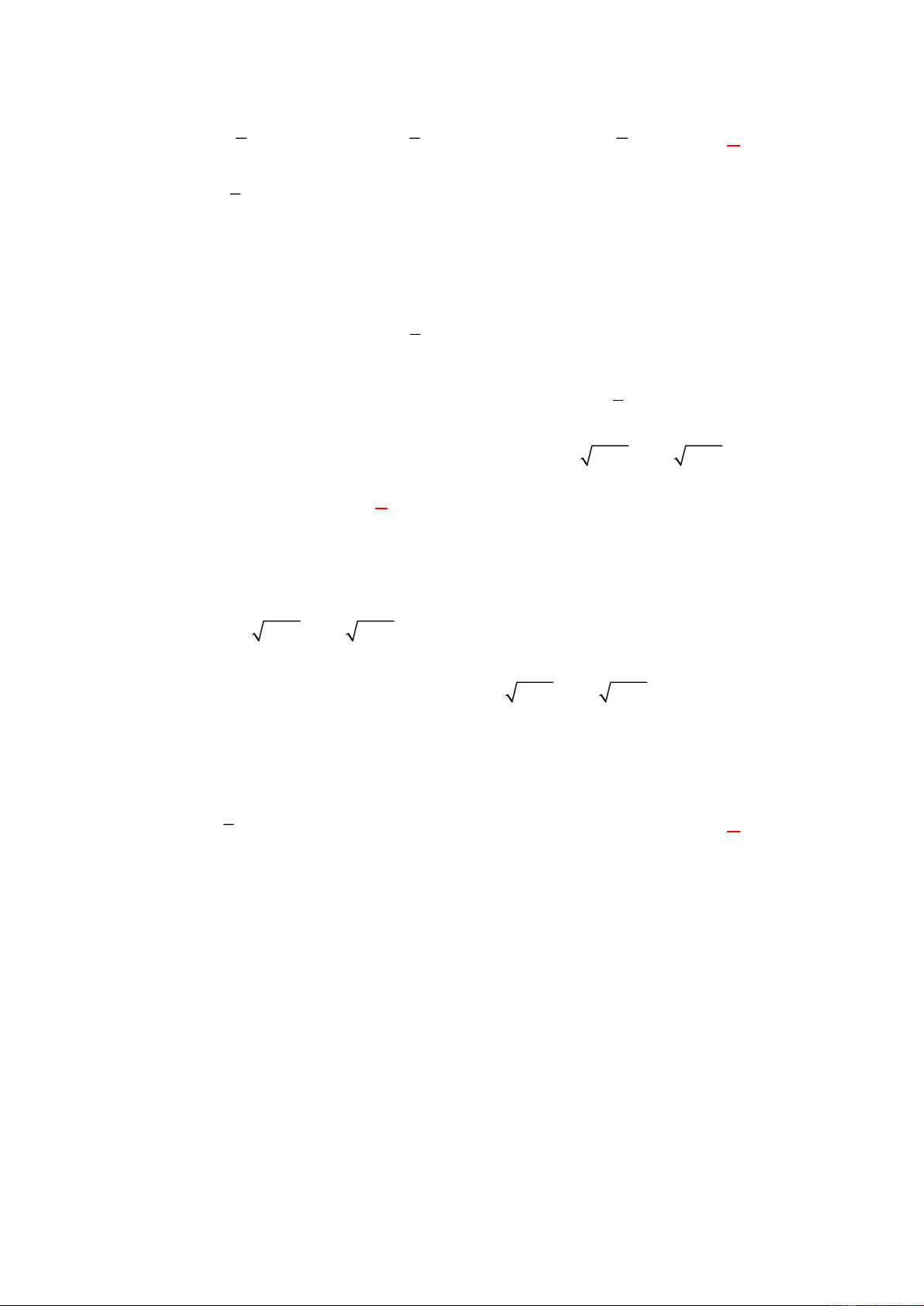
A.
5
;
2
. B.
5
;
8
. C.
5
;
4
. D.
5
;
8
.
Lời giải
Chọn D
5
3 5 1 8 5 .
8
x x x x
Vậy bt phương trnh đã cho có tập nghiệm là:
5
;.
8
S
Câu 19: [0D4-3-1] Tập nghiệm của bt phương trnh
3 2 2 2x x x x
là
A.
1;2
. B.
1;2
. C.
;1
. D.
1;
.
Lời giải
Chọn B
2 0 2
3 2 2 2
3 2 1
xx
x x x x
x x x
Tập nghiệm của bt phương trnh
3 2 2 2x x x x
là
1;2
.
Câu 20: [0D4-3-1] Tập nghiệm của hệ bt phương trnh
3 2 2 3
10
xx
x
là:
A.
1
;1
5
. B.
;1
. C.
1;
. D.
(tập
rỗng).
Lời giải
Chọn B
3 2 2 3 1
1 0 1
x x x
xx
. Do đó hệ bt phương trnh vô nghiệm, tập nghiệm
T
.
Câu 21: [0D4-3-1] Tập nghiệm của hệ bt phương trnh
2 1 3 2
30
xx
x
là:

A.
3;
. B.
;3
. C.
3;3
. D.
; 3 3;
.
Lời giải
Chọn C
2 1 3 2
30
xx
x
3
3
x
x
33x
.
Câu 22: [0D4-3-1] Tập nghiệm của hệ bt phương trnh
2 5 0
8 3 0
x
x
là:
A.
58
;
23
. B.
32
;
85
. C.
85
;
32
. D.
8
;
3
.
Lời giải
Chọn A
2 5 0
8 3 0
x
x
5
2
8
3
x
x
58
23
x
.
Câu 23: [0D4-3-1] Tập nghiệm của bt phương trnh
1
1
33
x
x
xx
là:
A.
. B.
1;3
. C.
;1
. D.
;3
.
Lời giải
Chọn C
1
1
33
x
x
xx
30
10
x
x
3
1
x
x
1x
.
Câu 24: [0D4-3-1] Tập hợp nghiệm của bt phương trnh
11xx
là:
A.
0;1
. B.
1;
. C.
0;
. D.
0;
.
Lời giải
Chọn C

11
0
1 1 0
x x x R
bpt x
x x x
.
Câu 25: [0D4-3-1] Tập hợp nghiệm của bt phương trnh
11xx
là:
A.
0;1
. B.
1;
. C.
0;
. D.
1;
.
Lời giải
Chọn D
11
1
1 1 1
x x x R
bpt x
x x x
.
Câu 26: [0D4-3-1] Tập nghiệm của bt phương trnh
1
1
3
x
x
là:
A.
. B. . C.
3;
. D.
;5
.
Lời giải
Chọn C
BPT
2
0
3x
30x
3x
.
Câu 27: [0D4-3-1] Nhị thức nào sau đây nhận giá trị âm với mi
x
nh hơn
2
?
A.
36f x x
. B.
6 – 3f x x
. C.
4 – 3f x x
. D.
3 – 6f x x
.
Lời giải
Chọn D
Cho
3 6 0 2xx
Du
fx
:
Câu 28: [0D4-3-1] Nhị thức nào sau đây nhận giá trị âm với mi số
x
nh hơn
2
3
?
x
fx
2
0
+
-
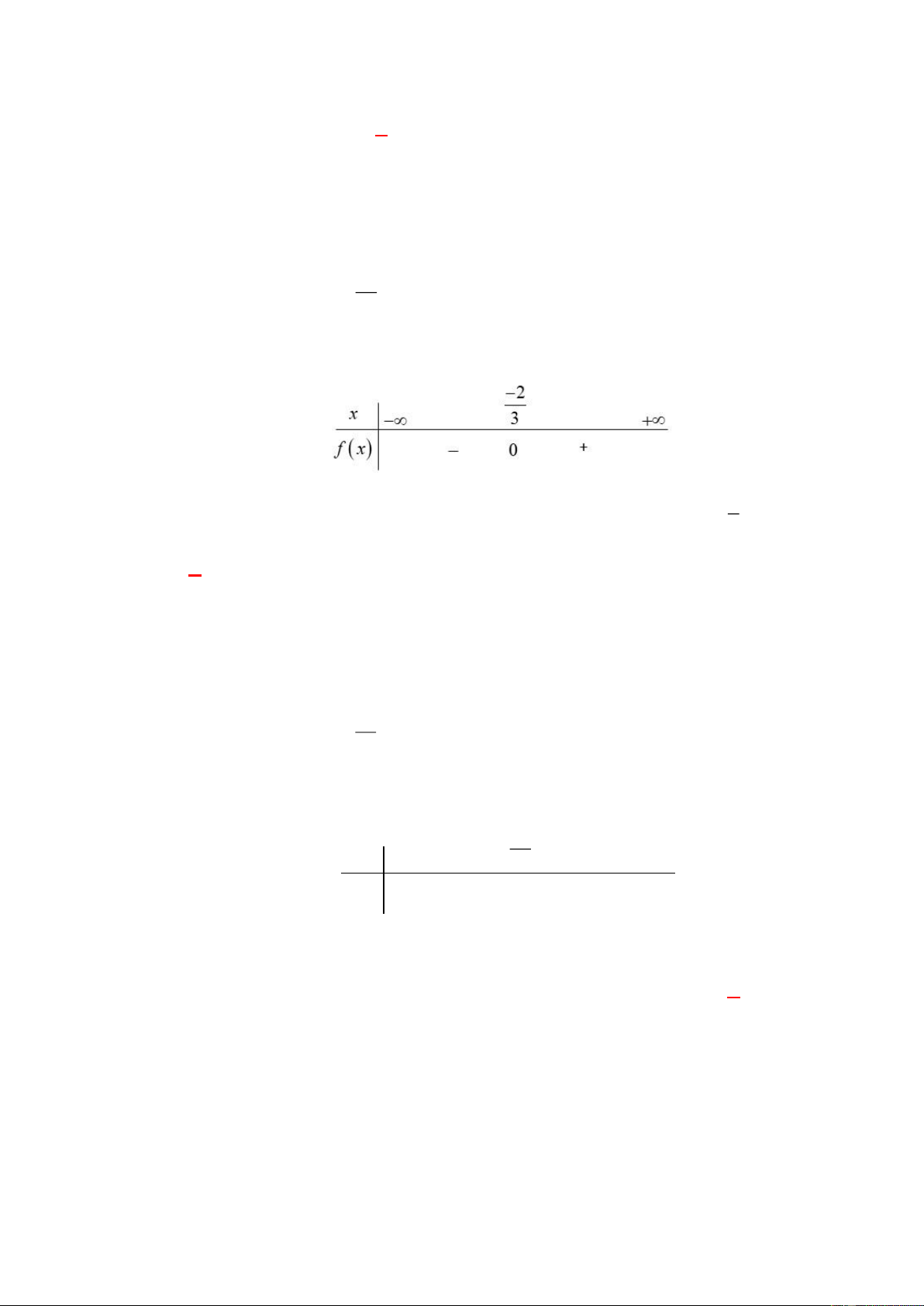
A.
6 – 4f x x
. B.
32f x x
. C.
3 – 2f x x
. D.
23f x x
.
Lời giải
Chọn B
Cho
2
3 2 0
3
xx
.
Du
fx
:
Câu 29: [0D4-3-1] Nhị thức nào sau đây nhận giá trị âm với mi số
x
nh hơn
3
2
?
A.
23f x x
. B.
23f x x
. C.
3 – 2f x x
. D.
23f x x
.
Lời giải
Chọn A
Cho
3
2 3 0
2
xx
.
Du
fx
:
Câu 30: [0D4-3-1] Nhị thức nào sau đây nhận giá trị âm với mi
x
lớn hơn
2
?
A.
2 –1f x x
. B.
–2f x x
. C.
25f x x
. D.
63f x x
.
Lời giải
Chọn D
Cho
6 3 0 2xx
.
3
2
x
fx
0
+
-
Du
fx
:
Câu 31: [0D4-3-1] Nhị thức
51x
nhận giá trị âm khi:
A.
1
5
x
. B.
1
5
x
. C.
1
5
x
. D.
1
5
x
.
Lời giải
Chọn D
Cho
1
5 1 0
5
xx
.
Du
fx
:
Câu 32: [0D4-3-1] Nhị thức
32x
nhận giá trị dương khi
A.
3
2
x
. B.
2
3
x
. C.
3
2
x
. D.
2
3
x
.
Lời giải
Chọn B
Cho
2
3 2 0
3
xx
.
Du
fx
:
Câu 33: [0D4-3-1] Nhị thức
23x
nhận giá trị dương khi và chỉ khi :
A.
3
2
x
. B.
2
3
x
. C.
3
2
x
. D.
2
3
x
.
2
3
x
fx
0
+
1
5
x
fx
0
+
2
x
fx
0
+
Lời giải
Chọn A
Cho
3
2 3 0
2
xx
Du
fx
:
Câu 34: [0D4-3-1] Nhị thức nào sau đây nhận giá trị dương với mi
x
nh hơn
2
?
A.
36f x x
. B.
6 – 3f x x
. C.
4 – 3f x x
. D.
3 – 6f x x
.
Lời giải
Chọn B
Cho
6 3 0 2xx
Du
fx
:
Câu 35: [0D4-3-1] Phương trnh
22
2( 2) 6 0x m x m m
có hai nghiệm đối nhau khi
và chỉ khi
A.
2m
. B.
–3 2m
. C.
–2m
hoặc
3m
. D.
–2 3.m
Lời giải
Chọn A
Ta có
22
2( 2) 6 0x m x m m
có hai nghiệm đối nhau khi và chỉ khi
2
60
2
20
c
P m m
m
a
m
Vậy
2m
.
2
x
fx
0
+
3
2
x
fx
0
+

Câu 36: [0D4-3-1] Các giá trị của m để phương trnh
22
3 (3 1) 4 0x m x m
có hai nghiệm
trái du là
A.
4.m
. B.
–2 2.m
.
C.
2.m
. D.
–2m
hoặc
2.m
Lời giải
Chọn B
Ta có
22
3 (3 1) 4 0x m x m
có hai nghiệm trái du khi và chỉ khi
2
2
4
0 4 0 2 2
3
cm
P m m
a
Vậy
–2 2.m
.
Câu 37: [0D4-3-1] Tập hợp tt c các giá trị của
m
để phương trnh bậc hai
2
2( 1) 3 0x m x m
có nghiệm là:
A.
0
.
B.
\0
.
C.
.
.
D.
.
Lời giải
Chọn C
2
2( 1) 3 0x m x m
có nghiệm khi và chỉ
2
2
' 0 1 3 0 1 0m m m m
Vì
2
2
13
10
24
m m m m
nên phương trnh luôn có nghiệm.
Vậy
.m
.
Câu 38: [0D4-3-1] Phương trnh
2
20mx mx
có nghiệm khi và chỉ khi
A.
0m
hoặc
8m
.
B.
0m
hoặc
8m
.
C.
08m
.
D.
08m
.
Lời giải
Chọn B.
0 2 0m
Phương trnh vô nghiệm
2
0 2 0m mx mx
có nghiệm khi và chỉ

2
2
0
0 8 0 8 0
8
m
m m m m
m
So với điều kiện ta có
0m
hoặc
8m
.

Câu 1: [0D4-3-2] Bất phương trình:
1 1 1 1
0
1 2 1 2x x x x
không thỏa mãn với
khoảng nào sau đây:
A.
1
0; .
3
B.
3; 5 .
C.
2; 3 .
D.
1
–1; .
2
Lời giải
Chọn A
Ta có BPT đã cho tương đương
22
22
0
14
xx
xx
2
22
2 2 5
0
14
xx
xx
2 2 5 2 5
0
1 1 2 2
x x x
x x x x
Lập bảng xét dấu các phần tử ta thấy B, C, D đều thỏa mãn.
Câu 2: [0D4-3-2] Nghiệm nguyên nhỏ nhất của bất phương trình:
5
0
( 7)( 2)
x
xx
là:
A.
–3x
. B.
–4x
. C.
–5x
. D.
–6x
.
Lời giải
Chọn D
Lập bảng xét dấu với các khoảng
;7
,
7;2
,
2;5
,
5;
ta thấy nghiệm
của bất phương trình là:
7;2 5;
. Vậy nghiệm nguyen nhỏ nhất của bất
phương trình trên là
6x
.
Câu 3: [0D4-3-2] Tập nghiệm của bất phương trình
12xx
là:
A.
( 1; )S
. B.
;1S
.
C.
1
;
2
S
. D.
1
;
2
S
.
Lời giải
Chọn C
Ta có
22
2
20
2
1
12
1
2 1 4 4
2
12
2
x
x
x
x x x
xx
x
xx
.
Câu 4: [0D4-3-2] Tập tất cả các giá trị của m để hệ bất phương trình
2 3 0
2
x
xm
vô nghiệm
là:
A.
1
;
2
. B.
1
;
2
. C.
1
;
2
. D.
1
;
2
.
Lời giải
Chọn B
Ta có
3
2 3 0
2
2
2
x
x
xm
xm
Hệ bất phương trình vô nghiệm khi
31
2
22
mm
.
Câu 5: [0D4-3-2] Tập hợp nghiệm của bất phương trinh sau:
1 3 5
3
22
x
xx
là:
A.
(2; )
. B.
\{2}
. C.
12
5
x
hoặc
22x
. D.
;2
.
Lời giải
Chọn C
2
1 3 5 1 3 5 5 12
3 3 0 0
2 2 2 2 4
x x x
x x x x x
Đặt:
2
5 12
4
x
fx
x
.
Bảng xét dấu:
x
12
5
2
2
5 12x
-
0
+ +
+
2
4x
+ +
0
-
0
+

fx
-
0
+ -
+
Kết luận:
12
5
x
hoặc
22x
.
Câu 6: [0D4-3-2] Giải bất phương trình:
2
1
21
x
xx
.
A.
1x
hoặc
2x
. B.
12x
. C.
12x
. D.
1x
hoặc
2x
.
Lời giải
Chọn B
2 2 2
2 2 4 4 2 6
1 1 0 0
2 1 2 1 2 1 2 1
x x x x x x x x
x x x x x x x x
12x
.
Câu 7: [0D4-3-2] Cho bất phương trình:
2
( 2)( 3) 6 (1)m x m m
. Xét các mệnh đề
sau:
I. Nếu
2m
: (1) có nghiệm là
xm
.
II. Nếu
2m
: (1) có nghiệm là
xm
.
III. Nếu
2m
: (1) vô nghiệm.
Mệnh đề nào đúng?
A. Chỉ I. B. Chỉ II. C. I và II. D. I, II và III.
Lời giải
Chọn D
Ta có
2
( 2)( 3) 6 m x m m
2 3 2 3m x m m
.
Nếu
2m
:
1 3 3 .x m x m
Nếu
2m
:
1 3 3 .x m x m
Nếu
2m
:
1 0 0
(vô lý). PT vô nghiệm.
[0D4-3-2] Bất phương trình nào sau đây không tương đương với bất phương trình
50x
?

A.
2
1 5 0xx
. B.
2
50xx
. C.
5 5 0xx
. D.
5 5 0xx
.
Lời giải
Chọn D
50x
5x
.
Tập nghiệm của bất phương trình là
1
5; +T
.
5 5 0xx
50
50
x
x
5
5
x
x
5x
.
Tập nghiệm của bất phương trình này là
2
5; +T
.
Vì hai bất phương trình này không có cùng tập nghiệm nên chúng không tương
đương nhau.
[0D4-3-2] Tập nghiệm của bất phương trình
2006 2006xx
là gì?
A.
. B.
2006,
. C.
,2006
. D.
2006
.
Lời giải
Chọn A
Điều kiện:
2006 0
2006 0
x
x
2006
2006
x
x
2006x
.
Thay
2006x
vào bất phương trình, ta được:
2006 2006 2006 2006
00
(sai).
Vậy bất phương trình vô nghiệm.
Câu 8: [0D4-3-2] Tìm tập nghiệm
S
của bất phương trình
2
14x x x
.
A.
3;
. B.
4;10
. C.
;5
. D.
2;
.
Lời giải
Chọn D
2
14x x x
2
2 1 4x x x x
32
24x x x x
32
2 2 4 0x x x
2
2 2 0xx
2
2 0 do 2 0,x x x
2x
.

Câu 9: [0D4-3-2] Tập nghiệm của hệ bất phương trình
21
1
3
43
3
2
x
x
x
x
là
A.
4
2;
5
. B.
4
2;
5
. C.
3
2;
5
. D.
1
1;
3
.
Lời giải
Chọn A
21
1
3
43
3
2
x
x
x
x
2 1 3 3
4 3 6 2
xx
xx
54
2
x
x
4
5
2
x
x
4
2;
5
x
.
Câu 10: [0D4-3-2] Cặp bất phương trình nào sau đây không tương đương
A.
1xx
và
2 1 1 2 1x x x x
. B.
11
21
33
x
xx
và
2 1 0x
.
C.
2
20xx
và
20x
. D.
2
20xx
và
20x
.
Lời giải
Chọn D
2
20xx
0
20
x
x
0
2
x
x
2; \ 0x
.
20xx
2x
2; x
.
Vậy hai bất phương trình này không tương đương.
Câu 11: [0D4-3-2] Cặp bất phương trình nào sau đây không tương đương:
A.
11
51
22
x
xx
và
5 1 0x
. B.
11
51
22
x
xx
và
5 1 0x
.
C.
2
30xx
và
30x
. D.
2
50xx
và
50x
.
Lời giải
Chọn B

11
51
22
x
xx
20
5 1 0
x
x
2
1
5
x
x
1
; \ 2
5
x
.
5 1 0x
1
5
x
1
;
5
x
.
Vậy hai bất phương trình này không tương đương.
Câu 12: [0D4-3-2] Bất phương trình
2 3 2xx
tương đương với:
A.
2
2 3 2xx
với
3
2
x
. B.
2
2 3 2xx
với
2x
.
C.
2 3 0
20
x
x
hoặc
2
2 3 2
20
xx
x
. D. Tất cả các câu trên đều đúng.
Lời giải
Chọn C
Ta sử dụng kiến thức sau
AB
2
0
0
0
A
B
AB
B
Câu 13: [0D4-3-2] Hệ bất phương trình
2 3 0
2 3 0
xx
xx
có nghiệm là
A.
23x
. B.
23x
.
C.
22x
,
33x
. D. Vô nghiệm.
Lời giải
Chọn A
2 3 0
2 3 0
xx
xx
2; 3
; 2 3;
x
x
2; 3x
.
Câu 14: [0D4-3-2] Hệ bất phương trình
43
6
25
1
2
3
x
x
x
x
có nghiệm là:

A.
5
3
2
x
. B.
5 33
28
x
. C.
73x
. D.
33
3
8
x
.
Lời giải
Chọn C
43
6
25
1
2
3
x
x
x
x
43
60
25
1
20
3
x
x
x
x
4 3 12 30
0
25
1 2 6
0
3
xx
x
xx
x
8 33
0
25
7
0
3
x
x
x
x
5 33
; ;
28
7; 3
x
x
7; 3x
.
Câu 15: [0D4-3-2] Bất phương trình
11xx
có nghiệm là
A.
,x
. B.
1x
. C.
1x
. D.
0x
.
Lời giải
Chọn A
, X X X
.
Câu 16: [0D4-3-2] Bất phương trình
31x
có nghiệm là:
A.
34x
. B.
23x
. C.
2x
hoặc
4x
. D.
3x
.
Lời giải
Chọn C
31x
31
31
x
x
4
2
x
x
.
Câu 17: [0D4-3-2] Tập nghiệm của bất phương trình
2
– 6 7 0xx
là
A.
; 1 7;
. B.
7;1
. C.
1;7
. D.
; 7 1;
.
Lời giải
Chọn C
Cách giải cũ dài dòng:

2
– 6 7 0 1;7x x x
.
Tập nghiệm bất phương trình là
1;7
Câu 18: [0D4-3-2] Hệ bất phương trình
2
2
2 3 0
11 28 0
xx
xx
có nghiệm là
A.
–1 x
hoặc
34x
hoặc
7x
. B.
4x
hoặc
7x
.
C.
–1 x
hoặc
7x
. D.
34x
.
Lời giải
Chọn C
2
2
2 3 0
11 28 0
xx
xx
3 1 0
7 4 0
xx
xx
; 1 3;
; 4 7;
x
x
; 1 7; x
.
Câu 19: [0D4-3-2] Cho các đa thức
2
16 4
4
12
1 1 1
21
x
fx
xx
gx
x x x
tìm các giá trị của
x
để
fx
luôn âm, và
gx
luôn dương
A.
2;0 1; 2 2; .
B.
4; 3 0;1 2;2 .
C.
3; 2 4; .
D.
4; 2 1; .
Lời giải
Chọn A
ĐK:
3; 1; 2; 4; 0x x x x x
.
2
16 4
40
12
x
xx
2
2
16 4 4 4 48
0
12
x x x
xx
2
4 16
0
43
x
xx
4
0
3
x
x
3
4
x
x
1 1 1
0
21x x x
1 2 1 2
0
21
x x x x x x
x x x
2
2
0
21
x
x x x
20
1 2 2
x
xx
Vậy
2;0 1; 2 2;x
Câu 20: [0D4-3-2] Xác định mệnh đề đúng.
A.
2 1 2 1 0x x x x
. B.
1 1 0x x x x
.
C.
2
2 3 2 2 3 2xx
. D.
1 1 0x x x x
.
Lời giải
Chọn B
A. Sai vì:
1
2 1 2 1 1
0
x
x x x x
x
.
B. Đúng vì:
1
1 1 0
0
x
x x x x
x
.
C. Sai vì:
2
3
3
35
2
2 3 2
2
5
22
2 3 2
2
x
x
xx
x
x
.
D. Sai vì:
1
1 1 1
0
x
x x x x
x
.
Câu 21: [0D4-3-2] Bất phương trình nào sau đây tương đương với bất phương trình
2 1 x
?
A.
2 2 1 2x x x
. B.
11
21
33
x
xx
.
C.
2
41x
. D.
2 2 1 2x x x
.
Lời giải
Chọn D
Ta có:
1
2 1
2
xx
A.
2
2 2 1 2 2
21
x
x x x x
x
.
B.
2
1
2
41
1
2
x
x
x
.
C.
3
11
21
1
33
2
x
x
xx
x
.

D.
2
1
2 2 1 2
1
2
2
x
x x x x
x
Từ tập nghiệm của các bất phương trình
Chọn D.
Câu 22: [0D4-3-2] Tập nghiệm của bất phương trình
3 2 xx
là
A.
;3
. B.
3;
. C.
;1
. D.
1;
.
Lời giải
Chọn D
3 2 3 3 1 .x x x x
Vậy bất phương trình đã cho có tập nghiệm là:
1; .S
.
Câu 23: [0D4-3-2] Tập xác định của hàm số
1
23
y
x
là:
A.
2
;
3
. B.
2
;
3
. C.
3
;
2
. D.
3
;
2
.
Lời giải
Chọn B
Điều kiện:
2
2 3 0 .
3
xx
Tập xác định:
2
;.
3
D
.
Câu 24: [0D4-3-2] Tập nghiệm của bất phương trình
21
0
3
x
x
là:
A.
1
3;
2
. B.
;3
. C.
1
;
2
. D.
1
; \ 3
2
.
Lời giải
Chọn D
21
0
3
x
x
30
2 1 0
x
x
3
1
2
x
x
.

Câu 25: [0D4-3-2] Hệ phương trình
2 1 0
3
x
xm
vô nghiệm khi và chỉ khi:
A.
5
2
m
. B.
5
2
m
. C.
7
2
m
. D.
5
2
m
.
Lời giải
Chọn B
Hệ pt
1
2
3
x
xm
Hệ vô nghiệm khi
15
3
22
mm
.
Câu 26: [0D4-3-2] Cho hệ bất phương trình
0 (1)
5 0 (2)
xm
x
. Hệ đã cho có nghiệm khi và chỉ
khi:
A.
5m
. B.
5m
. C.
5m
. D.
5m
.
Lời giải
Chọn A
1 xm
.
25x
Hệ có nghiệm khi
55mm
.
Câu 27: [0D4-3-2] Hệ bất phương trình
2 1 0
2
x
xm
có nghiệm khi và chỉ khi:
A.
3
2
m
. B.
3
2
m
. C.
3
2
m
. D.
3
2
m
.
Lời giải
Chọn C
Hệ BPT
1
2
2
x
xm
. Hệ có nghiệm khi
1
2
2
m
3
2
m
.

Câu 28: [0D4-3-2] Tập hợp các giá trị
m
để hệ bất phương trình
2 1 3
0
x
xm
có nghiệm duy
nhất là:
A.
. B.
2
. C.
2;
. D.
;2
.
Lời giải
Chọn B
Hệ BPT
2x
xm
. Hệ có nghiệm duy nhất
2m
.
Câu 29: [0D4-3-2] Tập nghiệm của bất phương trình
1
1
33
x
x
xx
là:
A.
;3
. B.
1;3
. C.
1;3
. D.
;1
.
Lời giải
Chọn D
Điều kiện
3 0 3xx
.
11
1
1
1 1 1
11
33
xx
x
x
x x x
xx
xx
.
KL:
1x
là nghiệm của bất phương trình.
Câu 30: [0D4-3-2] Tập xác định của hàm số
2
1
1
x
y
x
là :
A.
;1
. B.
1;
. C.
\1
. D.
;1
.
Lời giải
Chọn D
2
1
0 1 0 1
1
x
xx
x
.
TXĐ :
;1D
.
Câu 31: [0D4-3-2] Tập xác định của hàm số
21y m x x
là một đoạn trên trục số
khi và chỉ khi
A.
2m
. B.
2m
. C.
1
2
m
. D.
2m
.
Lời giải

Chọn D
Điều kiện
20
2
10
1
m
mx
x
x
x
. Để thỏa mãn điều kiện đề bài thì
12
2
m
m
.
Câu 32: [0D4-3-2] Nếu
28m
thì số nghiệm của phương trình
2
2 3 0x mx m
là:
A. 0. B. 1.
C. 2. D. Chưa xác định được.
Lời giải
Chọn D
2
8 12mm
.
2 6 0m
;
6 8 0m
.
Vậy với
28m
thì chưa xác định được số nghiệm của phương trình này.
Câu 33: [0D4--3-2] Phương trình
2
1 3 4 0m x x m
có hai nghiệm trái dấu khi và chỉ
khi
A.
–1m
hoặc
4
3
m
. B.
–1m
hoặc
3
4
m
.
C.
4
3
m
. D.
4
1
3
m
.
Lời giải
Chọn A
Phương trình có hai nghiệm trái dấu
1
1 4 3 0
4
3
m
mm
m
.
Câu 34: [0D4--3-2] Phương trình
2
20x mx m
có nghiệm khi và chỉ khi:
A.
2m
hoặc
0m
.
B.
0m
hoặc
8m
.
C.
80m
.
D.
8m
hoặc
0m
.
Lời giải
Chọn D
Phương trình có nghiệm
2
8
80
0
m
mm
m
.
Câu 35: [0D4--3-2] Phương trình
22
0x mx m m
có nghiệm khi và chỉ khi

A.
4
0
3
m
.
B.
4
0
3
m
.
C.
1
0
3
m
.
D.
1
0
3
m
.
Lời giải
Chọn B
Phương trình có nghiệm
2 2 2
4
4 0 3 4 0 0
3
m m m m m m
.
Câu 36: [0D4-3-2] Cho hệ bất phương trình
22
0 (1)
4 1 (2)
xm
x x x
Hệ đã cho có nghiệm khi và chỉ khi:
A.
–5.m
. B.
–5.m
. C.
5.m
. D.
5.m
Lời giải
Chọn A
Giải
2
ta được:
5x
.
Giải
1
ta được:
xm
.
Hệ có nghiệm
55mm
.
Câu 37: [0D4-3-2] Hai phương trình
2
10x x m
và
2
( 1) 1 0x m x
cùng vô
nghiệm khi và chỉ khi
A.
0 1m
. B.
3
1
4
m
.
C.
3
4
m
hoặc
1m
. D.
5
1
4
m
.
Lời giải
Chọn B
Đặt
2
1f x x x m
và
2
( 1) 1g x x m x
Ta có
2
10x x m
và
2
( 1) 1 0x m x
vô nghiệm khi và chỉ khi
2
2
3
0
1 4 1 0
3 4 0
3
1
4
0
4
2 3 0
1 4 0
31
fx
gx
m
m
m
m
mm
m
m

Vậy
3
1
4
m
.
Câu 38: [0D4-3-2] Tập hợp các giá trị của
m
để phương trình
22
( 1) ( 2) 2 1
44
m x m x m
xx
có nghiệm là
A.
73
;
22
.
B.
57
;
22
.
C.
57
;
22
.
D.
.
Lời giải
Chọn B
ĐK:
2
4 0 2 2xx
22
( 1) ( 2) 2 1 2 1
( 1) ( 2) 2 1 3 2 1
3
44
m x m x m m
m x m x m x m x
xx
Vì
2 1 5 7
2 2 2 2 6 2 1 6 5 2 7
3 2 2
m
x m m m
Vậy
57
;
22
m
.
Câu 39: [0D4-3-2] Tập hợp các giá trị của m để phương trình
2
1
11
x m m
x
xx
có
nghiệm là:
A.
1
;
3
.
B.
1
;
3
.
C.
1;
.
D.
1
;
3
.
Lời giải
Chọn A
ĐK
1 0 1xx
2 3 1
1 1 2 2 3 1
2
11
x m m m
x x x m m x m x
xx
Vì
3 1 1
1 1 2 3 1 1 3
23
m
x m m m
Vậy
1
;
3
m
.

Câu 40: [0D4-3-2] Tập hợp các giá trị của m để phương trình
2
( 1) 2 5 6m x x m
có
nghiệm dương là:
A.
; 1 6;
.
B.
–1;6 .
. C.
;2 3;
.
D.
2;3 .
Lời giải
Chọn C
2 2 2
( 1) 2 5 6 2 5 6.m x x m m x m m
Vì
2
2
2
56
20
2
mm
m m x
m
Ta có
2
2
2
2
56
0 5 6 0 .
3
2
m
mm
x m m
m
m
Vậy
;2 3; .m
.
Câu 41: [0D4-3-2] Tập hợp các giá trị của m để phương trình
22
52
11
xm
xx
có nghiệm là
A.
2;3 .
. B.
.
C.
2;3
.
D.
–1;1 .
Lời giải
Chọn A
ĐK
2
1 0 1 1xx
22
52
52
11
xm
xm
xx
Vì
1 1 1 5 2 1 6 2 4 2 3x m m m
Vậy
3 .2;m
Câu 42: [0D4-3-2] Nếu
13m
thì số nghiệm của phương trình
2
2 4 3 0x mx m
là.
A. 0. B. 1. C. 2. D. Chưa
xác định được
Lời giải
Chọn A
2
2 4 3 0x mx m
có nghiệm khi và chỉ
2
1
' 0 4 3 0
3
m
mm
m
Vì
13m
nên
'0
nên phương trình vô nghiệm.

Câu 43: [0D4-3-2] Nếu
12m
thì số nghiệm của phương trình
2
2 5 6 0x mx m
là
bao nhiêu.
A. 0. B. 1. C. 2. D. Chưa
xác định được
Lời giải
Chọn C
2
2 5 6 0x mx m
có nghiệm khi và chỉ
2
2
' 0 5 6 0 ;2 3;
3
m
m m m
m
Vì
1 2 1;2 ;2 3;mm
nên
'0
nên phương trình có 2
nghiệm phân biệt.
Câu 44: [0D4-3-2] Tam thức
2
( ) 2 2 1f x mx mx
nhận giá trị âm với mọi
x
khi và chỉ
khi.
A.
2m
hoặc
0m
. B.
–2m
hoặc
0m
.
C.
–2 0m
. D.
–2 0m
Lời giải
Chọn D
0 1 0m
(nhận)
0m
'2
2
20
( ) 2 2 1 0,
0
mm
f x mx mx x
m
20m
Vậy
2
( ) 2 2 1 0f x mx mx x
20m
.
Câu 45: [0D4-3-2] Bất phương trình
2
5 1 3
5
x
x
có nghiệm là:
A.
x
. B.
2x
. C.
5
2
x
. D.
20
23
x
.
Lời giải
Chọn D
2 23 20
5 1 3 4
5 5 23
x
x x x
.
Câu 46: [0D4-3-2] Tập nghiệm của bất phương trình
1
5 4 2 7
5
x
xx
là:
A.
. B. . C.
;1
. D.
1;
.
Lời giải
Chọn C
1
5 4 2 7 14 14 1
5
x
x x x x
.
Câu 47: [0D4-3-2] Tập nghiệm của hệ bất phương trình
30
10
x
x
là:
A.
. B.
;3
. C. . D.
1;3
.
Lời giải
Chọn D
3 0 3
13
1 0 1
xx
x
xx
.
Câu 48: [0D4-3-2] Tập nghiệm của hệ bất phương trình
5
6 4 7
7
83
25
2
xx
x
x
là:
A.
. B.
22
;
7
. C.
7
;
4
. D. .
Lời giải
Chọn C
5 22
6 4 7
7
77
8 3 7
4
25
24
x x x
x
x
xx
.
Câu 49: [0D4-3-2] Tập nghiệm của bất phương trình
3 2 1
11
xx
xx
là:

A.
7 57 7 57
; \ 1
22
S
. B.
7 57 7 57
1; 1;
22
S
.
C.
7 57 7 57
1; 1;
22
S
. D.
7 57 7 57
; ; \ 1
22
S
.
Lời giải
Chọn B
2
2
3 2 1 7 2
0
1 1 1
x x x x
x x x
Ta có:
2
7 57
7 1 0
2
x x x
,
2
1 0 1xx
Vậy
7 57 7 57
1; 1;
22
S
.
Câu 50: [0D4-3-2] Tìm m để bất phương trình
2
34m x mx
có nghiệm
A.
1m
. B.
0m
. C.
1m
hoặc
0m
. D.
m
.
Lời giải
Chọn D
22
3 4 1m x mx m m x
có nghiệm
m
.
Câu 51: [0D4-3-2] Bất phương trình
3mx
vô nghiệm khi:

A.
0m
. B.
0m
. C.
0m
. D.
0m
.
Lời giải
Chọn A
3mx
vô nghiệm
0m
.
Câu 52: [0D4-3-2] Khi giải bất phương trình
2
30
1
x
x
. Một học sinh làm như sau
(I)
22
3 0 3
11
xx
xx
(1)
(II)
(1) 2 3( 1)xx
(2)
(III)
(2) 2 3 3 1x x x
Vậy bất phương trình có tập nghiệm
( ;1)
Cách giải trên đúng hay sai? Nếu sau thì
A. Sai từ bước
I
. B. Sai từ bước
II
. C. Sai từ bước
III
. D. Hướng
dẫn giải đúng.
Lời giải
Chọn B
Sai từ bước
II
vì phép biến đổi đã làm thay đổi điều kiện của bpt và khi nhân hai
vế của bpt với
1x
mà chưa biết biểu thức này âm hay dương hay bằng không.
Câu 53: [0D4-3-2] Khi giải bất phương trình
5 1 1
2 1 1
x
x
xx
. Một học sinh làm như
sau
(I)
5 1 1 5
2 1 1 2
xx
xx
xx
(1)
(II)
(1) 5 2xx
(2)
(III)
(2) 5x
Vậy bất phương trình có tập nghiệm
( ;5)
Cách giải trên đúng hay sai? Nếu sau thì
A. Sai từ bước
I
. B. Sai từ bước
II
. C. Sai từ bước
III
. D. Hướng
dẫn giải đúng.
Lời giải

Chọn A
Sai từ bước
I
vì phép biến đổi đã làm thay đổi điều kiện của bpt.
Câu 54: [0D4-3-2] Bất phương trình
5 13 9 2
5 21 15 25 35
x x x
có nghiệm là
A.
0x
. B.
257
295
x
. C.
5
2
x
. D.
5x
.
Lời giải
Chọn B
Ta có
5 13 9 2 118 514 257
5 21 15 25 35 105 525 295
x x x
xx
.
Câu 55: [0D4-3-2] Bất phương trình
2
5 1 3
5
x
x
có nghiệm là
A.
x
. B.
2x
. C.
5
2
x
D.
20
23
x
.
Lời giải
Chọn D
Ta có
2 23 20
5 1 3 4
5 5 23
x
x x x
.
Câu 56: [0D4-3-2] Các nghiệm tự nhiên bé hơn 4 của bất phương trình
2
23 2 16
5
x
x
là
A.
4; 3; 2; 1;0;1;2;3
. B.
35
4
8
x
.
C.
0;1;2;3}
. D. Một kết quả khác.
Lời giải
Chọn C
Ta có
2 8 35
23 2 16 7
5 5 8
x
x x x
Câu 57: [0D4-3-2] Các nghiệm tự nhiên bé hơn 6 của bất phương trình
12
5 12
33
x
x
là
A.
2;3;4;5}
. B.
3;4;5}
. C.
0;1;2;3;4;5}
. D.
3;4;5;6}
.
Lời giải
Chọn B

Ta có
1 2 17 37 37
5 12
3 3 3 3 17
x
x x x
.
Câu 58: [0D4-3-2] Bất phương trình
2 1 3 1 2 5x x x x
có tập nghiệm là
A.
x
. B.
3, 24x
. C.
2,12x
. D. Vô
nghiệm.
Lời giải
Chọn A
Ta có
2 1 3 1 2 5 0 6x x x x
.
Câu 59: [0D4-3-2] Bất phương trình
3 5 2
1
23
xx
x
có nghiệm là
A. vô nghiệm. B. mọi
x
đều là nghiệm.
C.
4, 11x
. D.
5, 0x
.
Lời giải
Chọn D
Ta có
3 5 2 1 5
15
2 3 6 6
xx
x x x
.
Câu 60: [0D4-3-2] Bất phương trình
3
21
2
x x x
có tập nghiệm
A.
( 2; )
. B.
1
( ; )
2
. C.
3
( ; )
2
. D. (
9
;)
2
.
Lời giải
Chọn D
TH1
2x
Bpt
3 3 3
2 1 2 1
2 2 2
x x x x x x x
vô nghiệm vì
2x
.
TH2
21x
Bpt
3 3 5
2 1 2 1
2 2 2
x x x x x x x
vô nghiệm vì
21x
.
TH3
1x

Bpt
3 3 9
2 1 2 1
2 2 2
x x x x x x x
.
Vậy tập nghiệm của bpt là
9
;
2
S
.
Câu 61: [0D4-3-2] Hệ bất phương trình
3
32
5
63
21
2
xx
x
x
có nghiệm là
A.
5
2
x
. B.
75
10 2
x
. C.
7
10
x
D. Vô
nghiệm.
Lời giải
Chọn C
Ta có
37
32
7
5 10
6 3 5 10
21
22
x x x
x
x
xx
.

Câu 1: [0D4-3-3] Tìm tất cả các gi tr của
m
để vi mi
x
ta c
2
2
5
17
2 3 2
x x m
xx
A.
5 14
3 13
m
. B.
14 5
13 3
m
. C.
5
3
m
. D.
14
13
m
.
Lời giải
Chọn A
2
2
5
17
2 3 2
x x m
xx
2
2
2
2
5
1
2 3 2
5
7
2 3 2
x x m
xx
x x m
xx
(1)
Ta có:
2
2 3 2 0,x x x
(vì
2
3 4.2.2 7 0
và
20a
)
Do đ, ta c:
22
22
5 2 3 2
1
5 14 21 14
x x m x x
x x m x x
2
2
3 2 2 0
13 26 14 0
x x m
x x m
Từ đây suy ra để thỏa yêu cầu đề bài thì
2
2
3 2 2 0,
13 26 14 0,
x x m x
x x m x
'0
30
'0
13 0
a
a
2
2
1 3. 2 0
13 13 14 0
m
m
5
3
14
13
m
m
5 14
3 13
m
.
Câu 2: [0D4-3-3] Bất phương trình
(3 1) 2 (3 2) 5m x m m x
có tập hợp nghiệm là tập
con của
[2; )
khi và chỉ khi:
A.
11
2
m
. B.
11
2
m
. C.
5
2
m
. D.
5
2
m
.
Lời giải

Chọn B
25
(3 1) 2 (3 2) 5 3 2 5
3
m
m x m m x x m x
.
Để tập nghiệm là tập con của
[2; )
thì
2 5 11
2 2 11
32
m
mm
.
Câu 3: [0D4-3-3] Bất phương trình
22
( 1) 3 10 2m x x m m
:
A. Có vô số nghiệm khi và chỉ khi
3m
.
B. Có tập nghiệm là
1
;
3
m
m
khi và chỉ khi
3
3
m
m
.
C. Có tập nghiệm à
1
;
3
m
m
khi và chỉ khi
33m
D. Cả A và C đều đúng.
Lời giải
Chọn D
2 2 2 2
( 1) 3 10 2 9 2 3m x x m m m x m m
.
Vi
3m
bất phương trình trở thành
0 12x
(luôn đúng). Vậy bất phương trình
có vô số nghiệm khi
3m
. Vậy đp n A đúng.
Vi
2
3
90
3
m
m
m
bất phương trình trở thành
2
2
2 3 1
93
m m m
xx
mm
.
Vậy
1
;
3
m
S
m
. Đp n B sai.
Vi
2
9 0 3 3mm
bất phương trình trở thành
2
2
2 3 1
93
m m m
xx
mm
.
Vậy
1
;
3
m
S
m
. Đp n C đúng.
Vậy cả A và C đều đúng.
Câu 4: [0D4-3-3] Tập hợp nghiệm của bất phương trình
3 5 2 3xx
là:

A.
2
;8
5
. B.
2
;8
5
. C.
2
;8
5
. D.
2
8;
5
.
Lời giải
Chọn A
TH1:
5
3 5 0
3
xx
.
Bất phương trình trở thành
3 5 2 3 8x x x
. Vậy
1
5
;8
3
S
.
TH2:
5
3 5 0
3
xx
.
Bất phương trình trở thành
2
5 3 2 3 5 2
5
x x x x
. Vậy
2
25
;
53
S
.
Vậy tập nghiệm của bất phương trình là
2
;8
5
S
.
Câu 5: [0D4-3-3] Giải phương trình:
1 1 4xx
.
A.
{ 2}
. B.
2
. C.
2
. D. Vô
nghiệm.
Lời giải
Chọn C
TH1:
1x
. Phương trình trở thành
1 1 4 2 4 2x x x x
.
TH2:
11x
. Phương trình trở thành
1 1 4 2 4xx
(vô lý).
TH3:
1x
. Phương trình trở thành
1 1 4 2 4 2x x x x
.
Vậy
2;2S
.
Câu 6: [0D4-3-3] Vi điều kiện
1x
, bất phương trình
21
2
1
x
x
tương đương vi mệnh
đề nào sau đây:
A.
10x
hoặc
43
0
1
x
x
. B.
21
22
1
x
x
.
C.
21
2
1
x
x
. D. Tất cả cc câu trên đều đúng.

Lời giải
Chọn A
21
2
1
x
x
21
2
1
21
2
1
x
x
x
x
21
20
1
21
20
1
x
x
x
x
1
0
1
43
0
1
x
x
x
10
43
0
1
x
x
x
.
Câu 7: [0D4-3-3] Bất phương trình:
2
3 2 1 0xx
có tập nghiệm là:
A.
2
;
3
. B.
2
;
3
. C.
2
;
3
. D. .
Lời giải
Chọn D
2
3 2 0,
1 0,
xx
xx
2
3 2 1 0,x x x
.
Câu 8: [0D4-3-3] Giải bất phương trình
1 4 7xx
. Giá tr nghiệm nguyên dương nhỏ
nhất của
x
thoả bất phương trình là
A.
9x
. B.
8x
. C.
7x
. D.
6x
.
Lời giải
Chọn D
Xét dấu phá tr tuyệt đối:
TH1.
;1x
1 4 7xx
;1
1 4 7
x
xx
;1
2 3 7
x
x
;1
2
x
x
;2x
.
TH2.
1; 4x
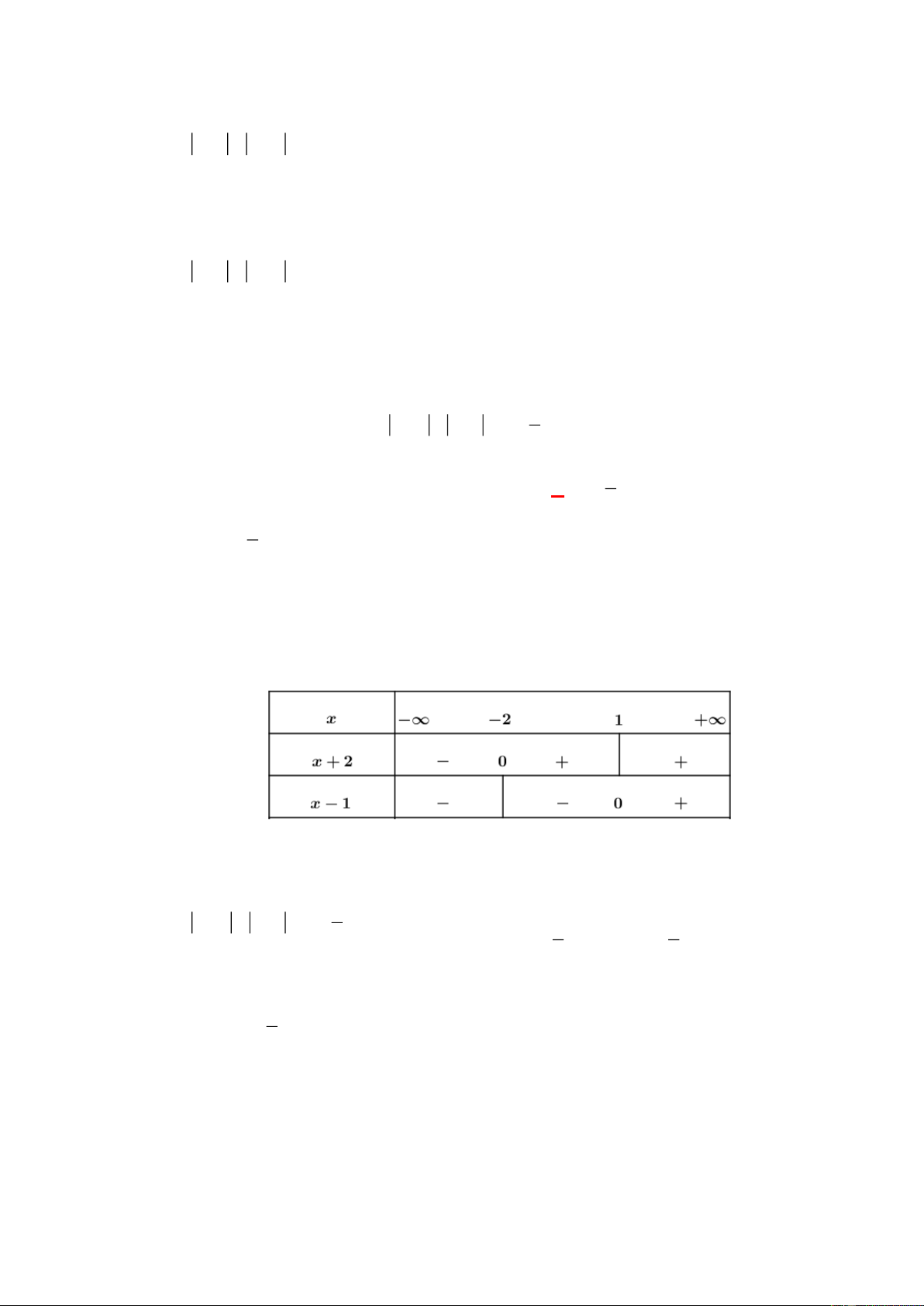
1 4 7xx
1; 4
1 4 7
x
xx
1; 4
57
x
x
.
TH3.
4; x
1 4 7xx
4;
1 4 7
x
xx
4;
2 3 7
x
x
4;
5
x
x
5; x
.
Tổng hợp lại, tập nghiệm của bất phương trình là:
; 2 5; .T
Câu 9: [0D4-3-3] Bất phương trình
3
21
2
x x x
có nghiệm là
A.
2x
. B.
1x
. C.
9
2
x
. D.
9
0
2
x
.
Lời giải
Chọn C
Xét dấu phá tr tuyệt đối:
TH1.
;2x
3
21
2
x x x
;2
3
21
2
x
x x x
;2
3
3
2
x
x
;2
3
2
x
x
x
.
TH2.
2; 1x

3
21
2
x x x
2; 1
3
21
2
x
x x x
2; 1
3
21
2
x
xx
2; 1
5
2
x
x
x
.
TH3.
1; x
3
21
2
x x x
1;
3
21
2
x
x x x
1;
3
3
2
x
x
1;
9
2
x
x
9
;
2
x
.
Tổng hợp lại, tập nghiệm của bất phương trình là:
9
;
2
T
.
Câu 10: [0D4-3-3] Bất phương trình
2
2
31
3
1
xx
xx
có nghiệm là
A.
35
2
x
hoặc
35
2
x
. B.
35
2
x
hoặc
35
2
x
.
C.
53
2
x
hoặc
53
2
x
. D.
53
2
x
hoặc
53
2
x
.
Lời giải
Chọn B
2
2
31
3
1
xx
xx
2
2
2
2
31
3
1
31
3
1
xx
xx
xx
xx
2
2
2
2
31
30
1
31
30
1
xx
xx
xx
xx
2
2
2
2
2 6 2
0
1
44
0
1
xx
xx
x
xx

2
2
2
3 5 3 5
2
22
0
13
24
41
0
13
24
xx
x
x
x
3 5 3 5
;;
22
;
x
x
3 5 3 5
;;
22
x
.
Câu 11: [0D4-3-3] Bất phương trình
2
2
54
1
4
xx
x
có nghiệm là
A.
0x
hoặc
85
52
x
,
2x
. B.
8
5
x
hoặc
8
2
5
x
.
C.
–2x
hoặc
8
0
5
x
. D.
20x
hoặc
5
2
x
.
Lời giải
Chọn A
2
2
54
1
4
xx
x
2
2
2
2
54
1
4
54
1
4
xx
x
xx
x
2
2
2
2
54
10
4
54
10
4
xx
x
xx
x
2
2
2
58
0
4
25
0
4
x
x
xx
x
58
0
22
25
0
22
x
xx
xx
xx
8
; 2 ; 2
5
5
2; 0 2;
2
x
x
85
; 2 2; 0 ; 2 2;
52
x
.
Câu 12: [0D4-3-3] Cho hệ bất phương trình
20
2 3 3
1
55
mx m
xx
. Xét các mệnh đề sau:
(I) Khi
0m
thì hệ bất phương trình đã cho vô nghiệm.
(II) Khi
0m
thì hệ bất phương trình đã cho c tập nghiệm là .

(III) Khi
0m
thì hệ bất phương trình đã cho c tập nghiệm là
2
;
5
.
(IV)Khi
0m
thì hệ bất phương trình đã cho có tập nghiệm là
2
;
5
.
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng?
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải
Chọn D
Ta có:
20
2 3 3
1
55
mx m
xx
2
2
5
mx m
x
.
Vi
0m
thì
2
2
5
mx m
x
2
2
5
x
x
x
. Vậy (I) đúng.
Vi
0m
thì
2
2
5
mx m
x
00
2
5
x
x
x
. Vậy (II) sai.
Vi
0m
thì
2
2
5
mx m
x
2
2
5
x
x
2
5
x
. Vậy (III), (IV) đúng.
Câu 13: [0D4-3-3] Hệ bất phương trình
3 4 0
1
xx
xm
vô nghiệm khi
A.
2m
. B.
2m
. C.
1m
. D.
0m
.
Lời giải
Chọn A
3 4 0
1
xx
xm
34
1
x
xm
.
Hệ bất phương trình vô nghiệm
13m
2m
.
Câu 14: [0D4-3-3] Tìm tất cả các giá tr thực của tham số
m
để hệ bất phương trình
3 6 3
5
7
2
x
xm
có nghiệm.

A.
11m
. B.
11m
. C.
11m
. D.
11m
.
Lời giải
Chọn A
3 6 3
5
7
2
x
xm
3 15
5 14
x
xm
5
14
5
x
m
x
.
Hệ bất phương trình c nghiệm
14
5
5
m
14 25m
11m
.
Câu 15: [0D4-3-3] Tìm tất cả các giá tr thực của tham số
m
để hệ bất phương trình
30
1
x
mx
vô nghiệm.
A.
4m
. B.
4m
. C.
4m
. D.
4m
.
Lời giải
Chọn D
30
1
x
mx
3
1
x
xm
.
Hệ bất phương trình vô nghiệm
13m
4m
.
[0D4-3-3] Cho bất phương trình:
22
21m x m x
(1). Xét các mệnh đề sau:
(I) Bất phương trình tương đương vi
21xx
(2).
(II) Vi
0m
, bất phương trình thoả
x
.
(III) Vi mi giá tr
m
thì bất phương trình vô nghiệm.
Mệnh đề nào đúng?
A. Chỉ (II). B. (I) và (II). C. (I) và (III). D. (I), (II)
và (III).
Lời giải
Chọn A
+) Vi
0m
thì (1) trở thành:
22
0 . 2 0 . 1xx
00
( đúng
x
).
Vậy (II) đúng,(III) sai.
+) Vi
0m
thì (2)
21
(sai). Bất phương trình vô nghiệm.
Vậy khi
0m
hai bất phương trình (1) và (2) không tương đương. (I) sai.

Câu 16: [0D4-3-3] Cho hệ bất phương trình
70
1
x
mx m
. Xét các mệnh đề sau
I
: Vi
0m
, hệ luôn có nghiệm.
II
: Vi
1
0
6
m
, hệ vô nghiệm.
III
: Vi
1
6
m
, hệ có nghiệm duy nhất.
Mệnh đề nào đúng?
A. Chỉ
I
. B.
II
và
III
. C. Chỉ
III
. D.
I
,
II
và
III
.
Lời giải
Chọn D
Vi
0m
thì
70
1
x
mx m
7
1
x
m
x
m
. Hệ này luôn có nghiệm. Vậy (I) đúng.
Vi
1
6
m
thì
70
11
1
66
x
x
7
7
x
x
7x
. Hệ này có nghiệm duy nhất. Vậy
(III) đúng.
Vi
0m
thì
70
1
x
mx m
7
1
x
m
x
m
.
Hệ này vô nghiệm nếu
1
7
m
m
1
70
m
m
16
0
m
m
1 6 0m
1
6
m
.
Vi
0m
thì
70
1
x
mx m
7
01
x
x
. Hệ này vô nghiệm.
Vậy (II) đúng.
Câu 17: [0D4-3-3] Tập nghiệm của bất phương trình
1
1
2
x
x
là
A.
,2S
. B.
1
,
2
S
.

C.
1
, 2 ,
2
S
D.
1; S
.
Lời giải
Chọn C
1
1
2
x
x
1
10
2
x
x
12
0
2
xx
x
10
12
0
2
10
12
0
2
x
xx
x
x
xx
x
1
21
0
2
1
3
0
2
x
x
x
x
x
1
; 2 ; 1
2
1;
x
x
1
; 2 ;
2
x
.
[0D4-3-3] Cho bất phương trình:
1 2 0x mx
(*). Xt cc mệnh đề sau:
I
Bất phương trình tương đương vi
20mx
.
II
0m
là điều kiện cần để mi
1x
là nghiệm của bất phương trình (*).
III
Vi
0m
, tập nghiệm của bất phương trình là
2
1x
m
.
Mệnh đề nào đúng?
A. Chỉ
I
. B. Chỉ
III
. C.
II
và
III
. D. Cả
I
,
II
,
III
.
Lời giải
Chọn C
Ta có:
1 2 0x mx
10
20
x
mx
. Vậy (I) sai.
Vi
0m
thì:
10
20
x
mx
1
02
x
x
1x
.
Vi
0m
thì:
10
20
x
mx
1
2
x
x
m
. Vậy (II) đúng.

Vi
0m
thì:
10
20
x
mx
1
2
x
x
m
2
1x
m
2
do 0 0 1m
m
.
Vậy (III) đúng.
Câu 18: [0D4-3-3] Đnh
m
để hệ sau c nghiệm duy nhất
3
39
mx m
m x m
.
A.
1m
. B.
2m
. C.
2m
. D.
1m
.
Lời giải
Chọn A
TH1.
30m
3m
.Khi đ:
3
39
mx m
m x m
3
9
3
m
x
m
m
x
m
.
Hệ bất phương trình c nghiệm duy nhất
39
3
mm
mm
3 3 9
0
3
m m m m
mm
99
0
3
m
mm
30
9 9 0
mm
m
0
3
1
m
m
m
1m
(không thỏa điều kiện
3m
).
Vậy
3m
không thỏa yêu cầu bài toán.
TH2.
3 0 3mm
.
Khi đ:
3
39
mx m
m x m
2
0 12
x
x
2x
.
Vậy
3m
không thỏa yêu cầu bài toán.
TH3.
3 0 3mm
.
30m
Khi đ:
3
39
mx m
m x m
3
9
3
m
x
m
m
x
m
. Hệ này có vô số nghiệm.
Vậy
30m
không thỏa yêu cầu bài toán.

0m
Khi đ:
3
39
mx m
m x m
03
39
x
x
0 3 sai
3x
.Hệ bất phương trình vô
nghiệm.
Vậy
0m
không thỏa yêu cầu bài toán.
0m
Khi đ:
3
39
mx m
m x m
3
9
3
m
x
m
m
x
m
.
Hệ bất phương trình c nghiệm duy nhất
39
3
mm
mm
3 3 9
0
3
m m m m
mm
99
0
3
m
mm
30
9 9 0
mm
m
0
3
1
m
m
m
1m
(thỏa điều kiện
0m
).
Kết luận:
1m
thỏa yêu cầu bài toán.
Câu 19: [0D4-3-3] Nghiệm của bất phương trình
2
2
xx
x
là
A.
01x
. B.
1x
,
2x
. C.
0x
,
1x
. D.
01x
.
Lời giải
Chọn C
2
2
xx
x
2
20
xx
x
23
0
xx
x
20
23
0
20
23
0
x
xx
x
x
xx
x
2
42
0
2
22
0
x
x
x
x
x
x
; 2
2; 0 1;
x
x
; 0 1; x
.

Câu 20: [0D4-3-3] Cho bất phương trình
28
13 9x
. Các nghiệm nguyên nhỏ hơn
13
của
bất phương trình là
A.
7x
và
8x
. B.
9x
và
10x
. C.
11x
và
12x
. D.
14x
và
15x
.
Lời giải
Chọn C
Vi
13x
13 0x
thì
28
13 9x
28
0
13 9x
18 8 13
0
9 13
x
x
8 86
0
9 13
x
x
8 86 0x
43
4
x
.
Vì
x
,
43
13
4
x
nên
11; 12x
.
Câu 21: [0D4-3-3] Vi giá tr nào của
m
để 2 bất phương trình sau là tương đương:
2 4 0mx m
và
( 1) 2 0m x m
.
A.
4 2 3m
. B.
4 2 3m
.
C.
4 2 3 4 2 3m
. D.
4 2 3m
.
Lời giải
Chọn A
2 4 0 1mx m
.
( 1) 2 0 2m x m
.
TH1: Khi
0m
hoặc
1m
thay trực tiếp vào
(1)
và
(2)
thấy không tương
đương.
TH2: Khi
0m
thì
1
42
;
m
D
m
và
2
2
;
1
m
D
m
.
Để
12
khi và chỉ khi
4 2 2
1
mm
mm
.
2
4 2 3
8 4 0
4 2 3
m
mm
m
(không thỏa mãn).

TH3: Khi
01m
thì
1
42
;
m
D
m
và
2
2
;
1
m
D
m
.
1
và
2
không tương đương.
TH4: Khi
1m
thì
1
42
;
m
D
m
và
2
2
;
1
m
D
m
.
Để
12
khi và chỉ khi
4 2 2
1
mm
mm
.
2
4 2 3 ( )
8 4 0
4 2 3
ml
mm
mn
Kết luận:
4 2 3m
.
Câu 22: [0D4-3-3] Vi giá tr nào của
m
để hệ bất phương trình sau c 1 nghiệm duy nhất:
( 2) 3 0
(2 5) 2 6 0
m x m
m x m
.
A.
1m
. B.
1m
. C.
4
3
m
. D.
3
4
m
.
Lời giải
Chọn A
( 2) 3 0 1m x m
.
(2 5) 2 6 0 2m x m
.
TH1: Khi
5
2
m
hoặc
2m
thay trực tiếp vào (1) và (2) thấy không có
nghiệm duy nhất.
TH2: Khi
5
2
m
thì
1
3
;
2
m
D
m
và
2
26
;
25
m
D
m
.
Không có giá tr nào của m để (1) và (2) thấy có nghiệm duy nhất.
TH3: Khi
5
2
2
m
thì
1
3
;
2
m
D
m
và
2
26
;
25
m
D
m
.
1
và
2
có nghiệm duy nhất
3 2 6
1
2 2 5
mm
m
mm
.
TH4: Khi
2m
thì
1
3
;
2
m
D
m
và
2
26
;
25
m
D
m
.
Không có giá tr nào của m để (1) và (2) thấy có nghiệm duy nhất.

Kết luận:
1m
.
Câu 23: [0D4-3-3] Tập nghiệm của bất phương trình
2
2
55
x
x
xx
là
A.
;2
. B.
2;
. C.
2;5
. D.
;2
.
Lời giải
Chọn A
22
5
20
50
5
2
2
2
20
22
2
55
22
x
x
x
x
x
x
x
x
xx
x
xx
xx
.
(loại trường hợp
22
22xx
)
Tập nghiệm của bất phương trình là
;2
.
Câu 24: [0D4-3-3] Tập hợp các giá tr của
m
để bất phương trình
22
2m m x m
thoả mãn
vi mi
x
là
A.
2;0
. B.
2;0
. C.
0
. D.
2;0
.
Lời giải
Chọn B
Nếu
2
20mm
thì
2
22
2
( 2 )
2
m
m m x m x
mm
không thỏa mãn yêu cầu đề
bài
Xt tương tự vi
2
20mm
cũng không thỏa mãn.
Vi
2
0
20
2
m
mm
m
thay vào phương trình ta thấy thoả mãn vi mi
x
00x
.
Câu 25: [0D4-3-3] Tập hợp các giá tr của
m
để bất phương trình
2
m m x m
vô nghiệm
là
A.
0;1
. B.
0
. C.
0;1
. D.
1
.
Lời giải
Chọn B

Nếu
2
0mm
thì
2
2
m
m m x m x
mm
không thỏa mãn yêu cầu đề bài
Xt tương tự vi
2
0mm
cũng không thỏa mãn.
Vi
2
0
0
1
m
mm
m
lần lượt thay vào phương trình ta thấy chỉ giá tr
0m
làm cho phương trình vô nghiệm (
00x
); loại giá tr
1m
.
Câu 26: [0D4-3-3] Bất phương trình:
2
30mx mx
vi mi
x
khi và chỉ khi.
A.
0m
hoặc
12m
. B.
0m
hoặc
12m
.
C.
0 12m
. D.
0 12m
Lời giải
Chọn C
0 3 0m
(nhận)
0m
2
2
12 0
30
0
mm
mx mx
m
0 12m
Vậy
2
30mx mx
0 12m
x
.
Câu 27: [0D4-3-3] Nghiệm nguyên ln nhất của hệ bất phương trình
4 2 3 9
2 1 2
xx
x
là:
A.
5
. B.
6
. C.
7
. D.
8
.
Lời giải
Chọn B
7
4 2 3 9
1
2 1 2
2
x
xx
x
x
. Nghiệm nguyên ln nhất là
6x
.
Câu 28: [0D4-3-3] Hệ phương trình
2 1 0
3
x
xm
vô nghiệm khi và chỉ khi:
A.
5
2
m
. B.
5
2
m
. C.
7
2
m
. D.
5
2
m
.
Lời giải
Chọn B

1
2 1 0
2
3
3
x
x
xm
xm
Hệ vô nghiệm thì
15
3
22
mm
.
Câu 29: [0D4-3-3] Cho hệ bất phương trình
0 (1)
5 0 (2)
xm
x
. Hệ đã cho c nghiệm khi và chỉ
khi:
A.
5m
. B.
5m
. C.
5m
. D.
5m
.
Lời giải
Chọn A
0 (1)
5 0 (2)
xm
x
5 xm
.
Hệ có nghiệm khi
55mm
.
Câu 30: [0D4-3-3] Tập hợp các giá tr
m
để hệ bất phương trình
2 1 3
0
x
xm
có nghiệm duy
nhất là:
A.
. B.
2
. C.
2;
. D.
;2
.
Lời giải
Chọn B
2 1 3 2
0
xx
x m x m
2 xm
.
Hệ có nghiệm duy nhất thì
2m
.
Câu 31: [0D4-3-3] Tập nghiệm của bất phương trình
2
1
1
x
là:
A.
;1
. B.
; 1 1;
. C.
1;
. D.
1;1
.
Lời giải
Chọn B
1
2 2 1
1 1 0 0 ; 1 1; .
1
1 1 1
x
x
x
x
x x x
.

Câu 32: [0D4-3-3] Bất phương trình
2
0
21
x
x
có tập nghiệm là:
A.
1
;2
2
. B.
1
;2
2
. C.
1
;2
2
. D.
1
;2
2
Lời giải
Chọn D
2 1 1
0 2 ;2 .
2 1 2 2
x
xx
x
Câu 33: [0D4-3-3] Tập nghiệm của bất phương trình
1
2
x
là
A.
1
;
2
. B.
1
0;
2
. C.
1
;0 ;
2
. D.
;0
.
Lời giải
Chọn C
1
1 1 1 2 1
2 2 0 0 ;0 ; .
2
2
0
x
x
x
x x x
x
.
Câu 34: [0D4-3-3] Tập xc đnh của hàm số
2 4 2 y x m x
là
1;2
khi và chỉ khi
A.
1
2
m
. B.
1m
. C.
1
2
m
. D.
1
2
m
.
Lời giải
Chọn C
ĐK :
20
2 2 2 ;2
4 2 0
xm
m x x m
x
YCBT
1
21
2
mm
.
Câu 35: [0D4-3-3] Tập xc đnh của hàm số
62 y x m x
là một đoạn trên trục số
khi và chỉ khi

A.
3m
. B.
3m
. C.
3m
. D.
1
3
m
.
Lời giải
Chọn B
ĐK :
0
3
6 2 0
xm
mx
x
YCBT
3m
.
Câu 36: [0D4-3-3] Tập xc đnh của hàm số
21 y m x x
là một đoạn trên trục số
khi và chỉ khi
A.
2m
. B.
2m
. C.
1
2
m
. D.
2m
.
Lời giải
Chọn D
ĐK :
2 0 2
1;
2
1 0 1
2
1
m
m x m x
x
m
x
xx
x
YCBT
12
2
m
m
.
Câu 37: [0D4-3-3] Bất phương trình
3mx
vô nghiệm khi:
A.
0m
. B.
0m
. C.
0m
. D.
0m
.
Lời giải
Chọn A
TH1:
0m
03
(vô nghiệm).
TH2:
0
3
m
x
m
( có nghiệm).
TH3:
0
3
m
x
m
( có nghiệm).
Câu 38: [0D4-3-3] Tìm tham số thực
m
để bất phương trình
2
34 m x mx
có nghiệm.
A.
1m
. B.
0m
. C.
1m
hoặc
0m
. D.
m
.

Lời giải
Chọn D
22
3 4 1m x mx m m x
TH1:
2
0
0
1
m
mm
m
bất phương trình nghiệm đúng vi mi
x
.
TH2:
2
0
0
1
m
mm
m
bất phương trình c nghiệm
2
1
x
mm
TH3:
2
0 0 1m m m
bất phương trình c nghiệm
2
1
x
mm
.
KL: bất phương trình c nghiệm
m
.
Câu 39: [0D4-3-3] Cho bất phương trình
1 m x m x
. Tìm tất cả các giá tr thực của
tham số
m
để tập nghiệm của bất phương trình đã cho là
;1Sm
.
A.
1m
. B.
1m
. C.
1m
. D.
1m
.
Lời giải
Chọn C
2
1 1 1m x m x m x m
TH1:
1 0 1mm
bất phương trình nghiệm đúng vi mi
x
.
TH2:
1 0 1mm
bất phương trình c nghiệm
2
1
1 1;
1
m
x m x m
m
TH3:
1 0 1mm
bất phương trình c nghiệm
2
1
1 ; 1
1
m
x m x m
m
Để tập nghiệm của bất phương trình đã cho là
;1Sm
thì
1m
.
Câu 40: [0D4-3-3] Tìm tất cả các giá tr thực của tham số
m
để bất phương trình
2mx m x
vô nghiệm.
A.
0m
. B.
2m
. C.
2m
. D.
m
.
Lời giải
Chọn B

22mx m x m x m
TH1:
2 0 2mm
bất phương trình vô nghiệm.
TH2:
2 0 2mm
bất phương trình c nghiệm
2
m
x
m
TH3:
2 0 2mm
bất phương trình c nghiệm
2
m
x
m
KL: giá tr cần tìm
2m
.
Câu 41: [0D4-3-3] Tìm
m
để
2
1 0, m x mx m x
?
A.
1m
. B.
1m
. C.
4
3
m
. D.
4
3
m
.
Lời giải
Chọn C
Trường hợp 1:
2
1 0 1 1 0,m m m x mx m x
0 1 , xxvô lí
.
Trường hợp 2:
1 0 1mm
Ta có:
2
2
10
1 0,
3 4 0
m
m x mx m x
mm
1
4
;
4
; 0;
3
3
m
m
m
.
Câu 42: [0D4-3-3] Tìm
m
để
2
( ) 2 2 3 4 3 0, f x x m x m x
?
A.
3
2
m
. B.
3
4
m
. C.
33
42
m
. D.
13m
.
Lời giải
Chọn D
Ta có:
2
2
1 0
( ) 2 2 3 4 3 0, 1;3
4 16
12 0
luôn đúng
f x x m x m x m
mm
.
Câu 43: [0D4-3-3] Vi giá tr nào của
m
thì bất phương trình
2
0 x x m
vô nghiệm?

A.
1m
. B.
1m
. C.
1
4
m
. D.
1
4
m
.
Lời giải
Chọn D
Ta có:
2
0 x x m
vô nghiệm
2
( ) 0,f x x x m x
.
1 0
0
1
4
14
luôn đúng
m
m
.
Câu 44: [0D4-3-3] Vi giá tr nào của
m
thì phương trình
2
( 1) 2( 2) 3 0 m x m x m
có hai nghiệm
12
,xx
và
1 2 1 2
1 x x x x
?
A.
12m
. B.
13m
. C.
2m
. D.
3m
.
Lời giải
Chọn B
Ta có:
2
( 1) 2( 2) 3 0 m x m x m
có hai nghiệm
12
,xx
và
1 2 1 2
1 x x x x
1 2 1 2
10
1
1
1 0
22
26
3
0
10
1
1
1
1
lu
am
m
m
m
m
m
m
x x x x
mm
ôn đúng
1
1;3
1;3
m
m
m
.
Câu 45: [0D4-3-3] Vi giá tr nào của m thì hai bất phương trình sau đây tương đương?
1 3 0a x a
;
1 2 0a x a
A.
1a
. B.
5a
. C.
1a
. D. Không
tồn tại
a
.
Lời giải
Chọn D
Ta có
1 3 0 1 3a x a a x a
1 2 0 1 2a x a a x a
Do
32
11
aa
aa
vô nghiệm, nên để hai bpt sau tương đương thì tập nghiệm của hai
bpt là
Vậy không tồn tại
m
để hai bất phương trình tương đương.

Câu 46: [0D4-3-3] Bất phương trình
22
4 2 4
9 3 3
xx
x x x x
có nghiệm nguyên ln nhất là
A.
2x
. B.
1x
. C.
2x
. D.
1x
.
Lời giải
Chọn A
Điều kiện
2
2
3
90
0
30
x
x
x
xx
Ta có
2 2 2 2 2
33
43
4 2 4 10 3 22
0
22
9 3 3 9 9 9
3
x
x
x x x x
x x x x x x x
x
.
Câu 47: [0D4-3-3] Bất phương trình
1 4 7xx
có nghiệm nguyên dương nhỏ nhất là
A.
4x
. B.
5x
. C.
6x
. D.
7x
.
Lời giải
Chọn C
TH1
1x
Bpt
1 4 7 1 4 7 2x x x x x
t/m.
TH2
14x
Bpt
1 4 7 1 4 7 0 2x x x x
vô nghiệm vì.
TH3
4x
Bpt
1 4 7 1 4 7 5x x x x x
t/m.
Vậy tập nghiệm của bpt là
; 2 5;S
. Do đ nghiệm nguyên dương nhỏ
nhất của phương trình là
6x
.
Câu 48: [0D4-3-3] Nghiệm của bất phương trình
1
1
2
x
x
là
A.
2x
;
1
2
x
B.
1
2
2
x
. C.
1
2
x
;
2x
. D. Vô
nghiệm.
Lời giải
Chọn A
ĐK
2x

TH1
1x
Bpt
1
1
12
21
1 0 0
2
2 2 2
2
x
xx
x
x
x x x
x
kết hợp đk, suy ra
1
1
2
2
x
x
TH2
1x
Bpt
1
12
3
1 0 0 2
2 2 2
x
xx
x
x x x
kết hợp đk, suy ra
1x
.
Vậy tập nghiệm của bpt là
1
; 2 [ ; )
2
S
.
Câu 49: [0D4-3-3] Nghiệm của bất phương trình
2
2
xx
x
là
A.
01x
. B.
1; 2xx
. C.
0; 1xx
. D.
01x
.
Lời giải
Chọn C
ĐK
0x
TH1
2x
Bpt
0
2
22
42
2 0 0
1
2
x
xx
x x x
x
x x x
x
kết hợp đk,
suy ra
2x
TH2
2x
Bpt
2
22
1
22
2 0 0
0
xx
x x x
x
x
x x x x
kết hợp đk, suy
ra
20
1
x
x
Vậy tập nghiệm của bpt là
;0 [1; )S
.
Câu 50: [0D4-3-3] Cho hệ bất phương trình
70
1
x
mx m
. Xét các mệnh đề sau

I) Vi
0m
hệ luôn có nghiệm.
II) Vi
1
0
6
m
hệ vô nghiệm
III) Vi
6m
hệ có nghiệm duy nhất.
Mệnh đề nào đúng
A. Chỉ I). B. II) và III). C. Chỉ III). D. I), II),
III)
Lời giải
Chọn A
Ta có
7 0 7
11
xx
mx m mx m
.
Xét bpt
1mx m
(1).
- Vi
0m
thì BPT (1) vô nghiệm.
- Vi
0m
bpt (1)
1m
x
m
. Để hệ bpt có nghiệm thì
1
7
m
x
m
đúng vi
moi
m
.
- Vi
0m
bpt (1)
1m
x
m
. Để hệ bpt có nghiệm thì
1
27
m
x
m
đúng
vi mi
m
.

Câu 1: [0D4-3-4] Với giá trị nào của
a
thì hai bất phương trình sau đây tương đương?
1 3 0a x a
(1)
1 2 0a x a
(2).
A.
1a
. B.
5a
. C.
1a
. D.
11a
.
Lời giải
Chọn B
TH1.
1 0 1aa
thì
1 2 0
( đúng
x
). Tập nghiệm của bất phương trình
1
T
.
2 2 1 0x
1
2
x
. Tập nghiệm của bất phương trình
2
1
;
2
T
.
Vậy
1a
không thỏa yêu cầu bài toán.
TH2.
1 0 1aa
thì
1 2 4 0x
2x
Tập nghiệm của bất phương trình
2
; 2T
.
2 3 0
( úng
x
).Tập nghiệm của bất phương trình
2
T
.
Vậy
1a
không thỏa yêu cầu bài toán.
TH3.
10
10
a
a
1
1
a
a
.
1 1 3a x a
.
2 1 2a x a
.
Hai bất phương trình tương đương
10
10
32
11
10
10
32
11
a
a
aa
aa
a
a
aa
aa
1
1
5
0
11
1
1
5
0
11
a
a
a
aa
a
a
a
aa
1
1
50
1
1
50
a
a
a
a
a
a
1
1
5
1
1
5
a
a
an
a
a
al
5a
.


Câu 1: [0D4-4-1] Cho nhị thức bậc nhất
23 20f x x
. Khẳng định nào sau đây đúng?
A.
0fx
với
x
. B.
0fx
với
20
;
23
x
.
C.
0fx
với
5
2
x
. D.
0fx
với
20
;
23
x
Lời giải
Chọn D
20
23 20 0
23
xx
.
Câu 2: [0D4-4-1] Với
x
thuộc tập hợp nào dưới đây thì đa thức
6 5 2 10 8f x x x x x x
luôn dương?
A.
. B. . C.
;5
. D.
5;
.
Lời giải
Chọn A
6 5 2 10 8 0 0 5x x x x x x
vô nghiệm.
Vậy
.x
Câu 3: [0D4-4-1] Bất phương trình
11xx
có nghiệm là
A.
;
. B.
1
. C.
1;
. D.
;0
.
Lời giải
Chọn A
Sử dụng tính chất
,a a a
để nhanh chóng có đáp số.

Câu 1: [0D4-4-2] Bất phương trình:
2 6 1) 0xx
có nghiệm là
A.
–3; –1.xx
B.
–3 .x
C.
–1 .x
D.
1.x
Lời giải
Chọn C
Điều kiện xác định
1x
BPT đã cho tương đương
2 6 0 3
1 0 1
xx
xx
Kết hợp điều kiện được đáp án đúng là C.
Câu 2: [0D4-4-2] Với
x
thuộc tập hợp nào dưới đây thì
2
1
1
fx
x
âm?
A.
;1
. B.
; 1 1;
.
C.
1;
. D.
1;1
.
Lời giải
Chọn B
2
10
1 x
21
0
1
x
x
1
1
0
1
1
x
x
x
x
.
Câu 3: [0D4-4-2] Với
x
thuộc tập hợp nào dưới đây thì
13f x x x
không âm?
A.
3,1
. B.
3,1
. C.
, 3 1,
. D.
, 3 1,
.
Lời giải
Chọn C
Ta có
1 3 0 , 3 1,xx
Câu 4: [0D4-4-2] Với
x
thuộc tập hợp nào dưới đây thì
41
3
31
x
fx
x
không dương?
A.
41
,
53
B.
41
,
53
C.
4
,
5
. D.
4
,
5
.
Lời giải
Chọn B

Ta có
41
30
31
x
x
5 4 4 1
0
3 1 5 3
x
x
x
.
Câu 5: [0D4-4-2] Với
x
thuộc tập hợp nào dưới đây thì
4
2
3
fx
x
không dương?
A.
, 3 1,
. B.
3, 1
. C.
1,
. D.
,1
.
Lời giải
Chọn A
Ta có
4
20
3x
3
22
0
1
3
x
x
x
x
.
Câu 6: [0D4-4-2] Với
x
thuộc tập hợp nào dưới đây thì nhị thức bậc nhất
2 5 3f x x
không dương?
A.
14x
. B.
5
2
x
. C.
0x
. D.
1x
.
Lời giải
Chọn A
Ta có
2 5 3 0x
2 5 3x
2 5 3
2 5 3
x
x
4
14
1
x
x
x
.
Vậy
1,4x
.
Câu 7: [0D4-4-2] Với
x
thuộc tập hợp nào dưới đây thì nhị thức bậc nhất
2
21
x
fx
x
không
âm?
A.
1
;2
2
S
. B.
1
; 2;
2
S
.
C.
1
; 2;
2
S
. D.
1
;2
2
S
.
Lời giải
Chọn D
Ta có
2 0 2xx
1
2 1 0
2
xx
+ Xét dấu
fx
:

+ Vậy
0fx
khi
1
;2
2
x
.
Câu 8: [0D4-4-2] Với
x
thuộc tập hợp nào dưới đây thì nhị thức bậc nhất
2 3 1f x x
không dương?
A.
13x
. B.
11x
. C.
12x
. D.
12x
.
Lời giải
Chọn C
2 3 1 0x
2 3 1x
1 2 3 1 1 2xx
.
Câu 9: [0D4-4-2] Với
x
thuộc tập hợp nào dưới đây thì đa thức
33
23
2 4 2 4
f x x
xx
âm?
A.
23x
. B.
3
2
x
và
2x
. C.
3
2
x
. D. Tất cả
đều đúng.
Lời giải
Chọn B
Ta có:
2
33
2 3 0
3
2 4 2 4
2
x
x
xx
x
.
Câu 10: [0D4-4-2] Với
x
thuộc tập hợp nào dưới đây thì đa thức
2 1 3 1 2 5f x x x x x
luôn dương
A.
x
. B.
3,24x
. C.
2,12x
. D. Vô
nghiệm.
Lời giải
Chọn A

Ta có
2 1 3 1 2 5 0x x x x
2 8 2 8xx
(luôn đúng).
Vậy
x
.
Câu 11: [0D4-4-2] Với
x
thuộc tập hợp nào dưới đây thì nhị thức bậc nhất
2
5 1 7 2f x x x x x x
luôn dương
A. Vô nghiệm. B.
.x
C.
2,5x
. D.
2,6x
.
Lời giải
Chọn A
Ta có
2
5 1 7 2 0x x x x x
22
5 5 7 2 5 0x x x x x
(vô
lý).
Vậy vô nghiệm.
Câu 12: [0D4-4-2] Với
x
thuộc tập hợp nào dưới đây thì nhị thức bậc nhất
2
5
x
fx
x
không dương
A.
2,5
. B.
2,5
C.
2,5
. D.
2,5
.
Lời giải
Chọn D
Ta có
2
0 2 5
5
x
x
x
.
Câu 13: [0D4-4-2] Với
x
thuộc tập hợp nào dưới đây thì nhị thức bậc nhất
11
11
fx
xx
luôn âm
A. . B.
. C.
1,1
. D. Một đáp
số khác.
Lời giải
Chọn C
Ta có
11
0
11xx
11
11xx
2
0 1 1
11
x
xx
.
Vậy
1,1x
.
Câu 14: [0D4-4-2] Với giá trị nào của
m
thì không tồn tại giá trị của
x
để
2f x mx m x
luôn âm?
A.
0m
. B.
2m
. C.
2m
. D.
m
.
Lời giải

Chọn B
2 0 2 0mx m x m x m
2m
bất phương trình trở thành
20
bất phương trình vô nghiệm.
Câu 15: [0D4-4-2] Tìm số nguyên nhỏ nhất của
x
để
5
72
x
fx
xx
luôn dương
A.
–3.x
B.
4.x
C.
–5.x
D.
–6.x
Lời giải
Chọn D
– Lập bảng xét dấu
5
( 7)( 2)
x
fx
xx
– Suy ra
7; 2 5;x
– Vậy
6x
Câu 16: [0D4-4-2] Với
x
thuộc tập hợp nào dưới đây thì
12
21
xx
fx
xx
không âm?
A.
1
2;
2
. B.
2;
. C.
1
2; 1;
2
. D.
1
; 2 ;1
2
.
Lời giải
Chọn D
Đkxđ:
2; 1xx
.
YCBT
12
0
21
xx
xx
22
12
0
12
xx
xx
63
0
12
x
xx
.
Cho
1
6 3 0
2
xx
.
Cho
1
1 2 0
2
x
xx
x
.
Bảng xét dấu

Căn cứ bảng xét dấu ta được
1
; 2 ;1
2
x
.
Câu 17: [0D4-4-2] Với giá trị nào của
m
thì nhị thức bậc nhất
3f x mx
luôn âm với mọi
x
?
A.
0m
. B.
0m
. C.
0m
. D.
0m
.
Lời giải
Chọn A
+ Nếu
0m
,
30mx
3
x
m
không thỏa mãn đề bài.
+ Nếu
0m
,
30mx
3
x
m
không thỏa mãn đề bài.
+ Nếu
0m
, bpt trở thành
30
luôn đúng với mọi
x
.
Câu 18: [0D4-4-2] Với
x
thuộc tập hợp nào dưới đây thì đa thức
1
1
2
x
fx
x
luôn âm
A.
1
2,
2
xx
. B.
1
2
2
x
. C.
1
,2
2
xx
. D. Vô
nghiệm.
Lời giải
Chọn A
11
1 0 1 *
22
xx
xx
Trường hợp
1x
, ta có
1
*1
2
x
x
3
0
2x
20x
2x
. So với
trường hợp đang xét ta có tập nghiệm bất phương trình là
1
1,S
.
Trường hợp
1x
, ta có
1
*1
2
x
x
12
0
2
x
x
.
Bảng xét dấu

Dựa vào bảng xét dấu, ta có
1
, 2 ,1
2
x
.
Vậy
12
1
, 2 ,
2
x S S
.
Câu 19: [0D4-4-2] Với
x
thuộc tập hợp nào dưới đây thì nhị thức bậc nhất
2 1 4f x x x
luôn dương?
A.
2x
. B.
2x
hoặc
2x
. C.
11x
. D. Một đáp
số khác.
Lời giải
Chọn B
2 1 4 0xx
2 1 4xx
40
40
2 1 4
2 1 4
x
x
xx
xx
4
4
2
2
x
x
x
x
4
42
2
x
x
x
.
Vậy
, 2 2,x
.
Câu 20: [0D4-4-2] Với
x
thuộc tập hợp nào dưới đây thì
21
2
1
x
fx
x
luôn dương?
A.
1,
. B.
3
, 3,
4
. C.
3
,1
4
. D.
3
, \ 1
4
.
Lời giải
Chọn D

Ta có
21
20
1
x
x
21
2
1
x
x
21
2
1
21
2
1
x
x
x
x
1
0
1
43
0
1
x
x
x
1
3
1
4
x
x
.
Tập
3
, \ 1
4
x
.
Câu 21: [0D4-4-2] Với
x
thuộc tập hợp nào dưới đây thì biểu thức
15
11
xx
fx
xx
không
âm
A.
1,
B.
, 1 1,3
. C.
3,5 6,16
. D.
6,4
.
Lời giải
Chọn B
Ta có
1 5 2 6
00
1 1 1 1
x x x
x x x x
.
Bảng xét dấu
Vậy
, 1 1,3x
.
Câu 22: [0D4-4-2] Giải hệ bất phương trình:
32
1 2 1
22
2 1 1
xx
x
xx
.
A.
15
1 v 0 1 v
22
x x x
. B.
11
2
24
xx
.
C.
1
1
2
x
. D.
11
24
xx
.
Lời giải
Chọn A
TXĐ:
1
\ 1;
2
D
.

HPT
2
41
32
0
1 2 1
1 2 1
22
25
0
2 1 1
1 2 1
x
xx
xx
x
xx
xx
xx
11
1v
24
15
1 v 0 1 v
22
15
v 0 1 v
22
xx
x x x
x x x
.
Câu 23: [0D4-4-2] Giải bất phương trình:
3
23
2
x
x
.
A.
9
7
2
xx
. B.
9
2
2
x
.
C.
9
7
2
x
. D.
9
2
2
xx
.
Lời giải
Chọn C
TXĐ:
\2D
.
BPT
37
20
22
3 2 9
30
22
xx
xx
xx
xx
27
9
7
9
2
2
2
x
x
xx
.
Kết luận:
9
7
2
x
.
Câu 24: [0D4-4-2] Ghép mỗi ý ở cột bên trái với một ý ở cột bên phải để được một mệnh đề
đúng:
A. Nghiệm của bất phương trình
–3 1 0x
là
(1)
1
3
x
B. Nhị thức
–3 1x
có dấu dương khi và chỉ khi
(2)
1
3
x
C. Nghiệm của nhị thức
3 –1x
là
(3)
1
3
x
(4)
1
3
x

A.
4, 3, 1A B C
. B.
3, 2, 1A B C
. C.
4, 1, 3A B C
. D.
4, 4, 1A B C
.
Lời giải
Chọn A
A4 vì
1
–3 1 0
3
xx
.
B3 vì
1
–3 1 0
3
xx
.
Xét dấu
C1 vì
1
3 1 0
3
xx
.
Câu 25: [0D4-4-2] Tập nghiệm của bất phương trình
1
2
x
là
A.
1
;
2
. B.
1
0;
2
.
C.
1
;0 ;
2
. D.
;0
.
Lời giải
Chọn C
Điều kiện :
0x
Bất phương trình đã cho tương đương với
11
2 2 0
xx
21
0
x
x
0
1
2
x
x
.
Kết hợp điều kiện, ta được tập nghiệm của bất phương trình
1
;0 ;
2
S
.
Câu 26: [0D4-4-2] Tập nghiệm của bất phương trình
2
1
x
là
A.
2;0
.
B.
;2
.
C.
2;
.
D.
; 2 0;
.
Lời giải
Chọn D
Điều kiện :
0m
.
1
3
x
fx
0
-
+

Bất phương trình đã cho tương đương với
2
2 2 2
1 1 0 0
0
m
m
m
m m m
Kết hợp điều kiện, ta được tập nghiệm của bất phương trình
; 2 0;S
.
Câu 27: [0D4-4-2] Nhị thức nào sau đây nhận giá trị âm với mọi
x
nhỏ hơn
2
?
A.
36f x x
. B.
63f x x
. C.
4–3f x x
. D.
3 – 6f x x
.
Lời giải
Chọn D
A.
3 6 0 2f x x x
. B.
6 – 3 0 2f x x x
.
C.
4
4 – 3 0
3
f x x x
. D.
3 – 6 0 2f x x x
.
Câu 28: [0D4-4-2] Nhị thức nào sau đây nhận giá trị âm với mọi số
x
nhỏ hơn
2
3
?
A.
6 – 4f x x
. B.
32f x x
. C.
3 – 2f x x
. D.
23f x x
.
Lời giải
Chọn B
2
3 2 3 2 0
3
x x x
.
Câu 29: [0D4-4-2] Nhị thức
32x
nhận giá trị dương khi:
A.
3
2
x
. B.
2
3
x
. C.
3
2
x
. D.
2
3
x
.
Lời giải
Chọn B
2
3 2 0 3 2
3
x x x
.
Câu 30: [0D4-4-2] Nhị thức
23x
nhận giá trị dương khi và chỉ khi :

A.
3
2
x
. B.
2
3
x
. C.
3
2
x
. D.
2
3
x
.
Lời giải
Chọn A
3
2 3 0 2 3
2
x x x
.
Câu 31: [0D4-4-2] Nhị thức nào sau đây nhận giá trị dương với mọi
x
nhỏ hơn
2
?
A.
36f x x
. B.
6 – 3f x x
. C.
4 – 3f x x
. D.
3 – 6f x x
.
Lời giải
Chọn B
2 2 0 3 6 0x x x
.
Câu 32: [0D4-4-2] Tập xác định của hàm số
2
1
1
x
y
x
là :
A.
;1
. B.
1;
. C.
\1
. D.
;1
.
Lời giải
Chọn D
ĐK :
1 0 1xx
.
Câu 33: [0D4-4-2] Tập nghiệm của bất phương trình
1 03xx
là
A.
3; 1
. B.
3;1
. C.
;3
. D.
( ; 3) [1; )
.
Lời giải
Chọn B
Lập bảng xét dấu biểu thức
1, 3xx
và
13xx
. Suy ra tập nghiệm cần tìm
là
3;1
Câu 34: [0D4-4-2] Tập nghiệm của bất phương trình
41
3
31
x
x
là

A.
41
;
53
. B.
41
;
53
. C.
4
;
5
. D.
4
;
5
.
Lời giải
Chọn A
ĐK
1
3
x
. Ta có
4 1 4 1 5 4
3 3 0 0
3 1 3 1 3 1
x x x
x x x
Lập bảng xét dấu biểu thức
54
31
x
x
. Suy ra tập nghiệm cần tìm là
41
;
53
Câu 35: [0D4-4-2] Tập nghiệm của bất phương trình
15
11
xx
xx
là
A.
1;
. B.
; 1 1;3
. C.
3;5 6;16
. D.
6;4
.
Lời giải
Chọn B
ĐK
1x
.
Ta có
1 5 1 5 2 6
00
1 1 1 1 1 1
x x x x x
x x x x x x
. Lập bảng xét dấu biểu
thức
26
11
x
xx
. Từ đó suy ra tập nghiệm bpt đã cho là
; 1 1;3
Câu 36: [0D4-4-2] Tập nghiệm của bất phương trình
2
0
5
x
x
là
A.
2;5
. B.
2;5
. C.
2;5
. D.
2;5
.
Lời giải
Chọn D
ĐK
5x
. Lập bảng xét dấu biểu thức
2
5
x
x
, ta được tập nghiệm bpt đã cho là
2;5
Câu 37: [0D4-4-2] Tập nghiệm của bất phương trình
11
11xx
là
A. . B.
. C.
1;1
. D.
0;1
.
Lời giải
Chọn B

ĐK
1x
. Ta có
1 1 1 1 2
00
1 1 1 1 1 1x x x x x x
. Lập bảng
xét dấu
2
11xx
, suy ra tập nghiệm cần tìm là
1;1
.
Câu 38: [0D4-4-2] Tập nghiệm của bất phương trình
4
2
3x
là
A.
; 3 1;
. B.
3; 1
. C.
1;
. D.
;1
.
Lời giải
Chọn A
ĐK
3x
.
Ta có
4 4 2 2
2 2 0 0 ; 3 1;
3 3 3
x
x
x x x
Câu 39: [0D4-4-2] Tập nghiệm của bất phương trình
1
1
2
x
x
là
A.
;2
. B.
1
;
2
.
C.
1
; 2 ( ;1]
2
. D.
1
; 2 ;
2
.
Lời giải
Chọn C
ĐK
2x
.
1
1
1
1
21
1
0
1
1
2
1
1 ; 2 ( ;1]
2
2
22
2
1
1
1
12
1
2
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
xx
x
Câu 40: [0D4-4-2] Bất phương trình
2 1 4xx
có tập nghiệm là
A.
; 1 2;
. B.
; 2 2;
. C.
2;
. D.
;1
.
Lời giải
Chọn B

11
2 2 4 2
2
2 1 4
2
11
2 2 4 2
xx
x x x
x
xx
x
xx
x x x
.
Câu 41: [0D4-4-2] Bất phương trình
33xx
có tập nghiệm là
A.
;
. B.
3
. C.
3;
. D.
;3
.
Lời giải
Chọn A
3
3
33
33
3
3
33
x
x
xx
x x x
x
x
x
xx
Ghi chú có thể sử dụng tính chất
,a a a
để nhanh chóng có đáp số.
Câu 42: [0D4-4-2] Bất phương trình
24xx
có tập nghiệm là
A.
2
. B.
6
. C.
1;
. D. .
Lời giải
Chọn C
2 2 2 2
2 4 2 4 2 4 0
6 2 2 0 1
x x x x x x
xx
Câu 43: [0D4-4-2] Bất phương trình
2 5 3x
có tập nghiệm là
A.
1;4
. B.
5
2
. C.
0
. D.
2;3
.
Lời giải
Chọn A
2 5 3 3 2 5 3 2 8 1 4x x x x
.
Câu 44: [0D4-4-2] Bất phương trình
1 3 2x
có tập nghiệm là
A.
1
; 1;
3
. B.
1;
. C.
1
;
3
. D.
1;
.
Lời giải

Chọn A
1
1 3 2
1 3 2
1
1 3 2
3
x
x
x
x
x
Câu 45: [0D4-4-2] Bất phương trình
52x
có tập nghiệm là
A.
5;7
. B.
5;7
. C.
3;7
. D.
3;7
.
Lời giải
Chọn D
5 2 2 5 2 3 7x x x
Câu 46: [0D4-4-2] Bất phương trình
31x
có tập nghiệm là
A.
3; 4
. B.
2;3
. C.
;2 4;
. D.
3
.
Lời giải
Chọn C
3 1 2
31
3 1 4
xx
x
xx
.
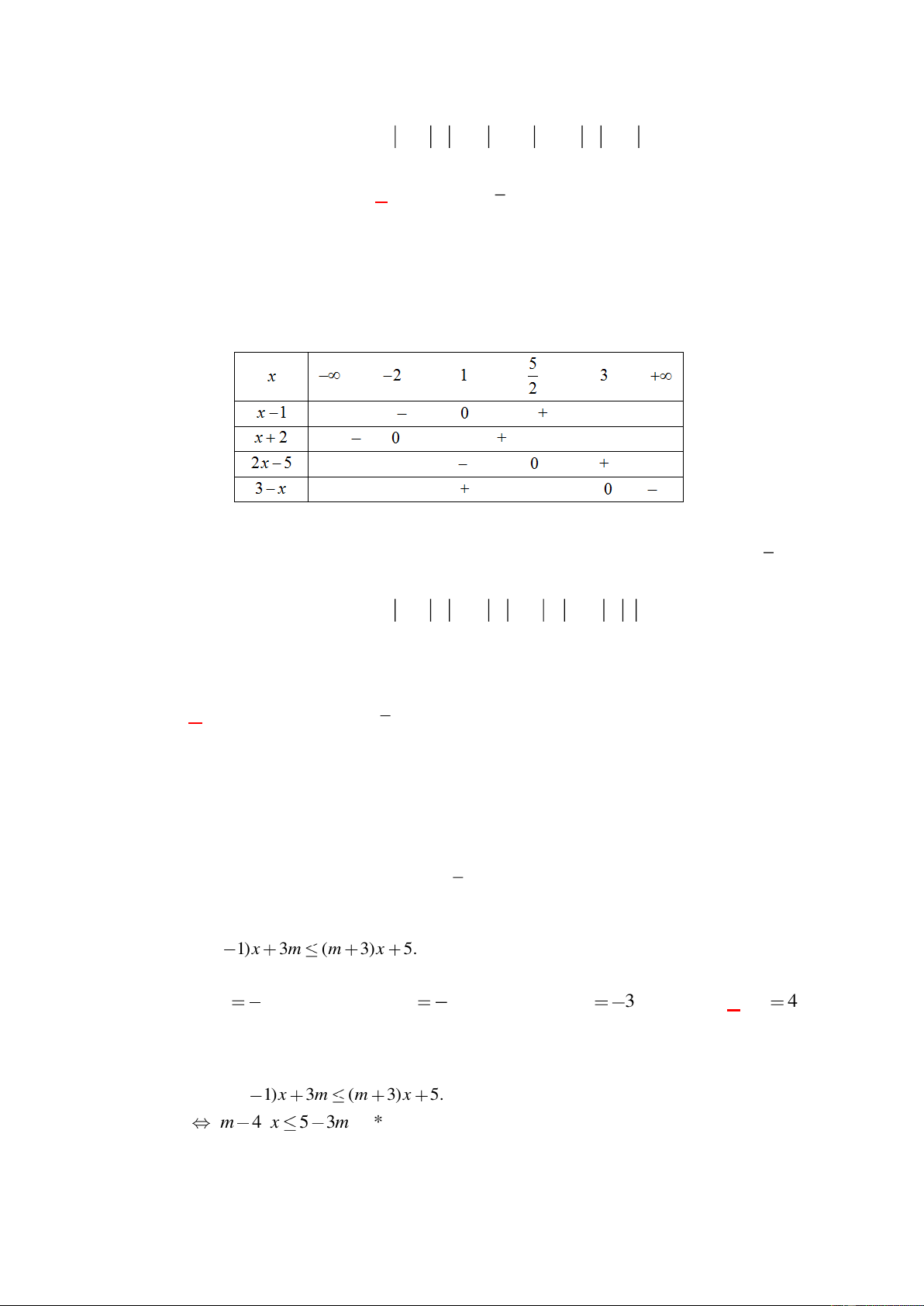
Câu 1: [0D4-4-3] Bất phương trình:
1 2 3 2 5 3x x x x
có tập nghiệm là:
A.
0;
. B.
8
4;0 2;
3
. C.
4;
. D.
0;2
.
Lời giải
Chọn B
Bảng xét dấu:
Giải với từng trường hợp được nghiệm của bất phương trình là:
8
4;0 2;
3
.
Câu 2: [0D4-4-3] Bất phương trình:
1 2 1 2 3x x x x x
có tập nghiệm là:
A.
2; .
B.
1; .
C.
1
–2; –1 –1; 0 0; .
3
D.
–2; –1 –1;1 .
Lời giải
Chọn C
Lập bảng xét dấu để phá các trị tuyệt đối, giải bất phương trình trên với từng khoảng
được nghiệm của BPT là:
1
2
3
x
.
Câu 3: [0D4-4-3] Với giá trị nào của m thì bất phương trình sau vô nghiệm:
(2 1) 3 ( 3) 5.m x m m x
A.
5
3
m
. B.
1
2
m
. C.
3m
. D.
4m
.
Lời giải
Chọn D
PT
(2 1) 3 ( 3) 5.m x m m x
4 5 3 *m x m

Bât phương trình
*
vô nghiệm khi và chỉ khi
40
5 3 0
m
m
4
4
5
3
m
m
m
Kết luận:
4m
.
Câu 4: [0D4-4-3] Với giá trị nào của m thì bất phương trình sau vô nghiệm:
2
( 4) 2 (3 2) .m x m x m
A.
1m
. B.
12mm
. C.
12mm
. D.
2m
.
Lời giải
Chọn D
PT
2
( 4) 2 (3 2) .m x m x m
2
3 2 2 *m m x m
Bât phương trình
*
vô nghiệm khi và chỉ khi
2
1
3 2 0
2
2
20
2
m
mm
m
m
m
m
Kết luận:
2m
.
Câu 5: [0D4-4-3] Định m để bất phương trình sau có nghiệm:
22
( 2) (2 1) 2.m x m m m x
A.
1m
và
3m
. B.
3m
và
2m
.
C.
1m
. D.
1m
và
2m
.
Lời giải
Chọn C
PT
22
( 2) (2 1) 2.m x m m m x
22
2 3 2m m x m m
1 3 1 2 *m m x m m
Xét
1m
thì
* 0 0x
(vô lí) Suy ra
*
vô nghiệm.
Xét
3m
thì
* 0 4x
(đúng) Suy ra
*
có tập nghiệm
Vậy bât phương trình
*
có nghiệm khi và chỉ khi
1m
Kết luận:
1m
.
Câu 6: [0D4-4-3] Định m để bất phương trình
( 3) 3 ( 2) 2m x m m x
có tập hợp
nghiệm là tập hợp con của
[2; ).
A.
4m
. B.
4m
. C.
4m
. D.
02m
.

Lời giải
Chọn B
PT
( 3) 3 ( 2) 2m x m m x
5 3 2xm
32
*
5
m
x
Để bất phương trình
( 3) 3 ( 2) 2m x m m x
có tập hợp nghiệm là tập hợp
con của
[2; ).
32
24
5
m
m
Kết luận:
4m
.
Câu 7: [0D4-4-3] Định m để bất phương trình
(3 4) 6 3 2m x mx m
có tập hợp nghiệm
là tập hợp con của
( ; 3].
A.
3m
. B.
7m
. C.
3m
. D.
3m
.
Lời giải
Chọn C
PT
(3 4) 6 3 2m x mx m
3
2
m
x
Để bất phương trình
(3 4) 6 3 2m x mx m
có tập hợp nghiệm là tập hợp con
của
( ; 3].
3
33
2
m
m
Kết luận:
3m
.
Câu 8: [0D4-4-3] Số các giá trị nguyên âm của
x
để đa thức
3 2 4f x x x x
không âm là
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn D
Ta có
3
3 2 4 0 4
2
x
x x x x
x
Bảng xét dấu
fx

Dựa vào bảng xét dấu, để
fx
không ấm thì
3,2 4,x
.
Vậy có 3 số nghiệm nguyên âm
x
thỏa YCBT.
Câu 9: [0D4-4-3] Với
x
thuộc tập hợp nào dưới đây thì nhị thức bậc nhất
11
32
fx
x
luôn âm?
A.
3x
hay
5x
. B.
5x
hay
3x
.
C.
3x
hay
5x
. D.
x
.
Lời giải
Chọn C
Ta có
1 1 1 1
00
3 2 3 2xx
5
0
2. 3
x
x
.
Đặt
tx
, bpt trở thành
5
0
23
t
t
.
Cho
5 0 5tt
.
Cho
3 0 3tt
.
Bảng xét dấu
Căn cứ bảng xét dấu ta được
3x
hay
5x
.

Câu 10: [0D4-4-3] Tìm tất cả các giá trị thực của tham số
m
để đa thức
1f x m x m x
không âm với mọi
; 1 .xm
A.
1m
. B.
1m
. C.
1m
. D.
1m
.
Lời giải
Chọn C
2
1 0 1 1m x m x m x m
.
1
+ Xét
1mx
. (thỏa)
+ Xét
1m
thì
11xm
không thỏa điều kiện nghiệm đã cho.
+ Xét
1m
thì
11xm
thỏa điều kiện nghiệm đã cho.
Vậy
1m
.
Câu 11: [0D4-4-3] Gọi
S
là tập tất cả các giá trị của
x
để đa thức
6 2 3f x mx x m
luôn âm khi
2m
. Hỏi các tập hợp nào sau đây là phần bù của tập
S
?
A.
3;
. B.
3;
. C.
;3
. D.
;3
.
Lời giải
Chọn D
6 2 3 0mx x m
2 6 3m x m
3x
(do
2m
)
Vậy
3;S
;3CS
.
Câu 12: [0D4-4-3] Tìm các giá trị thực của tham số
m
để không tồn tại giá trị nào của
x
sao
cho nhị thức
2f x mx m x
luôn âm.
A.
0m
. B.
2m
. C.
2m
. D.
m
.
Lời giải
Chọn B
0 2 0f x mx m x
20m x m
.
+ Xét
2m
thì
2 0,f x x
hay
0fx
vô nghiệm (thỏa mãn).
+ Xét
2m
thì
0fx
khi
2
m
x
m
(tồn tại nghiệm – loại).
+ Xét
2m
thì
0fx
khi
2
m
x
m
(tồn tại nghiệm – loại).

Vậy chỉ có
2m
thỏa mãn yêu cầu bài toán.
Câu 13: [0D4-4-3] Với
x
thuộc tập hợp nào dưới đây thì
21f x x x
luôn dương?
A.
1
; 1;
3
. B.
1
;1
3
. C. . D. vô
nghiệm.
Lời giải
Chọn A
+ Xét
1
2
x
thì ta có nhị thức
1f x x
để
0fx
thì
1x
.
+ Xét
1
2
x
thì ta có nhị thức
31f x x
để
0fx
thì
1
3
x
.
Vậy để
0fx
thì
1
; 1;
3
x
Câu 14: [0D4-4-3] Tìm số nguyên dương nhỏ nhất
x
để nhị thức bậc nhất
1 4 7f x x x
luôn dương
A.
4x
. B.
5x
. C.
6x
. D.
7x
.
Lời giải
Chọn C
Ta có
1 4 7 0 1 4 7 *x x x x
Bảng xét dấu
Trường hợp
1x
, ta có
* 1 4 7xx
4x
. So với trường hợp
đang xét ta có tập nghiệm
1
,4S
.
Trường hợp
14x
, ta có
* 1 4 7xx
57
(vô lý). Do đó, tập
nghiệm
2
S
.
Trường hợp
4x
, ta có
* 1 4 7xx
5x
. So với trường hợp đang
xét ta có tập nghiệm
3
5,S
.
Vậy
1 2 3
, 4 5,Sx S S
.
Nên
6x
thỏa YCBT.

Câu 15: [0D4-4-3] Với
x
thuộc tập hợp nào dưới đây thì
24f x x x
không dương?
A.
2x
. B.
6x
. C. Vô nghiệm. D.
1,
Lời giải
Chọn D
2 4 0xx
22
22
2 4 2 4 4 4 8 16x x x x x x x x
1x
.
Câu 16: [0D4-4-3] Nghiệm của bất phương trình
2 3 1x
là:
A.
13x
. B.
11 x
. C.
12x
. D.
12 x
.
Lời giải
Chọn C
Cách 1: Tính chất
0f x m m f x m m
2 3 1 1 2 3 1 1 2x x x
.
Cách 2:
2
22
2 3 1 2 3 1 4 12 8 0 3 2 0 1 2x x x x x x x
.
Câu 17: [0D4-4-3] Bất phương trình
21xx
có nghiệm là:
A.
1
; 1;
3
x
. B.
1
;1
3
x
.
C.
x
. D. Vô nghiệm.
Lời giải
Chọn A
Cách 1:
21xx
1
TH1:
0x
,
1
đúng với
0x
TH2:
0x
,
1
1
21
3
21
1
xx
x
xx
x
kết hợp
0x
ta được
1
0; 1;
3
x
Kết hợp
1
; 1;
3
x
.
Cách 2:
2
2
2
0
0
0
0
21
3 4 1 0
21
x
x
x
x
xx
xx
xx
0
0
0
1
1
; 1;
1
3
1
0
1
3
3
x
x
x
x
x
x
x
x
.
Cách 3: Casio
Ta có
2 1 2 1 0x x x x
sau đó sử dụng MTCT:
Nhập +
CALC
+
0=
(Loại. D.), tiếp tục bấm
CALC
+
2
3
( Loại B và C. Chọn A.
Câu 18: [0D4-4-3] Tập nghiệm của bất phương trình
2
2
1
0
3
x
x
là

A.
3; 1 1; 3
. B.
3; 1 1; 3
.
C.
; 3 1;1 3;
. D.
.
Lời giải
Chọn B
ĐK
3x
.
Ta có
2
2
11
1
00
3
33
xx
x
x
xx
.
Lập bảng xét dấu biểu thức
11
33
xx
xx
, ta suy ra tập nghiệm cần tìm là
3; 1 1; 3
.
Câu 19: [0D4-4-3] Cho bất phương trình
1 4 7xx
. Nghiệm nguyên dương nhỏ nhất
của bất phương trình là
A.
9x
. B.
8x
. C.
6x
. D.
3x
.
Lời giải
Chọn C
Cách 1. Giải bpt, ta được tập nghiệm
; 1 5;
. Từ đó, suy ra nghiệm
nguên dương nhỏ nhất là
6x
.
Cách 2. Lần lượt kiểm tra các giá trị của
x
ở mỗi phương án (từ nhỏ đến lớn), ta
được
6x
là một nghiệm.
Câu 20: [0D4-4-3] Bất phương trình
3
21
2
x x x
có tập nghiệm là
A.
2
. B.
1
. C.
9
;
2
. D.
9
0;
2
.
Lời giải
Chọn C
+) Trên
;2
, bpt đã cho trở thành
33
21
22
x x x x
(loại).
+) Trên
2;1
, bpt đã cho trở thành
35
21
22
x x x x
(loại).
+) Trên
1;
, bpt đã cho trở thành
39
21
22
x x x x
(nhận).
Vậy tập nghiệm cần tìm là
9
;
2
.


Câu 1: [0D4-4-4] Tìm
x
để
1 2 1 2 3f x x x x x x
luôn dương
A.
2x
B.
1;
C.
–3;–1 –1; 1 1; 3
D.
–3;–1 –1;1 1;3
Lời giải
Chọn C
1 2 1 2 3 0 1 2 2 1 3 0 *x x x x x x x x x
Chọn
3x
thay vào (*) ta thấy (*) thỏa mãn nên chọn đáp án C
Câu 2: [0D4-4-4] Tập nghiệm của bất phương trình
2
3
1
4
x
x
là
A.
; 4 1;1 4;
. B.
;4
.
C.
1;1
. D.
4;
.
Lời giải
Chọn A
2
2 2 2
2
2
22
2
14
3 3 3 4
0
1 1 0 0
22
3
4 4 4
1
4 3 3
14
34
1 1 0
0
0
44
4
22
xx
x x x x
xx
x
x x x
x x x
xx
xx
xx
x
xx
; 2 1;2 4;
; 4 1;1 4;
4 2;1 2;
x
x
x

Câu 1: [0D4-5-1] Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình
21xy
?
A.
2;1
. B.
3; 7
. C.
0;1
. D.
0;0
.
Lời giải
Chọn C
Nhận xét: chỉ có cặp số
0;1
không thỏa bất phương trình.
Câu 2: [0D4-5-1] Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình
4 5 0xy
?
A.
5;0
. B.
2;1
. C.
1; 3
. D.
0;0
.
Lời giải
Chọn B
Ta thay cặp số
2;1
vào bất phương trình
4 5 0xy
được
2 4 5 0
(sai)
đo dó cặp số
2;1
không là nghiệm của bất phương trình
4 5 0xy
.
Câu 3: [0D4-5-1] Cặp số
1; –1
là nghiệm của bất phương trình nào sau đây?
A.
– 3 0xy
. B.
– – 0xy
. C.
3 1 0xy
. D.
– – 3 –1 0xy
.
Lời giải
Chọn C
, 3 1f x y x y
. Thay
1, 1 1 3 1 1 0f
.
Câu 4: [0D4-5-1] Cặp số
2;3
là nghiệm của bất phương trình nào sau đây?
A.
2 – 3 –1 0xy
. B.
–0xy
. C.
43xy
. D.
– 3 7 0xy
.
Lời giải
Chọn B
,f x y x y
. Thay
2,3 2 3 1 0f
.
.
Câu 5: [0D4-5-1] Cặp số nào sau đây là nghiệm của bất phương trình
–2 – 3x y y
?
A.
4; –4
. B.
2;1
. C.
–1; –2
. D.
4;4
.
Lời giải
Chọn D
–2 – 3 2 3 3x y y x y
.
Thay giá trị từng cặp điểm vào, ta chọn đáp án. D.

Câu 6: [0D4-5-1] Bất phương trình
3 – 2 – 1 0x y x
tương đương với bất phương trình
nào sau đây?
A.
– 2 – 2 0xy
. B.
5 – 2 – 2 0xy
. C.
5 – 2 –1 0xy
. D.
4 – 2 – 2 0xy
.
Lời giải
Chọn B
3 – 2 – 1 0 3 2 2 2 0 5 2 2 0x y x x y x x y
.
Câu 7: [0D4-5-1] Cặp số nào sau đây không là nghiệm của bất phương trình
5 2 1 0xy
?
A.
0;1
. B.
1;3
. C.
–1;1
. D.
–1;0
.
Lời giải
Chọn B
Ta thế từng cặp
;xy
từ đáp án vào, nhận thấy đáp án B không thoả vì
5.1 2 3 1 1 0
.
Câu 8: [0D4-5-1] Điểm
0;0O
thuộc miền nghiệm của bất phương trình nào sau đây?
A.
3 2 0xy
. B.
20xy
. C.
2 5 2 0xy
. D.
2 2 0xy
.
Lời giải
Chọn D
Thay toạ độ điểm
0;0O
vào từng đáp án. Nhận thấy chỉ có mỗi đáp án D là thoả
20
.
Câu 9: [0D4-5-1] Điểm
0;0O
thuộc miền nghiệm của hệ bất phương trình nào sau đây?
A.
3 6 0
2 4 0
xy
xy
. B.
3 6 0
2 4 0
xy
xy
. C.
3 6 0
2 4 0
xy
xy
. D.
3 6 0
2 4 0
xy
xy
.
Lời giải
Chọn C
Thay điểm
0;0O
vào từng đáp án.
Đáp án
, AB
sai vì
0 3.0 6 0
.
Đáp án
D
sai vì
2.0 0 4 0
.
Nên ta chọn đáp án
C
.

Câu 10: [0D4-5-1] Trong các điểm sau đây, điểm nào thuộc miền nghiệm của hệ bất phương
trình
3 2 0
2 1 0
xy
xy
A.
0;1
. B.
–1;1
. C.
1;3
. D.
–1;0
.
Lời giải
Chọn B
Thay toạ độ
;xy
từ đáp án vào hệ bất phương trình. Ta dễ dàng tìm được đáp án
là. B.
Bài 5: Dấu tam thức bậc hai. Bất phương trình bậc hai.
Câu 11: [0D4-5-1] Cho bất phương trình
2 2 2 2 1x y x
. Khẳng định nào dưới
đây là khẳng định sai?
A. Điểm
0;0O
thuộc miền nghiệm của bất phương trình đã cho.
B. Điểm
1;1B
thuộc miền nghiệm của bất phương trình đã cho.
C. Điểm
4;2C
thuộc miền nghiệm của bất phương trình đã cho.
D. Điểm
1; 1D
thuộc miền nghiệm của bất phương trình đã cho.
Lời giải
Chọn C
Lần lượt thay toạ độ điểm ở mỗi phương án vào bất phương trình đã cho, ta thấy
00
; 4;2xy
không là nghiệm của bất phương trình đã cho.
Câu 12: [0D4-5-1] Cho bất phương trình
3 1 4 2 5 3x y x
. Khẳng định nào dưới
đây là khẳng định đúng?
A. Điểm
0;0O
thuộc miền nghiệm của bất phương trình đã cho.
B. Điểm
2;2B
thuộc miền nghiệm của bất phương trình đã cho.
C. Điểm
4;2C
thuộc miền nghiệm của bất phương trình đã cho.
D. Điểm
5;3D
thuộc miền nghiệm của bất phương trình đã cho.
Lời giải
Chọn A
Lần lượt thay toạ độ điểm ở mỗi phương án vào bất phương trình đã cho, ta thấy
00
; 0;0xy
là nghiệm của bất phương trình đã cho.
Câu 13: [0D4-5-1] Cho bất phương trình
3 2 2 5 2 1x y x
. Khẳng định nào dưới
đây là khẳng định sai?

A. Điểm
3; 4A
thuộc miền nghiệm của bất phương trình đã cho.
B. Điểm
2; 5B
thuộc miền nghiệm của bất phương trình đã cho.
C. Điểm
1; 6C
thuộc miền nghiệm của bất phương trình đã cho.
D. Điểm
0;0O
thuộc miền nghiệm của bất phương trình đã cho.
Lời giải
Chọn D
Lần lượt thay toạ độ điểm ở mỗi phương án vào bất phương trình đã cho, ta thấy
00
; 0;0xy
không là nghiệm của bất phương trình đã cho.
Câu 14: [0D4-5-1] Cho bất phương trình
4 1 5 3 2 9x y x
. Khẳng định nào dưới
đây là khẳng định đúng?
A. Điểm
0;0O
thuộc miền nghiệm của bất phương trình đã cho.
B. Điểm
1;1B
thuộc miền nghiệm của bất phương trình đã cho.
C. Điểm
1;1C
thuộc miền nghiệm của bất phương trình đã cho.
D. Điểm
2;5D
thuộc miền nghiệm của bất phương trình đã cho.
Lời giải
Chọn D
Lần lượt thay toạ độ điểm ở mỗi phương án vào bất phương trình đã cho, ta thấy
00
; 2;5xy
là nghiệm của bất phương trình đã cho.
Câu 15: [0D4-5-1] Cho hệ bất phương trình
0
4
2
3
)1(2
01
32
x
y
x
yx
.
Hỏi khẳng định nào dưới đây là khẳng định đúng?
A. Điểm
2;1A
thuộc miền nghiệm của hệ bất phương trình đã cho.
B. Điểm
0;0O
thuộc miền nghiệm của hệ bất phương trình đã cho.
C. Điểm
1;1C
thuộc miền nghiệm của hệ bất phương trình đã cho.
D. Điểm
3;4D
thuộc miền nghiệm của hệ bất phương trình đã cho.
Lời giải
Chọn A
Lần lượt thay toạ độ điểm ở mỗi phương án vào hệ bất phương trình đã cho, ta thấy
00
; 2;1xy
là nghiệm của hệ bất phương trình đã cho.
Câu 16: [0D4-5-1] Cho hệ bất phương trình

045
0132
yx
yx
.
Hỏi khẳng định nào dưới đây là khẳng định sai?
A. Điểm
1;4A
thuộc miền nghiệm của hệ bất phương trình đã cho.
B. Điểm
0;0O
thuộc miền nghiệm của hệ bất phương trình đã cho.
C. Điểm
2;4C
thuộc miền nghiệm của hệ bất phương trình đã cho.
D. Điểm
3;4D
thuộc miền nghiệm của hệ bất phương trình đã cho.
Lời giải
Chọn B
Lần lượt thay toạ độ điểm ở mỗi phương án vào hệ bất phương trình đã cho, ta thấy
00
; 0;0xy
không là nghiệm của hệ bất phương trình đã cho.
Câu 17: [0D4-5-1] Cho hệ bất phương trình
01
052
0152
yx
yx
yx
.
Hỏi khẳng định nào dưới đây là khẳng định đúng?
A. Điểm
0;0O
thuộc miền nghiệm của hệ bất phương trình đã cho.
B. Điểm
1;0B
thuộc miền nghiệm của hệ bất phương trình đã cho.
C. Điểm
0; 2C
thuộc miền nghiệm của hệ bất phương trình đã cho.
D. Điểm
0;2D
thuộc miền nghiệm của hệ bất phương trình đã cho.
Lời giải
Chọn C
Lần lượt thay toạ độ điểm ở mỗi phương án vào hệ bất phương trình đã cho, ta thấy
00
; 0; 2xy
là nghiệm của hệ bất phương trình đã cho.
Câu 18: [0D4-5-1] Cho hệ bất phương trình
05
033
0
yx
yx
yx
.
Hỏi khẳng định nào dưới đây là khẳng định đúng?
A. Điểm
0;0O
thuộc miền nghiệm của hệ bất phương trình đã cho.
B. Điểm
5;3B
thuộc miền nghiệm của hệ bất phương trình đã cho.
C. Điểm
1; 1C
thuộc miền nghiệm của hệ bất phương trình đã cho.
D. Điểm
2;2D
thuộc miền nghiệm của hệ bất phương trình đã cho.
Lời giải

Chọn B
Lần lượt thay toạ độ điểm ở mỗi phương án vào hệ bất phương trình đã cho, ta thấy
00
; 5;3xy
là nghiệm của hệ.
Câu 19: [0D4-5-1] Miền nghiệm của hệ bất phương trình
6
82
3
93
y
xy
yx
yx
là phần mặt phẳng
chứa điểm nào sau đây?
A.
0;0
. B.
1;2
. C.
2;1
. D.
8;4
.
Lời giải
Chọn D
Ta dùng máy tính lần lượt kiểm tra các đáp án để xem đáp án nào thỏa hệ bất
phương trình trên.
Câu 20: [0D4-5-1] Miền nghiệm của bất phương trình
3 2 3 4 1 3x y x y
là
phần mặt phẳng chứa điểm
A.
3;0
. B.
3;1
. C.
2;1
. D.
0;0
.
Lời giải
Chọn C
Ta có
3 2 3 4 1 3 3 1 0x y x y x y
.
Ta dùng máy tính lần lượt kiểm tra các đáp án để xem đáp án nào thỏa bất phương
trình trên.
Câu 21: [0D4-5-1] Miền nghiệm của bất phương trình
5 2 9 2 2 7x x y
không chứa
điểm nào trong các điểm sau?
A.
0;0
. B.
2; 1
. C.
2;1
. D.
2;3
.
Lời giải
Chọn D
Ta có
5 2 9 2 2 7 3 2 6 0x x y x y
.
Ta dùng máy tính lần lượt kiểm tra các đáp án để xem đáp án nào không thỏa bất
phương trình trên.

Câu 22: [0D4-5-1] Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình
21xy
?
A.
0;0
. B.
3; 7
. C.
2;1
. D.
0;1
.
Lời giải
Chọn D
Ta dùng máy tính lần lượt kiểm tra các đáp án để xem đáp án nào không thỏa bất
phương trình trên.
Câu 23: [0D4-5-1] Cặp số nào sau đây không là nghiệm của bất phương trình
4 5 0xy
?
A.
5;0
. B.
2;1
. C.
0;0
. D.
1; 3
.
Lời giải
Chọn B
Ta dùng máy tính lần lượt kiểm tra các đáp án để xem đáp án nào không thỏa bất
phương trình trên.
Câu 24: [0D4-5-1] Trong các cặp số sau, tìm cặp số không là nghiệm của hệ bất phương
trình
0232
02
yx
yx
A.
0;0
. B.
1;1
. C.
1;1
. D.
1; 1
.
Lời giải
Chọn C
Ta dùng máy tính lần lượt kiểm tra các đáp án để xem đáp án nào không thỏa hệ
bất phương trình trên với mọi x.
§ 6. DẤU CỦA TAM THỨC BẬC HAI.

Câu 1: [0D4-5-2] Giá trị nhỏ nhất của biết thức
F y x
trên miền xác định bởi hệ:
22
24
5
yx
yx
xy
là:
A.
min 1 2, 3F khi x y
. B.
min 2 0, 2F khi x y
.
C.
min 3 1, 4F khi x y
. D. Không tồn tại giá trị nhỏ nhất
của
F
.
Lời giải
Chọn A
Ta tìm giao điểm của các cặp đường thẳng trong miền xác định của hệ
22
24
5
yx
yx
xy
22
24
xy
xy
0
2
x
y
0;2A
.
22
5
xy
xy
3
2
7
2
x
y
37
;
22
B
.
5
24
xy
xy
2
3
x
y
2;3C
.
Ta tính giá trị của
F y x
tại các giao điểm:
Tại
0;2A
2 0 2F
.
Tại
37
;
22
B
73
2
22
F
.
Tại
2;3C
3 2 1F
.
Vậy
min 1 2, 3F khi x y
.

Câu 2: [0D4-5-2] Mệnh đề nào sau đây sai?
Miền nghiệm của bất phương trình
2 2 2 2 1x y x
là nửa mặt phẳng
chứa điểm
A.
0;0
. B.
1;1
. C.
4;2
. D.
1; 1
.
Lời giải
Chọn C
Ta có:
2 2 2 2 1x y x
2 2 4 2 2x y x
24xy
.
Dễ thấy tại điểm
4;2
ta có:
4 2.2 8 4
.
Câu 3: [0D4-5-2] Mệnh đề nào sau đây đúng?
Miền nghiệm của bất phương trình
3 1 4 2 5 3x y x
là nửa mặt phẳng
chứa điểm
A.
0;0
. B.
4;2
. C.
2;2
. D.
5;3
.
Lời giải
Chọn A
Ta có:
3 1 4 2 5 3x y x
3 3 4 8 5 3x y x
2 4 8 0xy
2 4 0xy
Dễ thấy tại điểm
0;0
ta có:
0 2.0 4 4 0
.
Câu 4: [0D4-5-2] Mệnh đề nào sau đây sai?.
Miền nghiệm của bất phương trình
3 2 2 5 2 1x y x
là nửa mặt phẳng
chứa điểm
A.
3; 4
. B.
2; 5
. C.
1; 6
. D.
0;0
.
Lời giải
Chọn D
Ta có:
3 2 2 5 2 1x y x
3 4 10 2 2x y x
3 4 11 0xy
.(rút gọn sai số)
Dễ thấy tại điểm
0;0
ta có:
3.0 4.0 8 0
(mâu thuẩn).
Câu 5: [0D4-5-2] Mệnh đề nào sau đây đúng?
Miền nghiệm của bất phương trình
4 1 5 3 2 9x y x
là nửa mặt phẳng
chứa điểm
A.
0;0
. B.
1;1
. C.
1;1
. D.
2;5
.
Lời giải
Chọn D
Ta có:
4 1 5 3 2 9x y x
4 4 5 15 2 9x y x
2 5 10 0xy
.
Dễ thấy tại điểm
2;5
ta có:
2.2 5.5 10 0
(đúng).

Câu 6: [0D4-5-2] Mệnh đề nào sau đây đúng?.
Miền nghiệm của hệ bất phương trình
10
23
3
2( 1) 4
2
0
xy
y
x
x
là phần mặt phẳng chứa
điểm
A.
2;1
. B.
0;0
. C.
1;1
. D.
3;4
.
Lời giải
Chọn A
Nhận xét: chỉ có điểm
2;1
thỏa mãn hệ.
Câu 7: [0D4-5-2] Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình
2 3 1 0
5 4 0
xy
xy
?
A.
1;4
. B.
2;4
. C.
0;0
. D.
3;4
.
Lời giải
Chọn C
Nhận xét : chỉ có điểm
0;0
không thỏa mãn hệ.
Câu 8: [0D4-5-2] Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình
2 5 1 0
2 5 0
10
xy
xy
xy
?
A.
0;0
. B.
1;0
. C.
0; 2
. D.
0;2
.
Lời giải
Chọn C
Nhận xét: chỉ có điểm
0; 2
thỏa mãn hệ.
Câu 9: [0D4-5-2] Miền nghiệm của hệ bất phương trình
0
3 3 0
50
xy
xy
xy
là phần mặt phẳng
chứa điểm
A.
5;3
. B.
0;0
. C.
1; 1
. D.
2;2
.
Lời giải
Chọn A
Nhận xét: chỉ có điểm
5;3
thỏa mãn hệ.
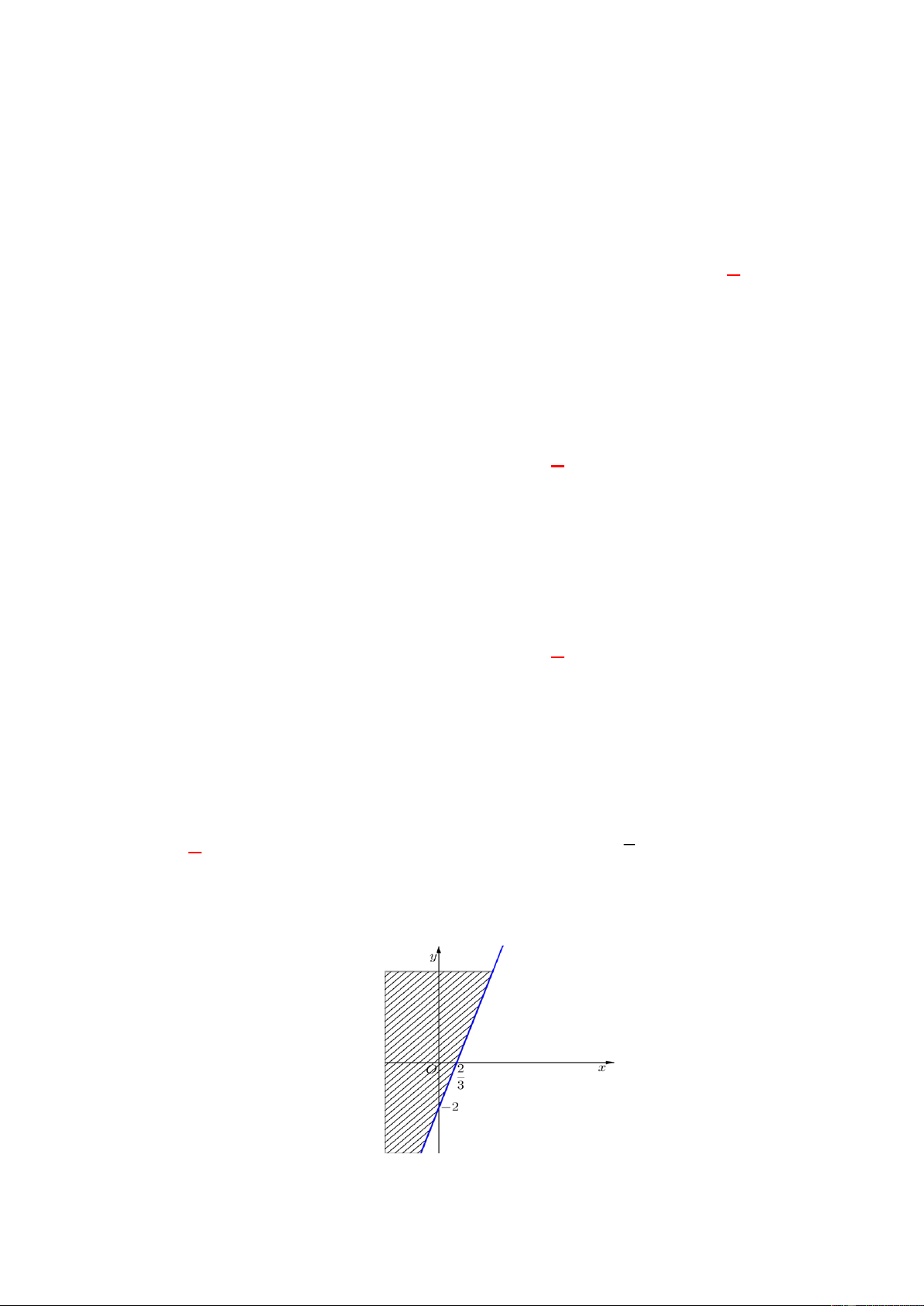
Câu 10: [0D4-5-2] Miền nghiệm của hệ bất phương trình
39
3
28
6
xy
xy
yx
y
là phần mặt phẳng chứa
điểm
A.
0;0
. B.
1;2
. C.
2;1
. D.
8;4
.
Lời giải
Chọn D
Nhận xét: chỉ có cặp số
8;4
thỏa bất phương trình
39xy
.
Câu 11: [0D4-5-2] Miền nghiệm của bất phương trình
3 2 3 4 1 3x y x y
là phần
mặt phẳng chứa điểm nào?
A.
3;0
. B.
3;1
. C.
1;1
. D.
0;0
.
Lời giải
Chọn C
Nhận xét: chỉ có cặp số
1;1
thỏa bất phương trình.
Câu 12: [0D4-5-2] Miền nghiệm của bất phương trình
5 2 9 2 2 7 x x y
là phần mặt
phẳng không chứa điểm nào?
A.
2;1
. B.
2;3
. C.
2; 1
. D.
0;0
.
Lời giải
Chọn C
Nhận xét: chỉ có cặp số
2; 1
không thỏa bất phương trình. (Đánh nhầm)
Câu 13: [0D4-5-2] Miền nghiệm của bất phương trình
3 2 0xy
không chứa điểm nào
sau đây?
A.
1 ; 2A
. B.
2 ; 1B
. C.
1
1;
2
C
. D.
3 ; 1D
.
Lời giải
Chọn A
Trước hết, ta vẽ đường thẳng
: 3 2 0.d x y
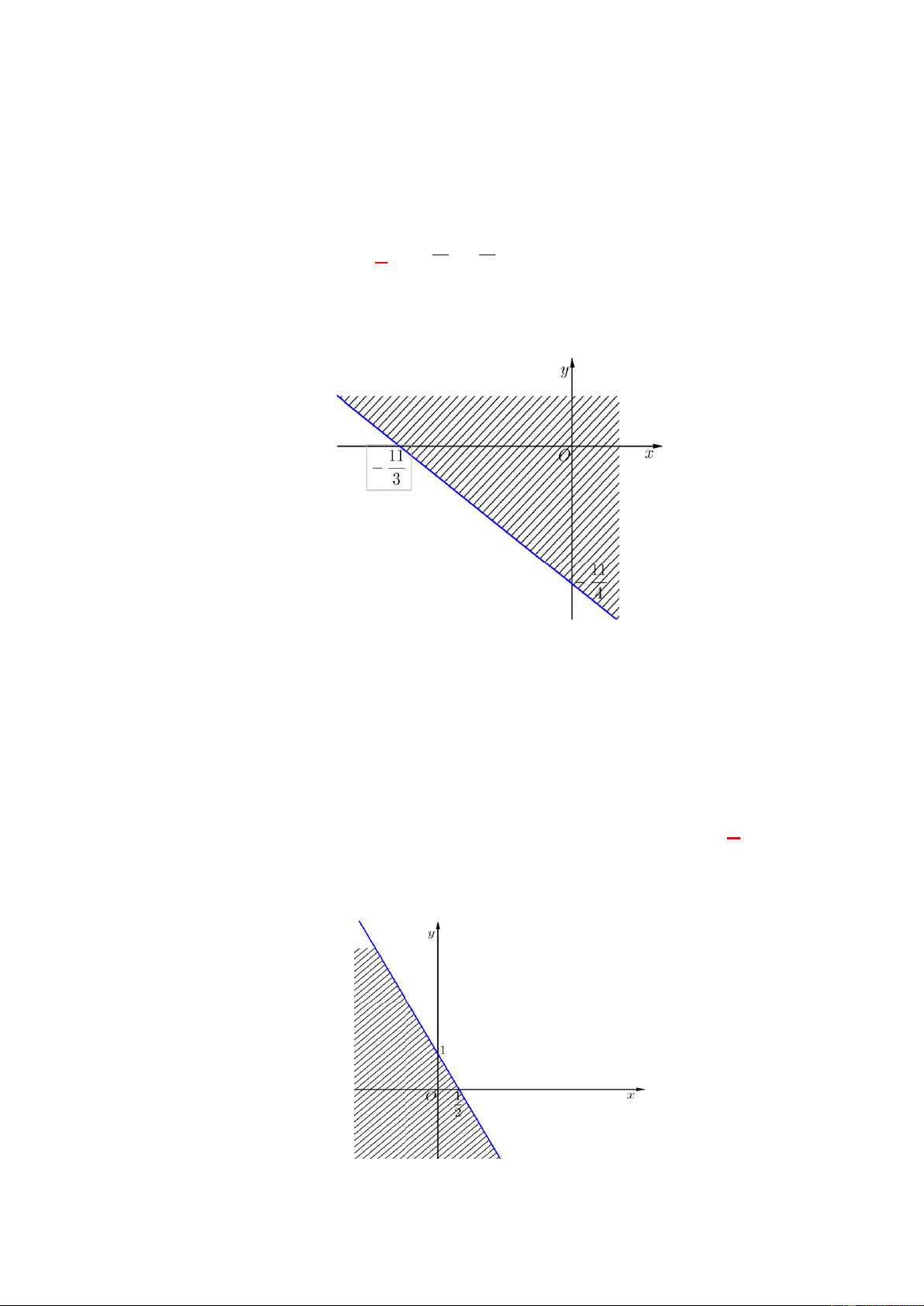
Ta thấy
0 ; 0
không là nghiệm của bất phương trình.
Vậy miền nghiệm là nửa mặt phẳng bờ
d
không chứa điểm
0 ; 0 .
Câu 14: [0D4-5-2] Miền nghiệm của bất phương trình
3 2(2 5) 2(1 )x y x
không chứa
điểm nào sau đây?
A.
1 ; 2A
. B.
12
;
11 11
B
. C.
0 ; 3C
. D.
4 ; 0D
.
Lời giải
Chọn B
Đầu tiên, thu gọn bất phương trình đề bài đã cho về thành
3 4 11 0.xy
Ta vẽ đường thẳng
:3 4 11 0.d x y
Ta thấy
0 ; 0
không là nghiệm của bất phương trình.
Vậy miền nghiệm là nửa mặt phẳng (không kể bờ
d
) không chứa điểm
0 ; 0 .
Câu 15: [0D4-5-2] Miền nghiệm của bất phương trình
21xy
không chứa điểm nào sau
đây?
A.
1 ; 1 .A
B.
2 ; 2B
. C.
3 ; 3C
. D.
1 ; 1D
.
Lời giải
Chọn D
Trước hết, ta vẽ đường thẳng
:2 1.d x y
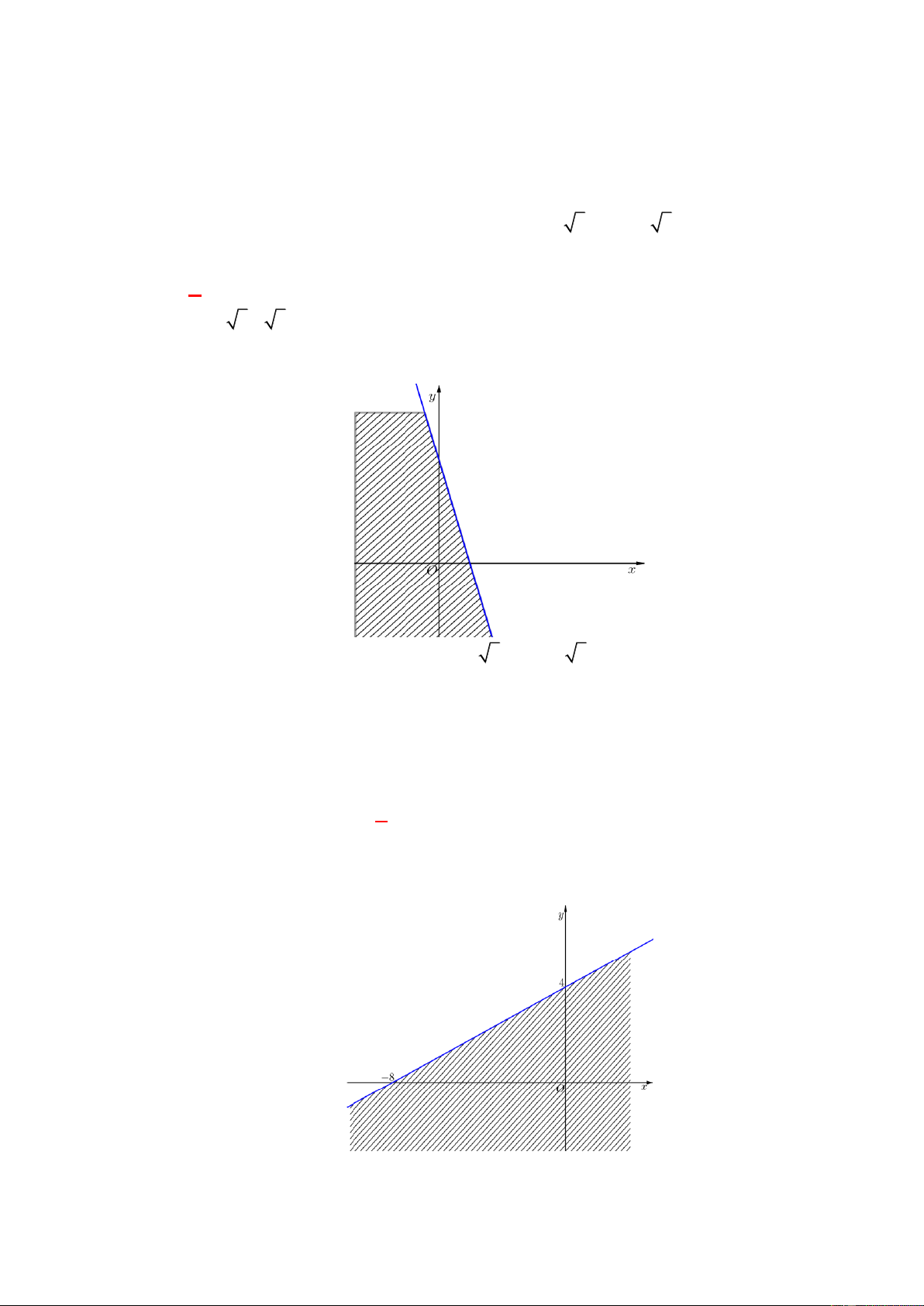
Ta thấy
0 ; 0
không là nghiệm của bất phương trình đã cho.
Vậy miền nghiệm của bất phương trình là nửa mặt phẳng (không kể bờ
d
)
không chứa điểm
0 ; 0 .
Câu 16: [0D4-5-2] Miền nghiệm của bất phương trình
1 3 1 3 2xy
chứa điểm
nào sau đây?
A.
1 ; 1A
. B.
1 ; 1B
. C.
1 ; 1C
. D.
3 ; 3D
.
Lời giải
Chọn A
Trước hết, ta vẽ đường thẳng
: 1 3 1 3 2.d x y
Ta thấy
0 ; 0
không là nghiệm của bất phương trình đã cho.
Vậy miền nghiệm là nửa mặt phẳng bờ
d
không chứa điểm
0 ; 0 .
Câu 17: [0D4-5-2] Miền nghiệm của bất phương trình
2 2 1 2 4x y x
chứa điểm nào
sau đây?
A.
1 ; 1 .A
B.
1 ; 5 .B
C.
4 ; 3 .C
D.
0 ; 4 .D
Lời giải
Chọn B
Đầu tiên ta thu gọn bất phương trình đã cho về thành
2 8 0.xy
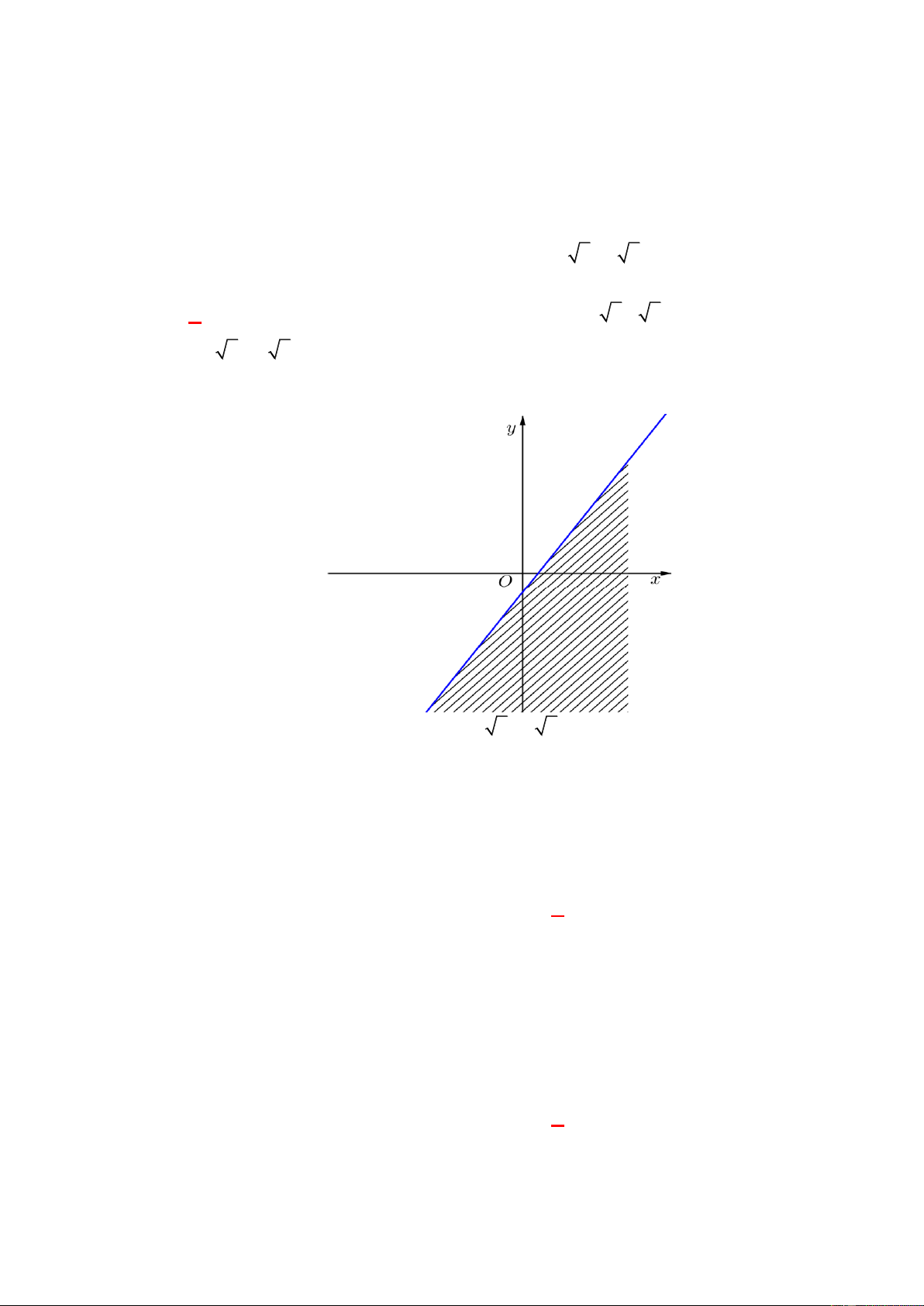
Vẽ đường thẳng
: 2 8 0.d x y
Ta thấy
0 ; 0
không là nghiệm của bất phương trình đã cho.
Vậy miền nghiệm cần tìm là nửa mặt phẳng (không kể bờ
d
) không chứa điểm
0 ; 0 .
Câu 18: [0D4-5-2] Miền nghiệm của bất phương trình
2 2 2 2 0xy
chứa điểm nào
sau đây?
A.
1 ; 1 .A
B.
1 ; 0B
. C.
2 ; 2C
. D.
2 ; 2 .D
Lời giải
Chọn A
Trước hết, ta vẽ đường thẳng
:2 2 2 2 0.d x y
Ta thấy
0 ; 0
là nghiệm của bất phương trình đã cho.
Vậy miền nghiệm cần tìm là nửa mặt phẳng bờ
d
chứa điểm
0 ; 0 .
Câu 19: [0D4-5-2] Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình
20
2 3 2 0
xy
xy
là
A.
0;0
. B.
1;1
. C.
1;1
. D.
1; 1
.
Lời giải
Chọn C
Ta thay cặp số
1;1
vào hệ ta thấy không thỏa mãn.
Câu 20: [0D4-5-2] Cho bất phương trình
2 4 5xy
có tập nghiệm là
S
. Khẳng định nào sau
đây là khẳng định đúng ?
A.
1;1 S
. B.
1;10 S
. C.
1; 1 S
. D.
1;5 S
.
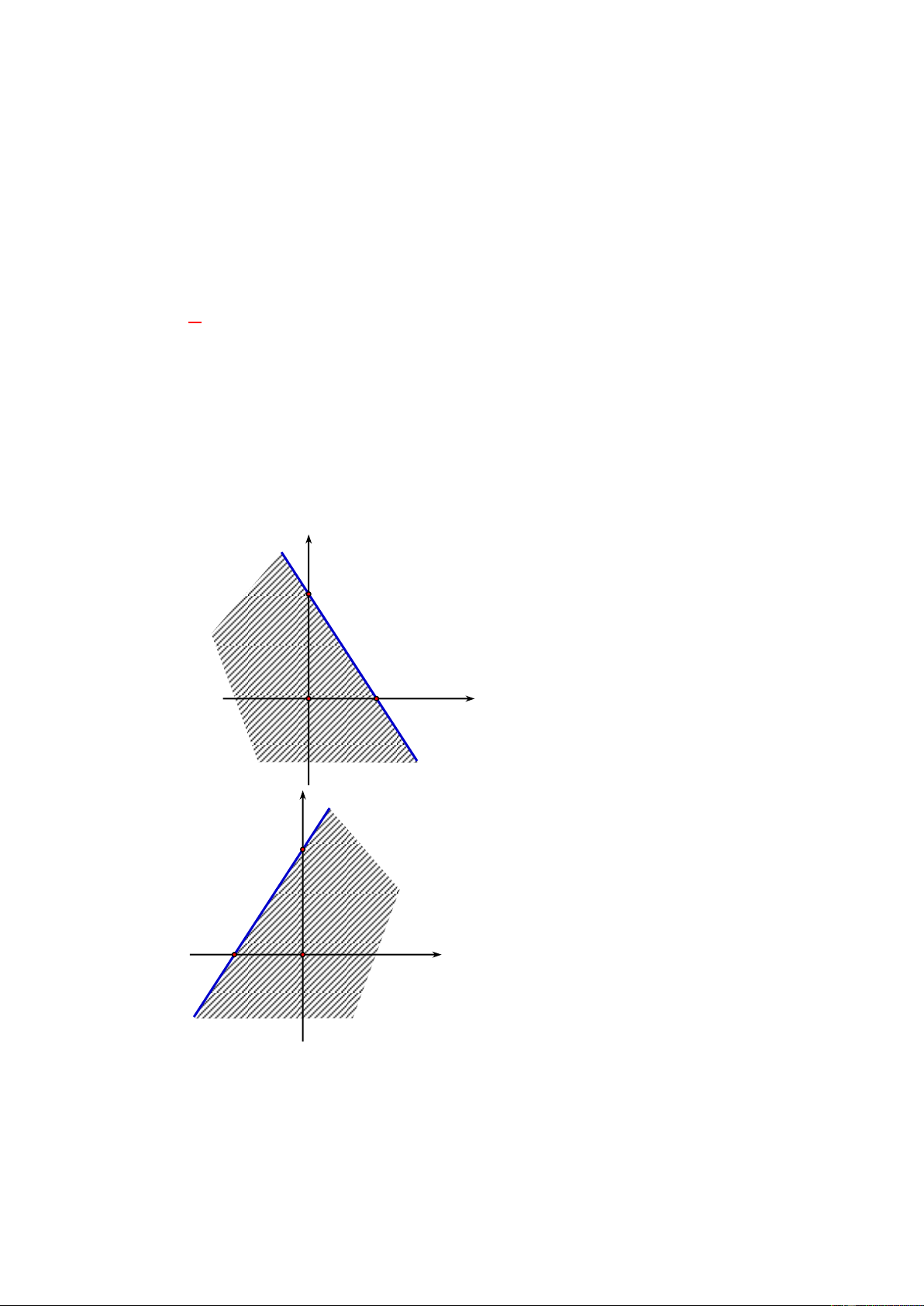
Lời giải
Chọn C
Ta thấy
1; 1
thỏa mãn hệ phương trình do đó
1; 1
là một cặp nghiệm của hệ
phương trình.
Câu 21: [0D4-5-2] Cho bất phương trình
2 5 0xy
có tập nghiệm là
S
. Mệnh đề nào sau
đây là đúng?
A.
2;2 S
. B.
1;3 S
. C.
2;2 S
. D.
2;4 S
.
Lời giải
Chọn A
Ta thấy
2;2 S
vì
2 2.2 5 0
.
Câu 22: [0D4-5-2] Miền nghiệm của bất phương trình
3 2 6xy
là
A.
B.
O
x
y
2
3
O
2
3
y
x
C.
D.
Lời giải
Chọn C
Trước hết, ta vẽ đường thẳng
:3 2 6.d x y
Ta thấy
0 ; 0
là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm
là nửa mặt phẳng bờ
d
chứa điểm
0 ; 0 .
Câu 23: [0D4-5-2] Miền nghiệm của bất phương trình
3 2 6xy
là
O
x
y
2
3
O
x
2
3
y
O
x
y
2
3
A.
B.
O
x
y
2
3
O
2
3
y
x
C.
D.
Lời giải
Chọn A
Trước hết, ta vẽ đường thẳng
:3 2 6.d x y
Ta thấy
0 ; 0
không phải là nghiệm của bất phương trình đã cho. Vậy miền nghiệm
cần tìm là nửa mặt phẳng (không kể bờ
d
) không chứa điểm
0 ; 0 .
Câu 24: [0D4-5-2] Miền nghiệm của bất phương trình
3 2 6xy
là
O
2
3
y
x
O
x
2
3
y
O
x
y
2
3
A.
B.
O
x
y
2
3
O
2
3
y
x
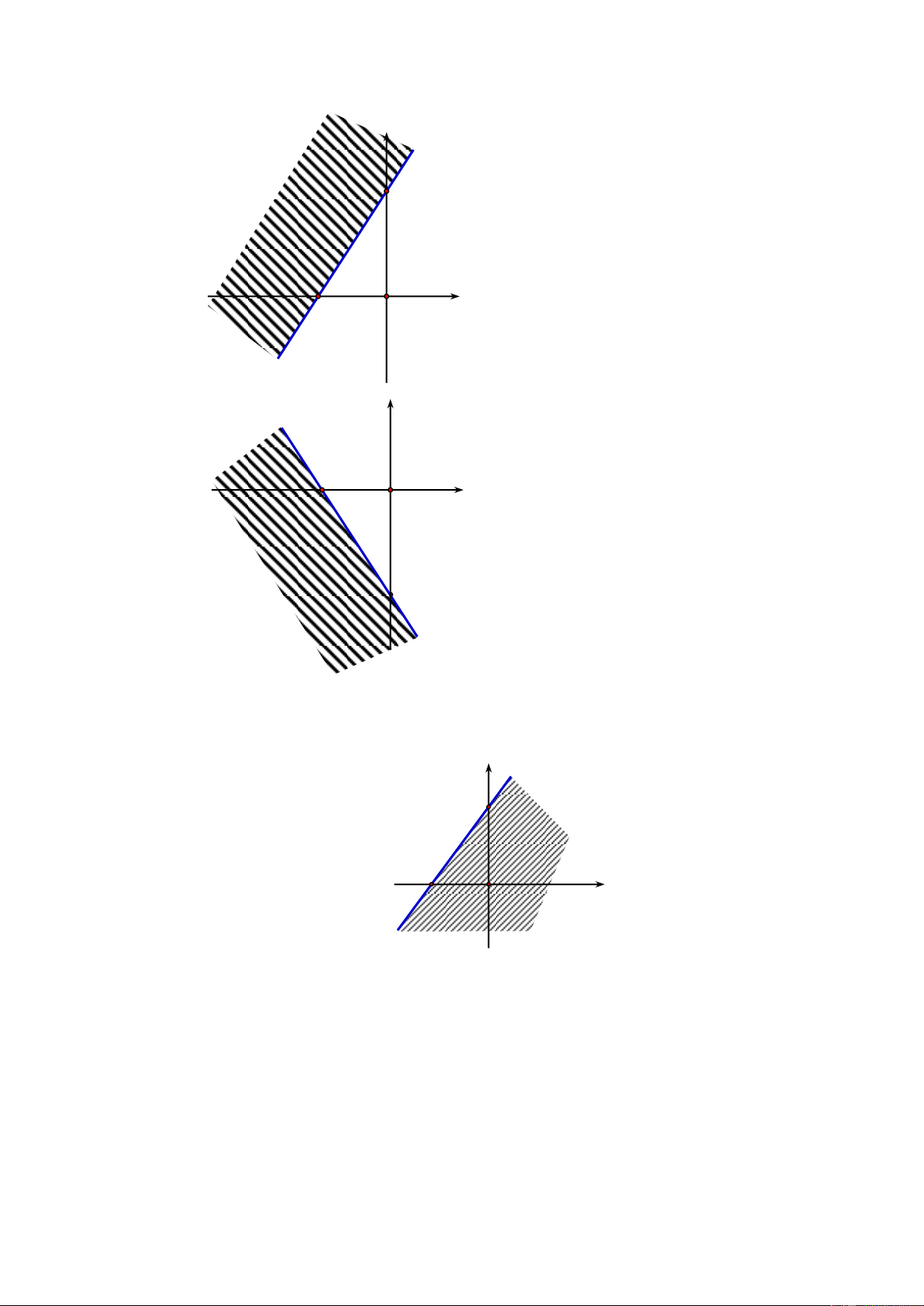
C.
D.
Lời giải
Chọn B
Trước hết, ta vẽ đường thẳng
:3 2 6.d x y
Ta thấy
0 ; 0
không phải là nghiệm của bất phương trình đã cho. Vậy miền nghiệm
cần tìm là nửa mặt phẳng (không kể bờ
d
) không chứa điểm
0 ; 0 .
Câu 25: [0D4-5-2] Miền nghiệm của bất phương trình
3 2 6xy
là
O
x
y
2
3
O
x
2
3
y
O
x
y
2
3
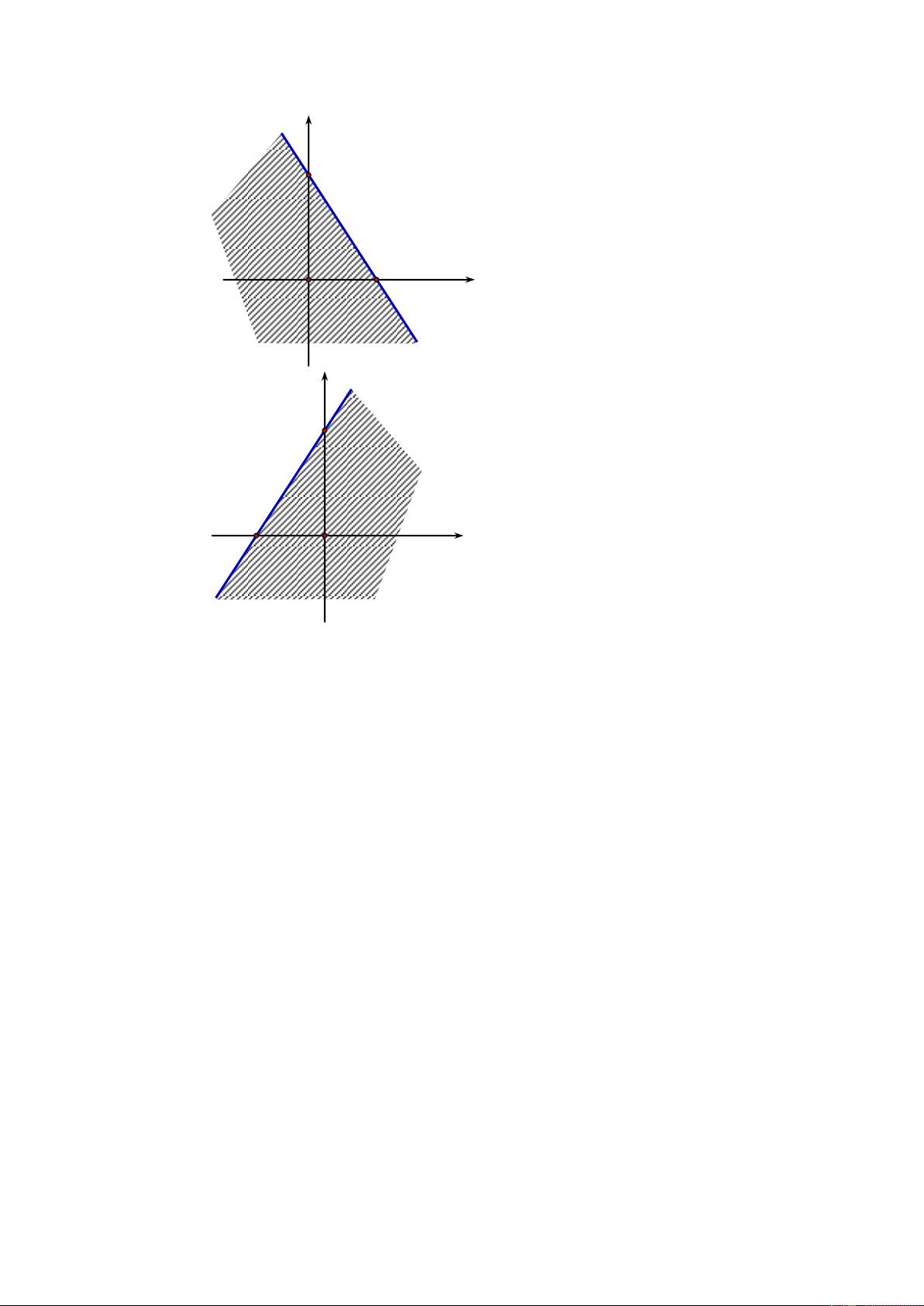
A.
B.
O
x
y
2
3
O
2
3
y
x
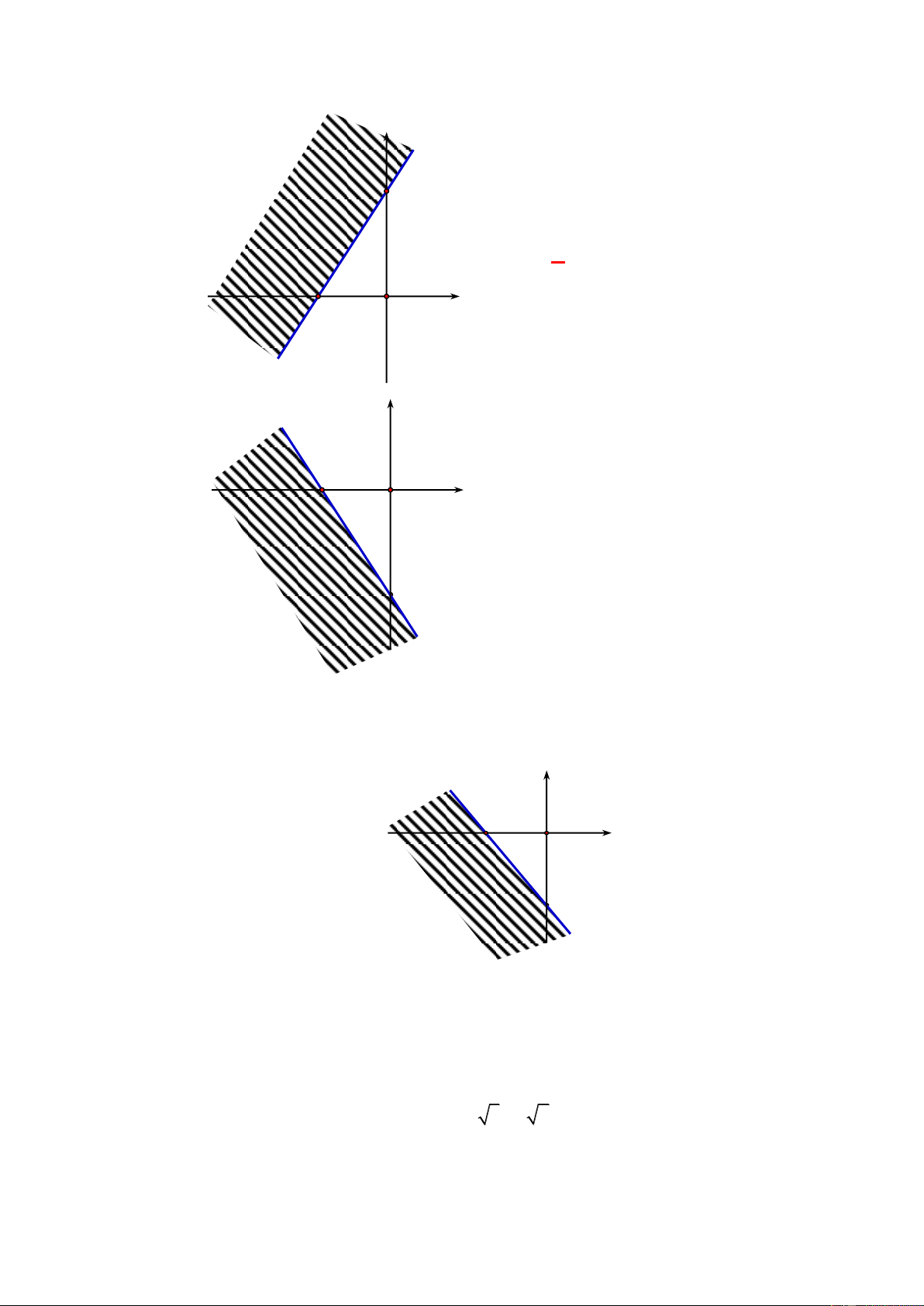
C.
D.
Lời giải
Chọn D
Trước hết, ta vẽ đường thẳng
:3 2 6.d x y
Ta thấy
0 ; 0
là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là
nửa mặt phẳng (không kể bờ
d
) chứa điểm
0 ; 0 .
Câu 26: [0D4-5-2] Cho bất phương trình
2 3 2 0xy
có tập nghiệm là
S
. Mệnh đề
nào sau đây là đúng?
O
x
2
3
y
O
x
2
3
y
O
x
y
2
3

A.
1;1 S
. B.
2
;0
2
S
. C.
1; 2 S
. D.
1;0 S
.
Lời giải
Chọn B
Ta thấy
2
;0
2
S
vì
2
2. 3.0 2 0
2
.
Câu 27: [0D4-5-2] Cho hệ bất phương trình
0
2 5 0
xy
xy
có tập nghiệm là
S
. Mệnh đề nào
sau đây là đúng?
A.
1;1 S
. B.
1; 1 S
. C.
1
1;
2
S
. D.
12
;
25
S
.
Lời giải
Chọn C
Ta thấy
1
1;
2
S
vì
1
10
2
1
2.1 5. 0
2
.
Câu 28: [0D4-5-2] Cho hệ bất phương trình
0
3 1 0
x
xy
có tập nghiệm là
S
. Mệnh đề
nào sau đây là đúng?
A.
1; 1 S
. B.
1; 3 S
. C.
1; 5 S
. D.
4; 3 S
.
Lời giải
Chọn C
Ta thấy
1; 5 S
vì
10
.
Câu 29: [0D4-5-2] Cho hệ bất phương trình
0
3 1 0
x
xy
có tập nghiệm là
S
. Mệnh đề
nào sau đây là đúng?

A.
1;2 S
. B.
2;0 S
. C.
1; 3 S
. D.
3;0 S
.
Lời giải
Chọn D
Ta thấy
3;0 S
vì
30
3 3.0 1 0
.
Câu 30: [0D4-5-2] Cho hệ bất phương trình
3
1
10
2
xy
xy
có tập nghiệm
S
. Mệnh đề nào
sau đây là đúng ?
A.
1; 2 S
. B.
2;1 S
. C.
5; 6 S
. D.
7;3 S
.
Lời giải
Chọn D
Câu 31: [0D4-5-2] Cho hệ bất phương trình
3
2 1 1
2
4 3 2 2
xy
xy
có tập nghiệm
S
. Mệnh đề
nào sau đây là đúng ?
A.
1
;1
4
S
.
B.
; | 4 3 2S x y x y
.
C.Biểu diễn hình học của
S
là nửa mặt phẳng chứa gốc tọa độ và kể cả bờ
d
, với
d
là là đường thẳng
4 3 2xy
.
D.Biểu diễn hình học của
S
là nửa mặt phẳng không chứa gốc tọa độ và kể cả bờ
d
, với
d
là là đường thẳng
4 3 2xy
.
Lời giải
Chọn B
Trước hết, ta vẽ hai đường thẳng:
1
3
:2 1
2
d x y
2
:4 3 2d x y
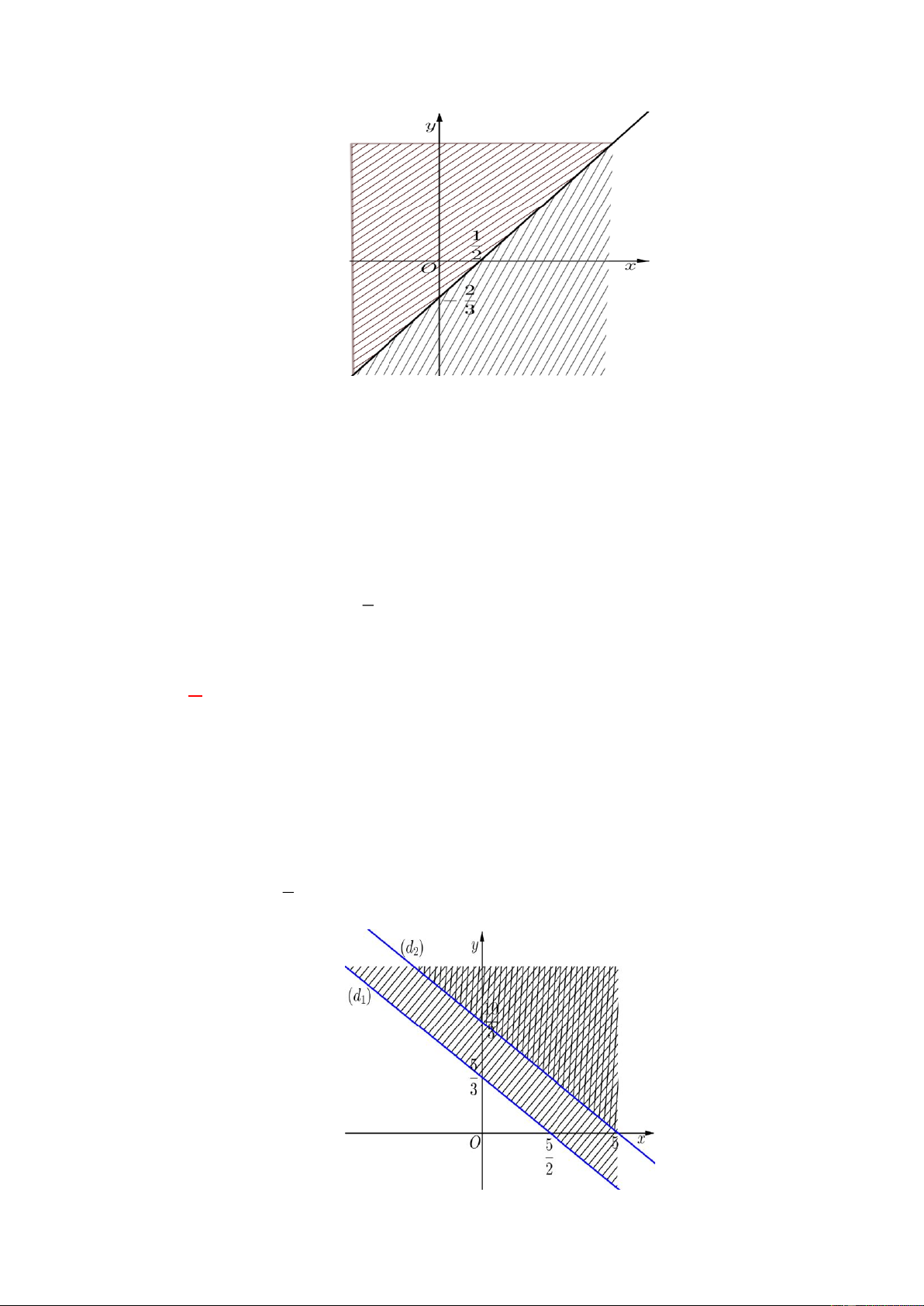
Thử trực tiếp ta thấy
0 ; 0
là nghiệm của bất phương trình (2) nhưng không phải
là nghiệm của bất phương trình (1). Sau khi gạch bỏ các miền không thích hợp, tập
hợp nghiệm của hệ bất phương trình chính là các điểm thuộc đường thẳng
:4 3 2.d x y
(Bổ sung)
Câu 32: [0D4-5-2] Cho hệ
2 3 5 (1)
3
5 (2)
2
xy
xy
. Gọi
1
S
là tập nghiệm của bất phương trình (1),
2
S
là tập nghiệm của bất phương trình (2) và
S
là tập nghiệm của hệ thì
A.
12
SS
. B.
21
SS
. C.
2
SS
. D.
1
SS
.
Lời giải
Chọn A
Trước hết, ta vẽ hai đường thẳng:
1
:2 3 5d x y
2
3
:5
2
d x y
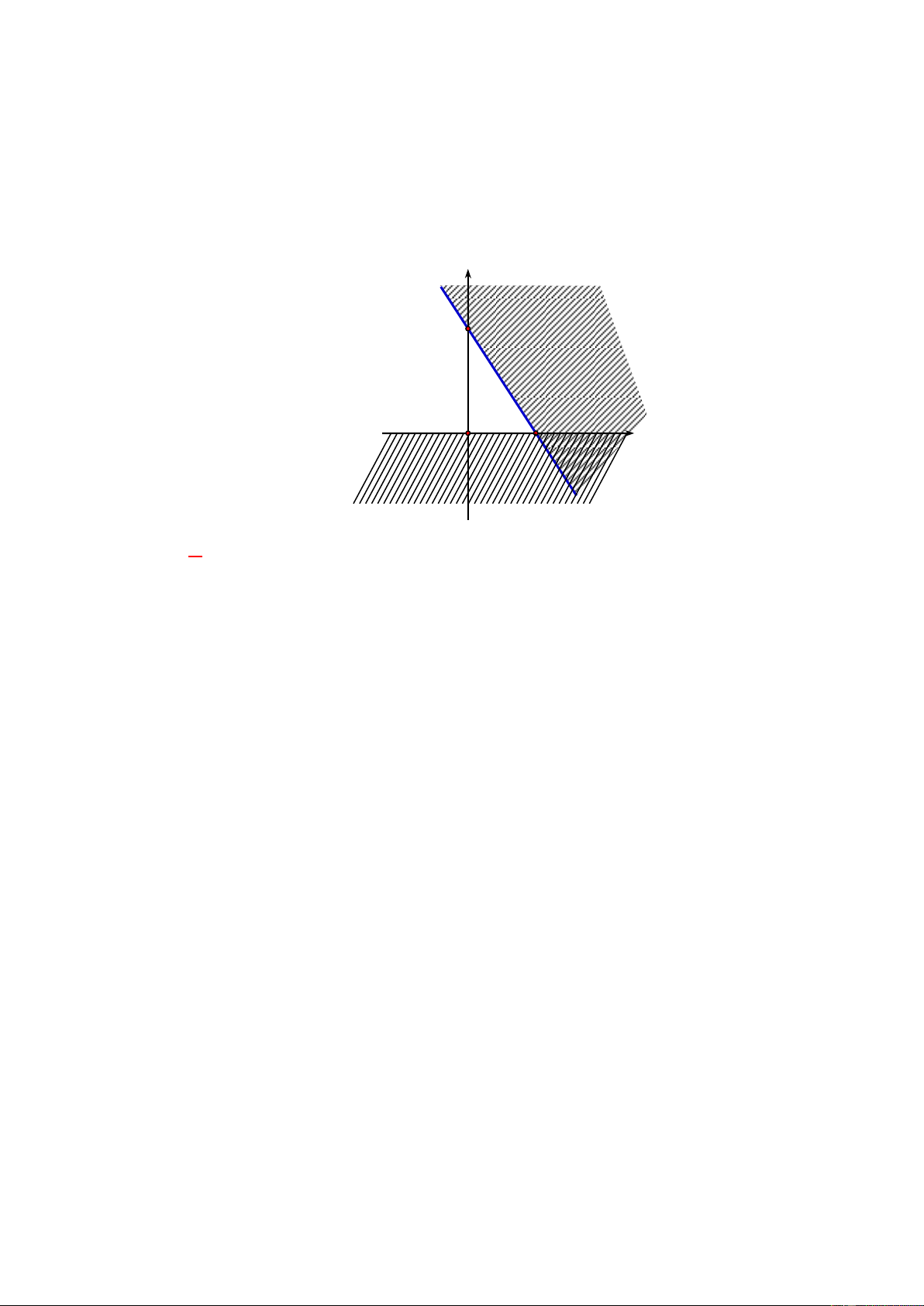
Ta thấy
0 ; 0
là nghiệm của cả hai bất phương trình. Điều đó có nghĩa gốc tọa độ
thuộc cả hai miền nghiệm của hai bất phương trình. Sau khi gạch bỏ các miền không
thích hợp, miền không bị gạch là miền nghiệm của hệ.
Câu 33: [0D4-5-2] Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất
phương trình nào trong bốn hệ A, B, C, D ?
A.
0
3 2 6
y
xy
. B.
0
3 2 6
y
xy
. C.
0
3 2 6
x
xy
. D.
0
3 2 6
x
xy
.
Lời giải
Chọn A
Dựa vào hình vẽ ta thấy đồ thị gồm hai đường thẳng
1
:0dy
và đường thẳng
2
:3 2 6.d x y
Miền nghiệm gồm phần
y
nhận giá trị dương.
Lại có
0 ; 0
thỏa mãn bất phương trình
3 2 6.xy
Câu 34: [0D4-5-2] Miền tam giác
ABC
kể cả ba cạnh sau đây là miền nghiệm của hệ bất
phương trình nào trong bốn hệ A, B, C, D ?
O
2
3
y
x
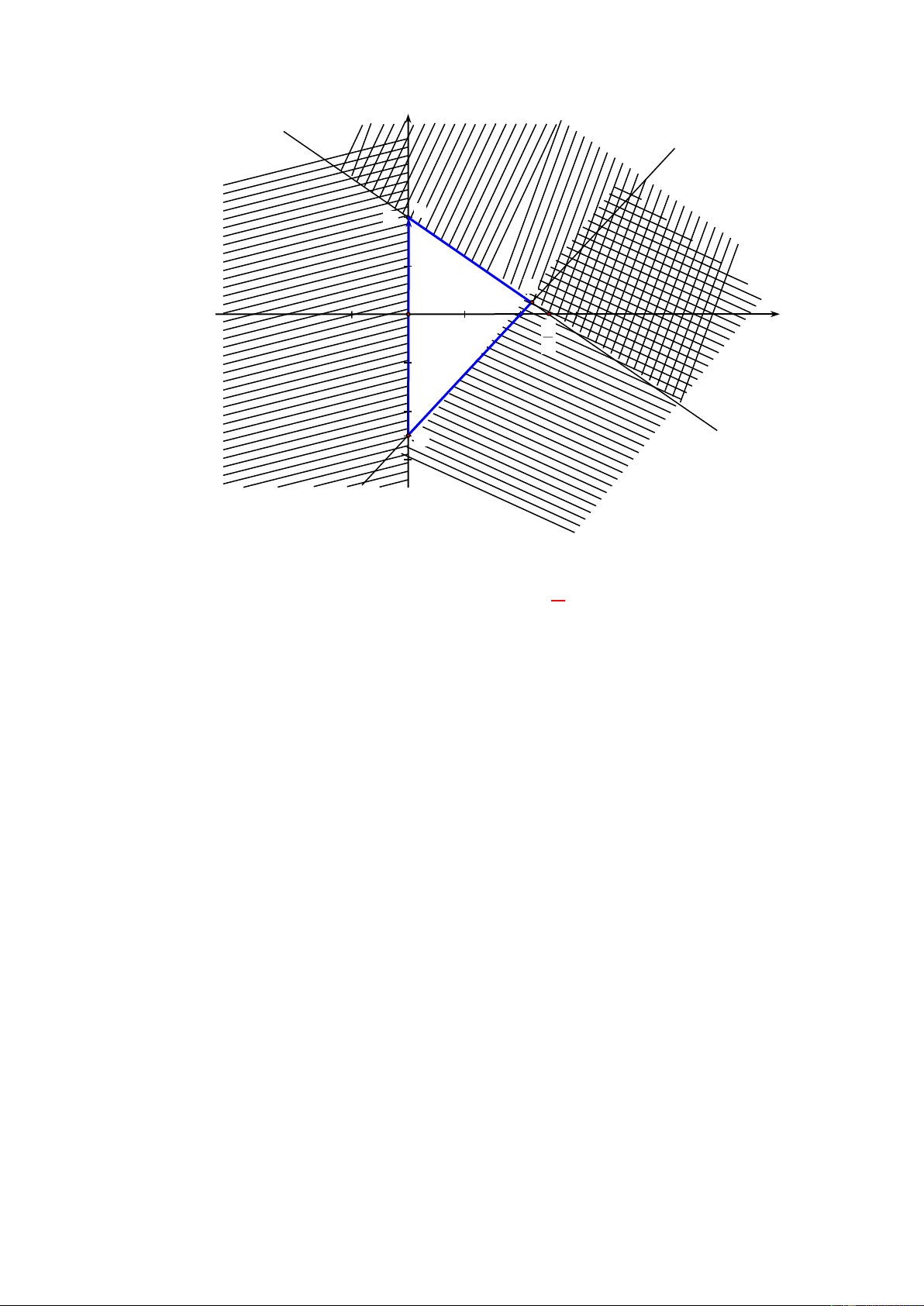
A.
0
5 4 10
5 4 10
y
xy
xy
. B.
0
4 5 10
5 4 10
x
xy
xy
. C.
0
5 4 10
4 5 10
x
xy
xy
. D.
0
5 4 10
4 5 10
x
xy
xy
.
Lời giải
Chọn C
Dựa vào hình vẽ, ta thấy đồ thị gồm các đường thẳng:
1
:0dx
2
:4 5 10d x y
3
:5 4 10d x y
Miền nghiệm gần phần mặt phẳng nhận giá trị
x
dương (kể cả bờ
1
d
).
Lại có
0 ; 0
là nghiệm của cả hai bất phương trình
4 5 10xy
và
5 4 10.xy
Câu 35: [0D4-5-2] Miền nghiệm của hệ bất phương trình
20
32
3
xy
xy
yx
chứa điểm nào sau
đây?
O
C
B
5
2
2
A
x
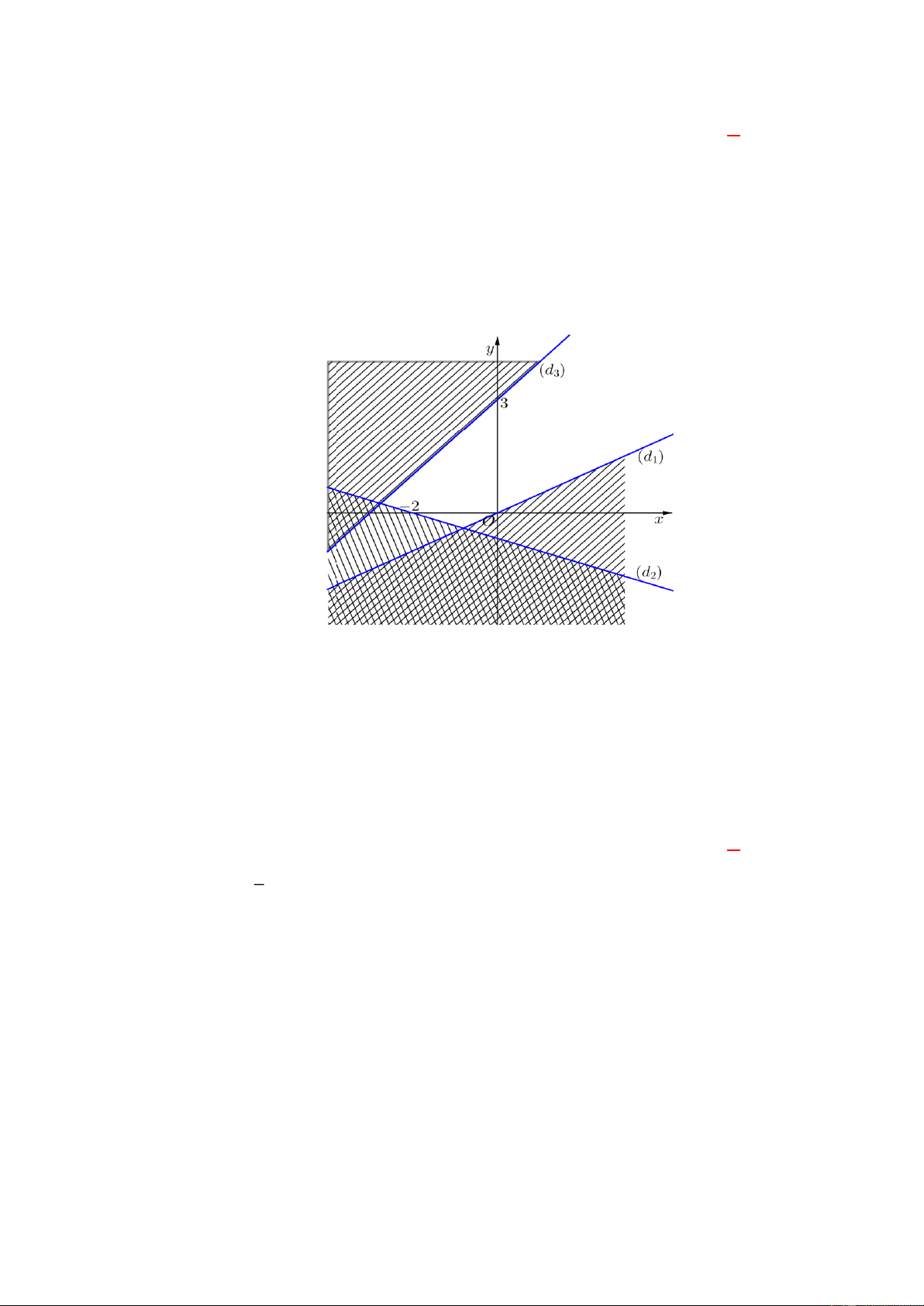
A.
1 ; 0A
. B.
2 ; 3B
. C.
0 ; 1C
. D.
1 ; 0 .D
Lời giải
Chọn D
Trước hết, ta vẽ ba đường thẳng:
1
: 2 0d x y
2
: 3 2d x y
3
:3d y x
Ta thấy
0 ; 1
là nghiệm của cả ba bất phương trình. Điều đó có nghĩa điểm
0 ; 1
thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ các miền không
thích hợp, miền không bị gạch là miền nghiệm của hệ.
Câu 36: [0D4-5-2] Miền nghiệm của hệ bất phương trình
2 3 6 0
0
2 3 1 0
xy
x
xy
chứa điểm nào sau
đây?
A.
1; 2 .A
B.
0 ; 2B
. C.
1 ; 3C
. D.
1
0 ; .
3
D
Lời giải
Chọn D
Trước hết, ta vẽ ba đường thẳng:
1
:2 3 6 0d x y
2
:0dx
3
:2 3 1 0d x y
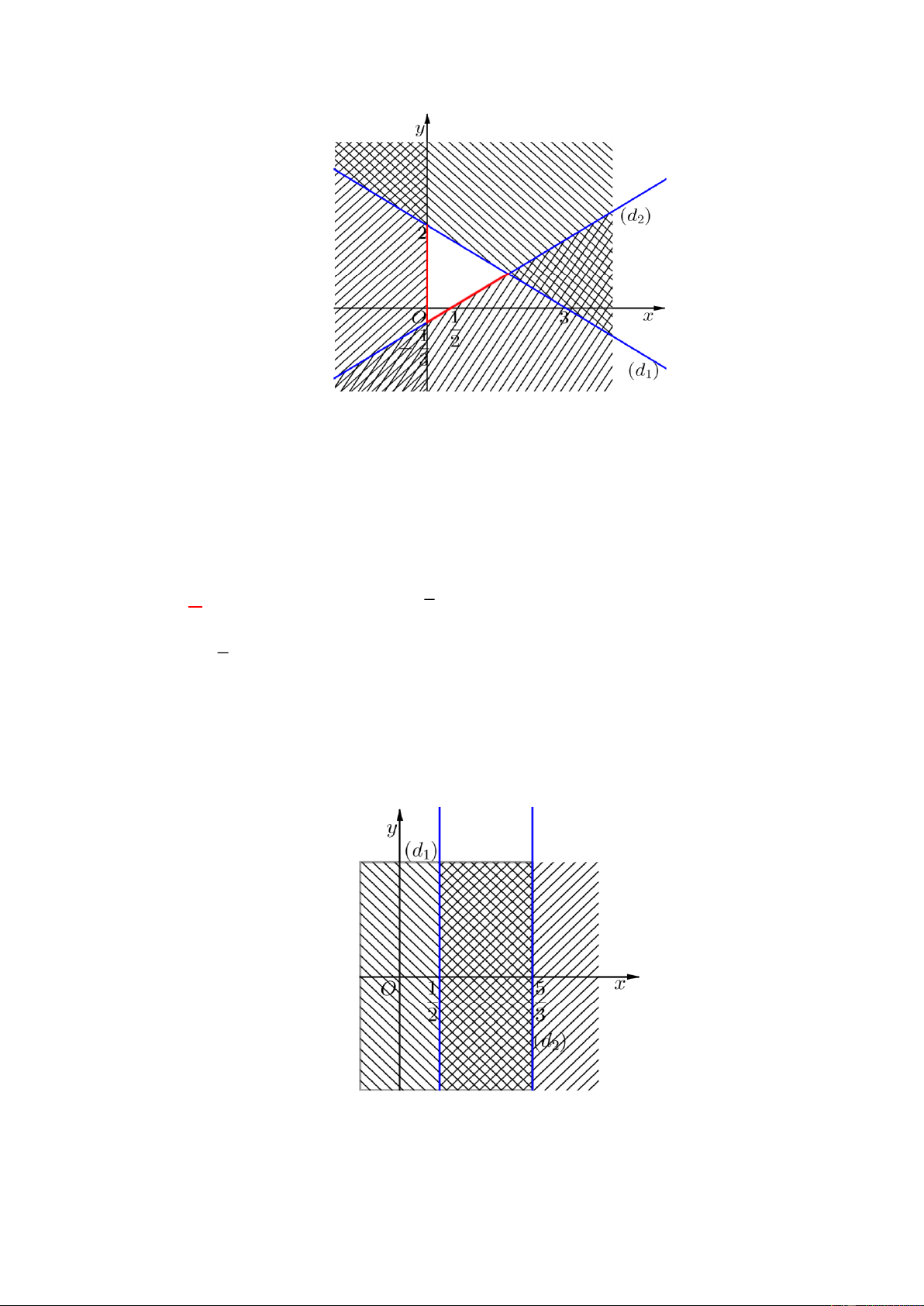
Ta thấy
1; 1
là nghiệm của các ba bất phương trình. Điều này có nghĩa là điểm
1; 1
thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ các miền
không thích hợp, miền không bị gạch là miền nghiệm của hệ.
Câu 37: [0D4-5-2] Miền nghiệm của hệ bất phương trình
2 1 0
3 5 0
x
x
chứa điểm nào sau
đây?
A. Không có. B.
5
; 2 .
3
B
C.
3 ; 1 .C
D.
1
; 10
2
D
.
Lời giải
Chọn A
Trước hết, ta vẽ hai đường thẳng:
1
:2 1 0dx
2
: 3 5 0dx
Ta thấy
1 ; 0
là không nghiệm của cả hai bất phương trình. Điều đó có nghĩa điểm
1 ; 0
không thuộc cả hai miền nghiệm của hai bất phương trình. Vậy không có
điểm nằm trên mặt phẳng tọa độ thỏa mãn hệ bất phương trình.
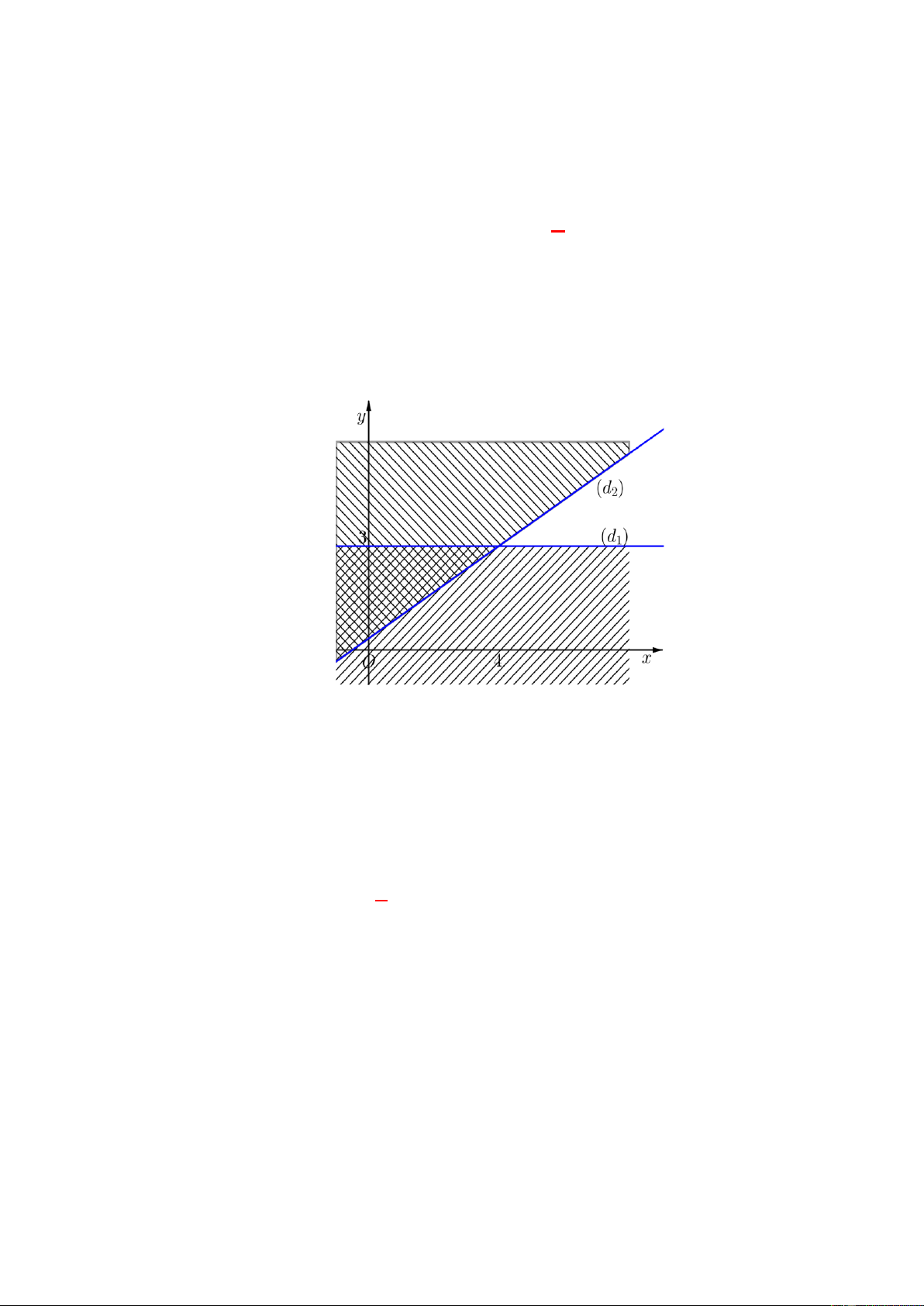
Câu 38: [0D4-5-2] Miền nghiệm của hệ bất phương trình
30
2 3 1 0
y
xy
chứa điểm nào sau
đây?
A.
3 ; 4A
. B.
4 ; 3B
. C.
7 ; 4C
. D.
4 ; 4 .D
Lời giải
Chọn C
Trước hết, ta vẽ hai đường thẳng:
1
:3 0dy
2
:2 3 1 0d x y
Ta thấy
6 ; 4
là nghiệm của hai bất phương trình. Điều đó có nghĩa điểm
6 ; 4
thuộc cả hai miền nghiệm của hai bất phương trình. Sau khi gạch bỏ các miền không
thích hợp, miền không bị gạch là miền nghiệm của hệ.
Câu 39: [0D4-5-2] Miền nghiệm của hệ bất phương trình
20
32
xy
xy
không chứa điểm nào
sau đây?
A.
1 ; 0 .A
B.
1 ; 0 .B
C.
3 ; 4C
. D.
0 ; 3 .D
Lời giải
Chọn B
Trước hết, ta vẽ hai đường thẳng:
1
: 2 0d x y
2
: 3 2d x y
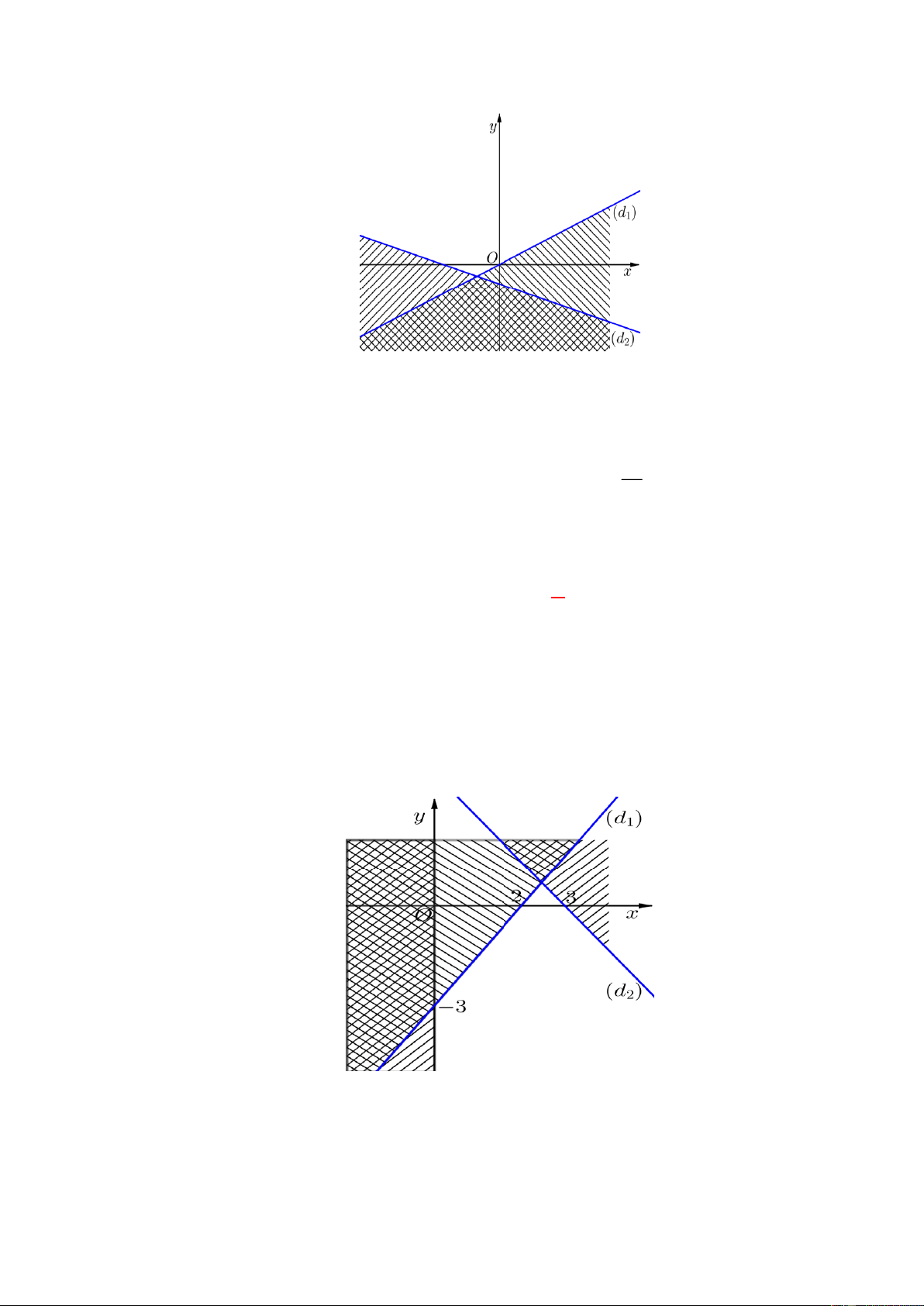
Ta thấy
0 ; 1
là nghiệm của hai bất phương trình. Điều đó có nghĩa điểm
0 ; 1
thuộc cả hai miền nghiệm của hai bất phương trình. Sau khi gạch bỏ phần không
thích hợp, phần không bị gạch là miền nghiệm của hệ.
Câu 40: [0D4-5-2] Miền nghiệm của hệ bất phương trình
3 2 6 0
3
2( 1) 4
2
0
xy
y
x
x
không chứa điểm
nào sau đây?
A.
2 ; 2A
. B.
3 ; 0 .B
C.
1 ; 1 .C
D.
2 ; 3 .D
Lời giải
Chọn C
Trước hết, ta vẽ ba đường thẳng:
1
:3 2 6 0d x y
2
:4 3 12 0d x y
3
:0dx
Ta thấy
2 ; 1
là nghiệm của cả ba bất phương trình. Điều đó có nghĩa điểm
2 ; 1
thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ các
miền không thích hợp, miền không bị gạch là miền nghiệm của hệ.
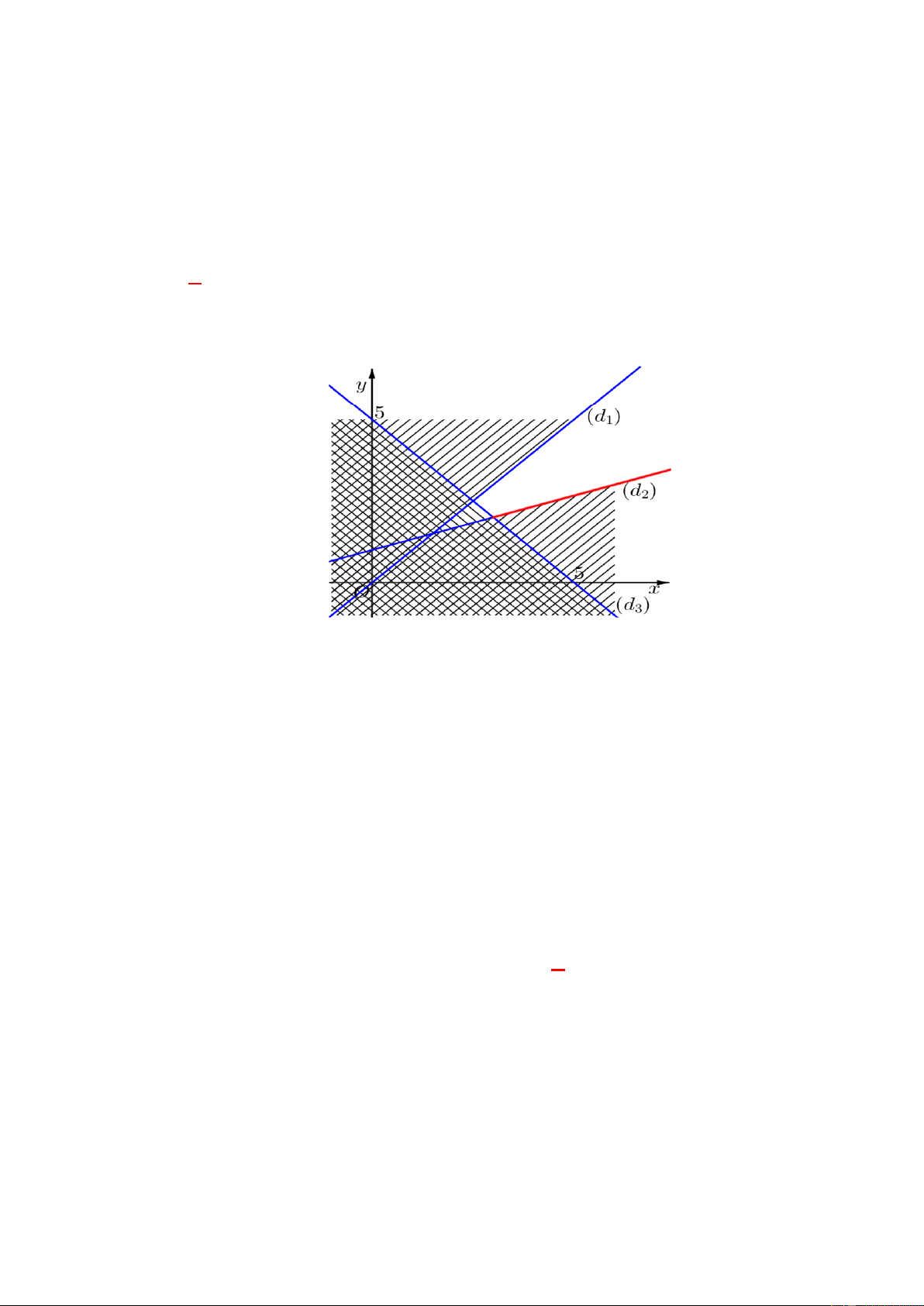
Câu 41: [0D4-5-2] Miền nghiệm của hệ bất phương trình
0
33
5
xy
xy
xy
không chứa điểm nào
sau đây?
A.
3 ; 2 .A
B.
6 ; 3 .B
C.
6 ; 4 .C
D.
5 ; 4 .D
Lời giải
Chọn A
Trước hết, ta vẽ ba đường thẳng:
1
:0d x y
2
: 3 3d x y
3
:5d x y
Ta thấy
5 ; 3
là nghiệm của cả ba bất phương trình. Điều đó có nghĩa điểm
5 ; 3
thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ miền
không thích hợp, miền không bị gạch là miền nghiệm của hệ.
Câu 42: [0D4-5-2] Miền nghiệm của hệ bất phương trình
30
23
2
xy
xy
yx
không chứa điểm nào
sau đây?
A.
0 ; 1 .A
B.
1; 1 .B
C.
3 ; 0 .C
D.
3 ; 1 .D
Lời giải
Chọn C
Trước hết, ta vẽ ba đường thẳng:
1
: 3 0d x y
2
: 2 3d x y
3
:2d x y
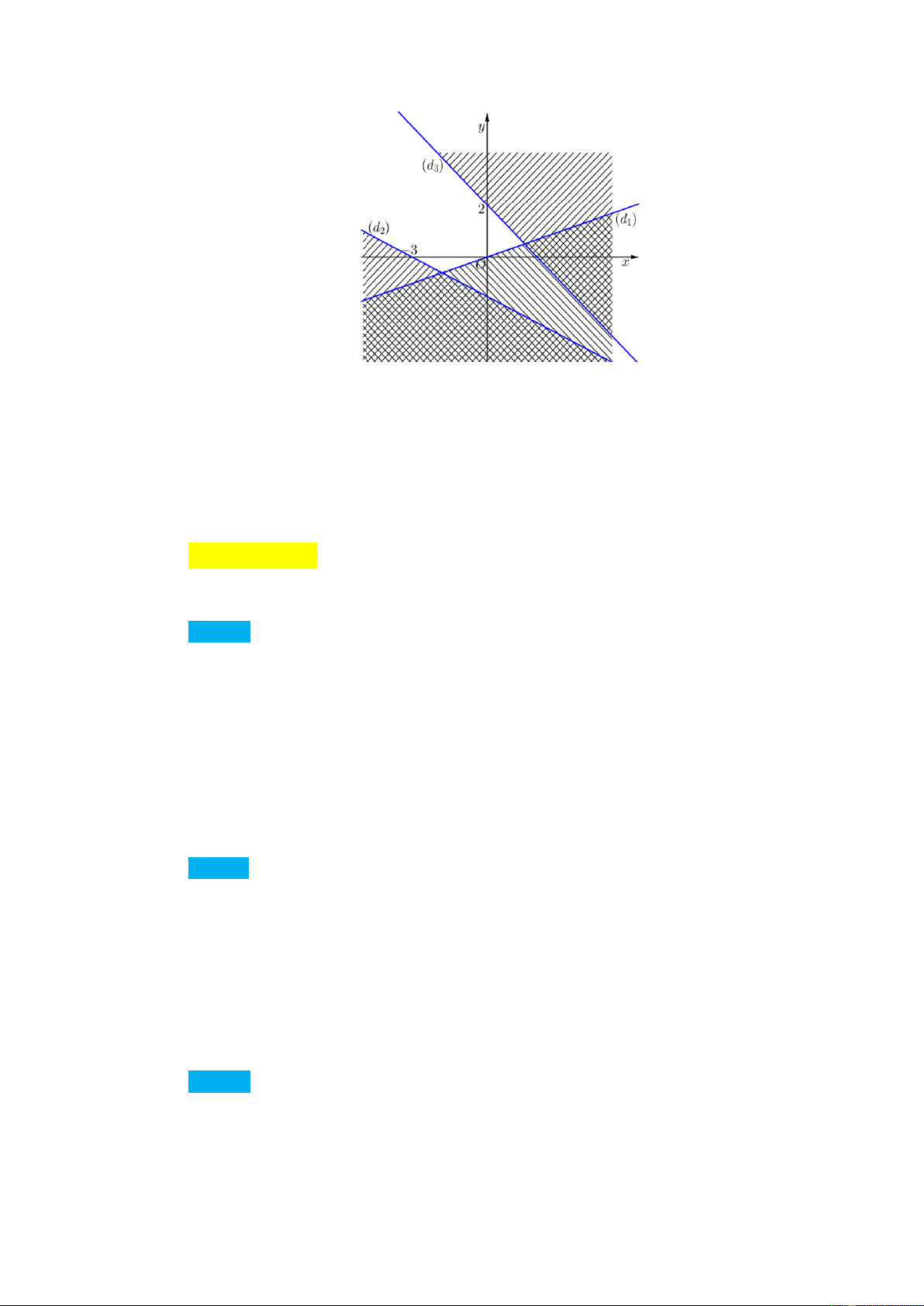
Ta thấy
1 ; 0
là nghiệm của cả ba bất phương trình. Điều đó có nghĩa điểm
1 ; 0
thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ miền
không thích hợp, miền không bị gạch là miền nghiệm của hệ.
Câu 43: [0D4-5-2] Cặp số
1;1
là nghiệm của bất phương trình nào sau đây?
A.
30xy
. B.
– – 0xy
.
C.
3 1 0 xy
. D.
– – 3 –1 0xy
.
Lời giải
Chọn C
Thay cặp số
;; 1 –1xy
vào từng bpt để kiểm tra.
Câu 44: [0D4-5-2] Cặp số
2;3
là nghiệm của bất phương trình nào sau đây?
A.
2 – 3 –1 0xy
. B.
–0xy
. C.
43xy
. D.
– 3 7 0xy
.
Lời giải
Chọn B
Thay cặp số
2; ;3xy
vào các bpt để kiểm tra.
Câu 45: [0D4-5-2] Cặp số nào sau đây là nghiệm của bất phương trình
–2 – 3x y y
?
A.
4; –4
. B.
2;1
. C.
–1;–2
. D.
4;4
.
Lời giải
Chọn D
–2 – 3 2 3 2 3 *x y y x y y x
Thay các đáp án vào bpt
*
để kiểm tra.

Câu 46: [0D4-5-2] Bất phương trình
3 – 2 – 1 0x y x
tương đương với bất phương trình
nào sau đây?
A.
– 2 – 2 0xy
. B.
5 – 2 – 2 0xy
.
C.
5 – 2 –1 0xy
. D.
4 – 2 – 2 0xy
.
Lời giải
Chọn B
Ta có
3 – 2 – 1 0x y x
3 2 2 2 0 5 2 2 0x y x x y
(chọn B.).
Câu 47: [0D4-5-2] Cặp số nào sau đây không là nghiệm của bất phương trình
5 2 1 0 xy
?
A.
0;1
. B.
1;3
. C.
–1;1
. D.
–1;0
.
Lời giải
Chọn B
Ta có
5 2 1 0 xy
5 2 2 0xy
; ta thay từng đáp án vào bất phương
trình, cặp
1;3
không thỏa mãn bất phương trình vì
5.1 2.3 2 0
là sai. Vậy
chọn B.
Câu 48: [0D4-5-2] Điểm
0;0O
thuộc miền nghiệm của bất phương trình nào sau đây?
A.
3 2 0 xy
. B.
20 xy
.
C.
2 5 2 0 xy
. D.
2 2 0 xy
.
Lời giải
Chọn D
Thay
0; 0xy
vào từng bất phương trình chỉ có D. Đúng :
20
. Vậy chọn D.
Câu 49: [0D4-5-2] Điểm
0;0O
thuộc miền nghiệm của hệ bất phương trình nào sau đây?
A.
3 6 0
2 4 0
xy
xy
. B.
3 6 0
2 4 0
xy
xy
.
C.
3 6 0
2 4 0
xy
xy
. D.
3 6 0
2 4 0
xy
xy
.
Lời giải
Chọn C

Thay
0; 0xy
vào từng đáp án ta được:
3 6 0 6 0
2 4 0 4 0
xy
xy
(loại A.) ;
3 6 0 6 0
2 4 0 4 0
xy
xy
( Loại B.)
3 6 0 6 0
2 4 0 4 0
xy
xy
(thỏa mãn). Vậy chọn C.
Câu 50: [0D4-5-2] Trong các điểm sau đây, điểm nào thuộc miền nghiệm của hệ bất phương
trình
3 2 0
2 1 0
xy
xy
A.
0;1
. B.
–1;1
. C.
1;3
. D.
–1;0
.
Lời giải
Chọn B
;xy
0;1
thì
3 2 0 3 2 0
2 1 0 1 1 0
xy
xy
( loại A.)
;xy
–1;1
thì
3 2 0 1 3 2 0
2 1 0 2 1 1 0
xy
xy
(thỏa mãn). Vậy chọn B.
Câu 51: [0D4-5-2] Xét biểu thức
F y x
trên miền xác định bởi hệ
5
42
22
yx
xy
xy
. Chọn
mệnh đề đúng.
A.
min 1F
khi
2, 3xy
. B.
min 2F
khi
0, 2xy
.
C.
min 3F
khi
1, 4xy
. D.
min 0F
khi
4, 4xy
.
Lời giải
Chọn A
Giải trắc nghiệm
Ta dùng máy tính lần lượt kiểm tra các đáp án để xem đáp án nào thỏa bất phương
trình trên loại đáp án D.
Ta lần lượt tính hiệu
F y x
được
min 1F
khi
2, 3xy
.
Giải tự luận
Giá trị tại các điểm
2;3 , 0;2 , 1;4A B C
lần lượt là
1,2,3
. Suy ra, giá trị
min 1F
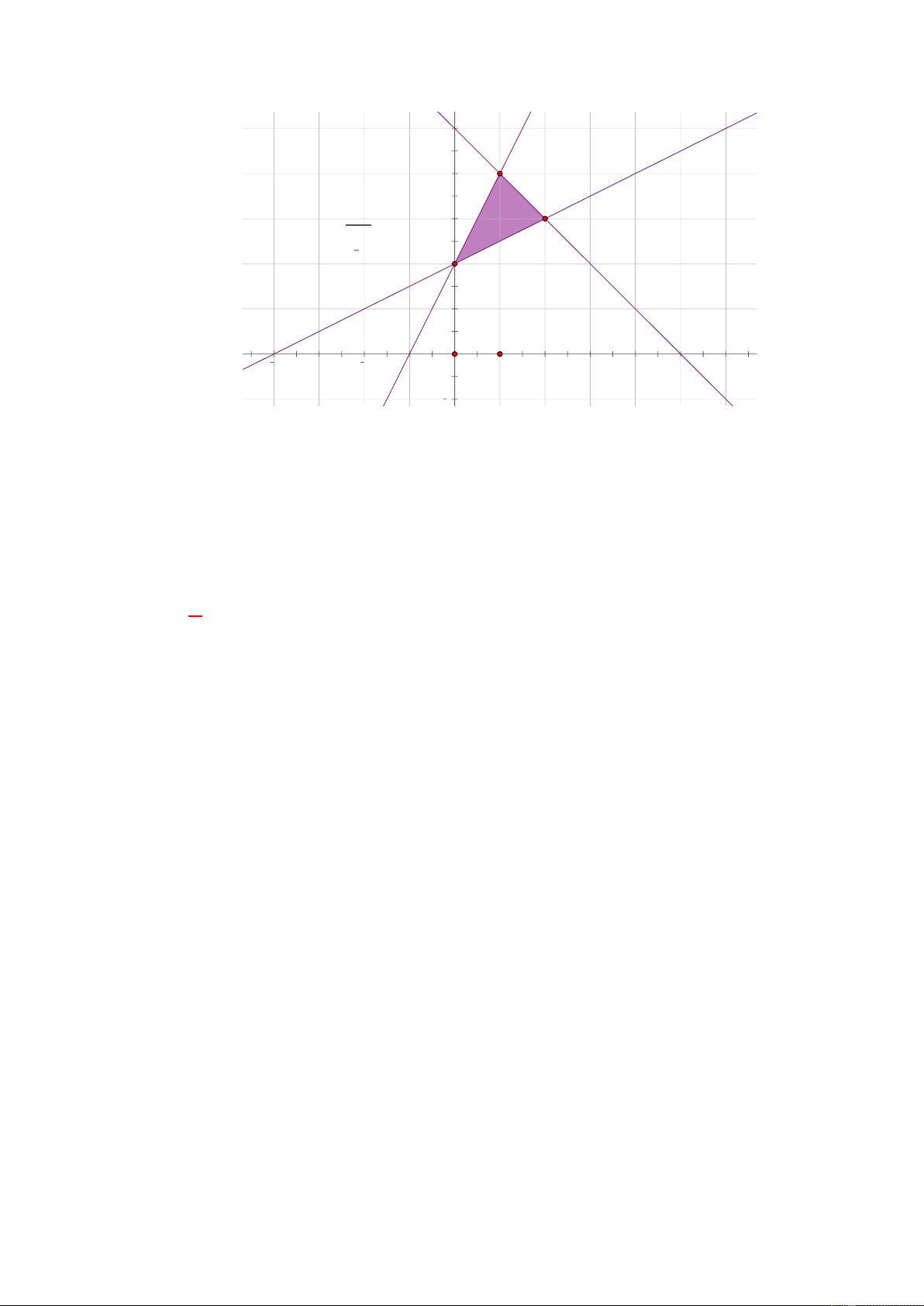
6
5
4
3
2
1
1
2
8
6
4
2
2
4
6
8
y
=
h
(
x
)
y
=
g
(
x
)
y
=
f
(
x
)
h
x
( )
= 5
x
g
x
( )
=
x
+ 4
2
f
x
( )
= 2
∙
x
+ 2
C
B
A
Câu 52: [0D4-5-2] Giá trị nhỏ nhất của biết thức trên
F y x
miền xác định bởi hệ
45
2
22
yx
yx
yx
là
A.
min 2F
khi
1, 1xy
. B.
min 2F
khi
0, 2xy
.
C.
min 2F
khi
1, 1xy
. D.
min 1F
khi
0, 1xy
.
Lời giải
Chọn C
Ta dùng máy tính lần lượt kiểm tra các đáp án để xem đáp án nào thỏa bất phương
trình trên.
Ta lần lượt tính hiệu
F y x
và
min 2F
khi
1, 1xy
.
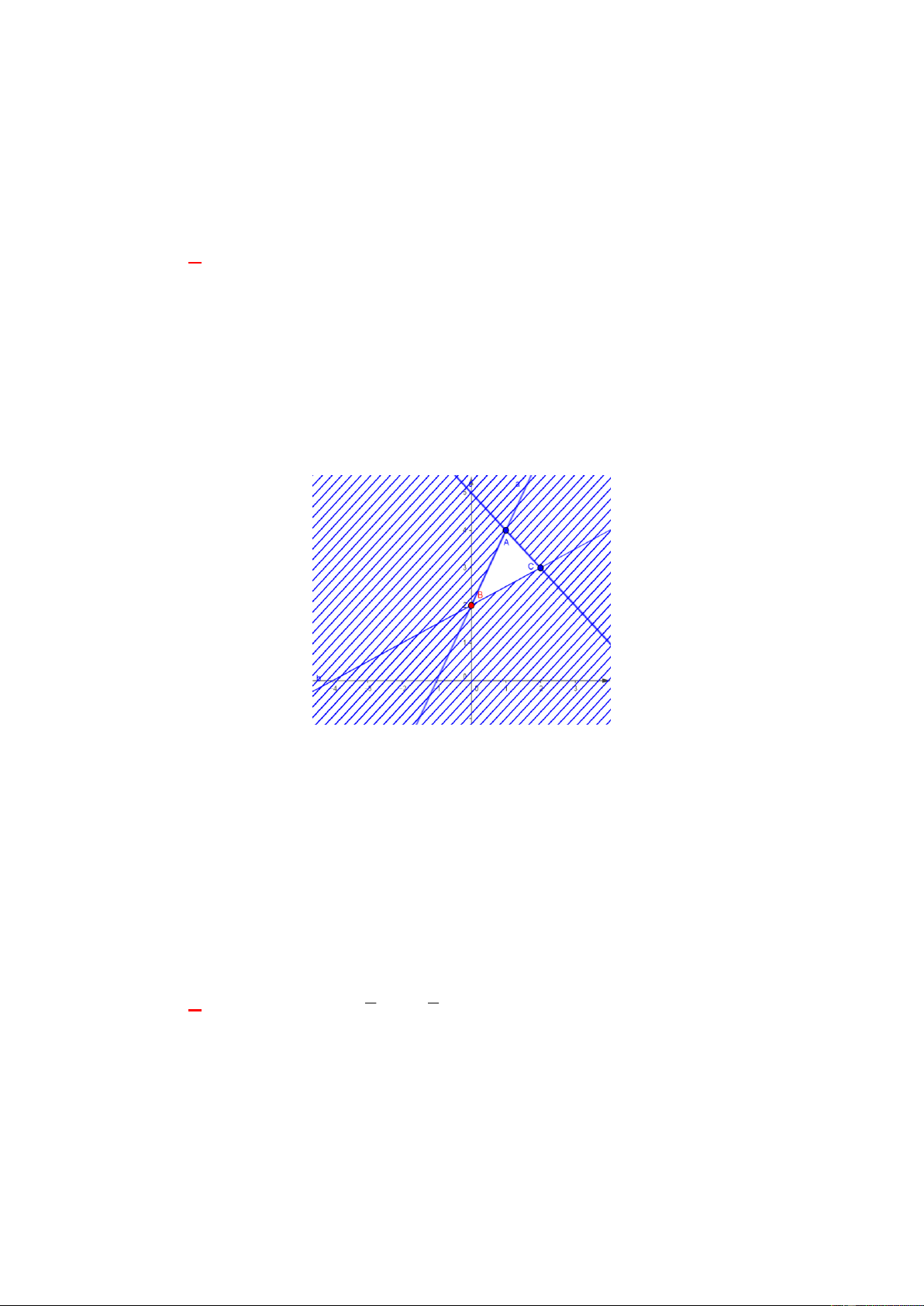
Câu 1: [0D4-5-3] Giá trị nhỏ nhất của biết thức
F y x
trên miền xác định bởi hệ
22
24
5
yx
yx
xy
là.
A.
min 1F
khi
2, 3xy
. B.
min 2F
khi
0, 2xy
.
C.
min 3F
khi
1, 4xy
. D.
min 0F
khi
0, 0xy
.
Lời giải
Chọn A
Biểu diễn miền nghiệm của hệ bất phương trình
22
24
5
yx
yx
xy
trên hệ trục tọa độ như
dưới đây:
Nhận thấy biết thức
F y x
chỉ đạt giá trị nhỏ nhất tại các điểm
,AB
hoặc
C
.
Ta có:
4 1 3; 2; 3 2 1F A F B F C
.
Vậy
min 1F
khi
2, 3xy
.
Câu 2: [0D4-5-3] Giá trị nhỏ nhất của biết thức
F y x
trên miền xác định bởi hệ
22
2
54
xy
xy
xy
là
A.
min 3F
khi
1, 2xy
. B.
min 0F
khi
0, 0xy
.
C.
min 2F
khi
42
,
33
xy
. D.
min 8F
khi
2, 6xy
.
Lời giải
Chọn C
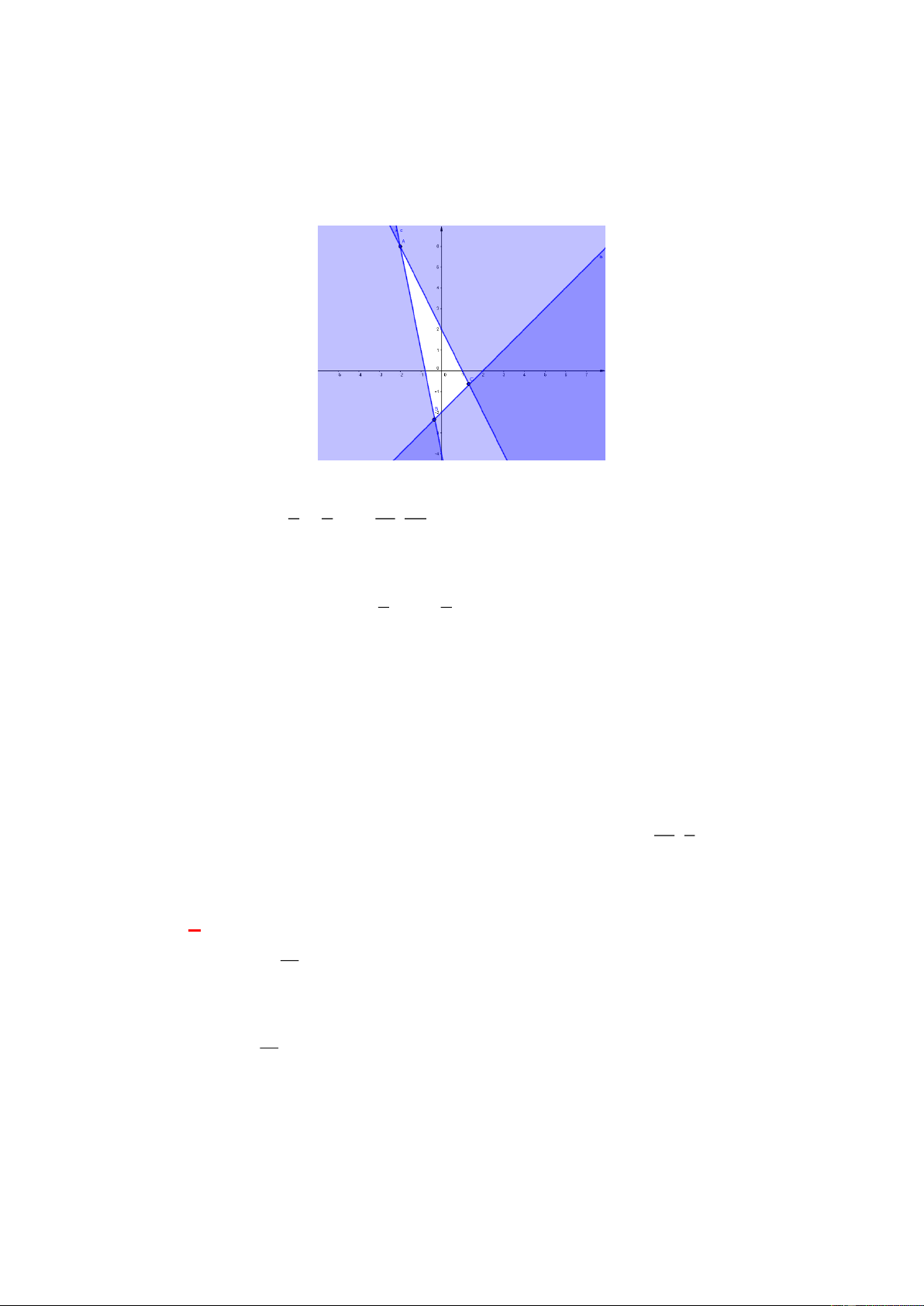
Biểu diễn miền nghiệm của hệ bất phương trình
22
2
54
xy
xy
xy
trên hệ trục tọa độ như
dưới đây:
Giá trị nhỏ nhất của biết thức
F y x
chỉ đạt được tại các điểm
4 2 1 7
2;6 , ; , ;
3 3 3 3
A C B
.
Ta có:
8; 2; 2F A F B F C
.
Vậy
min 2F
khi
42
,
33
xy
.
Câu 3: [0D4-5-3] Cho hệ bất phương trình
2
3 5 15
0
0
xy
xy
x
y
. Mệnh đề nào sau đây là sai ?
A. Trên mặt phẳng tọa độ
Oxy
, biểu diễn miền nghiệm của hệ bất phương trình đã
cho là miền tứ giác
ABCO
kể cả các cạnh với
0;3A
,
25 9
;
88
B
,
2;0C
và
0;0O
.
B. Đường thẳng
: x y m
có giao điểm với tứ giác
ABCO
kể cả khi
17
1
4
m
.
C. Giá trị lớn nhất của biểu thức
xy
, với
x
và
y
thỏa mãn hệ bất phương trình đã
cho là
17
4
.
D. Giá trị nhỏ nhất của biểu thức
xy
, với
x
và
y
thõa mãn hệ bất phương trình đã
cho là 0.
Lời giải
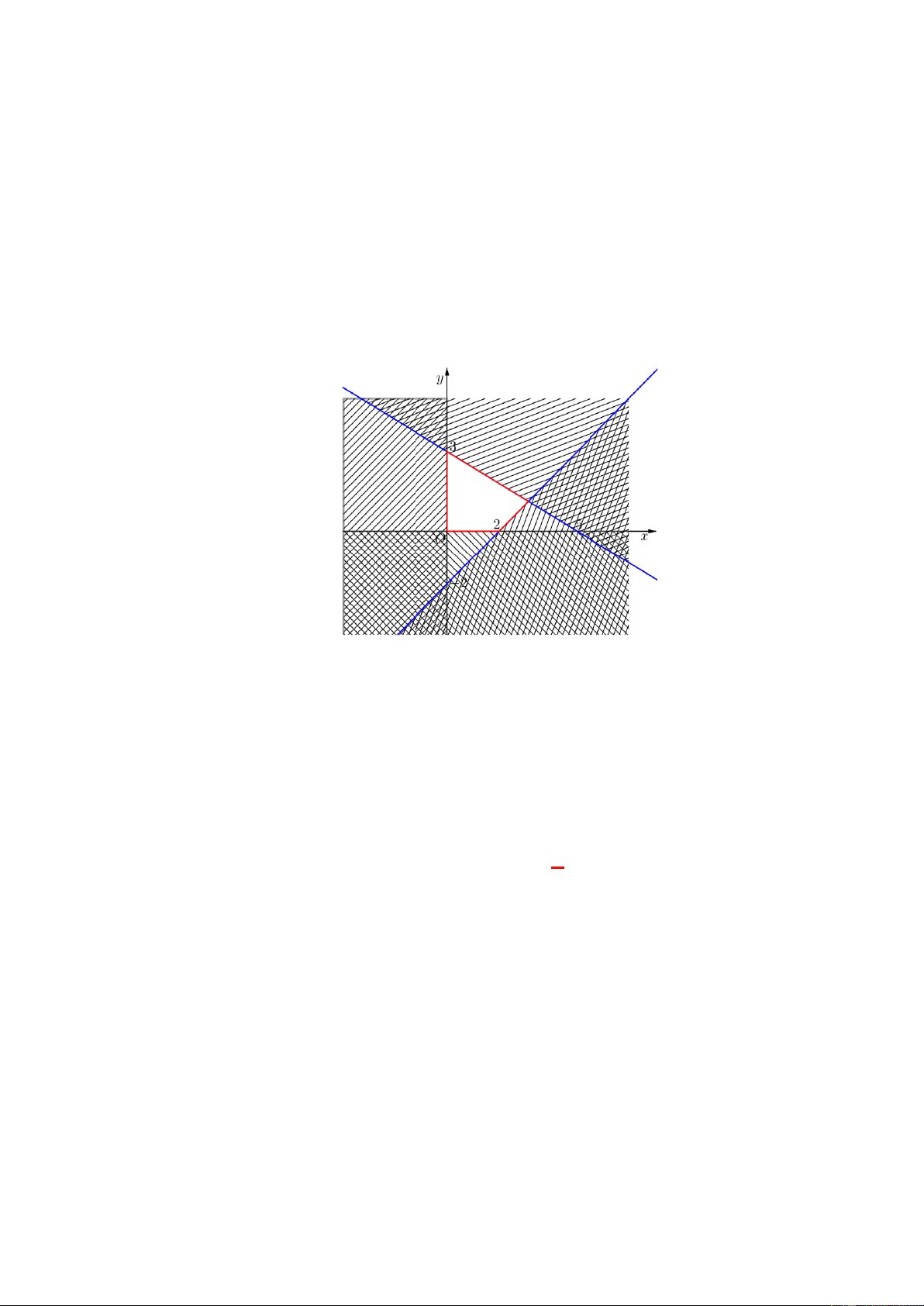
Chọn B
Trước hết, ta vẽ bốn đường thẳng:
1
:2d x y
2
:3 5 15d x y
3
:0dx
4
:0dy
Miền nghiệm là phần không bị gạch, kể cả biên.
Câu 4: [0D4-5-3] Giá trị lớn nhất của biết thức
;2F x y x y
với điều kiện
04
0
10
2 10 0
y
x
xy
xy
là
A.
6
. B.
8
. C.
10
. D.
12
.
Lời giải
Chọn C
Vẽ đường thẳng
1
: 1 0d x y
, đường thẳng
1
d
qua hai điểm
0; 1
và
1;0
.
Vẽ đường thẳng
2
: 2 10 0d x y
, đường thẳng
2
d
qua hai điểm
0;5
và
2;4
.
Vẽ đường thẳng
3
:4dy
.
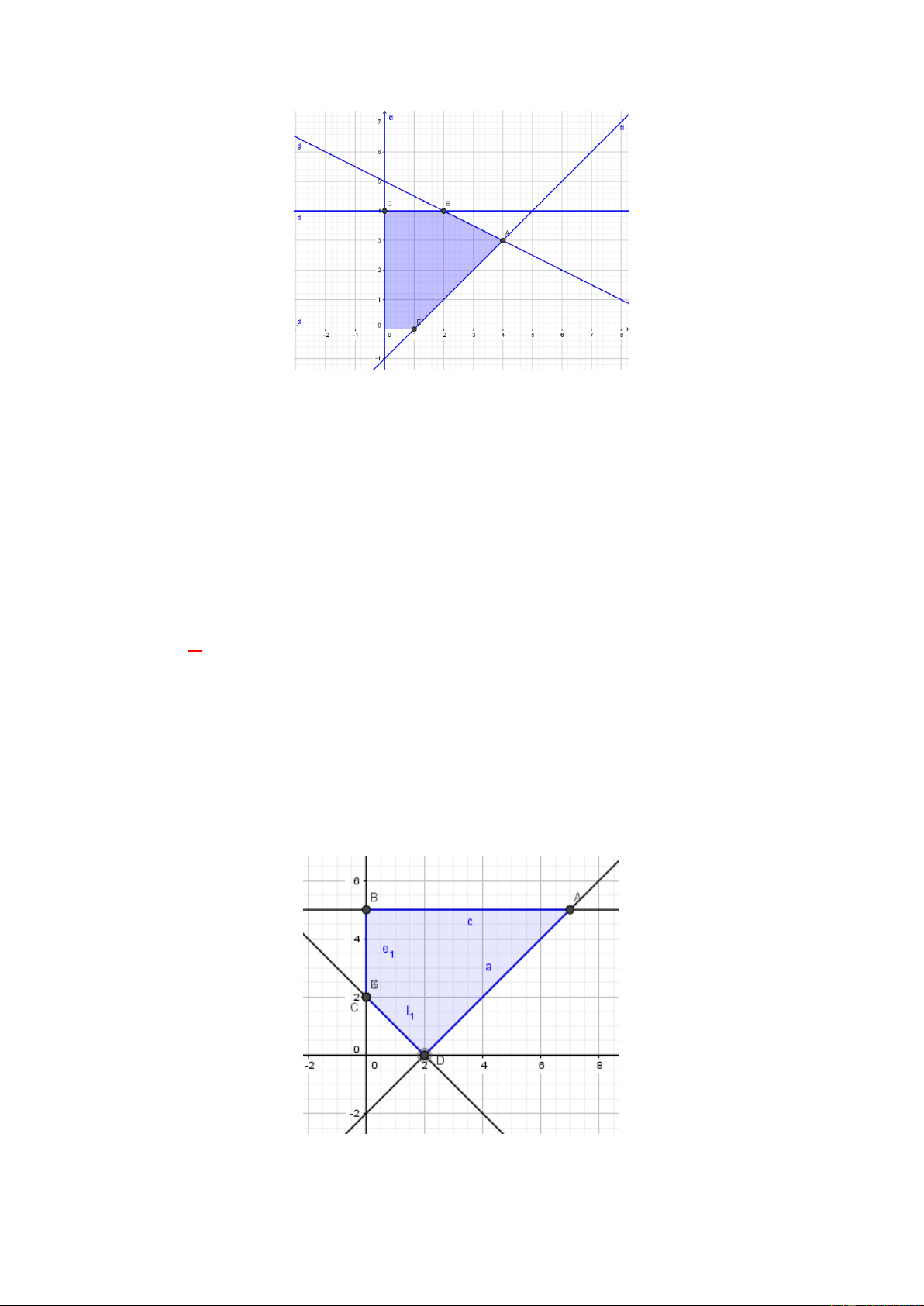
Miền nghiệm là ngũ giác
ABCOE
với
4;3 , 2;4 , 0;4 , 1;0A B C E
.
Ta có:
4;3 10F
,
2;4 10F
,
0;4 8F
,
1;0 1F
,
0;0 0F
.
Vậy giá trị lớn nhất của biết thức
;2F x y x y
bằng
10
.
Câu 5: [0D4-5-3] Giá trị nhỏ nhất của biết thức
;2F x y x y
với điều kiện
05
0
20
20
y
x
xy
xy
là
A.
10
. B.
12
. C.
8
. D.
6
.
Lời giải
Chọn A
Biểu diễn miền ngiệm của hệ bất phương trình
05
0
20
20
y
x
xy
xy
trên hệ trục tọa độ như
dưới đây:
Nhận thấy biết thức
;2F x y x y
chỉ đạt giá trị nhỏ nhất tại các điểm
,,A B C
hoặc
D
.
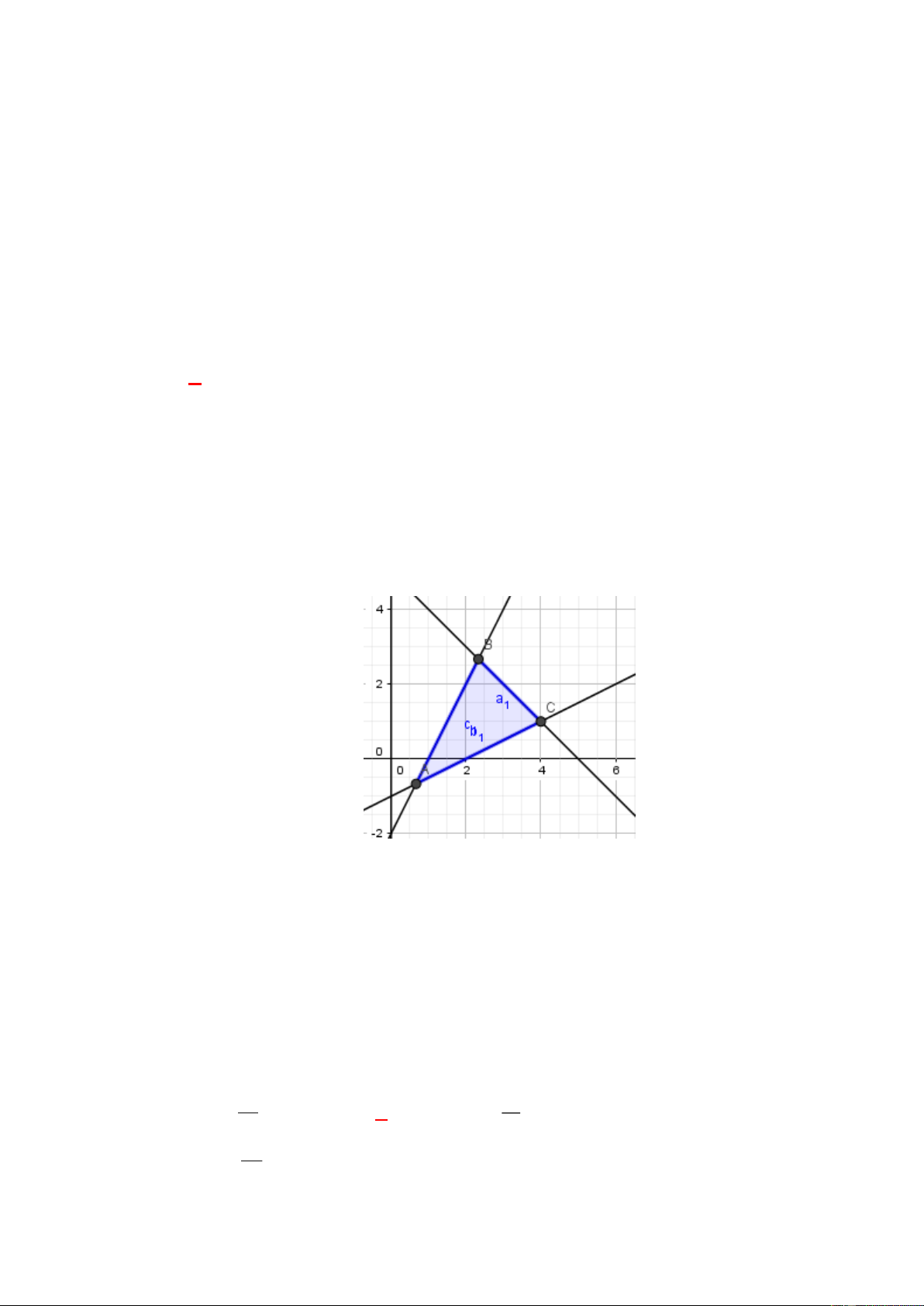
Ta có:
7 2 5 3; 2 5 10F A F B
.
2 2 4, 2 2 0 2F C F D
.
Vậy
min 10F
khi
0, 5xy
.
Câu 6: [0D4-5-3] Biểu thức
–F y x
đạt giá trị nhỏ nhất với điều kiện
22
22
5
0
xy
xy
xy
x
tại
điểm
;S x y
có toạ độ là
A.
4;1
. B.
3;1
. C.
2;1
. D.
1;1
.
Lời giải
Chọn A
Biểu diễn miền nghiệm của hệ bất phương trình
22
22
5
0
xy
xy
xy
x
trên hệ trục tọa độ
như dưới đây:
Nhận thấy biết thức
F y x
chỉ đạt giá trị nhỏ nhất tại các điểm
,AB
hoặc
C
.
Chỉ
4;1C
có tọa độ nguyên nên thỏa mãn.
Vậy
min 3F
khi
4, 1xy
.
Câu 7: [0D4-5-3] Biểu thức
L y x
, với
x
và
y
thỏa mãn hệ bất phương trình
2 3 6 0
0
2 3 1 0
xy
x
xy
, đạt giá trị lớn nhất là
a
và đạt giá trị nhỏ nhất là
b
. Hãy chọn kết
quả đúng trong các kết quả sau:
A.
25
8
a
và
2b
. B.
2a
và
11
12
b
. C.
3a
và
0b
. D.
3a
và
9
8
b
.
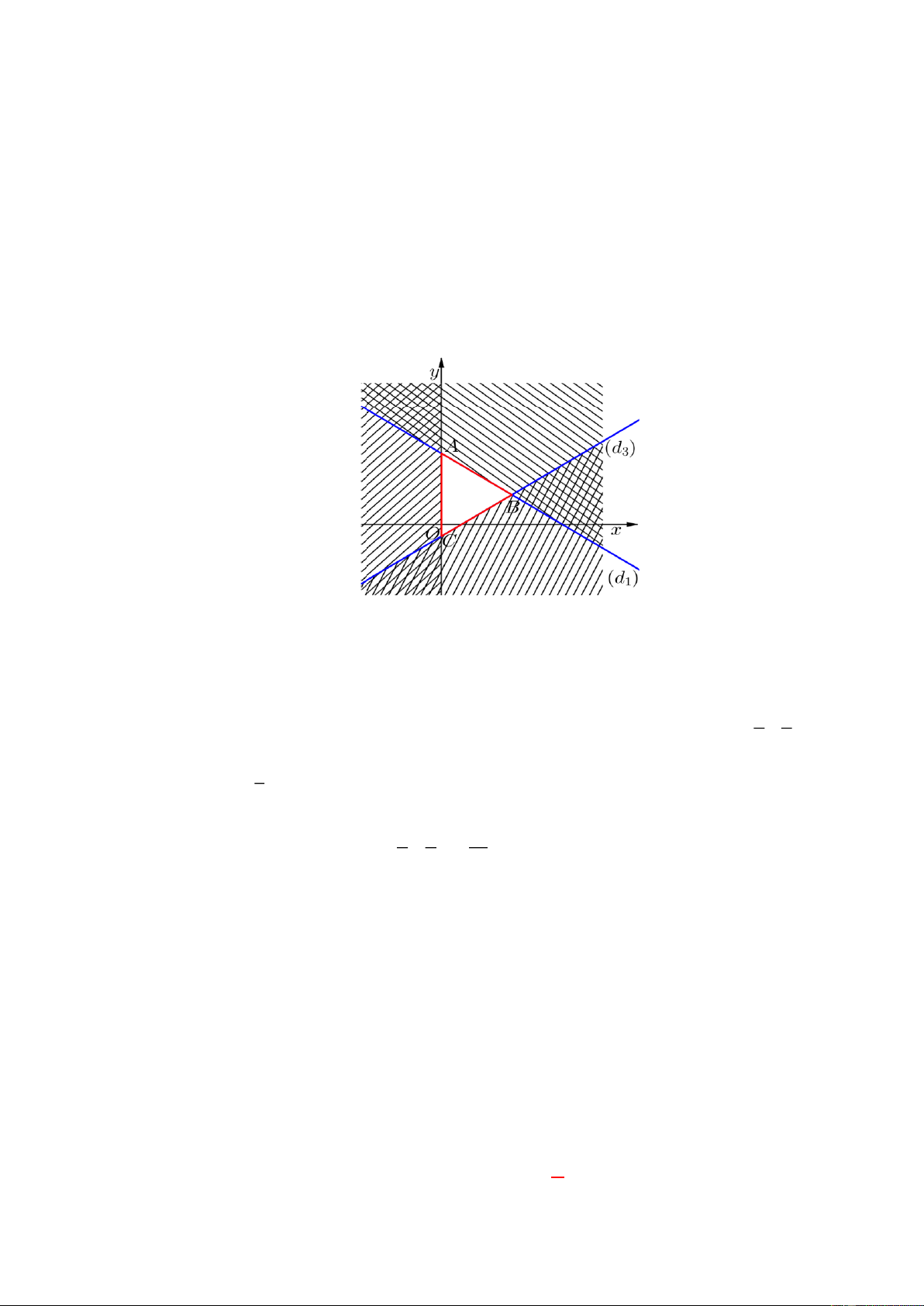
Lời giải
Chọn B
Trước hết, ta vẽ ba đường thẳng:
1
:2 3 6 0d x y
2
:0dx
3
:2 3 1 0d x y
Ta thấy
0 ; 0
là nghiệm của cả ba bất phương trình. Điều đó có nghĩa gốc tọa độ
thuộc cả ba miền nghiệm của cả ba bất phương trình. Sau khi gạch bỏ các miền
không thích hợp, miền không bị gạch là miền nghiệm của hệ (kể cả biên).
Miền nghiệm là hình tam giác
ABC
(kể cả biên), với
0 ; 2 ,A
75
;,
46
B
1
0 ; .
3
C
Vậy ta có
2 0 2,a
5 7 11
.
6 4 12
b
Câu 8: [0D4-5-3] Giá trị lớn nhất của biểu thức
;2F x y x y
, với điều kiện
0102
01
0
40
yx
yx
x
y
là
A.
6
. B.
8
. C.
10
. D.
12
.
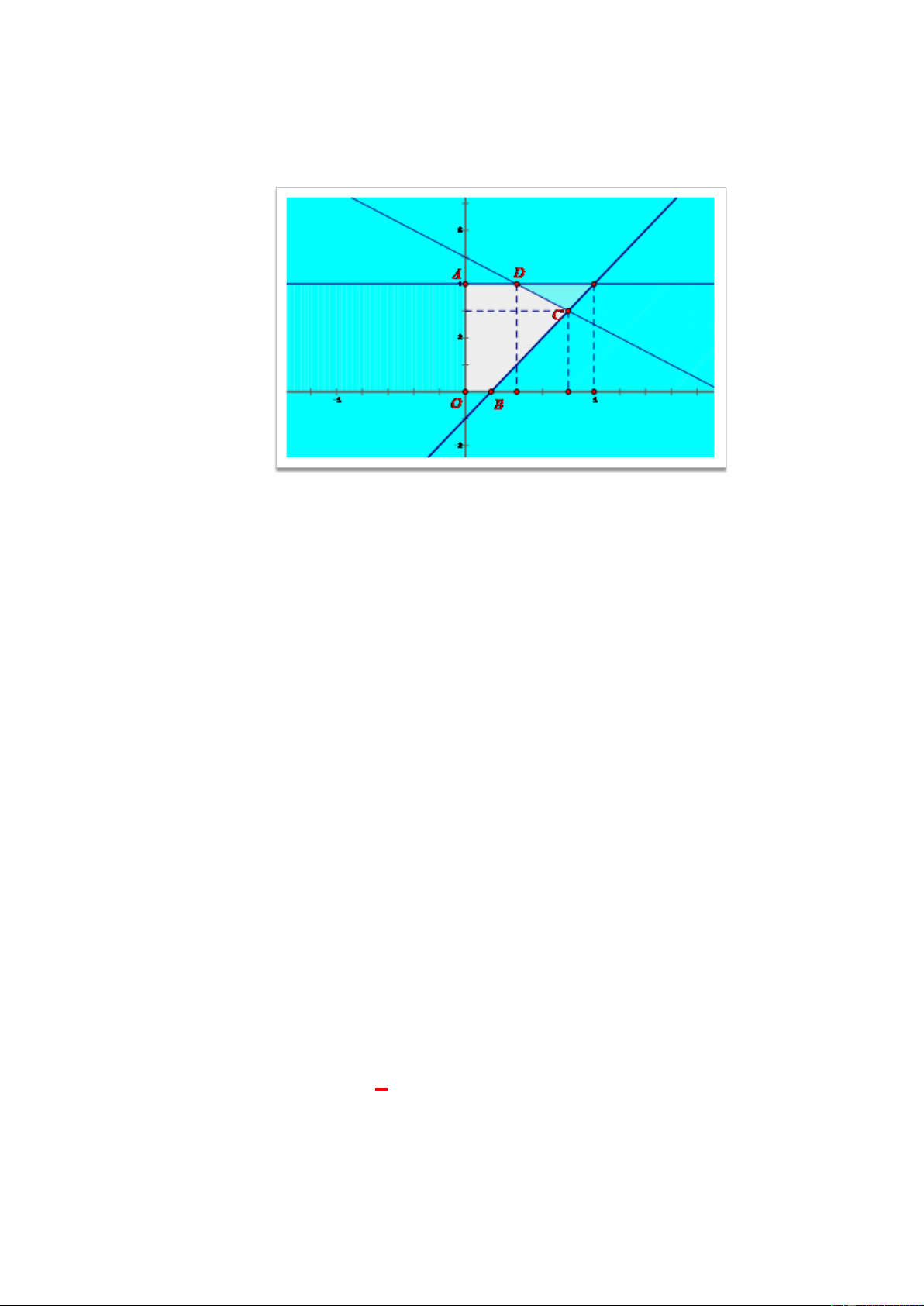
Lời giải
Chọn C
Vẽ các đường thẳng
1
:4dy
;
2
: 1 0d x y
;
3
: 2 10 0d x y
;
: 0; : 0Ox y Oy x
.
Các đường thẳng trên đôi một cắt nhau tại
0;4 , 0;0 , 1;0 , 4;3 , (2;4)A O B C D
Vì điểm
0
1;1M
có toạ độ thoả mãn tất cả các bất pt trong hệ nên ta tô đậm các nửa
mặt phẳng bờ
1 2 3
, , , ,d d d Ox Oy
không chứa điểm
0
M
. Miền không bị tô đậm là đa
giác
OADCB
kể cả các cạnh (hình bên) là miền nghiệm của hệ pt đã cho.
Kí hiệu
( ) ; 2
A A A A
F A F x y x y
, ta có
( ) 8,FA
( ) 0,FO
( ) 1,FB
( ) 10;FC
( ) 10FD
,
0 1 8 10
.
Giá trị lớn nhất cần tìm là
10
.
Câu 9: [0D4-5-3] Giá trị nhỏ nhất của biểu thức
;2F x y x y
, với điều kiện
02
02
0
50
yx
yx
x
y
là
A.
12
. B.
10
. C.
8
. D.
6
.
Lời giải
Chọn B

6
4
2
2
4
6
15
10
5
5
10
15
d
3
d
2
d
1
h
x
( )
=
x
2
g
x
( )
= 2
x
f
x
( )
= 5
B
A
D
C
O
Vẽ các đường thẳng
1
:5dy
;
2
: 2 0d x y
;
3
: 2 0d x y
;
: 0; : 0Ox y Oy x
.
Các đường thẳng trên đôi một cắt nhau tại
0;5A
Vì điểm
0
2;1M
có toạ độ thoả mãn tất cả các bất pt trong hệ nên ta tô đậm các nửa
mặt phẳng bờ
1 2 3
, , , ,d d d Ox Oy
không chứa điểm
0
M
. Miền không bị tô đậm là đa
giác
ABCD
kể cả các cạnh (hình bên) là miền nghiệm của hệ pt đã cho.
Kí hiệu
( ) ; 2
A A A A
F A F x y x y
, ta có
( ) 10, ( ) 4, ( ) 2; ( ) 3F A F B F C F D
,
10 4 3 2
.
Giá trị lớn nhất cần tìm là
10
.
Câu 10: [0D4-5-3] Biểu thức
F y x
đạt giá trị nhỏ nhất với điều kiện
0
5
22
22
x
yx
yx
yx
tại
điểm
;S x y
có toạ độ là
A.
4;1
. B.
3;1
. C.
2;1
. D.
1;1
.
Lời giải
Chọn A
Cách 1: Thử máy tínhTa dùng máy tính lần lượt kiểm tra các đáp án để xem đáp
án nào thỏa hệ bất phương trình trên loại được đáp án D.
Ta lần lượt tính hiệu
F y x
và
min 3F
tại
4,x
1y
.
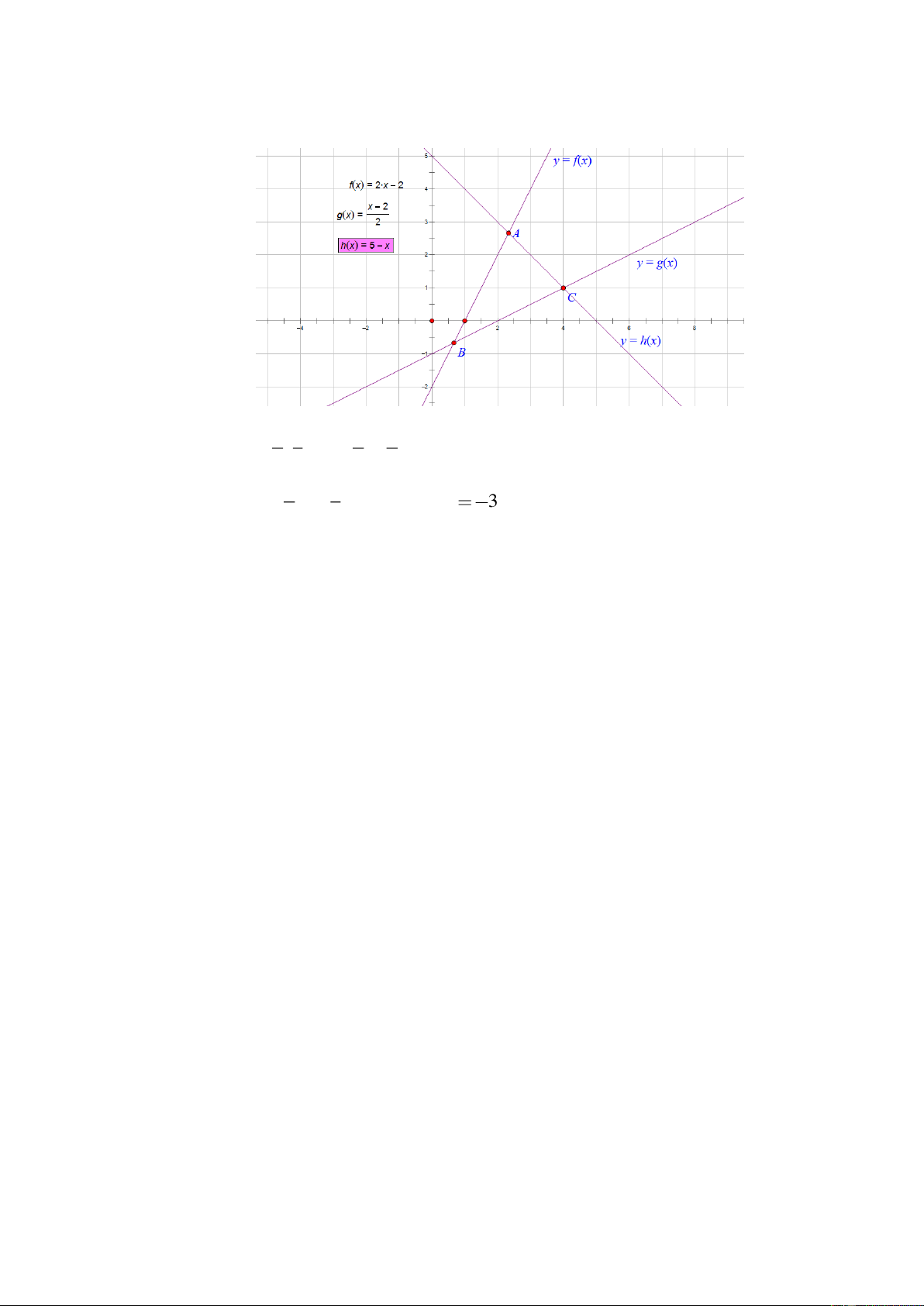
Cách 2: Tự luận:
Tọa độ
78
;
33
A
,
22
;
33
B
,
4;1C
. Giá trị
F
lần lượt tại toạ độ các điểm
,,B C A
là
41
, 3;
33
. Suy ra
min 3F
tại
4;1 .
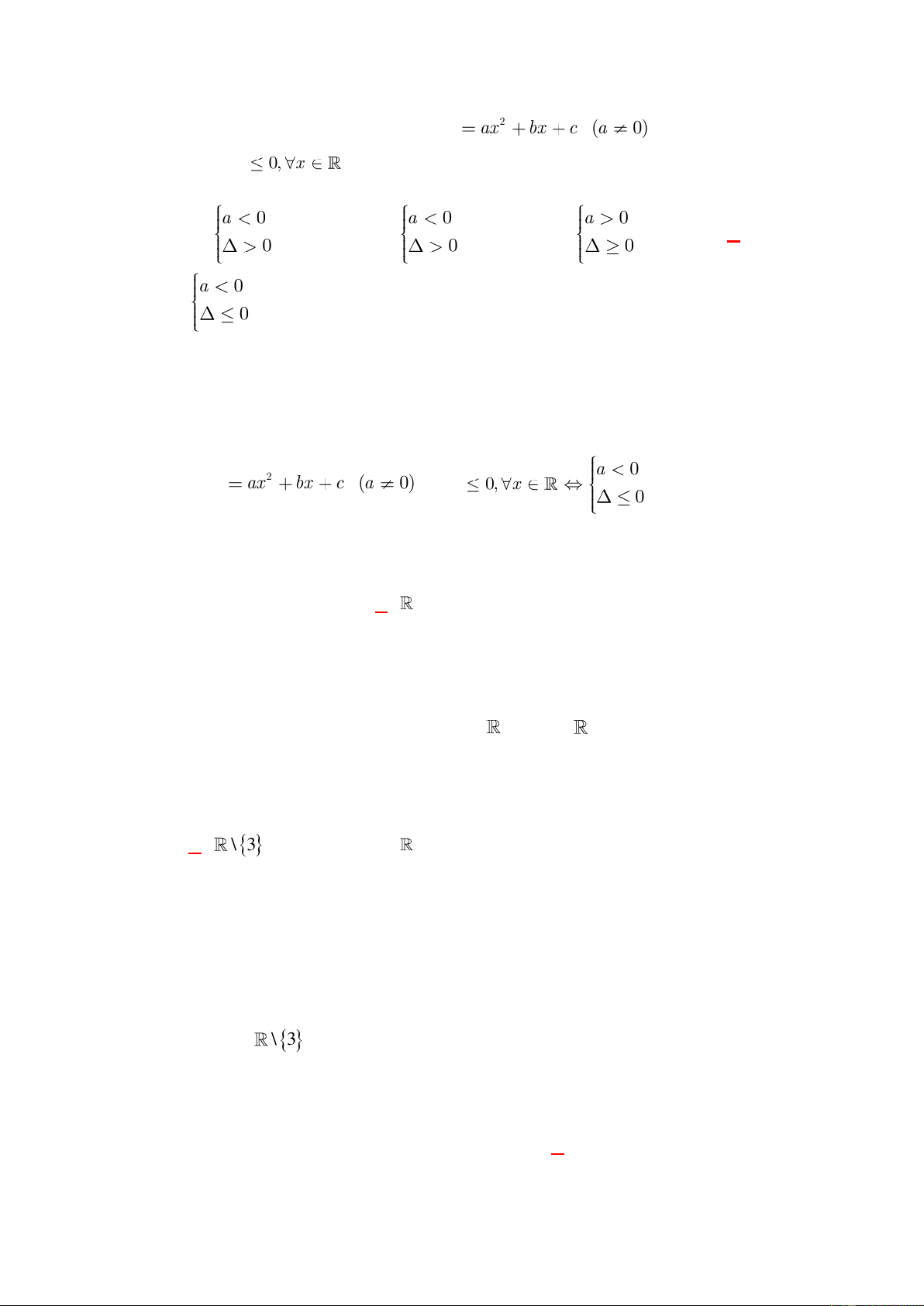
Câu 1: [0D4-6-1] Cho tam thức bậc hai
2
( ) ( 0)f x ax bx c a
. Điều kiện cần và đủ
để
( ) 0,f x x
là:
A.
0
0
a
. B.
0
0
a
. C.
0
0
a
. D.
0
0
a
.
Lời giải
Chọn D
2
( ) ( 0)f x ax bx c a
,
( ) 0,f x x
0
0
a
.
Câu 2: [0D4-6-1] Với
x
thuộc tập hợp nào dưới đây thì
2
23f x x x
luôn dương?
A.
. B. . C.
; 1 3;
. D.
1;3
.
Lời giải
Chọn B
Ta có
2
2
2 3 1 2 2,x x x x
.Vậy
x
.
Câu 3: [0D4-6-1] Với
x
thuộc tập hợp nào dưới đây thì đa thức
2
96f x x x
luôn
dương?
A.
\3
. B. . C.
3;
. D.
;3
.
Lời giải
Chọn A
Ta có
2
9 6 0xx
2
3 0 3xx
.
Vậy
\3x
.
Câu 4: [0D4-6-1] Với
x
thuộc tập hợp nào dưới đây thì đa thức
2
68f x x x
không
dương?
A.
2;3
. B.
;2 4;
. C.
2;4
. D.
1;4
.

Lời giải
Chọn C
Để
fx
không dương thì
2
6 8 0 2 4 0x x x x
Lập bảng xét dấu
fx
ta thấy để
0 2;4f x x
Câu 5: [0D4-6-1] Tam thức
2
23y x x
nhận giá trị dương khi và chỉ khi
A.
–3x
hoặc
–1x
. B.
–1x
hoặc
3x
. C.
–2x
hoặc
6x
. D.
–1 3x
.
Lời giải
Chọn B
2
2 3 0 1 3 0x x x x
1x
hoặc
3x
.
Câu 6: [0D4-6-1] Tam thức
2
12 13y x x
nhận giá trị âm khi và chỉ khi
A.
–13x
hoặc
1x
. B.
–1x
hoặc
13x
. C.
–13 1x
. D.
–1 13x
.
Lời giải
Chọn D
2
12 13 0 1 13 0 1 13x x x x x
.
Câu 7: [0D4-6-1] Tam thức
2
34y x x
nhận giá trị âm khi và chỉ khi
A.
–4x
hoặc
–1x
. B.
1x
hoặc
4x
. C.
–4 –4x
. D.
x
.
Lời giải
Chọn D
22
3 4 0 3 4 0x x x x x
.
Câu 8: [0D4-6-1] Tam thức nào sau đây nhận giá trị âm với mọi
2x
?
A.
2
56y x x
. B.
2
16yx
. C.
2
23y x x
. D.
2
56y x x
.
Lời giải
Chọn D
2
5 6 0 2 3x x x
. Nên loại. A.
2
16 0 4xx
hoặc
4x
. Nên loại. B.
2
2 3 0x x x R
nên loại. C.
22
5 6 0 5 6 0 2x x x x x
hoặc
3x
. Nên
2
5 6 0 2y x x x
.
Vậy đáp án là. D.
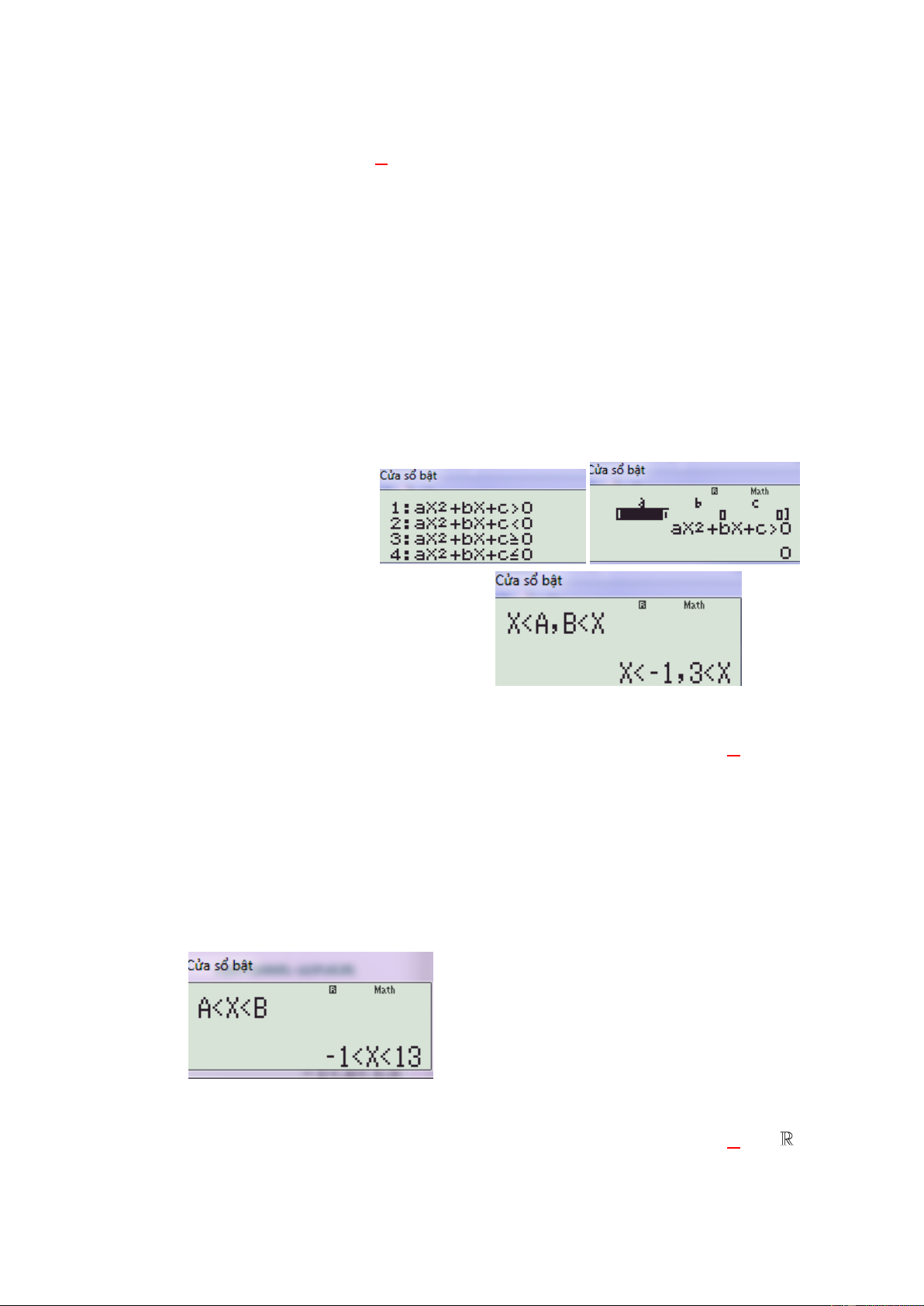
Câu 9: [0D4-6-1] Tam thức
2
23 y x x
nhận giá trị dương khi và chỉ khi
A.
–3x
hoặc
–1x
. B.
–1x
hoặc
3x
. C.
–2x
hoặc
6x
. D.
–1 3x
.
Lời giải
Chọn B
Cách 1: Ta có
2
23y x x
nhận giá trị dương tức là
2
2 3 0 1 3 0x x x x
10
30
3
1
10
30
x
x
x
x
x
x
. Vậy chọn B.
Cách 2: Casio
2
23y x x
nhận giá trị dương tức là
2
2 3 0xx
111MODE
Rồi nhập
1 2 3
; kết quả .
Câu 10: [0D4-6-1] Tam thức
2
12 13 y x x
nhận giá trị âm khi và chỉ khi
A.
–13x
hoặc
1x
. B.
–1x
hoặc
13x
. C.
–13 1x
. D.
–1 13x
.
Lời giải
Chọn D.
Cách 1:
2
12 13y x x
nhận giá trị âm tức là
2
12 13 0 1 13 0x x x x
1 13x
. Vậy chọn. D.
Cách 2: Casio: wR1121=p12=p13==
.
Câu 11: [0D4-6-1] Tam thức
2
34 y x x
nhận giá trị âm khi và chỉ khi
A.
–4x
hoặc
–1x
. B.
1x
hoặc
4x
. C.
–4 –4x
. D.
x
.
Lời giải
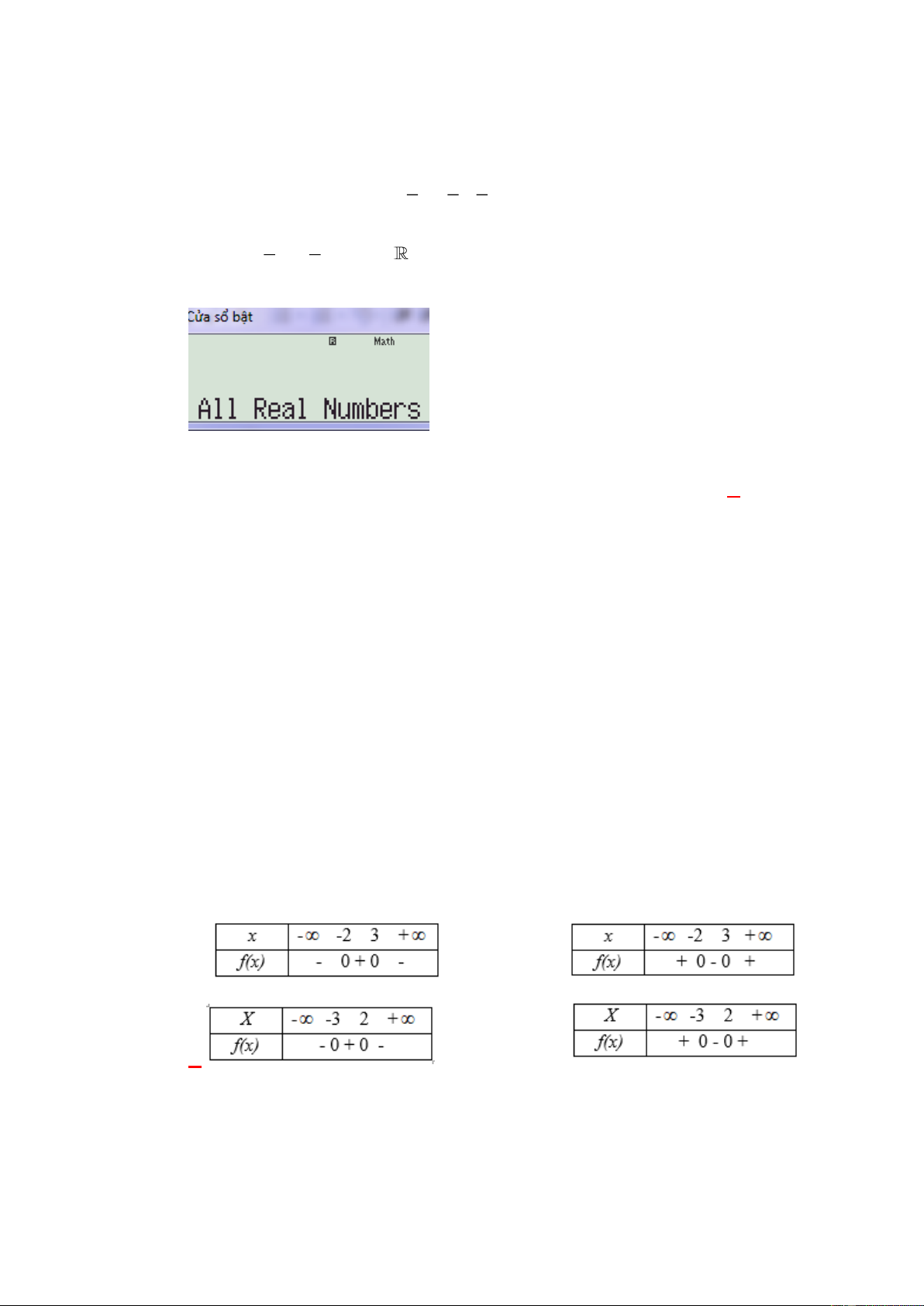
Chọn D
Cách 1:
2
34y x x
nhận giá trị âm khi
22
3 9 7
3 4 0 2. 0
2 4 4
x x x x
2
37
0,
24
xx
. Vậy chọn D.
Cách 2: Casio wR112p1=p3=p4==
( đúng với tất cả các số thực).
Câu 12: [0D4-6-1] Tam thức nào sau đây nhận giá trị âm với mọi
2x
?
A.
2
56 y x x
. B.
2
16yx
. C.
2
23 y x x
. D.
2
56 y x x
.
Lời giải
Chọn D
Cách 1: Ta có
2
5 6 2 3 0 2 3y x x x x x
(loại. A. );
2
4
16 4 4 0
4
x
y x x x
x
(loại B)
2
2
2 3 1 2 0,y x x x x
(loại C)
2
2
5 6 2 3 0
3
x
y x x x x
x
(Chọn D)
Cách 2: Thay
0x
vào từng đáp án; chỉ có D thỏa mãn
60
( đúng).
Câu 13: [0D4-6-1] Bảng xét dấu nào sau đây là bảng xét dấu của tam thức
2
6f x x x
?
A. . B. .
C. . D. .
Lời giải
Chọn C
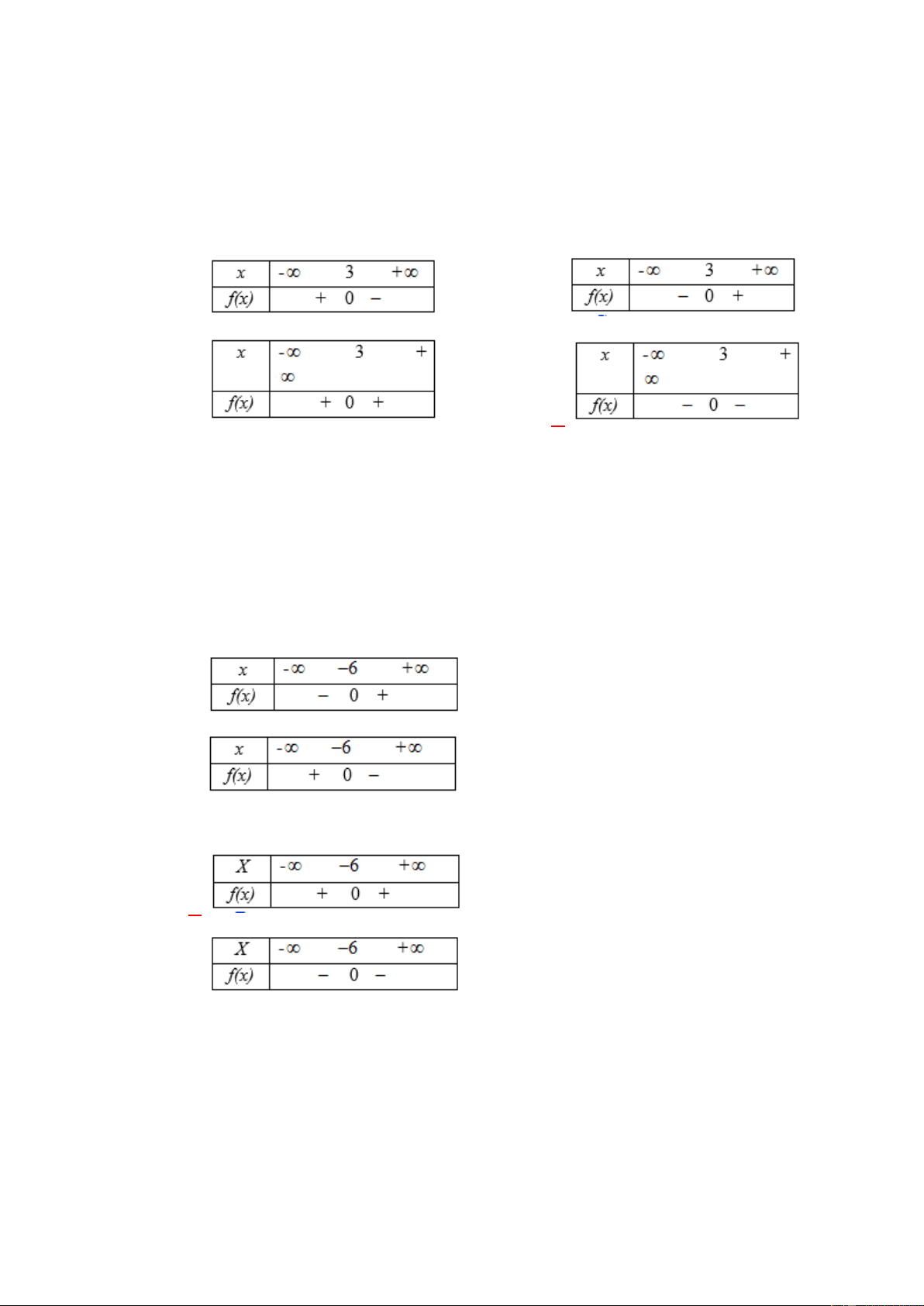
Ta có
2
2
60
3
x
xx
x
và
10a
.
Câu 14: [0D4-6-1] Bảng xét dấu nào sau đây là bảng xét dấu của tam thức
2
69f x x x
?
A. . B. .
C. . D.
.
Lời giải
Chọn D
Ta có
2
6 9 0 3x x x
và
10a
.
Câu 15: [0D4-6-1] Bảng xét dấu nào sau đây là bảng xét dấu của tam thức
2
12 36f x x x
?
A. .
B. .
C. .
D. .
Lời giải
Chọn C
Ta có
2
12 36 0xx
6x
và
10a
.

Câu 1: [0D4-6-2] Các giá trị
m
làm cho biểu thức
2
45f x x x m
luôn luôn dương là
A.
9m
. B.
9m
. C.
9m
. D.
m
.
Lời giải
Chọn C
2
22
4 5 4 4 9 2 9f x x x m x x m x m
.
Ta có:
2
2 0,xx
.
Để
0,f x x
thì
9 0 9mm
.
Câu 2: [0D4-6-2] Cho
2
21f x mx x
. Xc định
m
để
0fx
vi mọi
x
.
A.
1m
. B.
0m
. C.
10m
. D.
1m
và
0m
.
Lời giải
Chọn A
TH1.
0m
. Khi đó:
2 1 0f x x
1
2
x
.
Vậy
0m
không thỏa yêu cầu bài toán.
TH2.
0m
Giải TH2 dài dòng
22
22
1 1 1 1 1
2 1 2. . 1 1f x mx x m x x m x
m m m m m
.
Ta có:
2
1
0,xx
m
.
ycbt
0
1
10
m
m
0
1
0
m
m
m
10m
1m
thỏa điều kiện).
Cách 2:
TH2.
0m
0,f x x
00
1
0 1 0
mm
m
m
.
Câu 3: [0D4-6-2] Vi
x
thuộc tập hợp nào dưi đây thì nhị thức
2
1
43
x
fx
xx
không
dương?
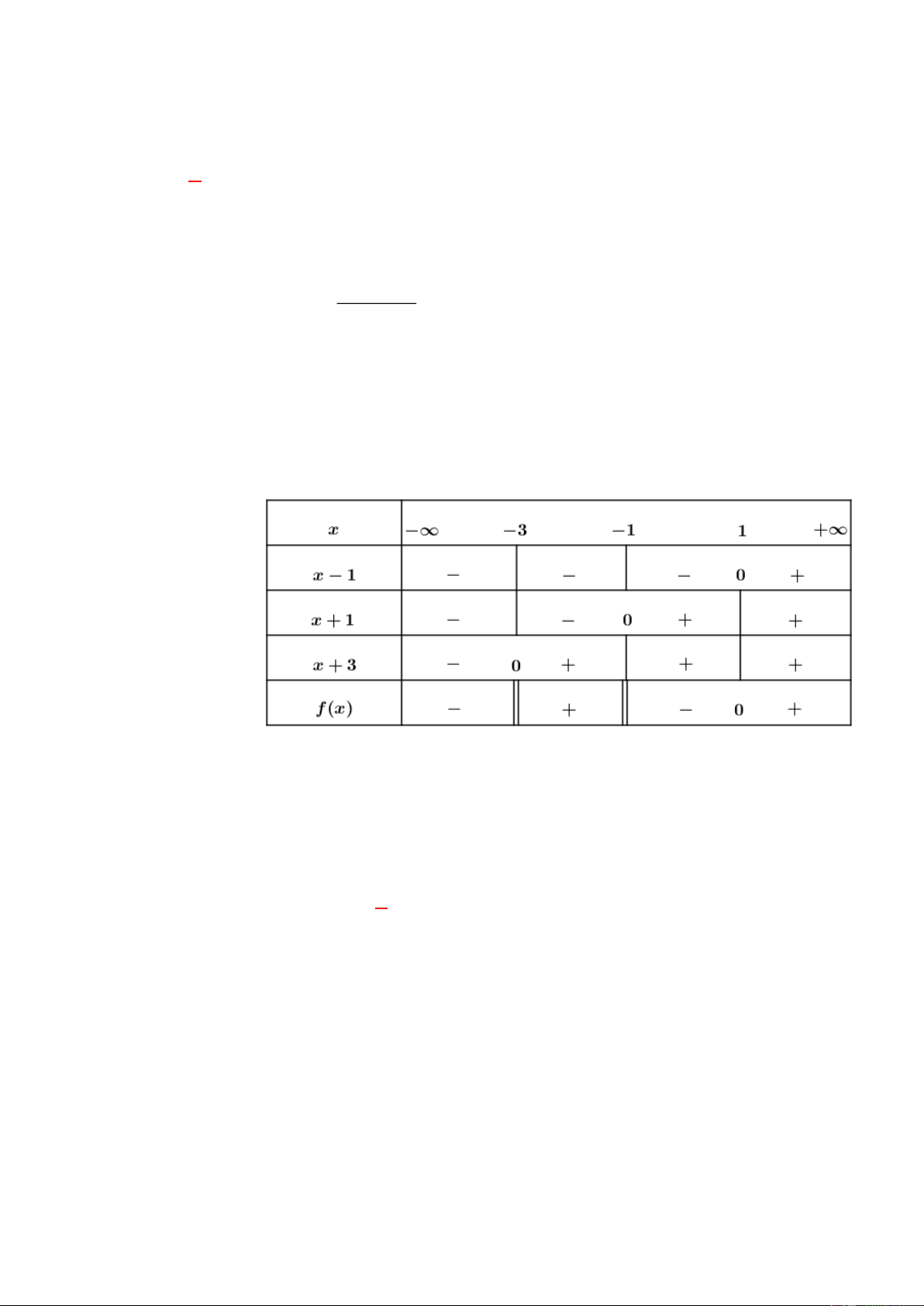
A.
;1S
. B.
3; 1 1;S
.
C.
; 3 1;1S
. D.
3;1S
.
Lời giải
Chọn C
+
2
1
43
x
fx
xx
.
Ta có
1 0 1xx
2
3
4 3 0
1
x
xx
x
+ Xét dấu
fx
:
+ Vậy
0fx
khi
; 3 1;1x
.
Vậy
; 3 1;1x
Câu 4: [0D4-6-2] Vi
x
thuộc tập hợp nào dưi đây thì nhị thức
2
1f x x x
không âm?
A.
; 1 1;
. B.
1;0 1;
. C.
; 1 0;1
. D.
1;1
.
Lời giải
Chọn B
Cho
2
0
1 0 1
1
x
x x x
x
.
Bảng xét dấu
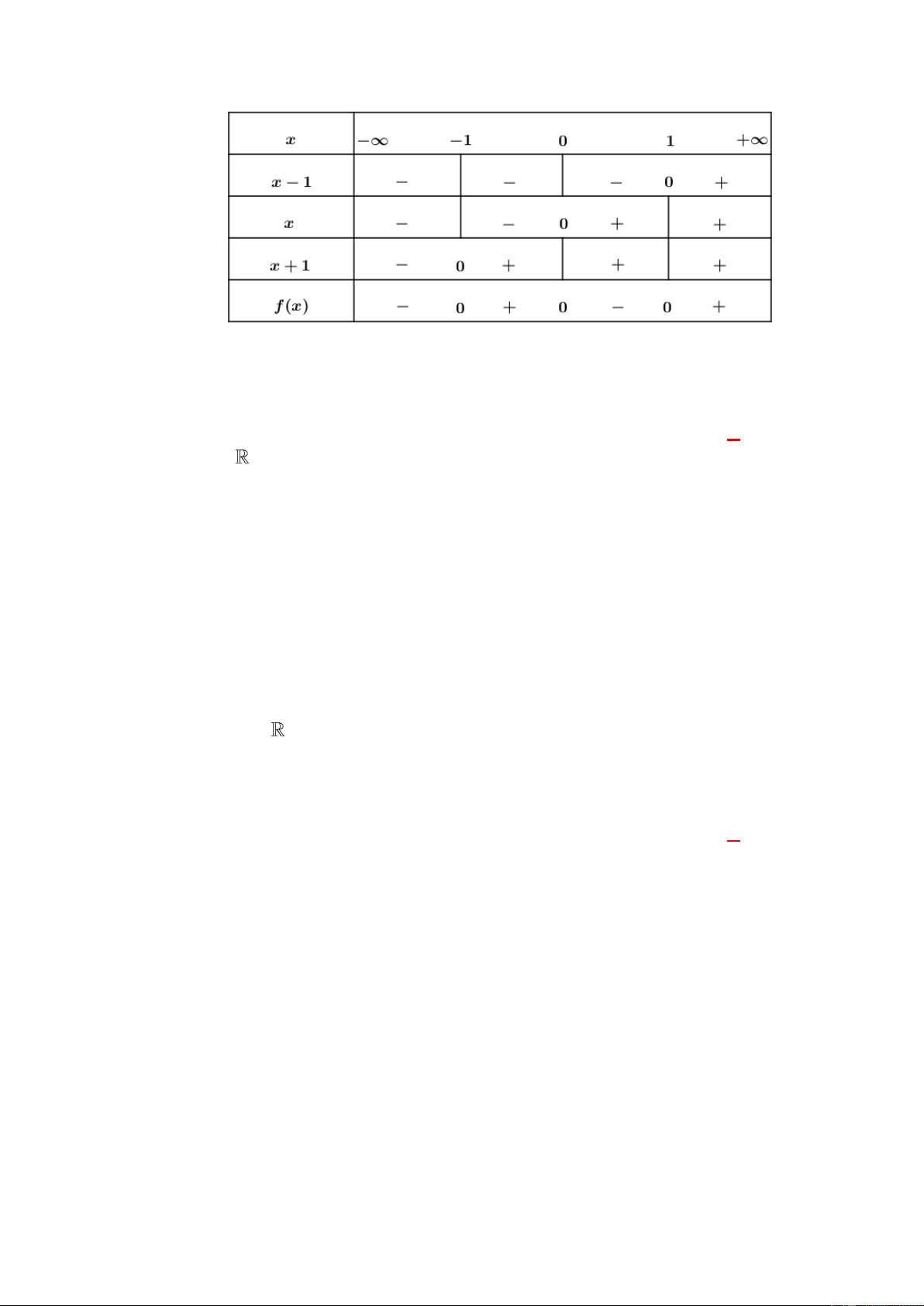
Căn cứ bảng xét dấu ta được
1;0 1;x
Câu 5: [0D4-6-2] Tìm tham số thực
m
để tồn tại
x
thỏa
2
34f x m x mx
âm?
A.
1m
. B.
0m
. C.
1m
hoặc
0m
. D.
m
.
Lời giải
Chọn D
22
3 4 0 1m x mx m m x
.
+ Xét
2
0
0
1
m
mm
m
thì bất phương trình đã cho có nghiệm.
+ Xét
2
0mm
thì bất phương trình đã cho luôn có nghiệm
Vậy
m
thỏa YCBT.
Câu 6: [0D4-6-2] Vi
x
thuộc tập hợp nào dưi đây thì
2
5 2 6f x x x x x
không
dương?
A.
;1 4;
. B.
1;4
. C.
1;4
. D.
0;1 4;
Lời giải
Chọn D
2 2
0 5 45 2 06x x x x x x x
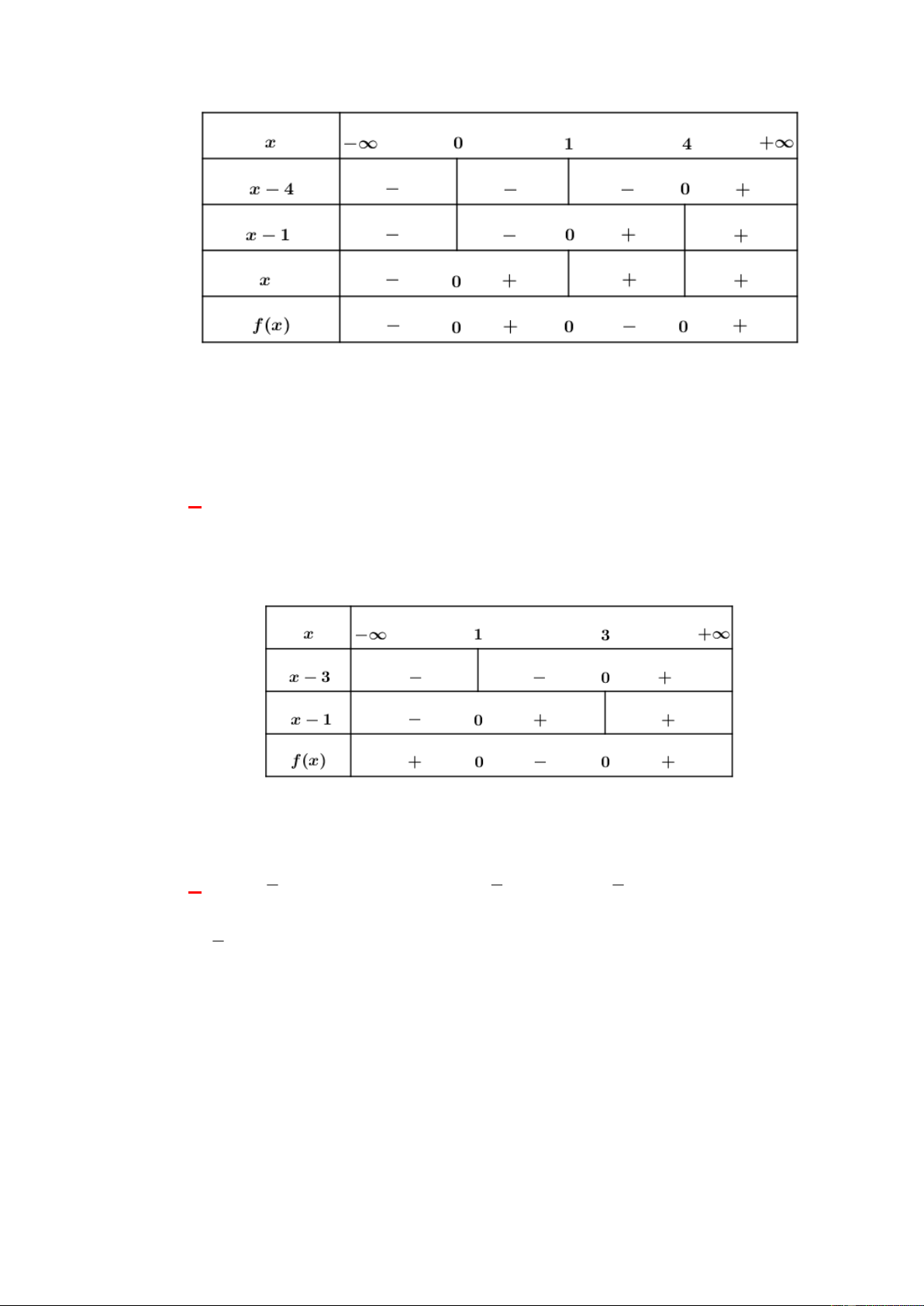
Vậy
0;1 4;x
.
Câu 7: [0D4-6-2] Vi
x
thuộc tập hợp nào dưi đây thì
2
– 4 3f x x x
luôn âm?
A.
;1 3;
. B.
;1 4;
.
C.
1;3
. D.
1;3
.
Lời giải
Chọn C
Vậy
1;3 .x
Câu 8: [0D4-6-2] Vi
x
thuộc tập hợp nào dưi đây thì
2
2 7 –15 f x x x
không âm?
A.
3
; 5;
2
. B.
3
; 5 ;
2
.C.
3
5;
2
. D.
3
;5
2
.
Lời giải
Chọn A

Vậy
3
; 5;
2
x
Câu 9: [0D4-6-2] Vi
x
thuộc tập hợp nào dưi đây thì nhị thức bậc nhất
2
67f x x x
không âm
A.
; 1 7;
B.
1;7
C.
; 7 1;
D.
7;1
.
Lời giải
Chọn B
2
6 7 0 1 7 0x x x x
1;7x
Câu 10: [0D4-6-2] Tìm
x
để
2
56
1
xx
fx
x
không âm.
A.
1;3
. B.
1;2 3;
. C.
2;3
. D.
;1 2;3
.
Lời giải
Chọn B
Điều kiện xc định:
1x
2
23
56
00
11
xx
xx
xx
Ta có:
2
2 3 0
3
x
xx
x
;
1 0 1xx
Bảng xét dấu:

Vậy
1;2 3;x
.
Câu 11: [0D4-6-2] Bảng xét dấu nào sau đây là của tam thức
2
6f x x x
?
A.
x
2
3
fx
0
0
B.
x
2
3
fx
0
0
C.
x
3
2
fx
0
0
D.
x
3
2
fx
0
0
Lời giải
Chọn C
Ta có
2
3
60
2
x
xx
x
Hệ số
10a
Áp dụng định lý về dấu của tam thức bậc hai ta có đp n C là đp n cần tìm.
Câu 12: [0D4-6-2] Bảng xét dấu nào sau đây là của tam thức
2
+ 6 9f x x x
?
A.
.
x
3
fx
0

B.
.
C.
.
D.
.
Lời giải
Chọn C
Tam thức có 1 nghiệm
3x
và hệ số
10a
Vậy đp n cần tìm là C
Câu 13: [0D4-6-2] Bảng xét dấu nào sau đây là của tam thức
2
12 36f x x x
?
A.
.
B.
.
C.
.
x
3
fx
0
x
3
fx
0
x
3
fx
0
x
6
fx
0
x
6
fx
0
x
6
fx
0

D.
.
Lời giải
Chọn C
Tam thức có một nghiệm
6, 1 0xa
đp n cần tìm là C
Câu 14: [0D4-6-2] Dấu của tam thức bậc 2:
2
( ) 5 6f x x x
được xc định như sau
A.
0fx
vi
23x
và
0fx
vi
2x
hoặc
3x
.
B.
0fx
vi
32x
và
0fx
vi
3x
hoặc
2x
.
C.
0fx
vi
23x
và
0fx
vi
2x
hoặc
3x
.
D.
0fx
vi
32x
và
0fx
vi
3x
hoặc
2x
.
Lời giải
Chọn C
Ta có bảng xét dấu
x
2
3
fx
0
0
Vậy
0fx
vi
23x
và
0fx
vi
2x
hoặc
3x
.
Câu 15: [0D4-6-2] Khi xt dấu biểu thức
2
2
4 21
1
xx
fx
x
ta có
A.
0fx
khi
71x
hoặc
13x
.
B.
0fx
khi
7x
hoặc
11x
hoặc
3x
.
C.
0fx
khi
10x
hoặc
1x
.
D.
0fx
khi
1x
.
Lời giải
Chọn B
x
6
fx
0
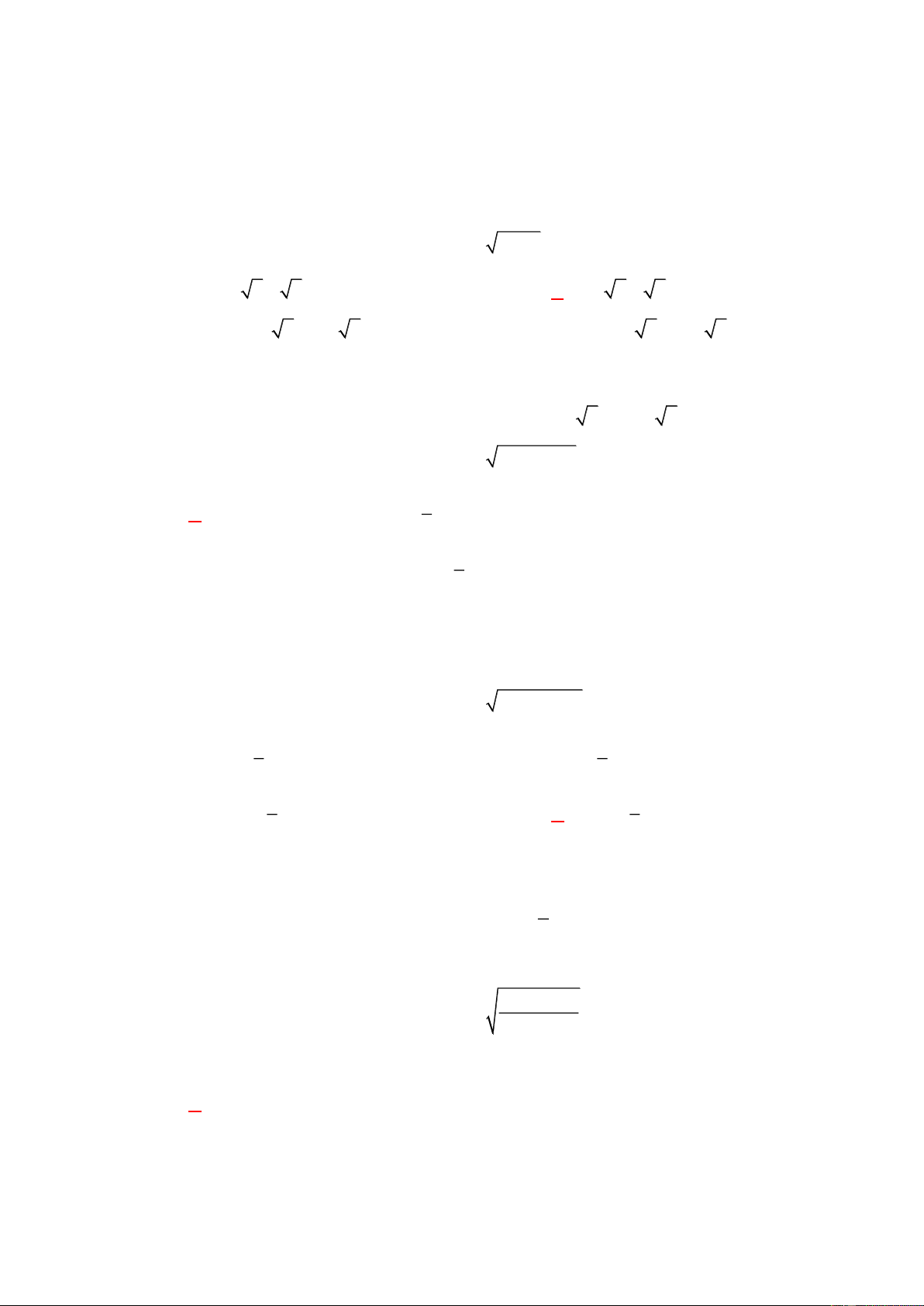
Ta có:
2
4 21 0 7; 3x x x x
và
2
1 0 1xx
. Lập bảng xét dấu ta
có
0fx
khi
7x
hoặc
11x
hoặc
3x
.
Câu 16: [0D4-6-2] Tập xc định của hàm số
2
8yx
là
A.
2 2;2 2
. B.
2 2;2 2
.
C.
; 2 2 2 2;
. D.
; 2 2 2 2;
.
Lời giải
Chọn B
Hàm số xc định khi
22
8 0 8 0 2 2 2 2x x x
.
Câu 17: [0D4-6-2] Tập xc định của hàm số
2
54y x x
là
A.
5;1
. B.
1
;1
5
.
C.
; 5 1;
. D.
1
; 1;
5
.
Lời giải
Chọn A
Hàm số xc định khi
22
5 4 0 4 5 0 5 1x x x x x
.
Câu 18: [0D4-6-2] Tập xc định của hàm số
2
5 4 1y x x
là
A.
1
; 1;
5
. B.
1
;1
5
.
C.
1
; 1;
5
. D.
1
; 1;
5
.
Lời giải
Chọn D
Hàm số xc định khi
2
1
5 4 1 0
4
1
x
xx
x
.
Câu 19: [0D4-6-2] Tập xc định của hàm số
2
2
56
y
xx
là:
A.
; 6 1;
. B.
6;1
.
C.
; 6 1;
. D.
; 1 6;
.
Lời giải
Chọn C
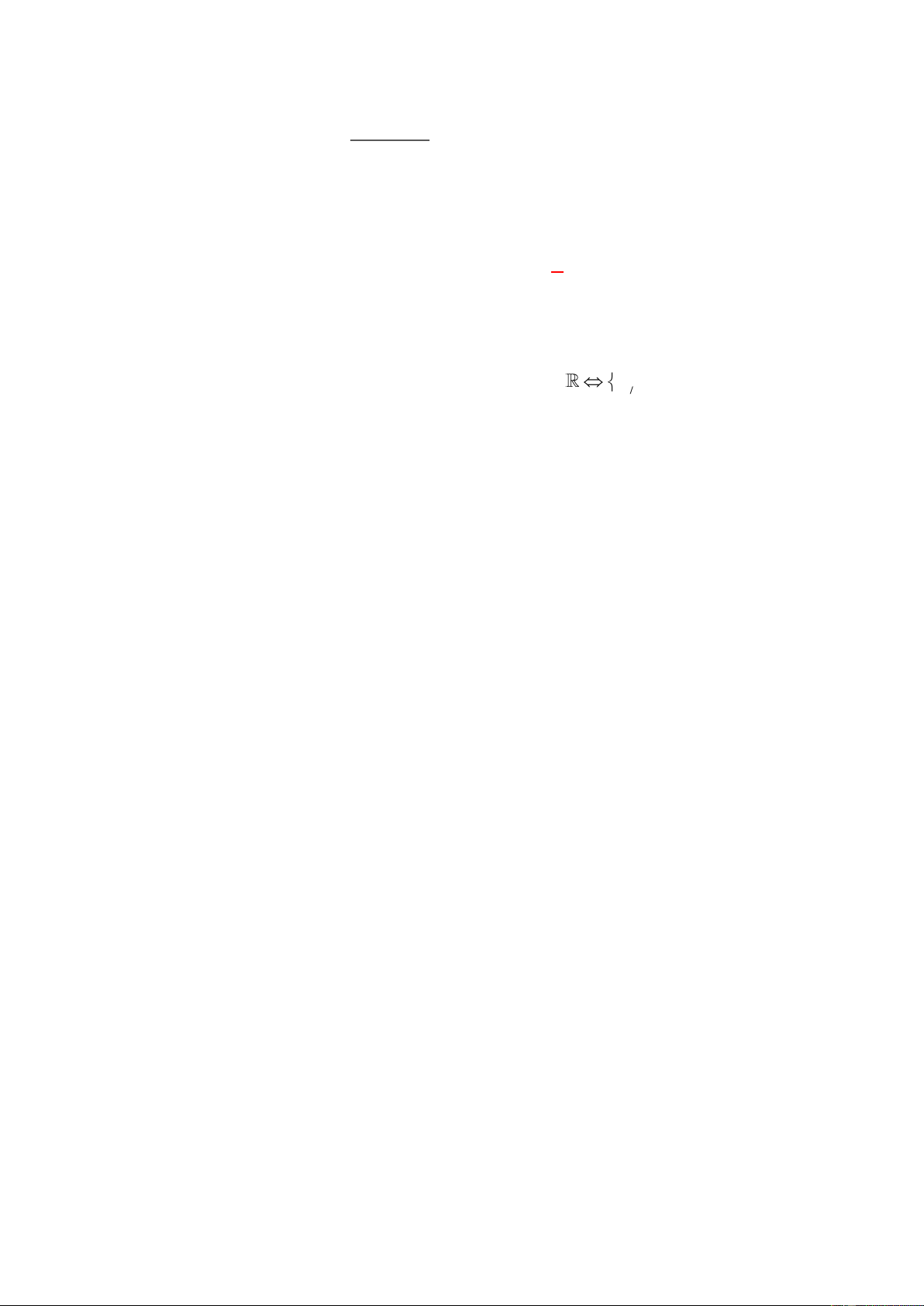
Hàm số xc định khi
2
2
6
2
0 5 6 0
1
56
x
xx
x
xx
.
Câu 20: [0D4-6-2] Biểu thức
22
2 2 2 2m x m x
luôn nhận giá trị dương khi và chỉ
khi:
A.
4m
hoặc
0m
. B.
4m
hoặc
0m
.
C.
40m
. D.
0m
hoặc
4m
.
Lời giải
Chọn B
Ta có
22
/
0
2 2 2 2 0,
0
a
m x m x x
2
2
20
40
m
mm
.
4
0
m
m
.

Câu 1: [0D4-6-3] Các giá trị
m
làm cho biểu thức
2
45 x x m
luôn luôn dương là:
A.
9m
. B.
9m
. C.
9m
. D.
m
.
Lời giải
Chọn C
Ta có:
2
45 x x m
luôn luôn dương
2
4 5 0,x x m x
1 0
9
90
luôn đú
m
nga
m
.
Câu 2: [0D4-6-3] Các giá trị
m
để tam thức
2
( ) ( 2) 8 1 f x x m x m
đổi dấu 2 lần là
A.
0m
hoặc
28m
. B.
0m
hoặc
28m
. C.
0 28m
. D.
0m
.
Lời giải
Chọn B
Ta có:
2
( ) ( 2) 8 1 f x x m x m
đổi dấu
2
lần khi:
2
28 0 ;0 28;0m m m
.
Câu 3: [0D4-6-3] Cho
2
( ) 2 1 f x mx x
. Xc định
m
để
( ) 0fx
vi
x
.
A.
1m
. B.
0m
. C.
10 m
. D.
1m
và
0m
.
Lời giải
Chọn A
TH1.
0m
. Khi đó
1
2 1 0, ,
2
f x x x x x
(vô lý)
TH2.
0m
.
Khi đó:
2
0
( ) 2 1 0, 1
0
am
f x mx x x m
m
Vậy
1m
thỏa mãn bài toán.
Câu 4: [0D4-6-3] Cho hàm số
2
( ) 2 3 2f x x mx m
. Tìm m để
( ) 0,f x m
?
A.
1;2m
. B.
1;2m
. C.
;1m
. D.
2;m
.
Lời giải
Chọn A
22
( ) 2 3 2 0, 3 2 0 1 2f x x mx m x m m m
.

Câu 5: [0D4-6-3] Cho hàm số
2
( ) 2 1f x mx mx m
. Tìm
m
để
( ) 0,f x m
?
A.
0m
. B.
0m
. C.
0m
. D.
0m
.
Lời giải
Chọn A
TH1.
0m
.Khi đó:
1 0,f x x
.
TH2.
0m
Khi đó:
2
2
0
0
( ) 2 1 0, 0
0
10
am
m
f x mx mx m x m
m
m m m
.
Vậy
0m
thỏa mãn bài toán.
Câu 6: [0D4-6-3] Tìm số nguyên ln nhất của
x
để đa thức
22
4 2 4
9 3 3
xx
fx
x x x x
luôn âm.
A.
2x
. B.
1x
. C.
2x
. D.
1x
.
Lời giải
Chọn A
Điều kiện
2
2
9 0 3
3 0 3
0
30
xx
xx
x
xx
.
Ta có
2 2 2 2
4 2 4 4 2 4
0
9 3 3 9 3 3
x x x x
x x x x x x x x
4 2 3 4 3
0
33
x x x
xx
3 22
0
33
x
xx
.
Bảng xét dấu

Dựa vào bảng xét dấu ta có
22
, 3,3
3
x
.
Vậy
2x
thỏa YCBT.
Câu 7: [0D4-6-3] Giá trị ln nhất của hàm số
2
2
59
fx
xx
bằng
A.
11
4
. B.
4
11
. C.
11
8
. D.
8
11
.
Lời giải
Chọn D
2
2
22
59
5 11
24
fx
xx
x
Ta có:
2
5 11
0
24
x
()fx
đạt giá trị ln nhất
2
5 11
24
x
nhỏ nhất
2
5 11
0
24
5
2
x
x
Khi đó
ax
8
11
m
fx
.
Câu 8: [0D4-6-3] Giá trị nhỏ nhất của hàm số
2
()
21
x
fx
x
vi
1 x
là
A.
2
. B.
5
2
. C.
22
. D. 3.
Lời giải
Chọn B
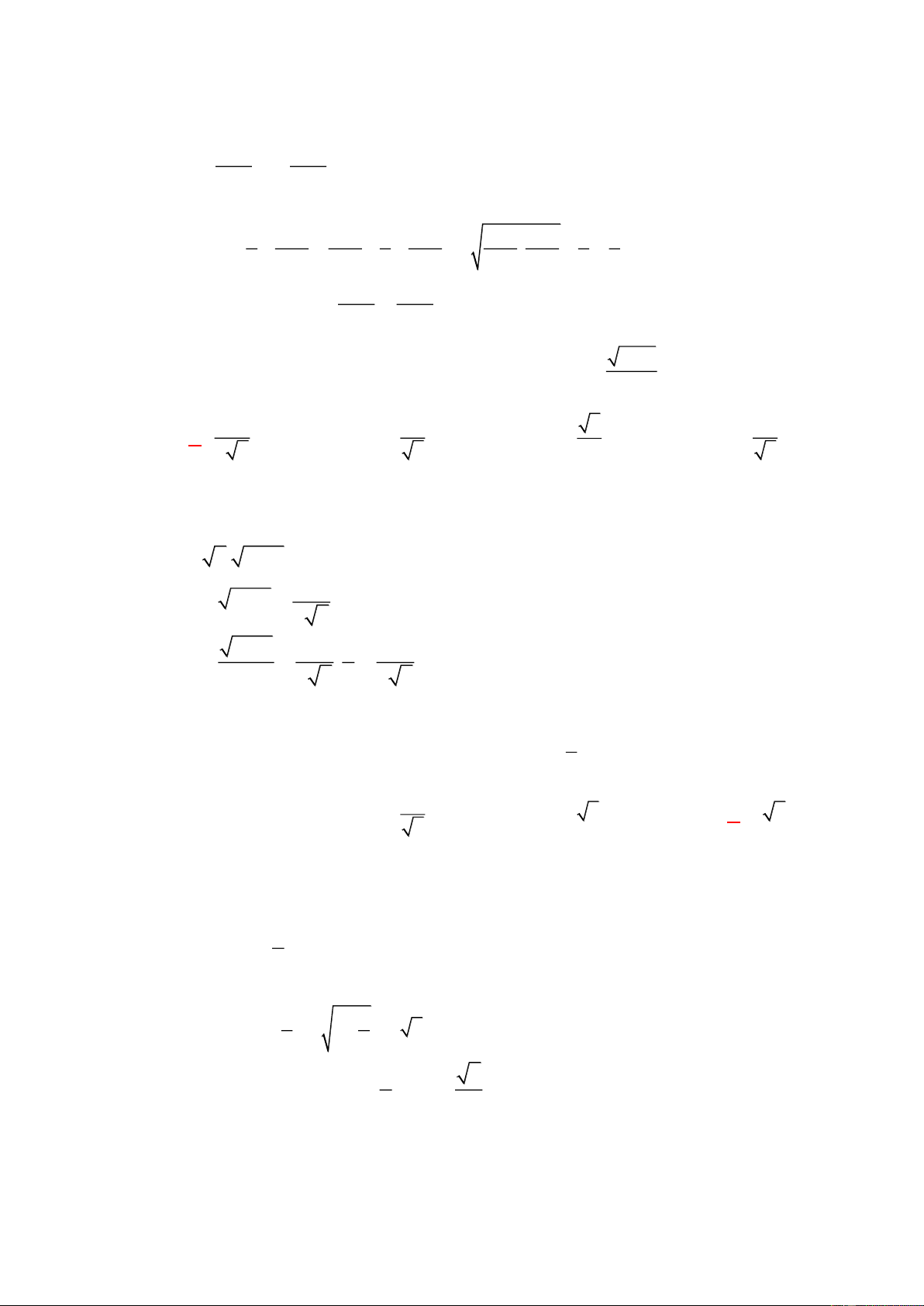
1
12
0; 0
21
x
x
x
Áp dụng bdt cosi ta có:
2 1 1 2 1 2 1 5
( ) 2 .
2 1 2 2 1 2 1 2 2
x x x
fx
x x x
.
Dấu “=” xảy ra khi
2
12
1 4 3( 1)
21
x
x x x
x
.
Câu 9: [0D4-6-3] Cho
2x
. Giá trị ln nhất của hàm số
2
()
x
fx
x
bằng
A.
1
22
. B.
2
2
. C.
2
2
. D.
1
2
.
Lời giải
Chọn A
Ta có:
2 2. 2 2 2 (cos )
2
22
2 1 1
.
2 2 2 2
x x x i
x
x
xx
xx
Dấu “=” xảy ra khi
4x
.
Câu 10: [0D4-6-3] Giá trị nhỏ nhất của hàm số
1
( ) 2f x x
x
vi
0x
là
A.
2
. B.
1
2
. C.
2
. D.
22
.
Lời giải
Chọn D
0
1
2 0; 0
x
x
x
Áp dụng bdt cosi ta có:
11
( ) 2 2 2 . 2 2f x x x
xx
.
Dấu “=” xảy ra khi
12
2 ( 0)
2
x x x
x
.

Câu 11: [0D4-6-3] Phương trình
2
2( 1) 3 0x m x m
có hai nghiệm đối nhau khi và chỉ
khi
A.
3m
. B.
1m
. C.
1m
. D.
13m
.
Lời giải
Chọn C
2
2( 1) 3 0x m x m
có 2 nghiệm đối nhau khi
2
0
3 4 0
1
0
10
mm
m
S
m
.
Câu 12: [0D4-6-3] Phương trình
2
0x x m
vô nghiệm khi và chỉ khi:
A.
3
4
m
. B.
3
4
m
. C.
1
4
m
. D.
5
4
m
.
Lời giải
Chọn C
2
0x x m
vô nghiệm khi
1
0 1 4 0
4
mm
.

Câu 1: [0D4-7-1] Tập nghiệm của bất phương trình
2
10x
là:
A.
1;
. B.
1;
. C.
1;1
. D.
; 1 1;
.
Lời giải
Chọn D
Cách 1: Ta có
2
1
1 0 1 1 0
1
x
x x x
x
( chọn D)
Cách 2 : Casio.
Câu 2: [0D4-7-1] Tập nghiệm của bất phương trình
2
9x
là:
A.
–3;3
. B.
;3
. C.
;3
. D.
; 3 3;
.
Lời giải
Chọn A
Ta có
2
9 3 3 3x x x
( chọn A).
Câu 3: [0D4-7-1] Tìm tập xác định của hàm số
2
2 5 2y x x
.
A.
1
;
2
D
. B.
[2; )
. C.
1
; [2; )
2
. D.
1
;2
2
.
Lời giải
Chọn C
Hàm số
2
2 5 2y x x
xác định khi và chỉ khi
2
1
2 5 2 0 ; 2;
2
x x x
.
Câu 4: [0D4-7-1] Tập xác định của hàm số
2
45y x x x
là:
A.
5;1D
. B.
5;1D
.
C.
; 5 1;D
. D.
; 5 1;D
.
Lời giải
Chọn C
Điều kiện xác định:
2
4 5 0xx
51xx

Tập xác định:
; 5 1;D
.
Câu 5: [0D4-7-1] Điều kiện của phương trình
1 4 3
2
1
2
x
x
x
x
là:
A.
2x
và
1x
. B.
2x
và
4
3
x
.
C.
2, 1xx
và
4
3
x
. D.
2x
và
1x
.
Lời giải
Chọn C
Điều kiện xác định của phương trình là
2
20
4
4 3 0
3
10
1
x
x
xx
x
x
.
Câu 6: [0D4-7-1] Tập nghiệm của bất phương trình
1 2 2 5 1 0x x x
là:
A.
1
1;
2
S
. B.
5
1;
2
S
.
C.
15
1; ;
22
S
. D.
1;S
.
Lời giải
Chọn C
Bất phương trình
2 1 2 5 1 0 x x x
Lập bảng xét dấu dễ dàng ta được
15
1; ;
22
S
.
Câu 7: [0D4-7-1] Tập nghiệm của bất phương trình
2
4 4 0xx
là:
A.
2;
. B. . C.
\2
.
D.
\2
.
Lời giải
Chọn C
2
2
4 4 0 2 0 2 0 2x x x x x
.
Tập nghiệm của bất phương trình là
\2
.
Câu 8: [0D4-7-1] Tập nghiệm của bất phương trình
2
6 9 0xx
là:
A.
3;
. B. .
C.
\3
.
D.
\3
.
Lời giải

Chọn D
2
2
6 9 0 3 0 3 0 3x x x x x
.
Vậy tập nghiệm của bất phương trình là
\3
.
Câu 9: [0D4-7-1] Tập nghiệm của bất phương trình
2
6 9 0xx
là:
A.
3;
. B. .
C.
\3
.
D.
\3
.
Lời giải
Chọn C
2
2
6 9 0 3 0 3 0 3x x x x x
.
Vậy tập nghiệm của bất phương trình là
\3
.
Câu 10: [0D4-7-1] Tập nghiệm của bất phương trình
2
2 1 0xx
là:
A.
1;
. B. .
C.
\1
.
D.
\1
.
Lời giải
Chọn D
2
2
2 1 0 1 0 1 0 1x x x x x
.
Vậy tập nghiệm của bất phương trình là
\1
.
Câu 11: [0D4-7-1] Tập nghiệm của bất phương trình
2
2 1 0xx
là:
A.
1;
. B. .
C.
\1
.
D.
\1
.
Lời giải
Chọn D
2
2
2 1 0 1 0 1 0 1x x x x x
.
Vậy tập nghiệm của bất phương trình là
\1
.
Câu 12: [0D4-7-1] Tập nghiệm của bất phương trình
2
10x
là:
A.
1;
. B.
1;
. C.
1;1
. D.
; 1 1;
.
Lời giải
Chọn D
2
1 0 1xx
hoặc
1x
.
Vậy tập nghiểm của bất phương trình là :
; 1 1;
.
Câu 13: [0D4-7-1] Tập nghiệm của bất phương trình
2
10xx
là:
A.
R
. B.
1 5 1 5
;;
22
.

C.
1 5 1 5
;
22
. D.
; 1 5 1 5;
.
Lời giải
Chọn B
2
15
10
2
x x x
hoặc
15
2
x
.
Vậy tập nghiệm của bất phương trình là
1 5 1 5
;;
22
.
Câu 14: [0D4-7-1] Tập nghiệm của bất phương trình
2
4 4 0xx
là:
A.
2;
. B. .
C.
\2
.
D.
\2
.
Lời giải
Chọn D
2
2
4 4 0 2 0 2x x x x
.
Vậy tập nghiệm của bất phương trình là
\2
.
Câu 15: [0D4-7-1] Tập nghiệm của bất phương trình
2
4 2 8 0xx
là:
A.
;2 2
. B.
\ 2 2
. C.
. D.
.
Lời giải
Chọn C
2
2
4 2 8 0 2 2 0x x x x
.
Vậy tập nghiệm của bất phương trình là
.
Câu 16: [0D4-7-1] Tập nghiệm của bất phương trình
2
60xx
là:
A.
; 3 2;
. B.
3;2
. C.
2;3
. D.
; 2 3;
.
Lời giải
Chọn C
2
6 0 2 3x x x
.
Vậy tập nghiệm của bất phương trình là
2;3
.
Câu 17: [0D4-7-1] Tập nghiệm của bất phương trình
2
9x
là:
A.
–3;3
. B.
;3
. C.
;3
. D.
; 3 3;
.
Lời giải
Chọn A
22
9 9 0 3 3x x x
.

Câu 18: [0D4-7-1] Tập nghiệm củabất phương trình
2
6 2 18 0xx
là:
A.
3 2;
. B.
3 2;
. C.
. D. .
Lời giải
Chọn D
2
2
6 2 18 3 2 0,x x x x
.
Cách khác : Ta có
2
2
/
10
6 2 18 0,
3 2 18 0
a
x x x
.
Câu 19: [0D4-7-1] Tập nghiệm của bất phương trình
2
3 2 6 0xx
là:
A.
2; 3
. B.
2; 3
. C.
3; 2
. D.
3; 2
.
Lời giải
Chọn D
2
3 2 6 0 3 2x x x
.
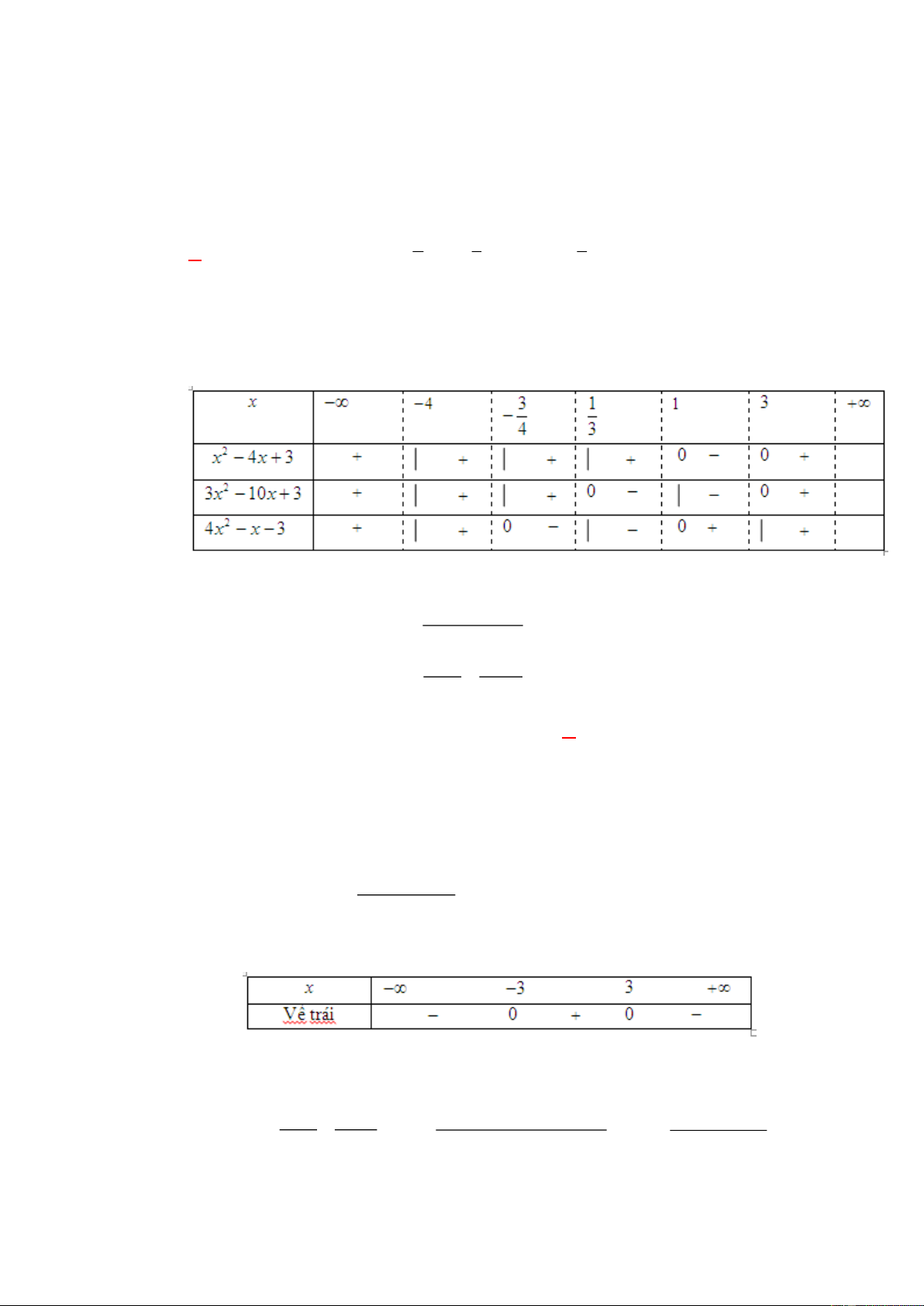
Câu 1: [0D4-7-2] Hệ bất phương trình:
2
2
2
4 3 0
3 10 3 0
4 3 0
xx
xx
xx
có nghiệm là:
A.
3x
. B.
31
43
x
. C.
1
1
3
x
. D.
13x
Lời giải
Chọn A
BXD chung :
Vậy hệ bpt có nghiệm
3x
.
Câu 2: [0D4-7-2] Hệ bất phương trình
2
2
9
0
3 12
7 3 1
0
52
x
xx
xx
x
có nghiệm là:
A.
3x
hoặc
1x
. B.
35x
. C.
13x
. D.
13x
.
Lời giải
Chọn C
Xét bất phương trình:
2
2
9
0
3 12
x
xx
.
Bảng xét dấu:
Vậy nghiệm bất phương trình là:
1
3;3S
.
Xét bất pt:
7 3 1
0
52
xx
x
2 14 (3 1)( 5)
0
2( 5)
x x x
x
2
3 12 9
0
25
xx
x
.
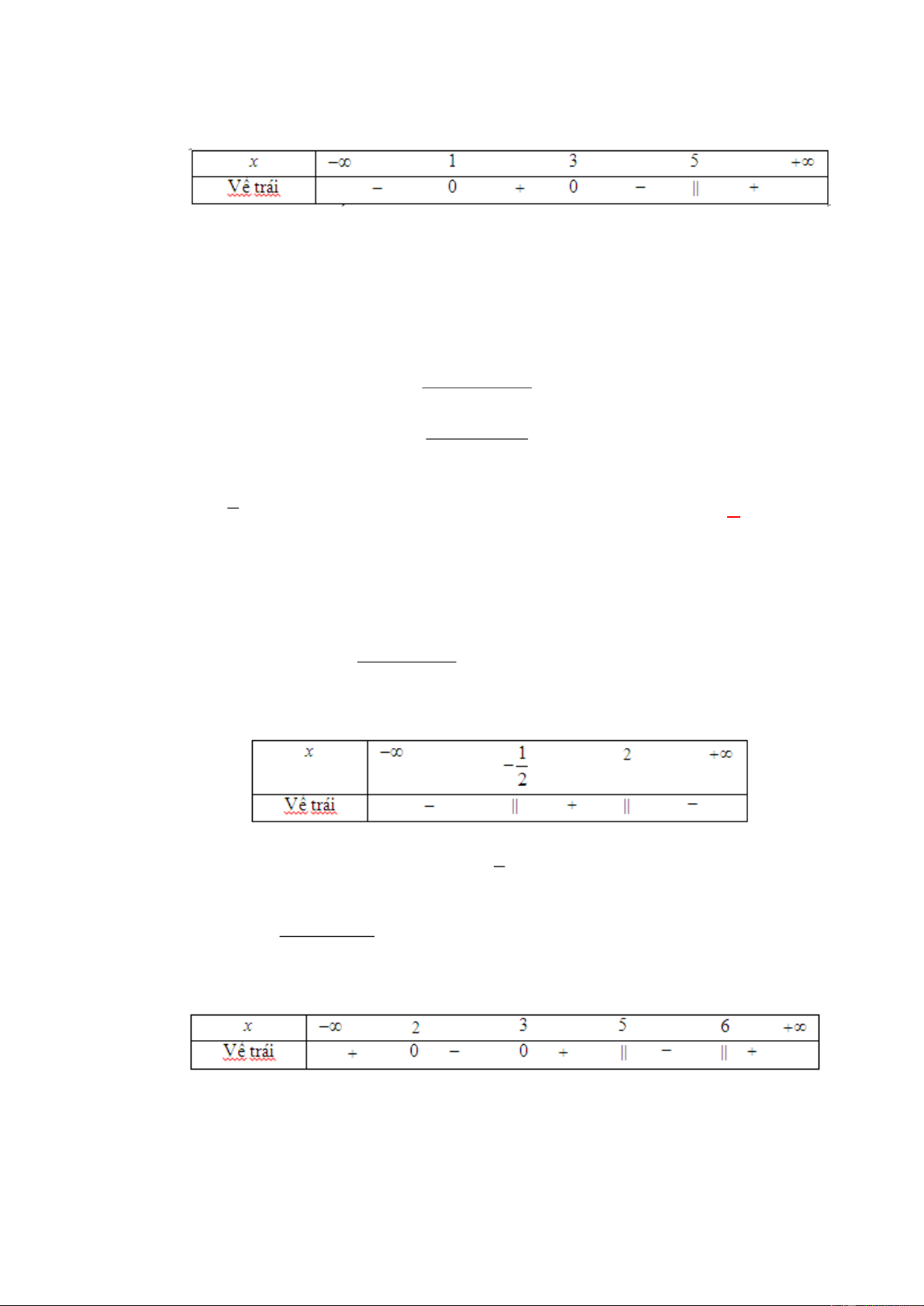
Bảng xét dấu:
Vậy nghiệm của bất phương trình là:
2
1;3 5;S
.
Vậy nghiệm của hệ bất phương trình là:
12
1;3S S S
.
Câu 3: [0D4-7-2] Hệ bất phương trình
0
30x11x
6x5x
0
2x3x2
7x5x
2
2
2
2
có nghiệm là:
A.
1
2
2
x
. B.
23x
. C.
03x
. D.Vô
nghiệm .
Lời giải
Chọn D
Xét bất phương trình:
2
2
57
0
2 3 2
xx
xx
.
Bảng xét dấu:
Tập nghiệm bất phương trình là:
1
1
;2
2
S
.
Xét bất pt:
2
2
56
0
11 30
xx
xx
.
Bảng xét dấu:
Tập nghiệm của bất phương trình là:
2
2;3 5;6S
.
Vậy nghiệm của hệ bất phương trình là:
12
S S S
.
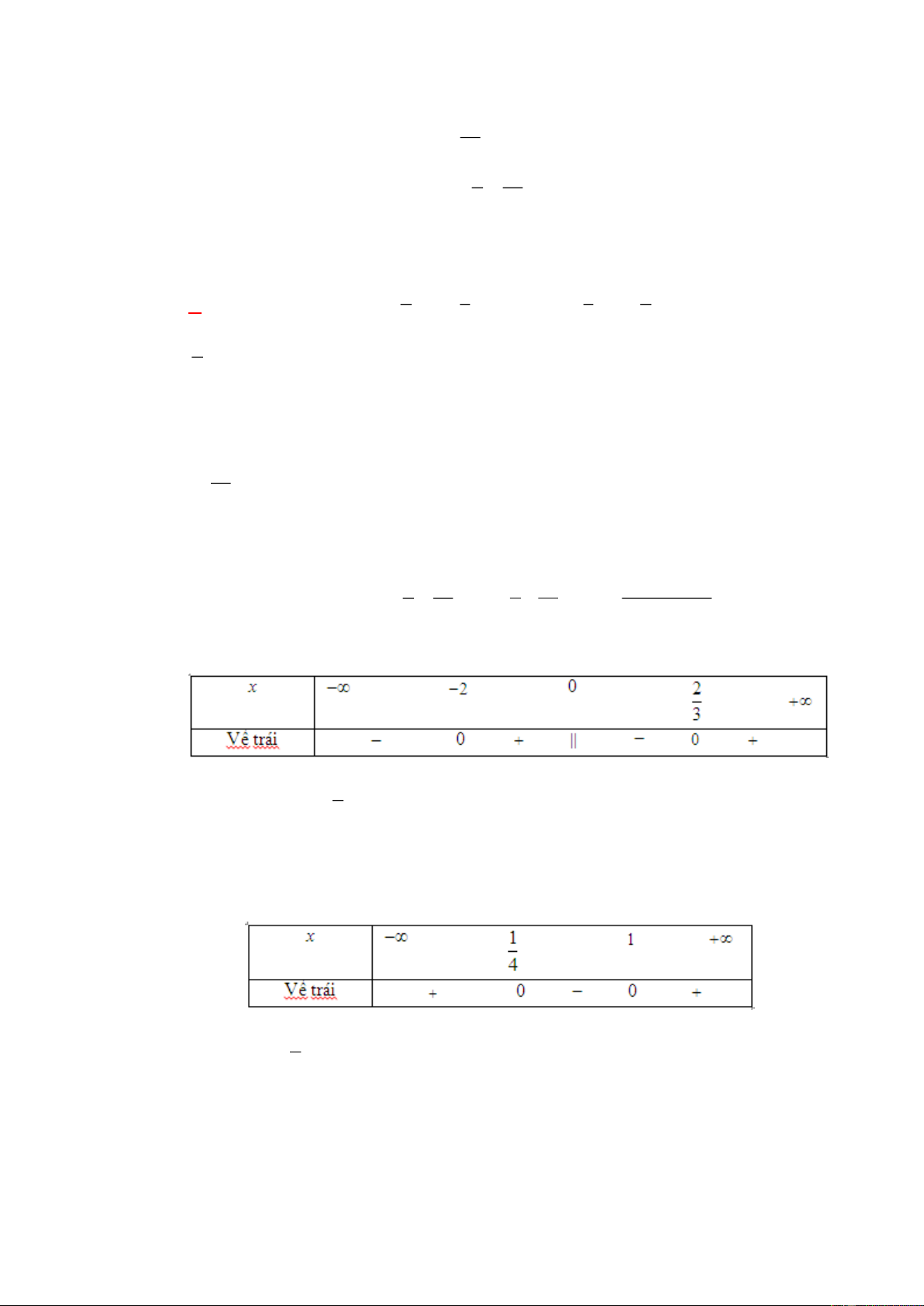
Câu 4: [0D4-7-2] Hệ bất phương trình:
2
1
0
3
44
33
4 5 1 0
x
x
x
xx
có nghiệm là:
A.
20x
. B.
11
43
x
C.
12
33
x
. D.
2
1
3
x
.
Lời giải
Chọn A
1
00
3
x
x
.
1
;0S
.
Xét bất phương trình:
44
33
x
x
44
0
33
x
x
2
3 4 4
0
3
xx
x
.
Bảng xét dấu:
2
2
2;0 ;
3
S
.
Xét bất pt:
2
4 5 1 0xx
.
Bảng xét dấu:
3
1
; 1;
4
S
.
Vậy nghiệm của hệ bất phương trình là:
1 2 3
2;0S S S S
.
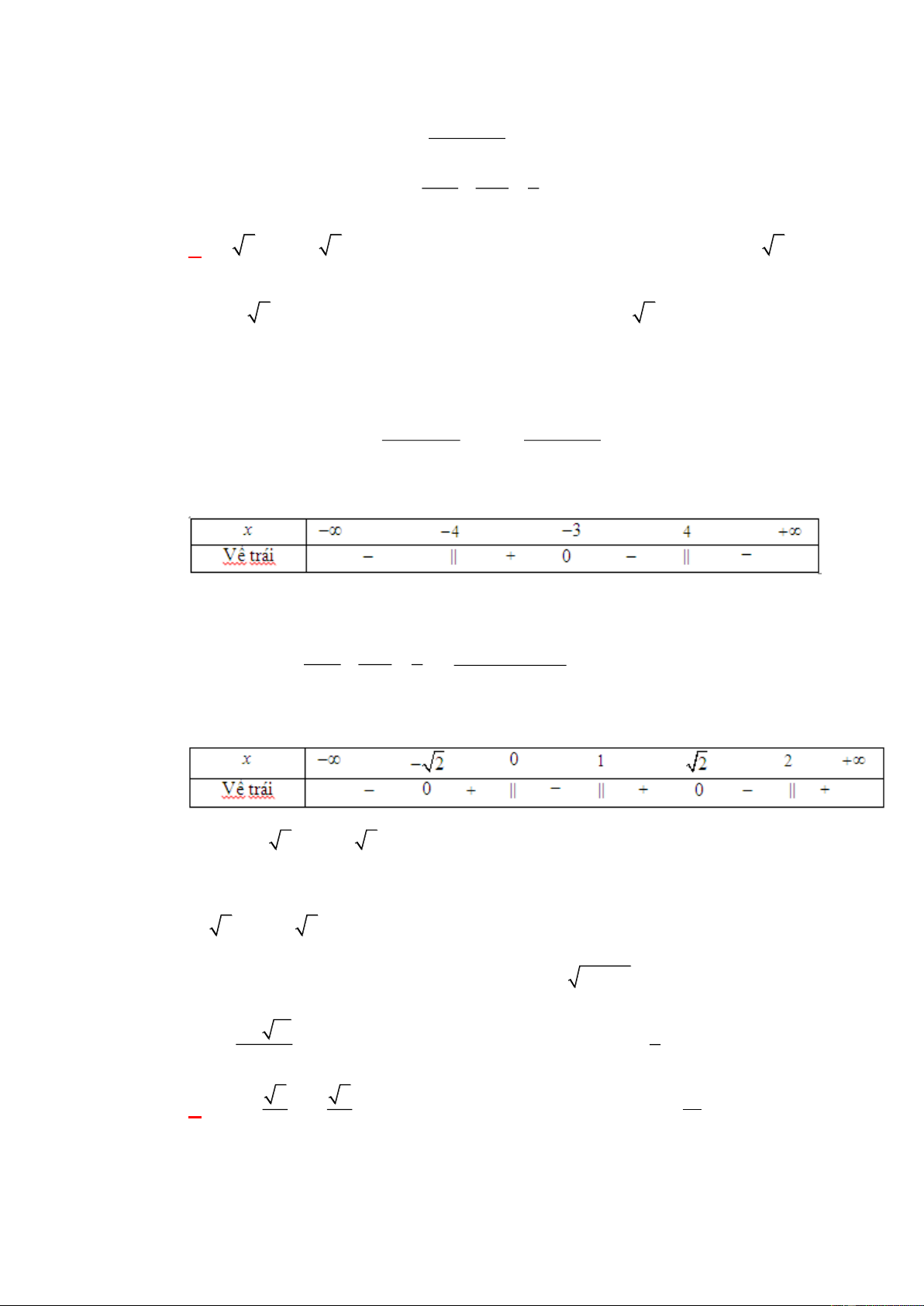
Câu 5: [0D4-7-2] Hệ bất phương trình
2
16 4
4
12
1 1 1
21
x
xx
x x x
có nghiệm là:
A.
2;0 1; 2 2;4 4;
. B.
4; 3 0;1 2;2
C.
3; 2 4;
. D.
4; 2 1;
.
Lời giải
Chọn A
Giải bất phương trình:
2
16 4
4
12
x
xx
2
2
4 64
0
12
x
xx
.
Bảng xét dấu:
1
; 4 3;4 4;S
.
Giải bất pt:
1 1 1
21x x x
2
2
0
12
x
x x x
.
Bảng xét dấu:
2
2;0 1; 2 2;S
.
Vậy nghiệm của hệ bất phương trình là:
12
S S S
2;0 1; 2 2;4 4;
.
Câu 6: [0D4-7-2] Nghiệm của bất phương trình
22
2 2 1 0x x x
là
A.
5 13
1; 2;
2
. B.
9
4; 5;
2
.
C.
22
2; ;1
22
. D.
17
; 5 5; 3 .
5
Lời giải

Chọn C
Điều kiện:
2
22
2 1 0
22
x x x
.
Bất phương trình trở thành:
2
2 0 2 1x x x
.
Kết hợp điều kiện ta được:
22
2; ;1 .
22
S
Câu 7: [0D4-7-2] Bất phương trình:
22
3 4 . 5 0x x x
có bao nhiêu nghiệm nguyên
dương?
A.
0
. B.
1
.
C.
2
. D. Nhiều hơn 2 nhưng hữu hạn.
Lời giải
Chọn B
Ta có điều kiện:
2
50x
55xx
.
22
3 4 . 5 0x x x
2
3 4 0xx
14x
.
Kết hợp với điều kiện ta được:
5; 4x
. Suy ra nghiệm nguyên dương của bất
phương trình đã cho là:
3x
. Vậy bất phương trình có 1 nghiệm nguyên dương.
Câu 8: [0D4-7-2] Tìm tất cả các gi tr của
a
để bất phương trình
2
. 0,a x x a x
A.
0a
. B.
0a
. C.
1
0
2
a
. D.
1
2
a
.
Lời giải
Chọn D
2
. 0,a x x a x
2
0
1 4. . 0
a
aa
2
0
1 4 0
a
a
0
11
22
a
aa
1
2
a
.

Câu 9: [0D4-7-2] Tìm tất cả các gi tr của
m
để bất phương trình
2
0x x m
vô
nghiệm?
A.
1m
. B.
1m
. C.
1
4
m
. D.
1
4
m
.
Lời giải
Chọn D
Bất phương trình
2
0x x m
vô nghiệm
2
0,x x m x
2
10
1 4.1. 0
a
m
1
4
m
.
Câu 10: [0D4-7-2] Tập xc đnh của hàm số
2
1
3
23
yx
xx
là:
A.
1;D
. B.
3;1D
. C.
3;D
. D.
;3D
.
Lời giải
Chọn A
Điều kiện xc đnh của hàm số là
2
3
3
30
1
1
2 3>0
3 1 >0
3
x
x
x
x
x
xx
xx
x
.
Câu 11: [0D4-7-2] Tập nghiệm của bất phương trình
2
2
1
x
x
là:
A.
1;0S
. B.
1;0S
.
C.
1;0S
. D.
; 1 0;S
.
Lời giải
Chọn C
Bất phương trình
2 2 2 2 2
2 2 0 0
1 1 1
x x x x
x x x
3
0 0 1;0
11
xx
x
xx
.

Câu 12: [0D4-7-2] Bất phương trình
2
(2 1) 1 0mx m x m
có nghiệm khi:
A.
2m
. B.
1m
. C.
0m
. D.
0,25m
.
Lời giải
Chọn C
Với
0m
phương trình
1 0 1xx
(bất phương trình có nghiệm).
Câu 13: [0D4-7-2] Giải bất phương trình sau:
12
13
xx
xx
A.
1x
hoặc
5
3
3
x
. B.
5
1
3
x
.
C.
5
1
3
x
hoặc
3x
. D.
13x
.
Lời giải
Chọn C
2
1 2 1 2 3 5
00
1 3 1 3 2 3
x x x x x
x x x x x x
.
Đặt:
2
35
23
x
fx
xx
.
Bảng xét dấu:
x
1
5
3
3
35x
+ +
0
-
-
2
23xx
+
0
- -
0
+
fx
+ -
0
+
-
Kết luận:
5
1
3
x
hoặc
3x
.
Câu 14: [0D4-7-2] Giải bất phương trình sau:
15
22
xx
x x x
.

A.
10 2x
hoặc
2x
. B.
20x
hoặc
2x
.
C.
2x
hoặc
02x
. D.
10x
hoặc
20x
hoặc
2x
.
Lời giải
Chọn D
2
1 5 1 5 10
00
2 2 2 2
4
x x x x x
x x x x x x
xx
10
2 0
2
x
x
x
.
Câu 15: [0D4-7-2] Giải bất phương trình sau:
2
23
1.
2
xx
x
x
A.
21x
B.
21x
. C.
2x
hoặc
1x
. D.
2x
hoặc
1x
.
Lời giải
Chọn A
22
2 3 2 3 1
1 1 0 0 2 1
2 2 2
x x x x x
x x x
x x x
.
Câu 16: [0D4-7-2] Giải bất phương trình sau:
2
2 4 3
1
2 ( 1)
xx
xx
.
A.
1x
hoặc
1
2
x
. B.
1x
hoặc
1
0
2
x
.
C.
10x
hoặc
1
2
x
. D.
0x
hoặc
1
2
x
.
Lời giải
Chọn C
22
2
10
2 4 3 2 4 3 6 3
1 1 0 0
1
2 ( 1) 2 ( 1) 2 2
2
x
x x x x x
x x x x x x
x
.

Câu 17: [0D4-7-2] Giải hệ bất phương trình:
3
2
2
4
3
1
x
x
x
x
.
A.
7 2 1xx
. B.
21x
.
C.
21xx
. D.
7
2
2
x
.
Lời giải
Chọn B
TXĐ:
\ 2; 1D
HPT
7
0
7 v 2
2
21
7
27
1
0
2
1
x
xx
x
x
x
x
x
.
Kết luận:
21x
.
Câu 18: [0D4-7-2] Giải hệ bất phương trình:
22
( 3) ( 2) 0
11
0
11
xx
xx
xx
.
A.
01x
. B.
1
10
2
xx
.
C.
01xx
. D.
1
01
2
xx
.
Lời giải
Chọn D
TX Đ:
\1D
HPT
2
1
10 5 0
1
2
0 1 .
4
2
0
1 0 v 1
1
x
x
xx
x
xx
x
.
Kết luận:
1
01
2
xx
.
Câu 19: [0D4-7-2] Giải hệ bất phương trình:
3
2
3
2
1
11
x
x
xx
xx
.
A.
39x
. B.
13x
.

C.
1 7 3xx
. D.
1 1 3 ( 9)x x x
.
Lời giải
Chọn D
TXĐ:
\ 1; 3D
.
BPT
2
2
9
0
39
3
1 1 3 ( 9)
21
11
0
1
x
xx
x
x x x
xx
xx
x
.
Kết luận:
1 1 3 ( 9)x x x
.
Câu 20: [0D4-7-2] Giải hệ bất phương trình:
22
(2 3) ( 1) 0
1 1 2
22
xx
xxx
.
A.
2
2
3
x
. B.
22x
.
C.
24xx
. D.
2
2
3
x
.
Lời giải
Chọn D
TXĐ:
\ 2; 0D
.
BPT
2
4 3 2 0
2
4
2
3
2
8
0
3
2 0 2
4
xx
x
x
xx
xx
.
Kết luận:
2
2
3
x
.
Câu 21: [0D4-7-2] Giải hệ bất phương trình:
2 1 1
2
12
21
x
x x x
xx
xx
.
A.
21xx
. B.
01x
.
C.
21x
. D.
20xx
.
Lời giải
Chọn B
TXĐ:
\ 2; 0;1D
.
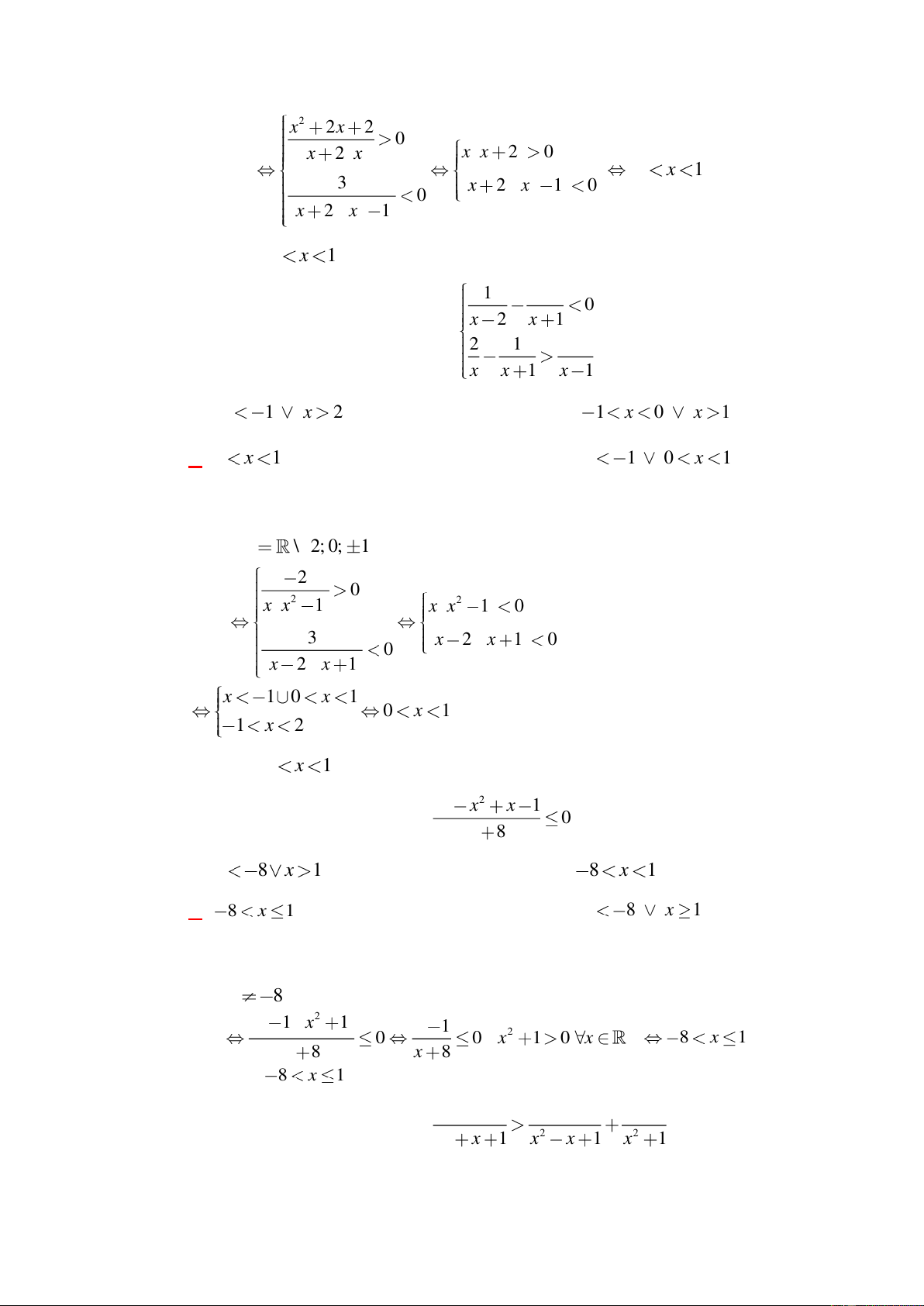
Hệ BPT
2
22
0
20
2
3
2 1 0
0
21
xx
xx
xx
xx
xx
01x
.
Kết luận:
01x
.
Câu 22: [0D4-7-2] Giải hệ bất phương trình:
11
0
21
2 1 1
11
xx
x x x
.
A.
12xx
. B.
1 0 1xx
.
C.
01x
. D.
1 0 1xx
.
Lời giải
Chọn C
TXĐ:
\ 2; 0; 1D
.
BPT
2
2
2
0
1
10
3
2 1 0
0
21
xx
xx
xx
xx
1 0 1
01
12
xx
x
x
.
Kết luận:
01x
.
Câu 23: [0D4-7-2] Giải bất phương trình:
32
1
0
8
x x x
x
.
A.
81xx
. B.
81x
.
C.
81x
. D.
81xx
.
Lời giải
Chọn A
ĐK:
8x
.
BPT
2
2
11
1
0 0 1 0
88
xx
x
xx
xx
81x
.
Kết luận:
81x
.
Câu 24: [0D4-7-2] Giải bất phương trình:
2 2 2
4 3 1
1 1 1x x x x x
.

A.
0x
. B.
0x
. C.
x
. D. Vô
nghiệm.
Lời giải
Chọn A
Đặt
2
10t x t
.
BPT
22
2
2 2 2
2 2 2
71
7
00
11
x x x
tx x
t x t
x x x
2
2
22
77
0 ( 1 0 )
11
x x x
xx
x x x x
2 2 2
7 7 0 1 1 0x x x x x x x x
2
0 7 7 0x x x x
.
Kết luận:
0x
.
Câu 25: [0D4-7-2] Giải bất phương trình:
2
7
2( 2) 2
2
xx
.
A.
3
2
x
. B.
3
2
x
. C. Vô nghiệm. D.
x
.
Lời giải
Chọn A
BPT:
2
22
7 9 3
2( 2) 2 2 6 0 2 0
2 2 2
x x x x x x
.
Kết luận:
x
.
Câu 26: [0D4-7-2] Giải bất phương trình:
2 2 2 2
2 1 3 4
1 2 ( 2)( 1)
x
x x x x x x
.
A.
x
. B. Vô nghiệm. C.
4
3
x
. D.
21x
.
Lời giải
Chọn B
22
2 2 2 2
22
2 2 1 3 4
2 1 3 4
0
1 2 ( 2)( 1)
21
x x x x
x
x x x x x x
x x x
2
22
47
0
21
xx
x x x
.
Nhận xét
2
4 7 0x x x
;
2
20xx
;
2
10x x x
.

Nên bất phương trình vô nghiệm.
Câu 27: [0D4-7-2] Giải bất phương trình:
2
4 2 1
4 3 3 2x x x
.
A.
73xx
. B.
73x
.
C.
51x
. D.
51xx
.
Lời giải
Chọn D
2
2
2
8 4 1 4 3
4 2 1
0
4 3 3 2
43
x x x
x x x
xx
2
2
8 15
0
43
xx
xx
Cho
2
5
8 15 0
3
x
xx
x
Cho
2
3
4 3 0
1
x
xx
x
Bảng xét dấu
51xx
.
Câu 28: [0D4-7-2] Giải bất phương trình:
2
2
5
13
3
xx
xx
.
A.
x
. B. Vô nghiệm.
C.
21x
. D.
21xx
.
Lời giải
Chọn A
Nhận xét :
2
30x x x
.
22
2
2
2
22
20
53
5
13
3
20
5 3 3 9
x x x x
xx
x
xx
xx
x x x x
.
Câu 29: [0D4-7-2] Tìm miền nghiệm của bất phương trình:
33
( 1)( 4 ) ( 2)( 3 2)x x x x x x
.

A.
2
1
3
x
B.
2
21
3
xx
.
C.
2
1
3
xx
. D.
2
21
3
xx
.
Lời giải
Chọn B
3 3 3
( 1)( 4 ) ( 2)( 3 2) 1 2 2 2 3 2 0x x x x x x x x x x x x x
3
2 1 2 3 2 0x x x x x x
3 2 3
2 3 2 3 2 0x x x x x x
2
2 3 2 0x x x
.
Cho
2 0 2xx
;
2
1
3 2 0
2
3
x
xx
x
Bảng xét dấu
2
21
3
xx
.
Câu 30: [0D4-7-2] Miền nghiệm của bất phương trình:
22
22
11
xx
x x x x
là:
A.
. B.
66
33
xx
.
C.
66
33
x
. D. .
Lời giải
Chọn D
Nhận xét
2
10x x x
;
2
10x x x
.

22
22
22
2 1 2 1
11
xx
x x x x x x
x x x x
3 2 3 2
3 3 2 3 3 2x x x x x x
2
6 4 0xx
.
Câu 31: [0D4-7-2] Giải hệ bất phương trình:
2
5 6 0
1 1 2
11
xx
x x x
.
A.
1
0 ( 1)
3
xx
. B.
1
0 (1 6)
3
xx
.
C.
( 1) ( 1)xx
. D.
( 1 0) ( 6)xx
.
Lời giải
Chọn B
2
5 6 0 1 6x x x
1
.
2
2
1 1 2 1
1 1 2
0
11
1
x x x x x
x x x
xx
2
31
0
1
x
xx
.
Cho
1
3 1 0
3
xx
;
0x
;
2
1
10
1
x
x
x
.
1
; 1 0; 1;
3
x
2
.
1
1 , 2 0; 1;6
3
x
.
Câu 32: [0D4-7-2] Giải bất phương trình:
2
2
23
12
1
xx
x
.
A.
1 2 ( 2)xx
. B.
1 2 2x
.
C.
1 2 1 2xx
. D.
1 2 1 2x
.
Lời giải

Chọn C
Nhận xét
2
10xx
.
2
22
2
2
22
2
2 2 4 0
2 3 1
23
12
1
2 3 2 2
2 1 0
x x Dung
x x x
xx
x
x x x
xx
12
12
x
x
.
Câu 33: [0D4-7-2] Giải hệ bất phương trình:
2
2
2
2
32
0
2
1
0
23
xx
xx
xx
xx
.
A.
3 2 ( 1 1)xx
. B.
21x
.
C.
32xx
. D.
21x
.
Lời giải
Chọn A
Nhận xét
2
20x x x
.
2
2
2
1
32
0 3 2 0
2
2
x
xx
xx
x
xx
1
.
Nhận xét
2
10x x x
.
2
2
2
1
0 2 3 0 3 1
23
xx
x x x
xx
2
.
32
1 , 2
11
x
x
.
Câu 34: [0D4-7-2] Giải hệ bất phương trình:
2
22
60
( 2) (2 1) 0
xx
xx
.
A.
3 ( 2)xx
. B.
33x
.
C.
1
2
3
x
. D.
32x
.
Lời giải
Chọn D

2
3
60
2
x
xx
x
1
.
2 2 2
1
( 2) (2 1) 0 3 8 3 0 3
3
x x x x x
2
.
1 , 2 3 2x
.
Câu 35: [0D4-7-2] Với số thực
a
bất kì, biểu thức nào sau đây có thể nhận giá tr âm?
A.
2
21aa
. B.
2
1aa
. C.
2
21aa
. D.
2
21aa
.
Lời giải
Chọn D
2
2
2 1 1 2 2a a a
nên
2
21aa
vẫn có thể nhận giá tr âm, ví dụ
như với
0a
thì
2
2 1 1 0aa
.
Câu 36: [0D4-7-2] Với số thực
a
bất kì, biểu thức nào sau đây luôn luôn dương.
A.
2
21aa
. B.
2
1aa
. C.
2
21aa
. D.
2
21aa
.
Lời giải
Chọn B
2
2
1 3 3
1 0,
2 4 4
a a a a
.
Câu 37: [0D4-7-2] Gọi
S
là tập nghiệm của bất phương trình
2
8 7 0xx
. Trong các tập
hợp sau, tập nào không là tập con của
S
?
A.
;0
. B.
8;
. C.
;1
. D.
6;
.
Lời giải
Chọn D
Ta có
2
7
8 7 0
1
x
xx
x
.
Câu 38: [0D4-7-2] Cho tam thức bậc hai
2
3f x x bx
. Với giá tr nào của
b
thì tam
thức
()fx
có hai nghiệm?
A.
2 3;2 3b
. B.
2 3;2 3b
.
C.
; 2 3 2 3;b
. D.
; 2 3 2 3;b
.
Lời giải
Chọn A

Ta có
2
3f x x bx
có nghiệm khi
2
23
12 0
23
b
b
b
.
Câu 39: [0D4-7-2] Giá tr nào của
m
thì phương trình
2
3 3 1 0m x m x m
(1)
có hai nghiệm phân biệt?
A.
3
; 1; \ 3
5
m
. B.
3
;1
5
m
.
C.
3
;
5
m
. D.
\3m
.
Lời giải
Chọn A
Ta có
1
có hai nghiệm phân biệt khi
0
'0
a
2
3
5 2 3 0
m
mm
3
5
3
1
m
m
m
.
Câu 40: [0D4-7-2] Tìm tập xc đnh của hàm số
2
2 5 2y x x
.
A.
1
;
2
. B.
2;
. C.
1
; 2;
2
. D.
1
;2
2
.
Lời giải
Chọn C
Điều kiện
2
2
2 5 2 0
1
2
x
xx
x
.
Vậy tập xc đnh của hàm số là
1
; 2;
2
.
Câu 41: [0D4-7-2] Các giá tr
m
để tam thức
2
( ) ( 2) 8 1f x x m x m
đổi dấu 2 lần là
A.
0m
hoặc
28m
. B.
0m
hoặc
28m
. C.
0 28m
. D.
0m
.
Lời giải
Chọn B
để tam thức
2
( ) ( 2) 8 1f x x m x m
đổi dấu 2 lần khi và chỉ khi
2
0 2 4 8 1 0mm
2
28 0mm
28
0
m
m
.

Câu 42: [0D4-7-2] Tập xc đnh của hàm số
2
( ) 2 7 15f x x x
là
A.
3
; 5;
2
. B.
3
; 5;
2
.
C.
3
; 5;
2
. D.
3
; 5;
2
.
Lời giải
Chọn B
Điều kiện
2
5
2 7 15 0
3
2
x
xx
x
.
Vậy tập xc đnh của hàm số là
3
; 5;
2
.
Câu 43: [0D4-7-2] Tập nghiệm của hệ bất phương trình
2
2
4 3 0
6 8 0
xx
xx
là
A.
;1 3;
. B.
;1 4;
. C.
;2 3;
. D.
1;4
.
Lời giải
Chọn B
Ta có:
2
2
4 3 0
6 8 0
xx
xx
1
3
2
4
x
x
x
x
1
4
x
x
.
Câu 44: [0D4-7-2] Hệ bất phương trình
2
2
2
4 3 0
2 10 0
2 5 3 0
xx
xx
xx
có nghiệm là
A.
11x
hoặc
35
22
x
. B.
21x
.
C.
43x
hoặc
13x
. D.
11x
hoặc
35
22
x
.
Lời giải
Chọn A

Ta có:
2
2
2
4 3 0
2 10 0
2 5 3 0
xx
xx
xx
3
1
5
2
2
1
3
2
x
x
x
x
x
11
35
22
x
x
.
Câu 45: [0D4-7-2] Tìm
m
để
2
2 2 3 4 3 0,f x x m x m x
?
A.
3
2
m
. B.
3
4
m
. C.
33
42
m
. D.
13m
.
Lời giải
Chọn D
2
2 2 3 4 3 0,f x x m x m x
0
2
4 16 12 0mm
13m
.
Câu 46: [0D4-7-2] Với giá tr nào của
a
thì bất phương trình
2
0,ax x a x
?
A.
0a
. B.
0a
. C.
1
0
2
a
. D.
1
2
a
.
Lời giải
Chọn D
Để bất phương trình
2
0,ax x a x
0
0a
2
1 4 0
0
a
a
1
2
1
2
0
a
a
a
1
2
a
.
Câu 47: [0D4-7-2] Với giá tr nào của
m
thì bất phương trình
2
0x x m
vô nghiệm?
A.
1m
. B.
1m
. C.
1
4
m
. D.
1
4
m
.
Lời giải
Chọn D
Bất phương trình
2
0x x m
vô nghiệm khi và chỉ khi bất phương trình
2
0,x x m x
0
10
1 4 0m
1
4
m
.
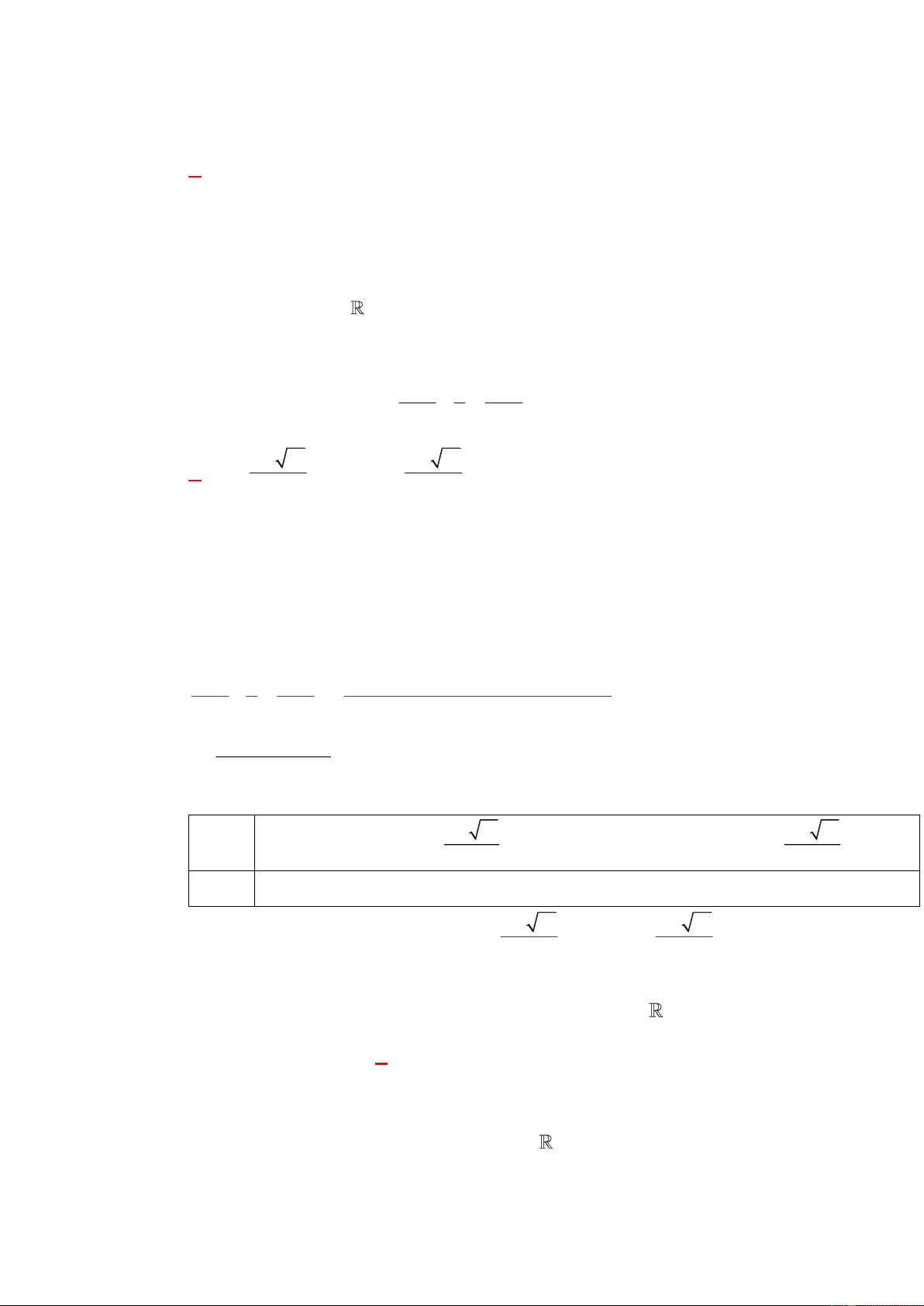
Câu 48: [0D4-7-2] Cho
2
( ) 2 ( 2) 4f x x m x m
. Tìm
m
để
()fx
âm với mọi
x
.
A.
14 2m
. B.
14 2m
.
C.
2 14m
. D.
14m
hoặc
2m
.
Lời giải
Chọn A
Ta có
0,f x x
0
0a
2
2 8 4 0mm
2
12 28 0mm
14 2m
.
Câu 49: [0D4-7-2] Bất phương trình
1 1 2
22x x x
có nghiệm là
A.
3 17 3 17
2, 0,2 ,
22
. B.
2,0,2x
.
C.
20x
. D.
02x
.
Lời giải
Chọn A
Điều kiện
0
2
x
x
.
Với điều kiện trên ta có
2 2 2 2 2
1 1 2
0
2 2 2 2
x x x x x x
x x x x x x
.
2
2 6 4
0
22
xx
x x x
.
Ta có bảng xét dấu
x
2
3 17
2
0
2
3 17
2
fx
0
0
0
0
0
Vậy nghiệm của bất phương trình là
3 17 3 17
2, 0,2 ,
22
.
Câu 50: [0D4-7-2] Tìm giá tr nguyên của
k
để bất phương trình
22
2 4 1 15 2 7 0x k x k k
nghiệm đúng với mọi
x
là
A.
2k
. B.
3k
. C.
4k
. D.
5k
.
Lời giải
Chọn B
Để bất phương trình nghiệm đúng với mọi
x
thì:

10
0
a
0
2
2
4 1 15 2 7 0k k k
24k
Vì
k
nên
3k
.
Câu 51: [0D4-7-2] Nghiệm của hệ bất phương trình:
2
32
2 6 0
10
xx
x x x
là:
A.
–2 3x
. B.
–1 3x
. C.
12x
hoặc
–1x
. D.
12x
.
Lời giải
Chọn C
Ta có
2
3
2 6 0 2,
2
x x x I
.
32
10x x x
2
1 1 0xx
2
1 1 0xx
1
.
1
x
II
x
Từ
I
và
II
suy ra nghiệm của hệ là
1; 2 1 S
.
Câu 52: [0D4-7-2] Hệ bất phương trình
2
10
0
x
xm
có nghiệm khi
A.
1m
. B.
1m
. C.
1m
. D.
1m
.
Lời giải
Chọn C
Ta có:
2
11
10
0
x
x
xm
xm
.
Do đó hệ có nghiệm khi
1m
.
Câu 53: [0D4-7-2] Tập xc đnh của hàm số
2
1
2
3
y x x
x
là
A.
3;
. B.
3;
. C.
;1 3;
. D.
1;2 3;
.
Lời giải
Chọn A
Hàm số xc đnh khi
2
2
20
3
1
30
3
x
xx
x
x
x
x
.
Câu 54: [0D4-7-2] Tập xc đnh của hàm số
2
1
32
3
y x x
x
là

A.
3;
. B.
3;1 2;
. C.
3;1 2;
. D.
3;1 2;
.
Lời giải
Chọn B
Hàm số xc đnh khi
2
1
31
3 2 0
2
2
30
3
x
x
xx
x
x
x
x
.
Câu 55: [0D4-7-2] Tập nghiệm của bất phương trình
2
1
1
xx
x
x
là
A.
1
;1
2
.
B.
1
;
2
.
C.
1;
.
D.
1
; 1;
2
.
Lời giải
Chọn A
Điều kiện :
1x
.
Bất phương trình đã cho tương đương với
2
1 2 1 1
0 0 1
1 1 2
x x x
xx
xx
Kết hợp điều kiện, ta được tập nghiệm của bất phương trình
1
;1
2
S
.
Câu 56: [0D4-7-2] Phương trình
2
2 3 2 3 0m x x m
có hai nghiệm trái dấu khi và chỉ
khi
A.
2.m
. B.
3
2
2
m
.
C.
3
2
m
. D.
2m
hoặc
3
2
m
.
Lời giải
Chọn B
Điều kiện cần và đủ để phương trình có hai nghiệm trái dấu là:
2 2 3 0mm
.
3
2
2
m
.
Câu 57: [0D4-7-2] Tập nghiệm của bất phương trình
2
4 4 0 xx
là:

A.
2;
. B. . C.
\2
. D.
\2
.
Lời giải
Chọn C
Cách 1 : Ta có
2
2
4 4 0 2 0 2x x x x
. Vậy chọn C.
Cách 2 : Casio : wR1111=4=4==
Kết quả: .
Câu 58: [0D4-7-2] Tập nghiệm của bất phương trình
2
4 2 8 0 xx
là:
A.
;2 2
. B.
\ 2 2
. C.
. D. .
Lời giải
Chọn C
Cách 1 :
22
22
4 2 8 0 2.2 2. 2 2 0 2 2 0x x x x x
( chọn
C)
Cách 2 : Casio: wR1121=p4s2=8==
( nghiệm rỗng).
Câu 59: [0D4-7-2] Tập nghiệm của bất phương trình
2
60 xx
là:
A.
; 3 2;
. B.
3;2
. C.
2;3
. D.
; 2 3;
.
Lời giải
Chọn C
Ta có:
2
6 0 2 3x x x
( chọn. C. ).
Câu 60: [0D4-7-2] Tập nghiệm của bất phương trình
2
6 2 18 0 xx
là:
A.
3 2;
. B.
3 2;
. C.
. D. .
Lời giải
Chọn D
Ta có
2
2
6 2 18 0 3 2 0,x x x x
(Chọn D).
Câu 61: [0D4-7-2] Tập nghiệm của bất phương trình
2
3 2 6 0 xx
là:

A.
2; 3
. B.
2; 3
. C.
3; 2
. D.
3; 2
.
Lời giải
Chọn D
Ta có
2
3 2 6 0 3 2x x x
( chọn D).
Câu 62: [0D4-7-2] Bất phương trình
2
1
0
43
x
xx
có tập nghiệm là:
A.
;1
. B.
3; 1 1;
. C.
; 3 1;1
. D.
3;1
.
Lời giải
Chọn C
Bảng xét dấu:
Vậy tập nghiệm của bất phương trình là:
; 3 1;1S
.
Câu 63: [0D4-7-2] Tập nghiệm bất phương trình
2
56
1
xx
x
0 là:
A.
1;3
. B.
1;2 3;
. C.
2;3
. D.
;1 2;3
.
Lời giải
Chọn B
Bảng xét dấu:
Vậy tập nghiệm của bất phương trình là:
1;2 3;S
.
Câu 64: [0D4-7-2] Bất phương trình
12
21
xx
xx
có tập nghiệm là:
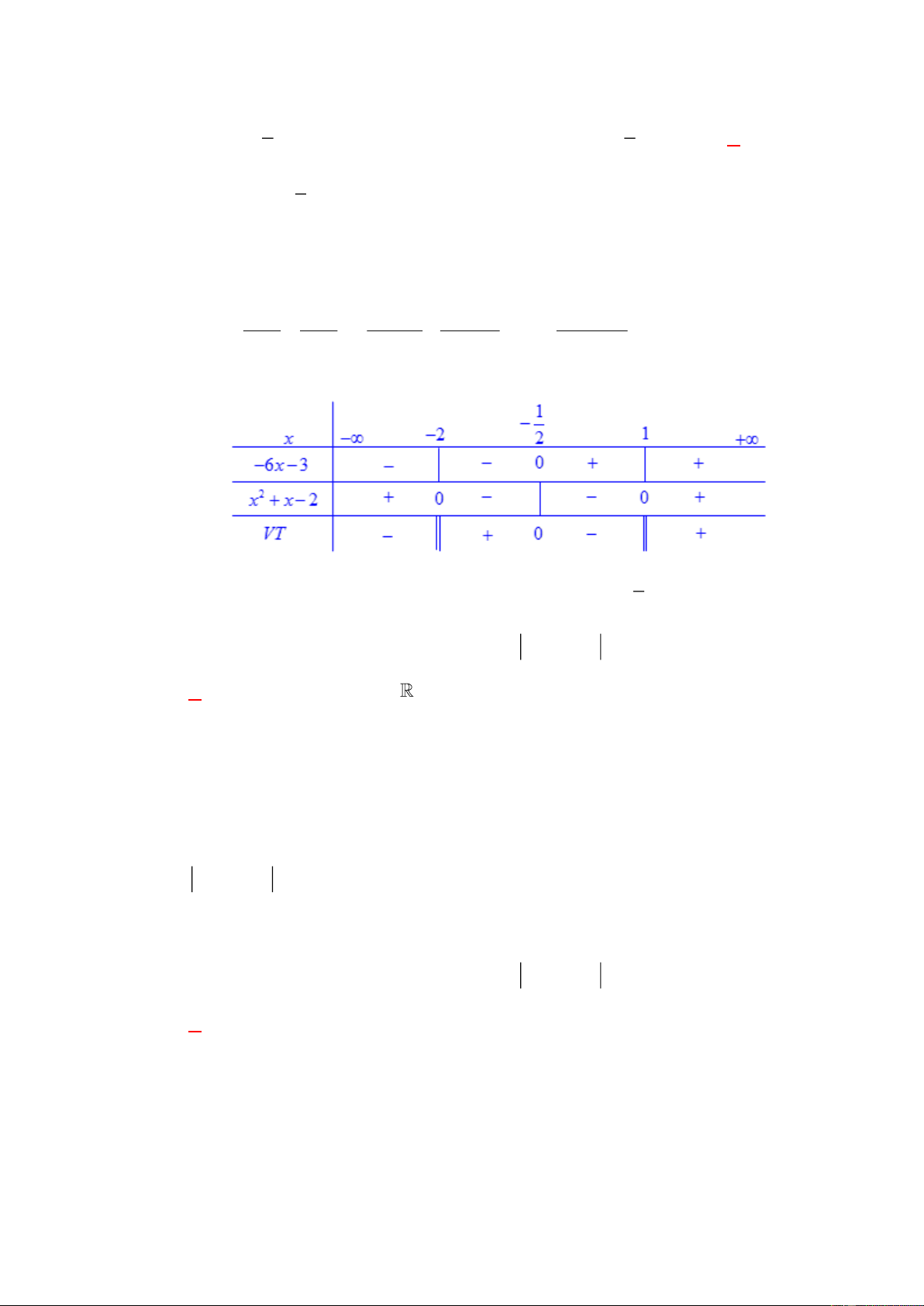
A.
1
2;
2
. B.
2;
. C.
1
2; 1;
2
. D.
1
; 2 ;1
2
.
Lời giải
Chọn D
Ta có:
22
2
12
1 2 6 3
00
2 1 2 1 2
xx
x x x
x x x x x x
Bảng xét dấu:
Vậy tập nghiệm của bất phương trình là:
1
; 2 ;1
2
S
.
Câu 65: [0D4-7-2] Tập nghiệm của bất phương trình
22
12 12 x x x x
là
A.
. B. .
C.
4; 3
. D.
; 4 3;
.
Lời giải
Chọn A
Ta có
22
22
2
22
0 0
12 12
12 12
2 2 24 0
12 12
x
x x x x
x x x
vô nghiem
v
x
xx
xx
ô ngh
x
e
x
im
Vậy tập nghiệm của bất phương trình là:
S
.
Câu 66: [0D4-7-2] Tập nghiệm của bất phương trình
22
12 12 x x x x
là
A.
; 3 4;
. B.
; 4 3;
. C.
6; 2 3;4
. D.
4;3
.
Lời giải
Chọn A

Ta có:
2
22
22
22
2 2 24 0
12 12
12 12
0 0
12 12
vô n
xx
x x x x
x x x x
x
x x x
ghi
x
em
; 3 4;
Vậy tập nghiệm của bất phương trình là:
; 3 4;S
.
Câu 67: [0D4-7-2] Tập nghiệm của hệ bất phương trình
2
7 6 0
2 1 3
xx
x
là:
A.
(1;2)
. B.
[1;2]
. C.
( ;1) (2; )
. D.
.
Lời giải
Chọn A
2
1 6 1 6
7 6 0
12
3 2 1 3 1 2
2 1 3
xx
xx
x
xx
x
.
Câu 68: [0D4-7-2] Tập nghiệm của hệ bất phương trình
2
2
3 2 0
10
xx
x
là:
A.
. B.
{1}
. C.
[1;2]
. D.
[ 1;1]
.
Lời giải
Chọn B
2
2
12
3 2 0
1
11
10
x
xx
x
x
x
.
Câu 69: [0D4-7-2] Tập nghiệm của hệ bất phương trình
2
2
4 3 0
6 8 0
xx
xx
là:
A.
( ;1) (3; )
. B.
( ;1) (4; )
. C.
( ;2) (3; )
. D.
(1;4)
.
Lời giải
Chọn B
2
2
;1 3;
4 3 0
;1 4;
6 8 0
;2 4;
x
xx
x
xx
x
.
Câu 70: [0D4-7-2] Hệ bất phương trình
( 3)(4 ) 0
1
xx
xm
có nghiệm khi:
A.
5m
. B.
2m
. C.
5m
. D.
5m
.
Lời giải

Chọn D
( 3)(4 ) 0 3 4
11
x x x
x m x m
. Hệ có nghiệm khi và chỉ khi
1 4 5mm
.
Câu 71: [0D4-7-2] Hệ bất phương trình
2
10
0
x
xm
có nghiệm khi:
A.
1m
. B.
1m
. C.
1m
. D.
1m
.
Lời giải
Chọn C
2
11
10
0
x
x
xm
xm
. Hệ có nghiệm khi và chỉ khi
1m
.
Chương VI: LƯỢNG GIÁC.
Câu 72: [0D4-7-2] Có bao nhiêu giá tr nguyên của
m
để bất phương trình sau có tập nghiệm
là ?
2 3 2
2 3 4 4 0x mx mx mx
A.
2
. B.
4
.
C.
1
. D. Nhiều hơn
6
nhưng hữu hạn.
Lời giải
Chọn C
Ta có
2 3 2 2
2 3 4 4 0 4 2 2 1x mx mx mx x x x x m
+ Với
0m
thỏa mãn yêu cầu bài toán.
+ Với
0m
Ta có VT dần tới dương vô cùng. VP khi
x
dần tới dương vô cùng thì
2
2 2 1 4x x x x
nên không tồn tại
m
để bpt đúng với mọi
x
.
+ Với
0m
Ta có VT dần tới dương vô cùng. VP khi
x
dần tới dương vô cùng thì
2
2 2 1 4x x x x
nên không tồn tại
m
để bpt đúng với mọi
x
.
Để phương trình có tập nghiệm là thì
0m
.
Câu 73: [0D4-7-2] Giải bất phương trình
2
5 1 7 2x x x x x
ta được
A. Vô nghiệm. B. Mọi
x
đều là nghiệm.

C.
2,5x
. D.
2,6x
.
Lời giải
Chọn A
Ta có
2
5 1 7 2 5 0x x x x x
vô lý. Vậy bất phương trình đã cho vô
nghiệm.
Câu 74: [0D4-7-2] Hệ bất phương trình
( 2)( 3) 0
( 2)( 3) 0
xx
xx
có nghiệm là
A.
23x
. B.
23x
.
C.
22x
;
33x
. D. Vô nghiệm.
Lời giải
Chọn A
Ta có
( 2)( 3) 0 2 3
23
( 2)( 3) 0 3 2
x x x
x
x x x x
.
Câu 75: [0D4-7-2] Tập nghiệm của bất phương trình
2
2
9
1
1
xx
xx
là
A.
2;1S
. B.
7
;2
2
S
. C.
2;1
. D.
2;1
.
Lời giải
Chọn A
Ta có
2
2
9
1
1
xx
xx
2
19xx
2
3 1 3xx
.
2
20xx
21x
.
Câu 76: [0D4-7-2] Tập xc đnh của hàm số
22
4 25y x x x
là
A.
5;0 4;5
. B.
5;0 4;5
. C.
5;5
. D.
;0 4;
.
Lời giải
Chọn A
ĐKXĐ
2
2
40
25 0
xx
x
40
55
xx
x
50
45
x
x
.

Câu 77: [0D4-7-2] Tập xc đnh của hàm số
2
3
6
2
x
y x x
x
là
A.
3;2
. B.
;3 2;
. C.
3;2
. D.
3;2
.
Lời giải
Chọn D
ĐKXĐ
2
60
20
xx
x
32
2
x
x
32x
.
Câu 78: [0D4-7-2] Tập xc đnh của hàm số
2
3y x x
là
A.
;0 3;
. B.
0;3
. C.
0;3
. D. .
Lời giải
Chọn B
ĐKXĐ
2
3 0 0 3x x x
.
Câu 79: [0D4-7-2] Tập xc đnh của hàm số
2
1
32
1
y x x
x
là
A.
;1 2;
. B.
1;
. C.
1;
. D.
1;2
.
Lời giải
Chọn B
ĐKXĐ
2
3 2 0
10
xx
x
21
1
xx
x
1x
.
Câu 80: [0D4-7-2] Bất phương trình
2 2 2
( ) 3( ) 2 0x x x x
có nghiệm là
A.
1 5 1 5
22
x
. B.
1 5 1 5
22
xx
.
C.
1
1 5 1 5
22
x
x
. D.Mọi số thực x.
Lời giải
Chọn D
Ta có
2 2 2
( ) 3( ) 2 0x x x x
2
2
2
1
xx
xx
2
2
20
10
xx
xx
đúng
x
.
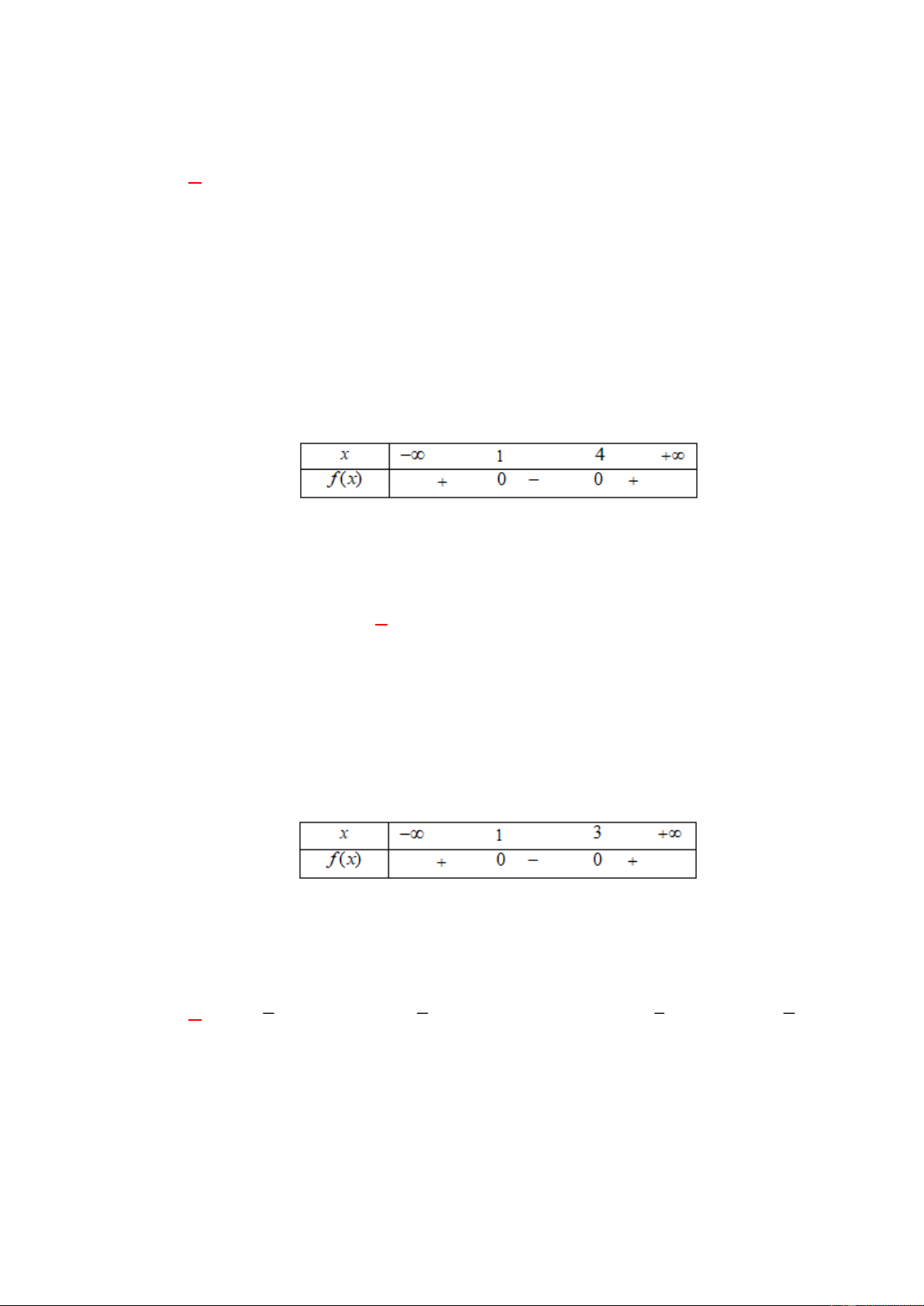
Câu 81: [0D4-7-2] Tập ngiệm của bất phương trình:
2
5 2( 2)x x x
là:
A.
– ;1 );( ] [4
. B.
1;4
. C.
– ;1 ));((4
. D.
(1;4)
.
Lời giải
Chọn A
Ta có:
2
5 2( 2)x x x
2
5 4 0xx
.
Đặt
2
54f x x x
1
0
4
x
fx
x
.
Ta có bảng xét dấu :
Vậy tập nghiệm của bpt là
S ( ] [– ;1 4 );
Câu 82: [0D4-7-2] Tập ngiệm của bất phương trình:
2
4 3 0xx
là:
A.
– ;1 );( ] [4
B.
1;3
C.
– ;1 ));([3
D.
1;3
Lời giải
Chọn B
Đặt
2
43xx xf
1
0
3
x
fx
x
.
Ta có bảng xét dấu :
0fx
1;3x
Câu 83: [0D4-7-2] Tập ngiệm của bất phương trình:
2
2 7 15 0xx
là:
A.
3
)– ; ;
2
[5
. B.
3
;5
2
C.
3
– ; 5 ;
2
. D.
3
5;
2
Lời giải
Chọn A
Đặt
2
2 7 15xfx x
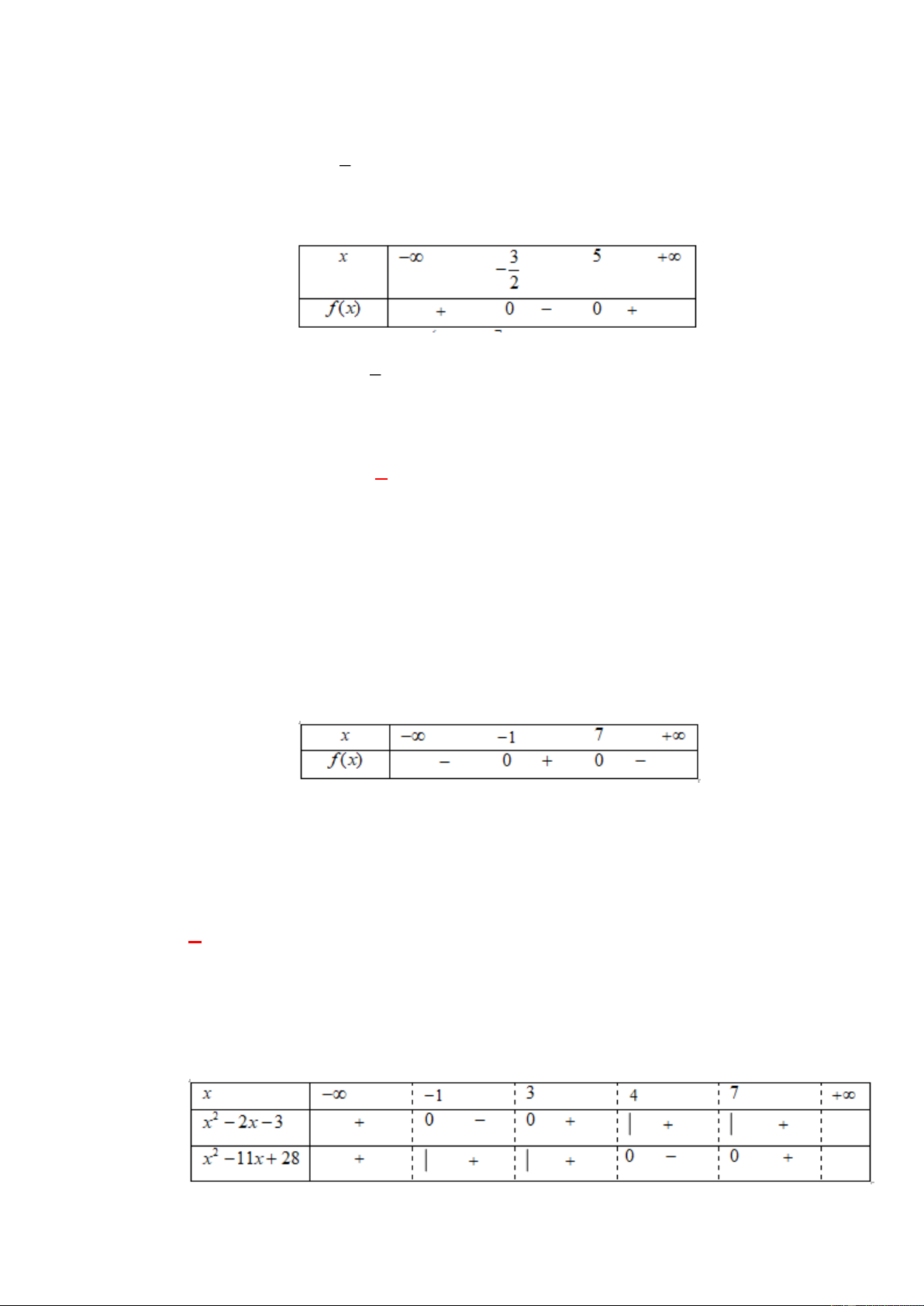
5
0
3
2
x
fx
x
Ta có bảng xét dấu :
0fx
3
–5
2
);;[x
Câu 84: [0D4-7-2] Tập ngiệm của bất phương trình:
2
6 7 0xx
là:
A.
[7; .1 )–;
B.
1;7 .
C.
1 .– ; 7 ;
D.
7;1 .
Lời giải
Chọn B
Đặt
2
67xxfx
1
0
7
x
fx
x
Ta có bảng xét dấu :
0fx
1;7x
Câu 85: [0D4-7-2] Hệ bất phương trình:
2
2
2 3 0
11 28 0
xx
xx
có nghiệm là:
A.
1x
hoặc
34x
hoặc
7.x
B.
4x
hoặc
7x
.
C.
1x
hoặc
7x
.
D.
1x
hoặc
34x
hoặc
7x
.
Lời giải
Chọn A
Cách 1: BXD chung :
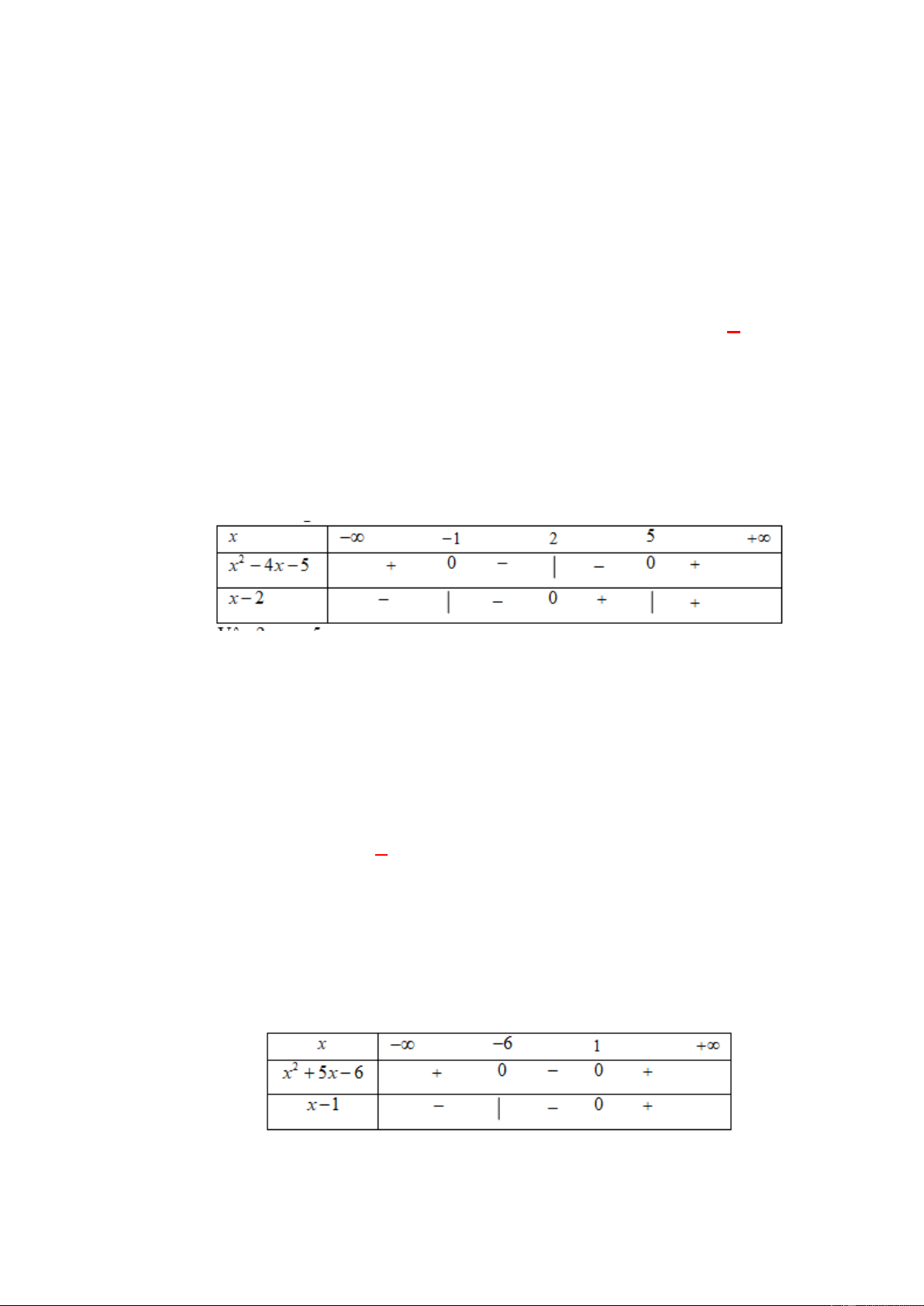
Vậy
1x
hoặc
34x
hoặc
7x
Cách 2 :Dùng MTCT :
2
2
2 3 0
11 28 0
xx
xx
1; 3
4; 7
xx
xx
1x
hoặc
34x
hoặc
7x
.
Câu 86: [0D4-7-2] Hệ bất phương trình:
2
45
13
xx
x
có nghiệm là:
A.
41x
. B.
11x
. C.
12x
. D.
25x
Lời giải
Chọn D
Cách 1:
31x
5x4x
2
2
4 5 0
2
xx
x
.
BXD chung :
Vậy
25x
.
Cách 2:Dùng MTCT:
2
45
13
xx
x
2
4 5 0
2
xx
x
15
2
x
x
25x
.
Câu 87: [0D4-7-2] Hệ bất phương trình:
2
56
12
xx
x
có nghiệm là:
A.
63x
.
B.
6x
. C.
21x
. D.
10x
Lời giải
Chọn B
Cách 1:
2
56
12
xx
x
2
5 6 0
10
xx
x
.
Bảng xét dấu chung :
Vậy
6x
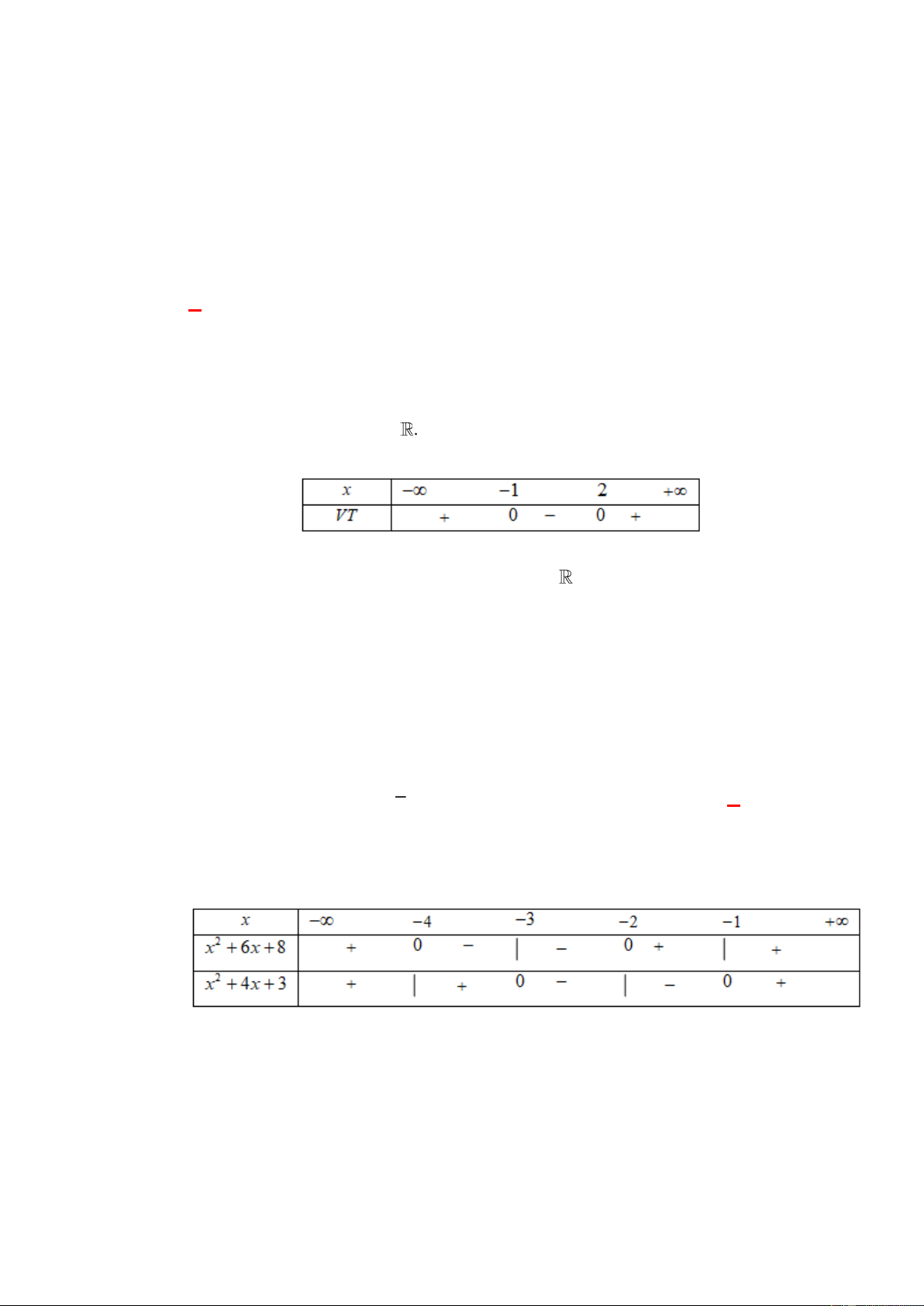
Cách 2:Dùng MTCT:
2
56
12
xx
x
2
5 6 0
1
xx
x
6; 1
1
xx
x
6x
.
Câu 88: [0D4-7-2] Hệ bất phương trình:
2
2
10
20
xx
xx
có nghiệm là:
A.
1x
hoặc
2x
. B.
12x
. C.Vô nghiệm. D.
12x
.
Lời giải
Chọn A
Cách 1:
Ta có (1) :
2
1 0, .xx
Giải (2) :
2
20xx
BXD:
Vậy
1x
hoặc
2x
Cách 2 :Dùng MTCT
2
2
10
20
xx
xx
1; 2
x
xx
1x
hoặc
2x
Câu 89: [0D4-7-2] Hệ bất phương trình sau có tập nghiệm là đoạn trên trục số có độ dài
bằng bao nhiêu?
2
2
6 8 0
4 3 0
xx
xx
A.
2
. B.
5
4
. C.
5
. D.
1
Lời giải
Chọn D
BXD chung :
Ta có :
32x
Vậy độ dài bằng
1
.

Câu 1: [0D4-7-3] Nghiệm của hệ bất phương trình:
2
32
2 6 0
10
xx
x x x
là:
A.
–2 3.x
B.
–1 3.x
C.
1 3x
hoặc
–1 .x
D.
1 2x
.
Lời giải
Chọn C
2
32
2 6 0
10
xx
x x x
3
2
2
1
x
x
12x
.
Câu 2: [0D4-7-3] Cho bất phương trình
2
2 4 5 0x x m
. Tìm
m
để bất phương trình
đúng
3x
?
A.
11m
. B.
11m
. C.
11m
. D.
11m
.
Lời giải
Chọn B
Ta có:
20a
. Do đó,
2
2 4 5 0x x m
,
3x
sẽ có trường hợp sau:
TH1.
'0
2
2 2 5 0m
3m
, khi đó
2
2 4 5 0,x x m x
. Do đó
2
2 4 5 0, 3x x m x
.
TH2.
'0
, khi đó phương trình
2
2 4 5 0x x m
sẽ có hai nghiệm
12
,xx
. Do đó, để
2
2 4 5 0,x x m
3x
12
'0
3xx
'0
30
3
2
af
S
2
3
2 2.3 4.3 5 0
13
m
m

3
11
m
m
11 3m
.
Kết hợp hai trường hợp lại ta được
11m
thì
2
2 4 5 0, 3x x m x
.
Câu 3: [0D4-7-3] Cho bất phương trình
22
(2 2) 2 0x m x m m
. Tìm
m
để bất
phương trình nghiệm đúng với mọi
x
thuộc đoạn
0;1
?
A.
10m
. B.
0
1
m
m
. C.
10m
. D.
1
2
m
m
.
Lời giải
Chọn C
Ta có:
10a
. Do đó,
22
(2 2) 2 0x m x m m
,
0;1x
12
'0
01xx
2
2
1 2 0
00
10
m m m
af
af
2
2
10
20
10
mm
m
20
11
m
m
10m
.
Câu 4: [0D4-7-3] Có bao nhiêu giá trị nguyên của
m
để bất phương trình sau có tập nghiệm
là ?
2 3 2
2 3 4 4 0x mx mx mx
A. 1. B. 4.
C. 6. D. Nhiều hơn 6 nhưng hữu hạn.
Lời giải
Chọn A

Ta có
2 3 2
2 3 4 4 0x mx mx mx
32
2 1 3 4 4 0mx m x mx
.
Để bất phương trình có tập nghiệm là thì
2
20
1 3 4 4 0,
m
m x mx x
2
0
1 3 0
' 4 12 4 0
m
m
mm
0
1
3
3 13 3 13
23
m
m
m
0m
.
Vậy có 1 giá trị nguyên của
m
để bất phương trình có tập nghiệm là .
Câu 5: [0D4-7-3] Cho phương trình
2
5 1 0m x m x m
(1). Tìm tất cả các gi
trị của
m
để (1) có 2 nghiệm
12
,xx
thỏa mãn
12
2xx
.
A.
22
5
7
m
. B.
22
5
7
m
. C.
22
5
7
m
. D.
22
5
7
m
.
Lời giải
Chọn B
Phương trình có hai nghiệm phân biệt
2
50
1 4. 5 . 0
m
m m m
2
5
3 18 1 0
m
mm
5
9 2 21 9 2 21
33
m
m
Khi đó, phương trình có hai nghiệm
12
,xx
thỏa mãn
12
2xx
12
2 2 0xx
1 2 1 2
2 4 0x x x x

1
2 4 0
55
mm
mm
7 22
0
5
m
m
22
5
7
m
Kết hợp với điều kiện ta được:
22
5
7
m
.
Câu 6: [0D4-7-3] Cho phương trình
2
20x x m
(1). Tìm tất cả các gi trị của
m
để
(1) có 2 nghiệm
12
,xx
thỏa mãn
12
2xx
.
A.
0m
. B.
1m
. C.
10m
. D.
1
4
m
.
Lời giải
Chọn C
Phương trình có hai nghiệm phân biệt
2
10
' 1 0m
1m
.
Khi đó, phương trình có hai nghiệm
12
,xx
thỏa mãn
12
2xx
12
12
2 2 0
2 2 0
xx
xx
12
1 2 1 2
40
2 4 0
xx
x x x x
2 4 0
2.2 4 0m
0m
.
Kết hợp với điều kiện ta được:
10m
.
Câu 7: [0D4-7-3] Cho hàm số
2
2 3 2 3y m x mx m
( m là tham số). Các giá trị của
m để đồ thị hàm số cắt trục hoành tại hai điểm phân biệt
,AB
sao cho gốc tọa độ
O
nằm giữa
A
và
B
là:
A.
2m
. B.
3
2
m
.
C.
3
2
2
m
. D.
3
2
m
hoặc
2m
.
Lời giải
Chọn C
Phương trình hoành độ giao điểm là
2
2 3 2 3 0 m x mx m

Điều kiện để đồ thị hàm số cắt trục hoành tại hai điểm phân biệt
,AB
sao cho gốc
tọa độ
O
nằm giữa
A
và
B
là
2 3 3
. 0 0 2
22
AB
m
x x m
m
.
Câu 8: [0D4-7-3] Hệ bất phương trình
2
2
8 20 0
2 1 9 4 0
xx
mx m x m
có nghiệm với mọi
x
khi và chỉ khi:
A.
1
;
2
m
. B.
1
;
2
m
.
C.
11
;
24
m
. D.
11
;
24
m
.
Lời giải
Chọn A
Hệ bất phương trình
2
2
2
2
8 20 0
4 4 0
2 1 9 4 0
2 1 9 4 0
xx
x
mx m x m
mx m x m
2
2 1 9 4 0 mx m x m
TH1:
0m
bất phương trình
2 +4 0x
không đúng khi
2x
, do đó khi
0m
không thỏa yêu cầu đề bài.
TH2:
0m
yêu cầu bài toán
2
2
0
0
8 2 1 0
' 1 9 4 0
m
m
mm
m m m
2
0
1
0
0
1
4
8 2 1 0
2 1 4 1 0
2
1
2
m
m
m
m
m
mm
mm
m
.
Câu 9: [0D4-7-3] Giải bất phương trình:
2 1 5
11
xx
xx
.
A.
41x
. B.
11x
.
C.
4 x
1x
. D.
1 x
1x
.
Lời giải
Chọn B
ĐK:
1; 1.xx

BPT
2 1 1 5 1
0
11
x x x x
xx
2
34
0
11
xx
xx
1 1 0xx
( vi
2
3 4 0x x x
)
11x
.
Câu 10: [0D4-7-3] Giải bất phương trình:
2
2
23
42
xx
xx
.
A.
4x
2x
. B.
42x
.
C.
22x
. D.
2 x
2x
.
Lời giải
Chọn D
BPT
2
2
2 3 2
0
4
x x x
x
2
2
28
0
4
xx
x
2
40x
(vi
2
2 8 0x x x
)
2 x
2x
.
.
Câu 11: [0D4-7-3] Miền nghiệm của bất phương trình:
2
2
38
12
1
xx
xx
là:
A.
6x
1x
. B.
7
1
4
x
.
C.
61x
. D.
6 x
7
1
4
x
.
Lời giải
Chọn D
Do
2
10x x x
nên BPT
22
22
3 8 1
3 8 2( 1)
x x x x
x x x x
2
4 7 0
5 6 0
x
xx
7
4
61
x
xx
6 x
7
1
4
x
.
Câu 12: [0D4-7-3] Giải bất phương trình:
2 2 2
( 4)( 2 ) 3( 4 4)x x x x x
.
A.
13x
. B.
1 3xx
.
C.
21x
. D.
2 1 3xx
.

Lời giải
Chọn D
BPT
22
2
2 2 3 2x x x x
2
2
2 2 3 0x x x
2
2
2 3 0
x
xx
2 1 3xx
.
Câu 13: [0D4-7-3] Giải bất phương trình:
3 2 2
( 1)( 2 ) ( 2)( 2 4)x x x x x x
.
A.
02xx
. B.
1 3 1 3x
. C. Vô nghiệm. D.
0x
và
2x
.
Lời giải
Chọn C
BPT
3 2 2
2 2 2 4x x x x x x
3
2 2 4 0x x x
2
2
2 2 2 0x x x
BPT vô nghiệm.
Câu 14: [0D4-7-3] Giải bất phương trình:
23
22
1 1 2
2 3 2
x x x x
x x x x x
.
A.
0 1 2xx
. B.
01x
. C.
0 1 2xx
. D.
12x
.
Lời giải
Chọn C
BPT
2 2 3
2
1 2 2
0
32
x x x x x x x
x x x
2
2
2
0 3 2 0
32
x x x
x x x
01x
2x
.
Câu 15: [0D4-7-3] Định m để bất phương trình
2
2( 2) 2 1 0x m x m
có miền nghiệm
là .
A.
15mm
. B.
5 1mx
. C.
15m
. D.
51m
.
Lời giải

Chọn C
BPT có miền nghiệm là
2
'
2 2 1 0mm
2
6 5 0mm
1 < 5m
.
Câu 16: [0D4-7-3] Bất phương trình
2
2
22
1
x mx m
xx
có miền nghiệm là khi và chỉ
khi
A.
22m
. B.
2 10m
. C.
2 10mm
. D.
2 10m
.
Lời giải
Chọn A
Do
2
1 0;x x x
nên BPT
22
22
21
21
x mx m x x
x mx m x x
2
2
3 2 2 0
2 2 0
x m x m
x m x m
BPT có miền nghiệm là
2
1
2
2
2 12 2 0
2 4 2 0
mm
mm
2
2
8 20 0
40
mm
m
2 10
22
m
m
22m
.
Câu 17: [0D4-7-3] Định m để phương trình
2
( 1) 2 2 0m x mx m
có 2 nghiệm phân
biệt x
1
, x
2
thỏa
12
11
3
xx
.
A.
2 6mm
. B.
21m
1 2 m
6m
.
C.
26m
. D.
26m
.
Lời giải
Chọn B

PT có hai nghiệm phân biệt
'2
10
1 2 0
m
m m m
1
(*)
2
m
m
.
Khi đó, theo Vi-ét ta có
12
12
2
1
2
1
m
xx
m
m
xx
m
.
Ta có
12
11
3
xx
12
12
2
33
.2
xx
m
x x m
12
11
3
xx
6
0 2 6
2
m
mm
m
.
Kết hợp (*) ta có
21m
1 2 m
6m
.
Câu 18: [0D4-7-3] Với điều kiện nào của m thì phương trình
2
2( 1) 2 0mx m x m
có
đúng 1 nghiệm thuộc khoảng (-1; 2)?
A.
21m
. B.
1 1mm
. C.
4
3
m
. D.
4
0
3
m
.
Lời giải
Chọn A
Khi
0m
, PT
1 1; 2x
. Ta có
0m
(tmyc).(*)
Khi
0m
, PT luôn có hai nghiệm
2
1;
m
xx
m
. PT có đúng 1 nghiệm thuộc
khoảng (-1; 2)
2
1
2
2
m
m
m
m
22
0
2
0
m
m
m
m
01
20
m
m
.
Kết hợp (*) ta có
21m
.
Câu 19: [0D4-7-3] Với điều kiện nào của m để phương trình
2
( 1) 2 0x m x m
có 2
nghiệm phân biệt x
1
, x
2
khác 0 thỏa mãn
22
12
11
1
xx
.
A.
27m
. B.
21m
.
C.
7
8
m
và
2m
. D.
2 1 m
7m
.
Lời giải
Chọn B

PT có 2 nghiệm phân biệt khác 0
2
20
1 4 2 0
m
mm
2
2
6 7 0
m
mm
2
*
17
m
mm
.
Theo Vi-et ta có
12
12
1
1
2
x x m
x x m
.
Ta có
22
12
11
1
xx
22
12
22
12
1
xx
xx
2
1 2 1 2
22
12
2
1
x x x x
xx
2
2
1 2 2
1
2
mm
m
2
8 7 7
0
8
2
m
m
m
.
Kết hợp (*) ta có
21m
.
Câu 20: [0D4-7-3] Với điều kiện nào của m để phương trình
2
( 1) 2 0x m x m
có 2
nghiệm phân biệt x
1
, x
2
khác 0 thỏa mãn
33
12
11
1
xx
.
A.
2 1 m
7m
. B.
2 m
7m
.
C.
1
1
2
m
. D.
1
7
2
m
.
Lời giải
Chọn A
PT có 2 nghiệm phân biệt khác 0
2
20
1 4 2 0
m
mm
2
2
6 7 0
m
mm
2
1
17
m
mm
.

Theo Vi-et ta có
12
12
1
2
x x m
x x m
.
Ta có
33
12
11
1
xx
33
12
33
12
1
xx
xx
2
1 2 1 2 1 2
33
12
3
1
x x x x x x
xx
2
3
1 1 3 2
1
2
m m m
m
2
3
12 7 3
0*
2
mm
m
.
Do
2
12 7 3 0;m m x
nên
* 2 0 2mm
.
Kết hợp
1
ta có
2 1 m
7m
.
Câu 21: [0D4-7-3] Định m để phương trình
22
(2 3) 3 2 0x m x m m
có 2 nghiệm
phân biệt thuộc khoảng
3;2 ?
A.
24m
. B.
2 m
4m
. C.
13m
. D.
13mm
.
Lời giải
Chọn C
Ta có
1
nên PT luôn có hai phân biệt
1
2
xm
xm
.
YCBT
3 2 1 2mm
13m
.
Câu 22: [0D4-7-3] Giải hệ phương trình: đề nghị sửa đề thành hệ bpt
2
7 10 0 (1)
1 1 1
(2)
81
xx
x x x
.
A.
85x
. B.
8 1xx
.
C.
8 x
10x
. D.
21x
.
Lời giải
Chọn C
Với
0; 1; 8x x x
. HBPT
2
7 10 0
8 1 1 8
0
81
xx
x x x x x x
x x x
2
2
7 10 0
28
0
81
xx
xx
x x x

Do
2
2 8 0;x x x
nên HBPT
2
2
7 10 0
80
xx
x x x
5 2
8 1 0
xx
xx
8 x
10x
.
Câu 23: [0D4-7-3] Giải hệ BPT phương trình:
22
2
(2 3) ( 3) 0 (1)
2 5 3 0 (2)
xx
xx
.
A.
3
2 1 0
2
xx
. B.
1 0xx
.
C.
2 x
1x
. D.
21x
.
Lời giải
Chọn C
HBPT
2
20
3 6 0
3
1
2 5 3 0
2
x
xx
xx
xx
3
2 1 0
2
xx
.
Câu 24: [0D4-7-3] Giải hệ BPT
2
2
2
2
45
0 (1)
32
43
0 (2)
1
xx
xx
xx
xx
A.
1 x
3x
. B.
3 x
2x
.
C.
32x
. D.
3 x
1 1 x
2x
.
Lời giải
Chọn D
Do
2
4 5 0 ;x x x
2
10x x x
nên HBPT
2
2
3 2 0
4 3 0
xx
xx
12
31
xx
xx
3 x
1 1 x
2x
.
Câu 25: [0D4-7-3] Giải hệ bphương trình:
2
2
4
0 (1)
2
1 2 1
0 (2)
22
x
xx
xx
xx

A.
22x
. B.
2 x
2x
. C. Vô nghiệm. D.
2 1xx
.
Lời giải
Chọn B
HBPT
2
2
2
2
4
0
2
3 2 4
0
4
x
xx
xx
x
. Do
22
2 0;3x 2 4 0;x x x x
nên
HBPT
2
40x
2 x
2x
.
Câu 26: [0D4-7-3] Giải bất phương trình:
2
2
32
23
1
xx
xx
.
A.
1 0xx
. B.
1 x
2x
. C.
12x
. D.
10x
.
Lời giải
Chọn D
Do Do
2
10x x x
nên BPT
22
22
3 2 3 1
3 2 2 1
x x x x
x x x x
2
2
2 1 0
0
x
xx
10x
.
Câu 27: [0D4-7-3] Miền nghiệm của hệ bất phương trình:
2
2
2
2 3 0
20
60
xx
xx
xx
.
A.
13x
. B.
1 3xx
. C.
23x
. D.
1 1 3xx
.
Lời giải
Chọn A
HBPT
13
21
23
x
xx
x
13x
.
Câu 28: [0D4-7-3] Miền nghiệm của hệ bất phương trình
2
32
2 8 0
2 2 0
xx
x x x
A.
21x
. B.
1 2x
. C.
2x
. D.
1 1 x
hoặc
2x
.
Lời giải
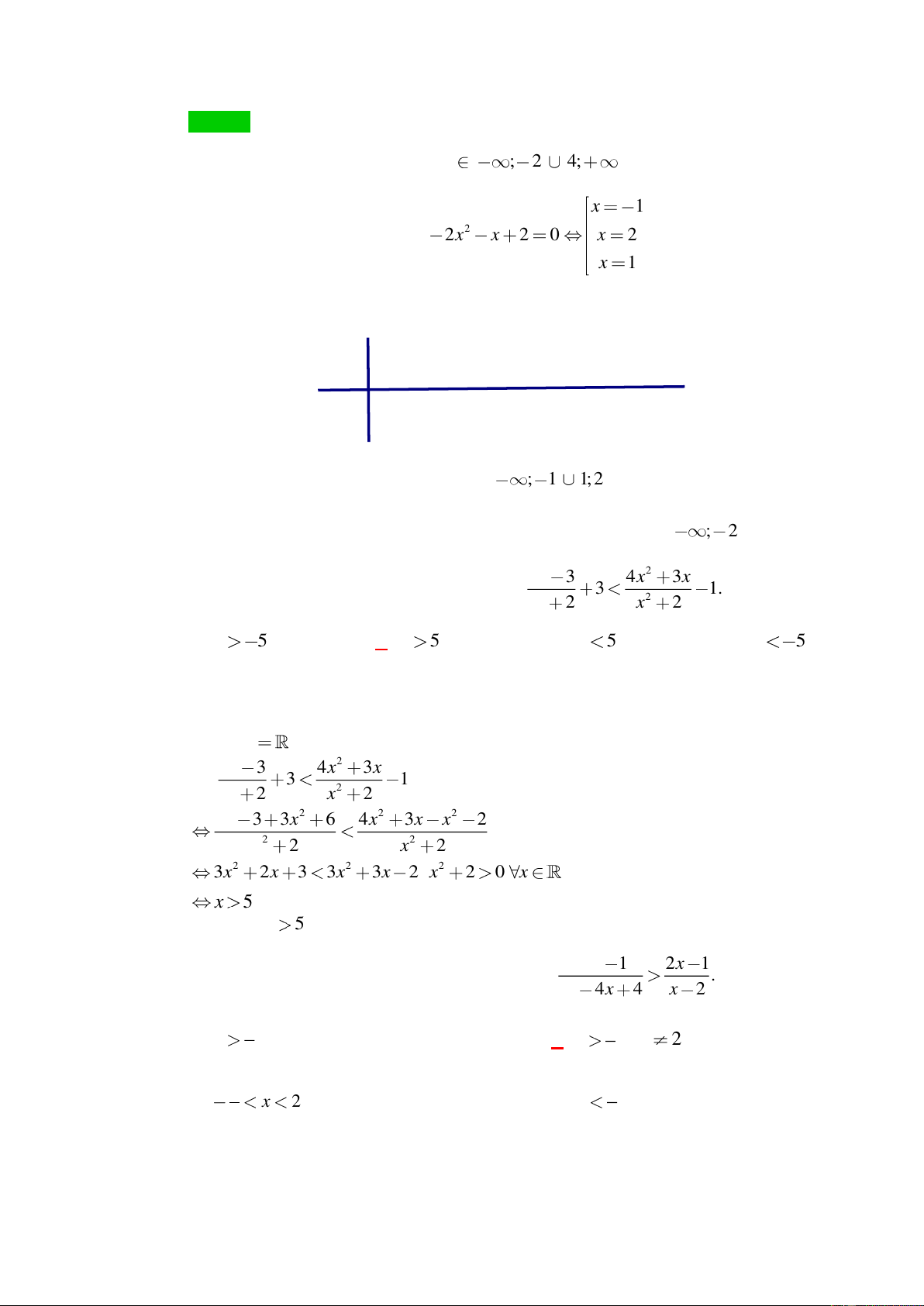
Chọn C
Giải bất phương trình (1) ta được
; 2 4;x
.
Xét bất phương trình (2) cho
32
1
2 2 0 2
1
x
x x x x
x
.
Lập bảng xét dấu vế tri (2) ta được
-
+
-
+
0
0
0
+
∞
2
1
-1
-
∞
VT
2
( )
x
Tập nghiệm của bất phương trình (2) là
; 1 1;2
.
Kết hợp tập nghiệm của (1) và (2) ta được tập nghiệm của hệ là
;2
.
Câu 29: [0D4-7-3] Tìm nghiệm của bất phương trình:
2
22
2 3 4 3
3 1.
22
x x x
xx
A.
5x
. B.
5x
. C.
5x
. D.
5x
.
Lời giải
Chọn B
TXĐ:
D
PT
2
22
2 3 4 3
31
22
x x x
xx
2 2 2
22
2 3 3 6 4 3 2
22
x x x x x
xx
2 2 2
3 2 3 3 3 2 2 0x x x x x x
5x
.
Kết luận:
5x
.
Câu 30: [0D4-7-3] Tập hợp nghiệm của bất phương trình:
2
2
2 1 2 1
.
4 4 2
xx
x x x
A.
3
5
x
. B.
3
5
x
và
2x
.
C.
3
2
5
x
. D.
3
5
x
.
Lời giải
Chọn B

TXĐ:
\2D
PT
2
2
2 1 2 1
.
4 4 2
xx
x x x
2
2
2
2 1 2
21
0
44
2
xx
x
xx
x
2
53
0
2
x
x
3
5
2
x
x
Kết luận:
3
5
x
và
2x
.
Câu 31: [0D4-7-3] Định m để phương trình:
2
( 1) 2( 2) 1 0m x m x m
có
2
nghiệm
phân biệt khác
0
sao cho
12
11
2
xx
.
A.
5
4
m
và
1m
. B.
1m
.
C.
5
1
4
m
. D.
5
1
4
m
và
1m
.
Lời giải
Chọn B
2
( 1) 2( 2) 1 0m x m x m
.
Phương trình có hai nghiệm phân biệt khác
0
khi
2
1
10
1
2 1 1 0 4 5 0
4
1
10
1
m
m
m
m m m m m
m
m
m
1
.
Viet
12
12
22
1
1
1
m
xx
m
m
xx
m
Khi đó
1 2 2 2
1 2 1 2
2
11
20
x x x x
x x x x
22
1
2
5
11
0 0 1
1
1
1
m
m
mm
m
m
m
m
2
.

Từ
1 ; 2 1m
.
Câu 32: [0D4-7-3] Giải bất phương trình:
22
2
8
( 2)
22
xx
xx
.
A.
( 0) ( 2)xx
. B.
02x
.
C.
( 2) ( 2)xx
. D.
22x
.
Lời giải
Chọn A
Nhận xét
2
2 2 0x x x
.
2 2 2 2
2
8
( 2) 2 2 2 4 4 8
22
x x x x x x
xx
2
2
22
2
2 2 2
2
2 2 4 2 0
0
2 2 2
xx
x
x x x x
x
x x VN
.
Câu 33: [0D4-7-3] Định
m
để bất phương trình:
2
2
21
32
1
x mx
xx
có miền nghiệm là
.
A.
5 11
20
22
mm
. B.
( 2) ( 0)mm
.
C.
20m
. D.
5 11
22
mm
.
Lời giải
Chọn C
Nhận xét
2
10x x x
.
22
2
2
22
2 1 3 3 3
21
32
1
2 1 2 2 2
x mx x x x
x mx
x
xx
x mx x x x
2
2
1
22
2
4 2 3 4 0 2 3 64 0
2 1 1 0
1 1 0
x m x m
x m x
m
2
2
5 11
4 12 55 0
2;0
22
20
20
mm
m
m
mm
m
.

Câu 34: [0D4-7-3] Định
m
để bất phương trình:
2
( 1) 2( 2) 2 0m x m x m
có miền
nghiệm là .
A.
12m
. B.
( 1) ( 2)mm
.
C.
3
2
2
mm
. D.
3
2
2
m
.
Lời giải
Chọn D
2
( 1) 2( 2) 2 0 1m x m x m x
.
Trường hợp
1
:
1 0 1mm
21xx
( Sai).
Trường hợp
2
:
1 0 1mm
.
Khi đó
2
2
1
10
1
3
12
3
2
2
2 7 6 0
2 1 2 0
2
m
m
m
m
m
mm
m m m
.
Vậy
3
2
2
m
.
Câu 35: [0D4-7-3] Xc định
m
để với mọi
x
ta có
2
2
5
17
2 3 2
x x m
xx
.
A.
5
1
3
m
. B.
5
1
3
m
. C.
5
3
m
. D.
1m
.
Lời giải
Chọn A
Ta có:
2
2
5
17
2 3 2
x x m
xx
có tập nghiệm là khi hệ sau có tập nghiệm là (do
2
2 3 2 0x x x
)
22
22
1 2 3 2 5
5 7 2 3 2
x x x x m
x x m x x
2
2
13 26 14 0 1
3 2 2 0 2
x x m
x x m
có tập nghiệm là
Ta có
1
có tập nghiệm là khi
' 0 13 13 0m
1m
(3)
2
có tập nghiệm là khi
' 0 5 3 0m
5
3
m
(4)

Từ (2) và (4), ta có
5
1
3
m
.
Câu 36: [0D4-7-3] Tìm
m
để
2
1 0,m x mx m x
?
A.
1m
. B.
1m
. C.
4
3
m
. D.
4
3
m
.
Lời giải
Chọn C
Với
1m
không thỏa mãn.
Với
1m
,
2
0
1 0,
0
a
m x mx m x
2
10
3 4 0
m
mm
1
4
3
0
m
m
m
4
3
m
.
Câu 37: [0D4-7-3] Có bao nhiêu giá trị
m
nguyên âm để mọi
0x
đều thoả bất phương trình
22
22
3x x m x x m
?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B
Ta có
2 2 2 2
2 2 2 2
3 3 0x x m x x m x x m x x m
4 2 1 0x x m x
Với
0m
ta có bảng xét dấu
TH1:
1
2
m
x
0
1
2
m
4x
-
0
+
||
+
||
+
1x
-
||
-
0
+
||
+
2xm
-
||
-
||
-
0
+
fx
-
0
+
0
-
0
+
Từ Bảng xét dấu ta thấy để BPT nghiệm đúng với
0x
thì
12
2
m
m
TH 2:
1
2
m

x
0
2
m
1
4x
-
0
+
||
+
||
+
2xm
-
||
-
0
+
||
+
1x
-
||
-
||
-
0
+
fx
-
0
+
0
-
0
+
Từ Bảng xét dấu ta thấy để BPT nghiệm đúng với
0x
thì
12
2
m
m
Vậy có 1 gi trị
Câu 38: [0D4-7-3] Xc định
m
để phương trình
2
1 2 3 4 12 0x x m x m
có ba
nghiệm phân biệt lớn hơn –1.
A.
7
2
m
. B.
21m
và
16
9
m
.
C.
7
1
2
m
và
16
9
m
. D.
7
3
2
m
và
19
6
m
.
Lời giải
Chọn D
Ta có
2
1 2 3 4 12 0x x m x m
2
1
2 3 4 12 0 *
x
x m x m
.
Giải sử phương trình
*
có hai nghiệm phân biệt
12
,xx
, theo Vi-et ta có
12
12
23
. 4 12
x x m
x x m
.
Để phương trình
2
1 2 3 4 12 0x x m x m
có ba nghiệm phân biệt lớn
hơn
–1
. thì phương trình
*
có hai nghiệm phân biệt
12
,xx
khác
1
và đều lớn hơn
1
.

21
0
1 2 3 4 12 0
1
mm
xx
2
12
12
3 4 12 0
6 19 0
1 1 0
1 1 0
mm
m
xx
xx
2
2 3 0
19
6
2 3 2 0
4 12 2 3 1 0
mm
m
m
mm
1
3
19
6
2
7
2
m
m
m
m
m
7
3
2
19
6
m
m
.
Câu 39: [0D4-7-3] Phương trình
22
1 2 1 4 5 0m x m x m m
có đúng hai nghiệm
12
,xx
thoả
12
2 xx
. Hy chọn kết quả đúng trong cc kết quả sau
A.
21m
. B.
1m
. C.
53m
. D.
21m
.
Lời giải
Chọn A
Để phương trình
22
1 2 1 4 5 0m x m x m m
có có đúng hai nghiệm
12
,xx
thoả
12
2 xx
.
21
0
10
2
m
xx
2
2
12
12
1 1 4 5 0
1
2 2 0
2 2 0
m m m m
m
xx
xx
.Theo Vi-et ta có
12
2
12
21
1
45
.
1
m
xx
m
mm
xx
m
.
2
2
1 5 6 0
1
21
40
1
21
45
2. 4 0
11
m m m
m
m
m
m
mm
mm
21
3
1
31
3
m
m
m
m
m
21m
.

Câu 40: [0D4-7-3] Cho hệ bất phương trình
2
32
3 4 0
3 6 0
xx
x x x m m
Để hệ có nghiệm, các giá trị thích hợp của tham số m là:
A.
2 8 m
. B.
–8 2 m
. C.
–2 8 m
. D.
–8 –2 m
.
Lời giải
Chọn C
Ta có
2
3 4 0 1 4x x x
.
Trường hợp 1:
0;4x
, bất phương trình hai trở thành
3 2 2
3 6 0x x m m
2 3 2
63m m x x
, mà
32
3 16 0;4x x x
suy ra
2
6 16mm
28m
.
Trường hợp 2:
1;0x
, bất phương trình hai trở thành
3 2 2
3 6 0x x m m
2 3 2
63m m x x
, mà
32
3 2 1;0x x x
suy ra
2
62mm
3 11 3 11m
.
Vậy
–2 8 m
thì hệ bất phương trình đ cho có nghiệm.
Câu 41: [0D4-7-3] Hệ bất phương trình:
2
2 2 2
5 4 0
( 3) 2( 1) 0
xx
x m x m
có tập nghiệm biểu
diễn trên trục số có độ dài bằng 1, với giá trị của
m
là:
A.
0m
. B.
2m
.
C.
2m
. D. Cả A, B, C đều đúng.
Lời giải
Chọn D
Thay
0m
vào ta có
2
2
5 4 0
3 2 0
xx
xx
14
12
12
x
x
x
. A đúng
Thay
2m
vào ta có
2
2
5 4 0
5 6 0
xx
xx
14
24
23
x
x
x
. B đúng
Tương tự C đúng.
Câu 42: [0D4-7-3] Tập nghiệm của bất phương trình
2
( 1) ( 3)
0
( 1)( 2)( 3)
xx
x x x
là:

A.
; 3 1;2 3;S
. B.
; 3 1;2 3;S
.
C.
; 3 1;2 3; \ 1S
. D.
; 3 1;2 3; \ 0S
.
Lời giải
Chọn B
Ta có:
2
1 0 1xx
,
3 0 3xx
1 0 1xx
,
2 0 2xx
,
3 0 3xx
.
Bảng xét dấu
Do đó:
; 3 1;2 3; \ 1S
.
Câu 43: [0D4-7-3] Cho bất phương trình
3
2
( 1) (2 1)
0
3 ( 1)
xx
xx
.Trong những tập sau, tập nào
không chứa nghiệm của bất phương trình trên.
A.
;2
. B.
1;1
. C.
1
;2
2
. D.
(0;1)
.
Lời giải
Chọn C
Ta có:
3
1 0 1xx
,
1
2 1 0
2
xx
,
3 0 0xx
,
2
1 0 1xx
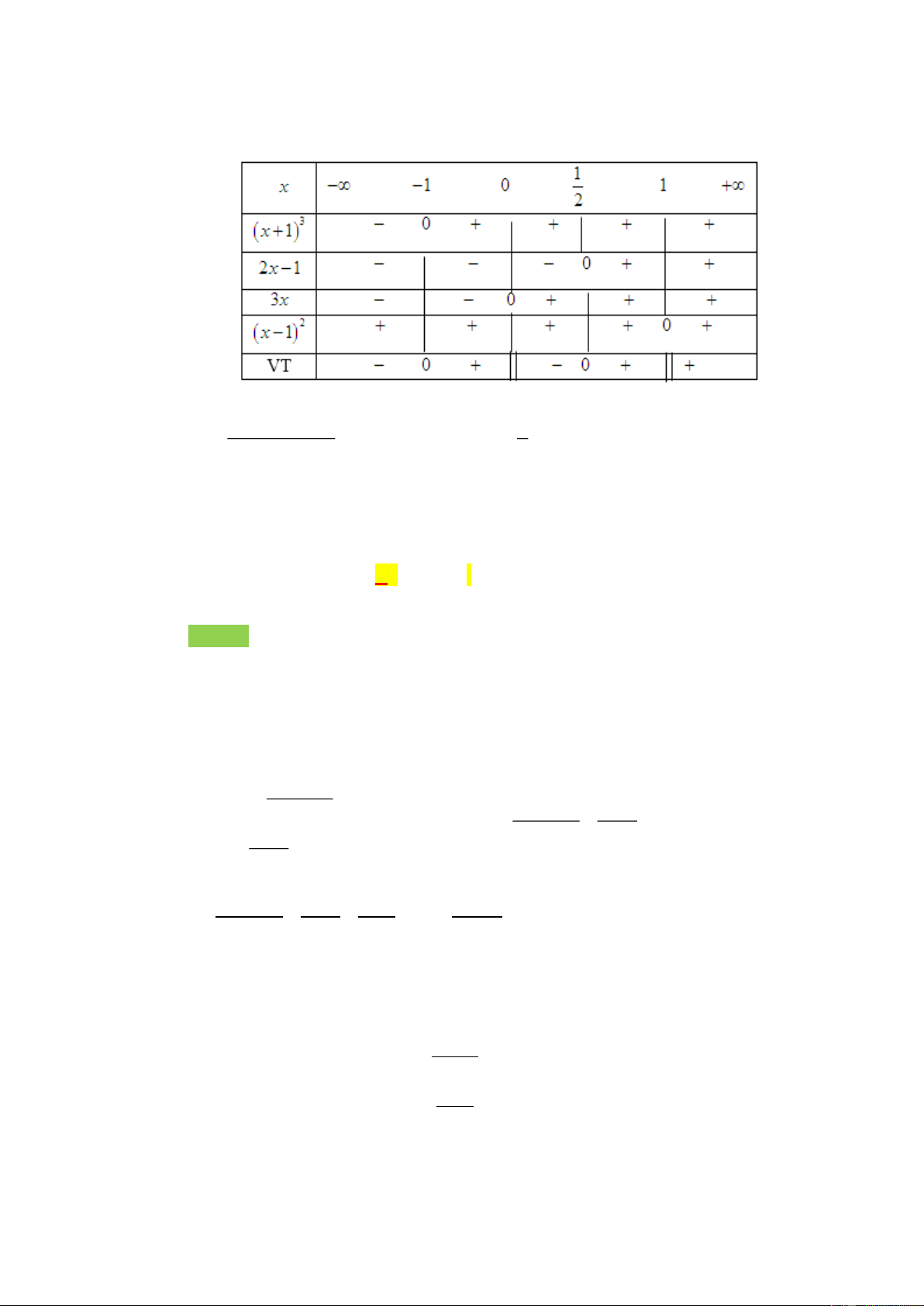
Bảng xét dấu
Vậy
3
2
( 1) (2 1) 1
0 ;0 0;
3 ( 1) 2
xx
x
xx
.
Câu 44: [0D4-7-3] Với giá trị nào của
m
thì pt:
2
( 1) 2( 2) 3 0m x m x m
có hai
nghiệm
12
,xx
và
1 2 1 2
1x x x x
?
A.
12m
. B.
13m
. C.
2m
. D.
3m
.
Lời giải
Chọn B
+ PT
2
( 1) 2( 2) 3 0m x m x m
có hai nghiệm
12
,xx
khi
0 1 0
1
0 1 0
am
m
m
. Khi đó, theo định lý Vi-ét ta có:
12
12
22
1
3
1
m
xx
m
m
xx
m
1 2 1 2
22
3
11
11
m
m
x x x x
mm
22
3 1 2 6
0 0 1 3
1 1 1 1
m
m m m
m
m m m m
.
Vậy
13m
.
Câu 45: [0D4-7-3] Hệ bất phương trình
43
6
25
1
2
3
x
x
x
x
có nghiệm là

A.
5
3
2
x
. B.
5 33
28
x
C.
73x
. D.
33
3
8
x
.
Lời giải
Chọn C
Ta có
4 3 6 2 5
4 3 8 33
33 5
6 0 0
2 5 2 5 2 5
73
82
17
1 2 3
73
20
0
33
3
xx
xx
xx
x x x
x
xx
xx
x
xx
x
.
Câu 46: [0D4-7-3] Hệ bất phương trình
45
3
25
74
23
3
x
x
x
x
x
có nghiệm là
A.
23
2
x
. B.
13x
. C.
13x
. D.
5
13
2
x
.
Lời giải
Chọn D
Ta có
2
4 5 3 2 5
45
30
2 7 10
0
2 5 2 5
25
74
7 4 3 2 3
23
13
0
3
3
x x x
x
x
xx
xx
x
x
xx
x
x
5
5
13
2
2
13
x
x
x
.
Câu 47: [0D4-7-3] Cho hai bất phương trình
2
2 3 0xx
1
và
2
2 9 0mx mx m
2
Xét mệnh đề P“ Mọi
x
là nghiệm của
1
hay nghiệm của
2
” câu nào sau đây
đúng
A. P đúng với mọi
0m
.

B. Giá trị nguyên lớn nhất của m để P đúng là 1.
C. Có vô số giá trị nguyên để P đúng.
D. Chỉ có hai câu đúng trong ba câu A, B, C.
Lời giải
Chọn D
1 1 3xx
.
2
2
99m m m m
. Với
0m
thì
33
2 1 1x
mm
Mệnh đề A đúng
3
13
39
2
3
4
11
m
m
m
m
nên có vô số giá trị
nguyên của m để A đúng trong đó
1m
là giá trị nguyên lớn nhất và mệnh đề A sẽ
không đúng với mọi
0m
.
Câu 48: [0D4-7-3] Để
2
1 2 7 0f x x m x m
với mọi x thì
A.
39m
. B.
39mm
. C.
39m
. D.
39mm
.
Lời giải
Chọn C
Ta có
0fx
x
2
10
6 27 0
a
mm
39m
.
Câu 49: [0D4-7-3] Bất phương trình
2
4 3 1 0f x mx x m
nghiệm đúng mọi
0x
khi
A.
0m
. B.
4
3
m
. C.
1m
. D.
2m
.
Lời giải
Chọn C
Chọn
1m
2
4 4 0f x x x
không đúng với
2x
nên ta loại A.
Chọn
4
3
m
2
4
4 5 0
3
f x x x
đúng
x
do
4
0
3
a
và
32
0
3
nên loại B.

Chọn
2m
2
2
2 4 7 2 1 5 0f x x x x
x
nên ta loại D.
Câu 50: [0D4-7-3] Cho bất phương trình
22
2 4 –1 15 2 7 0x k x k k
. Giá trị nguyên
của k để bất phương trình nghiệm đúng mọi
x
là
A.
2k
. B.
3k
. C.
4k
. D.
5k
.
Lời giải
Chọn B
Ta có
0fx
x
2
10
6 8 0
a
kk
24k
mà k nguyên nên
3k
.
Câu 51: [0D4-7-3] Có bao nhiêu giá trị m để mọi
0x
đều thoả bất pt
2 2 22
( ) ( ) 3x x m x x m
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B
Ta có
2 2 22
( ) ( ) 3x x m x x m
2
4 2 2 2 0f x x m x x
Các nghiệm
0;1;
2
m
. Ta nhận thấy nghiệm
1x
luôn nằm trước nghiệm
0x
sẽ
làm cho
fx
bị đổi dấu trong miền
0x
. Từ đó
1ycbt x
là nghiệm kép
12
2
m
m
.
Câu 52: [0D4-7-3] Tìm tất cả các giá trị thực của tham số để mọi nghiệm của bpt
2222
( ) ( 42)2x x m x x m
đều lớn hơn 1.
A.
0m
. B.
2m
. C.
02mm
. D.
02m
.
Lời giải
Chọn D
Ta có
2222
( ) ( 42)2x x m x x m
2
2 2 6 3 0x x m x m
.
Chọn
3m
2
2 2 3 6 9 0x x x
3
2
x
không thỏa ycbt nên loại B, C.

Chọn
4:m
2
2 2 4 6 12 0x x x
2 1 2xx
không thỏa ycbt nên
loại A.
Câu 53: [0D4-7-3] Tìmtất cả các giá trị thực của tham số m để bất phương trình sau vô
nghiệm
2
3 2 4 0m x xf mx
A.
22 2mm
. B.
22 2m
. C.
22 2m
. D.
22 2
3
m
m
.
Lời giải
Chọn B
Ta có
0fx
vô nghiệm
0f x x
.
Xét
3m
54f x x
nên loại
3m
.
Xét
3m
0f x x
2
30
20 44 0
am
mm
22 2m
.
Câu 54: [0D4-7-3] Tìm tất cả các giá trị thực của tham số m để bpt
22
1 2 1) 3 0(m x m x
(1) có nghiệm.
A.
12mm
. B.
12m
. C.
12m
. D.
12m
.
Lời giải
Chọn B
Ta giải bài ton tìm m để (1) vô nghiệm. Đặt
22
) 13( 12m x xfx m
.
0fx
vô nghiệm
0fx
x
.
Xét
1m
43f x x
nên loại
1m
.
Xét
1m
30f x x
nên nhận
1m
.
Xét
1m
0f x x
2
2
10
2 2 4 0
am
mm
1
2
m
m
Do đó (1) có nghiệm
12m
.
Câu 55: [0D4-7-3] Tập nghiệm của bất phương trình
222
3 1 3 5) 90(x x x x
là

A.
;1S
. B.
2;S
.
C.
;1 2;S
. D.
0;1S
.
Lời giải
Chọn C
Ta có
222
3 1 3 5) 90(x x x x
2
22
3 1 3 3 1 2 0x x x x
.
2
2
3 1 2
3 1 1
xx
xx
2
2
3 3 0
3 2 0
xx
xx
1
2
x
x
.
Câu 56: [0D4-7-3] Cho bất phương trình
2
2 1 1 0mx m x m
(1). Tìm tất cả các giá
thực của tham số m để bất phương trình (1) vô nghiệm.
A.
1
8
m
. B.
1
8
m
. C.
1
8
m
. D.
1
8
m
.
Lời giải
Chọn A
Đặt
2
2 1 1f x mx m x m
.
Ta có
0fx
vô nghiệm
0f x x
.
Xét
0m
1f x x
nên loại
0m
.
Xét
0m
0f x x
0
8 1 0
m
m
1
8
m
.
Câu 57: [0D4-7-3] Cho hai bất phương trình
2 2 4
1() 0x m m x m
(1) và
2
4 3 0 2xx
. Các giá trị của tham số msao cho nghiệm của bất phương trình
(1) đều là nghiệm của bất phương trình (2) là
A.
; 3 1; \ 0;1m
. B.
3m
.
C.
1m
và
0m
. D.
3m
và
0m
.
Lời giải
Chọn D
2 3 1xx
hay
2
; 3 1;S
. Ycbt
12
SS
22
2 2 4 2 2
1
1 4 1m m m m m
nên có 2 nghiệm
3
x m x m
.

Xét
3
mm
3
0mm
10
1
m
m
(*). Khi đó
3
1
;S m m
và với điều kiện
(*) nên hiển nhiên
12
SS
nhận
10
1
m
m
(*)
Xét
3
mm
3
0mm
01
1
m
m
3
1
;S m m
.
12
SS
3
3
; ; 3
; 1;
mm
mm
3
3
1
m
m
3
1
m
m
.
Kết hợp với
01
1
m
m
ta được
3
01
m
m
(**)
Kết hợp (*)(**) ta được
3
10
01
1
m
m
m
m
; 3 1; \ 0;1m
.
Câu 58: [0D4-7-3] Bất phương trình
3 3 3 3
(2 1) ( 1) (2 2) 0x x x x
có bao nhiêu
nghiệm nguyên âm?
A.
0
. B.
1
.
C.
2
. D.Nhiều hơn 2 nhưng hữu hạn.
Lời giải
Chọn A
Ta có
3 3 3 3
(2 1) ( 1) (2 2) 0x x x x
32
18 39 33 10 0x x x
.
2
3 2 6 9 5 0x x x
2
3
x
nên bất phương trình không có nghiệm
nguyên âm.
Câu 59: [0D4-7-3] Bất phương trình:
2
2
31
3
1
xx
xx
có nghiệm là:
A.
35
2
x
hoặc
35
.
2
x
B.
35
2
x
hoặc
35
.
2
x
C.
53
2
x
hoặc
53
.
2
x
D.
53
2
x
hoặc
53
2
x
.
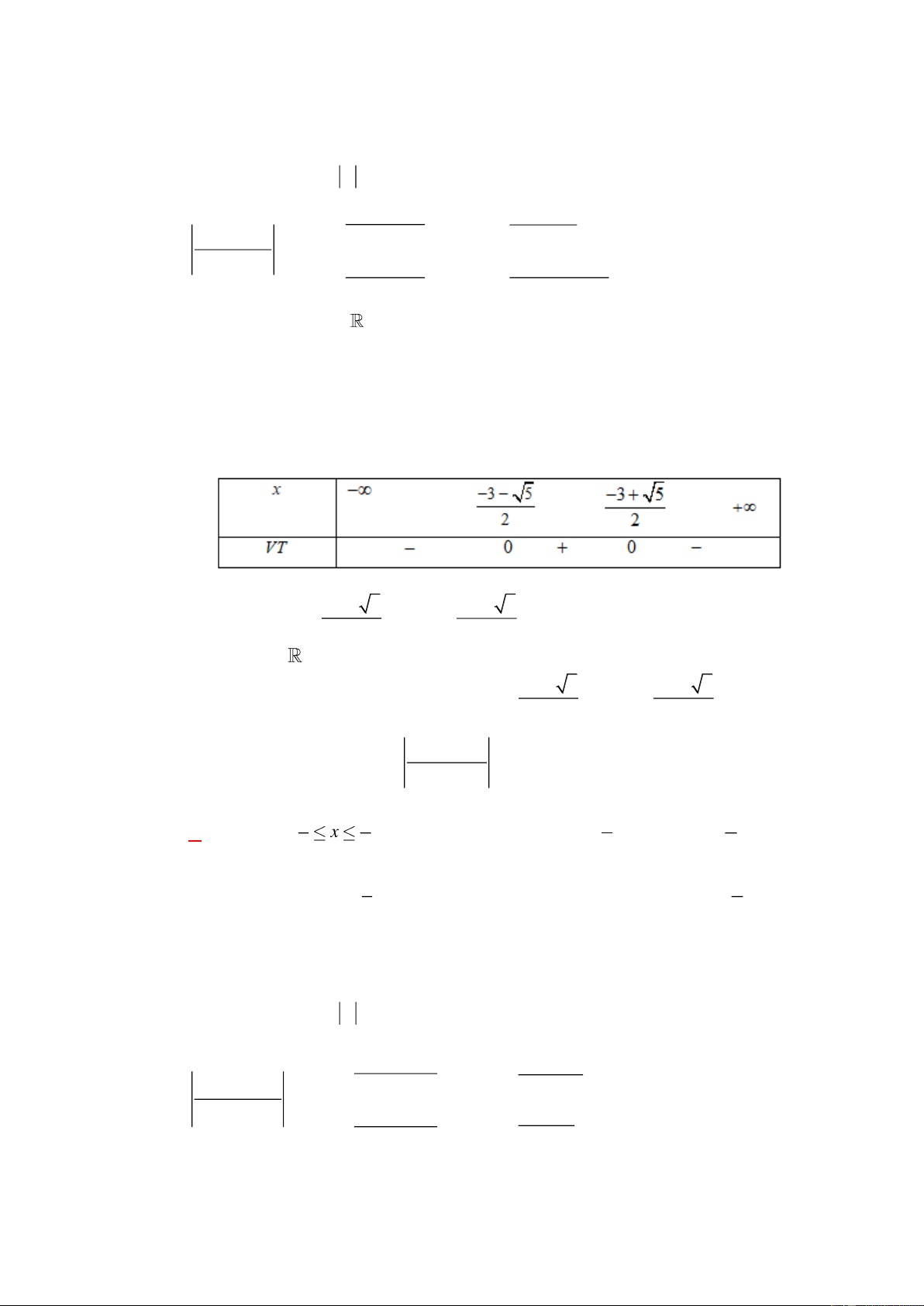
Lời giải
Chọn B
Áp dụng công thức
AB
B A B
2
2
31
3
1
xx
xx
2
2
2
2
31
3
1
31
3
1
xx
xx
xx
xx
2
2
2
2
44
0
1
2 6 2
0
1
x
xx
xx
xx
Vì
2
10x x x
.
Hệ bpt
2
2
2 6 2 0 (1)
4 4 0 (2)
xx
x
Giải (1) : BXD :
Ta có (1)
35
2
x
hoặc
35
2
x
(2)
x
Từ (1)(2) lấy giao hai tập nghiệm, ta có
35
2
x
hoặc
35
2
x
Câu 60: [0D4-7-3] Bất phương trình:
2
2
54
1
4
xx
x
có nghiệm là:
A.
0x
hoặc
85
52
x
,
2x
. B.
8
5
x
hoặc
5
2
2
x
.
C.
2x
hoặc
8
0
5
x
. D.
20x
hoặc
5
2
x
.
Lời giải
Chọn A
Áp dụng công thức
AB
AB
AB
1
4x
4x5x
2
2
2
2
2
2
54
1
4
54
1
4
xx
x
xx
x
2
2
2
25
0 (1)
4
58
0 (2)
4
xx
x
x
x
Giải (1) :
Bảng xét dấu:

Ta có (1)
20x
hoặc
5
2
2
x
Giải (2): Bảng xét dấu:
Ta có (2)
2x
hoặc
8
2
5
x
.
Lấy hợp tập nghiệm (1)(2)
0x
hoặc
2
5
x
5
8
,
2x

Câu 1: [0D4-7-4]Cho hệ bất phương trình
2
22
6 5 0
2( 1) 1 0
xx
x a x a
Để hệ bất phương trình có nghiệm, giá trị thích hợp của tham số
a
là:
A.
02a
. B.
04a
. C.
24a
. D.
08a
.
Lời giải
Chọn D
2
22
6 5 0 (1)
2( 1) 1 0 (2)
xx
x a x a
Giải (1) :
2
6 5 0xx
15x
Giải (2)
'2a
Th1 :
00a
thì
1x
là nghiệm của hệ pt.
Th2:
00a
thì (2) vô nghiệm nên hệ pt vô nghiệm.
Th3 :
00a
đặt
22
( ) 2( 1) 1f x x a x a
Giả sử
( ) 0fx
có 2 nghiệm
12
xx
vậy tập nghiệm
12
;xx
Hệ pt vô nghiệm khi.
12
1xx
hoặc
12
5 xx
.
Th3.1 :
12
1xx
đk là
2
(1) 0
20
11
0
f
aa
a
a
loại
Th3.2 :
12
5 xx
đk là
(5) 0
15
f
a
2
2, 8
10 16 0
4
4
aa
aa
a
a
Kết hợp với
0a
ta có:
8a
Vậy để có hai nghiệm thỏa đk là
08a
.
Câu 2: [0D4-7-4]Cho hệ bất phương trình
2
22
20
2(m 1) 0
xx
x x m
Đề hệ bất phương trình có nghiệm, giá trị cần tìm của tham số
m
là.
A.
1
2
m
. B.
1
2
m
. C.
0m
. D.
m
.
Lời giải
Chọn C
Giải (1):
2
2 0 0;2x x x
.
Giải (2) :
22
2(m 1) 0x x m
.
21m

Th1:
1
0
2
m
thì phương trình (2) có tập nghiệm là nên hệ phương trình
có tập nghiệm là
0;2
.
Th2 :
1
0
2
m
đặt
22
( ) 2(m 1)f x x x m
Giả sử
( ) 0fx
có 2 nghiệm
12
xx
thì tập nghiệm của (2) là
12
;;xx
Ta đi tìm
m
để hệ pt vô nghiệm.
Hệ vô nghiệm khi
12
;;xx
giao với
0;2
bằng tập rỗng hay
12
02xx
2
2
20
40
(0) 0
0
f
mm
f
m
4;0
0
0
m
m
m
Vậy hệ có nghiệm khi
0m
.
Câu 3: [0D4-7-4]Cho hệ bất phương trình
2
2
7 8 0
1 3 (3 2)
xx
ax a x
Đề hệ bất phương trình vô nghiệm, giá trị cần tìm của tham số
a
là:
A.
0a
hoặc
9
44
a
. B.
9
0
44
a
. C.
9
0
44
a
. D.
9
0
44
a
.
Lời giải
Chọn D
22
22
7 8 0 7 8 0 (1)
1 3 (3 2) (3 2) 2 0 (2)
x x x x
ax a x ax a x
Giải (1):
81x
Giải (2)
2
' 9 4 4 0 ,a a a
Th1 :
0a
(2)
1x
khi đó hệ đã cho vô nghiệm.
0a
thỏa.
Th2 :
0a
đặt
2
( ) (3 2) 2f x ax a x
Giả sử
( ) 0fx
có 2 nghiệm
12
xx
vậy tập nghiệm của (2) là
12
;xx
.

Để hệ vô nghiệm đk là :
12
12
8
1
xx
xx
80
16
10
2
f
S
f
S
88 18 0
32
16
20
32
2
a
a
a
a
a
a
9
44
2
19
0
2
a
a
a
a
Vì
0a
nên không có giá trị của
.a
Th3:
0a
lúc đó bpt (2) có tập nghiệm là
12
( ;x ) ;x
Để hệ vô nghiệm thì đk là
12
81xx
( 8) 0
(1) 0
f
f
88 18 0
9
0
20
44
a
a
a
Vậy
9
0
44
a
thỏa ycbt.
Câu 4: [0D4-7-4] Với giá trị nào của
m
thì hệ bất phương trình sau có nghiệm:
2
2 1 2
1
3 4 0
xx
xx
x x m
.
A.
01m
. B.
01m
. C.
3
0
4
m
. D.
4
3
m
.
Lời giải
Chọn D
2
2 1 2
1
1
3 4 0 2
xx
xx
x x m
.
Ta có:
2 1 2
10
1
xx
xx
.
2
1
0
1
xx
xx

Vì
2
1 0,x x x
nên
2
1
0 1 0 0;1
1
xx
x x x
xx
.
Đặt
2
34f x x x m
Để hệ bất phương trình có nghiệm thì phương trình
( ) 0fx
có 2 nghiệm
12
,xx
sao cho
12
01xx
hoặc
12
01xx
hoặc
12
01xx
hoặc
12
01xx
.
TH1 : Phương trình
( ) 0fx
có 2 nghiệm
12
,xx
sao cho
12
01xx
0
00
(1) 0
f
f
4 3 0
0
10
m
m
m
4
3
00
1
m
mm
m
TH2 : Phương trình
( ) 0fx
có 2 nghiệm
12
,xx
sao cho
12
01xx
0
4 3 0
0 0 0
10
(1) 0
m
fm
m
f
4
3
4
00
3
1
m
mm
m
TH3 : Phương trình
( ) 0fx
có 2 nghiệm
12
,xx
sao cho
12
01xx
0
4 3 0
0 0 0
10
(1) 0
m
fm
m
f
4
3
0
1
m
mm
m
Lấy hợp các trường hợp trên ta có
4
3
m
thỏa yêu cầu bài toán.
Câu 5: [0D4-7-4] Cho hệ:
42
22
5 4 0 1
(2 1) 2 0 2
xx
x a x a a
Để hệ có nghiệm duy nhất, các giá trị cần tìm của tham số a là:
A.
43a
hoặc
10a
hoặc
12a
.
B.
32a
hoặc
01a
hoặc
34a
.
C.
21a
hoặc
23a
hoặc
4a
.

D.
2a
hoặc
7
2
8
a
.
Lời giải
Chọn D
Ta có
21
1
12
x
x
Xét PT
2
có
87a
TH1:
7
0
8
a
khi đó
2
vô nghiệm nên hệ vô nghiệm
TH2:
7
0
8
a
khi đó
2
có nghiệm là
11
8
x
(thỏa mãn điều kiện có
nghiệm của
1
) Vậy hệ thỏa mãn có duy nhất nghiệm.
TH3:
7
0
8
a
khi đó
2
có hai nghiệm phân biệt
12
xx
.
Trong trường hợp này hệ đã cho có duy nhất nghiệm khi và chỉ khi
Khả năng 1: Một nghiệm thuộc
2; 1
và một nghiệm nằm ngoài
2; 1
, cả
hai đều không thuộc
1;2
.
2 1 0
10
ff
af
3
3
20
a
a
a
kết hợp điều kiện giả thiết ta được
3
7
2
8
a
a
Khả năng 2: Một nghiệm thuộc
1;2
và một nghiệm nằm ngoài
1;2
, cả hai
đều không thuộc
2; 1
.
1 2 0
10
ff
af
4
13
2
a
a
a
kết hợp điều kiện giả thiết ta được
2a
Kết luận hệ có nghiệm duy nhất khi và chỉ khi
7
8
a
và
2a
.
Câu 6: [0D4-7-4] Cho hệ bất phương trình:
2
32
3 4 0
3 6 0
xx
x x x m m
Để hệ có nghiệm, các giá trị thích hợp của tham số m là:
A.
2 8.m
B.
8 2.m
C.
2 8.m
D.
82m
.

Lời giải
Chọn C
Hệ có nghiệm khi và chỉ khi
32
3 6 0x x x m m
có nghiệm thỏa mãn
14x
.
Chia khoảng điều kiện thành 2 trường hợp
TH1:
10x
TH2:
04x
Để có thể xác định đáp án một cách nhanh chóng hơn, ta chọn 4 giá trị đặc biệt là
8; 2;2;8m
để thử vào các trường hợp và sử dụng máy tính để bấm nghiệm của
phương trình bậc 3.
Thấy
8m
khi thay vào không có nghiệm thỏa mãn nên loại.
2;8m
khi thay vào đều cho cùng một giá trị và có nghiệm
4x
thỏa mãn hệ.
Vậy cần chọn đáp án C là phù hợp.
Câu 7: [0D4-7-4] Cho hệ:
22
1
3
xy
x y m
Với giá trị nào của m thì hệ có nghiệm?
A.
1 m
. B.
2m
. C.
–2m
. D.
1m
.
Lời giải
Chọn B
Hệ có nghiệm khi và chỉ khi
2
13x x m
có nghiệm thỏa mãn
11x
2
13x x m
2
13x m x
22
1
4 2 3 0
m
x mx m
Xét
22
4 2 3 0x mx m
có
2
12 4m
Nếu
2
0
2
m
m
thì PT có nghiệm
x
nên sẽ có nghiệm thỏa mãn
11x
. kết hợp điều kiện suy ra
2m
.
Nếu
0
22m
khi đó
22
4 2 3 0x mx m
sẽ có nghiệm
2
12
1
xx
xx
xx

Hệ có nghiệm khi và chỉ khi
12
12
1
1
xx
xx
10
1
2
10
1
2
af
S
af
S
Giải hệ và kết hợp điều kiện ta thấy không có m thỏa mãn trường hợp này.
Vậy Hệ có nghiệm khi
2m
.
Câu 8: [0D4-7-4] Cho hệ:
2
2
2 0 1
4 6 0 2
x x a
x x a
Với giá trị nào của a thì hệ có nghiệm duy nhất:
A.
2
.
3
a
B.
1 .a
C.
5
.
6
a
D.
0 a
hoặc
1 a
.
Lời giải
Chọn D
Hệ có nghiệm duy nhất ở ba trường hợp sau:
TH1: BPT
1
có duy nhất nghiệm và nghiệm đó thỏa mãn BPT
2
1
có duy nhất nghiệm khi
2
20x x a
với
x
khi đó
1
chỉ có duy nhất
nghiệm thỏa mãn
2
20x x a
1a
.
Thay
1a
vào thấy hệ có nghiệm duy nhất là
1x
(Thỏa mãn).
TH2: BPT
2
có duy nhất nghiệm và nghiệm đó thỏa mãn
1
: giải tương tự trường
hợp 1 nhưng không cho nghiệm thỏa mãn.
TH3:
1
2
đều có hai khoảng nghiệm nhưng hai khoảng nghiệm này giao nhau
chỉ 1 phần tử hay nói cách khác phương trình
1
2
có chung nghiệm (nghiệm lớn
của
1
chính là nghiệm bé của
2
hoặc ngược lại )
Suy ra
1 1 2 4 6aa
với
2
1
3
a
0a
.

Câu 9: [0D4-7-4] Hệ bất phương trình:
2
2 2 2
5 4 0 1
( 3) 2( 1) 0 2
xx
x m x m
có tập nghiệm
biểu diễn trên trục số có độ dài bằng
1
, với giá trị của
m
là:
A.
0.m
B.
2.m
C.
2.m
D. Cả
, , abc
đều đúng.
Lời giải
Chọn D
Ta có
1 1 4x
2
có
2
2
10m
Hệ có nghiệm biểu diễn trên trục có độ dài bằng 1 trong các trường hợp sau
TH1:
2
có 2 nghiệm phân biệt, trong đó một nghiệm là 2, nghiệm còn lại nhỏ hơn
1
10
20
af
f
0m
TH2:
2
có 2 nghiệm phân biệt, trong đó một nghiệm là 3 nghiệm còn lại lớn hơn 4
40
30
af
f
giải và thấy vô nghiệm m thỏa mãn.
TH3:
2
có 2 nghiệm phân biệt có khoảng cách là 1 và hai nghiệm này thuộc
1;4
21
10
40
14
2
1
af
af
S
xx
0
2
2
m
m
m
.
Câu 10: [0D4-7-4] Định
m
để hệ bất phương trình sau có nghiệm
2
2
20
( 3) 2 0
xx
x m x m
A.
m
. B.
1m
. C.
0m
. D.
10m
.
Lời giải

Chọn A
Giải bất phương trình (1) ta được tập nghiệm
1;2
.
Để hệ bất phương trình có nghiệm khi và chỉ khi (2) có nghiệm
1;2x
.
Mặt khác (2) luôn có nghiệm
1 1;2x
. Vậy hệ có nghiêm với mọi
m
.
Câu 11: [0D4-7-4] Định
m
để hệ bất phương trình sau có nghiệm:
2
2 2 4 2
2 3 0
(2 1) 0
xx
x m x m m
A.
2 m
hoặc
2m
. B.
3 3.m
C.
3 m
hoặc
3m
. D.
m
.
Lời giải
Chọn B
Giải bất phương trình (1) ta được tập nghiệm
1;3
.
Giải bất phương trình (2) ta được tập nghiệm
22
;1mm
.
Để hệ bất phương trình có nghiệm khi và chỉ khi giao của hai tập nghiêm khác
2
3 3 3mm
.
Câu 12: [0D4-7-4] Tìm các giá trị của
a
sao cho với mọi
x
, ta luôn có:
2
2
5
1 7.
2 3 2
x x a
xx
A.
5
3
a
. B.
11a
. C.
01a
. D.
5
1
3
a
.
Lời giải
Chọn B
Ta có
2
2 3 2 0xx
với
x
.
Bất phương trình tương đương
2 2 2
1 2 3 2 5 7 2 3 2x x x x a x x
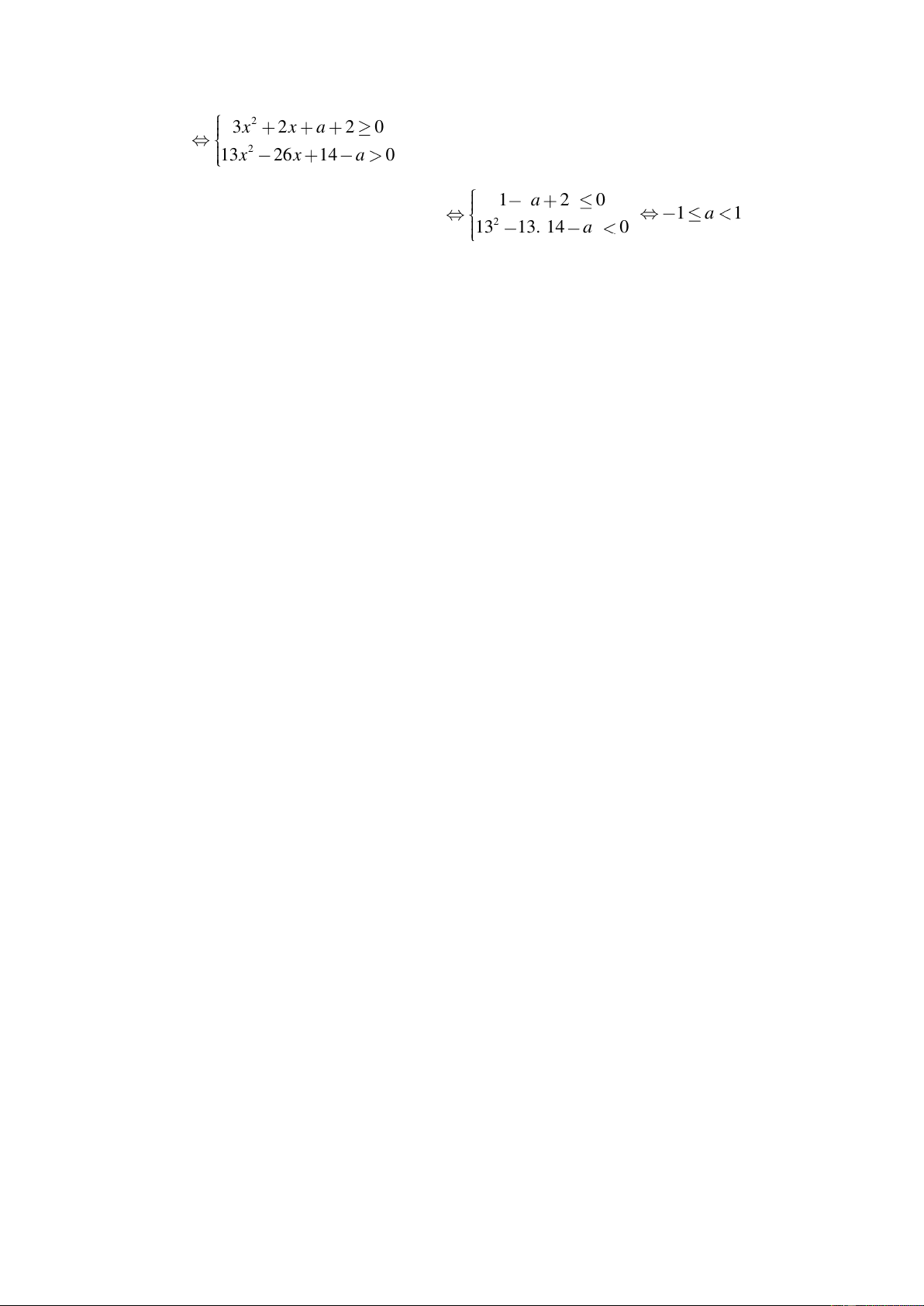
2
2
3 2 2 0
13 26 14 0
x x a
x x a
Để hệ bất phương trình với mọi
x
2
1 2 0
13 13. 14 0
a
a
11a
.

Câu 1: [0D4-8-1] Nghiệm của phương trình:
1 4 13 3 12x x x
là:
A.
1 .x
B.
–1 .x
C.
4 .x
D.
–4.x
Lời giải
Chọn B
Điều kiện xác định
1x
nên loại D.
Thử các giá trị A, B, C thấy
–1 x
là nghiệm của phương trình đã cho.
Câu 2: [0D4-8-1] Phương trình:
2 2 2
4 1 2 2 9x x x x x x
có các nghiệm là:
A.
–2; 1 xx
. B.
2; 3 xx
. C.
–1; 0 xx
. D.
–3; 4xx
.
Lời giải
Chọn C
Tập xác định , đặt
2
1 ; 0t x x t
PT đã cho trở thành
3 2 7t t t
32tt
1
4
t
t
Kết hợp điều kiện thấy
1t
2
11xx
0
1
x
x
.
Câu 3: [0D4-8-1] Tập nghiệm của phương trình:
22
3 2 1x x x x
là:
A.
1; 2 .
B.
0; 1 .
C.
13
.
2
D.
15
.
2
Lời giải
Chọn D
Điều kiện:
12x
Ta có
22
3 2 1x x x x
2 2 2
3 1 2 2 2x x x x x x
22
2 2 2 0x x x x
2
21xx
2
10xx
15
2
x
.

Câu 1: [0D4-8-2] Bất phương trình:
2
6 5 8 2x x x
có nghiệm là:
A.
35x
. B.
23x
C.
53x
. D.
32x
.
Lời giải
Chọn A
Ta có:
2
6 5 8 2x x x
2
2
2
8 2 0
6 5 0
8 2 0
6 5 8 2
x
xx
x
x x x
2
4
15
4
5 38 69 0
x
x
x
xx
4
15
4
23
3
5
x
x
x
x
45
35
34
x
x
x
.
Câu 2: [0D4-8-2] Bất phương trình:
2 1 3xx
có nghiệm là:
A.
1
– ;4 2 2
2
. B.
1
; 3
2
. C.
0; 3
. D.
1
;
2
.
Lời giải
Chọn A
Điều kiện xác định:
1
2
x
BPT đã cho tương đương
2
3
2 1 9 6
x
x x x
Giải hệ được nghiệm của BPT đã cho là:
1
4 2 2
2
x
.

Câu 3: [0D4-8-2] Bất phương trình:
2 4 0xx
có nghiệm là:
A.
2x
. B.
4.x
C.
2.x
D.
2.x
Lời giải
Chọn D
Bất phương trình tương đương
24xx
Dễ thấy
4x
là nghiệm của bất phương trình trên.
Với
4x
, ta bình phương hai vế, bất phương trình trở thành
2
9 14 0xx
27x
. Kết hợp điều kiện ta có nghiệm của bất phương trình lúc này là:
24x
Vậy nghiệm của bất phương trình ban đầu là:
2x
.
Câu 4: [0D4-8-2] Bất phương trình:
2
82xx
có nghiệm là:
A.
2; 2 2 .
B.
2; 2 2 .
C.
3; 2 2 .
D.
–3; 2 .
Lời giải
Chọn B
Điều kiện xác định:
2 2 2x
BPT tương đương
2
82xx
2
60xx
2
3
x
x
Kết hợp điều kiện được nghiệm của BPT là đáp án B.
Câu 5: [0D4-8-2] Nghiệm của phương trình:
2
2 4 6 11x x x x
là:
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Chọn C
Bài toán cho các phương án lựa chọn rất dễ để thử.
Thử các đáp án vào phương trình trên thấy C. 3 là nghiệm của phương trình.
Câu 6: [0D4-8-2] Bất phương trình:
2
( 3) 0xx
có nghiệm là:
A.
–3x
. B.
0 x
. C.
–3; 0xx
. D.
– 3x
.
Lời giải
Chọn C

Ta có
2
( 3) 0xx
2
30xx
0
3
x
x
.
Câu 7: [0D4-8-2] Bất phương trình
4 2 2
2 3 5x x x
có bao nhiêu nghiệm nghiệm
nguyên?
A.
0
. B.
1
.
C.
2
. D. Nhiều hơn
2
nhưng hữu hạn.
Lời giải
Chọn A
Nghiệm của bất phương trình thỏa điều kiện:
22
5 0 5 ; 5 5;x x x
Ta có
2
2
4 2 2
2 3 1 4 5 1 4 0x x x
.
Bất phương trình tương đương:
4 2 2 4 2
2 3 5 3 2 0 2; 1 1; 2x x x x x x
(không thỏa
điều kiện).
Vậy bất phương trình vô nghiệm.
Câu 8: [0D4-8-2] Cho bất phương trình
4 3 2
2 5 6 5 2 0x x x x
. Số nghiệm của bất
phương trình trên là:
A.
0
. B.
1
. C.
2
. D. Vô số.
Lời giải
Chọn B
Ta có:
4 3 2
2 5 6 5 2 0x x x x
2
2
1 2 2 0x x x
(1)
Ta thấy:
2
2 2 0,x x x
(vì
15 0
và
20a
).
Do đó, (1)
2
10x
1x
. Vậy bất phương trình có 1 nghiệm là
1x
.
Câu 9: [0D4-8-2] Bất phương trình
22
2
x x - 1
0
x + 5x + 6
có tập nghiệm là:
A.
3; 2 1;1
. B.
3; 2 1;1
.
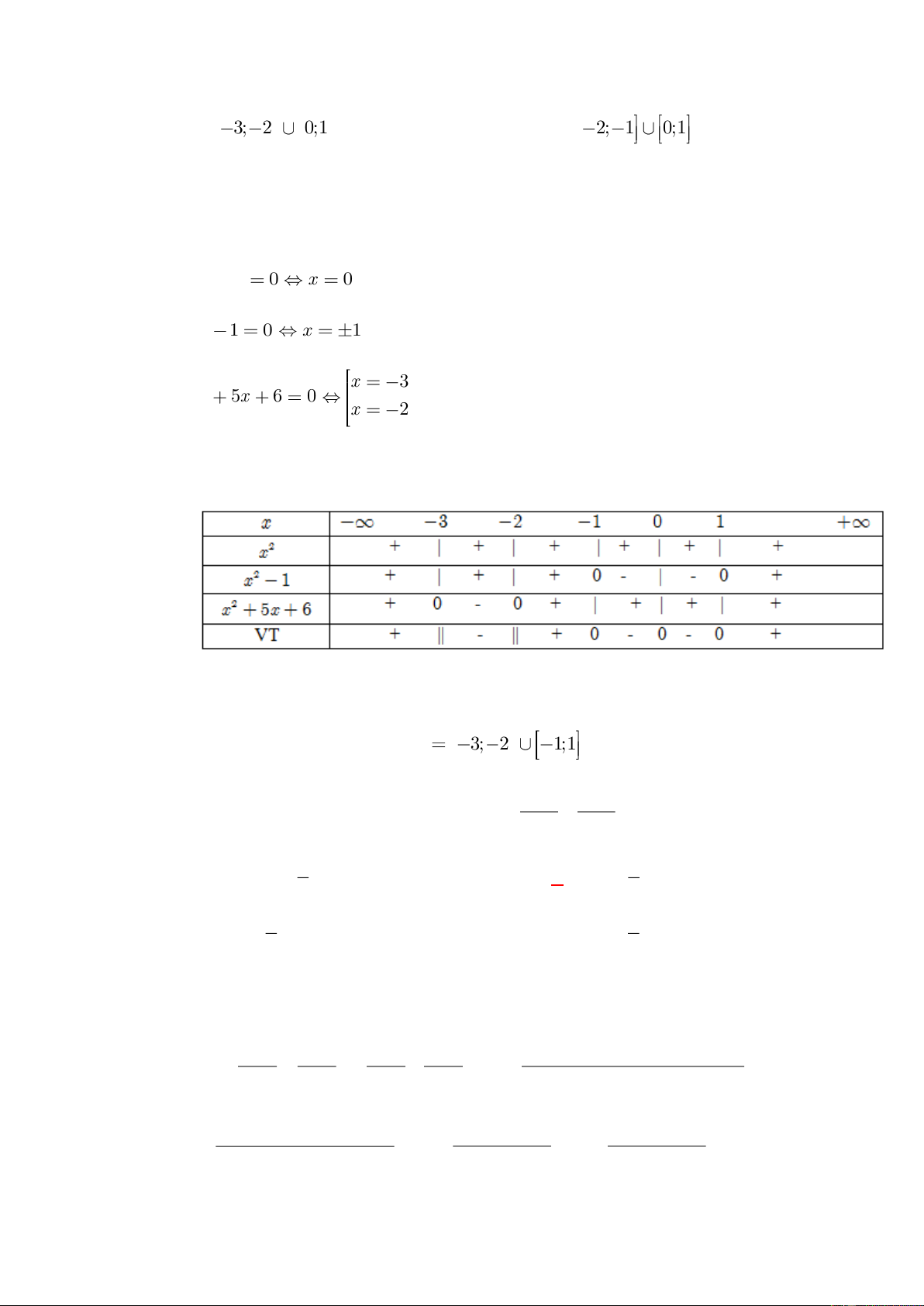
C.
3; 2 0;1
. D.
2; 1 0;1
.
Lời giải
Chọn A
Cho
2
00xx
2
1 0 1xx
2
3
5 6 0
2
x
xx
x
Lập bảng xét dấu ta được:
Dựa vào bảng xét dấu suy ra tập nghiệm bất phương trình đã cho là:
3; 2 1;1S
.
Câu 10: [0D4-8-2] Tập nghiệm của bất phương trình
24
13
xx
xx
là:
A.
1
; 1;3
2
S
. B.
1
; 1;3
2
.
C.
1
;1 1;3
2
S
. D.
1
;1 3;
2
S
.
Lời giải
Chọn B
Ta có
2 3 1 4
2 4 2 4
00
1 3 1 3 1 3
x x x x
x x x x
x x x x x x
22
6 3 4
0
13
x x x x
xx
4 2 2 1
00
1 3 1 3
xx
x x x x
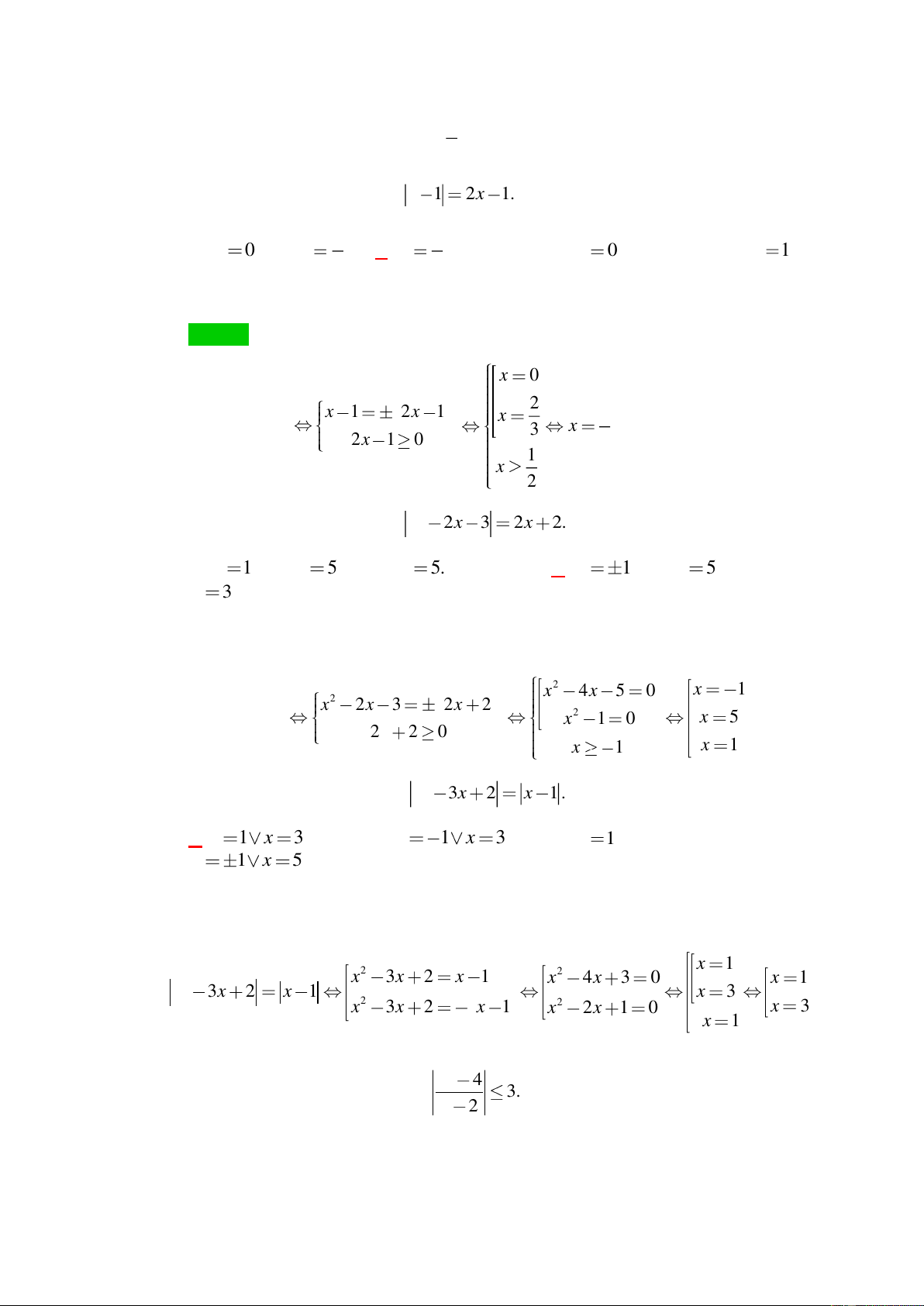
Lập bảng xét dấu ta có
1
; 1;3
2
x
.
Câu 11: [0D4-8-2] Giải phương trình
1 2 1.xx
A.
0x
hoặc
2
3
x
. B.
2
3
x
. C.
0x
. D.
1x
.
Lời giải
Chọn B
Phương trình
1 2 1
2 1 0
xx
x
0
2
3
1
2
x
x
x
2
3
x
.
Câu 12: [0D4-8-2] Giải phương trình
2
2 3 2 2.x x x
A.
1x
hoặc
5x
. B.
5.x
C.
1x
hoặc
5x
. D.
3x
.
Lời giải
Chọn C
Phương trình
2
2 3 2 2
2 2 0
x x x
x
2
2
4 5 0
10
1
xx
x
x
1
5
1
x
x
x
.
Câu 13: [0D4-8-2] Giải phương trình:
2
3 2 1.x x x
A.
13xx
. B.
13xx
. C.
1x
. D.
15xx
.
Lời giải
Chọn A
2
2
2
2
2
1
3 2 1
4 3 0 1
3 2 1
3
3
3 2 1
2 1 0
1
x
x x x
x x x
x x x
x
x
x x x
xx
x
.
Câu 14: [0D4-8-2] Giải bất phương trình
34
3.
2
x
x

A.
5
2
3
xx
. B.
2x
. C.
5
3
x
. D.
5
2
3
x
.
Lời giải
Chọn C
ĐK :
2x
5
3 4 3 4 6 10
3 3 0 0
3
3 4 5
2 2 2
3
2
3 4 3 4 2
23
3 3 0 0
2 2 2
2
x x x
x
x
x x x
x
x
xx
x
x x x
x
(t/m).
Câu 15: [0D4-8-2] Giải bất phương trình
2
2 5 2 4.x x x
A.
1x
. B.
11xx
. C.
11x
. D.
1x
.
Lời giải
Chọn B
Vì
2
2 4 0x x x
nên bất phương trình cho:
2
22
2
2 5 2 4
2 5 2 4 2 5 2 4
2 5 ( 2 4)
x x x
x x x x x x
x x x
2
2
1 0 1
1
4 9 0
xx
x
xx
.
Câu 16: [0D4-8-2] Giải phương trình
2
5 6 4 2( 1).x x x
A.
4x
. B.
2x
. C.
1x
. D.
42xx
.
Lời giải
Chọn B
2
5 6 4 2( 1)x x x
2
2
2 1 0
5 6 4 4 1
x
x x x
2
1
2 8 0
x
xx
1
2
2
4
x
x
x
x
.
Câu 17: [0D4-8-2] Giải phương trình
3 13 3.xx
A.
41xx
. B.
4x
. C.
14xx
. D.
1x
.
Lời giải

Chọn D
2
2
3
30
3
3 13 3 1
1
3 4 0
3 13 3
4
x
x
x
x x x
x
xx
xx
x
.
Câu 18: [0D4-8-2] Giải phương trình
22
5 1.xx
A.
1x
. B.
14xx
. C.
2x
. D.
4x
.
Lời giải
Chọn C
2
22
2
22
42
1
10
1
51
51
3 4 0
x
x
x
xx
xx
xx
2
2
1
1
1
1
2
2
12
2
4
x
x
x
x
x
x
xx
x
x
.
Câu 19: [0D4-8-2] Giải bất phương trình
2
4 12 4.x x x
A.
67x
. B.
2x
. C.
7x
. D.
26x
.
Lời giải .
Chọn A
2
4 12 4x x x
2
22
4 12 0
4 0 6 7
4 12 ( 4)
xx
xx
x x x
.
Câu 20: [0D4-8-2] Giải phương trình:
5 2 3xx
.
A.
8x
. B.
2
( 8)
3
xx
.
C.
2
3
x
. D.
2
( 8)
3
xx
.
Lời giải
Chọn B

8
5 2 3
5 2 3
2
5 2 3
3
x
xx
xx
xx
x
.
Câu 21: [0D4-8-2] Giải phương trình:
2 3 5xx
.
A.
3
4
x
. B.
7
2
x
.
C.
5
3
x
. D.
73
24
xx
.
Lời giải
Chọn A
5
3
3 5 0
3
7
2 3 5.
2 3 5
4
2
2 3 5
3
4
x
x
x x x
xx
x
xx
x
.
Câu 22: [0D4-8-2] Giải phương trình:
2
4 3 1x x x
.
A.
( 1) ( 2)xx
. B.
( 2) ( 4)xx
.
C.
( 1) ( 2) ( 4)x x x
. D.
( 1) ( 4)xx
.
Lời giải
Chọn C
2
2
2
1
4 3 1
4 3 1 2
4 3 1
4
x
x x x
x x x x
x x x
x
.
Câu 23: [0D4-8-2] Giải bất phương trình:
2
35x x x
.
A.
( 1) ( 5)xx
. B.
15x
.
C.
15x
. D.
( 5) ( 1)xx
.
Lời giải
Chọn B
2
22
2
2 5 0( )
3 5 5 3 5 1 5
4 5 0
x x dung
x x x x x x x x
xx
.

Câu 24: [0D4-8-2] Giải bất phương trình:
22
53x x x
A.
1x
. B.
5
( 1)
2
xx
.
C.
55
23
x
. D.
5
1
3
x
.
Lời giải
Chọn A
22
22
22
5
3
53
5 3 1
1
53
5
2
x
x x x
x x x x
x
x x x
x
.
Câu 25: [0D4-8-2] Giải phương trình:
2
2 6 4 2x x x
.
A.
( 2) ( 4)xx
. B.
2x
.
C.
2x
. D.
4x
.
Lời giải
Chọn B
2
2
2
2
20
2
2 6 4 2 2
20
2 6 4 2
x
x
x x x x
xx
x x x
.
Câu 26: [0D4-8-2] Giải phương trình:
2 7 4xx
.
A.
( 1) ( 9)xx
. B.
1x
.
C.
9x
. D.
( 1) ( 9)xx
.
Lời giải
Chọn C
2
2
40
4
2 7 4 9
10 9 0
2 7 4
x
x
x x x
xx
xx
.
Câu 27: [0D4-8-2] Giải bất phương trình:
2
2 15 3x x x
.
A.
5x
. B.
56x
. C.
36x
. D.
35x
.
Lời giải

Chọn B
22
2
2
3
30
5
2 15 3 2 15 0 5 6
3
2 15 3
6
x
x
x
x x x x x x
x
x x x
x
.
Câu 28: [0D4-8-2] Giải bất phương trình:
2
43xx
.
A.
13
6
x
. B.
13
3
6
x
. C.
3x
. D.
32x
.
Lời giải
Chọn C
2
2
2
2
3
30
2
40
2
43
30
3
43
13
6
x
x
x
x
x
xx
x
x
xx
x
3x
.
------------Hết----------------
Câu 29: [0D4-8-2] Tập nghiệm của bất phương trình
2
3
1
4
x
x
là
A.
, 4 1,1 4,S
. B.
,4S
.
C.
1,1S
. D.
4,S
.
Lời giải
Chọn A
Điều kiện
2x
2
3
1
4
x
x
2
3
11
4
x
x
2
2
3
1
4
3
1
4
x
x
x
x
2
2
3
10
4
3
10
4
x
x
x
x
2
2
2
2
34
0
4
34
0
4
xx
x
xx
x

Lập bảng xét dấu ta được nghiệm của bất phương trình là
4
11
4
x
x
x
Vậy tập nghiệm bất phương trình là:
, 4 1,1 4,S
.
Câu 30: [0D4-8-2] Bất phương trình:
2
6 5 8 2x x x
có nghiệm là:
A.
35x
. B.
23x
. C.
53x
. D.
32x
.
Lời giải
Chọn A
Ta có
2
6 5 8 2 x x x
2
2
2
6 5 0
8 2 0
8 2 0
6 5 8 2
xx
x
x
x x x
2
15
4
4
5 38 69 0
x
x
x
xx
15
4
4
25
3
3
x
x
x
x
3 5. x
Câu 31: [0D4-8-2] Bất phương trình:
2 1 3xx
có nghiệm là:
A.
1
;4 2 2
2
. B.
3;4 2 2
. C.
4 2 2;3
. D.
4 2 2;
.
Lời giải
Chọn A
Ta có:
2 1 3 xx
2
2 1 0
30
2 1 3
x
x
xx
2
1
2
3
8 8 0
x
x
xx
1
2
3
4 2 2
4 2 2
x
x
x
x
1
4 2 2.
2
x
Câu 32: [0D4-8-2] Bất phương trình:
4 2 2
2 3 5x x x
có bao nhiêu nghiệm nghiệm
nguyên?
A. 0. B. 1.
C. 2. D. Nhiều hơn 2 nhưng hữu hạn.

Lời giải
Chọn A
Đặt
2
0tx
Ta có
2
2 3 5t t t
.
Nếu
2
1
2 3 0
3
t
tt
t
thì ta có
2
3 2 0 1 2t t t
loại
Nếu
2
2 3 0 1 3t t t
thì ta có
2
1 33
2
80
1 33
2
t
tt
t
loại.
Câu 33: [0D4-8-2] Nghiệm của bất phương trình:
22
2 2 1 0x x x
là:
A.
5 13
1; 2;
2
. B.
9
4; 5;
2
.
C.
22
2; ;1
22
. D.
17
; 5 5; 3
5
.
Lời giải
Chọn C
22
2 2 1 0x x x
2
2
2 1 0
20
x
xx
2
2
2
2
21
x
x
x
22
2; ;1
22
x
.
Câu 34: [0D4-8-2] Tập nghiệm của bất phương trình
2
28
0
1
xx
x
là:
A.
4; 1 1;2
. B.
4; 1
. C.
1;2
. D.
2; 1 1;1
.
Lời giải
Chọn D

Trường hợp 1:
1x
, ta có
2
28
0
1
xx
x
, dựa vào xét dấu, suy ra tập nghiệm của
bất phương trình
1
1;2S
.
Trường hợp 2:
1x
, ta có
2
28
0
1
xx
x
, dựa vào xét dấu, suy ra tập nghiệm của
bất phương trình
2
4; 1S
.
Kết hợp 2 trường hợp, ta được tập nghiệm của bất phương trình đã cho:
4; 1 1;2S
.
Câu 35: [0D4-8-2] Tập nghiệm của bất phương trình
2
2 3 1
0
43
xx
x
là
A.
1 3 3
; ;1
2 4 4
. B.
1 3 3
; ;1
2 4 4
. C.
1
;1
2
. D.
1
; 1;
2
.
Lời giải
Chọn B
Trường hợp 1:
3
4
x
, ta có
2
2 3 1
0
43
xx
x
, dựa vào xét dấu, suy ra tập nghiệm của
bất phương trình
1
3
;1
4
S
.
Trường hợp 2:
3
4
x
, ta có
2
2 3 1
0
43
xx
x
, dựa vào xét dấu, suy ra tập nghiệm của
bất phương trình
2
13
;
24
S
.
Kết hợp 2 trường hợp, ta được tập nghiệm của bất phương trình đã cho:
1 3 3
; ;1
2 4 4
S
.
Câu 36: [0D4-8-2] Tập nghiệm của bất phương trình
22
12 12x x x x
là
A.
. B.
R
.
C.
4; 3
. D.
; 4 3;
.
Lời giải
Chọn A
Ta có :
2
2
1 47
12 0,
24
x x x x
Do đó :
22
12 12x x x x
Vậy bất phương trình đã cho vô nghiệm.

Câu 37: [0D4-8-2] Tập nghiệm của bất phương trình
22
12 12x x x x
là
A.
; 3 4;
. B.
; 4 3;
.
C.
6; 2 3;4
. D.
4;3
.
Lời giải
Chọn A
Trường hợp 1:
2
3
12 0
4
x
xx
x
ta có
2 2 2
3
12 12 2 2 24 0
4
x
x x x x x x
x
Do đó : tập nghiệm của bất phương trình
1
; 3 4;S
.
Trường hợp 2:
2
12 0 3 4x x x
Ta có
22
12 12 12 12x x x x
(vô lý)
Do đó : tập nghiệm của bất phương trình
2
S
.
Kết hợp 2 trường hợp, ta được tập nghiệm của bất phương trình đã cho:
12
; 3 4;S S S
.
Câu 38: [0D4-8-2] Tập nghiệm của bất phương trình
20xx
là
A.
1
;
4
. B.
1
0;
4
. C.
1
0;
4
. D.
1
0;
4
.
Lời giải
Chọn A
Điều kiện
0x
.
Bất phương trình tương đương với
22
0
2 4 4 0
1
4
x
x x x x x x
x
Kết hợp điều kiện, ta được nghiệm của bất phương trình
1
4
x
.
Vậy
1
;
4
S
.
Câu 39: [0D4-8-2] Tập nghiệm của bất phương trình
30xx
là
A.
1
;
9
.
B.
1
0;
9
.
C.
1
0;
9
.
D.
1
0;
9
.

Lời giải
Chọn C
Điều kiện
0x
.
Bất phương trình tương đương với
22
0
3 9 9 0
1
9
x
x x x x x x
x
Kết hợp điều kiện, ta được tập nghiệm của bất phương trình
1
0;
9
S
.
Câu 40: [0D4-8-2] Tập nghiệm của bất phương trình
11
4
x
là
A.
0;16
. B.
0;16
. C.
0;4
. D.
16;
.
Lời giải
Chọn A
Điều kiện:
0x
.
Bất phương trình
4 16xx
.
Tập nghiệm của bất phương trình là:
0;16S
.
Câu 41: [0D4-8-2] Tập nghiệm của bất phương trình
1
3
xx
x
là
A.
1;
. B.
0;
. C.
0;
. D.
0;1
.
Lời giải
Chọn C
Điều kiện:
0x
.
Bất phương trình
2
2 1 0 1 0x x x
đúng với mọi
0x
.
Tập nghiệm của bất phương trình là:
0;S
.
Câu 42: [0D4-8-2] Tập nghiệm của phương trình
22
5 6 5 6x x x x
là
A.
2;3
. B.
2;3
.
C.
;2 3;
. D.
;2 3;
.
Lời giải
Chọn D

22
5 6 5 6x x x x
22
22
2
5 6 5 6, 1
3
5 6 5 6, 2 3 2
x
x x x x
x
x x x x x
.
Giải
1
ta được tập nghiệm
1
;2 3;S
.
Giải
2
2
2 5 6 0
3
x
xx
x
không thỏa mãn.
Vậy tập nghiệm của phương trình
;2 3;S
.
Câu 43: [0D4-8-2] Tập nghiệm của phương trình
22
7 12 7 12x x x x
là
A.
3;4
. B.
3;4
. C.
3;4
. D.
;3 4;
.
Lời giải
Chọn C
22
7 12 7 12x x x x
22
22
3
7 12 7 12, 1
4
7 12 7 12, 3 4 2
x
x x x x
x
x x x x x
.
Giải
1
ta có phương trình:
2
3
7 12 0
4
x
xx
x
không thỏa mãn.
Giải
2
ta được tập nghiệm
3;4S
. Đây cũng là tập nghiệm của PT đã cho.
Câu 44: [0D4-8-2] Nghiệm của bất phương trình
11
32x
là:
A.
3x
hay
5x
. B.
5x
hay
3x
. C.
3x
hoặc
5x
. D.
x
.
Lời giải
Chọn C
5
5
11
0
32
23
3
x
x
x
x
x
.
Câu 45: [0D4-8-2] Tìm tập nghiệm của pt:
22
2 3 1 2 1x x x x
A.
{1; 1}
. B.
. C.
{0;1}
. D.
1
2
.

Lời giải
Chọn D
22
22
2
22
1
1
; 1;
; 1;
2
2
42
2 3 1 2 1
2 3 1 2 1
1
1
;1
;1
2
2
4 2 0
2 3 1 2 1
x
x
x
x x x x
x x x x
x
x
xx
x x x x
1
; 1;
2
1
2
1
1
;1
2
2
0
1
2
x
x tm
x
x
xl
xl
.
Câu 46: [0D4-8-2] Tìm tập nghiệm của bất phương trình:
2
40xx
A.
. B.
{}
. C.
(0;4)
. D.
( ;0) (4; )
Lời giải
Chọn A
2
40x x x
vì
2
4 0 x x x
.
Câu 47: [0D4-8-2] Bất phương trình
2 3 2xx
tương đương với
A.
2
2 3 2xx
với
3
.
2
x
B.
2
2 3 2xx
với
2x
.
C.
2 3 0
20
x
x
hoặc
2
2 3 ( 2)
20
xx
x
. D. Tất cả các câu trên đều đúng.
Lời giải
Chọn C
Câu 48: [0D4-8-2] Bất phương trình
32
3 10 24 0x x x
có bao nhiêu nghiệm nguyên âm?

A.
0
. B.
1
.
C.
2
. D. Nhiều hơn
2
nhưng hữu hạn.
Lời giải
Chọn D
Ta có
32
4
3 10 24 0 3 2 4 0
32
x
x x x x x x
x
.
Vậy phương trình có
3
nghiệm nguyên âm.
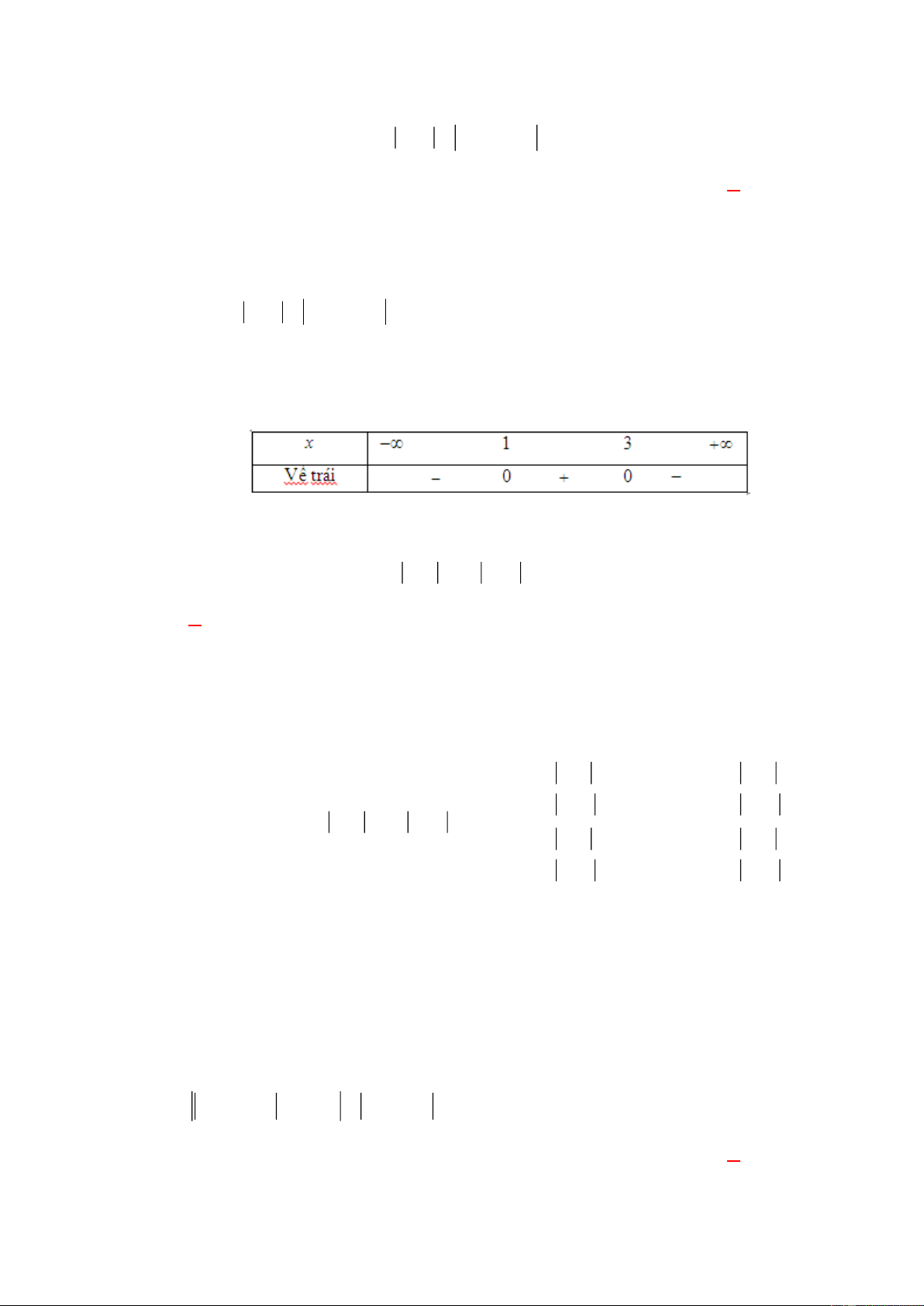
Câu 1: [0D4-8-3] Bất phương trình:
2
6 5 9x x x
có nghiệm là:
A.
31x
. B.
01x
. C.
13x
. D.
1x
hoặc
3x
.
Lời giải
Chọn C
Ta có:
2
6 5 9x x x
22
6 5 9 . 6 5 9 0x x x x x x
22
4 3 . 6 15 0x x x x
2
4 3 0xx
Bảng xét dấu:
Vậy nghiệm của bất phương trình là:
S
;1 3;
.
Câu 2: [0D4-8-3] Bất phương trình:
1 3 2 5 0xx
có nghiệm là:
A.
72x
hoặc
34x
. B.
21x
hoặc
12x
.
C.
03x
hoặc
45x
. D.
32x
hoặc
11x
.
Lời giải
Chọn A
Ta có:
1 3 2 5 0xx
1 3 0
2 5 0
1 3 0
2 5 0
x
x
x
x
13
25
13
25
x
x
x
x
24
73
24
73
x
xx
xx
x
34x
hoặc
72x
.
Câu 3: [0D4-8-3] Nghiệm dương nhỏ nhất của bất phương trình:
22
4 5 2 9 5x x x x x
gần nhất với số nào sau đây:
A.
2,8
. B.
3
. C.
3,5
. D.
4,2
.
Lời giải

Chọn D
Ta có:
22
4 5 2 9 5x x x x x
2 2 2 2
4 5 14 4 5 3 4 0x x x x x x x x
+TH1 :
1x
hoặc
5x
ta có bất phương trình :
2
2 3 9 1 0x x x
1x
Giao với điều kiện ta có nghiệm của bpt là :
1
1 5;S
.
TH2 :
15x
ta có bất phương trình là :
2
5 19 2 7 9 0x x x
19 9
; 1 ;
52
x
Giao với điều kiện ta có nghiệm của bpt là :
2
9
;5
2
S
.
Vậy tập nghiệm của bất phương trình là
12
9
1;
2
S S S
.
Câu 4: [0D4-8-3] Bất phương trình
4 1 2 0xx
có nghiệm là:
A.
1x
và
2x
. B.
1x
. C.
4x
. D.
2x
.
Lời giải
Chọn A
Điều kiện xác định:
1x
.
Bất phương trình trên tương đương
1 1 3 1 2 0x x x
2
1 1 1 2 0xx
1 1 0x
2x
Kết hợp điều kiện xác định ta có kết quả là đáp án A.
Câu 5: [0D4-8-3] Với giá trị nào của
m
thì phương trình sau vô nghiệm:
22
2 2 1x m x x
A.
2
.
3
m
B.
0m
hoặc
2
.
3
m
C.
2
0.
3
m
D.
0m
.
Lời giải
Chọn B

Thấy nếu
0m
phương trình trở thành
22
21x x x
. Phương trình này dễ
thấy có nghiệm bằng 1. Vậy nên
0m
không thỏa mãn yêu cầu đề bài.
Trong các đáp án trên, các đáp án A, C, D đều có
0m
. Vậy chọn B.
Câu 6: [0D4-8-3] Phương trình:
22
4 2 3 4x x x x
có bao nhiêu nghiệm lớn hơn
hoặc bằng
0
:
A.
2.
B.
3
. C.
1.
D.
0
.
Lời giải
Chọn A
Điều kiện:
22x
22
4 2 3 4x x x x
2 2 3 1 2 0x x x x
2
2
1
2 2 1 3
3
x
x x x x
Giải và kết hợp điều kiện được ba nghiệm thỏa mãn là:
12 504
2; 0;
18
x x x
.
Câu 7: [0D4-8-3] Bất phương trình:
2
4 7 12x x x
có tập nghiệm là:
A.
2;4S
. B.
2; 4S
. C.
;3 4;S
D.
.S
Lời giải
Chọn A
TH1
4x
khi đó BPT trở thành
2
4 7 12x x x
2
40x
4x
TH2
4x
khi đó BPT trở thành
2
4 7 12x x x
2
6 8 0xx
24x
Vậy nghiệm của BPT trên là
24x
.
Câu 8: [0D4-8-3] Bất phương trình:
22
( 3 ) 2 3 2 0x x x x
có nghiệm là:
A.
1
2
x
hoặc
3.x
B.
0x
hoặc
3.x
C.
1
3.
2
x
D.
1
2
x
hoặc
3x
.
Lời giải
Chọn A
22
( 3 ) 2 3 2 0x x x x
2
2
30
2 3 2 0
xx
xx
3
1
2
x
x
.
Câu 9: [0D4-8-3] Cho bất phương trình
2
2 2 6x x x ax
. Giá trị dương nhỏ nhất của
a để bất phương trình có nghiệm gần nhất với số nào sau đây
A.
0,5
. B.
1,6
. C.
2,2
. D.
2,6
.
Lời giải
Chọn D
Bất phương trình tương đương với
2
2 2 6 0x x x ax
Đặt
2
2
2
3 8 , 2 (1)
2 2 6
1 4 , 2 (2)
x a x x
f x x x x ax
x a x x
(1) và (2) là parabol có hoành độ đỉnh lần lượt là
3
2
a
x
và
1
2
a
x
TH1:
3
21
2
a
a
. Ta có bảng biến thiên của
fx
như sau:
Yêu cầu bài toán
2
2
3
1
1
0 0 1 16
5
24
a
a
a
fa
a
So điều kiện
1a
, ta được
5.a
TH2:
13
2
22
aa
a
. Ta có bảng biến thiên của
fx
như sau:
2
14x a x
2
38x a x
1
2
a
3
2
a
1
2
a
f
+
∞
2
∞
f
(
x
)
x
3
2
a
f
2
14x a x
2
38x a x
1
2
a
3
2
a
1
2
a
f
+
∞
2
∞
f
(
x
)
x

Yêu cầu bài toán
2
2
1
1
0
0
3
2
4
32 3.
3
32 3
3
0
80
2
4
a
a
f
a
a
a
a
a
f
So điều kiện
a
, ta được
32 3 3.a
TH3:
1
23
2
a
a
. Ta có bảng biến thiên của
fx
như sau:
Yêu cầu bài toán
2
3
3
0 8 0 32 3
24
a
a
fa
.
So điều kiện
3a
, ta được
3a
.
KẾT QUẢ:
32 3a
.
Câu 10: [0D4-8-3] Bất phương trình sau có nghiệm
22
2 18 13 3 4 18 13 0x x m x x m
với giá trị của tham số m là
A.
07m
. B.
0m
hoặc
7m
. C.
169
0
25
m
. D.
169
1
25
m
.
Lời giải
Chọn D
Bất phương trình tương đương với:
22
2 18 13 3 4 18 13x x m x x m
2
2 2 2
4 18 13 0
4 18 13 2 18 13 3 4 18 13
x x m
x x m x x m x x m
2
2
2
4 18 13
3 13
9
22
m x x f x
m x g x
m x x h x
2
14x a x
2
38x a x
1
2
a
3
2
a
+
∞
2
∞
f
(
x
)
x
3
2
a
f
Vẽ đồ thị các hàm
, , y f x y g x y h x
, ta được hình vẽ sau:
Yêu cầu bài toán
169
1
25
m
.
Câu 11: [0D4-8-3] Bất phương trình
2
2
21
21
12
xx
xx
xx
có bao nhiêu nghiệm nguyên?
A.
1
. B.
2
.
C.
3
. D. Nhiều hơn
3
nhưng hữu hạn.
Lời giải
Chọn B
Điều kiện
1
1
3
x
x
.
*
1
2
x
là một nghiệm không nguyên của bất phương trình.
* Nếu
2
1
2 0 1
2
x x x x x
. Bất phương trình trở thành
1 2 0
1
1 1 2
12
1 2 1
xx
x
xx
xx
.
So với điều kiện
12x
.
Khi đó nghiệm nguyên là
2.x
* Nếu
1
;1
2
x
. Bất phương trình trở thành
x
y
O
13
5
1
169
25
1
ym

1
1 1 2 1 1
12
x x x
xx
Nghiệm nguyên là
0.x
Vậy bất phương trình có 2 nghiệm nguyên.
Câu 12: [0D4-8-3] Tập nghiệm của phương trình
2 2 2
( ) ( ) 2 0x x x x
là:
A.
; 1 2;S
. B.
; 2 1;S
.
C.
; 1 2;S
. D.
; 2 1;S
.
Lời giải
Chọn D
Đặt
2
t x x
, khi đó ta có:
2
20Bpt t t
2
1
t
t
.
Với
2t
2
2xx
2
20xx
1
2
x
x
.
Với
1t
2
1xx
2
10xx
bpt vn
.
Vậy bất phương trình có tập nghiệm
; 2 1;S
.
Câu 13: [0D4-8-3] Trong một cuộc thi về “ bữa ăn dinh dưỡng”, ban tổ chức yêu cầu để đảm
bảo lượng dinh dưỡng hằng ngày thì mỗi gia đình có
4
thành viên cần ít nhất
900
đơn vị prôtêin và
400
đơn vị Lipít trong thức ăn hằng ngày. Mỗi kg thịt bò chứa
800
đơn vị prôtêin và
200
đơn vị Lipit,
1
kg thịt heo chứa
600
đơn vị prôtêin và
400
đơn vị Lipit. Biết rằng người nội trợ chỉ được mua tối đa
1, 6
kg thịt bò và
1,1
kg thịt heo. Biết rằng
1
kg thịt bò giá
100.000
đ,
1
kg thịt heo giá
70.000
đ. Tìm chi
phí thấp nhất cho khẩu phần thức ăn đảm bảo chất dinh dưỡng?
A.
100.000
đ. B.
107.000
đ. C.
109.000
đ. D.
150.000
đ.
Lời giải
Chọn B
Gọi
x
là số kg thịt bò,
y
là số kg thịt heo cần mua
0 1,6; 0 1,1xy
.
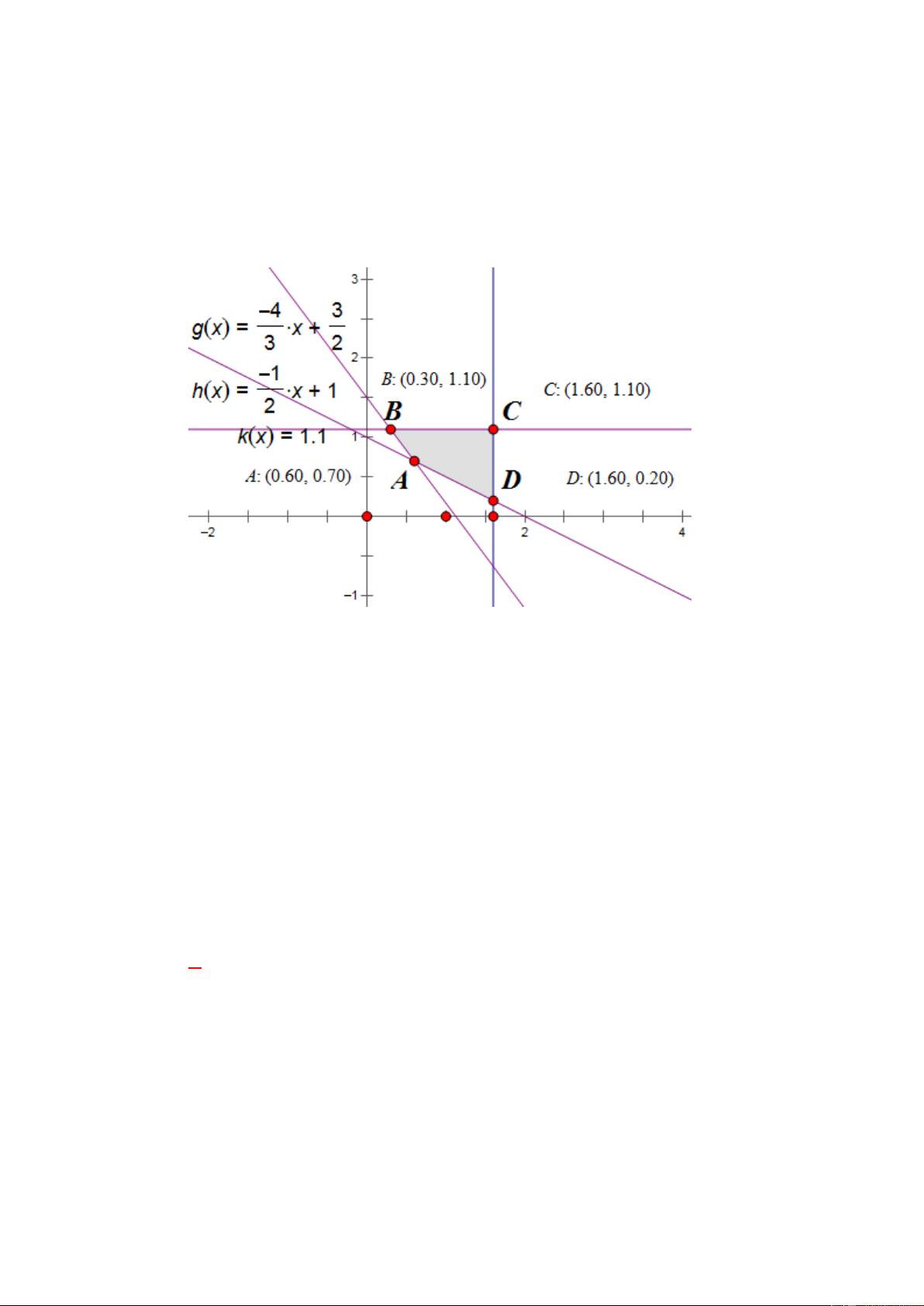
Chi phí để mua thức ăn là
; 100000 70000f x y x y
.
Lượng dinh dưỡng prôtêin của đồ ăn là
; 800 600 900g x y x y
.
Lượng dinh dưỡng Lipit của đồ ăn là
; 200 400 400h x y x y
.
Xét tại biên
,,,A B C D
ta có
Tại
A
,
0,6;0, 7 100000.0, 6 70000.0,7 109000f
Tại
B
,
0,6;0, 7 100000.0, 3 70000.1,1 107000f
Tại
C
,
0,6;0, 7 100000.1,6 70000.1,1 237000f
Tại
D
,
0,6; 0,7 100000.1,6 70000.0,2 174000f
Vậy chi phí thấp nhất cho khẩu phần thức ăn đảm bảo chất dinh dưỡng là
107000
đ.
Câu 14: [0D4-8-3] Giải bất phương trình:
4 3 2
8 23 28 12 0.x x x x
A.
13x
. B.
12x
3x
.
C.
13xx
. D.
1 x
2x
.
Lời giải
Chọn A
BPT
2
2
2 4 3 0x x x
2
4 3 0xx
13x
.

Câu 15: [0D4-8-3] đề nghị chuyển thành dạng 8.4 Miền nghiệm của bất phương trình:
2
2
2
4
( 1) 3
3
xx
x x x
xx
là:
A.
2x
12x
. B.
03x
.
C.
12x
. D.
21x
.
Lời giải
Chọn C
DK:
03x
.
BPT
22
(x 1)(3x x ) x 4x
32
4 4 0x x x
2
1 4 0xx
2 1 2.xx
Kết hợp điều kiện ta có
1 2.x
Câu 16: [0D4-8-3] Giải bất phương trình
22
3 6 3 .x x x x
A.
41x
. B.
20xx
.
C.
01x
. D.
4 3 0 1xx
.
Lời giải.
Chọn D
Đặt:
2
3 ( 0)t x x t
Bất phương trình đã cho trở thành:
2
6 0 3 2t t t
Kết hợp điều kiện ta có:
02t
. Từ đó suy ra:
2
2
2
3 0 4 3
0 3 2
01
34
x x x
xx
x
xx
.
Câu 17: [0D4-8-3] Giải phương trình:
2
3 2 2 8x x x
.
A.
2x
. B.
3x
. C.
2x
. D.
( 3) 2xx
.
Lời giải
Chọn D
2
22
22
2 8 0 4
2
3 2 2 8
3 2 2 8 6 0
3
3 2 2 8 5 10 0
xx
x
x x x
x x x x x
x
x x x x x
.

Câu 18: [0D4-8-3] Bất phương trình
1 3 2 5 0xx
có nghiệm là
A.
72
34
x
x
. B.
21
12
x
x
. C.
03
45
x
x
. D.
32
11
x
x
.
Lời giải
Chọn A
Lập bảng phá dấu giá trị tuyệt đối giải BPT trong từng khoảng ta được nghiệm là A.
Cách khác:
Trường hợp 1:
1 3 0
2 5 0
x
x
13
13
5 2 5
x
x
x
4
2
73
x
x
x
72x
Trường hợp 2:
1 3 0
2 5 0
x
x
3 1 3
25
25
x
x
x
24
3
7
x
x
x
34x
Câu 19: [0D4-8-3] Cho bất phương trình:
2
2 2 6x x x ax
. Giá trị dương nhỏ nhất của
a
để bất phương trình có nghiệm gần nhất với số nào sau đây:
A. 0,5. B. 1,6. C. 2,2. D. 2,6.
Lời giải
Chọn D
Trường hợp 1:
2;x
. Khi đó bất phương trình đã cho trở thành
2
3 8 0x a x
8
3 4 2 3 2,65ax
x
2;x
, dấu
""
xảy
ra khi
22x
.
Trường hợp 2:
;2x
. Khi đó bất phương trình đã cho trở thành
2
1 4 0x a x
4
1 0;2 1
4
1 ;0 2
a x khi x
x
a x khi x
x
. Giải
1
ta được
3a
(theo bất đẳng thức cauchy).
Giải
2
:
4
1ax
x
4
2 . 1 5ax
x
.
Vậy giá trị dương nhỏ nhất của
a
gần với số
2,6
.
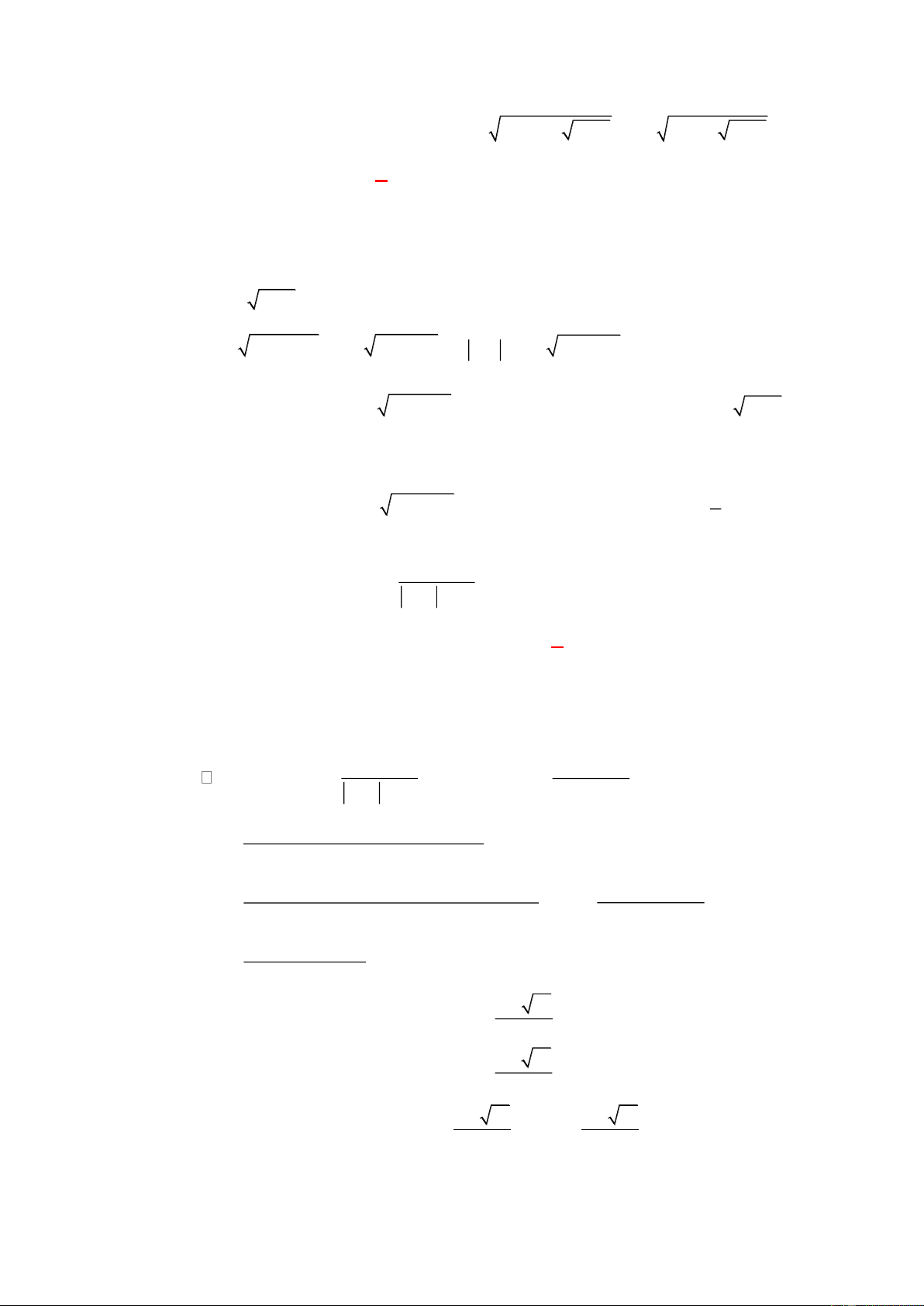
Câu 20: [0D4-8-3] Số nghiệm của phương trình:
8 2 7 2 1 7x x x x
là:
A. 0. B. 1. C. 2. D. 3.
Lời giải
Chọn B
Điều kiện
7x
.
Đặt
7tx
, điều kiện
0t
.
Ta có
22
1 2 2 6t t t t
2
1 2 6t t t
Nếu
1t
thì ta có
2
36t t t
22
6 9 6
3
t t t t
t
3t
73x
2x
Nếu
1t
thì ta có
2
16t t t
22
6 1 2
1
t t t t
t
7
3
tl
.
Câu 21: [0D4-8-3] Bất phương trình
2
2
21
21
12
xx
xx
xx
có bao nhiêu nghiệm nguyên?
A. 1. B. 2.
C. 3. D. Nhiều hơn 3 nhưng hữu hạn.
Lời giải
Chọn B
Nếu
1x
thì
2
2
21
21
12
xx
xx
xx
2
2
21
21
1
xx
xx
x
22
2 1 1 2 1
0
1
x x x x x
x
2 2 3 2
2 1 2 1 2
0
1
x x x x x x x
x
32
25
0
1
x x x
x
2
2 5 1
0
1
x x x
x
Cho
0x
;
2
2 5 1 0xx
5 17
4
5 17
4
x
x
;
1 0 1xx
Lập bảng xét dấu ta có:
5 17 5 17
01
44
xx
.
Vì là nghiệm nguyên nên có nghiệm là
0;2

Nếu
1x
thì
2
2
21
21
12
xx
xx
xx
2
2
21
21
13
xx
xx
x
22
2 1 1 3 2 1
0
13
x x x x x
x
2 2 3 2
2 1 2 1 6 3 3
0
13
x x x x x x x
x
32
63
0
13
x x x
x
2
63
0
13
x x x
x
Cho
0x
;
2
6 3 0xx
1 73
12
1 73
12
x
x
;
3 1 0x
1
3
x
Lập bảng xét dấu ta có:
1 73 1 1 73
0
12 3 12
xx
.
Vì là nghiệm nguyên nên có nghiệm là
0
(loại)
Vậy bất phương trình đã cho có 2 nghiệm nguyên.
Câu 22: [0D4-8-3] Nghiệm dương nhỏ nhất của bất phương trình
22
4 5 2 9 5x x x x x
gần nhất với số nào sau đây
A.
2,8
. B.
3
. C.
3,5
. D.
4,5
.
Lời giải
Chọn D
Lập bảng phá dấu giá trị tuyệt đối giải BPT trên ta được tập nghiệm là
1
9
2
x
x
vậy nghiệm dương nhỏ nhất là
4,5x
, đáp án D
Câu 23: [0D4-8-3] Tìm
m
để
2
11
4 2 2
22
x m x x m
với mọi
x
?
A.
3m
. B.
3
2
m
.
C.
3
2
m
. D.
23m
Lời giải
Chọn C

Ta thấy để
2
11
4 2 2
22
x m x x m
đúng với mọi
x
thì
2
1
2 0,
2
x x m x
Hay
2
1 1 3
2 , 1 0
2 2 2
x x m x m m
.
[0D4-8-3] Cho bất phương trình:
22
2x x a x x a x
( 1). Khi đó khẳng định nào sau
đây đúng nhất?
A. (1) có nghiệm khi
1
4
a
. B. Mọi nghiệm của( 1) đều không
âm.
C. ( 1) có nghiệm lớn hơn 1 khi
0a
. D. Tất cả A, B, C đều đúng.
Lời giải
Chọn D
Ta có
22
22
1 1 1 1
22
2 4 2 4
x x a x x a x x a x a x
Do vế trái luôn lớn hơn hoặc bằng
0
nên để BPT có nghiệm thì
2 0 0xx
nên
B đúng.
Với
1
4
a
BPT
2
2 2 2 0x x a
vô nghiệm hay BPT có nghiệm khi
1
4
a
nên
A đúng.
Khi
0a
ta có
22
0, 0x x a x x a
có 4 nghiệm xếp thứ tự
1 2 3 4
x x x x
Với
4
xx
hoặc
1
xx
ta có BPT:
2
2 2 2 0x x a
Có nghiệm
12
x x x
và
1 2 1 2
1; 0x x x x
Nên tồn tại nghiệm lớn hơn 1 vậy C đúng
Câu 24: [0D4-8-3] Cho bất phương trình:
22
2 2 3 3 1 0x x m mx m m
. Để bất
phương trình có nghiệm, các giá trị thích hợp của tham số
m
là:
A.
1
1
2
m
. B.
1
1
2
m
. C.
1
1
2
m
. D.
1
1
2
m
.
Lời giải
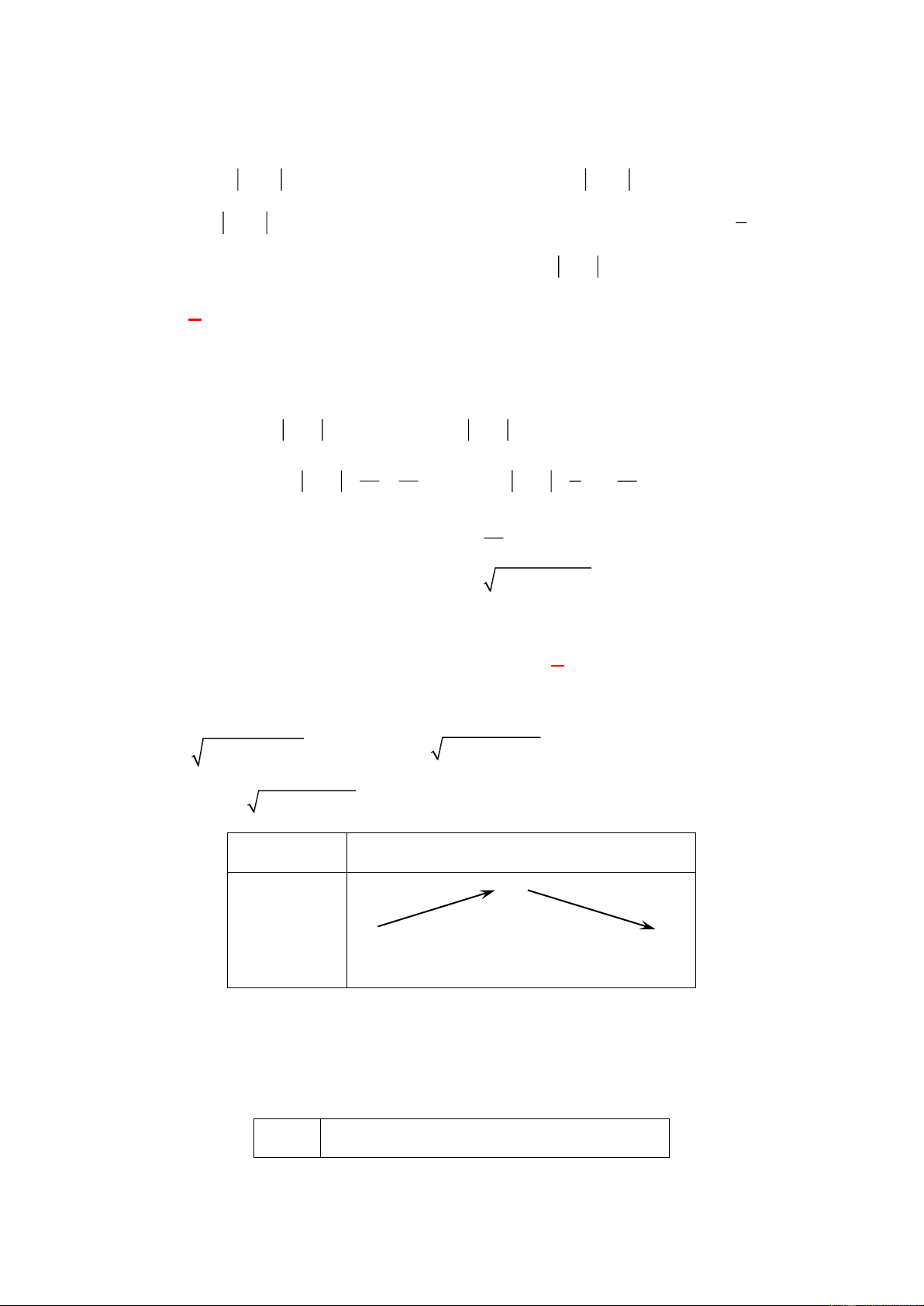
Chọn D
Ta có:
2
2 2 2
2 2 3 3 1 0 2 2 3 1 0x x m mx m m x m x m m m
2
2
1 2 3x m m m
có nghiệm khi và chỉ khi
2
1
2 3 1 1
2
m m m
Câu 25: [0D4-8-3] Tìm
a
để bất phương trình
2
4 2 1x x a x
có nghiệm?
A. Với mọi
a
. B. Không có
a
. C.
4a
. D.
4a
.
Lời giải
Chọn A
Ta có:
1a
2
2
4 2 1 2 2 4 0x x a x x a x a
22
2
2 2 4
44
aa
x a x a
2
2
24
24
aa
xa
Bất phương trình đã cho có nghiệm khi
2
40
4
a
a
luôn đúng với
a
.
Câu 26: [0D4-8-3] Để bất phương trình
2
( 5)(3 ) 2x x x x a
nghiệm đúng
5;3x
, tham số
a
phải thỏa điều kiện:
A.
3a
. B.
4a
. C.
5a
. D.
6a
.
Lời giải
Chọn C
2 2 2
5 3 2 2 15 2 x x x x a x x x x a
Đặt
2
2 15 t x x
, ta có bảng biến thiên
x
5
1
3
2
2 15 xx
16
0
0
Suy ra
0;4t
.Bất phương trình đã cho thành
2
15 t t a
.
Xét hàm
2
15 f t t t
với
0;4t
.
Ta có bảng biến thiên
t
0
4
ft
5
15
Bất phương trình
2
15 t t a
nghiệm đúng
0;4t
khi và chỉ khi
5.a
Câu 27: [0D4-8-3] Với giá trị nào của
m
thìphương trình
22
2 2 1x m x x
vô
nghiệm?
A.
2
3
m
. B.
0m
hoặc
2
3
m
. C.
2
0
3
m
. D.
0m
.
Lời giải
Chọn B
Điều kiện
2
2
20
10
xm
x
2
20
; 1 1;
xm
x
. Phương trình trở thành
22
2 2 1x m x x
22
2 3 4x m x
2
2 1 1xm
với
2 3 2 3
; 1 1;
33
x
. Phương trình đã cho vô nghiệm khi phương trình
1
vô nghiệm khi
0m
hoặc
2
3
m
.
Câu 28: [0D4-8-3] Để phương trình:
3 ( 2) 1 0x x m
có đúng một nghiệm, các giá trị
của tham số
m
là:
A.
1m
hoặc
29
4
m
. B.
21
–
4
m
hoặc
1m
.
C.
–1m
hoặc
21
4
m
. D.
29
–
4
m
hoăc
1m
.
Lời giải
Chọn A
Ta có
3 2 1 0 1 3 2x x m m x x
Xét hàm số
1 3 ( 2)y x x
Ta có
2
2
73
53
x x khi x
y
x x khi x
Bảng biến thiên của
1 3 ( 2)y x x
x
3
1
2
y
29
4
1
Dựa vào bảng trên phương trình có đúng 1 nghiệm khi và chỉ khi
1
29
4
m
m
Câu 29: [0D4-8-3] Phương trình
2 1 0x x m
có ba nghiệm phân biệt, giá trị thích
hợp của tham số
m
là:
A.
9
0
4
m
. B.
12m
. C.
9
–0
4
m
. D.
–2 1m
.
Lời giải
Chọn C
Xét
2 1 0 1x x m
Với
2x
, ta có:
2
1 2 1 0 2x x m m x x
Với
2x
, ta có:
2
1 2 1 0 2x x m m x x
Đặt
2
2
2 khi 2
2 khi 2
x x x
fx
x x x
Bảng biến thiên:
x
1
2
2
fx
0
9
4
Dựa vào bảng biến thiên ta có
9
0
4
m
.
Câu 30: [0D4-8-3] Để phương trình sau có 4 nghiệm phân biệt:
22
10 2 8 5x x x x a
.
Giá trị của tham số
a
là:
A.
1a
. B.
1; 10a
. C.
45
4;
4
a
. D.
43
4
4
a
.
Lời giải
Chọn D
Xét phương trình:
22
10 2 8 5x x x x a
(1)
22
10 2 8 5a x x x x
Xét
22
10 2 8 5f x x x x x
2 2 2
2 2 2
10 2 8 5 khi 10 2 8 0
10 2 8 5 khi 10 2 8 0
x x x x x x
x x x x x x
2
2
3 15 8 khi 1 4
5 8 khi 1 4
x x x
x x x x
Bảng biến thiên:
x
1
5
2
4
fx
43
4
4
4
Dựa vào bảng biến thiên ta có phương trình (1) có 4 nghiệm phân biệt
43
4
4
a
.
Câu 31: [0D4-8-3] Để phương trình sau cónghiệm duy nhất:
22
2 3 2 5 8x x a x x
, Giá
trị của tham số
a
là:
A.
15a
. B.
–12a
. C.
56
79
a
. D.
49
60
a
.
Lời giải
Chọn A
Xét phương trình:
22
2 3 2 5 8 1x x a x x
2 2 2
2 2 2
2 3 2 8 khi 2 3 2 0
5
2 3 2 8 khi 2 3 2 0
x x x x x x
a f x
x x x x x x
22
22
3 5 2 khi 2 3 2 0
11 2 khi 2 3 2 0
x x x x
x x x x
Bảng biến thiên:
x
5
6
1
2
2
fx
49
12
Dựa vào bảng biến thiên ta có: phương trình (1) có nghiệp duy nhất
49 49
5
12 60
aa
.
Câu 32: [0D4-8-3] Tập nghiệm của phương trình
2
2
7 10
7 10
33
xx
xx
xx
là
A.
5;
. B.
3;5
. C.
2;5
. D.
5;
.
Lời giải
Chọn A
Điều kiện:
3x
.
2
2
7 10
7 10
33
xx
xx
xx
22
2
7 10 7 10, 5 1
7 10 0, 3 5 2
x x x x x
x x x
.

Tập nghiệm của phương trình là:
5;S
.
Câu 33: [0D4-8-3] Tập nghiệm của bất phương trình
4 6 2 1 x x x
là:
A.
2;5
. B.
109 3
;6
5
. C.
1;6
. D.
0;7
.
Lời giải
Chọn B
Ta có:
22
2
2 1 0
1
4 6 2 1 4 6 0 4;6
2 24 4 8 4
5 6 20 0
x
x
x x x x x x
x x x x
xx
2
11
109 3
4;6 4;6 ;6
5
5 6 20 0
3 109 3 109
;;
55
xx
x x x
xx
Vậy tập nghiệm của bất phương trình là:
109 3
;6
5
S
.
Câu 34: [0D4-8-3] Tập nghiệm của bất phương trình
2 2 5 3 x x x
là:
A.
100;2
. B.
;1
.
C.
;2 6;
. D.
;2 4 5;
.
Lời giải
Chọn D
Ta có:
2
2
30
3
2 2 5 0
;2 5;
2 2 5 3
30
3
2 2 5 6 9
8 11 0
x
x
xx
x
x x x
x
x
x x x x
xx

2
3
3
;2 5;
;2
;2 5;
3
4 5;
3
;4 5 4 5;
8 11 0
x
x
x
x
x
x
x
x
x
xx
Vậy tập nghiệm của bất phương trình là:
;2 4 5;S
.
Câu 35: [0D4-8-3] nghiệm của bất phương trình
2
2 4 6 9 x x x
là:
A.
1
; 7 ;
3
. B.
1
7;
3
.
C.
1
; 7;
3
. D.
1
;7
3
.
Lời giải
Chọn A
Ta có:
2
22
22
6 9 0
2 4 6 9 3 22 7 0
4 16 16 6 9
xx
x x x x x
x x x x
1
; 7 ;
3
x
Vậy tập nghiệm của bất phương trình là:
1
; 7 ;
3
S
.
Câu 36: [0D4-8-3] Tập nghiệm của bất phương trình
20xx
là
A.
1
;
4
. B.
1
0;
4
. C.
1
0;
4
. D.
1
0;
4
.
Lời giải
Chọn A
Ta có:
2
0
0
1
2 0 2 2 0 ;
1
;0 ;
4
4
4
x
x
x x x x x x
x
xx
Vậy tập nghiệm của bất phương trình là:
1
;
4
S
.

Câu 37: [0D4-8-3] Tập nghiệm của bất phương trình
2
5 2 2 5 x x x
là:
A.
; 2 2;
. B.
2;2
. C.
0;10
. D.
;0 10;
.
Lời giải
Chọn C
Ta có:
22
2
2
2
2
2
5 2 0
5
5 2 2 5 5 2 5 2
5 2 5 2
10 0
5 2 5 2
40
x
x
x x x x x x
x x x
xx
x x x
x
2
5
0;10
0;10
x
x
x
Vậy tập nghiệm của bất phương trình là:
0;10S
.
Câu 38: [0D4-8-3] Một học sinh giải bất phương trình
2
1 13 3 2xx
(1) tuần tự như sau
(I)
2
(1) 1 2 13 3xx
(2)
(II)
22
(2) (1 2 ) 13 3xx
, với
1
2
x
(3)
(III)
2
(3) 4 12 0xx
, với
1
2
x
(4)
(IV)
(4) 2x
Lý luận trên nếu sai, thì sai từ bước nào?
A. (II). B. (III). C. (IV). D. Lý luận
đúng.
Lời giải
Chọn C
Sai từ bước
IV
vì
2
6
4 12 0
2
x
xx
x
.
Câu 39: [0D4-8-3] Bất phương trình (
22
3 4 ). 5 0x x x
có bao nhiêu nghiệm nguyên
dương?

A.
0
. B.
1
.
C.
2
. D. Nhiều hơn
2
nhưng hữu hạn.
Lời giải
Chọn B
Điều kiện của bpt là
2
55xx
.
Ta có
2 2 2
( 3 4). 5 0 3 4 0 1 4x x x x x x
.
Do
x
nguyên dương, thỏa mãn điều kiện nên
3x
.
Câu 40: [0D4-8-3] Bất phương trình
21
2
1
x
x
có tập nghiệm là
A.
1;
. B.
3
; 3;
4
C.
3
;1
4
D.
3
; \ {1}
4
.
Lời giải
Chọn D
ĐK
1x
TH1
1
1
2
x
x
Bpt
2 1 2 1
2 1 1
2 0 0 1
1 1 1
xx
x
x
x x x
kết hợp đk, suy ra
1x
.
TH2
1
1
2
x
Bpt
2 1 2 1
2 1 4 3 3
2 0 0 1
1 1 1 4
xx
xx
x
x x x
kết hợp đk,
suy ra
3
1
4
x
.
Vậy tập nghiệm của bpt là
3
; \ {1}
4
S
.
Câu 41: [0D4-8-3] Cho bất phương trình
28
13 9x
. Các nghiệm nguyên của bất phương
trình là

A.
7x
và
8x
. B.
9x
và
10x
.
C.
11; 12; 14; 15x x x x
. D.
13x
và
14x
.
Lời giải
Chọn C
ĐK
13x
TH1
13x
Bpt
8 8 86
2 13
2 8 43
9 9 9
0 0 13
13 9 13 13 4
xx
x
x x x
kết hợp
điều kiện, suy ra
43
13
4
x
.
TH2
13x
Bpt
8 8 122
2 13
2 8 61
9 9 9
0 0 13
13 9 13 13 4
xx
x
x x x
kết hợp điều
kiện, suy ra
61
13
4
x
.
Vậy tập nghiệm của BPT là
43 61
; \ {13}
44
S
.
Câu 42: [0D4-8-3] Bất phương trình
1 1 2
22x x x
có tập nghiệm là
A.
3 17 3 17
2; 0;2 ;
22
. B.
\ 2;0;2
.
C.
2;0
. D.
0;2
.
Lời giải
Chọn A
ĐK
2;0;2x
Ta có
2
2
2 4 2 2
1 1 2 2 6 4
00
2 2 2 2 2 2
x x x x x
xx
x x x x x x x x x
.
Lập bảng xét dấu biểu thức
2
2 6 4
22
xx
x x x
. Từ đó suy ra tập nghiệm cần tìm là
3 17 3 17
2; (0;2 ) ( ; )
22
.

Câu 1: [0D4-8-4] Định m để
2
11
4 2 2
22
x m x x m
với mọi
x
:
A.
1
3
4
m
hoặc
1
3
4
m
. B.
11
33
44
m
.
C.
3m
hoặc
2m
. D.
23m
.
Lời giải
Chọn A
Ta có:
2
11
4 2 2
22
x m x x m
2
2
11
4 2 2
22
11
4 2 2
22
x m x x m
x m x x m
2
2
2 1 0
6 3 0
x x m
x x m
2
2
21
1
2
3
m x x
m x x
Ta cần tìm giá trị của
m
sao cho
2
2
21
1
2
3
m x x
m x x
với mọi
x
.
Vẽ đồ thị các hàm số
2
21y x x
và
2
1
2
3
y x x
.
Dựa vào đồ thị ta có
1
3
4
m
hoặc
1
3
4
m
thỏa yêu cầu bài toán.
Câu 2: [0D4-8-4] Cho bất phương trình
22
2x x a x x a x
( 1).Khi đó:

A. (1) có nghiệm khi
1
4
a
. B. Mọi nghiệm của ( 1) đều không
âm.
C. (1) có nghiệm lớn hơn
1
khi
0a
. D. Tất cả A, B, C đều đúng.
Lời giải
Chọn D
* Vì vế trái của bất phương trình luôn lớn hơn hoặc bằng
0
nên
22
2x x a x x a x
có nghiệm thì nghiệm phải không âm
B
đúng.
+ Nếu
1
1 4 0
4
aa
thì
22
0, 0,x x a x x a x
.
Nên
22
2x x a x x a x
2
2 2 2x a x
22
2 2 2 0 0x x a x x a
( vô lí)
Do đó nếu
1
4
a
thì bpt vô nghiệm.
+ Nếu
1
4
a
,
2
1
2 2 0
2
bpt x x
1
2
x
+ Nếu
1
4
a
.
2
2
2 2 2 0
2 2 2 0
22
22
x x a
x x a
bpt
xx
xx
luôn có nghiệm.
Vậy bất phương trình có nghiệm khi
1
4
a
A đúng.
Khi
0a
+Phương trình
2
0x x a
có 2 nghiệm trái dấu là
1 1 4 1 1 4
;
22
aa
xx
+Phương trình
2
0x x a
có 2 nghiệm trái dấu là
1 1 4 1 1 4
;
22
aa
xx
Vì pt chỉ có nghiệm khi
0x
nên ta có bảng xét dấu.

Ta nhận thấy khi
0a
thì
1 1 4
1
2
a
và trên
1 1 4 1 1 4
;
22
aa
thì
22bpt x x
luôn đúng. Vậy với
0a
thì
22
2x x a x x a x
có nghiệm
lớn hơn 1.
C đúng.
Câu 3: [0D4-8-4] Cho bất phương trình:
22
2 3 1 0x x m m m
. Để bất phương trình
có nghiệm, các giá trị thích hợp của tham số
m
là:
A.
1
1
2
m
. B.
1
1
2
m
. C.
1
1
2
m
. D.
1
1
2
m
.
Lời giải
Chọn C
Xét
xm
.
Ta có:
22
2 3 1 0x x m m m
22
2 1 0x x m m
.
Đặt
22
21f x x x m m
2
mm
Bất phương trình có nghiệm khi phương trình
0fx
có 2 nghiệm
12
;xx
thỏa :
+TH1 :
12
x m x
2
2
0
0
0
2 3 1 0
mm
fm
mm
01
1
1
1
2
1
2
m
m
m
.

+TH2 :
12
m x x
12
0
0
2
fm
xx
m
2
2
0
2 3 1 0
2
2
mm
mm
m
01
1
1
2
1
m
mm
m
m
.
Xét
xm
.
Ta có:
22
2 3 1 0x x m m m
22
2 5 1 0x x m m
.
Đặt
22
2 5 1g x x x m m
2
5mm
Bất phương trình có nghiệm khi phương trình
0gx
có 2 nghiệm
12
;xx
thỏa :
+TH1 :
12
x m x
2
2
0
50
0
2 3 1 0
mm
gm
mm
05
1
1
1
2
1
2
m
m
m
.
+TH2 :
12
x x m
12
0
0
2
gm
xx
m
2
2
05
50
1
2 3 1 0 1
2
1
1
m
mm
m m m m
m
m
m
Vậy
1
1
2
m
thỏa ycbt.
Câu 4: [0D4-8-4] Định
a
để bất phương trình:
2
4 2 1x x a x
có nghiệm:
A.
a
. B. Không có
a
C.
4a
. D.
4a
.
Lời giải
Chọn C
Đặt
2tx
, điều kiện:
0t
Ta có pt theo
t
:
2
4t at a
2
40t at a
(1)
Đặt
2
4f t t at a
.

Ta thấy:
2
4 16 0,a a a
Để bất phương trình
2
4 2 1x x a x
có nghiệm thì bất phương trình (1) phải
có ít nhất một nghiệm
0t
.
+TH1: Phương trình
0ft
có 1 nghiệm
0t
4 0 4aa
+TH2 : Phương trình
0ft
có 2 nghiệm trái dấu
4 0 4aa
.
+TH3 : Phương trình
0ft
có 2 nghiệm dương
00
0 4 0
Sa
Pa
0
4
a
a
a
.
Kết hợp các trường hợp ta có
4a
thỏa ycbt.
Câu 5: [0D4-8-4] Định
m
để mọi
–2x
là nghiệm của bất phương trình:
22
2 1 2 1 1x mx x m x
.
A.
1
4
m
. B. Không có
m
. C.
1
4
m
. D.
5
4
m
.
Lời giải
Chọn D
Ta có:
22
2 1 2 1 1x mx x m x
22
2 1 2 1 2x mx x mx x
Xét
2
21f x x mx
TH1: Nếu
2
0 4 4 0 1;1mm
thì
2
2 1 0,x mx x
Khi đó
22
2 1 2 1 2x mx x mx x
2 0 2xx
.
Vậy
1;1m
thỏa ycbt.
TH2: Nếu
0
2
4 4 0 ; 1 1;mm
thì phương trình
( ) 0fx
luôn có 2 nghiệm
12
,xx
, ta có bảng xét dấu:
Khi đó ta có :

22
2 1 2 1 2x mx x mx x
1
12
12
2
2, 1
1
0 1 4 , ; 2
4
1
1 4 0, ;m 3
4
2, 4
x khi x x
x m khi x x x m
m x khi x x x
x khi x x
Ta thấy ở (2), (3), (4) phương trình không thể có nghiệm là
–2x
.
Với (1) ta có bpt có nghiệm là
–2x
khi
12
2 xx
0
20
4
f
S
2
4 4 0
4 5 0
2
m
m
m
11
5
4
2
mm
m
m
5
; 1 1;
4
m
Vậy
5
4
m
thỏa yêu cầu bài toán.
Câu 6: [0D4-8-4] Để bất phương trình:
2
( 5)(3 ) 2x x x x a
nghiệm đúng với mọi
x
thuộc tập xác định thì giá trị của tham số
a
phải thỏa điều kiện:
A.
3a
. B.
4a
. C.
5a
. D.
6a
.
Lời giải.
Chọn C.
Điều kiện:
5 3 0 5;3x x x
.
2
( 5)(3 ) 2x x x x a
(1)
22
2 15 2x x x x a
Đặt
2
2
2 15 1 16t x x x
04t
Ta có
22
2 15t x x
22
2 15x x t
Ta có bất phương trình theo
t
:
2
15t t a
2
15t t a
(2)
Để bất phương trình (1) nghiệm đúng với mọi
5;3x
thì bất pt (2) nghiệm
đúng với mọi
0;4t
0;4
maxa f t
với
2
15f t t t
.
Bảng biến thiên :
Vậy
0;4
max 5a f t
thỏa yêu cầu bài toán.
Câu 7: [0D4-8-4] Để phương trình:
3 ( 2) 1 0x x m
có đúng một nghiệm, các giá trị
của tham số m là:
A.
1 m
hoặc
29
.
4
m
B.
21
4
m
hoặc
29
.
4
m
C.
–1m
hoặc
21
.
4
m
D.
29
4
m
hoăc
1m
.
Lời giải
Chọn A
3 ( 2) 1 0x x m
3 2 1 0 3
3 2 1 0 3
x x m x
x x m x
2
2
7 0 1
5 0 2
x x m
x x m
PT có đúng một nghiệm khi và chỉ khi
1
có đúng một nghiệm và
2
vô nghiệm
hoặc ngược lại.
TH1:
1
có đúng 1 nghiệm và
2
vô nghiệm
2
vô nghiệm
21
4
m
1
có đúng 1 nghiệm thỏa mãn
3x
trong các khả năng sau
Khả năng 1:
1
có nghiệm
31xm
khi đó phương trình đã cho
có hai nghiệm nên không thỏa mãn yêu cầu đề bài (Loại)
Khả năng 2:
1
có nghiệm
12
3xx
3 0 1af m
(thỏa
mãn)
Khả năng 3:
1
có nghiệm kép
12
3xx
giải thấy không có m thỏa
mãn.
Vậy TH1 thỏa mãn khi và chỉ khi
1m
.
Giải tương tự với TH 2 ta có
29
4
m
.
Cách 2: Dùng pp biến đổi đồ thị:
3 ( 2) 1x x m
.
Câu 8: [0D4-8-4] Phương trình
2 ( 1) 0x x m
có ba nghiệm phân biệt, giá trị thích
hợp của tham số m là
A.
9
0.
4
m
B.
1 2.m
C.
9
0.
4
m
D.
2 1.m
Lời giải
Chọn C
2 ( 1) 0x x m
2 ( 1)x x m
Xét hàm số
21y x x
2
2
2 , 2
2 , 2
x x x
x x x
Suy ra bảng biến thiên của hàm số
21y f x x x
như sau:
Yêu cầu bài toán
99
0 0.
44
mm
Câu 9: [0D4-8-4] Để phương trình sau có 4 nghiệm phân biệt
22
10 2 8 5x x x x a
,
giá trị của tham số a là
A.
1.a
B.
1;10 .a
C.
45
4; .
4
a
D.
43
4; .
4
a
Lời giải
Chọn D
2
2xx
2
2xx
1
2
+
∞
2
∞
f
(
x
)
x
9
4
0

Đặt
2
2
5 25 25
5
2 4 4
t x x x
, phương trình trở thành:
2 8 2 8t t a t t a
2 8 , 4
25
2 8 , 4
4
t t a t
t t a t
8 , 4
8 25
, 4
34
t a t
a
tt
Để phương trình có 4 nghiệm phân biệt thì
84
25 8
4
43
8
8
3
a
a
a
a
4
43
4
4
4
a
a
a
43
4
4
a
.
Câu 10: [0D4-8-4] Định m để bất phương trình
2 2 2
( 1) ( 3) 8( 1)x x x m
thỏa
0x
A.
17m
. B.
17m
. C.
16m
. D. Không
có
m
Lời giải
Chọn D
Đặt
1xa
.
BPt đã cho có dạng
22
24
2 2 8 16a a a m a m
Vậy
16m
thì bất phương trình nghiệm đúng
0x
.
Bấm Tải xuống để xem toàn bộ.




