


































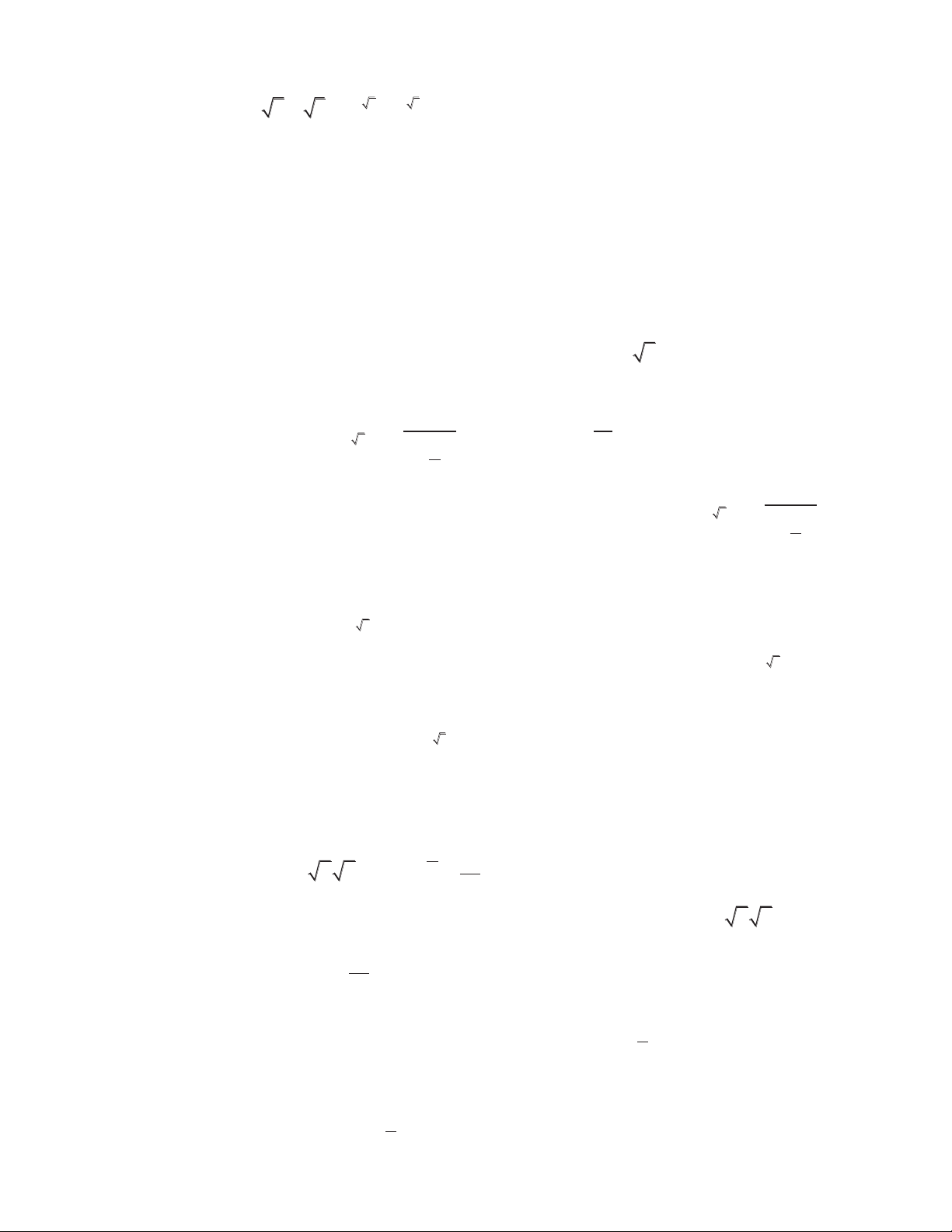



























































Preview text:
NỘI DUNG 1. LŨY THỪA 2. LOGARIT
3. HÀM SỐ LŨY THỪA – HÀM SỐ MŨ – HÀM SỐ LOGARIT
4. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH MŨ
5. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH LOGARIT LŨY THỪA
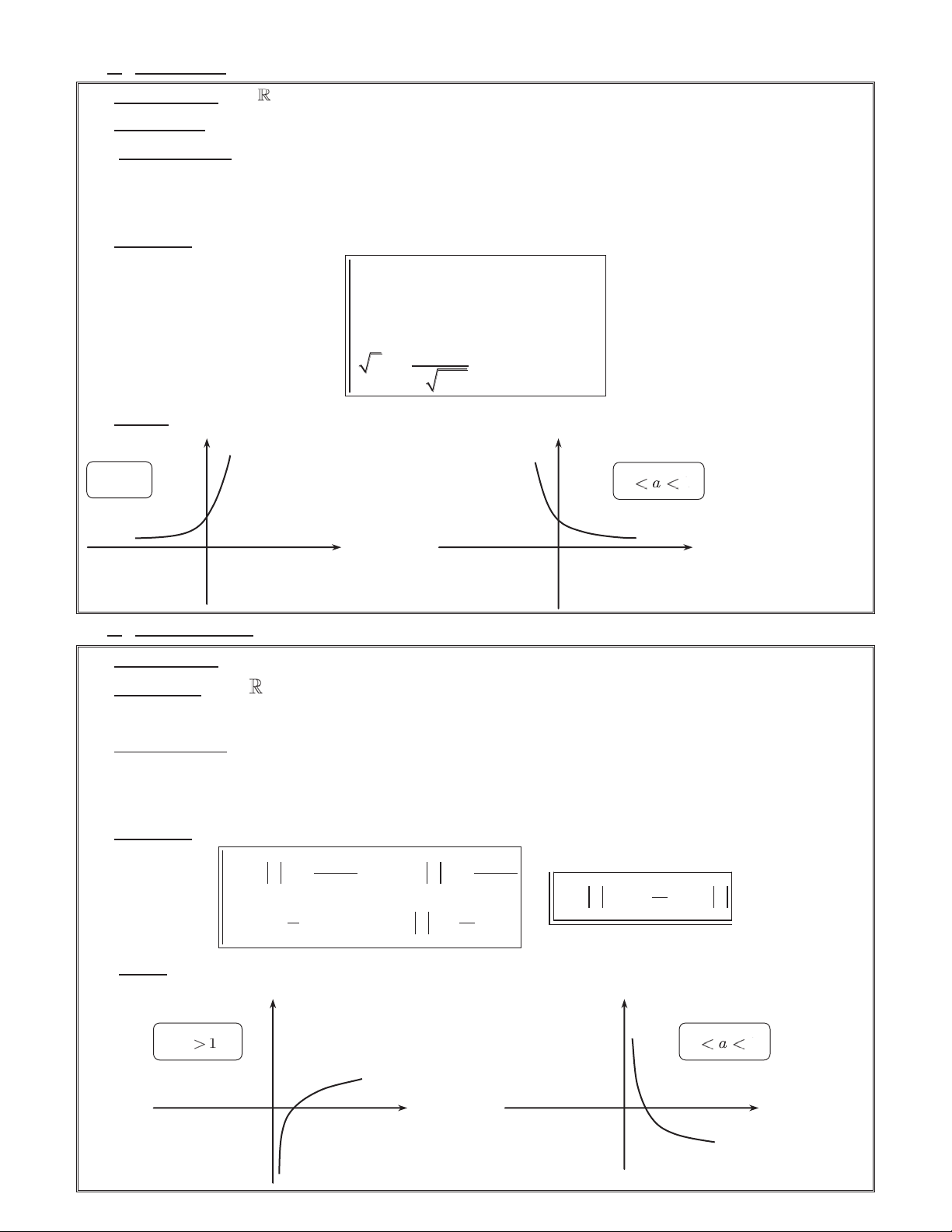
KIẾN THỨC CƠ BẢN
1. Định nghĩa lũy thừa và căn
x Cho số thực b và số nguyên dương n (n t 2) . Số a được gọi là căn bậc n của số b nếu n a b .
x Chú ý: q Với n lẻ và b : Có duy nhất một căn bậc n của b , kí hiệu là n b .
b 0 : Không tồn tại căn bậc n của b . q Với n chẵn:
b 0 : Có một căn bậc n của b là số 0 .
b ! 0 : Có hai căn bậc n của a là hai số đối nhau, căn có giá trị dương ký hiệu
là n b , căn có giá trị âm kí hiệu là n b . Số mũ D Cơ số a Lũy thừa α a * D D n * a n
a a a a
a ( n thừa số a ) D 0 a z 0 D 0 a a 1 D n 1 * D ,( n n ) a z 0 a a n a m * D ,(m ,n , ) a ! m 0 D n m n , (n n
a b a b ) n a a a *
D limr ,(r ,n , ) a ! 0 D a lim nr n n a
2. Một số tính chất của lũy thừa
x Giả thuyết rằng mỗi biểu thức được xét đều có nghĩa: D D D D D D E D E a D E D E D D D § a · a § a · § b · a a a ; D E a ; . (a ) a ; ( ) ab a b ; ; E ¨ ¸ D ¨ ¸ ¨ ¸ a © b ¹ b © b ¹ © a ¹ x Nếu D E D E
a ! 1 thì a ! a D ! E ; Nếu 0 a 1 thì a ! a D E .
x Với mọi 0 a b, ta có: m m
a b m ! 0 ; m m
a ! b m 0
x Chú ý: q Các tính chất trên đúng trong trường hợp số mũ nguyên hoặc không nguyên.
q Khi xét lũy thừa với số mũ 0 và số mũ nguyên âm thì cơ số a phải khác 0 .
q Khi xét lũy thừa với số mũ không nguyên thì cơ số a phải dương.
3. Một số tính chất của căn bậc n x Với * a,b ; n ;n , ta có: 2n 2n 2n 1 2n 1 q a a ~~ a ; q a a a . 2n 2n 2n 2n 1 2n 1 2n 1 q ab a ~~ b ~ , ~ ab t 0 ; q ab a b a ,b . 2n~~ 2n 1 a a a a q 2n , ab t 0,b z 0 ; q 2n 1 a , b z 0 . 2 2n 1 n b b ~~ b b
x Với a,b , ta có: m n m q n a a , a
! 0, n nguyên dương, m nguyên. n q m nm a a, a
t 0 , n , m nguyên dương. n p m q q Nếu p q
thì a a , a ! 0, , m n nguyên dương, ,
p q nguyên. Đặc biệt: n m n m a a . n m
BÀI TẬP TRẮC NGHIỆM
Câu 1. Khẳng định nào sau đây đúng : m A. n
a xác định với mọi a \^ ` 0 ^ ; n N B. n m n a a ; a m C. 0 a 1; a D. n m n a a ; a ; , m n Câu 2. Tìm
x để biểu thức x 2 2 1 có nghĩa: 1 1 § 1 · 1 A. x z B. x ! C. x ;2 ¨ ¸ D. x t 2 2 © 2 ¹ 2
Câu 3. Tìm x để biểu thức x 1 2 3 1 có nghĩa: B. x f @ ;1 >1;f. A. x ; f 1 1;f . C. x 1 ; 1 . D. x \^r ^ ` 1 .
Câu 4. Tìm x để biểu thức x x 2 2 3 1 có nghĩa: A. x
B. Không tồn tại x C. x !1 D. x \^ ` 0 ^
Câu 5. Các căn bậc hai của 4 là : A. 2 B. 2 C. 2 r D. 16
Câu 6. Cho a và * n 2k(k ) , n
a có căn bậc n là : n A. a . B. | a | . C. a . D. 2 a .
Câu 7. Cho a và *
n 2k 1(k ) , n
a có căn bậc n là : n A. 2n 1 a . B. | a | . C. a . D. a .
Câu 8. Phương trình 2016 x
2017 có tập nghiệm trong là : A. 2017 T={r 2016} B 2016 T={r 2017} C. 2016 T={ 2017} D. 2016 T={ 2017}
Câu 9. Các căn bậc bốn của 81 là : A. 3 B. 3 r C. 3 D. 9 r
Câu 10. Khẳng định nào sau đây đúng? A. Phương trình 2015 x 2 vô nghiệm. B. Phương trình 21 x
21 có 2 nghiệm phân biệt.
C. Phương trình e x S có 1 nghiệm. D. Phương trình 2015 x 2 có vô số nghiệm.
Câu 11. Khẳng định nào sau đây sai? 1 1
A. Có một căn bậc n của số 0 là 0.
B. là căn bậc 5 của . 3 243
C. Có một căn bậc hai của 4.
D. Căn bậc 8 của 2 được viết là 8 r 2 . 4 0,7 5 3 § 1 · § 1 ·
Câu 12. Tính giá trị ¨ ¸ ¨ ¸ , ta được : ©16 ¹ © 8 ¹ A. 12 B. 16 C. 18 D. 24
Câu 13. Viết biểu thức a a a ! 0 về dạng lũy thừa của a là. 5 1 3 1 A. 4 a B. 4 a C. 4 a D. 2 a 3 2 4
Câu 14. Viết biểu thức
về dạng lũy thừa 2m ta được m ?. 0,75 16 13 13 5 5 A. . B. . C. . D. . 6 6 6 6
Câu 15. Các căn bậc bảy của 128 là : A. 2 B. 2 r C. 2 D. 8 m § ·
Câu 16. Viết biểu thức b a a 5 3
, a,b ! 0 về dạng lũy thừa ¨ ¸ ta được m ?. a b © b ¹ 2 4 2 2 A. . B. . C. . D. . 15 15 5 15 2 2
Câu 17. Cho a ! 0 ; b ! 0. Viết biểu thức 3 a a về dạng m a và biểu thức 3
b : b về dạng n b . Ta có m n ? 1 1 A. B. 1 C. 1 D. 3 2 4 4
Câu 18. Cho x ! 0 ; y ! 0. Viết biểu thức 6 5 5 x . x
x ; về dạng m x và biểu thức 5 5 6 y : y
y ; về dạng n y . Ta có m n ? 11 11 8 8 A. B. C. D. 6 6 5 5 2 2 2 8
Câu 19. Viết biểu thức
về dạng 2x và biểu thức
về dạng 2y . Ta có 2 2 x y ? 4 8 3 4 2017 11 53 2017 A. B. C. D. 567 6 24 576 Câu 20. Cho 3 6 f (x)
x. x khi đó f (0, 09) bằng : A. 0,09 B. 0,9 C. 0,03 D. 0,3 3 2 Câu 21. Cho x x f x khi đó f 1,3 bằng: 6 x A. 0,13. B. 1,3 . C. 0,013. D. 13 .
Câu 22. Cho f x 3 4 12 5
x x x . Khi đó f (2,7) bằng A. 0,027 . B. 0, 27 . C. 2,7 . D. 27 .
Câu 23. Đơn giản biểu thức 4 2 81a b , ta được: A. 2 9 a b . B. 2 9a b . C. 2 9a b . D. 2 3a b .
Câu 24. Đơn giản biểu thức x x 4 8 4 1 , ta được: A. 2 x x 1 . B. 2 x x 1 C. 2 x x 1 . D. 2 x x 1 .
Câu 25. Đơn giản biểu thức x x 9 3 3 1 , ta được: A. xx 3 1 . B. xx 3 1 . C. x x 3 1 .
D. x x 3 1 .
Câu 26. Khẳng định nào sau đây đúng 1 2 § 1 · § 1 · A. 0 a 1 a . B. 2 a ! 1 a ! 1. C. 2 3 3 2 . D. ¨ ¸ ¨ ¸ . © 4 ¹ © 4 ¹ a Câu 27. Nếu 2 2 3 1 2 3 1 thì A. a 1 . B. a 1. C. a ! 1 . D. a t 1 .
Câu 28. Trong các khẳng định sau đây, khẳng định nào sai? A. 2 ! 2 0,01 10 . B. 2 2 0,01 10 . C. 2 2 0,01 10 . D. 0 a 1, a z 0 .
Câu 29. Trong các khẳng định sau đây , khẳng định nào đúng? 3 4 6 A. 2 2 2 2 . B. 11 2 ! 11 2 . 3 4 4 C. 4 2 4 2 . D. 3 2 3 2 . m Câu 30. Nếu 2 2 3 2 3 2 thì 3 1 1 3 A. m ! . B. m . C. m ! . D. m z . 2 2 2 2
Câu 31. Cho n nguyên dươngn t 2 khẳng định nào sau đây là khẳng định đúng? 1 1 A. n n a a a ! 0 . B. n n a a a z 0 . 1 1 C. n n a a a t 0 . D. n n a a a .
Câu 32. Khẳng định nào sau đây là khẳng định sai? A. 2n 2n ab a b , a b .
B. a t 0 a
, n nguyên dươngn t 1 .
C. 2n 2n . D. 4 2 a t 0 . a a a
, n nguyên dươngn t 1 a a
Câu 33. Cho a ! 0,b 0 , khẳng định nào sau đây là khẳng định sai? A. 4 4 4 3 3 3 a b ab .
B. a b ab . C. 2 2 . D. 4 2 2 . a b ab a b a b
Câu 34. Tìm điều kiện của a để khẳng định 2
(3 a) a 3 là khẳng định đúng ? A. a . B. a d 3. C. a ! 3. D. a t 3.
Câu 35. Cho a là số thực dương, ,
m n tùy ý. Phát biểu nào sau đây là phát biểu sai ? n A a n m. n m n a a a . B. n m a . C. n m m n a a . m m.n a a . D. m a 1 1 2 2 3 4
Câu 36. Bạn An trong quá trình biến đổi đã làm như sau: 2 3 6 3 6 27 27 27 27 3 bạn
đã sai ở bước nào? A. 4 . B. 2 . C. 3 . D. 1 . 1 1 Câu 37. Nếu 2 6 a ! a và 2 3 b ! b thì :
A. a 1;0 b 1.
B. a !1;b 1.
C. 0 a 1;b 1.
D. a !1;0 b 1. x
Câu 38. Nếu 3 2 ! 3 2 thì A. x . B. x 1. C. x ! 1 . D. x 1 . ax x a 1
Câu 39. Với giá trị nào của 2
a thì phương trình 4 2 2
có hai nghiệm thực phân biệt. 2 4 A. a z 0 B. a C. a t 0 D. a ! 0
Câu 40. Tìm biểu thức không có nghĩa trong các biểu thức sau: 0 § 1 · A. 4 3 . B. 1 4 3 3 . C. 0 . . D. ¨ 3 ¸ © 2 ¹ 2 1 1 § ·
Câu 41. Đơn giản biểu thức 2 P a .¨ ¸ được kết quả là © a ¹ A. 2 a . B. 2 2 1 a . C. 1 2 a . D. a . Câu 42. Biểu thức S
a 2 có nghĩa với : A. a ! 2 B. a C. a ! 0 D. a 2
Câu 43. Cho n N;n t 2 khẳng định nào sau đây đúng? 1 1 A. n n a a , a z 0. B. n n a a , a ! 0 . 1 1 C. n n a a , a t 0 . D. n n a a , a .
Câu 44. Khẳng định nào sau đây là khẳng định sai?
A. ab a b , a b 2n 2n
B. a t 0 a
, n nguyên dươngn t 2
C. 2n 2n n t 2 D. 4 2 a t 0 a a a , n nguyên dương a a
Câu 45. Cho a ! 0,b 0 , khẳng định nào sau đây là khẳng định sai? A. 4 4 4 3 3 3 2 2 2 4 2 a b ab
B. a b ab C. D. a b ab a b ab 1 1 Câu 46. Nếu 2 6 a ! a và 2 3 b ! b thì
A. a !1;0 b 1
B. a !1;b 1
C. 0 a 1;b 1
D. a 1;0 b 1 4 a .b 4 3 2
Câu 47. Cho a , b là các số dương. Rút gọn biểu thức P được kết quả là : 3 12 6 a .b A. 2 ab . B. 2 a b . C. ab . D. 2 2 a b .
Câu 48. Cho 3D 27 . Mệnh đề nào sau đây là đúng? D ª 3 A. . D ! . D . D . D « B. 3 C. 3 D. 3 3 ¬ ! 3
Câu 49. Giá trị của biểu thức
A a 1 b 1 1 1 a 1 2 3 và b 1 2 3 với A. 3. B. 2. C. 1. D. 4.
Câu 50. Với giá trị nào của x thì đẳng thức 2016 2016 x x đúng
A. Không có giá trị x nào. B. x t 0 . C. x 0 . D. x d 0 .
Câu 51. Với giá trị nào của x thì đẳng thức 2017 2017 x x đúng A. x t 0 . B. x . C. x 0 .
D. Không có giá trị x nào. 1
Câu 52. Với giá trị nào của 4 x thì đẳng thức 4 x đúng x A. x z 0 . B. x t 0 . C. x 1 r .
D. Không có giá trị x nào.
Câu 53. Căn bậc 4 của 3 là A 3 4 . B. 4 3 . C. 4 3 . D. 4 r 3 .
Câu 54. Căn bậc 3 của – 4 là A. 3 r 4 . B. 3 4 . C. 3 4 . D. Không có.
Câu 55. Căn bậc 2016 của –2016 là A. 2016 2016 . B. Không có. C. 2016 2016 . D. 2016 2016 .
Câu 56. Trong các mệnh đề sau, mệnh đề nào sai (I): 3 5 0. 4 ! 0 .3 (II): 5 3 5 ! 3 (III): 3 5 2 ! 4 (IV): 3 5 5 ! 3 A. (I) và (IV). B. (I) và (III). C. (IV). D. (II0 và (IV).
Câu 57. Trong các biểu thức sau biểu thức nào không có nghĩa A. 0 2016 . B. 2016 2016 . C. 2016 0 . D. 2016 2016 .
Câu 58. Với giá trị nào của x thì biểu thức 1 2 3 4 x sau có nghĩa A. x t 2 . B. 2 x 2 . C. x d 2 .
D. Không có giá trị x nào. 2 ª 1 1 4a 9a a 4 3 º a
Câu 59. Cho số thực dương a . Rút gọn biểu thức « » 1 1 1 1 « » 2 2 2 2 ¬2a 3a a a ¼ 1 1 A. 2 9a . B. 9a . C. 3a . D. 2 3a . § ·
Câu 60. Cho số thực dương a,b . Rút gọn biểu thức a b 2 2 3 3 3 3 3
¨ a b ab ¸ © ¹ 1 1 1 1 A. 3 3 a b .
B. a b .
C. a b . D. 3 3 a b . 11
Câu 61. Cho số thực dương a . Rút gọn biểu thức 16 a a a a : a 3 1 1 A. 4 a . B. 2 a . C. a . D. 4 a . 4a 4b
Câu 62. Cho a b 1 thì bằng 4a 2 4b 2 A. 4. B.2. C.3. D. 1. x x
Câu 63. Có bao nhiêu giá trị x thỏa mãn x x 2 6 2 3 3 1 A. 2 . B. 3 . C. 4 . D. 1. 2 x 3x 2x2
Câu 64. Có bao nhiêu giá trị x thỏa mãn 5 2 5 2 đúng A. 3. B.3. C. 2. D. 1.
LŨY THỪA VẬN DỤNG
Câu 65. Biết 4x 4x 23 tính giá trị của biểu thức 2x 2 x P : A. 5 . B. 27 . C. 23 . D. 25 .
Câu 66. Cho a là số thực dương. Biểu thức 4 3 8
a được viết dưới dạng lũy thừa với số mũ hữu tỉ là: 3 2 3 4 A. 2 a . B. 3 a . C. 4 a . D. 3 a .
Câu 67. Cho x là số thực dương. Biểu thức 4 2 3 x
x được viết dưới dạng lũy thừa với số mũ hữu tỉ là: 7 5 12 6 A. 12 x . B. 6 x . C. 7 x . D. 5 x . 5 2 Câu 68. Cho b b
b là số thực dương. Biểu thức
được viết dưới dạng lũy thừa với số mũ hữu tỉ là: 3 b b A. – 2. B. – 1. C. 2. D. 1.
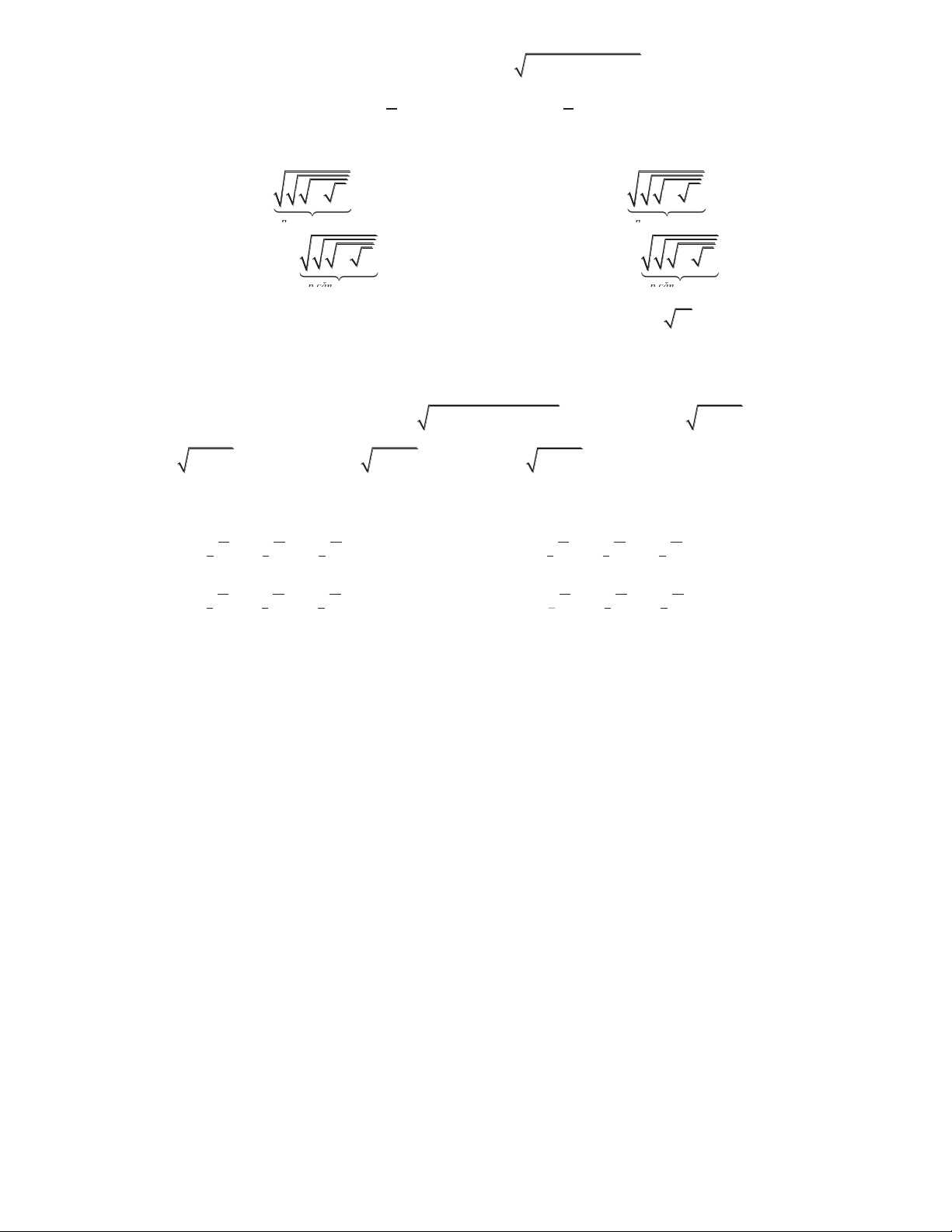
Câu 69. Cho x là số thực dương. Biểu thức x x x x x x x x được viết dưới dạng lũy thừa với số mũ hữu tỉ là: 256 255 127 128 A. 255 x . B. 256 x . C. 128 x . D. 127 x .
Câu 70. Cho hai số thực dương a b a
a và b . Biểu thức 5 3
được viết dưới dạng lũy thừa với số mũ b a b hữu tỉ là: 31 30 1 7 30 § · 31 § · 6 § · A. a a a 30 x . B. ¨ ¸ . C. ¨ ¸ . D. ¨ ¸ . © b ¹ © b ¹ © b ¹ P 1 2 a b 2 1 2 4 3 3 3 3 3 3
a a .b b
Câu 71. Cho các số thực dương a và b . Rút gọn biểu thức được kết quả là:
A. a b . B. 2 a b .
C. b a . D. 3 3 a b . 4
Câu 72. Cho các số thực dương a b a ab
a và b . Rút gọn biểu thức P được kết quả là: 4 4 4 4 a b a b A. 4 b . B. 4 4 a b .
C. b a . D. 4 a . § ·
Câu 73. Cho các số thực dương a b
a và b . Rút gọn biểu thức P
ab : a b 2 3 3 3 ¨ ¸ được 3 3 © a b ¹ kết quả là: A. 1 . B. 1. C. 2 . D. 2 . 1 1 3 3
Câu 74. Cho các số thực dương a b b a
a và b . Biểu thức thu gọn của biểu thức 3 P ab là 6 6 a b A. 0 . B. 1 . C. 1. D. 2 . 4 a 1 2 3 3 3 a a
Câu 75. Cho số thực dương a . Biểu thức thu gọn của biểu thức P là: 1 a 3 1 4 4 4 a a A. 1. B. a 1. C. 2a . D. a . 1 1 1 1 1 1 4 4 4 4 2 2 P a b a b a b
Câu 76. Cho a ! 0,b ! 0 . Biểu thức thu gọn của biểu thức là: A. 10 10 a b .
B. a b .
C. a b . D. 8 8 a b . 1 1 § · 3 3
Câu 77. Cho a ! 0,b ! 0 .Biểu thức thu gọn của biểu thức 3 3 : ¨ 2 a b P a b ¸ là: © b a ¹ 3 3 A. 3 ab ab ab . B. . C. . D. 3 3 3 ab a b . 3 3 3 a b 3 3 a b 3 3 Câu 78. Cho a b
a ! 0,b ! 0 và a z b . Biểu thức thu gọn của biểu thức P là: 6 6 a b A. 6 6 a b . B. 6 6 a b . C. 3 3 b a . D. 3 3 a b .
Câu 79. So sánh hai số m và n nếu 3, 2m 3, 2n thì:
A. m ! n .
B. m n .
C. m n .
D. Không so sánh được. m n
Câu 80. So sánh hai số m và n nếu 2 2
A m ! n .
B. m n .
C. m n .
D. Không so sánh được. 1 m 1 n § · § ·
Câu 81. So sánh hai số m và n nếu ¨ ¸ ! ¨ ¸ © 9 ¹ © 9 ¹
A. Không so sánh được.
B. m n .
C. m ! n .
D. m n . m n § 3 · § 3 ·
Câu 82. So sánh hai số m và n nếu ¨ ¸ ! ¨ ¸ © 2 ¹ © 2 ¹
A. m n .
B. m n .
C. m ! n .
D. Không so sánh được. m n
Câu 83. So sánh hai số m và n nếu 5 1 5 1
A. m n .
B. m n .
C. m ! n .
D. Không so sánh được. m n
Câu 84. So sánh hai số m và n nếu 2 1 2 1
A. m ! n .
B. m n .
C. m n .
D. Không so sánh được. 2 1
Câu 85. Kết luận nào đúng về số thực a nếu 3 3 (a 1) (a 1) A. a ! 2 . B. a ! 0 . C. a !1. D. 1 a 2.
Câu 86. Kết luận nào đúng về số thực a nếu 3 1 (2a 1) ! (2a 1) ª 1 a 0 1 ª0 a 1 A. « 2 . B. a 0 . C. . D. a 1 . « 2 « ¬a 1 ¬a 1 0, 2 § 1 ·
Câu 87. Kết luận nào đúng về số thực a nếu 2 ¨ ¸ a © a ¹ A. 0 a 1. B. a ! 0 . C. a !1. D. a 0 .
Do 0, 2 2 và có số mũ không nguyên nên 0,2 2 a
a khi a !1. 1 1
Câu 88. Kết luận nào đúng về số thực a nếu a 3! a 2 1 1 A. a 1. B. a ! 0 . C. 0 a 1. D. a !1. 3
Câu 89. Kết luận nào đúng về số thực 2 a nếu a 4 2 ! 2 a A. a !1. B. 0 a 1. C. 1 a 2. D. a 1. 1 1 2 2 § 1 · § 1 ·
Câu 90. Kết luận nào đúng về số thực a nếu ¨ ¸ ! ¨ ¸ © a ¹ © a ¹ A. 1 a 2. B. a 1. C. a !1. D. 0 a 1.
Câu 91. Kết luận nào đúng về số thực a nếu 3 7 a ! a A. a 1. B. 0 a 1. C. a !1. D. 1 a 2. 1 1
Câu 92. Kết luận nào đúng về số thực a nếu 17 8 a ! a A. a !1. B. a 1. C. 0 a 1. D. 1 a 2.
Câu 93. Kết luận nào đúng về số thực a nếu 0, 25 3 a ! a A. 1 a 2. B. a 1. C. 0 a 1. D. a !1. 1,5 1,5 a b 0,5 0,5 0,5 0,5 a b
Câu 94. Rút gọn biểu thức a b ta được : 0.5 0.5 a b
A. a b .
B. a b .
C. a b .
D. a b . 1 1 1 1 3 1 § · ¨ 2 2 2 2 ¸ 2 2 x y x y x y 2y
Câu 95. Rút gọn biểu thức ¨ ¸. được kết quả là: 1 1 1 1 x y x y ¨ ¸ 2 2 2 2
© xy x y xy x y ¹ 2
A. x y .
B. x y . C. 2 . D. . xy
Câu 96. Biểu thức f x 2 3 (x 3x 2)
2 x xác định với : A. x (0; ) f \{1;2}. B. x [0; ) f . C. x [0; ) f \{1;2}. D. x [0; ) f \{1}. 2 2 3 § 4x 3 · Câu 97. Biểu thức x f x ¨ xác định khi: 2 ¸ 2x 3x 1 © ¹ ª 1 º ª 4º § 1 · § 4 · A. x 1 ; 0; « . B. x ( ; f 1 ) ;0 ;f ¨ ¸ ¨ ¸ . 2» « 3» ¬ ¼ ¬ ¼ © 2 ¹ © 3 ¹ § 1 · § 4 · § 4 · C. x 1 ; 0; ¨ ¸ ¨ ¸ . D. x 1 ; ¨ ¸ . © 2 ¹ © 3 ¹ © 3 ¹
Câu 98. Biểu thức f x x x 1 3 2 4 3 2 chỉ xác định với : A. x 1 3;f. B. x ;1 f 3 1;1 3 . C. x 1 3;1. D. x 1 3; 1 1 3;f .
Câu 99. Biểu thức x x 2x 5x 6 2 3 2 1 với : A. x 2 . B. x 3.
C. x 2; x 3 .
D. Không tồn tại x .
Câu 100. Với giá trị nào của x thì ! 5 3 2 5 2 ( 4) 4 x x x x 1 1 1 1 A. x ! . B. x . C. x . D. x ! . 2 2 2 2 2 1 Câu 101. Cho a 1 3 a 1 3 khi đó A. a ! 2 . B. a 1. C. a !1. D. a 2 . Câu 102. Cho 1 2 x a , 1 2x b
. Biểu thức biểu diễn b theo a là: a 2 a 1 a 2 A. . B. . C. . D. a . a 1 a a 1 a 1 4 a 1 2 3 3 3 a a
Câu 103. Cho số thực dương a . Biểu thức thu gọn của biểu thức P là: 1 a 3 1 4 4 4 a a A. a . B. a 1. C. 2a . D. 1.
Câu 104. Cho các số thực dương a và b . Biểu thức thu gọn của biểu thức P 1 1 a b 1 1 a b 1 1 4 4 4 4 2 2 2 3 2 3
4a 9b có dạng là P xa yb . Tính x y ?
A. x y 97 .
B. x y 65 .
C. x y 56 .
D. y x 97 . 3 3
Câu 105. Cho các số thực dương phân biệt a b
a và b . Biểu thức thu gọn của biểu thức P là: 6 6 a b A. 6 6 a b . B. 6 6 a b . C. 3 3 b a . D. 3 3 a b . 1 1 3 3
Câu 106. Cho các số thực dương a b b a
a và b . Biểu thức thu gọn của biểu thức 3 P ab là: 6 6 a b A. 2 . B. 1 . C. 1. D. 0 .
Câu 107. Cho các số thực dương a và b . Biểu thức thu gọn của biểu thức § a b · P
ab : a b 2 3 3 3 ¨ ¸ 3 3 © a b ¹ A. 1 . B. 1. C. 2 . D. 2 .
Câu 108. Cho các số thực dương a và b . Biểu thức thu gọn của biểu thức 1 1 § · 3 3 3 3 : ¨ 2 a b P a b ¸ © b a ¹ 3 3 A. ab ab 3 3 3 . B. 3 ab . C. . D. ab a b . 3 3 a b 3 3 3 a b
Câu 109. Cho số thực dương x . Biểu thức x x x x x x x x được viết dưới dạng lũy thừa với a
số mũ hữu tỉ có dạng b
x , với a là phân số tối giản. Khi đó, biểu thức liên hệ giữa a và b là: b
A. a b 509 .
B. a 2b 767 .
C. 2a b 709 .
D. 3a b 510 .
Câu 110. Cho các số thực dương phân biệt a và b . Biểu thức thu gọn của biểu thức 4 a b 4a 16ab P có dạng 4 4
P m a n b . Khi đó biểu thức liên hệ giữa m và n 4 4 4 4 a b a b là:
A. 2m n 3 .
B. m n 2 .
C. m n 0 .
D. m 3n 1 . 1 1 § · ¨ a 2 a 2 1 2 2 2 ¸ a 1
Câu 111. Biểu thức thu gọn của biểu thức P ,(a ! 0,a z 1 r ), có dạng 1 1 ¨ a 1 ¸ 2 2 © a 2a 1 ¹ a m P
Khi đó biểu thức liên hệ giữa m và n là: a n
A. m 3n 1 .
B. m n 2 .
C. m n 0 .
D. 2m n 5 .
Câu 112. Một người gửi số tiền 2 triệu đồng vào một ngân hàng với lãi suất 0,65% / tháng. Biết rằng nếu
người đó không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào
vốn ban đầu (người ta gọi đó là lãi kép). Số tiền người đó lãnh được sau hai năm, nếu trong
khoảng thời gian này không rút tiền ra và lãi suất không đổi là: A. 24 (2,0065) triệu đồng. B. 24 (1,0065) triệu đồng. C. 24 2.(1,0065) triệu đồng. D. 24 2.(2,0065) triệu đồng.
Câu 113. Một người gửi số tiền M triệu đồng vào một ngân hàng với lãi suất 0,7% / tháng. Biết rằng
nếu người đó không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập
vào vốn ban đầu (người ta gọi đó là lãi kép). Sau ba năm, người đó muốn lãnh được số tiền là 5
triệu đồng, nếu trong khoảng thời gian này không rút tiền ra và lãi suất không đổi, thì người đó
cần gửi số tiền M là:
A. 3 triệu 600 ngàn đồng.
B. 3 triệu 800 ngàn đồng.
C. 3 triệu 700 ngàn đồng.
D. 3 triệu 900 ngàn đồng.
Câu 114. Lãi suất gửi tiết kiệm của các ngân hàng trong thời gian qua liên tục thay đổi. Bác An gửi vào
một ngân hàng số tiền 5 triệu đồng với lãi suất 0,7% / tháng. Sau sáu tháng gửi tiền, lãi suất
tăng lên 0,9% / tháng. Đến tháng thứ 10 sau khi gửi tiền, lãi suất giảm xuống 0,6% / tháng và
giữ ổn định. Biết rằng nếu bác An không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số
tiền lãi sẽ được nhập vào vốn ban đầu (người ta gọi đó là lãi kép). Sau một năm gửi tiền, bác
An rút được số tiền là (biết trong khoảng thời gian này bác An không rút tiền ra):
A. | 5436521,164 đồng.
B. | 5468994,09 đồng.
C. | 5452733,453 đồng.
D. | 5452771,729 đồng.
ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20
A A B A C B D B B A C D C A C D C B D D
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
B C B D B C A B C C A A A D C D D D A B
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
D A B A A A C D C D B A D B B C C D B C
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
D D C C A B A D B D B A B A D C B A C C
81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
D A B A A A C D C D B A D B B C C D B C
101 102 103 104 105 106 107 108 109 110 111 112 113 114 A D A B A D B C B A D C D C
II –HƯỚNG DẪN GIẢI
Câu 1. Khẳng định nào sau đây đúng : m A. n
a xác định với mọi a \^ ` 0 ^ ; n N B. n m n a a ; a m C. 0 a 1; a D. n m n a a ; a ; , m n Hướng dẫn giải:
Áp dụng tính chất của lũy thừa với số mũ thực ta có đáp án A là đáp án chính xác. Câu 2. Tìm
x để biểu thức x 2 2 1 có nghĩa: 1 1 § 1 · 1 A. x z B. x ! C. x ;2 ¨ ¸ D. x t 2 2 © 2 ¹ 2 Hướng dẫn giải: 1 Biểu thức x 2 2
1 có nghĩa 2x 1 z 0 x z 2
Câu 3. Tìm x để biểu thức x 1 2 3 1 có nghĩa: B. x f @ ;1 >1;f. A. x ; f 1 1;f . C. x 1 ; 1 . D. x \^r ^ ` 1 . Hướng dẫn giải: ªx !1 Biểu thức x 1 2 3 1 có nghĩa 2 x 1 ! 0 « ¬x 1
Câu 4. Tìm x để biểu thức x x 2 2 3 1 có nghĩa: A. x
B. Không tồn tại x C. x !1 D. x \^ ` 0 ^ Hướng dẫn giải:
Biểu thức x x 2 2 3 1 có nghĩa 2
x x 1! 0 x
Câu 5. Các căn bậc hai của 4 là : A. 2 B. 2 C. 2 r D. 16
Câu 6. Cho a và * n 2k(k ) , n
a có căn bậc n là : n A. a . B. | a | . C. a . D. 2 a . Hướng dẫn giải:
Áp dụng tính chất của căn bậc n
Câu 7. Cho a và *
n 2k 1(k ) , n
a có căn bậc n là : n A. 2n 1 a . B. | a | . C. a . D. a . Hướng dẫn giải:
Áp dụng tính chất của căn bậc n
Câu 8. Phương trình 2016 x
2017 có tập nghiệm trong là : A. 2017 T={r 2016} B 2016 T={r 2017} C. 2016 T={ 2017} D. 2016 T={ 2017} Hướng dẫn giải:
Áp dụng tính chất của căn bậc n
Câu 9. Các căn bậc bốn của 81 là : A. 3 B. 3 r C. 3 D. 9 r
Câu 10. Khẳng định nào sau đây đúng? A. Phương trình 2015 x 2 vô nghiệm. B. Phương trình 21 x
21 có 2 nghiệm phân biệt.
C. Phương trình e x S có 1 nghiệm. D. Phương trình 2015 x 2 có vô số nghiệm. Hướng dẫn giải:
Áp dụng tính chất của căn bậc n
Câu 11. Khẳng định nào sau đây sai? 1 1
A. Có một căn bậc n của số 0 là 0.
B. là căn bậc 5 của . 3 243
C. Có một căn bậc hai của 4.
D. Căn bậc 8 của 2 được viết là 8 r 2 . Hướng dẫn giải:
Áp dụng tính chất của căn bậc n 4 0,7 5 3 § 1 · § 1 ·
Câu 12. Tính giá trị ¨ ¸ ¨ ¸ , ta được : ©16 ¹ © 8 ¹ A. 12 B. 16 C. 18 D. 24 Hướng dẫn giải: 4 0,7 5 3 4 3 § 1 · § 1 ·
Phương pháp tự luận. 4 (2 ) ¨ ¸ ¨ ¸ 3 2 3 4 4 3 2 2 24 ©16 ¹ © 8 ¹
Phương pháp trắc nghiệm. Sử dụng máy tính
Câu 13. Viết biểu thức a a a ! 0 về dạng lũy thừa của a là. 5 1 3 1 A. 4 a B. 4 a C. 4 a D. 2 a Hướng dẫn giải 1 1 3
Phương pháp tự luận. 4 2 4 4
a a a. a a .a a
Phương pháp trắc nghiệm. Gán một hoặc hai giá trị để kiểm tra kết quả. Cụ thể gán a 2 rồi
sử dụng máy tính kiểm tra các đáp số bằng cách xét hiệu bằng không, sau đó để an toàn chọn 3
thêm một giá trị bất kỳ nữa, nhập vào máy tính 4
a a a được kết quả 0 suy ra A là đáp án đúng. 3 2 4
Câu 14. Viết biểu thức
về dạng lũy thừa 2m ta được m ?. 0,75 16 13 13 5 5 A. . B. . C. . D. . 6 6 6 6 Hướng dẫn giải 5 3 6 2 13 6 2 4 2. 2 2
Phương pháp tự luận. 6 2 . 0,75 16 2 3 3 4 2 4
Câu 15. Các căn bậc bảy của 128 là : A. 2 B. 2 r C. 2 D. 8 m § ·
Câu 16. Viết biểu thức b a a 5 3
, a,b ! 0 về dạng lũy thừa ¨ ¸ ta được m ?. a b © b ¹ 2 4 2 2 A. . B. . C. . D. . 15 15 5 15 Hướng dẫn giải 1 1 2 5 15 15 § · § · § ·
Phương pháp tự luận. b a b a a a a 5 3 5 15 . . ¨ ¸ ¨ ¸ ¨ ¸ . a b a b © b ¹ © b ¹ © b ¹ 2 2
Câu 17. Cho a ! 0 ; b ! 0. Viết biểu thức 3 a a về dạng m a và biểu thức 3
b : b về dạng n b . Ta có m n ? 1 1 A. B. 1 C. 1 D. 3 2 Hướng dẫn giải 2 2 1 5 5 2 2 1 1 1
Phương pháp tự luận. 3 3 2 6 a
a a .a a m ; 3 3 2 6
b : b b : b b n 6 6
m n 1 4 4
Câu 18. Cho x ! 0 ; y ! 0. Viết biểu thức 6 5 5 x . x
x ; về dạng m x và biểu thức 5 5 6 y : y
y ; về dạng n y . Ta có m n ? 11 11 8 8 A. B. C. D. 6 6 5 5 Hướng dẫn giải 4 4 5 1 103 103
Phương pháp tự luận. 5 6 5 5 6 12 60 x . x
x x .x .x x m 60 4 4 5 1 7 § · 7 11 5 5 6 5 6 12 60 y : y
y y : ¨ y .y ¸ y n m n 60 © ¹ 6 2 2 2 8
Câu 19. Viết biểu thức
về dạng 2x và biểu thức
về dạng 2y . Ta có 2 2 x y ? 4 8 3 4 2017 11 53 2017 A. B. C. D. 567 6 24 576 Hướng dẫn giải
Phương pháp tự luận. 3 4 3 2 2 2. 2 3 11 2 2 8 2.2 11 53 Ta có: 8 2 x ; 6 2 y 2 2 x y 4 8 3 8 2 8 2 3 4 6 24 3 2 Câu 20. Cho 3 6 f (x)
x. x khi đó f (0, 09) bằng : A. 0,09 B. 0,9 C. 0,03 D. 0,3 Hướng dẫn giải
Phương pháp tự luận. 1 1 1
Vì x 0,09 ! 0 nên ta có: f x 3 6 3 6 2
x. x x .x x x x t 0 f 0,09 0,3 3 2 Câu 21. Cho x x f x khi đó f 1,3 bằng: 6 x A. 0,13. B. 1,3 . C. 0,013. D. 13 . Hướng dẫn giải
Phương pháp tự luận. 1 2 3 2 2 3 x x x . Vì x
x 1,3 ! 0 nên ta có: f x x f 1,3 1,3 1 6 x 6 x
Câu 22. Cho f x 3 4 12 5
x x x . Khi đó f (2,7) bằng A. 0,027 . B. 0, 27 . C. 2,7 . D. 27 . Hướng dẫn giải
Phương pháp tự luận. 1 1 5
Vì x 2,7 ! 0 nên ta có: f x 3 4 12 5 3 4 12
x x x x .x .x x f 2,7 2,7 .
Câu 23. Đơn giản biểu thức 4 2 81a b , ta được: A. 2 9 a b . B. 2 9a b . C. 2 9a b . D. 2 3a b . Hướng dẫn giải
Phương pháp tự luận. a b a b2 4 2 2 2 2 81 9 9a b 9a b .
Câu 24. Đơn giản biểu thức x x 4 8 4 1 , ta được: A. 2 x x 1 . B. 2 x x 1 C. 2 x x 1 . D. 2 x x 1 . Hướng dẫn giải
Phương pháp tự luận. x x 4 x x 4 8 2 2 x x 2 4 4 1 1 1 x x 1 .
Câu 25. Đơn giản biểu thức x x 9 3 3 1 , ta được: A. xx 3 1 . B. xx 3 1 . C. xx 3 1 . D. x x 3 1 . Hướng dẫn giải 3
Phương pháp tự luận. x x 9 xx 3 xx 3 3 3 3 1 1 1
Câu 26. Khẳng định nào sau đây đúng 1 2 § 1 · § 1 · A. 0 a 1 a . B. 2 a ! 1 a ! 1. C. 2 3 3 2 . D. ¨ ¸ ¨ ¸ . © 4 ¹ © 4 ¹ Hướng dẫn giải
Đáp án A và B sai do áp dụng trực tiếp lí thuyết.
Dùng máy tính để kiểm tra kết quả đáp án A và D. a Câu 27. Nếu 2 2 3 1 2 3 1 thì A. a 1 . B. a 1. C. a ! 1 . D. a t 1 . Hướng dẫn giải a Do 2 3 1 !1nên 2 2 3 1
2 3 1 a 2 1 a 1
Câu 28. Trong các khẳng định sau đây, khẳng định nào sai? A. 2 ! 2 0,01 10 . B. 2 2 0,01 10 . C. 2 2 0,01 10 . D. 0 a 1, a z 0 . Hướng dẫn giải
Dùng máy tính kiểm tra kết quả.
Câu 29. Trong các khẳng định sau đây , khẳng định nào đúng? 3 4 6 A. 2 2 2 2 . B. 11 2 ! 11 2 . 3 4 4 C. 4 2 4 2 . D. 3 2 3 2 . Hướng dẫn giải
Dùng máy tính kiểm tra kết quả. m Câu 30. Nếu 2 2 3 2 3 2 thì 3 1 1 3 A. m ! . B. m . C. m ! . D. m z . 2 2 2 2 Hướng dẫn giải 1 2m2 1 1 Ta có 3 2 3 2 3 2 2m2 ! 1 m ! 3 2 2
Câu 31. Cho n nguyên dươngn t 2 khẳng định nào sau đây là khẳng định đúng? 1 1 A. n n a a a ! 0 . B. n n a a a z 0 . 1 1 C. n n a a a t 0 . D. n n a a a . Hướng dẫn giải
Áp dụng định nghĩa lũy thừa với số mũ hữu tỉ ta có đáp án A là đáp án chính xác.
Câu 32. Khẳng định nào sau đây là khẳng định sai? A. 2n 2n ab a b , a b .
B. a t 0 a
, n nguyên dươngn t 1 .
C. 2n 2n . D. 4 2 a t 0 . a a a
, n nguyên dươngn t 1 a a Hướng dẫn giải
Áp dụng tính chất căn bậc n ta có đáp án A là đáp án chính xác.
Câu 33. Cho a ! 0,b 0 , khẳng định nào sau đây là khẳng định sai? A. 4 4 4 3 3 3 a b ab .
B. a b ab . C. 2 2 . D. 4 2 2 . a b ab a b a b Hướng dẫn giải
Áp dụng tính chất căn bâc n ta có đáp án A là đáp án chính xác.
Câu 34. Tìm điều kiện của a để khẳng định 2
(3 a) a 3 là khẳng định đúng ? A. a . B. a d 3. C. a ! 3. D. a t 3. Hướng dẫn giải a3 neu a t 3 ° ° Ta có 2 (3 a) a 3 ® °a 3 neu a 3 °¯
Câu 35. Cho a là số thực dương, ,
m n tùy ý. Phát biểu nào sau đây là phát biểu sai ? n A a n m. n m n a a a . B. n m a . C. n m m n a a . m m.n a a . D. m a Hướng dẫn giải
Áp dụng tính chất của lũy thừa với số mũ thực ta có đáp án C là đáp án chính xác. 1 1 2 2 3 4
Câu 36. Bạn An trong quá trình biến đổi đã làm như sau: 2 3 6 3 6 27 27 27 27 3 bạn
đã sai ở bước nào? A. 4 . B. 2 . C. 3 . D. 1 . 1 1 Câu 37. Nếu 2 6 a ! a và 2 3 b ! b thì :
A. a 1;0 b 1.
B. a !1;b 1.
C. 0 a 1;b 1.
D. a !1;0 b 1. Hướng dẫn giải 1 1 ! ° ° 2 3 Vì 2 6 ® a !1 và ® 0 b 1 1 1 ° 2 3 b °¯ ! b 2 6 ¯a ! a Vậy đáp án D đúng. x
Câu 38. Nếu 3 2 ! 3 2 thì A. x . B. x 1. C. x ! 1 . D. x 1 . Hướng dẫn giải 1 Vì 3 2. 3 2 1 3 2 nên 3 2 x x x 3 2 ! 3 2 1 3 2 ! ! 1 3 2 3 2 . 3 2
Mặt khác 0 3 2 1 x 1
. Vậy đáp án A là chính xác. ax x a 1
Câu 39. Với giá trị nào của 2
a thì phương trình 4 2 2
có hai nghiệm thực phân biệt. 2 4 A. a z 0 B. a C. a t 0 D. a ! 0 Hướng dẫn giải ax x a 1 Ta có 2 4 2 2 ax x a 2 (*) 2 4 2 2 2 2
2 ax 4x 2a 2 ax 4x 2a 1 0 2 4 a z 0
PT (*) có hai nghiệm phân biệt 2
ax 4x 2a 1 0 ® a z 0 2
¯2a 2a 4 ! o
Vậy đáp án A là đáp án chính xác.
Câu 40. Tìm biểu thức không có nghĩa trong các biểu thức sau: 0 § 1 · A. 4 3 . B. 1 4 3 3 . C. 0 . . D. ¨ 3 ¸ © 2 ¹ Hướng dẫn giải 1 Vì nên 13 3
không có nghĩa. Vậy đáp án B đúng. 3 2 1 1 § ·
Câu 41. Đơn giản biểu thức 2 P a .¨ ¸ được kết quả là © a ¹ A. 2 2 2 1 1 2 a . B. a . C. a . D. a . Hướng dẫn giải 2 1 § 1 2 · 2 2 1 2 2 1 P a . a .a a a ¨ ¸ . Vậy đáp án D đúng. © a ¹ Câu 42. Biểu thức S
a 2 có nghĩa với : A. a ! 2 B. a C. a ! 0 D. a 2 Hướng dẫn giải S
a 2 có nghĩa khi a 2 ! 0 a ! 2 Vậy đáp án A đúng. .
Câu 43. Cho n N;n t 2 khẳng định nào sau đây đúng? 1 1 A. n n a a , a z 0. B. n n a a , a ! 0 . 1 1 C. n n a a , a t 0 . D. n n a a , a . Lời giải :
Đáp án B đúng. Đáp án A, C, D sai vì điều kiện của a
Câu 44. Khẳng định nào sau đây là khẳng định sai?
A. ab a b , a b 2n 2n
B. a t 0 a
, n nguyên dươngn t 2
C. 2n 2n n t 2 D. 4 2 a t 0 a a a , n nguyên dương a a
Câu 45. Cho a ! 0,b 0 , khẳng định nào sau đây là khẳng định sai? A. 4 4 4 3 3 3 2 2 2 4 2 a b ab
B. a b ab C. D. a b ab a b ab Hướng dẫn giải
Do a ! 0,b 0 nên 4 4 4 4 4 a b ( ) ab
ab ab . Đáp án A là đáp án chính xác. 1 1 Câu 46. Nếu 2 6 a ! a và 2 3 b ! b thì
A. a !1;0 b 1
B. a !1;b 1
C. 0 a 1;b 1
D. a 1;0 b 1 Hướng dẫn giải 1 1 1 1 Do ! nên 2 6
a ! a a ! 1. 2 6 Vì 2 3 nên 2 3 b
! b 0 b 1vậy đáp án A là đáp án chính xác. 4 a .b 4 3 2
Câu 47. Cho a , b là các số dương. Rút gọn biểu thức P được kết quả là : 3 12 6 a .b A. 2 2 2 2 ab . B. a b . C. ab . D. a b . Hướng dẫn giải 4 a .b 4 3 2 3 2 3 2 a .b a .b P
ab . Vậy đáp án C là chính xác. 2 6 12 6 3 12 6 . . a .b a b a b
Câu 48. Cho 3D 27 . Mệnh đề nào sau đây là đúng? D ª 3 A. . D ! . D . D . D « B. 3 C. 3 D. 3 3 ¬ ! 3 Hướng dẫn giải Ta có D D 3 3 27 3 3 D 3 3
D 3. Vậy đáp án D là đáp án chính xác.
Câu 49. Giá trị của biểu thức
A a 1 b 1 1 1 a 1 2 3 và b 1 2 3 với A. 3. B. 2. C. 1. D. 4. Hướng dẫn giải 1 1 A a b 1 1 1 1 1 1 2 3 1 2 3 1 1 3 3 3 3
Vậy đáp án C là đáp án chính xác.
Câu 50. Với giá trị nào của x thì đẳng thức 2016 2016 x x đúng
A. Không có giá trị x nào. B. x t 0 . C. x 0 . D. x d 0 . Hướng dẫn giải Do 2016 2016 x x nên 2016 2016 x
x x x khi x d 0
Câu 51. Với giá trị nào của x thì đẳng thức 2017 2017 x x đúng A. x t 0 . B. x . C. x 0 .
D. Không có giá trị x nào. Hướng dẫn giải n n
x x khi n lẻ nên 2017 2017 x x với x 1
Câu 52. Với giá trị nào của 4 x thì đẳng thức 4 x đúng x A. x z 0 . B. x t 0 . C. x 1 r .
D. Không có giá trị x nào. Hướng dẫn giải 1 Do 4 4 4 x x nên 4 x
khi x z 0 . Vậy đáp án A đúng. x
Câu 53. Căn bậc 4 của 3 là A 3 4 . B. 4 3 . C. 4 3 . D. 4 r 3 . Hướng dẫn giải
Theo định nghĩa căn bậc n của số b : Cho số thực b và số nguyên dương n n t 2 . Số a
được gọi là căn bậc n của số b nếu n a b
Nếu n chẵn và b ! 0 Có hai căn trái dấu, kí hiệu giá trị dương là n b , còn giá trị âm kí hiệu là n
b . Nên có hai căn bậc 4 của 3 là 4 r 3
Câu 54. Căn bậc 3 của – 4 là A. 3 r 4 . B. 3 4 . C. 3 4 . D. Không có. Hướng dẫn giải
Theo định nghĩa căn bậc n của số b : Cho số thực b và số nguyên dương n n t 2 . Số a
được gọi là căn bậc n của số b nếu n a b
n lẻ, b R : Có duy nhất một căn bậc n của b , kí hiệu n b
Câu 55. Căn bậc 2016 của -2016 là A. 2016 2016 . B. Không có. C. 2016 2016 . D. 2016 2016 . Hướng dẫn giải
n chẵn và b 0 Không tồn tại căn bậc n của b . -2016<0 nên không có căn bậc 2016 của - 2016
Câu 56. Trong các mệnh đề sau, mệnh đề nào sai (I): 3 5 0. 4 ! 0 .3 (II): 5 3 5 ! 3 (III): 3 5 2 ! 4 (IV): 3 5 5 ! 3 A. (I) và (IV). B. (I) và (III). C. (IV). D. (II0 và (IV). Hướng dẫn giải
Áp dụng tính chất với hai số a,b tùy ý 0 d a b và n nguyên dương ta có n n a b
Câu 57. Trong các biểu thức sau biểu thức nào không có nghĩa A. 0 2016 . B. 2016 2016 . C. 2016 0 . D. 2016 2016 . Hướng dẫn giải Ta có 0 0 , 0n D
n N không có nghĩa và a ,D Z xác định với a R D a ,D Z xác định với a z 0; D a ,D Z xác định với a ! 0 Vì vậy 2016 0
không có nghĩa. đáp A là đáp án đúng
Câu 58. Với giá trị nào của x thì biểu thức 1 2 3 4 x sau có nghĩa A. x t 2 . B. 2 x 2 . C. x d 2 .
D. Không có giá trị x nào. Hướng dẫn giải Điều kiện xác định 2 4 x ! 0 2 x 2 Vậy đáp án A đúng. 2 ª 1 1 4a 9a a 4 3 º a
Câu 59. Cho số thực dương a . Rút gọn biểu thức « » 1 1 1 1 « » 2 2 2 2 ¬2a 3a a a ¼ 1 1 A. 2 9a . B. 9a . C. 3a . D. 2 3a . Hướng dẫn giải 2 ª º 2 2 « » ª 1 1 º 2 2 4a 9a a 4 3a « 4a 9 a 4a 3 ª » 2a 3 a 3º « » « » 9a 1 1 1 1 « » « » 2a 3 a 1 1 « » 2 2 2 2 2 ¬2a 3a a a ¼ «a a » ¬ a ¼ 1 1 « » 2 2 ¬ a a ¼ Vậy đáp án B đúng. § ·
Câu 60. Cho số thực dương a,b . Rút gọn biểu thức a b 2 2 3 3 3 3 3
¨ a b ab ¸ © ¹ 1 1 1 1 A. 3 3 a b .
B. a b .
C. a b . D. 3 3 a b . Hướng dẫn giải 2 2 § · 3 3 ª º a
b ¨ a b ab ¸ a b « a 2 a b b2 ¬ » a 3 b 3 3 3 3 3 3 3 3 3 3 3 3 a b ¼ © ¹ Vậy đáp án A đúng. 11
Câu 61. Cho số thực dương a . Rút gọn biểu thức 16 a a a a : a 3 1 1 A. 4 a . B. 2 a . C. a . D. 4 a . Hướng dẫn giải 1 1 1 2 ½ 1 1 1 15 2 2 ª º ª º 11 ° 3 ° 11 3 11 7 11 1 2 2 2 16 ° § · « » ° § 1 · § 1 · a 16 2 16 « 4 » 6 8 16 4 a a a a : a
® ¨a ¸ a .a¾ : a ¨a ¸ .a : a ¨a ¸ : a a 11 « » « » ° © ¹ ° © ¹ © ¹ 16 «¬ »¼ «¬ »¼ ° a ¯ °¿ Vậy đáp án D đúng. 4a 4b
Câu 62. Cho a b 1 thì bằng 4a 2 4b 2 A. 4. B.2. C.3. D. 1. Hướng dẫn giải a b b a a 4 4 4 4 2 4 4 2
2.4 b 2.4a 4b 8 2.4a 4b a b a b a b
ab a b a b 1 4 2 4 2 4 2 4 2 4 2. 4 4 4 8 2. 4 4 x x
Câu 63. Có bao nhiêu giá trị x thỏa mãn x x 2 6 2 3 3 1 A. 2 . B. 3 . C. 4 . D. 1. Hướng dẫn giải Điều kiện xác định 2
x 3x 3 ! 0 x R 2 x x6 ªx 3x 3 1 ªx 1; x 2 Khi đó 2 x 3x 3 2 1 « « 2 ¬x x 6 0 ¬x 3; x 2 2 x 3x 2x2
Câu 64. Có bao nhiêu giá trị x thỏa mãn 5 2 5 2 đúng A. 3. B.3. C. 2. D. 1. Hướng dẫn giải 5 2. 5 2 1 5 2 5 2 1 x x x x x x 5 2 2 3 5 22 2 5 2 2 3 5 22 2 2
x 3x 2 2x x 1 ; x 2
LŨY THỪA VẬN DỤNG
Câu 65. Biết 4x 4x 23 tính giá trị của biểu thức 2x 2 x P : A. 5 . B. 27 . C. 23 . D. 25 . Hướng dẫn giải.
Do 2x 2x ! 0, x Nên x x x x 2 2x 2 2 2 2 2
2 2 2 x 4x 4x 2 23 2 5 .
Câu 66. Cho a là số thực dương. Biểu thức 4 3 8
a được viết dưới dạng lũy thừa với số mũ hữu tỉ là: 3 2 3 4 A. 2 a . B. 3 a . C. 4 a . D. 3 a . Hướng dẫn giải. 8 2 1 8 8 2 4 4 4 3 8 3 3 3 a a a a hoặc 4 3 8 12 8 12 3 a a a a
Câu 67. Cho x là số thực dương. Biểu thức 4 2 3 x
x được viết dưới dạng lũy thừa với số mũ hữu tỉ là: 7 5 12 6 A. 12 x . B. 6 x . C. 7 x . D. 5 x . Hướng dẫn giải. 4 3 3 3 3 1 1 7 7 7 4 4 4 2 2 12 x x x x x x x . 5 2 Câu 68. Cho b b
b là số thực dương. Biểu thức
được viết dưới dạng lũy thừa với số mũ hữu tỉ là: 3 b b A. – 2. B. – 1. C. 2. D. 1. Hướng dẫn giải. 5 2 2 b b b b b 2b1 1 5 5 1 5 5 5 2 2 2 b 1 3 3 3 b b 3b1 1 1 3 3 2 2 2 b bb b 2
Câu 69. Cho x là số thực dương. Biểu thức x x x x x x x x được viết dưới dạng lũy thừa với số mũ hữu tỉ là: 256 255 127 128 A. 255 x . B. 256 x . C. 128 x . D. 127 x . Hướng dẫn giải 1 3
Cách 1: x x x x x x x x 2
x x x x x x x x 2 x x x x x x x 7 7 1 3 2 2 x x x x x x x 4 x x x x x x 8 x x x x x x 15 15 31 31 63 8 x x x x x 16 x x x x x 16 x x x x 32 x x xx 32 x x x 63 127 127 255 255 255 64 x x x 64 x x 128 x x 128 x x 128 x 256 x . 8 2 1 255 Nhận xét: 8 2 256
x x x x x x x x x x .
Cách 2: Dùng máy tính cầm tay 1 Ta nhẩm 2
x x . Ta nhập màn hình 1a2=(M+1)1a2
Sau đó nhấn 7 lần (bằng với số căn bậc hai còn lại chưa xử lý) phím =.
Câu 70. Cho hai số thực dương a b a
a và b . Biểu thức 5 3
được viết dưới dạng lũy thừa với số mũ b a b hữu tỉ là: 31 30 1 7 30 § · 31 § · 6 § · A. a a a 30 x . B. ¨ ¸ . C. ¨ ¸ . D. ¨ ¸ . © b ¹ © b ¹ © b ¹ Hướng dẫn giải 1 1 1 5 5 1 1 a b a 2
a § a · § a · 2 a § a · 6 a § a · 6 § a · 6 § a · 6 § a · 5 3 5 3 ¨ ¸ ¨ ¸ 5 3 ¨ ¸ 5 ¨ ¸ 5 ¨ ¸ 5 ¨ ¸ ¨ ¸ b a b
b © b ¹ © b ¹ b © b ¹ b © b ¹ © b ¹ © b ¹ © b ¹ P 1 2 a b 2 1 2 4 3 3 3 3 3 3
a a .b b
Câu 71. Cho các số thực dương a và b . Rút gọn biểu thức được kết quả là:
A. a b . B. 2 a b .
C. b a . D. 3 3 a b . Hướng dẫn giải
P a b a a b b a 3 b 3 1 2 2 1 2 4 1 2 2 3 3 3 3 3 3 3 3 . a b 4
Câu 72. Cho các số thực dương a b a ab
a và b . Rút gọn biểu thức P được kết quả là: 4 4 4 4 a b a b A. 4 b . B. 4 4 a b .
C. b a . D. 4 a . Hướng dẫn giải a b a ab a2 b2 4 4 4 4 4 4 4 a a a b P . 4 4 4 4 4 4 4 4 a b a b a b a b 4 4 a b 4 4 a b 4 a 4 4 a b 4 4 4 4
a b a b . 4 4 4 4 a b a b § ·
Câu 73. Cho các số thực dương a b
a và b . Rút gọn biểu thức P
ab : a b 2 3 3 3 ¨ ¸ được 3 3 © a b ¹ kết quả là: A. 1 . B. 1. C. 2 . D. 2 . Hướng dẫn giải 3 3 ª º § a b · P
ab : a b 3 a 3 2 b «
ab»: a b 2 3 3 3 3 3 3 ¨ ¸ 3 3 3 3 © a b ¹ « a b » ¬ ¼ ª º ½
a b « a 2 a b ° b2 3 3 3 3 3 3 ¬ » ° ¼ ®
ab¾: a b 2 3 3 3 3 3 a b ° ° ¯ ¿ ª º 2 2 a 3 3 a b 3 3 : a b «
2 ab b2 ab a b2 3 3 3 3 3 3 : 1 ¬ »¼ 1 1 3 3
Câu 74. Cho các số thực dương a b b a
a và b . Biểu thức thu gọn của biểu thức 3 P ab là 6 6 a b A. 0 . B. 1 . C. 1. D. 2 . Hướng dẫn giải 1 1 1 1 1 1 1 1 3 3 3 2 3 2 1 3 3 a b b a a b b a a b 1 1 6 6 b a 1 1 3 P ab ab ab1 3 3 3
3 a b ab13 0 1 1 1 1 6 6 a b 6 6 6 6 a b a b 4 a 1 2 3 3 3 a a
Câu 75. Cho số thực dương a . Biểu thức thu gọn của biểu thức P là: 1 a 3 1 4 4 4 a a A. 1. B. a 1. C. 2a . D. a . Hướng dẫn giải 4 a 1 2 a a 2 3 3 3 a a a(a 1) P a 1 a 3 1 a 1 a 1 4 4 4 a a 1 1 1 1 1 1 4 4 4 4 2 2 P a b a b a b
Câu 76. Cho a ! 0,b ! 0 . Biểu thức thu gọn của biểu thức là: A. 10 10 a b .
B. a b .
C. a b . D. 8 8 a b . Hướng dẫn giải ª 2 2 1 1 1 1 1 1 1 1 º « » 1 1 1 1 1 1 4 4 4 4 2 2 4 4 2 2 2 2 2 2 P a b a b a b a b a b a b a b « » ¬ ¼ 2 2 1 1 2 2 a b a b . 1 1 § · 3 3
Câu 77. Cho a ! 0,b ! 0 .Biểu thức thu gọn của biểu thức 3 3 : ¨ 2 a b P a b ¸ là: © b a ¹ 3 3 A. 3 ab ab ab . B. . C. . D. 3 3 3 ab a b . 3 3 3 a b 3 3 a b Hướng dẫn giải § · § · § · P 1 1 a b a b 2 a b a b 3 3 a b 3 3 : ¨ 2 ¸ a b 3 3 : ¨ 2 ¸ a b 3 3 3 3 3 3 3 3 : ¨ ¸ 3 3 3 3 © b a ¹ © b a ¹ © a b ¹ 2 3 3 : a b 3 3 3 3 3 3 3 3 a b a b a b a b a b 2 3 3 3 3 3 3 a b a b 3 3 Câu 78. Cho a b
a ! 0,b ! 0 và a z b . Biểu thức thu gọn của biểu thức P là: 6 6 a b A. 6 6 a b . B. 6 6 a b . C. 3 3 b a . D. 3 3 a b . Hướng dẫn giải a b a2 b2 3 3 6 6 6 6 a b 6 6 a b 6 6 P a b 6 6 6 6 6 6 a b a b a b
Câu 79. So sánh hai số m và n nếu 3, 2m 3, 2n thì:
A. m ! n .
B. m n .
C. m n .
D. Không so sánh được. Hướng dẫn giải
Do 3, 2 !1 nên 3, 2m 3, 2n m n . m n
Câu 80. So sánh hai số m và n nếu 2 2
A m ! n .
B. m n .
C. m n .
D. Không so sánh được. Hướng dẫn giải m n
Do 2 !1 nên 2 2 m n . 1 m 1 n § · § ·
Câu 81. So sánh hai số m và n nếu ¨ ¸ ! ¨ ¸ © 9 ¹ © 9 ¹
A. Không so sánh được.
B. m n .
C. m ! n .
D. m n . Hướng dẫn giải 1 § 1 m · § 1 n ·
Do 0 1 nên ¨ ¸ ! ¨ ¸ m n . 9 © 9 ¹ © 9 ¹ m n § 3 · § 3 ·
Câu 82. So sánh hai số m và n nếu ¨ ¸ ! ¨ ¸ © 2 ¹ © 2 ¹
A. m n .
B. m n .
C. m ! n .
D. Không so sánh được. Hướng dẫn giải m n 3 § 3 · § 3 · Do 0 1 nên ¨ ¸ ! ¨
¸ m n . 2 © 2 ¹ © 2 ¹ m n
Câu 83. So sánh hai số m và n nếu 5 1 5 1
A. m n .
B. m n .
C. m ! n .
D. Không so sánh được. Hướng dẫn giải m n Do 5 1 !1 nên 5 1 5 1 m n . m n
Câu 84. So sánh hai số m và n nếu 2 1 2 1
A. m ! n .
B. m n .
C. m n .
D. Không so sánh được. Hướng dẫn giải m n Do 0 2 11 nên 2 1 2
1 m ! n . 2 1
Câu 85. Kết luận nào đúng về số thực a nếu 3 3 (a 1) (a 1) A. a ! 2 . B. a ! 0 . C. a !1. D. 1 a 2. Hướng dẫn giải 2 1 2 1
Do và số mũ không nguyên nên 3 3
(a 1) (a 1) khi a 1!1 a ! 2 . 3 3
Câu 86. Kết luận nào đúng về số thực a nếu 3 1 (2a 1) ! (2a 1) ª 1 a 0 1 ª0 a 1 A. « 2 . B. a 0 . C. . D. a 1 . « 2 « ¬a 1 ¬a 1 Hướng dẫn giải ª 1 ª0 2a 11 a 0 Do 3 1
và số mũ nguyên âm nên 3 1 (2a 1) (2a 1) ! khi « « 2 . ¬2a 1 1 « ¬a 1 0, 2 § 1 ·
Câu 87. Kết luận nào đúng về số thực a nếu 2 ¨ ¸ a © a ¹ A. 0 a 1. B. a ! 0 . C. a !1. D. a 0 . Hướng dẫn giải 0, 2 § 1 · 2 0,2 2 ¨ ¸
a a a © a ¹
Do 0, 2 2 và có số mũ không nguyên nên 0,2 2 a
a khi a !1. 1 1
Câu 88. Kết luận nào đúng về số thực a nếu a 3! a 2 1 1 A. a 1. B. a ! 0 . C. 0 a 1. D. a !1. Hướng dẫn giải 1 1 1 1
Do ! và số mũ không nguyên a 3! a 2 1 1 a !1. 3 2 3
Câu 89. Kết luận nào đúng về số thực 2 a nếu a 4 2 ! 2 a A. a !1. B. 0 a 1. C. 1 a 2. D. a 1. Hướng dẫn giải 3 3
Do 2 và có số mũ không nguyên a ! a2 4 2 2 4 0 2 a 1 2 a 1 2 ! a !1 1 1 2 2 § 1 · § 1 ·
Câu 90. Kết luận nào đúng về số thực a nếu ¨ ¸ ! ¨ ¸ © a ¹ © a ¹ A. 1 a 2. B. a 1. C. a !1. D. 0 a 1. Hướng dẫn giải 1 1 1 1 2 2 § 1 · § 1 · 1
Do ! và số mũ không nguyên ¨ ¸ ! ¨ ¸ !1 0 a 1. 2 2 © a ¹ © a ¹ a
Câu 91. Kết luận nào đúng về số thực a nếu 3 7 a ! a A. a 1. B. 0 a 1. C. a !1. D. 1 a 2. Hướng dẫn giải
Do 3 7 và số mũ không nguyên 3 7
a ! a 0 a 1. 1 1
Câu 92. Kết luận nào đúng về số thực a nếu 17 8 a ! a A. a !1. B. a 1. C. 0 a 1. D. 1 a 2. Hướng dẫn giải 1 1 1 1 Do
! và số mũ không nguyên nên 17 8 a
! a khi a !1. 17 8
Câu 93. Kết luận nào đúng về số thực a nếu 0, 25 3 a ! a A. 1 a 2. B. a 1. C. 0 a 1. D. a !1. Hướng dẫn giải Do 0,
25 ! 3 và số mũ không nguyên nên 0, 25 3 a ! a khi a !1. 1,5 1,5 a b 0,5 0,5 0,5 0,5 a b
Câu 94. Rút gọn biểu thức a b ta được : 0.5 0.5 a b
A. a b .
B. a b .
C. a b .
D. a b . Hướng dẫn giải a3 b a b 3 1,5 1,5 0,5 0,5 a b ab 0,5 0,5 a b a b
a 2 ab b a b 0.5 0.5 a b a b a b 1 1 1 1 3 1 § · ¨ 2 2 2 2 ¸ 2 2 x y x y x y 2y
Câu 95. Rút gọn biểu thức ¨ ¸. được kết quả là: 1 1 1 1 x y x y ¨ ¸ 2 2 2 2
© xy x y xy x y ¹ 2
A. x y .
B. x y . C. 2 . D. . xy Hướng dẫn giải 1 1 1 1 3 1 § · ¨ x y x y ¸ x y 2y § · x 3 2 2 2 2 2 2 y x y x y 2 ¨ ¸. ¨ ¸. y 1 1 1 1 x y x y ¨ ¸ x y y x x y y x x y x y ¨ ¸ © ¹ 2 2 2 2
© xy x y xy x y ¹ § ¨ · x
y 2 x y 2 ¸ x 3 y 2y 2 2y ¨ ¸
¨ xy x y x y . .x 2 x y x y x y x y ¸ © ¹
Câu 96. Biểu thức f x 2 3 (x 3x 2)
2 x xác định với : A. x (0; ) f \{1;2}. B. x [0; ) f . C. x [0; ) f \{1;2}. D. x [0; ) f \{1}. Hướng dẫn giải x z 2 2 x 3x 2 z 0 ° f x 2 3 (x 3x 2) 2 x xác định ® ®x z1 x [0;f) \{1;2} ¯x t 0 °x t 0 ¯ 2 2 3 § 4x 3x ·
Câu 97. Biểu thức f x ¨ xác định khi: 2 ¸ 2x 3x 1 © ¹ ª 1 º ª 4º § 1 · § 4 · A. x 1 ; 0; « . B. x ( ; f 1 ) ;0 ;f ¨ ¸ ¨ ¸ . 2» « 3» ¬ ¼ ¬ ¼ © 2 ¹ © 3 ¹ § 1 · § 4 · § 4 · C. x 1 ; 0; ¨ ¸ ¨ ¸ . D. x 1 ; ¨ ¸ . © 2 ¹ © 3 ¹ © 3 ¹ Hướng dẫn giải 2 2 3 § 4x 3x · 2 4x 3x 1 4 f x ¨ xác định khi ! 0 x ( 1 ; ) (0; ) 2 ¸ 2x 3x 1 © ¹ 2 2x 3x 1 2 3
Câu 98. Biểu thức f x x x 1 3 2 4 3 2 chỉ xác định với : A. x 1 3;f. B. x ;1 f 3 1;1 3 . C. x 1 3;1. D. x 1 3; 1 1 3;f . Hướng dẫn giải
f x x x 1 3 2 4 3 2 xác định khi 3 2
x 3x 2 ! 0 x 1 3; 1 1 3;f x x
Câu 99. Biểu thức x x 2 5 6 2 3 2 1 với : A. x 2 . B. x 3.
C. x 2; x 3 .
D. Không tồn tại x . Hướng dẫn giải 25 6 2 3 2 x x x x xác định 2
x 3x 2 ! 0 x ; f 1 2;f Khi đó x x x x ªx 2 loai 2 x 3x 2 2 1 2 x 3x 2 2 5 6 5 6 2x 3x20 2 x 5x 6 0 « «x 3 ¬ tmdk
Câu 100. Với giá trị nào của x thì ! 5 3 2 5 2 ( 4) 4 x x x x 1 1 1 1 A. x ! . B. x . C. x . D. x ! . 2 2 2 2 Hướng dẫn giải ! 5 3 2 5 2 ( 4) 4 x x x x xác định x x 2 x 1
Khi đó x 4 !1 x (x 4) ! x 45 3 2 2 5 2
x 5 ! 5x 3 x 2 2 1 Câu 101. Cho a 1 3 a 1 3 khi đó A. a ! 2 . B. a 1. C. a !1. D. a 2 . Hướng dẫn giải 2 1 2 1 Do a 1 3 a 1 3 a 1 !1 a ! 2 3 3 Câu 102. Cho 1 2 x a , 1 2x b
. Biểu thức biểu diễn b theo a là: a 2 a 1 a 2 A. . B. . C. . D. a . a 1 a a 1 a 1 Hướng dẫn giải x 1 Ta có: 1 2x a ! 1, x nên 2 a 1 1 Do đó: 1 a b a 1 a 1 4 a 1 2 3 3 3 a a
Câu 103. Cho số thực dương a . Biểu thức thu gọn của biểu thức P là: 1 a 3 1 4 4 4 a a A. a . B. a 1. C. 2a . D. 1. Hướng dẫn giải 4 a 1 2 a a 2 3 3 3 a a a(a 1) P a 1 a 3 1 a 1 a 1 4 4 4 a a
Câu 104. Cho các số thực dương a và b . Biểu thức thu gọn của biểu thức P 1 1 a b 1 1 a b 1 1 4 4 4 4 2 2 2 3 2 3
4a 9b có dạng là P xa yb . Tính x y ?
A. x y 97 .
B. x y 65 .
C. x y 56 .
D. y x 97 . Hướng dẫn giải § · ¨ ¸
P a b a b a b © a 2 b 2 1 1 1 1 1 1 1 1 ¹ 1 1 4 4 4 4 2 2 4 4 2 2 2 3 2 3 4 9 2 3 4a 9b Ta có: 2 a 2 2 4 9b 2 1 1 1 1 a b 1 1 2 2 2 2 4 9 4a 9b 16a 81b .
Do đó: x 16, y 8 1. 3 3
Câu 105. Cho các số thực dương phân biệt a b
a và b . Biểu thức thu gọn của biểu thức P là: 6 6 a b A. 6 6 a b . B. 6 6 a b . C. 3 3 b a . D. 3 3 a b . Hướng dẫn giải a b a2 b2 3 3 6 6 6 6 a b 6 6 a b 6 6 P a b 6 6 6 6 6 6 a b a b a b 1 1 3 3
Câu 106. Cho các số thực dương a b b a
a và b . Biểu thức thu gọn của biểu thức 3 P ab là: 6 6 a b A. 2 . B. 1 . C. 1. D. 0 . Hướng dẫn giải 1 1 1 1 1 1 1 1 3 3 3 2 3 2 1 3 3 a b b a a b b a a b 1 1 6 6 b a 1 1 3 P ab ab ab1 3 3 3 3 a b ab13 0 1 1 1 1 6 6 a b 6 6 6 6 a b a b
Câu 107. Cho các số thực dương a và b . Biểu thức thu gọn của biểu thức § a b · P
ab : a b 2 3 3 3 ¨ ¸ 3 3 © a b ¹ A. 1 . B. 1. C. 2 . D. 2 . Hướng dẫn giải 3 3 § · § a b · P
ab : a b 3 a 3 2 b ¨
ab ¸: a b 2 3 3 3 3 3 3 ¨ ¸ ¨ ¸ 3 3 3 3 © a b ¹ © a b ¹ § · a b 2 2 3 3 3 3 3 3
a a b b ¨
ab ¸: a b 2 3 3 3 ¨ ¸ 3 3 © a b ¹ 2 2 2 2 3 3 3 3
a ab b ab 3 3 : a b 2 3 3 a b 3 3 : a b 1
Câu 108. Cho các số thực dương a và b . Biểu thức thu gọn của biểu thức 1 1 § · 3 3 3 3 : ¨ 2 a b P a b ¸ © b a ¹ 3 3 A. ab ab 3 3 3 . B. 3 ab . C. . D. ab a b . 3 3 a b 3 3 3 a b Hướng dẫn giải § · § · § · P 1 1 a b a b 2 a b a b 3 3 a b 3 3 : ¨ 2 ¸ 3 3 a b 3 3 : ¨ 2 ¸ 3 3 a b 3 3 3 2 3 2 : ¨ ¸ 3 3 3 3 © b a ¹ © b a ¹ © a b ¹ 2 3 3 : a b 3 3 3 3 3 3 3 3 a b a b a b a b a b 2 3 3 3 3 3 3 a b a b
Câu 109. Cho số thực dương x . Biểu thức x x x x x x x x được viết dưới dạng lũy thừa với a
số mũ hữu tỉ có dạng b
x , với a là phân số tối giản. Khi đó, biểu thức liên hệ giữa a và b là: b
A. a b 509 .
B. a 2b 767 .
C. 2a b 709 .
D. 3a b 510 . Hướng dẫn giải 1 3
Cách 1: x x x x x x x x 2
x x x x x x x x 2 x x x x x x x 7 7 1 3 2 2 x x x x x x x 4 x x x x x x 8 x x x x x x 15 15 31 31 63 8 x x x x x 16 x x x x x 16 x x x x 32 x x xx 32 x x x 63 127 127 255 255 255 64 x x x 64 x x 128 x x 128 x x 128 x 256
x . Do đó a 255,b 256 . 8 2 1 255 Nhận xét: 8 2 256
x x x x x x x x x x .
Cách 2: Dùng máy tính cầm tay 1 Nhẩm 2
x x . Ta nhập màn hình 1a2=(M+1)1a2
Sau đó nhấn 7 lần (bằng với số căn bậc hai còn lại chưa xử lý) phím =. Chọn đáp án A.
Câu 110. Cho các số thực dương phân biệt a và b . Biểu thức thu gọn của biểu thức 4 a b 4a 16ab P có dạng 4 4
P m a n b . Khi đó biểu thức liên hệ giữa m và n 4 4 4 4 a b a b là:
A. 2m n 3 .
B. m n 2 .
C. m n 0 .
D. m 3n 1 . Hướng dẫn giải a b 4a 16ab a2 b2 4 4 4 4 4 4 4 2 a a 2 a b P . 4 4 4 4 4 4 4 4 a b a b a b a b 4 4 a b 4 4 a b 4 2 a 4 4 a b 4 4 4 4 4
a b 2 a b a . 4 4 4 4 a b a b Do đó m 1 ;n 1. 1 1 § · ¨ a 2 a 2 1 2 2 2 ¸ a 1
Câu 111. Biểu thức thu gọn của biểu thức P ,(a ! 0,a z 1 r ), có dạng 1 1 ¨ a 1 ¸ 2 2 © a 2a 1 ¹ a m P
Khi đó biểu thức liên hệ giữa m và n là: a n
A. m 3n 1 .
B. m n 2 .
C. m n 0 .
D. 2m n 5 . Hướng dẫn giải 1 1 § · ¨ a 2 a 2 1 2 2 2 ¸ a 1 § a 2 a 2 · a 1 P ¨ ¸ 1 1 ¨ a 1 ¸ ¨ ¸ © ¹ © a 1 a 1 a 1 2 2 2 a 2a 1 a a ¹ § a 2 a 2 · 1 2 a 1 2 ¨ ¸ © a 1 a 1 ¹ a a 1 a a 1
Do đó m 2;n 1 .
Câu 112. Một người gửi số tiền 2 triệu đồng vào một ngân hàng với lãi suất 0,65% / tháng. Biết rằng nếu
người đó không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào
vốn ban đầu (người ta gọi đó là lãi kép). Số tiền người đó lãnh được sau hai năm, nếu trong
khoảng thời gian này không rút tiền ra và lãi suất không đổi là: A. 24 (2,0065) triệu đồng. B. 24 (1,0065) triệu đồng. C. 24 2.(1,0065) triệu đồng. D. 24 2.(2,0065) triệu đồng. Hướng dẫn giải
Gọi số tiền gửi vào vào là M đồng, lãi suất là r /tháng.
q Cuối tháng thứ nhất: số tiền lãi là: Mr . Khi đó số vốn tích luỹ đượclà:
T M Mr M (1 r) . 1
q Cuối tháng thứ hai: số vốn tích luỹ được là: 2
T T T r T (1 r) M (1 r)(1 r) M (1 r) . 2 1 1 1
q Tương tự, cuối tháng thứ n: số vốn tích luỹ đượclà: T M (1 r)n . n
Áp dụng công thức trên với M 2, r 0,0065, n 24 , thì số tiền người đó lãnh được sau 2 năm (24 tháng) là: 24 24 T 2.(1 0,0065) 2.(1,0065) triệu đồng. 24
Câu 113. Một người gửi số tiền M triệu đồng vào một ngân hàng với lãi suất 0,7% / tháng. Biết rằng
nếu người đó không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập
vào vốn ban đầu (người ta gọi đó là lãi kép). Sau ba năm, người đó muốn lãnh được số tiền là 5
triệu đồng, nếu trong khoảng thời gian này không rút tiền ra và lãi suất không đổi, thì người đó
cần gửi số tiền M là:
A. 3 triệu 600 ngàn đồng.
B. 3 triệu 800 ngàn đồng.
C. 3 triệu 700 ngàn đồng.
D. 3 triệu 900 ngàn đồng. Hướng dẫn giải
Áp dụng công thức trên với T 5 , r 0,007, n 36 , thì số tiền người đó cần gửi vào ngân n T 5
hàng trong 3 năm (36 tháng) là: n M
| 3,889636925 triệu đồng. (1 r)n 1,00736
Câu 114. Lãi suất gửi tiết kiệm của các ngân hàng trong thời gian qua liên tục thay đổi. Bác An gửi vào
một ngân hàng số tiền 5 triệu đồng với lãi suất 0,7% / tháng. Sau sáu tháng gửi tiền, lãi suất
tăng lên 0,9% / tháng. Đến tháng thứ 10 sau khi gửi tiền, lãi suất giảm xuống 0,6% / tháng và
giữ ổn định. Biết rằng nếu bác An không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số
tiền lãi sẽ được nhập vào vốn ban đầu (người ta gọi đó là lãi kép). Sau một năm gửi tiền, bác
An rút được số tiền là (biết trong khoảng thời gian này bác An không rút tiền ra):
A. | 5436521,164 đồng.
B. | 5468994,09 đồng.
C. | 5452733,453 đồng.
D. | 5452771,729 đồng. Hướng dẫn giải
Số vốn tích luỹ của bác An sau 6 tháng gửi tiền với lãi suất 0,7% / tháng là:
T 5.1,0076 triệu đồng; 1
Số vốn tích luỹ của bác An sau 9 tháng gửi tiền ( 3 tháng tiếp theo với lãi suất 0,9% / tháng) là:
T T .1,0093 5.1,0076 .1,0093 triệu đồng; 2 1
Do đó số tiền bác An lãnh được sau 1 năm (12 tháng) từ ngân hàng ( 3 tháng tiếp theo sau đó
với lãi suất 0,6% / tháng) là:
T T .1,0063 5.1,0076 .1,0093 .1,0063 triệu đồng | 5452733,453 đồng 2 LOGARIT
A. KIẾN THỨC CƠ BẢN 1. Định nghĩa:
Cho hai số dương a, b với a z 1. Số D thỏa mãn đẳng thức D
a b được gọi là lôgarit cơ số a
của b và kí hiệu là log D
b . Ta viết: D log b a . b a a
2. Các tính chất: Cho ,
a b ! 0, a z 1, ta có: x log a 1, log 1 0 a a x logab a , b log ( D a ) D a
3. Lôgarit của một tích: Cho 3 số dương a, b , a z , ta có 1 2 b với 1
x log (b .b ) log b log b a 1 2 a 1 a 2
4. Lôgarit của một thương: Cho 3 số dương a, b , a z , ta có 1 2 b với 1 x 1
log b log b log b a a 1 a 2 2 b x 1 Đặc biệt : với ,
a b ! 0, a z 1 log log b a a b
5. Lôgarit của lũy thừa: Cho ,
a b ! 0, a z 1, với mọi D , ta có x log D b D log b a a x 1
Đặc biệt: log n b log b a a n
6. Công thức đổi cơ số: Cho 3 số dương , a ,
b c với a z 1,c z 1 , ta có x log log b b c a log a c x 1 1
Đặc biệt : log c và log b D z . D log b với 0 a log a D a a c
# Lôgarit thập phân và Lôgarit tự nhiên
Lôgarit thập phân là lôgarit cơ số 10. Viết : log b logb lg 10 b
Lôgarit tự nhiên là lôgarit cơ số e . Viết : log b lnb e
B. KỸ NĂNG CƠ BẢN
1. Tính giá trị biểu thức
2. Rút gọn biểu thức
3. So sánh hai biểu thức
4. Biểu diễn giá trị logarit qua một hay nhiều giá trị logarit khác
C. KỸ NĂNG SỬ DỤNG MÁY TÍNH
1. Tính giá trị của một biểu thức chứa logarit
Ví dụ : Cho a ! 0, a z 1, giá trị của biểu thức log 4 a a bằng bao nhiêu ? A. 16 B. 4 C. 8 D. 2
Ví dụ : Giá trị của biểu thức A 2log 12 3log 5 log 15 log 150 bằng: 2 2 2 2 A. 2 B. 3 C. 4 D. 5
2. Tính giá trị của biểu thức Logarit theo các biểu thức logarit đã cho
Ví dụ: Cho log 5 a; log 5 b . Khi đó log 5 tính theo a và b là 2 3 6 A. 1 B. ab C. a + b D. 2 2 a b a b a b
3. Tìm các khẳng định đúng trong các biểu thức logarit đã cho.
Ví dụ: Cho a ! 0,b ! 0 thỏa điều kiện 2 2
a b 7ab .Khẳng định nào sau đây đúng: 1 3
A. 3log a b log a logb
B. log(a b) (log a logb) 2 2 a b 1
C. 2(log a logb) log(7a ) b D. log (log a log ) b 3 2
4. So sánh lôgarit với một số hoặc lôgarit với nhau log2 5 log0,5 2 § · § ·
Ví dụ: Trong 4 số log34 2log32 1 1 3 ;3 ; ; ¨ ¸ ¨ ¸ số nào nhỏ hơn 1 © 4 ¹ ©16 ¹ log2 5 § 1 · log 0,5 2 § 1 · A. lo 3g 4 3 B. 2log3 2 3 C. ¨ ¸ D. ¨ ¸ © 4 ¹ ©16 ¹
D. BÀI TẬP TRẮC NGHIỆM
Câu 115. Với giá trị nào của x thì biểu thức f (x) log (2x 1) xác định? 2 § 1 · § 1 · 1 ½ A. x ;f ¨ ¸ . B. x ; f ¨ ¸ . C. x \ ® ¾. D. x ( 1 ; ) f . © 2 ¹ © 2 ¹ ¯2¿
Câu 116. Với giá trị nào của x thì biểu thức 2
f (x) ln(4 x ) xác định? A. x ( 2 ;2). B. x [ 2;2] . C. x \[ 2; 2 2] 2 . D. x \ ( 2 ; 2;2) 2 . x 1
Câu 117. Với giá trị nào của x thì biểu thức f (x) log xác định? 1 3 x 2 A. x [ 3;1]. B. x \[ 3; 3 1 ; ] 1 . C. x \ ( 3 ; 3 1 ; ) 1 . D. x ( 3 ;1) .
Câu 118. Với giá trị nào của x thì biểu thức: 2
f (x) log (2x x ) xác định? 6 A. 0 x 2. B. x ! 2 . C. 1 x 1. D. x 3 .
Câu 119. Với giá trị nào của x thì biểu thức: 3 2
f (x) log (x x 2x) xác định? 5 A. x (0;1). B x (1; ) f . C. x( 1 ;0) ( 2; ) f . D. x(0;2) (4; ) f .
Câu 120. Cho a ! 0, a z 1, giá trị của biểu thức log 4 a A a bằng bao nhiêu? A.8. B.16. C.4. D.2.
Câu 121. Giá trị của biểu thức B 2log 12 3log 5 log 15 log 150 bằng bao nhiêu? 2 2 2 2 A.5. B.2. C.4. D.3.
Câu 122. Giá trị của biểu thức P 22log 12 3log 5 log 15 log 150 bằng bao nhiêu? 2 2 2 2 A. 2 . B. 3. C. 4 . D. 5.
Câu 123. Cho a ! 0, a z 1, biểu thức D log
có giá trị bằng bao nhiêu? 3 a a 1 1 A.3. B. . C. 3 . D. . 3 3 1
Câu 124. Giá trị của biểu thức 3 C log 36 log 14 3log 21 bằng bao nhiêu ? 7 7 7 2 1 1 A. 2 . B.2. C. . D. . 2 2 Câu 125. Cho 4log 5
a ! 0, a z 1 , biểu thức 2 a E a
có giá trị bằng bao nhiêu? A. 5 . B. 625. C. 25 . D. 8 5 .
Câu 126. Trong các số sau, số nào lớn nhất? 5 5 6 6 A. log . B. log . C. log . D. log . 3 6 3 6 1 5 3 5 3
Câu 127. Trong các số sau, số nào nhỏ nhất ? 1 1 A. log . B. log 9 . C. log 17 . D. log . 5 12 1 1 5 15 5 5
Câu 128. Cho a ! 0, a z 1, biểu thức 2 2 2 A (ln a log ) e
ln a log e có giá trị bằng a a A. 2 2ln a 2. B. 4ln a 2. C. 2 2ln a 2 . D. 2 ln a 2 . Hướng dẫn giải 3 2
Câu 129. Cho a ! 0, a z 1, biểu thức B 2ln a 3log e có giá trị bằng a ln a log e a 3
A. 4ln a 6log 4 . B. 4ln a . C. 3ln a . D. 6log e . a log e a a Câu 130. Cho x y
a ! 0,b ! 0 , nếu viết log 5 3 a b log a log thì bằng bao nhiêu? 3 23 3 3 b x y 5 15 A.3. B.5. C.2. D.4. 0, 2 10 § · Câu 131. Cho a
a ! 0,b ! 0 , nếu viết log ¨ ¸
xlog a y log thì 5 5 5 b
xy bằng bao nhiêu ? 6 5 © b ¹ 1 1 A. 3 . B. . C. . D. 3 . 3 3
Câu 132. Cho log x 3log 2 log 25 log 3. Khi đó giá trị của 3 3 9 x là : 3 200 40 20 25 A. . B. . C. . D. . 3 9 3 9 1 Câu 133. Cho log 2log a 6log . Khi đó giá trị của 7 7 49 b x là : x 2 3 A. 2 a b a 6b . B. x . C. 2 3 x a b . D. x . 3 b 2 a Câu 134. Cho , a ,
b c ! 0; a z 1 và số D
, Trong các khẳng định sau, khẳng định nào sai? A. log c a c . B. log a 1. a a C. log D b D log b .
D. log (b c) log b log c . a a a a a Câu 135. Cho , a ,
b c ! 0; a z 1, Trong các khẳng định sau, khẳng định nào sai? 1 A. log b . B. log .
b log c log c . a log a a b a b
C. log b c b . D. log ( .
b c) log b log c . c loga a a a a Câu 136. Cho , a , b c ! 0 và ,
a b z 1, Trong các khẳng định sau, khẳng định nào sai? A. loga b a b .
B. log b log c b c . a a log C. log c a c .
D. log b ! log c b ! c . b log b a a a Câu 137. Cho , a ,
b c ! 0 và a ! 1. Trong các khẳng định sau, khẳng định nào sai?
A. log b log c b c .
B. log b ! log c b ! c . a a a a
C. log b ! c b ! c. D. b c
a ! a b ! c . a Câu 138. Cho , a ,
b c ! 0 và a 1.Trong các khẳng định sau, khẳng định nào sai?
A. log b ! log c b c . D. 2 3 a a . a a
C. log b log c b ! c .
D. log b ! 0 b 1. a a a
Câu 139. Số thực a thỏa điều kiện log (log a) 0 là: 3 2 1 1 A. . B. 3. C. . D. 2. 3 2
Câu 140. Biết các logarit sau đều có nghĩa. Khẳng định nào sau đây là khẳng định đúng ?
A. log b log c b c .
B. log b ! log c b ! c a a a a
C. log b ! log c b c .
D. log b log c 0 b c 0 . a a a a Câu 141. Cho , a ,
b c ! 0 và a z 1. Khẳng định nào sau đây là khẳng định sai ? A. log ( b
bc) log b log c .
B. log ( ) log b log c . a a a a a a c C. log c
b c b a . D. log (b )
c log b log c . a a a a
Câu 142. Số thực x thỏa mãn điều kiện log x log x log x 11 là :. 2 4 8 11 A. 64. B. 6 2 . C.8. D. 4.
Câu 143. Số thực x thỏa mãn điều kiện 3 log 2 2 4 là x 1 A. 3 2 . B. . C. 4. D. 2. 3 2 2 Câu 144. Cho , a b ! 0 và , a b z 1. Biểu thức 2 P log b
có giá trị bằng bao nhiêu? a log a a 2 b A. 6. B.3. C.4. D.2. Câu 145. Cho , a b ! 0 và , a b z 1, biểu thức 3 4 P log
b .log a có giá trị bằng bao nhiêu? b a A.6. B.24. C.12. D. 18.
Câu 146. Giá trị của biểu thức 3lo 8g3 2lo 1g65 4 là: A. 20. B.40. C. 45. D. 25 .
Câu 147. Giá trị của biểu thức P 3 5 log a a a là a 53 37 1 A. . B. . C.20. D. . 30 10 15
Câu 148. Giá trị của biểu thức A log 2.log 3.log 4...log 15 là: 3 4 5 16 1 3 1 A. . B. . C. 1. D. . 2 4 4 3 3 2 5 3 § ·
Câu 149. Giá trị của biểu thức log a a a ¨ ¸ là:. 1 ¨ 4 a a ¸ a © ¹ 1 3 211 91 A. . B. . C. . D. . 5 4 60 60
Câu 150. Trong 2 số log 2 và log 3 , số nào lớn hơn 1?. 3 2 A. log 3. B. log 2 . C. Cả hai số . D. Đáp án khác. 2 3
Câu 151. Cho 2 số log 2000 và log
2001. Khẳng định nào sau đây là khẳng định đúng? 1999 2000 A. log 2000 ! log 2001 .
B. Hai số trên nhỏ hơn 1. 1999 2000
C. Hai số trên lớn hơn 2. D. log 2000 t log 2001 . 1999 2000
Câu 152. Các số log 2 , log 3 , log 11 được sắp xếp theo thứ tự tăng dần là: 3 2 3
A. log 2, log 11, log 3 .
B. log 2, log 3, log 11. 3 3 2 3 2 3
C. log 3, log 2, log 11.
D. log 11, log 2, log 3 . 2 3 3 3 3 2
Câu 153. Số thực x thỏa mãn điều kiện log x 2 3 là: 3 A. 5 . B. 25 . C. 25 . D. 3 . 3
Câu 154. Số thực x thỏa mãn điều kiện log x log là : 3 9 x 2 A. 3 . B. 25 . C. 3. D. 9 .
Câu 155. Cho log x 4log a 7log b ,
a b ! 0 . Giá trị của 3 3 3
x tính theo a,b là: A. ab . B. 4 a b . C. 4 7 a b . D. 7 b . Câu 156. Cho log 2 2 x y
1 log xy xy ! 0 . Chọn khẳng định đúng trong các khẳng định sau ? 2 2
A. x ! y . B. x y . C. x y . D. 2 x y . 1 Câu 157. Cho log y x log =1 y ! 0, !
. Chọn khẳng định đúng trong các khẳng định sau? 1 4 y x y 4 3 3
A. 3x 4y .
B. x y .
C. x y . D. 3x 4 y . 4 4
Câu 158. Chọn khẳng định đúng trong các khẳng định sau? A. 2 x x 2 log 2log x ! 0 .
B. log xy log x log y . a a a a a
C. log xy log x log y xy ! 0 .
D. log xy log x log y xy ! 0 . a a a a a a Câu 159. Cho , x y ! 0 và 2 2
x 4y 12xy . Khẳng định nào sau đây là khẳng định đúng ? § x 2y · 1 A. log log x log log (x 2 ) y 2 (log x log ) 2 ¨ ¸ 2 2 y . B. y . © 4 ¹ 2 2 2 2
C. log (x 2y) log x log y 1.
D. 4log (x 2y) log x log 2 2 2 2 2 2 y . Câu 160. Cho , a b ! 0 và 2 2
a b 7ab . Khẳng định nào sau đây là khẳng định đúng ? § a b · A. 2log(a )
b log a log b . B. 4log log a log ¨ ¸ b . © 6 ¹ § a b · 1 § a b · C. log (loga logb ) ¨ ¸ . D. log 3(log a logb) ¨ ¸ . © 3 ¹ 2 © 3 ¹ Câu 161. Cho log 6 log 18 được tính theo 2
a . Khi đó giá trị của 3 a là: 2a 1 A. a a . B. . C. 2a 3. D. . a 1 a 1 Câu 162. Cho log 5 log 1250 được tính theo 2
a . Khi đó giá trị của 4 a là : 1 4a 1 4a A. . B. 2(1 4a) . C.1 4a . D. . 2 2 Câu 163. Biết log 2
log 28 được tính theo m là: 7
m , khi đó giá trị của 49 m 2 1 m 1 4m 1 2m A. . B. . C. . D. . 4 2 2 2
Câu 164. Biết a log 5,b log 3 ; khi đó giá trị của log 15 được tính theo a là: 2 5 10 a b ab 1 ab 1 a(b 1) A. . B. . C. . D. . a 1 a 1 a 1 a 1
Câu 165. Cho a log 15;b log 10 . Khi đó giá trị của log 50 được tính theo a, 3 3 b là : 3
A. 2(a b 1) .
B. 2(a b 1) .
C. 2(a b 1) .
D. 2(a b 1) . Câu 166. Biết log 3
log 75 được tính theo a là: 5
a , khi đó giá trị của 15 2 a 1 2a 1 a A. . B. . C. . D. 2 . 1 a a 1 2 a Câu 167. Biết log 7
log 7 được tính theo a là: 4
a , khi đó giá trị của 2 1 1 A. 2a . B. a . C. a . D. 4a . 2 4 27 Câu 168. Biết log 3 log được tính theo 5
a , khi đó giá trị của 3 a là: 25 3 3 3a 2 A. . B. a . C. . D. a . 2a 2 a 3a 2
Câu 169. Biết a log 5,b log 3 . Khi đó giá trị của log 15 được tính theo a là : 2 5 24 ab 1 ab 1 b 1 a(b 1) A. . B. . C. . D. . b a 1 a 1 3 ab Câu 170. Cho log 27
log 16 được tính theo a là: 12
a . Khi đó giá trị của 6 43 a 43 a 4 2 A. . B. . C. a . D. a . 3 a 3 a 3 a 3 a Câu 171. Cho lg3 ,
a lg 2 b . Khi đó giá trị của log
30 được tính theo a là: 125 1 43 a a a A. a . B. . C. . D. . 31 b 3 b 3 b 3 a 3 Câu 172. Cho b
log b 3 . Giá trị của biểu thức A log
được tính theo a là: a b a a 3 3 1 3 A. . B. . C. D. . 3 4 3 4 Câu 173. Cho log 5 , a log 7 , b log 3 log 35 được tính theo , a , b c là: 27 8 2 c . Giá trị của 6 ac ac 3ac b 3ac 3b A. . B. . C. . D. . 1 c 1 b 1 c 3 a 1 1 1
Câu 174. Cho x 2000!. Giá trị của biểu thức A ... là: log x log x log 2 3 2000 x 1 A.1. B. 1 . C. . D. 2000 . 5
Câu 175. Biết a log 12,b log 24 . Khi đó giá trị của log 168 được tính theo a là: 7 12 54 a(8 5b) ab 1 a(8 5b) ab 1 D. . B. a . C. . A. . 1 ab a a(8 5b) 1 ab a(8 5b) 2 3 a Câu 176. Biết log b b 2,log c 3
. Khi đó giá trị của bieeur thức log bằng: a a a 4 c 2 3 A. 20 . B. . C. 1 . D. . 3 2
Câu 177. Biết log b 3,log c 4
. Khi đó giá trị của biểu thức log a bc bằng: a 2 3 2 a a 16 3 A. . B. 5 . C. 16 . D. 48 . 3
Câu 178. Rút gọn biểu thức 3 5 A log a
a a , ta được kết quả là: a 37 35 3 1 A. . B. . C. . D. . 10 10 10 10 5 3 3 2 a a a
Câu 179. Rút gọn biểu thức B log
, ta được kết quả là : 1 4 a a a 91 60 16 5 A. . B. . C. . D. . 60 91 5 16
Câu 180. Biết a log 5,b log 5 . Khi đó giá trị của log 5 được tính theo , a b là : 2 3 6 1 A. ab . B. .
C. a b . D. 2 2 a b . a b a b
Câu 181. Cho a log 3;b log 5;c log 2 . Khi đó giá trị của biểu thức log 63 được tính theo a, , 2 3 7 140 b c là: 2ac 1 abc 2c 1 2ac 1 ac 1 A. . B. . C. . D. . abc 2c 1 2ac 1 abc 2c 1 abc 2c 1
Câu 182. Cho a log 2;b log 3 . Khi đó giá trị của log 72 được tính theo a, 5 5 5 b là :
A. 3a 2b . B. 3 2 a b .
C. 3a 2b . D. 6ab .
Câu 183. Biết a log 18,b log 54 . Khẳng định nào sau đây là khẳng định đúng? 12 24
A. ab 5(a ) b 1 .
B.5ab a b 1.
C. ab 5(a ) b 1.
D.5ab a b 0 .
Câu 184. Biết log log log y 0 , khi đó giá trị của biểu thức A 2y 1 là: 3 4 2 A.33. B. 17. C. 65. D. 133.
Câu 185. Cho log x ! 0 . Khẳng định nào sau đây là khẳng định đúng? 5 A. log 5 d log 4 . B. log 5 ! log 6 .
C. log x log 5 .
D. log x ! log x . x x x x 5 x 5 6
Câu 186. Cho 0 x 1. Khẳng định nào sau đây là khẳng định đúng? 1 A. 3 log 5 log 5 0 B. 3 log 5 ! log x 3 1 x x 2 2 1 1 1 C. log log . D. 3 log . log 5 ! 0 x 5 2 2 x 2 x log2 5 log0,5 2 § · § ·
Câu 187. Trong bốn số log34 2log32 1 1 3 , 3 , , ¨ ¸ ¨ ¸
số nào nhỏ hơn 1? © 4 ¹ ©16 ¹ log0,5 2 § 1 · log25 § 1 · A. ¨ ¸ . B. 2log32 3 . C. lo 3g 4 3 . D. ¨ ¸ . ©16 ¹ © 4 ¹ Câu 188. Gọi log0,5 4 log0,513 M 3 ; N = 3
. Khẳng định nào sau đây là khẳng định đúng?
A. M 1 N .
B. N M 1.
C. M N 1.
D. N 1 M . § S · § S ·
Câu 189. Biểu thức log 2sin log cos có giá trị bằng: 2 ¨ ¸ 2 ¨ ¸ © 12 ¹ © 12 ¹ A. 2 . B. 1 . C.1. D. log 3 1. 2
Câu 190. Với giá trị nào của m thì biểu thức f (x) log (x )
m xác định với mọi x ( 3 ; ) f ? 5 A. m ! 3 . B. m 3 . C. m d 3 . D. m t 3 .
Câu 191. Với giá trị nào của m thì biểu thức f (x) log (3 x)(x 2 ) x ? 1
m xác định với mọi [ 4;2] 2 3 A. m t 2. B. m t . C. m ! 2 . D. m t 1 . 2
Câu 192. Với giá trị nào của m thì biểu thức f (x) log (m x)(x 3 ) x ? 3
m xác định với mọi ( 5;4] 4 5 A. m z 0 . B. m ! . C. m . D. m . 3 3
Câu 193. Với mọi số tự nhiên n, Khẳng định nào sau đây là khẳng định đúng? A. n log log ... 2 . B. n log log ... 2 . 2 2 2 2 n c¨n bËc hai n c¨n bËc hai C. n 2 log log ... 2 . D. n 2 log log ... 2 . 2 2 2 2 n că c n ă bËc hai n că c n ă bËc hai
Câu 194. Cho các số thực , a ,
b c thỏa mãn: lo 3g7 log711 lo 11 g 25 a 27,b 49,c
11 . Giá trị của biểu thức 2 2 2 (log 11) (log 25) 7 11 (l 3 og 7) A a b c là: A. 519. B.729. C. 469. D.129.
Câu 195. Kết quả rút gọn của biểu thức C log b log a 2 b b b là: a b log log a ab loga A. 3 log b . B. . log b . C. b . D. log b . a 3 log a a a Câu 196. Cho , a ,
b c ! 0 đôi một khác nhau và khác 1, Khẳng định nào sau đây là khẳng định đúng? A. 2 c 2 a 2 log ;log ;log b 1. B. 2 c 2 a 2 log ;log ;log b !1 . a b c b c a a b c b c a b c a b c a C. 2 c 2 a 2 log ;log ;log b ! 1. D. 2 c 2 a 2 log ;log ;log b 1 . a b c b c a a b c b c a b c a b c a Câu 197. Gọi ( ;
x y) là nghiệm nguyên của phương trình 2x y 3 sao cho P x y là số dương nhỏ
nhất. Khẳng định nào sau đây đúng? A. log x log log (x ) y 1 . 2
3 y không xác định. B. 2
C. log (x y )! 1. D. log (x ) y ! 0 . 2 2
Câu 198. Có tất cả bao nhiêu số dương a thỏa mãn đẳng thức
log a log a log a log . a log . a log 2 3 5 2 3 5 a A. 3. B.1. C.2. D. 0.
E. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20
A A B A C B D B B A C D C A C D C B D D
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
C D C B D A D A A D B C B D B A A B C C
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
C B B C B C D D D D B A A C D B A A C A
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
D A B A A A C A C D B A D B B C C D B C 81 82 83 84 C A A A
II –HƯỚNG DẪN GIẢI 1
Câu 1. Biểu thức f (x) xác định 2x 1 ! 0 x ! . Ta chọn đáp án A 2
Câu 2. Biểu thức f (x) xác định 2 4 x ! 0 x( 2 ;2) . Ta chọn đáp án A x 1
Câu 3. Biểu thức f (x) xác định ! 0 x( ; f 3 ) (1; ) f . Ta chọn đáp án B 3 x
Câu 4. Biểu thức f (x) xác định 2
2x x ! 0 x(0;2) . Ta chọn đáp án A.
Câu 5. Biểu thức f (x) xác định 3 2
x - x 2x ! 0 x( 1 ;0) (2; )
f . Ta chọn đáp án C. Câu 6. Ta có log 4 log 1/2 4 2log 4 log 16 a a a a A a a a a 16 . Ta chọn đáp án B
Câu 7. Ta nhập vào máy tính biểu thức 2log 12 3log 5 log 15 log 150 , bấm =, được kết quả 2 2 2 2 B 3 Ta chọn đáp án D Câu 8. +Tự luận 2 3
P 2 log 12 3log 5 log 15 log 150 log 12 log 5 log (15.150) 2 2 2 2 2 2 2 2 3 12 .5 log 3 2 15.150 Đáp án B.
+Trắc nghiệm: Nhập biểu thức vào máy tính và nhấn calc ta thu được kết quả bằng 3. 1 1
Câu 9. Ta có D log a log . Ta chọn đáp án B 3 a 3 a a 3 1
Câu 10. Ta nhập vào máy tính biểu thức: 3 log 36 log 14 3log
21 bấm = , được kết quả C 2 . 7 7 7 2 Ta chọn đáp án A 4 4log 5 log 5 Câu 11. Ta có 2 a log 25 a 2 a E a a a 25 . Ta chọn đáp án C
Câu 12. + Tự luận: Đưa về cùng 1 cơ số và so sánh 6 5 6 5 Ta thấy log ! log log log .Ta chọn đáp án D 3 3 1 3 5 6 5 6 3
+ Trắc nghiệm: Sử dụng máy tính, lấy 1 số bất kỳ trừ đi lần lượt các số còn lại, nếu kết quả
! 0 thì giữ nguyên số bị trừ và thay đổi số trừ là số mới; nếu kết quả 0 thì đổi số trừ thành số
bị trừ và thay số trừ là số còn lại; lặp lại đến khi có kết quả.
Câu 13. + Tự luận : Đưa về cùng 1 cơ số và so sánh 1 1 Ta thấy log 17 log 15 log log 12 log
log 9 .Ta chọn đáp án C. 1 1 5 1 5 1 15 12 5 5 5 5
+ Trắc nghiệm: Sử dụng máy tính, lấy 1 số bất kỳ trừ đi lần lượt các số còn lại, nếu kết quả
0 thì giữ nguyên số bị trừ và thay đổi số trừ là số mới; nếu kết quả ! 0 thì đổi số trừ thành số
bị trừ và thay số trừ là số còn lại; lặp lại đến khi có kết quả.
Câu 14. +Tự luận : Ta có 2 2 2 2 2 2 A ln a 2ln .
a log e log e ln a log e 2ln a 2ln e 2ln a 2 . Ta chọn đáp a a a án A
+Trắc nghiệm : Sử dung máy tính, Thay a 2 rồi lấy biểu thức đã cho trừ đi lần lượt các
biểu thức có trong đáp số, nếu kết quả nào bằng 0 thì đó là đáp số.
Câu 15. +Tự luận : 3
Ta có B 2ln a 3log e 3log e 2ln a 0 3ln a . Ta chọn đáp án C a a log e a
+Trắc nghiệm : Sử dung máy tính, Thay a 2 rồi lấy biểu thức đã cho trừ đi lần lượt các
biểu thức có trong đáp số, nếu kết quả nào bằng 0 thì đó là đáp số. 2 2
Câu 16. Ta có: log 5 3 a b 2 2 3 3 15
log (a b) log a
log b x y 4 . Ta chọn đáp án D 3 3 3 3 5 15 0, 2 10 1 § a · 1 1 Câu 17. Ta có : 2 6 log ¨ ¸ log (a .b ) 2
log a log b . . Ta chọn đáp án C 5 5 5 5 x y 6 5 6 3 © b ¹ 40 40
Câu 18. Ta có: log x log 8 log 5 log 9 log . Ta chọn đáp án B 3 3 3 3 3 x 9 9 2 3 1 Câu 19. Ta có: 2 3 log
2log a 6log b log a log b log a b . Ta chọn đáp án D 7 7 49 7 7 7 x 3 2 x b a
Câu 20. Câu D sai, vì không có tính chất về logarit của một hiệu 1
Câu 21. Câu C sai, vì log b b c loga a c
Câu 22. Câu D sai, vì khẳng định đó chỉ đúng khi a !1, còn khi 0 a 1 log b ! log c b c a a
Câu 23. Câu C sai, vì log c
b ! c b ! a a
Câu 24. Câu D sai, vì 2 3 2 3 a ! a (do 0 a 1)
Câu 25. Ta có log (log )
a 0 log a 1 a 2 . Ta chọn đáp án D 3 2 2
Câu 26. Đáp án A đúng với mọi a, ,
b c khi các logarit có nghĩa
Câu 27. Đáp án D sai, vì không có logarit của 1 tổng.
Câu 28. Sử dụng máy tính và dùng phím CALC : nhập biểu thức log X log X log X 1 vào máy 2 4 8
và gán lần lượt các giá trị của x để chọn đáp án đúng. Với x 64 thì kquả bằng 0. Ta chọn D là đáp án đúng.
Câu 29. Sử dụng máy tính và dùng phím CALC : nhập biểu thức 3
log 2 2 4 vào máy và gán lần lượt x
các giá trị của x để chọn đáp án đúng. Với .. thì kquả bằng 0. Ta chọn A là đáp án đúng. 2
Câu 30. +Tự luận : Ta có 2 log 4log 2log a P b b 2 . Ta chọn đáp án A. 2 log a a a a b a 2 b 2
+Trắc nghiệm : Sử dụng máy tính, thay a b 2 , rồi nhập biểu thức 2 log b vào a log a a 2 b
máy bấm =, được kết quả P 2 . Ta chọn đáp án D.
Câu 31. + Tự luận : Ta có 3 4 P log
b .log a 2.3.4 24 . Ta chọn đáp án A. b a
+Trắc nghiệm : Sử dụng máy tính Casio, Thay a b 2 , rồi nhập biểu thức 3 4 log b .log a b a
vào máy bấm =, được kết quả P 24 . Ta chọn đáp án B. 2
Câu 32. + Tự luận : 3lo 8 g 3 2lo 1 g 65 log23 log2 5 4 2 .2 45
+ Trắc nghiệm : Sử dụng máy tính, rồi nhập biểu thức 3lo 8g3 2lo 1g65 4
vào máy, bấm =, được kết
quả bằng 45. Ta chọn đáp án C. 37
Câu 33. +Tự luận : log a a a a a 37 3 5 10 loga 10
+Trắc nghiệm : Sử dụng máy tính, Thay a 2 , rồi nhập biểu thức 3 5 log a a a vào máy a 37
bấm =, được kết quả P . Ta chọn đáp án B. 10 1
Câu 34. +Tự luận : A log 15.log 14...log 4.log 3.log 2 log 2 16 15 5 4 3 16 4
+Trắc nghiệm : Sử dụng máy tính Casio, rồi nhập biểu thức log 2.log 3.log 4...log 15 vào 3 4 5 16 1
máy bấm =, được kết quả A . Ta chọn đáp án D. 4 3 3 2 5 3 91 § a a a · 91
Câu 35. +Tự luận : 60 log ¨ ¸ log 1 a ¨ 4 a a a ¸ 60 a © ¹ 3 3 2 5 3 § ·
+Trắc nghiệm : Sử dụng máy tính, Thay a a a
a 2 , rồi nhập biểu thức log ¨ ¸ vào 1 ¨ 4 a a ¸ a © ¹ 211
máy bấm =, được kết quả . Ta chọn đáp án C. 60
Câu 36. Ta có: log 2 log 3 1, log 3 ! log 2 1 3 3 2 2 Câu 37. 2 2 2000 !1999.2001 log 2000 ! log 2001.1999 2000 2000 2 ! log 2001 log 1999 log 2000 ! log 2001 2000 2000 1999 2000
Câu 38. Ta có log 2 log 3=1=log 2< log 3 log 11 3 3 2 2 3
Câu 39. log x 2 3 3 x 2 3 x 25 3 3 1 3
Câu 40. log x log x log x log x x 3 3 9 3 3 2 2 2 Câu 41. Ta có 4 7 4 7
4log a 7log b log (a b ) . Ta chọn đáp án C. 3 3 3 x a b Câu 42. Ta có: log 2 2
x y 1 log xy log 2 2 x y 2 2
log 2xy x y 2x 2 2 2 2 y x y 1 y 3 Câu 43. log y x log =1 log 1 1 4 4 x y y y x 4 4 Câu 44. Do ! x , y 0
log xy log x log y , ta chọn đáp án D. a a a
Câu 45. Ta có : Chọn B là đáp án đúng, vì 2 2 2 2
x 4 y 12xy (x 2 y) 16xy log (x 2 y) log 16x 2 2 y 1
2log (x 2y) 4 log x log y log (x 2y) 2 log x log 2 2 2 2 2 2 y 2
Câu 46. Ta có: Chọn C là đáp án đúng, vì 2 2 2 2
a b 7ab (a b) 9ab log(a b) log 9ab a b 1
2log(a b) log9 log a logb log (loga logb) 3 2 1
Câu 47. +Tự luận : Ta có : a log 6 log (2.3) 1 log 3 log 2 2 2 2 3 a 1 1 2a 1 Suy ra 2 log 18 log (2.3 ) log 2 2 2 . Ta chọn đáp án A. 3 3 3 a 1 a 1 +Trắc nghiệm:
Sử dụng máy tính: Gán log 6 cho A 2
Lấy log 18 trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bẳng 0 thì đó là đáp án. 3 Ta chọn đáp án D 1 1 1 4
Câu 48. +Tự luận : Ta có : 4 4
log 1250 log (2.5 ) log (2.5 ) 2log 5 a . Ta chọn đáp 2 4 2 2 2 2 2 2 án A. +Trắc nghiệm:
Sử dụng máy tính: Gán log 5 cho A 2
Lấy log 1250 trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bằng 0 thì đó là đáp án. 4 Ta chọn đáp án D
Câu 49. Sử dụng máy tính: gán log 2 cho A 7
Lấy log 28 trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bẳng 0 thì đó là đáp án. 49 Ta chọn đáp án D
Câu 50. Sử dụng máy tính: gán lần lượt log 5; log 3 cho A, B 2 5
Lấy log 15 trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bẳng 0 thì đó là đáp án. 10 Ta chọn đáp án D
Câu 51. +Tự luận : Ta có : a log 15 log (3.5) 1 log 5 log 5 a 1 . 3 3 3 3
Khi đó : log 50 2log (5.10) 2(log 5 log 10) 2( 1 a )
b Ta chọn đáp án B. 3 3 3 3 +Trắc nghiệm
Sử dụng máy tính: gán lần lượt log 15;log 10 cho A, B. 3 3
Lấy log 50 trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bẳng 0 thì đó là đáp án. 3 Ta chọn đáp án B.
Câu 52. Sử dụng máy tính: Gán log 3 cho A 5
Lấy log 75 trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bẳng 0 thì đó là đáp án. 15 Ta chọn đáp án A. 1
Câu 53. Ta có: log 7 2. log 7 2log 7 2 2 2 4
a . Ta chọn đáp án A. 2 27 2 3a 2 Câu 54. Ta có: log log 27 log 25 3 2log 5 3 . Ta chọn đáp án C. 3 3 3 3 25 a a
Câu 55. Sử dụng máy tính: Gán lần lượt log 5;log 3 cho A, B 2 5
Lấy log 15 trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bẳng 0 thì đó là đáp án. 24 Ta chọn đáp án D. log 27 3log 3 2a 4 3 a 2 2
Câu 56. Ta có: a log 27 log 3 log 16 . 12 2 6 log 12 2 log 3 3 a 3 2 2 a lg30 1 lg3 1
Câu 57. Ta có: log 30 a . 125 lg125 31 lg 2 31b 3 3 3 1 D b D b 3 Câu 58. Ta có : 2 3 log b 3 a a a A . a a a 3 3 b a a b Câu 59. Ta có log 5 log 5 3 , log 7 log 7 log 5 3 27 3 8 3 2 ac c 3ac b log 35 . 6 1 c
Câu 60. Ta có: A log 2 log 3... log 2000 log x x x x x 1.2.3...2000 log 1 x
Câu 61. Sử dụng máy tính: Gán lần lượt log 12;log 24 cho A, B 7 12
Lấy log 168 trừ đi lần lượt các đáp số ở A, B, C, D. kết quả nào bẳng 0 thì đó là đáp án. 54 Ta chọn đáp án D. 2 3 a Câu 62. Ta có b 2 3 4 log
log a log b log c 2 3.2 4.( 3
) 20 . Ta chọn đáp án A. a 4 a a a c 1 1
Câu 63. Ta có log 2 3 2 a
bc 2log a log b 2log c 2 .3 2.( 4) 5 . Ta chọn đáp án B. a a 3 a a 3 37
Câu 64. Thay a e , rồi sử dụng máy tính sẽ được kết quả A . Ta chọn đáp án A. 10 91
Câu 65. Thay a e , rồi sử dụng máy tínhsẽ được kết quả B . Ta chọn đáp án A 60 1 1 1 log 5.log 5 ab Câu 66. Ta có: 2 3 log 5 . 6 log 6 log (2.3) log 2 log 3 log 5 log 5 a 5 5 5 5 2 3 b
Câu 67. Sử dụng máy tính: gán lần lượt log 3;log 5;log 2 cho A, B, C 2 3 7
Lấy log 63 trừ đi lần lượt các đáp số ở A, B, C, D. kết quả nào bẳng 0 thì đó là đáp án. 140 Ta chọn đáp án C.
Câu 68. Sử dụng máy tính: gán lần lượt log 2;log 3 cho A, B 5 5
Lấy log 72 trừ đi lần lượt các đáp số ở A, B, C, D. kết quả nào bẳng 0 thì đó là đáp án. 5 Ta chọn đáp án A.
Câu 69. Sử dụng máy tính Casio, gán lần lượt log 18;log 54 cho A và B. 12 24
Với đáp án C nhập vào máy : AB 5(A B) 1
, ta được kết quả bằng 0 . Vậy C là đáp án đúng.
Câu 70. Vì log log log y 0 nên 4
log (log y) 1 log y 4 y 2 2y 1 33. 3 4 2 4 2 2 Đáp án A.
Câu 71. Vì log x ! 0 x !1 . Khi đó log x ! log 5 5
6 x . Chọn đáp án D.
Câu 72. Sử dụng máy tính Casio, Chọn x 0,5 và thay vào từng đáp án, ta được đáp án A.
Câu 73. +Tự luận: log2 5 § 1 · 1 Ta có: 2 log3 4 2log3 2 log3 4 2log2 5 log2 5 2 3 4;3 3 4; 2 2 5 ¨ ¸ , © 4 ¹ 25 log0,5 2 § 1 · ¨ ¸ 4 2 log 2 4 2 log2 2 4 2 2 16 . ©16 ¹ Chọn : Đáp án D.
Trắc nghiệm: nhập vào máy tính từng biểu thức tính kết quả, chọn kết quả nhỏ hơn 1.
Câu 74. +Tự luận: Ta có log0,513 log0,5 4 log 13 log 4 0 3 3 1 N M 1. 0,5 0,5 Chọn : Đáp án B.
+ Trắc nghiệm: Nhập các biểu thức vào máy tính, tính kết quả rồi so sánh, ta thấy đáp án B đúng. § S · § S · § S S · § S · 1
Câu 75. Ta có log 2sin log cos log 2sin .cos log sin log 1 2 ¨ ¸ 2 ¨ ¸ 2 ¨ ¸ 2 ¨ ¸ 2 © 12 ¹ © 12 ¹ © 12 12 ¹ © 6 ¹ 2 Chọn: Đáp án B.
Câu 76. Biểu thức f (x) xác định x m ! 0 x ! m .
Để f (x) xác định với mọi x ( 3 ; ) f thì m d 3 Ta chọn đáp án C.
Câu 77. Thay m 2 vào điều kiện (3 x)(x 2 ) m ! 0 ta được (3 )(
x x 4) ! 0 x ( 4 ;3) mà [ 4;2] ( 4;
3) nên các đáp án B, A, D loại. Ta chọn đáp án đúng là C.
Câu 78. - Thay m 2 vào điều kiện (m x)(x 3 ) m ! 0 ta được (2 )(
x x 6) ! 0 x (2;6) mà ( 5
;4] (2;6) nên các đáp án B, A loại. - Thay m 2
vào điều kiện (m x)(x 3 ) m ! 0 ta được ( 2 )(
x x 6) ! 0 x ( 6 ; 2) mà ( 5 ;4] ( 6 ; 2
) nên các đáp án C loại. Do đó Ta chọn đáp án đúng là D. Câu 79. +Tự luận: Đặt -log log ... 2 . Ta có: 2 log ... 2 2 ... 2 2 m m . 2 2 m 2 n c¨n bËc hai 2 n 1 § 1 · § 1 · ¨ ¸ ¨ ¸ Ta thấy : 2 © 2 ¹ © 2 ¹ 2 2 2 , 2 2 ,....., ... 2 2 2 n .
Do đó ta được: 2m 2
n m n . Vậy n log log ... 2 . Đáp án B. 2 2 n c¨n bËc hai
+Trắc nghiệm: Sử dụng máy tính Casio, lấy n bất kì, chẳng hạn n 3. Nhập biểu thức log log
2 ( có 3 dấu căn ) vào máy tính ta thu được kết quả bằng – 3. 2 2 Vậy chọn B. Câu 80. Ta có log 7 a 1 log 7 log 11 log 25 3 log 11 b 7 3 7 lo 11g25 c log 2511 log3 7 log711 11 3 2 2 27 49 11 7 11 25 469 Suy ra : Đáp án C.
Câu 81. C log b log a 2 log b log b log b a b a ab a log b § b · b § b · a 2 1 loga loga 2 1 log ¨log b ¸ log a b ¨ ¸ log b b a a a loga 3 2 log b 1 log b log b 1 log b a © a ¹ a © a ¹ 1 2 b § c · c b § c · Câu 82. * 2 2 log log log log log log c a a ¨ ¸ a a ¨ a ¸ c © b ¹ b c © b ¹ a b
* log b.log c.log a 1 log b .log a log a 1 a b c a b a
* Từ 2 kết quả trên ta có : 2 c a b § b c a · 2 2 2 log log log a b c ¨log .log log a b c ¸ 1 b c a c a b b c a © b c a ¹ Chọn : Đáp án A.
Câu 83. Vì x y ! 0 nên trong hai số x và y phải có ít nhất một số dương mà
x y 3 x ! 0 nên suy ra x 3 mà x nguyên nên x 0; 1 r ; 2; r ...
+ Nếu x 2 suy ra y 1 nên x y 1
+ Nếu x 1 thì y 1 nên x y 2
+ Nếu x 0 thì y 3 nên x y 3
+ Nhận xét rằng : x 2 thì x y !1 . Vậy x y nhỏ nhất bằng 1. Suy ra: Chọn đáp án A.
Câu 84. (*) log a log 2.log a log 2.log a log . a log 5.log . a log 2 3 2 5 2 2 3 5 5 a log . a 1 log 2 log 2 2 log . a log 5.log 2 3 5 2 3 5 a log . a 2
1 log 2 log 2 log 5.log a 0 2 3 5 3 5 ªa 1 ªa 1 ªlog a 0 2 « « 1 log 2 log 2 « 1log 3 2 log5 2 2 « 3 5
1 log 2 log 2 log 5.log a 0 log a r r « log ¬ 3 5 3 5 3 5 5 « log 5 ¬a 5 ¬ 3 Chọn: Đáp án A.
HÀM SỐ LŨY THỪA – HÀM SỐ MŨ – HÀM SỐ LOGARIT
1. LÝ THUYẾT:Hàm lũy thừa:
1.1. Định nghĩa: Hàm số D y x với D
được gọi là hàm số lũy thừa.
1.2. Tập xác định: Tập xác định của hàm số D y x là:
x D nếu D là số nguyên dương. x D \^ ` 0
^ với D nguyên âm hoặc bằng 0. x D (0; ) f với D không nguyên.
1.3. Đạo hàm: Hàm số D D D
y x , (D ) có đạo hàm với mọi x ! 0 và 1 (x ) D.x c .
1.4. Tính chất của hàm số lũy thừa trên khoảng (0; ) f . D D y x , D ! 0 y x , D 0
a. Tập khảo sát: (0; ) f
a. Tập khảo sát: (0; ) f b. Sự biến thiên: b. Sự biến thiên: + D 1 D y Dx c ! 0, x ! 0. + 1 yc D x 0, x ! 0. + Giới hạn đặc biệt:
+ Giới hạn đặc biệt: lim D D D D x 0, lim x . f lim x , f lim x 0. x 0 o xof x 0 o xof + Tiệm cận: không có + Tiệm cận: - Trục Ox là tiệm cận ngang. - Trục Oy là tiệm cận đứng.
c. Bảng biến thiên:
c. Bảng biến thiên: x 0 f x 0 f yc yc f f y y 0 0 d. Đồ thị: y D
Đồ thị của hàm số lũy thừa y x luôn D !1 D 1
đi qua điểm I(1;1).
Lưu ý: Khi khảo sát hàm số lũy thừa với
số mũ cụ thể, ta phải xét hàm số đó trên
toàn bộ tập xác định của nó. Chẳng hạn: 3 2 S 0 D 1
y x , y x , y x . I 1 D 0 D 0 x O 1 2. Hàm số mũ: x
y a , (a ! 0, a 1 z ).
2.1.Tập xác định: D
2.2.Tập giá trị: T (0, )
f , nghĩa là khi giải phương trình mũ mà đặt f ( x) t a thì t ! 0.
2.3. Tính đơn điệu:
+ Khi a !1 thì hàm số x
y a đồng biến, khi đó ta luôn có: f (x) g ( x) a ! a
f (x) ! g(x).
+ Khi 0 a 1 thì hàm số x
y a nghịch biến, khi đó ta luôn có: f (x) g ( x) a ! a
f (x) g(x). 2.4.Đạo hàm: ( x a ) x
c a .ln a ( u
a )c u . u c a .ln a ( x e ) x c e ( u e ) u c e .uc c ( u n u )c n n 1 . n u
2.5.Đồ thị: Nhận trục hoành làm đường tiệm cận ngang. y y x y a x y a a ! 1 0 a 1 1 1 x x O O
3. Hàm số logarit: y log ,
x (a ! 0, a z 1) a
3.1.Tập xác định: D (0, ) f .
3.2.Tập giá trị: T , nghĩa là khi giải phương trình logarit mà đặt t log x thì t không có điều a kiện.
3.3.Tính đơn điệu:
+ Khi a !1 thì y log x đồng biến trên D, khi đó nếu: log f ( ) x ! log g( ) x f ( ) x ! g( ) x . a a a
+ Khi 0 a 1 thì y log x nghịch biến trên D, khi đó nếu log f ( ) x ! log g( ) x f ( ) x g( ) x . a a a 3.4.Đạo hàm: c c uc x u a 1 log loga .l x n a . u ln a uc n n 1
(ln u )c n ln u 1 c (ln )c , ( ! 0) (ln ) u u x x u c x u
3.5. Đồ thị: Nhận trục tung làm đường tiệm cận đứng. y y a 1 0 a 1 y log x a 1 x x O 1 O y log x a
A. BÀI TẬP TRẮC NGHIỆM:
Phần 1: Nhận biết – Thông hiểu
Câu 1. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Đồ thị hàm số x y
a và đồ thị hàm số y log x đối xứng nhau qua đường thẳng y x . a B. Hàm số x y
a với 0 a 1 đồng biến trên khoảng ( ; f ) f . C. Hàm số x y
a với a ! 1 nghịch biến trên khoảng ( ; f ) f .
D. Đồ thị hàm số x y
a với a ! 0 và a z 1 luôn đi qua điểm M ( ; a 1) .
Câu 2. Tập giá trị của hàm số x y a
(a ! 0;a z 1) là: A. (0; ) f B. [0; ) f C. \{0 \{ } 0 D.
Câu 3. Với a ! 0 và a z 1. Phát biểu nào sau đây không đúng? A. Hai hàm số x
y a và y log x có cùng tập giá trị. a B. Hai hàm số x
y a và y log x có cùng tính đơn điệu. a
C. Đồ thị hai hàm số x
y a và y log x đối xứng nhau qua đường thẳng y x . a
D. Đồ thị hai hàm số x
y a và y log x đều có đường tiệm cận. a x
Câu 4. Cho hàm số y 2
1 . Phát biểu nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng ( ; f ) f .
B. Hàm số đồng biến trên khoảng (0; ) f
C. Đồ thị hàm số có đường tiệm cận ngang là trục tung.
D. Đồ thị hàm số có đường tiệm cận đứng là trục hoành.
Câu 5. Tập xác định của hàm số 2017 y (2x 1) là: § 1 · ª1 º 1 ½ A. D B. D ;f ¨ ¸ C. D ;f D. D \ ® ¾ © 2 ¹ «2 » ¬ ¼ ¯2¿
Câu 6. Tập xác định của hàm số 2 2 y (3x 1) là: 1 ½ 1 ½ A. D \ ®r ¾ B. D ®r ¾ ¯ 3 ¿ ¯ 3 ¿ § 1 · § 1 · § 1 1 · C. D ; f ;f ¨ ¸ ¨ ¸ D. ; ¨ ¸ © 3 ¹ © 3 ¹ © 3 3 ¹
Câu 7. Tập xác định của hàm số 2 ( 3 2) e y x x là: A. D ( ; f 1) (2; ) f B. D \{1 \{ ; 1 2} 2 C. D (0; ) f
D. D (1;2)
Câu 8. Tập xác định của hàm số y log (x 1) là: 0,5 A. D ( 1 ; ) f B. D \{ \{1} 1 C. D (0; ) f D. ( ; f 1 )
Câu 9. Tìm x để hàm số 2
y log x x 12 có nghĩa. A. x( ; f 4 ) (3; ) f B. x( 4 ;3) x z 4 C. ®
D. x R ¯x z 3 x 3
Câu 10. Tập xác định của hàm số y log là: 2 2 x A. D ( 3 ;2) B. D \{ \{3; 3;2} 2} C. D ( ; f 3)(2; ) f
D. D [ 3;2] 1
Câu 11. Tập xác định của hàm số y ln(x 1) là: 2 x
A. D (1;2) B. D (1; ) f C. D (0; ) f
D. D [1;2] x
Câu 12. Tập xác định của hàm số e y là: x e 1 A. D \{ \ 0 { } 0 B. (0; ) f C. \{ \ 1 { } 1 D. D ( ; e ) f 1
Câu 13. Tập xác định 2 y 2 x 5x 2 ln là: 2 x 1
A. D (1;2]
B. D [1;2] C. D ( 1 ;1) D. D ( 1 ;2)
Câu 14. Tập xác định của hàm số y ln(ln x) là : A. D (1; ) f B. D (0; ) f C. D ( ; e ) f D. D [1; ) f
Câu 15. Tập xác định của hàm số x 2 y (3 9) là A. D \{ \ 2 { } 2 B. D \{ \ 0 { } 0 C. D (2; ) f D. D (0; ) f
Câu 16. Hàm số y log
x xác định khi và chỉ khi : x 1 x !1 A. ® B. x !1
C. x ! 0
D. x z 2 ¯x z 2
Câu 17. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? y 2 1 O 2 x x x A. y 2
B. y x C. 2x y D. y 2 1 Câu 18. Hàm số 3
y (x 1) có đạo hàm là: 1 1 3 2 (x 1) 3 (x 1) A. y ' B. y ' C. y ' D. y ' 3 2 3 (x 1) 3 3 (x 1) 3 3
Câu 19. Đạo hàm của hàm số 2 4 x y là: A. 2 ' 2.4 x y ln 4 B. 2 ' 4 .x y ln 2 C. 2 ' 4 x y ln 4 D. 2 ' 2.4 x y ln 2
Câu 20. Đạo hàm của hàm số y log , x x ! 0 là: 5 1 1 A. y '
B. y ' xln 5 C. ' 5x y ln 5 D. y ' x ln 5 5x ln 5 Câu 21. Hàm số 2 y log
x (x z 0) có công thức đạo hàm là: 0,5 2 1 2 1 A. y ' B. y ' C. y ' D. x ln 0,5 2 x ln 0,5 2 x ln 0,5 x ln 0,5
Câu 22. Đạo hàm của hàm số 3
y sin x log x (x ! 0) là: 3 3 3
A. y ' cos x
B. y ' cos x x ln 3 x ln 3 1 1
C. y ' cos x
D. y ' cos x 3 x ln 3 3 x ln 3
Câu 23. Cho hàm số f x 4 ( ) ln x 1 . Đạo hàm / f 0 bằng: A. 0 B. 1 C. 2 D. 3 Câu 24. Cho hàm số 2 2017 ( ) x f x e . Đạo hàm / f 0 bằng: A. 0 B. 1 C. e D. 2017 e
Câu 25. Cho hàm số ( ) x f x xe . Gọi / / f
x là đạo hàm cấp hai của f x . Ta có // f 1 bằng: A. 3e B. 2 3 e C. 3 e D. 2 5 e
Câu 26. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? y 1 x O 2 1 A. y log B. y log C. y log
D. y log 2 2 x 2 x 1 x x 2 2
Câu 27. Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai? A. Hàm số D
y x có tập xác định là D .
B. Đồ thị hàm số D
y x với D ! 0 không có tiệm cận. C. Hàm số D
y x với D 0 nghịch biến trên khoảng (0; ) f .
D. Đồ thị hàm số D
y x với D 0 có hai tiệm cận.
Câu 28. Trong các mệnh đề sau mệnh đề nào đúng?
A. Đồ thị hàm số lôgarit nằm bên phải trục tung.
B. Đồ thị hàm số lôgarit nằm bên trái trục tung.
C. Đồ thị hàm số mũ nằm bên phải trục tung.
D. Đồ thị hàm số mũ nằm bên trái trục tung.
Câu 29. Chọn phát biểu sai trong các phát biểu sau?
A. Đồ thị hàm số logarit nằm bên trên trục hoành.
B. Đồ thị hàm số mũ không nằm bên dưới trục hoành.
C. Đồ thị hàm số lôgarit nằm bên phải trục tung.
D. Đồ thị hàm số mũ với số mũ âm luôn có hai tiệm cận.
Câu 30. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? y O 1 2 x 1 1 1 A. y log B. y log y x D. y 3 x 1 0,5 x 2 x C. 3 3
Câu 31. Tìm a để hàm số y log x 0 a z
1 có đồ thị là hình bên dưới: a y 2 O x 1 2 1 1 A. a 2 B. a 2 C. a D. a 2 2
Phần 2: Vận dụng thấp 10
Câu 32. Tìm tập xác định D của hàm số log x y . 3 2 x 3x 2 A. D ( ;
f 1) (2;10) B. D (1; ) f C. D ( ; f 10) D. D (2;10)
Câu 33. Tìm tập xác định D của hàm số y log (x 2) 3 ? 3 A. D [29; ) f B. D (29; ) f
C. D (2;29) D. D (2; ) f
Câu 34. Tính đạo hàm của hàm số 2 ( 2 ) x y x x e ? A. 2 ' ( 2) x y x e B. 2 ' ( 2) x y x e C. ' x y xe D. ' (2 2) x y x e
Câu 35. Tìm tất cả các giá trị thực của tham số m để hàm số 2
y ln(x 2mx 4) có tập xác định D ? ªm ! 2 A. 2 m 2 B. « C. m ! 2 D. 2 d m d 2 ¬m 2 2017
Câu 36. Cho tập D (3;4) và các hàm số f (x) , g(x) log (4 ) x , 2 7 12 ( ) 3x x h x 2 x3 x 7x 12
D là tập xác định của hàm số nào?
A. f (x) và f (x) g(x)
B. f (x) và h(x)
C. g(x) và h(x)
D. f (x) (
h x) và h(x)
Câu 37. Biết hàm số 2x y
có đồ thị là hình bên. y y = 2x 1 O x Khi đó, hàm số 2 x y
có đồ thị là hình nào trong bốn hình được liệt kê ở bốn A, B, C, D dưới đây ? y y 1 1 x O O x Hình 1 Hình 2 y y 1 O 1 x x O Hình 3 Hình 4 A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4 Câu 38. Cho hàm số x y ex e
. Nghiệm của phương trình y ' 0 ? A. x 1 B. x 1 C. x 0 D. x ln 2
Câu 39. Tìm tất cả các giá trị thực của a để hàm số y log x 0 a z
1 có đồ thị là hình bên a y 2 O x 1 2 ? 1 1 A. a 2 B. a 2 C. a D. a 2 2
Câu 40. Tìm giá trị lớn nhất của hàm số 2 ( ) x
f x x e trên đoạn > 1; @ 1 ? 1 A. e B. C. 2e D. 0 e
Câu 41. Cho hàm số y log 2 . Khi đó, hàm số y log 2
có đồ thị là hình nào trong bốn hình 2 x 2 x
được liệt kê ở bốn phương án A, B, C, D dưới đây: y y 1 x O O x Hình 1 Hình 2 y y x O O x Hình 3 Hình 4 A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4
Phần 3: Vận dụng cao
Câu 42. Tìm điều kiện xác định của phương trình 4 2 2
log (x 1) log (x 1) 25 ? A. x !1 B. x z 1 C. x t1 D. x
Câu 43. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số | | 2 x y trên > 2; 2@? 1 1
A. max y 4;min y
B. max y 4; miny 4 4 1 C. max y 1 ;miny
D. max y 4;miny 1 4 ln
Câu 44. Chọn khẳng định đúng khi nói về hàm số x y x
A. Hàm số có một điểm cực tiểu.
B. Hàm số có một điểm cực đại.
C. Hàm số không có cực trị.
D. Hàm số có một điểm cực đại và một điểm cực tiểu.
Câu 45. Hình bên là đồ thị của ba hàm số y log x , y log x , y log x 0 , a , b c z 1 được vẽ a b c
trên cùng một hệ trục tọa độ. Khẳng định nào sau đây là khẳng định đúng? y y = logax y = logbx O 1 x y = logcx
A. b ! a ! c
B. a ! b ! c
C. b ! c ! a
D. a ! c ! b 1
Câu 46. Tìm tất cả các giá trị thực của tham số m để hàm số y log xác định 3 x m 2m 1 x trên 2;3. A.1d m d 2
B. 1 m d 2 C. 1 m 2 D. 1 d m d 2
Câu 47. Cho hàm số y x 2 x x 2 ln 1
1 x . Khẳng định nào sau đây là khẳng định đúng?
A.Hàm số giảm trên khoảng (0; ) f
B.Hàm số tăng trên khoảng (0; ) f
C.Tập xác định của hàm số là D
D.Hàm số có đạo hàm y 2 ' ln x 1 x 1
Câu 48. Đối với hàm số y ln
, Khẳng định nào sau đây là khẳng định đúng? x 1 A. '1 y xy e B. '1 y xy e C. '1 y xy e D. '1 y xy e x x
Câu 49. Đạo hàm của hàm số e e y là: x x e e 2 4 x 2x 2 2 x 2 3 x A. ' e e e e y B. y ' C. y ' D. y ' 2x 2 (e 1) 2x 2 (e 1) 2x 2 (e 1) 2x 2 (e 1)
Câu 50. Cho hàm số y xsin x . Khẳng định nào sau đây là khẳng định đúng?
A. xy '' 2y ' xy 2 sinx
B. xy ' yy '' xy ' 2sinx C. xy ' yy' xy' 2sin x
D. xy '' y ' xy 2cos x sin x
Câu 51. Hình bên là đồ thị của ba hàm số x y a , x y b , x y c 0 , a , b c z
1 được vẽ trên cùng một
hệ trục tọa độ. Khẳng định nào sau đây là khẳng định đúng? y y = bx y = cx y = ax O x
A. b ! a ! c
B. a ! b ! c
C. a ! c !b
D. c ! b ! a B. ĐÁP ÁN:
Câu 1. Chọn đáp án A Câu B sai vì hàm số x
y a với 0 a 1 nghịch biến trên khoảng ( ; f ) f . Câu C sai vì hàm số x
y a với a ! 1đồng biến trên khoảng ( ; f ) f .
Câu D sai vì đồ thị hàm số x
y a với a ! 0 và a z 1 luôn đi qua điểm ( ; a
M a a ) hoặc M (0;1)
chứ không phải M ( ; a 1) .
Câu 2. Chọn đáp án A
Với a ! 0; a z1 thì x a 0, x
. Suy ra tập giá trị của hàm số x y a
(a ! 0;a z 1) là (0; ) f
Câu 3. Chọn đáp án A
Tập giá trị của hàm số x y a là (0; )
f , tập giá trị của hàm số y log x là . a
Câu 4. Chọn đáp án A x
Vì 0 2 11 nên hàm số y 2
1 nghịch biến trên khoảng ( ; f ) f .
Câu 5. Chọn đáp án A Vì 2007
nên hàm số xác định với mọi x .
Câu 6. Chọn đáp án A 1 Vì 2 nên hàm số 2 2 y (3x 1) xác định khi 2 3x 1 z 0 x z r . 3
Câu 7. Chọn đáp án A ªx ! 2 Vì e
nên hàm số xác định khi 2 x 3x 2 ! 0 « . ¬x 1
Câu 8. Chọn đáp án A
Hàm số log (x 1) xác định khi x 1! 0 x ! 1 . 0,5
Câu 9. Chọn đáp án A ªx ! 3 Hàm số 2
log x x 12 có nghĩa khi 2 x x 12 ! 0 « . ¬x 4
Câu 10. Chọn đáp án A x 3 x 3 Hàm số log có nghĩa khi ! 0 3 x 2 . 2 2 x 2 x
Câu 11. Chọn đáp án A 1 2 x ! 0 Hàm số y
ln(x 1) xác định khi ® 1 x 2 . 2 x ¯x 1 ! 0
Câu 12. Chọn đáp án A x Hàm số e y xác định khi x e 1 z 0 x z 0 . x e 1
Câu 13. Chọn đáp án A 1 Hàm số 2 y 2 x 5x 2 ln xác định khi 2 x 1 1 d x d 2 2 ° 2x 5x 2 0 ° t °2 ® ® 1 x d 2 2 °¯ ! ªx !1 x 1 0 °« °¯¬x 1
Câu 14. Chọn đáp án A x ! 0 x ! 0
Hàm số y ln(ln(x)) xác định khi ® ® x !1 . ln ¯ x ! 0 ¯x !1
Câu 15. Chọn đáp án A Vì 2 nên hàm số x 2 y (3 9)
xác định khi 3x 9 z 0 x z 2 .
Câu 16. Chọn đáp án A x ! 0 x ! 0 ° ° x !1 Hàm số y log
x xác định khi ®x 1 ! 0 ®x ! 1 ® . x 1 ° ° ¯x z 2 x 1 z 1 x z 2 ¯ ¯
Câu 17. Chọn đáp án A
Nhận thấy đây là đồ thị hàm số dạng x y a . Ta có (0
A ;1) và B(2; 2) thuộc đồ thị hàm số. 0 a 1 ° x Suy ra, 2
®a 2 a 2 . Hàm số là y 2 . °a ! 0 ¯
Câu 18. Chọn đáp án A 1 1 2 1 1 1 1 3 3 3
y (x 1) y ' (x 1) '.(x 1) (x 1) . 3 3 3 2 3 (x 1)
Câu 19. Chọn đáp án A 2x 2x 2x y 4
y ' (2x)'.4 ln 4 2.4 ln 4.
Câu 20. Chọn đáp án A 1
y log x y ' . 5 x ln 5
Câu 21. Chọn đáp án A 1 2 2 2 y log
x y ' (x ) '. . 0,5 2 x ln 0,5 x ln 0,5
Câu 22. Chọn đáp án A 2 3x 3 3
y sin x log x y ' cos x cos x . 3 3 x ln 3 x ln 3
Câu 23. Chọn đáp án A 4 3 (x 1)' 4x 4
f (x) ln(x 1) f '(x) f '(0) 0 . 4 4 x 1 x 1
Câu 24. Chọn đáp án A 2 2 2017x 2017x f (x) e
f '(x) 2.2017x.e f '(0) 0 .
Câu 25. Chọn đáp án A ( ) . x '( ) x . x ''( ) x x . x f x x e f x e x e f x e e
x e f ''(1) 3e .
Câu 26. Chọn đáp án A § 1 ·
Nhận thấy đây là đồ thị hàm số y log x . Điểm ; 1
thuộc đồ thị hàm số nên a ¨ ¸ © 2 ¹ 1 1 1 1 1 1 log
a a 2 . Hàm số là y log x . a 2 2 2 a 2
Câu 27. Chọn đáp án A Hàm số D
y x có tập xác định thay đổi tùy theo D .
Câu 28. Chọn đáp án A
Hàm số lôgarit chỉ xác định khi x ! 0 nên đồ thị hàm số nằm bên phải trục tung.
Câu 29. Chọn đáp án A
Đồ thị hàm số lôgarit nằm bên phải trục tung và cả dưới, cả trên trục hoành.
Câu 30. Chọn đáp án A
Nhận thấy đây là đồ thị hàm số y log x . Điểm (2 A ; 1
) thuộc đồ thị hàm số nên a 1 1 1
log 2 a 2 2 a 0,5 . Hàm số y log x . a 0,5 a y O 1 2 x 1
Câu 31. Chọn đáp án A Đồ thị hàm số đi qua 2 (2
A ; 2) 2 log 2 a 2 a 2 . a y 2 O x 1 2
Câu 32. Chọn đáp án A 10 Hàm số xác định x
! 0 x 1hoặc 2 x 10 2 x 3x 2
Tập xác định D f ;1 2;10
Câu 33. Chọn đáp án A x 2 ! 0
Hàm số xác định log x 2 3 t 0 ® x t 29 3 3 ¯x 2 t 2
Tập xác định D >29;f
Câu 34. Chọn đáp án A x / x x y x x e y x x e e / 2 / 2 2 2 2 x 2x / x x 2 2 2 2 2 2 x y x e e x x x e
Câu 35. Chọn đáp án A
Hàm số có tập xác định là 2 x 2mx 4 ! 0, 0 x 2 '' m 4 0 2 m 2
Câu 36. Chọn đáp án A. Sử dụng điều kiện xác định của các hàm số.
Câu 37. Chọn đáp án A
Sử dụng lý thuyết phép suy đồ thị.
Câu 38. Chọn đáp án A x / x y ex e y e e . Suy ra / 0 x y e e 0 x 1
Câu 39. Chọn đáp án A Nhận dạng đồ thị:
- Dựa vào đồ thị thì hàm đã cho đồng biến loại C và D.
- Đồ thị đã cho qua điểm A2;
2 . Thử với hai đáp án còn lại loại B.
Câu 40. Chọn đáp án A Trên đoạn > 1 ; @ 1 , ta có: / x f
x xe x 2 ; /
f x 0 x 0 hoặc x 2 (loại). Ta có: f 1 1 ; f 0 0; f 1 e e
Suy ra: max f x e > 1; @ 1
Câu 41. Chọn đáp án A
Sử dụng lý thuyết phép suy đồ thị.
Câu 42. Chọn đáp án A x 1! 0 Hàm số xác định ® x !1 ¯x 1z 0
Tập xác định D 1;f
Câu 43. Chọn đáp án A
Đặt t x , với x> 2; @ 2 t >0; @ 2 Xét hàm 2t f t
trên đoạn >0;2@; f t đồng biến trên >0;2@
max y max f t 4 ; min y min f t 1 > 2; 2@ >0;2@ > 2; 2@ >0; @ 2 Hoặc với x x
x >2;2@ x >0;2 @ . Từ đây, suy ra: 0 2 2 d 2 d 2 1d 2 d 4
Câu 44. Chọn đáp án A
Tập xác định D 0;f 1 ln / x / ; y
; y 0 x e 2 ln x Hàm /
y đổi dấu từ âm sang dương khi qua x e nên x e là điểm cực tiểu của hàm số.
Câu 45. Chọn đáp án A
Do y log x và y log x là hai hàm dồng biến nên , a b ! 1 a b
Do y log x nghịch biến nên c 1. Vậy c bé nhất. c log x m a x a ° m
Mặt khác: Lấy y m, khi đó tồn tại x , x ! 0 để 1 1 ® 1 2 ® log x ¯ m ° m b b 2 ¯ 2 x Dễ thấy m m 1 x 2 x a b a b
Vậy b ! a ! c .
Câu 46. Chọn đáp án A 2m 1 x ! 0 x 2m 1 Hàm số xác định ® ® ¯x m ! 0 ¯x ! m
Suy ra, tập xác định của hàm số là D ;2 m m 1 , với m t 1 . m d m d
Hàm số xác định trên 2;3 suy ra 2 2 2;3 D ® ® ¯2m 1t 3 ¯m t1
Câu 47. Chọn đáp án A Tập xác định D Đạo hàm: / y 2 x / 2 ln 1 1
; y 0 1 1 x 1 x 0 Lập bảng biến thiên : x ∞ 0 +∞ y' + 0 y 1
Câu 48. Chọn đáp án A 1 y ln lnx 1 / 1 y x 1 x 1 1 Ta có: § 1 · x 1 ln y 1 xy '1 x 1 1 ¨ ¸ , x 1 e e . © x 1¹ x 1 x 1 x 1
Câu 49. Chọn đáp án A / / 2 2x 2x 2x 2 x e 1 e 1 e 1 x e 1 4 x / 2
Ta biến đổi hàm số về dạng e 1 e y y . 2 x e 1 x e 2 1 x e 2 2 2 1
Câu 50. Chọn đáp án A / //
y x sin x y sin x x cos x y 2cos x x sin x Ta có: // /
xy 2y xy x 2cos x xsin x 2sin x x cos x .
x xsin x 2s in x
Câu 51. Chọn đáp án A Do x y a và x
y b là hai hàm đồng biến nên , a b ! 1. Do x y
c nghịch biến nên c 1. Vậy x bé nhất. ° m a y
Mặt khác: Lấy x m , khi đó tồn tại y , y ! 0 để 1 1 2 ® ° m b ¯ y2 Dễ thấy m m 1 y 2 y a b a b
Vậy b ! a ! c .
PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH MŨ
A. KIẾN THỨC CƠ BẢN
1. Phương trình mũ cơ bản x
a b a ! 0, a z 1 .
● Phương trình có một nghiệm duy nhất khi b ! 0.
● Phương trình vô nghiệm khi b d 0 .
2. Biến đổi, quy về cùng cơ số 0 a z 1 ° f x g x a a a 1 hoặc ® . ° f ¯ x g x 3. Đặt ẩn phụ g x t ° a ! g x f ªa º a z 0 0 0 1 ® ¬ ¼ . ° f ¯ t 0
Ta thường gặp các dạng: ● 2 f x f x . m a . n a p 0 ● f x f x . m a . n b p 0, trong đó . a b 1. Đặt f x t a
, t ! 0 , suy ra f x 1 b . t f x § · ● 2 f x . 2 a m a . n . a b f x 2 f x . p b
0 . Chia hai vế cho f x b và đặt t ! 0 ¨ ¸ . © b ¹ 4. Logarit hóa 0 a z 1, b ! 0 °
● Phương trình f x a b ® . ° f ¯ x log b a
● Phương trình f x g x f x gx a b log a log b f x g x b a a .loga hoặc f x g x log a log b f x a g x b b .logb .
5. Giải bằng phương pháp đồ thị
o Giải phương trình: x
a f x 0 a z 1 .
o Xem phương trình là phương trình hoành độ giao điểm của hai đồ thị x
y a 0 a z 1 và
y f x . Khi đó ta thực hiện hai bước:
¾ Bước 1. Vẽ đồ thị các hàm số x
y a 0 a z
1 và y f x .
¾ Bước 2. Kết luận nghiệm của phương trình đã cho là số giao điểm của hai đồ thị.
6. Sử dụng tính đơn điệu của hàm số
o Tính chất 1. Nếu hàm số y f x luôn đồng biến (hoặc luôn nghịch biến) trên ;
a b thì số nghiệm của
phương trình f x k trên ;
a b không nhiều hơn một và f u f v u , v u ,v ; a b .
o Tính chất 2. Nếu hàm số y f x liên tục và luôn đồng biến (hoặc luôn nghịch biến) ; hàm số
y g x liên tục và luôn nghịch biến (hoặc luôn đồng biến) trên D thì số nghiệm trên D của phương
trình f x g x không nhiều hơn một.
o Tính chất 3. Nếu hàm số y f x luôn đồng biến (hoặc luôn nghịch biến) trên D thì bất phương trình
f u ! f v u ! v hoac u v, u ,v D .
7. Sử dụng đánh giá
o Giải phương trình f x g x . f ° x t m f ° x m
o Nếu ta đánh giá được ®
thì f x g x ® . °g ¯ x d m °g ¯ x m
8. Bất phương trình mũ
x Khi giải bất phương trình mũ, ta cần chú ý đến tính đơn điệu của hàm số mũ. ªa !1 ° «® f x g x ªa t a ° f
«¯ x ! g x « f x g x f x g x a ! a «
. Tương tự với bất phương trình dạng: «a a 0 a 1 ° « « ® f x g x « a d a « ¬° f ¯ x g x ¬
x Trong trường hợp cơ số a có chứa ẩn số thì: M N a ! a a 1 M N ! 0 .
x Ta cũng thường sử dụng các phương pháp giải tương tự như đối với phương trình mũ: + Đưa về cùng cơ số. + Đặt ẩn phụ. y f °
xđồng biến trênD thì: f u f v u v
+ Sử dụng tính đơn điệu: ® °y f ¯
xnghịch biến trên D thì: f u f v u ! v
B. BÀI TẬP TRẮC NGHIỆM
NHẬN BIẾT – THÔNG HIỂU
Câu 1. Cho phương trình 2x4x5 3
9 tổng lập phương các nghiệm thực của phương trình là: A. 28. B. 27. C. 26. D. 25. Hướng dẫn giải Ta có: ª 2 2 x 1 x 4 x5 x 4 x5 2 2 2 3 9 3
3 x 4x 5 2 x 4x 3 0 «¬x 3 Suy ra 3 3
1 3 28 . Chọn đáp án A
Câu 2. Cho phương trình : 2x3x8 2x 1 3 9
, khi đó tập nghiệm của phương trình là: ° 5 61 5 61½° A. S ^2; ` 5 B. S ® ; ¾ ° 2 2 ¯ °¿ °5 61 5 61½° C. S ® ; ¾ D. S ^ 2; ` 5 . ° 2 2 ¯ °¿ Hướng dẫn giải 2 x 3x8 2x 1 3 9 ª 2 x 5 x 3x8 4x2 2 2 3 3
x 3x 8 4x 2 x 7x 10 0 «¬x 2 Vậy S ^2; ` 5 § · x 1 x
Câu 3. Phương trình 1 3
2 ¨ ¸ có bao nhiêu nghiệm âm? © 9 ¹ A. 1. B. 3. C. 2. D. 0. Hướng dẫn giải x x 2 3 § 1 · § 1 · § 1 x ·
Phương trình tương đương với 2 3. 2 ¨ ¸ ¨ ¸ ¨ ¸ . 3x © 9 ¹ © 3 ¹ © 3 ¹ § 1 x · ªt 1
Đặt t ¨ ¸ , t ! 0. Phương trình trở thành 2 2
3t 2 t t 3t 2 0 . © 3 ¹ « ¬t 2 § 1 x ·
● Với t 1, ta được 1 x 0 ¨ ¸ . © 3 ¹ § 1 x ·
● Với t 2, ta được 2 x log 2 log 2 0 ¨ ¸ . 1 3 © 3 ¹ 3
Vậy phương trình có một nghiệm âm. 2x2 x § 1 ·
Câu 4. Số nghiệm của phương trình 2 9 9. 4 0 ¨ ¸ là: © 3 ¹ A. 2. B. 4. C. 1. D. 0. Hướng dẫn giải x 1 § · x 1
Phương trình tương đương với 3 9. 4 0 ¨ ¸ © 3 ¹ § 1 x · x x 1 2 3 3. 4 0 3 3.
4 0 3 x 4.3x 3 0 ¨ ¸ . © 3 ¹ 3x ªt 1 Đặt 3x t
, t ! 0. Phương trình trở thành 2 t 4t 3 0 « . ¬t 3
● Với t 1, ta được 3x 1 x 0 .
● Với t 3 , ta được 3x 3 x 1.
Vậy phương trình có nghiệm x 0 , x 1. 28 x4
Câu 5. Cho phương trình : 2 3 x 1 2 16
. Khẳng định nào sau đây là đúng ?
A. Tích các nghiệm của phương trình là một số âm.
B. Tổng các nghiệm của phương tình là một số nguyên .
C. Nghiệm của phương trình là các số vô tỉ.
D. Phương trình vô nghiệm. Hướng dẫn giải x d 1 x t1 x d 1 x t1 ° 28 ª 2 ª x 3 x4 ° ° 2 28 3 x 1 2 16 4 4 2 x x 3 2 1 ®ª 7 3 3x 3 x « « x x ® 3 7 . 3 °« « «x 2 ¯¬7 ° x 3 3 x 3 7 « ¬ 3 ° x 0 x « ¯¬ 3 7 ½
Nghiệm của phương trình là : S ® ;3¾ . ¯ 3 ¿ 7 Vì .3 7 0 . Chọn đáp án A 3 1
Câu 6. Phương trình 2 2 8 8 5 2 .5 0,001. 10 x x x
có tổng các nghiệm là: A. 5. B. 7. C. 7 . D. – 5 . Hướng dẫn giải 2 2 8x 3 55x 8x 25x 2 2.5 10 .10 10 10
8 x 2 5x x 1 ; x 6 Ta có : 1 6 5. Chọn đáp án A
Câu 7. Phương trình 9x 5.3x 6 0 có nghiệm là:
A. x 1, x log 2 . B. x 1
, x log 2 . C. x 1, x log 3. D. x 1 , x log 2 . 3 3 2 3 Hướng dẫn giải Đặt 3x t
( t ! 0), khi đó phương trình đã cho tương đương với ªt 2 ªx log 2 2 3 t 5t 6 0 « « ¬t 3 ¬x 1
Câu 8. Cho phương trình x x 1 4.4 9.2 8 0 . Gọi x ,1 2
x là hai nghiệm của phương trình trên. Khi đó, tích x .1 2 x bằng : A. 2 . B. 2 . C. 1 . D. 1. Hướng dẫn giải Đặt 2x t
( t ! 0), khi đó phương trình đã cho tương đương với ªt 4 ªx 2 2 1 4t 18t 8 0 « 1 « «t x 1 ¬ 2 ¬ 2 Vậy x .x 1 .2 2 . Chọn đáp án A 1 2
Câu 9. Cho phương trình x 1
4 4 x 3 . Khẳng định nào sau đây sai?
A. Phương trình vô nghiệm.
B. Phương trình có một nghiệm.
C. Nghiệm của phương trình là luôn lớn hơn 0.
D. Phương trình đã cho tương đương với phương trình: 2x 4 3.4x 4 0 . Hướng dẫn giải Đặt 4x t
( t ! 0), khi đó phương trình đã cho tương đương với ªt 4 2 t 3t 4 0 x 1 « ¬t 1( L) Chọn đáp án A
Câu 10. Cho phương trình 2 2 x x 1 x x2 9 10.3
1 0. Tổng tất cả các nghiệm của phương trình là: A. 2 . B. 2 . C. 1. D. 0 . Hướng dẫn giải Đặt 2 1 3x x t
( t ! 0), khi đó phương trình đã cho tương đương với ªx 2 2 x x 1 ªt 3 ª3 3 «x 1 2 3 « « t 10t 3 0 1 « 2 « « x x 1 1 t 3 «x 0 ¬ 3 «¬ 3 « ¬x 1
Vậy tổng tất cả các nghiệm của phương trình bằng 2.
Câu 11. Nghiệm của phương trình x x 1 x x 1 2 2 3 3 là: 3 2 A. x log . B. x 1. C. x 0 . D. x log . 3 4 4 3 2 3 Hướng dẫn giải § 3 x · x x x x x x 3 3 1 1 2 2 3 3 3.2 4.3 x log ¨ ¸ 3 © 2 ¹ 4 4 2
Câu 12. Nghiệm của phương trình 2x x2 2 3.2 32 0 là: A. x ^2; ` 3 . B. x ^4; ` 8 . C. x ^2; ` 8 . D. x ^3; ` 4 . Hướng dẫn giải ª2x 8 ªx 2 2x x2 2 2 3.2
32 0 2 x 12.2x 32 0 « « ¬2x 4 ¬x 3
Câu 13. Nghiệm của phương trình 6.4x 13.6x 6.9x 0 là: 2 3½ A. x ^1; ` 1 . B. x ® ; ¾. C. x ^ 1 ; ` 0 . D. x ^0; ` 1 . ¯3 2¿ Hướng dẫn giải 2 § · § · x x x 3 x 3 x 6.4 13.6 6.9 0 6 13 6 0 ¨ ¸ ¨ ¸ © 2 ¹ © 2 ¹ ª§ 3 x· 3 « ¨ ¸ «© 2 ¹ 2 ªx 1 « « § 3 x · 2 ¬x 1 « ¨ ¸ «¬© 2 ¹ 3
Câu 14. Nghiệm của phương trình x x x 1 12.3 3.15 5 20 là: A. x log 5 1. B. x log 5 . C. x log 5 1. D. x log 3 1. 3 3 3 5 Hướng dẫn giải x x x 1 12.3 3.15 5 20
3.3x 5x 4 55x 4 0 x x 1 5 4 3 5 0 x 1 3 5 x log 51 3
Câu 15. Phương trình 9x 5.3x
6 0 có tổng các nghiệm là: 2 3 A. log 6 . B. log . C. log . D. log 6 . 3 3 3 3 2 3 Hướng dẫn giải 9x 5.3x 6 0 1 x x x2 2 1 3 5.3 6 0 3 5.3x 6 0 1' ªt 2 N Đặt 3x t ! 0 . Khi đó: 1' 2 t 5t 6 0 « «t 3 ¬ N Với 2 3x t 2 x log 2 . 3 Với 3 3x t 3 x log 3 1 . 3
Suy ra 1 log 2 log 3 log 2 log 6 3 3 3 3
Câu 16. Cho phương trình 12
2 x 15.2x 8 0 , khẳng định nào sau dây đúng? A. Có một nghiệm. B. Vô nghiệm.
C. Có hai nghiệm dương.
D. Có hai nghiệm âm. Hướng dẫn giải 12 2 x 15.2x 8 0 2 x x x2 2 2 2.2 15.2 8 0 2. 2 15.2x 8 0 2' ª 1 t N Đặt 2x « t ! 0. Khi đó: 2' 2 2t 15t 8 0 2 « «t 8 ¬ L 1 x 1 1
Với t 2 x log x 1 2 2 2 2
Câu 17. Phương trình x 1
5 25 x 6 có tích các nghiệm là : §1 21 · §1 21 · §1 21 · A. log . B. log . C. 5. D. 5log . 5 ¨ ¸ ¨ ¨ ¸ ¨ ¸ 2 ¸ 5 ¨ ¸ 5 ¨ ¸ © ¹ 2 © ¹ 2 © ¹ Hướng dẫn giải x 1 5 25 x 6 1 x 25 x 25 x 25 1 5 6 0 5 6 0 5 6 0 6' . Đặt 5x t ! 0 . x x 2 25 25 5x ª «t 5 N « 25 « 1 21 Khi đó: 6' 3 t
6 0 t 6t 25 0 t 5 2t t 5 0 t N 2 t « 2 « « 1 21 t L «¬ 2 Với 5 5x t 5 x 1 . 1 21 § · x 1 21 1 21 Với t 5 x log . 5 ¨ ¸ 2 2 ¨ 2 ¸ © ¹ §1 21 · §1 21 · Suy ra: 1.log ¨ ¸ log 5 5 ¨ ¸ ¨ 2 ¸ ¨ 2 ¸ © ¹ © ¹ x x
Câu 18. Phương trình 7 4 3 2 3 6 có nghiệm là: A. x log
2 . B. x log 3 . C. x log 2 3 . D. x 1. 2 2 3 2 Hướng dẫn giải x
Đặt t 2 3 ( t ! 0), khi đó phương trình đã cho tương đương với ªt 2 2 t t 6 0 x log « ¬ 2 2 3 t 3(L) 1 x § ·
Câu 19. Tập nghiệm của bất phương trình ! 32 ¨ ¸ là: © 2 ¹ A. x ; f 5 . B. x ;5 f . C. x 5; f . D. x 5;f . Hướng dẫn giải 1 x § · x 5 ! § 1 · § 1 · 32 ¨ ¸ ! ¨ ¸ ¨ ¸ x 5 © 2 ¹ © 2 ¹ © 2 ¹ Câu 20. Cho hàm số 2 2x sin 2 .3 x f x
. Khẳng định nào sau đây là khẳng định đúng ? A. f x 2 1 x ln 4 sin x ln 3 0 . B. f x 1
2x 2sin xlog 3 0 . 2 C. f x 2
1 xlog 2 sin x 0. D. f x 2 1 2 x log 3 0 . 3 2 Hướng dẫn giải 2 2x sin x f x 2 1 ln 2 .3 ln1 xln 4 sin x ln3 0 Chọn đáp án A
Câu 21. Tập nghiệm của bất phương trình x x 1 x x 1 2 2 3 3 d A. x >2;f.
B. x 2;f . C. x ;2 f . D. 2;f . Hướng dẫn giải 3 x § · 9 x x 1 x x 1 2 2 3 3 d x 4 3.2 .3x d t ¨ ¸ x t 2 3 © 2 ¹ 4 x 2 § 1 x ·
Câu 22. Tập nghiệm của bất phương trình x 1 ! 3 ¨ ¸ là: © 9 ¹ ªx 2 A. « . B. x 2 . C. 1 x 0 . D. 1 d x 0 . ¬ 1 x 0 Hướng dẫn giải Điều kiện: x z 1 2x x x § · x 2 2 1 2 x 1 pt 3 ! 3 2 x ! 2x 0 2x 1 0 ¨ ¸ x 1 x 1 © x 1 ¹ 2x x 2 ªx 2 ªx 2 0 «
. Kết hợp với điều kiện « x 1 ¬ 1 x 0 ¬ 1 x 0
Câu 23. Tập nghiệm của bất phương trình 16x 4x 6 d 0 là A. x d log 3. B. x ! log 3. C. x t1. 4 4 D. x t 3 Hướng dẫn giải Đặt 4x t
( t ! 0), khi đó bất phương trình đã cho tương đương với 2 t t 6 d 0 2
d t d 3 0 t d 3 x d log 3. 4 3x
Câu 24. Tập nghiệm của bất phương trình 3 là: 3x 2 ªx !1 A. « . B. x ! log 2. C. x 1. D. log 2 x 1. x log 2 ¬ 3 3 3 Hướng dẫn giải 3x 3x 3 ª3x ! 3 ªx !1 3 ! 0 « 3 « x 2 3x 2 ¬3x 2 x log 2 ¬ 3
Câu 25. Tập nghiệm của bất phương trình x6 11 t11x là: A. 6 d x d 3. B. x 6 . C. x ! 3. D. . Hướng dẫn giải ªx 0 «® ª 6 d x 0 «¯x 6 t 0 « x6 11
t11x x 6 t x x t 0 6 d x d 3 « « x t 0 ® « « ® ¬¯ 2 d x d 3 2 «¬¯x 6 t x 1 1
Câu 26. Tập nghiệm của bất phương trình d là: x x 1 3 5 3 1 A. 1 x d1. B. x d 1. C. x !1. D. 1 x 2. Hướng dẫn giải Đặt 3x t
( t ! 0), khi đó bất phương trình đã cho tương đương với 1 1 3 t 1 ! 0 1 d ® t d 3 1 x d1. t 5 3t 1 3 ¯ t 1d t 5 3 2 x x 1 2x 1 5 5 § · § ·
Câu 27. Cho bất phương trình ! ¨ ¸ ¨ ¸
, tập nghiệm của bất phương trình có dạng S ; a b . © 7 ¹ © 7 ¹
Giá trị của biểu thức A b a nhận giá trị nào sau đây? A.1. B. 1. C. 2. D. 2. Hướng dẫn giải 2 x x 1 2x 1 5 5 § · § · 2 2 !
x x 1 2x 1 x 3x 2 0 1 x 2 ¨ ¸ ¨ ¸ © 7 ¹ © 7 ¹
Vậy tập nghiệm của bất phương trình là S 1;2 . Chọn đáp án A
Câu 28. Tập nghiệm của bất phương trình 4x 3.2x 2 ! 0 là: A. x ;0 f 1;f. B. x f ;1 2;f. C. x 0; 1 . D. x 1;2. Hướng dẫn giải ª2x ! 2 ªx !1
4x 3.2x 2 ! 0 « « ¬2x 1 ¬x 0
Câu 29. Tập nghiệm của bất phương trình x x 1 3 .2 t 72 là: A. x >2;f. B. x 2;f. C. x ;2 f . D. x ;2 f @. Hướng dẫn giải x x 1
3 .2 t 72 2.6x t 72 x t 2 x
Câu 30. Tập nghiệm của bất phương trình x 1 2x 1 2 3 2 12 0 là: A. x 0;f. B. x 1;f. C. x ;0 f . D. x f ;1 . Hướng dẫn giải x x x x x x § · § · x 1 2x 1 2 3 2 12 0 2 2 2 3.9 2.16 12 2 2 16 4 0 3. 2. 0 ¨ ¸ ¨ ¸ © 9 ¹ © 3 ¹ x 2 § 4 · !1 ¨ ¸ x ! 0 © 3 ¹ x x2 2.3 2
Câu 31. Tập nghiệm của bất phương trình d1 là: 3x 2x § º ª º
A. x ¨0;log 3». B. x 1;3. C. x 1; @ 3 .
D. x «0;log 3». 3 3 © 2 ¼ ¬ 2 ¼ Hướng dẫn giải § 3 x · § 3 x · 2. 4 2. 4 x x2 2.3 2 ¨ ¸ ¨ ¸ d1 © 2 ¹ d © 2 1 ¹ 1d 0 3x 2x § 3 x · x § 3 · 1 ¨ ¸ 1 ¨ ¸ © 2 ¹ © 2 ¹ § 3 x · 3 ¨ ¸ © 2 ¹ x d § 3 · 0 1 d 3 ¨ ¸ 0 x d log 3 § 3 x · © 2 ¹ 3 1 ¨ ¸ 2 © 2 ¹ 1 3 2 x § · § 2 ·
Câu 32. Tập nghiệm của bất phương trình d ¨ ¸ ¨ ¸ là: © 5 ¹ © 5 ¹ § 1º § 1 · § 1º § 1º A. 0; . ¨ B. 0; . ¨ ¸ C. ; f . ¨ D. ; f 0;f ¨ . 3» © ¼ © 3 ¹ 3» © ¼ 3» © ¼ Hướng dẫn giải 2 1 1 3x 1 Vì
1 nên bất phương trình tương đương với t 3 t 0 0 x d . 5 x x 3 § 1º
Vậy tập nghiệm của bất phương trình là 0; ¨ 3» © ¼
Câu 33. Tập nghiệm của bất phương trình 2x 4.5x 4 10x là: ªx 0 A. . « B. x 0. C. x ! 2. D. 0 x 2. ¬x ! 2 Hướng dẫn giải
2x 4.5x 4 10x
2x 10x 4.5x 4 0
2x 1 5x 41 5x 0 1 5x2x 4 0 ª 1 ° 5x 0 ª 5x ° !1 «® «® «°¯2x 4 ! 0 «°¯2x ! 4 ªx ! 2 x « « ; f 02;f « 1 «° 5x ! 0 5x «° 1 ¬x 0 ® ® « ¬°¯2x 4 0 « ¬°¯2x 4
Câu 34. Tập nghiệm của bất phương trình x 1 2 2 x 1 là: A. 1 d xd1. B. 8; 0. C. 1;9. D. 0; @ 1 . Hướng dẫn giải x 1 2 2 x 1
1 . Điều kiện: x t 0 x 2 1 2 1 2 . Đặt 2 x t . Do x t 0 t t1 2 x t t1 ° t t1 2 ® 2 ®
1d t 2 1d 2 x 2 0 d x1 2 t 1 t ° ¯ t 2 0 ¯ t VẬN DỤNG
Câu 35. Tìm tất cả các nghiệm của phương trình 2 2 2 x 3 x2 x 6x5 2x 3x7 4 4 4 1. A. x ^ 5 ; 1 ;1; ` 2 . B. x ^ 5 ; 1 ;1; ` 3 . C. x ^ 5 ; 1 ;1; ` 2 . D. x ^5; 1 ;1; ` 2 . Hướng dẫn giải 2 2 2 2 2 2 2 x 3 x2 x 6x5 2x 3x7 4 4 4 1 x 3x2 x 6x5 x 3 x2 x 6 x5 4 4 4 .4 1 2 2 2 x x 2x x 2 3 2 6 5 x 6 x5 4 1 4 1 4
0 x 3x2 x 6x5 4 1 1 4 0 2 x 3x2 ª4 1 0 2 ªx 3x 2 0 ªx 1 x 5 « « « 2 x 6 x5 1 « 2 ¬ 4 0 ¬x 6x 5 0 ¬x 1 x 2 x x x
Câu 36. Phương trình 3 2 3 2 10 có tất cả bao nhiêu nghiệm thực ? A. 1. B. 2. C. 3. D. 4. Hướng dẫn giải x x x x x § 3 2 · § 3 2 · 3 2 3 2 10 ¨ ¸ ¨ ¸ 1 ¨ 10 ¸ ¨ 10 ¸ © ¹ © ¹ x x § · § ·
Xét hàm số f x 3 2 3 2 ¨ ¸ ¨ ¸ ¨ 10 ¸ ¨ 10 ¸ © ¹ © ¹ Ta có: f 2 1 3 2 3 2
Hàm số f x nghịch biến trên do các cơ số 1; 1 10 10
Vậy phương trình có nghiệm duy nhất là x 2 .
Câu 37. Phương trình 2 3 x 2 3x 1 4.3x x
5 0 có tất cả bao nhiêu nghiệm không âm ? A. 1. B. 2. C. 0. D. 3. Hướng dẫn giải 2 3 x 2 3x 1 4.3x x 5 0 2 3 x 1 2 3x 1 4.3x x 4 0 3x 1 3x 1 2 43x x 1 0 3x 2 53x x 1 0 3x 2x 5 0 Xét hàm số 3x f x
2x 5 , ta có : f 1 0. ' 3x f x ln 3 2 ! 0; x
. Do đó hàm số f x đồng biến trên .
Vậy nghiệm duy nhất của phương trình là x 1
Câu 38. Phương trình 2 x3 x 5x6 2 3 có hai nghiệm x ,
, hãy chọn phát biểu đúng? 1 2 x trong đó 1 x 2 x
A. 3x 2x log 8 .
B. 2x 3x log 8 . 1 2 3 1 2 3
C. 2x 3x log 54.
D. 3x 2x log 54. 1 2 3 1 2 3 Hướng dẫn giải
Logarit hóa hai vế của phương trình (theo cơ số 2) ta được: 2 x3 x 5x6 3 log 2 log 3 2 2 x 3 log 2 2
x 5x 6 log 3 x 3 x 2 x 3 log 3 0 2 2 2 ªx 3 ª ª « x ª ¬ x x 3 0 x 3 3 . 1 2 log 3º 0 ¼ « « 1 2 1 ¬ x 2log 3 x 2 log 3 1 «x 2 2 ¬ 2 « log 3 ¬ 2 ªx 3 ªx 3 ªx 3 « « « x log 2 2 x log 2 log 9 x log 18 ¬ 3 ¬ 3 3 ¬ 3 x x
Câu 39. Cho phương trình 7 4 3 2 3 6 . Khẳng định nào sau đây là đúng?
A. Phương trình có một nghiệm vô tỉ.
B. Phương trình có một nghiệm hữu tỉ.
C. Phương trình có hai nghiệm trái dấu.
D. Tích của hai nghiệm bằng 6 . Hướng dẫn giải x x 7 4 3 2 3 6 8 x 2 ª« 2 x x x 8 2 3 º ¬ » 2 3 6 0 ª2 3 ¼ « º ¬ » 2 3 6 0 8' ¼ x Đặt t 2 3 ! 0 . ªt 2 N x Khi đó: 8' 2 t t 6 0 «
. Với t 2 2 3 2 x log 2 « 2 3 t 3 ¬ L Chọn đáp án A
Câu 40. Phương trình 33x 3 3 x 4x 4x 3 3 3 3 3
10 có tổng các nghiệm là ? A. 0. B. 2. C. 3. D. 4 . Hướng dẫn giải 33x 3 3 x 4x 4x 3 3 3 3 3 10 7 § · § · 7 x 27 x 81 x 1 x 1 3 3 3 3 27.3 81.3 10 27. 3 81. 3 10 7' 3 ¨ ¸ ¨ ¸ x x 3x x 3 3 © 3 ¹ © 3 ¹ Côsi x 1 x 1 Đặt t 3 t 2 3 . 2 3x 3x 3 § · x 1 x x 1 x 1 1 x 1 3 3 2 3 3 t 3 3 3.3 . 3.3 . 3 t 3t ¨ ¸ x x 2x 3x 3 © 3 ¹ 3 3 3 3 x 3 10 10
Khi đó: 7' 27 3t 3t 3 3 81t 10 t t ! 2 N 27 3 10 x 1 10 Với t 3 x 7' 3 3 3 ª y 3 N 1 10 Đặt 3x « y ! 0 . Khi đó: 7' 2 y 3y 10y 3 0 1 y 3 « y N «¬ 3 Với 3 3x y 3 x 1 1 x 1 Với y 3 x 1 3 3
Câu 41. Phương trình 2 2 sin x cos 9 9 x 6 có họ nghiệm là ? π kπ π kπ A. x , k . B. x , k . 4 2 2 2 π kπ π kπ C. x , k . D. x , k . 6 2 3 2 Hướng dẫn giải 2 2 sin x x 9 x cos 9 9 x 6 2 2 2 1 cos cos cos 9 9 6 9 x 6 0 * 2 cos 9 x 9 Đặt 2 cos 9 x t , 1d t d 9 . Khi đó: 2
* t 6 0 t 6t 9 0 t 3 t π kπ Với 2 2 cos x 2cos x 1 2 t 3 9 3 3
3 2cos x 1 0 cos 2x 0 x , k 4 2 x x
Câu 42. Với giá trị nào của tham số m thì phương trình 2 3 2 3 m vô nghiệm? A. m 2. B. m ! 2 . C. m 2 . D. m d 2 . x x
Câu 43. Với giá trị nào của tham số m thì phương trình 2 3 2 3 m có hai nghiệm phân biệt? A. m ! 2 . B. m 2. C. m 2 . D. m d 2 .
Hướng dẫn giải câu 8 & 9 x x
Nhận xét: 2 32 3 1 2 3 2 3 1. x x 1
Đặt t 2 3 2 3 , t 0,f . t 1
t m f t 1 1
t m 1', t 0,f . t t Xét hàm số 1
f t t xác định và liên tục trên 0, f . t 2 1 1 Ta có: ' 1 t f t
. Cho f 't 0 t 1 r . 2 2 t t Bảng biến thiên: t 1 0 1 f f 't 0 f f f t 2
Dựa vào bảng biến thiên:
+ Nếu m 2 thì phương trình 1' vô nghiệm pt 1 vô nghiệm.
Câu 8 chọn đáp án A
+ Nếu m 2 thì phương trình 1' có đúng một nghiệm t 1 pt 1 có đúng một nghiệm x t 2 3 1 x 0.
+ Nếu m ! 2 thì phương trình 1' có hai nghiệm phân biệt pt
1 có hai nghiệm phân biệt.
Câu 9 chọn đáp án A x 2 2 x 1 2 2 2 x 2 4 Câu 44. Gọi 2 x , x 3 2 2 2 2 1 . Khi đó, tổng hai 1 2
x là hai nghiệm của phương trình nghiệm bằng? A. 0. B. 2. C. 2. D. 1. Hướng dẫn giải 4 2 2 x 1 2 2 x 2 3 1 2 2 x 1 2 2 2 2 2 x x x x 1 2 x 1 2 2 2 2 1 8.2 2 4.2 4.2 1 Đặt 2 x 1 t 2
t t 2 , phương trình trên tương đương với 2 2 2
8t t 4t 4t 1 t 6t 1 0 t 3 10 (vì t t 2 ). Từ đó suy ra ª 3 10 «x log 1 2 2 x 1 « 2 2 3 10 « 3 10 «x log 2 2 «¬ 2
Vậy tổng hai nghiệm bằng 0 .
Câu 45. Với giá trị của tham số m thì phương trình 1 16x 22 34x m m 6m 5 0 có hai nghiệm trái dấu? 3 5 A. 4 m 1 .
B. Không tồn tại m . C. 1 m . D. 1 m . 2 6 Hướng dẫn giải
Đặt 4x t ! 0. Phương trình đã cho trở thành: m 2 1
1 t 22m 3t 6m 5 0. 0 * f t Yêu cầu bài toán * có hai nghiệm t , 0 t 1 1 t thỏa mãn 2 1 t2 m 1z 0 m 1z 0 ° ° ® m 1 f 1 0 ® m 1 3m 12 0 4 m 1 . ° ° m ¯ 1 6m 5 ! 0 m ¯ 1 6m 5 ! 0 1 1
Câu 46. Cho bất phương trình: t
. Tìm tập nghiệm của bất phương trình. x 1 5 1 5 5x A. S 1 ;0@1;f. B. S 1 ;0@1;f. C. S ;0 f @. D. S ;0 f . Hướng dẫn giải 615x 1 1 t t 0 (1) . x 1 5 1 5 5x 5.5x 155x 61t 61t Đặt 5x t , BPT (1) t f (t) t . Đặt t 0 5 1 5 5t 15 . t 61t
Lập bảng xét dấu f (t) 5t 15 , ta được nghiệm: t ª5 t ª5 5x 1 ª x « « 1 1 « « . t d 1 « 5x d1 ¬ 1 x d 0 ¬5 «¬5
Vậy tập nghiệm của BPT là S 1 ;0@1;f .
Câu 47. Bất phương trình 2 2 2 x 2x 1 x 2x 1 x 2 25 9 t 34.15
x có tập nghiệm là: A. S ;1 f 3º >0;2@ 1 ª 3;f ¼ ¬ . B. S 0;f. C. S 2;f. D. S 1 3;0. Hướng dẫn giải ª0 d x d 2 2 2 x 2x 1 2 x 2x 1 2 2 2 § · § · « x x x x x x 5 34 5 2 1 2 1 2 25 9 t 34.15 1t . x d1 3 ¨ ¸ ¨ ¸ « © 3 ¹ 15 © 3 ¹ «x t1 3 ¬
Câu 48. Với giá trị nào của tham số m thì phương trình x x 1 4 . m 2
2m 0 có hai nghiệm x , 1 2 x thoả mãn x x 3 ? 1 2 A. m 4 .
B. m 2 . C. m 1. D. m 3 . Hướng dẫn giải Ta có: x x x 2 1 4 .2 2 0 2 2 .2x m m m 2m 0 *
Phương trình * là phương trình bậc hai ẩn 2x có: ' m2 2 '
2m m 2m . ªm t 2
Phương trình * có nghiệm 2
m 2m t 0 mm 2 t 0 « ¬m d 0
Áp dụng định lý Vi-ét ta có: 1 x 2 x 1 x 2 2 .2 2 2 x m 2m Do đó 3
x x 3 2 2m m 4 . 1 2
Thử lại ta được m 4 thỏa mãn. Chọn A.
Câu 49. Với giá trị nào của tham số m thì bất phương trình 2 2 2 sin x cos x sin 2 3 t .3 x m có nghiệm? A. m d 4. B. m t 4. C. m d1. D. m t1. Hướng dẫn giải
Chia hai vế của bất phương trình cho 2 sin 3 x ! 0 , ta được 2 2 sin x sin § 2 · § 1 x · 3. t m ¨ ¸ ¨ ¸ © 3 ¹ © 9 ¹ 2 2 sin x sin § 2 · § 1 x · Xét hàm số y 3. ¨ ¸ ¨ ¸
là hàm số nghịch biến. © 3 ¹ © 9 ¹ Ta có: 2
0 d sin x d1 nên 1d y d 4
Vậy bất phương trình có nghiệm khi m d 4. Chọn đáp án A
Câu 50. Cho bất phương trình:9x 1 .3x m m ! 0
1 . Tìm tất cả các giá trị của tham số m để bất phương trình 1 nghiệm đúng x !1. 3 3 A. m t . B. m ! . C. m ! 3 2 2. m t 2 D. 3 2 2. 2 Hướng dẫn giải Đặt 3x t
Vì x !1 t ! 3 Bất phương trình đã cho thành: 2 t m
1 .t m ! 0 nghiệm đúng t t 3 2 t t
! m nghiệm đúng t ! 3. t 1 2 2
Xét hàm số g t t 2 , t ! 3, g 't 1 ! 0, t
! 3 . Hàm số đồng biến trên t 1 t 2 1 > 3 3 3;f và g 3
3 . Yêu cầu bài toán tương đương m d m t 2 2 2
C. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM I – ĐÁP ÁN 1.2 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119
PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH LOGARIT
A. KIẾN THỨC CƠ BẢN 1. Định nghĩa
x Phương trình lôgarit là phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.
x Bất phương trình lôgarit là bất phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.
2. Phương trình và bất phương trình lôgarit cơ bản: cho ,
a b ! 0, a z 1
x Phương trình lôgarit cơ bản có dạng: log f (x) b a
x Bất phương trình lôgarit cơ bản có dạng: log f ( ) x ! ; b log f ( ) x t ; b log f ( ) x ; b log f ( ) x d b a a a a
3. Phương pháp giải phương trình và bất phương trình lôgarit
x Đưa về cùng cơ số f (x) ! 0
¾ log f (x) log g(x) ® , với mọi 0 a z1 a a
¯ f (x) g(x) g(x) ! 0
¾ Nếu a !1 thì log f (x) ! log g(x) ® a a
¯ f (x) ! g(x) f (x) ! 0
¾ Nếu 0 a 1 thì log f (x) ! log g(x) ® a a
¯ f (x) g(x) x Đặt ẩn phụ x Mũ hóa
B. KỸ NĂNG CƠ BẢN Câu 1.
Điều kiện xác định của phương trình
Điều kiện xác định của phươg trình 2
log(x x 6) x log(x 2) 4 là A. x ! 3 B. x ! 2 C. \[ 2;3] D. x ! 2 Câu 2.
Kiểm tra xem giá trị nào là nghiệm của phương trình
Phương trình log (3x 2) 3 có nghiệm là: 3 29 11 25 A. x B. x C. x D. x 87 3 3 3 Câu 3.
Tìm tập nghiệm của phương trình Phương trình 2 log (x 1) 6log
x 1 2 0 có tập nghiệm là: 2 2 A. ^3;1 ` 5 B. ^1; ` 3 C. ^1; ` 2 D. ^1; ` 5 Câu 4.
Tìm số nghiệm của phương trình
Số nghiệm của phương trình log log x log log x 2 là: 4 2 2 4 A. 1 B. 2 C. 3 D. 0 Câu 5.
Tìm nghiệm lớn nhất, hay nhỏ nhất của phương trình
Tìm nghiệm lớn nhất của phương trình 3 2
log x 2log x log x 2 là 1 1 A. x B. x C. x 2 D. x 4 2 4 Câu 6.
Tìm mối quan hệ giữa các nghiệm của phương trình (tổng, hiệu, tích, thương…) Gọi x ,
log 2 log x 0 . Khi đó tích x . 1 2
x là nghiệm của phương trình x bằng: x 16 1 2 A. 1 B. 1 C. 2 D. 2 Câu 7.
Cho một phương trình, nếu đặt ẩn phụ thì thu được phương trình nào (ẩn t ) 1 2 Nếu đặt t log thì phương trình
1 trở thành phương trình nào 2 x 5 log x 1 log 2 2 x A. 2 t 5t 6 0 B. 2 t 5t 6 0 C. 2 t 6t 5 0 D. 2 t 6t 5 0 Câu 8.
Tìm điều kiện của tham số m để phương trình thỏa điều kiện về nghiệm số (có
nghiệm, vô nghiệm, 2 nghiệm thỏa điều kiện nào đó…)
1. Tìm m để phương trình 2
log x 2log x m 1 0 có nghiệm 3 3 A. m d 2 B. m 2 C. m t 2 D. m ! 2
2. Tìm m để phương trình 2 2
log x log x 1 2m 1 0 có ít nhất một nghiệm thuộc đoạn 3 3 3 1; ª 3 º ¬ ¼ A. m[0;2] B. m(0;2) C. m(0;2] D. m[0;2) Câu 9.
Điều kiện xác định của bất phương trình
Điều kiện xác định của bất phương trình log (4x 2) log (x 1) ! log là: 1 1 1 x 2 2 2 1 A. x !1 B. x ! 0 C. x ! D. x ! 1 2
Câu 10. Tìm tập nghiệm của bất phương trình
1. Bất phương trình log (2x 1) log (4x 2) d 2 có tập nghiệm: 2 3 A. ( ; f 0] B. ( ; f 0) C. [0; ) f D. 0;f 2. Bất phương trình log 2 x x 2 t log
x 1 1 có tập nghiệm là: 2 0,5 A. 1 ª 2;f ª ¬ B. 1 2;f ¬ C. ;1 f 2º¼ D. ;1 f 2º¼
Câu 11. Tìm nghiệm nguyên (tự nhiên) lớn nhất, nguyên (tự nhiên) nhỏ nhất của bất phương trình
Nghiệm nguyên nhỏ nhất của bất phương trình log log x ! log log là: 2 4 4 2 x A. 17 B. 16 C. 15 D. 18
Câu 12. Tìm điều kiện của tham số m để bất phương trình thỏa điều kiện về nghiệm số (có
nghiệm, vô nghiệm, nghiệm thỏa điều kiện nào đó…)
Tìm m để bất phương trình log (5x 1).log (2.5x 2) d có nghiệm x t1 2 2 m A. m t 3 B. m ! 3 C. m d 3 D. m 3
C. BÀI TẬP TRẮC NGHIỆM
NHẬN BIẾT – THÔNG HIỂU
Câu 1. Điều kiện xác định của phươg trình log 16 2 là: 2x3 ª3 º 3 3 A. x \ ;2 « . B. x z 2 . C. x z 2 . D. x ! . ¬«2 » ¬2 ¼ 2 2
Câu 2. Điều kiện xác định của phươg trình 2
log (2x 7x 12) 2 là: x A. x 0; 1 1;f . B. x ;0 f . C. x 0; 1 . D. x 0;f .
Câu 3. Điều kiện xác định của phương trình log (x 1) log x là: 5 5 x 1 A. x 1;f . B. x 1 ;0. C. x \[ 1; 1 0] 0 . D. x f ;1 . 2x 1
Câu 4. Điều kiện xác định của phươg trình log là: 9 x 1 2 A. x 1 ;f . B. x \[ 1; 1 0] 0 . C. x 1 ;0. D. x f ;1 .
Câu 5. Phương trình log (3x 2) 2 có nghiệm là: 2 4 2 A. x . B. x . C. x 1. D. x 2 . 3 3
Câu 6. Phương trình log (x 3) log (x 1) log 5 có nghiệm là: 2 2 2 A. x 2 . B. x 1. C. x 3. D. x 0 .
Câu 7. Phương trình 2
log (x 6) log (x 2) 1 có tập nghiệm là: 3 3 A. T {0;3}. B. T . C. T {3}. D. T {1;3}.
Câu 8. Phương trình log x log (x 1) 1 có tập nghiệm là: 2 2 A. ^ 1 ; ` 3 . B. ^1; ` 3 . C. ^ ` 2 . D. ^ ` 1 .
Câu 9. Phương trình 2 log (x 1) 6log
x 1 2 0 có tập nghiệm là: 2 2 A. ^3;1 ` 5 . B. ^1; ` 3 . C. ^1; ` 2 . D. ^1; ` 5 .
Câu 10. Số nghiệm của phương trình log log x log log x 2 là: 4 2 2 4 A. 0. B. 2. C. 3. D. 1.
Câu 11. Số nghiệm của phương trình log .
x log (2x 1) 2log là: 2 3 2 x A. 2. B. 0. C. 1. D. 3.
Câu 12. Số nghiệm của phương trình 3 2
log (x 1) log (x x 1) 2log x 0 là: 2 2 2 A. 0. B. 2. C. 3. D. 1.
Câu 13. Số nghiệm của phương trình log 5x log 5x 3 0 là : 5 25 A. 3. B. 4. C. 1. D. 2.
Câu 14. Phương trình 2
log (5x 3) log (x 1) 0 có 2 nghiệm x , .Giá trị của 3 1 1 2 x trong đó 1 x 2 x 3 P 2x 3 là 1 2 x A. 5. B. 14. C. 3. D. 13.
Câu 15. Hai phương trình 2log (3x 1) 1 log (2x 1) và 2
log (x 2x 8) 1 log (x 2) lần 3 5 5 2 1 2
lượt có 2 nghiệm duy nhất là x , là? 1 2 x . Tổng 1 x 2 x A. 8. B. 6. C. 4. D. 10.
Câu 16. Gọi x ,
log 2 log x 0 . Khi đó tích x . 1 2
x là nghiệm của phương trình x bằng: x 16 1 2 A. 1 . B. 1. C. 2. D. 2 . 1 2
Câu 17. Nếu đặt t log thì phương trình
1 trở thành phương trình nào? 2 x 5 log x 1 log 2 2 x A. 2 t 5t 6 0 . B. 2 t 5t 6 0 . C. 2 t 6t 5 0 . D. 2 t 6t 5 0 . 1 2
Câu 18. Nếu đặt t lg x thì phương trình
1 trở thành phương trình nào? 4 lg x 2 lg x A. 2 t 2t 3 0 . B. 2 t 3t 2 0 . C. 2 t 2t 3 0 . D. 2 t 3t 2 0 .
Câu 19. Nghiệm bé nhất của phương trình 3 2
log x 2log x log x 2 là: 2 2 2 1 1 A. x 4 . B. x . C. x 2 . D. x . 4 2
Câu 20. Điều kiện xác định của bất phương trình log (4x 2) log (x 1) ! log là: 1 1 1 x 2 2 2 1 A. x ! . B. x ! 0 . C. x !1. D. x ! 1 . 2
Câu 21. Điều kiện xác định của bất phương trình log (x 1) 2log (5 )
x 1 log (x 2) là: 2 4 2 A. 2 x 5. B.1 x 2. C. 2 x 3 . D. 4 x 3.
Câu 22. Điều kiện xác định của bất phương trình 2 log ªlog (2 x )º ! 0 1 ¬ 2 ¼ là: 2 A. x [ 1;1]. B. x 1 ;0 0; 1 . C. x 1 ; 1 2;f . D. x 1 ; 1 .
Câu 23. Bất phương trình log (2x 1) log (4x
2) d 2 có tập nghiệm là: 2 3 A. [0; ) f . B. ( ; f 0). C. ( ; f 0] . D. 0;f .
Câu 24. Bất phương trình log 2 x x 2 t log
x 1 1 có tập nghiệm là: 2 0,5 A. 1 ª 2;f ª ¬ . B. 1 2;f ¬ . C. ;1 f 2º¼ . D. ;1 f 2º¼ .
Câu 25. Nghiệm nguyên nhỏ nhất của bất phương trình log log x t log log là: 2 4 4 2 x A. 6. B. 10. C. 8. D. 9.
Câu 26. Nghiệm nguyên nhỏ nhất của bất phương trình log 2 1 x d log 1 là: 3 1 x 3 1 5 1 5 A. x 0 . B. x 1. C. x . D. x . 2 2
Câu 27. Tập nghiệm của bất phương trình 2
log (x 3x 1) d 0 là: 2 ª 3 5 · § 3 5 º § 3 5 · § 3 5 · A. S «0; ¸ ¨ ;3» . B. S ¨0; ¸ ¨ ;3¸ . 2 ¸ ¨ 2 ¨ ¸ ¨ ¸ ¬ ¹ © ¼ 2 2 © ¹ © ¹ ª3 5 3 5 º C. S « ; » . D. S . 2 2 ¬ ¼
Câu 28. Điều kiện xác định của phương trình log (x 5) log (x 2) 3 là: 2 3 A. x t 5. B. x ! 2 . C. 2 x 5 . D. x ! 5.
Câu 29. Điều kiện xác định của phương trình 2
log(x 6x 7) x 5 log(x 3) là: ªx ! 3 2 A. x ! 3 2 . B. x ! 3. C. « . D. x 3 2 . «¬x 3 2
Câu 30. Phương trình log x log x log x 6 có nghiệm là: 3 3 1 3 A. x 27 . B. x 9 . C. 12 x 3 .
D. . x log 6 .. 3 x 1
Câu 31. Phương trình ln
ln x có nghiệm là: x 8 ªx 4 A. x 2 . B. « . C. x 4 . D. x 1. ¬x 2
Câu 32. Phương trình 2
log x 4log x 3 0 có tập nghiệm là: 2 2 A. ^8; ` 2 . B. ^1; ` 3 . C. ^6; ` 2 . D. ^6; ` 8 . 1
Câu 33. Tập nghiệm của phương trình log x 22 1 0 là: 2 2 A. ^ ` 0 . B. ^0; ` 4 . C. ^ ` 4 . D. ^ 1 ; ` 0 . 1
Câu 34. Tập nghiệm của phương trình log log 2 x x 1 là: 2 1 x 2 1 ° 5 1 5 ½° A. ^1 2`.
B. ^1 2;1 2`. C. ® ; ¾ . D. ^1 2` . ° 2 2 ¯ °¿
Câu 35. Phương trình log 3.2x 1 2x 1có bao nhiêu nghiệm? 2 A. 1. B. 2. C. 3. D. 0.
Câu 36. Số nghiệm của phương trình 2
ln x 6x 7 lnx 3là: A. 0. B. 2. C. 3. D. 1.
Câu 37. Nghiệm nhỏ nhất của phương trình log x 2.log x 2log x 2 là: 3 5 3 1 A. . B. 3. C. 2. D. 1. 5
Câu 38. Nghiệm lớn nhất của phương trình 3 2
log x 2log x 2 log x là : A. 100. B. 2. C. 10. D. 1000.
Câu 39. Gọi x , 2
log x x 5 log 2x 5 . 1 2
x là 2 nghiệm của phương trình 3 3 Khi đó bằng: 1 x 2 x A. 5. B. 3. C. 2 . D. 7. 1 2
Câu 40. Gọi x , 1. Khi đó x . 1 2
x là 2 nghiệm của phương trình x bằng: 4 log 1 2 x 2 log 2 2 x 1 1 1 3 A. . B. . C. . D. . 2 8 4 4
Câu 41. Gọi x , log ªx x 3 º 1 bằng: 1 2
x là 2 nghiệm của phương trình 2 ¬
¼ . Khi đó 1x 2x 3 17 A. 3 . B. 2 . C. 17 . D. . 2
Câu 42. Nếu đặt t log
thì phương trình log 4x log 2 3 trở thành phương trình nào? 2 2 x x 1 1 A. 2 t t 1 0 . B. 2 4t 3t 1 0 . C. t 1 . D. 2t 3 . t t
Câu 43. Nếu đặt t log x thì phương trình 2 3
log x 20log x 1 0 trở thành phương trình nào? A. 2 9t 20 t 1 0 . B. 2 3t 20t 1 0 . C. 2 9t 1 0t 1 0 . D. 2 3t 10t 1 0 . 1 log x 1
Câu 44. Cho bất phương trình 9 d
t log x thì bất phương trình trở thành: 1 . Nếu đặt log 3 x 2 3 1 2t 1 1 1 2t 1
A. 21 2t d1 t . B. d .
C. 1 t d 1 t . D. t 0 . 1 t 2 2 2 1 t
Câu 45. Điều kiện xác định của bất phương trình log (x 2) log (x 2) ! log x 3 là: 5 1 5 5 A. x ! 3. B. x ! 2 . C. x ! 2 . D. x ! 0 .
Câu 46. Điều kiện xác định của bất phương trình log (5x 15)d log 2 x 6x 8 là: 0,5 0,5 ªx 4 A. x ! 2 . B. « . C. x ! 3 . D. 4 x 2 . ¬x ! 2 2 x 1
Câu 47. Điều kiện xác định của bất phương trình ln 0 là: x ª 1 x 0 ªx 1 A. « . B. x ! 1 . C. x ! 0 . D. « . ¬x !1 ¬x !1
Câu 48. Bất phương trình 2 log x 5log x 6 có tập nghiệm là: 0,2 0,2 § 1 1 · § 1 · A. S ; ¨ ¸ . B. S 2;3 . C. S 0; ¨ ¸ . D. S 0;3 . ©125 25 ¹ © 25 ¹
Câu 49. Tập nghiệm của bất phương trình log 2 x 6x 5 log x 1 t 0 là: 1 3 3 A. S >1;6@. B. S 5;6@ . C. S 5;f . D. S 1;f .
Câu 50. Bất phương trình log 2
2x x 1 0 có tập nghiệm là: 2 3 § 3 · § 3 · A. S 0; ¨ ¸ . B. S 1 ; ¨ ¸ . © 2 ¹ © 2 ¹ § · § · C. S f 1 ;0 ;f ¨ ¸ . D. S f 3 ;1 ;f ¨ ¸ . © 2 ¹ © 2 ¹ 4x 6
Câu 51. Tập nghiệm của bất phương trình log d 0 là: 3 x ª 3 · ª 3 º A. S 2; « ¸ . B. S > 2; 0 . C. S ;2 f @. D. S \ ;0 . ¬ 2 ¹ «¬ ;0 2 » ¬ 2 ¼
Câu 52. Nghiệm nguyên nhỏ nhất của bất phương trình log x log x 2 log 3 là: 0,2 5 0,2 A. x 6 . B. x 3. C. x 5. D. x 4 .
Câu 53. Nghiệm nguyên lớn nhất của bất phương trình log x 1 4.3 ! 2x 1 là: 3 A. x 3. B. x 2 . C. x 1. D. x 1 .
Câu 54. Điều kiện xác định của phương trình log 3 ª log 3x 1 1º 2 ¬ 2 x ¼ là: 3 2 1 1 A. x ! . B. x t . 3 3 C. x ! 0 . D. x (0; ) f \{1}.
Câu 55. Điều kiện xác định của phương trình log 2 x x 1.log 2 x x 1 2 log x x 1 2 3 6 là: A. x d 1 . B. x t1.
C. x ! 0, x z 1. D. x d 1 hoặc x t1.
Câu 56. Nghiệm nguyên của phương trình log 2 x x 1.log 2 x x 1 2
log x x 1 là: 2 3 6 A. x 1. B. x 1 . C. x 2 . D. x 3. 3 § x · § 32 ·
Câu 57. Nếu đặt t log thì bất phương trình 4 2 2 log x log ¨ ¸ 9log 4log trở 1 2 1 2 x ¨ 2 ¸ 2 x 2 © 8 ¹ © x ¹ 2
thành bất phương trình nào? A. 4 2 t 13t 36 0 . B. 4 2 t 5t 9 0 . C. 4 2 t 13t 36 0 . D. 4 2 t 13t 36 0 . 3 § x · § 32 ·
Câu 58. Nghiệm nguyên lớn nhất của bất phương trình 4 2 2 log x log ¨ ¸ 9log 4log 1 2 1 2 x ¨ 2 ¸ 2 © 8 ¹ © x ¹ 2 là: A. x 7 . B. x 8. C. x 4 . D. x 1.
Câu 59. Bất phương trình log d có tập nghiệm là: x log 9x 72 1 3 A. S ªlog 73;2º .
B. S log 72;2º . C. S log 73;2º . D. S ;2 f @. 3 ¬ ¼ 3 ¼ 3 ¼
Câu 60. Gọi x , log ªx x 1 º 1 x . 1 2
x là nghiệm của phương trình 2 ¬
¼ . Khi đó tích 1 2x bằng: A. 2 . B. 1. C. 1 . D. 2. Câu 61. Nếu đặt log 5x t
1 thì phương trình log 5x 1 .log 2.5x 2 1 trở thành phương 2 4 2 trình nào? A. 2 t t 2 0 . B. 2 2t 1. C. 2 t t 2 0 . D. 2 t 1.
Câu 62. Số nghiệm của phương trình log x 12 .log 2 1 là: 4 x A. 0. B. 2. C. 3. D. 1.
Câu 63. Phương trình 2 log (2x 1) 8log
2x 1 3 0 có tập nghiệm là: 5 5 A. ^ 1 ; ` 3 . B.^1; ` 3 . C. ^3;6 ` 3 . D.^1; ` 2 . x 1 x 1 x 1
Câu 64. Nếu đặt t log
thì bất phương trình log log log log trở thành bất 3 4 3 1 1 x 1 x 1 x 1 4 3 phương trình nào? 2 t 1 2 t 1 2 t 1 A. 0. B. 2 t 1 0 . C. ! 0 . D. 0 . t t t
Câu 65. Phương trình log x x có nghiệm là: x 2 3 7 3 2 0 2 3
A. x 2; x 3 . B. x 2 . C. x 3.
D. x 1; x 5 .
Câu 66. Nghiệm nguyên nhỏ nhất của bất phương trình log log x ! log log là: 2 4 4 2 x A. 18. B.16 . C.15 . D.17 . 1 2
Câu 67. Phương trình
1 có tích các nghiệm là: 4 ln x 2 ln x 1 A. 3 e . B. . C. e . D. 2 . e
Câu 68. Phương trình log9 2 9 x x
x có bao nhiêu nghiệm? A. 1. B.0. C.2. D.3.
Câu 69. Nghiệm nguyên nhỏ nhất của bất phương trình log 3 log 3 0 là: x x 3 A. x 3. B. x 1. C. x 2 . D. x 4 .
Câu 70. Phương trình ln7 ln 7 x x 98 có nghiệm là:
A. x e . B. x 2 . C. 2 x e .
D. x e .
Câu 71. Bất phương trình log 2 x x 2 t log
x 1 1 có tập nghiệm là: 2 0,5 A. S 1 ª 2;f S ª ¬ . B. 1 2;f ¬ . C. S ;1 f 2º¼. D. S ;1 f 2º¼ . 1 1 7
Câu 72. Biết phương trình
log x 0 có hai nghiệm x ,x . Khẳng định nào sau đây là 2 log x 2 6 1 2 2 đúng? 2049 2047 A. 3 3 x x . B. 3 3 x x . 1 2 4 1 2 4 2049 2047 C. 3 3 x x . D. 3 3 x x . 1 2 4 1 2 4
Câu 73. Số nghiệm nguyên dương của phương trình log 4x 4 x log x 1 2 3 là: 2 1 2 A. 2. B.1. C.3. D.0.
Câu 74. Tập nghiệm của bất phương trình log log 2x 1 ! 0 là: 1 2 2 § 3 · § 3 · § 3 · A. S 1; ¨ ¸ . B. S 0; ¨ ¸ . C. S 0;1 . D. S ; 2 ¨ ¸ . © 2 ¹ © 2 ¹ © 2 ¹
Câu 75. Tập nghiệm của bất phương trình log 2
2x 3x 1 ! log 2x 1 là: 4 2 § 1 · § 1 · § 1 · § 1 · A. S ;1 ¨ ¸ . B. S 0; ¨ ¸ . C. S ;1 ¨ ¸ . D. S ;0 ¨ ¸ . © 2 ¹ © 2 ¹ © 2 ¹ © 2 ¹ 3
Câu 76. Tập nghiệm của bất phương trình log x x ! x là: x 125 2 .log log 25 5 2 A. S 1; 5 . B. S 1 ; 5 . C. S 5;1 . D. S 5; 1 . 81
Câu 77. Tích các nghiệm của phương trình log . x log . x log . x log 2 4 8 16 x là : 24 1 A. . B. 2 . C. 1. D.3 . 2
Câu 78. Phương trình log
x 1 2 có bao nhiêu nghiệm ? 3 A. 2 . B. 0 . C.1. D.3 .
Câu 79. Biết phương trình 9 log x l 9 og x 3 log 27 4 6.2 2
0 có hai nghiệm x ,x . Khi đó 2 2 x x bằng : 1 2 1 2 82 A. 6642 . B. . C. 20 . D.90 . 6561 1 log
Câu 80. Tập nghiệm của bất phương trình 2 2 log2 2 x 10 x x 3 ! 0 là: § 1 · § · A. S 0; 2;f ¨ ¸ . B. S 1 2;0 ;f ¨ ¸ . © 2 ¹ © 2 ¹ § · § 1 · C. S f 1 ;0 ;2 ¨ ¸ . D. S ; f 2;f ¨ ¸ . © 2 ¹ © 2 ¹
Câu 81. Tập nghiệm của phương trình 2 log2 2x log2 6 log2 4 4 2.3 x x là: 4½ 1 ½ 1 ½ A. S ® ¾. B. S ® ¾ . C. S ® ¾. D. S ^ ` 2 . ¯9 ¿ ¯ 2¿ ¯4¿
Câu 82. Tìm tất cả các giá trị thực của tham số m để phương trình log x log x 2 log có 3 3 m 3 nghiệm? A. m !1. B. m t1. C. m 1. D. m d1.
Câu 83. Tìm tất cả giá trị thực của tham số m để bất phương trình log 2
x 4x m t 1 nghiệm đúng 3 với mọi x .? A. m t 7 . B. m ! 7 . C. m 4 . D. 4 m d 7 .
Câu 84. Tìm tất cả giá trị thực của tham số m để bất phương trình log 2 mx x d log 4 vô nghiệm? 1 1 5 5 ªm ! 4 A. 4 d m d 4 . B. « . C. m 4 . D. 4 m 4 . ¬m 4
Câu 85. Tìm tất cả các giá trị thực của tham số m để phương trình log 2 mx x 2 vô nghiệm? 2 ªm ! 4 A. m 4. B. 4 m 4 . C. « . D. m ! 4 . ¬m 4
Câu 86. Tìm tất cả các giá trị thực của tham số m để phương trình 2
log x 3log x 2m 1 0 có 2 4 4 nghiệm phân biệt? 13 13 13 13 A. m . B. m ! . C. m d . D. 0 m . 8 8 8 8
Câu 87. Tìm tất cả các giá trị thực của tham số m để bất phương trình log (5x 1).log (2.5x 2) t 2 2 m có nghiệm x t1? A. m t 6 . B. m ! 6. C. m d 6 . D. m 6 .
Câu 88. Tìm tất cả các giá trị thực của tham số m để phương trình 2
log x 2log x m 1 0 có 3 3 nghiệm? A. m 2. B. m d 2. C. m t 2 . D. m ! 2 .
Câu 89. Tìm tất cả các giá trị thực của tham số m để bất phương trình log (5x 1) d có nghiệm 2 m x t 1? A. m t 2. B. m ! 2 . C. m d 2 . D. m 2 .
Câu 90. Tìm tất cả các giá trị thực của tham số m để phương trình 2 2
log x log x 1 2m 1 0 có 3 3
ít nhất một nghiệm thuộc đoạn 3 1 ª ;3 º ¬ ¼ ? A. m[0;2]. B. m(0; 2). C. m(0;2] . D. m[0;2) .
Câu 91. Tìm tất cả các giá trị thực của tham số m để phương trình log 5x 1 .log 2.5x 2 có 2 4 m nghiệm x t1.? A. m>2;f . B. m>3;f. C. m( ; f 2] . D. mf @ ;3 .
Câu 92. Tìm tất cả các giá trị thực của tham số m để phương trình 2
log x m 2 log x 3m 1 0 3 3 có hai nghiệm x , x .x 27. ? 1 2 x thỏa mãn 1 2 A. m 2 . B. m 1 . C. m 1. D. m 2 .
Câu 93. Tìm tất cả các giá trị thực của tham số m để phương trình 2 2
log x log x 3 m 2
log x 3 có nghiệm thuộc >32;f ? 2 1 4 2 A. m1; 3º ª º ¼ . B. m 1; 3 ¬ . C. m ª 1 ; 3 ¬ . D. m 3;1¼ .
Câu 94. Tìm tất cả các giá trị thực của tham số m sao cho khoảng 2;3 thuộc tập nghiệm của bất phương trình log 2 x 1 ! log 2
x 4x m 1 (1) . 5 5 A. m> 12 ;1 @ 3 . B. m>12;1 @ 3 . C. m> 13 ;12 @. D. m> 13 ; 1 2@ .
Câu 95. Tìm tất cả các giá trị thực của tham số m để bất phương trình log 2 7x 7 t log 2
mx 4x m , x . 2 2 A. m2; @ 5 . B. m 2; @5. C. m>2;5 . D. m> 2; 5 .
Câu 96. Tìm tất cả các giá trị thực của tham số m để bất phương trình 1 log 2 x 1 t log 2 mx 4 có nghiệm đúng . x 5 5 x m A. m2; @ 3 . B. m 2; @3. C. m>2;3 . D. m> 2; 3 .
D. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM I – ĐÁP ÁN 3.5 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20
C A A B D A B C B D A A C B A B A B D C
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
A D C A C A A D A A C A B A B D B A D B
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
A A C D B A A A B C A D C A B A C A C A
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
A D C A C D A A D C B A B A D A C A A A
81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96
C A A D B A C B A A B C A A A A
II –HƯỚNG DẪN GIẢI
NHẬN BIẾT – THÔNG HIỂU
Câu 1. Điều kiện xác định của phươg trình log 16 2 là: 2x3 ª3 º 3 3 A. x \ ;2 « . B. x z 2 . C. x z 2 . D. x ! . ¬« ;2 2 » ¬2 ¼ 2 2 Hướng dẫn giải 3 2x 3 ! 0 °x ! 3 Biểu thức log 16 xác định ® ® 2 x z 2 2x3 ¯2x 3 z 1 2 °¯x z 2
Câu 2. Điều kiện xác định của phươg trình 2
log (2x 7x 12) 2 là: x A. x 0; 1 1;f . B. x ;0 f . C. x 0; 1 . D. x 0;f . Hướng dẫn giải Biểu thức 2
log (2x 7x 12) xác x ° x ! 0 x ! 0 ° ° ° định ®x z 1 ®x z1 x (0;1) (1;f) ° 2 ¯2 ° x 7x 12 ! 0 ª 7 47 2 º °2 (x ) ! 0 « ¯ 4 16 » ° ¬ ¼
Câu 3. Điều kiện xác định của phương trình log (x 1) log x là: 5 5 x 1 A. x 1;f . B. x 1 ;0. C. x \[ 1; 1 0] 0 . D. x f ;1 . Hướng dẫn giải x ° ! 0 x 1 x ! 0 Biểu thức log ( x x 1) và log xác định ® x 1 ® x !1 5 5 x 1 ° ¯x !1 ¯x 1 ! 0 chọn đáp án A. 2x 1
Câu 4. Điều kiện xác định của phươg trình log là: 9 x 1 2 A. x 1 ;f . B. x \[ 1; 1 0] 0 . C. x 1 ;0. D. x f ;1 . Hướng dẫn giải 2 Biểu thức log x xác định : 9 x 1 2x ! 0 x 1 x ! 0 x( ; f 1 ) (0;f) x 1
Câu 5. Phương trình log (3x 2) 2 có nghiệm là: 2 4 2 A. x . B. x . C. x 1. D. x 2 . 3 3 Hướng dẫn giải 3 3 x 2 ! 0 °x ! PT ® ® 2 x 2 . 3 ¯ x 2 4 °¯x 2
Câu 6. Phương trình log (x 3) log (x 1) log 5 có nghiệm là: 2 2 2 A. x 2 . B. x 1. C. x 3. D. x 0 . Hướng dẫn giải x !1 x 1 ! 0 x !1 ° PT ® ® ®ªx 8 x 2 . 2 ¯(x 3)(x 1) 5 ¯x 2x 8 0 °« ¯¬x 2
Câu 7. Phương trình 2
log (x 6) log (x 2) 1 có tập nghiệm là: 3 3 A. T {0;3}. B. T . C. T {3}. D. T {1;3}. Hướng dẫn giải ° 2 x 6 ! 0 x 6 x ! 6 ° ° ° PT ®x 3 ! 0 ®x ! 3 x . ° 2 ° x 6 3(x 3) ¯ ªx 0 °« °¯¬x 3
Câu 8. Phương trình log x log (x 1) 1 có tập nghiệm là: 2 2 A. ^ 1 ; ` 3 . B. ^1; ` 3 . C. ^ ` 2 . D. ^ ` 1 . Hướng dẫn giải x ! 0 x !1 ° x !1 ° PT ®x 1 ! 0 ® ®ªx 1
x 2 , chọn đáp án A. 2 ° ¯x x 2 0 °« log x(x 1) 1 ¯ ¯¬x 2 2 > @
Câu 9. Phương trình 2 log (x 1) 6log
x 1 2 0 có tập nghiệm là: 2 2 A. ^3;1 ` 5 . B. ^1; ` 3 . C. ^1; ` 2 . D. ^1; ` 5 . Hướng dẫn giải x ! 1 x ! 1 x 1 ! 0 ° ° ªx 1 PT ®
®ªlog (x 1) 1 ®ªx 1 . 2 2 «
log (x 1) 3log (x 1) 2 0 ¯ °« °« ¬x 3 2 2 log (x 1) 2 ¯¬ ¯¬x 3 2
Câu 10. Số nghiệm của phương trình log log x log log x 2 là: 4 2 2 4 A. 0. B. 2. C. 3. D. 1. Hướng dẫn giải x ! 0 ° x !1 log x ! 0 2 ° ° PT ® ®1 § 1 log · x ! 0 4 log log x log log x 2 ° ° 2 2 2 ¨ 2 ¸ ¯2 © 2 ¹
°log log x log log x 2 2 2 2 ¯ 2 22 x !1 x !1 ° ° ®1 1 ®3 log log x log log log x 2 log log x 1 2 ° 2 2 2 2 2 ° 2 2 ¯2 2 ¯2 x !1 ° x !1 x !1 ® ® ® x 16 . lo ° g log x 2 log x 4 ¯ ¯ ¯x 16 2 2 2
Câu 11. Số nghiệm của phương trình log .
x log (2x 1) 2log là: 2 3 2 x A. 2. B. 0. C. 1. D. 3. Hướng dẫn giải x ! 0 1 ° °x ! PT ®2x 1 ! 0 ® 2 °log . °
x log (2x 1) 2 log x
log x log (2x 1) 2 0 ¯ ¯ 2 > 3 @ 2 3 2 1 1 x ! x ! °° 2 °° 2 ªx 1 ® ® . ªlog x 0 « ªx 1 2 ° ° ¬x 5 «log (2 « ° x 1) 2 ° ¯¬ ¯¬x 5 3
Câu 12. Số nghiệm của phương trình 3 2
log (x 1) log (x x 1) 2log x 0 là: 2 2 2 A. 0. B. 2. C. 3. D. 1. Hướng dẫn giải x ! 0 ° ! 3 x 0 x 1 ! 0 ° ° PT 3 ® ® 2 x 1 x x 1 ! 0 0 ° ° 2 2
¯ x (x x 1) 3 2
°log (x 1) log (x x 1) 2log x 0 ¯ 2 2 2 x ! 0 ° x ! 0 x ! 0 2
®(x 1)(x x 1) ® ® x . 0 ° ¯x 1 0 ¯x 1 2 2
¯ x (x x 1)
Câu 13. Số nghiệm của phương trình log 5x log 5x 3 0 là : 5 25 A. 3. B. 4. C. 1. D. 2. Hướng dẫn giải x !1 x !1 x ! 0 ° ° PT ® ® 1 ®1
log (5x) log (5x) 3 0 ¯
log (5x) log (5x) 3 0 log (5x) 3 0 5 25 ° 5 5 ° 5 ¯ 2 ¯2 x !1 x !1 x !1 5 ® ® ® x 5 . 6 5 log (5x) 6 ¯ 5 ¯ x 5 ¯x 5 5
Câu 14. Phương trình 2
log (5x 3) log (x 1) 0 có 2 nghiệm x , .Giá trị của 3 1 1 2 x trong đó 1 x 2 x 3 P 2x 3 là 1 2 x A. 5. B. 14. C. 3. D. 13. Hướng dẫn giải 5 x 3 ! 0 3 ° °x ! PT 2 ® ® 5
log (5x 3) log (x 1) 0 3 1 2 ° ° ¯ 3
log (5x 3) log (x 1) 0 ¯ 3 3 3 3 3 3 x ! ° °x ! °x ! °x ! ° 5 ªx 1 ® 5 ® 5 ® 5 ® « Vậy ªx 1 ° ° ° ° ¬x 4 2 2 2
log (5x 3) log (x 1) 5 ¯ ¯ x 3 x 1 ¯x 5x 4 0 3 3 « °¯¬x 4
2x 3x 2.1 3.4 14 . 1 2
Câu 15. Hai phương trình 2log (3x 1) 1 log (2x 1) và 2
log (x 2x 8) 1 log (x 2) lần lượt 3 5 5 2 1 2
có 2 nghiệm duy nhất là x , là? 1 2 x . Tổng 1 x 2 x A. 8. B. 6. C. 4. D. 10. Hướng dẫn giải
PT1: 2log (3x 1) 1 log (2x 1) 3 5 5 3 x 1! 0 1 ° °x ! PT ®2x 1! 0 ® 3 2 °2log (3 °
x 1) 1 log (2x 1)
log (3x 1) log 5 3log (2x 1) 3 5 ¯ 5 5 5 ¯ 5 1 1 °x ! °x ! ® 3 ® 3 2 3 2 3
°log 5(3x 1) log (2x 1) 5( ° ¯ ¯ 3x 1) (2x 1) 5 5 1 1 °x ! °x ! ® 3 ® 3 2 3 2 3 2 5 °¯ (9 °
x 6x 1) 8x 12x 6x 1 8
¯ x 33x 36x 4 0 1 x ! ° 3 ° ®ª 1 x 2 1 x °« 8 °« ¯¬x 2 PT2: 2
log (x 2x 8) 1 log (x 2) 2 1 2 2 °x 2x 8 ! 0 x 2 x ! 4 ° ° PT ®x 2 ! 0 ®x ! 2 ° 2 ° 2
log (x 2x 8) 1 log (x 2)
log (x 2x 8) 1 log (x 2) 2 1 ° ¯ 2 2 ¯ 2 x ! 4 x ! 4 x ! 4 ® ® ® 2 2 2
log (x 2x 8) log 2(x 2) ¯
¯x 2x 8 2(x 2) ¯x 4x 12 0 2 2 x ! 4 ° ®ªx 2 x 6 2 °« ¯¬x 6
Vậy x x 2 6 8. 1 2
Câu 16. Gọi x ,
log 2 log x 0 . Khi đó tích x . 1 2
x là nghiệm của phương trình x bằng: x 16 1 2 A. 1 . B. 1. C. 2. D. 2 . Hướng dẫn giải
[Phương pháp tự luận]
Điều kiện: 0 x z1 1
PT log 2 log x 0 log 2 log x 0 log 2 log x 0 4 x 16 x x 2 2 4 2 1 4(log 2) 1 x 2 log 2 0 0 4(log 2) 1 0 x 4log 2 4log 2 x x x ª 1 1 log 2 ª ªx 4 « x 2 1 1 2 x 2 2 (log 2) « « « x 1 « 1 4 1 « « 2 x 2 log 2 « « ¬ ¬ x 2 x 4 ¬ 2 1
Vậy x .x 4. 1. 1 2 4
[Phương pháp trắc nghiệm]
Đáp án B,D có tích âm thì có thể x 0 hoặc x 0 thì không thỏa mãn điều kiện của 1 2 x nên loại. 1 2
Câu 17. Nếu đặt t log thì phương trình
1 trở thành phương trình nào? 2 x 5 log x 1 log 2 2 x A. 2 t 5t 6 0 . B. 2 t 5t 6 0 . C. 2 t 6t 5 0 . D. 2 t 6t 5 0 . Hướng dẫn giải Đặt t log 2 x 1 2 1 t 2(5 t) PT 1
1 1 t 2(5 t) (5 t)(1 t) 5 t 1 t (5 t)(1 t) 2 2
11t 5 4t t t 5t 6 0 . 1 2
Câu 18. Nếu đặt t lg x thì phương trình
1 trở thành phương trình nào? 4 lg x 2 lg x A. 2 t 2t 3 0 . B. 2 t 3t 2 0 . C. 2 t 2t 3 0 . D. 2 t 3t 2 0 . Hướng dẫn giải Đặt t lg x 1 2 2 t 2(4 t) PT 1
1 2 t 2(4 t) (4 t)(2 t) 4 t 2 t (4 t)(2 t) 2 2
10 t 8 2t t t 3t 2 0 .
Câu 19. Nghiệm bé nhất của phương trình 3 2
log x 2log x log x 2 là: 2 2 2 1 1 A. x 4 . B. x . C. x 2 . D. x . 4 2 Hướng dẫn giải TXĐ: x ! 0 PT 3 2 3 2
log x 2log x log x 2 log x 2log x log x 2 0 2 2 2 2 2 2 3 2 2 2
log x log x 2log x 2 0 log x(log x 1) 2(log x 1) 0 2 2 2 2 2 2 ªx 2 ªlog x 1 2 2 log « ª x 1 0 « 1 2 2
(log x 1)(log x 2) 0 « log x 1 « 2 2 2 x log « x 2 0 « 2 ¬ 2 «log x 2 ¬ 2 «x 4 ¬ 1
x là nghiệm nhỏ nhất. 2
Câu 20. Điều kiện xác định của bất phương trình log (4x 2) log (x 1) ! log là: 1 1 1 x 2 2 2 1 A. x ! . B. x ! 0 . C. x !1. D. x ! 1 . 2 Hướng dẫn giải x ! 0 x ! 0 ° ° ° 1
BPT xác định khi: ®4x 2 ! 0 ®x ! x !1. 2 ° ° x 1 ! 0 ¯ °x !1 ¯
Câu 21. Điều kiện xác định của bất phương trình log (x 1) 2log (5 )
x 1 log (x 2) là: 2 4 2 A. 2 x 5. B.1 x 2. C. 2 x 3 . D. 4 x 3. Hướng dẫn giải x 1 ! 0 x ! 1 ° ° BPT xác định khi : 5
® x ! 0 ®x 5 2 x 5 . ° ° x 2 ! 0 x ! 2 ¯ ¯
Câu 22. Điều kiện xác định của bất phương trình 2 log ªlog (2 x )º ! 0 1 ¬ 2 ¼ là: 2 A. x [ 1;1]. B. x 1 ;0 0; 1 . C. x 1 ; 1 2;f . D. x 1 ; 1 . Hướng dẫn giải 2 °2 x ! 0 ° 2 x 2 ° 2 x 2 BPT xác định khi : ® ® ® 2 2 2 lo ° g (2 x ) ! 0 ¯ °¯2 x !1 1 °¯ x ! 0 2 ° 2 x 2 ® 1 x 1. °¯ 1 x 1
Câu 23. Bất phương trình log (2x 1) log (4x
2) d 2 có tập nghiệm là: 2 3 A. [0; ) f . B. ( ; f 0). C. ( ; f 0] . D. 0;f . Hướng dẫn giải Xét x 0 0 2 2 1 2x 1 2 log 2x x ! ! ! 1 ! log 2 1 1 2 2 x 0 0 4 4 1 4x 2 2 1 3 log 4x x ! ! ! 2 ! log 3 1 2 3 3 Cộng vế với vế của
1 và 2 ta được: log (2x 1) log (4x 2) ! 2 2 3
Mà BPT: log (2x 1) log (4x
2) d 2 nên x ! 0loai 2 3 Xét x 0 0 2 2 1 2x 1 2 log 2x x d d d 1 d log 2 1 3 2 2 x 0 0 4 4 1 4x 2 2 1 3 log 4x x d d d 2 d log 3 1 4 3 3
Cộng vế với vế của 3 và4 ta được: log (2x 1) log (4x 2) d 2 2 3 tm
Vậy x d 0 hay x ;0 f @.
Câu 24. Bất phương trình log 2 x x 2 t log
x 1 1 có tập nghiệm là: 2 0,5 A. 1 ª 2;f ª ¬ . B. 1 2;f ¬ . C. ;1 f 2º¼ . D. ;1 f 2º¼ . Hướng dẫn giải 2 x x 2 ! 0 x 1 x ! 2 TXĐ ® ® x ! 2 ¯x 1 ! 0 ¯x !1 BPT log 2
x x 2 t log x 1 1 log 2 x x 2 t log x 1 1 2 0,5 2 1 2 2 x x x log 2 1 2 x x 2 log x 1 1 t 0 log t 0 2 2 2 2
2x x2x 1 t1 2
x x 2 x 1 t 2 x 2 x 2x 1 t 0 2 ªx d1 2 loai 2 x 2x 1t 0 « x t1 2 «x t1 2 ¬ tm
Câu 25. Nghiệm nguyên nhỏ nhất của bất phương trình log log x t log log là: 2 4 4 2 x A. 6. B. 10. C. 8. D. 9. Hướng dẫn giải x ! 0 ° x !1 log x ! 0 2 ° ° BPT ® ® § 1 · 1 log x ! 0 4 log log x t log log ° ° 2 ¨ 2 ¸ 2 2 x ¯ © 2 ¹ 2 °log log x t log log 2 ¯ 2 x 2 2 2 2 x !1 x !1 ° ° ® § 1 · 1 ® 1 log
log x t log log x ° ¨ ¸ log log x 1 t log log 2 2 2 2 ° 2 2 2 2 x ¯ © 2 ¹ 2 ¯ 2 x !1 ° x !1 ° x !1 x !1 ®1 ® ® ® x t 8 log log x t 1 ° lo ° g log x t 2 log x t 4 ¯ ¯ ¯x t 8 2 2 2 2 ¯2 2
Câu 26. Nghiệm nguyên nhỏ nhất của bất phương trình log 2 1 x d log 1 là: 3 1 x 3 1 5 1 5 A. x 0 . B. x 1. C. x . D. x . 2 2 Hướng dẫn giải 2 1 x ! 0 1 x 1 ° ° ° ° BPT 1 ® x ! 0 ®x 1 ° ° log °¯ 2 1 x d log 1 x log °¯ 2 1 x log 1 x d 0 3 3 3 3 1 x 1 1 x 1 1 x 1 ° ° ° ® ® ® log °¯ 2 1 x 1 x d 0 log °¯ 2 1 x 1 x d 0 2 1 x 1 x d1 3 3 °¯ 1 x 1 1 x 1 ° 1 5 ® ® 1 x d 0 d x 1 2 1 5 1 5
¯x(x x 1) d 0 °x d 0 d x d 2 ¯ 2 2
x 0 là nghiệm nguyên nhỏ nhất.
Câu 27. Tập nghiệm của bất phương trình 2
log (x 3x 1) d 0 là: 2 ª 3 5 · § 3 5 º § 3 5 · § 3 5 · A. S «0; ¸ ¨ ;3» . B. S ¨0; ¸ ¨ ;3¸ . 2 ¸ ¨ 2 ¨ ¸ ¨ ¸ ¬ ¹ © ¼ 2 2 © ¹ © ¹ ª3 5 3 5 º C. S « ; » . D. S . 2 2 ¬ ¼ Hướng dẫn giải 2 2 2 °x 3x 1! 0 °x 3x 1! 0 °x 3x 1! 0 BPT ® ® ® 2 2 2 lo
° g (x 3x 1) d 0 ¯ °¯x 3x 1d1 °¯x 3x 1d1 2 3 5 3 5 °x x ! ª 3 5 · § 3 5 º ® 2 2 x «0; ¸ ¨ ;3» 2 ¸ ¨ 2 °¯0 ¬ ¹ © ¼ d x d 3
Câu 28. Điều kiện xác định của phương trình log (x 5) log (x 2) 3 là: 2 3 A. x t 5. B. x ! 2 . C. 2 x 5 . D. x ! 5. Hướng dẫn giải
[Phương pháp tự luận] x 5 ! 0 x ! 5
PT xác định khi và chỉ khi: ® ® x ! 5 ¯x 2 ! 0 ¯x ! 2
[Phương pháp trắc nghiệm]
Nhập vào màn hình máy tính log (X 5) log (X 2) 3 2 3
Nhấn CALC và cho X 1 máy tính không tính đượC. Vậy loại đáp án B và C.
Nhấn CALC và cho X 5(thuộc đáp án D) máy tính không tính đượC. Vậy loại D.
Câu 29. Điều kiện xác định của phương trình 2
log(x 6x 7) x 5 log(x 3) là: ªx ! 3 2 A. x ! 3 2 . B. x ! 3. C. « . D. x 3 2 . «¬x 3 2 Hướng dẫn giải
[Phương pháp tự luận] ªx ! 3 2 2 x 6x+7 ! 0 °«
Điều kiện phương trình: ® ®«¬ x ! 3 2 x 3 2 ¯x 3 ! 0 ° ¯x ! 3
[Phương pháp trắc nghiệm]
Nhập vào màn hình máy tính 2
log(X 6X 7) X 5 log(X 3)
Nhấn CALC và cho X 1 máy tính không tính đượC. Vậy loại đáp án C và D.
Nhấn CALC và cho X 4 (thuộc đáp án B) máy tính không tính đượC. Vậy loại B.
Câu 30. Phương trình log x log x log x 6 có nghiệm là: 3 3 1 3 A. x 27 . B. x 9 . C. 12 x 3 .
D. . x log 6 .. 3 Hướng dẫn giải
[Phương pháp tự luận] Điều kiện: x ! 0
log x log x log x 6 log x 2log x log x 6 log x 3 x 27 3 3 1 3 3 3 3 3
[Phương pháp trắc nghiệm]
Nhập vào màn hình máy tính log X log X log X 6 3 3 1 3
Dùng chức năng CALC của máy tính ta gán từng giá trị của x trong 4 đáp án và ta chọn được đáp án đúng. x 1
Câu 31. Phương trình ln
ln x có nghiệm là: x 8 ªx 4 A. x 2 . B. « . C. x 4 . D. x 1. ¬x 2 Hướng dẫn giải
[Phương pháp tự luận] ! x ! 0 x 0 x 1 ° ° ln ln x ® x 1 ®ªx 4 x 4 x 8 x ° °« ¯ x 8 ¯¬x 2
[Phương pháp trắc nghiệm] X 1
Nhập vào màn hình máy tính ln ln X X 8
Dùng chức năng CALC của máy tính ta gán từng giá trị của x trong 4 đáp án và ta chọn được đáp án đúng.
Câu 32. Phương trình 2
log x 4log x 3 0 có tập nghiệm là: 2 2 A. ^8; ` 2 . B. ^1; ` 3 . C. ^6; ` 2 . D. ^6; ` 8 . Hướng dẫn giải
[Phương pháp tự luận]
Điều kiện: x ! 0 ªlog x 1 ªx 2 2 2
log x 4log x 3 0 2 2 «log « x 3 ¬ ¬x 8 2
[Phương pháp trắc nghiệm]
Nhập vào màn hình máy tính 2
log X 4log X 3 2 2
Dùng chức năng CALC của máy tính ta gán từng giá trị của x trong 4 đáp án và ta chọn được đáp án đúng. 1
Câu 33. Tập nghiệm của phương trình log x 22 1 0 là: 2 2 A. ^ ` 0 . B. ^0; ` 4 . C. ^ ` 4 . D. ^ 1 ; ` 0 . Hướng dẫn giải
[Phương pháp tự luận]
Điều kiện: x z 2 ªx 2 2 ªx 0
pt log x 2 1 x 2 2 2 « « ¬x 2 2 ¬x 4
[Phương pháp trắc nghiệm] 1
Nhập vào màn hình máy tính log X 22 1 2 2
Dùng chức năng CALC của máy tính ta gán từng giá trị của x trong 4 đáp án và ta chọn được đáp án đúng. 1
Câu 34. Tập nghiệm của phương trình log log 2 x x 1 là: 2 1 x 2 1 ° 5 1 5 ½° A. ^1 2`.
B. ^1 2;1 2`. C. ® ; ¾ . D. ^1 2` . ° 2 2 ¯ °¿ Hướng dẫn giải
[Phương pháp tự luận]
Điều kiện: x ! 0 và 2 x x 1 ! 0 1
Với điều kiện đó thì log log 2
1 x . Phương trình đã cho tương đương phương trình x 2 x ! 0 x ! ° log x log 0 2 x x 1 ® ª ® x 1 2 x 1 2 1 1 2
¯x x x 1 « 2 2 °«¯¬x 1 2
[Phương pháp trắc nghiệm] 1
Nhập vào màn hình máy tính log log 2 X X 1 2 1 X 2
Dùng chức năng CALC của máy tính ta gán từng giá trị của x trong 4 đáp án và ta chọn được đáp án đúng.
Câu 35. Phương trình log 3.2x 1 2x 1có bao nhiêu nghiệm? 2 A. 1. B. 2. C. 3. D. 0. Hướng dẫn giải
[Phương pháp tự luận] ª2x 1 ªx log 3.2x 0 x 2x 1 1 2 «
x 1 3.2 1 2 2.4x 3.2x 1 0 2 « x 1 «2 ¬x 1 «¬ 2
[Phương pháp trắc nghiệm]
Nhập vào màn hình máy tính log 3 2X x 1 2X 1 0 2
Ấn SHIFT CALC nhập X=5, ấn = . Máy hiện X=0. Ấn Alpha X Shift STO A log 3 2X x 1 2X 1 2
Ấn AC. Viết lại phương trình: 0 X A
Ấn SHIFT CALC. Máy hỏi A? ẤN = Máy hỏi X? Ấn 5 =. Máy hiện X=-1.
Ấn Alpha X Shift STO B. log 3x2X 1 2X 1 2
Ấn AC. Viết lại phương trình:
X A X B 0
Ấn SHIFT CALC. Máy hỏi A? ẤN = Máy hỏi B? Ấn =. Máy hỏi X? Ấn 1=
Máy không giải ra nghiệm. Vậy đã hết nghiệm.
Câu 36. Số nghiệm của phương trình 2
ln x 6x 7 lnx 3là: A. 0. B. 2. C. 3. D. 1. Hướng dẫn giải
[Phương pháp tự luận] x ! 3 x ! x ! ° ln 3 0 3 2
x 6x 7 ln x 3 ® ® ®ªx 5 x 5 2 2
¯x 6x 7 x 3 ¯x 7x 10 0 °« ¯¬x 2
[Phương pháp trắc nghiệm]
Nhập vào màn hình máy tính 2
ln X 6X 7 ln X 3 0
Ấn SHIFT CALC nhập X=4 (chọn X thỏa điều kiện xác định của phương trình), ấn = . Máy hiện X=5. Ấn Alpha X Shift STO A 2
ln X 6X 7 ln X 3
Ấn AC. Viết lại phương trình: 0 X A
Ấn SHIFT CALC. Máy hỏi A? ẤN = Máy hỏi X? Ấn 7 =.
Máy không giải ra nghiệm. Vậy đã hết nghiệm.
Câu 37. Nghiệm nhỏ nhất của phương trình log x 2.log x 2log x 2 là: 3 5 3 1 A. . B. 3. C. 2. D. 1. 5 Hướng dẫn giải
[Phương pháp tự luận]
Điều kiện: x ! 2
log x 2.log x 2log x 2 2
log x 2 .log x 2log x 2 3 5 3 3 5 3 ªx 3 ªlog x 2 0 ªlog x 2 0 3 3 « « « 1 log x 1 log x 1 «x ¬ 5 ¬ 5 ¬ 5
So điều kiện suy ra phương trình có nghiệm x 3.
[Phương pháp trắc nghiệm]
Nhập vào màn hình máy tính log X 2.log X 2log X 2 3 5 3 1
Nhấn CALC và cho X (số nhỏ nhất) ta thấy sai. Vậy loại đáp án A. 5
Nhấn CALC và cho X 1 ta thấy sai. Vậy loại đáp án D.
Nhấn CALC và cho X 2 ta thấy sai. Vậy loại đáp án C.
Câu 38. Nghiệm lớn nhất của phương trình 3 2
log x 2log x 2 log x là : A. 100. B. 2. C. 10. D. 1000. Hướng dẫn giải
[Phương pháp tự luận]
Điều kiện: x ! 0 ª 1 ªlog 1 x x « 10 « « 3 2
log x 2log x 2 log x log x 2 x 100 « « «log x 1 «x 10 ¬ « ¬
[Phương pháp trắc nghiệm]
Nhập vào màn hình máy tính 3 2
log X 2log X 2 log X
Nhấn CALC và cho X 1000 (số lớn nhất) ta thấy sai. Vậy loại đáp án D.
Nhấn CALC và cho X 100 ta thấy đúng.
Câu 39. Gọi x , 2
log x x 5 log 2x 5 . 1 2
x là 2 nghiệm của phương trình 3 3 Khi đó bằng: 1 x 2 x A. 5. B. 3. C. 2 . D. 7. Hướng dẫn giải
[Phương pháp tự luận] 5 x ! ° ! ° ªx log 2x 5 0 2 5 2 x x 5 log 2x 5 ® ® 3 3 2 « ¯ ªx 5 x x 5 2x 5 ° ¬x 2 « °¯¬x 2
[Phương pháp trắc nghiệm]
Dùng chức năng SOLVE trên máy tính bỏ túi tìm được 2 nghiệm là 5 và –2. 1 2
Câu 40. Gọi x , 1. Khi đó x . 1 2
x là 2 nghiệm của phương trình x bằng: 4 log 1 2 x 2 log 2 2 x 1 1 1 3 A. . B. . C. . D. . 2 8 4 4 Hướng dẫn giải
[Phương pháp tự luận] °x ! 0 °
Điều kiện: ®x z 4 . ° 1 °x z ¯ 16 t z 4 Đặt t log ,điều kiện
. Khi đó phương trình trở thành: 2 x ®t¯ z 2 ª 1 1 2 ª 1 x t « 2 2 1 t 3t 2 0 « « 4 t 2 t ¬t 2 1 « x «¬ 4 1 Vậy x . 1 2 x 8
[Phương pháp trắc nghiệm] 1 1
Dùng chức năng SOLVE trên máy tính bỏ túi tìm được 2 nghiệm là và . 2 4
Câu 41. Gọi x , log ªx x 3 º 1 bằng: 1 2
x là 2 nghiệm của phương trình 2 ¬
¼ . Khi đó 1x 2x 3 17 A. 3 . B. 2 . C. 17 . D. . 2 Hướng dẫn giải
[Phương pháp tự luận] ªx 3 Điều kiện: « ¬x ! 0 log ªx ¬ x 3 º 1 x ¼ x 3 2 2 x 3x 2 0 2 Vậy x x 3. 1 2
[Phương pháp trắc nghiệm]
Dùng chức năng SOLVE trên máy tính bỏ túi tìm được 2 nghiệm và lưu 2 nghiệm vào A và B. Tính A + B = – 3.
Câu 42. Nếu đặt t log
thì phương trình log 4x log 2 3 trở thành phương trình nào? 2 2 x x 1 1 A. 2 t t 1 0 . B. 2 4t 3t 1 0 . C. t 1 . D. 2t 3 . t t Hướng dẫn giải log 4x 1 2 log 2 3 log 4 log x
3 log x log x 1 0 2 x 2 2 2 2 log2 x
Câu 43. Nếu đặt t log x thì phương trình 2 3
log x 20log x 1 0 trở thành phương trình nào? A. 2 9t 20 t 1 0 . B. 2 3t 20t 1 0 . C. 2 9t 1 0t 1 0 . D. 2 3t 10t 1 0 . Hướng dẫn giải 2 3 2
log x 20log x 1 0 9log x 10log x 1 0 1 log x 1
Câu 44. Cho bất phương trình 9 d
t log x thì bất phương trình trở thành: 1 . Nếu đặt log 3 x 2 3 1 2t 1
A. 21 2t d1 t . B. d . 1 t 2 1 1 2t 1
C. 1 t d 1 t . D. t 0 . 2 2 1 t Hướng dẫn giải 1 1 log3 1 log 1 x x 1 2 log x 1 2 log x 2log x 1 9 2 3 3 3 d d d 1 t 0 t 0 1 log x 2 1 log x 2 2 1 log x 2 1 log x 1 log 3 3 3 3 3 x
Câu 45. Điều kiện xác định của bất phương trình log (x 2) log (x 2) ! log x 3 là: 5 1 5 5 A. x ! 3. B. x ! 2 . C. x ! 2 . D. x ! 0 . Hướng dẫn giải
[Phương pháp tự luận] x 2 ! 0 x ! 2 ° °
Điều kiện: ®x 2 ! 0 ®x ! 2 x ! 2 ° ° x ! 0 x ! 0 ¯ ¯
[Phương pháp trắc nghiệm]
Nhập vào màn hình máy tính log (X 2) log (X 2) log X 3 5 1 5 5
Nhấn CALC và cho X 1 máy tính không tính được. Vậy loại đáp án C và D. 5
Nhấn CALC và cho X (thuộc đáp án B) máy tính hiển thị 1,065464369. 2
Câu 46. Điều kiện xác định của bất phương trình log (5x 15) d log 2 x 6x 8 là: 0,5 0,5 ªx 4 A. x ! 2 . B. « . C. x ! 3 . D. 4 x 2 . ¬x ! 2 Hướng dẫn giải
[Phương pháp tự luận] x ! 3 5 x 15 ! 0 ° Điều kiện: ® ®ªx ! 2 x ! 2 2 ¯x 6x 8 ! 0 °« ¯¬x 4
[Phương pháp trắc nghiệm]
Nhập vào màn hình máy tính 2
log (5X 15) log (X 6X 8) 0,5 0,5
Nhấn CALC và cho X 3,
5 máy tính không tính được. Vậy loại đáp án C và D.
Nhấn CALC và cho X 5
(thuộc đáp án B) máy tính không tính được.
Vậy loại B, chọn A. 2 x 1
Câu 47. Điều kiện xác định của bất phương trình ln 0 là: x ª 1 x 0 ªx 1 A. « . B. x ! 1 . C. x ! 0 . D. « . ¬x !1 ¬x !1 Hướng dẫn giải
[Phương pháp tự luận] 2 x 1 ª 1 x 0 Điều kiện: ! 0 « x ¬x !1
[Phương pháp trắc nghiệm] 2 1
Nhập vào màn hình máy tính ln X X
Nhấn CALC và cho X 0,
5 (thuộc đáp án A và B) máy tính hiển thị 0,4054651081. Vậy loại đáp án C và D.
Nhấn CALC và cho X 0,5 (thuộc đáp án B) máy tính không tính đượC. Vậy loại B, chọn A.
Câu 48. Bất phương trình 2 log x 5log x 6 có tập nghiệm là: 0,2 0,2 § 1 1 · § 1 · A. S ; ¨ ¸ . B. S 2;3 . C. S 0; ¨ ¸ . D. S 0;3 . ©125 25 ¹ © 25 ¹ Hướng dẫn giải
[Phương pháp tự luận]
Điều kiện: x ! 0 1 1 2 log 5log x 6 2 log x 3 0,2 0,2 0,2 x 125 25
[Phương pháp trắc nghiệm]
Nhập vào màn hình máy tính log X 2 5log X 6 0,2 0,2
Nhấn CALC và cho X 2,5 (thuộc đáp án B và D) máy tính hiển thị 9.170746391. Vậy loại đáp án B và D. 1 Nhấn CALC và cho X
(thuộc đáp án C) máy tính hiển thị 0,3773110048. 200
Câu 49. Vậy loại C, chọn A.Tập nghiệm của bất phương trình log 2 x 6x 5 log x 1 t 0 là: 1 3 3 A. S >1;6@. B. S 5;6@ . C. S 5;f . D. S 1;f . Hướng dẫn giải
[Phương pháp tự luận] °x x !
log x 6x 5 log x 1 t 0 log x 1 t log x 6x 5 2 6 5 0 2 2 1 3 3 3 ® 2 °¯
x 1 t x 6x 5 3 x 1 x ! 5 ® 5 x d 6 1 ¯ d x d 6
[Phương pháp trắc nghiệm]
Nhập vào màn hình máy tính log 2 X 6X 5 log X 1 1 3 3
Nhấn CALC và cho X 2 (thuộc đáp án A và D) máy tính không tính được. Vậy loại đáp án A và D.
Nhấn CALC và cho X 7 (thuộc đáp án C) máy tính hiển thị – 0,6309297536.
Vậy loại C, chọn B.
Câu 50. Bất phương trình log 2
2x x 1 0 có tập nghiệm là: 2 3 § 3 · § 3 · A. S 0; ¨ ¸ . B. S 1 ; ¨ ¸ . © 2 ¹ © 2 ¹ § · § · C. S f 1 ;0 ;f ¨ ¸ . D. S f 3 ;1 ;f ¨ ¸ . © 2 ¹ © 2 ¹ Hướng dẫn giải
[Phương pháp tự luận] ªx 0 log 2 2x x 2 1 0 2x x 1 1 « ! 2 1 « ! 3 x ¬ 2
[Phương pháp trắc nghiệm]
Nhập vào màn hình máy tính log 2 2X X 1 2 3
Nhấn CALC và cho X 5
(thuộc đáp án A và D) máy tính hiển thị – 9,9277…. Vậy loại đáp án A và B.
Nhấn CALC và cho X 1(thuộc đáp án C) máy tính hiển thị – 1,709511291. Vậy chọn C. 4x 6
Câu 51. Tập nghiệm của bất phương trình log d 0 là: 3 x ª 3 · ª 3 º A. S 2; « ¸ . B. S > 2; 0 . C. S ;2 f @. D. S \ ;0 ;0 . ¬ 2 ¹ «¬ ;0 2 » ¬ 2 ¼ Hướng dẫn giải
[Phương pháp tự luận] 4x 6 ! 0 3 4x 6 °° x °x x ! 0 3 log d 0 ® ® 2 2 d 3 x x 4x 6 2 ° d1 °¯ 2 d x 0 °¯ x
[Phương pháp trắc nghiệm] 4 6
Nhập vào màn hình máy tính log X 3 X
Nhấn CALC và cho X 1 (thuộc đáp án C và D) máy tính hiển thị 2,095903274. Vậy loại đáp án C và D.
Nhấn CALC và cho X 1
(thuộc đáp án B) máy tính không tính đượC. Vậy loại B, chọn A.
Câu 52. Nghiệm nguyên nhỏ nhất của bất phương trình log x log x 2 log 3 là: 0,2 5 0,2 A. x 6 . B. x 3. C. x 5. D. x 4 . Hướng dẫn giải
[Phương pháp tự luận]
Điều kiện: x ! 2 ªx
log x log x 2 log 3 log ªx ¬ x 2 1 2
º log 3 x 2x 3 ! 0 0,2 5 0,2 0,2 ¼ 0,2 « ¬x ! 3
So điều kiện suy ra x ! 3
[Phương pháp trắc nghiệm]
Nhập vào màn hình máy tính log X log X 2 log 3 0,2 5 0,2
Nhấn CALC và cho X 3 (nhỏ nhất) máy tính hiển thị 0. Vậy loại đáp án B.
Nhấn CALC và cho X 4 máy tính hiển thị -0.6094234797.Vậy chọn D.
Câu 53. Nghiệm nguyên lớn nhất của bất phương trình log x 1 4.3 ! 2x 1 là: 3 A. x 3. B. x 2 . C. x 1. D. x 1 . Hướng dẫn giải
[Phương pháp tự luận] log x 1 4.3 x 1 2x 1 2 ! 2 1 4.3 ! 3
3 x 4.3x 0 0 3x x 4 x log 4 3 3
[Phương pháp trắc nghiệm]
Nhập vào màn hình máy tính log X 1 4.3 2X 1 3
Nhấn CALC và cho X 3 (lớn nhất) máy tính hiển thị –1.738140493. Vậy loại đáp án A.
Nhấn CALC và cho X 2 máy tính hiển thị – 0.7381404929. Vậy loại B.
Nhấn CALC và cho X 1 máy tính hiển thị 0.2618595071. Vậy chọn C.
Câu 54. Điều kiện xác định của phương trình log 3 ª log 3x 1 1º 2 ¬ 2 x ¼ là: 3 2 1 1 A. x ! . B. x t . C. x ! 0 . D. x (0; ) f \{1}. 3 3 Hướng dẫn giải
[Phương pháp tự luận] Biểu thức log 3 ª log 3x 1 1º 2 ¬ 2 x ¼
xác định khi và chỉ khi: 1 1 1 log 3 3 x 1 ! 1 ° ° 2 1 2 3l ° og 3x 1 1! 0 3 3 ° x 1 ! 2 x ! 3 2 ° 3 ° 2 1 ® ® ® 3 ® x ! 3 °¯ x 1! 0 1 ° 1 3 x ! °x ! ° 1 °¯ 3 ¯ 3 x ! °¯ 3
[Phương pháp trắc nghiệm] 1
Thay x (thuộc B, C, D) vào biểu thức log 3x 1 được log (0) không xác định, vậy loại 2 3 2
B, C, D, chọn đáp án A.
Câu 55. Điều kiện xác định của phương trình log 2 x x 1.log 2 x x 1 2
log x x 1 là: 2 3 6 A. x d 1 . B. x t1.
C. x ! 0, x z 1. D. x d 1 hoặc x t1. Hướng dẫn giải
[Phương pháp tự luận] 2 x x 1 ! 0 °°
Phương trình xác định khi và chỉ khi : 2
®x x 1 ! 0 x t1 ° 2 x 1 t 0 °¯
[Phương pháp trắc nghiệm] Thay x 1
(thuộc A, D) vào biểu thức log 2
x x 1 được log ( 1 ) không xác định, 2 2 1 3
Thay x (thuộc C) vào biểu thức 2 x 1 được không xác định 2 4
Vậy loại A, C, D chọn đáp án B.
Câu 56. Nghiệm nguyên của phương trình log 2 x x 1.log 2 x x 1 2
log x x 1 là: 2 3 6 A. x 1. B. x 1 . C. x 2 . D. x 3. Hướng dẫn giải
[Phương pháp tự luận]
Điều kiện: x t1 log 2 x x 1.log 2 x x 1 2 log x x 1 2 3 6 log 2 x x 1.log 2 x x 1 log 2 x x 1 2 3 6 log 6.log 2
x x 1.log 6.log 2 x x 1 log 2 x x 1 0 2 6 3 6 6 Đặt t log 2 x x 1 ta được 6 2
log 6.log 6.t t 0 2 3 ª ªt 0 log « 2 x x 1 0 6 « 1 « « 1 t «log x x 1 log 6.log 6 « 6 ¬ 2 3 2 « log 6.log 6 ¬ 2 3 ª « 2 x x 1 1 1 « «log ¬ 2 x x 1 log 3 2 2 6 2 °x x 1 1 1 ® x 1 2 °¯x x 1 1 2 log 3 log 3 log 3 6 6 6 °x x 1 2 2 2 2 ® x 2 log6 3 2 °¯x x 1 2
[Phương pháp trắc nghiệm]
Thay x 1 vào phương trình ta được VT VP chọn đáp án A. 3 § x · § 32 ·
Câu 57. Nếu đặt t log thì bất phương trình 4 2 2 log x log ¨ ¸ 9log 4log trở thành 1 2 1 2 x ¨ 2 ¸ 2 x 2 © 8 ¹ © x ¹ 2 bất phương trình nào? A. 4 2 t 13t 36 0 . B. 4 2 t 5t 9 0 . C. 4 2 t 13t 36 0 . D. 4 2 t 13t 36 0 . Hướng dẫn giải
[Phương pháp tự luận]
Điều kiện: x ! 0 3 § x · § 32 4 2 · 2 log x log ¨ ¸ 9log 4log 1 2 1 2 x ¨ 2 ¸ 2 © 8 ¹ © x ¹ 2
log x 3log x 32 4 95 2log x 2 4log x 0 2 2 2 2 4 2
log x 13log x 36 0 2 2 3 § x · § 32 ·
Câu 58. Nghiệm nguyên lớn nhất của bất phương trình 4 2 2 log x log ¨ ¸ 9log 4log là: 1 2 1 2 x ¨ 2 ¸ 2 © 8 ¹ © x ¹ 2 A. x 7 . B. x 8. C. x 4 . D. x 1. Hướng dẫn giải
[Phương pháp tự luận]
Điều kiện: x ! 0 3 § x · § 32 4 2 · 2 log x log ¨ ¸ 9log 4log 1 2 1 2 x ¨ 2 ¸ 2 © 8 ¹ © x ¹ 2
log x 3log x 32 4 95 2log x 2 4log x 0 2 2 2 2 4 2 log x 13log x 36 0 2 2 ª4 x 8 ª2 log x 3 2 2 4 log « x 9 2 « 1 1 3 log x 2 « ¬ 2 x ¬8 4 chọn đáp án A.
[Phương pháp trắc nghiệm]
Lần lượt thay x 7; x 8; x 4; x 1thấy x 7 đúng, chọn đáp án A.
Câu 59. Bất phương trình log d có tập nghiệm là: x log 9x 72 1 3 A. S ªlog
73;2º . B. S log 72;2º . C. S log 73;2º . D. S ;2 f @. 3 ¬ ¼ 3 ¼ 3 ¼ Hướng dẫn giải
[Phương pháp tự luận]
Điều kiện x ! log 73 3 log d d x d d x d x log 9x 72 1 log 9x 72 9x 3x 72 0 3x 9 2 3 3 Chọn đáp án A.
[Phương pháp trắc nghiệm] Thay x log
73 (thuộc B, C, D) vào biểu thức log được log (0) không xác x log 9x 72 3 3 x
định, vậy loại B, C, D, chọn đáp án A.
Câu 60. Gọi x , log ªx x 1 º 1 x . 1 2
x là nghiệm của phương trình 2 ¬
¼ . Khi đó tích 1 2x bằng: A. 2 . B. 1. C. 1 . D. 2. Hướng dẫn giải
[Phương pháp tự luận]
Điều kiện x 0 hoặc x !1 ªx 1
log ªx x 1 º 1 x x 2 0 x .x 2 2 ¬ 2 1 ¼ « 1 2 x 2 ¬ 2
Vậy chọn đáp án A. Câu 61. Nếu đặt log 5 x t 1
thì phương trình log 5x 1 .log 2.5x
2 1 trở thành phương trình 2 4 2 nào? A. 2 t t 2 0 . B. 2 2t 1. C. 2 t t 2 0 . D. 2 t 1. Hướng dẫn giải
Điều kiện: x ! 0
log 5x 1 .log 2.5x 2 1 2 4 log 5x 1 . 1 ª log 5x 1 º 2 0 2 2 ¬ ¼
Vậy chọn đáp án A.
Câu 62. Số nghiệm của phương trình log x 12 .log 2 1 là: 4 x A. 0. B. 2. C. 3. D. 1. Hướng dẫn giải
Điều kiện : 0 x z 1 ªx
log x 12.log 2 1 log x x x x x 12 3 2 2 log 12 0 4 2 2 « ¬x 4 Loại x 3 chọn đáp án A
Câu 63. Phương trình 2 log (2x 1) 8log
2x 1 3 0 có tập nghiệm là: 5 5 A. ^ 1 ; ` 3 . B. ^1; ` 3 . C. ^3;6 ` 3 . D. ^1; ` 2 . Hướng dẫn giải
[Phương pháp tự luận] 1 Điều kiện : x ! 2 2 2 log (2x 1) 8log
2x 1 3 0 log (2x 1) 4log 2x 1 3 0 5 5 5 5 ªlog 2x 1 1 ª 5 x 3 « « «log 2x 1 3 ¬ ¬x 63 5
[Phương pháp trắc nghiệm]
Thay x 1(thuộc B, D) vào vế trái ta được 3 0 vô lý, vậy loại B, D, Thay x 1
vào log 2x 1 ta được log 3
không xác định, nên loại A 5 5 Vậy chọn đáp án C. x 1 x 1 x 1
Câu 64. Nếu đặt t log
thì bất phương trình log log log log trở thành bất phương 3 4 3 1 1 x 1 x 1 x 1 4 3 trình nào? 2 t 1 2 t 1 2 t 1 A. 0. B. 2 t 1 0 . C. ! 0 . D. 0 . t t t Hướng dẫn giải
Điều kiện: x( ; f 1 ) (1; ) f
Sau khi đưa về cùng cơ số 4, rồi tiếp tục biến đổi về cùng cơ số 3 ta được bất phương trình x 1 1 log 0 3 x 1 x 1 log3 x1 Chọn đáp án A.
Câu 65. Phương trình log x x có nghiệm là: x 2 3 7 3 2 0 2 3
A. x 2; x 3 . B. x 2 . C. x 3.
D. x 1; x 5 . Hướng dẫn giải
[Phương pháp tự luận] 3
Điều kiện x ! ; x z 2 2 ªx log x x x x x x x x 3 7 3 2 0 3 7 3 2 32 2 2 2 2 5 6 0 2 3 « ¬x 3
Lần lượt thay x 1; x 2 (thuộc B,A, D) vào vê trái ta được đẳng thức sai, vậy loại B, A, D. Vậy chọn đáp án C.
Câu 66. Nghiệm nguyên nhỏ nhất của bất phương trình log log x ! log log là: 2 4 4 2 x A. 18. B. 16 . C. 15 . D. 17 . Hướng dẫn giải
[Phương pháp tự luận]
Điều kiện: x ! 1
log log x ! log log x log log x ! 2 log x ! 4 x !16 2 4 4 2 2 2 2
Phương pháp trắc nghiệm]
Thay x 16;15(thuộc B, C) vào phương trình ta được bất dẳng thức sai nên loại B, C
Thay x 17;18 vào phương trình ta được bất đẳng thức đúng Vậy chọn đáp án D. 1 2
Câu 67. Phương trình
1 có tích các nghiệm là: 4 ln x 2 ln x 1 A. 3 e . B. . C. e . D. 2 . e Hướng dẫn giải
[Phương pháp tự luận] Điều kiện: 2 4
x ! 0,x z e ;x z e 1 2 ªln x 1 ªx e 2
1 ln x 3ln x 2 0 « « 2 4 ln x 2 ln x ¬ln x 2 ¬x e
Vậy chọn đáp án A.
Câu 68. Phương trình log9 2 9 x x
x có bao nhiêu nghiệm? A. 1. B. 0. C. 2. D. 3. Hướng dẫn giải
[Phương pháp tự luận]
Điều kiện : x ! 0; x z 1 9 log x 2 9 log l 9 og 9 x x x x log 2x 2
1 log x 2log x 0 log x 1 x 9 9 9 9 9 9
Vậy chọn đáp án A.
Câu 69. Nghiệm nguyên nhỏ nhất của bất phương trình log 3 log 3 0 là: x x 3 A. x 3. B. x 1. C. x 2 . D. x 4 . Hướng dẫn giải
[Phương pháp tự luận]
Điều kiện : x ! 0; x z1; x z 3 1 ªlog x 0 ª0 x 1 3 log 3 log 3 0 0 x x « log . « x log x 1 log x !1 ¬ ¬x ! 3 3 3 3 3
[Phương pháp trắc nghiệm]
Loại B, A vì x z 1; x z 3
Loại C vì x 2 log 3 log 3 ! 0 Vậy chọn đáp án D. 2 2 3
Câu 70. Phương trình ln7 ln 7 x x 98 có nghiệm là:
A. x e . B. x 2 . C. 2 x e .
D. x e . Hướng dẫn giải
[Phương pháp tự luận]
Điều kiện : x ! 0; x z 1 Đặt t x e ln7 ln .ln7 ln 7 98 7 t x t e 98 2.7t x e 98 t 2
[Phương pháp trắc nghiệm]
Lần lượt thay x 2; x ;
e x e vào phương trình ta được đẳng thức sai, vậy loại A, B, D, vậy chọn đáp án C.
Câu 71. Bất phương trình log 2 x x 2 t log
x 1 1 có tập nghiệm là: 2 0,5 A. S 1 ª 2;f S ª ¬ . B. 1 2;f ¬ . C. S ;1 f 2º¼. D. S ;1 f 2º¼ . Hướng dẫn giải
[Phương pháp tự luận]
Điều kiện : x ! 2 log 2
x x 2 t log x
1 1 log ª¬ 2x x 2x 1 º t 1 ¼
2x x2 x1 2 t 0 2 0,5 2 1 ª 2 d x d 0 [ 3 2
x 2x x t 0 ««¬xt1 2
Phương pháp trắc nghiệm]
Dựa vào điều kiện ta loại A, C, D. Vậy chọn đáp án B. 1 1 7
Câu 72. Biết phương trình
log x 0 có hai nghiệm x ,x . Khẳng định nào sau đây là 2 log x 2 6 1 2 2 đúng? 2049 2047 2049 2047 A. 3 3 x x . B. 3 3 x x . C. 3 3 x x . D. 3 3 x x . 1 2 4 1 2 4 1 2 4 1 2 4 Hướng dẫn giải x ! 0 x ! 0 Điều kiện: ® ® . log x z 0 ¯ ¯x z 1 2
Đặt t log . Phương trình đã cho trở thành 2 3t 7t 6 0 . 2 x 3 ªt 3 ªlog x 3 ªx 2 9 2 « « « 2 2 2 « (thỏa mãn điều kiện) « « 1 3 t log x x 2 2 ¬ ¬ « 3 3 3 ¬ 4 1 ½ 2049
Vậy tập nghiệm của phương trình đã cho là 3 3 S 8; ® ¾ x x 1 2 3 ¯ 4 ¿ 4
Câu 73. Số nghiệm nguyên dương của phương trình log 4x 4 x log x 1 2 3 là: 2 1 2 A. 2. B. 1. C. 3. D. 0. Hướng dẫn giải Điều kiện: x 1 2 3 ! 0 x ! log 31. 2 4x 4 4x x x 4
Ta có: log 4 4 x log 1 2 3 log x 2x 1 2 1 2 x 1 x 1 2 3 2 3 2 Đặt 2x t ,t ! 0. Ta có 2 2 2
1 t 4 2t 3t t 3t 4 0 t 4. x 2
2 2 x 2 (thỏa mãn điều kiện)
Vậy nghiệm của phương trình đã cho là x 2 .
Câu 74. Tập nghiệm của bất phương trình log log 2x 1 ! 0 là: 1 2 2 § 3 · § 3 · § 3 · A. S 1; ¨ ¸ . B. S 0; ¨ ¸ . C. S 0; 1 . D. S ; 2 ¨ ¸ . © 2 ¹ © 2 ¹ © 2 ¹ Hướng dẫn giải 2x 1 ! 0 Điều kiện: ® x !1. log (2x 1) ! 0 ¯ 2
Ta có: log log 2x 1 ! 0 log log 2x 1 ! log 1 1 2 1 2 1 2 2 2 lo g (2x 1) 1 0 2x 1 2 2 3 ® ®
1 x . (thỏa mãn điều kiện) log (2x 1) ! 0 ¯ ¯2x 1 !1 2 2 § 3 ·
Vậy tập nghiệm của bất phương trình đã cho là S 1; ¨ ¸ . © 2 ¹
Câu 75. Tập nghiệm của bất phương trình log 2
2x 3x 1 ! log 2x 1 là: 4 2 § 1 · § 1 · § 1 · § 1 · A. S ;1 ¨ ¸ . B. S 0; ¨ ¸ . C. S ;1 ¨ ¸ . D. S ;0 ¨ ¸ . © 2 ¹ © 2 ¹ © 2 ¹ © 2 ¹ Hướng dẫn giải 1 ! 2 x 1 2 3 1 ! 0 x x x °° 2 1 Điều kiện: ® ® x ! . ¯2x 1 ! 0 1 2 °x ! °¯ 2
Ta có: log 2x 3x 1 ! log 2x 1 log 2x 3x 1 ! log 2x 2 2 2 1 4 2 4 4 1 2 2 2
2x 3x 1 ! 4x 4x 1 2x x 0 x 0. (thỏa mãn điều kiện) 2 § 1 ·
Vậy tập nghiệm của bất phương trình đã cho là S ;0 ¨ ¸ . © 2 ¹ 3
Câu 76. Tập nghiệm của bất phương trình log x x ! x là: x 125 2 .log log 25 5 2 A. S 1; 5 . B. S 1 ; 5 . C. S 5; 1 . D. S 5; 1 . Hướng dẫn giải
Điều kiện: 0 x z 1 * . 3 3 Ta có: 2
log (125x).log x ! log x log 5 log x .log x ! log x x 25 5 3 x x 2 2 5 5 2 2 § · 3log 5 x ! x x ! x x x x 1 3 3 1 3 2 2 2 1 . log log log log 2log log 0 ¨ 5 ¸ 5 5 5 5 5 © 2 ¹ 2 2 2 2 1 1 0 2
0 log x 5 x 5 1 x 5. (thỏa mãn điều kiện) 5 2
Vậy tập nghiệm của bất phương trình đã cho là S 1; 5 . 81
Câu 77. Tích các nghiệm của phương trình log . x log . x log . x log 2 4 8 16 x là : 24 1 A. . B. 2 . C. 1. D. 3 . 2 Hướng dẫn giải Điều kiện: x ! 0. 81 § 1 ·§ 1 ·§ 1 · 81 Ta có: log . x log . x log . x log x log x log x log x log 2 4 8 16 2 ¨ 2 ¸¨ 2 ¸¨ 2 x ¸ 24 © 2 ¹© 3 ¹© 4 ¹ 24 1 4 log 81 log x 3 r x 8 hoặc 2 2 x
. (thỏa mãn điều kiện) 8 1 ½
Vậy tập nghiệm của phương trình đã cho là S ® ;8¾ x .x 1. 1 2 ¯8 ¿
Câu 78. Phương trình log
x 1 2 có bao nhiêu nghiệm ? 3 A. 2 . B. 0 . C. 1. D. 3 . Hướng dẫn giải Điều kiện: x z 1 Ta có: log
x 1 2 x 1 3 x 1 3
r x 2 hoặc x 4. (thỏa mãn điều kiện) 3
Vậy tập nghiệm của phương trình đã cho là S ^ 4; ` 2 .
Câu 79. Biết phương trình 9 log x l 9 og x 3 log 27 4 6.2 2
0 có hai nghiệm x ,x . Khi đó 2 2 x x bằng : 1 2 1 2 82 A. 6642 . B. . C. 20 . D. 90 . 6561 Hướng dẫn giải Điều kiện: x ! 0.
Ta có phương trình tương đương 2lo 9g x lo 9 g x 3 2 6.2 2 0. (1) ªt 2 Đặt log9 2 x t ,t ! 0. 2 1 t 6t 8 0 « ¬t 4 - Với log9 2 2 x t
2 log x 1 x 9. 9 - Với log9 x 2 t 4 2
2 log x 2 x 81. 9
Vậy tập nghiệm của phương trình đã cho là S ^9; ` 2 2 81 x x 6642 . 1 2 1 log
Câu 80. Tập nghiệm của bất phương trình 2 2 log2 2 x 10 x x 3 ! 0 là: § 1 · § · A. S 0; 2;f ¨ ¸ . B. S 1 2;0 ;f ¨ ¸ . © 2 ¹ © 2 ¹ § · § 1 · C. S f 1 ;0 ;2 ¨ ¸ . D. S ; f 2;f ¨ ¸ . © 2 ¹ © 2 ¹ Hướng dẫn giải
Điều kiện: x ! 0 (*) . Đặt log 2u u x x . 2 u u u u 10
Bất phương trình đã cho trở thành 2 2 102 2 3 ! 0 2 3 ! 0 (1) 2 2u ªt 5 (l) Đặt 2
t 2u , t t 1. 2 2 u 2 1 t 3t 10 ! 0 2 ! 2 u !1 u !1 « hoặc u 1 ¬t ! 2
- Với u !1 log x !1 x ! 2 2 1 - Với u 1 log x 1 x . 2 2 1
Kết hợp điều kiện (*), ta được nghiệm của bất phương trình đã cho là x ! 2 hoặc 0 x . 2
Câu 81. Tập nghiệm của phương trình 2 log2 2x log2 6 log2 4 4 2.3 x x là: 4½ 1 ½ 1 ½ A. S ® ¾. B. S ® ¾ . C. S ® ¾. D. S ^ ` 2 . ¯9 ¿ ¯ 2¿ ¯4¿ Hướng dẫn giải
Điều kiện: 0 x z 1 2 Ta có: log 2 2 x log2 6 log2 4x 1 log2 x log2 x 2 2log2 x log2 x log2 x log2 4 2.3 4 6 2.3 4.4 6 19.9 x x (1) Chia 2 vế cho log2 4 x . ª 4 log x t 2 x log2 9 3 x § · § · log2 3 « § · (1) 18. 4 0 9 ¨ ¸ ¨ ¸ . Đặt 2 t
! 0. PT 18t t 4 0 ¨ ¸ « © 4 ¹ © 2 ¹ © 2 ¹ 1 «t (l) «¬ 2 log 2 x 2 § 3 · § 4 · § 3 · 1 2 log x 2 x 2 . ¨ ¸ ¨ ¸ ¨ ¸ (thỏa mãn điều kiện) 2 © 2 ¹ © 9 ¹ © 2 ¹ 4 1 ½
Vậy tập nghiệm của phương trình đã cho là S ® ¾. ¯4¿ VẬN DỤNG CAO
Câu 82. Tìm tất cả các giá trị thực của tham số m để phương trình log x log x 2 log có 3 3 m 3 nghiệm? A. m !1. B. m t1. C. m 1. D. m d1. Hướng dẫn giải
[Phương pháp tự luận]
Điều kiện x ! 2;m ! 0 2 2 log m x log x 2 log x x 2 2 x 3 3 m m 3 2 m 1
Phương trình có nghiệm x ! 2 khi m !1,chọn đáp án A
[Phương pháp trắc nghiệm]
Thay m 0(thuộc C, D) vào biểu thức log m không xác định, vậy loại C, D, 3
Thay m 1 (thuộc B) ta được phương trình tương đương x x 2 vô nghiệm
Vậy chọn đáp án A.
Câu 83. Tìm tất cả giá trị thực của tham số m để bất phương trình log 2
x 4x m t 1 nghiệm đúng 3 với mọi x .? A. m t 7 . B. m ! 7 . C. m 4 . D. 4 m d 7 . Hướng dẫn giải log 2 x 4x m 2 t1 x
x 4x m 3 t 0 x ' d 0 m t 7 3 Vậy chọn A.
Câu 84. Tìm tất cả giá trị thực của tham số m để bất phương trình log 2 mx x d log 4 vô nghiệm? 1 1 5 5 ªm ! 4 A. 4 d m d 4 . B. « . C. m 4 . D. 4 m 4 . ¬m 4 Hướng dẫn giải log 2 mx x 2 2
d log 4 mx x t 4 x mx 4 d 0 1 1 5 5 2
x mx 4 d 0 vô nghiệm 2
x mx 4 ! 0 x R ' 0 4 m 4
Câu 85. Tìm tất cả các giá trị thực của tham số m để phương trình log 2 mx x 2 vô nghiệm? 2 ªm ! 4 A. m 4. B. 4 m 4 . C. « . D. m ! 4 . ¬m 4 Hướng dẫn giải log 2 mx x 2 2 x mx 4 0(*) 2
Phương trình (*) vô nghiệm 2 ' 0 m 16 0 4 m 4
Câu 86. Tìm tất cả các giá trị thực của tham số m để phương trình 2
log x 3log x 2m 1 0 có 2 4 4 nghiệm phân biệt? 13 13 13 13 A. m . B. m ! . C. m d . D. 0 m . 8 8 8 8 Hướng dẫn giải 13
Phương trình có 2 nghiệm phân biệt ' ! 0 138m ! 0 m 8
Câu 87. Tìm tất cả các giá trị thực của tham số m để bất phương trình log (5x 1).log (2.5x 2) t 2 2 m có nghiệm x t1? A. m t 6 . B. m ! 6. C. m d 6 . D. m 6 . Hướng dẫn giải
BPT log (5x 1).log (2.5x 2)d m log (x5 1). 1 log x ª (5 º 1) d 2 2 2 ¬ 2 ¼ Đặt t log 2
x x 1 do x t 1 t >2;f 6 BPT 2
t(1 t) t m t t t m f (t) t m Với 2
f (t) t t ,
f (t) 2t 1 ! 0 với t >2;f nên hàm đồng biến trên t >2;f
Nên Minf (t) f (2) 6
Do đó để để bất phương trình log (5x 1).log (2.5x
2) t m có nghiệm x t1thì : 2 2
m d Minf (t) m d 6
Câu 88. Tìm tất cả các giá trị thực của tham số m để phương trình 2
log x 2log x m 1 0 có 3 3 nghiệm? A. m 2. B. m d 2. C. m t 2 . D. m ! 2 . Hướng dẫn giải TXĐ: x ! 0 PT có nghiệm khi c
' t 0 1 (m1) t 0 2 m t 0 m d 2 .
Câu 89. Tìm tất cả các giá trị thực của tham số m để bất phương trình log (5x 1) d có nghiệm 2 m x t 1? A. m t 2. B. m ! 2 . C. m d 2 . D. m 2 . Hướng dẫn giải
[Phương pháp tự luận]
t1 5x 1t 4 log 5x x 1 t 2 m t 2 2
Câu 90. Tìm tất cả các giá trị thực của tham số m để phương trình 2 2
log x log x 1 2m 1 0 có ít 3 3
nhất một nghiệm thuộc đoạn 3 1; ª 3 º ¬ ¼ ? A. m[0;2]. B. m(0;2) . C. m(0;2] . D. m[0;2) . Hướng dẫn giải Với 3 x 1 ª ;3 º ¬ ¼ hay 3 2 2 2 3
1d x d 3 log 11 d log x 1 d log 3 1 hay 1d t d 2 . 3 3 3
Khi đó bài toán được phát biểu lại là: “Tìm m để phương trình có ít nhất một nghiệm thuộc đoạn >1;2@”. Ta có 2
PT 2m t t 2. t 1 2 Xét hàm số fc(t) 2
f (t) t t 2, t
>1;2@, f '(t) 2t 1! 0, t >1;2@ 4
Suy ra hàm số đồng biến trên >1;2@. f (t) 0
Khi đó phương trình có nghiệm khi 0 d 2m d 4 0 d m d 2.
Vậy 0 d m d 2 là các giá trị cần tìm.
Câu 91. Tìm tất cả các giá trị thực của tham số m để phương trình log 5x 1 .log 2.5x 2 có 2 4 m nghiệm x t1.? A. m>2;f . B. m>3;f. C. m( ; f 2]. D. mf @ ;3 . Hướng dẫn giải Với 1 5x 5 log 5x x t t
1 t log 51 2 hay t t 2. 2 2
Khi đó bài toán được phát biểu lại là: “Tìm m để phương trình có nghiệm t t 2 ”. Xét hàm số 2
f (t) t t, t
t 2, f '(t) 2t 1! 0, t t 2 t 2 f
Suy ra hàm số đồng biến với t t 2. fc(t)
Khi đó phương trình có nghiệm khi 2m t 6 m t 3. f
Vậy m t 3 là các giá trị cần tìm. f (t) 6
Câu 92. Tìm tất cả các giá trị thực của tham số m để phương trình 2
log x m 2 log x 3m 1 0 có 3 3 hai nghiệm x , x .x 27. ? 1 2 x thỏa mãn 1 2 A. m 2 . B. m 1 . C. m 1. D. m 2 . Hướng dẫn giải
Điều kiện x ! 0. Đặt t log . Khi đó phương trình có dạng: 2
t m 2t 3m 1 0 . 3 x
Để phương trình có hai nghiệm phân biệt thì ª m ' m 22 43m 4 2 2 2 1 m 8m 8 ! 0 « * «¬m ! 4 2 2
Với điều kiện * ta có: t t log x log x log x .x log 27 3. 1 2 3 1 3 2 3 1 2 3
Theo Vi-ét ta có: t t m 2 m 2 3 m 1 (thỏa mãn điều kiện) 1 2
Vậy m 1 là giá trị cần tìm. Câu 93. Tìm tất cả các giá trị thực của tham số m để phương trình 2 2
log x log x 3 m 2
log x 3 có nghiệm thuộc >32;f ? 2 1 4 2 A. m1; 3º ª º ¼ . B. m 1; 3 ¬ . C. m ª 1 ; 3 ¬ . D. m 3;1¼ . Hướng dẫn giải
Điều kiện: x ! 0. Khi đó phương trình tương đương: 2
log x 2log x 3 m log x 3 . 2 2 2 Đặt t log
với x t 32 log x t log 32 5 hay t t 5. 2 x 2 2 Phương trình có dạng 2
t 2t 3 mt 3 * .
Khi đó bài toán được phát biểu lại là: “Tìm m để phương trình (*) có nghiệm t t 5 ”
Với t t 5 thì (*) t 3.t
1 mt 3 t 3. t 1m t 3 0 t 1
t 1 m t 3 0 m t 3 t 1 4 4 4 t 1 t 1 Ta có 1 . Với t t 5 11 d1 3 hay 1 d 3 1 d 3 t 3 t 3 t 3 5 3 t 3 t 3
suy ra 1 m d 3. Vậy phương trình có nghiệm với 1 m d 3.
Câu 94. Tìm tất cả các giá trị thực của tham số m sao cho khoảng 2;3 thuộc tập nghiệm của bất phương trình log 2 x 1 ! log 2
x 4x m 1 (1) . 5 5 A. m> 12 ;1 @ 3 . B. m>12;1 @ 3 . C. m> 13 ;1 @ 2 . D. m> 13 ; 1 2@ . Hướng dẫn giải 2 x 4 2 x m 2 °x 1 !
°m ! x 4x f (x) (1) ® 5 ® 2 ° °¯ 2 m 4x 4x 5 g(x)
¯x 4x m ! 0
m t Max f (x) 12 khi x 2 ° Hệ trên thỏa mãn x 2;3 2 x 3 ® 1 2 d m d13.
m d Min f (x) 13 khi x 2 °¯ 2x3
Câu 95. Tìm tất cả các giá trị thực của tham số m để bất phương trình log 2 7x 7 t log 2
mx 4x m , x . 2 2 A. m2; @ 5 . B. m 2; @ 5 . C. m>2;5 . D. m> 2; 5 . Hướng dẫn giải
Bất phương trình tương đương 2 2
7x 7 t mx 4x m ! 0, x ° 7 m 2
x 4x 7 m t 0 (2) ® , x . 2
°¯mx 4x m ! 0 (3)
9 m 7 : (2) không thỏa x
9 m 0: (3) không thỏa x 7 m ! 0 m 7 ° °' 4 7 ° c m d 0 °m d 5 2 2 (1) thỏa x ® ® 2 m d 5. m ! 0 m ! 0 ° ° ° 2 ° 'c ¯m ! 2 4 m 0 ¯ 3
Câu 96. Tìm tất cả các giá trị thực của tham số m để bất phương trình 1 log 2 x 1 t log 2 mx 4 có nghiệm đúng . x 5 5 x m A. m2; @ 3 . B. m 2; @3. C. m>2;3 . D. m> 2; 3 . Hướng dẫn giải
Bất phương trình tương đương 2 x 2 7
1 t mx 4x m ! 0, x ° 5 m 2
x 4x 5 m t 0 (2) ® (*), x . 2
°¯mx 4x m ! 0 (3)
9 m 0 hoặc m 5 : (*) không thỏa x 5 m ! 0 ° °'c 4 5 m d 0 2 2
9 m z 0 và m z 5: (*) ® 2 m d 3. m ! 0 ° ° 2 'c 4 m 0 ¯ 3




