
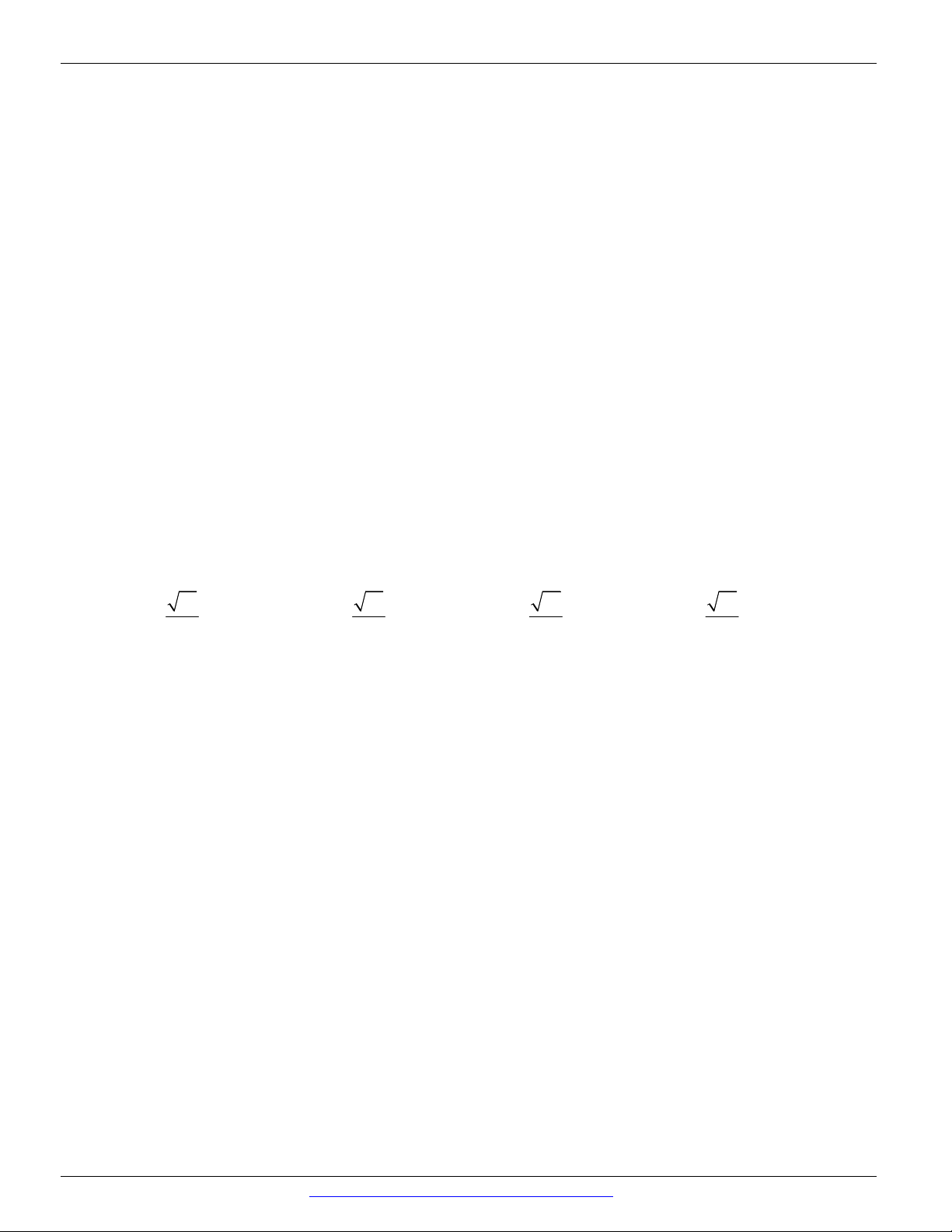




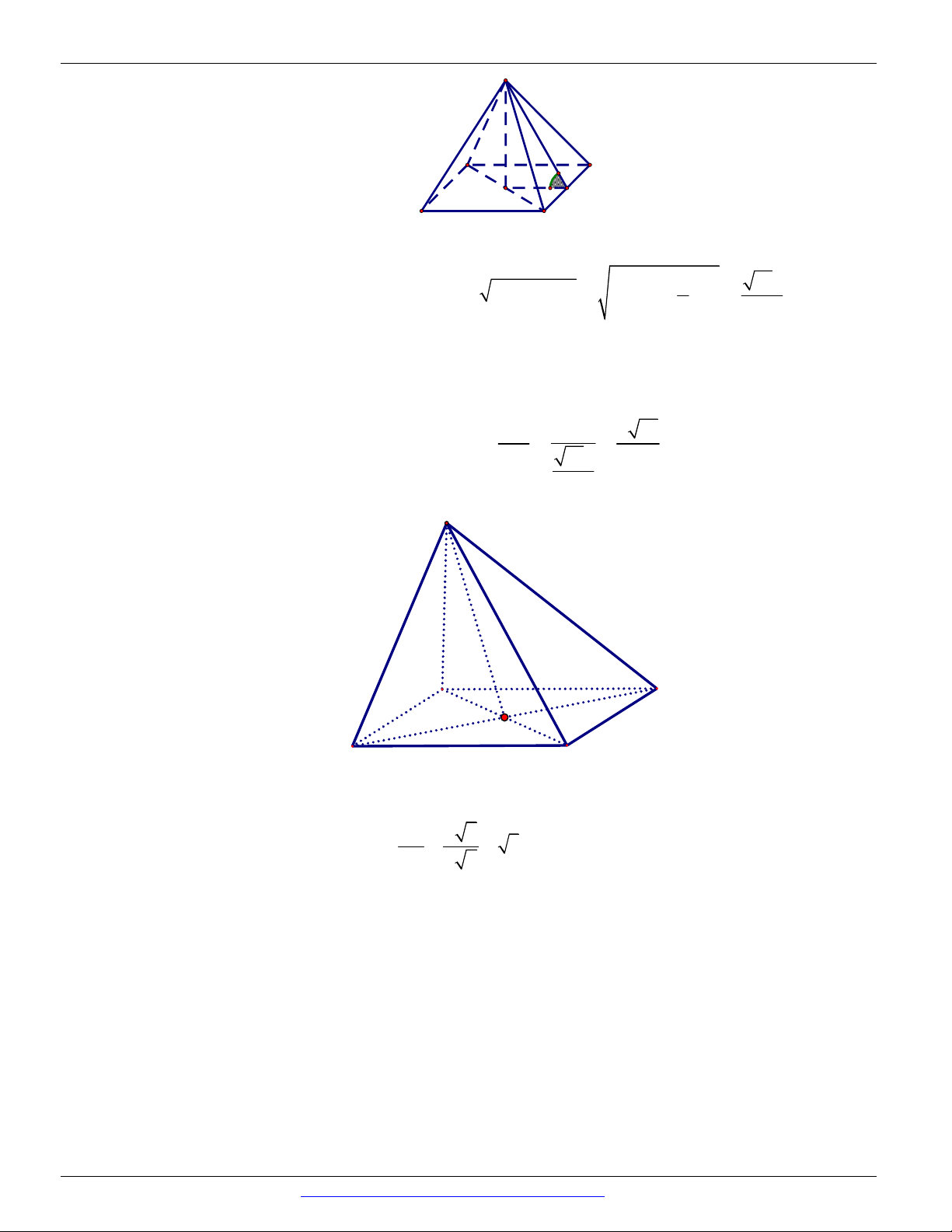

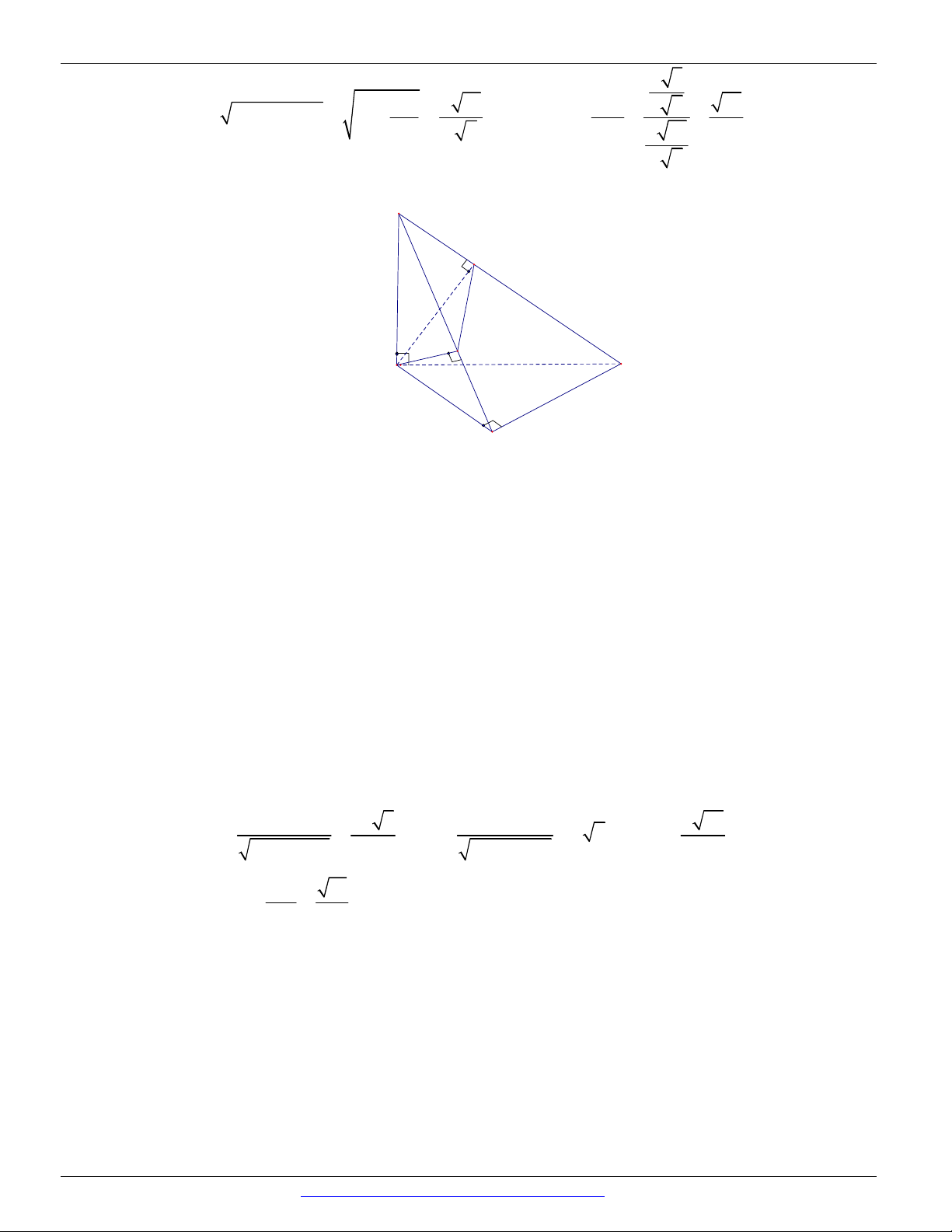
Preview text:
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 TOÁN 11
HAI MẶT PHẲNG VUÔNG GÓC 1H3-4 Contents
A. CÂU HỎI .................................................................................................................................................................... 1
DẠNG 1. CÂU HỎI LÝ THUYẾT .................................................................................................................................. 1
DẠNG 2. XÁC ĐỊNH QUAN HỆ VUÔNG GÓC GIỮA HAI MẶT PHẲNG, MẶT PHẲNG VỚI ĐƯỜNG
THẲNG, ĐƯỜNG THẲNG VỚI ĐƯỜNG THẲNG .................................................................................................. 4
Dạng 2.1 Đường thẳng vuông góc với mặt phẳng, đường thẳng vuông góc với đường thẳng .................................... 4
Dạng 2.2 Hai mặt phẳng vuông góc ............................................................................................................................. 4
DẠNG 3. XÁC ĐỊNH GÓC GIỮA HAI MẶT PHẲNG ................................................................................................. 6
Dạng 3.1 Góc của mặt phẳng bên với mặt phẳng đáy .................................................................................................. 6
Dạng 3.2 Góc của hai mặt phẳng bên ..................................................................................................................... 10
Dạng 3.3 Góc của hai mặt phẳng khác ....................................................................................................................... 13
DẠNG 4. MỘT SỐ CÂU HỎI LIÊN QUAN ................................................................................................................ 15
B. LỜI GIẢI ................................................................................................................................................................... 18
DẠNG 1. CÂU HỎI LÝ THUYẾT ................................................................................................................................ 18
DẠNG 2. XÁC ĐỊNH QUAN HỆ VUÔNG GÓC GIỮA HAI MẶT PHẲNG, MẶT PHẲNG VỚI ĐƯỜNG
THẲNG, ĐƯỜNG THẲNG VỚI ĐƯỜNG THẲNG ................................................................................................ 19
Dạng 2.1 Đường thẳng vuông góc với mặt phẳng, đường thẳng vuông góc với đường thẳng .................................. 19
Dạng 2.2 Hai mặt phẳng vuông góc ........................................................................................................................... 21
DẠNG 3. XÁC ĐỊNH GÓC GIỮA HAI MẶT PHẲNG ............................................................................................... 26
Dạng 3.1 Góc của mặt phẳng bên với mặt phẳng đáy ................................................................................................ 26
Dạng 3.2 Góc của hai mặt phẳng bên ..................................................................................................................... 42
Dạng 3.3 Góc của hai mặt phẳng khác ....................................................................................................................... 53
DẠNG 4. MỘT SỐ CÂU HỎI LIÊN QUAN ................................................................................................................ 62 A. CÂU HỎI
DẠNG 1. CÂU HỎI LÝ THUYẾT Câu 1.
Khẳng định nào sau đây đúng?
A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
B. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
C. Hai mặt phẳng song song khi và chỉ khi góc giữa chúng bằng 00.
D. Hai đường thẳng trong không gian cắt nhau khi và chỉ khi góc giữa chúng lớn hơn 00 và nhỏ hơn 900. Câu 2.
Chọn mệnh đề đúng trong các mệnh đề sau:
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
A. Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng tùy ý nằm trong mỗi mặt phẳng.
B. Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
C. Góc giữa hai mặt phẳng luôn là góc nhọn.
D. Góc giữa hai mặt phẳng bằng góc giữa hai vec tơ chỉ phương của hai đường thẳng lần lượt vuông
góc với hai mặt phẳng đó. Câu 3.
Trong các mệnh đề dưới đây, mệnh đề nào sai?
A. Hình chóp tứ giác đều có tất cả các cạnh bằng nhau.
B. Hình chóp tứ giác đều có các cạnh bên bằng nhau.
C. Hình chóp tứ giác đều có đáy là hình vuông.
D. Hình chóp tứ giác đều có hình chiếu vuông góc của đỉnh lên đáy trùng với tâm của đáy. Câu 4.
Cho các đường thẳng a,b và các mặt phẳng , . Chọn mệnh đề đúng trong các mệnh đề sau a a b A.
. B. b// . a a a b
C. a .
D. a a b . b b Câu 5.
Trong các mệnh đề sau đây, mệnh đề nào là đúng?
A. Cho hai mặt phẳng vuông góc với nhau, nếu một đường thẳng nằm trong mặt phẳng này và
vuông góc với giao tuyến của hai mặt phẳng thì vuông góc với mặt phẳng kia.
B. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước
C. Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
D. Đường thẳng d là đường vuông góc chung của hai đườngthẳng chéo nhau a, b khi và chỉ khi
d vuông góc với cả a và . b Câu 6.
Cho đường thẳng a không vuông góc với mặt phẳng . có bao nhiêu mặt phẳng chứa a và
vuông góc với . A. 2 . B. 0 . C. Vô số. D. 1 . Câu 7.
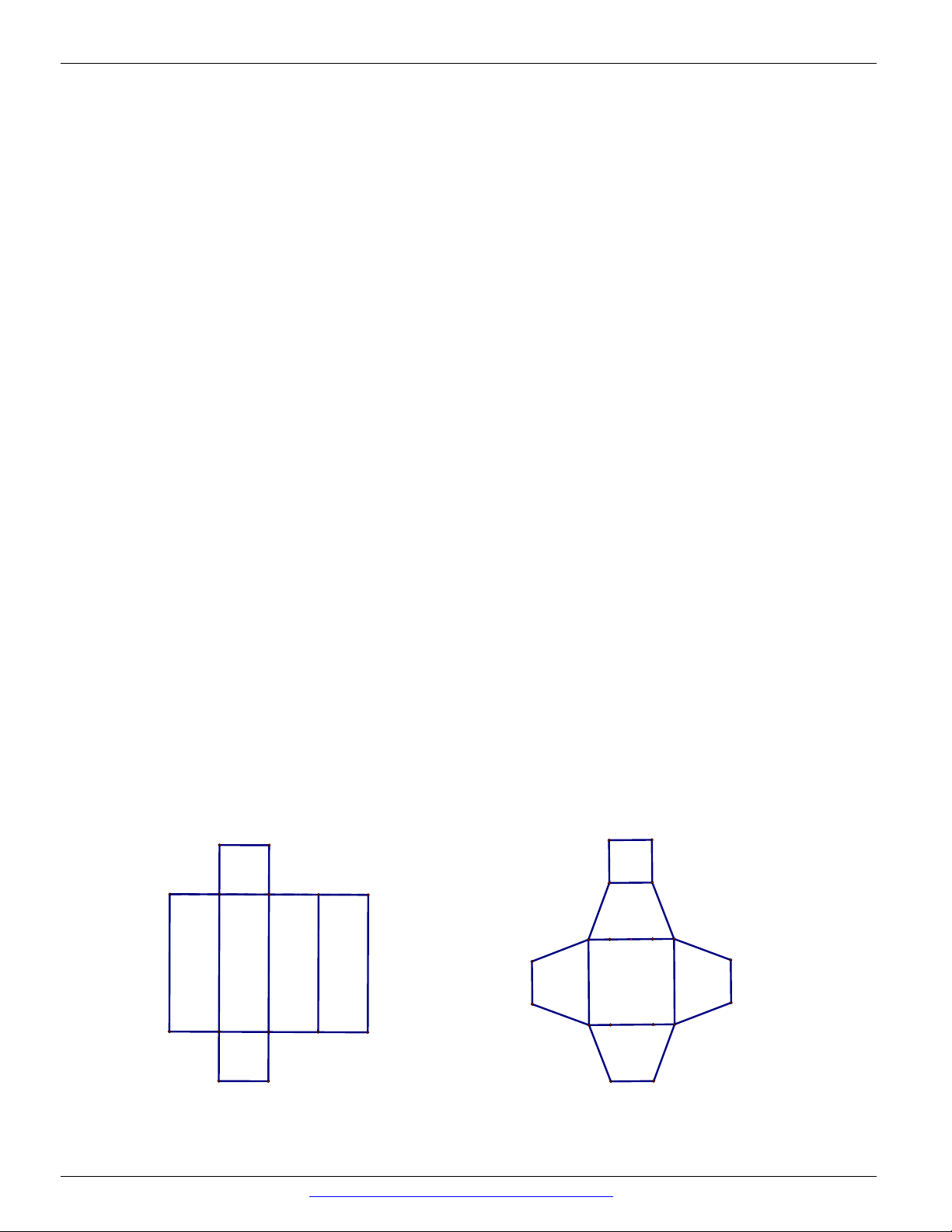
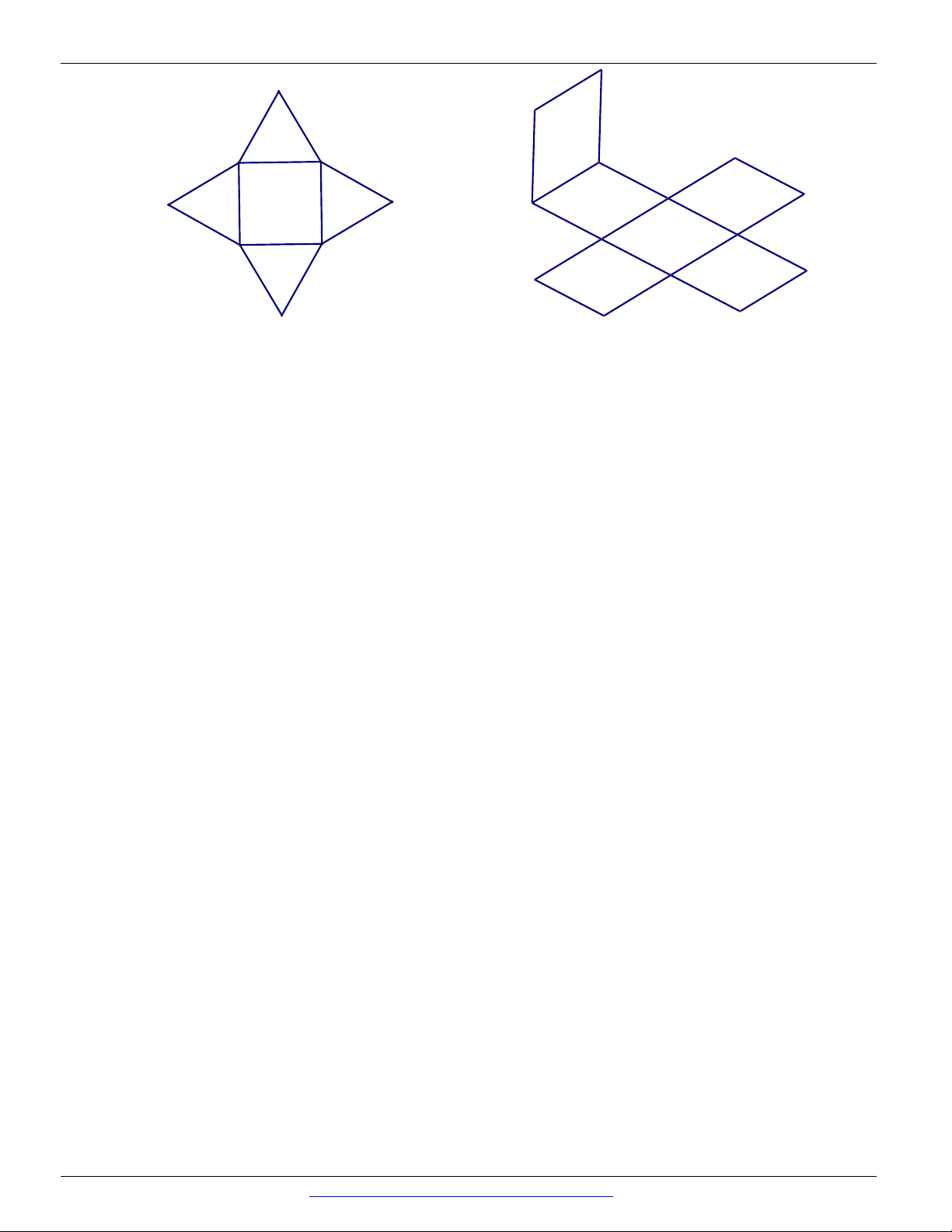
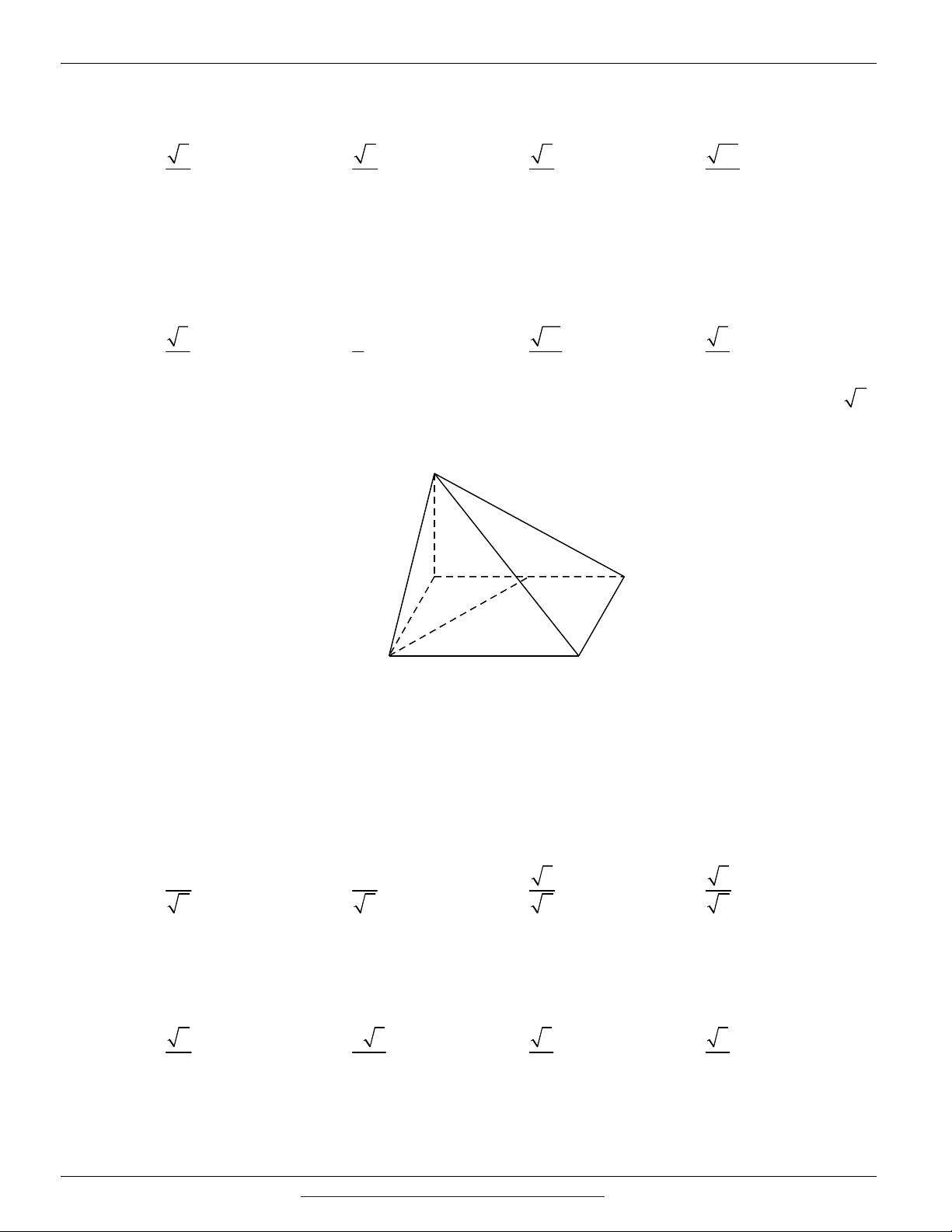
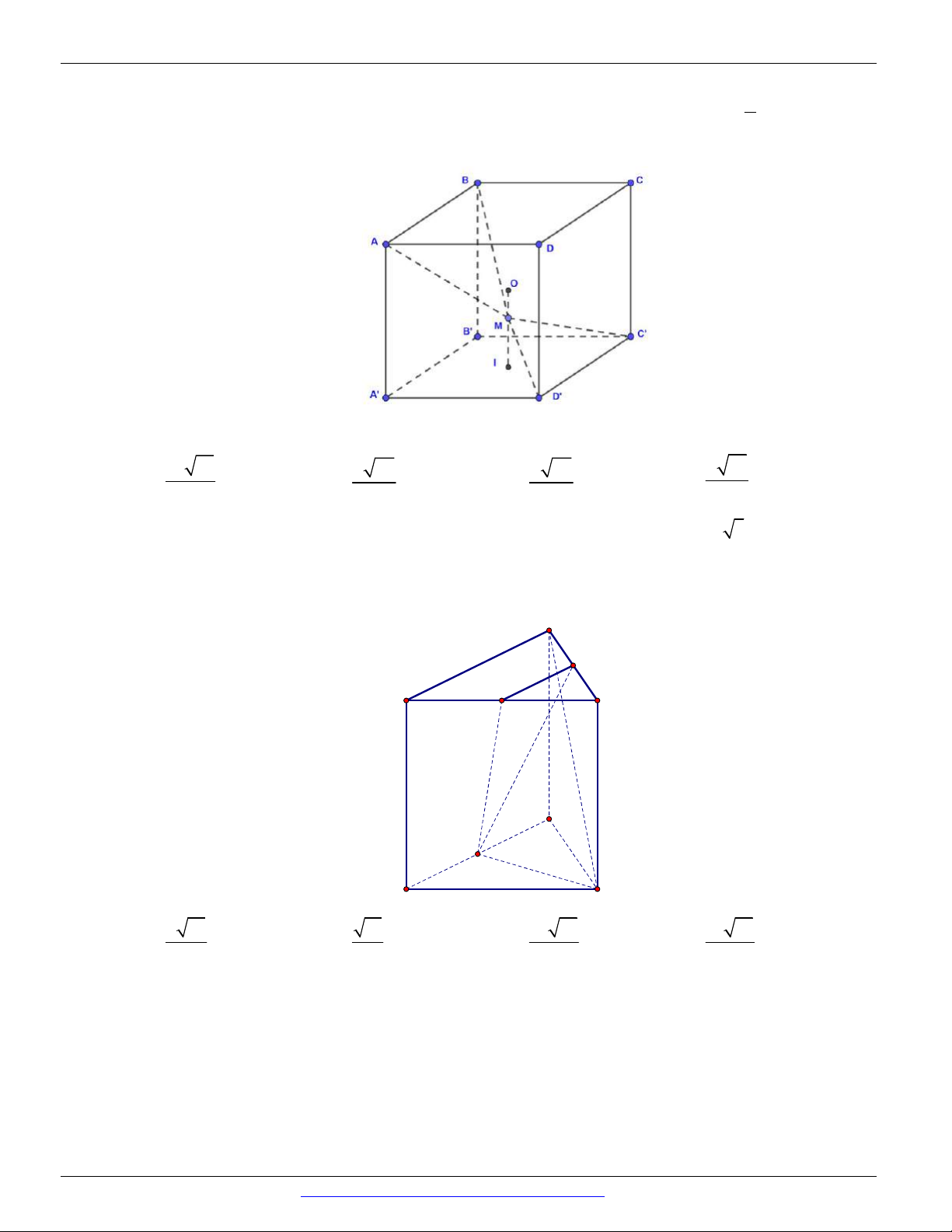
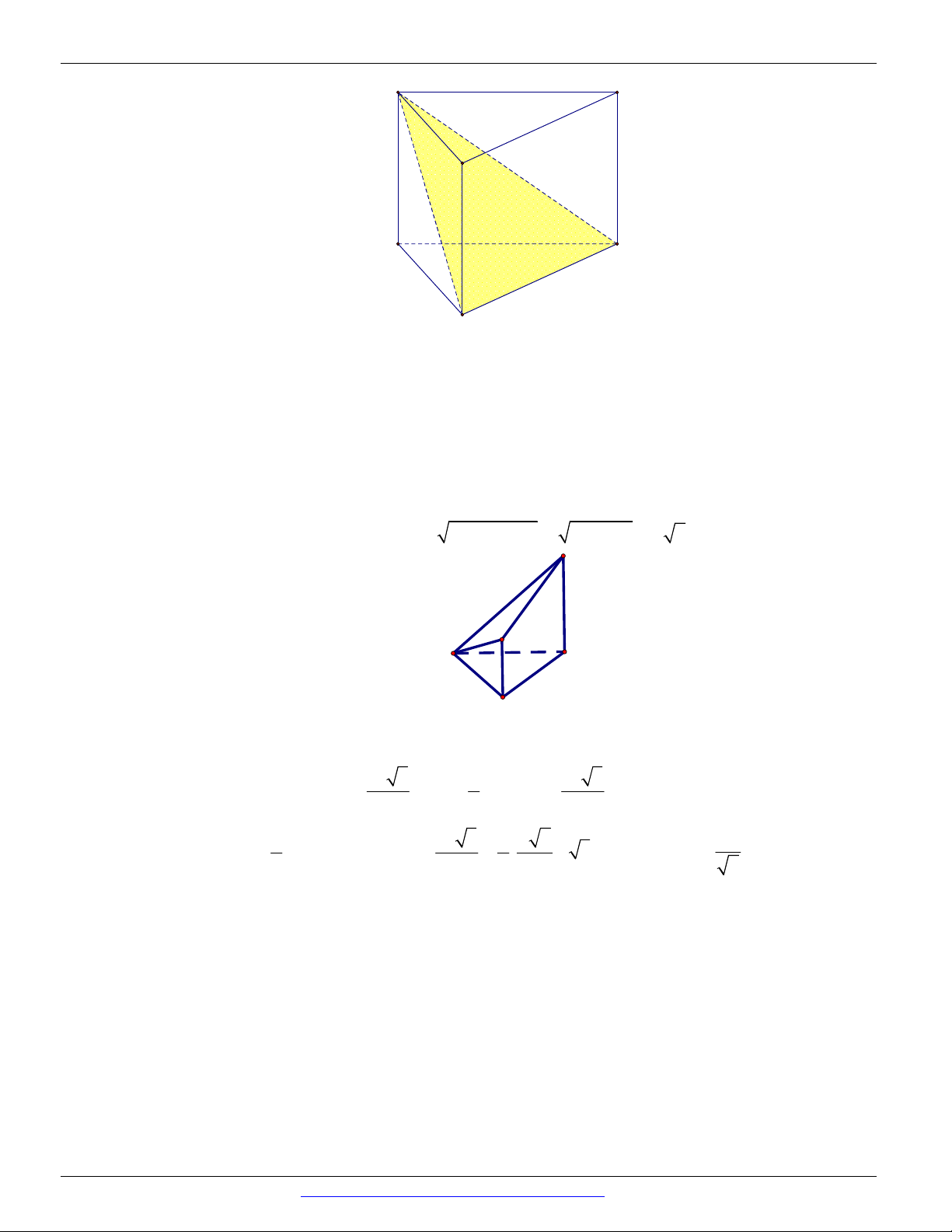
Mảnh bìa phẳng nào sau đây có thể xếp thành lăng trụ tứ giác đều? A. B.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 C. D. Câu 8.
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu một đường thẳng nằm trong mặt phẳng này và vuông góc với mặt phẳng kia thì hai mặt phẳng vuông góc nhau.
B. Nếu hai mặt phẳng cùng vuông góc với mặt phẳng thứ ba thì chúng song song với nhau.
C. Nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này đều vuông
góc với mặt phẳng kia.
D. Nếu hai mặt phẳng cùng vuông góc với mặt phẳng thứ ba thì chúng vuông góc với nhau. Câu 9.
Cho đường thẳng a không vuông góc với mặt phẳng . Có bao nhiêu mặt phẳng chứa a và
vuông góc với ? A. 2 . B. 0 . C. Vô số. D. 1.
Câu 10. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau đây?
i) Hình hộp đứng có đáy là hình vuông là hình lập phương
ii) Hình hộp chữ nhật có tất cả các mặt là hình chữ nhật
iii) Hình lăng trụ đứng có các cạnh bên vuông góc với đáy
iv) Hình hộp có tất cả các cạnh bằng nhau là hình lập phương A. 1. B. 2 . C. 3 . D. 4 .
Câu 11. (Nông Cống - Thanh Hóa - Lần 1 - 1819) Trong không gian cho hai đường thẳng a, b và mặt
phẳng (P) , xét các phát biểu sau:
(I). Nếu a / / b mà a (P) thì luôn có b (P) .
(II). Nếu a (P) và a b thì luôn có b / / (P) .
(III). Qua đường thẳng a chỉ có duy nhất một mặt phẳng (Q) vuông góc với mặt phẳng (P) .
(IV). Qua đường thẳng a luôn có vô số mặt phẳng (Q) vuông góc với mặt phẳng (P) .
Số khẳng định đúng trong các phát biểu trên là A. 1. B. 4 . C. 2 . D. 3 .
Câu 12. Trong các khẳng định sau, khẳng định nào là khẳng định sai?
A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
B. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì cũng vuông góc
với đường thẳng còn lại.
C. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
D. Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng vuông góc với một
đường thẳng thì song song với nhau.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 13. Cho hai mặt phẳng P và Q song song với nhau và một điểm M không thuộc P và Q .
Qua M có bao nhiêu mặt phẳng vuông góc với P và Q . A. 3 . B. Vô số. C. 1. D. 2 .
DẠNG 2. XÁC ĐỊNH QUAN HỆ VUÔNG GÓC GIỮA HAI MẶT PHẲNG, MẶT PHẲNG
VỚI ĐƯỜNG THẲNG, ĐƯỜNG THẲNG VỚI ĐƯỜNG THẲNG
Dạng 2.1 Đường thẳng vuông góc với mặt phẳng, đường thẳng vuông góc với đường thẳng
Câu 14. Cho hình chóp S.ABCD đều. Gọi H là trung điểm của cạnh AC . Tìm mệnh đề sai?
A. SAC SBD .
B. SH ABCD .
C. SBD ABCD . D. CD SAD .
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O và SA SC, SB SD . Mệnh
đề nào sau đây sai?
A. SC SBD .
B. SO ABCD .
C. SBD ABCD . D. SAC ABCD .
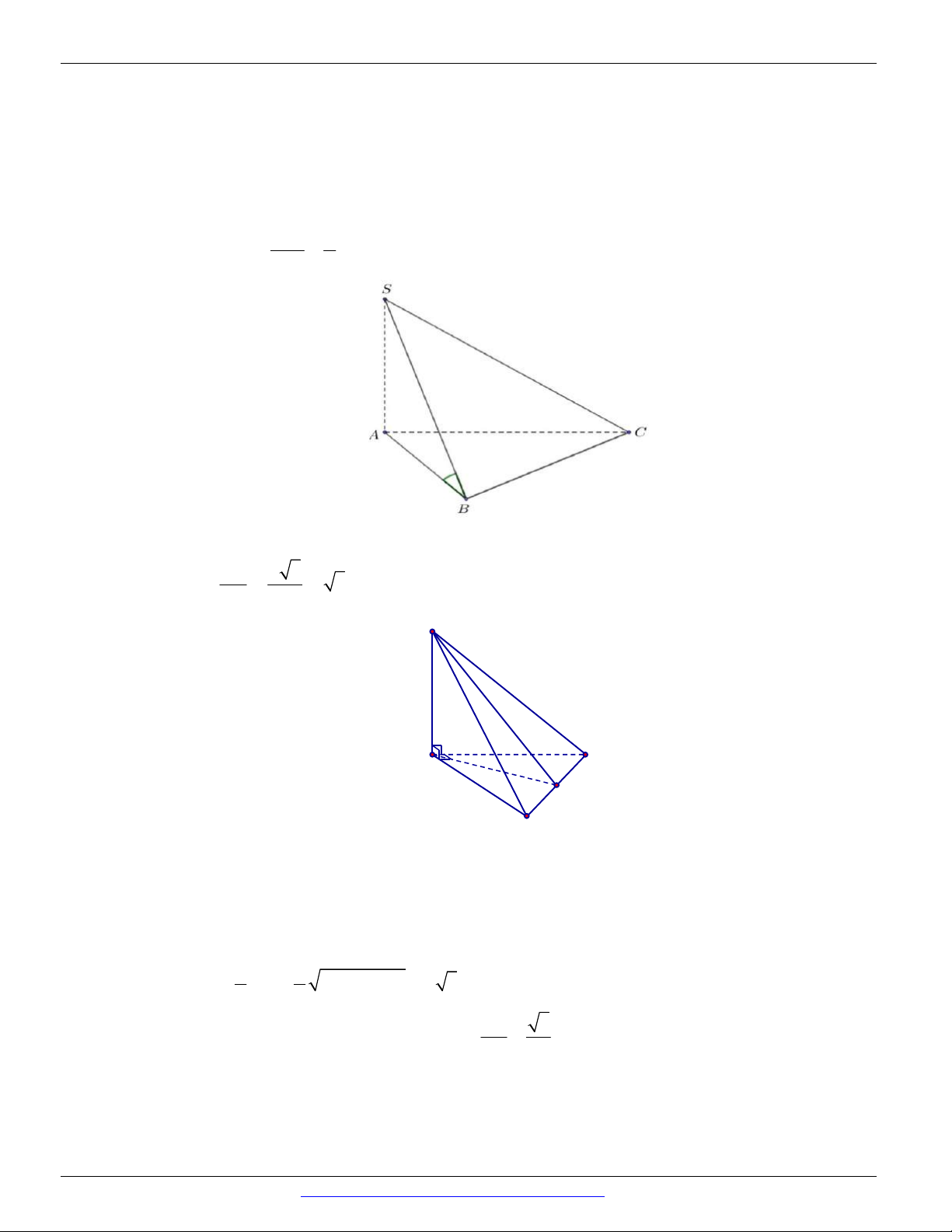
Câu 16. Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B và cạnh bên SA vuông góc với mặt
phẳng ABC . Mệnh đề nào sau đây sai?
A. SA BC .
B. AB BC .
C. AB SC .
D. SB BC .
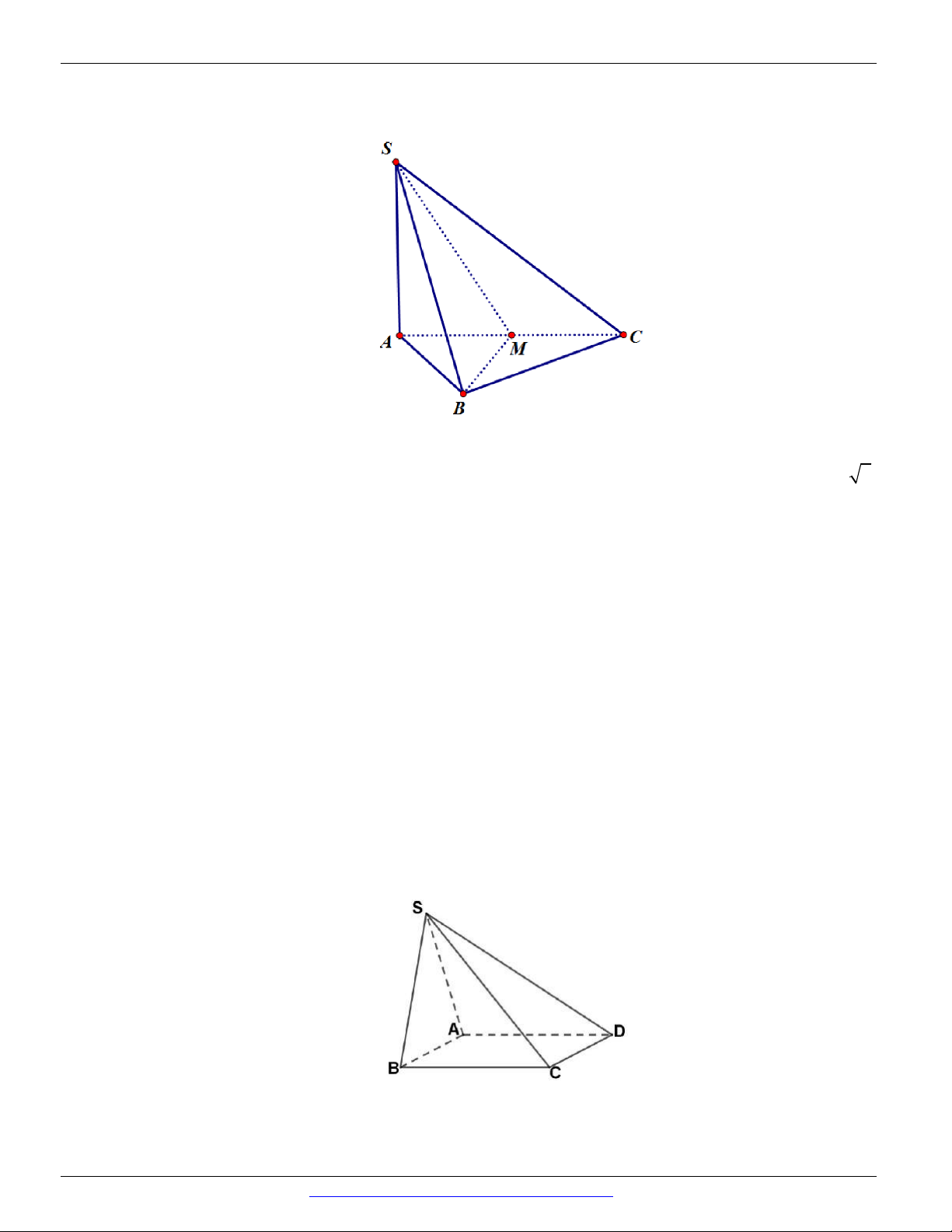
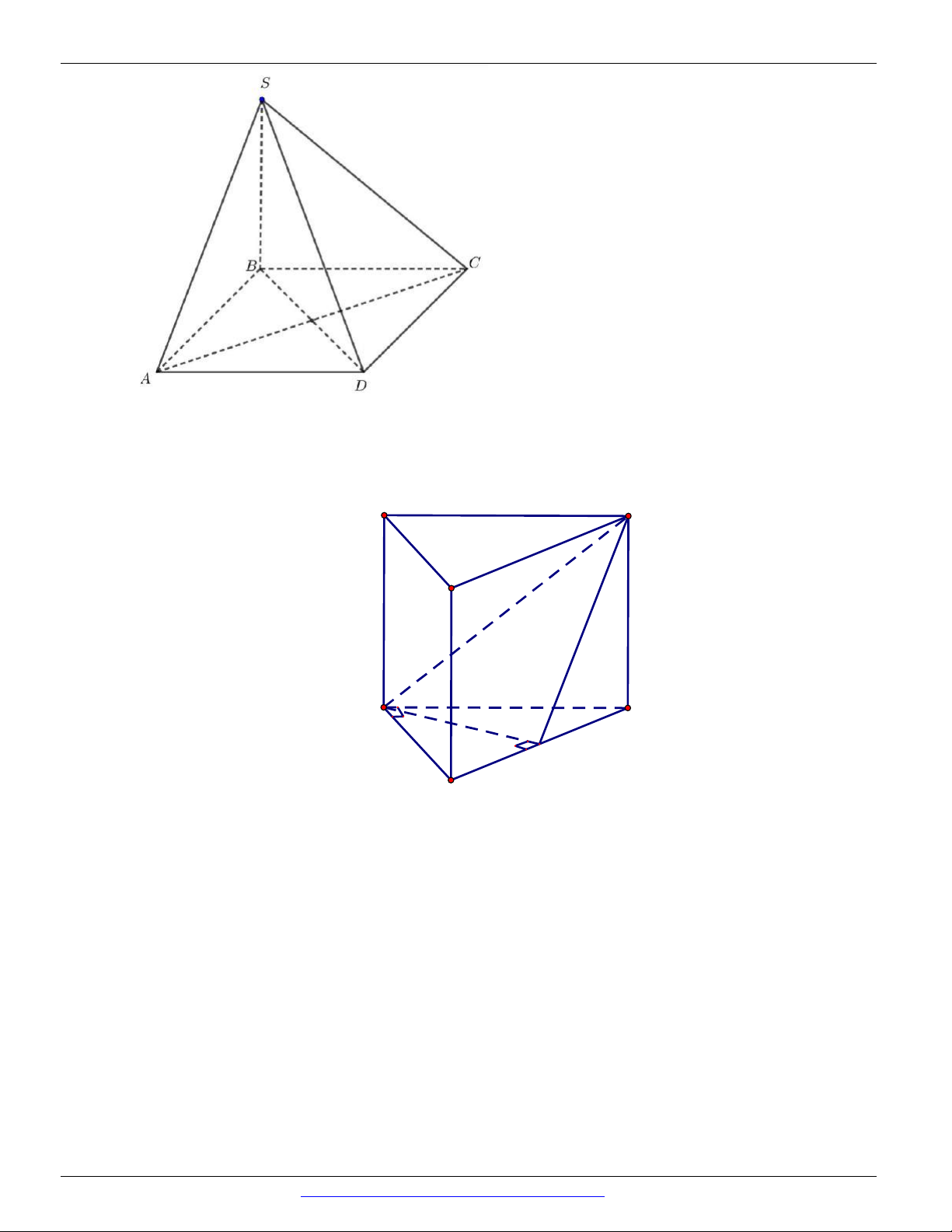
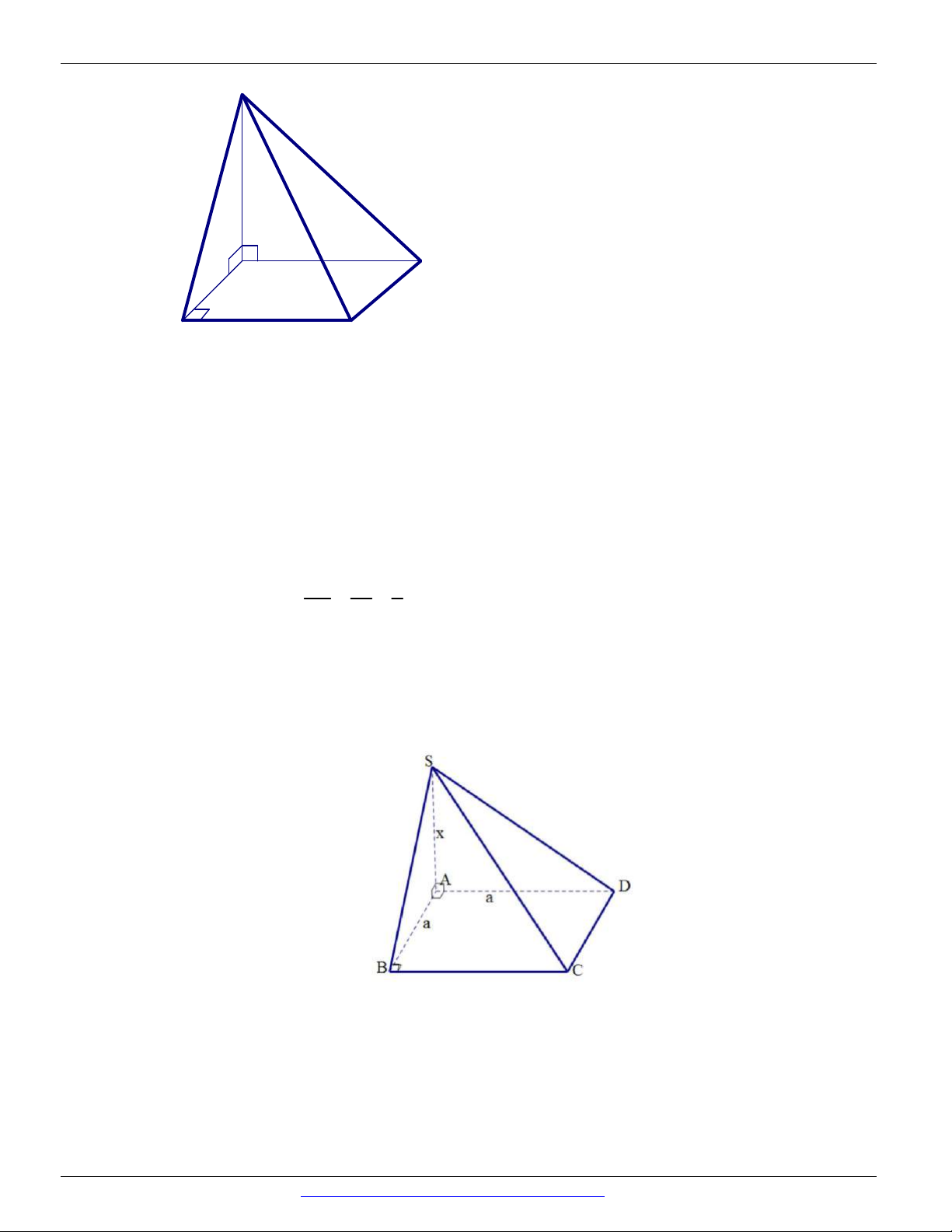
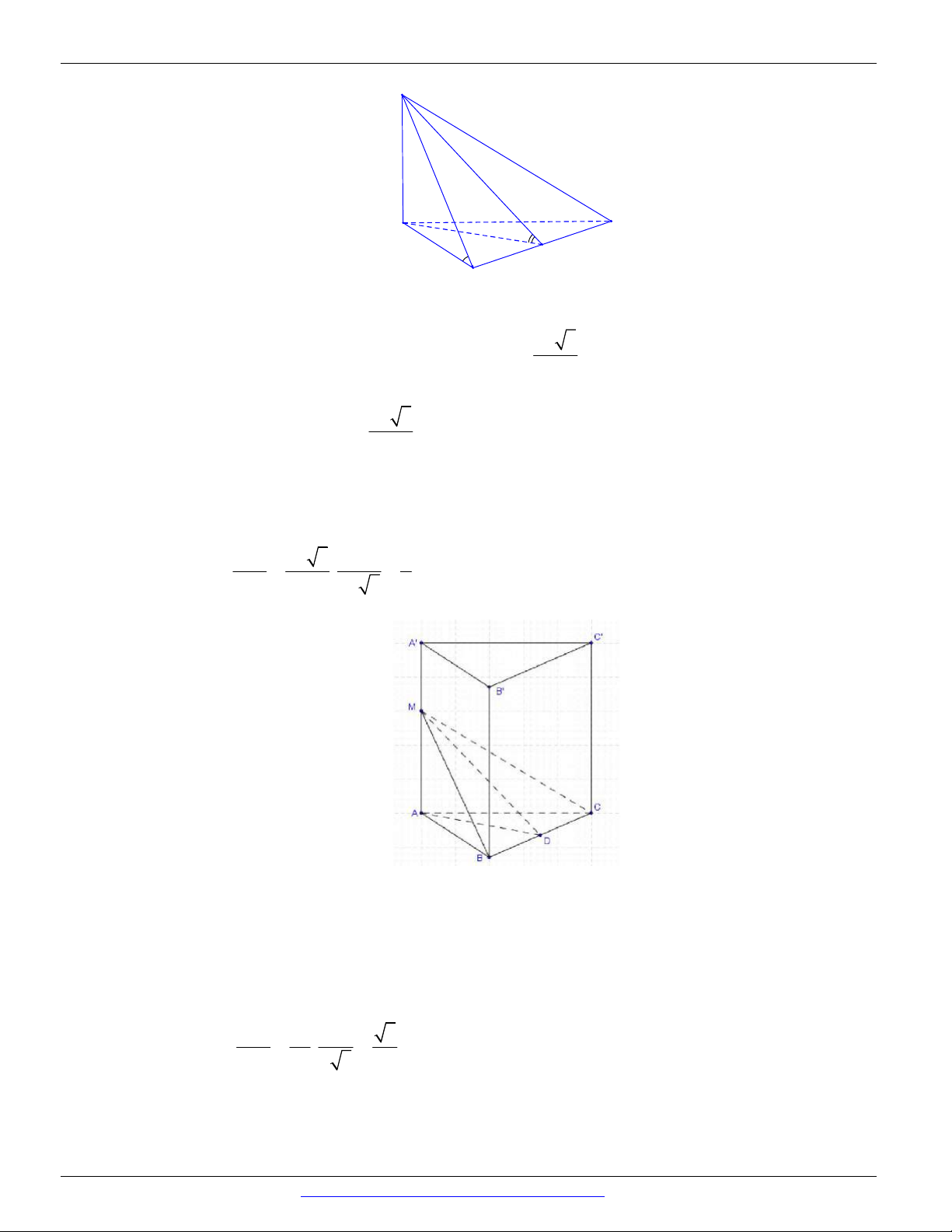
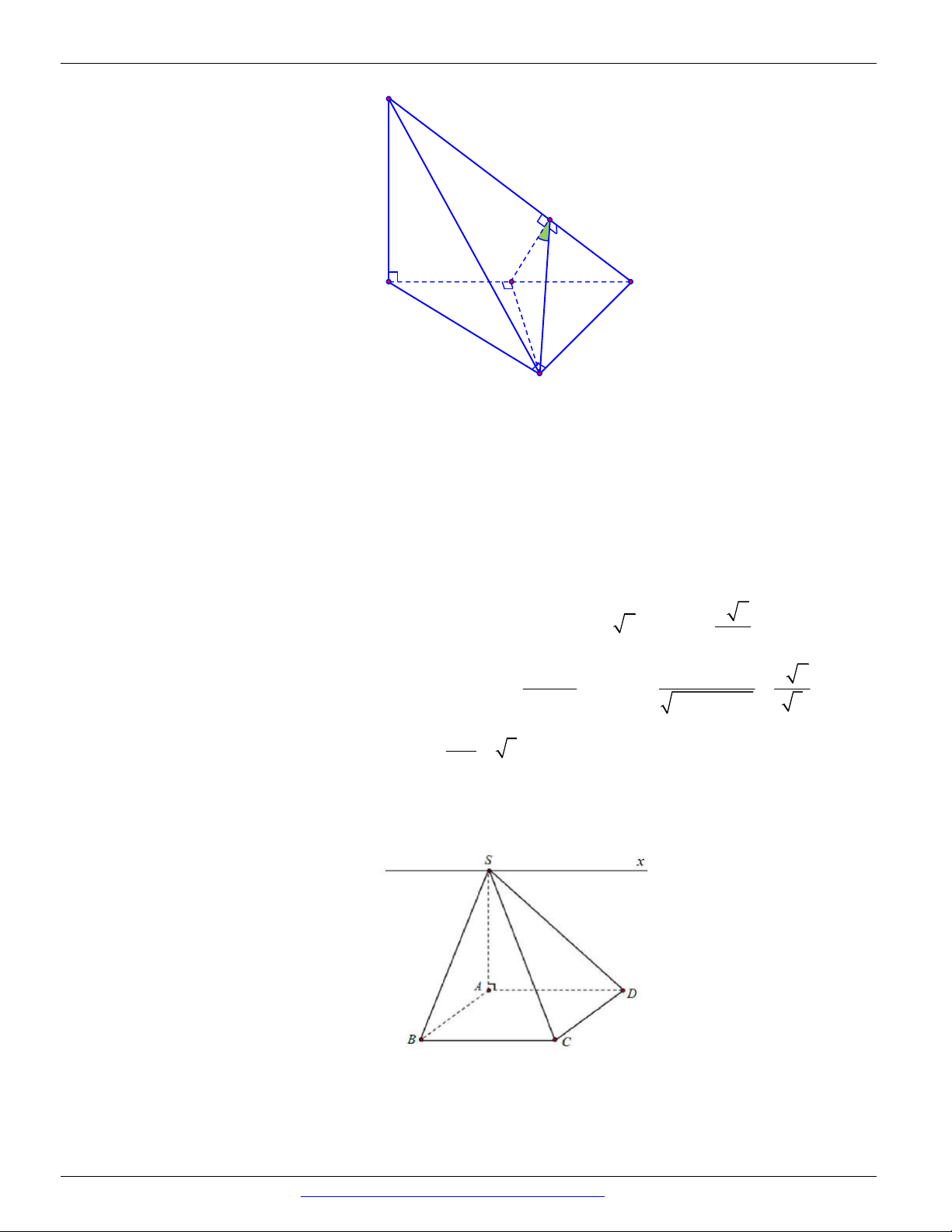
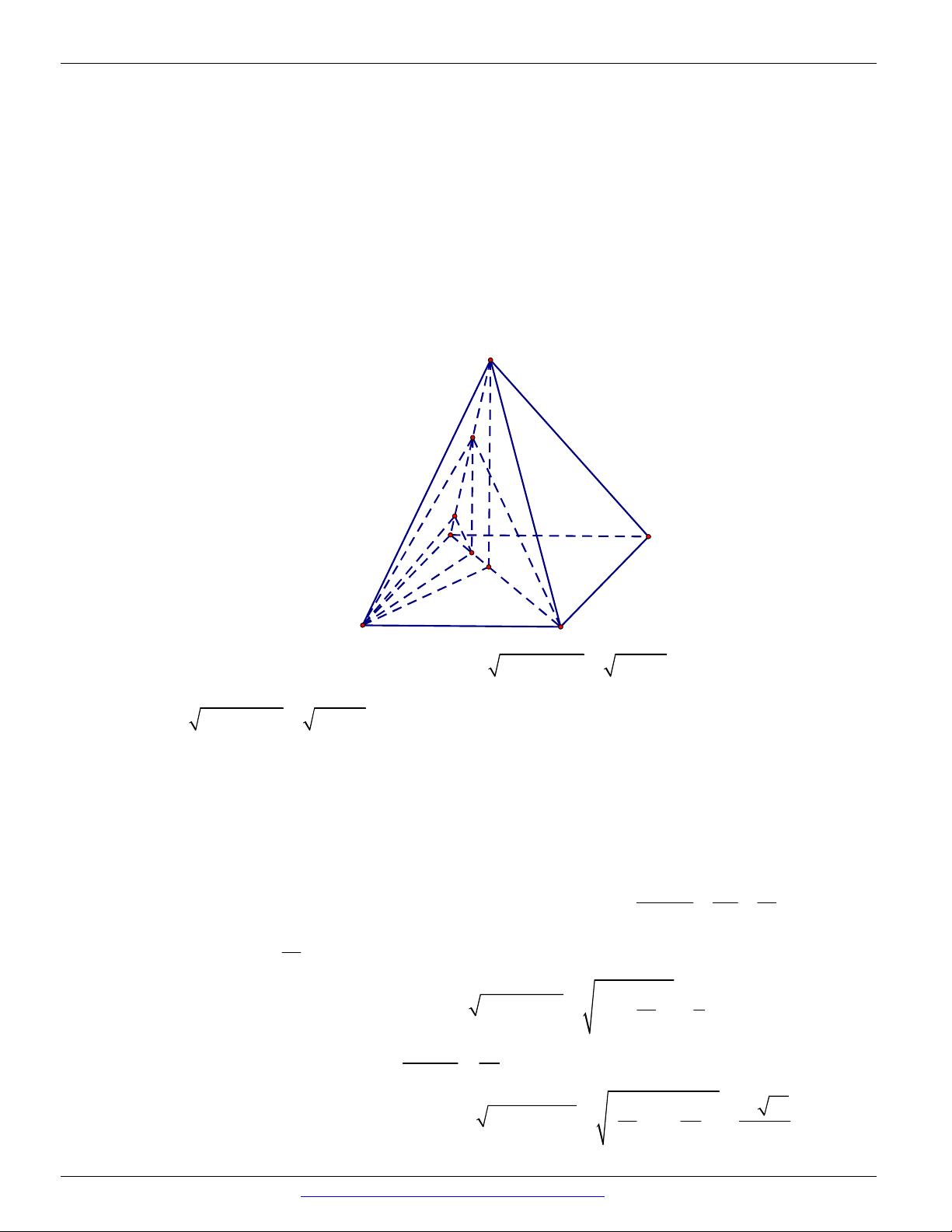
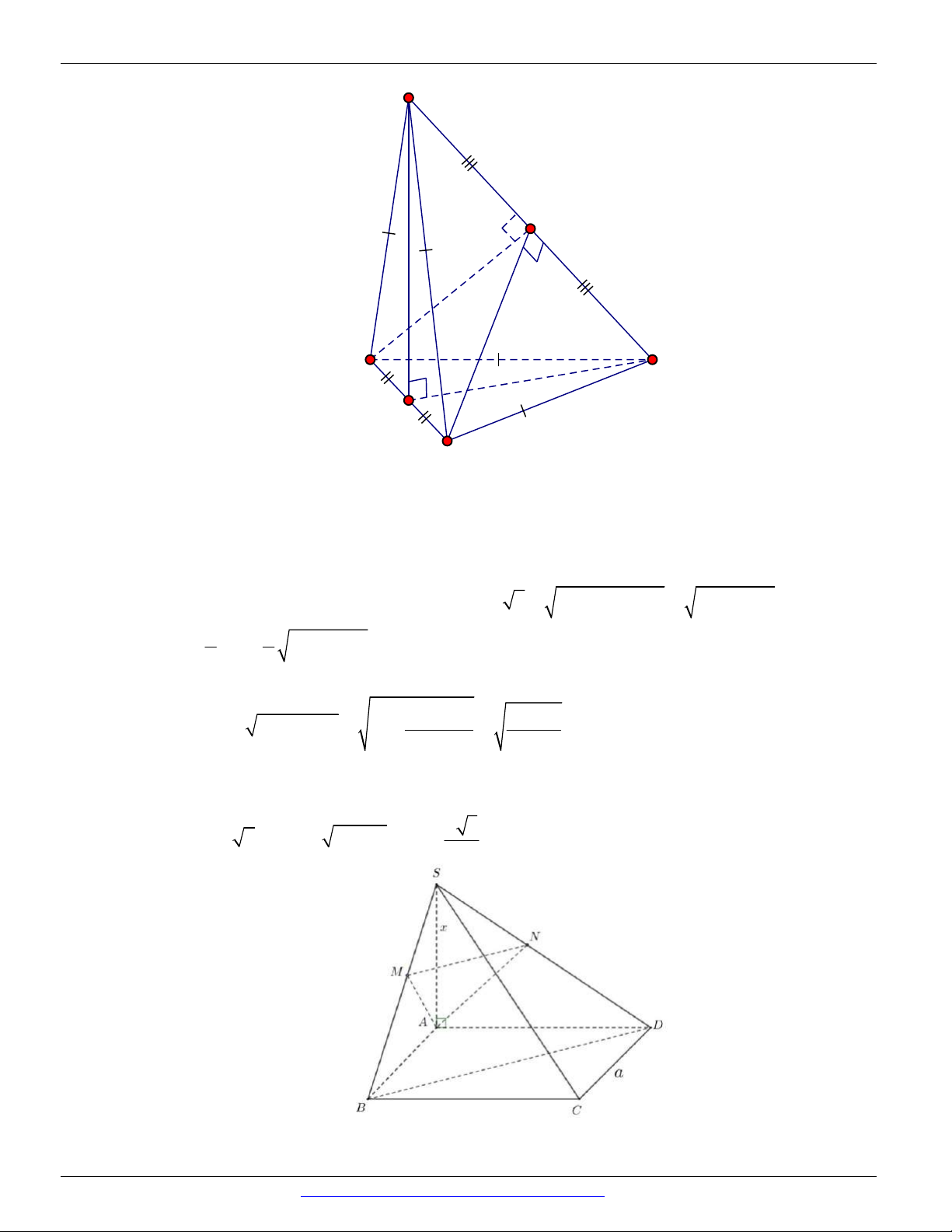
Câu 17. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , tam giác SAB đều và nằm trong
mặt phẳng vuông góc với mặt phẳng đáy. Tính sin của góc tạo bởi đường MD và mặt phẳng SBC . 13 13 15 15 A. . B. . C. . D. . 5 3 5 3
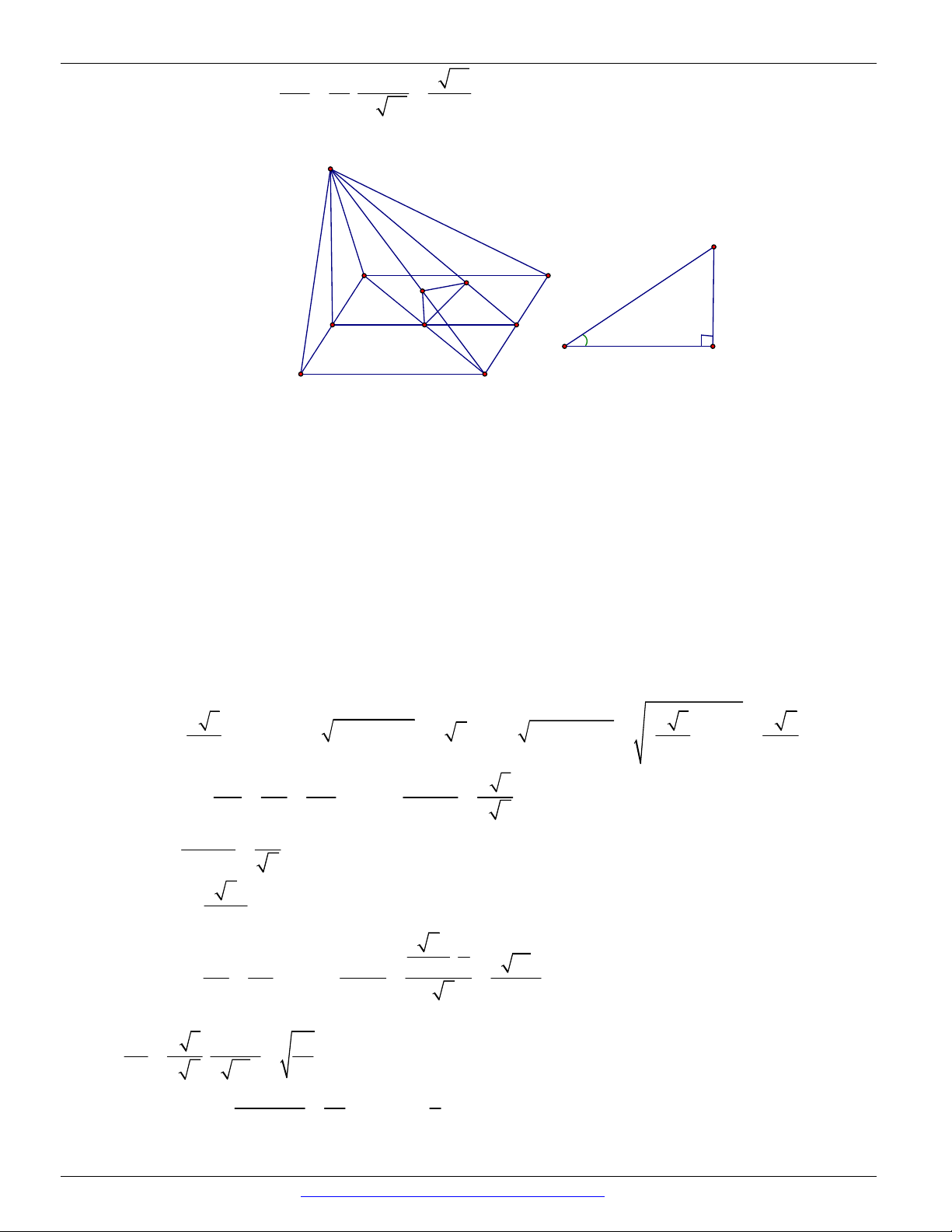
Câu 18. (THPT TRIỆU THỊ TRINH - LẦN 1 - 2018) Cho hình chóp S.ABCD có đáy ABCD là hình
vuông, hai mặt bên SAB và SAD vuông góc với mặt đáy. AH , AK lần lượt là đường cao của
tam giác SAB , SAD . Mệnh đề nào sau đây là sai?
A. BC AH .
B. SA AC .
C. HK SC .
D. AK BD .
Dạng 2.2 Hai mặt phẳng vuông góc
Câu 19. Cho hình chóp S.ABCD có đáy ABCD là hình thoi và SB vuông góc với mặt phẳng ABCD .
Mặt phẳng nào sau đây vuông góc với mặt phẳng SBD ?
A. SBC . B. SAD . C. SCD .
D. SAC .
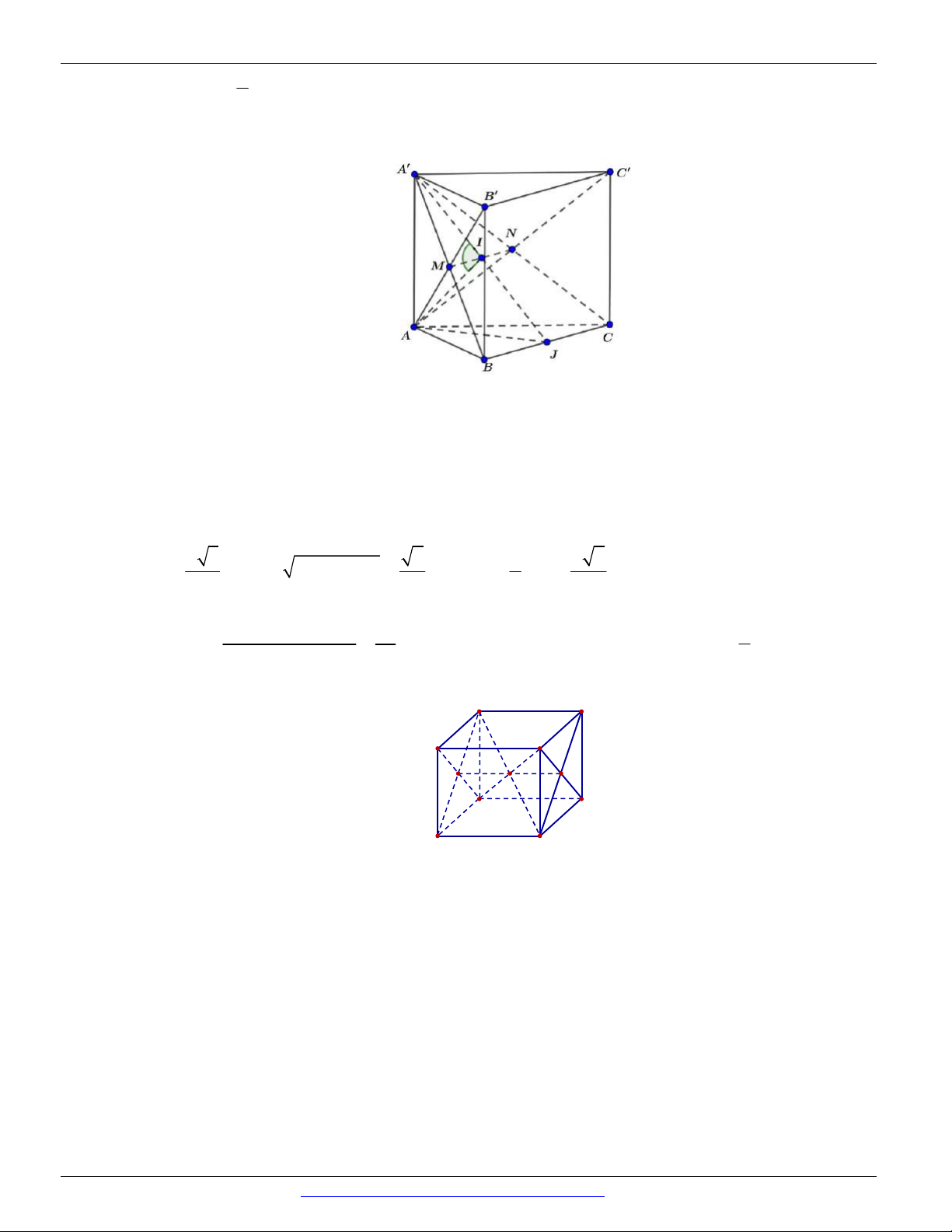
Câu 20. Cho lăng trụ đứng ABC.AB C
có đáy là tam giác ABC vuông cân tại A . Gọi M là trung điểm
của BC , mệnh đề nào sau đây sai ?
A. ABB ACC . B. AC M ABC .
C. AMC BCC . D. ABC ABA .
Câu 21. (THPT TỨ KỲ - HẢI DƯƠNG - LẦN 2 - 2018).Cho hình chóp S.ABC có đáy ABC là tam giác
cân tại B , cạnh bên SA vuông góc với đáy, I là trung điểm AC , H là hình chiếu của I lên SC
. Khẳng định nào sau đây đúng?
A. BIH SBC .
B. SAC SAB .
C. SBC ABC . D. SAC SBC .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
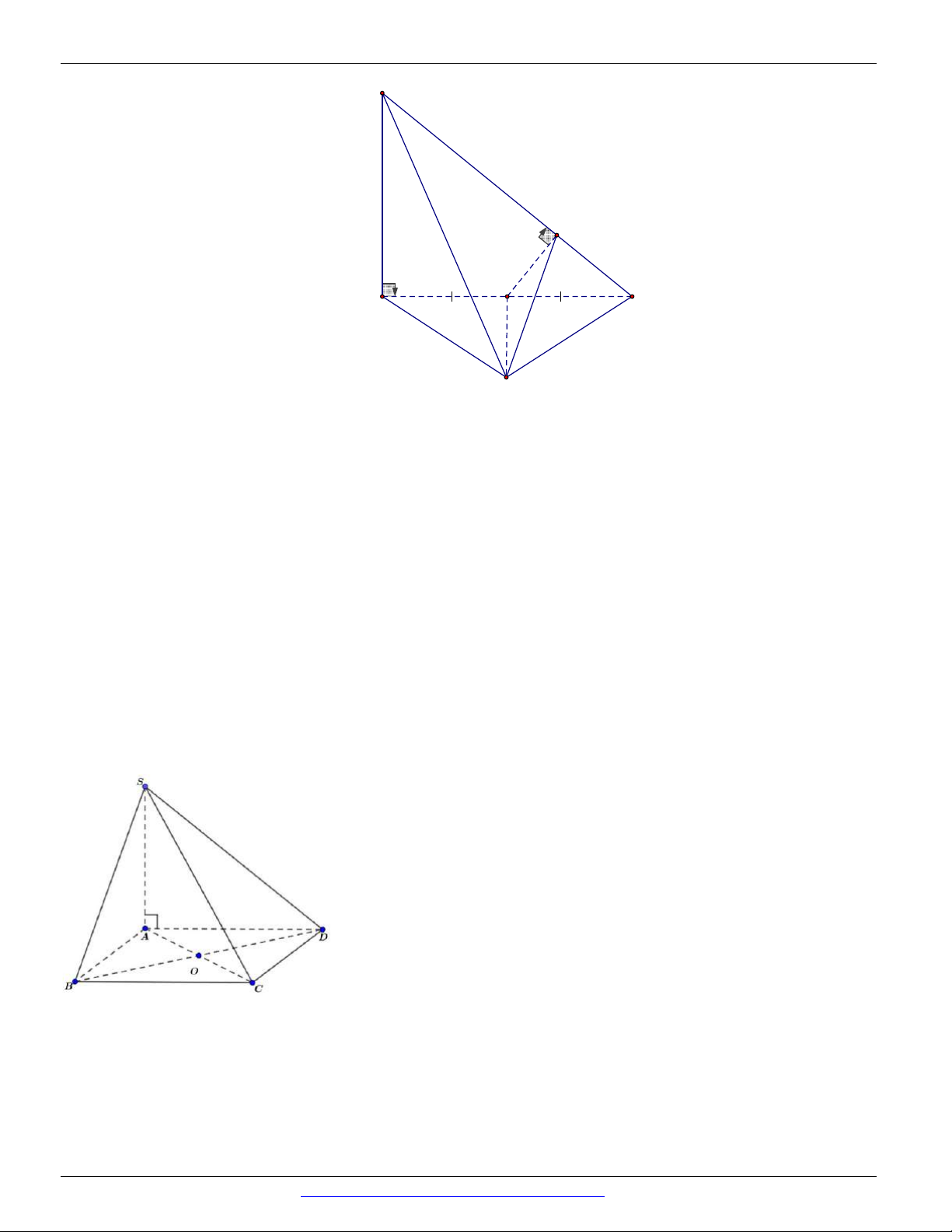
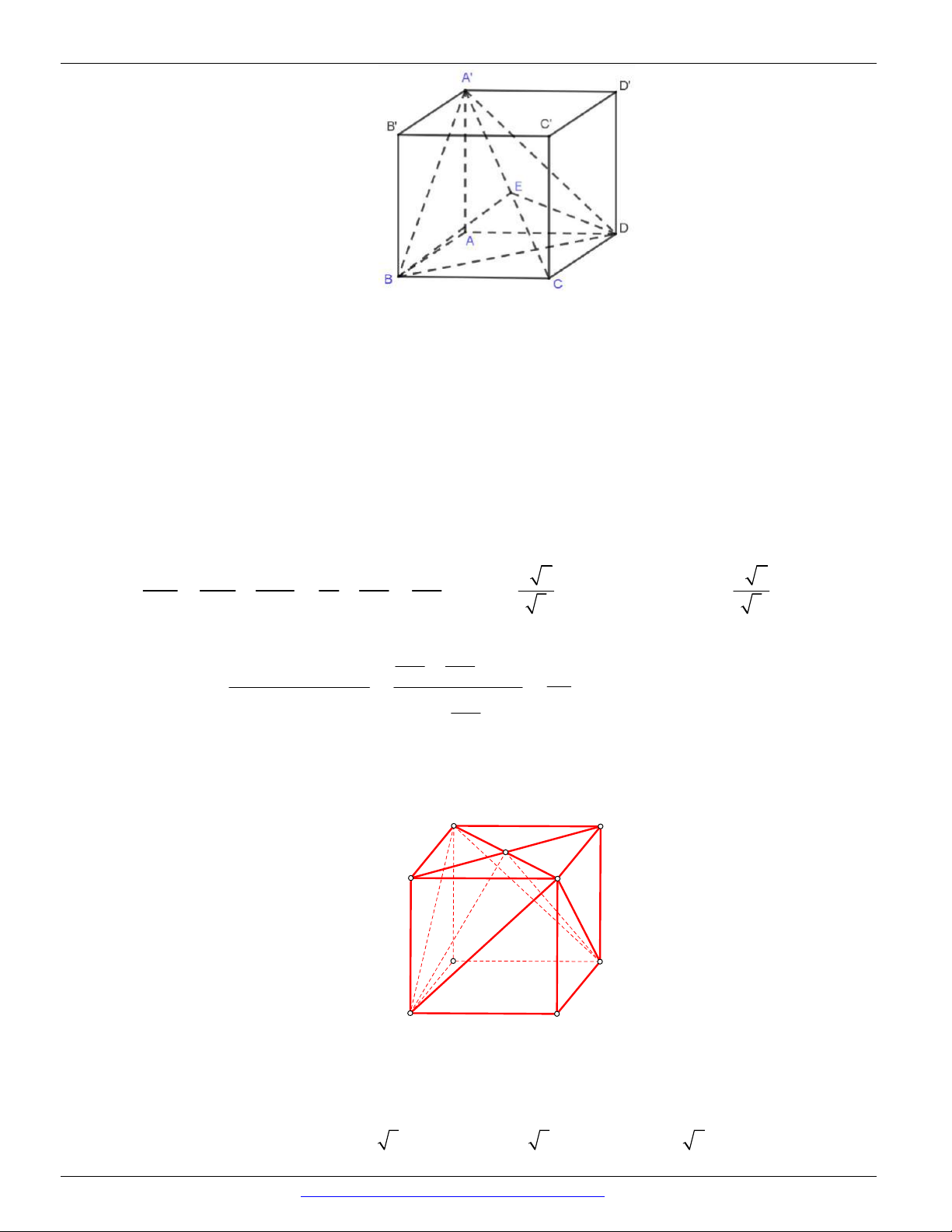
Câu 22. Cho hình chóp S .ABC có đáy ABC là tam giác vuông cân tại B , SA ABC , gọi M là trung
điểm của AC . Mệnh đề nào sai ?
A. SAB SAC . B. BM AC .
C. SBM SAC . D. SAB SBC .
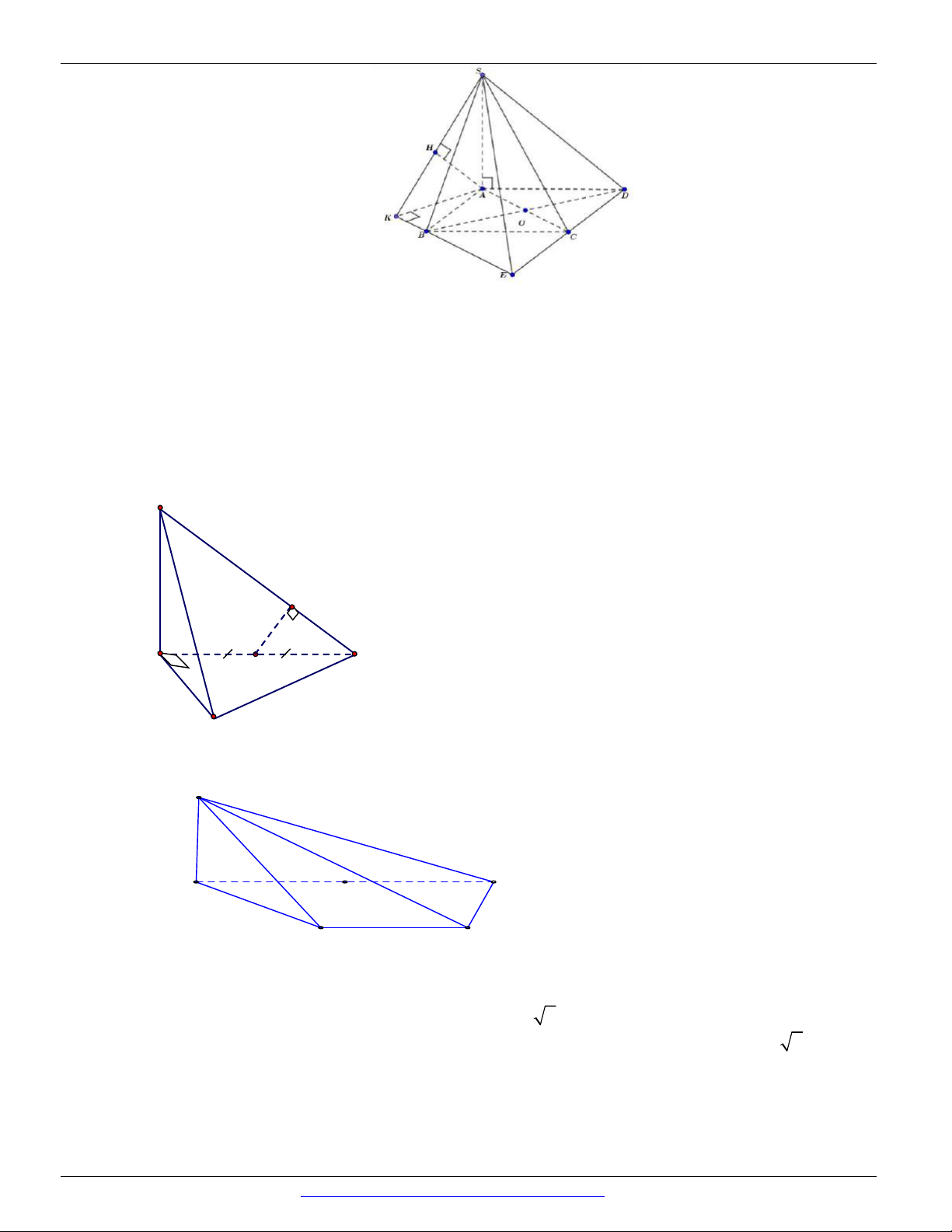
Câu 23. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , tâm O , SA ABCD , SA a 6
(như hình vẽ). Mệnh đề nào sau đây là đúng?.
A. SBC ABCD . B. SBC SCD . C. SBC SAD
D. SBC SAB .
Câu 24. Cho hình lăng trụ tứ giác đều ABC .
D A ' B 'C ' D ' . Mặt phẳng AB 'C vuông góc với mặt phẳng nào sau đây?
A. D ' BC .
B. B ' BD .
C. D ' AB .
D. BA'C ' .
Câu 25. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , cạnh bên SA vuông góc với ABC
. Gọi I là trung điểm cạnh AC , H là hình chiếu của I trên SC . Khẳng định nào sau đây đúng?
A. SBC IHB .
B. SAC SAB .
C. SAC SBC . D. SBC SAB .
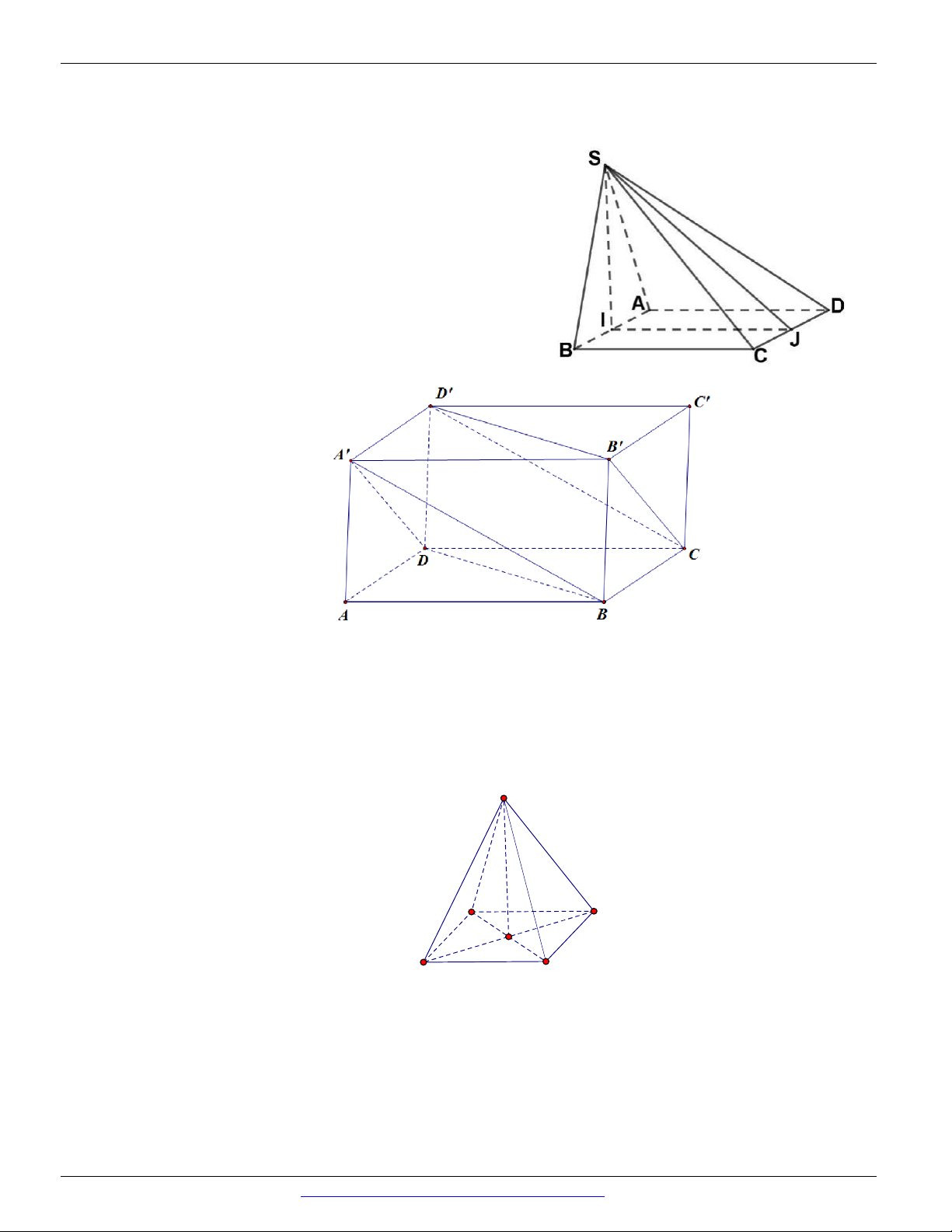
Câu 26. Cho hình chóp S.ABCD có SA ABCD , đáy ABCD là hình thang vuông tại A và D . Biết
SA AD DC a , AB 2a . Khẳng định nào sau đây sai?
A. SBD SAC .
B. SAB SAD .
C. SAC SBC .
D. SAD SCD .
Câu 27. Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với mặt phẳng đáy.Trong số các mặt phẳng chứa mặt đáy và các mặt
bên của hình chóp, có bao nhiêu mặt phẳng vuông góc với mặt phẳng (SAB) ? A. 4 . B. 3 . C. 1. D. 2 .
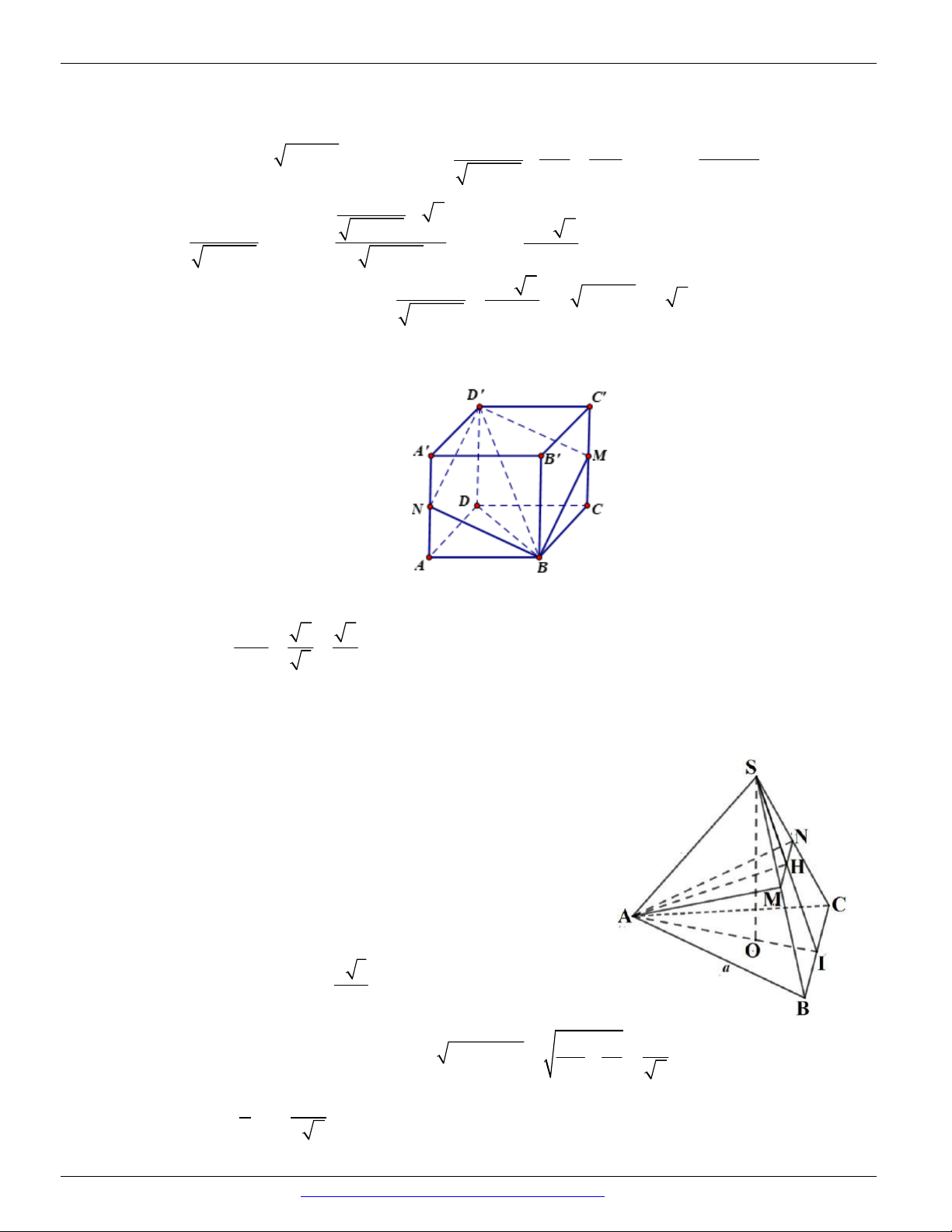
Câu 28. (THPT THANH MIỆN I - HẢI DƯƠNG - LẦN 1 - 2018) Cho hình hộp ABC . D AB C D , khẳng
định nào đúng về hai mặt phẳng A BD và CB D .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
A. ABD CB D
. B. ABD // CB D .
C. ABD CB D
. D. ABD CB D BD .
Câu 29. (SGD&ĐT BRVT - 2018) Cho hình chóp S.ABCD có đáy ABCD là hình thoi, SA SC . Khẳng
định nào sau đây đúng?
A. Mặt phẳng SBD vuông góc với mặt phẳng ABCD .
B. Mặt phẳng SBC vuông góc với mặt phẳng ABCD .
C. Mặt phẳng SAD vuông góc với mặt phẳng ABCD .
D. Mặt phẳng SAB vuông góc với mặt phẳng ABCD .
DẠNG 3. XÁC ĐỊNH GÓC GIỮA HAI MẶT PHẲNG
Dạng 3.1 Góc của mặt phẳng bên với mặt phẳng đáy
Câu 30. [KIM LIÊN - HÀ NỘI - LẦN 1 - 2018] Cho hình lập phương ABC . D ABC D
. Tính góc giữa mặt
phẳng ABCD và ACC A . A. 45 . B. 60 . C. 30 . D. 90 .
Câu 31. (Thi thử SGD Hưng Yên) Cho hình lập phương ABCD.AB C D
. Góc giữa ABCD và A B C D bằng A. 45 . B. 60 . C. 0 . D. 90 .
Câu 32. (THPT QUỲNH LƯU - NGHỆ AN - 2018) Cho hình chóp tứ giác đều có cạnh đáy bằng a 2 và a 2 chiều cao bằng
. Tang của góc giữa mặt bên và mặt đáy bằng: 2 1 3 A. 1. B. . C. 3 . D. . 3 4
Câu 33. (SỞ GD&ĐT QUẢNG NAM - 2018) Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA
vuông góc với mặt đáy (tham khảo hình vẽ bên). Góc giữa hai mặt phẳng SCD và ABCD bằng S A D B C A. Góc SDA . B. Góc SCA . C. Góc SCB . D. Góc ASD .
Câu 34. (THPT QUẢNG YÊN - QUẢNG NINH - 2018) Cho hình chóp tứ giác S.ABCD có đáy là hình
chữ nhật cạnh AB 4a , AD 3a . Các cạnh bên đều có độ dài 5a . Tính góc giữa SBC và ABCD .
A. 7546 .
B. 7121 .
C. 6831 .
D. 6521 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 35. (SỞ GD&ĐT HƯNG YÊN - 2018) Cho hình chóp S.ABCD với đáy ABCD là hình vuông có
cạnh 2a , SA a 6 và vuông góc với đáy. Góc giữa SBD và ABCD bằng? A. 0 90 . B. 0 30 . C. 0 45 . D. 0 60 .
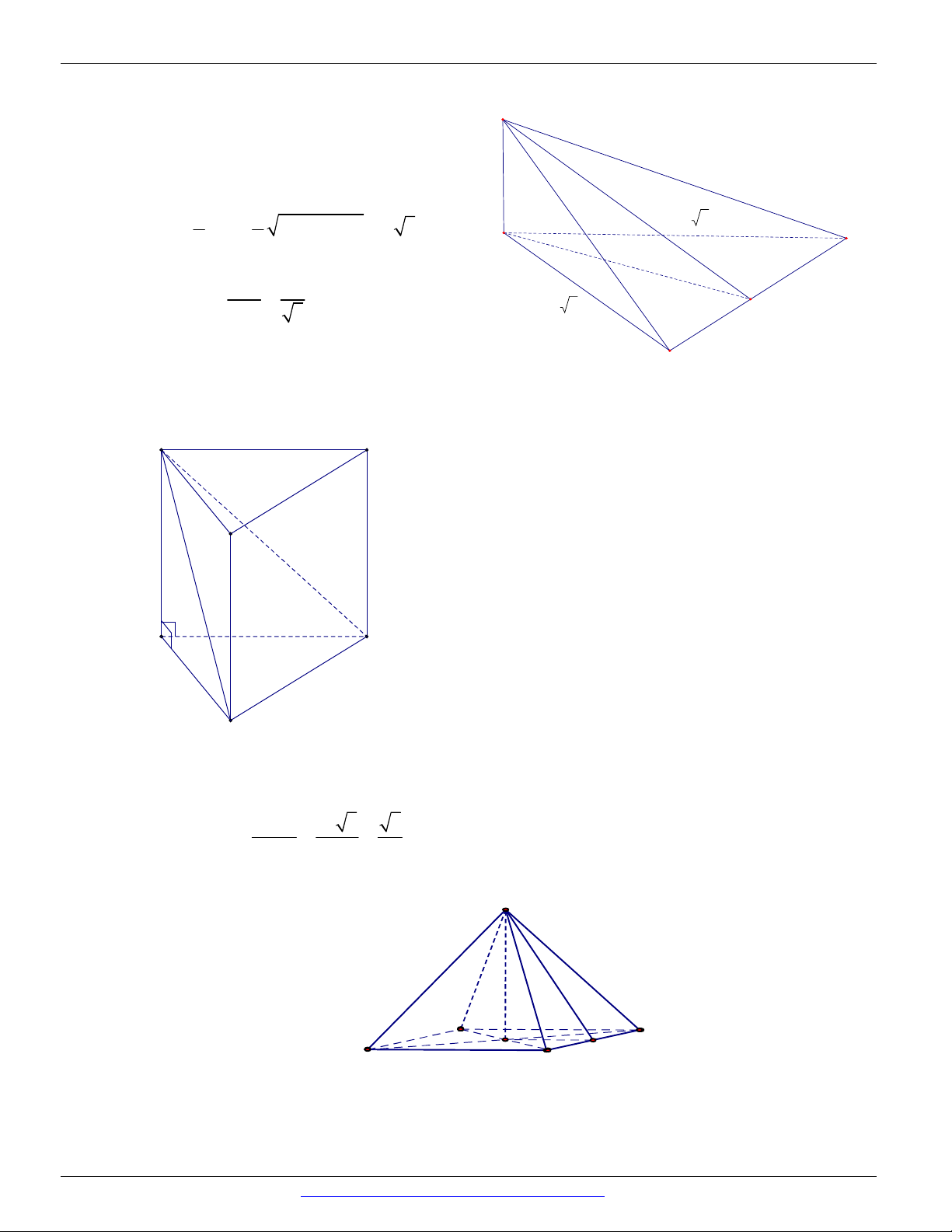
Câu 36. (THPT PHÚ LƯƠNG - THÁI NGUYÊN - 2018) Cho hình lăng trụ ABC.AB C có đáy là tam
giác đều cạnh bằng a , cạnh bên AA 2a . Hình chiếu vuông góc của A lên mặt phẳng ABC
trùng với trung điểm của đoạn BG (với G là trọng tâm tam giác ABC ). Tính cosin của góc
giữa hai mặt phẳng ABC và ABB A . 1 1 1 1 A. cos . B. cos . C. cos . D. cos . 95 165 134 126
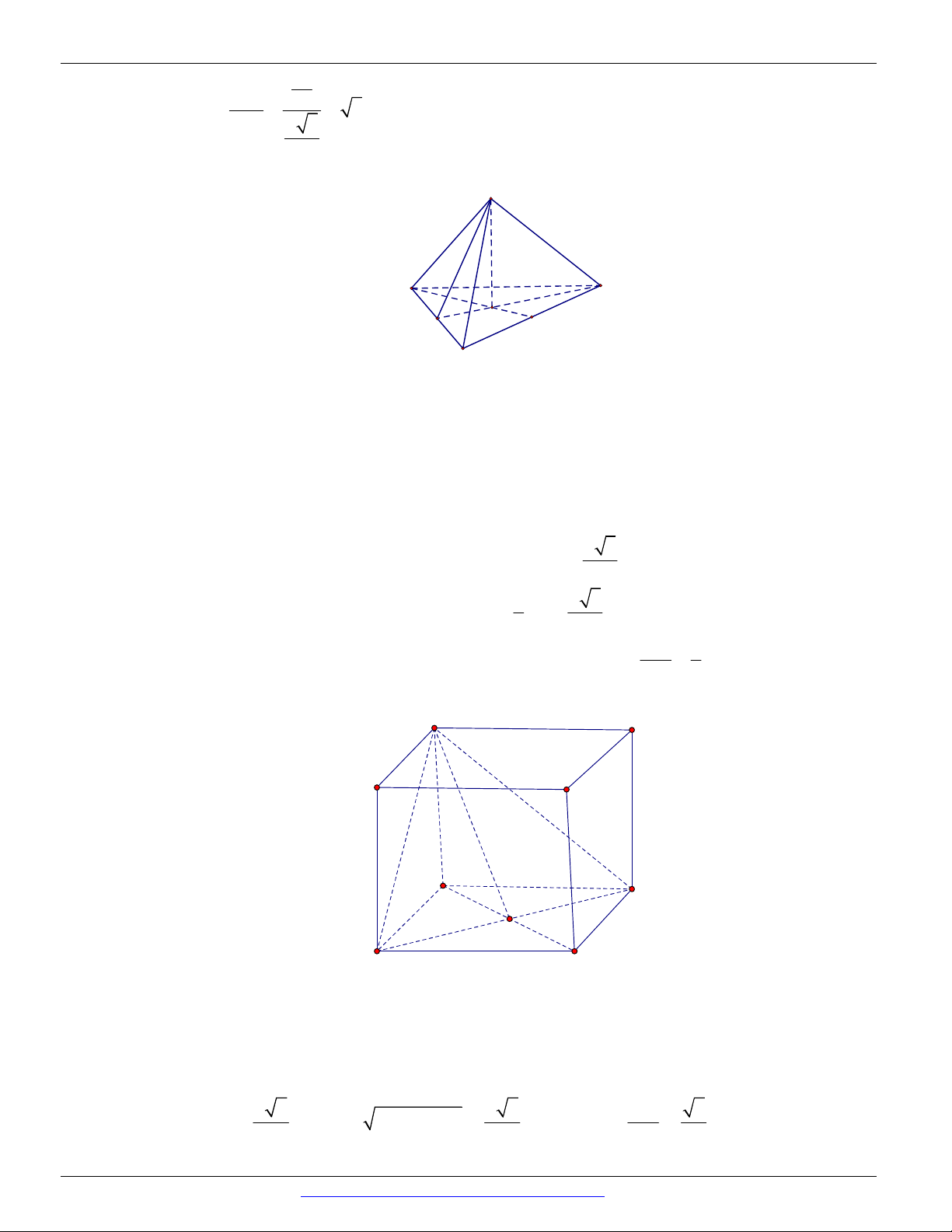
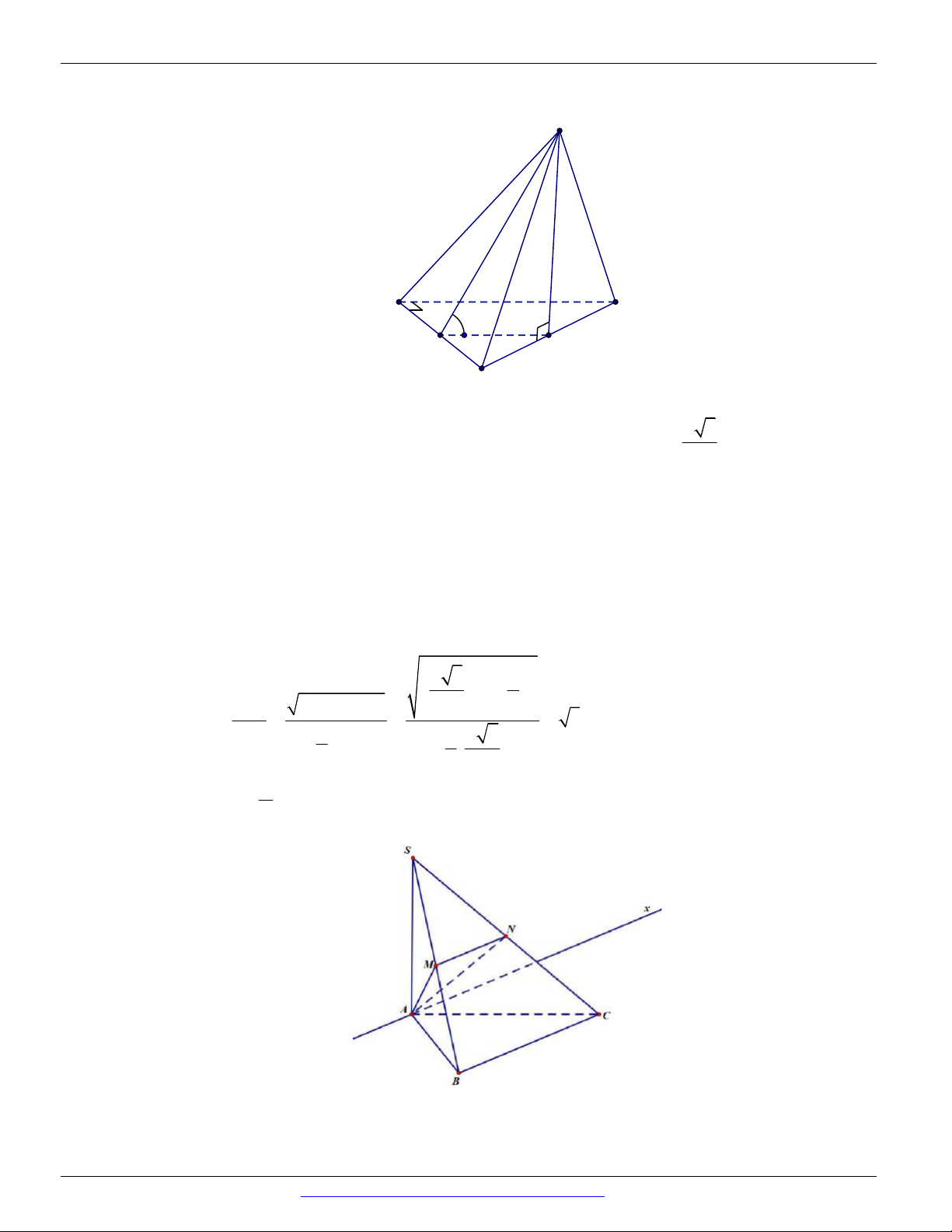
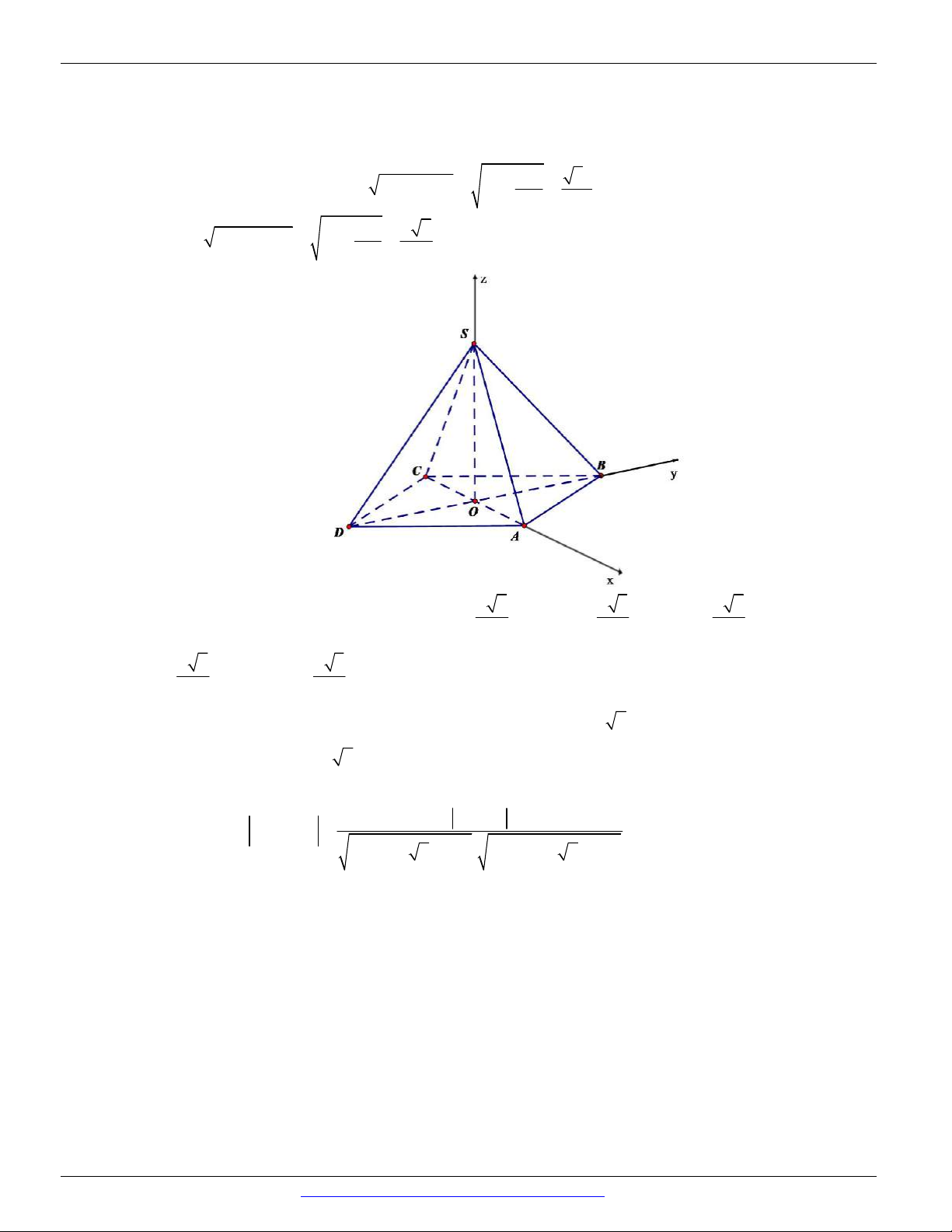
Câu 37. (THTP LÊ QUÝ ĐÔN - HÀ NỘI - LẦN 1 - 2018) Cho tứ diện S.ABC có các cạnh SA , SB ; SC
đôi một vuông góc và SA SB SC 1 . Tính cos , trong đó là góc giữa hai mặt phẳng SBC và ABC ? 1 1 1 1 A. cos . B. cos . C. cos . D. cos . 2 2 3 3 2 3
Câu 38. (CHUYÊN KHTN - LẦN 1 - 2018) Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân
tại A và AB a 2 . Biết SA ABC và SA a . Góc giữa hai mặt phẳng SBC và ABC bằng A. 30 . B. 45 . C. 60 . D. 90 .
Câu 39. (THPT LÊ XOAY - LẦN 3 - 2018) Cho hình chóp S.ABC có tam giác ABC vuông cân tại B ,
AB BC a , SA a 3 , SA ABC . Góc giữa hai mặt phẳng SBC và ABC là A. o 45 . B. o 60 . C. o 90 . D. o 30 .
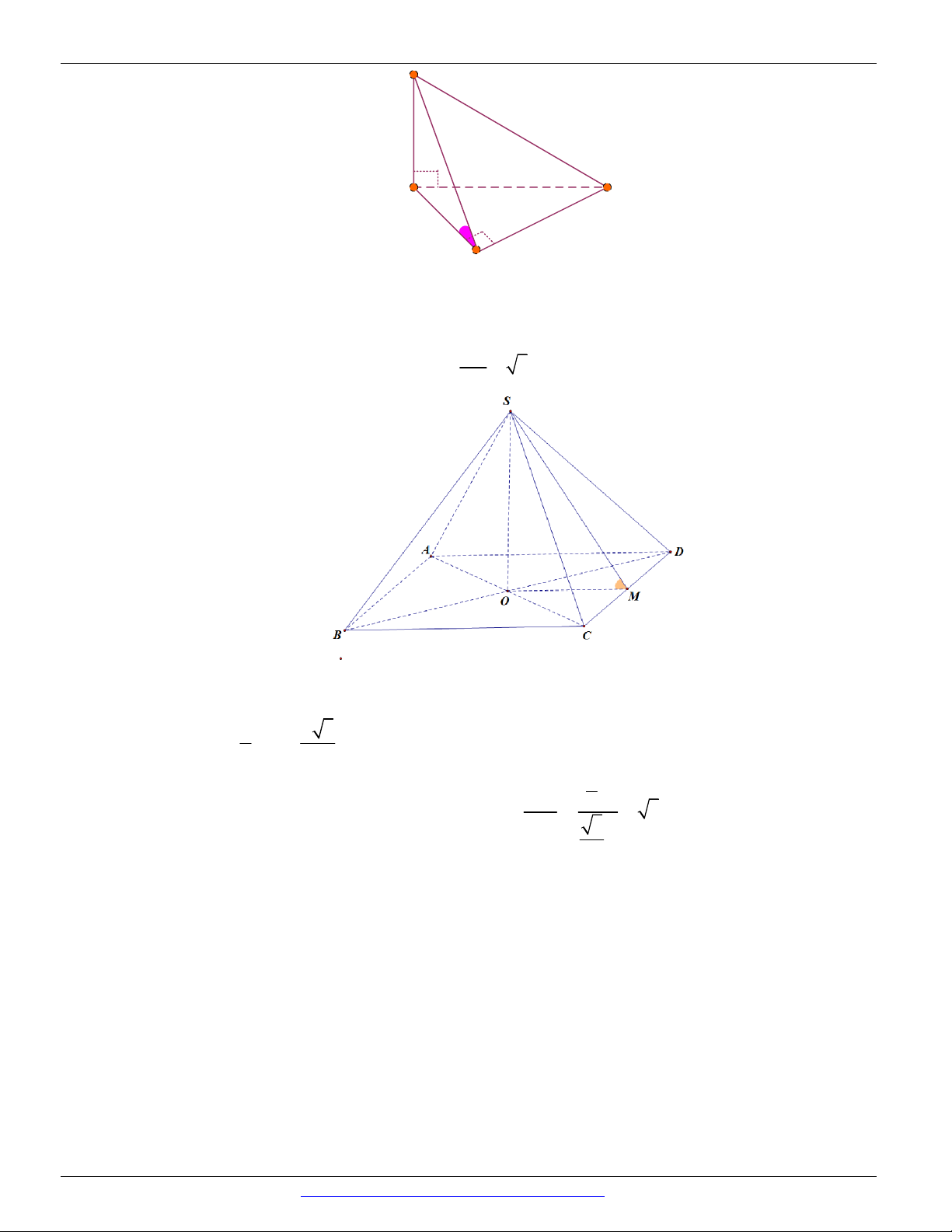
Câu 40. (THPT HOA LƯ A - LẦN 1 - 2018) Cho tứ diện OABC có OA , OB , OC đôi một vuông góc
và OB OC a 6 , OA a . Tính góc giữa hai mặt phẳng ABC và OBC . A. 60 . B. 30 . C. 45 . D. 90 .
Câu 41. (TT DIỆU HIỀN - CẦN THƠ - 2018) Cho hình chóp S.ABC có đáy là tam giác vuông tại B ,
SA ABC , SA 3 cm , AB 1 cm , BC 2 cm . Mặt bên SBC hợp với đáy một góc bằng: A. 30 . B. 90 . C. 60 . D. 45 .
Câu 42. (THPT HẬU LỘC 2 - TH - 2018) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a 3 , 3a đường cao bằng
. Góc giữa mặt bên và mặt đáy bằng: 2 A. 30 . B. 45 . C. 60 . D. 75 .
Câu 43. (TRƯỜNG THPT THANH THỦY 2018 -2019) Cho tứ diện OABC có O ,
A OB, OC đôi một
vuông góc và OB OC a 6 , OA a . Khi đó góc giữa hai mặt phẳng ( ABC) và (OBC) bằng A. 0 90 B. 0 60 C. 0 45 D. 0 30
Câu 44. (LƯƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Cho lăng trụ tam giác đều ABC.A B C có diện tích đáy bằng 2
3a (đvdt), diện tích tam giác A B C bằng 2
2a (đvdt). Tính góc giữa hai mặt phẳng A B
C và ABC ? A. 120 . B. 60 . C. 30 . D. 45 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 45. (Nông Cống - Thanh Hóa - Lần 1 - 1819) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 3a
a 3 , đường cao bằng
. Góc giữa mặt bên và mặt đáy bằng 2 A. 45 . B. 30 . C. 60 . D. 75 .
Câu 46. (THPT NGUYỄN TRÃI-THANH HOÁ - Lần 1.Năm 2018&2019) Cho hình chóp tứ giác đều
có tất cả các cạnh bằng a . Côsin của góc giữa mặt bên và mặt đáy bằng 1 1 1 1 A. . B. . C. . D. . 3 3 2 2
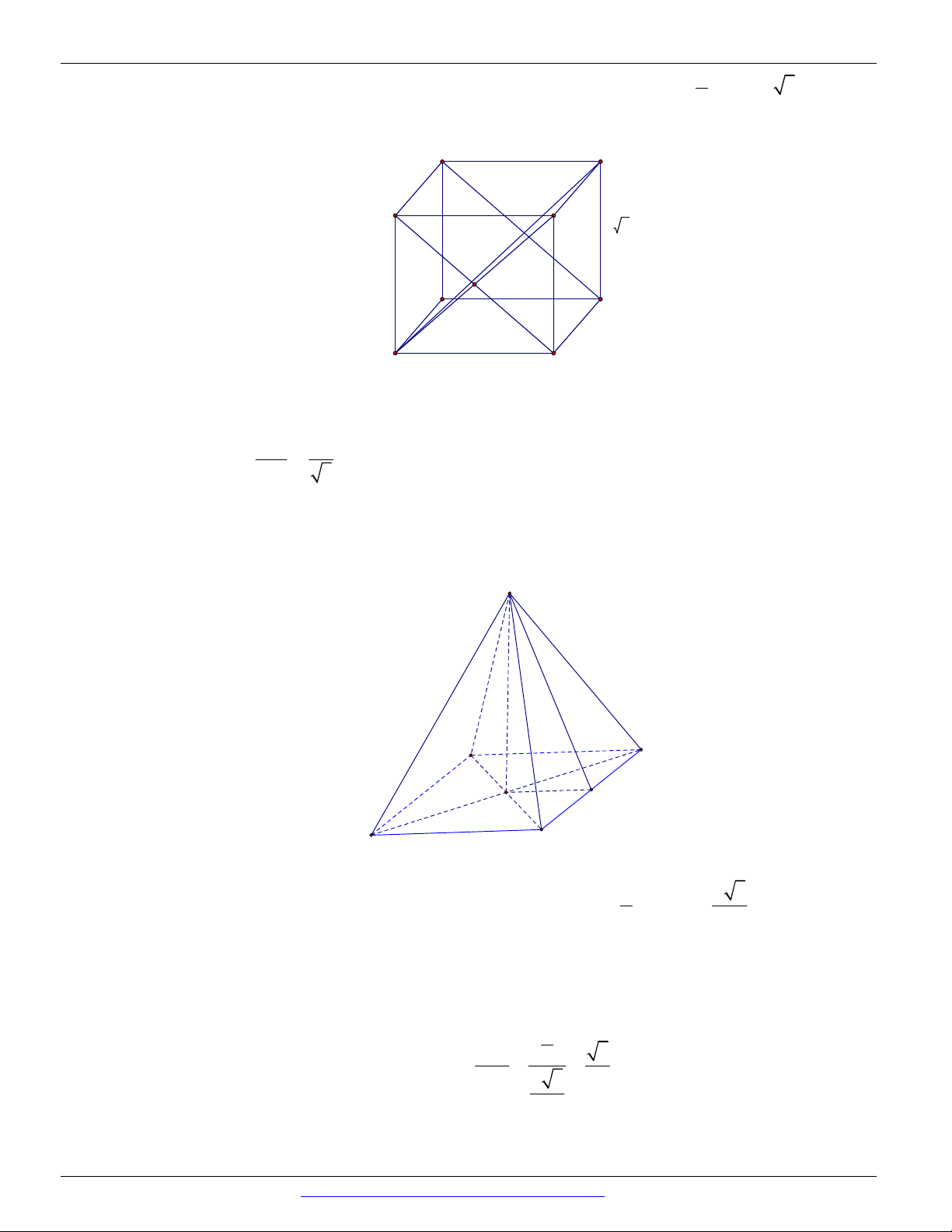
Câu 47. (Thi thử Bạc Liêu – Ninh Bình lần 1) Cho hình lập phương A . BCD AB C D
có cạnh bằng a .
Giá trị sin của góc giữa hai mặt phẳng BDA và ABCD bằng 3 6 6 3 A. . B. . C. . D. . 4 4 3 3
Câu 48. (THPT Quỳnh Lưu- Nghệ An- 2019) Cho hình chóp S.ABCD có đáy là hình chữ nhật cạnh AB
= a , SA vuông góc với mặt phẳng đáy và SB 2a . Góc giữa mặt phẳng SBC mặt phẳng đáy bằng A. o 90 . B. o 60 . C. o 45 . D. o 30 .
Câu 49. (THPT Đoàn Thượng – Hải Dương) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a ,
đường cao SA x . Góc giữa SBC và mặt đáy bằng 0
60 . Khi đó x bằng a 6 a 3 a A. . B. a 3 . C. . D. . 2 2 3
Câu 50. (TRƯỜNG CHUYÊN QUANG TRUNG- BÌNH PHƯỚC 2018-2019) Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' có BC a, BB ' a 3 . Góc giữa hai mặt phẳng A' B 'C và ABC ' D ' bằng A. o 60 . B. o 45 . C. o 30 . D. o 90 .
Câu 51. (THI THỬ L4-CHUYÊN HOÀNG VĂN THỤ-HÒA BÌNH-2018-2019)Cho hình chóp tứ giác
đều có tất cả các cạnh đều bằng a . Tính cosin của góc giữa một mặt bên và mặt đáy. 3 2 1 1 A. . B. . C. . D. . 3 2 2 3
Câu 52. (Kim Liên - Hà Nội lần 2 năm 2019) Cho hình chóp tứ giác đều có cạnh đáy bằng 2a , cạnh bên
bằng 3a . Gọi là góc giữa mặt bên và mặt đáy, mệnh đề nào dưới đây đúng? 2 10 2 14 A. cos . B. cos . C. cos . D. cos . 4 10 2 14
Câu 53. (Thi thử Lômônôxốp - Hà Nội lần V 2019) Cho lăng trụ tam giác đều ABC.A' B 'C ' có tất cả
các cạnh đều bằng a . Gọi là góc giữa hai mặt phẳng AB 'C ' và A' B 'C ' . Tính giá trị của tan ? 2 3 3 3 2 3 A. . B. . C. . D. . 3 3 2 2
Câu 54. (SP Đồng Nai - 2019) Cho hình lăng trụ đều AB .
C A' B 'C ' có cạnh đáy bằng 2a , cạnh bên bằng
a . Tính góc giữa hai mặt phẳng AB 'C ' và A'B 'C ' .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A. 30 . B. 60 . C. 45 . D. 90 .
Câu 55. (Kim Liên - Hà Nội - L1 - 2018-2019) Cho hình chóp tứ giác đều S.ABCD với O là tâm của 3
đáy và chiều cao SO
AB . Tính góc giữa mặt phẳng SAB và mặt phẳng đáy. 2 A. 90 . B. 60 . C. 30 . D. 45 .
Câu 56. (THPT Yên Dũng 3 - Bắc Giang lần 1- 18-19) Cho hình chop S.ABC có SA ( ABC) , tam giác
ABC đều cạnh 2a , SB tạo với mặt phẳng đáy một góc 30 . Khi đó mpSBC tạo với đáy một
góc x . Tính tan x . 1 3 2
A. tan x 2 . B. tan x . C. tan x . D. tan x . 3 2 3
Câu 57. (LẦN 01_VĨNH YÊN_VĨNH PHÚC_2019) Lăng trụ tam giác đều AB . C A B C có cạnh đáy 3a
bằng a . Gọi M là điểm trên cạnh AA sao cho AM
. Tang của góc hợp bởi hai mặt phẳng 4
MBC và ABC là: 1 3 2 A. 2 . B. . C. . D. . 2 2 2
Câu 58. (THPT Mai Anh Tuấn_Thanh Hóa - Lần 1 - Năm học 2018_2019) Cho hình chóp S.ABCD có a 6
đáy ABCD là hình vuông cạnh ,
a SA vuông góc với đáy và SA
. Khi đó góc giữa mặt phẳng 6
SBD và mặt đáy ABCD là. A. 60 B. 45 C. 30 D. 75
Câu 59. (HKII-CHUYÊN NGUYỄN HUỆ-HN-2018-2019) Cho hai tam giác ACD và BCD nằm trên
hai mặt phẳng vuông góc với nhau và AC AD BC BD a, CD 2x . Tìm giá trị của x để
hai mặt phẳng ABC và ABD vuông góc với nhau. a a 3 a 2 a A. x . B. x . C. x . D. x . 3 3 3 2
Câu 60. (Thi thử Đại học Hồng Đức –Thanh Hóa – 07-05 - 2019) Cho tứ diện ABCD có BCD là tam a 6 a 3
giác vuông tại đỉnh B , cạnh CD a , BD
, AB AC AD . Tính góc tạo bởi các 3 2
mặt phẳng ABC và mặt phẳng BCD . A. . B. . C. . D. arctan 3 . 4 3 6
Câu 61. (Chu Văn An - Hà Nội - lần 2 - 2019) Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại
B , cạnh bên SA vuông góc với đáy ABC , AB a , SA 2a . Gọi M , N lần lượt là trung điểm của S ,
B SC . Côsin của góc giữa hai mặt phẳng AMN và ABC bằng 1 2 5 5 1 A. . B. . C. . D. . 2 5 5 4
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 62. (Thi thử Nguyễn Huệ- Ninh Bình- Lần 3- 2019)Cho lăng trụ đứng ABC.A B C có cạnh bên
AA 2a , AB AC a , góc 0
BAC 120 . Gọi M là trung điểm BB thì côsin của góc tạo bởi hai
mặt phẳng ( ABC) và ( AC M ) là 3 5 3 93 A. . B. . C. . D. . 31 5 15 31
Dạng 3.2 Góc của hai mặt phẳng bên
Câu 63. (THPT LÝ THÁI TỔ - BẮC NINH - 2018) Hình chóp S.ABC có đáy là tam giác vuông tại B
có AB a , AC 2a , SA vuông góc với mặt phẳng đáy, SA 2 .
a Gọi là góc tạo bởi hai mặt
phẳng SAC ,SBC . Tính cos ? 3 1 15 3 A. . B. . C. . D. . 2 2 5 5
Câu 64. (SỞ GD&ĐT PHÚ THỌ - 2018) Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB a 2 ,
AD a và SA ABCD . Gọi M là trung điểm của đoạn thẳng AB (tham khảo hình vẽ). S A M B D C
Góc giữa hai mặt phẳng SAC và SDM bằng A. 45 . B. 60 . C. 30 . D. 90 .
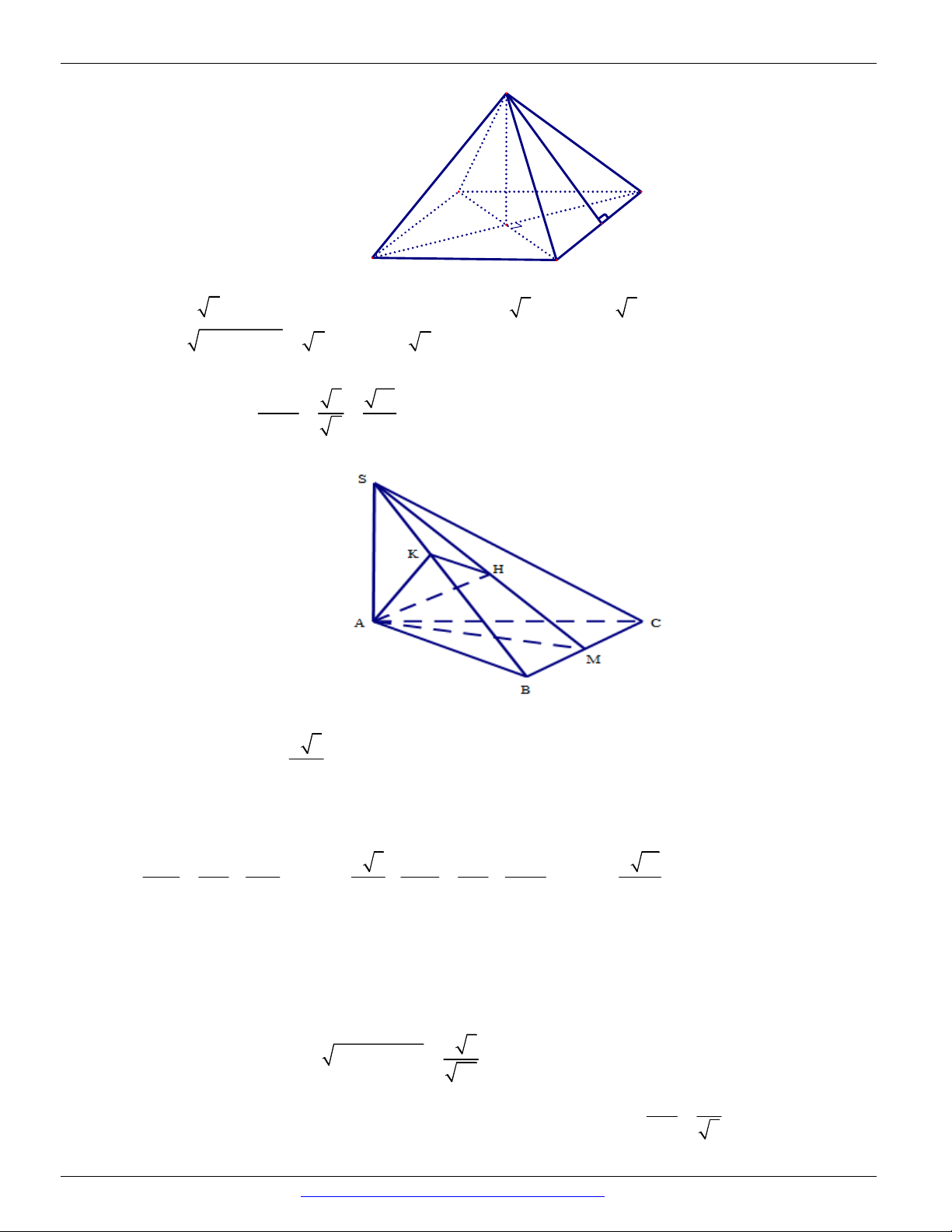
Câu 65. (THPT NGUYỄN ĐỨC THUẬN - NAM ĐỊNH - LẦN 1 - 2018) Cho hình chóp S.ABCD có
đáy ABCD là hình thang vuông tại A và D , AD DC a . Biết SAB là tam giác đều cạnh 2a
và mặt phẳng SAB vuông góc với mặt phẳng ABCD . Tính cosin của góc giữa hai mặt phẳng
SAB và SBC . 2 2 3 5 A. . B. . C. . D. . 7 6 7 7
Câu 66. (THPT NGUYỄN ĐỨC THUẬN - NAM ĐỊNH - LẦN 1 - 2018) Cho hình chóp S.ABCD có
đáy là hình vuông cạnh a , tam giác đều SAB nằm trong mặt phẳng vuông góc với đáy. Gọi H ,
K lần lượt là trung điểm của AB , CD . Ta có tan của góc tạo bởi hai mặt phẳng SAB và SCD bằng 2 2 3 3 3 A. . B. . C. . D. . 3 3 3 2
Câu 67. (THPT GANG THÉP - LẦN 3 - 2018) Trong không gian cho tam giác đều SAB và hình vuông
ABCD cạnh a nằm trên hai mặt phẳng vuông góc. Góc là góc giữa hai mặt phẳng SAB và
SCD . Mệnh đề nào sau đây đúng?
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 3 3 3 2 A. tan . B. tan . C. tan . D. tan . 3 3 2 3
Câu 68. (THPT CHUYÊN PHAN BỘI CHÂU - NGHỆ AN - LẦN 2 - 2018) Cho hình chóp S.ABCD có
đáy ABCD là hình vuông cạnh a . Cạnh SA vuông góc với mặt phẳng đáy, SA a 3 . Góc tạo
bởi SAB và SCD bằng A. 30 . B. 60 . C. 90 . D. 45 .
Câu 69. (THPT LƯƠNG VĂN TỤY - NINH BÌNH - LẦN 1 - 2018) Cho hình chóp S.ABCD có đáy a 3
ABCD là hình chữ nhật, AB a ; AD
. Mặt bên SAB là tam giác cân đỉnh S và nằm trong 2
mặt phẳng vuông góc với mặt phẳng ABCD . Biết
ASB 120 . Góc giữa hai mặt phẳng SAD và SBC bằng: A. 60 . B. 30 . C. 45 . D. 90 .
Câu 70. (THPT KIẾN AN - HẢI PHÒNG - LẦN 1 - 2018) Cho hình chóp S.ABC có cạnh SA vuông
góc với mặt phẳng ABC , biết AB AC a , BC a 3 . Tính góc giữa hai mặt phẳng SAB và SAC . A. 30 . B. 150 . C. 60 . D. 120 .
Câu 71. (SGD&ĐT BẮC GIANG - LẦN 1 - 2018) Cho hình chóp S.ABCD có đáy ABCD là hình vuông
cạnh a , SA vuông góc với đáy và SA a (tham khảo hình vẽ bên dưới). Góc giữa hai mặt phẳng
SAB và SCD bằng? S A D B C A. 60 . B. 45 . C. 30 . D. 90 .
Câu 72. (CHUYÊN ĐHSPHN - 2018) Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , cạnh
bên SA vuông góc với mặt phẳng đáy, AB BC a và SA a . Góc giữa hai mặt phẳng SAC và SBC bằng A. 60 . B. 90 . C. 30 . D. 45 .
Câu 73. (THPT CHUYÊN LAM SƠN - THANH HÓA - 2018) Cho hình chóp S.ABCD có đáy ABCD
là hình chữ nhật với AB a , cạnh bên SA vuông góc với đáy và SA a (hình vẽ). Góc giữa hai
mặt phẳng SAD và SBC bằng: A. 45 . B. 30 . C. 60 . D. 90 .
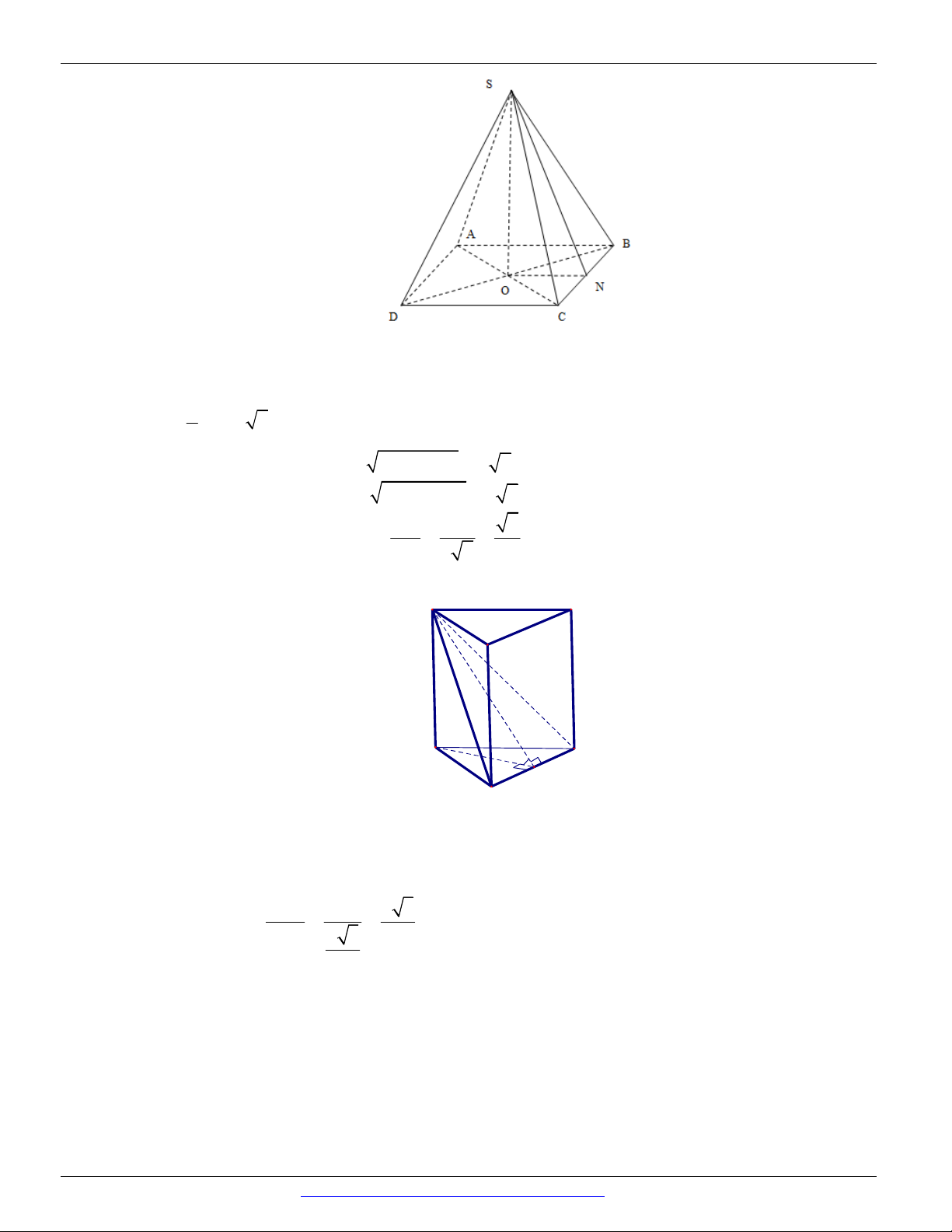
Câu 74. (Trường THPT Chuyên Lam Sơn_2018-2019) Cho hình chóp S.ABCD đáy là hình thoi tâm O a 6
và SO ( ABCD) , SO
, BC SB a .Số đo góc giữa hai mặt phẳng (SBC) và (SCD) là: 3 A. 0 90 . B. 0 60 . C. 0 30 . D. 0 45 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 75. (Chuyên Nguyễn Trãi Hải Dương thi thử lần 1 (2018-2019)) Cho hình chóp đều S.ABCD có
cạnh đáy bằng 2 và cạnh bên bằng 2 2 . Gọi là góc của mặt phẳng (SAC) và mặt phẳng (SAB)
. Khi đó cos bằng 5 2 5 21 5 A. . B. . C. . D. . 7 5 7 5
Câu 76. (TRƯỜNG THPT HÀM RỒNG NĂM HỌC 2018 – 2019) Cho hình chóp S.ABC có đáy là tam
giác đều cạnh bằng a , SA ABC , SA a 3 . Cosin của góc giữa hai mặt phẳng SAB và SBC là 2 1 2 1 A. . B. . C. . D. . 5 5 5 5
Câu 77. (THPT Cộng Hiền - Lần 1 - 2018-2019) Cho hình chóp tam giác đều S.ABC có cạnh bên bằng
2a , cạnh đáy bằng a . Gọi là góc giữa hai mặt bên của hình chóp đó. Hãy tính cos . 8 3 7 1 A. cos . B. cos . C. cos . D. cos . 15 2 15 2
Câu 78. [THPT NINH BÌNH-BẠC LIÊU-2019] Cho hình chóp S.ABCD có đáy ABCD là hình chữ
nhật, AB a , cạnh bên SA vuông góc với đáy và SA a . Góc giữa hai mặt phẳng SBC và SAD bằng S a A D a B C A. 60 . B. 30 . C. 90 . D. 45 .
Câu 79. (SGD Điện Biên - 2019) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB 3 ,
BC 4 . Tam giác SAC nằm trong mặt phẳng vuông góc với đáy, khoảng cách từ điểm C đến
đường thẳng SA bằng 4 . S A D B C
Côsin của góc giữa hai mặt phẳng SAB và SAC bằng 3 17 3 34 2 34 5 34 A. . B. . C. . D. . 17 34 17 17
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 80. (Lương Thế Vinh - Hà Nội - Lần 1 - 2018-2019) Cho hình chóp S.ABCD có đáy ABCD là hình
vuông cạnh a , SAB là tam giác đều và SAB vuông góc với ABCD . Tính cos với là góc
tạo bởi SAC và SCD . 3 6 5 2 A. . B. . C. . D. . 7 7 7 7
Dạng 3.3 Góc của hai mặt phẳng khác
Câu 81. (THPT MỘ ĐỨC - QUẢNG NGÃI - 2018) Cho hình lăng trụ đều ABC.AB C
có tất cả các cạnh
bằng nhau. Gọi là góc giữa hai mặt phẳng AB C
và ABC , tính cos 1 21 7 4 A. . B. . C. . D. . 7 7 7 7
Câu 82. (Tham khảo THPTQG 2019) Cho hình lập phương ABC . D
A BCD . Góc giữa hai mặt phẳng
A BCD và ABCD bằng A. 30 . B. 60 . C. 45 . D. 90 .
Câu 83. (THPT Quỳnh Lưu- Nghệ An- 2019) Cho hình lập phương ABC . D AB C D
. Tính góc giữa hai
mặt phẳng ABC và ACD. A. 90 . B. 120 . C. 60 . D. 45 .
Câu 84. (Hậu Lộc 2-Thanh Hóa-L1-2019) Cho hình lăng trụ đứng AB D C .A B C D
có đáy ABCD là
hình thoi, AC 2 AA 2a 3 . Góc giữa hai mặt phẳng A' BD và C BD bằng A. 0 90 . B. 0 60 . C. 0 45 . D. 0 30 .
Câu 85. (Chuyên Nguyễn Trãi Hải Dương thi thử lần 1 (2018-2019)) Cho lăng trụ đều AB .
C A' B 'C ' có
AB 2 3, BB ' 2. Gọi M , N , P tương ứng là trung điểm của A ' B ', A 'C ', BC. Nếu gọi là độ
lớn của góc giữa hai mặt phẳng MNP và ACC ' thì cos bằng 4 2 3 2 3 A. . B. . C. . D. . 5 5 5 5
Câu 86. (THPT Phan Bội Châu - Nghệ An - L2 - 2019) Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' có mặt AB 6
ABCD là hình vuông, AA '
. Xác định góc giữa hai mặt phẳng A' BD và C ' BD . 2 A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
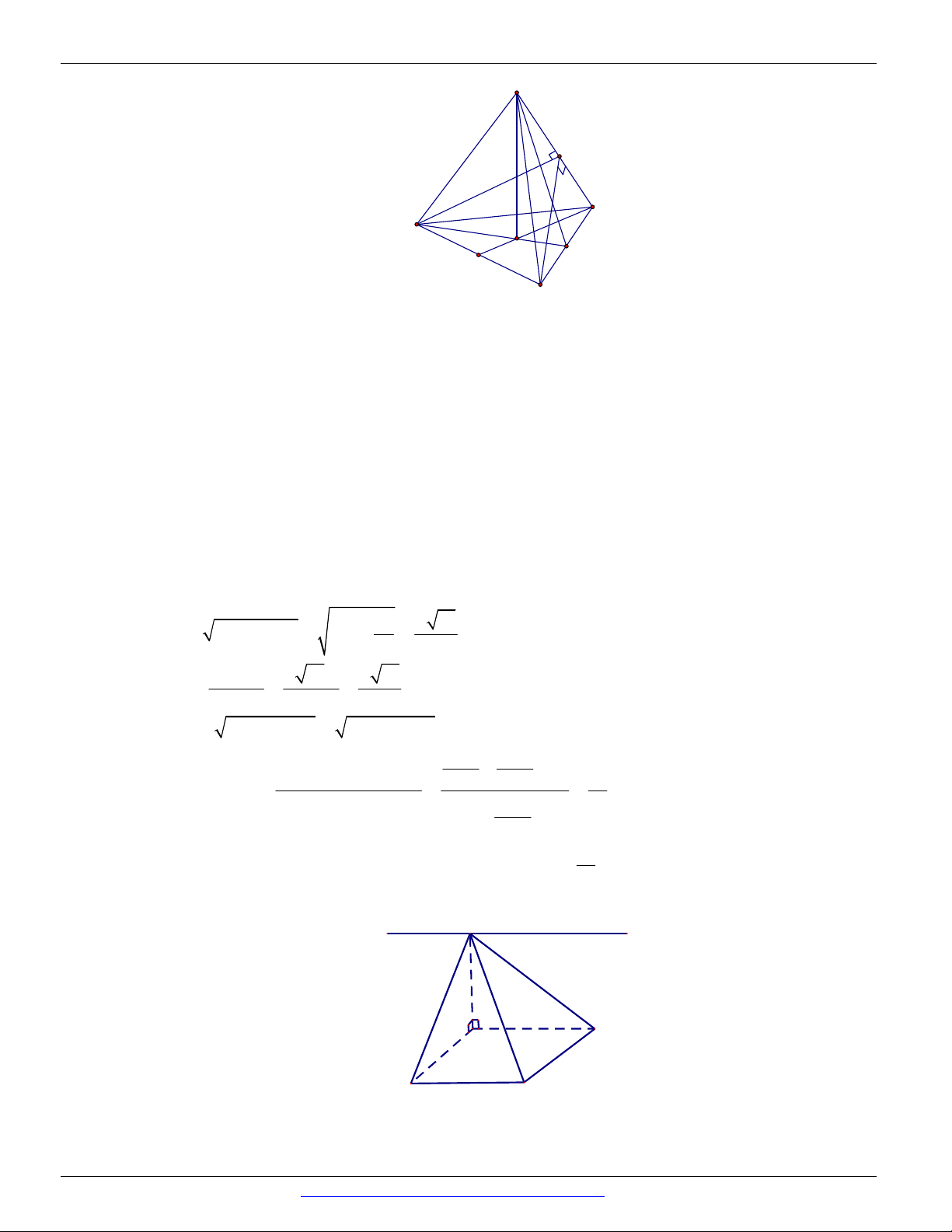
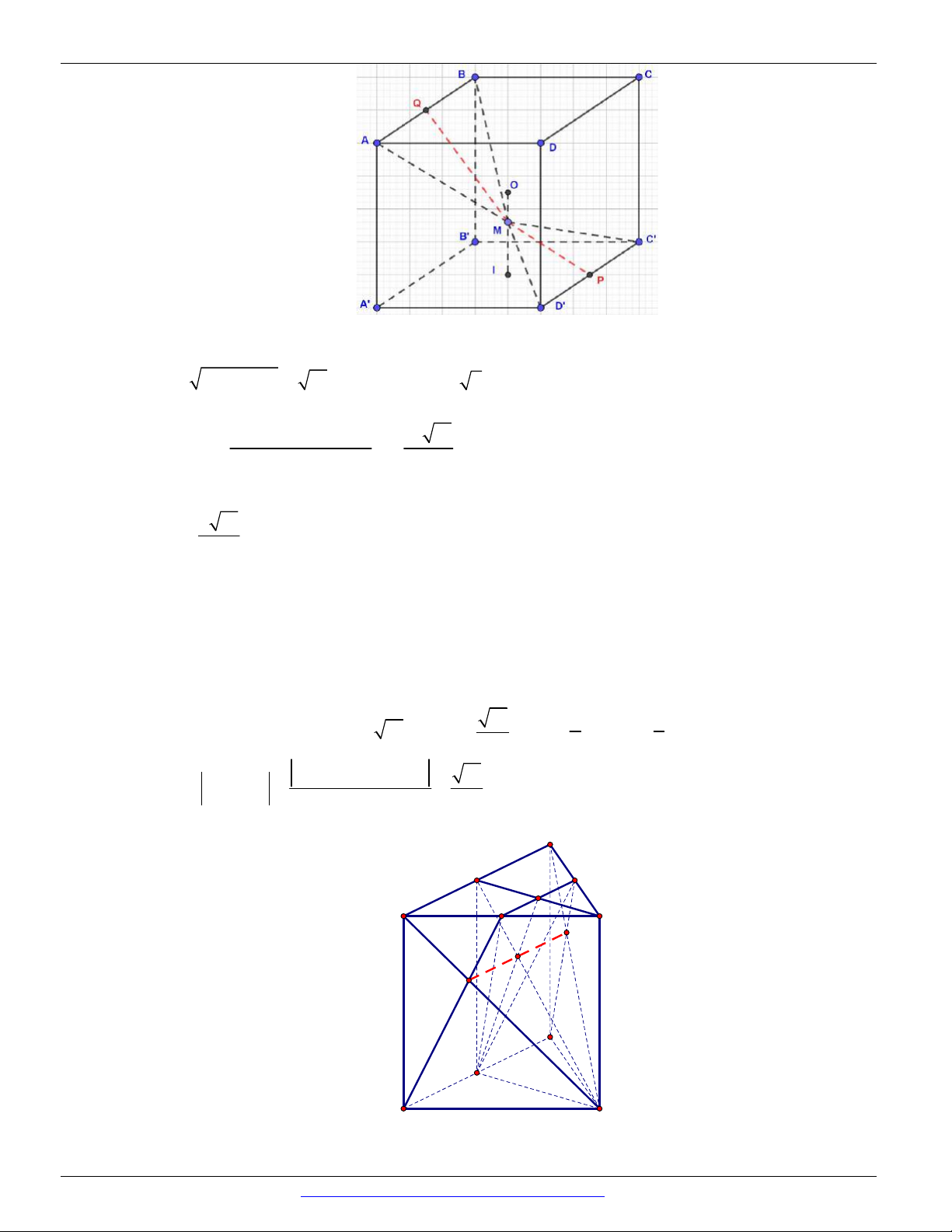
Câu 87. (Mã đề 104 BGD&ĐT NĂM 2018) Cho hình lập phương ABC . D AB C D
có tâm O . Gọi I là 1
tâm của hình vuông AB C D
và M là điểm thuộc đoạn thẳng OI sao cho MO MI (tham khảo 2 hình vẽ).
Khi đó sin của góc tạo bởi hai mặt phẳng MC D
và MAB bằng. 17 13 6 85 7 85 6 13 A. . B. . C. . D. . 65 85 85 65
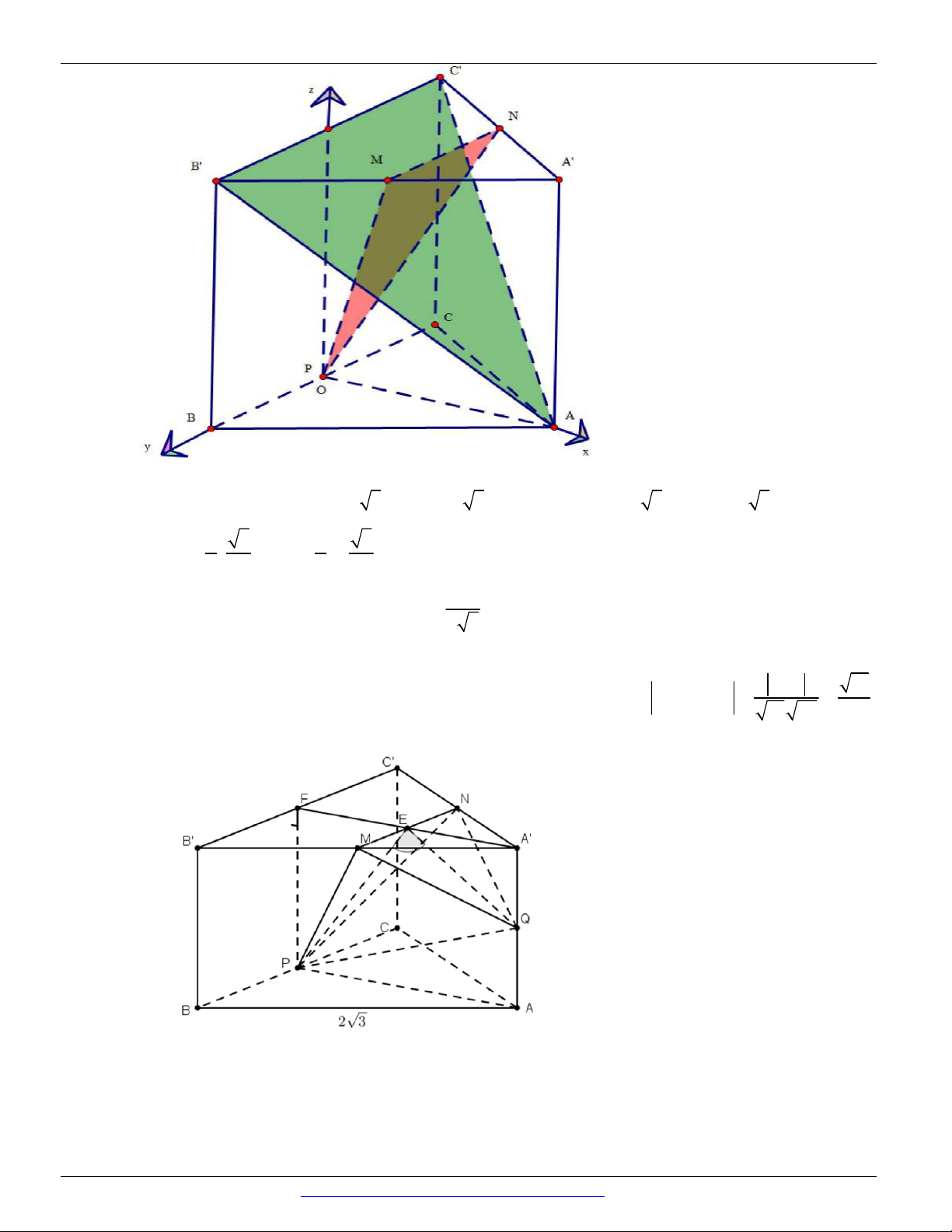
Câu 88. (Tham khảo 2018) Cho hình lăng trụ tam giác đều ABC.AB C
có AB 2 3 và AA 2. Gọi
M , N, P lần lượt là trung điểm các cạnh A B , A C
và BC (tham khảo hình vẽ bên). Côsin của
góc tạo bởi hai mặt phẳng AB C
và MNP bằng C' N M B' A' C P B A 6 13 13 17 13 18 13 A. . B. . C. . D. . 65 65 65 65
Câu 89. (Thi thử lần 4-chuyên Bắc Giang_18-19) Cho hình hộp chữ nhật ABC . D AB C D có các cạnh
AB 2 ; AD 3 ; AA 4 . Góc giữa hai mặt phẳng BC D
và AC D
là , (tham khảo hình vẽ
bên dưới). Tính giá trị gần đúng của ?
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A B D C B' A' D' C' A. 38,1 . B. 45, 2 . C. 53, 4 . D. 61, 6 .
Câu 90. (KSCL Sở Hà Nam - 2019) Cho hình lăng trụ đứng ABC . D A B C D
có đáy ABCD là hình thoi.
Biết AC 2, AA 3 . Tính góc giữa hai mặt phẳng AB D và CB D . A. 0 60 . B. 0 90 . C. 0 45 . D. 0 30 .
Câu 91. (Mã đề 101 BGD&ĐT NĂM 2018) Cho hình lập phương ABC . D AB C D
có tâm O . Gọi I là
tâm của hình vuông AB C D
và M là điểm thuộc đoạn thẳng OI sao cho MO 2MI (tham khảo hình vẽ). B C N J A D O H M K B' C' I L A' D'
Khi đó côsin của góc tạo bởi hai mặt phẳng (MC D ) và (MA ) B bằng 6 85 7 85 17 13 6 13 A. . B. . C. . D. . 85 85 65 65
Câu 92. (Bình Minh - Ninh Bình - Lần 4 - 2018) Cho hình hộp chữ nhật ABC . D AB C D có các cạnh
AB 2 , AD 3 , AA 4 . Góc giữa hai mặt phẳng ( AB ' D ') và ( A'C ' D) là . Tính giá trị gần đúng của góc . A. 45, 2 . B. 38,1 . C. 53, 4 . D. 61, 6 .
DẠNG 4. MỘT SỐ CÂU HỎI LIÊN QUAN
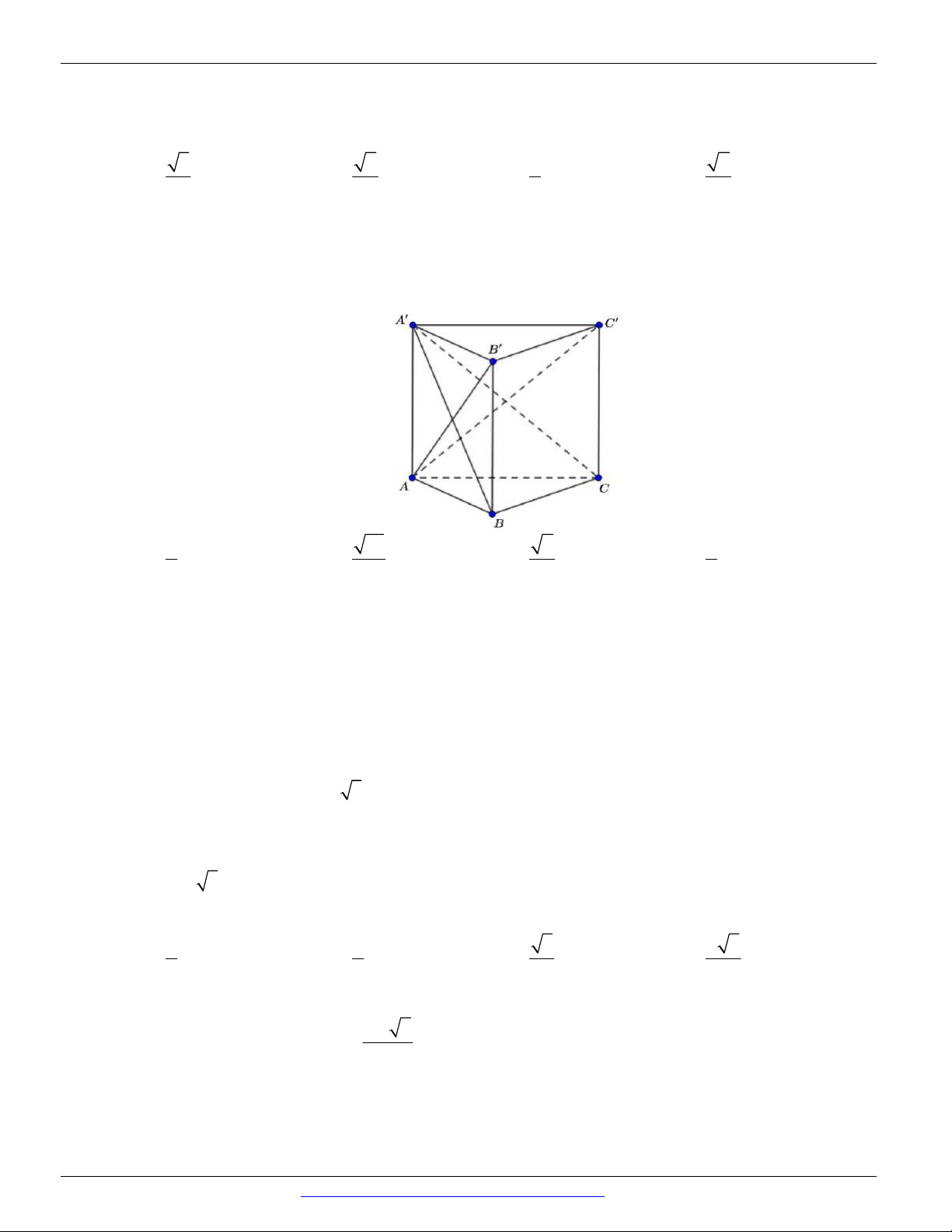
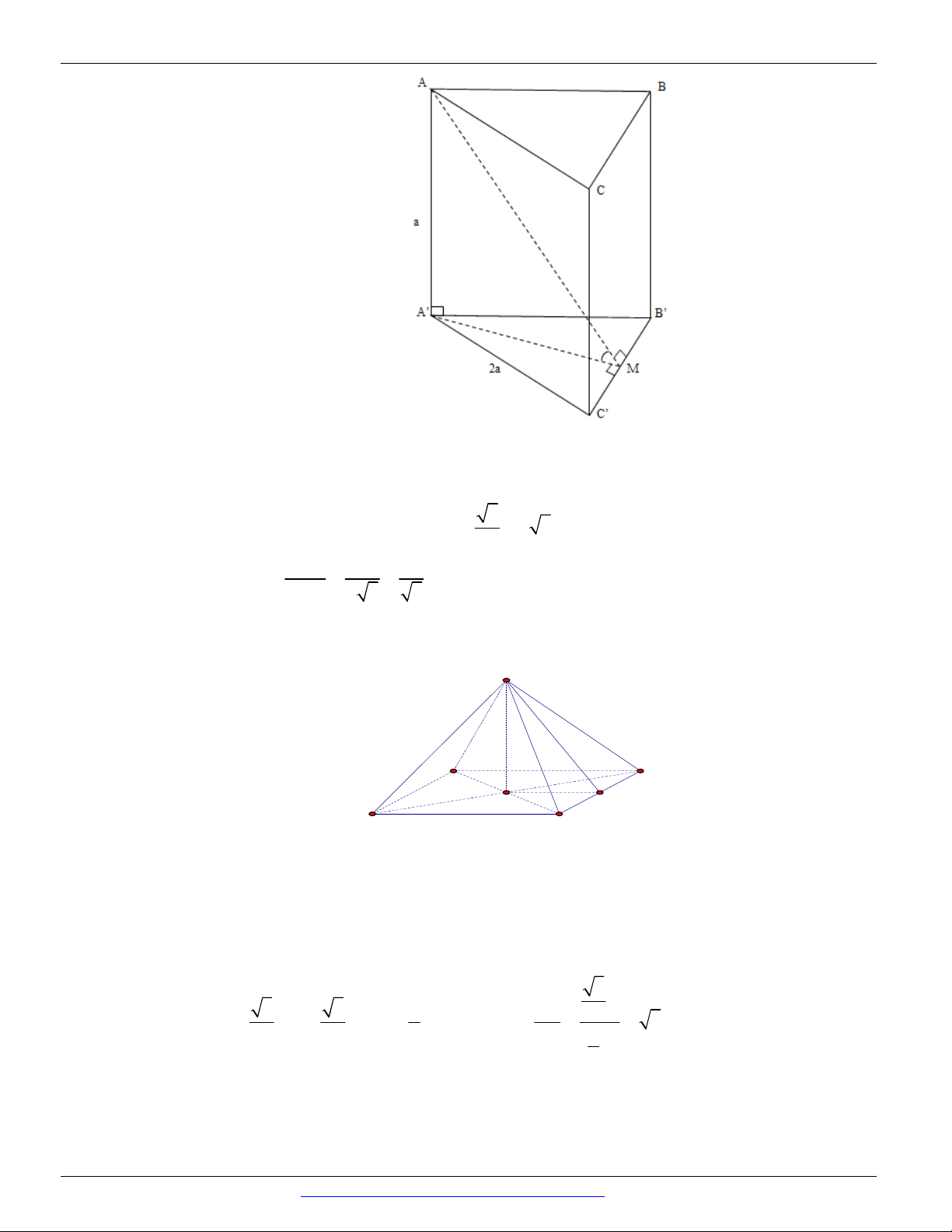
Câu 93. (THPT CHUYÊN VĨNH PHÚC - LẦN 3 - 2018) Trong hình lăng trụ đứng ABC.AB C có
AB AA a , BC 2a , AC a 5 . Khẳng định nào sau đây sai?
A. Góc giữa hai mặt phẳng ABC và ABC có số đo bằng 45 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
B. Hai mặt phẳng AAB ' B và BB C
vuông góc với nhau.
C. AC 2a 2 .
D. Đáy ABC là tam giác vuông.
Câu 94. (THPT QUẢNG YÊN - QUẢNG NINH - 2018) Cho tam giác đều ABC cạnh a . Gọi d , d lần B C
lượt là các đường thẳng đi qua B , C và vuông góc với ABC . P là mặt phẳng đi qua A và a 6
hợp với ABC một góc bằng 60 . P cắt d , d tại D và E . Biết AD , AE a 3 . B C 2
Đặt DAE . Khẳng định nào sau đây là đúng? 2 6 A. 30 . B. sin . C. sin . D. 60 . 6 2
Câu 95. (CHUYÊN TRẦN PHÚ - HẢI PHÒNG - LẦN 2 - 2018) Cho tứ diện ABCD có
ACD BCD , AC AD BC BD a và CD 2x . Gọi I , J lần lượt là trung điểm của
AB và CD . Với giá trị nào của x thì ABC ABD ? a 3 a A. x .
B. x a .
C. x a 3 . D. x . 3 3
Câu 96. (ĐẶNG THÚC HỨA - NGHỆ AN - LẦN 1 - 2018)Cho hình chóp S.ABCD có đáy ABCD là
hình vuông cạnh a và SA ABCD , SA x . Xác định x để hai mặt phẳng SBC và SDC
tạo với nhau một góc 60 . a 3 a
A. x a 3 .
B. x a . C. x . D. x . 2 2
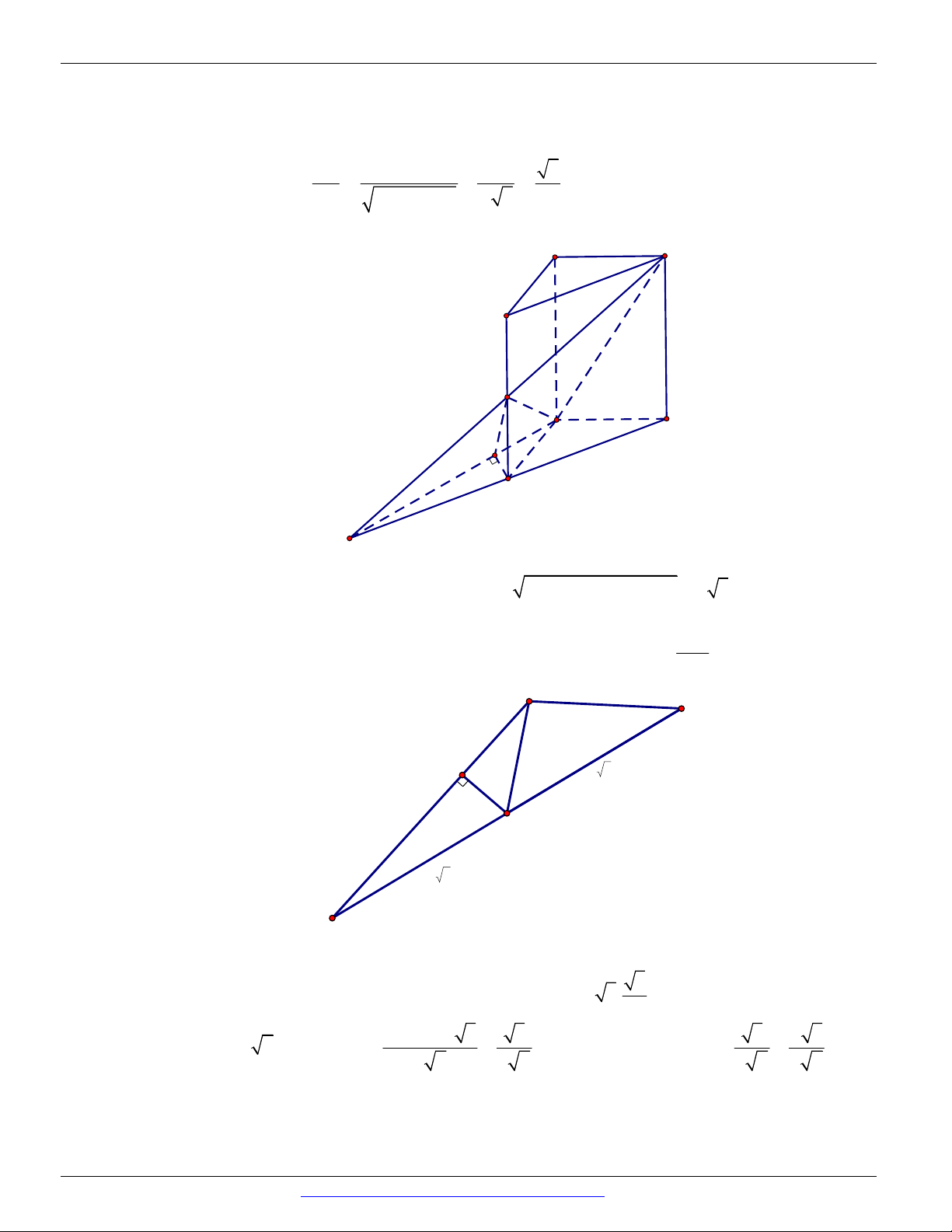
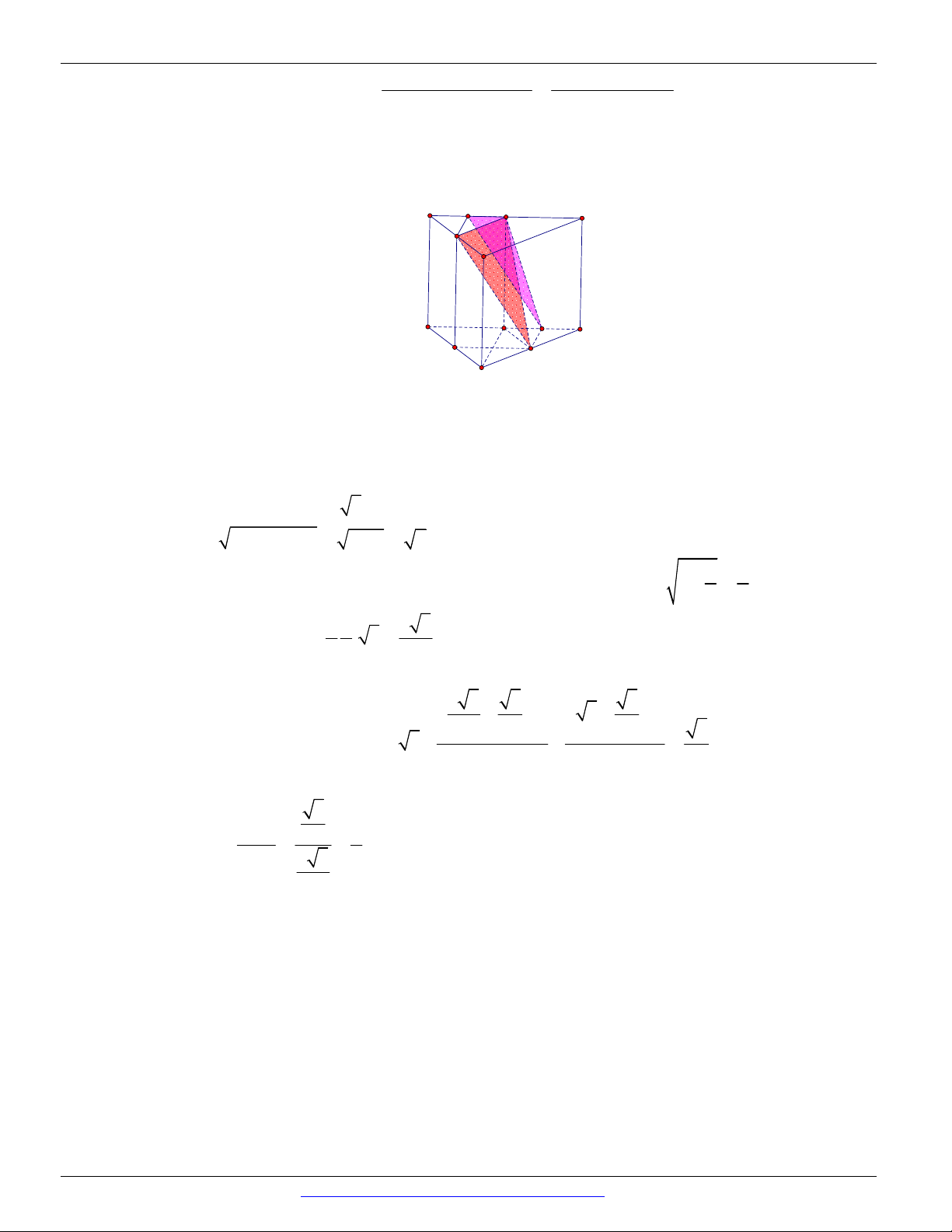
Câu 97. (THPT THÁI PHIÊN - HẢI PHÒNG - LẦN 1 - 2018) Cho hình lập phương / / / / AB . CD A B C D
có cạnh bằng 1. Cắt hình lập phương bằng một mặt phẳng (P) đi qua dường chéo / BD , khi diện
tích thiết diện đạt giá trị nhỏ nhất, côsin góc tạo bởi (P) và mặt phẳng ( ABCD) bằng 6 6 6 2 2 A. . B. . C. . D. . 3 4 6 3
Câu 98. (THPT CHUYÊN KHTN - LẦN 3 - 2018) Cho hình chóp tam giác đều S.ABC đỉnh S, có độ dài
cạnh đáy bằng a . Gọi M và N lần lượt là trung điểm của các cạnh SB và SC . Biết mặt phẳng
AMN vuông góc với mặt phẳng SBC. Tính diện tích tam giác AMN theo a . 2 a 10 2 a 10 2 a 5 2 a 5 A. . B. . C. . D. . 24 16 8 4
Câu 99. (THPT CHUYÊN VĨNH PHÚC - LẦN 4 - 2018)Cho tứ diện ABCD có V
AC AD BC BD a và hai mặt phẳng ACD , BCD vuông góc với nhau. Tính độ dài
cạnh CD sao cho hai mặt phẳng ABC , ABD vuông góc. 2a a a A. . B. . C. . D. a 3 . 3 3 2
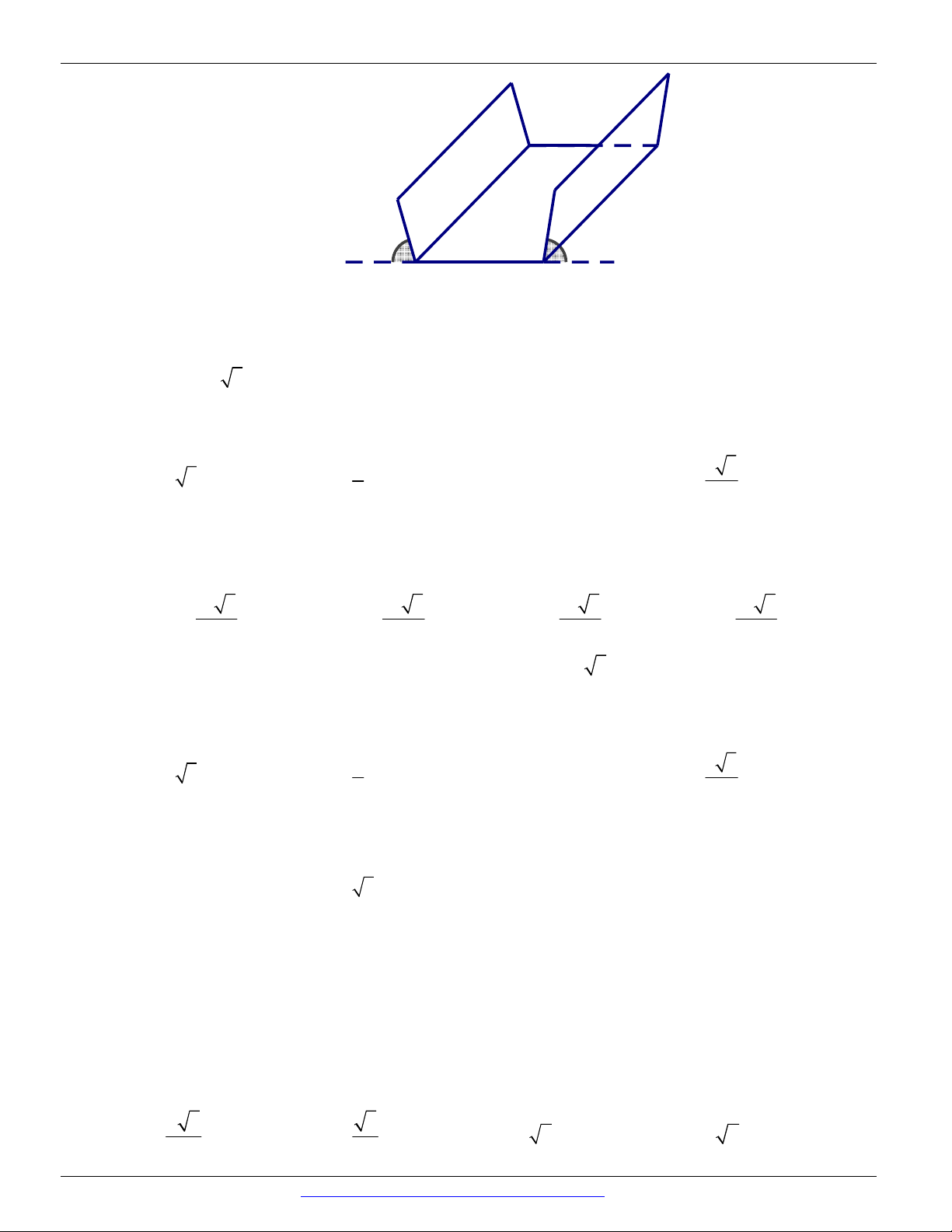
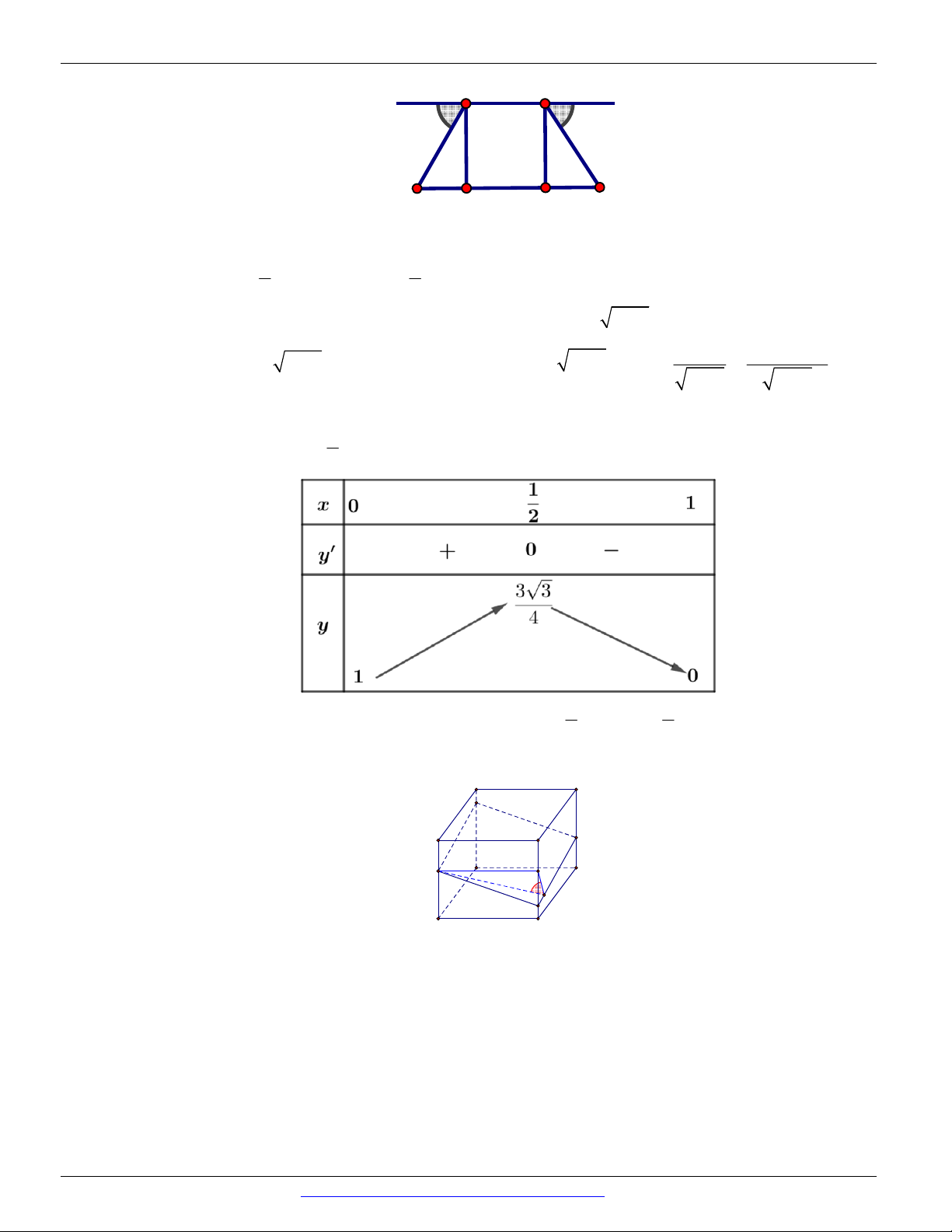
Câu 100. (THPT CHU VĂN AN - HÀ NỘI - HKI - 2018) Bạn Nam làm một cái máng thoát nước mưa,
mặt cắt là hình thang cân có độ dài hai cạnh bên và cạnh đáy đều bằng 20 cm , thành máng nghiêng
với mặt đất một góc 0 90 . Bạn Nam phải nghiêng thành máng một góc trong khoảng
nào sau đây để lượng nước mưa thoát được là nhiều nhất?
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 20cm 20cm φ φ 20cm A. 50 ; 70 . B. 10 ; 30 . C. 30 ; 50 . D. 70 ; 90 .
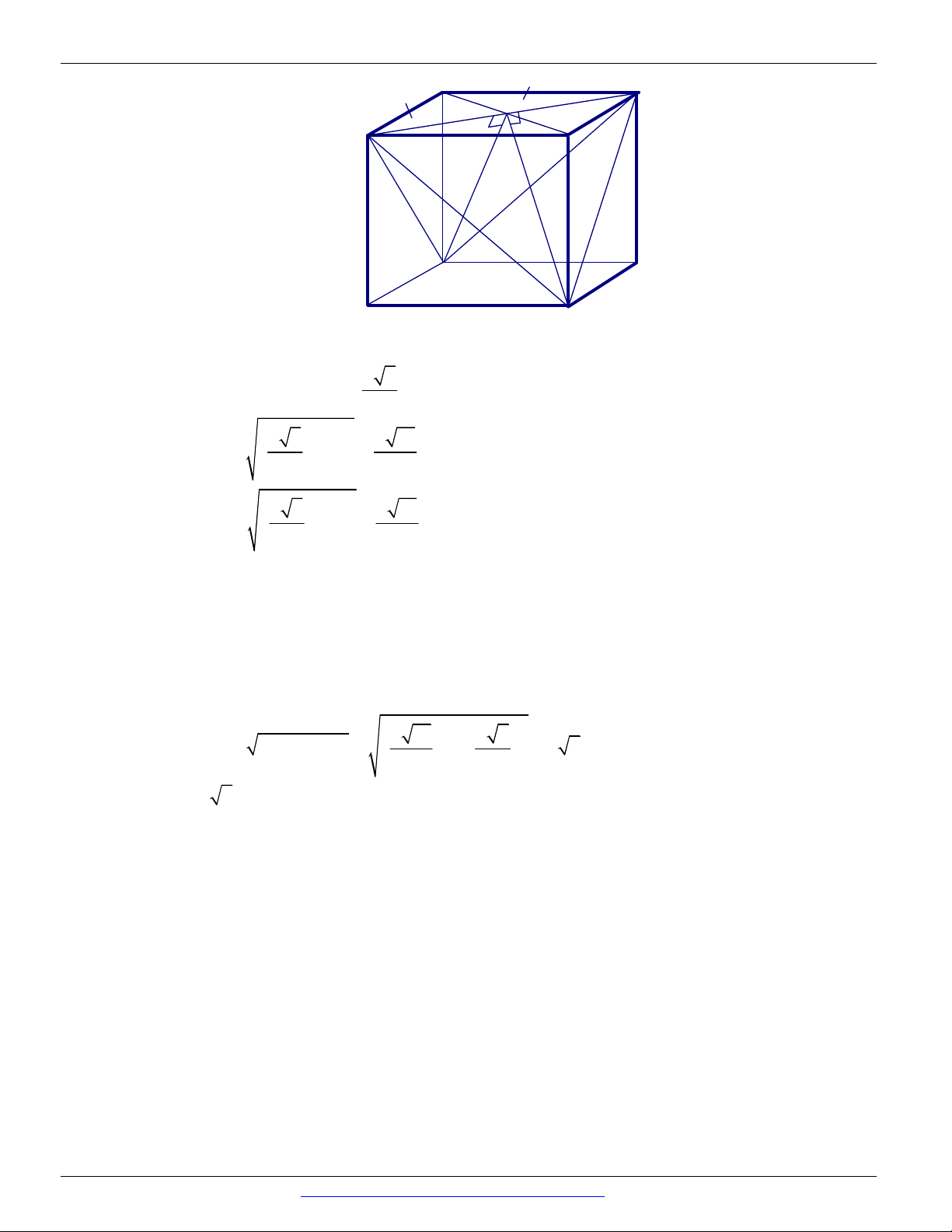
Câu 101. (Trường THPT Thăng Long Lần 1 năm 2018-2019) Cho hình lập phương ABC . D AB C D có
cạnh bằng 3 . Mặt phẳng cắt tất cả các cạnh bên của hình lập phương. Tính diện tích thiết
diện của hình lập phương cắt bởi mặt phẳng biết tạo với mặt phẳng ABB A một góc 60 . 3 3 3 A. 2 3 . B. . C. 6 . D. . 2 2
Câu 102. Cho hình lập phương ABCD.A' B' C' D' có cạnh bằng 3. Gọi M , N ,P là ba điểm lần lượt thuộc
ba cạnh BB',C ' D', AD sao cho BM C ' N DP 1. Tính diện tích S của thiết diện cắt bởi mặt
phẳng ( M N P ) với hình lập phương đã cho. 13 3 17 3 15 3 13 3 A. S . B. S . C. S . D. S . 3 3 2 2
Câu 103. Cho hình hình lập phương ABC . D A B C
D có cạnh bằng 3 . Mặt phẳng cắt tất cả các cạnh
bên của hình lập phương. Tính diện tích thiết diện của hình lập phương cắt bởi biết tạo với ABB
A một góc 60 . 3 3 3 A. 2 3 . B. . C. 6 . D. . 2 2
Câu 104. Cho hình chóp S.ABC có SA vuông góc với đáy, góc giữa mặt phẳng ABC và mặt phẳng SBC bằng 0
60 . Tính diện tích A
BC , biết diện tích S BC bằng 2. A. 1. B. 3 . C. 4. D. 2.
Câu 105. (Bình Giang-Hải Dương lần 2-2019) Bác Bình muốn làm một ngôi nhà mái lá cọ như trong hình
với diện tích mặt nền nhà (tính theo viền tường bên ngoài ngôi nhà) là 2
100 m , mỗi mặt phẳng mái
nhà nghiêng so với mặt đất 0 30 , để lợp một 2
m mái nhà cần mua 100 nghìn đồng lá cọ. Hỏi số tiền
bác Bình sử dụng mua lá cọ để lợp tất cả mái nhà gần nhất với số nào sau đây? (coi như các mép
của mái lá cọ chỉ chớm đến viền tường bên ngoài ngôi nhà, chỗ thò ra khỏi tường không đáng kể).
A. 11,547 triệu đồng.
B. 12,547 triệu đồng. C. 18,547 triệu đồng. D. 19,547 triệu đồng.
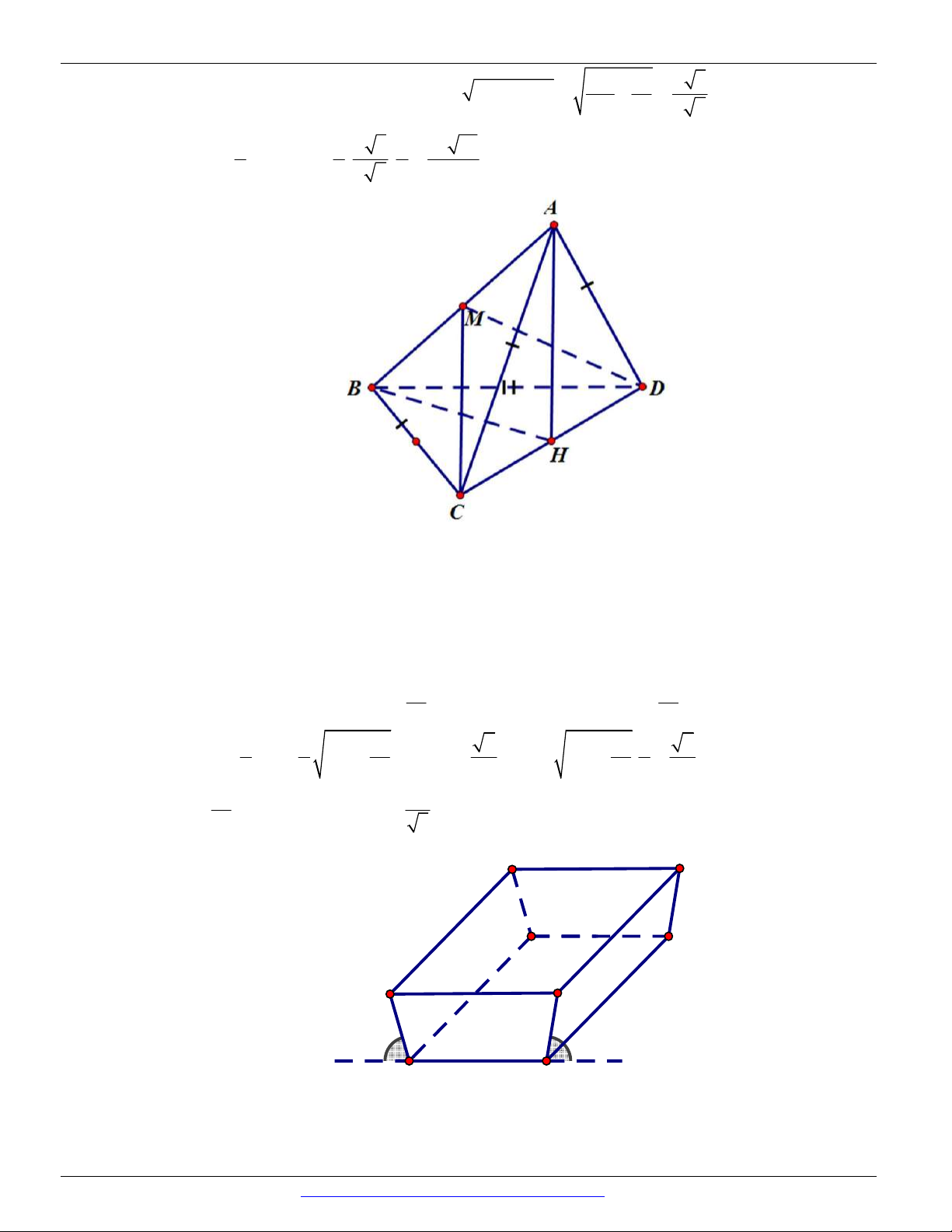
Câu 106. Cho tứ diện ABCD AC AD BC BD a , ACD BCD và ABC ABD . Tính độ
dài cạnh CD. 2 3 3 A. a . B. a . C. 2a . D. 2 2a . 3 3
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
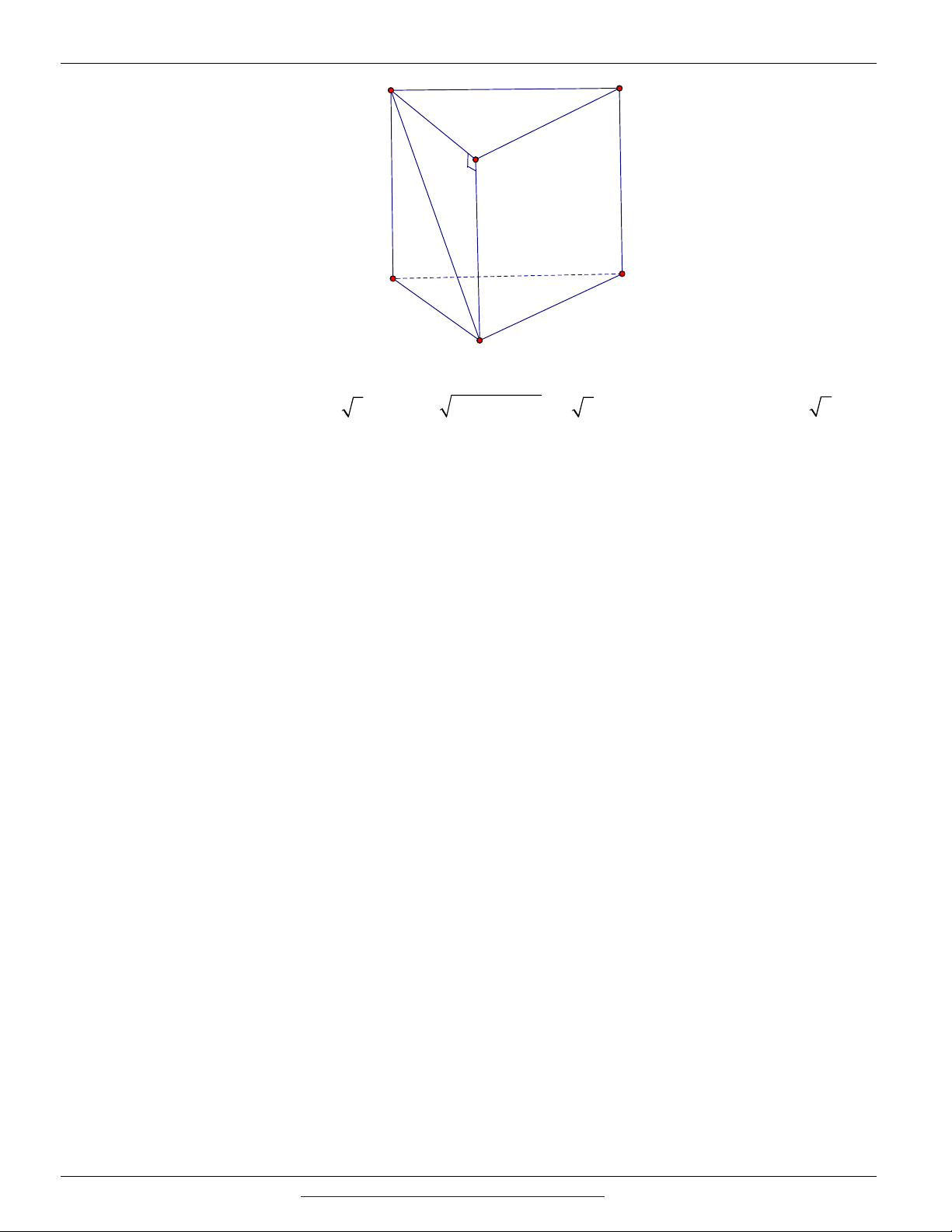
Câu 107. Cho hình hộp chữ nhật ABCB.AB C D
có AB a, AD a 3, AA a . Gọi M , N lần lượt là
trung điểm của AD, AA . Góc giữa hai đường thẳng MN và BB bằng A. 45 . B. 90 . C. 60 . D. 30 .
Câu 108. (Bình Giang-Hải Dương lần 2-2019) Cho hình lăng trụ đứng ABC.A B C có
AB AA a, BC 2a; AC a 5 . Khẳng định nào sau đây sai?
A. AC 2a 2 .
B. Góc giữa hai mặt phẳng ABC và A B
C có số đo bằng 45 .
C. Đáy ABC là tam giác vuông.
D. Hai mặt phẳng AA B B và BB C
vuông góc với nhau. B. LỜI GIẢI
DẠNG 1. CÂU HỎI LÝ THUYẾT Câu 1. Chọn B
A sai vì hai mặt phẳng đó có thể cắt nhau.
C Sai vì hai đường thẳng đó có thể trùng nhau.
D Sai vì hai đường thẳng đó có thể cheo nhau. Câu 2. Chọn B Câu 3. Chọn A Lý thuyết. Câu 4. Chọn A Câu 5. Chọn A Câu 6. Chọn D Câu 7. Chọn A Câu 8. Chọn A Câu 9. Chọn D
Câu 10. Chọn B
Có hai mệnh đề đúng là ii) và iii)
Câu 11. Chọn A
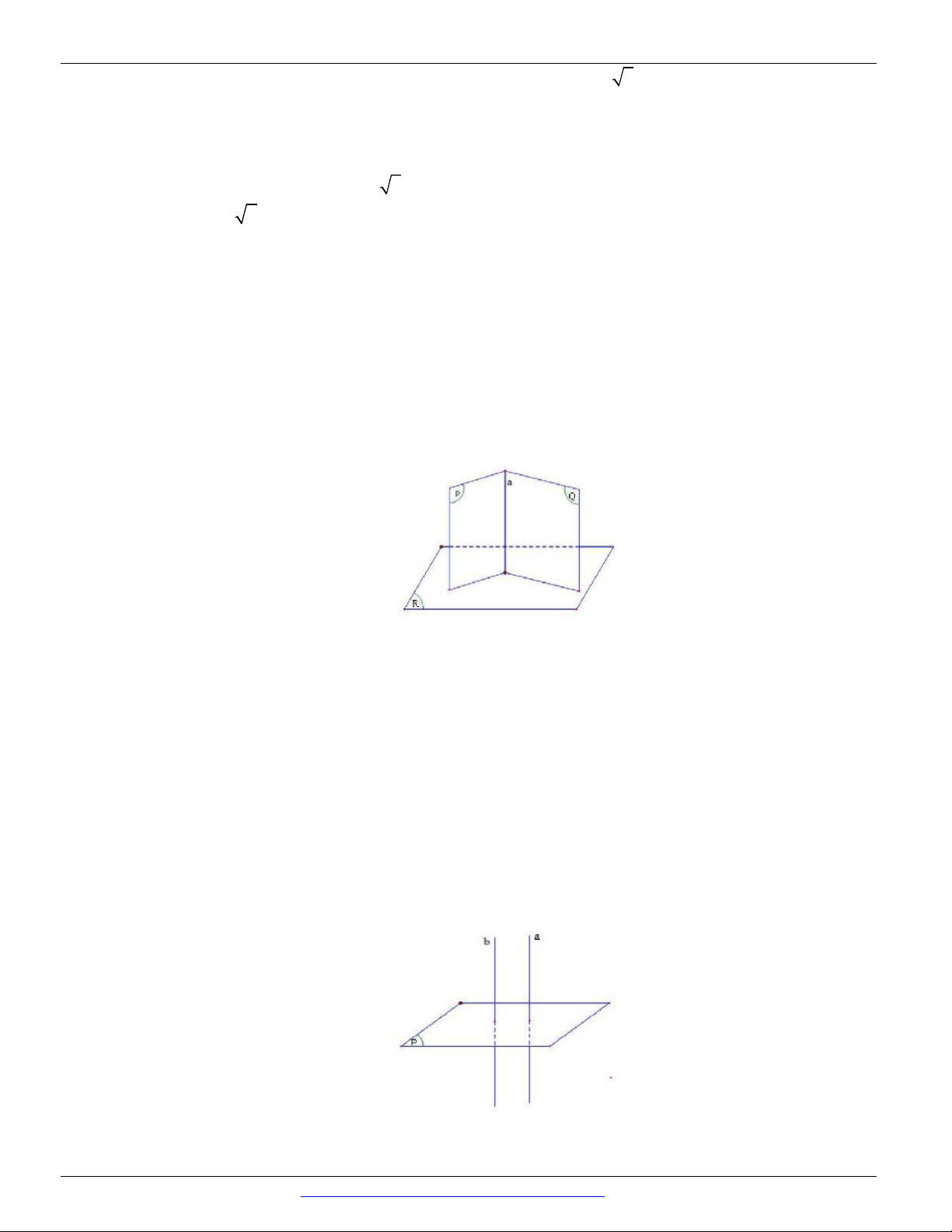
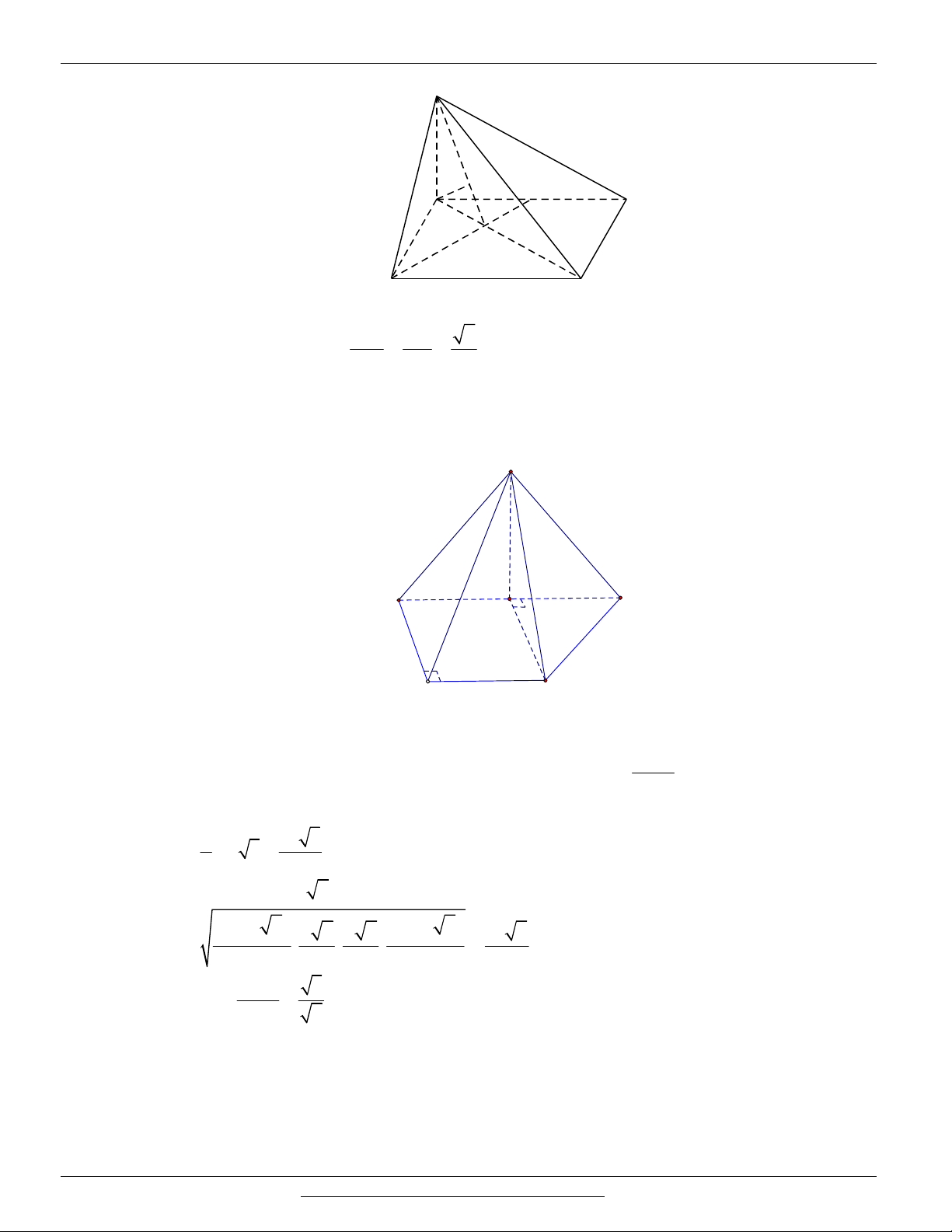
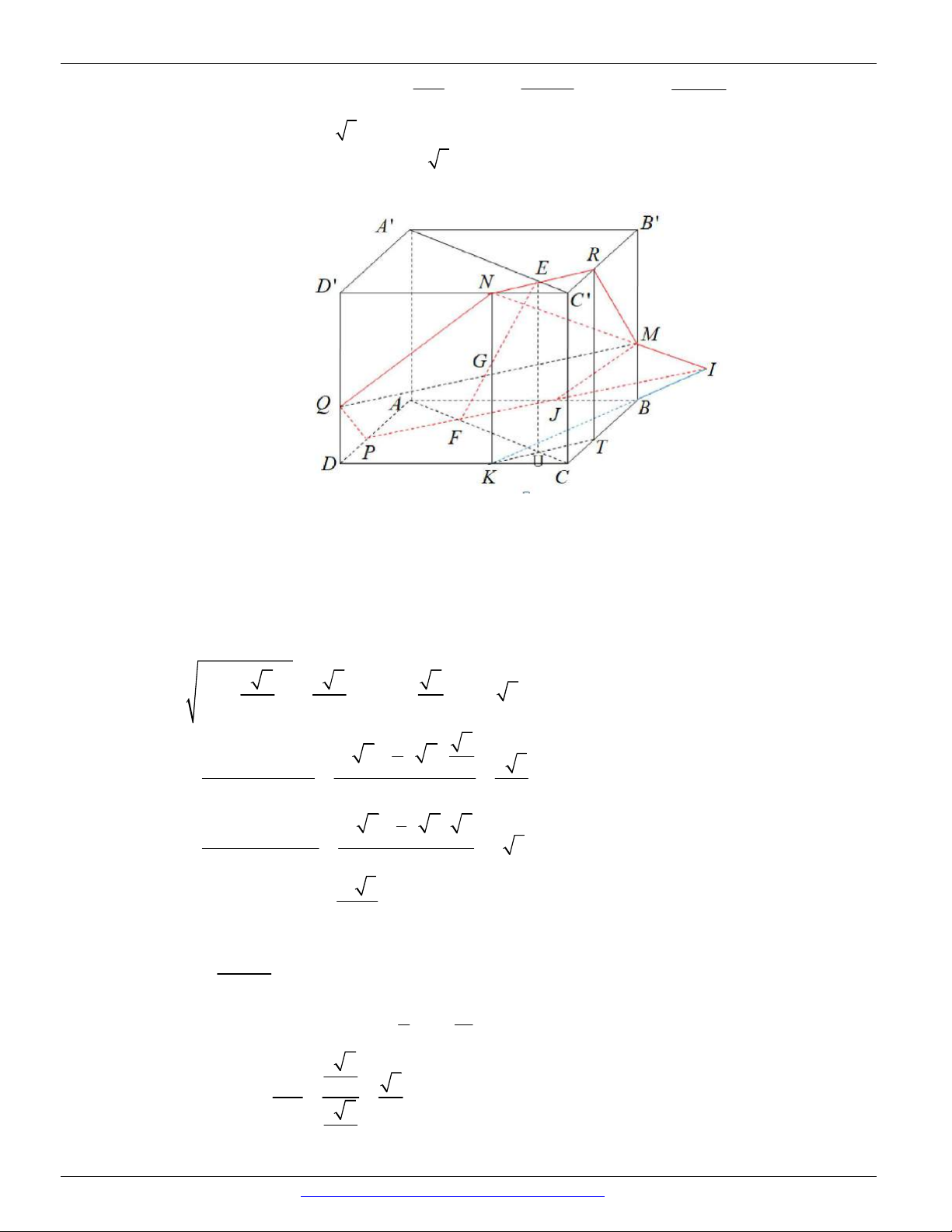
Khẳng định (I) đúng (Hình vẽ trên)
Khẳng định (II) sai vì nếu a P và a b thì b / / P hoặc b P
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
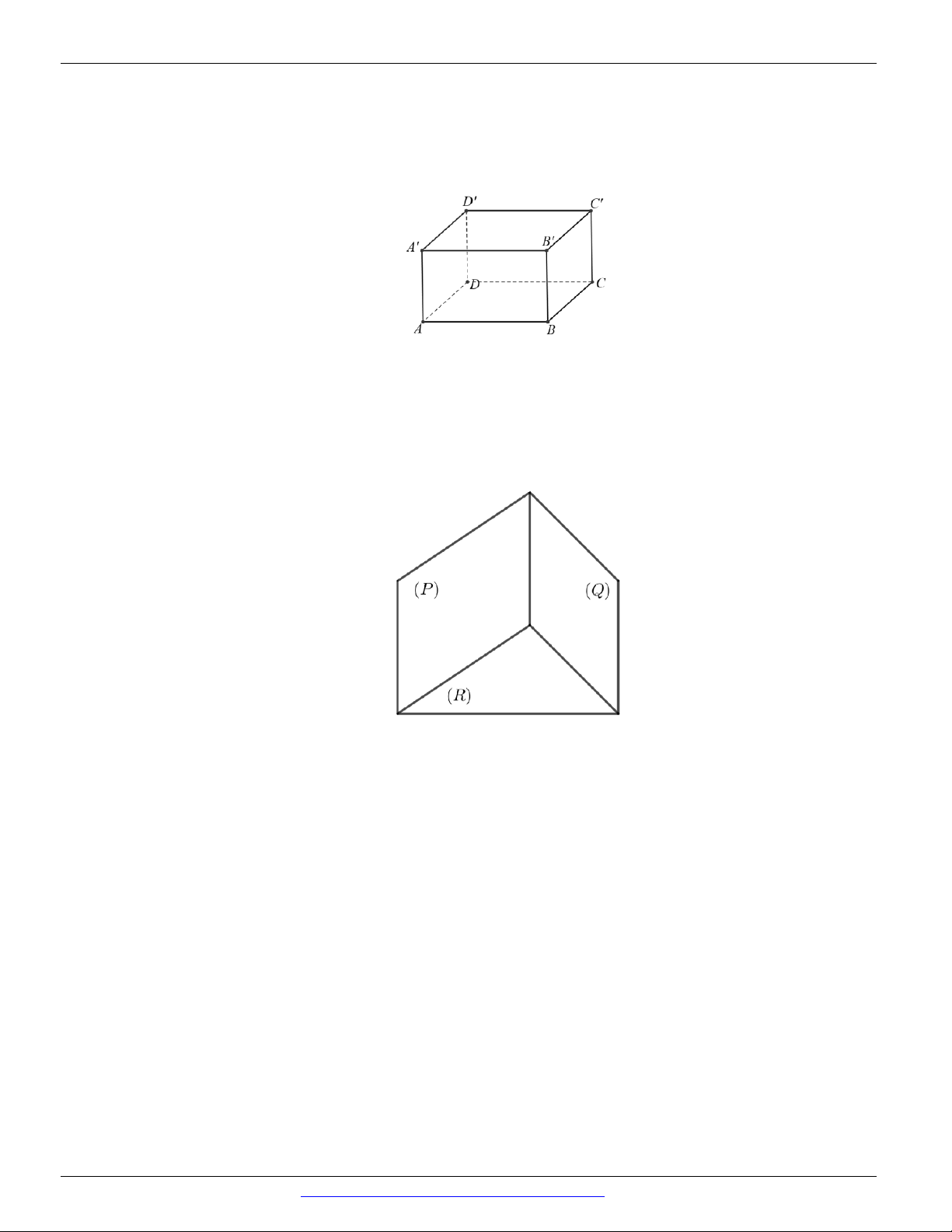
Khẳng định (III) sai trong trường hợp đường thẳng a vuông góc với mặt phẳng P . Khi đó có
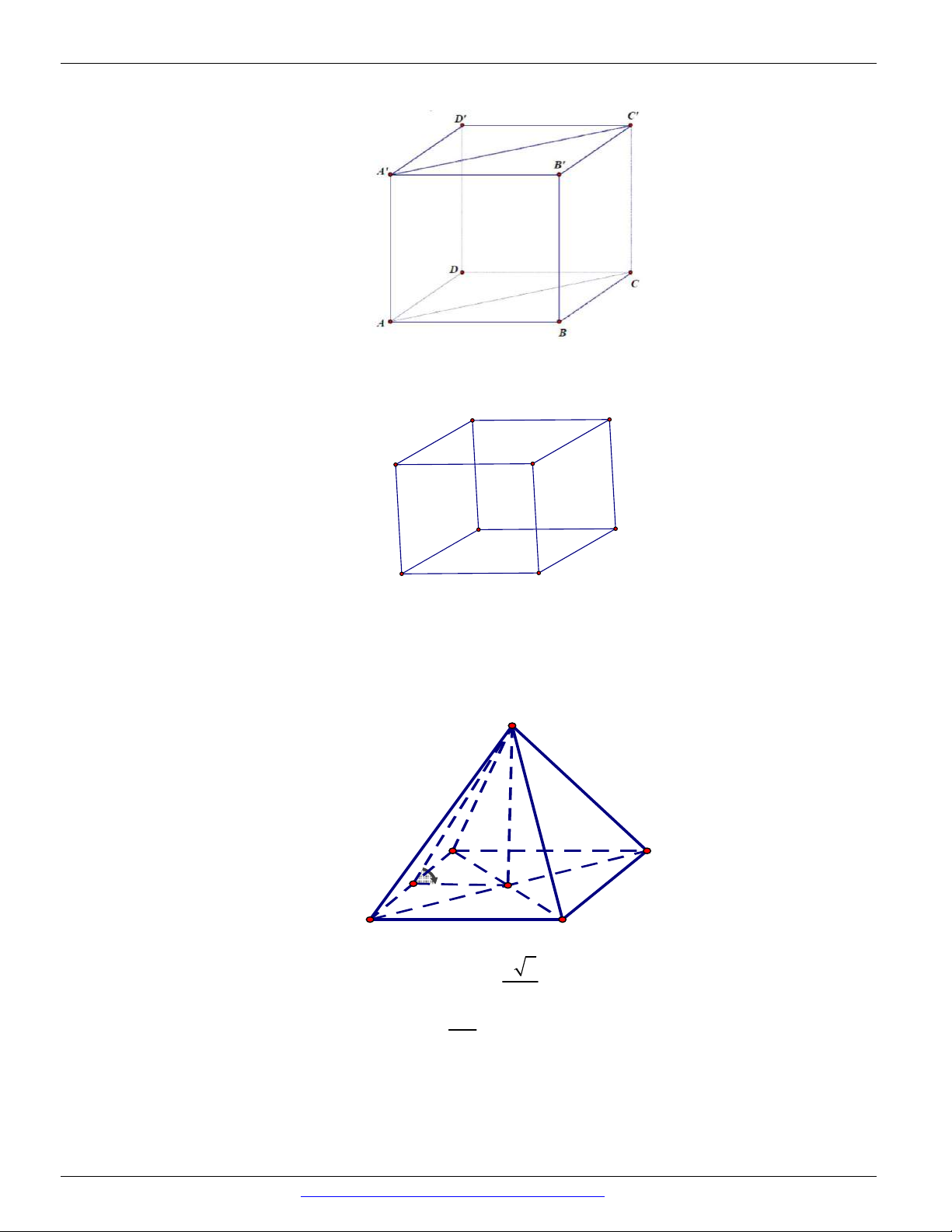
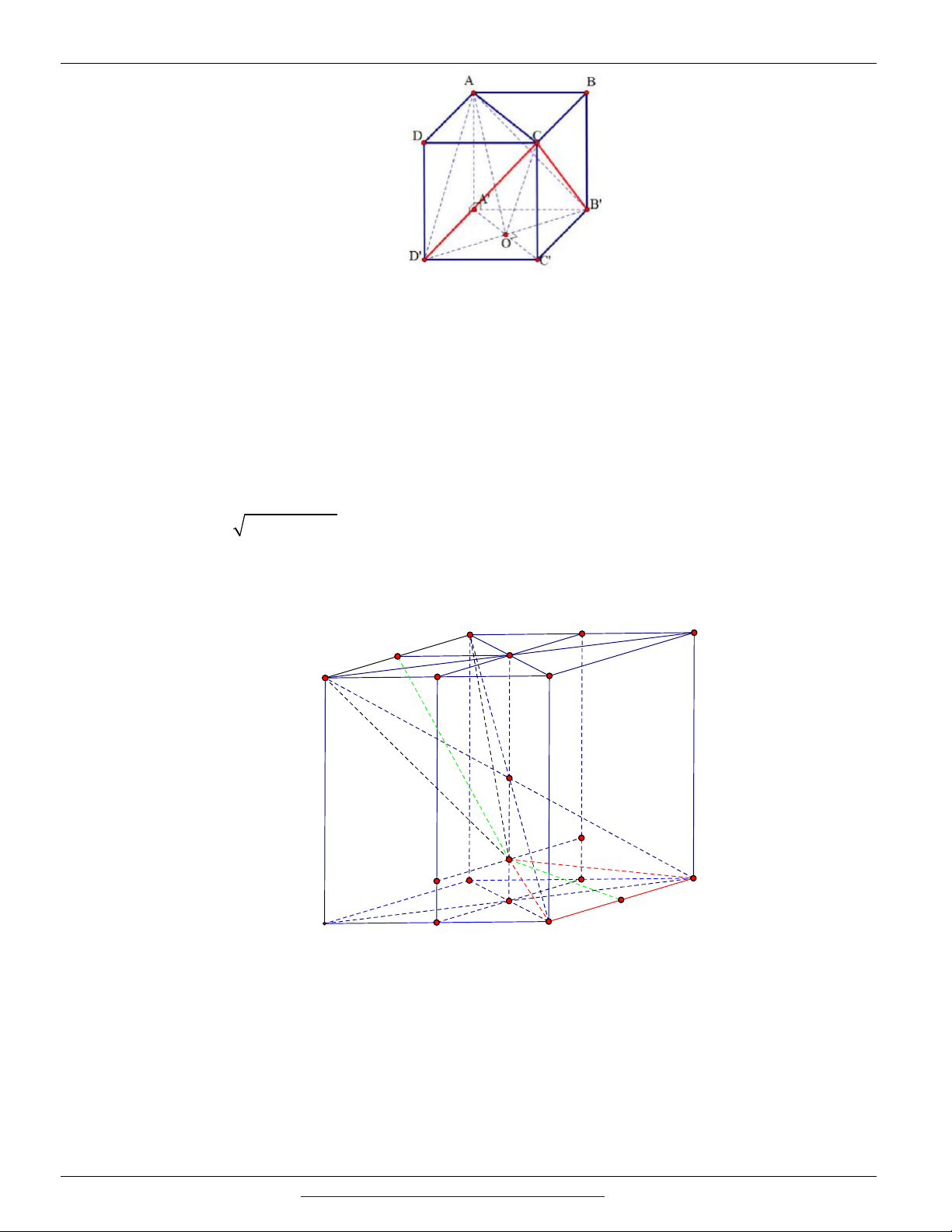
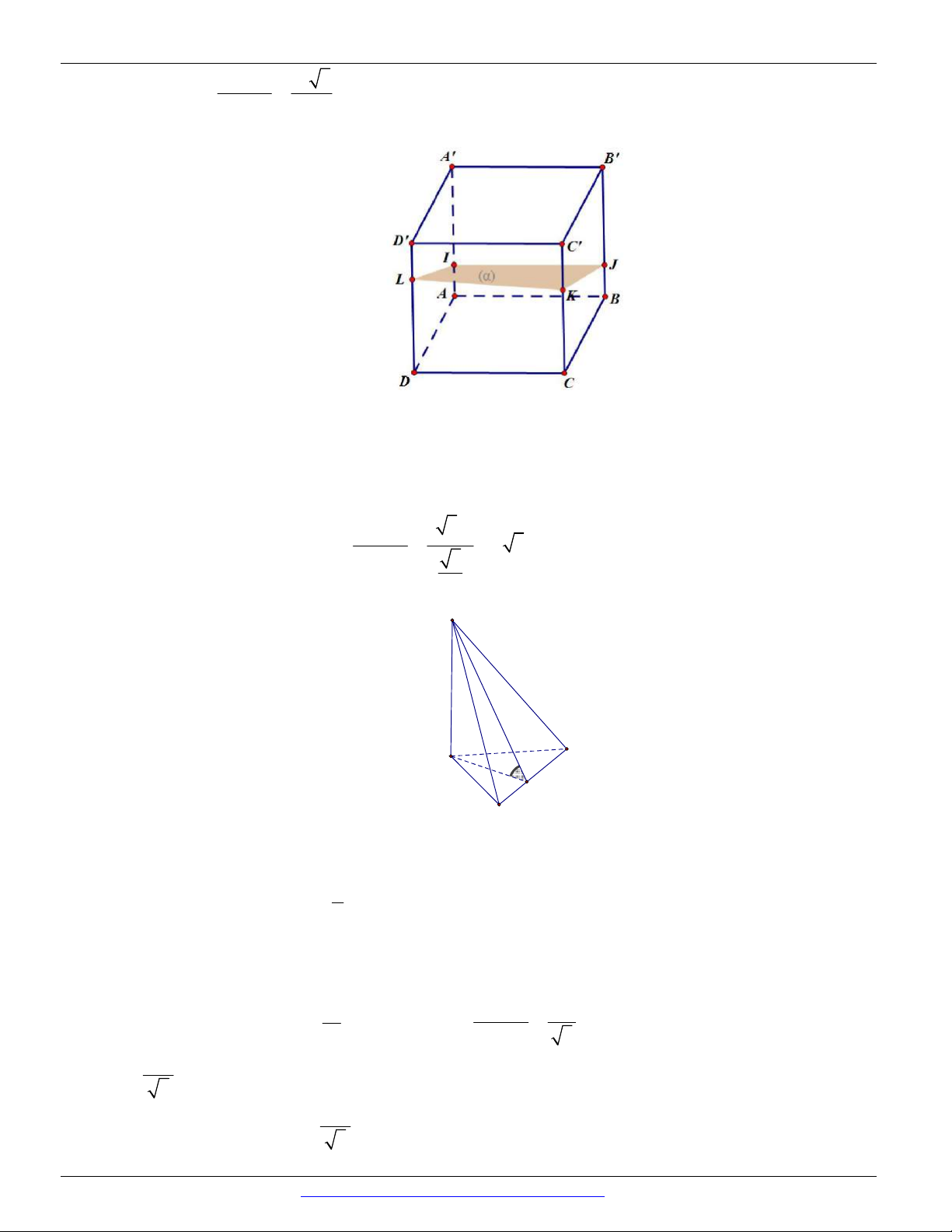
vô sô mặt phẳng chứa đường thẳng a và vuông góc với mặt phẳng P . Ví dụ hình hộp chữ nhật ABC . D A B C D
thì qua đường thẳng AA ta chỉ ra được ít nhất ba mặt phẳng cùng vuông góc với
mặt phẳng ABCD .
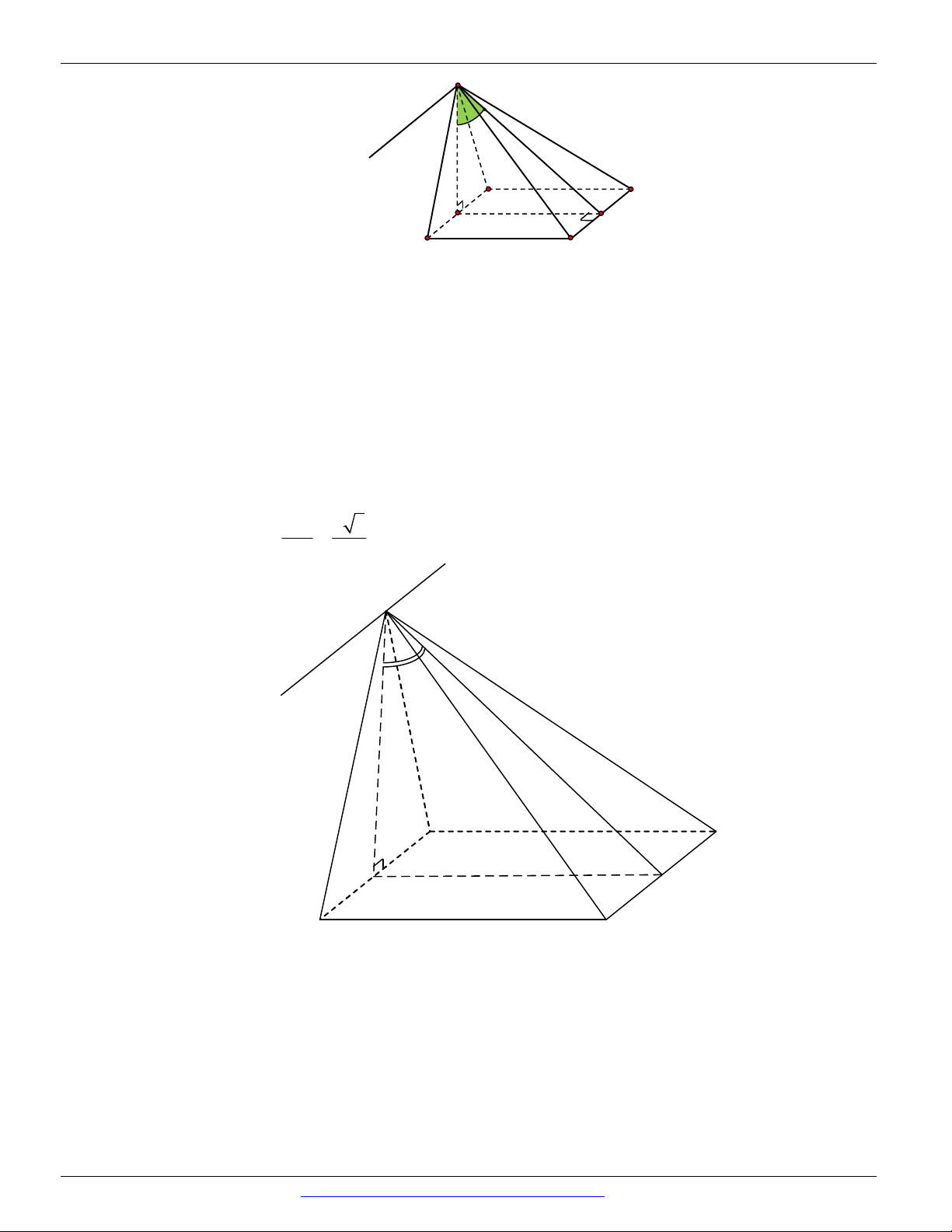
Khẳng định (IV) sai trong trường hợp đường thẳng a không vuông góc với mặt phẳng P . Khi
đường thẳng a không vuông góc với mặt phẳng P thì qua đường thẳng a có duy nhất một mặt
phẳng Q vuông góc với mặt phẳng P .
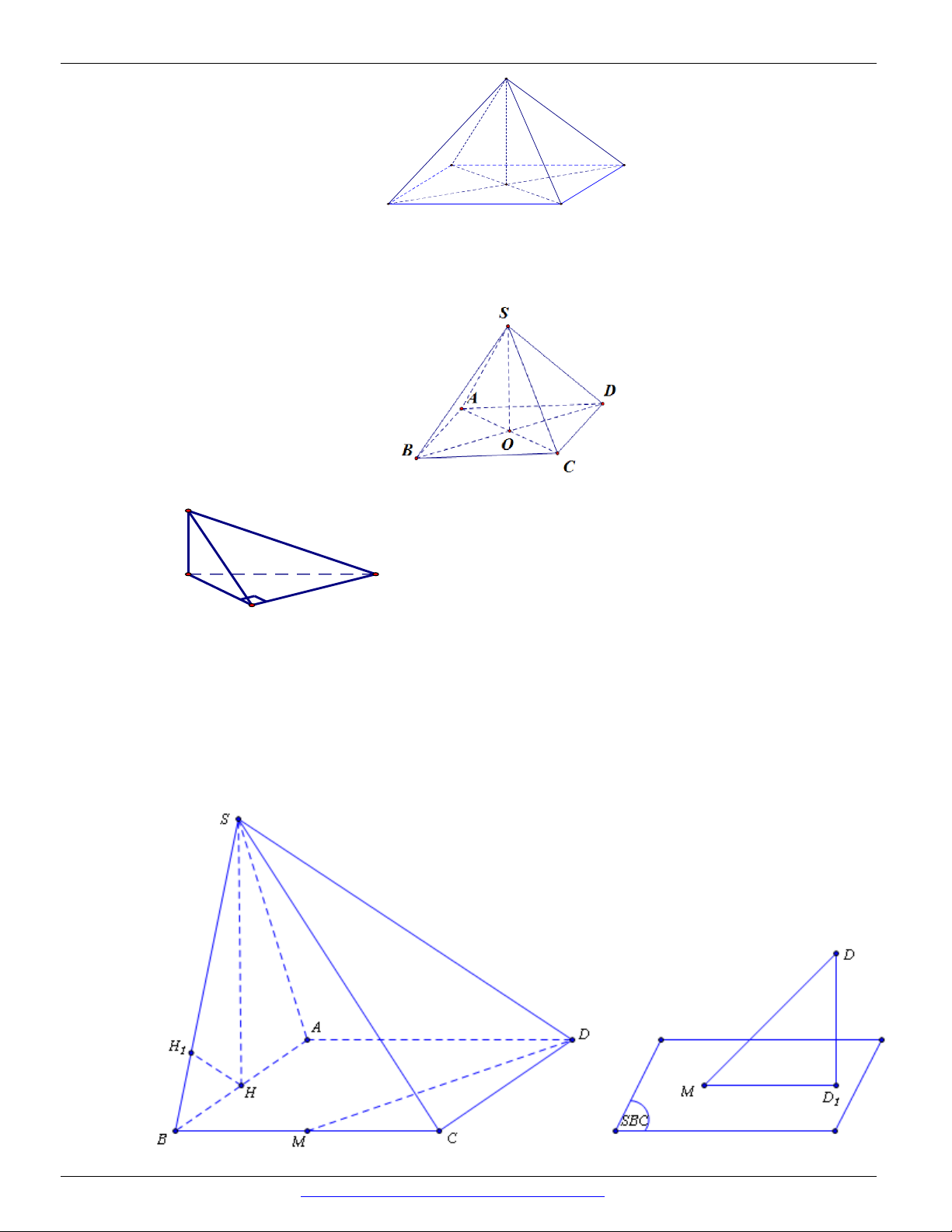
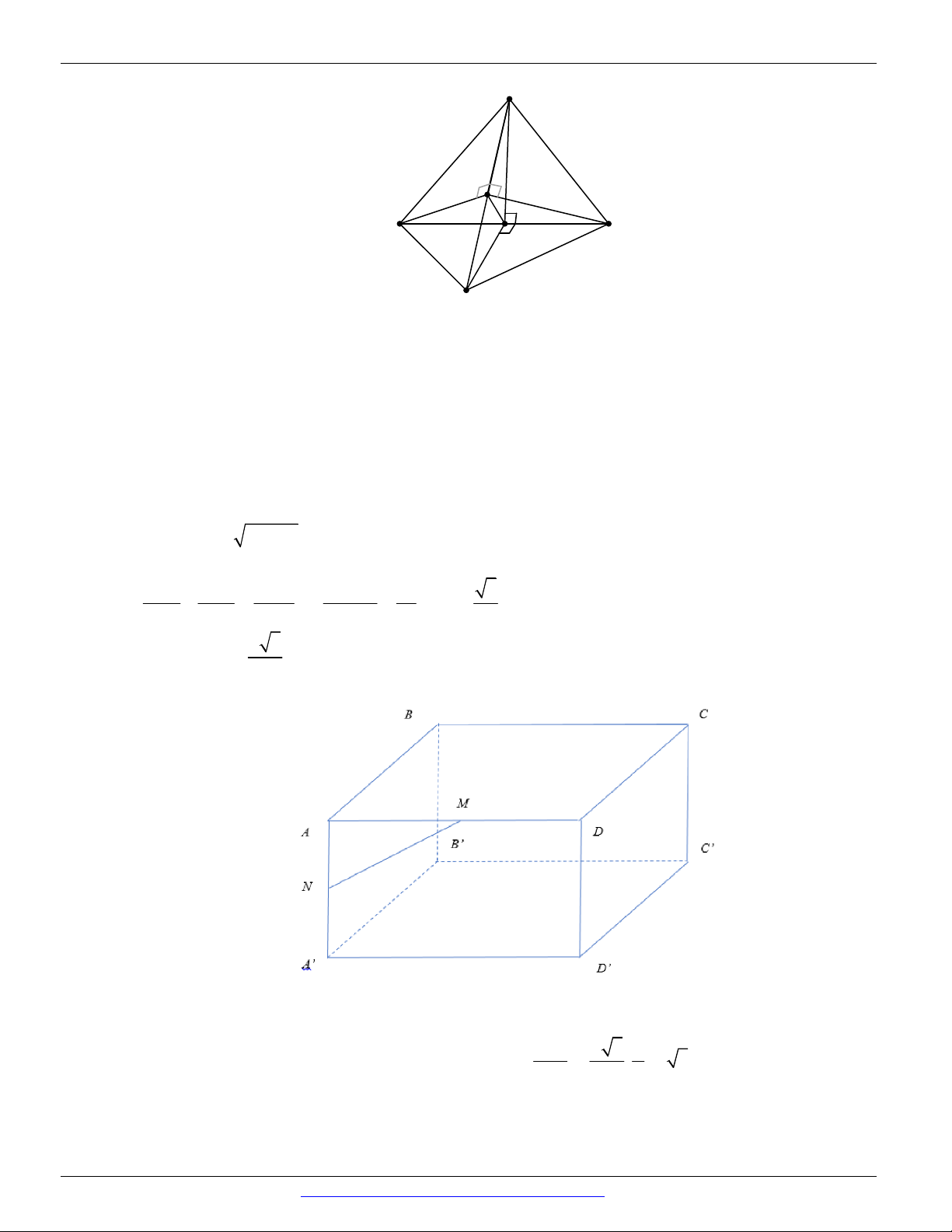
Câu 12. Chọn A
Hình ảnh minh họa hai mặt phẳng P và Q cùng vuông góc với mặt phẳng R nhưng không song song với nhau.
Câu 13. Chọn B
+ Qua M có duy nhất một đường thẳng d vuông góc với P và Q .
+ Mọi mặt phẳng chứa d đều vuông góc với P và Q nên có vô số mặt phẳng qua M vuông
góc với P và Q
DẠNG 2. XÁC ĐỊNH QUAN HỆ VUÔNG GÓC GIỮA HAI MẶT PHẲNG, MẶT PHẲNG
VỚI ĐƯỜNG THẲNG, ĐƯỜNG THẲNG VỚI ĐƯỜNG THẲNG
Dạng 2.1 Đường thẳng vuông góc với mặt phẳng, đường thẳng vuông góc với đường thẳng Câu 14. Lời giải Chọn D
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 S A D H B C
Câu 15. Chọn A
Từ giả thiết suy ra SO AC; SO BD SO ABCD mà SO SBD, SO SAC
SBD ABCD; SAC ABCD . Vậy SC SBD là mệnh đề sai.
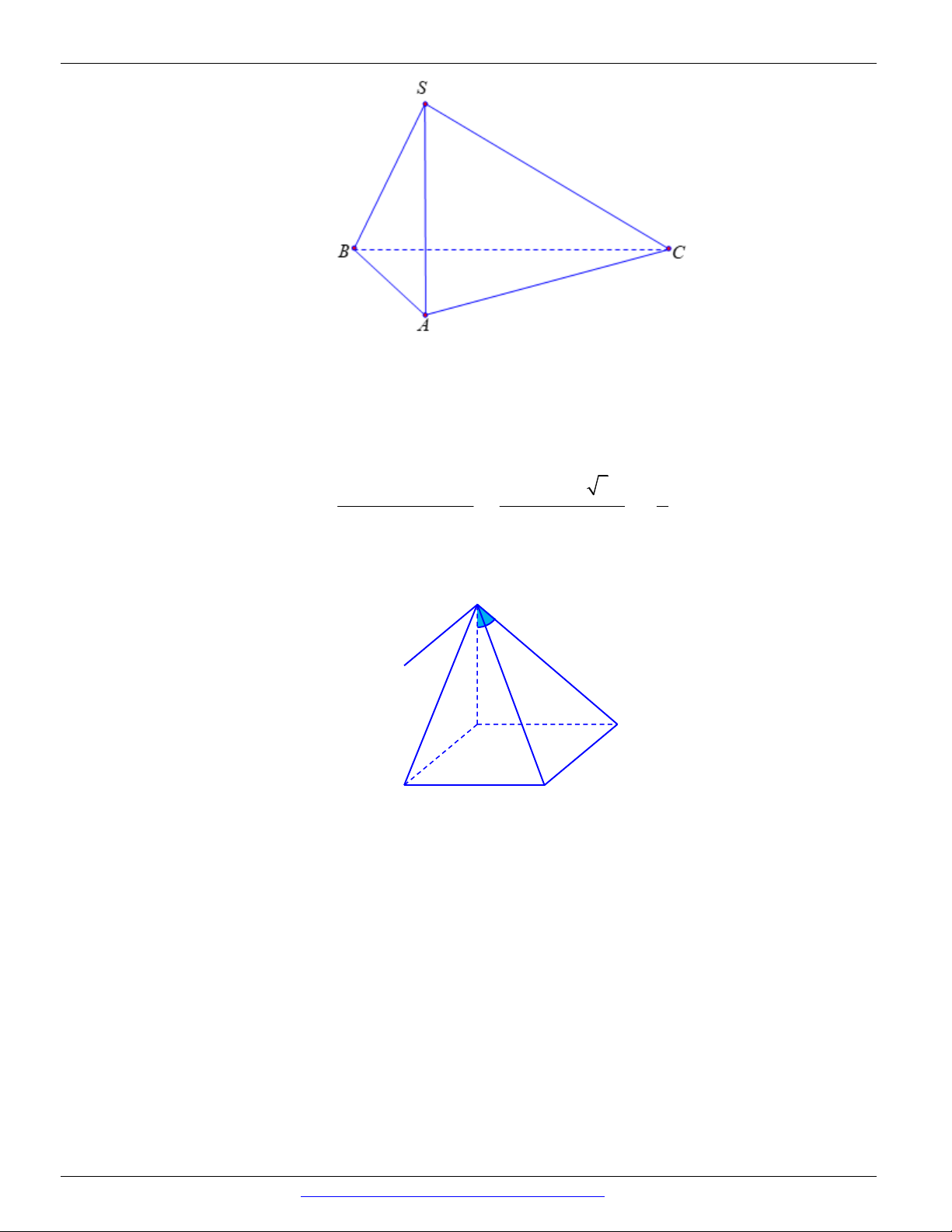
Câu 16. Chọn C S A C B
SA BC đúng vì SA ABC .
AB BC đúng vì A
BC vuông tại B . AB BC
SB BC đúng vì
BC SAB . SA BC
Câu 17. Chọn C
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Gọi D là hình chiếu vuông góc của D trên SBC . 1
Gọi là góc tạo bởi đường MD và mặt phẳng SBC . Khi đó: DD1 sin . MD 2 a a 5 Ta có 2 2 2
MD CD CM a . 4 2
Gọi H là chân đường cao kẻ từ S của SAB . Khi đó do tam giác SAB đều và a 3
SAB ABCD SH ABCD và SH . 2
Kẻ HH SB HH SBC d H , SBC HH và ta có 1 1 1 1 1 1 1 1 a 3 HH . 2 2 2 2 2 1 HH SH BH a 4 1 a 3 2 2 a 3
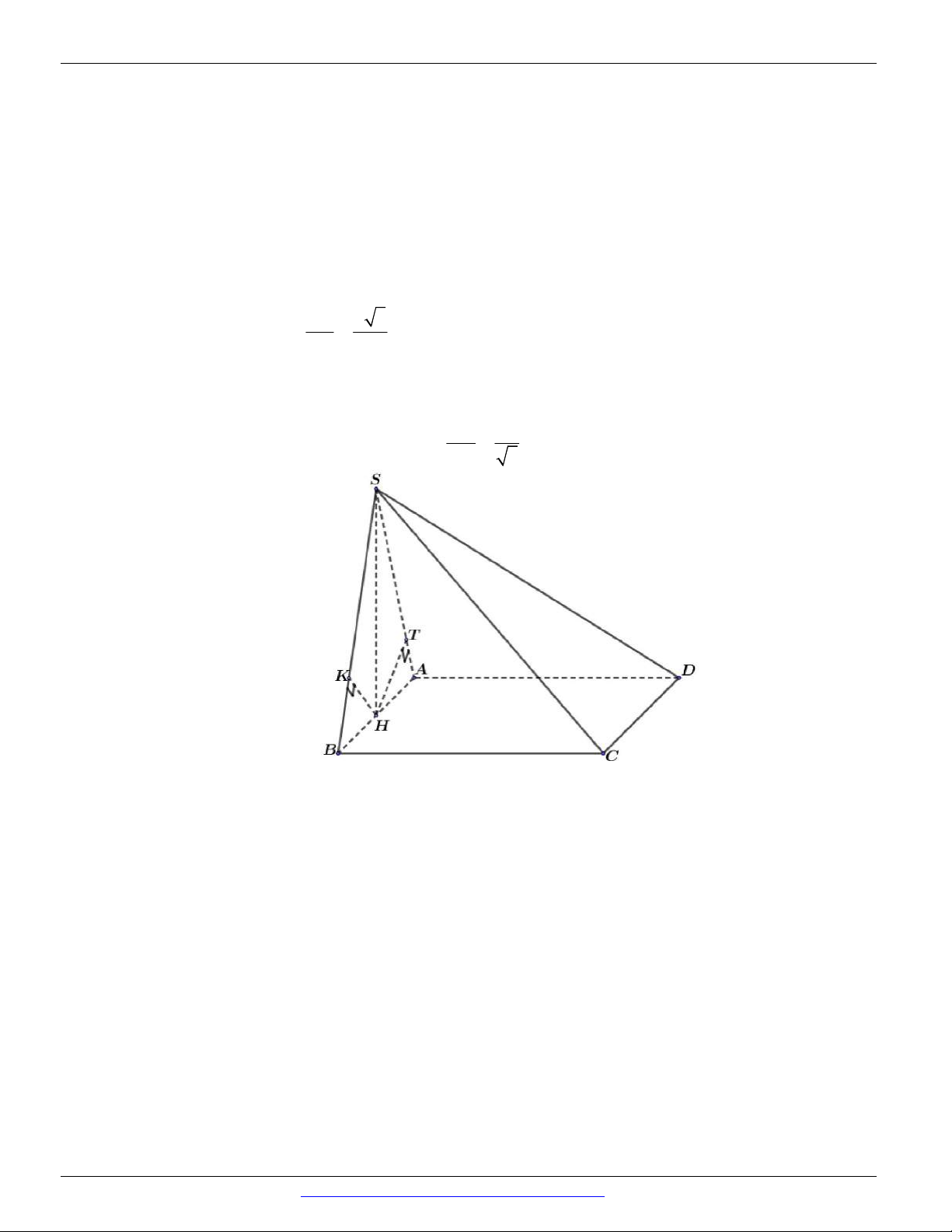
Ta có DD d D, SBC d , A SBC 2d H , SBC 2HH . 1 1 2 DD 15 Do đó 1 sin . MD 5 Câu 18. SAB ABCD Ta có
nên SA ABCD SAD ABCD
Suy ra SA AC (B đúng); SA BC ; SA BD .
Mặt khác BC AB nên BC SAB suy ra BC AH (A đúng).
và BD AC nên BD SAC suy ra BD SC ;
Đồng thời HK // BD nên HK SC (C đúng).
Vậy mệnh đề sai là AK BD (vì không đủ điều kiện chứng minh).
Dạng 2.2 Hai mặt phẳng vuông góc
Câu 19. Chọn D
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 AC BD Ta có
AC SBD SAC SBD . AC SB
Câu 20. Chọn B A' C' B' A C M B
Ta có BC AM và BC AA nên BC AAM ABC AAB B . Nếu AC M
ABC thì suy ra AC M
AAB B : Vô lý. Do đó B sai.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 S H I A C B Câu 21.
BI AC gt Ta có:
BI SAC SC SC BI 1 .
BI SA SA ABC
Theo giả thiết: SC IH 2 . Từ
1 và 2 suy ra: SC BIH . Mà SC SBC nên BIH SBC .
Câu 22. Chọn A
+ Có tam giác ABC là tam giác vuông cân tại B , M là trung điểm của AC BM AC BM AC + Có
BM SAC SBM SAC . BM SA BC SA + Có
BC SAB SBC SAB BC AB Vậy A sai. Câu 23. Chọn D
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
BC SA do SA ABCD
BC AB gt
BC SAB mà BC SBC . Vậy SBC SAB .
SA AB A
Câu 24. Chọn B AC BD Ta có:
AC BB ' D mà AC AB 'C AB 'C BB ' D . AC BB '
Câu 25. Chọn B. S H A I C B
Vì AB SAC nên SAC SAB .
Câu 26. Chọn A S A M B D C AB AD Ta có
AB SAD SAB SAD , suy ra phương án B đúng. AB SA Lại có 2 2 2 2 2 2
AC AD DC a a 2a AC a 2 .
Gọi M là trung điểm của AB . Khi đó 2 2 2 2 2 2
BC MB MC a a 2a BC a 2 . Ta thấy 2 2 2
AB AC CB BC AC . BC AC Như vậy
BC SAC SBC SAC , suy ra phương án C đúng. BC SA
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 DC AD Ta có
DC SAD SCD SAD , suy ra phương án D đúng. DC SA
Câu 27. Chọn B
(SAB) ( ABCD)
(SAB) ( ABCD) AB BC (SAB) BC AB (SBC) (SAB)
Tương tự suy ra (SAD) (SAB).
SCD SAB 0 ; ISJ 90
Vậy có 3 mặt phẳng ( ABCD);(SAD); (SBC) vuông góc với (SAB). Câu 28.
Ta có CD // AB mà A B
ABD nên CD // ABD . CB // A D mà A D A B
D nên CB// ABD . Vậy CB D
chứa hai đường thẳng CD , CB cắt nhau và cùng song song với A BD từ đó ta
có ABD // CB D . S Câu 29. A B O D C
Gọi O AC BD .
Tứ giác ABCD là hình thoi nên AC BD (1).
Mặt khác tam giác SAC cân tại S nên SO AC (2).
Từ (1) và (2) suy ra AC SBD nên SBD ABCD .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
DẠNG 3. XÁC ĐỊNH GÓC GIỮA HAI MẶT PHẲNG
Dạng 3.1 Góc của mặt phẳng bên với mặt phẳng đáy Câu 30.
Do AA ABCD ACC A
ABCD .
Câu 31. Chọn C A ' D' B' C ' A D B C
Ta thấy hai mặt phẳng ABCD và A B C D
là hai mặt đáy của hình lập phương nên chúng song song với nhau.
Vậy góc giữa ABCD và A B C D
bằng ABCD, AB C D 0. S B C E O A D Câu 32. a 2
Góc giữa mặt bên và mặt đáy bằng SEO ; EO 2 SO
Xét SEO vuông tại O , ta có tan SEO 1. EO CD SAD Câu 33. Ta có
ABCD SCD , SDA . ABCD
SCD CD
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 S B A O H C D Câu 34.
Gọi O , H lần lượt là trung điểm của AC và BC . 2 2 3 91a
Xét tam giác SHC vuông tại H ta có: 2 2
SH SC HC 5a a . 2 2
Vì SA SB SC SD 5a nên SO ABCD .
Ta có: SBC ABCD BC , SH BC , OH BC , suy ra góc giữa SBC và ABCD bằng SHO . OH 2a 4 91
Xét tam giác SOH vuông tại O , ta có: cos 6521 . SH 91a 91 2 S A B D Câu 35. C
Từ A ta kẻ đường vuông góc tới BD , thì chân đường vuông góc là tâm O của hình vuông, từ đây
dễ thấy SO BD , nên góc giữa hai mặt phẳng là góc SOA . SA a 6 Xét tam giác SO
A có tan SOA
3 . Vậy góc cần tìm bằng 0 60 . OA a 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A' C' B' A G C M H K B Câu 36.
- Gọi H là trung điểm BG , theo giả thiết AH ABC .
- Gọi M , K lần lượt là trung điểm của AB và BM CM AB
HK AB AHK AB HK / /CM
AKH là góc giữa hai mặt phẳng ABC và ABB A a 3 2 2 2 2 AB AG BG 7a
- Ta có: AB a , AG BG 2 AH 3 2 4 12 2 41a 1 a 3 2 165a 2 2 2
AH AA AH ; HK GM 2 2 2
AK AH HK 12 2 12 48 HK 1 cos . AK 165
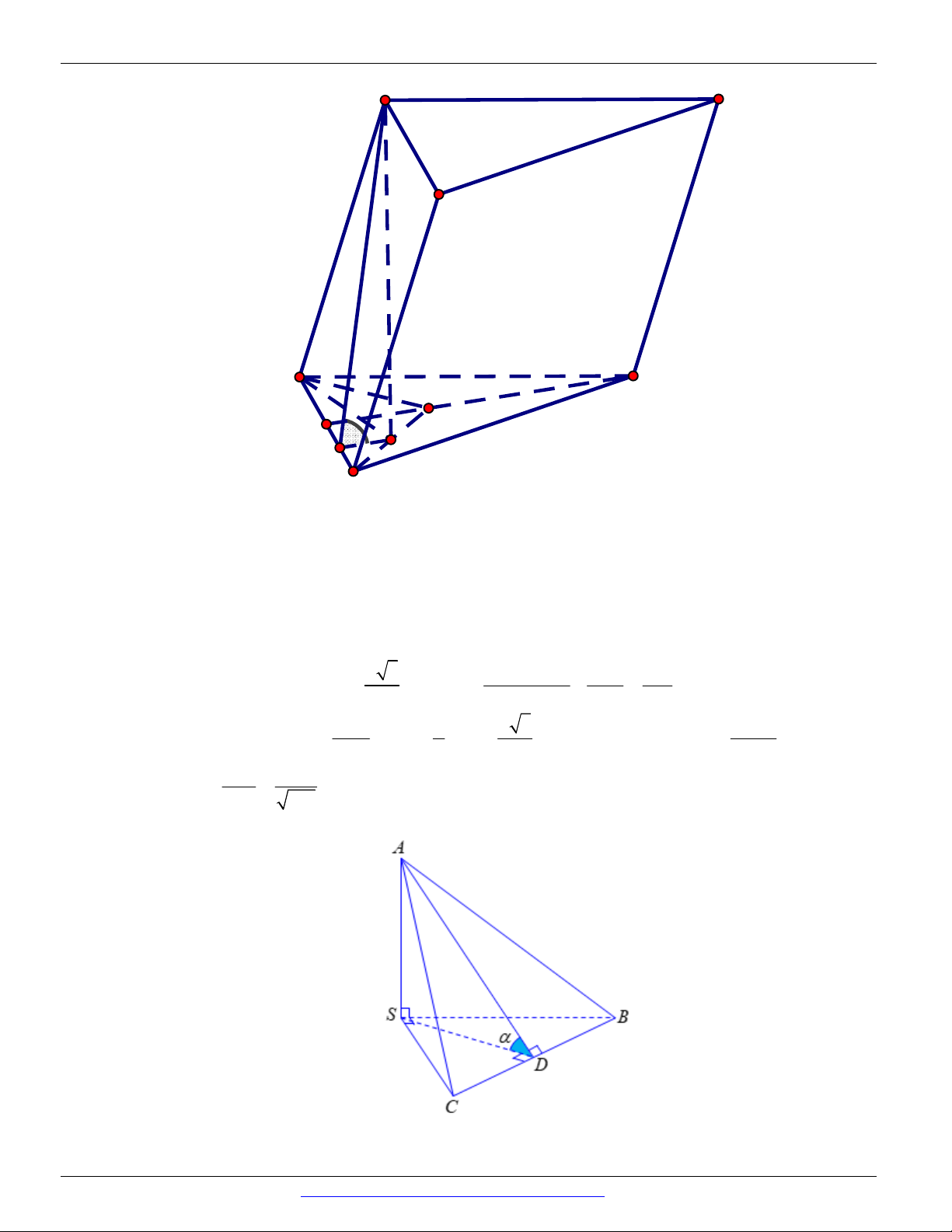
Câu 37. Cách 1:
Gọi D là trung điểm cạnh BC .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 SA SB Ta có
SA SBC SA BC . SA SC
Mà SD BC nên BC SAD .
SBC ABC , SDA . 1 3 SD 1
Khi đó tam giác SAD vuông tại S có SD ; AD và cos cos . 2 2 AD 3 Cách 2:
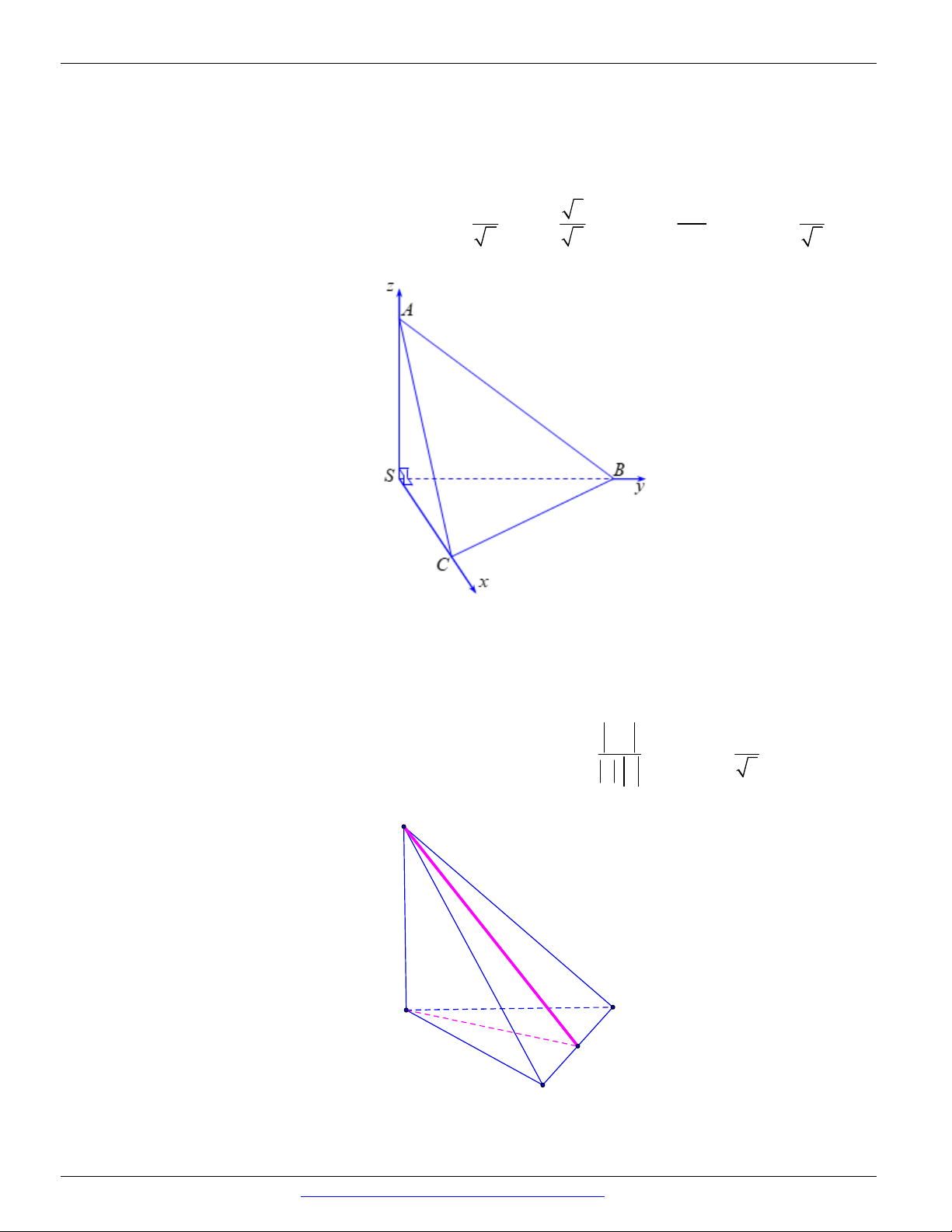
Chọn hệ trục Oxyz như hình vẽ
Ta có S 0;0;0 , A0;0
;1 , B 0;1;0 , C 1;0;0
phương trình mặt phẳng ABC : x y z 1 0 có VTPT n 1;1 ;1 .
Mặt phẳng SBC Oxy : z 0 có VTPT là k 0;0 ;1 . .nk 1
Khi đó góc giữa hai mặt phẳng SBC và ABC là cos cos . n . k 3 S C A M B Câu 38.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
SBC ABC BC SAM BC
Kẻ AM BC tại M . Ta có
SBC , ABC
SM , AM . SAM
SBC SM
SAM ABC AM
Suy ra góc giữa SBC và ABC bằng góc SMA . SA a Ta có tan SMA
1 SMA 45 . AM a Câu 39.
Ta có BC SAB BC SA . Góc giữa hai mặt phẳng SBC và ABC là góc SBA . SA a 3 tan SBA 3 o SBA 60 . AB a A O C I Câu 40. B
Gọi I là trung điểm của BC AI BC . Mà OA BC nên AI BC .
OBC ABC BC
Ta có: BC AI
OBC ABC OI AI , , OIA . BC OI 1 1 Ta có: 2 2 OI BC
OB OC a 3 . 2 2 OA 3
Xét tam giác OAI vuông tại A có tan OIA OIA 30 . OI 3
Vậy OBC ABC , 30 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 S A C Câu 41. B
Theo giả thiết vì SA ABC nên SA AB , SA BC . Mặt khác BC AB nên BC SB . Vậy
góc giữa SBC và đáy là góc SBA . SA
Trong tam giác vuông SAB ta có: tan 3 60 . AB Câu 42.
Gọi O là tâm của hình vuông ABCD ; M là trung điểm của CD .
Góc giữa mặt bên và mặt đáy là SMO . 1 a 3 Ta có OM AD . 2 2 3 a SO
Xét tam giác SOM vuông tại O , ta có tan SMO 2 3
SMO 60 . OM 3 a 2 Câu 43.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Lời giải Chọn D
Gọi M là trung điểm của BC . Suy ra A
OM BC . Nên góc giữa hai mặt phẳng
( ABC ) và (OBC ) chính là góc OMA . a
Ta có: Tam giác OBC vuông cân tạ O nên 1 1 2 2 a 6 OM BC
OB OC a 3 2 2 O C
Xét tam giác OAM vuông tại O có OA 1 tan OMA . Suy ra OM a 6 3 M 0 OMA 30
Vây, góc giữa hai mặt phẳng ( ABC) và B (OBC ) bằng 0 30
Câu 44. Chọn C A' C' B' A C B +) Ta có A
BC là hình chiếu vuông góc của A B
C trên mặt phẳng ABC
+) Gọi là góc giữa A B
C và ABC . 2 S a 3 3 Ta có: cos ABC 30 . 2 S 2a 2 ABC
Câu 45. Chọn C S D O C M A B
Gọi O AC BD thì SO ABCD .
Gọi M là trung điểm của BC thì
SMO là góc cần tìm. Xét S
MO vuông tại O có:
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 3a SO 2 tan SMO 3 SMO 60 . OM a 3 2
Câu 46. Chọn D A D B H I C
Hình chóp tứ giác đều ABCD có H là trọng tâm của tam giác đáy BCD và DH cắt BC tại I
Ta có AH BCD
Tam giác BCD đều và H là trọng tâm của tam giác BCD nên DI BC . AH BC AI BC DI BC
góc giữa mặt bên ABC và mặt đáy BCD là AID a 3
Tam giác ABC đều có AI là đường trung tuyến nên AI 2 1 a 3
Tam giác BCD đều có H là trọng tâm nên IH DI . 3 6 IH
AH BCD nên tam giác AIH vuông tại H . Khi đó 1 cos AIH AH 3
Câu 47. Chọn C A' D' B' C' A D I B C BD AI
Gọi I AC BD . Ta có:
BD AIA; BD BDAABCD. BD AA
Do đó góc giữa hai mặt phẳng BDA và ABCD là AIA . Ta có: A AI vuông tại A , có: a 2 a 6 AA 6 2 2
AA a; AI
AI AA AI sin AIA . 2 2 AI 3
Câu 48. Chọn B
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 S 2 a D A a B C
Ta có BC AB
BC SA vì SA ABCD .
BC SAB BC SB .
SBC ABCD BC
SB SBC , SB BC
AB ABCD , AB BC
góc giữa mặt phẳng SBC mặt phẳng ABCD bằng góc giữa SB, AB bằng góc SBA . AB a 1 0
SAB : cos SBA SBA 60 . v SB 2a 2
Vậy góc giữa mặt phẳng SBC mặt phẳng đáy bằng o 60 . Câu 49. Lời giải Chọn B
SBC ABCD BC BC SA SAB BC
BC SAB . Ta có BC AB SAB
SBC SB
SAB ABCD AB
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 x
Suy ra góc giữa SBC và mặt đáy bằng góc 0 ˆ SBA 60 . Do đó 0 tan 60 x a 3 . a
Câu 50. Chọn A D' A' C' B' a 3 I D A C a B Ta có:
A'B'C;ABC 'D 'BC ';B'C
Gọi I là giao điểm của hai đường chéo BC ' và B 'C . CB 1 +) o tan CB ' B
CB ' B 30 . BB ' 3
Tam giác IBB ' cân tại I , suy ra: o o
BIB ' 120 CIB 60 . Vậy
A B ABC D o ' 'C ; ' ' 60 .
Câu 51. Chọn A S A D M O B C
Giả sử S.ABCD là hình chóp tứ giác đều có tất cả các cạnh bằng a . a a 3
Gọi O AC BD và M là trung điểm của cạnh CD OM và SM . 2 2 CD SO Theo giả thiết ta có
CD SOM CD SM . CD OM
Vậy SCD ABCD OM SM , , SMO . a OM
Xét tam giác vuông SOM ta có 3 2 cos SOM . SM a 3 3 2
Câu 52. Chọn A
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Gọi O là giao điểm của AC và BD , N là trung điểm của BC .
SBC ABC SN ON , D , SNO 1 OB BD 2a 2 Xét S OB vuông tại O: 2 2 SO
SB OB a 7 Xét SO N vuông tại O: 2 2 SN
SO ON 2 2a ON 1 2 Xét SO
N vuông tại O: cos SN 2 2 4
Câu 53. Chọn A A C B A' C' H B'
Gọi H là trung điểm của B 'C '
AH B 'C ' (do A
B 'C ' cân tại A ) và A' H B 'C ' (do A
' B 'C ' đều).
Suy ra AB C A B C AH A H ' ' , ' ' ' , ' AHA ' . AA a Vậy ' 2 3 tan AHA ' . A' H a 3 3 2
Câu 54. Chọn A
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 36
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Gọi M là trung điểm B 'C ' . Do lăng trụ đều nên ta có: A'M B'C ', AM B'C ' .
Do đó góc giữa hai mặt phẳng AB 'C ' và A'B 'C ' là góc AMA'. 3
Lại có tam giác đều A' B 'C ' nên A ' M 2a a 3 . 2 AA a 1 Từ đó: ' t n a AMA ' A' M a 3 3
Vậy góc giữa hai mặt phẳng AB 'C ' và A'B 'C ' bằng 30 .
Câu 55. Chọn B S D A I O C B
Đặt AB a , gọi I là trung điểm của AB . Ta có:
SAB ABCD AB SI AB
SAB ABCD SI OI , , SIO O I AB Mặt khác, ta lại có: 3 a 3 3 1 SO 2
AB a, SO AB a, OI
a tan SIO
3 SIO 60o 2 2 2 OI 1 a 2
Câu 56. Chọn D
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 37
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 S C A x 2a 30° M B
Ta có SA (ABC) AB là hình chiếu của AB lên (ABC) . 2a 3
Do đó SBA (S ;
B (ABC)) 30 , SA AB tan 30 . 3
Gọi M là trung điểm của BC , ta có 2a 3 A
BC đều cạnh 2a AM 2
(SBC) ( ABC) BC Và AM BC
SMA (SBC; ABC) x . SM BC SA 2a 3 2 2 Vậy tan x . . AM 3 2a 3 3
Câu 57. Chọn C
Gọi D là trung điểm của BC .
Ta có MBC ABC BC . BC AD Và
BC AMD . BC AM
Do đó MBC ABC DM AD , ,
MDA , (vì tam giác MAD vuông tại A ). AM 3a 2 3 Vậy tan . . AD 4 a 3 2
Câu 58. Chọn C
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 38
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 S A D O B C
Gọi O AC BD ta có SO B , D AO BD
Góc giữa mặt phẳng SBD và mặt phẳng ABCD là góc SOA a 6 a 2
Xét tam giác vuông SOA có SA ;OA 6 2 a 6 SA 3 Nên 6 tan SOA , suy ra góc SOA 30 OA a 2 3 2
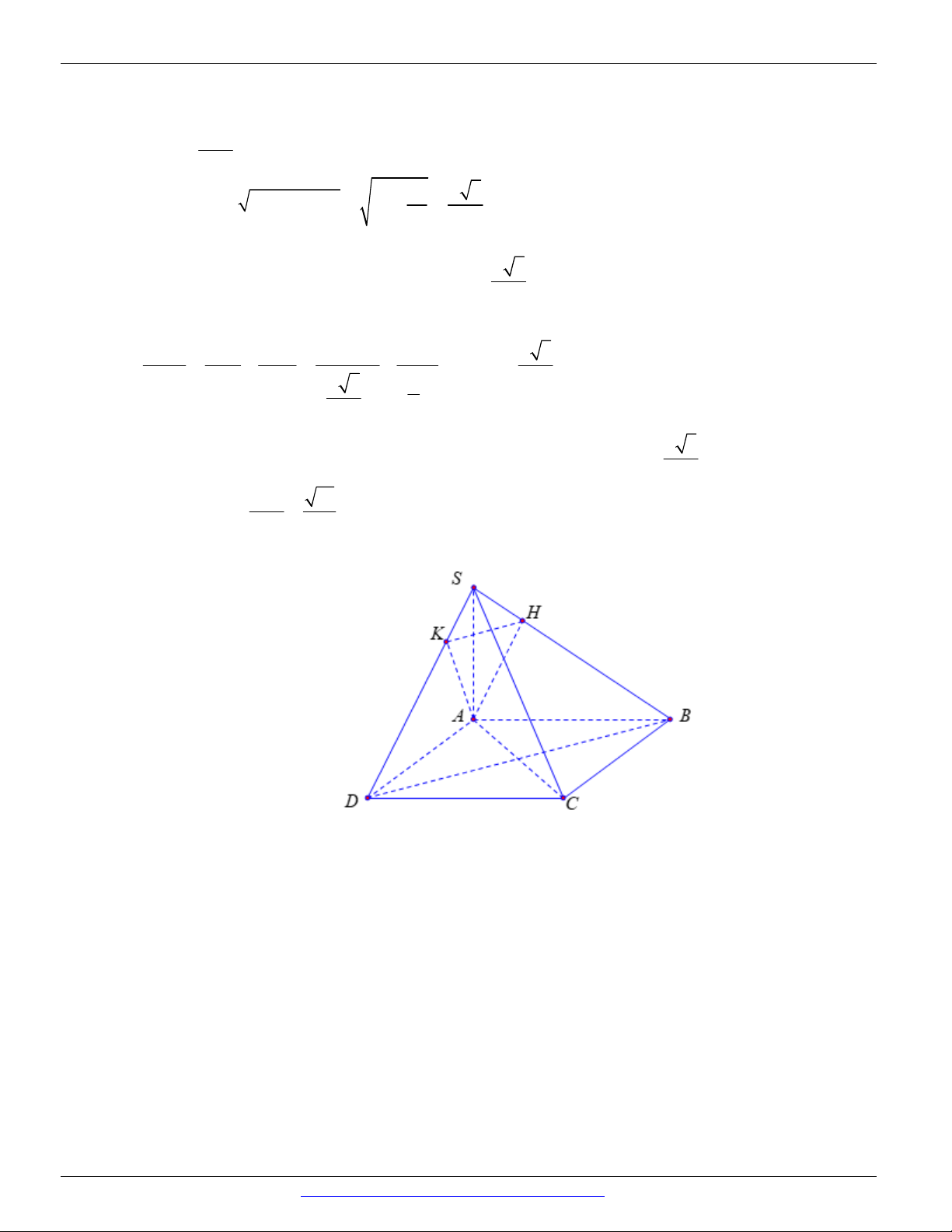
Vậy góc giữa hai mặt phẳng SBD và ABCD bằng 30 Câu 59. Chọn B A K B D H C
Gọi H , K lần lượt là trung điểm của CD và AB .
Do tam giác ACD cân tại A nên AH CD mà ACD BCD AH BCD AH HB 2 2 2 a x AB 2 2 AB HA HB 2 2
2 a x và HK . 2 2
Do các tam giác ABC, ABD cân tại C và D nên CK AB, DK AB góc giữa hai mặt phẳng
ABC và ABDlà góc KC KD , . Khi đó: 2 2 2 a x CD a 3
ABC ABD
CKD 90 KH x x . 2 2 3 a 3 Vậy x . 3
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 39
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 60. Chọn B A B D M H C a 3
Gọi M và H lần lượt là trung điểm BC và CD . Do AB AC AD và H là chân 2
đường tròn ngoại tiếp tam giác đáy BCD nên AH BCD . BC MH
Ta có BC AH
BC AMH .
MH, AH AMH BC MH Suy ra
ABC BCD , AMH . BC AM 2 2 a 3 a 2 2 2 2 AH AB BH tan AMH 3 . MH 1 1 a 6 BD . 2 2 3 Suy ra AMH . 3
Câu 61. Chọn C
Ta có: MN //BC (tính chất đường trung bình) MN // ABC AMN ABC Ax .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 40
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Ax AB
Dễ thấy, BC SAB Ax SAB
. Vậy góc giữa hai mặt phẳng AMN và Ax AM ABC
là MAB . Vì tam giác SAB vuông, nên MAB SBA . Ta có: AB a a 5
cosMAB cosSBA . 2 2 SB SA AB a 5 5
Câu 62. Chọn D A' C' B' 2a M A a C K a B D
Kéo dài BC cắt C M
tại D , khi đó giao tuyến của ( ABC) và ( AC M ) là AD .
Do M là trung điểm của BB suy ra 2 2 2
DB BC a a 2a cos120 a 3
Trong mặt phẳng ( ABC) kẻ BK AD, K AD . BK
Gọi là góc tạo bởi hai mặt phẳng ( ABC) và ( AC M ) . Ta có cos . MK A a C a K a 3 B a 3 D
Do tam giác ABC cân tại A và góc 0 BAC 120 nên 0
ABC ACB 30 suy ra 0 ABD 150 . 3 Ta có 2 2 2 0 2 2 2 2
AD BD AB 2B . D A .
B cos150 3a a 2a 3. 7a . 2 a a
Suy ra AD a 7 0 sin150 . 3 3 sin DAB 3 3 BK .
AB sin DAB a . a 7 2 7 2 7 2 7
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 41
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 a 3 2 3a a 31 BK 2 7 93 2 2 2 MK
BM BK a . Vậy cos . 28 2 7 MK a 31 31 2 7
Dạng 3.2 Góc của hai mặt phẳng bên S K H A C Câu 63. B
Ta có SA ABC SA BC
Mặt khác BC AB BC SAB BC AH (1).
Gọi H , K lần lượt là hình chiếu vuông góc của A trên các cạnh SB , SC khi đó ta có. AH SC (2).
Từ (1) và (2) ta có AH SBC AH SC (3).
Mặt khác ta lại có AK SC (4).
Từ (3) và (4) ta có SC AHK SC HK .
Vậy SAC SBC AK HK , , AKH .
Do AH SBC AH HK hay tam giác AHK vuông tại H . . AB SA 2a 5 AC.SA a 30 Ta có AH ; AK
a 2 HK . 2 2 5 AB SA 2 2 AC SA 5 HK 15 Vậy cos AKH . AK 5
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 42
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 S H A M B N D C Câu 64. AM AD 2
Gọi N AC DM . Ta có
, do đó hai tam giác ABC và DAM đồng dạng, suy BC AB 2 ra
AMN MAN 90 . Vậy AC DM DM SAC mà DM SDM nên góc giữa hai
mặt phẳng SAC và SDM là 90 . S H A B D C Câu 65.
Theo giả thuyết H là hình chiếu của C lên AB nên hình chiếu của mặt phẳng SBC lên mặt S
phẳng SAB là SBH . Đặt SBC SAB , ta có: cos SBH . S SB C Mặt khác ta có: 2 1 a 3 S . a a 3 . SH B 2 2
SB SC 2 ; a BC a 2 . a a a a 2 4 2 4 2 2 2 a 7 S . . . . SBC 2 2 2 2 2 S 3 Vậy cos SBH . S SB C 7
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 43
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 S x B C H K A Câu 66. D
Ta có: H là trung điểm AB thì SH AB (vì tam giác SAB đều) SAB ABCD Mà
SH ABCD SAB
ABCD AB AB CD Mặt khác
SAB SCD Sx // AB // CD
S SAB SCD Sx SH
Mà Sx SHK
, với K là trung điểm CD . Sx SK
SAB SCD , HSK . HK 2 3 Khi đó tan HSK . SH 3 S x A D H I B Câu 67. C
Gọi H là trung điểm của AB SH là trung tuyến đồng thời là đường cao của tam giác SAB
SAB ABCD
Ta có: AB SAB
ABCD SH ABCD
SH SAB,SH AB
Gọi I là trung điểm của CD HI là đường trung bình của hình vuông ABCD
HI a, HI CD CD SH Do
CD SHI CD SI CD HI
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 44
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
S SAB SCD
Lại có AB SAB; CD SCD Sx SAB SCD với Sx / / AB / /CD AB / /CD Sx / / AB Ta có:
SH Sx . Chứng minh tương tự: Sx SI . AB SH
Sx SCD SAB Khi đó: SH
SAB, SH AB SAB SCD SH SI , , HSI
SI SCD,SI CD HI 2 3 Xét S
HI có: tan . SH 3
Câu 68. Giao tuyến của hai mặt phẳng SAB và SCD là đường thẳng d đi qua S và d //AB, d //CD .
Do đó d S ,
A d SD , góc giữa hai mặt phẳng SAB và SCD là góc giữa SA và SD AD
Tam giác SAD vuông tại A , 1 tan ASD
, do đó góc cần tìm bằng 30 . AS 3 Câu 69.
Gọi H là trung điểm của AB , theo đề ra ta được SH ABCD .
Dựng T , K lần lượt là hình chiếu của H lên SA , SB HT SAD và HK SBC .
Vậy SAD; SBC
HT; HK .
Xét tứ giác SKHT có hai góc vuông đối diện nhau nên SKHT là tứ giác nội tiếp KHT 60 do ASB 120 .
Vậy SAD SBC HT HK ; ; KHT 60 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 45
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Câu 70.
Vì SA ABC nên SA AB và SA AC .
SAB SAC SA
ta có: SA AB
SAB SAC AB AC , , BAC . SA AC
AB AC BC
a a a 2 2 2 3 1 Xét ABC có 2 2 2 cos BAC BAC 120 . 2. . AB AC 2. . a a 2
Vậy SAB,SAC 120. S x A D Câu 71. B C CD SAD Sx SA Ta có
Sx SAD
và SAB SCD Sx // AB //CD CD // Sx Sx SD
SAB SCD , ASD .
Tam giác SAD vuông tại A có SA AD a SAD vuông cân tại A 45
Vậy SAB,SCD 45.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 46
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 S K H A C Câu 72. B
Gọi H là trung điểm cạnh AC
Ta có SAC ABC (vì SA ABC ) và BH AC BH SAC .
Trong mặt phẳng SAC , kẻ HK SC thì SC BHK SC BK .
SAC SBC , SKH . Mặt khác a 2
Tam giác ABC vuông cân tại B có AB BC a nên AC a 2 và BH . 2 HC.SA HC.SA a 2
Hai tam giác CKH và CAS đồng dạng nên HK HK . SC 2 2 SA AC 3 BH
Tam giác BHK vuông tại H có tan 3 60 . BK
Vậy SAC ,SBC 60. Câu 73.
Ta có: SBC SAD Sx // BC // AD .
Ta chứng minh được BC SAB BC SB Sx SB .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 47
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Lại có: SA ABCD SA AD SA Sx .
Vậy góc giữa mặt phẳng SBC và SAD là góc BSA 45 .
Câu 74. Chọn A 2 a a Theo bài ra ta có 2 2 2 6 3 OB SB SO a 9 3 2 a a và 2 2 2 3 6 OA AB OB a . 9 3 a 6 a 3 a 6
Chọn hệ trục Oxyz , với O0;0;0 , A ;0;0, B 0; ;0 , S 0;0; , 3 3 3 a 6 a 3 C ;0;0 , D 0; ;0 . 3 3
Phương trình mặt phẳng (SBC) có vectơ pháp tuyến là n 1 ; 2;
1 và vectơ pháp tuyến của mặt
phẳng (SCD) là n ' 1 ; 2; 1 .
Gọi là góc giữa hai mặt phẳng (SBC) và (SCD) ta có:
cos cos n n 1 2 1 , ' 0 ( 1
) 2 2 1 . ( 1 ) 2 2 2 1 2 1 1 Suy ra góc 0 90
Vậy góc giữa hai mặt phẳng (SBC) và (SCD) là 0 90
Câu 75. Chọn C
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 48
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 S C B O H D A AC 2 2 S
AC là tam giác đều S 2 3 S 3 SA C SA O 2 2 SH SA AH 7 S 7 . SAB
Hình chiếu vuông góc của S
AB lên mặt phẳng (SAC) là S AO . S 3 21 Suy ra: cos SAO . S SAB 7 7
Câu 76. Chọn B
Gọi M là trung điểm của BC . Do tam giác ABC đều nên AM BC và a 3
AM AB sin 60 2
Gọi H , K lần lượt là hình chiếu của A trên SM, SB .
Vì SA ABC SA A ,
B SA AM . Trong các tam giác vuông SAB , SAM , ta có: 1 1 1 a 3 1 1 1 a 15 AK AH 2 2 2 ; AK SA AB 2 2 2 2 AH SA AM 5
BC SAdo SA ABC
BC SAM BC AH AM BC AH SM AH KH SB AH
AH SBC .
SB AHK SB HK . AH BC AH SB SB AK a 3 Từ 2 2
AH KH KH AK AH 20 SB AK HK Từ
SAB SBC AKH
SAB SBC 1 , cos , SB HK AK 5
Câu 77. Chọn C
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 49
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 S M C A H N B
Gọi M , N là chân đường cao hạ từ các đỉnh B, S của tam giác SBC . H là hình chiếu của S trên
mặt phẳng ABC .
Ta có: AB SHC AB SC
Mặt khác SC BM SC ABM SC AM
SAC SBC SC
AM SAC Vậy
SAC ;SBC AM ; BM . BM SBC
SC AM , SC BM
Ta tính góc AMB . Xét tam giác AMB .
Tam giác SBC cân tại S nên N là trung điểm của BC . 2 a a 15 +) 2 2 2 SN SC NC 4a . 4 2 SN.BC a 15.a a 15 +) BM . SC 2.2a 4 +) 2 2 2 2 AM AC MC
BC MC BM . 2 2 15a 15a 2 a 2 2 2
AM BM AB 7 Ta có 16 16 cos AMB
0 , suy ra góc AMB nhọn. 2 2.M . A MB 15a 15 2. 16
Vậy SAC SBC AM BM 7 ; ; AMB cos . 15
Câu 78. Chọn D S x a A D a B C
S SAD SBC Ta có:
SAD SBC Sx //BC , Sx //AD . BC // AD
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 50
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 BC AB Ta có:
BC SAB BC SB . BC SA
Mà Sx//BC Sx SB tại S . (1) SA AD Ta lại có:
SA Sx tại S . (2) Sx//AD
Từ (1) và (2) SBC SAD SB SA , , ASB .
Xét tam giác SAB vuông tại A có: SA AB SAB vuông cân tại
A ASB 45
SBC,SAD 45.
Câu 79. Chọn B S K M D A P H B C
Xét tam giác ABC vuông tại B ta có: 2 2 2 2 2 AC
AB BC 3 4 5 .
Gọi K là chân đường vuông góc kẻ từ C xuống SA . Xét tam giác CAK vuông tại K ta có: 2 2 2 2
AK CA CK 5 4 3.
Kẻ SH AC , H AC và KP//SH , P AC thì KP ABCD .
Xét tam giác BAC vuông tại B và tam giác KAC vuông tại K ta thấy các cạnh tương ứng bằng
nhau và KP là đường cao của tam giác KAC nên BP là đường cao của tam giác BAC .
Kẻ PM KA , M KA . Vì KA PB và KA PM nên KA PMB . Suy ra KA MB .
Như vậy, góc giữa mặt phẳng SAC và SAB bằng góc PMB . . KA KC 3.4 12
Xét tam giác KAC vuông tại K ta có: K . P AC K . A KC KP . AC 5 5 12
Suy ra BP KP . 5 2 12 9
Xét tam giác KPA vuông tại P ta có 2 2 2 PA
KA KP 3 . 5 5 P . A PK 36
Lại có PM .AK P . A PK PM . AK 25 2 2 12 36 12 34
Xét tam giác PMB vuông tại P ta có 2 2 MB PB PM . 5 25 25
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 51
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 MP Ta có: 36 25 3 34 cos PMB . . MB 25 12 34 34
Câu 80. Chọn C S O D A K I H J O K I B C
Gọi H , O, J lần lượt là trung điểm của AB, AC, CD .
I là hình chiếu vuông góc của O lên SJ , K là hình chiếu vuông góc của I lên SC .
SAB ABCD
SAB ABCD AB SH ABCD . SH AB SH CD .
Mặt khác, CD HJ CD SHJ CD OI . OI SJ SC OI
OI SCD OI SC , Có SC OK. OI CD SC IK
Suy ra SAC SCD KO KI , , OKI (do O
KI vuông tại I nên OKI nhọn) 2 a 3 a 3 a 7 SH , 2 2
SC SD SB BC a 2 , 2 2 2 SJ
SH HJ a . 2 2 2 OI OJ IJ OJ .SH a 3 S HJ ∽ O IJ OI . SH SJ H J SJ 2 7 OJ .HJ a IJ . SJ 7 5 7a
Có SI SJ IJ . 14 5 7a a . SI KI SI.JC 5 14a S KI S JC 14 2 KI . SC JC SC a 2 56 O
KI vuông tại I OI a 3 56 24 tan . KI 2 7 5 14a 25 1 25 5 Có 2 cos cos (do cos 0 ) 2 1 tan 49 7
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 52
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 5 Vậy cos . 7
Dạng 3.3 Góc của hai mặt phẳng khác Câu 81.
Giả sử cạnh của hình lăng trụ đều ABC.AB C
có độ dài bằng a . Gọi M A B
AB và N AC AC . Khi đó AB C
ABC MN . Kẻ A I
MN I MN mà AA BC , BC//MN AA MN . Vậy AI MN . Khi đó AB C
, ABC AI, AI .
Gọi J là trung điểm BC . a 3 7 1 a 7 AJ , 2 2 AJ AA AJ
a AI AJ . 2 2 2 4 Xét tam giác A I A có: 2 2 2
AI AI AA 1 cos AIA AI AI AIA 1 cos cos , cos 180 .
2.AI.AI 7 7
Câu 82. Chọn D A B C D I J O A B D C
Ta có: CD AD D
A CD A D A D AD AD A BCD CD AD Mà
AD ABCD ABCD A BCD
Do đó: góc giữa hai mặt phẳng
A BCD và ABCD bằng 90 .
Câu 83. Chọn C
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 53
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 BD AC
Ta có: ABC ACD AC . Do BD A C . BD AA
Kẻ BE AC E , thì BDE AC .
BDEABC EB ;BDEACD ED .
Vậy ABC; AC D E ; B ED. BC BA Có
BC AAB B BC A B . BC BB
Giả sử hình lập phương ABC . D AB C D
có cạnh bằng a . Tam giác ABC vuông tại B với
đường cao là BE , ta có: 1 1 1 1 1 3 a 2 a 2 BE
. Tương tự ta có DE . 2 2 2 BE BC BA 2 2 a 2a 2 2a 3 3
Áp dụng định lý hàm số cosin trong tam giác BDE : 2 2 2a 2a 2 2a 2 2 2
BE DE BD cos BED 3 3 1 BED 120 . 2.BE.DE 2 2a 2 2. 3
Vậy ABC; AC D E ; B ED
180 BED 60 .
Câu 84. Chọn A B C O A D B' C' A' D' BD AC Ta có:
BD ACC A
BD OA , BD OC BD A A
Suy ra góc giữa hai mặt phẳng ABD và C BD
là góc giữa hai đường thẳng OA và OC.
Theo giả thiết: AC 2 AA 2a 3 AO AA a 3 OA OC a 6
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 54
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 2 2 2 2 2
OA OC AC
6a 6a 12a Trong tam giác OA C : cos O 0 2 2.OA .OC 2.6a Suy ra 0
AOC 90 .
Chú ý: có thể suy ra góc
AOC vuông bằng cách nhận xét 2 tam giác AOA ,
COC vuông cân.
Câu 85. Chọn B A' H N C' M B' L A K C E P B Do AB .
C A' B 'C ' là lăng trụ đều nên nó là lăng trụ đứng và có đáy là tam giác đều. Ta lấy thêm
các trung điểm của AB, AC lần lượt là các điểm E, L. Gọi H , K lần lượt là trung điểm của
A ' N , C .
L Khi đó thực hiện phép chiếu vuông góc tam giác MNP lên mặt phẳng ACC ' A' ta
được tam giác KNH .
Tam giác MNP có MN 3, MP NP với 2 2 MP
PE ME 3 4 7 . 3 5
Tam giác MNP cân tại P nên độ dài đường cao kẻ từ P tính được là 7 . 4 2 1 5 5 3
Nên diện tích là: S . 3 . MNP 2 2 4
Tam giác KHN có diện tích được tính là 3 3 3 3 .2 3 .2 2 2 2 3 S S S S 4 3 . KHN ACC ' A' AKHA' KCC ' N 2 2 2
Áp dụng công thức hình chiếu ta có S S .cos . KHN MNP 3 S 2 Vậy KHN 2 cos . SMNP 5 3 5 4
Câu 86. Chọn C
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 55
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A D O B C A' D' B' C'
+ Gọi O là giao điểm của hai đường chéo hình vuông ABCD . x 6
Đặt AB x BC ; x AA' . 2 2 x 6 x 10 2
A' B A ' D x
A ' BD cân A'O BD . 2 2 2 x 6 x 10 2
C ' B C ' D x
C ' BD cân C 'O BD . 2 2
+ A' BD C ' BD BD
A'O B ,
D A'O A' BD
C 'O BD, C 'O C ' BD
góc giữa hai mặt phẳng A' BD và C ' BD bằng góc giữa A'O và C 'O . + Tính A'OC ' . 2 2 x 10 x 2 2 2
A'O C 'O
A ' B BO x 2 . 2 2
A'C ' x 2 .
A 'OC ' đều 0 A'OC ' 60 .
Vậy góc giữa hai mặt phẳng A' BD và C ' BD bằng 0 60 .
Cách khác: Gắn hệ trục tọa độ Oxyz vào hình hộp chữ nhật ABC .
D A' B 'C ' D ' để tìm góc giữa hai
mặt phẳng A' BD và C ' BD .
Câu 87. Chọn D
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 56
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Ta chọn hình lập phương có cạnh bằng 6 . Gọi ,
P Q lần lượt là trung điểm các cạnh C D
và AB . Khi đó ta có 2 2
MP MI IP 13 , MQ 5, PQ 6 2
Áp dụng định lý hàm cos ta được: 2 2 2
MP MQ PQ 17 13 cos PMQ . 2M . P MQ 65
Gọi là góc giữa MC D
và MAB : 6 13 sin . 65
Câu 88. Chọn B Gọi ,
P Q lần lượt là trung điểm của BC và B C
; I BM AB , J CN AC , E MN A . Q
Suy ra, MNP AB C
MNCB AB C
IJ và gọi K IJ PE K AQ với E là
trung điểm MN (hình vẽ).
AAQP IJ AQ IJ , PE IJ MNP, AB C
AQ, PE 13 5 5
Ta có AP 3, PQ 2 AQ 13 QK ; PE PK . 3 2 3 2 2 2
KQ KP PQ 13 cos cos QKP . 2K . Q KP 65 C' Q N E M B' A' J K I C P B A Cách 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 57
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Gắn hệ trục tọa độ Oxyz như hình vẽ
P 0;0;0, A3;0;0, B 0; 3;0,C 0; 3;0, A3;0;2, B0; 3;2,C0; 3;2 3 3 3 3 nên M ; ; 2 , N ; ; 2 2 2 2 2
1
Ta có vtpt của mp AB C là n
AB , AC 2;0;3 và vtpt của mp MNP là 1 2 3 n 4; 0; 3 2 8 9 13
Gọi là góc giữa hai mặt phẳng AB C
và mp MNP os c o
c s n ,n 1 2 13 25 65 Cách 3
Gọi Q là trung điểm của AA ' , khi đó mặt phẳng AB 'C ' song song với mặt phẳng MNQ nên
góc giữa hai mặt phẳng AB 'C ' và MNP cũng bằng góc giữa hai mặt phẳng MNQ và MNP . Ta có:
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 58
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
MNP MNQ MN 0
PE MNP PE MN MNP MNQ ; ;
PEQ hoặc MNP;MNQ 180 PEQ
QE MNQ; QE MN
Tam giác ABC đều có cạnh 2 3 AP 3 .
Tam giác APQ vuông tại A nên ta có: 2 2 2 2 PQ
AP AQ 3 1 10 2 3 13
Tam giác A 'QE vuông tại A ' nên ta có: 2 2 2 QE
A ' E A 'Q 1 2 2 2 3 5
Tam giác PEF vuông tại F nên ta có: 2 2 2 PE FP FE 2 2 2
Áp dụng định lý hàm số côsin vào tam giác PQE ta có: 25 13 10 2 2 2
EP EQ PQ 13 4 4 cos PEQ 2. . EP EQ 5 13 65 2. . 2 2 13
Do đó: cos MNP; AB 'C ' 0
cos 180 PEQ cos PEQ . 65
Câu 89. Chọn D
Chọn hệ trục tọa độ như hình vẽ sau. z A' D' C' B' A D y B C x
Theo cách chọn hệ trục tọa độ và theo bài ra ta có: A0;0;0 ; B 2;0;0 ; D0;3;0 ; C 2;3;0 ;
C2;3;4 ; A0;0;4 .
Ta có: BC 0;3; 4 ; BD 2;3;0 n BC ; BD
n 6; 4; 3 là 1 12; 8;6 BC D
một vectơ pháp tuyến của BC D .
Tương tự ta có: n 6; 4; 3 là một vectơ pháp tuyến của AC D . 2 n .n 6.6 16 9 29 Ta có: 1 2 cos . n n 6 4 3 2 . 6 4 2 3 2 2 2 2 61 1 2 61, 6 . Câu 90. Lời giải Chọn A
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 59
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Gọi O A C B D . AB D CB D B D Mà B D ACC A AC CA AB D AO Mặt khác: AC CA CB D CO
suy ra góc giữa hai mặt phẳng AB D và CB D
là góc giữa AO và CO . 2 2 CO AO
AA AO 2 AC AOC là tam giác đều. Vậy góc cần tìm bằng 0 60 .
Câu 91. Chọn B B C N J A D O H M K B' C' I L A' D'
Giao tuyến của (MA ) B và (MC D )
là đường thẳng KH như hình vẽ.
Gọi J là tâm hình vuông ABCD . ,
L N lần lượt là trung điểm của C D và AB . Ta có: C D
(LIM ) C D
LM LM KH .
Tương tự AB (NJM ) AB MN MN KH .
Suy ra góc giữa hai mặt phẳng (MA ) B và (MC D )
chính là góc giữa 2 đường thẳng (MN, M ) L .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 60
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 10 34
Gọi cạnh hình lập phương là 1. Ta có LM , MN , NL 2 . 6 6
MN ML NL Ta có: 2 2 2 7 85 cos LMN . 2MN.ML 85 7 85
Suy ra cosin của góc giữa hai mặt phẳng (MA ) B và (MC D ) là . 85
Câu 92. Chọn D
Gọi M và N là tâm của các hình chữ nhật AA' D ' D và A ' B 'C ' D ' .
Dễ thấy A ' MN D ' MN .
Gọi H là chân đường cao từ đỉnh A' của tam giác A ' MN . Thế thì D ' H MN . Suy ra
cos cos A ' HD ' . 5 13
Ta có: A ' D 5 ; A ' M ; A' N ; MN 5 . 2 2
Xét tam giác A ' MN . 2 2 2
A ' M A ' N MN 9 2 61 Ta có cos A ' 2
sin A ' 1 cos A' .
2.A ' M .A ' N 5 13 5 13 1 61 1 61 S
A ' M .A ' N.sin A '
MN.A' H A ' H D ' H . A ' MN 2 4 2 2 5 2 2 2
A' H D ' H A' D ' 29
Trong tam giác A' HD ' có cos H
2.A' H.D ' H 61 29 Vậy cos 61, 6 . 61
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 61
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
DẠNG 4. MỘT SỐ CÂU HỎI LIÊN QUAN A' C' B' A C Câu 93. B
Xét tam giác ABC có AB BC a a2 2 2 2 2 2 5a 2
AC tam giác ABC vuông tại B .
Đáp án D đúng.
Do ABC.AB C
là lăng trụ đứng và tam giác ABC vuông tại B nên AB BB C
AAB ' B BB C
Đáp án B đúng.
Do ABC.AB C
là lăng trụ đứng và tam giác ABC vuông tại B nên
ABC , ABC AB, AB ABA 45 Đáp án A đúng.
Xét tam giác vuông AAC ta có 2 2 AC AA AC 2 2
a 5a a 6 Đáp án C sai. E D A C B Câu 94.
Ta có: ABC là hình chiếu của A
DE trên mặt phẳng ABC . 2 a 3 1 2 a 3 Do đó S S .cos 60 S . S . ABC ADE 4 ADE 2 ADE 2 1 2 a 3 1 a 6 2 Mặt khác S .
AD AE.sin DAE .
.a 3 sin sin . ADE 2 2 2 2 6
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 62
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A I a a a C B x J a D Câu 95.
ACD BCD Theo giả thiết ta có:
ACD BCD CD AJ BCD AJ BJ . AJ CD
ACD BCD (c.c.c) AJ BJ AB AJ 2 2
AC CJ 2 2 2 2 2 a x 1 1 AI AB 2 2 2 a x 2 2
Dễ thấy CAB và D
AB bằng nhau và cân tại các đỉnh C và D . 2 2 a x 2 2 a x 2 2 2
DI CI
AC AI a . 2 2 CI AB Có
, nên để ABC ABD thì CI DI hay ICD vuông tại I . DI AB a 3 2 2
CD CI 2 2x a x x . 3 Câu 96.
Ta có SCD SAD , vẽ AN SD tại N AN SCD .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 63
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
SAB SBC , vẽ AM SB tại M AM SBC .
SBC SCD ,
AM AN MAN . ax SM MN SM .BD Ta có SB SD 2 2
x a , AM AN , MN 2 2 x a SB BD SB 2 x .a 2 2 x 2 2 x a 2 x a 2 SM MN MN . 2 2 2 2 x a 2 2 x a x a 2 xa x a 2
AMN đều cho ta MN AM 2 2
x a x 2 x a . 2 2 2 2 x a x a
Câu 97. Gọi là góc tạo bởi (P) và mặt phẳng ( ABCD)
Diện tích thiết diện đạt giá trị nhỏ nhất / BD ABCD / , ( ) D BD BD 2 6 / cos D BD / BD 3 3
Câu 98. Ta thấy do hình chóp S.ABC đỉnh S là chóp tam giác đều nên AB BC AC . a
SAB SAC . c .
c c AM AN.
Do đó tam giác AMN cân tại
A. Gọi H
là trung điểm của MN thì AH MN và I là trung điểm của BC.
AMN SBC
AMNSBC MN AH SBC AH SH; AH SI
Trong AMN:AH MN
Xét tam giác SAI có đường AH vừa là trung tuyến vừa là đường cao
nên tam giác SAI cân tại A. a 3
Tam giác ABC đều cạnh a AI SA S . B 2 2 2 3a a a
Xét tam giác SBI vuông tại I nên 2 2 SI SB BI . 4 4 2 1 a Ta có: SH SI . 2 2 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 64
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 2 3a a a 5
Xét tam giác ASH vuông tại H nên 2 2 AH SA SH . 4 8 2 2 2 1 1 a 5 a a 10 Vậy S .AH.MN . . . AMN 2 2 2 2 2 16 Câu 99.
Gọi H là trung điểm của CD nên AH CD
AH BCD (do ACD BCD ) và ACD BCD CD
Gọi M là trung điểm của AB nên CM AB
Vì ABC ABD và ABC ABD AB CM . MD
ABC ABD MC MD MCD vuông cân tại M . 2 2 x x
Đặt CD x 2 2 2 2 2 2 2
AH BH a
AB AH BH 2a 4 2 2 2 1 1 x 2 x 1 2 Ta có 2 2 MH AB 2a MH CD 2a . x 2 2 2 2 2 2 2 2 x 2a 2 2 2 2 2a
2x 4a 3x x . 2 3
Câu 100. Chọn A D C 20cm 20cm φ φ A 20cm B
Để lượng mưa thoát được nhiều nhất khi diện tích hình thang cân ABCD lớn nhất.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 65
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A B φ φ D C H K
Khi đó ta có: HK AB 20cm , DH CK cos.20 , AH BK sin .20 . 1 1 Do đó: S AB CD AH
20 20 2.20.cos .20.sin 400.1 cos.sin ABCD . 2 2
Đặt t cos , vì 0 ;1
80 cos 0 S t 2 400 1 1 t . t 2 2 t t 1
Xét f t t 2 1
1 t với t 0
;1 . Khi đó: f t 2
1 t 1 t . 2 1 t 2 1 t t 1
Do đó: f t 0 1 .Bảng biến thiên: t 2 1 1
Từ bảng biến thiên ta có f t đạt giá trị lớn nhất tại t cos 60 . 2 2
Câu 101. Chọn A C' B' P A' D' N K Q B C H M D A
Gọi M , N , P, Q lần lượt là giao điểm của với các cạnh bên AA, BB ,
CC, DD .
Thiết diện của với hình lập phương là hình bình hành MNPQ . Kẻ QH vuông góc với MN ,
QK vuông góc với AA . Suy ra HK MN .
MNPQABB A MN Vì Q H MN
MNPQ ABB A QH HK , , QHK 60 . HK MN
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 66
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 QK QK QK
QKH vuông tại K nên sin 60 QH 2 ; KH 1. QH sin 60 tan 60
Do đó ta tìm được MN 3 .
Vậy diện tích của thiết diện S 2 3 . MNPQ
Câu 102. Đáp án. D.
Dựng NK 3MB,MN KB I
PI AB J , NQ 2MJ MR 2PQ
Thiết diện là lục giác MRNQPJ . Cách 1: S S S MRNQPJ MJPQ MQNR 2 3 2 3 6 6 2 FE 3 FG ,GE 6 2 2 2 2 6 ( 3 2 3 2 ) ( MQ JP )FG 5 3 3 2 S MJPQ 2 2 2 1
( 3 2 3 2 ) 6 ( MQ NR )EG 3 S 4 3 MJPQ 2 2 13 3 S S S . MRNQPJ MJPQ MQNR 2
Cách 2: Gọi là góc giữa hai mặt phẳng( MRNQPJ );( PJBTKD ) SPJBTKD S MRNQPJ cos 1 13 S S S S 9 2 PJBTKD ABCD KCT APJ 2 2 3 2 FU 3 2
cos cosEFU= FE 3 6 3 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 67
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 S 13 3 PJBTKD S . MRNQPJ cos 2
Câu 103. Chọn A
Giả sử cắt tất cả các cạnh bên như hình vẽ.
Do góc giữa và ABB
A bằng 60 nên suy ra góc giữa và mặt đáy ABCD bằng 90 60 30 .
Gọi S là diện tích tứ giác IJKL và S là diện tích của hình vuông ABCD . S 2 3
Ta có S S.cos 30 S 2 3 . cos 30 3 2 S C A 60 M B Câu 104. Chọn A
Áp dụng công thức diện tích hình chiếu: 1 S S .cos 60 2. 1 A BC S BC 2
Câu 105. Chọn A
Ngôi nhà có hai mái đối xứng nhau và có diện tích bằng nhau, diện tích một nửa mặt nền nhà bằng 2
S 50 m . Gọi S ' là diện tích một mái, khi đó một mái nhà có hình chiếu vuông góc là một S S 100
nửa mặt nền nhà. Ta có 0 cos 30 2 S '
m . Vậy tổng diện tích mái nhà là S ' 0 cos 30 3 200 2 m . 3 200
Số tiền bác Bình cần là
.100 11547 nghìn đồng 11, 547 triệu đồng. 3
Câu 106. Chọn A
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 68
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 C a a N A M B a a D
Gọi M, N lần lượt là trung điểm của AB, CD. A BC A
BD CM DM .
ABC ABD o CMD 90 . M
CD vuông cân tại M. MN CD .
Tương tự, ta cũng có ABN
vuông cân tại N MN AB Đặt CD 2 ,
x 0 x a ta có:
CN DN MN x . 2 2
AN BN a x .
Áp dụng hệ thức lượng trong tam giác vuông ABN ta có: 1 1 1 2 1 3 x a . 2 2 2 2 2 2 AN BN MN a x x 3 2 3
CD 2x a . 3
Câu 107. Chọn C
Vì AA / / BB nên góc giữa hai đường thẳng MN và BB bằng góc giữa MN và AA và bằng góc ANM . AM a 3 2
Xét tam giác ANM vuông tại A , ta có: tan ANM .
3 ANM 60 . AN 2 a
Câu 108. Chọn A
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 69
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A B C B' A' C'
Ta có: Tam giác ACC vuông tại C . Mà 2 2
CC AA ;
a AC a 5 AC
AC CC a 6 do đó khẳng định AC 2a 2 là sai. +) Ta có 2 2 2 2 2 2
AB BC a 4a 5a AC chứng tỏ tam giác ABC vuông tại B
+) Ta có AB BC; AB BB AB BB C
mà AB AAB B
AAB B BB C
+) Ta có AB AA ABB A
là hình vuông do đó A B A 45 .
Mặt khác: ABC A B
C BC
BC AB và BC BB BC ABB A ABB A
ABC AB; ABB A
ABC AB góc giữa hai mặt phẳng ABC và ABC bằng
góc giữa AB và AB và bằng
ABA . Vậy góc giữa hai mặt phẳng ABC và A B
C có số đo bằng 45 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 70




