Bài tập trắc nghiệm lũy thừa – mũ – lôgarit vận dụng cao

Tài liệu gồm 127 trang, tuyển chọn các bài tập trắc nghiệm lũy thừa – mũ – lôgarit vận dụng cao, có đáp án và lời giải chi tiết, giúp học sinh lớp 12 tham khảo khi học chương trình Toán 12 phần Giải tích chương 2: Hàm Số Lũy Thừa, Hàm Số Mũ Và Hàm Số Logarit.

58 29 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

127 trang 7 tháng trước

Tác giả:

Profile Kim Oanh
1
HÀM SỐ LŨY THỪA
HÀM SỐ MŨ – HÀM SỐ LOGARIT
120 câu – Vận dụng cao
Phần 1. Tính chất và các phép toán…………………………………………
Phần 2. Đồ thị …………………………………………………………………………………..
Phần 3. Dãy logarit ………………………………………………………………….…….
Phần 4. Cực trị nghiệm ………………………………………………………………..
Phần 5. Bài toán tìm GTLN – GTNN …………………….…………………
2
Phần 1. Tính chất và các phép toán
Câu 1. Tìm tất cả các giá trị của tham số
a
để hàm số
2
21
log
aa
yx

đồng biến trên
khoảng
0; .
A.
0;2 .a
B.
0;2 \ 1 .a
C.
\ 0;2 .a
D.
\ 0;2 .a
Câu 2. Cho hàm số
Khẳng định nào sau đây đúng?
A. Hàm số
y fx
nghịch biến trên
;0 .
B. Hàm số
y fx
đồng biến trên
;0 .
C. Hàm số
y fx
nghịch biến trên
; 1.
D. Hàm số
y fx
đồng biến trên
; 1.
Câu 3. Số giá trị nguyên của
10m
để hàm số
2
ln 1
y x mx 
đồng biến trên
khoảng
0;
là
A.
8.
B.
9.
C.
10.
D.
11.
Câu 4. Có bao nhiêu số nguyên âm
m
để hàm số
3
ln 2
y x mx

đồng biến trên
nửa khoảng
1; 
?
A.
1.
B.
2.
C.
3.
D.
4.
Câu 5. Cho
, , abc
là các số thực dương thỏa mãn
37
11
log 7 log 11
log 25
27, 49, 11ab c
.
Giá trị của biểu thức
22
2
37
11
log 7 log 11
log 25
Ta b c

bằng
A.
76 11.
B.
469.
C.
2017.
D.
31141.
Câu 6. Cho
, , abc
là các số thực khác
0
thỏa mãn
4 25 10
abc

. Tính
.
cc
T
ab

A.
1
.
10
T
B.
1
.
2
T
C.
2.T
D.
10.T
Câu 7. Cho
,xy
là các số thực dương thỏa mãn
964
log log logx y xy
và
2
x ab
y

với
,
a
b
là hai số nguyên dương. Tổng
ab
bằng
A.
4.
B.
6.
C.
8.
D.
11.
Câu 8. Cho các số thực dương
, , xy z
theo thứ tự lập thành một cấp số nhân, đồng
thời với mỗi số thực dương
1a
thì
3
log , log , log
a
aa
xyz
theo thứ tự lập thành một
cấp số cộng. Giá trị biểu thức
3 7 2020xy z
P
yz x

bằng
A.
2030
.
3
B.
1015.
C.
2030.
D.
4038.
Câu 9. Cho
, , xyz
là các số thực dương thỏa
log xy z
và
22
log 1.xy z 
Giả sử
, ab
là các số thực sao cho
33 3 2
. ..10 10
zz
xya b
Tổng
ab
bằng
3
A.
31
.
2
B.
25
.
2
C.
29
.
2
D.
31
.
2
Câu 10. Cho
, , xyz
là các số thực thỏa mãn
2017
3 5 15 .
x
xy
xy

Gọi
.S xy yz zx
Khẳng định nào sau đây đúng?
A.
1;2016 .S
B.
0;2017 .S
C.
0;2018 .S
D.
2016;2017 .S
Câu 11. Tìm bộ ba số nguyên dương
;;abc
thỏa mãn
log1 log 1 3 log 1 3 5 ... log 1 3 ... 19 2 log 5040 log 2 log 3.ab c
A.
1; 3; 2 .
B.
2;4;3 .
C.
2;4;4 .
D.
2;6;4 .
Câu 12. Cho
11
f
và
fm n fm fn mn
với mọi
*
,.
mn
Giá trị biểu
thức
96 69 241
log
2
ff
T





bằng
A.
3.
B.
4.
C.
6.
D.
9.
Câu 13. Cho
, , abc
là ba số thực dương không cùng bằng nhau, đồng thời khác
1
và
thỏa mãn
log log log
.
bca
cab
abc
Giá trị nhỏ nhất của biểu thức
abc

bằng
A.
2 2.
B.
2 3.
C.
3 2.
D.
3 3.
Câu 14. Cho
0a
và
0b
thỏa mãn
22
4 51 8 1
log 16 1 log 4 5 1 2.
a b ab
ab ab


Giá trị của biểu thức
2ab
bằng
A.
20
.
3
B.
27
.
4
C.
6.
D.
9.
Câu 15. Cho
1a
và
1b
thỏa
32 2
3
log 4 4 log 16 64 2.
ba
aa b b b b
Giá trị của biểu thức
21ab
P
ab

bằng
A.
15
.
10
B.
17
.
10
C.
19
.
10
D.
21
.
10
Câu 16. Cho
0x
và số thực
y
thỏa mãn
1
2
2 log 14 2 1 .
x
x
yy




Giá trị của
biểu thức
22
1P x y xy

bằng
A.
1.
B.
2.
C.
3.
D.
4.
Câu 17. Cho
0x
và
0y
thỏa mãn
32
2
2
1
2 log .
2
xxx
y
y




Giá trị của biểu
thức
22
2P x y xy
bằng
A.
1
.
2
B.
1.
C.
2.
D.
2.
Câu 18. Cho hàm số
4
.
42
x
x
fx
Tổng
1 2 2016
...
2017 2017 2017
Sf f f
 







 
bằng
A.
1007.
B.
1008.
C.
2016.
D.
2017.
4
Câu 19. Cho hàm số
92
.
93
x
x
fx
Tổng
1 2 2017
...
2017 2017 2017
Pf f f
 







 
bằng
A.
1009.
B.
4035
.
4
C.
4039
.
12
D.
12103
.
12
Câu 20. Xét hàm số
2
9
9
t
t
ft
m
với
m
là tham số thực. Gọi
S
là tập hợp tất cả
các giá trị của
m
sao cho
1fx fy
với mọi
, xy
thỏa mãn
xy
e ex y

. Tìm
số phần tử của
S
.
A.
0.
B.
1.
C.
2.
D. Vô số.
Câu 21. Xét hàm số
4
4
t
t
ft
m
với
0m
là tham số thực. Biết
1fx fy

với
mọi số thực dương
,xy
thỏa mãn
1
2
11
..
22
xy xy

Giá trị nhỏ nhất của hàm
số
ft
trên đoạn
1
;1
2




bằng
A.
1
.
2
B.
1
.
4
C.
3
.
4
D.
5
.
4
Câu 22. Cho
a
là số thực dương. Xét hàm số
x
x
a
fx
am
với
0m
là tham số
thực. Biết
1
fx fy
với mọi
1
.
2
xy
Khẳng định nào sau đây đúng?
A.
4
.ma
B.
.ma
C.
.ma
D.
2
.
ma
Câu 23. Xét hàm số
4
9
9
x
x
fx
m
với
m
là tham số thực. Gọi
S
là tập hợp tất cả
các giá trị của
m
sao cho
1fa fb
với mọi
, ab
thỏa mãn
2
1.
ab
e eab

Tích các phần tử của
S
bằng
A.
3.
B.
9.
C.
81.
D.
81.
Câu 24. Xét hàm số
2
log 2 4
x
fx
và
, ab
là hai số thực dương thỏa mãn
1.fa fb


Đặt
27 2018
12 2017
.Ta b
Khẳng định nào sau đây là đúng?
A.
1
0.
4
T
B.
11
.
42
T
C.
1
1.
2
T
D.
1.T
Câu 25. Cho hàm số
2
12
log
21
x
fx
x


. Tính tổng
1 2 3 2015 2016
... .
2017 2017 2017 2017 2017
Sfff ff
 
 
 

 
 
 
 
 
A.
1008.S
B.
2016.S
C.
2017.S
D.
4032.S
Câu 26. Xét hàm số
2018
2018 ln .
x
fx e e



Tính
1 2 ... 2017 .Tf f f


A.
1008.T
B.
1009.T
C.
2017
.
2
T
D.
2019
.
2
T
5
Câu 27. Xét hàm số
2
3
log
1
mx
fx
x
với
m
là tham số thực. Gọi
S
là tập hợp tất cả
các giá trị của
m
sao cho
3fa fb
với mọi
,ab
thỏa mãn
.
ab
e ea b

Tích
các phần tử của
S
bằng
A.
27.
B.
3 3.
C.
3 3.
D.
27.
Câu 28. Cho hàm số
2019 2
.log 1 sin .cos 2018 6fx a x x b x x

với
, .ab
Biết
ln 2019
2018 10.f
Giá trị của biểu thức
ln 2018
2019f
bằng
A.
10.
B.
2.
C.
8.
D.
10.
Câu 29. Cho hàm số
2
.log 2 4 1 .sin .
x
f x a x x b x ce 
với
, , .abc
Biết
rằng
1
ln 2 ln 2.
2
ff



Khi đó hằng số
c
thuộc khoảng nào sau đây?
A.
1
0; .
2


B.
1
;1 .
2


C.
3
1; .
2


D.
3
;2 .
2


Câu 30. Cho hàm số
32
.ln 1 .cos 5 1f x a x x bx x

với
, .ab
Biết
log log . log ln10 .
f ef m
Gọi
S
là tập các giá trị của tham số
m
thỏa mãn
22 2
log log log ln10 8.f e f mm 
Số phần tử của tập
S
bằng
A.
0.
B.
1.
C.
2.
D. Vô số.
Phần 2. Đồ thị và các vấn đề liên quan
Câu 1. Cho bốn hàm số
3 1,
x
y
1
2,
3
x
y


4 3,
x
y
1
4
4
x
y


có đồ thị là bốn đường cong
như hình bên. Tương ứng hàm số - đồ thị đúng là
A.
4 13 2
3 ,2 ,1 , 4 .C CC C 
B.
413 2
1 ,3 ,2 ,4 .
CCC C
C.
413 2
1,2,3,4.C CC C

D.
41 3 2
2 ,1 ,3 ,4 .CCC C
Câu 2. Cho các hàm số
,
x
fx a
log
b
gx x
và
log
b
hx x c
(trong đó
, ab
lớn hơn
0
và khác
1;
c
) có đồ thị như hình vẽ. Khẳng định nào sau đây
đúng?
A.
.acb
B.
.abc
C.
1 , 0.a bc
D.
.cab
6
Câu 3. Cho
, , abc
là các số thực dương khác
1
và đồ thị
của ba hàm số
,
x
ya
log ,
b
yx
x
yc
trên cùng một
hệ trục tọa độ như hình vẽ bên. Mệnh đề nào sau đây
đúng?
A.
.
aba
B.
.
cab
C.
.cba
D.
.
bca
Câu 4. Cho
, , abc
là các số thực dương khác
1
và đồ thị
của ba hàm số
,
x
ya
log ,
b
yx
log
c
yx
trên cùng
một hệ trục tọa độ như hình vẽ bên. Mệnh đề nào sau đây
đúng?
A.
.bca

B.
.acb
C.
.cba
D.
.cab
Câu 5. Biết hàm số
y fx
có đồ thị đối xứng với đồ thị
hàm số
3
x
y
qua đường thẳng
1.x

Chọn khẳng định
đúng trong các khẳng định sau
A.
1
.
3.3
x
fx
B.
1
.
9.3
x
fx
C.
11
.
2
3
x
fx

D.
1
2.
3
x
fx

Câu 6. Biết hàm số
y gx
có đồ thị đối xứng với đồ thị hàm số
x
ya
qua điểm
1;1 .I
Giá trị của biểu thức
1
2 log
2018
a
g


bằng
A.
2020.
B.
2016.
C.
2016.
D.
2020.
Câu 7. Biết hàm số
y fx
có đồ thị đối xứng với đồ thị hàm số
2018
1
logy
x


qua
gốc tọa độ. Tính giá trị của biểu thức
2018 .f
A.
1.
B.
0.
C.
1.
D. Không tồn tại.
Câu 8.
Cho hai hàm số
x
ya
và
y fx
có đồ thị như
hình vẽ đồng thời đồ thị của hai hàm số này đối xứng
nhau qua đường
:.dy x
Giá trị của
3
fa
bằng
A.
3
1
.
a
a
B.
1
.
3
C.
3.
D.
3
.
a
a
Câu 9.
Cho
, ab
là các số thực dương khác
1.
Các hàm số
x
ya
và
x
yb
có đồ thị như hình vẽ bên. Đường thẳng bất
kỳ song song với trục hoành và cắt đồ thị hàm số
,
x
ya
,
x
yb
trục tung lần lượt tại
, , MNA
đều thỏa mãn
2.AN AM
Mệnh đề nào sau đây đúng?
A.
2.ba
B.
2
.ab
C.
1
.
2
ab
D.
2
1.ab
7
Câu 10. Cho các hàm số
log
a
yx
và
log
b
yx
có đồ
thị như hình vẽ bên. Đường thẳng
5x
cắt trục hoành,
đồ thị hàm số
log
a
yx
và
log
b
yx
lần lượt tại
, AB
và
C
. Biết rằng
2.CB AB
Mệnh đề nào sau đây đúng?
A.
2
.ab
B.
3
.
ab
C.
3
.ab
D.
5.ab
Câu 11.
Cho hai hàm số
2,
x
y
2
logyx
có đồ thị như
hình vẽ. Đường thẳng
cắt trục tung, đồ thị hàm số
2,
x
y
đồ thị hàm số
2
logyx
và trục hoành lần lượt
tại
, , , ABCD
thỏa mãn
.AB BC CD
Hỏi có bao nhiêu
đường thẳng
như thế ?
A.
1.
B.
2.
C.
3.
D. Vô số.
Câu 12. Gọi
B
và
C
lần lượt là các điểm thuộc đồ thị hàm số
2
x
y
và
2
logyx
sao cho tam giác
OBC
đều. Giả sử điểm
B
có hoành độ là
a
khi đó tỉ số
2
x
a
bằng
A.
2 3.
B.
2 3.
C.
2 2.
D.
2 2.
Câu 13. Gọi
,
AB
là các điểm lần lượt thuộc đồ thị các hàm số
x
ye
và
x
ye
sao
cho tam giác
OAB
nhận điểm
1;1M
làm trọng tâm. Khi đó tổng các giá trị của
hoành độ và tung độ điểm
A
gần với giá trị nào sau đây nhất?
A.
3.
B.
3, 5.
C.
4.
D.
4,5.
Câu 14.
Gọi
A
và
B
lần lượt là hai điểm di động trên
hai đồ thị hàm số
x
ye
và
lnyx
như hình vẽ.
Khoảng cách giữa hai điểm
,A
B
nhỏ nhất gần với giá
trị nào nhất trong các giá trị sau
A.
1, 2.
B.
1, 3 .
C.
1, 4 .
D.
1, 5 .
Câu 15. Cho đồ thị hàm số
2
x
ye
như hình vẽ.
ABCD
là một hình chữ nhật thay đổi sao cho
B
và
C
luôn thuộc đồ thị hàm số đã cho,
A
và
D
thuộc
trục hoành. Giá trị lớn nhất của diện tích của hình
chữ nhật
ABCD
bằng
A.
2
.
e
B.
2
.
e
C.
2
.
e
D.
2
.
e
8
Phần 3. Dãy loga
Câu 1. Cho dãy số
n
u
thỏa mãn

2
2 4 24
log 3log 2 0uu
và

1
2
nn
uu
với mọi
*
.n
Giá trị lớn nhất của
n
để
2018
n
u
bằng
A.
999.
B.
1000.
C.
1010.
D.
1011.
Câu 2. Cho dãy số
n
u
thỏa mãn

1 1 8 10
log 2 log 2 log 2 logu uu u
và
1
10
nn
uu
với mọi
*
.n
Khi đó
2018
u
bằng
A.
2000
10 .
B.
2008
10 .
C.
2017
10 .
D.
2018
10 .
Câu 3. Cho dãy số
n
u
thỏa mãn
2 2 22
21 21 2 2
log 5 log 7 log 5 log 7.
uu 
Biết số hạng
đầu
1
1u
và
1
7
nn
uu
với mọi
*
.
n
Giá trị nhỏ nhất của
n
để
1111111
n
u
là
A.
8.
B.
9.
C.
10.
D.
11.
Câu 4. Cho dãy số
n
u
thỏa mãn
9 9 19
11
2
2
4 24 3
u u uu
uu
e e e ee

và
1
3
nn
uu

với mọi
*
.
n
Khi đó giá trị nhỏ nhất của
n
để
3
n
u
là
A.
9.
B.
10.
C.
11.
D.
12.
Câu 5. Cho cấp số cộng
n
u
có tất cả các số hạng đều dương và thỏa mãn
1 2 2018 1 2 1009
... 4 ... .uu u uu u  
Giá trị nhỏ nhất của biểu thức
222
3 2 3 5 3 14
log log logPu u u
bằng
A.
1.
B.
2.
C.
3.
D.
4.
Câu 6. Cho dãy số
n
u
thỏa mãn
32
1 11
log 2 log log 2 0u uu 
và
1
2 10
nn
uu

với mọi
*
.n
Giá trị nhỏ nhất của
n
để
100
10 10
n
u 
là
A.
225.
B.
226.
C.
326.
D.
327.
Câu 7. Cho dãy số
n
u
thỏa mãn
19
3
1119
log log log log 33uu uu

và
1
2
nn
uu
với mọi
*
.n
Tìm số tự nhiên
n
lớn nhất sao cho
100
3 5 .
n
u
A.
71.n
B.
72.n
C.
73.n
D.
74.n
Câu 8. Cho dãy số
n
u
thỏa
22 2 2
12 1 1
ln ln ... ln ln ln 1 3
n nn
u u u uu


và
2
1nn
uu
với mọi
*
.n
Tìm giá trị nhỏ nhất của
n
để
2018
2017 .
n
u
A.
11.
B.
12.
C.
14.
D.
15.
Câu 9. Cho dãy số
n
u
có tất cả các số hạng đều dương và thỏa
2
1
.log 1
,
10
n
n
un
u
với mọi
1.n
Gọi
a
là giá trị nhỏ nhất của
.
n
u
Có bao nhiêu số tự nhiên
n
để
n
ua
A.
1.
B.
2.
C.
3.
D.
4.
Câu 10. Cho cấp số cộng
n
a
thỏa
21
0;aa
cấp số nhân
n
b
thỏa
21
1bb
và
hàm số

3
3fx x x
sao cho
21
2;fa fa
22 21
log 2 log .fb fb
Tìm số
nguyên dương
n
nhỏ nhất sao cho
2018 .
nn
ba
A.
15.n
B.
16.n
C.
17.n
D.
18.n
9
Phần 4. Cực trị nghiệm
Câu 1. Xét các số nguyên dương
,a
b
sao cho phương trình
2
ln ln 5 0
a xbx

1
có hai nghiệm phân biệt
1
,x
2
x
và phương trình
2
5 log log 0xb xa 
2
có hai
nghiệm phân biệt
3
,
x
4
x
thỏa mãn
12 34
.
xx xx
Giá trị nhỏ nhất của biểu thức
23S ab
bằng
A.
17.
B.
25.
C.
30.
D.
33.
Câu 2. Với
,mn
là các số nguyên dương sao cho phương trình
2
ln 1 ln 0x m xn 
1
có hai nghiệm phân biệt
12
,
xx
và phương trình
2
ln 1 ln 0x n xm 
2
có hai nghiệm phân biệt
34
,
xx
thỏa mãn
2
12 34
.xx xx
Giá trị nhỏ nhất của biểu thức
23P mn
bằng
A.
46.
B.
48.
C.
51.
D.
53.
Câu 3. Cho hai phương trình
2
ln 1 ln 0 1
x m xn 
và
2
ln 1 ln 0 2 .x n xm
Biết phương trình
1
có hai nghiệm phân biệt là
01
,
xx
và phương trình
2
có hai
nghiệm phân biệt là
02
, xx
(tức là
0
x
là nghiệm chung của hai phương trình) Giá trị
nhỏ nhất của biểu thức
22
12
Sx x
bằng
A.
1.
B.
2.
C.
3.
D.
4.
Câu 4. Xét các số nguyên dương
, ab
sao cho phương trình
.4 .2 50 0
xx
ab 
1
có
hai nghiệm phân biệt
12
,
xx
và phương trình
9 .3 50 0
xx
ba
2
có hai nghiệm
phân biệt
34
, xx
thỏa mãn
34 12
.xx xx
Giá trị nhỏ nhất của biểu thức
32S ab
bằng
A.
49.
B.
51.
C.
59.
D.
81.
Câu 5. Cho
, ab
là hai số thực dương lớn hơn
1.
Biết phương trình
2
1
1
xx
ab
có hai
nghiệm phân biệt
12
, .xx
Giá trị nhỏ nhất của biểu thức
2
12
12
12
4
xx
S xx
xx



bằng
A.
3
4.
B.
3
3 4.
C.
3
3 2.
D.
4.
Câu 6. Cho
, ab
là hai số nguyên dương lớn hơn
1.
Biết phương trình
2
1xx
ab
có
hai nghiệm phân biệt
12
, xx
và phương trình
2
1
9
x
x
ba
có hai nghiệm phân biệt
34
, xx
thỏa mãn

1 23 4
3.x xx x 
Giá trị nhỏ nhất của biểu thức
32S ab

bằng
A.
40.
B.
41.
C.
44.
D.
46.
Câu 7. Cho
,
ab
là hai số thực lớn hơn
1.
Biết phương trình
2
1
1
xx
ab
có nghiệm
thực. Giá trị nhỏ nhất của biểu thức
4
log
log
a
a
P ab
b

bằng
A.
4.
B.
5.
C.
6.
D.
10.
10
Câu 8. Cho
, ab
là hai số thực lớn hơn
1
thỏa mãn
10.
ab
Gọi
, mn
là hai
nghiệm của phương trình

log log 2 log 3log 1 0.
ab a b
xx x x 
Giá trị nhỏ nhất
của biểu thức
S mn
bằng
A.
16875
.
16
B.
4000
.
27
C.
3456.
D.
15625.
Câu 9. Cho
,
ab
là các số thực lớn hơn
1
và phương trình
log .log 2018
ab
ax bx
có
hai nghiệm phân biệt
, .mn
Giá trị nhỏ nhất của biểu thức
2 2 22
4 9 36 1P a b mn

bằng
A.
36.
B.
72.
C.
144.
D.
288.
Câu 10. Cho
, ,
abc
là các số thực lớn hơn
1
thỏa mãn
100.
abc

Gọi
, mn
là
hai nghiệm của phương trình
2
log 1 2 log 3 log log 1 0.
a a aa
x b cx 
Tính
23Sa b c
khi
mn
đạt giá trị lớn nhất.
A.
200.
S
B.
500
.
3
S
C.
650
.
3
S
D.
700
.
3
S
Phần 5. Bài toán tìm GTNN-GTLN
Câu 1. Cho hai số thực
, xy
thỏa mãn
log 3 log 3 1.xy xy
Giá trị nhỏ nhất
của biểu thức
Sxy
bằng
A.
22
.
3
B.
1.
C.
45
.
3
D.
10.
Câu 2. Cho
,
xy
là các số thực dương thỏa mãn
22
23
log 11 20 40 1.
x xy y
xy


Gọi
, ab
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
.
y
S
x
Tổng
ab
bằng
A.
10.
B.
2 14.
C.
11
.
6
D.
7
.
2
Câu 3. Cho
,,abc
là các số thực dương khác
1
thỏa
22
log log log 2 log 3.
ab a b
cc
bc
bb

Gọi
,
Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
log log .
ab
P bc
Giá trị
của biểu thức
23S mM
bằng
A.
1
.
3
S
B.
2
.
3
S
C.
2.S
D.
3.S
Câu 4. Cho
,
a
,
b
c
là các số thực lớn hơn
1.
Giá trị nhỏ nhất của biểu thức
3
41 8
log
log 3 log
ac ab
bc
P
a
bc

bằng
A.
10.
B.
12.
C.
18.
D.
20.
Câu 5. Cho
, xy
là các số thực dương thỏa mãn
22 4
log log log .x y xy
Giá trị
nhỏ nhất của biểu thức
22
Sx y
bằng
11
A.
2 2.
B.
3
2 4.
C.
3
4 2.
D.
4.
Câu 6. Cho
,
ab
là hai số thực dương. Giá trị nhỏ nhất của biểu thức
33 3
4
log 1 2 log 1 2 log 1
2
b
Pa
a
b






A.
1.
B.
4.
C.
7.
D.
9.
Câu 7. Cho
, ab
là các số thực lớn hơn
1
thỏa mãn
23
log log 1.ab
Giá trị lớn nhất
của biểu thức
32
log logPab

bằng
A.
23
log 3 log 2.
B.
32
log 2 log 3.
C.
32
1
log 2 log 3 .
2
D.
23
2
.
log 3 log 2
Câu 8. Cho
, , xyz
là các số thực thỏa mãn
4 9 16 2 3 4 .
xy z xyz

Giá trị lớn
nhất của biểu thức
111
234
xy z
P


bằng
A.
3 87
.
2
B.
5 87
.
2
C.
7 87
.
2
D.
9 87
.
2
Câu 9. Cho
, ab
là các số thực thỏa mãn
22
1ab
và
22
log 1.
ab
ab

Giá trị lớn
nhất của biểu thức
243P ab
bằng
A.
1
.
10
B.
10
.
2
C.
10.
D.
2 10.
Câu 10. Cho hai số thực
, xy
thỏa mãn
22
2
log 2 1
xy
xy

*.
Biết giá trị lớn nhất
của biểu thức
2P xy
là
a
b
với
, ab
và
a
b
tối giản. Tổng
ab
bằng
A.
11.
B.
13.
C.
15.
D.
17.
Câu 11. Cho các số thực
, , abc
thỏa
2
222
log 4 4 4 .
2
abc
aa bb cc
abc

 

Giá trị lớn nhất của biểu thức
23abc
P
abc


bằng
A.
4 30
.
3
B.
8 30
.
3
C.
6 30
.
3
D.
12 30
.
3
Câu 12. Cho các số thực
, xy
thỏa mãn
22 22 22 22
4 41 3 4 2 4
4 2 2 4.
xy xy xy xy
 

Gọi
,m
M
lần lượt là giá trị nhỏ nhất và lớn nhất của
21
4
xy
P
xy


. Tổng
Mm
bằng
A.
36
.
59
B.
18
.
59
D.
18
.
59
C.
36
.
59
Câu 13. Cho các số thực dương
, , abc
thỏa mãn
222
222
5 log 16 log 27 log 1.abc
Giá
trị lớn nhất của biểu thức
22 22 22
log log log log log logS ab bc ca

bằng
A.
1
.
16
B.
1
.
12
C.
1
.
9
D.
1
.
8
12
Câu 14. Cho các số thực
, , abc
lớn hơn
1
thỏa mãn
2 22
log 1 log log log 2.
bc
a bc
Giá trị nhỏ nhất của biểu thức
2 22
2 22
10 log 10 log logP a bc
bằng
A.
7
.
2
B.
9
.
2
C.
3.
D.
4.
Câu 15. Cho
, ab
là hai số thực dương. Giá trị nhỏ nhất của biểu thức
22
55
81
log logP ab
ab



bằng
A.
1
.
2
B.
1.
C.
3
.
2
D.
2.
Câu 16. Cho
log
x
y
m
x
với
1,x
0 1.y

Giá trị của lớn nhất của biểu thức
log log
xy
T yx
bằng
A.
2.
B.
1.
C.
0.
D.
2.
Câu 17. Cho các số thực dương
, ab
thỏa mãn
2
log 2 2 .
b
ab a
Giá trị nhỏ nhất của
biểu thức
312
1
a
b
Sa
a

bằng
A.
3 1.
B.
1 3.
C.
2 3 2.
D.
2 3 4.
Câu 18. Xét các số thực
, ab
thỏa mãn
1.ab
Biết rằng
1
log
log
a
ab
a
P
ab

đạt
giá trị lớn nhất khi
k
ba
. Khẳng định nào sau đây đúng?
A.
3
0; .
2
k


B.
1; 0 .k 
C.
3
;2 .
2
k


D.
2;3 .k
Câu 19. Cho
, ax
là các số thực dương,
1a
và thỏa mãn
log log .
x
a
xa
Giá trị lớn
nhất của
a
bằng
A.
1.
B.
log 2 1 .
e
C.
ln10
.
e
e
D.
log
10 .
e
e
Câu 20. Cho hai số thực
, 1ab
sao cho tồn tại số thực
01x
thỏa
2
log log
.
ba
xx
ab
Giá trị nhỏ nhất của biểu thức
22
ln ln lnP a b ab 
bằng
A.
3 22
.
12
B.
1 33
.
4
C.
.
2
e
D.
1
.
4
Câu 21. Cho
, ab
là các số thực thỏa mãn
0 1,ab
1.ab
Giá trị lớn nhất của
biểu thức
4
log
1 log . log
a
aa
b
P ab
b ab

bằng
A.
4.
B.
2.
C.
3.
D.
4.
Câu 22. Cho
, xy
là các số thực thỏa mãn
1
4, , 1.
2
xy x y
Gọi
, Mm
lần lượt là
giá trị lớn nhất và nhỏ nhất của
2
2
22
log log 1 .Px y
Tổng
2Mm
bằng
13
A.
6.
B.
11.
C.
11
.
2
D.
21
.
2
Câu 23. Xét các số thực
, ab
thỏa mãn
1.
ab
Giá trị nhỏ nhất của biểu thức
22
log 3 log
a
b
b
a
Pa
b



bằng
A.
13.
B.
14.
C.
15.
D.
19.
Câu 24. Xét các số thực
, ab
thỏa
1,b
.aba
Biểu thức
log 2 log
a
b
b
a
Pa
b



đạt giá trị khỏ nhất khi
A.
2
.ab
B.
23
.ab
C.
32
.ab
D.
2
.ab
Câu 25. Xét các số thực
, ab
thỏa mãn
2
ab
và
1.b
Giá trị nhỏ nhất của biểu thức
log log
ab
b
a
Pa
b

bằng
A.
1
.
3
B.
1.
C.
3.
D.
9.
Câu 26. Cho
,xy
là hai số thực thỏa mãn
ye
và
ln
ln .
ln
xx
yy
Giá trị nhỏ nhất của
biểu thức
P xy
bằng
A.
322
.e
B.
3
42
2
.e
C.
6
.e
D.
8
.
e
Câu 27. Cho
, ab
là các số thực dương thỏa mãn
22
12
log log .
2
a
b
Giá trị nhỏ nhất
của biểu thức
33 33
2
4 4 log 4P ab ab

bằng
A.
4.
B.
2
4 log 6.
C.
2
4 1 log 3 .
D.
2
44
4 log .
ln 2 ln 2


Câu 28. Cho
, xy
là hai số thực dương thỏa
4 1.xy y
Giá trị nhỏ nhất của biểu
thức
62
ln
y xy
P
xy



bằng
A.
3 ln 4.
B.
12 ln 4.
C.
3
ln 6.
2
D.
24 ln 6.
Câu 29. Cho
,xy
là hai số thực dương thỏa
33
11
log 2 1 log .
xy
xy
yx




Biết giá trị nhỏ nhất của
22
xy
xy
là
a
b
với
, ab
và
, 1.ab
Tổng
ab
bằng
A.
2.
B.
9.
C.
12.
D.
13.
Câu 30. Cho
, xy
là hai số thực dương thỏa mãn
2
ln l nn l.
xy xy
Giá trị nhỏ
nhất của biểu thức
Pxy
bằng
A.
2 2 3.
B.
3 2 2.
C.
17 3.
D.
6.
14
Câu 31. Cho
,
xy
là hai số thực dương thỏa mãn
22 2
log log 3 2 2 log .x xy y 
Biết giá trị lớn nhất của biểu thức
22
23
2
2
xy x y
P
xy
x xy y



là
b
a
c
với
, , abc
là các số nguyên dương và
b
c
là phân số tối giản. Tổng
abc

bằng
A.
10.
B.
15.
C.
17.
D.
30.
Câu 32. Cho
, , abc
là các số thực lớn hơn
1
và
, , xyz
là các số thực dương thỏa mãn
.
x yz
a b c abc
Giá trị lớn nhất của biểu thức
2
16 16
Pz
xy

bằng
A.
3
3
20 .
4
B.
3
3
24 .
4
C.
20.
D.
24.
Câu 33. Xét các số thực
, ab
thỏa mãn
1.ab
Giá trị nhỏ nhất của biểu thức
4
2
log 32 3log
128
ba
b
aa
P
b






bằng
A.
13.
B.
14.
C.
15.
D.
19.
Câu 34. Giá trị nhỏ nhất của biểu thức
32
22 2
9
log log 16 64 3 log 7
2
Pa a a 
với
1;16a
bằng
A.
20.
B.
13.
C.
7.
D.
8.
Câu 35. Cho
, ab
là các số thực thỏa mãn điều kiện
0 1.ba
Khi biểu thức
2
43 1
log 8log 1
9
ab
a
b
Pa

đạt giá trị nhỏ nhất, tổng
3
2ab
bằng
A.
1.
B.
2.
C.
6.
D.
7.
Câu 36. Xét các số thực
, ab
thỏa mãn điều kiện
1
1.
4
ba
Biểu thức
1
log log
4
aa
b
Pb b



đạt giá trị nhỏ nhất khi
log
a
b
bằng
A.
2
.
3
B.
3
.
2
C.
2
.
9
D.
9
.
2
Câu 37. Cho
, ab
là hai số thực thuộc
1; 2
và
.
ab
Biết giá trị nhỏ nhất của biểu
thức
22
2 log 4 4 log
ab
a
P bb a 
là
3
mn
với
, .mn
Tổng
mn
bằng
A.
37
.
3
B.
12.
C.
15.
D.
249.
Câu 38. Cho
, ab
là hai số thực thỏa
1
1
3
ba
và giá trị nhỏ nhất của biểu thức
2
3
31
log 12 log
4
ab
a
b
Pa
a



là
m
khi
.
n
ba
Tổng
mn
bằng
15
A.
12.
B.
15.
C.
37
.
3
D.
46
.
3
Câu 39. Cho
, ab
là hai số thực thỏa
4
3
ab
và
3
2
16 log 3 log
12 16
aa
b
a
Pa
b



có
giá trị nhỏ nhất. Tổng
ab
bằng
A.
7
.
2
B.
11
.
2
C.
4.
D.
6.
Câu 40. Cho
, ab
là hai số thực thỏa
34 0ab
và
2
3
3
4
3
log log
4 16
aa
b
a
Pa
b





đạt
giá trị nhỏ nhất. Tổng
3ab
bằng
A.
13
.
2
B.
25
.
2
C.
8.
D.
14.
Câu 41. Cho hai số thực
, xy
thỏa mãn
2 22
2
41 1
.
4
xy x y x
yx
e ey
 

Giá trị lớn
nhất của biểu thức
322
228 2P x y x yx 
bằng
A.
2.
B.
58
.
27
C.
115
.
27
D.
122
.
27
Câu 42. Cho
, xy
là hai số thực thuộc
0;1
và thỏa mãn
2
1
2
2018
2017 .
2 2019
xy
x
yy


Tổng giá trị lớn nhất và nhỏ nhất của biểu thức

22
4 3 4 3 25P x y y x xy 
bằng
A.
25
.
2
B.
136
.
3
C.
383
.
16
D.
391
.
16
Câu 43. Cho
, xy
là hai số thực không âm thỏa mãn
2
2
21
2 1 log .
1
y
x xy
x

Giá trị nhỏ nhất của biểu thức
21 2
4 21
x
Pe x y

bằng
A.
1.
B.
1
.
2
C.
1
.
2
D.
1.
Câu 44. Xét các số thực dương
, xy
thỏa
22
3
log 3 3 .
2
xy
x x y y xy
x y xy
 

Giá trị lớn nhất của biểu thức
321
6
xy
P
xy


bằng
A.
1.
B.
2.
C.
3.
D.
4.
Câu 45. Cho hai số thực dương
,xy
thỏa mãn
 
1
3
log 11 9 11.
y
xy xy



Giá trị nhỏ nhất của biểu thức
2Px y
bằng
A.
5 6 3.
B.
3 6 2.
C.
11
.
2
D.
27
.
5
Câu 46. Cho
, xy
là các số thực thỏa mãn
2
2
log 3 1 .
21
y
y xyx
x

Giá trị
nhỏ nhất của biểu thức
P xy
bằng
16
A.
3
.
4
B.
5
.
4
C.
2.
D.
1.
Câu 47. Cho
,
xy
là các số thực thỏa mãn
22
2
22
1
3 log 1 log 1 .
2
xy
x y xy




Giá
trị lớn nhất của biểu thức
33
23P x y xy

bằng
A.
13
.
2
B.
17
.
2
C.
3.
D.
7.
Câu 48. Cho
, xy
là hai số dương thỏa mãn
2
2
2
41
2.4 ln 4 .
2
x xy
x
xy



Giá trị lớn nhất
của biểu thức
222P xy x x y 
bằng
A.
1 2 3.
B.
1 3.
C.
1 3.
D.
1 2 3.
Câu 49. Cho
, xy
là hai số thực dương thỏa mãn
2 22
2 22 2
4 9.3 4 9 .7 .
xy xy yx 

Giá
trị nhỏ nhất của biểu thức
2 18xy
P
x

bằng
A.
32
.
2
B.
1 9 2.
C.
9.
D.
17.
Câu 50. Gọi
S
là tập các số thực
;
xy
sao cho
0;x 
và
11
2 2.
22
yx
xy
xy









Biết rằng giá trị nhỏ nhất của biểu thức
2
cos 2 2
2
y
x
Pe y x 
với
;xy S
đạt
được tại
00
;.xy
Mệnh đề nào sau đây đúng?
A.
0
0; 1 .x
B.
0
1.x
C.
0
1; 2 .x
D.
0
2.x
Câu 51. Gọi
S
là tập các số thực
;xy
sao cho
1;1x 
và
2018
ln 2017 ln 2017 .
xy
xy x xy ye
Biết rằng giá trị lớn nhất của biểu thức
2018 2
1 2018
x
Pe y x

với
;xy S
đạt
được tại
00
;.xy
Mệnh đề nào sau đây đúng?
A.
0
1.x

B.
0
1; 0 .x

C.
0
0;1 .x
D.
0
1.x
Câu 52. Cho các số thực dương
, xy
thỏa mãn
22
1 22
3
2 log 1 3.
xy
xy


Biết giá
trị lớn nhất của biểu thức
33
S xy x y
là
6
a
b
với
*
, ab
và
a
b
tối giản.
Tổng
2ab
bằng
A.
25.
B.
32.
C.
34.
D.
41.
Câu 53. Cho
, , abc
là các số thực khác
0
thỏa mãn
3 5 15 .
ab c

Giá trị nhỏ nhất
của biểu thức
222
4P a b c abc 
bằng
A.
5
3 log 3.
B.
3
2 log 5.
C.
2 3.
D.
4.
17
Câu 54. Cho
, , xyz
là các số thực không âm thỏa
5 25 125 2018.
xy z

Giá trị nhỏ
nhất của biểu thức
632
xyz
S 
bằng
A.
5
1
log 2018.
3
B.
5
1
log 2016.
6
C.
5
log 2016.
D.
5
1
log 2017.
2
Câu 55. Cho
, , xyz
là các số thực dương thỏa
1
1
1
2018
64 8 4 3.4 .
y
x
z

Giá trị lớn nhất
của biểu thức
1 1 1 3029
43223 26 2
P
x yz x yzx yz

 
bằng
A.
2017.
B.
2018.
C.
2019.
D.
2020.
1
HÀM SỐ LŨY THỪA
HÀM SỐ MŨ – HÀM SỐ LOGARIT
120 câu – Vận dụng cao
Phần 1. Tính chất và các phép toán………………………………………… 2
Phần 2. Đồ thị ………………………………………………………………………………….. 11
Phần 3. Dãy logarit ………………………………………………………………….……. 16
Phần 4. Cực trị nghiệm ……………………………………………………………….. 20
Phần 5. Bài toán tìm GTLN – GTNN …………………….………………… 23
2
Phần 1. Tính chất và các phép toán
Câu 1. Tìm tất cả các giá trị của tham số
a
để hàm số
2
21
log
aa
yx

đồng biến trên
khoảng
0; .
A.
0;2 .a
B.
0;2 \ 1 .a
C.
\ 0;2 .a
D.
\ 0;2 .a
Lời giải. Điều kiện xác định:
2
0
.
0 2 11
x
aa

Theo tính chất của hàm số logarit, ta có hàm số
2
21
log
aa
yx

đồng biến khi và chỉ
khi
2
0
2 11 .
2
a
aa
a

Chọn C.
Câu 2. Cho hàm số
Khẳng định nào sau đây đúng?
A. Hàm số
y fx
nghịch biến trên
;0 .
B. Hàm số
y fx
đồng biến trên
;0 .

C. Hàm số
y fx
nghịch biến trên
; 1.
D. Hàm số
y fx
đồng biến trên
; 1.
Lời giải. Điều kiện xác định:
0.x
Ta có
1
0, ;0 .
ln 2018
fx x
x

Lại có
0 1.fx x 
Lập BBT và kết luận được hàm số
y fx
nghịch biến trên
; 1.
Chọn C.
Câu 3. Số giá trị nguyên của
10m
để hàm số
2
ln 1y x mx 
đồng biến trên
khoảng
0;
là
A.
8.
B.
9.
C.
10.
D.
11.
Lời giải. Điều kiện xác định:
2
1 0.x mx 
Ta có
2
2
.
1
xm
y
x mx

Yêu cầu bài toán
2
2
20
2
0, 0; , 0;
1
10
xm
xm
xx
x mx
x mx

 


10
2
0
, 0; 0
1
2
m
m
mx
m
xm
m
mx
x







có
10
giá trị. Chọn C.
Câu 4. Có bao nhiêu số nguyên âm
m
để hàm số
3
ln 2y x mx 
đồng biến trên
nửa khoảng
1; 
?
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải. Điều kiện xác định:
3
2 0.x mx 
Ta có
2
3
3
.
2
xm
y
x mx

3
Yêu cầu bài toán
2
2
3
3
30
3
0, 1; , 1;
2
20
xm
xm
xx
x mx
x mx

 


2
2
3
3
, 1; 3
2
3
m
mx
m
xm
m
mx
x









có
2
giá trị. Chọn B.
Câu 5. Cho
, ,
abc
là các số thực dương thỏa mãn
37
11
log 7 log 11
log 25
27, 49, 11ab c

.
Giá trị của biểu thức
22
2
37
11
log 7 log 11
log 25
Ta b c
bằng
A.
76 11.
B.
469.
C.
2017.
D.
31141.
Lời giải. Có
11
37
11
37
37
11
log 25
log 7 log 11
log 25
log 7 log 11
log 7 log 11
log 25
27 49 11 .
Ta b c

Áp dụng
log
a
b
ab
, ta được
3
3
3
7
7
7
11
11
11
3
log 7
log 7
log 7
33
2
log 11
log 11
log 11
22
log 25
11
1
log 25
log 25
22
2
27 3 3 7 343
49 7 7 11 121 .
11 11 11 25 25 5





Vậy
343 121 5 469.
T

Chọn B.
Câu 6. Cho
, , abc
là các số thực khác
0
thỏa mãn
4 25 10
abc

. Tính
.
cc
T
ab

A.
1
.
10
T
B.
1
.
2
T
C.
2.
T
D.
10.T
Lời giải. Giả sử
4
25
10
log
4 25 10 log .
log
abc
at
tb t
ct

Ta có
10 10
10 10
4 25
log log log 4 log 25
log 4 log 25
log log log 10 log 10
tt
tt
tt
cc
T
ab t t

10 10
log 4.25 log 100 2. 
Chọn C.
Câu 7. Cho
,xy
là các số thực dương thỏa mãn
964
log log logx y xy

và
2
x ab
y

với
,
a
b
là hai số nguyên dương. Tổng
ab
bằng
A.
4.
B.
6.
C.
8.
D.
11.
Lời giải. Ta có
964
9
log log log 6 9 6 4
4
t
t tt t
t
x
x y xy t y
xy


93
2
2
6
1
3 3 3 15
1 0 6.
5
22 2 2
t
t
t
x
tt t
y
a
ab
b



  








  
Chọn
B.
4
Câu 8. Cho các số thực dương
, , xy z
theo thứ tự lập thành một cấp số nhân, đồng
thời với mỗi số thực dương
1a
thì
3
log , log , log
a
aa
xyz
theo thứ tự lập thành một
cấp số cộng. Giá trị biểu thức
3 7 2020xy z
P
yz x

bằng
A.
2030
.
3
B.
1015.
C.
2030.
D.
4038.
Lời giải. Theo giả thiết ta có
3
2
2
34
log log 2 log
log . log
a
aa
aa
xz y
xz y
xz y
xz y




2
34
0.
xz y
xyz
xz y

Khi đó
3 7 2020 2030.P 
Chọn C.
Câu 9. Cho
, , xyz
là các số thực dương thỏa
log xy z
và
22
log 1.
xy z 
Giả sử
,
ab
là các số thực sao cho
33 3 2
. ..10 10
zz
xya b

Tổng
ab
bằng
A.
31
.
2
B.
25
.
2
C.
29
.
2
D.
31
.
2
Lời giải. Đặt
10 .
z
t
Khi đó
33 3 2
.
xyatbt
Từ giả thiết
2
22
22
log
10
10
.
2
log 1
10.10 10
z
z
xy z
xy t
tt
xy
xy z
xy t









Khi đó
2
3
33 3 3 2
1
3 10
1
3 15 .
2
22
15
tt t
a
x y xy xyxy t t t
b

 
Vậy
29
.
2
ab
Chọn C.
Câu 10. Cho
, ,
xyz
là các số thực thỏa mãn
2017
3 5 15 .
x
xy
xy

Gọi
.S xy yz zx
Khẳng định nào sau đây đúng?
A.
1;2016 .
S
B.
0;2017 .S
C.
0;2018 .S
D.
2016;2017 .S
Lời giải. Đặt
2017
3 5 15 .
x
xy
xy
t

Từ giả thiết ta có
3
5
15
log
log
.
2017
log
xt
yt
zt
xy

Suy ra
15
2017 1 1 1
log .
11
log 15 log 3 log 5
t tt
xy
zt
xy xy
xy


Suy ra
2017
2017 .
xy x y z
xy yz zx
xy xy



Chọn C.
Câu 11. Tìm bộ ba số nguyên dương
;;abc
thỏa mãn
log1 log 1 3 log 1 3 5 ... log 1 3 ... 19 2 log 5040 log 2 log 3.ab c
5
A.
1; 3; 2 .
B.
2;4;3 .
C.
2;4;4 .
D.
2;6;4 .
Lời giải. Ta có công thức quy nạp:
2
1 3 5 ... 2 1 .
nn
Khi đó vế trái của giả thiết bằng:
22 2
log 2 log 3 ... log10 2 log 5040 
10!
2 log10! 2 log 5040 2 log 2 log 720 2 6 log 2 4 log 3.
5040

Chọn D.
Câu 12. Cho
11f
và
fm n fm fn mn
với mọi
*
,.mn
Giá trị biểu
thức
96 69 241
log
2
ff
T





bằng
A.
3.
B.
4.
C.
6.
D.
9.
Lời giải. Theo giải thiết, ta có
2 1 1 1.1
3 2 1 2.1
4 3 1 3.1
1 1 .1
f ff
fff
f ff
fn fn f n





Suy ra
1
2 3 4 ... 1 1 2 3 ... . 1
2
nn
f f f fn f f f fn nf

  

96 4656
1
1 11 .
2
69 2415
f
nn
fn n f
f

Vậy
96 69 241
4656 2415 241
log log 3.
22
ff
T







Chọn A.
Câu 13. Cho
, , abc
là ba số thực dương không cùng bằng nhau, đồng thời khác
1
và
thỏa mãn
log log log
.
bca
cab
abc
Giá trị nhỏ nhất của biểu thức
abc
bằng
A.
2 2.
B.
2 3.
C.
3 2.
D.
3 3.
Lời giải. Giả thiết
222
ln . ln ln .ln ln .ln
ln ln ln .
ln ln ln
ac ba cb
abc
bca

1
Vì
, , abc
không cùng bằng nhau, nên
1
ln ln ln
1
1 ln ln ln .
ln ln ln
1
ab
c
ab c
a b c bc
a
ac b
ac
b


 


Với
1
,ab
c

khi đó
11 2
2 2.abc c c
cc c
  
Dấu
""
xảy ra khi và chỉ
khi
11
;; ; ; 2.
22
abc


Tương tự cho các trường hợp còn lại. Chọn A.
Câu 14. Cho
0a
và
0b
thỏa mãn
22
4 51 8 1
log 16 1 log 4 5 1 2.
a b ab
ab ab


Giá trị của biểu thức
2ab
bằng
6
A.
20
.
3
B.
27
.
4
C.
6.
D.
9.
Lời giải. Ta có
22
4 51 8 1
log 16 1 log 4 5 1
a b ab
ab ab


4 51 8 1
4 51 8 1
log 8 1 log 4 5 1
2 log 8 1 .log 4 5 1 2.
a b ab
a b ab
ab a b
ab a b




Dấu
'' ''
xảy ra
22
81
3
16
27
2.
4
4
log 4 5 1 1
3
ab
ab
a
ab
ab
b





Chọn B.
Câu 15. Cho
1a
và
1b
thỏa
32 2
3
log 4 4 log 16 64 2.
ba
aa b b b b
Giá trị của biểu thức
21
ab
P
ab

bằng
A.
15
.
10
B.
17
.
10
C.
19
.
10
D.
21
.
10
Lời giải. Ta có
2
32 3
2
2
33
log 4 4 log 2 3log
.
1
log 16 64 log 8 log
3
b bb
a aa
aa a a a a
b b b bb b








Suy ra
32 2
3
log 4 4 log 16 64
ba
aa b b b b
11
3 log log 2 3 log . log 2.
33
b a ba
a b ab

Dấu
'' ''
xảy ra
2
.
8
a
b
Chọn C.
Câu 16. Cho
0
x
và số thực
y
thỏa mãn
1
2
2 log 14 2 1 .
x
x
yy




Giá trị của
biểu thức
22
1
P x y xy 
bằng
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải. Theo BĐt Côsi:
11
2 . 2.
xx
xx

Suy ra
1
2 4.
x
x
Ta có
10
3
14 2 1 14 1 1 3 1 3 14.
ty
y y y y y tt


Xét hàm
3
3 14ft t t
trên
0;
có kết quả
0;
max 1 16.ft f


Suy ra
14 2 1 16.yy 
Do đó
2
log 14 2 1 4.yy




Vậy
1
2
1
2 log 14 2 1 2.
0
x
x
x
yy P
y




Chọn B.
Câu 17. Cho
0x
và
0y
thỏa mãn
32
2
2
1
2 log .
2
xxx
y
y




Giá trị của biểu
thức
22
2P x y xy
bằng
A.
1
.
2
B.
1.
C.
2.
D.
2.
Lời giải. Với
0,x
ta có
32
21
1
2 2.
2
xxx 

7
Với
0,y
ta có
22
1 11
log log 2 . .
2 22
yy
yy





Vậy
32
32
2
2
21
1
11 1
2 log .
2
22 2
2
,0
xxx
xxx
x
yy P
yy
y
xy










Chọn A.
Câu 18. Cho hàm số
4
.
42
x
x
fx
Tổng
1 2 2016
...
2017 2017 2017
Sf f f
 







 
bằng
A.
1007.
B.
1008.
C.
2016.
D.
2017.
Lời giải. Dễ dàng chứng minh được
''
Nếu
1ab

thì
1fa fb
''
.
Do đó
1 2016 2 2015 1008 1009
...
2017 2017 2017 2017 2017 2017
Sff ff ff

 
  
  


  
  
  
  

 

1 1 ... 1 1008
. Chọn B.
Bài toán tổng quát: Nếu
0
x
x
M
fx M
MM

thì ta có kết quả
a)
1 1.fx f x 
b)
22
sin cos 1.
ff

c)
21fa fb 
với
3.ab

Câu 19. Cho hàm số
92
.
93
x
x
fx
Tổng
1 2 2017
...
2017 2017 2017
Pf f f
 







 
bằng
A.
1009.
B.
4035
.
4
C.
4039
.
12
D.
12103
.
12
Lời giải. Ta tính được
1
1
9 29 2 1
1.
3
9 39 3
xx
xx
fx f x



Do đó
1 2016 2 2015
...
2017 2017 2017 2017
Pff ff


 
 


 
 
 
 



1008 1009 2017
2017 2017 2017
ff f














3 7 4039
1008. 1 336 .
4 12 12
f 
Chọn C.
Câu 20. Xét hàm số
2
9
9
t
t
ft
m
với
m
là tham số thực. Gọi
S
là tập hợp tất cả
các giá trị của
m
sao cho
1
fx fy
với mọi
, xy
thỏa mãn
xy
e ex y

. Tìm
số phần tử của
S
.
A.
0.
B.
1.
C.
2.
D. Vô số.
Lời giải. Xét hàm
,.
t
g t e et t 
Ta có
; 0 1.
t
gt e egt t


Lập bảng biến thiên ta thấy
0,gt t 
và đẳng thức xảy ra
1.t
Ta có
0.
x xyy
gxy e exy e ex y


Kết hợp với giải thiết
,
xy
eye x

suy ra
1.
xy
e exy xy

8
Khi đó
22
99
11
99
xy
xy
fx fy
mm


2 2 44
2.9 . 9 9 9 . 9 9 9 9 3.
xy x y xy x y xy
m m mm m


Chọn C.
Câu 21. Xét hàm số
4
4
t
t
ft
m
với
0
m
là tham số thực. Biết
1
fx fy
với
mọi số thực dương
,
xy
thỏa mãn
1
2
11
..
22
xy xy 
Giá trị nhỏ nhất của hàm
số
ft
trên đoạn
1
;1
2




bằng
A.
1
.
2
B.
1
.
4
C.
3
.
4
D.
5
.
4
Lời giải. Từ điều kiện bài toán ta có:
1xy
(đưa về hằng đẳng thức).
Như các bài trên ta dễ dàng suy ra
2
.
2
m
n

loaïi
Khi đó
1
;1
2
1 11
min .
2
22
1
4
t
ft ft f







Chọn A.
Câu 22. Cho
a
là số thực dương. Xét hàm số
x
x
a
fx
am
với
0m
là tham số
thực. Biết
1
fx fy
với mọi
1
.
2
xy
Khẳng định nào sau đây đúng?
A.
4
.ma
B.
.ma
C.
.ma
D.
2
.ma
Lời giải. Ta có
11
xy
xy
aa
fx fy
a ma m


11
22
24
2. . . .
xy x y xy x y xy
a ma a a ma a m m a a m a


Chọn A.
Câu 23. Xét hàm số
4
9
9
x
x
fx
m
với
m
là tham số thực. Gọi
S
là tập hợp tất cả
các giá trị của
m
sao cho
1fa fb
với mọi
, ab
thỏa mãn
2
1.
ab
e eab

Tích các phần tử của
S
bằng
A.
3.
B.
9.
C.
81.
D.
81.
Lời giải. Theo giả thiết ta có:
22
1 1 2.
ab ab
e ab e ab
 
 
Tương tự như Câu 20, ta có
2
1 2.
ab
e ab


Do đó dấu bằng phải xảy ra
2 0 2.ab ab
Biến đổi như câu trên ta được
4
3
9 81 .
3
ab
m
m
m


Vậy tích các phần tử của tập hợp
S
là
3. 3 9. 
Chọn B.
Câu 24. Xét hàm số
2
log 2 4
x
fx
và
, ab
là hai số thực dương thỏa mãn
1.fa fb


Đặt
27 2018
12 2017
.Ta b
Khẳng định nào sau đây là đúng?
9
A.
1
0.
4
T
B.
11
.
42
T
C.
1
1.
2
T

D.
1.T
Lời giải. Ta có
4
.
42
x
x
fx
Do đó
44
11
4 14 1
ab
ab
fa fb



01
44 1 .
01
ab
a
ab
b

 

Khi đó ta có
4 2017
27 2018
12 2017
9 2018
1T a b a b ab 
với mọi
, 0;1 .ab
Chọn D.
Câu 25. Cho hàm số
2
12
log
21
x
fx
x


. Tính tổng
1 2 3 2015 2016
... .
2017 2017 2017 2017 2017
Sfff ff
 
 
 

 
 
 
 
 
A.
1008.S
B.
2016.S
C.
2017.S
D.
4032.S
Lời giải. Xét
22
21
1 21
1 log log
2 1 2 11
x
x
fx f x
xx









22 2 2
21 21
1 21 1 2 1
log log log . log 4 1
21 2 21 2
xx
xx
x x xx









.
Áp dụng tính chất trên, ta được
1 2016 2 2015 1008 1009
...
2017 2017 2017 2017 2017 2017
Sff ff ff

 
  
  


  
  
  
  

 

1 1 ... 1 1008.
Chọn A.
Câu 26. Xét hàm số
2018
2018 ln .
x
fx e e



Tính
1 2 ... 2017 .Tf f f


A.
1008.T
B.
1009.
T
C.
2017
.
2
T
D.
2019
.
2
T
Lời giải. Ta có
2018
2018
x
x
e
fx
ee
và
1
2018
1
2018 2018
2018 .
x
xx
ee
fx
e ee e


Suy ra
2018 1.fx f x


Lại có
1
1009 .
2
f
Vậy
1 2017
1 2 ... 2017 1008 .
22
Tf f f

 
Chọn C.
Câu 27. Xét hàm số
2
3
log
1
mx
fx
x
với
m
là tham số thực. Gọi
S
là tập hợp tất cả
các giá trị của
m
sao cho
3fa fb
với mọi
,ab
thỏa mãn
.
ab
e ea b

Tích
các phần tử của
S
bằng
A.
27.
B.
3 3.
C.
3 3.
D.
27.
Lời giải. Điều kiện xác định:
01
0
.
1
0
0
x
x
x
m
m




Như Câu 20 ta được
1.ab
10
Ta có
2
2
3 3 33
log log log log 1 .
1
mx
fx m x x
x

Suy ra
3 13fa fb fa f a 
22
333 33 3
log log log 1 log log 1 log 3m a a m aa 
2
3
3
log
2
m
2
27 0m

27.m 
Chọn B.
Câu 28. Cho hàm số
2019 2
.log 1 sin .cos 2018 6fx a x x b x x

với
, .ab
Biết
ln 2019
2018 10.f
Giá trị của biểu thức
ln 2018
2019f
bằng
A.
10.
B.
2.
C.
8.
D.
10.
Lời giải. Đặt
2019 2
6 .log 1 sin .cos 2018 .gx f x a x x b x x 
Dễ dàng chứng minh
gx
là hàm lẻ nên
ln 2018 ln 2019 ln 2019
2019 2018 2018gg g 
hay
ln 2018 ln 2019
2019 6 2018 6 .ff




Mà
ln 2019
2018 10f
nên suy ra
ln 2018
2019 2.f 
Chọn B.
Câu 29. Cho hàm số
2
.log 2 4 1 .sin .
x
f x a x x b x ce 
với
, , .abc
Biết
rằng
1
ln 2 ln 2.
2
ff



Khi đó hằng số
c
thuộc khoảng nào sau đây?
A.
1
0; .
2


B.
1
;1 .
2


C.
3
1; .
2


D.
3
;2 .
2


Lời giải. Đặt
..
x
g x f x ce

Dễ dàng chứng minh
gx
là hàm lẻ nên
1
ln 2 ln 0
2
gg



suy ra
1
ln
ln 2
2
1
ln 2 . ln . 0
2
f ce f ce



1
ln
ln 2
2
1 14
ln 2 ln . . 0 2 2 0 .
2 25
f f ce ce c c c






 








Chọn B.
Câu 30. Cho hàm số
32
.ln 1 .cos 5 1
f x a x x bx x 
với
, .ab
Biết
log log . log ln10 .f ef m
Gọi
S
là tập các giá trị của tham số
m
thỏa mãn
22 2
log log log ln10 8.f e f mm 
Số phần tử của tập
S
bằng
A.
0.
B.
1.
C.
2.
D. Vô số.
Lời giải. Chứng minh
1gx f x
là hàm lẻ nên
log log log ln10 0g eg
(do
1
log loge log log ln10
ln10



). Suy ra
log log log ln10 2.f ef
Bình
phương hai vế ta được
22
log log log ln10 2 log log . log ln10 4f e f ef
22
1
82 4 3 4 0
4
m
mm m m m
m


loaïi
Chọn B.
11
Phần 2. Đồ thị và các vấn đề liên quan
Câu 1. Cho bốn hàm số
3 1,
x
y
1
2,
3
x
y


4 3,
x
y
1
4
4
x
y


có đồ thị là bốn đường cong
như hình bên. Tương ứng hàm số - đồ thị đúng là
A.
4 13 2
3 ,2 ,1 , 4 .C CC C 
B.
413 2
1 ,3 ,2 ,4 .CCCC
C.
413 2
1,2,3,4.C CC C 
D.
41 3 2
2 ,1 ,3 ,4 .CCC C
Lời giải. Kẻ đường
1x
để so sánh cơ số. Ta thấy cơ số của
2
C
nhỏ nhất nên
2
4,C
tiếp theo là
1
C
nên
1
2 C
và cơ số lớn nhất là của
3
.
C
Chọn C.
Câu 2. Cho các hàm số
,
x
fx a
log
b
gx x
và
log
b
hx x c

(trong đó
, ab
lớn hơn
0
và khác
1;
c
) có đồ thị như hình vẽ. Khẳng định nào sau đây
đúng?
A.
.
acb
B.
.abc

C.
1 , 0.a bc
D.
.
cab
Lời giải. Dễ dàng nhận thấy
01a
và
1.b
Đồ thị hàm số
log
b
hx x c
được suy từ đồ thị của hàm
log
b
gx x
qua phép
tịnh tiến sang phải
c
đơn vị nên
0.c
Vậy
.cab
Chọn D.
Câu 3.
Cho
, , abc
là các số thực dương khác
1
và đồ thị
của ba hàm số
,
x
ya
log ,
b
yx
x
yc
trên cùng một
hệ trục tọa độ như hình vẽ bên. Mệnh đề nào sau đây
đúng?
A.
.
aba
B.
.cab
C.
.cba
D.
.bca
Lời giải.
Dựa vào đồ thị ta thấy: Hàm số
x
ya
và
log
b
yx
là các hàm đồng biến nên
1,a
1.b
Hàm số
x
yc
là hàm nghịch biến nên
0 1.c
Vẽ đồ thị hàm số
log
a
yx
bằng cách lấy đối xứng đồ thị
hàm số
x
ya
qua đường thẳng
yx
(như hình vẽ). Đến
đây ta kẻ đường thẳng
1y
dễ dàng so sánh được
.ab
Vậy
.cab
Chọn B.
12
Câu 4. Cho
, , abc
là các số thực dương khác
1
và đồ thị
của ba hàm số
,
x
ya
log ,
b
yx
log
c
yx
trên cùng
một hệ trục tọa độ như hình vẽ bên. Mệnh đề nào sau đây
đúng?
A.
.bca

B.
.acb
C.
.cba
D.
.cab
Lời giải. Tương tự như câu trên. Chọn D.
Câu 5.
Biết hàm số
y fx
có đồ thị đối xứng với đồ thị
hàm số
3
x
y
qua đường thẳng
1.x 
Chọn khẳng định
đúng trong các khẳng định sau
A.
1
.
3.3
x
fx
B.
1
.
9.3
x
fx
C.
11
.
2
3
x
fx
D.
1
2.
3
x
fx
Lời giải. Gọi
;M xy
và
;M xy

là hai điểm đối xứng nhau qua đường thẳng
1x 
nên
22
.
xx x x
yy yy


 








Khi đó
2
1
33 .
9.3
xx
x
yy


Chọn B.
Trắc nghiệm: Chọn
0;1 3
x
Ay


ñoái xöùng qua 1x
2; 1A
chỉ có đáp án B thỏa.
Câu 6. Biết hàm số
y gx
có đồ thị đối xứng với đồ thị hàm số
x
ya
qua điểm
1;1 .I
Giá trị của biểu thức
1
2 log
2018
a
g


bằng
A.
2020.
B.
2016.
C.
2016.
D.
2020.
Lời giải. Gọi
;M xy
và
;
M xy

là hai điểm đối xứng nhau qua điểm
1;1I
nên
ta có
22
.
22
xx x x
yy y y











Khi đó
22
2 2.
xx x
ya y a y a




Suy ra
1
2 2 log
2
2018
1
2 2 log 2 2016.
2018
a
x
a
y gx a g a




 

Chọn B.
Câu 7. Biết hàm số
y fx
có đồ thị đối xứng với đồ thị hàm số
2018
1
logy
x


qua
gốc tọa độ. Tính giá trị của biểu thức
2018 .f
A.
1.
B.
0.
C.
1.
D. Không tồn tại.
Lời giải. Gọi
;M xy
và
;M xy

là hai điểm đối xứng nhau qua gốc tọa độ
0;0O
nên ta có
0
.
0
xx x x
yy y y











Khi đó
2018 2018
11
log log .yy
xx









Suy ra
2018
1
log 2018 1.y fx f
x



Chọn C.
13
Câu 8. Cho hai hàm số
x
ya
và
y fx
có đồ thị như
hình vẽ đồng thời đồ thị của hai hàm số này đối xứng
nhau qua đường
:.
dy x
Giá trị của
3
fa
bằng
A.
3
1
.
a
a
B.
1
.
3
C.
3.
D.
3
.
a
a
Lời giải. Ta có




ñoái xöùng qua
ñoái xöùng qua
1
.
x
x Oy x
Oy
ya ya
a
yfx yfx
Theo giả thiết, ta có đồ thị hai hàm số
x
ya
và
y fx
đối xứng nhau qua đường
thẳng
yx
nên suy ra đồ thị của hai hàm số
1
x
y
a


và
yfx
đối xứng nhau
qua đường thẳng
yx
.
1
Mà
x
ya
và
log
a
yx
đối xứng nhau qua đường thẳng
.
yx
2
Từ
1
và
2,
suy ra
3
33
11
log log 3.
xa
aa
fx x fa a

Chọn C.
Câu 9.
Cho
, ab
là các số thực dương khác
1.
Các hàm số
x
ya
và
x
yb
có đồ thị như hình vẽ bên. Đường thẳng bất
kỳ song song với trục hoành và cắt đồ thị hàm số
,
x
ya
,
x
yb
trục tung lần lượt tại
, , MNA
đều thỏa mãn
2.AN AM
Mệnh đề nào sau đây đúng?
A.
2.ba
B.
2
.ab
C.
1
.
2
ab
D.
2
1.ab
Lời giải. Gọi
0;At
với
0.t
Suy ra
log ;
.
log ;
a
b
M tt
N tt
Theo giả thiết
2AN AM
nên
suy ra
log 2 log
ba
tt

, khaùc phía vôùi M N Oy
1
log 2 lo .g
ba
t tb
a

Chọn D.
Câu 10. Cho các hàm số
log
a
yx
và
log
b
yx
có đồ
thị như hình vẽ bên. Đường thẳng
5
x
cắt trục hoành,
đồ thị hàm số
log
a
yx
và
log
b
yx
lần lượt tại
,
AB
và
C
. Biết rằng
2.CB AB
Mệnh đề nào sau đây đúng?
A.
2
.ab
B.
3
.ab
C.
3
.ab
D.
5.ab
Lời giải. Theo giả thiết, ta có
5; 0 , 5; log 5 , 5; log 5
ab
AB C
.
Do
2 2 log 5 log 5 2. log 5
ab a
CB AB CB BA 
 
3
.ab 
Chọn C.
14
Câu 11. Cho hai hàm số
2,
x
y
2
logyx
có đồ thị như
hình vẽ. Đường thẳng
cắt trục tung, đồ thị hàm số
2,
x
y
đồ thị hàm số
2
logyx
và trục hoành lần lượt
tại
, , , ABCD
thỏa mãn
.AB BC CD
Hỏi có bao nhiêu
đường thẳng
như thế ?
A.
1.
B.
2.
C.
3.
D. Vô số.
Lời giải. Gọi
22
;2 2
;log log
bx
Bb y
Cc c y x




1
2
2
2 ;2 log do B laø trung ñieåm AC
.
2 ;2log 2 do C laø trung ñieåm DB
b
b
Abc c
Dcb c
Vì
1
1
2
22
2
20 2
1, 2
.
2, 4
2 log 2 0 log 2
2
b
bb
cb
bc c b
A Oy b c
D Ox b c
cc
c












Vậy có hai bộ
điểm
, , , ABCD
thỏa yêu cầu bài toán. Hay có hai đường thẳng
như thế. Chọn B.
Câu 12. Gọi
B
và
C
lần lượt là các điểm thuộc đồ thị hàm số
2
x
y
và
2
logyx
sao cho tam giác
OBC
đều. Giả sử điểm
B
có hoành độ là
a
khi đó tỉ số
2
x
a
bằng
A.
2 3.
B.
2 3.
C.
2 2.
D.
2 2.
Lời giải.
Đồ thị hai hàm số
2
x
y
và
2
logyx
đối xứng qua đường thẳng
yx
và theo yêu
cầu bài toán là tam giác
OBC
đều nên suy ra
;2 , 2 ;
aa
Ba C a
(theo đề điểm
B
có
hoành độ là
a
).
Tam giác
OBC
đều
2 22 2
2 4 .2 0.
aa
OB BC OB B C a a 
Đấy là phương
trình đẳng cấp và tìm được
2
2 3.
x
a

Vì
B
là điểm nằm trên đồ thị hàm số
2
x
y
suy ra
2
a
a
nên
2
2 3.
x
a

Chọn B.
Câu 13. Gọi
,AB
là các điểm lần lượt thuộc đồ thị các hàm số
x
ye
và
x
ye
sao
cho tam giác
OAB
nhận điểm
1;1M
làm trọng tâm. Khi đó tổng các giá trị của
hoành độ và tung độ điểm
A
gần với giá trị nào sau đây nhất?
A.
3.
B.
3, 5.
C.
4.
D.
4,5.
Lời giải.
Gọi
;, ; .
ab
Aae B be
Vì tam giác
OAB
nhận
15
điểm
1;1M
làm trọng tâm nên
3
3
ab
ab
ee


33
3
33
33
3 ln .
11
aa a
ee
ee e a
ee


Khi đó tổng hoành độ và tung độ điểm
A
là
33
33
33
ln 4.
11
ee
ee


Chọn C.
Câu 14. Gọi
A
và
B
lần lượt là hai điểm di động trên
hai đồ thị hàm số
x
ye
và
lnyx
như hình vẽ.
Khoảng cách giữa hai điểm
,A
B
nhỏ nhất gần với giá
trị nào nhất trong các giá trị sau
A.
1, 2.
B.
1, 3 .
C.
1, 4 .
D.
1, 5 .
Lời giải. Đồ thị của hai hàm số
x
ye
và
lnyx
đối xứng nhau qua đường thẳng
yx
nên
AB
đạt giá trị nhỏ nhất
, AB
đối xứng nhau qua đường thẳng
:.dy x
Gọi
;,
a
Aae
khi đó
2 , 2 2 2 min 2 0 2.
a
AB d A d a e f a f x f 
Chọn C.
Câu 15.
Cho đồ thị hàm số
2
x
ye
như hình vẽ.
ABCD
là một hình chữ nhật thay đổi sao cho
B
và
C
luôn thuộc đồ thị hàm số đã cho,
A
và
D
thuộc
trục hoành. Giá trị lớn nhất của diện tích của hình
chữ nhật
ABCD
bằng
A.
2
.
e
B.
2
.
e
C.
2
.
e
D.
2
.
e
Lời giải. Hàm số
2
x
ye
là hàm số chẵn nên đồ thị hàm số nhận trục
Oy
làm trục
đối xứng. Giả sử
2
;
x
C xe
với
0.x
Suy ra
2
;0
.
;
x
Dx
B xe
Diện tích của hình chữ nhật
ABCD
là
2
0;
12
. 2 . max .
2
x
ABCD
S CB CD x e f x f x f
e




Chọn A.
16
Phần 3. Dãy loga
Câu 1. Cho dãy số
n
u
thỏa mãn

2
2 4 24
log 3 log 2 0uu
và

1
2
nn
uu
với mọi
*
.n
Giá trị lớn nhất của
n
để
2018
n
u
bằng
A.
999.
B.
1000.
C.
1010.
D.
1011.
Lời giải. Do

1
2
nn
uu
nên
n
u
là một cấp số cộng với công sai
2.d
Ta có
24 4 1 1
2
2 4 24
24 4 1 1
log 1 2 3 2 4
log 3 log 2 0 .
log 2 4 3 4 2
u u ud u
uu
u u ud u







• Với
2
1
4 4 1 2.
d
n
u un
 
Khi đó
2018
n
u
 4 1 .2 2018n

1012n
nên giá trị lớn nhất của
n
là
1011.
• Với
2
1
2 2 1 2.
d
n
u un
 
Khi đó
2018
n
u
2 1 .2 2018n
1011n
nên giá trị lớn nhất của
n
là
1010.
Vậy giá trị lớn nhất thỏa mãn yêu cầu đề bài là
1011.n
Chọn D.
Câu 2. Cho dãy số
n
u
thỏa mãn

1 1 8 10
log 2 log 2 log 2 logu uu u
và
1
10
nn
uu
với mọi
*
.
n
Khi đó
2018
u
bằng
A.
2000
10 .
B.
2008
10 .
C.
2017
10 .
D.
2018
10 .
Lời giải. Do
1
10
nn
uu
nên
n
u
là cấp số nhân có công bội
7
81
9
10 1
10
10 .
10
uu
q
uu

Ta có
1 1 8 10
log 2 log 2 log 2 logu uu u
79
1 11 1
log 2 log 2 log 10 2 log 10u uu u

.
1 11 1
log 2 log 2 7 log 2 9 logu uu u 
1
11
2
11
log 18
log 16 log 18
log 16 log 18
u
uu
uu



1
17
11
2
11
log 18
log 17 10 .
log 37 log 340 0
u
uu
uu



Số hạng tổng quát của
n
u
là
1 17 18
10 .10 10 .
nn
n
u


Do đó
2000
2018
10 .u
Chọn A.
Câu 3. Cho dãy số
n
u
thỏa mãn
2 2 22
21 21 2 2
log 5 log 7 log 5 log 7.uu 
Biết số hạng
đầu
1
1u
và
1
7
nn
uu
với mọi
*
.
n
Giá trị nhỏ nhất của
n
để
1111111
n
u
là
A.
8.
B.
9.
C.
10.
D.
11.
Lời giải. Do
1
7
nn
uu
nên dãy số
n
u
là cấp số nhân với công bội
7.q
Ta có
2 2 22
21 21 2 2
log 5 log 7 log 5 log 7uu

.
22
22
2 21 2 21 2 2
log 5 log log 7 log log 5 log 7uu 
1
21
2
21 2 2 21
21
1
1
log 0
2 log 2 log 5 log 7 log 0 .
1
log 35
35
u
u
uu
u
u


loaïi
17
Số hạng tổng quát của dãy số
n
u
là
1
1
.7 .
35
n
n
u
Ta có
1
1
1111111 .7 1111111 10.
35
n
n
un

Do đó giá trị nhỏ nhất của
n
là
10.
Chọn C.
Câu 4. Cho dãy số
n
u
thỏa mãn
9 9 19
11
2
2
4 24 3
u u uu
uu
e e e ee

và
1
3
nn
uu

với mọi
*
.
n
Khi đó giá trị nhỏ nhất của
n
để
3
n
u
là
A.
9.
B.
10.
C.
11.
D.
12.
Lời giải. Do
1
3
nn
uu

nên
n
u
là cấp số cộng với công sai
91
3 24.d uu
Ta có
9 9 19 9 9
11 1 1
2
2
2
4 2 4 3 2 2 30
u u uu u u
uu u u
e e e ee ee ee

9
1 11 1
9
1 11 1
24
24
24
24
1 13 1 13 1 13
2 2 21
22 2
.
1 13 1 13 1 13
2 2 21
22 2
u
u uu u
u
u uu u
ee e e ee
ee e e ee

  

 




  

 


loaïi
Suy ra
1
1
24 24
1 13 13 1
ln .
42 42
u
eu
ee





Số hạng tổng quát của dãy số
n
u
là
24
13 1
ln 3 1 .
42
n
un
e



Ta có
24
13 1 1 13 1
3 ln 3 1 3 6 ln 10,142.
3 42
42
n
u nn
a
e






 






Do đó giá trị nhỏ nhất của
n
là
11.
Chọn C.
Câu 5. Cho cấp số cộng
n
u
có tất cả các số hạng đều dương và thỏa mãn
1 2 2018 1 2 1009
... 4 ... .uu u uu u  
Giá trị nhỏ nhất của biểu thức
222
3 2 3 5 3 14
log log logPu u u
bằng
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải. Vì
n
u
là cấp số cộng nên
1 2 2018 1 2 1009
... 4 ...uu u uu u  
11
1
2018 2 2017 1009 2 1008
4. .
2 22
ud ud
d
u


Do đó
21
3
,
2
d
u ud 
51
9
4,
2
d
uu d
14 1
27
13 .
2
d
uu d
Ta có
222 2 2 2
3 2 3 5 3 14 3 3 3
3 9 27
log log log log log log
22 2
dd d
Pu u u









222 2
3 3 33
1 log 2 log 3 log 3 log 2 2 2.
2 2 22
d d dd
 







 
Chọn B.
Câu 6. Cho dãy số
n
u
thỏa mãn
32
1 11
log 2 log log 2 0u uu 
và
1
2 10
nn
uu

với mọi
*
.n
Giá trị nhỏ nhất của
n
để
100
10 10
n
u 
là
A.
225.
B.
226.
C.
326.
D.
327.
18
Lời giải. Ta có
32
1 11
log 2 log log 2 0
u uu

2
1 21 1 1
log 2 log 1 0 log 2 100.u u uu  
Ta có
11
2 10 10 2 10 .
nn n n
uu u u


Đặt
11
1
10 110
10
2
nn
nn
vu
vu
vv


là cấp số nhân với công bội
1
2 110.2 .
n
n
qv

Mà
10
nn
vu
suy ra
1
110.2 10.
n
n
u

Ta có
100 100
100 1 100 1
2
10 10
10 10 110.2 10 10 10 2 log 1
110 110
nn
n
un


 

Ta có
100 100
98
222 2
10 10
log 1 log 1 log 10 1 98 log 10 1 326,54.
110 100
 



   





 
Do đó giá trị nhỏ nhất của
n
là
327.
Chọn D.
Câu 7. Cho dãy số
n
u
thỏa mãn
19
3
1119
log log log log 3
3uu uu 
và
1
2
nn
uu
với mọi
*
.n
Tìm số tự nhiên
n
lớn nhất sao cho
100
3 5 .
n
u
A.
71.n
B.
72.n
C.
73.n
D.
74.n
Lời giải. ĐK
1 19
19 1
0, 0
.
log log 3 0
uu
uu


Đặt
19
3
1
32
1 19
log log
3.
log log 3 0
a uu
ab
b uu



Ta được hệ phương trình









2
32
3
3
1
1 60
2
3
ba
ab
a
aa
b
ab
(thỏa mãn).
Do
1
2
nn
uu
nên
n
u
là cấp số cộng với công sai
19 11
18 36.2 uud
du 
Với
1a
suy ra
19
19 19 1 1 1 1
1
1
1 log 1 10 36 10 4.log log
u
u uu uu
u
uu 
Số hạng tổng quát của
n
u
là
1
1 4 2 1 2 2.
n
uu n d n n

Ta có
100 2 2 100 100
3
1
3 5 3 5 log 5 2 72,2.
2
n
u
n
n

Do đó giá trị lớn nhất của
n
là
72.n
Chọn B.
Câu 8. Cho dãy số
n
u
thỏa
22 2 2
12 1 1
ln ln ... ln ln ln 1 3
n nn
u u u uu


và
2
1nn
uu
với mọi
*
.n
Tìm giá trị nhỏ nhất của
n
để
2018
2017 .
n
u
A.
11.
B.
12.
C.
14.
D.
15.
Lời giải. Vì
2
1nn
uu
nên
2
1
ln ln 2 ln .
nnn
uuu

Khi đó
22
1
ln ln 1 ln 2 ln 1 ln 1 .
nn n n n
uu u u u
 
• Nếu
1
11
n
uu
thì không tồn tại
n
thỏa yêu cầu bài toán.
• Nếu
1
11
n
uu
thì
ln 1 ln 1
nn
uu
với mọi
*
.n
Tiếp tục quá trình như thế ta được
19
22 2 2
12 1 1
ln ln ... ln ln ln 1 3
n nn
u u u uu

 
22
12 1 1 1
ln ln 1 3 ln 1 3 ln 2 .
u u u u ue  
Ta có
1
1
2
248 2 2 2
123 1
...
n
nn
nn n n
uu u u u e e


Theo giả thiết
2018 2 2018 2018
2017 2017 2 ln 2017 2 2018 ln 2017
n
nn
n
ue  
13,9.n
Do đó giá trị nhỏ nhất của
n
là
14.
Chọn C.
Câu 9. Cho dãy số
n
u
có tất cả các số hạng đều dương và thỏa
2
1
.log 1
,
10
n
n
un
u
với mọi
1.
n
Gọi
a
là giá trị nhỏ nhất của
.
n
u
Có bao nhiêu số tự nhiên
n
để
n
ua
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải. Từ giả thiết có
12
.log
.
10
n
n
un
u
Do
a
là giá trị nhỏ nhất của
n
u
nên khi
n
ua
2
1
2
10 10
1
12
2
1
.log 1
log 1 10
10
2 1 2.
.log
log 10
10
n
n
nn
nn
n
n
un
u
uu
n
n
uu
un
n
u






Vậy có
hai số tự nhiên
n
là
10
21
và
10
2
thỏa yêu cầu bài toán. Chọn B.
Câu 10. Cho cấp số cộng
n
a
thỏa
21
0;
aa
cấp số nhân
n
b
thỏa
21
1bb

và
hàm số

3
3fx x x
sao cho
21
2;
fa fa
22 21
log 2 log .fb fb
Tìm số
nguyên dương
n
nhỏ nhất sao cho
2018 .
nn
ba
A.
15.n
B.
16.n
C.
17.n
D.
18.n
Lời giải. Ta có
2
3 3;fx x

1
0.
1
x
fx
x


Bảng biến thiên
• Ta có
12
12
0
20
aa
fa fa



Keát hôïp BTT
1
2
0
1
1
n
a
an
a

(do
n
a
là cấp số cộng).
• Lại có

21
1b b
nên
22 21
log log 0.
bb
Vì
22 21
21 22
log log 0
log log 2 0
bb
fbfb



Keát hôïp BTT
21 1
22 2
log 0 1
log 1 2
bb
bb



1
2
n
n
b
(do
n
b
là cấp số nhân).
Khi đó yêu cầu bài toán:
2018
nn
ba
1
2 2018 1 .
n
n

Thử cả bốn đáp án ta được
16n
là giá trị nguyên dương nhỏ nhất thỏa mãn. Chọn B.
20
Phần 4. Cực trị nghiệm
Câu 1. Xét các số nguyên dương
,a
b
sao cho phương trình
2
ln ln 5 0
a xbx

1
có hai nghiệm phân biệt
1
,x
2
x
và phương trình
2
5 log log 0xb xa 
2
có hai
nghiệm phân biệt
3
,
x
4
x
thỏa mãn
12 34
.
xx xx
Giá trị nhỏ nhất của biểu thức
23S ab
bằng
A.
17.
B.
25.
C.
30.
D.
33.
Lời giải. Điều kiện
0.x
Để



2
2
2
1 coù 2 nghieäm phaân bieät 20
20 .
2 coù 2 nghieäm phaân bieät 20
ba
ba
ba
Ta có
12 1 2 12
5
34 3 4 34
ln ln ln
.
log log log 10
5
b
a
b
b
xx x x xx e
a
b
xx x x xx


Yêu cầu bài toán:
5
12 34
5
10 ln10 3.
5 ln10
bb
a
a
bb
xx xx e a a
a


Suy ra
2
20 60 8
b
ba b

.
Khi đó
2 3 2.3 3.8 30.S ab
Dấu
'' ''
xảy ra
3
.
8
a
b
Chọn C.
Câu 2. Với
,mn
là các số nguyên dương sao cho phương trình
2
ln 1 ln 0x m xn 
1
có hai nghiệm phân biệt
12
,xx
và phương trình
2
ln 1 ln 0x n xm 
2
có hai nghiệm phân biệt
34
,xx
thỏa mãn
2
12 34
.xx xx
Giá trị nhỏ nhất của biểu thức
23P mn
bằng
A.
46.
B.
48.
C.
51.
D.
53.
Lời giải. Điều kiện
0.x
Để


2
2
1 coù 2 nghieäm phaân bieät 1 4 0
.
2 coù 2 nghieäm phaân bieät 1 4 0
mn
nm
*
Ta có
2
Vi-et
12 34 1 2 3 4
ln ln 2 ln ln 1 2 1 2 1.xx xx x x x x m n m n 
Thay
21mn
vào
*
ta được
3 2 3 7.
n
nn

Khi đó
2 3 2 2 1 3 7 2 51.P mn n n n  
Chọn C.
Câu 3. Cho hai phương trình
2
ln 1 ln 0 1x m xn 
và
2
ln 1 ln 0 2 .x n xm
Biết phương trình
1
có hai nghiệm phân biệt là
01
, xx
và phương trình
2
có hai
nghiệm phân biệt là
02
,
xx
(tức là
0
x
là nghiệm chung của hai phương trình) Giá trị
nhỏ nhất của biểu thức
22
12
Sx x
bằng
A.
1.
B.
2.
C.
3.
D.
4.
21
Lời giải. Điều kiện:
.
mn
Để hai phương trình đã cho mỗi phương trình có hai
nghiệm phân biệt là
2
2
140
.
14 0
mn
nm


Gọi
0
x
là nghiệm chung của hai phương trình
1
và
2.
Khi đó
2
00
00
2
00
ln 1 ln 0
ln 0 ln 1 0.
ln 1 ln 0
x m xn
mn x mn x mn
x n xm


 
Theo Vi-et, ta có
0
01
11
ln 1
02 2
2
ln ln 1
ln
.
ln ln 1 ln
m
x
n
x xm
xm xe
x xn xn
xe









Khi đó
2 2 2 2 22
12
2 2.
m n mn
xxe e e

Chọn B.
Câu 4. Xét các số nguyên dương
, ab
sao cho phương trình
.4 .2 50 0
xx
ab 
1
có
hai nghiệm phân biệt
12
,
xx
và phương trình
9 .3 50 0
xx
ba
2
có hai nghiệm
phân biệt
34
,
xx
thỏa mãn
34 12
.xx xx
Giá trị nhỏ nhất của biểu thức
32S ab
bằng
A.
49.
B.
51.
C.
59.
D.
81.
Lời giải. Ta có
22
32
1 50 0 1
.
2 50 0 2
x
x
t
at bt
ba



Để

2
1 coù 2 nghieäm phaân bieät 1 coù 2 nghieäm döông phaân bieät
200 0.
2 coù 2 nghieäm phaân bieät 2 coù 2 nghieäm döông phaân bieät
ba
Ta có
12 1 2
3
12 4
12 2
34 3
50 50
2 2 .2 log
.
3 3 .3 50 log 50
xx x x
x
xx x
xx
aa
axx a


Yêu cầu bài toán:
34 12 3 2
50
log 50 log 3.
a
xx xx a a
a



Suy ra
2
200 600 25.
b
ba b

Khi đó
3 2 3.3 2.25 59.S ab
Chọn C.
Câu 5. Cho
, ab
là hai số thực dương lớn hơn
1.
Biết phương trình
2
1
1
xx
ab
có hai
nghiệm phân biệt
12
, .xx
Giá trị nhỏ nhất của biểu thức
2
12
12
12
4
xx
S xx
xx



bằng
A.
3
4.
B.
3
3 4.
C.
3
3 2.
D.
4.
Lời giải. Ta có



2
1 laáy logarit cô soá hai veá 2
12
12
log
1 log 1 0 .
1
xx b
b
b
xx a
ab x x a
xx
Khi đó
3
3
22
11
2 log 2 log 3 .2 log .2 log 3 4.
log log
b b bb
bb
S a a aa
aa

22
Dấu
'' ''
xảy ra
1
3
2
2
3
11
2 log log .
2
log
bb
b
a a ab
a

Chọn B.
Câu 6. Cho
, ab
là hai số nguyên dương lớn hơn
1.
Biết phương trình
2
1
xx
ab
có
hai nghiệm phân biệt
12
, xx
và phương trình
2
1
9
x
x
ba
có hai nghiệm phân biệt
34
, xx
thỏa mãn

1 23 4
3.x xx x 
Giá trị nhỏ nhất của biểu thức
32
S ab
bằng
A.
40.
B.
41.
C.
44.
D.
46.
Lời giải. Ta có
2
12 2
1 log log 1 0.
xx
aa
a bx xbxxb
 
Phương trình này có
hai nghiệm phân biệt
2
2
log 4 0 log 2 .
aa
b b ba  
Tương tự từ phương trình
2
1
9
x
x
ba
ta có
log 9 4 0 :
b
a

luôn đúng.
Theo Vi-ét
12
34
log
log . log 9 3
log 9
a
ab
b
xx b
ba
xx a



3
log 9 3 9 3 4.
a
a
a aa a a
 
Suy ra
2
16 17.
b
ba b

Khi đó
3 2 3.4 2.17 46.S ab

Chọn D.
Câu 7. Cho
, ab
là hai số thực lớn hơn
1.
Biết phương trình
2
1
1
xx
ab
có nghiệm
thực. Giá trị nhỏ nhất của biểu thức
4
log
log
a
a
P ab
b

bằng
A.
4.
B.
5.
C.
6.
D.
10.
Lời giải. Ta có
2
12 2
1 1 log 0 log log 0.
xx
a aa
ab x x b x x b b
 
Để phương trình có nghiệm
2
log 0
log 4 log 0 .
log 4
a
aa
a
b
bb
b

*
Vì
1a
và
1b
nên
log 0.
a
b
Do đó
* log 4.
a
b
Khi đó
2
log
4;
4 44
1 log 1 min 6.
log
a
tb
a
a
tt
P b t ft ft
b tt



Chọn C.
Câu 8. Cho
, ab
là hai số thực lớn hơn
1
thỏa mãn
10.ab
Gọi
, mn
là hai
nghiệm của phương trình

log log 2 log 3log 1 0.
ab a b
xx x x 
Giá trị nhỏ nhất
của biểu thức
S mn
bằng
A.
16875
.
16
B.
4000
.
27
C.
3456.
D.
15625.
Lời giải. Phương trình tương đương với
2
log . log 2 3 log .log 1 0.
ba b a
ax a x 
Theo Vi-ét ta có
32 32
2 3 log
log log 2 log 3 log .
log
b
aa a a
b
a
m n b ab mn ab
a

Khi đó
2
32 3
1;9
10 max 6 3456.S ab a a fa fa f 
Chọn C.
Câu 9. Cho
, ab
là các số thực lớn hơn
1
và phương trình
log .log 2018
ab
ax bx
có
hai nghiệm phân biệt
, .mn
Giá trị nhỏ nhất của biểu thức

2 2 22
4 9 36 1P a b mn
bằng
23
A.
36.
B.
72.
C.
144.
D.
288.
Lời giải. Ta có
log .log 2018 1 log 1 log 2018
ab a b
ax bx x x 
2
log log log .log 2017
log . log log 1 log 2017 0.
a b ab
ab a b
x x xx
bx b x


Theo Vi-et:
11
log log log 1 log .
log
b bb b
a
mn m n
b ab

Suy ra
1
.mn
ab
Khi đó

22 22 22 2 2
22 2 2
36 144 324
4936 149 1 4 9P ab mn ab a b
ab b a

 

22
22
324 144
2 4 . 2 .9 72 72 144.ab
ab

Chọn C.
Câu 10. Cho
, , abc
là các số thực lớn hơn
1
thỏa mãn
100.abc
Gọi
, mn
là
hai nghiệm của phương trình
2
log 1 2 log 3log log 1 0.
a a aa
x b cx 
Tính
23Sa b c
khi
mn
đạt giá trị lớn nhất.
A.
200.
S
B.
500
.
3
S
C.
650
.
3
S
D.
700
.
3
S
Lời giải. Theo Vi-et
23
log log log 1 2 log 3log log .
a a a a aa
mn m n b c ab c 
Suy ra
3
2 3 100. 2
100
abc
mn ab c mn ab a b



4 33
3 . . (100 ) 100 100
27 2 2
bb
a ab ab ab


  


6
8
3
3 2 3 100
4 625.10
2
.
27 6 27
b
a ab







Dấu
'' ''
xảy ra
3
3 100
2
b
a ab

50 100 150
, , .
33 3
ab c
Khi đó
700
.
3
S
Chọn D.
Phần 5. Bài toán tìm GTNN-GTLN
Câu 1. Cho hai số thực
, xy
thỏa mãn
log 3 log 3 1.xy xy
Giá trị nhỏ nhất
của biểu thức
Sxy
bằng
A.
22
.
3
B.
1.
C.
45
.
3
D.
10.
Lời giải. Điều kiện xác định:
30
.
30
xy
xy


(suy ra
0x
)
Ta có
22
log 3 log 3 1 9 10.xy xy x y 
Ta từ
Sxy
suy ra
.y xS
Thay vào trên ta được
2
2
9 10x xS
22
8 18 9 10 0.x Sx S 
24
Để phương trình có nghiệm dương
2
2
18 4.8. 9 10 0
45
.
3
0
SS
S
S


Chọn C.
Câu 2. Cho
, xy
là các số thực dương thỏa mãn
22
23
log 11 20 40 1.
x xy y
xy


Gọi
,
ab
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
.
y
S
x
Tổng
ab
bằng
A.
10.
B.
2 14.
C.
11
.
6
D.
7
.
2
Lời giải. Giả thiết tương đương với
22
2 3 11 20 40 0.
x xy y x y
Từ
.
y
S y Sx
x

Thay vào trên ta được
2 22 22
2 3 11 20 40 0x Sx Sx x Sx 
22
4 2 20 11 40 0.Sx Sx 
*
Nhận xét: Vì
0, 0xy

nên
0.S
Suy ra
12
2
12
2
20 11
0
42
.
40
0
42
S
xx
S
xx
S


Khi phương trình
*
có nghiệm thì luôn có hai nghiệm dương.
Để phương trình
*
có nghiệm
2
0 240 440 199 0.SS
Suy ra
440 11
.
240 6
ab

Chọn C.
Câu 3. Cho
,,ab c
là các số thực dương khác
1
thỏa
22
log log log 2 log 3.
ab a b
cc
bc
bb

Gọi
,
Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
log log .
ab
P bc
Giá trị
của biểu thức
23S mM
bằng
A.
1
.
3
S
B.
2
.
3
S
C.
2.S
D.
3.S
Lời giải. Đặt
log
log
a
b
xb
P xy
yc

và giả thiết trở thành
22
2 1.x y xy x y 
Suy ra
22
22
2 1 3 1 0.
x xP xxP x xP x Px P
 
Phương trình có nghiệm khi
5
01 .
3
P 
Chọn D.
Câu 4. Cho
,a
,b
c
là các số thực lớn hơn
1.
Giá trị nhỏ nhất của biểu thức
3
41 8
log
log 3 log
ac ab
bc
P
a
bc

bằng
A.
10.
B.
12.
C.
18.
D.
20.
Lời giải. Ta có
4 18
2 log 2 log 8 log
1
2 log log
log
2
abc
bc ab
ac
P bc ac ab
ac
b

25
2 log 2 log 2 log 2 log 8 log 8 log
aab bc c
bcacab 
2 log 2 log 2 log 8 log 2 log 8 log .
ab ac bc
ba ca cb
Vì
,a
,
b
c
là các số thực lớn hơn
1
nên
log ,
a
b log ,
b
a log ,
a
c log ,
c
a
log ,
b
c
log
c
b
đều là
những số dương. Do đó áp dụng bất đẳng thức Côsi, ta có
2 2 log .2 log 2 2 log .8 log 2 2 log .8 log 4 8 8 20.
ab ac bc
P ba ca cb

Dấu
'' ''
xảy ra
2
2
log log
log 4 log 1.
log 4 log
ab
ac
bc
ab
ba
c a ca ab c
cb
cb







Chọn D.
Câu 5. Cho
, xy
là các số thực dương thỏa mãn
22 4
log log log .x y xy
Giá trị
nhỏ nhất của biểu thức
22
Sx y
bằng
A.
2 2.
B.
3
2 4.
C.
3
4 2.
D.
4.
Lời giải. Ta có
22 4 2 2
log log log log log .x y xy xy xy xy xy 
Mà
2
3
3
3
4 0 4 16.
4
xy
xy xy xy xy xy xy

 



Do đó
2
3
22 2
3
11
16 2 4.
22
Sx y xy
Chọn B.
Câu 6. Cho
, ab
là hai số thực dương. Giá trị nhỏ nhất của biểu thức
33 3
4
log 1 2 log 1 2 log 1
2
b
Pa
a
b






A.
1.
B.
4.
C.
7.
D.
9.
Lời giải. Ta có
2
3
4
log 1 2 1 1 .
2
b
Pa
a
b











•
2
12 1 1 2 12 1
22
bb
a ab bb b
aa



.
•
2
22
2
4 44
1 2 1 1 1 1 1 4 1 2.2 4 81.
2
b
a bb
a
b bb

 













 

Suy ra
3
log 81 4.P 
Chọn B.
Câu 7. Cho
,
ab
là các số thực lớn hơn
1
thỏa mãn
23
log log 1.ab

Giá trị lớn nhất
của biểu thức
32
log logPab
bằng
A.
23
log 3 log 2.
B.
32
log 2 log 3.
C.
32
1
log 2 log 3 .
2
D.
23
2
.
log 3 log 2
Lời giải. Ta có
22
2
3 2 32 23
log log log 2.log log 3.logP ab a b

3223 32
log 2 log 3 log log log 2 log 3.ab 
Suy ra
32
log 2 log 3.P 
Chọn A.
26
Câu 8. Cho
, , xyz
là các số thực thỏa mãn
4 9 16 2 3 4 .
xy z xyz

Giá trị lớn
nhất của biểu thức
111
234
xy z
P


bằng
A.
3 87
.
2
B.
5 87
.
2
C.
7 87
.
2
D.
9 87
.
2
Lời giải. Đặt
2 , 3 , 4 .
xyz
abc
Ta có
222
222
, , 0
, , 0
.
1 1 13
2 2 24
abc
abc
a b c abc
abc


 










 
*
Ta cần tìm GTNN của
1 1 19
234 2 3 4 .
2 2 22
P abc a b c



   





Áp dụng bất đẳng thức Bunhiacopxky, ta có
2
222
22 2
1 1 1 1113
2 3 4 2 3 4 29. .
2 2 2 2224
a b c abc


 




 






 



Suy ra
9 87
2
P
. Chọn D.
Cách khác. Ta xem
*
là mặt cầu và
234 :234 0P abc abcP  
là
mặt phẳng. Tìm điều kiện để mặt phẳng cắt mặt cầu.
Câu 9. Cho
, ab
là các số thực thỏa mãn
22
1ab
và
22
log 1.
ab
ab

Giá trị lớn
nhất của biểu thức
243P ab
bằng
A.
1
.
10
B.
10
.
2
C.
10.
D.
2 10.
Lời giải. Ta có
22
22
22
1 22
1 11
log 1 .
2 22
ab
ab
ab ab a b a b










Ta có
1 13
2 2.
2 22
ab a b













Áp dụng bất đẳng thức Bunhiacopxky, ta có
2
22
22
1 1 1 1 15
2 1 2 5. .
2 2 2 2 22
a b ab


 




 






 



Do đó
1 1 10 10 3
2 2 2 4 3 10.
2 2 2 22
a b ab P ab



 





Dấu
""
xảy ra
5 10 5 2 10
; .
10 10
ab


Chọn C.
Cách 2. Ta thấy
1
là hình tròn tâm
11
;
22
I


, bán kính
2
.
2
R
Ta có
243 :243 0.P ab ab P 
Xem đây là phương trình đường thẳng.
Để đường thẳng và hình tròn có điểm chung
,dI R 
27
11
2. 4. 3
2
22
10 10.
2
4 16
P
PP


Câu 10. Cho hai số thực
, xy
thỏa mãn
22
2
log 2 1
xy
xy

*.
Biết giá trị lớn nhất
của biểu thức
2P xy

là
a
b
với
, ab
và
a
b
tối giản. Tổng
ab
bằng
A.
11.
B.
13.
C.
15.
D.
17.
Lời giải. Với
22
0 21xy
thì
22
*2 2 1
xyx y 
hay
1.P
Với
22
21xy
thì
2
2
22
19
*2 2 1 2 .
8
22
xyx y x y



Khi đó
1 19
2 21 2
4
2 22
P xy x y

 

2
2
9
1 1 99
4. 1 2 .
2
2 42
22
a
xy
b



Chọn A.
Cách khác. Từ
22
22xyx y
ta đặt
2ty
thì trở thành phương trình hình
tròn
2
2
22
1 19
2 01
8
2 22
xt x t x t



(ta dùng phương pháp hình học).
Câu 11. Cho các số thực
, , abc
thỏa
2
222
log 4 4 4 .
2
abc
aa bb cc
abc

 

Giá trị lớn nhất của biểu thức
23
a bc
P
abc


bằng
A.
4 30
.
3
B.
8 30
.
3
C.
6 30
.
3
D.
12 30
.
3
Lời giải. Ta có
2
222
log 4 4 4
2
abc
aa bb cc
abc

 

222 222
22
log 4 4 4 4 4 4 log 2 2.ab c ab c abc abc 
Xét hàm
2
logft t t
với
0t
ta đi đến kết quả
222
444 2a b ca b c 
222
2 2 2 10.abc
Ta lại có
23
1 2 3 0.
a bc
P P aP b P c
abc

 

Đến đây ta dùng điều kiện
để mặt phẳng và mặt cầu có điểm chung. Chọn C.
Câu 12. Cho các số thực
, xy
thỏa mãn
22 22 22 22
4 41 3 4 2 4
4 2 2 4.
xy xy xy xy  

Gọi
,m
M
lần lượt là giá trị nhỏ nhất và lớn nhất của
21
4
xy
P
xy


. Tổng
Mm
bằng
A.
36
.
59
B.
18
.
59
D.
18
.
59
C.
36
.
59
Lời giải. Đặt
22
4,tx y
ta được

8 16
4 2.2 2 2 8 8 0 1.
24
tt t t
tt
t 
28
Suy ra
2 2 2 22
4 1 1.
Yy
x y xY

*
Từ
21
4
xy
P
xy


suy ra
1 2 14P xP y P 
2 1 2 2 8.
P xP Y P

**
Sử dụng điều kiện có nghiệm (đường thẳng có điểm chung với đường tròn) ta thu được
kết quả
2
22
28
1 59 36 4 0.
4 21 4 4
P
PP
PP PP


Chọn A.
Câu 13. Cho các số thực dương
, , abc
thỏa mãn
222
222
5 log 16 log 27 log 1.
abc
Giá
trị lớn nhất của biểu thức
22 22 22
log log log log log logS ab bc ca 
bằng
A.
1
.
16
B.
1
.
12
C.
1
.
9
D.
1
.
8
Lời giải. Đặt
2 22
log , log , log .x ay bz c
Giả thiết trở thành
222
5 16 27 1.xyz
Ta đi tìm GTLN của
.S xy yz zx
Sử dụng bất đẳng thức Cauchy – Schwarz dạng phân thức ta có
2
222
2
2 22
11 22 33 6 .
1 1 1 111
11 22 33 11 22 33
xyz
xyz
x y z xyz



Suy ra
222
5 16 27 12 .x y z xy yz zx 
Do đó
1
.
12
S
Chọn B.
Cách 2. Ghép cặp và dùng BĐT Cauchy. Cụ thể
22
22
22
3 12 12
2 18 12
4 9 12
xyxy
x z xz
y z yz



(đpcm).
Câu 14. Cho các số thực
, , abc
lớn hơn
1
thỏa mãn
2 22
log 1 log log log 2.
bc
a bc

Giá trị nhỏ nhất của biểu thức
2 22
2 22
10 log 10 log logP a bc
bằng
A.
7
.
2
B.
9
.
2
C.
3.
D.
4.
Lời giải. Đặt
2 22
log , log , log .x ay bz c
Suy ra
, , 0.xyz
Khi đó ta có
1
11x yz xy yz xz
yz

và
22 2
10 .P xy z

Sử dụng bất đẳng thức Cauchy – Schwarz dạng phân thức ta có
2
2 22
2
2 22
12 12 3 2 .
1 1 1 1 11
12 12 3 12 12 3
xyz
x yz
x y z xyz



Suy ra
22 2
10 4 4.x y z xy yz xz 
Chọn D.
Câu 15. Cho
, ab
là hai số thực dương. Giá trị nhỏ nhất của biểu thức
22
55
81
log logP ab
ab



bằng
29
A.
1
.
2
B.
1.
C.
3
.
2
D.
2.
Lời giải. Ta có
2
2
2
22
22
41
81 4 1
81 5
22
.
5
25
ab ab ab
ab
ab
ab a b
 


Do đó
22
22
55 5
22
5 53
log log log .
2
5
5
P ab
ab

Chọn C.
Cách khác.
22
22
55
22
81
log log 8 1 1 .
ba
P ab
ab
ab









Đặt
2
2
b
t
a
và xét
hàm số
1
81 1ft t
t

trên
0;
và có
1
5 5.
4
ft f



Câu 16. Cho
log
x
y
m
x
với
1,x
0 1.y
Giá trị của lớn nhất của biểu thức
log log
xy
T yx
bằng
A.
2.
B.
1.
C.
0.
D.
2.
Lời giải. Ta có
1
log log 1 .
2
xx
y
my
x

Suy ra
log 2 1.
x
ym
Vì
1,
x
01y
nên
1
log 0 2 1 0 .
2
x
ym m 
Khi đó
1
;
2
11
log 2 1 max 1 2.
log 2 1
x
x
y m fm fm f
ym




Chọn A.
Câu 17. Cho các số thực dương
, ab
thỏa mãn
2
log 2 2 .
b
ab a
Giá trị nhỏ nhất của
biểu thức
312
1
a
b
Sa
a

bằng
A.
3 1.
B.
1 3.
C.
2 3 2.
D.
2 3 4.
Lời giải. Có
.2
2
log 2 2 2 2 .2 2 1 1 2 .
a
b
ab a b ab a a a
a
ab b a b
b


Khi đó
0;
312
3
min 1 3 2 3 4.
11
a
b
a
S a a fa fa f
aa



Chọn D.
Cách 2. Biến đổi
3
14
1
Sa
a

sau đó dùng Côsi.
Câu 18. Xét các số thực
, ab
thỏa mãn
1.ab
Biết rằng
1
log
log
a
ab
a
P
ab

đạt
giá trị lớn nhất khi
k
ba
. Khẳng định nào sau đây đúng?
A.
3
0; .
2
k


B.
1; 0 .k 
C.
3
;2 .
2
k


D.
2;3 .k
30
Lời giải. Ta có
1
log log 1 log 1 log 1 log
log
aa a a a
ab
a
P ab b b b
ab
 
Khi
11
k
ba P k k 
.
Đặt
1 1t kk

, ta được
2
2
1 99
2.
2 44
P tt t

 

Dấu
'' ''
xảy ra
1 33
0;
2 42
tk



. Chọn A.
Câu 19. Cho
, ax
là các số thực dương,
1
a
và thỏa mãn
log log .
x
a
xa
Giá trị lớn
nhất của
a
bằng
A.
1.
B.
log 2 1 .
e
C.
ln10
.
e
e
D.
log
10 .
e
e
Lời giải. Ta có
2
log log
log log log log log log .
log
x
aa
xx
x a xxa xa a
ax
 
Do
2
log 0a
nên suy ra
1.x
Xét hàm
log x
fx
x
trên
1; 
ta tìm được
1
log
max .
x
e
fx
e
Ssuy ra
log
2
log
log 10 .
e
e
e
aa
e

Chọn D.
Câu 20. Cho hai số thực
, 1ab
sao cho tồn tại số thực
01x
thỏa
2
log log
.
ba
xx
ab
Giá trị nhỏ nhất của biểu thức
22
ln ln lnP a b ab 
bằng
A.
3 22
.
12
B.
1 33
.
4
C.
.
2
e
D.
1
.
4
Lời giải. Ta có
2
log log
2
ln ln
log . ln log .ln . ln 2 .ln
ln ln
ba
xx
ba
xx
a b xa x b a b
ba

22
ln ln 2 ln 0 ln ln 2 ln ln 2 ln 0.x a b xa b a b 
*
Theo giả thiết
, 1ab
và
1
x
nên
2
* ln 2 ln 0 .a b ab 
Khi đó
22 2
ln ln ln 3 ln 2 1 ln .
P a b ab b b 
Đặt
lntb
với
0.t
Xét hàm ta được
min
3 22
12
P

tại
21
.
6
t
Chọn A.
Câu 21. Cho
,
ab
là các số thực thỏa mãn
0 1,ab 
1.ab
Giá trị lớn nhất của
biểu thức
4
log
1 log .log
a
aa
b
P ab
b ab

bằng
A.
4.
B.
2.
C.
3.
D.
4.
Lời giải. Dễ dàng biến đổi được
4
1 log .
1 log
a
a
Pb
b

Do
01ab 
và
1ab
nên suy ra
log 0.
a
b
31
Xét hàm
;0
4
1 max 3 4.
1
ft t ft f
t


Chọn A.
Câu 22. Cho
, xy
là các số thực thỏa mãn
1
4, , 1.
2
xy x y
Gọi
, Mm
lần lượt là
giá trị lớn nhất và nhỏ nhất của
2
2
22
log log 1 .Px y
Tổng
2Mm
bằng
A.
6.
B.
11.
C.
11
.
2
D.
21
.
2
Lời giải. Từ giả thiết suy ra
1
8.
42
y
xy

Ta có
2 2 22
22
22 2 2 2 2
4
log log 1 log log 1 log 2 log 1 .Px y y y y
y

Vì
18y
nên
2
0 log 3.
y
Xét hàm
22
21ft t t 
trên
0;3
ta được
1
;5 .
2
ft




Chọn A.
Câu 23. Xét các số thực
, ab
thỏa mãn
1.ab
Giá trị nhỏ nhất của biểu thức
22
log 3 log
a b
b
a
Pa
b



bằng
A.
13.
B.
14.
C.
15.
D.
19.
Lời giải. Dễ dàng biến đổi được
2
4 1 log 3 log .
a b
b
a
Pb
b






Do
1ab
nên suy ra
log 0.
a
b
b
Xét hàm
2
3
41ft t
t

trên
0;
, ta được
1
15.
2
t
fPf



Chọn C.
Câu 24. Xét các số thực
, ab
thỏa
1,b
.aba
Biểu thức
log 2 log
a
b
b
a
Pa
b



đạt giá trị khỏ nhất khi
A.
2
.ab
B.
23
.ab
C.
32
.ab
D.
2
.ab
Lời giải. Dễ dàng biến đổi được
14
4.
1 log log
aa
P
bb

Từ điều kiện, suy ra
1a
.
Do
1
log log log
a
a aa
aba a b a

hay
1
log 1.
2
a
b
Xét hàm
14
4
1
ft
tt

trên
1
;1 ,
2

ta được
ft
đạt giá trị nhỏ nhất bằng
5
khi
23
2
log .
3
a
b ab
Chọn B.
Câu 25. Xét các số thực
, ab
thỏa mãn
2
ab
và
1.b
Giá trị nhỏ nhất của biểu thức
log log
ab
b
a
Pa
b

bằng
32
A.
1
.
3
B.
1.
C.
3.
D.
9.
Lời giải. Dễ dàng biến đổi được
1 log
1
.
1 log log
a
aa
b
P
bb

Từ điều kiện, suy ra
1
1 log 0.
b
a
ab

Do
21 2
log log 2
b
bb
ab a b

hay
log 0
11
2 log .
log 2
a
b
a
a
b
b

Xét hàm
11
1
t
ft
tt

trên
1
0; ,
2

ta được
1
3
2
P ft f



. Chọn C.
Câu 26. Cho
,xy
là hai số thực thỏa mãn
ye
và
ln
ln .
ln
xx
yy
Giá trị nhỏ nhất của
biểu thức
P xy
bằng
A.
322
.e
B.
3
42
2
.e
C.
6
.e
D.
8
.e
Lời giải. Đặt
ln ,ax
ln .by
Do
1.ye b

Từ giả thiết ta có
2
.
1
ab
ab a
bb

Suy ra
2
1
2 1 3 2 2 3.
11
b
ab b b
bb
  

Khi đó
ln ln ln 2 2 3
.
xy x y a b
P xy e e e e


Chọn A.
Câu 27. Cho
, ab
là các số thực dương thỏa mãn
22
12
log log .
2
a
b
Giá trị nhỏ nhất
của biểu thức
33 33
2
4 4 log 4P ab ab 
bằng
A.
4.
B.
2
4 log 6.
C.
2
4 1 log 3 .
D.
2
44
4 log .
ln 2 ln 2


Lời giải. Từ giả thiết ta có
2
4
.a
b
Đặt
33
33 3
3
66
256 256
4 3 . . 12.
22
bb
t ab b
bb
 
Khi đó
22
12;
4 log min 12 4 1 log 3 .P ft t t ft ft f


Chọn C.
Câu 28. Cho
, xy
là hai số thực dương thỏa
4 1.xy y
Giá trị nhỏ nhất của biểu
thức
62
ln
y xy
P
xy



bằng
A.
3 ln 4.
B.
12 ln 4.
C.
3
ln 6.
2
D.
24 ln 6.
Lời giải. Có
2
22
41 41 1
4 1 4 4 4 2 4.
x
xy y
yy y y
yy



Đặt
0;4 .
x
t
y

Khi đó
0;4
63
ln 2 min 4 ln 6.
2
P t ft ft f
t
 
Chọn C.
33
Câu 29. Cho
,xy
là hai số thực dương thỏa
33
11
log 2 1 log .
xy
xy
yx




Biết giá trị nhỏ nhất của
22
xy
xy
là
a
b
với
, ab
và
, 1.ab
Tổng
ab
bằng
A.
2.
B.
9.
C.
12.
D.
13.
Lời giải. Ta có
33
1 1 11
log 2 1 log 2 3
x y xy
xy xy
y x yxxy





 






33
3 2 3 2 3 2.
xy xy x y
xy
yx y x yx y x

 









 

Đặt
2
2.
x y xy
tt
y x yx

Ta được
2
4
3 2 23 2 .
3
t tt 
Khi đó
22
2
10
10
2 13.
3
3
a
x y xy
t ab
b
xy y x
 
Chọn D.
Câu 30. Cho
, xy
là hai số thực dương thỏa mãn
2
ln l nn
l.xy xy

Giá trị nhỏ
nhất của biểu thức
Pxy
bằng
A.
2 2 3.
B.
3 2 2.
C.
17 3.
D.
6.
Lời giải. Ta có
2022
lnln ln 1 1 0
x
xy xyxyx y yx x yx
 
0
1.
y
x

Do đó
2
2
1.
1
x
yx x y
x
 
Khi đó
2
1;
22
mi
1
n 2 2 3.
2
P x y fx
x
x ffx
x





Chọn A.
Câu 31. Cho
, xy
là hai số thực dương thỏa mãn
22 2
log log 3 2 2 log .
x xy y 
Biết giá trị lớn nhất của biểu thức
22
23
2
2
xy x y
P
xy
x xy y



là
b
a
c
với
, , abc
là các số nguyên dương và
b
c
là phân số tối giản. Tổng
abc
bằng
A.
10.
B.
15.
C.
17.
D.
30.
Lời giải. Ta có
2 2 0, 0
22
log 3 log 4 4 0 .
xy
x xy y x y x y x y


Khi đó
22 2
2
13
23
.
2
2
2
2
xx
xy x y
yy
P
x
xy
x xy y
xx
y
yy







Đặt
0;1 .
x
t
y

Xét hàm
2
0;1
1 23 5
min 1 2 10.
23
2
tt
ft ft f a b c
t
tt



Chọn A.
Câu 32. Cho
, , abc
là các số thực lớn hơn
1
và
, , xyz
là các số thực dương thỏa mãn
.
x yz
a b c abc
Giá trị lớn nhất của biểu thức
2
16 16
Pz
xy

bằng
34
A.
3
3
20 .
4
B.
3
3
24 .
4
C.
20.
D.
24.
Lời giải. Có
1
log
log
1
log
log
.
1
log
log
11 1
log
2 log log log log
a
t
b
t
x yz
c
t
abc
t ttt
xt
a
yt
b
a b c abc t
zt
c
t
abc a b c






Suy ra
1 1 11 1
2.
111
2
xy z
xyz


Khi đó
2
16
32 2 20.P z fz f
z

Chọn C.
Câu 33. Xét các số thực
, ab
thỏa mãn
1.ab

Giá trị nhỏ nhất của biểu thức
4
2
log 32 3 log
128
ba
b
aa
P
b






bằng
A.
13.
B.
14.
C.
15.
D.
19.
Lời giải. Ta có
44
2
32 2 .32 .
128 128
aa
a

Do
1ab
suy ra
1.
a
b
Khi đó
2
2
2
log 3 log 4 1 log 3 log .
bbaa
bb
aa
Pa b
bb

 









 

Đặt
log 0
a
b
tb
(vì
1ab
), ta có
2
31
4 1 15.
2
P t ft
t
f



Chọn C.
Câu 34. Giá trị nhỏ nhất của biểu thức
32
22 2
9
log log 16 64 3 log 7
2
Pa a a 
với
1;16a
bằng
A.
20.
B.
13.
C.
7.
D.
8.
Lời giải. Ta có
2
2
82 8
16 64 8 2 8 .
2
a
aa a




Khi đó
32
222
log 9 log 3 log 7.Pa a a
Đặt
1;16
2
log 0; 4 .
a
ta t

Ta có
32
3 9 7 3 20.P t t t ft f 
Chọn A.
35
Câu 35. Cho
, ab
là các số thực thỏa mãn điều kiện
0 1.
ba
Khi biểu thức
2
43 1
log 8 log 1
9
ab
a
b
Pa

đạt giá trị nhỏ nhất, tổng
3
2ab
bằng
A.
1.
B.
2.
C.
6.
D.
7.
Lời giải. Ta có
2
43112 49.b bb 
Dấu
'' ''
xảy ra
2
.
3
b
Vì
01a
nên
2
12 4 9
log log 2 log
99
a aa
bb
b

Khi đó
22
12 4 8 8
log 1 2 log 1.
9
log 1 log 1
aa
aa
b
Pb
bb


Do
01ba
nên suy ra
log log 1.
aa
ba
Đặt
log 1
a
t bt

ta được
3
2 22
8 88
2 1 ( 1) ( 1) 1 3 ( 1)( 1) 1 7.
( 1) ( 1) ( 1)
Pt t t t t
t tt


Dấu
'' ''
xảy ra
3
2
8
1 3.
( 1)
t t ba
t

Chọn B.
Câu 36. Xét các số thực
, ab
thỏa mãn điều kiện
1
1.
4
ba

Biểu thức
1
log log
4
aa
b
Pb b



đạt giá trị nhỏ nhất khi
log
a
b
bằng
A.
2
.
3
B.
3
.
2
C.
2
.
9
D.
9
.
2
Lời giải. Ta có
2
1
.
4
bb
Dấu
'' ''
xảy ra
1
.
2
b
Do
1a
nên
2
1
log log 2 log .
4
a aa
b bb



Khi đó
log
11
log
1 39
2 log . 2 .
2 1 log 2 2 2 2
a
tb
a
a
ba t
a
b
t
P b t ft f
bt





Chọn D.
Câu 37. Cho
, ab
là hai số thực thuộc
1; 2
và
.ab
Biết giá trị nhỏ nhất của biểu
thức
22
2 log 4 4 log
ab
a
P bb a 
là
3
mn
với
, .mn
Tổng
mn
bằng
A.
37
.
3
B.
12.
C.
15.
D.
249.
Lời giải. Có
 
32
4 4 1 2 2 0 1; 2 .bb b b b b b 
Suy ra
32
4 4.bb b
Do
1a
nên
23
log 4 4 log .
aa
bb b
Khi đó
32
2
1
2 log log 6 log
log 1
aa a
b
a
P ba b
b

33
2
1
3 log 1 3 log 1 6 3 9 6 6 243.
log 1
aa
a
bb
b
 
Chọn D.
36
Câu 38. Cho
,
ab
là hai số thực thỏa
1
1
3
ba

và giá trị nhỏ nhất của biểu thức
2
3
31
log 12 log
4
ab
a
b
Pa
a



là
m
khi
.
n
ba
Tổng
mn
bằng
A.
12.
B.
15.
C.
37
.
3
D.
46
.
3
Lời giải. Ta có
2
3
1
4 3121 10, .
3
bb b b b 
Suy ra
3
1
3
1
31
3
33 3
314 31
4 3 1 log log .
44 4
a
a
aa
bb b b
bb
a
aa a





 





Khi đó
3
2
2
12
log 12 log 3 log 1
log 1
a aa
b
a
b
P ab
a
b



2
3 3 12
log 1 log 1 9
22
log 1
aa
a
bb
b
 
(vì
1
1
3
ba
nên
log 1
a
b
).
Dấu
'' ''
xảy ra
3
log 3 .
a
b ba 
Suy ra
9
12.
3
m
mn
n

Chọn A.
Câu 39. Cho
, ab
là hai số thực thỏa
4
3
ab

và
3
2
16 log 3 log
12 16
aa
b
a
Pa
b



có
giá trị nhỏ nhất. Tổng
ab
bằng
A.
7
.
2
B.
11
.
2
C.
4.
D.
6.
Lời giải. Ta có
2
3
12 16 2 4 0b bb b 
luông đúng
4
.
3
b
Suy ra
3
1,
12 16
aa
b
b

suy ra
3
log log log 1 0.
12 16
a aa
aa
b
b



Do đó
22
3
48 log 3log 48 log 3 log .
12 16
a a aa
bb
aa
P aa
b
b



Đặt
log
a
a
t
b
, vì
log log 1 0
aa
a
b

nên
0.t
Khi đó
2
0;
31
48 min 36.
2
P t ft ft f
t




Dấu
'' ''
xảy ra
2
2
6.
1
4
log
2
a
b
b
ab
a
a
b




Chọn D.
Câu 40. Cho
, ab
là hai số thực thỏa
34 0ab
và
2
3
3
4
3
log log
4 16
aa
b
a
Pa
b





đạt
giá trị nhỏ nhất. Tổng
3ab
bằng
A.
13
.
2
B.
25
.
2
C.
8.
D.
14.
37
Lời giải. Ta có
3
4 2 2 3 4.bb b
*
Do
3
*
3
3
4
4
3
4
4
log log .
3 4 0
3
3 4 0 3 41 1
4
aa
b
b
a
a
aa
b
b
aa
a b ab
b


Khi đó
3
2
3
4
3
log log
4 16
aa
b
a
Pa
b





Đặt
3
log 0,
4
a
a
t
b

ta được
2
2
3
22
3 3 3 27
22
16 64
31 9
3 . 3. .
16 4
tt t
t
t
t
t
P 

Dấu
'' ''
xảy ra
2
1
2
b
t
4
3 14.
2
a
ab
b

Chọn D.
Câu 41. Cho hai số thực
, xy
thỏa mãn
2 22
2
41 1
.
4
xy x y x
yx
e ey
 

Giá trị lớn
nhất của biểu thức
322
228 2P x y x yx 
bằng
A.
2.
B.
58
.
27
C.
115
.
27
D.
122
.
27
Lời giải. Điều kiện:
1 1.
x
Từ giả thiết ta có
2 22
41 2 1 2 2
4 4 1 4 1.
xy x y x
e xy x e y x
 
 
Xét hàm
4
t
ft e t
trên
và đi đến kết quả
22 2
41 1xy x y x 
hay
2
4.xy y
Khi đó
32
1;1
1 58
2 2 max .
3 27
P x x x fx fx f



Chọn B.
Câu 42. Cho
, xy
là hai số thực thuộc
0;1
và thỏa mãn
2
1
2
2018
2017 .
2 2019
xy
x
yy


Tổng giá trị lớn nhất và nhỏ nhất của biểu thức

22
4 3 4 3 25P x y y x xy

bằng
A.
25
.
2
B.
136
.
3
C.
383
.
16
D.
391
.
16
Lời giải. Từ giả thiết ta có
22
2017 2017
1 log 2018 log 2 2019xy x y y
2
2
2017 2017
log 2018 log 1 2018 1 .xx y y




Xét
2
2017
log 2018
ft t t
trên
0;1
và đi đến kết quả
1xy

hay
1.yx
Khi đó
2
2
191 25
4 3 1 4 1 3 25 1 ;
16 2
P x x x x xx











với
0;1 .
x
Suy ra
391
.
16
Mm
Chọn D.
Câu 43. Cho
, xy
là hai số thực không âm thỏa mãn
2
2
21
2 1 log .
1
y
x xy
x

Giá trị nhỏ nhất của biểu thức
21 2
4 21
x
Pe x y

bằng
38
A.
1.
B.
1
.
2
C.
1
.
2
D.
1.
Lời giải. Từ giả thiết ta có
22
22
2 1 log 2 1 log 2 1 2 1.x x yy 
Xét hàm số
2
log
ft t t
trên
0;

và đi đến kết quả
2
2 1 2 1.xy
Khi đó
21 2
2 42 .
x
P e x x gx

Ta có
21 21
2 4 4; 0 2 4 4 .
xx
gx e x gx e x



Ta thấy vế trái là hàm nghịch
biến, vế phải là hàm đồng biến nên phương trình có nghiệm duy nhất. Vì
1
0
2
g


nên
1
2
x
là nghiệm duy nhất của
0.gx
Lập bảng biến thiên của
gx
trên
0;
và kết luận được giá trị nhỏ nhất của
P
bằng
1
.
2
Chọn B.
Câu 44. Xét các số thực dương
, xy
thỏa
22
3
log 3 3 .
2
xy
x x y y xy
x y xy
 

Giá trị lớn nhất của biểu thức
321
6
xy
P
xy


bằng
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải. Ta có
22
3
log 3 3
2
xy
x x y y xy
x y xy
 

22 22
33
3 log 3 2 log 2 .x y x y x y xy x y xy

 

Xét hàm
3
logft t t
trên
0;
và đi đến kết quả
22
32x y x y xy 
2
3 2.xy xy xy 
Suy ra
2 22 2
22
2 2 6 4 5 3 5.x y xy xy xy xy xy xy 
Từ
321
3 2 1 6.
6
xy
P P xP y P
xy



Suy ra
Bunhiacopxkia
2
2 22
22
16 3 2 3 2P P xP y x yP P


 



2
5 2 10 13 .PP

Hay
2
26 38 64 0PP 
suy ra
1.P
Dấu
'' ''
xảy ra
2
.
1
x
y
Chọn A.
Câu 45. Cho hai số thực dương
,xy
thỏa mãn
 
1
3
log 11 9 11.
y
xy xy



Giá trị nhỏ nhất của biểu thức
2Px y
bằng
A.
5 6 3.
B.
3 6 2.
C.
11
.
2
D.
27
.
5
Lời giải. Từ giả thiết ta có
 
3
1log 119 11y xy xy




3 33
9 99
log 1 1 1 log 1 1 log .
1 11
xy x x x
y yy

 


39
Xét hàm
3
logft t t
trên
0;
và đi đến kết quả
9
1
1
x
y

hay
8
.
1
y
x
y
Vì
0
8
0 0 8.
1
y
y
xy
y

Khi đó
2
0;8
8 28
2 2 min 3 6 2.
11
y yy
P x y y gy gy
yy

 

Chọn B.
Câu 46. Cho
, xy
là các số thực thỏa mãn
2
2
log 3 1 .
21
y
y xyx
x

Giá trị
nhỏ nhất của biểu thức
P xy
bằng
A.
3
.
4
B.
5
.
4
C.
2.
D.
1.
Lời giải. Điều kiện:
1
.
0
x
y

Từ giả thiết ta có
2
22
log 1 log 1 3 3 1y x y xy x
2
2
22
3 log 1 3 1 log 1 .yy y x x x 
Xét hàm
2
2
3 logft t t t
trên
0;
và đi đến kết quả
1.yx
Khi đó
1;
35
1 min .
44
P x y x x gx gx g




Chọn B.
Câu 47. Cho
, xy
là các số thực thỏa mãn
22
2
22
1
3 log 1 log 1 .
2
xy
x y xy




Giá
trị lớn nhất của biểu thức
33
23P x y xy 
bằng
A.
13
.
2
B.
17
.
2
C.
3.
D.
7.
Lời giải. Điều kiện:
.
1
xy
xy
Từ giả thiết ta có
2
2
22
22
3 log 3 log 2 2 .
xy
xy
x y xy

Xét hàm
2
3 . log
t
ft t
trên
0;
và đi đến kết quả
2
22
x y xy 
2
2
2
22 .
2
xy
x y xy xy


Đặt
.txy
Ta có
2 12
2 2 4 2;2 .
xy
t xy t t

Khi đó
22
3
2;2
2 2 13
2 6 3 max .
22 2
tt
P t t gt gt












Chọn A.
Câu 48. Cho
, xy
là hai số dương thỏa mãn
2
2
2
41
2.4 ln 4 .
2
x xy
x
xy



Giá trị lớn nhất
của biểu thức
222P xy x x y 
bằng
A.
1 2 3.
B.
1 3.
C.
1 3.
D.
1 2 3.
Lời giải. Điều kiện
0.xy
Giả thiết
2
41 2 2
2 ln 4 1 2 ln 2 .
x xy
x xy

40
Xét hàm
2 ln
t
ft t
trên
0;
và đi đến kết quả
2
1
4 12 2 .
2
x xy y x
x

Ta có
13
2 2 2 123 12.2 123.
22
P xy x x y x
x

  

Chọn A.
Câu 49. Cho
,
xy
là hai số thực dương thỏa mãn
2 22
2 22 2
4 9.3 4 9 .7 .
xy xy yx 

Giá
trị nhỏ nhất của biểu thức
2 18xy
P
x

bằng
A.
32
.
2
B.
1 9 2.
C.
9.
D.
17.
Lời giải. Đặt
2
2,tx y
khi đó giả thiết tương đương với
22
2 2 22
22
43 43
4 9.3 4 9 .7 4 3 4 3 .7 .
77
tt
t tt t tt
tt


 
Xét hàm
43 1 3
4.
77
7
aa
a
a
fa
 







 
là hàm số nghịch biến trên
nên đi đến kết
qủa
22 2t tt 
suy ra
22
2 2 2 2.x y yx

Khi đó
2
2 18 16
1 2 14 1 9.
xx
Px
xx

 
Chọn C.
Câu 50. Gọi
S
là tập các số thực
;xy
sao cho
0;
x 
và
11
2 2.
22
yx
xy
xy









Biết rằng giá trị nhỏ nhất của biểu thức
2
cos 2 2
2
y
x
Pe y x

với
;xy S
đạt
được tại
00
;.xy
Mệnh đề nào sau đây đúng?
A.
0
0; 1 .x
B.
0
1.x
C.
0
1; 2 .x
D.
0
2.x
Lời giải. Giả thiết
41 41
41 41
22
yx
xy
yx
xy
xy












ln 1 4 ln 1 4
.ln 4 1 .ln 4 1 .
xy
xy
yx
xy


1
Xét hàm
ln 1 4
t
ft
t
trên
0; .
Ta có
2
.4 .ln 4 1 4 . ln 1 4
0
14
tt t t
t
t
ft
t


với mọi
0.t
Do đó
ft
nghịch biến trên
0; .
Nhận thấy
1
có dạng
.fx fy x y 
Khi đó
2
cos 2 2 .
2
x
x
Pe x x 
Xét hàm số
2
cos 2 2 .
2
x
x
gx e x x 
TXĐ:
D.
Đạo hàm
sin 2 ;
x
gx e x x

1 cos 0
x
gx e x


với mọi
x
nên
gx
đồng biến trên
.
41
Ta có
0
0 10
0;1
1 1 sin1 0
g
x
ge



sao cho
0
0.gx
Lập bảng biến thiên ta thấy
gx
đạt giá trị nhỏ nhất tại
0
0;1 .x
Chọn A.
Câu 51. Gọi
S
là tập các số thực
;
xy
sao cho
1;1x

và
2018
ln 2017 ln 2017 .
xy
xy x xy ye
Biết rằng giá trị lớn nhất của biểu thức
2018 2
1 2018
x
Pe y x 
với
;xy S
đạt
được tại
00
;.xy
Mệnh đề nào sau đây đúng?
A.
0
1.x

B.
0
1; 0 .
x 
C.
0
0;1 .
x
D.
0
1.x
Lời giải. Điều kiện :
0.xy
Giả thiết tương đương với
2018
ln 2017 ln 2017x xy x y xy ye 
2018
2018
ln 2017 ln 2017 0.
e
xy xy xy e xy
xy
 
*
Xét hàm
2018
ln 2017
e
ft t
t

trên
0; .
Đạo hàm
2018
2
1
0
e
ft
t
t

với mọi
0.t
Suy ra hàm
ft
đồng biến trên
0; .
Mà
2018
0fe
nên
2018 2018 2018
*.fxy fe xye y xe  
Khi đó
2018 2018 2
1 2018 .
x
P e x e x gx 
Xét hàm
gx
có
0gx

với mọi
1; 1x 
nên
gx
nghịch biến trên
1; 1 .
Mà
2018
2018
1 2018 0
0 2019 2018 0
ge
ge


nên tồn
tại
0
1; 0x 
sao cho
0
0gx
và khi đó
0
1;1
max .
gx gx
Chọn B.
Câu 52. Cho các số thực dương
, xy
thỏa mãn
22
1 22
3
2 log 1 3.
xy
xy


Biết giá
trị lớn nhất của biểu thức
33
S xy x y
là
6a
b
với
*
, ab
và
a
b
tối giản.
Tổng
2ab
bằng
A.
25.
B.
32.
C.
34.
D.
41.
Lời giải. Xét hàm
1
3
2 log 1
t
ft t

là hàm đồng biến trên
0; .
Mà
22 22
23 2 .f fxy xy
Khi đó

2
22
2 22
1 22 3 .S x y x xy y xy xy




Đặt
,t xy
vì
22
1
2
xy
xy

nên
1;1 .t 
Do đó

2
2
1;1
1 512 16 6
2 2 3 max .
3 27 9
S ft t t ft f S



Chọn C.
42
Câu 53. Cho
, , abc
là các số thực khác
0
thỏa mãn
3 5 15 .
ab c

Giá trị nhỏ nhất
của biểu thức
222
4P a b c abc 
bằng
A.
5
3 log 3.
B.
3
2 log 5.
C.
2 3.

D.
4.
Lời giải. Theo giả thiết
3 5 15 .
ab c
t

Suy ra
3 5 15
log ; log ; log .a tb t c t 
Ta có
15
11
log .
11
log 15
t
ct
ab

Suy ra
0.ab bc ca
Khi đó
22
2 4 4 4.P abc abbcca abc abc abc

   


Chọn D.
Câu 54. Cho
, , xyz
là các số thực không âm thỏa
5 25 125 2018.
xy z

Giá trị nhỏ
nhất của biểu thức
632
xyz
S

bằng
A.
5
1
log 2018.
3
B.
5
1
log 2016.
6
C.
5
log 2016.
D.
5
1
log 2017.
2
Lời giải. Đặt
23
5 ; 5 ; 5 .
x yz
ab c
Ta có
2018
.
, , 1
abc
abc

Suy ra

1 1 0 1.a b ab a b 
1
Nhân
c
hai vế ta được
.abc ac bc c

2
Tương tự
1,
ta cũng có
1ac a c
và
1.bc b c
3
Từ
2
và
3
ta có
2.
abc a b c 
Ta có
23 2 3
5 5 .5 .5 2 2018 2 2016.
x yz x y z
abc a b c

 
Suy ra
5
2 3 log 2016xyz
hay
55
1
6 log 2016 .log 2016.
6
SS 
Chọn B.
Câu 55. Cho
, , xyz
là các số thực dương thỏa
1
1
1
2018
64 8 4 3.4 .
y
x
z

Giá trị lớn nhất
của biểu thức
1 1 1 3029
43223 26 2
P
x yz x yzx yz

 
bằng
A.
2017.
B.
2018.
C.
2019.
D.
2020.
Lời giải. Ta có
16 1 1 1 1
43 2 2 3
16 1 1 1 1 1 4 3 3 1 3029
..
223 2 3 163 2 2
16 1 1 1 1
26 2 33
x y zx y y z
P
xyzxxyz xyz
x y zx y z z



 




Mà
1 331
1
1
3
2018
2
3.4 64 8 4 3 4
y x yz
x
z


suy ra
3
2018
4
3 3 1 3.4
log 3.2018.
23x yz



Suy ra
2018 3029
2019.
42
P 
Chọn C.
1
Ứng dụng
HÀM SỐ MŨ – HÀM SỐ LOGARIT
Sự phân rã của các chất phóng xạ
Phần 1.
Một số bài toán áp dụng
(tăng trưởng, phóng xạ, động đất,…)
Phần 2. Bài toán lãi suất
2
Phần 1. Một số bài toán áp dụng
Dạng 1. Áp dụng công thức có sẵn
Câu 1. Một lon nước soda
0
80
F
được đưa vào một máy làm lạnh chứa đá tại
0
32 .
F
Nhiệt độ của soda ở phút thứ
t
được tính theo định luật Newton bởi công thức
32 48. 0,9 .
t
Tt
Phải làm mát soda trong bao lâu để nhiệt độ là
0
37 .F
Chọn đáp
án gần nhất với kết quả?
A.
15, 6
phút. B.
17
phút. C.
21, 5
phút. D.
25, 6
phút.
Câu 2. với
t
là khoảng thời gian tính bằng giờ và
0
Q
là dung lượng nạp tối đa (pin
đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là
0%
) thì sau bao lâu sẽ nạp được
90%
(kết quả làm tròn đến hàng phần trăm)?
A.
1, 21t
giờ. B.
1, 22t
giờ. C.
1, 3 4
t
giờ. D.
1, 5 4t
giờ.
Câu 3. Một loài cây xanh trong quá trình quang hợp sẽ nhận một lượng nhỏ Carbon
14
(một đơn vị của Carbon). Khi cây đó chết đi thì hiện tượng quang hợp cũng sẽ
ngưng và nó sẽ không nhận Carbon
14
nữa. Lượng Carbon
14
của nó sẽ phân hủy
chậm chạp và chuyển hóa thành Nitơ
14.
Gọi
Pt
là số phần trăm Carbon
14
còn lại
trong một bộ phận của cây sinh trưởng
t
năm trước đây thì
Pt
được cho bởi công
thức
5750
100. 0,5 %.
t
Pt
Phân tích một mẫu gỗ từ công trình kiến trúc gỗ, người ta
thấy lượng Carbon
14
còn lại trong gỗ là
65,21%.
Hãy xác định số tuổi của công trình
kiến trúc đó.
A.
3475
(năm). B.
3547
(năm). C.
3574
(năm). D.
3754
(năm).
Câu 4. Cường độ một trận động đất được tính bởi công thức
0
log log ,
M AA
với
A
là biên độ rung chấn tối đa và
0
A
là một biên độ chuẩn (hằng số). Đầu thế kỷ
,XX
một trận động đất ở Nhật Bản có cường độ đo được là
9
độ Richter. Trong cùng năm
đó, trận động đất khác ở Trung Quốc có cường độ đo được là
7
độ Richter. Hỏi trận
động đất ở Nhật Bản có biên độ gấp bao nhiêu lần trận động đất ở Trung Quốc ?
A.
10
lần. B.
20
lần. C.
100
lần. D.
200
lần.
Câu 5. Cường độ một trận động đất được tính bởi công thức
0
log log ,M AA
với
A
là biên độ rung chấn tối đa và
0
A
là một biên độ chuẩn (hằng số). Đầu thế kỷ
,XX
một trận động đất ở San Francisco có cường độ
8
độ Richter. Trong cùng năm đó,
trận động đất khác Nam Mỹ có biên độ mạnh hơn gấp
4
lần. Cường độ của trận động
đất ở Nam Mỹ xấp xỉ
A.
8, 4
Richter. B.
8, 6
Richter. C.
10
Richter. D.
12
Richter.
Câu 6. Các khí thải gây hiệu ứng nhà kính là nguyên nhân chủ yếu làm trái đất nóng
lên. Theo OECD (Tổ chức hợp tác và phát triển kinh tế thế giới), khi nhiệt độ trái đất
tăng lên thì tổng giá trị kinh tế toàn cầu giảm. Người ta ước tính rằng khi nhiệt độ
3
trái đất tăng thêm
2 C
thì tổng giá trị kinh tế toàn cầu giảm 3%, còn khi nhiệt độ
trái đất tăng thêm
5 C
thì tổng giá trị kinh tế toàn cầu giảm
10%
. Biết rằng nếu
nhiệt độ trái đất tăng thêm
tC
, tổng giá trị kinh tế toàn cầu giảm
ft
% thì
.
t
f t ka
(trong đó
,
ak
là các hằng số dương). Nhiệt độ trái đất tăng thêm bao nhiêu
độ
C
thì tổng giá trị kinh tế toàn cầu giảm
20%
?
A.
6,7
C
. B.
7, 6
C
. C.
8, 4 C
. D.
9,3 C
.
Câu 7. Cho biết chu kì bán rã của chất phóng xạ radi
226
Ra
là
1602
năm (tức là một
lượng
226
Ra
sau
1602
năm phân hủy thì chỉ còn lại một nửa). Sự phân hủy được tính
theo công thức
.,
rt
S Ae
trong đó
A
là lượng chất phóng xạ ban đầu,
r
là tỉ lệ phân
hủy hàng năm
0,r
t
là thời gian phân hủy,
S
là lượng còn lại sau thời gian phân
hủy. Hỏi
5
gam
226
Ra
sau
4000
năm phân hủy sẽ còn lại bao nhiêu gam (làm tròn
đến
3
chữ số phần thập phân)?
A.
0,795 gam .
B.
0,886 gam .
C.
0,923 gam .
D.
1, 023 gam .
Câu 8. Số lượng của loại vi khuẩn A trong một phòng thí nghiệm ước tính theo công
thức
.2 ,
t
to
SS
trong đó
0
S
là số lượng vi khuẩn A ban đầu,
t
S
là số lượng vi khuẩn A
có sau
t
phút. Biết sau
3
phút thì số lượng vi khuẩn A là
625
nghìn con. Hỏi sau bao
lâu, kể từ lúc ban đầu, số lượng vi khuẩn A là
10
triệu con?
A.
6
phút. B.
7
phút. C.
8
phút. D.
9
phút.
Câu 9. Sự tăng trưởng của một loại vi khuẩn ước tính theo công thức
.,
rt
S Ae
trong
đó
A
là số lượng vi khuẩn ban đầu,
r
là tỉ lệ tăng trưởng
0,r
t
là thời gian tăng
trưởng. Biết rằng số lượng vi khuẩn ban đầu có
100
con và sau
5
giờ có
300
con. Hỏi
sau bao lâu thì số lượng vi khuẩn tăng gấp
10
lần?
A.
5
log 3
t
giờ. B.
3
log 5
t
giờ. C.
5 ln 3
ln10
t
giờ. D.
3 ln 5
ln10
t
giờ.
Câu 10. Biết rằng cuối năm
2001,
dân số Việt Nam là
78685800
người và tỉ lệ tăng
dân số năm đó là
1, 7 % .
Cho biết sự tăng dân số được ước tính theo công thức
.
.
Nr
S Ae
(trong đó
:
A
là dân số của năm lấy làm mốc tính,
S
là dân số sau
N
năm,
r
là tỉ lệ tăng dân số hàng năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào
dân số nước ta ở mức
120
triệu người?
A.
2020.
B.
2022.
C.
2025.
D.
2026.
Câu 11. Cho biết sự tăng dân số được ước tính theo công thức
.
.
Nr
S Ae
(trong đó
:A
là dân số của năm lấy làm mốc tính,
S
là dân số sau
N
năm,
r
là tỉ lệ tăng dân số
hàng năm). Theo số liệu thực tế, dân số của tỉnh A đầu năm
2010
là
1.038.229
người,
tính đến đầu năm năm
2015
là
1.153.600
người. Hỏi nếu tỉ lệ tăng dân số hàng năm
giữ nguyên thì đầu năm
2025
dân số của tỉnh trong khoảng nào?
A.
1.424.000;1.424.100 .
B.
1.424.100;1.424.200 .
4
C.
1.424.200;1.424.300 .
D.
1.424.300;1.424.400 .
Câu 12. Các nhà khoa học thực hiện nghiên cứu trên một nhóm học sinh bằng cách
cho họ xem một danh sách các loài động vật và sau đó kiểm tra xem họ nhớ được bao
nhiêu
%
mỗi tháng. Sau
t
tháng, khả năng nhớ trung bình của nhóm học sinh tính
theo công thức
75 20 ln 1 , Mt t t

(đơn vị
%
). Hỏi khoảng thời gian ngắn
nhất bao lâu thì số học sinh trên nhớ được danh sách đó dưới
10%
?
A. Khoảng
22
tháng. B. Khoảng
24
tháng.
C. Khoảng
25
tháng. D. Khoảng
32
tháng.
Câu 13. Giả sử
0
.2
t
n ft n
là số lượng cá thể trong một đám vi khuẩn tại thời
điểm
t
giờ,
0
n
là số lượng cá thể lúc ban đầu. Biết tốc độ phát triển về số lượng của vi
khuẩn tại thời điểm
t
chính là
.ft
Giả sử mẫu thử ban đầu có
0
100n
con vi
khuẩn. Vậy tốc độ phát triển sau
4
giờ là bao nhiêu con vi khuẩn?
A.
500
con. B.
1109
con. C.
1600
con. D.
3200
con.
Dạng 2. Sử dụng công thức lãi kép
Câu 14. Tỉ lệ tăng dân số hàng năm ở Việt Nam được duy trì ở mức
1,05%.
Theo số
liệu của tổng cục thống kê, dân số của Việt Nam giữa năm
2014
là
90728900
người.
Với tốc độ tăng dân số như thế thì vào giữa năm
2030
thì dân số của Việt Nam xấp xỉ
là bao nhiêu người?
A.
107026537
người. B.
107232574
người.
C.
105971355
người. D.
106118331
người.
Câu 15. Hết ngày
31
tháng
12
năm
2017,
dân số tỉnh
X
là
1, 5
triệu người. Với tốc
độ tăng dân số hàng năm không thay đổi là
1, 5 %
và chỉ có sự biến dộng do sinh - tử
thì trong năm
2027
(từ
1/1/ 2017
đến hết
31/12 / 2027
) tại tỉnh
X
có tất cả bao
nhiêu trẻ em được sinh ra, giả sử rằng tổng số người tử vong trong năm
2027
là
2700
người và chỉ là những người trên hai tuổi.
A.
28812.
B.
28426.
C.
23026.
D.
23412.
Câu 16. Một khu rừng ban đầu có trữ lượng gỗ là
53
4.10 m .
Gọi tốc độ sinh trưởng
mỗi năm của khu rừng đó là
%.r
Biết sau
5
năm thì sản lượng gỗ là xấp xỉ
53
4,8666.10 m .
Giá trị của
r
xấp xỉ bằng
A.
3, 5.
B.
4.
C.
4,5.
D.
5.
Câu 17. Số lượng động vật nguyên sinh tăng trưởng với tốc độ
0,7944
con/ngày. Giả
sử vào cuối ngày đầu tiên, số lượng động vật nguyên sinh là
2
con. Hỏi sau
6
ngày
(kể cả ngày đầu tiên), số lượng động vật nguyên sinh là bao nhiêu con?
A.
37
con. B.
48
con. C.
67
con. D.
106
con.
Câu 18. Cục điều tra dân số thế giới cho biết: Trong chiến tranh thế giới thứ hai (kéo
dài 6 năm); dân số mỗi năm giảm đi
2%
so với dân số năm liền trước đó. Vào thời hòa
5
bình sau chiến tranh thế giới thứ hai thì dân số tăng
4%
so với dân số năm liền trước
đó. Giả sử rằng, vào cuối năm thứ
2
diễn ra chiến tranh dân số thế giới là
4
tỷ người.
Kể từ thời điểm đó thì
10
năm sau thì dân số thế giới khoảng bao nhiêu tỷ người (làm
tròn đến chữ số thập phân thứ hai)?
A.
4,40.
B.
4,67.
C.
4,88.
D.
4,95.
Câu 19. Biết thể tích khí
2
CO
đầu năm
2002
là
3
m.V
Thời gian
10
năm tiếp theo,
thể tích khí
2
CO
tăng
%;m
thời gian
10
năm tiếp theo nữa, thể tích
2
CO
tăng
%.n
Thể tích khí
2
CO
đầu năm
2020
là
A.
10
3
20
100 100
m.
10
mn
V



B.
10 8
3
36
100 . 100
m.
10
mn
V

C.
18
3
1 1 m.V mn




D.
18
3
1 m.V mn
Dạng 3. Thiết lập công thức
Câu 20. Quan sát quá trình sao chép tế bào trong phòng thí nghiệm sinh học, nhà
sinh vật học nhận thấy các tế bào tăng gấp đôi mỗi phút. Biết sau một thời gian
t
phút thì có
100000
tế bào và ban đầu có
1
tế bào duy nhất. Khẳng định nào sau đây
đúng?
A.
14 15.t

B.
15 16.t

C.
16 17.t
D.
17 18.t
Câu 21. E.coli là vi khuẩn đường ruột gây tiêu chảy, đau bụng dữ dội. Cứ sau
20
phút thì số lượng vi khuẩn E.coli lại tăng gấp đôi. Ban đầu, chỉ có
60
vi khuẩn E.coli
trong đường ruột. Sau
8
giờ, số lượng vi khuẩn E.coli là bao nhiêu?
A.
158.159.469
vi khuẩn. B.
1.006.632.960
vi khuẩn.
C.
2.108.252.760
vi khuẩn. D.
3.251.603.769
vi khuẩn.
Câu 22. Một quần thể vi khuẩn bắt đầu với
100
con. Cứ sau
3
giờ đồng hồ thì số
lượng vi khuẩn lại tăng gấp đôi. Hỏi khi nào số lượng vi khuẩn đạt đến
50000
con?
A.
26,06
giờ. B.
26,6
giờ. C.
26,09
giờ. D.
26,9
giờ.
Câu 23. Một bể nước có dung tích
3
1 m
(không có nước). Người ta mở vòi cho nước
chảy vào bể. Trong giờ đầu, vận tốc nước chảy vào bể là
1
lít/phút. Trong các giờ tiếp
theo, vận tốc nước chảy giờ sau gấp đôi giờ trước. Hỏi sau khoảng thời gian bao lâu thì
bể nước đầy ?
A.
3,14
giờ. B.
5,14
giờ. C.
350
phút. D.
14915
giây.
Câu 24. Một người thả một lượng bèo hoa dâu chiếm
4%
diện tích mặt hồ. Biết rằng
cứ sau đúng một tuần bèo phát triển thành
3
lần lượng đã có và tốc độ phát triển của
bèo ở mọi thời điểm như nhau. Sau bao nhiêu ngày, lượng bèo sẽ vừa phủ kín mặt hồ?
A.
3
7 log 25.
B.
25
7
3.
C.
24
7.
3
D.
3
log 25.
6
Câu 25. Người ta thả một lượng bèo vào một hồ nước. Kết quả cho thấy sau
9
giờ bèo
sẽ sinh sôi kín cả mặt hồ. Biết rằng sau mỗi giờ, lượng bèo tăng gấp
10
lần lượng bèo
trước đó và tốc độ tăng không đổi. Hỏi sau mấy giờ thì lượng bèo phủ kín
1
3
mặt hồ?
A.
3
giờ. B.
9 log 3
giờ. C.
9
10
3
giờ. D.
9
log 3
giờ.
Phần 2. Bài toán lãi suất
Dạng 1. Cho vay một lần (lãi kép)
Câu 1. (ĐỀ THAM KHẢO 2017 – 2018) Một người gửi
100
triệu đồng vào một ngân
hàng với lãi suất
0, 4%
/tháng. Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ
sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho tháng tiếp
theo. Hỏi sau đúng
6
tháng, người đó được lĩnh số tiền (cả vốn ban đầu và lãi) gần
nhất với số tiền nào dưới đây, nếu trong khoảng thời gian này người đó không rút tiền
ra và lãi suất không thay đổi?
A.
102.016.000
đồng. B.
102.017.000
đồng.
C.
102.423.000
đồng. D.
102.424.000
đồng.
Câu 2. Một người gửi
10
triệu đồng vào ngân hàng với lãi suất
5%
/năm trong thời
gian
10
năm. Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ sau định kỳ, số tiền
lãi sẽ được nhập vào vốn ban đầu để tính lãi cho định kỳ tiếp theo. Hỏi rằng người đó
nhận được số tiền nhiều hơn hay ít hơn bao nhiêu nếu ngân hàng trả lãi suất
5
%
12
/tháng (lãi suất tháng so với lãi suất năm)?
A. Ít hơn 1.811.486,1 đồng. B. Ít hơn 1.911.486,1 đồng.
C. Bằng nhau. D. Nhiều hơn 1.811.486,1 đồng.
Câu 3. Một người lần đầu gửi vào ngân hàng
100
triệu đồng với kì hạn
3
tháng, lãi
suất
2%
/quý. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi quý, số
tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho quý tiếp theo. Sau đúng 6 tháng,
người đó gửi thêm
100
triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền
người đó nhận được một năm sau khi gửi tiền (cả vốn lẫn lãi) gần nhất với kết quả
nào sau đây?
A. 210 triệu. B. 212 triệu. C. 216 triệu. D. 220 triệu.
Câu 4. Một người dự định sẽ mua xe Honda SH với giá
80.990.000
đồng. Người đó gửi
tiết kiệm vào ngân hàng với số tiền
60.000.000
đồng với lãi suất
0,8%
/tháng. Biết
rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được
nhập vào vốn ban đầu để tính lãi cho tháng tiếp theo. Do sức ép thị trường nên mỗi
tháng loại xe Honda SH giảm
500.000
đồng. Vậy sau bao lâu người đó sẽ đủ tiền mua
xe máy?
A.
20
tháng. B.
21
tháng. C.
22
tháng. D.
23
tháng.
7
Câu 5. Một người muốn gửi tiền vào ngân hàng để đến ngày
15/ 3/ 2020
rút được
khoản tiền là
50.000.000
đồng. Lãi suất ngân hàng là
0,55%
/tháng. Biết rằng nếu
không rút tiền khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn
ban đầu để tính lãi cho tháng tiếp theo. Hỏi vào ngày
15/ 4 / 2018
người đó phải gửi
ngân hàng số tiền là bao nhiêu để đáp ứng nhu cầu trên, nếu lãi suất không thay đổi
trong thời gian người đó gửi tiền?
A.
43.593.000
đồng. B.
43.833.000
đồng.
C.
44.316.000
đồng. D.
44.074.000
đồng.
Câu 6. Ông Việt dự định gửi vào ngân hàng một số tiền với lãi suất
6,5%
/năm. Biết
rằng nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập
vào vốn ban đầu để tính lãi cho năm tiếp theo. Tính số tiền tối thiểu
x
triệu đồng
x
ông Việt gửi vào ngân hàng để sau
3
năm số tiền lãi đủ mua một chiếc xe gắn
máy trị giá
30
triệu đồng.
A.
140
x
triệu đồng. B.
145x
triệu đồng.
C.
150
x
triệu đồng. D.
154x
triệu đồng.
Câu 7. Một người gửi tiết kiệm vào ngân hàng
200
triệu đồng theo thể thức lãi kép
(tức là tiền lãi được cộng vào vốn kỳ tiếp theo). Ban đầu người đó gửi với kỳ hạn
3
tháng, lãi suất
2%
/ kỳ hạn, sau hai năm người đó thay đổi phương thức gửi, chuyển
thành kỳ hạn một tháng với lãi suất
0, 6%
/tháng. Tính tổng số tiền lãi và gốc nhận
được sau
5
năm (kết quả làm tròn tới đơn vị nghìn đồng).
A.
290.640.000
đồng. B.
290.642.000
đồng.
C.
290.646.000
đồng. D.
290.644.000
đồng.
Câu 8. (ĐỀ CHÍNH THỨC 2016 – 2017) Một người gửi 50 triệu đồng vào ngân hàng
với lãi suất
6% /
năm. Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi
năm, số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho năm tiếp theo. Hỏi sau
ít nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn 100 triệu đồng bao gồm
cả gốc và lãi? Giả sử trong suốt thời gian gửi lãi suất không đổi và người đó không rút
tiền ra.
A. 11 năm. B. 12 năm. C. 13 năm. D. 14 năm.
Câu 9. Ông An gửi
320
triệu đồng vào ngân hàng ACB và VietinBank theo phương
thức lãi kép. Số tiền thứ nhất gửi vào ngân hàng ACB với lãi suất
2,1%
/quý trong
thời gian
15
tháng. Số tiền còn lại gửi vào ngân hàng VietinBank với lãi suất
0,73%
/tháng trong thời gian
9
tháng. Biết tổng số tiền lãi ông An nhận được ở hai
ngân hàng là
26670725,95
đồng. Hỏi số tiền ông An lần lượt ở hai ngân hàng ACB và
VietinBank là bao nhiêu?
A.
120
triệu đồng và
200
triệu đồng. B.
140
triệu đồng và
180
triệu đồng.
C.
180
triệu đồng và
140
triệu đồng. D.
200
triệu đồng và
120
triệu đồng.
Câu 10. (ĐỀ CHÍNH THỨC 2016 – 2017) Đầu năm 2016, ông An thành lập một
công ty. Tổng số tiền ông An dùng để trả lương cho nhân viên trong năm 2016 là 1 tỷ
8
đồng. Biết rằng cứ sau mỗi năm thì tổng số tiền dùng để trả lương cho nhân viên
trong cả năm đó tăng thêm
15%
so với năm trước. Hỏi năm nào dưới đây là năm đầu
tiên mà tổng số tiền ông An dùng để trả lương cho nhân viên trong cả năm lớn hơn 2
tỷ đồng?
A. Năm 2020. B. Năm 2021. C. Năm 2022. D. Năm 2023.
Dạng 2. Gửi tiền đầu mỗi định kỳ (gửi tiết kiệm)
Cứ đầu mỗi định kỳ gửi vào ngân hàng
M
triệu, lãi suất kép
%r
/định kỳ. Hỏi sau
n
định kỳ số tiền thu được là bao nhiêu?
Ta xây dựng bảng sau:
Định kỳ
Đầu định kỳ
Cuối định kỳ
1
M
1Mr
2
1M rM
2
11
11
M rM r
Mr r







3
2
11M r rM




2
32
1 1 .1
111
M r rM r
Mr r r








 


n
1 ... 1 .
n
Mr r




Vậy sau
n
định kỳ ta được số tiền:
11
1 ... 1 1 . .
n
n
r
TM r r M r
r





Từ đó suy ra
11 1
n
Tr
M
rr




và
1
log 1 .
1
r
Tr
n
Mr






Câu 11. Một người gửi tiết kiệm ngân hàng, mỗi tháng gửi đều đặn vào ngân hàng
1
triệu đồng với lãi suất kép
1%
/tháng. Gửi được hai năm ba tháng người đó rút toàn
bộ tiền vốn và lãi. Số tiền người đó nhận được là
A.
26
100. 1,01 1



triệu đồng. B.
27
100. 1,01 1



triệu đồng.
C.
26
101. 1,01 1



triệu đồng. D.
27
101. 1,01 1



triệu đồng.
Câu 12. Một người mỗi đầu tháng đều đặn gửi vào ngân hàng một khoản tiền
M
theo hình thức lãi kép với lãi suất
0, 6%
/tháng. Biết đến cuối tháng thứ
15
thì người
đó có số tiền là
10
triệu đồng (cả vốn và lãi). Hỏi số tiền
M
gần với số tiền nào nhất
trong các số sau?
A.
535.000
đồng. B.
613.000
đồng. C.
635.000
đồng. D.
643.000
đồng.
Câu 13. Một người muốn có
2
tỷ tiền tiết kiệm sau
6
năm gửi ngân hàng bằng cách
môi năm gửi vào ngân hàng số tiền bằng nhau với lãi suất ngân hàng là
8%
/năm và
lãi hàng năm được nhập vào vốn. Hỏi số tiền mà người đó phải gửi vào ngân hàng sô
9
tiên hàng năm là bao nhiêu? Giả thiết rằng lãi suât không thay đôi và sô tiên đươc
làm tròn đên đơn vị nghìn đông.
A.
251
triệu. B.
252,5
triệu. C.
253
triệu. D.
253,5
triệu.
Câu 14. Đúng ngày
01
mỗi tháng anh A gửi vào ngân hàng
3
triệu đồng với lãi suất
0,7%
/tháng. Biết không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng tiền lãi sẽ
nhập vào gốc để tính lãi cho tháng tiếp theo. Hỏi sau ít nhất bao nhiêu tháng thì anh
A có được số tiền cả gốc và lãi nhiều hơn
100
triệu đồng? Giả định trong suốt thời
gian gửi, lãi suất không đổi, được tính lãi ngay từ ngày gửi và anh A không rút tiền
ra.
A.
28
tháng. B.
29
tháng. C.
30
tháng. D.
33
tháng.
Dạng 3. Vay trả góp
Vay ngân hàng
M
triệu đồng, lãi suất
%r
/định kỳ. Cứ cuối mỗi định kỳ trả ngân
hàng
m
triệu. Hỏi sau
n
định kỳ số tiền còn nợ là bao nhiêu?
Ta xây dựng bảng sau:
Định kỳ
Đầu định kỳ
Cuối định kỳ
1
M
1M rm
2
1M rm
2
11
1 11
M rm rm
M rm r

 




3
2
32
1 1 11
1 1 11
M r m r rm
M rm r r










n
12
1 1 11
n nn
M rm r r





Vậy sau
n
định kỳ, số tiền còn nợ
12
1 1 11
n nn
TM r m r r





1 1 1.
nn
m
Mr r
r

 


Từ đó suy ra nếu định kỳ thứ
n
mà trả hết nợ thì
1
0.
11
n
n
M rr
Tm
r


Câu 15. (ĐỀ MINH HỌA 2016 – 2017) Ông Việt vay ngân hàng
100
triệu đồng, với
lãi suất
1%
/tháng. Ông muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một tháng
kể từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một
tháng, số tiền hoàn nợ ở mỗi lần là như nhau và trả hết tiền nợ sau đúng
3
tháng kể
từ ngày vay. Hỏi theo cách đó, số tiền
m
mà ông Việt sẽ phải trả cho ngân hàng trong
mỗi lần hoàn nợ là bao nhiêu? Biết rằng lãi suất ngân hàng không thay đổi trong thời
gian ông Việt hoàn nợ.
10
A.
3
100. 1,01
3
m
(triệu đồng). B.
3
3
1, 01
1, 01 1
m
(triệu đồng).
C.
100 1,03
3
m
(triệu đồng). D.
3
3
120. 1,12
1, 12 1
m
(triệu đồng).
Câu 16. Một người vay ngân hàng
500
triệu đồng, với lãi suất
1, 2%
/tháng. Sau đúng
một tháng kể từ ngày vay, người đó bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách
nhau đúng một tháng, số tiền hoàn nợ ở mỗi lần là như nhau và bằng
10
triệu đồng.
Hỏi sau ít nhất bao nhiêu tháng thì người đó trả hết nợ? Biết rằng, lãi suất ngân
hàng không thay đổi trong thời người đó hoàn nợ.
A.
70
tháng. B.
77
tháng. C.
80
tháng. D.
85
tháng.
Câu 17. Bạn Hùng trúng tuyển Đại học nhưng vì do không đủ tiền nộp học phí nên
Hùng quyết định vay ngân hàng trong
4
năm, mỗi năm
4.000.000
đồng để nộp học
phí với lãi suất
3%
/ năm. Sau khi tốt nghiệp Đại học, bạn Hùng phải trả góp hàng
tháng cho ngân hàng số tiền
m
(không đổi) cùng với lãi suất
0,25%
/tháng trong vòng
5
năm. Tính số tiền
m
hàng tháng mà bạn Hùng phải trả cho ngân hàng (làm tròn
đến kết quả hàng đơn vị).
A.
309.604,14
đồng. B.
309.718,166
đồng.
C.
312.518,166
đồng. D.
398.402,12
đồng.
Dạng 4. Bài tập tổng hợp
Câu 18. [Lãi suất tăng dần] Ông Bách dự định đầu tư khoản tiền
20
triệu đồng vào
một dự án với lãi suất tăng dần:
3,35%
/năm trong
3
năm đầu,
3,75%
/năm tong
2
năm kế tiếp và
4,8%
/năm ở
5
năm cuối. Khoản tiền mà ông Bách nhận được (cả vốn
và lãi) cuối năm thứ
10
là
A.
25
triệu. B.
30
triệu. C.
35
triệu. D.
40
triệu.
Câu 19. Năm
2017
số tiền để đổ đầy bình xăng cho một chiếc xe máy trung bình là
70000
đồng. Giả sử tỉ lệ lạm phát hàng năm của Việt Nam trong 10 năm tới không
đổi với mức
5%,
tính số tiền để đổ đầy bình xăng cho chiếc xe đó vào năm
2022.
A.
5
70000.0,05
đồng. B.
6
70000.0,05
đồng.
C.
5
70000.1,05
đồng. D.
6
70000.1,05
đồng.
Câu 20. Một người mua chiếc xe máy Air Blade với giá
45
triệu đồng. Biết rằng giá
trị khấu hao tài sản xe giảm
60%
mỗi năm. Biết rằng sau
n
năm thì giá trị xe chỉ
còn
5
triệu đồng. Giá trị
n
gần nhất với đáp án nào sau đây?
A.
2
năm. B.
2,5
năm. C.
3
năm. D.
3, 5
năm.
Câu 21. Đầu năm
2017,
anh Hùng có xe công nông trị giá
100
triệu đồng. Biết mỗi
tháng thì xe công nông hao mòn mất
0, 4%
giá trị, đồng thời anh Hùng làm ra được
6
triệu đồng (số tiền làm ra mỗi tháng là không đổi). Hỏi sau đúng một năm, tổng số
11
tiền (bao gồm tiền giá xe công nông và tiền anh Hùng làm ra) mà anh Hùng có là bao
nhiêu?
A.
172
triệu. B.
167,3042
triệu. C.
144
triệu. D.
120,3042
triệu.
Câu 22. Theo thống kê tài chính của thị xã An Nhơn, tỉnh Bình Định, trong dịp Tết
Nguyên Đán năm
2015,
làng nghề trồng mai cảnh xã An Nhơn đạt tổng doanh thu
khoảng
15
tỷ đồng nhờ vào việc bán mai cảnh. Biết rằng trong các năm tiếp theo tổng
doanh thu luôn tăng ổn định và doanh thu trong năm đó cao hơn so với năm trước
6,27%.
Hỏi tổng doanh thu của làng nghề trồng mai cảnh xã An Nhơn vào dịp Tết
Nguyên Đán năm
2018
là bao nhiêu? (làm tròn đến tỷ đồng)
A.
17
tỷ đồng. B.
18
tỷ đồng. C.
19
tỷ đồng. D.
20
tỷ đồng.
Câu 23. [Tiền lương tăng theo chu kỳ] Một kỹ sư được nhận lương khởi điểm là
8000000
đồng/tháng. Cứ sau hai năm lương mỗi tháng của kỹ sư đó được tăng thêm
10%
so với mức lương hiện tại. Tổng số tiền kỹ sư đó nhận được sau
6
năm làm việc
A.
633600000
đồng. B.
635520000
đồng.
C.
696960000
đồng. D.
766656000
đồng.
Câu 24. Theo dự báo với mức tiêu thụ dầu không đổi như hiện nay thì trữ lượng dầu
của nước A sẽ hết sau
100
năm tới. Nhưng do nhu cầu thực tế, mức tiêu thụ tăng lên
4%
mỗi năm. Hỏi sau bao nhiêu năm số dầu dự trữ của nước A sẽ hết?
A.
40.
B.
41.
C.
42.
D.
43.
Câu 25. Sau một tháng thi công công trình xây dựng Nhà học thể dục của Trường X
đã thực hiện được một khối lượng công việc. Nếu tiếp tục với tiến độ như vậy thì dự
kiến sau đúng
23
tháng nữa công trình sẽ hoàn thành. Để sớm hoàn thành công
trình và kịp thời đưa vào sử dụng, công ty xây dựng quyết định từ tháng thứ
2
, mỗi
tháng tăng
4%
khối lượng công việc so với tháng kề trước. Hỏi công trình sẽ hoàn
thành ở tháng thứ mấy sau khi khởi công?
A.
17.
B.
18.
C.
19.
D.
20.
Câu 26. [So sánh lãi không kỳ hạn và lãi có kỳ hạn] Ngân hàng BIDV Việt Nam
đang áp dụng hình thức lãi kép với mức lãi suất: không kỳ hạn là
0, 2%
/năm, kỳ hạn
3
tháng là
1, 2%
/quý. Ông A đến ngân hàng BIDV để gửi tiết kiệm với số tiền ban
đầu là
300
triệu đồng. Nếu gửi không kỳ hạn mà ông A muốn thu về cả vốn và lãi
bằng hoặc vượt quá
305
triệu đồng thì ông A phải gửi ít nhất
n
tháng
*
.n
Hỏi
nếu cùng số tiền ban đầu và cũng số tháng đó, ông A gửi tiết kiệm có kỳ hạn
3
tháng
thì ông A sẽ nhận được số tiền cả vốn lẫn lãi là bao nhiêu?
A.
444.785.421
đồng. B.
444.711.302
đồng.
C.
446.490.147
đồng. D.
447.190.465
đồng.
Câu 27. [Gửi tiết kiệm nhưng số tiền tăng dần] Một người lập kế hoạch gửi tiết
kiệm ngân hàng như sau: Đầu tháng
01
năm
2018,
người đó gửi
10
triệu đồng; sau
mỗi đầu tháng tiếp theo, người đó gửi số tiền nhiều hơn
10%
so với số tiền đã gửi ở
tháng liền trước đó. Biết rằng lãi suất ngân hàng không đổi là
0,5%
mỗi tháng và
12
được tính theo hình thức lãi kép. Với kế hoạch như vậy, đến hết tháng
12
năm
2019,
số tiền của người đó trong tài khoản tiết kiệm là bao nhiêu? (Làm tròn đến hàng
nghìn)
A.
832.765.000
đồng. B.
918.165.000
đồng.
C.
922.756.000
đồng. D.
926.281.000
đồng.
Câu 28. [Gửi và rút hàng tháng] Ngày
01
tháng
01
năm
2017,
ông An gửi
800
triệu đồng vào một ngân hàng với lãi suất
0,5%
/tháng. Từ đó, cứ tròn mỗi tháng ông
đến ngân hàng rút
6
triệu để chi tiêu cho gia đình. Hỏi đến ngày
01
tháng
01
năm
2018,
sau khi rút tiền, số tiền tiết kiệm của ông An còn lại là bao nhiêu? Biết rằng lãi
suất trong suốt thời gian ông An gửi không thay đổi.
A.
11
800. 1,005 72
(triệu đồng). B.
12
800. 1,005 72
(triệu đồng).
C.
11
1200 400. 1,005
(triệu đồng). D.
12
1200 400. 1,005
(triệu đồng).
Câu 29. [Gửi và rút hàng tháng] Một hội khuyến học đã kêu gọi sự ủng hộ của các
nhà hảo tâm được
120
triệu đồng. Hội khuyến học gửi số tiền đó vào ngân hàng với
lãi suất
0,75%
/tháng với dự định hàng tháng rút
m
triệu đồng làm khuyến học cho
học sinh nghèo vượt khó. Hội khuyến học bắt đầu trao quà cho học sinh sau một
tháng gửi tiền vào ngân hàng. Để số tiền (cả lãi và
120
triệu đồng tiền gốc) đủ trao
cho học sinh trong
10
tháng thì số tiền
m
mà hàng tháng Hội khuyến học rút ra tối
đa (lấy kết quả chính xác đến chữ số thập phân thứ nhất) là
A.
12,3.
B.
12,4.
C.
12,5.
D.
12,6.
Câu 30. [Trả góp nhưng bị điều chỉnh lãi suất] Một người vay ngân hàng
40
triệu đồng, với lãi suất
0,85%
/tháng. Sau đúng một tháng kể từ ngày vay, người đó
bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ
ở mỗi lần là như nhau và bằng
500
nghìn đồng. Sau một năm mức lãi suất của ngân
hàng được điều chỉnh lên là
1,15%
/tháng và người vay muốn nhanh chóng hết nợ nên
đã thỏa thuận trả
1
triệu
500
nghìn đồng cho mỗi tháng. Hỏi phải mất bao nhiêu lâu
người đó mới trả hết nợ?
A.
30
tháng. B.
31
tháng. C.
42
tháng. D.
43
tháng.
1
HUỲNH ĐỨC KHÁNH
0975120189
Ứng dụng
HÀM SỐ MŨ – HÀM SỐ LOGARIT
Sự phân rã của các chất phóng xạ
Phần 1.
Một số bài toán áp dụng
(tăng trưởng, phóng xạ, động đất,…)
Phần 2. Bài toán lãi suất
2
Phần 1. Một số bài toán áp dụng
Dạng 1. Áp dụng công thức có sẵn
Câu 1. Một lon nước soda
0
80
F
được đưa vào một máy làm lạnh chứa đá tại
0
32 .
F
Nhiệt độ của soda ở phút thứ
t
được tính theo định luật Newton bởi công thức
32 48. 0,9 .
t
Tt
Phải làm mát soda trong bao lâu để nhiệt độ là
0
37 .F
Chọn đáp
án gần nhất với kết quả?
A.
15, 6
phút. B.
17
phút. C.
21, 5
phút. D.
25, 6
phút.
Lời giải. Thay vào công thức ta được:
37 32 48. 0,9 21,5.
t
t

Chọn C.
Câu 2. với
t
là khoảng thời gian tính bằng giờ và
0
Q
là dung lượng nạp tối đa (pin
đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là
0%
) thì sau bao lâu sẽ nạp được
90%
(kết quả làm tròn đến hàng phần trăm)?
A.
1, 21t
giờ. B.
1, 22t
giờ. C.
1, 3 4t
giờ. D.
1, 5 4t
giờ.
Lời giải. Với
0
90
,
100
QQ
thay vào ta được
3
2
90
1 1,535
100
t
et

giờ. Chọn D.
Câu 3. Một loài cây xanh trong quá trình quang hợp sẽ nhận một lượng nhỏ Carbon
14
(một đơn vị của Carbon). Khi cây đó chết đi thì hiện tượng quang hợp cũng sẽ
ngưng và nó sẽ không nhận Carbon
14
nữa. Lượng Carbon
14
của nó sẽ phân hủy
chậm chạp và chuyển hóa thành Nitơ
14.
Gọi
Pt
là số phần trăm Carbon
14
còn lại
trong một bộ phận của cây sinh trưởng
t
năm trước đây thì
Pt
được cho bởi công
thức
5750
100. 0,5 %.
t
Pt
Phân tích một mẫu gỗ từ công trình kiến trúc gỗ, người ta
thấy lượng Carbon
14
còn lại trong gỗ là
65,21%.
Hãy xác định số tuổi của công trình
kiến trúc đó.
A.
3475
(năm). B.
3547
(năm). C.
3574
(năm). D.
3754
(năm).
Lời giải. Thay số ta được
5750
65,21% 100. 0,5 % 3547.
t
t 
Chọn B.
Câu 4. Cường độ một trận động đất được tính bởi công thức
0
log log ,M AA
với
A
là biên độ rung chấn tối đa và
0
A
là một biên độ chuẩn (hằng số). Đầu thế kỷ
,XX
một trận động đất ở Nhật Bản có cường độ đo được là
9
độ Richter. Trong cùng năm
đó, trận động đất khác ở Trung Quốc có cường độ đo được là
7
độ Richter. Hỏi trận
động đất ở Nhật Bản có biên độ gấp bao nhiêu lần trận động đất ở Trung Quốc ?
A.
10
lần. B.
20
lần. C.
100
lần. D.
200
lần.
Lời giải. Cường độ trân động đất ở Nhật Bản là:
9
1
10
9 log log 10 .
o
A
AA
A

1
Cường độ trân động đất ở Trung Quốc là:
7
2
20
7 log log 10 .
o
A
AA
A

2
Từ
1
và
2,
suy ra
12
100 .AA
Chọn C.
3
Câu 5. Cường độ một trận động đất được tính bởi công thức
0
log log ,M AA
với
A
là biên độ rung chấn tối đa và
0
A
là một biên độ chuẩn (hằng số). Đầu thế kỷ
,XX
một trận động đất ở San Francisco có cường độ
8
độ Richter. Trong cùng năm đó,
trận động đất khác Nam Mỹ có biên độ mạnh hơn gấp
4
lần. Cường độ của trận động
đất ở Nam Mỹ xấp xỉ
A.
8, 4
Richter. B.
8, 6
Richter. C.
10
Richter. D.
12
Richter.
Lời giải. Trận động đất ở San Francisco có cường độ
8
độ Richter, khi đó áp dụng
công thức
10 0
log log 8 log log .M AA AA 
1
Trận động đất ở Nam Mỹ có biên độ là
4,A
khi đó cường độ của trận động đất ở Nam
Mỹ là:
1
2 02 0 2
log 4 log log 4 log log log 4 8 8, 6M A AM A A M  
độ
Richter. Chọn B.
Câu 6. Các khí thải gây hiệu ứng nhà kính là nguyên nhân chủ yếu làm trái đất nóng
lên. Theo OECD (Tổ chức hợp tác và phát triển kinh tế thế giới), khi nhiệt độ trái đất
tăng lên thì tổng giá trị kinh tế toàn cầu giảm. Người ta ước tính rằng khi nhiệt độ
trái đất tăng thêm
2 C
thì tổng giá trị kinh tế toàn cầu giảm 3%, còn khi nhiệt độ
trái đất tăng thêm
5 C
thì tổng giá trị kinh tế toàn cầu giảm
10%
. Biết rằng nếu
nhiệt độ trái đất tăng thêm
tC
, tổng giá trị kinh tế toàn cầu giảm
ft
% thì
.
t
f t ka
(trong đó
, ak
là các hằng số dương). Nhiệt độ trái đất tăng thêm bao nhiêu
độ
C
thì tổng giá trị kinh tế toàn cầu giảm
20%
?
A.
6,7 C
. B.
7, 6 C
. C.
8, 4 C
. D.
9,3 C
.
Lời giải. Theo đề bài, ta có
2
5
. 3%
1.
. 10%
ka
ka
Cần tìm
t
thỏa mãn
. 20%
t
ka
.
Từ
2
3%
1 k
a

và
3
10
3
a
.
Khi đó
3
2
2
10
3
3% 20 20
. 20% . 20% 2 log 6,7.
33
t tt
ka a a t
a
 
Chọn A.
Câu 7. Cho biết chu kì bán rã của chất phóng xạ radi
226
Ra
là
1602
năm (tức là một
lượng
226
Ra
sau
1602
năm phân hủy thì chỉ còn lại một nửa). Sự phân hủy được tính
theo công thức
.,
rt
S Ae
trong đó
A
là lượng chất phóng xạ ban đầu,
r
là tỉ lệ phân
hủy hàng năm
0,r
t
là thời gian phân hủy,
S
là lượng còn lại sau thời gian phân
hủy. Hỏi
5
gam
226
Ra
sau
4000
năm phân hủy sẽ còn lại bao nhiêu gam (làm tròn
đến
3
chữ số phần thập phân)?
A.
0,795 gam .
B.
0,886 gam .
C.
0,923 gam .
D.
1, 023 gam .
Lời giải. Khi
tT
(chu kỳ bán rã) thì
.
2
A
S
Thay vào công thức ta được
.
1 ln 2
..
2
rT
A Ae r
T

4
Khi đó
ln 2
ln 2 5
4000, 1602
1
. . . . 0,886 gam .
2
t
t
T
t
rt A
T
T
tT
S Ae Ae A e A





Chọn B.
Chú ý:
0
1
..
2
t
T
rt S m
Am
S Ae A



công thức trở thành
0
1
.
2
t
T
mm


Câu 8. Số lượng của loại vi khuẩn A trong một phòng thí nghiệm ước tính theo công
thức
.2 ,
t
to
SS
trong đó
0
S
là số lượng vi khuẩn A ban đầu,
t
S
là số lượng vi khuẩn A
có sau
t
phút. Biết sau
3
phút thì số lượng vi khuẩn A là
625
nghìn con. Hỏi sau bao
lâu, kể từ lúc ban đầu, số lượng vi khuẩn A là
10
triệu con?
A.
6
phút. B.
7
phút. C.
8
phút. D.
9
phút.
Lời giải. Vì sau
3
phút thì số lượng vi khuẩn A là
625
nghìn con nên ta có phương
trình
3
0
625.000 .2 78125
o
SS 
con.
Để số lượng vi khuẩn A là
10
triệu con thì
7
10 78125.2 7.
t
t 
Chọn B.
Câu 9. Sự tăng trưởng của một loại vi khuẩn ước tính theo công thức
.,
rt
S Ae
trong
đó
A
là số lượng vi khuẩn ban đầu,
r
là tỉ lệ tăng trưởng
0,
r
t
là thời gian tăng
trưởng. Biết rằng số lượng vi khuẩn ban đầu có
100
con và sau
5
giờ có
300
con. Hỏi
sau bao lâu thì số lượng vi khuẩn tăng gấp
10
lần?
A.
5
log 3
t
giờ. B.
3
log 5
t
giờ. C.
5 ln 3
ln10
t
giờ. D.
3 ln 5
ln10
t
giờ.
Lời giải. Thay các dữ kiện ta có phương trình
5
ln 3
300 100. .
5
r
er 
Để số lượng vi khuẩn tăng
10
lần (tức
1000
con), ta có
ln 3
5
5
1000 100. .
log 3
t
et 
Chọn A.
Câu 10. Biết rằng cuối năm
2001,
dân số Việt Nam là
78685800
người và tỉ lệ tăng
dân số năm đó là
1, 7 % .
Cho biết sự tăng dân số được ước tính theo công thức
.
.
Nr
S Ae
(trong đó
:A
là dân số của năm lấy làm mốc tính,
S
là dân số sau
N
năm,
r
là tỉ lệ tăng dân số hàng năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào
dân số nước ta ở mức
120
triệu người?
A.
2020.
B.
2022.
C.
2025.
D.
2026.
Lời giải. Ta có
6
.
1 100 120.10
. .ln .ln 24,825.
1,7 78685800
Nr
S
S Ae N
rA

Lúc đấy là năm
2001 25 2026.
Chọn D.
Câu 11. Cho biết sự tăng dân số được ước tính theo công thức
.
.
Nr
S Ae
(trong đó
:A
là dân số của năm lấy làm mốc tính,
S
là dân số sau
N
năm,
r
là tỉ lệ tăng dân số
hàng năm). Theo số liệu thực tế, dân số của tỉnh A đầu năm
2010
là
1.038.229
người,
tính đến đầu năm năm
2015
là
1.153.600
người. Hỏi nếu tỉ lệ tăng dân số hàng năm
giữ nguyên thì đầu năm
2025
dân số của tỉnh trong khoảng nào?
5
A.
1.424.000;1.424.100 .
B.
1.424.100;1.424.200 .
C.
1.424.200;1.424.300 .
D.
1.424.300;1.424.400 .
Lời giải. Gọi
1
S
là dân số đầu năm
2015,
ta có
1
1.153.600 ngöôøi
5 naêm .
1.038.229 ngöôøi
S
N
A
Từ hệ thức
11
.
1
ln ln
..
5
Nr
SS
AA
S Ae r
N

Gọi
2
S
là dân số đầu năm
2025,
ta có
1
ln
15.
15.
5
2
. 1.038.229. 1.424.227,71.
S
A
r
S Ae e
Chọn C.
Câu 12. Các nhà khoa học thực hiện nghiên cứu trên một nhóm học sinh bằng cách
cho họ xem một danh sách các loài động vật và sau đó kiểm tra xem họ nhớ được bao
nhiêu
%
mỗi tháng. Sau
t
tháng, khả năng nhớ trung bình của nhóm học sinh tính
theo công thức
75 20 ln 1 , Mt t t
(đơn vị
%
). Hỏi khoảng thời gian ngắn
nhất bao lâu thì số học sinh trên nhớ được danh sách đó dưới
10%
?
A. Khoảng
22
tháng. B. Khoảng
24
tháng.
C. Khoảng
25
tháng. D. Khoảng
32
tháng.
Lời giải. Yêu cầu bài toán tương đương với
75 20 ln 1 10t 
13 13
44
min
13
ln 1 1 1 25.
4
t
t t e te t

Chọn C.
Câu 13. Giả sử
0
.2
t
n ft n
là số lượng cá thể trong một đám vi khuẩn tại thời
điểm
t
giờ,
0
n
là số lượng cá thể lúc ban đầu. Biết tốc độ phát triển về số lượng của vi
khuẩn tại thời điểm
t
chính là
.ft
Giả sử mẫu thử ban đầu có
0
100n
con vi
khuẩn. Vậy tốc độ phát triển sau
4
giờ là bao nhiêu con vi khuẩn?
A.
500
con. B.
1109
con. C.
1600
con. D.
3200
con.
Lời giải. Tốc độ phát triển của vi khuẩn tại thời điểm
t
là
0
.2 .ln 2.
t
ft n
Khi đó tốc độ phát triểu sau
4
giờ là
4
4 100.2 .ln 2 1109f

con. Chọn B.
Dạng 2. Sử dụng công thức lãi kép
Câu 14. Tỉ lệ tăng dân số hàng năm ở Việt Nam được duy trì ở mức
1,05%.
Theo số
liệu của tổng cục thống kê, dân số của Việt Nam giữa năm
2014
là
90728900
người.
Với tốc độ tăng dân số như thế thì vào giữa năm
2030
thì dân số của Việt Nam xấp xỉ
là bao nhiêu người?
A.
107026537
người. B.
107232574
người.
C.
105971355
người. D.
106118331
người.
6
Lời giải. Với bài này khác với hai bài trước là đề không cho công thức
.
..
Nr
S Ae
Do
đó ta áp dụng cách tính lãi kép
1
n
TM r
với
90728900, 1,05%, 16.rM n
Ta
tính được
107232574,1.T
Chọn B.
Câu 15. Hết ngày
31
tháng
12
năm
2017,
dân số tỉnh
X
là
1, 5
triệu người. Với tốc
độ tăng dân số hàng năm không thay đổi là
1, 5 %
và chỉ có sự biến dộng do sinh - tử
thì trong năm
2027
(từ
1/1/ 2017
đến hết
31/12 / 2027
) tại tỉnh
X
có tất cả bao
nhiêu trẻ em được sinh ra, giả sử rằng tổng số người tử vong trong năm
2027
là
2700
người và chỉ là những người trên hai tuổi.
A.
28812.
B.
28426.
C.
23026.
D.
23412.
Lời giải. Đề không cho công thức
.
.
Nr
S Ae
nên ta sử dụng công thức tính lãi kép.
Dân số tỉnh
X
đến cuối năm
2026
là
9
2026
1,5. 1 1,5% 1.715.085T

người.
Dân số tỉnh
X
đến cuối năm
2027
là
10
2027
1,5. 1 1,5% 1.740.811
T 
người.
Suy ra dân số tỉnh
X
tăng lên trong năm
2027
là
2027 2026
25.726TT
người.
Mà số dân tăng trong thời gian từ
2026
đến
2027
là số trẻ em được sinh ra trừ số
người tử vong. Do đó số trẻ em sinh ra trong năm
2027
là:
25726 2700 28426
người. Chọn B.
Câu 16. Một khu rừng ban đầu có trữ lượng gỗ là
53
4.10 m .
Gọi tốc độ sinh trưởng
mỗi năm của khu rừng đó là
%.r
Biết sau
5
năm thì sản lượng gỗ là xấp xỉ
53
4,8666.10 m .
Giá trị của
r
xấp xỉ bằng
A.
3, 5.
B.
4.
C.
4,5.
D.
5.
Lời giải. Trữ lượng gỗ sau một năm của khu rừng là:
55 5
1
4.10 4.10 . % 4.10 1 % .T rr

Trữ lượng gỗ sau năm thứ hai của khu rừng là:
2
5
2
4.10 1 % .Tr

Trữ lượng gỗ sau
5
năm của khu rừng là:
5
55
5
4.10 1 % 4,8666.10 4.Tr r 
Chọn B.
Câu 17. Số lượng động vật nguyên sinh tăng trưởng với tốc độ
0,7944
con/ngày. Giả
sử vào cuối ngày đầu tiên, số lượng động vật nguyên sinh là
2
con. Hỏi sau
6
ngày
(kể cả ngày đầu tiên), số lượng động vật nguyên sinh là bao nhiêu con?
A.
37
con. B.
48
con. C.
67
con. D.
106
con.
Lời giải. Ta xem đây là bài toán lãi kép với công thức
1.
n
TM r

Với
2, 0,7944Mr
và
5n
(chú ý) nên
5
2. 1 0,7944 37T 
con. Chọn A.
Câu 18. Cục điều tra dân số thế giới cho biết: Trong chiến tranh thế giới thứ hai (kéo
dài 6 năm); dân số mỗi năm giảm đi
2%
so với dân số năm liền trước đó. Vào thời hòa
bình sau chiến tranh thế giới thứ hai thì dân số tăng
4%
so với dân số năm liền trước
đó. Giả sử rằng, vào cuối năm thứ
2
diễn ra chiến tranh dân số thế giới là
4
tỷ người.
7
Kể từ thời điểm đó thì
10
năm sau thì dân số thế giới khoảng bao nhiêu tỷ người (làm
tròn đến chữ số thập phân thứ hai)?
A.
4,40.
B.
4,67.
C.
4,88.
D.
4,95.
Lời giải.
10
năm đó gồm
4
năm chiến tranh và
6
năm hòa bình. Do đó, dân số sẽ
được tính là:
46
46
24
4. 1 . 1 4. 0,98 . 1,04 4,67
100 100









tỷ người. Chọn B.
Câu 19. Biết thể tích khí
2
CO
đầu năm
2002
là
3
m.V
Thời gian
10
năm tiếp theo,
thể tích khí
2
CO
tăng
%;m
thời gian
10
năm tiếp theo nữa, thể tích
2
CO
tăng
%.n
Thể tích khí
2
CO
đầu năm
2020
là
A.

10
3
20
100 100
m.
10
mn
V



B.
10 8
3
36
100 . 100
m.
10
mn
V

C.
18
3
1 1 m.
V mn




D.
18
3
1 m.V mn
Lời giải. Đầu năm
2003
thể tích khí
2
CO
là:
2003
100
...
100 100
mm
V VV V

Đầu năm
2004
thể tích khí
2
CO
là:
2
2004
100
.
100
m
VV


Vậy ta có quy luật nên sẽ
nhẩm nhanh như sau: từ đầu năm
2002
đến đầu năm
2020
là
18
năm, trong đó
10
năm đầu chỉ số tăng là
%,
m
8
năm sau chỉ số tăng là
%.n
Vậy thể tích cần tính
10 8
10 8
2020
36
100 100
100 100
.
100 100
10
mn
mn
VV V











Chọn B.
Dạng 3. Thiết lập công thức
Câu 20. Quan sát quá trình sao chép tế bào trong phòng thí nghiệm sinh học, nhà
sinh vật học nhận thấy các tế bào tăng gấp đôi mỗi phút. Biết sau một thời gian
t
phút thì có
100000
tế bào và ban đầu có
1
tế bào duy nhất. Khẳng định nào sau đây
đúng?
A.
14 15.t
B.
15 16.t
C.
16 17.t
D.
17 18.t
Lời giải. Do ban đầu có một tế bào duy nhất nên:
Sau phút sao chép thứ nhất số tế bào là:
1
2;T
Sau phút sao chép thứ hai số tế bào là:
2
2
2;T
Sau phút sao chép thứ
t
số tế bào là:
2 100000 16,61.
t
t
Tt 
Chọn C.
Câu 21. E.coli là vi khuẩn đường ruột gây tiêu chảy, đau bụng dữ dội. Cứ sau
20
phút thì số lượng vi khuẩn E.coli lại tăng gấp đôi. Ban đầu, chỉ có
60
vi khuẩn E.coli
trong đường ruột. Sau
8
giờ, số lượng vi khuẩn E.coli là bao nhiêu?
A.
158.159.469
vi khuẩn. B.
1.006.632.960
vi khuẩn.
8
C.
2.108.252.760
vi khuẩn. D.
3.251.603.769
vi khuẩn.
Lời giải. Tương tự như bài trên, sau
n
lần
20
phút thì số vi khuẩn có là
60.2 .
n
n
T
Vì
8
giờ tương đương với
24
lần
20
phút. Do đó số lượng vi khuẩn E.coli sau
8
giờ là
24
24
60.2 1.006.632.960T 
vi khuẩn. Chọn B.
Câu 22. Một quần thể vi khuẩn bắt đầu với
100
con. Cứ sau
3
giờ đồng hồ thì số
lượng vi khuẩn lại tăng gấp đôi. Hỏi khi nào số lượng vi khuẩn đạt đến
50000
con?
A.
26,06
giờ. B.
26,6
giờ. C.
26,09
giờ. D.
26,9
giờ.
Lời giải. Tương tự như bài trên, sau
n
lần
3
giờ thì số vi khuẩn có là
100.2 .
n
n
T
Theo đề bài, ta có
2
50000
50000 50000 100.2 log 8,9657.
100
n
n
Tn



Suy ra số thời gian cần thiết là
3 8,9657 3 26,9n 
giờ. Chọn D.
Câu 23. Một bể nước có dung tích
3
1 m
(không có nước). Người ta mở vòi cho nước
chảy vào bể. Trong giờ đầu, vận tốc nước chảy vào bể là
1
lít/phút. Trong các giờ tiếp
theo, vận tốc nước chảy giờ sau gấp đôi giờ trước. Hỏi sau khoảng thời gian bao lâu thì
bể nước đầy ?
A.
3,14
giờ. B.
5,14
giờ. C.
350
phút. D.
14915
giây.
Lời giải. Gọi
n
là số giờ vòi nước chảy để đầy bể.
Trong giờ đầu vòi chảy được
60
lit;
Trong giờ thứ hai vòi chảy được
60.2
lit;
Trong giờ thứ ba vòi chảy được
2
60.2
lit;
Trong giờ thứ
n
vòi chảy được
1
60.2
n
lit;
Tổng lượng nước chảy sau
n
giờ là
21
60. 1 2 2 ...2 1000
n

2
53 53
60 2 1 1000 2 log 4,142957
33
nn
n



giờ
14915
giây. Chọn D.
Câu 24. Một người thả một lượng bèo hoa dâu chiếm
4%
diện tích mặt hồ. Biết rằng
cứ sau đúng một tuần bèo phát triển thành
3
lần lượng đã có và tốc độ phát triển của
bèo ở mọi thời điểm như nhau. Sau bao nhiêu ngày, lượng bèo sẽ vừa phủ kín mặt hồ?
A.
3
7 log 25.
B.
25
7
3.
C.
24
7.
3
D.
3
log 25.
Lời giải. Gọi
A
là lượng bèo ban đầu

phủ kín mặt hồ thì cần lượng bèo
100
.
4
A
Sau một tuần số lượng bèo là
3A 
sau
n
tuần lượng bèo là
3.
n
A
Lượng bèo phủ kín mặt hồ khi
3
100
3 log 25
4
n
A An 
tuần
3
7 log 25
ngày.Chọn A.
Câu 25. Người ta thả một lượng bèo vào một hồ nước. Kết quả cho thấy sau
9
giờ bèo
sẽ sinh sôi kín cả mặt hồ. Biết rằng sau mỗi giờ, lượng bèo tăng gấp
10
lần lượng bèo
trước đó và tốc độ tăng không đổi. Hỏi sau mấy giờ thì lượng bèo phủ kín
1
3
mặt hồ?
9
A.
3
giờ. B.
9 log 3
giờ. C.
9
10
3
giờ. D.
9
log 3
giờ.
Lời giải. Gọi
A
là lượng bèo ban đầu. Sau mỗi giờ, lượng lá bèo tăng gấp
10
lần nên
sau
9
giờ ta có lượng bèo là
9
.10 .
A
Gọi
t
là số giờ để lượng bèo trong hồ phủ kín
1
3
mặt hồ. Khi đó ta có phương trình
9
9
1 10
.10 .10 log 9 log3.
33
t
A At

Chọn B.
Phần 2. Bài toán lãi suất
Dạng 1. Cho vay một lần (lãi kép)
Câu 1. (ĐỀ THAM KHẢO 2017 – 2018) Một người gửi
100
triệu đồng vào một ngân
hàng với lãi suất
0, 4%
/tháng. Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ
sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho tháng tiếp
theo. Hỏi sau đúng
6
tháng, người đó được lĩnh số tiền (cả vốn ban đầu và lãi) gần
nhất với số tiền nào dưới đây, nếu trong khoảng thời gian này người đó không rút tiền
ra và lãi suất không thay đổi?
A.
102.016.000
đồng. B.
102.017.000
đồng.
C.
102.423.000
đồng. D.
102.424.000
đồng.
Lời giải. Công thức lãi kép
1
n
n
TA r
với
A
số tiền gửi vào lần đầu tiên,
r
là lãi
suất mỗi kỳ,
n
là số kỳ hạn. Ta được
6
6
6
0, 4
100 10 1 102.424.000
100
T



đồng.
Chọn D.
Câu 2. Một người gửi
10
triệu đồng vào ngân hàng với lãi suất
5%
/năm trong thời
gian
10
năm. Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ sau định kỳ, số tiền
lãi sẽ được nhập vào vốn ban đầu để tính lãi cho định kỳ tiếp theo. Hỏi rằng người đó
nhận được số tiền nhiều hơn hay ít hơn bao nhiêu nếu ngân hàng trả lãi suất
5
%
12
/tháng (lãi suất tháng so với lãi suất năm)?
A. Ít hơn 1.811.486,1 đồng. B. Ít hơn 1.911.486,1 đồng.
C. Bằng nhau. D. Nhiều hơn 1.811.486,1 đồng.
Lời giải. Số tiền nhận được sau
10
năm với
• Lãi suất là
5%
/năm
10
1628
5
10000000. 1
10
47
0
89 6,2



đồng.
• Lãi suất là
5
%
12
/tháng
120
5
10000000. 1
12.
16470
100
094,98



đồng.
Suy ra số tiền gửi theo lãi suất tháng nhiều hơn: 1.811.486,1 đồng. Chọn D.
Câu 3. Một người lần đầu gửi vào ngân hàng
100
triệu đồng với kì hạn
3
tháng, lãi
suất
2%
/quý. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi quý, số
tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho quý tiếp theo. Sau đúng 6 tháng,
người đó gửi thêm
100
triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền
10
người đó nhận được một năm sau khi gửi tiền (cả vốn lẫn lãi) gần nhất với kết quả
nào sau đây?
A. 210 triệu. B. 212 triệu. C. 216 triệu. D. 220 triệu.
Lời giải. Số tiền nhận về sau 1 năm của 100 triệu gửi trước là
4
100 1 2%
triệu.
Số tiền nhận về sau 6 tháng của 100 triệu gửi sau là
2
100 1 2%
triệu.
Vậy tổng số tiền nhận là
42
100 1 2% 100 1 2% 212,283216
triệu. Chọn B.
Câu 4. Một người dự định sẽ mua xe Honda SH với giá
80.990.000
đồng. Người đó gửi
tiết kiệm vào ngân hàng với số tiền
60.000.000
đồng với lãi suất
0,8%
/tháng. Biết
rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được
nhập vào vốn ban đầu để tính lãi cho tháng tiếp theo. Do sức ép thị trường nên mỗi
tháng loại xe Honda SH giảm
500.000
đồng. Vậy sau bao lâu người đó sẽ đủ tiền mua
xe máy?
A.
20
tháng. B.
21
tháng. C.
22
tháng. D.
23
tháng.
Lời giải. Áp dụng công thức lãi kép, ta có số tiền người đó nhận được (cả vốn ban đầu
và lãi) sau
n
tháng là:
6
0,8
1 60.10 . 1 .
100
n
n
TA r



Số tiền xe Honda SH giảm trong
n
tháng là:
80990000 500000 .pn
Để người đó mua được xe Honda SH thì:
Tp
6
0,8
60.10 1 80990000 500000 20,58771778.
100
n
nn



Chọn B.
Câu 5. Một người muốn gửi tiền vào ngân hàng để đến ngày
15/ 3/ 2020
rút được
khoản tiền là
50.000.000
đồng. Lãi suất ngân hàng là
0,55%
/tháng. Biết rằng nếu
không rút tiền khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn
ban đầu để tính lãi cho tháng tiếp theo. Hỏi vào ngày
15/ 4 / 2018
người đó phải gửi
ngân hàng số tiền là bao nhiêu để đáp ứng nhu cầu trên, nếu lãi suất không thay đổi
trong thời gian người đó gửi tiền?
A.
43.593.000
đồng. B.
43.833.000
đồng.
C.
44.316.000
đồng. D.
44.074.000
đồng.
Lời giải. Áp dụng công thức lãi kép
1
n
n
TA r

với
A
số tiền gửi vào lần đầu tiên,
0,55%r
là lãi suất mỗi tháng,
23n
tháng và
50.000.000
n
T
đồng. Ta được
23
0,55
50000000 . 1 44074000
100
AA



đồng. Chọn D.
Câu 6. Ông Việt dự định gửi vào ngân hàng một số tiền với lãi suất
6,5%
/năm. Biết
rằng nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập
vào vốn ban đầu để tính lãi cho năm tiếp theo. Tính số tiền tối thiểu
x
triệu đồng
x
ông Việt gửi vào ngân hàng để sau
3
năm số tiền lãi đủ mua một chiếc xe gắn
máy trị giá
30
triệu đồng.
A.
140x
triệu đồng. B.
145x
triệu đồng.
11
C.
150x
triệu đồng. D.
154
x
triệu đồng.
Lời giải. Áp dụng công thức lãi kép
1
n
n
TA r
với
Ax
số tiền gửi vào lần đầu
tiên,
5%6,r
là lãi suất mỗi năm,
3
n
năm. Suy ra số tiền người đó nhận được (cả
vốn ban đầu và lãi) là:
3
6,5
1.
100
Tx



Suy ra số tiền lãi người đó nhận được là:
3
6,5
1.
100
Tx x x



Theo đề, ta có
3
6,5
30 1 30 144,27
100
Tx x x x

 

triệu đồng. Chọn B.
Câu 7. Một người gửi tiết kiệm vào ngân hàng
200
triệu đồng theo thể thức lãi kép
(tức là tiền lãi được cộng vào vốn kỳ tiếp theo). Ban đầu người đó gửi với kỳ hạn
3
tháng, lãi suất
2%
/ kỳ hạn, sau hai năm người đó thay đổi phương thức gửi, chuyển
thành kỳ hạn một tháng với lãi suất
0, 6%
/tháng. Tính tổng số tiền lãi và gốc nhận
được sau
5
năm (kết quả làm tròn tới đơn vị nghìn đồng).
A.
290.640.000
đồng. B.
290.642.000
đồng.
C.
290.646.000
đồng. D.
290.644.000
đồng.
Lời giải. Áp dụng công thức lãi kép, ta có
• Sau
2
năm đầu tiên người đó có số tiền cả gốc và lãi là:
8
2
200 1 .
100
T



• Sau
5
năm người đó có số tiền cả gốc và lãi là:
36
0, 6
1
100
TT



8 36
2 0, 6
200 1 . 1 290642000
100 100









đồng. Chọn B.
Câu 8. (ĐỀ CHÍNH THỨC 2016 – 2017) Một người gửi 50 triệu đồng vào ngân hàng
với lãi suất
6% /
năm. Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi
năm, số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho năm tiếp theo. Hỏi sau
ít nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn 100 triệu đồng bao gồm
cả gốc và lãi? Giả sử trong suốt thời gian gửi lãi suất không đổi và người đó không rút
tiền ra.
A. 11 năm. B. 12 năm. C. 13 năm. D. 14 năm.
Lời giải. Áp dụng công thức lãi kép
1.
n
n
TA r
Theo đề bài ta cần có:
100 50. 1 6% 100 1,06 2 11.
n
n
n
Tn
 
Vì
n
là số
tự nhiên và người đó chỉ được nhận lãi vào cuối năm nên ta chọn
12.n
Chọn B.
Câu 9. Ông An gửi
320
triệu đồng vào ngân hàng ACB và VietinBank theo phương
thức lãi kép. Số tiền thứ nhất gửi vào ngân hàng ACB với lãi suất
2,1%
/quý trong
thời gian
15
tháng. Số tiền còn lại gửi vào ngân hàng VietinBank với lãi suất
0,73%
/tháng trong thời gian
9
tháng. Biết tổng số tiền lãi ông An nhận được ở hai
12
ngân hàng là
26670725,95
đồng. Hỏi số tiền ông An lần lượt ở hai ngân hàng ACB và
VietinBank là bao nhiêu?
A.
120
triệu đồng và
200
triệu đồng. B.
140
triệu đồng và
180
triệu đồng.
C.
180
triệu đồng và
140
triệu đồng. D.
200
triệu đồng và
120
triệu đồng.
Lời giải. Gọi số tiền ông An gửi ở ngân hàng ACB là
x
triệu đồng. Suy ra số tiền ông
An gửi ở ngân hàng VietinBank là
320 x
triệu đồng.
• Số tiền cả vốn và lãi ông An nhận được khi gửi ở ngân hàng ACB sau
15
tháng là:
5
2,1
1.
100
x


Suy ra số tiền lãi ông An nhận được khi gửi ở ngân hàng ACB sau
15
tháng là:
5
2,1
1.
100
xx



• Số tiền cả vốn và lãi ông An nhận được khi gửi ở ngân hàng VietinBank sau
9
tháng là:
9
0,73
320 1 .
100
x



Suy ra số tiền lãi ông An nhận được khi gửi ở ngân
hàng VietinBank sau
9
tháng là:
9
0,73
320 1 320 .
100
xx



Tổng số tiền lãi ông An nhận được ở hai ngân hàng là
26670725,95
đồng nên ta có
phương trình
59
2,1 0,73
1 320 1 320 26,67072595 120.
100 100
x xx x x









Vậy ông An gửi ở ACB là
120
triệu và VietinBank
200
triệu. Chọn A.
Câu 10. (ĐỀ CHÍNH THỨC 2016 – 2017) Đầu năm 2016, ông An thành lập một
công ty. Tổng số tiền ông An dùng để trả lương cho nhân viên trong năm 2016 là 1 tỷ
đồng. Biết rằng cứ sau mỗi năm thì tổng số tiền dùng để trả lương cho nhân viên
trong cả năm đó tăng thêm
15%
so với năm trước. Hỏi năm nào dưới đây là năm đầu
tiên mà tổng số tiền ông An dùng để trả lương cho nhân viên trong cả năm lớn hơn 2
tỷ đồng?
A. Năm 2020. B. Năm 2021. C. Năm 2022. D. Năm 2023.
Lời giải. Áp dụng công thức lãi kép
1.
n
n
TA r
Trong năm
2016
ông An trả lương nhân viên là
1
tỷ đồng.
Trong năm
2017
ông An trả lương nhân viên là
1
15
1 1 1, 1 5
100



tỷ đồng.
Trong năm
2018
ông An trả lương nhân viên là
2
15
1 1 1, 3 2
100



tỷ đồng.
Trong năm
2019
ông An trả lương nhân viên là
3
15
1 1 1, 5 2
100



tỷ đồng.
Trong năm
2020
ông An trả lương nhân viên là
4
15
1 1 1, 75
100



tỷ đồng.
13
Trong năm
2021
ông An trả lương nhân viên là
5
15
1 1 2,011
100



tỷ đồng. Chọn B.
Bình luận. Nếu xem là bài toán lãi kép thì từ đầu năm
2017
mới sinh lãi.
Dạng 2. Gửi tiền đầu mỗi định kỳ (gửi tiết kiệm)
Cứ đầu mỗi định kỳ gửi vào ngân hàng
M
triệu, lãi suất kép
%r
/định kỳ. Hỏi sau
n
định kỳ số tiền thu được là bao nhiêu?
Ta xây dựng bảng sau:
Định kỳ
Đầu định kỳ
Cuối định kỳ
1
M
1Mr
2
1M rM
2
11
11
M rM r
Mr r







3
2
11M r rM




2
32
1 1 .1
111
M r rM r
Mr r r








 


n
1 ... 1 .
n
Mr r




Vậy sau
n
định kỳ ta được số tiền:
11
1 ... 1 1 . .
n
n
r
TM r r M r
r





Từ đó suy ra
11 1
n
Tr
M
rr




và
1
log 1 .
1
r
Tr
n
Mr






Câu 11. Một người gửi tiết kiệm ngân hàng, mỗi tháng gửi đều đặn vào ngân hàng
1
triệu đồng với lãi suất kép
1%
/tháng. Gửi được hai năm ba tháng người đó rút toàn
bộ tiền vốn và lãi. Số tiền người đó nhận được là
A.
26
100. 1,01 1



triệu đồng. B.
27
100. 1,01 1



triệu đồng.
C.
26
101. 1,01 1



triệu đồng. D.
27
101. 1,01 1



triệu đồng.
Lời giải. Áp dụng công thức
11
1.
n
r
TM r
r


với
1
1%.
27
M
r
n
Chọn D.
Câu 12. Một người mỗi đầu tháng đều đặn gửi vào ngân hàng một khoản tiền
M
theo hình thức lãi kép với lãi suất
0, 6%
/tháng. Biết đến cuối tháng thứ
15
thì người
đó có số tiền là
10
triệu đồng (cả vốn và lãi). Hỏi số tiền
M
gần với số tiền nào nhất
trong các số sau?
A.
535.000
đồng. B.
613.000
đồng. C.
635.000
đồng. D.
643.000
đồng.
14
Lời giải. Áp dụng
11 1
n
Tr
M
rr




với
10
0, 6%.
15
T
r
n
Chọn C.
Câu 13. Một người muốn có
2
tỷ tiền tiết kiệm sau
6
năm gửi ngân hàng bằng cách
môi năm gửi vào ngân hàng số tiền bằng nhau với lãi suất ngân hàng là
8%
/năm và
lãi hàng năm được nhập vào vốn. Hỏi số tiền mà người đó phải gửi vào ngân hàng sô
tiên hàng năm là bao nhiêu? Giả thiết rằng lãi suât không thay đôi và sô tiên đươc
làm tròn đên đơn vị nghìn đông.
A.
251
triệu. B.
252,5
triệu. C.
253
triệu. D.
253,5
triệu.
Lời giải. Áp dụng
11 1
n
Tr
M
rr




với
10
2.10
8% .
6
T
r
n
Chọn B.
Câu 14. Đúng ngày
01
mỗi tháng anh A gửi vào ngân hàng
3
triệu đồng với lãi suất
0,7%
/tháng. Biết không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng tiền lãi sẽ
nhập vào gốc để tính lãi cho tháng tiếp theo. Hỏi sau ít nhất bao nhiêu tháng thì anh
A có được số tiền cả gốc và lãi nhiều hơn
100
triệu đồng? Giả định trong suốt thời
gian gửi, lãi suất không đổi, được tính lãi ngay từ ngày gửi và anh A không rút tiền
ra.
A.
28
tháng. B.
29
tháng. C.
30
tháng. D.
33
tháng.
Lời giải. Áp dụng
1
log 1
1
r
Tr
n
Mr






với
6
100.10
0,7% .
3
T
r
M
Chọn C.
Dạng 3. Vay trả góp
Vay ngân hàng
M
triệu đồng, lãi suất
%
r
/định kỳ. Cứ cuối mỗi định kỳ trả ngân
hàng
m
triệu. Hỏi sau
n
định kỳ số tiền còn nợ là bao nhiêu?
Ta xây dựng bảng sau:
Định kỳ
Đầu định kỳ
Cuối định kỳ
1
M
1M rm
2
1M rm
2
11
1 11
M rm rm
M rm r

 




3
2
32
1 1 11
1 1 11
M r m r rm
M rm r r










n
12
1 1 11
n nn
M rm r r





15
Vậy sau
n
định kỳ, số tiền còn nợ
12
1 1 11
n nn
TM r m r r





1 1 1.
nn
m
Mr r
r

 


Từ đó suy ra nếu định kỳ thứ
n
mà trả hết nợ thì
1
0.
11
n
n
M rr
Tm
r


Câu 15. (ĐỀ MINH HỌA 2016 – 2017) Ông Việt vay ngân hàng
100
triệu đồng, với
lãi suất
1%
/tháng. Ông muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một tháng
kể từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một
tháng, số tiền hoàn nợ ở mỗi lần là như nhau và trả hết tiền nợ sau đúng
3
tháng kể
từ ngày vay. Hỏi theo cách đó, số tiền
m
mà ông Việt sẽ phải trả cho ngân hàng trong
mỗi lần hoàn nợ là bao nhiêu? Biết rằng lãi suất ngân hàng không thay đổi trong thời
gian ông Việt hoàn nợ.
A.
3
100. 1,01
3
m
(triệu đồng). B.
3
3
1, 01
1, 01 1
m
(triệu đồng).
C.
100 1,03
3
m
(triệu đồng). D.
3
3
120. 1,12
1, 12 1
m
(triệu đồng).
Lời giải. Áp dụng công thức
1
11
n
n
M rr
m
r

với
100
1% .
3
M
r
n
Chọn B.
Câu 16. Một người vay ngân hàng
500
triệu đồng, với lãi suất
1, 2%
/tháng. Sau đúng
một tháng kể từ ngày vay, người đó bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách
nhau đúng một tháng, số tiền hoàn nợ ở mỗi lần là như nhau và bằng
10
triệu đồng.
Hỏi sau ít nhất bao nhiêu tháng thì người đó trả hết nợ? Biết rằng, lãi suất ngân
hàng không thay đổi trong thời người đó hoàn nợ.
A.
70
tháng. B.
77
tháng. C.
80
tháng. D.
85
tháng.
Lời giải. Áp dụng công thức
1 11
nn
m
TM r r
r

 


với
0
500
.
10
1, 2%
T
M
m
r
Đặt
1,ar
ta được
1,012
15 5
0 500. 10. log 76,8.
12 2
n
nn
a
a an
a

Chọn B.
Câu 17. Bạn Hùng trúng tuyển Đại học nhưng vì do không đủ tiền nộp học phí nên
Hùng quyết định vay ngân hàng trong
4
năm, mỗi năm
4.000.000
đồng để nộp học
phí với lãi suất
3%
/ năm. Sau khi tốt nghiệp Đại học, bạn Hùng phải trả góp hàng
tháng cho ngân hàng số tiền
m
(không đổi) cùng với lãi suất
0,25%
/tháng trong vòng
5
năm. Tính số tiền
m
hàng tháng mà bạn Hùng phải trả cho ngân hàng (làm tròn
đến kết quả hàng đơn vị).
A.
309.604,14
đồng. B.
309.718,166
đồng.
16
C.
312.518,166
đồng. D.
398.402,12
đồng.
Lời giải. Giai đoạn 1: Số tiền bạn Hùng nợ ngân hàng sau 4 năm. Ta xem đây
là bài toán gửi tiết kiệm (Dạng 2) với người cho vay là ngân hàng. Áp dụng công thức
gửi tiết kiệm
11
1.
n
r
TM r
r


với
4000000
3%
4
M
r
n
được
17236543,24T
đồng.
Giai đoạn 2. Ta coi như bạn Hùng nợ ngân hàng khoản tiền ban đầu
17236543,24
đồng. Số tiền này bắt đầu được tính lãi và được trả góp trong
5
năm (
60
tháng).
Áp dụng
1
11
n
n
M rr
m
r

với
17236543,24
0,25%
60
M
r
n
ta được
309718,166.
m
Chọn B.
Dạng 4. Bài tập tổng hợp
Câu 18. [Lãi suất tăng dần] Ông Bách dự định đầu tư khoản tiền
20
triệu đồng vào
một dự án với lãi suất tăng dần:
3,35%
/năm trong
3
năm đầu,
3,75%
/năm tong
2
năm kế tiếp và
4,8%
/năm ở
5
năm cuối. Khoản tiền mà ông Bách nhận được (cả vốn
và lãi) cuối năm thứ
10
là
A.
25
triệu. B.
30
triệu. C.
35
triệu. D.
40
triệu.
Lời giải. Số tiền ông Bách nhận được sau
3
năm đầu là
3
1
3, 35
20. 1 .
100
T



Số tiền ông Bách nhận được sau
2
năm tiếp theo là
2
21
3, 75
.1 .
100
TT



Số tiền ông Bách nhận được vào cuối năm thứ
10
là
5 3 25
32
4,8 3,35 3,75 4,8
.1 20.1 .1 .1 30
100 100 100 100
TT
 







 
triệu đồng. Chọn B.
Câu 19. Năm
2017
số tiền để đổ đầy bình xăng cho một chiếc xe máy trung bình là
70000
đồng. Giả sử tỉ lệ lạm phát hàng năm của Việt Nam trong 10 năm tới không
đổi với mức
5%,
tính số tiền để đổ đầy bình xăng cho chiếc xe đó vào năm
2022.
A.
5
70000.0,05
đồng. B.
6
70000.0,05
đồng.
C.
5
70000.1,05
đồng. D.
6
70000.1,05
đồng.
Lời giải. Số tiền để đổ đầy bình xăng vào năm
2018
là
1
70000. 1 0,05 .
T 
Số tiền để đổ đầy bình xăng vào năm
2019
là
2
21
. 1 0,05 70000. 1 0,05 .TT
Số tiền để đổ đầy bình xăng vào năm
2022
là
5
5
70000. 1 0,05 .T 
Chọn C.
Câu 20. Một người mua chiếc xe máy Air Blade với giá
45
triệu đồng. Biết rằng giá
trị khấu hao tài sản xe giảm
60%
mỗi năm. Biết rằng sau
n
năm thì giá trị xe chỉ
còn
5
triệu đồng. Giá trị
n
gần nhất với đáp án nào sau đây?
17
A.
2
năm. B.
2,5
năm. C.
3
năm. D.
3, 5
năm.
Lời giải. Theo đề bài suy ra giá trị còn lại của chiếc xe sau mỗi năm là
40%.
Giá trị của chiếc xe sau
1
năm là
1
45 40%.T 
Giá trị của chiếc xe sau
2
năm là
2
2
45 40% 40% 45 40% .T

Giá trị của chiếc xe sau
n
năm là
45 40% .
n
n
T 
Theo đề bài, ta có
0,4
1
5 45 40% 5 log 2,39.
9
n
n
Tn

 

Chọn B.
Câu 21. Đầu năm
2017,
anh Hùng có xe công nông trị giá
100
triệu đồng. Biết mỗi
tháng thì xe công nông hao mòn mất
0, 4%
giá trị, đồng thời anh Hùng làm ra được
6
triệu đồng (số tiền làm ra mỗi tháng là không đổi). Hỏi sau đúng một năm, tổng số
tiền (bao gồm tiền giá xe công nông và tiền anh Hùng làm ra) mà anh Hùng có là bao
nhiêu?
A.
172
triệu. B.
167,3042
triệu. C.
144
triệu. D.
120,3042
triệu.
Lời giải. Số tiền anh Hùng làm ra sau
1
năm là
6.12 72
triệu đồng.
Sau
1
năm giá trị xe công nông còn
12
100. 1 0,4 95,3042
triệu đồng.
Vậy sai một năm số tiền anh Hùng có
167,3042
triệu. Chọn B.
Câu 22. Theo thống kê tài chính của thị xã An Nhơn, tỉnh Bình Định, trong dịp Tết
Nguyên Đán năm
2015,
làng nghề trồng mai cảnh xã An Nhơn đạt tổng doanh thu
khoảng
15
tỷ đồng nhờ vào việc bán mai cảnh. Biết rằng trong các năm tiếp theo tổng
doanh thu luôn tăng ổn định và doanh thu trong năm đó cao hơn so với năm trước
6,27%.
Hỏi tổng doanh thu của làng nghề trồng mai cảnh xã An Nhơn vào dịp Tết
Nguyên Đán năm
2018
là bao nhiêu? (làm tròn đến tỷ đồng)
A.
17
tỷ đồng. B.
18
tỷ đồng. C.
19
tỷ đồng. D.
20
tỷ đồng.
Lời giải. Tổng doanh thu vào dịp tết năm
2016
là
1
15 1 6,27% .T 
Tổng doanh thu vào dịp tết năm
2017
là
2
21
1 6,27% 15 1 6,27% .TT
Tổng doanh thu vào dịp tết năm
2018
là
3
3
15 1 6,27% 18
T 
tỷ đồng. Chọn B.
Câu 23. [Tiền lương tăng theo chu kỳ] Một kỹ sư được nhận lương khởi điểm là
8000000
đồng/tháng. Cứ sau hai năm lương mỗi tháng của kỹ sư đó được tăng thêm
10%
so với mức lương hiện tại. Tổng số tiền kỹ sư đó nhận được sau
6
năm làm việc
A.
633600000
đồng. B.
635520000
đồng.
C.
696960000
đồng. D.
766656000
đồng.
Lời giải. Tổng tiền lương
2
năm đầu tiên:
66
1
8.10 24 192.10T 
đồng.
Theo công thức tính lãi kép, tổng tiền lương
2
năm tiếp theo công nhân đó nhận được
là:
1
66
2
8.10 24. 1 10% 212,2.10
T 
đồng.
Tổng tiền lương
2
năm cuối cùng:
2
66
3
8.10 24 1 10% 232,32.10T

đồng.
Vậy tổng số tiền lương kỹ sư đó nhận được sau
6
năm làm việc là
18
123
635.520.000TTT T

đồng. Chọn B.
Câu 24. Theo dự báo với mức tiêu thụ dầu không đổi như hiện nay thì trữ lượng dầu
của nước A sẽ hết sau
100
năm tới. Nhưng do nhu cầu thực tế, mức tiêu thụ tăng lên
4%
mỗi năm. Hỏi sau bao nhiêu năm số dầu dự trữ của nước A sẽ hết?
A.
40.
B.
41.
C.
42.
D.
43.
Lời giải. Gọi mức tiêu thụ dầu hàng năm của nước A theo dự báo là
M

lượng dầu của nước A là
100 .M
Trên thực tế ta có
Lượng dầu tiêu thụ năm thứ
2
là:
2
4% 1 4% 1,04 .x M MM M
Lượng dầu tiêu thụ năm thứ
3
là:
2
3
1 4% 1 4% .4% 1,04 .xM M M 

Lượng dầu tiêu thụ năm thứ
n
là:
1
1, 04 .
n
n
xM
Theo đề bài ta có phương trình
123
... 100
n
xxx x M 
21
1, 04 1
1 1,04 1,04 ... 1,04 100 100 41,0354.
0, 04
n
n
MM n

Chọn B.
Câu 25. Sau một tháng thi công công trình xây dựng Nhà học thể dục của Trường X
đã thực hiện được một khối lượng công việc. Nếu tiếp tục với tiến độ như vậy thì dự
kiến sau đúng
23
tháng nữa công trình sẽ hoàn thành. Để sớm hoàn thành công
trình và kịp thời đưa vào sử dụng, công ty xây dựng quyết định từ tháng thứ
2
, mỗi
tháng tăng
4%
khối lượng công việc so với tháng kề trước. Hỏi công trình sẽ hoàn
thành ở tháng thứ mấy sau khi khởi công?
A.
17.
B.
18.
C.
19.
D.
20.
Lời giải. Dự kiến hoàn thành công việc trong
24
tháng.
Như bài trên ta có phương trình
21
1 1,04 1,04 ... 1,04 24
n
MM

1,04
1, 04 1
24 1,04 1,96 log 1,96 17,2.
0, 04
n
n
n

Chọn B.
Câu 26. [So sánh lãi không kỳ hạn và lãi có kỳ hạn] Ngân hàng BIDV Việt Nam
đang áp dụng hình thức lãi kép với mức lãi suất: không kỳ hạn là
0, 2%
/năm, kỳ hạn
3
tháng là
1, 2%
/quý. Ông A đến ngân hàng BIDV để gửi tiết kiệm với số tiền ban
đầu là
300
triệu đồng. Nếu gửi không kỳ hạn mà ông A muốn thu về cả vốn và lãi
bằng hoặc vượt quá
305
triệu đồng thì ông A phải gửi ít nhất
n
tháng
*
.n
Hỏi
nếu cùng số tiền ban đầu và cũng số tháng đó, ông A gửi tiết kiệm có kỳ hạn
3
tháng
thì ông A sẽ nhận được số tiền cả vốn lẫn lãi là bao nhiêu?
A.
444.785.421
đồng. B.
444.711.302
đồng.
C.
446.490.147
đồng. D.
447.190.465
đồng.
Lời giải. Áp dụng công thức lãi kép:
305; 300
0,2%
1 99,18.
n
n
TA
n
n
TA r n


Như vậy,
khi gửi không kỳ hạn để được số tiền gồm cả vốn lẫn lãi lớn hơn hoặc bằng
305
triệu
đồng thì ông A phải gửi tối thiểu là
100
tháng.
19
Nếu cũng gửi với số tiền ban đầu là
300
triệu đồng với lãi suất
1, 2%
/quý trong thời
gian
100
năm (gồm
33
kỳ hạn và
1
tháng không kỳ hạn)
• Số tiền ông A có được sau
33
định kỳ là:
33
1, 2
300000000. 1
100
T



đồng.
• Số tiền ông A có được sau
100
tháng là
33
0,2 1,2 0,2
. 1 300000000. 1 . 1
100 100 100
T
 







 
444.785.421
đồng. Chọn A.
Câu 27. [Gửi tiết kiệm nhưng số tiền tăng dần] Một người lập kế hoạch gửi tiết
kiệm ngân hàng như sau: Đầu tháng
01
năm
2018,
người đó gửi
10
triệu đồng; sau
mỗi đầu tháng tiếp theo, người đó gửi số tiền nhiều hơn
10%
so với số tiền đã gửi ở
tháng liền trước đó. Biết rằng lãi suất ngân hàng không đổi là
0,5%
mỗi tháng và
được tính theo hình thức lãi kép. Với kế hoạch như vậy, đến hết tháng
12
năm
2019,
số tiền của người đó trong tài khoản tiết kiệm là bao nhiêu? (Làm tròn đến hàng
nghìn)
A.
832.765.000
đồng. B.
918.165.000
đồng.
C.
922.756.000
đồng. D.
926.281.000
đồng.
Lời giải. Với
10A
triệu đồng,
10%a
và
0,5%.r
Ta có
Số tiền gửi ban đầu
Số tiền cuối tháng
1
Đầu tháng
2
gửi thêm
A
1Ar
1Aa
• Suy ra số tiền đầu tháng
2
(sau khi đã gửi thêm) là:
1 1.ArAa
• Số tiền đầu tháng
3
(sau khi đã gửi thêm):

22
1 11 1.ArAa rAa
• Số tiền đầu tháng
4
(sau khi đã gửi thêm):

3 22 3
1 11 1 1 1.ArAa rAa rAa 

• Số tiền đầu tháng
n
(sau khi đã gửi thêm):

12 21
1 1 1 ... 1 1 1 .
nn n n
Ar r a r a a


  


Cuối tháng
:n

12 21
1 1 1 ... 1 1 1 1
nn n n
Ar r a r a a r


  


24
11
1 922756396,2
nn
n
ar
Ar
ar


đồng. Chọn C.
Câu 28. [Gửi và rút hàng tháng] Ngày
01
tháng
01
năm
2017,
ông An gửi
800
triệu đồng vào một ngân hàng với lãi suất
0,5%
/tháng. Từ đó, cứ tròn mỗi tháng ông
đến ngân hàng rút
6
triệu để chi tiêu cho gia đình. Hỏi đến ngày
01
tháng
01
năm
2018,
sau khi rút tiền, số tiền tiết kiệm của ông An còn lại là bao nhiêu? Biết rằng lãi
suất trong suốt thời gian ông An gửi không thay đổi.
A.
11
800. 1,005 72
(triệu đồng). B.
12
800. 1,005 72
(triệu đồng).
C.
11
1200 400. 1,005
(triệu đồng). D.
12
1200 400. 1,005
(triệu đồng).
20
Lời giải. Gọi
800M
triệu đồng,
0,5%,r
6
m
triệu đồng.
• Số tiền cuối tháng
1
(sau khi đã rút):
1.M rm
• Số tiền cuối tháng
2
(sau khi đã rút):
11M rm rm

 

2
1 1 1.
M rm r



• Số tiền cuối tháng
n
(sau khi đã rút):
12
1 1 11
n nn
M rm r r





12
1 11
nn
n
m
Mr r
r

 


Chọn D.
Câu 29. [Gửi và rút hàng tháng] Một hội khuyến học đã kêu gọi sự ủng hộ của các
nhà hảo tâm được
120
triệu đồng. Hội khuyến học gửi số tiền đó vào ngân hàng với
lãi suất
0,75%
/tháng với dự định hàng tháng rút
m
triệu đồng làm khuyến học cho
học sinh nghèo vượt khó. Hội khuyến học bắt đầu trao quà cho học sinh sau một
tháng gửi tiền vào ngân hàng. Để số tiền (cả lãi và
120
triệu đồng tiền gốc) đủ trao
cho học sinh trong
10
tháng thì số tiền
m
mà hàng tháng Hội khuyến học rút ra tối
đa (lấy kết quả chính xác đến chữ số thập phân thứ nhất) là
A.
12,3.
B.
12,4.
C.
12,5.
D.
12,6.
Lời giải. Áp dụng công thức như câu trên. Số tiền cuối tháng
n
(sau khi đã rút) là:
1 1 1.
nn
m
Mr r
r

 


Vì trao tới tháng thứ
10
thì hết tiền nên
1 1 1 0.
nn
m
Mr r
r

 


Suy ra
120; 0,75%; 10
1.
12,5.
11
n
Mr n
n
M rr
mm
r



Chọn C.
Câu 30. [Trả góp nhưng bị điều chỉnh lãi suất] Một người vay ngân hàng
40
triệu đồng, với lãi suất
0,85%
/tháng. Sau đúng một tháng kể từ ngày vay, người đó
bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ
ở mỗi lần là như nhau và bằng
500
nghìn đồng. Sau một năm mức lãi suất của ngân
hàng được điều chỉnh lên là
1,15%
/tháng và người vay muốn nhanh chóng hết nợ nên
đã thỏa thuận trả
1
triệu
500
nghìn đồng cho mỗi tháng. Hỏi phải mất bao nhiêu lâu
người đó mới trả hết nợ?
A.
30
tháng. B.
31
tháng. C.
42
tháng. D.
43
tháng.
Lời giải. Sau
1
năm số tiền còn nợ ngân hàng là:
1 11
nn
m
TM r r
r

 


với
40000000
500000
0,85%
12
M
m
r
n
ta được
37987647T
đồng.
Để trả hết số nợ còn lại ta cần có
21
11
1
11 1
1
1 1 10
nn
m
Mr r
r

 


với
1
37987647
1500000
1,15%
MT
m
r

ta được
1
30,1n
tháng.
Vậy cần
12 31 43
tháng để trả hết nợ. Chọn D.
1
PHƯƠNG TRÌNH MŨ
PHƯƠNG TRÌNH LOGARIT
Phần 1. Phương trình mũ – phương trình logarit………………………………….………
Phần 2. Phương trình mũ chứa tham số…………………………………………………………….
Phần 3. Phương trình logarit chứa tham số…………………………………………………..…
2
Phần 1. Phương trình mũ–Phương trình logarit
Câu 1. Số nghiệm của phương trình
21
2
2
1
2 log log 1 log 2 2
2
x x xx

là
A.
0.
B.
1.
C.
2.
D.
4.
Câu 2. Cho
0 1,
a
phương trình
2
2
24 2
1
log 1 log
xx
aa
a ax a
a



có bao
nhiêu nghiệm?
A.
0.
B.
1.
C.
3.
D.
4.
Câu 3. Phương trình
32
2 log cot log cosxx
có tất cả bao nhiêu nghiệm thuộc khoảng
0;2018
?
A.
321.
B.
322.
C.
642.
D.
643.
Câu 4. Phương trình
3
32
log 2 2 log 1xx
có bao nhiêu nghiệm?
A.
0.
B.
1.
C.
2.
D.
4.
Câu 5. Gọi
0
x
là nghiệm của phương trình
22 2
3 3 4 4 3 4 7.
x x xx

Khẳng
định nào sau đây đúng?
A.
0
0.x
B.
0
0;1 .x
C.
0
3
; 2.
2
x


D.
0
2; 3 .x
Câu 6. Tập nghiệm của bất phương trình
21032 5 132
5 4.5 5
xx x x

là đoạn
;.
ab
Tổng
ab
bằng
A.
14.
B.
16.
C.
18.
D.
20.
Câu 7. Phương trình
23
3 2 3 31 2 3 2
1 3 2 .2018 3 1 .2018
xx xx
xx x x x x
 
  
có
bao nhiêu nghiệm?
A.
1.
B.
2.
C.
3.
D.
4.
Câu 8. Số nghiệm của phương trình
44
log log
2
3 5 .3 5 1
xx
xx 
là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 9. Trên
0;2018
phương trình
3
sin sin
11
sin 3
27 81
xx
x









có bao nhiêu nghiệm?
A.
1925.
B.
1927.
C.
1928.
D.
1930.
Câu 10. Trên khoảng
0;
2


phương trình
2
sin 2 cos 1 log sinxx x 
có bao nhiêu
nghiệm ?
A.
0.
B.
1.
C.
2.
D.
3.
Câu 11. Bất phương trình
2 11
2
3 3 43
x
x
xx


có bao nhiêu nghiệm nguyên nhỏ
hơn
10
?
A.
6.
B.
7.
C.
8.
D.
9.
3
Câu 12. Biết phương trình
53
21 1
log 2 log
2
xx
x
x

có nghiệm duy nhất
2
x ab
trong đó
,
ab
là các số nguyên. Tổng
ab
bằng
A.
1.
B.
1.
C.
2.
D.
5.
Câu 13. Tổng các nghiệm của phương trình
sin
4
tan
x
ex


trên đoạn
0;50
bằng
A.
1853
.
2
B.
2105
.
2
C.
2475
.
2
D.
2671
.
2
Câu 14. Tổng các nghiệm của phương trình
2
log 1 2 1
x
x xx 
bằng
A.
0.
B.
1.
C.
2.
D.
3.
Câu 15. Tích các nghiệm của phương trình
3
3 2 3 43
2 3 22 1 0
xx x
xx


bằng
A.
2.
B.
1.
C.
1.
D.
2.
Câu 16. Phương trình
2 22
22
log211 log21121xxx x 
có bao
nhiêu nghiệm nguyên?
A.
0.
B.
1.
C.
2.
D.
4.
Câu 17. Số nghiệm của phương trình
11
2
ln 1
x
xx

là
A.
1.
B.
2.
C.
3.
D.
4.
Câu 18. Phương trình
2
22
log 4 log 8 16
xx x 
có bao nhiêu nghiệm?
A.
0.
B.
1.
C.
2.
D.
3.
Câu 19. Cho phương trình
22 2
22
5 6 log log 5 5 6 .xx xx x x x x xx
 
Gọi
;
S ab
là tập nghiệm của bất phương trình đã cho. Khi đó
ba
bằng
A.
1
.
2
B.
2.
C.
5
.
2
D.
7
.
2
Câu 20. Tích các nghiệm của phương trình
2
2 31
3
log 3 2 2 5 2
xx
xx


bằng
A.
1.
B.
2.
C.
4.
D.
9.
Câu 21. Số nghiệm của phương trình
12
3 22 1
x
xx x

là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 22. Cho phương trình
22
23
log 5 5 1 log 5 7 2.xx xx 
Tổng tất cả
các nghiệm của phương trình đã cho bằng
A.
5.
B.
9.
C.
10.
D.
15.
Câu 23. Số nghiệm của phương trình
13
2
2
8
22
log 2 3
xx
xx



là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 24. Số nghiệm của phương trình
32 2
22
2 3 log 1 log 0xx x x 
là
A.
0.
B.
1.
C.
2.
D.
3.
4
Câu 25. Cho phương trình
2
12
2016 1 .2017 1.
xx
x

Khẳng định sau đây đúng?
A. Phương trình có tổng các nghiệm bằng
0.
B. Phương trình có nghiệm duy nhất.
C. Phương trình có hai nghiệm dương phân biệt.
D. Phương trình có nhiều hơn hai nghiệm.
Phần 2. Phương trình mũ chứa tham số
Câu 1. Cho phương trình
2
22
log log
2
3 2 3 .3 3 0
xx
mm 
với
m
là tham số. Tập
hợp tất cả các giá trị của
m
để phương trình đã cho có hai nghiệm phân biệt
12
,
xx
thỏa mãn
12
2xx
là
A.
0; .
B.
\ 1;1 .
C.
1; . 
D.
1; \ 0 . 
Câu 2. Biết phương trình
1
4 12 8 0
xx
m

có hai nghiệm
12
,
xx
thỏa mãn điều
kiện

12
1 1 6.
xx 
Khẳng định nào sau đây đúng?
A.
0.
m
B.
0 2.m
C.
1 3.
m
D.
3.
m
Câu 3. Có bao nhiêu giá trị nguyên của tham số
m
trên khoảng
2018;2018
để
phương trình
21 2
6.2 7 48 .2 2 16 0
xx
m mm

có hai nghiệm dương
12
, xx
thỏa
mãn
12
15xx
?
A.
1993.
B.
1994.
C.
3986.
D.
3988.
Câu 4. Cho phương trình
22
21 22
4 .2 3 2 0.
xx xx
mm
 

Tập tất cả các giá trị của
tham số
m
để phương trình đã cho có
4
nghiệm phân biệt là
A.
2; .
B.
2, .
C.
1; .
D.
;1 2; . 
Câu 5. Có bao nhiêu giá trị nguyên
m
thuộc đoạn
2018;2018
để phương trình
2 22
2 22
.9 2 1 .6 .4 0
xx xx xx
mm m


có nghiệm thuộc khoảng
0;2
?
A.
2010.
B.
2011
. C.
2012.
D.
2013.
Câu 6. Cho phương trình
22
2
2
51 51 2 .
xx
x
m

Tập tất cả các giá trị của
tham số
m
để phương trình có đúng bốn nghiệm phân biệt là
;.ab
Hiệu
ba
bằng
A.
3
.
4
B.
1
.
16
C.
1
.
64
D.
49
.
64
Câu 7. Cho phương trình
22
2
1
4 7 4 7 3 0.
xx
x
m

Gọi
S
là tập tất cả các
giá trị của tham số
m
sao cho
36m
và phương trình đã cho có đúng hai nghiệm
phân biệt. Số phần tử của
S
bằng
A.
1.
B.
24.
C.
25.
D.
26.
5
Câu 8. Cho phương trình
.9 2 1 6 .4 0.
x xx
mm m
Tìm tất cả các giá trị của tham
số
m
để bất phương trình nghiệm đúng với mọi
x
thuộc
0;1 .
A.
6.
m 
B.
6 4.m 
C.
4.m 
D.
6.m
Câu 9. Tập tất cả các giá trị của tham số
m
để phương trình
3 3 .9 1
xx
m
có
đúng
1
nghiệm có dạng
;.ab c
Tổng
abc
bằng
A.
4.
B.
11.
C.
14.
D.
15.
Câu 10. Tìm tất cả các giá trị thực của tham số
m
để phương trình
2
4
2
1
x
x
me e
có nghiệm thực.
A.
1 0.m
B.
0 1.
m
C.
2
0.m
e

D.
1
1.m
e

Câu 11. Cho hàm số
47
3 1 2 6 3.
xx
fx x x


Khi phương trình
2
7 46 9 3 1 0f xx m 
có số nghiệm nhiều nhất thì giá trị nhỏ nhất của tham
số
0
.
mm
Khẳng định nào sau đây đúng?
A.
0
0;1 .m
B.
0
1; 2 .m
C.
0
2;3 .m
D.
0
3; 4 .m
Câu 12. Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
5;5
để phương
trình
1
x
e mx
có nghiệm duy nhất?
A.
5.
B.
6.
C.
7.
D.
10.
Câu 13. Có bao nhiêu giá trị nguyên của tham số
m
thuộc
2000;2000
để
log log
2 log 1
ab
ba
a
a b mb
với
, ab
là các số thực lớn hơn
1
?
A.
1999.
B.
2000.
C.
2001.
D.
2199.
Câu 14. Tìm tất cả các giá trị của tham số
m
để phương trình
22
2
x
mx

có hai
nghiệm thực phân biệt.
A.
1
.
1
m
m

B.
1
.
2
m
m

C.
2
.
2
m
m

D.
3 1.m 
Câu 15. Phương trình
3
23 3 2 2 1
2 69 2 21
x mx x x
x x xm


có ba nghiệm phân
biệt khi và chỉ khi
;.m ab
Giá trị biểu thức
22
Tb a
bằng
A.
36.
B.
48.
C.
64.
D.
72.
Câu 16. Cho phương trình
3 22
2 1 11 .
mm
ee x x x x 
Tập hợp tất cả các
giá trị thực của tham số
m
để phương trình có nghiệm là
A.
1
0; ln 2 .
2


B.
1
0; .
e


C.
1
; ln 2 .
2


D.
1
ln 2; .
2


Câu 17. Có bao nhiêu giá trị nguyên dương của
m
nhỏ hơn
2018
để phương trình
2
2
11
32
4
1
x xm
x
x
x mx x
e
x


có nghiệm thực dương?
6
A.
2014.
B.
2015.
C.
2016.
D.
2017.
Câu 18. Có bao nhiêu giá trị nguyên của tham số
m
nhỏ hơn
10
để phương trình
xx
m me e 
có nghiệm thực?
A.
9.
B.
10.
C.
11.
D. Vô số.
Câu 19. Biết rằng
a
là số thực để phương trình
9 9 .3 cos
xx
ax

có nghiệm duy
nhất. Hỏi
a
thuộc khoảng nào sau đây?
A.
8; 4 .
B.
4;2 .
C.
4;10 .
D.
12;18 .
Câu 20. Cho tham số thực
,a
biết phương trình
2 cos
xx
e e ax

1
có
5
nghiệm
thực phân biệt. Hỏi phương trình
2 cos 4
xx
e e ax

2
có bao nhiêu nghiệm
thực phân biệt?
A.
5.
B.
10.
C.
11.
D.
20.
Phần 3. Phương trình loagarit chứa tham số
Câu 1. Cho phương trình
22
22
log 5 1 log 4 0.x m x mm

Biết phương trình có
2
nghiệm phân biệt
12
, xx
thỏa
12
165.xx
Giá trị của
12
xx
bằng
A.
16.
B.
119.
C.
120.
D.
159.
Câu 2. Giá trị thực của tham số
m
để phương trình

2
33
log 3 log 2 7 0x xm
có
hai nghiệm thực
12
,
xx
thỏa mãn


12
3 3 72xx
thuộc khoảng nào sau đây?
A.


7
;0 .
2
B.


7
0; .
2
C.


7
;7 .
2
D.


21
7; .
2
Câu 3. Cho phương trình
2
33
2 log 4 log 2 0.m x xm 
Tập tất cả các giá trị
của tham số thực
m
đê phương trình có hai nghiệm
12
,xx
thỏa
12
01xx 
là
A.
; 2.

B.
2;2 .
C.
2; .
D.
\ 2;2 .
Câu 4. Cho phương trình
22
22
log 2 1 log 2 0.
x m xm m 
Tập tất cả các giá trị
của tham số
m
để bất phương trình nghiệm đúng với mọi
1; 2x
là
A.
1 0.m
B.
1 0.m
C.
2
.
1
m
m

D.
2
.
1
m
m

Câu 5. Cho phương trình
2 22
42
log 2 2 2 log 2 .
xx
m




Có bao nhiêu giá trị
nguyên của tham số
m
để phương trình vô nghiệm?
A.
3.
B.
4.
C.
5.
D.
6.
Câu 6. Cho phương trình
2 22 2
41
2
2 log 2 2 4 log 2 0.x x m m x mx m
Tập tất
cả các giá trị của tham số
m
để phương trình có hai nghiệm phân biệt
12
, xx
thỏa
mãn
22
12
1xx
có dạng
;;ab cd
với
.abcd
Tổng
52ab c d
bằng
A.
0.
B.
1.
C.
2.
D.
3.
7
Câu 7. Cho phương trình
2 22
log cos log cos 4 0.
x m xm 
Có bao nhiêu giá trị
nguyên của tham số
m
để phương trình đã cho vô nghiệm?
A.
0.
B.
1.
C.
3.
D.
4.
Câu 8. Cho phương trình
22
5
5
2 log 2 5 4 log 2 6 .
mx
mx
xx x x

Gọi
S
là tập
tất cả các giá trị
m
sao cho
10m
và phương trình có nghiệm duy nhất. Số phần tử
của
S
bằng
A.
13.
B.
14.
C.
15.
D.
16.
Câu 9. Cho phương trình
2
31
3
log 2 log 2 1 0.x mx x m 
Có bao nhiêu giá trị
nguyên của tham số
m
để phương trình có nghiệm duy nhất?
A.
0.
B.
1.
C.
2.
D.
3.
Câu 10. Có bao nhiêu giá trị nguyên của tham số
m
để bất phương trình
22
log 5 log 1 log 4x mx x m 
đúng với mọi
x
?
A.
1.
B.
2.
C.
4.
D. Vô số.
Câu 11. Tìm
m
để bất phương trình
2
log 2 1 0
m
x xm 
đúng với mọi
x
.
A.
0.m
B.
1.
m
C.
1.
m
D.
1.
m
Câu 12. Cho phương trình
2
22
2
2
log 5 6 log 3 1 .
a
ax x x x




Có bao nhiêu
giá trị của biến
x
để phương trình có nghiệm đúng với mọi số thực
a
?
A.
0.
B.
1.
C.
2.
D.
4.
Câu 13. Cho phương trình
5
5 log
x
m xm
với
m
là tham số. Có bao nhiêu giá
trị nguyên của
20;20m

để phương trình đã cho có nghiệm?
A.
9.
B.
19.
C.
20.
D.
21.
Câu 14. Cho phương trình
ln 2 sin ln 3sin sinm xm x x



với
m
là tham số
thực. Có bao nhiêu số nguyên
m
để phương trình có nghiệm?
A.
3.
B.
4.
C.
5.
D.
6.
Câu 15. Cho phương trình
2
1
2
22
2 . log 2 3 4 .log 2 2
x xm
x x xm


với
m
là
tham số thực. Tìm tất cả các giá trị của
m
để phương trình có đúng hai nghiệm phân
biệt.
A.
13
; ;.
22
m









B.
13
; ;.
22
m






C.
; 1 1; .m  
D.
;1 1; .m  
Câu 16. Cho phương trình
32
21
2
log log 14 29 2 0mx x x x 
với
m
là tham số
thực. Gọi
,S ab
là tập tất cả các giá trị của
m
để phương trình có ba nghiệm phân
biệt. Hiệu
ba
bằng
A.
1
.
2
B.
5
.
2
C.
2
.
3
D.
5
.
3
8
Câu 17. Cho phương trình
22
33
log log 1 2 1 0.
x xm

Tập tất cả các giá trị của
tham số
m
để phương trình có nghiệm thuộc đoạn
3
1; 3



là
A.
01
m
. B.
02
m

. C.
13
0
6
m
. D.
12
m
.
Câu 18. Cho phương trình
ln ln 1 .mx x m 
Tập tất cả các giá trị của tham số
m
để phương trình có nghiệm thuộc khoảng
0;1
là
A.
.
eme
B.
1.me
C.
0.m
D.
0.m
Câu 19. Cho phương trình
2
22 2
log 2 log 3 log 3x x mx 
với
m
là tham số thực.
Tập tất cả các giá trị của
m
để phương trình có nghiệm thuộc
16;
là
A.
12
m

. B.
15m

. C.
15m
. D.
3
5
4
m

.
Câu 20. Cho phương trình
22 2
25
log 1 .log 1 log 1
m
xx xx xx 
với
m
là tham số dương khác
1.
Có bao nhiêu giá trị nguyên của
m
để phương trình đã
cho có nghiệm
2;x 
?
A.
1.
B.
2.
C.
3.
D. Vô số.
Câu 21. Cho phương trình
2 22 2 2
1 .log 1 2 1 .log 1 4 0.x x mx x m 
Có
bao nhiêu số nguyên
m
thuộc
10;10
để phương trình đã cho có hai nghiệm phân
biệt thỏa mãn
13x
?
A.
7.
B.
9.
C.
12.
D.
14.
Câu 22. Cho bất phương trình
32
log 2 1 1.
x
x x mx m




Có bao nhiêu giá trị
m
nguyên trong đoạn
2017;2017
để bất phương trình luôn đúng với
2x
?
A.
2010.
B.
2017.
C.
2018.
D.
2019.
Câu 23. Cho phương trình
2
2
22
2
2018 1 ln 1 2018.
x mx
x mx x





Có bao
nhiêu giá trị nguyên
m
thuộc đoạn
2018;2018
để phương trình có nghiệm duy nhất
thuộc khoảng
1; 
?
A.
2017.
B.
2018.
C.
2019.
D.
2020.
Câu 24. Cho phương trình
2
2 2 43
2
7
2 sin 3cos log 2 .
2
mm
xx




Có bao nhiêu giá trị
nguyên của tham số
m
để phương trình đã cho có nghiệm?
A.
0.
B.
1.
C.
2.
D.
3.
Câu 25. Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
10;10
để phương
trình
32
23
log 2 log 1x xm
có ba nghiệm phân biệt?
A.
8.
B.
10.
C.
11.
D.
12.
1
PHƯƠNG TRÌNH MŨ
PHƯƠNG TRÌNH LOGARIT
Phần 1. Phương trình mũ – phương trình logarit………………………………….……… 02
Phần 2. Phương trình mũ chứa tham số……………………………………………………………. 10
Phần 3. Phương trình logarit chứa tham số…………………………………………………..…18
2
Phần 1. Phương trình mũ – phương trình logarit
Câu 1. Biết phương trình
21
2
2
1
2 log log 1 log 2 2
2
x x xx

có nghiệm
x a bc
với
, 1.ac
Tổng
abc
bằng
A.
2.
B.
1
C.
1.
D.
5.
Lời giải. Điều kiện:
0 1.x
Phương trình
2
22 2
log log 1 log 2 2x x xx 
2 22
22
2
log log 2 2 2 2 2 0
11 1
1
x x xx
xx xx
xx x
x
 

1
1
x
x

(vô nghiệm) hoặc
2 2 2 0 4 2 3.
1
x
xx x
x
 
Chọn D.
Câu 2. Cho
0 1,
a
phương trình
2
2
24 2
1
log 1 log
xx
aa
a ax a
a



có bao
nhiêu nghiệm?
A.
0.
B.
1.
C.
3.
D.
4.
Lời giải. Phương trình
2
24 2 2 2
log 2 log 1
xx
aa
a ax x a

22
22
24 2 2 2
2
2 2 22
log log log 1
1
xx xx
a aa
xx xx
aa a a
a aa a





22
2
22 2
2
0
22
1 2.
20
13
xx xx
x
xx
a aa x
xx
x





Chọn D.
Câu 3. Phương trình
32
2 log cot log cosxx
có tất cả bao nhiêu nghiệm thuộc khoảng
0;2018
?
A.
321.
B.
322.
C.
642.
D.
643.
Lời giải. Điều kiện:
cos 0
cot 0 2 ; 2 , .
2
sin 0
x
x xk k k
x




Đặt
22
32
2
1
cot 3 tan
cot 3
2 log cot log cos .
3
cos 2
cos 4
t
t
t
t
t
xx
x
x xt
x
x







Do
2
2
1
1 tan
cos
x
x

nên ta có
11
1 1.
34
tt
t

3
Suy ra
1
cot
3
3
2 , .
3
1
2
cos
3
2
x
xk
x kk
xk
x









Vì
0;2018x
nên
1 1 2018
0 2 2018 0;1,...,321 .
3 6 62
k
kk k

Chọn B.
Câu 4. Phương trình
3
32
log 2 2 log 1xx
có bao nhiêu nghiệm?
A.
0.
B.
1.
C.
2.
D.
4.
Lời giải. Điều kiện:
1.x 
Phương trình
32
3 log 2 2 log 1 .xx

Đặt
2
32
3
23
81
3 log 2 2 log 1 6 9 8 1 1 .
99
12
tt
t
tt
t
x
x xt
x

 







 

*
Vế phải là hàm nghịch biến-Vế trái là hằng số nên phương trình có nghiệm duy nhất.
Mà
11
81
11
99
t
 







 
là nghiệm duy nhất của phương trình
*.
Suy ra
7x
là
nghiệm duy nhất của phương trình đã cho. Chọn B.
Câu 5. Gọi
0
x
là nghiệm của phương trình
22 2
3 3 4 4 3 4 7.
x x xx

Khẳng
định nào sau đây đúng?
A.
0
0.x
B.
0
0;1 .x
C.
0
3
; 2.
2
x


D.
0
2; 3 .
x
Lời giải. Đặt
33
.
44
x
x
a
b


Phương trình trở thành
2
22
a b ab

22 2 2 2
0
2 22 0 0 .
b
a b a b ab b ab b a b
ab
 

•
0 4 4 0 1.
x
bx 
•
3 4 7.
xx
ab
Phương trình có nghiệm duy nhất
1.x
Vậy phương trình có nghiệm
0
1.x
Chọn C.
Câu 6. Tập nghiệm của bất phương trình
21032 5 132
5 4.5 5
xx x x

là đoạn
;.ab
Tổng
ab
bằng
A.
14.
B.
16.
C.
18.
D.
20.
Lời giải. Điều kiện
2.x
Đặt
5
32
50
,
50
x
x
u
v


ta được
2
45
u
uv
v


22
4 5 0 5 0 5.
u uv v u v u v u v  
Hay
5 3 21
5 5 6 3 2 2;18 .
xx
xx S


Chọn D.
Câu 7. Phương trình
23
3 2 3 31 2 3 2
1 3 2 .2018 3 1 .2018
xx xx
xx x x x x
 
  
có
bao nhiêu nghiệm?
4
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải. Đặt
2
3
31
,
32
ax x
bx x


phương trình trở thành
.2018 .2018 2018 1 2018 1 0.
ab b a
ab b a a b
• Nếu
0, 0ab
chia hai vế cho
,ab
ta được
2018 1 2018 1
0.
ab
ab


Phương trình
này vô nghiệm do
2018 1
0
a
a
và
2018 1
0
b
b
với mọi
, 0.ab
Thật vậy: nếu
0a
thì
2018 1 0;
a

nếu
0a
thì
2018 1 0.
a

• Kiểm tra thấy
0a
hoặc
0b
thỏa mãn. Suy ra
2
3
3 10
.
3 20
xx
xx


Chọn D.
Câu 8. Số nghiệm của phương trình
44
log log
2
3 5 .3 5 1
xx
xx

là
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải. Điều kiện:
0.
x
Ta có
4
4
4
log
log
log
4
35 .
35
35
x
x
x
x



Do đó phương trình tương đương với
4
4
2
log
2
log
35 1
35
x
x
x
x 
.
Đặt
4
log
2
35 0
,
0
x
a
bx


phương trình trở thành
1
b
ab
a

1
10 1 0 .
1
ab
b
ab ab
a
aa
 


 




 
•
4
log
4
1 3 5 1 log 0 1.
x
a xx
•
4
4
log
log 3 5
22
3 5 1.
x
ab x x x x

Chọn B.
Câu 9. Trên
0;2018
phương trình
3
sin sin
11
sin 3
27 81
xx
x









có bao nhiêu nghiệm?
A.
1925.
B.
1927.
C.
1928.
D.
1930.
Lời giải. Phương trình
3
3sin 4 sin
3
11
3sin 4 sin
33
xx
xx
 







 
3
3sin 4 sin
3
11
3sin 4 sin .
33
xx
xx
 







 
Xét hàm
1
()
3
t
ft t



trên
và đi đến kết quả
3
3sin 4 sin .
3
k
x xx

Vì
0;2018x
nên
2018.3
2018 0
3
0 0;1927 .
k
k
k k

Chọn C.
5
Câu 10. Trên khoảng
0;
2


phương trình
2
sin 2 cos 1 log sinxx x

có bao nhiêu
nghiệm ?
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải. Vì
sin 0
0; .
cos 0
2
x
x
x



Do đó phương trình tương đương với
2 22
sin 2 cos log cos 1 log sin log cos
xx x x x 
22
log cos cos log sin 2 sin 2 .xx x x 
Xét
2
logft t t
trên
0;1
và đi đến kết quả
0;
2
cos sin 2 .
6
x
xx x



Chọn B.
Câu 11. Bất phương trình
2 11
2
3 3 43
x
x
xx


có bao nhiêu nghiệm nguyên nhỏ
hơn
10
?
A.
6.
B.
7.
C.
8.
D.
9.
Lời giải. Điều kiện:
1.x
Phương trình
2 11
2
3 2 13 2 1
x
x
x xx


2
2 11
11
3 2 1 3 1.
x
x
xx



Xét hàm
12
3
t
ft t

trên
0;
và đi đến kết quả
3
21 1 .
1
x
xx
x

Mà
10x
và
x
nên có
8
giá trị nguyên thỏa mãn bất phương trình. Chọn C.
Câu 12. Biết phương trình
53
21 1
log 2 log
2
xx
x
x

có nghiệm duy nhất
2x ab

trong đó
, ab
là các số nguyên. Tổng
ab
bằng
A.
1.
B.
1.
C.
2.
D.
5.
Lời giải. Điều kiện:
1.x
Phương trình
5 53 3
log 2 1 log 2 log 1 log 2x xx x

 


5 3 53
log 2 1 2 log 2 log 2 log 1 .x xx x 
Xét
53
log 2 log 1ft t t
với
1,t
ta được
2 1 3 2 2.x xx
Chọn D.
Câu 13. Tổng các nghiệm của phương trình
sin
4
tan
x
ex


trên đoạn
0;50
bằng
A.
1853
.
2
B.
2105
.
2
C.
2475
.
2
D.
2671
.
2
Lời giải. Điều kiện:
cos 0.
x
Phương trình
1
sin
1
2
sin cos
2
1
cos
2
sin sin
.
cos cos
x
xx
x
xe x
e
xx
e

*
Do
, xkk
không là nghiệm của phương trình nên
11
sin cos
22
*.
sin cos
xx
ee
xx

6
Xét hàm
2
t
e
ft
t
trên
1;1 \ 0 .
Ta có
2
2
1
2
0, 1;1 \ 0 .
t
t
e
ft t
t



Suy ra hàm số
ft
nghịch biến trên từng khoảng
1; 0
và
0;1 .
Mà
sin cos sin cos
4
f x f x x xx k

mà
0;50 0; 49 .xk 
Vậy tổng các nghiệm cần tính
49 49
00
2475
50. .
44 2
kk
kk







Chọn C.
Câu 14. Tổng các nghiệm của phương trình
2
log 1 2 1
x
x xx 
bằng
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải. Điều kiện:
0.x
Phương trình
2
log 1 1 2
x
xx x 
22
log 1 1 log 2 2 .
xx
xx 
Xét hàm
2
logft t t
với
0
t
và đi đến kết quả
0
12 .
1
x
x
x
x

Chọn B.
Câu 15. Tích các nghiệm của phương trình
3
3 2 3 43
2 3 22 1 0
xx x
xx


bằng
A.
2.
B.
1.
C.
1.
D.
2.
Lời giải. Phương trình
3
32
3 34
43
2
3 22 0
2
xx
x
x
xx


3
2 3 34
2 2 2 3 4.
xx
xx


Xét hàm
2
t
ft t
trên
và đi đến kết quả
3
2
23 4 .
1
x
xx
x


Chọn A.
Câu 16. Phương trình
2 22
22
log211 log21121xxx x 
có bao
nhiêu nghiệm nguyên?
A.
0.
B.
1.
C.
2.
D.
4.
Lời giải. Điều kiện:
0.x
Phương trình đã cho
2
22
22
2
2
log log 2 1 1 2 1
2 11
x
xx x
x


22 2 2
22 2
22
22
22
22
log 2 log 2 1 1 log 2 1 1 2 1
1 2 log 2 log 2 1 1 2 1
2 log 2 log 2 1 1 2 1 1 .
x xxx x
xx x x
xx x x
 

 
Xét hàm
2
2 logft t t

trên
0;
và đi đến kết quả
2
2 11xx 
2
1 2 1 2.x xx 
Chọn C.
Sai lầm hay gặp là biến đổi
2
22
22
2
2
log 2 1 1 log 2 1
2 11
x
xx x
x


7
22
22
2 log 2 1 1 2 1 1 2 log
x x xx
 
và xét hàm
2
2 log
ft t t
trên
0;
nhưng hàm này không đơn điệu trên
0; .
Câu 17. Số nghiệm của phương trình
11
2
ln 1
x
xx

là
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải. Điều kiện:
1 2.x
Xét hàm
11
2.
ln 1
fx x
xx

Ta có
22
11
10
1 ln 1
fx
xx x


với
mọi
x
thuộc tập xác định. Suy ra
fx
nghịch biến trên từng khoảng xác định.
Dựa vào BBT suy ra phương trình đã cho có hai nghiệm phân biệt. Chọn B.
Câu 18. Phương trình
2
22
log 4 log 8 16xx x 
có bao nhiêu nghiệm?
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải. Điều kiện:
2.
x
Phương trình tương đương
2
22
log 2 4 log 8 16
x
xx




22
8
2 4 8 16 2 2 8 2 .
2
x x xx
xx x
x

Ta có
2
x
fx
là hàm đồng biến;
8
2
gx
x
là hàm nghịch biến nên phương trình có
nghiệm duy nhất. Mà
33fg
suy ra
3x
là nghiệm duy nhất. Chọn B.
Câu 19. Cho phương trình
22 2
22
5 6 log log 5 5 6 .xx xx x x x x xx
 
Gọi
;S ab
là tập nghiệm của bất phương trình đã cho. Khi đó
ba
bằng
A.
1
.
2
B.
2.
C.
5
.
2
D.
7
.
2
Lời giải. Điều kiện
0 3.x
Bất phương trình đã cho
22
2
log 16 5 16 0x xx xx x xx  
2
2
log 5 1 6 0.x x x xx




*
Xét
2
logfx x x
trên
0;3 .
Lập BBT ta có
2
0;3
max 3 3 log 3 5.fx f
Suy ra
2
log 5 0, 0;3 .xx x 
Do đó
2
* 1 6 0.x xx 
Giải bất phương
trình này và kết hợp với điều kiện ta được tập nghiệm
5
;3 .
2
S

Chọn A.



2
2
1
f
f
x

8
Câu 20. Tích các nghiệm của phương trình
2
2 31
3
log 3 2 2 5 2
xx
xx


bằng
A.
1.
B.
2.
C.
4.
D.
9.
Lời giải. Điều kiện:
2
3 2 0.xx 
Đặt
2
2 .3 0txx 
Khi đó phương trình trở thành
2
1
3
log 2 5 2.
t
t

*
Xét
2
1
3
log 2 5
t
ft t

với
0.t
Ta có
2
1
1
2 .5 ln 5 0, 0.
2 ln 3
t
ft t t
t

Suy ra hàm số
ft
đồng biến trên
0; .
Mà
1
ft f
suy ra
1t
là nghiệm
của phương trình
*.
Với
1,
t
ta có
2
12
– 3 1 0 . 1.
x x xx
Chọn B.
Câu 21. Số nghiệm của phương trình
12
3 22 1
x
xx x

là
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải. Đặt
1.tx
Phtrình trở thành
22
3 1 3 1 1.
tt
tt tt

*
Xét
2
3 1 1.
t
ft t t

Ta có
22
22
1
1
1 3 3 ln 3 1 3 1 ln 3 0.
11
tt t
t
ft tt tt
tt





 








Do đó phương trình
0ft
có tối đa
1
nghiệm. Mà
0 0.f
Do đó
0t
là nghiệm duy nhất của phương trình
*.
Hay phương trình đã cho có nghiệm duy nhất
1.x
Chọn B.
Câu 22. Cho phương trình
22
23
log 5 5 1 log 5 7 2.xx xx 
Tổng tất cả
các nghiệm của phương trình đã cho bằng
A.
5.
B.
9.
C.
10.
D.
15.
Lời giải. Đặt
2
5 5 0.
txx

Phương trình trở thành
2
23
log 1 log 2 2.tt
• Xét
1,t
ta có
22
2
23
2
33
log 1 log 2 1
log 1 log 2 2.
log 2 log 3 1
t
tt
t



• Xét
0 1,t
ta có
22
2
23
2
33
log 1 log 2 1
log 1 log 2 2.
log 2 log 3 1
t
tt
t



Dấu
'' ''
xảy ra
2 22
12
551 551 540 5.xx xx xx xx 
Chọn A.
Câu 23. Số nghiệm của phương trình
13
2
2
8
22
log 2 3
xx
xx



là
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải. Áp dụng bất đẳng thức Côsi, ta có
1 3 13
2 2 2 2 .2 8 VT 8.
x x xx 

Lại có
2
2
2 3 1 22xx x 
nên suy ra
2
22
log 2 3 log 2 1 VP 8.xx 
9
Do đó
13
13
2
2
2
2
22 8
8
2 2 1.
log 2 3 1
log 2 3
xx
xx
x
xx
xx






Chọn B.
Câu 24. Số nghiệm của phương trình
32 2
22
2 3 log 1 log 0xx x x 
là
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải. Điều kiện:
0.
x
Phương trình tương đương
32
2
1
2 3 log 0.xx x
x



Áp dụng bất đẳng thức Côsi, ta có
1
2x
x

suy ra
22
1
log log 2 1.x
x



Do đó
2
32 32
2
1
23log 231 1210, 0.xx x xx x x x
x

 

Dấu
""
xảy ra khi
1.x

Chọn B.
Câu 25. Cho phương trình
2
12
2018 1 .2019 1.
xx
x

Khẳng định sau đây đúng?
A. Phương trình có tổng các nghiệm bằng
0.
B. Phương trình có nghiệm duy nhất.
C. Phương trình có hai nghiệm dương phân biệt.
D. Phương trình có nhiều hơn hai nghiệm.
Lời giải. Nếu
; 1 1;x  
thì
2
1
2
2
2018 1
10 .
1 .2019 0
x
x
x
x


Suy ra
2
12
2018 1 .2019 1
xx
x

Phương trình đã cho vô nghiệm.
Nếu
1;1x 
thì
2
1
2
2
2018 1
10 .
1 .2019 0
x
x
x
x


Suy ra
2
12
2018 1 .2019 1
xx
x

Phương trình đã cho vô nghiệm.
Kiểm tra thấy
1x 
là nghiệm của phương trình đã cho.
Vậy phương trình đã cho có tổng các nghiệm bằng
0.
Chọn A.
10
Phần 2. Phương trình mũ chứa tham số
Câu 1. Cho phương trình
2
22
log log
2
3 2 3 .3 3 0
xx
mm 
với
m
là tham số. Tập
hợp tất cả các giá trị của
m
để phương trình đã cho có hai nghiệm phân biệt
12
,
xx
thỏa mãn
12
2xx
là
A.
0; .
B.
\ 1;1 .
C.
1; . 
D.
1; \ 0 . 
Lời giải. Điều kiện:
0.x
Đặt
2
log
3 0.
x
t 
Phương trình trở thành
22
2 3 3 0.
t m tm 
*
Nhận xét: 1) Cứ một nghiệm
0t
thì cho một nghiệm
0.x
2) Ta có
21 22 21 22 212 2
log log log log log log 2
3 .3 3 3 3 3
xxxxxx

hay
12
3.tt
Do đó để phương trình đã cho có hai nghiệm phân biệt
12
,
xx
thỏa mãn
12
2xx
khi
và chỉ khi phương trình
*
có hai nghiệm dương phân biệt
12
,
tt
thỏa mãn
12
3tt
2
2
2
3 30
0
1
3 33 .
0
0
2 30
mm
m
Pm
m
S
m










Chọn D.
Câu 2. Biết phương trình
1
4 12 8 0
xx
m

có hai nghiệm
12
, xx
thỏa mãn điều
kiện

12
1 1 6.xx 
Khẳng định nào sau đây đúng?
A.
0.m
B.
0 2.m

C.
1 3.
m
D.
3.m
Lời giải. Đặt
1
2 0.
x
t

Phương trình trở thành
2
4 1 32 0.t mt

*
Phương trình đã cho có hai nghiệm
12
, xx
khi và chỉ khi phương trình
*
có hai
nghiệm
12
, tt
đều dương
2
0
2 70
.
10
1
mm
m
m









1
Gọi
12
0tt

là hai nghiệm của phương trình
*,
suy ra
1 21
2 22
1 log
1 log
xt
xt



1 2 21 22
1 1 6 log . log 6.xx tt 
Lại có
2 1 2 2 2 12 2
log log log log 32 5.t t tt
Từ đó suy ra
21 1
22 2
log 3 8
log 2 4
tt
tt









hoặc
21 1
22 2
log 2 4
.
log 3 8
tt
tt









Với hai trường hợp ta đều có
12
41 2tt m m 
(thỏa mãn
1
). Chọn C.
Cách khác. Đặt
2 0,
x
t 
ta được
2
2 1 8 0.t mt 
Ta thấy
12
8tt
nên suy ra
12
3.xx
Đến đây kết hợp với giả thiết

12
1 16xx 
để tìm
12
, .xx
Câu 3. Có bao nhiêu giá trị nguyên của tham số
m
trên khoảng
2018;2018
để
phương trình
21 2
6.2 7 48 .2 2 16 0
xx
m mm

có hai nghiệm dương
12
, xx
thỏa
mãn
12
15xx
?
11
A.
1993.
B.
1994.
C.
3986.
D.
3988.
Lời giải. Đặt
2,
x
t
vì
0 1.xt 
Phương trình trở thành
22
2 16
3 7 48 2 16 0 .
3
tm
t m tm m
m
t


Để phương trình đã cho có hai nghiệm dương
1
2
2 16 1
1
17
.
1
2
1
3
m
t
m
m
t





Khi đó
12
12 2 2
22
log 2 16
15 log 2 16 .log 15.
3
log
3
xm
m
xx m
m
x


*
Xét hàm
22
log 2 16 .log
3
m
fm m
là hàm đồng biến trên
17
;.
2



Nhận thấy
*
có dạng
2018;2018
24 24
m
m
fm f m


có
1994
giá trị. Chọn B.
Câu 4. Cho phương trình
22
21 22
4 .2 3 2 0.
xx xx
mm
 

Tập tất cả các giá trị của
tham số
m
để phương trình đã cho có
4
nghiệm phân biệt là
A.
2; .
B.
2, .
C.
1; .
D.
;1 2; . 
Lời giải. Đặt
2
1
2 1.
x
t

Phtrình trở thành
2
2
2
2. 3 2 0 .
23
t
t mt m m
t

*
Xét hàm
2
2
23
t
ft
t
trên
3
1; \ .
2








Phương trình đã cho có bốn nghiệm phân
biệt khi và chỉ khi phương trình
*
có
hai nghiệm phân biệt lớn hơn
1
và khác
3
2
BBT
2.m 
Chọn A.
Câu 5. Có bao nhiêu giá trị nguyên
m
thuộc đoạn
2018;2018
để phương trình
2 22
2 22
.9 2 1 .6 .4 0
xx xx xx
mm m


có nghiệm thuộc khoảng
0;2
?
A.
2010.
B.
2011
. C.
2012.
D.
2013.
Lời giải. Phương trình đã cho tương đương với
22
22 2
33
. 2 1 . 0.
22
xx xx
mm m

 







 
Đặt
2
2
3
,
2
xx
t


vì
0;2x
nên
2
;1 .
3
t

Phương trình trở thành
2
2
21 0 .
21
t
mt m t m m
tt


0
0

2
t
f
f
1

2

1

1, 5
12
Xét hàm
2
21
t
ft
tt

trên
2
;1 .
3

Từ bảng biến thiên suy ra phương trình có
nghiệm khi
6.m
Kết hợp với giả thiết ta có
6;7;...2018 :m
có
2013
giá trị. Chọn D.
Câu 6. Cho phương trình
22
2
2
51 51 2 .
xx
x
m

Tập tất cả các giá trị của
tham số
m
để phương trình có đúng bốn nghiệm phân biệt là
;.ab
Hiệu
ba
bằng
A.
3
.
4
B.
1
.
16
C.
1
.
64
D.
49
.
64
Lời giải. Phương trình đã cho tương đương với
22
51 51 1
..
2 24
xx
m













Đặt
2
51
2
x
t


0 1.t
Phương trình trở thành
2
11
.
44
m
t m tt
t

*
Nhận xét: 1) Cứ một nghiệm
0;1t
cho ta hai nghiệm
.x
2) Với
1t
cho ta một nghiệm
0.
x
Do đó yêu cầu bài toán tương đương với phương trình
*
có hai nghiệm
12
,
tt
phân
biệt thuộc khoảng
0;1 .
Xét hàm
2
1
4
ft t t
trên
0;1 .
Dựa vào BBT ta có
1
0
64
m

thỏa mãn yêu cầu.
Suy ra
1
.
64
ba
Chọn C.
Câu 7. Cho phương trình
22
2
1
4 7 4 7 3 0.
xx
x
m

Gọi
S
là tập tất cả các
giá trị của tham số
m
sao cho
36m
và phương trình đã cho có đúng hai nghiệm
phân biệt. Số phần tử của
S
bằng
A.
1.
B.
24.
C.
25.
D.
26.
Lời giải. Phương trình đã cho tương đương với
22
47 47 1
0.
3 33
xx
m













Đặt
2
47
3
x
t


0 1.t
Phương trình trở thành
2
1
0.
33
mt
t mt
t
 
*
f
1
2/3
f
t
6

1
64
f
1
0
f
t
0
0
1
8
3
4
13
Xét hàm
2
3
t
ft t
trên
0;1 .
Dựa vào BBT ta có
1
36
2
0
3
m
m

thỏa yêu cầu bài
toán, suy ra
36 1
.
24 36 0
m
m

Vậy có tất cả
25
giá trị thỏa mãn. Chọn C.
Câu 8. Cho phương trình
.9 2 1 6 .4 0.
x xx
mm m
Tìm tất cả các giá trị của tham
số
m
để bất phương trình nghiệm đúng với mọi
x
thuộc
0;1 .
A.
6.m 
B.
6 4.m 
C.
4.m 
D.
6.m
Lời giải. Bất phương trình đã cho
93
. 2 1 0.
42
xx
mm m









Đặt
3
2
x
t


với
3
1.
2
t
Bất phương trình trở thành
2
21 0mt m t m

2
3
1;
2
33
, 1; min 6 .
22
1
t
m ft t m ft f
t



 



Chọn D.
Câu 9. Tập tất cả các giá trị của tham số
m
để phương trình
3 3 .9 1
xx
m
có
đúng
1
nghiệm có dạng
;.
ab c
Tổng
abc
bằng
A.
4.
B.
11.
C.
14.
D.
15.
Lời giải. Đặt
3 0.
x
t 
Phương trình trở thành
2
2
3
31 .
1
t
t mt m
t
 
*
Xét hàm
2
3
1
t
ft
t
trên
0; .
Ta có
22
13 1
; 0 .
3
11
t
ft ft t
tt



Để phương trình đã cho có đúng
1
nghiệm
phương trình
*
có đúng
1
nghiệm dương
BBT
13
.
10
m
m

Chọn C.
Câu 10. Tìm tất cả các giá trị thực của tham số
m
để phương trình
2
4
2
1
x
x
me e
có nghiệm thực.
A.
1 0.m
B.
0 1.m
C.
2
0.
m
e

D.
1
1.m
e

Lời giải. Đặt
2
4
1,
x
te
vì
2
0
x
e
nên
1.t
Suy ra
4
4
42 4 4
22
1 11
xx
x
te e t e t



.
Khi đó phương trình trở thành
44
44
1 1.m t t mt t 
10
f
0
f
t
3
0
1/3
1

1
36
f
1
0
f
t
0
0
1
6
2
3
14
Xét hàm
4
4
1ft t t
trên
1; 
. Ta có
3
3
4
4
1 0, 1.
1
t
ft t
t

Suy ra hàm số
ft
nghịch biến
trên
1; 
.
Dựa vào bảng biến thiên, ta thấy
phương trình có nghiệm khi và chỉ
khi
01
m

. Chọn B.
Câu 11. Cho hàm số
47
3 1 2 6 3.
xx
fx x x


Khi phương trình
2
7 46 9 3 1 0f xx m 
có số nghiệm nhiều nhất thì giá trị nhỏ nhất của tham
số
0
.mm
Khẳng định nào sau đây đúng?
A.
0
0;1 .
m
B.
0
1; 2 .m
C.
0
2;3 .m
D.
0
3; 4 .m
Lời giải. Đặt
2
2
746 9 741 3 1 3;7.t xx x 
Khi đó
1 3.
ft m
Xét hàm số
47
3 12 6 3
tt
ft t t


trên đoạn
3;7 .
Ta có
47 7
3 ln 3 2 1 2 ln 2 6;
tt t
ft t


22
4 77 7
3 ln 3 2 ln 2 2 ln 2 1 2 ln 2
t tt t
ft t



2
47
0, 3;7
3 ln 3 2 1 ln 2 2 ln 2 0.
tt
t
t






Suy ra hàm số
ft
đồng biến trên
3;7 .
Lại có
30
0
70
f
fx
f

có nghiệm duy nhất
0
t
thuộc
3;7 .
Dựa vào BBT, ta thấy phương trình
13ft m
có số nghiệm nhiều nhất
0
0
1
5
13 4 .
33
ft
ft m m

Suy ra
0
5
1; 2 .
3
m 
Chọn B.
Câu 12. Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
5;5
để phương
trình
1
x
e mx

có nghiệm duy nhất?
A.
5.
B.
6.
C.
7.
D.
10.
Lời giải. Vì
0
x
e
nên
0.m
Khi đó:
1
x
e mx
11
x
x
m
e

1
1
x
x e fx
m

.
Xét hàm
1.
x
fx x e

Ta có
' 0 0.
x
f x xe x

0
4
0
ft
f
7
3
f
t
148
3
0
t
0
1
t
f
f

1
15
Dựa vào BBT, ta thấy phương trình có nghiệm duy
nhất
1
1
0
11
0
m
m
m
m

5;5
5;4;3;2;1;1.
m
m
m


Chọn B.
Cách 2. Ta có
x
ye
là hàm đồng biến trên
và
0
x
ye
với mọi
x
có đồ thị
C
(xem hình 1).
Hình 1 Hình 2
Do đó:
Nếu
0m
thì
1y mx
là hàm số nghịch biến trên
, có đồ thị là một đường
thẳng luôn qua điểm
1; 0
nên luôn cắt đồ thị
:
x
Cye
tại duy nhất một điểm.
Nếu
0:m
phương trình vô nghiệm (do
0
x
ye
).
Nếu
0:m
để phương trình có duy nhất một nghiệm khi và chỉ khi đường thẳng
:1
y mx
là tiếp tuyến của
C
(như hình 2)
1
x
x
e mx
em

0
1.
1
x
m
m

Câu 13. Có bao nhiêu giá trị nguyên của tham số
m
thuộc
2000;2000
để
log log
2 log 1
ab
ba
a
a b mb
với
, ab
là các số thực lớn hơn
1
?
A.
1999.
B.
2000.
C.
2001.
D.
2199.
Lời giải. Đặt
log
a
tb
vì
, 1;ab 
nên
0.t
Suy ra
2
.
1
log
t
b
ba
a
t
Bất phương trình trở thành
2
1
1
2 1 1 , 0.
t
tt t
t
a
a a mt a mt m t
t
 
Xét hàm
1
t
a
ft
t
trên
0; .
Ta có
2
ln 1
.
tt
ta a a
ft
t

•
ln 1
tt
g t ta a a 
trên
0; .
Đạo hàm
2
ln 0, 0.
t
g t ta a t

• Suy ra
gt
đồng biến trên
0;
nên
0 0, 0.gt g t 
Suy ra
0, 0.ft t

Suy ra hàm số
ft
đồng biến trên
0; .
1
f

f
x

0
0
0

16
Dựa vào BBT ta thấy
ln
ma
thỏa mãn yêu
cầu bài toán. Do đúng với mọi
1
a
và
m
là
số nguyên thuộc
2000;2000
nên
1999; 1998;...;0 .
m

Chọn B.
Câu 14. Tìm tất cả các giá trị của tham số
m
để phương trình
22
2
x
mx
có hai
nghiệm thực phân biệt.
A.
1
.
1
m
m

B.
1
.
2
m
m

C.
2
.
2
m
m

D.
3 1.m 
Lời giải. Đặt
0.
tx
Phương trình trở thành
22 2
2.
t
tm
Nhận xét: Với mỗi nghiệm
0t
ta tìm được tương ứng hai nghiệm
.
x
Xét hàm
22
2
t
ft t

trên
0;
Ta có
2
2.2 .ln 2 2 0, 0.
t
ft t t

Dựa vào bảng biên thiên, ta thấy yêu cầu bài
toán
2
1
1.
1
m
m
m


Chọn A.
Cách 2. Phương pháp hình học. Nhận thấy phương trình
22
2
x
mx
là phương trình hoành độ giao điểm của đồ
thị hàm số
2
x
y
và nửa đường tròn
22 2
xym
(phần
phía trên trục hoành) như hình vẽ. Dựa vào hình vẽ ta
thấy để hai đường này cắt nhau tại hai điểm phân biệt khi
2
1m
1m
hoặc
1.m 
Câu 15. Phương trình
3
23 3 2 2 1
2 69 2 21
x mx x x
x x xm


có ba nghiệm phân
biệt khi và chỉ khi
;.m ab
Giá trị biểu thức
22
Tb a
bằng
A.
36.
B.
48.
C.
64.
D.
72.
Lời giải. Phương trình
3
3
23 2
2 2 32 1
x mx x
x mx





3
3
3
32
3
2 3 2 2.
mx x
mx x


Xét hàm
3
2
t
ft t
với
t
và đi đến kết quả
3
3
32 3 2mx xmx x

3 2 BBT 2 2
4
6 9 8 4;8 48.
8
a
m x x x m Tb a
b

Chọn B.
Câu 16. Cho phương trình
3 22
2 1 11 .
mm
ee x x x x 
Tập hợp tất cả các
giá trị thực của tham số
m
để phương trình có nghiệm là
A.
1
0; ln 2 .
2


B.
1
0; .
e


C.
1
; ln 2 .
2


D.
1
ln 2; .
2


Lời giải. Điều kiện:
1 1.x
t
f
f
0

ln a

t
f
f
0

1

17
Phương trình
3 22
1 22 1
mm
ee x x x x

3 22 2 2
3
3
22
1 21 1 1
1 1.
mm
mm
e e x xx x x x
eexxxx




 
Xét hàm
3
ft t t
với
t
và đi đến kết quả
2 BBT
12
mm
ex x e 
1
ln 2 ln 2.
2
mm 
Chọn C.
Câu 17. Có bao nhiêu giá trị nguyên dương của
m
nhỏ hơn
2018
để phương trình
2
2
11
32
4
1
x xm
x
x
x mx x
e
x


có nghiệm thực dương?
A.
2014.
B.
2015.
C.
2016.
D.
2017.
Lời giải. Phương trình
2
2
2
2
1
1
1
2
2
1
2
2
1
11
.
1
x
x
x
xm
xx
xm
x
xm
e
x
x e x me
x
x
x
e
x












Xét hàm
t
f t te
với
0t
và đi đến kết quả
2
2
11
x xm
x
x

2
1
2
2 BBT
do 0
11
2 2 0 0.
tx
x
x
mx x tt m
xx




 





Mà
m
là số nguyên dương nhỏ hơn
2018
nên
1;2;3...2016;2017 .m
Chọn D.
Câu 18. Có bao nhiêu giá trị nguyên của tham số
m
nhỏ hơn
10
để phương trình
xx
m me e 
có nghiệm thực?
A.
9.
B.
10.
C.
11.
D. Vô số.
Lời giải. Phương trình
22
.
xx x xxx
m me e me me e e 
Xét hàm
2
ft t t
với
0t
và đi đến kết quả
2xx x x
me e me e

2 BBT
10
1
4
xx m
m
me e m
 
có
10
giá trị thỏa mãn. Chọn B.
Câu 19. Biết rằng
a
là số thực để phương trình
9 9 .3 cos
xx
ax
có nghiệm duy
nhất. Hỏi
a
thuộc khoảng nào sau đây?
A.
8; 4 .
B.
4;2 .
C.
4;10 .
D.
12;18 .
Lời giải. Phương trình tương đương với
2
3 3 .cos .
xx
ax

*
Nhận thấy rằng nếu
0
x
là nghiệm của phương trình
*
thì
0
2 x
cũng là nghiệm
của phương trình
*.
Thật vậy
0
0 00
22
22
00
3 3 .cos 2 3 3 .cos .
x
x xx
a x ax





Vậy phương trình
*
có nghiệm duy nhất khi
00 0
2 1.xx x
Suy ra
6.a 
Thử lại
6,a 
ta được
2
9 9 6.3 cos 3 3 6.3 1 cos 0
x x xx
xx



18
3 30
1.
1 cos 0
x
x
x



Vậy
6
a

thỏa mãn bài toán. Chọn A.
Câu 20. Cho tham số thực
,a
biết phương trình
2 cos
xx
e e ax

1
có
5
nghiệm
thực phân biệt. Hỏi phương trình
2 cos 4
xx
e e ax

2
có bao nhiêu nghiệm
thực phân biệt?
A.
5.
B.
10.
C.
11.
D.
20.
Lời giải. Phương trình
22
2
2
22
22
2 cos 2.1
2
2 4 cos .
2
2 cos 2.2
2
xx
xx
xx
ax
ee
ax
ee
ax
ee












Nhận xét: 1)
0x
không là nghiệm của
1.
2) Nếu
0
0x
là nghiệm của
1
thì
0
2x
là nghiệm
2.1
và
0
2x
là nghiệm
2.2 .
Vậy phương trình
2
có
10
nghiệm thực phân biệt. Chọn B.
Phần 3. Phương trình logarit chứa tham số
Câu 1. Cho phương trình
22
22
log 5 1 log 4 0.
x m x mm 
Biết phương trình có
2
nghiệm phân biệt
12
, xx
thỏa
12
165.xx
Giá trị của
12
xx
bằng
A.
16.
B.
119.
C.
120.
D.
159.
Lời giải. Điều kiện:
0.
x
Đặt
2
log ,tx
phương trình trở thành
22
5 1 4 0.t m t mm

*
Phương trình đã cho có
2
nghiệm phân biệt
phương trình
*
có
2
nghiệm phân
biệt
2
2
1
9 6 10 3 1 0 .
3
mm m m  
Khi đó phương trình
*
có
2
nghiệm là
11
41
2
2
2
.
41
2
m
m
tm x
tm
x





Ycbt:
41
12
165 2 2 165 2 3.
mm m
xx
 
Suy ra
12
3 162.xx

Khi đó
12
159.xx
Chọn D.
Câu 2. Giá trị thực của tham số
m
để phương trình

2
33
log 3 log 2 7 0x xm
có
hai nghiệm thực
12
,xx
thỏa mãn


12
3 3 72xx
thuộc khoảng nào sau đây?
A.


7
;0 .
2
B.


7
0; .
2
C.


7
;7 .
2
D.


21
7; .
2
Lời giải. Điều kiện:
0.x
Đặt
3
log ,tx
phương trình trở thành
2
3 2 7 0.t tm 
*
19
Phương trình đã cho có
2
nghiệm phân biệt
phương trình
*
có
2
nghiệm phân
biệt
37
9 42 7 0 .
8
mm
Áp dụng Vi-et ta có
1 2 3 1 3 2 3 12 12
3 log log 3 log 3 27.
t t x x xx xx   
Kết
hợp với giả thiết ta được
1
2
3
.
9
x
x
Lại có
12 3 1 3 2 3 3
9
2 7 log .log 2 7 log 3.log 9 2 7 .
2
tt m x x m m m  
Chọn C.
Câu 3. Cho phương trình
2
33
2 log 4 log 2 0.m x xm 
Tập tất cả các giá trị
của tham số thực
m
đê phương trình có hai nghiệm
12
,xx
thỏa
12
01xx 
là
A.
; 2.

B.
2;2 .
C.
2; .
D.
\ 2;2 .
Lời giải. Điều kiện:
0.x
Đặt
3
log ,tx
vì
1 2 31 3 3 2
0 1 log log 1 log
xx x x 
nên
12
0.tt
Phương trình trở thành
2
2 4 2 0.m t tm 
*
Khi đó ycbt
phương trình
*
có hai nghiệm trái dấu

2 20mm 
2 2.m
Chọn B.
Câu 4. Cho phương trình
22
22
log 2 1 log 2 0.x m xm m 
Tập tất cả các giá trị
của tham số
m
để bất phương trình nghiệm đúng với mọi
1; 2x
là
A.
1 0.m
B.
1 0.m
C.
2
.
1
m
m

D.
2
.
1
m
m

Lời giải. Điều kiện:
0.
x
Đặt
2
log ,tx
vì
1; 2x
nên
0;1 .t
Bất phương trình trở thành
22
12
0
2 1 2 0, 0;1
01
t m tm m t
tt




2
2
2
2
12
1 20
20
0 1 0.
2 2 1 10
1 10
m mm
mm
Pm
mmm
tt








Chọn B.
Câu 5. Cho phương trình
2 22
42
log 2 2 2 log 2 .
xx
m




Có bao nhiêu giá trị
nguyên của tham số
m
để phương trình vô nghiệm?
A.
3.
B.
4.
C.
5.
D.
6.
Lời giải. Điều kiện:
2.m
Phương trình
2
42
log 2 2 log 2
x
m




22
22 2 2 4
log22log 2 22 2 .
2 22 2
xx
xx
xx
mm
mm
mm

 

 




Phương trình vô nghiệm
40 4
0 4.
00
mm
m
mm










2
0;1; 3; 4 .
m
m
m

Chọn B.
20
Câu 6. Cho phương trình
2 22 2
41
2
2 log 2 2 4 log 2 0.x x m m x mx m
Tập tất
cả các giá trị của tham số
m
để phương trình có hai nghiệm phân biệt
12
, xx
thỏa
mãn
22
12
1xx
có dạng
;;ab cd
với
.abcd

Tổng
52ab c d
bằng
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải. Phương trình
2 22 2
22
log 2 2 4 log 2x x m m x mx m

22
22
22
2 22 2
20
20
1 22 0
2 24 2
x mx m
x mx m
x m x mm
x x m m x mx m








1
2
.
Phương trình
2
có hai nghiệm là
12
1 , 2
x mx m
nên yêu cầu bài toán
22
2
2
2
2
12
10
1 21
.
21
1 1 20
52
2 22 0
mm
m
mm
m
mmmm
m mm m







Chọn C.
Câu 7. Cho phương trình
2 22
log cos log cos 4 0.x m xm

Có bao nhiêu giá trị
nguyên của tham số
m
để phương trình đã cho vô nghiệm?
A.
0.
B.
1.
C.
3.
D.
4.
Lời giải. Phương trình
22
log cos 2 log cos 4 0.x m xm 
Đặt
log cos
tx
0.t
Phương trình trở thành
22
2 4 0.t mt m 
*
Phương trình đã cho vô nghiệm khi
• Phương trình
*
vô nghiệm
22
4 4 4 0 2 2.
mm m 
• Phương trình
*
có hai nghiệm
12
, tt
đều dương
0
0 2 2.
0
Sm
P

 
Hợp hai trường hợp ta được
2;2m 
thỏa ycbt
có
3
giá trị nguyên. Chọn C.
Câu 8. Cho phương trình
22
5
5
2 log 2 5 4 log 2 6 .
mx
mx
xx xx

Gọi
S
là tập
tất cả các giá trị
m
sao cho
10m
và phương trình có nghiệm duy nhất. Số phần tử
của
S
bằng
A.
13.
B.
14.
C.
15.
D.
16.
Lời giải. Phương trình
22
55
log 2 5 4 log 2 6
mx mx
xx x x


22
0 51
2 54 26
mx
xx xx




0 51
.
2 hoaëc 5
mx
xx
• Chỉ
2x
là nghiệm thỏa bài toán


 
02 51
.
5 5 0 hoaëc 5 5 1
m
m
mm
• Chỉ
5x
là nghiệm thỏa bài toán

 
05 51
2 5 0 hoaëc 2 5 1
m
mm
21
10
6
1
5
10 10 12
65
12 10 25 10 11;13;14; 25;30 .
52
10 30
3
m
m
m
mm m
m
m



Chọn C.
Câu 9. Cho phương trình
2
31
3
log 2 log 2 1 0.
x mx x m 
Có bao nhiêu giá trị
nguyên của tham số
m
để phương trình có nghiệm duy nhất?
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải. Phương trình
2
33
log 2 log 2 1x mx x m 
2
2
1
2 10
1
2
22 1
2 1 10 *
.
m
xm
x
x mx x m
x m xm




Yêu cầu bài toán
phương trình
*
có một nghiệm thỏa mãn
1:
●
*
có nghiệm kép thỏa
/
*
0
0.
1
22
1 m
bm
x
a



●
*
có hai nghiệm
12
, xx
thỏa
12
1
1
.
1
2
5
m
m
xx
m



●
*
có hai nghiệm
12
, xx
thỏa
12
11
1.
25
m
x xm

Vậy
0
1
1
5
m
m

thỏa yêu cầu bài toán: Có
2
giá trị nguyên thỏa mãn. Chọn C.
Câu 10. Có bao nhiêu giá trị nguyên của tham số
m
để bất phương trình
22
log 5 log 1 log 4x mx x m 
đúng với mọi
x
?
A.
1.
B.
2.
C.
4.
D. Vô số.
Lời giải. Để bất phương trình đúng với mọi
x
khi và chỉ khi:
● Bất phương trình xác định với mọi
2
4 0, x mx x m x 
2
0
0
2.
'0
40
m
m
m
m







1
● Bất phương trình nghiệm đúng với mọi
22
log 5 5 log 4 , x x mx x m x 
22
2
2
5 5 4 ,
5
50
5 4 5 0, 3.
'0
10 21 0
x mx x m x
m
m
mx x m x m
mm



 





2
Từ
1
và
2
, ta được
2 3 3.
m
mm

Chọn A.
22
Câu 11. Tìm
m
để bất phương trình
2
log 2 1 0
m
x xm 
đúng với mọi
x
.
A.
0.m
B.
1.m
C.
1.m
D.
1.m
Lời giải. Điều kiện:
2
2
2 10
10
01
01
01
x xm
xm
m
m
m








.
Nhận xét. Với dạng

log 0 1 1 0.
a
b ab 
Bất phương trình
2
1 2 0.m x xm 
*
Để
*
đúng với mọi
:
x
● Nếu
1m
thì
2
10
* 2 0,
10
x xm x
m


: vô lí.
● Nếu
1m
thì
2
10
* 2 0, 1
10
x xm x m
m


: (thỏa).
Vậy
1m
thỏa mãn yêu cầu bài toán. Chọn D.
Câu 12. Cho phương trình
2
22
2
2
log 5 6 log 3 1 .
a
ax x x x




Có bao nhiêu
giá trị của biến
x
để phương trình có nghiệm đúng với mọi số thực
a
?
A.
0.
B.
1.
C.
2.
D.
4.
Lời giải. Vì đúng với mọi
a
nên ta chọn
0.a
Với
0,a
phương trình trở thành
22
2
log 6 log 3 1 .
5
x
xx
x

Thử lại chỉ có
5x
thỏa mãn. Chọn B.
Câu 13. Cho phương trình
5
5 log
x
m xm
với
m
là tham số. Có bao nhiêu giá
trị nguyên của
20;20m 
để phương trình đã cho có nghiệm?
A.
9.
B.
19.
C.
20.
D.
21.
Lời giải. Đặt
5
5 log .
x
m xm t
Ta được hệ
5
5 5.
5
t
xt
x
xm
xt
mt



Xét hàm
5
x
fx x
trên
và đi đến kết quả
.xt
Khi đó
5.
x
m x gx
Ta có bảng biến thiên của hàm
gx
như sau
Từ bảng biến thiên suy ra phương trình có nghiệm khi
5
1
log .
ln 5
mg





5
1
log
ln 5
g






0


g
g
x
5
1
log
ln 5



23
20;20
19; 18; 17;...; 1 .
m
m
m


Có
19
giá trị. Chọn B.
Câu 14. Cho phương trình
ln 2 sin ln 3sin sin
m xm x x



với
m
là tham số
thực. Có bao nhiêu số nguyên
m
để phương trình có nghiệm?
A.
3.
B.
4.
C.
5.
D.
6.
Lời giải: Phương trình
2 sin ln 3 sin ln 2 sin ln 3 sinm xm x m xm x

 

3sin ln 3sin .mxmx
Xét hàm
lnft t t
với
0t
và có được
2 sin ln 3sin 3sin
mxmxmx

sin
1;1 .
1
ln 3 sin sin ln 3 3 3; 3 .
ax a
a
m x x m a a me ae
e






Chọn B.
Câu 15. Cho phương trình
2
1
2
22
2 . log 2 3 4 .log 2 2
x xm
x x xm


với
m
là
tham số thực. Tìm tất cả các giá trị của
m
để phương trình có đúng hai nghiệm phân
biệt.
A.
13
; ;.
22
m









B.
13
; ;.
22
m






C.
; 1 1; .m  
D.
;1 1; .m  
Lời giải. Phương trình
2
22
23 2
22
2 .log 2 3 2 .log 2 2 .
xm
xx
x x xm



Xét hàm
2
2 .log
t
ft t
trên
2;
và đi đến kết quả
2
2 32 2x x xm 
2
2
2
22
1 2 4 2 10 1
12 .
21 2
12
x xm x x m
x xm
xm
x xm




Phương trình đã cho có hai nghiệm phân biệt khi:
TH1. Phương trình
1
và
2
đều có nghiệm kép và hai nghiệm này khác nhau
1
2
0
.
2 10
m
xm



TH2. Phương trình
1
có hai nghiệm phân biệt, phương trình
2
vô nghiệm
1
2
0
42 10
1
.
2
2 10
2 10
m
m
m
xm









TH3. Phương trình
1
vô nghiệm, phương trình
2
có hai nghiệm phân biệt
1
2
0
42 10
3
.
2
2 10
2 10
m
m
m
xm









TH4. Phương trình
1
có hai nghiệm phân biệt, phương trình
2
cũng có hai
nghiệm phân biệt và hai nghiệm của
1
giống hai nghiệm của
2
(hay nói cách khác
hai phương này trình tương đương)
.m 
Vậy
13
;;
22
m









là giá trị cần tìm. Chọn A.
24
Câu 16. Cho phương trình
32
21
2
log log 14 29 2 0
mx x x x

với
m
là tham số
thực. Gọi
,S ab
là tập tất cả các giá trị của
m
để phương trình có ba nghiệm phân
biệt. Hiệu
ba
bằng
A.
1
.
2
B.
5
.
2
C.
2
.
3
D.
5
.
3
Lời giải. Phương trình
32
22
log log 14 29 2mx x x x 
2
32
2
1
2
14 29 2 0
4
2
14 29 2
6 14 29
x
xx
mx x x x
mx x
x










Xeùt haøm
39
19; .
2
m


Chọn A.
Câu 17. Cho phương trình
22
33
log log 1 2 1 0.x xm  
Tập tất cả các giá trị của
tham số
m
để phương trình có nghiệm thuộc đoạn
3
1; 3



là
A.
01m
. B.
02m
. C.
13
0
6
m
. D.
12m
.
Lời giải. Điều kiện:
0.x
Đặt
2
3
log 1,tx
vì
3
1; 3x



nên
1; 2t
.
Phương trình trở thành
2
2
2
1 2 1 0 0;2
2
tt
t t m m ft


với
1; 2 .t
Do đó yêu cầu bài toán
0 2.
m
Chọn B.
Câu 18. Cho phương trình
ln ln 1 .mx x m 
Tập tất cả các giá trị của tham số
m
để phương trình có nghiệm thuộc khoảng
0;1
là
A.
.eme

B.
1.me

C.
0.m
D.
0.
m
Lời giải. Phương trình
ln 1
ln 1 ln 1
ln 1
x
mx x m
x

.
Xét
ln 1
ln 1
x
fx
x
trên
0;1 .
Có
2
ln 1
ln 1 1
. 0.
1
ln 1
x
x
fx
xx
x





Dựa vào BBT suy ra phương trình đã cho có
nghiệm
0.m
Chọn D.
Câu 19. Cho phương trình
2
22 2
log 2 log 3 log 3x x mx 
với
m
là tham số thực.
Tập tất cả các giá trị của
m
để phương trình có nghiệm thuộc
16;
là
A.
12m
. B.
15m
. C.
15m
. D.
3
5
4
m
.
Lời giải. Đặt
2
log ,tx
vì
16x
nên
4.t
Phtrình trở thành
2
2
23
2 3 3 1; 5
3
tt
t t mt m f t
t


với
4.t
f
1
0
f
x
0

25
Do đó yêu cầu bài toán
1 5.
m
Chọn B.
Câu 20. Cho phương trình
22 2
25
log 1 .log 1 log 1
m
xx xx xx 
với
m
là tham số dương khác
1.
Có bao nhiêu giá trị nguyên của
m
để phương trình đã
cho có nghiệm
2;x 
?
A.
1.
B.
2.
C.
3.
D. Vô số.
Lời giải. Phương trình đã cho xác định trên khoảng
2; .
Phương trình
1
22 2
25 2
log 1 .log 1 log 2. log 1
m
xx xx xx
  
22
25
log 1 . log 1 log 2 0.
m
xx xx

 


•
2
2
log 1 0xx 
vô nghiệm do
2.x
•
22
55
log 1 log 2 0 log 2 log 1 .
mm
xx xx 
Xét hàm
2
1
fx x x
trên
2; .
Ta có
2
2
1 0, 2.
1
fx x
x
 
Suy ra
fx
đồng biến nên
22 3fx f

với mọi
2.x
Suy ra
2
55
log 1 log 2 3 .
xx

Do đó để phương trình có nghiệm
2;x 
khi và chỉ khi
5
log 2 log 2 3
m

1
2:
m
m
m

Có duy nhất
1
giá trị. Chọn A.
Câu 21. Cho phương trình
2 22 2 2
1 .log 1 2 1 .log 1 4 0.x x mx x m 
Có
bao nhiêu số nguyên
m
thuộc
10;10
để phương trình đã cho có hai nghiệm phân
biệt thỏa mãn
13
x
?
A.
7.
B.
9.
C.
12.
D.
14.
Lời giải. Phương trình
2 22 2 2
2 1 .log 1 2 2 1 . log 1 2 8 0.x x mx x m 
Đặt
2 2 BBT
2 1 .log 1 0;4tx x t 
với
1 3.x
Nhận xét: Với mỗi nghiệm
t
ta có tương ứng
2
nghiệm
.x
Phương trình đã cho trở thành
2
2
8
2 2 80 .
22
t
t mt m m
t

*
Do đó để phương trình đã cho có
2
nghiệm thực
x
thỏa
13x
thì
phương trình
*
có đúng một nghiệm
0;4 .t
Xét hàm
2
8
22
t
ft
t
trên
0;4 .
Dựa
26
vào bảng biến thiên ta thấy
4
4
m
m

thỏa yêu cầu bài toán. Chọn D.
Câu 22. Cho bất phương trình
32
log 2 1 1.
x
x x mx m




Có bao nhiêu giá trị
m
nguyên trong đoạn
2017;2017
để bất phương trình luôn đúng với
2x
?
A.
2010.
B.
2017.
C.
2018.
D.
2019.
Lời giải. Bất phương trình
32
1
2 1 , 2x x mx m x
x

2
11
1 1 , 2 1 , 2.
1
xx mx x xx m x
x xx
 
Đặt
1 2, 2.t xx x 
Khi đó
1
, 2.m t ft t
t

Lập BBT của hàm
ft
ta
được
3
, 2.
2
ft t 
Suy ra
2017;2017
3
2
m
m
m


có
2019
giá trị. Chọn D.
Câu 23. Cho phương trình
2
2
22
2
2018 1 ln 1 2018.
x mx
x mx x





Có bao
nhiêu giá trị nguyên
m
thuộc đoạn
2018;2018
để phương trình có nghiệm duy nhất
thuộc khoảng
1;

?
A.
2017.
B.
2018.
C.
2019.
D.
2020.
Lời giải. Phương trình
2
21
22
1 2018 .2018 2 1 .ln 1 .
x mx
x mx x





• Nếu
2
2 10x mx 
thì
VT 0
VP 0
phương trình vô nghiệm.
• Nếu
2
2 10x mx 
thì
VT 0
VP 0
phương trình vô nghiệm.
• Thử thấy
2
2 10x mx 
*
thỏa mãn phương trình. Do đó yêu cầu bài toán
phương trình
*
có nghiệm duy nhất trên
1; . 
Bằng cách dùng tam thức
bậc hai hoặc xét hàm số cho ta kết quả
2018;2018
4
0
m
m
m
m


có
2019
giá trị. Chọn C.
Câu 24. Cho phương trình
2
2 2 43
2
7
2 sin 3cos log 2 .
2
mm
xx




Có bao nhiêu giá trị
nguyên của tham số
m
để phương trình đã cho có nghiệm?
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải. Phương trình
2
2 43
2
7
5sin log 2 3.
2
mm
x




Ta có


t
f
f
0
1
3
4
4
27
•
2
5sin 5.x
•
2
2
4 3 211mm m 
nên
2
43 1
22
77
log 2 log 2 2.
22
mm



 





Do đó phương trình
2
2
2
43
2
2
5sin 5
sin 1
2.
7
log 2 2
431
2
mm
x
x
m
mm










Chọn B.
Câu 25. Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
10;10
để phương
trình
32
23
log 2 log 1x xm
có ba nghiệm phân biệt?
A.
8.
B.
10.
C.
11.
D.
12.
Lời giải. Điều kiện:
1 2.
x
Phương trình
33
22
log 2 log 1x xm 
3
2
3
log 21 21 .
2
m
xx mxx



*
Phương trình
*
là phương trình hoành độ giao điểm của đồ thị hàm số
21fx x x
và đường thẳng
3
2
m
y


(cùng phương với trục hoành).
Xét hàm số
21fx x x
xác định trên
1; 2 2; 
.
Ta có

2
2
2 1 2 khi 2
21
2 1 2 khi 1 2
hx x x x x x
fx x x
gx x x x x x


 
.
Dựa vào đồ thị, ta thấy để phương
trình
*
có ba nghiệm phân biệt khi
1;2
3 39
0 max 2
2 24
mm
gx m
 







 
10;10
10; 9;...;1 .
m
m
m


Chọn D.
| 1/127
| | Tải xuống

Có thể bạn quan tâm:

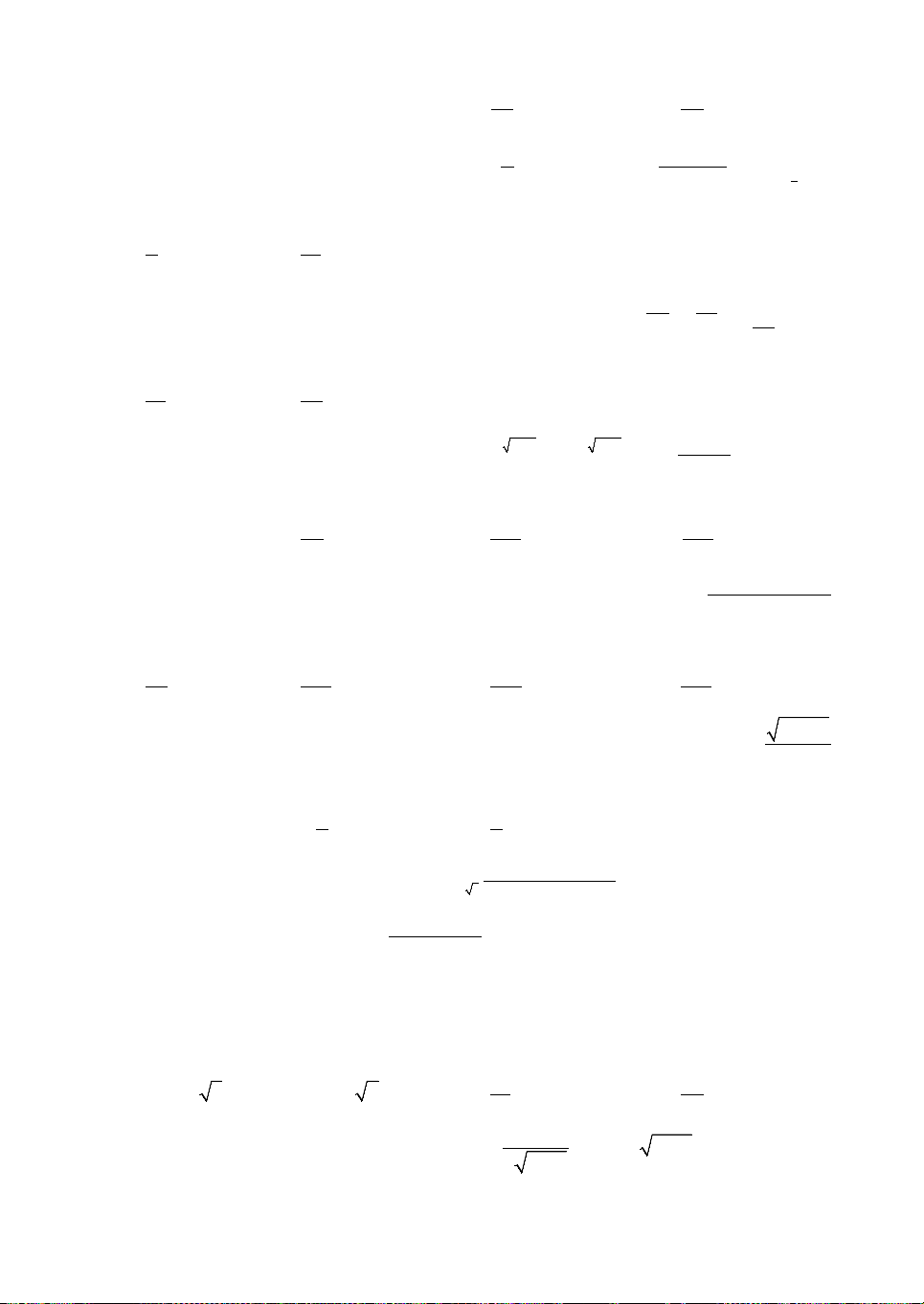
Preview text:

HÀM SỐ LŨY THỪA
HÀM SỐ MŨ – HÀM SỐ LOGARIT
120 câu – Vận dụng cao
Phần 1. Tính chất và các phép toán…………………………………………
Phần 2. Đồ thị …………………………………………………………………………………..
Phần 3. Dãy logarit ………………………………………………………………….…….
Phần 4. Cực trị nghiệm ………………………………………………………………..
Phần 5. Bài toán tìm GTLN – GTNN …………………….………………… 1
Phần 1. Tính chất và các phép toán
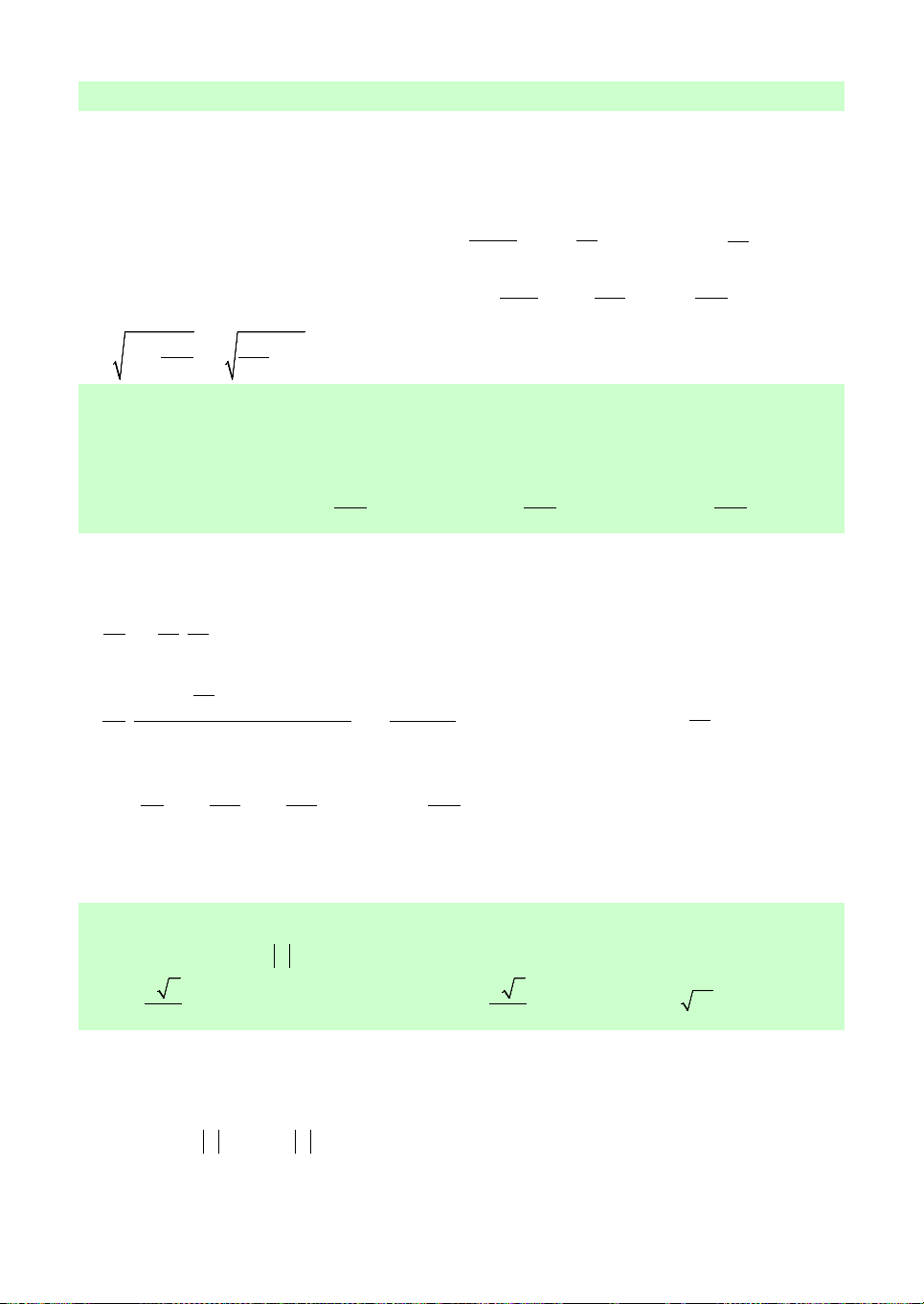
Câu 1. Tìm tất cả các giá trị của tham số a để hàm số y  log
x đồng biến trên 2 a 2a 1  khoảng 0;.
A. a 0;2.
B. a 0;2\  1 .
C. a   \0;2.
D. a   \0;2.  
Câu 2. Cho hàm số y f x 1  log    
. Khẳng định nào sau đây đúng? 2018  x 
A. Hàm số y f x nghịch biến trên  ;  0.
B. Hàm số y f x đồng biến trên  ;  0.
C. Hàm số y f x nghịch biến trên  ;    1 .
D. Hàm số y f x đồng biến trên  ;    1 .
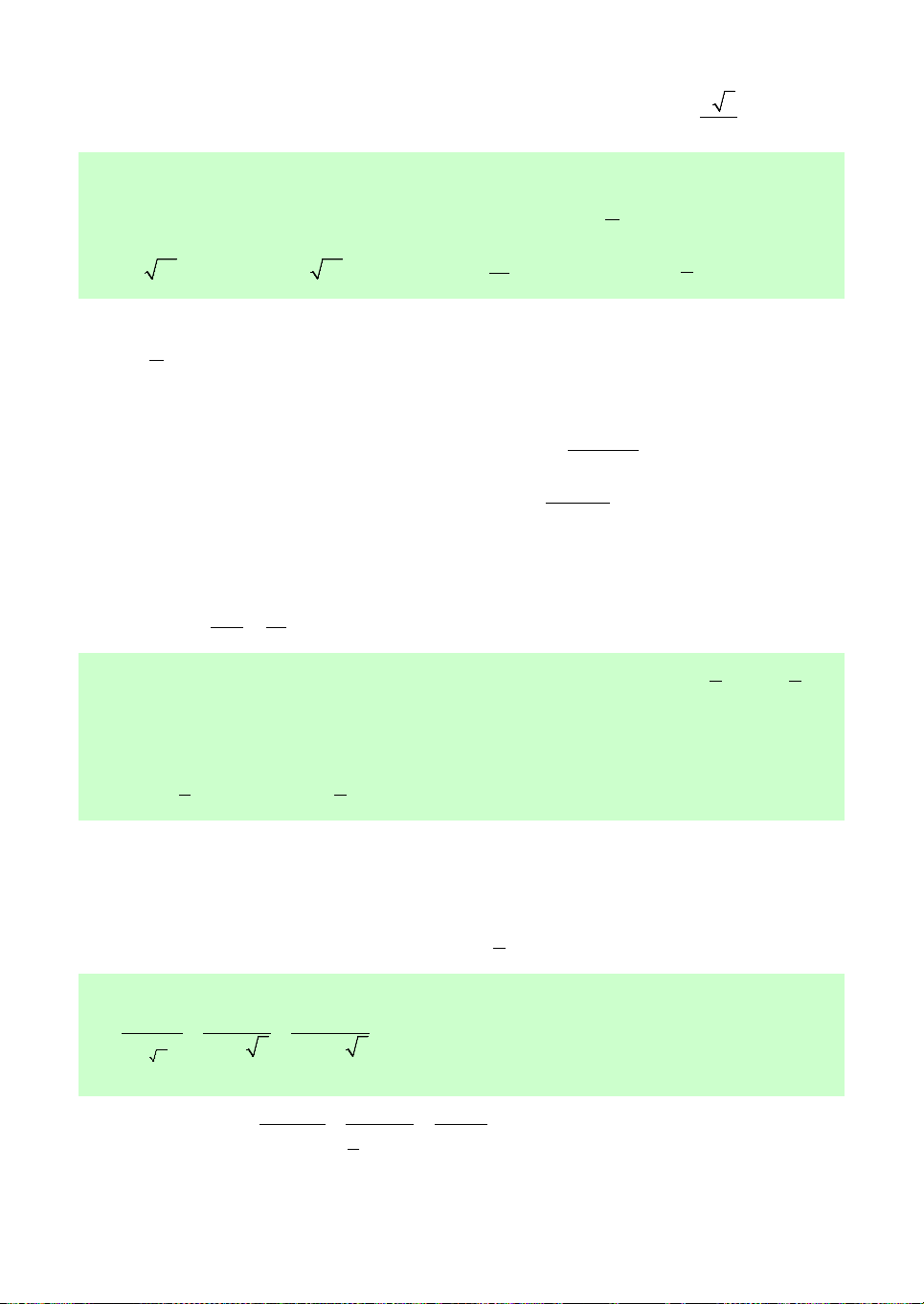
Câu 3. Số giá trị nguyên của m 10 để hàm số y   2
ln x mx   1 đồng biến trên khoảng 0; là A. 8. B. 9. C. 10. D. 11.
Câu 4. Có bao nhiêu số nguyên âm m để hàm số y   3
ln x mx  2 đồng biến trên
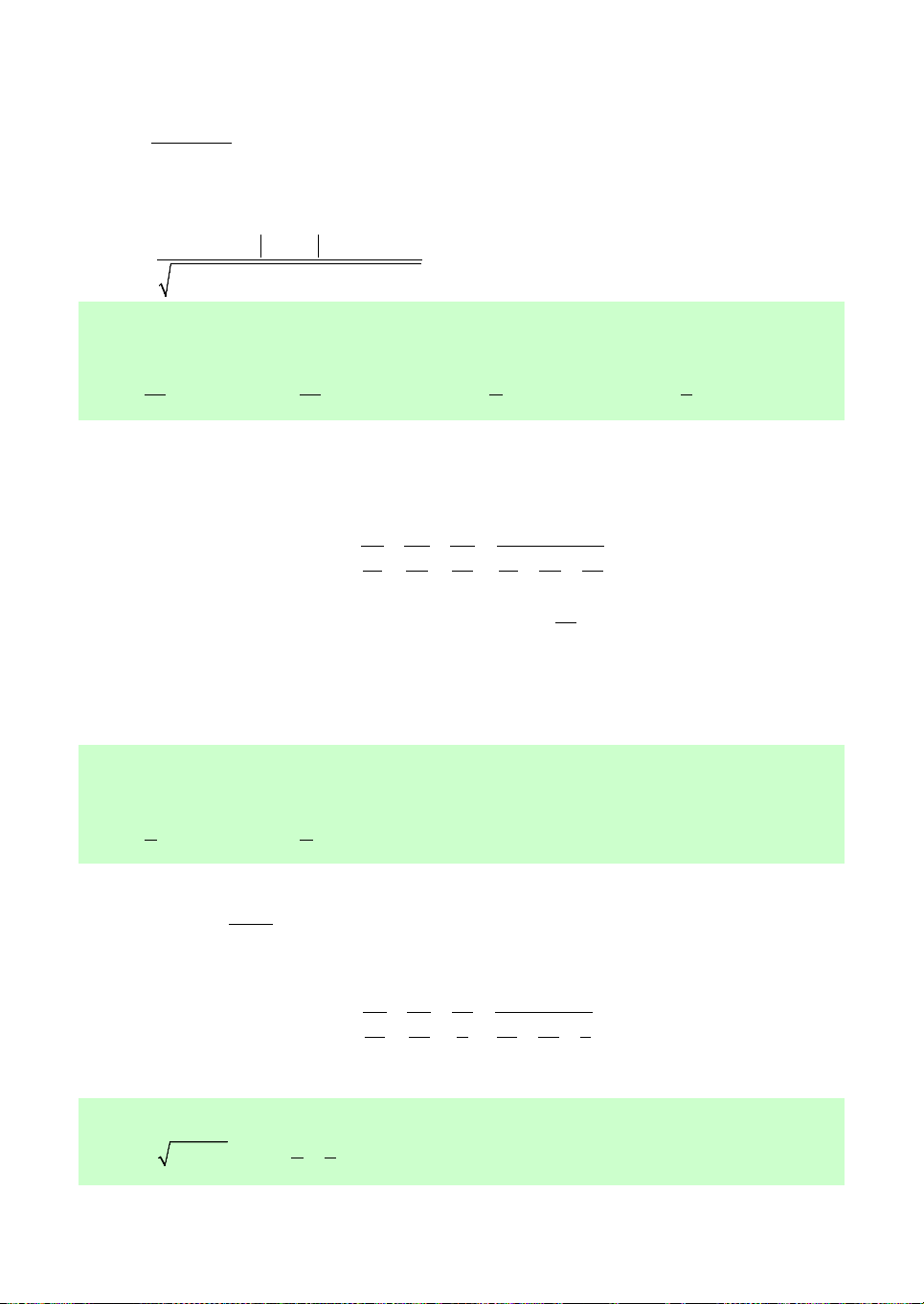
nửa khoảng 1; ? A. 1. B. 2. C. 3. D. 4. Câu 5. Cho ,
a b, c là các số thực dương thỏa mãn log3 7 log7 11 l 11 og 25 a  27, 49 b  , c  11 .
Giá trị của biểu thức 2 2 2 log3 7 log7 11 l 11 og 25 T abc bằng A. 76  11. B. 469. C. 2017. D. 31141. Câu 6. Cho c c ,
a b, c là các số thực khác 0 thỏa mãn 4a 25b 10c   . Tính T   . a b A. 1 T  . B. 1 T  . C. T  2. D. T  10. 10 2
Câu 7. Cho x, y là các số thực dương thỏa mãn log x  log y  log x y và 9 6 4   x a   b  với ,
a b là hai số nguyên dương. Tổng a b bằng y 2 A. 4. B. 6. C. 8. D. 11.
Câu 8. Cho các số thực dương x, y, z theo thứ tự lập thành một cấp số nhân, đồng
thời với mỗi số thực dương a 1 thì log x, log y, log z theo thứ tự lập thành một 3 a a a
cấp số cộng. Giá trị biểu thức 3x 7 y 2020z P    bằng y z x A. 2030 . B. 1015. C. 2030. D. 4038. 3
Câu 9. Cho x, y, z là các số thực dương thỏa logx y z và  2 2
log x y  z 1. Giả sử ,
a b là các số thực sao cho 3 3 3z 2   .10  .10 z x y a b
. Tổng a b bằng 2 A. 31  . B. 25  . C. 29 . D. 31. 2 2 2 2 2017x
Câu 10. Cho x, y, z là các số thực thỏa mãn 3x  5y  15xy . Gọi S xy yz zx.
Khẳng định nào sau đây đúng?
A. S 1;2016. B. S 0;2017.
C. S 0;2018.
D. S 2016;2017.
Câu 11. Tìm bộ ba số nguyên dương a;b;c thỏa mãn log1 log1  3  log13 
5 ... log13...192 log 5040  a b log 2  c log 3.
A. 1;3;2. B. 2;4;  3 . C. 2;4;4.
D. 2;6;4.
Câu 12. Cho f  
1  1 và f m n  f m f n mn với mọi * ,
m n   . Giá trị biểu
f 96 f 69241 thức T  log    bằng 2    A. 3. B. 4. C. 6. D. 9. Câu 13. Cho ,
a b, c là ba số thực dương không cùng bằng nhau, đồng thời khác 1 và thỏa mãn log c log a log b c a b abc
. Giá trị nhỏ nhất của biểu thức a b c bằng A. 2 2. B. 2 3. C. 3 2. D. 3 3.
Câu 14. Cho a  0 và b  0 thỏa mãn log a b   a b   ab  2 2 16 1 log 4 5 1 2. 4 5 1  8ab 1   
Giá trị của biểu thức a  2b bằng A. 20 . B. 27 . C. 6. D. 9. 3 4
Câu 15. Cho a 1 và b 1 thỏa  3 2
a a b    2 3 log 4 4
log b b 16b  64  2. b a
Giá trị của biểu thức a  2b 1 P  bằng a b A. 15 . B. 17 . C. 19 . D. 21. 10 10 10 10 1 Câu 16. Cho x
x  0 và số thực y thỏa mãn 2 x log 1  4 y 2 y 1     . Giá trị của 2     biểu thức 2 2
P x y xy 1 bằng A. 1. B. 2. C. 3. D. 4.   Câu 17. Cho
x x x 1
x  0 và y  0 thỏa mãn 3 2 2 2  log y   . Giá trị của biểu 2  2 y  thức 2 2
P x y  2xy bằng A. 1 . B. 1. C. 2. D. 2. 2 x      
Câu 18. Cho hàm số f x 4  . Tổng 1 2 2016 S f     f      ... f   bằng       4x  2 2017 2017 2017 A. 1007. B. 1008. C. 2016. D. 2017. 3 x       Câu 19. Cho hàm số  f x 9 2  . Tổng 1 2 2017 P f     f      ... f   bằng       9x  3 2017 2017 2017 A. 1009. B. 4035. C. 4039 . D. 12103. 4 12 12 t
Câu 20. Xét hàm số f t 9 
với m là tham số thực. Gọi S là tập hợp tất cả t 2 9  m
các giá trị của m sao cho f x f y1 với mọi x, y thỏa mãn xy e
ex y. Tìm
số phần tử của S . A. 0. B. 1. C. 2. D. Vô số. t
Câu 21. Xét hàm số f t 4 
với m  0 là tham số thực. Biết f x f y1 với 4t m 1 mọi số thực dương 1 1
x, y thỏa mãn x y2  .x y . Giá trị nhỏ nhất của hàm 2 2  
số f t trên đoạn 1  ;1 bằng 2    A. 1 . B. 1 . C. 3 . D. 5 . 2 4 4 4 x Câu 22. Cho a
a là số thực dương. Xét hàm số f x 
với m  0 là tham số x a m
thực. Biết f x f y1 với mọi 1
x y  . Khẳng định nào sau đây đúng? 2 A. 4 m a.
B. m a. C. m  . a D. 2 m a . x
Câu 23. Xét hàm số f x 9 
với m là tham số thực. Gọi S là tập hợp tất cả x 4 9  m
các giá trị của m sao cho f a f b1 với mọi ,
a b thỏa mãn ab 2 e
e a b   1 .
Tích các phần tử của S bằng A. 3. B. 9. C. 81. D. 81.
Câu 24. Xét hàm số   log 2 4x f x   và ,
a b là hai số thực dương thỏa mãn 2
f a f b  1. Đặt 27 12 2018 2017 T a b
. Khẳng định nào sau đây là đúng? A. 1
0 T  . B. 1 1 T  . C. 1 T 1. D. T 1. 4 4 2 2  
Câu 25. Cho hàm số   1 2x f x  log    . Tính tổng 2 2 1 x   1   2   3  2015 2016 S f     f       f        ... f         f        . 2017 2017 2017 2017 2017 A. S  1008. B. S  2016. C. S  2017. D. S  4032. x  
Câu 26. Xét hàm số f x  2018  2018 lnee . 
 Tính T f  
1  f 2... f 2017.     A. T  1008. B. T  1009. C. 2017 T  . D. 2019 T  . 2 2 4 2
Câu 27. Xét hàm số   m x f x  log
với m là tham số thực. Gọi S là tập hợp tất cả 3 1 x
các giá trị của m sao cho f a f b 3 với mọi ,
a b thỏa mãn ab e
ea b. Tích
các phần tử của S bằng A. 27. B. 3 3. C. 3 3. D. 27.
Câu 28. Cho hàm số f x 2019  a  2 .log
x 1  xb sin x.cos2018x6 với ,a b  .  Biết f  ln 2019 2018
10. Giá trị của biểu thức f  ln 2018 2019  bằng A. 10. B. 2. C. 8. D. 10.
Câu 29. Cho hàm số    2 .log 2  4
1 .sin . x f x a x x b x c e với ,
a b, c  .  Biết   rằng f   1
ln 2  f ln   2. 
Khi đó hằng số c thuộc khoảng nào sau đây?  2         A. 1 0; .        B. 1  ;1. C. 3 1;  . D. 3  ;2.  2 2   2 2 
Câu 30. Cho hàm số f x 3  a  2
.ln x x 1bx.cos5x1 với ,a b  .  Biết
f loglog e. f logln10  .
m Gọi S là tập các giá trị của tham số m thỏa mãn 2 f   e 2  f    2 log log log ln10  m
m 8. Số phần tử của tập S bằng A. 0. B. 1. C. 2. D. Vô số.
Phần 2. Đồ thị và các vấn đề liên quan x  
Câu 1. Cho bốn hàm số  x 1 y  3   1 , y      2,   3 1 x  4x y    3 , y       4 
có đồ thị là bốn đường cong 4
như hình bên. Tương ứng hàm số - đồ thị đúng là A.  
3 C , 2  C , 1  C , 4  C . 4   
 1    3    2 B.  
1 C , 3  C , 2  C , 4  C . 4   
 1    3    2 C.  
1 C , 2  C , 3  C , 4  C . D. 2C , 1  C , 3  C , 4  C . 4   
 1    3    2 4   
 1    3    2
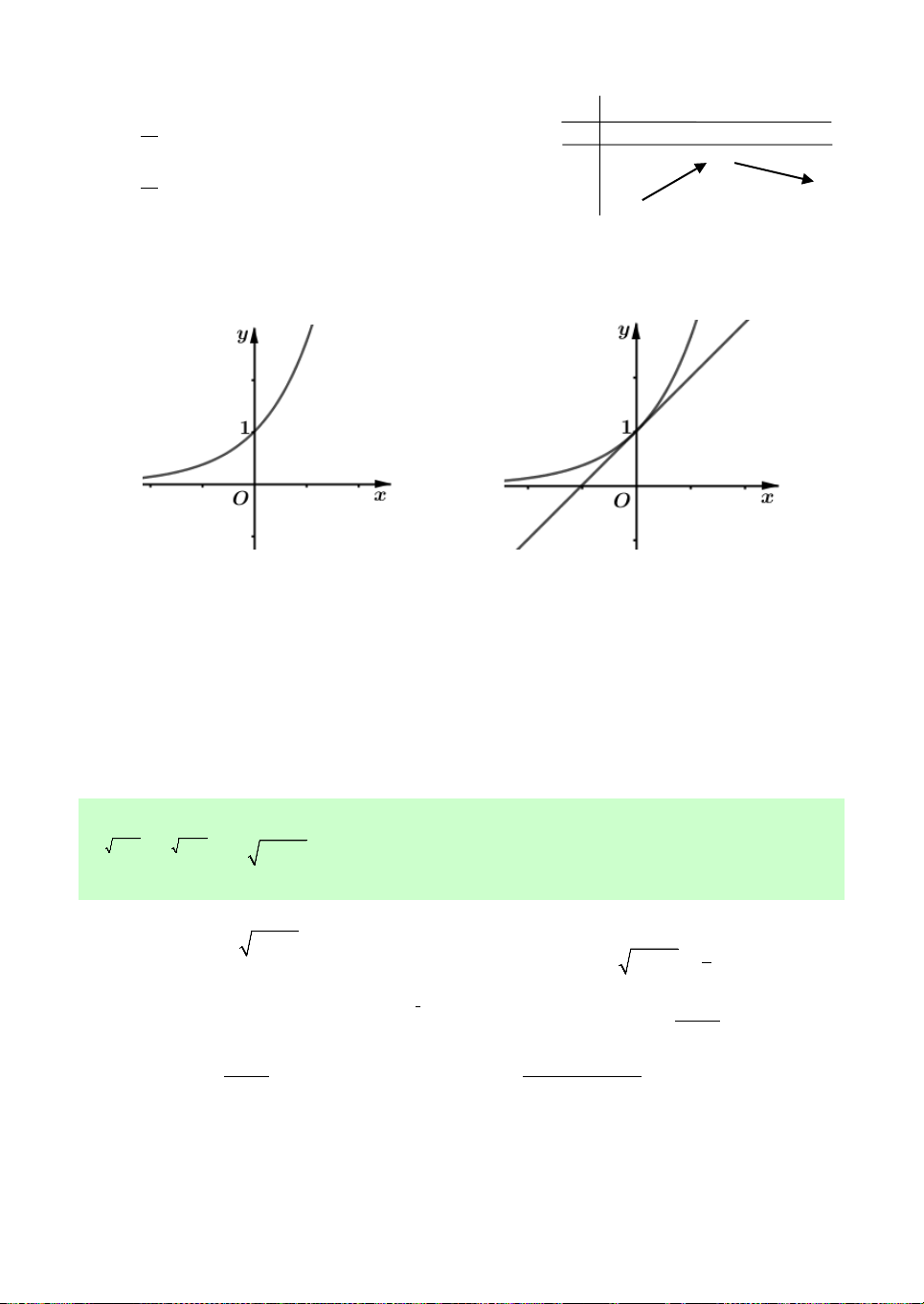
Câu 2. Cho các hàm số   x
f x a , g x  log x và b
hx  log x c (trong đó ,
a b lớn hơn 0 và khác 1; b  
c   ) có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
A. a c  . b
B. a b c.
C. a 1 b, c  0.
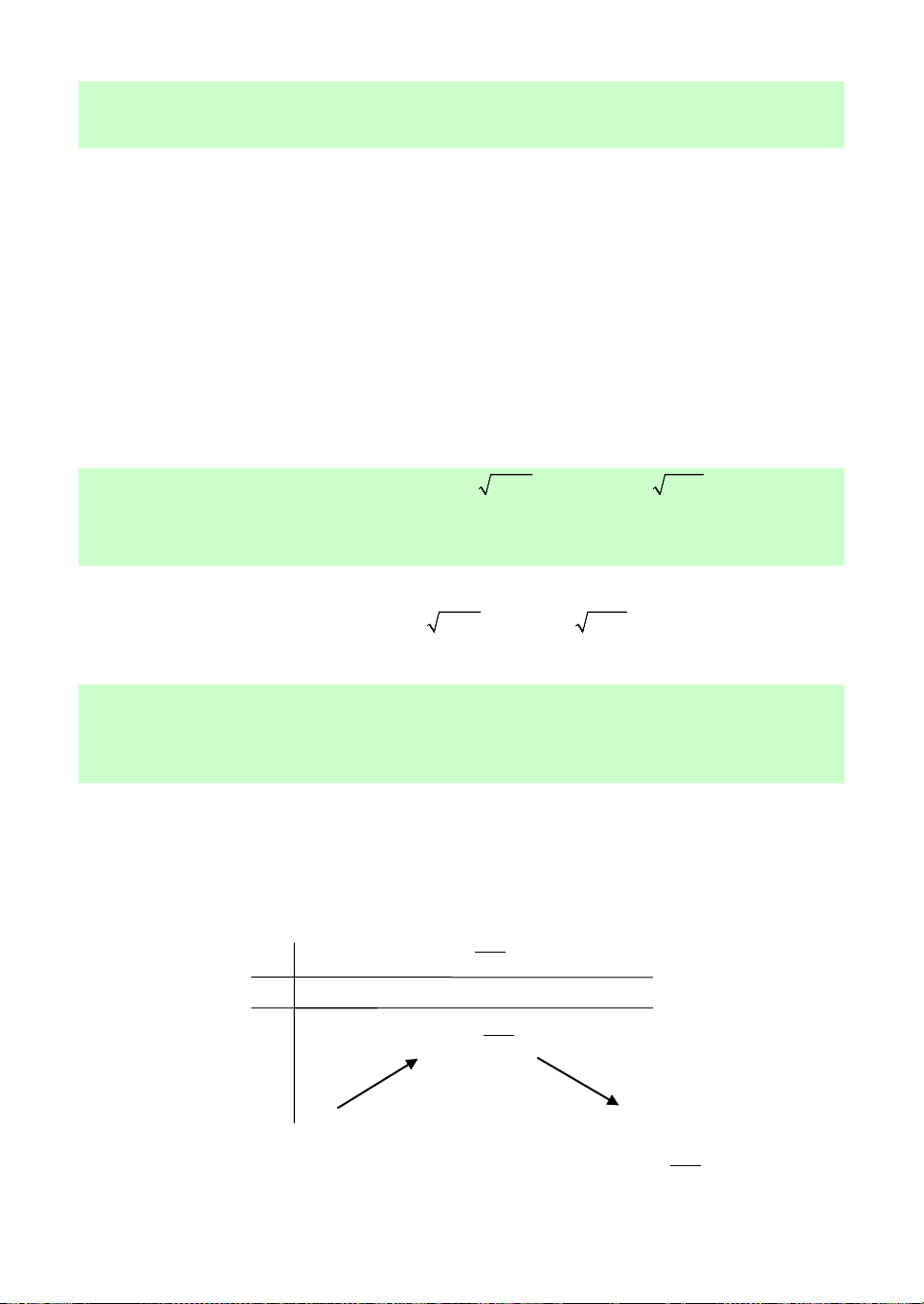
D. c a  . b 5 Câu 3. Cho ,
a b, c là các số thực dương khác 1 và đồ thị của ba hàm số x
y a , y  log x, x
y c trên cùng một b
hệ trục tọa độ như hình vẽ bên. Mệnh đề nào sau đây đúng?
A. a b  . a
B. c a  . b
C. c b  . a
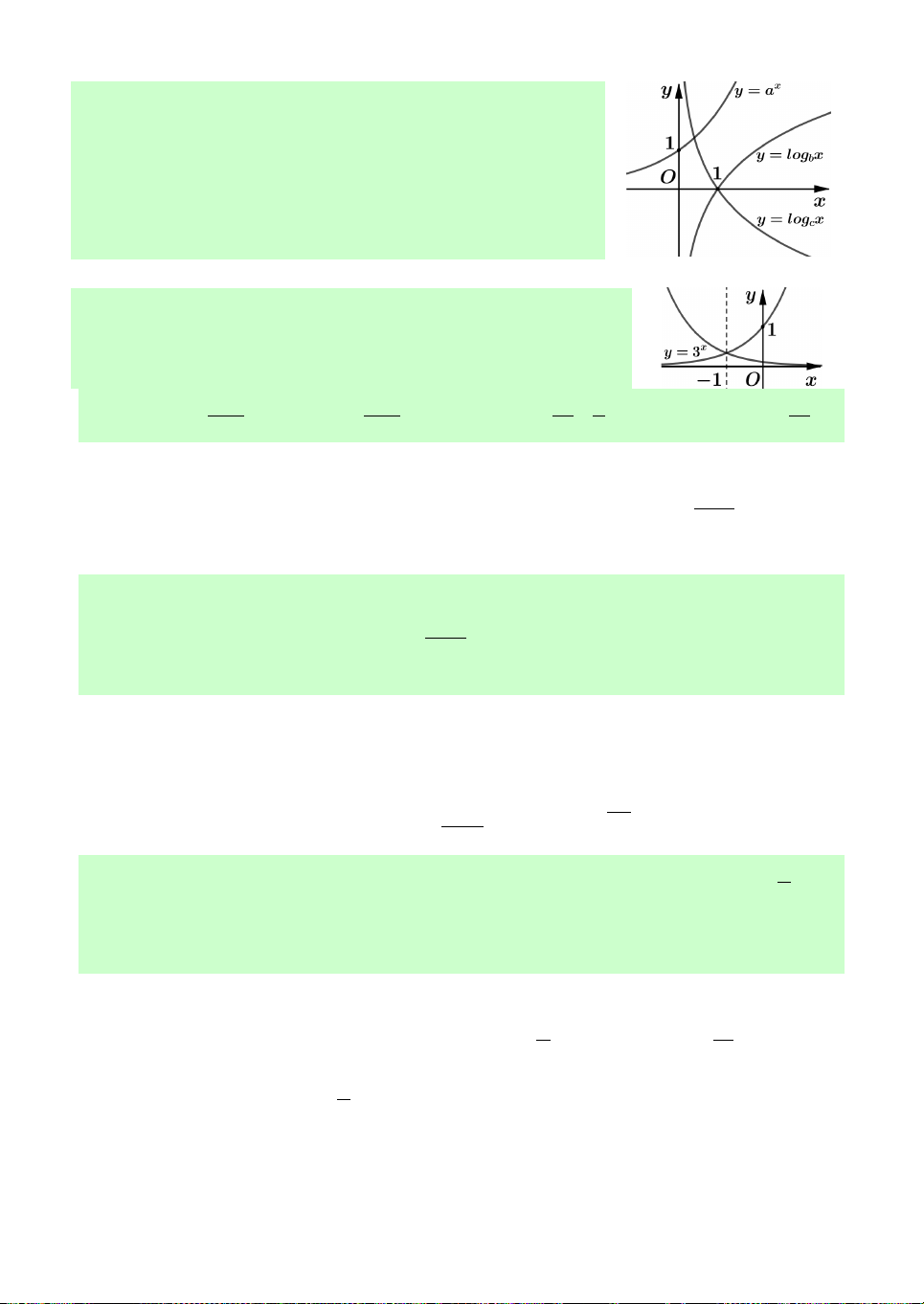
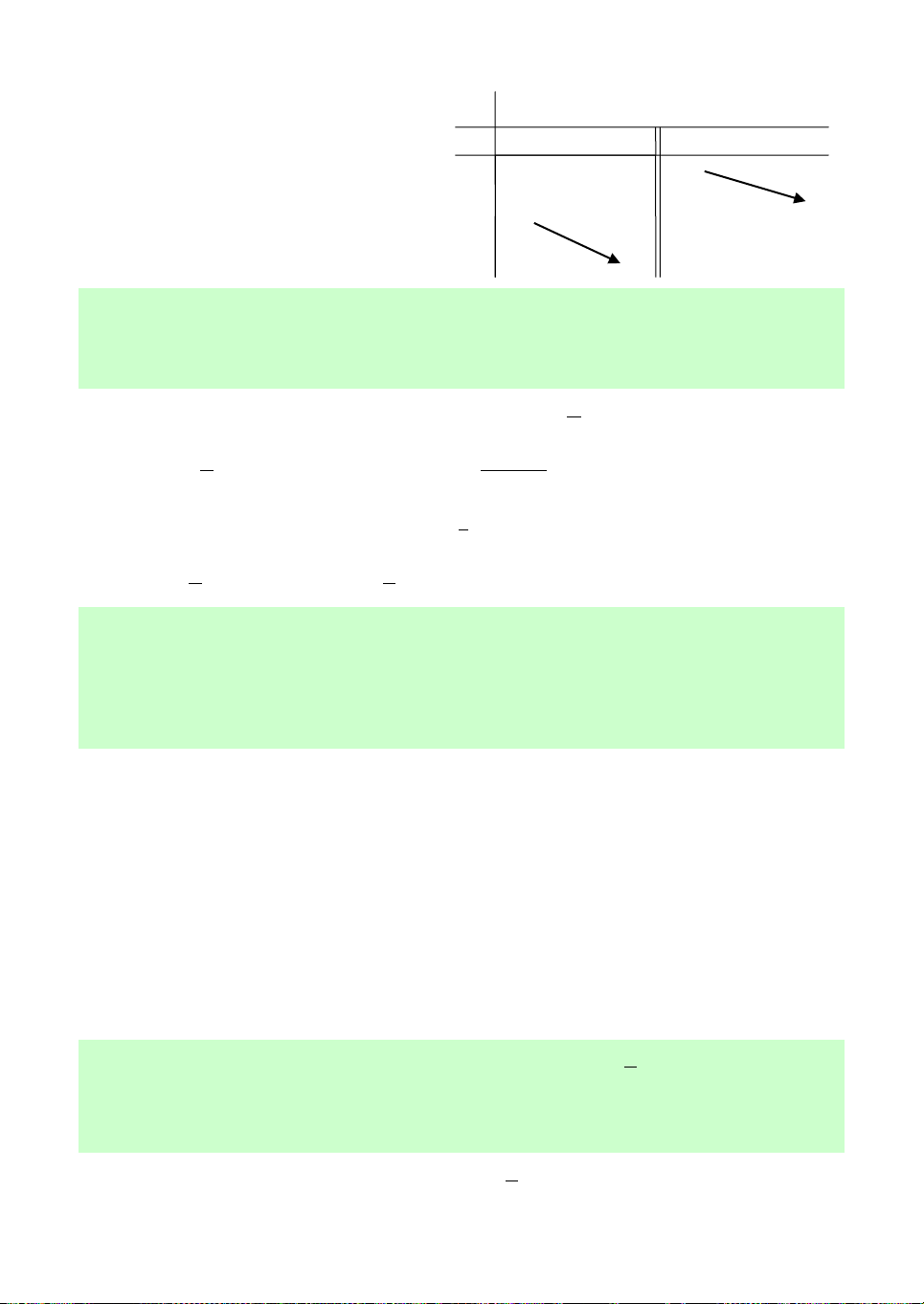
D. b c  . a Câu 4. Cho ,
a b, c là các số thực dương khác 1 và đồ thị của ba hàm số x
y a , y  log x, y  log x trên cùng b c
một hệ trục tọa độ như hình vẽ bên. Mệnh đề nào sau đây đúng?
A. b c  . a
B. a c  . b
C. c b  . a
D. c a  . b
Câu 5. Biết hàm số y f x có đồ thị đối xứng với đồ thị hàm số 3x y
qua đường thẳng x  1. Chọn khẳng định
đúng trong các khẳng định sau
A. f x 1 
. B. f x 1  .
C. f x 1 1   .
D. f x 1  2  . 3.3x 9.3x 3x 2 3x
Câu 6. Biết hàm số y gx có đồ thị đối xứng với đồ thị hàm số x
y a qua điểm   I 1; 
1 . Giá trị của biểu thức 1 g 2  log  bằng a  2018 A. 2020. B. 2016. C. 2016. D. 2020.  
Câu 7. Biết hàm số 1
y f x có đồ thị đối xứng với đồ thị hàm số y  log     qua 2018  x 
gốc tọa độ. Tính giá trị của biểu thức f 2018. A. 1. B. 0. C. 1.
D. Không tồn tại.
Câu 8. Cho hai hàm số x
y a và y f x có đồ thị như
hình vẽ đồng thời đồ thị của hai hàm số này đối xứng
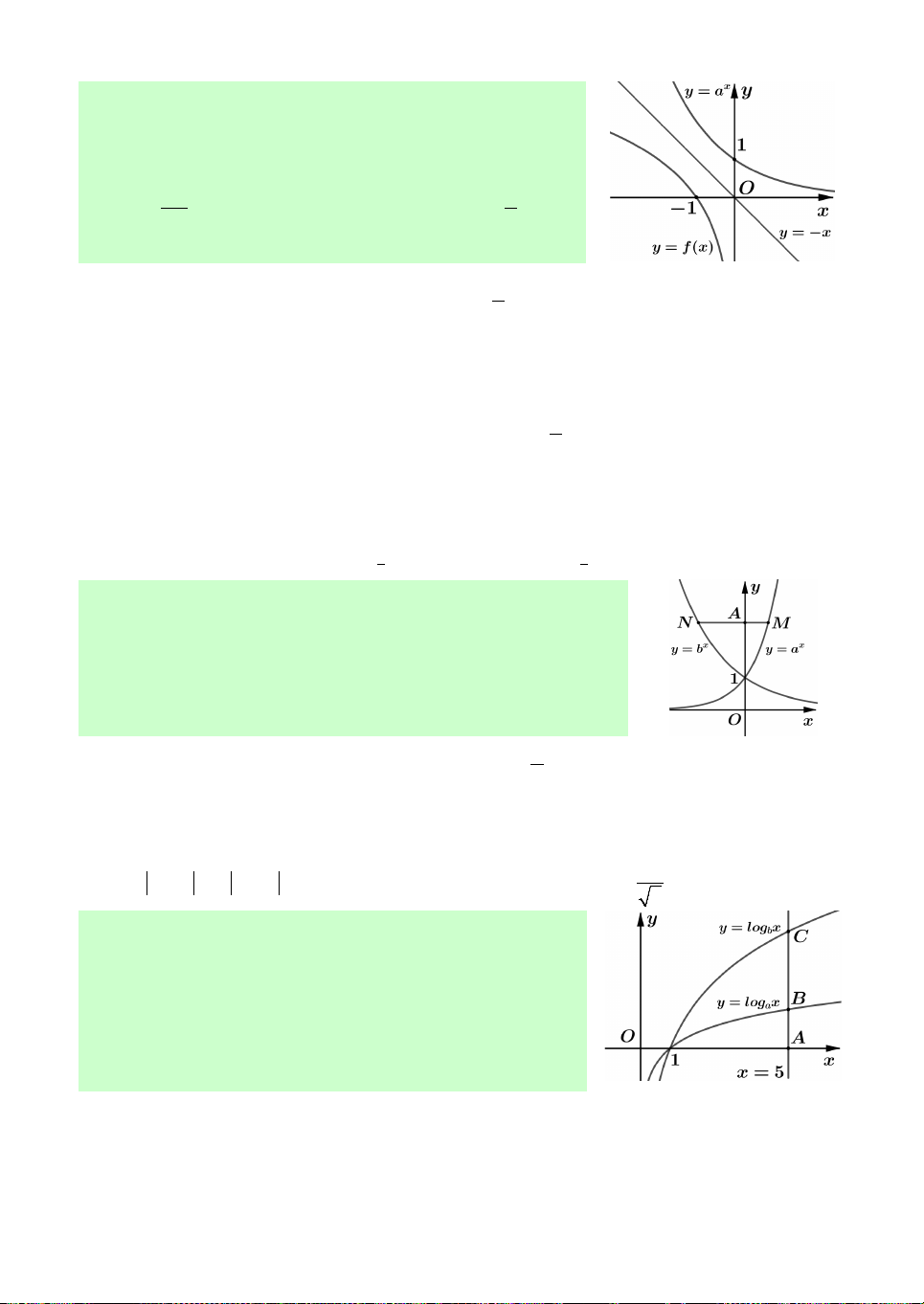
nhau qua đường d : y  x. Giá trị của  3 f a   bằng A. 1  . B. 1  . 3a a 3 C. 3. D. 3a a  . Câu 9. Cho ,
a b là các số thực dương khác 1. Các hàm số x y a và x
y b có đồ thị như hình vẽ bên. Đường thẳng bất
kỳ song song với trục hoành và cắt đồ thị hàm số x y a , x
y b , trục tung lần lượt tại M , N, A đều thỏa mãn
AN  2AM. Mệnh đề nào sau đây đúng? A. b  2 . a B. 2 a  . b C. 1 ab  . D. 2 ab  1. 2 6
Câu 10. Cho các hàm số y  log x và y  log x có đồ a b
thị như hình vẽ bên. Đường thẳng x  5 cắt trục hoành,
đồ thị hàm số y  log x và y  log x lần lượt tại , A B a b
và C . Biết rằng CB  2AB. Mệnh đề nào sau đây đúng? A. 2 a b . B. 3 a  . b C. 3 a b . D. a  5 . b
Câu 11. Cho hai hàm số 2x y
, y  log x có đồ thị như 2
hình vẽ. Đường thẳng  cắt trục tung, đồ thị hàm số 2x y
, đồ thị hàm số y  log x và trục hoành lần lượt 2 tại ,
A B, C, D thỏa mãn AB BC CD. Hỏi có bao nhiêu
đường thẳng  như thế ? A. 1. B. 2. C. 3. D. Vô số.
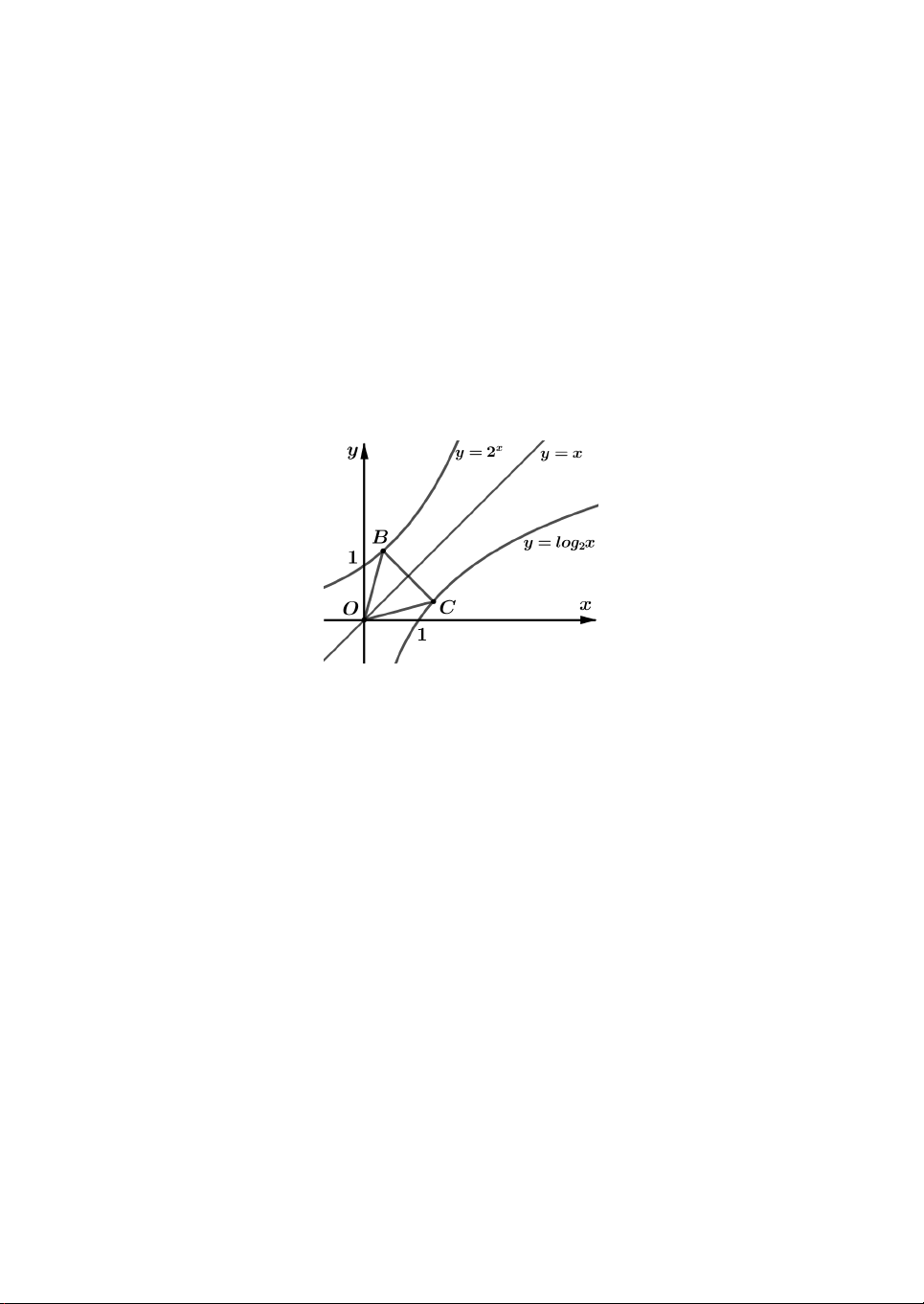
Câu 12. Gọi B và C lần lượt là các điểm thuộc đồ thị hàm số 2x y
và y  log x 2
sao cho tam giác OBC đều. Giả sử điểm B có hoành độ là a khi đó tỉ số 2x bằng a A. 2 3. B. 2  3. C. 2 2. D. 2  2. Câu 13. Gọi ,
A B là các điểm lần lượt thuộc đồ thị các hàm số x y e và x y e  sao
cho tam giác OAB nhận điểm M 1; 
1 làm trọng tâm. Khi đó tổng các giá trị của
hoành độ và tung độ điểm A gần với giá trị nào sau đây nhất? A. 3. B. 3,5. C. 4. D. 4,5.
Câu 14. Gọi A và B lần lượt là hai điểm di động trên hai đồ thị hàm số x
y e và y  ln x như hình vẽ.
Khoảng cách giữa hai điểm ,
A B nhỏ nhất gần với giá
trị nào nhất trong các giá trị sau A. 1,2. B. 1,3. C. 1,4. D. 1,5.
Câu 15. Cho đồ thị hàm số 2 x y e  như hình vẽ.
ABCD là một hình chữ nhật thay đổi sao cho B và
C luôn thuộc đồ thị hàm số đã cho, A và D thuộc
trục hoành. Giá trị lớn nhất của diện tích của hình
chữ nhật ABCD bằng A. 2 . B. 2 . e e C. 2 . D. 2 . e e 7 Phần 3. Dãy loga
Câu 1. Cho dãy số u thỏa mãn 2
log u 3 log u  2  0 và u
u  2 với mọi n  2 4 2 4 n1 n *
n   . Giá trị lớn nhất của n để u  2018 bằng n A. 999. B. 1000. C. 1010. D. 1011.
Câu 2. Cho dãy số u thỏa mãn log u  2  log u 2 log u  2 log u và n  1 1 8 10 u  10u với mọi *
n   . Khi đó u bằng n 1  n 2018 A. 2000 10 . B. 2008 10 . C. 2017 10 . D. 2018 10 .
Câu 3. Cho dãy số u thỏa mãn 2
log 5u  log 7u  log 5  log 7. Biết số hạng 2  1  2 2  1  2 2 n  2 2
đầu u 1 và u  7u với mọi *
n   . Giá trị nhỏ nhất của n để u 1111111 là 1 n 1  n n A. 8. B. 9. C. 10. D. 11.
Câu 4. Cho dãy số u thỏa mãn 2 9u 9 u 1 u  9 u 1 u 2 1 4  2  4 u e e e
e e  3 và uu 3 n n 1  n với mọi *
n   . Khi đó giá trị nhỏ nhất của n để u  3 là n A. 9. B. 10. C. 11. D. 12.
Câu 5. Cho cấp số cộng u có tất cả các số hạng đều dương và thỏa mãn n
u u ... u
 4 u u ...u
. Giá trị nhỏ nhất của biểu thức 1 2 2018  1 2 1009  2 2 2
P  log u  log u  log u bằng 3 2 3 5 3 14 A. 1. B. 2. C. 3. D. 4.
Câu 6. Cho dãy số u thỏa mãn 3 2
log u 2 log u  log u 2  0 và u  2u 10 n  1 1 1 n 1  n với mọi *
n   . Giá trị nhỏ nhất của n để 100 u 10 10 là n A. 225. B. 226. C. 326. D. 327.
Câu 7. Cho dãy số u thỏa mãn 3 logu logu  logu logu 3  3 và n  19 1 19 1 u
u  2 với mọi *
n   . Tìm số tự nhiên n lớn nhất sao cho 100 3 nu  5 . n1 n
A. n  71.
B. n  72.
C. n  73.
D. n  74.
Câu 8. Cho dãy số u thỏa 2 2 2 2
ln u  ln u ...  ln u
 ln u  ln u 1  3 n  1 2 n 1  n n 1  và 2 uu với mọi *
n   . Tìm giá trị nhỏ nhất của n để 2018 u  2017 . n 1  n n A. 11. B. 12. C. 14. D. 15. u .log n 1 n 2  
Câu 9. Cho dãy số u có tất cả các số hạng đều dương và thỏa u  , n n 1  10
với mọi n 1. Gọi a là giá trị nhỏ nhất của u . Có bao nhiêu số tự nhiên n để u a n n A. 1. B. 2. C. 3. D. 4.
Câu 10. Cho cấp số cộng a thỏa a a  0; cấp số nhân b thỏa b b 1 và n n  2 1 2 1
hàm số f x 3
x 3x sao cho f a  2  f a ; f log b  2  f log b . Tìm số 2 2   2 1 2   1
nguyên dương n nhỏ nhất sao cho b  2018a . n n A. n  15. B. n  16. C. n  17.
D. n  18. 8
Phần 4. Cực trị nghiệm
Câu 1. Xét các số nguyên dương ,
a b sao cho phương trình 2
a ln x b ln x  5  0   1
có hai nghiệm phân biệt x , x và phương trình 2
5 log x b log x a  0 2 có hai 1 2
nghiệm phân biệt x , x thỏa mãn x x x x . Giá trị nhỏ nhất của biểu thức 3 4 1 2 3 4
S  2a  3b bằng A. 17. B. 25. C. 30. D. 33. Câu 2. Với ,
m n là các số nguyên dương sao cho phương trình 2
ln x m  
1 ln x n  0  
1 có hai nghiệm phân biệt x , x và phương trình 1 2 2
ln x n  
1 ln x m  0 2 có hai nghiệm phân biệt x , x thỏa mãn x x x x . 1 2  3 4 2 3 4
Giá trị nhỏ nhất của biểu thức P  2m 3n bằng A. 46. B. 48. C. 51. D. 53.
Câu 3. Cho hai phương trình 2
ln x m  
1 ln x n  0   1 và 2
ln x n  
1 ln x m  0 2. Biết phương trình  
1 có hai nghiệm phân biệt là x , x và phương trình 2 có hai 0 1
nghiệm phân biệt là x , x (tức là x là nghiệm chung của hai phương trình) Giá trị 0 2 0
nhỏ nhất của biểu thức 2 2
S x x bằng 1 2 A. 1. B. 2. C. 3. D. 4.
Câu 4. Xét các số nguyên dương ,
a b sao cho phương trình .4x  .2x a b 50  0   1 có
hai nghiệm phân biệt x , x và phương trình 9x  .3x b
50a  0 2 có hai nghiệm 1 2
phân biệt x , x thỏa mãn x x x x . Giá trị nhỏ nhất của biểu thức 3 4 3 4 1 2
S  3a  2b bằng A. 49. B. 51. C. 59. D. 81. Câu 5. Cho ,
a b là hai số thực dương lớn hơn 1. Biết phương trình 2 x x 1 a b   1 có hai 2   nghiệm phân biệt x x x ,
x . Giá trị nhỏ nhất của biểu thức  1 2 S     4   x x 1 2  1 2
x x  1 2  bằng A. 3 4. B. 3 3 4. C. 3 3 2. D. 4. Câu 6. Cho ,
a b là hai số nguyên dương lớn hơn 1. Biết phương trình 2x 1  x ab có
hai nghiệm phân biệt x , x và phương trình 2 1   9 x x b
a có hai nghiệm phân biệt 1 2
x , x thỏa mãn x x
x x  3. Giá trị nhỏ nhất của biểu thức S  3a  2b bằng 1 2  3 4  3 4 A. 40. B. 41. C. 44. D. 46. Câu 7. Cho ,
a b là hai số thực lớn hơn 1. Biết phương trình 2 x x 1
a b   1 có nghiệm
thực. Giá trị nhỏ nhất của biểu thức P ab  bằng a   4 log log b a A. 4. B. 5. C. 6. D. 10. 9 Câu 8. Cho ,
a b là hai số thực lớn hơn 1 thỏa mãn a b  10. Gọi , m n là hai
nghiệm của phương trình log xlog x2 log x 3log x 1 0. Giá trị nhỏ nhất a b a b
của biểu thức S mn bằng A. 16875. B. 4000 . C. 3456. D. 15625. 16 27 Câu 9. Cho ,
a b là các số thực lớn hơn 1 và phương trình log ax.log bx  2018 có a b hai nghiệm phân biệt , m .
n Giá trị nhỏ nhất của biểu thức P   2 2 a b  2 2 4 9 36m n   1 bằng A. 36. B. 72. C. 144. D. 288. Câu 10. Cho ,
a b, c là các số thực lớn hơn 1 thỏa mãn a b c  100. Gọi , m n là
hai nghiệm của phương trình  x2 log
1 2 log b 3log clog x 1  0. Tính a a a a
S a  2b  3c khi mn đạt giá trị lớn nhất.
A. S  200. B. 500 S  . C. 650 S  . D. 700 S  . 3 3 3
Phần 5. Bài toán tìm GTNN-GTLN
Câu 1. Cho hai số thực x, y thỏa mãn logx 3y logx 3y1. Giá trị nhỏ nhất
của biểu thức S x y bằng A. 2 2 . B. 1. C. 4 5 . D. 10. 3 3
Câu 2. Cho x, y là các số thực dương thỏa mãn log
11x  20y  40  1. Gọi 2 2  
2 x xy3 y y ,
a b lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của S  . Tổng a b bằng x A. 10. B. 2 14. C. 11. D. 7 . 6 2 Câu 3. Cho c c ,
a b,c là các số thực dương khác 1 thỏa 2 2
log b  log c  log 2 log 3. a b a b b b
Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P  log b log c. Giá trị a b
của biểu thức S  2m 3M bằng A. 1 S  . B. 2 S  .
C. S  2.
D. S  3. 3 3 Câu 4. Cho ,
a b, c là các số thực lớn hơn 1. Giá trị nhỏ nhất của biểu thức 4 1 8 P    bằng 3 log a log b 3 log c bc ac ab A. 10. B. 12. C. 18. D. 20.
Câu 5. Cho x, y là các số thực dương thỏa mãn log x  log y  log x y . Giá trị 2 2 4  
nhỏ nhất của biểu thức 2 2
S x y bằng 10 A. 2 2. B. 3 2 4. C. 3 4 2. D. 4. Câu 6. Cho ,
a b là hai số thực dương. Giá trị nhỏ nhất của biểu thức     b 4
P  log 1 2a  log 1      2 log 1      3   3 3  2a  b  A. 1. B. 4. C. 7. D. 9. Câu 7. Cho ,
a b là các số thực lớn hơn 1 thỏa mãn log a  log b  1. Giá trị lớn nhất 2 3
của biểu thức P  log a  log b bằng 3 2
A. log 3 log 2.
B. log 2  log 3. 2 3 3 2 C. 1  2 log 2  log 3 . D. . 3 2  2 log 3  log 2 2 3
Câu 8. Cho x, y, z là các số thực thỏa mãn 4x 9y 16z 2x 3y 4z      . Giá trị lớn nhất của biểu thức x 1  y 1  z 1 P 2 3 4     bằng A. 3 87    . B. 5 87 . C. 7 87 . D. 9 87 . 2 2 2 2 Câu 9. Cho ,
a b là các số thực thỏa mãn 2 2
a b 1 và log
a b 1. Giá trị lớn 2 2   a b
nhất của biểu thức P  2a  4b 3 bằng A. 1 . B. 10 . C. 10. D. 2 10. 10 2
Câu 10. Cho hai số thực x, y thỏa mãn log
2x y 1 *. Biết giá trị lớn nhất 2 2   x 2 y
của biểu thức P  2x y là a với , a b
  và a tối giản. Tổng a b bằng b b A. 11. B. 13. C. 15. D. 17.
Câu 11. Cho các số thực
a b c ,
a b, c thỏa log
a a 4 b b 4  c c  4 . 2 2 2 2      
a b c  2
Giá trị lớn nhất của biểu thức
a  2b  3c P  bằng
a b c A. 4  30    . B. 8 30 . C. 6 30 . D. 12 30 . 3 3 3 3
Câu 12. Cho các số thực x, y thỏa mãn 2 2 2 2 2 2 2 2 x 4 y x 4 y 1  3x 4 y 2x 4 4 2  2 4 y . Gọi , m x y
M lần lượt là giá trị nhỏ nhất và lớn nhất của 2 1 P
. Tổng M m bằng x y  4 A. 36  . B. 18  . D. 18 . C. 36 . 59 59 59 59
Câu 13. Cho các số thực dương ,
a b, c thỏa mãn 2 2 2
5 log a 16 log b  27 log c  1. Giá 2 2 2
trị lớn nhất của biểu thức S  log a log b  log b log c  log c log a bằng 2 2 2 2 2 2 A. 1 . B. 1 . C. 1 . D. 1 . 16 12 9 8 11
Câu 14. Cho các số thực ,
a b, c lớn hơn 1 thỏa mãn log a  1 log b log c log 2. 2  2 2  bc
Giá trị nhỏ nhất của biểu thức 2 2 2
P  10 log a 10 log b  log c bằng 2 2 2 A. 7 . B. 9 . C. 3. D. 4. 2 2 Câu 15. Cho ,
a b là hai số thực dương. Giá trị nhỏ nhất của biểu thức 8 1 2 2 P  log
a b  log      bằng 5 5 a b A. 1 . B. 1. C. 3 . D. 2. 2 2 Câu 16. Cho y m  log
với x 1, 0  y 1. Giá trị của lớn nhất của biểu thức x x
T  log y  log x bằng x y A. 2. B. 1. C. 0. D. 2.
Câu 17. Cho các số thực dương ,
a b thỏa mãn log ab a
Giá trị nhỏ nhất của b 2 2 . 2   3 12a b
biểu thức S a  bằng a 1 A. 3 1. B. 1 3. C. 2 3 2. D. 2 3 4.
Câu 18. Xét các số thực 1 a ,
a b thỏa mãn ab1. Biết rằng P   log đạt log a a bab giá trị lớn nhất khi k
b a . Khẳng định nào sau đây đúng?     A. 3 k 0; .   
B. k 1;0. C. 3 k  ;2.
D. k 2;  3 .  2 2  Câu 19. Cho ,
a x là các số thực dương, a  1 và thỏa mãn log x  log x a Giá trị lớn a . nhất của a bằng ln10 log e A. 1.
B. log2e   1 . C. e e . D. 10 e .
Câu 20. Cho hai số thực , a
b 1 sao cho tồn tại số thực 0  x  1 thỏa 2 log x log b a x ab .
Giá trị nhỏ nhất của biểu thức 2 2
P  ln a  ln b  lnab bằng A. 3 2 2  e  . B. 1 3 3 . C. . D. 1 . 12 4 2 4 Câu 21. Cho ,
a b là các số thực thỏa mãn 0  a 1  b, ab 1. Giá trị lớn nhất của biểu thức 4 P  log ab  bằng a 1log b ab a .loga b A. 4. B. 2. C. 3. D. 4.
Câu 22. Cho x, y là các số thực thỏa mãn 1 xy  4, x  ,
y 1. Gọi M , m lần lượt là 2
giá trị lớn nhất và nhỏ nhất của P  log x log y  2 2
1 . Tổng M  2m bằng 2 2 12 A. 6. B. 11. C. 11. D. 21. 2 2
Câu 23. Xét các số thực ,
a b thỏa mãn a b 1. Giá trị nhỏ nhất của biểu thức   2   2 a P
log a 3log     bằng a b b  b A. 13. B. 14. C. 15. D. 19.  
Câu 24. Xét các số thực a ,
a b thỏa b  1, a b  .
a Biểu thức P  log a  2 log     a b b  b
đạt giá trị khỏ nhất khi A. 2 a b . B. 2 3 a b . C. 3 2 a b . D. 2 a  . b
Câu 25. Xét các số thực ,
a b thỏa mãn 2
a b và b 1. Giá trị nhỏ nhất của biểu thức a
P  log a  log bằng a b b b A. 1. B. 1. C. 3. D. 9. 3 Câu 26. Cho x x
x, y là hai số thực thỏa mãn y e và ln ln 
. Giá trị nhỏ nhất của y ln y
biểu thức P xy bằng 3 A. 3 2 2 4 2  e  . B. 2 e . C. 6 e . D. 8 e . Câu 27. Cho 1 2 ,
a b là các số thực dương thỏa mãn log a  log . Giá trị nhỏ nhất 2 2 2 b của biểu thức 3 3
P  4a b  4 log  3 3
4a b bằng 2    A. 4 4 4. B. 4 log 6. C. 41log 3 . D. 4 log    . 2  2 2 ln 2 ln 2
Câu 28. Cho x, y là hai số thực dương thỏa xy  4y 1. Giá trị nhỏ nhất của biểu    thức 6 y x 2y P   ln    bằng x  y  A. 3 ln 4. B. 12  ln 4. C. 3  ln 6.
D. 24  ln 6. 2     Câu 29. Cho x 1 y 1
x, y là hai số thực dương thỏa log x y  2  1 log     . 3   3  y x  2 2
Biết giá trị nhỏ nhất của x y là a với , a b    và  ,
a b  1. Tổng a b bằng xy b A. 2. B. 9. C. 12. D. 13.
Câu 30. Cho x, y là hai số thực dương thỏa mãn x  n y  l  2 ln l
n x y. Giá trị nhỏ
nhất của biểu thức P x y bằng A. 2 2 3. B. 3 2  2. C. 17  3. D. 6. 13
Câu 31. Cho x, y là hai số thực dương thỏa mãn log x  log x 3y  2  2 log . y 2 2   2
Biết giá trị lớn nhất của biểu thức x y 2x  3y P   là b a  với , a b, c 2 2
x xy  2y x  2y c
là các số nguyên dương và b là phân số tối giản. Tổng a b c bằng c A. 10. B. 15. C. 17. D. 30. Câu 32. Cho ,
a b, c là các số thực lớn hơn 1 và x, y, z là các số thực dương thỏa mãn 16 16 x y z
a b c abc. Giá trị lớn nhất của biểu thức 2 P    z bằng x y A. 3 3 20  . B. 24  . C. 20. D. 24. 3 4 3 4
Câu 33. Xét các số thực ,
a b thỏa mãn a b 1. Giá trị nhỏ nhất của biểu thức 4     2 a   a P  log  323log       bằng a 128 b    b  b A. 13. B. 14. C. 15. D. 19.
Câu 34. Giá trị nhỏ nhất của biểu thức 9 3
P  log a  log 16a 64 2 3log a 7 với 2 2 2 2
a 1;16 bằng A. 20. B. 13. C. 7. D. 8. Câu 35. Cho ,
a b là các số thực thỏa mãn điều kiện 0  b a 1. Khi biểu thức 43b   1 2 P  log
8 log a 1 đạt giá trị nhỏ nhất, tổng 3
a  2b bằng a 9 b a A. 1. B. 2. C. 6. D. 7.
Câu 36. Xét các số thực ,
a b thỏa mãn điều kiện 1  b a 1. Biểu thức 4  1 P  log b     log
b đạt giá trị nhỏ nhất khi log b bằng a  4 a  a b A. 2 . B. 3 . C. 2 . D. 9 . 3 2 9 2 Câu 37. Cho ,
a b là hai số thực thuộc 1;2 và a  .
b Biết giá trị nhỏ nhất của biểu thức P
 2b b  2 2 log 4 4  log a là 3 m n với , m n
  . Tổng m n bằng a b a A. 37 . B. 12. C. 15. D. 249. 3 Câu 38. Cho ,
a b là hai số thực thỏa 1  b a 1 và giá trị nhỏ nhất của biểu thức 3 3b 1 2 P  log   
12 log a là m khi n
b a . Tổng m n bằng a 3  4 b a  a 14 A. 12. B. 15. C. 37 . D. 46 . 3 3 3   Câu 39. Cho a ,
a b là hai số thực thỏa 4 a b  và   2 P  16 log  3log a có 3
a 12b 16 a  b
giá trị nhỏ nhất. Tổng a b bằng A. 7 . B. 11. C. 4. D. 6. 2 2 2 3     Câu 40. Cho a 3 ,
a b là hai số thực thỏa 3a  4  b  0 và P  log      log a đạt a   3     4b  16 a    4b
giá trị nhỏ nhất. Tổng 3a b bằng A. 13. B. 25. C. 8. D. 14. 2 2 2
Câu 41. Cho hai số thực x, y thỏa mãn 2 2 2
x4 y 1x y  1  x y x eey  . Giá trị lớn 4 nhất của biểu thức 3 2 2
P x  2y 2x  8y x  2 bằng A. 2. B. 58 . C. 115. D. 122 . 27 27 27 2 Câu 42. Cho x  y x 2018
x, y là hai số thực thuộc 0;  1 và thỏa mãn 1 2017  . 2 y 2y  2019
Tổng giá trị lớn nhất và nhỏ nhất của biểu thức P   2 x y 2 4 3
4 y  3x25xy bằng A. 25. B. 136 . C. 383. D. 391. 2 3 16 16 Câu 43. Cho 2 y 1
x, y là hai số thực không âm thỏa mãn 2
x  2x y 1  log . 2 x 1
Giá trị nhỏ nhất của biểu thức 2 x 1  2 P e
 4x 2y 1 bằng A. 1. B. 1  . C. 1 . D. 1. 2 2
Câu 44. Xét các số thực dương x y x, y thỏa log
x x 3  y y 3  . xy 3 2 2    
x y xy  2
Giá trị lớn nhất của biểu thức 3x  2y 1 P  bằng x y  6 A. 1. B. 2. C. 3. D. 4.
Câu 45. Cho hai số thực dương x, y thỏa mãn log x  
1 y   y 1 1   
 9  x 1 y 1 . 3     
Giá trị nhỏ nhất của biểu thức P x  2y bằng A. 5 6 3.
B. 3 6 2. C. 11. D. 27 . 2 5 Câu 46. Cho y
x, y là các số thực thỏa mãn log
 3y  1 x  2
y x. Giá trị 2 2 1 x
nhỏ nhất của biểu thức P x y bằng 15 A. 3  . B. 5  . C. 2. D. 1. 4 4 Câu 47. Cho x y  1
x, y là các số thực thỏa mãn 2 2 2 3
log x y  1
  log 1 xy . 2   2   2   Giá
trị lớn nhất của biểu thức P   3 3
2 x y 3xy bằng A. 13. B. 17 . C. 3. D. 7. 2 2 2    Câu 48. Cho x 4x 1
x, y là hai số dương thỏa mãn 2 2 2.4  ln     4xy.  Giá trị lớn nhất  2xy 
của biểu thức P  2x y 2x 2 x y bằng A. 12 3. B. 1 3. C. 1 3. D. 1 2 3.
Câu 49. Cho x, y là hai số thực dương thỏa mãn 2 x y    2 x y   2 2 2 2 yx 2 4 9.3 4 9 .7 . Giá
trị nhỏ nhất của biểu thức x  2y 18 P  bằng x A. 3 2 . B. 1 9 2. C. 9. D. 17. 2 y x    
Câu 50. Gọi S là tập các số thực x; y sao cho x 0; và x 1 y 1 2        2    .  2x   2y  2
Biết rằng giá trị nhỏ nhất của biểu thức y x
P e  cos y 2 2x
với x; y S đạt 2
được tại x ; y . Mệnh đề nào sau đây đúng? 0 0  A. x  0; 1 . B. x  1.
C. x  1;2 . D. x  2. 0   0   0 0
Câu 51. Gọi S là tập các số thực x; y sao cho x 1;  1 và
x yx
x  x yy 2018 ln 2017 ln 2017y e .
Biết rằng giá trị lớn nhất của biểu thức 2018x P ey   2
1 2018x với x; y S đạt
được tại x ; y . Mệnh đề nào sau đây đúng? 0 0  A. x  1.
B. x  1;0 .
C. x  0;1 . D. x  1. 0   0   0 0
Câu 52. Cho các số thực dương x, y thỏa mãn 2 2 x y 1 2   log  2 2
x y 1  3. Biết giá 3 
trị lớn nhất của biểu thức 3 3 a
S x y x y là 6 với * ,
a b   và a tối giản. b b
Tổng a  2b bằng A. 25. B. 32. C. 34. D. 41. Câu 53. Cho ,
a b, c là các số thực khác 0 thỏa mãn 3a  5b  15c. Giá trị nhỏ nhất của biểu thức 2 2 2
P a b c  4a b c bằng
A. 3log 3. B. 2log 5. C. 2 3. D. 4. 5 3 16
Câu 54. Cho x, y, z là các số thực không âm thỏa 5x 25y 125z    2018. Giá trị nhỏ nhất của biểu thức x y z
S    bằng 6 3 2 A. 1 1 1 log 2018. B. log 2016. C. log 2016. D. log 2017. 5 3 5 6 5 5 2 1 1 1
Câu 55. Cho x, y, z là các số thực dương thỏa x y 2018 64 8 4 z    3.4 . Giá trị lớn nhất của biểu thức 1 1 1 3029 P     bằng
x  4 y  3z
2x  2y  3z
x  2y  6z 2 A. 2017. B. 2018. C. 2019. D. 2020. 17 HÀM SỐ LŨY THỪA
HÀM SỐ MŨ – HÀM SỐ LOGARIT
120 câu – Vận dụng cao
Phần 1. Tính chất và các phép toán………………………………………… 2
Phần 2. Đồ thị ………………………………………………………………………………….. 11
Phần 3. Dãy logarit ………………………………………………………………….……. 16
Phần 4. Cực trị nghiệm ……………………………………………………………….. 20
Phần 5. Bài toán tìm GTLN – GTNN …………………….………………… 23 1
Phần 1. Tính chất và các phép toán
Câu 1. Tìm tất cả các giá trị của tham số a để hàm số y  log
x đồng biến trên 2 a 2a 1  khoảng 0;.
A. a 0;2.
B. a 0;2\  1 .
C. a   \0;2.
D. a   \0;2. x  0
Lời giải. Điều kiện xác định:  . 2 0
  a 2a 11 
Theo tính chất của hàm số logarit, ta có hàm số y  log
x đồng biến khi và chỉ 2 a 2a 1  a  0 khi 2
a 2a 11   . Chọn C.a  2   
Câu 2. Cho hàm số y f x 1  log    
. Khẳng định nào sau đây đúng? 2018  x 
A. Hàm số y f x nghịch biến trên  ;  0.
B. Hàm số y f x đồng biến trên  ;  0.
C. Hàm số y f x nghịch biến trên  ;    1 .
D. Hàm số y f x đồng biến trên  ;    1 .
Lời giải. Điều kiện xác định: x  0.
Ta có f x 1   0, x  ;
 0. Lại có f x  0  x  1. x ln 2018
Lập BBT và kết luận được hàm số y f x nghịch biến trên  ;    1 . Chọn C.
Câu 3. Số giá trị nguyên của m 10 để hàm số y   2
ln x mx   1 đồng biến trên khoảng 0; là A. 8. B. 9. C. 10. D. 11.
Lời giải. Điều kiện xác định: 2  2 x m
x mx 1 0. Ta có y  . 2 x mx 1 2x m 2
 x m  0 Yêu cầu bài toán 0, 0; x         , 0; x   2     2 x mx 1
x mx 1 0  m  2xm     0  1 , x  0;          m  0 m 
  có 10 giá trị. Chọn C. m 1  0 m   x m   2  x  
Câu 4. Có bao nhiêu số nguyên âm m để hàm số y   3
ln x mx  2 đồng biến trên
nửa khoảng 1; ? A. 1. B. 2. C. 3. D. 4. 2
Lời giải. Điều kiện xác định: 3  3 x m
x mx  2  0. Ta có y  . 3 x mx  2 2 2 2 3x m 3
 x m  0 Yêu cầu bài toán 0, 1; x         , 1; x   3     3 x mx  2
x mx 2  0  2 m  3xm     3      2 , x  1;  
m  3 m 
  có 2 giá trị. Chọn B. 2 m  x m   3   x Câu 5. Cho ,
a b, c là các số thực dương thỏa mãn log3 7 log7 11 l 11 og 25 a  27, 49 b  , c  11 .
Giá trị của biểu thức 2 2 2 log3 7 log7 11 l 11 og 25 T abc bằng A. 76  11. B. 469. C. 2017. D. 31141.
Lời giải. Có T   7 a log 7 log 11 log 25 log 25 3  log 11 b  7  log 25 c
 11 27log37 49log711 log3 7 11  11 11 . 27  log 7   3 3 log37 3 3   log37 3  3  7  343  Áp dụng  log log 11 log7 11 2  a b ab , ta được   49 7   2 7    log711 7  2  11  121 .  l 11 og 25     11   1 1 1 l 11 og 25  11         l 11 og 25 2 11 2 2  25  25  5      
Vậy T  3431215  469. Chọn B. Câu 6. Cho c c ,
a b, c là các số thực khác 0 thỏa mãn 4a 25b 10c   . Tính T   . a b A. 1 T  . B. 1 T  . C. T  2. D. T  10. 10 2 a   log t 4 
Lời giải. Giả sử  4a 25b 10c t     
 b  log t . 25
c  log t  10 Ta có c c log t log t log 4 log 25 10 10 t t T        log 4  log 25 10 10 a b log t log t log 10 log 10 4 25 t t
 log 4.25  log 100  2. Chọn C. 10   10
Câu 7. Cho x, y là các số thực dương thỏa mãn log x  log y  log x y và 9 6 4   x a   b  với ,
a b là hai số nguyên dương. Tổng a b bằng y 2 A. 4. B. 6. C. 8. D. 11. x  9t 
Lời giải. Ta có log x log y log x y t    
  y  6t
 9t  6t  4t 9 6 4  
xy4t  2t t t
x 9t 3 t 3 3 3 1 5              a t 1 y                 6 2 1 0   Chọn B.        
a b  6. 2 2 2 2 b   5  3
Câu 8. Cho các số thực dương x, y, z theo thứ tự lập thành một cấp số nhân, đồng
thời với mỗi số thực dương a 1 thì log x, log y, log z theo thứ tự lập thành một 3 a a a
cấp số cộng. Giá trị biểu thức 3x 7 y 2020z P    bằng y z x A. 2030 . B. 1015. C. 2030. D. 4038. 3 2 2 xz y xz y
Lời giải. Theo giả thiết ta có      3 4
log x log z  2 log y   a
log x.z  log y 3  a aa   a  2 xz y   
x y z  0. Khi đó P  3 7  2020  2030. Chọn C. 3 4 xz y
Câu 9. Cho x, y, z là các số thực dương thỏa logx y z và  2 2
log x y  z 1. Giả sử ,
a b là các số thực sao cho 3 3 3z 2   .10  .10 z x y a b
. Tổng a b bằng A. 31  . B. 25  . C. 29 . D. 31. 2 2 2 2 Lời giải. Đặt 10z t  . Khi đó 3 3 3 2
x y at bt .
logx yz 2  z  
x y  10  t Từ giả thiết t 10t        xy  log   . 2 2 x y  2 2  z 1
x y 10.10z 10t 2   t  2  1 3 t 10t  3 1 a   3 3 3  Khi đó x y
x y 3xyx y 3 2 t t 15t              2 . 2 2 b 15  Vậy 29 a b  . Chọn C. 2 2017x
Câu 10. Cho x, y, z là các số thực thỏa mãn 3x  5y  15xy . Gọi S xy yz zx.
Khẳng định nào sau đây đúng?
A. S 1;2016. B. S 0;2017.
C. S 0;2018.
D. S 2016;2017.
x  log t 3
y log t 2017x 5 
Lời giải. Đặt 3x  5y  15xy t. Từ giả thiết ta có  . 2017   z  log t 15 x y  Suy ra 2017 1 1 1 xy
z  log t     . 15 x y log 15 log 3  log 5 1 1 x y t t tx y 2017
xy x yz Suy ra 
 2017  xy yz zx. Chọn C. x y x y
Câu 11. Tìm bộ ba số nguyên dương a;b;c thỏa mãn log1 log1  3  log13 
5 ... log13...192 log 5040  a b log 2  c log 3. 4
A. 1;3;2. B. 2;4;  3 . C. 2;4;4.
D. 2;6;4.
Lời giải. Ta có công thức quy nạp: 2
1 3  5 ... 2n 1  n .
Khi đó vế trái của giả thiết bằng: 2 2 2
log 2  log 3 ... log10 2 log 5040 10!
 2 log10!2 log 5040  2 log
 2 log720  2  6 log 2  4 log 3. Chọn D. 5040
Câu 12. Cho f  
1  1 và f m n  f m f n mn với mọi * ,
m n   . Giá trị biểu
f 96 f 69241 thức T  log    bằng 2    A. 3. B. 4. C. 6. D. 9.
Lời giải. Theo giải thiết, ta có
f 2  f   1  f   1 1.1 f  
3  f 2 f   1  2.1
f 4  f   3  f   1  3.1  f n  
1  f n f   1  . n 1 Suy ra nn  
f   f   f    f n    f   f   f    f n  n f   1 2 3 4 ... 1 1 2 3 ... . 1    2 nn   1
 f 96 4656 f n  1 n  1 f   1         . 2
 f 69 2415 
f 96 f 69241 Vậy 4656 2415241 T  log    log  3.  Chọn A. 2  2   Câu 13. Cho ,
a b, c là ba số thực dương không cùng bằng nhau, đồng thời khác 1 và thỏa mãn log c log a log b c a b abc
. Giá trị nhỏ nhất của biểu thức a b c bằng A. 2 2. B. 2 3. C. 3 2. D. 3 3.
Lời giải. Giả thiết ln . a ln c ln . b ln a ln c.ln b 2 2 2   
 ln a  ln b  ln c.   1 ln b ln c ln a  1 a b  ln  ln  ln  c a b c   Vì  1 ,
a b, c không cùng bằng nhau, nên   1 
 ln a  ln b  ln c  b c  .   a
ln a  ln c  lnb    1 a c   b Với 1
a b  , khi đó 1 1 2
a b c    c   c  2 2. Dấu "  " xảy ra khi và chỉ c c c c   khi a b c 1 1 ; ;    ;
; 2. Tương tự cho các trường hợp còn lại.  Chọn A.  2 2 
Câu 14. Cho a  0 và b  0 thỏa mãn log a b   a b   ab  2 2 16 1 log 4 5 1 2. 4 5 1  8ab 1   
Giá trị của biểu thức a  2b bằng 5 A. 20 . B. 27 . C. 6. D. 9. 3 4
Lời giải. Ta có log a b   a b ab  2 2 16 1 log 4 5 1 4 5 1  8ab 1     log 8ab 1  log 4a  5b 1 4a5b 1    8ab 1     2 log 8ab 1 .log
4a  5b 1  2. 4a5b 1    8ab 1     2 2  3 16  a b  Dấu a  27 ''  '' xảy ra      
4  a  2b  . Chọn B. log
4a  5b 1  1  4  8ab 1     b   3 
Câu 15. Cho a 1 và b 1 thỏa  3 2
a a b    2 3 log 4 4
log b b 16b  64  2. b a
Giá trị của biểu thức a  2b 1 P  bằng a b A. 15 . B. 17 . C. 19 . D. 21. 10 10 10 10
log a a a    a a    a b  4 4 logb    22 3 2 3 3 log  b  
Lời giải. Ta có  . log b b bb b           ba  16 64 loga   82 1 2 3 3 log      3 a Suy ra  3 2
a a b    2 3 log 4 4
log b b 16b  64 b aa   2 1 1
 3log a  log b  2 3log .
a log b  2. Dấu ''  '' xảy ra    . Chọn C. b 3 a b 3 a b   8  1 Câu 16. Cho x
x  0 và số thực y thỏa mãn 2 x log 1  4 y 2 y 1     . Giá trị của 2     biểu thức 2 2
P x y xy 1 bằng A. 1. B. 2. C. 3. D. 4. 1
Lời giải. Theo BĐt Côsi: 1 1 x
x   2 x.  2. Suy ra 2 x  4. x x Ta có
y   y   y   ty 1  0 3 14 2 1 14 1
y 1  3 y 1  t  3t 14.
Xét hàm f t 3  t
 3t 14 trên 0; có kết quả max f t  f   1  16. 0;
Suy ra 14 y 2 y 1 16. Do đó log 14  y 2 y 1     4. 2     1 x  x 1 Vậy 2 x  log 14
  y 2 y 1   
P  2. Chọn B. 2     y  0    Câu 17. Cho
x x x 1
x  0 và y  0 thỏa mãn 3 2 2 2  log y   . Giá trị của biểu 2  2 y  thức 2 2
P x y  2xy bằng A. 1 . B. 1. C. 2. D. 2. 2 Lời giải. Với
x x x  1 x  0, ta có 3 2 2 1 2  2  . 2 6     Với 1 1     1
y  0, ta có log y    log 2 . y         . 2 2 2 y   2 y  2 3 2
x x x 2  1  x 1     Vậy 3 2
x x x 1    1   1 2 2  log y      y    
P  . Chọn A. 2 2  2 y   2 y   y  2     2 x, y  0  x      
Câu 18. Cho hàm số f x 4  . Tổng 1 2 2016 S f     f      ... f   bằng       4x  2 2017 2017 2017 A. 1007. B. 1008. C. 2016. D. 2017.
Lời giải. Dễ dàng chứng minh được '' Nếu a b  1 thì f a f b1 '' .                Do đó 1 2016 2 2015 1008 1009 S   f     f          f         f          ...  f         f          2017 2017 2017 2017 2017 2017      
 11...1  1008 . Chọn B. x
Bài toán tổng quát: Nếu   M f x   0
M   thì ta có kết quả x M M
a) f x f 1 x1.
b) f  2  f  2 sin cos 1.
c) f a f b 21 với a b  3. x       Câu 19. Cho hàm số  f x 9 2  . Tổng 1 2 2017 P f     f      ... f   bằng       9x  3 2017 2017 2017 A. 1009. B. 4035. C. 4039 . D. 12103. 4 12 12 x 1x
Lời giải. Ta tính được  
f x f   x 9 2 9 2 1 1    . x 1 9  3 9 x  3 3           Do đó 1 2016 2 2015        P   f   1008 1009 2017   f                         f   f f f             f          ... 2017 2017 2017 2017         2017 2017 2017   3   f   7 4039 1008. 1  336   . Chọn C. 4 12 12 t
Câu 20. Xét hàm số f t 9 
với m là tham số thực. Gọi S là tập hợp tất cả t 2 9  m
các giá trị của m sao cho f x f y1 với mọi x, y thỏa mãn xy e
ex y. Tìm
số phần tử của S . A. 0. B. 1. C. 2. D. Vô số.
Lời giải. Xét hàm   t
g t e et, t  .  Ta có   t
g t e e; gt 0
  t  1.
Lập bảng biến thiên ta thấy gt 0, t   và đẳng thức xảy ra  t 1. Ta có    x y g x y e
ex y 0 x ye
ex y.
Kết hợp với giải thiết xy e
ex y, suy ra xy e
ex y  x y  1. 7 x y
Khi đó f x f y 9 9  1    1 x 2 y 2 9  m 9  m x y 2    x y   x y 2    x y   4 4 2.9 . 9 9 9 . 9 9    9xy m m m m
 9  m   3. Chọn C. t
Câu 21. Xét hàm số f t 4 
với m  0 là tham số thực. Biết f x f y1 với 4t m 1 mọi số thực dương 1 1
x, y thỏa mãn x y2  .x y . Giá trị nhỏ nhất của hàm 2 2  
số f t trên đoạn 1  ;1 bằng 2    A. 1 . B. 1 . C. 3 . D. 5 . 2 4 4 4
Lời giải. Từ điều kiện bài toán ta có: x y  1 (đưa về hằng đẳng thức). m  2
Như các bài trên ta dễ dàng suy ra  .  n  2   loaïi  
Khi đó f t 1   f t 1 1 min  f  
   . Chọn A. 2 1       ;1 2 2 1 2  4tx Câu 22. Cho a
a là số thực dương. Xét hàm số f x 
với m  0 là tham số x a m
thực. Biết f x f y1 với mọi 1
x y  . Khẳng định nào sau đây đúng? 2 A. 4 m a.
B. m a. C. m  . a D. 2 m a . x y
Lời giải. Ta có     a a f x f y  1    1 x y a m a m 1 1 x yam x y a a x yam x y a a  2 2 x y 2 4 2. . .
m m a
a m a . Chọn A. x
Câu 23. Xét hàm số f x 9 
với m là tham số thực. Gọi S là tập hợp tất cả x 4 9  m
các giá trị của m sao cho f a f b1 với mọi ,
a b thỏa mãn ab 2 e
e a b   1 .
Tích các phần tử của S bằng A. 3. B. 9. C. 81. D. 81.
Lời giải. Theo giả thiết ta có: ab2 ab2 e
a b 1  e
1a b 2.
Tương tự như Câu 20, ta có ab2 e
1a b 2. Do đó dấu bằng phải xảy ra m  3
a b 2  0  a b  2. Biến đổi như câu trên ta được 4
m  9ab  81   . m  3 
Vậy tích các phần tử của tập hợp S là 3.  3  9. Chọn B.
Câu 24. Xét hàm số   log 2 4x f x   và ,
a b là hai số thực dương thỏa mãn 2
f a f b  1. Đặt 27 12 2018 2017 T a b
. Khẳng định nào sau đây là đúng? 8 A. 1
0 T  . B. 1 1 T  . C. 1 T 1. D. T 1. 4 4 2 2 x a b
Lời giải. Ta có f x 4 
. Do đó f a f b 4 4  1    1 4x  2 4a 1 4b 1 0   a 1 4ab 4 a b 1          . 0   b 1  4 2017 Khi đó ta có 27 12 2018 2017 9 2018 T a ba b
a b  1 với mọi , a b  0;  1 . Chọn D.  
Câu 25. Cho hàm số   1 2x f x  log    . Tính tổng 2 2 1 x   1   2   3  2015 2016 S f     f       f        ... f         f        . 2017 2017 2017 2017 2017 A. S  1008. B. S  2016. C. S  2017. D. S  4032. 1  2x  1  21x 
Lời giải. Xét f x f 1 x log     log   2 2 2 1 x  2 1  1 x   1  2x  1 21 x 1
 2x 21 x 1  log     log    log  .   log 4 1. 2 2 2 2 2 1 x  2  x  2 1 x x  2    
Áp dụng tính chất trên, ta được   1  2016    2  2015   1008 1009  S   f     f          f         f          ...  f         f          2017 2017 2017 2017 2017 2017      
 11...1  1008. Chọn A. x  
Câu 26. Xét hàm số f x  2018  2018 lnee . 
 Tính T f  
1  f 2... f 2017.     A. T  1008. B. T  1009. C. 2017 T  . D. 2019 T  . 2 2 x x 1 2018 2018
Lời giải. Ta có   e e e f x
và f 2018 x  . x x x 1 2018 ee 2018 2018 ee ee
Suy ra f x f 2018 x1. Lại có f   1 1009  . 2
Vậy T f   f    f   1 2017 1 2 ... 2017  1008   . Chọn C. 2 2 2
Câu 27. Xét hàm số   m x f x  log
với m là tham số thực. Gọi S là tập hợp tất cả 3 1 x
các giá trị của m sao cho f a f b 3 với mọi ,
a b thỏa mãn ab e
ea b. Tích
các phần tử của S bằng A. 27. B. 3 3. C. 3 3. D. 27.  x   0 0     x 1
Lời giải. Điều kiện xác định: 1   x   
. Như Câu 20 ta được a b  1.  m   0 m  0    9 2 Ta có f xm x 2  log
 log m  log x log 1 x . 3 3 3 3   1 x
Suy ra f a f b 3  f a f 1a 3   2
log m  log a  log 1a 2
log m  log 1a  log a  3 3 3 3 3 3   3  3 2  log m  2
m  27  0  m   27 . Chọn B. 3 2
Câu 28. Cho hàm số f x 2019  a  2 .log
x 1  xb sin x.cos2018x6 với ,a b  .  Biết f  ln 2019 2018
10. Giá trị của biểu thức f  ln 2018 2019  bằng A. 10. B. 2. C. 8. D. 10.
Lời giải. Đặt gx f x 2019   a  2 6 .log
x 1  xbsin x.cos2018x.
Dễ dàng chứng minh gx là hàm lẻ nên g ln 2018   g ln 2019  g ln 2019 2019 2018 2018  hay f  ln 2018   f  ln 2019 2019 6 2018  6      .   Mà f  ln 2019 2018
10 nên suy ra f  ln 2018 2019  2. Chọn B.
Câu 29. Cho hàm số    2 .log 2  4
1 .sin . x f x a x x b x c e với ,
a b, c  .  Biết   rằng f   1
ln 2  f ln   2. 
Khi đó hằng số c thuộc khoảng nào sau đây?  2         A. 1 0; .        B. 1  ;1. C. 3 1;  . D. 3  ;2.  2 2   2 2 
Lời giải. Đặt     . x g x f x
c e . Dễ dàng chứng minh g x là hàm lẻ nên   1  1 ln g   1
ln 2  g ln   0 ln 2     2 
suy ra f ln 2 c.e ln f  c.e  0  2  2 1          f ln 2 1 ln      1 4 ln 2 2 ln f    c.e
c.e   0  2  Chọn B.       
2c c  0  c  . 2         2  5
Câu 30. Cho hàm số f x 3  a  2
.ln x x 1bx.cos5x1 với ,a b  .  Biết
f loglog e. f logln10  .
m Gọi S là tập các giá trị của tham số m thỏa mãn 2 f   e 2  f    2 log log log ln10  m
m 8. Số phần tử của tập S bằng A. 0. B. 1. C. 2. D. Vô số.
Lời giải. Chứng minh gx f x1 là hàm lẻ nên gloglog e glogln10  0   (do   1 log loge  log     logln10 
). Suy ra f loglog e f logln10 2. Bình ln10
phương hai vế ta được 2 f   e 2 log log
f logln102loglog e. f logln10  4 m  1 2 2  m
m 8  2m  4  m 3m 4  0   Chọn B. m  4   loaïi 10
Phần 2. Đồ thị và các vấn đề liên quan x  
Câu 1. Cho bốn hàm số  x 1 y  3   1 , y      2,   3 1 x  4x y    3 , y       4 
có đồ thị là bốn đường cong 4
như hình bên. Tương ứng hàm số - đồ thị đúng là A.  
3 C , 2  C , 1  C , 4  C . 4   
 1    3    2 B.  
1 C , 3  C , 2  C , 4  C . 4   
 1    3    2 C.  
1 C , 2  C , 3  C , 4  C . D. 2C , 1  C , 3  C , 4  C . 4   
 1    3    2 4   
 1    3    2
Lời giải. Kẻ đường x  1 để so sánh cơ số. Ta thấy cơ số của C nhỏ nhất nên 2 
4C , tiếp theo là C nên 2C và cơ số lớn nhất là của C . Chọn C. 3  1  1  2 
Câu 2. Cho các hàm số   x
f x a , g x  log x và b
hx  log x c (trong đó ,
a b lớn hơn 0 và khác 1; b  
c   ) có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
A. a c  . b
B. a b c.
C. a 1 b, c  0.
D. c a  . b
Lời giải. Dễ dàng nhận thấy 0  a 1 và b 1.
Đồ thị hàm số hx log x c được suy từ đồ thị của hàm gx log x qua phép b   b
tịnh tiến sang phải c đơn vị nên c  0. Vậy c a  . b Chọn D. Câu 3. Cho ,
a b, c là các số thực dương khác 1 và đồ thị của ba hàm số x
y a , y  log x, x
y c trên cùng một b
hệ trục tọa độ như hình vẽ bên. Mệnh đề nào sau đây đúng?
A. a b  . a
B. c a  . b
C. c b  . a
D. b c  . a
Lời giải. Dựa vào đồ thị ta thấy: Hàm số x y a và
y  log x là các hàm đồng biến nên a 1, b 1. Hàm số b x
y c là hàm nghịch biến nên 0  c 1.
Vẽ đồ thị hàm số y  log x bằng cách lấy đối xứng đồ thị a hàm số x
y a qua đường thẳng y x (như hình vẽ). Đến
đây ta kẻ đường thẳng y  1 dễ dàng so sánh được a  . b
Vậy c a  . b Chọn B. 11 Câu 4. Cho ,
a b, c là các số thực dương khác 1 và đồ thị của ba hàm số x
y a , y  log x, y  log x trên cùng b c
một hệ trục tọa độ như hình vẽ bên. Mệnh đề nào sau đây đúng?
A. b c  . a
B. a c  . b
C. c b  . a
D. c a  . b
Lời giải. Tương tự như câu trên. Chọn D.
Câu 5. Biết hàm số y f x có đồ thị đối xứng với đồ thị hàm số 3x y
qua đường thẳng x  1. Chọn khẳng định
đúng trong các khẳng định sau
A. f x 1 
. B. f x 1  .
C. f x 1 1   .
D. f x 1  2  . 3.3x 9.3x 3x 2 3x
Lời giải. Gọi M x; y và M x ; y là hai điểm đối xứng nhau qua đường thẳng
x x  2
x  2 xx  x  1 x  1 nên      . Khi đó 2
y  3  y  3  . Chọn B.y y y y   x   9.3
Trắc nghiệm: Chọn 0;  1   3x A y
ñoái xöùng qua x   1 A2; 
1 chỉ có đáp án B thỏa.
Câu 6. Biết hàm số y gx có đồ thị đối xứng với đồ thị hàm số x
y a qua điểm   I 1; 
1 . Giá trị của biểu thức 1 g 2  log  bằng a  2018 A. 2020. B. 2016. C. 2016. D. 2020.
Lời giải. Gọi M x; y và M x ; y là hai điểm đối xứng nhau qua điểm I 1;  1 nên
x x  2
x  2 x ta có      . Khi đó x 2x  2   2       2 x y a y a ya .
y y  2
y  2 y    1  2     2log 
Suy ra y gx  1 2 a x  2018  2 a   g2  log  2a
  2016. Chọn B. a  2018  
Câu 7. Biết hàm số 1
y f x có đồ thị đối xứng với đồ thị hàm số y  log     qua 2018  x 
gốc tọa độ. Tính giá trị của biểu thức f 2018. A. 1. B. 0. C. 1.
D. Không tồn tại.
Lời giải. Gọi M x; y và M x ; y là hai điểm đối xứng nhau qua gốc tọa độ O0;0
x x  0
x  x     nên ta có   1 1    . Khi đó y  log  
   y  log       .
y y  0 y  y 2018 2018       xx   
Suy ra y f x 1  log      
f 2018  1. Chọn C. 2018    x  12
Câu 8. Cho hai hàm số x
y a và y f x có đồ thị như
hình vẽ đồng thời đồ thị của hai hàm số này đối xứng
nhau qua đường d : y  x. Giá trị của  3 f a   bằng A. 1  . B. 1  . 3a a 3 C. 3. D. 3a a  .   x Oy x 1x  ñoái xöùng qua    
y a  y a    
Lời giải. Ta có      a .
y f x
ñoái xöùng qua Oyy f   x 
Theo giả thiết, ta có đồ thị hai hàm số x
y a và y f x đối xứng nhau qua đường  
thẳng y  x nên suy ra đồ thị của hai hàm số 1 x y      
và y f x đối xứng nhau a
qua đường thẳng y x .   1 Mà x
y a và y  log x đối xứng nhau qua đường thẳng y x. 2 a Từ  
1 và 2, suy ra f x 3  log x a x   f  3 a   3
 log a  3. Chọn C. 1 1 a a Câu 9. Cho ,
a b là các số thực dương khác 1. Các hàm số x y a và x
y b có đồ thị như hình vẽ bên. Đường thẳng bất
kỳ song song với trục hoành và cắt đồ thị hàm số x y a , x
y b , trục tung lần lượt tại M , N, A đều thỏa mãn
AN  2AM. Mệnh đề nào sau đây đúng? A. b  2 . a B. 2 a  . b C. 1 ab  . D. 2 ab  1. 2
M log t;t a
Lời giải. Gọi A0;t với t  0. Suy ra 
. Theo giả thiết AN  2AM nên
N log t;t b  
suy ra log t  2 log t 
M, N khaùc phía vôùi O y 1
 log t  2 log t b  . Chọn D. b a b a a
Câu 10. Cho các hàm số y  log x và y  log x có đồ a b
thị như hình vẽ bên. Đường thẳng x  5 cắt trục hoành,
đồ thị hàm số y  log x và y  log x lần lượt tại , A B a b
và C . Biết rằng CB  2AB. Mệnh đề nào sau đây đúng? A. 2 a b . B. 3 a  . b C. 3 a b . D. a  5 . b
Lời giải. Theo giả thiết, ta có A5;0, B 5;log  5 , C  5;log  5 . a b  
Do CB  2AB 
CB  2BA  log 5log 5  2.log  5 3 
a b . Chọn C. a b a 13
Câu 11. Cho hai hàm số 2x y
, y  log x có đồ thị như 2
hình vẽ. Đường thẳng  cắt trục tung, đồ thị hàm số 2x y
, đồ thị hàm số y  log x và trục hoành lần lượt 2 tại ,
A B, C, D thỏa mãn AB BC CD. Hỏi có bao nhiêu
đường thẳng  như thế ? A. 1. B. 2. C. 3. D. Vô số.   b  1
  ;2b   2x B b yA2b ;
c 2 log c do B laø trung ñieåm AC 2   
Lời giải. Gọi    . C
 c;log c y  log x  bD2c ;
b 2 log c2 do C laø trung ñieåm DB 2    2  2   A Oy 2
 b c  0 c   2b c   2b
b  1,c  2 Vì              Vậy có hai bộ  . 1 1  2 D Ox 2  log  c 2  0 log c  2    c     2 b b b
b  2,c  4 2 2   điểm ,
A B, C, D thỏa yêu cầu bài toán. Hay có hai đường thẳng  như thế. Chọn B.
Câu 12. Gọi B và C lần lượt là các điểm thuộc đồ thị hàm số 2x y
và y  log x 2
sao cho tam giác OBC đều. Giả sử điểm B có hoành độ là a khi đó tỉ số 2x bằng a A. 2 3. B. 2  3. C. 2 2. D. 2  2. Lời giải. Đồ thị hai hàm số 2x y
và y  log x đối xứng qua đường thẳng y x và theo yêu 2
cầu bài toán là tam giác OBC đều nên suy ra  ;2a ,  2a B a C
;a (theo đề điểm B có
hoành độ là a ).
Tam giác OBC đều 2 2 2a a 2 
OB BC OB BC  2 4 .
a 2  a  0. Đấy là phương x
trình đẳng cấp và tìm được 2  2  3. Vì B là điểm nằm trên đồ thị hàm số 2x y a x
suy ra 2a a nên 2  2  3. Chọn B. a Câu 13. Gọi ,
A B là các điểm lần lượt thuộc đồ thị các hàm số x y e và x y e  sao
cho tam giác OAB nhận điểm M 1; 
1 làm trọng tâm. Khi đó tổng các giá trị của
hoành độ và tung độ điểm A gần với giá trị nào sau đây nhất? A. 3. B. 3,5. C. 4. D. 4,5.
Lời giải. Gọi  ; a ,  ; b A a e
B b e . Vì tam giác OAB nhận 14 a  b  3 điểm M 1; 
1 làm trọng tâm nên  a b e  e  3  3 3 a aa 3e 3 3 ee e  3  e   a  ln . 3 3 1 e 1 e
Khi đó tổng hoành độ và tung độ điểm A là 3 3 3e 3e ln   4. Chọn C. 3 3 1 e 1 e
Câu 14. Gọi A và B lần lượt là hai điểm di động trên hai đồ thị hàm số x
y e và y  ln x như hình vẽ.
Khoảng cách giữa hai điểm ,
A B nhỏ nhất gần với giá
trị nào nhất trong các giá trị sau A. 1,2. B. 1,3. C. 1,4. D. 1,5.
Lời giải. Đồ thị của hai hàm số x
y e và y  ln x đối xứng nhau qua đường thẳng
y x nên AB đạt giá trị nhỏ nhất  ,
A B đối xứng nhau qua đường thẳng d : y x. Gọi  ; a A a e , khi đó  2  ,   2 a AB d A d
a e  2 f a  2 min f x  2 f 0  2. Chọn C.
Câu 15. Cho đồ thị hàm số 2 x y e  như hình vẽ.
ABCD là một hình chữ nhật thay đổi sao cho B và
C luôn thuộc đồ thị hàm số đã cho, A và D thuộc
trục hoành. Giá trị lớn nhất của diện tích của hình
chữ nhật ABCD bằng A. 2 . B. 2 . e e C. 2 . D. 2 . e e
Lời giải. Hàm số 2 x y e 
là hàm số chẵn nên đồ thị hàm số nhận trục Oy làm trục Dx;0
đối xứng. Giả sử  2  ; x
C x e  với x  0. Suy ra  B . 2 x; x e  
Diện tích của hình chữ nhật ABCD là   2 x S
CB CD x ef x f x f      Chọn A. ABCD     1 2 . 2 . max .    0;  2  e 15 Phần 3. Dãy loga
Câu 1. Cho dãy số u thỏa mãn 2
log u 3 log u  2  0 và u
u  2 với mọi n  2 4 2 4 n1 n *
n   . Giá trị lớn nhất của n để u  2018 bằng n A. 999. B. 1000. C. 1010. D. 1011.
Lời giải. Do u u  2 nên u là một cấp số cộng với công sai d  2. n n1 n log u  1 u  2 u 3d  2 u  4 Ta có 2 2 4 4 1 1
log u 3log u  2  0         . 2 4 2 4 log u  2 u  4 u 3d  4 u  2  2 4  4  1  1 • Với d 2 u  4 
u  4  n 1 2. Khi đó u  2018  4 n   1 .2  2018 1 n   n
n 1012 nên giá trị lớn nhất của n là 1011. • Với d 2 u  2 
u  2  n 1 2. Khi đó u  2018  2 n   1 .2  2018 1 n   n
n 1011 nên giá trị lớn nhất của n là 1010.
Vậy giá trị lớn nhất thỏa mãn yêu cầu đề bài là n  1011. Chọn D.
Câu 2. Cho dãy số u thỏa mãn log u  2  log u 2 log u  2 log u và n  1 1 8 10 u  10u với mọi *
n   . Khi đó u bằng n 1  n 2018 A. 2000 10 . B. 2008 10 . C. 2017 10 . D. 2018 10 . 7 u  10 u
Lời giải. Do u  10u nên u là cấp số nhân có công bội  8 1 q  10   . n n 1  n 9 u  10 u  10 1
Ta có log u  2  log u 2 log u  2 log u 1 1 8 10
 log u  2  log u 2 log 7 10 u   2 log 9 10 u . 1 1 1 1 
 log u  2  log u 2 7  log u  2 9  log u 1 1  1   1  logu 18 1 log u 16 log u 18        1 1 log 
u 16  log u 182 1 1  logu 18 1  17  
 log u  17  u  10 . 2 1 1
log u 37 logu 340  0  1 1
Số hạng tổng quát của u là n 1  17 n 1  8 u  10 .10  10 . Do đó 2000 u  10 . Chọn A. n n 2018
Câu 3. Cho dãy số u thỏa mãn 2
log 5u  log 7u  log 5  log 7. Biết số hạng 2  1  2 2  1  2 2 n  2 2
đầu u 1 và u  7u với mọi *
n   . Giá trị nhỏ nhất của n để u 1111111 là 1 n 1  n n A. 8. B. 9. C. 10. D. 11.
Lời giải. Do u  7u nên dãy số u là cấp số nhân với công bội q  7. n n 1  n Ta có 2 log 5u  2  log 7u  2 2  log 5  log 7 . 2 1 2 1 2 2
 log 5  log u 2 log 7  log u 2 2 2  log 5  log 7 2 2 1 2 2 1 2 2 u 1 loaïi 1   log u  0  2
 2 log u  2 log 5 log 7 log u  0     . 2 1  2 2  2 1 2 1 1 log u  35   2 1 u  1  35 16
Số hạng tổng quát của dãy số  1 u là n 1 u .7   . n n 35 Ta có 1 n 1 u 1111111 .7   
1111111  n 10. n 35
Do đó giá trị nhỏ nhất của n là 10. Chọn C.
Câu 4. Cho dãy số u thỏa mãn 2 9u 9 u 1 u  9 u 1 u 2 1 4  2  4 u e e e
e e  3 và uu 3 n n 1  n với mọi *
n   . Khi đó giá trị nhỏ nhất của n để u  3 là n A. 9. B. 10. C. 11. D. 12.
Lời giải. Do u u  3 nên u là cấp số cộng với công sai d  3  u u  24. n n 1  n 9 1 Ta có 2 2 9 u 9 u 1 u  9 u 1 u 2 1 4  2 4 u   3   9u 1 2 u    9u 1 2 u e e e e e e e
e e 3  0    u       u 1 13 u u 1 13 u 1 13  9 1  1 24 1  1 2e e  2ee e  24 2e   1     2 2 2       .    u        u 1 13  u u 1 13  u 1 13 9 1 1 24 1 1 2e e  2ee e     24 2e   1  loaïi  2  2  2   Suy ra     u 1 13 13 1  1 e   u  ln . 24 1  24  4e 2 4e 2  
Số hạng tổng quát của dãy số  13  1 u là u  ln      3 n 1 . n 24   n  4e 2     Ta có 13  1  1 13  1 u  3  ln  
3 n 1  3  n  6 ln        10,142. n 24   4e 2 3  4a 2 
Do đó giá trị nhỏ nhất của n là 11. Chọn C.
Câu 5. Cho cấp số cộng u có tất cả các số hạng đều dương và thỏa mãn n
u u ... u
 4 u u ...u
. Giá trị nhỏ nhất của biểu thức 1 2 2018  1 2 1009  2 2 2
P  log u  log u  log u bằng 3 2 3 5 3 14 A. 1. B. 2. C. 3. D. 4.
Lời giải. Vì u là cấp số cộng nên u u ...u
 4 u u ...u 1 2 2018  1 2 1009  n
20182u  2017d 1009 2u 1008d 1   1  d   4.  u  . 1 2 2 2 Do đó 3d 9d 27d
u u d
, u u  4d
, u u 13d  . 2 1 2 5 1 2 14 1 2       Ta có 3d 9d 27 2 2 2 2 2 2 d
P  log u  log u  log u  log     log       log         3 2 3 5 3 14 3 3 3 2  2   2  2 2 2 2  d   d   d   d   1  log     2  log   3  Chọn B.       log   3     log  2  2  2. 3 3 3 3 2 2  2   2 
Câu 6. Cho dãy số u thỏa mãn 3 2
log u 2 log u  log u 2  0 và u  2u 10 n  1 1 1 n 1  n với mọi *
n   . Giá trị nhỏ nhất của n để 100 u 10 10 là n A. 225. B. 226. C. 326. D. 327. 17 Lời giải. Ta có 3 2
log u 2 log u  log u 2  0 1 1 1
 logu 2 2
log u 1  0  log u  2  u  100. 1 2 1  1 1 Ta có u
 2u 10  u 10  2 u 10 . n 1  n n 1   nv
  u 10 110 Đặt 1 1 v u 10    
là cấp số nhân với công bội n 1 q 2 v 110.2     . n nv  2v n  n 1  n
Mà v u 10 suy ra n 1 u 110.2   10. n n n 100 100   Ta có 100 n 1  100 n 1  10 10 u 10 10  110.2 10 10 10  2   n  log    1 n 2 110  110  100 100     Ta có 10 10 log    1  log      1  log      98 10
1  98 log 10 1  326,54. 2 2 2  2 110   100 
Do đó giá trị nhỏ nhất của n là 327. Chọn D.
Câu 7. Cho dãy số u thỏa mãn 3 logu logu  logu logu 3  3 và n  19 1 19 1 u
u  2 với mọi *
n   . Tìm số tự nhiên n lớn nhất sao cho 100 3 nu  5 . n1 n
A. n  71.
B. n  72.
C. n  73.
D. n  74. u   0,u  0  3 a
  log u log u Lời giải. ĐK 1 19    . Đặt 19 1  3 2 
a b  3.
log u log u 3  0   19 1 b
  log u log u 3  0 19 1   a b 3     b  3 a    a  1
Ta được hệ phương trình       (thỏa mãn). 3 a  2 b   2  3 a     1 a  6     0 b      2
Do u u  2 nên u là cấp số cộng với công sai d  2  u u 18d u 36. n n1 n 19 1 1 Với u a  1 suy ra 19
log u  log u  1  log
 1  u  10u u 36  10u u  4. 19 1 19 1 1 1 1 u1
Số hạng tổng quát của u là u u n1 d  4 2 n1  2n 2. n 1     n  Ta có n 1 100 2 2 100 3 nu  5  3  5  n   100
log 5 2  72,2. Do đó giá trị lớn nhất của n 3  2
là n  72. Chọn B.
Câu 8. Cho dãy số u thỏa 2 2 2 2
ln u  ln u ...  ln u
 ln u  ln u 1  3 n  1 2 n 1  n n 1  và 2 uu với mọi *
n   . Tìm giá trị nhỏ nhất của n để 2018 u  2017 . n 1  n n A. 11. B. 12. C. 14. D. 15. Lời giải. Vì 2 uu nên 2 ln u
 ln u  2 ln u . n 1  n n 1  n n Khi đó 2 2 ln u  ln u
1  ln u  2 ln u 1  ln u 1 . n n 1  n n n
• Nếu u 1  u 1 thì không tồn tại n thỏa yêu cầu bài toán. 1 n
• Nếu u 1  u 1 thì ln u 1  ln u 1 với mọi * n   . 1 n n n
Tiếp tục quá trình như thế ta được 18 2 2 2 2
ln u  ln u ... ln u
 ln u  ln u 1  3 1 2 n 1  n n 1  2 2
 ln u  ln u 1  3  ln u 1  3  ln u  2  u e . 1 2 1 1 1 n
Ta có u u uu  ... nu   ee nn   1 1 2 2 4 8 2 2 2n n n 1 2 3 1 Theo giả thiết 2018 2n 2018 n u   e      n  2018 2017 2017 2 ln 2017  2n 2018ln2017
n 13,9. Do đó giá trị nhỏ nhất của n là 14. Chọn C. u .log n 1 n 2  
Câu 9. Cho dãy số u có tất cả các số hạng đều dương và thỏa u  , n n 1  10
với mọi n 1. Gọi a là giá trị nhỏ nhất của u . Có bao nhiêu số tự nhiên n để u a n n A. 1. B. 2. C. 3. D. 4.
Lời giải. Từ giả thiết có u .log n n 1 2 u  
. Do a là giá trị nhỏ nhất của u nên khi n 10 n  u .log n 1 n 2   u    n u   u  log    n 1 10 n n 1   10 2   u a  10 10      
 2 1 n  2 . Vậy có n u   u     u nn n n .log log 10 1 n 1  2  2   un 1  10 
hai số tự nhiên n là 10 2 1 và 10
2 thỏa yêu cầu bài toán. Chọn B.
Câu 10. Cho cấp số cộng a thỏa a a  0; cấp số nhân b thỏa b b 1 và n n  2 1 2 1
hàm số f x 3
x 3x sao cho f a  2  f a ; f log b  2  f log b . Tìm số 2 2   2 1 2   1
nguyên dương n nhỏ nhất sao cho b  2018a . n n A. n  15. B. n  16. C. n  17. D. n  18. x  1
Lời giải. Ta có f x 2
 3x 3; f x  0   . x  1  Bảng biến thiên 0
  a a a   0 • Ta có 1 2   Keát hôïp BTT 1 
a n 1 (do a là cấp số cộng). n   f
 a f a  2  0 a   1 n 1   2    2
log b  log b  0
• Lại có b b 1 nên log b  log b  0. Vì 2 2 2 1  2 1 2 2 2 1  f
 log b f log b  2  0 2 1   2 2  
log b  0  b 1  Keát hôïp BTT 2 1 1    b  1
2n (do b là cấp số nhân). n
log b  1  b  2 n  2 2 2
Khi đó yêu cầu bài toán: b  2018a n 1 2    2018n  
1 . Thử cả bốn đáp án ta được n n
n  16 là giá trị nguyên dương nhỏ nhất thỏa mãn. Chọn B. 19
Phần 4. Cực trị nghiệm
Câu 1. Xét các số nguyên dương ,
a b sao cho phương trình 2
a ln x b ln x  5  0   1
có hai nghiệm phân biệt x , x và phương trình 2
5 log x b log x a  0 2 có hai 1 2
nghiệm phân biệt x , x thỏa mãn x x x x . Giá trị nhỏ nhất của biểu thức 3 4 1 2 3 4
S  2a  3b bằng A. 17. B. 25. C. 30. D. 33.  2  
1 coù 2 nghieäm phaân bieät  b  20a
Lời giải. Điều kiện x  0. Để   2 b  20 . a  
2 coù 2 nghieäm phaân bieät  2 b   a  20 b  b
lnx x  ln x ln a x     x x e 1 2  1 2 1 2  Ta có  a  . b  b  logx x  5
 log x  log x     x x  10  3 4 3 4 3 4  5 b b Yêu cầu bài toán:   b b 5  5 x x x x e 10 ln10 a a a            a  3. 1 2 3 4 a 5 ln10 Suy ra 2 20 60 b b a      b  8 . a   3
Khi đó S  2a 3b  2.33.8  30. Dấu ''  '' xảy ra    . Chọn C. b   8  Câu 2. Với ,
m n là các số nguyên dương sao cho phương trình 2
ln x m  
1 ln x n  0  
1 có hai nghiệm phân biệt x , x và phương trình 1 2 2
ln x n  
1 ln x m  0 2 có hai nghiệm phân biệt x , x thỏa mãn x x x x . 1 2  3 4 2 3 4
Giá trị nhỏ nhất của biểu thức P  2m 3n bằng A. 46. B. 48. C. 51. D. 53.  2  
1 coù 2 nghieäm phaân bieät  m   1 4n  0
Lời giải. Điều kiện x  0. Để  . *   2
2 coù 2 nghieäm phaân bieät  n  1 4m   0
Ta có x x  x x 2  ln x  ln x  2ln x  ln x  Vi-et 
m 1  2 n 1  m  2n 1. 1 2 3 4 1 2 3 4  
Thay m  2n 1 vào * ta được 3 2 3 n n      n  7.
Khi đó P  2m 3n  22n  
1  3n  7n  2  51. Chọn C.
Câu 3. Cho hai phương trình 2
ln x m  
1 ln x n  0   1 và 2
ln x n  
1 ln x m  0 2. Biết phương trình  
1 có hai nghiệm phân biệt là x , x và phương trình 2 có hai 0 1
nghiệm phân biệt là x , x (tức là x là nghiệm chung của hai phương trình) Giá trị 0 2 0
nhỏ nhất của biểu thức 2 2
S x x bằng 1 2 A. 1. B. 2. C. 3. D. 4. 20
Lời giải. Điều kiện: m  .
n Để hai phương trình đã cho mỗi phương trình có hai   m 2 1  4n  0
nghiệm phân biệt là  .   n 2 1  4m  0 
Gọi x là nghiệm chung của hai phương trình   1 và 2. Khi đó 0 2
ln x m1 ln x n  0  0   0 
 m nln x m n  0  ln x  1 
m n  0.
ln x n  0 0 2
1 ln x m  0 0 0 
ln x  ln x m1 ln m x m x e Theo Vi-et, ta có 0 1  ln x   0 1 1 1      .
ln x  ln x n 1 ln n x n   0 2  2 x e  2 Khi đó 2 2 2m 2n 2m 2 2 n x x e e e       2. Chọn B. 1 2
Câu 4. Xét các số nguyên dương ,
a b sao cho phương trình .4x  .2x a b 50  0   1 có
hai nghiệm phân biệt x , x và phương trình 9x  .3x b
50a  0 2 có hai nghiệm 1 2
phân biệt x , x thỏa mãn x x x x . Giá trị nhỏ nhất của biểu thức 3 4 3 4 1 2
S  3a  2b bằng A. 49. B. 51. C. 59. D. 81. 
  t2x 2 1 
at bt 50  0 1
Lời giải. Ta có  .   2 3x 2 
  b 50a  0 2 
 1 coù 2 nghieäm phaân bieät  
 1 coù 2 nghieäm döông phaân bieät Để   2
b 200a  0.  
2 coù 2 nghieäm phaân bieät  2 
coù 2 nghieäm döông phaân bieät  x x x x 50 50 1 2 1 2 2   2 .2 
x x  log Ta có  1 2 2  a a .  1xx2 x3 x4 3 
 3 .3  50a x x  log 50a 3 4 3      Yêu cầu bài toán: 50     log 50  log a x x x x a        a  3. 3 4 1 2 3   2  a  Suy ra 2 200 600 b b a     
b  25. Khi đó S  3a  2b  3.3  2.25  59. Chọn C. Câu 5. Cho ,
a b là hai số thực dương lớn hơn 1. Biết phương trình 2 x x 1 a b   1 có hai 2   nghiệm phân biệt x x x ,
x . Giá trị nhỏ nhất của biểu thức  1 2 S     4   x x 1 2  1 2
x x  1 2  bằng A. 3 4. B. 3 3 4. C. 3 3 2. D. 4. x x log a 2    
Lời giải. Ta có x x 1
laáy logarit cô soá b hai veá 2  a b
 1 x x log a1  0  b  1 2 b . x x    1 1 2 Khi đó 1 1 3 S
 2 log a  2 log a  3 .2 log .
a 2 log a  3 4. log a 3 2 b b log a2 b b b b 21 1 Dấu ' 3 1 1  ' xảy ra 2 
 2 log a  log a
a b . Chọn B. log a b 2 b b 3 2 Câu 6. Cho ,
a b là hai số nguyên dương lớn hơn 1. Biết phương trình 2x 1  x ab có
hai nghiệm phân biệt x , x và phương trình 2 1   9 x x b
a có hai nghiệm phân biệt 1 2
x , x thỏa mãn x x
x x  3. Giá trị nhỏ nhất của biểu thức S  3a  2b bằng 1 2  3 4  3 4 A. 40. B. 41. C. 44. D. 46.
Lời giải. Ta có 2x 1  x 2 2 a
b x 1  x log b x x log b 1  0. Phương trình này có a a
hai nghiệm phân biệt     b2 2 log
4  0  log b  2  b a . a a
Tương tự từ phương trình 2 1   9 x x b
a ta có log 9a  4  0 : luôn đúng. b
x x  log b Theo Vi-ét 1 2 a   log . b log a a b 9  3
x x  log 9a  3 4 b    a a a a          a a   3 log 9 3 9 3 a 4. Suy ra 2 16 b b a     
b 17. Khi đó S  3a  2b  3.4  2.17  46. Chọn D. Câu 7. Cho ,
a b là hai số thực lớn hơn 1. Biết phương trình 2 x x 1
a b   1 có nghiệm
thực. Giá trị nhỏ nhất của biểu thức P ab  bằng a   4 log log b a A. 4. B. 5. C. 6. D. 10.
Lời giải. Ta có 2x x 1  2 a b
  x x   2 1
1 log b  0  x x log b  log b  0. a a ab
Để phương trình có nghiệm     b b    * a 2 log 0 log 4 log 0 a . a log b  4  a
Vì a 1 và b 1 nên log b  0. Do đó *  log b  4. a a tlog b 2 Khi đó 4 a 4 t t  4
P  1 log b   1 t    f t
f t Chọn C. a   min   6. 4; log b t t a Câu 8. Cho ,
a b là hai số thực lớn hơn 1 thỏa mãn a b  10. Gọi , m n là hai
nghiệm của phương trình log xlog x2 log x 3log x 1 0. Giá trị nhỏ nhất a b a b
của biểu thức S mn bằng A. 16875. B. 4000 . C. 3456. D. 15625. 16 27
Lời giải. Phương trình tương đương với a x2 log . log
2 3log a.log x 1  0. b a b a Theo Vi-ét ta có 2  3log a log m  log b n
 2 log b 3  log a b mn a b a a a a  3 2  3 2 . log a b
Khi đó S a b a 10a2 3 2 3
f a max f a  f 6  3456. Chọn C. 1;9 Câu 9. Cho ,
a b là các số thực lớn hơn 1 và phương trình log ax.log bx  2018 có a b hai nghiệm phân biệt , m .
n Giá trị nhỏ nhất của biểu thức P   2 2 a b  2 2 4 9 36m n   1 bằng 22 A. 36. B. 72. C. 144. D. 288.
Lời giải. Ta có log ax.log bx 2018  1 log x1 log x 2018 a b a b
 log x  log x  log x.log x  2017 a b a b  log . b x b x   a
logb 2 loga  1 log 2017 0. b Theo Vi-et: mn m n     Suy ra 1 mn  . b   1 1 log log log 1 log . b b log b b ab ab a   Khi đó P   36 144 324 2 2 4a  9b  2 2 36m n   1   2 2 4a  9b  2 2  1   4a   9b 2 2   2 2 a bb a 324 144 2 2  2 4a .  2
.9b  72 72  144. Chọn C. 2 2 a b Câu 10. Cho ,
a b, c là các số thực lớn hơn 1 thỏa mãn a b c  100. Gọi , m n là
hai nghiệm của phương trình  x2 log
1 2 log b 3log clog x 1  0. Tính a a a a
S a  2b  3c khi mn đạt giá trị lớn nhất.
A. S  200. B. 500 S  . C. 650 S  . D. 700 S  . 3 3 3
Lời giải. Theo Vi-et mn m n   b c   2 3 log log log 1 2 log 3 log log ab c . a a a a a a Suy ra abc mn ab c    mn ab  a b3 2 3 100. 2 100 4  3b 3b   3 . a .
(100 a b)100a b100a b 27  2 2    6  3b  3a 2 
 3100a b     8 4   2   625.10  b     . Dấu ''  '' xảy ra 3  3a
 100 a b 27  6  27   2       50 100 150  a  , b  , c  . Khi đó 700 S  . Chọn D. 3 3 3 3
Phần 5. Bài toán tìm GTNN-GTLN
Câu 1. Cho hai số thực x, y thỏa mãn logx 3y logx 3y1. Giá trị nhỏ nhất
của biểu thức S x y bằng A. 2 2 . B. 1. C. 4 5 . D. 10. 3 3
x 3y  0
Lời giải. Điều kiện xác định: 
. (suy ra x  0 ) x 3y  0  Ta có x y x y 2 2 log 3 log
3  1  x 9y  10.
Ta từ S x y suy ra y x S.
Thay vào trên ta được x  x S2 2 9  10 2 2
 8x 18Sx  9S 10  0. 23   S2    2 18 4.8. 9S 10 0
Để phương trình có nghiệm dương 4 5    S  . Chọn C.  3 S   0 
Câu 2. Cho x, y là các số thực dương thỏa mãn log
11x  20y  40  1. Gọi 2 2  
2 x xy3 y y ,
a b lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của S  . Tổng a b bằng x A. 10. B. 2 14. C. 11. D. 7 . 6 2
Lời giải. Giả thiết tương đương với 2 2
2x xy  3y 11x 20y  40  0. Từ y
S   y Sx. Thay vào trên ta được 2 2 2 2 2
2x S x  3S x 11x 20Sx  40  0 x   2 S   2 4
2 x 20S  
11 x  40  0. *  20S 11 x x   0  1 2 2 Nhận xét: Vì  4S  2 x  0, 0
y  nên S  0. Suy ra  . Khi phương trình  40 x x   0 1 2 2  4S  2
* có nghiệm thì luôn có hai nghiệm dương.
Để phương trình * có nghiệm 2
   0  240S 440S 199  0. Suy ra 440 11 a b   . Chọn C. 240 6 Câu 3. Cho c c ,
a b,c là các số thực dương khác 1 thỏa 2 2
log b  log c  log 2 log 3. a b a b b b
Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P  log b log c. Giá trị a b
của biểu thức S  2m 3M bằng A. 1 S  . B. 2 S  .
C. S  2.
D. S  3. 3 3
x  log b
Lời giải. Đặt  a
P x y và giả thiết trở thành 2 2
x y xy x 2y 1. y  log c  b
Suy ra x x P2  x x P x  x P  x  Px P  2 2 2 2 1 3 1  0.
Phương trình có nghiệm khi 5
  0  1 P  . Chọn D. 3 Câu 4. Cho ,
a b, c là các số thực lớn hơn 1. Giá trị nhỏ nhất của biểu thức 4 1 8 P    bằng 3 log a log b 3 log c bc ac ab A. 10. B. 12. C. 18. D. 20. Lời giải. Ta có 4 1 8 P   
 2 log bc  2 log ac 8 log ab 2 log a 1 log a b c c bc log ab b 2 ac 24
 2 log b  2 log c  2 log a  2 log c  8 log a  8 log b a a b b c c
 2 log b  2 log a2 log c 8 log a2 log c 8 log b. a b a c b c Vì ,
a b, c là các số thực lớn hơn 1 nên log b, log a, log c, log a, log c, log b đều là a b a c b c
những số dương. Do đó áp dụng bất đẳng thức Côsi, ta có P  2 2 log .
b 2 log a  2 2 log c.8 log a  2 2 log c.8 log b  4  8  8  20. a b a c b c
log b  log a a   b a b     Dấu ''  '' xảy ra   2
 log c  4 log a c
  a a b c 1. Chọn D. a c     2
log c  4 log b   b c c b 
Câu 5. Cho x, y là các số thực dương thỏa mãn log x  log y  log x y . Giá trị 2 2 4  
nhỏ nhất của biểu thức 2 2
S x y bằng A. 2 2. B. 3 2 4. C. 3 4 2. D. 4.
Lời giải. Ta có log x  log y  log x y  log xy  log
x y x y x . y 2 2 4   2 2 x y2 Mà  
x y xy
x y  x y3 3 3
4  0  x y  4  x y  16. 4   Do đó 1 1 2 2
S x y  x y2 3 2 3  16  2 4. Chọn B. 2 2 Câu 6. Cho ,
a b là hai số thực dương. Giá trị nhỏ nhất của biểu thức     b 4
P  log 1 2a  log 1      2 log 1      3   3 3  2a  b  A. 1. B. 4. C. 7. D. 9. 2      Lời giải. Ta có b 4
P  log  1 2a 1       1       . 3   2  a b         •    b b a       
a b   b b     b  2 1 2 1 1 2 1 2 1 .  2a 2a 2 2 2         •   ab 4                b      4 4 1 2 1 1 1 1       1      b
 4 1 2.2  42  81. 2a b   b     b   
Suy ra P  log 81  4. Chọn B. 3 Câu 7. Cho ,
a b là các số thực lớn hơn 1 thỏa mãn log a  log b  1. Giá trị lớn nhất 2 3
của biểu thức P  log a  log b bằng 3 2
A. log 3 log 2.
B. log 2  log 3. 2 3 3 2 C. 1  2 log 2  log 3 . D. . 3 2  2 log 3  log 2 2 3
Lời giải. Ta có P   log a  log b2  log 2.log a  log 3.log b2 2 3 2 3 2 2 3
log 2  log 3 log a  log b  log 2  log 3. 3 2  2 3  3 2
Suy ra P  log 2  log 3. Chọn A. 3 2 25
Câu 8. Cho x, y, z là các số thực thỏa mãn 4x 9y 16z 2x 3y 4z      . Giá trị lớn nhất của biểu thức x 1  y 1  z 1 P 2 3 4     bằng A. 3 87    . B. 5 87 . C. 7 87 . D. 9 87 . 2 2 2 2
Lời giải. Đặt  2x ,  3y,  4z a b c .  ,
a b, c  0  ,
a b, c  0  Ta có    2 2 2   1  1  1 3 . * 2 2 2 a
 b c a b c      a     b              c     2  2  2 4        Ta cần tìm GTNN của 1 1 1 9
P  2a  3b  4c  2a   3 b        4     c    . 2  2  2 2
Áp dụng bất đẳng thức Bunhiacopxky, ta có 2 2 2 2   1  1  1           2a   3 b         4     c          1 1 1 3 2 2 2
2  3  4 a     b                 c      29. . 2 2 2 2  2  2   4     Suy ra 9  87 P  . Chọn D. 2
Cách khác. Ta xem * là mặt cầu và P  2a 3b  4c  : 2a 3b  4c P  0 là
mặt phẳng. Tìm điều kiện để mặt phẳng cắt mặt cầu. Câu 9. Cho ,
a b là các số thực thỏa mãn 2 2
a b 1 và log
a b 1. Giá trị lớn 2 2   a b
nhất của biểu thức P  2a  4b 3 bằng A. 1 . B. 10 . C. 10. D. 2 10. 10 2 2 2    
Lời giải. Ta có log a b 2 2 a b  1 1 1 1 2 2 1
a b a b  a     b         . 2 2 a b  2  2 2     Ta có 1 1 3
a  2b  a    2 b   
Áp dụng bất đẳng thức Bunhiacopxky, ta có       .  2  2 2   2 2 2  1  1         a    2 b               1 1 1 5 2 2 1  2 a     b              5.  . 2 2  2  2   2 2         Do đó 1 1 10 10 3 a    2 b          a  2b   
P  2a  4b 3  10.  2  2 2 2 2 Dấu   "  " xảy ra 5 10 5 2 10  a  ; . b Chọn C. 10 10  
Cách 2. Ta thấy   1 là hình tròn tâm 1 1 I  ;   , bán kính 2 R  . 2 2 2
Ta có P  2a  4b 3   : 2a  4b 3 P  0. Xem đây là phương trình đường thẳng.
Để đường thẳng và hình tròn có điểm chung  d I, R 26 1 1 2.  4. 3 P 2 2 2    P  10   P  10. 4 16 2
Câu 10. Cho hai số thực x, y thỏa mãn log
2x y 1 *. Biết giá trị lớn nhất 2 2   x 2 y
của biểu thức P  2x y là a với , a b
  và a tối giản. Tổng a b bằng b b A. 11. B. 13. C. 15. D. 17. Lời giải. Với 2 2
0  x  2y 1 thì   2 2
*  2x y x  2y 1 hay P 1. 2   Với 1 9 2 2
x  2y 1 thì * 2x y x 2 yx 2 2 2 1         2y     .  2 2  8   Khi đó P x yx  1 1 9 2 2 1        2y    2  2 2  4 2   a   1 4 . x 2 1 9 9 9 1      2y         . Chọn A. 2  2 2  4 2 b   2  Cách khác. Từ 2 2
2x y x  2y ta đặt t  2y thì trở thành phương trình hình 2   tròn 1 x t 2x t 0 x 2 1 9 2 2 1        t  
  (ta dùng phương pháp hình học). 2  2 2  8
Câu 11. Cho các số thực
a b c ,
a b, c thỏa log
a a 4 b b 4  c c 4 . 2 2 2 2      
a b c  2
Giá trị lớn nhất của biểu thức
a  2b  3c P  bằng
a b c A. 4  30    . B. 8 30 . C. 6 30 . D. 12 30 . 3 3 3 3 Lời giải. Ta có
a b c log
a a 4 b b 4  c c  4 2 2 2 2      
a b c  2
 log 4a  4b  4c4a  4b  4c  log  2 2 2
a b c  2 2 2 2
a b c  2. 2 2
Xét hàm f t log t t với t  0 ta đi đến kết quả 2 2 2
4a  4b  4c a b c  2 2
 a  2 b  2 c  2 2 2 2  10. Ta lại có
a  2b  3c P   P  
1 a P 2b P  
3 c  0. Đến đây ta dùng điều kiện
a b c
để mặt phẳng và mặt cầu có điểm chung. Chọn C.
Câu 12. Cho các số thực x, y thỏa mãn 2 2 2 2 2 2 2 2 x 4 y x 4 y 1  3x 4 y 2x 4 4 2  2 4 y . Gọi , m x y
M lần lượt là giá trị nhỏ nhất và lớn nhất của 2 1 P
. Tổng M m bằng x y  4 A. 36  . B. 18  . D. 18 . C. 36 . 59 59 59 59 Lời giải. Đặt t t 8 16 2 2
t x  4 y , ta được 4 2.2        t t t
2t 28t 8 0 1. 2 4 27 Suy ra 2 2 Y 2 y 2 2
x  4 y  1  x Y  1. * Từ x 2y 1 P  suy ra P  
1 x P  2 y  14P x y  4  2P  
1 x P  2Y  28P. * *
Sử dụng điều kiện có nghiệm (đường thẳng có điểm chung với đường tròn) ta thu được 2  8P kết quả 2
1  59P 36P 4  0. Chọn A. 4 2 P 2P   1  2
P  4P  4
Câu 13. Cho các số thực dương ,
a b, c thỏa mãn 2 2 2
5 log a 16 log b  27 log c  1. Giá 2 2 2
trị lớn nhất của biểu thức S  log a log b  log b log c  log c log a bằng 2 2 2 2 2 2 A. 1 . B. 1 . C. 1 . D. 1 . 16 12 9 8
Lời giải. Đặt x  log a, y  log b,
z  log c. Giả thiết trở thành 2 2 2
5x 16y  27z  1. 2 2 2
Ta đi tìm GTLN của S xy yz zx.
Sử dụng bất đẳng thức Cauchy – Schwarz dạng phân thức ta có x y z
x y z2 2 2 2 x y z    
 x y z2 2 2 2 11 22 33 6 . 1 1 1 1 1 1   11 22 33 11 22 33 Suy ra 2 2 2
5x 16y  27z 12xy yz zx. Do đó 1 S  . Chọn B. 12 2 2 3
 x 12y 12xy 
Cách 2. Ghép cặp và dùng BĐT Cauchy. Cụ thể  2 2 2
x 18z 12xz  (đpcm).  2 2
4 y  9z 12yz 
Câu 14. Cho các số thực ,
a b, c lớn hơn 1 thỏa mãn log a  1 log b log c log 2. 2  2 2  bc
Giá trị nhỏ nhất của biểu thức 2 2 2
P  10 log a 10 log b  log c bằng 2 2 2 A. 7 . B. 9 . C. 3. D. 4. 2 2
Lời giải. Đặt x  log a, y  log b,
z  log c. Suy ra x, y, z  0. 2 2 2 Khi đó ta có 1 x
1 yz  xy yz xz 1 và P   2 2 x y  2 10  z . y z
Sử dụng bất đẳng thức Cauchy – Schwarz dạng phân thức ta có x y z
x y z2 2 2 2 x y z    
 x y z2 2 2 2 12 12 3 2 . 1 1 1 1 1 1   12 12 3 12 12 3 Suy ra  2 2 x y  2 10
z  4xy yz xz  4. Chọn D. Câu 15. Cho ,
a b là hai số thực dương. Giá trị nhỏ nhất của biểu thức 8 1 2 2 P  log
a b  log      bằng 5 5 a b 28 A. 1 . B. 1. C. 3 . D. 2. 2 2 8 1 4 1 4 2 2 1  2    
Lời giải. Ta có  8 1 5
a b 2a b 2a b    .  2 2 a b   2a b   5 2 2 a b  5a b   2 2 Do đó 5 5 3 2 2 P  log a b  log  log  . Chọn C. 5 5 5a b  5 2 2 5 2  2 2     2 Cách khác. 8 1 2 2  b ab
P  log  a b       log 8  1  1 Đặt     . t  và xét 5 5 2 2 a b     a b    2 a  
hàm số f t 1  8 1 t
1 trên 0; và có f t 1  f      5 5. t 4 Câu 16. Cho y m  log
với x 1, 0  y 1. Giá trị của lớn nhất của biểu thức x x
T  log y  log x bằng x y A. 2. B. 1. C. 0. D. 2. Lời giải. Ta có y 1 m  log  y
Suy ra log y  2m 1. x logx  1 . x 2 x
Vì x 1, 0  y 1 nên 1
log y  0  2m 1  0  m   . x 2 Khi đó 1 y   m    f m
f m f    Chọn A. x   1 log 2 1   max     1 2.  1 log y 2m 1  x   ;     2
Câu 17. Cho các số thực dương ,
a b thỏa mãn log ab a
Giá trị nhỏ nhất của b 2 2 . 2   3 12a b
biểu thức S a  bằng a 1 A. 3 1. B. 1 3. C. 2 3 2. D. 2 3 4.
Lời giải. Có log 2ab a b.2  2  2 a ab a a a a
a b ba b      b 2 .2 2 1 1 2 . 2   b 3 12a b  Khi đó 3a S a   a
f a min f a  f 1 3 2 3 4. Chọn D. 0; a 1 a 1
Cách 2. Biến đổi S  a   3 1  4 sau đó dùng Côsi. a 1
Câu 18. Xét các số thực 1 a ,
a b thỏa mãn ab1. Biết rằng P   log đạt log a a bab giá trị lớn nhất khi k
b a . Khẳng định nào sau đây đúng?     A. 3 k 0; .   
B. k 1;0. C. 3 k  ;2.
D. k 2;  3 .  2 2  29 Lời giải. Ta có 1 a P   log
 log ab 1log b  1 log b  1log b log a a a a a a bab Khi k b a 
P  1 k  1k . 2   Đặt 1 9 9 t  1 k k   1 , ta được 2 P t
  t  2  t      .   2 4 4   Dấu ''  '' xảy ra 1 3 3  t  
k  0;  . Chọn A. 2 4  2 Câu 19. Cho ,
a x là các số thực dương, a  1 và thỏa mãn log x  log x a Giá trị lớn a . nhất của a bằng ln10 log e A. 1.
B. log2e   1 . C. e e . D. 10 e . Lời giải. Ta có x x
log x  log x a x x a   x a   a a  log log 2 log log log log . a log a x Do 2
log a  0 nên suy ra x 1. Xét hàm   log x log e f x
trên 1; ta tìm được max f x . x x 1  e log e Ssuy ra log 2 e log a  
a  10 e . Chọn D. e
Câu 20. Cho hai số thực , a
b 1 sao cho tồn tại số thực 0  x  1 thỏa 2 log x log b a x ab .
Giá trị nhỏ nhất của biểu thức 2 2
P  ln a  ln b  lnab bằng A. 3 2 2  e  . B. 1 3 3 . C. . D. 1 . 12 4 2 4
Lời giải. Ta có 2 log x log x ln x ln 2 x b a ab
 log x.ln a  log x .ln b  .ln a  2 .ln b b a ln b ln ax  2 2 ln
ln a 2 ln b 0  ln x ln a 2 lnbln a  2 lnb  0. * Theo giả thiết , a
b 1 và x  1 nên   2
*  ln a  2 ln b  0  a b . Khi đó 2 2 P a b  ab 2 ln ln ln
 3ln b  2   1 ln . b Đặt 3  2 2 
t  ln b với t  0. Xét hàm ta được P   tại 2 1 t  . Chọn A. min 12 6 Câu 21. Cho ,
a b là các số thực thỏa mãn 0  a 1  b, ab 1. Giá trị lớn nhất của biểu thức 4 P  log ab  bằng a 1log b ab a .loga b A. 4. B. 2. C. 3. D. 4.
Lời giải. Dễ dàng biến đổi được 4
P  1 log b  . a 1 log b a
Do 0  a 1 b và ab 1 nên suy ra log b  0. a 30
Xét hàm f t 4  1 t
 max f t  f   3  4. Chọn A. 1  ;0  t 
Câu 22. Cho x, y là các số thực thỏa mãn 1 xy  4, x  ,
y 1. Gọi M , m lần lượt là 2
giá trị lớn nhất và nhỏ nhất của P  log x log y  2 2
1 . Tổng M  2m bằng 2 2 A. 6. B. 11. C. 11. D. 21. 2 2
Lời giải. Từ giả thiết suy ra y 1
x    y  8. 4 2 Ta có P x  y  2 4 log log 1  log log y  2
1  log y 22 log y  2 2 2 1 . 2 2 2 2 2 2 y
Vì 1 y  8 nên 0  log y  3. 2  
Xét hàm f t t  2 t  2 2
1 trên 0;3 ta được f t 1
  ;5. Chọn A. 2   
Câu 23. Xét các số thực ,
a b thỏa mãn a b 1. Giá trị nhỏ nhất của biểu thức   2   2 a P
log a 3log     bằng a b b  b A. 13. B. 14. C. 15. D. 19.  
Lời giải. Dễ dàng biến đổi được 2 a P  4 1
  log b 3log    . a b   b  b
Do a b 1 nên suy ra log b  0. a b  
Xét hàm f t  t2 3 4 1
 trên 0; , ta được P f t 1  f  
   15. Chọn C. t 2  
Câu 24. Xét các số thực a ,
a b thỏa b  1, a b  .
a Biểu thức P  log a  2 log     a b b  b
đạt giá trị khỏ nhất khi A. 2 a b . B. 2 3 a b . C. 3 2 a b . D. 2 a  . b
Lời giải. Dễ dàng biến đổi được 1 4 P   4. 1 log b log b a a
Từ điều kiện, suy ra a 1 . Do a 1 a b a     log
a  log b  log a hay 1  log b 1. a a a 2 a  
Xét hàm f t 1 4   4 trên 1 ;1 
, ta được f t đạt giá trị nhỏ nhất bằng 5 khi 1t t 2     2 2 3
log b   a b . Chọn B. a 3
Câu 25. Xét các số thực ,
a b thỏa mãn 2
a b và b 1. Giá trị nhỏ nhất của biểu thức a
P  log a  log bằng a b b b 31 A. 1. B. 1. C. 3. D. 9. 3
Lời giải. Dễ dàng biến đổi được 1 1 log b a P   . 1 log b log b a a Từ điều kiện, suy ra b 1 a 1 
  log b  0. a Do 1  1 2 b 1  2
a b  log a  log b  2 hay log 0  2 a b   log b  . b b log a b 2 a     Xét hàm   1 1t f t   trên 1
0; , ta được P f t 1  f  
   3 . Chọn C. 1t t  2 2 Câu 26. Cho x x
x, y là hai số thực thỏa mãn y e và ln ln 
. Giá trị nhỏ nhất của y ln y
biểu thức P xy bằng 3 A. 3 2 2 4 2  e  . B. 2 e . C. 6 e . D. 8 e .
Lời giải. Đặt a  ln x, b  ln .
y Do y e b 1. 2 Từ giả thiết ta có a b
a b   a  . b b 1 2 Suy ra b a b
b  b   1 2 1  3  2 2 3. b 1 b 1 Khi đó ln xy ln x ln y ab 2 2 3
P xy eeee . Chọn A. Câu 27. Cho 1 2 ,
a b là các số thực dương thỏa mãn log a  log . Giá trị nhỏ nhất 2 2 2 b của biểu thức 3 3
P  4a b  4 log  3 3
4a b bằng 2    A. 4 4 4. B. 4 log 6. C. 41log 3 . D. 4 log    . 2  2 2 ln 2 ln 2 3 3
Lời giải. Từ giả thiết ta có 4 256 256 b b a  . Đặt 3 3 3 3
t  4a b  b  3 . .  12. 2 b 6 6 b b 2 2
Khi đó P f t t 4 log t f t  min f t f 12  4 1log 3 . Chọn C. 2        2  12;
Câu 28. Cho x, y là hai số thực dương thỏa xy  4y 1. Giá trị nhỏ nhất của biểu    thức 6 y x 2y P   ln    bằng x  y  A. 3 ln 4. B. 12  ln 4. C. 3  ln 6.
D. 24  ln 6. 2 2   Lời giải. Có x 4 1 4 1 1
xy  4 y 1     4    4  4 
 2  4. 2 2 y y y y y  y  Đặt x 6 3
t   0;4. Khi đó P   lnt  2  f t min f t f 4   ln 6. Chọn C. y 0;4 t 2 32     Câu 29. Cho x 1 y 1
x, y là hai số thực dương thỏa log x y  2  1 log     . 3   3  y x  2 2
Biết giá trị nhỏ nhất của x y là a với , a b    và  ,
a b  1. Tổng a b bằng xy b A. 2. B. 9. C. 12. D. 13.       Lời giải. Ta có x 1 y 1 x y 1 1
log x y  2  1 log    
  x y  2  3         3   3  y x     y x x y   x y  3 3  x y        x y
 3    x   y   2  3       2 3              2. y x y x y x   y x  Đặt x y x y 4 2 t  
   t 2. Ta được 3 2t 2 2 3t 2  t  . y x y x 3 2 2 x y x y 10 a  10 Khi đó 2 t 2        
a b  13. Chọn D. xy y x 3 b   3 
Câu 30. Cho x, y là hai số thực dương thỏa mãn x  n y  l  2 ln l
n x y. Giá trị nhỏ
nhất của biểu thức P x y bằng A. 2 2 3. B. 3 2  2. C. 17  3. D. 6.
Lời giải. Ta có ln x  ln y   2 x y 2 ln
xy x y yx   2 x0 1  x 
yx   1  0 2 y0 x 
x 1. Do đó yx   2
1  x y  . x 1 2   Khi đó x  
P x y x   f x n f x 2 2 mi  f    
  2 2 3. Chọn A. 1; x 1  2 
Câu 31. Cho x, y là hai số thực dương thỏa mãn log x  log x 3y  2  2 log . y 2 2   2
Biết giá trị lớn nhất của biểu thức x y 2x  3y P   là b a  với , a b, c 2 2
x xy  2y x  2y c
là các số nguyên dương và b là phân số tối giản. Tổng a b c bằng c A. 10. B. 15. C. 17. D. 30.
Lời giải. Ta có log  2 3  2 log 4  4   x0, 0 0 y x xy y x y x y          x  . y 2 2 x 2x 1 3 Khi đó x y 2x  3y y y x P    
. Đặt t   0;  1 . 2 2 2
x xy  2y x  2y xx x y    2     2   yy  y Xét hàm   f tt 1 2t 3   
f t  f   5 min
1  2   a b c  10. Chọn A. 2 0  ;1 t t  2 t  2 3 Câu 32. Cho ,
a b, c là các số thực lớn hơn 1 và x, y, z là các số thực dương thỏa mãn 16 16 x y z
a b c abc. Giá trị lớn nhất của biểu thức 2 P    z bằng x y 33 A. 3 3 20  . B. 24  . C. 20. D. 24. 3 4 3 4  1
x  log t   a  log at  1
y  log t   b  log b
Lời giải. Có x y zt a b c abc t        .  1
z  log t c  log c t 1 1 1   log t   2 abc log abc
log a  log b  log c  t t t t Suy ra 1 1 1 1 1     2  . 2 1 1 1 x y z   x y z Khi đó 16 2 P  32 
z f z f 2  20. Chọn C. z
Câu 33. Xét các số thực ,
a b thỏa mãn a b 1. Giá trị nhỏ nhất của biểu thức 4     2 a   a P  log  323log       bằng a 128 b    b  b A. 13. B. 14. C. 15. D. 19. 4 4
Lời giải. Ta có a a 2 a 32  2
.32  a . Do a b 1 suy ra 1. 128 128 b 2       Khi đó 2 a a P a         b         a  2 log  3log 4 1 log 3 log . b a b b    b bb    Đặt 1
t  log b  0 (vì a b 1 ), ta có P  41 t2 3
  f t f  
   15. Chọn C. a t 2 b
Câu 34. Giá trị nhỏ nhất của biểu thức 9 3
P  log a  log 16a 64 2 3log a 7 với 2 2 2 2
a 1;16 bằng A. 20. B. 13. C. 7. D. 8. 2     Lời giải. Ta có a
16a 64  82a 8 8 2 8 2      a .   2  Khi đó 3 2
P  log a 9 log a 3log a 7. 2 2 2 Đặt a   1;16
t  log a t  0;4 . Ta có 3 2
P t 3t 9t 7  f t f   3  20. Chọn A. 2   34 Câu 35. Cho ,
a b là các số thực thỏa mãn điều kiện 0  b a 1. Khi biểu thức 43b   1 2 P  log
8 log a 1 đạt giá trị nhỏ nhất, tổng 3
a  2b bằng a 9 b a A. 1. B. 2. C. 6. D. 7.
Lời giải. Ta có  b   2 4 3
1  12b  4  9b . Dấu ''  '' xảy ra 2  b  . 3 2 Vì 12b  4 9b 0  a 1 nên log  log  2 log b a 9 a 9 a Khi đó 12b  4 8 8 P  log  1 2 log b  1. a 9 log b  2 1 a b a loga 2 1
Do 0  b a 1 nên suy ra log b  log a  1. Đặt t  log b t  ta được a   1 a a 8 8 8 P  2t
1  (t 1)  (t 1) 
1 33 (t 1)(t 1) 1  7. 2 2 2 (t 1) (t 1) (t 1) Dấu 8 ''  '' xảy ra 3  t 1 
t  3  b a . Chọn B. 2 (t 1)
Câu 36. Xét các số thực ,
a b thỏa mãn điều kiện 1  b a 1. Biểu thức 4  1 P  log b     log
b đạt giá trị nhỏ nhất khi log b bằng a  4 a  a b A. 2 . B. 3 . C. 2 . D. 9 . 3 2 9 2 Lời giải. Ta có 1 2
b   b . Dấu ''  '' xảy ra  1 b  . 4 2   Do 1 a 1 nên 2 log b  
    log b  2 log . b a  4 a a    Khi đó 1 log bt a t loga b P b
 t
f t f      Chọn D. a   3 9 2 log . 2 . ba 1   t 1 2 1 log b  2t 2 2 2 a Câu 37. Cho ,
a b là hai số thực thuộc 1;2 và a  .
b Biết giá trị nhỏ nhất của biểu thức P
 2b b  2 2 log 4 4  log a là 3 m n với , m n
  . Tổng m n bằng a b a A. 37 . B. 12. C. 15. D. 249. 3 Lời giải. Có 3 2
b b  4b  4  b  
1 b  2b 2 0 b  1;2. Suy ra 3 2
b b  4b  4. Do a 1 nên
 2b b  3 log 4 4  log b . a a Khi đó 1 3 2
P  2 log b  log a  6 log b a a a b log b a 2 1  3log b   b        Chọn D. a  1 3loga  1 3 3 1 6 3 9 6 6 243. log b a 2 1 35 Câu 38. Cho ,
a b là hai số thực thỏa 1  b a 1 và giá trị nhỏ nhất của biểu thức 3 3b 1 2 P  log   
12 log a là m khi n
b a . Tổng m n bằng a 3  4 b a  a A. 12. B. 15. C. 37 . D. 46 . 3 3
Lời giải. Ta có 4b 3b 1  2b  2 1 3 1 b   1  0, b  . 3 1 3 3       Suy ra a 1  3b 1 4b a 3b 1 3 b 3 1
4b  3b 1    log      log       . 3 3 a 3 4a 4a  4 a a  a 3   Khi đó b 12 2 P  log  
  12 log a  3 b   a a loga  1 a b log b a 2 1 3   b   b  
 (vì 1  b a 1 nên log b 1 ). a  3 a  12 log 1 log 1 9 2 2 log b  3 a a 2 1 m   9 Dấu ''  '' xảy ra 3
 log b  3  b a . Suy ra 
m n  12. Chọn A. a n   3  3   Câu 39. Cho a ,
a b là hai số thực thỏa 4 a b  và   2 P  16 log  3log a có 3
a 12b 16 a  b
giá trị nhỏ nhất. Tổng a b bằng A. 7 . B. 11. C. 4. D. 6. 2 2
Lời giải. Ta có b   b  b  2 3 12 16
2 b  4 0 luông đúng 4 b  . 3   Suy ra a a a a  1, suy ra log      log  log 1  0. 3 12b 16 b a  3  12b 16  a a  b   Do đó a   2 a 2 P  48 log  3log a  48 log 3log . a a  3  12b 16  a a a  b b b Đặt a a t  log , vì log
 log 1  0 nên t  0. a b a a b   Khi đó 3 1 P  48t
f t  min f t f      36. 2     0;  t  2 b   2  b     2 Dấu ''  '' xảy ra  a 1    
a b  6. Chọn D. log  a   4  a b 2   2 3     Câu 40. Cho a 3 ,
a b là hai số thực thỏa 3a  4  b  0 và P  log      log a đạt a   3     4b  16 a    4b
giá trị nhỏ nhất. Tổng 3a b bằng A. 13. B. 25. C. 8. D. 14. 2 2 36 Lời giải. Ta có 3
b  4  b  2  2  3 4b. * *  3a a 3  a4  0    3 Do  b  4 4b   log a  log . a 3  3 a a a 3 b4 4 3
a 4  b  0  3a b  4 1  1 b  b  4 2 3     Khi đó a 3     P  log   log aa     4b 16 a     3 4b  2 Đặt a 3 1 3t 3t 3 27t 9 t  log  0, ta được 3 P  3t  .     3.  . a 3 4b 2 2 2 16 t 2 2 16t 64t 4 b   2  a   4 Dấu ''  '' xảy ra    1   
 3a b  14. Chọn D. t    b   2    2  2
Câu 41. Cho hai số thực x, y thỏa mãn 2 2 2
x4 y 1x y  1  x y x eey  . Giá trị lớn 4 nhất của biểu thức 3 2 2
P x  2y 2x  8y x  2 bằng A. 2. B. 58 . C. 115. D. 122 . 27 27 27
Lời giải. Điều kiện: 1 x 1. Từ giả thiết ta có 2 2 2
x4 y 1x 2 y  1x 2 2 4e
x 4 y  1 x  4e
y  1 x .
Xét hàm   4 t f t
e t trên  và đi đến kết quả 2 2 2
x  4 y  1 x y  1 x hay 1 58 2
x y  4 . y Khi đó 3 2
P x 2x x  2  f x max f x  f      . Chọn B. 1  ;1 3 27 2 Câu 42. Cho x  y x 2018
x, y là hai số thực thuộc 0;  1 và thỏa mãn 1 2017  . 2 y 2y  2019
Tổng giá trị lớn nhất và nhỏ nhất của biểu thức P   2 x y 2 4 3
4 y  3x25xy bằng A. 25. B. 136 . C. 383. D. 391. 2 3 16 16
Lời giải. Từ giả thiết ta có 1 x y  log
 2x 2018log  2y 2y 2019 2017 2017  log
x 2018 x log 1 y  2 2 2018       1 . y 2017 2017   
Xét f t t  log
 2t 2018 trên 0; 1 và đi đến kết quả x 1 y hay y 1x. 2017   
Khi đó P  4x 3  1 x 4 
  1 x2 191 25 2 3x  25x  1 x  ;
 với x 0;  1 .    16 2    Suy ra 391 M m  . Chọn D. 16 Câu 43. Cho 2 y 1
x, y là hai số thực không âm thỏa mãn 2
x  2x y 1  log . 2 x 1
Giá trị nhỏ nhất của biểu thức 2 x 1  2 P e
 4x 2y 1 bằng 37 A. 1. B. 1  . C. 1 . D. 1. 2 2
Lời giải. Từ giả thiết ta có 2x  2
1  log 2x  2
1  log 2y 1  2y 1. 2 2  
Xét hàm số f t t  log t trên 0; và đi đến kết quả x  2 2 1  2y 1. 2 Khi đó 2 x 1  2 P e
 2x 4x 2  gx. Ta có g x 2 x 1
e   x g x 2 x 1 2 4 4; 0   2e   
 4 4x. Ta thấy vế trái là hàm nghịch  
biến, vế phải là hàm đồng biến nên phương trình có nghiệm duy nhất. Vì 1 g     0  2 nên 1
x  là nghiệm duy nhất của gx  0. Lập bảng biến thiên của gx trên 2
0; và kết luận được giá trị nhỏ nhất của P bằng 1  . Chọn B. 2
Câu 44. Xét các số thực dương x y x, y thỏa log
x x 3  y y 3  . xy 3 2 2    
x y xy  2
Giá trị lớn nhất của biểu thức 3x  2y 1 P  bằng x y  6 A. 1. B. 2. C. 3. D. 4. Lời giải. Ta có x y log
x x 3  y y 3  xy 3 2 2    
x y xy  2
 3x y log 3x y     2 2
x y xy  2 log  2 2
x y xy  2 . 3 3 
Xét hàm f t t  log t trên 0; và đi đến kết quả x y 2 2 3
x y xy  2 3
xy  x y2 3x y 2.
Suy ra x y  x y2  xy  x y2  x y2  x y  x y  2 2 2 2 2 6 4 5 3  5. Từ 3x  2y 1 P   P  
3 x P 2 y  16P. x y  6 Bunhiacopxkia
Suy ra   P2  P  x P   2 y   
x y  P  2 P   2 2 2 1 6 3 2 3 2      2
5 2P 10P   13 . x  2 Hay 2
26P  38P 64  0 suy ra P 1. Dấu ''  '' xảy ra    . Chọn A.y  1 
Câu 45. Cho hai số thực dương x, y thỏa mãn log x  
1 y   y 1 1   
 9  x 1 y 1 . 3     
Giá trị nhỏ nhất của biểu thức P x  2y bằng A. 5 6 3.
B. 3 6 2. C. 11. D. 27 . 2 5
Lời giải. Từ giả thiết ta có y  
1 log  x 1 y 1   9  x 1 y 1 3         9 9 9
 log  x 1 y 1  
x 1  log x 1  x 1  log  . 3      3     3   y 1 y 1 y 1 38 Xét hàm  y
f t  t  log t trên 0; và đi đến kết quả 9 x 1  hay 8 x  . 3 y 1 y 1 Vì 8 y y0 x  0   0   y  8. y 1 2 Khi đó 8 y 2 y y  8
P x  2y   2y
gy min gy  3 6 2. Chọn B. 0;8 y 1 y 1 Câu 46. Cho y
x, y là các số thực thỏa mãn log
 3y  1 x  2
y x. Giá trị 2 2 1 x
nhỏ nhất của biểu thức P x y bằng A. 3  . B. 5  . C. 2. D. 1. 4 4 x  1
Lời giải. Điều kiện:  . y  0  Từ giả thiết ta có 2 log y 1 log
1 x  3y 3 1 x y x 2 2
y 3y  log y   1 x 2 2
3 1 x  log 1 x. 2 2
Xét hàm f t 2
t 3t  log t trên 0; và đi đến kết quả y  1 x. 2  
Khi đó P x y x   x gx g x 3 5 1 min  g   
   . Chọn B. 1;  4 4 Câu 47. Cho x y  1
x, y là các số thực thỏa mãn 2 2 2 3
log x y  1
  log 1 xy . 2   2   2   Giá
trị lớn nhất của biểu thức P   3 3
2 x y 3xy bằng A. 13. B. 17 . C. 3. D. 7. 2 2 x y
Lời giải. Điều kiện:  2 
. Từ giả thiết ta có xy 3 log   2 22  3 xy x y log 2 2xy . 2 2   xy 1  Xét hàm   3t f t
.log t trên 0; và đi đến kết quả x y2  22xy 2 2
x y2 2
 x y  2  2xy xy  . 2
Đặt t x  . y Ta có 2 xy 1  2
t  2  2xy 
t  4  t 2;2. 2 2         Khi đó t 2 t 2 13 3
P  2t 6t  3       g Chọn A.    
t max gt . 2   2  2;2  2 2    Câu 48. Cho x 4x 1
x, y là hai số dương thỏa mãn 2 2 2.4  ln     4xy.  Giá trị lớn nhất  2xy 
của biểu thức P  2x y 2x 2 x y bằng A. 12 3. B. 1 3. C. 1 3. D. 1 2 3.
Lời giải. Điều kiện xy  0. Giả thiết 2 4 x 1     2   2 2 ln 4 1  2 xy x  ln2xy. 39 Xét hàm   1  2t f t
 ln t trên 0; và đi đến kết quả 2
4x 1  2xy y  2x  . 2x  
Ta có P x y x x y 1 3 2 2 2  1 2 3  x    1 2.2  12 3.  Chọn A.  2x  2
Câu 49. Cho x, y là hai số thực dương thỏa mãn 2 x y    2 x y   2 2 2 2 yx 2 4 9.3 4 9 .7 . Giá
trị nhỏ nhất của biểu thức x  2y 18 P  bằng x A. 3 2 . B. 1 9 2. C. 9. D. 17. 2 Lời giải. Đặt 2
t x 2y, khi đó giả thiết tương đương với t 2 2t  
4  9.3t  4 9t  t t tt 4 3 4 3 2 2 .7  4 3   2 4  3  2 .7   . t 2 2 7 7 t a a a     
Xét hàm f a 4 3 1 3   4.       
  là hàm số nghịch biến trên  nên đi đến kết 7a 7 7
qủa t  2  2t t  2 suy ra 2 2
x 2y  2  2y x 2. 2 Khi đó
x x 2 18 16 P   x
1 2 14 1  9. Chọn C. x x y x    
Câu 50. Gọi S là tập các số thực x; y sao cho x 0; và x 1 y 1 2        2    .  2x   2y  2
Biết rằng giá trị nhỏ nhất của biểu thức y x
P e  cos y 2 2x
với x; y S đạt 2
được tại x ; y . Mệnh đề nào sau đây đúng? 0 0  A. x  0; 1 . B. x  1.
C. x  1;2 . D. x  2. 0   0   0 0 y x x y        
Lời giải. Giả thiết 4 1 4 1               x y     4 1y 4 1x x y 2   2 
ln1 4x  ln1 4y x y   . y ln4   1  x.ln4   1   .   1 x y ln1 4t
t.4t.ln 4t 1 4t .ln1 4t
Xét hàm f t
trên 0;. Ta có f t  0 t 14t  2t
với mọi t  0. Do đó f t nghịch biến trên 0;. 2 Nhận thấy  
1 có dạng f x  f y  x  . y Khi đó x x
P e  cos x 2 2x  . 2 2 Xét hàm số   x x
g x e  cos x 2 2x  . TXĐ: D  .  2 Đạo hàm   x
g x e sin x 2  x;   x
g x e 1cos x  0 với mọi x   nên gx đồng biến trên .  40
g0 1 0 Ta có 
 x  0;1 sao cho gx  0. 0  0   g 
1  e 1sin1 0 
Lập bảng biến thiên ta thấy gx đạt giá trị nhỏ nhất tại x  0;1 . Chọn A. 0  
Câu 51. Gọi S là tập các số thực x; y sao cho x 1;  1 và
x yx
x  x yy 2018 ln 2017 ln 2017y e .
Biết rằng giá trị lớn nhất của biểu thức 2018x P ey   2
1 2018x với x; y S đạt
được tại x ; y . Mệnh đề nào sau đây đúng? 0 0  A. x  1.
B. x  1;0 .
C. x  0;1 . D. x  1. 0   0   0 0
Lời giải. Điều kiện : x y  0.
Giả thiết tương đương với x x y
x y x y 2018 ln 2017 ln 2017y e 2018
    x y x y 2018 e x y ln 2017  e
 lnx y2017  0. * x y 2018 Xét hàm   e
f t  ln t 2017 
trên 0; . t 2018
Đạo hàm   1 e f t  
 0 với mọi t  0. Suy ra hàm f t đồng biến trên 0; . 2 t t Mà f  2018 e
 0 nên   f x y f  2018 e  2018 2018 *
x y e
y x e . Khi đó 2018x P e  2018  x e  2 1
2018x gx. Xét hàm gx có g x 0 với mọi g  2018 1  e  2018  0 x 1; 
1 nên gx nghịch biến trên 1;  1 . Mà  nên tồn g0 2018  2019 2018e  0 
tại x  1; 0 sao cho gx  0 và khi đó max gx gx . Chọn B. 0  0  0   1;  1
Câu 52. Cho các số thực dương x, y thỏa mãn 2 2 x y 1 2   log  2 2
x y 1  3. Biết giá 3 
trị lớn nhất của biểu thức 3 3 a
S x y x y là 6 với * ,
a b   và a tối giản. b b
Tổng a  2b bằng A. 25. B. 32. C. 34. D. 41.
Lời giải. Xét hàm f tt 1 2  
 log t 1 là hàm đồng biến trên 0;. 3  
Mà f    f  2 2 x y  2 2 2 3
 2  x y . Khi đó S
x y  x xy y  2 2      
   xy  xy2 2 2 2 1 2 2 3 .   2 2 Đặt x y
t xy, vì xy
 1 nên t 1;  1 . 2  
Do đó S f t 22t3t2 1 512 16 6 2
 max f t  f        S  . Chọn C. 1  ;1  3 27 9 41 Câu 53. Cho ,
a b, c là các số thực khác 0 thỏa mãn 3a  5b  15c. Giá trị nhỏ nhất của biểu thức 2 2 2
P a b c  4a b c bằng
A. 3log 3. B. 2log 5. C. 2 3. D. 4. 5 3
Lời giải. Theo giả thiết 3a  5b  15c t. Suy ra a  log t; lo b  g t; c  log t. 3 5 15 Ta có 1 1 c   log t  
. Suy ra ab bc ca  0. 15 log 15 1 1 ta b Khi đó P a b c  2 ab bc ca        
a b c a b c2 2 4
4a b c 4.   Chọn D.
Câu 54. Cho x, y, z là các số thực không âm thỏa 5x 25y 125z    2018. Giá trị nhỏ nhất của biểu thức x y z
S    bằng 6 3 2 A. 1 1 1 log 2018. B. log 2016. C. log 2016. D. log 2017. 5 3 5 6 5 5 2 a
 b c  2018 Lời giải. Đặt x 2 y 3  5 ;  5 ; 5 z a b c  . Ta có  .  ,
a b, c 1  Suy ra a   1 b  
1  0  ab a b 1.  1
Nhân c hai vế ta được abc ac bc c. 2 Tương tự  
1 , ta cũng có ac a c 1 và bc b c 1.   3 Từ 2 và  
3 ta có abc a b c 2.
Ta có x2y3z x 2 y 3 5
 5 .5 .5 z abc a b c 2  20182  2016. Suy ra 1
x  2y  3z  log 2016 hay 6S  log 2016 
S  .log 2016. Chọn B. 5 5 5 6 1 1 1
Câu 55. Cho x, y, z là các số thực dương thỏa x y 2018 64 8 4 z    3.4 . Giá trị lớn nhất của biểu thức 1 1 1 3029 P     bằng
x  4 y  3z
2x  2y  3z
x  2y  6z 2 A. 2017. B. 2018. C. 2019. D. 2020.  16 1 1 1 1     
x 4y 3z x 2y 2y 3z    Lời giải. Ta có 16 1 1 1 1 1 4 3 3 1 3029       P  .       .
2x  2y 3z x x 2 y 3z 16 3  x 2 y z  2  16 1 1 1 1     
x 2y 6z x 2y 3z 3z  1 1 1 3 3 1 3   2018   Mà 3 3 3 1 3.4 2018 x y z x 2 3.4  64 8  4  3 4 y z suy ra    log      3.2018. 4 x 2 y z  3  Suy ra 2018 3029 P    2019. Chọn C. 4 2 42 Ứng dụng
HÀM SỐ MŨ – HÀM SỐ LOGARIT
Sự phân rã của các chất phóng xạ
Phần 1. Một số bài toán áp dụng
(tăng trưởng, phóng xạ, động đất,…)
Phần 2. Bài toán lãi suất 1
Phần 1. Một số bài toán áp dụng
Dạng 1. Áp dụng công thức có sẵn
Câu 1. Một lon nước soda 0
80 F được đưa vào một máy làm lạnh chứa đá tại 0 32 F.
Nhiệt độ của soda ở phút thứ t được tính theo định luật Newton bởi công thức
  32 48.0,9t T t  
. Phải làm mát soda trong bao lâu để nhiệt độ là 0 37 F. Chọn đáp
án gần nhất với kết quả? A. 15,6 phút. B. 17 phút. C. 21,5 phút. D. 25,6 phút.
Câu 2. với t là khoảng thời gian tính bằng giờ và Q là dung lượng nạp tối đa (pin 0
đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là
0% ) thì sau bao lâu sẽ nạp được 90% (kết quả làm tròn đến hàng phần trăm)?
A. t  1,21 giờ. B. t  1,22 giờ.
C. t  1,34 giờ.
D. t  1,54 giờ.
Câu 3. Một loài cây xanh trong quá trình quang hợp sẽ nhận một lượng nhỏ Carbon
14 (một đơn vị của Carbon). Khi cây đó chết đi thì hiện tượng quang hợp cũng sẽ
ngưng và nó sẽ không nhận Carbon 14 nữa. Lượng Carbon 14 của nó sẽ phân hủy
chậm chạp và chuyển hóa thành Nitơ 14. Gọi P t là số phần trăm Carbon 14 còn lại
trong một bộ phận của cây sinh trưởng t năm trước đây thì P t được cho bởi công t
thức P t  5750 100. 0,5
%. Phân tích một mẫu gỗ từ công trình kiến trúc gỗ, người ta
thấy lượng Carbon 14 còn lại trong gỗ là 65,21%. Hãy xác định số tuổi của công trình kiến trúc đó.
A. 3475 (năm). B. 3547 (năm). C. 3574 (năm). D. 3754 (năm).
Câu 4. Cường độ một trận động đất được tính bởi công thức M  log Alog A , với A 0
là biên độ rung chấn tối đa và A là một biên độ chuẩn (hằng số). Đầu thế kỷ XX, 0
một trận động đất ở Nhật Bản có cường độ đo được là 9 độ Richter. Trong cùng năm
đó, trận động đất khác ở Trung Quốc có cường độ đo được là 7 độ Richter. Hỏi trận
động đất ở Nhật Bản có biên độ gấp bao nhiêu lần trận động đất ở Trung Quốc ? A. 10 lần. B. 20 lần. C. 100 lần. D. 200 lần.
Câu 5. Cường độ một trận động đất được tính bởi công thức M  log Alog A , với A 0
là biên độ rung chấn tối đa và A là một biên độ chuẩn (hằng số). Đầu thế kỷ XX, 0
một trận động đất ở San Francisco có cường độ 8 độ Richter. Trong cùng năm đó,
trận động đất khác Nam Mỹ có biên độ mạnh hơn gấp 4 lần. Cường độ của trận động
đất ở Nam Mỹ xấp xỉ
A. 8,4 Richter. B. 8,6 Richter. C. 10 Richter. D. 12 Richter.
Câu 6. Các khí thải gây hiệu ứng nhà kính là nguyên nhân chủ yếu làm trái đất nóng
lên. Theo OECD (Tổ chức hợp tác và phát triển kinh tế thế giới), khi nhiệt độ trái đất
tăng lên thì tổng giá trị kinh tế toàn cầu giảm. Người ta ước tính rằng khi nhiệt độ 2
trái đất tăng thêm 2 C
 thì tổng giá trị kinh tế toàn cầu giảm 3%, còn khi nhiệt độ
trái đất tăng thêm 5 C
 thì tổng giá trị kinh tế toàn cầu giảm 10% . Biết rằng nếu
nhiệt độ trái đất tăng thêm t C
 , tổng giá trị kinh tế toàn cầu giảm f t % thì   . t f t k a (trong đó ,
a k là các hằng số dương). Nhiệt độ trái đất tăng thêm bao nhiêu
độ C thì tổng giá trị kinh tế toàn cầu giảm 20% ? A. 6,7 C  . B. 7,6 C  . C. 8,4 C  . D. 9,3 C  .
Câu 7. Cho biết chu kì bán rã của chất phóng xạ radi 226
Ra là 1602 năm (tức là một lượng 226
Ra sau 1602 năm phân hủy thì chỉ còn lại một nửa). Sự phân hủy được tính
theo công thức  . rt S
A e , trong đó A là lượng chất phóng xạ ban đầu, r là tỉ lệ phân
hủy hàng năm r  0, t là thời gian phân hủy, S là lượng còn lại sau thời gian phân hủy. Hỏi 5 gam 226
Ra sau 4000 năm phân hủy sẽ còn lại bao nhiêu gam (làm tròn
đến 3 chữ số phần thập phân)? A. 0,795  gam. B. 0,886  gam. C. 0,923 gam. D. 1,023  gam.
Câu 8. Số lượng của loại vi khuẩn A trong một phòng thí nghiệm ước tính theo công
thức S S .2t , trong đó S là số lượng vi khuẩn A ban đầu, S là số lượng vi khuẩn A t o 0 t
có sau t phút. Biết sau 3 phút thì số lượng vi khuẩn A là 625 nghìn con. Hỏi sau bao
lâu, kể từ lúc ban đầu, số lượng vi khuẩn A là 10 triệu con? A. 6 phút. B. 7 phút. C. 8 phút. D. 9 phút.
Câu 9. Sự tăng trưởng của một loại vi khuẩn ước tính theo công thức  . rt S A e , trong
đó A là số lượng vi khuẩn ban đầu, r là tỉ lệ tăng trưởng r  0, t là thời gian tăng
trưởng. Biết rằng số lượng vi khuẩn ban đầu có 100 con và sau 5 giờ có 300 con. Hỏi
sau bao lâu thì số lượng vi khuẩn tăng gấp 10 lần? A. 5 t  giờ. B. 3 t  giờ. C. 5 ln 3 t  giờ. D. 3 ln 5 t  giờ. log 3 log 5 ln10 ln10
Câu 10. Biết rằng cuối năm 2001, dân số Việt Nam là 78685800 người và tỉ lệ tăng
dân số năm đó là 1,7%. Cho biết sự tăng dân số được ước tính theo công thức .  . N r S A e
(trong đó A : là dân số của năm lấy làm mốc tính, S là dân số sau N năm,
r là tỉ lệ tăng dân số hàng năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào
dân số nước ta ở mức 120 triệu người? A. 2020. B. 2022. C. 2025. D. 2026.
Câu 11. Cho biết sự tăng dân số được ước tính theo công thức .  . N r S A e (trong đó A :
là dân số của năm lấy làm mốc tính, S là dân số sau N năm, r là tỉ lệ tăng dân số
hàng năm). Theo số liệu thực tế, dân số của tỉnh A đầu năm 2010 là 1.038.229 người,
tính đến đầu năm năm 2015 là 1.153.600 người. Hỏi nếu tỉ lệ tăng dân số hàng năm
giữ nguyên thì đầu năm 2025 dân số của tỉnh trong khoảng nào?
A. 1.424.000;1.424.100.
B. 1.424.100;1.424.200. 3
C. 1.424.200;1.424.300.
D. 1.424.300;1.424.400.
Câu 12. Các nhà khoa học thực hiện nghiên cứu trên một nhóm học sinh bằng cách
cho họ xem một danh sách các loài động vật và sau đó kiểm tra xem họ nhớ được bao
nhiêu % mỗi tháng. Sau t tháng, khả năng nhớ trung bình của nhóm học sinh tính
theo công thức M t 7520 lnt   1 , 
t   (đơn vị % ). Hỏi khoảng thời gian ngắn
nhất bao lâu thì số học sinh trên nhớ được danh sách đó dưới 10% ? A. Khoảng 22 tháng. B. Khoảng 24 tháng. C. Khoảng 25 tháng. D. Khoảng 32 tháng.
Câu 13. Giả sử    .2t n f t n
là số lượng cá thể trong một đám vi khuẩn tại thời 0
điểm t giờ, n là số lượng cá thể lúc ban đầu. Biết tốc độ phát triển về số lượng của vi 0
khuẩn tại thời điểm t chính là f t. Giả sử mẫu thử ban đầu có n 100 con vi 0
khuẩn. Vậy tốc độ phát triển sau 4 giờ là bao nhiêu con vi khuẩn? A. 500 con. B. 1109 con. C. 1600 con. D. 3200 con.
Dạng 2. Sử dụng công thức lãi kép
Câu 14. Tỉ lệ tăng dân số hàng năm ở Việt Nam được duy trì ở mức 1,05%. Theo số
liệu của tổng cục thống kê, dân số của Việt Nam giữa năm 2014 là 90728900 người.
Với tốc độ tăng dân số như thế thì vào giữa năm 2030 thì dân số của Việt Nam xấp xỉ là bao nhiêu người?
A. 107026537 người.
B. 107232574 người.
C. 105971355 người.
D. 106118331 người.
Câu 15. Hết ngày 31 tháng 12 năm 2017, dân số tỉnh X là 1,5 triệu người. Với tốc
độ tăng dân số hàng năm không thay đổi là 1,5% và chỉ có sự biến dộng do sinh - tử
thì trong năm 2027 (từ 1/1/ 2017 đến hết 31/12 / 2027 ) tại tỉnh X có tất cả bao
nhiêu trẻ em được sinh ra, giả sử rằng tổng số người tử vong trong năm 2027 là 2700
người và chỉ là những người trên hai tuổi. A. 28812. B. 28426. C. 23026. D. 23412.
Câu 16. Một khu rừng ban đầu có trữ lượng gỗ là 5  3
4.10 m . Gọi tốc độ sinh trưởng
mỗi năm của khu rừng đó là r%. Biết sau 5 năm thì sản lượng gỗ là xấp xỉ 5  3
4,8666.10 m . Giá trị của r xấp xỉ bằng A. 3,5. B. 4. C. 4,5. D. 5.
Câu 17. Số lượng động vật nguyên sinh tăng trưởng với tốc độ 0,7944 con/ngày. Giả
sử vào cuối ngày đầu tiên, số lượng động vật nguyên sinh là 2 con. Hỏi sau 6 ngày
(kể cả ngày đầu tiên), số lượng động vật nguyên sinh là bao nhiêu con? A. 37 con. B. 48 con. C. 67 con. D. 106 con.
Câu 18. Cục điều tra dân số thế giới cho biết: Trong chiến tranh thế giới thứ hai (kéo
dài 6 năm); dân số mỗi năm giảm đi 2% so với dân số năm liền trước đó. Vào thời hòa 4
bình sau chiến tranh thế giới thứ hai thì dân số tăng 4% so với dân số năm liền trước
đó. Giả sử rằng, vào cuối năm thứ 2 diễn ra chiến tranh dân số thế giới là 4 tỷ người.
Kể từ thời điểm đó thì 10 năm sau thì dân số thế giới khoảng bao nhiêu tỷ người (làm
tròn đến chữ số thập phân thứ hai)? A. 4,40. B. 4,67. C. 4,88. D. 4,95.
Câu 19. Biết thể tích khí CO đầu năm 2002 là V  3
m . Thời gian 10 năm tiếp theo, 2
thể tích khí CO tăng m%; thời gian 10 năm tiếp theo nữa, thể tích CO tăng n%. 2 2
Thể tích khí CO đầu năm 2020 là 2
100 m100 n 10 
100 m10 .100 n8 A. V     3 m . B. V   3 m . 36  20  10 10 C. V   m n18      18 3    3 1 1 m . D. V
 1 m n m .  
Dạng 3. Thiết lập công thức
Câu 20. Quan sát quá trình sao chép tế bào trong phòng thí nghiệm sinh học, nhà
sinh vật học nhận thấy các tế bào tăng gấp đôi mỗi phút. Biết sau một thời gian t
phút thì có 100000 tế bào và ban đầu có 1 tế bào duy nhất. Khẳng định nào sau đây đúng?
A. 14  t 15. B. 15  t 16.
C. 16  t 17.
D. 17  t 18.
Câu 21. E.coli là vi khuẩn đường ruột gây tiêu chảy, đau bụng dữ dội. Cứ sau 20
phút thì số lượng vi khuẩn E.coli lại tăng gấp đôi. Ban đầu, chỉ có 60 vi khuẩn E.coli
trong đường ruột. Sau 8 giờ, số lượng vi khuẩn E.coli là bao nhiêu?
A. 158.159.469 vi khuẩn.
B. 1.006.632.960 vi khuẩn.
C. 2.108.252.760 vi khuẩn.
D. 3.251.603.769 vi khuẩn.
Câu 22. Một quần thể vi khuẩn bắt đầu với 100 con. Cứ sau 3 giờ đồng hồ thì số
lượng vi khuẩn lại tăng gấp đôi. Hỏi khi nào số lượng vi khuẩn đạt đến 50000 con? A. 26,06 giờ. B. 26,6 giờ. C. 26,09 giờ. D. 26,9 giờ.
Câu 23. Một bể nước có dung tích  3
1 m  (không có nước). Người ta mở vòi cho nước
chảy vào bể. Trong giờ đầu, vận tốc nước chảy vào bể là 1 lít/phút. Trong các giờ tiếp
theo, vận tốc nước chảy giờ sau gấp đôi giờ trước. Hỏi sau khoảng thời gian bao lâu thì bể nước đầy ? A. 3,14 giờ. B. 5,14 giờ. C. 350 phút. D. 14915 giây.
Câu 24. Một người thả một lượng bèo hoa dâu chiếm 4% diện tích mặt hồ. Biết rằng
cứ sau đúng một tuần bèo phát triển thành 3 lần lượng đã có và tốc độ phát triển của
bèo ở mọi thời điểm như nhau. Sau bao nhiêu ngày, lượng bèo sẽ vừa phủ kín mặt hồ? 25 A. 7log 25. B. 7 3 . C. 24 7 . D. log 25. 3 3 3 5
Câu 25. Người ta thả một lượng bèo vào một hồ nước. Kết quả cho thấy sau 9 giờ bèo
sẽ sinh sôi kín cả mặt hồ. Biết rằng sau mỗi giờ, lượng bèo tăng gấp 10 lần lượng bèo
trước đó và tốc độ tăng không đổi. Hỏi sau mấy giờ thì lượng bèo phủ kín 1 mặt hồ? 3 9 A. 10 3 giờ.
B. 9log 3 giờ. C. giờ.
D. 9 giờ. 3 log 3
Phần 2. Bài toán lãi suất
Dạng 1. Cho vay một lần (lãi kép)
Câu 1. (ĐỀ THAM KHẢO 2017 – 2018) Một người gửi 100 triệu đồng vào một ngân
hàng với lãi suất 0,4% /tháng. Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ
sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho tháng tiếp
theo. Hỏi sau đúng 6 tháng, người đó được lĩnh số tiền (cả vốn ban đầu và lãi) gần
nhất với số tiền nào dưới đây, nếu trong khoảng thời gian này người đó không rút tiền
ra và lãi suất không thay đổi?
A. 102.016.000 đồng.
B. 102.017.000 đồng.
C. 102.423.000 đồng.
D. 102.424.000 đồng.
Câu 2. Một người gửi 10 triệu đồng vào ngân hàng với lãi suất 5% /năm trong thời
gian 10 năm. Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ sau định kỳ, số tiền
lãi sẽ được nhập vào vốn ban đầu để tính lãi cho định kỳ tiếp theo. Hỏi rằng người đó
nhận được số tiền nhiều hơn hay ít hơn bao nhiêu nếu ngân hàng trả lãi suất
5 %/tháng (lãi suất tháng so với lãi suất năm)? 12
A. Ít hơn 1.811.486,1 đồng.
B. Ít hơn 1.911.486,1 đồng. C. Bằng nhau.
D. Nhiều hơn 1.811.486,1 đồng.
Câu 3. Một người lần đầu gửi vào ngân hàng 100 triệu đồng với kì hạn 3 tháng, lãi
suất 2% /quý. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi quý, số
tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho quý tiếp theo. Sau đúng 6 tháng,
người đó gửi thêm 100 triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền
người đó nhận được một năm sau khi gửi tiền (cả vốn lẫn lãi) gần nhất với kết quả nào sau đây? A. 210 triệu. B. 212 triệu. C. 216 triệu. D. 220 triệu.
Câu 4. Một người dự định sẽ mua xe Honda SH với giá 80.990.000 đồng. Người đó gửi
tiết kiệm vào ngân hàng với số tiền 60.000.000 đồng với lãi suất 0,8% /tháng. Biết
rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được
nhập vào vốn ban đầu để tính lãi cho tháng tiếp theo. Do sức ép thị trường nên mỗi
tháng loại xe Honda SH giảm 500.000 đồng. Vậy sau bao lâu người đó sẽ đủ tiền mua xe máy? A. 20 tháng. B. 21 tháng. C. 22 tháng. D. 23 tháng. 6
Câu 5. Một người muốn gửi tiền vào ngân hàng để đến ngày 15/3/ 2020 rút được
khoản tiền là 50.000.000 đồng. Lãi suất ngân hàng là 0,55% /tháng. Biết rằng nếu
không rút tiền khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn
ban đầu để tính lãi cho tháng tiếp theo. Hỏi vào ngày 15/ 4 / 2018 người đó phải gửi
ngân hàng số tiền là bao nhiêu để đáp ứng nhu cầu trên, nếu lãi suất không thay đổi
trong thời gian người đó gửi tiền? A. 43.593.000 đồng. B. 43.833.000 đồng. C. 44.316.000 đồng. D. 44.074.000 đồng.
Câu 6. Ông Việt dự định gửi vào ngân hàng một số tiền với lãi suất 6,5% /năm. Biết
rằng nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập
vào vốn ban đầu để tính lãi cho năm tiếp theo. Tính số tiền tối thiểu x triệu đồng
x   ông Việt gửi vào ngân hàng để sau 3 năm số tiền lãi đủ mua một chiếc xe gắn
máy trị giá 30 triệu đồng.
A. x  140 triệu đồng.
B. x  145 triệu đồng.
C. x  150 triệu đồng.
D. x  154 triệu đồng.
Câu 7. Một người gửi tiết kiệm vào ngân hàng 200 triệu đồng theo thể thức lãi kép
(tức là tiền lãi được cộng vào vốn kỳ tiếp theo). Ban đầu người đó gửi với kỳ hạn
3 tháng, lãi suất 2% / kỳ hạn, sau hai năm người đó thay đổi phương thức gửi, chuyển
thành kỳ hạn một tháng với lãi suất 0,6% /tháng. Tính tổng số tiền lãi và gốc nhận
được sau 5 năm (kết quả làm tròn tới đơn vị nghìn đồng).
A. 290.640.000 đồng.
B. 290.642.000 đồng.
C. 290.646.000 đồng.
D. 290.644.000 đồng.
Câu 8. (ĐỀ CHÍNH THỨC 2016 – 2017) Một người gửi 50 triệu đồng vào ngân hàng
với lãi suất 6% / năm. Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi
năm, số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho năm tiếp theo. Hỏi sau
ít nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn 100 triệu đồng bao gồm
cả gốc và lãi? Giả sử trong suốt thời gian gửi lãi suất không đổi và người đó không rút tiền ra. A. 11 năm. B. 12 năm. C. 13 năm. D. 14 năm.
Câu 9. Ông An gửi 320 triệu đồng vào ngân hàng ACB và VietinBank theo phương
thức lãi kép. Số tiền thứ nhất gửi vào ngân hàng ACB với lãi suất 2,1% /quý trong
thời gian 15 tháng. Số tiền còn lại gửi vào ngân hàng VietinBank với lãi suất
0,73% /tháng trong thời gian 9 tháng. Biết tổng số tiền lãi ông An nhận được ở hai
ngân hàng là 26670725,95 đồng. Hỏi số tiền ông An lần lượt ở hai ngân hàng ACB và VietinBank là bao nhiêu?
A. 120 triệu đồng và 200 triệu đồng. B. 140 triệu đồng và 180 triệu đồng.
C. 180 triệu đồng và 140 triệu đồng. D. 200 triệu đồng và 120 triệu đồng.
Câu 10. (ĐỀ CHÍNH THỨC 2016 – 2017) Đầu năm 2016, ông An thành lập một
công ty. Tổng số tiền ông An dùng để trả lương cho nhân viên trong năm 2016 là 1 tỷ 7
đồng. Biết rằng cứ sau mỗi năm thì tổng số tiền dùng để trả lương cho nhân viên
trong cả năm đó tăng thêm 15% so với năm trước. Hỏi năm nào dưới đây là năm đầu
tiên mà tổng số tiền ông An dùng để trả lương cho nhân viên trong cả năm lớn hơn 2 tỷ đồng? A. Năm 2020. B. Năm 2021. C. Năm 2022. D. Năm 2023.
Dạng 2. Gửi tiền đầu mỗi định kỳ (gửi tiết kiệm)
Cứ đầu mỗi định kỳ gửi vào ngân hàng M triệu, lãi suất kép r% /định kỳ. Hỏi sau n
định kỳ số tiền thu được là bao nhiêu? Ta xây dựng bảng sau: Định kỳ Đầu định kỳ Cuối định kỳ 1 M M 1r 2
M 1 r M
M 1r M 1r  
M 1 r2 1 r         3 M  r 2      2 1 1 r     M    M  1r
 1r  M .   1 r     
M 1 r3 1 r2 1 r              n  1  n M r ... 1 r     .   1 n n r 1
Vậy sau n định kỳ ta được số tiền: T M 1 r   ... 1 r       M  1r. .   r   Từ đó suy ra Tr Tr M  và n log  1   .  1r  
1 r  1 rn 1      M  1r     
Câu 11. Một người gửi tiết kiệm ngân hàng, mỗi tháng gửi đều đặn vào ngân hàng 1
triệu đồng với lãi suất kép 1% /tháng. Gửi được hai năm ba tháng người đó rút toàn
bộ tiền vốn và lãi. Số tiền người đó nhận được là A.  26 100. 1,01 1      triệu đồng. B.  27
100. 1,01 1 triệu đồng.      C.  26 101. 1,01 1      triệu đồng. D.  27
101. 1,01 1 triệu đồng.     
Câu 12. Một người mỗi đầu tháng đều đặn gửi vào ngân hàng một khoản tiền M
theo hình thức lãi kép với lãi suất 0,6% /tháng. Biết đến cuối tháng thứ 15 thì người
đó có số tiền là 10 triệu đồng (cả vốn và lãi). Hỏi số tiền M gần với số tiền nào nhất trong các số sau?
A. 535.000 đồng. B. 613.000 đồng. C. 635.000 đồng. D. 643.000 đồng.
Câu 13. Một người muốn có 2 tỷ tiền tiết kiệm sau 6 năm gửi ngân hàng bằng cách
mỗi năm gửi vào ngân hàng số tiền bằng nhau với lãi suất ngân hàng là 8% /năm và
lãi hàng năm được nhập vào vốn. Hỏi số tiền mà người đó phải gửi vào ngân hàng số 8
tiền hàng năm là bao nhiêu? Giả thiết rằng lãi suất không thay đổi và số tiền được
làm tròn đến đơn vị nghìn đồng. A. 251 triệu. B. 252,5 triệu. C. 253 triệu. D. 253,5 triệu.
Câu 14. Đúng ngày 01 mỗi tháng anh A gửi vào ngân hàng 3 triệu đồng với lãi suất
0,7% /tháng. Biết không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng tiền lãi sẽ
nhập vào gốc để tính lãi cho tháng tiếp theo. Hỏi sau ít nhất bao nhiêu tháng thì anh
A có được số tiền cả gốc và lãi nhiều hơn 100 triệu đồng? Giả định trong suốt thời
gian gửi, lãi suất không đổi, được tính lãi ngay từ ngày gửi và anh A không rút tiền ra. A. 28 tháng. B. 29 tháng. C. 30 tháng. D. 33 tháng.
Dạng 3. Vay trả góp
Vay ngân hàng M triệu đồng, lãi suất r% /định kỳ. Cứ cuối mỗi định kỳ trả ngân
hàng m triệu. Hỏi sau n định kỳ số tiền còn nợ là bao nhiêu? Ta xây dựng bảng sau: Định kỳ Đầu định kỳ Cuối định kỳ 1 M
M 1rm 2
M 1 rm
M 1rm1rm  
M 1 r2 m 1 r1   3 M
 1 r 2 m 1 r 1  
1 r m
M 1 r 3 m 1 r2 1 r 1               n
M 1 rn m 1 rn 1  1 rn2 1          
Vậy sau n định kỳ, số tiền còn nợ T M r n m  r n 1   rn2 1 1 1 1             m
M 1 r n 1 r  n 1      . r   
M 1 rn r
Từ đó suy ra nếu định kỳ thứ n mà trả hết nợ thì T  0  m  .
1rn 1
Câu 15. (ĐỀ MINH HỌA 2016 – 2017) Ông Việt vay ngân hàng 100 triệu đồng, với
lãi suất 1% /tháng. Ông muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một tháng
kể từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một
tháng, số tiền hoàn nợ ở mỗi lần là như nhau và trả hết tiền nợ sau đúng 3 tháng kể
từ ngày vay. Hỏi theo cách đó, số tiền m mà ông Việt sẽ phải trả cho ngân hàng trong
mỗi lần hoàn nợ là bao nhiêu? Biết rằng lãi suất ngân hàng không thay đổi trong thời gian ông Việt hoàn nợ. 9  3 100. 1,01 1,0 3 1 A. m  (triệu đồng). B. m  (triệu đồng). 3 1,0 3 1 1 120.1,123 C. 100 1  ,03 m  (triệu đồng). D. m  (triệu đồng). 3 1,123 1
Câu 16. Một người vay ngân hàng 500 triệu đồng, với lãi suất 1,2% /tháng. Sau đúng
một tháng kể từ ngày vay, người đó bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách
nhau đúng một tháng, số tiền hoàn nợ ở mỗi lần là như nhau và bằng 10 triệu đồng.
Hỏi sau ít nhất bao nhiêu tháng thì người đó trả hết nợ? Biết rằng, lãi suất ngân
hàng không thay đổi trong thời người đó hoàn nợ. A. 70 tháng.
B. 77 tháng. C. 80 tháng. D. 85 tháng.
Câu 17. Bạn Hùng trúng tuyển Đại học nhưng vì do không đủ tiền nộp học phí nên
Hùng quyết định vay ngân hàng trong 4 năm, mỗi năm 4.000.000 đồng để nộp học
phí với lãi suất 3% / năm. Sau khi tốt nghiệp Đại học, bạn Hùng phải trả góp hàng
tháng cho ngân hàng số tiền m (không đổi) cùng với lãi suất 0,25% /tháng trong vòng
5 năm. Tính số tiền m hàng tháng mà bạn Hùng phải trả cho ngân hàng (làm tròn
đến kết quả hàng đơn vị).
A. 309.604,14 đồng.
B. 309.718,166 đồng.
C. 312.518,166 đồng.
D. 398.402,12 đồng.
Dạng 4. Bài tập tổng hợp
Câu 18. [Lãi suất tăng dần] Ông Bách dự định đầu tư khoản tiền 20 triệu đồng vào
một dự án với lãi suất tăng dần: 3,35% /năm trong 3 năm đầu, 3,75% /năm tong 2
năm kế tiếp và 4,8% /năm ở 5 năm cuối. Khoản tiền mà ông Bách nhận được (cả vốn
và lãi) cuối năm thứ 10 là A. 25 triệu. B. 30 triệu. C. 35 triệu. D. 40 triệu.
Câu 19. Năm 2017 số tiền để đổ đầy bình xăng cho một chiếc xe máy trung bình là
70000 đồng. Giả sử tỉ lệ lạm phát hàng năm của Việt Nam trong 10 năm tới không
đổi với mức 5%, tính số tiền để đổ đầy bình xăng cho chiếc xe đó vào năm 2022. A. 5
70000.0,05 đồng. B. 6 70000.0,05 đồng. C. 5
70000.1,05 đồng. D. 6 70000.1,05 đồng.
Câu 20. Một người mua chiếc xe máy Air Blade với giá 45 triệu đồng. Biết rằng giá
trị khấu hao tài sản xe giảm 60% mỗi năm. Biết rằng sau n năm thì giá trị xe chỉ
còn 5 triệu đồng. Giá trị n gần nhất với đáp án nào sau đây? A. 2 năm. B. 2,5 năm. C. 3 năm. D. 3,5 năm.
Câu 21. Đầu năm 2017, anh Hùng có xe công nông trị giá 100 triệu đồng. Biết mỗi
tháng thì xe công nông hao mòn mất 0,4% giá trị, đồng thời anh Hùng làm ra được 6
triệu đồng (số tiền làm ra mỗi tháng là không đổi). Hỏi sau đúng một năm, tổng số 10
tiền (bao gồm tiền giá xe công nông và tiền anh Hùng làm ra) mà anh Hùng có là bao nhiêu? A. 172 triệu.
B. 167,3042 triệu. C. 144 triệu.
D. 120,3042 triệu.
Câu 22. Theo thống kê tài chính của thị xã An Nhơn, tỉnh Bình Định, trong dịp Tết
Nguyên Đán năm 2015, làng nghề trồng mai cảnh xã An Nhơn đạt tổng doanh thu
khoảng 15 tỷ đồng nhờ vào việc bán mai cảnh. Biết rằng trong các năm tiếp theo tổng
doanh thu luôn tăng ổn định và doanh thu trong năm đó cao hơn so với năm trước
6,27%. Hỏi tổng doanh thu của làng nghề trồng mai cảnh xã An Nhơn vào dịp Tết
Nguyên Đán năm 2018 là bao nhiêu? (làm tròn đến tỷ đồng)
A. 17 tỷ đồng. B. 18 tỷ đồng.
C. 19 tỷ đồng. D. 20 tỷ đồng.
Câu 23. [Tiền lương tăng theo chu kỳ] Một kỹ sư được nhận lương khởi điểm là
8000000 đồng/tháng. Cứ sau hai năm lương mỗi tháng của kỹ sư đó được tăng thêm
10% so với mức lương hiện tại. Tổng số tiền kỹ sư đó nhận được sau 6 năm làm việc A. 633600000 đồng. B. 635520000 đồng. C. 696960000 đồng. D. 766656000 đồng.
Câu 24. Theo dự báo với mức tiêu thụ dầu không đổi như hiện nay thì trữ lượng dầu
của nước A sẽ hết sau 100 năm tới. Nhưng do nhu cầu thực tế, mức tiêu thụ tăng lên
4% mỗi năm. Hỏi sau bao nhiêu năm số dầu dự trữ của nước A sẽ hết? A. 40. B. 41. C. 42. D. 43.
Câu 25. Sau một tháng thi công công trình xây dựng Nhà học thể dục của Trường X
đã thực hiện được một khối lượng công việc. Nếu tiếp tục với tiến độ như vậy thì dự
kiến sau đúng 23 tháng nữa công trình sẽ hoàn thành. Để sớm hoàn thành công
trình và kịp thời đưa vào sử dụng, công ty xây dựng quyết định từ tháng thứ 2 , mỗi
tháng tăng 4% khối lượng công việc so với tháng kề trước. Hỏi công trình sẽ hoàn
thành ở tháng thứ mấy sau khi khởi công? A. 17. B. 18. C. 19. D. 20.
Câu 26. [So sánh lãi không kỳ hạn và lãi có kỳ hạn] Ngân hàng BIDV Việt Nam
đang áp dụng hình thức lãi kép với mức lãi suất: không kỳ hạn là 0,2% /năm, kỳ hạn
3 tháng là 1,2% /quý. Ông A đến ngân hàng BIDV để gửi tiết kiệm với số tiền ban
đầu là 300 triệu đồng. Nếu gửi không kỳ hạn mà ông A muốn thu về cả vốn và lãi
bằng hoặc vượt quá 305 triệu đồng thì ông A phải gửi ít nhất n tháng  * n   . Hỏi
nếu cùng số tiền ban đầu và cũng số tháng đó, ông A gửi tiết kiệm có kỳ hạn 3 tháng
thì ông A sẽ nhận được số tiền cả vốn lẫn lãi là bao nhiêu?
A. 444.785.421 đồng.
B. 444.711.302 đồng.
C. 446.490.147 đồng.
D. 447.190.465 đồng.
Câu 27. [Gửi tiết kiệm nhưng số tiền tăng dần] Một người lập kế hoạch gửi tiết
kiệm ngân hàng như sau: Đầu tháng 01 năm 2018, người đó gửi 10 triệu đồng; sau
mỗi đầu tháng tiếp theo, người đó gửi số tiền nhiều hơn 10% so với số tiền đã gửi ở
tháng liền trước đó. Biết rằng lãi suất ngân hàng không đổi là 0,5% mỗi tháng và 11
được tính theo hình thức lãi kép. Với kế hoạch như vậy, đến hết tháng 12 năm 2019,
số tiền của người đó trong tài khoản tiết kiệm là bao nhiêu? (Làm tròn đến hàng nghìn)
A. 832.765.000 đồng.
B. 918.165.000 đồng.
C. 922.756.000 đồng.
D. 926.281.000 đồng.
Câu 28. [Gửi và rút hàng tháng] Ngày 01 tháng 01 năm 2017, ông An gửi 800
triệu đồng vào một ngân hàng với lãi suất 0,5% /tháng. Từ đó, cứ tròn mỗi tháng ông
đến ngân hàng rút 6 triệu để chi tiêu cho gia đình. Hỏi đến ngày 01 tháng 01 năm
2018, sau khi rút tiền, số tiền tiết kiệm của ông An còn lại là bao nhiêu? Biết rằng lãi
suất trong suốt thời gian ông An gửi không thay đổi. A.  11
800. 1,005 72 (triệu đồng). B.  12
800. 1,005 72 (triệu đồng). C.   11
1200 400. 1,005 (triệu đồng). D.   12 1200 400. 1,005 (triệu đồng).
Câu 29. [Gửi và rút hàng tháng] Một hội khuyến học đã kêu gọi sự ủng hộ của các
nhà hảo tâm được 120 triệu đồng. Hội khuyến học gửi số tiền đó vào ngân hàng với
lãi suất 0,75% /tháng với dự định hàng tháng rút m triệu đồng làm khuyến học cho
học sinh nghèo vượt khó. Hội khuyến học bắt đầu trao quà cho học sinh sau một
tháng gửi tiền vào ngân hàng. Để số tiền (cả lãi và 120 triệu đồng tiền gốc) đủ trao
cho học sinh trong 10 tháng thì số tiền m mà hàng tháng Hội khuyến học rút ra tối
đa (lấy kết quả chính xác đến chữ số thập phân thứ nhất) là A. 12,3. B. 12,4. C. 12,5. D. 12,6.
Câu 30. [Trả góp nhưng bị điều chỉnh lãi suất] Một người vay ngân hàng 40
triệu đồng, với lãi suất 0,85% /tháng. Sau đúng một tháng kể từ ngày vay, người đó
bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ
ở mỗi lần là như nhau và bằng 500 nghìn đồng. Sau một năm mức lãi suất của ngân
hàng được điều chỉnh lên là 1,15% /tháng và người vay muốn nhanh chóng hết nợ nên
đã thỏa thuận trả 1 triệu 500 nghìn đồng cho mỗi tháng. Hỏi phải mất bao nhiêu lâu
người đó mới trả hết nợ? A. 30 tháng. B. 31 tháng. C. 42 tháng. D. 43 tháng. 12 HUỲNH ĐỨC KHÁNH 0975120189 Ứng dụng
HÀM SỐ MŨ – HÀM SỐ LOGARIT
Sự phân rã của các chất phóng xạ
Phần 1. Một số bài toán áp dụng
(tăng trưởng, phóng xạ, động đất,…)
Phần 2. Bài toán lãi suất 1
Phần 1. Một số bài toán áp dụng
Dạng 1. Áp dụng công thức có sẵn
Câu 1. Một lon nước soda 0
80 F được đưa vào một máy làm lạnh chứa đá tại 0 32 F.
Nhiệt độ của soda ở phút thứ t được tính theo định luật Newton bởi công thức
  32 48.0,9t T t  
. Phải làm mát soda trong bao lâu để nhiệt độ là 0 37 F. Chọn đáp
án gần nhất với kết quả? A. 15,6 phút. B. 17 phút. C. 21,5 phút. D. 25,6 phút.
Lời giải. Thay vào công thức ta được: 37  32  48.0,9t t  21,5. Chọn C.
Câu 2. với t là khoảng thời gian tính bằng giờ và Q là dung lượng nạp tối đa (pin 0
đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là
0% ) thì sau bao lâu sẽ nạp được 90% (kết quả làm tròn đến hàng phần trăm)?
A. t  1,21 giờ. B. t  1,22 giờ.
C. t  1,34 giờ.
D. t  1,54 giờ. 3t Lời giải. Với 90 90  Q
Q , thay vào ta được 2  1e
t  1,535 giờ. Chọn D. 0 100 100
Câu 3. Một loài cây xanh trong quá trình quang hợp sẽ nhận một lượng nhỏ Carbon
14 (một đơn vị của Carbon). Khi cây đó chết đi thì hiện tượng quang hợp cũng sẽ
ngưng và nó sẽ không nhận Carbon 14 nữa. Lượng Carbon 14 của nó sẽ phân hủy
chậm chạp và chuyển hóa thành Nitơ 14. Gọi P t là số phần trăm Carbon 14 còn lại
trong một bộ phận của cây sinh trưởng t năm trước đây thì P t được cho bởi công t
thức P t  5750 100. 0,5
%. Phân tích một mẫu gỗ từ công trình kiến trúc gỗ, người ta
thấy lượng Carbon 14 còn lại trong gỗ là 65,21%. Hãy xác định số tuổi của công trình kiến trúc đó.
A. 3475 (năm). B. 3547 (năm). C. 3574 (năm). D. 3754 (năm). t
Lời giải. Thay số ta được   5750 65,21% 100. 0,5
%  t  3547. Chọn B.
Câu 4. Cường độ một trận động đất được tính bởi công thức M  log Alog A , với A 0
là biên độ rung chấn tối đa và A là một biên độ chuẩn (hằng số). Đầu thế kỷ XX, 0
một trận động đất ở Nhật Bản có cường độ đo được là 9 độ Richter. Trong cùng năm
đó, trận động đất khác ở Trung Quốc có cường độ đo được là 7 độ Richter. Hỏi trận
động đất ở Nhật Bản có biên độ gấp bao nhiêu lần trận động đất ở Trung Quốc ? A. 10 lần. B. 20 lần. C. 100 lần. D. 200 lần.
Lời giải. Cường độ trân động đất ở Nhật Bản là: A1 9
9  log A  log A   10 .   1 1 0 Ao
Cường độ trân động đất ở Trung Quốc là: A2 7
7  log A  log A   10 . 2 2 0 Ao Từ  
1 và 2, suy ra A  100A . Chọn C. 1 2 2
Câu 5. Cường độ một trận động đất được tính bởi công thức M  log Alog A , với A 0
là biên độ rung chấn tối đa và A là một biên độ chuẩn (hằng số). Đầu thế kỷ XX, 0
một trận động đất ở San Francisco có cường độ 8 độ Richter. Trong cùng năm đó,
trận động đất khác Nam Mỹ có biên độ mạnh hơn gấp 4 lần. Cường độ của trận động
đất ở Nam Mỹ xấp xỉ
A. 8,4 Richter. B. 8,6 Richter. C. 10 Richter. D. 12 Richter.
Lời giải. Trận động đất ở San Francisco có cường độ 8 độ Richter, khi đó áp dụng
công thức M  log Alog A  8  log Alog A .   1 1 0 0
Trận động đất ở Nam Mỹ có biên độ là 4 ,
A khi đó cường độ của trận động đất ở Nam
Mỹ là: M  log4A   1
log A M  log 4  log A log A  M  log 4 8  8,6 độ 2 0 2 0 2 Richter. Chọn B.
Câu 6. Các khí thải gây hiệu ứng nhà kính là nguyên nhân chủ yếu làm trái đất nóng
lên. Theo OECD (Tổ chức hợp tác và phát triển kinh tế thế giới), khi nhiệt độ trái đất
tăng lên thì tổng giá trị kinh tế toàn cầu giảm. Người ta ước tính rằng khi nhiệt độ
trái đất tăng thêm 2 C
 thì tổng giá trị kinh tế toàn cầu giảm 3%, còn khi nhiệt độ
trái đất tăng thêm 5 C
 thì tổng giá trị kinh tế toàn cầu giảm 10% . Biết rằng nếu
nhiệt độ trái đất tăng thêm t C
 , tổng giá trị kinh tế toàn cầu giảm f t % thì   . t f t k a (trong đó ,
a k là các hằng số dương). Nhiệt độ trái đất tăng thêm bao nhiêu
độ C thì tổng giá trị kinh tế toàn cầu giảm 20% ? A. 6,7 C  . B. 7,6 C  . C. 8,4 C  . D. 9,3 C  . 2 k.a  3%
Lời giải. Theo đề bài, ta có   
1 . Cần tìm t thỏa mãn . t k a  20% . 5 k.a 10%  Từ   3% 10 1  k  và 3 a  . 2 a 3 Khi đó t 3% t t 20 20 2
k.a  20%   .a  20%  a   t  2  log  6,7. Chọn A. 2 10 3 a 3 3 3
Câu 7. Cho biết chu kì bán rã của chất phóng xạ radi 226
Ra là 1602 năm (tức là một lượng 226
Ra sau 1602 năm phân hủy thì chỉ còn lại một nửa). Sự phân hủy được tính
theo công thức  . rt S
A e , trong đó A là lượng chất phóng xạ ban đầu, r là tỉ lệ phân
hủy hàng năm r  0, t là thời gian phân hủy, S là lượng còn lại sau thời gian phân hủy. Hỏi 5 gam 226
Ra sau 4000 năm phân hủy sẽ còn lại bao nhiêu gam (làm tròn
đến 3 chữ số phần thập phân)? A. 0,795  gam. B. 0,886  gam. C. 0,923 gam. D. 1,023  gam. Lời giải. Khi A
t T (chu kỳ bán rã) thì S  . 2
Thay vào công thức ta được 1  r T ln 2 . A  . A er  . 2 T 3 t ln 2 t   Khi đó  t T S  . rt A e  . T A e  . A   1 ln 2 eA5 T  . A        0,886 gam .   Chọn B. t4000, T 1  602   2 t t     Chú ý: 1 rt 1 T T S  . A e  . S m A           
công thức trở thành m m   . A 0   0 2 m  2
Câu 8. Số lượng của loại vi khuẩn A trong một phòng thí nghiệm ước tính theo công
thức S S .2t , trong đó S là số lượng vi khuẩn A ban đầu, S là số lượng vi khuẩn A t o 0 t
có sau t phút. Biết sau 3 phút thì số lượng vi khuẩn A là 625 nghìn con. Hỏi sau bao
lâu, kể từ lúc ban đầu, số lượng vi khuẩn A là 10 triệu con? A. 6 phút. B. 7 phút. C. 8 phút. D. 9 phút.
Lời giải. Vì sau 3 phút thì số lượng vi khuẩn A là 625 nghìn con nên ta có phương trình 3
625.000  S .2  S  78125 con. o 0
Để số lượng vi khuẩn A là 10 triệu con thì 7
10  78125.2t t  7. Chọn B.
Câu 9. Sự tăng trưởng của một loại vi khuẩn ước tính theo công thức  . rt S A e , trong
đó A là số lượng vi khuẩn ban đầu, r là tỉ lệ tăng trưởng r  0, t là thời gian tăng
trưởng. Biết rằng số lượng vi khuẩn ban đầu có 100 con và sau 5 giờ có 300 con. Hỏi
sau bao lâu thì số lượng vi khuẩn tăng gấp 10 lần? A. 5 t  giờ. B. 3 t  giờ. C. 5 ln 3 t  giờ. D. 3 ln 5 t  giờ. log 3 log 5 ln10 ln10
Lời giải. Thay các dữ kiện ta có phương trình r ln 3 5
300  100.e r  . 5 ln 3
Để số lượng vi khuẩn tăng t 5
10 lần (tức 1000 con), ta có 5 1000  100.et  . log 3 Chọn A.
Câu 10. Biết rằng cuối năm 2001, dân số Việt Nam là 78685800 người và tỉ lệ tăng
dân số năm đó là 1,7%. Cho biết sự tăng dân số được ước tính theo công thức .  . N r S A e
(trong đó A : là dân số của năm lấy làm mốc tính, S là dân số sau N năm,
r là tỉ lệ tăng dân số hàng năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào
dân số nước ta ở mức 120 triệu người? A. 2020. B. 2022. C. 2025. D. 2026. 6 Lời giải. Ta có N r 1 S 100 120.10 . S  . A e   N  .ln  .ln  24,825. r A 1,7 78685800
Lúc đấy là năm 2001 25  2026. Chọn D.
Câu 11. Cho biết sự tăng dân số được ước tính theo công thức .  . N r S A e (trong đó A :
là dân số của năm lấy làm mốc tính, S là dân số sau N năm, r là tỉ lệ tăng dân số
hàng năm). Theo số liệu thực tế, dân số của tỉnh A đầu năm 2010 là 1.038.229 người,
tính đến đầu năm năm 2015 là 1.153.600 người. Hỏi nếu tỉ lệ tăng dân số hàng năm
giữ nguyên thì đầu năm 2025 dân số của tỉnh trong khoảng nào? 4
A. 1.424.000;1.424.100.
B. 1.424.100;1.424.200.
C. 1.424.200;1.424.300.
D. 1.424.300;1.424.400. S   1.153.600 ngöôøi 1    Lời giải. Gọi 
S là dân số đầu năm 2015, ta có N   5 naêm . 1
A1.038.229  ngöôøi  S S 1 1 ln ln Từ hệ thức N .  . r A A S A er   . 1 N 5 1 S ln A Gọi 15.
S là dân số đầu năm 2025, ta có 15.r 5 S  . A e  1.038.229.e  1.424.227,71. 2 2 Chọn C.
Câu 12. Các nhà khoa học thực hiện nghiên cứu trên một nhóm học sinh bằng cách
cho họ xem một danh sách các loài động vật và sau đó kiểm tra xem họ nhớ được bao
nhiêu % mỗi tháng. Sau t tháng, khả năng nhớ trung bình của nhóm học sinh tính
theo công thức M t 7520 lnt   1 , 
t   (đơn vị % ). Hỏi khoảng thời gian ngắn
nhất bao lâu thì số học sinh trên nhớ được danh sách đó dưới 10% ? A. Khoảng 22 tháng. B. Khoảng 24 tháng. C. Khoảng 25 tháng. D. Khoảng 32 tháng.
Lời giải. Yêu cầu bài toán tương đương với 7520 lnt   1 10 13 13 ln  13 4 4 1 1 1 t t t e t e            t
 25. Chọn C. min 4
Câu 13. Giả sử    .2t n f t n
là số lượng cá thể trong một đám vi khuẩn tại thời 0
điểm t giờ, n là số lượng cá thể lúc ban đầu. Biết tốc độ phát triển về số lượng của vi 0
khuẩn tại thời điểm t chính là f t. Giả sử mẫu thử ban đầu có n 100 con vi 0
khuẩn. Vậy tốc độ phát triển sau 4 giờ là bao nhiêu con vi khuẩn? A. 500 con. B. 1109 con. C. 1600 con. D. 3200 con.
Lời giải. Tốc độ phát triển của vi khuẩn tại thời điểm t là   .2t f t n .ln 2. 0
Khi đó tốc độ phát triểu sau 4 giờ là f   4
4  100.2 .ln 2  1109 con. Chọn B.
Dạng 2. Sử dụng công thức lãi kép
Câu 14. Tỉ lệ tăng dân số hàng năm ở Việt Nam được duy trì ở mức 1,05%. Theo số
liệu của tổng cục thống kê, dân số của Việt Nam giữa năm 2014 là 90728900 người.
Với tốc độ tăng dân số như thế thì vào giữa năm 2030 thì dân số của Việt Nam xấp xỉ là bao nhiêu người?
A. 107026537 người.
B. 107232574 người.
C. 105971355 người.
D. 106118331 người. 5
Lời giải. Với bài này khác với hai bài trước là đề không cho công thức N .  . r S A e . Do
đó ta áp dụng cách tính lãi kép  1 n T M
r với M  90728900, 1 r  ,05%, n  16. Ta
tính được T  107232574,1. Chọn B.
Câu 15. Hết ngày 31 tháng 12 năm 2017, dân số tỉnh X là 1,5 triệu người. Với tốc
độ tăng dân số hàng năm không thay đổi là 1,5% và chỉ có sự biến dộng do sinh - tử
thì trong năm 2027 (từ 1/1/ 2017 đến hết 31/12 / 2027 ) tại tỉnh X có tất cả bao
nhiêu trẻ em được sinh ra, giả sử rằng tổng số người tử vong trong năm 2027 là 2700
người và chỉ là những người trên hai tuổi. A. 28812. B. 28426. C. 23026. D. 23412.
Lời giải. Đề không cho công thức .  . N r S A e
nên ta sử dụng công thức tính lãi kép.
Dân số tỉnh X đến cuối năm 2026 là T
 1,5.11,5%9  1.715.085 người. 2026
Dân số tỉnh X đến cuối năm 2027 là T
 1,5.11,5%10  1.740.811 người. 2027
Suy ra dân số tỉnh X tăng lên trong năm 2027 là T T   25.726 người. 2027 2026
Mà số dân tăng trong thời gian từ 2026 đến 2027 là số trẻ em được sinh ra trừ số
người tử vong. Do đó số trẻ em sinh ra trong năm 2027 là: 25726  2700  28426 người. Chọn B.
Câu 16. Một khu rừng ban đầu có trữ lượng gỗ là 5  3
4.10 m . Gọi tốc độ sinh trưởng
mỗi năm của khu rừng đó là r%. Biết sau 5 năm thì sản lượng gỗ là xấp xỉ 5  3
4,8666.10 m . Giá trị của r xấp xỉ bằng A. 3,5. B. 4. C. 4,5. D. 5.
Lời giải. Trữ lượng gỗ sau một năm của khu rừng là: 5 5 5
T  4.10  4.10 .r %  4.10 1 r % . 1  
Trữ lượng gỗ sau năm thứ hai của khu rừng là: T  4.10 1r%2 5 . 2
Trữ lượng gỗ sau 5 năm của khu rừng là: T  4.10 1r%5 5 5
 4,8666.10  r  4. 5 Chọn B.
Câu 17. Số lượng động vật nguyên sinh tăng trưởng với tốc độ 0,7944 con/ngày. Giả
sử vào cuối ngày đầu tiên, số lượng động vật nguyên sinh là 2 con. Hỏi sau 6 ngày
(kể cả ngày đầu tiên), số lượng động vật nguyên sinh là bao nhiêu con? A. 37 con. B. 48 con. C. 67 con. D. 106 con.
Lời giải. Ta xem đây là bài toán lãi kép với công thức  1 n T M r . Với M  2, 0
r  ,7944 và n  5 (chú ý) nên T    5
2. 1 0,7944  37 con. Chọn A.
Câu 18. Cục điều tra dân số thế giới cho biết: Trong chiến tranh thế giới thứ hai (kéo
dài 6 năm); dân số mỗi năm giảm đi 2% so với dân số năm liền trước đó. Vào thời hòa
bình sau chiến tranh thế giới thứ hai thì dân số tăng 4% so với dân số năm liền trước
đó. Giả sử rằng, vào cuối năm thứ 2 diễn ra chiến tranh dân số thế giới là 4 tỷ người. 6
Kể từ thời điểm đó thì 10 năm sau thì dân số thế giới khoảng bao nhiêu tỷ người (làm
tròn đến chữ số thập phân thứ hai)? A. 4,40. B. 4,67. C. 4,88. D. 4,95.
Lời giải. 10 năm đó gồm 4 năm chiến tranh và 6 năm hòa bình. Do đó, dân số sẽ 4 6     được tính là: 2 4 4. 1      . 1      
  4.0,984 .1,046  4,67 tỷ người. Chọn B.  100  100
Câu 19. Biết thể tích khí CO đầu năm 2002 là V  3
m . Thời gian 10 năm tiếp theo, 2
thể tích khí CO tăng m%; thời gian 10 năm tiếp theo nữa, thể tích CO tăng n%. 2 2
Thể tích khí CO đầu năm 2020 là 2
100 m100 n 10 
100 m10 .100 n8 A. V     3 m . B. V   3 m . 36  20  10 10 C. V   m n18     18 3    3 1 1 m . D. V
 1 m n m .  
Lời giải. Đầu năm m 100  m
2003 thể tích khí CO là: VV V . V . . 2 2003 100 100 2    Đầu năm 100 m
2004 thể tích khí CO là: VV   
 . Vậy ta có quy luật nên sẽ 2 2004  100 
nhẩm nhanh như sau: từ đầu năm 2002 đến đầu năm 2020 là 18 năm, trong đó 10
năm đầu chỉ số tăng là m%, 8 năm sau chỉ số tăng là n%. 10 8
100  m 100  n
100 m10 100 n8
Vậy thể tích cần tínhVV           V  . Chọn B. 2020     36 100  100  10
Dạng 3. Thiết lập công thức
Câu 20. Quan sát quá trình sao chép tế bào trong phòng thí nghiệm sinh học, nhà
sinh vật học nhận thấy các tế bào tăng gấp đôi mỗi phút. Biết sau một thời gian t
phút thì có 100000 tế bào và ban đầu có 1 tế bào duy nhất. Khẳng định nào sau đây đúng?
A. 14  t 15. B. 15  t 16.
C. 16  t 17.
D. 17  t 18.
Lời giải. Do ban đầu có một tế bào duy nhất nên:
Sau phút sao chép thứ nhất số tế bào là: T  2; 1
Sau phút sao chép thứ hai số tế bào là: 2 T  2 ; 2 
Sau phút sao chép thứ t số tế bào là: T  2t  100000  t  16,61. Chọn C. t
Câu 21. E.coli là vi khuẩn đường ruột gây tiêu chảy, đau bụng dữ dội. Cứ sau 20
phút thì số lượng vi khuẩn E.coli lại tăng gấp đôi. Ban đầu, chỉ có 60 vi khuẩn E.coli
trong đường ruột. Sau 8 giờ, số lượng vi khuẩn E.coli là bao nhiêu?
A. 158.159.469 vi khuẩn.
B. 1.006.632.960 vi khuẩn. 7
C. 2.108.252.760 vi khuẩn.
D. 3.251.603.769 vi khuẩn.
Lời giải. Tương tự như bài trên, sau n lần 20 phút thì số vi khuẩn có là T  60.2n. n
Vì 8 giờ tương đương với 24 lần 20 phút. Do đó số lượng vi khuẩn E.coli sau 8 giờ là 24
T  60.2  1.006.632.960 vi khuẩn. Chọn B. 24
Câu 22. Một quần thể vi khuẩn bắt đầu với 100 con. Cứ sau 3 giờ đồng hồ thì số
lượng vi khuẩn lại tăng gấp đôi. Hỏi khi nào số lượng vi khuẩn đạt đến 50000 con? A. 26,06 giờ. B. 26,6 giờ. C. 26,09 giờ. D. 26,9 giờ.
Lời giải. Tương tự như bài trên, sau n lần 3 giờ thì số vi khuẩn có là T  100.2n. n   Theo đề bài, ta có n 50000
T  50000  50000  100.2  n  log      8,9657. n 2  100 
Suy ra số thời gian cần thiết là n3  8,96573  26,9 giờ. Chọn D.
Câu 23. Một bể nước có dung tích  3
1 m  (không có nước). Người ta mở vòi cho nước
chảy vào bể. Trong giờ đầu, vận tốc nước chảy vào bể là 1 lít/phút. Trong các giờ tiếp
theo, vận tốc nước chảy giờ sau gấp đôi giờ trước. Hỏi sau khoảng thời gian bao lâu thì bể nước đầy ? A. 3,14 giờ. B. 5,14 giờ. C. 350 phút. D. 14915 giây.
Lời giải. Gọi n là số giờ vòi nước chảy để đầy bể.
Trong giờ đầu vòi chảy được 60 lit;
Trong giờ thứ hai vòi chảy được 60.2 lit;
Trong giờ thứ ba vòi chảy được 2 60.2 lit; 
Trong giờ thứ n vòi chảy được 1 60.2n lit;
Tổng lượng nước chảy sau n giờ là  2 n 1 60. 1 2 2 ...2     1000     n   n 53 53 60 2 1  1000  2   n  log  
   4,142957 giờ  14915 giây. Chọn D. 2 3  3 
Câu 24. Một người thả một lượng bèo hoa dâu chiếm 4% diện tích mặt hồ. Biết rằng
cứ sau đúng một tuần bèo phát triển thành 3 lần lượng đã có và tốc độ phát triển của
bèo ở mọi thời điểm như nhau. Sau bao nhiêu ngày, lượng bèo sẽ vừa phủ kín mặt hồ? 25 A. 7log 25. B. 7 3 . C. 24 7 . D. log 25. 3 3 3
Lời giải. Gọi A là lượng bèo ban đầu 
 phủ kín mặt hồ thì cần lượng bèo 100 . A 4
Sau một tuần số lượng bèo là 3A 
 sau n tuần lượng bèo là 3n . A
Lượng bèo phủ kín mặt hồ khi n 100 3 A
A n  log 25 tuần  7 log 25 ngày.Chọn A. 3 4 3
Câu 25. Người ta thả một lượng bèo vào một hồ nước. Kết quả cho thấy sau 9 giờ bèo
sẽ sinh sôi kín cả mặt hồ. Biết rằng sau mỗi giờ, lượng bèo tăng gấp 10 lần lượng bèo
trước đó và tốc độ tăng không đổi. Hỏi sau mấy giờ thì lượng bèo phủ kín 1 mặt hồ? 3 8 9 A. 10 3 giờ.
B. 9log 3 giờ. C. giờ.
D. 9 giờ. 3 log 3
Lời giải. Gọi A là lượng bèo ban đầu. Sau mỗi giờ, lượng lá bèo tăng gấp 10 lần nên
sau 9 giờ ta có lượng bèo là 9 .
A 10 . Gọi t là số giờ để lượng bèo trong hồ phủ kín 1 3 9
mặt hồ. Khi đó ta có phương trình t 1 10 9 . A 10   .
A 10  t  log
 9 log 3. Chọn B. 3 3
Phần 2. Bài toán lãi suất
Dạng 1. Cho vay một lần (lãi kép)
Câu 1. (ĐỀ THAM KHẢO 2017 – 2018) Một người gửi 100 triệu đồng vào một ngân
hàng với lãi suất 0,4% /tháng. Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ
sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho tháng tiếp
theo. Hỏi sau đúng 6 tháng, người đó được lĩnh số tiền (cả vốn ban đầu và lãi) gần
nhất với số tiền nào dưới đây, nếu trong khoảng thời gian này người đó không rút tiền
ra và lãi suất không thay đổi?
A. 102.016.000 đồng.
B. 102.017.000 đồng.
C. 102.423.000 đồng.
D. 102.424.000 đồng.
Lời giải. Công thức lãi kép T A1rn với A số tiền gửi vào lần đầu tiên, r là lãi n 6   suất mỗi kỳ, 0,4
n là số kỳ hạn. Ta được 6 T  100 10  1       102.424.000 đồng. 6  100 Chọn D.
Câu 2. Một người gửi 10 triệu đồng vào ngân hàng với lãi suất 5% /năm trong thời
gian 10 năm. Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ sau định kỳ, số tiền
lãi sẽ được nhập vào vốn ban đầu để tính lãi cho định kỳ tiếp theo. Hỏi rằng người đó
nhận được số tiền nhiều hơn hay ít hơn bao nhiêu nếu ngân hàng trả lãi suất
5 %/tháng (lãi suất tháng so với lãi suất năm)? 12
A. Ít hơn 1.811.486,1 đồng.
B. Ít hơn 1.911.486,1 đồng. C. Bằng nhau.
D. Nhiều hơn 1.811.486,1 đồng.
Lời giải. Số tiền nhận được sau 10 năm với 10   • Lãi suất là 5 5% /năm  10000000. 1       16288946,27  đồng.  100 120   • Lãi suất là 5 5 % /tháng  10000000. 1    
  16470094,98 đồng. 12  12.100
Suy ra số tiền gửi theo lãi suất tháng nhiều hơn: 1.811.486,1 đồng. Chọn D.
Câu 3. Một người lần đầu gửi vào ngân hàng 100 triệu đồng với kì hạn 3 tháng, lãi
suất 2% /quý. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi quý, số
tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho quý tiếp theo. Sau đúng 6 tháng,
người đó gửi thêm 100 triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền 9
người đó nhận được một năm sau khi gửi tiền (cả vốn lẫn lãi) gần nhất với kết quả nào sau đây? A. 210 triệu. B. 212 triệu. C. 216 triệu. D. 220 triệu.
Lời giải. Số tiền nhận về sau 1 năm của 100 triệu gửi trước là   4 100 1 2% triệu.
Số tiền nhận về sau 6 tháng của 100 triệu gửi sau là   2 100 1 2% triệu.
Vậy tổng số tiền nhận là   4    2 100 1 2%
100 1 2%  212,283216 triệu. Chọn B.
Câu 4. Một người dự định sẽ mua xe Honda SH với giá 80.990.000 đồng. Người đó gửi
tiết kiệm vào ngân hàng với số tiền 60.000.000 đồng với lãi suất 0,8% /tháng. Biết
rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được
nhập vào vốn ban đầu để tính lãi cho tháng tiếp theo. Do sức ép thị trường nên mỗi
tháng loại xe Honda SH giảm 500.000 đồng. Vậy sau bao lâu người đó sẽ đủ tiền mua xe máy? A. 20 tháng. B. 21 tháng. C. 22 tháng. D. 23 tháng.
Lời giải. Áp dụng công thức lãi kép, ta có số tiền người đó nhận được (cả vốn ban đầu n   và lãi) sau n 0,8
n tháng là: T A1 r  6  60.10 . 1      .   100
Số tiền xe Honda SH giảm trong n tháng là: p  80990000500000 . n
Để người đó mua được xe Honda SH thì: T p  0,8 n  6  60.10 1    
  80990000500000n  n  20,58771778.  Chọn B.  100
Câu 5. Một người muốn gửi tiền vào ngân hàng để đến ngày 15/3/ 2020 rút được
khoản tiền là 50.000.000 đồng. Lãi suất ngân hàng là 0,55% /tháng. Biết rằng nếu
không rút tiền khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn
ban đầu để tính lãi cho tháng tiếp theo. Hỏi vào ngày 15/ 4 / 2018 người đó phải gửi
ngân hàng số tiền là bao nhiêu để đáp ứng nhu cầu trên, nếu lãi suất không thay đổi
trong thời gian người đó gửi tiền? A. 43.593.000 đồng. B. 43.833.000 đồng. C. 44.316.000 đồng. D. 44.074.000 đồng.
Lời giải. Áp dụng công thức lãi kép T A1rn với A số tiền gửi vào lần đầu tiên, n
r  0,55% là lãi suất mỗi tháng, n  23 tháng và T  50.000.000 đồng. Ta được n 23  0,55 50000000  . A 1        A  44074000  đồng. Chọn D.  100 
Câu 6. Ông Việt dự định gửi vào ngân hàng một số tiền với lãi suất 6,5% /năm. Biết
rằng nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập
vào vốn ban đầu để tính lãi cho năm tiếp theo. Tính số tiền tối thiểu x triệu đồng
x   ông Việt gửi vào ngân hàng để sau 3 năm số tiền lãi đủ mua một chiếc xe gắn
máy trị giá 30 triệu đồng.
A. x  140 triệu đồng.
B. x  145 triệu đồng. 10
C. x  150 triệu đồng.
D. x  154 triệu đồng.
Lời giải. Áp dụng công thức lãi kép T A1rn với A x số tiền gửi vào lần đầu n
tiên, r  6,5% là lãi suất mỗi năm, n  3 năm. Suy ra số tiền người đó nhận được (cả 3  
vốn ban đầu và lãi) là: 6,5 T x 1      .   100 3  
Suy ra số tiền lãi người đó nhận được là: 6,5
T x x 1       x.   100 3   Theo đề, ta có 6,5
T x  30  x 1       x  30   x  144,27 
triệu đồng. Chọn B.  100
Câu 7. Một người gửi tiết kiệm vào ngân hàng 200 triệu đồng theo thể thức lãi kép
(tức là tiền lãi được cộng vào vốn kỳ tiếp theo). Ban đầu người đó gửi với kỳ hạn
3 tháng, lãi suất 2% / kỳ hạn, sau hai năm người đó thay đổi phương thức gửi, chuyển
thành kỳ hạn một tháng với lãi suất 0,6% /tháng. Tính tổng số tiền lãi và gốc nhận
được sau 5 năm (kết quả làm tròn tới đơn vị nghìn đồng).
A. 290.640.000 đồng.
B. 290.642.000 đồng.
C. 290.646.000 đồng.
D. 290.644.000 đồng.
Lời giải. Áp dụng công thức lãi kép, ta có 8   • Sau 2
2 năm đầu tiên người đó có số tiền cả gốc và lãi là: T  200 1      .   100 36   • Sau 0,6
5 năm người đó có số tiền cả gốc và lãi là: T  T 1        100 8 36  2   0,6   200 1      . 1      
  290642000 đồng. Chọn B.  100  100
Câu 8. (ĐỀ CHÍNH THỨC 2016 – 2017) Một người gửi 50 triệu đồng vào ngân hàng
với lãi suất 6% / năm. Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi
năm, số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho năm tiếp theo. Hỏi sau
ít nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn 100 triệu đồng bao gồm
cả gốc và lãi? Giả sử trong suốt thời gian gửi lãi suất không đổi và người đó không rút tiền ra. A. 11 năm. B. 12 năm. C. 13 năm. D. 14 năm.
Lời giải. Áp dụng công thức lãi kép T A r n 1 n .
Theo đề bài ta cần có: T 100  50.      n  Vì n là số n
1 6%n 100 1,06n 2 11.
tự nhiên và người đó chỉ được nhận lãi vào cuối năm nên ta chọn n  12. Chọn B.
Câu 9. Ông An gửi 320 triệu đồng vào ngân hàng ACB và VietinBank theo phương
thức lãi kép. Số tiền thứ nhất gửi vào ngân hàng ACB với lãi suất 2,1% /quý trong
thời gian 15 tháng. Số tiền còn lại gửi vào ngân hàng VietinBank với lãi suất
0,73% /tháng trong thời gian 9 tháng. Biết tổng số tiền lãi ông An nhận được ở hai 11
ngân hàng là 26670725,95 đồng. Hỏi số tiền ông An lần lượt ở hai ngân hàng ACB và VietinBank là bao nhiêu?
A. 120 triệu đồng và 200 triệu đồng. B. 140 triệu đồng và 180 triệu đồng.
C. 180 triệu đồng và 140 triệu đồng. D. 200 triệu đồng và 120 triệu đồng.
Lời giải. Gọi số tiền ông An gửi ở ngân hàng ACB là x triệu đồng. Suy ra số tiền ông
An gửi ở ngân hàng VietinBank là 320 x triệu đồng.
• Số tiền cả vốn và lãi ông An nhận được khi gửi ở ngân hàng ACB sau 15 tháng là: 5  2,1  x 1      . 
Suy ra số tiền lãi ông An nhận được khi gửi ở ngân hàng ACB sau 15  100 5   tháng là: 2,1 x 1       x.   100
• Số tiền cả vốn và lãi ông An nhận được khi gửi ở ngân hàng VietinBank sau 9 9   tháng là:   x 0,73 320 1      . 
Suy ra số tiền lãi ông An nhận được khi gửi ở ngân  100  9   hàng VietinBank sau 0,73
9 tháng là: 320 x 1      320 x.   100 
Tổng số tiền lãi ông An nhận được ở hai ngân hàng là 26670725,95 đồng nên ta có 5 9     phương trình 2,1 x       x   x 0,73 1 320 1      
 320 x  26,67072595  x  120.  100  100 
Vậy ông An gửi ở ACB là 120 triệu và VietinBank 200 triệu. Chọn A.
Câu 10. (ĐỀ CHÍNH THỨC 2016 – 2017) Đầu năm 2016, ông An thành lập một
công ty. Tổng số tiền ông An dùng để trả lương cho nhân viên trong năm 2016 là 1 tỷ
đồng. Biết rằng cứ sau mỗi năm thì tổng số tiền dùng để trả lương cho nhân viên
trong cả năm đó tăng thêm 15% so với năm trước. Hỏi năm nào dưới đây là năm đầu
tiên mà tổng số tiền ông An dùng để trả lương cho nhân viên trong cả năm lớn hơn 2 tỷ đồng? A. Năm 2020. B. Năm 2021. C. Năm 2022. D. Năm 2023.
Lời giải. Áp dụng công thức lãi kép T A r n 1 n .
Trong năm 2016 ông An trả lương nhân viên là 1 tỷ đồng. 1   Trong năm 15
2017 ông An trả lương nhân viên là 1 1       1,15  tỷ đồng.  100 2   Trong năm 15
2018 ông An trả lương nhân viên là 1 1       1,32  tỷ đồng.  100 3   Trong năm 15
2019 ông An trả lương nhân viên là 1 1       1,52  tỷ đồng.  100 4   Trong năm 15
2020 ông An trả lương nhân viên là 1 1       1,75  tỷ đồng.  100 12 5   Trong năm 15
2021 ông An trả lương nhân viên là 1 1       2,011 
tỷ đồng. Chọn B.  100
Bình luận. Nếu xem là bài toán lãi kép thì từ đầu năm 2017 mới sinh lãi.
Dạng 2. Gửi tiền đầu mỗi định kỳ (gửi tiết kiệm)
Cứ đầu mỗi định kỳ gửi vào ngân hàng M triệu, lãi suất kép r% /định kỳ. Hỏi sau n
định kỳ số tiền thu được là bao nhiêu? Ta xây dựng bảng sau: Định kỳ Đầu định kỳ Cuối định kỳ 1 M M 1r 2
M 1 r  M
M 1r M 1r  
M 1 r2 1 r         3 M  r 2      2 1 1 r     M    M  1r
 1r  M .   1 r     
M 1 r3 1 r2 1 r              n  1  n M r ... 1 r     .   1 n n r 1
Vậy sau n định kỳ ta được số tiền: T M 1 r   ... 1 r       M  1r. .   r   Từ đó suy ra Tr Tr M  và n log  1   .  1r  
1 r  1 r n 1      M  1r     
Câu 11. Một người gửi tiết kiệm ngân hàng, mỗi tháng gửi đều đặn vào ngân hàng 1
triệu đồng với lãi suất kép 1% /tháng. Gửi được hai năm ba tháng người đó rút toàn
bộ tiền vốn và lãi. Số tiền người đó nhận được là A.  26 100. 1,01 1      triệu đồng. B.  27
100. 1,01 1 triệu đồng.      C.  26 101. 1,01 1      triệu đồng. D.  27
101. 1,01 1 triệu đồng.      M 1 1 n r 1 
Lời giải. Áp dụng công thức 
T M 1 r . với r
 1%. Chọn D. rn  27 
Câu 12. Một người mỗi đầu tháng đều đặn gửi vào ngân hàng một khoản tiền M
theo hình thức lãi kép với lãi suất 0,6% /tháng. Biết đến cuối tháng thứ 15 thì người
đó có số tiền là 10 triệu đồng (cả vốn và lãi). Hỏi số tiền M gần với số tiền nào nhất trong các số sau?
A. 535.000 đồng. B. 613.000 đồng. C. 635.000 đồng. D. 643.000 đồng. 13 T  10 
Lời giải. Áp dụng TrM  với r
  0,6%. Chọn C.
1 r 1 rn 1         n  15 
Câu 13. Một người muốn có 2 tỷ tiền tiết kiệm sau 6 năm gửi ngân hàng bằng cách
mỗi năm gửi vào ngân hàng số tiền bằng nhau với lãi suất ngân hàng là 8% /năm và
lãi hàng năm được nhập vào vốn. Hỏi số tiền mà người đó phải gửi vào ngân hàng số
tiền hàng năm là bao nhiêu? Giả thiết rằng lãi suất không thay đổi và số tiền được
làm tròn đến đơn vị nghìn đồng. A. 251 triệu. B. 252,5 triệu. C. 253 triệu. D. 253,5 triệu. 10 T   2.10 
Lời giải. Áp dụng Tr M  với r
  8% . Chọn B.
1 r 1 rn 1         n   6 
Câu 14. Đúng ngày 01 mỗi tháng anh A gửi vào ngân hàng 3 triệu đồng với lãi suất
0,7% /tháng. Biết không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng tiền lãi sẽ
nhập vào gốc để tính lãi cho tháng tiếp theo. Hỏi sau ít nhất bao nhiêu tháng thì anh
A có được số tiền cả gốc và lãi nhiều hơn 100 triệu đồng? Giả định trong suốt thời
gian gửi, lãi suất không đổi, được tính lãi ngay từ ngày gửi và anh A không rút tiền ra. A. 28 tháng. B. 29 tháng. C. 30 tháng. D. 33 tháng. 6    T 100.10 
Lời giải. Áp dụng Tr n log  1   với r
  0,7% . Chọn C.
1r M 1 r     M 3 
Dạng 3. Vay trả góp
Vay ngân hàng M triệu đồng, lãi suất r% /định kỳ. Cứ cuối mỗi định kỳ trả ngân
hàng m triệu. Hỏi sau n định kỳ số tiền còn nợ là bao nhiêu? Ta xây dựng bảng sau: Định kỳ Đầu định kỳ Cuối định kỳ 1 M
M 1rm 2
M 1 rm
M 1rm1rm  
M 1 r2 m 1 r1   3 M
 1 r 2 m 1 r 1  
1 r m
M 1 r 3 m 1 r2 1 r 1               n
M 1 rn m 1 rn 1  1 rn2 1           14
Vậy sau n định kỳ, số tiền còn nợ T M r n m  r n 1   r n2 1 1 1 1             m
M 1 r n 1 r  n 1      . r   
M 1 rn r
Từ đó suy ra nếu định kỳ thứ n mà trả hết nợ thì T  0  m  .
1rn 1
Câu 15. (ĐỀ MINH HỌA 2016 – 2017) Ông Việt vay ngân hàng 100 triệu đồng, với
lãi suất 1% /tháng. Ông muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một tháng
kể từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một
tháng, số tiền hoàn nợ ở mỗi lần là như nhau và trả hết tiền nợ sau đúng 3 tháng kể
từ ngày vay. Hỏi theo cách đó, số tiền m mà ông Việt sẽ phải trả cho ngân hàng trong
mỗi lần hoàn nợ là bao nhiêu? Biết rằng lãi suất ngân hàng không thay đổi trong thời gian ông Việt hoàn nợ.  3 100. 1,01 1,0 3 1 A. m  (triệu đồng). B. m  (triệu đồng). 3 1,0 3 1 1 120.1,123 C. 100 1  ,03 m  (triệu đồng). D. m  (triệu đồng). 3 1,123 1 M 100
M 1 rn r
Lời giải. Áp dụng công thức  m  với r
 1% . Chọn B.
1rn 1 n 3 
Câu 16. Một người vay ngân hàng 500 triệu đồng, với lãi suất 1,2% /tháng. Sau đúng
một tháng kể từ ngày vay, người đó bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách
nhau đúng một tháng, số tiền hoàn nợ ở mỗi lần là như nhau và bằng 10 triệu đồng.
Hỏi sau ít nhất bao nhiêu tháng thì người đó trả hết nợ? Biết rằng, lãi suất ngân
hàng không thay đổi trong thời người đó hoàn nợ. A. 70 tháng.
B. 77 tháng. C. 80 tháng. D. 85 tháng. T   0 M 500
Lời giải. Áp dụng công thức  m T
M 1 r n 1 r   n 1      với  . r    m   10 r 1,2%  n Đặt  n a 1 n 5 5
a  1 r, ta được 0  500.a 10.
a   n  log  76,8. Chọn B. 1,012 a 1 2 2
Câu 17. Bạn Hùng trúng tuyển Đại học nhưng vì do không đủ tiền nộp học phí nên
Hùng quyết định vay ngân hàng trong 4 năm, mỗi năm 4.000.000 đồng để nộp học
phí với lãi suất 3% / năm. Sau khi tốt nghiệp Đại học, bạn Hùng phải trả góp hàng
tháng cho ngân hàng số tiền m (không đổi) cùng với lãi suất 0,25% /tháng trong vòng
5 năm. Tính số tiền m hàng tháng mà bạn Hùng phải trả cho ngân hàng (làm tròn
đến kết quả hàng đơn vị).
A. 309.604,14 đồng.
B. 309.718,166 đồng. 15
C. 312.518,166 đồng.
D. 398.402,12 đồng.
Lời giải. Giai đoạn 1: Số tiền bạn Hùng nợ ngân hàng sau 4 năm. Ta xem đây
là bài toán gửi tiết kiệm (Dạng 2) với người cho vay là ngân hàng. Áp dụng công thức M  4000000 1 n r 1  gửi tiết kiệm 
T M 1 r . với r   3%
được T  17236543,24 đồng. rn  4 
Giai đoạn 2. Ta coi như bạn Hùng nợ ngân hàng khoản tiền ban đầu 17236543,24
đồng. Số tiền này bắt đầu được tính lãi và được trả góp trong 5 năm (  60 tháng). M 17236543,24
M 1 r n r  Áp dụng  m  với r   0,25%
ta được m  309718,166. Chọn B.
1rn 1 n  60 
Dạng 4. Bài tập tổng hợp
Câu 18. [Lãi suất tăng dần] Ông Bách dự định đầu tư khoản tiền 20 triệu đồng vào
một dự án với lãi suất tăng dần: 3,35% /năm trong 3 năm đầu, 3,75% /năm tong 2
năm kế tiếp và 4,8% /năm ở 5 năm cuối. Khoản tiền mà ông Bách nhận được (cả vốn
và lãi) cuối năm thứ 10 là A. 25 triệu. B. 30 triệu. C. 35 triệu. D. 40 triệu. 3  
Lời giải. Số tiền ông Bách nhận được sau 3,35
3 năm đầu là T  20. 1      . 1  100  2  
Số tiền ông Bách nhận được sau 3,75
2 năm tiếp theo là T T . 1      . 2 1  100 
Số tiền ông Bách nhận được vào cuối năm thứ 10 là 5 3 2 5  4,8   3,35  3,75  4,8  T T . 1       20. 1        . 1   
triệu đồng. Chọn B.        . 1          30 3 2 100 100  100   100
Câu 19. Năm 2017 số tiền để đổ đầy bình xăng cho một chiếc xe máy trung bình là
70000 đồng. Giả sử tỉ lệ lạm phát hàng năm của Việt Nam trong 10 năm tới không
đổi với mức 5%, tính số tiền để đổ đầy bình xăng cho chiếc xe đó vào năm 2022. A. 5
70000.0,05 đồng. B. 6 70000.0,05 đồng. C. 5
70000.1,05 đồng. D. 6 70000.1,05 đồng.
Lời giải. Số tiền để đổ đầy bình xăng vào năm 2018 là T  70000. 1 0,05 . 1  
Số tiền để đổ đầy bình xăng vào năm 2019 là T T .10,  05  70000.1 0, 2 05 . 2 1 
Số tiền để đổ đầy bình xăng vào năm 2022 là T  70000.10, 5 05 . Chọn C. 5
Câu 20. Một người mua chiếc xe máy Air Blade với giá 45 triệu đồng. Biết rằng giá
trị khấu hao tài sản xe giảm 60% mỗi năm. Biết rằng sau n năm thì giá trị xe chỉ
còn 5 triệu đồng. Giá trị n gần nhất với đáp án nào sau đây? 16 A. 2 năm. B. 2,5 năm. C. 3 năm. D. 3,5 năm.
Lời giải. Theo đề bài suy ra giá trị còn lại của chiếc xe sau mỗi năm là 40%.
Giá trị của chiếc xe sau 1 năm là T  4540%. 1
Giá trị của chiếc xe sau 2 năm là T  4540%40%  45   40%2 . 2
Giá trị của chiếc xe sau n năm là T  45 n 40%n .  
Theo đề bài, ta có T      n       Chọn B. n  n 1 5 45 40% 5 log 2,39. 0,4 9
Câu 21. Đầu năm 2017, anh Hùng có xe công nông trị giá 100 triệu đồng. Biết mỗi
tháng thì xe công nông hao mòn mất 0,4% giá trị, đồng thời anh Hùng làm ra được 6
triệu đồng (số tiền làm ra mỗi tháng là không đổi). Hỏi sau đúng một năm, tổng số
tiền (bao gồm tiền giá xe công nông và tiền anh Hùng làm ra) mà anh Hùng có là bao nhiêu? A. 172 triệu.
B. 167,3042 triệu. C. 144 triệu.
D. 120,3042 triệu.
Lời giải. Số tiền anh Hùng làm ra sau 1 năm là 6.12  72 triệu đồng.
Sau 1 năm giá trị xe công nông còn   12 100. 1 0,4  95,3042 triệu đồng.
Vậy sai một năm số tiền anh Hùng có 167,3042 triệu. Chọn B.
Câu 22. Theo thống kê tài chính của thị xã An Nhơn, tỉnh Bình Định, trong dịp Tết
Nguyên Đán năm 2015, làng nghề trồng mai cảnh xã An Nhơn đạt tổng doanh thu
khoảng 15 tỷ đồng nhờ vào việc bán mai cảnh. Biết rằng trong các năm tiếp theo tổng
doanh thu luôn tăng ổn định và doanh thu trong năm đó cao hơn so với năm trước
6,27%. Hỏi tổng doanh thu của làng nghề trồng mai cảnh xã An Nhơn vào dịp Tết
Nguyên Đán năm 2018 là bao nhiêu? (làm tròn đến tỷ đồng)
A. 17 tỷ đồng. B. 18 tỷ đồng.
C. 19 tỷ đồng. D. 20 tỷ đồng.
Lời giải. Tổng doanh thu vào dịp tết năm 2016 là T  15 1 6,27% . 1  
Tổng doanh thu vào dịp tết năm 2017 là T T 16,27%1516,27%2 . 2 1
Tổng doanh thu vào dịp tết năm 2018 là T  1516,27%3 18 tỷ đồng. Chọn B. 3
Câu 23. [Tiền lương tăng theo chu kỳ] Một kỹ sư được nhận lương khởi điểm là
8000000 đồng/tháng. Cứ sau hai năm lương mỗi tháng của kỹ sư đó được tăng thêm
10% so với mức lương hiện tại. Tổng số tiền kỹ sư đó nhận được sau 6 năm làm việc A. 633600000 đồng. B. 635520000 đồng. C. 696960000 đồng. D. 766656000 đồng.
Lời giải. Tổng tiền lương 2 năm đầu tiên: 6 6
T  8.10 24  192.10 đồng. 1
Theo công thức tính lãi kép, tổng tiền lương 2 năm tiếp theo công nhân đó nhận được
là: T  8.10 24.110%1 6 6  212,2.10 đồng. 2
Tổng tiền lương 2 năm cuối cùng: T  8.10 24110%2 6 6  232,32.10 đồng. 3
Vậy tổng số tiền lương kỹ sư đó nhận được sau 6 năm làm việc là 17
T T T T  635.520.000 đồng. Chọn B. 1 2 3
Câu 24. Theo dự báo với mức tiêu thụ dầu không đổi như hiện nay thì trữ lượng dầu
của nước A sẽ hết sau 100 năm tới. Nhưng do nhu cầu thực tế, mức tiêu thụ tăng lên
4% mỗi năm. Hỏi sau bao nhiêu năm số dầu dự trữ của nước A sẽ hết? A. 40. B. 41. C. 42. D. 43.
Lời giải. Gọi mức tiêu thụ dầu hàng năm của nước A theo dự báo là M 
 lượng dầu của nước A là 100M. Trên thực tế ta có
Lượng dầu tiêu thụ năm thứ 2 là: x M  4%M M 1 4%  1,04M. 2  
Lượng dầu tiêu thụ năm thứ 3 là: x M 1 4% M 1 4% 2 .4%  1,04 M. 3 
Lượng dầu tiêu thụ năm thứ n là: n 1 x 1,04   M. n
Theo đề bài ta có phương trình x x x ... x  100M 1 2 3 n n    n 1,04 1 2 1 11,04 1,04 ...1,04 M 100M   100 
n  41,0354. Chọn B. 0,04
Câu 25. Sau một tháng thi công công trình xây dựng Nhà học thể dục của Trường X
đã thực hiện được một khối lượng công việc. Nếu tiếp tục với tiến độ như vậy thì dự
kiến sau đúng 23 tháng nữa công trình sẽ hoàn thành. Để sớm hoàn thành công
trình và kịp thời đưa vào sử dụng, công ty xây dựng quyết định từ tháng thứ 2 , mỗi
tháng tăng 4% khối lượng công việc so với tháng kề trước. Hỏi công trình sẽ hoàn
thành ở tháng thứ mấy sau khi khởi công? A. 17. B. 18. C. 19. D. 20.
Lời giải. Dự kiến hoàn thành công việc trong 24 tháng.
Như bài trên ta có phương trình  2 n 1 1 1,04 1,04 ... 1,04       M  24M 1,04n 1 
 24  1,04n  1,96  n  log
1,96  17,2. Chọn B. 1,04 0,04
Câu 26. [So sánh lãi không kỳ hạn và lãi có kỳ hạn] Ngân hàng BIDV Việt Nam
đang áp dụng hình thức lãi kép với mức lãi suất: không kỳ hạn là 0,2% /năm, kỳ hạn
3 tháng là 1,2% /quý. Ông A đến ngân hàng BIDV để gửi tiết kiệm với số tiền ban
đầu là 300 triệu đồng. Nếu gửi không kỳ hạn mà ông A muốn thu về cả vốn và lãi
bằng hoặc vượt quá 305 triệu đồng thì ông A phải gửi ít nhất n tháng  * n   . Hỏi
nếu cùng số tiền ban đầu và cũng số tháng đó, ông A gửi tiết kiệm có kỳ hạn 3 tháng
thì ông A sẽ nhận được số tiền cả vốn lẫn lãi là bao nhiêu?
A. 444.785.421 đồng.
B. 444.711.302 đồng.
C. 446.490.147 đồng.
D. 447.190.465 đồng.
Lời giải. Áp dụng công thức lãi kép: T A r   n  Như vậy, n 1 n T 305; 3 A 00 n 99,18. n0,2%
khi gửi không kỳ hạn để được số tiền gồm cả vốn lẫn lãi lớn hơn hoặc bằng 305 triệu
đồng thì ông A phải gửi tối thiểu là 100 tháng. 18
Nếu cũng gửi với số tiền ban đầu là 300 triệu đồng với lãi suất 1,2% /quý trong thời
gian 100 năm (gồm 33 kỳ hạn và 1 tháng không kỳ hạn) 33  
• Số tiền ông A có được sau 1,2
33 định kỳ là: T  300000000. 1       đồng.  100 33      
• Số tiền ông A có được sau 0,2 1,2 0,2 100 tháng là T. 1       300000000. 1        . 1          100  100  100
 444.785.421 đồng. Chọn A.
Câu 27. [Gửi tiết kiệm nhưng số tiền tăng dần] Một người lập kế hoạch gửi tiết
kiệm ngân hàng như sau: Đầu tháng 01 năm 2018, người đó gửi 10 triệu đồng; sau
mỗi đầu tháng tiếp theo, người đó gửi số tiền nhiều hơn 10% so với số tiền đã gửi ở
tháng liền trước đó. Biết rằng lãi suất ngân hàng không đổi là 0,5% mỗi tháng và
được tính theo hình thức lãi kép. Với kế hoạch như vậy, đến hết tháng 12 năm 2019,
số tiền của người đó trong tài khoản tiết kiệm là bao nhiêu? (Làm tròn đến hàng nghìn)
A. 832.765.000 đồng.
B. 918.165.000 đồng.
C. 922.756.000 đồng.
D. 926.281.000 đồng.
Lời giải. Với A  10 triệu đồng, a  10% và r  0,5%. Ta có Số tiền gửi ban đầu Số tiền cuối tháng 1 Đầu tháng 2 gửi thêm A A1 rA1 a
• Suy ra số tiền đầu tháng 2 (sau khi đã gửi thêm) là: A1 r A1 a.
• Số tiền đầu tháng 3 (sau khi đã gửi thêm): A  r2  A  a  r A  a2 1 1 1 1 .
• Số tiền đầu tháng 4 (sau khi đã gửi thêm):
A  r 3  A  a  r 2  A  a2   r  A  a3 1 1 1 1 1 1 . 
• Số tiền đầu tháng n (sau khi đã gửi thêm): A r  n 1  r n 2   a  r  an 2   an 1 1 1 1 ... 1 1 1              .    Cuối tháng n : A r  n 1  r n2  a  r  an2  an 1 1 1 1 ... 1 1 1              1 r   
 an  rn n24 1 1  A
1r  922756396,2 đồng. Chọn C. a r
Câu 28. [Gửi và rút hàng tháng] Ngày 01 tháng 01 năm 2017, ông An gửi 800
triệu đồng vào một ngân hàng với lãi suất 0,5% /tháng. Từ đó, cứ tròn mỗi tháng ông
đến ngân hàng rút 6 triệu để chi tiêu cho gia đình. Hỏi đến ngày 01 tháng 01 năm
2018, sau khi rút tiền, số tiền tiết kiệm của ông An còn lại là bao nhiêu? Biết rằng lãi
suất trong suốt thời gian ông An gửi không thay đổi. A.  11
800. 1,005 72 (triệu đồng). B.  12
800. 1,005 72 (triệu đồng). C.   11
1200 400. 1,005 (triệu đồng). D.   12 1200 400. 1,005 (triệu đồng). 19
Lời giải. Gọi M  800 triệu đồng, r  0,5%, m  6 triệu đồng.
• Số tiền cuối tháng 1 (sau khi đã rút): M 1r . m
• Số tiền cuối tháng 2 (sau khi đã rút): M 1rm1rm  
M  r2 1
m 1 r1.   
• Số tiền cuối tháng n (sau khi đã rút): M r n m  r n 1   rn2 1 1 1 1              n m M r   r  nn 1  2 1 1 1   Chọn D. r   
Câu 29. [Gửi và rút hàng tháng] Một hội khuyến học đã kêu gọi sự ủng hộ của các
nhà hảo tâm được 120 triệu đồng. Hội khuyến học gửi số tiền đó vào ngân hàng với
lãi suất 0,75% /tháng với dự định hàng tháng rút m triệu đồng làm khuyến học cho
học sinh nghèo vượt khó. Hội khuyến học bắt đầu trao quà cho học sinh sau một
tháng gửi tiền vào ngân hàng. Để số tiền (cả lãi và 120 triệu đồng tiền gốc) đủ trao
cho học sinh trong 10 tháng thì số tiền m mà hàng tháng Hội khuyến học rút ra tối
đa (lấy kết quả chính xác đến chữ số thập phân thứ nhất) là A. 12,3. B. 12,4. C. 12,5. D. 12,6.
Lời giải. Áp dụng công thức như câu trên. Số tiền cuối tháng n (sau khi đã rút) là:  m
M 1 r n 1 r  n 1     . r    Vì trao tới tháng thứ m
10 thì hết tiền nên M 1 r n 1 r  n 1      0. r   
M 1 rn .r Suy ra M 1  20; 0 r  ,75%; n 1  0 m
m  12,5. Chọn C.
1rn 1
Câu 30. [Trả góp nhưng bị điều chỉnh lãi suất] Một người vay ngân hàng 40
triệu đồng, với lãi suất 0,85% /tháng. Sau đúng một tháng kể từ ngày vay, người đó
bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ
ở mỗi lần là như nhau và bằng 500 nghìn đồng. Sau một năm mức lãi suất của ngân
hàng được điều chỉnh lên là 1,15% /tháng và người vay muốn nhanh chóng hết nợ nên
đã thỏa thuận trả 1 triệu 500 nghìn đồng cho mỗi tháng. Hỏi phải mất bao nhiêu lâu
người đó mới trả hết nợ? A. 30 tháng. B. 31 tháng. C. 42 tháng. D. 43 tháng.
Lời giải. Sau 1 năm số tiền còn nợ ngân hàng là: M  40000000 m   500000  m T
M 1 r n 1 r   n 1      với 
ta được T  37987647 đồng. r    r   0,85% n12 
Để trả hết số nợ còn lại ta cần có 20
M T  37987647 1   m
M 1 r  1n 1  1 n r 1      0 với m  1500000
ta được n  30,1 tháng. 1 1  1  1 r     1 1 r  1,15% 
Vậy cần 12 31  43 tháng để trả hết nợ. Chọn D. 21 PHƯƠNG TRÌNH MŨ
PHƯƠNG TRÌNH LOGARIT
Phần 1. Phương trình mũ – phương trình logarit………………………………….………
Phần 2. Phương trình mũ chứa tham số…………………………………………………………….
Phần 3. Phương trình logarit chứa tham số…………………………………………………..… 1
Phần 1. Phương trình mũ–Phương trình logarit
Câu 1. Số nghiệm của phương trình 1
2 log x  log 1 x  log
x 2 x  2 là 2 1   2   2 2 A. 0. B. 1. C. 2. D. 4.   Câu 2. Cho x x 1
0  a  1, phương trình log aa x   a    có bao a  2   2 2 4 2 1
loga  a nhiêu nghiệm? A. 0. B. 1. C. 3. D. 4.
Câu 3. Phương trình 2 log cot x  log cos x có tất cả bao nhiêu nghiệm thuộc khoảng 3 2 0;2018 ? A. 321. B. 322. C. 642. D. 643.
Câu 4. Phương trình log x 23  2 log x 1 có bao nhiêu nghiệm? 3 2   A. 0. B. 1. C. 2. D. 4. Câu 5. Gọi 2 2 2
x là nghiệm của phương trình 3x  3
4x 4 3x 4x      7 . Khẳng 0
định nào sau đây đúng?   A. 3 x  0. B. x  0;1 . C. x   ; 2. D. x   2; 3 . 0   0   0 0    2  
Câu 6. Tập nghiệm của bất phương trình 2x 1  0 3  x2 x 5  13 x2 5 4.5  5
là đoạn a;b.
Tổng a b bằng A. 14. B. 16. C. 18. D. 20.
Câu 7. Phương trình x x   x x   2
x x x x   3 3 2 3 3 1 2 x 3  x 2 1 3 2 .2018 3 1 .2018 có bao nhiêu nghiệm? A. 1. B. 2. C. 3. D. 4.
Câu 8. Số nghiệm của phương trình   log4 x x   log4 x 2 3 5 . 3 5  x 1 là A. 0. B. 1. C. 2. D. 3. 3 sin x sin x     Câu 9. Trên  1 1
0;2018 phương trình          
 sin 3x có bao nhiêu nghiệm? 27 81 A. 1925. B. 1927. C. 1928. D. 1930.  
Câu 10. Trên khoảng 0;    
phương trình sin 2x cos x  1 log sin x có bao nhiêu 2    2  nghiệm ? A. 0. B. 1. C. 2. D. 3.
Câu 11. Bất phương trình 2x 1 1  x 2 3
3  x 4x 3 có bao nhiêu nghiệm nguyên nhỏ hơn 10 ? A. 6. B. 7. C. 8. D. 9. 2
Câu 12. Biết phương trình 2 x 1 x 1 log  2 log
có nghiệm duy nhất x a b 2 5 3 x 2 x trong đó ,
a b là các số nguyên. Tổng a b bằng A. 1. B. 1. C. 2. D. 5.   sinx   
Câu 13. Tổng các nghiệm của phương trình  4 e
  tan x trên đoạn 0;50 bằng A. 1853 . B. 2105 . C. 2475 . D. 2671 . 2 2 2 2
Câu 14. Tổng các nghiệm của phương trình log 1  2x x
x x 1 bằng 2   A. 0. B. 1. C. 2. D. 3.
Câu 15. Tích các nghiệm của phương trình 3x 3
x 2  3    4 3 2 3 2 2  x x x 1  0 bằng A. 2. B. 1. C. 1. D. 2.
Câu 16. Phương trình log  2 2x 1   1  x  log  2 2x 1   2 1  2x 1 có bao 2 2 nhiêu nghiệm nguyên? A. 0. B. 1. C. 2. D. 4.
Câu 17. Số nghiệm của phương trình 1 1   x 2 là x lnx   1 A. 1. B. 2. C. 3. D. 4.
Câu 18. Phương trình log  2
x  4  x  log 8x 16 có bao nhiêu nghiệm? 2  2   A. 0. B. 1. C. 2. D. 3.
Câu 19. Cho phương trình 2
5x x 6  x x log x   2 x x 2
log x  5  5 6  x x . 2 2
Gọi S  a;b là tập nghiệm của bất phương trình đã cho. Khi đó b a bằng A. 1 . B. 2. C. 5 . D. 7 . 2 2 2
Câu 20. Tích các nghiệm của phương trình log  x 3x 2 2 2 2 x 3  x 1 5       2 bằng 3 A. 1. B. 2. C. 4. D. 9.
Câu 21. Số nghiệm của phương trình x 1  2 3
x 2x  2  x 1 là A. 0. B. 1. C. 2. D. 3.
Câu 22. Cho phương trình log  2x 5x 5  1log  2x 5x 7  2. Tổng tất cả 2 3 
các nghiệm của phương trình đã cho bằng A. 5. B. 9. C. 10. D. 15.
Câu 23. Số nghiệm của phương trình x x 8 1 3 2  2  là log  2 x 2x  3 2  A. 0. B. 1. C. 2. D. 3.
Câu 24. Số nghiệm của phương trình 3 2
2x 3x  log  2
x 1  log x  0 là 2  2 A. 0. B. 1. C. 2. D. 3. 3
Câu 25. Cho phương trình 2 x 1   2 2016   1 .2017x x
 1. Khẳng định sau đây đúng?
A. Phương trình có tổng các nghiệm bằng 0.
B. Phương trình có nghiệm duy nhất.
C. Phương trình có hai nghiệm dương phân biệt.
D. Phương trình có nhiều hơn hai nghiệm.
Phần 2. Phương trình mũ chứa tham số
Câu 1. Cho phương trình 2
log2 x  m   log2 x 2 3 2 3 .3
m 3  0 với m là tham số. Tập
hợp tất cả các giá trị của m để phương trình đã cho có hai nghiệm phân biệt x , x 1 2
thỏa mãn x x  2 là 1 2 A. 0;. B.  \1;  1 .
C. 1;.
D. 1;\0.
Câu 2. Biết phương trình x mx 1 4 1 2   
8  0 có hai nghiệm x , x thỏa mãn điều 1 2
kiện x 1 x 1  6. Khẳng định nào sau đây đúng? 1  2 
A. m  0.
B. 0  m  2.
C. 1 m  3. D. m  3.
Câu 3. Có bao nhiêu giá trị nguyên của tham số m trên khoảng 2018;2018 để phương trình 2 x 1
  m   x 2 6.2 7
48 .2  2m 16m  0 có hai nghiệm dương x , x thỏa 1 2 mãn x x 15 ? 1 2 A. 1993. B. 1994. C. 3986. D. 3988.
Câu 4. Cho phương trình 2 2 x 2x 1  x 2x 2 4  . m 2
3m 2  0. Tập tất cả các giá trị của
tham số m để phương trình đã cho có 4 nghiệm phân biệt là A. 2;. B. 2,.
C. 1;. D.  ;   1 2;.
Câu 5. Có bao nhiêu giá trị nguyên m thuộc đoạn 2018;2018 để phương trình 2 x x    2 2 2 x 2 x x 2 .9 2 1 .6  .4 x m m m
 0 có nghiệm thuộc khoảng 0;2? A. 2010. B. 2011 . C. 2012. D. 2013. 2 2
Câu 6. Cho phương trình   x m  x 2 x 2 5 1 5 1  2
. Tập tất cả các giá trị của
tham số m để phương trình có đúng bốn nghiệm phân biệt là a;b. Hiệu b a bằng A. 3 . B. 1 . C. 1 . D. 49 . 4 16 64 64 2 2
Câu 7. Cho phương trình  x m x 2 x 1 4 7 4 7 3     
 0. Gọi S là tập tất cả các
giá trị của tham số m sao cho 36m   và phương trình đã cho có đúng hai nghiệm
phân biệt. Số phần tử của S bằng A. 1. B. 24. C. 25. D. 26. 4
Câu 8. Cho phương trình .9x 2   1 6x  .4x m m m
 0. Tìm tất cả các giá trị của tham
số m để bất phương trình nghiệm đúng với mọi x thuộc 0;  1 .
A. m  6.
B. 6  m  4.
C. m  4.
D. m  6.
Câu 9. Tập tất cả các giá trị của tham số m để phương trình 3x 3  . 9x m 1 có
đúng 1 nghiệm có dạng a;b c. Tổng a b c bằng A. 4. B. 11. C. 14. D. 15. x
Câu 10. Tìm tất cả các giá trị thực của tham số m để phương trình 2 4 2 x
m e e 1 có nghiệm thực.
A. 1 m  0. B. 0  m 1. C. 2 0  m  .
D. 1  m 1. e e Câu 11. Cho hàm số   x4     7 3 1 2 x f x x
6x 3. Khi phương trình f  2
7  4 6x 9x 3m1 0 có số nghiệm nhiều nhất thì giá trị nhỏ nhất của tham
số m m . Khẳng định nào sau đây đúng? 0
A. m  0;1 . B. m  1;2 .
C. m  2;3 .
D. m  3;4 . 0   0   0   0  
Câu 12. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 5;5 để phương trình x
e mx   1 có nghiệm duy nhất? A. 5. B. 6. C. 7. D. 10.
Câu 13. Có bao nhiêu giá trị nguyên của tham số m thuộc 2000;2000 để log b log 2 a b a ab
m log b 1 với ,
a b là các số thực lớn hơn 1? a A. 1999. B. 2000. C. 2001. D. 2199.
Câu 14. Tìm tất cả các giá trị của tham số m để phương trình 2 2
2 x m x có hai nghiệm thực phân biệt. m  1 m  1 m  2 A.  . B.C.D.  . . 3  m  1. m 1  m  2  m  2 
Câu 15. Phương trình 3 x2 m 3  x  3 2 x x x mx2 x 1 2 6 9 2 2       1 có ba nghiệm phân
biệt khi và chỉ khi m a;b. Giá trị biểu thức 2 2
T b a bằng A. 36. B. 48. C. 64. D. 72.
Câu 16. Cho phương trình 3m m e e   2 x   x  2 2 1
1 x 1 x . Tập hợp tất cả các
giá trị thực của tham số m để phương trình có nghiệm là         A. 1 0; ln2.      B. 1 0; . C. 1 ;   ln 2. D. 1  ln 2;.  2   e  2  2    
Câu 17. Có bao nhiêu giá trị nguyên dương của m nhỏ hơn 2018 để phương trình 2 1 1 3 2 x   xm  2
x mx x x x e
có nghiệm thực dương? 4 x 1 5 A. 2014. B. 2015. C. 2016. D. 2017.
Câu 18. Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để phương trình x x
m m e e có nghiệm thực? A. 9. B. 10. C. 11. D. Vô số.
Câu 19. Biết rằng a là số thực để phương trình 9x  9  .3x a
cosx có nghiệm duy
nhất. Hỏi a thuộc khoảng nào sau đây? A. 8;4. B. 4;2. C. 4;10.
D. 12;18.
Câu 20. Cho tham số thực ,
a biết phương trình xx e e
 2 cosax   1 có 5 nghiệm
thực phân biệt. Hỏi phương trình xx e e
 2 cosax 4 2 có bao nhiêu nghiệm thực phân biệt? A. 5. B. 10. C. 11. D. 20.
Phần 3. Phương trình loagarit chứa tham số
Câu 1. Cho phương trình 2
log x 5m   2
1 log x  4m m  0. Biết phương trình có 2 2 2
nghiệm phân biệt x , x thỏa x x  165. Giá trị của x x bằng 1 2 1 2 1 2 A. 16. B. 119. C. 120. D. 159.
Câu 2. Giá trị thực của tham số m để phương trình 2
log x 3 log x  2m 7  0 có 3 3
hai nghiệm thực x , x thỏa mãn x  3 x 3
72 thuộc khoảng nào sau đây? 1   2  1 2  7   7 7   21 A.     ;0        . B. 0; . C.  ;7. D. 7; .  2     2   2     2 
Câu 3. Cho phương trình m 2 2
log x  4 log x m 2  0. Tập tất cả các giá trị 3 3  
của tham số thực m để phương trình có hai nghiệm x , x thỏa 0  x 1 x là 1 2 1 2 A.  ;  2.
B. 2;2. C. 2;. D.  \2;2.
Câu 4. Cho phương trình 2
log x 2m   2
1 log x m  2m  0. Tập tất cả các giá trị 2 2
của tham số m để bất phương trình nghiệm đúng với mọi x 1;2 là m  2 m  2
A. 1 m  0. B. 1 m  0. C.  . D.   . m 1  m 1 
Câu 5. Cho phương trình 2 x x 2 2 log 2  2
 2   log m 2 . 4   2  Có bao nhiêu giá trị
nguyên của tham số m để phương trình vô nghiệm? A. 3. B. 4. C. 5. D. 6.
Câu 6. Cho phương trình 2 log  2 2
2x x  2m  4m  log  2 2
x mx 2m  0. Tập tất 4 1  2
cả các giá trị của tham số m để phương trình có hai nghiệm phân biệt x , x thỏa 1 2 mãn 2 2
x x 1 có dạng a;bc;d với a b c d. Tổng a b 5c  2d bằng 1 2 A. 0. B. 1. C. 2. D. 3. 6
Câu 7. Cho phương trình 2 2 2
log cos x m log cos x m  4  0. Có bao nhiêu giá trị
nguyên của tham số m để phương trình đã cho vô nghiệm? A. 0. B. 1. C. 3. D. 4.
Câu 8. Cho phương trình 2 log  2
2x 5x  4 log x x
Gọi S là tập  mx  2 2 6 . mx 5 5 
tất cả các giá trị m sao cho 10m   và phương trình có nghiệm duy nhất. Số phần tử của S bằng A. 13. B. 14. C. 15. D. 16.
Câu 9. Cho phương trình log  2
x  2mx  log 2x m 1  0. Có bao nhiêu giá trị 3  1   3
nguyên của tham số m để phương trình có nghiệm duy nhất? A. 0. B. 1. C. 2. D. 3.
Câu 10. Có bao nhiêu giá trị nguyên của tham số m để bất phương trình   2x    2 log 5 log 1
log mx  4x m đúng với mọi x   ? A. 1. B. 2. C. 4. D. Vô số.
Câu 11. Tìm m để bất phương trình  2 log
x  2x m  
1  0 đúng với mọi x . m A. m  0. B. m  1. C. m 1. D. m 1.
Câu 12. Cho phương trình 2 2 log a x x 5 6 x      log
3 x 1 . Có bao nhiêu 2   2   2a   
giá trị của biến x để phương trình có nghiệm đúng với mọi số thực a ? A. 0. B. 1. C. 2. D. 4.
Câu 13. Cho phương trình 5x m  log x m với m là tham số. Có bao nhiêu giá 5  
trị nguyên của m 20;20 để phương trình đã cho có nghiệm? A. 9. B. 19. C. 20. D. 21.
Câu 14. Cho phương trình ln m  2 sin x  lnm 3sin x  sin x  
với m là tham số
thực. Có bao nhiêu số nguyên m để phương trình có nghiệm? A. 3. B. 4. C. 5. D. 6.
Câu 15. Cho phương trình x 2 1 2
.log  2 2 3  4 xm x x
.log 2 x m  2 với m là 2  2  
tham số thực. Tìm tất cả các giá trị của m để phương trình có đúng hai nghiệm phân biệt.         A. 1 3 m   ;         ;  . B. 1 3 m  ;
    ;.  2 2   2 2    C. m  ;    1 1;. D. m  ;   1 1;.
Câu 16. Cho phương trình log  3
mx x  log  2
14x  29x 2  0 với m là tham số 2 1  2
thực. Gọi S   ,
a b là tập tất cả các giá trị của m để phương trình có ba nghiệm phân
biệt. Hiệu b a bằng A. 1 . B. 5 . C. 2 . D. 5. 2 2 3 3 7
Câu 17. Cho phương trình 2 2
log x  log x 1 2m 1  0. Tập tất cả các giá trị của 3 3
tham số m để phương trình có nghiệm thuộc đoạn  3 1;3   là  
A. 0  m 1.
B. 0  m  2 . C. 13 0  m  .
D. 1 m  2 . 6
Câu 18. Cho phương trình m ln x  ln1 x .
m Tập tất cả các giá trị của tham số m
để phương trình có nghiệm thuộc khoảng 0;  1 là A. e
  m e.
B. 1 m e. C. m  0. D. m  0.
Câu 19. Cho phương trình 2
log x 2 log x 3  m log x 3 với m là tham số thực. 2 2  2 
Tập tất cả các giá trị của m để phương trình có nghiệm thuộc 16; là
A. 1 m  2 .
B. 1 m  5 .
C. 1 m  5 .
D. 3  m  5 . 4
Câu 20. Cho phương trình log  2
x x 1.log  2
x x 1 log x x  với m  2 1 2 5 
m là tham số dương khác 1. Có bao nhiêu giá trị nguyên của m để phương trình đã
cho có nghiệm x 2; ? A. 1. B. 2. C. 3. D. Vô số.
Câu 21. Cho phương trình  2 x   2  2
x  m  2 x    2 1 .log 1 2 1 .log x  
1  m  4  0. Có
bao nhiêu số nguyên m thuộc 10;10 để phương trình đã cho có hai nghiệm phân
biệt thỏa mãn 1 x  3 ? A. 7. B. 9. C. 12. D. 14.
Câu 22. Cho bất phương trình 3 2
log x 2x  
1mx m  1. x   Có bao nhiêu giá trị
m nguyên trong đoạn 2017;2017 để bất phương trình luôn đúng với x  2 ? A. 2010. B. 2017. C. 2018. D. 2019.
Câu 23. Cho phương trình 2 x
 2mx 2 x  2 mx      2 2018 1 ln x   1  2018. Có bao  
nhiêu giá trị nguyên m thuộc đoạn 2018;2018 để phương trình có nghiệm duy nhất
thuộc khoảng 1;? A. 2017. B. 2018. C. 2019. D. 2020.  
Câu 24. Cho phương trình 2 m m 7 2 2 4 3
2 sin x 3cos x  log 2 
 . Có bao nhiêu giá trị 2  2
nguyên của tham số m để phương trình đã cho có nghiệm? A. 0. B. 1. C. 2. D. 3.
Câu 25. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 10;10 để phương
trình log x 2 log x 1  m có ba nghiệm phân biệt? 3 2   2 3 A. 8. B. 10. C. 11. D. 12. 8 PHƯƠNG TRÌNH MŨ
PHƯƠNG TRÌNH LOGARIT
Phần 1. Phương trình mũ – phương trình logarit………………………………….……… 02
Phần 2. Phương trình mũ chứa tham số……………………………………………………………. 10
Phần 3. Phương trình logarit chứa tham số…………………………………………………..…18 1
Phần 1. Phương trình mũ – phương trình logarit
Câu 1. Biết phương trình 1
2 log x  log 1 x  log
x 2 x  2 có nghiệm 2 1   2   2 2
x a b c với  ,
a c  1. Tổng a b c bằng A. 2. B. 1 C. 1. D. 5.
Lời giải. Điều kiện: 0  x 1. Phương trình 2
 log x log 1 x  log x 2 x  2 2 2   2   2 x x x x  log
 log x 2 x 2 2 2 
x 2 x  2    2  0 2 2 1 x 1 x   2 1 1  x x x x
 1 (vô nghiệm) hoặc
 2  x  2 x 2  0  x  4 2 3. Chọn D. 1 x 1 x   Câu 2. Cho x x 1
0  a  1, phương trình log aa x   a    có bao a  2   2 2 4 2 1
loga  a nhiêu nghiệm? A. 0. B. 1. C. 3. D. 4.
Lời giải. Phương trình a  
a x x a a  2 2 x 4 x 2  2 a  2 log 2 log 1
 log a   a a   a a  2 2 x 4 x 2  2 x 2 log x log a a  2 1   2xx a 2 2 2
a   2x2x a  2a  1 x  0   2   2 x  2x  2 x 2 x 2 a
a  2x2x a   1     x  2 .  Chọn D. 2 
x  2x  0   x  1 3 
Câu 3. Phương trình 2 log cot x  log cos x có tất cả bao nhiêu nghiệm thuộc khoảng 3 2 0;2018 ? A. 321. B. 322. C. 642. D. 643. cos  x  0   
Lời giải. Điều kiện:  cot 
x  0  x k2;  k2, . k     2  s  in x  0  t     cot  x    3 t 1 2 2 cot 
x  3  tan x
Đặt 2 log cot x log cos x t        3t . 3 2  t     2 cos x 2  cos  x  4t  Do 1 2 1 tan x  nên ta có 1 1 1   t  1. 2 cos x 3t 4t 2  1  cot  x    x   k  Suy ra  3  3   
x   k2 , k  .   1  3 cos  x  
x    k2  2  3 Vì 1 1 2018
x 0;2018 nên 0 22018 k k k            k  0;1,...,  321 . 3 6 6 2 Chọn B.
Câu 4. Phương trình log x 23  2 log x 1 có bao nhiêu nghiệm? 3 2   A. 0. B. 1. C. 2. D. 4.
Lời giải. Điều kiện: x  1. Phương trình  3log x  2  2 log x 1 . 3   2   2
x 2  3 t t t     Đặt  t t 8 1
3 log x  2  2 log x 1  6t  
 9  8 1  1        *      . 3   2   3
x 1  2 t 9 9 
Vế phải là hàm nghịch biến-Vế trái là hằng số nên phương trình có nghiệm duy nhất. 1 1     Mà 8 1 1         
   t  1 là nghiệm duy nhất của phương trình *. Suy ra x  7 là 9 9
nghiệm duy nhất của phương trình đã cho. Chọn B. Câu 5. Gọi 2 2 2
x là nghiệm của phương trình 3x  3
4x 4 3x 4x      7 . Khẳng 0
định nào sau đây đúng?   A. 3 x  0. B. x  0;1 . C. x   ; 2. D. x   2; 3 . 0   0   0 0    2   3x  3  a
Lời giải. Đặt 
. Phương trình trở thành     2 2 2 a b a b
4x 4  b  b  0 2 2 2 2 2
a b a b  2ab  2b  2ab  0  ba b  0   . a b   •  0  4x b
4  0  x  1.
•    3x  4x a b
 7. Phương trình có nghiệm duy nhất x  1.
Vậy phương trình có nghiệm x 1. Chọn C. 0
Câu 6. Tập nghiệm của bất phương trình 2x 1  0 3  x2 x 5  13 x2 5 4.5  5
là đoạn a;b.
Tổng a b bằng A. 14. B. 16. C. 18. D. 20. x 5 u   5   0 2
Lời giải. Điều kiện u x  2. Đặt  , ta được 4u  5v 3 x2 v   5  0  v 2 2
u 4uv 5v  0  u 5vu v 0  u  5v. Hay x 5  3 x2 1 5 5  
x 6  3 x 2 
S  2;18. Chọn D.
Câu 7. Phương trình x x   x x   2
x x x x   3 3 2 3 3 1 2 x 3  x 2 1 3 2 .2018 3 1 .2018 có bao nhiêu nghiệm? 3 A. 1. B. 2. C. 3. D. 4. 2 a
  x 3x 1
Lời giải. Đặt 
, phương trình trở thành 3 b
  x 3x 2 
  .2018a  .2018b  2018b   1  2018a a b b a a b   1  0. a b • Nếu   a  0, 0
b  chia hai vế cho ab, ta được 2018 1 2018 1   0. Phương trình a b a b này vô nghiệm do 2018 1   0 và 2018
1  0 với mọi ,ab  0. Thật vậy: nếu a  0 a b
thì 2018a 1 0; nếu a  0 thì 2018a 1 0. 2
x 3x 1 0
• Kiểm tra thấy a  0 hoặc b  0 thỏa mãn. Suy ra  .  Chọn D. 3
x 3x  2  0 
Câu 8. Số nghiệm của phương trình   log4 x x   log4 x 2 3 5 . 3 5  x 1 là A. 0. B. 1. C. 2. D. 3. log4 x  
Lời giải. Điều kiện: log x 4 x
x  0. Ta có 3 5 4       .  3 5  x 3  5log4 2
Do đó phương trình tương đương với  x x 3  5log4 2   x 1 . x 3  5log4     x a 3  5log4  0 Đặt b
, phương trình trở thành a   b 1  2 b   x  0 a            b a b  
     a b 1 a b 1 0 1         0   . a   a a 1  • x
a  1  3 5log4 1  log x  0  x 1. 4 •    x a b 3  5log4 log4 3 5 2 2 
x x x
x  1. Chọn B. 3 sin x sin x     Câu 9. Trên  1 1
0;2018 phương trình          
 sin 3x có bao nhiêu nghiệm? 27 81 A. 1925. B. 1927. C. 1928. D. 1930. 3 3sin x 4 sin x    
Lời giải. Phương trình 1 1 3           
 3sin x  4 sin x 3 3 3 3sin x 4 sin x     1 1 3      3sin x        4 sin x. 3 3 t   Xét hàm 1 k
f (t)       t
trên  và đi đến kết quả 3
3sin x  4 sin x   x  . 3 3 Vì k 2018.3
x 0;2018 nên 0 2018 0 k k       
k 0;1927. Chọn C. 3 4  
Câu 10. Trên khoảng 0;    
phương trình sin 2x cos x  1 log sin x có bao nhiêu 2    2  nghiệm ? A. 0. B. 1. C. 2. D. 3.   s  in x  0
Lời giải. Vì x 0;      . 
Do đó phương trình tương đương với  2  cos  x  0 
sin 2x cos x  log cos x  1 log sin x  log cos x 2   2   2  
 log cos x cos x  log sin 2x sin 2x. 2   2    x  0;  Xét    
f t  log t t trên0;  1 và đi đến kết quả 2
cos x  sin 2x  x  . Chọn B. 2 6
Câu 11. Bất phương trình 2x 1 1  x 2 3
3  x 4x 3 có bao nhiêu nghiệm nguyên nhỏ hơn 10 ? A. 6. B. 7. C. 8. D. 9.
Lời giải. Điều kiện: x 1. Phương trình 2x  1 1    x   x 2 3 2
1  3  x 2x 1 2x  1 1  x  x  1 1 3 2 1 3      x  2 1 . x  3 Xét hàm   1  2  3t f t
t trên 0; và đi đến kết quả 2x   1  x 1   . x 1 
Mà x 10 và x   nên có 8 giá trị nguyên thỏa mãn bất phương trình. Chọn C.
Câu 12. Biết phương trình 2 x 1 x 1 log  2 log
có nghiệm duy nhất x a b 2 5 3 x 2 x trong đó ,
a b là các số nguyên. Tổng a b bằng A. 1. B. 1. C. 2. D. 5.
Lời giải. Điều kiện: x 1. Phương trình log 2 x 1 log x 2 log x 1 log 2 x        5   5 3   3  
 log 2 x 1  2 log 2 x  log x  2 log x 1 . 5   3 5 3  
Xét f t log t 2 log t 1 với t 1, ta được 2 x 1 x x  32 2. Chọn D. 5 3     sinx   
Câu 13. Tổng các nghiệm của phương trình  4 e
  tan x trên đoạn 0;50 bằng A. 1853 . B. 2105 . C. 2475 . D. 2671 . 2 2 2 2 1 sin 1 x
sin xcos x 2
Lời giải. Điều kiện: sin x e sin x
cos x  0. Phương trình 2  e    . * 1 cos x cos x cos x 2 e 1 1 sin x cos x 2 2 Do e e x k ,
k   không là nghiệm của phương trình nên *   . sin x cos x 5 t   t t 2 e  1 2    Xét hàm   ef t  trên 1; 
1 \0. Ta có f t 2   0, 1; t  1 \ 0 . 2     t t
Suy ra hàm số f t nghịch biến trên từng khoảng 1;0 và 0;  1 . Mà
f sin x  f cos x  sin x  cos x x   k mà x 0;50 k 0;49. 4 49 49  
Vậy tổng các nghiệm cần tính 2475
 k 50. k  .   Chọn C.   k 4 4 k 2 0 0
Câu 14. Tổng các nghiệm của phương trình log 1  2x x
x x 1 bằng 2   A. 0. B. 1. C. 2. D. 3.
Lời giải. Điều kiện: x  0. Phương trình  log 1  1  2x x xx 2      log 1 
1  log 2x  2x x x . 2     2 x  0
Xét hàm f t log t t với t  0 và đi đến kết quả x 1 2x   . Chọn B. 2 x 1 
Câu 15. Tích các nghiệm của phương trình 3x 3
x 2  3    4 3 2 3 2 2  x x x 1  0 bằng A. 2. B. 1. C. 1. D. 2. 3 x 3  x 2
Lời giải. Phương trình 2 3 3x4 
x 3x  2 2  0 4 3 2  x 3 x 2   3 x   3x4 2 2  2
3x 4. x  2 Xét hàm   2t f t
t trên  và đi đến kết quả 3
x 2  3x  4   . Chọn A.x 1 
Câu 16. Phương trình log  2 2x 1   1  x  log  2 2x 1   2 1  2x 1 có bao 2 2 nhiêu nghiệm nguyên? A. 0. B. 1. C. 2. D. 4.
Lời giải. Điều kiện: x  0. 2 Phương trình đã cho 2x  log  x  log  2 2x 1   2 1  2x 1 2 2 2 2x 1 1  log  2 2x log  2 2x 1   1  x  log  2 2x 1   2 1  2x 1 2 2 2
 1 2 log x x  2 log  2 2x 1   2 1  2x 1 2 2
 2 log x x  2 log  2 2x 1   1  2 2x 1 1 . 2 2 
Xét hàm f t 2 log t t trên 0; và đi đến kết quả 2
x  2x 1 1 2 2
x 1  2x 1  x  2. Chọn C.
Sai lầm hay gặp là biến đổi x log  2x 1  2 2 2 2 1  x  log  2x 1 2 2 2 2x 1 1 6  2 log  2 2x 1   1  2
2x 1 1  2 log x x và xét hàm f t  2 log t t trên 2  2 2
0; nhưng hàm này không đơn điệu trên 0;.
Câu 17. Số nghiệm của phương trình 1 1   x 2 là x lnx   1 A. 1. B. 2. C. 3. D. 4.
Lời giải. Điều kiện: 1 x  2. Xét hàm 1 1 f x 1 1  
x  2. Ta có f x    1 0 với x lnx   1 2 xx   2 1 ln x   1
mọi x thuộc tập xác định. Suy ra f x nghịch biến trên từng khoảng xác định. x 1 2  f     f 2  
Dựa vào BBT suy ra phương trình đã cho có hai nghiệm phân biệt. Chọn B.
Câu 18. Phương trình log  2
x  4  x  log 8x 16 có bao nhiêu nghiệm? 2  2   A. 0. B. 1. C. 2. D. 3.
Lời giải. Điều kiện: x  2. Phương trình tương đương log 2x   2 x 4    log 8x 16 2  2      2x xx x 8 2 x  4 2  8x 16 
x 22  8  2  . x 2 Ta có   2x f x
là hàm đồng biến; gx 8 
là hàm nghịch biến nên phương trình có x 2
nghiệm duy nhất. Mà f   3  g  
3 suy ra x  3 là nghiệm duy nhất. Chọn B.
Câu 19. Cho phương trình 2
5x x 6  x x log x   2 x x 2
log x  5  5 6  x x . 2 2
Gọi S  a;b là tập nghiệm của bất phương trình đã cho. Khi đó b a bằng A. 1 . B. 2. C. 5 . D. 7 . 2 2 2
Lời giải. Điều kiện 0  x  3.
Bất phương trình đã cho  x log x  2
x 1 6  x x 5 2
x 1 6  x x  0 2  x log x  5 x   2 1 6 x x         0. * 2   
Xét f x x log x trên 0;3. Lập BBT ta có max f x f   3  3log 3  5. 2   2 0;3
Suy ra x log x 5  0, 0
x  ;3 . Do đó   2
*  x 1 6  x x  0. Giải bất phương 2    
trình này và kết hợp với điều kiện ta được tập nghiệm 5 S   ;3.  Chọn A. 2  7
Câu 20. Tích các nghiệm của phương trình log  x 3x 2 2 2 2 x 3  x 1 5       2 bằng 3 A. 1. B. 2. C. 4. D. 9.
Lời giải. Điều kiện: 2
x 3x  2  0. Đặt 2
t x 3x  2  0.
Khi đó phương trình trở thành log t 2 2 t 1 5     2. * 3 Xét   1 log  2 2 1 5t f t t    
với t  0. Ta có f t 2 t 1 2t.5    
ln 5  0, t  0. 3 t 2ln3
Suy ra hàm số f t đồng biến trên 0;. Mà f t f  
1 suy ra t  1 là nghiệm
của phương trình *. Với t 1, ta có 2
x – 3x 1  0  x .x  1. Chọn B. 1 2
Câu 21. Số nghiệm của phương trình x 1  2 3
x 2x  2  x 1 là A. 0. B. 1. C. 2. D. 3.
Lời giải. Đặt t x 1. Phtrình trở thành t 2 t
t   t   2 3 1 3
t 1 t1. * Xét   t f t   2 3
t 1 t1.     Ta có    t f t   1  3t 3t ln 3    t  1 2
t 1 t 3  2t 1t ln3      0. 2  2     1 t 1    t 1
Do đó phương trình f t 0 có tối đa 1 nghiệm. Mà f 0 0.
Do đó t  0 là nghiệm duy nhất của phương trình *.
Hay phương trình đã cho có nghiệm duy nhất x  1. Chọn B.
Câu 22. Cho phương trình log  2x 5x 5  1log  2x 5x 7  2. Tổng tất cả 2 3 
các nghiệm của phương trình đã cho bằng A. 5. B. 9. C. 10. D. 15. Lời giải. Đặt 2
t x 5x  5  0. Phương trình trở thành log t  
1  log  2t 2  2. 2 3 
log t 1  log 2 1 2  
• Xét t 1, ta có 2  2 
 log t 1  log t  2  2. log  t  2  log 3  1 3   2   3 2   3 
log t 1  log 2 1 2   • Xét 0  2 t 1, ta có  2 
 log t 1  log t  2  2. Dấu ''  '' log  t  2  log 3  1 3   2   3 2   3  xảy ra 2 2 2
x 5x 5  1  x 5x 5  1  x 5x  4  0 
x x  5. Chọn A. 1 2
Câu 23. Số nghiệm của phương trình x x 8 1 3 2  2  là log  2 x 2x  3 2  A. 0. B. 1. C. 2. D. 3.
Lời giải. Áp dụng bất đẳng thức Côsi, ta có x 1  3x x 1  3 2  2
 2 2 .2 x  8   VT  8.
Lại có x x   x  2 2 2 3
1  2  2 nên suy ra log  2
x 2x  3  log 2  1   VP  8. 2  2 8 x 1  3 2   2 x  8 Do đó x x 8 1 3 2 2     
x  1. Chọn B.
log x 2x  3
log x 2x 3 1 2  2   2  2  
Câu 24. Số nghiệm của phương trình 3 2
2x 3x  log  2
x 1  log x  0 là 2  2 A. 0. B. 1. C. 2. D. 3.  
Lời giải. Điều kiện: 1
x  0. Phương trình tương đương 3 2
2x 3x  log x     0. 2  x   
Áp dụng bất đẳng thức Côsi, ta có 1 1
x   2 suy ra log x     log 2  1. x 2 2  x    Do đó 1
2x 3x  log x
   2x 3x 1  x  2 3 2 3 2 1
2x 1  0, x  0. 2    x 
Dấu "  " xảy ra khi  x  1. Chọn B.
Câu 25. Cho phương trình 2 x 1   2 2018   1 .2019x x
 1. Khẳng định sau đây đúng?
A. Phương trình có tổng các nghiệm bằng 0.
B. Phương trình có nghiệm duy nhất.
C. Phương trình có hai nghiệm dương phân biệt.
D. Phương trình có nhiều hơn hai nghiệm. 2  x 1 2018   1
Lời giải. Nếu x  ;    1 1; thì 2 x 1 0      . 2  x   1 .2019x  0  Suy ra 2 x 1   2 2018   1 .2019x x
1  Phương trình đã cho vô nghiệm. 2  x 1 2018   1 Nếu x 1;  1 thì 2 x 1 0      . 2  x   1 .2019x  0  Suy ra 2 x 1   2 2018   1 .2019x x
1  Phương trình đã cho vô nghiệm.
Kiểm tra thấy x  1 là nghiệm của phương trình đã cho.
Vậy phương trình đã cho có tổng các nghiệm bằng 0. Chọn A. 9
Phần 2. Phương trình mũ chứa tham số
Câu 1. Cho phương trình 2
log2 x  m   log2 x 2 3 2 3 .3
m 3  0 với m là tham số. Tập
hợp tất cả các giá trị của m để phương trình đã cho có hai nghiệm phân biệt x , x 1 2
thỏa mãn x x  2 là 1 2 A. 0;. B.  \1;  1 .
C. 1;.
D. 1;\0.
Lời giải. Điều kiện: x  0. Đặt log2 3 x t   0. Phương trình trở thành 2
t  m   2 2
3 t m  3  0. *
Nhận xét: 1) Cứ một nghiệm t  0 thì cho một nghiệm x  0.
2) Ta có log2 1x log2 x2 log2 1 x log2 x2 log2 1 x x2 log2 2 3 .3  3  3  3  3 hay t t  3. 1 2
Do đó để phương trình đã cho có hai nghiệm phân biệt x , x thỏa mãn x x  2 khi 1 2 1 2
và chỉ khi phương trình * có hai nghiệm dương phân biệt t , t thỏa mãn t t  3 1 2 1 2        m  2 3  2 m   3  0 0     m   1   2 P 3 m  3 3         . Chọn D.   m   0 S   0 2   m   3  0   
Câu 2. Biết phương trình x mx 1 4 1 2   
8  0 có hai nghiệm x , x thỏa mãn điều 1 2
kiện x 1 x 1  6. Khẳng định nào sau đây đúng? 1  2 
A. m  0.
B. 0  m  2.
C. 1 m  3. D. m  3. Lời giải. Đặt x 1 t 2  
 0. Phương trình trở thành 2
t  4m  
1 t  32  0. *
Phương trình đã cho có hai nghiệm x , x khi và chỉ khi phương trình * có hai 1 2 2      nghiệm 0
m  2m 7  0
t , t đều dương       .   1 1 2 m  1 0 m   1  
x 1 log t
Gọi t t  0 là hai nghiệm của phương trình *, suy ra 1 2 1  1 2
x 1 log t  2 2 2
 x 1 x 1  6  log t .log t  6. 1  2  2 1 2 2
Lại có log t  log t  log t t  log 32  5. 2 1 2 2 2  1 2  2 log t  3 t   8 log t  2 t   4 Từ đó suy ra 2 1 1      hoặc 2 1 1      . log t  2 t   4  log t  3 t   8 2 2  2  2 2  2
Với hai trường hợp ta đều có t t  4 m 1  m  2 (thỏa mãn   1 ). Chọn C. 1 2   Cách khác. Đặt 2x t   0, ta được 2
t 2m  
1 t  8  0. Ta thấy t t  8 nên suy ra 1 2
x x  3. Đến đây kết hợp với giả thiết x 1 x 1  6 để tìm x , x . 1  2  1 2 1 2
Câu 3. Có bao nhiêu giá trị nguyên của tham số m trên khoảng 2018;2018 để phương trình 2 x 1
  m   x 2 6.2 7
48 .2  2m 16m  0 có hai nghiệm dương x , x thỏa 1 2 mãn x x 15 ? 1 2 10 A. 1993. B. 1994. C. 3986. D. 3988. Lời giải. Đặt 2x t
, vì x  0  t 1.
t  2m 16  Phương trình trở thành 2
3t 7m 48 2
t  2m 16m  0   m . t   3 2  m16 1 t  1 
Để phương trình đã cho có hai nghiệm dương 1 17      mm  . t  1  1 2  2  3
x  log 2m16 1 2    Khi đó  m 
x x 15  log 2m 16 .log 15. m * 1 2 2   2 x  log 3 2 2  3   Xét hàm   m
f m  log 2m 16 .log
là hàm đồng biến trên 17  ;  . 2   2 3  2 
Nhận thấy * có dạng f m f 24  m  24 m  
 có 1994 giá trị. Chọn B. m   2018;2018
Câu 4. Cho phương trình 2 2 x 2 x 1  x 2 x 2 4  . m 2
3m 2  0. Tập tất cả các giá trị của
tham số m để phương trình đã cho có 4 nghiệm phân biệt là A. 2;. B. 2,.
C. 1;. D.  ;   1 2;. 2 Lời giải. Đặt x 2 1 t 2 t  2 1. Phtrình trở thành 2 t 2 .
m t  3m 2  0  m  . * 2t 3 2   Xét hàm 
f tt 2  trên   3 1; \    . t 1 1,5 2  2t 3 2   f 0   0 
Phương trình đã cho có bốn nghiệm phân  
biệt khi và chỉ khi phương trình * có f 2 1
hai nghiệm phân biệt lớn hơn 1 và khác 3  BBT 
m  2. Chọn A. 2
Câu 5. Có bao nhiêu giá trị nguyên m thuộc đoạn 2018;2018 để phương trình 2 x x    2 2 2 x 2 x x 2 .9 2 1 .6  .4 x m m m
 0 có nghiệm thuộc khoảng 0;2? A. 2010. B. 2011 . C. 2012. D. 2013.  2xx 2 2 2 x 2x    
Lời giải. Phương trình đã cho tương đương với 3 m      m   3 . 2 1 .       m  0. 2 2 2 x 2x     Đặt 3 t      ,  
vì x 0;2 nên 2 t   ;1. 2 3     Phương trình trở thành 2  t mt 2m  
1 t m  0  m  . 2 t 2t 1 11   Xét hàm   t f t  trên 2 ;1  . t 2 /3 1 2 t 2t 1 3     f  
Từ bảng biến thiên suy ra phương trình có 
nghiệm khi m  6. Kết hợp với giả thiết ta có f m  6;7;...201 
8 : có 2013 giá trị. Chọn D. 6 2 2
Câu 6. Cho phương trình   x m  x 2 x 2 5 1 5 1  2
. Tập tất cả các giá trị của
tham số m để phương trình có đúng bốn nghiệm phân biệt là a;b. Hiệu b a bằng A. 3 . B. 1 . C. 1 . D. 49 . 4 16 64 64 2 2 x x    
Lời giải. Phương trình đã cho tương đương với 5  1 5  1 1      . m        .  2   2  4 2 x   Đặt 5  1 m 1 1 t       0  t  
1 . Phương trình trở thành 2 t
  m t t . *  2  t 4 4
Nhận xét: 1) Cứ một nghiệm t 0; 
1 cho ta hai nghiệm x.
2) Với t  1 cho ta một nghiệm x  0.
Do đó yêu cầu bài toán tương đương với phương trình * có hai nghiệm t , t phân 1 2
biệt thuộc khoảng 0;  1 . Xét hàm 1 f t 1 2
t t trên 0;  1 . t 0 1 8 4 f   0  Dựa vào BBT ta có 1 0  m  thỏa mãn yêu cầu. 1 f 64 64 0 3  Suy ra 1 b a  . Chọn C. 4 64 2 2
Câu 7. Cho phương trình  x m x 2 x 1 4 7 4 7 3     
 0. Gọi S là tập tất cả các
giá trị của tham số m sao cho 36m   và phương trình đã cho có đúng hai nghiệm
phân biệt. Số phần tử của S bằng A. 1. B. 24. C. 25. D. 26. 2 2 x x    
Lời giải. Phương trình đã cho tương đương với 4   7  4   7  1      m        0.  3   3  3 2 x   Đặt 4   7 m 1 t t       0  t  
1 . Phương trình trở thành 2 t
  0  m  t . *  3  t 3 3 12 Xét hàm 1
f tt 2
 t trên 0;  1 . t 0 1 6 3 f   0   1 m  1 f 36 Dựa vào BBT ta có  36  thỏa yêu cầu bài 2  2 0     m  0 3   3 36m  1 toán, suy ra  . Vậy có tất cả 
25 giá trị thỏa mãn. Chọn C. 24  36m  0 
Câu 8. Cho phương trình .9x 2   1 6x  .4x m m m
 0. Tìm tất cả các giá trị của tham
số m để bất phương trình nghiệm đúng với mọi x thuộc 0;  1 .
A. m  6.
B. 6  m  4.
C. m  4.
D. m  6. x x    
Lời giải. Bất phương trình đã cho 9  m  
   m   3 . 2 1        m  0. 4 2 x   Đặt 3 t      2  với 3
1  t  . Bất phương trình trở thành mt 2m   1 t m  0 2 2 t  3 3  m   f t , 1; t 
  m  min f t f  
   6. Chọn D. 2     t       3 1 2       1;   2  2
Câu 9. Tập tất cả các giá trị của tham số m để phương trình 3x 3  . 9x m 1 có
đúng 1 nghiệm có dạng a;b c. Tổng a b c bằng A. 4. B. 11. C. 14. D. 15. Lời giải. Đặt t  3 3x t
 0. Phương trình trở thành 2
t  3  m t 1  m  . * 2 t 1 Xét hàm  13t 1 f tt 3 
trên 0;. Ta có f t f t ;  0  t  . 2 t 1  2t   2 1 t 1 3
Để phương trình đã cho có đúng 1 nghiệm  t 0 1/ 3 
phương trình * có đúng 1 nghiệm dương f   0  1   m  3 10 BBT    . f Chọn C.m  10  3 1 x
Câu 10. Tìm tất cả các giá trị thực của tham số m để phương trình 2 4 2 x
m e e 1 có nghiệm thực.
A. 1 m  0. B. 0  m 1. C. 2 0  m  .
D. 1  m 1. e e Lời giải. Đặt 4 2 x
t e 1, vì 2x
e  0 nên t 1. 4 x x   Suy ra 4 2 x   4 4 4 2 2
t e 1  e   t 1  e t 1   .    
Khi đó phương trình trở thành 4 4 4 4
m t 1  t m t t 1.    13 3 Xét hàm t f t 4 4
t t 1 trên 1; . Ta có f t  1  0, 1 t  . t  3 4 4 1
Suy ra hàm số f t nghịch biến t 1  trên 1; . f  
Dựa vào bảng biến thiên, ta thấy 1
phương trình có nghiệm khi và chỉ f
khi 0  m 1. Chọn B. 0 Câu 11. Cho hàm số   x4     7 3 1 2 x f x x
6x 3. Khi phương trình f  2
7  4 6x 9x 3m1 0 có số nghiệm nhiều nhất thì giá trị nhỏ nhất của tham
số m m . Khẳng định nào sau đây đúng? 0
A. m  0;1 . B. m  1;2 .
C. m  2;3 .
D. m  3;4 . 0   0   0   0  
Lời giải. Đặt t   x x    x  2 2 7 4 6 9 7 4 1 3
1 3;7. Khi đó f t  13 . m Xét hàm số   t4     7 3 1 2 t f t t
6t 3 trên đoạn 3;7. Ta có   t4 7t      7 3 ln 3 2 1 2 t f t t ln 2 6;    t   2 tt      t f t t  2 4 7 7 7 3 ln 3 2 ln 2 2 ln 2 1 2 ln 2  3t ln 2 4
3  2 t   7
1 ln 2 2 t ln 2  0.  
 0,t   3;7
Suy ra hàm số f t đồng biến trên 3;7.  f   3  0 Lại có 
f x  0 có nghiệm duy nhất t thuộc 3;7.  0  f 7 0 
Dựa vào BBT, ta thấy phương trình t 3 t 0 7
f t  13m có số nghiệm nhiều nhất f   0  5 1 f t0 
f t 13m  4   m  . 148 0  3 3 f 4 3 Suy ra 5
m   1;2 . Chọn B. f t 0  0   3
Câu 12. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 5;5 để phương trình x
e mx   1 có nghiệm duy nhất? A. 5. B. 6. C. 7. D. 10.
Lời giải. Vì x
e  0 nên m  0. Khi đó: x 1 x 1 1
e mx   1        1 x x ef x . x m e m Xét hàm     1 x f x x e   . Ta có '  x f x  xe  0  x  0. 14
Dựa vào BBT, ta thấy phương trình có nghiệm duy x   0   1  1  f   0  mm  0 nhất    1  1 m 1 f  0   0 m  m   
m  5;4;3;2;1;1 . Chọn B. m 5;5     Cách 2. Ta có x
y e là hàm đồng biến trên  và x
y e  0 với mọi x   có đồ thị
C (xem hình 1). Hình 1 Hình 2 Do đó:
 Nếu m  0 thì y mx  
1 là hàm số nghịch biến trên  , có đồ thị là một đường
thẳng luôn qua điểm 1;0 nên luôn cắt đồ thị  : x C
y e tại duy nhất một điểm.
 Nếu m  0 : phương trình vô nghiệm (do x
y e  0 ).
 Nếu m  0 : để phương trình có duy nhất một nghiệm khi và chỉ khi đường thẳng x e
  mx   1 x  0
 : y mx  
1 là tiếp tuyến của C  (như hình 2)        m  1. x e   mm   1 
Câu 13. Có bao nhiêu giá trị nguyên của tham số m thuộc 2000;2000 để log b log 2 a b a ab
m log b 1 với ,
a b là các số thực lớn hơn 1? a A. 1999. B. 2000. C. 2001. D. 2199. 2  t b   a
Lời giải. Đặt t  log b vì ,
a b  1; nên t  0. Suy ra  . a 1  log a b  t 1 t
Bất phương trình trở thành  t a  2t a a t t 1 2
mt 1  a mt 1  m  , t  0. t t t t Xét hàm 
ta ln a a 1
f ta 1 
trên 0;. Ta có f t . t 2 t •   t  ln t g t ta
a a 1 trên 0;. Đạo hàm gtt 2
ta ln a  0, t  0.
• Suy ra gt đồng biến trên 0; nên gt g0 0,t  0.
Suy ra f t 0,t  0. Suy ra hàm số f t đồng biến trên 0;. 15
Dựa vào BBT ta thấy m  ln a thỏa mãn yêu t 0 
cầu bài toán. Do đúng với mọi a 1 và m là f
số nguyên thuộc 2000;2000 nên  f
m  1999;1998;...;0. Chọn B. ln a
Câu 14. Tìm tất cả các giá trị của tham số m để phương trình 2 2
2 x m x có hai nghiệm thực phân biệt. m  1 m  1 m  2 A.  . B.C.D.  . . 3  m  1. m 1  m  2  m  2 
Lời giải. Đặt t x  0. Phương trình trở thành 2t 2 2 2  t m .
Nhận xét: Với mỗi nghiệm t  0 ta tìm được tương ứng hai nghiệm x. Xét hàm   2 2  2 t f t
t trên 0; Ta có t 0    2  2.2 t f t .ln 2  2t  0, 0. t f  
Dựa vào bảng biên thiên, ta thấy yêu cầu bài f m 1 toán 2 m 1   . Chọn A. m 1 1 
Cách 2. Phương pháp hình học. Nhận thấy phương trình 2 2
2 x m x là phương trình hoành độ giao điểm của đồ thị hàm số 2 x y  và nửa đường tròn 2 2 2
x y m (phần
phía trên trục hoành) như hình vẽ. Dựa vào hình vẽ ta
thấy để hai đường này cắt nhau tại hai điểm phân biệt khi 2
m 1  m 1 hoặc m  1.
Câu 15. Phương trình 3 x2 m 3  x  3 2 x x x mx2 x 1 2 6 9 2 2       1 có ba nghiệm phân
biệt khi và chỉ khi m a;b. Giá trị biểu thức 2 2
T b a bằng A. 36. B. 48. C. 64. D. 72.
Lời giải. Phương trình 3
x  mx   x   3 2 3  x2 2 2  m 3x 2  1    3 mx  3 2 3 3  2 x m x 2 x3 3 2 . Xét hàm   3  2t f t
t với t   và đi đến kết quả m x   x m x    x3 3 3 2 3 2 a   4 3 2 BBT
m  x  6x 9x 8  m 4;8  2 2  
T b a  48. Chọn B. b   8 
Câu 16. Cho phương trình 3m m e e   2 x   x  2 2 1
1 x 1 x . Tập hợp tất cả các
giá trị thực của tham số m để phương trình có nghiệm là         A. 1 0; ln2.      B. 1 0; . C. 1 ;   ln 2. D. 1  ln 2;.  2   e  2  2    
Lời giải. Điều kiện: 1 x 1. 16 Phương trình 3m m
e e   2 x   x  2 1
2  2x 1 x  3m m e e  2 x 1 x   2 2 2  x 2x 1 x 1 x  1                m e m
e  x  1x 3 3 2  2
x  1 x . Xét hàm   3
f t t t với t   và đi đến kết quả m 2 BBT   1 m e xx  e  2 1
m  ln 2  m  ln 2. Chọn C. 2
Câu 17. Có bao nhiêu giá trị nguyên dương của m nhỏ hơn 2018 để phương trình 2 1 1 3 2 x   xm  2
x mx x x x e
có nghiệm thực dương? 4 x 1 A. 2014. B. 2015. C. 2016. D. 2017. 2 1 1 x  2 x m  2 1 1 x x     
Lời giải. Phương trình e 1 x  m 2 1 x 2      x       x x e  
x   me . 1 2     x  m 2 1 xxx x e  2 x Xét hàm   1 1 t
f t te với t  0 và đi đến kết quả 2 x
x   m 2 x x 2 1     tx  2 1 1 2 BBT
m  x       x   2 x
t t 2  0  m  0.     do 0 x xx  
Mà m là số nguyên dương nhỏ hơn 2018 nên m  1;2;3...2016;2017. Chọn D.
Câu 18. Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để phương trình x x
m m e e có nghiệm thực? A. 9. B. 10. C. 11. D. Vô số.
Lời giải. Phương trình x 2 x x x 2 x x
m m e e m e m e e e . Xét hàm   2
f t t t với t  0 và đi đến kết quả x x x 2 x
m e e m e e x x 1 2 BBT m
m e e  m    
  có 10 giá trị thỏa mãn. Chọn B. m 1  0 4
Câu 19. Biết rằng a là số thực để phương trình 9x  9  .3x a
cosx có nghiệm duy
nhất. Hỏi a thuộc khoảng nào sau đây? A. 8;4. B. 4;2. C. 4;10.
D. 12;18.
Lời giải. Phương trình tương đương với x 2 3  3 x  .
a cosx. *
Nhận thấy rằng nếu x là nghiệm của phương trình * thì 2 x cũng là nghiệm 0 0
của phương trình *. Thật vậy 2x 2 2x 0  0  3 3  .cos 2
  3 x 3x a x  . a cos x . 0  2 0 0 0  
Vậy phương trình * có nghiệm duy nhất khi 2 x x x 1. Suy ra a  6. 0 0 0 Thử lại 2
a  6, ta được 9x  9  6.3x cos  3x   3  6.3x x 1
 cosx  0   17 3x  3  0   
x  1. Vậy a  6 thỏa mãn bài toán. Chọn A. 1  cos  x 0 
Câu 20. Cho tham số thực ,
a biết phương trình xx e e
 2 cosax   1 có 5 nghiệm
thực phân biệt. Hỏi phương trình xx e e
 2 cosax 4 2 có bao nhiêu nghiệm thực phân biệt? A. 5. B. 10. C. 11. D. 20. x x   ax  2 2      2 e e 2 cos  2.  1 x x         
Lời giải. Phương trình     ax 2 2 2 2 2
 e e   4 cos         .       2   x x     ax  2 2 e e  2 cos     2.2    2  
Nhận xét: 1) x  0 không là nghiệm của   1 .
2) Nếu x  0 là nghiệm của  
1 thì 2x là nghiệm 2. 
1 và 2x là nghiệm 2.2. 0 0 0
Vậy phương trình 2 có 10 nghiệm thực phân biệt. Chọn B.
Phần 3. Phương trình logarit chứa tham số
Câu 1. Cho phương trình 2
log x 5m   2
1 log x  4m m  0. Biết phương trình có 2 2 2
nghiệm phân biệt x , x thỏa x x  165. Giá trị của x x bằng 1 2 1 2 1 2 A. 16. B. 119. C. 120. D. 159.
Lời giải. Điều kiện: x  0.
Đặt t  log x, phương trình trở thành 2
t  m   2 5
1 t  4m m  0. * 2
Phương trình đã cho có 2 nghiệm phân biệt  phương trình * có 2 nghiệm phân
biệt    9m  6m 1 0  3m  2 1 2
1  0  m   . 3 t   m x  2m
Khi đó phương trình * có 2 nghiệm là 1   1    . 4m 1 t   4m 1    2 x  2  2 Ycbt: m 4m 1 165 2 2 165 2m x x         3. 1 2
Suy ra x  3  x  162. Khi đó x x  159. Chọn D. 1 2 1 2
Câu 2. Giá trị thực của tham số m để phương trình 2
log x 3 log x  2m 7  0 có 3 3
hai nghiệm thực x , x thỏa mãn x  3 x 3
72 thuộc khoảng nào sau đây? 1   2  1 2  7   7 7   21 A.     ;0        . B. 0; . C.  ;7. D. 7; .  2     2   2     2 
Lời giải. Điều kiện: x  0.
Đặt t  log x, phương trìn h trở thành 2
t 3t  2m 7  0. * 3 18
Phương trình đã cho có 2 nghiệm phân biệt  phương trình * có 2 nghiệm phân
biệt      m  37 9 4 2 7  0  m  . 8
Áp dụng Vi-et ta có t t  3  log x  log x  3  log x x  3  x x  27. Kết 1 2 3 1 3 2 3  1 2  1 2 x  3
hợp với giả thiết ta được 1  . x  9  2 Lại có 9
t t  2m 7  log x .log x  2m 7  log 3.log 9  2m 7  m  . Chọn C. 1 2 3 1 3 2 3 3 2
Câu 3. Cho phương trình m 2 2
log x  4 log x m 2  0. Tập tất cả các giá trị 3 3  
của tham số thực m để phương trình có hai nghiệm x , x thỏa 0  x 1 x là 1 2 1 2 A.  ;  2.
B. 2;2. C. 2;. D.  \2;2.
Lời giải. Điều kiện: x  0.
Đặt t  log x, vì 0  x 1 x  log x  log 1 log x nên t  0  t . 3 1 2 3 1 3 3 2 1 2
Phương trình trở thành m   2
2 t  4t m 2  0. *
Khi đó ycbt  phương trình * có hai nghiệm trái dấu  m 2m2 0
 2  m  2. Chọn B.
Câu 4. Cho phương trình 2
log x 2m   2
1 log x m  2m  0. Tập tất cả các giá trị 2 2
của tham số m để bất phương trình nghiệm đúng với mọi x 1;2 là m  2 m  2
A. 1 m  0. B. 1 m  0. C.  . D.   . m 1  m 1 
Lời giải. Điều kiện: x  0. Đặt t  log x, vì x 1;2 nên t 0;  1 . 2     0
Bất phương trình trở thành 2 t 2m  2 1 t m 2m 0, t  0;  1           t   0 1 t  1 2   m 2 2
1 m 2m  0 2  m   2m  0   P  0   
 1 m  0. Chọn B. 2  m   2m 2   m   1 1  0 
t 1 t 1  0   1  2  
Câu 5. Cho phương trình 2 x x 2 2 log 2  2
 2   log m 2 . 4   2  Có bao nhiêu giá trị
nguyên của tham số m để phương trình vô nghiệm? A. 3. B. 4. C. 5. D. 6.
Lời giải. Điều kiện: m  2. Phương trình log 2x 2  2     log m 2 4 2  
2x 2  m2 2x m4 log 2x 2 log m 2 2x 2 m 2             . 2   2
2x 2 2 m      2x m   m  4  0 m   4 Phương trình vô nghiệm        0  m  4.  m   0 m   0   m 
m  0;1;3;4 . Chọn B. m2   19
Câu 6. Cho phương trình 2 log  2 2
2x x  2m  4m  log  2 2
x mx 2m  0. Tập tất 4 1  2
cả các giá trị của tham số m để phương trình có hai nghiệm phân biệt x , x thỏa 1 2 mãn 2 2
x x 1 có dạng a;bc;d với a b c d. Tổng a b 5c  2d bằng 1 2 A. 0. B. 1. C. 2. D. 3.
Lời giải. Phương trình  log  2 2
2x x  2m  4m  log  2 2
x mx 2m 2 2  2 2 2 2
x mx 2m  0
x mx 2m  0     1     . 2 2 2 2 2 2
 x x 2m4m x mx 2mx    m   2
1 x  2m 2m  0  2
Phương trình 2 có hai nghiệm là x 1 , m
x  2m nên yêu cầu bài toán 1 2 1
 m  2m
 m2  m2 1 m  0 1 2 1       2 1 . Chọn C.   1
 m2  m1m 2 2m  0   m     5 2 
 2m2 m2m 2 2m  0 
Câu 7. Cho phương trình 2 2 2
log cos x m log cos x m  4  0. Có bao nhiêu giá trị
nguyên của tham số m để phương trình đã cho vô nghiệm? A. 0. B. 1. C. 3. D. 4.
Lời giải. Phương trình 2 2
 log cos x 2m log cos x m  4  0.
Đặt t  log cos x t  0. Phương trình trở thành 2 2
t 2mt m  4  0. *
Phương trình đã cho vô nghiệm khi
• Phương trình * vô nghiệm 2    m   2 4 4 m
 4 0   2  m  2.    0  • Phương trình  
* có hai nghiệm t , t đều dương S
   0  2  m  2. 1 2 P 0 
Hợp hai trường hợp ta được m  2;2 thỏa ycbt có 3 giá trị nguyên. Chọn C.
Câu 8. Cho phương trình 2 log  2
2x 5x  4 log x x
Gọi S là tập  mx  2 2 6 . mx 5 5 
tất cả các giá trị m sao cho 10m   và phương trình có nghiệm duy nhất. Số phần tử của S bằng A. 13. B. 14. C. 15. D. 16.
Lời giải. Phương trình  log  2
2x 5x  4 log x x mx  2 2 6 mx 5 5  0   mx 5 1 
0  mx 5 1      . 2 2 2
x 5x  4  x 2x 6 
x  2 hoaëc x   5 0 2m 5 1 • Chỉ   
x  2 là nghiệm thỏa bài toán     m  .
5m5  0 hoaëc 5m5   1 0 5m 5 1 • Chỉ   
x  5 là nghiệm thỏa bài toán   
2m5  0 hoaëc 2m5   1 20  6 1   m   5  10  10m 12 6 5   10
   m   12  10m  25 m 
10m  11;13;14;25;30. Chọn C. 5 2   10   m  30 m  3   
Câu 9. Cho phương trình log  2
x  2mx  log 2x m 1  0. Có bao nhiêu giá trị 3  1   3
nguyên của tham số m để phương trình có nghiệm duy nhất? A. 0. B. 1. C. 2. D. 3.
Lời giải. Phương trình  log  2
x  2mx  log 2x m 1 3  3    m 1 2
 x m1 0 x     1      2 . 2
x 2mx  2x m1  2 
x 2m 
1 x m 1 0 *  
Yêu cầu bài toán  phương trình * có một nghiệm thỏa mãn   1 : /   0  *
● * có nghiệm kép thỏa   1      m  0. b m 1 x     2a 2 m  1   ●  m 1
* có hai nghiệm x , x thỏa x   x   1 . 1 2 1 2 2 m    5 ●  m 1 1
* có hai nghiệm x , x thỏa x
x  1 m   . 1 2 1 2 2 5 m  0  Vậy 
1 thỏa yêu cầu bài toán: Có 2 giá trị nguyên thỏa mãn. Chọn C. 1 m   5
Câu 10. Có bao nhiêu giá trị nguyên của tham số m để bất phương trình   2x    2 log 5 log 1
log mx  4x m đúng với mọi x   ? A. 1. B. 2. C. 4. D. Vô số.
Lời giải. Để bất phương trình đúng với mọi x   khi và chỉ khi:
● Bất phương trình xác định với mọi 2
x    mx  4x m  0, x   m   0 m   0        m  2.   1 2 '  0 4  m  0  
● Bất phương trình nghiệm đúng với mọi x   2x    2 log 5 5
log mx  4x m, x   2 2
 5x 5  mx  4x  , m x   5  m  0 m   5 2 5 m 2 x 4x 5 m 0, 3 x                 m  . 2 '  0   m  10m 21 0   Từ   1 và 2 , ta được 2 3 m m    
m  3. Chọn A. 21
Câu 11. Tìm m để bất phương trình  2 log
x  2x m  
1  0 đúng với mọi x . m A. m  0. B. m  1. C. m 1. D. m 1. 2        
Lời giải. Điều kiện: x 2x m 1 0    x  2 1  m  0     0  m  1 . 0   m 1  0   m 1 
Nhận xét. Với dạng log b  0  a   1 b   1  0. a
Bất phương trình  m  2
1 x  2x m 0. *
Để * đúng với mọi x   : 1   0
● Nếu m 1 thì * 2 x 2x m 0, x           : vô lí.   1m  0  1   0
● Nếu m 1 thì * 2 x 2x m 0, 1 x          
m  : (thỏa).   1m  0 
Vậy m 1 thỏa mãn yêu cầu bài toán. Chọn D.
Câu 12. Cho phương trình 2 2 log a x x 5 6 x      log
3 x 1 . Có bao nhiêu 2   2   2a   
giá trị của biến x để phương trình có nghiệm đúng với mọi số thực a ? A. 0. B. 1. C. 2. D. 4.
Lời giải. Vì đúng với mọi a   nên ta chọn a  0. x  2
Với a  0, phương trình trở thành log 6 x  log 3 x 1   . 2 2   x 5 
Thử lại chỉ có x  5 thỏa mãn. Chọn B.
Câu 13. Cho phương trình 5x m  log x m với m là tham số. Có bao nhiêu giá 5  
trị nguyên của m 20;20 để phương trình đã cho có nghiệm? A. 9. B. 19. C. 20. D. 21.
x m  5t
Lời giải. Đặt 5x m  log x m t. Ta được hệ 
 5x x  5t t. 5   5x
 m t  Xét hàm   5x f x
x trên  và đi đến kết quả x t. Khi đó  5x m x
gx. Ta có bảng biến thiên của hàm gx như sau  1  log     x  5 ln 5  g  0    1   g log       5 g    ln 5        
Từ bảng biến thiên suy ra phương trình có nghiệm khi 1
m g log       . 5    ln 5   22 m   20;20
m     
Có 19 giá trị. Chọn B. m  19; 18; 17;...;  1 . 
Câu 14. Cho phương trình ln m  2 sin x  lnm 3sin x  sin x  
với m là tham số
thực. Có bao nhiêu số nguyên m để phương trình có nghiệm? A. 3. B. 4. C. 5. D. 6.
Lời giải: Phương trình  m  2 sin x  lnm 3sin x  ln m 2sin x  lnm 3sin x    
 m 3sin x lnm 3sin x.
Xét hàm f t t  ln t với t  0 và có được m 2sin x  lnm 3sin x m 3sin x  
 lnm 3sin xax a 1 sin  sin x 
 ln m 3a a m e 3a  e 3; 3. Chọn B. a 1  ;1 .      e   
Câu 15. Cho phương trình x 2 1 2
.log  2 2 3  4 xm x x
.log 2 x m  2 với m là 2  2  
tham số thực. Tìm tất cả các giá trị của m để phương trình có đúng hai nghiệm phân biệt.         A. 1 3 m   ;         ;  . B. 1 3 m  ;
    ;.  2 2   2 2    C. m  ;    1 1;. D. m  ;   1 1;.
Lời giải. Phương trình 2 x 2x 3  2 .log  2
x 2x  3  2 xm  .log 2 x m  2 . 2  2 2 2   Xét hàm   2t f t
.log t trên 2; và đi đến kết quả 2
x 2x  3  2 x m  2 2 x   2
1  2x m 2
x 4x 2m 1 0 1 2   x  1 2 x m         .    x  2
1  2x m 2 x  2m 1 2  
Phương trình đã cho có hai nghiệm phân biệt khi:
TH1. Phương trình  
1 và 2 đều có nghiệm kép và hai nghiệm này khác nhau     0   1     m  .  2
x  2m1 0 
TH2. Phương trình  
1 có hai nghiệm phân biệt, phương trình 2 vô nghiệm     0    1 4 2m   1  0 1        m  . 2
x  2m1 0 2    m 1 0 2 
TH3. Phương trình  
1 vô nghiệm, phương trình 2 có hai nghiệm phân biệt     0    1 4 2m   1  0 3        m  . 2
x  2m1 0 2    m 1 0 2 
TH4. Phương trình  
1 có hai nghiệm phân biệt, phương trình 2 cũng có hai
nghiệm phân biệt và hai nghiệm của  
1 giống hai nghiệm của 2 (hay nói cách khác
hai phương này trình tương đương)  m  .      Vậy 1 3 m   ;       ; 
 là giá trị cần tìm. Chọn A.  2 2  23
Câu 16. Cho phương trình log  3
mx x  log  2
14x  29x 2  0 với m là tham số 2 1  2
thực. Gọi S   ,
a b là tập tất cả các giá trị của m để phương trình có ba nghiệm phân
biệt. Hiệu b a bằng A. 1 . B. 5 . C. 2 . D. 5. 2 2 3 3
Lời giải. Phương trình  log  3
mx x  log  2
14x  29x 2 2 2  1  2  x  2
14x 29x 2  0   4        Xeùt  haøm 39 m  1
 9; .Chọn A. 3 2 mx    
x  14x  29x 2  2   2  2 m
  6x 14x  29  x
Câu 17. Cho phương trình 2 2
log x  log x 1 2m 1  0. Tập tất cả các giá trị của 3 3
tham số m để phương trình có nghiệm thuộc đoạn  3 1;3   là  
A. 0  m 1.
B. 0  m  2 . C. 13 0  m  .
D. 1 m  2 . 6
Lời giải. Điều kiện: x  0. Đặt 2
t  log x 1, vì  3 x 1;3   nên t 1;2 . 3   2 Phương trình trở thành t t 2 2
t 1 t 2m 1  0  m
f t0;2 với t 1;2. 2
Do đó yêu cầu bài toán  0  m  2. Chọn B.
Câu 18. Cho phương trình m ln x  ln1 x .
m Tập tất cả các giá trị của tham số m
để phương trình có nghiệm thuộc khoảng 0;  1 là A. e
  m e.
B. 1 m e. C. m  0. D. m  0. ln1 x
Lời giải. Phương trình  mln x  
1  ln1 x  m  . ln x 1 ln1 x
Xét f x trên 0;  1 . x 0 1 ln x 1  f  
ln x 1 ln1 x Có f x 1    .  0.   x 1 x   f   ln x  2 1
Dựa vào BBT suy ra phương trình đã cho có 0
nghiệm  m  0. Chọn D.
Câu 19. Cho phương trình 2
log x 2 log x 3  m log x 3 với m là tham số thực. 2 2  2 
Tập tất cả các giá trị của m để phương trình có nghiệm thuộc 16; là
A. 1 m  2 .
B. 1 m  5 .
C. 1 m  5 .
D. 3  m  5 . 4
Lời giải. Đặt t  log x, vì x 16 nên t  4. 2 2 Phtrình trở thành t 2t 3 2 t 2t 3 mt  3 m
f t 1; 5         với t  4. t 3  24
Do đó yêu cầu bài toán  1 m  5. Chọn B.
Câu 20. Cho phương trình log  2
x x 1.log  2
x x 1 log x x  với m  2 1 2 5 
m là tham số dương khác 1. Có bao nhiêu giá trị nguyên của m để phương trình đã
cho có nghiệm x 2; ? A. 1. B. 2. C. 3. D. Vô số.
Lời giải. Phương trình đã cho xác định trên khoảng 2;. 
Phương trình  log x x 1.log x x 1 log 2.log x x 1 m  1 2 2 2 2 5 2 log  2 x x 1.log  2 x x 1 log 2         0. 2 5  m   • log  2
x x 1  0 vô nghiệm do x  2. 2  • log  2
x x 1log 2  0  log 2  log x x m m  2 1 . 5 5  Xét hàm 2 f x 2
x x 1 trên 2;. Ta có f x  1  0, 2 x  . 2 x 1
Suy ra f x đồng biến nên f x f 2 2  3 với mọi x  2. Suy ra log  2
x x 1  log 2  3 . 5  5  
Do đó để phương trình có nghiệm x 2; khi và chỉ khi log 2  log 2  3 m 5   m   
 m  2 : Có duy nhất 1 giá trị. Chọn A. m 1 
Câu 21. Cho phương trình  2 x   2  2
x  m  2 x    2 1 .log 1 2 1 .log x  
1  m  4  0. Có
bao nhiêu số nguyên m thuộc 10;10 để phương trình đã cho có hai nghiệm phân
biệt thỏa mãn 1 x  3 ? A. 7. B. 9. C. 12. D. 14.
Lời giải. Phương trình   2 x   2  2
x   m  2 x    2 2 1 .log 1 2 2 1 .log x   1  2m  8  0. Đặt t
 2x    2x   BBT 2 1 .log 1 
t 0;4 với 1 x  3.
Nhận xét: Với mỗi nghiệm t ta có tương ứng 2 nghiệm x. 2
Phương trình đã cho trở thành t  8 2
t 2mt  2m  8  0  m  . * 2t 2
Do đó để phương trình đã cho có 2
nghiệm thực x thỏa 1 x  3 thì
phương trình * có đúng một nghiệm t 0;4. 2 Xét hàm 
f tt 8  trên 0;4. Dựa 2t 2 25 m  4
vào bảng biến thiên ta thấy  m 4 t 0 1 3  f   
thỏa yêu cầu bài toán. Chọn D.  f 4 4 
Câu 22. Cho bất phương trình 3 2
log x 2x  
1mx m  1. x   Có bao nhiêu giá trị
m nguyên trong đoạn 2017;2017 để bất phương trình luôn đúng với x  2 ? A. 2010. B. 2017. C. 2018. D. 2019.
Lời giải. Bất phương trình 1 3 2
x 2x 1mx m  , x  2 x
x x  2 1
  mx   x   x x   1 1 1 , 2 1   , m x  2. x x x   1 Đặt 1
t x x   1  2, 2
x  . Khi đó m t   f t, 2.
t  Lập BBT của hàm f t ta t được 3 f t 3  , 2. t  Suy ra m m    
 có 2019 giá trị. Chọn D. 2 m   2  017;2017 2
Câu 23. Cho phương trình 2 x
 2mx 2 x  2 mx      2 2018 1 ln x   1  2018. Có bao  
nhiêu giá trị nguyên m thuộc đoạn 2018;2018 để phương trình có nghiệm duy nhất
thuộc khoảng 1;? A. 2017. B. 2018. C. 2019. D. 2020.
Lời giải. Phương trình 2 x   2m   x 1    2
 x  mx    2 1 2018 .2018 2 1 .ln x    1.  VT  0 • Nếu 2
x 2mx 1 0 thì 
 phương trình vô nghiệm. VP  0  VT  0 • Nếu 2
x 2mx 1 0 thì 
 phương trình vô nghiệm. VP  0  • Thử thấy 2
x 2mx 1  0 * thỏa mãn phương trình. Do đó yêu cầu bài toán
 phương trình * có nghiệm duy nhất trên 1;. Bằng cách dùng tam thức m  4
bậc hai hoặc xét hàm số cho ta kết quả m   
 có 2019 giá trị. Chọn C. m   2018;2018 m  0   
Câu 24. Cho phương trình 2 m m 7 2 2 4 3
2 sin x 3cos x  log 2 
 . Có bao nhiêu giá trị 2  2
nguyên của tham số m để phương trình đã cho có nghiệm? A. 0. B. 1. C. 2. D. 3.  
Lời giải. Phương trình 2 m m 7 2 4 3 5sin x  log 2   3. Ta có 2  2 26 • 2 5sin x  5.     •  m m 7  7
m m   m  2 2 4 3 2 1  1 nên 2 4 3 1 log 2     log    2     2. 2 2  2  2 2 5  sin x  5 2  s  in x 1 Do đó phương trình       
m   Chọn B. m m 7 2. 2 4 3    2 log  2    2 m       4m 3  1 2  2   
Câu 25. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 10;10 để phương
trình log x 2 log x 1  m có ba nghiệm phân biệt? 3 2   2 3 A. 8. B. 10. C. 11. D. 12.
Lời giải. Điều kiện: 1 x  2. Phương trình  log x 2  log x 1  m 3 3   2 2 3 m   log
x 2 x 1  m x 2 x 1      . * 3      2 2
Phương trình * là phương trình hoành độ giao điểm của đồ thị hàm số m  
f x  x 2 x   1 và đường thẳng 3 y   
  (cùng phương với trục hoành). 2
Xét hàm số f x x 2 x  
1 xác định trên 1;22;. h
 xx 2x   2
1  x x 2 khi x  2
Ta có f x x 2 x   1   . g
 x  x 2x   2
1  x x  2 khi 1   x  2 
Dựa vào đồ thị, ta thấy để phương
trình * có ba nghiệm phân biệt khi 3 m m         g x 3 9 0 max          m  2 2 1;2 2 4 m  
m  10;9;...;1 . Chọn D. m 10;10     27
Document Outline

  • 0 DE1
  • 0 DAP AN1
  • 1 DE_Ungdung
  • 2 DAP AN_Ungdung
  • 3 DE_Phtrinh
  • 4 DAP AN_Phtrinh